-1.0 / 3.0 вычисляется как (от 8 до – 1 или 0,125), деленное на 3,0, что приведет к 0.041666666666666666666666666666667.

См. также

Контрольная работа по теме степени и корни

Контрольная работа №1

Вариант 1

1. Вычислите:

а) б) в)

2. Расположите числа в порядке убывания:

3. Постройте график функции:

а) б)

4. Вычислите:

5. Найдите значение выражения: при

6. Решите уравнение:

Контрольная работа №1

Вариант 2

1. Вычислите:

а) б) в)

2. Расположите числа в порядке возрастания:

3. Постройте график функции:

а) б)

4. Вычислите:

5. Найдите значение выражения: при

6. Решите уравнение:

Контрольная работа №1

Вариант 3

1. Вычислите:

а) б) в)

2. Расположите числа в порядке убывания:

3. Постройте график функции:

а) б)

4. Вычислите:

5. Найдите значение выражения: при

6. Решите уравнение:

Контрольная работа №1

Вариант 4

1. Вычислите:

а) б) в)

2. Расположите числа в порядке возрастания:

3. Постройте график функции:

а) б)

4. Вычислите:

5. Найдите значение выражения: при

6. Решите уравнение:

Контрольная работа №2

Вариант 1

1. Вычислите:

а) б) в) г)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Составьте уравнение касательной к графику функции в точке х=1.

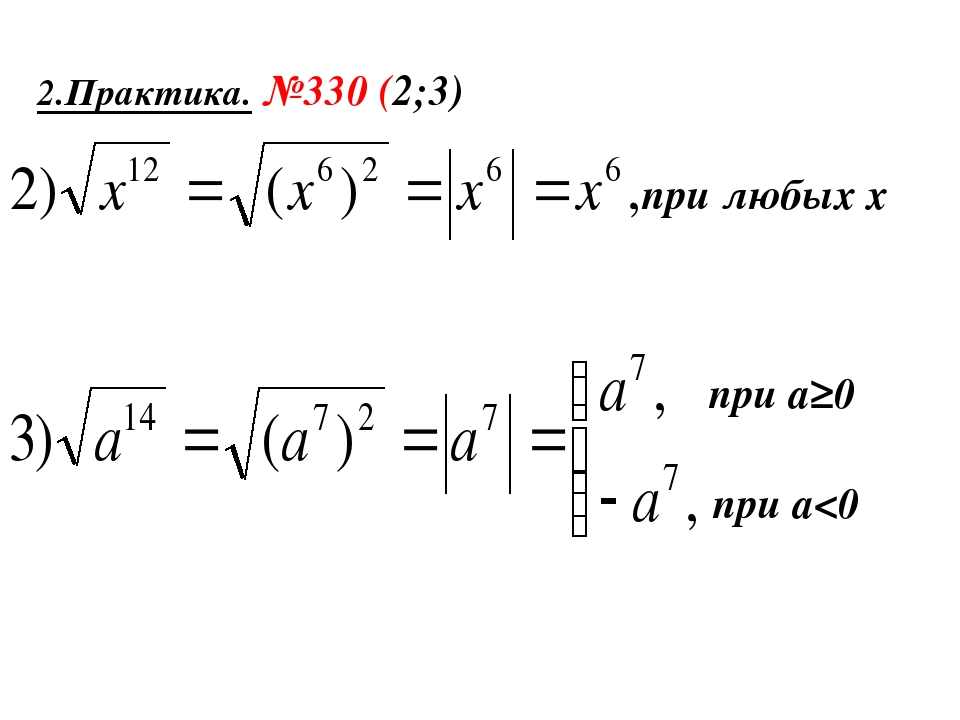
6. Дана функция , где

а) Вычислите: f(-1), f (3).

б) Постройте график функции.

в) Найдите область значений функции.

г) Выясните, при каких значениях параметра уравнение имеет два корня.

Контрольная работа №2

Вариант 2

1. Вычислите:

а) б) в) г)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Найдите наибольшее и наименьшее значения функции на отрезке [0;8].

6. Дана функция , где а) Вычислите: f(-2), f (7).

б) Постройте график функции.

в) Найдите область значений функции.

г) Выясните, при каких значениях параметра уравнение имеет два корня.

Контрольная работа №2

Вариант 3

1. Вычислите:

а) б) в) г)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Составьте уравнение касательной к графику функции в точке х=1.

6. Дана функция , где

а) Вычислите: f(-4), f (31).

б) Постройте график функции.

в) Найдите область значений функции.

г) Выясните, при каких значениях параметра уравнение имеет два корня.

Контрольная работа №2

Вариант 4

1. Вычислите:

а) б) в) г)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Найдите наибольшее и наименьшее значения функции на отрезке [1;9].

6. Дана функция , где

а) Вычислите: f(-1), f (4).

б) Постройте график функции.

в) Найдите область значений функции.

г) Выясните, при каких значениях параметра уравнение имеет два корня.

Контрольная работа №3

Вариант 1

1. Вычислите: а) б)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Решите уравнение:

Контрольная работа №3

Вариант 2

1. Вычислите: а) б)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Решите уравнение:

Контрольная работа №3

Вариант 3

1. Вычислите: а) б)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Решите уравнение:

Контрольная работа №3

Вариант 4

1. Вычислите: а) б)

2. Постройте график функции: а) б)

3. Решите уравнение: а) б)

4. Решите неравенство:

5. Решите уравнение:

Контрольная работа №4

Вариант 1

1. Решите неравенство:

2. Исследуйте функцию на монотонность и экстремумы.

3. Напишите уравнение касательной к графику функции

в точке x=1.

4. Решите уравнение:

5. Решите систему уравнений

Контрольная работа №4

Вариант 2

1. Решите неравенство:

2. Исследуйте функцию на монотонность и экстремумы.

3. Напишите уравнение касательной к графику функции

в точке x=3.

4. Решите уравнение:

5. Решите систему уравнений

Контрольная работа №4

Вариант 3

1. Решите неравенство:

2. Исследуйте функцию на монотонность и экстремумы.

3. Напишите уравнение касательной к графику функции

в точке x=4.

4. Решите уравнение: 2

5. Решите систему уравнений

Контрольная работа №4

Вариант 4

1. Решите неравенство:

2. Исследуйте функцию на монотонность и экстремумы.

3. Напишите уравнение касательной к графику функции

в точке x=2.

4. Решите уравнение:

5. Решите систему уравнений

Контрольная работа №5

Вариант 1

1. Докажите, что функция является первообразной для функции .

2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А (-π;0).

3. Вычислите интеграл: а) ; б) .

4. Вычислите площадь фигуры, ограниченной линиями .

5. Известно, что функция – первообразная для функции . Исследуйте функцию на монотонность и экстремумы.

Контрольная работа №5

Вариант 2

1. Докажите, что функция является первообраз-ной для функции .

2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А (-).

3. Вычислите интеграл: а) ; б) .

4. Вычислите площадь фигуры, ограниченной линиями .

5. Известно, что функция – первообразная для функции . Исследуйте функцию на монотонность и экстремумы.

Контрольная работа №5

Вариант 3

1. Докажите, что функция является первообразной для функции .

2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А ().

3. Вычислите интеграл: а) ; б) .

4. Вычислите площадь фигуры, ограниченной линиями .

5. Известно, что функция – первообразная для функции . Сравните числа F (6) и F (7).

Контрольная работа №5

Вариант 4

1. Докажите, что функция является первообразной для функции .

2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А ().

3. Вычислите интеграл: а) ; б) .

4. Вычислите площадь фигуры, ограниченной линиями.

5. Известно, что функция – первообразная для функции . Сравните числа F (3) и F (4).

Контрольная работа №6

Вариант 1

1. В клубе 25 спортсменов. Сколькими способами из них можно составить команду из четырёх человек для участия в четырёхэтапной эстафете с учётом порядка пробега этапов?

2. Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 0 при условии, что каждая цифра может встретиться в записи числа один раз?

3. Решите уравнение .

4. Напишите разложение степени бинома.

5. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом карты одинаковой масти?

6. На прямой взяты шесть точек, а на параллельной ей прямой – 7 точек. Сколько существует треугольников, вершинами которых являются данные точки?

Контрольная работа №6

Вариант 2

1. Сколькими способами можно составить трёхцветный полосатый флаг, если имеется ткань пяти различных цветов?

2. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3 при условии, что цифры могут повторяться?

3. Решите уравнение .

4. Напишите разложение степени бинома.

5. Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?

6. Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 10-угольника?

Контрольная работа №6

Вариант 3

1. В городской думе 30 человек. Из них на общем заседании надо выбрать председателя, а также его первого, второго и третьего заместителей. Сколькими способами это можно сделать?

2. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6 при условии, что цифры могут повторяться?

3. Решите уравнение .

4. Напишите разложение степени бинома.

5. В урне находятся 3 белых и 4 чёрных шара. Какова вероятность того, что вынутые из неё наудачу два шара окажутся белыми?

6. На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?

Контрольная работа №6

Вариант 4

1. В яхт-клубе состоит 9 человек. Из них на общем собрании надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?

2. Сколько четырёхзначных чисел можно составить из цифр 1, 2, 3, 0 при условии, что каждая цифра может встретиться в записи числа один раз?

3. Решите уравнение .

4. Напишите разложение степени бинома.

5. В урне находятся 2 белых, 3 красных и 16 чёрных шаров. Какова вероятность того, что из вынутых наудачу двух шаров один окажется белым, а другой красным?

6. Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 8-угольника, а стороны не совпадают со сторонами этого многоугольника?

Контрольная работа №7 (2 часа)

Вариант 1

1. Решите уравнение: а) б)

в)

2. Решите неравенство: а) б)

в)

3. Решите уравнение в целых числах:

4. Решите систему уравнений:

5. Решите уравнение:

Контрольная работа №7 (2 часа)

Вариант 2

1. Решите уравнение: а) б)

в)

2. Решите неравенство: а) б)

в)

3. Решите уравнение в целых числах:

4. Решите систему уравнений:

5. Решите уравнение:

Контрольная работа №7 (2 часа)

Вариант 3

1. Решите уравнение: а) б)

в)

2. Решите неравенство: а) б)

в)

3. Решите уравнение в целых числах:

4. Решите систему уравнений:

5. Решите уравнение:

Контрольная работа №7 (2 часа)

Вариант 4

1. Решите уравнение: а) б)

в)

2. Решите неравенство: а) б)

в)

3. Решите уравнение в целых числах:

4. Решите систему уравнений:

5. Решите уравнение:

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Константин Берков (7), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2),

Как сделать знак корня в excel?

Извлечение корня из числа является довольно распространенным математическим действием. Оно применяется и для различных расчетов в таблицах. В Microsoft Excel есть несколько способов посчитать данное значение. Давайте подробно рассмотрим различные варианты осуществления подобных расчетов в этой программе.

Способы извлечения

Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.

Способ 1: применение функции

Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:

=КОРЕНЬ(число)

Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.

Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.

Кроме того, можно применить данную формулу через мастер функций.

1. Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.
2. В открывшемся списке выбираем пункт «КОРЕНЬ». Кликаем по кнопку «OK».
3. Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена. Достаточно кликнуть по этой ячейке, чтобы её адрес был внесен в поле. После ввода данных жмем на кнопку «OK».

В итоге в указанной ячейке будет отображаться результат вычислений.

Также функцию можно вызвать через вкладку «Формулы».

1. Выделяем ячейку для отображения результата расчета. Переходим во вкладку «Формулы».
2. В блоке инструментов «Библиотека функций» на ленте кликаем по кнопке «Математические». В появившемся списке выбираем значение «КОРЕНЬ».
3. Открывается окно аргументов. Все дальнейшие действия в точности такие же, как и при действии через кнопку «Вставить функцию». 1/n

   n – это степень возведения.

   Таким образом, этот вариант является намного универсальнее, чем использование первого способа.

   Как видим, несмотря на то, что в Excel нет специализированной функции для извлечения кубического корня, данное вычисление можно провести, используя возведение в дробную степень, а именно — 1/3. Для извлечения квадратного корня можно воспользоваться специальной функцией, но существует также возможность сделать это путем возведения числа в степень. На этот раз нужно будет возвести в степень 1/2. Пользователь сам должен определить, какой способ вычислений для него удобнее.

   Мы рады, что смогли помочь Вам в решении проблемы.

   Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

   Помогла ли вам эта статья?

   Да Нет

   Программа Microsoft Excel имеет широкий набор математических функций, позволяющих решать непростые задачи. Ряд простейших действий — сложение, умножение и другие — выполнить очень легко, воспользовавшись специальными символами. Однако есть и те, которые требуют особого описания — так, далеко не все знают, как вычислить корень квадратный в Excel.

   Что такое корень квадратный?

   Перед началом изучения процесса, как найти корень квадратный в Excel, стоит поближе ознакомиться с тем, что собой представляет эта математическая функция. По определению, квадратный корень из числа а — это некоторое число, квадрат которого равен числу а. В математических науках можно встретить не только квадратные корни. Они также бывают и любой другой степени, поэтому квадратный корень часто называют корнем второй степени.

   Функция корня

   При решении задачи, связанной с нахождением квадратного корня в «Экселе», получить желаемый результат можно несколькими способами. Функционал программы позволяет как воспользоваться встроенными алгоритмами решений, так и написать его самостоятельно, пользуясь специальными теоремами и свойствами корня. Самым простым способом нахождения ответа является функция квадратного корня. В Excel её можно вызвать, открыв меню функций или же прописав вручную.

   Синтаксис функции очень прост — после указания использования одной из функций (знака равенства) необходимо прописать ключевое слово «КОРЕНЬ», обозначающее вызов соответствующей команды. Далее в скобках останется записать переменную, из которой требуется извлечь квадратный корень. В Excel в качестве аргумента функции может использоваться как явное числовое значение, так и ссылка на ячейку, а также некоторое математическое выражение, результатом которого является число.

   Использование математических свойств

   Корень квадратный в Excel можно вычислить и рядом других методов, которые не требуют глубоких познаний в математических науках. Для этого достаточно знать, что такое корень, — эта тема была затронута в первом разделе статьи. Воспользовавшись определением квадратного корня, его можно представить в виде обратной степени двойки искомого числа. (0,5)». Результат этого действия будет аналогичен возведению в степень с помощью функции, а также использованию функции «КОРЕНЬ».

   Стоит отметить, что способ нахождения корня с возведением в степень является более удобным. Причиной тому является тот факт, что с помощью этих операций можно получить корень любой степени, не применяя каких-то специальных дополнительных вычислений.

   Примеры

   Чтобы окончательно разобраться с тем, как вычислить корень квадратный в Excel, стоит рассмотреть пару примеров для двух описанных выше способов.

   В первом случае воспользуемся функцией «КОРЕНЬ», вызвав её с помощью кнопки «Вставить функцию». В открывшемся окне останется указать данные для вычисления, например разность значений двух ячеек, и нажать «Ок».

   Во втором случае, используя более удобочитаемый вариант, с явным заданием степени числа, получим следующее выражение для нахождения квадратного корня из числа, например, 9:

   Результатом выполнения этого действия станет значение «3».

   Для извлечения корня в Excel и возведения числа в степень используются встроенные функции и математические операторы. Рассмотрим на примерах.

   Примеры функции КОРЕНЬ в Excel

   Встроенная функция КОРЕНЬ возвращает положительное значение квадратного корня. В меню «Функции» она находится в категории «Математические».

   Синтаксис функции: =КОРЕНЬ(число).

   Единственный и обязательный аргумент представляет собой положительное число, для которого функция вычисляет квадратный корень. Если аргумент имеет отрицательное значение, Excel вернет ошибку #ЧИСЛО!.

   В качестве аргумента можно указывать конкретное значение либо ссылку на ячейку с числовым значением.

   Рассмотрим примеры.

   Функция вернула квадратный корень числа 36. Аргумент – определенное значение.

   Аргумент функции – ссылка на ячейку с положительным значением 36.

   Функция вернула ошибку, т.к. аргумент – ссылка на ячейку с отрицательным значением.

   Функция ABS возвращает абсолютное значение числа -36. ».

   Обратите внимание! Дробная степень пишется в скобках.

   Выполнили ту же задачу, но с использованием функции СТЕПЕНЬ.

   Извлекли корень девятой степени из значения ячейки h2.

   Извлекли корень пятой степени из суммы числа 9 и значения ячейки h2.

   Те же математические операции можно выполнить с помощью функции СТЕПЕНЬ:

   Таким образом, возвести в степень и извлечь корень n-й степени в Excel можно с помощью одной функции.

   Как написать число в степени

   Для корректного отображения числа в степени при демонстрации файла или его печати, необходимо произвести ряд манипуляций:

   1. Щелкаем по ячейке с числом правой кнопкой мыши. Выбираем «Формат ячеек» (или нажмите CTRL+1).
   2. В открывшемся меню переходим на вкладку «Число». Задаем «Текстовый» формат. Текстовый формат для значения в ячейке можно также задать через панель инструментов («Главная» – «Число»). После установки текстового формата цифра в ячейке становится слева.
   3. Рядом с цифрой вводим в ячейку значение со знаком «минус».
   4. Выделяем только значение степени («-3»). Вызываем меню «Формат ячеек». Устанавливаем видоизменение «Надстрочный». И нажимаем ОК.

   Получили корректное отображение числа 5 в -3 степени.

   В разделе Прочее компьютерное на вопрос Как в excel вставить ЗНАЧОК корня?… заданный автором Благосостояние лучший ответ это Вставка -> Символ и выбирай там что твоей душе угодно.

   Ответ от

   22 ответа

   Привет! Вот подборка тем с ответами на Ваш вопрос: Как в excel вставить ЗНАЧОК корня?…

   Как ввести формулу в Excel, чтобы вычислить корень третьей степени?

   Ответ от Гигроскопичный
   держи — √ . копируй и вставляй хоть куда. его можно найти в шрифте verdana. Удачи!

   Ответ от Џна Розова
   Если надо вычислить корень числа, то используй функцию SQRT() или КОРЕНЬ () в зависимости от версии excel

   Разложение на множители многочлена третьей степени

   Пример 1. Разложить на множители многочлен x³ — 3x² — 4x + 6.

   Решение.

   Делители свободного члена: ±1, ±2, ±3, ±6. Значит, корни многочлена нужно искать среди них. Простой подстановкой убеждаемся, что корнем многочлена является число 1. Значит, исходный многочлен надо разделить на x — 1.

   Воспользуемся схемой Горнера.

   Таким образом, x³ — 3x² — 4x + 6 = (x — 1)(x² — 2x — 6). Чтобы найти оставшиеся 2 корня многочлена, решаем квадратное уравнение x² — 2x — 6 = 0.

   Но обычно в разложении на множители нас не интересуют иррациональные корни (то есть, такое разложение квадратичного многочлена на множители

   Ответ: x³ — 3x² — 4x + 6 = (x — 1)(x² — 2x — 6).

   Пример 2. Разложить на множители многочлен -2x³ + 3x² — 4x — 9.

   Решение.

   Делители свободного члена: ±1, ±3, ±9. Делители старшего коэффициента: ±1, ±2.
   Значит, корни исходного многочлена будем искать среди чисел: ±1, ±3, ±9,

   .

   Снова простой подстановкой убеждаемся, что -1 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x + 1.

   Таким образом, -2x³ + 3x² — 4x — 9 = (x + 1)(-2x² + 5x — 9). Решая квадратное уравнение -2x² + 5x — 9 = 0, получаем, что его дискриминант

   Ответ: -2x³ + 3x² — 4x — 9 = (x + 1)(-2x² + 5x — 9).

   Пример 3. Разложить на множители многочлен 2x³ — x² — 8x + 4.

   Решение.

   Простой подстановкой убеждаемся, что 2 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x — 2.

   Таким образом, 2x³ — x² — 8x + 4 = (x — 2)(2x² + 3x — 2).
   Решая квадратное уравнение 2x² + 3x — 2 = 0, получаем,

   Следовательно, 2x² + 3x — 2 = 2(x — 

   )(x + 2).

   Ответ: 2x³ — x² — 8x + 4 = 2(x — 2)(x — 

   )(x + 2) = (2x — 1)(x — 2)(x + 2).

   Разложение на множители многочлена третьей степени методом неопределенных коэффициентов

   Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он достаточно трудоемкий, но иногда бывает очень полезным, причем для разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x₀)*(a₃x² + bx + c).

   Раскрывая скобки, получим a(x) = a₃x³ + x²(b — a₃x₀) + x*(c — bx₀) — cx₀.

   Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a₃,b,c и x₀. Рассмотрим применение метода неопределенных коэффициентов на примерах.

   Пример 4. Разложить на множители многочлен x³ + 2x² — 5x — 6.

   Решение.

   Приравнивая соответствующие коэффициенты, получаем следующую систему уравнений

   Выразим из первого уравнения x₀ = b — 2 и подставим в два оставшихся. Получим

   Теперь из первого уравнения выразим переменную c и подставим во второе.

   Раскрывая скобки во втором уравнении и решая его, находим b:

   Если b=4, то c=3, x₀ = 2. Следовательно, x³ + 2x² — 5x — 6 = (x — 2)(x² — 4x + 3)=(x — 2)(x + 1)(x + 3).

   Если b = 1, то c = -6, x₀ = -1. Следовательно, x³ + 2x² — 5x — 6 = (x + 1)(x² + x — 6)=(x + 1)(x + 3)(x — 2).

   Если b = -1, то c = -2, x₀ = -3. Следовательно, x³ + 2x² — 5x — 6=(x + 3)(x² — x — 2) = (x + 3)(x — 2)(x + 1).

   Ответ: x³ + 2x² — 5x — 6 = (x — 2)(x + 1)(x + 3).

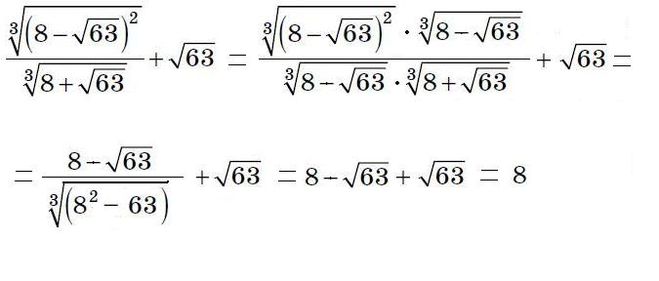
   30 60 90 Правые треугольники

   Треугольник особого вида

   Прямоугольный треугольник 30-60-90 (буквально произносится как «тридцать шестьдесят девяносто») — это особый тип прямоугольного треугольника, в котором три угла составляют 30 градусов, 60 градусов и 90 градусов. Треугольник важен, потому что стороны существуют в легко запоминающемся соотношении: 1: \ (\ sqrt {3} \): 2. Иными словами, гипотенуза в два раза длиннее более короткого отрезка, а более длинное отрезок представляет собой квадратный корень из 3-кратного более короткого отрезка.Вы также можете помнить это как «корни X, 2X и X из 3», как я это помню, но тогда вы должны помнить, что на самом деле самая длинная сторона — это 2X, а не X корней из 3.

   Какая сторона какая? Сторона, противоположная углу 30 градусов, будет иметь наименьшую длину. Сторона, противоположная углу 60 градусов, будет в \ (\ sqrt {3} \) раз длиннее, а сторона, противоположная углу 90 градусов, будет вдвое длиннее. Треугольник ниже показывает эту взаимосвязь. Помните, что самая длинная сторона будет противоположна наибольшему углу, а самая короткая — противоположному наименьшему углу.

   Мы можем использовать соотношение между углами и сторонами треугольника 30-60-90, чтобы найти недостающие углы или длины сторон. Взгляните на этот пример:

   Пример 1

   Для треугольника 30-60-90 ниже найдите длины недостающих сторон:

   Поскольку это прямоугольный треугольник 30-60-90, мы знаем, что стороны существуют в пропорции 1: \ (\ sqrt {3} \): 2. Самая короткая сторона, 1, находится напротив угла 30 градусов. Поскольку сторона X противоположна углу в 60 градусов, мы знаем, что он равен \ (1 * \ sqrt {3} \), или примерно 1.73. Наконец, сторона Y противоположна прямому углу, и это в два раза короче сторона, или 2.

   Откуда взялась формула?

   Это еще одна выдуманная математическая формула? Нет! Это просто приложение базовой тригонометрии. В приведенном выше примере мы могли бы взять синус крайнего левого угла: sin (30) = 1/2. Поскольку синус дает нам отношение противоположности к гипотенузе, мы бы знали, что гипотенуза должна быть 2. По сути, вся причина, по которой треугольник 30-60-90 легко решить, заключается в том, что синус и косинус этих углов равны тоже очень просто.

   Пример 2

   Используйте те же принципы для поиска неизвестных переменных X и Y.

   Известная сторона — 4, и это самая длинная сторона. Помните, как длинная сторона в два раза длиннее самой короткой стороны для треугольника 30-60-90? Это означает, что Y должно быть 2!

   Теперь мы можем найти оставшуюся сторону. Так как сторона , противоположная углу в 60 градусов, равна меньшей стороне, умноженной на квадратный корень из 3 , мы можем вычислить, что X равно \ (2 * \ sqrt {3} \).

   Сводка

   Для прямоугольного треугольника с углами, равными 30, 60 и 90 градусов, стороны будут иметь длину в соотношении 1: \ (\ sqrt {3} \): 2, как показано на этой диаграмме:

   Дополнительная справка

   Как всегда, вы можете задать свои конкретные вопросы на нашей доске сообщений справки по математике, выполнить поиск в Google или пройти этот урок по 30-60-90 треугольникам или этот. Или, чтобы вычислить стороны и углы треугольника, используйте интерактивный инструмент ниже:

   Суммы и произведения корней

   Корни многочлена

   «Корень» (или «ноль») — это полином , равный нулю. :

   Проще говоря: корень — это значение x, где значение y равно нулю.

   Общий полином

   Если у нас есть такой общий многочлен:

   f (x) = ax ⁿ + bx ^n-1 + cx ^n-2 + … + z

   Тогда:

   • Складывая корни дает −b / a
   • Умножение корней дает:
     • z / a (для полиномов четной степени, таких как квадратичные)
     • −z / a (для многочленов нечетной степени, таких как кубики)

   Что иногда может помочь нам решить проблемы.

   Как работает эта магия? Давайте узнаем …

   Факторы

   Мы можем взять многочлен, например:

   f (x) = ax ⁿ + bx ^n-1 + cx ^n-2 + . .. + z

   А затем разложите на множители так:

   f (x) = a (x − p) (x − q) (x − r) …

   Тогда p, q, r и т. Д. Являются корнями (где многочлен равен нулю)

   Квадратичный

   Давайте попробуем это с помощью квадратичного уравнения (где наибольший показатель переменной равен 2):

   топор ² + bx + c

   Когда корни равны p и q , то же квадратичное значение становится:

   а (х-р) (х-д)

   Есть ли связь между a, b, c и p, q ?

   Давайте расширим a (x − p) (x − q):

   a (x − p) (x − q)
   = a (x ² — px — qx + pq)
   = ax ² — a (p + q) x + apq

   А теперь сравним:

   Квадратичный:	топор 2	+ bx	+ с
   Коэффициенты расширения:	топор 2	−a (p + q) x	+ apq

   Теперь мы видим, что −a (p + q) x = bx, поэтому:

   -a (p + q) = b

   р + д = -b / а

   И apq = c, поэтому:

   pq = c / a

   И получаем такой результат:

   • Сложение корней дает −b / a
   • Умножение корней дает c / a

   Это поможет нам ответить на вопросы.

   Пример: что такое уравнение, корни которого равны 5 + √2 и 5 — √2

   Сумма корней равна (5 + √2) + (5 — √2) = 10
   Произведение корней равно (5 + √2) (5 — √2) = 25-2 = 23

   И нам нужно уравнение вроде:

   топор ² + bx + c = 0

   Когда a = 1 , мы можем вычислить, что:

   • Сумма корней = −b / a = -b
   • Произведение корней = c / a = c

   Что дает нам этот результат

   x ² — (сумма корней) x + (произведение корней) = 0

   Сумма корней равна 10, а произведение корней равно 23, поэтому мы получаем:

   x ² — 10x + 23 = 0

   А вот его сюжет:

   (Вопрос: что произойдет, если мы выберем a = −1 ?)

   кубический

   Теперь давайте посмотрим на кубический (на один градус выше квадратичного):

   топор ³ + bx ² + cx + d

   Как и в случае квадратичной, расширим коэффициенты:

   a (x − p) (x − q) (x − r)
   = ax ³ — a (p + q + r) x ² + a (pq + pr + qr) x — a (pqr )

   И получаем:

   Кубический:	топор 3	+ bx 2	+ сх	+ d
   Коэффициенты расширения:	топор 3	−a (p + q + r) x 2	+ a (pq + pr + qr) x	−apqr

   Теперь мы видим, что −a (p + q + r) x ² = bx ² , поэтому:

   -a (p + q + r) = b

   р + д + г = -b / а

   И −apqr = d, поэтому:

   pqr = -d / a

   Это интересно. .. получаем то же самое:

   • Сложение корней дает -b / a (точно так же, как квадратичный)
   • Умножение корней дает -d / a (аналогично + c / a для квадратичного)

   (Мы также получаем pq + pr + qr = c / a, что само по себе может быть полезно.)

   Высшие полиномы

   Тот же самый образец продолжается с более высокими полиномами.

   В целом:

   • Сложение корней дает −b / a
   • Умножение корней дает (где z — константа в конце):
     • z / a (для полиномов четной степени, таких как квадратичные)
     • −z / a (для многочленов нечетной степени, таких как кубики)

   Квадраты: многочлены второй степени

   10

   Решение квадратного уравнения с множителем

   Двойной корень

   Квадратичное неравенство

   Сумма и произведение корней

   КВАДРАТИКА — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени. 2 — самый высокий показатель степени.

   1. Какой вид имеет полиномиальная функция 2-й степени?

   y = ax ² + bx + c

   2. Какой вид имеет квадратное уравнение?

   ось ² + bx + c = 0

   3. Что мы подразумеваем под корнем квадратичного?

   Решение квадратного уравнения.

   4. Сколько корней всегда у квадратичной?

   Два, реальные или сложные.

   5. График квадратичной всегда имеет форму, называемую -?

   Парабола.

   6. Каковы три метода решения квадратного уравнения,
   6. То есть поиска корней?

   1. Факторинг. 2. Завершение квадрата.

   3.Квадратичная формула.

   Начнем с метода факторинга. В следующей теме мы представим как Завершение квадрата, так и формулу квадратного уравнения.

   7. Если произведение множителей равно 0 — если ab = 0 — то что вы можете
   
   7. сделать вывод о факторах a , b ?

   Либо a = 0, либо b = 0.

   Пример 1. Решение по факторингу.

   f ( x ) = x ² −2 x −3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).

   Решение . x ² −2 x −3 = ( x + 1) ( x — 3).

   Следовательно, корни — это −1 и 3. (См. Урок 37 по алгебре.) Они представляют собой точки пересечения x графа.

   Перехват y — постоянный член −3.

   В каждом полиноме пересечение y является постоянным членом, потому что постоянный член представляет собой значение y , когда x = 0.

   Пример 2. Двойной корень

   f ( x ) = x ² −10 x + 25. Найдите корни
   f ( x ) и нарисуйте график y = f ( х ).

   Решение . x ² −10 x + 25 =
   ( x — 5) ( x — 5) = ( x — 5) ² . Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)

   При двойном корне график не пересекает ось x . Это просто трогает.

   Двойной корень возникает, когда квадратичный является трехчленом полного квадрата: x ² ± 2 ax + a ² ; то есть, когда квадратичная величина является квадратом бинома: ( x ± a ) ² .

   Пример 3. Сколько действительных корней, т.е. корней, которые являются действительными числами, имеет квадратичный элемент каждого графа?

   Ответ . График а) имеет два действительных корня. Он имеет два перехватчика x .

   График б) не имеет реальных корней. У него нет x -перехватов. Оба корня сложные.

   График c) имеет два действительных корня. Но они двойной корень.

   Пример 4.Квадратичное неравенство.

   Решите это неравенство:

   x ² — 4 x — 5

   Для этого осмотрите график

   y = x ² — 4 x — 5.

   Решение . Для каких значений x эта квадратичная будет отрицательной? То есть где график под осью x ?

   График отрицательный между корнями, которые равны -1 и 5.Решение неравенства равно −1 x. Мы также можем заметить, что квадратичная функция будет иметь положительные значения — график будет выше оси x — слева и справа от корней:

   х х> 5.

   В то время как квадратичный будет иметь значение 0 в корнях.

   Мы рассмотрели три возможности:

   Эта квадратичная величина равна 0 в двух корнях.

   Это на меньше, чем 0 между двумя корнями.

   Это на больше, чем 0 слева и справа от двух корней.

   Эти три возможности, которые верны для любого действительного числа, имеют причудливое название Закона трихотомии. Любое число должно быть либо равно, меньше или больше 0.

   Закон трихотомии также принимает такую ​​форму:

   Для любых действительных чисел a, b , либо a = b , a b, либо a > b .

   Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».

   Задача 1. Нарисуйте график y = x ² — 2 x −8. То есть покажите точки пересечения x и y .

   Чтобы увидеть ответ, наведите указатель мыши на цветную область.
   Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

   x ² −2 x — 8 = ( x + 2) ( x — 4). Следовательно, корни равны −2, 4. 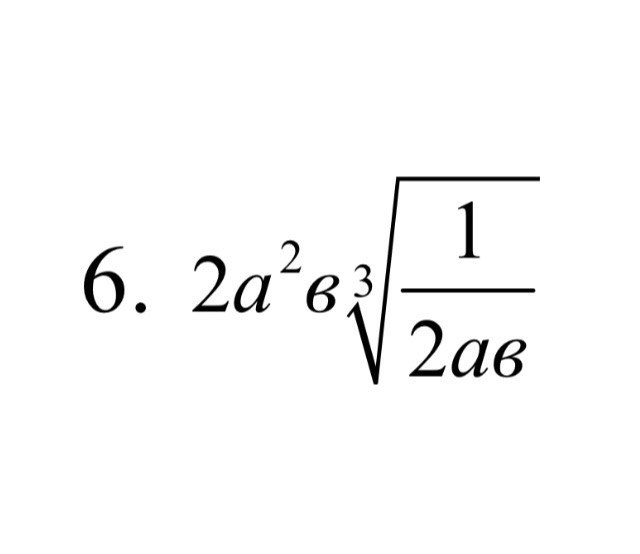Пересечение y является постоянным членом −8.

   Задача 2. Нарисуйте график

   .

   y = x ² + 4 x + 4.

   x ² + 4 x + 4 = ( x + 2) ² .В −2 есть двойной корень. Перехват y — постоянный член, 4.

   Проблема 3.

   а) Чтобы решить это квадратное неравенство —

   x ² + 2 x — 3> 0

   —проверьте график

   y = x ² + 2 x — 3.

   Квадратичное значение будет положительным — выше оси x — для значений x слева и справа от корней.Решение:
   x x> 1.

   б) Решите это квадратное неравенство:

   x ² + 2 x — 3

   −3 х

   Квадратичный будет отрицательным между корнями.

   Проблема 4. Квадратичная имеет следующие корни. Запишите каждую квадратичную как произведение линейных множителей.

   а) 3, 4
   ( x — 3) ( x — 4)

   б) −3, −4
   ( х + 3) ( х + 4)

   в) — р , с
   ( x + r ) ( x — s )

   г) 3+, 3 —
   ( x -3 -) ( x −3 +)

   Сумма и произведение корней

   Теорема. В квадратичной системе со старшим коэффициентом 1:

   Сумма корней равна отрицательному значению коэффициента x ;

   произведение корней — постоянный член.

   То есть, если

   x ² + bx + c = 0,

   и корни r и s , затем

   r + s	=	— б ,
   RS	=	с .

   Ибо, если корни равны r и s , то квадратичный равен

   ( x — r ) ( x — s )	=	x 2 — rx — sx + rs
   	=	x 2 — ( r + s ) x + rs .

   Коэффициент x равен — ( r + s ), что является отрицательным значением суммы корней. Постоянный член составляет рупий , что является их произведением.

   Пример 5. Построить квадратичную с корнями 2 и 3.

   Решение . Сумма корней равна 5, их произведение равно 6, следовательно, квадратичный равен x ² -5 x + 6.

   Сумма корней равна отрицательному значению коэффициента x . Произведение корней — постоянный член.

   Пример 6. Построить квадратичную с корнями 2 +, 2 -.

   Решение . Сумма корней равна 4. Их произведение — разность двух квадратов: 2 ² — () ² = 4 — 3 = 1.

   Следовательно, квадратичный равен x ² -4 x + 1.

   Пример 7. Построить квадратичный, корни которого равны 2 + 3 i , 2 — 3 i , где i — комплексная единица.

   Решение . Сумма корней равна 4. Произведение снова является разностью двух квадратов: 4–9 i ² = 4 + 9 = 13.

   Квадратичная с этими корнями равна

   .

   x ² -4 x + 13.

   Задача 5. Построить квадратичную с корнями −3, 4.

   Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичный равен x ² — x — 12.

   Задача 6. Построить квадратичную с корнями 3 +, 3 -.

   Сумма корней равна 6. Их произведение равно 9 — 3 = 6.
   Следовательно, квадратичный равен x ² — 6 x + 6.

   Задача 7. Построить квадрат, корни которого равны 2 + i , 2 — i .

   Сумма корней равна 4. Их произведение равно 4 — ( i ) ² = 4 + 5 = 9.
   Следовательно, квадратичный равен x ² — 4 x + 9.

   *

   В более общем смысле, для любого коэффициента x ² , то есть, если квадратичный равен

   ось ² + bx + c ,

   и корни r и s , затем

   r + s	=	–	b a	,
   RS	=	c a	.

   Когда a = 1, мы имеем теорему выше.

   Следующая тема: Завершение квадрата

   Содержание | Дом

   ---

   Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
   Даже 1 доллар поможет.

   ---

   Авторские права © 2021 Лоуренс Спектор

   Вопросы или комментарии?

   Эл. Почта: [email protected]

   Корневой топологический изолятор с неквантованными индексами, реализованный с помощью фотонных клеток Ааронова-Бома

   Теоретическая модель

   Рассматривается цепочка из клеток Ааронова-Бома, т.е.{4} {d} _ {i} {\ lambda} _ {3 + i}, $$

   (1)

   , где λ _i , где i = 1,. . , 8, восемь матриц Гелл-Манна (определенные в дополнительном примечании 5) и d = ( d ₁ , d ₂ , d ₃ , d ₄ ) представляет собой 4-компонентный вещественнозначный вектор с \ ({d} _ {1} = 1 + \ cos k \), \ ({d} _ {2} = \ sin k \), \ ({d} _ {3} = \ cos \ phi + \ cos k \) и \ ({d} _ {4} = \ sin \ phi + \ sin k \). 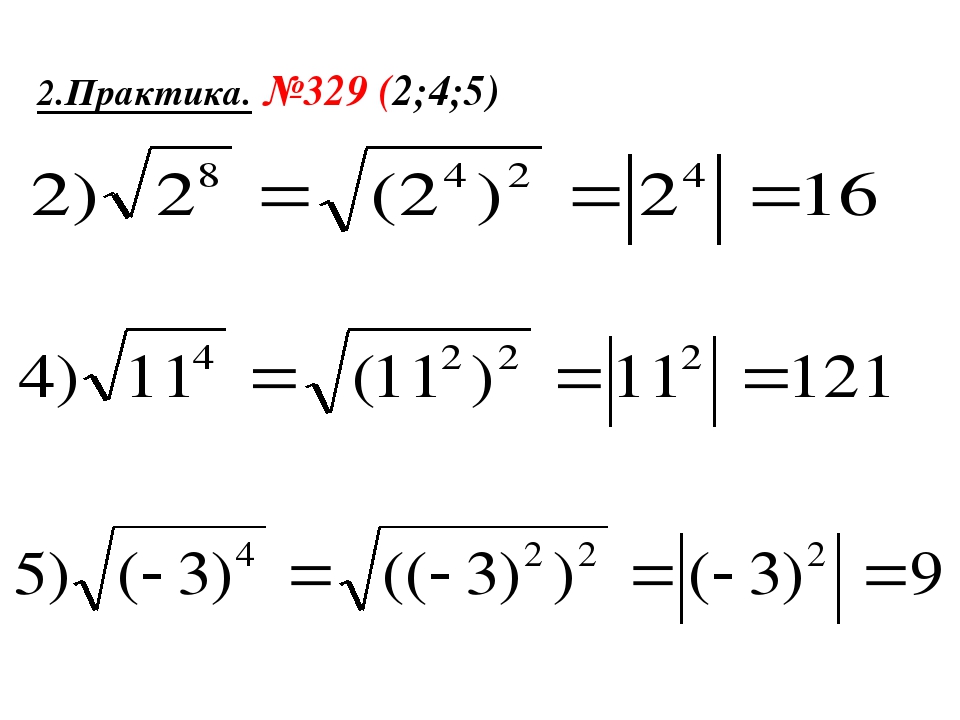Спектр H ( k ) имеет три полосы: центральную полосу, которая остается недисперсной при всех значениях потока ϕ , и две дополнительные частица-дырочные симметричные полосы. При ϕ = 0 три полосы пересекаются, а при ϕ = π спектр перекрывается тремя плоскими полосами при энергиях E _i ∈ {−2 t , 0, 2 т }, см. Рис. 1б. Последний случай соответствует эффекту клетки Ааронова – Бома, когда частицы становятся неподвижными из-за деструктивной интерференции ^20,21,22 .

   Рис. 1: Клетки Ааронова – Бома.

   a Цепь клеток Ааронова – Бома [ср. Уравнение (1)], с тремя участками a _n , b _n , c _n в элементарной ячейке n и потоком ϕ в каждой резьбе плакетка. b Энергетическая дисперсия E ( k ) цепи как функция потока ϕ . 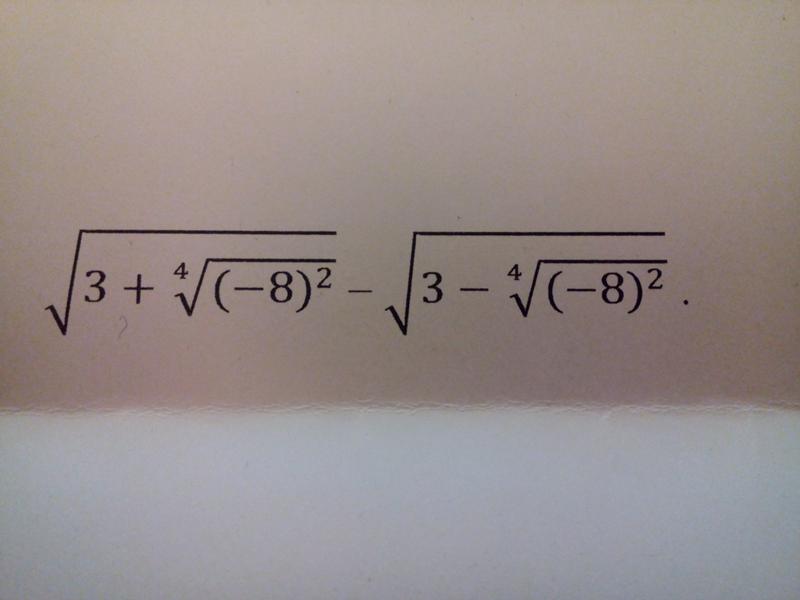c Энергетическая дисперсия E ( k ) при ϕ = π состоит из трех плоских полос при энергиях 0 и ± 2 t .Полоса на E = 0 имеет квантованную фазу Зака ​​ γ = π , в то время как две другие полосы показывают неквантованную обмотку π 2. В конце цепочки с участком a _n , два граничных состояния в промежутке появляются в \ (E = \ pm \ sqrt {2} t \). d Возведение гамильтониана (1) в квадрат дает модель (2) с одной плоской полосой при E = 0 и двумя вырожденными плоскими полосами при E = 4 t ² .Обе полосы имеют квантованную фазу Вильзчека – Зи γ ∣ = π .

   Для каждой полосы мы можем оценить одномерный топологический инвариант, фазу намотки Зака ​​\ ({\ gamma} _ {i} = {\ int} _ {\ text {BZ}} {\ rm {d}} k {{ \ mathcal {A}}} _ {i} (k) \), где \ ({{\ mathcal {A}}} _ {i} (k) = {\ rm {i}} \ left \ langle {v } _ {i} (k) \ right | {\ partial} _ {k} \ left | {v} _ {i} (k) \ right \ rangle \) — это соединение Берри диапазона i -го и \ (\ left | {v} _ {i} (k) \ right \ rangle \) — соответствующее собственное состояние ²³ . {{\ rm {i}} k} {\ lambda} _ {3} — \ frac {1} {3} {\ lambda} _ {8} \) (преобразование для общего потока ϕ см. в дополнительном примечании 1).{{\ rm {i}} k} {\ lambda} _ {3} — \ frac {1} {3} {\ lambda} _ {8} \) (см. дополнительное примечание 1 для преобразования для общего ϕ ), который квантует фазы обмотки до γ ₂ ∈ {0, π } mod 2 π и γ ₁ + γ ₃ ∈ {0, π } мод 2 π ²⁵ . Таким образом, член, разрушающий χ в гамильтониане H ( k ), делает фазы γ ₁ и γ ₃ спектрально разделенных полос неквантованными и непрерывно смешанными.

   Цепочка AB-каркасов с ϕ = π и открытыми граничными условиями имеет два внутризонных состояния с энергиями \ (\ pm \! \ Sqrt {2} t \), локализованные на одной и той же границе. Интересно, что их локализация и энергия устойчивы к беспорядку, который не нарушает-или χ -симметрию (см. Рис. 2 и дополнительное примечание 7). Следовательно, цепочка AB-клеток имеет устойчивые граничные состояния, даже когда фазы намотки γ ₁ и γ ₃ не квантованы.{2} \ rangle \) между энергией граничного состояния β _edge при наличии беспорядка и энергией невозмущенной системы \ ({\ beta} _ {0} = \ sqrt {2} t \), как функция силы разупорядочения σ . Используются три различных типа беспорядка, которые либо не нарушают одну из симметрий (χ или), либо нарушают обе. Все три типа беспорядка выбираются таким образом, чтобы в среднем сохранялись обе симметрии χ и, т.е.распределение беспорядка имеет исчезающее среднее значение. Вертикальная сплошная линия указывает размер зазора между граничным состоянием и ближайшей объемной зоной.{2}} \), \ ({m} _ {1} = 1 + \ cos (k) + \ cos (\ phi) + \ cos (k- \ phi) \), \ ({m} _ { 2} = \ sin (k) + \ sin (\ phi) — \ sin (k- \ phi) \) и \ ({m} _ {3} = \ cos (k) — \ cos (k- \ фи) \). Квадрат гамильтониана является блочно-диагональным с одной полосой \ (\ left | {w} _ {1} \ right \ rangle \) при энергии Λ ₁ = 2 t ² m ₀ и Подблок 2 × 2 с собственными состояниями \ (\ left | {w} _ {2} \ right \ rangle \) и \ (\ left | {w} _ {3} \ right \ rangle \) при энергиях Λ ₂ = 0 и Λ ₃ = 2 t ² m ₀ соответственно. {{\ rm {i}} {\ lambda} _ {2} \ frac {\ pi} {4}} \). В частности, при ϕ = π результирующий субблок 2 × 2 эквивалентен SSH-цепи с 0 внутриклеточным взаимодействием, 2 t ² межклеточного взаимодействия и константой 2 t ² сдвиг энергии (см. Дополнительный рис. 3).

   Важно отметить, что \ (\ left | {w} _ {1} \ right \ rangle \) и \ (\ left | {w} _ {3} \ right \ rangle \) образуют вырожденное подпространство с энергией Λ ₁ = Λ ₃ = 2 т ² м ₀ .{nm} = \ langle {v} _ {n} (k) | {\ partial} _ {k} | {v} _ {m} (k) \ rangle \), и n , m пробегают вовлеченные государства. Для квадрата гамильтониана H ² ( k ) фаза Вильзчека-Зи как полосы с нулевой энергией, так и вырожденного подпространства квантуется до {0, π } mod 2 π из-за -И χ-преобразования (см. Дополнительное примечание 3). В результате стандартное соответствие объем-граница одномерных ТИ применяется ²⁷ , а спектр открытой границы гамильтониана (2) поддерживает состояния средней щели, локализованные на границе. Когда ϕ = π , энергия этих состояний закреплена на 2 t ² . Следовательно, два энергетически разделенных состояния, появляющиеся на границе клеток AB, отображаются при операции возведения в квадрат на топологические граничные состояния квадрата гамильтониана. Это приводит к их характерной устойчивости, как по локализации, так и по энергии, к беспорядку, который сохраняет соответствующую симметрию, которая квантует топологические фазы в H ² ( k ) (см.рис.2).

   Экспериментальная реализация

   Реализуем цепочку AB-каркасов (1) в решетках фотонных волноводов, изготовленных методом фемтосекундной лазерной записи в объемном стекле ²⁸ . Эволюция света, распространяющегося в направлении z массива одномодовых волноводов, может быть хорошо описана в параксиальном приближении с помощью набора уравнений связанных мод i∂ _z ψ = H ψ . Волновая функция ψ представляет возбужденный оптический волновой пакет как суперпозицию связанных мод волноводов. 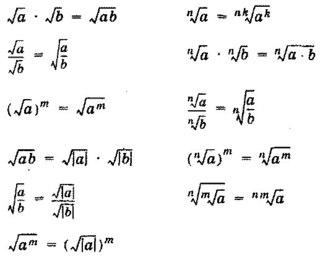Матрица H имеет диагональные элементы, соответствующие показателям преломления волноводов, и недиагональные элементы связи, пропорциональные перекрытию между связанными модами соседних волноводов. Таким образом, дискретные уравнения Шредингера можно моделировать в решетках волноводов с тем преимуществом, что временная координата в квантовом режиме отображается на расстояние пространственного распространения в оптической системе. Другими словами, распространение оптического волнового пакета через систему волноводов моделирует временную динамику электрона в потенциальном ландшафте.Примечательно, что с помощью флуоресцентной микроскопии мы можем напрямую отображать распространение света вдоль устройства ²⁹ .

   Чтобы создать эффективную фазу AB, пронизывающую каждую клетку, мы используем подстановку Пайерлса и связываем эффективную фазу с одной из скачкообразных амплитуд, см. Рис. 3. Разработка скачкообразной фазы для фотонов является сложной задачей, поскольку положительный показатель преломления каждого волновода всегда приводит к реальной положительной связи между волноводами. Тем не менее, размещая вспомогательный волновод с хорошо настроенным показателем преломления между двумя волноводами ³⁰ , создается эффективная отрицательная связь между двумя исходными волноводами (см. Дополнительное примечание 8).Важно отметить, что вспомогательный волновод сконструирован таким образом, что он не вносит значительного вклада в динамику системы, см. Рис. 3a. Выбрав показатель преломления двух исходных волноводов для энергетического согласования эффективной двухуровневой системы с остальной частью решетки (см. Дополнительное примечание 8) и разместив отрицательную связь в каждом плакете нашей волноводной структуры (см. Рис. 3b), создается общий поток π внутри плакеток, что приводит к желаемому эффекту АВ-каркаса (см.рис.3в для иллюстрации устройства).

   Рис. 3: Экспериментальная реализация.

   a Динамика света в трехуровневой системе из двух волноводов и вспомогательного волновода с тщательно подобранным показателем преломления. Поскольку большая часть амплитуды находится в исходных волноводах, мы можем проследить динамику вспомогательного волновода и получить двухуровневую систему с эффективными отрицательными прыжками — t . Горизонтальная шкала соответствует 1 см, а вертикальная шкала — 25 мкм. b Размещение такого дефекта в каждой пластине решетчатой ​​структуры создает общий поток ϕ = π . c Иллюстрация квазиодномерного массива быстро связанных волноводов, использованных в эксперименте. Свет выборочно вводится во входную грань устройства и визуализируется непосредственно с помощью флуоресцентной микроскопии.

   Мы сначала устанавливаем нашу способность генерировать эффект AB-каркаса в основной части цепи, исследуя динамику света, чтобы проверить плоскостность полос, см. Рис.4. Возбуждение одиночного волновода внутри плакета возбудит все k -состояния полос Блоха, которые перекрываются с этим участком. В случае плоских лент свет остается привязанным к точке впрыска и не рассеивается. Мы проводим два эксперимента, соответствующие двум различным местам инжекции в элементарной ячейке, см. Рис. 4a – c. Действительно, несмотря на некоторое остаточное растекание из-за несовершенной инжекции и слабого беспорядка в устройстве, в обоих экспериментах распространяющийся волновой пакет остается ограниченным инжектированной элементарной ячейкой.Экспериментальные измерения хорошо согласуются с моделированием сильной связи цепи AB. Напротив, распространение света для случая исчезающего потока ϕ = 0 не показывает локализации, и волновой пакет распространяется на всю решетку (см. Дополнительный рис. 7).

   Рис. 4: Массовая динамика.

   a Динамика света при возбуждении верхнего волновода в объемной пластине. Полная оболочка остается локализованной и показывает дыхание только внутри плакетки. Различия между моделированием и экспериментом возникают в основном из-за небольшого количества света, просачивающегося в соседние волноводы во время возбуждения волновода.Это порождает несколько иное начальное состояние, запущенное в систему, что приводит к небольшим отклонениям в динамике распространения. Горизонтальная шкала соответствует 1 см, а вертикальная шкала — 50 мкм. b Два волновода, которые исследуются в экспериментах, демонстрирующих плоскостность объемного спектра. c Динамика света в конструкции при возбуждении волновода между двумя плакетками. Общий конверт показывает местное дыхание, локализованное внутри плакетки.Горизонтальная шкала соответствует 1 см, а вертикальная шкала — 50 мкм. d Амплитудное распределение трех собственных состояний системы.

   По распространению света вдоль образца (см. Рис. 4) мы можем дополнительно измерить энергию полос: направляя свет в волновод, соединяющий два плакета, возбуждает только два состояния в полосах при E = ± 2 t , так как состояние из полосы E = 0 не имеет веса в этом узле, см. Рис.4в, г. Таким образом, результирующая диаграмма биений создается двумя модами с длиной биений l _b , которые связаны с разностью энергий Δ E участвующих мод посредством ³¹ \ ({l} _ { b} = \ frac {\ pi} {\ Delta E} \). По биению на рис. 4в, мы измеряем l _b = 0,9 см, что соответствует Δ E = ± 3,4 см ⁻¹ . Принимая во внимание симметрию модели частица-дырка, измеренная энергия двух зон составляет E = ± 1.7 см ⁻¹ , а третья зона лежит при E = 0.

   Теперь мы продемонстрируем существование граничных состояний в нашей модели квадратного корня. Распределение амплитуд предсказанных граничных мод показано на рис. 5а, б. Два состояния отличаются фазовым переворотом и появляются при двух неэквивалентных собственных энергиях, ср. Рис. 1в. Следовательно, как и в описанных выше объемных экспериментах, свет, инжектируемый во внешний волновод, одновременно возбуждает обе граничные моды, и в результирующем световом шаблоне наблюдается биение с частотой, соответствующей разнице между их собственными энергиями, см. Рис.{2}} \ sim 2 \), что соответствует предсказаниям модели (1).

   Рис. 5: Граничная динамика и защита симметрии.

   a Распределение амплитуд граничного состояния с энергией \ (E = \ sqrt {2} t \). b Распределение амплитуд граничного состояния с энергией \ (E = — \ sqrt {2} t \). c Картина биений между двумя граничными состояниями, возбуждаемая путем попадания света во внешний волновод структуры. Горизонтальная шкала соответствует 1 см, а вертикальная шкала — 50 мкм. d Моделирование плотного связывания, подтверждающее поведение.

   Нулей полиномиальных функций | Безграничная алгебра

   Основная теорема алгебры

   Основная теорема утверждает, что каждый непостоянный многочлен от одной переменной с комплексными коэффициентами имеет по крайней мере один комплексный корень.

   Цели обучения

   Обсудить основную теорему алгебры

   Ключевые выводы

   Ключевые моменты

   • Основная теорема алгебры утверждает, что каждый непостоянный многочлен от одной переменной с комплексными коэффициентами имеет по крайней мере один комплексный корень. 2 + 1 [/ latex], не имеют действительных нулей.{n-1} + \ ldots c_0 [/ латекс]

     , где [latex] n> 0 [/ latex] и [latex] c_n \ not = 0 [/ latex], имеет по крайней мере один комплексный корень.

     Есть много доказательств основной теоремы алгебры. Однако, несмотря на свое название, чисто алгебраического доказательства не существует, поскольку каждое доказательство использует тот факт, что [latex] \ mathbb {C} [/ latex] является полным.

     В частности, поскольку каждое действительное число также является комплексным числом, каждый многочлен с действительными коэффициентами допускает комплексный корень.3 (x + \ pi) [/ латекс]

     допускает один комплексный корень кратности [latex] 4 [/ latex], а именно [latex] x_0 = 0 [/ latex], один комплексный корень кратности [latex] 3 [/ latex], а именно [latex] x_1 = i [ / latex] и один комплексный корень из кратности [latex] 1 [/ latex], а именно [latex] x_2 = — \ pi [/ latex]. Сумма кратностей корней равна степени многочлена, [латекс] 8 [/ латекс]. Для ненулевых комплексных многочленов это в общем случае оказывается верным и непосредственно следует из основной теоремы алгебры.

     Действительно, многочлен степени [latex] 0 [/ latex] принимает форму [latex] c_0 [/ latex], где [latex] c_0 \ not = 0 [/ latex], и, следовательно, не имеет нулей.

     Для общего многочлена [latex] f (x) [/ latex] степени [latex] n [/ latex] основная теорема алгебры гласит, что мы можем найти один корень [latex] x_0 [/ latex] из [latex] ] f (x) [/ латекс]. Таким образом, мы можем разложить [латекс] f (x) [/ latex] на

     [латекс] f (x) = (x-x_0) f_1 (x) [/ латекс]

     , где [латекс] f_1 (x) [/ latex] — ненулевой многочлен степени [латекс] n-1.[/ latex] Итак, если кратности корней [латекса] f_1 (x) [/ latex] добавить к [latex] n-1 [/ latex], кратность корней [latex] f [/ latex] добавить в [латекс] н [/ латекс].

     Итак, поскольку свойство верно для всех многочленов степени [latex] 0 [/ latex], оно также верно для всех многочленов степени [latex] 1 [/ latex]. И поскольку это верно для всех многочленов степени [latex] 1 [/ latex], это также верно для всех многочленов степени [latex] 2 [/ latex]. В общем, для любого [латекса] n \ in \ mathbb {N} [/ latex] мы сможем сделать вывод, что свойство верно для всех многочленов степени [латекс] n.[/ latex] Таким образом, свойство верно для всех многочленов.

     И наоборот, если кратности корней многочлена складываются с его степенью, и если его степень не менее [latex] 1 [/ latex] (т.е. она не постоянна), то из этого следует, что он имеет хотя бы один ноль. .

     Итак, альтернативная формулировка фундаментальной теоремы алгебры:

     Кратности комплексных корней ненулевого многочлена с комплексными коэффициентами добавляют к степени указанного многочлена.2 [/ latex], мы получаем еще один действительный многочлен, для которого снова применима теорема о комплексном сопряженном корне. Таким образом, мы видим, что общая кратность невещественных комплексных корней многочлена с действительными коэффициентами всегда должна быть четной .

     Это последнее замечание, вместе с альтернативным утверждением основной теоремы алгебры, говорит нам, что четность действительных корней (с учетом кратности) многочлена с действительными коэффициентами должна быть такой же, как четность степени указанного многочлена. .Следовательно, многочлен четной степени допускает четное число действительных корней, а многочлен нечетной степени допускает нечетное число действительных корней (считая с кратностью). В частности, каждый многочлен нечетной степени с действительными коэффициентами допускает по крайней мере один действительный корень. [латекс] [/ латекс]

     Нахождение многочленов с заданными нулями

     Чтобы построить многочлен из заданных нулей, установите [latex] x [/ latex] равным каждому нулю, переместите все в одну сторону, затем умножьте каждое полученное уравнение.3 [/ латекс].

   • Каждый заданный нуль будет одним членом факторизованного полинома. Найдя все разложенные на множители члены, просто перемножьте их, чтобы получить полином целиком. 0 [/ латекс].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс].
   • ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].

   Один из типов задач — построить многочлен из заданных нулей. Это может быть решено с помощью того свойства, что если [latex] x_0 [/ latex] является нулем многочлена, то [latex] (x-x_0) [/ latex] является делителем этого многочлена, и наоборот.

   Мы предполагаем, что постановка задачи следующая: нам даны нули. Если не указано, какова кратность нулей, мы хотим, чтобы нули имели кратность один. Других нулей нет, т.е. если число не упомянуто в постановке задачи, оно не может быть нулем найденного нами многочлена.

   Степень полинома

   Помните, что степень полинома, наивысший показатель степени, определяет максимальное количество корней, которое он может иметь. Таким образом, степень многочлена с заданным числом корней равна или больше числа заданных корней.Если в этом числе уже посчитать кратность, то степень равна количеству корней. Например, если нам даны два нуля, то нужно построить многочлен второй степени.

   Решение и константы

   Если [latex] x_1, x_2, \ ldots x_n [/ latex] — это нули [latex] f (x) [/ latex], а ведущий коэффициент [latex] f (x) [/ latex]] равен [latex] ] 1 [/ latex], тогда [latex] f (x) [/ latex] разлагается на

   [латекс] f (x) = (x-x_1) (x-x_2) \ cdots (x-x_n) [/ латекс]

   Это уже дает нам решение нашей проблемы: ответ на наш вопрос — это просто произведение всех факторов [латекс] (x-x_i) [/ latex], где [latex] x_i [/ ​​latex] — это заданные нули. ! Однако мы видим, что этот многочлен не единственный:

   Для любой ненулевой константы [latex] a [/ latex] мы имеем, что [latex] (af) (x) = af (x) [/ latex] разлагается на

   [латекс] af (x) = a (x-x_1) (x-x_2) \ cdots (x-x_n) [/ латекс]

   Таким образом, если мы найдем решение [latex] g (x) [/ latex] для нашей проблемы, мы фактически найдем бесконечно много решений [latex] cg (x) [/ latex], по одному для каждого ненулевого числа [latex ] c [/ латекс].2 + 2cx [/ латекс]

   На рисунке ниже синий график представляет решение для [latex] c [/ latex], равное [latex] 1 [/ latex]. Красный график представляет решение для [latex] c [/ latex], равное [latex] -1/2 [/ latex].

   Пример: Два полинома с одинаковыми нулями: Оба [latex] f (x) [/ latex] и [latex] g (x) [/ latex] имеют нули [latex] 0, 1 [/ latex] и [ латекс] 2 [/ латекс]. Они равны с точностью до константы. Изменение значения и знака константы не меняет нулей, так как ноль, умноженный на любую константу, по-прежнему равен нулю.

   Нахождение нулей факторизованных многочленов

   Факторизованная форма многочлена показывает его нули, которые определяются как точки, в которых функция касается оси [latex] x [/ latex].

   Цели обучения

   Используйте факторизованную форму многочлена, чтобы найти его нули

   Ключевые выводы

   Ключевые моменты

   • Полиномиальная функция может иметь ноль, один или несколько нулей.
   • Все полиномиальные функции положительного нечетного порядка имеют по крайней мере один нуль, в то время как полиномиальные функции положительного четного порядка могут не иметь нуля.
   • Независимо от четности или нечетности, любой многочлен положительного порядка может иметь максимальное количество нулей, равное его порядку.

   Ключевые термины

   • ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].

   Факторизованная форма многочлена может показать, где функция пересекает ось [latex] x [/ latex]. Значение [latex] x [/ latex], при котором это происходит, называется «нулем» или «корнем».

   Число нулей полинома

   Рассмотрим факторизованную функцию:

   [латекс] f (x) = (x-a_1) (x-a_2)… (x-a_n) [/ latex]

   Каждое значение [латекс] a_1, a_2 [/ latex] и т. Д. Равно нулю.

   Полиномиальная функция может иметь много нулей, один или не иметь нулей. 2 — 5x — 6 = (x + 3) (x + 1) (x-2).[/ latex] Мы видим, что его корни равны отрицательным вторым коэффициентам его первой степени факторов

   Факторинг и нули

   В общем, мы знаем из теоремы об остатке, что [latex] a [/ latex] является нулем [latex] f (x) [/ latex] тогда и только тогда, когда [latex] xa [/ latex] делит [latex] f (x). [/ latex] Таким образом, если мы можем разложить [latex] f (x) [/ latex] на многочлены настолько малой степени, насколько это возможно, мы узнаем его нули, посмотрев на все линейные члены в факторизации. Вот почему факторизация так важна: возможность быстро распознавать нули многочлена.

   Из основной теоремы алгебры и факта, называемого теоремой о комплексном сопряженном корне, следует, что каждый многочлен с действительными коэффициентами может быть разложен на линейные многочлены и квадратичные многочлены без действительных корней. Таким образом, если вы нашли такую ​​факторизацию данной функции, вы можете быть полностью уверены, каковы нули этой функции.

   Целочисленные коэффициенты и теорема о рациональных нулях

   Каждое решение многочлена, выраженного как [latex] x = \ frac {p} {q} [/ latex], должно удовлетворять тому, что [latex] p [/ latex] и [latex] q [/ latex] являются целочисленными множителями. of [latex] a_0 [/ latex] и [latex] a_n [/ latex] соответственно.{n-1} +… + a_0 = 0 [/ latex] с целыми коэффициентами.

4. Если [latex] a_0 [/ latex] и [latex] a_n [/ latex] не равны нулю, то каждое рациональное решение [latex] x [/ latex], записанное в виде дроби [latex] x = \ frac { p} {q} [/ latex] в наименьших терминах (т.е. наибольший общий делитель [latex] p [/ latex] и [latex] q [/ latex] равен [latex] 1 [/ latex]), удовлетворяет следующее: [латекс] 1 [/ латекс]) [латекс] p [/ латекс] является целочисленным множителем постоянного члена [латекс] a_0 [/ латекс] и [латекс] 2 [/ латекс]) [латекс] q [/ latex] — это целочисленный коэффициент ведущего коэффициента [latex] a_n [/ latex].

Ключевые термины

• Лемма Евклида : Одно из фундаментальных свойств простых чисел. Утверждает, что если простое число делит произведение двух чисел, оно должно делить хотя бы один из множителей. Например, поскольку 133 × 143 = 19019 делится на 19, одно или оба из 133 или 143 также должны быть. Фактически, 19 × 7 = 133. Оно используется при доказательстве основной теоремы арифметики.
• coprime : Отсутствие положительных целочисленных факторов, кроме [latex] 1 [/ latex], общих с одним или несколькими заданными другими положительными целыми числами.{n-1} +… + a_0 = 0 [/ latex]

  С целыми коэффициентами [латекс] a_n, a_ {n-1}, \ ldots, a_0. [/ Latex]

  Если [latex] a_0 [/ latex] и [latex] a_n [/ latex] не равны нулю, то каждое рациональное решение [latex] x = \ frac {p} {q} [/ latex], где [latex] p [ / latex] и [latex] q [/ latex] являются взаимно простыми целыми числами (т.е. их наибольший общий делитель равен [latex] 1 [/ latex]), удовлетворяет:

  • [латекс] п [/ латекс] является делителем постоянного члена [латекс] а_0 [/ латекс] _.
  • [latex] q [/ latex] является делителем ведущего коэффициента [latex] a_n [/ latex].

  Итак, [latex] a_0 [/ latex] должен быть кратным [latex] p [/ latex], а [latex] a_n [/ latex] должен быть кратным [latex] q [/ latex].

  Поскольку у любого целого числа есть только конечное число делителей, теорема о рациональном корне дает нам конечное число кандидатов в рациональные корни. Получив многочлен с целыми коэффициентами, мы можем подключить всех этих кандидатов и посмотреть, являются ли они нулем данного многочлена. После того, как мы нашли все рациональные нули (и посчитали их кратность, например, делением с использованием длинного деления), мы узнаем количество иррациональных и комплексных корней.2 + 5x-2 [/ latex] имеет один настоящий корень между [latex] 0 [/ latex] и [latex] 1 [/ latex]. Мы можем использовать Rational Root Test, чтобы проверить, является ли этот корень рациональным.

  то есть его числитель должен делить [латекс] 2 [/ латекс], а его знаменатель должен делить [латекс] 3 [/ латекс]. Это дает список возможных ответов

  [латекс] 1, -1,2, -2, \ frac 13, — \ frac 13, \ frac 23, — \ frac 23 [/ латекс]

  Эти корневые кандидаты можно проверить, подключив их напрямую или разделив и проверив, есть ли остаток, например, с помощью деления в столбик.Преимущество этого состоит в том, что как только мы нашли корень, мы сразу же нашли полином меньшей степени, для которого мы снова хотим найти корни, и теорема о рациональном корне предоставит нам еще меньше кандидатов на этот корень. Более того, как только мы установили корень, мы все равно должны использовать деление, чтобы проверить, является ли он множественным корнем.

  Минус в том, что приходится чаще использовать длинное деление. Когда есть много нулевых кандидатов для полинома малой степени, мы можем просто включить кандидатов и использовать деление только тогда, когда мы нашли корень.k [/ latex] для всех положительных целых чисел [latex] k [/ latex], мы можем заменить [latex] x [/ latex] на [latex] t + x_0 [/ latex], чтобы найти многочлен с тем же старшим коэффициентом, что и наш исходный многочлен и постоянный член, равный значению многочлена в [latex] x_0 [/ latex]. В этом случае мы заменяем [latex] x [/ latex] на [latex] t + 1 [/ latex] и получаем многочлен от [latex] t [/ latex] с ведущим коэффициентом [latex] 3 [/ latex] и константой термин [латекс] 1 [/ латекс]. Таким образом, кандидатами на нули в этом многочлене от [latex] t [/ latex] являются

  [латекс] t = \ pm \ frac 1 {1,3} [/ латекс]

  Таким образом, кандидаты в корни многочлена в [latex] x [/ latex] должны быть на единицу больше, чем один из этих кандидатов:

  [латекс] x = 1 + t = 2,0, \ frac 43, \ frac 23 [/ латекс]

  Кандидаты на корень, которых нет в обоих списках, исключаются.Таким образом, список рациональных корневых кандидатов сократился до [latex] x = 2 [/ latex] и [latex] x = 2/3 [/ latex]. После проверки этих кандидатов мы видим, что единственный рациональный корень (с кратностью [latex] 1) [/ latex] — это [latex] 2/3 [/ latex], что также можно увидеть на графике выше.

  Правило знаков

  Правило знаков дает верхнюю границу числа положительных или отрицательных корней многочлена.

  Цели обучения

  Используйте правило знаков, чтобы определить максимальное количество положительных и отрицательных корней многочлена

  Ключевые выводы

  Ключевые моменты

  • Правило знаков дает нам верхнюю границу положительных или отрицательных корней многочлена.Это не полный критерий, то есть он не указывает точное количество положительных или отрицательных корней.
  • Правило гласит, что если члены многочлена с действительными коэффициентами упорядочены по убывающей переменной экспоненты, то количество положительных корней многочлена либо равно количеству знаков различия между последовательными ненулевыми коэффициентами, либо меньше на несколько из 2.
  • Как следствие правила, количество отрицательных корней — это количество смен знака после умножения коэффициентов членов с нечетной степенью на [латекс] -1 [/ латекс] или меньше на кратное 2.

  Ключевые термины

  • знак : положительная или отрицательная полярность. 4 [/ латекс]).Как только вы их найдете, умножьте каждый на [latex] -1 [/ latex]. Затем процедура такая же; подсчитать количество изменений знака между последовательными ненулевыми коэффициентами. Это число или любое число, кратное 2, может быть вашим числом отрицательных корней. Снова важно отметить, что несколько корней одного и того же значения следует считать отдельно.

    Это также можно сделать, взяв функцию [latex] f (x) [/ latex] и заменив [latex] x [/ latex] на [latex] -x [/ latex], чтобы получить функция [латекс] f (-x) [/ латекс].2-х-1 [/ латекс]

    У этой функции есть одно изменение знака между вторым и третьим членами. Следовательно, он имеет ровно один положительный корень. Не забывайте, что у первого члена есть знак, который в данном случае положительный.

    Далее мы переходим к поиску отрицательных корней. Измените экспоненты коэффициентов с нечетной степенью, не забывая менять знак первого члена. Как только вы это сделали, вы получили второй многочлен и готовы найти количество отрицательных корней.2 + x-1 [/ латекс]

    Знак этого многочлена меняется дважды после первого и третьего слагаемых. Следовательно, мы знаем, что он имеет не более двух отрицательных корней. Мы знаем, что количество корней любого знака равно количеству смен знака или кратному на два меньше этого числа. Итак, этот многочлен имеет отрицательные корни [latex] 2 [/ latex] или [latex] 0 [/ latex]. Мы можем проверить это алгебраически, как показано ниже.

    Сначала разложите многочлен на множители:

    [латекс] f (x) = (x + 1) (x + 1) (x-1) [/ латекс].2 + б [/ латекс]

    Чтобы найти положительные корни, мы подсчитываем смену знака. В этом примере мы предположим, что [latex] b> 0 [/ latex]. Поскольку нет смены знака, нет положительных корней [латекс] (p = 0) [/ latex]. Теперь ищем отрицательные корни. Поскольку нечетные коэффициенты мощности отсутствуют, перед поиском изменений знака не нужно вносить никаких изменений; следовательно, нет отрицательных корней [латекс] (q = 0) [/ латекс]. Теперь применим уравнение комплексного корня: [латекс] n — (p + q) = 2 — (0 + 0) = 2 [/ latex]. {n} = x [/ latex].3 = у [/ латекс].

  Ключевые термины

  • корень : Число, возведение которого в указанную степень дает указанное число или выражение.
  • радикальное выражение : математическое выражение, содержащее корень, записанный в форме [латекс] \ sqrt [n] {a} [/ latex].
  • кубический корень : корень степени 3, записанный в форме [латекс] \ sqrt [3] {a} [/ latex].
  • квадратный корень : корень степени 2, записанный в форме [латекс] \ sqrt {a} [/ latex].2 = 7 \ cdot 7 = 49 [/ латекс]

    Поскольку корни являются обратной операцией возведения в степень, они позволяют нам работать в обратном направлении от решения экспоненциального выражения к числу в основе выражения.

    Например, следующее радикальное выражение, которое переворачивает вышеприведенное решение, работая в обратном порядке от 49 до квадратного корня:

    [латекс] \ sqrt {49} = 7 [/ латекс]

    В этом выражении символ известен как «радикал», а решение 7 называется «корнем». {n} = a [/ latex].4 = 7 \ cdot 7 \ cdot 7 \ cdot 7 = 2401 [/ латекс].

    Сложение, вычитание и умножение радикальных выражений

    Радикалы и экспоненты предъявляют особые требования к сложению и вычитанию, тогда как умножение выполняется более свободно.

    Цели обучения

    Различать правильное и неправильное использование операций над радикальными выражениями

    Ключевые выводы

    Ключевые моменты

    • Чтобы добавить радикалы, подкоренное выражение (число под радикалом) должно быть одинаковым для каждого радикала.
    • Вычитание выполняется по тем же правилам, что и сложение: подкоренное выражение должно быть таким же.
    • Умножение радикалов просто требует, чтобы мы умножили член под радикальными знаками.

    Ключевые термины

    • radicand : число или выражение, квадратный корень или другой корень которого рассматривается; например, 3 дюйма [латекс] \ sqrt [n] {3} [/ latex]. Проще говоря, число под корнем.
    • радикальное выражение : выражение, представляющее корень числа или величины.

    Корни — это операция, обратная экспонентам. Выражение с корнями называется радикальным выражением . Легко, хотя, возможно, и утомительно, вычислить экспоненты с учетом корня. Например [латекс] 7 \ cdot7 \ cdot7 \ cdot7 = 49 \ cdot49 = 2401 [/ латекс]. Итак, мы знаем, что корень четвертой степени из 2401 равен 7, а квадратный корень из 2401 равен 49. Что такое корень третьей степени из 2401? Найти значение для конкретного корня сложно. Это связано с тем, что возведение в степень — это другой вид функции, чем сложение, вычитание, умножение и деление.

    Давайте рассмотрим некоторые основные математические операции с радикалами и показателями.

    Сложение и вычитание радикальных выражений

    Чтобы добавить радикалы, подкоренный элемент и (число под радикалом) должны быть одинаковыми для каждого радикала, поэтому общее уравнение будет иметь вид:

    [латекс] a \ sqrt {b} + c \ sqrt {b} = (a + c) \ sqrt {b} [/ латекс]

    Давайте подставим некоторые числа вместо переменных:

    [латекс] \ sqrt 3 +2 \ sqrt 3 = 3 \ sqrt 3 [/ латекс]

    Вычитание выполняется по тем же правилам, что и сложение:

    [латекс] a \ sqrt b — c \ sqrt b = (a-c) \ sqrt b [/ латекс]

    Например:

    [латекс] 3 \ sqrt 3 -2 \ sqrt 3 = \ sqrt 3 [/ латекс]

    Умножение радикальных выражений

    Умножение радикалов просто требует, чтобы мы умножили переменную под знаками радикала.

    [латекс] \ sqrt a \ cdot \ sqrt b = \ sqrt {a \ cdot b} [/ латекс]

    Несколько примеров с действительными числами:

    [латекс] \ sqrt 3 \ cdot \ sqrt 6 = \ sqrt {18} [/ латекс]

    Это уравнение можно еще больше упростить; мы рассмотрим упрощение в другом разделе.

    Упрощение радикальных выражений

    Радикальное выражение можно упростить, если:

    1. значение под знаком корня можно записать как показатель степени,
    2. есть дроби под знаком корня,
    3. в знаменателе стоит радикальное выражение.2} {3}} = 4 \ sqrt {\ frac {1} {3}} [/ латекс]

       Тогда можно обратиться к дроби под знаком корня и упростить радикал в числителе.

       [латекс] \ displaystyle 4 \ sqrt {\ frac {1} {3}} = \ frac {4 \ sqrt {1}} {\ sqrt {3}} = \ frac {4} {\ sqrt {3}} [/ латекс]

       Наконец, нужно вычеркнуть радикал из знаменателя.

       [латекс] \ displaystyle \ frac {4} {\ sqrt {3}} = \ frac {4} {\ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} = \ frac {4 \ sqrt {3}} {3} = \ frac {4} {3} \ sqrt {3} [/ latex]

       Дроби, содержащие радикалы

       Рационализация корня — это процесс, с помощью которого исключаются любые корни в знаменателе иррациональной дроби.

       Цели обучения

       Преобразование между дробями с рационализированным знаменателем и без него

       Ключевые выводы

       Ключевые моменты

       • Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на радикал в знаменателе.

       Ключевые термины

       • рационализация : Процесс удаления радикалов в знаменателе дроби.

       В математике нам часто дают члены в виде дробей с радикалами в числителе и / или знаменателе.Когда нам задают выражения, которые включают радикалы в знаменателе, это упрощает оценку выражения, если мы переписываем его таким образом, чтобы радикал больше не был в знаменателе. Этот процесс называется , рационализируя знаменатель .

       Прежде чем мы начнем, помните, что все, что мы делаем с одной стороной алгебраического уравнения, мы должны делать и с другой стороной. Тот же принцип можно применить и к дробям: что бы мы ни делали с числителем, мы должны делать и со знаменателем, и наоборот. 2}} = {\ frac {10 \ sqrt {3}} {3}} [/ латекс]

       Мнимые числа

       Не существует такого значения, возведение которого в квадрат дает отрицательное значение; поэтому мы классифицируем корни отрицательных чисел как «мнимые».2 = -1 [/ latex] для [latex] x [/ latex] приводит к «числу», которое не может быть действительным числом, называемым мнимым числом.

    4. Мнимое число [латекс] i [/ latex] определяется как квадратный корень из -1: [latex] i = \ sqrt {-1} [/ latex].

  Ключевые термины

  • мнимое число : квадратный корень из -1.
  • подкоренное выражение : значение под знаком корня.

  Радикальное выражение представляет собой корень заданной величины.2 = -1 [/ latex] истинное утверждение.

  Вот здесь и появляются мнимые числа. Когда подкоренное выражение (значение под знаком радикала) отрицательное, корень этого значения считается мнимым числом. В частности, мнимое число , [latex] i [/ latex], определяется как квадратный корень из -1: таким образом, [latex] i = \ sqrt {-1} [/ latex].

  Мы можем записать квадратный корень из любого отрицательного числа через [латекс] i [/ латекс]. Вот несколько примеров:

  • [латекс] \ sqrt {-25} = \ sqrt {25 \ cdot-1} = \ sqrt {25} \ cdot \ sqrt {-1} = 5i [/ латекс]
  • [латекс] \ sqrt {-18} = \ sqrt {2 \ cdot9 \ cdot-1} = \ sqrt {2} \ cdot \ sqrt {9} \ cdot \ sqrt {-1} = 3i \ sqrt {2} [/ латекс]

  Треугольник 30 ° -60 ° -90 ° — пояснения и примеры

  Когда вы закончите и поймете, что такое прямоугольный треугольник и другие специальные прямоугольные треугольники, пора пройти через последний специальный треугольник — треугольник 30 ° -60 ° -90 °.

  Он также имеет такое же значение, как и треугольник 45 ° -45 ° -90 ° из-за соотношения сторон. У него два острых угла и один прямой.

  Что такое треугольник 30-60-90?

  Треугольник 30-60-90 — это специальный прямоугольный треугольник, углы которого составляют 30º, 60º и 90º. Треугольник особенный, потому что его стороны всегда находятся в соотношении 1: √3: 2.

  Любой треугольник формы 30-60-90 может быть решен без применения длинных шагов , таких как теорема Пифагора и тригонометрические функции.

  Самый простой способ запомнить соотношение 1: √3: 2 — это запомнить числа; «1, 2, 3» . Одна из мер предосторожности при использовании этой мнемоники — помнить, что 3 находится под знаком квадратного корня.

  Из приведенного выше рисунка мы можем сделать следующие наблюдения относительно треугольника 30-60-90:

  • Более короткая часть, противоположная углу 30 градусов, помечена как x.
  • Гипотенуза, противоположная углу в 90 градусов, вдвое больше короткой длины ноги (2x).
  • Более длинная полка, противоположная углу в 60 градусов, равна произведению более короткой ветви и квадратному корню из трех (x√3).

  Как решить треугольник 30-60-90?

  Решая задачи с треугольниками 30-60-90, всегда знаешь одну сторону, по которой можно определить другие стороны. Для этого вы можете умножить или разделить эту сторону на соответствующий коэффициент.

  Вы можете резюмировать различные сценарии как:

  • Если известна более короткая сторона, вы можете найти более длинную, умножив более короткую сторону на квадратный корень из 3.После этого вы можете применить теорему Пифагора, чтобы найти гипотенузу.
  • Когда длинная сторона известна, вы можете найти более короткую, погрузив длинную сторону на квадратный корень из 3. После этого вы можете применить теорему Пифагора, чтобы найти гипотенузу.
  • Когда известна более короткая сторона, вы можете найти гипотенузу, умножив более короткую сторону на 2. После этого вы можете применить теорему Пифагора, чтобы найти более длинную сторону.
  • Когда гипотенуза известна, вы можете найти более короткую сторону, разделив гипотенузу на 2.После этого вы можете применить теорему Пифагора, чтобы найти более длинную сторону.

  Это означает, что более короткая сторона действует как шлюз между другими двумя сторонами прямоугольного треугольника . Вы можете найти более длинную сторону, когда задана гипотенуза, или наоборот, но вам всегда нужно сначала найти более короткую сторону.

  Кроме того, для решения задач , связанных с треугольниками 30-60-90 , вам необходимо знать следующие свойства треугольников:

  • Сумма внутренних углов в любом треугольнике составляет 180 °.Следовательно, если вы знаете размер двух углов, вы можете легко определить третий угол, вычтя два угла из 180 градусов.
  • Самая короткая и самая длинная стороны в любом треугольнике всегда противоположны наименьшему и наибольшему углам. Это правило касается и треугольника 30-60-90.
  • Треугольники с одинаковыми углами похожи, и их стороны всегда будут в одинаковом соотношении друг с другом. Таким образом, концепция подобия может использоваться для решения задач, связанных с треугольниками 30-60-90.
  • Поскольку треугольник 30-60-90 является прямоугольным, то теорема Пифагора a ² + b ² = c ² также применима к треугольнику. Например, мы можем доказать, что гипотенуза треугольника равна 2x следующим образом:

  ⇒ c ² = x ² + (x√3) ²

  ⇒ c ² = x ² + (x√3) (x√3)

  ⇒ c ² = x ² + 3x ²

  ⇒ c ² = 4x ²

  Найдите квадратный корень из обеих частей.

  √c ² = √4x ²

  c = 2x

  Следовательно, доказано.

  Давайте поработаем над некоторыми практическими задачами.

  Пример 1

  У прямоугольного треугольника с одним углом 60 градусов длинная сторона равна 8√3 см. Вычислите длину его более короткой стороны и гипотенузу.

  Решение

  Из отношения x: x√3: 2x длинная сторона равна x√3. Итак, у нас есть;

  x√3 = 8√3 см

  Возвести обе части уравнения в квадрат.

  ⇒ (x√3) ² = (8√3) ²

  ⇒ 3x ² = 64 * 3

  ⇒ x ² = 64

  Найдите квадрат обеих сторон.

  √x ² = √64

  x = 8 см

  Заменитель.

  2x = 2 * 8 = 16 см.

  Следовательно, более короткая сторона равна 8 см, а гипотенуза — 16 см.

  Пример 2

  Лестница, прислоненная к стене, образует угол 30 градусов с землей.Если длина лестницы 9 м, найти;

  а. Высота стены.

  г. Рассчитайте длину между подножием лестницы и стеной.

  Раствор

  Один угол составляет 30 градусов; тогда это должен быть прямоугольный треугольник 60 ° — 60 ° — 90 °.

  Соотношение = x: x√3: 2x.

  ⇒ 2x = 9

  ⇒ x = 9/2

  = 4,5

  Заменитель.

  а. Высота стены = 4,5 м.

  б. x√3 = 4,5√3 м

  Пример 3

  Диагональ прямоугольного треугольника равна 8 см.Найдите длины двух других сторон треугольника, учитывая, что один из его углов равен 30 градусам.

  Решение

  Это должен быть треугольник 30 ° -60 ° -90 °. Поэтому мы используем соотношение x: x√3: 2x.

  Диагональ = гипотенуза = 8 см.

  ⇒2x = 8 см

  ⇒ x = 4cm

  Заменитель.

  x√3 = 4√3 см

  Более короткая сторона прямоугольного треугольника равна 4 см, а длинная сторона — 4√3 см.

  Пример 4

  Найдите значения x и z на диаграмме ниже:

  Решение

  Длина 8 дюймов будет более короткой ногой, потому что она противоположна углу 30 градусов .Чтобы найти значение z (гипотенуза) и y (более длинный отрезок), мы действуем следующим образом;

  Из отношения x: x√3: 2x;

  x = 8 дюймов.

  Заменитель.

  ⇒ x√3 = 8√3

  ⇒2x = 2 (8) = 16.

  Следовательно, y = 8√3 дюймов и z = 16 дюймов.

  Пример 5

  Если один угол прямоугольного треугольника равен 30º, а длина самой короткой стороны равна 7 м, каковы размеры двух оставшихся сторон?

  Решение

  Это треугольник 30-60-90, в котором длины сторон находятся в соотношении x: x√3: 2x.

  Замените x = 7 м для более длинного отрезка и гипотенузы.

  ⇒ x √3 = 7√3

  ⇒ 2x = 2 (7) = 14

  Следовательно, другие стороны равны 14 м и 7√3 м

  Пример 6

  В прямоугольном треугольнике гипотенуза составляет 12 см, а меньший угол — 30 градусов. Найдите длину длинной и короткой ноги.

  Решение

  Дано соотношение сторон = x: x√3: 2x.

  2x = 12 см

  x = 6 см

  Заменить x = 6 см для длинной и короткой ножки, чтобы получить;

  Короткая штанина = 6 см.

  длинная ножка = 6√3 см

  Пример 7

  Две стороны треугольника 5√3 мм и 5 мм. Найдите длину его диагонали.

  Решение

  Проверьте соотношение длин сторон, если оно соответствует соотношению x: x√3: 2x.

  5: 5√3 😕 = 1 (5): √3 (5) 😕

  Следовательно, x = 5

  Умножьте 2 на 5.

  2x = 2 * 5 = 10

  Следовательно, гипотенуза равна 10 мм.

  Пример 8

  Пандус, образующий угол 30 градусов с землей, используется для разгрузки грузовика высотой 2 фута.Рассчитайте длину пандуса.

  Решение

  Это должен быть треугольник 30-60-90.

  x = 2 фута.

  2x = 4 фута

  Следовательно, длина пандуса составляет 4 фута.

  Пример 9

  Найдите гипотенузу треугольника 30 ° — 60 ° — 90 °, длинная сторона которого составляет 6 дюймов.

  Решение

  Соотношение = x: x√3: 2x.

  ⇒ x√3 = 6 дюймов.

  Квадрат с обеих сторон

  ⇒ (x√3) ² = 36

  ⇒ 3x ² = 36

  x ² = 12

  x = 2√3 дюйма.

  Практические задачи

  1. В треугольнике 30 ° — 60 ° — 90 ° пусть сторона, лежащая напротив угла 60 °, равна 9√3. Найдите длину двух других сторон.
  2. Если гипотенуза треугольника 30 ° — 60 ° — 90 ° равна 26, найдите две другие стороны.