область определения, нули функции, четность функции и все остальные.

Функция — это одно из важнейших математических понятий.
Функция — зависимость переменной у от переменной x, если каждому значению
х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом.
Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции.
Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.

Графиком функции называют множество всех точек
координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по
оси ординат откладываются значения переменной y. Для
построения графика функции необходимо знать свойства функции.
Основные свойства функции будут рассмотрены далее!

Для построения графика функции советуем использовать нашу программу —
Построение графиков функций онлайн.
Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем
форуме. Также на форуме Вам помогут
решить задачи по математике, химии,
геометрии,
теории вероятности
и многим другим предметам!

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при
которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых
значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) — функция, у которой большему
значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению
аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция — функция, у которой область определения симметрична относительно
начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен
относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала
координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен
относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число
M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции.

Функция f(x) — периодическая, если существует такое отличное от нуля число T,
что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции.
Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по
свойствам функции сможете построить график функции. Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.

Слишком сложно?

Свойства функции не по зубам? Тебе ответит эксперт через 10 минут!

Федеральная служба исполнения наказаний

Федеральная служба исполнения наказаний Российской Федерации (далее — ФСИН России) — федеральный орган исполнительной власти, подведомственный Министерству юстиции РФ, который осуществляет правоприменительные функции, функции по контролю и надзору в сфере исполнения уголовных наказаний в отношении осуждённых, функции по содержанию лиц, подозреваемых либо обвиняемых в совершении преступлений, и подсудимых, находящихся под стражей, их охране и конвоированию, а также функции по контролю за поведением условно осуждённых и осуждённых, которым судом предоставлена отсрочка отбывания наказания.

Основные задачами ФСИН России:

1. Исполнение в соответствии с законодательством Российской Федерации уголовных наказаний, содержание под стражей лиц, подозреваемых либо обвиняемых в совершении преступлений, и подсудимых (далее — лица, содержащиеся под стражей).
2. Контроль за поведением осуждённых к наказаниям и мерам уголовно-правового характера без изоляции от общества.




3. Обеспечение охраны прав, свобод и законных интересов осуждённых и лиц, содержащихся под стражей.




4. Обеспечение правопорядка и законности в учреждениях, исполняющих уголовные наказания в виде лишения свободы (далее — учреждения, исполняющие наказания), и в следственных изоляторах, обеспечение безопасности содержащихся в них осуждённых, лиц, содержащихся под стражей, а также работников уголовно-исполнительной системы, должностных лиц и граждан, находящихся на территориях этих учреждений и следственных изоляторов.




5. Охрана и конвоирование осуждённых и лиц, содержащихся под стражей, по установленным маршрутам конвоирования, конвоирование граждан Российской Федерации и лиц без гражданства на территорию Российской Федерации, а также иностранных граждан и лиц без гражданства в случае их экстрадиции.




6. Создание осуждённым и лицам, содержащимся под стражей, условий содержания, соответствующих нормам международного права, положениям международных договоров Российской Федерации и федеральных законов.




7. Организация деятельности по оказанию осуждённым помощи в социальной адаптации;
8. Управление территориальными органами ФСИН России и непосредственно подчинёнными учреждениями.

из чего она состоит и как она работает

автор: Maria Yiallouros, erstellt am: 2016/12/01,
редактор: Dr. Natalie Kharina-Welke, Переводчик: Dr. Natalie Kharina-Welke, Последнее изменение: 2021/01/20

У человека нервная система‎ – это система высшего уровня в организме. Она состоит из различных органов. Через них она взаимодействует с внешним миром и одновременно она управляет всей работой, которая протекает внутри организма. Многочисленные нервы в теле составляют у человека так называемую периферическую нервную систему [периферическая нервная система‎]. Головной мозг и спинной мозг называют центральной нервной системой [ЦНС‎].

Часть нервной системы, которую называют автономная или вегетативная нервная система‎, управляет всей работой организма, на которую не может повлиять воля человека (то есть эти действия организма не находятся под сонательным контролем человека).

Автономная нервная система контролирует все жизненноважные основные функции организма. Она работает и днём, и ночью, и управляет такими самопроизвольными процессами как биение сердца, пищеварение и дыхание, уровень давления и работу мочевого пузыря.

Когда при физической нагрузке у человека выделяется пот и учащается пульс, то это тоже регулирует автономная нервная система.

Сама автономная нервная система состоит из двух отделов: это симпатическая нервная система (она также может называться симпатический отдел) и парасимпатическая нервная система (также может называться парасимпатический отдел). Оба этих отдела регулируют работу одних и тех же органов, но противоположным образом:

• Симпатическая нервная система, когда идёт интенсивная работа или организм находится в стрессовой ситуации, стимулирует затраты энергии. Например, она усиливает у человека работу сердца (учащается пульс), ускоряется дыхание и повышается давление.
• Парасимпатическая нервная система наоборот отвечает за то, чтобы организм во время сна, покая и отдыха накапливал и восстанавливал запасы энергии. Например, она ослабляет работу сердца (частота ритма сердца снижается) и стимулирует работ желез и мускулатуры в пищеварительном тракте.

Основные функции философии | Мудрый Философ

Все статьи сайта → Философия → Основные функции философии

Философия, как особый вид духовной деятельности, оказывает непосредственное влияние на различные сферы деятельности человека. Ниже кратко рассмотрим основные философские функции.

Мировоззренческая функция философии

Одной из основных и наиболее значимых функций философии является мировоззренческая. Философия формирует представления людей о мире и его устройстве, о человеке и обществе, о принципах взаимоотношения с окружающим миром и месте человека в нем, тем самым формируя его мировоззрение. Философия проясняет взгляды человека, его цели, интересы и потребности и их связь с окружающей действительностью, вырабатывает универсальную философскую картину мира и раскрывает природу человека в результате осмысления и систематизации научного знания, а также содержания остальных форм общественного знания.

В категориях философии происходит рефлексия ми­ровоззренческих проблем, вырабатывается понятийный инстру­ментарий для анализа и сравнения различных типов мировоззре­ний. Таким образом, данная функция способствует построению единой и обобщенной системы знаний человека и выработке мировоззренческих идеалов.

Фундаментальная функция философии

Суть фундаментальной функции философии заключается в раскрытии формировании общих понятий, законов и принципов реальной действительности, применяемых как в науке, так и в практической деятельности людей. Философия изучает не объекты, не эмпирическую реальность, а то, как эта реальность «живет» в общественном сознании; она изучает смыслы реальности для общества и человека.

Философия ищет в мире его онтологические, методологические, нравственные, эстетические основания. Философ всегда строит систему ценностей мира, и тем самым показывает исходные основания человеческой деятельности. Философия, в отличие от любой другой науки, начинается с человека.

Методологическая функция философии

Методологическая функция философии характеризуется формированием общих принципов и норм познавательной деятельности, а также содействует приросту научных знаний и созданию предпосылок для научных открытий.

Метод и методология познания — это та «нить Ариадны», кото­рая помогает исследователю успешно выйти из лабиринта про­блем познания, — а их всегда предостаточно. Однако методоло­гическая функция не сводится к методологии познания: в ней речь идет о стратегическом уровне методологии человеческой деятельности в целом. Философия сопоставляет и оценивает раз­личные средства этой деятельности, указывает на наиболее опти­мальные из них. Философская методология определяет направле­ние научных исследований, дает возможность ориентироваться в бесконечном многообразии фактов и процессов, происходящих в объективном мире.

Гносеологическая функция философии

Гносеологическая функция философии подталкивает мышление человека к познанию окружающего мира и поиску истины.

Благодаря теории философского познания раскрываются закономерности естественных и общест­венных явлений, исследуются формы продвижения человеческо­го мышления к истине, пути и средства ее достижения, обобща­ются результаты других наук. Овладение философскими знания­ми имеет важное значение для развития культуры мышления человека, для решения им разнообразных теоретических и прак­тических задач.

Логическая функция философии

Логическая функция философии проявляется в формировании определенной позиции человека в межличностных и социально-культурных отношениях, а также определяет культуру человеческого мышления. Также она заключается в разработке самого философского метода, его нормативных принципов, в логическом обосновании тех или иных понятийных и теоретических структур научного знания.

Если общая гносеология убеждает в возможности и необходимости адекватного научного познания объекта, то логика призвана обеспечить достижение этой адекватности. Она разрабатывает средства наиболее полного, точного отражения развивающейся, непрерывно изменяющейся сущности объекта.

Воспитательная функция философии

Воспитательная функция философии направлена на формирование в человеке моральных, нравственных и культурных ценностей, стремления самосовершенствоваться, творить и искать жизненные приоритеты.

Знание философии способствует формированию у человека важных качеств культурной личности: ориентации на истину, правду, доброту. Философия способна оградить человека от поверхностных и узких рамок обыденного типа мышления; она динамизирует теоретические и эмпирические понятия частных наук с целью максимально адекватного отражения противоречивой, изменяющейся сущности явлений.

Формирование философского мышления есть одновременно формирование таких ценных качеств культурной личности, как самокритичность, критичность, сомнение. Выработка сомнения не есть, однако, развитие скепсиса (и в данном смысле — скептицизма). Сомнение является одним из активных средств научного поиска. Философия дает прочное общеметодологическое и гносеологическое основание для последовательного саморазвития сомнения в научную уверенность, для гармоничного сочетания его с верой в преодоление ошибок, заблуждений, в получение более полных, глубоких, объективных истин.

Философия дает людям общий язык, вырабатывает у них единые, общезначимые представления о главных ценностях жизни. Она выступает одним из важных факторов, содействующих устранению «барьеров коммуникации», порождаемых узостью специализации.

Аксиологическая функция философии

Аксиологическая функция философии представляет собой отражение явлений окружающей действительности с точки зрения различных ценностей, определяющих выбор людей, их поступки, идеалы, нормы поведения.

Философия не может избавить общество от порождаемых со­циально-экономической системой негативных явлений. Но она может оградить систему ценностей от проникновения в нее ложного и критического непроверенного, порочного и политически авантюрного, примитивного и радикалистского.

Несомненной заслугой современной философской мысли является выдвижение ее представителями новых ценностей. К ним относятся общегуманистические, экологические ценности и ценности качества жизни. Ценность качества жизни противопоставляется уровню жизни, массовому производству и потреблению. Для человека, его здоровья и счастья не так важен уровень жизни, как ее качество. Оно определяется не столько ее комфортом, сколько добрыми и гуманными отношениями в обществе, социальным ра­венством и близостью к природе. Быть в гармонии с самим собой, с окружающими и природой — для многих людей становится приоритетным ориентиром и мотивом поведения.

Интегративная функция философии

Суть интегративной функции философии состоит в соединении воедино практического, познавательного и ценностного жизненного опыта людей. Философия старается обобщить, оценить осмыслить как интеллектуальные, духовные и практические достижения всего человечества, так и отрицательный исторический опыт.

Знания, доставляемые отдельными дисциплинами столь разнообразны, что они нуждаются в сведе­нии в единую целостную научную картину мира. Но разработка теоретических основ научного познания не сво­дится к механическому объединению данных различных дисциплин. Сам синтез научных открытий возможен лишь на более высоком теоретическом фундаменте, чем сами открытия. Если философия не есть основание отдельных наук, а целиком осно­вывается на этих дисциплинах, то при таком подходе философия превращается в побочное приложение к естествознанию, в некото­рый необязательный довесок для науки. Этот подход опровергается самой наукой. Крупнейшие ученые разных эпох, работавшие в об­ласти фундаментальных исследований от Ломоносова до Эйнштей­на, настойчиво и плодотворно работали над методологическими и мировоззренческими проблемами, не имея в наличной философии соответствующего обоснования для своих естественнонаучных иссле­дований. Таким образом, философия образует методологическую ос­нову для каждой научной дисциплины, достигшей высот самосозна­ния. И неразвита та наука, которая не поднялась до самосознания и не имеет методологической основы.

Критическая функция философии

Философия выполняет и критическую функцию, стремясь разрушить старые идеалы и взгляды, сформировать новое мировоззрение, что сопровождается сомнениями и критикой принятых догм и стереотипов.

Философ постоянно сталкивается с расхождением социальной действительности с идеалами. Размышления над социальной действительностью, ее сопоставление с общественным идеалом приводят к критике этой действительности. В критике выражается неудовлетворенность субъекта объектом, желание его изменить. Философия критична по своему существу. Основой и сущностью критической работы философа является обнаружение и раскрытие противоречий, несоответствия между принятой системой понятий и ценностей и тем содержанием, которое в них вносится новым этапом развития мировой истории.

Регулятивная функция философии

С помощью регулятивной функции философия влияет на взаимосогласо­ванность конкретных действий и направлений жизнедеятельно­сти человека на основе понимания общих принципов и целей, определяемых с помощью философского мировосприятия.

Прогностическая функция философии

Прогностическая функция философии основывается на прогнозировании форм и направлений развития будущих объектов, процессов, явлений, материи, сознания, человека и общества на основании имеющейся системы знаний об окружающей действительности.

Искренне благодарны всем, кто поделился полезной статьей с друзьями:

Основы Python — кратко. Часть 5. Определение функций, основы. / Хабр

Начав писать главу про ООП, понял что совсем забыл освятить такой большой и нужный раздел Пайтона как функции. Тема это большая и обширная, потому, чтобы не сильно растягивать паузу между уроками, решил разделить ее на 2 части. Сначала расскажу основы, потом уже углубленные особенности Пайтоновского функциестроения.

Функции в Пайтоне объявляются не просто, а очень просто. Вот пример самой простой:

def empty_func():
    pass

Начинается объявление с ключевого слова def, что как не сложно догадаться является сокращением от define. После него идет имя функции. После имени в круглых скобках задается список параметров, в данном случае отсутствующих.
Тело функции пишется с отступом со следующей строки. учтите, что в Пайтоне функции с пустым телом запрещены, потому в качестве тела приведенной выше функции используется «пустой оператор» pass.
Теперь рассмотрим пример посерьезнее.

def safe_div(x, y):
    """Do a safe division :-)
for fun and profit"""
    if y != 0:
        z = x / y
        print z
        return z
    else:
        print "Yippie-kay-yay, motherf___er!"

В этом примере есть несколько нововведений. первое, что бросается в глаза — это строка документации (docstring), идущая сразу после тела функции.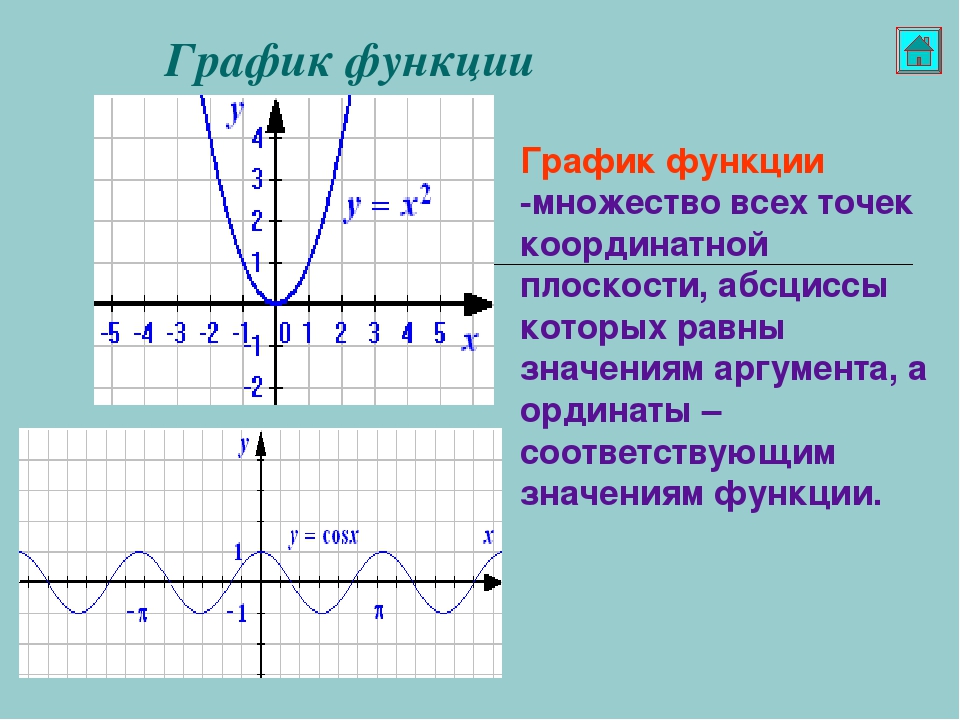
Обычно эта строка занимает не одну строку исходного текста (простите за каламбур) и потому задается в тройных кавычках. Она предназначена для описания функции, ее предназначения, параметров и т.п. Все хорошие ИДЕ умеют с этой строкой работать. Получить к ней доступ можно и из самой программы, используя свойство __doc__:

print safe_div.__doc__

Этим свойством (да, да, именно свойством, в Пайтоне даже функции на самом деле — классы) удобно пользоваться во время сеансов работы интерактивной консоли.

>>> from ftplib import FTP
>>> print FTP.__doc__
An FTP client class.

    To create a connection, call the class using these argument:
            host, user, passwd, acct
    These are all strings, and have default value ''.
    Then use self.connect() with optional host and port argument.
# дальнейшее почикано мною :-)

Вернемся к нашей исходной функции. Суть ее очень проста, она принимает 2 параметра: х и у. Если у не равен 0, она делит х на у, выводит результат на экран и возвращает свое частное в виде результата. Результат функции возвращают с помощью команды return. Благодаря механизму кортежей, описанному в прошлом уроке, функции в Пайтоне могут возвращать одновременно множество объектов.
Если же делитель все-таки равен нулю, функция выводит сообщение об ошибке. Неверно было бы предположить что в этом случае функция ничего не вернет. Правильнее будет сказать что функция вернет «ничего» 🙂 Иначе говоря, если в функции отсутствует оператор return, или же он вызван без параметров, то функция возвращает специальное значение None. В этом легко убедиться вызвав что-то типа print safe_div(10, 0).

Вот пример слегка посложнее, он взят из доклада-презентации Гвидо ван Россума.

def gcd(a, b):
   "Нахождение НОД"
   while a != 0:
      a,b = b%a,a # параллельное определение
   return b

Данная функция находит наибольший общий делитель двух чисел.

В общем, следует учитывать, что параметры в функции Пайтоном передаются по ссылке. Еще одним, возможно нетривиальным фактом к которому придется привыкать — является тот факт что сами функции являются значением, которое можно присваивать. Если воспользоваться нашей функцией safe_div для дальнейших экспериментов, то можно написать следующий код.

mystic_function = safe_div
print mystic_function(10, 4)

Вот на этот раз и все, «за бортом» осталось еще много аспектов определения функций в Пайтоне, которые будут освещены в следующий раз.

Упражнения для проверки.

1. На основе существующей функции нахождения НОД, напишите функцию поиска НОК двух чисел.

2. Напишите подпрограмму табулирования функции, переданной в качестве аргумента. Так же аргументами задается начальное, конечное значение и шаг табуляции.

PS кстати, каков оптимальный объем «урока»? Что лучше — реже выходящие большие главы, или «лучше меньше да чаще».

Три главные функции денег

Что такое деньги? Казалось бы, все знают ответ. Однако, можете ли вы дать однозначное и короткое определение этого явления? Самый верный способ понять, что человечество на самом деле вкладывает в понятие «деньги», – это описать их функции: деньги определяют меру стоимости вещей, являются средством платежа и одним из средств накопления.

Согласно Гражданскому кодексу, «рубль является законным платежным средством, обязательным к приему по нарицательной стоимости на всей территории Российской Федерации». Какие же функции выполняют деньги и что это значит? 

Мера стоимости

Цены, выраженные в деньгах, позволяют нам сравнить: насколько одни товары дороже других, сколько мы можем позволить себе на те деньги, которые зарабатываем и накопили.

Если бы одни цены были обозначены, скажем, в баночках зеленого горошка, другие – в соболиных шкурках, а третьи – в яблоках, как бы мы вообще могли бы что-то оценивать?

Средство платежа

Рубль – универсальная денежная единица. Куда бы мы ни пришли в России, везде с его помощью можно расплатиться. При этом в современном мире деньги могут быть не только наличными, но и безналичными. Простейший пример последних – банковская карта. С ее помощью можно заплатить за нужный товар или услугу не только в России, но и по всему миру – рубль уже давно свободно-конвертируемая валюта.

Средство накопления

Есть крупные покупки, которые невозможно сделать на одну зарплату – например, автомобиль или жилье. Есть ситуации, когда зарабатываешь сейчас, а тратить придется потом. Один из смыслов денег – чтобы они не теряли со временем своей покупательной способности. Или хотя бы теряли не слишком быстро. С последней функцией сложнее всего. Мы живем в мире необеспеченных денег, их создает банковская система, и почти всегда это сопровождается инфляцией. Цены постепенно растут, а деньги, соответственно, обесцениваются. Впрочем, эта же система позволяет вкладывать деньги под проценты и, как минимум, защищать их от инфляции. А часто еще и зарабатывать в реальном выражении (когда ставка процента по вкладу выше инфляции). За то, чтобы рубль не терял покупательную способность слишком быстро, отвечает Центральный банк. В его распоряжении целый арсенал инструментов денежно-кредитной политики, главный из которых – процентная ставка. Подробнее об этом можно почитать в разделе ДКП на сайте ЦБ

Президент ∙ Структура ∙ Президент России

В соответствии с Конституцией права и свободы человека и гражданина определяют смысл, содержание и применение законов, деятельность всех органов государственной власти, местного самоуправления. Соблюдение прав и свобод обеспечивается правосудием. Особую роль в этой сфере Конституция отводит Президенту. Слова об обязанности защищать Конституцию, уважать и охранять права и свободы человека и гражданина, верно служить народу есть в тексте присяги Президента, которую он приносит народу при вступлении в должность.

Необходимым условием соблюдения прав и свобод человека и гражданина является положение, при котором все органы государственной власти выполняют свои конституционные обязанности в пределах своей компетенции. Обеспечить такое положение в государстве должен Президент. Для этого Конституцией ему предоставлены особые полномочия по обеспечению согласованного функционирования и взаимодействия органов государственной власти.

Защищая права и свободы человека и гражданина, Президент опирается на всю систему органов государственной власти. Функции гаранта прав и свобод человека и гражданина требуют от Президента постоянной заботы об эффективности исполнительной, законодательной и судебной властей, разумеется, без вторжения в сферу их компетенции.

Будучи юридически дистанцирован от всех ветвей власти, Президент участвует в нормотворчестве, управляет, разрешает споры, осуществляет функции конституционного контроля. Реализуя полномочия по защите прав и свобод, глава государства взаимодействует с Правительством, федеральными судами, прокуратурой, правоохранительными органами, общественными объединениями.

Президент обязан добиваться того, чтобы Конституция и нормативные акты субъектов Федерации полностью соответствовали Конституции страны, федеральному законодательству, задачам обеспечения и защиты прав и свобод человека и гражданина. В противном случае Президент имеет право потребовать от любого федерального органа власти либо органа власти субъекта федерации соблюдения прав и свобод человека и гражданина, а в случае их попрания – требовать восстановления нарушенных прав в полном объеме. При этом Президент может предпринять самые решительные меры, вплоть до принудительных.

Конституционные полномочия гаранта прав и свобод человека и гражданина Президент реализует, используя своё право законодательной инициативы. Он также издаёт указы по защите правового положения личности в целом и отдельных групп населения, а также по обеспечению граждан всей полнотой личных, политических и социально-экономических прав.

Власть Президента ограничивается пределами Конституции. Многие россияне воспринимают обязанности Президента гарантировать Конституцию, права и свободы человека и гражданина достаточно широко. Часто они адресуют Президенту свои жалобы на решения, например, правоохранительных органов или даже приговоры судов. Однако Президент, исходя из конституционного принципа разделения властей, не имеет права подменять функции и полномочия этих органов. Общие рамки полномочий Президента определяются принципом разделения властей и требованием Конституции, согласно которому указы и распоряжения Президента не должны противоречить Конституции и федеральным законам.

Функция

| Определение, типы, примеры и факты

Функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной). Функции повсеместно используются в математике и необходимы для формулирования физических соотношений в естественных науках. Современное определение функции было впервые дано в 1837 году немецким математиком Петером Дирихле:

Британская викторина

Определить: математические термины

Вот ваша миссия, если вы решите принять ее: Определите следующие математические термины до того, как истечет время.

Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y считается функцией независимой переменной x .

Это соотношение обычно обозначается как y = f ( x ). Помимо f ( x ), для представления функций независимой переменной x часто используются другие сокращенные символы, такие как g ( x ) и P ( x ), особенно когда природа функции неизвестна или не указана.

Общие функции

Многие широко используемые математические формулы являются выражениями известных функций. Например, формула для площади круга A = π r ² дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных, также распространены в математике, что можно увидеть в формуле для площади треугольника: A = b h /2, которая определяет A как функцию обоих b (основание) и h (высота).В этих примерах физические ограничения вынуждают независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Формула площади круга является примером полиномиальной функции. Общий вид таких функций:
P ( x ) = a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n х ^н ,
где указаны коэффициенты ( a ₀ , a ₁ , a ₂ ,…, a _n ), x может быть любым действительным числом, и все степени x — это счетные числа (1, 2, 3,…).(Когда степень x может быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любые отношения, включающие действительные числа, можно точно аппроксимировать с помощью полиномиальная функция. Полиномиальные функции характеризуются наивысшей степенью независимой переменной. Для степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартичная и квинтическая.

Полиномиальным функциям можно дать геометрическое представление с помощью аналитической геометрии. Независимая переменная x нанесена вдоль оси x (горизонтальная линия), а зависимая переменная y нанесена вдоль оси y (вертикальная линия). График функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x ³ — 3 x + 2.

График кубического уравнения f ( x ) = x ³ — 3 x + 2. Точки на графике показывают изменения кривизны.

Британская энциклопедия, Inc.

Другой распространенный тип функции, который изучается с древних времен, — это тригонометрические функции, такие как sin x и cos x , где x — это мера угла ( см. Рисунок ). Из-за своей периодической природы тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».Негебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.

графики некоторых тригонометрических функций

Обратите внимание, что каждая из этих функций периодическая. Таким образом, функции синуса и косинуса повторяются каждые 2π, а функции тангенса и котангенса повторяются через каждые π.

Encyclopædia Britannica, Inc.

Комплексные функции

Практическое применение функций, переменные которых являются комплексными числами, не так легко проиллюстрировать, но, тем не менее, они очень обширны.Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена ​​в виде z = x + i y , где i — мнимая единица (квадратный корень из -1), а x и y — действительные переменных ( см. рисунок ), можно разделить сложную функцию на действительную и мнимую части: f ( z ) = P ( x , y ) + i Q ( x , y ).

точка на комплексной плоскости

Точка на комплексной плоскости. В отличие от действительных чисел, которые могут быть расположены одним знаком (положительным или отрицательным) числом вдоль числовой прямой, для комплексных чисел требуется плоскость с двумя осями, одна ось для компонента действительного числа и одна ось для мнимого компонента. Хотя комплексная плоскость выглядит как обычная двумерная плоскость, где каждая точка определяется упорядоченной парой действительных чисел ( x , y ), точка x + i y является единственной номер.

Британская энциклопедия, Inc.

Меняя ролями независимых и зависимых переменных в заданной функции, можно получить обратную функцию. Обратные функции делают то, что подразумевает их название: они отменяют действие функции, возвращая переменную в исходное состояние. Таким образом, если для данной функции f ( x ) существует функция g ( y ) такая, что g ( f ( x )) = x и f ( g ( y )) = y , тогда g называется обратной функцией для f и обозначается обозначением f ^-1 , где по соглашению переменные меняются местами.Например, функция f ( x ) = 2 x имеет обратную функцию: f ^-1 ( x ) = x /2.

Прочие функциональные выражения

Функция может быть определена с помощью степенного ряда. Например, бесконечный ряд

можно использовать для определения этих функций для всех комплексных значений x . При необходимости можно использовать другие типы серий, а также бесконечное количество продуктов. Важным случаем является ряд Фурье, выражающий функцию через синусы и косинусы:

Такие представления имеют большое значение в физике, особенно при изучении волнового движения и других колебательных явлений.

Иногда функции удобнее всего определять с помощью дифференциальных уравнений. Например, y = sin x является решением дифференциального уравнения d ² y / d x ² + y = 0, где y = 0, d y / d x = 1, когда x = 0; y = cos x является решением того же уравнения, имеющего y = 1, d y / d x = 0, когда x = 0.

Редакторы Британской энциклопедии
Эта статья была недавно отредактирована и обновлена ​​Адамом Августином, управляющим редактором, справочное содержание.

Узнайте больше в этих связанных статьях Britannica:

Гомоморфизм | математика | Britannica

Гомоморфизм , (от греческого homoios morphe , «подобная форма»), особое соответствие между элементами (элементами) двух алгебраических систем, таких как две группы, два кольца или два поля.Две гомоморфные системы имеют одинаковую базовую структуру, и, хотя их элементы и операции могут казаться совершенно разными, результаты для одной системы часто применимы и к другой системе. Таким образом, если можно показать, что новая система гомоморфна известной системе, некоторые известные особенности одной могут быть применены к другой, что упрощает анализ новой системы.

В гомоморфизме соответствующие элементы двух систем очень похожи друг на друга в сочетании с другими соответствующими элементами.Например, пусть G и H будут группами. Элементы G обозначены g , g ′,…, и они подлежат некоторой операции ⊕. (Хотя символ можно рассматривать как некоторую операцию, например умножение, он может также указывать на вращение или другую неарифметическую операцию.) Аналогичным образом, элементы H обозначаются как h , h ‘,… , и они подлежат некоторой операции ⊗. Гомоморфизм от G до H — это соответствие g → h между всеми элементами G и некоторыми элементами H , которое имеет следующее свойство: если g → h и g ′ → h ′, то g ⊕ g ′ → h ⊗ h ′.Другими словами, элемент H , соответствующий произведению элементов в G , является произведением в том же порядке элементов H , соответствующих двум элементам в G . Выражаясь более компактно, «образ» продукта является продуктом изображений, или соответствие сохраняет работу.

Соответствие между элементами двух алгебраических систем может быть записано как функция f от G до H , и можно говорить о f как о «отображении» G на H .Условие, что f является гомоморфизмом группы G группе H , может быть выражено как требование, чтобы f ( g ⊕ g ′) = f ( g ) ⊗ f ( г, ′).

Гомоморфизмы накладывают условия на отображение f : если e является тождеством G , то g ⊕ e = g , поэтому f ( g ⊕ e ) = f ( г ).Кроме того, поскольку f является гомоморфизмом, f ( g ⊕ e ) = f ( g ) ⊗ f ( e ), поэтому f ( g ) = f ( g ) ⊗ f ( e ). По законам отмены для групп это означает, что f ( e ) совпадает с идентификатором в H . Таким образом, гомоморфизмы отображают уникальный единичный элемент одной группы в уникальный единичный элемент другой группы.Точно так же гомоморфизмы отображают инверсию элемента g в одной группе в инверсию элемента f ( g ). Вот почему гомоморфизмы называются отображениями, сохраняющими структуру.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Специальные типы гомоморфизмов имеют свои собственные названия. Взаимнооднозначный гомоморфизм от G до H называется мономорфизмом, а гомоморфизм, который «на» или покрывает каждый элемент H , называется эпиморфизмом.Особенно важным гомоморфизмом является изоморфизм, в котором гомоморфизм от G до H является как взаимно однозначным, так и включенным. В этом последнем случае G и H по сути являются одной и той же системой и отличаются только названиями своих элементов. Таким образом, гомоморфизмы полезны при классификации и перечислении алгебраических систем, поскольку они позволяют идентифицировать, насколько тесно связаны разные системы.

Формулы Excel: функции

/ ru / excelformulas / относительные-абсолютные-ссылки-ячейки / содержание /

Введение

Функция — это предопределенная формула , которая выполняет вычисления с использованием определенных значений в определенном порядке.Все программы для работы с электронными таблицами включают общие функции, которые можно использовать для быстрого поиска суммы , среднего , счетчика , максимального значения и минимального значения для диапазона ячеек. Чтобы правильно использовать функции, вам необходимо понимать различные части функции и понимать, как создавать аргументов для вычисления значений и ссылок на ячейки.

Посмотрите видео ниже, чтобы узнать больше об использовании функций в Excel.

Части функции

Для правильной работы функция должна быть написана особым способом, который называется синтаксисом . Базовый синтаксис функции — это знак равенства (=) , имя функции (например, SUM) и один или несколько аргументов . Аргументы содержат информацию, которую вы хотите вычислить. Функция в примере ниже добавит значения диапазона ячеек A1: A20.

Работа с аргументами

Аргументы могут относиться как к отдельным ячейкам , так и к диапазонам ячеек и должны быть заключены в круглых скобок .Вы можете включить один аргумент или несколько аргументов, в зависимости от синтаксиса, необходимого для функции.

Например, функция = СРЕДНЕЕ (B1: B9) вычислит среднее значений в диапазоне ячеек B1: B9. Эта функция содержит только один аргумент.

Несколько аргументов должны быть разделены запятой . Например, функция = СУММ (A1: A3, C1: C2, E2) добавит к значениям всех ячеек в трех аргументах.

Использование функций

Есть множество функций. Вот некоторые из наиболее часто используемых функций:

• СУММ : эта функция добавляет всех значений ячеек в аргументе.
• СРЕДНЕЕ : Эта функция определяет средних значений, включенных в аргумент. Он вычисляет сумму ячеек, а затем делит это значение на количество ячеек в аргументе.
• COUNT : Эта функция подсчитывает числа ячеек с числовыми данными в аргументе.Эта функция полезна для быстрого подсчета элементов в диапазоне ячеек.
• MAX : Эта функция определяет наивысшее значение ячейки , включенное в аргумент.
• MIN : эта функция определяет наименьшее значение ячейки , включенное в аргумент.

Чтобы использовать функцию:

В нашем примере ниже мы будем использовать базовую функцию для расчета средней цены за единицу для списка недавно заказанных товаров с помощью функции СРЕДНИЙ.

1. Выберите ячейку , которая будет содержать функцию. В нашем примере мы выберем ячейку C11 .
2. Введите знак равенства (=) и введите желаемое имя функции . В нашем примере мы введем = СРЕДНЕЕ .
3. Введите диапазон ячеек для аргумента в круглых скобках . В нашем примере мы введем (C3: C10) . Эта формула добавит значения ячеек C3: C10, а затем разделит это значение на общее количество ячеек в диапазоне, чтобы определить среднее значение.
4. Нажмите Введите на клавиатуре. Функция будет рассчитана , а результат появится в ячейке. В нашем примере средняя цена за единицу заказанного товара составила $ 15,93 .

Ваша электронная таблица не всегда сообщит вам , если ваша функция содержит ошибку, поэтому вам нужно проверить все свои функции. Чтобы узнать, как это сделать, ознакомьтесь с уроком «Двойная проверка формул».

Работа с незнакомыми функциями

Если вы хотите узнать, как работает функция, вы можете начать вводить эту функцию в пустую ячейку , чтобы увидеть, что она делает.

Затем вы можете ввести открывающую скобку, чтобы увидеть , какие аргументы ему нужны.

Общие сведения о вложенных функциях

Всякий раз, когда формула содержит функцию, она обычно вычисляется перед любыми другими операторами, такими как умножение и деление. Это потому, что формула рассматривает всю функцию как одно значение — прежде чем она сможет использовать это значение в формуле, ей необходимо запустить функцию. Например, в приведенной ниже формуле функция СУММ будет вычислена до деления:

Давайте посмотрим на более сложный пример, в котором используется несколько функций:

= РАБОЧИЙ ДЕНЬ (СЕГОДНЯ (), 3)

Здесь у нас есть две разные функции, работающие вместе: функция РАБДЕНЬ и функция СЕГОДНЯ.Они известны как вложенных функций , поскольку одна функция помещается, или вложенных в аргументы другой. Как правило, вложенная функция всегда вычисляется первой , точно так же, как скобки ставятся первыми в порядке операций. В этом примере функция СЕГОДНЯ будет вычислена первой, поскольку она вложена в функцию РАБДЕНЬ.

Другие общие функции

Есть многих других функций , которые вы можете использовать для быстрого вычисления различных вещей с вашими данными.Изучение того, как использовать другие функции, позволит вам решать сложные проблемы с вашими электронными таблицами, и мы будем больше говорить о них в этом руководстве. Вы также можете ознакомиться с нашими статьями ниже, чтобы узнать о конкретных функциях:

/ ru / excelformulas / resolve-reallife-issues-in-excel / content /

Excel 2016: функции

/ ru / excel2016 / относительные-абсолютные-ссылки-ячейки / контент /

Введение

Функция — это предопределенная формула , которая выполняет вычисления с использованием определенных значений в определенном порядке.Excel включает множество общих функций, которые можно использовать для быстрого поиска суммы , среднего , счетчика , максимального значения и минимального значения для диапазона ячеек. Чтобы правильно использовать функции, вам необходимо понимать различные части функции и понимать, как создавать аргументов для вычисления значений и ссылок на ячейки.

Необязательно: Загрузите нашу рабочую тетрадь.

Посмотрите видео ниже, чтобы узнать больше о работе с функциями.

Части функции

Для правильной работы функция должна быть написана особым способом, который называется синтаксисом . Базовым синтаксисом функции является знак равно (=) , имя функции (например, SUM) и один или несколько аргументов . Аргументы содержат информацию, которую вы хотите вычислить. Функция в примере ниже добавит значения диапазона ячеек A1: A20.

Работа с аргументами

Аргументы могут относиться как к отдельным ячейкам , так и к диапазонам ячеек и должны быть заключены в круглых скобок .Вы можете включить один аргумент или несколько аргументов, в зависимости от синтаксиса, необходимого для функции.

Например, функция = СРЕДНЕЕ (B1: B9) вычислит среднее значений в диапазоне ячеек B1: B9. Эта функция содержит только один аргумент.

Несколько аргументов должны быть разделены запятой . Например, функция = СУММ (A1: A3, C1: C2, E1) добавит значений всех ячеек в трех аргументах.

Создание функции

В Excel доступно множество функций. Вот некоторые из наиболее часто используемых функций:

• СУММ : эта функция добавляет всех значений ячеек в аргументе.
• СРЕДНЕЕ : Эта функция определяет средних значений, включенных в аргумент. Он вычисляет сумму ячеек, а затем делит это значение на количество ячеек в аргументе.
• COUNT : Эта функция подсчитывает числа ячеек с числовыми данными в аргументе. Эта функция полезна для быстрого подсчета элементов в диапазоне ячеек.
• MAX : Эта функция определяет наивысшее значение ячейки , включенное в аргумент.
• MIN : эта функция определяет наименьшее значение ячейки , включенное в аргумент.

Чтобы создать функцию с помощью команды Автосумма:

Команда AutoSum позволяет автоматически вставлять в формулу наиболее распространенные функции, включая СУММ, СРЕДНЕЕ, СЧЁТ, МИН и МАКС.В приведенном ниже примере мы будем использовать функцию СУММ для расчета общей стоимости для списка недавно заказанных товаров.

1. Выберите ячейку , которая будет содержать функцию. В нашем примере мы выберем ячейку D13 .
2. В группе Редактирование на вкладке Домашняя страница щелкните стрелку рядом с командой Автосумма . Затем выберите желаемую функцию из раскрывающегося меню.В нашем примере мы выберем Sum .
3. Excel поместит функцию в ячейку и автоматически выберет диапазон ячеек в качестве аргумента. В нашем примере ячейки D3: D12 были выбраны автоматически; их значения будут , добавлено для расчета общей стоимости. Если Excel выберет неправильный диапазон ячеек, вы можете вручную ввести нужные ячейки в аргумент.
4. Нажмите Введите на клавиатуре. Функция будет рассчитана , а результат появится в ячейке.В нашем примере сумма D3: D12 составляет $ 765,29 .

Команда AutoSum также доступна на вкладке Formulas на ленте .

Вместо команды Автосумма можно также использовать сочетание клавиш Alt + = . Чтобы использовать этот ярлык, удерживайте нажатой клавишу Alt , а затем нажмите знак равенства .

Посмотрите видео ниже, чтобы увидеть этот ярлык в действии.

Чтобы ввести функцию вручную:

Если вы уже знаете имя функции, вы можете легко ввести его самостоятельно.В приведенном ниже примере (подсчет продаж файлов cookie) мы будем использовать функцию СРЕДНЕЕ для расчета среднего числа единиц, проданных каждым отрядом.

1. Выберите ячейку , которая будет содержать функцию. В нашем примере мы выберем ячейку C10 .
2. Введите знак равенства (=), и введите желаемое имя функции . Вы также можете выбрать нужную функцию из списка предлагаемых функций , который появляется под ячейкой по мере ввода.В нашем примере мы введем = СРЕДНЕЕ .
3. Введите диапазон ячеек для аргумента в круглых скобках . В нашем примере мы введем (C3: C9) . Эта формула добавит значения ячеек C3: C9, а затем разделит это значение на общее количество значений в диапазоне.
4. Нажмите Введите на клавиатуре. Функция будет рассчитана, и в ячейке появится результат . В нашем примере среднее количество единиц, проданных каждым отрядом, составляет 849 .

Excel не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вам нужно проверить все свои формулы. Чтобы узнать, как это сделать, прочитайте урок «Двойная проверка формул» в нашем руководстве по формулам Excel.

Библиотека функций

Хотя в Excel есть сотни функций, те из них, которые вы будете использовать чаще всего, будут зависеть от типа данных , которые содержатся в ваших книгах. Нет необходимости изучать каждую функцию, но изучение некоторых из различных типов функций поможет вам при создании новых проектов.Вы даже можете использовать библиотеку функций на вкладке Формулы для просмотра функций по категориям, например Financial , Logical , Text и Date & Time .

Чтобы получить доступ к библиотеке функций , выберите вкладку Формулы на ленте . Найдите группу Function Library .

Нажмите кнопки в интерактивном меню ниже, чтобы узнать больше о различных типах функций в Excel.

Чтобы вставить функцию из библиотеки функций:

В приведенном ниже примере мы будем использовать функцию COUNTA для подсчета общего количества элементов в столбце Items . В отличие от COUNT, COUNTA можно использовать для подсчета ячеек, содержащих данные любого типа, а не только числовые.

1. Выберите ячейку , которая будет содержать функцию. В нашем примере мы выберем ячейку B17 .

2. Щелкните вкладку Формулы на ленте , чтобы получить доступ к библиотеке функций .
3. В группе Function Library выберите желаемую категорию функции . В нашем примере мы выберем More Functions , th и наведем указатель мыши на Statistical .
4. Выберите нужную функцию из раскрывающегося меню. В нашем примере мы выберем функцию COUNTA , которая будет подсчитывать количество непустых ячеек в столбце Items .
5. Откроется диалоговое окно « аргументы функции ».Выберите поле Value1 , затем введите или выберите нужные ячейки. В нашем примере мы введем диапазон ячеек A3: A12 . Вы можете продолжать добавлять аргументы в поле Value2 , но в этом случае мы хотим подсчитать только количество ячеек в диапазоне ячеек A3: A12 .
6. Когда вы будете удовлетворены, щелкните OK .
7. Функция будет рассчитана , а результат появится в ячейке. В нашем примере результат показывает, что всего было заказано 10 штук .

Команда «Вставить функцию»

Хотя Библиотека функций — отличное место для поиска функций, иногда вы можете предпочесть поиск для поиска вместо . Это можно сделать с помощью команды Вставить функцию . Это может занять некоторое время методом проб и ошибок, в зависимости от типа функции, которую вы ищете; однако со временем команда «Вставить функцию» может стать мощным способом быстрого поиска функции.

Чтобы использовать команду «Вставить функцию»:

В приведенном ниже примере мы хотим найти функцию, которая будет рассчитывать рабочих дней , которые потребовались для получения товаров после того, как они были заказаны.Мы будем использовать даты в столбцах E и F для расчета времени доставки в столбце G .

1. Выберите ячейку , которая будет содержать функцию. В нашем примере мы выберем ячейку G3 .
2. Щелкните вкладку Formulas на ленте , затем щелкните команду Insert Function .
3. Откроется диалоговое окно Вставить функцию .
4. Введите несколько ключевых слов , описывающих вычисления, которые должна выполнять функция, затем щелкните Go .В нашем примере мы введем count days , но вы также можете выполнить поиск, выбрав категорию из раскрывающегося списка.
5. Просмотрите результаты , чтобы найти нужную функцию, затем щелкните ОК . В нашем примере мы выберем NETWORKDAYS , что будет считать количество рабочих дней между датой заказа и датой получения.
6. Откроется диалоговое окно « аргументы функции ». Отсюда вы сможете вводить или выбирать ячейки, которые будут составлять аргументы функции.В нашем примере мы введем E3 в поле Start_date и F3 в поле End_date .
7. Когда вы будете удовлетворены, щелкните OK .
8. Функция будет рассчитана , а результат появится в ячейке. В нашем примере результат показывает, что на получение заказа ушло четыре рабочих дня .

Как и формулы, функции можно копировать в соседние ячейки. Просто выберите ячейку , содержащую функцию, затем щелкните и перетащите маркер заполнения на ячейки, которые вы хотите заполнить.Функция будет скопирована, и значения для этих ячеек будут вычислены относительно их строк или столбцов.

Подробнее:

Если вам удобны основные функции, вы можете попробовать более продвинутые, например VLOOKUP . Ознакомьтесь с нашей статьей о том, как использовать функцию ВПР в Excel для получения дополнительной информации.

Чтобы узнать больше о работе с функциями, посетите наш учебник по формулам Excel.

Вызов!

1. Откройте нашу рабочую тетрадь.
2. Щелкните вкладку Challenge в нижнем левом углу книги.
3. В ячейке F3 вставьте функцию для вычисления среднего из четырех оценок в ячейках B3: E3 .
4. Используйте дескриптор заполнения , чтобы скопировать функцию из ячейки F3 в ячейки F4: F17 .
5. В ячейке B18 используйте AutoSum , чтобы вставить функцию, которая вычисляет наименьшее значение в ячейках B3: B17 .
6. В ячейке B19 используйте библиотеку функций , чтобы вставить функцию, которая вычисляет медианное значение оценок в ячейках B3: B17 . Подсказка : Вы можете найти медианную функцию, перейдя в Дополнительные функции> Статистические .
   
7. В ячейке B20 создайте функцию для вычисления наивысшего балла в ячейках B3: B17 .
8. Выберите ячейки B18: B20 , затем используйте маркер заполнения , чтобы скопировать все три функции, которые вы только что создали, в ячейки C18: F20 .
9. Когда вы закончите, ваша рабочая тетрадь должна выглядеть так:

/ ru / excel2016 / basic-tips-for-work-with-data / content /

Представляем деньги | Безграничная экономика

Определение денег

Деньги — это любой предмет, который обычно принимается в качестве оплаты товаров и услуг и погашения долга.

Цели обучения

Различают три основные функции денег: средство обмена, расчетную единицу и средство сбережения

Основные выводы

Ключевые моменты

• Деньги бывают трех видов: товарные деньги, бумажные деньги и фидуциарные деньги.Большинство современных денежных систем основаны на бумажных деньгах.
• Товарные деньги получают свою стоимость от товара, из которого они сделаны, в то время как бумажные деньги имеют ценность только по приказу правительства.
• Деньги функционируют как средство обмена, расчетная единица и средство сбережения.

Ключевые термины

• Fiat money : Деньги, которым придается ценность, потому что те, кто их использует, считают, что они имеют ценность; значение не является производным от какой-либо присущей ему характеристики.

Деньги — это любой предмет, который обычно используется в качестве оплаты товаров и услуг и погашения долгов в данном социально-экономическом контексте или стране. Деньги бывают трех видов: товарные деньги, бумажные деньги и фидуциарные деньги.

Многие предметы исторически использовались в качестве товарных денег, включая редкие в природе драгоценные металлы, раковины, ячменные бусы и другие предметы, которые считались ценными. Стоимость товарных денег определяется товаром, из которого они сделаны.Сам товар составляет деньги, а деньги — товар.

Товарные деньги : Раковины из раковин раньше использовались в качестве товарных денег. Стоимость товарных денег определяется товаром, из которого они сделаны.

Фиатные деньги — это деньги, стоимость которых не зависит от внутренней стоимости или гарантии того, что они могут быть конвертированы в ценный товар (например, золото). Вместо этого он имеет ценность только по государственному заказу (фиат). Обычно правительство объявляет фиатную валюту законным платежным средством, что делает незаконным отказ от фиатной валюты в качестве средства выплаты всех долгов.Бумажные деньги — это пример бумажных денег.

Фидуциарные деньги включают депозиты до востребования (например, текущие счета) банков. Фидуциарные деньги принимаются на основании доверительного управления их эмитентом (банком).

Большинство современных денежных систем основаны на бумажных деньгах. Однако на протяжении большей части истории почти все деньги были товарными деньгами, такими как золотые и серебряные монеты.

Функции денег

Деньги выполняют три основные функции. Это средство обмена, расчетная единица и средство сбережения:

1. Средство обмена: Когда деньги используются для посредничества при обмене товарами и услугами, они выполняют функцию средства обмена.
2. Расчетная единица: это стандартная числовая единица измерения рыночной стоимости товаров, услуг и других операций. Это стандарт относительной стоимости и отсрочки платежа, и как таковой является необходимым предварительным условием для заключения коммерческих соглашений, связанных с задолженностью. Чтобы функционировать в качестве расчетной единицы, деньги должны делиться на более мелкие единицы без потери стоимости, быть взаимозаменяемыми (одна единица или единица должна восприниматься как эквивалент любой другой), а также иметь определенный вес или размер, чтобы их можно было проверяемо исчислить.
3. Средство сбережения: чтобы действовать как средство сбережения, деньги должны надежно сохраняться, храниться и извлекаться. При извлечении он должен быть предсказуемо пригодным для использования в качестве средства обмена. Кроме того, стоимость денег должна оставаться стабильной с течением времени.

Экономисты иногда отмечают дополнительные функции денег, такие как стандарт отсрочки платежа и функция измерения стоимости. «Стандарт отсрочки платежа» — приемлемый способ урегулирования долга — единица, в которой выражены долги.Статус денег как законного платежного средства означает, что деньги можно использовать для погашения долгов. Деньги также могут выступать в качестве стандартной меры и общего наименования торговли. Таким образом, это основа для котировок и заключения сделок. Его наиболее важное использование — это метод сравнения значений разнородных объектов.

Функции денег

Денежная экономика является значительным усовершенствованием бартерной системы, при которой товары обменивались напрямую на другие товары.

Цели обучения

Проанализировать, как характеристики денег делают их эффективным средством обмена

Основные выводы

Ключевые моменты

• Бартерная система имеет ряд ограничений, включая двойное совпадение желаний, отсутствие общей меры стоимости, неделимость определенных товаров, сложность отсроченных платежей и сложность хранения богатства.
• Несмотря на многочисленные ограничения, бартерная система работает хорошо, когда валюта нестабильна или недоступна для ведения торговли.
• Деньги долговечные, делимые, портативные, жидкие и устойчивые к подделке.
• Деньги служат средством обмена, расчетной единицей, средством сбережения и стандартом отсрочки платежа.

Ключевые термины

• бартер : Обмен товаров или услуг без привлечения денег.

Бартер — это система обмена, при которой товары или услуги напрямую обмениваются на другие товары или услуги без использования средства обмена, например денег.Взаимный обмен происходит мгновенно и не откладывается по времени. Обычно он двусторонний, хотя может быть многосторонним и обычно существует параллельно с валютными системами в большинстве развитых стран, хотя и в очень ограниченной степени. Бартерная система имеет ряд ограничений, которые делают транзакции очень неэффективными, в том числе:

Бартер : В системе бартера люди, обладающие чем-то ценным, могут обменять это на что-то аналогичное или более ценное.

• Двойное совпадение желаний: потребности продавца товара должны соответствовать потребностям покупателя.В противном случае транзакция не состоится.
• Отсутствие общей меры стоимости: В денежной экономике деньги играют роль меры стоимости всех товаров, позволяя сравнивать ценности товаров друг с другом. Это невозможно в бартерной экономике.
• Неделимость определенных товаров: если человек хочет купить определенное количество товаров другого лица, но имеет платеж только за один неделимый товар, стоимость которого превышает то, что человек хочет получить, бартерная сделка невозможна.
• Сложность отсроченных платежей: невозможно производить платежи в рассрочку и сложно производить платежи в более поздний момент времени.
• Сложность хранения богатства: если общество полагается исключительно на скоропортящиеся товары, хранить богатство на будущее может быть непрактично.

Несмотря на длинный список ограничений, бартерная система имеет ряд преимуществ. Он может заменить деньги в качестве метода обмена во время валютного кризиса, например, когда валюта нестабильна (например,грамм. гиперинфляция или дефляционная спираль) или просто недоступны для ведения торговли. Это также может быть полезно, когда имеется мало информации о кредитоспособности торговых партнеров или когда отсутствует доверие.

Денежная система является значительным улучшением по сравнению с бартерной системой. Он позволяет количественно оценить стоимость товаров и сообщить об этом другим. Деньги имеют несколько определяющих характеристик. Это:

• Долговечный.
• Делимый.
• Портативный.
• Жидкость.
• Учетная единица.
• Законное платежное средство.
• Устойчив к подделкам.

Деньги служат четырем основным целям. Это:

• Средство обмена: объект, который обычно принимается в качестве формы платежа.
• Учетная единица: средство отслеживания того, сколько что-то стоит.
• Средство сбережения: его можно сохранить и впоследствии обменять на товары и услуги по приблизительной стоимости.
• Стандарт отсроченных платежей (не все экономисты считают это определяющим назначением денег).

Использование денег в качестве средства обмена устранило основную трудность двойного совпадения потребностей в бартерной системе. Он разделяет акт купли-продажи товаров и услуг и помогает обеим сторонам независимо друг от друга получить максимальное удовлетворение и прибыль.

Измерение денежной массы: M1

M1 охватывает наиболее ликвидные компоненты денежной массы, включая валюту, находящуюся у населения, и чековые депозиты в банках.

Цели обучения

Определить M1

Основные выводы

Ключевые моменты

• Федеральная резервная система измеряет денежную массу с помощью трех денежных агрегатов: M1, M2 и M3.
• M1 — это самая узкая мера денежной массы, включающая только деньги, которые можно потратить напрямую.
• M2 — более широкая мера, охватывающая M1 и почти деньги.
• M3 включает M2 плюс относительно меньше ликвидных денег. Однако на практике эта мера больше не используется.

Ключевые термины

• M1 : сумма наличных денег в обращении плюс сумма на текущих банковских счетах.

Федеральная резервная система измеряет денежную массу с помощью трех основных денежных агрегатов: M1, M2 и M3.

M1 — это самая узкая мера денежной массы, включающая только деньги, которые можно потратить напрямую. В частности, M1 включает валюту и все чековые депозиты. Под валютой понимаются монеты и бумажные деньги, находящиеся в руках населения. Чековые депозиты относятся ко всем расходуемым депозитам в коммерческих банках и сберегательных кассах.

M1 : Мера M1 включает наличные деньги в руках населения и чековые депозиты в коммерческих банках.

Более широкий показатель денег, чем M1, включает не только все расходуемые остатки в M1, но и некоторые дополнительные активы, называемые «почти денежными».Почти деньги нельзя потратить так же легко, как деньги или деньги на текущих счетах, но их можно превратить в потраченные остатки с очень небольшими усилиями или затратами. Ближайшие деньги включают то, что находится на сберегательных счетах и ​​паевых инвестиционных фондах денежного рынка. Более широкая категория денег, охватывающая все эти активы, называется M2. M3 включал M2 плюс относительно менее ликвидный, близкий к деньгам. На практике мера M3 больше не используется Федеральной резервной системой.

Представьте, что Лаура кладет 900 долларов на свой текущий счет в мире, в котором нет других денег (M1 = 900 долларов).Банк выделяет 10% суммы на обязательные резервы, а оставшиеся 810 долларов могут быть предоставлены банком в качестве кредита. Денежная масса M1 увеличивается на 810 долларов при выдаче ссуды (M1 = 1710 долларов). Тем временем Лаура выписывает чек на 400 долларов. Общая денежная масса M1 не изменилась; он включает чек на 400 долларов и 500 долларов, оставшихся на текущем счете (M1 = 1710 долларов). Чек Лауры случайно испорчен в прачечной. M1 и ее текущий счет не меняются, потому что чек никогда не обналичивается (M1 = 1710 долларов).Тем временем банк ссужает Мэнди созданный им кредит в размере 810 долларов. Мэнди кладет деньги на текущий счет в другом банке. Банк должен держать 10% в качестве резервов и иметь 729 долларов для ссуд. Это создает деньги с обещанием заплатить из предыдущего обещания заплатить, увеличивая денежную массу M1 (M1 = 2439 долларов). Теперь банк Мэнди ссужает деньги кому-то другому, который кладет их на текущий счет в другом банке, и процесс повторяется.

Измерение денежной массы: M2

M2 — это более широкий показатель денежной массы, чем M1, включая все деньги M1 и те, которые могут быть быстро преобразованы в жидкие формы.

Цели обучения

Определить M2

Основные выводы

Ключевые моменты

• M2 состоит из всех компонентов M1 плюс почти деньги.
• Почти деньги — это относительно ликвидные финансовые активы, которые можно быстро конвертировать в деньги М1.
• Ближайшие денежные средства включают сберегательные вклады, небольшие срочные вклады и паевые инвестиционные фонды денежного рынка.

Ключевые термины

• M2 : сумма наличных денег в обращении плюс банковские счета, сберегательные счета и небольшие депозиты.

Не существует единого «правильного» показателя денежной массы. Вместо этого существует несколько показателей, классифицированных по континууму между узкими и широкими денежными агрегатами. К узким критериям относятся только наиболее ликвидные активы, наиболее легко используемые для расходования (например, валюта и чековые депозиты). Более широкие меры добавляют менее ликвидные виды активов (депозитные сертификаты и т. Д.). Континуум соответствует тому, как различные типы денег более или менее контролируются денежно-кредитной политикой.Узкие меры включают меры, более непосредственно затрагиваемые и контролируемые денежно-кредитной политикой, тогда как более широкие меры менее тесно связаны с действиями денежно-кредитной политики.

Различные типы денег обычно классифицируются как «M». Во всем мире они варьируются от M0 (самый узкий) до M3 (самый широкий), но какая из мер фактически является основным направлением разработки политики, зависит от центрального банка страны.

M2 — это один из агрегатов, по которым Федеральная резервная система измеряет денежную массу.Это более широкая классификация денег, чем M1, и ключевой экономический индикатор, используемый для прогнозирования инфляции. M2 состоит из всех жидких компонентов M1 плюс почти деньги. Почти деньги — это относительно ликвидные финансовые активы, которые можно легко конвертировать в деньги М1. В частности, к почти денежным средствам относятся сберегательные вклады, небольшие срочные вклады (менее 100 000 долларов США), которые становятся доступными при наступлении срока погашения, и паевые инвестиционные фонды денежного рынка.

Федеральный резерв : Исторически Федеральный резерв измерял денежную массу, используя агрегаты M1, M2 и M3.Совокупность M2 включает M1 плюс почти деньги.

Представьте, что Лаура выписывает чек на 1000 долларов и приносит его в банк, чтобы открыть счет на денежном рынке. Это приведет к уменьшению M1 на 1000 долларов, но M2 останется прежним. Это связано с тем, что M2 включает счет денежного рынка в дополнение ко всем деньгам, учитываемым в M1.

Другие измерения денежной массы

В дополнение к обычно используемым агрегатам M1 и M2 также используется несколько других показателей денежной массы.

Цели обучения

Объясните, как измеряется денежная масса

Основные выводы

Ключевые моменты

• M0 — это мера всех физических денег и монет, находящихся в обращении в экономике.
• МБ — это мера, которая охватывает всю физическую валюту, монеты и депозиты Федеральной резервной системы (специальные депозиты, которые могут иметь только банки в ФРС).
• Различные формы денег в статистике денежной массы правительства возникают в результате практики банковского обслуживания с частичным резервированием.Каждый раз, когда банк выдает ссуду в банковской системе с частичным резервированием, создается новая сумма денег, которая составляет компоненты, не относящиеся к M0, в статистике M1 -M3.

Ключевые термины

• M0 : количество монет и банкнот в обращении.
• MB : Доля резервов коммерческих банков, которая хранится на счетах в их центральном банке, плюс общая валюта, обращающаяся среди населения.

В дополнение к обычно используемым агрегатам M1 и M2, также используется несколько других измерений денежной массы.Более конкретно:

Денежная масса в евро : Все показатели денежной массы взаимосвязаны, но использование разных показателей может привести экономистов к разным выводам.

• M0: Общая сумма всей физической валюты, включая монеты. M0 = Банкноты Федерального Резерва + Банкноты США + Монеты.
• МБ: означает «денежная база», относящаяся к базе, на которой создаются все другие формы денег. МБ — это сумма всей физической валюты плюс депозиты Федерального резерва (специальные депозиты, которые могут иметь только банки в ФРС).MB = Монеты + Банкноты США + Банкноты Федерального Резерва + Депозиты Федерального Резерва.
• M1: Общая сумма M0 (наличные / монеты) вне системы частного банковского обслуживания плюс сумма депозитов до востребования, дорожных чеков и других проверяемых депозитов.
• M2: M1 + большинство сберегательных счетов, счетов денежного рынка, паевые инвестиционные фонды розничного денежного рынка и срочные вклады небольшого номинала (депозитные сертификаты на сумму менее 100 000 долларов США).
• M3: M2 + все остальные депозитные сертификаты (крупные срочные вклады, остатки паевых инвестиционных фондов институционального денежного рынка), депозиты в евродолларах и соглашения РЕПО.
• M4-: M3 + коммерческая бумага.
• M4: M4- + казначейские векселя (или M3 + коммерческие бумаги + казначейские векселя)
• MZM: «Деньги с нулевым сроком погашения» — один из самых популярных агрегатов, используемых ФРС, поскольку его скорость исторически является наиболее точным предсказателем инфляции. Это М2 — срочные вклады + фонды денежного рынка.
• L: Самый широкий показатель ликвидности, который Федеральная резервная система больше не отслеживает. M4 + Банковское согласие.

Различные формы денег в статистике денежной массы правительства возникают в результате практики банковского обслуживания с частичным резервированием.Банковское обслуживание с частичным резервированием — это практика, при которой банк сохраняет только часть депозитов своих клиентов в качестве доступных резервов для удовлетворения требований о снятии средств. Каждый раз, когда банк выдает ссуду в банковской системе с частичным резервированием, создается новая сумма денег. Этот новый тип денег составляет компоненты, не относящиеся к M0, в статистике M1-M3.

Функции денег

Деньги часто определяются в терминах трех функций , или услуг , которые они предоставляют.Деньги служат средством обмена , хранилищем стоимости и расчетной единицей .

Средство обмена. Самая важная функция денег — это средство обмена для облегчения транзакций. Без денег все операции пришлось бы проводить по бартеру , который предполагает прямой обмен одного товара или услуги на другой. Сложность бартерной системы заключается в том, что для получения определенного товара или услуги от поставщика необходимо иметь товар или услугу равной стоимости, что также необходимо поставщику.Другими словами, в бартерной системе обмен может иметь место только , если есть двойного совпадения желаний между двумя сторонами сделки. Однако вероятность двойного совпадения желаний мала и затрудняет обмен товарами и услугами. Деньги эффективно устраняют проблему двойного совпадения желаний, выступая в качестве средства обмена, которое принимается во всех транзакциях всеми сторонами, независимо от того, желают ли они товаров и услуг друг друга.

Накопитель. Чтобы быть средством обмена, деньги должны сохранять свою ценность с течением времени; то есть это должно быть средство сбережения. Если бы деньги не могли храниться в течение некоторого периода времени и по-прежнему оставаться ценными при обмене, это не решило бы проблему двойного совпадения желаний и, следовательно, не было бы принято в качестве средства обмена. Как средство сбережения деньги не уникальны; существует множество других средств сбережения, таких как земля, произведения искусства и даже бейсбольные карточки и марки.Деньги могут быть даже не лучшим средством сбережения, потому что они обесцениваются с инфляцией. Однако деньги на более ликвидны, чем на других средств сбережения, потому что как средство обмена они легко принимаются повсюду. Кроме того, деньги — это легко транспортируемое средство сбережения, доступное в нескольких удобных номиналах.

Учетная единица. Деньги также функционируют как расчетная единица, обеспечивая общую меру стоимости обмениваемых товаров и услуг.Знание стоимости или цены товара в денежном выражении позволяет как поставщику, так и покупателю товара принимать решения о том, сколько товара нужно поставить, а какое — купить.

Функции менеджеров

Все менеджеры на всех уровнях каждой организации выполняют эти функции, но количество времени, которое менеджер тратит на каждую из них, зависит как от уровня управления, так и от конкретной организации.

Менеджер носит много шляп. Менеджер является не только лидером команды, но и планировщиком, организатором, чирлидером, тренером, специалистом по решению проблем и лицом, принимающим решения — все в одном лице.И это лишь некоторые из ролей менеджера.

Кроме того, графики менеджеров обычно забиты. Независимо от того, заняты ли они встречами сотрудников, неожиданными проблемами или стратегическими сессиями, менеджеры часто находят немного свободного времени в своих календарях. (И это даже не включает ответы на электронную почту!)

В своей классической книге « Природа управленческой работы», Генри Минцберг описывает набор из десяти ролей, которые выполняет менеджер. Эти роли делятся на три категории:

• Межличностное общение: Эта роль предполагает взаимодействие с людьми.

• Информационный: Эта роль включает обмен и анализ информации.

• Принятие решений: Эта роль включает принятие решений.

Таблица 1 содержит более подробный анализ каждой категории ролей, которые помогают менеджерам выполнять все пять функций, описанных в предыдущем разделе «Функции менеджеров».

Не каждый может быть менеджером. Определенные навыки , или способности воплощать знания в действия, которые приводят к желаемой производительности, необходимы, чтобы помочь другим сотрудникам стать более продуктивными.Эти навыки подпадают под следующие категории:

• Технический: Этот навык требует способности использовать особые навыки или опыт для выполнения определенных задач. Бухгалтеры, инженеры, исследователи рынка и компьютерные специалисты, например, обладают техническими навыками. Руководители приобретают эти навыки сначала в рамках формального образования, а затем развивают их в процессе обучения и получения опыта работы. Технические навыки наиболее важны на более низких уровнях управления.

• Человек: Этот навык демонстрирует способность хорошо работать в сотрудничестве с другими. Человеческие навыки проявляются на рабочем месте в духе доверия, энтузиазма и подлинного участия в межличностных отношениях. Менеджер с хорошими человеческими навыками обладает высокой степенью самосознания и способностью понимать чувства других или сопереживать им. Некоторые менеджеры от природы рождаются с большими человеческими навыками, в то время как другие улучшают свои навыки с помощью занятий или опыта.Независимо от того, как приобретаются человеческие навыки, они имеют решающее значение для всех менеджеров из-за в высшей степени межличностного характера управленческой работы.

• Концептуальный: Этот навык требует способности мыслить аналитически. Аналитические навыки позволяют менеджерам разбивать проблемы на более мелкие части, видеть отношения между частями и распознавать последствия одной проблемы для других. По мере того, как менеджеры берут на себя все более высокие обязанности в организации, им приходится иметь дело с более неоднозначными проблемами, которые имеют долгосрочные последствия.Опять же, менеджеры могут сначала приобрести эти навыки в рамках формального образования, а затем развивать их, обучаясь и работая. Чем выше уровень управления, тем важнее становятся концептуальные навыки.

Хотя все три категории содержат навыки, необходимые для менеджеров, их относительная важность имеет тенденцию варьироваться в зависимости от уровня управленческой ответственности.

Преподаватели бизнеса и менеджмента все больше заинтересованы в том, чтобы помогать людям приобретать технические, человеческие и концептуальные навыки, а также развивать определенные компетенции или специализированные навыки, которые способствуют высокой производительности на управленческой работе.Ниже приведены некоторые навыки и личные качества, которые Американская ассамблея университетских школ бизнеса (AACSB) призывает бизнес-школы помогать своим ученикам развиваться.

• Лидерство — способность влиять на других для выполнения задач

• Самообъективность — способность реалистично оценивать себя

• Аналитическое мышление — способность интерпретировать и объяснять закономерности в информации

• Поведенческая гибкость — способность изменять личное поведение для объективной, а не субъективной реакции для достижения целей организации

• Устное общение — способность ясно выражать идеи словами

• Письменное общение — способность ясно выражать идеи в письменной форме

• Личное влияние — способность производить хорошее впечатление и вселять уверенность

• Стрессоустойчивость — способность работать в стрессовых условиях

• Допуск на неопределенность — способность действовать в неоднозначных ситуациях

.