2 с помощью параллельного переноса.
Содержание
Нужна помощь в учебе?
Предыдущая тема: Разложение квадратного трехчлена на множители: теорема и формулы
Следующая тема:   Графики функции: от чего зависит вид графика функции
Урок «Квадратичная функция и её график»
МБОУ Алтунинская ООШ
Обобщающий урок по алгебре 9 класс
по теме «Квадратичная функция и её график»
Автор: учитель первой
квалификационной категории
Рушева Татьяна Борисовна
с.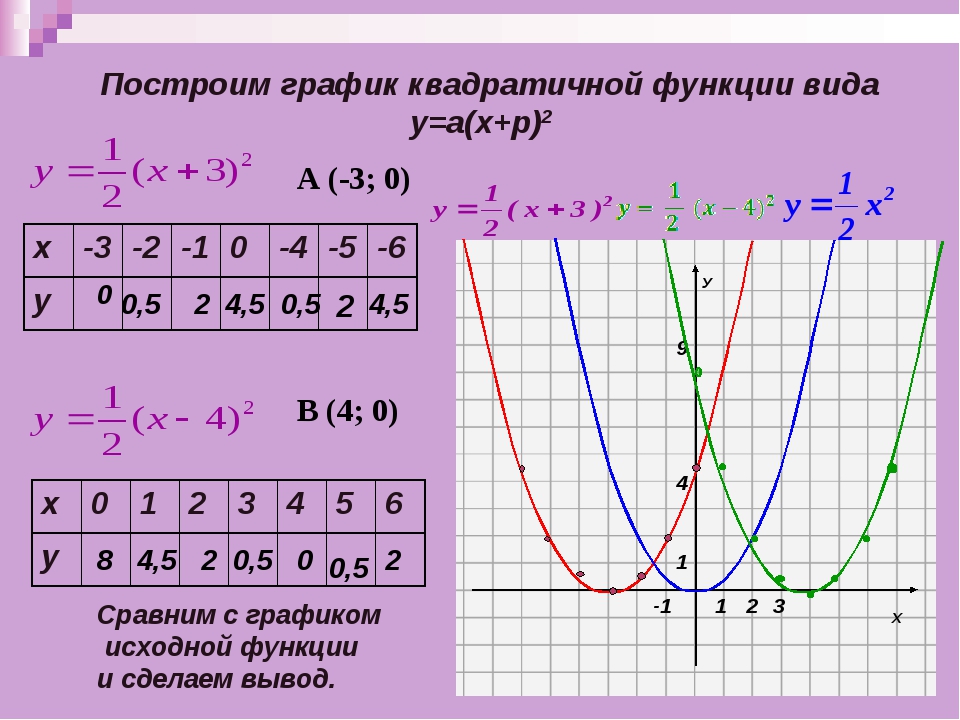 Алтунино
Алтунино
2020 год
Цель урока: повторить тему «Квадратичная функция и её график» , использовать её для решения задач, входящих в раздел «Алгебра » ОГЭ, подготовить учащихся к написанию контрольной работе.
Задачи:
-образовательные: повторить определение и свойства квадратичной функции, как влияют коэффициенты а, и с на расположение графика квадратичной функции ,нахождение наибольшего и наименьшего значения квадратичной функции, нахождение области значения функции ; рассмотреть задачи, входящие в ОГЭ по данной теме.
-развивающие: Развивать умения анализировать, сопоставлять, логически мыслить, обобщать, развивать память, активность и самостоятельность, способность к самоорганизации.
-воспитательные: Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата.
Тип урока: Урок систематизации знаний и умений.
Формы работы учащихся: Фронтальная, самостоятельная, групповая.
Необходимое техническое оборудование: интерактивная доска, компьютер, раздаточный и справочный материал.
Учебник: Ю.Н.Макарычев, Н.Г.Миндюк и др.Алгебра-9.
Ход урока:
1.Организационный момент.
Мотивационная беседа с учащимися.
— Доброе утро, ребята! Мне бы хотелось начать урок со следующих слов. Француский писатель Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы переварить знания, надо поглощать их с аппетитом».
Давайте следовать совету писателя. Будем активны,внимательны,будем поглощать знания с большим желанием, ведь они вам пригодятся в дальнейшей жизни.
А девизом нашего урока пусть будут следующие слова: слушать и слышать, смотреть и видеть, думать и рассуждать.
Тема нашего урока «Квадратичная функция и её график»(записываем в тетрадях число, классная работа и тему урока).
2. Постановка целей урока.
Цель нашего урока: повторить тему «Квадратичная функция и её график» , использовать её для решения задач, входящих в раздел «Алгебра » ОГЭ, подготовиться к написанию контрольной работе.
3.Фронтальная работа с использованием интерактивной доски.
Актуализация опорных знаний и умений. (Работа с презентацией)
(Работа с презентацией)
Ученик выполняет тест на компьютере
(проверка домашнего задания)
Для того, чтобы успешно справиться с поставленными целями нам необходимо вспомнить некоторый теоретический материал:
-
Квадратичная функция- это… -
Область определения функции – это… -
Множество значений функции – это… -
Нули функции – это… -
Промежутки знакопостоянства – это… -
Промежутки убывания функции — … -
Промежутки возрастания функции — … -
График квадратичной функции –
Историческая справка- Александров Павел.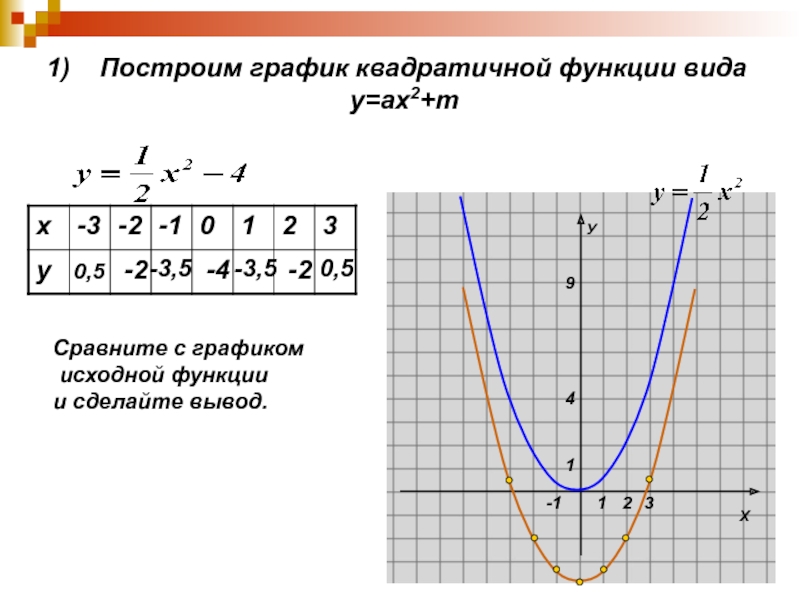
Работа с презентацией-фронтальная работа
4.Работа с тестовыми заданиями ОГЭ- стр.31 №2,№3,№5
5.Входной контроль. Индивидуальная работа.
1 вариант.
№1 №2
№3 №4
2 вариант
№1 №2
№3 №4
Ответы.
|
|
|
Оценить работу соседа по следующему критерию:
«5» — нет ошибок;
«4» — 1 ошибка;
«3» — 2 ошибки;
«2» — 3 и более ошибки.
6. Решение задачи на построение графика квадратичной функции.
Белова Н. ч.2 №23 ОГЭ в.2 стр.19.
Задание1. Постройте график функции y = x2 – 2x — 3.
(Ученик выполняет задание у доски все работают в тетрадях, строим график на миллиметровой бумаге)
С помощью графика найдите (работа в парах):
-
Значение функции, при x = 1,5____________ -
Значение x, при которых y = -2____________ -
Нули функции______________ -
Промежутки, в которых у>0______________________
y<0______________________
5. Промежутки возрастания ________________________
Промежутки возрастания ________________________
убывания __________________________
6.Наибольшее (наименьшее) значение функции________
7.Облость значения функции_________
(проверка)
7.Физкультминутка
Отвели свой взгляд направо,
Отвели свой взгляд налево,
Оглядели потолок,
Посмотрели все вперёд.
8. Повторить свойство квадратичной функции о наибольшем и наименьшем значении и выполнить задание.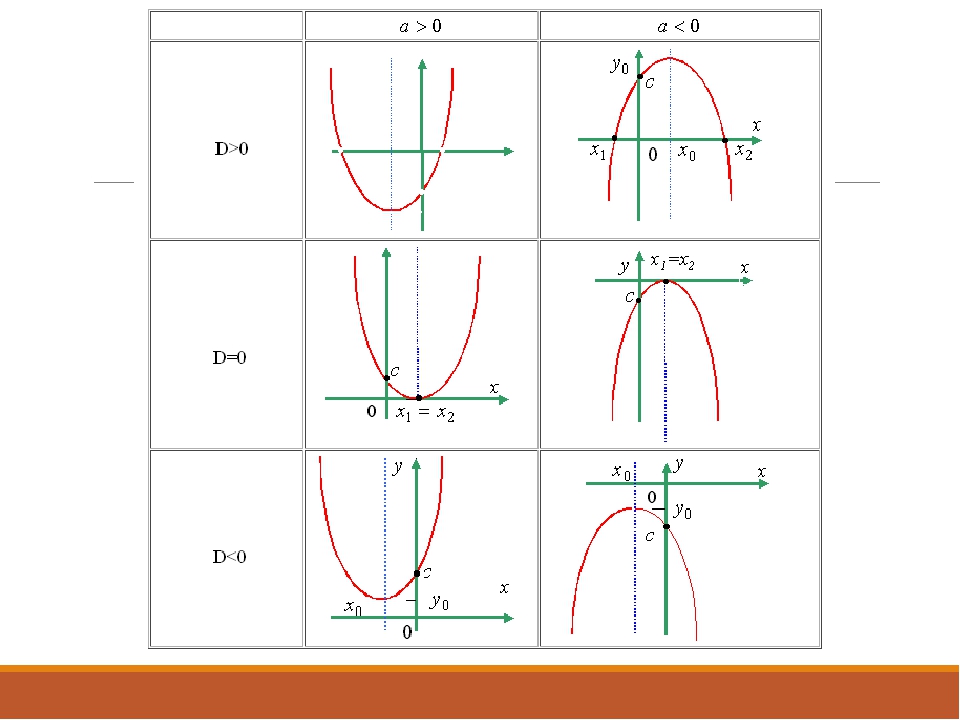 2+4x+11
2+4x+11
Вывод: 1.Если а>0, то функция имеет наименьшее значение:
yнаим.=yв(yв-ордината вершины параболы, yв=y(xв), xв= —b/2а)
2.Если а<0, то функция имеет наибольшее значение:
yнаиб.=yв(yв-ордината вершины параболы, yв=y(xв), xв= —b/2а)
9. 2-3x+3 и прямая y=2x-3. Если точки пересечения существуют. То найдите их координаты.
2-3x+3 и прямая y=2x-3. Если точки пересечения существуют. То найдите их координаты.
11.Итог урока. Объявление оценок.
Опрос.
-Что такое область определения и область значений функции?
— Функцию какого вида называют квадратичной?
— Что за линия является графиком квадратичной функции?
— От чего зависит направление ветвей параболы?
— Как определить координаты вершины параболы?
12. Домашнее задание.
№243(г),№244(г)
№257(б, в, е)
Ч.1 №3 в.26 (ОГЭ)
Ч.2 №23 в.17(ОГЭ)
13. Рефлексия. Выбери утверждение, которое соответствует тому, как тебе работалось на уроке. Выведены на интерактивную доску.
Выведены на интерактивную доску.
1) Мне было всё понятно, я смог повторить теоретический материал и могу решать задачи без посторонней помощи.
2) Я вспомнил теоретический материал, решил задачи, но некоторые задачи требуют посторонней помощи.
3) Я плохо знаю теоретический материал, не смог его вспомнить и не могу решать задачи по данной теме.
(учащиеся дают учителю фигуру соответствующего цвета)
Раздел 8.3A: Квадратичная функция | Школа: Назарбаев Интеллектуальная школа химико-биологического направления г. | |||||||||||
Дата: | Ф.И.О. Шарипова АС | |||||||||||
КЛАСС: 8 | Количество присутствующих: | отсутствующие: | ||||||||||
Тема урока: | Квадратичная функция и ее график. | |||||||||||
Цель (цели) обучения, на что направлен урок | 8.5.1.4 находить значения функции по заданным значениям аргумента и обратно; 8.5.1.5 устанавливать связи между коэффициентами а, b, с квадратичной функции и расположением ее графика на координатной плоскости. | |||||||||||
Цели урока | Учащийся знает алгоритм построения графика квадратичной функции; Учащийся умеет строить график квадратичной функции. | |||||||||||
Критерии оценивания |
| |||||||||||
Языковая цель | Лексика/терминология: Квадратичная функция, парабола, выделение полного квадрата, ось симметрии, координаты вершины параболы, старший коэффициент, алгоритм построения. | |||||||||||
Развитие навыков | Коммуникативные навыки:
| |||||||||||
Привитие ценностей | Связи с ценностями НИШ:
Ценности ГГ:
| |||||||||||
Межпредметные связи | Информатика :умение использовать интерактивную доску, использовать программу «Графический калькулятор». | |||||||||||
Навыки использования ИКТ | Умение использовать интерактивную доску, использовать программу «Графический калькулятор». | |||||||||||
Предварительные знания | Знают, как строить график квадратичной функции с помощью параллельного переноса и по алгоритму. | |||||||||||
План | ||||||||||||
Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | ||||||||||
Начало урока 0 –5 мин Вызов. |
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 10 раз. Сделайте глубокий вздох и медленный выдох. Здравствуйте.Садитесь.
-совместно с учащимися определить тему урока; Запишите дату и тему урока в тетрадь. — совместно с учащимися определить цели урока; — совместно с учащимися определить критерии оценивания. Цели урока и критерии оценивания записать на доске. | РРТ | ||||||||||
Середина урока 23мин |
| |||||||||||
Работа в парах кластер | Итак, функция вида y = ax2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax2. То есть а не должно равняться нулю, остальные коэффициенты (b и с) нулю равняться могут. Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов. Самая простая зависимость для коэффициента а. y = 0,5x2 — 3x + 1 В данном случае а = 0,5 А теперь для а
y = — 0,5×2 — 3x + 1 В данном случае а = – 0,5 Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу: y = a 02 + b 0 + c = c. Получается, что у = с. То есть с – это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с 0 или с с 0: y = x2 + 4x + 3 с y = x2 + 4x – 3
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат: y = x2 + 4x Сложнее с параметром b. Однако это не все. Надо еще обратить внимание на знак коэффициента а. То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = — 2ахв определить знак b. Рассмотрим пример: Ветви направлены вверх, значит а 0, парабола пересекает ось у ниже нуля, значит с хв 0. Значит b = — 2ахв = -++ = -. b а 0, b с Рассмотрим еще один график: Ветви направлены вниз, значит а с 0, вершина параболы лежит правее нуля. А теперь такой: Ветви направлены вверх, значит а 0, парабола пересекает ось у ниже нуля, значит с хв b = — 2ахв = -+- = +. b 0. Окончательно имеем: а 0, b 0, с Если b = 0, то вершина параболы лежит на оси у. Она может лежать выше нуля (с 0) y = x2 + 3: Или ниже нуля (с у: y = x2 — 4: | Раздаточный материал | ||||||||||
Устная работа. | Определите, график какой функции изображен на рисунке:
| PPT | ||||||||||
Устно | По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с: а) б) Р е ш е н и е а) Ветви параболы направлены вверх, поэтому а 0. Парабола пересекает ось ординат в нижней полуплоскости, поэтому с b воспользуемся формулой для нахождения абсциссы вершины параболы: т = . По графику видно, что т а 0. Поэтому b 0. б) Аналогично определяем знаки коэффициентов а, b и с: а с 0, b | |||||||||||
Письменно в тетради | ||||||||||||
ФО №3 | 1. Ответ: , , . 2. По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с: Ответ: , , . 3.При каком значении аргумента значение функции
равно 0? Решение: При y=0
Решаем квадратное уравнение.
4. Найдите значение функции при х=2. | |||||||||||
Рефлексия 2 мин | Как влияют коэффициенты а, b и с на расположение графика квадратичной функции? | |||||||||||
Д/з 1 мин | 1) График какой из функций изображен на рисунке | |||||||||||
Дополнительная информация | ||||||||||||
Дифференциация — как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся? Дифференциация на уроке основана на принципах проблемного обучения и самостоятельного открытия знаний при изучении нового материала, а так же заданий более высокого уровня сложности на этапе закрепления. | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? При объяснении нового материала самооценивание по готовым ответам учащихся и словесное оценивание учителем, при первичном закреплении материала самооценивание по листу с готовым решением. На этапе закрепления самооценивание по чертежу построенному на компьютере. | Здоровье и соблюдение техники безопасности Физминутка в начале урока. Повторение правил ТБ при работе с ноутбуками. | ||||||||||
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Цели урока были реалистичными, так как учащимся удалось самостоятельно вывести формулы и составить алгоритм построения графика квадратичной функции. Конечно, были учащиеся которые не совсем поняли материал, но тема имеет продолжение на следующем уроке. Дифференциация для учащихся при изучений нового материала была предусмотрена в виде задания более высокого уровня сложности, в котором необходимо было синтезировать знания из предыдущих тем с новым материалом и провести анализ при решении задачи. Временные рамки были выдержаны. Отступлении от плана урока не было. | |||||||||||
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: Удачным была постановка вызова в начале урока . 2: Самостоятельное исследование учащимися поставленной задачи и самостоятельное составление алгоритма построения графика квадратичной функции. 3 .Использованеие ИКТ при проверке заданий Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: Больше времени уделить на рефлексию. Каждый ученик должен осознать, какое значение урок имел лично для него и записать это. Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках? В классе есть учащиеся у которых задания более высокого уровня сложности вызывают интерес и повышают мотивацию к учению, но и есть учащиеся которым необходима поддержка. | ||||||||||||
Урок по теме «Квадратичная функция и ее график»
Цели урока:
Образовательные:
- повторить понятие квадратичной функции;
- повторить алгоритм построения графика квадратичной функции;
- повторить свойства данной функции;
- закрепить умение определять свойства квадратичной функции по графику;
- закрепить навыки построения квадратичной функции;
- систематизировать знания по теме;
Воспитательные:
- учить работать самостоятельно;
- воспитание внимания;
- воспитание на уроке воли и упорства для достижения цели;
- воспитание, уважительного отношения друг к другу;
Развивающие:
- Развить навыки самоконтроля;
- развивать математическую речь;
- развить устойчивое внимание;
- развить умение переключать внимание.

Тип урока: урок обобщения и систематизации знаний.
Оборудование урока:
- Компьютер;
- мультимедийный проектор;
- карточки с заданиями.
План урока:
- Организационный момент.
- Сообщение темы и цели урока.
- Повторить основные свойства квадратичной функции (устная работа).
- Применение знаний, умений и навыков учащихся при построении графиков квадратичной функции.
- Самостоятельная работа (Тест).
- Рефлексия (“Что знаю?”, “Чего не знаю?”, “Что получилось?”, “Что нет?”).
- Подведение итогов урока.
Ход урока
I. Организационный момент.
II. Сообщение темы и цели урока.
III. Устная работа.
для того чтобы достичь целей урока вспомним теоретический материал по теме «Квадратичная функция».
- Функцию какого вида называют квадратичной? (слайд 2)
- Что является графиком квадратичной функции? (слайд 3)
- Как зависит направление ветвей параболы от коэффициента а? (слайд 4)
- Как определить координаты вершины параболы? (слайд 5)
- Каков алгоритм построения квадратичной функции? (слайд 6)
- Для каждой из функций укажите координаты вершины параболы, направление ее ветвей, уравнение оси симметрии.

- у = х2 – 1;
- у = + 5;
- у = ;
- у = ;
IV. Применение знаний, умений и навыков учащихся при построении графиков квадратичной функции.
V. Тест.
Вариант 1.
-
Для неравенства х2 > 4 найдите верную запись:
а) х > 2;
б) х > 2 или x > –2;
в) –2 < x < 2;
г) х < –2 или x > 2. -
На рисунке 1 показан график некоторой функции у = ах2 + bx + c Укажите верную комбинацию:
а) а > 0; D > 0;
б) а < 0; D > 0;
в) а > 0; D < 0;
г) а < 0; D < 0.
Рис. 1. -
На рисунке 2 показан график некоторой функции у = ах2 + bx + c Найдите формулу, задающую эту функцию
а) у = – х2 + 4х +2;
б) у = х2 – 4х +2;
в) у = – х2 – 4х +2;
г) у = х2 – 4х – 2.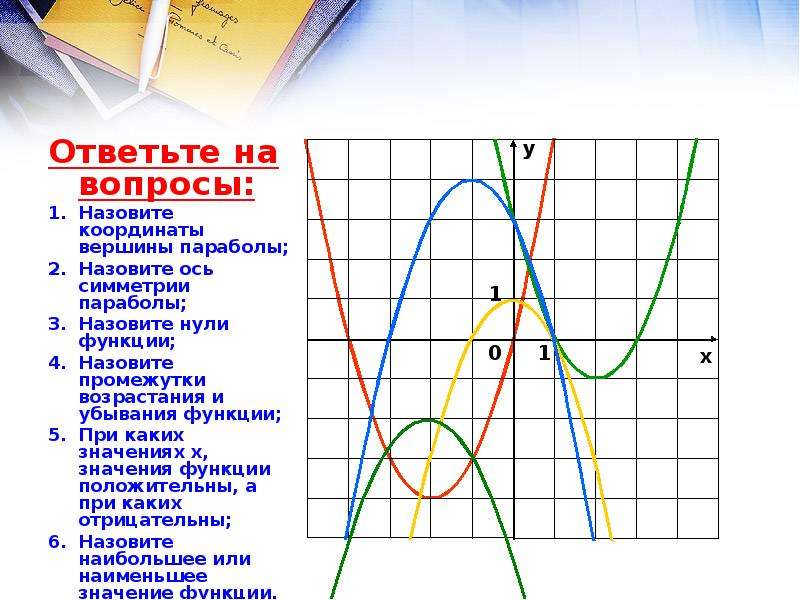
Рис. 2.
Вариант 2.
-
Для неравенства х2 < 9 найдите верную запись:
а) х < 3;
б) х < 3 или x < –3;
в) –3 < x < 3;
г) х < –3 или x > 3. -
На рисунке 3 показан график некоторой функции у = ах2 + bx + c Укажите верную комбинацию:
а) а > 0; D > 0;
б) а < 0; D > 0;
в) а > 0; D < 0;
г) а < 0; D < 0.
Рис. 3. -
На рисунке 4 показан график некоторой функции у = ах2 + bx + c Найдите формулу, задающую эту функцию
а) у = – х2 + 6х +9;
б) у = х2 – 6х +9;
в) у = – х2 – 6х – 9;
г) у = х2 – 6х – 9.
Рис 4.
Взаимопроверка результатов теста.
Дети меняются тетрадями и проверяют работу.
VI. Рефлексия.
Ответьте на вопросы:
- Какие знания понадобились тебе на уроке?
- Что понравилось на уроке больше всего?
- Где во время урока у тебя всё получалось хорошо?
- Какими словами можешь выразить своё настроение как результат работы на уроке?
VII. Подведение итогов урока.
Используемый материал:
- Алгебра 9 класс. Авторы: Ю.Н. Макарычев и др.
- Алгебра 8 класс. Авторы: Ю.Н. Макарычев и др.
- Алгебра 7 класс. Авторы: Ю.Н. Макарычев и др.
- Тесты по алгебре. Автор: П.И. Алтынов.
- gimn7matem.narod.ru
- fgraphiks.narod.ru
- findmapplaces.com
Презентация.
Квадратичная функция и её график
Зеленая парабола.
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 — он отрицательный. Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.
И остается Б-2.
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 — верно. Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида , где называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
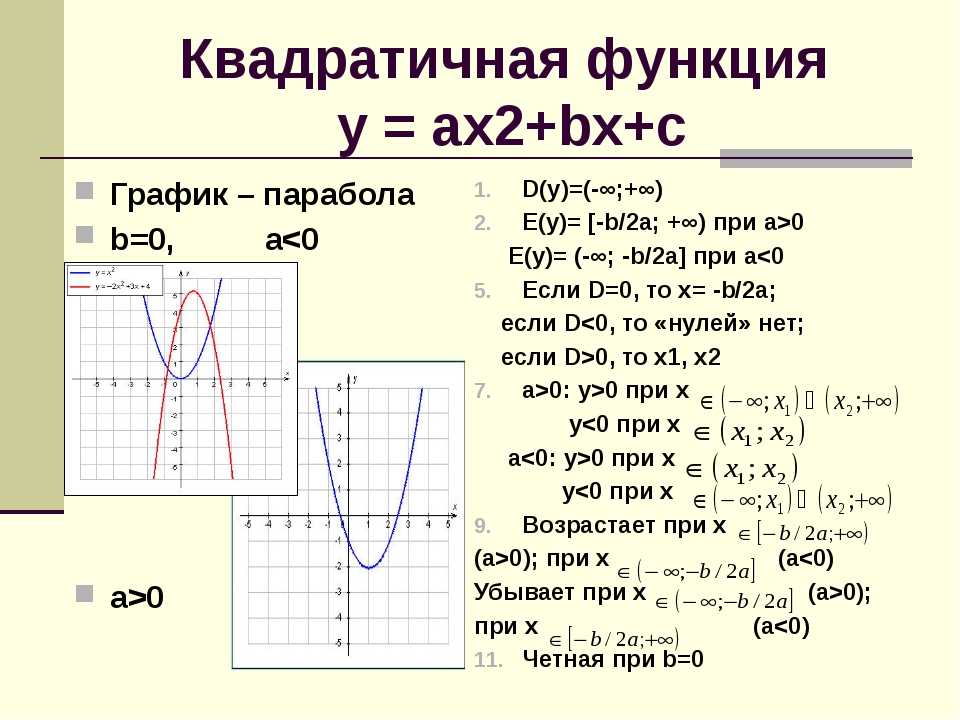
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
Квадратичная функция, ее график и свойства. П1
Данный модуль состоит из 5 заданий. Задания предназначены для отработки умений и навыков учащихся находить область определения и область значений квадратичной функции, а также вычислять значения квадратичной функции по заданным значениям аргумента и наоборот. При решении заданий учащемуся предоставляется возможность использовать подсказки. Все задания данного учебного модуля параметризированы. Это позволяет формировать индивидуальные задания для каждого учащегося.
Категория пользователей
Обучаемый, Преподаватель
Дисциплины
Математика
/ Квадратичная функция, ее график и свойства
Уровень образования
Профессионально-техническая подготовка, повышение квалификации
Статус
Завершенный вариант (готовый, окончательный)
Тип ИР сферы образования
информационный модуль
Ключевые слова
функция
Издатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Правообладатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.
Характеристики информационного ресурса
Тип используемых данных:
text/plain, text/html, image/jpeg
Объем цифрового ИР
1 266 225 байт
Проигрыватель
Категория модифицируемости компьютерного ИР
Признак платности
бесплатный
Наличие ограничений по использованию
нет ограничений
Рубрикация
Ступени образования
Основное общее образование
Целевое назначение
Учебное
Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)
Классы общеобразовательной школы
9
Уровень образовательного стандарта
Федеральный
Характер обучения
Базовое
College Algebra Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
Нахождение квадратичной функции с параболой
Нахождение квадратичной функции для заданных парабол
Квадратичные уравнения:
На этом этапе вы должны быть относительно знакомы с тем, что такое параболы и как они выглядят. Но, чтобы убедиться, что вы в курсе, парабола — это тип U-образной кривой, которая формируется из уравнений, включающих член x2x ^ {2} x2.{2} у = х2.
Пример графика простого квадратичного выражения
Существует так много разных типов задач, которые вам могут задать относительно квадратных уравнений. В этой статье основное внимание будет уделено тому, как мы можем построить квадратное уравнение из квадратичного графа, используя несколько различных методов. Но, прежде чем мы перейдем к подобным проблемам, найдите время поиграться с квадратичными выражениями в этом замечательном онлайн-калькуляторе для построения графиков. Чем удобнее вы будете работать с квадратичными графиками и выражениями, тем проще будет эта тема!
Теперь давайте приступим к решению задач с этими знаниями, а именно, как найти уравнение параболы!
Как найти квадратное уравнение из графика:
Чтобы найти квадратное уравнение из графика, можно использовать два простых метода: с использованием 2 точек или с использованием 3 точек.{2} \ mp dy = a (x ± f) 2∓d
Используя эту формулу, все, что нам нужно сделать, это перебрать вершину и другую точку, решить для a, а затем переписать наше окончательное уравнение. {2} 8 = a (−2) 2
8 = 4a8 = 4a8 = 4a
а = 2а = 2а = 2
Решите значение a, используя координату
Шаг 3. Запишите квадратное уравнение
После решения «а» у нас теперь есть вся информация, необходимая для написания нашего окончательного ответа.{2} + 4y = 2 (x + 1) 2 + 4
На этом урок о форме вершин и о том, как найти квадратное уравнение по двум точкам, завершен! Если вы хотите освежить свою память на связанные темы, такие как, как решать квадратные выражения в форме вершин, как преобразовать регулярное квадратное уравнение из стандартной формы в форму вершины, заполнив квадрат, и как использовать формулу вершины, убедитесь, что чтобы посмотреть наши уроки.
2) Найдите квадратное уравнение по 3 точкам
В некоторых случаях нам не повезет получить точку на вершине.Если это так, мы больше не сможем найти квадратичное выражение, используя всего две точки, и нам нужно сделать что-то немного другое. В случае, если нам дана информация о пересечениях параболы по оси x, а также об одной другой точке, мы можем найти квадратное уравнение, используя уравнение, которое называется «факторизованной формой». Общее уравнение для формулы факторизованной формы выглядит следующим образом, где b и c являются значениями x-координат пересечений x:
y = a (x − b) (x − c) y = a (x — b) (x — c) y = a (x − b) (x − c)
Используя эту формулу, все, что нам нужно сделать, это подставить координаты x точек пересечения с x, другую точку, а затем найти a, чтобы мы могли записать наш окончательный ответ.Опять же, лучший способ освоить эту форму квадратных уравнений — это решить задачу-пример.
Пример:
Определите уравнение параболы, показанное на изображении ниже:
Найдите уравнение параболы
Шаг 1: Определите точки
Поскольку нам даны три точки в этой задаче, x-точки пересечения и еще одна точка, мы можем использовать факторизованную форму для решения этого вопроса.
Из графика мы видим, что точки пересечения по оси x равны -2 и 5, а точка на параболе — (8,6).
Шаг 2. Подточки в форме вершины и решение относительно «a»
Теперь все, что нам нужно сделать, это подставить наши значения в формулу факторизованной формы и решить для «a», чтобы получить всю информацию для написания нашего окончательного квадратного уравнения. Напомним, факторизованная форма:
y = a (x − b) (x − c) y = a (x — b) (x — c) y = a (x − b) (x − c)
Использование координат точек пересечения по оси x:
ххх-перехват = -2-2-2
х = −2x = -2x = −2
(х + 2) = 0 (х + 2) = 0 (х + 2) = 0
ххх-перехват = 555
х = 5х = 5х = 5
(х-5) = 0 (х — 5) = 0 (х-5) = 0
y = (x + 2) (x − 5) y = (x + 2) (x — 5) y = (x + 2) (x − 5)
Затем мы можем использовать точку на параболе (8,6), чтобы найти «a»:
6 = a (8 + 2) (8−5) 6 = a (8 + 2) (8-5) 6 = a (8 + 2) (8−5)
6 = а (10) (3) 6 = а (10) (3) 6 = а (10) (3)
6 = 30a6 = 30a6 = 30a
a = 15a = \ frac {1} {5} a = 51
Шаг 3. Запишите квадратное уравнение
После решения «а» у нас теперь есть вся информация, необходимая для написания нашего окончательного ответа.
y = 15 (x + 2) (x − 5) y = \ frac {1} {5} (x + 2) (x — 5) y = 51 (x + 2) (x − 5)
И это все! Это два наиболее важных метода нахождения квадратичной функции по заданной параболе. Для дальнейшего изучения квадратичных функций и их графиков посмотрите эти полезные видео, посвященные дискриминанту и построению графиков квадратичных неравенств.
, и конические сечения.
Графические квадратные уравнения
Квадратное уравнение в стандартной форме
( a , b и c может иметь любое значение, за исключением того, что a не может быть 0.)
Вот пример:
Графики
Вы можете построить квадратное уравнение с помощью Function Grapher, но чтобы действительно понимал, что происходит, вы можете составить график самостоятельно. Читать дальше!
Простейший квадратичный
Простейшее квадратное уравнение:
f (x) = x 2
И график у него тоже простой:
Это кривая f (x) = x 2
Это парабола.
Теперь давайте посмотрим, что произойдет, когда мы введем значение «a»:
f (x) = ах 2
- Большие значения сгибают кривую внутрь
- Меньшие значения a расширяют его наружу
- И отрицательные значения переворачивают вверх дном
«Генерал» квадратичный
Перед построением графика мы переставляем уравнение, из этого:
f (x) = ax 2 + bx + c
К этому:
f (x) = a (x-h) 2 + k
Где:
Другими словами, вычислите h (= −b / 2a), затем найдите k , вычислив все уравнение для x = h
Но почему?
В этой новой форме замечательно то, что h и k показывают нам самую низкую (или самую высокую) точку, называемую вершиной :
А также кривая симметрична (зеркальное отображение) относительно оси , которая проходит через x = h , что упрощает построение графика
Итак…
- h показывает, насколько далеко влево (или вправо) кривая сместилась от x = 0
- k показывает, насколько далеко вверх (или вниз) кривая сместилась от y = 0
Давайте посмотрим, как это сделать:
Пример: График f (x) = 2x
2 — 12x + 16
Сначала отметим:
- а = 2,
- b = −12, и
- с = 16
Итак, что мы знаем?
- a положительный, значит, это «восходящий» график (U-образный)
- a равно 2, поэтому он немного «раздавлен» по сравнению с графиком x 2
Далее посчитаем h:
h = −b / 2a = — (- 12) / (2×2) = 3
И теперь мы можем вычислить k (используя h = 3):
k = f ( 3 ) = 2 (3) 2 — 12 · 3 + 16 = 18−36 + 16 = −2
Итак, теперь мы можем построить график (с настоящим пониманием!):
Мы также знаем: вершина равна (3, −2), а ось равна x = 3
От графика к уравнению
Что делать, если у нас есть график и мы хотим найти уравнение?
Пример: вы только что построили некоторые интересные данные, и они выглядят квадратично:
Просто зная эти два момента, мы можем придумать уравнение.
Во-первых, мы знаем h и k (в вершине):
(ч, к) = (1, 1)
Итак, давайте представим это в следующей форме уравнения:
f (x) = a (x-h) 2 + k
f (x) = a (x − 1) 2 + 1
Затем вычисляем «а»:
Мы знаем точку (0, 1.5) , поэтому: f (0) = 1.5
И a (x − 1) 2 + 1 при x = 0 равно: f (0) = a (0−1) 2 + 1
Оба они равны f (0) , поэтому сделайте их равными: a (0-1) 2 + 1 = 1.5
Упростить: a + 1 = 1,5
а = 0,5
Итак, вот результирующее квадратное уравнение:
f (x) = 0,5 (x − 1) 2 + 1
Примечание. Это может быть не правильное уравнение для данных, но это хорошая модель и лучшее, что мы можем придумать.
Как найти уравнение квадратичной функции по ее графику
Читатель недавно спросил:
Я хотел бы знать, как найти уравнение квадратичной функции по ее графику, в том числе когда он не пересекает ось x .Спасибо.
Моделирование
Это хороший вопрос, потому что он лежит в основе многих «настоящих» математических расчетов. Часто у нас есть набор точек данных из наблюдений, скажем, в эксперименте, но мы не знаем функцию, которая проходит через наши точки данных. (В большинстве случаев математика из учебников неверна — она сначала дает вам функцию и просит вас вставить значения в эту функцию.)
График квадратичной функции представляет собой параболу
График квадратичной функции — парабола.Парабола может иметь ориентацию «ноги вверх» или «ноги вниз».
Мы знаем, что квадратное уравнение будет иметь вид:
y = ax 2 + bx + c
Наша задача — найти значения a , b и c после первого наблюдения за графиком . Иногда легко определить точки, через которые проходит кривая, но часто нам нужно оценить точки.
Начнем с самого простого случая.(Предположим, что ось данной параболы вертикальна.)
Парабола разрезает график на 2 места
На графике видно, что корни квадратичного уравнения равны:
x = −2 (поскольку график срезает ось x на x = — 2); и
x = 1 (так как график сокращает ось x на x = 1)
Теперь мы можем записать нашу функцию для квадратичной функции следующим образом (поскольку, если мы решим следующую задачу для 0, мы получим две точки пересечения):
f ( x ) = ( x + 2) ( x — 1)
Мы можем расширить это, чтобы получить:
f ( x ) = x 2 + x -2
Это квадратичная функция, которая проходит через ось x в необходимых точках.
Но правильный ли это ответ?
Обратите внимание, что мой график проходит через −3 на оси y . Давайте подставим x = 0 в уравнение, которое мне нужно было проверить, правильно ли оно.
f (0) = 0 2 + 0-2 = −2
Неправильно!
Оказывается, существует бесконечных парабол, проходящих через точки (−2,0) и (1,0).
Вот некоторые из них (зеленые):
И не забудьте параболы в ориентации «ноги вниз»:
Итак, как нам найти правильную квадратичную функцию для нашего исходного вопроса (синего цвета)?
Метод системы уравнений
Чтобы найти уникальную квадратичную функцию для нашей синей параболы, нам нужно использовать 3 точки на кривой.Затем мы можем составить 3 уравнения с 3 неизвестными и решить их, чтобы получить требуемый результат.
На исходной синей кривой мы видим, что она проходит через точку (0, −3) на оси y . Мы будем использовать это как нашу третью известную точку.
Используя нашу общую форму квадратичной, y = ax 2 + bx + c , мы заменяем известные значения на x и y , чтобы получить:
Подставляем (−2,0):
0 = a (−2) 2 + b (−2) + c = 4 a -2 b + c
Заменяя (1,0):
0 = a (1) 2 + b (1) + c = a + b + c
Подставляя (0, −3):
— 3 = a (0) 2 + b (0) + c = c
Итак, получаем c = — 3.
Подстановка c = — 3 в первую строку дает:
4 a -2 b = 3; и подставив во вторую строку, получим:
a + b = 3
Умножение последней строки на 2 дает:
2 a + 2 b = 6
Добавляя это к 4 a -2 b = 3, получаем:
6 a = 9
Это дает = 1.5.
Подставляя a = 1,5 в a + b = 3, получаем b = 1,5.
Итак, правильная квадратичная функция для синего графика —
.
f ( x ) = 1,5 x 2 + 1,5 x — 3
Отметим, что значение « a » положительное, что, как и ожидалось, приводит к ориентации «ноги вверх».
Вершинный метод
Другой способ сделать это — наблюдать вершину («заостренный конец») параболы.
Мы можем записать параболу в «форме вершины» следующим образом:
y = a ( x — h ) 2 + k
Для этой параболы вершина находится в точке ( h, k ).
В нашем примере выше мы не можем точно сказать, где находится вершина. Это около (-0,5, -3,4), но «около» не даст нам правильного ответа. (Если нет других «хороших» точек, через которые мы можем видеть проходящий график, тогда нам придется использовать нашу оценку.)
В следующем примере показано, как мы можем использовать метод вершин, чтобы найти нашу квадратичную функцию.
Одна точка, касающаяся оси
x
Эта парабола касается оси x только в точке (1, 0).
Если мы используем y = a ( x — h ) 2 + k , мы можем увидеть из графика, что h = 1 и k = 0.
Это дает нам y = a ( x — 1) 2 .Какое значение имеет « a «?
Но, как и в предыдущем случае, мы имеем бесконечное количество парабол, проходящих через (1, 0). Вот некоторые из них:
В этом примере синяя кривая проходит через (0, 1) на оси y , поэтому мы можем просто заменить x = 0, y = 1 на y = a ( x -1) 2 следующим образом:
1 = a (- 1) 2
Это дает нам a = 1.
Итак, наша квадратичная функция для этого примера —
.
f ( x ) = ( x — 1) 2 = x 2 -2 x + 1
Примечание: Мы также могли бы использовать тот факт, что x -значение вершины параболы y = ax 2 + bx + c определяется как:
Нет точек касания оси
x
Вот пример отсутствия перехвата x .
Мы видим, что вершина находится в точке (-2, 1), а точка пересечения y находится в точке (0, 2).
Мы просто подставляем, как и раньше, в вершинную форму нашей квадратичной функции.
У нас есть ( h , k ) = (-2, 1) и при x = 0, y = 2.
Так
y = a ( x — h ) 2 + k
становится
2 = a (0 — (−2)) 2 + 1
2 = 4 a +1
a = 0.25
Итак, наша квадратичная функция:
f ( x ) = 0,25 ( x — (- 2)) 2 + 1 = 0,25 ( x + 2) 2 + 1 = 0,25 ( x 2 + 4 x + 4) + 1
f ( x ) = 0,25 x 2 + x + 2
Использование математического программного обеспечения для нахождения функции
а. Wolfram | Альфа
Этот поиск Wolfram | Alpha дает ответ на мой последний пример.
г. Excel
Вы можете использовать MS Excel, чтобы найти уравнение. Введите точки в ячейки, как показано, и заставьте Excel построить график с помощью «диаграммы рассеяния X-Y». Это дает показанную черную кривую. Затем щелкните правой кнопкой мыши кривую и выберите «Добавить линию тренда». Выберите «Многочлен» и «Порядок 2». (Это дает синюю параболу, как показано ниже).
На вкладке «Параметры» выберите «Отображать уравнение на диаграмме».
Получаем следующий результат.
г.GeoGebra
GeoGebra оказалась не очень полезной для этой задачи. GeoGebra предоставит нам уравнение параболы, но сначала вам нужно знать фокус и направляющую. Это не так просто из наблюдений за графиком.
Заключение
Нахождение уравнения параболы по определенным точкам данных — полезный математический навык. Параболы очень полезны для математического моделирования из-за своей простоты.
См. 82 комментария ниже.
6.{2} + k \) форма.
Пример \ (\ PageIndex {10} \)
- Перепишите \ (f (x) = 2 x ^ {2} +4 x + 5 \) в виде \ (f (x) = a (x-h) ^ {2} + k \)
- Постройте график функции, используя свойства
Решение :
| Перепишите функцию в форме \ (f (x) = a (x-h) ^ {2} + k \), заполнив квадрат.{2} +3 \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определите константы \ (a, h, k \). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поскольку \ (a = 2 \), парабола открывается вверх. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ось симметрии \ (x = h \). | Ось симметрии — \ (x = -1 \). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вершина равна \ ((h, k) \). | Вершина равна \ ((- 1,3) \). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найдите точку пересечения \ (y \), найдя \ (f (0) \).{2} +4 \ cdot 0 + 5 \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \ (f (0) = 5 \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \ (y \) — точка пересечения \ ((0,5) \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найдите точку, симметричную \ ((0,5) \) поперек оси симметрии. | \ ((- 2,5) \) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найдите \ (x \) — точки пересечения. | Дискриминант отрицательный, поэтому \ (x \) — точки пересечения отсутствуют. {2} + k \).{2} -1 \) Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в построении графиков квадратичных функций с помощью преобразований. Обратная квадратичная функция — ChiliMathЗдесь мы хотим найти обратную функцию , которая подразумевает, что обратная функция ДОЛЖНА быть самой функцией. В противном случае мы получили инверсию, не являющуюся функцией. Не всем функциям, естественно, «везет» иметь обратные функции.{- 1}} \ left (x \ right), если ни одна горизонтальная линия не пересекает его график более одного раза.
Ниже приведены основные стратегии алгебраического решения обратной функции. Основные этапы поиска функции, обратной квадратичной функции
|

 Петропавловска
Петропавловска



 Большинство школьников уверенно отвечает: » если а 0, то ветви параболы направлены вверх, а если а а 0.
Большинство школьников уверенно отвечает: » если а 0, то ветви параболы направлены вверх, а если а а 0. Точка, по которой мы будем его находить, зависит не только от b но и от а. Это вершина параболы. Ее абсцисса (координата по оси х) находится по формуле хв = — b/(2а). Таким образом, b = — 2ахв. То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (хв 0) или левее (хв
Точка, по которой мы будем его находить, зависит не только от b но и от а. Это вершина параболы. Ее абсцисса (координата по оси х) находится по формуле хв = — b/(2а). Таким образом, b = — 2ахв. То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (хв 0) или левее (хв  Следовательно, хв 0. Значит b = — 2ахв = —+ = +. b 0. Окончательно имеем: а b 0, с 0.
Следовательно, хв 0. Значит b = — 2ахв = —+ = +. b 0. Окончательно имеем: а b 0, с 0.
 По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с:
По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с:
 Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
Ответьте на самые важные вопросы о Вашем уроке из левой колонки. 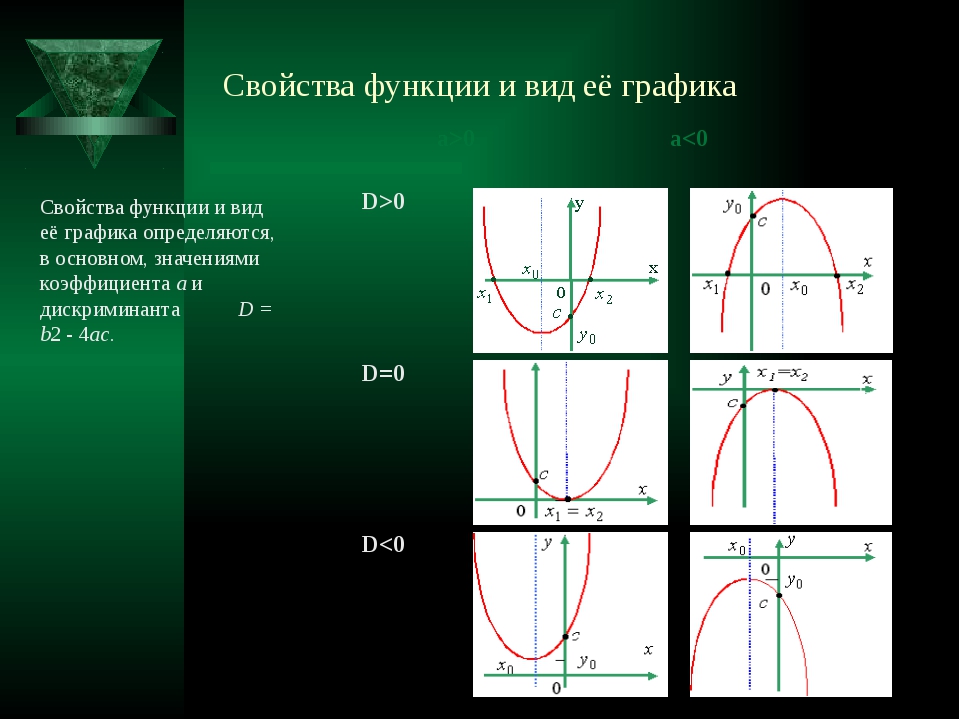 .
.