Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Парабола на координатной плоскости

      Определение 1. Параболой называют график функции

где   a   – любое число, не равное нулю. Точку   О (0;0)   называют вершиной параболы (1).

      При   a > 0   и   a < 0   график функции (1) изображён на рисунках 1 и 2 соответственно.

Рис.1

Рис.2

Рис.1

Рис.2

      Функция (1) обладает следующими свойствами:

      Рассмотрим теперь функцию, заданную формулой

где   a,   b,   c   – любые числа, но число   a   не равно нулю.

      Поскольку выражение, стоящее в правой части формулы (2), является квадратным трёхчленом, то, в соответствии с материалом, изложенным в разделе «Квадратные уравнения», формулу (2) можно переписать в виде

(3)

      Из формулы (3) вытекает, что график функции (2) может быть получен из графиков, изображенных на рисунках 1 или 2 (в зависимости от знака числа   a)   при помощи параллельного переноса, в результате которого вершина параболы (1) передвигается из начала координат в точку   V   (рис. 3, 4) с координатами

(4)

Рис.3	Рис.4

Рис.3

Рис.4

Рис.3

Рис. 4

      Поскольку дискриминант квадратного трёхчлена вычисляется по формуле

то координаты вершины параболы (3), определяемые по формуле (4), можно записать так:

(6)

      Замечание. При   a > 0   ветви параболы (2) направлены вверх, при   a < 0   ветви параболы (2) направлены вниз. Парабола (2) пересекает ось ординат в точке с координатами   (0; c).

Решение квадратных неравенств

      Зная расположение параболы (2) на координатной плоскости, можно, в частности, решать квадратные неравенства

как показано в следующей таблице.

      На нашем сайте можно также ознакомиться нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике. 2 — 4ac}}{2a}$

Парабола

График квадратного уравнения называется параболой.
Если a > 0 тогда ветви параболы направлены вниз:

если a < 0 тогда ветви параболы направлены вверх:

Середина любой параболы есть точкой $x = — \frac{b}{2a}$.

Задачи с квадратными уравнениями

1) x² — 4 = 0; x = ?
Решение: x² — 4 = (x — 2)(x + 2)
x = 2 or x = -2

2) 3x² + 4x + 5 = 0; x = ?
Решение: Дискриминант это уравнения равен 4² — 4⋅3⋅5 = 16 — 60 = -44

3) x² + 4x — 5 = 0; x = ?
Решение: Дискриминант это уравнения равен 4² — (-4⋅1⋅5) = 16 + 20 = 36 > 0
Поэтому, здесь есть два решения: $\frac{-4 \pm \sqrt{36}}{2}$
x = 1 или x = -5

4) x² + 4x + 4 = 0; x = ?
Решение: Дискриминант это уравнения равен 4² — (4⋅1⋅4) = 16 — 16 = 0
Поэтому, здесь есть одно решение: $x = \frac{-4}{2}$
x = -2

5) x² — 13x + 12 = 0
Решение: 1; 12
Построить график функции: f(x) = x² — 13x + 12

6) 8x² — 30x + 7 = 0
Решение: 3,5; 0,25
Построить график функции: f(x) = 8x² — 30x + 7

Квадратные уравнения на страницах математического форума

Форум о квадратных уравнениях

Квадратное уравнение с комплексными корнями

Рассмотрим решение уравнений с комплексными корнями и коэффициентами. {3} =\sqrt{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} )\]

При $k=0$ получаем $x_{0} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4}{3} +i\cdot \sin \frac{\pi /4}{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)=\sqrt[{6}]{2} \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.

При $k=1$ получаем

\[\begin{array}{l} {x_{1} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+2\pi }{3} +i\cdot \sin \frac{\pi /4+2\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)} \end{array}\]

При $k=2$ получаем

\[\begin{array}{l} {x_{2} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+4\pi }{3} +i\cdot \sin \frac{\pi /4+4\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)} \end{array}\]

Определение 2

Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами. {2} +4+4i=1-4+4=1.\]

Так как $D>0$, уравнение имеет два корня:

\[x_{1} =\frac{-(1-2i))-\sqrt{1} }{2} =\frac{-1+2i-1}{2} =\frac{-2+2i}{2} =-1+i.\] \[x_{2} =\frac{-(1-2i))+\sqrt{1} }{2} =\frac{-1+2i+1}{2} =\frac{2i}{2} =i.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

Рис. 2

Примечание 4

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

 

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению. ..

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

 

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

 

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

 

Арифметическая прогрессия

К оглавлению. ..

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

 

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

 

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

 

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

 

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

 

Тригонометрические уравнения

К оглавлению. ..

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

 

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

 

Геометрия в пространстве (стереометрия)

К оглавлению. ..

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

 

Координаты

К оглавлению. ..

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

 

Таблица умножения

К оглавлению…

 

Таблица квадратов двухзначных чисел

К оглавлению…

 

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Квадратный трёхчлен / math5school.ru

 

 

Немного теории

В большинстве задач, сводящихся к исследованию квадратичной функции

у = f(х) = ax² + bx + c,

полезно представить себе её график:

• если он пересекает ось Ох в двух точках (корнях) х₁ и х₂, то между корнями значения функции у = f(х) противоположны по знаку числу а, а вне отрезка [х₁; х₂] – совпадают по знаку с числом а;
• при этом вершина параболы у = f(х) (абсцисса которой равна полусумме корней) соответствует точке экстремума функции у = f(х): минимума, если а > 0, и максимума, если а < 0.

В ряде задач полезно использовать такой факт:

• если непрерывная на отрезке [а, b] функция у = f(х) принимает в концах этого отрезка значения разных знаков, то между точками a и b лежит хотя бы один корень уравнения f(х) = 0.

 

Задачи с решениями

 

1. Известно, что a + b + c < 0 и что уравнение ax² + bx + c = 0 не имеет действительных корней. Определить знак коэффициента с.

Решение

Квадратный трёхчлен f(x) = ax² + bx + c не имеет действительных корней, значит, он сохраняет один и тот же знак для всех значений аргумента х. Так как  f(1) = a  + b + c < 0, то f(0) = c < 0.

Ответ: c < 0.

 

2. Может ли квадратное уравнение ax² + bx + c = 0 с целыми коэффициентами иметь дискриминант равный 23?

Решение

Допустим, что дискриминант указанного уравнения равен числу 23. Тогда можно записать:

b² – 4ac = 23,

и

b² – 25 = 4ac – 2

или

(b – 5) ·(b + 5) = 2(2ас – 1).

Заметим, что b – 5 и b + 5 – числа одинаковой чётности, поэтому их произведение, если оно чётно, делится на 4. Правая часть последнего равенства есть чётное число, не делящееся на 4. Полученно противоречие, значит, сделаное допущение ложно. 

Ответ: нет.

 

3. Найти все пары действительных чисел p, q, для которых многочлен x⁴ + px² + q, имеет 4 действительных корня, образующих арифметическую прогрессию.

Решение

Многочлен x⁴ + px² + q, имеет 4 действительных корня в том и только в том случае, если многочлен у² + pу  + q (относительно у = x²) имеет два неотрицательных корня, т. е. числа р и q удовлетворяют условиям 

p² > 4q,   q > 0,   p < 0. 

Если исходный многочлен имеет 4 действительных корня (а именно: –х₁, –х₂, х₁, х₂, где без ограничения общности считаем, что х₁> х₂> 0), то они образуют арифметическую прогрессию тогда и  только  тогда,   когда   совместна система 

–2х₂ = – х₁ + х₂,   x₁² + x₂² = –p,   x₁² · x₂² = q 

(смотрите теорему Виета и обратную к ней), т.е. когда q = 0,09 · р².   Таким образом, все искомые пары чисел р, q описываются условиями 

p < 0,   q = 0,09 · р²

(неравенства p² > 4q и q > 0,вытекают из последнего равенства).

 

4. Пусть a, b, c – действительные числа. Доказать, что уравнение 

(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0 

всегда имеет хотя бы один действительный корень. Выяснить, когда таких корня два.

Решение

Обозначим 

f (x) = (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a). 

Без ограничения общности рассуждений можно считать, что a < b < c. Рассмотрим все возможные случаи:

– если a = b = c, то можно записать f(x) = 3(x – a)², и, очевидно, f(а) = 0: а – корень;

– если a = b, то f(x) = (x – a)²+ 2 (x – а)(x – c), и f(а) = 0: а – корень;

– если b = c, то f(x) = 2(x – a)(x – b) + (x – b)², и f(b) = 0: b – корень;

– если a < b < c, то 

f(a) = (a – b) (a – c) > 0,

f(b) = (b – a) (b – c) < 0,

f(c) = (c – a) (c – b) > 0.

Так как f(x) – непрерывная квадратичная функция, принимающая значения разного знака на концах интервалов (a; b) и (b; c), то она имеет два различных действительных корня х₁ и х₂. Более того  

a < х₁ < b < х₂ < c.

Решение задачи окончено.

 

5. Дан многочлен ax² + bx + c. За один ход разрешается заменить х на (х – k) или заменить многочлен целиком на многочлен

cx² + (b + 2c)x + (a + b + c).

Можно ли после нескольких ходов из многочлена x² – 3x – 4 получить многочлен x² – 2x – 5?

Решение

Нетрудно убедиться, что при указанных заменах исходного многочлена его дискриминант не изменяется. Значит, если из многочлена  x² – 3x – 4 можно получить многочлен x² – 2x – 5, то их дискриминанты должны быть равны. Однако это не так.

Ответ: нет.

 

6. Найдите все значения a и b, такие, что для любого х из отрезка [–1; 1] будет выполняться неравенство

| 2x² + ax + b| < 1.

Решение

Пусть числа а и b такие, что для любого х из отрезка [–1; 1] выполняется данное неравенство, т. е,

–1 < 2x² + ax + b < 1.

Полагая здесь последовательно х = 0, х = 1, х = – 1, получаем, что а и b удовлетворяют следующей системе неравенств:

–1 < b < 1,

–3 < a + b < –1,

–3 < b – а < – 1.

Сложив почленно два последних неравенства, подучим 

–3 < b < – 1. 

Отсюда и из первого неравенства следует, что b = –1. Тогда а удовлетворяет следующим двум неравенствам:

–2 < a < 0,

0 < a < –2, 

и поэтому, а = 0. Таким образом, если существуют числа а и b, удовлетворяющие условию задачи, то

а = 0, b = – 1

и других решений задача не имеет.

Чтобы доказать, что найденные значения а = 0, b = – 1 являются решением задачи, остается проверить, что для любого х из отрезка [–1; 1] верно двойное неравенство 

–1 < 2x² – 1 < 1. 

А оно равносильно неравенству

0 < 2x² < 2,

которое, очевидно, справедливо на числовом промежутке [–1; 1].

Ответ: а = 0, b = – 1.

 

7. По трём прямолинейным дорогам с постоянными скоростями идут три пешехода. В начальный момент времени они не находились на одной прямой. Докажите, что они могут оказаться на одной прямой не более двух раз.

Решение

Поставим каждому из пешеходов в соответствие точку в прямоугольной системе координат. Точки (х₁; у₁), (х₂; у₂), (х₃; у₃)  лежат на одной прямой тогда и только тогда, когда 

(х₁ – х₃)(у₂ – у₃) = (х₂ – х₃) (у₁ – у₃).

Так как скорости пешеходов постоянны, то х₁(t), у₁(t), х₂ (t), у₂(t), х₃(t) и у₃(t)  – линейные функции от времени t и последнее равенство является квадратным уравнением относительно t, которое может иметь не более двух решений t₁ и t₂. Это и есть те два возможных момента времени, когда все три пешехода могут оказаться на одной прямой.

 

8. На координатной плоскости Oхy нарисован график функции y = x².  Потом оси координат стёрли, осталась только парабола. Как при помощи циркуля и линейки восстановить оси координат и единицу длины?

Решение

Докажем следующую лемму.

Лемма. Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы.

Доказательство. Пусть хорды AB и CD параболы лежат на параллельных прямых 

y = kx + a   и   y = kx + b,

тогда абсциссы точек  A, B, C, D  – это корни уравнений 

x² = kx + a  и  x² = kx + b,

а абсциссы точек M и N – полусуммы корней этих уравнений, то есть по теореме Виета равны k/2.   Следовательно, точки M и N лежат на прямой х = k/2, которая параллельна оси Oy. Лемма доказана.

Вернёмся к исходной задаче.

Последовательно осуществляем следующие построения:

1) две параллельные прямые, каждая из которых пересекает параболу в двух точках;

2) прямую через середины получающихся отрезков;

3) перпендикуляр к этой прямой, пересекающий параболу в двух точках А и В;

4) серединный перпендикуляр к отрезку АВ – это ось Оу;

5) ось Ох перпендикулярна Оу в точке пересечения с параболой;

6) единичный отрезок – абсцисса пересечения прямой у = х с параболой.

 

9. Учитель написал на доске квадратный трехчлен х² + 10х + 20, после чего по очереди каждый из учеников увеличил или уменьшил на единицу либо коэффициент при х, либо свободный член, но не оба сразу. В результате на доске оказался написан квадратный трехчлен х² + 20х+10. Верно ли, что в некоторый момент на доске был написан квадратный трехчлен с целыми корнями?

Решение

Первый способ.

Заметим, что при каждом изменении трехчлена его значение в точке х = – 1 изменяется на 1 (в ту или другую сторону). Значение первого трехчлена

f(x) = х² + 10х + 20

в этой точке равно f(–1) = 11, а последнего,

g(x) = х² + 20х+10,

— g(–1) = –9. Поэтому в какой-то промежуточный момент на доске был написан трехчлен

h(х) = х² + pх + q,

для которого h(–1)=0. Оба его корня – целые числа: один равен –1, другой по теореме Виета равен –q.

 

Второй способ.

Каждому квадратному трёхчлену

x² + bx + c

поставим в соответствие точку координатной плоскости Оbc, где вдоль оси  Оb будем откладывать значения второго коэффициента, а вдоль Ос – свободного члена. Многочленам

х² + 10х + 20  и  х² + 20х +10

будут соответствовать точки

А(10; 20) и В(20; 10),

соответственно. Предложенные в условии операции предполагают перемещение от точки А к точке В вдоль узлов некоторой ломаной L. Узлы L – некоторые целочисленные точки плоскости Оbc, а длина каждого звена L равна 1 (соседние звенья могут лежать на одной прямой).

Так как точки А и В расположены в разных полуплоскостях относительно прямой

с = b – 1,

то ломаная L одним из своих узлов имеет точку этой прямой. Значит, одним из промежуточных многочленов будет многочлен вида

х² + b₀х + (b₀– 1)

с целым b₀ и целыми корнями –1 и 1 – b₀ .

 

10. Какова вероятность того, что корни квадратного уравнения x² + 2bx + c = 0 действительны?

Решение

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b; c) равномерно распределена на квадрате с центром в начале координат и стороной 2B. Решим задачу при фиксированном значении B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

 

На рисунке более тёмная выделенная область отвечает случаю действительных корней,

более светлая – комплексных.

 

Для того чтобы уравнение имело действительные корни, необходимо и достаточно, чтобы

b² — c > 0.

На приведенном рисунке изображена парабола с = b² и показана область, где наше уравнение имеет действительные корни для B = 4.  

Нетрудно подсчитать, что площадь «комплексной» области равна (4 · B^3/2)/3 (при B > 1), а площадь всего квадрата, конечно, равна 4B². Следовательно, вероятность того, что корни комплексные, равна 1/(3√В). При B = 4 она составляет 1/6. Действительно,

(4 · B3/2) / 3	=	1	=	1
4B2		3 · √В		3 · √4

С ростом B значение дроби 1/√В стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1. 

Замечание. Рассмотренная задача отличается от такой же задачи, связанной с уравнением

ax² + 2bx + c = 0.

Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

 

Задачи без решений

1. Корни уравнения х² + pх + q = 0, у которого p + q = 198, являются целыми числами. Найдите эти корни.

 

2. В квадратном уравнении х² + pх + q = 0 коэффициенты p и q независимо пробегают все значения от –1 до +1 включительно. Найти множество значений, которые при этом могут принимать действительные корни данного уравнения.

 

3. Квадратный трёхчлен f(х) = ax² + bx + c таков, что уравнение f (х) = x не имеет действительных корней. Докажите, что уравнение f (f (х)) = х так же не имеет вещественных корней.

 

4. Найдите уравнение общей касательной к параболам у = x² + 4x + 8 и у = x² + 8x + 4.

 

5. 2+20=0.$

Ответ: $z_{1,2}=\pm 2i$ $z_{3,4}=\pm\sqrt 5i.$ 

 

Решение квадратных уравнений через производные / Хабр

Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.

Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:

Перейдем от квадратного уравнения к квадратичной функции:

Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.

Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!

Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.

Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:

На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.

Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:

Где — время, — начальная скорость, — ускорение.

Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.

Разве формула перемещения для РУД не является следствием решения квадратного уравнения?Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.

Теперь осталось разобраться что есть что, и чего нам не хватает.

«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.

В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:

В таком случае составим уравнение для поиска :

[подставили в производную первого порядка ]

Корнем такого уравнения относительно будет:

А значением исходной функции при таком аргументе будет:

Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль». Иными словами, нам от положения необходимо «дойти до нуля».

Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:

, также как и

Тогда, подставив все известные величины, получим:

Поделим все на :

Теперь становится очевидно, что:

Соединим все «детали пазла» воедино:

Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).

Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.

С вами был Петр, спасибо за внимание!

5.6: Квадратичные поверхности — математика LibreTexts

Мы изучали векторы и векторные операции в трехмерном пространстве и разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями , для изучения множества других поверхностей, которые могут быть построены в трехмерной системе координат.

Идентификационные цилиндры

Первая поверхность, которую мы рассмотрим, — это цилиндр.2 = 9 \) представляет собой цилиндр радиуса \ (3 \) с центром на оси \ (z \). Это продолжается бесконечно в положительном и отрицательном направлениях.

Определение: цилиндры и линейки

Набор линий, параллельных заданной линии, проходящей через заданную кривую, известен как цилиндрическая поверхность или цилиндр . Параллельные линии называются постановлениями .

Из этого определения мы можем видеть, что у нас все еще есть цилиндр в трехмерном пространстве, даже если кривая не является окружностью.2 = 25 \) представляет собой цилиндр радиуса \ (5 \) с центром на оси \ (y \).

г. В этом случае уравнение содержит все три переменные — \ (x, y, \) и \ (z \) — поэтому ни одна из переменных не может изменяться произвольно. Самый простой способ визуализировать эту поверхность — использовать компьютерную утилиту для построения графиков (рис. \ (\ PageIndex {4} \)).

Рисунок \ (\ PageIndex {4} \)

c. В этом уравнении переменная \ (z \) может принимать любое значение без ограничений. Следовательно, линии, составляющие эту поверхность, параллельны оси \ (z \).2 \).

Подсказка

Переменная \ (x \) может принимать любое значение без ограничений.

Ответ

При рисовании поверхностей мы увидели, что полезно рисовать пересечение поверхности с плоскостью, параллельной одной из координатных плоскостей. Эти кривые называются следами. Мы можем увидеть их на графике цилиндра на рисунке \ (\ PageIndex {6} \).

Определение: следы

Следы поверхности — это поперечные сечения, созданные, когда поверхность пересекает плоскость, параллельную одной из координатных плоскостей.

Трассы полезны при рисовании цилиндрических поверхностей. Однако для трехмерного цилиндра полезен только один набор следов. Обратите внимание на рис. \ (\ PageIndex {6} \), что след графика \ (z = \ sin x \) на плоскости xz полезен при построении графика. Однако кривая на плоскости xy представляет собой просто серию параллельных линий, а кривая на плоскости yz — это просто одна линия.

Рисунок \ (\ PageIndex {6} \): (a) Это один вид графика уравнения \ (z = \ sin x \). (b) Чтобы найти след графа на плоскости \ (xz \), положим \ (y = 0 \). След — это просто двумерная синусоида.

Цилиндрические поверхности образованы набором параллельных линий. Однако не все поверхности в трех измерениях строятся так просто. Теперь мы исследуем более сложные поверхности, и следы являются важным инструментом в этом исследовании.

Поверхности Quadric

Мы узнали о трехмерных поверхностях, описываемых уравнениями первого порядка; это самолеты. 2} = 1.2} = 1 \) в плоскости \ (xy \), когда мы положим \ (z = 0 \). (b) Когда мы устанавливаем \ (y = 0 \), мы получаем след эллипсоида в плоскости \ (xz \), который является эллипсом. (c) Когда мы устанавливаем \ (x = 0 \), мы получаем след эллипсоида в плоскости \ (yz \), который также является эллипсом.

Теперь, когда мы знаем, как выглядят следы этого твердого тела, мы можем нарисовать поверхность в трех измерениях (рис. \ (\ PageIndex {8} \)).

Рисунок \ (\ PageIndex {8} \): (a) Следы служат основой для поверхности. (б) Центр этого эллипсоида — начало координат.2} = 1 \) (см. Следующий рисунок).

Гиперболоиды одного листа обладают удивительными свойствами. Например, они могут быть построены с использованием прямых линий, как в скульптуре на рисунке \ (\ PageIndex {1a} \). Фактически градирни для атомных электростанций часто имеют форму гиперболоида. Строители могут использовать в конструкции прямые стальные балки, что делает башни очень прочными при использовании относительно небольшого количества материала (рис. 2} {100} = \ dfrac {z} {4}, \), где — фокус точка рефлектора?

Рисунок \ (\ PageIndex {12} \): Энергия отражается от параболического отражателя и собирается в фокусной точке.2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0. \]

На следующих рисунках приведены наиболее важные из них.

Рисунок \ (\ PageIndex {13} \): Характеристики общих квадратичных поверхностей: эллипсоид, гиперболоид одного листа, гиперболоид двух листов. Рисунок \ (\ PageIndex {14} \): Характеристики общих квадратичных поверхностей: эллиптический конус, эллиптический Параболоид, гиперболический параболоид.

Пример \ (\ PageIndex {5} \): определение уравнений квадратичных поверхностей

Определите поверхности, представленные данными уравнениями.2} {9} = 1. \ nonumber \]

Итак, это, на самом деле, эллипсоид с центром в начале координат.

г. Сначала заметим, что член \ (z \) возведен только в первую степень, так что это либо эллиптический параболоид, либо гиперболический параболоид. {2} + bx + c = 0}, где a не равно 0.{2} + bx + c = 0}, где коэффициенты a , b и c являются действительными числами. Есть разные способы узнать значение x. Построение функции на графике — это один из способов. На рисунке справа функция пересекает ось x в точках (−1,0) {\ displaystyle (-1,0)} и (2,0) {\ displaystyle (2,0)}.

Построение графика квадратного уравнения позволяет очень легко найти корни, но это не всегда удобно. Так что есть разные способы сделать это с помощью математики.{2} -x-1 = 0}, можно разложить на множители. Это уравнение можно записать как (2x + 1) (x − 1) = 0 {\ displaystyle (2x + 1) (x-1) = 0}, что дает два отдельных уравнения, 2x + 1 = 0 {\ displaystyle 2x + 1 = 0} и x − 1 = 0 {\ displaystyle x-1 = 0}. Это потому, что, когда любое из двух уравнений равно нулю, исходное уравнение равно нулю, потому что два уравнения умножаются вместе, чтобы сформировать квадратное уравнение. Из этого уравнения легко вычислить значение x с помощью алгебры. В первом из двух уравнений x = −1 / 2 {\ displaystyle x = -1 / 2}, а во втором — x = 1 {\ displaystyle x = 1}.{2} = {\ frac {14} {25}}}

Найдите квадратный корень из обеих частей. ± {\ displaystyle \ pm} существует, поскольку квадратный корень предназначен как для положительных, так и для отрицательных значений: x − 25 = ± 1425 {\ displaystyle x — {\ frac {2} {5}} = \ pm {\ sqrt { \ frac {14} {25}}}}

Наконец, переместите числовой член на другую сторону, чтобы получить значение для x : x = ± 1425 + 25 {\ displaystyle x = \ pm {\ sqrt {\ frac {14} {25}}} + {\ frac {2} {5}}}

Последнее значение для x имеет два значения: x = 1425 + 25≈1,148 {\ displaystyle x = {\ sqrt {\ frac {14} {25}}} + {\ frac {2} {5}} \ приблизительно 1.148} и x = −1425 + 25≈ − 0,348 {\ displaystyle x = — {\ sqrt {\ frac {14} {25}}} + {\ frac {2} {5}} \ приблизительно -0,348}. Это x-координаты в точках, где y-координаты равны нулю, и поэтому функция пересекает ось x.

Также интересно отметить, что вершина функции, (25, −1425) {\ displaystyle \ left ({\ frac {2} {5}}, — {\ frac {14} {25}} \ right)}, можно найти из уравнения в шаге 3 выше. ^[2]

квадратное уравнение на графике

Хотя заполнение квадрата можно использовать для решения многих квадратных уравнений, оно работает не со всеми уравнениями.{2} -4ac}}} {2a}}}

Числа, представленные как a , b и c , такие же, как и в исходном уравнении, ax ² + bx + c = 0. Чтобы эта формула работала правильно, a не может быть равно 0 для формулы (но на самом деле, когда a = 0 в исходном уравнении, оно не является квадратичным, поскольку нет x-квадрат).

Факторизованная форма этого уравнения: y = a ( x — s ) ( x — t ), где s и t — нули, a — константа, а y и два значения x являются упорядоченными парами, которые удовлетворяют уравнению. {2} -4ac}, известно как дискриминант .Он может сказать, настоящие корни или мнимые. Есть три случая:

1. Если дискриминант положительный, будет два значения для x и, следовательно, два отдельных корня, по одному в каждом месте, где график пересекает ось x.
2. Если дискриминант равен нулю, существует только одно значение для x , но на самом деле есть два равных корня. График касается оси x в своей вершине, но не пересекает ее.
3. Если дискриминант отрицательный, не существует действительного значения x .На графике функция даже не касается оси x, но корни все еще там. Значение корней здесь — комплексное число, которое использует значение i для представления -1 {\ displaystyle {\ sqrt {-1}}}. ^[5]

Решение приложений квадратных уравнений · Промежуточная алгебра

Решение приложений квадратных уравнений · Промежуточная алгебра

К концу этого раздела вы сможете:

• Решение приложений, моделируемых квадратными уравнениями

Прежде чем начать, пройдите тест на готовность.

1. Сумма двух последовательных нечетных чисел равна −100. Найдите числа.
   

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

2. Решить:
   2x + 1 + 1x − 1 = 1×2−1.

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

3. Найдите длину гипотенузы прямоугольного треугольника с катетами 5 и 12 дюймов.
   

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

Решение приложений, моделируемых квадратными уравнениями

Ранее мы решили некоторые приложения, моделируемые квадратными уравнениями, когда единственным методом их решения было разложение на множители.Теперь, когда у нас есть больше методов для решения квадратных уравнений, мы еще раз рассмотрим приложения.

Давайте сначала резюмируем методы, которые у нас теперь есть для решения квадратных уравнений.

Методы решения квадратных уравнений

1. Факторинг
2. Свойство квадратного корня
3. Завершение площади
4. Квадратичная формула

Решая каждое уравнение, выбирайте метод, наиболее удобный для вас. Напоминаем, что мы скопируем здесь нашу обычную стратегию решения проблем, чтобы мы могли следовать инструкциям.

Используйте стратегию решения проблем.

1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
2. Определите , что мы ищем.
3. Имя то, что мы ищем. Выберите переменную, чтобы представить это количество.
4. Переведите в уравнение. Может быть полезно сформулировать проблему одним предложением со всей важной информацией.Затем переведите английское предложение в алгебраическое уравнение.
5. Решите уравнение, используя методы алгебры.
6. Отметьте ответ в проблеме и убедитесь, что он имеет смысл.
7. Ответьте на вопрос полным предложением

Мы решили числовые приложения, которые включали последовательные четные и нечетные целые числа, моделируя ситуацию с помощью линейных уравнений. Помните, мы заметили, что каждое четное целое число на 2 больше, чем предшествующее ему.Если мы назовем первый n , то следующий будет n + 2. Следующим будет n + 2 + 2 или n + 4. Это также верно, когда мы используем нечетные целые числа. Ниже показаны один набор четных целых чисел и один набор нечетных целых чисел.

Последовательные четные целые числа Последовательные нечетные целые 64,66,6877,79,81n1стевен целые n1стодд целыеn + 22последовательные четные целыеn + 22последовательные нечетные целыеn + 43rdпоследовательные четные целыеn + 43рые последовательные нечетные целые

Некоторые применения нечетных или четных последовательных целых чисел моделируются квадратными уравнениями.Приведенные выше обозначения будут полезны при присвоении имен переменным.

Произведение двух последовательных нечетных целых чисел равно 195. Найдите целые числа.

Шаг 1. Прочтите задачу. Шаг 2. Определите, что мы ищем. Мы ищем два последовательных нечетных целых числа. Шаг 3. Назовите то, что мы ищем. Пусть n = первое нечетное целое число. N + 2 = следующее нечетное целое число. Шаг 4. Переведите в уравнение. Сформулируйте задачу одним предложением: «Произведение двух последовательных нечетных чисел равно 195.Произведение первого нечетного целого числа и второго нечетного целого числа равно 195. Преобразуйте в уравнение. Шаг 5. Решите уравнение. Распределите. Запишите уравнение в стандартной форме. Фактор. Используйте свойство нулевого произведения. Решите каждое уравнение. N (n + 2) = 195n2 + 2n = 195n2 + 2n − 195 = 0 (n + 15) (n − 13) = 0n + 15 = 0n − 13 = 0n = −15, n = 13 Есть два значения, которые являются решениями. Это даст нам две пары последовательных нечетных целых чисел для нашего решения. Первое нечетное целое n = 13 Первое нечетное целое n = −15 следующее нечетное целое n + 2 следующее нечетное целое n + 213 + 2−15 + 215−13 Шаг 6.Проверьте ответ. Работают ли эти пары? Являются ли они последовательными нечетными целыми числами? 13,15 Да − 13, −15 Да Является ли их произведение 195? 13 · 15 = 195 Да − 13 (−15) = 195 Да Шаг 7. Ответьте на вопрос. Два последовательных нечетных целых числа, произведение которых is195 равны 13, 15 и −13, −15.

Произведение двух последовательных нечетных целых чисел равно 99. Найдите целые числа.

Два последовательных нечетных целых числа, произведение которых равно 99: 9, 11 и −9, −11

Произведение двух последовательных четных целых чисел равно 168.Найдите целые числа.

Два последовательных четных целых числа, произведение которых равно 128: 12, 14 и −12, −14.

Мы будем использовать формулу площади треугольника для решения следующего примера.

Площадь треугольника

Для треугольника с основанием b и высотой h площадь A определяется формулой A = 12bh.

Напомним, что когда мы решаем геометрические приложения, полезно рисовать фигуры.

Архитектор проектирует вход в ресторан. Она хочет поставить треугольное окно над дверным проемом. Из-за ограничений по энергии окно может иметь площадь не более 120 квадратных футов, а архитектор хочет, чтобы основание было на 4 фута больше, чем в два раза выше. Найдите основание и высоту окна.

Factor. The product of h minus 10 and h plus 12 equals 0. Use the Zero Product Property. H – 10 equals 0 or h plus 12 equals 0. Simplify. H equals 10 or h equals negative 12. Since h is the height of a window, a value of h equals negative 12 does not make sense. The height of the triangle is h equals 10. The base of the triangle is 2 h plus 4, or 2 times 10 plus 4 which equals 24. Step 6. Check the answer. Does a triangle with height 10 and base 24 have area 120? Yes. Step 7. Answer the question. The height of the triangular window is 10 feet and the base is 24 feet.»>

Шаг 1. Прочтите проблему. Нарисуйте картинку.
Шаг 2.Определите , что мы ищем.		Ищем базу и высоту.
Шаг 3. Назовите то, что мы ищем.		Пусть h = высота треугольника. 2 h + 4 = основание треугольника
Шаг 4. Переведите в уравнение. Мы знаем местность. Напишите формулу для площади треугольника.		А = 12bh
Шаг 5.Решите уравнение. Подставить значения.		120 = 12 (2ч + 4) ч
Распространить.		120 = h3 + 2h
Это квадратное уравнение, перепишите его в стандартном виде.		h3 + 2h − 120 = 0
Фактор.		(ч-10) (ч + 12) = 0
Используйте свойство нулевого произведения.		ч-10 = 0ч + 12 = 0
Упростить.		ч = 10, ч = −12
Поскольку h — это высота окна, значение h = −12 не имеет смысла.
Высота треугольника h = 10.
Основание треугольника 2h + 4. 2 · 10 + 4 24
Шаг 6. Отметьте ответ. Имеет ли треугольник с высотой 10 и основанием 24 площадь 120? Да.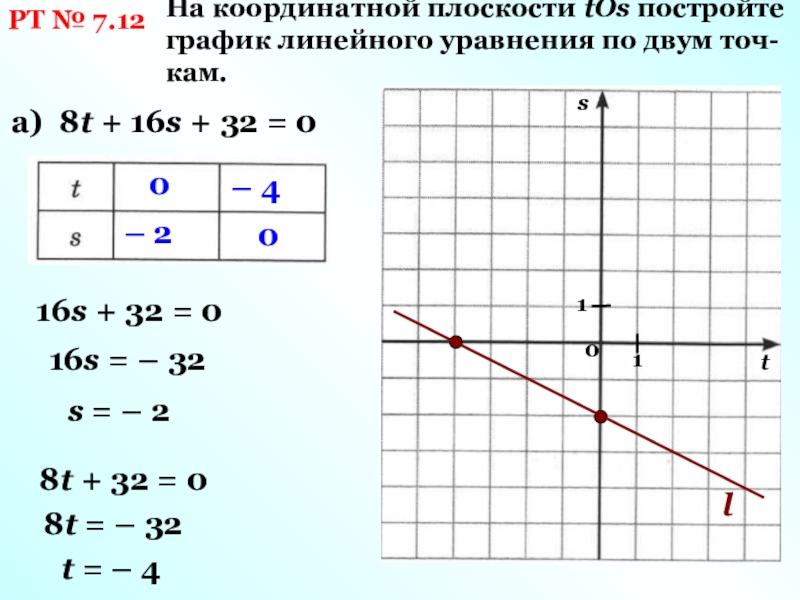
Шаг 7. Ответьте на вопрос.		Высота треугольного окна составляет 10 футов, а основание — 24 фута.

Найдите основание и высоту треугольника, основание которого на четыре дюйма больше, чем в шесть раз его высоты, и имеет площадь 456 квадратных дюймов.

Высота треугольника 12 дюймов, основание 76 дюймов.

Если у треугольника площадью 110 квадратных футов основание на два фута меньше двойной высоты, каковы длина его основания и высота?

Высота треугольника 11 футов, основание 20 футов.

В двух предыдущих примерах число в корне квадратичной формулы было полным квадратом, поэтому решениями были рациональные числа.Если мы получим иррациональное число как решение проблемы приложения, мы воспользуемся калькулятором, чтобы получить приблизительное значение.

Мы будем использовать формулу площади прямоугольника для решения следующего примера.

Площадь прямоугольника

Для прямоугольника длиной L и шириной W площадь A определяется по формуле A = LW .

Майк хочет засаживать 150 квадратных футов искусственного газона во дворе своего дома.Это максимальная площадь искусственного газона, разрешенная ассоциацией его домовладельцев. Он хочет иметь прямоугольный участок дерна длиной на один фут меньше, чем в 3 раза ширины. Найдите длину и ширину. Округлите до ближайшей десятой доли фута.

Длина прямоугольного огорода площадью 200 квадратных футов на четыре фута меньше, чем в два раза его ширина. Найдите длину и ширину сада с точностью до десятых долей фута.

Длина сада составляет примерно 18 футов, а ширина — 11 футов.

Прямоугольная скатерть имеет площадь 80 квадратных футов. Ширина на 5 футов короче длины. Каковы длина и ширина скатерти с точностью до десятых долей фута?

Длина скатерти составляет приблизительно 11,8 футов, а ширина — 6,8 футов.

Теорема Пифагора устанавливает связь между катетами и гипотенузой прямоугольного треугольника. Мы воспользуемся теоремой Пифагора для решения следующего примера.

Теорема Пифагора

В любом прямоугольном треугольнике, где a и b — длина катетов, а c — длина гипотенузы, a ² + b ² = c ² .

Рене настраивает праздничный световой дисплей. Он хочет сделать «дерево» в форме двух прямоугольных треугольников, как показано ниже, и имеет две 10-футовые гирлянды огней, которые можно использовать по бокам.Он прикрепит фонари к вершине столба и к двум столбам на земле. Он хочет, чтобы высота шеста была такой же, как расстояние от основания шеста до каждой стойки. Какой высоты должен быть шест?

Шаг 1. Прочтите проблему. Нарисуйте картинку.
Шаг 2. Определите , что мы ищем.	Ищем высоту шеста.
Шаг 3.Назовите то, что мы ищем.	Расстояние от основания шеста до любой стойки равно высоте шеста. Пусть x = высота шеста. x = расстояние от шеста до стойки Каждая сторона представляет собой прямоугольный треугольник. Рисуем изображение одного из них.
Шаг 4. Переведите в уравнение. Мы можем использовать теорему Пифагора, чтобы найти x . Напишите теорему Пифагора.	а2 + Ь2 = с2
Шаг 5. Решите уравнение. Заменять.	х2 + х2 = 102
Упростить.	2×2 = 100
Разделите на 2, чтобы изолировать переменную.	2×22 = 1002
Упростить.	x2 = 50
Используйте свойство квадратного корня.	х = ± 50
Упростим корень.	х = ± 52
Перепишите, чтобы показать два решения.	х = 52, х = -52
	Если мы аппроксимируем это число до ближайшей десятой с помощью калькулятора, мы получим x≈7,1.
Шаг 6. Отметьте ответ. Самостоятельно проверьте теорему Пифагора.
Шаг 7. Ответьте на вопрос.	Высота шеста должна быть около 7,1 футов.

Солнце отбрасывает тень от флагштока.Высота флагштока в три раза больше его тени. Расстояние между концом тени и вершиной флагштока составляет 20 футов. Найдите длину тени и длину флагштока. Округлите до ближайшей десятой.

Длина тени флагштока составляет примерно 6,3 фута, а высота флагштока — 18,9 фута.

Расстояние между противоположными углами прямоугольного поля в четыре раза больше ширины поля.Длина поля вдвое больше ширины. Найдите расстояние между противоположными углами. Округлите до ближайшей десятой.

Расстояние между противоположными углами составляет примерно 7,2 фута.

Высота снаряда, выпущенного вверх от земли, моделируется квадратным уравнением. Начальная скорость, v ₀ , продвигает объект вверх до тех пор, пока сила тяжести не заставит объект снова упасть.

Движение снаряда

Высота в футах, h , объекта, взлетающего в воздух с начальной скоростью v0

, после т

секунды задается формулой

h = −16t2 + v0t

Мы можем использовать эту формулу, чтобы определить, сколько секунд потребуется фейерверку, чтобы достичь определенной высоты.

Фейерверк взлетает вверх с начальной скоростью 130 футов в секунду. Сколько секунд потребуется, чтобы достичь высоты 260 футов? Округлите до ближайшей десятой доли секунды.

Стрела запускается с земли в воздух с начальной скоростью 108 фут / с. Используйте формулу h = −16 t ² + v ₀ t , чтобы определить, когда стрела будет на высоте 180 футов от земли. Округлите ближайшую десятую.

Стрела достигнет 180 футов по пути вверх через 3 секунды и снова опустится примерно через 3,8 секунды.

Мужчина бросает мяч в воздух со скоростью 96 фут / с. Используйте формулу h = −16 t ² + v ₀ t , чтобы определить, когда высота шара будет 48 футов. Округлите до ближайшей десятой.

Мяч достигнет 48 футов по пути примерно через.6 секунд и снова через 5,4 секунды.

Мы решили задачи равномерного движения, используя формулу D = rt в предыдущих главах. Мы использовали таблицу, подобную приведенной ниже, чтобы систематизировать информацию и привести нас к уравнению.

Формула D = rt предполагает, что мы знаем r и t и используем их, чтобы найти D . Если мы знаем D и r и нам нужно найти t , мы решим уравнение для t и получим формулу t = Dr.

Некоторые задачи равномерного движения также моделируются квадратными уравнениями.

Профессор Смит только что вернулся с конференции, которая находилась в 2000 милях к востоку от его дома. Его общее время в самолете за перелет туда и обратно составило 9 часов. Если самолет летел со скоростью 450 миль в час, какова была скорость реактивного потока?

Это ситуация с равномерным движением. Диаграмма поможет нам наглядно представить ситуацию. * * *

---

Заполняем диаграмму, чтобы систематизировать информацию.

Мы ищем скорость струи. Буква = скорость струи.

Когда самолет летит вместе с ветром, скорость ветра увеличивается, поэтому коэффициент равен 450 + r .

Когда самолет летит против ветра, скорость ветра уменьшается и составляет 450 — r .

Пишите в ставках. Пишите на расстоянии. С D = r · t, мы решаем для т и получаем t = Dr. Мы делим расстояние на скорость в каждой строке, и помещаем выражение в столбец времени .
Мы знаем, что время складывается с 9 , поэтому мы пишем наше уравнение.	2000450 − r + 2000450 + r = 9
Умножаем обе стороны на ЖКИ.	(450 − r) (450 + r) (2000450 − r + 2000450 + r) = 9 (450 − r) (450 + r)
Упростить.	2000 (450 + r) +2000 (450 − r) = 9 (450 − r) (450 + r)
Выведите множитель на 2,000.	2000 (450 + r + 450 − r) = 9 (4502 − r2)
Решить.	2000 (900) = 9 (4502 − r2)
Разделить на 9.	2000 (100) = 4502 − r2
Упростить.	200000 = 202500 − r2 −2500 = −r2 50 = r Скорость струйной струи.
Чек: 50 миль в час — разумная скорость для реактивного потока? Да. Если самолет движется со скоростью 450 миль в час, а ветер 50 миль в час, Попутный ветер 450 + 50 = 500 миль / ч 3000500 = 4 часа Встречный ветер 450-50 = 400 миль / ч 3000400 = 5 часов Время складывается с 9 часами, поэтому проверяется.
	Скорость струи 50 миль в час.

Мэри-Энн только что вернулась из поездки с внуками на восток. Путешествие было в 2400 милях от ее дома, и ее общее время в самолете в оба конца составило 10 часов. Если самолет летел со скоростью 500 миль в час, какова была скорость реактивного потока?

Скорость струи 100 миль в час.

Джерри только что вернулся из поездки по стране. Поездка находилась в 3000 милях от его дома, и его общее время в самолете в оба конца составило 11 часов.Если самолет летел со скоростью 550 миль в час, какова была скорость реактивного потока?

Скорость струи 50 миль в час.

Рабочие приложения также можно моделировать квадратными уравнениями. Мы настроим их, используя те же методы, которые мы использовали, когда решали их с помощью рациональных уравнений. Сейчас мы воспользуемся аналогичным сценарием.

Еженедельный журнал сплетен рассказывает о президентских выборах, и редактор хочет, чтобы журнал был напечатан как можно скорее.Она попросила типографию запустить дополнительный печатный станок, чтобы печатать быстрее. Пресс № 1 занимает на 12 часов больше, чем Пресс № 2, чтобы выполнить задание, и когда оба пресса работают, они могут распечатать задание за 8 часов. Сколько времени требуется каждой печатной машине для печати одного задания?

Это рабочая проблема. Диаграмма поможет нам организовать информацию.

Мы ищем, сколько часов потребуется каждой печатной машине в отдельности для выполнения работы.

В еженедельном новостном журнале есть большая статья о Человеке года, и редактор хочет, чтобы журнал был напечатан как можно скорее.Она попросила типографию запустить дополнительный печатный станок, чтобы печатать быстрее. Пресс # 1 занимает на 6 часов больше, чем Пресс # 2, чтобы выполнить задание, и когда оба пресса работают, они могут распечатать задание за 4 часа. Сколько времени требуется каждой печатной машине для печати одного задания?

Пресс № 1 займет 12 часов, а нажатие № 2 займет 6 часов, чтобы выполнить работу в одиночку.

Эрлинда устраивает вечеринку и хочет наполнить свою горячую ванну. Если она использует только красный шланг, это займет на 3 часа больше, чем если бы она использовала только зеленый шланг.Если она использует оба шланга вместе, ванна наполняется за 2 часа. Сколько времени нужно, чтобы каждый шланг наполнял гидромассажную ванну?

Красный шланг занимает 6 часов, а зеленый — 3 часа.

Ключевые понятия

• Методы решения квадратных уравнений
  • Факторинг
  • Свойство квадратного корня
  • Завершение площади
  • Квадратичная формула
• Как использовать стратегию решения проблем.
  1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
  2. Определите , что мы ищем.
  3. Имя то, что мы ищем. Выберите переменную, чтобы представить это количество.
  4. Переведите в уравнение. Может быть полезно сформулировать проблему одним предложением со всей важной информацией. Затем переведите английское предложение в алгебраическое уравнение.
  5. Решите уравнение, используя хорошие методы алгебры.
  6. Отметьте ответ в проблеме и убедитесь, что он имеет смысл.
  7. Ответьте на вопрос полным предложением.
• Площадь треугольника
  • Для треугольника с основанием b и высотой h площадь A определяется по формуле
    А = 12bh.

  ---

• Площадь прямоугольника
  • Для прямоугольника длиной L и шириной W площадь A определяется по формуле A = LW .
    

    ---

• Теорема Пифагора
  • В любом прямоугольном треугольнике, где a и b — длина катетов, а c — длина гипотенузы, a ² + b ² = c ² .
    

    ---

• Движение снаряда
  • Высота в футах, h , объекта, взлетающего в воздух с начальной скоростью v ₀ , через t секунды определяется формулой h = −16 t ² + v ₀ t .

Практика делает идеальным

Решение приложений, моделируемых квадратными уравнениями

В следующих упражнениях решите любым методом.

Произведение двух последовательных нечетных чисел равно 255. Найдите числа.

Два последовательных нечетных числа, произведение которых равно 255: 15 и 17, а также −15 и −17.

Произведение двух последовательных четных чисел равно 360. Найдите числа.

Произведение двух последовательных четных чисел равно 624. Найдите числа.

Первое и второе последовательные нечетные числа — 24 и 26, а также –26 и –24.

Произведение двух последовательных нечетных чисел равно 1023. Найдите числа.

Произведение двух последовательных нечетных чисел равно 483. Найдите числа.

Два последовательных нечетных числа, произведение которых равно 483: 21 и 23, а также −21 и −23.

Произведение двух последовательных четных чисел равно 528. Найдите числа.

В следующих упражнениях решите любым методом. При необходимости округлите ответы до ближайшей десятой.

Треугольник площадью 45 квадратных дюймов имеет высоту, которая вдвое меньше четырех оснований. Найдите основание и высоту треугольника.

Ширина треугольника 5 дюймов, высота 18 дюймов.

Основание треугольника на шесть больше, чем в два раза высоты.Площадь треугольника 88 квадратных ярдов. Найдите основание и высоту треугольника.

Площадь треугольной клумбы в парке составляет 120 квадратных футов. Основание на 4 фута длиннее, что в два раза больше высоты. Каковы основание и высота треугольника?

Основание составляет 24 фута, а высота треугольника — 10 футов.

В спортивном зале висит треугольный баннер чемпионата по баскетболу. Его площадь составляет 75 квадратных футов.Какова длина основания и высота, если основание составляет две трети высоты?

Длина прямоугольной проезжей части на пять футов больше ширины в три раза. Площадь 50 квадратных футов. Найдите длину и ширину проезжей части.

Длина проезжей части составляет 15,0 футов, а ширина — 3,3 фута.

Прямоугольный газон площадью 140 квадратных ярдов. Его ширина в шесть раз меньше длины вдвое. Какая длина и ширина газона?

Прямоугольный стол для столовой имеет площадь 24 квадратных фута.Его длина на два фута больше, чем ширина стола в два раза. Найдите длину и ширину стола.

Длина стола 8 футов, ширина 3 фута.

Новый компьютер имеет площадь 168 квадратных дюймов. Если ширина на 5,5 дюймов меньше длины, каковы размеры компьютера?

Гипотенуза прямоугольного треугольника в два раза длиннее одной из его катетов. Длина другой ноги — три фута.Найдите длины трех сторон треугольника.

Длина ног прямоугольного треугольника 3,2 и 9,6 см.

Гипотенуза прямоугольного треугольника 10 см. Одна из ножек треугольника в три раза длиннее другой. Округлите до ближайшей десятой. Найдите длины трех сторон треугольника.

Прямоугольный сад разделят на два участка, огородив его по диагонали. Расстояние по диагонали от одного угла сада до противоположного на пять ярдов больше ширины сада.Длина сада в три раза больше ширины. Найдите длину диагонали сада.

Длина диагонального ограждения — 7,3 ярда.

Морские флаги используются для обозначения букв алфавита. Флаг для буквы O состоит из желтого прямоугольного треугольника и красного прямоугольного треугольника, которые сшиты вместе вдоль своей гипотенузы, образуя квадрат. Гипотенуза двух треугольников на три дюйма длиннее стороны флага.Найдите длину стороны флага.

Джерри планирует установить 25-футовую лестницу сбоку от своего дома, чтобы очистить желоба. Низ лестницы будет на расстоянии 5 футов от дома. Как подняться по стене дома?

Лестница будет достигать 24,5 футов сбоку от дома.

У Джона есть 10-футовый кусок веревки, который он хочет использовать для поддержки своего 8-футового дерева. Как далеко от основания дерева он должен закрепить веревку?

Ракета-фейерверк взлетает вверх со скоростью 640 фут / сек.Используйте формулу снаряда h = −16 t ² + v ₀ t , чтобы определить, когда высота ракеты-фейерверка будет 1200 футов.

Стрела достигнет 400 футов по пути вверх за 2,8 секунды и вниз за 11 секунд.

Стрела выпускается вертикально вверх со скоростью 220 футов в секунду. Используйте формулу снаряда h = −16 t ² + v ₀ t , чтобы определить, когда высота стрелы будет 400 футов.

Пуля выстреливается прямо из пулемета BB с начальной скоростью 1120 футов в секунду на начальной высоте 8 футов. Используйте формулу h = −16 t ² + v ₀ t + 8, чтобы определить, сколько секунд потребуется пуле, чтобы поразить землю. (То есть, когда ч = 0?)

Пуля упадет на землю за 70 секунд.

Камень падает с 196-футовой платформы.Используйте формулу h = −16 t ² + v ₀ t + 196, чтобы определить, сколько секунд потребуется, чтобы камень упал на землю. (Поскольку камень упал, v ₀ = 0.)

Бизнесмен на небольшом самолете быстро перелетел вдоль побережья на обеденную встречу, а затем вернулся домой. Самолет налетал в общей сложности 4 часа, а путь в каждую сторону составлял 200 миль. Какая скорость ветра поразила самолет, летевший со скоростью 120 миль в час?

Скорость ветра была 49 миль в час.

Пара села на небольшой самолет, чтобы быстро полететь в винную страну для романтического ужина, а затем вернулась домой. Самолет налетал в общей сложности 5 часов, а путь в каждую сторону составлял 300 миль. Если самолет летел со скоростью 125 миль в час, какая скорость ветра влияла на самолет?

Рой плыл по реке на байдарке, а затем вернулся в общей сложности за 6 часов. Поездка составляла 4 мили в каждую сторону, и течение было трудным. Если Рой катался на каяке со скоростью 5 миль в час, какова была скорость течения?

Скорость тока была 4.3 миль / ч.

Рик поплыл вверх по реке, ночевал в кемпинге, а затем поплыл обратно. Он провел 10 часов в гребле, а палаточный лагерь находился в 24 милях от него. Если Рик каяки со скоростью 5 миль в час, какова скорость течения?

Два художника могут покрасить комнату за 2 часа, если работают вместе. Менее опытному маляру требуется на 3 часа больше, чем более опытному маляру, чтобы закончить работу. Сколько времени нужно каждому художнику, чтобы расписать комнату индивидуально?

Менее опытному маляру требуется 6 часов, а опытному маляру требуется 3 часа, чтобы выполнить работу в одиночку.

Два садовника могут проводить еженедельное обслуживание двора за 8 минут, если они работают вместе. Старшему садовнику требуется на 12 минут больше, чем младшему, чтобы закончить работу в одиночку. Сколько времени нужно каждому садовнику для индивидуального еженедельного обслуживания двора?

Две машины производят 10 000 деталей за два часа. Если машина №1 может выполнить работу в одиночку за один час меньше, чем машина №2 может выполнить эту работу, сколько времени потребуется каждой машине, чтобы изготовить 10 000 деталей в одиночку?

Машина № 1 занимает 3.6 часов, а Машине № 2 требуется 4,6 часа, чтобы сделать работу в одиночку.

Салли устраивает вечеринку и хочет наполнить бассейн. Если он использует только шланг, это займет на 2 часа больше, чем если бы он использовал только шланг своего соседа. Если он использует оба шланга вместе, бассейн заполняется за 4 часа. Сколько времени нужно, чтобы каждый шланг наполнял гидромассажную ванну?

Письменные упражнения

Составьте задачу, состоящую из произведения двух подряд идущих нечетных целых чисел.

ⓐ Начните с выбора двух подряд идущих нечетных целых чисел.Какие у вас целые числа?

ⓑ Каково произведение ваших целых чисел?

ⓒ Решите уравнение n ( n + 2) = p , где p — это продукт, который вы нашли в части (b).

ⓓ Вы получили числа, с которых начали?

Составьте задачу, состоящую из произведения двух последовательных четных целых чисел.

ⓐ Начните с выбора двух последовательных четных целых чисел. Какие у вас целые числа?

ⓑ Каково произведение ваших целых чисел?

ⓒ Решите уравнение n ( n + 2) = p , где p — это продукт, который вы нашли в части (b).

ⓓ Вы получили числа, с которых начали?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

Ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?

---

Эта работа находится под международной лицензией Creative Commons Attribution 4.0.

Вы также можете бесплатно скачать по адресу http: // cnx.org/contents/[email protected]

Атрибуция:

Комплексные числа и квадратичная формула

Комплекс Числа и квадратичная формула (стр. 3 из 3) Разделы: Введение, Операции с комплексами, Квадратичная формула Вы, вероятно, будете использовать только комплексы в контексте решения квадраты для свои нули.(Есть много других практических применений комплексов, но вам придется подождать более интересных занятий, таких как «Инженерное дело» 201 «, чтобы добраться до» хороших вещей «.) Помните, что квадратичный Формула решает «a x 2 + b x + c = 0 » для значений x . Также помните, что это означает, что вы пытаетесь найти перехваты x графа.Когда Формула дает отрицательный результат внутри квадрата root, теперь вы можете упростить этот ноль, используя комплексные числа. Ответ вы придумываете правильный «ноль», «корень» или «решение» для «a x 2 + b x + c = 0 «, потому что, если вы снова включите его в квадратичный, вы получите ноль после вы упрощаете. Но вы не можете изобразить комплексное число на плоскости x , y . Таким образом, это «решение уравнения» не является перехватом x .Вы можете установить эту связь между квадратной формулой, комплексными числами, и построение графиков: Кроме того, вы можете построить график комплексов, но не в плоскости x , y . Вам нужен «сложный» самолет. Для комплексной плоскости ось x здесь вы строите реальную часть, а ось y здесь вы изобразите мнимую часть.Например, вы построили бы график комплексное число 3 2 i вот так: Это приводит к интересному факт: когда вы узнали об обычных («настоящих») числах, вы также узнали об их порядке (это то, что вы показываете в числовой строке). Но x , y -точек не приходите в каком-то определенном порядке. Вы не можете сказать, что приходит одна точка » после «другой точки, так же, как вы можете сказать, что одно число идет после другого числа.Например, нельзя сказать, что (4, 5) «приходит после» (4, 3) в том смысле, что вы можете сказать, что 5 приходит после 3. Практически все, что вы можете сделать, это сравнить «размер», а для сложных числа, «размер» означает «насколько далеко от источника». К сделайте это, вы используете Distance Формула и сравнить какие комплексы находятся ближе к источнику или дальше от него. Этот «размер» понятие называется «модуль упругости». Например, глядя на наши комплексное число, построенное выше, его модуль вычисляется с использованием расстояния Формула: Авторское право Элизабет Стапель 2000-2011 Все права защищены Обратите внимание, что все точки на это расстояние от начала координат имеют одинаковый модуль.Все точки на круг радиусом sqrt (13) рассматриваются как комплексные числа, имеющие тот же «размер», что и 3 2 и . << Предыдущая Вверх | 1 | 2 | 3 | Возвращаться в индекс Цитируйте эту статью как: Стапель, Елизавета.«Комплексные числа и квадратная формула». Purplemath . Доступно по номеру https://www.purplemath.com/modules/complex3.htm . Дата обращения [Дата] [Месяц] 2016 г.

Расстояние, середина и парабола

Конические секции

Коническое сечение Кривая, полученная на пересечении прямого кругового конуса и плоскости.кривая, полученная из пересечения прямого кругового конуса и плоскости. Конические сечения — это парабола, круг, эллипс и гипербола.

Цель состоит в том, чтобы нарисовать эти графики на прямоугольной координатной плоскости.

Формулы расстояния и средней точки

Начнем с обзора формулы расстояния. Для двух точек (x1, y1) и (x2, y2) расстояние d между ними определяется как d = (x2 − x1) 2+ (y2 − y1) 2.. Для двух точек (x1, y1) и (x2, y2) в прямоугольной координатной плоскости расстояние d между ними определяется формулой расстояния

д = (х2-х1) 2+ (у2-у1) 2

Кроме того, точка, которая делит пополам отрезок прямой, образованный этими двумя точками, называется средней точкой. Учитывая две точки (x1, y1) и (x2, y2), средняя точка представляет собой упорядоченную пару, заданную формулой (x1 + x22, y1 + y22) . и определяется формулой

(x1 + x22, y1 + y22)

Средняя точка — это упорядоченная пара, образованная средним значением x и средним значением y .

Пример 1

Даны (−2, −5) и (−4, −3) вычислить расстояние и среднюю точку между ними.

Решение:

В данном случае мы будем использовать формулы со следующими точками:

(x1, y1) (x2, y2) (- 2, −5) (- 4, −3)

Рекомендуется включать формулу в ее общем виде перед заменой значений переменных; это улучшает читаемость и снижает вероятность ошибок.

d = (x2 − x1) 2+ (y2 − y1) 2 = [- 4 — (- 2)] 2 + [- 3 — (- 5)] 2 = (- 4 + 2) 2 + (- 3 +5) 2 = (- 2) 2+ (2) 2 = 4 + 4 = 8 = 22

Затем определите среднюю точку.

(x1 + x22, y1 + y22) = (- 2 + (- 4) 2, −5 + (- 3) 2) = (- 62, −82) = (- 3, −4)

Нанося эти точки на имеющийся график,

Ответ: Дистанция: 22 единицы; средняя точка: (−3, −4)

Пример 2

Диаметр круга определяется двумя точками (−1,2) и (1, −2).Определите радиус круга и используйте его для вычисления его площади.

Решение:

Найдите диаметр по формуле расстояния.

d = (x2 − x1) 2+ (y2 − y1) 2 = [1 — (- 1)] 2 + (- 2−2) 2 = (2) 2 + (- 4) 2 = 4 + 16 = 20 = 25

Напомним, что радиус круга равен половине диаметра круга. Следовательно, если d = 25 единиц, то

г = d2 = 252 = 5

Площадь круга определяется формулой A = πr2, и мы имеем

А = π (5) 2 = π⋅5 = 5π

Площадь измеряется в квадратных единицах.

Ответ: Радиус: 5 единиц; площадь: 5π квадратных единиц

Попробуй! Учитывая (0,0) и (9, −3), вычислите расстояние и среднюю точку между ними.

Ответ: Дистанция: 310 единиц; середина: (92, −32)

Парабола

Парабола Множество точек на плоскости, равноудаленных от заданной линии, называемой директрисой, и точки, не лежащей на линии, называемой фокусом.- это набор точек на плоскости, равноотстоящих от заданной линии, называемый директрисой, и точка не на прямой, называемая фокусом. Другими словами, если дана прямая L директриса, а точка F фокус, то (x, y) будет точкой на параболе, если кратчайшее расстояние от нее до фокуса и от нее до линии равно как на картинке ниже:

Вершина параболы — это точка, в которой кратчайшее расстояние до директрисы минимально.Кроме того, парабола образуется при пересечении конуса с наклонной плоскостью, параллельной стороне конуса:

Напомним, что график квадратичной функции, полиномиальной функции степени 2, является параболическим. Мы можем записать уравнение параболы в общем виде Уравнение параболы, записанное в виде y = ax2 + bx + c или x = ay2 + by + c, где a , b и c являются действительными числа и 0. или мы можем записать уравнение параболы в стандартной форме Уравнение параболы, записанное в виде y = a (x − h) 2 + k или x = a (y − k) 2 + h.:

Стандарт общего вида Formy = ax2 + bx + c y = a (x − h) 2 + k

Здесь a , b и c — действительные числа, a 0. Обе формы полезны для определения общей формы графика. Однако в этом разделе мы сосредоточимся на получении стандартной формы, которую часто называют вершинной формой. Уравнение параболы, записанное в стандартной форме, часто называют вершинной формой. В этой форме вершина очевидна: (h, k) .. Для квадратичной функции в стандартной форме вершиной является (h, k).Чтобы убедиться в этом, рассмотрим построение графика y = (x + 3) 2 + 2 с использованием преобразований.

y = x2 Базовая функция возведения в квадрат. Y = (x + 3) 2 Горизонтальный сдвиг влево на 3 единицы. Y = (x + 3) 2 + 2 Вертикальный сдвиг вверх на 2 единицы.

Используйте эти переводы, чтобы нарисовать график,

Здесь мы видим, что вершина равна (−3,2). Это можно определить непосредственно из уравнения в стандартной форме:

y = a (x − h) 2 + k ↓ ↓ y = [x — (- 3)] 2 + 2

В таком виде мы видим, что вершина равна (−3,2).Однако это уравнение обычно не приводится в стандартной форме. Преобразование общей формы в стандартную путем завершения квадрата — это основной процесс, с помощью которого мы нарисуем все конические сечения.

Пример 3

Перепишем уравнение в стандартной форме и определим вершину его графика: y = x2−8x + 15.

Решение:

Начните с того, что освободите место для постоянного члена, завершающего квадрат.

y = x2−8x + 15 = x2−8x + ___ + 15 −___

Идея состоит в том, чтобы сложить и вычесть значение, завершающее квадрат, (b2) 2, а затем разложить на множители.В этом случае сложите и вычтите (b2) 2 = (- 82) 2 = (- 4) 2 = 16.

y = x2−8x + 15 Сложить и вычесть 16. = (x2−8x +16) +15 −16Factor. = (X − 4) (x − 4) −1 = (x − 4) 2−1

Добавление и вычитание одного и того же значения в выражении не меняют его. Это эквивалентно добавлению 0. Когда уравнение имеет такую ​​форму, мы можем легко определить вершину.

y = a (x — h) 2 + k ↓ ↓ y = (x − 4) 2 + (- 1)

Здесь у нас есть перевод вправо на 4 единицы и вниз на 1 единицу.Следовательно, h = 4 и k = −1.

Ответ: y = (x − 4) 2−1; вершина: (4, −1)

Если есть ведущий коэффициент, отличный от 1, то начните с вынесения этого ведущего коэффициента из первых двух членов трехчлена.

Пример 4

Перепишем уравнение в стандартной форме и определим вершину графика: y = −2×2 + 12x − 16.

Решение:

Поскольку a = −2, вычтите это из первых двух членов, чтобы завершить квадрат.Оставьте место в круглых скобках для добавления и вычитания значения, завершающего квадрат.

y = −2×2 + 12x − 16 = −2 (x2−6x + ___ − ___) — 16

Теперь используйте −6, чтобы определить значение, завершающее квадрат. В этом случае (b2) 2 = (- 62) 2 = (- 3) 2 = 9. Сложите и вычтите 9 и разложите множители следующим образом:

y = −2×2 + 12x − 16 = −2 (x2−6x + ___ −___) −16 Сложить и вычесть 9. = — 2 (x2−6x + 9−9) −16 Фактор. = — 2 [(x− 3) (x − 3) −9] −16 = −2 [(x − 3) 2−9] −16 Распределите −2. = — 2 (x − 3) 2 + 18−16 = −2 (x −3) 2 + 2

В таком виде мы легко можем определить вершину.

y = a (x − h) 2 + k ↓↓ y = −2 (x − 3) 2 + 2

Здесь h = 3 и k = 2.

Ответ: y = −2 (x − 3) 2 + 2; вершина: (3,2)

Используйте как общую, так и стандартную форму при построении графика параболы.

Пример 5

График: y = −2×2 + 12x − 16.

Решение:

Из предыдущего примера у нас есть две эквивалентные формы этого уравнения:

Общая форма Стандартная форма: y = −2×2 + 12x − 16 y = −2 (x − 3) 2 + 2

Напомним, что если старший коэффициент a> 0, парабола открывается вверх, а если a <0, парабола открывается вниз.В этом случае a = −2, и мы заключаем, что парабола открывается вниз. Используйте общую форму для определения точки перехвата и . Когда x = 0, мы видим, что интервал y равен (0, −16). Из уравнения в стандартной форме видно, что вершина равна (3,2). Чтобы найти перехват x , мы могли бы использовать любую форму. В этом случае мы будем использовать стандартную форму для определения значений x , где y = 0,

.

y = −2 (x − 3) 2 + 2 Положим y = 0 и решим: 0 = −2 (x − 3) 2 + 2 −2 = −2 (x − 3) 21 = (x − 3) 2 Примените свойство квадратного корня.± 1 = х-33 ± 1 = х

Здесь x = 3−1 = 2 или x = 3 + 1 = 4, и поэтому x -перехватывания равны (2,0) и (4,0). Используйте эту информацию, чтобы нарисовать график.

Ответ:

До сих пор мы рисовали параболы, которые открываются вверх или вниз, потому что эти графики представляют функции. На этом этапе мы расширяем наше исследование, включив параболы, которые открываются вправо или влево. Если мы возьмем уравнение, определяющее параболу в предыдущем примере,

у = −2 (х − 3) 2 + 2

и переключая значения x и y , получаем

х = -2 (у-3) 2 + 2

Это создает новый график с симметрией относительно прямой y = x.

Обратите внимание, что полученный график не является функцией. Однако он имеет ту же общую параболическую форму, которая открывается влево. Мы можем распознать уравнения парабол, которые открываются влево или вправо, заметив, что они квадратичны в y вместо x . Графическое изображение парабол, открывающихся влево или вправо, аналогично графическому изображению парабол, открывающихся вверх и вниз. В целом у нас

Во всех случаях вершина равна (h, k).Обратите внимание на размещение h и k в каждом уравнении.

Пример 6

График: x = y2 + 10y + 13.

Решение:

Поскольку коэффициент при y2 положительный, a = 1, мы заключаем, что график представляет собой параболу, которая открывается вправо. Кроме того, когда y = 0, ясно, что x = 13, и поэтому интервал x равен (13,0). Заполните квадрат, чтобы получить стандартную форму. Здесь мы будем складывать и вычитать (b2) 2 = (102) 2 = (5) 2 = 25.

x = y2 + 10y + 13 = y2 + 10y + 25−25 + 13 = (y + 5) (y + 5) −12 = (y + 5) 2−12

Следовательно,

x = a (y − k) 2 + h ↓↓ x = (y — (- 5)) 2 + (- 12)

Отсюда видно, что вершина (h, k) = (- 12, −5). Затем используйте стандартную форму для поиска перехватов y , задав x = 0.

x = (y + 5) 2−120 = (y + 5) 2−1212 = (y + 5) 2 ± 12 = y + 5 ± 23 = y + 5−5 ± 23 = y

y -перехват: (0, −5−23) и (0, −5 + 23). Используйте эту информацию, чтобы нарисовать график.

Ответ:

Пример 7

График: x = −2y2 + 4y − 5.

Решение:

Поскольку коэффициент при y2 равен a = −2, мы заключаем, что график представляет собой параболу, которая открывается влево. Кроме того, когда y = 0, ясно, что x = −5, и поэтому интервал x равен (−5,0). Начните с вычитания ведущего коэффициента следующим образом:

x = −2y2 + 4y − 5 = −2 (y2−2y + ___ − ___) — 5

Здесь мы будем складывать и вычитать (b2) 2 = (- 22) 2 = (- 1) 2 = 1.

x = −2y2 + 4y − 5 = −2 (y2−2y + 1−1) −5 = −2 [(y − 1) 2−1] −5 = −2 (y − 1) 2 + 2− 5 = −2 (y − 1) 2−3

Следовательно, из формы вершины x = −2 (y − 1) 2−3, мы можем видеть, что вершина равна (h, k) = (- 3,1). Поскольку вершина находится в точке (−3,1), а парабола открывается влево, мы можем заключить, что не существует пересечений y -перехвата. Поскольку у нас есть только две точки, выберите несколько значений y и найдите соответствующие значения x .

xyx = −2 (y − 1) 2−3−11−1x = −2 (−1−1) 2−3 = −2 (−2) 2−3 = −11−52x = −2 (2− 1) 2−3 = −2 (1) 2−3 = −5−113x = −2 (3−1) 2−3 = −2 (2) 2−3 = −11

Ответ:

Попробуй! График: x = y2 − y − 6.

Ответ:

Основные выводы

• Используйте формулу расстояния, чтобы определить расстояние между любыми двумя заданными точками. Используйте формулу средней точки, чтобы определить среднюю точку между любыми двумя заданными точками.
• Парабола может открываться вверх или вниз, в этом случае это функция. В этом разделе мы расширяем наше исследование парабол, чтобы включить те, которые открываются влево или вправо.Такие графики не представляют функций.
• Уравнение параболы, которая открывается вверх или вниз, квадратично относительно x , y = ax2 + bx + c. Если a> 0, то парабола открывается вверх, а если a <0, то парабола открывается вниз.
• Уравнение параболы, которая открывается влево или вправо, квадратично относительно y , x = ay2 + by + c. Если a> 0, то парабола открывается вправо, а если a <0, то парабола открывается влево.
• Уравнение параболы в общем виде y = ax2 + bx + c или x = ay2 + by + c может быть преобразовано к стандартной форме y = a (x − h) 2 + k или x = a (y − k) 2 + ч, завершив пл.
• При заполнении квадрата убедитесь, что ведущий коэффициент группировки переменных равен 1, прежде чем добавлять и вычитать значение, завершающее квадрат.
• При построении парабол полезны как общие, так и стандартные формы. В стандартной форме вершина очевидна (h, k). Чтобы найти перехват x , установите y = 0 и решите для x , а чтобы найти перехват y , установите x = 0 и найдите y .

Тематические упражнения

Часть A: Формулы расстояния и средней точки

Вычислить расстояние и среднюю точку между заданными двумя точками.

1. (−1, −3) и (5, −11)

4. (−5, −6) и (−3, −4)

6. (−6, −4) и (−12,1)

12. (-43,2) и (-13, -12)

13. (15, -95) и (310, -52)

14. (-12,43) и (-23,56)

Определите площадь круга, диаметр которого определяется двумя заданными точками.

Определите периметр треугольника по координатам вершин.

23. (5,3), (2, −3) и (8, −3)

24. (−3,2), (−4, −1) и (−1,0)

25. (3,3), (5,3−23) и (7,3)

Найдите a так, чтобы расстояние d между точками было равно заданной величине.

27. (1,2) и (4, а); d = 5 шт.

28. (−3, а) и (5,6); d = 10 шт.

29. (3,1) и (а, 0); d = 2 шт.

30. (а, 1) и (5,3); d = 13 шт.

Часть B: Парабола

График.Обязательно найдите вершину и все пересечения.

Перепишем в стандартном виде и дадим вершину.

Перепишите в стандартной форме и графике.Обязательно найдите вершину и все пересечения.

Часть C: Обсуждение

87. Исследуйте и обсуждайте реальные приложения, использующие параболу.

88. Все ли параболы имеют точки пересечения x ? Объяснять.

89. Все ли параболы имеют точки пересечения и ? Объяснять.

90. Составьте свою собственную параболу, которая открывается влево или вправо, запишите ее в общем виде и нанесите на график.

ответов

1. Дальность: 10 единиц; середина: (2, −7)

3. Дистанция: 213 единиц; средняя точка: (1, −4)

5. Дальность: 52 единицы; середина: (192,52)

7. Дальность: 5 единиц; середина: (22,32)

9. Дальность: 5 единиц; середина: (352, −3)

11. Дистанция: 522 единицы; средняя точка: (-34,14)

13. Дальность: 22 единицы; средняя точка: (14, −4320)

15. Дистанция: юниты a2 + b2; середина: (a2, b2)

45. у = (х — 3) 2 + 9; вершина: (3,9)

47. х = (у + 10) 2−13; вершина: (−13, −10)

49. у = (х − 7) 2; вершина: (7,0)

51. х = 2 (у — 1) 2 + 3; вершина: (3,1)

53. у = 6 (х + 3) 2; вершина: (−3,0)

55. y = 2 (x − 12) 2−32; вершина: (12, −32)

57. х = — (у-52) 2 + 54; вершина: (54,52)

59. y = (x − 2) 2−9;

61. у = — (х − 6) 2 + 4;

63. у = 2 (х + 1) 2 + 7;

65. y = −5 (x − 3) 2;

67. х = (y − 1) 2−9;

69. x = (y − 1) 2−4;

71. х = — (у + 5) 2 + 1;

73. х = 3 (у + 2) 2;

75. x = (y − 2) 2−7;

77. х = — (у − 1) 2 + 6;

79. y = −3 (x − 13) 2 + 43;

81. x = −4 (y + 12) 2−4;

83. y = (x + 52) 2−294;

85. х = 2 (у + 52) 2−12;

ORCCA Подробнее о сложных решениях квадратных уравнений

Подраздел 11. 2-4 (\ replace {\ sfrac {1} {2}}) (\ replace { 12})}} {2 (\ replace {\ sfrac {1} {2}})} \\
\ amp = \ frac {5 \ pm \ sqrt {25-24}} {1} \\
\ amp = 5 \ pm \ sqrt {1} \\
\ amp = 5 \ pm1
\ end {выровнять *}

Итак, либо:

\ begin {align *}
t = 6 \ amp \ amp \ text {или} \ amp \ amp t = 4
\ end {выровнять *}

Рисунок 11.2-4ac \ text {,} \) называется дискриминантом . Знак дискриминанта подскажет нам, сколько горизонтальных пересечений будет иметь график квадратичной функции

• При использовании квадратной формулы для решения уравнения \ (h (t) = 0 \ text {,} \), если дискриминант является положительным числом, это говорит нам, что уравнение имеет два действительных решения и что график квадратичной функции \ (h \) имеет два горизонтальных пересечения.

• При использовании формулы квадратного уравнения для решения уравнения \ (h (t) = 0 \ text {,} \), если дискриминант равен нулю, это говорит нам, что уравнение имеет только одно действительное решение и что график квадратичной функции \ (h \) имеет одно горизонтальное пересечение.2-4 (\ replace {6}) (\ replace {-1}) \\
  \ amp = 36 + 24 \\
  \ amp = 60
  \ end {выровнять *}

  Таким образом, дискриминант положительный, что означает, что график \ (h \) имеет два горизонтальных пересечения.

Пример 11.3.5.


Футзал ¹ — это разновидность того, что в США обычно называют футболом. Игра ведется на твердом корте и обычно проходит в помещении. Потолок находится за пределами поля, поэтому, если мяч попадает в потолок, он переходит к противоположной команде.

Борна отбивает мяч от земли со скоростью \ (8 \) метров в секунду.2 + 8t \ text {,} \) с \ (t \), обозначающим время в секундах после удара по мячу. Если высота потолка составляет \ (4 \) метра, минимальная высота, разрешенная правилами, определяет, попадет ли мяч в потолок.

Объяснение

Чтобы увидеть, ударится ли их мяч в потолок, мы решим уравнение \ (h (t) = 4 \ text {.} \). Мы могли бы заполнить квадрат или использовать формулу корней квадратного уравнения. Поскольку это уравнение имеет десятичные коэффициенты, мы будем использовать формулу корней квадратного уравнения. Приведем уравнение в стандартной форме и укажем, что \ (a = \ replace {-4.2-4 (\ replace {-4.9}) (\ replace {-4})}} {2 (\ replace {-4.9})} \\
\ amp = \ frac {-8 \ pm \ sqrt {64-78.4}} {- 9.8} \\
\ amp = \ frac {-8 \ pm \ sqrt {-14.4}} {- 9,8}
\ end {выровнять *}

Подкоренное выражение отрицательное, поэтому мы можем заключить, что реальных решений уравнения \ (h (t) = 4 \ text {.} \) Не существует. Это означает, что парабола не пересечет линию \ (y = 4 \) и мяч не ударится о потолок.

Пример 11.3.6.


Эмма отбивает мяч от земли со скоростью \ (10 ​​\) метров в секунду.2 + 10t \ text {,} \) с \ (t \), обозначающим время в секундах после удара по мячу. Если высота потолка составляет \ (4,5 \) метра, определите, попадет ли мяч в потолок.

Объяснение

Чтобы увидеть, ударится ли ее мяч в потолок, мы решим уравнение \ (h (t) = 4.5 \ text {.} \). Мы будем использовать формулу корней квадратного уравнения, потому что это уравнение имеет десятичные коэффициенты. Мы приводим уравнение в стандартную форму и определяем, что \ (a = \ replace {-4.9} \ text {,} \) \ (b = \ substitute {10} \) и \ (c = \ replace {-4.2-4 (\ replace {-4.9}) (\ replace {-4.5})}} {2 (\ replace {-4.9})} \\
\ amp = \ frac {-10 \ pm \ sqrt {100-88.2}} {- 9.8} \\
\ amp = \ frac {-10 \ pm \ sqrt {11.8}} {- 9.8}
\ end {выровнять *}

Подкоренное выражение положительное, поэтому есть два реальных решения уравнения \ (h (t) = 4.5 \ text {.} \). Это означает, что парабола пересечет линию \ (y = 4.5 \), и мяч попадет в потолок.

Подраздел 11.3.2 Решение уравнений с комплексными решениями


В физическом контексте мы можем только хотеть знать, являются ли решения реальными или сложными.Или мы можем захотеть найти решения. Когда подкоренное выражение отрицательное, нам нужно перейти в комплексную систему счисления. Сначала мы вернемся к определению комплексных чисел. Напомним, что \ (i \) определяется как \ (\ sqrt {-1} \ text {.} \)

Определение 11.3.7. Комплексное число.


Комплексное число ² — это число, которое может быть выражено в форме \ (a + bi \ text {,} \), где \ (a \) и \ (b \) — действительные числа, а \ (i \) — мнимая единица. В этом выражении \ (a \) — это действительная часть , а \ (b \) (не \ (bi \)) — это мнимая часть .2 \ amp = -9
\ end {выровнять *}

\ begin {align *}
s-5 \ amp = — \ sqrt {-9} \ amp \ amp \ text {или} \ amp s-5 \ amp = \ sqrt {-9} \\
s-5 \ amp = — \ sqrt {9} \ cdot \ sqrt {-1} \ amp \ amp \ text {или} \ amp s-5 \ amp = \ sqrt {9} \ cdot \ sqrt {-1} \\
s-5 \ amp = -3i \ amp \ amp \ text {или} \ amp s-5 \ amp = 3i \\
s \ amp = 5-3i \ amp \ amp \ text {или} \ amp s \ amp = 5 + 3i
\ end {выровнять *}

Набор решений: \ (\ {5-3i, 5 + 3i \} \ text {.} \)

КПП 11.3.9.


Квадратичная формула также может использоваться для нахождения сложных решений. Вот пример, в котором имеет смысл использовать формулу корней квадратного уравнения.2-4 (\ replace {5}) (\ replace {3})}} {2 (\ replace {5})} \\
\ amp = \ frac {2 \ pm \ sqrt {4-60}} {10} \\
\ amp = \ frac {2 \ pm \ sqrt {-56}} {10} \\
\ amp = \ frac {2 \ pm \ sqrt {-1 \ cdot4 \ cdot14}} {10} \\
\ amp = \ frac {2 \ pm \ sqrt {-1} \ cdot \ sqrt {4} \ cdot \ sqrt {14}} {10} \\
\ amp = \ frac {2 \ pm i \ cdot2 \ cdot \ sqrt {14}} {10}
\ end {выровнять *}

Теперь нам нужно оформить решения в стандартном виде: \ (a + bi \ text {.} \)

\ begin {align *}
x \ amp = \ frac {2} {10} \ pm \ frac {2i \ sqrt {14}} {10} \\
х \ amp = \ frac {1} {5} \ pm \ frac {\ sqrt {14}} {5} я
\ end {выровнять *}

Набор решений: \ (\ left \ {\ frac {1} {5} — \ frac {\ sqrt {14}} {5} i, \ frac {1} {5} + \ frac {\ sqrt {14) }} {5} i \ right \} \ text {.} \)

KangAssgn3

KangAssgn3

Задание III: Параметры квадратных уравнений

по

Руи Кан

---

Расследование 1.

Построение графиков, учитывающих уравнение

, стало довольно стандартным упражнением с доступными технологиями.

и наложить несколько графиков

для разных значений a, b или c, так как два других остаются постоянными.

На этих графиках обсуждаются закономерности корней

.

можно отслеживать.

Следующий график демонстрирует, что происходит, если мы сохраняем b и c постоянными, в частности, b = c = 1, и меняем значение параметра a:

Обратите внимание на приведенный выше график, отметим, что это семейство парабол всегда проходит через точку (0,1), что понятно, потому что, когда x = 0,

подставляем x в квадратное уравнение, получаем y = 1;

, таким образом, (0,1) всегда является решением этого семейства парабол, даже если мы позволим a принимать другие значения, такие как -4, 5, 37, -104 и т. Д.

Заключение 1: Из этого наблюдения мы можем обобщить, что если мы изменим значение a на положительное, мы получим семейство раскрывающихся парабол;

для отрицательного a получаем семейство парабол, раскрывающихся вниз; и наконец, но все эти параболы проходят через общую точку, т.е. (0, c).

(Примечание: когда a = 0, график больше не является параболой, потому что он нарушает одно из условий квадратного уравнения.

В этом частном случае, когда a = 0, график представляет собой линию y = 1, но обратите внимание, что график все еще проходит через точку (0,1).)

---

Следующая пара графиков исследует, что произойдет, если мы изменим параметр b, сохраняя постоянные a и c. Например, если мы установим

и пусть b принимает значения -3, -2, -1, 0, 1, 2, 3 и накладывает графики, получается следующая картина:

Теперь мы можем обсудить «движение» параболы при изменении b. Парабола всегда проходит через одну и ту же точку (0, C) на оси y (точка (0,1) с этим уравнением).

• Для b <-2 парабола будет пересекать ось x в двух точках с положительными значениями x (т. Е. Исходное уравнение будет иметь два действительных корня, оба положительные).
• Для b = -2 (желтая парабола) парабола касается оси x, поэтому исходное уравнение имеет один действительный положительный корень в точке касания.
• Для -2
• Аналогично, для b = 2 (красная парабола) парабола касается оси x, поэтому исходное уравнение имеет один действительный положительный корень в точке касания.
• И для b> 2 парабола дважды пересекает ось x с отрицательными значениями x (т. Е. Исходное уравнение будет иметь два отрицательных корня, оба отрицательные).

Далее, давайте рассмотрим геометрическое место вершин этого семейства парабол, построенное на графике из

В частности, мы хотим показать, что геометрическое место является параболой.

Воспользуйтесь методом «завершающего квадрата», чтобы переписать приведенное выше уравнение,

получаем

Факторинг и замена b на n для анимации графика получаем

Это говорит о том, что вершина находится в

Если мы назовем эту точку вершины как (d, f), то d и f удовлетворяют

d =, f =,

подставляем d в уравнение f, получаем f = или параболу.

Мы показали, не прибегая к исчислению, что геометрическое место вершин множества парабол, построенных на графике из

действительно парабола.

Следующий график дополнительно иллюстрирует этот факт:

Вывод 2: При изменении b параболы все еще проходят через ту же точку (0, C) на оси y (точка (0,1) с этим уравнением).

Когда парабола пересекает ось x в двух точках, квадратное уравнение имеет два корня.

Когда парабола касается оси x, квадратное уравнение имеет один корень.

Когда парабола вообще не пересекает ось x, квадратное уравнение не имеет корней. Кроме того, геометрическое место вершин множества парабол — это еще одна парабола.

---

На следующем графике мы исследуем, что произойдет, если мы сохраним a и b постоянными и изменим значения c:

Заключение 3: При изменении c парабола перемещается вверх и вниз, но остается той же формы с одним вложением внутри другого.

---

Расследование 2.

Рассмотрим снова уравнение

,

, но на этот раз, вместо того, чтобы строить график в нашей стандартной системе координат, мы строим график этого отношения в плоскости xb.

Если мы возьмем какое-либо конкретное значение b, скажем, b = 5, и наложим это уравнение на график, мы добавим линию, параллельную оси x.

Если линия пересекает кривую в плоскости xb, точки пересечения соответствуют корням исходного уравнения для этого значения b.У нас есть следующий график:

Для каждого выбранного значения b мы получаем горизонтальную линию.

На одном графике видно, что мы получаем два отрицательных действительных корня исходного уравнения, когда b> 2 (обратите внимание на красную линию, b = 5),

один отрицательный действительный корень, когда b = 2 (обратите внимание на синюю линию, b = 2),

нет реальных корней для -2

один положительный действительный корень, когда b = -2 (обратите внимание на серую линию, b = -2),

и два положительных действительных корня, когда b <-2 (обратите внимание на черную линию, b = -4).

Теперь попробуем разные значения c вместо c = + 1:

Во-первых, мы замечаем, что при изменении значения c мы получаем набор вложенных кривых.

Во-вторых, наше внимание привлекает конкретное значение c, то есть c = 0. Эта кривая соответствует уравнению:

Если мы разложим это уравнение на множители, мы получим x (x + y) = 0. Это говорит о том, что мы получаем две линии: x = 0 (то есть ось y) и y = -x (красная линия на нашем графике)

Если мы проследим связь между этими двумя линиями и набором кривых, мы обнаружим, что эти две прямые фактически являются двумя асимптотами парабол.

В-третьих, мы можем снова взять любое конкретное значение b, скажем, b = 5, и наложить это уравнение на график, а затем добавить линию, параллельную оси x.

Если линия пересекает кривую в плоскости xb, точки пересечения соответствуют корням исходного уравнения для этого значения b.

Интересно, что мы наблюдаем, что когда c отрицательно (посмотрите на синюю или зеленую линию), уравнение всегда имеет два корня, один положительный и один отрицательный.

Это потому, что мы знаем, что для любого квадратного уравнения, когда оно имеет два действительных корня; когда он имеет один настоящий корень;

, когда у него нет настоящих корней.

Так для

,

всегда имеет два настоящих корня, когда

.

Но когда c <0, указанное выше неравенство всегда верно. Это причина того, что мы наблюдаем, что когда c отрицательно, уравнение всегда имеет два корня.

Для положительных значений c, с другой стороны, нам нужно использовать тот же метод ранее, позволив b принимать разные значения

и наблюдайте, когда горизонтальная линия пересекает кривую в двух точках (два корня), одной точке (один корень) или без точки (без корня).

И мы можем назвать этот метод «горизонтальным тестом».

---

Расследование 3:

Теперь давайте добавим к рисунку график 2x + b = 0 и обсудим его связь с формулой корней квадратного уравнения:

Ясно, что эта прямая проходит через все вершины множества парабол при c> 0.

Небольшой расчет может помочь нам объяснить, почему это так.

Обратите внимание на набор квадратных уравнений на графике, и мы увидим, что 2x + y = 0 является первой производной каждой из функций, представленных на графике.

Мы также наблюдаем, что когда c> 0, кривые / параболы меняют направление, когда они пересекают линию, 2x + y = 0.

И, согласно тесту первой производной, именно здесь происходит относительный максимум или минимум.

(Примечание: для c <0 или c = 0 кривые не имеют относительного максимума и минимума. И линия 2x + y = 0 не проходит через эти кривые.)

---

Расследование 4:

Пока мы только построили квадратное уравнение в плоскости xb, вы можете спросить, что происходит, если графики находятся в плоскости xc или xa.

В этом конкретном исследовании мы рассмотрим случай для плоскости xc. В исследовании 5 мы рассматриваем случай для плоскости xa.

В частности, на следующем графике мы позволяем b варьироваться от -3, -2, -1, 0 до 1, 2 и 3 и наблюдаем, что происходит:

В этом случае мы видим, что все параболы проходят через начало координат (0, 0), что понятно

, потому что, когда x = 0, y = 0, т.е. (0, 0) всегда является общим корнем для этой системы уравнений.

Еще одно довольно интересное наблюдение, которое мы можем получить из этого набора графов, заключается в том, что координата y вершин этого набора парабол имеет особые отношения с

, есть ли у квадратного уравнения решения и сколько у него решений. Это покажется намного проще, если мы посмотрим на пример:

Обратите внимание на желтую кривую

,

его вершина находится в точке (1,1), координата y которой равна 1.

Если мы используем свои знания в алгебре, мы знаем, что это квадратное уравнение будет иметь реальное решение, если

, г.е., или для b = -2. В частности, квадратное уравнение будет иметь два действительных корня, если y <1,

и ровно один действительный корень, если y = 1, и никакого реального решения, если y> 1.

Следовательно, наблюдая, где находится вершина параболы в плоскости xc,

мы можем определить, какие значения c должен принимать, чтобы соответствующее квадратное уравнение имело два действительных корня, один действительный корень или не имело действительных корней.

Попробуйте это с любой из других кривых на изображении выше и посмотрите, применимо ли вышеприведенное наблюдение ко всем из них!

---

Расследование 5:

Наконец, давайте посмотрим, что происходит, если наши графики находятся в плоскости xa.В частности, давайте изменим c от -3, -2, -1, 0, 1, 2 и 3:

На самом деле этот график не дает нам столько информации, сколько в плоскости xb и xc.

Тем не менее, мы можем заметить, что при c = 0 график

никогда не пересекает ось x (зеленая), тогда как на всех остальных графиках половина из них пересекает ось x.

Для c> 0, когда x стремится к 0, y стремится к отрицательной бесконечности; для c <0, когда x стремится к 0, y стремится к положительной бесконечности.

При более внимательном рассмотрении квадратного уравнения мы находим, что,

, в отличие от остальных уравнений, всегда имеет реальные решения, потому что, когда x = 0, y может принимать любое значение.

Но для остальных уравнений для некоторых значений y уравнение имеет два действительных корня или один действительный корень; тогда как для других значений y уравнение может не иметь действительных корней.

Мы наконец подошли к концу этого долгого расследования.

Надеюсь, эта статья даст вам больше информации о взаимосвязях между свойствами квадратного уравнения и тем, как выглядит его график.

---

Вернуться на главную

.