2{(x+1)}+10≤11 \lg{(x+1)}\)
Содержание
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
Примеры:
|
Решение:
|
Решение:
|
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства. 2-24≥-x\) невозможен.
2-24≥-x\) невозможен.
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
Раскладываем левую часть неравенства на множители. |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
Ответ: \((0; \frac{1}{3})∪(9;∞)\)
Смотрите также:
Показательные неравенства
Скачать статью
Логарифмические неравенства — подготовка к ЕГЭ по Математике
Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.
Также мы используем определение логарифма и основные логарифмические формулы.
Давайте повторим, что такое логарифмы:
Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .
При этом
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Алгоритм решения логарифмических неравенств
Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.
И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .
Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение
Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.
Перейдем к практике. Как всегда, начнем с самых простых неравенств.
1. Рассмотрим неравенство log3x > log35.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.
Только при таких x неравенство имеет смысл.
Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»
Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?
Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.
Так почему же мы все-таки «отбрасываем логарифмы»?
Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log3x1 > log3x2 следует, что x1 > x2.
Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.
Итак, x > 5.
Следующее логарифмическое неравенство тоже простое.
2. log5(15 + 3x) > log52x
Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому
Решая эту систему, получим: x > 0.
Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.
15 + 3x > 2x.
Получаем: x > −15.
Итак,
Ответ: x > 0.
А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.
Приведем пример.
3.
Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть
Решая эту систему, получим: x > 4,5.
Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента:
А это значит, что большему значению функции отвечает меньшее значение аргумента:
И если , то
2x − 9 ≤ x.
Получим, что x ≤ 9.
Учитывая, что x > 4,5, запишем ответ:
x ∈ (4,5; 9].
В следующей задаче показательное неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.
Теперь более сложные неравенства:
4. Решите неравенство
Ответ:
5. Решите неравенство
ОДЗ:
Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.
Сделаем замену
Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!
Ответ:
6.
Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:
Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:
Упростим эту систему:
Это область допустимых значений неравенства.
Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что
В данном случае удобно перейти к основанию 4.
Сделаем замену
Упростим неравенство и решим его методом интервалов:
Итак,
Вернемся к переменной x:
Мы добавили условие x > 0 (из ОДЗ).
Ответ:
7. Следующая задача тоже решается с помощью метода интервалов
Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае
Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:
Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:
Видим, что условие (то есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение неравенства.
Что ж, это упрощает решение неравенства.
Решаем неравенство методом интервалов:
Ответ:
Получилось? Что же, повышаем уровень сложности:
8. Решите неравенство:
Неравенство равносильно системе:
Ответ:
9. Решите неравенство:
Выражение 5—x2навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:
Поскольку показательная функция принимает только положительные значения, t > 0. Тогда
Неравенство примет вид:
Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, (t − 3) (59 · t − 1) > 0
Если это условие выполнено, то и частное будет положительным.
А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625t − 2)2.
Это означает, что 625t − 2 ≠ 0, то есть
Аккуратно запишем ОДЗ
и решим получившуюся систему, применяя метод интервалов.
Итак,
Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:
«Отбросим» логарифмы. Знак неравенства сохраняется.
Перенесем все в левую часть и разложим по известной формуле разности квадратов:
Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.
Получим, что
Вернемся к переменной x
Поскольку
Ответ:
10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.
Запишем ОДЗ:
Воспользуемся формулой и перейдем к основанию 10:
Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию
Выражение в левой части неравенства можно записать как функцию
Эта функция может менять знак в точках, где она равна нулю или не существует.
Выражение lg |x − 3| равно нулю, если |x − 3| = 1, то есть x = 4 или x = 2.
Выражение lg (|x| − 2) равно нулю, если |x| = 3, то есть в точках 3 и −3.
Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.
Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.
Ответ:
11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.
Запишем ОДЗ:
Итак, Это ОДЗ.
Обратите внимание, что .
Это пригодится вам при решении неравенства.
Упростим исходное неравенство:
Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x < 18.
В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x < 18.
Как же быть? Вспомним, что (x — 18)2=(18 — x)2. Тогда:
Вторая ловушка – попроще. Запись означает, что сначала надо вычислить логарифм, а потом возвести полученное выражение в квадрат. Поэтому:
Дальше – всё просто. Сделаем замену
Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда
— не удовлетворяет ОДЗ;
Ответ: 2.
Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье.
Читайте также: Неравенства. Метод замены множителя (метод рационализации)
Метод замены множителя (метод рационализации)
Логарифмические неравенства повышенной сложности
Решение логарифмических неравенств
Решение логарифмических неравенств имеет много общего с решением показательных неравенств:
а) При переходе от логарифмов к выражениям, стоящим под знаком логарифма, мы также сравниваем основание логарифма с единицей;
б) Если мы решаем логарифмическое неравенство с помощью замены переменных, то нужно решать относительно замены до получения простейшего неравенства.
Однако, есть одно очень важное отличие: поскольку логарифмическая функция имеет ограниченную область определения, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, необходимо учитывать область допустимых значений.
Если при решении логарифмического уравнения можно найти корни уравнения, а потом сделать проверку, то при решении логарифмического неравенства этот номер не проходит: при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать ОДЗ неравенства.
Итак. Простейшее логарифмическое неравенство имеет вид:
V , где V — один из знаков неравенства: <,>, ≤ или ≥.
Если основание логарифма больше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
равносильно системе:
Если основание логарифма больше нуля и меньше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
равносильно системе:
Рассмотрим примеры решения логарифмических неравенств.
1. Решим неравенство:
Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:
Перейдем к системе:
Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.
Решим систему неравенств:
Корни квадратного трехчлена: ,
Отсюда:
Ответ:
2. Решим неравенство:
Мы видим, что в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:
Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).
Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:
Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма. Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:
Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:
Отсюда:
Ответ:
3. Решим неравенство:
В нашем неравенстве логарифм стоит в квадрате, поэтому это логарифмическое неравенство мы будем решать с помощью замены переменных.
Сначала приведем логарифмы к одному основанию:
Введем замену переменных:
.
Получим квадратное неравенство:
Значит, .
Запишем это двойное неравенство в виде системы:
Вот только теперь, когда мы получили систему простейших неравенств относительно , мы можем вернуться к исходной переменной.
Перейдем к выражениям, стоящим под знаком логарифма:
Последнее неравенство системы — это ОДЗ неравенства. Заметим, что оно выполняется, если выполняется второе неравенство системы, поэтому нет необходимости его решать.
Решим систему.
Первое неравенство системы преобразуется к виду
Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значениях .
Второе неравенства преобразуется к виду , отсюда
Ответ:
И.В. Фельдман, репетитор по математике.
Урок 28. логарифмические неравенства — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №28.Логарифмические неравенства.
Перечень вопросов, рассматриваемых в теме
1) Понятие логарифмического неравенства
2) Основные способы решения логарифмических неравенств
Глоссарий по теме
Логарифмические неравенства – это неравенства вида , где и неравенства, сводящиеся к этому виду.
Решение логарифмических неравенств:
(знак неравенства сохраняется)
(знак неравенства меняется)
Основная литература:
Колягин Ю.М., Ткачева М.В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.
Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.
Дополнительная литература:
Лысенко Ф. Ф. Тематические тесты. Математика. ЕГЭ-2008. Под редакцией – Ростов-на-Дону: Легион, 2007. 256 с.
Шестаков С.А., Трепалин А.С., Ященко И.В., Захаров П.И.; под ред. Ященко И. В. ЕГЭ 2016. Математика. 20 вариантов тестов. Тематическая рабочая тетрадь – М.: МЦНМО, Издательство «Экзамен», 2016. – 295, [1] c.
Теоретический материал для самостоятельного изучения
Логарифмические неравенства – это неравенства вида , где и неравенства, сводящиеся к этому виду.
Способы решения логарифмических неравенств основаны на монотонности логарифмической функции в зависимости от основания логарифма. Функция возрастает, если и убывает, если .
(знак неравенства сохраняется)
(знак неравенства меняется)
Пример 1.
Решить неравенство.
Решение:
Основание логарифма 3 > 1, значит используем 1 схему.
; ; .
Ответ: (6; 14)
Пример 2.
Решить неравенство .
Решение:
Выполним преобразование правой части: заменим и используем свойство суммы логарифмов.
Основание логарифма , значит используем 2 схему.
;; ; .
Ответ:
Решение логарифмических уравнений и неравенств встречается в заданиях ГИА.
Задача 1. Решите неравенство
.
Решение:
Замена: .
Рассмотрим функцию: .
Нули:
Обратная замена:
Используем определение логарифма, учитывая, что основание 2 >1.
; ; ;
Ответ:
Задача 2. Решите неравенство
.
Решение:
;
Квадраты противоположных чисел равны, поэтому применяя свойство логарифма степени, не забываем поставить модуль.
;
Т. к. основание логарифма содержит переменную, необходимо рассмотреть 2 случая.
1.
; ; ;
; .
2. .
; ; ;
; .
Ответ:
Примеры и разбор решения заданий тренировочного модуля
№1.Найдите наименьшее целочисленное решение неравенства .
Решение:
- Упростим левую часть неравенства, используя основное логарифмическое тождество:
- Приведем подобные слагаемые.
- Разделим неравенство на 2. (2 > 0, знак неравенства не меняем):
- Основание логарифма 0 <0,5< 1, значит логарифмическая функция убывает и знак неравенства меняем:
; ;
Ответ: 3.
№2Сколько натуральных чисел являются решениями неравенства
.
Решение:
- Двойное неравенство равносильно системе неравенств:
- Основание логарифма 0 <0,5< 1, значит логарифмическая функция убывает и знак неравенства меняем:
; ; ; .
Ответ: 1. {-1}$ или $x-1<2 \Rightarrow x<3$
{-1}$ или $x-1<2 \Rightarrow x<3$
В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$
Ответ. $x \in(1 ; 3)$
Больше примеров решений
2. Решение логарифмического неравенства вида $$\log _{a} f(x) \lt \log _{a} g(x)$$ равносильно решению следующих систем:
а) б)
Неравенство $\log _{a} f(x)>\log _{a} g(x)$ в каждом из двух случаев сводится к одной из систем:
$$00
\end{array}\right.$$
$$a>1:\left\{\begin{array}{l}
f(x)>g(x) \\
g(x)>0
\end{array}\right.$$
Слишком сложно?
Логарифмические неравенства не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Решить неравенство $\log _{5} 5>\log _{5} x$
Решение. Данное неравенство равносильно системе:
$$\left\{\begin{array}{l}
5>x, \\
x>0
\end{array} \Rightarrow\left\{\begin{array}{l}
x0
\end{array} \Rightarrow x \in(0 ; 5)\right. {\log_ba}\\
{\log_ba}\\
&&\\
\log_a{bc}=\log_a{|b|}+\log_a{|c|}&& \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\\
&&\\
\log_ab\cdot \log_bc=\log_ac & \Longleftrightarrow & \log_bc=\dfrac{\log_ac}{\log_ab}\\
&&\\
\log_ab\cdot \log_ba=1 & \Longleftrightarrow & \log_ab=\dfrac1{\log_ba}\\
&&\\
\hline
\end{array}}\]
\(\blacktriangleright\) Стандартное логарифмическое неравенство \[{\Large{\log_a{h(x)}\geqslant \log_a{g(x)} \quad
(*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
Логарифмическая функция \(f(x)=\log_ax\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех положительных \(x\) (то есть ее область определения \(x\in (0;+\infty)\)).
На графике приведен пример возрастающей логарифмической функции \(f_1(x)=\log_2x\) и убывающей логарифмической функции \(f_2(x)=\log_{\,0,5}x\).
Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).
Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).
Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:
если \({\large{a>1}}\), то данное неравенство равносильно системе (не забываем про ОДЗ!) \[{\Large{\begin{cases} h(x)\geqslant g(x)\\ g(x)>0 \end{cases}}}\] Заметим, что условие \(h(x)>0\) учитывается автоматически в такой системе, т.к. если \(h\geqslant g\), а \(g>0\), то и \(h>0\).
если \({\large{0<a<1}}\), то данное неравенство равносильно системе \[{\Large{\begin{cases} h(x)\leqslant g(x)\\ h(x)>0 \end{cases}}}\]
Заметим, что условие \(g(x)>0\) учитывается автоматически в такой системе. 2-9>0 \Leftrightarrow
2-9>0 \Leftrightarrow
(x-3)(x+3)>0 \Rightarrow x\in (-\infty;-3)\cup(3;+\infty)\).
Таким образом, после пересечения решений обоих неравенств системы решением исходного неравенства будут \(x\in
(-\infty;-3)\cup(3;+\infty)\).
\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{\log_{h(x)}{f(x)}\geqslant \log_{h(x)}{g(x)}}}\] (на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
То есть когда в основании логарифма находится не конкретное число, а функция, зависящая от \(x\).
Данное неравенство равносильно совокупности: \[{\Large{\left[\begin{gathered}
\begin{aligned}
&\begin{cases}
h(x)>1\\
f(x)\geqslant g(x)\\
g(x)>0
\end{cases}\\[4pt]
&\begin{cases}
0<h(x)<1\\
f(x)\leqslant g(x)\\
f(x)>0
\end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
Иногда удобно выписать ОДЗ отдельно. Тогда неравенство будет равносильно системе: \[{\Large{\begin{cases}
f(x)>0 \quad (\textbf{ОДЗ})\\
g(x)>0 \quad (\textbf{ОДЗ})\\[3pt]
\left[\begin{gathered}
\begin{aligned}
&\begin{cases}
h(x)>1\\
f(x)\geqslant g(x)
\end{cases}\\[3pt]
&\begin{cases}
0<h(x)<1\\
f(x)\leqslant g(x)
\end{cases}
\end{aligned}
\end{gathered}
\right. 2\geqslant 0
2\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
(x-1)(x+1)>0\\
(x+1-x)(x+1+x)\leqslant 0
\end{cases}\\[2pt]
&\begin{cases}
(x-1)(x+1)<0\\
x\ne 0\\
(x+1-x)(x+1+x)\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad\]
\[\quad \Leftrightarrow \quad
\left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x\in (-\infty;-1)\cup(1;+\infty)\\
x\in (-\infty;-\dfrac12\big]
\end{cases}\\[2pt]
&\begin{cases}
x\in (-1;1)\\
x\ne 0\\
x\in\big[-\dfrac12;+\infty)
\end{cases}
\end{aligned}
\end{gathered}
\right. \quad \Leftrightarrow \quad x\in
\Big(-\infty;-1\Big)\cup\Big[-\dfrac12;0\Big)\cup\Big(0;1\Big)\]
Пересекая данный ответ с ОДЗ (\(x\ne -1\)), получим тот же ответ.
\(\blacktriangleright\) Таким образом, как правило, для того, чтобы система (совокупность) не выглядела слишком огромной, удобно записывать ОДЗ неравенства отдельно, а затем просто пересекать решение системы (совокупности) с этим ОДЗ. Что мы и сделали в примере \(3\).
Что мы и сделали в примере \(3\).
Как решать логарифмические неравенства: формулы, примеры
Логарифмическое неравенство – это неравенство, в котором неизвестная величина находится под знаком логарифма.
Формулы логарифмических неравенств
1. Значение логарифма больше нуля (loga x > 0) при условии, что и основание, и подлогарифмическое выражение находятся по одному сторону от числа 1. Здесь могут быть два варианта:
- a>1 и x>1
- 0<a<1 и 0<x<1
Соответственно, если a и x стоят по разные стороны от единицы, значение логарифма logax отрицательно.
2. Для логарифмического неравенства loga f(x) > b справедливо:
- f(x) < ab при 0<a<1
- f(x) > ab при a>1
Аналогичным образом, для logaf(x) < b верно:
- f(x) > ab при 0<a<1
- f(x) < ab при a>1
3. Неравенство вида loga f(x) > loga g(x) сводится к:
Неравенство вида loga f(x) > loga g(x) сводится к:
- 0 < f(x) < g(x) при 0<a<1
- f(x) > g(x) > 0 при a>1
Подобным образом, для loga f(x) < loga g(x) можно утверждать:
- f (x) > g(x) > 0 при 0<a<1
- 0 < f(x) < g(x) при a>1
Примеры заданий
Задача 1
Решите неравенство log0,7(x-3) > 3.
Решение:
Основание логарифма больше нуля, но меньше единицы (0<0,7<1). Применив соответствующую формулу (f(x) < ab при 0<a<1), получаем:
(x-3) < 0,73
(x-3) < 0,343
x<3,343
Одновременно с этим подлогарифмическое выражение любого логарифма должно быть больше нуля. Следовательно, (x-3) > 0, а значит, x>3.
Таким образом, совместив оба условия определяем x∈(3;3,343).
Задача 2
Решите неравенство log28 < log2x.
Решение:
Т.к. основание логарифма больше единицы, для заданного неравенства верно: 0<8<x. То есть x∈(8;∞).
Логарифмических неравенств | Блестящая вики по математике и науке
Имейте в виду, что основание логарифма может быть меньше 1, что связано с равенством
logab = −log1ab, \ large \ log_ab = — \ log _ {\ frac {1} {a}} b, loga b = −loga1 b,
, так что не забывайте об этом футляре!
Решите неравенство
logx + 42 (log22x − 13 + x) <0. \ log _ {\ frac {x + 4} {2}} \ left (\ log_ {2} \ frac {2x-1} {3+ x} \ right) <0. log2x + 4 (log2 3 + x2x − 1) <0.
Во-первых, основание должно быть положительным и не равным 1, поэтому сразу x> −4x> -4x> −4 и x ≠ −2x \ neq -2x = −2.Аналогично, аргумент log22x − 13 + x \ log_2 \ frac {2x-1} {3 + x} log2 3 + x2x − 1 должен быть положительным, поэтому 2x − 1x + 3> 0 ⟹ x> 12 или x <−3 \ frac {2x-1} {x + 3}> 0 \ подразумевает x> \ frac12 \ text {или} x <-3x + 32x − 1> 0⟹x> 21 или x <−3 .
Таким образом, единственные возможных значений xxx — это x> 12 или −4
\ frac12 \, \ text {or} \, -4 21 или −4 Теперь рассмотрим два случая:
Случай 1. 0
В этом случае необходимо, чтобы log22x − 13 + x> 1 \ log_2 \ frac {2x-1} {3 + x}> 1log2 3 + x2x − 1> 1, или 2x − 13 + x > 2 \ frac {2x-1} {3 + x}> 23 + x2x − 1> 2, поэтому 2x − 13 + x − 2 = −73 + x> 0 \ frac {2x-1} {3 + x } -2 = \ frac {-7} {3 + x}> 03 + x2x − 1 −2 = 3 + x − 7> 0.Следовательно, 3 + x3 + x3 + x отрицательно, или x <−3x <-3x <−3. Таким образом, все xxx такие, что −4
Помните, что эта стратегия вычитания двух сторон, а не умножения позволяет избежать рассмотрения дел, связанных с умножением, поскольку больше нет необходимости рассматривать последствия того, что умноженная величина отрицательна.
Случай 2. x + 42> 1 ⟺ x> −2 \ frac {x + 4} {2}> 1 \ iff x> -22x + 4> 1⟺x> −2
В этом случае необходимо, чтобы log22x − 13 + x <1 \ log_2 \ frac {2x-1} {3 + x} <1log2 3 + x2x − 1 <1, или 2x − 13 + x <2 \ frac {2x-1} {3 + x} <23 + x2x − 1 <2, поэтому 2x − 13 + x − 2 = −73 + x <0 \ frac {2x-1} {3 + x } -2 = \ гидроразрыва {-7} {3 + x} <03 + x2x − 1 −2 = 3 + x − 7 <0.Это всегда верно, поскольку x> −2x> -2x> −2, поэтому любой x> −2x> -2x> −2 будет работать. Однако помните, что только x> 12 или −4
\ frac12 \ text {или} -4 21 или −4 12x> \ frac12x> 21 делать. Следовательно, набор решений —
х> 12, -4 <х <-3. □ x> \ frac12, \ -4
21, −4
Типичная стратегия решения проблем использует формулу замены основания, чтобы все логарифмы имели одинаковое основание.Это значительно упрощает применение других неравенств, таких как AM-GM. 2> \ log n \ log (n + 2).\ end {align} logn (n + 1)> logn + 1 (n + 2) ⟺lognlog (n + 1)> log (n + 1) log (n + 2) ⟺ (log (n +1)) 2> lognlog (n + 2).
2> \ log n \ log (n + 2).\ end {align} logn (n + 1)> logn + 1 (n + 2) ⟺lognlog (n + 1)> log (n + 1) log (n + 2) ⟺ (log (n +1)) 2> lognlog (n + 2).
Произведение логарифмов — отличный знак для использования AM-GM, поскольку с суммой логарифмов очень легко работать.
В частности,
logn + log (n + 2) 2≥lognlog (n + 2) ⟹ log (n (n + 2)) 2≥lognlog (n + 2). \ Frac {\ log n + \ log (n + 2)} {2} \ geq \ sqrt {\ log n \ log (n + 2)} \ подразумевает \ frac {\ log \ big (n (n + 2) \ big)} { 2} \ geq \ sqrt {\ log n \ log (n + 2)}. 2logn + log (n + 2) ≥lognlog (n + 2) ⟹2log (n (n + 2)) ≥lognlog ( п + 2).2> \ log n \ log (n + 2), (журнал (n + 1)) 2> lognlog (n + 2),
, доказывающее исходное неравенство. □ _ \ квадрат □
Логарифмические неравенства — Бесплатные задания по математике
Логарифмические неравенства — это неравенства, в которых одна или обе стороны содержат логарифм. Решая логарифмические неравенства, мы должны помнить следующие факты:
Решая логарифмические неравенства, мы должны помнить следующие факты:
1) Если $ a> 1 $ и $ x Если $ a> 1 $ и $ log_ {a} x Точнее, логарифмическая функция $ f (x) = log_ {a} x $ — это , монотонно возрастающая для $ a> 1 $ . 2) Если $ 0 log_ {a} y $. Если $ 0 log_ {a} y $, то $ x Точнее, логарифмическая функция $ f (x) = log_ {a} x $ — это , монотонно убывающая для $ 0 . 3) аргумент логарифма должен быть положительным числом ! Логарифмические неравенства — те же основания Пример 1: $$ log_ {2} (2x + 1)> log_ {2} (x + 3) $$ Решение: База равна $ a = 2 $, что больше 1 $. $$ 2x + 1> x + 3 $$ $$ 2x-x> 3-1 $$ $$ x> 2 $$ Чек: 1) $ 2x + 1> 0 \ Rightarrow 2x> -1 \ Rightarrow x> — \ frac {1} {2} $ 2) $ x + 3> 0 \ Rightarrow x> -3 $ У нас $ x> 2 $, поэтому оба условия выполнены. Решение — $ x> 2 $, т.е. $ x \ in \ left <2, + \ infty \ right> $. Пример 2: $$ журнал _ {\ frac {1} {2}} (x + 3)> журнал _ {\ frac {1} {2}} (2x + 1) $$ Решение: База равна $ a = \ frac {1} {2} $, что меньше $ 0 $.2> -2, $$ , что выполняется для каждого $ x \ in \ mathbf {R} $. Следовательно, каждое $ x \ in \ mathbf {R} $ является решением. Пример 4: $$ log_ {7} (x + 6)> log_ {5} (x + 6) $$ Решение: Здесь мы должны использовать правило изменения базы , то есть $ log_ {a} x = \ frac {log_ {b} x} {log_ {b} a} $ $$ \ frac {log (x + 6)} {log7}> \ frac {log (x + 6)} {log5} $$ $$ log5 \ cdot log (x + 6)> log7 \ cdot log (x + 6) $$ $$ (log5-log7) \ cdot log (x + 6)> 0 $$ Поскольку $ log5-log7 $ — отрицательное число, $ log (x + 6) $ также должно быть отрицательным. $$ журнал (x + 6) Поскольку база равна $ a = 10> 0 $, $$ x + 6 <1 $$ $$ x <-5 $$ Чек: $$ x + 6> 0 \ Rightarrow x> -6 $$ Поскольку у нас $ x <-5 $, решение будет $ -6 Пример 5: $$ log_ {5} (x + 3)> 1 $$ Решение: В этом неравенстве есть логарифм только с одной стороны.Мы хотели бы иметь логарифм с одинаковым основанием с обеих сторон. Для этого воспользуемся правилом (логарифм от основания ) $$ log_ {a} a = 1 $$ Теперь у нас $$ log_ {5} (x + 3)> log_ {5} 5 $$ База равна $ a = 5 $, что больше 0 $. Это означает, что $ x + 3> 5 $. Следовательно, $ x> 2 $. Чек: $ x + 3> 0 \ Rightarrow x> -3 $ У нас $ x> 2 $, значит, условие выполнено. Теперь у нас есть логарифмы с обеих сторон, которые мы хотели.2} {t-1} <0 $$ Эта дробь, очевидно, является отрицательным числом, а значение числителя — положительным числом. Это означает, что знаменатель принимает отрицательное число, т.е. . $$ t-1 <0 $$ $$ t <1, $$ , что означает $$ logx <1 $$ $$ logx Так как база равна $ a = 10> 1 $, $$ x <10. $$ Чек: $$ x> 0 $$ Так как у нас $ x <10 $, решение будет $ 0 Давайте сначала сформулируем некоторые конкретные определения, которые различают экспоненциальные и логарифмические неравенства. Проще говоря, экспоненциальных неравенства имеют показатели степени, а логарифмических неравенства имеют логарифмы. Прежде чем показывать метод решения, давайте решим аналогичную математическую задачу, начав с ответа. Звучит интересно? Что 25? Ответ: 2 (2) (2) (2) (2) = 32. Это ответ, но в чем вопрос? Возникает вопрос: найти x , чтобы 2 x > 32. Поскольку 25 равно 32, подойдет любое значение x , большее 5. Теперь о способе решения: Шаг 1: Замените неравенство знаком равенства. Из 2 x > 32 запись Шаг 2: В показателях степени используйте логарифмы. Взять журнал: Шаг 3: Решить. Из собственности, войдите x = x войдите a, вынесите x вперед: Разделить на лог 2: Шаг 4: Оценить. Используя калькулятор, лог 32 = 1,505 и лог 2 = 0.301. Таким образом, x = 1,505 / 0,301 = 5. Шаг 5: Определите домен. Какие значения x дают 2 x > 32? Попробуйте число больше 5, например, x = 6. Тогда 26 = 64 больше 32. Итак, числа больше 5 работают. На всякий случай, как насчет числа меньше 5, например, x = 4? Итак, 24 = 16 не больше 32. Таким образом, x > 5 удовлетворяет неравенству 2 x > 32. Шаг 6: (необязательный шаг) График. В числовой строке укажите значения решения для x : Кружок показывает пропущенное значение при x = 5, а значения x простираются до положительной бесконечности. Значение 5 не включено, потому что исходное неравенство было строго «больше чем», а не «больше или равно». Логарифмы и экспоненты — это обратные операции .Другими словами, одна операция отменяет другую. Например, 102 = 100, а журнал 100 = 2. Также 10log x = x . Примечание: log — это база 10. Найдите значения x для log x <2. Шаг 1: Замените неравенство знаком равенства. Из журнала x <2, записать Шаг 2: Используя логарифм, возвести в степень основания. Возвести в степень 10: Шаг 3: Решить. Используя обратное свойство, alog x = x : Шаг 4: Оценить. Шаг 5: Определите домен. x = 101, log 101 = 2,004 больше 2 и не в домене. Шаг 6: График. Кружки показывают недостающие значения при x = 0 и x = 100.0 не включен, потому что log (0) не определен, а 100 не включен, потому что исходная проблема неравенства указала, что меньше, чем ‘, а не’ меньше или равно ‘. Давайте вернемся к примеру, с которого мы начали наш урок, посмотрев на Саманту, изучающую сохранение стоимости ее нового автомобиля. Она может начать с написания уравнения, основанного на амортизации 16,8% в год. За сколько лет текущая стоимость больше половины того, что заплатила Саманта? Используя неравенство, найдите x , где y ≥.5лет. От y ≥ .5 лет, заменить y o (.832) x на y : y o (.832) x ≥ .5yo Отменить yo: (.832) x ≥ 0,5 Это экспоненциальное неравенство, которое необходимо решить. Поскольку начальное значение больше не находится в неравенстве, рекомендованная производителем розничная цена не повлияет на результаты. Шаг 1: Заменить неравенство знаком равенства. Из (.832) x ≥ .5 запись: Шаг 2: Для экспоненты используйте логарифмы. Шаг 3: Решить. Вынесите x вперед: Разделить на лог. 832: Шаг 4: Оценить. лог. 5 = -0,301 и лог. 832 = -0,0799. Таким образом, x = -0,301 / -0,0799 = 3,77 года. Шаг 5: Определите домен. Проверьте число больше 3,77, например, x = 4. Тогда (0,832) 4 = 0,48 меньше 0,5. Числа больше 3,77 не работают. Как насчет числа меньше 3,77, например x = 3? Хорошо, (.832) 3 = .58 работает, потому что .58 больше, чем .5. Шаг 6: График. Значения x = 0 и x = 3. Саманта может хранить автомобиль в течение 3,77 года, в течение которых стоимость автомобиля будет ≥ половины его первоначальной стоимости. Давайте рассмотрим то, что мы узнали. Экспоненциальные неравенства содержат экспоненты, а логарифмические неравенства содержат логарифмы.Оба используют один из четырех типов неравенства : больше, больше или равно, меньше и меньше или равно. Логарифмирование и возведение в степень — это обратные операции , поскольку одна операция отменяет другую. Это ясно видно из 10log x = x . Шаги решения для этого процесса следующие: Шаг 1: Замените неравенство знаком равенства. Шаг 2: Для экспоненты используйте логарифмы; с логарифмом возвести в степень основания. Шаг 3: Решить. Шаг 4: Оценить. Шаг 5: Определите домен. Шаг 6: График. Решая логарифмические неравенства, важно понимать направление изменения неравенства, если основание логарифмов меньше 1. Решить \ (\ log_ {3} {(x-3)} \ gt \ log_ {3} {(x-1)}. \) \ (\ begin {align} \ displaystyle \ require {color} Решите \ (\ log_ {3} {(x-3)} \ gt \ log_ {9} {(x-1)} \). Алгебра абсолютных значений Алгебраические дроби Биномиальное расширение Цепи Правило Круг Геометрия Общая разность Общее отношение Составной угол Формула Циклическое четырехстороннее дифференцирование Дискриминант Двойной угол Формула Уравнение Экспонента Экспоненциальная функция Факториалы Факториалы Геометрическая последовательность Геометрические ряды Индексные законы Интегрирование неравенства Кинематика Преобразование длины Логарифм Логарифмические функции Математическая индукция Идеальная квадратная факторизация Правило квадратичной квантования Правило скетча Правило корректора квадратов Преобразование Сурда Тригонометрические функции Тригонометрические свойства Объем Используя свойства логарифма, мы можем разделить начальный член на две части (спасибо @egreg за указание на точку об абсолютных значениях, которая часто упускается из виду, но очень важна): $$ \ log (3 — 2x) (1 — x) \ geq 0 \ подразумевает \ log | 3 — 2x | + \ log | 1 — х | \ geq 0 \ подразумевает $ $$ \ log | 3 — 2x | \ geq — \ log | 1 — x | \ подразумевает \ log | 3 — 2x | \ geq \ log | 1 — x | ^ {- 1} \ подразумевает $$ $$ 3 ^ {\ log | 3 — 2x |} \ geq 3 ^ {\ log | 1 — x | ^ {- 1}} \ подразумевает | 3 — 2x | \ geq | 1 — x | ^ {- 1} \ подразумевает $$ $$ | 3-2x || 1-x | \ geq 1 $$ Теперь нам нужно немного поработать, чтобы определить правильный домен. $$ <----------- \ пробел \ пробел 1 \ пробел ++++ ---- \ пробел \ пробел \ гидроразрыв {3} {2} \ пробел ++++++ ++++> $ Для значений $ x <1 $ имеем: $$ \ bigl (- (3-2x) \ bigr) \ bigl (- (1-x) \ bigr) \ geq 1 \ подразумевает (3-2x) (1-x) \ geq 1 $$ Из приведенного выше ограничения у нас должно быть $ x \ leq 1/2 $.{2} -5x + 4 \ leq 0 \ подразумевает $ $$ x = \ frac {5 \ pm \ sqrt {25–32}} {4} \ подразумевает x \ in \ mathbb {C} $$ Таким образом, на этом интервале нет реального решения. И, наконец, для нашего последнего интервала мы имеем то же самое, что и первый интервал выше, но с оговоркой, что $ x> 3/2 $. Таким образом, получаем $ x \ geq 2 $. Итак, домен $ (- \ infty, \ tfrac {1} {2} \ bigr] \ cup [2, \ infty) $. Обновление $$ \ bigl [\ log (3 — 2x) \ bigr] (1 — x) \ quad \ text {эквивалентно} \ quad (1-x) \ log (3-2x) $$ В разделе \ ref {ExpEquations} мы решили уравнения и неравенства, включающие экспоненциальные функции, используя одну из двух основных стратегий. Теперь мы обратим наше внимание на уравнения и неравенства, включающие логарифмические функции, и неудивительно, что есть две основные стратегии на выбор. Например, предположим, что мы хотим решить \ (\ log_ {2} (x) = \ log_ {2} (5) \).{3} = x \) или \ (x = 8 \). Мы резюмируем два распространенных способа решения логарифмических уравнений ниже. Этапы решения уравнения с логарифмическими функциями Пример \ (\ PageIndex {1} \): Решите следующие уравнения.2-3 \ right)} {\ ln (117)} \) и мы видим, что они пересекаются только в точке \ (x = -4 \). \ [\ begin {array} {rclr} 1 & = & 2 \ log_ {2} (x) — 2 \ left (\ frac {1} {2} \ log_ {2} (x + 1) \ right ) & \\ 1 & = & 2 \ log_ {2} (x) — \ log_ {2} (x + 1) & \\ 1 & = & \ log_ {2} \ left (x ^ 2 \ right) — \ log_ {2} (x + 1) & \ text {Правило мощности} \\ 1 & = & \ log_ {2} \ left (\ dfrac {x ^ {2}} {x + 1} \ right) & \ текст {Правило частного} \\ \ end {array} \] Переписывая это в экспоненциальной форме, мы получаем \ (\ frac {x ^ {2}} {x + 1} = 2 \) или \ (x ^ 2 -2x-2 = 0 \). По крайней мере, Пример \ ref {LogEqnsEx1} демонстрирует важность проверки на наличие посторонних решений \ footnote {Напомним, что постороннее решение — это полученный аналитически ответ, который не удовлетворяет исходному уравнению.} при решении уравнений, содержащих логарифмы. Несмотря на то, что мы проверили наши ответы графически, посторонние решения легко обнаружить — любое предполагаемое решение, которое вызывает отрицательное число внутри логарифма, необходимо отбросить. Как и в случае с уравнениями в примере \ ref {expeqnsex1}, многое можно узнать, проверив все ответы в примере \ ref {LogEqnsEx1} аналитически. Оставим это читателю и обратим внимание на неравенства, содержащие логарифмические функции. Поскольку логарифмические функции непрерывны в своей области определения, мы можем использовать знаковые диаграммы.2 <2 \ log_ {2} (x) + 3 \) Решение \ item Мы начинаем решать \ (\ frac {1} {\ ln (x) +1} \ leq 1 \), получая \ (0 \) на одной стороне неравенства: \ (\ frac {1} {\ ln (x) +1} — 1 \ leq 0 \). Получение общего знаменателя дает \ (\ frac {1} {\ ln (x) +1} — \ frac {\ ln (x) +1} {\ ln (x) +1} \ leq 0 \), который сводится к \ (\ frac {- \ ln (x)} {\ ln (x) +1} \ leq 0 \) или \ (\ frac {\ ln (x)} {\ ln (x) +1} \ geq 0 \). Мы определяем \ (r (x) = \ frac {\ ln (x)} {\ ln (x) +1} \) и приступаем к поиску области и нулей \ (r \).2 \) находится ниже графика \ (y = g (x) = \ frac {2 \ ln (x)} {\ ln (2)} + 3 \) на интервале решения. В следующем примере мы вновь возвращаемся к понятию pH, впервые представленному в упражнениях в Разделе \ ref {IntroExpLogs}.{-1} (x) \) и проверьте свой ответ графически с помощью калькулятора. Решение Сначала мы пишем \ (y = f (x) \), затем меняем местами \ (x \) и \ (y \) и решаем относительно \ (y \). {\ frac { x} {x + 1}} & \ mbox {Перепишите в виде экспоненциального уравнения.{-1} \) в том же окне просмотра дает Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон Или заполните форму ниже: . Отсюда следует $ 2x + 1> x + 3 $.
Отсюда следует $ 2x + 1> x + 3 $. 0 $$
0 $$ Другие примеры
 {- 2 } $$
{- 2 } $$ Как решить логарифмические и экспоненциальные неравенства — урок математики [видео 2021 года]
Экспоненциальные неравенства
 Оба используют один из четырех типов неравенства. Словами: больше, больше или равно, меньше, меньше или равно.
Оба используют один из четырех типов неравенства. Словами: больше, больше или равно, меньше, меньше или равно.

Логарифмические неравенства
 x = 99, log 99 = 1.995 меньше 2 и находится в домене. Таким образом, наш вывод должен быть x <100. В отличие от экспонент, есть особое соображение с логарифмами: log x действителен для x больше нуля. Таким образом, x <100 и x > 0. Комбинируя эти неравенства, получаем: 0 < x <100.
x = 99, log 99 = 1.995 меньше 2 и находится в домене. Таким образом, наш вывод должен быть x <100. В отличие от экспонент, есть особое соображение с логарифмами: log x действителен для x больше нуля. Таким образом, x <100 и x > 0. Комбинируя эти неравенства, получаем: 0 < x <100. Вернуться к исходному примеру
 Ей нужно рассмотреть уравнение, y = y o (1 -.168) х . Исходное значение — y o, текущее значение — y , а x — количество лет, прошедших с момента покупки. Имеет ли смысл это уравнение? Вначале x = 0 лет и y = y o (1 — 0,168) 0 = y o, как и ожидалось. Через год x = 1 и y = y o (1 — 0,168) 1 = 0,832 y o, что имеет смысл.
Ей нужно рассмотреть уравнение, y = y o (1 -.168) х . Исходное значение — y o, текущее значение — y , а x — количество лет, прошедших с момента покупки. Имеет ли смысл это уравнение? Вначале x = 0 лет и y = y o (1 — 0,168) 0 = y o, как и ожидалось. Через год x = 1 и y = y o (1 — 0,168) 1 = 0,832 y o, что имеет смысл.
 77 включены. Значение 3,77 включено, потому что в неравенстве используется значение «меньше» или «равно», а 0 включен, поскольку начальный момент времени для определения приведенной стоимости автомобиля — это момент, когда Саманта покупает автомобиль в момент, «равный» нулю.
77 включены. Значение 3,77 включено, потому что в неравенстве используется значение «меньше» или «равно», а 0 включен, поскольку начальный момент времени для определения приведенной стоимости автомобиля — это момент, когда Саманта покупает автомобиль в момент, «равный» нулю. Резюме урока

Логарифмические неравенства — iitutor
$$ \ log_ {2} {x} \ lt \ log_ {2 } {y}, \ text {then} x \ lt y \\
\ log_ {0.5} {x} \ lt \ log_ {0.5} {y}, \ text {then} x \ gt y \\
$$
Также область логарифма положительна.
$$ \ log_ {10} {(x-2)}, \ text {then} x-2 \ gt 0 $$ Вопрос 1
\ text {domain:} x-3 & \ gt 0 \ text { или} x-1 \ gt 0 \\
\ text {то есть} x & \ gt 3 \ color {green} \ cdots (1) \\
x-3 & \ gt x-1 \\
x & \ gt 2 \ color {зеленый} \ cdots (2) \\
\, следовательно, x & \ gt 3 & \ color {green} \ text {by (1) и (2)} \\
\ end {выровнено} \\ \) Вопрос 2
 3 \\
3 \\
\ следовательно \ frac {1} {2} & \ lt x \ lt 8 \\
\ end {align} \) логарифмов — Как решить логарифмическое неравенство?
 Ниже мы устанавливаем нашу числовую линию с «поворотными точками» (то есть значениями, которые делают каждое выражение равным нулю), чтобы установить наши интервалы (отрицательные значения слева от $ 1 $ означают, что оба выражения отрицательны, знак $ + — $ в средний означает, что член $ (1-x) $ положительный, а другое выражение отрицательное, и что-либо справа от
Ниже мы устанавливаем нашу числовую линию с «поворотными точками» (то есть значениями, которые делают каждое выражение равным нулю), чтобы установить наши интервалы (отрицательные значения слева от $ 1 $ означают, что оба выражения отрицательны, знак $ + — $ в средний означает, что член $ (1-x) $ положительный, а другое выражение отрицательное, и что-либо справа от
$ \ frac {3} {2} $ означает, что оба выражения положительны.
$$ (2x — 1) (x — 2) \ geq 0 \ подразумевает x \ geq 2 \ space \ space \ space x \ leq 1/2 $$
Я проверил все выше и ниже в поисках такой постановки логарифмической задачи, как эта, и не нашел точных совпадений.Однако, просмотрев сотни задач логарифмирования, я склоняюсь к тому, чтобы НЕ включать $ (1-x) $ в аргумент логарифма. В этом случае решений, предоставленных @ B, Goddard или @egreg, будет достаточно. Обычно в учебниках для устранения двусмысленности эта проблема выглядела бы как одна из следующих:
$$ (т.е. (1 — x) \ space \ text {не является частью аргумента для логарифма}) $$
$$ — \ text {OR} — $$
$$ \ log \ bigl ((3 — 2x) (1 — x) \ bigr) \ quad (я.е. (1 — x) \ space \ text {является частью аргумента логарифма}) $$ 6.
 3: Экспоненциальные уравнения и неравенства
3: Экспоненциальные уравнения и неравенства Чтобы увидеть, что случилось с решением \ (x = 1 \), мы подставляем его в наше исходное уравнение, чтобы получить \ (\ log_ {117} (- 2) = \ log_ {117} (- 2) \). Хотя эти выражения выглядят одинаково, ни одно из них не является действительным числом, \ footnote {Однако они представляют одно и то же \ textbf {семейство} комплексных чисел. Мы останавливаемся на этом и отсылаем читателя к хорошему курсу комплексных переменных.} Что означает, что \ (x = 1 \) не входит в область определения исходного уравнения и не является решением.2 + x-6 = 0 \), что дает \ (x = -3 \) и \ (x = 2 \). Построение графика \ (y = f (x) = \ frac {\ ln (x + 4)} {\ ln (6)} + \ frac {\ ln (3-x)} {\ ln (6)} \) и \ (y = g (x) = 1 \), мы видим, что они пересекаются дважды, в точках \ (x = -3 \) и \ (x = 2 \).
Чтобы увидеть, что случилось с решением \ (x = 1 \), мы подставляем его в наше исходное уравнение, чтобы получить \ (\ log_ {117} (- 2) = \ log_ {117} (- 2) \). Хотя эти выражения выглядят одинаково, ни одно из них не является действительным числом, \ footnote {Однако они представляют одно и то же \ textbf {семейство} комплексных чисел. Мы останавливаемся на этом и отсылаем читателя к хорошему курсу комплексных переменных.} Что означает, что \ (x = 1 \) не входит в область определения исходного уравнения и не является решением.2 + x-6 = 0 \), что дает \ (x = -3 \) и \ (x = 2 \). Построение графика \ (y = f (x) = \ frac {\ ln (x + 4)} {\ ln (6)} + \ frac {\ ln (3-x)} {\ ln (6)} \) и \ (y = g (x) = 1 \), мы видим, что они пересекаются дважды, в точках \ (x = -3 \) и \ (x = 2 \). {3} = \ frac { x + 3} {6-x} \] Это сводится к линейному уравнению \ (8 (6-x) = x + 3 \), которое дает нам \ (x = 5 \).Когда мы строим график \ (f (x) = \ frac {\ ln (x + 3)} {\ ln (2)} \) и \ (g (x) = \ frac {\ ln (6-x)} { \ ln (2)} + 3 \), мы находим, что они пересекаются в точке \ (x = 5 \).
{3} = \ frac { x + 3} {6-x} \] Это сводится к линейному уравнению \ (8 (6-x) = x + 3 \), которое дает нам \ (x = 5 \).Когда мы строим график \ (f (x) = \ frac {\ ln (x + 3)} {\ ln (2)} \) и \ (g (x) = \ frac {\ ln (6-x)} { \ ln (2)} + 3 \), мы находим, что они пересекаются в точке \ (x = 5 \). Используя формулу корней квадратного уравнения, получаем \ (x = 1 \ pm \ sqrt {3} \). Построение графика \ (f (x) = 1 + \ frac {2 \ ln (x + 1)} {\ ln (4)} \) и \ (g (x) = \ frac {2 \ ln (x)} { \ ln (2)} \), мы видим, что графики пересекаются только в точке \ (x = 1 + \ sqrt {3} \ приблизительно 2.732 \). Решение \ (x = 1 — \ sqrt {3} <0 \), что означает, что если подставить в исходное уравнение, член \ (2 \ log_ {2} \ left (1 - \ sqrt {3} \ right) \) не определено.
Используя формулу корней квадратного уравнения, получаем \ (x = 1 \ pm \ sqrt {3} \). Построение графика \ (f (x) = 1 + \ frac {2 \ ln (x + 1)} {\ ln (4)} \) и \ (g (x) = \ frac {2 \ ln (x)} { \ ln (2)} \), мы видим, что графики пересекаются только в точке \ (x = 1 + \ sqrt {3} \ приблизительно 2.732 \). Решение \ (x = 1 — \ sqrt {3} <0 \), что означает, что если подставить в исходное уравнение, член \ (2 \ log_ {2} \ left (1 - \ sqrt {3} \ right) \) не определено. Авторы и авторство
Использование логарифмов для решения экспоненциальных уравнений и неравенств
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
в виде
ChillingEffects.org.
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

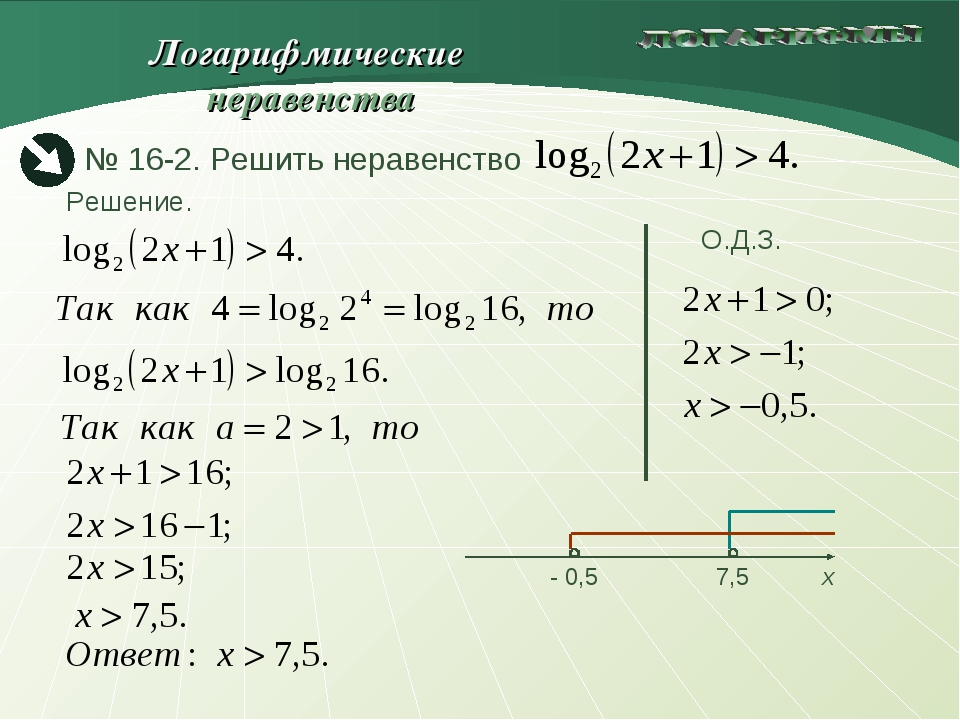 {-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).
{-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).

 2-t-2>0\)
2-t-2>0\)
