Любую ли трапецию можно вписать в окружность: В любую равнобедренную трапецию можно вписать окружность — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Анализ геометрических высказываний. ОГЭ по математике — Разное

Утверждение	Верно?
Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.	Да
Внешний угол треугольника больше каждого не смежного с ним внутреннего угла.	Да
В прямоугольном треугольнике катет больше гипотенузы.	Нет
В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший.	Да
Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам.	Нет
Биссектриса равнобедренного треугольника, проведённая из вершины перпендикулярна основанию.	Да
Биссектриса треугольника делит пополам сторону, к которой проведена?	Нет
Биссектриса угла делит угол пополам.	Да
Биссектриса угла любого параллелограмма является его диагональю.	Нет
Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.	Да
Биссектрисы смежных углов взаимно перпендикулярны.	Да
Биссектрисы треугольника не могут пересекаться в одной точке	Нет
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, описанной около этого треугольника.	Нет
Биссектрисы треугольника пересекаются в центре его вписанной окружности.	Да
Биссектрисы углов параллелограмма прилежащих к одной стороне, пересекаются под прямым углом.	Да
Вертикальные углы равны.	Да
В каждом треугольнике углы при основании равны.	Нет
В квадрате диагонали пересекаются под прямым углом.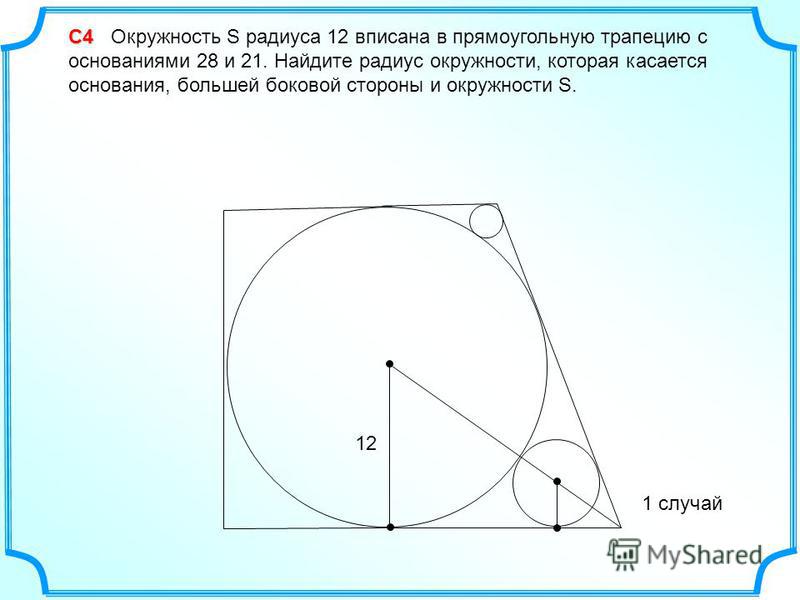	Да
В любой выпуклый семиугольник можно вписать окружность.	Нет
В любой прямоугольник можно вписать окружность.	Нет
В любой прямоугольный треугольник можно вписать окружность.	Да
В любой ромб можно вписать окружность.	Да
В любой трапеции диагонали перпендикулярны.	Нет
В любой трапеции диагонали равны.	Нет
В любой треугольник можно вписать окружность.	Да
В любой четырёхугольник можно вписать не более одной окружности.	Да
В любой четырёхугольник можно вписать окружность.	Нет
В любом выпуклом четырёхугольнике все углы острые.	Нет
В любом выпуклом четырёхугольнике все углы прямые.	Нет
В любом выпуклом четырёхугольнике все углы тупые.	Нет
В любом описанном около окружности четырехугольнике суммы противоположных сторон равны.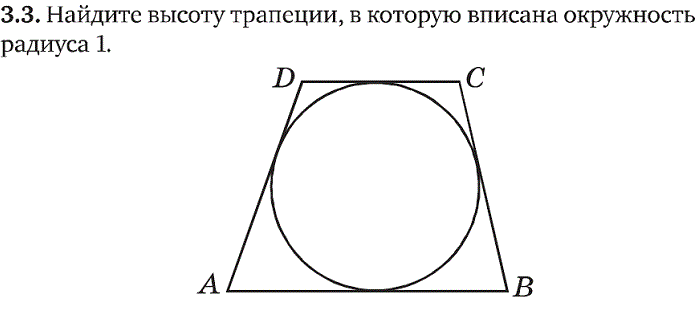	Да
В любом описанном четырёхугольнике сумма противоположных углов равна 180°.	Да
В любом параллелограмме диагонали равны.	Нет
В любом параллелограмме диагонали точкой пересечения делятся пополам.	Да
В любом прямоугольнике все стороны равны.	Нет
В любом прямоугольнике диагонали взаимно перпендикулярны.	Нет
В любом прямоугольнике диагонали равны.	Да
В любом равнобедренном треугольнике медиана, проведённая из вершины основания, является биссектрисой и высотой.	Да
В любом ромбе диагонали перпендикулярны.	Да
В любом треугольнике выполняется теорема Пифагора.	Нет
В любом треугольнике против большего угла лежит большая сторона.	Да
В любом треугольнике против большей стороны лежит меньший угол.	Нет
В любом треугольнике сумма двух сторон больше третьей стороны.	Да
В любом треугольнике сумма двух сторон меньше третьей стороны.	Нет
В любом тупоугольном треугольнике есть острый угол.	Да
В любую окружность можно вписать два подобных, но неравных треугольника.	Нет
В любую окружность можно вписать прямоугольник.	Да
В любую равнобедренную трапецию можно вписать окружность.	Нет
Внешний угол треугольника больше каждого внутреннего угла.	Нет
Внешний угол треугольника больше не смежного с ним внутреннего угла.	Да
Внешний угол треугольника всегда тупой.	Нет
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.	Да
Внешний угол треугольника равен сумме его внутренних углов.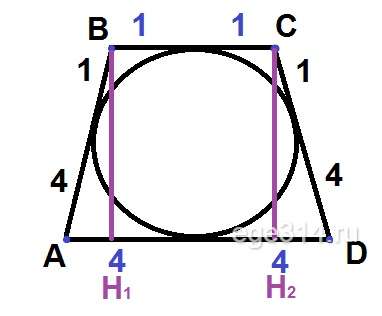	Нет
Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.	Да
Во всякий четырёхугольник можно вписать окружность.	Нет
Во всяком треугольнике биссектриса угла равна его медиане.	Нет
Во всяком треугольнике высота проведённая к основанию, совпадает с медианой.	Нет
Вокруг любого выпуклого восьмиугольника можно описать окружность.	Нет
Вокруг любого параллелограмма можно описать окружность.	Нет
Вокруг любого треугольника можно описать окружность.	Да
Вокруг любого четырёхугольника можно описать окружность.	Нет
Вокруг параллелограмма всегда можно описать окружность.	Нет
Вокруг равнобедренной трапеции можно описать окружность.	Да
Вокруг тупоугольного треугольника нельзя описать окружность.	Нет
В окружности на диаметр опирается прямой угол.	Да
В окружности радиуса 2 можно провести хорду длиной 3.	Да
В окружность можно вписать угол, равный 200°	Нет
В параллелограмме все стороны равны.	Нет
В параллелограмме диагонали точкой пересечения делятся пополам.	Да
В параллелограмме есть два равных угла.	Да
В параллелограмме противоположные углы равны.	Да
Вписанные углы окружности равны.	Нет
Вписанные углы, опирающиеся на одну и ту же дугу, равны.	Да
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.	Нет
Вписанный угол измеряется дугой, на которую он опирается.	Нет
Вписанный угол измеряется половиной дуги, на которую он опирается.	Да
Вписанный угол, опирающийся на диаметр окружности, прямой.	Да
Вписанный угол, опирающийся на диаметр окружности, равен 90°.	Да
Вписанный угол, опирающийся на полуокружность — развёрнутый.	Нет
Вписанный угол равен половине угловой величины дуги, на которую он опирается.	Да
Вписанный угол равен половине центрального, опирающегося на туже дугу.	Да
В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.	Да
В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.	Да
В подобных треугольниках соответствующие стороны равны.	Нет
В подобных треугольниках сходственные стороны пропорциональны.	Да
В правильном многоугольнике все стороны равны.	Да
В правильном многоугольнике все углы равны.	Да
В правильном треугольнике все углы прямые.	Нет
В прямоугольнике диагонали являются биссектрисами.	Нет
В прямоугольнике диагонали являются биссектрисами его углов.	Нет
В прямоугольной трапеции основания параллельны.	Да
В прямоугольном треугольнике гипотенуза больше катета.	Да
В прямоугольном треугольнике гипотенуза меньше катета.	Нет
В прямоугольном треугольнике гипотенуза в два раза больше каждого из катетов.	Нет
В прямоугольном треугольнике гипотенуза всегда меньше суммы его катетов.	Да
В прямоугольном треугольнике гипотенуза равна сумме катетов.	Нет
В прямоугольном треугольнике катет больше гипотенузы.	Нет
В прямоугольном треугольнике катет, лежащий против угла к 30° равен половине гипотенузы.	Да
В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.	Нет
В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов.	Нет
В прямоугольном треугольнике любой катет меньше гипотенузы.	Да
В прямоугольном треугольнике синус одного из углов равен 0.	Нет
В прямоугольном треугольнике тангенсом острого угла а называется отношение sin a / cos a.	Да
В равнобедренной трапеции диагонали равны.	Да
В равнобедренной трапеции углы при основании равны.	Да
В равнобедренном прямоугольном треугольнике все стороны равны.	Нет
В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.	Да
В равнобедренном треугольнике все стороны равны.	Нет
В равнобедренном треугольнике все углы равны.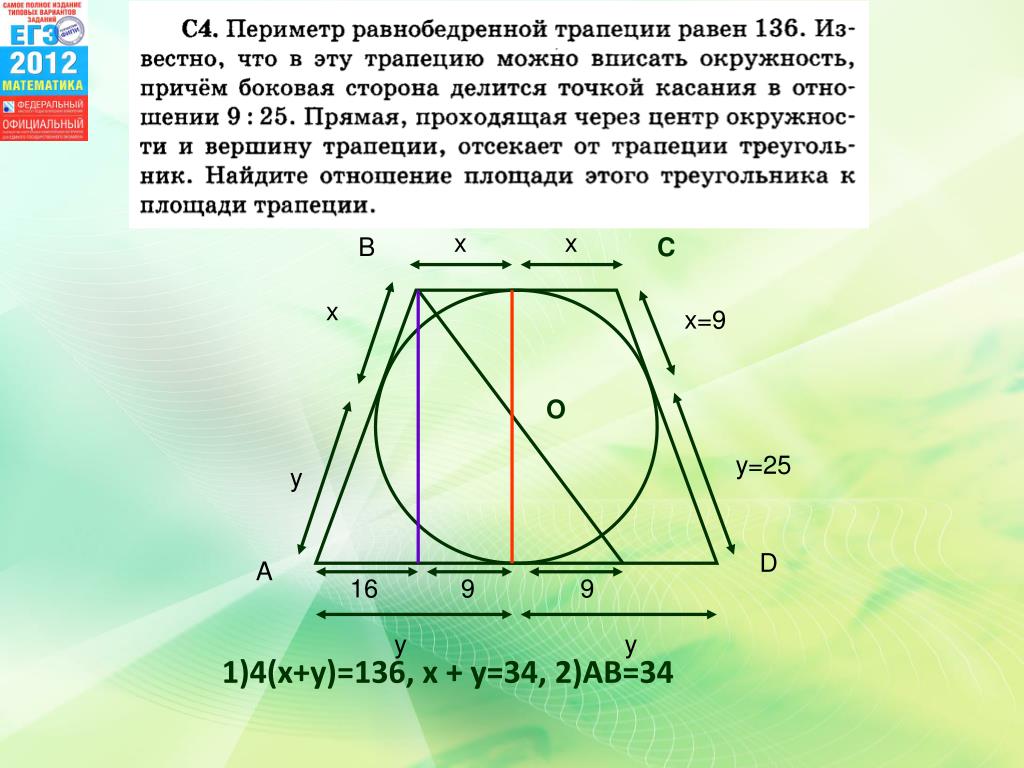	Нет
В равнобедренном треугольнике имеется не более двух равных углов.	Нет
В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и биссектрисой.	Да
В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и высотой.	Да
В равнобедренном треугольнике углы при основании равны.	Да
В равностороннем треугольнике АВС медиана AK равна высоте CH.	Да
В равностороннем треугольнике все углы острые.	Да
В равностороннем треугольнике все углы равны.	Да
В равностороннем треугольнике каждый угол равен 45°.	Нет
В равностороннем треугольнике медианы пересекаются в одной точке.	Да
В ромбе все углы прямые.	Нет
В ромбе диагонали пересекаются под прямым углом.	Да
В ромбе противоположные углы равны.	Да
В ромб нельзя вписать окружность.	Нет
Все вписанные углы окружности равны.	Нет
Все высоты равностороннего треугольника равны.	Да
Все диаметры окружности равны между собой.	Да
Все квадраты имеют равные площади.	Нет
Все прямоугольные треугольники подобны.	Нет
Все прямоугольные треугольники подобны друг другу.	Нет
Все равнобедренные треугольники подобны.	Нет
Все равнобедренные треугольники равны.	Нет
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.	Да
Все углы квадрата прямые.	Да
Все углы правильного пятиугольника равны 112°.	Нет
Все углы правильного шестиугольника равны 135°.	Нет
Все углы пятиугольника равны.	Да
Все углы ромба равны.	Нет
Все хорды одной окружности равны между собой.	Нет
Всякий равнобедренный треугольник является остроугольным.	Нет
Всякий равносторонний треугольник является остроугольным.	Да
Всякий равносторонний треугольник является равнобедренным.	Да
В трапеции боковые стороны параллельны.	Нет
В трапеции сумма длин боковых сторон всегда меньше суммы оснований.	Нет
В трапецию АВCD с основаниями ВС = 7, AD = 10, и боковыми сторонами AB = CD = 8 можно вписать окружность.	Нет
В трапецию с основаниями 6 и 3 и боковыми сторонами 4 и 4 можно вписать окружность.	Нет
В треугольнике ABC, для которого AB = 3, BC = 4, АС = 5, угол С наименьший.	Да
В треугольнике АВС, для которого АВ = 4, BC = 5, AC = 6, угол A наибольший.	Нет
В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший	Да
В треугольнике АВС, для которого АВ = 6, BC = 8, АС = 11, угол при вершине С — наименьший.	Да
В треугольнике АВС, для которого ∠A = 40°, ∠B = 60°, ∠C = 80°, сторона AC — наибольшая.	Нет
В треугольнике АВС, для которого ∠A = 40°, ∠B = 55°, ∠C = 85° сторона AC — наименьшая.	Нет
В треугольнике АВС, для которого ∠A = 44°, ∠B = 55°, ∠C = 81° сторона BC — наибольшая.	Нет
В треугольнике АВС, для которого ∠A = 45°, ∠B = 55°, ∠C = 80° сторона AC — наименьшая	Нет
В треугольнике АВС, для которого ∠A = 47°, ∠B — 64°, сторона АВ — наибольшая.	Да
В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона AB — наибольшая	Да
В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона BC — наименьшая.	Да
В треугольнике любая сторона меньше суммы двух других сторон.	Да
В треугольнике может быть только один тупой угол.	Да
В треугольнике против большего угла лежит большая сторона.	Да
В треугольнике против большего угла лежит меньшая сторона.	Нет
В треугольнике против большей стороны лежит больший угол.	Да
В треугольнике против большей стороны лежит меньший угол.	Нет
В треугольнике против меньшего угла лежит меньшая сторона.	Да
В треугольнике против меньшего угла лежит большая сторона.	Нет
В треугольнике против меньшей стороны лежит больший угол.	Нет
В треугольнике против меньшей стороны лежит меньший угол.	Да
В треугольнике сумма двух сторон больше третьей стороны.	Да
В тупоугольном треугольнике все углы тупые.	Нет
В тупоугольном треугольнике сумма углов больше 180 градусов.	Нет
Высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных треугольника.	Да
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.	Да
Высота равнобедренного треугольника проведённая к основанию, является медианой и биссектрисой.	Да
Гипотенуза длиннее катета.	Да
Гипотенуза прямоугольного треугольника, вписанного в окружность, в два раза больше её радиуса.	Да
Гипотенуза равна сумме квадратов катетов.	Нет
Гипотенуза — самая длинная сторона в прямоугольном треугольнике.	Да
Два угла с общей стороной называются смежными.	Нет
Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.	Нет
Две прямые всегда пересекаются.	Нет
Две прямые, параллельные третьей прямой, перпендикулярны друг другу.	Нет
Две прямые, перпендикулярные к третьей, не пересекаются.	Да
Две прямые, перпендикулярные одной и той же прямой, не пересекаются.	Да
Две прямые, перпендикулярные третьей прямой, параллельны друг другу.	Да
Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу.	Нет
Диагонали квадрата взаимно перпендикулярны.	Да
Диагонали квадрата делят его углы пополам.	Да
Диагонали квадрата пересекаются под прямым углом.	Да
Диагонали квадрата равны.	Да
Диагонали квадрата точкой пересечения делятся пополам.	Да
Диагонали любого прямоугольника делят его на 4 равных треугольника.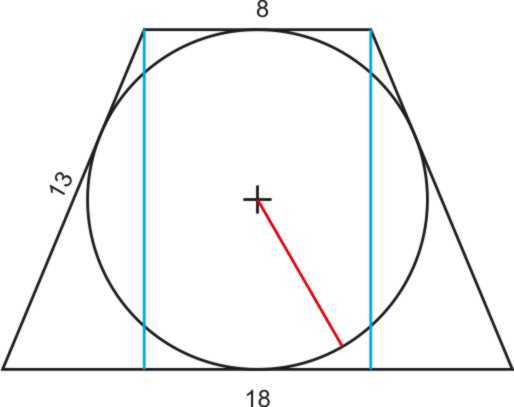	Нет
Диагонали любого прямоугольника равны.	Да
Диагонали параллелограмма делят его углы пополам.	Нет
Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам.	Нет
Диагонали параллелограмма перпендикулярны.	Нет
Диагонали параллелограмма равны.	Нет
Диагонали прямоугольника взаимно перпендикулярны.	Нет
Диагонали прямоугольника пересекаются под прямым углом и точкой пересечения делятся пополам.	Нет
Диагонали прямоугольника равны.	Да
Диагонали прямоугольника точкой пересечения делятся пополам.	Да
Диагонали прямоугольной трапеции равны.	Нет
Диагонали равнобедренной трапеции равны.	Да
Диагонали ромба взаимно перпендикулярны.	Да
Диагонали ромба в точке пересечения делятся пополам.	Да
Диагонали ромба пересекаются под прямым углом.	Да
Диагонали ромба пересекаются под углом 60°.	Нет
Диагонали ромба перпендикулярны.	Да
Диагонали ромба равны.	Нет
Диагонали ромба точкой пересечения делятся пополам.	Да
Диагонали трапеции пересекаются и делятся точкой пересечения пополам.	Нет
Диагонали трапеции пересекаются под прямым углом.	Нет
Диагонали трапеции равны.	Нет
Диагонали трапеции точкой пересечения делятся пополам.	Нет
Диагональ квадрата равна его стороне.	Нет
Диагональ параллелограмма делит его на два равных треугольника	Да
Диагональ параллелограмма делит его углы пополам.	Нет
Диагональ равнобедренной трапеции делит её на два равных треугольника.	Нет
Диагональ трапеции делит её на два равных треугольника.	Нет
Диагональ трапеции равна квадратному корню из суммы квадратов её оснований.	Нет
Диаметр делит окружность на две равные дуги.	Да
Диаметр окружности в два раза больше её радиуса.	Да
Диаметр окружности в два раза меньше его радиуса.	Нет
Длина вектора равна квадратному корню из суммы его координат.	Да
Длина вектора, равного сумме двух векторов, не превосходит сумму длин этих векторов.	Нет
Длина гипотенузы прямоугольного треугольника больше суммы длин его катетов.	Нет
Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.	Да
Длина катета прямоугольного треугольника равна длине гипотенузы, умноженной на косинус угла, образованного этим катетом и гипотенузой.	Да
Длина окружности вычисляется по формуле С = 2πR.	Да
Длина окружности равна её удвоенному радиусу.	Нет
Длина окружности равна πR.	Нет
Длина окружности радиуса R равна 2πR.	Да
Длина суммы двух векторов равна сумме их длин.	Нет
Для любого четырёхугольника, вписанного в окружность, сумма углов, прилежащих к одной стороне, равна 180°	Нет
Для любого числа к и любых векторов а, b справедливо равенство	Да
Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.	Да
Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.	Да
Если в выпуклом четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.	Нет
Если в параллелограмме две высоты равны, то этот параллелограмм — ромб.	Да
Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.	Да
Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.	Да

13 вопрос ОГЭ | Олимпиадный Центр МатРИЦА

1. Любые две прямые имеют ровно одну общую точку

неверно

верно

2. В тупоугольном треугольнике все углы тупые

верно

неверно

3. Через любые три точки проходит не более одной прямой

неверно

верно

4. Если угол равен 60 градусов, то смежный с ним равен 120 градусов

верно

неверно

5. Любая биссектриса равнобедренного треугольника является его медианой

неверно

верно

6. Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8

неверно

верно

7. Если один из углов, прилежащих к стороне параллелограмма, равен 50 градусов, то другой угол, прилежащий к той же стороне, равен 50 градусов

неверно

верно

8. Вертикальные углы равны

верно

неверно

9. Один из углов треугольника всегда не превышает 60 градусов

верно

неверно

10. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой

верно

неверно

11. Если диагонали ромба равны 3 и 4, то его площадь равна 6

верно

неверно

12. Если угол острый, то смежный с ним угол также является острым

неверно

верно

13. Треугольник АВС, у которого АВ=5, ВС=6, АС=7, является остроугольным

верно

неверно

14. Если при пересечении двух прямых третьей прямой соответственные углы равны 37 градусов, то эти две прямые параллельны

неверно

верно

15. В любую равнобедренную трапецию можно вписать окружность

неверно

верно

16. Через любые три точки проходит ровно одна прямая

верно

неверно

17. Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам

верно

неверно

18. Диагонали ромба перпендикулярны

верно

неверно

19. Вокруг любого треугольника можно описать окружность

верно

неверно

20. Центром симметрии ромба является точка пересечения его диагоналей

неверно

верно

21. Существует квадрат, который не является ромбом

верно

неверно

22. Диагональ параллелограмма делит его угол пополам

верно

неверно

23. Около любого правильного многоугольника можно описать не более одной окружности

верно

неверно

24. Все углы ромба равны

неверно

верно

25. Около всякого треугольника можно описать не более одной окружности

неверно

верно

26. Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу

неверно

верно

27. Через любые три точки проходит более одной прямой

неверно

верно

28. Около любого ромба можно описать окружность

неверно

верно

29. Если радиусы двух окружностей равны 5 и 7, а расстояние между центрами равно 3, то эти окружности не имеют общих точек

неверно

верно

30. Если площади фигур равны, то равны и сами фигуры

верно

неверно

31. Любые три прямые имеют не более одной общей точки

верно

неверно

32. Окружность имеет бесконечно много центров симметрии

верно

неверно

33. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30 градусов, то площадь этого параллелограмма равна 10

верно

неверно

34. Площадь трапеции меньше произведения суммы оснований на высоту

неверно

верно

35. Если один из углов параллелограмма равен 60 градусов, то противоположный ему угол равен 120 градусов

неверно

верно

36. Центром окружности, описанной около квадрата, является точка пересечения его диагоналей

неверно

верно

37. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник

верно

неверно

38. Любые две прямые имеют не менее одной общей точки

верно

неверно

39. Диагональ трапеции делит ее на два равных треугольника

верно

неверно

40. Если угол равен 45 градусов, то вертикальный с ним угол равен 45 градусов

верно

неверно

41. Если угол равен 120 градусов, то смежный с ним равен 120 градусов

верно

неверно

42. Площадь прямоугольного треугольника равна половине произведения его катетов

неверно

верно

43. Площадь трапеции равна произведению средней линии на высоту

верно

неверно

44. Через заданную точку плоскости можно провести только одну прямую

неверно

верно

45. Каждая из биссектрис равнобедренного треугольника является его медианой

верно

неверно

46. Центры вписанной и описанной окружностей равностороннего треугольника совпадают

неверно

верно

47. Треугольник со сторонами 1, 2, 4 существует

верно

неверно

48. Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника

верно

неверно

49. Центром симметрии равнобедренной трапеции является точка пересечения его диагоналей

верно

неверно

50. Всегда один из смежных углов острый, а другой тупой

неверно

верно

51. Любые два равнобедренных треугольника подобны

верно

неверно

52. Через любые две точки можно провести прямую

неверно

верно

53. Средняя линия трапеции равна полусумме ее оснований

верно

неверно

54. Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности

верно

неверно

55. Если вписанный угол равен 30, то дуга окружности, на которую опирается этот угол, равна 60 градусам

неверно

верно

56. Через любую точку проходит не менее одной прямой

неверно

верно

57. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны

верно

неверно

58. Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек

неверно

верно

59. Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружности пересекаются

неверно

верно

60. Диагонали квадрата взаимно перпендикулярны

неверно

верно

61. Площадь квадрата равна произведению двух его смежных сторон

неверно

верно

62. Треугольник АВС, у которого АВ=3, ВС=4, АС=5, является тупоугольным

неверно

верно

63. Квадрат не имеет центра симметрии

верно

неверно

64. Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70 градусов и 110 градусов, то две прямые параллельны

верно

неверно

65. Сумма углов выпуклого четырехугольника равна 180 градусов

неверно

верно

66. Любой прямоугольник можно вписать в окружность

верно

неверно

67. Центром симметрии прямоугольника является точка пересечения его диагоналей

неверно

верно

68. Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны

неверно

верно

69. Прямая не имеет осей симметрии

верно

неверно

70. Любые два прямоугольных треугольника подобны

неверно

верно

71. Любая высота равнобедренного треугольника является его биссектрисой

верно

неверно

72. Сумма вертикальных углов равна 180 градусов

верно

неверно

73. Любые три прямые имеют не менее одной общей точки

неверно

верно

74. Центром окружности, описанной около треугольника, является точка пересечения биссектрис

верно

неверно

75. У любой трапеции боковые стороны равны

неверно

верно

76. Площадь ромба равна произведению его стороны на высоту, проведенную к этой стороне

неверно

верно

77. Смежные углы равны

неверно

верно

78. Если два угла треугольника равны, то равны и противолежащие им стороны

верно

неверно

79. Треугольника со сторонами 1, 2,4 не существует

неверно

верно

80. Центром симметрии ромба является точка пересечения его диагоналей

неверно

верно

81. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм

неверно

верно

82. При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180 градусов

неверно

верно

83. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб

верно

неверно

84. Равнобедренный треугольник имеет три оси симметрии

верно

неверно

85. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой

верно

неверно

86. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов

верно

неверно

87. Если в ромбе один из углов равен 90 градусов, то такой ромб -квадрат

верно

неверно

88. Средняя линия трапеции параллельна ее основаниям

неверно

верно

89. Площадь прямоугольного треугольника равна произведению длин его катетов

верно

неверно

90. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны

верно

неверно

91. Диагонали трапеции пересекаются и делятся точкой пересечения пополам

неверно

верно

92. Если катеты прямоугольного треугольника равны соответственно 5 и 12, то его гипотенуза этого треугольника равна 13

неверно

верно

93. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника

верно

неверно

94. Стороны треугольника пропорциональны косинусам противолежащих углов

верно

неверно

95. Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1

верно

неверно

96. Если угол равен 108 градусов, то вертикальный с ним равен 108 градусов

неверно

верно

97. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними

неверно

верно

98. Если сумма трех углов выпуклого четырехугольника равна 200 градусов, то его четвертый угол равен 160 градусов

верно

неверно

99. Биссектриса, равнобедренного треугольника, проведенная из вершины, противолежащей основанию, делит основание на две равные части

верно

неверно

100. Диагонали прямоугольника равны

верно

неверно

101. Через любые три точки проходит не более одной окружности

верно

неверно

102. Прямая не имеет осей симметрии

верно

неверно

103. Сумма углов любого треугольника равна 180 градусов

верно

неверно

104. В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета

верно

неверно

105. В плоскости все точки, равноудаленные от заданной точки, лежат на одной окружности

верно

неверно

106. Сумма смежных углов равна 180 градусов

неверно

верно

107. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны

верно

неверно

108. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат

неверно

верно

109. Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности

неверно

верно

110. Точка пересечения двух окружностей равноудалена от центров этих окружностей

верно

неверно

111. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30 градусов, то площадь этого треугольника равна 10

неверно

верно

112. Правильный пятиугольник имеет пять осей симметрии

неверно

верно

113. Если угол равный 47 градусов, то смежный с ним равен 153 градусов

неверно

верно

114. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

верно

неверно

115. Правильный шестиугольник имеет шесть осей симметрии

верно

неверно

116. Диагональ трапеции делит ее на два равных треугольника

верно

неверно

117. Все хорды одной окружности равны между собой

неверно

верно

118. В любой треугольник можно вписать не менее одной окружности

верно

неверно

119. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны

неверно

верно

120. Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются

неверно

верно

121. Смежные углы равны

верно

неверно

122. Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой

верно

неверно

123. В любом прямоугольнике диагонали взаимно перпендикулярны

верно

неверно

124. Любые две прямые имеют ровно одну общую точку

верно

неверно

125. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 градусов, то эти две прямые параллельны

верно

неверно

126. Площадь прямоугольного треугольника меньше произведения его катетов

неверно

верно

127. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны

верно

неверно

128. Диагонали квадрата делят его углы пополам

неверно

верно

129. Вписанные углы, опирающиеся на одну и ту же хорду окружности равны

верно

неверно

130. Через любую точку проходит более одной прямой

верно

неверно

131. Площадь трапеции равна произведению суммы оснований на высоту

неверно

верно

132. Все диаметры окружности равны между собой

верно

неверно

133. Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведенной из данной точки к прямой больше 3

верно

неверно

134. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны

неверно

верно

135. Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны

неверно

верно

136. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними

неверно

верно

137. Существует квадрат, который не является прямоугольником

верно

неверно

138. Если в ромбе один из углов равен 90 градусов, то такой ромб — квадрат

неверно

верно

139. Если стороны одного четырехугольника соответственно равны сторонам другого четырехугольника, то такие четырехугольники равны

неверно

верно

140. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности

верно

неверно

141. Длина гипотенузы прямоугольного треугольника меньше сумм длин его катетов

верно

неверно

142. В параллелограмме есть два равных угла

неверно

верно

143. Площадь трапеции равна половине высоты, умноженной на разность оснований

верно

неверно

144. Диагонали параллелограмма равны

неверно

верно

145. Если дуга окружности составляет 80 градусов, то вписанный угол, опирающийся на эту дугу окружности, равен 40 градусов

неверно

верно

146. Сумма углов любого треугольника равна 360 градусов

верно

неверно

147. Если при пересечении двух прямых третьей прямой соответственные углы равны, то эти две прямые параллельны

верно

неверно

Спонсор плагина: Тесты для девочек

Все вопросы и предложения Вы сможете задать в контактной форме:

Варианты ответов и пояснения к заданию №13 ОГЭ по математике здесь >>>

Можно ли описать окружность около трапеции. Трапеция. Полный иллюстрированный гид (2019). Защита персональной информации

Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года

Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.

Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к

Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с

Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К

Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О

Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д

Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h

1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен

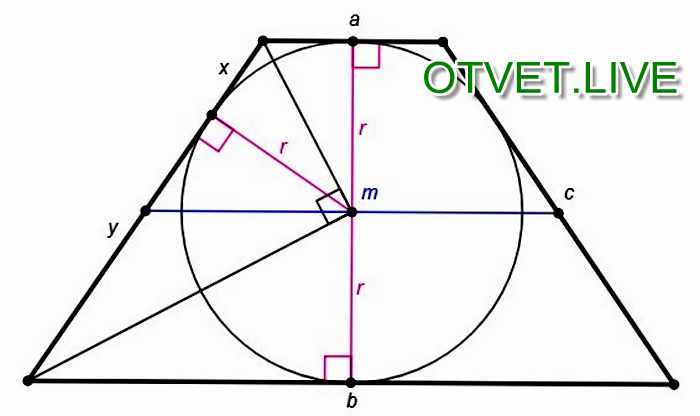
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC

Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.

I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.

Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна

Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь

27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:

*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.

И решение будет «второго варианта» будет следующим.

По теореме Пифагора вычисляем OF:

Также вычислим OE:

Таким образом EF=FO–OE=4–3=1.

Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.

27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:

Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.

Добрый вечер! Ох уж эти описанные, или вписанные окружности, геометрические фигуры. Так сложно запутаться. что да когда.

Давайте попробуем разобраться для начала с формулировкой. Нам дана окружность описанная около . Иными словами — данная трапеция вписана в окружность.

Давайте вспомним, что описать окружность мы можем только вокруг . А равнобедренная трапеция в свою очередь — это трапеция, у которой боковые стороны равны.

Давайте попробуем решить задачку. Нам известно, что основания равнобедренной трапеции ADCB равны 6 (DC) и 4 (AB). А радиус описанной окружности равен 4. Нужно найдите высоту трапеции FK.

FK — высота трапеции. её нам нужно найти, но перед этим вспомним, что точка О — это центр окружности. А ОС, ОD, OA, OB — известные радиусы .

В OFC нам известна гипотенуза, которая является радиусом окружности, а катет FC = половине основания DC = 3 см (так как DF = FC).

Теперь по найдём OF:

А в прямоугольном треугольнике OKB нам тоже известна гипотенуза, так как это радиус окружности. А KB равняется половине AB; KB = 2 см. И, используя теорему Пифагора вычислим отрезок OK:

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 .
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.

Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».

Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.

Элементы, виды и признаки геометрической фигуры трапеция

Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.

У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:

Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.

Свойства трапеции, описанной около окружности

Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.

Итак, подробнее о свойствах трапеции, описанной около окружности:

Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.

Еще немного о свойствах трапеции, заключенной в окружность

Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.

Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.

На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.

Тренировочный тест по геометрии для 9 класса

Тренировочный тест по геометрии для 9 класса

Укажите номера верных утверждений.

1) Площадь треугольника меньше произведения двух его сторон.

2) Если диагонали параллелограмма равны, то это ромб.

3) Вертикальные углы равны.

Ответ:______________________.

1) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольники равны.

2) Диагонали прямоугольника равны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Ответ:_________________.

1) Сумма двух углов параллелограмма, прилежащих к одной стороне, равна 180 градусов.

2) Любая биссектриса равнобедренного треугольника является его медианой.

3) Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны.

Ответ:___________________.

1) Любая сторона треугольника меньше суммы двух других его сторон.

2) Если диагонали параллелограмма равны, то это квадрат.

3) Сумма смежных углов равна 180 градусов.

Ответ:_________________.

1) Любую трапецию можно вписать в окружность.

2) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

3) Тангенс любого острого угла меньше единицы.

Ответ:_________________________.

1) В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов.

2) Если в ромбе один из углов равен 90 градусов, то такой ромб — квадрат.

3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности

Ответ:______________________.

1) В параллелограмме есть да равных угла.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

3) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

Ответ:__________________.

1) В любом тупоугольном треугольнике есть острый угол.

2) Все диаметры окружности равны между собой.

3) Средняя линия трапеции равна сумме её оснований.

Ответ:______________________.

Ответы.

Комбинации цилиндра и призмы — урок. Геометрия, 11 класс.

Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.

Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.

Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.

Окружность основания цилиндра описана около многоугольника основания призмы.

Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны 180°.

Формулы вычисления радиуса $R$ описанной окружности

$a, b, c$ — стороны, $h$ — высота, $d$ — диагональ.

Правильный треугольник	$R =$ 23h; $R=$ a33
Прямоугольный треугольник	$R=$ 12 гипотенузы
Произвольный треугольник	R=abc4S;R=a2sinα
Квадрат	$R =$ a22
Прямоугольник	$R =$ d2
Правильный шестиугольник	$R = a$

Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.

Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.

Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.

Окружность основания цилиндра вписана в многоугольник основания призмы.

Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.

Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.

Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.

Формулы вычисления радиуса $r$ вписанной окружности

Где $h$ — высота, $S$ — площадь, $p$ — полупериметр, $a$ — сторона.

Правильный треугольник	r=13h;r=a36
Произвольный (и прямоугольный) треугольник	$r =$ Sp
Квадрат	$r =$ 12$a$
Ромб	$r =$ Sp или $r =$ 12 от $h$
Правильный шестиугольник	$r =$ a32

В какую трапецию можно вписать окружность. Интересные свойства трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.

Задача
.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение
.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b) 2 + (24 — b) 2 = 169

-(64 + 16b + b) 2 + (24 — b) 2 = -256

-64 — 16b — b 2 + 576 — 48b + b 2 = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b — основания трапеции, h — высота трапеции

S = (24 + 8) * 5 / 2 = 80 см 2

Ответ
: площадь трапеции равна 80 см 2 .

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 .
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.

Свойства трапеции, вписанной в окружность

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.

Свойства трапеции, описанной около окружности

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

Задача для повторения

Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .

Послесловие

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь

Отрезок EF является высотой трапеции, его нам нужно найти.

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

А если бы в условии не было дано эскиза?

*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.

И решение будет «второго варианта» будет следующим.

По теореме Пифагора вычисляем OF:

Также вычислим OE:

Таким образом EF=FO–OE=4–3=1.

27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:

Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.

ФГКОУ «МКК «Пансион воспитанниц МО РФ»

«УТВЕРЖДАЮ»

Руководитель отдельной дисциплины

(математика, информатика и ИКТ)

Ю. В. Крылова _____________

«___» _____________ 2015 г.

«Трапеция и ее свойства
»

Методическая разработка

преподавателя математики

Шаталиной Елены Дмитриевны

Рассмотрено и

на заседании ПМО от _______________

Протокол №______

Москва

2015 год

Оглавление

Введение 2

Определения 3

Свойства равнобедренной трапеции 4

Вписанные и описанные окружности 7

Свойства вписанных и описанных трапеций 8

Средние величины в трапеции 12

Свойства произвольной трапеции 15

Признаки трапеции 18

Дополнительные построения в трапеции 20

Площадь трапеции 25

10. Заключение

Список используемой литературы

Приложение

Доказательства некоторых свойств трапеции 27

Задачи для самостоятельных работ

Задачи по теме «Трапеция» повышенной сложности

Проверочный тест по теме «Трапеция»

Введение

Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.

Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.

В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.

Трапеция.

Определения

Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.

Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.

Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.

Расстояние между основаниями называется высотой
трапеции
.

. Свойства равнобедренной трапеции

3. Диагонали равнобедренной трапеции равны.

1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.

3. Вписанная и описанная окружность

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.

Е
сли трапеция равнобедренная, то около неё можно описать окружность.

4
. Свойства вписанных и описанных трапеций

2.Если в равнобедренную
трапецию можно вписать окружность, то

сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.

.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.

Е
сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m
и n,
тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.

1

0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.

5.
Средние величины в трапеции

Среднее геометрическое

В любой трапеции с основаниями

a

для

справедливо неравенство

:

b
˂
h
˂
g
˂
m
˂
s
˂
a

6.
Свойства произвольной трапеции

1

. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.

2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.

Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.

5.
При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).

6.
Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.

1

2

+

d

2

2

=

c

2

+

d

2

+ 2

ab

В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований

d

—

–

8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.

7
. Признаки трапеции

8
. Дополнительные построения в трапеции

1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.

2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.

3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.

4

. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.

5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.

6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований

7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.

8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

9. Биссектриса угла трапеции отсекает равнобедренный треугольник.

1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.

13.
Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.

9. Площадь трапеции

1

. Площадь трапеции равна произведению полусуммы оснований на высоту
S

= ½(a

+
b

)
h

или

П

лощадь трапеции равна произведению средней линии трапеции на высоту S

=
m

h

.

2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:

10.
Заключение

ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?

Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.

Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.

Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.

Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.

Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.

Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн

В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.

Список используемой литературы

Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.

Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004

Гордин Р.К. Планиметрия. Задачник.

Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN
5-89155-188-3

Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).

Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.

Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.

Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.

Приложение

1.Доказательство некоторых свойств трапеции.

1.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках
K

Доказать, что если основания трапеции равны

а

, то

длина отрезка

KL

равна среднему геометрическому оснований трапеции.

Доказательство

Пусть

— точка пересечения диагоналей,
AD

а, ВС

Прямая

параллельна основанию
AD

, следовательно,

║

треугольники

BAD

подобны, поэтому

(1)

(2)

Подставим (2) в (1)
, получим KO =

Аналогично LO

= Тогда K

KO

+

LO

=

о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.

Через точку

и точку

пересечения диагоналей
проведём прямую

КО.

Окажем, что эта прямая делит основания пополам.

Обозначим
ВМ

х, МС

у,

и,

Имеем:

∆

ВКМ

∆AKN

→

∆
MК

∆NKD

→

Теперь по найдём OF:

Комбинация шара с другими телами

Тема “Разные задачи на многогранники, цилиндр,
конус и шар” является одной из самых сложных в
курсе геометрии 11 класса. Перед тем, как решать
геометрические задачи, обычно изучают
соответствующие разделы теории, на которые
ссылаются при решении задач. В учебнике
С.Атанасяна и др. по данной теме (стр. 138) можно
найти только определения многогранника,
описанного около сферы, многогранника,
вписанного в сферу, сферы, вписанной в
многогранник, и сферы, описанной около
многогранника. В методических рекомендациях к
этому учебнику (см. книгу “Изучение геометрии в
10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159)
сказано, какие комбинации тел рассматриваются
при решении задач № 629–646, и обращается внимание
на то, что “при решении той или иной задачи
прежде всего нужно добиться того, чтобы учащиеся
хорошо представляли взаимное расположение
указанных в условии тел”. Далее приводится
решение задач №638(а) и №640.

Учитывая все выше сказанное, и то, что наиболее
трудными для учащихся являются задачи на
комбинацию шара с другими телами, необходимо
систематизировать соответствующие
теоретические положения и сообщить их учащимся.

Определения.

1. Шар называется вписанным в многогранник, а
многогранник описанным около шара, если
поверхность шара касается всех граней
многогранника.

2. Шар называется описанным около
многогранника, а многогранник вписанным в шар,
если поверхность шара проходит через все вершины
многогранника.

3. Шар называется вписанным в цилиндр, усеченный
конус (конус), а цилиндр, усеченный конус (конус) –
описанным около шара, если поверхность шара
касается оснований (основания) и всех образующих
цилиндра, усеченного конуса (конуса).

(Из этого определения следует, что в любое
осевое сечение этих тел может быть вписана
окружность большого круга шара).

4. Шар называется описанным около цилиндра,
усеченного конуса (конуса), если окружности
оснований (окружность основания и вершина)
принадлежат поверхности шара.

(Из этого определения следует, что около
любого осевого сечения этих тел может быть
описана окружность большего круга шара).

Общие замечания о положении центра
шара.

1. Центр шара, вписанного в многогранник, лежит в
точке пересечения биссекторных плоскостей всех
двугранных углов многогранника. Он расположен
только внутри многогранника.

2. Центр шара, описанного около многогранника,
лежит в точке пересечения плоскостей,
перпендикулярных ко всем ребрам многогранника и
проходящих через их середины. Он может быть
расположен внутри, на поверхности и вне
многогранника.

Комбинация шара с призмой.

1. Шар, вписанный в прямую призму.

Теорема 1. Шар можно вписать в прямую
призму в том и только в том случае, если в
основание призмы можно вписать окружность, а
высота призмы равна диаметру этой окружности.

Следствие 1. Центр шара, вписанного в прямую
призму, лежит в середине высоты призмы,
проходящей через центр окружности, вписанной в
основание.

Следствие 2. Шар, в частности, можно вписать
в прямые: треугольную, правильную,
четырехугольную (у которой суммы
противоположных сторон основания равны между
собой) при условии Н = 2r, где Н – высота призмы, r –
радиус круга, вписанного в основание.

2. Шар, описанный около призмы.

Теорема 2. Шар можно описать около
призмы в том и только в том случае, если призма
прямая и около ее основания можно описать
окружность.

Следствие 1. Центр шара, описанного около
прямой призмы, лежит на середине высоты призмы,
проведенной через центр круга, описанного около
основания.

Следствие 2. Шар, в частности, можно описать:
около прямой треугольной призмы, около
правильной призмы, около прямоугольного
параллелепипеда, около прямой четырехугольной
призмы, у которой сумма противоположных углов
основания равна 180 градусов.

Из учебника Л.С.Атанасяна на комбинацию шара с
призмой можно предложить задачи № 632, 633, 634, 637(а),
639(а,б).

Комбинация шара с пирамидой.

1. Шар, описанный около пирамиды.

Теорема 3. Около пирамиды можно описать
шар в том и только в том случае, если около ее
основания можно описать окружность.

Следствие 1. Центр шара, описанного около
пирамиды лежит в точке пересечения прямой,
перпендикулярной основанию пирамиды, проходящей
через центр окружности, описанной около этого
основания, и плоскости, перпендикулярной любому
боковому ребру, проведенной через сере дину
этого ребра.

Следствие 2. Если боковые ребра пирамиды
равны между собой (или равно наклонены к
плоскости основания), то около такой пирамиды
можно описать шар.Центр этого шара в этом случае
лежит в точке пересечения высоты пирамиды (или ее
продолжения) с осью симметрии бокового ребра,
лежащей в плоскости бокового ребра и высоты.

Следствие 3. Шар, в частности, можно описать:
около треугольной пирамиды, около правильной
пирамиды, около четырехугольной пирамиды, у
которой сумма противоположных углов равна 180
градусов.

2. Шар, вписанный в пирамиду.

Теорема 4. Если боковые грани пирамиды
одинаково наклонены к основанию, то в такую
пирамиду можно вписать шар.

Следствие 1. Центр шара, вписанного в
пирамиду, у которой боковые грани одинаково
наклонены к основанию, лежит в точке пересечения
высоты пирамиды с биссектрисой линейного угла
любого двугранного угла при основании пирамиды,
стороной которого служит высота боковой грани,
проведенная из вершины пирамиды.

Следствие 2. В правильную пирамиду можно
вписать шар.

Из учебника Л.С.Атанасяна на комбинацию шара с
пирамидой можно предложить задачи № 635, 637(б), 638,
639(в),640, 641.

Комбинация шара с усеченной
пирамидой.

1. Шар, описанный около правильной усеченной
пирамиды.

Теорема 5. Около любой правильной
усеченной пирамиды можно описать шар. (Это
условие является достаточным, но не является
необходимым)

2. Шар, вписанный в правильную усеченную
пирамиду.

Теорема 6. В правильную усеченную
пирамиду можно вписать шар в том и только в том
случае, если апофема пирамиды равна сумме апофем
оснований.

На комбинацию шара с усеченной пирамидой в
учебнике Л.С.Атанасяна есть всего лишь одна
задача (№ 636).

Комбинация шара с круглыми телами.

Теорема 7. Около цилиндра, усеченного
конуса (прямых круговых), конуса можно описать
шар.

Теорема 8. В цилиндр (прямой круговой)
можно вписать шар в том и только в том случае,
если цилиндр равносторонний.

Теорема 9. В любой конус (прямой
круговой) можно вписать шар.

Теорема 10. В усеченный конус (прямой
круговой) можно вписать шар в том и только в том
случае, если его образующая равна сумме радиусов
оснований.

Из учебника Л.С.Атанасяна на комбинацию шара с
круглыми телами можно предложить задачи № 642, 643,
644, 645, 646.

Для более успешного изучения материала данной
темы необходимо включать в ход уроков устные
задачи:

1. Ребро куба равно а. Найти радиусы шаров:
вписанного в куб и описанного около него. (r = a/2, R =
a3).

2. Можно ли описать сферу (шар) около: а) куба; б)
прямоугольного параллелепипеда; в) наклонного
параллелепипеда, в основании которого лежит
прямоугольник; г) прямого параллелепипеда; д)
наклонного параллелепипеда? (а) да; б) да; в) нет;
г) нет; д) нет)

3. Справедливо ли утверждение, что около любой
треугольной пирамиды можно описать сферу? (Да)

4. Можно ли описать сферу около любой
четырехугольной пирамиды? (Нет, не около любой
четырёхугольной пирамиды)

5. Какими свойствами должна обладать пирамида,
чтобы около нее можно было описать сферу? (В её
основании должен лежать многоугольник, около
которого можно описать окружность)

6. В сферу вписана пирамида, боковое ребро
которой перпендикулярно основанию. Как найти
центр сферы? (Центр сферы – точка пересечения
двух геометрических мест точек в пространстве.
Первое – перпендикуляр, проведённый к плоскости
основания пирамиды, через центр окружности,
описанной около него. Второе – плоскость
перпендикулярная данному боковому ребру и
проведённая через его середину)

7. При каких условиях можно описать сферу около
призмы, в основании которой – трапеция? (Во-первых,
призма должна быть прямой, и, во-вторых, трапеция
должна быть равнобедренной, чтобы около неё
можно было описать окружность)

8. Каким условиям должна удовлетворять призма,
чтобы около нее можно было описать сферу?
(Призма должна быть прямой, и её основанием
должен являться многоугольник, около которого
можно описать окружность)

9. Около треугольной призмы описана сфера, центр
которой лежит вне призмы. Какой треугольник
является основанием призмы? (Тупоугольный
треугольник)

10. Можно ли описать сферу около наклонной
призмы? (Нет, нельзя)

11. При каком условии центр сферы, описанной
около прямой треугольной призмы, будет находится
на одной из боковых граней призмы? (В основании
лежит прямоугольный треугольник)

12. Основание пирамиды – равнобедренная
трапеция .Ортогональная проекция вершины
пирамиды на плоскость основания – точка,
расположенная вне трапеции. Можно ли около такой
трапеции описать сферу? (Да, можно. То что
ортогональная проекция вершины пирамиды
расположена вне её основания, не имеет значения.
Важно, что в основании пирамиды лежит
равнобедренная трапеция – многоугольник, около
которого можно описать окружность)

13. Около правильной пирамиды описана сфера. Как
расположен ее центр относительно элементов
пирамиды? (Центр сферы находится на
перпендикуляре, проведенном к плоскости
основания через его центр)

14. При каком условии центр сферы, описанной
около прямой треугольной призмы, лежит: а) внутри
призмы; б) вне призмы? (В основании призмы: а)
остроугольный треугольник; б) тупоугольный
треугольник)

15. Около прямоугольного параллелепипеда, ребра
которого равны 1 дм, 2 дм и 2 дм, описана сфера.
Вычислите радиус сферы. (1,5 дм)

16. В какой усеченный конус можно вписать сферу? (В
усечённый конус, в осевое сечение которого можно
вписать окружность. Осевым сечением конуса
является равнобедренная трапеция, сумма её
оснований должна равняться сумме её боковых
сторон. Другими словами, у конуса сумма радиусов
оснований должна равняться образующей)

17. В усеченный конус вписана сфера. Под каким
углом образующая конуса видна из центра сферы? (90
градусов)

18. Каким свойством должна обладать прямая
призма, чтобы в нее можно было вписать сферу? (Во-первых,
в основании прямой призмы должен лежать
многоугольник, в который можно вписать
окружность, и, во-вторых, высота призмы должна
равняться диаметру вписанной в основание
окружности)

19. Приведите пример пирамиды, в которую нельзя
вписать сферу? (Например, четырёхугольная
пирамида, в основании которой лежит
прямоугольник или параллелограмм)

20. В основании прямой призмы лежит ромб. Можно
ли в эту призму вписать сферу? (Нет, нельзя, так
как около ромба в общем случае нельзя описать
окружность)

21. При каком условии в прямую треугольную
призму можно вписать сферу? (Если высота призмы
в два раза больше радиуса окружности, вписанной в
основание)

22. При каком условии в правильную
четырехугольную усеченную пирамиду можно
вписать сферу? (Если сечением данной пирамиды
плоскостью, проходящей через середину стороны
основания перпендикулярно ей, является
равнобедренная трапеция, в которую можно вписать
окружность)

23. В треугольную усеченную пирамиду вписана
сфера. Какая точка пирамиды является центром
сферы? (Центр вписанной в данную пирамиду сферы
находится на пересечении трёх биссектральных
плоскостей углов, образованных боковыми гранями
пирамиды с основанием)

24. Можно ли описать сферу около цилиндра
(прямого кругового)? (Да, можно)

25. Можно ли описать сферу около конуса,
усеченного конуса (прямых круговых)? (Да, можно,
в обоих случаях)

26. Во всякий ли цилиндр можно вписать сферу?
Какими свойствами должен обладать цилиндр, чтобы
в него можно было вписать сферу? (Нет, не во
всякий: осевое сечение цилиндра должно быть
квадратом)

27. Во всякий ли конус можно вписать сферу? Как
определить положение центра сферы, вписанной в
конус? (Да, во всякий. Центр вписанной сферы
находится на пересечении высоты конуса и
биссектрисы угла наклона образующей к плоскости
основания)

Автор считает, что из трех уроков, которые
отводятся по планированию на тему “Разные
задачи на многогранники, цилиндр, конус и шар”,
два урока целесообразно отвести на решение задач
на комбинацию шара с другими телами. Теоремы,
приведенные выше, из-за недостаточного
количества времени на уроках доказывать не
рекомендуется. Можно предложить учащимся,
которые владеют достаточными для этого навыками,
доказать их, указав (по усморению учителя) ход или
план доказательства.

Автор надеется, что материал этой статьи
поможет молодым коллегам при подготовке к урокам
по данной теме.

{2} -4x + 4 = 0 $$

итак я получил:
$$ x = -2 \ quad или \ quad x = \ frac {2} {3} $$

$ x = -2 $ не имеет смысла, поэтому я выбрал $ x = \ frac {2} {3} $ и снова подключил его к моей исходной формуле для площади этой трапеции, но мой ответ, похоже, не совпадает любое из решений с множественным выбором. Где я ошибся?

Четырехугольников по кругу — объяснения и примеры

Мы изучили, что четырехугольник — это четырехугольник с четырьмя углами и четырьмя вершинами.Подробнее читайте в статье «Четырёхугольники» в разделе «Многоугольник».

На экзамене по геометрии экзаменаторы усложняют вопросы, вписывая фигуру внутри другой фигуры и прося вас найти недостающий угол, длину или площадь. Один пример из предыдущей статьи показывает, как вписанный треугольник внутри круга образует две хорды, и следует определенным теоремам.

В этой статье мы обсудим, что такое четырехугольник, вписанный в круг, и теорема о вписанном четырехугольнике.

Что такое четырехугольник, вписанный в круг?

В геометрии четырехугольник, вписанный в круг, также известный как вписанный четырехугольник или хордовый четырехугольник, представляет собой четырехугольник с четырьмя вершинами на окружности круга. В четырехугольной вписанной окружности четыре стороны четырехугольника являются хордами окружности.

На приведенном выше рисунке четыре вершины четырехугольника ABCD лежат на окружности окружности.В этом случае диаграмма выше называется вписанным в окружность четырехугольником.

Теорема о вписанном четырехугольнике

Есть две теоремы о вписанном четырехугольнике. Давайте взглянем.

Теорема 1

Первая теорема о круговом четырехугольнике утверждает, что:

Противоположные углы в круговом четырехугольнике являются дополнительными. т.е. сумма противоположных углов равна 180˚.

Рассмотрим диаграмму ниже.

Если a, b, c и d — внутренние углы вписанного четырехугольника, то

a + b = 180˚ и c + d = 180˚.

Давайте это докажем;

Соедините вершины четырехугольника с центром круга.

Вспомните теорему о вписанном угле (центральный угол = 2 x вписанный угол).

∠ COD = 2∠ CBD

∠ COD = 2b

Аналогично, по теореме о перехвате дуги,

∠ COD = 2 ∠ CAD

∠ COD = 2

∠ COD + reflex ∠ COD = 360 ^o

2a + 2b = 360 ^o

2 (a + b) = 360 ^o

Разделив обе стороны на 2, мы получим

a + b = 180 ^o.

Значит доказано!

Теорема 2

Вторая теорема о круговых четырехугольниках утверждает, что:

Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведения двух его пар противоположных сторон.

Рассмотрим следующую диаграмму, где a, b, c и d — стороны вписанного четырехугольника, а D ₁ и D ₂ — диагонали четырехугольника.

На приведенном выше рисунке

(a * c) + (b * d) = (D ₁ * D ₂)

Свойства четырехугольника, вписанного в круг

Существуют несколько интересных свойств вписанного четырехугольника.

Все четыре вершины четырехугольника, вписанного в круг, лежат на окружности круга.
Сумма двух противоположных углов в циклическом четырехугольнике равна 180 градусам (дополнительные углы)
Мера внешнего угла равна размеру противоположного внутреннего угла.
Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведений двух его пар противоположных сторон.
Серединные перпендикуляры четырех сторон вписанного четырехугольника пересекаются в центре O.
Площадь четырехугольника, вписанного в круг, определяется формулой Брета Шнайдера как:

Площадь = √ [s (sa) (sb) (s — c) (s — c)]

где a , b, c и d — длины сторон четырехугольника.

s = Полупериметр четырехугольника = 0,5 (a + b + c + d)

Давайте рассмотрим теорему, решив несколько примеров задач.

Пример 1

Найдите величину недостающих углов x и y на диаграмме ниже.

Решение

x = 80 ^o (внешний угол = противоположный внутренний угол).

y + 70 ^o = 180 ^o (противоположные углы являются дополнительными).

Вычтем 70 ^o с обеих сторон.

y = 110 ^o

Следовательно, размеры углов x и y равны 80 ^o и 110 ^o, соответственно.

Пример 2

Найдите угол ∠Q PS в круговом четырехугольнике, показанном ниже.

Решение

∠ QPS — это угол, противоположный ∠ SRQ .

Согласно теореме о вписанном четырехугольнике,

∠ QPS + ∠ SRQ = 180 ^o (Дополнительные углы)

∠ QPS + 60 ^o = 180 ^o

60 ^{Вычесть o} с обеих сторон.

∠ QPS = 120 ^o

Итак, величина угла ∠Q PS составляет 120 ^o.

Пример 3

Найдите размер всех углов следующего вписанного четырехугольника.

Решение

Сумма противоположных углов = 180 ^o

(y + 2) ^o + (y — 2) ^o = 180 ^o

Simplify.

y + 2 + y — 2 = 180 ^o

2y = 180 ^o

Разделим на 2 с обеих сторон, чтобы получить,

y = 90 ^o

При замене

(y + 2) ^o ⇒ 92 ^o

(y — 2) ^o ⇒ 88 ^o

Аналогично

(3x — 2) ^o = (7x + 2) ^o

3x — 2 + 7x + 2 = 180 ^o

10x = 180 ^o

Разделить на 10 с обеих сторон,

x = 18 ^o

Заменить.

(3x — 2) ^o ⇒ 52 ^o

(7x + 2) ^o ⇒ 128 ^o

Практические вопросы

1. Все многоугольники можно вписать в круг. .

A. Да

B. Нет

2. Вписанные четырехугольники также называются _____

A. Захваченные четырехугольники

B. Циклические четырехугольники

C. Касательные четырехугольники

D. Ни одного из них.

3.Четырехугольник вписан в круг тогда и только тогда, когда противоположные углы равны ______

A. Соседний

B. Альтернативный

C. Дополнительный

D. Ни один из них.

Ответы

Нет
B
C

Предыдущий урок | Главная страница | Следующий урок

Вписанные и описанные круги и многоугольники в GMAT

Вписанные и описанные

Еще один сложный тип геометрической диаграммы включает многоугольники «внутри» окружностей или окружности «внутри» многоугольников.Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на нем:

На этой диаграмме неправильный пятиугольник ABCDE равен вписанному в круг, а круг — , описанному вокруг пятиугольника. Можно также сказать: круг ограничивает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «ограниченный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.

Обратите внимание, что каждая сторона этого неправильного пятиугольника составляет касательной к окружности.Теперь пятиугольник — это , описанный вокруг круга , а круг — это , вписанный в , вписанный в пятиугольник . В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.

Треугольники

Как это часто бывает при обсуждении многоугольников, треугольники — это особый случай в обсуждении вписанных и описанных. Каждый возможный треугольник можно вписать в один круг и описать другой круг. .Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.

Обратите внимание, что, когда один угол особенно тупой, близкий к 180 °, разница в размерах между описанной окружностью и вписанной окружностью становится довольно большой. Также обратите внимание: в случае прямоугольного треугольника, второго изображения, гипотенуза треугольника равна диаметру описанной окружности.Мы вернемся к этому моменту.

Четырехугольники

Многие четырехугольники нельзя ни вписать в круг, ни описать кругом: то есть невозможно построить круг, проходящий через все четыре вершины, а также невозможно построить круг, к которому все четыре стороны касаются друг друга.

Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в круг, но нельзя описать круг. Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в круг.

Несколько элитных четырехугольников могут описывать один круг и вписываться в другой круг. Конечно, квадрат (внизу слева), самый элитный из четырехугольников, обладает этим свойством. Другой пример — «правый воздушный змей» (внизу справа), воздушный змей с парой противоположных прямых углов:

Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми особыми случаями с четырехугольниками.

Высшие многоугольники

То, что было верно для четырехугольников, верно и для всех высших многоугольников.

а. Большинство, подавляющее большинство, не могут ни описать круг, ни вписать круг.

г. Некоторые можно вписать в круг, но нельзя описать круг.

г. Некоторые могут описать круг, но не могут быть вписаны в круг.

г. Некоторые избранные могут как описать круг, так и вписаться в него.

Последняя категория, элитные члены, всегда включает правильный многоугольник. Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.Вот галерея правильных многоугольников, как с вписанной, так и с описанной окружностью.

Очевидно, что с увеличением количества сторон размеры двух окружностей становятся все ближе и ближе.

GMAT вопросы о вписанных и описанных многоугольниках встречаются редко и могут проверить как ваше понимание терминологии, так и ваши навыки визуализации, описывая геометрическую ситуацию (например, «прямоугольник JKLM вписан в круг») и , а не , давая вам оценку диаграмма.

Особый случай: треугольник, вписанный в полукруг.

Это особый случай, который нравится GMAT. Он появляется в OG13 (DS # 118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.

Если все, что вы знаете, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90 ° и что треугольник JKL является прямоугольным треугольником с KL в качестве гипотенузы. С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром.Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.

Кстати, этот пост — четвертый в серии из пяти статей. Вот вся серия.

1) Введение в окружности в GMAT

2) Геометрия GMAT: круги и углы

3) Круговые и линейные диаграммы в GMAT

4) Вписанные и замкнутые круги и многоугольники в GMAT

5) Разбиение на части GMAT Circles: Arclengths, Sectors, and Pi

Практический вопрос

1) На диаграмме выше S — центр круга.Если QS = 5 и QR = 6, что такое PQ?

A. 7

B. 8

C. 9

D. 10

E. 11

Практическое объяснение вопроса

1) Прежде всего, QS — это радиус, поэтому если QS = 5 , это означает, что PS = SR = 5 и диаметр PR = 10. Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64

PQ = sqrt {64} = 8

Ответ = B

Готовы получить отличный результат GMAT? Начните здесь.

Самые популярные ресурсы

О Майке МᶜГарри

Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах.Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы болеть за Нью-Йорк Метс.

Четырехугольники — Четырехугольники циклические | Shmoop

Циклический четырехугольник

Всю жизнь нас учили, что коробки — это плохо. Мы не должны складывать вещи в коробки (по крайней мере, по мнению Розенкранца и Гильденстерна). Лучше мыслить нестандартно. И это не совсем комплимент, когда бабушка говорит вам, что ваша фигура становится «квадратной».»

Итак, если мы не можем складывать вещи в коробки, давайте попробуем складывать их в круги.

Циклический четырехугольник — это четырехугольник, все вершины которого лежат на окружности. Неважно, углы или стороны параллельны или конгруэнтны, либо нет ни одного из вышеперечисленных. Если мы можем нарисовать круг, соединяющий все вершины этого четырехугольника, он будет циклическим. Никаких вопросов.

Пример задачи

Какой из следующих четырехугольников является круговым?

Самый простой способ определить, какие четырехугольники являются циклическими, — это просто нарисовать вокруг них наименьший из возможных кругов.

Когда мы рисуем самые маленькие окружности вокруг каждого четырехугольника, мы видим, что все вершины (B) и (C) находятся на окружности. Четырехугольник в (A) имеет только две вершины на своей окружности. Итак, (B) и (C) циклические, а (A) — нет. Просто как тот.

Ну, а что же такого особенного в круговых четырехугольниках? Можно целый день вплетать четырехугольники в круги, но какой в этом смысл?

Противоположные углы вписанных четырехугольников всегда являются дополнительными.Это означает, что если мы можем нарисовать круг вокруг четырехугольника, который соединяет все его вершины, то мы сразу знаем, что противоположные углы имеют меры, которые в сумме составляют 180 °. Как , что за точку? И мы только начинаем.

Также верно, что если две противоположные стороны вписанного четырехугольника равны, то две другие стороны параллельны. Возможно, мы этого не ожидали, но, тем не менее, это правда. Точно так же, как мы, возможно, не ожидали, что Наполеон Бонапарт страдает айлурофобией (страхом перед кошками).Но он это сделал.

Допустим, четырехугольник вписанный. Если у него есть пара конгруэнтных и параллельных противоположных сторон, то это должен быть прямоугольник. Если у него есть пара конгруэнтных и непараллельных сторон , это должна быть равнобедренная трапеция.

Пример задачи

Четырехугольник PQRS является циклическим. Что такое ∠ PSR ?

Из рисунка видно, что PS ≅ QR .Поскольку противоположные стороны этого кругового четырехугольника совпадают, мы знаем, что две другие стороны (а именно, PQ и SR ) параллельны. Мы также знаем, что ∠ QPS и ∠ PSR являются дополнительными, потому что последовательные углы, которые разделяют одно и то же плечо в трапеции, являются дополнительными. Таким образом, мы можем составить следующее уравнение:

м∠ QPS + m∠ PSR = 180 °
75 ° + м∠ PSR = 180 °
м∠ PSR = 180 ° — 75 °
м∠ PSR = 105 °

Игра, набор и матч.

Что, если нас попросят определить, является ли данный четырехугольник циклическим? Что же нам тогда делать? Мы могли бы просунуть голову между колен и поцеловать задницу на прощание, но мы бы этого не сделали. Вместо этого у нас есть два варианта:

Докажите, что все вершины четырехугольника лежат на окружности. (Они называют это «методом компаса», потому что нам, вероятно, понадобится компас.)
Докажите, что любые два противоположных угла являются дополнительными.

Пример задачи

Является ли квадрат вписанным четырехугольником?

Все внутренние углы квадрата равны 90 °.Противоположные пары составляют в сумме 180 °, что означает, что они дополняют друг друга. Поскольку мы доказали, что противоположные углы являются дополнительными, мы знаем, что квадраты циклические. Вы также можете попробовать это с помощью компаса, но мы рекомендуем рисовать его на бумаге, а не на экране компьютера. Просто предложение.

Квадрат, вписанный в круг

Когда квадрат вписан в круг, мы можем вывести формулы для всех его свойств — длины сторон, периметра, площади и длины диагоналей, используя только радиус круга.

И наоборот, мы можем найти радиус, диаметр, длину окружности и площадь круга, используя только сторону квадрата.

Задача 1

Квадрат вписан в круг с радиусом ‘r’. Найдите формулы для длины стороны, длины диагонали, периметра и площади квадрата через r.

Стратегия

Ключевым моментом для решения этой проблемы является то, что диагональ квадрата — это диаметр круга. Мы можем показать это, используя аргумент симметрии — квадрат симметричен по диагонали, поэтому диагональ должна проходить через центр круга.

В качестве альтернативы мы знаем, что все внутренние углы квадрата являются прямыми углами, составляющими 90 °. Поскольку эти углы вписаны в круг, они измеряют половину центрального угла на той же дуге. Таким образом, центральный угол составляет 180 °, что означает диаметр.

Вооружившись этим знанием, длина диагонали квадрата равна просто 2r, каждая сторона измеряет r · √2 (теорема Пифагора, примененная к треугольнику 45-45-90), тогда площадь равна 2r ², а периметр равно 4 · r · √2.

Теперь давайте сделаем обратное, найдя свойства круга по длине стороны вписанного квадрата.

Задача 2

Квадрат со стороной a вписан в круг. Найдите формулы для радиуса, диаметра, длины окружности и площади круга через a.

Стратегия

У нас уже есть ключевой вывод сверху — диаметр — это диагональ квадрата. Мы уже видели, как найти длину диагонали квадрата со стороны: это · √2.Радиус равен половине диаметра, поэтому r = a · √2 / 2 или r = a / √2. Окружность равна 2 · r · π, значит, это · √2 · π. А площадь равна π · r ², поэтому это π · a ²/2.

Теперь, когда мы это сделали, мы можем применить наши знания для решения различных задач «найти область заштрихованной формы», связанных с квадратом, вписанным в круг, например, этот:

Задача 3

A квадрат со стороной а вписан в круг. Найдите область заштрихованной формы.

Стратегия

Стратегия поиска области неправильных форм обычно состоит в том, чтобы увидеть, можем ли мы выразить эту область как разницу между областями, образованными двумя или более правильными формами.

Вот это очень просто — все четыре неправильные формы имеют одинаковый размер (из-за симметрии). Сумма их площадей — это разница между площадью круга и площадью квадрата.

Итак, заштрихованная область A _{заштрихована} = (A _круг -A _{квадрат}) / 4

Если у нас есть сторона квадрата, a, мы получим A _{заштрихованный} = (_круг -A _{квадрат}) / 4 = (π · a ²/2 -a ²) / 4 = (π-2) · a ²/8.

И если у нас есть радиус, A _{закрашенный} = (A _круг -A _{квадрат}) / 4 = (π · r ² -2r ²) / 4 = (π-2) · r ²/4

Теперь, когда мы это сделали, мы можем решить аналогичную задачу, где вместо квадрата, вписанного в круг, у нас есть круг, вписанный в квадрат.

Вписанная окружность многоугольника — математическая открытая ссылка

Вписанная окружность многоугольника — математическая открытая ссылка

Определение: самый большой круг, который поместится внутри многоугольника, который касается каждой стороны.

Попробуй это
Отрегулируйте правильный многоугольник ниже, перетащив любую оранжевую точку, или измените количество сторон.Обратите внимание на поведение вписанной окружности многоугольника.

Вписанная окружность правильного многоугольника — это наибольшая окружность, которая помещается внутри многоугольника и касается каждой стороны.
только в одном месте (см. рисунок выше), и поэтому каждая из сторон представляет собой
касательная к вписанной окружности.
Если количество сторон 3, это
равносторонний треугольник и вписанная в него окружность ровно
такой же, как описанный в Введении треугольника.

Внутренний радиус правильного многоугольника точно такой же, как и его апофема.Формулы ниже такие же, как для апофемы.
Для начала используйте формулу, в которой используются предоставленные вам факты.

Inradius с учетом длины стороны

По определению, все стороны правильного многоугольника равны по длине. Если вам известна длина одной из сторон, внутренний радиус определяется по формуле:

где
s — длина любой стороны
n — количество сторон
tan — тангенциальная функция, вычисленная в градусах (см. Обзор тригонометрии)

Inradius с учетом радиуса (описанной окружности)

Если ты знаешь радиус
(расстояние от центра до вершины):

где
r — радиус (окружной радиус)
n — количество сторон
cos — функция косинуса, вычисленная в градусах (см. Обзор тригонометрии)

Неправильные многоугольники

Неправильные многоугольники не считаются вписанной окружностью или даже центром.Если бы вы нарисовали многоугольник наугад, он
маловероятно, что существует круг, каждая сторона которого является касательной.
Исключение составляет трехсторонний многоугольник (треугольник). У всех треугольников всегда есть вписанная окружность.
(См. Окружность треугольника)

Однако может произойти и обратное. Вы можете начать с круга и нарисовать вокруг него неправильный многоугольник, как на рисунке справа.
Это можно было бы назвать ограниченным многоугольником.

Некоторые математики считают вписанную окружность наибольшей окружностью, которая помещается внутри многоугольника,
без требования, чтобы он касался всех сторон.Понятно, что согласно этому определению всегда можно нарисовать такой круг.

Другие темы многоугольников

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

Видео: кадрирование изображения по форме

Используйте инструменты кадрирования в PowerPoint, чтобы обрезать и удалять ненужные части изображений или обрезать изображение по размеру формы.

Обрезка изображения по форме

Если вы хотите изменить контур изображения и придать ему форму (например, круг или звезду), используйте инструменты обрезки на вкладке ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ .

Выберите изображение (или изображения), которое вы хотите обрезать.
Если вы обрезаете сразу много изображений, вы должны использовать одну и ту же форму для всех из них.Чтобы кадрировать до разных форм, кадрируйте каждое изображение по одному
На вкладке ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ щелкните Обрезать > Обрезать по фигуре , а затем выберите нужную форму.

Обрезать по фигуре или заполнить ее

В качестве заливки фигуры можно использовать изображение. Просто щелкните фигуру, к которой вы хотите добавить изображение, затем в разделе ИНСТРУМЕНТЫ ДЛЯ РИСОВАНИЯ на вкладке ФОРМАТ щелкните Стили формы > Заливка формы > Изображение и выберите нужное изображение.

Щелкните нужный рисунок внутри фигуры.
Щелкните ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЙ > ФОРМАТ > Размер и щелкните стрелку под Обрезать . Если вы не видите вкладки Работа с изображениями и Формат, убедитесь, что вы выбрали изображение.
Нажмите Заполните или Подогните .
- Заливка устанавливает размер изображения в соответствии с высотой или шириной фигуры, в зависимости от того, что больше. Это заполнит фигуру изображением.
- Подгонка устанавливает размер изображения таким образом, чтобы высота и ширина изображения соответствовали границам фигуры. Это максимально поместит изображение в форму.Некоторые области фигуры могут остаться пустыми.
Когда вы закончите, нажмите ESC.

Хотите больше?

Обрезать картинку

Вы можете улучшить изображение, придав ему другую форму. Быстрый способ сделать это — использовать Crop to Shape .

Сначала выберите картинку на слайде.

Затем найдите вкладку ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЯ ФОРМАТ , которая появляется при выборе изображения. Щелкните FORMAT .

На вкладке ФОРМАТ в группе Размер щелкните стрелку под Обрезать и укажите на Обрезать до формы .

Это открывает галерею фигур, где вы можете выбрать форму для изображения.

Ищите форму, которая хорошо сочетается с изображением и ориентацией изображения.Для этого изображения давайте попробуем прямоугольник с закругленными углами.

Эта форма прекрасно работает, вырезая небольшую часть изображения и придавая ему закругленные углы.

Обратите внимание, что Обрезать по форме сохраняет соотношение сторон изображения, то есть пропорции его высоты к ширине.

Чтобы поэкспериментировать с другой формой, просто щелкните стрелку под Обрезать и укажите на Обрезать до формы .

Давайте поищем совершенно другую форму.А как насчет звезды?

Интересно, но я думаю, что он вырезает слишком много из изображения, особенно из центральной фигуры.

Я нажму Отменить , чтобы вернуться к форме прямоугольника со скругленными углами, которая лучше соответствует этому изображению.

Теперь, когда изображение все еще выбрано и отображается вкладка FORMAT , я сделаю небольшое форматирование изображения.

Например, я нажимаю Граница изображения и выбираю цвет границы.

Затем я снова нажму Граница изображения , наведу указатель на Толщина и увеличу ширину границы до 4 ½ пункта, чтобы она была более заметной.

Это приятный простой акцент.

Если вам нужно более сложное форматирование изображения, вот быстрый способ его применения и использование Обрезать по форме .

Вернемся к исходной картинке.

На этот раз, прежде чем использовать Обрезать по фигуре , я выделю изображение, нажмите ФОРМАТ и нажмите Еще , чтобы открыть галерею Стили изображения .

Стили галереи сочетают в себе разные вещи — тип формы изображения, цвета и стили границ, а также такие эффекты, как отражения и тени.

Я найду стиль изображения, который мне нравится, например этот, с белой рамкой и тенью в перспективе, и нажму, чтобы применить его.

Затем, не снимая выделения с изображения, я нажимаю стрелку Crop , наведу указатель на Crop to Shape и выберу прямоугольник с закругленными углами.

После этого процесса я быстро получил более сложный стиль изображения, затем я выбрал нужную форму, используя Crop to Shape .

Для получения дополнительных сведений см. Краткое содержание курса и поэкспериментируйте с PowerPoint.

Правильный треугольник	\(R =\) 23h; \(R=\) a33
Прямоугольный треугольник	\(R=\) 12 гипотенузы
Произвольный треугольник	R=abc4S;R=a2sinα
Квадрат	\(R =\) a22
Прямоугольник	\(R =\) d2
Правильный шестиугольник	\(R = a\)