Содержание
Урок 3. масштаб — Математика — 6 класс
Математика
6 класс
Урок № 3
Масштаб
Перечень рассматриваемых вопросов:
- Понятие масштаба.
- Находить масштаб по заданному расстоянию на местности и расстоянию на карте (плане).
- При заданном масштабе и расстоянии на местности определять расстояние на карте (плане).
- При заданном масштабе и расстоянии на карте (плане) определять расстояние на местности.
Тезаурус
Частное двух не равных нулю чисел a и b называется отношением чисел a и b.
Числа a и b называются членами отношения.
Отношения 2 к 3 и 3 к 2 называются взаимно обратными.
Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.
Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т. д.) есть новая величина.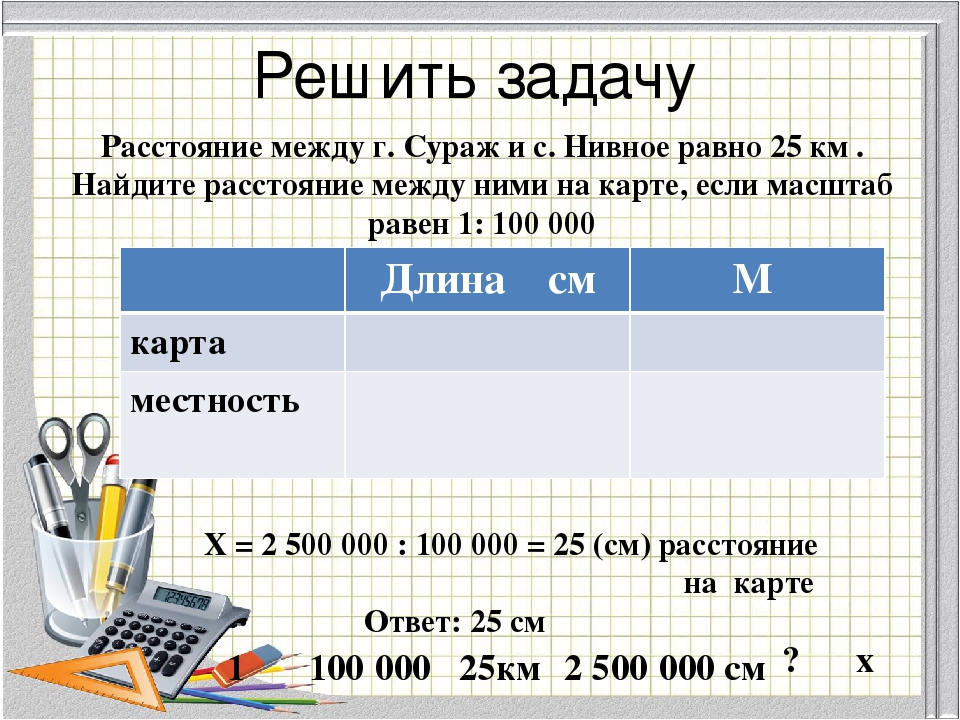
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Масштаб, выраженный отношением чисел, называется численным.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.
Теоретический материал для самостоятельного изучения
Сегодня мы с вами разберём, что означает масштаб.
Давайте сначала вспомним, что отношение величин одного наименования – это число.
Составим отношения:
Все мы хорошо знаем, что участки земной поверхности, детали машин и многое другое изображается на бумаге в уменьшенном виде.
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Рассмотрим пример:
Длина отрезка на карте равна 8 см.
Ответ: 800 м.
Ещё один пример:
Длина отрезка на местности равна 130 километров.
Ответ: 13 см.
Что же означает данный масштаб:
Говорят: карта сделана в масштабе одна двухтысячная. Объект на карте уменьшен в 2000 раз.
Что будет означать такой масштаб:
Рассмотрим ещё несколько примеров.
Огород имеет вид прямоугольника, длина которого 60 м, а ширина 10 м.
Ответ: Огород на плане будет иметь размеры: ширина 20 см, длина 12 см.
Разбор заданий тренировочного модуля
№ 1. Тип задания: Установление соответствий между элементами двух множеств.
Расстояние между двумя городами равно 150 км. Определите расстояние между изображениями этих городов на карте при трёх разных масштабах карты.
№ 2. Тип задания: Выбор элемента из выпадающего списка.
Тип задания: Выбор элемента из выпадающего списка.
Значит, выбираем ответ 15 км.
3.3.2. Численный и линейный масштаб
Масштаб карты — степень уменьшения линии на карте или плане относительно горизонтального проложения соответствующей линии на местности.
При работе с картой, планами или аэрофотоснимками местности пользуются различными масштабами: численным или линейным.
Численный масштаб — масштаб длин, выраженный отвлеченным числом, в котором числитель — единица, а знаменатель — число, показывающее, во сколько раз уменьшены линейные размеры карты (формула 1):
| d | | 1 | |
D | D / d | |||
|
|
где d — длина линии на карте;
М — знаменатель масштаба карты;
D — длина горизонтального проложения этой линии на местности.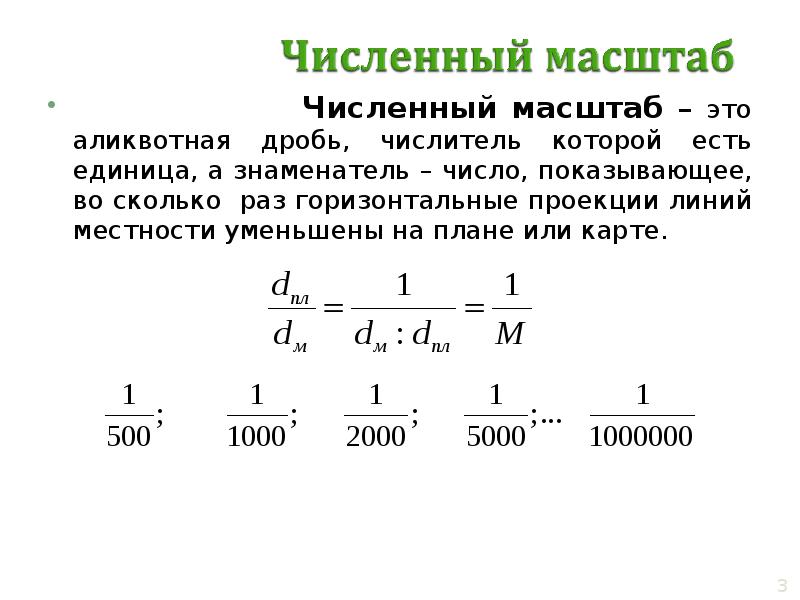 Масштаб карты или плана определяет подробность изображения на них
Масштаб карты или плана определяет подробность изображения на них
элементов местности. Чем больше значение знаменателя численного масштаба М, тем больше степень уменьшения горизонтальных проекций линий местности, тем мельче масштаб плана или карты и менее подробно изображены элементы местности. И наоборот, чем знаменатель М меньше, тем масштаб будет крупнее, тем с большей подробностью и детальностью могут быть показаны на них элементы местности.
Например, численный масштаб 1:50 000 является более мелким, чем масштаб 1:25 000, но более крупным, чем масштаб 1:100 000.
Для удобства знаменатель численного масштаба принимают равным круглому числу: 1:500, 1:1 000, 1:2 000, 1:5 000 и 1:10 000 — для планов,
1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000, 1:1 000 000 — для топографических карт. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены соответственно в 500, 1000, 2000 раз и т. д., то есть отрезку 1 см на плане соответствуют на местности длины: 500 см или 5 м; 1000 см или 10 м; 2000 см или 20 м и т. д.
д.
Расстояние на местности в метрах или километрах, соответствующее 1 см карты или плана, называется величиной масштаба. Численный масштаб и величина масштаба размещаются под южной стороной рамки листа карты.
Численный масштаб — безразмерная величина, поэтому им можно пользоваться при измерениях в любых линейных мерах (метрах, милях и т.д.). Величина отношения 1:М сохраняет силу для всех линий плана или карты. Следовательно, масштаб является постоянной величиной.
Непосредственное использование численного масштаба в практической работе связано с вычислениями, которые необходимы для перехода от горизонтальных проекций линий местности к соответствующим линиям плана или карты, и наоборот.
При пользовании численным масштабом расстояния на карте или плане могут быть измерены в сантиметрах линейкой или курвиметром. Полученное при этом число сантиметров умножают на знаменатель масштаба.
Например, линия на карте d = 13,14 см, а масштаб карты 1:100 000. Используя формулу перехода от линий карты (плана) к горизонтальным проекциям соответствующих линий местности D = dM, получим D = 13,14 100 000 = 1314 000 см = 13 140 м = 13,14 км.
Для нанесения на карту или план линий, измеренных на местности, используют (равенство 2):
| d | D | (2) |
| M | ||
|
|
| |
|
| . |
|
Например, D = 3750м; 1:М = 1:50 000, тогда d = 3750:50 000 = 0,075м | |||
= 7,5см. |
|
|
|
|
| Линейным масштабом называется | |
| графическое | изображение численного | |
| масштаба в виде прямой линии с | ||
| делениями для отсчета расстояний. | ||
Рис. 40. Линейн6ый масштаб | построения | линейного масштаба на | |
| прямой линии откладывают ряд отрезков | ||
одинаковой длины, называемой основанием линейного масштаба (рис. 40). Основание масштаба обычно соответствует целому числу километров или сотен метров.
| Для повышения точности измерения первое основание разделено на | ||||
более | мелкие | части. | Для | карты | масштаба |
1:50 000 наименьшее деление на линейном масштабе будет соответствовать
50 м.
Измерения по линейному масштабу производят циркулем- измерителем. При измерении циркуль следует держать одной рукой, наклоняя от себя так, чтобы были хорошо видны одновременно обе иглы. И определяя с помощью линейного масштаба длину линии, взятой с карты или плана, нужно правую ножку циркуля поставить на одну из черточек справа от нуля с таким расчетом, чтобы вторая его ножка точно совпала с крайним левым основанием масштаба.
И определяя с помощью линейного масштаба длину линии, взятой с карты или плана, нужно правую ножку циркуля поставить на одну из черточек справа от нуля с таким расчетом, чтобы вторая его ножка точно совпала с крайним левым основанием масштаба.
США намерены увеличить масштаб гуманитарной помощи штату Тыграй — Международная панорама
ООН, 4 марта. /ТАСС/. Соединенные Штаты направили специальную команду, которая будет руководить увеличением масштаба гуманитарной помощи США штату Тыграй (Эфиопия). Об этом в четверг в видеообращении сообщила постоянный представитель США при ООН Линда Томас-Гринфилд после проведения закрытых консультаций Совета Безопасности ООН по ситуации в этом регионе.
«На этой неделе мы направили в Эфиопию команду помощи в реагировании на чрезвычайные ситуации, чтобы руководить расширением гуманитарной помощи американского правительства. Нашей целью является помощь пострадавшим в регионе Тыграй, и мы надеемся, что другие присоединятся к нашим неотложным, необходимым усилиям по спасению жизней», — сказала она.
Томас-Гринфилд отметила, что происходящее в регионе «приводит к разрушительным последствиям для тысяч людей и представляет собой региональную угрозу миру и безопасности». Американский дипломат добавила, что США «встревожены гуманитарной ситуацией и в сфере соблюдения прав человека в Эфиопии» и призывают правительство страны «поддержать немедленное прекращение столкновений в регионе Тыграй».
По информации ТАСС от источников в ООН, Совбез на закрытой встрече не пришел к единому мнению по ситуации в Тыграе.
Военная операция федеральных войск началась в штате Тыграй 4 ноября после того, как мятежники из Народного фронта освобождения Тыграя (НФОТ) напали накануне на объекты Северного командования, убили оставшихся верными центральному правительству военных и захватили тяжелое вооружение. Боевая фаза операции завершилась 28 ноября взятием федеральными войсками столицы Тыграя Мэкэле и возвращением Аддис-Абебой контроля над всеми крупными городами и стратегическими объектами штата.
Лидеры НФОТ покинули Мэкэле за несколько часов до вхождения в него федеральных войск. Геберемайкл заявил, что борьба с федеральным правительством за самоопределение Тыграя будет продолжена. Во время проходящей в Тыграе полицейской операции были задержаны несколько десятков членов руководства НФОТ, некоторые из них погибли во время перестрелок с силовиками.
Масштаб чертежей по ГОСТ: виды масштаба, полезные советы
Масштаб (размер) чертежа – параметр, о котором должен знать каждый инженер, геодезист, программист, ведь без его определения невозможно начать чертить проект.
При выборе размера «самовольничать» не получится, так как масштабы чертежей стандартизованы, подбираются по ГОСТ. Действующим стандартом для всех отраслей строительства и промышленности является ГОСТ 2.302-68.
Слово «масштаб» пришло в русский язык из немецкого, где «masstab» – это мерная палка, масштаб, размер, мерило.
Виды масштаба
Указанный выше ГОСТ определяет 3 вида масштаба: натуральный, уменьшенный и увеличенный. Оптимальным является масштаб, который соответствует реальным параметрам, обозначается он 1:1.
Оптимальным является масштаб, который соответствует реальным параметрам, обозначается он 1:1.
Лучший масштаб — реальный
Тем не менее, не всегда получается воспроизвести объект в натуральную величину, если он слишком большой или маленький.
В таких случаях используются увеличивающий и уменьшающий масштабы.
Масштабы уменьшения применяются, когда габариты объекта слишком большие (например, в строительных чертежах, графических изображениях в сфере геодезии).
ГОСТ предлагает около десятка вариантов увеличения, с которыми можно ознакомиться в пункте 5.2 данного нормативного документа или в таблице, предоставленной ниже (составлена по ГОСТ).
Слишком крупные объекты, например, для генеральных планов, можно изображать в соотношениях 1:50000, 1:25000, 1:20000, 1:10000, 1:5000, 1:2000.
Если же деталь очень маленькая (гайка, болт, деталь компьютера, ноутбука и другой техники), для ее изображения на бумаге нужно использовать масштаб увеличения, варианты которого также предоставлены государственным стандартом (см. таблицу).
таблицу).
https://drive.google.com/file/d/0BxbM7O7fIyPcOFdNYlZlQnVDUWM/view?usp=sharing
Обратите внимание! Первая цифра в соотношениях указывает на величину реального объекта, а вторая – на размер на чертеже. Например, соотношение 1:2 указывает на то, изображение уменьшило деталь в 2 раза, а если на чертеже обозначено 2:1 – деталь наоборот увеличили в 2 раза.
ГОСТом предусмотрена и ситуация, когда автору нужно самостоятельно рассчитать увеличенный масштаб. Для этого используется формула 100n:1 (букву n при расчете меняем на целое число).
Некоторые заметки к оформлению
После того, как масштаб рассчитан, его нужно обязательно нанести на чертеж. Записывается он в графе основной надписи по такому шаблону М 1:2, М 2:1. Параметры шрифта такие же, как и для остального текста в основной надписи.
Когда масштаб какого-то изображения на чертеже имеет параметры, отличающиеся от тех, что указаны в основной надписи, такой масштаб нужно написать сразу после надписи, которая относится к соответствующему графическому объекту.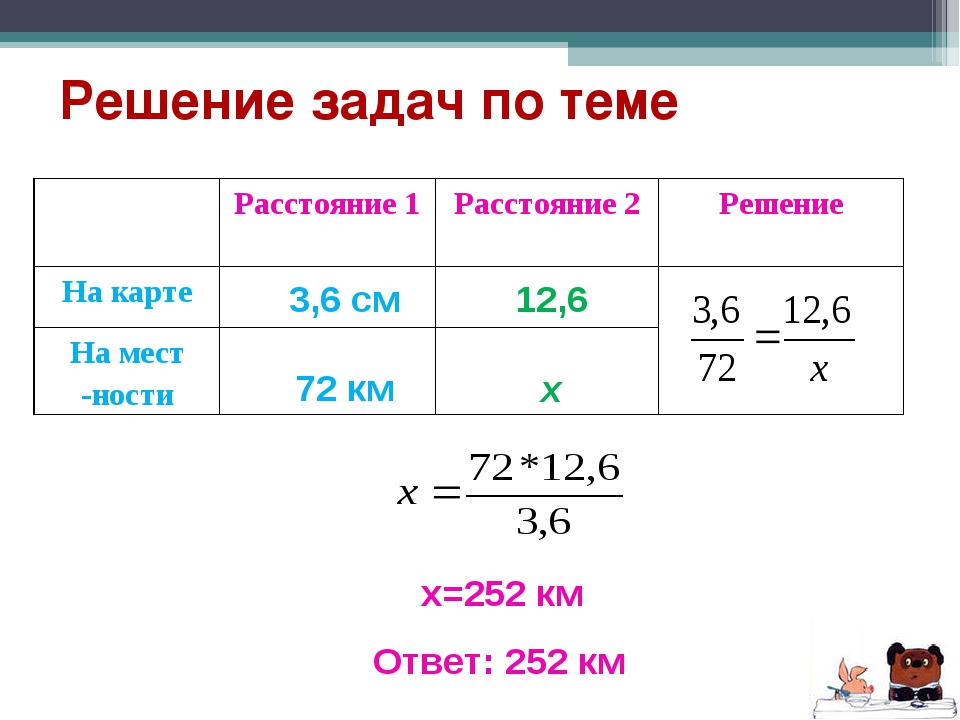
Примеры записи: А (3:1), Б(1:10). Эта ситуация также прописана ГОСТом 2.316-68.
Как определить масштаб на уже готовом чертеже
Очень часто людям, работающим в промышленной или строительной отраслях, студентам технических ВУЗов приходится работать с чужими чертежами.
Нужно научиться определять масштаб на чужих чертежах
Предоставим алгоритм, который поможет быстро справляться с данной задачей:
- Ознакомиться с основной надписью чертежа, там должен быть указан масштаб. Располагается он в нижнем углу изображения справа. Если масштаб обозначен, дальнейшие действия данного алгоритма выполнять не придется, в противном случае придется засучить рукава и определить соотношение размеров самостоятельно. Для самостоятельных расчетов предлагаем инструкцию, отображенную в следующих пунктах.
- Определить, что именно изображено в графическом документе, узнать реальные размеры объекта.
- Если деталь имеется под рукой, а габариты ее неизвестны, их нужно измерить самостоятельно.
 Для этого применяются рулетка, штангенциркуль, линейка и другие инструменты.
Для этого применяются рулетка, штангенциркуль, линейка и другие инструменты. - На чертеже нужно определить, в каком разрезе изображена деталь.
- На графических изображениях найти тот вид объекта, где прописаны габаритные параметры. На изображении такого вида должна быть размерная линия (она имеет стрелки на концах и указание размеров по середине). К размерной линии нужно приложить рулетку или линейку и определить числовое значение.
- Сравнить полученные в ходе измерений результаты (результат самостоятельного измерения делим на число, указанное на размерной линии, например самостоятельное измерение дало показатель – «27», на линии написано «3», значит масштаб увеличен в 9 раз).
Этот алгоритм поможет научиться определять масштаб изображений.
Парочка советов на заметку
При определении или выборе масштаба важно учитывать то, что все величины на чертежах рассчитываются и прописываются в миллиметрах. Если удобно работать с сантиметрами, можно сначала измерять все в них, а потом перевести в миллиметры.
Если не удалось найти нужные параметры на строительном чертеже, стоит попробовать выяснить реальные размеры реального объекта (проекта). Можно сделать приблизительные расчеты, учитывая этажность постройки.
Делая замеры детали для чертежа, необходимо учитывать основные параметры: высоту, длину и ширину. Далее они отображаются в натуральном, уменьшенном или увеличенном масштабах.
Как видим, определять масштаб и записывать его по ГОСТу совсем не сложно, нужно лишь вооружиться измерительными приспособлениями, нормативным документом и терпением.
В этом видео вы узнаете о масштабах и размерах чертежей в Автокад:
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Масштаб площади
Масштаб площади
Масштаб площади на карте
Масштабом площади в данной точке карты называется отношение площади бесконечно малого эллипса на карте к площади соответствующего бесконечно малого круга на земном эллипсоиде.
Известно, что площадь эллипса с полуосями А и B вычисляется по формуле
,
а площадь круга—по формуле
.
Обозначив масштаб площади буквой Р и взяв отношение площади эллипса к’ площади круга, будем иметь
Или
Из последнего выражения видно, что масштаб площади в данной точке карты равен произведению масштабов по главным направлениям в этой же точке.
Считая главный масштаб карты и приравняв радиус бесконечно малого круга с на эллипсоиде к единице, будем иметь
(4)
Где А и B—числа отвлеченные, выражающие собой длины большой и малой полуосей эллипса искажений на карте в радиусах бесконечно малого круга на эллипсоиде.
Для определения масштаба площади можно поступить и иначе. Пусть направлениям меридиана MoNo и параллели МoEo в бесконечно малом круге на эллипсоиде (рис. 12 а) соответствуют на карте в эллипсе искажений расположенные под углом в направления, MN и ME (рис.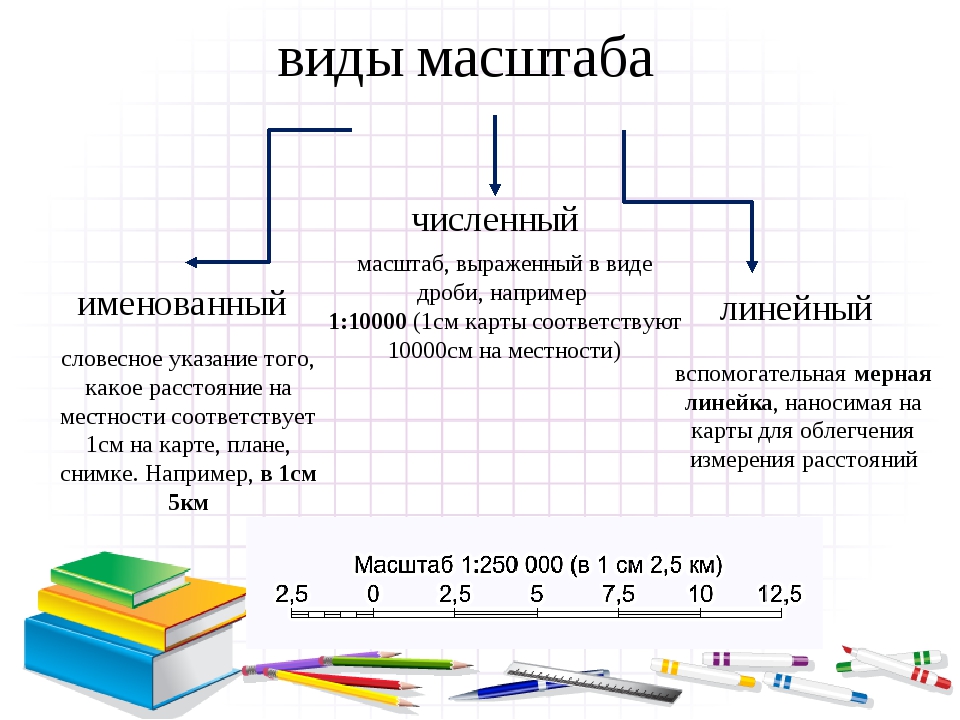 126), точкам Ho, Аo, Fo соответствуют точки H, А и F, а направлениям AoDo и СoBo —главные направления (оси эллипса) AD и СВ. Тогда масштаб площади можно определить как отношение площади бесконечно малого параллелограмма MHAF к площади бесконечно малого прямоугольника MoHo AoFo, и получить равенство
126), точкам Ho, Аo, Fo соответствуют точки H, А и F, а направлениям AoDo и СoBo —главные направления (оси эллипса) AD и СВ. Тогда масштаб площади можно определить как отношение площади бесконечно малого параллелограмма MHAF к площади бесконечно малого прямоугольника MoHo AoFo, и получить равенство
Но
а
Следовательно,
Т. е. масштаб площади равен произведению масштабов по меридиану и параллели на синус угла между ними. Итак, для определения масштаба площади можно пользоваться как формулой (4), так и формулой (5).
Рис. 1. Направления меридиана и параллели в бесконечно малом круге на эллипсоиде и соответствующем ему эллипсе на карте
Зная масштаб площади, можно определить и относительное искажение площади по формуле
= Р-1
Относительное искажение площадей так же, как и относительное искажение длин, выражается в процентах. Так например, если р=1,23, то =0,23, или =23%
Следует отметить, что, кроме понятия масштаба площади, существует также понятие увеличения масштаб а площади, под которым понимают отношение площади бесконечно малой фигуры на карте к площади соответствующей бесконечно малой фигуры на глобусе, масштаб которого равен главному масштабу карты. Именно это увеличение и характеризует собой искажение площадей. При Увеличение масштаба площади равно масштабу площади. Поэтому в дальнейшем изложении термин «увеличение масштаба площади» будет заменяться термином «масштаб площади».
Именно это увеличение и характеризует собой искажение площадей. При Увеличение масштаба площади равно масштабу площади. Поэтому в дальнейшем изложении термин «увеличение масштаба площади» будет заменяться термином «масштаб площади».
Масштаб площади — 5.0 out of
5
based on
1 vote
Как рассчитать масштаб изображения? | Астрономические мероприятия, наблюдения звездного неба в Крыму!
День добрый, любители астрономии и астрофотографии! В этой статье — короткий, но очень полезный расчет, который однажды пригодится даже тем, кто снимает небо редко. Ну а те кто занимается этим приятным ночным делом постоянно, должны знать его назубок! 🙂 Речь пойдет о масштабе изображения получаемой с вашй техникой. У вас, наверное спрашивают — какое увеличение дает этот телескоп? И по сути ответить людям нечего, тк обычное понятие увеличение предполагает наличие окуляра, ибо считается оно по формуле F/f, где F — фокус объектива, а f — фокус окуляра. Как же быть в случае с одним лишь объективом и фотокамерой? Давайте посчитаем!
Как же быть в случае с одним лишь объективом и фотокамерой? Давайте посчитаем!
Предположим, у вас есть классический телескоп системы Ньютона с зеркалом D=200 мм и фокусным расстоянием F=1000мм. Съемка ведется на матрицу QHY5-L-II-M. Каков же будет масштаб изображения? Фактически вопрос заключается в том насколько большую картинку мы увидим на экране монитора. Но помимо визуального эффекта вопрос имеет и практическую составляющую. К примеру, зная сколько секунд дуги неба приходится на один пиксель матрицы можно оценить влияние турбуленции на изображение или понять какую выдержку надо дать чтобы движущийся с известной скоростью в кадре астероид/комета еще не успел размазаться в черточку. Также можно оценить видимость деталей на планетах, к примеру — сможем ли мы наблюдать в данный телескоп вулкан Олимп на Марсе в момент великого противостояния.
Поскольку нас известен из документации фокус нашего телескопа, начнем с него. Из геометрии известно, что 1 угловая секунда — это угловой размер объекта на расстоянии равном 206265 его линейных размеров.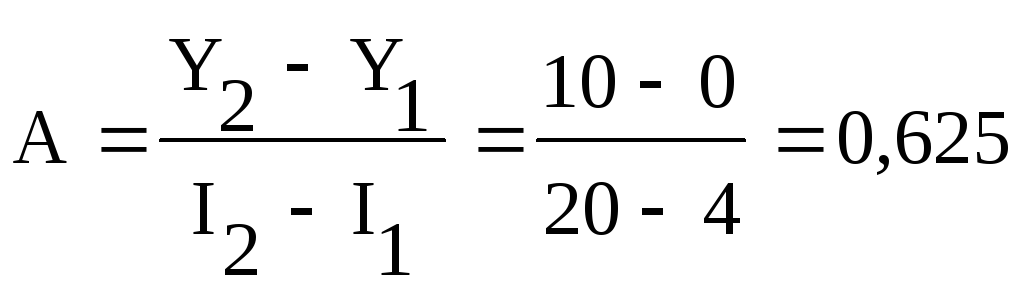 Отсюда масштаб изображения в секундах на миллиметр s = 206265/F, где F — фокус в миллиметрах, то есть s = 206,265″/мм. Обратите внимание, ответ в секундах дуги на миллиметр.
Отсюда масштаб изображения в секундах на миллиметр s = 206265/F, где F — фокус в миллиметрах, то есть s = 206,265″/мм. Обратите внимание, ответ в секундах дуги на миллиметр.
Но нам нужен масштаб в секундах на пиксель. Это легко! Из документации к матрице узнаем, что размер ее пикселя 3,75 мкм, то бишь миллионных долей метра или тысячных долей миллиметра. Значит, в одном миллиметре умещается 267 таких пикселей и окончательный масштаб s = 206,265/267 = 0,77″/px.
Отсюда выходит, что у астрофотографов для получения большого масштаба есть два пути: взять телескоп с большим фокусным расстоянием (или линзу барлоу), либо достать матрицу с меньшим размером пикселя. У каждого из способов есть свои недостатки: больший фокус потребует большего диаметра зеркала при сохранении светосилы, а меньший пиксель будет принимать меньшее количество фотонов в единицу времени, значит потребует большей выдержки для получения той же величины отношения сигнала к шуму. И конечно же картинка с большим масштабом будет более чувствительна к атмосфере и механике телескопа.
октябрь 2015,
Ваш Назаров Сергей.
Расчет поля зрения телескопа
Астробиблиотека
P.S. Если не охота считать ручками, забейте размер пикселя и фокус телескопа в Максимке, там есть кнопка «PinPoint Astrometry» и программа выдаст Вам масштаб автоматически 🙂 Этот процесс разобран в статье АСТРОМЕТРИЯ.
P.P.S. Масштаб изображения в виде угловых секунд на пиксель также выдает сайт nova.astrometry.net. Загрузите туда снимок, дождитесь отождествления и вуаля! Результат весьма точен, ему смело можно доверять.
P.P.P.S. Полезная ссылочка на инглише: https://www.peterzelinka.com/blog/2020/2/choosing-your-first-dedicated-a…
Шоссейный автомобиль HPI Формула Q32 (красный) HPI-116710 2WD RTR 2.4G в масштаб 1:32
Шоссейный автомобиль HPI Формула Q32 на радиоуправлении
Миниатюрная модель машины на радиоуправлении в стиле формулы 1 специально разработаны для заездов внутри помещения. Модель полностью готова к эксплуатации, все что нужно — вставить батарейки в пульт управления и зарядить аккумулятор.
Модель полностью готова к эксплуатации, все что нужно — вставить батарейки в пульт управления и зарядить аккумулятор.
Радиоуправляемая модель имеет задний привод и умещается на ладне, что делает ее идеальным вариантом для заездов по квартире или в загородном доме. Вы можете загрузить изображения трека и распечатать их на свем принтереи создать уникальную трассу у себя дома.
Пульт управления работает на помехоустойчивой частоте 2,4 GHz, в него так же встроено зарядное устройство для самой модели. Покрышки модели сделаны из высококачественной микропористой резины которая дает великолепное сцепление как на кафельной плитке, так и на ковровом покрытии.
ХАРАКТЕРИСТИКИ
- Масштаб: 1/32
- Длина: 110мм
- Ширина: 75мм
- Высота: 44мм
- Колесная база: 82мм
ОСОБЕННОСТИ
- Компактный размер, задний привод и реальное управление
- Можно устроить гонки где угодно, хоть на обеденном столе
- Зарядка аккумулятора прямо от пульта управления
- Полнофункциональный пульт управления 2,4ГГц с реалистичным рулевым колесом
- Как и большие Р/У автомодели, машины Formula Q32 можно модернизировать и чинить с помощью выпускаемых дополнительно запасных частей.

- Вы можете загрузить, распечатать и создать свою собственную гоночную трассу
КОМПЛЕКТ ПОСТАВКИ
- Автомодель синего цвета в сборе с регулятором, бортовой аппаратурой и аккумулятором
- Аппаратура управления 2.4ГГц
- Элементы трассы
- Инструкция
Рекомендуется докупить: 4 батарейки размер AA для передатчика.
Что такое формула шкалы и как ее использовать для гитары
Последнее обновление 14 мая 2019 г., автор: Клаус Кроу
Bigstock photo
Все развивается вокруг масштабов. Мы используем гаммы для создания музыки, изучения теории музыки, понимания музыки, построения аккордов, прогрессий, арпеджио и обучения соло и импровизации.
Итак, как построить шкалу с помощью формулы, как определить примечания для конкретной шкалы, что еще можно сделать с формулой шкалы и как разобраться во всем этом?
Что ж, давайте выясним.
Формула гаммы позволяет лучше понять исполняемые ноты. Он дает вам четкое представление о том, как шкалы соотносятся друг с другом, и показывает, как легко построить любую шкалу за секунды.
Это также отличный инструмент для изучения и понимания построения аккордов и соло. Как только вы узнаете логику шкалы и научитесь пользоваться формулой, многие части головоломки встанут на свои места, шаг за шагом.
Для построения или построения шкалы нам нужны большая шкала и формула шкалы.Мы используем основную шкалу в качестве основы и ориентира для построения всех остальных шкал, а затем применяем соответствующую формулу шкалы для заполнения примечаний.
Что такое формула шкалы?
Формула гаммы показывает ноты гаммы в сравнении с нотами мажорной гаммы.
Поясним:
Ноты мажорной гаммы обозначаются цифрами 1 2 3 4 5 6 7
См. Здесь ноты мажорной гаммы:
В Г Д Е Ж А Б 1 2 3 4 5 6 7 См. Изображение ниже, первые две масштабные диаграммы.Затем вы выбираете формулу шкалы. Построение минорной шкалы пентатоники Возьмем, к примеру, пентатонику до минор. Формула основной шкалы = 1 2 3 4 5 6 7 Масштаб C = C D E F G A B Формула гаммы минорной пентатоники = 1 b3 4 5 b7 Пентатоника до минор = C Eb F G Bb Таким образом, вы играете первую ноту мажорной гаммы, затем третью ноту, пониженную на полшага, четвертую, пятую и седьмую ноты, пониженную на полтона. b3 (три плоских) означает, что вы берете третью ноту мажорной гаммы только на половину шага вниз.Третья нота до мажор - это ми, поэтому, если вы опускаетесь на полтона вниз, ми становятся Eb (ми-бемоль). b7 (плоская семерка) означает, что вы берете седьмую ноту мажорной гаммы только на полшага вниз. Седьмая нота до мажорной шкалы - это си, поэтому, если вы опускаетесь на полтона вниз, си становится Bb (си-бемоль). Ноты пентатоники до минор состоят из нот C Eb F G Bb (1 b3 4 5 b7) См. Изображение ниже, схемы три и четыре. Сделать это можно с любым масштабом в любой тональности.
Выберите подходящий крупный ключ масштаба и формулу масштабирования ниже: Основные масштабы в каждой тональности: Крупный масштаб = A B C # D E F # G # A Большой масштаб Bb = Bb C D Eb F G A Bb B мажорная шкала = B C # D # E F # G # A # B Масштаб C = C D E F G A B C Основной масштаб Db = Db Eb F Gb Ab Bb C Db D мажорная шкала = D E F # G A B C # D Eb мажорная шкала = Eb F G Ab Bb C D Eb Мажорная шкала E = E F # G # A B C # D # E F мажорная гамма = F G A Bb C D E F Большой масштаб Gb = Gb Ab Bb Cb (= B) Db Eb F Gb Масштаб G = G A B C D E F # G Масштаб Ab major = Ab Bb C Db Eb F G Ab Формулы общей шкалы: Основной масштаб = 1 2 3 4 5 6 7 (C D E F G A B) Малый масштаб = 1 2 b3 4 5 b6 b7 (C D Eb F G Ab Bb) Минорная пентатоника = 1 b3 4 5 b7 (C Eb F G Bb) Шкала блюза = 1 b3 4 b5 5 b7 (C Eb F Gb G Bb) Основная пентатоника = 1 2 3 5 6 (C D E G A) Гармоническая минорная шкала = 1 2 b3 4 5 b6 7 (C D Eb F G Ab B) Мелодический минор = 1 2 b3 4 5 6 7 (C D Eb F G A B) Ионический масштаб = 1 2 3 4 5 6 7 (C D E F G A B) Шкала дориана = 1 2 b3 4 5 6 b7 (C D Eb F G A Bb) Фригийская шкала = 1 b2 b3 4 5 b6 b7 (C Db Eb F G Ab Bb) Лидийская шкала = 1 2 3 # 4 5 6 7 (C D E F # G A B) Миксолидийская шкала = 1 2 3 4 5 6 b7 (C D E F G A Bb) Эоловый масштаб = 1 2 b3 4 5 b6 b7 (C D Eb F G Ab Bb) Шкала Локрия = 1 b2 b3 4 b5 b6 b7 (C Db Eb F Gb Ab Bb) Вся шкала тонов = 1 2 3 # 4 # 5 b7 (C D E F # G # Bb) Уменьшено на половину = 1 2 b3 4 b5 b6 6 7 (C D Eb F Gb Ab A B) Половина всего уменьшенного = 1 b2 b3 3 b5 5 6 b7 (C Db Eb E F # G A Bb) Задания 1 - Создайте гармоническую минорную гамму: * Найдите в приведенном выше списке крупную шкалу A.
* Найдите формулу гаммы «гармонический минор» и запишите ее. * Заполните примечания для гаммы ля минор. * Ищите ноты гармонической минорной гаммы на шее гитары. * Сыграйте на гитаре гармонический минор. * Теперь играйте в разных тональностях. 2 - Постройте крупную шкалу. 3 - Постройте гамму ля минор. 4 - Постройте пентатонику ля минор. 5 - Создайте мажорную пентатонику. 6 - Запишите разницу между формулой мажорной и минорной гаммы? 7 - Запомните формулы мажорной, минорной и минорной пентатоники.8 - Научитесь обращать внимание на номера нот при игре на гамме. Повеселись!
возврат Согласно Гарвардскому словарю
возврат Что такое формула интервалов? Шкалы построены по формулам интервалов. Диатонический Первая нота гаммы называется ее корнем:
Использование только белых клавиш, крупная шкала, начинающаяся с C, не имеет
Формула основной шкалы: Теперь, если вы воспользуетесь клавиатурой и сделаете крупную шкалу Попробуйте эти:
возврат Формулы весов
|
Как создаются аккорды и гаммы с использованием «формул»
Формулы весов для 6 важных весов
Major Scale : 1-2-3-4-5-6-7
Natural Minor Scale : 1-2 — b3 — 4-5 — b6 — b7
Harmonic Minor Scale : 1-2 — b3 — 4 — 5 — b6 — 7
Минорная пентатоническая шкала : 1 — b3 — 4 — 5 — b7
Минорная шкала блюза : 1 — b3 — 4 — b5 — 5 — b7
Большая пентатоническая шкала : 1-2-3-5-6
Формулы аккордов для всех аккордов
Major (C) : 1-3-5
Minor (Cm) : 1 — b3 — 5
Доминант 7 (C7) : 1-3-5 — b7
Major 7-й (Cmaj7) : 1 — 3 — 5 — 7
Незначительный 7-й (Cm7) : 1 — b3 — 5 — b7
Sus2 (Csus2) : 1 — 2 — 5
Sus4 (Csus4) : 1 — 4 — 5
Мажор 6-й (C6) : 1-3-5-6
Младший 6-й (Cm6) : 1 — b3 — 5-6
Add9 (Cadd9) : 1-3-5-9
9-й (C9) : 1 — 3 — 5 — b7 — 9
Add11 (Cadd11) : 1 — 3 — 5 — 11
11-й (C11) : 1 — 3 — 5 — b7 — 9 — 11
Add13 (Cadd13) : 1 — 3 — 5 — 13
13 (C13) : 1 — 3 — 5 — b7 — 9 — 11 — 13
Уменьшено (Cdim) : 1 — b3 — b5 — bb7 ( DOUBLE Flat 7-е)
Half Diminished (C7b5) : 1 — b3 — b5 — b7
Augmented (Caug) : 1-3 — # 5
ВСЕ в музыке исходит из мажорной шкалы
Как я уже много раз говорил ранее, все в музыке происходит от мажорной гаммы.
Мажорная гамма состоит из 7 нот. Если бы вы присвоили «градусы» каждой из 7 нот, у вас была бы формула шкалы , которая выглядит так:
- Формула основной шкалы: 1-2-3-4-5-6-7
Если бы мы использовали в качестве примера шкалу до мажор, состоящую из нот:
- C Основная шкала: C — D — E — F — G — A — B
1 — C
2 — D
3 — E
4 — F
5 — G
6 — A
7 — B
Любая другая шкала — это просто изменение основной шкалы.Изменение для каждой конкретной шкалы определяется с помощью формулы шкалы.
Итак, если вы хотите применить формулу натуральной минорной шкалы, вы просто измените степени большой шкалы в соответствии с формулой…
Глядя выше, мы видим, что формула шкалы для натурального минорного строя:
- Формула натуральной младшей шкалы: 1-2 — b3 — 4-5 — b6 — b7
Применяя эту формулу гаммы к нотам до мажор, чтобы получить естественную минорную шкалу до:
- C Минор натуральный Шкала: C — D — Eb — F — G — Ab — Bb
Эта новая гамма является естественной минорной гаммой C (которая для краткости обычно обозначается просто как C-минорная гамма ).
Этот же метод может быть использован для получения любой шкалы из основной шкалы. Поскольку вы знаете формулу шкалы, вы можете легко определить, какие ноты содержит шкала.
Это можно сделать с помощью любого из 12 ключей
Если бы я хотел выяснить, каковы ноты пентатоники соль минор, я бы просто начал с мажорной гаммы G , а затем применил формулу шкалы . Попробуем:
- G Основная шкала: G — A — B — C — D — E — F #
1 — G
2 — A
3 — B
4 — C
5 — D
6 — E
7 — F #
- Формула минорной пентатоники: 1 — b3 — 4-5 — b7
Следовательно, ноты гаммы пентатоники соль минор:
- Пентатоника соль минор: G — Bb — C — D — F
1 — G
b3 — Bb (на полшага ниже, чем примечание «B»)
4 — C
5 — D
b7 — F (на полшаг ниже, чем примечание «F #»)
Довольно просто, да?
Попробуйте сами несколько раз, и вы быстро поймете.
Полезный образец шкалы
Мне нравится использовать этот крупный масштаб, глядя на гриф гитары, чтобы понять это:
Используя этот крупный образец шкалы, очень очевидно, где расположен каждый градус шкалы. Предполагая, что вы знаете ноты на грифе (по крайней мере, на низких струнах E, A и D), вы можете легко определить новые гаммы.
Знание реальных нот может быть важно для вас, а может и не быть, так как многие гитаристы просто запоминают подвижные паттерны гаммы, а затем используют слух, чтобы вычислить остальное.Однако если вы когда-нибудь задумывались, откуда взялась чешуя, теперь вы знаете!
Это также относится к аккордам
Попробуем разобраться, что за ноты аккорда…
A7 аккорд
Сначала мы начнем с крупной шкалы A :
- A Основная шкала: A — B — C # — D — E — F # — G #
1 — A
2 — B
3 — C #
4 — D
5 — E
6 — F #
7 — G #
Затем мы применяем соответствующую формулу аккорда для аккорда «7» (также известного как «доминантный 7-й аккорд»):
- Формула доминирующего седьмого аккорда: 1-3-5 — b7
Что дает,
- A7 аккорд: A — C # — E — G
Теперь вы знаете ноты аккорда A7!
Опять же, это работает для всех клавиш и всех аккордов.
Расширенные аккорды
Иногда встречаются аккорды, которые содержат числа больше 7. Например, вы можете увидеть такие аккорды, как:
Это лишь некоторые примеры типов аккордов, с которыми вы можете столкнуться, и я рассмотрю происхождение каждого из них, используя эту диаграмму:
Поскольку мажорная гамма состоит только из 7 нот, все числа после 7 происходят из следующей октавы . На примере шкалы до мажор:
1 — C
2 — D
3 — E
4 — F
5 — G
6 — A
7 — B
8 — C 9 — D
10 — E
11 — F
12 — G
13 — A
13 — это наибольшее число, которое вы увидите в аккордах!
Теперь, когда вы это знаете, давайте разберемся, что это за 3 забавных аккорда выше:
B9 аккорд
Начнем с мажорной шкалы B:
- B Основная шкала: B — C # — D # — E — F # — G # — A #
Теперь мы присваиваем степень каждой заметке:
1 — B
2 — C #
3 — D #
4 — E
5 — F #
6 — G #
7 — A #
9 — C #
10 — D #
11 — E
12 — F #
13 — G #
Затем мы рассмотрим формулу аккорда для аккорда «9» (ака. «Доминантный 9-й аккорд»), то есть
«Доминантный 9-й аккорд»), то есть
- 9 Формула аккорда: 1 — 3 — 5 — b7 — 9
А затем мы знаем ноты аккорда B9:
- B9 аккорд: B — D # — F # — A — C #
А теперь попробуем еще…
Dadd11 аккорд
Начнем со шкалы ре мажор:
- D Основная шкала: D — E — F # — G — A — B — C #
Теперь мы присваиваем степень каждой заметке:
1 — D
2 — E
3 — F #
4 — G
5 — A
6 — B
7 — C #
9 — D
9 — D 9 — E
10 — F #
11 — G
12 — A
13 — B
Теперь посмотрим на формулу аккорда «add11», которая выглядит так:
- Добавить 11 формул аккорда: 1 — 3 — 5 — 11
Затем мы знаем ноты аккорда Dadd11:
- Dadd11 Аккорды: D — F # — A — G
Неплохо, да?
Давайте попробуем последний пример…
Ab13 аккорд
Начнем с крупной шкалы Ab:
- D Основная шкала: Ab — Bb — C — Db — Eb — F — G
Далее мы присваиваем каждой ноте степень:
1 — Ab
2 — Bb
3 — C
4 — Db
5 — Eb
6 — F
7 — G
8 — Ab 9 — Bb
10 — C
11 — Db
12 — Eb
13 — F
Теперь посмотрим на формулу аккорда «13», которая выглядит так:
- 13 Формула аккорда: 1 — 3 — 5 — b7 — 9 — 11 — 13
Затем мы знаем ноты аккорда Ab13:
- Ab13 Аккорды: Ab — C — Eb — Gb — Bb — Db — F
Major Chords vs.
 Минорные аккорды (также известные как «Качество»)
Минорные аккорды (также известные как «Качество»)
Способ определения того, является ли аккорд мажорным или минорным, — это посмотреть на 3-ю степень. Это также известно как качества аккорда.
- Аккорд с мажорным качеством будет иметь тройку в формуле аккорда.
- Аккорд минорного качества будет иметь в своей формуле аккорда b3.
Если в символе аккорда НЕТ «м», то это мажорный аккорд.
Если — это в символе аккорда, то это минорный аккорд.
Некоторые примеры:
G: G мажорный аккорд
Bm: Минорный аккорд B
Abadd13: Мажорный аккорд Ab с добавленной 13-й степенью
F # m7: F # минорный аккорд с добавленной степенью b7
Понять?
Когда вы видите «мажор» в символе аккорда
Теперь, когда вы знаете, как создавать аккорды, используя формулы аккордов, будьте осторожны, когда видите аккорд «maj7».
«мажор» НЕ имеет ничего общего с мажорным или минорным качеством аккорда, независимо от того, является ли аккорд мажорным или минорным.Скорее, «май» относится к 7-й степени шкалы.
Итак,
- Cmaj7 — аккорд до мажор, который также содержит 7
- a C7 — аккорд до мажор, который также содержит b7
- a Cm7 — аккорд до минор , который также содержит b7
- a Cm (maj7) — аккорд до минор , который также содержит 7
Итак, «мажор» не говорит вам, является ли аккорд мажорным или минорным. Скорее, это относится к 7-й ступени шкалы.
Аккорд «maj7» просто содержит 7-ю ступень гаммы.
Аккорда «7» содержит ступень шкалы b7.
Это сбивает с толку, я знаю, но так оно и есть.
«Слэш-аккорды»
Когда вы видите символ аккорда со знаком «/», это просто означает, что самая низкая нота аккорда больше не является основным тоном. Скорее, это то, что обозначено под символом «/» или справа от него.
Скорее, это то, что обозначено под символом «/» или справа от него.
Примеры:
C / G: Аккорд до мажор с «G» в качестве самой нижней ноты (также называемый «G в басу»)
F # 11 / A: F # 11 аккорд с «A» в басу
Bbsus2 / E: Аккорд Bbsus2 с «E» в басу
Неплохо, да?
Это может быть много, поэтому не помешает перечитать этот пост несколько раз, чтобы действительно понять.
Классная картинка зомби
Итак, на сегодня все. Спасибо, что прочитали весь этот пост!
Как всегда, получайте удовольствие!
Об авторе:
Я играю в группах и занимаюсь обучением игре на грифе с 11 лет. Я уже стар и до сих пор занимаюсь этим!
Масштабный коэффициент
| Определение, формула и как найти
Определение масштабного коэффициента
Масштабный коэффициент в математике — это соотношение между соответствующими измерениями объекта и представлением этого объекта. Если масштабный коэффициент — целое число, копия будет больше. Если коэффициент масштабирования дробный, копия будет меньше.
Если масштабный коэффициент — целое число, копия будет больше. Если коэффициент масштабирования дробный, копия будет меньше.
Коэффициент масштабного коэффициента может быть выражен дробью 12 или двоеточием 1: 2.
Коэффициент измеряет взаимосвязь между двумя вещами. Вы можете создать соотношение студентов-левшей ко всем студентам, но это соотношение будет , а не , как коэффициент масштабирования.
Как найти коэффициент масштабирования
Чтобы найти масштабный коэффициент, вы сначала решаете, в каком направлении вы масштабируете:
| Направление шкалы | Формула |
|---|---|
| Масштаб Вверх (от меньшего к большему) | = размер большей фигуры меньший размер фигуры |
| Масштаб Вниз (от большего к меньшему) | = измерение меньшего размера фигуры большее измерение фигуры |
Масштабный коэффициент для при увеличении масштаба — это коэффициент , больший, чем 1 . Масштабный коэффициент для при уменьшении составляет коэффициент меньше 1 .
Масштабный коэффициент для при уменьшении составляет коэффициент меньше 1 .
Как только вы узнаете, в каком направлении вы масштабируете, вы сравниваете соответствующие стороны, используя правильное базовое уравнение. Сравните длину стороны реального объекта с длиной соответствующей стороны изображения.
Определение масштабного коэффициента аналогичных цифр
Вот два похожих треугольника. Какой масштабный коэффициент используется для создания второй, большей фигуры?
Поскольку мы увеличиваем до , мы делим большее число на меньшее:
3612 = 31 = 3
Масштабный коэффициент равен 3 .Чтобы перейти от ножек 12 см к ножкам 36 см, нам потребовалось умножить 12 см на 3.
А теперь попробуем уменьшить масштаб. Вот два похожих пятиугольника. Какой масштабный коэффициент используется для создания второй, меньшей фигуры?
Поскольку мы уменьшаем масштаб, мы делим соответствующие длины сторон (меньшее число на большее число):
321 = 17
Масштабный коэффициент равен 17 . Чтобы получить вторую, меньшую фигуру, умножаем 21 × 17; на рисунке справа используется масштабный коэффициент 1: 7, 17 или одна седьмая.
Чтобы получить вторую, меньшую фигуру, умножаем 21 × 17; на рисунке справа используется масштабный коэффициент 1: 7, 17 или одна седьмая.
Давайте рассмотрим еще один пример и увеличим и уменьшим масштаб. Рассмотрим эти два похожих прямоугольных треугольника с помеченными сторонами.
Если у нас есть маленький прямоугольный треугольник наверху и мы хотим масштабировать его до большего треугольника, мы напишем это:
, 18537 = 51; масштабный коэффициент равен 5: 1
Таким образом, любая другая линейная мера умножается на 5.
Если у нас есть большой прямоугольный треугольник и мы хотим уменьшить его, чтобы сделать меньший, мы напишем это:
37185 = 15; масштабный коэффициент 1: 5
Таким образом, любая другая линейная мера умножается на 15; или делится на 5
Масштабный коэффициент по геометрии
Масштаб используется в геометрии для точного воспроизведения фигур; они разных размеров, но не пропорции. Цифры похожи, но в масштабе.
Цифры похожи, но в масштабе.
Масштабный коэффициент используется на подобных геометрических фигурах. Вы можете найти масштабный коэффициент соответствующих углов, сторон и даже диагоналей.
Как уменьшить форму с помощью коэффициента масштабирования?
Предположим, вам дали цифру и сказали уменьшить ее на 25% . Думайте поэтапно:
- Вы делаете большее или меньшее расширение?
- Вы уменьшаете оригинал, поэтому коэффициент масштабирования будет меньше целого числа.
- Затем измерьте (или прочтите) любую сторону фигуры и произведите вычисления.
Предположим, у нас есть прямоугольник шириной 16 дюймов, и нам нужно уменьшить его на 25%, или на одну четверть (14).
Это означает, что это будет 75% оригинала (100% — 25% = 75%). В качестве масштабного коэффициента мы будем использовать или 3: 4.
Умножьте 16 × масштабный коэффициент (34):
161 × 34 = 484
Теперь мы упрощаем наш ответ:
484 = 121 = 12 дюймов
Ширина нашей новой меньшей формы должна быть 12 дюймов. . Мы повторяем эти шаги с другим размером, 6 дюймов:
. Мы повторяем эти шаги с другим размером, 6 дюймов:
61 × 34 = 184
Упрощать:
184 × 4,51 = 4,5 дюйма
Высота нашего меньшего прямоугольника должна быть 4,5 дюйма.
Как сделать масштабную модель
Модель в масштабе — это модель с точностью до коэффициента масштабирования. Если копия реального объекта не масштабирована, она будет выглядеть нереально, как маленькая детская игрушка.
Один объект тоже может иметь разный масштаб. Чем больше разница между двумя числами отношения, тем меньше будет модель.Модель 1:87, как правило, будет намного меньше модели с соотношением 1:12.
Для изготовления масштабных моделей вам нужны точные планы исходного предмета, такие как масштабный чертеж . Чертеж в масштабе — это точный план реального объекта, нарисованный с использованием масштабного коэффициента, позволяющего сделать чертеж достаточно маленьким для обработки.
Вы умножаете каждый напечатанный размер на масштабном чертеже на масштабный коэффициент, чтобы получить правильные размеры для деталей модели. Если, например, вы хотите построить простой сарай для своей модели железной дороги, вы должны использовать коэффициент 187, чтобы получился сарай длиной 32 фута 4.4 дюйма в длину!
Если, например, вы хотите построить простой сарай для своей модели железной дороги, вы должны использовать коэффициент 187, чтобы получился сарай длиной 32 фута 4.4 дюйма в длину!
Примеры масштабного коэффициента
Попробуйте свои силы в этих вопросах, чтобы понять, понимаете ли вы концепцию масштабного коэффициента в математике. Не уклоняйся от этого! Сделайте огромные усилия!
- Что такое масштабный коэффициент?
- Как найти масштабный коэффициент подобных фигур?
- Какую информацию дает масштабный коэффициент?
- Определите чертеж в масштабе.
Пожалуйста, не заглядывайте вперед, пока не постараетесь найти ответы изо всех сил.
- Определение масштабного коэффициента состоит в том, что это число, умноженное на заданное количество, чтобы получить меньшую или большую версию исходного числа. Это отношение рисунка, карты, модели или чертежа к фактическому объекту или расстоянию.
- Вы вычисляете масштабный коэффициент аналогичных фигур, беря соотношение соответствующих частей двух фигур.
 При увеличении формы большее значение является числителем, а меньшее значение — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем.
При увеличении формы большее значение является числителем, а меньшее значение — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем. - Масштабный коэффициент дает отношение изображения к реальному объекту.
- Чертеж в масштабе — это точный чертеж объекта, выполненный с использованием масштабного коэффициента для уменьшения размеров исходного объекта.
Как использовать масштабный коэффициент
Масштабирование объекта помогает визуализировать большие объекты реального мира в небольших помещениях или увеличивать небольшие объекты для лучшего просмотра.Коэффициент масштабирования — это то, как мы гарантируем, что представление объекта отличается только по размеру от исходного объекта.
Мы используем масштаб до:
- Нарисуйте аналогичные фигуры в геометрии
- Сделать масштабные модели
- Нарисовать масштабные чертежи архитектуры и машинного оборудования
В реальной жизни масштабный коэффициент часто используется для того, чтобы представить обширные площади суши на небольших листах бумаги, как на карте.
Масштаб
используется, чтобы позволить дизайнерам, архитекторам и машинистам обрабатывать модели объектов, которые были бы слишком большими, чтобы сохранить их, если бы они имели фактический размер.
The Major Scale »Уроки игры на соло-гитаре
Мажорная гамма — основа почти всей западной музыки. Если бы мы назвали одну гамму самой важной в музыке, это была бы мажорная гамма.
В этой статье мы рассмотрим, как создается мажорная гамма, несколько форм, которые вы можете использовать, чтобы играть на ней на гитаре, и как она соотносится с некоторыми другими важными гитарными гаммами.
Прежде чем приступить к изучению этих гамм, вам необходимо иметь базовую технику игры на соло-гитаре.Изучите их в этой статье: Техника игры на соло-гитаре для начинающих
Формула большой шкалы
Основная шкала состоит из серии целых шагов ( W, ) и полушагов ( H ). Шаг на гитаре — это расстояние в два лада. Полушаг — это расстояние в один лад. Это порядок целых и полушаговых шагов, составляющих основную гамму.
Это порядок целых и полушаговых шагов, составляющих основную гамму.
Ноты до мажор гаммы
Чтобы найти ноты гаммы, мы применяем формулу мажорной гаммы к музыкальному алфавиту.Если бы мы делали гамму G-мажор, мы бы начали с ноты G. Если бы мы делали мажорную гамму Bb, мы бы начали с Bb. В данном случае мы будем делать гамму до мажор. Итак, первая нота будет C. Остальные ноты определяются с применением формулы мажорной гаммы.
Градусы до мажор Шкала
Теперь, когда у нас есть ноты нашей шкалы до мажор, важно выработать привычку назначать числа на шкалу. Знание степеней шкалы помогает нам найти взаимосвязь между основной шкалой и другими гаммами, а также будет важно для распознавания взаимосвязи между нотами внутри шкалы.
Относительная мажорная и малая гаммы
В музыке каждая мажорная гамма имеет относительную минорную гамму. И наоборот, у каждой минорной гаммы есть относительная мажорная гамма. Чтобы найти относительную минорную гамму, вам нужно понимать основные ноты. Основная нота гаммы или тональности — это 1-я ступень гаммы. В этом случае основная нота до мажор — это нота до.
Основная нота гаммы или тональности — это 1-я ступень гаммы. В этом случае основная нота до мажор — это нота до.
Есть два способа найти относительную минорную шкалу. Первый способ — найти ноту на полтора шага (3 полутона / лада) ниже нашей основной основной ноты.Нота на полтора шага ниже до — это A. Это означает, что относительная минорная шкала до мажор — это ля минор.
Другой способ найти относительную малую шкалу — найти шестую ступень большой шкалы. Шестая ступень шкалы до мажор — это A. Делая ля минор нашей относительной минорной шкалой.
Pro Совет: Каждой мажорной и минорной гамме соответствует одноименная тональность. Например, гамма до мажор происходит от тональности до мажор, а шкала ля минор — от тональности ля минор.
Шкалы до мажор и ля минор
Вот наиболее часто используемые формы для гаммы до мажор и ля минор. Черными точками отмечены основные ноты (ноты C в гамме C-мажор и ноты A в гамме A-минор) каждой гаммы.
Расширенная шкала до мажор
Важно понять, что мажорная и минорная гаммы содержат одни и те же ноты. Единственная реальная разница заключается в том, что традиционно они играются в разных позициях на грифе и что первая ступень шкалы / основная нота изменяется между двумя гаммами.Шкала до мажор содержит ноты 1C 2D 3E 4F 5G 6A 7B, а шкала ля минор содержит ноты 1A 2B 3C 4D 5E 6F 7G.
Единственная реальная разница заключается в том, что традиционно они играются в разных позициях на грифе и что первая ступень шкалы / основная нота изменяется между двумя гаммами.Шкала до мажор содержит ноты 1C 2D 3E 4F 5G 6A 7B, а шкала ля минор содержит ноты 1A 2B 3C 4D 5E 6F 7G.
Благодаря этому мы можем объединить стандартную форму основной шкалы и стандартную форму вспомогательной шкалы в одну большую «расширенную» шкалу.
Обратите внимание на расположение нот черного корня. Эти примечания C могут помочь вам ориентироваться и понимать эту форму расширенной шкалы.
Расширенные звукоряды до мажор и ля минор
Здесь вы можете видеть, что комбинированные версии гамм до мажор и ля минор практически идентичны.Единственная разница — расположение основной ноты. В форме C мажор ноты C являются нашими корневыми нотами. В форме ля минор ноты ля — это наши корневые ноты.
Невероятно важно держать такую чешуйку под пальцами. Это позволяет вам охватить массу вопросов, когда вы начинаете разучивать свои любимые гитарные соло, писать собственные соло и когда вы импровизируете.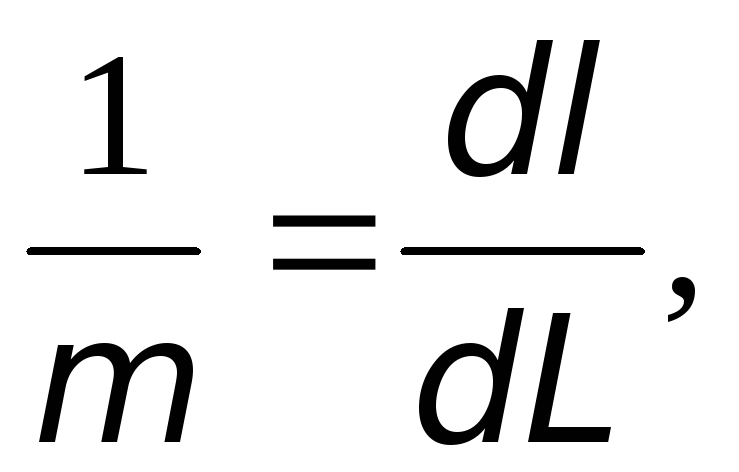 Когда вы играете на соло-гитаре, думайте об этой форме как о своей «опорной базе».
Когда вы играете на соло-гитаре, думайте об этой форме как о своей «опорной базе».
Горизонтальный вид в увеличенном масштабе
Чтобы помочь вам понять эту фигуру, вот еще один способ взглянуть на эту расширенную фигуру до мажорной шкалы.
Использование формы расширенной основной шкалы в других клавишах
Если вы хотите использовать эту масштабную фигуру в другой тональности, сами формы не меняются, они просто перемещаются вверх или вниз по ладу. Из-за этого всегда важно знать, где находится ваша основная нота. Чтобы изменить тональность, вам просто нужно переместить фигуру так, чтобы ваши корневые ноты совпадали с корневыми нотами любой клавиши, в которой вы хотите быть. Если вы хотите играть в тональности ре мажор, вы бы переместили эту фигуру так, чтобы ваша Основные ноты крупной шкалы — это ноты D.
Вы ищете больше уроков соло-гитары и актуальных джем-треков? Guitareo — это пошаговая система видеообучения Нейта Сэвиджа. В нем есть несколько отличных песен для соло-гитары, а также многие другие важные стили музыки, включая рок, кантри, фингеринг, металл, классику, блюграсс, джаз и другие. Лучше всего, что он включает в себя огромную библиотеку оригинальных джем-треков, так что вы можете применить все к музыке.
Лучше всего, что он включает в себя огромную библиотеку оригинальных джем-треков, так что вы можете применить все к музыке.
Введите свой адрес электронной почты и нажмите синюю кнопку, чтобы БЕСПЛАТНО получить 50 пошаговых видеоуроков для начинающих!
Формула основной шкалы
и ее использование: Studio Notes Online
В теории музыки шкала — это серия высот (нот), отображаемых в возрастающей или убывающей последовательности.В этом уроке вы узнаете, как построить крупную шкалу, используя формулу основной шкалы . Музыкантам начинающего и среднего уровня необходимо изучать гаммы, чтобы совершенствовать свои навыки как исполнителей, так и студентов-теоретиков. Изучение того, как построить мажорную гамму, подготовит почву для освоения других гамм. Щелкните здесь, чтобы просмотреть «Что такое гаммы в музыке».
Музыкальные термины
Важно отслеживать музыкальные термины, которые вы изучаете.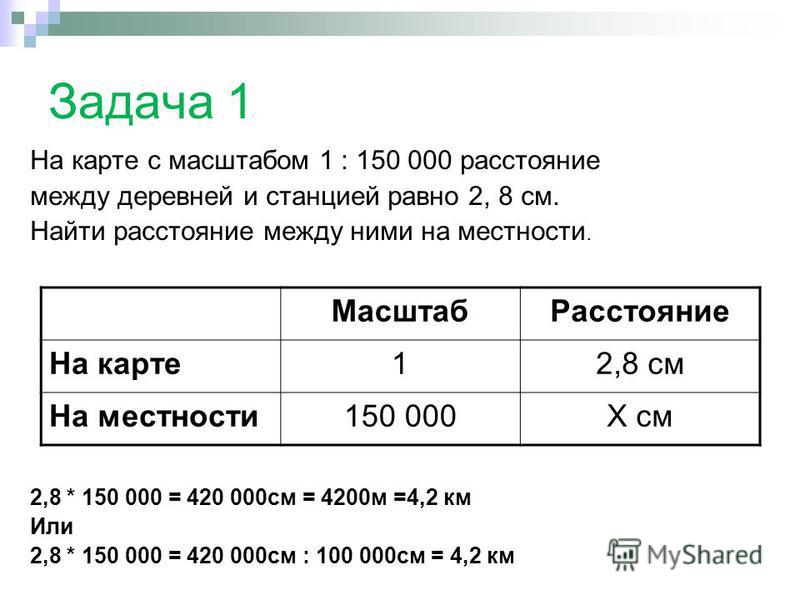 На прошлых и будущих уроках теории музыки вы заметите совпадение некоторых терминов.Это хорошо, так как в будущем укрепит ваше музыкальное мастерство.
На прошлых и будущих уроках теории музыки вы заметите совпадение некоторых терминов.Это хорошо, так как в будущем укрепит ваше музыкальное мастерство.
Запомните следующий список музыкальных терминов, затронутых в этом уроке.
- Масштаб
- Подпись ключа
- Несчастные случаи
- Весь шаг
- Полушаг
Ниже приведен список других музыкальных гамм, которые мы будем изучать на будущих уроках теории музыки:
- Незначительный
- Гармонический минор
- Мелодический минор
- Пентатоника
- Полный тон
- Блюз
- Хроматический
Целые и половинные шаги и формула большой шкалы
В предыдущем уроке, посвященном нотам и клавишам на фортепиано , мы обсудили и показали, как работают целые шаги и полушаги.Нажмите, если вам нужно просмотреть этот материал.
Помните, что на фортепиано имеется 12 различных тембров, которые называются полутонами . Формула мажорной шкалы состоит из целых и полушаговых значений. Используя случайных чисел (плоские, диез, натуральные), мы можем построить любой крупный масштаб и воспроизвести их.
БОНУС!
Пожалуйста, посмотрите это короткое видео ниже, так как оно очень ясно иллюстрирует концепции этого урока. Нажмите на видео для просмотра.
Люк! Используйте формулу большой шкалы
Термин «масштаб» происходит от латинского слова «Scala» и означает «лестница» .Итак, давайте представим шкалу как лестницу нот. Вы можете подниматься или спускаться по лестнице. Мы можем начать с любой ноты и построить или сконструировать крупную шкалу.
Масштаб ре мажор, например , начинается с ноты D .
Eb (бемоль) мажор начинается и заканчивается нотой Eb.
Построить этот тип шкалы довольно просто, если мы воспользуемся простой формулой. Эта формула имеет отношение к расстоянию (интервалам) между нотами.
Ниже приведена формула, которую мы используем для построения этих шкал с использованием целых шагов (W) и полушагов (H).
Ш Ш В Ш Ш В
Все гаммы имеют семь разных нот плюс еще одна в октаве .
Градусы шкалы 1 2 3 4 5 6 7 8
Формула большой шкалы W W H W W W H
Итак, давайте вспомним, что для всех основных масштабов промежутки между 3–4 и 7–8 всегда составляют шага H alf, а остальные — шага W отверстия.
Ниже вы увидите шкалу, основанную на ноте «C». Если следовать установленной формуле, расстояние между нотами E — F и B — C составляет половину шагов. Все остальные шаги — это целые шаги. Следовательно, у нас есть правильное построение этой шкалы.
Загрузить (PDF, 10KB)
Использование формулы большой шкалы на любой ноте.
Используя формулу мажорной шкалы, мы можем построить мажорную шкалу на любой ноте. Пример ниже показывает мажорную шкалу F.Чтобы понять, как это было построено, нам нужно взглянуть на каждую записку: F G A Bb C D E F .
Обратите внимание, что есть банкнота под названием Bb или B-flat. Причина, по которой он называется Bb, заключается в том, что расстояние между нотами A и B (шаги 3 и 4) составляет целый шаг. Формула требует полшага. Следовательно, нам нужно изменить одну из нот случайно. (плоский или острый). Мы не можем изменить ноту «A», поэтому мы должны изменить ноту «B». Изменив си-бемоль на си-бемоль, мы снизили высоту звука на полшага.Теперь у нас есть мажорная гамма F по формуле.
Загрузить (PDF, 13 КБ)
Освоение нот
Любой изучающий теорию музыки захочет овладеть искусством нотной грамоты. Эта статья касается этого, но чтобы освоить это, я рекомендую иметь программу Music Notation Software. Программа такого рода позволит вам развивать больше навыков в более быстром темпе. Ниже приведены несколько доступных примеров.
Программа для нотной записи PreSonus Notion 6
Программа Sibelius First Music Notation
Еще две основные шкалы
В следующем примере мы начнем с ноты «G».Последовательность нот не меняется, пока мы не дойдем до ноты «F». Согласно нашей формуле, расстояние между «E» и «F» составляет полушага , но формула требует всего шага . Значит, нам нужно сделать пространство больше. Итак, используя диез (#), он поднимет высоту на половину шага, и у нас есть целый шаг. Это мажорная шкала G .
В последнем примере мы начнем с ноты «D». Ноты в этой последовательности: D E F # G A B C # D .Обратите внимание, что у нас есть два острых предмета. (F # и C #) К настоящему времени я уверен, что вы уже понимаете концепцию формулы основной шкалы. Но давайте рассмотрим это.
Расстояние между D и E составляет целый шаг. Прохладный! Нам нужен целый шаг. Расстояние между E и F составляет полшага, и формула говорит, что нам нужен целый шаг. Что делать? Поднимите ноту F до F #, и она у вас есть.
Откуда появился C #? В нашей формуле между шагами 6 и 7 это две ноты: B и C.Это полшага, а нам нужен целый шаг. Мы повысим C до C #, что даст нам целый шаг. Он также выполняет шаги 7 и 8, которые требуют полушага. Фантастический!
Прочтите эту замечательную статью под названием «Руководство по прослушиванию музыки», чтобы получить от своей музыки максимум удовольствия.
Ключевая подпись
Ключевая подпись — это визуальное устройство, используемое в музыке для предупреждения музыканта о «тональном центре» музыки. Он также служит формой музыкальной стенографии, определяющей масштаб, который используется в музыкальном произведении.
Большинство гамм требуют использования случайностей в музыке. Ключевая подпись избавляет от необходимости последовательно выписывать в нотной записи бемоль и диез. В качестве примера, единственным диезом в гамме G мажор является F-диез, поэтому подпись ключа , связанная с ключом G мажор , является подпись ключа с одним диезом.
Ключ соль мажор
Практикуйте информацию, которую вы узнали здесь, заполнив Рабочий лист теории музыки: основные весы.
При закрытии
Концепция формулы большой шкалы относительно проста для понимания. Ключ к этому — практика, практика, практика. В кратчайшие сроки вы обнаружите, что очень хорошо разбираетесь в написании и игре мажорных гамм. Следующий урок — «Понимание минорной шкалы».
Пожалуйста, поставьте лайк этой статье и упомяните ее на одной из кнопок социальных сетей выше.
Связанные
Формулы шкалы
Формулы минорной шкалы, построенные с учетом
к мажорной шкале.
Этот символ часто указывает на уменьшенное
аккорд.Этот символ + часто указывает на усиленный аккорд.
Этот символ b обозначает квартиру.
Примеры будут проиллюстрированы с использованием тональности ля мажор.
построить каждую минорную гамму.
Крупная шкала | ||||||||
| Вт | Вт | H | Вт | Вт | Вт | H | шагов | |
Я | II | iii | IV | В | vi | vii | I | Роман |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | Формула |
| А | B | C # | D | E | F # | G # | A | Банкноты |
| А | Bm | C # м | D | E | F # m | G # | A | Аккорды |
Посмотрите на иллюстрацию выше и обратите внимание на аккорды в 1, 4, 5
прогрессия.Обратите внимание, что все аккорды A, D и E являются мажорными. Сравните каждый из
эти аккорды к каждой минорной гамме ниже. Обратите внимание, как у каждой шкалы разные
прогрессии. Например, в большой шкале 1, 4, 5 ступеней будут A,
D, E — мажорные аккорды. В Am прогрессия i, iv, v будет Am, Dm и
Эм.
Эолийская мода также известна как естественный или относительный минор и является
показано ниже.
Эолийский режим можно записать или выразить по следующей формуле с
уважение к мажорной шкале.Например, мы используем тональность ля мажор для
вычислить шкалу Am. Используйте формулу ниже, чтобы построить эту шкалу.
Эоловый режим или шкала Am | ||||||||
| Вт | H | Вт | Вт | H | Вт | Вт | ступеней | |
я | II | bIII | iv | v | bVI | bVII | и | Роман |
| 1 | 2 | b3 | 4 | 5 | b6 | b7 | Формула | |
| А | B | С | D | E | F | G | A | Банкноты |
| Am | B | С | Дм | Em | F | G | Am | Аккорды |
Посмотрите на иллюстрацию выше и обратите внимание на последовательность 1, 4, 5.Каждый аккорд
в этой прогрессии — минорный аккорд. Сравните все шкалы с разными
аккорды — это каждая гамма. Заметки, выделенные серым, — это заметки, которые
изменен в большой шкале, чтобы сформировать меньшую шкалу.
Чтобы построить гармонический минор, используйте следующую формулу относительно
в крупном масштабе.
Все, что вам нужно сделать, это опустить 3-ю и 6-ю ноты в мажорной тональности, чтобы получить гармонический минорный строй.
Основные ноты: A B C # D E F # G # A
Гармонический минор: A B C D E F G # A.Он имеет ноты b3 и b6 по сравнению с мажорной гаммой.
Гармонический минор | ||||||||
| Вт | H | Вт | Вт | H | Вт + В | H | ступеней | |
я | II | bIII + | iv | В | bVI | vii | и | Роман |
| 1 | 2 | b3 | 4 | 5 | b6 | 7 | Формула | |
| А | B | С | D | E | F | G # | A | Банкноты |
| Am | B | C + | Дм | E | F | G # | Am | Аккорды |
Посмотрите на иллюстрацию выше и обратите внимание на последовательность 1, 4, 5.D — это
минор, а ми — мажорный аккорд. В относительной минорной шкале у вас есть Am,
Dm и Em прогрессия.
Мелодический минор может быть построен по следующей формуле с учетом
в крупном масштабе. Все, что вам нужно сделать, это понизить 3-ю ноту в мажорной тональности, чтобы получить мелодическую минорную гамму.
Крупная шкала. A B C # D E F # G # A
Мелодический минор. A B C D E F # G # A. Мелодический минор будет иметь b3.
Мелодический минор | ||||||||
| Вт | H | Вт | Вт | Вт | Вт | H | ||
я | II | bIII + | IV | В | vi | vii | и | |
| 1 | 2 | b3 | 4 | 5 | 6 | 7 | Формула | |
| А | B | С | D | E | F # | G # | A | Банкноты |
| Am | Bm | C + | D | E | F # | G # | Am | Аккорды |
Посмотрите на прогрессию 1, 4, 5 выше.

 Для
Для «(Большая гамма и естественный минор
«(Большая гамма и естественный минор C # и Db энгармоничны
C # и Db энгармоничны Посмотрите на клавиатуру и увидите, что это
Посмотрите на клавиатуру и увидите, что это