Содержание
Определение массовой доли
Определение массовой доли (ω) вещества
Многие характеристики вещества являются суммой нескольких составляющих, каждая из которых представляет определенную долю от целого.
Математически долю каждой составляющей определяют как частное от деления части на целое (меньшей величины на большую).
Важными характеристиками состава многокомпонентных систем (молекул, смесей веществ, растворов, сополимеровСополимеры – высокомолекулярные соединения, макромолекулы которых содержат два (и более) типа структурных звеньев.) являются массовые, мольные и объёмные доли отдельных компонентов.
Массовая доля компонента (вещества, химического элемента) – содержание компонента в многокомпонентной системе (смеси веществ, растворе, молекуле), определяемое как отношение массы этого компонента к суммарной массе всех компонентов системы.
Таким образом, для нахождения массовой доли вещества в смеси (и решения обратной задачи) служит соотношение:
ω(вещества) = m(вещества) / m(смеси).
Массовую долю элемента в веществе можно определить, используя молярные массы:
ω(элемента) = M(элемента) / M(вещества).
Например, массовая доля водорода ω(H) в этиловом спирте С2Н5ОН вычисляется следующим образом:
Часто долю выражают в процентах. Для этого полученный результат умножают на 100. То есть в данном случае ω(H)=13%. Это означает, что в каждом г (кг, т) С2Н6O содержится 0,13 г (кг, т) водорода или каждые 100 г (кг, т) С2Н6O содержат 13 г (кг, т) водорода.
Задача 1. Вычислить массовые доли каждого из элементов, входящих в состав углеводорода, формула которого C6H12.
Задача 2. Из нефти получают бензин (массовая доля его в нефти составляет 25%) и мазут (55%). При дальнейшей переработке мазута получают еще некоторое количество бензина (60% от массы мазута). Рассчитайте массу бензина, который будет получен из нефти массой 200 кг.
Задача 3. Смесь ацетата натрия с избытком гидроксида натрия прокалили. После прокаливания масса сухого остатка оказалась в 1,136 раза меньше массы исходной смеси. Вычислите массовые доли компонентов исходной смеси.
Смесь ацетата натрия с избытком гидроксида натрия прокалили. После прокаливания масса сухого остатка оказалась в 1,136 раза меньше массы исходной смеси. Вычислите массовые доли компонентов исходной смеси.
Решение
При сплавлении ацетата натрия CH3COONa с гидроксидом натрия образуется метан CH4 (реакция Дюма).
Уравнение реакции:
Масса, относительные массы, молярная масса, массовые доли — урок. Химия, 8–9 класс.
Особенности применения физической величины «масса»
Масса обозначается буквой m и измеряется в граммах, килограммах или миллиграммах.
Пример:
m(h3SO4)= \(98\) г — масса серной кислоты равна \(98\) г.
Обрати внимание!
Связь между единицами измерения массы:
\(1\) кг \(=\) \(1000\) г, \(1\) г \(= 1000\) мг, \(1\) г \(= 0,001\) кг, \(1\) мг \(= 0,001\) г.
Массу атомов и молекул тоже можно выражать в граммах, килограммах или миллиграммах.
Пример:
масса одного атома серы:
ma(S)= 5,312⋅10−23 г.
Масса одной молекулы серной кислоты:
mm(h3SO4)= 1,627⋅10−22 г.
Это очень маленькие числа, которыми пользоваться неудобно. Поэтому для характеристики масс атомов и молекул введена атомная единица массы.
Атомная единица массы (а. е. м.) — 112 часть массы атома углерода. Её международное обозначение — u («unit»).
\(1\) u \(= 1\) а. е. м. \(=\) 1,66⋅10−24 г \(=\) 1,66⋅10−27 кг.
В атомных единицах массы атомов и молекул равны небольшим целым числам.
Пример:
ma(S)= \(32\) а. е. м. \(= 32\) u,
mm(h3SO4)= \(98\) а. е. м. \(= 98\) u.
Относительные массы
Применяются также относительные массы. Эти величины показывают, во сколько раз масса атома или молекулы больше одной атомной единицы массы.
Относительная атомная масса Ar — это отношение массы атома к \(1\) атомной единице массы. Величина безразмерная.
Величина безразмерная.
Пример:
Ar(S)= \(32\).
Относительная молекулярная масса Mr — это отношение массы молекулы к \(1\) атомной единице массы. Величина безразмерная.
Пример:
Mr(h3SO4)= \(98\).
Молярная масса
В расчётах используется также понятие «молярная масса».
Молярная масса численно равна массе \(1\) моль вещества. Она обозначается буквой M и измеряется в г/моль.
Пример:
M(h3SO4)= \(98\) г/моль.
Массовые доли
Массовая доля — это отношение массы компонента к массе образца вещества, в котором он содержится. Вычисляют массовую долю химического элемента в веществе, вещества в смеси, растворённого вещества в растворе, примесей и т. д.
Массовая доля обозначается буквой w. Это безразмерная величина. Может вычисляться также в %.
Молекула. Молекулярная масса. Массовая доля элемента.
На данный момент известно около 120 разных химических элементов, из которых в природе можно обнаружить не более 90. Многообразие же различных химических веществ вокруг нас несоизмеримо больше этого числа.
Многообразие же различных химических веществ вокруг нас несоизмеримо больше этого числа.
Связано это с тем, что крайне редко химические вещества состоят из отдельных, не связанных между собой атомов химических элементов. Таким строением в обычных условиях обладает лишь небольшой ряд газов называемых благородными — гелий, неон, аргон, криптон, ксенон и радон. Чаще же всего, химические вещества состоят не из разрозненных атомов, а из их объединений в различные группировки.
То есть атомы большинства химических элементов способны связываться друг с другом. Чаще всего в результате этого получаются молекулы – частицы, представляющие собой группировки из двух или более атомов. Например, химическое вещество водород состоит из молекул водорода, которые образуются из атомов следующим образом:
Рисунок 3. Образование молекулы водорода
Образовывать связи друг с другом могут и атомы разных химических элементов, так, например, при взаимодействии атома кислорода с двумя атомами водорода образуется молекула воды:
Рисунок 4.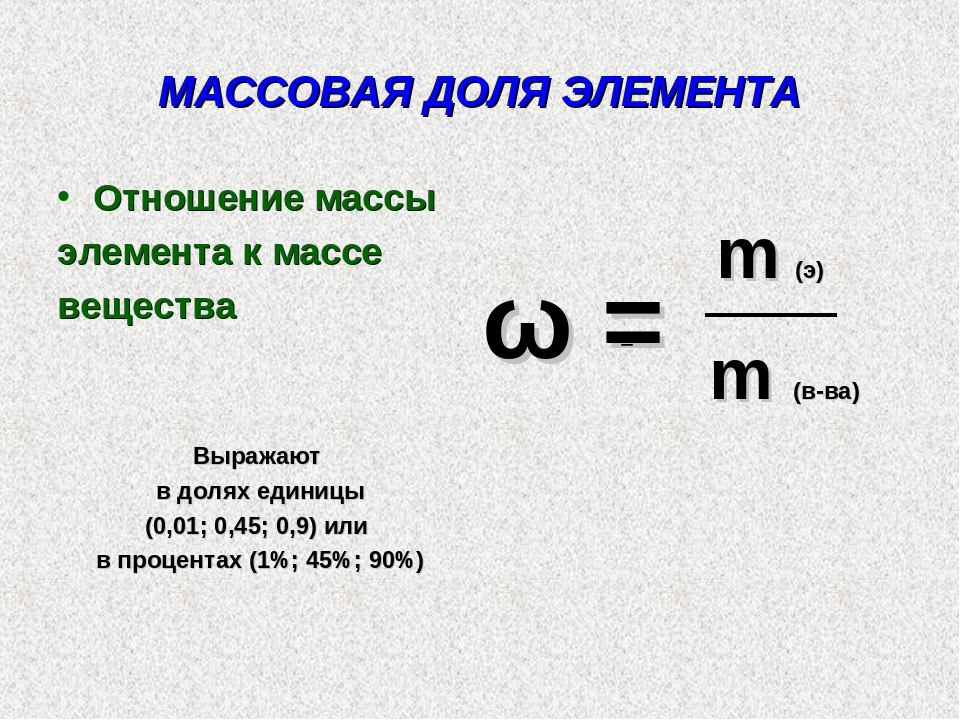 Образование молекулы воды
Образование молекулы воды
Поскольку каждый раз рисовать атомы химических элементов и подписывать их неудобно, для отражения состава молекул были придуманы химические формулы. Так, например, формула молекулярного водорода записывается как Н2, где число 2, написанное подстрочным шрифтом справа от символа атома водорода, означает количество атомов данного типа в молекуле. Таким образом, формулу воды можно записать как H2O. Единица, которая должна показывать количество атомов кислорода в молекуле, согласно принятым в химии правилам, не пишется. Числа, обозначающие количества атомов в составе одной молекулы называют индексами.
Рассмотрим еще несколько примеров химических формул веществ. Так, формула аммиака записывается как NH3, что говорит о том, что каждая молекула аммиака состоит из одного атома азота и трех атомов водорода.
Нередко встречаются молекулы, в которых можно насчитать несколько одинаковых групп атомов. Например, из формулы сульфата алюминия Al2(SO4)3, можно сделать вывод о том, что в составе молекулы данного вещества находятся две группы атомов SO4.
Таким образом, химические формулы веществ однозначно характеризуют как их качественный, так и количественный состав.
Из всего вышесказанного логично вытекает закон постоянства состава вещества, установленный еще в 1808 году французским ученым Жозефом Луи Прустом, и звучит он следующим образом:
Любое чистое химическое вещество имеет постоянный качественный и количественный состав, не зависящий от способа получения этого вещества.
Поскольку любое химическое вещество является совокупностью молекул одинакового состава, это приводит к тому, что пропорции между атомами химических элементов в любой порции вещества такие же, как и в одной молекуле данного вещества. Все различия в химических свойствах веществ зависят от количественного и качественного состава молекул и кроме того, от порядка связей атомов между собой, если таковое возможно.
Таким образом, можно дать следующее определение термина молекула:
Молекула – это наименьшая частица какого-либо химического вещества обладающая его химическими свойствами.
Аналогично относительной атомной массе, существует также и такое понятие как относительная молекулярная масса Mr:
Относительная молекулярная масса (Mr) вещества это отношение массы одной молекулы этого вещества к одной двенадцатой массы одного атома углерода (1 атомной единице массы).
Таким образом, очевидно, что относительная молекулярная масса складывается из относительных атомных масс элементов, каждая из которых помножена на количество атомов данного конкретного типа в одной молекуле. Так, например, относительная молекулярная масса молекулы азотной кислоты HNO3 складывается из относительной атомной массы водорода, относительной атомной массы азота и трех относительных атомных масс кислорода:
Для описания качественного и количественного состава вещества используют такое понятие как массовая доля химического элемента w(X):
Массовая доля (ω) химического элемента в веществе — это отношение относительной атомной массы Ar(X) данного элемента, помноженной на число его атомов в молекуле, к относительной молекулярной массе Ar(X) данного вещества.
где ω(Х) — массовая доля элемента X; Аr(Х) — его относительная атомная масса; n — число атомов X в одной молекуле вещества; Мr — относительная молекулярная масса химического вещества.
Чаще всего, массовую долю химического элемента выражают в процентах, в этом случае формульное выражение массовой доли в процентах ω%(Х) будет иметь вид:
Рассчитаем в качестве примера массовые доли водорода, азота и кислорода в молекуле азотной кислоты (НNO3):
Массовые доли элементы — Справочник химика 21
Массовые доли элементов в минерале изумруде равны 5,06% Ве, 10,05% А1, 31,49% 51 и 53,40% О. Опре- [c.118]
В состав химического соединения входят натрий, фосфор и кислород. Массовые доли элементов составляют (%) натрия — 34,6, фосфора — 23,3, кислорода 42,1. Определите простейшую формулу соединения. [c.13]
С помощью химической формулы можно рассчитать массовые доли атомов различных элементов в веществе. Массовая доля элемента А ы(А) в веществе А В С определяется по формуле [c.240]
Массовая доля элемента А ы(А) в веществе А В С определяется по формуле [c.240]
Вычисление массовой доли элементов по формулам веществ [c.208]
Нахождение формулы химического соединения по его известным массовым долям элементов. (Звездочкой отмечены задачи повышенной трудности.) [c.209]
I, Вычисление массовой доли элементов (в процентах) по формулам [c.171]
На основе данных о соотношении масс или о массовых долях элементов, входящих в состав вещества, можно определить химическую формулу этого вещества. [c.241]
Решение. Эквивалентом элемента называется такое его количество, которое соединяется с 1 моль атомов водорода или замешает его в химических реакциях. Эквивалентная масса — масса 1 эквивалента, выраженная в г/моль. Массовая доля элемента в гидриде йу (эл.) =(100 —8,87) = 91,13%. Согласно закону эквивалентов [c. 7]
7]
В соединении калия, хлора и кислорода массовые доли элементов равны соответственно 31,8 29,0 39,2 . Установите простейшую формулу этого соединения. [c.25]
Определите простейшую формулу соединения калия с марганцем и кислородом, если массовые доли элементов в этом веществе составляют соответственно 24,7, 34,8 и 40,5%. Ответ КМпО . [c.14]
Массовые доли элементов в минерале изумруда равны 5,06% Ве, 10,05% А1, 31,49% 51 и 53,40% О. Определите формулу минерала и представьте ее в В1вде соединения оксидов металлов. Ответ ЗВе0-Л120з-65102. [c.147]
Задача. Рассчитать массовую долю элементов в сульфате кальция Са804. [c.208]
Температура термообработки, Массовая дола элементов, % [c.473]
Массовая доля элемента (%), соответствующая появлению линии в спектре [c.114]
Чаще массовую долю элемента в веществе выражают не в долях единицы, а в процентах [c. 17]
17]
В зависимости от поставленной задачи, свойств анализируемого вещества и других условий состав веществ выражается по-разному. Химический состав вещества может быть охарактеризован массовой долей элементов или их оксидов или других соединений, а также содержанием реально присутствующих в пробе индивидуальных химических соедииений или фаз, содержанием изотопов и т. д. Состав сплавов обычно выражают массовой долей (%) составляющих элементов состав горных пород, руд, минералов и т. д. — содержанием элементов в пересчете на какие-либо их соединения, чаще всего оксиды. Наиболее сложен так называемый фазовый или вещественный анализ, целью которого является определение содержания в пробе индивидуальных химических соединений, форм, в виде которых присутствует тот или иной элемент в анализируемом образце. При анализе органических соединений наряду с определением отдельных элементов (углерода, водорода, азота и т. д.) нередко выполняется молекулярный и функциональный анализ (устанавливаются индивидуальные химические соединения, функциональные группировки и т. д.). [c.5]
д.). [c.5]
П. В состав химического соединения входят Ка, Р и О. Массовые доли элементов, % N3 — 34,6, Р — 23,3 О — 42,1. Определите простейшую формулу. [c.7]
Массовая доля элемента в сложном веществе-безразмерная величина, она всегда меньше единицы (wg [c.16]
Упр. 25. Рассчитать массовые доли элементов в сульфате железа (III). [c.56]
Массовая доля элемента в данном веществе — это отношение относительной атомной массы данного элемента, умноженной на ч ело его атомов в молекуле, к относительной молекулярной массе веш,ества [c.13]
Нахождение молекулярной формулы газообразного вещества основании его плотности и массовых долей элементов (процентного [c.179]
Молекула Массовая доля. % Элемент с.близким содержанием в морской воде [c.215]
О 1, Найдите формулы веществ, массовые доли элементов в которых следующие а) С — [c. 14]
14]
Рассчитайте массовые доли элементов в соединениях а) СО2, б) Н28, в) СаС12. [c.237]
Что такое массовая доля элемента в данном веществе [c.13]
Для выражения элементного состава сложного вещества используются массовые доли элементов, представляющие собой отношение части (массы элемента) к целому (массе вещества). Для того, чтобы эти величины стали более понятны, рассмотрим понятие моль атомов в сложном веществе . [c.55]
Таким образом, без применения специальных приемов непосредственно спектрофотометрически возможно определение массовой доли элементов не ниже 5-10-5%, фотоколориметрически — н е ниже 1-10- % . Меньшие содержания находятся ниже чувствительности большинства абсолютных фотометрических методов анализа. На практике эти пределы могут быть снижены до Ы0 —Ы0 % за счет увеличения навески пробы, концентрирования и других приемов. [c.185]
Массовая доля элемента X в сложном веществе, обозначаемая греческой буквой а (омега), равна отношению молярной массы атомов данного элемента М(Х), умноженной на число его молей п в моле вещества, к молярной массе вещества М(в-бй) [c. 56]
56]
Массовые доли элементов в сложном веществе. Обычно элементный состав вещества выражают в массовых долях, выраженных процентах. Вычислим, например, содержание магния в карбонате магния Mg Oa. Для этого подсчитаем молярную массу этого соединения. Она равна 24,3-1- 12-1-3-1б = 84,3 г/моль. Приняв эту величину за 100%, найдем содержание магния х = 24,3 100/84,3 = 28,8% (масс.). [c.35]
Решение. Выше мы уже вычислили молярную массу Fe2(S04)g она равна 400 г/моль. Массовые доли элементов равны [c.56]
Для любого сложного вещества, находится ли оно в мо-номолекулярном или ассоциированном виде, можно определить количественный состав, т.е. содержание отдельных элементов, входящих в это вещество. Количественный состав сложного вещества, с одной стороны, передается отношением числа атомов элементов в молекуле (например, 1 Fe 3 С1 для РеС1з и Fe2 le), а с другой стороны, массовой долей элемента Э в этом веществе (wg) — отношением массы данного элемента Э (т ) во взятой порцни вещества к массе этой порщш (т,. ) [c.16]
) [c.16]
Определите массовые доли элементов (в процентах) А12О3 и Н О в гидроксиде алюминия А1(ОН)з. [c.238]
Однако, зная только массовые доли элементов, мы можем установить лишь простейшую (или так называемую эмпирическую) формулу вещества. Поясним это на конкретном примере. Если вы уже изучали органическую химию, то вам известно о существовании веществ, имеющих молекулярные формулы jHg (ацетилен) и gHg (бензол). Соотношение числа атомов углерода и числа атомов водорода в молекулах этих веществ одинаково и равно 1 1. Поэтому массовые доли углерода и водорода в этих веществах также одинаковы. Таким образом, простейшая химическая формула, которую мы можем установить, исходя из массовых долей элементов, — это СН. Понятно, что эта формула противоречит нашим знаниям о валентности элементов, тем не менее, именно она выражает простейшее целочисленное отношение между числами атомов углерода и водорода в обоих веществах. [c.57]
[c.57]
Что же еще, кроме массовых долей элементов, необходимо знать для установления молекулярной (истинной) форп1улы вещества Нужно знать его молекулярную массу В химии существуют различные экспериментальные способы определения молекулярных масс веществ. Что касается задач, в которых требуется установить молекулярные формулы, то в их условиях молекулярная масса либо просто указывается, либо приводятся данные, позволяющие рассчитать ее. [c.58]
Массовая доля химического элемента в сложном веществе —
1. Заполните пропуски в предложениях.
а) В математике «доля» — это отношенеи части к целому. Для расчета массовой доли элемента нужно его относительную атомную массу умножить на число атомов данного элемента в формуле и разделить на относительную молекулярную массу вещества.
б) Сумма массовых долей всех элементов, входящих в состав вещества, равна 1 или 100%.
2. Запишите математические формулы для нахождения массовых долей элементов, если:
а) формула вещества — P2O5, Mr = 2*31+5*16=142
w(P) = 2*31/132 *100% = 44%
w(O) = 5*16/142*100% = 56% или w(O) = 100-44=56.
б) формула вещства — AxBy
w(A) = Ar(A)*x/Mr(AxBy) * 100%
w(B) = Ar(B)*y / Mr(AxBy) *100%
3. Рассчитывайте массовые доли элементов:
а) в метане (СН4)
б) в карбонате натрия (Na2CO3)
4. Сравните массовые доли указанных элементов в веществах и поставьте знак <, > или = :
5. В соединении кремния с водородом массовая доля кремния равна 87,5%, водорода 12,5%. Относительная молекулярная масса вещества равна 32. Определите формулу этого соединения.
6. Массовые доли элементов в соединении отражены в диаграмме:
Определите формулу этого вещества, если известно, что его относительная молекулярная масса равна 100.
7. Этилен является природным стимулятором созревания плодов: его накопление в плодах ускоряет их созревание. Чем раньше начинается накопление этилена, тем раньше созревают плоды. Поэтому этилен используют для искусственного ускорения созревания плодов. Выведите формулу этилена, если известно, что массовая доля углерода составляет 85,7%, массовая доля водорода -14,3%. Относительная молекулярная масса этого вещства равна 28.
Чем раньше начинается накопление этилена, тем раньше созревают плоды. Поэтому этилен используют для искусственного ускорения созревания плодов. Выведите формулу этилена, если известно, что массовая доля углерода составляет 85,7%, массовая доля водорода -14,3%. Относительная молекулярная масса этого вещства равна 28.
8. Выведите химическую формулу вещества, если известно, что
а) w(Ca) = 36%, w(Cl) = 64%
б) w(Na) 29,1%, w(S) = 40,5%, w(O) = 30,4%.
9. Ляпис обладает противомикробными свойствами. Раньшего его применяли для прижигания бородавок. В небльших концентрациях он действует как противовоспалительное и вяжущее вредство, но может вызвать ожоги. Выведите формулу ляписа, если известно, что в его состав входит 63,53% серебра, 8,24% азота, 28,23% кислорода.
Массовая доля элемента в сложном веществе
С
XIX
века химия перестала быть описательной наукой. Учёные широко стали использовать
Учёные широко стали использовать
методы измерения различных параметров веществ.
Массовая
доля элемента – это отношение массы этого элемента в
сложном веществе к массе всего вещества, выраженное в долях единицы (или в
процентах).
Массовая
доля элемента в веществе обозначается латинской буквой ω (дубль-вэ) и показывает
долю (часть массы), приходящуюся на данный элемент в общей массе вещества.
Массовая доля элемента в веществе выражается в долях единицы или в процентах.
Часть от целого всегда меньше целого, как долька апельсина меньше всего
апельсина.
Например,
в состав оксида ртути HgO входит два элемента –
ртуть и кислород. При нагревании этого вещества массой 50 г получается 46,3 г
ртути и 3,7 г кислорода. Рассчитаем массовую долю ртути в сложном веществе:
Рассчитаем
массовую долю кислорода в веществе. Для этого массу кислорода разделим на массу
смеси. Подставим значения масс веществ. Получаем:
Получаем:
Учитывая,
что сумма массовых долей элемента в веществе равна единице, или 100 %, массовую
долю кислорода можно найти по разности:
Для
того, чтобы найти массовую долю элемента в веществе, нужно относительную
атомную массу этого элемента умножить на число атомов данного химического
элемента в веществе и разделить на относительную молекулярную массу вещества.
Определим
массовую долю кислорода в серной кислоте. Для этого найдём относительную
молекулярную массу серной кислоты. Необходимо значения все относительных
атомных масс элементов сложить.
Mr
(H2SO4)
= Ar
(H)
· 2 + Ar
(S)
+ Ar
(O)
· 4 = 1 · 2 + 32 + 16 · 4 = 98
Найдём массовую долю кислорода. Для
этого нужно относительную атомную массу кислорода умножить на 4 и разделить на
относительную молекулярную массу всего вещества. Получается 0,653, или 65,3 %.
Рассчитаем
массовые доли элементов в метане, формула которого CH4.
Для этого определим относительную молекулярную массу метана. Подставим значения
относительных атомных масс и получим 16.
Mr (CH4) = Ar (C) +
Ar (H) · 4 = 12 + 1 · 4 = 16
Затем
найдём массовую долю углерода в метане. Для этого 12 умножим на 1 и разделим на
16. В результате образуется 0,75, или 75 %.
Для
того, чтобы найти массовую долю водорода в метане, следует от 1 вычесть
массовую долю углерода. Получается 0,25, или 25 %.
Пирит,
или золотая обманка, имеет ярко-жёлтый золотистый цвет, похож на золото,
поэтому и получил название «золото дураков». Испанские завоеватели грабили
индейцев ради изделий из пирита и увозили их домой в Европу. Пирит путали с
золотом и во время золотой лихорадки на Аляске. Это хорошо описано в книге
Джека Лондона. Минерал пирит, состоящий из 46,6 % железа и 53,4 % серы, внешним
видом очень напоминает золото. Вычислим химическую формулу пирита.
Вычислим химическую формулу пирита.
Обозначим
формулу пирита FexSy. Затем найдём
соотношение индексов x
и y.
Для этого значения массовых долей разделим на относительные атомные массы
элементов. Подставим значения и получим соотношение 0,0083 :
0,0167.
Приведём
соотношения индексов к целым числам. Для этого нужно каждое значение разделить
на меньшее число в соотношении. Получим 1 : 2. Значит,
формула пирита FeS2.
Массовая доля химического вещества онлайн
| Формула химического вещества |
| Молярная масса вещества (Грамм/Моль) |
| Процентное содержание элементов в заданном веществе |
| Массовое содержание элементов в веществе |
Массовая доля элемента
Что же такое массовая доля? Например, массовая доля химического элемента — это отношении массы элемента к массе всего вещества. Массовая доля может выражаться как в процентах, так и долях.
Массовая доля может выражаться как в процентах, так и долях.
Где же может применятся массовая доля?
Вот одни из направлений:
— определение элементарного состава сложного химического вещества
— содержание массовых долей элементов
— нахождение массы элемента по массе сложного вещества
Для расчетов используется калькулятор Молярная масса вещества онлайн с расширенными данными которые можно увидеть если пользоватся XMPP запросом.
Расчет подобных задач, что указаны выше, при примении этой страницы становятся еще проще, удобнее и точнее. Кстати про точность. В школьных учебниках почему то молярные массы элементов округлены до целых значений, что для решения школьных задач это вполне пригодится, хотя на самом деле молярные массы каждого химического элемента периодически предаются корректировке.
Наш калькулятор не стремится показать высокую точность (выше 5-ти знаков после запятой), хотя в этом нет ничего сложного. В большинстве своем, те атомные массы элементов, которые используют калькулятор, достаточны для решения поставленных задач на определение массовых долей элементов
В большинстве своем, те атомные массы элементов, которые используют калькулятор, достаточны для решения поставленных задач на определение массовых долей элементов
Но для тех педантов 🙂 , которым важна точность, хотелось бы порекомендовать ссылку Atomic Weights and Isotopic Compositions for All Elements в которой отображены все химические элементы, их относительные атомные массы, а также массы всех изотопов каждого из элемента.
Вот и все, что хотелось бы сказать. Теперь будем рассматривать конкретные задачи и как их решать. Заметьте что несмотря на то, что они все разнородны, они в своей сути опираются на молярную массу вещества и массовые доли элементов в этом веществе
На начало осени 2017 года, я добавил еще один калькульятор Мольные доли вещества и количество атомов, который поможет решать задачи на массу чистого вещества в сложном веществе, количество моль в веществе и в каждом элементе, а также количество атомов/молекул в веществе.
Примеры
Вычислит массовую долю элементов в меди сульфате CuSO4
Запрос очень простой, просто пишем формулу и получаем результат который и будет нашим ответом
|
Формула химического вещества |
|
Молярная масса вещества (Грамм/Моль) |
|
|
|
Процентное содержание элементов в заданном веществе |
|
|
|
Массовое содержание элементов в веществе |
|
|
Как уже сказано в школьных учебниках идет достаточно угрубленные значения, поэтому не удивляйтесь если в ответах бумажных книг Вы увидите Cu = 40% ,O = 40%, S = 20%. Это скажем так «побочные эффекты» упрощения школьного материала, для учеников. Для реальных задач наш ответ (ответ бота) естественно более точен.
Если речь шла о том , что бы выразить в долях а не процентах, то делим проценты каждого из элементов на 100 и получаем ответ в долях.
Сколько натрия содержится в 10 тоннах криолина Na3[AlF6]?
Введем формулу криолина и получим следующие данные
|
Формула химического вещества |
|
Молярная масса вещества (Грамм/Моль) |
|
|
|
Процентное содержание элементов в заданном веществе |
|
|
|
Массовое содержание элементов в веществе |
|
|
Из полученных данных мы видим, что в 209,9412 количестве вещества содержится 68,96931 количества натрия.
В граммах ли мы будем это измерять, в килограммах или тоннах для соотношения это ничего не меняется.
Теперь осталось построить другое соответствие где у нас есть 10 тон исходного вещества и неизвестное количество натрия
Это получилась типичная пропорция. Можно конечно воспользоваться ботом Расчет пропорций и соотношений но данная пропорция настолько проста, что сделаем это ручками.
209,9412 относится к 10(тоннам) как 68,96391 к неизвестному числу.
Таким образом количество натрия (в тоннах) в криолине составит 68.96391*10/209.9412=3.2849154906231 тонны натрия.
Опять же для школы иногда придется округлять до целого числа массовое содержание элементов в веществе, но ответ фактически не сильно отличается от предыдущего
69*10/210=3.285714
Точность до сотых долей совпадает.
Вычислить сколько кислорода содержится в 50 тоннах фосфата кальция Ca3(PO4)2 ?
Массовые доли заданного вещества следующие
|
Формула химического вещества |
|
Молярная масса вещества (Грамм/Моль) |
|
|
|
Процентное содержание элементов в заданном веществе |
|
|
|
Массовое содержание элементов в веществе |
|
|
Та же самая пропорция что и в предыдущей задаче 310.18272 относится к 50 (тоннам) так же как и 127.9952 к неизвестной величине
ответ 20,63 тонны кислорода находится в заданной массе вещества.
Если же мы добавим к формуле служебный символ восклицательный знак, говорящий нам о том что задача школьная(используются грубые округления атомных масс до целых чисел), то ответ получим следующий:
|
Формула химического вещества |
|
Молярная масса вещества (Грамм/Моль) |
|
|
|
Процентное содержание элементов в заданном веществе |
|
|
|
Массовое содержание элементов в веществе |
|
|
Пропорция будет уже вот такой
310 относится к 50 (тоннам) так же как и 128 к неизвестной величине. И ответ
20,64 тонны
Как то так 🙂
Удачи в расчетах!!
- Металлы и неметаллы >>
Определение, примеры, проблемы, расчет ~ ChemistryGod
Массовая доля — это свойство смеси. Смесь — это физическая комбинация двух или более разных веществ. Типы смесей — растворы, суспензии и коллоиды.
Рисунок 1: Типы смесей: растворы (соль и вода), суспензии (почва и вода) и коллоиды (молоко) (слева направо)
[Источники изображений: Викимедиа, Flickr и общественное достояние]
По химии, большинство смесей представляют собой растворы, гомогенную смесь растворенного вещества и растворителя.Но приведенное ниже определение массовой доли применимо и к другим типам.
Содержание
Определение и формула
Массовая доля вещества в смеси — это отношение массы вещества к общей массе смеси. Он также известен как массовый процент или массовый процент при выражении в процентах. Поскольку массовая доля представляет собой отношение массы к массе, это безразмерная величина.
Для смеси
Здесь w i — массовая доля компонента i th , m i — масса компонента i th , и м T — общая масса смеси.
Общая масса смеси — это сумма масс каждого компонента.
Используя два приведенных выше уравнения,
Примечание: сумма всех массовых долей равна единице.
Примечание: массовая доля вещества не зависит от давления, температуры и местоположения; это интенсивное количество. Он остается постоянным, если не происходит химического изменения или чистого физического переноса какого-либо вещества. Итак, массовый процент вина (в приведенном выше примере) постоянен во всем мире.
Массовая доля растворенного вещества в растворе определяется как отношение массы растворенного вещества к массе раствора.
Пусть m растворенного вещества будет массой растворенного вещества, а m раствора массой раствора. Массовая доля растворенного вещества следующая:
Массовый процент
Массовая доля также известна как массовый процент, массовый процент, массовый процент или массовый процент, когда выражается в процентах.Это сокращенно мас.% Или мас.%.
Для раствора:
Связь с другими величинами
Массовая доля — это одна из величин, используемых для выражения состава смеси. Но есть также другие величины, такие как мольная доля, молярность, массовая концентрация и другие. Некоторые из них обсуждаются ниже.
Пропорция смешивания
Пропорция смешивания компонента — это относительное содержание этого компонента в смеси по сравнению с другими компонентами. Пусть m 1 будет массой чистого вещества 1 и m 2 , чистого вещества 2.Соотношение смеси составляет r m .
Теперь мы можем выразить w 1 и w 2 через r m .
Молярная доля
Мольная доля широко используется в химии и технике. Это также безразмерная величина, представляющая собой отношение молей компонента к общему количеству молей смеси. Обычно обозначается как x и .
Пусть n i будет моль i th компонента смеси.Общее количество моль в смеси
. Мольная доля компонента i th составляет x i .
Мы также знаем, что моль вещества — это отношение массы ( m i ) к молярной массе ( M i ).
Используя два приведенных выше уравнения,
Здесь
— средняя молярная масса смеси. Но мы тоже это знаем.
Подставив
,
Таким образом, мы установили связь между мольной долей и массовой долей.
Объемная доля
Объемная доля ( v i ) — это объем компонента ( V i ) к общему объему смеси ( V mix ).
Объем — это масса, разделенная на плотность.
Массовая концентрация
Массовая концентрация растворенного вещества ( ρ i ) — это отношение массы растворенного вещества ( m i ) к объему раствора ( V ).
Здесь
— плотность раствора ( ρ ).
Из приведенного выше уравнения массовая концентрация растворенного вещества — это массовая доля растворенного вещества, умноженная на плотность раствора.
Молярность или молярная концентрация
Молярность или молярная концентрация ( C i ) — это моль растворенного вещества ( n i ) на единицу объема раствора ( V ). Объем раствора обычно выражается в дециметровых кубах (дм 3 ).
Моль вещества — это масса, деленная на молярную массу. А плотность — это масса, разделенная на объем.
Процентный состав
Соединение состоит из различных элементов. Когда рассчитывается массовая доля элемента, она называется процентным составом этого элемента. Короче говоря, массовая доля и процентный состав одинаковы, когда речь идет об элементах соединения.
Решенные проблемы
Проблема 1: Воздух
Заявление: Воздух содержит 21% кислорода и 79% азота.Молярная масса кислорода и азота составляет 15,999 г моль -1 и 14,007 г моль -1 .
Решение: Вышеуказанные проценты даны не по массе, а в молях. Итак, в 100 моль воздуха содержится 21 моль кислорода и 79 моль азота.
Преобразуя моль в грамм,
Пусть w O 2 и w N 2 будут массовыми долями кислорода и азота соответственно.
Таким образом, массовая доля кислорода и азота составляет 23% и 77%.
Проблема 2: Газовая труба
Утверждение: Газовая труба содержит 2 моля диоксида углерода, 10 моль кислорода, 52 моль азота и 1,3 моль метана. Молярная масса водорода, углерода, азота и кислорода составляет 1,008 г-моль -1 , 12,011 г-моль -1 , 14,007 г-моль -1 и 15,999 г-моль -1 .
Решение: молярная масса диоксида углерода, кислорода, азота и метана должна быть M CO 2 , M O 2 , M N 2 и М СН 4 .
Преобразование моля в грамм,
Массовая доля рассчитывается как:
Задача 3: Серная кислота
Утверждение: Молярная концентрация серной кислоты составляет 2,0 М или 2 моль дм −3 . Молярная масса серной кислоты составляет 98,08 г · моль -1 . Плотность раствора 1,19 г · см −3 .
Решение: Рассмотрим 1 л (или 1 дм −3 ) раствора.
Моль серной кислоты в 1 л раствора составляет
Если перевести моль в грамм,
Таким образом, в 1 л раствора содержится 196.16 г серной кислоты.
Плотность раствора 1,19 г см −3 . На 1 л раствора масса раствора составляет
Массовая доля серной кислоты в 1190 г раствора составляет
Практические задачи
Найдите массовую долю в следующих задачах.
Задача 1: Изопропиловый спирт
Раствор изопропилового спирта содержит 40 г изопропилового спирта и 20 г воды. Молярная масса изопропилового спирта и воды составляет 60 г моль -1 и 18 г моль -1 .
Задача 2: гидроксид натрия
Молярность раствора гидроксида натрия составляет 0,51 М. Молярная масса гидроксида натрия составляет 40 г · моль -1 . Плотность раствора 1,02 г · см −3 .
Проблема 3: Выхлоп из дымохода
Выхлоп из дымохода содержит 10 моль кислорода (O 2 ), 53 моль азота (N 2 ) и 37 моль диоксида углерода (CO 2 ). Молярная масса кислорода, азота и диоксида углерода составляет 32 г моль -1 , 28 г моль -1 и 44 г моль -1 .
Показать ответы
- 0,67 изопропилового спирта и 0,33 воды.
- 0,020 гидроксида натрия.
- 0,09 кислорода, 0,43 азота и 0,48 диоксида углерода.
Сопутствующие статьи
Молярная фракция — обзор
3 Имидазол, бензимидазол и их производные
В растворе и в твердом состоянии имидазол и его N2-незамещенные производные образуют большие ассоциаты с водородными связями 13 (Схема 8) [76AHC (S1), с.266; 84CHEC-I (5) 345,84JPC5882; 96CHEC-II (3) 77; 97JST (415) 187].
Схема 8.
Благодаря идеальному линейному расположению водородных мостиков NH ⋯ N в 13 в растворе происходят чрезвычайно быстрые кооперативные переносы протонов, которые приводят к усреднению положений 4 и 5 в кольце по времени ЯМР. шкала. В отличие от пиразолов, только усредненные спектры ЯМР 1 H, 13 C и 15 N с эффективной симметрией C 2v были зарегистрированы до сих пор для имидазола, бензимидазола и многих их производных [75T1461, 82JOC5132, 96CHEC-II (3) 77, 97MRC35].Медленная прототропная кольцевая таутомерия 2-перфторалкилими-дазолов приписана внутримолекулярным связям N-H ⋯ F, реализованным в этих соединениях (82JOC2867; 95OPP33). Реакция протонного обмена подлежит общему и специфическому кислотному и основному катализу [76AHC (S1), p. 266; 87AHC (41) 187],
Как и в случае пиразола, относительные энергии неароматических 2 H 14c и 4 (или 5) 14d, e (R 1 = R 2 = R 3 = H) изомеров имидазола слишком много, чтобы они вносили вклад в таутомерное равновесие (схема 9).По расчетам STO-3G (86BSF429) эти значения равны 60,4 и 67,7 кДж моль −1 соответственно относительно 14a, b (R 1 = R 2 = R 3 = H).
Схема 9.
Большая часть доступной информации о положениях таутомерных равновесий 14a ⇌ 14b имидазолов основана на измерениях основности N-незамещенных имидазолов и N-метилированных производных таутомеров 14a и 14b. Данные, полученные ранее [76AHC (S1), с. 272] и более поздние [96CHEC-II (3) 77] исследования собраны в Таблице III. Как правило, они соответствуют полученным с использованием ЯМР 1 H и 13 C ЯМР [79JOC3864; 83T3797; 86JHC921; 92JCS (P1) 2779; 98JCS (P2) 1665], 15 N ЯМР (79JOC3864; 83HCA1537) и УФ-спектральный (86ZC378) методы.
Таблица III. Константы равновесия ( K T = 14a / 14b ) для кольцевой таутомерии имидазола, как определено из p K a Измерения
| Соединение a | 904 904 904 904 T Каталожный номер | |
|---|---|---|
| 4-канальный 3 | 1.1 | 96CHEC-II (3) 77 |
| 4 фазы | 10-37 | 76AHC (S1), стр. 278 |
| 4-NO 2 | 320-500 | 76AHC (S1), стр. 278 |
| 4-класс | 90 | 96CHEC-II (3) 77 |
| 4-Br | 47 | 96CHEC-II (3) 77 |
| 4-I | 96CHEC-II (3) 77 | |
| 2-Br-4-NO 2 | 210 | 76AHC (S1), стр.278 |
| 4-NO 2 -5-Cl | 118 | 76AHC (S1), стр. 278 |
| 2,4- (NO 2 ) 2 | 1.1-3.1 | 76AHC (S1), стр. 278 |
Главный вывод о влиянии заместителей в имидазольном кольце на состояние таутомерных равновесий 14a ⇌ 14b состоит в том, что электроноакцепторные группы благоприятствуют 4-положению, т. Е. Таутомерам 14a с R 2 = Hal, NO 2 и так далее, являются энергетически предпочтительными видами.Применение уравнения Чартона, K T = [4-R Im] / [5-R Im] = 3,2 σ м , подробно обсуждалось [76AHC (S1); 96CHEC-II (3) 77]. Было обнаружено, что уравнение качественно согласуется с экспериментальными данными, представленными в таблице III.
Теоретические исследования относительной устойчивости таутомеров 14a и 14b проводились в основном на полуэмпирическом уровне. Расчеты AM1 и PM3 [98JST (T) 249] относительной стабильности, проведенные для серии из 4 (5) — замещенных имидазолов 14 (R 3 = H, R 2 = H, CH 3 , OH, F, NO 2 , Ph) в основном согласуются с выводом, основанным на уравнении Чартона.Из сравнения электронных спектров 4 (5) -фенилимидазола 14 (R 2 = Ph, R 1 = R 3 = H) и 2,4 (5) -дифенилимидазола 14 ( R 1 = R 2 = Ph, R 3 = H) в этаноле с рассчитанными с использованием метода π -электронного PPP для каждой из таутомерных форм, следует, что расчеты для таутомеров типа 14a лучше соответствуют экспериментально наблюдаемым спектрам (86ZC378).Расчеты AM1 [92JCS (P1) 2779] энтальпий образования 4 (5) — аминоимидазола 14 (R 2 = NH 2 , R 1 = R 3 = H) и 4 ( 5) -нитроимидазол 14 (R 2 = NO 2 , R 1 = R 3 = H) указывает на таутомеры 14a и 14b соответственно как энергетически предпочтительные в газовой фазе. Оба прогноза не согласуются с ожиданиями, основанными на уравнении Чартона и данными, относящимися к измерениям основности (таблица III).Эти несоответствия можно объяснить тем, что таутомеры 14b 4 (5) -аминоимидазола и 14a 4 (5) -нитроимидазола обладают более высокими значениями дипольных моментов по сравнению с их более стабильными газофазными таутомерами. Учет энергии сольватации должен перекрыть внутреннюю энергетическую щель.
Утверждая, что метод MNDO более подходит, чем метод AM1 для прогнозирования теплоты образования пятичленных азотированных ароматических колец, Гарсия и Виларраса (88h2803) вычислили, что 4-фторимидазол 14a (R 2 = F, R 1 = R 3 = H) равно 2.На 5 кДж моль −1 более стабилен, чем его таутомер 14b , тогда как 2,4-дифторимидазол 14a (R 1 = R 2 = F, R 3 = H) составляет 2,1 кДж моль −1 менее стабильно, чем 14b. Различия в энергии очень малы и исчезают, если принять во внимание поправочные члены, относящиеся к отталкиванию неподеленной пары между вицинальными пиридиноподобными атомами азота и фторными заместителями.
Теоретическое исследование ab initio основности метилдиазолов (90JA1303) в газовой фазе включало обсуждение таутомерии 4 (5) -метилимидазола.Расчеты RHF / 4-31G привели к выводу, что 4-метилтаутомерная форма 14a (R 2 = Me, R 1 = R 3 = H) составляет 5,2 кДж моль −1 больше стабильнее, чем его 5-метиловый аналог 14b. Было подчеркнуто, что этот результат следует рассматривать как зависимый от базового набора. Однако недавнее теоретическое исследование [94JST (T) 45] показало, что, начиная с уровня RHF / 6-31G *, все более точные приближения указывают на более высокую внутреннюю стабильность 4-метилтаутомера.На уровне MP2 / 6–31G * полная энергия 4-метилтаутомера на 0,7 кДж / моль –1 ниже, чем у 5-метилтаутомера. Таким образом, учет сольватационных эффектов может сильно повлиять на положение таутомерного равновесия 14a ⇌ 14b. Недавно было проведено систематическое теоретическое исследование, направленное на оценку молекулярных свойств и таутомерного равновесия 4- и 5-метилимидазолов [98JST (T) 197]. Было обнаружено, что значение K T для газофазного равновесия весьма чувствительно как к базисному набору, так и к эффектам корреляции.Для достижения хорошего согласия с экспериментальными данными требуется использование расширенных базисных наборов (6-31 + G *, 6-311 + G * и 6-31 ++ G **) на уровнях MP2 и DFT.
В последние годы не так много информации было добавлено к более ранним исследованиям таутомерных равновесий бензимидазолов, основанным на измерениях основности [76AHC (S1), p. 292], для 5 (6) — и 4 (7) -замещенных бензимидазолов и 2-метил-5 (6) -замещенных бензимидазолов K T значения очень близки к 1, что указывает на почти эквивалентную стабильность Таутомеры N1 (H) и N3 (H).Таутомерные равновесия 2-замещенных (H, NH 2 , OMe, CN) 5-нитробензимидазолов и 4-нитробензимидазолов анализировали с помощью полуэмпирических методов MINDO / 3 и INDO. Было предсказано, что высвобождающие электроны группы в положении 2 сдвигают равновесие к таутомерам 6-NO 2 и 4-NO 2 соответственно.
Как уже упоминалось, частоты скачков протонов, приводящие к установлению равновесия 14a ⇌ 14b в растворах имидазолов и бензимидазолов, слишком высоки для того, чтобы эти формы наблюдались на шкале времени ЯМР с 13 C [ Различия химического сдвига для C4 и C5 в N -алкильных производных составляют около 10 ppm (88MRC134)] и даже для 15 N ЯМР, где азотные резонансы пирролоподобных и пиридиноподобных атомов азота имеют различия в химическом сдвиге до 100 ppm (97MRC35).Это указывает на то, что среднее время жизни индивидуального таутомера до его прототропной перегруппировки составляет примерно 10 -4 -10 -5 с. Эта перегруппировка заморожена в твердом состоянии. Хорошо разрешенные твердотельные спектры ЯМР 13 C CPMAS были записаны для имидазола [81JA6011, 81JCS (CC) 1207], 2-метилимидазола [87H (26) 333], бензимидазола [83h2713; 96CHEC-II (3) 77] и 2,2′-бис-1 H -имидазол [96CHEC-II (3) 77]: сигналы C (4) и C (5) были отнесены к спектры соответствующих N -метильных производных.Недавно было проведено спектроскопическое исследование ЯМР 1 H и 13 C 2,2′-бисбензимидазолила в растворе ДМСО в диапазоне температур от 293 до 383 К и энергии активации 67-69 кДж моль. — 1 был оценен для процесса переноса протона [98JPOC411]. Это значение попадает в диапазон значений, характерных для таутомеризации других циклических оксаламидинов (89JA5946; 94JA1230), что предполагает возможность двухступенчатого межмолекулярного механизма таутомерной перегруппировки. .
Спектр ЯМР 15 N твердого имидазола показывает два отдельных сигнала для NH (–210 м.д.) и пиридиноподобного (–138 м.д.) азота, что указывает на то, что протонный обмен в твердом состоянии замедлен (82JA1192). Принимая во внимание очень большую разницу между химическими сдвигами 15 N двух атомов азота в имидазольном кольце, спектроскопия ЯМР 15 N может рассматриваться как наиболее точный и надежный подход для определения K T значения для таутомерных равновесий 14a ⇌ 14b (82JA3945).
Мольные доли таутомеров 14a ( X a ) и 14b ( X b ) можно рассчитать по уравнению
Pobs = XaPa + XbPb,
где P obs — наблюдаемый усредненный химический сдвиг (или константа взаимодействия), а P a и P b — химические сдвиги (или константы взаимодействия) пирролоподобных и пиридиноподобных атомов азота в 14 в условиях медленного протона. обмен (e.g., в твердом виде) или в его производном NMe. Процедура не очень точна, потому что всегда существует неопределенность относительно того, насколько хорошо значения модели соответствуют значениям отдельных таутомеров; однако он обычно считается (80JA2881; 82JA3945, 82JOC5132; 93JA6813) более точным, чем тот, который основан на измерениях основности. Используя усредненные значения химических сдвигов 15 N атомов азота N1 и N3 гистамина 15 и ряда его аналогов, обладающих способностью образовывать циклическую водородную связь внутри определенного таутомера, Roberts et al. (82JA3945) рассчитал значения K T для диапазона pH, который соответствует существованию соединений 15 — 21 в водном растворе в форме, подчиняющейся таутомерному равновесию N1 (H) ⇌ N3 (H). 1
Как видно из значений K T , влияние циклических водородных связей в соединениях 15,17 и 18 недостаточно сильное, чтобы сдвинуть таутомерные равновесия к N3 ( H) сторона.Этот факт был приписан неблагоприятному затмению метиленовых групп в боковой цепи и конкуренции воды с группой боковой цепи за образование водородной связи с группой N-H. Устранение первого фактора в цис -урокановой кислоте 19 и 20 привело к заметной стабилизации таутомеров N (3) H, что подтверждено измерениями p K a [98JCS (P2) 1665] .
Особое внимание было уделено изучению таутомерных равновесий в растворах гистидина 22 , поскольку признана ключевая функциональная роль таких равновесий в белках.В водных растворах таутомеры гистидина быстро взаимопревращаются, и для каждого кольцевого азота наблюдается только один усредненный сигнал (схема 10).
Схема 10.
В более ранних исследованиях значения этих 15 химических сдвигов N были оценены по модельным N-метилированным соединениям (78JA8041; 80JA2881; 82JA3945) или по 15 N ЯМР-спектроскопии таутомерных форм гистидина в твердое состояние, в котором таутомерный обмен является медленным (82JA1192). Использование смеси 80% этанол / вода в качестве растворителя позволило Bachovchin et al. (93JA6813) для непосредственного наблюдения отдельных таутомерных форм гистидина в спектрах ЯМР 15 N при –55 ° C. Было обнаружено, что растворитель оказывает небольшое влияние на собственные сдвиги 15 N индивидуальных таутомеров и таутомерные равновесия имидазольного кольца. В интервале pH, где имидазольное кольцо является нейтральным, в спектрах ЯМР 15 N наблюдались три из четырех возможных форм гистидина при –55 ° C. Только 22b напрямую не обнаружен.Примечательно, что только формы 22a и 23a наблюдались в твердотельных спектрах ЯМР 15 N гистидина (82JA1192). Мольная доля таутомерной формы 22b , рассчитанная из химических сдвигов 15 N в растворах при pH ~ 8,2, где преобладает цвиттерион 22 , составляет 0,18. Это значение хорошо согласуется с более ранними оценками (80JA2881), основанными на значениях констант связи 2 J NH . Стабилизация 22a над 22b , по-видимому, вызвана образованием водородной связи с участием N3-центра.При pH выше 9,2, когда депротонирование α-аминогруппы не передает водородную связь центру N3, таутомер 23a по-прежнему остается энергетически предпочтительной формой. Расчетная мольная доля составила 0,35 (93JA6813). Недавно был разработан эффективный метод определения протонированных и депротонированных форм и таутомерных состояний остатков гистидина даже в белках с большой молекулярной массой (до 30-40 кДа), основанный на измерениях констант связи между 15 N и 13 C в имидазольном кольце (98JA10998).Было обнаружено, что во всех гистидин-содержащих белках доминируют таутомерные формы типа 22a и 23a .
Таутомерные равновесия между двумя вырожденными парами ( A ′, A ″ ⇌ B ′, B ″) наблюдались в растворах бензодиимид-азолов с низкой концентрацией DMSO-d 6 , содержащих аналогичные заместители. в обоих имидазольных кольцах [98H (48) 113]. В этих равновесиях преобладают несимметричные таутомеры A ‘и A ″.
Objectives_template
Массовые доли :
Позвольте и быть массой волокон, матрицы и композита, соответственно. Мы знаем, что
(7,6) |
Массовые доли, аналогичные объемным долям, определяются как отношение массы соответствующей фазы к массе композита.Таким образом, мы можем написать,
(7,7) |
где — массовая доля волокна, а — массовая доля матрицы. Теперь давайте запишем массу каждой фазы через плотность и объем соответствующей фазы как
(7,8) |
где, и — плотности волокна, матрицы и композита соответственно.Теперь массовые доли могут быть записаны через плотность и объемные доли как
(7,9) |
Это соотношение между массовой и объемной долями задается в терминах свойств отдельных составляющих (с использованием уравнений (7.6) и (7.8)) как
(7.10) |
Таким образом, из приведенного выше уравнения ясно, что объемная и массовая доли не совпадают. Всегда следует указывать основу для расчета содержания волокна в композите.
Плотность :
Плотность композита рассчитывается на основе плотностей и объемных долей отдельных фаз следующим образом. Масса композита определяется уравнением (7.6). Мы можем записать это в терминах соответствующих объемных долей и плотностей (с перегруппировкой) как
(7,11) |
Это записано с использованием определения объемной доли для волокна и матрицы как
(7,12) |
Мы запишем плотность композита через массовую долю из уравнения (7.9) как
(7,13) |
Массовые доли в недрах звезды во время предсверхновой эволюции
Ауфдерхайде, М.Б., Фушики, И., Вусли, С.Е., Хартманн, Д.Х .: Поиск важных ядер слабого взаимодействия в эволюции предсверхновой. Astrophys. J. Suppl. Сер. 91 , 389 (1994)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Бор, А., Моттельсон, Б.Р .: Структура ядра, т. 1. Бенджамин, Нью-Йорк (1969)
Google Scholar
Браво, Э., Гарсия-Сенз, Д .: Кулоновские поправки к уравнению состояния ядерной статистической равновесной материи: последствия для нуклеосинтеза SNIa и индуцированного аккрецией коллапса белых карликов. Пн. Нет. R. Astron. Soc. 307 , 984 (1999)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Чамель, Н., Наими, С., Хан, Э., Маргерон, Дж .: Применимость приближения Вигнера-Зейтца в коре нейтронной звезды. Phys. Ред. C 75 , 055806 (2007)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Клиффорд Ф.Э., Тайлер Р.Д .: Равновесное распределение нуклидов в веществе при высоких температурах. Пн. Нет. R. Astron. Soc. 129 , 104 (1965)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Димарко, А., Барберо, К., Диас, Х., Гарка, Ф., Хорват, Дж., Лосано, Л .: Влияние низколежащих дискретных ядерных состояний на изотопные содержания в ядрах предсверхновой. J. Phys. G, Nucl. Часть. Phys. 28 , 121 (2002)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Эпштейн, Р.И., Арнетт, У.Д .: Нейтронизация и термический распад плотной звездной материи. Astrophys. J. 201 , 202 (1975)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Фишер, Т., Хемпель, М., Сагерт, И., Сува, Ю., Шаффнер-Белич, Дж .: Симметрия энергетического воздействия при моделировании сверхновых с коллапсом ядра. Евро. Phys. J. A 50 , 1 (2014)
Артикул
Google Scholar
Фаулер, В.А., Коулэн, Г.Р., Циммерман, Б.А.: Скорости термоядерных реакций. Анну. Rev. Astron. Astrophys. 5 , 525 (1967)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Фуллер, Г.М .: Нейтронная оболочка, блокирующая захват электрона при гравитационном коллапсе. Astrophys. J. 252 , 741 (1982)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Хартманн Д., Вусли С.Е., Эль Эйд М.Ф .: Нуклеосинтез в нейтронно-избыточных выбросах сверхновой. Astrophys. Дж. 297 , 837 (1985)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Хикс, В.Р., Тилеманн, Ф.-К., Сжигание кремния, I. Нейтронизация и физика квазиравновесия. Astrophys. J. 460 , 869 (1996)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Хойл, Ф .: О ядерных реакциях, происходящих в очень горячих ЗВЕЗДАХ. I. Синтез элементов от углерода до никеля. Astrophys. J. Suppl. Сер. 1 , 121 (1954)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Ишизука, К., Охниши, А., Сумиёси, К .: Фазовый переход жидкого газа сверхновой материи и его связь с нуклеосинтезом. Nucl. Phys. А 723 , 517 (2003)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Кодама, Т., Такахаши, К .: R-процесс нуклеосинтеза и ядра вдали от области \ (\ beta \) — стабильности. Nucl. Phys. А 239 , 489 (1975)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Мен-Куан, Л., Цзе, З., Чжи-Цюань, Л .: Ядерное статистическое равновесие при сверхновой с коллапсом ядра. Подбородок. Phys. 16 , 3146 (2007)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Мёллер, П., Никс, Дж. Р., Майерс, В. Д., Святецки, В. Дж.: Ядерные массы в основном состоянии и деформации. В. Data Nucl. Таблицы данных 59 , 185 (1995)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Муто, К.А.З.У.О., Бендер, Э., Ода, Т., Клапдор-Клейнгротхаус, Х.В.: Протонно-нейтронная квазичастичная RPA с разделяемыми силами Гамова-Теллера. Z. Phys. А 341 (4), 407 (1992)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Наби, J.-U., Klapdor-Kleingrothaus, H.V .: Микроскопические расчеты скоростей слабого взаимодействия ядер в звездной среде для \ (A = 18 \) до 100. Eur. Phys. J. A 5 , 337 (1999)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Наби, Дж.-U., Klapdor-Kleingrothaus, H.V .: Микроскопические расчеты скоростей слабого взаимодействия звезд и потерь энергии для ядер fp- и fpg-оболочек. В. Data Nucl. Таблицы данных 88 , 237 (2004)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Наби, Дж. У., Тауфик, А. Н., Эззелараб, Н., Хан, А. А.: Плотности ядерных уровней, статистические суммы и содержание в недрах звезды. Phys. Scr. (2015, отправлено)
Надёжин, Д.К., Панов И.В., Блинников С.И. Нейтрино-индуцированный источник нейтронов в гелиевой оболочке и r-процесс нуклеосинтеза. Astron. Astrophys. 335 , 207 (1998)
ADS
Google Scholar
Пирсон, Дж. М., Наяк, Р. К., Гориели, С.: Формула ядерной массы с усиленной Боголюбовым гашением оболочки: применение к r-процессу. Phys. Lett. В 387 , 455 (1996)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Птицын, Д.{10} ~ \ mbox {K} \). Astrophys. J. Suppl. Сер. 147 , 403 (2003)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Раушер, Т., Тилеманн, Ф.-К .: Скорости астрофизических реакций из статистических расчетов модели. В. Data Nucl. Таблицы данных 75 , 1 (2000)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
Вусли, С.Е., Хоффман, Р.Д .: Альфа-процесс и r-процесс. Astrophys. J. 395 , 202 (1992)
Артикул
ОБЪЯВЛЕНИЯ
Google Scholar
массовых долей газа
массовых долей газа
АСТРОФИЗИЧЕСКИЙ ЖУРНАЛ, 481: 689702, 1997 1 июня
© 1997. Американское астрономическое общество. Все права защищены. Напечатано в США.
Департамент земного магнетизма, Институт Карнеги в Вашингтоне, 5241 Broad Branch Road, NW, Вашингтон, округ Колумбия 20015
И
Астрономический институт Каптейна, Университет Гронингена, Postbus 800, 9700 AV Groningen, Нидерланды
Поступила 13 мая 1996 г .; принята к печати 1996 г. 31 декабря
РЕФЕРАТ
Мы показываем, что массовая доля газа в спиральных галактиках сильно коррелирует со светимостью и поверхностной яркостью.Это не коррелирует с линейным размером. Доля газа изменяется в зависимости от светимости и поверхностной яркости с одинаковой скоростью, что указывает на эволюцию при фиксированном размере.
Тусклые галактики явно менее развиты, чем яркие, поскольку они потребляют только свой газ. Это разрешает парадокс потребления газа, поскольку существует множество галактик с большими газовыми резервуарами. Эти богатые газом галактики, должно быть, сформировали основную часть своего звездного населения во второй половине хаббловского времени. Существование таких незрелых галактик в точке z = 0 указывает на то, что либо формирование галактик является длительным или даже продолжающимся процессом, либо начало значительного звездообразования может быть отложено на произвольные периоды в разреженных газовых дисках.
Предметные рубрики: галактики: эволюциягалактики: фундаментальные параметрыгалактики: ISMгалактики: спиральные
Об эволюционной истории галактик можно судить по-разному. Один из подходов — использовать обширные знания об эволюции звезд, полученные из диаграммы HR, для построения модельных галактик (например, Tinsley 1968; Bruzual & Charlot 1993). В последнее время стало возможным получать соответствующую информацию статистическим способом из обследований глубокого красного смещения (например,г., Lilly et al. 1995; Эллис и др. 1996). Соединение различных линий доказательств воедино не является тривиальным делом, и из одинаково действенных подходов можно получить довольно разные картины.
Важно, чтобы вопрос был правильно поставлен. Что подразумевается под эволюцией галактики? Обычно мы представляем, что галактики образуются из газа, образовавшегося в результате горячего Большого взрыва. Независимо от деталей формирования галактик, единицы, которые мы наблюдаем сегодня как галактики, преобразовали некоторую часть этого газа в звезды.Массовая доля газа f g , таким образом, является естественным параметром для количественной оценки степени эволюции галактики.
Этот очевидный путь практически не использовался по той простой причине, что большинство хорошо наблюдаемых галактик имеют низкие газовые фракции ( f g 0,2). Их эволюция хорошо развита, и небольшой динамический диапазон f g не накладывает никаких ограничений на модели. В самом деле, это приводит к загадке, поскольку мы, кажется, живем в особенное время, когда большинство дисков почти исчерпали свои газовые резервуары (например.г., Робертс 1963; Kennicutt, Tamblyn, & Condon 1994).
Однако хорошо изученные объекты не обязательно должны быть репрезентативными. Недавно было продемонстрировано, что дисковые галактики с низкой поверхностной яркостью довольно распространены (McGaugh, Bothun, & Schombert 1995a; de Jong 1996; McGaugh 1996a; Impey et al. 1996). Эти галактики обычно богаты газом (Schombert et al.1992; de Blok, McGaugh, & van der Hulst 1996), и M H I / L систематически увеличивается с уменьшением поверхностной яркости (рис.1). Это соотношение зависит только от относительного количества атомарного водорода и звездного света и должно быть эволюционным эффектом. Попытка понять эту эволюцию и ее сильную зависимость от поверхностной яркости является предметом данной статьи.
рисунок 1
Подчеркнем, что наше обсуждение ограничивается дисковыми галактиками, в первую очередь спиральными. Мы не рассматриваем эллиптические или карликовые сфероидальные галактики, хотя тщательно изучаем соответствующие эффекты отбора. При необходимости, зависящие от расстояния величины предполагают H 0 = 75 км с -1 Мпк -1 .
Данные состоят из оптического потока и потока 21 см. Данные выбираются для обеспечения как можно большей базы данных для исследования связи между содержанием газа и оптическими свойствами спиральных галактик, в частности яркостью поверхности. Обязательным условием является то, что каждая интересующая величина действительно измеряется. Поверхностная яркость, под которой мы понимаем центральную поверхностную яркость диска, определенную путем экстраполяции к R = 0 экспоненциального соответствия наблюдаемому световому профилю, обычно не измеряется и поэтому является наиболее ограничивающим фактором.Из исследований, которые специально измеряют поверхностную яркость соответствующим образом, измерения H I не всегда доступны, что еще больше ограничивает доступные данные. Было бы желательно также иметь измерения CO в качестве индикатора молекулярного газа, но по существу нет опубликованных данных, которые удовлетворяют этому дополнительному критерию, а галактики с низкой поверхностной яркостью еще не обнаружены в CO (Schombert et al. 1990). ). Вместо этого мы воспользуемся соотношением газовая фаза и морфологическим типом молекулярного газосодержания Янга и Кнезека (1989).Дополнительная информация, необходимая для оценки звездной массы, — это звездная величина I или цвет B — V (см. § 3.1). Таким образом, нам необходимо знать морфологический тип M B , 0 , h , M H I и B — V или I .
Большие наборы данных, отвечающие этим требованиям, принадлежат Romanishin et al. (1982; Романишин, Стром и Стром, 1983), Макго и Ботун (1994), де Йонг и ван дер Круит (1994), де Йонг (1995, 1996) и де Блок и др.(1996; де Блок, Макгоу и ван дер Хульст 1995). Фотометрия поверхности была выполнена на всех изображениях галактик для определения параметров диска 0 (центральная поверхностная яркость) и h (длина шкалы), как описано в различных источниках. Большинство данных для более высокой поверхностной яркости ( 0 <23 B mag arcsec -2 ) получены от де Йонга, тогда как большая часть данных для 0 > 23 — из нашей собственной работы. Очевидный разрыв, видимый на Рисунке 1 b при промежуточной яркости поверхности между этими двумя наборами данных, заполнен данными Романишина на Рисунке 1 a .Там, где это используется, данные для особого случая Малина 1 взяты из Bothun et al. (1987) и Импи и Ботун (1989).
Никаких тенденций с M H I / L не наблюдается только в одном наборе данных. Только после их объединения становится очевидной сильная связь на Рисунке 1. Данные о поверхностной яркости в этом большом динамическом диапазоне (100 раз) ранее не были доступны.
§2.1.
Эффекты выбора
Данные были выбраны как можно более всеобъемлющими с учетом требований, предъявляемых к информационному содержанию.Мы не утверждаем, что эти данные являются полными в каком-либо ограниченном по объему смысле. Для наших настоящих целей это менее важно, чем наличие данных, представляющих все морфологические типы, светимости и т. Д. Это потому, что нас больше интересует эволюция галактик как физических систем, чем численная плотность любого данного типа. Тем не менее, потенциальное влияние отбора на интерпретацию требует дальнейшего обсуждения.
Оптические свойства галактик представлены на рисунках 2 и 3.Это иллюстрирует некоторые важные основные факты о спиральных галактиках. Диски бывают самых разных по яркости, поверхностной яркости и размеру. Ни для одного из них не характерно никакой особой ценности; у каждого есть какое-то распределение (McGaugh 1996a; de Jong 1996). Диски с более низкой поверхностной яркостью имеют тенденцию быть более синими (рис. 3), а не краснее, чем ожидалось, если они имеют затухающую эволюционную историю (McGaugh & Bothun et al. 1994). Отсутствие красных галактик с низкой поверхностной яркостью само по себе может быть эффектом отбора (McGaugh 1996a), но все же хочется понять, почему те, о которых мы знаем, такие синие.
Рис.2 Рис.3
Обзоры с ограничением потока
наиболее эффективны для идентификации самых ярких ( L * ) и самых контрастных () галактик, которые существуют в собственных распределениях в данной полосе пропускания. Как прямое следствие, в каталогах галактик численно преобладают такие объекты, несоразмерные их действительным числам. Образцы, отобранные для подробного изучения из таких каталогов, естественно, имеют тенденцию концентрироваться на этих наиболее выдающихся галактиках. Мы избежали этого, дополнив такие данные нашими собственными данными для галактик с низкой поверхностной яркостью.В результате объединенные данные обеспечивают максимально полное представление о спиральных галактиках в этой области, насколько это возможно в настоящее время, охватывая весь диапазон морфологий диска от Sa до Sm / Im с 0 <25 и h > 1 кпк.
Хотя эта процедура добавляет крайне необходимый вес поздним типам и низкой яркости поверхности, она никоим образом не гарантирует однородность образца. Одним из свидетельств этого является очевидное отсутствие галактик с низкой светимостью и высокой поверхностной яркостью с M B > -18 и 0 <23.Этот пробел не очевиден, когда 0 сопоставлены с ч (Макгоу, 1996b), и не обязательно указывает на реальное отсутствие таких галактик. Фактически, выборка де Йонга содержит только яркие ( M B <-18) галактики, а наша собственная содержит только галактики с низкой поверхностной яркостью ( 0 > 23). Исключенная область вполне может быть заполнена, но в этой области пространства параметров нет данных, которые удовлетворяют всем нашим требованиям к информации.
Чтобы проверить, может ли это оказать серьезное влияние на наши результаты, мы проводим анализ, описанный ниже, как для всей выборки, так и для подвыборки, ограниченной M B <-18. Хотя плечо рычага для более слабых галактик, конечно, слабее, никаких серьезных различий между параметрами, связанными с газом, не наблюдается. Причина этого проста: галактики оптически выделены. Выводы о связи между оптическими параметрами, имеющими отношение к отбору ( M B , 0 и h ), трудно сделать в отсутствие строго полной выборки.Однако исследование эволюции галактик не сильно затруднено, поскольку, по крайней мере, представлен широкий диапазон этих параметров. Более того, первоначальный выбор галактик не зависит от M H I . Эти данные довольно много говорят нам об эволюции типов галактик, о которых мы знаем, и разграничивают то, что еще может отсутствовать.
Массовая доля барионного газа равна
, где M г — полная масса в форме газа, а M * — в звездах.Чтобы связать их с наблюдениями, нам нужны M * = * L и M g = M H I . Параметр * — это отношение массы к световому потоку звездного населения, в то время как он играет аналогичную роль для газа. Он учитывает как гелий, так и любую массу в металлах и газовую фазу, кроме атомной.
С этими определениями легко получить
Коэффициент магнитного потока M H I / L не зависит от расстояния и в большинстве случаев имеет небольшие ошибки.Однако коэффициенты пересчета * и должны оцениваться на основе другой информации.
§3.1.
Отношение массы к световому потоку звездного населения
Мы хотим использовать наблюдаемый свет звезды как индикатор звездной массы. Наше отношение массы звезды к свету * включает всю массу живых или мертвых звезд, поскольку мы хотим различать резервуары газовой и звездной массы. Значение * можно оценить с помощью моделей популяционного синтеза, но они весьма неопределенны и зависят от многих факторов, таких как ММП, история звездообразования, металличность, рециркуляция газа, малоизвестное поведение некоторых поздних стадий звездной эволюции и т. Д. .Что еще хуже для наших целей, это итеративно зависит от интересующего количества, f g . Хотя такие модели по-прежнему очень полезны, очевидный интерес представляет независимые средства ограничения * .
Мы используем динамические ограничения, налагаемые наблюдениями за вертикальной дисперсией звездных скоростей (Bottema, 1993), в том виде, в котором они обобщены де Блоком и Макго (1997). Это дает
в диапазоне B .Это выражение получено из дискового соотношения Талли-Фишера с нормировкой, наложенной наблюдениями за дисперсией скоростей. В абсолютной нормировке есть некоторая неопределенность, но она значительно меньше, чем в оценках без граничных условий, налагаемых динамическими измерениями. Цветовой термин имеет остаточную зависимость от синтеза населения, что в ожидаемом смысле означает, что более красные галактики имеют более высокие * . Это хорошо воспроизводит наблюдаемую тенденцию (рис. 4), даже несмотря на то, что нельзя ожидать, что B — V будет идеальным индикатором вариации * с множеством основных переменных.
Рис. 4
Наиболее важным аспектом уравнения (3) является нормализация динамических ограничений, которые дают наиболее надежную оценку массы, содержащейся в звездах. Без этого всегда можно изобрести модели, в которых звезды содержат всю или никакую барионную массу, а f g остается весьма неопределенным. При этом f g достаточно хорошо определяется.
Числа, возвращаемые уравнением (3), согласуются как с моделями звездного населения (например,g., van den Hoek et al. 1997) и анализ кривой вращения (Sanders 1996; de Blok & McGaugh 1997), которые не зависят от измерений дисперсии скорости. В качестве дополнительной независимой проверки наших результатов мы также вычислим f g из оценки чисто популяционного синтеза в полосе I . Полоса – считается наиболее надежным индикатором звездной массы (Worthey 1994), хотя все еще не ожидается универсального значения для всех популяций.Модели Bruzual и Charlot (1993) для галактики с постоянным звездообразованием предлагают значение 1,2 для широкого диапазона возрастов с довольно скромными вариациями. Хотя как абсолютная нормализация, так и универсальная применимость этого значения сомнительны, использование этого фиксированного числа в диапазоне I дает неотличимые результаты от результатов уравнения (3) в диапазоне B (рис. 5).
Рис. 5
§3.2.
Газовые фазы
Для газа необходимо внести поправку как на массовую долю водорода X , так и на фазы газа, отличные от атомной.Мы предполагаем массовую долю солнечного водорода, давая = X = 1,4. Хотя это не всегда верно, большая часть этого связана с изначальным гелием. Вариации содержания гелия и металлов приводят к отклонениям от этого значения менее чем на 10%. Это очень небольшой эффект по сравнению с другими газовыми фазами. Ионизированный газ в областях H II и более горячая плазма имеет пренебрежимо малую массу в спиральных галактиках, но не такой молекулярный газ. Следовательно,
Соотношение молекулярного и атомарного газа систематически меняется в зависимости от типа Хаббла (Young & Knezek 1989).Мы параметризуем их среднее отношение как
(рис. 6). Для очень поздних типов мы вынудили подгонку приближаться к M (H 2 ) / M (HI) 0 как 10. Уравнение (5) хорошо соответствует тенденции данных Young & Knezek. (1989), за исключением, возможно, очень ранних типов, но в выборке мало галактик с = 1. Большую озабоченность вызывает то, что большое количество реального рассеяния для каждого типа ни в коем случае не является идеальным индикатором M (H 2 ) / M (HI), поэтому уравнение (5) является только статистической оценкой относительного содержания молекулярного газа.
Рис. 6
Нормализация уравнения (5) зависит от коэффициента преобразования CO в H 2 , точное значение и универсальность которого являются предметом многочисленных споров. Коэффициент преобразования, по-видимому, зависит от металличности (Wilson, 1995), и более поздние типы, как правило, более бедны металлом, чем ранние. Если бы можно было исправить зашумленную корреляцию M (H 2 ) / M (HI) с для зашумленной корреляции Z с, это оказало бы лишь умеренное влияние на уравнение (5), поскольку предполагаемое изменение коэффициента преобразования в зависимости от металличности довольно мало по сравнению с диапазоном на рисунке 6.Немногое изменится, потому что ранние типы имеют приблизительно солнечную металличность и не получат поправки от канонического значения коэффициента преобразования. Последние типы — это примерно 0,1 Z (McGaugh 1994a), что соответствует 5-кратному увеличению коэффициента преобразования. Однако M (H 2 ) / M (HI) считается очень маленьким для поздних типов, а пятикратное увеличение небольшого числа все же приводит к очень небольшой поправке к окончательному f г .Вместо того, чтобы сводить воедино все эти неопределенности, мы просто используем уравнение (5), понимая, что это, вероятно, самая большая неопределенность в процессе.
Неопределенность поправки на молекулярный газ мало повлияет на наши окончательные результаты. Коррекция важна только для ранних типов, которые относительно бедны газом f g 0,3. Предполагается, что именно поздние типы являются богатыми газом на основании одного только HI. Если мы упустим огромное количество молекулярного газа в поздних типах, это приведет только к образованию еще более богатых газом галактик, которые, как уже предполагается, очень богаты газом.Следовательно, наши качественные результаты очень надежны, даже если количественные данные могут быть улучшены в данных по CO. Более того, для нашего анализа имеет значение только соотношение * / (уравнение [2]). Это соотношение не сильно меняется и не коррелирует с поверхностной яркостью. Чтобы повлиять на наши результаты, это соотношение должно систематически меняться в зависимости от поверхностной яркости на порядок, чтобы компенсировать сильную наблюдаемую тенденцию в M H I / L .Это не только кажется маловероятным, но и просто невозможным. Газовые фракции галактик с низкой поверхностной яркостью не могут быть уменьшены на большие * , поскольку они не допускаются данными кривой вращения (de Blok & McGaugh, 1996), а также не могут быть увеличены для галактик с высокой поверхностной яркостью, где легко обнаруживается CO. Следовательно, большая наблюдаемая вариация в M H I / L должна соответствовать единице в f g .
§3.2.1.
Роль молекулярного и атомарного газа
Обычно считается, что звездообразование происходит только в молекулярном газе. Однако похоже, что в галактиках с самой низкой поверхностной яркостью молекулярного газа очень мало или, возможно, нет вообще (Шомберт и др., 1990). Поэтому мы должны учитывать возможность того, что звезды образуются непосредственно из атомного газа. Однако не очевидно, что это необходимо. Скорость звездообразования низкая, и в качестве промежуточного этапа может существовать очень небольшое количество молекулярного газа.Действительно, можно утверждать, что недостаток молекулярного газа препятствует звездообразованию и сохраняет низкую поверхностную яркость. Хотя это интересные возможности, они не имеют значения для нашего настоящего анализа, который касается только глобальных поставок газа, а не деталей его местного потребления. В этом контексте, возможно, лучше всего думать о H I как о резервуаре для будущего звездообразования, независимо от того, является ли молекулярный газ обязательным промежуточным этапом. В самом деле, постепенное радиальное падение из расширенных дисков спиралей H I может быть источником предполагаемой аккреции необработанного материала, поскольку нет свидетельств существования значительных резервуаров H I в сферических гало (Bothun 1985).
Массовые доли газа, рассчитанные, как описано выше, приведены в таблице 1 вместе с исходными данными. В целом существует тесное соответствие между f g , вычисленным на основе данных диапазона B и данных I -диапазона. Это обнадеживает, поскольку для оценки * используются независимые методы, что является более важным фактором в уравнении (2). Различия в двух разных определениях f g дают некоторое представление об их неопределенностях.
На рис. 7 мы построили график зависимости газовых фракций от свойств галактик в полосе B . Очевидна сильная связь между долей газа и общей светимостью, яркостью поверхности диска и цветом. Такие же отношения со светимостью и поверхностной яркостью видны и в данных полосы I (рис. 8). Никакой связи с размером оптического диска нет. Соответствие данным диапазона B дает
, где погрешность наклона составляет ± 0.07 для M B , ± 0,04 для 0 и ± 0,5 для цвета. Эти соотношения, конечно, могут незначительно изменяться с улучшением соотношений * и, но ясно, что более тусклые галактики систематически более богаты газом. Уклоны f g — M B и — 0 отношения неразличимы.
Рис.7 Рис.8
Важным следствием систематического увеличения газовой фракции с увеличением поверхностной яркости является конец парадоксу газопотребления.Поскольку при каждой поверхностной яркости существует примерно равное количество галактик, существует множество галактик, которые все еще сохраняют значительные газовые резервуары (функции распределения см. В McGaugh 1996a). Возможно, неудивительно, что наиболее заметными в оптическом отношении галактиками являются те, которые превратили большую часть своего газа в звезды.
§4.1.
Корреляции
Коэффициенты корреляции из анализа основных компонентов данных B -диапазона приведены в таблице 2.Читая эту таблицу, обязательно помните обратное соглашение в определении величин. Это влияет на знаки коэффициентов корреляции: = -0,59 между M B и h означает, что более яркие галактики имеют тенденцию быть больше, а не меньше.
Во-первых, обратите внимание, что f g хорошо коррелирует с M H I / L , из которого оно получено. Это не было полностью предрешенным выводом, поскольку отношения для * , вероятно, могли бы компенсировать это.Использование этих соотношений вносит шум, который снижает коэффициент корреляции с единицы.
Среди независимых переменных самая сильная корреляция находится между M H I / L и 0 . Эта связь более значима, чем любая из хорошо известных связей между M HI / L и M B (Rao & Briggs 1993; Salpeter & Hoffman 1996) или M HI. / L и (Roberts 1963), хотя они также очевидны в таблице 2.Это сильное соотношение M H I / L — 0 превращается в сильное соотношение между f g и 0 . Центральная поверхностная яркость галактики является хорошим индикатором совокупного потребления газа и, следовательно, ее эволюционного состояния.
Доля газа также коррелирует с M B и B — V . Хотя оба они используются при вычислении f g , эта корреляция не является артефактом.Это проистекает из основного факта, что светимость относительно больше 21 см в спиралях с низкой оптической светимостью, которые также имеют тенденцию быть более голубыми. Связь с цветом заключается в том, что голубые галактики, как и следовало ожидать, более богаты газом. Более того, тот же результат получается, когда цвет не используется в вычислении f g с данными диапазона I .
Данные, по-видимому, занимают довольно узкую структуру в пространстве f g — 0 -color- M B .По аналогии с фундаментальной плоскостью для эллиптических тренажеров, это может указывать на существование эволюционной гиперповерхности, ограничивающей эволюцию спиралей. Однако это нарушает крайняя галактика Малин 1, которая чрезвычайно богата газом из-за своей светимости. Более фундаментальной может быть плоскость в f g — 0 — цветовое пространство, но это тоже может быть изменено с помощью дополнительных эффектов выбора (см. Ниже).
Доля газа плохо коррелирует с размером.Скорость эволюции спиральных галактик, по-видимому, не зависит от масштаба. Также f g не коррелирует с типом Хаббла, несмотря на соотношение M H I / L -. Это связано с тем, что преобладающая газовая фаза быстро изменяется по типу Хаббла (Young & Knezek 1989), компенсируя в общей газовой фракции тенденцию, наблюдаемую только в атомарной фазе.
Среди оптических параметров тип Хаббла больше всего зависит от M B и 0 .Хотя неудивительно, что они имеют отношение к морфологическому внешнему виду галактики, они не обеспечивают точного измерения каких-либо физических параметров (Naim et al. 1995; McGaugh 1995b; de Jong 1995). Тип не очень хорошо коррелирует с размером, хотя есть некоторая тенденция для более ранних типов быть более красными.
Линейный размер дисковой галактики плохо коррелирует ни с чем, кроме абсолютной величины. Абсолютная величина кажется достаточно хорошо коррелированной с поверхностной яркостью в том очевидном смысле, что галактики с более высокой поверхностной яркостью ярче.Однако это может быть иллюзией, поскольку это отношение наиболее подвержено эффектам отбора. В частности, практически все галактики с низкой светимостью имеют низкую поверхностную яркость (вспомните рис. 2). Это может или не может быть репрезентативным. Если мы ограничим выборку объектами ярче -18, где более полно покрыта плоскость M B — 0 , этот коэффициент корреляции упадет до = 0,34. Что между 0 и ч увеличивается до = 0.44 галактики большего размера имеют тенденцию иметь более низкую поверхностную яркость. Это единственные существенные изменения в корреляционной матрице, когда выборка ограничена яркими галактиками.
Выбор оптических галактик зависит совместно от M B , 0 и h (Disney & Phillipps 1983; McGaugh et al. 1995a), поэтому корреляции между этими переменными очень чувствительны к отбору выборки и должны относиться с осторожностью. Корреляции с другими переменными не так напрямую зависят от эффектов отбора и могут быть разумно проанализированы, если доступны репрезентативные данные в разумном динамическом диапазоне.В частности, корреляции, включающие f g , кажутся надежными.
§4.2.
Дополнительные эффекты выбора
Тем не менее, мы должны рассмотреть, не влияют ли на полученные выше отношения эффекты отбора, которые в прошлом помогали их скрыть. Мы обратились к проблеме изофотальной селекции, насколько это возможно в настоящее время, путем целенаправленного нацеливания на галактики с низкой поверхностной яркостью. Это увеличивает динамический диапазон, доступный в 0 , но очевидно, что такие эффекты остаются от усечения данных как 0 25.Изучаемые здесь галактики выбираются оптически, но, конечно, галактика должна была обнаружить H I, чтобы провести этот анализ. Отсутствие малой доли газа и галактики с низкой поверхностной яркостью может быть дополнительным эффектом отбора.
Отношения кажутся непрерывными во всех выборках, что, казалось бы, является аргументом против сильных эффектов отбора в этом смысле. Скорость обнаружения 21 см очень высока (80%) для галактик с низкой поверхностной яркостью в исследовании Schombert et al. (1992), поэтому нам не кажется, что мы упускаем из виду значительное количество этих преимущественно спиральных галактик.Однако тот факт, что эти галактики очень синие (рис. 3), сам по себе может быть эффектом отбора, поскольку они были выбраны на голубых чувствительных пластинах (см. McGaugh 1996a). Для того чтобы это было важно для рис. 7, также должно существовать дополнительных бедных газом красных галактик с низкой поверхностной яркостью.
Несомненно, существуют другие типы галактик (например, dE и dSph), которые имеют низкую поверхностную яркость и низкую долю газа. Эти конкретные типы не имеют очевидного отношения к более крупным спиралям низкой поверхностной яркости, каталогизированным Schombert et al.(1992), или к спиралям с более высокой поверхностной яркостью. Тем не менее, вполне может быть, что наблюдаемые зависимости представляют только верхние оболочки, и еще предстоит обнаружить значительную популяцию бедных газом галактик с низкой поверхностной яркостью. Действительно, такая популяция может потребоваться из-за быстрой эволюции плотности светимости (Dalcanton 1993; Lilly et al. 1995 см. § 6). Отсутствие богатых газом галактик с высокой поверхностной яркостью — это , а не эффект отбора: такие объекты были бы заметны как оптически, так и в H I.
Независимо от этих предостережений, существуют четкие эволюционные тенденции. Более низкая поверхностная яркость и спирали меньшей светимости, о которых мы знаем, потребляли меньше газа и менее развиты, чем более яркие системы. Этот результат согласуется с другими линиями доказательств по порогам звездообразования (van der Hulst et al. 1993), численности (McGaugh 1994a; Rönnback & Bergvall 1995), цветам (McGaugh & Bothun 1994; Rönnback & Bergvall 1994; Bergvall & Rönnback 1995). ; де Блок и др.1995) и окружающей среде (Bothun et al. 1993; Mo, McGaugh, & Bothun 1994), все это указывает на то, что галактики с низкой поверхностной яркостью эволюционируют медленно и, возможно, поздно формируются.
Сами по себе рисунки 7 и 8 предлагают простую картину: дисковые галактики формируются, а затем эволюционируют с постоянным размером, превращая газ в звезды и, следовательно, изменяя их светимость и поверхностную яркость с той же скоростью. Это обеспечивает надежные отношения f g — M B и f g — 0 с одинаковым уклоном.Нет необходимости в корреляции между M B и 0 , поскольку галактики существуют в диапазоне размеров. Таким образом, эволюция дисковых галактик, кажется, протекает упорядоченно, без чрезмерного количества слияний, эволюции размеров, сильных стохастических звездных вспышек или других экзотических явлений.
Эволюционная траектория галактики на рисунках 7 или 8 зависит от эволюции содержащихся в ней звезд и скорости образования этих звезд. Скорость звездообразования (SFR) является просто отрицательной величиной скорости потребления газа: = -, по крайней мере, до тех пор, пока рециркуляция газа не станет важной при низком уровне f г .Фотометрическая эволюция звезд зависит от многих факторов (например, их металличности), что приводит к множеству осложнений, но основная физика хорошо изучена и позволяет оценить светимость, которую будет производить данная масса звезд. Это дает абсциссу. Ордината следует из SFR, который традиционно параметризуется как некоторая удобная функция времени (например, Guideroni & Rocca-Volmerange 1987). Для падающих SFR, в которых большая часть звездообразования произошла в прошлом, обычно принимается форма
SFR нормирована на полную барионную массу данной галактики, так что 0 f * 1.Шкала времени складывания e обычно составляет несколько млрд лет, что считается подходящим для галактик ранних типов. Для постоянных SFR (подходящих для спиралей позднего типа) или восходящих (как, возможно, имеет место для неправильных галактик) полезная форма:
В этом случае г — это время до полного потребления газа. . Это не совсем то же самое, что шкала времени сгибания e , но в обоих случаях -1 задает скорость эволюции.
Мы не заблуждаемся по поводу того, что любой из этих простых SFR точно отражает то, что действительно происходит в любой данной галактике.Тем не менее, они предоставляют очень полезный способ параметризации диапазона возможных средних историй звездообразования. Этот простой аналитический подход действительно позволяет вывести несколько интересных ограничений для более сложной реальности, когда доступен большой динамический диапазон в f g .
Интеграция этих SFR позволяет нам определить несколько представляющих интерес величин (а также показывает, почему эти формы просты и популярны). Под возрастом галактики T G мы будем понимать время, прошедшее с начала звездообразования.Это очевидное рабочее определение образования галактик в данном контексте. Конечно, здесь не указано, как именно образовалась галактика. Звездообразование вполне может начаться в то время, когда продолжается коллапс газа, или могло начаться отдельными подразделениями, которые впоследствии сливаются в единое целое, наблюдаемое сегодня. Удобно представить случай, в котором временной масштаб для таких событий формирования является коротким по сравнению с эволюционным временным масштабом, так что формирование происходит одновременно с началом звездообразования, а T G является истинным возрастом галактики для все практические цели.Это не обязательно, поэтому следует иметь в виду, что T G действительно измеряет время, прошедшее с начала звездообразования.
Еще одна интересная величина — средний возраст звезд T * . Часто можно изменить форму SFR, чтобы получить любую желаемую f g с вырожденным набором возрастов T G и темпами эволюции. Однако правдоподобные комбинации этих двух параметров иногда имеют неправдоподобные последствия для T * .Эти и другие представляющие интерес количества и пределы приведены в Таблице 3.
Обладая этим формализмом, мы почти готовы интерпретировать положения галактик на рисунке 8. Значение f g происходит из условия SFR, но точная траектория, по которой галактика следует по светимости, зависит от деталей. звезд, для которых требуется популяционная модель. Это дает изменение * со временем. Количество света на единицу массы, производимого одним поколением звезд, быстро уменьшается по мере того, как светящиеся массивные звезды эволюционируют и умирают.Однако, если звездообразование продолжается в течение какого-то периода времени, этот эффект компенсируется рождением новых звезд. Чтобы оценить интерполяцию этих эффектов, нам нужно выбрать конкретную модель популяции. На данный момент мы используем модели Guideroni & Rocca-Volmerange (1987), кратко описанные в таблице 4. Этот конкретный выбор сделан по той простой причине, что они опубликовали полный диапазон f g для интересного разнообразие SFR. С тех пор были внесены различные улучшения в моделирование, но пока нет единого набора моделей для всего необходимого нам динамического диапазона.Более того, здесь мы пытаемся по возможности избежать серьезной астрономической проблемы зависимости модели; конкретные модели приняты только для иллюстрации различных проблем. По сравнению с динамическим диапазоном в f g , звездное население претерпевает довольно умеренную эволюцию * во всех правдоподобных моделях. Таким образом, хотя детальная форма эволюционных следов сильно зависит от модели, основная суть — нет.
Например, рисунок 8 сам по себе не представляет прямой эволюционной последовательности.Галактики не начинаются на слабых M и 0 , а просто становятся ярче в наблюдаемой последовательности. Наклон наблюдаемых соотношений на порядок отличается от того, что ожидается от эволюционных моделей для скорости изменения абсолютной величины ( м ) с долей газа ( f g ). Вместо наклона, наблюдаемого в уравнениях (6a) (6c), m / f g = 8, очень широкий диапазон моделей эволюционирует по светимости медленно по сравнению со скоростью потребления газа с -2 < м / f g <2 (рис.9). Эта разница между наблюдаемыми и модельными наклонами требует систематического изменения скорости эволюции в зависимости от поверхностной яркости. Все более тусклые галактики либо эволюционируют медленнее, либо моложе, либо их комбинация.
Рис.9.
Изохроны моделей Guideroni и Rocca-Volmerange (1987) примерно параллельны наблюдаемому уклону м / f g для возрастов T G > 10 млрд лет.Это достигается путем систематического изменения шкалы времени потребления газа с типом Хаббла (Таблица 4). Поскольку на момент построения моделей было доступно очень мало этих данных, это успех стандартной картины эволюции галактик, которую представляют модели. С другой стороны, корреляция между M H I / L и типом была известна, и модели были построены для соответствия этим данным.
Из рисунка 9 можно определить суммарный SFR возраста любой данной галактики.Если один может быть ограничен другой информацией, такой как цвета, другой следует. Тип коррелирует с поверхностной яркостью (таблица 2; de Blok et al. 1995; de Jong 1996), поэтому можно сделать все спирали одного и того же возраста (15 млрд лет) и удовлетворить наблюдаемые газовые фракции, просто изменив временную шкалу. Изменение поверхностной яркости должно быть достаточно систематическим и настолько большим, что необходимо изменить функциональную форму SFR, чтобы приспособиться к нему. (В принципе, можно сохранить экспоненциальный SFR, допуская, а затем становясь отрицательным.)
Разброс данных велик по сравнению с разделением изохрон. Это может указывать на большой разброс по возрасту. Скорее всего, это просто результат перекрытия диапазона барионных масс любого данного типа SFR. То есть, определенный тип SFR, такой как Sd, может ощущаться галактиками разного диапазона масс, а не только одной конкретной, как показано на рисунке 9. Поскольку такое перекрытие неизбежно, мы не придаем особого значения изгибу в сетка модели для SFR Sa и Sb при низком уровне f g перекрытие размывает его, даже если модели заслуживают доверия на этом уровне детализации.Отсутствие каких-либо соответствующих характеристик в данных может указывать на то, что они не различаются так широко, как предполагается в моделях, так что для спиральных дисков отклонения от постоянного SFR не являются огромными (8 млрд лет).
Стандартная картина эволюции галактик, представленная моделями Guideroni и Rocca-Volmerange (1987), должна связывать наблюдаемое изменение f g с поверхностной яркостью с вариациями, поскольку T G принято одинаковым для всех галактик.Как только это искусственное граничное условие будет наложено, выбора нет. Не очевидно, что это действительно разумное предположение. Если образование галактик происходит в результате гравитационного коллапса первичных флуктуаций в поле плотности, то эпоха коллапса любого данного объекта зависит от контраста плотности флуктуации, из которой он возникает. Большинство наблюдательных данных (McGaugh 1992, 1996b) предполагает, что это происходит очевидным образом: большие контрасты плотности приводят к галактикам с высокой поверхностной яркостью, а небольшие контрасты плотности приводят к галактикам с низкой поверхностной яркостью.Если это действительно так, то можно ожидать, что галактики с более низкой поверхностной яркостью будут моложе, как следует из их цвета (McGaugh & Bothun 1994; de Blok et al. 1995). Абсолютная величина разницы в возрасте может быть или не быть большой; очень сложно указать абсолютное число. Судя по цветам, относительный сдвиг обычно составляет порядка нескольких (35) миллиардов лет. Если спирали с высокой поверхностной яркостью имеют возраст 13 или 14 миллиардов лет, то диски с низкой поверхностной яркостью имеют возраст примерно 8 или 10 миллиардов лет.
Чтобы изучить эту возможность в контексте данных о газовой фракции, рассмотрим в качестве тривиального предельного случая сценарий, в котором все спиральные диски имеют одинаковую форму истории звездообразования.Все эволюционные траектории будут выглядеть одинаково на рисунке 9, и (по выбору) изохроны будут горизонтальными линиями. Вместо систематического изменения эволюционной шкалы времени потребуются реальные возрастные различия для объяснения тенденции данных. В случае постоянного звездообразования с той же относительной скоростью (трек Sd) яркие галактики с f g 0,3 имели бы возраст T G 17 млрд лет, а тусклые — лет. f г 0.6 будет T G 10 млрд лет.
Любой из этих сценариев кажется правдоподобным, и реальность, по-видимому, более сложна, и возраст, и скорость эволюции могут играть роль. Сами по себе газовые фракции не позволяют различить, какой фактор доминирует. Они действительно показывают, что существуют явные различия. Это может помочь снять вырождение, которое преследовало только анализ цветов. Если это так, возможно, появится возможность датировать возраст спиральных галактик.
Различие между галактикой, которая сегодня богата газом, потому что она сформировалась рано и медленно эволюционировала, или потому, что сформировалась поздно, неясно.Некоторые ограничения могут быть наложены на эти крайние случаи из-за правдоподобия требуемого SFR и среднего звездного возраста. Если мы будем настаивать на том, что все галактики имеют одинаковый возраст, единственный способ получить очень богатые газом голубые галактики ( f g > 0,4) при z = 0 — это иметь темпы звездообразования, которые сильно увеличиваются с увеличением время. Сегодня они удерживают много газа просто потому, что в первую половину времени Хаббла произошло очень мало. Для трека Im на Рисунке 9 только 10% газа потребляется за первые 9 млрд. Лет.Различие между этой галактикой и галактикой, которая формируется поздно, неочевидно и возвращает нас к щекотливому вопросу определения образования галактики. Возможно, длительный коллапс из-за постепенного рассеивания и медленная эволюция тесно связаны.
Для более количественной иллюстрации рассмотрим консервативный случай снижения скорости звездообразования. Сохранение доли газа больше, чем расходуется на одну складку e ( f г > e -1 = 0.37, что соответствует 0 > 22) требует эволюционной шкалы времени> T U больше возраста Вселенной, со средним звездным возрастом T * <0,6 T U . Это просто следует из требования, чтобы галактика была моложе Вселенной: T G < T U . Если мы примем историю восходящего звездообразования, предложенную моделью Im на рисунке 9, эволюционная шкала времени может быть очень (но не произвольно) длинной.Это достигается только за счет того, что звезды становятся очень молодыми: T < T U , т. Е. T * = 3 млрд лет для T G = 12 млрд лет. . В любом случае, большая часть звездообразования в галактиках, богатых газом, должна быть отнесена к более поздним эпохам (см. McGaugh & Bothun, 1994), независимо от того, сформировалась ли галактика рано и ничего не сделала или сформировалась поздно. Действительно, галактики с f g > 0.5 еще предстоит реализовать большую часть своего потенциала звездообразования, который должен быть отнесен к будущим эпохам.
Картина, которая появляется на данный момент, кажется довольно разумной, подтверждая и расширяя устоявшиеся представления об эволюции местных галактик. Связанную информацию можно получить из обзоров глубоких красных смещений, и значительный прогресс был достигнут в измерении свойств галактик в интересном диапазоне красного смещения. Эти исследования указывают на значительный прогресс в обеих областях (Lilly et al.1995; Эллис и др. 1996) и скопления (Schade et al. 1996) галактик. Получение изображений с высоким разрешением с помощью HST показывает, что большая часть этой эволюции происходит за счет морфологически поздних типов галактик (Глейзбрук и др., 1995; Драйвер, Виндхорст и Гриффитс, 1995; Абрахам и др., 1996). Это согласуется с эволюцией функции светимости, построенной на основе глубоких обзоров: красные галактики, кажется, мало эволюционируют, в то время как синие галактики исчезают очень быстро (Лилли и др., 1995; Эллис и др., 1996).
Имеются убедительные доказательства прямой эволюции яркости поверхности ярких дисков (Schade et al. 1995, 1996). Похоже, что их поверхностная яркость на 1 маг. Дугу -2 ярче на z 0,5, чем на z = 0. Это полностью согласуется с рисунком 9: эти галактики предположительно были более газовыми на z = 0,5. и с тех пор эволюционировали по траектории, подобной той, которая была нанесена для спиралей раннего типа (Sa-Sc).
Таким образом, подходы локального и большого красного смещения к эволюции спиралей ранних типов дают хорошо согласованные результаты.Чего нельзя сказать о поздних типах. Многие исследования теперь показывают, что избыток слабых голубых галактик — это преимущественно поздние типы, которые быстро эволюционируют. Если искать локально слабые голубые галактики позднего типа, можно найти галактики с низкой поверхностной яркостью. Действительно, сходство между физическими свойствами этих двух популяций привело к предположению, что одно может объяснять другое (McGaugh 1994b). Это сходство теперь распространяется и на морфологию: эти галактики буквально похожи друг на друга (см. Dalcanton & Shectman 1996).Однако простой связи один-к-одному недостаточно: хотя глубокие обзоры более чувствительны к галактикам с низкой поверхностной яркостью, чем локальные, они все же выбираются по потоку. В обзорах с ограниченной звездной величиной всегда численно преобладают галактики с самой высокой поверхностной яркостью, независимо от того, насколько распространены на самом деле галактики с низкой поверхностной яркостью (McGaugh et al. 1995a), поэтому для большинства вероятных сценариев галактики с низкой поверхностной яркостью не вносят значительного вклада в слабую считается (Ferguson & McGaugh 1995; McLeod & Rieke 1995), если они не претерпят существенного развития.
Возникает соблазн сделать вывод, что именно это и происходит: голубые галактики поздних типов быстро эволюционируют, постепенно теряя свою поверхностную яркость к нынешней эпохе (Phillipps & Driver 1995). Хотя это разумно в контексте данных о большом красном смещении, оно не имеет смысла для известных местных галактик. Сценарии замирания для немарликовых галактик с низкой поверхностной яркостью в настоящей выборке сильно исключаются как по цвету (McGaugh & Bothun, 1994; рис. 3), так и по газовым фракциям.Чтобы иметь траекторию сильного затухания (Sa или даже более экстремальную) на рисунке 9 и сохранять высокие наблюдаемые газовые фракции, такие галактики должны быть чрезвычайно молодыми: T G <2 млрд лет для = 3 млрд лет и f g > 0,5. Они еще не сформировались бы на красных смещениях, где происходит предполагаемая эволюция.
Действительно, эволюционные истории, обсуждаемые в разделе 5, прямо противоположны: галактики позднего типа с низкой поверхностной яркостью эволюционируют медленно, а не быстро.Фотометрически они развиваются примерно с постоянной светимостью или даже со временем становятся ярче . Остается загадка: существуют две популяции: слабые голубые галактики с большим красным смещением и галактики с низкой поверхностной яркостью локально, которые имеют очень похожие цвета, свойства кластеризации и морфологию: они буквально похожи друг на друга, но не могут быть одинаковыми. .
Возможно, картина, которая вырисовывается в результате глубокого исследования, обманчиво проста. Разделение функции яркости на ячейки по цвету (Lilly et al.1995) или спектрального типа (Heyl et al. 1996) дает видимость медленно или даже не эволюционирующей красной популяции и быстро развивающейся синей. Тем не менее, для красных галактик можно ожидать более значительного эволюционного затухания, что согласуется с величиной эволюции поверхностной яркости, наблюдаемой Шаде и др. (1996). Возможно, между подборками цветов есть кроссовер. На определенном уровне это ожидается, поскольку даже галактики ранних типов должны были быть голубыми в какой-то момент на раннем этапе своей эволюции.
Не очевидно, что кроссовер адекватен для объяснения эволюции ранних типов, но вполне может быть (Pozzetti, Bruzual, & Zamorani 1996).Более серьезная проблема — понимание быстрой эволюции плотности синей светимости, относящейся к поздним типам. Поскольку слабые голубые галактики, о которых мы знаем локально, кажется неспособными объяснить это, возможно, вывод о быстро развивающейся популяции карликов верен и локально существует дополнительная остаточная популяция (Phillipps & Driver 1995; Babul & Ferguson 1996). Такая популяция, по-видимому, теперь выцветла бы и стала красной, с низкой поверхностной яркостью и бедным газом. Это как раз та часть самолета f g — 0 , не ограниченная наблюдением.Потребовалась бы очень большая популяция таких объектов, но вполне возможно, что такая популяция осталась бы до сих пор незамеченной (McGaugh 1996a), особенно если типичный объект по своей природе мал, на что указывает глубокая визуализация HST (Im et al. al. 1995). Эту картину можно считать привлекательной, поскольку она позволяет избежать противоположного парадокса потребления газа: если богатые газом галактики существуют так же, как и те, которые близки к тому, чтобы их запасы газа истощились, почему нет галактик далеко за этой точкой? Неизбежным следствием такого сценария является то, что наши знания о местном населении галактик остаются явно неполными.
Исследование массовых долей газа в спиральных галактиках в большом диапазоне светимости и поверхностной яркости дает ряд возможностей для понимания эволюции галактик.
1. Доля барионной массы спиральных галактик, преобразованная из газа в звезды, коррелирует со светимостью, поверхностной яркостью и цветом. Это не коррелирует с масштабом диска.
2. Наиболее сильная корреляция между газосодержанием и центральной поверхностной яркостью диска.Поверхностная яркость диска — фундаментальный параметр и хороший индикатор эволюционного статуса галактики. Тусклые галактики развиваются медленно, имеют относительно молодое звездное население и, возможно, сформировались поздно.
3. Поскольку светимость определяет барионную массу, а поверхностная яркость определяет плотность поверхностной массы, сила соотношения f g — 0 предполагает, что поверхностная плотность по крайней мере так же важна, как и общая масса в определении эволюции галактика.
4. Отношения f g — M B и f g — 0 имеют одинаковый наклон. Любая эволюция размера вызовет эволюцию поверхностной яркости сверх того, что из-за эволюции светимости, что приведет к разнице в этих наклонах. Отсутствие такой разницы указывает на то, что спирали развиваются примерно с фиксированным размером.
5. Большое количество богатых газом галактик с низкой поверхностной яркостью разрешает парадокс потребления газа.
6. Население местных галактик с низкой поверхностной яркостью и слабых голубых галактик с большим красным смещением физически и морфологически схожи, но сильно различаются по способу эволюции. Это представляет собой сложную головоломку. Одно из возможных решений — это дополнительная популяция местных красных бедных газом галактик с низкой поверхностной яркостью.
Нет никаких оснований полагать, что мы достигли самых слабых пределов поверхностной яркости или что еще более богатых газом галактик не существует.Учитывая барьер, налагаемый изофотными ограничениями отбора, определенно могут быть и другие галактики с очень низкой поверхностной яркостью, которые еще предстоит обнаружить. Некоторые из них могут быть даже более газовыми (путем экстраполяции наблюдаемых тенденций), а другие могут быть бедными газом (§ 6).
Предлагается еще несколько направлений работы.
1. Дальнейшие исследования галактик с низкой поверхностной яркостью, как до более глубоких изофотических пределов, так и в более красных полосах пропускания. Также были бы интересны слепые 21-сантиметровые обзоры с оптическим контролем для измерения поверхностной яркости.
2. Детальное моделирование отдельных галактик для соответствия цвету, металличности, скорости звездообразования и массовым долям газа.
3. Изучение этих свойств как на местном, так и на глобальном уровне.
Эти проекты позволят решить некоторые из поставленных головоломок и еще больше углубят наше понимание эволюции галактик.
По сути, мы должны понять, как галактики с низкой поверхностной яркостью могут оставаться богатыми газом до нынешней эпохи. Можно призвать либо покой, либо молодость, либо некоторую их комбинацию.Если в первую очередь это связано с покоем, то должна быть возможность подавить крупномасштабное звездообразование в газовых дисках на многие млрд лет, возможно, за счет явлений, зависящих от критической плотности (например, Kennicutt 1989). Если молодость является фактором, существование таких неэволюционировавших галактик предполагает, что процесс формирования галактик продолжается или завершился совсем недавно.
Мы благодарны J. M. van der Hulst и L. B. van den Hoek за полезные обсуждения, и мы благодарим рецензента за предложение более расширенного обсуждения.
- Абрахам, Р. Г., Танвир, Н. Р., Сантьяго, Б. X., Эллис, Р. С., Глейзбрук, К., и ван ден Берг, С. 1996, MNRAS, 279, 47 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Бабул, А., & Фергюсон, Х. К. 1996, ApJ, 458, 100 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Bergvall, N., & Rönnback, J. 1995, MNRAS, 273, 603 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Bruzual, A. G., & Charlot, S. 1993, ApJ, 405, 538 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Ботун, Г.D. 1985, AJ, 90, 1982 Первая цитата в статье | Crossref | ОБЪЯВЛЕНИЕ
- Ботун, Г. Д., Импи, К. Д., Малин, Д. Ф., и Молд, Дж. Р. 1987, AJ, 94, 23 Первое упоминание в статье | Crossref | ОБЪЯВЛЕНИЕ
- Bothun, G. D., Schombert, J. M., Impey, C. D., Sprayberry, D., & McGaugh, S. S. 1993, AJ, 106, 530 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Bottema, R. 1993, A&A, 275, 16 Первое цитирование в статье | ОБЪЯВЛЕНИЕ
- . 1995 г., канд. диссертация, Univ. Гронинген Первое упоминание в статье | ОБЪЯВЛЕНИЕ
- Далкантон, Дж.J. 1993, ApJ, 415, L87 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Далкантон, Дж. Дж., И Шектман, С. А. 1996, ApJ, 465, L9 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЕ
- de Blok, W. J. G., & McGaugh, S. S. 1996, ApJ, 469, L89 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЕ
- . 1997, MNRAS, первое цитирование в статье
- de Blok, W. J. G., McGaugh, S. S., & van der Hulst, J. M. 1996, MNRAS, 283, 18 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- де Блок, В.J. G., van der Hulst, J. M., & Bothun, G. D. 1995, MNRAS, 274, 235 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- де Йонг, Р.С. 1995, доктор философии. диссертация, Univ. Гронинген Первое упоминание в статье | ОБЪЯВЛЕНИЕ
- . 1996, A&A, 313, 45 Первое цитирование в статье | ОБЪЯВЛЕНИЕ
- de Jong, R. S., & van der Kruit, P. C. 1994, A&AS, 106, 451 Первое цитирование в статье | ОБЪЯВЛЕНИЕ
- Disney, M. J., & Phillipps, S. 1983, MNRAS, 205, 1253 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Драйвер, С., Виндхорст, Р. А., & Гриффитс, Р. Э. 1995, ApJ, 453, 48 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Эллис, Р. С., Коллесс, М., Бродхерст, Т. Дж., Хейл, Дж. С., & Глейзбрук, К. 1996, MNRAS, 280, 235 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Фергюсон, Х. К., & Макгоу, С. С. 1995, ApJ, 440, 470 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Глейзбрук, К., Эллис, Р., Сантьяго, Б., и Гриффитс, Р. 1995, MNRAS, 275, L19 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Гайдрони, Б., & Rocca-Volmerange, B. 1987, A&A, 186, 1 Первое упоминание в статье | ОБЪЯВЛЕНИЕ
- Heyl, J., Colless, M., Ellis, R. S., & Broadhurst, T. 1997, MNRAS, в печати Первое упоминание в статье
- Им, М., Ратнатунга, К. У., Гриффитс, Р. Э., & Казертано, С. 1995, ApJ, 445, L15 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Импей, С. Д., & Ботун, К. Д. 1989, ApJ, 341, 89 Первое упоминание в статье | Crossref | ОБЪЯВЛЕНИЕ
- Импей, С. Д., Спрейберри, Д., Ирвин, М., & Bothun, C. D. 1996, препринт Первое упоминание в статье
- Kennicutt, R.C.1989, ApJ, 344, 685 Первое упоминание в статье | Crossref | ОБЪЯВЛЕНИЕ
- Kennicutt, R. C., Tamblyn, P., & Congdon, C. E. 1994, ApJ, 435, 22 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Лилли, С. Дж., Тресс, Л., Хаммер, Ф., Крэмптон, Д., и Ле Февр, О. 1995, ApJ, 455, 108 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- McGaugh, S. S. 1992, доктор философии. диссертация, Univ. Мичиган Первое упоминание в статье | ОБЪЯВЛЕНИЕ
- .1994a, ApJ, 426, 135 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- . 1994b, Nature, 367, 538 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- . 1996а, МНРАС, 280, 337 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- . 1996b, в IAU Symp. 171, Новый свет в эволюции галактик, изд. Р. Бендер и Р. Л. Дэвис (Дордрехт: Клувер), 97 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- McGaugh, S. S., & Bothun, G. D. 1994, AJ, 107, 530 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Макгоу, С.С., Ботун, Г. Д., & Шомберт, Дж. М. 1995a, AJ, 110, 573 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- McGaugh, S. S., Schombert, J. M., & Bothun, G. D. 1995b, AJ, 109, 2019 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- McLeod, B.A., & Rieke, M. J. 1995, ApJ, 454, 611 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Мо, Х. Дж., Макгоу, С. С. и Ботун, Г. Д. 1994, MNRAS, 267, 129 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Наим, А., Лахав, О., Содре, Л., & Сторри-Ломбарди, М. С. 1995, MNRAS, 275, 567 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Филлиппс, С., & Драйвер, С. 1995, MNRAS, 274, 832 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Поццетти, Л., Брузуаль, Г., & Заморани, Г. 1996, MNRAS, 281, 953 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Rao, S., & Briggs, F. 1993, ApJ, 419, 515 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Робертс, М. С. 1963, AR&A, 1, 149 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Романишин, В., Крумм, Н., Солпитер, Э. Э., Кнапп, Г. Р., Стром, К. М., & Стром, С. Э. 1982, ApJ, 263, 94 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Романишин В., Стром, К. М., & Стром, С. Е. 1983, ApJS, 53, 105 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Rönnback, J., & Bergvall, N. 1994, A&AS, 108, 193 Первое цитирование в статье | ОБЪЯВЛЕНИЕ
- . 1995, A&A, 302, 353 Первое цитирование в статье | ОБЪЯВЛЕНИЕ
- Salpeter, E. E., & Hoffman, G. L. 1996, 465, 595 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Сандерс, Р.H. 1996, ApJ, 473, 117 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЕ
- Шаде, Д., Карлберг, Р. Г., Йи, Х. К. К., Лопес-Крус, О., и Эллингсон, Э. 1996, ApJ, 465, 103 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЕ
- Шаде, Д., Лилли, С. Дж., Крэмптон, Д., Хаммер, Ф., Ле Февр, О., & Тресс, Л. 1995, ApJ, 451, L1 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЕ
- Шомберт, Дж. М., Ботун, Г. Д., Импи, К. Д., & Манди, Л. Г. 1990, AJ, 100, 1523 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Шомберт, Дж.М., Ботун, Г. Д., Шнайдер, С. Э., & Макго, С. С. 1992, AJ, 103, 1107 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Тинсли, Б. М. 1968, ApJ, 151, 547 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- van den Hoek, L. B., de Blok, W. J. G., & van der Hulst, J. M. 1997, препринт Первое упоминание в статье
- van der Hulst, J. M., Skillman, E. D., Smith, T. R., Bothun, G. D., McGaugh, S. S., & de Blok, W. J. G. 1993, AJ, 106, 548 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Уилсон, К.D. 1995, ApJ, 448, L97 Первая ссылка в статье | IOPscience | ОБЪЯВЛЕНИЕ
- Worthey, G. 1994, ApJS, 95, 107 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЕ
- Янг, Дж. С., & Кнезек, П. М. 1989, ApJ, 347, L55 Первая ссылка в статье | Crossref | ОБЪЯВЛЕНИЕ
Изображение целиком (63kb) Изображение целиком (54kb) | Обсуждение в тексте
РИС. 1. Отношение массы к световому потоку H I как функция яркости центральной поверхности диска: ( a ) полоса B , полоса ( b ) I .Существует сильная корреляция между газосодержанием спиральных галактик и их поверхностной яркостью. Это очевидно в обеих полосах пропускания, хотя в I меньше данных. То, что есть разброс, отражает реальные различия между галактиками, поскольку погрешности невелики по сравнению с нанесенным диапазоном: обычно 0,20,3 звездной величины. в 0 и 0,2 dex в отношении магнитного потока, не зависящего от расстояния M H I / L . Обратите внимание на острый конец данных как 0 25 B mag arcsec -2 , наложенный изофотальными пределами выбора.Без наших данных для галактик с низкой поверхностной яркостью это происходит ярче, чем 0 23 дюйма ( a ). Это также очевидно в разрыве в ( b ) на 21. Изучение только галактик ярче этого значения скрывает корреляцию из-за отсутствия динамического диапазона. Гигант с очень низкой поверхностной яркостью Малин 1 [ панель ( a ), треугольник ] преодолевает этот изофотальный барьер, потому что он был случайно обнаружен, отчасти из-за высокого содержания газа.
Полное изображение (72кб) Полное изображение (64кб) | Обсуждение в тексте
РИС.2. Оптические (полоса B ) свойства спиральных галактик: ( a ) центральная поверхностная яркость в зависимости от абсолютной звездной величины и ( b ) масштабная длина в зависимости от абсолютной звездной величины. Различные символы представляют разные типы Хаббла, переходящие от ранних к поздним типам в порядке увеличения количества точек на символе [ панель (a), вставка ].
Изображение полностью (57кб) | Обсуждение в тексте
РИС. 3. Яркость центральной поверхности полосы I = 0 — ( B — I ) vs. V — I цвет. Символы соответствуют типу Хаббла согласно рис. 2. Обратите внимание, что диски с более низкой поверхностной яркостью систематически более голубые, чем диски с более высокой поверхностной яркостью, они не являются результатом выцветания после прекращения звездообразования.
Изображение полностью (68кб) | Обсуждение в тексте
РИС. 4. Дисперсия вертикальной скорости спиральных дисков в зависимости от цвета. Данные взяты из Bottema (1993, 1995). Линия — это наша оценка для * , отображенная на дисперсию скоростей по формуле.(8) из Bottema (1993). Нормализация выбрана для соответствия данным, но форма линии не соответствует им (см. De Blok & McGaugh 1997). Тем не менее, это соответствует наблюдаемой тенденции, которая в ожидаемом смысле означает, что более красные галактики имеют более высокие * .
Изображение полностью (71кб) | Обсуждение в тексте
РИС. 5.Звездная масса галактик выборки (в массах Солнца), вычисленная из * = * L независимо в полосах B ( абсцисса ) и I ( ордината ).Отдельные меры светимости ( L B и L I ) используются вместе с оценками для * , обсуждаемыми в тексте. Данные четко следуют линии единства, что указывает на разумное согласие между двумя методами.
Изображение полностью (56кб) | Обсуждение в тексте
РИС. 6. Отношение массы молекулярного газа к массе атомарного газа как функция типа Хаббла. Данные (среднее значение и ошибка среднего) взяты из Young & Knezek (1989).Как обычно, ошибка среднего занижает величину реального разброса для данного типа. Линия соответствует нашим данным (см. Текст).
Полное изображение (52кб) Полное изображение (57кб) Полное изображение (63кб) Полное изображение (55кб) | Обсуждение в тексте
РИС. 7. Доля газа спиральных галактик в зависимости от ( a ) абсолютной величины B , ( b ) яркости центральной поверхности диска, ( c ) масштабной длины диска и ( d ) цвета. На графике нанесен полный возможный диапазон 0 f g 1, и впервые требуется, чтобы самые тусклые галактики в основном газообразные с f g 0.5. Существует сильная связь между f g и M B , 0 и цветом. Нет никакой связи между f g и размером диска. Обратите внимание, что отношения f g — M B и — 0 имеют одинаковый наклон. Малин 1 ( треугольник ) — это крайний случай, когда газовая фракция аномально высока для его светимости, но нормальна для его поверхностной яркости.
Полное изображение (50кб) Полное изображение (53кб) Полное изображение (62кб) Полное изображение (44кб) | Обсуждение в тексте
РИС. 8. То же, что и на рис. 7, за исключением данных диапазона I . На рисунке показано f против ( a ) абсолютной величины I , ( b ) I -полосная яркость центральной поверхности диска, ( c ) длина шкалы и ( d ) V — I цвет. Газовая доля определяется независимо от показанной на рис.7, предполагая, что это постоянное значение для всех спиралей. Это дает неотличимые результаты от диапазона B , хотя использовалась совершенно другая оценка звездной массы.
Изображение целиком (111кб) | Обсуждение в тексте
РИС. 9. Данные на рис. 7 a и 7 b наложены поверх графика после смещения пересечением ур. (3). Круги , M B ; квадратов , 0 . Линии представляют собой модельные эволюционные треки из Guideroni & Rocca-Volmerange (1987).Горизонтальные линии — изохроны каждые 2 млрд лет от 1 до 15 млрд лет. Вертикальные линии — это эволюционные траектории для конкретных историй звездообразования, помеченные типом Хаббла, который модель пытается представить. Ранние типы (от Sa до Sc) имеют экспоненциально снижающиеся темпы звездообразования, в то время как Sd постоянна, а Im растет со временем (Таблица 4). Положение этих линий зависит от полной барионной массы галактики. Они нарисованы с разделениями, соответствующими среднему для каждого типа, как предусмотрено Guideroni & Rocca-Volmerange (1987); абсолютное положение результирующей сетки было скорректировано, чтобы оно совпадало с данными.Хотя эти (или любые другие) модели популяционного синтеза ни в коем случае не идеальны, они действительно иллюстрируют, как f g ограничивает комбинацию скорости эволюции и возраста. С большим динамическим диапазоном в f g и традиционными ограничениями цвета и металличности, возможно, удастся построить многомерный внегалактический аналог HR-диаграммы, который может позволить датировать возраст спиральных галактик.
Изображений наборной таблицы: 1 2 | Обсуждение в тексте
Изображение наборной таблицы | Обсуждение в тексте
a Снижение SFR с> 0.
b Плоский или восходящий SFR с g и x 0.
c = e — шкала времени складывания; г = шкала времени потребления газа.
d Глобальный SFR, нормированный на полную барионную массу.
e L T G определяется началом звездообразования = возрастом самых старых звезд.
f Пределы, полученные при требовании T G < T U , возраста вселенной.
Изображение наборной таблицы | Обсуждение в тексте
ПРИМЕЧАНИЕ. Тип Хаббла используется здесь для обозначения моделей Guideroni & Rocca-Volmerange 1987. Строго говоря, они только определяют форму истории модельного звездообразования.
Изображение наборной таблицы | Обсуждение в тексте
Распределения изотопов, соотношения элементов и массовые доли элементов по результатам измерений гамма-излучения МОХ с помощью измерителя обогащения (Конференция)
Клоуз Д. А., Паркер Дж. Л., Хейкок Д. Л. и Драгнев Т. Изотопные распределения, соотношения элементов и массовые доли элементов по результатам измерений гамма-излучения MOX прибором для обогащения. США: Н. П., 1991.
Интернет.
Клоуз, Д. А., Паркер, Дж. Л., Хейкок, Д. Л., и Драгнев, Т. Изотопные распределения, отношения элементов и массовые доли элементов по результатам измерений гамма-излучения МОХ с помощью измерителя обогащения.Соединенные Штаты.
Клоуз Д. А., Паркер Дж. Л., Хейкок Д. Л. и Драгнев Т. Вт.
«Изотопные распределения, отношения элементов и массовые доли элементов по результатам измерений гамма-излучения МОХ с помощью измерителя обогащения». Соединенные Штаты. https://www.osti.gov/servlets/purl/5213010.
@article {osti_5213010,
title = {Изотопные распределения, соотношения элементов и массовые доли элементов по результатам измерений гамма-излучения МОХ с помощью измерителя обогащения},
author = {Клоуз, Д. А. и Паркер, Д. Л. и Хейкок, Д. Л. и Драгнев, Т.},
abstractNote = {Измерены спектры гамма-излучения от бесконечно '' толстых образцов смешанных оксидов.Изотопы плутония, отношение U / Pu, массовые доли с высоким Z (при условии только плутония, урана и америция) и массовые доли с низким Z (при условии, что матрица состоит только из кислорода) могут быть определены путем тщательного анализа данных. . Результаты хорошо согласуются с химическим определением этих параметров. 8 исх., 3 рис., 3 таб.},
doi = {},
url = {https://www.osti.gov/biblio/5213010},
журнал = {},
номер =,
объем =,
place = {United States},
год = {1991},
месяц = {1}
}
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
