Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

1. использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

2. логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

3. последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

4. высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

1. Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

2. Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

3. Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

4. Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

5. Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

6. Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

7. Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «… Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый — отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй — подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т.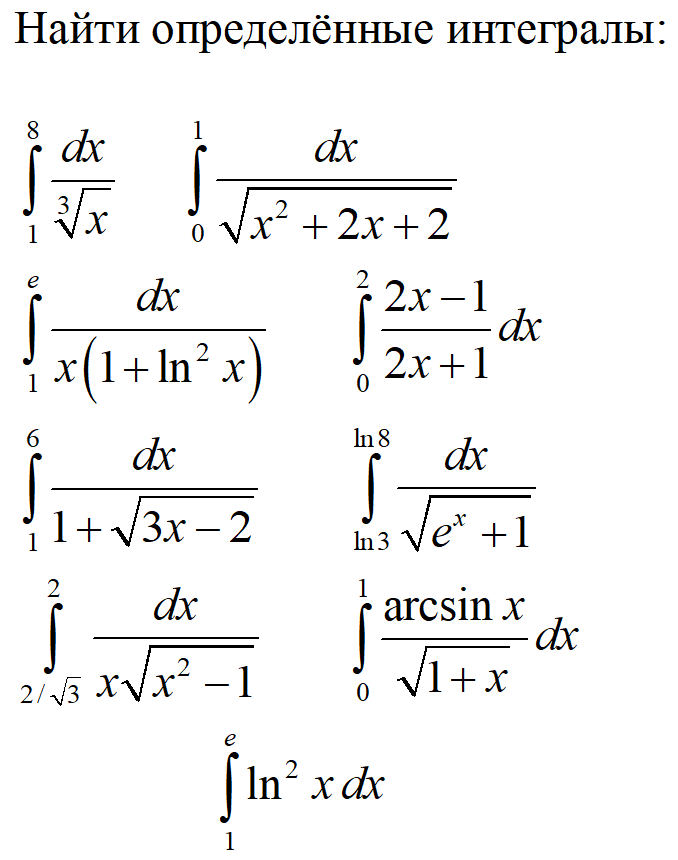 д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

• В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

• В случае с вещественными числами.

  • Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

  • Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

  • В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.

• В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

• Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

• Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

1. Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при , , а значение . Если. Тогда, при , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

Высшая математика в 3 т. Том 3. В 2 кн. Книга 1. Дифференциальные уравнения. Кратные интегралы

Учебники курса «Высшая математика» авторов Я. С. Бугрова и С. М. Никольского получили широкое признание как в нашей стране, так и за рубежом; они были апробированы специалистами многих высших учебных заведений и научных учреждений. Данное издание является третьим томом учебно-методического комплекcа учебников «Высшая математика». В состав тома входят две книги. В первой книге излагаются следующие разделы: «Обыкновенные дифференциальные уравнения», «Кратные интегралы», «Векторный анализ»; во второй книге излагаются: «Ряды», «Уравнения математической физики», «Функции комплексного переменного», «Операционное исчисление» и «Обобщенные функции».

Высшее образование

Укажите параметры рабочей программы

Дисциплина

Высшая математика

УГС

24.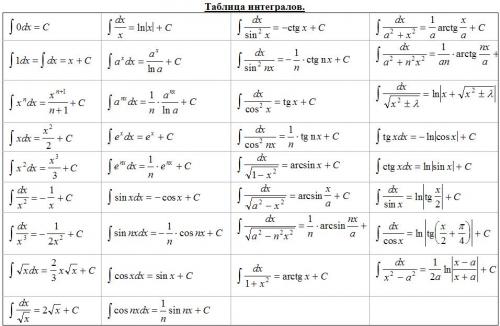 00.00 «АВИАЦИОННАЯ И РАКЕТНО-КОСМИЧЕСКАЯ ТЕХНИКА»07.00.00 «АРХИТЕКТУРА»25.00.00 «АЭРОНАВИГАЦИЯ И ЭКСПЛУАТАЦИЯ АВИАЦИОННОЙ И РАКЕТНО-КОСМИЧЕСКОЙ ТЕХНИКИ»06.00.00 «БИОЛОГИЧЕСКИЕ НАУКИ»36.00.00 «ВЕТЕРИНАРИЯ И ЗООТЕХНИЯ»58.00.00 «ВОСТОКОВЕДЕНИЕ И АФРИКАНИСТИКА»09.00.00 «ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА»10.00.00 «ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ»31.00.00 «КЛИНИЧЕСКАЯ МЕДИЦИНА»02.00.00 «КОМПЬЮТЕРНЫЕ И ИНФОРМАЦИОННЫЕ НАУКИ»01.00.00 «МАТЕМАТИКА И МЕХАНИКА»15.00.00 «МАШИНОСТРОЕНИЕ»28.00.00 «НАНОТЕХНОЛОГИИ И НАНОМАТЕРИАЛЫ»05.00.00 «НАУКИ О ЗЕМЛЕ»44.00.00 «ОБРАЗОВАНИЕ И ПЕДАГОГИЧЕСКИЕ НАУКИ»17.00.00 «ОРУЖИЕ И СИСТЕМЫ ВООРУЖЕНИЯ»41.00.00 «ПОЛИТИЧЕСКИЕ НАУКИ И РЕГИОНОВЕДЕНИЕ»21.00.00 «ПРИКЛАДНАЯ ГЕОЛОГИЯ, ГОРНОЕ ДЕЛО, НЕФТЕГАЗОВОЕ ДЕЛО И ГЕОДЕЗИЯ»19.00.00 «ПРОМЫШЛЕННАЯ ЭКОЛОГИЯ И БИОТЕХНОЛОГИИ»37.00.00 «ПСИХОЛОГИЧЕСКИЕ НАУКИ»35.00.00 «СЕЛЬСКОЕ, ЛЕСНОЕ И РЫБНОЕ ХОЗЯЙСТВО»43.00.00 «СЕРВИС И ТУРИЗМ»39.00.00 «СОЦИОЛОГИЯ И СОЦИАЛЬНАЯ РАБОТА»42.00.00 «СРЕДСТВА МАССОВОЙ ИНФОРМАЦИИ И ИНФОРМАЦИОННО-БИБЛИОТЕЧНОЕ ДЕЛО»48. 00.00 «ТЕОЛОГИЯ»26.00.00 «ТЕХНИКА И ТЕХНОЛОГИИ КОРАБЛЕСТРОЕНИЯ И ВОДНОГО ТРАНСПОРТА»23.00.00 «ТЕХНИКА И ТЕХНОЛОГИИ НАЗЕМНОГО ТРАНСПОРТА»08.00.00 «ТЕХНИКА И ТЕХНОЛОГИИ СТРОИТЕЛЬСТВА»29.00.00 «ТЕХНОЛОГИИ ЛЕГКОЙ ПРОМЫШЛЕННОСТИ»22.00.00 «ТЕХНОЛОГИИ МАТЕРИАЛОВ»20.00.00 «ТЕХНОСФЕРНАЯ БЕЗОПАСНОСТЬ И ПРИРОДООБУСТРОЙСТВО»27.00.00 «УПРАВЛЕНИЕ В ТЕХНИЧЕСКИХ СИСТЕМАХ»03.00.00 «ФИЗИКА И АСТРОНОМИЯ»16.00.00 «ФИЗИКО-ТЕХНИЧЕСКИЕ НАУКИ И ТЕХНОЛОГИИ»47.00.00 «ФИЛОСОФИЯ, ЭТИКА И РЕЛИГИОВЕДЕНИЕ»12.00.00 «ФОТОНИКА, ПРИБОРОСТРОЕНИЕ, ОПТИЧЕСКИЕ И БИОТЕХНИЧЕСКИЕ СИСТЕМЫ И ТЕХНОЛОГИИ»30.00.00 «ФУНДАМЕНТАЛЬНАЯ МЕДИЦИНА»18.00.00 «ХИМИЧЕСКИЕ ТЕХНОЛОГИИ»04.00.00 «ХИМИЯ»38.00.00 «ЭКОНОМИКА И УПРАВЛЕНИЕ»13.00.00 «ЭЛЕКТРО- И ТЕПЛОЭНЕРГЕТИКА»11.00.00 «ЭЛЕКТРОНИКА, РАДИОТЕХНИКА И СИСТЕМЫ СВЯЗИ»14.00.00 «ЯДЕРНАЯ ЭНЕРГЕТИКА И ТЕХНОЛОГИИ»

Направление подготовки

Уровень подготовки

определение, история развития, применение интегралов на практике

Содержание:

Имеется несколько типов интегралов: неопределенный и определенный интегралы, интеграл Римана и Римана-Стилтьеса, интеграл
Лебега и Лебега-Стилтьеса, интеграл Даниэля. По области интегрирования интегралы подразделяются на кратные, криволинейные и
поверхностные интегралы.

Историческая справка

Интегрирование берет свое начало ещё в древнем Египте примерно с 1800 года до н. э., о чем свидетельствует Московский математический
папирус (или математический папирус Голенищева). Первым известным методом для расчёта интегралов является метод для исследования
площади или объёма криволинейных фигур — метод исчерпывания Евдокса (Евдокс Книдский (ок. 408 г. до н.э. — ок. 355 г. до н.э.) —
древнегреческий математик, механик и астроном), который был предложен примерно в 370 до н. э. Суть этого метода заключается в следующем:
фигура, площадь или объем которой пытались найти, разбивалась на бесконечное множество частей, для которых площадь или объём уже известны.
Этот метод получил свое дальнейшее развитие в работах древнегреческого математика, физика и инженера Архимеда (287 до н.э. — 212 до н.э.)
для расчёта площадей парабол и приближенного расчёта площади круга. {a} \sqrt{x} d x$

Используя математическую индукцию,
он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску
общей формулы для интегралов от полиномов не выше четвёртой степени.

Следующий значительный толчок в исчислении интегралов состоялся лишь в 16 веке в работах итальянского математика Бонавентура
Франческо Кавальери (1598 — 1647), в которых описывался предложенный им метод неделимых, а также в работах французского математика
Пьера де Ферма (1601 — 1665). Этими учеными были заложены основы современного интегрального исчисления. Дальнейшее развитие связано
с деятельностью английского математика, физика и богослова Исаака Барроу (1630 — 1677) и итальянского математика и физика, ученика
Галилея Эванджелиста Торричелли (1608 — 1647), которые представили первые намеки на связь между интегрированием и дифференцированием.

За время становления интегрального исчисления менялось и обозначение интеграла. Английский физик, механик, математик и астроном Исаак
Ньютон (1643 — 1727) использовал, правда не во всех своих работах, в качестве символа интегрирования значок квадрата перед
обозначением функции или вокруг него, а также вертикальную черту над функцией, но эти обозначения не получили широкого распространения.
Современное обозначение неопределённого интеграла было введено немецким философом, логиком, математиком, механиком,
физиком, юристом, историком, дипломатом, изобретателем и языковедом Готфридом Вильгельмом Лейбницем (1646 — 1716) в 1675 году.
Он образовал символ интеграла из буквы «длинная s» (от первой буквы слова Summa — сумма) Современное обозначение определённого
интеграла, с указанием пределов интегрирования, было впервые предложено французским математиком и физиком Жаном Батистом
Жозефом Фурье (1768 — 1830) в 1819-20 годах. Сам термин «интеграл» придумал швейцарский математик Якоб
Бернулли (1654 — 1705) в 1690 году.

Применение интегралов на практике

Основной задачей дифференциального исчисления является определение для заданной функции
$F(x)$ ее
производной
$F^{\prime}(x)=f(x)$ или ее дифференциала
$F^{\prime}(x) d x=f(x) d x$ . Обратная задача, состоящая в определении функции
$F(x)$ по ее известным производной
$f(x)$ или
дифференциалу
$f(x) d x$, представляет собой основную задачу интегрального исчисления.

Читать дальше: неопределенный интеграл и понятие первообразной.

Интегралы для чайников — что это, как решать, примеры

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

• вычисление площади фигуры.
• вычисление массы тела с неравномерной плотностью.
• определение пройденного пути при движении с непостоянной скоростью.
• и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Пример решения неопределенного интеграла.

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Пример решения определенного интеграла

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Интегралы – что это, как решать, примеры решений и объяснение для чайников обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Высшая математика. Интегралы, ряды, ТФКП, дифференциальные уравнения

Настоящая книга вместе с другой книгой автора, >, охватывает весь комплекс вопросов, которые изучаются в рамках курса > в высших учебных заведениях, за исключением вопросов линейной алгебры и аналитической геометрии. Она содержит следующие разделы высшей математики: >, >, > и >. Для студентов инженерно-технических и экономических специальностей вузов, а также для изучающих в том или ином объеме высшую математику.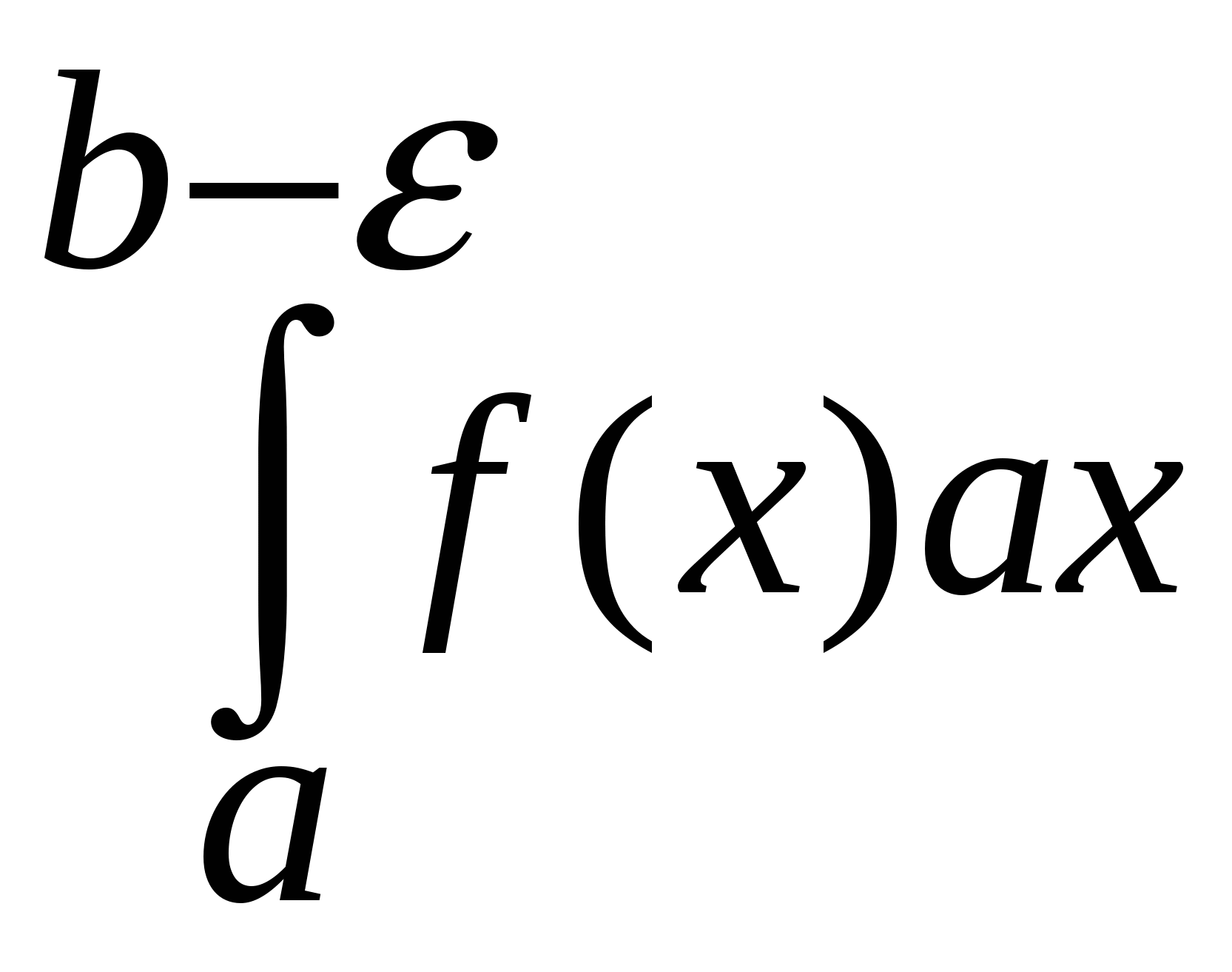 Допущено Министерством образования и науки Российской Федерации в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям и специальностям в области экономики и управления, техники и технологии. begincentersooРецензенты:par д.ф.-м.н., проф. Петрушко И.М., д.ф.-м.н., проф. Смирнов Ю.М.endcenter

Автор	Геворкян Павел Самвелович
Издательство	ООО «Физматлит»
Дата издания	2007
Кол-во страниц	272
Номер тома	2
ISBN	978-5-9221-0710-5
Тематика	Математика. Прикладная математика
№ в каталоге	710

Категории:
Учебная литература

📝Что такое интеграл?

В переводе с латинского языка интеграл означает «целый». Это одно из наиболее важных и распространенных понятий в высшей математике, которое появилось из-за необходимости находить функции по их производным или измерять объёмы, площади, работу нескольких сил за конкретный промежуток времени, длины дуг и т. д. В соответствии с этими задачами принято выделять определённые и неопределенные интегралы.

Содержание статьи:

Обозначение

Первым символ для обозначения интегрирования придумал Ньютон. Он применял для этого небольшой квадрат. Однако данное обозначение не получило серьезного распространения. Сегодняшнее обозначение неопределенного интеграла было придумано в 1675 году Лейбницем:

Что касается обозначения определённого интеграла, где указаны пределы интегрирования, то его в 1819 году предложил Жан Батист Фурье.

Виды интегралов

Первообразная функции f(x) — функция F(x), производная которой при любом значении х равняется f(x). Добавляя постоянную к первообразной определенной функции, снова можно получить первообразную этой же функции. Соответственно, имея единственную первообразную F(x) функции f(x), можно получить единое выражение всех первообразных данной функции в виде F(x) + С. Подобное выражение первообразных принято называть неопределённым интегралом функции f(x):

Одно из главных правил интегрального исчисления определяет, что любая непрерывная функция f(x) имеет неопределённый интеграл.

Что касается определённого интеграл от функции f(x) с верхним пределом b и нижним пределом а, то он определяется в качестве разности:

где F(x) является первообразной функции f(x).

Определённый интеграл можно выразить посредством любой первообразной F(x). Верным является и обратное. Первообразную F(x) можно записать в следующем виде:

В этой формуле а – это произвольная константа. Таким образом, интеграл можно записать в виде:

История возникновения интеграла

Если углубиться в историю, то можно утверждать, что интегрирование зародилось в древнем Египте, приблизительно в 1800 году до нашей эры. Первой известной методикой вычисления интегралов считается способ исчерпывания Евдокса. Он предпринимал попытки найти объёмы и площади фигур, разрывая их на несколько частей, для которых уже известны площадь или объём. Через некоторое время данная методика была развита Архимедом. Он применял ее для вычислений площадей парабол и примерного расчёта площади круга. Подобные методы независимо разрабатывались в Китае в 3 столетии нашей эры Лю Хуэйем. Он использовал их с целью определения площади круга.

Следующий внушительный прогресс в исчислении интегралов произошел только в XVI веке. В работах с методом неделимых Кавальери, а также в научных трудах Ферма, были заложены основы сегодняшнего интегрального исчисления.

Последующие шаги были сделаны в середине XVII столетия Торричелли и Барроу, которые предоставили первые намеки на взаимосвязь между дифференцированием и интегрированием.

Зачем и кому нужны интегралы?

Ученые стремятся любые физические явления выражать в виде математических формул. Когда в руках есть определенная формула, то в дальнейшем уже можно с ее помощью посчитать все, что необходимо. А интеграл является одним из главных инструментов работы с любыми функциями.

К примеру, имея формулу круга, можно посредством интеграла вычислить его площадь. Если есть формула шара, то можно вычислить его объем.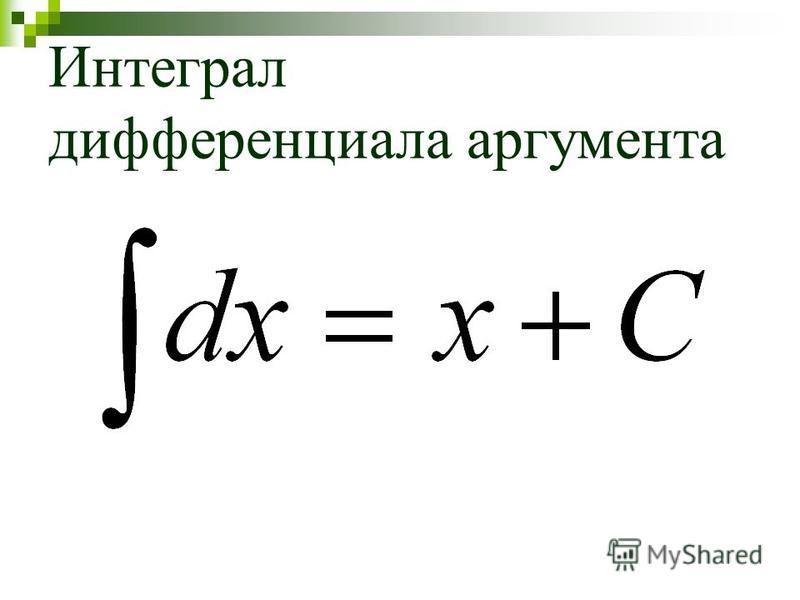 Посредством интегрирования можно найти работу, энергию, массу, давление, электрический заряд и прочие важные величины.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Урок 25. применение интегралов для решения геометрических и физических задач — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №25. Применение интегралов для решения геометрических и физических задач.

Перечень вопросов, рассматриваемых в теме

1) Знакомство с применением определенного интеграла в различных предметных областях

2) Знакомство с прикладными задачами, связанными с вычислением определенного интеграла в физике, экономике, геометрии.

3) Решение задач, с помощью определенных интегралов

путь, пройденный телом

Прирост численности популяции N(t) за промежуток времени от t₀ до T равен .

Объем тела вращения

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

путь, пройденный телом

Прирост численности популяции N(t) за промежуток времени от t₀ до T равен .

Объем тела вращения

Примеры и разбор решения заданий тренировочного модуля

№1 Найти объем тела вращения вокруг оси 0х , ограниченной прямыми у=0, х=0ю у= х², х=4.

Решение: Построим тело вращения, образованного вращением фигуры вокруг оси 0х

Воспользуемся формулой Ньютона-Лейбница.

и формулой нахождения объемов тел вращения.

Далее подставляем значения в формулу и рассчитываем объем тела вращения.

Ответ 51,2 ед³

№2. Сила в 1 Н растягивает пружину на 3 см. Какую работу она при этом производит?

Решение.

Если F–сила, А – работа S– перемещение, то F = A’(S).

Обратимся к физике.

По закону Гука сила пропорциональна растяжению или сжатию пружины, т. е. F = kx, где k – коэффициент пропорциональности, х – величина растяжения или сжатия.

Используя данные задачи, найдите коэффициент k. Подставим данные в задаче величины в уравнение, выражающее закон Гука. Получим: .

Следовательно, сила, растягивающая нашу пружину, выразится следующим образом:.

Так как сила начинает действовать на пружину в состоянии покоя, то работа

Ответ: 0,015 Дж

№3. Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м³), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.

Решение.

Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой

Р=

Стенка имеет форму прямоугольника, поэтому f(x)=0.7x, xϵ [0;0.4]  Так как пределы интегрирования а=0 и b=0,4, то получим:

Ответ: 549 Н

№4 Скорость прямолинейного движения тела выражается формулой . Найти путь, пройденный телом за 5 секунд от начала движения.

Решение.

Физический смысл производной: если тело движется по закону S = S(t), то скорость тела в момент времени t₀ равна значению производной функции S(t) в этой точке, т. е. v = S’(t₀). Тогда обратное утверждение: если скорость движения тела задана уравнением v = v(t), то путь, пройденный телом от момента времени t = a до момента времени t = b равен . Подставим уравнение скорости в формулу и рассчитаем путь.

Ответ 150м

Введение в интеграцию

Интеграция — это способ добавления фрагментов для поиска целого.

Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но проще всего начать с поиска области между функцией и осью x следующим образом:

Что это за площадь?

Ломтики

Это много сложностей!

Но складывать их не нужно, есть «ярлык», потому что …

… нахождение интеграла — это , обратный нахождения производной.

(Так что вам действительно следует знать о производных финансовых инструментах, прежде чем читать больше!)

Как здесь:

Пример: 2x

Интеграл от 2x равен x ² …

… потому что производная x ² равна 2x

(Подробнее о «+ C» позже.)

Этот простой пример можно подтвердить вычислением площади:

Площадь треугольника = 1 2 (основание) (высота) = 1 2 (x) (2x) = x ²

Иногда интеграция может быть такой простой!

Обозначение

После символа интеграла мы помещаем функцию, интеграл которой мы хотим найти (называемую интегралом),

, а затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).

А вот как пишем ответ:

плюс C

Мы написали ответ как x ² , но почему + C?

Это «Константа интеграции». Это из-за всех функций, производная которых равна 2x :

• производная от x ² составляет 2x ,
• и производная от x ² +4 также равна 2x ,
• и производная x ² +99 также 2x ,
• и так далее!

Поскольку производная константы равна нулю.

Итак, когда мы перевернем операцию (чтобы найти интеграл), мы знаем только 2x , но могла быть константа любого значения .

Итак, мы завершаем идею, просто написав + C в конце.

Практический пример: кран и резервуар

Давайте воспользуемся краном, чтобы наполнить бак.

Вход (до интегрирования) — расход от крана.

Мы можем интегрировать этот поток (сложить все маленькие кусочки воды), чтобы получить объема воды в резервуаре.

Представьте себе постоянный расход из 1:

При расходе 1 объем резервуара увеличивается на x . Это Интеграция !

Интеграл от 1 равен x

При скорости потока 1 литр в секунду объем увеличивается на 1 литр каждую секунду, поэтому будет увеличиваться на 10 литров через 10 секунд, 60 литров через 60 секунд и т. Д.

Скорость потока остается на уровне 1 , а объем увеличивается на x

И наоборот:

Если объем резервуара увеличивается на x , то расход должен быть 1.

Производная x равна 1

Это показывает, что интегралы и производные противоположны!

Теперь для увеличения расхода

Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, двигатель медленно открывает кран):

По мере увеличения расхода резервуар наполняется все быстрее и быстрее:

• Интеграция: при расходе 2x объем резервуара увеличивается на x ²
• Производная: если объем резервуара увеличивается на x ² , то расход должен быть 2x

Мы можем записать это так:

И, привет, мы даже получили хорошее объяснение этого значения «C». .. может быть, в баке уже есть вода!

• Поток по-прежнему увеличивает объем на ту же величину
• И увеличение объема может вернуть нам скорость потока.

Которая учит всегда помнить «+ C».

Прочие функции

Как мы интегрируем другие функции?

Если нам посчастливится найти функцию на стороне результата производной, то (зная, что производные и интегралы противоположны), у нас есть ответ.Но не забудьте добавить C.

Пример: что такое ∫cos (x) dx?

Из таблицы Rules of Derivatives мы видим, что производная sin (x) равна cos (x), поэтому:

∫cos (x) dx = sin (x) + C

Но многое из этого «обращения» уже сделано (см. Правила интеграции).

Пример: Что такое ∫x

³ dx?

В правилах интеграции есть «Правило власти», которое гласит:

∫x ⁿ dx = x ^{n + 1} n + 1 + C

Мы можем использовать это правило с n = 3:

∫x ³ dx = x ⁴ 4 + C

Знание того, как использовать эти правила, — ключ к успешной интеграции.

Так что изучайте правила и получайте много практики .

Изучите правила интеграции и практикуйтесь! Упражняться! Упражняться!
(для начала вам нужно задать несколько вопросов)

Определенные и неопределенные интегралы

До сих пор мы выполняли неопределенных интегралов .

Определенный интеграл имеет фактические значения для вычисления между ними (они помещаются внизу и вверху буквы «S»):

Прочтите Определенные интегралы, чтобы узнать больше.

Исчисление I — Интегралы

Показать общее уведомление

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST. Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Глава 5: Интегралы

В этой главе мы рассмотрим интегралы. Интегралы — третья и последняя основная тема, которая будет рассмотрена в этом классе. Как и в случае с производными, эта глава будет посвящена почти исключительно поиску и вычислению интегралов. Заявки будут представлены в следующей главе. На самом деле в этой главе мы рассмотрим два типа интегралов: неопределенные интегралы и определенные интегралы. Первая половина этой главы посвящена неопределенным интегралам, а вторая половина посвящена определенным интегралам. Как мы увидим во второй половине главы, если мы не знаем неопределенных интегралов, мы не сможем делать определенные интегралы.

Вот краткий список материалов этой главы.

Неопределенные интегралы — В этом разделе мы начнем главу с определения и свойств неопределенных интегралов. В этом разделе мы не будем вычислять много неопределенных интегралов. Этот раздел посвящен простому определению того, что такое неопределенный интеграл, и описанию многих свойств неопределенного интеграла. Фактически вычисление неопределенных интегралов начнется в следующем разделе.

Вычисление неопределенных интегралов — В этом разделе мы вычислим некоторые неопределенные интегралы. Интегралы в этом разделе, как правило, будут такими, которые не требуют большого количества манипуляций с функцией, которую мы интегрируем, чтобы фактически вычислить интеграл. Как мы увидим в следующем разделе, многие интегралы действительно требуют некоторых манипуляций с функцией, прежде чем мы действительно сможем выполнить интеграл. Мы также кратко рассмотрим применение неопределенных интегралов.

Правило замещения для неопределенных интегралов — в этом разделе мы начнем использовать один из наиболее распространенных и полезных методов интеграции — правило замещения. С помощью правила подстановки мы сможем интегрировать более широкий спектр функций. Все интегралы в этом разделе потребуют некоторых манипуляций с функцией перед интегрированием, в отличие от большинства интегралов из предыдущего раздела, где все, что нам действительно нужно, это основные формулы интегрирования.

Дополнительные правила замены — в этом разделе мы продолжим рассмотрение правила замены.Проблемы в этом разделе, как правило, будут немного сложнее, чем в предыдущем разделе.

Проблема с областью — В этом разделе мы начинаем с мотивации определенных интегралов и даем одну из интерпретаций определенных интегралов. Мы будем аппроксимировать площадь, которая находится между функцией и осью \ (x \). Как мы увидим в следующем разделе, эта проблема приведет нас к определению определенного интеграла и будет одной из основных интерпретаций определенного интеграла, которую мы рассмотрим в этом материале.

Определение определенного интеграла — В этом разделе мы формально определим определенный интеграл, дадим многие из его свойств и обсудим несколько интерпретаций определенного интеграла. Мы также рассмотрим первую часть фундаментальной теоремы исчисления, которая показывает очень тесную связь между производными и интегралами

.

Вычисление определенных интегралов — В этом разделе мы рассмотрим вторую часть фундаментальной теоремы исчисления.Это покажет нам, как мы вычисляем определенные интегралы без использования (часто очень неприятного) определения. Все примеры в этом разделе могут быть выполнены с базовыми знаниями неопределенных интегралов и не требуют использования правила подстановки. В примеры этого раздела включены вычисления определенных интегралов от кусочных и абсолютных функций.

Правило замещения для определенных интегралов — В этом разделе мы еще раз рассмотрим правило замены, поскольку оно применяется к определенным интегралам.Единственные реальные требования к умению выполнять примеры в этом разделе — это умение выполнять правило замены для неопределенных интегралов и понимание того, как вычислять определенные интегралы в целом.

Исчисление I — Вычисление определенных интегралов

Показать общее уведомление

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-7: Вычисление определенных интегралов

В этом разделе мы сосредоточимся на том, как мы фактически вычисляем определенные интегралы на практике. Для этого нам понадобится Фундаментальная теорема исчисления, часть II.б = F \ влево (б \ вправо) — F \ влево (а \ вправо) \]

Чтобы увидеть доказательство этого, см. Раздел «Доказательство различных интегральных свойств» в главе «Дополнительные возможности».

Напомним, что когда мы говорим об антипроизводной функции, на самом деле мы говорим о неопределенном интеграле для функции. Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, это вычислить неопределенный интеграл для функции. Это должно объяснить сходство обозначений неопределенного и определенного интегралов.

Также обратите внимание, что мы требуем, чтобы функция была непрерывной в интервале интегрирования. Это также было требованием при определении определенного интеграла. В последнем разделе мы не особо особо задумывались об этом. Однако в этом разделе нам нужно будет помнить об этом условии при проведении наших оценок.

Теперь давайте обратимся к тому факту, что мы можем использовать любую антипроизводную от \ (f \ left (x \ right) \) в оценке. Давайте в последний раз взглянем на следующий интеграл.3} + 0 — \ frac {{18}} {{31}}} \ right) \\ & = \ frac {{14}} {3} — \ frac {{18}} {{31}} + \ гидроразрыв {{18}} {{31}} \\ & = \ frac {{14}} {3} \ end {align *} \]

Константа, которую мы добавили ко второй антипроизводной, аннулирована на этапе оценки. Итак, выбирая антипроизводную для использования в процессе оценки, упростите себе жизнь и не беспокойтесь о константе, поскольку в конечном итоге она только отменится.

Также обратите внимание, что нам нужно быть очень осторожными со знаками минус и круглыми скобками в этих задачах.{- 2}} \, dy}} \) Показать решение

Вспомните из нашего первого примера выше, что все, что нам действительно нужно, это любая антипроизводная подынтегрального выражения. Мы просто вычислили самую общую антипроизводную в первой части, поэтому мы можем использовать ее, если захотим. Однако помните, что, как мы отметили выше, любые константы, которые мы добавляем, в конечном итоге просто отменяются, и поэтому мы будем использовать ответ из (a) без «+ \ (c \)». {- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]

Помните, что оценка всегда выполняется в порядке оценки на верхнем пределе минус оценка на нижнем пределе. Также будьте очень осторожны со знаками минус и круглыми скобками. Их очень легко забыть или неправильно использовать и получить неправильный ответ.

Также обратите внимание, что для облегчения вычисления мы немного переписали неопределенный интеграл.{- 2}} \, dy}} \) Показать решение

Этот интеграл здесь, чтобы указать на важность. Напомним, что для того, чтобы мы могли сделать интеграл, подынтегральное выражение должно быть непрерывным в пределах диапазона. В этом случае второй член будет иметь деление на ноль в точке \ (y = 0 \), и поскольку \ (y = 0 \) находится в интервале интегрирования, , т.е. , он находится между нижним и верхним пределом, это подынтегральное выражение равно не непрерывна в интервале интегрирования, поэтому мы не можем сделать этот интеграл.

Обратите внимание, что эта проблема не помешает нам выполнить интеграл в (b), поскольку \ (y = 0 \) не находится в интервале интегрирования.

Итак, что мы узнали из этого примера?

Во-первых, чтобы получить определенный интеграл, первое, что нам нужно сделать, это неопределенный интеграл. Итак, мы не собираемся отказываться от вычисления неопределенных интегралов, они будут в каждом интеграле, который мы будем делать в оставшейся части этого курса, поэтому убедитесь, что вы хорошо умеете их вычислять.

Во-вторых, нам нужно внимательно следить за функциями, которые не являются непрерывными ни в одной точке между пределами интеграции.Также важно отметить, что это будет проблемой только в том случае, если точка (точки) разрыва возникает между пределами интеграции или на самих границах. Если точка разрыва возникает за пределами интегрирования, интеграл все еще может быть вычислен.

В следующих наборах примеров мы не будем уделять слишком много внимания проблемам непрерывности или отсутствию непрерывности, если это не влияет на оценку интеграла. Не позволяйте этому убедить вас, что вам не стоит беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \]

Сравните этот ответ с предыдущим, особенно с нулевой оценкой. Очень легко выработать привычку записывать ноль при вычислении функции. Это особенно проблема, когда многие из функций, которые мы интегрируем, включают только \ (x \), возведенные в положительные целые числа; эти оценки нулевая конечно.{\, ​​{\ pi} / {4} \;} \\ & = 5 \ left ({\ frac {\ pi} {4}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {4}} \ right) — \ left ({5 \ left ({\ frac {\ pi} {6}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {6}} \ right) )} \ right) \\ & = \ frac {{5 \ pi}} {{12}} — 2 \ sqrt 2 + \ frac {4} {{\ sqrt 3}} \ end {align *} \]

Для оценки напомним, что

\ [\ sec z = \ frac {1} {{\ cos z}} \]

, и поэтому, если мы можем вычислить косинус под этими углами, мы сможем вычислить секанс под этими углами.6} — 10t + \ frac {1} {t} \; dt}} \) Показать решение

Этот интеграл не может быть выполнен. В третьем члене при \ (t = 0 \) есть деление на ноль, а \ (t = 0 \) лежит в интервале интегрирования. Тот факт, что первые два члена могут быть объединены, не имеет значения. Если даже одно слагаемое в интеграле не может быть интегрировано, то и весь интеграл не может быть выполнен.

Итак, на данный момент мы вычислили изрядное количество определенных интегралов. Помните, что большая часть работы по их вычислению — это сначала поиск неопределенного интеграла.{{\, 22}} {{f \ left (x \ right) \, dx}} \) Показать решение

Для этого интеграла обратите внимание, что \ (x = 1 \) не находится в интервале интегрирования, и поэтому нам не нужно беспокоиться об этом в этой части.

Также обратите внимание, что пределы интеграла полностью лежат в диапазоне для первой функции. Для нас это означает, что при выполнении интеграла все, что нам нужно сделать, это вставить первую функцию в интеграл.

Вот интеграл.{{\, 3}} {{f \ left (x \ right) \, dx}} \) Показать решение

В этой части \ (x = 1 \) находится в пределах интегрирования. Это означает, что подынтегральная функция больше не является непрерывной в интервале интегрирования, и это, с нашей точки зрения, сдерживающий фактор. Как отмечалось выше, мы просто не можем интегрировать функции, которые не являются непрерывными в интервале интегрирования.

Кроме того, даже если бы функция была непрерывной в точке \ (x = 1 \), у нас все еще была бы проблема, заключающаяся в том, что функция на самом деле представляет собой два разных уравнения в зависимости от того, где мы находимся в интервале интегрирования.

Давайте сначала рассмотрим проблему того, что функция не является непрерывной при \ (x = 1 \). Как мы увидим, в этом случае, если мы сможем найти способ обойти эту проблему, вторая проблема также будет решена одновременно. {3} {{\ left | {3t — 5} \ right | \, dt}} \]

Показать решение

Напомним, что смысл неопределенного интегрирования (который нам нужно будет сделать в этой задаче) состоит в том, чтобы определить, какую функцию мы дифференцировали, чтобы получить подынтегральное выражение.На данный момент мы не видели никаких функций, которые будут дифференцироваться для получения абсолютного значения, и мы никогда не увидим функцию, которая будет дифференцировать, чтобы получить абсолютное значение.

Единственный способ решить эту проблему — избавиться от абсолютного значения. Для этого нам нужно вспомнить определение абсолютной величины.

\ [\ left | х \ право | = \ left \ {{\ begin {array} {* {20} {l}} x & {{\ mbox {if}} x \ ge 0} \\ {- x} & {{\ mbox {if}} x

Как только мы вспомним, что можем определить абсолютное значение как кусочную функцию, мы можем использовать работу из примера 4 в качестве руководства для вычисления этого интеграла. {{\, 3}} {{\ left | {3t — 5} \ right | \, dt}} \]

Теперь в первых интегралах \ (t <\ frac {5} {3} \) и, следовательно, \ (3t - 5 <0 \) в этом интервале интегрирования.2} - 5 \ left ({\ frac {5} {3}} \ right)} \ right)} \ right) \\ & = \ frac {{25}} {6} + \ frac {8} {3} \\ & = \ frac {{41}} {6} \ end {align *} \]

Неплохо интегрировать функции абсолютного значения. Это немного больше работы, чем «стандартный» определенный интеграл, но на самом деле это не так уж и много работы. Во-первых, определите, где количество внутри столбцов абсолютного значения отрицательное, а где положительное. Когда мы определили эту точку, все, что нам нужно сделать, это разбить интеграл так, чтобы в каждом диапазоне пределов количество внутри столбцов абсолютного значения всегда было положительным или всегда отрицательным.Как только это будет сделано, мы можем отбросить столбцы абсолютного значения (добавив отрицательные знаки, когда количество отрицательное), а затем мы можем выполнить интеграл, как мы всегда делали. 2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \]

Мораль здесь — быть осторожным и не злоупотреблять этими фактами.

Калькулятор интегралов

: интеграция с Wolfram | Alpha

Что такое интегралы?

Интеграция — важный инструмент в исчислении, который может дать первообразную или представить площадь под кривой.

Неопределенный интеграл от, обозначенный, определяется как первообразная от.Другими словами, производная от is. Поскольку производная константы равна 0, неопределенные интегралы определяются только с точностью до произвольной константы. Например, так как производная от. Определенный интеграл от до, обозначенный, определяется как область со знаком между и осью, от до.

Оба типа интегралов связаны основной теоремой исчисления. Это означает, что если непрерывен на и является его непрерывным неопределенным интегралом, то. Это означает .Иногда требуется приближение к определенному интегралу. Обычный способ сделать это — разместить под кривой тонкие прямоугольники и сложить области со знаком. Wolfram | Alpha может решать широкий спектр интегралов.

Как Wolfram | Alpha вычисляет интегралы

Wolfram | Alpha вычисляет интегралы иначе, чем люди. Он вызывает функцию Integrate системы Mathematica, которая представляет собой огромное количество математических и вычислительных исследований. Integrate не выполняет интегралы, как это делают люди.Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые используются чаще всего. Один из них включает разработку общей формы интеграла, затем дифференцирование этой формы и решение уравнений для сопоставления неопределенных символьных параметров. Даже для довольно простых подынтегральных выражений уравнения, сгенерированные таким образом, могут быть очень сложными и для их решения требуются сильные алгебраические вычислительные возможности Mathematica. Другой подход, который Mathematica использует при вычислении интегралов, состоит в том, чтобы преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений об этих очень общих математических функциях.

Хотя эти мощные алгоритмы дают Wolfram | Alpha возможность очень быстро вычислять интегралы и обрабатывать широкий спектр специальных функций, понимание того, как будет интегрироваться человек, также важно. В результате в Wolfram | Alpha также есть алгоритмы для пошаговой интеграции. В них используются совершенно разные методы интеграции, имитирующие подход человека к интегралу. Это включает интегрирование путем подстановки, интегрирование по частям, тригонометрическую замену и интегрирование по частям.

Исчисление — свойства определенных интегралов

Это устройство не может отображать анимацию Java. Вышеупомянутое статическое изображение заменяет

1. Правило нуля и обратные пределы

Аплет показывает график экспоненциальной функции с площадью под кривой от a до b зеленым цветом. Перетащите ползунок a или b , чтобы сделать a = b . Какой район? Это иллюстрирует правило нуля :

Теперь перетащите ползунки так, чтобы b < a .Что происходит с районом? Как видите, меняет пределы определенного интеграла на противоположный, или:

.

2. Постоянное множественное правило

Выберите второй пример из раскрывающегося меню. Это показывает линию и область под кривой от a до b
в зеленом. Также показана вторая функция (красным цветом), которая является постоянным кратным c первой функции.
(т.е. h ( x ) = c f ( x )).Первоначально c = 2. Что вы заметили в областях (значения областей показаны в верхнем левом углу графика)? Перетащите ползунок c или введите другие значения для c в поле ввода c . Что ты заметил? Попробуйте сделать c равным -1. Это иллюстрирует правило для постоянных множественных чисел :

Другими словами, если подынтегральное выражение в определенном интеграле умножить на константу, вы можете «вытащить константу за пределы» интеграла.

3. Дополнительное правило

Выберите третий пример. Зеленая кривая — это линия f ( x ) = x , синяя кривая — экспоненциальная функция g ( x ) = e ^x
а красная функция — их сумма, h ( x ) = f ( x ) + g ( x ). Что вы замечаете в областях? Переместите ползунки a и b и посмотрите, сохраняется ли эта связь.Вы должны заметить, что площадь под красной кривой представляет собой сумму площадей под синей и зеленой кривыми. Это имеет смысл, поскольку суммы Римана состоят только из высоких тонких прямоугольников, а высота красных прямоугольников — это просто сумма высот зеленого и синего прямоугольников.
Итак, правило добавления гласит:

Это говорит о том, что интеграл от суммы двух функций является суммой интегралов каждой функции.
Показывает плюс / минус, так как это правило работает для разницы двух функций.
(попробуйте, отредактировав определение для h ( x ) как f ( x ) — g ( x )).

4. Дополнение внутреннее

Выберите четвертый пример. Здесь показана одна функция: f ( x ) = e ^x . Зеленая область — от a до c , а синяя область — от c до b . Значения этих двух областей плюс значение области от a до b отображаются в верхнем левом углу. Что вы заметили во взаимосвязи между этими тремя областями? Попробуйте перетащить ползунок c , чтобы проверить, сохраняется ли эта связь, в то время как c находится между a и b .Теперь попробуйте перетащить c мимо a или b ; отношения все еще сохраняются? Это называется внутренним добавлением :

Другими словами, вы можете разделить определенный интеграл на два интеграла с одним и тем же подынтегральным выражением, но с разными пределами, если соблюдается шаблон, показанный в правиле.

5. Доминирование

Выберите пятый пример. Зеленая кривая представляет собой экспоненту, f ( x ) = ½ e ^x , а синяя кривая также является экспоненциальной, g ( x ) = e ^x .В интервале от a до b , g ( x ) всегда больше, чем f ( x ). Это означает, что прямоугольники в сумме Римана для г ( x ) всегда будут выше, чем прямоугольники для f ( x ). Следовательно, площадь под g будет больше, чем площадь под f , как вы можете видеть, в данном случае верно.

Если g ( x ) ≥ f ( x ) на отрезке [ a , b ], то

В качестве особого случая установите f ( x ) = 0, введя в поле определения для f и нажав Enter.Это означает, что если g положителен всюду на некотором интервале, то определенный интеграл также положителен на этом интервале.

6. Мин. — Макс. Неравенство

Выберите шестой пример. Функция: f ( x ) = e ^x , показано зеленым цветом. Высота меньшего зеленовато-серого прямоугольника соответствует минимальному значению f на интервале [ a , b ], а высота темно-серого прямоугольника является максимальным значением f на том же интервале. интервал.Ясно, что область под f находится где-то между площадью этих двух прямоугольников. Формально мы говорим, что

где min f — минимальное значение f на [ a , b ], а max f — максимальное значение f на этом интервале. ( b — a ) — ширина интервала (и показанных прямоугольников).

7. Площадь между кривыми

Выберите седьмой пример. Здесь показана область между двумя линейными функциями: f ( x ) в качестве верхней функции зеленым цветом и g ( x ) в качестве нижней функции синим цветом.Вы можете думать о площади между двумя кривыми двумя разными способами. Вы можете найти площадь верхней функции и вычесть из нее площадь нижней функции, или

Вы также можете подумать о сумме Римана, в которой вершины прямоугольников относятся к верхней функции, а нижняя часть прямоугольников — к нижней функции. Тогда высота прямоугольников будет f ( x ) — g ( x ), поэтому площадь

Попробуйте отредактировать определение g ( x ), поставив знак минус впереди (т.е.е., сделайте — 0,5 x ) и нажмите Enter. Есть ли смысл в увеличении площади между кривыми? Удалите только что добавленный минус (т.е.
g ( x ) = 0,5 x ) и получим f ( x ) = — x (т.е. поставьте знак минус перед определением для f и нажмите Enter). Что происходит с районом? Почему он отрицательный, если «верхняя» функция фактически находится ниже «нижней» функции?

8.Пересечение кривых

Выберите восемь примеров. Это показывает более сложную ситуацию, когда две функции пересекаются. Площадь слева от точки пересечения будет считаться отрицательно, потому что g ( x ) больше в этой области, а площадь справа от точки пересечения будет считаться положительно, потому что f ( x ) больше.

Исследуйте

Вы можете поэкспериментировать с собственными примерами, выбрав свойство в поле выбора; это настроит поля ввода, ползунки и график соответствующим образом.Затем вы можете ввести определения функций, значения для a , b и c (в соответствии с примером) и масштабировать / панорамировать график.

Прочие темы «Определенный интеграл»

(C) Открытый справочник по математике, 2011 г.

Все права защищены.

Производные и интегралы

Поиск определенных интегралов — математика для старших классов

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.