Свойства числа 40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Математические настройки для вашего сайта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свойства числа 173 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Математические настройки для вашего сайта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свойства числа 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Математические настройки для вашего сайта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сумма цифр | 4 |
| Произведение цифр | 0 |
| Произведение цифр (без учета ноля) | 4 |
| Все делители числа | 1, 2, 4, 5, 8, 10, 20, 40 |
| Наибольший делитель из ряда степеней двойки | 8 |
| Количество делителей | 8 |
| Сумма делителей | 90 |
| Простое число? | Нет |
Полупростое число? | Нет |
| Обратное число | 0. 025 025 |
| Римская запись | XL |
| Индо-арабское написание | ٤٠ |
| Азбука морзе | ….- —— |
Факторизация | 2 * 2 * 2 * 5 |
| Двоичный вид | 101000 |
| Троичный вид | 1111 |
| Восьмеричный вид | 50 |
| Шестнадцатеричный вид (HEX) | 28 |
| Перевод из байтов | 40 байтов |
| Цвет | RGB(0, 0, 40) или #000028 |
| Наибольшая цифра в числе (возможное основание) | 4 (5) |
| Число Фибоначчи? | Нет |
Нумерологическое значение | 4 энергия земли, постоянство, однообразие, практичность, упорство, надежность, терпеливость, усердие, стойкость |
| Синус числа | 0.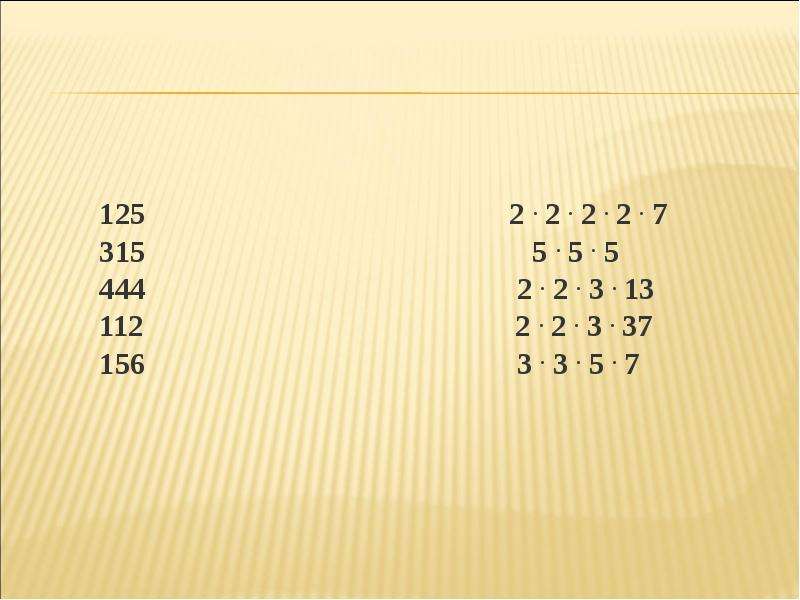 7451131604793488 7451131604793488 |
| Косинус числа | -0.6669380616522619 |
| Тангенс числа | -1.117214930923896 |
| Натуральный логарифм | 3.6888794541139363 |
| Десятичный логарифм | 1.6020599913279625 |
| Квадратный корень | 6. 324555320336759 324555320336759 |
| Кубический корень | 3.4199518933533937 |
| Квадрат числа | 1600 |
| Перевод из секунд | 40 секунд |
| Дата по UNIX-времени | Thu, 01 Jan 1970 00:00:40 GMT |
| MD5 | d645920e395fedad7bbbed0eca3fe2e0 |
| SHA1 | af3e133428b9e25c55bc59fe534248e6a0c0f17b |
| Base64 | NDA= |
| QR-код числа 40 |
77, 78.
 Разложение числа на простые множители
Разложение числа на простые множители
Это надо знать
Разложить натуральное число на множители – значит представить его в виде произведения натуральных чисел.
Разложить натуральное число на простые множители – значит представить его в виде произведения простых чисел.
При разложении больших чисел на простые множители используют запись в столбик:
Пример: Разложить число 84 на простые множители.
При разложении числа на простые множители делим его на простые множители, начиная с 2, затем берем 3, 5, 7, 11,…, пока в частном не получим число 1.
84 | 2 Делим на 2, т.к. число 84 делится на 2
42 | 2 Делим на 2, т.к. число 42 делится на 2
21 | 3 Делим на 3, т.к. число 21 делится на 3
7 | 7 Делим на 7, т.к. число 7 делится на 7
1 |
Ответ: 84 = 2∙ 2∙ 3∙ 7
Видеоурок
Домашнее задание
К уроку 77 (на 22.12)
П. 5.2
№ 1.175
Представьте число в виде произведения простых множителей:
1) 20; 2) 27; 3) 32; 4) 40; 5) 74; 6) 118.
№ 1.185
Найдите три натуральных числа, которые имеют простые делители:
1) 2; 2) 2, 3; 3) 2, 3, 5; 4) 2, 5, 7, 11.
№ 1.213
Найдите два простых числа, сумма и разность которых являются простыми числами.
К уроку 78 (на 23.12)
П. 5.2
№ 1.174
Найдите все простые делители числа:
1) 8; 2) 18; 3) 24; 4) 60; 5) 100; 6) 300.
№ 1.196
Не выполняя умножения, определите, делится ли произведение на 3, на 9. (Указание: разложите произведение на простые множители):
(Указание: разложите произведение на простые множители):
1) 3 ∙ 4 ∙ 5 ∙ 6
2) 11 ∙ 12 ∙ 13 ∙ 14
4) 42 ∙ 44 ∙ 46 ∙ 48
№ 1.216
Найдите сумму двузначных чисел, соседями которых в натуральном ряду являются простые числа.
Разложение чисел на простые множители. Онлайн калькулятор.
Разложить число на простые множители значит представить это число в виде произведения простых чисел. Любое составное натуральное число можно представить единственным образом в виде произведения простых чисел, если не учитывать порядка записей простых множителей.
Введите число
Алгоритм разложения чисел на простые множители
Проводим вертикальную черту
Слева от черты пишем число
Справа от черты пишем простой делитель этого числа
Слева записываем число которое образовалось в результате деления
Продолжаем процесс пока слева не останется 1
Рассмотрим пример
Разложим число 36
Проводим черту, записываем 36 слева. Самым маленьким простым делителем числа 36 является 2. Делим 36/2 = 18. 18 записываем под числом 36. Далее повторяем. Самым маленьким делителем числа 18 является 2. Дилим 18/2 = 9. 9 записываем под числом 18. Опять повторяем. Самым маленьким простым множителем числа 9 является 3. Делим 9/3 получается 3. Тройку записываем под 9. Тройка это простое число у которого делить только 3 и 1. Записываем 3 напротив тройки. Делим 3/3 = 1. 1 записывам под 3. Разложение закончено.
Делим 36/2 = 18. 18 записываем под числом 36. Далее повторяем. Самым маленьким делителем числа 18 является 2. Дилим 18/2 = 9. 9 записываем под числом 18. Опять повторяем. Самым маленьким простым множителем числа 9 является 3. Делим 9/3 получается 3. Тройку записываем под 9. Тройка это простое число у которого делить только 3 и 1. Записываем 3 напротив тройки. Делим 3/3 = 1. 1 записывам под 3. Разложение закончено.
Целое положительное число называется простым, если оно делится только на 1 и на само себя.
Целое положительное число называется составным, если у него есть хоть один делитель, отличный от 1 и самого себя.
Таблица составных чисел
| 4 | 6 | 8 | 9 | 10 | 12 | 14 | 15 | 16 | 18 |
| 20 | 21 | 22 | 24 | 25 | 26 | 27 | 28 | 30 | 32 |
| 33 | 34 | 35 | 36 | 38 | 39 | 40 | 42 | 44 | 45 |
| 46 | 48 | 49 | 50 | 51 | 52 | 54 | 55 | 56 | 57 |
| 58 | 60 | 62 | 63 | 64 | 65 | 66 | 68 | 69 | 70 |
| 72 | 74 | 75 | 76 | 77 | 78 | 80 | 81 | 82 | 84 |
| 85 | 86 | 87 | 88 | 90 | 91 | 92 | 93 | 94 | 95 |
| 96 | 98 | 99 | 100 | 102 | 104 | 105 | 106 | 108 | 110 |
| 111 | 112 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 |
| 122 | 123 | 124 | 125 | 126 | 128 | 129 | 130 | 132 | 133 |
| 134 | 135 | 136 | 138 | 140 | 141 | 142 | 143 | 144 | 145 |
| 146 | 147 | 148 | 150 | 152 | 153 | 154 | 155 | 156 | 158 |
| 159 | 160 | 161 | 162 | 164 | 165 | 166 | 168 | 169 | 170 |
| 171 | 172 | 174 | 175 | 176 | 177 | 178 | 180 | 182 | 183 |
| 184 | 185 | 186 | 187 | 188 | 189 | 190 | 192 | 194 | 195 |
| 196 | 198 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 |
| 208 | 209 | 210 | 212 | 213 | 214 | 215 | 216 | 217 | 218 |
| 219 | 220 | 221 | 222 | 224 | 225 | 226 | 228 | 230 | 231 |
| 232 | 234 | 235 | 236 | 237 | 238 | 240 | 242 | 243 | 244 |
| 245 | 246 | 247 | 248 | 249 | 250 | 252 | 253 | 254 | 255 |
| 256 | 258 | 259 | 260 | 261 | 262 | 264 | 265 | 266 | 267 |
| 268 | 270 | 272 | 273 | 274 | 275 | 276 | 278 | 279 | 280 |
| 282 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 |
| 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 |
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
| 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 |
| 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 |
| 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 |
| 269 | 271 | 277 | 281 | 283 | 293 | 307 | 311 |
| 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 |
| 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 |
| 571 | 577 | 587 | 593 | 599 | 601 | 607 | 613 |
| 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 |
| 727 | 733 | 739 | 743 | 751 | 757 | 761 | 769 |
| 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 |
| 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Похожие калькуляторы
Урок 3.
 простые и составные числа. разложение натурального числа на множители — Алгебра — 7 класс
простые и составные числа. разложение натурального числа на множители — Алгебра — 7 класс
Алгебра
7 класс
Урок № 3
Простые и составные числа. Разложение натурального числа на множители
Перечень рассматриваемых вопросов:
- Определения простого и составного числа, примеры простых и составных чисел.
- Разложение числа на простые множители.
- Таблица простых чисел.
Тезаурус:
Делителем натурального числа n называют натуральное число, на которое n делится без остатка
Натуральное число называют простым, если оно имеет ровно два делителя: единицу и само это число.
Натуральное число называют составным, если оно имеет более двух делителей.
Основная теорема арифметики.
Любое натуральное число, большее единицы, можно разложить на произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
Теорема 1.
Каждое отличное от единицы натуральное число имеет делитель – простое число.
Теорема 2. (теорема Евклида)
Простых чисел бесконечно много.
Разложить натуральное число на простые множители – значит представить его в виде произведения простых чисел.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
На уроке будем формулировать определения, конструировать несложные определения самостоятельно. Сформулируем определения простого и составного числа, приведём примеры простых и составных чисел. Выполним разложение числа на простые множители. Выясним, является ли число составным. Будем использовать таблицу простых чисел.
Сформулируем определения простого и составного числа, приведём примеры простых и составных чисел. Выполним разложение числа на простые множители. Выясним, является ли число составным. Будем использовать таблицу простых чисел.
Натуральные числа, имеющие только два делителя, называют простыми.
Пример:
числа 2; 3; 5; 7; 11 – простые, т. к. делятся только на 1 и сами на себя, т. е. имеют ровно два делителя.
Натуральные числа, имеющие более двух делителей, называют составными.
Пример:
числа 4; 6; 8; 10 – составные, т. к. делятся не только на 1 и сами на себя, а ещё, например, на 2, т. е. имеют более двух делителей.
Число 1 не относится ни к простым, ни к составным числам.
Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители.
Простых чисел бесконечно много.
Основная теорема арифметики.
Любое натуральное число (кроме 1) либо является простым, либо его можно разложить на простые множители, причём единственным способом.
Рассмотрим, как раскладывать составные числа на простые множители.
Число 57 – составное, т. к. кроме 1 и 57 оно делится, например, ещё на 3.
Покажем это.
Согласно признаку делимости на 3, сумма цифр должна делиться на 3. Проверяем:
5 + 7 = 12,
12 : 3 = 4.
Число 57 можно представить в виде произведения простых чисел.
При разложении числа на простые множители используют признаки делимости и применяют запись столбиком, при которой делитель располагают справа от вертикальной черты, а частное записывают под делимым.
Получаем:
57 = 3 · 12.
Рассмотрим разложение еще одного составного числа на простые множители.
120.
120 – чётное число, значит, делится на 2.
120 : 2 = 60.
60 – чётное число
60 : 2 = 30.
30 – чётное число.
30 : 2 = 15.
15 – нечётное число,
Следовательно, не делится на 2,
но делится на 3.
15 : 3 = 5.
5 – простое число.
Получаем:
120 = 2 · 2 · 2 · 3 · 5 = 23 · 3 · 5.
При выполнении задания по определению простых и составных чисел удобно использовать таблицу простых чисел.
Выясним, является ли число 337 простым или составным.
Будем считать, что каждое простое число уже разложено на множители.
Например, простое число 13 равно произведению само числа 13 и единицы.
13 = 13 · 1.
Рассмотрим задачу.
Определите самое маленькое натуральное число, которое не имеет простых делителей кроме 2 и 3.
Решение.
Не имеет простых делителей кроме 2 и 3 – это означает, что в разложении может быть 2 в любой степени и 3 любой степени.
Самое маленькое натуральное число, не является ни простым не сложным.
2, 3, 5 – натуральные числа, они есть в таблице простых чисел.
4 – составное число, которое делится на 2, но не делится на 3. Нам не подходит.
6 – составное число, которое делится на 2 и на 3. Оно удовлетворяет нашему условию.
Ответ: 6.
Итак, мы с вами узнали, какие числа называют простыми и составными.
Узнали основную теорему арифметики.
Узнали, как разложить натуральное число на простые множители.
Углубим наши знания.
Делимость на 3.
Докажем, что одно из трёх последовательных чётных чисел делится на 3
Доказательство.
Чётные числа должны делиться на 2.
Предположим противное не делиться на 3.
Тогда получаем:
первое чётное число представим в виде:
2 · 3n + 2,
тогда второе чётное число представим в виде:
2 · 3n + 4
а третье чётное число представим в виде:
2 · 3n + 6
Видим первое и второе не делятся на 3, а третье делится, так как
(2 · 3n) делится на 3 и 6 делится на 3, значит и сумма 2 · 3n + 6.
Делится на 3, по свойствам делимости.
Значит, предположение неверно и из трёх последовательных чётных чисел одно обязательно будет делиться на 3.
Разбор заданий тренировочного модуля.
1. Выберите правильный ответ.
Сколько чисел в ряду от 1 до 100 одновременно не делятся ни на 2, ни на 7?
Варианты ответа:
40
43
57
67
Решение.
Для решения задачи нужно вспомнить признаки делимости на 2.
Если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.
То есть делятся на 2 чётные числа. Таких чисел в ряду от 1 до 100 – 50 штук.
Значит, из 100 вычитаем 50 чётных чисел, которые нам не подходят.
Далее рассматриваем в ряду числа от 1 до 100, которые делятся на 7 и являются нечётными. Это: 7, 21, 35, 49, 63, 77, 91. Всего их 7 штук. Вычтем их из 50 и получим 43.
Ответ: 43.
2. Впишите правильный ответ.
Определите, какую цифру, являющуюся простым числом, нужно подставить вместо звёздочки, чтобы число f делилось на число k без остатка, если:
f = 3 ⋅ 2 ⋅ 2 ⋅ 5
и
k = 3 * 5.
Решение.
Для того чтобы одно число делилось без остатка на другое, необходимо, чтобы они имели в разложении общие множители. Чтобы число k делилось без остатка на f , необходимо, чтобы оно было меньше f и содержало только делители f. Значит, нам подходит только 2.
Ответ: 2.
множителей из 40 — из нашего калькулятора множителей
Какие множители 40?
Это целые числа, которые можно без остатка разделить на 40; они могут быть выражены как отдельные
факторы или как пары факторов. В данном случае мы представляем их обоими способами. Это математическое разложение определенного числа.
Хотя обычно это положительное целое число, обратите внимание на комментарии ниже об отрицательных числах.
Что такое факторизация 40 на простые множители?
Факторизация на простые множители — это результат разложения числа на набор компонентов, каждый член которого является простым числом.Обычно это записывается путем отображения 40 как произведения его основных множителей.
Для
40, этот результат будет:
40 = 2 x 2 x 2 x 5
(это также известно как разложение на простые множители; наименьшее простое число в этой серии описывается как наименьшее простое множитель)
40 — составное число?
Да! 40 — составное число. Это произведение двух положительных чисел, кроме 1 и самого себя.
40 — квадратное число?
Нет! 40 — это не квадратное число.Квадратный корень из этого числа (6.32) не является целым числом.
Сколько факторов у 40?
Это число состоит из 8 факторов: 1, 2, 4, 5, 8, 10, 20, 40
Более конкретно, показаны парами …
(1 * 40) (2 * 20) (4 * 10) ( 5 * 8) (8 * 5) (10 * 4) (20 * 2) (40 * 1)
Какой наибольший общий делитель 40 и другого числа?
Наибольший общий делитель двух чисел может быть определен путем сравнения факторизации на простые множители (факторизации в некоторых текстах) двух чисел.
и беря наивысший общий простой множитель.Если нет общего множителя, gcf равен 1.
Это также называется наивысшим общим множителем и является частью общих простых множителей двух чисел.
Это самый большой множитель (наибольшее число), которое два числа делят в качестве основного множителя.
Наименьший общий множитель (наименьшее общее число) любой пары целых чисел равен 1.
Как найти наименее распространенное кратное 40 и другое число?
У нас есть калькулятор наименьшего общего кратного. Решение — наименьшее общее кратное.
из двух номеров.
Что такое факторное дерево
Факторное дерево — это графическое представление возможных факторов числа и их подфакторов.
Он предназначен для упрощения факторизации.
Он создан
найти множители числа, а затем найти множители множителей числа. Процесс продолжается рекурсивно
до тех пор, пока вы не получите набор простых множителей, который является факторизацией исходного числа на простые множители.При построении дерева обязательно запомните второй элемент в факторной паре.
Как найти множители отрицательных чисел? (например, -40)
Чтобы найти множители -40, найдите все положительные множители (см. Выше), а затем продублируйте их с помощью
Выше), а затем продублируйте их с помощью
добавляя знак минус перед каждым (фактически умножая их на -1). Это устраняет негативные факторы.
(обработка отрицательных целых чисел)
40 — целое число?
Да.
Каковы правила делимости?
Делимость относится к данному целому числу, которое делится на данный делитель. Правило делимости — это сокращение
система для определения того, что делится, а что нет. Сюда входят правила о нечетных и четных числовых множителях.
Этот пример предназначен для того, чтобы учащийся мог оценить статус данного числа без вычислений.
прайм-факторизация. Калькулятор | Определение
Обратите внимание на приведенный ниже список факторизаций на простые множители, которые можно проверить с помощью нашего калькулятора разложения на простые множители.
Разложение на простые множители 2: это простое число!
Разложение на простые множители 3: это простое число!
Разложение на простые множители 4: 2 * 2
Разложение на простые множители 5: это простое число!
Разложение на простые множители 6: 2 * 3
Разложение на простые множители 7: это простое число!
Разложение на простые множители 8: 2 * 2 * 2
Разложение на простые множители 9: 3 * 3
Разложение на простые множители 10: 2 * 5
Разложение на простые множители 11: это простое число!
Разложение на простые множители 12: 2 * 2 * 3
Разложение на простые множители 13: это простое число!
Разложение на простые множители 14: 2 * 7
Разложение на простые множители 15: 3 * 5
Разложение на простые множители 16: 2 * 2 * 2 * 2
Разложение на простые множители 17: это простое число!
Разложение на простые множители 18: 2 * 3 * 3
Разложение на простые множители 19: это простое число!
Разложение на простые множители 20: 2 * 2 * 5
Разложение на простые множители 21: 3 * 7
Разложение на простые множители 22: 2 * 11
Разложение на простые множители 23: это простое число!
Разложение на простые множители 24: 2 * 2 * 2 * 3
Разложение на простые множители 25: 5 * 5
Разложение на простые множители 26: 2 * 13
Разложение на простые множители 27: 3 * 3 * 3
Разложение на простые множители 28: 2 * 2 * 7
Разложение на простые числа 29: это простое число!
Разложение на простые множители 30: 2 * 3 * 5
Разложение на простые множители 31: это простое число!
Разложение на простые множители 32: 2 * 2 * 2 * 2 * 2
Разложение на простые множители 33: 3 * 11
Разложение на простые множители 34: 2 * 17
Разложение на простые множители 35: 5 * 7
Разложение на простые множители 36: 2 * 2 * 3 * 3
Разложение на простые множители 37: это простое число!
Разложение на простые множители 38: 2 * 19
Разложение на простые множители 39: 3 * 13
Разложение на простые множители 40: 2 * 2 * 2 * 5
Разложение на простые множители 41: это простое число!
Разложение на простые множители 42: 2 * 3 * 7
Разложение на простые множители 43: это простое число!
Разложение на простые множители 44: 2 * 2 * 11
Разложение на простые множители 45: 3 * 3 * 5
Разложение на простые множители 46: 2 * 23
Разложение на простые множители 47: это простое число!
Разложение на простые множители 48: 2 * 2 * 2 * 2 * 3
Разложение на простые множители 49: 7 * 7
Разложение на простые множители 50: 2 * 5 * 5
Разложение на простые множители 51: 3 * 17
Разложение на простые множители 52: 2 * 2 * 13
Разложение на простые множители 53: это простое число!
Разложение на простые множители 54: 2 * 3 * 3 * 3
Разложение на простые множители 55: 5 * 11
Разложение на простые множители 56: 2 * 2 * 2 * 7
Разложение на простые множители 57: 3 * 19
Разложение на простые множители 58: 2 * 29
Разложение на простые множители 59: это простое число!
Разложение на простые множители 60: 2 * 2 * 3 * 5
Разложение на простые множители 61: это простое число!
Разложение на простые множители 62: 2 * 31
Разложение на простые множители 63: 3 * 3 * 7
Разложение на простые множители 64: 2 * 2 * 2 * 2 * 2 * 2
Разложение на простые множители 65: 5 * 13
Разложение на простые множители 66: 2 * 3 * 11
Разложение на простые множители 67: это простое число!
Разложение на простые множители 68: 2 * 2 * 17
Разложение на простые множители 69: 3 * 23
Разложение на простые множители 70: 2 * 5 * 7
Разложение на простые множители 71: это простое число!
Разложение на простые множители 72: 2 * 2 * 2 * 3 * 3
Разложение на простые множители 73: это простое число!
Разложение на простые множители 74: 2 * 37
Разложение на простые множители 75: 3 * 5 * 5
Разложение на простые множители 76: 2 * 2 * 19
Разложение на простые множители 77: 7 * 11
Разложение на простые множители 78: 2 * 3 * 13
Разложение на простые множители 79: это простое число!
Разложение на простые множители 80: 2 * 2 * 2 * 2 * 5
Разложение на простые множители 81: 3 * 3 * 3 * 3
Разложение на простые множители 82: 2 * 41
Разложение на простые множители 83: это простое число!
Разложение на простые множители 84: 2 * 2 * 3 * 7
Разложение на простые множители 85: 5 * 17
Разложение на простые множители 86: 2 * 43
Разложение на простые множители 87: 3 * 29
Разложение на простые множители 88: 2 * 2 * 2 * 11
Разложение на простые множители 89: это простое число!
Разложение на простые множители 90: 2 * 3 * 3 * 5
Разложение на простые множители 91: 7 * 13
Разложение на простые множители 92: 2 * 2 * 23
Разложение на простые множители 93: 3 * 31
Разложение на простые множители 94: 2 * 47
Разложение на простые множители 95: 5 * 19
Разложение на простые множители 96: 2 * 2 * 2 * 2 * 2 * 3
Разложение на простые множители 97: это простое число!
Разложение на простые множители 98: 2 * 7 * 7
Разложение на простые множители 99: 3 * 3 * 11
Разложение на простые множители 100: 2 * 2 * 5 * 5
Разложение на простые множители 104: 2 * 2 * 2 * 13
Разложение на простые множители 105: 3 * 5 * 7
Разложение на простые множители 108: 2 * 2 * 3 * 3 * 3
Разложение на простые множители 117: 3 * 3 * 13
Разложение на простые множители 120: 2 * 2 * 2 * 3 * 5
Разложение на простые множители 121: 11 * 11
Разложение на простые множители 125: 5 * 5 * 5
Разложение на простые множители 126: 2 * 3 * 3 * 7
Разложение на простые множители 130: 2 * 5 * 13
Разложение на простые множители 132: 2 * 2 * 3 * 11
Разложение на простые множители 135: 3 * 3 * 3 * 5
Разложение на простые множители 140: 2 * 2 * 5 * 7
Разложение на простые множители 144: 2 * 2 * 2 * 2 * 3 * 3
Разложение на простые множители 147: 3 * 7 * 7
Разложение на простые множители 150: 2 * 3 * 5 * 5
Разложение на простые множители 162: 2 * 3 * 3 * 3 * 3
Разложение на простые множители 175: 5 * 5 * 7
Разложение на простые множители 180: 2 * 2 * 3 * 3 * 5
Разложение на простые множители 196: 2 * 2 * 7 * 7
Разложение на простые множители 200: 2 * 2 * 2 * 5 * 5
Разложение на простые множители 210: 2 * 3 * 5 * 7
Разложение на простые множители 216: 2 * 2 * 2 * 3 * 3 * 3
Разложение на простые множители 225: 3 * 3 * 5 * 5
Разложение на простые множители 245: 5 * 7 * 7
Разложение на простые множители 250: 2 * 5 * 5 * 5
Разложение на простые множители 256: 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2
Разложение на простые множители 300: 2 * 2 * 3 * 5 * 5
Разложение на простые множители 375: 3 * 5 * 5 * 5
Разложение на простые множители 400: 2 * 2 * 2 * 2 * 5 * 5
Разложение на простые множители 500: 2 * 2 * 5 * 5 * 5
Разложение на простые множители 625: 5 * 5 * 5 * 5
Вначале 1 считалось простым числом. Только в начале 20 века большинство математиков исключили 1 из числа простых чисел. Обратите внимание, что калькулятор факторизации простых чисел не включает 1 в результаты простых чисел.
Только в начале 20 века большинство математиков исключили 1 из числа простых чисел. Обратите внимание, что калькулятор факторизации простых чисел не включает 1 в результаты простых чисел.
Наибольший общий множитель 40 и 56 (GCF 40, 56)
Ищете ли вы GCF 40 и 56? Поскольку вы находитесь на этой странице, я так и думаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий множитель для любых чисел, которые вам нужно проверить. Давайте прыгнем!
Хотите быстро узнать или показать студентам, как найти GCF двух или более чисел? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Во-первых, если вы спешите, вот ответ на вопрос «каков GCF 40 и 56?» :
GCF из 40 и 56 = 8
Каков наибольший общий фактор?
Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т. e целое число, а не десятичное), которое делится на все числа в наборе. Это также широко известно как:
e целое число, а не десятичное), которое делится на все числа в наборе. Это также широко известно как:
- Наибольший общий знаменатель (НОД)
- Наивысший общий коэффициент (HCF)
- Наибольший общий делитель (НОД)
Существует несколько различных способов вычисления GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.
Для меньших чисел вы можете просто посмотреть множители или кратные для каждого числа и найти их наибольшее общее кратное.
Для 40 и 56 эти коэффициенты выглядят так:
- Факторы для 40: 1, 2, 4, 5, 8 , 10, 20 и 40
- Факторы для 56: 1, 2, 4, 7, 8 , 14, 28 и 56
Как вы можете видеть, когда перечисляете множители каждого числа, 8 — это наибольшее число, на которое делятся 40 и 56.
Подводящие факторы
По мере того, как числа становятся больше или вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, как перечисление всех факторов станет слишком большим. Чтобы исправить это, вы можете использовать простые множители.
Перечислите все простые множители для каждого числа:
- Основные факторы для 40: 2, 2, 2 и 5
- Основные факторы для 56: 2, 2, 2 и 7
Теперь, когда у нас есть список основных факторов, нам нужно найти любые, которые общий для каждого номера.
Глядя на случаи появления общих простых множителей в числах 40 и 56, мы видим, что обычно встречающиеся простые множители — это 2, 2 и 2.
Чтобы вычислить простой множитель, умножим эти числа вместе:
GCF = 2 x 2 x 2 = 8
Найдите GCF с помощью алгоритма Евклида
Последний метод вычисления GCF 40 и 56 — использовать алгоритм Евклида. Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами GCD.
Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами GCD.
Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.
Надеюсь, сегодня вы немного научились математике и понимаете, как вычислять НОД чисел. Возьмите карандаш и бумагу и попробуйте сами. (или просто воспользуйтесь нашим калькулятором НОД — никому не скажем!)
Цитируйте, дайте ссылку или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Наибольший общий множитель 40 и 56».
 VisualFractions.com . По состоянию на 9 мая 2021 г. https://visualfractions.com/calculator/greatest-common-factor/gcf-of-40-and-56/.
VisualFractions.com . По состоянию на 9 мая 2021 г. https://visualfractions.com/calculator/greatest-common-factor/gcf-of-40-and-56/.«Наибольший общий множитель 40 и 56». VisualFractions.com , https://visualfractions.com/calculator/greatest-common-factor/gcf-of-40-and-56/. По состоянию на 9 мая 2021 г.
Наибольший общий множитель 40 и 56. VisualFractions.com. Получено с https://visualfractions.com/calculator/greatest-common-factor/gcf-of-40-and-56/.
Факторов числа
Если число может быть выражено как произведение двух целых чисел, то
целые числа называются множителями этого числа.
Итак, множители 6 равны 1, 2, 3 и 6.
Пример 1
Найдите все множители 45.
Решение:
Итак, множители 45 равны 1, 3, 5, 9, 15 и 45.
Общие факторы
10 = 2 5 = 1 10
Таким образом, делители 10 равны 1, 2, 5 и 10.
15 = 1 15 = 3 5
Таким образом, множители 15 равны 1, 3, 5 и 15.
Ясно, что 5 является множителем как 10, так и 15. Говорят, что 5 является общим числом .
коэффициент из 10 и 15.
Пример 2
Найдите общий множитель для:
a. 6 и 8
b. 14 и 21
Решение:
Простые числа
Если число имеет только два разных фактора, 1 и само,
тогда число называется простым числом .
Например, 31 = 1 31
31 — простое число, поскольку у него всего два разных множителя.
Примечание:
Но 1 не является простым числом, поскольку у него нет двух разных
факторы.
Пример 3
Выразите 150 как произведение простых чисел, т.е.е. найти свой главный фактор
разложение.
Решение:
Примечание:
Мы пробуем простые числа в порядке их величины.
Мы видим, что:
Разложение на простые множители числа является уникальным.
Это называется основной теоремой арифметики . Это
дает нам вескую причину для определения простых чисел, чтобы исключить
1.Если бы 1 было простым числом, то разложение на простые множители потеряло бы
его уникальность. Это потому, что мы могли умножить на 1 столько раз
как нам нравится в разложении.
Наивысший общий коэффициент
наивысший общий множитель (HCF) двух чисел (или
выражений) — это наибольшее число (или выражение), которое является фактором
оба.
Рассмотрим наибольший общий множитель 16 и 24.
Общие множители 2, 4 и 8. Итак, самый высокий общий множитель
составляет 8.
Примечание:
Наивысший общий делитель — произведение простого простого числа.
факторы.
Всего:
Чтобы найти наивысший общий делитель двух (или более) чисел, составьте простые множители чисел и определите общие простые множители.
Тогда наивысший общий делитель — это произведение общих простых множителей.
Пример 4
Найдите наибольший общий делитель 60 и 150.
Решение:
Разложив 60 на простые множители, получится:
Разложим 150 на простые множители:
Примечание:
Наивысший общий множитель также может быть получен методом проб и ошибок
метод .
Например, наибольший общий множитель 40 и 45 равен 5, потому что 5 — это
наибольшее число, которое точно делится на 40 и 45.
Аналогично, наибольший общий делитель 27 и 36 равен 9, потому что 9 — это
наибольшее число, которое точно делится на 27 и 36.
Ключевые термины
множителя, общие множители, простые
числа, разложение на простые множители, фундаментальный
Теорема арифметики, старший общий множитель, HCF
Калькулятор простых множителей — разложение на простые множители
Примеры разложения на простые множители
Разложение на простые множители 100:
100 = 2 * 2 * 5 * 5
Разложение 100 на простые множители с использованием показателей степени 100 = 2 2 * 5 2 .
Факторизация на простые множители 76:
76 = 2 * 2 * 19
Факторизация на простые числа 76 с использованием показателей 76 = 2 2 * 19.
Факторизация на простые числа 48:
48 = 2 * 2 * 2 * 2 * 3
Факторизация на простые числа 48 с использованием показателей 48 = 2 4 * 3.
Разложение на простые множители 36:
36 = 2 * 2 * 3 * 3
Разложение на простые множители 36 с использованием показателей 36 = 2 2 * 3 2 .
Разложение на простые множители 18:
18 = 2 * 3 * 3
Разложение на простые множители 18 с использованием показателей 18 = 2 * 3 2 .
Факторизация на простые множители 20:
20 = 2 * 2 * 5
Факторизация на простые числа 20 с использованием показателей 20 = 2 2 * 5.
Факторизация на простые числа 24:
24 = 2 * 2 * 2 * 3
Разложение на простые множители 24 с использованием показателей 24 = 2 3 * 3.
Разложение на простые множители 28:
28 = 2 * 2 * 7
Разложение на простые множители 28 в экспоненциальной форме 28 = 2 2 * 7.
Разложение на простые множители 30:
30 = 2 * 3 * 5
Разложение на простые множители 32:
32 = 2 * 2 * 2 * 2 * 2
Разложение на простые множители 32 в экспоненциальной форме 32 = 2 5 .
Факторизация на простые числа 36:
36 = 2 * 2 * 3 * 3
Факторы на простые числа 36 в экспоненциальной форме 36 = 2 2 * 3 2 .
Разложение на простые множители 40:
40 = 2 * 2 * 2 * 5
Разложение на простые множители 40 в экспоненциальной форме 40 = 2 3 * 5.
Разложение на простые множители 42:
42 = 2 * 3 * 7
Разложение на простые множители 45:
45 = 3 * 3 * 5
Разложение на простые множители 45 в экспоненциальной форме 45 = 3 2 * 5.
Разложение на простые множители 48:
48 = 2 * 2 * 2 * 2 * 3
Разложение на простые множители 48 в экспоненциальной форме 48 = 2 4 * 3.
Разложение на простые множители 50:
50 = 2 * 5 * 5
Разложение на простые множители 50 в экспоненциальной форме 50 = 2 * 5 2 .
Разложение на простые множители 52:
52 = 2 * 2 * 13
Разложение на простые множители 52 в экспоненциальной форме 52 = 2 2 * 13.
Разложение на простые множители 54:
54 = 2 * 3 * 3 * 3
Разложение на простые множители 54 в экспоненциальной форме 52 = 2 * 3 3 .
Разложение на простые множители 56:
56 = 2 * 2 * 2 * 7
Разложение на простые множители 56 с использованием показателей 56 = 2 3 * 7.
Разложение на простые множители 60:
60 = 2 * 2 * 3 * 5
Факторизация на простые множители 60 с использованием показателей 60 = 2 2 * 3 * 5.
Разложение на простые множители 63:
63 = 3 * 3 * 7
Разложение на простые множители 63 в экспоненциальной форме 63 = 3 2 * 7.
Разложение на простые множители 64:
64 = 2 * 2 * 2 * 2 * 2 * 2
Разложение на простые множители 64 в экспоненциальной форме 64 = 2 6 .
Разложение на простые множители 68:
68 = 2 * 2 * 17
Разложение на простые множители 68 в экспоненциальной форме 64 = 2 2 * 17.
Разложение на простые множители 70:
70 = 2 * 5 * 7
Разложение на простые множители 75:
75 = 3 * 5 * 5
Разложение на простые множители 75 в экспоненциальной форме 75 = 3 * 5 2 .
Разложение на простые множители 78:
78 = 2 * 3 * 13
Разложение на простые множители 80:
80 = 2 * 2 * 2 * 2 * 5
Разложение на простые множители 80 с использованием показателей 80 = 2 4 * 5.
Разложение на простые множители 81:
81 = 3 * 3 * 3 * 3
Разложение на простые множители 81 с использованием показателей 81 = 3 4 .
Разложение на простые множители 84:
84 = 2 * 2 * 3 * 7
Разложение на простые множители 84 с использованием показателей 84 = 2 2 * 3 * 7.
Разложение на простые множители 85:
85 = 5 * 17
Разложение на простые множители 90:
90 = 2 * 3 * 3 * 5
Разложение на простые множители 90 с использованием показателей 90 = 2 * 3 2 * 5.
Разложение на простые множители 96:
96 = 2 * 2 * 2 * 2 * 2 * 3
Разложение на простые множители 96 с использованием показателей 96 = 2 5 * 3.
Разложение на простые множители 98:
98 = 2 * 7 * 7
Разложение 96 на простые множители с использованием показателей 98 = 2 * 7 2 .
Факторизация на простые множители 99:
99 = 3 * 3 * 11
Факторизация на простые числа 99 с использованием показателей 99 = 3 2 * 11.
Факторы урока четвертого класса: первичное факторизация
Цель
Чтобы начать сегодняшний урок, я представил цель: Я могу найти множители для 21-40. Я объяснил: Вчера вы определили факторы для всех чисел до 20. Сегодня мы перейдем к числам 21-40. Воздух наполнился чувством волнения. Мои ученики любят, когда задачи постепенно усложняются!
Я объяснил: Вчера вы определили факторы для всех чисел до 20. Сегодня мы перейдем к числам 21-40. Воздух наполнился чувством волнения. Мои ученики любят, когда задачи постепенно усложняются!
Простые стихи Составные числа
Прежде чем приступить к нашему уроку, я хотел рассказать ученикам о простых и составных числах. Вместо того, чтобы рассказывать им значения, я хотел, чтобы они сами открыли для себя значения! Я раздал простые и не простые числа каждой группе из 2-3 студентов.У меня есть студенты, стратегически распределенные по настольным группам, чтобы их было легко объединить в пары по всем предметам!
Затем я попросил студентов разделить свои белые доски пополам. По обе стороны от белых досок ученики написали следующие вопросы: Что такое простое число? Что не является простым числом? Студенты начали изучать простые числа. Некоторые студенты начали складывать числа. Другие, «Нечетное против Четного», указывали: «Сначала я думал, что все простые числа четные, но потом я увидел два.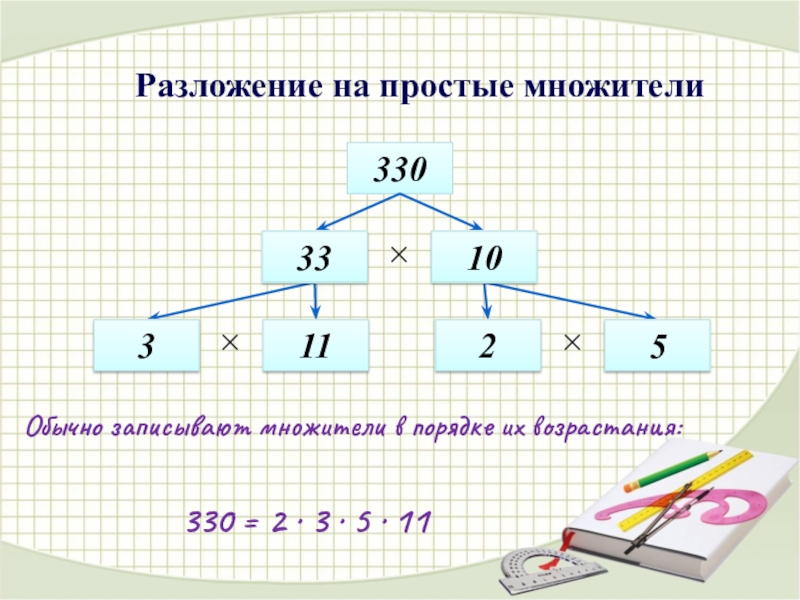 «
«
Через несколько минут я решил постепенно предоставить ученикам больше примеров и не примеров простых чисел, чтобы ускорить расследование: Пять — простое число. Через минуту я сказал: Но 8 — не простое число. Студенты добавили каждую из этих подсказок на свои листы. С каждой подсказкой ученики ахали: «О! Теперь я знаю!» Я подбегал к их столам и часто говорил: «Продолжайте думать! Вы почти у цели». Я также попросил студентов достать свои цветные плитки (ниже) и начать моделировать простые числа с помощью массивов: Конференция со студентом.
Это было тогда, когда студенты поняли это! Здесь, Студент, объясняющий простые числа, студент объясняет свое открытие! Я гордился своими учениками, которые практиковали математическую практику 1, поскольку они постоянно «анализировали данные, ограничения, отношения и цели», а также постоянно спрашивали: «Имеет ли это смысл?»
Мы обсудили определения учащихся простых и непростых чисел (пример объяснения учащегося A.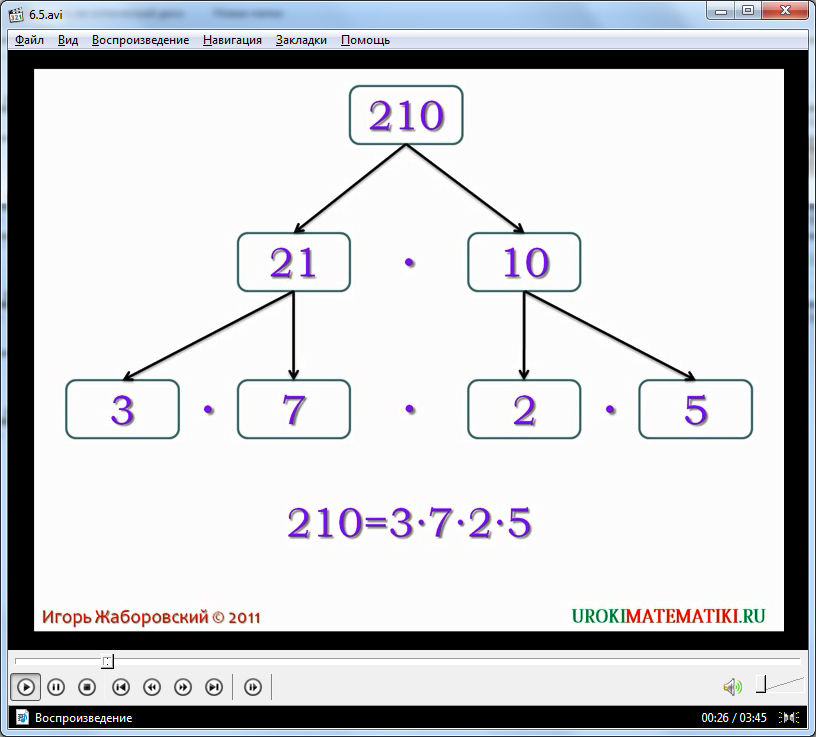 и пример объяснения учащегося B.Затем я показал следующие плакаты со словарным запасом: Простые числа и Составные числа. Мне нравилось наблюдать, как студенты связывают свои исследования, рассуждения и формальные определения.
и пример объяснения учащегося B.Затем я показал следующие плакаты со словарным запасом: Простые числа и Составные числа. Мне нравилось наблюдать, как студенты связывают свои исследования, рассуждения и формальные определения.
Словарь
Мы быстро просмотрели плакаты со словарным запасом со вчерашнего урока: умножение, множители, факторные пары и множители. Я попросил студентов повернуться и поговорить: Объясните разницу между множителем и множителем. Я знал, что поощрение студенческих разговоров повысит уровень понимания вновь усвоенной информации.Я также знал, что это поддержит математическую практику 3: создавайте жизнеспособные аргументы и критикуйте рассуждения других.
Выпечка кексов и строительство помещений
Чтобы помочь студентам разобраться в реальном приложении (Math Practice 4: Model with Mathematics), в котором факторы действительно имеют значение, я разыграл роль выпечки кексов. Я надел бейкерскую кепку и разложил мини-кексы. Затем я объяснил: Помните, как мы говорили о важности понимания факторов, если вы пекарь кексов ?! Мы обсудили, как понимание факторов помогает пекарю решить, как разложить кексы на противне для кексов (или в прямоугольной коробке).Вчера мы также говорили о важности размещения кексов идеальными прямоугольными формами (или рядами). Мне понравилось, как один студент заметил, что в противном случае кексы могут опрокинуться и покатиться!
Затем я объяснил: Помните, как мы говорили о важности понимания факторов, если вы пекарь кексов ?! Мы обсудили, как понимание факторов помогает пекарю решить, как разложить кексы на противне для кексов (или в прямоугольной коробке).Вчера мы также говорили о важности размещения кексов идеальными прямоугольными формами (или рядами). Мне понравилось, как один студент заметил, что в противном случае кексы могут опрокинуться и покатиться!
Использование уравнения простой факторизации для поиска множителей
Я попросил студентов подойти к парадному ковру со своими белыми досками. Я начал с объяснения: Сегодня мы собираемся использовать уравнения разложения на простые множители, чтобы найти делители чисел.Вот уравнение разложения на простые множители для 12: 2 x 2 x 3 = 12.
Затем я смоделировал, как умножить простые множители в уравнении простой факторизации, чтобы найти пары факторов для 12: Поиск пар факторов для 12. Я объяснил: Посмотрите, как мы можем умножить два простых множителя, например 2 x 2, на получить 4. Сколько 4 умножить на 12? (Три!) Что остается в нашем уравнении разложения на простые множители, когда мы закрываем 2 x 2? (Три!) Мы также можем умножить 2 x 3, чтобы получить 6. Сколько 6 будет 12? (Два!) Что остается в нашем уравнении разложения на простые множители, когда мы закрываем 2 x 3? (Два!)
Сколько 4 умножить на 12? (Три!) Что остается в нашем уравнении разложения на простые множители, когда мы закрываем 2 x 2? (Три!) Мы также можем умножить 2 x 3, чтобы получить 6. Сколько 6 будет 12? (Два!) Что остается в нашем уравнении разложения на простые множители, когда мы закрываем 2 x 3? (Два!)
Затем я проделал те же шаги, чтобы смоделировать пары факторов для 36. Студенты были поражены!
Использование факторного дерева для определения уравнения простой факторизации
Я объяснил и смоделировал плакат по первичной факторизации: Когда вы используете метод первичной факторизации, вы всегда выполняете следующие шаги.Студенты выполнили те же действия на своих белых досках.
1. Напишите целевое число, 24, вверху доски.
2. Задайте вопрос: какие два множителя при умножении равняются 24? Поскольку этот метод называется факторизацией PRIME, цель состоит в том, чтобы найти все простые множители для 24. Я всегда спрашиваю: входит ли 2 в 24 равномерно? Это потому, что 2 — это простой множитель, и его легко умножать и делить на! Итак … 2 равно 24? Студенты ответили: «Да! 2 x 12!» Я смоделировал, как написать 2 x 12 на плакате первичной факторизации.
Я всегда спрашиваю: входит ли 2 в 24 равномерно? Это потому, что 2 — это простой множитель, и его легко умножать и делить на! Итак … 2 равно 24? Студенты ответили: «Да! 2 x 12!» Я смоделировал, как написать 2 x 12 на плакате первичной факторизации.
3. Всякий раз, когда вы используете метод разложения на простые множители , я хотел бы, чтобы вы обвели все простые числа. Кто-нибудь пока видит простое число в нашем фактор-дереве? (Два!) А как насчет 12? 12 — простое или составное? (Составной!) Откуда ты знаешь? (поскольку у него более двух факторов)
4. Когда у вас останется составное число, спросите: « Что входит в это число равномерно?» Итак … что входит в 12 равномерно? (два… 2 х 6!) Что обвести? (2!) Почему? (2 простое!)
5. Что входит в 6 равномерно? (2! …. 2 x 3) Что следует обвести? (2 и 3!) Почему? (2 и 3 простые числа!)
6. Теперь мы готовы написать уравнение разложения на простые множители! Я смоделировал, как написать 2 x 2 x 2 x 3 = 24. Я также протестировал уравнение со студентами, указывая на каждый фактор: Посмотрим, работает ли оно! Что 2 х 2? (4) Что такое 4 x 2? (8) Что такое 8 x 3? Студенты взволнованно сказали: «24!»
Теперь мы готовы написать уравнение разложения на простые множители! Я смоделировал, как написать 2 x 2 x 2 x 3 = 24. Я также протестировал уравнение со студентами, указывая на каждый фактор: Посмотрим, работает ли оно! Что 2 х 2? (4) Что такое 4 x 2? (8) Что такое 8 x 3? Студенты взволнованно сказали: «24!»
Соединение метода первичной факторизации с методом U-Turn
В этот момент я попросил студентов вернуться к своим партам.Я попросил руководителей групп раздать наши цветные бумаги в защитных пленках. Студенты назвали одну страницу «Первичная факторизация», а другую — «Разворот». Затем я смоделировал, как использовать метод простой факторизации и метод разворота вместе, чтобы найти множители для 24. Пока я моделировал это на доске: Моделирование простой факторизации и разворота, студенты выполняли те же шаги за своими партами: Студент Пример первичной факторизации и разворота для 24.
Метод разворота для 24
1. Нарисуйте t-диаграмму.
Нарисуйте t-диаграмму.
2. Напишите целевой номер 24 в верхней части строки.
3. Правило номер один … ученик закончили мое предложение: «Всегда начинайте с 1!»
4. Спросите себя: сколько раз 1 переходит в 24? Или, другими словами: сколько 1 равно 24? Студенты сказали: «24!» Хорошо! Идеально! Напишите 24 в правом столбце напротив первого.
5. Мы продолжили писать 2 (левый столбец). Я закрыл 2 в уравнении разложения на простые множители для 24 (2 x 2 x 2 x 3 = 24).Я спросил: Если я закрою 2, что останется? (2 x 2 x 3) Что такое 2 x 2? (4) Что такое 4 x 3? ( 12) Затем я смоделировал, как вернуться к диаграмме разворота и записать 12 в правом столбце напротив множителя 2.
6. Затем мы написали 3 в левом столбце диаграммы разворота. Я спросил: Вы видите тройку в уравнении разложения на простые множители для 24? (Да!) Давайте закроем 3 и посмотрим, что осталось! Что такое 2 х 2? (4) Что такое 4 x 2? (8). Возвращаясь к диаграмме разворота, я спросил: Итак, сколько 3 умножить на 24? (8) Мы написали 8 в правом столбце напротив множителя 3.
Возвращаясь к диаграмме разворота, я спросил: Итак, сколько 3 умножить на 24? (8) Мы написали 8 в правом столбце напротив множителя 3.
7. Я написал 4 в левом столбце диаграммы разворота и спросил студентов: Кто-нибудь видит, как мы можем умножить два множителя вместе в простой факторизации, чтобы получить 4? Студенты сказали: «Да! Мы можем умножить 2 x 2. Что бы осталось? (2 x 3 … что равно 6!) Затем мы написали 6 в правом столбце диаграммы разворота напротив фактор 4.
8. Я написал 5 в левом столбце таблицы разворота и спросил студентов: Как насчет 5? Кто-нибудь знает, как мы можем умножить два множителя в разложении на простые множители, чтобы получить 5? Один студент сказал: «Да! 2 и 3!» Другой студент сказал: «Но это же умножение!» Затем я снова задал вопрос, подчеркнув слово «умножить»: Кто-нибудь знает, как мы можем умножить два множителя вместе в простой факторизации, чтобы получить 5? (Нет!)
Практика с инструкциями
Я раздал таблицу факторов B, чтобы студенты могли начать документировать факторы. Проектируя факторную диаграмму, я спросил: Какие факторы снова были для 24? Я смоделировал, как это сделать в диаграмме.
Проектируя факторную диаграмму, я спросил: Какие факторы снова были для 24? Я смоделировал, как это сделать в диаграмме.
Сегодня для управляемой практики я хотел полностью заполнить первую строку таблицы факторов B. Сначала мы начали с нахождения множителей для 21, используя методы разложения на простые множители и разворота. Я смоделировал каждую задачу на доске, в то время как студенты моделировали стратегии разложения на простые множители и разворота на своих партах: пример ученика 21 и пример ученика 22.
За это время мы также вместе заполнили верхнюю строку факторной таблицы B: завершенная таблица.
За это время я возлагал на учеников все больше и больше ответственности, давая все меньше и меньше указаний при выполнении каждой задачи. К тому времени, когда мы закончили верхний ряд, ученики были готовы продолжить самостоятельно!
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov. | |

 3245553203368
3245553203368
 152946437966
152946437966
 3862943611199
3862943611199 Si le problème persiste,
Si le problème persiste,