Содержание
Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
| (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
где
Мы будем предполагать, что матрица A имеет обратное, т. е. определитель матрицы A не равен нулю.
е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
Учитывая определение обратной матрицы, имеем A−1A=E, где E— единичная матрица. Следовательно (4) можно записать так:
или, учитывая, что Ex=x:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
Матричный вид записи системы линейных уравнений: Ax=b, где
| . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
Для этого заменяем местами строки 1 и 2:
| . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
| . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
| . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
| . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
| . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
. |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
| . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
| . |
Ответ:
Пример 2. Решить следующую систему линейных уравнений матричным методом:
| . |
Матричный вид записи системы линейных уравнений: Ax=b, где
| . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
| . |
Вычислим все алгебраические дополнения матрицы A:
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| , |
. |
Обратная матрица вычисляется из следующего выражения:
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
Ответ:
Решение системы линейных уравнений (матричный метод)
Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) матричным методом.
Для того чтобы решить систему линейных уравнений матричным методом, выберите количество неизвестных величин:
2345
Заполните систему линейных уравнений
Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Решить систему
Воспользуйтесь также:
Решение системы линейных уравнений (метод подстановки)
Решение системы линейных уравнений (метод Гаусса)
Решение системы линейных уравнений (метод Крамера)
Решение системы линейных уравнений матричным методом
Матричный метод решения СЛУ
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то система линейных уравнения сведется к следующему матричному уравнению
A · X = B,
которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю (в противном случае система уравнений будет иметь либо бесконечное количество решений, либо не иметь решений вовсе).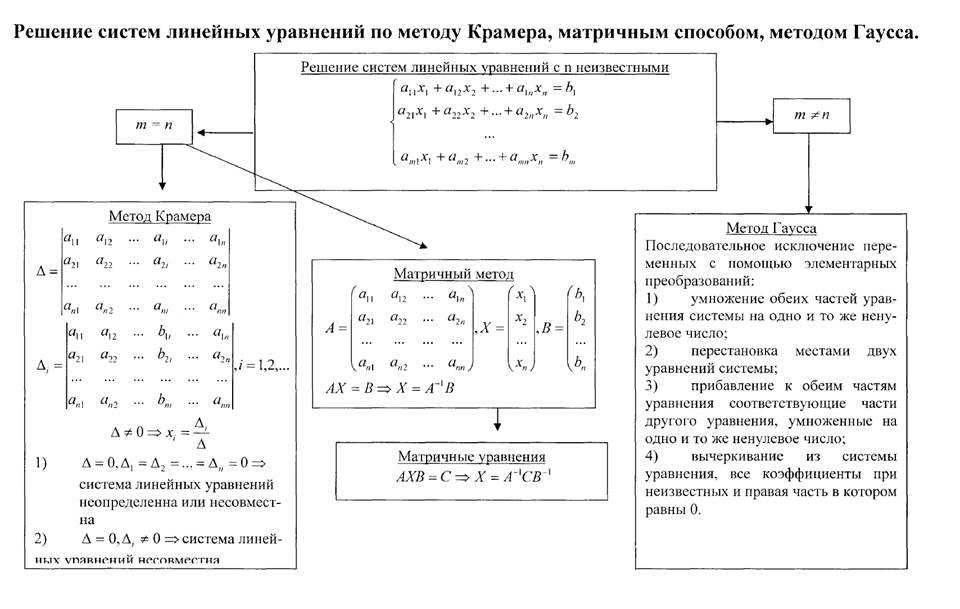
Если определитель матрицы A отличен от нуля, то решение системы уравнений можно найти следующим способом
X = A-1 · B,
где A-1 обратная матрица, которую можно найти используя, например, Онлайн сервис для вычисления обратной матрицы на нашем сайте.
Таким образом, задача решения системы линейных уравнений матричным способом сводится к нахождению обратной матрицы A-1 и последующему умножению её на матрицу-столбец B. Именно эта задача и выполняется с помощью предложенного вам онлайн калькулятора.
Решение систем линейных уравнений методом обратной матрицы онлайн
Одним из популярных методов решения систем линейных алгебраических уравнений (СЛАУ) является
метод обратной матрицы.
Рассмотрим этот метод подробнее на примере решения СЛАУ, состоящей из двух уравнений с двумя неизвестными.
a11xa12yb1a21xa22yb2
Введем обозначения:
A
— матрица СЛАУ, которая имеет вид:
Aa11a12a21a22
X
— вектор столбец неизвестных, которые нам нужно найти:
Xxy
B
— вектор столбец свободных коэффициентов:
Bb1b2
В результате, исходную СЛАУ можно записать в матричной форме:
AXB
Решим это матричное уравнение, для чего домножим его обе части слева на матрицу
A-1:
A1AXA1B
Здесь,
A-1
— это матрица, обратная к матрице
A.
Такая матрица существует для любой квадратной невырожденной матрицы (т.е. такой, определитель которой не равен нулю).
Эти условия показывают границы применимости метода обратной матрицы для решения СЛАУ. Во-первых: матрица СЛАУ
A
должна быть квадратной. Это означает, что количество уравнений должно быть равно количеству неизвестных. Во-вторых: определитель матрицы
A
должен быть отличен от нуля:
A0
Кроме того, обратная матрица обладает ещё одним замечательным свойством: её произведение на исходную матрицу коммутативно и равно единичной матрице:
A1AAA1E
Возвращаясь к решению нашего матричного уравнения, получаем:
EXXA1B
Таким образом, для того, чтобы решить СЛАУ методом обратной матрицы, сначала нам нужно убедиться, что обратная матрица существует, затем найти её и умножить на вектор
B.
Наш онлайн калькулятор предназначен для
решения СЛАУ методом обратной матрицы.
Калькулятор выдаёт пошаговое решение с описанием действий на русском языке. Уравнения СЛАУ вводятся в калькулятор в естественном виде. В качестве коэффициентов уравнения можно вводить не только числа и дроби, но и параметры — в этом случае калькулятор выдаст решение в общем виде.
Матричный метод решения систем линейных уравнений
Матричный метод может применяться в решении систем линейных
уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с
квадратной матрицей коэффициентов при неизвестных.
Другое условие применимости матричного метода — невырожденность матрицы коэффициентов
при неизвестных, то есть неравенство нулю определителя этой матрицы.
Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в
матричном виде, а затем решить её путём отыскания обратной матрицы
к матрице системы.
Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной
матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица
обозначается символом .
Пусть нужно решить систему линейных уравнений:
Запишем эту систему уравнений в матричном виде:
Обозначим отдельно как A матрицу коэффициентов
при неизвестных и как B матрицу неизвестных и матрицу свободных членов
.
Тогда
То есть, для нахождения решений системы нужно обе части уравнения
умножить на матрицу, обратную матрице коэффициентов при неизвестных
и приравнять соответствующие элементы полученных матриц.
Алгоритм решения системы линейных уравнений матричным методом разберём на следующем
примере системы линейных уравнений второго порядка.
Пример 1. Решить матричным методом систему линейных уравнений:
Решение состоит из следующих шагов.
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:
По выведенному выше последнему равенству и будем вычислять решения данной системы.
Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть
можем ли вообще применять матричный метод:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Для второго примера выберем систему линейных уравнений третьего порядка.
Пример 2. Решить матричным методом систему линейных уравнений:
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение
Всё по теме «Системы уравнений и неравенств»
Начало темы «Линейная алгебра»
Поделиться с друзьями
Матричный метод решения уравнений онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Довольно часто матричный метод используют для решения систем линейных уравнений, поскольку любую
такую систему можно представить в матричном виде, после чего, определив ее обратную матрицу, легко
решить.
Решения таких систем основано на определенном свойстве обратной матрицы: произведение обратной матрицы (А-1)
и исходной матрицы равно единичной матрице.
Так же читайте нашу статью «Решить уравнения
методом простой итерации онлайн»
Допустим, нам дана следующая система:
\[ \left\{\begin{matrix} 2x_1-x_2+3x_3=1\\ -2x_2+2x_3=2\\ 3x_1+x_2+x_3=0 \end{matrix}\right.\]
Данную систему можно решить всего за три шага:
1 шаг
Составляем матрицу:
Матрица коэффициентов при неизвестных
\[A=\begin{pmatrix} 2 & -1&3\\ 0&-2&2\\ 3&1&1 \end{pmatrix}\]
Матрица неизвестных:
\[x=\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}\]
Матрица свободных членов:
\[ B=\begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix} \]
2 шаг
Все, что мы делали в 1 шаге, было сделано для того, чтобы получить обратную матрицу коэффициентов при
неизвестных:
\[ A^{-1}=\frac{1}{4}\cdot \begin{pmatrix} -4&4&4\\ 6&-7&-4\\ 6&-5&-4 \end{pmatrix} \]
3 шаг
Определяем матрицу неизвестных:
\[ x=\frac{1}{4}\cdot \begin{pmatrix} -4&4&4\\ 6&-7&-4\\ 6&-5&-4 \end{pmatrix}\cdot \begin{pmatrix} 1\\ 2\\ 0
\end{pmatrix}=\begin{pmatrix} 1\\ -2\\ -1 \end{pmatrix} \]
Ответ:
\[x_1=1;x_2=-2;x_3=-1\]
Поскольку математика точная наука, нужно быть уверенным в правильности решения. Для этого сделаем стандартную
Для этого сделаем стандартную
проверку:
\[\left\{\begin{matrix} 2\cdot1-(-2)+3\cdot (-1)=1\\ -2\cdot(-2)+2\cdot (-1)=2\\ 3\cdot 1+(-2)+(-1)=0
\end{matrix}\right.\]
Проверка подтвердила правильность решения.
Где можно решить уравнение матричным методом онлайн с решением?
Решить уравнение матричным способом онлайн вы можете на нашем сайте https://pocketteacher.ru.
Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что
вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть
видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте
в нашу группу, мы всегда рады помочь вам.
решение неоднородной системы линейных алгебраических уравнений через обратную матрицу
Калькулятор основан на решении неоднородной системы линейных алгебраических уравнений при помощи матричного метода ( другими словами данный метод еще называют решением через обратную матрицу).
Кто еще не знаком с решениями неоднородной системы алгебраических уравнений, то вы можете ознакомится с теорией на данной страничке:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B. C.
C.
%1 century
An error occurred while importing data on line% 1.
Value: ‘%2’.
Error:
%3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Матричный метод онлайн калькулятор с подробным решением. Матричный метод онлайн
Для
решения произвольной системы линейных
уравнений нужно уметь решать системы,
в которых число уравнений равно числу
неизвестных, — так называемые
системы крамеровского типа
:
a 11
x 1
+
a 12
x 2
+…
+ a 1n
x n
=
b 1 ,
a 21
x 1
+ a 22
x 2
+…
+ a 2n
x n
=
b 2 ,
(5.3)
…
… … …
… …
a n1
x 1
+ a n1
x 2
+… + a nn
x n
= b n .
Системы (5.3) решаются
одним из следующих способов: 1) методом
Гаусса, или методом исключения неизвестных;
2) по формулам Крамера;
3) матричным
методом.
Пример
2.12
. Исследовать
систему уравнений и решить ее, если она
совместна:
5x 1
— x 2
+ 2x 3
+ x 4
= 7,
2x 1
+ x 2
+ 4x 3 —
2x 4
= 1,
x 1
— 3x 2
— 6x 3
+ 5x 4
= 0.
Решение.
Выписываем
расширенную матрицу системы:
.
Вычислим
ранг основной матрицы системы. Очевидно,
что, например, минор второго порядка в
левом верхнем углу
=
7
0; содержащие его миноры третьего порядка
равны нулю:
Следовательно,
ранг основной матрицы системы равен 2,
т.е. r(A) = 2. Для вычисления ранга расширенной
матрицы A
рассмотрим окаймляющий минор
значит,
ранг расширенной матрицы r(A)
= 3. Поскольку r(A)
r(A),
то система несовместна.
Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица — таблица элементов. О такой таблице, где m
строк и n
столбцов, говорят, что это матрица имеет размерность m
на n
.
Общий вид матрицы:
Для решения матриц
необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:
- Главная диагональ, состоящая из элементов а 11 ,а 22 …..а mn
. - Побочная диагональ, состоящая из элементов а 1n ,а 2n-1 …..а m1
.
Основные виды матриц:
- Квадратная — такая матрица, где число строк = числу столбцов (m=n
). - Нулевая — где все элементы матрицы = 0.
- Транспонированная матрица — матрица В
, которая была получена из исходной матрицы A
путем замены строк на столбцы. - Единичная — все элементы главной диагонали = 1, все остальные = 0.
- Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.
Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а 12 =а 21
, а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1
, то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.
Методы решения матриц.
Почти все методы решения матрицы
заключаются в нахождении ее определителя n
-го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.
Нахождение определителей 2-го порядка.
Для вычисления определителя матрицы А
2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:
Методы нахождения определителей 3го порядка.
Ниже приведены правила для нахождения определителя 3го порядка.
Упрощенно правило треугольника, как одного из методов решения матриц
, можно изобразить таким образом:
Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «+»; так же, для 2го определителя — соответствующие произведения берутся со знаком «-«, то есть по такой схеме:
При решении матриц правилом Саррюса
, справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком «+»; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком «-«:
Разложение определителя по строке или столбцу при решении матриц.
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Приведение определителя к треугольному виду при решении матриц.
При решении матриц
методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.
Теорема Лапласа при решении матриц.
Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ
— это определитель n
-го порядка. Выбираем в нем любые k
строк (либо столбцов), при условии k
≤
n — 1
. В таком случае сумма произведений всех миноров k
-го порядка, содержащихся в выбранных k
строках (столбцах), на их алгебраические дополнения будет равна определителю.
Решение обратной матрицы.
Последовательность действий для решения обратной матрицы
:
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Вычисляем алгебраические дополнения.
- Составляем союзную (взаимную, присоединённую) матрицу C
. - Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C
делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной. - Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.
Решение систем матриц.
Для решения систем матриц
наиболее часто используют метод Гаусса.
Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т.е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
Метод Гаусса
является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.
Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный — метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.
Матричный метод
решения СЛАУ
применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы,
называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения
СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n
неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B
, где A
— основная матрица системы, B
и X
— столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1
— обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E
, значит, X=A −1 B
. Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A
. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A
:
detA≠0.
Для однородной системы линейных уравнений
, т.е. если вектор B=0
, выполняется обратное правило: у системы AX=0
есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0
. Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы
A −1
.
Известно, что у квадратной матрицы А
порядка n
на n
есть обратная матрица A −1
только в том случае, если ее определитель ненулевой. Таким образом, систему n
линейных алгебраических уравнений с n
неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Теперь находим союзную матрицу
, транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
Итак, x=2; y=1; z=4.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например
:
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 ,
x 2 , …, x n
могут оказаться другие буквы. К примеру
:
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод
вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
×
Предупреждение
Очистить все ячейки?
Закрыть
Очистить
Инструкция ввода данных.
Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
Учитывая определение обратной матрицы, имеем A
−1 A
=E
, где E
— единичная матрица. Следовательно (4) можно записать так:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A
матрицу на вектор ограничений b
.
Примеры решения системы линейных уравнений матричным методом
Пример 1.
Решить следующую систему линейных уравнений матричным методом:
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A
запишем единичную матрицу:
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A
:
Матричный вид записи системы линейных уравнений: Ax=b
, где
Вычислим все алгебраические дополнения матрицы A
:
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| . |
Обратная матрица вычисляется из следующего выражения.
Калькулятор системы уравнений
Добро пожаловать в калькулятор системы , где мы узнаем, как решить систему линейных уравнений . Наш удобный калькулятор быстро найдет решение любой проблемы, которую вы ему дадите, и, если существует бесконечное количество решений, , он даже скажет вам, как они выглядят ! Решатель системы уравнений использует так называемый метод исключения Гаусса , но это не единственный метод, поэтому ниже мы представляем пять различных ответов на вопрос «Как решить систему уравнений?»
Давайте не будем терять ни секунды и займемся этим, не так ли?
Что такое система линейных уравнений?
Запомните все те загадки в Facebook или Instagram. , знаете, те, где три яблока равны 30, яблоко и два банана равны 18, а банан минус кокос равен двум, и вам нужно было вычислить сколько стоят яблоко, банан и кокос? Это то, что математики называют системой линейных уравнений .« Но как? Математики не используют яблоки и бананы, не так ли? » Ну, им тоже нравится держать доктора подальше и время от времени кусать яблоко, но вы правы, они не делают посчитать в яблоках . Однако нет никакой разницы, если вы правы: « Три яблока равны 30 » или 3x = 30 .
Отображенное выше значение x — это то, что мы называем переменной . Он обозначает число или элемент, значение которого мы не знаем, но о котором мы знаем и что-то .В нашем случае мы знаем, что три яблока равно 30 , но яблоко — это просто переменная, например x , поскольку мы не знаем ее значения. По сути, «, что является решением системы уравнений … » — это то же самое, что « дать мне значение яблока (или x ), , которое удовлетворяет …» Честно говоря , мы знаем, что большинство ученых хотели бы использовать бананы вместо x , но они всего не уверены в своих навыках рисования .
« Но что, черт возьми, означает linear ? » Мы говорим, что уравнение является линейным, если его переменные (будь то x или кокосы) находятся в первой степени. Это означает, что, например, они не возведены в квадрат x² , как в квадратных уравнениях, или знаменатель дроби, или квадратный корень. Однако их можно умножить на любое число, как мы имели 3 в нашем уравнении 3x = 30 . Это относится к всем переменным в уравнении .Например, уравнение -2x + 14y - 0,3z = 0 является линейным, а 10x - 7y + z² = 1 — нет.
Наконец, если у нас есть несколько уравнений, которые нужно решить вместе, мы называем их системой уравнений . Обозначим это, нарисовав фигурную скобку (или повернутый набор усов, как вам больше нравится) слева от них. Это означает, что нас интересуют только решений всех уравнений в системе . Если мы найдем значения, которые работают для первого уравнения, но не для второго, мы не будем называть это решением.
Как решить систему уравнений?
Существует различных способов решения системы линейных уравнений. Кратко опишем несколько наиболее распространенных методов.
- Замена
Первый метод, которому обучают студентов, и наиболее универсальный метод , работает, выбирая одно из уравнений, выбирая одну из переменных в нем, и делая эту переменную объектом этого уравнения .Затем мы используем это преобразованное уравнение и подставляем его каждый раз, когда эта переменная появляется в других уравнениях. Таким образом, в других уравнениях теперь на одну переменную меньше , что упрощает их решение.
Например, если у нас есть уравнение 2x + 3y = 6 и мы хотим получить из него x , то мы начинаем с , избавляясь от всего, что не содержит x с левой стороны. . Для этого мы должны вычесть 3y с обеих сторон (потому что это выражение находится слева).Это означает, что левая сторона будет 2x + 3y - 3y , что просто 2x , а правая сторона будет 6 - 3y . Другими словами, мы преобразовали наше уравнение в 2x = 6 - 3y .
Поскольку мы хотим получить x , а не 2x , нам все равно нужно избавиться от 2 . Для этого мы делим обе стороны на 2. Таким образом, слева мы получаем (2x) / 2 , что составляет всего лишь x , а справа мы имеем (6 - 3y) / 2 , что составляет 3 - 1.5лет . В итоге мы получили x = 3 - 1,5y , и мы можем использовать эту новую формулу для замены 3 - 1,5y in на каждые x в других уравнениях.
- Исключение переменных
Решение систем уравнений методом исключения означает, что мы пытаемся уменьшить количество переменных в некоторых уравнениях, чтобы упростить их решение . Для этого мы начнем с преобразования двух уравнений так, чтобы они выглядели одинаково.Чтобы быть точным, мы хотим сделать коэффициент (число рядом с переменной) одной из переменных уравнения противоположным коэффициенту той же переменной в другом уравнении . Затем мы складываем два уравнения, чтобы получить новое, в котором нет этой переменной, поэтому его легче вычислить.
Например, если у нас есть система уравнений,
2x + 3y = 6 и
4x - y = 3 ,
, то мы можем попытаться сделать коэффициент x в первом уравнении противоположным коэффициенту во втором уравнении.В нашем случае это означает, что мы хотим преобразовать 2 в противоположность 4 , то есть -4 . Для этого нам нужно умножить обе части первого уравнения на -2 , так как 2 * (-2) = -4 . Это изменяет первое уравнение на
2x * (-2) + 3y * (-2) = 6 * (-2) ,
, то есть
-4x - 6y = -12 .
Теперь мы можем добавить это уравнение ко второму ( 4x - y = 3 ), добавив левую часть к левой и правую к правой.Это дает
4x - y + (-4x - 6y) = 3 + (-12) ,
, то есть
-7y = -9 .
Мы получили новое уравнение только с одной переменной, что означает, что мы можем легко решить y . Затем мы можем подставить это число в любое из исходных уравнений, чтобы получить x .
- Метод исключения Гаусса
Это метод, используемый нашим калькулятором системы уравнений. Названный в честь немецкого математика Иоганна Гаусса, он представляет собой алгоритмическое расширение метода исключения, представленного выше. В случае всего двух уравнений это одно и то же. Однако решение систем уравнений путем регулярного исключения становится все сложнее и сложнее с появлением все большего числа уравнений и переменных. Вот где приходит на помощь метод исключения Гаусса.
Допустим, у нас есть четырех уравнений с четырьмя переменными . Чтобы найти решение нашей системы, мы хотим попытаться получить значения наших переменных одно за другим, последовательно удаляя все остальные.Для этого мы возьмем первое уравнение и первую из переменных . Мы используем его коэффициент для , чтобы исключить все вхождения этой конкретной переменной в трех других уравнениях , точно так же, как мы это сделали при обычном исключении. Таким образом, у нас остается первое уравнение, такое же, как и было, и три уравнения, теперь каждое с только тремя переменными .
Теперь посмотрим на первое уравнение, поставим его «вверх» и оставим как есть до самого конца .Мы повторяем процесс для остальных трех уравнений. Другими словами, мы берем вторую переменную и ее коэффициент из второго уравнения , чтобы исключить все вхождения этой переменной в последних двух уравнениях. Это оставляет нам первое уравнение с четырьмя переменными, второе — с тремя, а последние два — с только двумя переменными .
Затем мы объявляем второе уравнение красивым и красивым и оставляем его в покое. Мы переходим к двум оставшимся уравнениям и берем третью переменную и ее коэффициент в третьем уравнении, чтобы исключить эту переменную из четвертого равенства.
В итоге мы получаем систему из четырех уравнений, в которой первая имеет четыре переменных, вторая — три, третья — две, а последняя — только одну . Это означает, что мы можем легко получить значение четвертой переменной из четвертого уравнения (поскольку в нем нет других переменных). Затем мы подставляем это значение в третье уравнение и получаем значение третьей переменной (поскольку теперь у нее нет других переменных) и так далее.
- Графическое представление
Возможно, наименее используемый метод, но тем не менее метод.Он берет каждое из уравнений в нашей системе, и переводит их в функцию . Точки на графике такой функции соответствуют координатам, которые удовлетворяют этому уравнению. Следовательно, если мы хотим решить систему линейных уравнений, то достаточно найти всех точек пересечения линии на графике , то есть координаты, удовлетворяющие всем уравнениям.
Однако это может быть непросто. Если у нас есть только два уравнения и две переменные, то функции представляют собой линии на двумерной плоскости.Следовательно, нам просто нужно найти точку, где эти две линии пересекают .
Для трех переменных функции теперь находятся в трехмерном пространстве, а больше не линии, а плоскости . Это означает, что нам нужно будет нарисовать три плоскости (что само по себе сложно), а затем также найти, где эти плоскости пересекаются. И, если вы думаете, что это сложно, попробуйте представить четырех переменных и четырех измерений . Если это произойдет естественным образом, свяжитесь с нами, и мы направим вас к ближайшему объекту, удостоенному Нобелевской премии, или к неврологу для тщательной проверки состояния головы.
- Правило Крамера
Достаточно простой и очень простой способ решить систему линейных уравнений. Однако для этого требуется хорошее понимание матриц и их определителей . В качестве поощрения отметим, что он не нуждается ни в какой замене, ни в играх с уравнениями, это просто старая добрая базовая арифметика . Например, для системы трех уравнений с тремя переменными мы подставляем коэффициенты из этих уравнений, чтобы сформировать четыре матрицы размером три на три и вычислить их детерминанты.Мы заканчиваем делением соответствующих значений, которые мы только что получили, чтобы получить окончательное решение.
Пример: Использование решателя системы уравнений
Давайте посмотрим на одну из загадок с картинками и попробуем решить ее с помощью нашего калькулятора системы уравнений .
Первое, что нам нужно сделать, это записать все вкусные сладости в виде буквенных переменных. Мы знаем, что выражение, которое мы получим, будет далеко от , сладкого для глаза , но математики не имеют особого вкуса .Ладно, приступим к работе и оставим каламбуры на десерт .
В нашей загадке есть три символа — пончик, печенье и конфета. Мы не знаем значения ни одного из них, поэтому нам понадобятся три переменные — по одной для каждого изображения. Обычно используются такие буквы, как x , y и z , но вы можете свободно использовать другие буквы. Обозначим пончик x , печенье y , и конфету z .Это позволяет нам написать загадку выше в виде:
х + х + х = у
y + y - z = 25
z + z - x = 16 .
Итак, каково решение системы уравнений? Теперь держите лошадей. Прежде всего, мы попытаемся упростить каждое из трех выражений , прежде чем мы даже подумаем о том, как решить эту систему уравнений. Обратите внимание, что наш решатель системы уравнений не использует формулы в том виде, в котором мы имеем сейчас .В частности, у него нет никаких переменных справа от знака = , как в первом выражении. Итак, нам действительно нужно сначала поработать.
Мы берем каждое из уравнений и перемещаем все переменные в левую часть . Затем мы складываем вместе все слагаемые с той же переменной ( x , y или z ) в этом уравнении. Наконец, мы записываем слагаемые, которые мы получили, в алфавитном порядке , в терминах переменных.Это означает, что мы сначала записываем выражение с x , затем выражение с y , а затем с z .
В нашем случае это означает, что мы должны сначала переместить y в первом уравнении справа налево. Для этого вычтем y из обеих частей равенства. Это дает
х + х + х - у = у - у ,
, то есть
x + x + x - y = 0 .
Теперь вся система выглядит так:
x + x + x - y = 0
y + y - z = 25
г + г - х = 16
Теперь мы складываем все слагаемые, содержащие одну и ту же переменную .Это означает, что в первом уравнении мы складываем три x , во втором — две y , а в третьем — две z . Получаем
3x - y = 0
2y - z = 25
2z - x = 16 .
Помните, что когда мы пишем 3x , , мы имеем в виду 3 * x , или «три копии x » . Теперь мы записываем переменные в алфавитном порядке .Первые два уравнения уже имеют желаемую форму, но в последнем нам нужно переместить выражение с размером x перед выражением с z . Это дает
3x - y = 0
2y - z = 25
-x + 2z = 16
Обратите внимание, что, на первый взгляд, не похоже на выражение, которое есть в калькуляторе системы уравнений . Однако это так. Например, в первом уравнении нет никаких z .Но помните, что «нет z » означает «ноль копий z ». Следовательно, мы можем записать недостающие переменные с коэффициентами 0. Таким образом, мы получаем
3x - y + 0z = 0
0x + 2y - z = 25
-x + 0y + 2z = 16
Теперь это больше похоже на — это просто форма решателя системы уравнений! Чтобы быть уверенным, помните, что когда у нас нет числа перед переменной, тогда принято говорить, что число равно 1.Например, -y в первом уравнении фактически равно -1y .
Наконец, нам нужно определить, какие данные нам нужно взять из системы, которую мы получили, и куда поместить их в калькуляторе системы уравнений . Что ж, давайте посмотрим на первое равенство, которое у нас есть, и на верхнее равенство решателя и сравним их:
3x - y + 0z = 0
a₁x + b₁y + c₁z = d₁
Соответствие выглядит так, как выглядит: a₁ — это число рядом с x в уравнении, b₁ — это число рядом с y , c₁ — число рядом с z и d₁ — это номер справа.В нашем случае это означает, что мы должны положить a₁ = 3 , b₁ = -1 , c₁ = 0 и d₁ = 0 . Повторим это со вторым и третьим уравнениями: a₂ = 0 , b₂ = 2 , c₂ = -1 , d₂ = 25 , a₃ = -1 , b₃ = 0 , c₃ = 2 , d₃ = 16 . Как только мы дадим все эти числа , решатель системы уравнений даст нам решение . В следующем разделе мы опишем , как это сделать, шаг за шагом .
Пример: решение систем уравнений методом исключения Гаусса
Работа с печеньем и пончиками — это развлечение и игра, но давайте теперь попробуем сжечь некоторые из этих сладких калорий, описав , как решить систему уравнений , которую мы получили в предыдущем разделе:
3x - y + 0z = 0
0x + 2y - z = 25
-x + 0y + 2z = 16
Мы хотим, чтобы оставило первое уравнение равным , поскольку оно имеет ненулевой коэффициент рядом с переменной x .Однако мы будем использовать этот коэффициент для , чтобы избавиться от x в других уравнениях . Обратите внимание, что нам не нужно беспокоиться о втором, потому что его коэффициент x равен нулю. Чтобы справиться с третьим, мы удалим из него -x , сначала преобразовав его в противоположность 3x из первого уравнения. Фактически, достаточно умножить обе части третьего уравнения на 3 .
3x - y + 0z = 0
0x + 2y - z = 25
-3x + 0y + 6z = 48
Теперь у нас есть противоположные числа рядом с x в первом и последнем равенстве, мы складываем два выражения вместе
(3x - y + 0z) + (-3x + 0y + 6z) = 0 + 48 ,
, то есть
0x -y + 6z = 48 .
Теперь мы можем заменить третье уравнение на то, что мы только что получили , чтобы получить
3x - y + 0z = 0
0x + 2y - z = 25
0x - y + 6z = 48
В результате мы получили то, что в двух последних выражениях нет x , и всегда легче решить систему линейных уравнений с двумя переменными вместо трех.
Следующим шагом в методе исключения Гаусса является повторение того же процесса для последних двух уравнений .По сути, мы будем использовать ненулевой коэффициент y во втором равенстве, чтобы избавиться от y из последнего. Как мы уже делали выше, мы начинаем с преобразования -y в противоположность 2y , то есть в -2y . Для этого достаточно обе части последнего уравнения умножить на 2.
3x - y + 0z = 0
0x + 2y - z = 25
0x - 2y + 12z = 96
Теперь мы можем сложить два последних уравнения , чтобы получить
(0x + 2y - z) + (0x - 2y + 12z) = 25 + 96 ,
, то есть
0x + 0y + 11z = 121 .
Пора заменить третье уравнение
3x - y + 0z = 0
0x + 2y - z = 25
0x + 0y + 11z = 121 .
Это конечная форма системы уравнений, которую мы получаем из метода исключения Гаусса . Теперь решить систему линейных уравнений стало намного проще. Как так? Что ж, начнем с последнего равенства. В нем есть только одна переменная с ненулевым коэффициентом, а именно z .Мы можем забыть о нулевых членах, что дает нам
11z = 121 ,
, а это значит, что у нас должно быть z = 11 . Теперь, когда мы знаем, какова первая часть решения системы уравнений, мы можем использовать это знание, чтобы заменить это число на z в двух других уравнениях :
3x - y + 0 = 0
0x + 2y - 11 = 25 ,
, то есть
3x - y = 0
0x + 2y = 36 .
Теперь у нас есть второе уравнение только с одной переменной с ненулевым коэффициентом. Если забыть о нулевых членах, получим
2y = 36 ,
и, следовательно, должно быть y = 18 . Опять же, мы заменяем этим числом на y в первом уравнении :
3x - 18 = 0 ,
, что дает
3x = 18 ,
, а это означает, что x = 6 .В общем, нам удалось решить систему линейных уравнений, и нашли решение
х = 6
y = 18
г = 11
Если мы теперь посмотрим на нашу загадку с картинками, все это решение системы уравнений методом исключения приведет нас к ответу, что пончик равняется 6 , печенье равно 18 , и конфета равна 11 .
Кусок торта, не так ли?
Решение систем линейных уравнений с использованием матриц
Привет! Эта страница будет иметь смысл только тогда, когда вы немного знаете о системах линейных уравнений и матриц, поэтому, пожалуйста, пойдите и узнайте о них, если вы их еще не знаете!
Пример
Одним из последних примеров систем линейных уравнений был этот:
Пример: Решить
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y — z = 27
Затем мы решили его, используя метод «исключения»… но мы можем решить это с помощью Матриц!
Использование матриц упрощает жизнь, потому что мы можем использовать компьютерную программу (например, Матричный калькулятор), чтобы выполнять всю «обработку чисел».
Но сначала нам нужно написать вопрос в матричной форме.
в матричной форме?
ОК. Матрица — это массив чисел, верно?
Матрица
Ну, подумайте об уравнениях:
| x | + | y | + | z | = | 6 |
| 2 года | + | 5z | = | −4 | ||
| 2x | + | 5лет | – | z | = | 27 |
Их можно было бы превратить в таблицу чисел вот так:
| 1 | 1 | 1 | = | 6 | ||
| 0 | 2 | 5 | = | −4 | ||
| 2 | 5 | -1 | = | 27 |
Мы могли бы даже разделить числа до и после знака «=» на:
| 1 | 1 | 1 | 6 | |
| 0 | 2 | 5 | и | −4 |
| 2 | 5 | -1 | 27 |
Теперь похоже, что у нас есть 2 матрицы.
На самом деле у нас есть третий, это [x y z]:
Почему [x y z] идет туда? Потому что, когда мы умножаем матрицы, левая сторона становится:
Это исходная левая часть приведенных выше уравнений (вы можете это проверить).
Матричное решение
Мы можем написать это:
как это:
AX = B
где
- A — это матрица 3×3 коэффициентов x, y и z
- X — это x, y и z и
- B — это 6, −4 и 27
Тогда (как показано на странице инверсии матрицы) решение следующее:
X = A -1 B
Что это значит?
Это означает, что мы можем найти значения x, y и z (матрица X), умножив , инверсную матрицу A , на матрицу B .
Итак, давайте продолжим и сделаем это.
Во-первых, нам нужно найти , обратную матрице A (при условии, что она существует!)
Используя Матричный калькулятор, получаем:
(для упрощения чисел я оставил определитель 1 / вне матрицы)
Затем умножьте A -1 на B (мы снова можем использовать Матричный калькулятор):
И готово! Решение:
x = 5,
y = 3,
z = −2
Как и на странице Системы линейных уравнений.
Довольно изящный и элегантный, человек думает, а компьютер производит вычисления.
Просто для развлечения … Сделай это снова!
Для удовольствия (и для того, чтобы помочь вам учиться), давайте проделаем все это снова, но сначала поставим матрицу «X».
Я хочу показать вам этот способ, потому что многие люди думают, что вышеприведенное решение настолько изящно, что это, должно быть, единственный способ.
Так что решим так:
XA = B
И из-за способа умножения матриц нам нужно настроить матрицы по-другому.Строки и столбцы необходимо поменять местами («транспонировать»):
И XA = B выглядит так:
Матричное решение
Тогда (также показано на странице инверсии матрицы) решение следующее:
X = BA -1
Это то, что мы получаем для A -1 :
Фактически, это то же самое, что и обратное, которое мы получили раньше, но транспонированное (строки и столбцы меняются местами).
Затем мы умножаем B на A -1 :
И решение то же:
x = 5, y = 3 и z = −2
Это выглядело не так красиво, как предыдущее решение, но оно показывает нам, что существует более одного способа составления и решения матричных уравнений.Только будьте осторожны со строками и столбцами!
| Матрица и определитель: онлайн калькуляторы |
| Анимированный Умножение матрицы на вектор |
| Калькулятор определителя 2 неизвестных Калькулятор определителя онлайн Калькулятор определителя |
| Калькулятор определителя 3 неизвестных Детерминантный калькулятор Три уравнения с тремя неизвестными, a Утилита для численного решения |
| Калькулятор определителя 4 неизвестных Детерминантный калькулятор Четыре уравнения с четырьмя неизвестными, a Утилита для численного решения |
| Калькулятор определителя 5 неизвестных Детерминантный калькулятор Пять уравнений с пятью неизвестными, a Утилита для численного решения |
| Собственные значения матрицы 4 на 4 |
| Собственные значения матрицы 5 на 5 |
| Собственные значения матрицы 6 на 6 |
| Интерактивный Упражнения по матричной алгебре |
| Линейная алгебра Набор инструментов |
| Программа решения линейных уравнений 3 неизвестных, программа для решения линейных уравнений |
| Решатель линейных уравнений n неизвестных , программа решения линейных уравнений |
Решатель линейных, квадратичных, кубических и четвертых уравнений Линейные, квадратичные, |
| Линейный решатель это приложение решает ваши линейные системы, Решая линейное уравнение система до 20 неизвестных |
| Линейный решатель это приложение решает ваши линейные системы |
| линейный система из 3-х уравнений решает линейную систему из 3-х уравнений и 3-х неизвестных |
| Программа для решения линейных систем Решает системы линейных уравнений |
| Матрица алгебра Пошаговые линейные уравнения, матрицы и определители |
| Матричный калькулятор Решите любую систему линейных уравнений, используя метод расширенной матрицы.В калькулятор может быстро решать уравнения, определяя точки поворота и выполнение строковых операций для получения решений |
| Инструмент матричной алгебры утилита для вычисления формул с матрицами |
Матричный калькулятор |
| Матрица калькулятор матричный калькулятор, который имеет возможность вычислять определитель, сопряженная и обратная матрица 3 x 3 |
| Матрица калькулятор матричный калькулятор |
| Матрица калькулятор матричный калькулятор |
| Матрица калькулятор добавить, вычесть, произведение, транспон, обратный, Апплет матричного калькулятора |
| Матричный калькулятор вычисляет определитель, обратный вектор, собственные векторы, апплет матричного калькулятора |
| Матричный калькулятор апплет вычисляет обратные, собственные значения и собственные векторы матриц 2 x 2, 3 x 3, 4 x 4 и 5 x 5, умножает матрицу и вектор и решает матрично-векторное уравнение A x = b |
| Матричная цепь множитель |
| Матричный умножитель эта страница представляет собой инструмент, позволяющий быстро вычислить умножение (или другую формулу) двух матриц.Вам нужно только ввести свои матрицы, и щелкни! умножение двух матриц |
| Незначительный и сомножитель калькулятор |
| N X N Solver Utility — исполняемая консольная программа, которая решает N уравнений в N неизвестных |
Инструмент Pivot & Gauss-Jordan Утилита для работы со строками, поворота, |
| Инструмент Pivot & Gauss-Jordan Утилита для работы со строками, поворота, и уменьшение строк |
Инструмент решения Simplex Method Tool для линейного программирования |
| Решение линейной системы уравнений Решить данную линейную систему m уравнений с n неизвестными |
| Решение линейной системы уравнений Инструмент для решения системы линейных уравнений |
Решение системы линейных уравнений с применением обращения к матрице |
| Horizontaal |
Дом Карта сайта Электронная почта: support [at] karadimov.инфо Последнее обновление: http://educypedia.karadimov.info |
Калькулятор правила Крамерса
Как найти неизвестные переменные по правилу Крамерса?
Понятие матричного определителя появилось в Германии и Японии практически в одно и то же время.Секи впервые написал об этом в 1683 году в своем «Метод решения разрозненных проблем ». Секи разработал шаблон для определителей для $ 2 \ times 2 $, $ 3 \ times 3 $,
Матрицы $ 4 \ times 4 $ и $ 5 \ times 5 $ и использовали их для решения уравнений. В том же году Г. Лейбниц написал о методе решения
система уравнений. Этот метод хорошо известен как правило Крамера . Определитель квадратной матрицы $ A $ — это уникальное действительное число, которое является атрибутом матрицы $ A $.Определитель матрицы $ A $ обозначается $ det (A) $ или $ | A | $.
Правило Крамера — это формула для решения системы линейных уравнений. Он выводит решение в терминах определителей матрицы и матриц, полученных из нее, путем замены одного столбца вектором-столбцом правых частей уравнений. Он назван Габриэлем Крамером (17041752), и правило для произвольного числа неизвестных опубликовано в статье [Cramer, G. (1750), Introduction a l’Analyse des lignes Courbes alg ‘ebriques »(на французском ).{th} $ столбец основной матрицы вектором правых частей уравнений и вычисляем его определитель, $ D_x $.
Если главный определитель равен нулю, система линейных уравнений либо несовместна, либо имеет бесконечно много решений.
Правило Крамера в двух переменных : Рассмотрим систему уравнений:
$$ \ begin {align} & a_1x + b_1y = \ color {синий} {c_1} \\
& a_2x + b_2y = \ color {синий} {c_2} \ end {align} $$
Главный определитель $$ D = \ left |
\ begin {array} {cc}
a_1 и b_1 \\
a_2 и b_2 \\
\ end {массив}
\ right | $$
и два других детерминанта
$$ D_x = \ left |
\ begin {array} {cc}
\ color {blue} {c_1} & b_1 \\
\ color {синий} {c_2} & b_2 \\
\ end {массив}
\ right | \ quad \ mbox {и} \ quad D_y = \ left |
\ begin {array} {cc}
a_1 & \ color {синий} {c_1} \\
a_2 & \ color {синий} {c_2} \\
\ end {массив}
\ right | $$
С помощью определителей можно найти $ x $ и $ y $ по правилу Крамера как
$$ x = \ frac {D_x} {D} =
\ frac {\ left |
\ begin {array} {cc}
\ color {blue} {c_1} & b_1 \\
\ color {синий} {c_2} & b_2 \\
\ end {массив}
\ right |} {\ left |
\ begin {array} {cc}
a_1 и b_1 \\
a_2 и b_2 \\
\ end {массив}
\ right |} \ quad \ mbox {and} \ quad y = \ frac {D_y} {D} = \ frac {\ left |
\ begin {array} {cc}
a_1 & \ color {синий} {c_1} \\
a_2 & \ color {синий} {c_2} \\
\ end {массив}
\ right |} {\ left |
\ begin {array} {cc}
a_1 и b_1 \\
a_2 и b_2 \\
\ end {массив}
\ right |} $$
Если каждый определитель равен нулю, система согласована, а уравнения зависимы.У системы бесконечно много решений. Если $ D = 0 $ и $ D_x $ или $ D_y $ не равны нулю, система несовместима и не имеет решения.
Правило Крамера в трех переменных : Рассмотрим систему уравнений:
$$ \ begin {align} & a_1x + b_1y + c_1z = \ color {синий} {d_1} \\
& a_2x + b_2y + c_2z = \ цвет {синий} {d_2} \\
& a_3x + b_3y + c_3z = \ color {синий} {d_3} \\
\ end {align} $$
Главный определитель $$ D = \ left |
\ begin {array} {ccc}
a_1 и b_1 и c_1 \\
a_2 и b_2 и c_2 \\
a_3 & b_3 & c_3 \\
\ end {массив}
\ right | $$
а остальные три детерминанта
$$ D_x = \ left |
\ begin {array} {ccc}
\ color {синий} {d_1} & b_1 & c_1 \\
\ цвет {синий} {d_2} & b_2 & c_2 \\
\ color {blue} {d_3} & b_3 & c_3 \\
\ end {массив}
\ right | \ quad D_y = \ left |
\ begin {array} {ccc}
a_1 & \ color {синий} {d_1} & c_1 \\
a_2 & \ цвет {синий} {d_2} & c_2 \\
a_3 & \ color {синий} {d_3} & c_3 \\
\ end {массив}
\ right | \ quad \ mbox {и} \ quad D_z = \ left |
\ begin {array} {ccc}
a_1 & b_1 & \ color {синий} {d_1} \\
a_2 & b_2 & \ color {синий} {d_2} \\
a_3 & b_3 & \ color {синий} {d_3} \\
\ end {массив}
\ right | $$
Решение системы трех уравнений есть
$$ x = \ frac {D_x} {D}, \ quad y = \ frac {D_y} {D}, \ quad \ mbox {и} \ quad z = \ frac {D_z} {D} $$
Например, решим систему линейных уравнений:
$$ \ begin {align} & 3x + 4y + 5z = 10 \\
& 5x + 6y + 7z = 12 \\
& 4x + 5y + 0z = 15 \\
\ end {align} $$
Сначала вычисляем главный определитель:
$$ \ begin {align} D & = \ left |
\ begin {array} {ccc}
3 и 4 и 5 \\
5 и 6 и 7 \\
4 и 5 и 0 \\
\ end {массив}
\ right | \ & = \ left | \ begin {array} {ccc | cc}
3 и 4 и 5 и 3 и 4 \\
5 и 6 и 7 и 5 и 6 \\
4 и 5 и 0 и 4 и 5 \\
\ end {массив}
\верно.= 3 \ cdot6 \ cdot0 + 4 \ cdot7 \ cdot4 + 5 \ cdot5 \ cdot 5-5 \ cdot6 \ cdot4-3 \ cdot7 \ cdot5-4 \ cdot6 \ cdot0 = 12 \ end {align} $$
По аналогии,
$$ D_x = \ left |
\ begin {array} {ccc}
\ color {blue} {10} & 4 и 5 \\
\ color {blue} {12} & 6 и 7 \\
\ color {blue} {15} & 5 & 0 \\
\ end {массив}
\ right | = -80, \ quad D_y = \ left |
\ begin {array} {ccc}
3 & \ color {синий} {10} & 5 \\
5 & \ color {blue} {12} & 7 \\
4 & \ color {blue} {15} & 0 \\
\ end {массив}
\ right | = 100, \ quad D_z = \ left |
\ begin {array} {ccc}
3 и 4 & \ color {синий} {10} \\
5 и 6 & \ color {синий} {12} \\
4 и 5 & \ color {синий} {15} \\
\ end {массив}
\ right | = -8 $$
Решатель линейных уравнений
| Система m линейных уравнений от n неизвестных имеет решение тогда и только тогда, когда ранг r расширенной матрицы равен рангу матрицы коэффициентов. Если две матрицы имеют одинаковый ранг r и r = n, решение уникально. Если две матрицы имеют одинаковый ранг r и r
| |||||||||
| Другой способ решения линейной системы уравнений — это правило Крамера, которое включает только детерминанты. Рассмотрим систему уравнений:
| |||||||
Поскольку r n = 4 2 = 2, две переменные зависят от двух других переменных, и мы должны выбрать определенные значения для двух переменных
например: w = a и y = b (a, b — любое число), тогда:
| z = 1 + 2a |
| x = 4 2b + a |
Вектор пространства решений равен (4 + a 2b, b, 1 + 2a, a)
например, если мы выберем: a = 1 b = 1, то решение будет:
(7, 1, 3, 1).
Я занимаюсь математикой · Программа для решения одновременных линейных уравнений
См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование
Калькулятор, представленный ниже, решит одновременные линейные уравнения с двумя, тремя и до 10 переменными, если система уравнений имеет единственное решение.
Для систем уравнений с множеством решений используйте метод исключения Гаусса-Жордана.
Прокрутите вниз, чтобы прочитать о различных методах решения одновременных линейных уравнений.
Программа для решения одновременных линейных уравнений
Выберите размер системы.
загрузка. . .
Расчет. . .
Сообщайте о любых ошибках на [адрес электронной почты] .
Методы решения одновременных линейных уравнений
Существует как минимум пять методов решения одновременных линейных уравнений.
Например, давайте попробуем найти решение для следующего набора одновременных линейных уравнений с 3 переменными
{x & plus; y − z = 1 (1) 8x & plus; 3y − 6z = 1 (2) −4x − y & plus; 3z = 1 (3)
Метод исключения
Как следует из названия, этот метод пытается исключить переменные, пока не останется только 1 переменная.
Во-первых, посмотрите на уравнения и попытайтесь найти 2 уравнения с одинаковым коэффициентом (плюс или минус) для одинаковых переменных. Например, см. Уравнения (1) и (3). Коэффициент для y равен 1 и -1 соответственно. Мы можем сложить два уравнения, чтобы исключить y, и мы получим уравнение (4).
x & plus; y − z = 1 (1) −4x − y & plus; 3z = 1 (3) ———————— & plus ; −3x & plus; 0 & plus; 2z = 2 (4)
Обратите внимание, что уравнение (4) состоит из переменных x и z. Теперь нам нужно другое уравнение, которое имеет те же переменные, что и уравнение (4).Чтобы получить это, мы исключим y из уравнений (1) и (2). В уравнениях (1) и (2) коэффициенты при y равны 1 и 3 соответственно. Чтобы исключить y, мы умножаем уравнение (1) на 3, а затем вычитаем уравнение (2) из уравнения (1).
x & plus; y − z = 1 (1) × 3 8x & plus; 3y − 6z = 1 (2)
3x & plus; 3y − 3z = 3 (1) 8x & plus; 3 Y − 6z = 1 (2) ———————— −−5x & plus; 0y & plus; 3z = 2 (5)
Теперь, используя уравнения (4) и (5), мы можем исключить z.
−3x & plus; 2z = 2 (4) × 3 −5x & plus; 3z = 2 (5) × 2
−9x & plus; 6z = 6 (4) −10x & plus; 6 Z = 4 (5) ———————— — & plus; 01x & plus; 0z = 2 (6)
Из уравнения ( 6) получаем x = 2.Теперь мы можем подставить это значение x в уравнение (4), чтобы получить значение z.
−3 (2) & plus; 2z = 2 (4) −6 & plus; 2z = 22z = 2 & plus; 62z = 8z = 8 ÷ 2z = 4
Наконец, мы можем подставить значения x и z в уравнение (1), чтобы получить y.
2 & plus; y − 4 = 1 (1) y = 1−2 & plus; 4y = 3
Следовательно, решение системы линейных уравнений имеет вид
х = 2,
у = 3,
г = 4.
Метод замещения
Во-первых, давайте перегруппируем уравнение (1) так, чтобы только 1 переменная находилась в левой части.
x = 1 − y & plus; z (1)
Теперь давайте подставим этот x в уравнение (2).
8 (1 − y & plus; z) & plus; 3y − 6z = 1 (2) 8−8y & plus; 8z & plus; 3y − 6z = 1−5y & plus; 2z = 1−8−5y & plus; 2z = −7 (4)
Аналогичным образом подставим x в уравнение (3).
−4 (1 − y & plus; z) −y & plus; 3z = 1 (3) −4 & plus; 4y − 4z − y & plus; 3z = 13y − z = 1 & plus; 43y− z = 5 (5)
Теперь давайте перегруппируем уравнение (5) так, чтобы только 1 переменная находилась в левой части.
z = 3y − 5 (5)
Затем подставляем это значение z в уравнение (4).
−5y & plus; 2 (3y − 5) = — 7 (4) −5y & plus; 6y − 10 = −7y = −7 & plus; 10y = 3
Теперь, когда мы нашли y, мы можем подставьте это в уравнение (5), чтобы найти z.
z = 3 (3) −5 (5) z = 9−5z = 4
Наконец, мы можем подставить значение y и z в уравнение (1), чтобы получить значение x.
х = 1-3 & плюс; 4 (1) х = 2
Графический метод
Решение системы линейных уравнений с использованием графического метода выполняется путем рисования линий или плоскостей, которые представляют каждое уравнение.Решение — это координаты пересечения линий или плоскостей.
Для простоты рассмотрим систему линейных уравнений с двумя переменными.
{x & plus; y = 32x − y = −3
Постройте линии этих двух уравнений.
Как показано на графике, две прямые пересекаются в точке (0,3). Это решение системы линейных уравнений, т.е. x = 0,
у = 3.
Для системы линейных уравнений с тремя переменными решением является точка пересечения трех плоскостей, представляющих каждое уравнение.
Метод обратной матрицы
Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в матричной форме следующим образом.
AB = C12−183−6−4−13xyz = 111
Множеством решений является матрица B. Чтобы выделить только B на одной стороне уравнения, мы умножаем обе части уравнения на матрицу, обратную матрице A
A − 1AB = A − 1CB = A − 1C
Теперь, чтобы найти B, нам нужно найти A − 1. Пожалуйста, проверьте страницу матрицы, чтобы узнать, как найти обратную матрицу.
A − 1 = −323012−435B = −323012−435111B = 234
Следовательно, множество решений
х = 2,
у = 3,
г = 4.
Исключение Гаусса / Исключение Гаусса-Джордана
Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в форме расширенной матрицы следующим образом.
A = 11−1 | 183−6 | 1−4−13 | 1
Выполняя серию операций со строками (исключение Гаусса), мы можем привести указанную выше матрицу к ее эшелонированной форме по строкам.
A = 10,375−0,75 | 0,12501−0,4 | 1.4001 | 4
Затем мы можем выполнить обратную подстановку, чтобы получить значения всех неизвестных / переменных, или мы можем выполнять дальнейшие операции со строками, пока
матрица приведена в виде приведенного ряда строк (с использованием метода исключения Гаусса-Жордана).
A = 100 | 2010 | 3001 | 4
Выполняя исключение Гаусса-Жордана, мы получаем решение системы уравнений в последнем столбце: x = 2,
у = 3,
г = 4.
Чтобы просмотреть пошаговые операции со строками, см. Страницу исключения Гаусса-Джордана.
Запутались, есть вопросы? У нас есть ответы.С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области.
Джимми Си
См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование
Система двух линейных уравнений с двумя переменными Калькулятор
- Цель использования
- Исследование Руководство
- Комментарий / запрос
- Очень полезно для быстрых ответов на 2 уравнения.
[1] 2021.01.28 10:36 Мужчина / До 20 лет / Начальная школа / Ученик средней школы / Очень /
- Цель использования
- , чтобы узнать, как его использовать.
[2] 2021.01.20 20:31 Женский / 20-летний уровень / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- Для проекта строительства моста
- Комментарий / Запрос
- полезно для инженеры
[3] 2020/12/01 19:17 Мужчина / 60 лет и старше / Инженер / Полезно /
- Цель использования
- Решающая статистика
- Комментарий / запрос
- Довольно хорошо
[4] 2020/07/23 14:40 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Комментарий / Запрос
- Невозможно вычислить с помощью корневого
[5] 2020/06/23 12:09 Женский / Моложе 20 лет / Начальная школа / Младший ученик средней школы / Немного /
- Цель использования
- Математическое представление / застрял на двух линейных уравнениях
[6] 2020/03/21 05:46 Женский / До 20 лет / Начальная школа / Младший школьник / Полезно /
- Назначение
- Не терять время.
[7] 2019/11/23 21:00 Мужчины / До 20 лет ars old / Высшая школа / ВУЗ / Аспирант / Очень /
