Содержание
принцип, теорема и примеры решения задач
Задание. Решить СЛАУ
$\left\{\begin{array}{l}
2 x_{1}+x_{2}+x_{3}=2 \\
x_{1}-x_{2}=-2 \\
3 x_{1}-x_{2}+2 x_{3}=2
\end{array}\right.$ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее
строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса
(сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся 1 (это мы делаем для упрощения
вычислений):
$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r}
2 & 1 & 1 & 2 \\
1 & -1 & 0 & -2 \\
3 & -1 & 2 & 2
\end{array}\right) \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
2 & 1 & 1 & 2 \\
3 & -1 & 2 & 2
\end{array}\right)$$
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых,
Для этого от второй строки отнимаем две первых,
от третьей — три первых:
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 3 & 1 & 6 \\
0 & 2 & 2 & 8
\end{array}\right)$$
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 3 & 1 & 6 \\
0 & 1 & 1 & 4
\end{array}\right)$$
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений
поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
$$\tilde{A} \sim\left(\begin{array}{ccc|c}
1 & -1 & 0 & -2 \\
0 & 1 & 1 & 4 \\
0 & 3 & 1 & 6
\end{array}\right)$$
От третьей строки отнимаем вторую, умноженную на 3:
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 1 & 1 & 4 \\
0 & 0 & -2 & -6
\end{array}\right)$$
Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 1 & 1 & 4 \\
0 & 0 & 1 & 3
\end{array}\right)$$
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю.
Начнем с элементов третьего столбца. Надо обнулить элемент $a_{23}$, для этого от второй строки отнимем третью:
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 1 & 0 & 1 \\
0 & 0 & 1 & 3
\end{array}\right)$$
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
$$\tilde{A} \sim\left(\begin{array}{ccc|c}
1 & 0 & 0 & -1 \\
0 & 1 & 0 & 1 \\
0 & 0 & 1 & 3
\end{array}\right)$$
Полученной матрице соответствует система
$\left\{\begin{array}{l}x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3\end{array}\right.$
или $\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$
Ответ. $\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$
Метод Гаусса — примеры c решением, теоремы и формулы
Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.
Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.
Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ
Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.
Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.
Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.
У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.
Определения и обозначения
Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.
Для начала систематизируем знания о системах линейных уравнений.
Обратите внимание!
СЛАУ в зависимости от её элементов может иметь:
- Одно решение;
- много решений;
- совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.
Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:
- перемена мест уравнений системы;
- почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
- сложение к обеим частям одного из уравнений определённых частей другого уравнения.
Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.
Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:
где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.
Коэффициенты и свободные члены уравнения можно называть его элементами.
Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.
Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.
Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:
– это основная матрица СЛАУ.
– матрица столбец неизвестных переменных.
– матрица столбец свободных членов.
Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:
Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.
Обратите внимание!
Если с системой уравнений:
Произвести такие действия:
- умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
- менять местами уравнения;
- к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,
тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.
Теперь можно перейти непосредственно к методу Гаусса.
Нужна работа? Есть решение!
Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.
Подробнее Гарантии Отзывы
Простейшие преобразования элементов матрицы
Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:
Из уравнения запишем расширенную матрицу:
Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.
Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.
Определение
Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.
На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:
1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:
.
2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).
3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.
4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.
Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.
5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:
Для удобства умножаем первую строку на (-3):
Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:
В итоге получилось такое преобразование:
Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:
В матрице верхняя строка преобразовалась:
Первую строку делим на и преобразовалась нижняя строка:
И верхнюю строку поделили на то же самое число :
Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.
Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:
На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:
.
Обратите внимание!
Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.
Алгоритм решения методом Гаусса пошагово
После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:
Шаг 1. Переписываем систему в виде матрицы
Записываем матрицу:
Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю
Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .
Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .
Шаг 3. Приводим матрицу к ступенчатому виду
Теперь вторую строку можно поделить на 2 и получается:
Верхнюю строку делим на и приводим матрицу к ступенчатому виду:
Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.
Шаг 4. Записываем эквивалентную систему
После наших элементарных преобразований получилась эквивалентная система:
Шаг 5. Производим проверку (решение системы обратным путём)
Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:
находим : ,
,
.
После находим :
,
.
Тогда:
.
Как видим, уравнение решено правильно, так как ответы в системе совпадают.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений
Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.
Дана система уравнений:
Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.
Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :
Из последнего, третьего уравнения мы видим, что .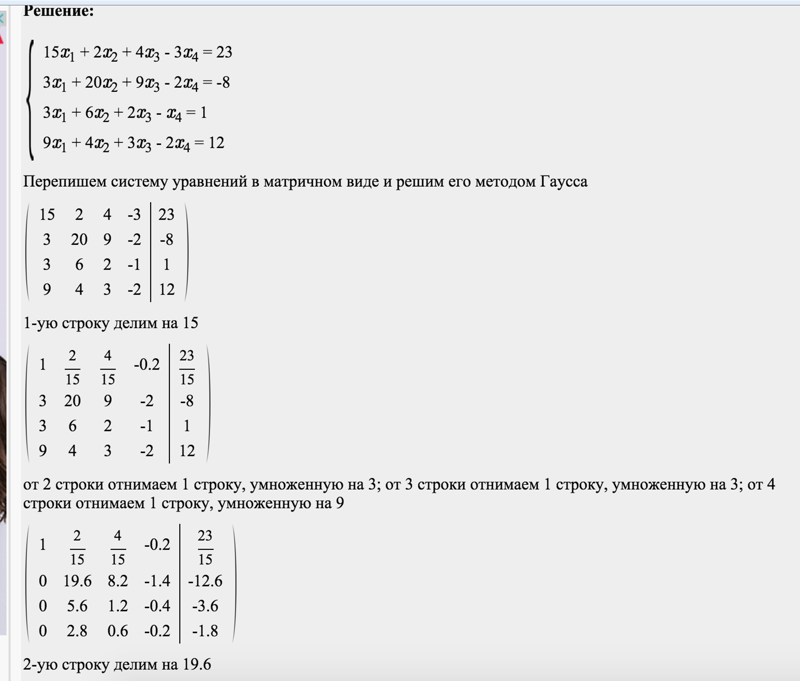 Из второго уравнения находим . И последнее, находим первое уравнение .
Из второго уравнения находим . И последнее, находим первое уравнение .
Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.
Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:
- берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
- берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .
И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:
Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:
Рассмотрим такую систему:
В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.
Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.
В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.
Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений
Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.
Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.
В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:
1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.
Например, вам попалась подобная система:
У нас получается такая ситуация
Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.
Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.
2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:
Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:
В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.
3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же уже исключались, тогда переходим к , и т. д.
Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :
Такая система уравнений после преобразования выглядит так:
Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:
Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:
Допусти, что система уравнений стала:
В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:
Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:
В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:
Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , , – произвольные числа.
Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.
В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:
= =
В итоге, получился результат, который можно и записать.
Ответ
,
,
,
,
,
.
Примеры решения методом Гаусса
Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.
Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.
Пример 1
Задача
Решить систему линейных алгебраических уравнений методом Гаусса:
Решение
Выписываем матрицу, куда добавляем столбец свободных членов:
Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:
Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).
Соответственно, первая строка остаётся неизменной, а вторая поменяется:
Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:
. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:
Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.
Итак, у нас получился ступенчатый вид матрицы:
Записываем новую систему уравнений:
Для проверки решаем систему обратным ходом. Для этого находим сначала :
Так как найден, находим :
.
Подставляем в изначальную нашу систему уравнений найденные и :
и .
Как видите из решения, система уравнений решена верно. Запишем ответ.
Ответ
Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.
Пример 2
Задача
Решить систему уравнений методом Гаусса:
Решение
Составляем матрицу, куда вписываем и свободные члены:
Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:
Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:
То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:
Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:
В результате получилась ступенчатая система уравнений:
Сначала находим : ,
.
Обратный ход:
Итак, уравнение системы решено верно.
Ответ
,
,
.
Пример 3
Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.
Задача
Решите систему уравнений методом Гаусса:
Решение
В уравнении , то есть – ведущий член и пусть ≠ 0
Из данного уравнения составим расширенную матрицу:
Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.
Поменяем вторую и третью строку местами и получим:
Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:
Получилась такая матрица:
Также, учитывая, что = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:
Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,
из третьего: = = =
второе уравнение находим: = = = 2,
из первого уравнения: = .
Значит, решение системы такое: (1, 2, -1, -2).
Ответ
,
,
,
.
Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.
Пример 4
Задача
Решить систему уравнений методом Гаусса:
Решение
Записываем расширенную матрицу системы:
Сначала смотрим на левое верхнее число:
Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:
Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:
Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:
Получился ступенчатый вид уравнения:
Проверяем:
,
,
,
,
.
.
Ответ
,
,
.
Заключение
Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.
Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.
Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.
Литература для общего развития:
Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.
Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.
пособие – Казанский университет – 2012 – 302 с.
Метод Гаусса – теорема, примеры решений обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру
в чем суть, решение системы уравнений, примеры с объяснением
Благодаря великим ученым было открыто множество эффективных теорем для работы со сложными математическими задачами. Один из таких примеров — метод Гаусса.
Метод Гаусса — что это такое
Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.
Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:
- Нет необходимости сравнивать уравнения для оценки совместимости.
- Решение систем равенств, в которых число определителей совпадает или не совпадает с количеством неизвестных переменных.
- Поиск решений для уравнений с нулевым определителем.

- Сравнительно небольшое количество вычислительных операций для получения результата.
Основные определения и обозначения
Матрицы: определение и свойства
Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.
Важным параметром матрицы является размер:
- ширина — это количество строк, обозначают буквой m;
- длину выражают числом столбцов, записывают буквой n.
Источник: bigpicture. ru
ru
Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.
Определитель
Матрица обладает крайне важной характеристикой. Таким параметром является определитель. Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:
- Если диагональ обладает наклоном в правую сторону, то знак «+».
- Для диагоналей, наклоненных влево, знак «–».
Источник: wp.com
Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.
Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:
- из числа строк и числа столбцов выбрать наименьшее и обозначить его k;
- отметить в матрице произвольным образом k столбцов и k строк.

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.
Классификация систем
Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:
По этой причине совместные системы подразделяют на следующие типы:
- определенные, обладающие одним решением, в которых наблюдается равенство ранга матрицы и количество неизвестных;
- неопределенные;
- обладающие бесконечным числом решений с рангом матрицы, который меньше количества неизвестных.
В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.
Источник: asiaplustj.info
Основные правила и разрешаемые преобразования при использовании метода Гаусса
Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:
Список элементарных преобразований:
- Перестановка строк. При перемене записей в системе местами ее решение не меняется. Можно менять место строк в матрице, учитывая столбец со свободными членами.
- Произведение всех элементов строк и некоторого коэффициента. Сокращаются большие числа в матрице, и исключаются нули. При этом множество решений сохраняется без изменений, а дальнейшие манипуляции существенно упрощаются. Важным условием является отличие от нуля коэффициента.
- Удаление строк, которые содержат пропорциональные коэффициенты. Данное преобразование следует из предыдущего пункта. При условии, что две или более строк в матрице обладают пропорциональными коэффициентами, то при произведении или делении одной из строк на коэффициент пропорциональности получают две или более абсолютно одинаковые строки. В этом случае лишние строки исключают, оставляя только одну.
- Удаление нулевой строки. Бывают случаи, когда в процессе манипуляций с уравнениями возникает строка, все элементы которой, в том числе свободный член, равны нулю.
 Нулевую строку допустимо исключать из матрицы.
Нулевую строку допустимо исключать из матрицы. - Суммирование элементов одной строки с элементами другой, умноженными на некоторый коэффициент, в соответствующих столбцах. Данное преобразование имеет наиболее важное значение из всех перечисленных.
Особенности использования метода Гаусса для решения СЛАУ
На первом этапе система уравнений записывается в определенном виде. Пример выглядит следующим образом:
Источник: wp.com
Коэффициенты необходимо представить в виде таблицы. С правой стороны в отдельном столбце записаны свободные члены. Данный блок отделен для удобства решения. Матрицу со столбцом со свободными членами называют расширенной.
Источник: wp.com
Затем основная матрица с коэффициентами приводится к верхней треугольной форме. Данное действие является ключевым моментом при решении системы уравнений с помощью метода Гаусса. По итогам преобразований матрица должна приобрести такой вид, чтобы слева внизу находились одни нули:
Источник: wp. com
com
При записи новой матрицы в виде системы уравнений можно отметить, что последняя строка уже содержит значение одного из корней, которое в дальнейшем подставляется в уравнение выше для нахождения следующего корня и так далее. Подобное описание позволяет разобраться в методе Гаусса в общих чертах.
Обратный и прямой ход метода Гаусса
В первом случае необходимо представить запись расширенной матрицы системы. При выполнении обратного метода Гаусса далее в главную матрицу добавляют столбец со свободными членами.
Источник: wp.com
Суть такого способа заключается в выполнении элементарных преобразований, по итогам которых данная матрица приводится к ступенчатому или треугольному виду. В этом случае над или под главной диагональю матрицы располагаются только нули.
Источник: wp.com
Варианты дальнейших действий:
- перемена строк матрицы местами, при наличии одинаковых или пропорциональных строк их можно исключить, кроме одной;
- деление либо умножение строки на любое число, не равное нулю;
- удаление нулевых строк;
- добавление строки, умноженной на число, не равное нулю, к другой строке.

Имея преобразованную систему с одной неизвестной Xn, которая становится известной, можно выполнить поиск в обратном порядке остальных неизвестных с помощью подстановки известных х в уравнения системы, вплоть до первого. Данный способ называют обратным методом Гаусса.
Примеры решений с объяснением
Пример 1
Требуется решить с помощью метода Гаусса систему линейных уравнений, которая выглядит следующим образом:
Источник: wp.com
Решение
Необходимо записать расширенную матрицу:
Источник: wp.com
Затем нужно выполнить преобразования. В результате матрица должна приобрести треугольный вид. Для этого следует умножить первую строку на (3) и умножить вторую строку на (-1). В результате суммирования второй и первой строк получается следующее:
Источник: wp.com
Далее следует умножить третью строку на (-1). После добавления третьей строки ко второй получаем следующие преобразования:
Источник: wp. com
com
После этого необходимо умножить первую строку на (6) и вторую строку на (13). Далее следует добавить вторую строку к первой:
Источник: wp.com
После того, как система преобразована, остается вычислить неизвестные:
\(x_{3}=\frac{98}{49}=2\)
\(x_{2}=\frac{14-7x_{3}}{6}=\frac{14-7*2}{6}=0\)
\(x_{3}=\frac{-9+5x_{2}+6x_{3}}{3}=\frac{-9+5*0+6*2}{3}=1\)
Данный пример демонстрирует единственное решение системы.
Источник: supertics.com
Пример 2
Необходимо решить систему уравнений, которая выглядит следующим образом:
Источник: wp.com
Решение
Необходимо составить матрицу:
Источник: wp.com
Согласно методу Гаусса уравнение первой строки по итогам преобразований не меняется. Удобнее, когда левый верхний элемент матрицы обладает наименьшим значением. В таком случае первые элементы остальных строк после преобразований будут равны нулю. Таким образом, составленная матрица будет решаться проще, если на место первой строки поставить вторую:
вторая строка:
\(k = (-a_{21} /a_{11}) = (-3/1) = -3\)
\(a»_{21} = a_{21} + k×a_{11} = 3 + (-3)×1 = 0\)
\(a» _{22} = a_{22} + k×a _{12} = -1 + (-3)×2 = -7\)
\(a»_{ 23} = a_{23} + k×a_{13} = 1 + (-3)×4 = -11\)
b» 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24
третья строка:
\(k = (-a_{31} /a_{11}) = (-5/1) = -5\)
\(a»_{31} = a_{31} + k×a_{11} = 5 + (-5)×1 = 0\)
\(a»_{32} = a_{32} + k×a_{12} = 1 + (-5)×2 = -9\)
\( a»_{33} = a_{33} + k×a_{13} = 2 + (-5)×4 = -18\)
\( b»_3 = b_3 + k×b_1 = 3 + (-5)×12 = -57\)
Матрица с промежуточными результатами манипуляций будет иметь следующий вид:
Источник: wp. com
com
Благодаря некоторым операциям можно придать матрице наиболее удобный вид. К примеру, вторую строку можно избавить от всех «минусов» путем умножения каждого элемента на «-1». Можно заметить, что для третьей строки характерны все элементы, кратные трем. В этом случае строка сокращается с помощью произведения каждого элемента на «-1/3». Минус позволит удалить отрицательные значения.
Источник: wp.com
Далее следует приступить к манипуляциям со второй и третьей строками. Необходимо суммировать третью и вторую строки. Вторая строка при этом умножается на такой коэффициент, при котором элемент а 32 будет равен нулю.
\(k = (-a_{32} /a_{22}) = (-3/7) = -3/7\)
В случае, когда некоторые преобразования приводят в результате к получению не целого числа, следует оставить его в этом виде. Таким образом, вычисления будут более точными. Затем при получении ответов можно определиться с его дальнейшем округлением или переводом в другую форму записи.
\(a»_{32} = a_{32} + k×a_{22} = 3 + (-3/7)×7 = 3 + (-3) = 0\)
\(a»_{33} = a_{33} + k×a_{23} = 6 + (-3/7)×11 = -9/7\)
\(b»_3 = b_3 + k×b_2 = 19 + (-3/7)×24 = -61/7\)
Преобразованная матрица будет иметь следующий вид:
Матрица обладает ступенчатым видом. Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».
Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».
Источник: wp.com
Затем необходимо представить запись матрицы в виде системы уравнений для вычисления корней.
x + 2y + 4z = 12 (1)
7y + 11z = 24 (2)
Найти корни можно обратным методом Гаусса. Уравнение (3) содержит значение z:
y = (24 — 11×(61/9))/7 = -65/9
С помощью первого уравнения можно определить х:
x = (12 — 4z — 2y)/1 = 12 — 4×(61/9) — 2×(-65/9) = -6/9 = -2/3
Подобная система является совместной и определенной, для которого характерно единственное решение. Ответ будет следующим:
x 1 = -2/3, y = -65/9, z = 61/9.
Метод Гаусса предполагает последовательное исключение неизвестных. Методика справедлива в случае решения квадратных систем линейных алгебраических уравнений. Несмотря на простоту метода, многие студенты сталкиваются с некоторыми трудностями в процессе поиска правильного решения. Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.
Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными — это система уравнений вида
(1)
Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m — уравнений, n — количество неизвестных. x1, x2,…, xn — неизвестные, которые следует определить.
В системе (1) – фиксированные коэффициенты, b1, b2, …, bm — свободные члены — предполагаются известными.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .
Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.
Система линейных уравнений может быть представлена в матричной форме как:
или:
Ax = b
Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:
(2)
Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.
Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:
(3)
Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b1:A = A1, b=b1.
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
Имеем систему уравнений A2x = b2:
где
3 шаг.
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на
При этом получим систему A3x = b3:
(k+1)-ый шаг:
Здесь
Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:
и вектор
Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения
(5)
эквивалентного начальной системе линейных алгебраических уравнений.
При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
.
Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A — квадратная NxN — матрица.
Рассмотрим задачу Ax = b.
Пусть также некоторая норма в пространстве RN
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина называется числом обусловленности.
Очевидно:
- если A — диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.
Тогда справедливо следующее неравенство:
Доказательство. Имеем:
Имеем:
Так как
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
В начало
Содержание портала
Решение уравнений методом Гаусса | matematicus.ru
С помощью метода Гаусса можно решить любую систему линейных уравнений с различным числом уравнений и неизвестных переменных. И именно этим свойством этот метод превосходит матричный метод и метод Крамера.
Суть метода состоит в приведении системы линейных уравнений к ступенчатому (треугольному) виду за счет последовательного исключения неизвестных. Затем её решения с помощью обратной подстановки.
Допустимые преобразования матрицы:
- Перестановка местами двух строк или двух столбцов;
- Умножение строки на число, которое не равно 0;
- Прибавление одной строки к другой.

- Исключение или добавление нулевой строки
Допустим, дана система линейных алгебраических уравнений с четырьмя уравнениями и четырьмя неизвестными.
Составим расширенную матрицу СЛАУ:
Затем первое уравнение СЛАУ делим на a11. При этом a11≠0, если равно нуля, то переставляем две строки или два столбца местами так, чтобы избавится от нуля. После полученное уравнение умножаем на a21 и вычитаем из второго уравнения, дальше, умножаем на a31 и вычитаем из третьего уравнения и т.д.
Также поступаем и с оставшемся уравнениями, т.е. со вторым, третьем и четвёртым. В итоге должна получится матрица ступенчатого или треугольного вида.
Система уравнений примет вид
Такую систему элементарно решить обратным ходом, т.е. последовательным решением уравнений от нижнего к верхнему.
Рассмотрим наиболее подробно метод Гаусса при решении СЛАУ на практике.
Пример 1
Решить методом Гаусса систему уравнений
Решение
Составим расширенную матрицу системы уравнений:
Первую строку разделим на a11, но так как в этой строке a11=0, то необходимо поменять строку у которой первый элемент не равен нулю. Выберем по модулю наибольшей элемент, это a41=2 Поэтому поменяем первую и четвёртую строки местами.
Получаем:
Первую строку разделим на a11=2. Получим матрицу:
Умножаем элементы первой строки на -1 и прибавляем к элементам второй строк. Получим матрицу:
Умножаем элементы первой строки на -1 и прибавляем к элементам третьей строки.
Четвёртую строку оставляем без изменений, так как её первый элемент равен нулю.
Теперь первый столбец не трогаем.
Начинаем повторять действия, которые применяли ранее.
Второе уравнение разделим на a22=-1/2, тогда
Умножаем элементы второй строки на -1/2 и прибавляем к элементам третьей строки.
Умножаем элементы второй строки на -1 и прибавляем к элементам четвёртой строки.
Первый и второй столбец не трогаем.
Третьей столбец разделим на 2.
Умножаем элементы третьей строки на -1 и прибавляем к элементам четвёртой строки.
Получаем ступенчатую систему алгебраических уравнений:
Отсюда, решая систему снизу вверх, получаем корни системы уравнений
Приведём простой пример краткой записи решения СЛАУ методом Гаусса
Пример 2
Решить систему линейных уравнений с тремя неизвестными методом Гаусса.
Решение
Составим расширенную матрицу системы линейных уравнений .
Следовательно, искомая система может быть представлена в ступенчатом виде:
Решая последовательно уравнение, получаем:
Ответ: z = 3; y = 2; x = 1
Метода Гаусса: примеры решения СЛАУ: понятия, определения, примеры задач
Найти решение этого же примера методом Гаусса в матричной форме записи:
3×1+2×2+x3+x4=-2×1-x2+4×3-x4=-1-2×1-2×2-3×3+x4=9×1+5×2-x3+2×4=4
Как решать?
Расширенная матрица системы представлена в виде:
x1 x2 x3 x432111-14-1-2-2-3115-12-2-194
Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.
Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на -a21a11=-13, -a31a11=—23=23 и на -а41а11=-13.
Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на -а32(1)а22(1)=-23-53=-25 и -а42(1)а22(1)=-133-53=135:
x1 x2 x3 x43211|-20-53113-43|-130-23-7353|2330133-4353|143~
x1 x2 x3 x4~3211|-20-53113-43|-130-23+(-25)(-53)-73+(-25)11353+(-25)(-43)|233+(-25)(-13)0133+135(-53)-43+135×11353+135(-43)|143+135(-13)~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415-95|195
Теперь исключаем переменную x3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а43(2)а33(2)=-415-195=4119.
x1 x2 x3 x43211|-20-53113-43|-1300-195115|39500415-95|195~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415+4119(-195)-95+4119×115|195+4119×395~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|3950005619|39219
Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:
x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219
стала диагональной, т.е. приняла следующий вид:
x1 x2 x3 x43000|а10-5300|а200-1950|а30005619|39219, где а1, а2, а3 — некоторые числа.
Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на
-1155619=-209280, на —435619=1942 и на -15619=1956.
x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219~
x1 x2 x3 x4~3211+(-1956)5619|-2+(-1956)392190-53113-43+1942×5619|-13+1942×3921900-195115+(-209280)5619|395+(-209280)392190005619|39219~
x1 x2 x3 x4~3210|-90-531130|900-1950|-3850005619|39219
Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на
-113-195=5557 и на -1-195=519.
x1 x2 x3 x43210|-90-531130|900-1950|-3850005619|39219~
x1 x2 x3 x4~321+519(-195)0|-9+519(-385)0-53113+5557(-195)0|9+5557(-385)00-1950|-3850005619|39219~
x1 x2 x3 x4~3210|-110-5300|5300-1950|-3850005619|39219
На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на -2-53=65.
x1 x2 x3 x43210|-110-5300|5300-1950|-3850005619|39219~
x1 x2 x3 x4~32+65(-53)00|-11+65×53)0-5300|5300-1950|-3850005619|39219~
x1 x2 x3 x4~3000|-90-5300|5300-1950|-3850005619|39219
Полученная матрица соответствует системе уравнений
3×1=-9-53×2=53-195×3=-3855619×4=39219, откуда находим неизвестные переменные.
Ответ: x1=-3, x2=-1,x3=2,x4=7.
МЕТОД ГАУССА — Системы линейных уравнений
Ме́тод Га́усса
– классический метод решения системы линейных алгебраических уравнений (СЛАУ).
Это метод последовательного исключения переменных, когда с помощью элементарных
преобразований система уравнений приводится к равносильной системе треугольного
вида, из которой последовательно, начиная с последних (по номеру), находятся
все переменные системы.
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он
был известен и до К. Ф. Гаусса. Первое известное описание данного
метода – в китайском трактате «Математика в девяти книгах».
Пусть исходная
система выглядит следующим образом
Матрица A называется основной матрицей системы, – столбцом свободных членов.
Тогда, согласно
свойству элементарных преобразований над строками, основную матрицу этой
системы можно привести к ступенчатому виду (эти же преобразования нужно
применять к столбцу свободных членов):
При этом будем
считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы
находится в верхнем левом углу, то есть в него входят только коэффициенты при
переменных .
Тогда переменные называются главными
переменными. Все остальные называются свободными.
Если хотя бы одно
число , где , то рассматриваемая система несовместна,
т.е. у неё нет ни одного решения.
Пусть для любых .
Перенесём
свободные переменные за знаки равенств и поделим каждое из уравнений системы на
свой коэффициент при самом левом (, где — номер строки):
где
Если свободным
переменным системы (2) придавать все возможные значения и решать новую систему
относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к
верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена
путём элементарных преобразований над исходной системой (1), то по теореме об
эквивалентности при элементарных преобразованиях системы (1) и (2)
эквивалентны, то есть множества их решений совпадают.
Условие
совместности
Упомянутое выше
условие для всех может быть сформулировано в
качестве необходимого и достаточного условия совместности:
Напомним, что
рангом совместной системы называется ранг её основной матрицы (либо
расширенной, так как они равны).
Алгоритм
решения СЛАУ методом Гаусса подразделяется на два этапа.
- На первом этапе осуществляется так называемый
прямой ход, когда путём элементарных преобразований над строками систему
приводят к ступенчатой или треугольной форме, либо устанавливают, что
система несовместна. А именно, среди элементов первого столбца матрицы
выбирают ненулевой, перемещают его на крайнее верхнее положение
перестановкой строк и вычитают получившуюся после перестановки первую
строку из остальных строк, домножив её на величину, равную отношению
первого элемента каждой из этих строк к первому элементу первой строки,
обнуляя тем самым столбец под ним. После того, как указанные
преобразования были совершены, первую строку и первый столбец мысленно
вычёркивают и продолжают пока не останется матрица нулевого размера. Если
на какой-то из итераций среди элементов первого столбца не нашёлся
ненулевой, то переходят к следующему столбцу и проделывают аналогичную
операцию. - На втором этапе осуществляется так называемый
обратный ход, суть которого заключается в том, чтобы выразить все
получившиеся базисные переменные через небазисные и построить фундаментальную
систему решений, либо, если все переменные являются базисными, то выразить
в численном виде единственное решение системы линейных уравнений. Эта
процедура начинается с последнего уравнения, из которого выражают
соответствующую базисную переменную (а она там всего одна) и подставляют в
предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.
Каждой строчке соответствует ровно одна базисная переменная, поэтому на
каждом шаге, кроме последнего (самого верхнего), ситуация в точности
повторяет случай последней строки.
Метод Гаусса требует арифметических операций.
В простейшем случае алгоритм выглядит так:
- Обратный ход. Из последнего ненулевого уравнения
выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения.
Повторяя эту процедуру для всех базисных переменных, получаем
фундаментальное решение.
Пример 1
Покажем, как
методом Гаусса можно решить следующую систему:
Обнулим
коэффициенты при во второй и третьей строчках. Для
этого прибавим к ним первую строчку, умноженную на и 1, соответственно:
Теперь обнулим
коэффициент при в третьей строке, вычтя из неё
вторую строку, умноженную на 4:
В результате мы
привели исходную систему к треугольному виду, тем самым закончим первый этап
алгоритма.
На втором этапе
разрешим полученные уравнения в обратном порядке. Имеем:
из третьего;
из второго, подставив
полученное
из первого, подставив
полученные и .
Таким образом
исходная система решена.
В случае, если
число уравнений в совместной системе получилось меньше числа неизвестных, то
тогда ответ будет записываться в виде фундаментальной системы решений.
Систем линейных уравнений: исключение Гаусса
Системы
линейных уравнений:
Решение методом исключения Гаусса (стр.
6 из 7)
Разделы: Определения,
Решение по графику, Подстановка,
Исключение / добавление, исключение по Гауссу.
Решение трех переменных,
линейных систем с тремя уравнениями сложнее, по крайней мере, на начальном этапе, чем
решение систем с двумя переменными, потому что требуемые вычисления
более грязный.Вам нужно будет очень аккуратно работать, и вам следует
планируйте использовать много бумаги для заметок. Метод решения этих систем
является расширением метода сложения двух переменных, поэтому сделайте
конечно ты знаешь это
метод хорошо и
может использовать его последовательно правильно.
Хотя метод решения
основан на добавлении / исключении, попытка выполнить фактическое добавление имеет тенденцию
становится очень запутанным, поэтому существует систематизированный метод решения трех или более переменных
системы.Этот метод называется «исключением по Гауссу» (с
уравнения заканчиваются так называемой «строковой формой»).
Начнем с простого, и
работаем над более сложными примерами.
- Решите следующие проблемы
система уравнений.
Достаточно легко увидеть
как действовать в этом случае. Я просто подставлю обратно значение z -value
из третьего уравнения во второе, решите результат для
л , г.
а затем подключите z
и y в
первое уравнение и решите результат для x .
10 л
3 (3) = 11
10 y 9 = 11
10 y = 20
y
= 2
5x +
4 (2) (3) = 0
5 x + 8 3 = 0
5 x + 5 = 0
5 x = 5
x = 1
Тогда решение
( х ,
y , z ) = (1, 2, 3).
Причина, по которой эта система была
Легко решить, что система была «треугольной»; это относится
к уравнениям, имеющим форму треугольника, из-за нижних уравнений
содержащий только более поздние переменные.
Дело в том, что в этом
формат, система проста в решении. И гауссовское исключение — это
метод, который мы будем использовать для преобразования систем в эту верхнетреугольную форму, используя
операции со строками, которые мы изучили, когда применили метод сложения.
- Решите следующие проблемы
система уравнений с использованием исключения Гаусса.
Уравнение не решается
для переменной, поэтому мне нужно будет выполнить умножение и сложение
чтобы упростить эту систему. Чтобы отслеживать свою работу, напишу
вниз на каждом шагу, когда я иду. Но я сделаю свои вычисления на бумаге для заметок.
Вот как я это сделал:
Первое, что нужно сделать
состоит в том, чтобы избавиться от ведущих x -термов
в два ряда.А пока я просто посмотрю, какие строки будут легко
расчистить; Я могу поменять строки позже, чтобы перевести систему в «верхний
треугольной «формы. Нет правила, которое гласит, что я должен использовать
x — срок
из первой строки, и в этом случае, думаю, будет проще
используйте термин x
из третьей строки, так как его коэффициент просто «1».
Поэтому я умножу третью строку на 3,
и добавьте его в первую строку.Я делаю вычисления на бумаге для заметок:
… а потом записываю
результатов:
(Когда мы решали
системы с двумя переменными, мы могли умножить строку, переписав систему
в сторону, а затем добавить. Для этого нет места в
система с тремя переменными, поэтому нам и нужна бумага для заметок.)
Предупреждение: поскольку я не
на самом деле ничего не делаю с третьей строкой, я скопировал ее без изменений,
в новую матрицу уравнений.Я б / у
третий ряд, но я на самом деле не менял
Это. Не путайте «использование» с «изменением».
Чтобы получить меньшие числа
для коэффициентов умножу первую строку пополам:
Теперь умножу
третий ряд на 5
и добавьте это ко второму
строка. Работаю на бумаге для заметок:
… а потом записываю
результаты: Авторские права
Элизабет Стапель 2003-2011 Все права защищены
Я ничего не делал
с первым рядом, поэтому я скопировал его без изменений. Я работал с
третий ряд, но я работал только на
вторая строка, поэтому вторая строка обновляется, а третья строка копируется
более без изменений.
Хорошо, теперь
x — столбец
удаляется, за исключением ведущего члена в третьей строке.Так что дальше
Приходится работать над колонкой и .
Предупреждение: Начиная с третьего
уравнение имеет член x ,
Я больше не могу использовать его ни в одном из двух других уравнений (или я
отменить мой прогресс). Я могу работать с уравнением, но не с
Это.
Если я добавлю в два раза больше первого
строки во вторую строку, это даст мне ведущую 1
во втором ряду.Я не буду
избавились от ведущего y -терм
во втором ряду, но я его преобразовал (не вмешиваясь
дробями) в более простую форму. (Вы должны сохранить
обратите внимание на такого рода упрощения.) Сначала я делаю царапину
работа:
… а потом записываю
результатов:
Теперь могу использовать второй
ряд, чтобы убрать и -семестр
в первом ряду.Вторую строку умножу на 7
и добавить. Сначала я царапаю
работа:
… а потом записываю
результатов:
Я могу сказать что
z
сейчас, но для большей точности я разделю первую строку на
43.
Затем я переставляю ряды, чтобы придать им верхнетреугольную форму:
Теперь я могу начать процесс
обратного решения:
Тогда решение
( х ,
y , z ) = ( 2,
3, 1 ) .
Примечание: нет ничего священного
о шагах, которые я использовал для решения указанной выше системы; там ничего не было
Особо о том, как я решил эту систему. Вы могли бы работать в другом
упорядочивайте или упрощайте разные строки, и все равно получите правильный ответ.
Эти системы достаточно сложны, поэтому вряд ли
один правильный способ вычисления ответа. Так что не беспокойтесь о том, «как
она знала, что делать дальше? », потому что здесь нет правила.я просто
делал все, что пришло мне в голову; Я делал то, что казалось самым простым или что-то в этом роде
пришла в голову первая. Не волнуйтесь, если бы вы использовали совершенно другой
шаги. Если каждый шаг на этом пути верен, вы придумаете
Такой же ответ.
В приведенном выше примере я мог
пошли дальше в своих вычислениях и более тщательно проработали
строковые операции, очищая все термины и
кроме этого во второй строке и во всех терминах z
кроме того, что в первой строке.Это то, что процесс тогда
выглядело так:
Так я могу просто читать
от значений x ,
л , г.
и z ,
и мне не нужно заморачиваться с обратной заменой. Это более полное
метод решения называется «методом исключения Гаусса-Жордана» (с
уравнения, попадающие в так называемый «пониженный ряд-эшелон»
форма»).Многие тексты доходят до исключения Гаусса, но я
всегда было легче продолжать и делать Гаусс-Джордан.
Обратите внимание, что я выполнил две строковые операции
сразу на этом последнем шаге перед переключением строк. Пока я не
работая с и работая на в той же строке на том же шаге,
это нормально. В этом случае я работал с первой строкой и
рабочая по второй и третий ряды.
<< Предыдущая
Вверх | 1
| 2 | 3 | 4
| 5 | 6 | 7 |
Вернуться к указателю Далее
>>
Цитируйте эту статью | Стапель, Елизавета. |
Системы линейных уравнений: исключение Гаусса
Решение линейной системы с матрицами с использованием исключения Гаусса
После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.
Что такое гауссовское исключение
Исключение Гаусса — это название метода, который мы используем для выполнения трех типов операций со строками матрицы над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы. Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.
Эти два шага метода исключения Гаусса различаются не операциями, которые вы можете использовать с их помощью, а результатом, который они производят.Шаг прямого исключения относится к сокращению строки, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Цель такого этапа — продемонстрировать, имеет ли система уравнений, изображенная в матрице, единственное возможное решение, бесконечное множество решений или просто отсутствие решения. Если обнаружено, что система не имеет решения, то нет причин продолжать сокращение строки матрицы на следующем этапе.
Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой.На этом последнем шаге будет получена сокращенная форма матрицы, которая, в свою очередь, дает общее решение системы линейных уравнений.
Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически оперировать строками матрицы следующими тремя способами (или комбинацией):
- Перестановка двух рядов
- Умножение строки на константу (любую константу, отличную от нуля)
- Добавление строки в другую строку
Итак, решение линейной системы с матрицами с использованием исключения Гаусса оказывается структурированным, организованным и довольно эффективным методом.
Как выполнить исключение по Гауссу
На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, это все о матрице, которая у вас есть в ваших руках, и необходимых операциях со строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:
Пример 1
Обратите внимание, что в этот момент мы можем заметить, что эта система линейных уравнений разрешима с единственным решением для каждой из ее переменных.То, что мы выполнили до сих пор, — это первый этап сокращения строк: прямое исключение. Мы можем продолжить упрощение этой матрицы еще больше (что приведет нас ко второму этапу обратной подстановки), но нам это действительно не нужно, поскольку на этом этапе система легко разрешима. Таким образом, мы смотрим на получившуюся систему, чтобы решить ее напрямую:
Уравнение 5: Полученная линейная система уравнений для решения
Из этого набора мы можем автоматически заметить, что значение переменной z равно: z = -2.Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:
В последний раздел этого урока добавлено больше задач исключения Гаусса. Обязательно проработайте их, чтобы практиковаться.
Разница между исключением по Гауссу и по Гауссу Иордану
Разница между гауссовым исключением и гауссовым методом исключения Жордана состоит в том, что один создает матрицу в форме эшелона строк, а другой — матрицу в форме уменьшенного ряда.Матрица формы эшелона строк имеет верхнюю треугольную композицию, где любые нулевые строки находятся внизу, а ведущие члены находятся справа от ведущего члена из строки выше. Уменьшенная форма эшелона выходит за рамки еще большего упрощения (иногда даже достигая формы единичной матрицы).
Уравнение 8: Разница между формой эшелона и формой ряда эшелонов
История исключения Гаусса и его названия довольно интересны, вы будете удивлены, узнав, что название «Гауссовский» было присвоено этой методологии по ошибке в прошлом веке.На самом деле было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому уроку, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал эту технику, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.
На самом деле нет никакой физической разницы между исключением Гаусса и исключением Гаусса Джордана, оба процесса следуют одному и тому же типу операций со строками и их комбинациям, их различие зависит от результатов, которые они производят. Многие математики и учителя во всем мире будут относиться к исключению Гаусса и исключению Гаусса Джордана как к методам создания матрицы эшелонированной формы по сравнению с методом создания матрицы уменьшенной эшелонированной формы, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно рассматривать также как поворотное исключение Гаусса).
Мы оставим подробное объяснение форм сокращения строк и эшелонирования для следующего урока, поскольку сейчас вам нужно знать это, если у вас нет единичной матрицы в левой части расширенной матрицы, которую вы решаете (в этом случае вы не используете не нужно ничего делать для решения системы уравнений, относящейся к матрице), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была записана в виде матрицы.
Примеры исключения Гаусса
В качестве последнего раздела давайте поработаем еще несколько упражнений по исключению Гаусса (сокращение строк), чтобы вы могли больше попрактиковаться в этой методологии.На протяжении многих будущих уроков этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из самых важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все этапы решения следующих проблем.
Пример 2
Пример 3
Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных).В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, — это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.
Уравнение 15: Строка, уменьшающая расширенную матрицу
Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, поскольку третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая предоставит уравнение 2y — 6z = 0 , подставив в это уравнение значение z = 0 \, в результате получится y \, также равное нулю.Таким образом, мы, наконец, подставляем оба значения y и z \ в уравнение, которое получается из первой строки матрицы: x + 4y + 3z = 1 , поскольку и y , и z \ , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:
Уравнение 16: Окончательное решение системы уравнений
Пример 4
Из чего видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2.Мы подставляем это в уравнения, полученные во второй и первой строках (в указанном порядке), чтобы вычислить значения переменных x и y:
Пример 5
- Решите следующую линейную систему, используя метод исключения Гаусса:
Уравнение 21: Система линейных уравнений с двумя переменными
- Транскрипция линейной системы в виде расширенной матрицы и редукции строк:
Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически говорит нам y = 8 .Итак, подставляя это значение в уравнение из первой строки, получаем: 4x — 5y = 4x — 5 (8) = 4x — 40 = -6 4x = 34 \, и поэтому значение x равно: x = 172 \ frac {\ small17} {\ small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений
Пример 6
Чтобы завершить наш урок на сегодня, у нас есть рекомендация по ссылке, чтобы дополнить ваши исследования: Исключение Гаусса — статья, которая содержит некоторую дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров.Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на протяжении всего курса линейной алгебры, так что до встречи на следующем уроке!
Исключение Гаусса
Тип 2. Умножьте строку на ненулевую константу.
Тип 3. Добавьте одну строку, кратную одной, в другую.
Цель этих операций — преобразовать — или уменьшить — исходную расширенную матрицу в одну из форм, где A ′ является верхним треугольником ( a ij ′ = 0 для i> j ), любые нулевые строки появляются внизу матрицы, и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица, как говорят, имеет форму эшелон .Решения системы, представленные более простой расширенной матрицей, [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку элементарные операции со строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, являются в точности теми, которые удовлетворяют исходной системе, A x = Ь .
Пример 3 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица, которая представляет эту систему:
Первая цель — получить нули под первой записью в первом столбце , что означает исключение первой переменной x из второго и третьего уравнений.Для этого выполняются следующие операции со строками:
Вторая цель — получить ноль под второй записью во втором столбце, что означает исключение второй переменной y из третьего уравнения. Один из способов добиться этого — добавить -1/5 второй строки к третьей строке. Однако, чтобы избежать дробей, есть еще один вариант: сначала поменять местами второй и третий ряды. Замена двух строк просто меняет местами уравнения, что явно не меняет решения системы:
Теперь прибавьте −5 раз вторую строку к третьей строке:
Поскольку матрица коэффициентов преобразована в эшелонированную форму, «прямая» часть исключения Гаусса завершена.Теперь остается использовать третью строку для оценки третьего неизвестного, затем выполнить обратную подстановку во вторую строку для оценки второго неизвестного и, наконец, выполнить обратную замену в первой строке для оценки первого неизвестного.
Третья строка финальной матрицы переводится в 10 z = 10, что дает z = 1. Обратная подстановка этого значения во вторую строку, которая представляет уравнение y — 3 z = — 1, дает y = 2.Обратная подстановка обоих этих значений в первую строку, которая представляет уравнение x — 2 y + z = 0, дает x = 3. Таким образом, решение этой системы ( x, y, z ) = (3, 2, 1).
Пример 4 : Решите следующую систему с помощью исключения Гаусса:
Для этой системы расширенная матрица (вертикальная линия опущена) —
Сначала умножьте строку 1 на 1/2:
Теперь добавление -1 первой строки ко второй строке дает нули под первой записью в первом столбце:
Перестановка второй и третьей строк дает желаемую матрицу коэффициентов верхней треугольной формы:
В третьей строке теперь указано z = 4.Обратная подстановка этого значения во вторую строку дает y = 1, а обратная подстановка обоих этих значений в первую строку дает x = −2. Решение этой системы, следовательно, ( x, y, z ) = (−2, 1, 4).
Исключение Гаусса-Джордана . Исключение Гаусса осуществляется путем выполнения элементарных операций со строками для получения нулей ниже диагонали матрицы коэффициентов, чтобы привести ее к эшелонированной форме. (Напомним, что матрица A ′ = [ a ij ′] имеет эшелонированную форму, когда a ij ′ = 0 для i> j , любые нулевые строки появляются в нижней части матрицы , а первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке.Как только это будет сделано, проверка нижней строки (строк) и обратная подстановка в верхние строки определяют значения неизвестных.
Однако можно сократить (или полностью исключить) вычисления, связанные с обратной подстановкой, выполнив дополнительные операции со строками для преобразования матрицы из эшелонированной формы в сокращенную форму . Матрица находится в форме сокращенного эшелона, когда, помимо того, что она находится в форме эшелона, каждый столбец, содержащий ненулевую запись (обычно равную 1), имеет нули не только под этой записью, но и над этой записью.Грубо говоря, исключение Гаусса работает сверху вниз, чтобы создать матрицу в форме эшелона, тогда как исключение Гаусса-Жордана продолжается с того места, где остановилось Гаусса, а затем работает снизу вверх для создания матрицы в форме сокращенного эшелона. Техника будет проиллюстрирована на следующем примере.
Пример 5 : Известно, что высота, y , брошенного в воздух объекта задается квадратичной функцией от t (время) в форме y = at 2 + bt + c .Если объект находится на высоте y = 23/4 в момент времени t = 1/2, при y = 7 в момент времени t = 1 и при y = 2 при t = 2 , определите коэффициенты a, b и c .
Так как t = 1/2 дает y = 23/4
, а два других условия, y ( t = 1) = 7 и y ( t = 2) = 2, дают следующие уравнения для a, b и c :
Следовательно, цель — решить систему
Расширенная матрица для этой системы сокращается следующим образом:
На этом прямая часть исключения Гаусса завершена, поскольку матрица коэффициентов приведена к эшелонированной форме.Однако, чтобы проиллюстрировать исключение Гаусса-Жордана, выполняются следующие дополнительные элементарные операции со строками:
Эта окончательная матрица сразу дает решение: a = −5, b = 10 и c = 2.
Пример 6 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица для этой системы —
Кратные значения первой строки добавляются к другим строкам, чтобы получить нули под первой записью в первом столбце:
Затем −1 раз вторая строка добавляется к третьей строке:
В третьей строке теперь указано 0 x + 0 y + 0 z = 1, уравнение, которому не могут удовлетворять никакие значения x, y и z .Процесс останавливается: у этой системы нет решений.
Предыдущий пример показывает, как метод исключения по Гауссу обнаруживает противоречивую систему. Небольшое изменение этой системы (например, изменение постоянного члена «7» в третьем уравнении на «6») проиллюстрирует систему с бесконечным числом решений.
Пример 7 : Решите следующую систему с помощью исключения Гаусса:
Те же операции, которые применяются к расширенной матрице системы в примере 6, применяются к расширенной матрице для данной системы:
Здесь третья строка переводится в 0 x + 0 y + 0 z = 0, уравнение, которому удовлетворяют любые x, y и z .Поскольку здесь нет ограничений на неизвестные, на неизвестные не три условия, а только два (представленные двумя ненулевыми строками в окончательной расширенной матрице). Поскольку есть 3 неизвестных, но только 2 константы, 3–2 = 1 неизвестных, z , скажем, произвольно; это называется свободной переменной . Пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = −6) дает
Обратная подстановка z = t и y = 6 + 5 t в первую строку ( x + y — 3 z = 4) определяет x :
Следовательно, каждое решение системы имеет вид
, где t — любое действительное число.Существует бесконечно много решений, поскольку каждое действительное значение t дает отдельное конкретное решение. Например, выбор t = 1 дает ( x, y, z ) = (−4, 11, 1), а t = 3 дает ( x, y, z ) = (4, — 9, −3) и т. Д. Геометрически эта система представляет собой три плоскости в R 3 , которые пересекаются по линии, и (*) является параметрическим уравнением для этой линии.
Пример 7 дает иллюстрацию системы с бесконечным множеством решений, как возникает этот случай и как записывается решение.Каждая линейная система, имеющая бесконечно много решений, должна содержать хотя бы один произвольный параметр (свободная переменная). После того, как расширенная матрица была приведена к эшелонированной форме, количество свободных переменных равно общему количеству неизвестных минус количество ненулевых строк:
Это согласуется с теоремой B выше, которая гласит, что линейная система с меньшим количеством уравнений, чем неизвестных, если она согласована, имеет бесконечно много решений. Условие «меньше уравнений, чем неизвестных» означает, что количество строк в матрице коэффициентов меньше количества неизвестных.Следовательно, приведенное выше уравнение в рамке подразумевает, что должна быть хотя бы одна свободная переменная. Поскольку такая переменная по определению может принимать бесконечно много значений, система будет иметь бесконечно много решений.
Пример 8 : Найти все решения для системы
Во-первых, обратите внимание, что есть четыре неизвестных, но только три уравнения. Следовательно, если система непротиворечива, гарантировано, что у нее будет бесконечно много решений, а это состояние характеризуется по крайней мере одним параметром в общем решении.После того, как соответствующая расширенная матрица построена, исключение Гаусса дает
Тот факт, что в эшелонированной форме расширенной матрицы остались только две ненулевые строки, означает, что 4-2 = 2 переменных свободны:
Следовательно, выбрав y и z в качестве свободных переменных, пусть y = t 1 и z = t 2 . Во второй строке сокращенной расширенной матрицы следует
, а первая строка дает
Таким образом, решения системы имеют вид
, где t 1 t 2 могут принимать любые реальные значения.
Пример 9 : Пусть b = ( b 1 , b 2 , b 3 ) T и пусть A будет матрицей
Для каких значений b 1 , b 2 и b 3 будет ли система A x = b согласованной?
Расширенная матрица для системы A x = b читает
, который гауссовский элиминатин сокращает следующим образом:
Нижняя строка теперь означает, что b 1 + 3 b 2 + b 3 должен быть равен нулю, чтобы эта система была согласованной.Следовательно, в данной системе есть решения (фактически бесконечно много) только для тех векторов-столбцов b = ( b 1 , b 2 , b 3 ) T , для которых b 1 + 3 b 2 + b 3 = 0.
Пример 10 : Решите следующую систему (сравните с Примером 12):
Такая система, как эта, где постоянный член в правой части каждого уравнения равен 0, называется однородной системой .В матричной форме он читается как A x = 0 . Поскольку каждая гомогенная система непротиворечива — потому что x = 0, всегда является решением, — однородная система имеет либо ровно одно решение (простое решение , x = 0 ) или бесконечно много. Сокращение строки матрицы коэффициентов для этой системы уже было выполнено в примере 12. Нет необходимости явно дополнять матрицу коэффициентов столбцом b = 0 , поскольку никакая элементарная операция со строкой не может повлиять на эти нули.То есть, если A ‘является эшелонированной формой A , то операции элементарной строки преобразуют [ A | 0 ] в [ A ′ | 0 ]. По результатам Примера 12,
Поскольку последняя строка снова подразумевает, что z можно принять как свободную переменную, пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = 0) дает
и обратная подстановка z = t и y = 5 t в первую строку ( x + y -3 z = 0) определяет x :
Следовательно, каждое решение этой системы имеет вид ( x, y, z ) = (−2 t , 5 t, t ), где t — любое действительное число.Существует бесконечно много растворяющих веществ, поскольку каждое действительное значение t дает уникальное частное решение.
Обратите внимание на разницу между набором решений для системы в Примере 12 и здесь. Хотя у обоих была одна и та же матрица коэффициентов A , система в примере 12 была неоднородной ( A x = b , где b ≠ 0 ), а здесь — соответствующая однородная система, A x = 0 .Помещая свои решения рядом,
общее решение для Ax = 0 : ( x, y, z ) = (−2 t , 5 t , t )
общее решение для Ax = b : ( x, y, z ) = (−2 t , 5 t , t ) + (−2, 6, 0)
иллюстрирует важный факт:
Теорема C . Общие решения для согласованной неоднородной лиенарной системы, A x = b , равны общему решению соответствующей однородной системы, A x = 0 , плюс частное решение неоднородная система.То есть, если x = x h представляет собой общее решение A x = 0 , тогда x = x h + x представляет общее решение A x + b , где x — любое конкретное решение (согласованной) неоднородной системы A x = b .
[Техническое примечание: теорема C, которая касается линейной системы , имеет аналог в теории линейных дифференциальных уравнений .Пусть L — линейный дифференциальный оператор; то общее решение разрешимого неоднородного линейного дифференциального уравнения, L (y) = d (где d ≢ 0), равно общему решению соответствующего однородного уравнения, L (y) = 0 плюс частное решение неоднородного уравнения. То есть, если y = y h повторно отображает общее решение L (y) = 0, то y = y h + y представляет общее решение L (y ) = d , где y — любое частное решение (решаемого) неоднородного линейного уравнения L (y) = d .]
Пример 11 : Определить все решения системы
Запишите расширенную матрицу и выполните следующую последовательность операций:
Поскольку в этой финальной (эшелонированной) матрице остаются только 2 ненулевые строки, есть только 2 ограничения, и, следовательно, 4-2 = 2 из неизвестных (скажем, y и z ) являются свободными переменными. Пусть y = t 1 и z = t 2 .Обратная подстановка y = t 1 и z = t 2 во второй строке ( x — 3 y + 4 z = 1) дает
Наконец, обратная замена x = 1 + 3 t 1 — 4 2 , y = t 1 и z = t 2 в первый строка (2 w — 2 x + y = −1) определяет w :
Следовательно, каждое решение этой системы имеет вид
, где t 1 и t 2 — любые действительные числа.Другой способ написать решение:
, где t 1 , t 2 ∈ R .
Пример 12 : Определите общее решение
, которая является однородной системой, соответствующей неоднородной в примере 11 выше.
Поскольку решением неоднородной системы в примере 11 является
Из теоремы C следует, что решение соответствующей однородной системы (где t 1 , t 2 ∈ R ) получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
Пример 13 : Докажите теорему A: независимо от ее размера или количества неизвестных, содержащихся в ее уравнениях, линейная система не будет иметь решений, ровно одно решение или бесконечно много решений.
Доказательство . Пусть данная линейная система записана в матричной форме A x = b . Теорема действительно сводится к следующему: если A x = b имеет более одного решения, то на самом деле их бесконечно много.Чтобы установить это, пусть x 1 и x 2 будут двумя разными решениями A x = b . Теперь будет показано, что для любого действительного значения t вектор x 1 + t ( x 1 — x 2 ) также является решением A x = b ; Поскольку t может принимать бесконечно много различных значений, из этого следует желаемый вывод.Поскольку A x 1 = b и A x 2 ,
Следовательно, x 1 + t ( x 1 — x 2 ) действительно является решением A x = b , и теорема доказана.
2.2: Системы линейных уравнений и метод Гаусса-Жордана
Цели обучения
В этом разделе вы узнаете о
- Представьте систему линейных уравнений в виде расширенной матрицы
- Решите систему, используя элементарные операции со строками.
В этом разделе мы учимся решать системы линейных уравнений, используя процесс, называемый методом Гаусса-Жордана. Процесс начинается с того, что сначала система выражается в виде матрицы, а затем сводится к эквивалентной системе с помощью простых операций со строками. Процесс продолжается до тех пор, пока решение не станет очевидным из матрицы. Матрица, представляющая систему, называется расширенной матрицей , а арифметические операции, которые используются для перехода от системы к сокращенной эквивалентной системе, называются операцией строки .
Пример \ (\ PageIndex {1} \)
Запишите следующую систему как расширенную матрицу.
\ [\ begin {array} {l}
2 x + 3 y-4 z = 5 \\
3 x + 4 y-5 z = -6 \\
4 x + 5 y-6 z = 7
\ конец {массив} \ nonumber \]
Решение
Мы выражаем вышеуказанную информацию в матричной форме. Поскольку система полностью определяется своей матрицей коэффициентов и матрицей постоянных членов, расширенная матрица будет включать только матрицу коэффициентов и постоянную матрицу.Итак, расширенная матрица, которую мы получаем, выглядит следующим образом:
\ [\ left [\ begin {array} {ccc | c}
2 & 3 & -4 & 5 \\
3 & 4 & -5 & -6 \\
4 & 5 & -6 & 7
\ конец {массив} \ nonumber \ right] \ nonumber \]
В последнем разделе мы выразили систему уравнений как \ (AX = B \), где \ (A \) представляет матрицу коэффициентов, а \ (B \) — матрицу постоянных членов. В качестве расширенной матрицы мы записываем матрицу как \ (\ left [\ begin {array} {l | l} A & B \ end {array} \ right] \).Ясно, что вся информация сохраняется в этой матричной форме, и отсутствуют только буквы \ (x \), \ (y \) и \ (z \). Учащийся может написать \ (x \), \ (y \) и \ (z \) поверх первых трех столбцов, чтобы облегчить переход.
Пример \ (\ PageIndex {2} \)
Для следующей расширенной матрицы запишите систему уравнений, которую она представляет.
\ [\ left [\ begin {array} {ccccc}
1 & 3 & -5 & | & 2 \\
2 & 0 & -3 & | & -5 \\
3 & 2 & -3 & | & -1
\ end {array} \ right] \ nonumber \]
Решение
Легко получить систему, как показано ниже.
\ [\ begin {array} {l}
x + 3 y-5 z = 2 \\
2 x-3 z = -5 \\
3 x + 2 y-3 z = -1
\ end { массив} \ nonumber \]
После того, как система выражена как расширенная матрица, метод Гаусса-Жордана сокращает систему до ряда эквивалентных систем с помощью строковых операций. Это сокращение строк продолжается до тех пор, пока система не будет выражена в так называемой сокращенной форме эшелона строк . Уменьшенная ступенчатая форма матрицы коэффициентов имеет единицы по главной диагонали и нули в других местах.Решение легко получить из этой формы.
Этот метод не сильно отличается от алгебраических операций, которые мы использовали в методе исключения в первой главе. Основное отличие состоит в том, что он носит алгоритмический характер и, следовательно, может быть легко запрограммирован на компьютере.
Далее мы решим систему двух уравнений с двумя неизвестными, используя метод исключения, а затем покажем, что этот метод аналогичен методу Гаусса-Жордана.
Пример \ (\ PageIndex {3} \)
Решите следующую систему методом исключения.
\ [\ begin {array} {l}
x + 3 y = 7 \\
3 x + 4 y = 11
\ end {array} \ nonumber \]
Решение
Умножаем первое уравнение на — 3 и добавляем его ко второму уравнению.
\ begin {выравнивается}
-3 x-9 y & = — 21 \\
3 x + 4 y & = 11 \\ \ hline
-5y & = — 10
\ end {выравнивается}
Таким образом мы преобразовали нашу исходную систему в эквивалентную систему:
\ begin {выравнивается}
x + 3 y & = 7 \\
-5 y & = — 10
\ end {выравнивается}
Разделим второе уравнение на — 5 и получим следующую эквивалентную систему.
\ начало {выровнено}
x + 3 y & = 7 \\
y & = 2
\ end {выровнено}
Теперь мы умножаем второе уравнение на — 3 и прибавляем к первому, получаем
\ [\ begin {array} {l}
x = 1 \\
y = 2
\ end {array} \ nonumber \]
Пример \ (\ PageIndex {4} \)
Решите следующую систему из примера 3 методом Гаусса-Жордана и покажите сходство в обоих методах, написав уравнения рядом с матрицами.
\ begin {array} {l}
x + 3 y = 7 \\
3 x + 4 y = 11
\ end {array}
Решение
Расширенная матрица для системы выглядит следующим образом.
\ [\ left [\ begin {array} {cccc}
1 & 3 & | & 7 \\
3 & 4 & | & 11
\ end {array} \ right] \ quad \ left [\ begin {array} {c}
x + 3 y = 7 \\
3 x + 4 y = 11
\ end {array} \ right] \ nonumber \]
Умножаем первую строку на — 3, и прибавляем ко второй строке.
\ [\ left [\ begin {array} {cccc}
1 & 3 & | & 7 \\
0 & -5 & | & -10
\ end {array} \ right] \ quad \ left [\ begin {array} {c}
x + 3 y & = 7 \\
-5 y & = — 10
\ end {array} \ right] \ nonumber \]
Делим вторую строку на — 5, получаем,
\ [\ left [\ begin {array} {llll}
1 & 3 & | & 7 \\
0 & 1 & | & 2
\ end {array} \ right] \ quad \ left [\ begin {array} {rl}
x + 3 y & = 7 \\
y & = 2
\ end {array} \ right] \ nonumber \]
Наконец, мы умножаем вторую строку на — 3 и прибавляем к первой строке, и получаем
\ [\ left [\ begin {array} {llll}
1 & 0 & | & 1 \\
0 & 1 & | & 2
\ end {array} \ right] \ quad \ left [\ begin {array} {l}
x = 1 \\
y = 2
\ end {array} \ right] \ nonumber \]
Теперь мы перечислим три операции со строками, которые использует метод Гаусса-Жордана.
Операции со строками
- Любые две строки в расширенной матрице можно поменять местами.
- Любая строка может быть умножена на ненулевую константу.
- Постоянное кратное одной строке может быть добавлено к другой строке.
Легко видеть, что эти операции с тремя строками могут изменить внешний вид системы, но они не меняют решения системы.
Операция первой строки утверждает, что если любые две строки системы поменять местами, полученная новая система имеет то же решение, что и старая.Давайте посмотрим на пример в двух уравнениях с двумя неизвестными. Рассмотрим систему
\ begin {выравнивается}
x + 3 y & = 7 \\
3 x + 4 y & = 11
\ end {выравнивается}
Меняем ряды местами, и получаем,
\ begin {выравнивается}
3 x + 4 y & = 11 \\
x + 3 y & = 7
\ end {выравнивается}
Очевидно, что эта система имеет то же решение, что и предыдущая.
Вторая операция утверждает, что если строка умножается на любую ненулевую константу, полученная новая система имеет то же решение, что и старая.Снова рассмотрим указанную выше систему,
\ begin {выравнивается}
x + 3 y & = 7 \\
3 x + 4 y & = 11
\ end {выравнивается}
Умножаем первую строку на –3, получаем
\ begin {выравнивается}
-3 x-9 y & = — 21 \\
3 x + 4 y & = 11
\ end {выравнивается}
Опять же, очевидно, что эта новая система имеет то же решение, что и исходная.
Операция третьей строки утверждает, что любое постоянное кратное одной строки, добавленной к другой, сохраняет решение.Рассмотрим нашу систему,
\ begin {выравнивается}
x + 3 y & = 7 \\
3 x + 4 y & = 11
\ end {выравнивается}
Если мы умножим первую строку на –3 и прибавим ее ко второй строке, мы получим
\ begin {выравнивается}
x + 3 y & = 7 \\
-5 y & = — 10
\ end {выравнивается}
И снова сохраняется то же самое решение.
Теперь, когда мы понимаем, как работают операции с тремя строками, пора ввести метод Гаусса-Жордана для решения систем линейных уравнений.Как упоминалось ранее, метод Гаусса-Жордана начинается с расширенной матрицы и с помощью серии операций со строками заканчивается матрицей, которая находится в сокращенном эшелоне строк формы .
Матрица находится в сокращенном эшелоне строк формирует , если первая ненулевая запись в каждой строке равна 1, а столбцы, содержащие эти единицы, имеют все остальные записи как нули. Форма сокращенного эшелона строк также требует, чтобы ведущая запись в каждой строке была справа от ведущей записи в строке над ней, а строки, содержащие все нули, были перемещены вниз.Сформулируем метод Гаусса-Жордана следующим образом.
Метод Гаусса-Джордана
- Запишите расширенную матрицу.
- Поменяйте местами строки, если необходимо, чтобы получить ненулевое число в первой строке, первом столбце.
- Используйте строковую операцию, чтобы получить 1 в качестве записи в первой строке и первом столбце.
- Используйте операции со строками, чтобы сделать все остальные записи нулями в первом столбце.
- Поменяйте местами строки, если необходимо, чтобы получить ненулевое число во второй строке, втором столбце.Используйте строковую операцию, чтобы сделать эту запись 1. Используйте строковую операцию, чтобы сделать все остальные записи нулями во втором столбце.
- Повторите шаг 5 для строки 3, столбца 3. Продолжайте двигаться по главной диагонали, пока не дойдете до последней строки или пока число не станет равным нулю.
Итоговая матрица называется сокращенной формой строки-эшелона.
Пример \ (\ PageIndex {5} \)
Решите следующую систему методом Гаусса-Жордана.
\ begin {выравнивается}
2 x + y + 2 z & = 10 \\
x + 2 y + z & = 8 \\
3 x + y-z & = 2
\ end {выравнивается}
Решение
Пишем расширенную матрицу.
\ [\ left [\ begin {array} {ccccc}
2 & 1 & 2 & | & 10 \\
1 & 2 & 1 & | & 8 \\
3 & 1 & -1 & | & 2
\ end {array} \ right] \ nonumber \]
Нам нужна 1 в первой строке, первом столбце. Этого можно добиться, разделив первую строку на 2 или поменяв местами вторую строку с первой. Перестановка строк — лучший выбор, потому что таким образом мы избегаем дробей.
\ [\ left [\ begin {array} {ccccc}
1 & 2 & 1 & | & 8 \\
2 & 1 & 2 & | & 10 \\
3 & 1 & -1 & | & 2
\ end {array} \ right] \ quad \ text {мы поменяли местами строку 1 (R1) и строку 2 (R2)} \ nonumber \]
Нам нужно обнулить все остальные записи в столбце 1.Чтобы сделать запись (2) нулем в строке 2, столбце 1, мы умножаем строку 1 на — 2 и добавляем ее ко второй строке. Получаем,
\ [\ left [\ begin {array} {ccccc}
1 & 2 & 1 & | & 8 \\
0 & -3 & 0 & | & -6 \\
3 & 1 & -1 & | & 2
\ end {array} \ right] \ quad-2 R 1 + R 2 \ nonumber \]
Чтобы сделать запись (3) нулем в строке 3, столбце 1, мы умножаем строку 1 на — 3 и добавляем ее в третью строку. Получаем,
\ [\ left [\ begin {array} {ccccc}
1 & 2 & 1 & | & 8 \\
0 & -3 & 0 & | & -6 \\
0 & -5 & -4 & | & -22
\ end {array} \ right] \ quad-3 R 1 + R 3 \ nonumber \]
Пока что мы поставили 1 в левом углу, а все остальные записи в этом столбце — нули.Теперь мы переходим к следующей диагональной записи, строке 2, столбцу 2. Нам нужно сделать эту запись (–3) равной 1 и обнулить все остальные записи в этом столбце. Чтобы сделать запись строки 2, столбца 2 равной 1, мы делим всю вторую строку на –3.
\ [\ left [\ begin {array} {ccccc}
1 & 2 & 1 & | & 8 \\
0 & 1 & 0 & | & 2 \\
0 & -5 & -4 & | & -22
\ end {array} \ right] \ quad \ mathrm {R} 2 \ div (-3) \ nonumber \]
Затем мы обнуляем все остальные записи во втором столбце.
\ [\ left [\ begin {array} {ccccc}
1 & 0 & 1 & | & 4 \\
0 & 1 & 0 & | & 2 \\
0 & 0 & -4 & | & -12
\ end {array} \ right] \ quad-2 R 2 + R 1 \ text {и} 5 R 2 + R 3 \ nonumber \]
Сделаем последнюю диагональную запись равной 1, разделив строку 3 на — 4.
\ [\ left [\ begin {array} {ccccc}
1 & 0 & 1 & | & 4 \\
0 & 1 & 0 & | & 2 \\
0 & 0 & 1 & | & 3
\ end {array} \ right] \ quad \ quad R 3 \ div (-4) \ nonumber \]
Наконец, мы обнуляем все остальные записи в столбце 3.
\ [\ left [\ begin {array} {ccccc}
1 & 0 & 0 & | & 1 \\
0 & 1 & 0 & | & 2 \\
0 & 0 & 1 & | & 3
\ end {array} \ right] \ quad- \ mathrm {R} 3+ \ mathrm {R} 1 \ nonumber \]
Ясно, что решение читается как \ (x = 1 \), \ (y = 2 \) и \ (z = 3 \).
Прежде чем мы закончим этот раздел, мы упомянем некоторые термины, которые могут нам понадобиться в четвертой главе.
Процесс получения 1 в местоположении и затем обнуления всех остальных записей в этом столбце называется поворотным .
Число, равное 1, называется сводным элементом , , , а строка, которая содержит сводный элемент, называется сводной строкой .
Мы часто умножаем сводную строку на число и добавляем его к другой строке, чтобы получить в последней ноль. Строка, к которой добавляется кратная сводная строка, называется целевой строкой .
M.7 Устранение Гаусса-Джордана | STAT ONLINE
Исключение Гаусса-Жордана — это алгоритм, который можно использовать для решения систем линейных уравнений и поиска обратной матрицы для любой обратимой матрицы.Он полагается на три операции с элементарной строкой , которые можно использовать с матрицей:
- Поменять местами две строки
- Умножить одну из строк на ненулевой скаляр.
- Добавить или вычесть скалярное кратное одной строки из другой строки.
В качестве примера операции с первой элементарной строкой поменяйте местами 1-ю и 3-ю строки.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \ end {pmatrix} \]
Для примера операции со второй элементарной строкой умножьте вторую строку на 3.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9 \\ 7 & 5 & 0 \ end {pmatrix} \]
В качестве примера операции с третьей элементарной строкой добавьте дважды первую строку ко второй строке.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \ end {pmatrix} \]
Редукторный эшелон формы
Цель исключения Гаусса-Жордана состоит в том, чтобы использовать три операции элементарных строк для преобразования матрицы в эшелонированную форму сокращенных строк.Матрица находится в форме уменьшенного ряда строк , также известной как каноническая форма строки , если выполняются следующие условия:
- Все строки с нулевыми записями находятся внизу матрицы
- Первая ненулевая запись в строке, называемая ведущей записью или поворотной точкой каждой ненулевой строки, находится справа от ведущей записи строки над ней.
- Начальная запись, также известная как точка поворота, в любой ненулевой строке — 1.
- Все остальные записи в столбце, содержащие в начале 1, являются нулями.
Например
\ [A = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \ end {pmatrix}, B = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix}, C = \ begin {pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}, D = \ begin {pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix} \]
Матрицы A, и B имеют форму уменьшенного ряда, а матрицы C и D — нет. C не находится в форме пониженного ряда, поскольку нарушает условия два и три. D не находится в форме пониженного ряда, поскольку нарушает четвертое условие. Кроме того, операции с элементарными строками могут использоваться для уменьшения матрицы D в матрицу B .
Шаги для исключения Гаусса-Джордана
Для выполнения исключения Гаусса-Джордана:
- Поменяйте местами строки так, чтобы все строки со всеми нулевыми записями находились внизу
- Поменяйте местами строки так, чтобы строка с самой большой левой ненулевой записью была наверху.
- Умножьте верхнюю строку на скаляр так, чтобы ведущая запись верхней строки стала 1.
- Сложить / вычесть кратные числа верхней строки из других строк, чтобы все остальные записи в столбце, содержащем ведущую запись верхней строки, были равны нулю.
- Повторите шаги 2–4 для следующей самой левой ненулевой записи, пока все ведущие записи не станут 1.
- Поменяйте местами строки так, чтобы ведущая запись каждой ненулевой строки находилась справа от ведущей записи строки над ней.
Выбранные примеры видео показаны ниже:
Чтобы получить инверсию матрицы n × n A :
- Создайте разделенную матрицу \ ((A | I) \), где I — единичная матрица.{-1} = I \).
Решение системы с исключением Гаусса
Результаты обучения
- Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
- Интерпретировать решение системы уравнений, представленной в виде расширенной матрицы.
Мы увидели, как написать систему уравнений с расширенной матрицей , а затем, как использовать строковые операции и обратную подстановку, чтобы получить форму рядов строк .Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.
Пример: решение системы 2 X 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]
Показать решение
Во-первых, мы запишем это как расширенную матрицу.
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]
Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.
[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]
Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Этого можно добиться, умножив строку 1 на [latex] -2 [/ latex] и затем прибавив результат к строке 2.
[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]
У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]
Использовать обратную замену.Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.
[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]
Решение — точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].
Попробуй
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x — 3y = -1 \ hfill \ end {array} [/ latex]
Показать решение
[латекс] \ влево (2,1 \ вправо) [/ латекс]
В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex]. Мы также рассмотрим написание общего решения для зависимой системы.
Пример: решение зависимой системы
Решите систему уравнений.
[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]
Показать решение
Выполните строковых операций на расширенной матрице, чтобы попытаться получить строковой формы .
[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]
[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} — \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].
[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 — 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]
Итак, решение этой системы — [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].
Теперь мы перейдем на следующий шаг к решению системы линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Пример: решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x — 2y — 9z = 9 \ end {array} [/ latex]
Показать решение
Сначала мы пишем расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]
Затем мы выполняем операции со строками для получения формы «строка-эшелон».
[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]
Самый простой способ получить 1 в строке 2 столбца 1 — это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].
[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill — 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill — \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]
Последняя матрица представляет собой эквивалентную систему.
[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y — 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]
Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].
Напомним, что есть три возможных исхода решений для линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.
Пример: решение зависимой системы 3 x 3
Решите следующую систему линейных уравнений, используя метод исключения Гаусса.
[латекс] \ begin {array} {r} \ hfill -x — 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y — 2z = 0 \ end {array} [/ latex]
Показать решение
Запишите расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками , чтобы получить форму строки-эшелон.
[латекс] — {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]
[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
Последняя матрица представляет следующую систему.
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y — 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]
По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [latex] y [/ latex] и подставив его в первое уравнение, мы можем решить для [latex] z [/ latex] через [latex] x [/ latex].
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]
Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].
[латекс] \ begin {массив} {l} \ text {} y — 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y — 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 — 2x} {3} \ hfill \ end {array} [/ latex ]
Общее решение — [latex] \ left (x, \ frac {2 — 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].
Общее решение для зависимой системы 3 X 3
Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].
Попробуй
Решите систему методом исключения Гаусса.
[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y — 3z = 1 \ end {array} [/ latex]
Показать решение
[латекс] \ левый (1,1,1 \ правый) [/ латекс]
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Пример: решение систем уравнений с помощью калькулятора
Решите систему уравнений.
[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x — 4y + 5z = 1 \ end { array} [/ latex]
Показать решение
Напишите расширенную матрицу для системы уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill — 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]
Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]
Оценить.
[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill — \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill — \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = — \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = — \ frac {4} {7} \ hfill \\ \ text {} z = — \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]
При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, — \ frac {92} {187}, — \ frac {24} {187} \ right) [/ latex] .
Приложения систем уравнений
Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.
Пример: применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?
Показать решение
У нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.
[латекс] \ begin {массив} {l} \ text {} x + y = 12 000 \ hfill \\ 0,105x + 0,12y = 1,335 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12 000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]
Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]
Затем,
[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]
Итак [латекс] 12 000 — 5 000 = 7 000 [/ латекс].
Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.
Пример: применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Показать решение
У нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,
[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill — \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Третья строка сообщает нам [латекс] — \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].
Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].
Подставляя [латекс] z = 6,000 [/ латекс], получаем
[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]
Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставляя [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получаем
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3 000 \ text {} \ hfill \ end {array} [/ latex]
Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.
Попробуй
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Показать решение
150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Решающих систем с исключением Гаусса — College Algebra
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполняет операции со строками в матрице.
- Решите систему линейных уравнений, используя матрицы.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные.В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства.Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термы идут в первый столбец, — -термы во втором столбце и z -термы в третьем столбце.Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x как числа в первом столбце.
- Запишите коэффициенты членов и в виде чисел во втором столбце.
- Если имеется z -термов, запишите коэффициенты как числа в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Запишите расширенную матрицу данной системы уравнений.
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение строковых операций над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение 🙂
- Умножить строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения многоуровневой формы матрицы. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1. Поменяйте местами строки или умножьте их на константу, если необходимо.
- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решение системы методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
Решите данную систему методом исключения Гаусса.
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений.
Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3×3 для получения формы Row-Echelon
Выполняет операции со строками с заданной матрицей, чтобы получить форму строки-эшелона.
Запишите систему уравнений в виде строк.
Решение системы линейных уравнений с использованием матриц
Мы увидели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Решите систему с помощью матриц.
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Для данной системы уравнений решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 евро. Сколько было вложено по каждой ставке?
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 фунтов стерлингов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
В третьей строке указано usthus
Вторая строка сообщает нам Подставляя, мы получаем
Первая строка говорит нам о подстановке и получаем
Ответ: 3000 евро вложены под 5%, 1000 евро вложены под 8% и 6000 евро вложены под 9%.
Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 фунтов стерлингов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
— 150 000 фунтов стерлингов при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%
Ключевые понятия
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений.См. (Рисунок).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Устный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.
Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
.
Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
Алгебраические
Для следующих упражнений напишите расширенную матрицу для линейной системы.
Для следующих упражнений запишите линейную систему из расширенной матрицы.
Для следующих упражнений решите систему методом исключения Гаусса.
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если шоколадный ароматизатор в 3 раза популярнее ванильного, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата — 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
860 красный бархат, 1340 шоколадный
Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой — с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?
Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2.Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
4% на счет 1, 6% на счет 2
Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Производитель обошелся в 180 фунтов стерлингов за велосипед плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по цене 86 фунтов стерлингов каждый, с оплатой доставки в размере 9 200 фунтов стерлингов, независимо от того, сколько пылесосов будет продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
Три самых популярных вкуса мороженого — это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
В магазине мороженого растет спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы — на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
Банан — 3%, тыква — 7%, а каменистая дорога — 2%
Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
100 миндальных орехов, 200 кешью, 600 фисташек
Глоссарий
- расширенная матрица
- матрица коэффициентов, примыкающая к постоянному столбцу, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Исключение по Гауссу
- с использованием элементарных операций со строками для получения матрицы в форме строка-эшелон
- главная диагональ
- записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент строки
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой, умножение строки на константу, перестановка строк и т.

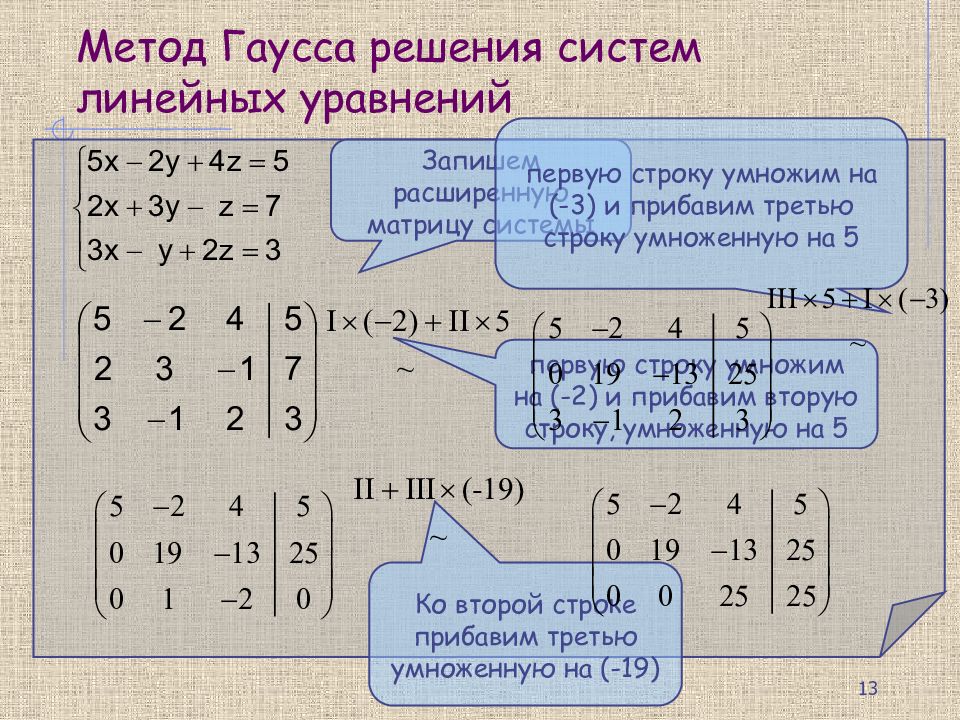


 Нулевую строку допустимо исключать из матрицы.
Нулевую строку допустимо исключать из матрицы.
