Содержание
Тригонометрические уравнения с модулем
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а < 0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим образом:
№1. Решить уравнение.
№2. Решить уравнение.
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx<0,
получаем х =
Серии ответов можно записать объединяя
№3. Решить уравнение.
Решение. Раскрывая знак модуля, получаем системы:
Решая уравнение первой системы, получим
Из значений
нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это
при n=0, 1, 2, 3…
Это
при n=0, 1, 2, 3…
Решая уравнение второй системы, получим Из этого множества значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это значения при m= -1, -2, -3…
Ответ: при n=0, 1, 2, 3…; при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения на отрезке [0;4].
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии
Решая вторую систему, получим систему
, которая не имеет решений.
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Обратная замена:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно
сразу отбросить. Второй модуль раскрываем по определению.
Выражение под первым модулем всегда неотрицательно, и его можно
сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
В промежутке только одно целое нечетное число 3, т.е
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида можно решать и следующим способом:
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx <0, тогда уравнение равносильно системе
Рассмотрим две системы:
Решая уравнение первой системы получим: cosx-2sinx=0
Учитывая, что cosx≤0, x = arctg Вторая система решений не имеет.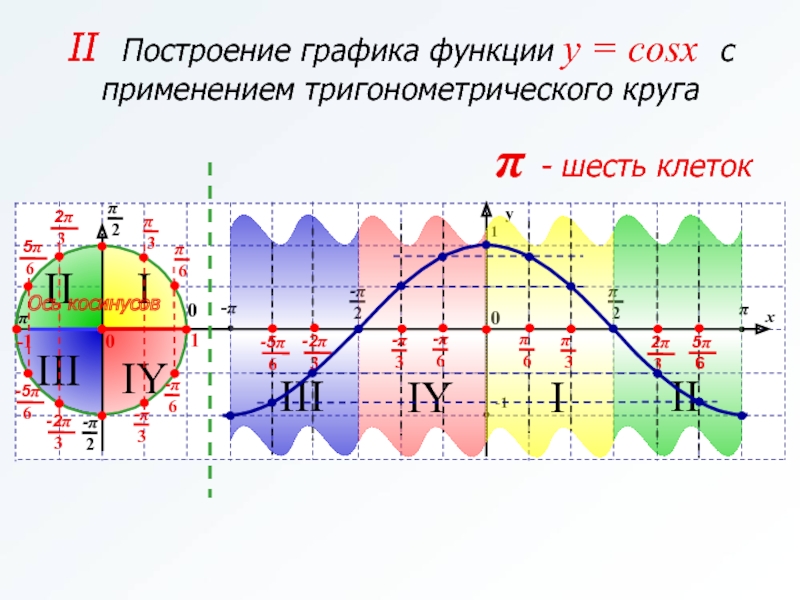
Ответ: x = arctg.
№11. Решить уравнение.
cosx
Решение.
№12. Решить уравнение.
Решение. Уравнение равносильно sinx = ± cosx
Ответ:
Задачи для самостоятельного решения:
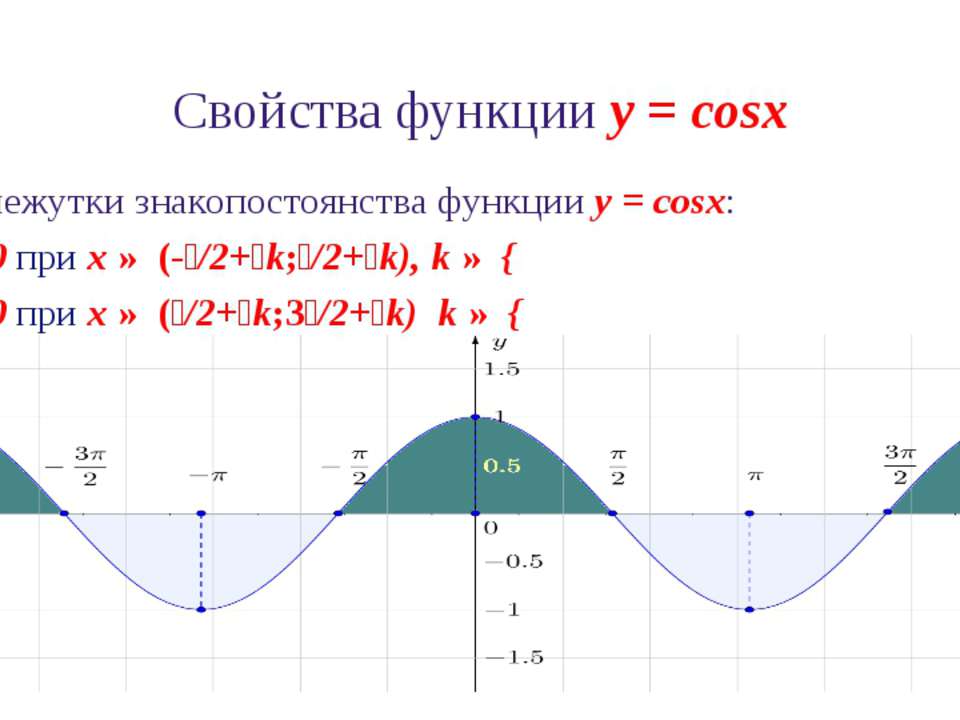
Уравнение cosx=a
Итак,
уравнение, которое содержит переменную под знаком тригонометрических функций,
называется тригонометрическим уравнением. Уравнения вида , , и , где –
переменная, а число , называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида .
Напомним,
что косинусом угла называется
абсцисса точки , полученной
поворотом точки вокруг начала
координат на угол . При этом не
забудем отметить, что так как координаты и точек единичной
окружности удовлетворяют неравенствам и , то для справедливо
неравенство . Из этого
Из этого
следует, что уравнение имеет корни
только при .
Так
как же решают такие уравнения? Давайте рассмотрим два уравнения: и . Чтобы найти х
в первом уравнении, нам нужно ответить на вопрос, чему равен косинус точки . Для этого нам
достаточно вспомнить таблицу значений косинуса.
Тогда
. Давайте покажем
это на единичной окружности. Отметим точку . У этой точки,
как и у любой другой, есть свои координаты. Если мы опустим перпендикуляр из
точки на ось абсцисс,
то попадём в .
А
теперь вернёмся ко второму уравнению – . Чтобы здесь найти
х, нам нужно ответить на вопрос, косинус каких точек равен .
Давайте
ненадолго отвлечёмся от тригонометрии. Начертим координатную плоскость. А
теперь найдём все те точки, у которых абсцисса равна . Несложно
догадаться, что таких точек будет бесконечное множество и все они будут лежать
на вертикальной прямой, проходящей через точки с абсциссой, равной .
А
теперь вернёмся к тригонометрии. Нас будут интересовать все точки, которые
лежат на единичной окружности и пересекаются вертикальной прямой, проходящей
через точки, имеющие абсциссу, равную . Заметим, что
наша прямая пересекает единичную окружность в двух точках – и . Исходя из
таблицы значений косинусов, точка получается из
начальной точки поворотом на угол
, а тогда точка – поворотом на
угол . Тогда решением нашего
уравнения будут два корня – и . Но ведь в эти
точки мы можем попасть не по одному разу. Если мы сделаем полный оборот по
единичной окружности, то снова попадём в эти точки. Сделав ещё полный оборот,
снова попадём в эти точки и так далее. Отсюда уравнение имеет две серии
решений:
.
Как
правило, эти серии решений совмещают и записывают как .
Вообще
при решении уравнений вида возможны четыре
случая.
Первый
случай: . Раскрывая
модуль, имеем .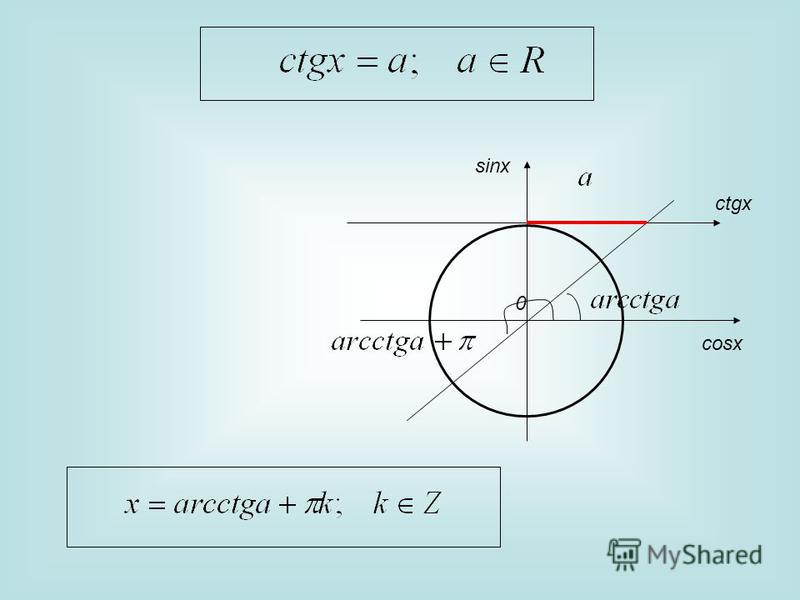 В этом случае на
В этом случае на
единичной окружности будут располагаться две точки – и , абсциссы которых
равны а. Эти точки получаются путём поворота начальной точки на угол и
соответственно. Тогда
решения уравнения можно записать в
виде: , и . Заметим, что эти
точки симметричны относительно оси абсцисс. Следовательно, . Тогда все
решения уравнения можно объединить
в одно: .
Например,
решим следующие уравнения и . Абсциссу, равную
, имеют две точки
единичной окружности. Так как , то угол , а потому угол . Следовательно,
все корни уравнения можно найти по
формуле .
Перейдём
к уравнению . Абсциссу, равную
, имеют две точки
единичной окружности. Так как , то угол , а потому угол . Следовательно,
все корни уравнения можно найти по
формуле .
Заметим,
что каждое из уравнений и
к имеет бесконечное
множество корней. Однако на отрезке каждое из этих
уравнений имеет только один корень. Так, , – это корень
Так, , – это корень
уравнения , а , – это корень
уравнения . Число называют арккосинусом
числа . Записывают так: . Число называют
арккосинусом числа . Записывают так: .
Кстати,
«арккосинус» в переводе с латинского означает «дуга» и «косинус». Это обратная
функция.
Вообще
уравнение , где , на отрезке имеет только один
корень. Если ,
то этот корень заключён в промежутке ;
если
же , то корень располагается
в промежутке .
Этот
корень называют арккосинусом числа а и обозначают так .
Запомните! Арккосинусом
числа а, , называется такое
число , косинус которого
равен а.
, если и
Например,
, так как , . , так как , .
Возвращаясь
к нашему уравнению , где , можно утверждать,
что все корни уравнения можно найти по формуле: .
Запомните!
Для любого справедлива
формула . Эта формула
Эта формула
позволяет находить значения арккосинусов отрицательных чисел через значения арккосинусов
положительных чисел.
Например,
.
Второй
случай: . Раскрывая модуль,
имеем и . Поскольку для справедливо
неравенство , то понятно, что
в этом случае уравнение не будет иметь
корней.
Например,
уравнения и не имеют корней.
Третий
случай (частный): . В этом случае
есть две точки тригонометрической окружности, которые имеют абсциссу, равную 0.
Точка получается из
начальной точки поворотом на угол
, а точка – поворотом на
угол . Тогда уравнение имеет две серии
решений:
Однако
эти две серии решений можно выразить одной формулой: . Полученная
формула задаёт множество корней уравнения .
И
последний, четвёртый случай (тоже частный): . Раскрывая
модуль, имеем , и . В этом случае
вертикальные прямые, проходящие через точки, имеющие абсциссы, равные –1 и 1,
будут касаться единичной окружности в точках с координатами (–1;0) и (1;0). Эти
Эти
точки получаются путём поворота начальной точки на угол , и . Тогда решением
уравнения будет , а решением
уравнения будет .
А
теперь давайте приступим к практической части нашего урока.
Задание
первое. Решите уравнение .
Решение. По
формуле нахождения корней уравнения , имеем: . Значение вычислим с
помощью калькулятора. .
Задание
второе. Решите уравнение .
Решение. По
формуле нахождения корней уравнения , имеем: . . Перенесём в правую часть
равенства. Затем разделим обе части равенства на 2: . Отсюда .
Модуль math — Питошка
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами.
math.ceil(X) – округление до ближайшего большего числа.
math.copysign(X, Y) — возвращает число, имеющее модуль такой же, как и у числа X, а знак — как у числа Y.
math.fabs(X) — модуль X.
math.factorial(X) — факториал числа X.
math.floor(X) — округление вниз.
math.fmod(X, Y) — остаток от деления X на Y.
math.frexp(X) — возвращает мантиссу и экспоненту числа.
math.ldexp(X, I) — X * 2i. Функция, обратная функции math.frexp().
math.fsum(последовательность) — сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.
math.isfinite(X) — является ли X числом.
math.isinf(X) — является ли X бесконечностью.
math.isnan(X) — является ли X NaN (Not a Number — не число).
math.modf(X) — возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.
math.trunc(X) — усекает значение X до целого.
math.exp(X) — eX.
math.expm1(X) — eX — 1. При X → 0 точнее, чем math.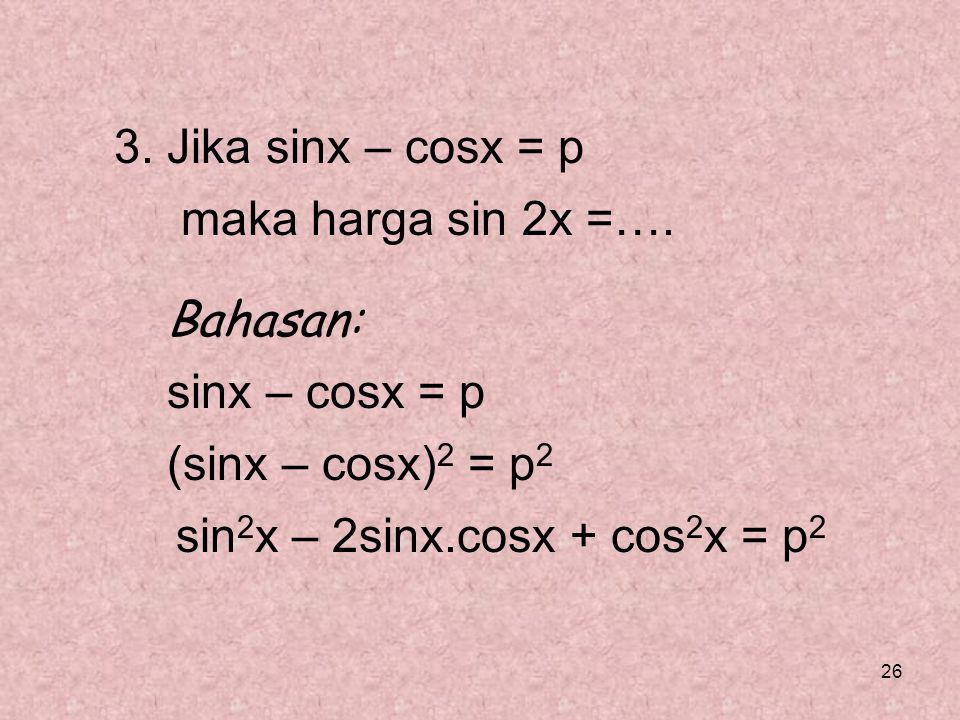 exp(X)-1.
exp(X)-1.
math.log(X, [base]) — логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.
math.log1p(X) — натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).
math.log10(X) — логарифм X по основанию 10.
math.log2(X) — логарифм X по основанию 2. Новое в Python 3.3.
math.pow(X, Y) — XY.
math.sqrt(X) — квадратный корень из X.
math.acos(X) — арккосинус X. В радианах.
math.asin(X) — арксинус X. В радианах.
math.atan(X) — арктангенс X. В радианах.
math.atan2(Y, X) — арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).
math.cos(X) — косинус X (X указывается в радианах).
math.sin(X) — синус X (X указывается в радианах).
math.tan(X) — тангенс X (X указывается в радианах).
math.hypot(X, Y) — вычисляет гипотенузу треугольника с катетами X и Y (math. sqrt(x * x + y * y)).
sqrt(x * x + y * y)).
math.degrees(X) — конвертирует радианы в градусы.
math.radians(X) — конвертирует градусы в радианы.
math.cosh(X) — вычисляет гиперболический косинус.
math.sinh(X) — вычисляет гиперболический синус.
math.tanh(X) — вычисляет гиперболический тангенс.
math.acosh(X) — вычисляет обратный гиперболический косинус.
math.asinh(X) — вычисляет обратный гиперболический синус.
math.atanh(X) — вычисляет обратный гиперболический тангенс.
math.erf(X) — функция ошибок.
math.erfc(X) — дополнительная функция ошибок (1 — math.erf(X)).
math.gamma(X) — гамма-функция X.
math.lgamma(X) — натуральный логарифм гамма-функции X.
math.pi — pi = 3,1415926…
math.e — e = 2,718281…
E | Представляет основание натурального логарифма, определяемое константой |
PI | Представляет отношение длины окружности к ее диаметру, определяемое константой π.Represents the ratio of the circumference of a circle to its diameter, specified by the constant, π. |
Tau | Представляет число радианов в полном обороте, заданное константой τ.Represents the number of radians in one turn, specified by the constant, τ. |
Abs(Decimal) | Возвращает абсолютное значение числа Decimal. |
Abs(Double) | Возвращает абсолютное значение числа двойной точности с плавающей запятой.Returns the absolute value of a double-precision floating-point number. |
Abs(Int16) | Возвращает абсолютное значение 16-битового целого числа со знаком.Returns the absolute value of a 16-bit signed integer. |
Abs(Int32) | Возвращает абсолютное значение 32-битового целого числа со знаком.Returns the absolute value of a 32-bit signed integer. |
Abs(Int64) | Возвращает абсолютное значение 64-битового целого числа со знаком.Returns the absolute value of a 64-bit signed integer. |
Abs(SByte) | Возвращает абсолютное значение 8-битового целого числа со знаком.Returns the absolute value of an 8-bit signed integer. |
Abs(Single) | Возвращает абсолютное значение числа одинарной точности с плавающей запятой.Returns the absolute value of a single-precision floating-point number. |
Acos(Double) | Возвращает угол, косинус которого равен указанному числу.Returns the angle whose cosine is the specified number. |
Acosh(Double) | Возвращает угол, гиперболический косинус которого равен указанному числу.Returns the angle whose hyperbolic cosine is the specified number. |
Asin(Double) | Возвращает угол, синус которого равен указанному числу.Returns the angle whose sine is the specified number. |
Asinh(Double) | Возвращает угол, гиперболический синус которого равен указанному числу.Returns the angle whose hyperbolic sine is the specified number. |
Atan(Double) | Возвращает угол, тангенс которого равен указанному числу.Returns the angle whose tangent is the specified number. |
Atan2(Double, Double) | Возвращает угол, тангенс которого равен отношению двух указанных чисел.Returns the angle whose tangent is the quotient of two specified numbers. |
Atanh(Double) | Возвращает угол, гиперболический тангенс которого равен указанному числу.Returns the angle whose hyperbolic tangent is the specified number. |
BigMul(Int32, Int32) | Умножает два 32-битовых числа.Produces the full product of two 32-bit numbers. |
BigMul(Int64, Int64, Int64) | Формирует полное произведение двух 64-битовых чисел.Produces the full product of two 64-bit numbers. |
BigMul(UInt64, UInt64, UInt64) | Формирует полное произведение двух 64-битовых чисел без знака.Produces the full product of two unsigned 64-bit numbers. |
BitDecrement(Double) | Возвращает ближайшее самое маленькое значение, которое меньше, чем |
BitIncrement(Double) | Возвращает ближайшее самое большое значение, превышающее |
Cbrt(Double) | Возвращает кубический корень из указанного числа.Returns the cube root of a specified number. |
Ceiling(Decimal) | Возвращает наименьшее целое число, которое больше или равно заданному десятичному числу.Returns the smallest integral value that is greater than or equal to the specified decimal number. |
Ceiling(Double) | Возвращает наименьшее целое число, которое больше или равно заданному числу с плавающей запятой двойной точности.Returns the smallest integral value that is greater than or equal to the specified double-precision floating-point number. |
Clamp(Byte, Byte, Byte) | Возвращает |
Clamp(Decimal, Decimal, Decimal) | Возвращает |
Clamp(Double, Double, Double) | Возвращает |
Clamp(Int16, Int16, Int16) | Возвращает |
Clamp(Int32, Int32, Int32) | Возвращает |
Clamp(Int64, Int64, Int64) | Возвращает |
Clamp(SByte, SByte, SByte) | Возвращает |
Clamp(Single, Single, Single) | Возвращает |
Clamp(UInt16, UInt16, UInt16) | Возвращает |
Clamp(UInt32, UInt32, UInt32) | Возвращает |
Clamp(UInt64, UInt64, UInt64) | Возвращает |
CopySign(Double, Double) | Возвращает значение с величиной |
Cos(Double) | Возвращает косинус указанного угла.Returns the cosine of the specified angle. |
Cosh(Double) | Возвращает гиперболический косинус указанного угла.Returns the hyperbolic cosine of the specified angle. |
DivRem(Int32, Int32, Int32) | Вычисляет частное двух 32-разрядных знаковых целых чисел и возвращает остаток в выходном параметре. |
DivRem(Int64, Int64, Int64) | Вычисляет частное двух 64-битовых целых чисел со знаком и возвращает остаток в выходном параметре.Calculates the quotient of two 64-bit signed integers and also returns the remainder in an output parameter. |
Exp(Double) | Возвращает |
Floor(Decimal) | Возвращает наибольшее целое число, которое меньше или равно указанному десятичному числу.Returns the largest integral value less than or equal to the specified decimal number. |
Floor(Double) | Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности. |
FusedMultiplyAdd(Double, Double, Double) | Возвращает значение (x * y) + z, округленное в рамках одной тернарной операции.Returns (x * y) + z, rounded as one ternary operation. |
IEEERemainder(Double, Double) | Возвращает остаток от деления одного указанного числа на другое указанное число.Returns the remainder resulting from the division of a specified number by another specified number. |
ILogB(Double) | Возвращает целочисленный логарифм с основанием 2 указанного числа.Returns the base 2 integer logarithm of a specified number. |
Log(Double) | Возвращает натуральный логарифм (с основанием |
Log(Double, Double) | Возвращает логарифм указанного числа в системе счисления с указанным основанием.Returns the logarithm of a specified number in a specified base. |
Log10(Double) | Возвращает логарифм с основанием 10 указанного числа.Returns the base 10 logarithm of a specified number. |
Log2(Double) | Возвращает логарифм с основанием 2 указанного числа.Returns the base 2 logarithm of a specified number. |
Max(Byte, Byte) | Возвращает большее из двух 8-битовых целых чисел без знака.Returns the larger of two 8-bit unsigned integers. |
Max(Decimal, Decimal) | Возвращает большее из двух десятичных чисел. |
Max(Double, Double) | Возвращает большее из двух чисел двойной точности с плавающей запятой.Returns the larger of two double-precision floating-point numbers. |
Max(Int16, Int16) | Возвращает большее из двух 16-битовых целых чисел со знаком.Returns the larger of two 16-bit signed integers. |
Max(Int32, Int32) | Возвращает большее из двух 32-битовых целых чисел со знаком.Returns the larger of two 32-bit signed integers. |
Max(Int64, Int64) | Возвращает большее из двух 64-битовых целых чисел со знаком.Returns the larger of two 64-bit signed integers. |
Max(SByte, SByte) | Возвращает большее из двух 8-битовых целых чисел со знаком.Returns the larger of two 8-bit signed integers. |
Max(Single, Single) | Возвращает большее из двух чисел одинарной точности с плавающей запятой.Returns the larger of two single-precision floating-point numbers. |
Max(UInt16, UInt16) | Возвращает большее из двух 16-битовых целых чисел без знака.Returns the larger of two 16-bit unsigned integers. |
Max(UInt32, UInt32) | Возвращает большее из двух 32-битовых целых чисел без знака.Returns the larger of two 32-bit unsigned integers. |
Max(UInt64, UInt64) | Возвращает большее из двух 64-битовых целых чисел без знака.Returns the larger of two 64-bit unsigned integers. |
MaxMagnitude(Double, Double) | Возвращает большую величину из двух чисел двойной точности с плавающей запятой. |
Min(Byte, Byte) | Возвращает меньшее из двух 8-битовых целых чисел без знака.Returns the smaller of two 8-bit unsigned integers. |
Min(Decimal, Decimal) | Возвращает меньшее из двух десятичных чисел.Returns the smaller of two decimal numbers. |
Min(Double, Double) | Возвращает меньшее из двух чисел двойной точности с плавающей запятой.Returns the smaller of two double-precision floating-point numbers. |
Min(Int16, Int16) | Возвращает меньшее из двух 16-битовых целых чисел со знаком.Returns the smaller of two 16-bit signed integers. |
Min(Int32, Int32) | Возвращает меньшее из двух 32-битовых целых чисел со знаком.Returns the smaller of two 32-bit signed integers. |
Min(Int64, Int64) | Возвращает меньшее из двух 64-битовых целых чисел со знаком.Returns the smaller of two 64-bit signed integers. |
Min(SByte, SByte) | Возвращает меньшее из двух 8-битовых целых чисел со знаком.Returns the smaller of two 8-bit signed integers. |
Min(Single, Single) | Возвращает меньшее из двух чисел одинарной точности с плавающей запятой.Returns the smaller of two single-precision floating-point numbers. |
Min(UInt16, UInt16) | Возвращает меньшее из двух 16-битовых целых чисел без знака.Returns the smaller of two 16-bit unsigned integers. |
Min(UInt32, UInt32) | Возвращает меньшее из двух 32-битовых целых чисел без знака.Returns the smaller of two 32-bit unsigned integers. |
Min(UInt64, UInt64) | Возвращает меньшее из двух 64-битовых целых чисел без знака. |
MinMagnitude(Double, Double) | Возвращает меньшую величину из двух чисел двойной точности с плавающей запятой.Returns the smaller magnitude of two double-precision floating-point numbers. |
Pow(Double, Double) | Возвращает указанное число, возведенное в указанную степень.Returns a specified number raised to the specified power. |
Round(Decimal) | Округляет десятичное значение до ближайшего целого значения; значения посередине округляются до ближайшего четного числа.Rounds a decimal value to the nearest integral value, and rounds midpoint values to the nearest even number. |
Round(Decimal, Int32) | Округляет десятичное значение до указанного числа знаков после запятой; значения посередине округляются до ближайшего четного числа. |
Round(Decimal, Int32, MidpointRounding) | Округляет десятичное значение до указанного числа знаков после запятой; использует указанное соглашение для округления значений посередине.Rounds a decimal value to a specified number of fractional digits, and uses the specified rounding convention for midpoint values. |
Round(Decimal, MidpointRounding) | Округляет десятичное значение до ближайшего целого числа; использует указанное соглашение для округления значений посередине.Rounds a decimal value to the nearest integer, and uses the specified rounding convention for midpoint values. |
Round(Double) | Округляет значение с плавающей запятой двойной точности до ближайшего целого значения; значения посередине округляются до ближайшего четного числа. |
Round(Double, Int32) | Округляет значение с плавающей запятой двойной точности до указанного числа знаков после запятой; значения посередине округляются до ближайшего четного числа.Rounds a double-precision floating-point value to a specified number of fractional digits, and rounds midpoint values to the nearest even number. |
Round(Double, Int32, MidpointRounding) | Округляет значение с плавающей запятой двойной точности до указанного числа знаков после запятой; использует указанное соглашение для округления значений посередине.Rounds a double-precision floating-point value to a specified number of fractional digits, and uses the specified rounding convention for midpoint values. |
Sign(Decimal) | Возвращает целое число, указывающее знак десятичного числа.Returns an integer that indicates the sign of a decimal number. |
Sign(Double) | Возвращает целое число, обозначающее знак числа двойной точности с плавающей запятой.Returns an integer that indicates the sign of a double-precision floating-point number. |
Sign(Int16) | Возвращает целое число, указывающее знак 16-разрядного целого числа со знаком.Returns an integer that indicates the sign of a 16-bit signed integer. |
Sign(Int32) | Возвращает целое число, указывающее знак 32-разрядного целого числа со знаком.Returns an integer that indicates the sign of a 32-bit signed integer. |
Sign(Int64) | Возвращает целое число, указывающее знак 64-разрядного целого числа со знаком. |
Sign(SByte) | Возвращает целое число, указывающее знак 8-разрядного целого числа со знаком.Returns an integer that indicates the sign of an 8-bit signed integer. |
Sign(Single) | Возвращает целое число, обозначающее знак числа с плавающей запятой одиночной точности.Returns an integer that indicates the sign of a single-precision floating-point number. |
Sin(Double) | Возвращает синус указанного угла.Returns the sine of the specified angle. |
Sinh(Double) | Возвращает гиперболический синус указанного угла.Returns the hyperbolic sine of the specified angle. |
Sqrt(Double) | Возвращает квадратный корень из указанного числа.Returns the square root of a specified number. |
Tan(Double) | Возвращает тангенс указанного угла.Returns the tangent of the specified angle. |
Tanh(Double) | Возвращает гиперболический тангенс указанного угла.Returns the hyperbolic tangent of the specified angle. |
Truncate(Decimal) | Вычисляет целую часть заданного десятичного числа. |
Truncate(Double) | Вычисляет целую часть заданного числа двойной точности с плавающей запятой.Calculates the integral part of a specified double-precision floating-point number. |
Используйте обратный cos в функции lambda без дополнительного модуля
Фон
Я выполняю задачу на codewar, которая просит меня использовать функцию 1 line lambda, чтобы закончить ее. В частности, я хочу использовать
В частности, я хочу использовать math.acos в своей функции lambda .
# Code contains 2 lines, so it will fail
import math # line 1
fun1 = lambda x: math.acos(x) # line 2
fun1(1)
Из:
0.0
Приведенный выше код не работает, потому что он содержит 2 строки. То, что я хочу, — это использовать аналогичную функцию внутри lambda function :
fun1 = lambda x: XXXX # line 1
fun1(1)
Из:
0.0
Мой вопрос
Можно ли использовать math.acos в функции lambda? Если это не так, возможно, мне следует изменить свою идею, чтобы закончить задачу.
python
python-3.x
math
lambda
Поделиться
Источник
Travis
10 февраля 2020 в 07:57
2 ответа
- Проверьте наличие дополнительного модуля
Я пишу проект в C# для Unity, который представляет собой своего рода фреймворк, состоящий из нескольких модулей, одного основного модуля и нескольких дополнительных модулей.
 В основном модуле некоторый код должен проверить, существует ли один из дополнительных модулей, чтобы иметь возможность…
В основном модуле некоторый код должен проверить, существует ли один из дополнительных модулей, чтобы иметь возможность… - функции sin & cos без math.h
Я не могу использовать функции c++ sin() и cos() из-за некоторых проблем компилятора, вызванных PS3 3.40 SDK. Каковы вычисления sin() & cos() , чтобы я мог использовать функции без необходимости math.h ? Я до сих пор придумывал их, но они, похоже, функционируют неправильно? float sin(float…
4
Вот ты где:
fun1 = lambda x: __import__('math').acos(x)
Поделиться
Zaraki Kenpachi
10 февраля 2020 в 08:10
3
Здесь нет необходимости даже в lambda:
from math import acos as fun1
Но если вам действительно нужно, чтобы он был lambda, вы можете использовать точку с запятой ; , чтобы поместить его в ту же строку, что и import :
import math; fun1 = lambda x: math. acos(x)
acos(x)
Поделиться
kaya3
10 февраля 2020 в 08:46
Похожие вопросы:
Python flask jinja2 используйте математический модуль sin() cos() в шаблоне
В настоящее время я внедряю систему фильтров radius. Пользователь может найти номер в городе,и на основе широты и долготы искомого города страница результатов покажет все остальные номера в радиусе…
Определение функции схемы как это сделать
Используйте comp для определения функции pos-cos: pos-cos(x) = cos(x) if cos(x) ≥ 0 else −cos(x) if cos(x) < 0 (define (comp f g) (lambda (x) (f (g x)))) (define (pos-cos x) (if (< (comp (cos…
абстрактные функции в python без использования lambda
У меня только один вопрос. как использовать абстрактные функции без lambda? скажем, у меня есть два списка a = [1,2,3,4,5] b = [2,4,6] если я хочу напечатать все элементы, они появляются в A и B, с. ..
..
Проверьте наличие дополнительного модуля
Я пишу проект в C# для Unity, который представляет собой своего рода фреймворк, состоящий из нескольких модулей, одного основного модуля и нескольких дополнительных модулей. В основном модуле…
функции sin & cos без math.h
Я не могу использовать функции c++ sin() и cos() из-за некоторых проблем компилятора, вызванных PS3 3.40 SDK. Каковы вычисления sin() & cos() , чтобы я мог использовать функции без необходимости…
AWS Lambda-обратный вызов(«некоторый тип ошибки») эквивалентен в Java 8
Как сделать так, чтобы функция lambda сообщала о сбое в Java 8? Я вижу, что это возможно в Node.js. http://docs.aws.amazon.com/lambda/ последний/ДГ/nodejs-прог-модель-handler.html Использование…
XML синтаксический анализ в функции AWS Lambda
Можно ли выполнить синтаксический анализ XML в функции AWS Node.js Lambda без использования стороннего модуля, такого как xml2js? Мне интересно, есть ли у AWS какая-либо встроенная функциональность. ..
..
Как читать изображение RGB (JPG) без дополнительного модуля в python
Я пытаюсь прочитать image.jpg (RGB) в массив в python без какого-либо дополнительного модуля, но это не работает? pic = open(‘image.jpg’) array=[] with open(p, ‘rb’) as inf: jpgdata = inf.read()…
Xbee3 — вычисление тригонометрических величин без математического модуля
Я использую MicroPython на Xbee3-24, и у него нет внутреннего модуля math . Мне нужно вычислить значения sin , cos и arctan . Как я могу использовать тригонометрические функции без использования…
Используйте группы пулов пользователей Cognito для вызова функции Lambda без федеративных удостоверений
Я новичок и чувствую, что мне не хватает связи между ролью IAM в группе пула пользователей Cognito и вызовом функции lambda. Пример использования: я хотел бы использовать Cognito для управления…
Способы решения тригонометрических уравнений /модуль «Тригонометрические уравнения/
Итоговая контрольная работа
План – конспект урока
Преподаватель математики
ГБПОУ Строгановский колледж
Пешкова Ольга Алексеевна
Тема: «Решение тригонометрических уравнений» / модульная технология/
Тип занятия: занятие по повторению и обобщению знаний, закрепление умений
Цели и задачи занятия:
Образовательные– сформировать у студентов умение различать тригонометрические уравнения по способам решения, отработать навыки решения различных видов тригонометрических уравнений;
Развивающие– развивать умение работать с книгой, самостоятельно добывать знания; развивать и совершенствовать умения применять знания в измененной ситуации; развивать логическое мышление, умение делать выводы;
Воспитательные – воспитывать трудолюбие, умение работать в парах, аккуратность, культуру поведения, чувство ответственности.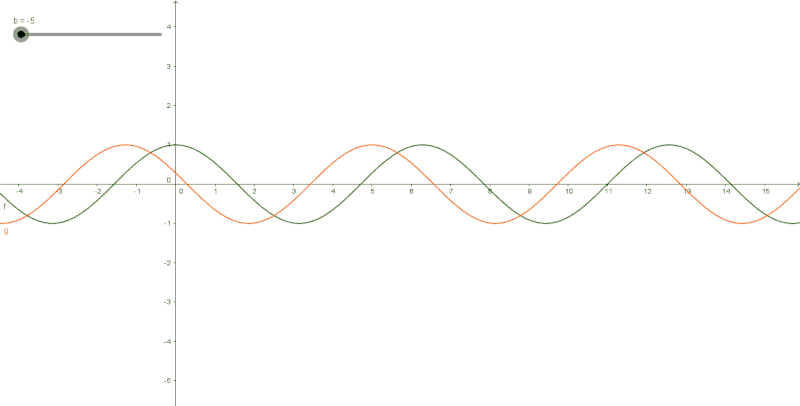
Оборудование занятия: учебники, опорные конспекты, карточки с заданиями, чистые листы для самостоятельной работы, справочный материал (значения тригонометрических функций, решение простейших тригонометрических уравнений, основные формулы тригонометрии).
Литература:
М.И.Башмаков Математика, учебник для начального и среднего профессионального образования, М., 2013 г
Ш.А.Алимов Алгебра и начала анализа, учебник 10 – 11 класс, М., 2012 г.
В.С.Крамор Повторение курса алгебры, М., 2010 г
М.Л.Галицкий Углубленное изучение алгебры и математического анализа /пособие для учителя/, М., 2011 г.
Структура занятия
Организационный этап
Мотивация
Этап применения знаний и способов деятельности
Подведение итогов. Рефлексия
Ход урока:
Учебный элемент, хронометраж времени | Учебный материал, задания для студентов | Руководство по усвоению материала занятия |
УЭ 0 2 минуты | Задача: подготовка студентов к работе. Взаимное приветствие, проверка готовности группы к занятию, организация внимания. Великий физик, математик и политик А. Эйнштейн заметил: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно» Сегодня мы повторяем, приводим в систему знания по способам решения тригонометрических уравнений. Ваша задача: показать свои знания и умения по их решению. Пояснить, что в процессе работы над учебными элементами /модулями/ студенты должны уметь: 1 уровень – решать простейшие тригонометрические уравнения; использовать алгоритмы решения различных тригонометрических уравнений; 2 уровень – решать тригонометрические уравнения, самостоятельно выбирая метод решения; 3 уровень – все, что достигнуто на 1 и 2 уровнях, необходимо применить в нестандартной ситуации 1 уровень – общий, знаниями данного уровня должны овладеть все студенты группы; 2 уровень включает все, что достигнуто на 1 уровне, но более сложного вида; 3 уровень – все, что достигнуто на 1 и 2 уровнях, должно применяться в нестандартных ситуациях. | УЭ 1 – УЭ 4 – соответствует 1 уровню подготовки. УЭ 5 – обеспечивает 2 уровень подготовки. УЭ 6 – 3 уровень подготовки. Вся работа над данным модулем сопровождается оценочным листом. |
1 вариант | 2 вариант |
3sin2x +2sin x – 8 = 0 (2 б) tg2 x – 3tg x – 4 = 0 (3 б) 2cos2x-sinx+1 = 0 (3б) | 2cos2 x – cos x – 1 = 0 (2 б) 2cos23x+cos3x– 6 = 0 (3 б) 2sin2(x2) +3 cos ( x2) = 0 (3б) |
Алгоритм решения оформлен в виде опорного конспекта на формате А4.
Каждый опорный конспект иллюстрируется решенным уравнением.
Работа в парах.
Указание: прочитать пояснения, разобрать решение и самостоятельно выполнить задания.
Объяснить способ решения партнеру (и наоборот)
УЭ 4
14 минут
Цель: закрепить навык решения однородных уравнений
Рассмотрим примеры решения:
однородное уравнение 1 степени
sin 2x + cos 2x = 0 : cos 2x ≠ 0
tg 2x + 1 = 0
tg 2x = — 1
2x = + n : 2
x = + n; nZ
Ответ; x = + n;nZ
Однородное уравнение II степени
–sin2x – 5sinx cosx + 6 cos2x = 0: cos2x ≠ 0
— tg2x – 5 tgx + 6 = 0
пусть tgx = y, где y – любое число
-y2 – 5 y + 6 = 0
D = 49 y1 = — 6 y2 = — 1
tg x = — 6 x = — arctg 6 + n; n Z
tgx = — 1 x = — /4 + n;nZ
Далее решает квадратное тригонометрическое уравнение, заменив tqx = y, где у – любое число
/см. сведение к квадратным уравнениям/
сведение к квадратным уравнениям/
Самостоятельная работа
1 вариант | 2 вариант |
(2 бал) (3 балла) | (2 бал) ( 3 балла) |
Работа в парах
Карточки – информаторы дают возможность повторить метод решения.
Самостоятельное решение уравнений, если набрано менее 5 баллов, то необходимо решить уравнение из другого варианта, где была допущена ошибка.
УЭ 5
3 мин
Физкультминутка
Примите удобную позу, сидя на стуле. В положении сидя, ноги согнуты в коленях, под углом приблизительно 100 градусов. Согните стопу, опираясь на пятку и приведя к голени, свободно отпустите. Вместе и попеременно.
УЭ 6
25 мин
Вы освоили решение уравнений 2 уровня сложности. Целью дальнейшей вашей работы является применение знаний и умений в более сложных ситуациях.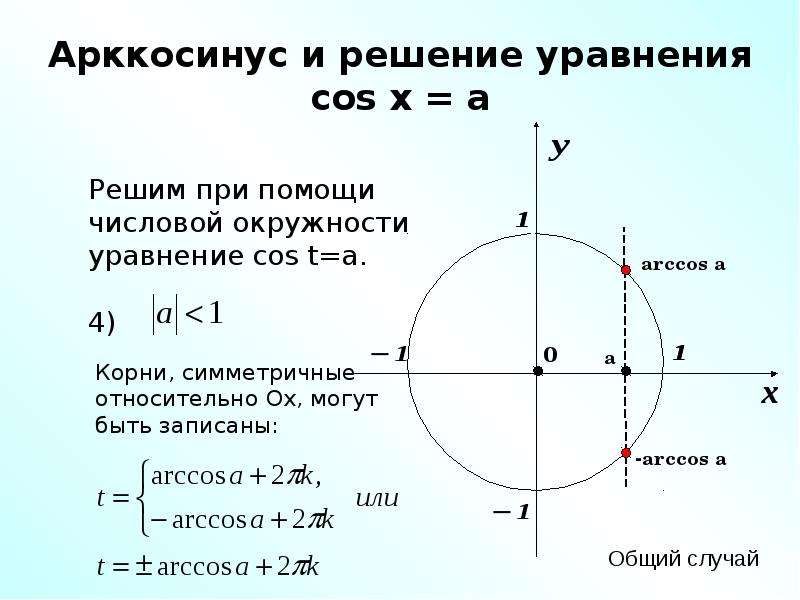
Самостоятельная работа
(задания не ограничиваются временными рамками, т.к. их решают не все учащиеся)
Sin6x+cos6x = 1-2sin2x
1 — sin2x = cosx — sinx
Каждое задание – 2 балла.
Максимально – 16 баллов
Проверьте и оцените свои работы. Исправьте ошибки, если они есть. Проставьте количество набранных баллов в оценочный лист.
УЭ 7
3 мин
Дифференцированная домашняя работа
На «3»
Sin x = ½
Cos 2x – 9cos x + 8 = 0
3cos x*sin x – sin x = 0
На «4»
Cos 2x -9cos x + 8 = 0
3cos x + sin x = 0
3sin 2x + sin x*cos x – 2cos 2x = 0
На «5»
2cos 2x + 3sin x = 0
3sin x *cos x – cos 2x = 0
2sin 2x – 3 sin x*cos x + 4cos 2x = 4
Уровень учащиеся выбирают сами
3 мин
Подведение итогов. Выставление оценок.
Выставление оценок.
Оценка за модуль «Способы решения тригонометрических уравнений» зависит от суммы баллов по всем учебным элементам.
Критерии:
Оценка «5» — более 31 балла
Оценка «4» — от 25 до 30 баллов
Оценка «3» — от 21 до 24 баллов
Оценка «2» — менее 20 баллов
5 минут
Рефлексия
Прочитайте еще раз требования к уровню подготовки и ответьте на вопрос:
— Достигли ли вы намеченной цели? В какой степени достигли?
— Оцените свое самочувствие, поставив какой либо смайлик на графике функцииy= sin x, изображенный на доске. Где вы себя видите: на гребне волны или во впадине, а может на подьеме?
Заключительное слово преподавателя:
«Считай несчастным тот день и час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» /Я.А.Коменский/
Приложение 1. Оценочный лист учащегося
Фамилия | |||
Имя | |||
УЭ | Кол – во баллов за основные задания | Корректирующие задания | Всего баллов |
№ 1 | |||
№ 2 | |||
№ 3 | |||
№ 4 | |||
№ 6 | |||
Итоговое количество баллов | |||
Оценка | |||
Приложение 2. Схема «Способы решения тригонометрических уравнений»
Схема «Способы решения тригонометрических уравнений»
Приложение 3. Карточки – информаторы /для помощи при решении уравнений/
Простейшие тригонометрические уравнения
| ||||||||||||||||||||||||||||
Сведение тригонометрического уравнения к квадратному уравнению Заменитьcosx новой переменной, например cosx = y, причем новая переменная имеет ограничение, а именно Исходное уравнение с новой переменной имеет вид Решить квадратное уравнение Вернуться к старой переменной, т. Формулы корней простейших уравнений Записать ответ |
Сведение тригонометрического уравнения к квадратному уравнению Используя основное тригонометрическое тождество заменить Исходное уравнение принимает вид Раскрыть скобки, привести подобные слагаемые и привести уравнение к виду Заменитьcosx новой переменной, например cosx = y, причем новая переменная имеет ограничение, а именно Исходное уравнение с новой переменной имеет вид Решить квадратное уравнение Вернуться к старой переменной, т.е. перейти к решению простейших тригонометрических уравнений: и . Найти корни простейших тригонометрических уравнений или доказать что корней нет. Формулы корней простейших уравнений Записать ответ |
Метод введения вспомогательного аргумента Уравнения вида решаем способом введения вспомогательного аргумента , используя формулу (1) Выписать коэффициенты и Вычислить Разделить коэффициенты уравнения на , после чего уравнение будет выглядеть Исходное уравнение по формуле (1) представимо в виде ; (2) Угол находим из условия , где угол — угол первой координатной четверти. В значении корня уравнения (2) заменим его величиной. |
Однородное уравнение Iстепени (1) поделим каждое слагаемое уравнения на cosx ≠ 0, тогда уравнение (1) корень уравнения находим по формуле простейшего тригонометрического уравнения: |
Однородное уравнение II степени (1) поделим каждое слагаемое уравнения на cos2x ≠ 0. Тогда уравнение (1) будет выглядеть, Решаем квадратное тригонометрическое уравнение относительно тангенса, заменив tqx = y |
Универсальная подстановка При решении уравнения данным способом произведем замену: Исходное уравнение после замены содержит переменную х под единственной функциейtq и имеет вид тригонометрического квадратного уравнения. |
Равенство одноименных функций Данный способ помогает решать тригонометрические уравнения, где в обеих частях находятся одинаковые тригонометрические функции, но аргументами являются различные значения. При решении следует использовать следующие схемы: 2) 3) |
Разложение на множители Данный способ решения приводит уравнение к виду , где итригонометрические функции. Каждая из функций является множителем, произведение которых равно нулю. Так как произведение равно нулю, значит каждый из множителей тоже может быть равен нулю. Поэтому переходим к простейшим тригонометрическим уравнениям, где a = 0 (частные случаи решения простейших тригонометрических уравнений). При разложении на множители используем формулы сокращенного умножения, вынесения общего множителя, тригонометрические формулы. |
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/111469-sposoby-reshenija-trigonometricheskih-uravnen
Функция y = (x) — online presentation
1. Функция
y | x |
Подготовил Кожемяко Никита,
9 класс
2008г.
Актуальность – собрать сведения по теме в связи с
подготовкой к экзамену
Проблема – в школьном курсе алгебры недостаточно
задач с модулем
Объект исследования – функция
Предмет исследования – функция у=|x|
Цель – рассмотреть решение распространённых
задач с модулем
Гипотеза – я предполагал, что задачи с модулем
решаются только графически
Задачи –
1. Вспомнить известную мне информацию о задачах
с модулем
2.Придумать новые задачи
3.Проконсультироваться с учителем
4.Создать презентацию
5.Защитить работу
3. Определение модуля
В математике через |x| обозначается абсолютная
величина, или модуль числа х.
Абсолютная величина числа х равна этому числу, если
х>0, равна противоположному числу –х, если x
равна нулю, если х=0.
Таким образом, функция |x| определена для всех
х (-∞;+∞).
Множество её значений совпадает с множеством
неотрицательных чисел.
|x|=
х, если х≥0,
-х, если х
График функции
у
0
Свойства функции
y | x |
х
1.D(f)=(-∞;+∞)
2.E(f)=[0;+∞)
3.Ограничена снизу
4.Возрастает
на[0;+∞)
убывает на(-∞;0]
5.Чётная функция
6. У наиб нет У наим. 0
7.Непрерывна
Решение уравнений
с модулем графическим методом
|x-3|-1=x3
y=|x-3|-1
0
Ответ: x=1
у
y=x3
1
4
x
Решение неравенств
с модулем графическим методом
Решим неравенство |x|-2 ≥
y=|x|-2
0
Ответ: [4;+∞)
y=
y
1
x
x
4
x
Решение уравнения с параметром и
модулем графическим способом
Сколько решений имеет уравнение
у
|x+2|+1 =c
y=|x+2|+1
y=c
Рассмотрим 3 случая
1
Iсл. c>1, 2 решения
c>1, 2 решения
IIсл. c
IIIсл. c=1, 1 решение
0
x
8. Аналитический метод решения уравнения с модулем
Решим уравнение|x-3|=5
I способ
Рассмотрим два случая
1 случай
2 случай
x-3≥0
x-3=5
x-3
3-x=5
x=5+3
-x=5-3
x=8, 8-3≥0 (и) x=-2, -2-3
Ответ:-2, 8
II способ
x-3=5 или x-3=-5
x=8
x=-2
9. Показательные уравнения с модулем
2|x+2| = 16
2|x+2| = 24
|x+2| = 4
I случай
x+2=4
x=2
Ответ: 2;-6
II случай
x+2=-4
x=-6
10. Логарифмическое уравнение с модулем
log2(|x-2| — 1) = 1
ОДЗ: (|x-2| — 1) > 0:
|x-2| — 1 = 2
|x-2| = 3
I случай
II случай
x-2 = 3
x-2 = -3
x=5
x = -1
Ответ: 5;-1
11. Алгоритм решения уравнений с модулем
1. Найти нули модулей.
2. Отметить нули на координатной
прямой.
3. Решить уравнение на каждом из
промежутков с помощью системы.
4. Написать ответ.
12. Решение уравнений с двумя модулями
|x|=|x-3|+4-x
|x|=0,|x-3|=0
Нули модулей: 0;3
0
3
1сл.
2сл.
3сл.
x
-x=3-x+4-x
0≤x≤3
x=-x+3+4-x
x>3
x=x-3+4-x
x=7, 7
x=7/3 ,0≤7/3≤3 (и)
x=1 ,1>3 (л)
Решений нет
Ответ: 7/3.
7/3 — корень
Решений нет
х
13. Решение неравенств с модулем аналитическим методом
|x+2|≥1
Рассмотрим два случая
I случай
II случай
x+2≥0
x+2≥1
x+2
-2-x
x≥-2
x≥-1
x
x>-3
-2
x
-1
x
[-1;+∞)
-3
x
Ответ:
[-3;-2]
(-3;-2)U[-1;+∞).
-2
x
Решение неравенств с модулем
различными методами
Третий способ. Имеем: |x-2.5|>2.
Геометрически выражение |x-2.5| означает расстояние р(x-2.5)
на координатной прямой между точками х и 2.5. Значит, нам
нужно
Найти все такие точки х, которые удалены от точки 2. 5 более, чем
5 более, чем
на 2это точки из промежутков (-∞;0.5) и (4.5;+∞)
Итак, получили следующее решения неравенства: х4.5.
Четвёртый способ.
Поскольку обе части заданного неравенства неотрицательны,
то возведение их в квадрат есть равносильное преобразование
неравенства. Получим |2x-5|2>42
Воспользовавшись тем что |x|2=x2, получим
(2x-5-4)(2x-5+4)>0
Применив метод интервалов получим тот же ответ.
15. Алгоритм решения неравенств с модулем
1. Найти нули модулей.
2. Отметить нули на координатной
прямой.
3. Решить неравенство на каждом из
промежутков с помощью системы.
4. Написать ответ.
16. Решение неравенств с двумя модулями
|x+1|≥|x-2|
-1
Нули модулей: -1;2
1сл.
2сл.
2
3сл.
x
-x-1≥-х+2
-1≤x≤2
х+1≥-x+2
x>2
х+1≥х-2
0x≥3, 0≥3 (л)
2х≥1
х≥0,5
0,5
0x≥-3,0≥3 (и)
Решений нет
-1
Ответ:(0,5;+∞)
х
х
х
2
2
Тригонометрические уравнения с
модулем
|sin(x+
)|=1
I случай
sin(x+ )=1
-sinx=1
sinx=-1
x=3 /2+2 n
/2+ n
Ответ:
II случай
sin(x+ )=-1
-sinx=-1
sinx=1
x= /2+2 n
Тригонометрические уравнения с
модулем
)
|cosx|=cos(x+
I cлучай
cosx
-cosx=cos(x+ )
cos( +x)=cos(x+ )
x+ =x+ +2
или -x- =x+
x=x+
-2x=2
0x=
x=
решений нет
2
Ответ:
+2
Тригонометрические уравнения с
модулем
)
|cosx|=cos(x+
II cлучай
cosx≥0
cosx=cos(x+ )
cos(x)=cos(x+ )
x =x+ +2
или -x=x+ +2
x=x+
-2x= +2
0x=
x=
—
решений нет
Ответ:
2
График функции у=|x+1|-|x-2|
Нули модулей: -1;2
1сл.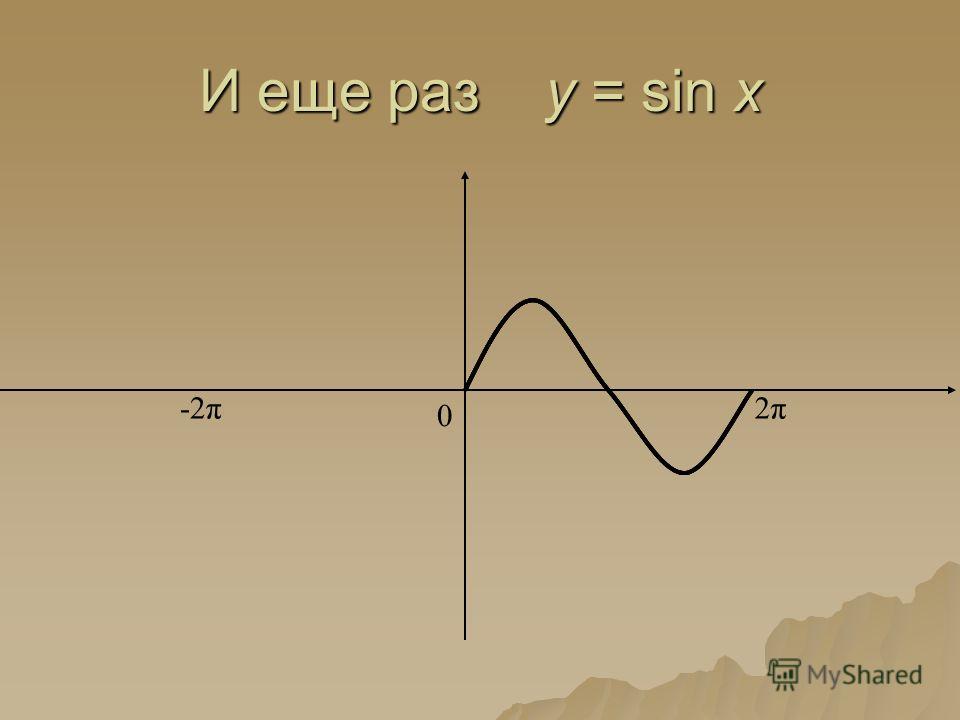
2сл.
x
у=-x-1+х-2
-1≤x≤2
x>2
у=х+1+x-2 у=х+1-х+2
x
у=-3
-1≤x≤2
у=2х-1
у=
-3, x
2х-1, -1≤x≤2
3, x>2
3сл.
2
-1
х
у
x>2
у=3
0
х
Считают, что термин предложил использовать Котс, ученик
Ньютона. Знак модуля введен в XIX веке Вейерштрассом.
Роджер Котс (Roger Cotes;
10 июля 1682 — 5 июня
1716) — английский
математик и философ.
В двадцать четыре года был
назначен профессором
астрономии и
экспериментальной
философии в Кембриджском
университете. В 1713 он
подготовил второе издание
«Principia» Ньютона. Котс
оставил серию подробных
исследований по оптике.
Карл Те́одор Ви́льгельм
Ве́йерштрасс (нем. Karl
Theodor Wilhelm Weierstraß;
31 октября 1815 — 19
февраля 1897) —
выдающийся немецкий
математик, «отец
современного анализа».
22. Выводы
В ходе работы над проектом моя гипотеза не
подтвердилась.
Я не только вспомнил графический способ, но и
научился решать уравнения и неравенства
аналитическим методом и строить графики с
несколькими модулями.
В дальнейшем можно рассмотреть аналитический
метод решения неравенств и уравнений с
модулем и параметром.
23. Список литературы
Алгебра:Для 8 кл.:учеб. пособие для учащихся
шк. и классов с углуб.изуч математики/
Н.Я.Виленкин, Г.С.Сурвило и др., под ред.
Н.Я.Виленкина – М.: Просвещение.
Мордкович А.Г. И др. Алгебра.9кл.: В двух
частях. Ч.2: Задачник для общеообразоват.
учреждений/М.:Мнемозина, 2004 г.
Мордкович А.Г. И др. Алгебра.9кл.: В двух
частях. Ч.2: Учебник для общеообразоват.
учреждений/М.:Мнемозина, 2004 г.
Мордкович А.Г. И др.Алгебра и начала анализа
10-11кл.: В двух частях. Ч.1: Задачник для
общеообразоват. учреждений/М.:Мнемозина,
2004 г.
Математика: Учеб. Для 6 кл. сред. шк./Н.Я.
Виленкин и др. М.: Просвещение, 1993.
Разложение Маклорена cos (x)
Предыдущая: Maclaurin Expansion of sin (x)
Следующая: Список Maclaurin Expansions
Пример
Найдите разложение в ряд Маклорена для cos ( x ) при x = 0 и определите его радиус сходимости.
Полное решение
Шаг 1. Найдите серию Maclaurin
Шаг 2: Найдите радиус схождения
Тест соотношения дает нам:
Поскольку этот предел равен нулю для всех реальных значений x , радиус сходимости расширения — это набор всех действительных чисел.
Объяснение каждого шага
Шаг 1
Чтобы найти расширение серии, мы могли бы использовать здесь тот же процесс, который мы использовали для sin ( x ) и e x . Но есть способ попроще. Мы можем дифференцировать известное нам разложение для синусоидальной функции.
Если вы, , хотели бы увидеть вывод разложения в ряд Маклорена для косинуса, следующий видеоролик предоставляет этот вывод.
| Косинус серии Тейлора в 0 |
|---|
| Вывод разложения в ряд Маклорена для косинуса. |
| Это видео можно найти на веб-сайте Академии Кана, и оно защищено авторскими правами Creative Commons (CC BY-NC-SA 3.0). |
Шаг 2
Этот шаг был не чем иным, как подстановкой нашей формулы в формулу для теста отношения.
Возможные проблемы
Когда мы можем дифференцировать серию Power?
В рамках этого модуля мы всегда предполагаем, что можем.Однако существует теорема о дифференцировании и интегрировании степенных рядов, которую вы не должны знать, которая говорит нам, что степенной ряд можно дифференцировать только в том случае, если он имеет радиус сходимости больше нуля.
Скоро в этом модуле будет страница, посвященная этой теореме. А пока эта страница в Википедии может помочь.
А пока эта страница в Википедии может помочь.
Приходилось ли нам проверять конвергенцию?
Короткий ответ: нет. Упомянутая выше теорема говорит нам, что, поскольку
- мы вывели ряд для cos (x) из ряда для sin (x) посредством дифференцирования, и
- мы уже знаем радиус сходимости sin (x),
радиус сходимости cos (x) будет таким же, как sin (x).Однако мы не вводили эту теорему в этом модуле. Вы можете спросить своего инструктора, должны ли вы знать эту теорему.
Сводка
| Разложение Маклорена cos (x) |
|---|
| Разложение в ряд Маклорена для cos ( x ) дается выражением Эта формула действительна для всех действительных значений x . |
Предыдущая: Maclaurin Expansion of sin (x)
Следующая: Список Maclaurin Expansions
patrick-kidger / sympytorch: превращение выражений SymPy в модули PyTorch.

Микробиблиотека для удобства превращения выражений SymPy в модули PyTorch.
поплавков SymPy (опционально) становятся обучаемыми параметрами. Символы SymPy являются входными данными для модуля.
Установка
pip install git + https: //github.com/patrick-kidger/sympytorch.git
Пример
импортный sympy, torch, sympytorch
x = sympy.symbols ('x_name')
cosx = 1.0 * sympy.cos (x)
sinx = 2,0 * sympy.sin (x)
mod = sympytorch.SymPyModule (выражения = [cosx, sinx])
x_ = факел.ранд (3)
out = mod (x_name = x_) # out имеет форму (3, 2)
assert torch.equal (out [:, 0], x_.cos ())
утверждать torch.equal (out [:, 1], 2 * x_.sin ())
assert out.requires_grad # из двух параметров, инициализированных как 1.0 и 2.0
assert {x.item () для x в mod.parameters ()} == {1.0, 2.0} API
sympytorch.SymPyModule (*, выражения, extra_funcs = None)
Где:
-
выражений— это список выражений SymPy.
-
extra_funcs— отображение словаря из пользовательского sympy.Функцияс их реализацией PyTorch. По умолчанию никаких дополнительных функций.
Можно вызывать экземпляры SymPyModule , передавая значения символов, как в приведенном выше примере.
SymPyModule имеет метод .sympy () , который возвращает соответствующий список выражений SymPy. (Что может не совпадать с выражениями, которыми оно было инициализировано, если значения его параметров были изменены, т.е. были изучены.)
Обертывание поплавков в sympy.UnevaluatedExpr заставит их не обучаться, зарегистрировав их как буферы, а не параметры.
sympytorch.hide_floats (выражение)
Для удобства hide_floats будет принимать выражение и возвращать новое выражение с каждым веществом с плавающей запятой, обернутым в sympy.UnevaluatedExpr , так что оно интерпретируется как буфер, а не параметр.
Расширения
Поддерживаются не все операции PyTorch или SymPy — только те, которые мне нужны! Здесь есть словарь, в котором перечислены поддерживаемые операции.Не стесняйтесь отправлять PR для любых дополнительных операций, которые, по вашему мнению, должны выполняться по умолчанию. Вы также можете использовать аргумент extra_funcs для указания дополнительных функций, включая пользовательские функции.
PPLATO | Учебники | Дифференциальные уравнения
Рассмотрим обыкновенное дифференциальное уравнение (о. Д. Е.), Которое мы хотим решить, чтобы выяснить, как переменная y зависит от переменной x.
Если уравнение первого порядка , тогда самая высокая производная является первой производной.
Если это также линейное уравнение , то это означает, что каждый член может включать y либо как производную dy / dx ИЛИ через единственный множитель y.
Любой такой линейный н.о. первого порядка. могут быть преобразованы в следующую стандартную форму:
— где P ( x ) и Q ( x ) — функции
x, а в некоторых случаях могут быть константами.
Линейный н.о. первого порядка. может быть решена с использованием метода интегрирующего множителя .
После записи уравнения в стандартной форме , можно идентифицировать P ( x ). Один тогда
умножает уравнение на следующий «интегрирующий коэффициент»:
Этот коэффициент определяется таким образом, что уравнение становится эквивалентным:
d / dx (IF y ) = IF Q ( x ) dx
Интегрирование обеих сторон по x дает:
IF z = ∫IF Q 1 ( x ) dx
Наконец, деление на интегрирующий коэффициент (IF) дает y явно через x, i.е. дает решение уравнения.
В каждом случае выведите общее решение. Если также задано граничное условие, выведите частное решение.
Нажмите на вопросы, чтобы узнать их решения
Упражнение 1:
Решение:
Сравните с формой: dy / dx + P ( x ) y = Q ( x ) ⇒ P ( x ) = 1.
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e ∫ dx = e x | |
| Умножьте уравнение на ЕСЛИ: | e x dy / dx + e x y | = | e x x | |
| я.е. | д / dx [e x y ] | = | e x x | |
| Объедините обе стороны относительно x : | e x y | = | e x ( x — 1) + C | |
| {Примечание: интегрировать по частям, т.е.э .: | ∫ u дв / dx dx = мкв — ду / dx dx с u ≡ x и дв / dx ≡ e x | |||
| → | x e x — ∫e x dx | |||
| → | x e x — e x = e x ( x — 1) } | |||
| я.е. | y | = | ( x — 1) + C e — x | |
Частное решение с y (0) = 2:
| 2 | = | (0 — 1) + С e 0 | |
| = | -1 + С | ||
| i.е. | К | = | 3 |
| ∴ | y | = | ( x — 1) + 3 e — x |
Упражнение 2:
dy / dx
+ y = e — x ; y (0) = 1
Решение:
P ( x ) = 1.
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e ∫ dx = e x | |
| Умножить уравнение на IF: | e x dy / dx + e x y | = | e x e — x | |
| я.е. | d / dx [e x y ] | = | 1 | |
| Интегрировать: | e x y | = | x + С | |
| то есть | y | = | e — x ( x + C ) |
Частное решение с x = 0, y = 1:
| 1 | = | e 0 (0 + C ) | |
| = | 1⋅ С | ||
| i.е. | К | = | 1 |
| ∴ | y | = | e — x ( x + 1) |
Упражнение 3:
x dy / dx
+ 2 y = 10 x 2 ; y (1) = 3
Решение:
Уравнение линейное, 1-го порядка, т.е.е.
dy / dx
+ P ( x ) y = Q ( x )
⇒
dy / dx
+ 2/ x y
= 10 x , поэтому: P ( x ) =
2/ x , Q ( x ) = 10
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e 2∫ dx / x = e 2 ln x = e ln x 2 = x 2 | |
| Умножить уравнение на IF: | x 2 dy / dx + 2 xy | = | 10 x 3 | |
| я.е. | d / dx [ x 2 ⋅ y ] | = | 10 x 3 | |
| Интегрировать: | x 2 y | = | 5/2 x 4 + C | |
| я.е. | y | = | 5/2 x 2 + С / x 2 |
Частное решение: y (1) = 3, т.е. y ( x ) = 3, когда x = 1:
| т.е. | 3 | = | 5 / 2⋅1 + 1/2 |
| i.е. | 6/2 | = | 5/2 + К |
| т.е. | К | = | 1/2 |
| ∴ | y | = | 5/2 x 2 + 1/2 x 2 = 1/2 (5 x 2 + 1/ x 2 ) |
Упражнение 4:
x dy / dx
— y = x 2 ; y (1) = 3
Решение:
Приведите уравнение в стандартную форму: dy / dx — (1/ x ) y = x
Сравнить с:
dy / dx + P ( x ) y = Q ( x )
⇒ P ( x ) = — 1/ x
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e — ∫ dx / x = e — ln x = e ln ( x −1 ) = 1/ х | |
| Умножить уравнение на IF: | 1/ х dy / dx — 1/ х 2 л | = | 1 | |
| я.е. | d / dx [1/ x y ] | = | 1 | |
| Интегрировать: | 1/ x y | = | x + С | |
| я.е. | y | = | x 2 + Cx |
Частное решение с y (1) = 3:
| т.е. | 3 | = | 1 + К |
| т.е. | К | = | 2 |
| ∴ | y | = | x 2 + 2 x ) |
Упражнение 5:
x dy / dx
— 2 y = x 4 sin x
Решение:
Сделайте уравнение линейным по оси y: dy / dx —
2/ x y
= x 3 sin x ⇒ P ( x ) =
— 2/ х
.
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e −2∫ dx / x = e −2 ln x = e ln ( x −2 ) = 1/ x 2 | |
| Умножить уравнение на IF: | 1/ х 2 dy / dx — 2/ х 3 л | = | x sin x | |
| я.е. | d / dx [1/ x 2 y ] | = | x sin x | |
| Интегрировать: | y / x 2 | = | — x cos x — ∫1⋅ (- cos x ) dx + C ‘ | |
| {Примечание: интегрировать по частям, т.е.э .: | ∫ u dv / dx dx = uv — du / dx dx с u ≡ x и dv / sin x } | |||
| то есть | y / x 2 | = | — x cos x + sin x + C | |
| я.е. | y | = | x 3 cos x + x 2 sin x + Сх 2 | |
Упражнение 6:
x dy / dx
— 2 л
= х 2
Решение:
Стандартная форма: dy / dx — (2/ x ) y = x ⇒ P ( x ) =
— 2/ х .
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e −2 ∫ dx / x = e −2 ln x = e ln ( x −2 ) = 1/ x 2 | |
| Умножить уравнение на IF: | 1/ x 2 dy / dx — 2/ x 3 y | = | 1/ х | |
| я.е. | d / dx [1/ x 2 y ] | = | 1/9000 9 x | |
| Интегрировать: | 1/ x 2 y | = | ∫ dx / x | |
| я.е. | 1/ x 2 y | = | лин x + C | |
| то есть | y | = | x 2 ln x + Cx 2 |
Упражнение 7:
dy / dx
+ y Детская кроватка x
= cosec x
Решение:
Уравнение уже имеет стандартную форму: dy / dx + P ( x ) y = Q ( x ), т.е.е. линейный 1-го порядка н.у.
, поэтому P ( x ) = детская кроватка x
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e ∫ cos x / sin x dx ≡ e ∫ ƒ ′ ( x ) / ƒ ( x ) dx = e ln (sin x ) = грех х | |
| Умножьте уравнение: | sin x ⋅ dy / dx + sin x (cos x / sin x ) л | = | грех х / грех х | |
| я.е. | sin x ⋅ dy / dx + cos x ⋅ y | = | 1 | |
| то есть | d / dx [sin x ⋅ y ] | = | 1 | |
| Интегрировать: | sin x ⋅ y | = | x + С |
Упражнение 8:
dy / dx
+ y Детская кроватка x
= cos x
Решение:
P ( x ) = детская кроватка x =
cos x / sin x
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e ∫ cos x / sin x dx ≡ e ∫ ƒ ′ ( x ) / ƒ ( x ) dx = e ln (sin x ) = sin x | |
| Умножьте уравнение: | sin x ⋅ dy / dx + sin x (cos x / sin x ) y | = | sin x ⋅cos x | |
| я.е. | d / dx [sin x ⋅ y ] | = | sin x ⋅cos x | |
| Интегрировать: | y sin x | = | sin x cos x | |
| {Примечание: ∫sin x cos x ≡ ∫ ƒ ( x ) ƒ ′ ( x ) dx ≡ ∫ ƒ ( x ) dƒ / dx ⋅ dx ≡ ∫ ƒ dƒ = 1/2 ƒ 2 + C } | ||||
| я.е. | y sin x | = | 1/2 sin 2 x + C | |
| = | 1 / 2⋅ 1/2 (1 — cos 2 x ) + C | |||
| я.е. | 4 y sin x + cos 2 x | = | С ‘ = 4 С + 1 | |
Упражнение 9:
( x 2 — 1) dy / dx
+ 2 xy
= х
Решение:
Стандартная форма: dy / dx
+ (2 x / x 2 — 1) y
= x / x 2 — 1
⇒ P ( x ) =
2 x / x 2 — 1
| Интегрирующий коэффициент: | IF | = | e ∫ P ( x ) dx = e ∫2 x / x 2 — 1 dx = e ln x 2 — 1 = x 2 — 1 | |
| Умножить уравнение на IF: | ( x 2 — 1) dy / dx + 2 xy | = | х | |
| я.е. | d / dx [( x 2 — 1) y ] | = | х | |
| Интегрировать: | ( x 2 — 1) y | = | 1/2 x 2 + С |
Упражнение 10:
dy / dx
= y tan x — сек x ; y (0) = 1
Решение:
P ( x ) = — загар x и Q ( x ) = — sec x
Интегрирующий коэффициент IF =
e −∫tan x dx
= e −∫ sin x / cos x dx
= e + ∫ — sin x / cos x dx
= e ln (cos x ) = cos x
| Умножить уравнение на IF: | cos x dy / dx — cos x ⋅ sin x / cos x y | = | — cos x мкс x | |
| я.е. | d / dx [cos x ⋅ y ] | = | -1 | |
| Интегрировать: | y cos x | = | — x + С |
Частное решение с y (0) = 1, т.е.е. y = 1, когда x = 0:
| cos 0 | = | 0 + К | |
| ∴ | К | = | 1 |
| т.е. | y cos x | = | — х + 1 |
| ƒ ( x ) | ∫ ƒ ( x ) dx | ƒ ( x ) | ∫ ƒ ( x ) dx | |
|---|---|---|---|---|
| x n | x n +1 / n +1 ( n ≠ −1) | [ г ( x )] n г ‘ ( x ) | [ г ( x )] n +1 / n +1 ( n −1) | |
| 1/9000 9 x | лин x | г ‘ ( x ) / г ( x ) | лин г ( x ) | |
| e x | e x | а x | a x / ln a ( a > 0) | |
| sin x | −cos x | sinh x | цвет x | |
| cos x | грех x | цвет x | sinh x | |
| желто-коричневый x | — ln cos x | танх x | ln cosh x | |
| код x | ln загар x /2 | cosech x | ln tanh x /2 | |
| сек x | лн сек x + загар x | сек x | 2 желто-коричневый −1 e x | |
| сек 2 x | коричневый x | сек 2 x | танх x | |
| детская кроватка x | лин. Sin x | Детская кроватка x | линз x | |
| sin 2 x | x /2 — sin 2 x /4 | sinh 2 x | sinh 2 x /4 — x /2 | |
| cos 2 x | x /2 + sin 2 x /4 | cosh 2 x | sinh 2 x /4 + x /2 | |
| 1/ a 2 + x 2 | 1/ a tan −1 x / a ( a > 0) | √ a 2 + x 2 | a 2 /2 [sinh −1 ( x / a ) + x √ a 2 — x 2 / a 2 ] | |
| 1/ a 2 — x 2 | 1/2 a ln a + x / a — x (0 < x < a ) | √ a 2 — x 2 | a 2 /2 [sin −1 ( x / a ) + x √ a 2 — x 2 / a 2 ] | |
| 1/ x 2 — a 2 | 1/2 a ln x — a / x + a ( x > a > 0) | √ x 2 — a 2 | a 2 /2 [−cosh −1 ( x / a ) + x √ x 2 — a 2 / a 2 ] | |
| 1 / √ a 2 + x 2 | ln x + √ a 2 + x 2 / a ( a > 0) | |||
| 1 / √ a 2 — x 2 | sin −1 x / a (- a < x < a ) | 1 / √ x 2 — a 2 | ln x + √ x 2 — a 2 / a ( x > a > 0) |
Линейное дифференциальное уравнение первого порядка:
dy / dx
+ P ( x ) y = Q ( x )
имеет интегрирующий коэффициент IF = e ∫ P ( x ) dx .
Метод интегрирующих множителей иногда объясняется в терминах более простых форм дифференциального уравнения. Например, при постоянном
коэффициенты a и b, уравнение можно записать как:
а
dy / dx
+ b P ( x ) y = Q ( x )
В нашей стандартной форме это:
dy / dx
+
b / a
л
знак равно
Q ( x ) / a
— с интегрирующим фактором:
ЕСЛИ = e ∫
b / a
dx
= e bx / a
Сегодня: лямбда-разминка, модули 1.0, модуль wordcount, превью HW7, конкурс синего экрана
Лямбда-прогрев
Сделайте это в интерпретаторе
Предположим, есть список строк. Как отсортировать их по возрастанию по длине? Какой однострочник / лямбда вытянет струну с наибольшей длиной?
>>> strs = ['яблоко', 'пончик глазурь', 'груша', 'банан'] >>>
Решение
>>> # выводить len (s) для каждой строки >>> отсортировано (strs, key = lambda s: len (s)) ["груша", "яблоко", "банан", "глазурь для пончика"] >>> >>> # макс вытаскивает самую большую >>> max (strs, key = lambda s: len (s)) 'пончик глазурь'
Модули
- «модуль» — используемая единица кода, «библиотека»
- У каждого модуля есть имя, например.грамм. «математика»
- Модуль содержит множество функций, решающих общие проблемы
- Современная кодировка:
1. Часть, созданная на основе кода модуля
2. Часть вы пишете кастом
Стандартные модули — импортная математика
- Python поставляется со «стандартными» модулями
- Стандартные модули устанавливаются при установке Python, поэтому дополнительных действий не требуется
- например модуль «математика» — математика
- например модуль «sys» — интерфейс с операционной системой
- импортный модуль по имени
- Используйте точку для обозначения функций и т. Д.в модуле
math.sqrt (2)— вызов функции
math.pi— константа Пи в математике - Показано здесь в интерпретаторе, но работает и в .py
- Распространенная ошибка: забыть выполнить импорт
- Кроме того: есть и другие формы импорта, но эта форма имени / точки является наиболее важной.
>>> импорт математики >>> math.sqrt (2) # вызов sqrt () fn 1,4142135623730951 >>> math.sqrt >>> >>> math.log (10) 2.3025850046 >>> math.pi # тоже в модуле константы 3,1415589793
Перезапустить интерпретатор без импорта, увидеть общую ошибку:
>>> # выйти и перезапустить интерпретатор >>> math.sqrt (2) # OOPS забыл импорт Отслеживание (последний вызов последний): NameError: имя 'math' не определено >>> >>> импорт математики >>> math.sqrt (2) # теперь работает 1,4142135623730951
Хакер: используйте dir () и help ()
- Почувствуйте себя хакером, используйте dir () и help () в модуле
- В интерпретаторе >>>
-
dir (module)— показывает список всех defs в модуле -
справка (модуль.fn)— показывает текст справки для этой функции
>>> импорт математики
>>> dir (математика)
['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', ' atanh ',' ceil ',' copysign ',' cos ',' cosh ',' градусы ',' e ',' erf ',' erfc ',' exp ',' expm1 ',' fabs ',' factorial ' , 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', ' ldexp ',' lgamma ',' log ',' log10 ',' log1p ',' log2 ',' modf ',' nan ',' pi ',' pow ',' радианы ',' остаток ',' sin ' , 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc']
>>>
>>> справка (математика.sqrt)
Справка по встроенной функции sqrt в модуле math:
sqrt (х, /)
Верните квадратный корень из x.
>>>
>>> справка (math.cos)
Справка по встроенной функции cos в модуле math:
соз (х, /)
Верните косинус x (измеренный в радианах).
Обзор модуля
- Что такое модуль?
- Имеет имя
- Содержит множество функций
т.е. «библиотека» функций - Используйте
import math, чтобы ввести его - Используйте математику
.sqrt (5)синтаксис для вызова функции в модуле
wordcount.py Это модуль
- Предположим, вы создали несколько полезных функций
- Кто-то еще в вашей лаборатории хочет их использовать ….
Их вставка в собственную копию не идеальна - Что содержит модуль?
- У нас есть wordcount.py
- python3 wordcount.py — запускает main ()
- wordcount.py — это также модуль , названный просто «wordcount»
- Подумайте обо всех определениях в wordcount: read_counts (), clean (), print_counts (),
- import работает с wordcount (в том же каталоге)
- Функции доступа как модуль.ххх как обычно
- Запустите интерпретатор Python в каталоге wordcount, чтобы попробовать это
- Попробуйте импортировать wordcount, вызвав функцию read_counts ()
- Вызвать wordcount.clean ()
>>> # Запускаем интерпретатор в каталоге wordcount
>>> импортировать количество слов
>>>
>>> wordcount.read_counts ('test1.txt')
{'a': 2, 'b': 2}
- Модуль / файл содержит много определений
- Может импортировать модуль / файл, вызвать его defs:
- модуль.fn_name ()
- Стиль: чтобы функцию можно было использовать из другого модуля …
он должен принимать данные в качестве параметров и возвращать значение
т.е. стиль черного ящика
мы делали это все время, теперь посмотрим на более широкую картину - HW7 детская графика:
рассматривает babynames.py как модуль
импортных babynames
вызовите babynames.read_files () и т. Д.
dir () и help () тоже работают с wordcount.
- dir () и help () тоже работают
- Посмотрите, куда идет «» «Pydoc» «»!
>>> dir (количество слов)
['__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'clean', 'main', 'print_counts', 'print_top', ' read_counts ',' sys ']
>>>
>>> справка (wordcount.read_counts)
Справка по функции read_counts в модуле wordcount:
read_counts (имя файла)
Данное имя файла читает его текст, разбивает его на слова.
Возвращает "счетчик", в котором каждое слово
...
Два способа использования wordcount.py
- Два способа использования этого файла
- 1.
python3 wordcount.py poem.txt
загрузить весь код wordcount.py
запустить main () … он запускает все функции - 2. Некоторый код
импортирует wordcount
В этом случае:
Загрузить все wordcount.py-код
не запускать основной
Модуль сидит там
Ожидание вызова типа wordcount.read_counts () - Как различаются эти два случая?
- (1) — обычное дело, кстати, (2) — редко, но должно работать
Как Python знает, как запустить main ()?
- Есть специальная переменная
__name__ - Python в сторону: когда имя начинается с подчеркивания
Обозначает внутреннюю деталь, с которой нормальный код не должен связываться. - Когда __name__ имеет специальное значение __main__
Это означает, что у нас есть случай (1), мы должны запустить main () - Вот почему внизу файла есть этот сумасшедший if-оператор!
Типичные последние 2 строки.py файл:
если __name__ == '__main__':
основной()
Эксперимент: поместите эти строки в конец wordcount.py. Затем попробуйте запустить wordcount из командной строки и загрузить его в интерпретатор.
если __name__ == '__main__':
print ("Мне хочется запустить main ()")
основной()
еще:
print ("Не работает main ()")
Идея дизайна: простые вещи должны быть легкими
Идея дизайна: делать обычные вещи должно быть легко, не требуя размышлений. Сделать что-то сложное должно быть возможно, но может потребоваться работа.
Этот бизнес __name__ кажется слабым местом в дизайне Python. Это не здорово, что каждая ванильная программа на питоне должна содержать эти 2 малоизвестные строки. Должен быть менее неясный способ получить поведение по умолчанию, которого хотят 99% программ на Python.
Демо HW7 Детская графика
- Он просто вызывает ваши функции babynames.xxx
- Код здесь рисует линии, цвета
Демо HW7 Ghost
- Посмотрите на серию изображений — подумайте о выбросах
часовая башня
монстр - Алгоритмический взгляд на пиксели
Конкурс Bluescreen Art (по желанию!)
- У нас будет дополнительный арт-проект HW7c, которым можно заняться в свое удовольствие
Небольшой дополнительный балл, не влияющий на кривую
Действительно просто для удовольствия после того, как вы закончите с HW7
Художественная выставка в классе, призы - Recall — Алгоритм Bluescreen
- 1.«фронтальная» стратегия
- Обнаружение синих пикселей — средний метод
- Заменить синие пиксели в изображении пикселями фона
- Подробнее Понедельник (сначала сделайте HW7)
- Демо здесь — закомментируйте строки pixel.red = xxx, чтобы увидеть исходное изображение
>
синяя обезьяна
Общие ошибки и проблемы ORCA
На этой странице перечислены общие ошибки и проблемы, возникающие при выполнении вычислений с ORCA.
Внезапное завершение работы ORCA
Если ORCA завершается с общим сообщением: «ORCA завершено из-за ошибки завершения в [модуле ORCA]» без другого полезного сообщения выше,
причина зависит от того, какой модуль ORCA был запущен.Если запущенный модуль был модулем с интенсивным использованием памяти, например: orca_mp2, orca_scfhess, orca_mdci, orca_mrci и т. Д., Возможно, что для задания не хватило памяти или места на диске, либо возникла проблема с доступом к памяти или диску. Это также может быть вопрос выполнения расчета небольшой системы со слишком большим количеством ядер (выполнение расчета 60 ядер системы всего с несколькими атомами не имеет смысла и приводит к непредсказуемым результатам).
— Для управления памятью см. Сообщения об ошибках «Недостаточно памяти» ниже.Также рекомендуется отслеживать использование памяти для выполняемого задания в реальном времени (например, с помощью команды free в Linux / Unix).
— Чтобы проверить, не возникла ли проблема с диском, войдите в рабочее пространство вычислительного узла и проверьте, сколько рабочего пространства было создано ORCA. Обратите внимание, что скрипт задания, возможно, уже удалил царапины, в случае чего вам, возможно, придется перезапустить задание и отслеживать, сколько царапин создается прямо перед царапиной ORCA. Если ORCA создает больше царапин, чем доступно на диске узла, вы можете быть вынуждены инвестировать в диск большего размера для таких вычислений.
— Также обратите внимание, что случайные ошибки чтения / записи на диск могут возникать с ORCA, если ORCA запускается на сетевом диске. Сетевой диск не идеален для расчетов ORCA, когда на диск записывается много царапин.
— Если проблема не в диске или памяти, возможно, это ошибка. Задайте вопрос на форуме ORCA и с самого начала предоставьте всю необходимую информацию. Рекомендуется показывать входной файл в сообщении на форуме, так как это поможет разработчикам быстрее диагностировать проблему.Это также полезная информация для разработчика, если вы можете воспроизвести ошибку в молекулярной системе, которая настолько проста, насколько это возможно (например, двухатомная молекула) или с входным файлом, который содержит как можно меньше параметров.
Сообщения об ошибках «Недостаточно памяти»
ORCA требуется больше памяти для завершения вычислений, если вы получаете сообщение «Недостаточно памяти» в конце выходного файла. Управляющая память обычно необходима для различных расчетов теории волновых функций (MP2, CCSD (T), CASSCF, MRCI и т. Д.) или при расчете возбужденных состояний (TDDFT, CIS, EOM-CC, CASSCF, MRCI) или сложных молекулярных свойств (Hessian, химические сдвиги ЯМР или спин-спиновые связи). Знание того, как правильно управлять памятью, часто позволяет выполнять более эффективные вычисления, поскольку это сокращает количество пакетов в некоторой части кода.
Использование памяти в ORCA контролируется ключевым словом% maxcore, где пользователь должен указать объем памяти в мегабайтах для каждого ядра, который программе разрешено использовать.
Пример:
! DLPNO-CCSD (T) def2-TZVP def2-TZVP / C
% maxcore 3000
% pal
nprocs 6
end
Здесь ORCA отдает 3000 МБ памяти на каждое ядро.Поскольку было запрошено использование 6 ядер ЦП, это означает, что общая потребность ORCA в памяти составляет 6×3000 = 18000 МБ = 18 ГБ
. Убедитесь, что на вычислительном узле имеется доступный общий объем физической памяти.
В общем, вам не следует запрашивать более 75% доступной физической памяти (поскольку ORCA иногда будет использовать больше, чем установлено maxcore). Так что, если на компьютере в этом случае доступно 24 ГБ или более физической памяти, все должно быть в порядке.
Если используемый вами вычислительный узел также используется другими пользователями, убедитесь, что не запрашиваете больше памяти, чем вы имеете право.Например, если 12-ядерный узел имеет 120 ГБ памяти и вы отправляете 6-ядерное задание, то вы имеете право, например, на половину этой памяти (также обратите внимание, что иногда системы очередей требуют, чтобы вы указывали, сколько памяти вы хотите). Таким образом, для вашей 6-ядерной задачи должно быть разрешено использовать только 60 ГБ памяти или maxcore (память на ядро) в размере 10 000 МБ (10 ГБ). Поскольку использование памяти в ORCA часто превышает maxcore, снижая maxcore до ~ 75% доступной физической памяти: рекомендуется установка maxcore% maxcore 7500.
Мнимые колебательные моды из частотного задания оптимизированной структуры (минимум)
Маленькие мнимые моды (~ менее 100 см-1), например:
————— ———
ЧАСТОТА КОЛЕБАНИЙ
————————
0: 0,00 см ** — 1
1: 0,00 см ** — 1
2: 0,00 см ** — 1
3: 0,00 см ** — 1
4: 0,00 см ** — 1
5: 0.00 см ** — 1
6: -70,85 см ** — 1 *** мнимый режим ***
7: -50,05 см ** — 1 *** мнимый режим ***
8: 48,60 см ** — 1
9: 169,21 см ** — 1
10: 176,59 см ** — 1
11: 241,39 см ** — 1
обычно указывают на числовой шум. Шум, вызывающий это, мог присутствовать только в гессиане или он мог присутствовать в энергии или градиенте при оптимизации геометрии, что приводило к неоптимальной геометрии.В этом случае проблема устраняется увеличением сетки интеграции путем добавления ключевых слов «Grid4 FinalGrid5». Если приближение RIJCOSX использовалось либо в оптимизации геометрии, либо в расчете Гессе, числовой шум также мог быть связан с сеткой COSX. Дополнительные сведения см. На странице «Числовая точность».
Также может быть, что вам просто нужно немного снизить пороговые значения для оптимизации геометрии (возможно, поверхность энергии немного плоская), чтобы вы более точно сходились к минимуму.TightOpt — удобный способ сделать это.
Более крупные воображаемые режимы, например:
ЧАСТОТА КОЛЕБАНИЙ
————————
0: 0,00 см ** — 1
1: 0,00 см ** — 1
2: 0,00 см ** — 1
3: 0,00 см ** — 1
4: 0,00 см ** — 1
5: 0,00 см ** — 1
6: -646,34 см ** — 1 *** мнимый режим ***
7: -467,58 см ** — 1 *** мнимый режим ***
8: -109.76 см ** — 1 *** мнимая мода ***
9: 7,86 см ** — 1
, однако, как правило, не указывают на числовой шум, а скорее указывают на геометрию, которая не сведена к минимуму. В этом случае причиной этих мнимых режимов является то, что оптимизация геометрии сходилась к седловой точке более высокого порядка. Это может произойти, если начальная геометрия для работы по оптимизации была близка к такой точке перевала, в частности, если геометрия точки перевала симметрична. Это был пример замещенной бифенильной структуры, которая имеет неплоский минимум, но поскольку исходная геометрия была плоской, оптимизация вместо этого сходилась к плоской седловой точке.Чтобы решить эту проблему, просто измените геометрию так, чтобы она больше не выглядела как геометрия седловой точки.
Если использовалась сольватация континуума (CPCM), то также возможно, что виновата конструкция полости (или поверхностные заряды), что приводит к неоднородностям. Отключение континуума может решить проблему, но если континуум необходим, может потребоваться настройка параметров CPCM (например, конструкции полости). ORCA 4.2 имеет более сложную конструкцию полости, которая уменьшает эту проблему.
Молекула взрывается
В редких случаях оптимизация геометрии молекулы вызывает взрыв молекулы, то есть координаты атомов повсюду, как показывает программа визуализации.
Это может быть вызвано несколькими причинами:
— Исходная структура неправильная. Атомы могут быть слишком близко. Может быть, смешение единиц Ангстремов и Бора.
Решение: Исправить конструкцию.
— У тяжелых элементов отсутствуют базисные функции или эффективный потенциал ядра для описания электронов ядра.
Решение: Тщательно проверьте, какие базовые функции и ECP назначены каждому элементу (используйте ключевое слово! Printbasis для получения дополнительной информации).
— Плохое поведение оптимизатора из-за внутренних координат.
Решение: Переключитесь на декартову систему координат для оптимизации (используйте ключевое слово COpt вместо ключевого слова Opt). Это займет больше времени, но исправлены редкие случаи несоответствия внутренней системы координат.
Проблемы сходимости SCF
Если SCF пытается сойтись, существует несколько возможных причин.
Однако, прежде чем исследовать другую стратегию конвергенции SCF, стоит проверить такие базовые вещи, как:
— приемлемы ли координаты? Визуализируйте координаты в программе визуализации. Совкомфлот будет бороться со слишком длинными или слишком короткими облигациями и т. Д.
— Вы перепутали Ангстрема и Бора?
— Верна ли кратность заряда и вращения?
— У тяжелых элементов отсутствуют базовые функции или эффективные основные потенциалы?
— У вас есть сложная структура с открытой оболочкой с несколькими открытыми оболочками, возможно, требующая стратегии ДПФ с нарушенной симметрией? См. Страницу BS-DFT.- Используете ли вы диффузный базисный набор, такой как aug-cc-pVTZ? Такой диффузный базисный набор может быть трудным в использовании из-за линейных зависимостей в базисном наборе. См. Обсуждение внизу этой страницы. Лучшее решение — часто избегать таких рассеянных базисных наборов, если это действительно не нужно. См. Страницу базового набора для других альтернатив (например, ma-def2-TZVP, хотя он не застрахован от проблем с линейной зависимостью). Хорошая идея — провести исследование сходимости базисного набора. — Вы рассчитываете анион в газовой фазе? Анионы иногда нестабильны в газовой фазе, и для стабилизации самых высоких занятых орбиталей может потребоваться модель континуума (CPCM).Если ничего не работает, опубликуйте свою проблему на форуме ORCA. Чтобы диагностировать проблему, экспертам ORCA обычно требуется видеть весь выходной или входной файл, в идеале с координатами.
Оптимизация геометрии не может сходиться и / или энергия увеличивается во время оптимизации
Это может произойти по нескольким причинам.
— Если энергия во время оптимизации не уменьшается (как должно), то, вероятно, есть числовой шум в градиенте. Таким образом, на каждом этапе вычисления градиента шум в градиенте заставляет оптимизатор предпринимать неверные шаги.Этот числовой шум, скорее всего, связан с использованием сетки интегрирования в члене обменно-корреляционной обработки DFT или сетки COSX в приближении RIJCOSX. Часто виноват термин обмен-корреляция DFT, и решение состоит в том, чтобы немного увеличить интегральную сетку (например, Grid4 Finalgrid5). Также возможно, что виновата сетка COSX, и тогда увеличение сетки COSX с GridXS2 по умолчанию до GridX4, GridX5, GridX6 и т. Д. Может уменьшить числовой шум, исходящий от сетки COSX.Дополнительные сведения см. На странице «Числовая точность».
SCF энергия или свойство странные (например, отличается от предыдущего расчета или другой программы, или заряды, спиновые населенности или орбитали странные)
Что может случиться в любом вычислении SCF (DFT или HF), так это то, что оно сходится к возбужденное состояние (то есть другое заполнение орбиталей) или даже седловая точка в орбитальном пространстве вместо минимума. Такие случаи редки, но более вероятны в случаях высокой симметрии (например,грамм. атомы, диатомики или другие высокосимметричные геометрии, например бензол и ферроцен). Эта проблема может впоследствии повлиять на расчет после HF, например MP2, связанный кластер.
В качестве примера этот входной файл для двухатомного I 2 :
! B3LYP def2-TZVPP tightscf kdiis
* xyz 0 1
I -0,8112688 -0,2430916 0,0150128
I 1,8686027 -0,3386353 -0,0757158
*
энергии в результате решения с SC-
95 будет.256765 хартри.
Хотя в этом прямом ограниченном вычислении ДПФ нет ничего подозрительного, энергия (как будет показано ниже) здесь слишком высока. Этот проблемный пример был обнаружен, когда при расчете с использованием B3LYP / def2-TZVPP с KDIIS была обнаружена необычно большая энергия реакции: Metalcomplex + I 2 => Metal-I 2 -complex.
Чтобы выяснить, подходит ли решение SCF, можно попробовать следующее.
— Попробуйте разные преобразователи SCF.
Если в этом случае KDIIS выключен, энергия будет равна: -595,4364778 а.е. На 112,8 ккал / моль меньше по энергии.
Таким образом, кажется, что использование алгоритма KDIIS (вместо DIIS по умолчанию) по какой-то причине (вероятно, случайной) заставило вычисление сходиться к чему-то другому. Плохое решение SCF может быть весьма чувствительным к используемой стратегии преобразования.
— Попробуйте разные предположения для начальных орбиталей.
Если предположение переключено с предположения PModel по умолчанию на! Патом или! Хюккель догадывается, что SCF сходится (с KDIIS) в этом случае к правильному -595.4364778 а.е. энергии. Часто плохое решение SCF сильно зависит от начальных орбиталей предположения.
-Попробуйте повернуть валентные орбитали (например, HOMO-LUMO) подозрительного раствора
Распространенной причиной неправильного решения SCF является то, что расположенные выше электроны занимают неправильную орбиталь.
Путем считывания орбиталей ранее сведенного решения и замены орбиталей HOMO и LUMO (или, возможно, HOMO и LUMO + 1, HOMO и LUMO + 2, HOMO-1 и LUMO и т. Д.)) SCF может быть преобразован в правильное решение. Здесь HOMO нет. 24, а LUMO — нет. 25.
! B3LYP def2-TZVPP tightscf kdiis MOREAD
% moinp «previous.gbw»
% scf
rotate {24,25,90,0,0} end
end
Для этого примера поменять местами орбитали HOMO и LUMO и повторное схождение приводит к правильной сведенной энергии -595,43648 а.е. Примечание : это работает только для этого примера, если орбитали меняются местами в ранее сходящемся решении через MOREAD (не если орбитали меняются местами в начале с использованием обычных орбиталей предположения по умолчанию).
— Анализируйте электронную структуру
Проверяя электронную структуру вручную, обычно можно определить, что что-то не так. Часто заряды Малликена или спиновые популяции могут уже выявить, если что-то не так, хотя в случае двухатомного йода нечего проверять, поскольку атомные заряды равны нулю и нет спиновой плотности.
Однако, если проанализировать молекулярные орбитали, проблема становится ясной для нашего примера. Для решения с более высокой энергией HOMO выглядит как орбиталь σ *, в то время как LUMO является несвязывающей орбиталью.Химическая интуиция, очевидно, подсказывает нам, что орбиталь σ * не должна быть занята для I 2 .
Для решения с более низкой энергией это наоборот, где HOMO является несвязывающей орбиталью (одиночная пара йода, как и ожидалось), а LUMO является орбиталью σ *. Таким образом, орбитальный анализ показывает, что произошло: SCF подошел к решению, в котором орбитали HOMO и LUMO поменялись местами, а разрыхляющая LUMO занята 2 электронами. Этот разрыхляющий характер этого неправильного раствора SCF увеличивает полную энергию молекулы на 112.8 ккал / моль.
— Выполните вычисление TDDFT поверх SCF.
Решая уравнения TDDFT и анализируя энергии первых переходов, можно определить, сошлись ли вы к чему-то странному; либо седловая точка, либо возбужденное состояние (разная электронная конфигурация).
Добавьте конец% tddft nroots 4 во входной файл и снова запустите вычисление.
Вывод TDDFT показывает:
СОСТОЯНИЕ 1: E = -0,098115 а.е. -2,670 эВ -21533.7 см ** — 1
24a -> 25a: 0,997998 (c = -0,99899838)
СОСТОЯНИЕ 2: E = -0,010974 au -0,299 эВ -2408,6 см ** — 1
23a -> 25a: 0,998581 (c = -0,993)
СОСТОЯНИЕ 3: E = 0,044783 au 1,219 эВ 9828,6 см ** — 1
22a -> 25a: 0,998823 (c = 0,995)
СОСТОЯНИЕ 4: E = 0,0
20a -> 25a: 0,994562 (c = -0,99727746)
, показывающий, что первые возбужденные состояния имеют отрицательную энергию перехода, что не имеет смысла, поскольку они должны быть положительными для вычисления TDDFT, выполняемого для основного состояния.
Это говорит о том, что вы пришли в возбужденное состояние или в седловую точку. Фактически, доминирующая пара орбитальных дырок для СОСТОЯНИЯ 1 с отрицательной энергией перехода -2,67 эВ предполагает, что HOMO (24) и LUMO (25) должны быть поменяны местами, как мы ранее выяснили.
Примечание : Отсутствие отрицательных энергий перехода не исключает, что ваш SCF является возбужденным состоянием. Истинное основное состояние может быть просто недоступно из уравнений линейного отклика TDDFT, выполненных для текущего решения SCF.
— Выполните анализ стабильности волновой функции SCF.
Добавьте:
% scf Stabperform true end
во входной файл. После схождения SCF вычисляется электронный гессиан, и ORCA сообщит, сошелся ли SCF к седловой точке в орбитальном пространстве:
РЕЗУЛЬТАТ АНАЛИЗА СТАБИЛЬНОСТИ SCF
————— —————
RHF / RKS-> UHF / UKS — триплет — внешний
Корневое собственное значение (au)
0-0.132711
1 -0,045713
2 -0,021069
Анализ устойчивости показывает НЕСТАБИЛЬНУЮ волновую функцию HF / KS с НЕСКОЛЬКИМИ отрицательными собственными значениями.
———————————————— ———————
WARNING
Хотя ваша волновая функция сходится, анализ устойчивости
выявил нестабильность по отношению к решению UHF / UKS.
Вам решать, использовать ли волновую функцию.
При желании его можно получить через файл gbw для
, которое можно использовать в качестве предположения для расчета UHF / UKS или для RHF / RKS post-SCF.
———————————————— ———————
Анализ устойчивости здесь ясно показывает, что SCF сходится к седловой точке n -го порядка вместо минимума.
Для волновых функций UHF / UKS программа может сдвинуть решение в направлении собственного вектора, связанного с отрицательным собственным значением, и попытаться снова сходиться.Это невозможно для RHF / RKS.
Здесь это невозможно, и правильное решение должно быть найдено другими способами (как описано выше).
Примечание: Анализ устойчивости может только сказать вам, сошлись ли вы в седловой точке или нет. Он не может показать, дошли ли вы до возбужденного состояния. Возбужденное состояние, найденное путем решения уравнений ССП, может выглядеть совершенно корректно с точки зрения анализа устойчивости.
Результаты расчета ORCA отличаются от программы X
Если вы переключаетесь на ORCA из другой программы, вы можете убедиться, что две программы дают одинаковые результаты для типичного расчета.При проведении этого сравнения следует учитывать несколько моментов:
— Начните со сравнения одноточечных вычислений для одной и той же геометрии. Делает вещи проще, чем оптимизация геометрии, поскольку программы могут иметь разные алгоритмы оптимизации и разные пороговые значения для сходимости сигналов.
— Обратите внимание на сходимость SCF, а также на использование приближений RI / RIJK / RIJCOSX (возможно, лучше всего отключить эти приближения для начала в обеих программах).
— Легче сначала сравнить вычисление Хартри-Фока, чем вычисление ДПФ.
Метод Хартри-Фока должен быть реализован одинаково во всех программах, но это не всегда так для вычисления ДПФ. Расчеты ДПФ выполняются в виде множества различных функционалов, которые иногда по-разному реализуются в разных программах. Кроме того, термин обмен-корреляция DFT требует численного интегрирования с использованием сетки. Численное интегрирование может выполняться по-разному в разных программах и вносит числовой шум, который необходимо минимизировать. Расчет HF не должен иметь подобных ошибок численного интегрирования.
Если вы можете воспроизвести высокочастотные энергии с помощью обеих программ, но не можете воспроизвести энергии ДПФ, тогда вам следует подумать о сетке или, возможно, другой реализации функционала.
— Если вы хотите сравнить результаты DFT, обратите особое внимание на интегральную сетку в обеих программах. Вероятно, слишком сложно воспроизвести одну и ту же сетку интеграции в обеих программах, поэтому более простой стратегией будет запускать сетку интеграции в обеих программах (используя их соответствующие ключевые слова) до тех пор, пока общая энергия не прекратит (до разумного порога) изменяться для каждой программы, как сетка увеличивается.После уменьшения числового шума энергии должны быть сопоставимы.
— Если вы хотите сравнить вычисления B3LYP в обеих программах, то важна точная реализация B3LYP. Существуют как минимум две разные реализации, в которых функционал отличается точным используемым функционалом корреляции LDA. Один из них иногда называют «B3LYP в гауссовском стиле», а другой — «B3LYP в стиле турбомоля». ORCA имеет обе реализации: используйте! B3LYP / G для стиля Гаусса и! B3LYP для стиля Турбомола.Эти два определения будут иметь значительные различия в общей энергии, но не огромные различия в относительных энергиях (т.е. оба функционала примерно одинаково хороши / плохи).
— Если вы хотите сравнить функционалы wB97X, обратите внимание, что эти функционалы бывают разных форм: wB97X, wB97X-D, wB97X-D3, wB97X-D3BJ, wB97X-V и т. Д. Эти функционалы различаются не только с точки зрения дисперсии. но некоторые из них имеют очень разные параметры (как параметры разделения диапазонов, так и функциональные параметры обмена и корреляции).
— Расчеты на атомах (и иногда диатомовых или других молекулах высокой симметрии) склонны к поиску альтернативных решений SCF, в зависимости от орбитального предположения. Попробуйте различные предположения, анализ устойчивости или поменяйте орбитали вручную, как описано выше.
— Может быть разница между реализациями базисных наборов в программах. Базовые наборы в стиле Попла (6-31G и 6-311G и т. Д.) Могут, например, сильно отличаться, поскольку они были разработаны с учетом декартовых базисных функций (например, 6 d-функций и 10 f-функций), в то время как ORCA использует сферические гармоники ( 5 d-функций и 7 f-функций).См. Дополнительную информацию в руководстве. Чтобы избежать этой неопределенности, можно выбрать базовый набор, который реализован одинаково в обеих программах, например def2-SVP или cc-pVDZ. Используйте! PrintBasis в ORCA (и соответствующее ключевое слово в другой программе), чтобы распечатать базисный набор и напрямую сравнить функции (обратите внимание, что коэффициент сжатия может отличаться с точки зрения нормализации).
— Если вы рассчитываете тяжелые элементы, убедитесь, что эффективный потенциал ядра одинаков в обеих программах.Def2-ECP может, например, различаются между программами.
— Если вы используете приближения ZORA или DKH, обратите внимание на возможные различия в реализации. Также обратите внимание, включена или выключена аппроксимация 1 центра в ORCA.
— Если вы сравниваете результаты TDDFT, проверьте, используется ли приближение Тамма-Данкова или нет. Он используется по умолчанию в ORCA, но не всегда в других программах.
— Модели сольватации континуума могут быть по-разному реализованы в разных программах.Определение полости имеет особое значение. Сравните атомные радиусы, которые используются для определения полости, и то, используется ли GEPOL SES / SAS.
— Если вы сравните расчеты после HF, то определение замороженного керна в обеих программах является решающим аспектом. Определения замороженных ядер в ORCA недавно были обновлены и должны быть надежными. В других программах могут быть совершенно другие значения по умолчанию, особенно для переходных металлов или тяжелых элементов p-блока. — Если вы сравниваете результаты связанных кластеров, обратите внимание на то, как генерируется опорная волновая функция.Это особенно важно для расчетов связанных кластеров с открытой оболочкой. См. Страницу связанных кластеров. Обратите внимание, что в вычислениях связанных кластеров с открытой оболочкой DLPNO по умолчанию используются опорные орбитали QRO.
Программа для построения функции косинуса?
Программа для построения функции косинуса?
Косинусная функция в математике: В математике тригонометрические функции также называются круговыми функциями, угловыми функциями или гониометрическими функциями. Эти функции являются фактическими функциями, которые связывают положение прямоугольного треугольника с соотношением двух сторон.
Эти функции используются во всех науках, связанных с геометрией, таких как навигация, механика твердого тела, небесная механика, геодезия и многих других областях. Они относятся к числу очень простых периодических функций и, как таковые, также широко используются для считывания периодических явлений с помощью анализа Фурье.
Наиболее широко используемые тригонометрические функции — это синус, косинус и тангенс.
Функция косинуса в Python:
cos (): — В Python математический модуль содержит различные математические операции, которые можно выполнять с помощью этого модуля.Функция math.cos () возвращает косинус значения, переданного в качестве аргумента. Функция math.cos () взята из стандартной математической библиотеки языка программирования Python.
Цель этой функции — вычислить положительный или отрицательный косинус любого заданного числа. Эта функция недоступна напрямую, поэтому нам нужно импортировать математический модуль, а затем нам нужно вызвать эту функцию, используя математический статический объект.
Синтаксис: — Синтаксис функции cos () в Python:
математика.cos (x)
В Python функция cos () возвращает косинус x радиан. Значение, переданное в эту функцию, должно быть в радианах. Эта функция возвращает косинус значения, переданного в качестве аргумента.
Но в этой статье мы реализуем функцию Cosine с помощью matplotlib и numpy. вы также можете использовать математический модуль, когда он дает результаты в радианах. поэтому мы можем реализовать, используя numpy. мы обсуждаем здесь, как использовать numpy.cos () в Python вместе с кодом, а также обсуждаем программу для построения функции косинуса? в программировании на Python.
numpy.cos () в Python
numpy.cos (x [, out]) = ufunc ‘cos’): Это математическая функция, используемая для вычисления тригонометрического косинуса для всех x (являющихся элементами массива).
Косинусные волны — это периодические волны, генерируемые колебаниями. Косинусоидальные волны аналогичны синусоидальным волнам, с другой стороны, косинусоидальные волны опережают синусоидальные волны на 90 градусов фазового угла.
Кривая косинуса не проходит через начало координат.Приливы в океане — пример косинусных волн. Кривая косинуса может быть построена с помощью функции cosine () в массиве numpy и функции plot () модуля pyplot библиотеки matplotlib.
Код Python:
import numpy as np
from matplotlib import pyplot as plt
x = np.arange (0,3 * np.pi, 0,01)
a = 5
b = 4
y = np .cos (a * x + b)
plt. участок (x, y)
plt.xlabel ( ‘x values’ )
plt.ylabel ( ‘y values’ )
plt.title ( ‘cos function’ )
plt.grid ( True )
plt.show ()
Выход:
| Программа для построения графика функции косинуса |
Резюме: В этой статье мы подробно обсуждаем функцию косинуса. Прежде всего, мы обсуждаем функцию синуса в математике, определение функции косинуса и то, как на самом деле она используется в математике.затем мы обсуждаем синусоидальную функцию в Python вместе с синтаксисом косинусной функции в Python.
Есть два способа использования функции cosine () в Python. Первый — math.cosine (x), в этом случае нам нужно импортировать математический модуль. второй — numpy.cosine (), использующий numpy и matplotlib для построения графика функции косинуса.
В последнем мы обсудим код для построения графика функции косинуса с выходом. В этом коде сначала нам нужно импортировать numpy, и мы использовали numpy как np, затем нам нужно импортировать matplotlib, который необходим для построения графика.поэтому мы определили matplotlib как plt.
В этом matplotlib.pyplot — это набор функций, которые заставляют matplotlib работать как MATLAB. Каждая функция pyplot вносит некоторые изменения в фигуру: например, создает фигуру, создает область построения на фигуре, строит некоторые линии в области построения, украшает график метками и т. Д.
Математическая библиотека Python
Введение
Математическая библиотека Python предоставляет нам доступ к некоторым общим математическим функциям и константам в Python, которые мы можем использовать в нашем коде для более сложных математических вычислений.Библиотека является встроенным модулем Python, поэтому вам не нужно выполнять установку, чтобы использовать ее. В этой статье мы покажем пример использования наиболее часто используемых функций и констант математической библиотеки Python.
Специальные константы
Математическая библиотека Python содержит две важные константы.
Пирог
Первая — это Pie (π), очень популярная математическая константа. Он обозначает отношение длины окружности к диаметру круга и имеет значение 3.1415589793. Чтобы получить к ней доступ, мы сначала импортируем математическую библиотеку следующим образом:
импорт математики
Затем мы можем получить доступ к этой константе, используя pi :
math.pi
Выход
3,1415589793
Эту константу можно использовать для вычисления площади или длины окружности. Следующий пример демонстрирует это:
импорт математики
радиус = 2
print ('Площадь круга радиусом 2 равна:', math.пи * (радиус ** 2))
Выход
Площадь круга радиусом 2 равна: 12,566370614359172
Мы увеличили значение радиуса до степени 2, а затем умножили его на круговую диаграмму в соответствии с формулой площади πr 2 .
Число Эйлера
Число Эйлера (e), являющееся основанием натурального логарифма, также определено в библиотеке Math. Мы можем получить к нему доступ следующим образом:
math.e
Выход
2.718281828459045
В следующем примере показано, как использовать указанную выше константу:
импорт математики
печать ((math.e + 6/2) * 4.32)
Выход
24.7029774984
Показатели и логарифмы
В этом разделе мы исследуем функции библиотеки Math, используемые для поиска различных типов показателей и логарифмов.
Функция exp ()
Математическая библиотека Python поставляется с функцией exp () , которую мы можем использовать для вычисления степени e .Например, e x , что означает экспоненту x. Значение e равно 2,718281828459045.
Метод может использоваться со следующим синтаксисом:
math.exp (x)
Параметр x может быть положительным или отрицательным числом. Если x не является числом, метод вернет ошибку. Продемонстрируем использование этого метода на примере:
импорт математики
# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00
# Передаем значения методу exp () и распечатаем
печать (math.exp (an_int))
печать (math.exp (a_neg_int))
печать (math.exp (a_float))
Выход
403.42879341
0,000335462627185
7,38 98
Мы объявили три переменные и присвоили им значения с разными числовыми типами данных. Затем мы передали их методу exp () для вычисления их показателей.
Мы также можем применить этот метод к встроенным константам, как показано ниже:
импорт математики
печать (математ.ехр (math.e))
печать (math.exp (math.pi))
Выход
15.154262241479262
23.1406779267
Если вы передадите методу нечисловое значение, он выдаст ошибку, как показано здесь:
импорт математики
печать (math.exp ("20"))
Выход
Traceback (последний вызов последний):
Файл "C: /Users/admin/mathe.py", строка 3, в
печать (math.exp ("20"))
TypeError: требуется float
Ошибка TypeError была сгенерирована, как показано в выходных данных выше.
Функция log ()
Эта функция возвращает логарифм указанного числа. Натуральный логарифм вычисляется по основанию e . Следующий пример демонстрирует использование этой функции:
импорт математики
print ("math.log (10.43):", math.log (10.43))
print ("math.log (20):", math.log (20))
print ("math.log (math.pi):", math.log (math.pi))
В приведенном выше сценарии мы передали методу числовые значения с разными типами данных.Мы также вычислили натуральный логарифм постоянной пи . Результат выглядит так:
Выход
math.log (10.43): 2.3446862681
math.log (20): 2.995732273553991
math.log (math.pi): 1.14472988584
Функция log10 ()
Этот метод возвращает десятичный логарифм указанного числа. Например:
импорт математики
# Возвращает log10 из 50
print ("Лог 10 из 50:", math.log10 (50))
Выход
Логарифм 10 из 50: 1.6989700043360187
Функция log2 ()
Эта функция вычисляет логарифм числа по основанию 2. Например:
импорт математики
# Возвращает log2 из 16
print ("Журнал2 из 16 равен:", math.log2 (16))
Выход
Лог2 из 16: 4,0
Функция log (x, y)
Эта функция возвращает логарифм x, где y является основанием.Например:
импорт математики
# Возвращает лог 3,4
print ("Журнал 3 с основанием 4:", math.log (3, 4))
Выход
Бревно 3 с основанием 4: 0,63035714574
Функция log1p (x)
Эта функция вычисляет логарифм (1 + x), как показано здесь:
импорт математики
print ("Значение 10 логарифма (1 + x):", math.log1p (10))
Выход
Значение логарифма (1 + x) 10: 2.3978952727983707
Арифметические функции
Арифметические функции используются для представления чисел в различных формах и выполнения над ними математических операций. Некоторые из наиболее распространенных арифметических функций описаны ниже:
-
ceil () : возвращает максимальное значение указанного числа. -
fabs () : возвращает абсолютное значение указанного числа. -
floor () : возвращает минимальное значение указанного числа.х) -1. -
exp (x) -1 : когда значение x мало, вычисление exp (x) -1 может привести к значительной потере точности. expm1 (x) может возвращать выходные данные с полной точностью.
Следующий пример демонстрирует использование вышеуказанных функций:
импорт математики
число = -4,28
а = 14
б = 8
num_list = [10, 8.25, 75, 7.04, -86.23, -6.43, 8.4]
x = 1e-4 # Маленькое значение x
print ('Число:', число)
print ('Минимальное значение:', math.x (с использованием функции expml ()): 0,00010000500016667084
К другим математическим функциям относятся следующие:
-
pow () : принимает два аргумента с плавающей запятой, переводит первый аргумент во второй и возвращает результат. Например, pow (2,2) эквивалентно 2 ** 2 . -
sqrt () : возвращает квадратный корень указанного числа.
Эти методы можно использовать, как показано ниже:
Мощность:
математ.pow (3, 4)
Выход
81,0
Квадратный корень:
math.sqrt (81)
Выход
9,0
Тригонометрические функции
Модуль Python Math поддерживает все тригонометрические функции. Некоторые из них занесены в список ниже:
-
sin (a) : возвращает синус "a" в радианах. -
cos (a) : возвращает косинус «a» в радианах. .
-
tan (a) : возвращает тангенс «a» в радианах. .
-
asin (a) : возвращает значение, обратное синусу.Также есть «атан» и «акос». -
градусов (a) : Преобразует угол «a» из радиана в градусы. -
радиан (a) : преобразует угол «a» из градусов в радианы.
Рассмотрим следующий пример:
импорт математики
angle_In_Degrees = 62
angle_In_Radians = математические радианы (angle_In_Degrees)
print ('Значение угла:', angle_In_Radians)
print ('sin (x) is:', math.sin (angle_In_Radians))
print ('tan (x) is:', math.tan (angle_In_Radians))
print ('cos (x) is:', math.cos (угол_In_Radians))
Выход
Значение угла: 1.0821041362364843
sin (x) равен: 0.88294759269
tan (x) равен: 1.8807264653463318
cos (x) равен: 0.46947156278589086
Обратите внимание, что мы сначала преобразовали значение угла из градусов в радианы перед выполнением других операций.
Преобразование типа
Вы можете преобразовать число из одного типа в другой. Этот процесс известен как «принуждение». Python может внутренне преобразовывать число из одного типа в другой, если выражение имеет значения смешанных типов.Следующий пример демонстрирует это:
3 + 5.1
Выход
8,1
В приведенном выше примере целое число 3 было приведено к значению 3,0 (число с плавающей запятой) для операции сложения, и результатом также является число с плавающей запятой.
Однако иногда необходимо явно привести число от одного типа к другому, чтобы удовлетворить требованиям параметра функции или оператора. Это можно сделать с помощью различных встроенных функций Python.Например, чтобы преобразовать целое число в число с плавающей запятой, мы должны вызвать функцию float () , как показано ниже:
а = 12
b = с плавающей точкой (a)
печать (б)
Выход
12,0
Целое число преобразовано в число с плавающей запятой. Число с плавающей запятой можно преобразовать в целое число следующим образом:
а = 12,65
б = int (а)
печать (б)
Выход
12
Число с плавающей запятой было преобразовано в целое путем удаления дробной части и сохранения основного числа.

 The following example uses several mathematical and trigonometric functions from the Math class to calculate the inner angles of a trapezoid.
The following example uses several mathematical and trigonometric functions from the Math class to calculate the inner angles of a trapezoid. Returns the absolute value of a Decimal number.
Returns the absolute value of a Decimal number.

 Returns
Returns  Returns
Returns  Returns
Returns  Returns
Returns  Returns
Returns 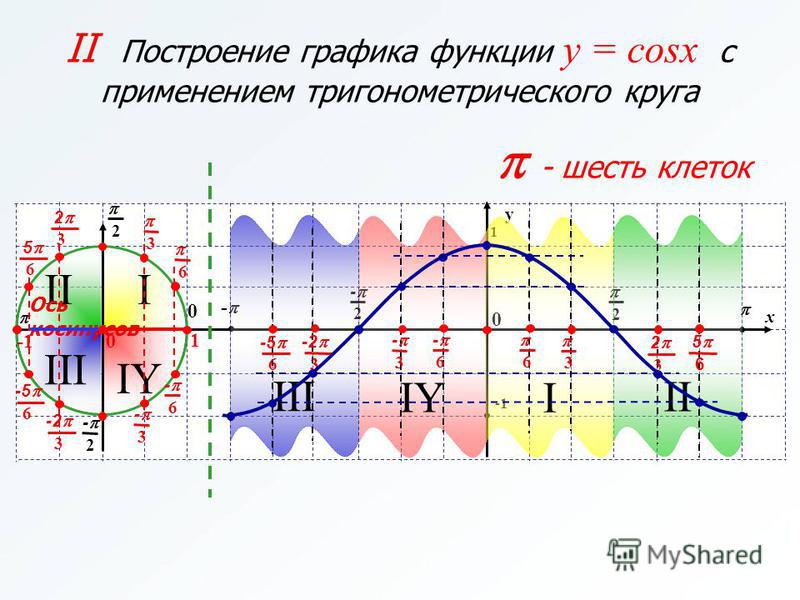 Returns a value with the magnitude of
Returns a value with the magnitude of  Calculates the quotient of two 32-bit signed integers and also returns the remainder in an output parameter.
Calculates the quotient of two 32-bit signed integers and also returns the remainder in an output parameter.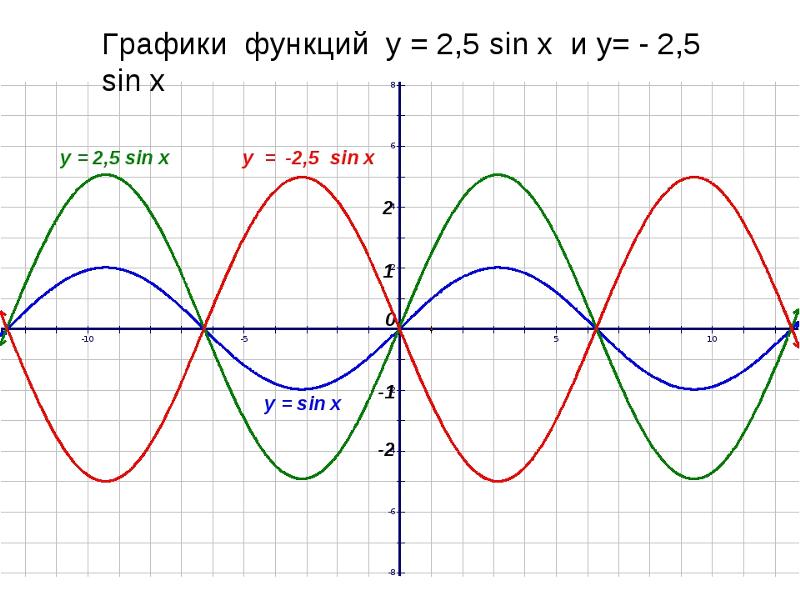 Returns
Returns  Returns the largest integral value less than or equal to the specified double-precision floating-point number.
Returns the largest integral value less than or equal to the specified double-precision floating-point number.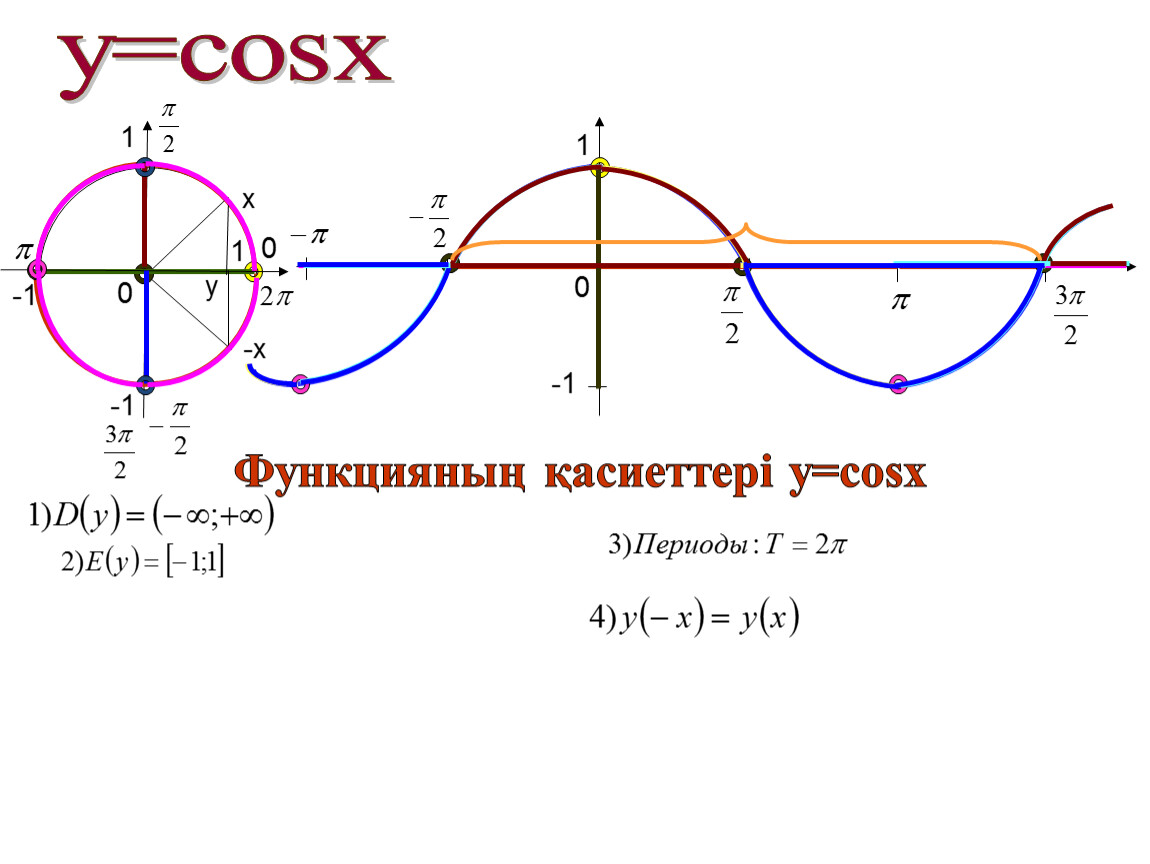 Returns the natural (base
Returns the natural (base  Returns the larger of two decimal numbers.
Returns the larger of two decimal numbers.
 Returns the larger magnitude of two double-precision floating-point numbers.
Returns the larger magnitude of two double-precision floating-point numbers. Returns the smaller of two 64-bit unsigned integers.
Returns the smaller of two 64-bit unsigned integers. Rounds a decimal value to a specified number of fractional digits, and rounds midpoint values to the nearest even number.
Rounds a decimal value to a specified number of fractional digits, and rounds midpoint values to the nearest even number.
 Rounds a double-precision floating-point value to the nearest integral value, and rounds midpoint values to the nearest even number.
Rounds a double-precision floating-point value to the nearest integral value, and rounds midpoint values to the nearest even number. Returns an integer that indicates the sign of a 64-bit signed integer.
Returns an integer that indicates the sign of a 64-bit signed integer.
 Calculates the integral part of a specified decimal number.
Calculates the integral part of a specified decimal number.
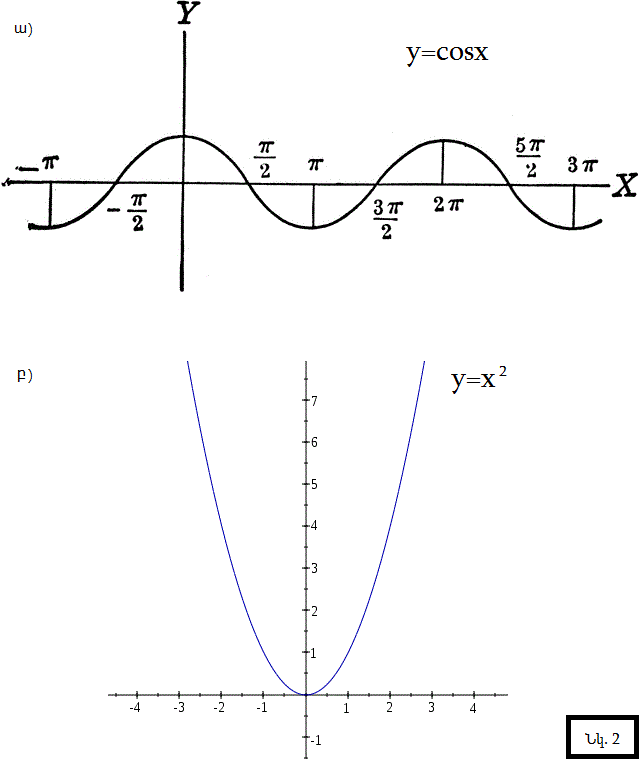
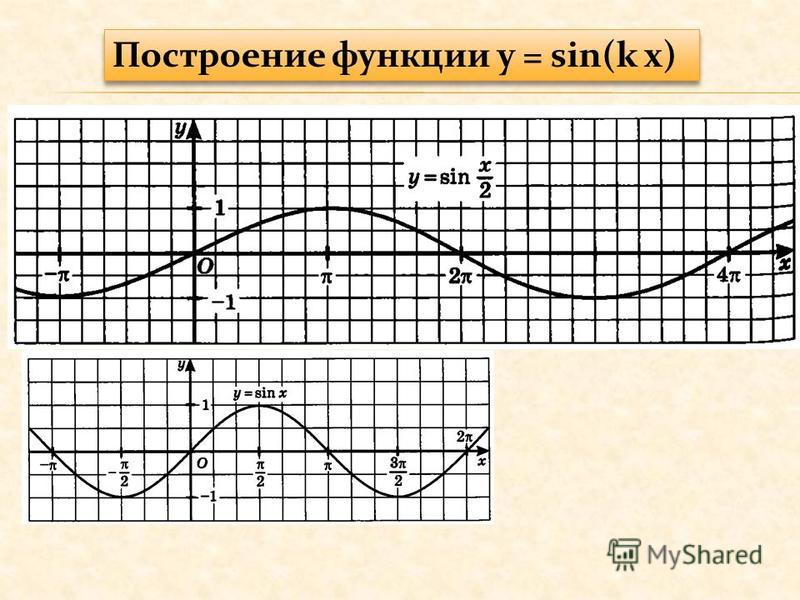 е. перейти к решению простейших тригонометрических уравнений: и . Найти корни простейших тригонометрических уравнений или доказать что корней нет.
е. перейти к решению простейших тригонометрических уравнений: и . Найти корни простейших тригонометрических уравнений или доказать что корней нет.
