|
1. |
Вычисления
|
1 |
|
2. |
Нахождение значения выражения
|
1 |
|
3. 
|
Уравнение
|
1 |
|
4. |
Построение графика функции
|
2 |
|
5. 
|
Значение функции
|
2 |
|
6. |
Упрощение выражения
|
2 |
|
7. 
|
Использование формул
|
3 |
|
8. |
Выражение
|
3 |
|
9. 
|
Вычисление значения выражения
|
3 |
Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.
Числовая прямая, числовая ось, — это прямая на которой изображаются действительные числа. На прямой выбирают начало отсчета – точку О (точка О изображает 0) и точку L, изображающую единицу. Точка L обычно стоит справа от точки О. Отрезок ОL называют единичным отрезком.
Точки, стоящие справа от точки О изображают положительные числа. Точки стоящие слева от точки. О, изображают отрицательные числа. Если точка Х изображает положительное число х, то расстояние ОХ = х. Если точка Х изображает отрицательное число х, то расстояние ОХ = — х.
Точки стоящие слева от точки. О, изображают отрицательные числа. Если точка Х изображает положительное число х, то расстояние ОХ = х. Если точка Х изображает отрицательное число х, то расстояние ОХ = — х.
Число, показывающее положение точки на прямой, называется координатой этой точки.
Точка V изображенная на рисунке имеет координату 2, а точка H имеет координату -2,6.
Модулем действительного числа называется расстояние от начала отсчета до точки, соответствующей этому числу. Обозначают модуль числа х, так: | х |. Очевидно, что | 0 | = 0.
Если число х больше 0, то | х | = х, а если х меньше 0, то | х | = — х. На этих свойствах модуля, основано решение многих уравнений и неравенств с модулем.
Пример: Решить уравнение | х – 3 | = 1.
Решение: Рассмотрим два случая – первый случай, когда х -3 > 0, и второй случай, когда х — 3 0.
1. х — 3 > 0, х > 3.
В этом случае | х – 3 | = х – 3.
Уравнение принимает вид х – 3 = 1, х = 4. 4 > 3 – удовлетворят первому условию.
4 > 3 – удовлетворят первому условию.
2. х -3 0, х 3.
В этом случае | х – 3 | = — х + 3
Уравнение принимает вид х + 3 = 1, х = — 2. -2 3 – удовлетворят второму условию.
Ответ: х = 4, х = -2.
Числовые выражения.
Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками.
Примеры числовых выражений:
Значением числового выражения является число.
Операции в числовом выражении выполняются в следующей последовательности:
1. Действия в скобках.
2. Вычисление функций.
3. Возведение в степень
4. Умножение и деление.
5. Сложение и вычитание.
6. Однотипные операции выполняются слева на право.
Так значением первого выражения будет само число 12,3
Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности:
1. Выполним действия в скобках в следующей последовательности — сначала 2 возведем в третью степень, затем от полученного числа отнимем 11:
Выполним действия в скобках в следующей последовательности — сначала 2 возведем в третью степень, затем от полученного числа отнимем 11:
3 • 4 + (23 — 11) = 3 • 4 + (8 — 11) = 3 • 4 + (-3)
2. Умножим 3 на 4:
3 • 4 + (-3) = 12 + (-3)
3. Выполним последовательно операции слева направо:
12 + (-3) = 9.
Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.
Алгебраические выражения.
Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности этих действий (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение должно быть конечным. [1]
Пример алгебраического выражения:
«Алгебраическое выражение» — понятие синтаксическое, то есть нечто является алгебраическим выражением тогда и только тогда, когда подчиняется некоторым грамматическим правилам (см. Формальная грамматика). Если же буквы в алгебраическом выражении считать переменными, то алгебраическое выражение обретает смысл алгебраической функции.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Модуль действительного числа, урок по алгебре в 8 классе, презентация
Дата публикации: . 2$.
2$.
5. $|a|=|-a|$.
Геометрический смысл модуля действительного числа
Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние $ρ(a; b)$ между этими точками. Очевидно, что это расстояние равно $b-a$, если $b>a$.
Если $a>b$, то расстояние будет равно $a-b$.
Если $a=b$, то расстояние равно нулю, так как получается единая точка.
Все три случая мы можем описать единообразно: $ρ(a;b)=|a-b|$.
Пример.
Решите уравнение:
а) $|x-3|=6$;
б) $|x+5|=3$;
в) $|x|=2,8$;
г) $|x-\sqrt{3}|=2$.
Решение.
а) Надо найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6.
$ρ(x;3)=6$.
Это точки – 9 и -3 (прибавили и отняли шестерку от тройки).
Ответ: $х=9$ и $х=-3$.
б) $|x+5|=3$, перепишем уравнение в виде $|x-(-5)|=3$.
$ρ(x;-5)=3$.
Найдем расстояние от точки -5, удаленное на 3. Такое расстояние, получается от двух точек: $х=2$ и $х=-8$.
Ответ: $х=2$ и $х=-8$.
в) $|x|=2,8$ можно представить в виде $|х-0|=2,8$ или $ρ(x;0)=2,8$.
Очевидно, что $х=-2,8$ или $х=2,8$.
Ответ: $х=-2,8$ и $х=2,8$.
г) $|x-√3|=2$ эквивалентно $ρ(x; \sqrt{3})=2$.
Очевидно, что $х=\sqrt{3}-2$ или $х=\sqrt{3}+2$.
Ответ: $x=\sqrt{3}-2$ или $x=\sqrt{3}+2$.
Пример.
Решить уравнения:
а) $|2x-8|=4$;
б) $|3-3x|=6$;
в) $|10x+5|=-2$.
Решение.
а) Преобразуем левую часть уравнения: $|2x-8|=|2(x-4)|=|2||x-4|=2|x-4|$.
Тогда уравнение можно переписать в виде: $|x-4|=2$.
Или $ρ(x;4)=2$.
Ответ: $х=6$ или $х=2$.
б) Опять же преобразуем левую часть: $|3-3x|=|-3(x-1)|=|-3||(x-1)|=3|x-1|$.
Тогда уравнение можно переписать в виде: $|x-1|=2$.
Или $ρ(x;1)=2$.
Ответ: $х=3$ или $х=-1$.
в)$|10x+5|=-2 $.
Модуль не может быть отрицательным числом, тогда, очевидно, что корней нет.
Ответ: нет корней.
График функции $y=|x|$.
Вычислить модуль мы можем из любого числа. 2}$.
2}$.
Модуль действительного числа | Презентация к уроку по алгебре (8 класс) по теме:
Слайд 1
Модуль действительного числа Автор материала: Дудниченко Татьяна Анатольевна, учитель математики первой квалификационной категории ГАОУ СОШ МГПУ, г . Москва
Слайд 2
Цели и задачи урока Ввести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля; Ввести функцию y = |x | , показать правила построения ее графика; Научить разными способами решать уравнения, содержащие модуль; Развивать интерес к математике, самостоятельность, логическое мышление, математическую речь, прививать аккуратность и трудолюбие.
Слайд 3
Определение . Например: |8|=8 ; | -8 | =-(-8)=8;
Слайд 4
Свойства модуля
Слайд 5
Геометрический смысл модуля Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние ρ( a ; b ) между этими точками. Очевидно что это расстояние равно b-a , если b>a Если поменять местами, то есть a > b , расстояние будет равно a — b . Если a = b то расстояние равно нулю, так как получается точка. Все три случая мы можем описать единообразно:
Очевидно что это расстояние равно b-a , если b>a Если поменять местами, то есть a > b , расстояние будет равно a — b . Если a = b то расстояние равно нулю, так как получается точка. Все три случая мы можем описать единообразно:
Слайд 6
Пример. Решите уравнение: а) |x-3|=6 б) |x+5|=3 в) |x|=2.8 г) Решение. а) Нам нужно найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6. Такие точки 9 и -3. (Прибавили и отняли шестерку от тройки.) Ответ: х=9 и х=-3 б) | x +5|=3, перепишем уравнение в виде | x -(-5)|=3. Найдем расстояние от точки -5 удаленное на 3. Такое расстояние, получается, от двух точек: х=2 и х=-8 Ответ: х=2 и х=-8. в) | x |=2.8, можно представить в виде |х-0|=2.8 или Очевидно, что х=-2.8 или х=2.8 Ответ: х=-2.8 и х=2.8. г) эквивалентно Очевидно, что
Слайд 8
Функция y = |x|
Слайд 10
Решить уравнение |x-1| = 4 1 способ (аналитический) Задание 2
Слайд 11
2 способ (графический)
Слайд 12
3 способ
Слайд 13
Модуль действительного числа. Тождество Рассмотрим выражение , если а>0, то мы знаем что . Но как быть, в случае если a 0. 2. Давайте обобщим: По определению модуля: То есть
Тождество Рассмотрим выражение , если а>0, то мы знаем что . Но как быть, в случае если a 0. 2. Давайте обобщим: По определению модуля: То есть
Слайд 14
Модуль действительного числа . Пример. Упростить выражение если: а) а-2≥0 б) a -2
Слайд 15
Модуль действительного числа. Пример. Вычислить Решение. Мы знаем что: Осталось раскрыть модули Рассмотрим первое выражение:
Слайд 16
Рассмотрим второе выражение: Используя определение раскроем знаки модулей: В итоге получили: Ответ: 1.
Слайд 17
Закрепление нового материала. № 16.2, №16.3, №16.4, №16.12, №16.16 ( а, г ), №16.19
Слайд 18
Задачи для самостоятельного решения. 1. Решите уравнение: а) | x -10|=3 б) | x +2|=1 в) | x |=2.8 г) 2. Решить уравнение: а) |3 x -9|=33 б) |8-4 x |=16 в) | x +7|=-3 3. Упростить выражение если а) а-3≥0 б) a -3
Слайд 19
Список использованной литературы: Звавич Л.И. Алгебра. Углубленное изучение. 8 кл .: задачник / Л.И. Звавич , А.Р. Рязановский. – 4-е изд., испр . – М.: Мнемозина, 2006. – 284 с. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2014. – 215 с. Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр . и доп. – М.: Мнемозина, 2014. – 271 с.
– 4-е изд., испр . – М.: Мнемозина, 2006. – 284 с. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2014. – 215 с. Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр . и доп. – М.: Мнемозина, 2014. – 271 с.
«Модуль действительного числа». — математика, уроки
Учитель математики высшей квалификационной категории
Ужачкина Надежда Павловна.
Урок №3 по теме «Модуль действительного числа».
Цели:
повторить понятие модуля, его свойства, геометрический смысл модуля, правила построения графика функции у = |х| и случаи примениния графического способа решения; проверить умение обучающихся применять определение модуля при упрощении выражений и решении уравнений, содержащих модули; проверить умение обучающихся строить график функции у = |х| и решать графическим способом уравнения, системы уравнений, неравенства, содержащие модуль;
развивать речевую культуру обучающихся; продолжать развивать умение систематизировать полученные знания, описывать ситуацию математическим языком, переводить математический язык на обыкновенный; развивать навыки самоконтроля и взаимоконтроля, учиться оценивать результаты выполненных действий;
воспитывать организованность, дисциплинированность, самостоятельность, внимательность, воспитание мотивов добросовестного отношения к труду.
1. Организационный момент.
Приветствие, оформление тетрадей, урока (привлечь учеников к постановке цели урока), повторение правил к уроку (работа в парах).
2. Актуализация знаний.
1. Что называют модулем действительного числа?
2. Как упростить выражение ?
3. Какими свойствами обладает модуль?
4. При выполнении каких заданий можно применять свойства модуля?
5. В чем заключается геометрический смысл модуля?
6. Как найти расстояние между точками А(а) и В(в) на числовой прямой?
7. Сколько корней может иметь уравнение вида |х| = а?
8. Какого вида функция у = |х|?
9. Какая линия является графиком этой функции?
10. При выполнении каких заданий применяют построение графиков?
3. Самостоятельная работа.
Давайте проверим, как на прошлых уроках и дома вы научились упрощать выражения, содержащие модуль.
Выполняем задание 1) из карточек. На эту работу отводится 4 минуты.
Самостоятельная работа по теме «Модуль действительного числа».
Вариант 1.
1) Найдите значение выражения:
а) |-5|; б) |7,2|; в) ||- 2; г) ; д) — + 4.
2) Решите уравнение: а) |х| = 3; б) |х + 2| = 4; в) |х — 7| = 0;
г) |4х + 1| = 5; д) 2|х| + |- х| = 15.
3) Постройте графики функций у = |х| и у = .
С помощью графиков решите : а) уравнение |х| = ;
б) систему уравнений у = |х|,
у =
в) неравенство |х| ≥ ;
г) неравенство |х|
Самостоятельная работа по теме «Модуль действительного числа».
Вариант 2.
1) Найдите значение выражения:
а) |5|; б) |-7,2|; в) ||; г) ; д) + — 1.
2) Решите уравнение: а) |х| = 4; б) |х — 2| = 3; в) |х + 7| = -1;
г) |2х + 2| = 6; д) 3|х| — |- х| = 16.
3) Постройте графики функций у = |х| и у = — .
С помощью графиков решите : а) уравнение |х| = — ;
б) систему уравнений у = |х|,
у = —
в) неравенство |х| ≤ — ;
г) неравенство |х| —
Поменяйтесь работами с соседом по парте, оцените работу и поставьте оценку за этот этап работы. Готовые ответы смотрите на экране.
Готовые ответы смотрите на экране.
Верно выполнены все 5 случаев – «5»,
4 – «4»,
3 – «3»,
2-1 – «2».
Ответы: а) 5; б) 7,2; в) 2 — ; г) 5 — ; д) 2.
4. Самостоятельная работа.
Проверим, как научились решать простейшие уравнения с модулем. Выполняем задание 2), для этой работы у вас есть 7 минут.
Поменяйтесь тетрадями с соседом позади себя, проверьте получившиеся корни уравнений по готовым ответам на экране. Оцените работу.
Верно выполнены все 5 случаев – «5»,
4 – «4»,
3 – «3»,
2-1 – «2».
Ответы:
Вариант 1. Вариант 2.
а) – 3; 3; а) – 4; 4;
б) – 6; 2; б) – 1; 5;
в) 7; в) корней нет;
г) – 1,5; 1; г) – 4; 2;
д) – 5; 5; д) – 8; 8.
5. Только ли в математике мы встречаемся с понятием модуля?
Посмотрите, что еще означает этот термин в других сферах деятельности.
— Модуль упругости (в физике) – величина, характеризующая упругие свойства твердых тел, коэффициент деформации.
— Модуль (в архитектуре и строительстве) – исходная мера, принятая для выражения кратных соотношений размеров комплексов, сооружений и их частей.
— Модуль (в радиоэлектронике) – унифицированный функциональный узел радиоэлектронной аппаратуры, выполненный в виде самостоятельного изделия.
— Модуль зубчатого колеса (в технике) – геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса.
6. Самостоятельная работа.
Осталось проверить умение строить графики и умения решать графически уравнения, системы уравнений, неравенства. На обороте доски работают два человека по вариантам, остальные в тетрадях. Выполняем задание 3), для этого у вас 10 минут.
Поменяйтесь тетрадями с соседом впереди себя, проверьте построение графиков и ответы на поставленные вопросы, оцените работу.
Если все верно, то заработана оценка «5»,
допущена одна ошибка – «4»,
допущены две ошибки – «3»,
допущены три ошибки при ответах – «2»,
неверно построены графики – «1».
7. Итоги урока, домашнее задание.
Подсчитайте среднее арифметическое трех оценок. Это ваша предварительная оценка за самостоятельную работу сегодня.
— Кто получил «5»? «4»? «3»? «2»?
— Довольны ли вы своей оценкой?
— Те, кто желает улучшить результат, или чувствует, что недостаточно хорошо отработал навыки, выполняют следующие задания.
Уровень «3 – 4»: №16.1 – 4 вг, 16.27 вг, 16.13, 16.38 б, 16.21 – 24 б.
Уровень «4 – 5»: №16.33 вг, 16.27 вг, 16.41 бг, 16.38 б, 16.29 – 30 аб.
На дополнительную оценку: 16.36, 16.42.
— Какие вопросы у вас возникли при выполнении самостоятельной работы?
— Просмотрите домашнее задание. Все ли понятно?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 — 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| — 5; б) |х| — 5?
Математика
Программа вступительных испытаний по математике на направления подготовки высшего образования
Основные математические понятия и формулы
Арифметика, алгебра и начала анализа
- Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель, наименьшее общее кратное.
- Целые числа (Z). Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.
- Действительные числа (R), их представление в виде десятичных дробей. Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.
- Числовые выражения. Выражения с переменными. Формулы сокращенного умножения.
 Степень с натуральным и рациональным показателем. Арифметический корень.
Степень с натуральным и рациональным показателем. Арифметический корень. - Логарифмы и их свойства.
- Одночлен и многочлен. Разложение квадратного трехчлена на линейные множители.
- Понятие функции. Способы задания функции. Область определения. Множество значений функции.
- График функции. Возрастание и убывание функции; периодичность, четность, нечетность. Экстремумы функции.
- Определение , основные свойства и графики функций:
линейной y=kх+b, квадратичной у=ах2+bx+с, гиперболической у=k/х,
степенной у=ахn, показательной у=ах, логарифмической у=lоgах, тригонометрических: у=sinх, у=соsх, у=tgх
- Уравнение. Корни уравнения.
- Неравенства. Решение неравенств.
- Системы уравнений и неравенств.
- Арифметическая и геометрическая прогрессия.
- Определение производной.
 Ее физический и геометрический смысл. Производные функций у = sin х, у = соs х,у = tg х, у = ах, у = хn .
Ее физический и геометрический смысл. Производные функций у = sin х, у = соs х,у = tg х, у = ах, у = хn . - Формулы приведения. Зависимости между тригонометрическими функциями одного и того же аргумента. Тригонометрические функции двойного аргумента.
Геометрия
- Прямая, луч, отрезок, ломаная; длина отрезка. Угол, величина угла. Вертикальные и смежные углы. Параллельные прямые. Окружность, круг.
- Примеры преобразования фигур, виды симметрии. Преобразование подобия и его свойства.
- Векторы. Операции над векторами.
- Многоугольник, его вершины, стороны, диагонали.
- Треугольник. Его медиана, биссектриса, высота. Виды треугольников. Соотношения между сторонами и углами прямоугольного треугольника.
- Четырехугольники: параллелограмм, прямоугольник, ромб, квадрат, трапеция.
- Окружность и круг.
 Центр, хорда, диаметр, радиус. Касательная к окружности. Дуга окружности. Сектор.
Центр, хорда, диаметр, радиус. Касательная к окружности. Дуга окружности. Сектор. - Центральные и вписанные углы.
- Вписанные и описанные многоугольники.
- Формулы площади: треугольника, прямоугольника, параллелограмма, ромба, квадрата, трапеции.
- Длина окружности и длина дуги окружности. Радианная мера угла.
- Площадь круга и площадь сектора.
- Подобие. Подобные фигуры. Отношение площадей подобных фигур.
- Плоскость. Параллельные и пересекающиеся плоскости.
- Параллельность прямой и плоскости.
- Угол прямой с плоскостью. Перпендикуляр к плоскости.
- Двугранные углы. Линейный угол двугранного угла. Перпендикулярность двух плоскостей.
- Многогранники. Их вершины, ребра, грани, диагонали. Прямая и наклонная призмы; пирамиды. Правильная призма и правильная пирамида. Параллелепипеды, их виды.
- Фигуры вращения: цилиндр, конус, сфера, шар. Центр, диаметр, радиус сферы и шара.
 Плоскость, касательная к сфере.
Плоскость, касательная к сфере. - Объем параллелепипеда.
- Площадь поверхности и объем призмы, пирамиды, цилиндра, конуса.
- Объема шара и его частей, площадь поверхности сферы.
Основные умения и навыки
Абитуриент должен уметь:
- Производить арифметические действия над числами, заданными в виде обыкновенных и десятичных дробей; с требуемой точностью округлять данные числа и результаты вычислений; пользоваться калькуляторами или таблицами для вычислений.
- Проводить тождественные преобразования многочленов, дробей, содержащих переменные, выражений, содержащих степенные, показательные, логарифмические и тригонометрические функции.
- Строить графики линейной, квадратичной, степенной, показательной, логарифмической и тригонометрических функций.
- Решать уравнения и неравенства первой и второй степени, уравнения и неравенства, приводящиеся к ним; решать системы уравнений и неравенств первой и второй степени и приводящиеся к ним.
 Сюда, в частности, относятся простейшие уравнения и неравенства, содержащие степенные, показательные, логарифмические и тригонометрические функции.
Сюда, в частности, относятся простейшие уравнения и неравенства, содержащие степенные, показательные, логарифмические и тригонометрические функции. - Решать задачи на составление уравнений и систем уравнений.
- Изображать геометрические фигуры на чертеже и производить простейшие построения на плоскости.
- Использовать геометрические представления при решении алгебраических задач, а методы алгебры и тригонометрии применять при решении геометрических задач.
- Проводить на плоскости операции над векторами (сложение и вычитание векторов, умножение вектора на число) и пользоваться свойствами этих операций.
- Пользоваться понятием производной при исследовании функций на возрастание (убывание), на экстремумы и при построении графиков функций.
Список литературы для подготовки к вступительным испытаниям
- ЕГЭ. Математика: тематический сборник заданий / Под ред. А.Л. Семенова, И.
 В. Ященко. – М.: Издательство «Национальное образование», 2014. – (ЕГЭ. ФИПИ-школе)
В. Ященко. – М.: Издательство «Национальное образование», 2014. – (ЕГЭ. ФИПИ-школе) - ЕГЭ-2014 : Математика : Самое полное издание типовых вариантов заданий / авт.-сост. И.В. Ященко, И.Р. Высоцкий; под ред. А.Л. Семенова, И.В. Ященко. — Москва: АСТ : Астрель, 2014. — (Федеральный институт педагогических измерений).
- Математика. ЕГЭ 2014. Книга 1,2. / Д.А. Мальцев, А.А. Мальцев, Л.И. Мальцева. – Ростов н/Д: Издатель Мальцев Д.А.; М.: Народное образование, 2014. – 320 с.
- Сканави М.И., Егерев В.К. Сборник задач по математике для поступающих во втузы. (2013,608 с.)
- Математика. Подготовка к ЕГЭ в 2014 году. Диагностические работы. Высоцкий И.Р., Семенов А.В. и др. (2014, 72с.)
- Математика. 5-11 классы. Справочник школьника / Гусев В.А., Мордкович А.Г. — Москва: АСТ : Астрель,2014
СИСТЕМА И КРИТЕРИИ
оценки знаний поступающих на вступительных испытаниях
на программы высшего образования бакалавриата
Выполненное экзаменационное задание по всем предметам оценивается по стобалльной системе.
Одно правильно выполненное задание частей экзаменационного теста оценивается:
| Предмет | Номера/части заданий | Количество баллов, выставляемых за одно правильно выполненное задание | Количество баллов за все правильно выполненные задания данной части | Минимальное количество баллов, подтверждающее успешное прохождение вступительного испытания |
| Математика | 1-14 | 3 | 42 | 27 |
| 15-16 | 7 | 14 | ||
| 17-18 | 10 | 20 | ||
| 19-20 | 12 | 24 |
За неправильные ответы баллы не начисляются.
В целом за экзаменационную работу выставляется итоговый балл как сумма баллов за отдельные задания.
Программа одобрена на Ученом совете Университета протокол № 7 от 28 сентября 2017 г.
Конспект урока по теме: «Модуль действительного числа»
Тема урока: «Длина окружности».
Муниципальное общеобразовательное учреждение «Заречная средняя общеобразовательная школа» Открытый урок по математике в 6 классе Тема урока: «Длина окружности». Урок подготовила и провела учитель математики
Подробнее
Урок математики в 3 «б» классе
Урок математики в 3 «б» классе Тема: Переменная. Запись выражений и предложений с помощью переменной Цели: 1. Дать понятие о переменной, как букве, обозначающей меняющиеся (переменные) значения элементов
Запись выражений и предложений с помощью переменной Цели: 1. Дать понятие о переменной, как букве, обозначающей меняющиеся (переменные) значения элементов
Подробнее
ПЛАН-КОНСПЕКТ УРОКА 1. ФИО
ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет
Подробнее
КОНСПЕКТ УРОКА МАТЕМАТИКИ
КОНСПЕКТ УРОКА МАТЕМАТИКИ Учитель: Вихрова Оксана Николаевна Класс: 4. Дата проведения: 13.10.15 г. Тема: Доли. Получение и образование долей. Тип урока: Открытие нового знания. Цели урока: Предметные:
Подробнее
Конспект урока по математике.
Конспект урока по математике. Класс: 1 В, учитель Шелякина Н.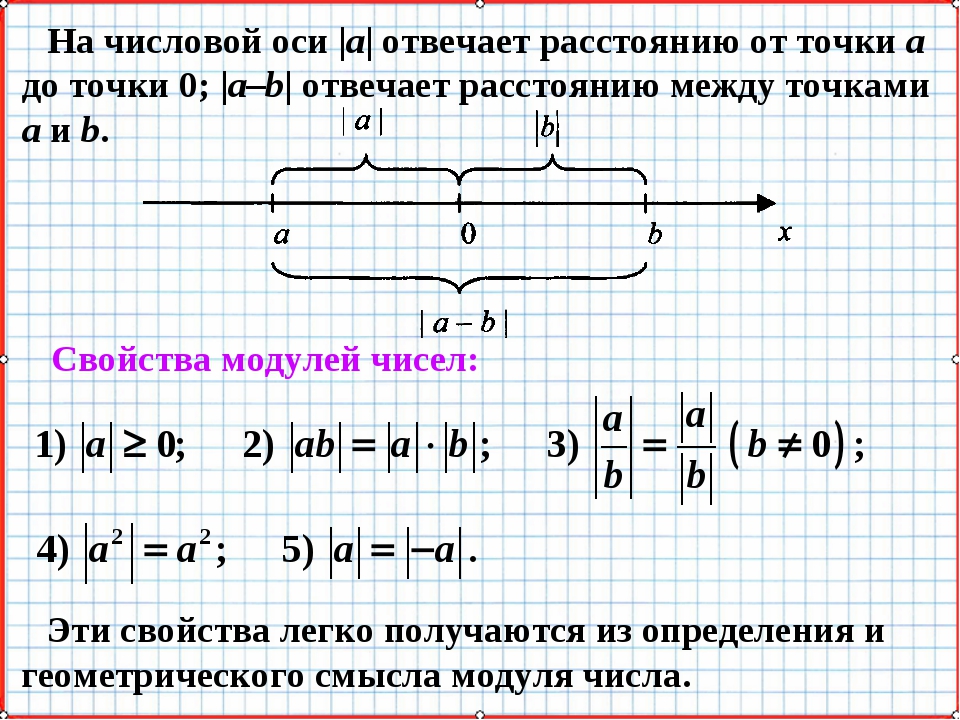 А. Тема урока: «Дециметр». Дидактическая цель: создать условия для открытия детьми новых знаний. Тип урока: открытие новых знаний. Задачи урока:
А. Тема урока: «Дециметр». Дидактическая цель: создать условия для открытия детьми новых знаний. Тип урока: открытие новых знаний. Задачи урока:
Подробнее
Урок алгебры в 10 классе. Белорукова М.В. 2
Урок алгебры в 10 классе Белорукова М.В. 2 Белорукова Марина Васильевна Белорукова М.В. 3 п/п Комплексные числа — 10 часов Содержание материала Количество часов 1. Комплексные числа и арифметические операции
Подробнее
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
Подробнее
Тема: «Сложение дробей с одинаковыми
Урок по математике. 4 класс. Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.
Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.
Подробнее
Технологическая карта урока
Технологическая карта урока Тема урока: «Прямоугольник» Класс: 5 Учитель: Рыжова Лидия Петровна Тип урока: урок «открытия» нового знания Цели по содержанию: обучающие: изучить свойства прямоугольника развивающие:
Подробнее
Технологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
Подробнее
Методическая разработка открытого урока
Довлатбегян Виктория Александровна, учитель математики МБОУ «Лицей» г. протвино, МО Методическая разработка открытого урока «Разложение многочлена на множители с помощью комбинации различных приемов» Алгебра.
протвино, МО Методическая разработка открытого урока «Разложение многочлена на множители с помощью комбинации различных приемов» Алгебра.
Подробнее
Технологическая карта урока
Технологическая карта урока Класс: 8 Предмет: алгебра Тема урока: Погрешность и точность измерения. Дидактическая цель урока: создать условия для восприятия и осознания понятий абсолютная и относительная
Подробнее
Технологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнее
Занятие 1 (2 часа) Ход занятия.
Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие
Подробнее
Комарова Е.
 И., МБОУ СОШ 3 г. Сасово
И., МБОУ СОШ 3 г. Сасово
Комарова Е.И., МБОУ СОШ 3 г. Сасово Тема: Площадь треугольника. Класс — 5 1. Учебник: С. Козлова «Математика. 5 класс» «БАЛАСС», 2013. 2. Цели урока: для учителя Содержательная цель: расширение знаний
Подробнее
Оборудование: проектор, ноутбуки, рабочие листы, тетради, учебники, раздаточный материал
Достаточно часто в школах мы встречаем ситуацию, когда учитель прекрасно объясняет материал, учащиеся его внимательно слушают, но через несколько минут, выходя из кабинета, забывают, о чем шла речь на
Подробнее
Тема: Решение систем уравнений
Цель урока: МОУ гимназия 11 г. Елец Липецкой области Разработчик: учитель информатики Губина Т.Н. Методическая разработка системы интегрированных уроков по информатике и математике в 10 классе Урок 7 Тема:
Подробнее
МАОУ Побединская СОШ
МАОУ Побединская СОШ Учитель математики Новодворская Лилия Андреевна. 2015г. Обобщающий урок по математике в 6 классе «Сложение и вычитание положительных и отрицательных чисел» Цели и задачи урока: Обобщить
2015г. Обобщающий урок по математике в 6 классе «Сложение и вычитание положительных и отрицательных чисел» Цели и задачи урока: Обобщить
Подробнее
Конспект урока по математике в 7 классе
Муниципальное специальное (коррекционное) образовательное учреждение для обучающихся с ограниченными возможностями здоровья, Кольская специальная (коррекционная) общеобразовательная школа VIII вида Муниципального
Подробнее
Технологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
Подробнее
Технологическая карта урока
Технологическая карта урока Предмет: математика Класс: 5 Учебник (УМК): Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5 класс: Учебник для общеобразовательных учреждений. — М.:
Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5 класс: Учебник для общеобразовательных учреждений. — М.:
Подробнее
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Дата: 08.02.2019г. Учитель:
Подробнее
Тема: Упрощение выражений
Цель урока: МОУ гимназия г. Елец Липецкой области Разработчик: учитель информатики Губина Т.Н. Методическая разработка системы интегрированных уроков по информатике и математике в 0 классе Урок Тема: Упрощение
Подробнее
Конспект урока по математике в 6 классе
Конспект урока по математике в 6 классе УМК: Н.Я.Виленкина, В.И.Жохова, А. С.Чеснокова, С.И.Шварцбурда «Математика 5», «Математика 6», издательства М.: «Мнемозина». Тема урока: Умножение обыкновенных дробей.
С.Чеснокова, С.И.Шварцбурда «Математика 5», «Математика 6», издательства М.: «Мнемозина». Тема урока: Умножение обыкновенных дробей.
Подробнее
Схема конспекта урока «Что обозначают буквы Е, Ё, Ю, Я» Возраст учащихся: 5 класс. Тема урока: «Что обозначают буквы Е, Ё, Ю, Я»
Учитель: Фирсова Наталья Михайловна. Предмет: русский язык. Возраст учащихся: 5 класс. Тема урока: «Что обозначают буквы Е, Ё, Ю, Я» Схема конспекта урока «Что обозначают буквы Е, Ё, Ю, Я» 1) Образовательная:
Подробнее
Сложение и вычитание смешанных чисел
Предмет: Математика Класс: 5 «Б» класс Сложение и вычитание смешанных чисел Учебник: Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Подробнее
Технологическая карта урока
Технологическая карта урока Предмет, класс Математика, 5А Автор (ы) УМК Н. Я. Виленкин, М.; Мнемозина, 2012 год ФИО учителя, школа Страшнова Г. А. МОУ СОШ 2 Тема урока Умножение десятичных дробей на натуральные
Я. Виленкин, М.; Мнемозина, 2012 год ФИО учителя, школа Страшнова Г. А. МОУ СОШ 2 Тема урока Умножение десятичных дробей на натуральные
Подробнее
Модуль или абсолютное значение комплексного числа?
На моей странице полярной формы комплексного числа в IntMath я указываю:
Для комплексного числа x + yj = r (cos θ + j sin θ), r — это абсолютное значение (или модуль ) комплексного числа.
Читатель Саншайн из Филиппин оспорил это утверждение, сказав:
Абсолютное значение
не имеет того же определения, что и модуль
.
Мне нравится такая обратная связь, потому что она заставляет меня глубже задуматься о том, как я написал определения (или, возможно, обозначения) на сайте.Нам нужно быть ясными, точными и точными, но при этом сделать это понятным.
Итак, Sunshine верна?
Это был мой ответ ей.
В случае комплексных чисел термины обычно взаимозаменяемы, но я согласен, что это может быть небрежно.
В этих других математических ресурсах оба термина также используются для обозначения одного и того же:
Комплексные числа отрубного узла
Абсолютное значение Википедии
Абсолютное значение комплексного числа Mathwords
Тем не менее, Pauls Online Notes (Университет Ламара) проводит некоторое различие между модулем комплексного числа и абсолютным значением действительного числа (последнее является вырожденным случаем первого).
Но в том смысле, что «абсолютное значение» означает расстояние от начала координат для действительного числа (на одномерной числовой прямой), а «модуль» означает расстояние от начала координат для комплексного числа (на двумерной комплексной плоскости ), Я не думаю, что существует большая проблема с взаимозаменяемостью терминов. Концепция, безусловно, та же, и это не приводит к большой путанице.
Я бы, вероятно, не стал писать «абсолютное значение комплексного числа» — это, конечно, менее распространено, и предпочитаю «модуль комплексного числа».
Спасибо, что побудили меня подумать об этом!
Читатели, что вы думаете по этому поводу? Что написано в вашем учебнике или конспектах лекций?
См. 6 комментариев ниже.
Комплексные числа: абсолютное значение
Комплексные числа: абсолютное значение
Важным понятием для чисел, действительных или комплексных, является абсолютное значение . Напомним, что абсолютное значение | x | действительного числа x есть само, если оно положительное или ноль, но если x отрицательно, то его абсолютное значение | x | это его отрицание — x, то есть соответствующее положительное значение.Например, | 3 | = 3, но | –4 | = 4. Функция абсолютного значения лишает знак действительного числа.
Для комплексного числа z = x + yi, мы определяем абсолютное значение | z | как расстояние от z до 0 в комплексной плоскости C . Это расширит определение абсолютного значения для действительных чисел, поскольку абсолютное значение | x | действительного числа x можно интерпретировать как расстояние от x до 0 на строке действительного числа.Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси). Горизонтальная сторона треугольника имеет длину | | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно,
Это расширит определение абсолютного значения для действительных чисел, поскольку абсолютное значение | x | действительного числа x можно интерпретировать как расстояние от x до 0 на строке действительного числа.Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси). Горизонтальная сторона треугольника имеет длину | | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно,
| z | 2 = x 2 + y 2 .
(Обратите внимание, что для вещественных чисел, таких как x, , мы можем опустить абсолютное значение при возведении в квадрат, поскольку | x | 2 = x 2 . ) Это дает нам формулу для | z |, а именно,
) Это дает нам формулу для | z |, а именно,
Единичный круг.
Некоторые комплексные числа имеют абсолютное значение 1. Конечно, 1 — это абсолютное значение как 1, так и –1, но это также абсолютное значение как i , так и — i , поскольку они оба на одну единицу от 0 на мнимая ось.Единичный круг — это круг радиуса 1 с центром в 0. Он включает в себя все комплексные числа с абсолютным значением 1, поэтому он имеет уравнение | z | = 1.
Комплексное число z = x + yi будет лежать на единичной окружности, когда x 2 + y 2 = 1. Некоторые примеры, кроме 1, –1, i, и — 1 — это ± √2 / 2 ± i √2 / 2, где плюсы и минусы могут быть взяты в любом порядке.Это четыре точки на пересечении диагональных линий y = x и y = x с единичной окружностью. Позже мы увидим их как квадратные корни из i и — i.
Вы можете найти другие комплексные числа на единичной окружности из троек Пифагора. Пифагорова тройка состоит из трех целых чисел a, b, и c , так что a 2 + b 2 = c 2 Если разделить это уравнение на c 2 , тогда вы обнаружите, что
( в / в ) 2 + ( в / в ) 2 = 1.Это означает, что a / c + i b / c — комплексное число, лежащее на единичной окружности. Самая известная тройка Пифагора — 3: 4: 5. Эта тройка дает нам комплексное число 3/5 + i 4/5 на единичной окружности. Некоторые другие пифагорейские тройки: 5:12:13, 15: 8: 17, 7:24:25, 21:20:29, 9:40:41, 35:12:27 и 11:60:61. Как и следовало ожидать, их бесконечно много. (Для
еще немного о троек Пифагора см. в конце страницы по адресу http: // www.clarku.edu/~djoyce/trig/right.html.)
Неравенство треугольника.
Существует важное свойство комплексных чисел, относящееся к сумме абсолютного значения, называемое неравенством треугольника. Если z и w — любые два комплексных числа, то
Если z и w — любые два комплексных числа, то
Вы можете увидеть это из правила сложения параллелограмма. Рассмотрим треугольник с вершинами 0, z, и z + w.
Одна сторона треугольника от 0 до z + w имеет длину | z + w |.Вторая сторона треугольника от 0 до z, имеет длину | z |. И третья сторона треугольника, от z до z + w, параллельна и равна прямой от 0 до w, и, следовательно, имеет длину | w |. Итак, в любом треугольнике любая сторона меньше или равна сумме двух других сторон, и, следовательно, мы имеем неравенство треугольника, показанное выше.
Абсолютное значение | Психология Вики
Оценка |
Биопсихология |
Сравнительный |
Познавательная |
Развивающий |
Язык |
Индивидуальные различия |
Личность |
Философия |
Социальные |
Методы |
Статистика |
Клиническая |
Образовательная |
Промышленное |
Профессиональные товары |
Мировая психология |
Статистика:
Научный метод ·
Методы исследования ·
Экспериментальная конструкция ·
Курсы бакалавриата по статистике ·
Статистические тесты ·
Теория игры ·
Теория принятия решений
В математике абсолютное значение (или модуль 1 ) действительного числа является его числовым значением безотносительно знака. Так, например, 3 — это абсолютное значение как 3, так и −3. В компьютерах математической функции, используемой для выполнения этого вычисления, обычно присваивается имя abs () .
Так, например, 3 — это абсолютное значение как 3, так и −3. В компьютерах математической функции, используемой для выполнения этого вычисления, обычно присваивается имя abs () .
Обобщения абсолютного значения действительных чисел происходят в самых разных математических условиях. Например, абсолютное значение также определено для комплексных чисел, кватернионов, упорядоченных колец, полей и векторных пространств.
Абсолютное значение тесно связано с понятиями величины, расстояния и нормы в различных математических и физических контекстах.
График функции абсолютного значения действительных чисел.
Для любого действительного числа абсолютное значение или модуль обозначается 2 и определяется как
Как видно из приведенного выше определения, абсолютное значение всегда либо положительно, либо равно нулю, но никогда не отрицательно.
С геометрической точки зрения абсолютное значение действительного числа — это расстояние вдоль линии действительного числа этого числа от нуля, а в более общем смысле абсолютное значение разности двух действительных чисел — это расстояние между ними. Действительно, понятие абстрактной функции расстояния в математике можно рассматривать как обобщение свойств абсолютного значения (см. «Расстояние» ниже).
Действительно, понятие абстрактной функции расстояния в математике можно рассматривать как обобщение свойств абсолютного значения (см. «Расстояние» ниже).
Следующее предложение дает тождество, которое иногда используется как альтернативное (и эквивалентное) определение абсолютного значения:
ПРЕДЛОЖЕНИЕ 1 :
Абсолютное значение имеет следующие четыре основных свойства:
ПРЕДЛОЖЕНИЕ 2 :
Другие важные свойства абсолютного значения включают:
ПРЕДЛОЖЕНИЕ 3 :
Два других полезных неравенства:
Вышеупомянутое часто используется при решении неравенств; Например:
Поскольку комплексные числа не упорядочены, приведенное выше определение действительного абсолютного значения не может быть напрямую обобщено для комплексного числа.Однако тождество, указанное в предложении 1:
можно рассматривать как мотивирующее следующее определение.
Для любого комплексного числа
Абсолютное значение или модуль обозначается и определяется как
Отсюда следует, что абсолютное значение действительного числа x равно его абсолютному значению, рассматриваемому как комплексное число, поскольку:
Подобно геометрической интерпретации абсолютного значения для действительных чисел, из теоремы Пифагора следует, что абсолютное значение комплексного числа — это расстояние в комплексной плоскости этого комплексного числа от начала координат, и в более общем смысле , что абсолютное значение разности двух комплексных чисел равно расстоянию между этими двумя комплексными числами.
Комплексное абсолютное значение разделяет все свойства действительного абсолютного значения, данные в предложениях 2 и 3 выше. Кроме того, если
и
— комплексное сопряжение, тогда легко видеть, что
Реальная функция абсолютного значения везде непрерывна. Он дифференцируемый везде, кроме x = 0.Он монотонно убывает на интервале (-∞, 0] и монотонно возрастает на интервале [0, ∞). Поскольку действительное число и его отрицательное значение имеют одинаковое абсолютное значение, это четная функция и, следовательно, не обратима.
Он дифференцируемый везде, кроме x = 0.Он монотонно убывает на интервале (-∞, 0] и монотонно возрастает на интервале [0, ∞). Поскольку действительное число и его отрицательное значение имеют одинаковое абсолютное значение, это четная функция и, следовательно, не обратима.
Комплексная функция абсолютного значения непрерывна везде, но дифференцируема нигде (Один из способов убедиться в этом — показать, что она не подчиняется уравнениям Коши-Римана).
И действительная, и комплексная функции идемпотентны.
Определение абсолютного значения, данное для действительных чисел выше, может быть легко распространено на любое упорядоченное кольцо.То есть, если является элементом упорядоченного кольца, то абсолютное значение , обозначаемое, определяется как:
где — аддитивная величина, обратная величине, а — аддитивный элемент идентичности.
Абсолютная величина тесно связана с идеей расстояния. Как отмечалось выше, абсолютное значение действительного или комплексного числа — это расстояние от этого числа до начала координат, вдоль линии действительного числа, для действительных чисел или в комплексной плоскости, для комплексных чисел, и, в более общем смысле, абсолютное значение разницы двух действительных или комплексных чисел — это расстояние между ними.
Стандартное евклидово расстояние между двумя точками
и
в евклидовом пространстве n определяется как:
Это можно рассматривать как обобщение того факта, что если они действительны, то согласно предложению 1
а если
и
— комплексные числа, тогда
Выше показано, что расстояние «абсолютного значения» для действительных или комплексных чисел согласуется со стандартным евклидовым расстоянием, которое они наследуют в результате рассмотрения их как одно- и двумерного евклидова пространства соответственно.
Свойства абсолютного значения разности двух действительных или комплексных чисел: неотрицательность, тождество неразличимых, симметрия и неравенство треугольника, данные в предложениях 2 и 3 выше, можно рассматривать как мотивирующие более общее понятие функция расстояния следующим образом:
Действительная функция на множестве называется функцией расстояния (или метрикой ) для, если она удовлетворяет следующим четырем аксиомам:
Неотрицательность Личность неразличимых Симметрия Неравенство треугольника
Основные свойства абсолютного значения для действительных чисел, приведенные в предложении 2 выше, могут быть использованы для обобщения понятия абсолютного значения на произвольное поле следующим образом.
Действительная функция поля называется абсолютным значением (также модулем , величиной , значением или оценкой ), если она удовлетворяет следующим четырем аксиомам:
Неотрицательность Положительная определенность Мультипликативность Субаддитивность или неравенство треугольника
Из вышеизложенного следует, что, где обозначает мультипликативный тождественный элемент.Определенные выше действительные и комплексные абсолютные значения являются примерами абсолютных значений для произвольного поля.
Если — абсолютное значение on, то функция on, определенная с помощью, является метрикой, а если — мультипликативным тождеством в, то следующие эквиваленты:
- на каждые
- на все
Абсолютное значение, которое удовлетворяет любому (следовательно, всем) из вышеперечисленных условий, называется неархимедовым , в противном случае оно называется архимедовым. 3
Опять же, фундаментальные свойства абсолютного значения для действительных чисел могут быть использованы, с небольшими изменениями, для обобщения этого понятия на произвольное векторное пространство.
Действительная функция || · || в векторном пространстве a над полем называется абсолютным значением (или, чаще, нормой ), если оно удовлетворяет следующим аксиомам:
Для всех в, и, в,
Неотрицательность Положительная определенность Положительная однородность или положительная масштабируемость Субаддитивность или неравенство треугольника
Норма вектора также называется его длиной или величиной .
В случае евклидова пространства R n функция
— норма, называемая евклидовой нормой. Когда действительные числа R рассматриваются как одномерное векторное пространство R 1 , абсолютное значение является нормой и является нормой p для любого p . Фактически абсолютное значение является «единственной» нормой в R 1 в том смысле, что для каждой нормы || · || в R 1 , || x || = || 1 || · | x |.Комплексное абсолютное значение — это частный случай нормы во внутреннем пространстве продукта. Она идентична евклидовой норме, если комплексная плоскость отождествляется с евклидовой плоскостью R 2 .
На языке программирования C функции abs () , labs () , llabs () (в C99), fabs () , fabsf () и fabsl () вычисляют абсолютное значение операнда. Кодирование целочисленной версии функции тривиально, игнорируя граничный случай, когда вводится наибольшее отрицательное целое число:
интервал абс (интервал i)
{
если (я <0)
return -i;
еще
вернуть я;
}
Версии с плавающей запятой сложнее, поскольку им приходится иметь дело со специальными кодами для бесконечности и не-чисел.
Используя язык ассемблера, можно взять абсолютное значение регистра всего в трех инструкциях (пример показан для 32-битного регистра в архитектуре x86, синтаксис Intel):
кд xor eax, edx sub eax, edx
cdq расширяет знаковый бит eax в edx . Если eax неотрицательно, тогда edx становится равным нулю, а последние две инструкции не действуют, оставляя eax без изменений.Если eax отрицательно, то edx становится 0xFFFFFFFF или -1. Следующие две инструкции затем становятся инверсией дополнения до двух, давая абсолютное значение отрицательного значения в eax .
Неравенство абсолютных значений
Неравенство абсолютных значений
Определение абсолютного значения "забудьте знак минус":
бесполезны для наших целей. Вместо этого мы в основном будем использовать геометрические
определение абсолютного значения:
Абсолютное значение числа измеряет его расстояние до начала координат.
на действительной числовой строке.
Поскольку 5 находится на расстоянии 5 единиц от начала координат 0, абсолютное значение
из 5 равно 5, | 5 | = 5
Поскольку -5 также находится на расстоянии 5 единиц от начала координат,
абсолютное значение -5 равно 5, | -5 | = 5:
Мы готовы к нашему первому неравенству. Найдите набор решений для
| x | <5.
Переведем на английский: ищем те действительные числа x , расстояние от которых до начала координат меньше 5 единиц.
Очевидно, речь идет об интервале (-5,5):
Что насчет решений?
На английском языке: какие числа, x , отстоят как минимум на 2 единицы от
источник? Слева действительные числа меньше или равны -2.
квалифицировать, справа все действительные числа больше или равные 2:
Мы можем записать это обозначение интервала как
Каков геометрический смысл | x - y |?
| x - y | - это расстояние между x и y на прямой числовой прямой.
Рассмотрим пример | (-4) -3 |. Расстояние по действительной числовой прямой
между точками -4 и +3 равно 7, поэтому
| (-4) -3 | = 7.
Найдем решения неравенства:
По-английски: Какие действительные числа не более чем на 1 единицу, кроме 2?
Речь идет о числах в интервале [1,3].
Как насчет примера
Давайте перепишем это как
что мы можем перевести в поиск тех чисел x , чьи
расстояние до -1 не менее 3.
Набор решений
После небольшой настройки наш метод также может справиться с неравенствами.
такой как
| 2 x -5 | <2.
Сначала разделим обе стороны на 2.Обратите внимание, что абсолютные значения взаимодействуют
красиво с умножением и делением:
до тех пор, пока , положителен.
Таким образом, мы получаем
после упрощения получаем неравенство
задавая вопрос, какие числа меньше, чем на 1 единицу, кроме
Таким образом, исходное неравенство имеет в качестве множества решений интервал
.
Рассмотрим пример
Разделим на 3:
который совпадает с
Какие числа имеют расстояние не менее
из
? Набор решений дается формулой
Наш метод не годится для более надуманных примеров.
Рассмотрим неравенство
| x -3 | <2 x -4
Это возвращение к базовой алгебре с изюминкой.
Стандартное определение функции абсолютного значения дается следующим образом:
Таким образом мы можем избавиться от
войдите в наше неравенство, если мы
знать, положительное или отрицательное выражение внутри, x -3.
Мы именно так и поступим!
Давайте сначала рассмотрим только те значения x , для которых:
Дело 1 :
В этом случае мы знаем, что | x -3 | = x -3, поэтому наше неравенство становится
x -3 <2 x -4
Решая неравенство, получаем
x > 1.
Мы нашли несколько решений нашего неравенства:
x - решение, если
и x > 1 одновременно! Разговаривали
по поводу цифр.
Что делать, если x -3 <0?
Случай 2 : x <3
На этот раз x -3 <0, поэтому | x -3 | = - ( x -3) = 3- x ,
поэтому наше неравенство читается как
3- x <2 x -4.
Применяя стандартные методы, это можно упростить до
У нашего неравенства есть еще несколько решений:
В нашем случае предположение x <3, решения - те действительные числа которые удовлетворяют .
Мы говорим о числах в интервале
Объединяя решения, которые мы нашли для обоих случаев, мы заключаем, что
множество решений неравенства
| x -3 | <2 x -4
числа в интервале
Упражнение 1.
Найдите решения неравенства
Отвечать.
Упражнение 2.
Найдите решения неравенства
Отвечать.
Упражнение 3.
Найдите решения неравенства
| x -3 |> 5.
Отвечать.
Упражнение 4.
Найдите решения неравенства
Отвечать.
Упражнение 5.
Найдите решения неравенства
| 2 x -5 |> x +1.
Отвечать.
[Назад]
[Следующий]
[Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] С.Домашняя страница O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
Гельмут КнаустАвторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. - П.О. Box 12395 - El Paso TX 79913 - США
пользователя онлайн за последний час
Праймер для комплексных чисел
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с "узкой" шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Сопряжение и модуль
В предыдущем разделе мы рассмотрели алгебраические операции над комплексными числами.Есть несколько других операций, на которые мы должны обратить внимание, поскольку они, как правило, появляются время от времени. Мы также рассмотрим довольно много интересных фактов об этих операциях.
Комплексный конъюгат
Первое, что мы рассмотрим, это комплексное сопряжение (или просто сопряжение). С учетом комплексного числа \ (z = a + bi \) комплексное сопряжение обозначается \ (\ overline z \) и определяется как,
\ begin {уравнение} \ overline z = a - bi \ end {уравнение}
Другими словами, мы просто меняем знак мнимой части числа.
Вот несколько основных фактов о конъюгатах.
\ begin {align} \ overline {\ overline {z}} & = z \\
\ overline {{z_1} \ pm {z_2}} & = {\ overline z_1} \ pm {\ overline z_2} \ label {eq: consum} \\
\ overline {{z_1} {z_2}} & = {\ overline z_1} \, {\ overline z_2} \ label {eq: conprod} \\
\ overline {\ left ({\ frac {{{z_1}}} {{{z_2}}}} \ right)} & = \ frac {{{{\ overline z} _1}}} {{{{\ overline z} _2}}}
\ end {align}
Первый просто говорит, что если мы спрягаем дважды, мы вернемся к тому, с чего начали, и, надеюсь, в этом есть какой-то смысл.Остальные три просто говорят, что мы можем разбить сумму, разницы, продукты и частные на отдельные части, а затем соединить их.
Итак, чтобы мы могли сказать, что мы проработали несколько примеров, давайте сделаем пару примеров, иллюстрирующих приведенные выше факты.
Пример 1 Рассчитайте каждое из следующих значений.
- \ (\ overline {\ overline {z}} \) для \ (z = 3 - 15i \)
- \ (\ overline {{z_1} - {z_2}} \) для \ ({z_1} = 5 + i \) и \ ({z_2} = - 8 + 3i \)
- \ ({\ overline {z_1}} - {\ overline {z_2}} \) для \ ({z_1} = 5 + i \) и \ ({z_2} = - 8 + 3i \)
Показать решение
На самом деле с этим особо нечего делать, кроме как работать так,
а \ (\ overline {z} = 3 + 15i \ hspace {0.5 дюймов} \ Rightarrow \ hspace {0,5 дюйма} \ overline {\ overline {z}} = \ overline {3 + 15i} = 3 - 15i = z \)
Конечно, мы видим, что после двойного спряжения мы возвращаемся к нашему исходному числу.
b \ ({z_1} - {z_2} = 13 - 2i \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,5 дюйма} \ overline {{z_1} - {z_2}} = \ overline {13 - 2i} = 13 + 2i \)
c \ ({\ overline z_1} - {\ overline z_2} = \ overline {5 + i} - \ left ({\ overline {- 8 + 3i}} \ right) = 5 - i - \ left ({- 8 - 3i} \ right) = 13 + 2i \)
Мы видим, что результаты (b), и (c) совпадают с предполагаемым фактом.
Есть еще один интересный факт, в котором используются конъюгаты, на которые, вероятно, стоит обратить внимание. Однако вместо того, чтобы просто выдавать этот факт, давайте выведем его. Мы начнем с комплексного числа \ (z = a + bi \), а затем выполните каждую из следующих операций.
\ [\ begin {array} {rlcrl} z + \ overline {z} & = a + bi + \ left ({a - bi} \ right) & \ hspace {0,5in} & z - \ overline {z} & = a + bi - \ left ({a - bi} \ right) \\
& = 2a & \ hspace {0.5in} & & = 2bi \ end {array} \]
Теперь, вспоминая, что \ ({\ mathop {\ rm Re} \ nolimits} \, z = a \) и \ ({\ mathop {\ rm Im} \ nolimits} \, z = b \), мы видим, что иметь,
\ begin {Equation} {\ mathop {\ rm Re} \ nolimits} z = \ frac {{z + \ overline z}} {2} \ hspace {0,75in} {\ mathop {\ rm Im} \ nolimits} z = \ frac {{z - \ overline z}} {{2i}} \ label {eq: ReImDefn} \ end {уравнение}
Модуль
T Другая операция, которую мы хотим рассмотреть в этом разделе, - это модуль комплексного числа.2} \]
Если мы извлечем квадратный корень из обеих частей, получим
\ [\ left | г \ право | \ ge \ left | {{\ mathop {\ rm Re} \ nolimits} \, z} \ right | \]
, где \ (\ left | {\, \, \ cdot \,} \ right | \) на \ (z \) - это модуль комплексного числа, а \ (\ left | {\, \, \ cdot \,} \ right | \) на \ ({\ mathop {\ rm Re} \ nolimits} \, z \) - столбцы абсолютного значения. Наконец, для любого действительного числа \ (a \) мы также знаем, что \ (a \ le \ left | a \ right | \) (абсолютное значение…), и поэтому мы получаем
\ begin {Equation} \ left | г \ право | \ ge \ left | {{\ mathop {\ rm Re} \ nolimits} \, z} \ right | \ ge {\ mathop {\ rm Re} \ nolimits} \, z \ label {eq: zRez} \ end {уравнение}
Мы можем использовать аналогичный аргумент, чтобы прийти к
\ begin {Equation} \ left | г \ право | \ ge \ left | {{\ mathop {\ rm Im} \ nolimits} \, z} \ right | \ ge {\ mathop {\ rm Im} \ nolimits} \, z \ label {eq: zImz} \ end {уравнение}
Существует очень хорошая связь между модулем комплексного числа и его сопряженным.2} \ label {eq: zConjz} \ end {уравнение}
Иногда бывает приятный и удобный факт.
Также обратите внимание, что при вычислении модуля знак действительной и мнимой части комплексного числа не влияет на значение модуля, поэтому мы также можем видеть, что,
\ begin {Equation} \ left | г \ право | = \ left | {\ overline z} \ right | \ label {eq: MzMzbar} \ end {уравнение}
и
\ begin {Equation} \ left | {- z} \ right | = \ left | z \ right | \ end {уравнение}
Теперь мы можем формализовать процесс деления из предыдущего раздела, теперь, когда у нас есть модуль и сопряженные обозначения.2}}} {{164}} = \ frac {{21}} {{41}} - \ frac {9} {{82}} i \]
Вот еще несколько интересных фактов о модуле комплексного числа.
\ begin {align} {\ rm {If}} \ left | г \ право | & = 0 \, \, \, {\ rm {then}} \, z = 0 \ label {eq: Mzero} \\
\ left | {{z_1} \, {z_2}} \ right | & = \ left | {{z_1}} \ right | \, \ left | {{z_2}} \ right | \ label {eq: MProd} \\
\ left | {\ frac {{{z_1}}} {{{z_2}}}} \ right | & = \ frac {{\ left | {{z_1}} \ right |}} {{\ left | {{z_2}} \ right |}} \ label {eq: MQuot}
\ end {align}
Свойство \ (\ eqref {eq: Mzero} \) должно иметь для вас некоторый смысл.2} \]
Наконец, напомним, что мы знаем, что модуль всегда положителен, поэтому извлеките квадратный корень из обеих частей, чтобы получить
.
\ [\ left | {{z_1} \, {z_2}} \ right | = \ left | {{z_1}} \ right | \, \, \ left | {{z_2}} \ right | \]
Свойство \ (\ eqref {eq: MQuot} \) можно проверить с помощью аналогичного аргумента.
Неравенство треугольника и варианты
Свойства \ (\ eqref {eq: MProd} \) и \ (\ eqref {eq: MQuot} \) связывают модуль произведения / частного двух комплексных чисел с произведением / частным модуля отдельных чисел.Теперь нам нужно взглянуть на аналогичное соотношение для сумм комплексных чисел, которое называется неравенством треугольника и равно
.
\ begin {Equation} \ left | {{z_1} + {z_2}} \ вправо | \ le \ left | {{z_1}} \ right | + \ влево | {{z_2}} \ right | \ label {экв: треугольник} \ end {уравнение}
Мы также сможем использовать это, чтобы получить соотношение для разности комплексных чисел.
Неравенство треугольника на самом деле довольно просто доказать, так что давайте сделаем это.2} = {z_1} \, {\ overline z_1} + {z_1} \, {\ overline z_2} + {z_2} \, {\ overline z_1} + {z_2} \, {\ overline z_2} \ label {eq : tripfone} \ end {уравнение}
Затем обратите внимание, что,
\ [\ overline {{z_2} {{\ overline z} _1}} = {\ overline z_2} {\ overline {\ overline {z_1}}} = {\ overline z_2} {z_1} \]
и поэтому, используя \ (\ eqref {eq: ReImDefn} \), \ (\ eqref {eq: zRez} \) и \ (\ eqref {eq: MzMzbar} \), мы можем написать два средних члена правой части \ (\ eqref {eq: tripfone} \) как
\ [{z_1} \, {\ overline z_2} + {z_2} \, {\ overline z_1} = {z_1} \, {\ overline z_2} + \ overline {{z_1} \, {{\ overline z} _2 }} = 2 {\ mathop {\ rm Re} \ nolimits} \ left ({{z_1} \, {{\ overline z} _2}} \ right) \ le 2 \ left | {{z_1} \, {{\ overline z} _2}} \ right | = 2 \ влево | {{z_1}} \ right | \, \ left | {{{\ overline z} _2}} \ right | = 2 \ влево | {{z_1}} \ right | \, \ left | {{z_2}} \ right | \]
Также используйте \ (\ eqref {eq: zConjz} \) в первом и четвертом членах в \ (\ eqref {eq: tripfone} \), чтобы записать их как,
\ [{z_1} \, {\ overline z_1} = {\ left | {{z_1}} \ right | ^ 2} \ hspace {0.2} \]
Теперь, вспоминая, что модуль всегда положителен, мы можем извлекать квадратный корень из обеих сторон и прийти к неравенству треугольника.
\ [\ left | {{z_1} + {z_2}} \ вправо | \ le \ left | {{z_1}} \ right | + \ влево | {{z_2}} \ right | \]
Существует несколько вариантов неравенства треугольника, которые легко вывести.
Давайте сначала начнем с предположения, что \ (\ left | {{z_1}} \ right | \ ge \ left | {{z_2}} \ right | \). Это не требуется для вывода, но поможет получить более общая версия того, что мы собираемся здесь получить.Итак, давайте начнем с \ (\ left | {{z_1}} \ right | \) и поработаем над ним.
\ begin {align *} \ left | {{z_1}} \ right | & = \ left | {{z_1} + {z_2} - {z_2}} \ вправо | & \\ & \ le \ left | {{z_1} + {z_2}} \ вправо | + \ влево | {- {z_2}} \ right | & \ hspace {0.25in} {\ text {Используя неравенство треугольника}} \\ & = \ left | {{z_1} + {z_2}} \ вправо | + \ влево | {{z_2}} \ right | & \ end {выровнять *}
Теперь немного перепишем, и мы получим
\ begin {Equation} \ left | {{z_1} + {z_2}} \ вправо | \ ge \ left | {{z_1}} \ right | - \ left | {{z_2}} \ right | \ ge 0 \ label {eq: revtrione} \ end {уравнение}
Если теперь предположить, что \ (\ left | {{z_1}} \ right | \ le \ left | {{z_2}} \ right | \), мы можем проделать тот же процесс, что и выше, за исключением этого переключателя времени \ ({ z_1} \) и \ ({z_2} \), и мы получаем
\ begin {Equation} \ left | {{z_1} + {z_2}} \ вправо | \ ge \ left | {{z_2}} \ right | - \ left | {{z_1}} \ right | = - \ left ({\ left | {{z_1}} \ right | - \ left | {{z_2}} \ right |} \ right) \ ge 0 \ label {eq: revtritwo} \ end {уравнение}
Теперь, вспоминая определение абсолютного значения, мы можем объединить \ (\ eqref {eq: revtrione} \) и \ (\ eqref {eq: revtritwo} \) в следующий вариант неравенства треугольника.
\ begin {Equation} \ left | {{z_1} + {z_2}} \ вправо | \ ge \ left | {{\ kern 1pt} \ left | {{z_1}} \ right | - \ left | {{z_2}} \ right | {\ kern 1pt}} \ right | \ label {eq: revtrithree} \ end {уравнение}
Кроме того, если мы заменим \ ({z_2} \) на \ (- {z_2} \) в \ (\ eqref {eq: треугольник} \) и \ (\ eqref {eq: revtrithree} \), мы получим два больше вариаций неравенства треугольника.
\ begin {Equation} \ left | {{z_1} - {z_2}} \ right | \ le \ left | {{z_1}} \ right | + \ влево | {{z_2}} \ right | \ end {уравнение}
\ begin {Equation} \ left | {{z} _ {1}} - {{z} _ {2}} \ right | \ ge \ left | \ left | {{z} _ {1}} \ right | - \ left | {{z} _ {2}} \ right | \ право | \ label {eq: revtri} \ end {уравнение}
Иногда вы увидите \ (\ eqref {eq: revtri} \), называемое неравенством обратного треугольника .
Комплексные числа | Безграничная алгебра
Введение в комплексные числа
Комплексное число имеет вид [латекс] a + bi [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] - действительные числа, а [latex] i [/ latex] - это мнимая единица.
Цели обучения
Описание свойств комплексных чисел и комплексной плоскости
Основные выводы
Ключевые моменты
- Комплексное число - это число, которое может быть выражено в форме [latex] a + bi [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] - действительные числа, а [latex] ] i [/ latex] - мнимая единица.
- Действительное число [латекс] a [/ latex] называется действительной частью комплексного числа [latex] z = a + bi [/ latex] и обозначается [latex] \ text {Re} \ {a + bi \ } = [/ латекс]. Действительное число [латекс] b [/ latex] называется мнимой частью [latex] z = a + bi [/ latex] и обозначается [латекс] \ text {Im} \ {a + bi \} = b [ /латекс].
Ключевые термины
- вещественное число : элемент набора действительных чисел. Набор действительных чисел включает рациональные числа и иррациональные числа, но не все комплексные числа.
- мнимое число : число вида [latex] ai [/ latex], где [latex] a [/ latex] - действительное число, а [latex] i [/ latex] - мнимая единица
- комплексный : число в форме [латекс] a + bi [/ латекс], где [латекс] a [/ латекс] и [латекс] b [/ латекс] являются действительными числами, а [латекс] i [/ латекс] - квадратный корень из [латекс] -1 [/ латекс]. 2 = -1 [/ latex].В этом выражении [латекс] а [/ латекс] называется действительной частью, а [латекс] b [/ латекс] мнимой частью комплексного числа. Мы будем писать [latex] \ text {Re} \ {a + bi \} = a [/ latex], чтобы указать действительную часть комплексного числа, и [latex] \ text {Im} \ {a + bi \} = b [/ latex] для обозначения мнимой части.
Например, чтобы указать, что действительная часть числа [латекс] 2 + 3i [/ латекс] равна [латекс] 2 [/ латекс], мы должны написать [латекс] \ text {Re} \ {2 + 3i \ } = 2 [/ латекс]. Чтобы указать, что мнимая часть [latex] 4-5i [/ latex] равна [latex] -5 [/ latex], мы должны написать [latex] \ text {Im} \ {4-5i \} = -5 [ /латекс].
Комплексные числа расширяют идею одномерной числовой прямой до двухмерной комплексной плоскости, используя горизонтальную ось для действительной части и вертикальную ось для мнимой части. Комплексное число [латекс] а + би [/ латекс] можно идентифицировать с помощью точки [латекс] (a, b) [/ латекс]. Таким образом, например, комплексное число [латекс] -2 + 3i [/ latex] будет связано с точкой [латекс] (- 2,3) [/ latex] и будет нанесено на комплексную плоскость, как показано ниже.
Комплексная точка [латекс] -2 + 3i [/ latex]: Комплексное число [латекс] -2 + 3i [/ latex] нанесено на комплексную плоскость [латекс] 2 [/ латекс] слева. на действительной оси, и [латекс] 3 [/ латекс] вверх на мнимой оси.
Комплексное число, действительная часть которого равна нулю, называется чисто мнимым, а комплексное число, мнимая часть которого равна нулю, является действительным числом. Таким образом, набор обычных действительных чисел можно рассматривать как подмножество набора комплексных чисел. Полезно думать о множестве комплексных чисел как о расширении набора действительных чисел. Это расширение позволяет решать определенные проблемы, которые не могут быть решены в рамках набора действительных чисел.
Комплексные числа используются во многих областях науки, включая инженерию, электромагнетизм, квантовую физику и прикладную математику, например теорию хаоса.2 \\ & = - 9 \ end {align} [/ latex]
Оказывается, если мы позволим [latex] x [/ latex] быть комплексным числом, то любое полиномиальное уравнение в [latex] x [/ latex] степени [latex] n [/ latex] будет иметь [latex] n [/ latex] (не обязательно уникальных) решений.
Сложение и вычитание комплексных чисел
Комплексные числа можно складывать и вычитать, складывая отдельно действительные и мнимые части.
Цели обучения
Вычисление сумм и разностей комплексных чисел путем раздельного сложения действительных и мнимых частей
Основные выводы
Ключевые моменты
- Комплексные числа можно складывать и вычитать для получения других комплексных чисел.Это делается путем добавления соответствующих реальных частей и соответствующих мнимых частей.
- Два нереальных комплексных числа можно сложить с действительным числом. Однако сложение двух действительных чисел никогда не может быть нереальным комплексным числом.
Суммы комплексных чисел
Комплексные числа можно складывать и вычитать для получения других комплексных чисел. Это делается путем добавления соответствующих реальных частей и соответствующих мнимых частей.
Например, сумма [латекс] 2 + 3i [/ латекс] и [латекс] 5 + 6i [/ латекс] может быть вычислена путем сложения двух реальных частей [латекс] (2 + 5) [/ латекс] и две мнимые части [латекс] (3 + 6) [/ латекс] для получения комплексного числа [латекс] 7 + 9i [/ латекс].Обратите внимание, что это всегда возможно, поскольку действительная и мнимая части являются действительными числами, а сложение действительных чисел определено и понятно.
В качестве другого примера рассмотрим сумму [латекс] 1-3i [/ латекс] и [латекс] 4 + 2i [/ латекс]. В этом случае мы добавили бы [латекс] 1 [/ латекс] и [латекс] 4 [/ латекс], чтобы получить [латекс] 5 [/ латекс], а также добавили бы [латекс] -3 [/ латекс] и [латекс] ] 2 [/ latex] для производства [латекса] -1 [/ latex]. Таким образом, мы бы написали:
[латекс] (1-3i) + (4 + 2i) = 5-i [/ латекс]
Различия (вычитание) комплексных чисел
Аналогичным образом можно вычесть комплексные числа.Ключевым моментом снова является объединение реальных частей вместе и мнимых частей вместе, на этот раз путем их вычитания.
Таким образом, чтобы вычислить:
[латекс] (4-3i) - (2 + 4i) [/ латекс]
, мы вычислим [латекс] 4-2 [/ latex], получив [latex] 2 [/ latex] для реальной части, и вычислим [latex] -3-4 = -7 [/ latex] для мнимой части.
Таким образом, мы могли бы написать [латекс] (4-3i) - (2 + 4i) = 2-7i [/ латекс].
Обратите внимание, что то же самое можно сделать, представив, что вы распределяете знак вычитания по сумме [латекс] 2 + 4i [/ latex], а затем складываете, как определено выше.Таким образом, вы могли написать:
[латекс] (4-3i) - (2 + 4i) = (4-3i) + (- 2-4i) = 2-7i. [/ Latex]
Обратите внимание, что два нереальных комплексных числа можно сложить с действительным числом. Например, [латекс] (1-3i) + (1 + 3i) = 2 + 0i = 2 [/ латекс]. Однако сложение двух действительных чисел никогда не может быть нереальным комплексным числом.
Умножение комплексных чисел
Комплексные числа можно умножать с помощью алгоритма FOIL.
Цели обучения
Вычислить произведение комплексных чисел с использованием ФОЛЬГИ и свойств [латекс] i [/ латекс]
Основные выводы
Ключевые моменты
- Мнимая единица [латекс] i [/ latex] имеет свойство [latex] i ^ 2 = -1 [/ latex]
- Комплексные числа можно умножать с помощью алгоритма FOIL
Квадрат мнимой единицы [латекс] и [/ латекс]
В следующих расчетах важно помнить, что [латекс] i ^ 2 = -1 [/ латекс].2 [/ latex] появляется в расчетах, его можно заменить действительным числом [latex] -1. [/ Latex]
Умножение комплексных чисел
Два комплексных числа можно умножить, чтобы получить другое комплексное число. Ключ к выполнению умножения - запомнить аббревиатуру FOIL, которая расшифровывается как First, Outer, Inner, Last. Таким образом, мы умножаем [latex] a + bi [/ latex] и [latex] c + di [/ latex], записывая [latex] (a + bi) (c + di) [/ latex] и умножая первые члены [ латекс] а [/ латекс] и [латекс] с [/ латекс], а затем внешние термины [латекс] а [/ латекс] и [латекс] ди [/ латекс], а затем внутренние термины [латекс] би [/ латекс] и [латекс] с [/ латекс], а затем последние термины [латекс] би [/ латекс] и [латекс] ди [/ латекс].2 = bd \ cdot (-1) = -bd [/ latex]
Обратите внимание, что алгоритм FOIL производит два действительных члена (из первого и последнего умножения) и два мнимых члена (из внешнего и внутреннего умножения). Затем мы объединяем их, чтобы записать наше комплексное число в стандартной форме. 2) \\ & = 2 + 2i - (- 4 ) \\ & = 6 + 2i \ end {align} [/ latex]
Обратите внимание, что если число имеет действительную часть [latex] 0 [/ latex], то метод FOIL не нужен.5 [/ латекс]
Это, в свою очередь, можно записать как:
[латекс] 32 + 80i-80-40i + 10 + i = -38 + 41i [/ латекс]
Комплексные конъюгаты
Комплексное сопряжение числа [латекс] а + би [/ латекс] есть [латекс] а-би [/ латекс]. Два комплексных конъюгата друг друга умножаются, чтобы получить действительное число с геометрическим значением.
Цели обучения
Объясните, как найти сопряжение комплексного числа и что оно используется для получения
.
Основные выводы
Ключевые моменты
- Комплексный конъюгат [латекс] а + би [/ латекс] представляет собой [латекс] а-би [/ латекс], и наоборот.2} [/ латекс]
- комплексный конъюгат : Для числа [латекс] а + би [/ латекс] это [латекс] а-би [/ латекс].
Комплексные конъюгаты
Комплексное сопряжение (иногда называемое просто конъюгатом ) комплексного числа [латекс] а + би [/ латекс] - это комплексное число [латекс] а-би [/ латекс]. 2}.2} [/ латекс]
Мультипликативные символы, обратные комплексным числам
Мы видели, как складывать, вычитать и умножать комплексные числа, но осталось научиться их делить. Ключ в том, чтобы думать о делении на число [latex] z [/ latex] как о умножении на мультипликативную обратную величину [latex] z [/ latex]. Вы, вероятно, уже знакомы с этой концепцией для обычных действительных чисел: деление на [латекс] 2 [/ латекс] аналогично умножению на [латекс] \ frac12 [/ латекс], деление на 3 такое же, как умножение на [латекс ] \ frac13 [/ latex] и так далее.2} [/ латекс]
Пример 1
Множитель, обратный [latex] 1 + 2i [/ latex], равен:
[латекс] \ frac {1-2i} {1 + 4} = (1/5) - (2/5) i [/ латекс]
Чтобы убедиться, что это правильно, мы можем умножить эти числа, чтобы увидеть, получим ли мы мультипликативный идентификационный номер [latex] 1 [/ latex]. Используя FOIL, получаем:
[латекс] \ begin {align} (1 + 2i) ((1/5) - (2/5) i) & = 1/5 - (2/5) i + (2/5) i + 4/5 \\ & = 1/5 + 4/5 \\ & = 1 \ end {align} [/ latex]
Пример 2
Множитель, обратный [latex] 3-4i [/ latex], равен:
[латекс] \ frac {3 + 4i} {9 + 16} = (3/25) + (4/25) i [/ латекс]
Опять же, проверяя умножение, имеем:
[латекс] \ begin {align} (3-4i) ((3/25) + (4/25) i & = 9/25 - (12/25) i + (12/25) i + 16/25 \\ & = \ frac {25} {25} \\ & = 1 \ end {align} [/ latex]
Деление комплексных чисел
Предположим, вы хотите разделить комплексное число [latex] z = 2 + 3i [/ latex] на число [latex] 1 + 2i [/ latex]. {i \ theta} [/ latex].2} [/ latex] - это модуль [latex] z [/ latex], а [latex] \ phi [/ latex] - это угол, который образует отрезок линии от начала до [latex] z [/ latex] с горизонтальный.
Иногда полезно думать о комплексных числах другим геометрическим способом. Предыдущая геометрическая идея, в которой число [латекс] z = a + bi [/ latex] связано с точкой [latex] (a, b) [/ latex] в обычной системе координат [latex] xy [/ latex]. называется прямоугольными координатами.2} = | z | [/ латекс]
Другой параметр - это угол [латекс] \ phi [/ latex], который линия от исходной точки до точки образует с горизонталью, измеряется в радианах.
Параметры полярных координат: Точка в первом квадранте с декартовыми координатами [latex] (x, y) [/ latex] и полярными координатами [latex] (r, \ phi) [/ latex].
Угол [латекс] \ phi [/ latex] может быть вычислен с помощью тригонометрии из чисел [latex] a [/ latex] и [latex] b [/ latex], но мы просто рассмотрим следующий альтернативный способ записи [ латекс] з = а + би [/ латекс]. {3i \ pi / 4} = -1. + я [/ латекс].
Итак, [latex] z [/ latex] - это комплексное число, которое находится в единицах [latex] \ sqrt2 [/ latex] от начала координат и чей угол с горизонтали равен [latex] \ pi / 4 [/ latex] радианам, что составляет [латекс] 45 [/ латекс] градусов.
Тогда [latex] w [/ latex] - это число, расстояние от которого до начала координат равно [latex] \ sqrt2 [/ latex], а угол с началом координат равен [latex] 3 \ pi / 4 [/ latex] радианам, что равно [латекс] 135 [/ латекс] градусов.
Когда мы умножаем [latex] (1 + i) (- 1 + i) [/ latex] на FOILing, мы получаем [latex] -1 + i-i-1 = -2 [/ latex].{-i \ pi / 2} = -i [/ латекс]
Результат - одна единица от начала координат и под углом [латекс] - \ pi / 2 [/ latex] (или [латекс] -90 [/ latex]] градусов) к горизонтали.
Такой способ размышления об умножении и делении комплексных чисел дает геометрический образ мыслей об этих операциях.
Геометрическая интерпретация сложных уравнений | Что такое геометрическая интерпретация сложных уравнений - примеры и решения
Этот раздел даст вам больше опыта работы с комплексными числами с геометрической точки зрения.Мы будем использовать полученные к этому моменту знания для геометрической интерпретации уравнений и неравенств, включающих комплексные числа. В частности, мы нарисуем областей , соответствующих уравнениям и неравенствам на комплексной плоскости; Что это означает, станет ясно из следующих примеров.
Пример - 16
Интерпретируйте уравнение \ (\ left | z \ right | = 1 \) геометрически.
Решение: \ (z \) - (переменное) комплексное число, модуль которого равен 1.Это означает, что независимо от направления, в котором лежит \ (z \) (т.е. независимо от его аргумента), расстояние \ (z \) от начала координат всегда равно 1. Следовательно, какой путь может \ (z \) , возможно, начертить на комплексной плоскости или, другими словами, каково геометрическое место \ (z? \). Очевидно, круг радиуса 1 с центром в начале координат.
Пример - 17
Постройте области, которые представляет \ (z \) , если:
(a) \ (\ left | z \ right | <1 \) (b) \ (\ left | z \ right |> 2 \) (c) \ (1 <\ left | z \ right | <2 \)
Решение: (a) \ (\ left | z \ right | <1 \) означает, что расстояние \ (z \) от начала координат должно быть меньше 1.Следовательно, \ (z \) должен лежать (где угодно) внутри круга радиуса 1 с центром в начале координат.
(b) \ (\ left | z \ right |> 2 \) означает, что расстояние \ (z \) от начала координат должно быть больше 2. Следовательно, \ (z \) должно лежать (где угодно) вне круга радиуса 2 с центром в начале координат.
(c) \ (1 <\ left | z \ right | <2 \) геометрически означает, что \ (z \) должен лежать вне круга радиуса 1, но внутри круга радиуса 2, как круги с центром в начале координат.
Пример - 18
Постройте область, представленную \ (z \) , если \ (z \) удовлетворяет
\ [\ begin {align} {} \ left | {\ arg (z)} \ right | <\ frac {\ pi} {6} \\\ влево | г \ право | <3 \ end {align} \]
Решение: Поскольку \ (\ begin {align} \ left | {\ arg (z)} \ right | <\ frac {\ pi} {6} \ end {align} \) это означает, что \ (\ begin {align} \ frac {{- \ pi}} {6} <\ arg (z) <\ frac {\ pi} {6} \ end {align} \).

