Что такое модуль числа в математике

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.

Графически абсолютное значение а обозначается как |a|.

Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.

Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Это интересно: умножение на 0 — правило для любого числа.

Геометрическое значение

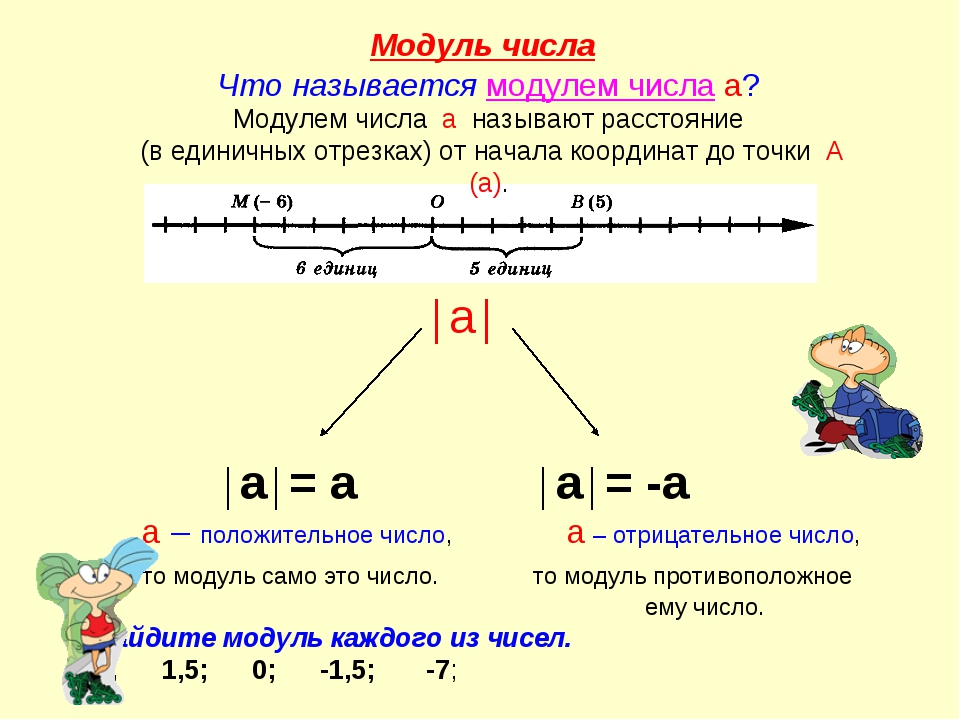
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

1. Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
2. Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
3. В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
4. Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.

Графически это можно выразить следующим образом: |a| = OA.

Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

1. Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
2. Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
3. Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
4. Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
5. Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
6. Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
7. Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
8. Такое же правило распространяется и на показатель степени выражения.

Это интересно: что такое разность в математике?

Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.

К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.

|А + 5| = А + 5, если, А больше или равняется нулю.

5-А, если, А значение меньше нуля.

В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.

Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.

Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.

Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.

Видео: Модуль числа. Математика 6 класс.

Модуль числа. Абсолютная величина | Математика

Модуль числа обозначается двумя вертикальными чертами, между которыми заключается число:

|-7|  —  модуль числа  -7.

Модуль числа — это абсолютная величина числа. Абсолютная величина — это неотрицательное число, удовлетворяющее условиям:

|x| = x,   если   x ⩾ 0;

|x| = —x,   если   x < 0.

Следовательно, модуль числа – это положительное число или нуль.

Модуль на координатной прямой

Модуль числа — это расстояние от начальной точки до соответствующей точки на координатной прямой. Рассмотрим координатную прямую с точками  A  и  B:

Точка  A  соответствует числу  -5,  которое находится в пяти единичных отрезках от начальной точки, то есть длина отрезка  AO  равна  5. Так как модуль равен расстоянию от начала координат до точки, то модуль числа  -5  равен  5,  это можно записать так:

|-5| = 5.

Точка  B  соответствует числу  4,5,  значит длина отрезка  OB  равна  4,5. Следовательно, модуль числа  4,5  равен  4,5:

|4,5| = 4,5.

Точка  O  соответствует числу  0  и является начальной точкой, следовательно, модулем нуля будет нуль:

|0| = 0.

Следует иметь ввиду, что чем дальше от нуля точка, изображающая данное число, тем больше модуль этого числа.

Свойства абсолютной величины

Абсолютной величиной нуля является число нуль.

Пример:

|+0| = |-0| = 0.

Модулем положительного числа называется само это число.

Пример:

|+2| = 2;   |+35| = 35   и т. д.

Модулем отрицательного числа называется противоположное ему числу.

Пример:

|-10| = 10,

потому что  -(-10) = 10.

Модули противоположных чисел равны.

Пример:

|+7| = |-7| = 7,   |-5| = |+5| = 5.

Модуль числа. — tutomath репетитор по математике

Модуль числа вводится новое понятие в математике. Разберем подробно, что такое модуль числа и как с ним работать?

Рассмотрим пример:

Мы вышли из дома в магазин. Прошли 300 м, математически это выражение можно записать как +300, смысл числа 300 от знака “+” не поменяется. Расстояние или модуль числа в математике это одно и тоже можно записать так: |300|=300. Знак модуля числа обозначается двумя вертикальными линиями.

А потом в обратном направлении прошли 200м. Математически обратный путь мы можем записать как -200. Но мы не говорим так “мы прошли минус двести метров”, хотя мы вернулись, потому что расстояние как величина остается положительной. Для этого в математике ввели понятие модуля. Записать расстояние или модуль числа -200 можно так: |-200|=200.

Свойства модуля.

Определение:
Модуль числа или абсолютная величина числа – это расстояние от отправной точки до точки назначения.

Модуль целого числа не равного нулю, всегда положительное число.

Записывается модуль так:

1. Модуль положительного числа равно самому числу.
|a|=a

2. Модуль отрицательного числа равно противоположному числу.
|-a|=a

3. Модуль нуля, равен нулю.
|0|=0

4. Модули противоположных чисел равны.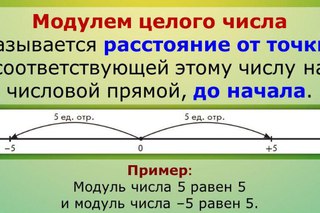
|a|=|-a|=a

Вопросы по теме:
Что такое модуль числа?
Ответ: модуль — это расстояние от отправной точки до точки назначения.

Если перед целым числом поставить знак “+” , что произойдет?
Ответ: число не поменяет свой смысл, например, 4=+4.

Если перед целым числом поставить знак “-” , что произойдет?
Ответ: число изменится на противоположное число, например, 4 и -4.

У каких чисел одинаковый модуль?
Ответ: у положительных чисел и нуля модуль будет тот же. Например, 15=|15|.

У каких чисел модуль – противоположное число?
Ответ: у отрицательных чисел, модуль будет равен противоположному числу. Например, |-6|=6.

Пример №1:
Найдите модуль чисел: а) 0 б) 5 в) -7?

Решение:
а) |0|=0
б) |5|=5
в)|-7|=7

Пример №2:
Существуют ли два различных числа, модули которых равны?

Решение:
|10|=10
|-10|=10

Модули противоположных чисел равны.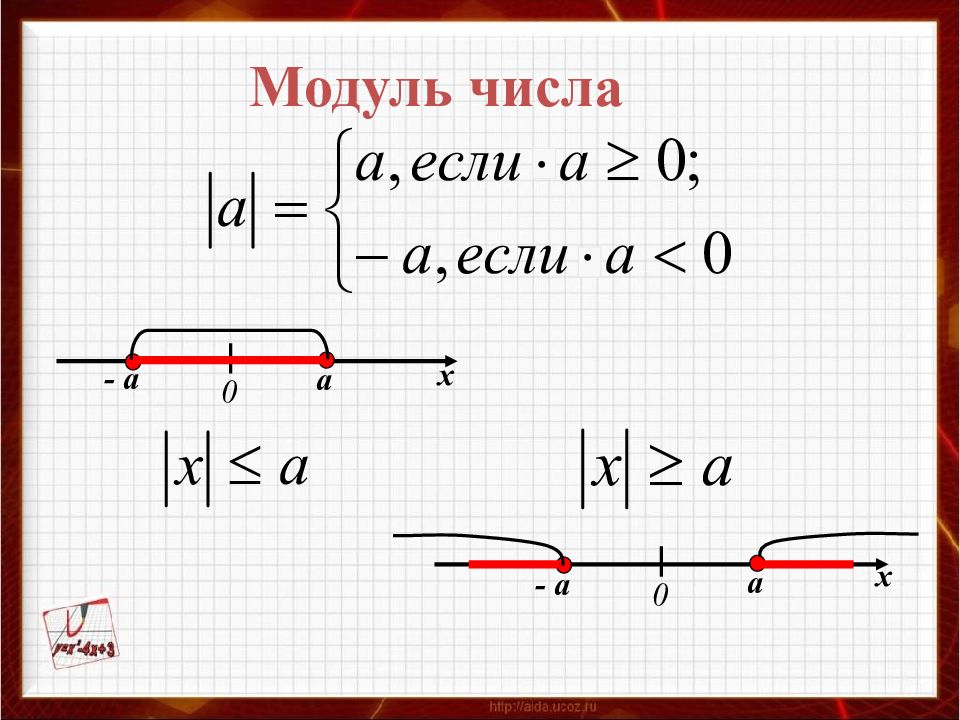

Пример №3:
Какие два противоположных числа, имеют модуль 9?

Решение:
|9|=9
|-9|=9

Ответ: 9 и -9.

Пример №4:
Выполните действия: а) |+5|+|-3| б) |-3|+|-8| в)|+4|-|+1|

Решение:
а) |+5|+|-3|=5+3=8
б) |-3|+|-8|=3+8=11
в)|+4|-|+1|=4-1=3

Пример №5:
Найдите: а) модуль числа 2 б) модуль числа 6 в) модуль числа 8 г) модуль числа 1 д) модуль числа 0.
Решение:

а) модуль числа 2 обозначается как |2| или |+2| это одно и тоже.
|2|=2

б) модуль числа 6 обозначается как |6| или |+6| это одно и тоже.
|6|=6

в) модуль числа 8 обозначается как |8| или |+8| это одно и тоже.
|8|=8

г) модуль числа 1 обозначается как |1| или |+1| это одно и тоже.
|1|=1

д) модуль числа 0 обозначается как |0|, |+0| или |-0| это одно и тоже.
|0|=0

Модуль числа

Модуль числа — это расстояние от этого числа до нуля на координатной прямой.

Модуль обозначается с помощью символа: | |.

• Запись |6| читается как «модуль числа 6», или «модуль шести».
• Запись |8| читается как «модуль 8-ми».

Модуль положительного числа равен самому числу. Например, |2| = 2.
Модуль отрицательного числа равен противоположному числу <=> |-3| = 3.
Модуль нуля равен нулю, то есть |0| = 0.
Модули противоположных чисел равны, то есть |-a| = |a|.

---

Для лучшего понимания

темы: «модуль числа» предлагаем воспользоваться методом ассоциаций.

Представим, что модуль числа — это баня

, а знак «минус» — грязь .

Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется»

, и выходит без знака «минус» — чистым .Модуль

В бане могут «мыться»

(то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют !Модуль числа

 

---

История модуля числа или 6 интересных фактов о модуле числа

1. Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x.
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
который изучается в курсе высшей математики.

---

Решение задач на тему «Модуль числа»

Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания.

Решение:

Для начала раскроем скобки и модули:

— | 12 | = — 12
| — ( — 2) | = 2

Далее осталось расположить числа: -12, 0, 54, 2, -17 в порядке возрастания. Получим следующее неравенство:

-17 < -12 < 0 < 2 < 54, что будет равносильно:
-17 < -|12| < 0 < | — ( — 2) | < 54.

Ответ: -17 < -|12| < 0 < | — ( — 2) | < 54.

Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
в порядке убывания.

Решение:

Для начала раскроем скобки и модули:

— | — 14| = — 14
— |30| = -30
|-16| = 16
| -(-9) | = 9

Далее осталось расположить числа: -14, -30, 16, -21, 9 в порядке убывания. Получим следующее неравенство:

16 > 9 > -14 > — 21 > — 30 что будет равносильно:
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.

Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30|

Модуль числа, сравнение чисел

Модуль числа

Модуль числа а обозначают $|a|$. Вертикальные черточки справа и слева от числа образуют знак модуля.

Например, модуль любого числа (натурального, целого, рационального или иррационального) записывается так: $|5|$, $|-11|$, $|2,345|$, $|\sqrt[4]{45}|$.

Определение 1

Модуль числа a равен самому числу $a$, если $a$ является положительным, числу $−a$, если $a$ является отрицательным, или $0$, если $a=0$.

Данное определение модуля числа можно записать следующим образом:

$|a|= \begin{cases} a, & a > 0, \\ 0, & a=0,\\ -a, &a

Можно использовать более краткую запись:

$|a|=\begin{cases} a, & a \geq 0 \\ -a, & a

Пример 1

Вычислить модуль чисел $23$ и $-3,45$.

Решение.

Найдем модуль числа $23$.

Число $23$ – положительное, следовательно, по определению модуль положительного числа равен этому числу:

$|23|=23$.

Найдем модуль числа $–3,45$.

Число $–3,45$ – отрицательное число, следовательно согласно определению модуль отрицательного числа равен числу, противоположному данному:

$|-3,45|=3,45$. 2}=14$.

Ответ: $|-14|=14$.

Сравнение отрицательных чисел

Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.

Замечание 1

Правило сравнения отрицательных чисел:

• Если модуль одного из отрицательных чисел больше, то такое число является меньшим;
• если модуль одного из отрицательных чисел меньше, то такое число является большим;
• если модули чисел равны, то отрицательные числа равны.

Замечание 2

На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа.

Пример 4

Сравнить отрицательные числа $−27$ и $−4$.

Решение.

Согласно правилу сравнения отрицательных чисел найдем сначала модули чисел $–27$ и $–4$, а затем сравним полученные положительные числа.

$|-27|=27$

$|-4|=4$

Сравним полученные натуральные числа:

$27 > 4$.

Таким образом, получаем, что $–27 |-4|$.

Ответ: $–27

При сравнении отрицательных рациональных чисел необходимо преобразовать оба числа к виду обыкновенных дробей или десятичных дробей.

Сравнение чисел с противоположными знаками

Замечание 3

Правило сравнения чисел с противоположными знаками:

Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.

Пример 5

Сравнить целые числа $−53$ и $8$.

Решение.

Числа имеют противоположные знаки. Согласно правилу сравнения чисел с противоположными знаками получаем, что отрицательное число $−53$ меньше положительного числа $8$.

Ответ: $−53

Пример 6

Сравнить числа $3 \frac{11}{13}$ и $–5,(123)$.

Решение.

Согласно правилу сравнения чисел с противоположными знаками отрицательное число всегда меньше положительного. Следовательно, $–5,(123)

Ответ: $–5,(123)

По данному правилу можно сравнивать также и действительные числа с противоположными знаками.

Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.

что это такое и как его найти?

Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.

Модуль с точки зрения геометрии

Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.

Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.

Как найти модуль числа?

Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.

Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.

Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.

• Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
• Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
• Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
• То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.

Похожие статьи

Конспект урока по математике на Тему: «Модуль числа»

Краткосрочный план урока по математике 6класс

Школа: №4. Г. Текели

Дата:«__12__»____10________2018_г.

ФИО учителя: Безус Н.В.

Класс: «___6_» класс.

Количество присутствующих:

отсутствующих:

Тема урока:

Модуль числа

Цели обучения6.1.1.9Знать определение модуля и находить его значение

6.1.1.9

знать определение модуля числа и уметь находить его значение;

Цели урока:

Ввести определение модуля числа, обозначение модуля числа,научиться находить модуль числа.

Критерии

оценивания

Учащиеся выполняют задания находят модуль положительного числа,отрицательного числа,ему противоположному,знаюм чему равен модульнуля,модуль любого рационального числа.

Привитие

ценностей

Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество;образование в течение всей жизни.

Межпредметные

связи

Взаимосвязь с предметами: физика

Навыки

использования

ИКТ

На данном уроке учащиеся используют флеш-презентацию, которую можно загрузить на планшет или мобильный телефон через QR-код

Предварительные

знания

Знают основные понятия координатной прямой, противоположные числа,

Уровень мышления

Знание,понимание,применение.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

Актуализация знаний уч-ся

Орг. Момент.

Психологический настрой:Повернитесь друг к другу, улыбнитесь друг другу, пожелайте друг другу хорошего настроения на уроке.Теперь посмотрите на меня я тоже желаю вам работать дружно,и открыть для себя чт-то новое.

Деление на группы:Собери букет.

Ребята, запишите в тетрадях число, классная работа.

Для того, чтобы узнать тему нашего урока, укажите число, противоположное данному , а во второй таблице найдите букву, соответствующую этому числу.

Задание №1(слайд №2

Обратная связь:

Метод «Большого пальца»

Задача :

От остановки автобуса магазин находится на расстоянии 100 метров вправо, а кафе – на расстоянии 100 м влево.

записать условие задачи на математическом языке:

магазин – (+100)

кафе – (–100).

Запишите чему равно расстояние от остановки до обоих объектов. Введите обозначение |100|; |–100|.

Проблемная ситуация:/задание для всех /

Середина урока

Начертите координатную прямую, отметьте на ней точк М (.) Знак минус указывает, что точка М лежит левее начала отсчета. Число шесть говорит о том, что расстояние от точки О до точки М равно шесть единичных отрезков.

Число 6 называют модулем числа . Записывают это так: 

 

Определение.

Модулем числа a называют расстояние от начала координат до точки с координатой А(a.)

Мы помним, что расстояние на координатной прямой измеряется в единичных отрезках.

Примеры.

Модуль числа 5 равен 5, так как точка с координатой пять удалена от точки начала отсчета на пять единичных отрезков.

Модуль 0 равен 0, так как точка с координатой ноль – это и есть начало отсчета.

2. Модуль противоположных чисел

Модуль числа – это расстояние. Поэтому он не может быть отрицательным. Для положительного числа его модуль равен самому числу, а для отрицательного – противоположному.

Примеры:

Заметим, что противоположные числа имеют равные модули. В общем виде это можно записать так:

 

 Обозначение:

Например:

І5 І=5 І-5 І=5 І3 І=3 І-3 І=3

Чему равен модуль числа 0? Почему?

І0 І=0

Каким числом не может быть модуль числа?

Чему равен модуль положительного числа? Приведи пример.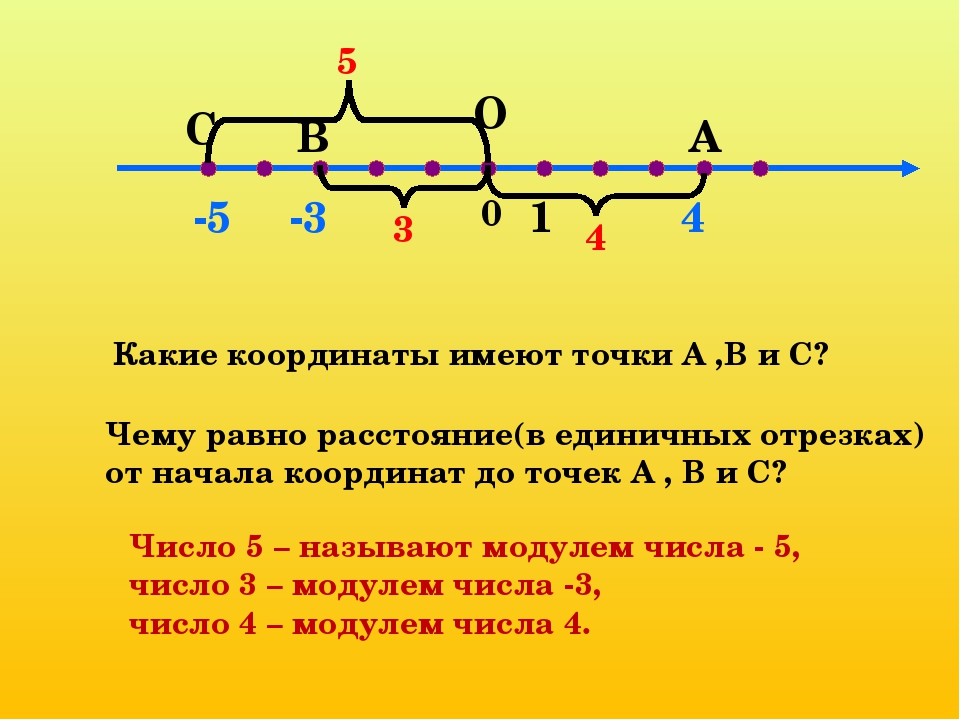

Чему равен модуль отрицательного числа? Приведите пример модуль -85=

Чему равен модуль 0?

Работа в группах метод «Ключевые слова»:запись нового слова модуль- в переводе с латинского означает мера, величина.или абсолютная величина.

«Я начну, а ты закончи»-рассказывают правила.

IV. Закрепление изученного: делаем самостоятельно и проверяем

1.(слайд №6):

Даны числа: 4 и — 4; 94 и — 94; — 42 и 42

Найдите модуль каждого из чисел.

Дискрипторы: Знает что такое модуль числа 1б

Умеет находить модуль отрицательного числа 1б

Умеет находить модуль положительного числа 1б

|4|=4 и |-4|=4

|94|=94 и |-94|=94

|-42|=42 и |42|=42

Сравните эти модули.

Какой вывод можно сделать?

|-а|=|a| — запишите в тетрадь.

2. (слайд №8):

Делаем и проверяем /работа в парах/

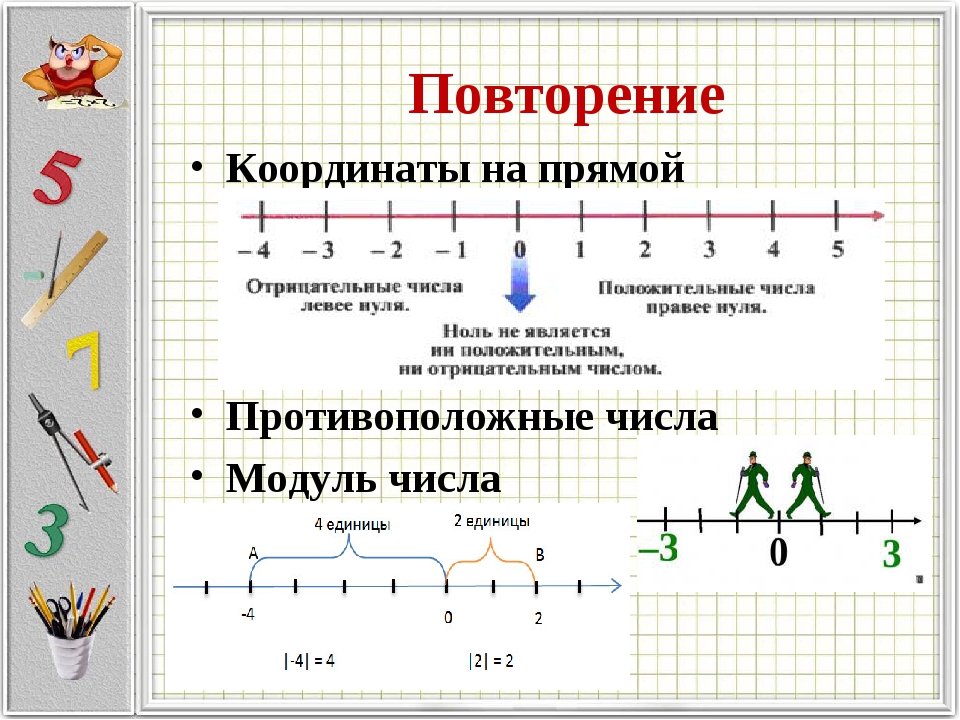
Найдите координаты точек А,В,С, изображённых на числовой оси и запишите расстояние от точек до начала отсчёта, используя знак модуля

|-5|=5

|-2|=2

|-3|=3

|5|=5

3. Задание

Отметьте на координатной прямой числа, модуль которых равен 2.

Решение.

Начертим координатную прямую. Для этого на прямой выберем начало отсчета, единичный отрезок и направление.

Поставим точки на расстоянии 2 единичных отрезка от начала отсчета.

Таких точки две. Одной соответствует число  , а другой число 2.

4. Задание

Найдите значение выражений:

Дискрипторы:

Умеет находить модуль числа

Находит числовое значение

        ;           

Решение.

1)      

Модуль числа  равен 8. Модуль числа 5 равен 5.

2)          

Модуль числа 10 равен 10. Модуль числа  равен 15.

3)      .

  Раскрыв модули, получим сумму чисел 2,3 и 3,7

4)      

Модули данных чисел равны соответственно 24 и 80.

№5 .задание работа с учебником

Выполните №279, №280,№2

Учебн

ик:

тетрадь:

Взаимопро-верка, правильные ответы

на слайде.

Решают все

У доски проверяем задания групп

Критерии успеха

ученики самостоятельно изучают новый материал.

Ученики делают выводы по увиденному.

Конец урока

По методу «Ассоциативная карта» проводит закрепление урока.

1 группа самостоятельная работа 1в

2 группа :2 вариант

3группа 3-вариант

4группа—4 вариант

Решают самостоятельно, азатем один ученик решает у доски, затем решение проверятся

Дом задание пар2.4 читать стр 89 №292

Подведение итогов урока

Что такое модуль числа?

Как обозначают модуль числа?Верно ли, что для любого числа а справедливо равенство |а|=|-а|?

Может ли модуль какого-нибудь числа быть отрицательным числом?

— «барометр настроения»

Барометр настроения

На числовой прямой дети отмечают как они работали на уроке

Примерз. Равнодушен. Закипел

_-100__________50____________0_________+50__________+100___

— Что узнали нового?

— Что уже знали?

Критерии успеха

Умеют находить модуль любого числа.,отмечать на координатной прямой положительные и отрицательные числа.

Дифференциация

Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание

. Метод большого пальца-согласен, не согласен.

Взаимооценивание,

Барометр настроения.,конструктив

но-эмонациональная связь.

Здоровье и соблюдение техники безопасности

Здоровьесберегающие технологии.

Используемые физминутки и активные виды деятельности.

{-1}} $
$ \ Renewcommand {\ Im} {\ operatorname {Im}} $
$ \ DeclareMathOperator {\ Mod} {Mod} $
$ \ DeclareMathOperator {\ Ker} {Ker} $
$ \ DeclareMathOperator {\ Coker} {Coker} $
$ \ DeclareMathOperator {\ Coim} {Coim} $

An
Абелева группа с дистрибутивным действием кольца. Модуль — это обобщение (линейного)
векторное пространство над
поле $ K $, когда $ K $ заменяется
звенеть.

Пусть дано кольцо $ A $. Аддитивная абелева группа $ M $ называется левым $ A $ -модулем, если существует отображение $ A \ times M \ to M $, значение которого на паре $ (a, m) $ для $ a \ in A $ , $ m \ in M ​​$, записанное $ am $, удовлетворяет аксиомам:

1) $ a (m_1 + m_2) = am_1 + am_2 $;

2) $ (a_1 + a_2) m = a_1 m + a_2 m $;

3) $ a_1 (a_2 m) = (a_1 a_2) m $.\ text {opp} $ — модули, и наоборот. Когда $ A $ коммутативен, любой левый $ A $ -модуль можно рассматривать как правый $ A $ -модуль, и различие между левым и правым модулями исчезает. Ниже обсуждаются только левые $ A $ -модули.

Простейшие примеры модулей (конечные абелевы группы; они являются $ \ ZZ $ -модулями) были известны еще К.Ф. Гаусс как группы классов бинарных квадратичных форм. Общее понятие модуля впервые встретилось в 1860–1880-х годах в работах Р. Дедекинда и Л. Кронекера, посвященный арифметике алгебраических числовых и функциональных полей. Примерно в то же время исследования конечномерных ассоциативных алгебр, в частности групповых алгебр конечных групп (Б. Пирс, Ф. Фробениус), привели к изучению идеалов некоторых некоммутативных колец. Сначала теория модулей развивалась в первую очередь как теория идеалов кольца. Лишь позже, в работах Э. Нётер и У. Крулля, было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных модулей, а не только идеалов.Дальнейшее развитие теории модулей было связано с применением методов и идей теории категорий (ср.
Категория), в частности, методы
гомологическая алгебра.

Примеры модулей.

1) Любая абелева группа $ M $ является модулем над кольцом целых чисел $ \ ZZ $. Для $ a \ in \ ZZ $ и $ m \ in M ​​$ произведение $ am $ определяется как результат добавления $ m $ к самому себе $ a $ раз.

2) Когда $ A $ — поле, понятие унитарного $ A $ -модуля в точности эквивалентно понятию линейного векторного пространства над $ A $.

3) $ n $ -мерное векторное пространство $ V $ над полем $ K $ (снабженное координатами) можно рассматривать как модуль над кольцом $ M_n (K) $ всех $ (n \ times n) $ -матрицы с коэффициентами в $ K $. Для $ v \ in V $ и $ X \ in M_n (K) $ произведение $ Xv $ определяется как умножение матрицы $ X $ на столбец координат вектора $ v $.

4) Ассоциативное кольцо (ср.
Ассоциативные кольца и алгебры) $ A $ — левый $ A $ -модуль. Умножение элементов кольца на элементы модуля является обычным умножением в $ A $.

5) Множество дифференциальных форм на гладком многообразии $ X $ имеет естественную структуру модуля над кольцом всех гладких функций на $ X $.

6) С любой абелевой группой $ M $ связано ассоциативное кольцо с единицей $ \ End (M) $ всех эндоморфизмов группы $ M $. Группа $ M $ имеет естественную $ \ End (M) $ -модульную структуру.

Если на $ M $ существует структура $ A $ -модуля для некоторого кольца $ A $, то отображение $ m \ mapsto am $ является эндоморфизмом $ M $ для любого $ a \ in A $. Сопоставляя элементу $ a \ in A $ эндоморфизм $ M $, который он порождает, получаем гомоморфизм $ \ phi $ элемента $ A $ в $ \ End (M) $.Наоборот, любой гомоморфизм $ \ phi: A \ to \ End (M) $ определяет структуру $ A $ -модуля на $ M $. Таким образом, задание структуры $ A $ -модуля на абелевой группе $ M $ эквивалентно заданию гомоморфизма колец $ \ phi: A \ to \ End (M) $. Такой гомоморфизм также называется представлением кольца $ A $, а $ M $ модулем представления. С любым представлением $ \ phi $ связан двусторонний идеал $ \ Ann (M) = \ Ker \ phi $, состоящий из таких $ a \ in A $, что $ am = 0 $ для всех $ m \ in M $.Этот идеал называется аннулятором модуля $ M $. Когда $ \ Ann (M) = 0 $, представление называется точным, а $ M $ — точным модулем (или точным представлением).

Очевидно, что модуль $ M $ можно рассматривать и как модуль над факторкольцом $ A / \ Ann (M) $. В частности, хотя определение модуля не предполагает ассоциативности $ A $, кольцо $ A / \ Ann (M) $ всегда ассоциативно. Поэтому в большинстве случаев обсуждение может ограничиться модулями над ассоциативными кольцами.Везде ниже, если не указано иное, $ A $ считается ассоциативным.

$ G $ -модули.

Пусть $ G $ —
группа. Аддитивная абелева группа $ M $ называется левым $ G $ -модулем, если существует отображение $ G \ times M \ to M $, значение которого на паре $ (g, m) $, где $ g \ in G $ , $ m \ in M ​​$, записывается как $ gm $, и где для любого $ g \ in G $ отображение $ m \ mapsto gm $ является эндоморфизмом $ M $; для любых $ g_1, g_2 \ in G $, $ m \ in M ​​$, $ (g_1 g_2) m = g_1 (g_2 m) $; и для всех $ m \ in M ​​$ $ 1m = m $, где 1 — единица $ G $.Для любого $ g \ in G $ отображение $ m \ mapsto gm $ является автоморфизмом группы $ M $.

Правые $ G $ -модули могут быть определены аналогично.

Примеры $ K $ -модулей.

1) Пусть $ k $ —
Расширение Галуа поля $ G $ с
Группа Галуа $ K $. Тогда аддитивная и мультипликативная группы $ K $ имеют естественную структуру $ G $ -модулей. g $ также используется вместо $ gm $, что есть, действие $ G $ записывается экспоненциально.

Пусть дан $ G $ -модуль $ M $. Сопоставляя элементу $ g \ in G $ автоморфизм $ m \ mapsto gm $ кольца $ M $, получается гомоморфизм $ G $ в группу обратимых элементов кольца $ \ End (M) $. Наоборот, любые гомоморфимы $ G $ в группу обратимых элементов $ \ End (M) $ дают $ M $ структуру $ G $ -модуля.

Понятия модуля над кольцом и $ G $ -модуля тесно связаны. А именно, любой $ G $ -модуль $ M $ можно рассматривать как модуль над групповым кольцом (ср.Групповая алгебра) $ \ ZZ G $, если действие $ G $ на $ M $ линейно продолжено, т. Е. Если положить

$$ \ left (\ sum a_i g_i \ right) m = \ sum a_i (g_i m), $$
где $ a_i \ in \ ZZ $, $ g_i \ in G $, $ m \ in M ​​$. Наоборот, при наличии унитарной структуры $ \ ZZ G $ -модуля на $ M $, $ M $ можно рассматривать как $ G $ -модуль.

Когда $ M $ является одновременно $ K $ -модулем над коммутативным кольцом $ K $ и $ G $ -модулем, где действие элементов $ G $ на $ M $ коммутирует с действием элементов $ K $, то $ M $ можно задать структуру $ KG $ -модуля путем линейного продолжения действия с $ G $ на $ KG $. Например, если $ V $ — линейное векторное пространство над полем $ K $, то спецификация структуры $ KG $ -модуля на $ V $ эквивалентна заданию представления $ G $ в $ V $.

Используя стандартную инволюцию $ g \ mapsto g \ inv $ в $ G $, любой левый $ G $ -модуль $ M $ можно превратить в правый $ G $ -модуль, положив $ mg = g \ inv m $ для $ m \ in M ​​$, $ g \ in G $. Аналогично любой правый $ G $ -модуль можно превратить в левый $ G $ -модуль.

Модули над алгеброй Ли.

Пусть $ \ lieg $ —
Алгебра Ли над коммутативным кольцом $ K $, и пусть $ M $ — $ K $ -модуль.Спецификация структуры $ \ lieg $ -модуля на $ M $ состоит из спецификации $ K $ -эндоморфизма $ m \ mapsto gm $ группы $ M $ для каждого $ g \ in \ lieg $, где аксиома

$$ [g_1, g_2] m = g_1 (g_2 m) — g_2 (g_1 m) $$
выполняется для $ g_1, g_2 \ in \ lieg $, $ m \ in M ​​$. Это определение отличается от приведенного ранее для $ A $ -модуля. Создание структуры $ \ lieg $ -модуля на $ M $ равносильно заданию гомоморфизма алгебры Ли $ \ lieg $ в алгебру Ли кольца $ \ End (M) $. Модуль над алгеброй Ли $ \ lieg $ также можно рассматривать как модуль в обычном смысле
универсальная обертывающая алгебра $ \ lieg $.

Построения в теории модулей.

Начиная с заданного $ A $ -модуля можно получить новые $ A $ -модули с помощью ряда стандартных конструкций. Таким образом, любому модулю $ M $ соответствует
решетка его подмодулей. Например, если $ A $ рассматривается как левый модуль над собой, то его левые подмодули являются в точности левыми идеалами в $ A $. Ряд важных типов модулей определяется в терминах решетки подмодулей. Например, условие завершения нисходящей (восходящей) цепочки подмодулей определяет артиновы модули (соответственно, нётеровы модули, ср.Артинианский модуль;
Нетеровский модуль). Условие отсутствия нетривиальных подмодулей, то есть подмодулей, отличных от 0 или $ M $, определяет неприводимые или простые модули (см.
Неприводимый модуль).

Для модуля $ M $ и любого подмодуля $ N $ фактор-группе $ M / N $ можно задать структуру $ A $ -модуля. Этот модуль называется фактор-модулем $ M $ над $ N $.

Гомоморфизм $ A $ -модулей определяется как абелева группа
гомоморфизм $ f: M \ to N $, коммутирующий с умножением на элементы из $ A $, то есть $ f (am) = af (m) $ для всех $ m \ in M ​​$, $ a \ in A $.Если даны два гомоморфизма $ f_1, f_2: M \ to N $, то их сумма, определенная формулой $ (f_1 + f_2) (m) = f_1 (m) = f_2 (m) $, снова является гомоморфизмом $ A $ -модули. Это дополнение дает структуру абелевой группы множеству $ \ Hom_A (M, N) $ всех гомоморфизмов $ M $ в $ N $. Для любого гомоморфизма $ f: M \ to N $ подмодули $ \ Ker f $ (ядро $ f $) и $ \ Im f $ (образ $ f $), а также фактормодули $ \ Coker f = N / \ Im f $ (коядро $ f $) и $ \ Coim f = M / \ Ker f $ (кообраз $ f $).Модули $ \ Im f $ и $ \ Coim f $ канонически изоморфны и поэтому обычно отождествляются. Например, для любого левого идеала $ J $ в $ A $ определен фактормодуль $ A / J $. Модуль $ A / J $ неприводим тогда и только тогда, когда $ J $ — максимальный левый идеал (ср.
Максимальный идеал). Если $ M $ — неприводимый $ A $ -модуль, не аннулирующий кольцо $ A $, то $ M $ изоморфен $ A / J $ для некоторого максимального левого идеала $ J $.

Для любого семейства $ A $ -модулей $ \ {M_i \} $, где $ i $ пробегает некоторый набор индексов $ J $, прямая сумма и прямое произведение $ \ {M_i \} $ существуют в категории $ A $ -модулей.Здесь элемент прямого произведения $ \ prod_ {i \ in J} M_i $ можно интерпретировать как вектор $ (ldots, m_i, \ ldots) $, компоненты которого индексируются $ J $ и где для каждого $ i $, $ m_i \ in M_i $. Сумма таких векторов и их умножение на элементы кольца определяются покомпонентно. Прямая сумма $ \ sum_ {i \ in J} M_i $ семейства $ \ {M_i \} $ может быть интерпретирована как подмодуль прямого произведения, состоящего из векторов, все компоненты которых, за исключением конечного числа, равны до нуля.

Для проективной (индуктивной) системы $ A $ -модулей проективный (индуктивный) предел этой системы можно естественным образом снабдить структурой $ A $ -модуля. Прямое произведение и прямая сумма могут рассматриваться как частные случаи понятий проективного и индуктивного пределов.

Генераторы и отношения.

Пусть $ X $ — подмножество $ A $ -модуля $ M $. Подмодуль, порожденный $ X $, является пересечением подмодулей модуля $ M $, содержащих $ X $. Если этот подмодуль совпадает с $ M $, то $ X $ называется семейством (системой) образующих модуля $ M $.Модуль, допускающий конечное семейство образующих, называется конечно порожденным модулем. Например, в нётеровом кольце любой идеал является конечно порождённым модулем. Прямая сумма конечного числа конечно порожденных модулей снова конечно порождена. Любой фактор-модуль конечно порожденного модуля также конечно порожден. Для построения системы образующих модуля $ M $
Лемма Накаямы часто оказывается полезной: для любого идеала $ \ frakA $, содержащегося в радикале кольца $ A $, из условия $ \ frakA M = M $ следует $ M = 0 $.В частности, в условиях леммы Накаямы элементы $ m_1, \ ldots, m_r $ образуют систему образующих для $ M $, если их образы порождают модуль $ M / \ frakA M $. Это особенно часто используется, когда $ A $ является
локальное кольцо, а $ \ frakA $ — максимальный идеал в $ A $.

Пусть $ M $ — модуль с системой образующих $ \ {x_i \} _ {i \ in J} $. Тогда отображение $ \ phi: y_i \ to x_i $ определяет эпиморфизм свободного $ A $ -модуля $ F $ с образующими $ \ {y_i \} _ {i \ in I} $ на $ M $ ($ F $ можно определить как набор формальных конечных сумм $ \ sum a_i y_i $, $ a_i \ in A $, а $ \ phi $ расширяется от образующих до $ F $ по линейности).Элементы $ R = \ Ker \ phi $ называются отношениями между образующими $ \ {x_i \} $ $ M $. Если $ M $ можно представить как фактор-модуль конечно порожденного свободного модуля $ F $, так что модуль отношений $ R $ также конечно порожден, то $ M $ называется конечно-определенным модулем. Например, над нётеровым кольцом $ A $ любой конечно порожденный модуль конечно представим. В общем, быть конечно порожденным не означает быть конечно представленным.

Замена колец.

Существуют стандартные конструкции, позволяющие рассматривать $ A $ -модуль $ M $ как модуль над каким-то другим кольцом. Например, пусть $ \ phi: B \ to A $ — гомоморфизм колец. Тогда, полагая $ bm = \ phi (b) m $, $ M $ можно рассматривать как $ B $ -модуль. Результирующий $ B $ -модуль называется полученным заменой базы или, в частности, в случае, когда $ B $ является подкольцом в $ A $, ограничением скаляров. Если $ M $ — унитарный $ A $ -модуль, а $ \ phi $ переводит тождество в тождество, $ M $ становится унитарным $ B $ -модулем.

Пусть дан гомоморфизм колец $ \ phi: A \ to B $ и $ A $ -модуль $ M $. Тогда $ B $ может быть задана структура $ (B, A) $ — модуля (см.Бимодуль), положив $ ba = b \ phi (a) $ для $ b \ in B $, $ a \ in A $ и левый $ B $ -модуль $ B \ tensor_A M $. Говорят, что этот модуль получается из $ M $ расширением скаляров.

Категория модулей.

Класс всех модулей над данным кольцом $ A $ с гомоморфизмами модулей как морфизмов образует
Абелева категория, обозначаемая, например, $ A $ -mod или $ \ Mod_A $. Наиболее важными функторами, определенными в этой категории, являются $ \ Hom $ (гомоморфизм) и $ \ tensor $ (тензорное произведение). Функтор $ \ Hom $ принимает значения в категории абелевых групп и ставит в соответствие паре $ A $ -модулей $ M, N $ группу $ \ Hom_A (M, N) $. Для $ f: M_1 \ to M $ и $ \ phi: N \ to N_1 $ отображения

$$ f ‘: \ Hom_A (M, N) \ to \ Hom_A (M_1, N) $$
а также

$$ \ phi ‘: \ Hom_A (M, N) \ to \ Hom_A (M, N_1) $$
определены очевидным образом; т.е. функтор $ \ Hom $ контравариантен по первому аргументу и ковариантен по второму. Когда $ M $ или $ N $ несут бимодульную структуру, группа $ \ Hom_A (M, N) $ имеет дополнительную модульную структуру.Если $ N $ — $ (A, B) $ — модуль, $ \ Hom_A (M, N) $ — правый $ B $ -модуль и если $ M $ — $ (A, B) $ — модуль, тогда $ \ Hom_A (M, N) $ — левый $ B $ -модуль.

Функтор $ \ tensor_A $ переводит пару $ M, N $, где $ M $ — правый $ A $ -модуль, а $ N $ — левый $ A $ -модуль, в тензорное произведение $ M \ tensor_A N $ из $ M $ и $ N $ больше $ A $. Этот функтор принимает значения в категории абелевых групп и ковариантен как по отношению к $ M $, так и по отношению к $ N $. Когда $ M $ или $ N $ — бимодуль, группа $ M \ tensor_A N $ может быть снабжена дополнительной структурой.А именно, если $ M $ — $ (B, A) $ — модуль, $ M \ tensor_A N $ — $ B $ -модуль, а если $ N $ — $ (A, B) $ — модуль, то $ M \ tensor_A N $ — правый $ B $ -модуль. Изучение функторов $ \ Hom $ и $ \ tensor $, а также производных от них функторов является одной из фундаментальных проблем гомологической алгебры.

Многие важные типы модулей можно охарактеризовать в терминах $ \ Hom $ и $ \ tensor $. Таким образом,
проективный модуль $ M $ определяется требованием точности функтора $ \ Hom_A (M, X) $ (как функтора в $ X $) (см.Точный функтор). Аналогичным образом
инъективный модуль $ N $ определяется требованием точности $ \ Hom_A (X, N) $ (в $ X $). А
плоский модуль $ M $ определяется требованием точности функтора $ M \ tensor_A X $.

Модуль над данным кольцом $ A $ можно рассматривать с двух точек зрения.

A) Модули можно изучать с точки зрения их внутренней структуры. Основной проблемой здесь является полная классификация модулей, то есть построение для каждого модуля системы инвариантов, которая характеризует модуль с точностью до изоморфизма, и, учитывая набор инвариантов, возможность построить модуль с этими инвариантами. .Для некоторых типов колец такое описание возможно. Например, если $ M $ — конечно порожденный модуль над групповым кольцом $ KG $ конечной группы $ G $, где $ K $ — поле характеристики, взаимно простой с порядком $ G $, то $ M $ представимо в виде конечной прямой суммы неприводимых подмодулей ($ M $ вполне приводимо, ср.
Полностью приводимый модуль). Это представление единственно с точностью до изоморфизма (выбор неприводимых модулей, вообще говоря, не единственный). Все неприводимые подмодули также допускают простое описание: все они содержатся в
регулярное представление группы $ G $ и находятся во взаимно однозначном соответствии с неприводимыми характерами группы.Модули над кольцами главных идеалов и над кольцами Дедекинда также имеют простое описание. А именно, любой конечно порожденный модуль $ M $ над
кольцо главных идеалов $ A $ изоморфно конечной прямой сумме модулей вида $ A / \ frakA_i $, где $ \ frakA_i $ — идеалы $ A $ (возможно, нулевые), а $ \ frakA_1 \ substeq \ cdots \ substeq \ frakA_m \ ne A $. Этим последним условием однозначно определяются идеалы $ \ frakA_i $. Таким образом, набор инвариантов $ \ {\ frakA_i \} $ полностью определяет $ M $. Если $ M $ — конечно порожденный модуль над
Кольцо Дедекинда $ A $, то $ M = M_1 \ oplus M_2 $, где $ M_2 $ — торсионный модуль (периодический модуль), а $ M_1 $ —
модуль без кручения (выбор $ M_1 $ не единственен).n $ — $ n $ -кратная прямая сумма. Модуль $ M_1 $ с точностью до изоморфизма определяется двумя инвариантами: числом $ n $ и классом $ \ frakB $ в группе классов идеалов.

B) Другой подход к изучению модулей состоит в изучении категории $ A $ -mod и рассмотрении данного модуля $ M $ как объекта этой категории. Такое исследование является предметом
гомологическая алгебра и
алгебраическая $ K $ -теория. На этом пути было найдено много важных и глубоких результатов.

Часто рассматриваются модули, которые несут некоторую дополнительную структуру.Таким образом, рассматриваются градуированные модули, фильтрованные модули, топологические модули, модули с
полуторалинейная форма и т. д. (ср.
Градуированный модуль;
Топологический модуль;
Фильтрованный модуль).

Список литературы

[1]	Н. Бурбаки, «Элементы математики. Алгебра: алгебраические структуры. Линейная алгебра», 1 , Addison-Wesley (1974), стр. 1; 2 (перевод с французского) MR0354207
[2]	Н. Бурбаки, «Элементы математики.Коммутативная алгебра », Аддисон-Уэсли (1972) (перевод с французского) MR0360549 Zbl 0279.13001
[3]	Н. Бурбаки, «Элементы математики. Группы Ли и алгебры Ли», Addison-Wesley (1975) (перевод с французского) MR0682756 Zbl 0319. 17002
[4]	С. Ланг, «Алгебра», Эддисон-Уэсли (1984) MR0783636 Zbl 0712.00001
[5]	B.L. ван дер Варден, «Алгебра», 1-2 , Springer (1967–1971) (перевод с немецкого) MR1541390 Zbl 1032.00002 Zbl 1032.00001 Zbl 0903.01009 Zbl 0781.12003 Zbl 0781.12002 Zbl 0724.12002 Zbl 0724.12001 Zbl 0569.01001 Zbl 0534.01001 Zbl 0997.00502 Zbl 00997.00501 Zbl 0316.22001 Zbl 0297.01014 Zbl2402.25 Zbl2198.100 0297.01014 Zbl021981200
[6]	А. Кострикин, «Введение в алгебру», Springer (1982) MR0661256 Zbl 0482.00001
[7]	Н.Якобсон, «Строение колец», Америк. Математика. Soc. (1956) MR0081264 Zbl 0073.02002
[8]	И. Герштейн, «Некоммутативные кольца», Матем. Доц. Амер. (1968) MR1535024 MR0227205 Zbl 0177.05801
[9]	C. Faith, «Алгебра: кольца, модули и категории», 1-2 , Springer (1981–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001
[10]	Х. Картан, С. Эйленберг, «Гомологическая алгебра», Princeton Univ.Пресс (1956) MR0077480 Zbl 0075.24305
[11]	С. Маклейн, «Гомология», Спрингер (1963) Zbl 0818.18001 Zbl 0328.18009
[12]	Х. Басс, «Алгебраическая $ K $ -теория», Бенджамин (1968) MR249491
[13]	J.W. Милнор, «Введение в алгебраическую $ K $ -теорию», Princeton Univ. Пресс (1971) MR349811

Как процитировать эту запись:
Module.2): Математика для понимания обучения и воспитания для средних школ

В рамках проекта MODULE (S ² ) создаются учебные материалы для преподавателей математики.
с возможностью предоставить потенциальным учителям возможность развивать математические
знания для обучения (MKT), пока они изучают материалы по университетской алгебре, геометрии,
курсы моделирования и статистики.Материалы предназначены для преподавания на основе принципов справедливости, в том числе:
углубляясь в математику и подтверждая личность учащихся, изучающих математику.

Как вы можете принять участие

Мы ищем преподавателей для пилотных материалов МОДУЛЯ (S ² ) в университетских курсах математики, которые будущие учителя средней школы
брать. Мы ищем пилотов на 2021-2022 учебный год. Факультет пилотирования будет
получать стипендию за: участие в летнем институте; участие
в педагогическом сообществе в течение учебного года; обучение с материалами для
полный семестр; и участие в мероприятиях в течение всего срока, в течение которого
курс преподается, включая сбор домашних заданий, видеосъемку занятий,
и проведение мероприятий в начале и в конце срока.Пожалуйста, укажите ваш
интерес, заполнив форму здесь.

Совместное усилие

Мы содействуем сотрудничеству между заинтересованными сторонами, включая преподавателей пилотирования, учебную программу.
дизайнеры, профессиональные разработчики, исследователи, руководство и члены совета директоров.
Мы собираем отзывы, анализируем преподавание и обучение с помощью материалов и координируем профессиональные
развивающая деятельность для ППС с использованием материалов МОДУЛЯ (S ² ).

Кто мы

PI Team: Cynthia Anhalt, University of Arizona Джейсон Обри, Университет Аризоны Стефани Кейси, Университет Восточного Мичигана Ховард Гобштейн, Ассоциация государственных университетов и университетов, предоставляющих земельные участки, Бринья Колер, Университет штата Юта Ивонн Лай, Университет Небраски — Линкольн Элисон Лишка, Государственный университет Среднего Теннесси Эндрю Росс, Университет Восточного Мичигана Джереми Страйер, Государственный университет Среднего Теннесси

Консультанты: Emina Alibegovic, Rowland Hall Джеймс Харт, Государственный университет Среднего Теннесси Саманта Мэддокс, школы Джефферсон-Сити Коди Паттерсон, Техасский университет в Сан-Антонио Джеймс Таттл, средний технический колледж Ваштено, Майкл Вайс, Мичиганский университет Джон Вомак, средняя школа Sky View

Консультативный совет: Рикардо Кортес, Тулейнский университет Кристин Франклин, Американская статистическая ассоциация Гэри Мартин, Обернский университет (председатель) Маргарет Мор-Шредер, Университет Кентукки Мэтью Ондрус, Государственный университет Вебера

Аспиранты: Мелоди Уилсон, Университет Восточного Мичигана Кэндис Куинн, Государственный университет Среднего Теннесси, Линдси Чап, Государственный университет Среднего Теннесси Рэйчел Зигтерман, Университет Небраски — Линкольн

МОДУЛЬ

(S

² ) Характеристики

Подготовка студентов к внесению вклада в области науки, статистики, инженерии
математика и технологии имеют решающее значение для нашей страны, чтобы оставаться мировым лидером. Для этого важно, чтобы учителя математики средней и старшей школы.
быть хорошо подготовленным к преподаванию математики. Математика действия, понимания,
В рамках проекта «Обучение и образование для средних школ» (MODULE (S ² )) создаются учебные материалы, которые открывают возможности для будущих учителей.
развивать математические знания, особенно связанные с преподавательской деятельностью
геометрия, статистика, алгебра и моделирование.Эти модули можно использовать в университете.
курсы математики преподавателями университетов и колледжей всех типов по всей
Соединенные Штаты. Проект способствует эффективному обучению, предлагая профессиональные
развивающие мероприятия для преподавателей с использованием модулей летом и в школе
год. Кроме того, проект исследует влияние инструкций с модулями.
на знаниях будущих учителей — тем самым информируя общенациональные усилия учителей
образование.Этот пятилетний проект основан на усилиях Департамента образования учителей математики.
Партнерство (MTE-P) для создания золотого стандарта подготовки средней математики
преподаватели из более чем 90 университетов-членов.

В последние десятилетия появились доказательства того, что для внедрения надежных инструкций по математике
учителя должны обладать пониманием содержания, которое конкретно применяется в
педагогическая работа (математические знания для обучения — МКТ).Развивать МКТ, перспективный
учителям нужны возможности использовать математические знания, чтобы распознавать, реагировать на
и понимать математические вопросы, возникающие в контексте обучения. Выводы
из циклов «планирование-выполнение-изучение-действие», в которых использовались начальные модули, разработанные в рамках проекта, указывают
увеличение MKT будущих учителей средней школы. МОДУЛЬ (S ² ) в настоящее время расширяет эти материалы и изучает условия обучения, которые
влияют на MKT будущих учителей, развитие MKT, а также на ожидания и ценность в
использование MKT в качестве ресурса для обучения.В проекте используются смешанные методы для получения эмпирически обоснованных
учет влияния факторов качества обучения и учебных ресурсов
МКТ для будущих учителей. Кроме того, результаты используются несколько раз в год для
улучшить материалы МОДУЛЯ (S ² ) с помощью циклов улучшения, проводимых как часть Сетевого улучшения
Дизайн сообщества.

Образцы материалов

Здесь вы можете найти образцы материалов Geometry MODULE (S ² ).

Здесь вы можете найти образцы материалов для МОДУЛЯ алгебры (S ² ).

Здесь вы можете найти образцы материалов МОДУЛЯ статистики (S ² ).

Здесь вы можете найти образцы материалов МОДУЛЯ МОДУЛЯ (S ² ).

Вопросы?

Если у вас есть вопросы о МОДУЛЕ (S ² ), свяжитесь с Джереми Страйером.

Любые мнения, выводы и заключения или рекомендации, выраженные в этом материале
принадлежат авторам и не обязательно отражают точку зрения Национального
Научный фонд.

MST124 | Основы математики 1

Счет бюджета студентов Открытого университета

The Open University Student Budget Accounts Ltd (OUSBA) предлагает удобный вариант оплаты по мере использования для оплаты взносов в OU, который является безопасным, быстрым и простым способом оплаты. Обратите внимание, что Открытый университет работает исключительно с OUSBA и не может предложить вам кредитные услуги от любого другого поставщика.Все кредиты зависят от статуса и подтверждения того, что вы можете позволить себе выплаты.

Вы платите OU через OUSBA одним из следующих способов:

• Зарегистрируйтесь сейчас, платите позже — OUSBA платит за модуль напрямую организационному подразделению. Затем вы выплачиваете OUSBA беспроцентную выплату в полном объеме непосредственно перед началом вашего модуля. 0% годовых представительских. Этот вариант может дать вам дополнительное время, которое может потребоваться для обеспечения финансирования для выплаты OUSBA.
• Оплата в рассрочку — OUSBA рассчитывает вашу ежемесячную плату и количество взносов на основе стоимости модуля, который вы изучаете. годовая процентная ставка 5,1% представительская.

Совместные заявки на кредит

Если вы чувствуете, что не сможете получить ссуду OUSBA самостоятельно из-за кредитной истории или проблем с доступностью, OUSBA предлагает возможность подать заявку на совместную ссуду с третьей стороной. Например, ваш муж, жена, партнер, родитель, брат или сестра или друг. В таких случаях OUSBA будет необходимо провести дополнительные проверки доступности по отдельности и / или коллективно для обоих совместных заявителей, которые будут нести солидарную ответственность за погашение кредита.

Поскольку при обработке совместных кредитных заявок требуются дополнительные проверки доступности, к сожалению, мгновенное решение не может быть принято. В среднем время обработки совместной кредитной заявки составляет пять рабочих дней с момента получения необходимой документации.

Узнайте больше о счетах бюджета студентов Открытого университета (OUSBA).

Кредитная / дебетовая карта

Вы можете полностью или частично оплатить обучение дебетовой или кредитной картой при регистрации на каждый модуль.

Мы принимаем карты American Express, Mastercard, Visa и Visa Electron.

Смешанные выплаты

Мы знаем, что иногда вам может понадобиться комбинировать способы оплаты. Например, вы можете оплатить часть платы за обучение с помощью дебетовой карты, а оставшуюся часть оплатить частями через счет бюджета студента Открытого университета (OUSBA).

STEP Math — Помощь учителям в совершенствовании их практики

Организация и дизайн

ШАГ состоит из шести учебных модулей.Первый модуль представляет собой введение, которое знакомит учащихся с общими целями, рамками и основными идеями учебного процесса. Остальные пять модулей сосредоточены на областях ранней математики — счетах, операциях, геометрии и пространственном чувстве, построении паттернов, измерениях. В рамках каждого модуля 30-минутные занятия исследуют конкретный навык и то, как этот навык взаимосвязан с одним или несколькими навыками исполнительной функции (EF).

Учебные модули STEP предназначены для дополнения процессом коучинга STEP, но также могут использоваться сами по себе для более традиционных подходов к онлайн-обучению.Учебные модули предоставляют участникам множество возможностей увидеть, как выглядят ранние математические и EF, участвовать в интерактивных мероприятиях, чтобы укрепить свое понимание нового контента, и обсудить идеи со сверстниками. Модули также предназначены для привлечения внимания учащегося, актуальны для учителей дошкольных учреждений и предоставляют возможности для практики, чтобы учителя укрепляли уверенность в себе и чувствовали себя успешными.

Модуль 1:

Введение в STEP

Модуль 2:

Счисление

Модуль 3:

Операции

Модуль 4:

Геометрия и пространственное чувство

Модуль 5:

Узор

Модуль 6:

Измерение

---

Поток сеанса

Каждое занятие длится около 30 минут, с отдельными небольшими видео-уроками, в которых рассматриваются разные темы и стратегии.

1. Что это?

Сессия всегда начинается с знакомства с каждым навыком. Основное внимание уделяется не только объяснению навыка, но и тому, почему он актуален и как выглядит в контексте дошкольных классов. Например, введение в умение копировать, расширять и создавать шаблоны помогает учащимся понять, над какими типами шаблонов обычно работают дошкольники, а также идею о том, что шаблоны являются не только визуальными, но также слуховыми и кинестетическими.

2. Как развивается

Как только учащиеся поймут, что это за навык, они получат представление о том, как он развивается у маленьких детей от рождения до пяти лет. Учащиеся видят, как дети демонстрируют свои навыки в действии на разных этапах развития. Особое внимание уделяется дошкольному возрасту от 3 до 5 лет.

3. Целевые стратегии

Каждое занятие предлагает от одной до трех целевых стратегий, которые поддерживают развитие ребенка в определенных математических навыках.Учителя не только знакомятся с шагами или передовыми методами на этих уроках, но и получают возможность наблюдать, как разные учителя применяют их в классе.

4. Вы попробуете

Каждое занятие предоставляет учащимся несколько возможностей проверить свои знания и понимание. Короткие вопросы «Проверьте свои знания» встроены в течение всего занятия. Кроме того, одно более длинное интерактивное упражнение побуждает учащихся посмотреть сценарий в классе и определить соответствующие математические стратегии.Некоторые упражнения также направлены на устранение распространенных заблуждений о том или ином навыке.

5. В течение дня и в дальнейшем

Учащиеся получают возможность увидеть, как математику можно использовать в течение дня. Это дает учителям идеи по интеграции математических моментов в повседневные дела, такие как обеденное время, перекус, переходы или игра вне игры.

6. Математические и исполнительные функции

Для каждого навыка учащиеся получают возможность увидеть, как один или несколько из трех навыков EF — тормозящий контроль, рабочая память и когнитивная гибкость — связаны с развивающимися математическими способностями детей. Это позволяет учащимся увидеть, как математика и навыки EF работают вместе, а также как учителя могут намеренно разрабатывать математические задания, способствующие развитию в обеих областях.

7. Составление плана!

На всех занятиях учителям предоставляется возможность либо выбрать собственное задание по математике, либо то, которое мы предложили. Если учителя выбирают свой собственный урок, им предоставляется шаблон, который помогает им продумать, как они будут применять изученные стратегии в своей деятельности.

Модули профессиональной разработки прототипов

Чтобы действительно соответствовать требованиям Общих государственных стандартов, необходимо
недостаточно просто пересмотреть список математического содержания
включены в учебную программу. Стандарты уделяют особое внимание математике
Практика требует от учащихся способности думать
математически и применять изученные методы к богатым
проблемы в различных контекстах. Для этого необходимы изменения в
способ преподавания и оценки математики в большинстве школ.

В рамках проекта оценки по математике были разработаны задания Classroom Challenges , чтобы проиллюстрировать типы необходимых занятий.
для дополнения традиционной практики в классе и поддержки
Стандарты. Модули профессионального развития предназначены для помощи
учителей с практическими и педагогическими проблемами, представленными
эти уроки.

Модуль
1 представляет модель формирующего оценивания , используемую в
уроки, их теоретические основы и практическое применение. Модули
2 и 3
подробно рассмотрите два типа задач в классе .
Модули
4 и 5
изучить две важнейшие педагогические особенности уроков: задавать вопросы
вопросы и совместное обучение.

Модули основаны на деятельности; построен вокруг коллекции
пример классной деятельности. Цель состоит в том, чтобы привлечь группы учителей
в конструктивном обсуждении собственных практик и того, как они
может измениться. Затем они планируют и проводят урок, используя эти идеи в
их собственный класс, и встретимся снова, чтобы поразмышлять над своим опытом.

Каждый модуль включает руководство по занятию PD и раздаточные материалы для учителей,
а также образцы учебных материалов и предлагаемые планы уроков.Также включены видео с настоящими учителями, пробующими эти методы.
со своими классами, часто впервые, и обсуждая
полученные результаты.

Примечание: это черновые материалы. Видео с участием студентов
в Англии работает над проектами со схожими целями. Многие из
показанные действия теперь были преобразованы в задачи или формирующие
уроки оценки для школ США. В конечном итоге мы надеемся, что сможем
снимать видеоролики, демонстрирующие актуальные материалы для среднего и высокого уровня США.
школы.

Модули профессионального развития могут распространяться под
творческий
Некоммерческая лицензия на совместное использование с авторством Commons Attribution. Пожалуйста
любые запросы о коммерческом использовании направляйте по адресу [email protected].

Технические требования

Для этих страниц требуется современный веб-браузер с включенным Javascript. Для печати материалов требуется программа для просмотра PDF-файлов.
и / или текстовый процессор, совместимый с MS Office.Модули могут быть
загружается для использования в автономном режиме, если это необходимо.

(PDF) Дизайн математического модуля Разработка дизайна модели обучения Номер модели обучения «Голова вместе» для улучшения обучения студентов Результат

Международный саммит по науке, технологиям и человечеству (ISETH 2018)

Интеграция знаний для будущего устойчивого развития

Международный саммит по науке Технологии и гуманность

102ISETH

p-ISSN: 2477-3328

e-ISSN: 2615-1588

Дизайн разработки математического модуля

Обучающая модель №

Голова вместе для улучшения обучения

студентов и результатов обучения

Ика Путри Астрияна. S, 1 Магистр математического образования, Университет Ахмада Дахлана, Индонезия

Супарман, Магистр математического образования, Университет Ахмада Дахлана, Индонезия

Аннотация: Способность к сотрудничеству — одна из важных компетенций, которыми студенты должны обладать при обучении

21st математика века. Учащиеся, не умеющие сотрудничать, не получат опыта, не смогут самостоятельно развить

и не получат новых навыков. Это исследование преследует две цели.Во-первых, это исследование призвано проанализировать потребности

модулей, которые соответствуют характеристикам учащихся. Во-вторых, это исследование направлено на разработку модулей, которые

могут улучшить возможности совместной работы. Данное исследование представляет собой исследование с использованием Модели исследования дизайна, которое состоит из двух этапов

: предварительный этап и этап формирующей оценки. Объектами исследования выступили

учителя и

ученика VII класса. В инструментах сбора данных используются листы проверки, инструкции по проведению интервью и анкеты

.Листы валидации выдаются экспертам для получения критических замечаний и предложений по материалам.

Правила собеседования используются для получения информации о состоянии школ, учащихся и СМИ, используемых в школах

. Анкета предоставляется учителям и ученикам для получения критических замечаний и предложений, касающихся средств массовой информации.

Данные проанализированы с помощью описательного анализа. Это исследование показывает, что учащимся и учителям нужны модули, которые

могут улучшить возможности сотрудничества между учащимися.В этом исследовании сделан вывод о том, что необходимо разработать модели обучения

Number Head Together с помощью математических модулей для улучшения совместной работы учащихся по социальным арифметическим материалам

.

Ключевые слова: Разработка модулей, Сотрудничество, Number Head Together

ВВЕДЕНИЕ

Развитие 21 века требует развития четырех способностей учащихся, одна из которых — способность

сотрудничества. Это потому, что умение сотрудничать очень важно в жизни.Способность к сотрудничеству

очень важна, чтобы владеть всеми, включая студентов. Сотрудничество — это хорошая способность к развитию, потому что в сущности

люди — это индивидуальные существа и социальные существа, которые нуждаются друг в друге (Norscia, Ivan & Palagi, Elisabetta,

2011). Это сотрудничество также является формой приобретения опыта, развития самосовершенствования за счет приобретения новых знаний и навыков

(Камаль, Сристи и Гродзинска-Юрчак, Малгожата, 2014; Джоан Р.Рентч и др., 1994).

Способность к сотрудничеству важна в процессе изучения математики (Дэвид У. Джонсон, 2006; Сертель,

Алтун, 2018). Однако, на самом деле, на основании наблюдений, проведенных в школах Мухаммадия Плэрет и Мухаммадия Миддл

в Бангантапане, практика обучения, проводимая в школах, до сих пор не прилагалась учителями для обучения

учеников совместной работе на хороших уроках математики во время дискуссий. По этой причине необходим новый прорывный шаг

для улучшения навыков совместной работы учащихся.Благодаря сотрудничеству студенты будут приобретать опыт,

развивать себя и приобретать новые навыки. Это означает, что способность студентов к сотрудничеству важна для развития

. Усиление результатов наблюдений в поле также наблюдается в результатах исследования MANCIU,

Ionela, et al, 2018. Это согласуется с результатами исследования Sormunen, Eero, et al, 2014, что низкий уровень обучения

На

результатов влияет низкий уровень сотрудничества студентов.

Учебные ресурсы, которые могут быть разработаны учителями для улучшения совместной работы, — это модули

(Сингх, Чаранджит Каур Сваран, 2018). Модули можно интерпретировать как один из источников обучения:

систематически организованы на языке, который легко понимается учащимися в соответствии с уровнем способностей

учащихся при минимальном руководстве со стороны учителя (Maike, Wiesenfarth, 2018).

Наличие модулей может помочь студентам получить информацию об учебных материалах.

Чтобы модуль мог систематически разрабатываться учителем в качестве источника обучения ученика

, модуль, предоставленный учителем, также может помочь ученикам быть более отзывчивыми в

, предоставляя информацию о материале во время процесса обучения в классная (Mohamed

Hamada, Mohammed Hassan, 2017). Создать хороший модуль и уметь улучшить ученика

1 Ика Путри Астрияна Сари, магистр математического образования, Университет Ахмада Дахлана, Индонезия.Эл. Почта: ikaputriastriyanasarii @

gmail.com Astriyana

Математические модули | Математический факультет

Шаг 1: Ma 080 — Модули гуманитарной математики

Почему мы здесь? Исследования показали, что хорошее знание математики может помочь студентам добиться успеха в колледже. Это касается даже студентов, не специализирующихся в области математики. Почему это могло быть? Потому что в нашем ядре Liberal Arts есть много классов, которые требуют как вычислительных навыков, так и навыков рассуждения, которые исходят непосредственно из математического мира. Одним из примеров может быть Essential Science (неудивительно). Экономика — еще один пример курса, где хорошие математические навыки могут помочь вам добиться успеха. Удивительно, но даже на 102-м английском и на занятиях по Библии и философии высшего уровня требуется хорошее понимание математической логики и рассуждений, чтобы иметь возможность устанавливать связи и делать правильные выводы.

Команда «Развивающая математика» провела время с преподавателями гуманитарных наук, чтобы разработать модули, в которых для вас четко обозначены связи математики с их различными курсами.В разработанных нами прикладных задачах наша цель — показать вам, как приобретаемые вами математические навыки будут использоваться в будущих курсах, а также в реальной жизни. Когда вы туда доберетесь, мы хотим, чтобы он казался вам знакомым! Конечно, каждый видел (и, вероятно, наслаждался) подобные мемы со скелетом на скамейке, который «все еще ждет того дня, когда он начнет использовать алгебру в реальной жизни», но правда в том, что «алгебра в реальной жизни» — нет ». Они всегда напоминают то, что мы находим в математическом тексте.

Ma 080 Описание модулей

Шаг 2: Ma 090 — Подготовительные модули по математике

Если вы планируете посещать какие-либо курсы математики на уровне колледжа (по выбору или потому, что этого требует ваша специальность), вам также необходимо будет пройти модули Ma 090.Профессора этих курсов ожидают, что у вас будет сильный опыт в алгебре, помимо того, что необходимо для общих курсов гуманитарных наук.

Ma 090 Описание модулей

Если вам просто нужно соревноваться с модулями 080 или 090, прелесть этой модульной системы в том, что каждый сможет работать в своем собственном темпе. Некоторым просто нужно заполнить некоторые пробелы, в то время как другим нужно потратить некоторое время на основы и отталкиваться от них. Модули составлены таким образом, что вам нужно будет делать уроки и домашнее задание только по тому, что вам нужно повторить или изучить.После того, как вы завершите все модули, вам больше не нужно будет посещать математическую лабораторию.