Содержание
Урок 10. силы трения — Физика — 10 класс
Физика, 10 класс
Урок 10. Силы трения
Перечень вопросов, рассматриваемых на уроке:
- Сухое и жидкое (вязкое) трение.
- Максимальная сила трения покоя.
- Формула для вычисления силы трения скольжения.
- Особенности сил сопротивления при движении твердых тел в жидкостях и газах.
- Формулы вычисления сил сопротивления при движении твердых тел в жидкостях и газах.
Глоссарий по теме:
Сухое трение — трение, возникающее при соприкосновении двух твёрдых тел при отсутствии между ними жидкой или газообразной прослойки.
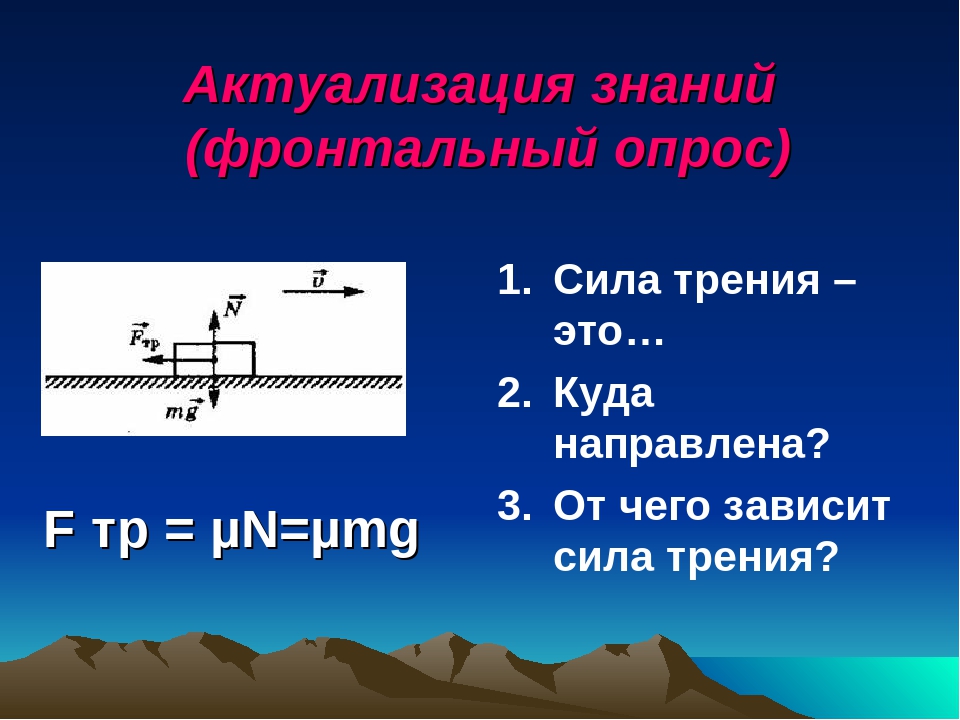
Сила трения покоя — сила трения, действующая между двумя телами, неподвижными относительно друг друга.
Максимальная сила трения покоя — наибольшее значение силы трения, при котором скольжение еще не наступает.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.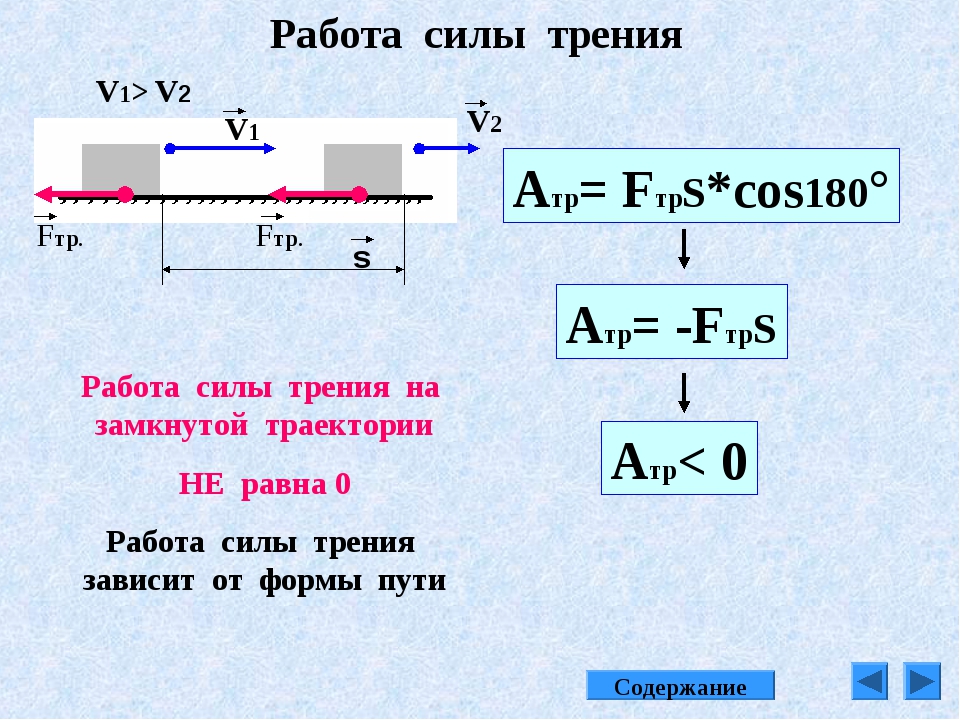
Трение качения — сопротивление движению, возникающее при перекатывании тел друг по другу т.е. сопротивление качению одного тела (катка) по поверхности другого
Основная и дополнительная литература по теме урока:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 113 – 122.
- Парфентьева Н. А. Сборник задач по физике. 10-11 классы. Базовый уровень.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1978/05/kuda_napravlena_sila_treniya.htm
http://kvant.mccme.ru/1985/10/trenie_vrednoe_poleznoe_intere.htm
Теоретический материал для самостоятельного изучения
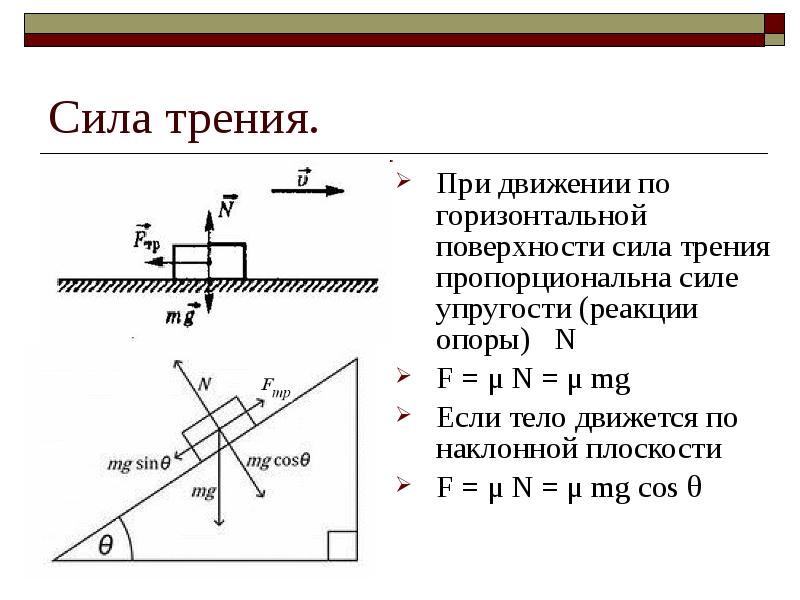
Трение – физическое явление, сопровождающее всякое движение на Земле. При любом механическом движении тела соприкасаются либо друг с другом, либо с окружающей их сплошной жидкой или газообразной средой. В результате соприкосновения возникает сила трения, которая препятствует движению.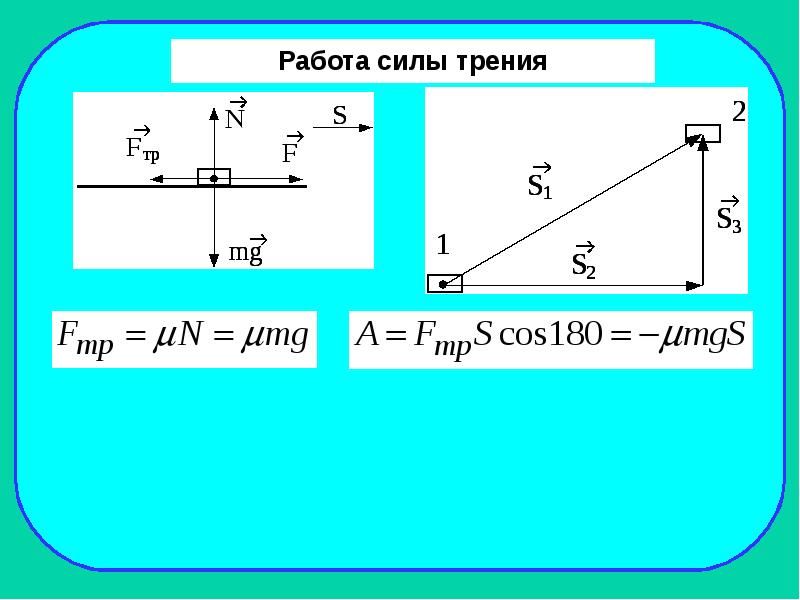 Трение может быть полезно, и тогда мы стремимся его увеличить. В случаях, когда трение вредно, принимаются меры для его уменьшения.
Трение может быть полезно, и тогда мы стремимся его увеличить. В случаях, когда трение вредно, принимаются меры для его уменьшения.
История открытия. Свой вклад в попытки объяснить природу трения внесли многие ученые, начиная с Аристотеля, Леонардо да Винчи, Амонтона, Леонарда Эйлера, Кулона. Дальнейший вклад в теорию трения сделали Майер, Джоуль, Гельмгольц, Кузнецов, Дерягин, Томлинсон, Рейнольдс, Штрибек, Боуден и другие.
Различают следующие виды трения:
- сухое;
- жидкое (вязкое).
Сухое трение бывает трех видов:
- трение покоя;
- трение скольжения;
- трение качения.
Причины возникновения силы трения:
- шероховатость поверхностей соприкасающихся тел.
- взаимное притяжение молекул соприкасающихся тел.
Сухое трение − трение, возникающее при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Силы сухого трения всегда направлены по касательной к соприкасающимся поверхностям.
Сухое трение, возникающее при относительном покое тел, называют трением покоя.
Сухое трение, возникающее при относительном движении тел, называют трением скольжения.
Трение качения возникает, когда одно тело катится по поверхности другого тела.
Закон, выражающий зависимость максимального значения модуля силы трения покоя от модуля силы нормальной реакции опоры впервые экспериментально установил французский военный инженер и учёный-физик Шарль Огюстен де Кулон. Согласно этому закону, максимальное значение модуля силы трения покоя прямо пропорционально модулю силы нормальной реакции опоры
Fтр.макс = µN,
где Fтр.макс — модуль максимальной силы трения покоя, µ- коэффициент пропорциональности, называемый коэффициентом трения покоя.
Коэффициент трения µ характеризует обе трущиеся поверхности и зависит не только от материала этих поверхностей, но и от качества их обработки. Коэффициент трения определяется экспериментально.
Трение скольжения. Сила трения скольжения также направлена вдоль поверхности соприкосновения тел, но в отличие от силы трения покоя, которая противоположна внешней силе, стремящейся сдвинуть тело, сила трения скольжения всегда направлена противоположно относительной скорости. Модуль силы трения скольжения, как и максимальной силы трения покоя, тоже пропорционален прижимающей силе, а значит, нормальной силе реакции опоры:
При не слишком больших относительных скоростях движения сила трения скольжения мало отличается от максимальной силы трения покоя. Поэтому приближенно можно считать ее постоянной и равной максимальной силе трения покоя:
Fтр ≈ Fтр.макс = µN.
Важно! Сила трения зависит от относительной скорости движения тел. В этом ее главное отличие от сил тяготения и упругости, зависящих только от расстояний.
При движении твердого тела в жидкости или газе возникает силa жидкого (вязкого) трения.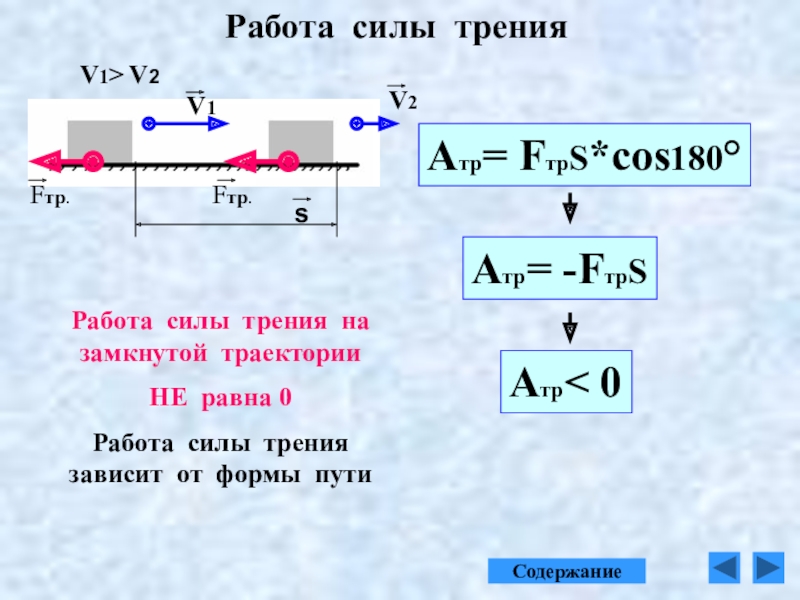 Сила жидкого трения значительно меньше силы сухого трения. Эта сила направлена против скорости тела относительно среды и тормозит движение.
Сила жидкого трения значительно меньше силы сухого трения. Эта сила направлена против скорости тела относительно среды и тормозит движение.
Главная особенность силы сопротивления состоит в том, что она появляется только при наличии относительного движения тела и окружающей среды. Сила трения покоя в жидкостях и газах полностью отсутствует. Поэтому усилием рук можно сдвинуть тяжелую баржу в воде, а сдвинуть поезд усилием рук невозможно.
Модуль силы сопротивления Fc зависит от размеров, формы и состояния поверхности тела, свойств среды (жидкости или газа), в которой тело движется, и, наконец, от относительной скорости движения тела и среды.
Примерный характер зависимости модуля силы сопротивления от модуля относительной скорости тела показан на рисунке
При относительной скорости, равной нулю, сила сопротивления не действует на тело (Fc=0). С увеличением относительной скорости сила сопротивления сначала растет медленно, а затем все быстрее и быстрее.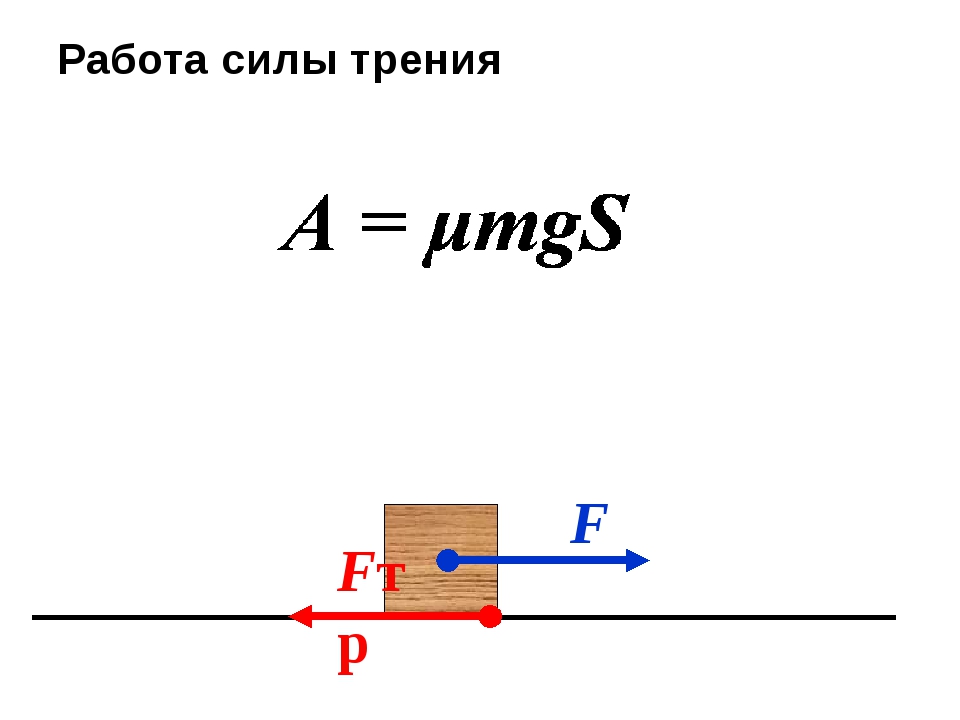 При малых скоростях движения силу сопротивления можно считать прямо пропорциональной скорости движения тела относительно среды:
При малых скоростях движения силу сопротивления можно считать прямо пропорциональной скорости движения тела относительно среды:
Fc = k1v, (1)
где k1— коэффициент сопротивления, зависящий от формы, размеров, состояния поверхности тела и свойств среды — ее вязкости.
Вычислить коэффициент k1 теоретически для тел сколько-нибудь сложной формы не представляется возможным, его определяют опытным путем.
При больших скоростях относительного движения сила сопротивления пропорциональна квадрату скорости:
Fc = k2v2, (2)
где k2 — коэффициент сопротивления, отличный от k1.
Только опытным путём можно определить, какая из формул — (1) или (2) — подходит для использования в конкретной практической задаче.
Итак, основными особенностями силы сопротивления, действующей на тело, являются:
1) отсутствие силы трения покоя; 2) зависимость от относительной скорости движения.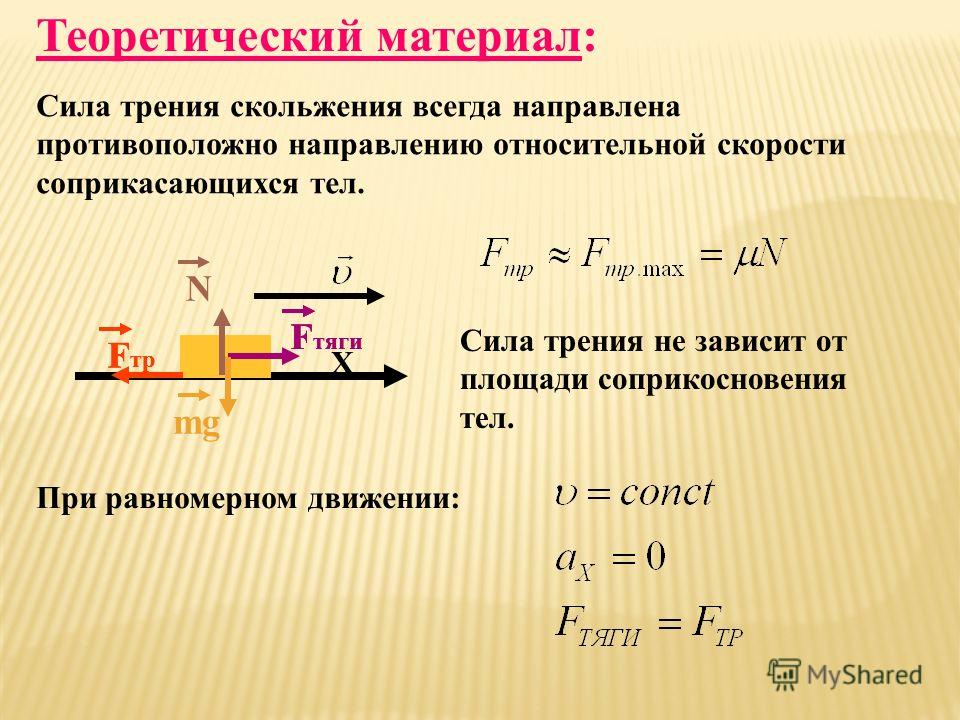
Примеры и разбор решения заданий
1. Какая сила не позволяет человеку сдвинуть с места дом?
- Силы трения скольжения;
- сила трения покоя;
- сила тяжести.
Ответ: 2) Сила трения покоя.
2. Деревянный ящик равномерно движется по поверхности длинного стола. Сила давления ящика на поверхность равна 30 Н, сила трения 6 Н. Найдите коэффициент трения скольжения.
Решение.
Воспользуемся формулой, которая связывает силу давления на плоскость, силу трения и коэффициент трения Fтр = µP. Из этой формулы легко получить формулу для расчёта коэффициента трения µ = Fтр / P. Подставляя в неё численные значения, получаем:
µ = Fтр / P = 6Н/30Н = 0,2.
Ответ: 0,2.
3. Кубик из детского конструктора покоится на наклонной плоскости, образующей угол α = 40° с горизонтом. Сила трения покоя равна 0,32 Н. Определите значение силы тяжести, которая действует на кубик.
Решение.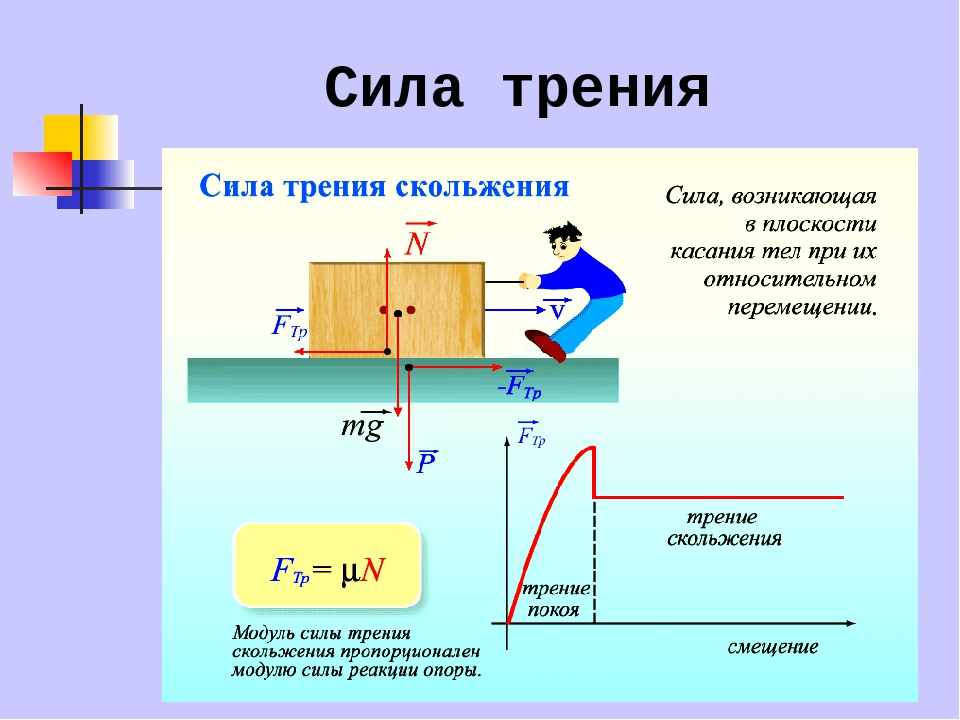
По условию задачи кубик покоится. Следовательно, сумма всех действующих на него сил равна нулю. В проекции на ось, идущей вдоль склона плоскости, получаем соотношение: mg sin α – Fтр = 0. Из него выражаем формулу для расчета силы тяжести, действующей на кубик
Ответ: 0,5 Н.
Механическая работа. Мощность | Физика
1. Определение работы
С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.
Если сила направлена так же, как перемещение тела, то работа силы
A = Fs (1)
В этом случае работа силы положительна.
Если сила направлена противоположно перемещению тела, то работа силы
A = –Fs (2)
В этом случае работа силы отрицательна.
Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:
A = 0 (3)
Работа – скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:
Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:
1 Дж = 1 Н * м.
? 1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском и столом равен 0,2. Чему равна работа действующей на брусок:
а) силы тяжести m?
б) силы нормальной реакции ?
в) силы упругости ?
г) силы трения скольжения тр?
Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами:
1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.
Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.
? 2. Чему равна:
а) сумма работ всех действующих на брусок сил?
б) равнодействующая всех действующих на брусок сил?
в) работа равнодействующей? В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.
Работа A постоянной силы равна произведению модуля силы F на модуль перемещения s и на косинус угла α между направлением силы и направлением перемещения:
A = Fs cos α (4)
? 3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.
? 4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) –3 Дж; в) –3 Дж; г) –6 Дж? Сделайте пояснительные чертежи.
2. Работа силы тяжести
Пусть тело массой m движется вертикально от начальной высоты hн до конечной высоты hк.
Если тело движется вниз (hн > hк, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (hн < hк, рис.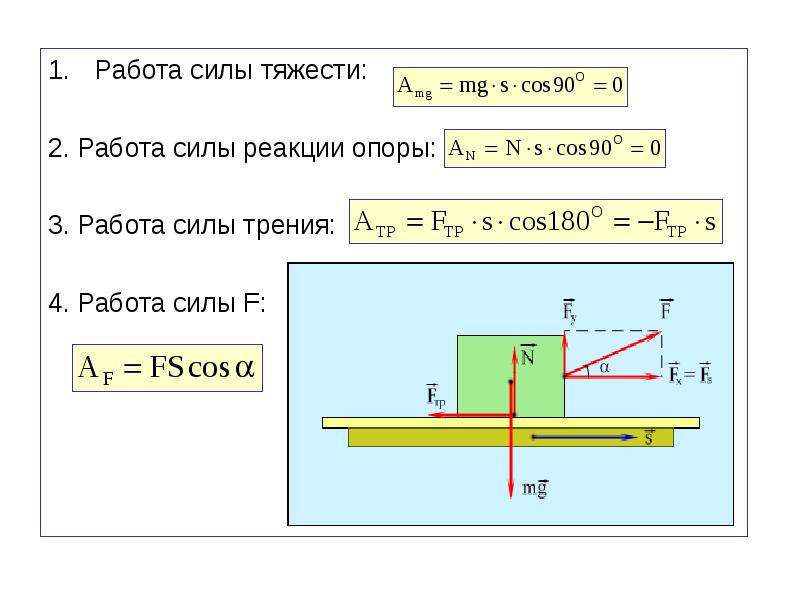 28.2, б), то работа силы тяжести отрицательна.
28.2, б), то работа силы тяжести отрицательна.
В обоих случаях работа силы тяжести
A = mg(hн – hк). (5)
Найдем теперь работу силы тяжести при движении под углом к вертикали.
? 5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.
а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж.
б) Выразите работу силы тяжести через m, g, s, α.
в) Выразите s через h и α.
г) Выразите работу силы тяжести через m, g, h.
д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?
Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали – как вниз, так и вверх.
Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).
28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).
Таким образом,
работа силы тяжести при движении но любой траектории выражается формулой
Aт = mg(hн – hк),
где hн – начальная высота тела, hк – его конечная высота.
Работа силы тяжести не зависит от формы траектории.
Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.
? 6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?
3.
 Работа силы упругости
Работа силы упругости
Когда пружина возвращается в недеформированное состояние, сила упругости совершает всегда положительную работу: ее направление совпадает с направлением перемещения (рис. 28.7).
Найдем работу силы упругости .
Модуль этой силы связан с модулем деформации x соотношением (см. § 15)
F = kx. (6)
Работу такой силы можно найти графически.
Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).
На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.
Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.
Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).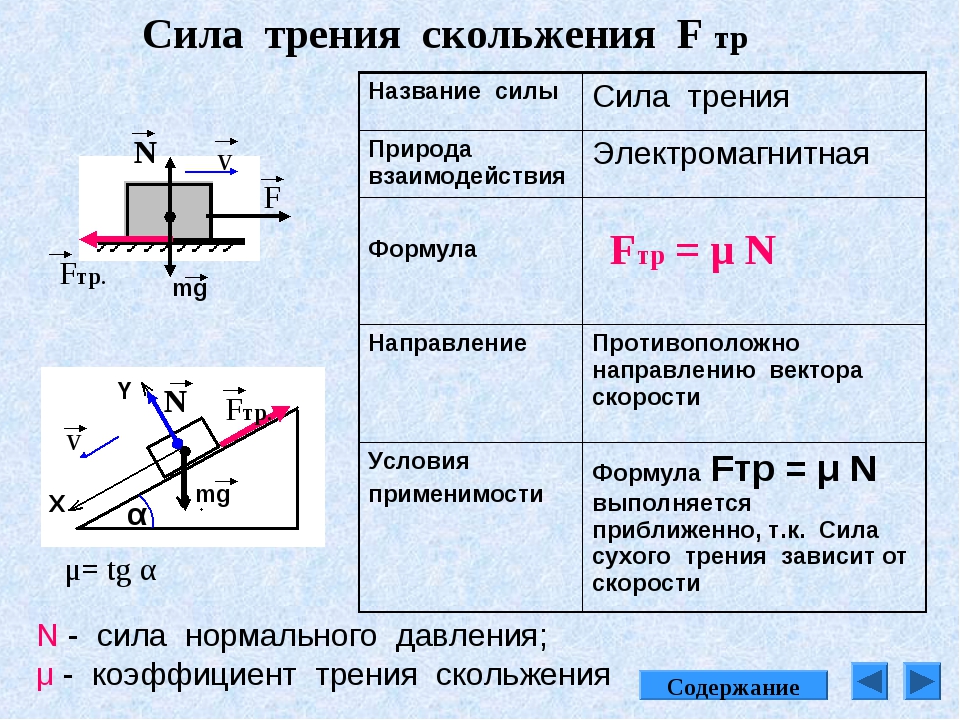
? 7. Используя рисунок 28.10, докажите, что
работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой
A = (kx2)/2. (7)
? 8. Используя график на рисунке 28.11, докажите, что при изменении деформации пружины от xн до xк работа силы упругости выражается формулой
Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.
? 9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см.
а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?
? 10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?
Чему равна работа силы упругости пружины?
4. Работа силы трения
Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).
Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.
? 11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см.
а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.
5.
 Мощность
Мощность
Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.
Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:
P = A/t. (9)
(Иногда мощность в механике обозначают буквой N, а в электродинамике – буквой P. Мы считаем более удобным одинаковое обозначение мощности.)
Единица мощности – ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что
1 Вт = 1 Дж/c.
? 12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?
Часто мощность удобно выражать не через работу и время, а через силу и скорость.
Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:
P = (Fs)/t = F(s/t) = Fv. (10)
? 13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?
При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?
Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.
? 14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?
Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.
Дополнительные вопросы и задания
15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю.
а) Чему равна работа силы тяжести при подъеме мяча?
б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча?
г) Есть ли в условии лишние данные?
16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия?
в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?
17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.
а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности?
б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м?
в) Чему равен модуль силы трения при движении санок по горе?
г) Чему равна работа силы трения при спуске санок?
д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?
18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м3, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м3, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.
Закон силы трения: объясняем сложную тему простыми словами
Определение силы трения
Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.
Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.
Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел.
Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.
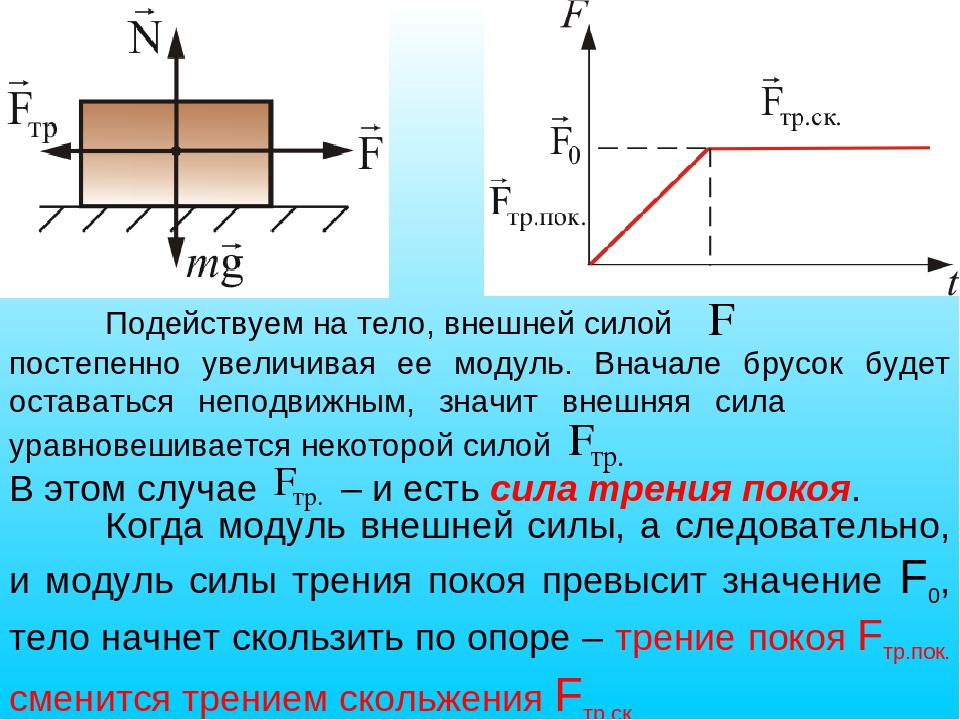
Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Откуда берётся трение
Трение возникает по двум причинам:
- Все тела имеют шероховатости.
 Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения. - Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Виды силы трения
В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.
- Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
- трение скольжения,
- трение покоя,
- трение качения.
- Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.
Сила трения покоя
Рассмотрим силу трения покоя подробнее.
Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.
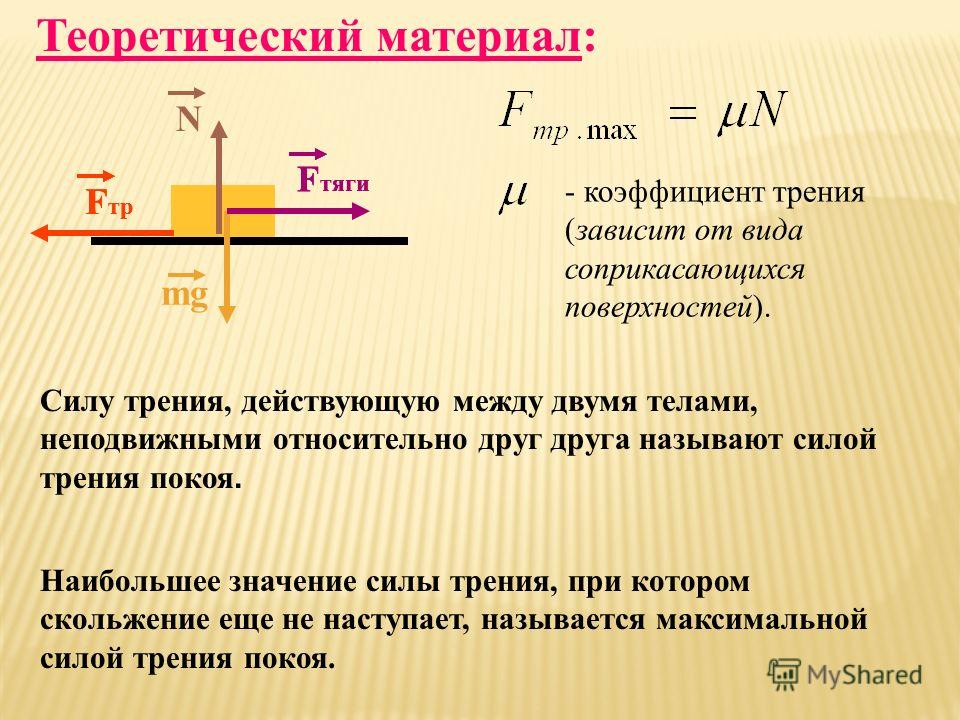
Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Пока силы равны, холодильник остаётся на месте:
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя.
Сила трения скольжения
Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности?
Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.
Она возникает при относительном движении контактирующих твёрдых тел.
Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.
Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:
Как рассчитать и измерить силу трения
Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!
Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Сила реакции опоры обозначается N. Можно сделать вывод
Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.
Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.
Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
где μ — коэффициент трения, N — сила нормальной реакции опоры.
Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:
Сила трения качения
Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Причина трения качения — деформация катка и опорной поверхности.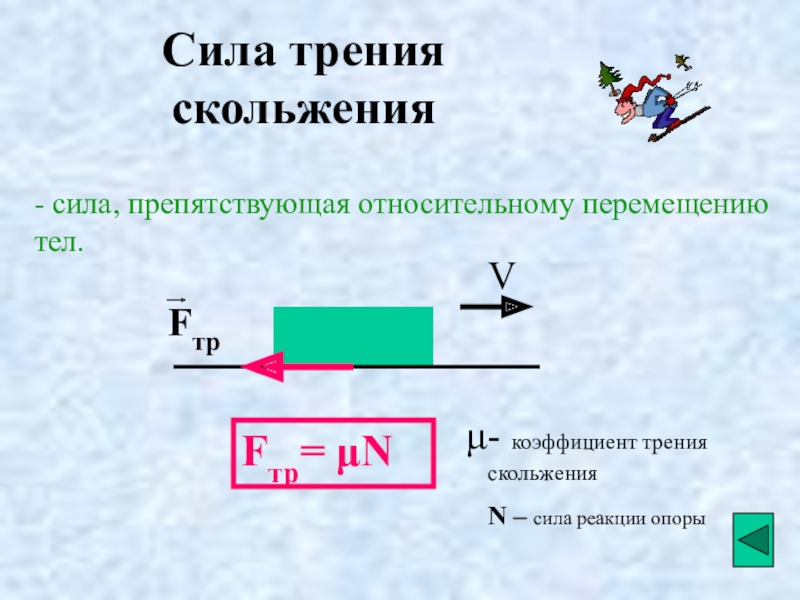 Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Направление силы трения
Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.
Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.
Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.
Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля сила трения покоя и вовсе направлена к центру окружности.
Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.
Подведём итоги
- Сила трения покоя меняется от нуля до максимального значения 0 < Fтр.покоя < Fтр.пок.макс в зависимости от внешнего воздействия.
- Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.
 макс
макс - Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N, где μ — коэффициент трения, N — сила нормальной реакции опоры.
- При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
- Коэффициент трения μ зависит от рода и степени обработки поверхностей 0 < μ < 1 .
- При одинаковых силе нормального давления и коэффициенте трения сила трения качения всегда меньше силы трения скольжения.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду
PHYSICS72020 вы получите бесплатный доступ к курсу физики 7 класса, в котором изучается закон силы трения.
Задачи на силу трения
Проверьте, насколько хорошо вы разобрались в теме «Сила трения», — решите несколько задач. Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
- Однажды в день открытия железной дороги произошёл конфуз: угодливый чиновник, желая выслужиться перед Николаем I, приказал выкрасить рельсы белой масляной краской.
 Какая возникла проблема и как её удалось решить с помощью сажи?
Какая возникла проблема и как её удалось решить с помощью сажи? - В один зимний день бабушка Нюра катала внука Алексея по заснеженной горизонтальной дороге. Чему равен коэффициент трения полозьев о снег, если сила трения, действующая на санки, равна 250 Н, а их масса вместе с Алексеем составляет 50 кг?
- На брусок массой m = 5 кг, находящийся на горизонтальной шероховатой поверхности μ = 0,7, начинает действовать сила F = 25 Н, направленная вдоль плоскости. Чему при этом равна сила трения, действующая на брусок?
Решения
- Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.
- Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g.
 Получаем формулу Fтр. = μ ⋅ m ⋅ g , откуда выразим искомую величину
Получаем формулу Fтр. = μ ⋅ m ⋅ g , откуда выразим искомую величину
Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .
Как решать 2 задание ЕГЭ по физике, примеры решения (Ростов-на-Дону)
Из
последних КИМов ЕГЭ по физике следует, что задание 2 относится к
разделу «Динамика» и может содержать расчетные задачи по
следующим темам: «Законы Ньютона, закон всемирного тяготения,
закон Гука, сила трения».
Основные
формулы, которые необходимо знать для успешного решения задания 2.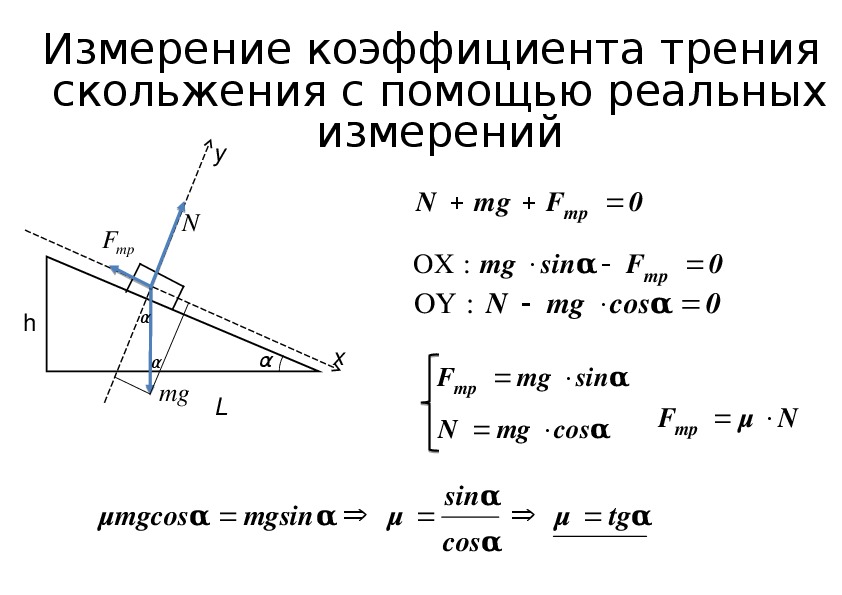
|
|
g=10
|
|
|
k
|
|
|
N
|
|
|
V
g=10
|
|
|
m1
r
|
|
|
R
a
|
При
решении задач из раздела «Динамика» желательно
придерживаться следующего алгоритма решения:
1.
Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
2.
Если тело двигается с ускорением, указать направление этого
ускорения. Если тело покоится или двигается равномерно, его ускорение
a=0.
3.
Составить уравнение движения (второй закон Ньютона) для
рассматриваемого тела в его векторном виде.
3.
Выбрать систему координат и спроецировать полученное уравнение на
выбранные оси координат.
4.
Расшифровать неизвестные величины, вошедшие в уравнение движения.
5.
Решить полученную систему уравнений.
Задание
2
– это расчётные задачи базового уровня сложности, и для решения
некоторых из них этот алгоритм будет чересчур подробным и
перегруженным, так как их можно решить и без вспомогательного рисунка
или даже без записи второго закона Ньютона. Это касается, например,
заданий, в которых на тело действует только одна сила. Но привычка
решать задания по приведенному выше алгоритму поможет ученикам
успешно справиться с расчетными задачами по разделу «Динамика»
повышенного и высокого уровней сложности – такие задания могут
стоять в ЕГЭ под номерами 25 и 29.
Ответом
на задание 2 является число, именно его нужно вписать в бланк ответов
1, не указывая единицы измерения.
Примеры
решения
1.
(ЕГЭ-2019)
Пружина
жёсткостью 2*104
Н/м одним концом закреплена в штативе. На какую величину она
растянется под действием силы 400 Н?
Ответ:
___________________________ см.
Решение:
Сделаем
чертёж
Пружина
под действием силы F
привели в растянутое состояние. Кроме растягивающей силы F
и силы упругости
,
стремящейся вернуть пружину в нерастянутое состояние, больше никакие
силы на нее не действуют.
Запишем
проекции сил на вертикальную ось Oy
F=Fупр
По
закону Гука, сила упругости Fупр
=
k
*Δx,
следовательно,
k
— коэффициент
жёсткости пружины,
Δx
– её
удлинение.
Выразим
величину растяжения пружины
Ответ:
2
(ЕГЭ
– 2020. Вариант 1 досрочного ЕГЭ)
Тело
движется по горизонтальной плоскости. Нормальная составляющая силы
воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н.
Определите коэффициент трения скольжения.
Ответ:
_______ .
Решение:
Силу
трения можно найти по формуле
Fтр=
µN,
где
N
–
сила реакции опоры, или по-другому нормальная составляющая силы
воздействия тела на плоскость.
Ответ:
0,25.
(ЕГЭ
– 2020. Демонстрационный вариант)
Два
одинаковых маленьких шарика массой m
каждый,
расстояние между центрами которых равно r,
притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков
Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?
Ответ:
_______ пН.
Решение:
По
закону Всемирного тяготения шары массами m1и
m2,
находящиеся друг от друга на расстоянии r,
притягиваются друг к другу с силой
.
В
первом случае
Во
втором случае
Ответ:
0,2
(ЕГЭ
– 2019. Демонстрационный вариант)
По
горизонтальному полу по прямой равномерно тянут ящик, приложив к нему
горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и
ящиком равен 0,25. Чему равна масса ящика?
Ответ
_______ кг.
Решение:
Сделаем
чертёж, на котором обозначим все силы, действующие на тело.
По
второму закону Ньютона, равнодействующая всех сил, действующих на
тело, будет равна нулю, так как по условию задачи тело движется
равномерно, то есть ускорение тела a=0.
Запишем
это в проекциях на оси Ox
и Oy
Ox:
Fтр
– F = 0,
Oy:
N — m g=0.
Откуда
N
= mg,
следовательно,
Fтр
=
µ N
= µ mg.
Масса
тела
Ответ:
14
(ЕГЭ
– 2018)
К
пружине подвесили груз массой 150 г, вследствие чего пружина
удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к
ней подвесить груз 450 г?
Ответ:
__________ см.
Решение:
Переведём
единицы измерения физических величин в систему СИ
m1
=
150 г = 0,15 кг, m2
=
450 г = 0,45 кг, Δx=1
см = 0,01 м.
Сделаем
чертёж, на котором обозначим все силы, действующие на тело.
На
тело действует сила тяжести (Fт
= mg),
направленная вертикально вниз, и сила упругости со стороны пружины
(Fупр
= k
Δx),
направленная вертикально вверх.
В
проекции на вертикальную ось Oy.
Fт
=Fупр
mg
= kΔx
(1)
k
— коэффициент
жёсткости пружины,
Δx
– её
удлинение.
Найдём,
чему равен коэффициент жёсткости пружины
Выразим
из выражения (1) удлинение пружины во втором случае
Ответ:
3
РЕКОМЕНДУЕМЫЕ ТОВАРЫ
Механическая работа и мощность 🐲 СПАДИЛО.РУ
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести | Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения | Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости | Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство | Работа полезная и полная | КПД |
| Неподвижный блок, рычаг | Aполезн = mgh Асоверш. | |
| Наклонная плоскость | Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт.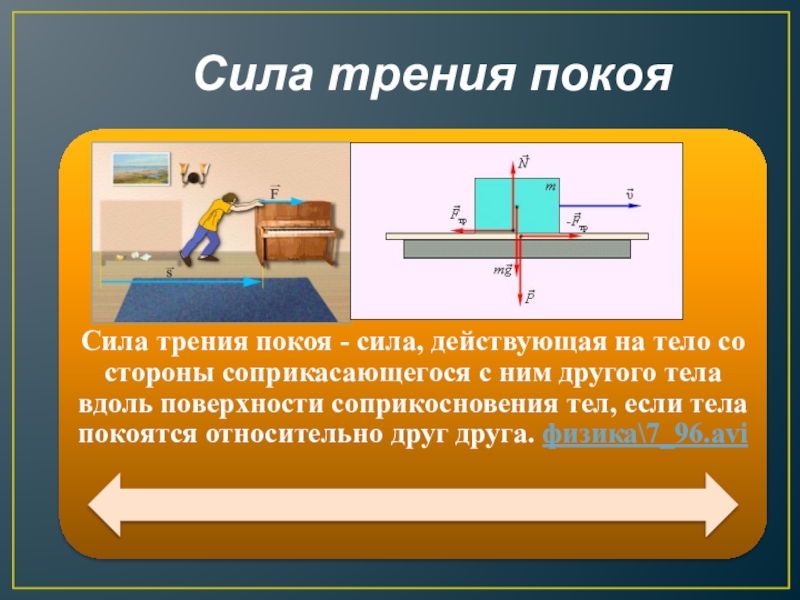 Из этой формулы выразим полезную мощность:
Из этой формулы выразим полезную мощность:
Задание EF17557 Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН? Ответ: а) 916 Вт б) 3300 Вт в) 82500 Вт г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At..
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst..=Fv=16,5·103·5=82500 (Вт)
.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17574 С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Время движения | Ускорение | Модуль работы силы трения |
. | . | . |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22..
y=yo+v0yt+ayt22..
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
.
.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится 2) уменьшится 3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа.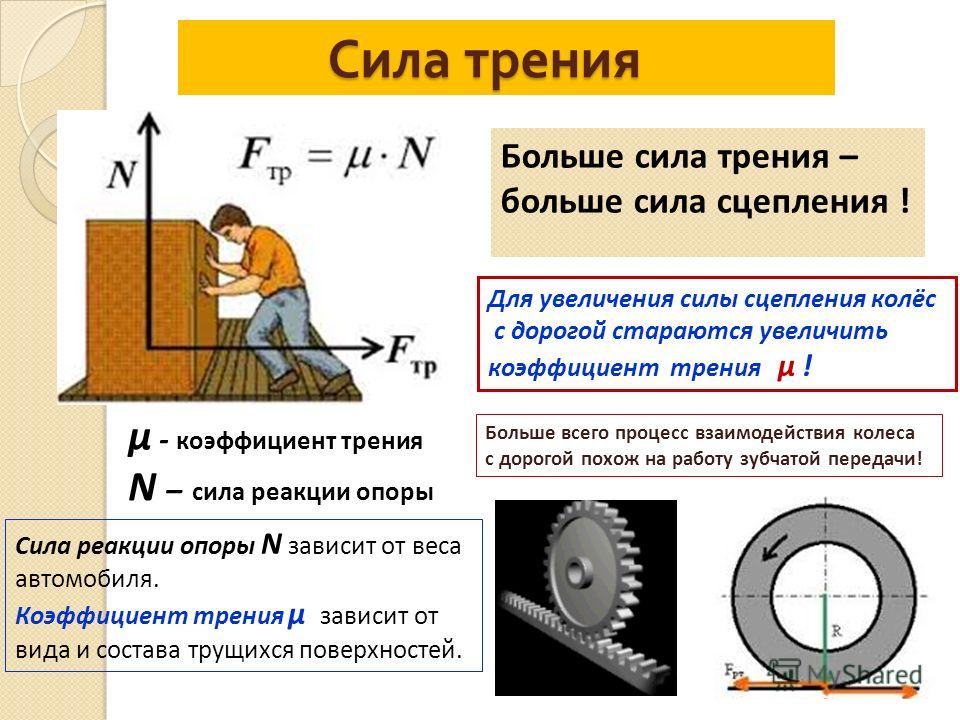 Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18271 Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 235.92U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ..100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Сила трения скольжения — урок.
 Физика, 9 класс.
Физика, 9 класс.
Сила трения скольжения возникает, если одно тело скользит по поверхности другого тела. Трение скольжения характеризуется силой трения, которая тормозит движение скольжения.
Сила трения скольжения прямо пропорциональна силе реакции опоры и коэффициенту трения скольжения.
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры и вычисляется по формуле: Fтр=μ⋅Fр.
При увеличении веса тела и коэффициента трения увеличивается сила трения. Сила трения скольжения действует в тех случаях, когда тело движется или его пытаются сдвинуть с места.
Сила реакции опоры — сила, при помощи которой опора действует на тело. Сила реакции опоры — сила, при помощи которой опора давит на тело, которое находится на ней. Из третьего закона Ньютона следует, что сила реакции опоры всегда равна силе, при помощи которой тело воздействует на опору. На неподвижной горизонтальной поверхности сила реакции опоры всегда равна весу тела или силе тяжести: Fр=Fт.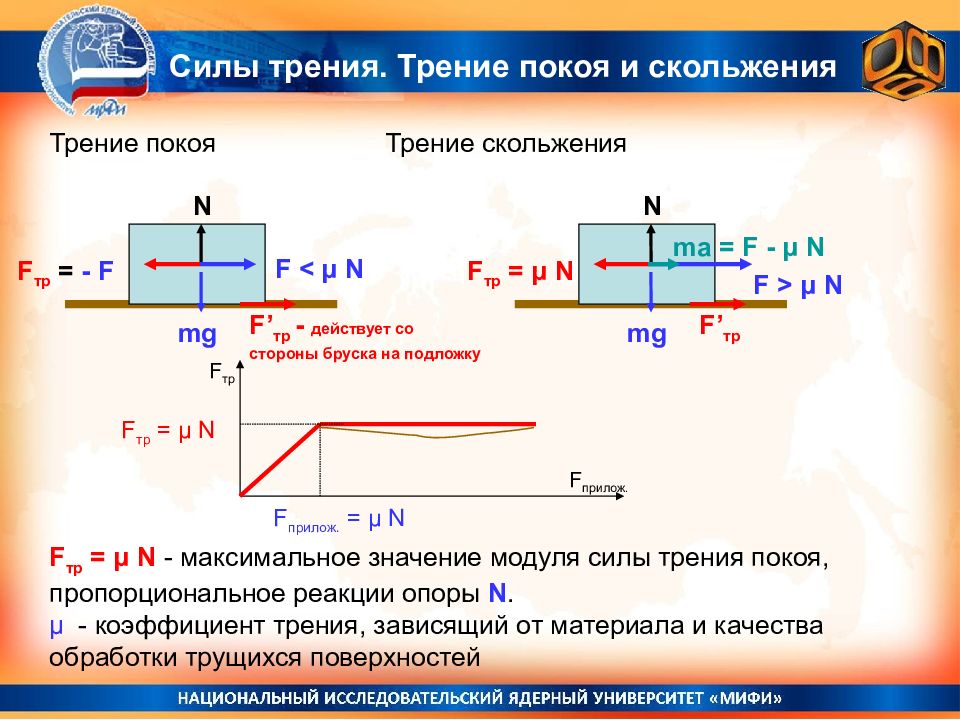 На наклонной плоскости сила тяжести и сила, при помощи которой тело воздействует на опору, различаются.
На наклонной плоскости сила тяжести и сила, при помощи которой тело воздействует на опору, различаются.
Обрати внимание!
Сила реакции опоры всегда направлена перпендикулярно поверхности опоры.
Коэффициент трения скольжения — отношение силы трения к силе реакции опоры. Коэффициент трения между двумя любыми материалами легко определить, если возможно измерить силу трения, которая равна силе тяги, при которой тело перемещается равномерно, и силу тяжести, которая на горизонтальной поверхности равна силе реакции опоры. В таблице представлены различные коэффициенты трения скольжения.
| Пары материалов | Коэффициент трения скольжения |
| Сталь — лёд (коньки) | \(0,015\) |
| Древесина — древесина | \(0,2\)–\(0,5\) |
| Покрышка — мокрый асфальт | \(0,35\)–\(0,45\) |
| Покрышка — сухой асфальт | \(0,50\)–\(0,75\) |
Обрати внимание!
Коэффициент трения скольжения не имеет размерности.
Если сравнивать коэффициенты трения покрышки на сухом и мокром асфальте, то на мокром асфальте у одной и той же машины коэффициент трения, а также сила трения почти в \(2\) раза меньше, чем на сухом асфальте. В результате также увеличивается замедление торможения почти в \(2\) раза, поэтому тормозной путь может увеличиться почти в \(4\) раза.
У силы трения имеются как положительные, так и отрицательные свойства. Если бы не было силы трения, то мы не могли бы оттолкнуться при ходьбе от земли, а машина не могла бы «оттолкнуться» от поверхности дороги. Но в технике трение между различными вращающимися и скользящими поверхностями весьма нежелательно, поэтому такое оборудование смазывают, чтобы снизить влияние силы трения.
Решаем задачи по физике. Механика
Предлагаем разобрать три задачи, приведенные ниже. Это задание №6 из ЕГЭ прошлых лет, рекомендованные как тренировочные.
Задача № 1
Школьник скатывается на санках со склона широкого оврага и затем с разгона сразу же начинает заезжать на санках вверх, на противоположный склон оврага. Коэффициент трения полозьев санок о снег всюду одинаков, углы наклона склонов оврага к горизонту всюду одинаковы. Как в результате переезда с одного склона на другой изменяются следующие физические величины: модуль действующей на санки силы трения, модуль ускорения санок, модуль работы силы тяжести при перемещении санок вдоль склона на 1 метр?
Коэффициент трения полозьев санок о снег всюду одинаков, углы наклона склонов оврага к горизонту всюду одинаковы. Как в результате переезда с одного склона на другой изменяются следующие физические величины: модуль действующей на санки силы трения, модуль ускорения санок, модуль работы силы тяжести при перемещении санок вдоль склона на 1 метр?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ИХ ИЗМЕНЕНИЕ |
A) Модуль действующей на санки силы трения Б) Модуль ускорения санок B) Модуль работы силы тяжести при перемещении вдоль склона на 1 метр |
| 1) Увеличивается 2) Уменьшается 3) Не изменяется |
Решение
Санки скользят, поэтому на них действует сила трения скольжения, которая определяется силой реакции опоры:
Fтр = μN
Поскольку оба склона имеют одинаковый угол наклона, сила реакции в обоих случаях имеет одинаковую величину:
N = mg·cosα
Где:
α — угол наклона.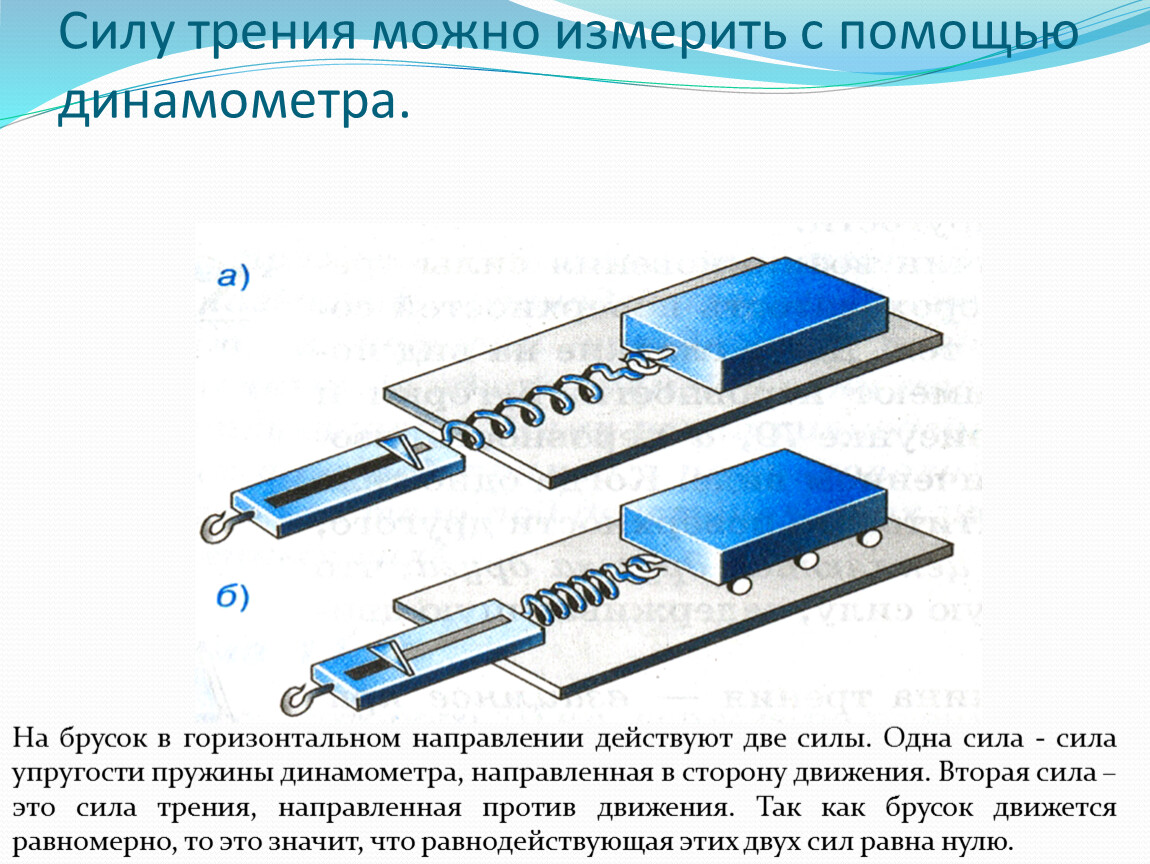
Таким образом, модуль действующей на санки силы трения остается неизменным (А — 3).
Модуль ускорения санок увеличивается (Б — 1), так как на первом склоне сила тяжести его разгоняла, а сила трения — тормозила:
mg·sinα – Fтр = m ǀa1ǀ
а на втором склоне его тормозят и сила тяжести, и сила трения:
mg·sinα + Fтр = m ǀa2ǀ
Работа силы есть скалярное произведение силы на перемещение. Сила тяжести все время направлена вниз, угол наклона склонов одинаков, поэтому модуль работы силы тяжести при перемещении вдоль склона на 1 метр не изменяется (В — 3).
Ответ: 313.
Задача № 2
Школьник скатывается на санках со склона оврага. Сначала он едет по шероховатому снегу, а потом въезжает на очень гладкий обледеневший участок склона. Угол наклона склона оврага к горизонту всюду одинаков. Как при этом изменяются следующие физические величины: модуль действующей на санки силы трения, модуль ускорения санок, модуль работы силы тяжести при перемещении санок вдоль склона на 1 метр?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.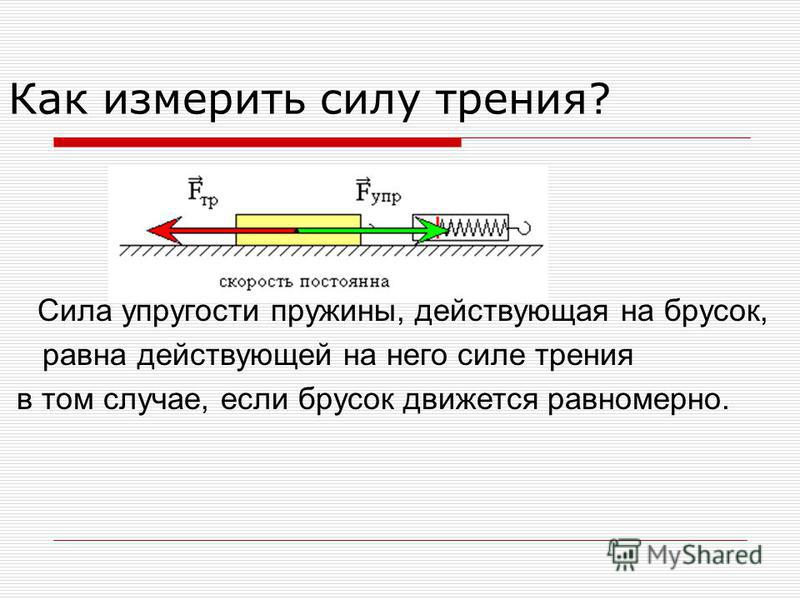
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ИХ ИЗМЕНЕНИЕ |
A) Модуль действующей на санки силы трения Б) Модуль ускорения санок B) Модуль работы силы тяжести при перемещении вдоль склона на 1 метр |
| 1) Увеличивается 2) Уменьшается 3) Не изменяется |
Решение
Санки скользят, поэтому на них действует сила трения скольжения, которая определяется силой реакции опоры:
Fтр = μN
Поскольку склон имеет постоянный наклон, сила реакции в обоих случаях имеет одинаковую величину:
N = mg·cosα
Где:
α — угол наклона.
Коэффициент трения уменьшается при выезде с шероховатого снега на обледеневший участок, поэтому модуль действующей на санки силы трения уменьшается (А — 2).
Модуль ускорения санок увеличивается (Б — 1), так как уменьшается тормозящая его сила трения:
ma = mg·sinα – Fтр
Работа силы есть скалярное произведение силы на перемещение. Сила тяжести всё время направлена вниз, угол наклона склона постоянен, поэтому модуль работы силы тяжести при перемещении вдоль склона на 1 метр не изменяется (В — 3).
Ответ: 213.
Задача № 3
Груз изображённого на рисунке (Рис. 1) пружинного маятника совершает гармонические колебания между точками 1 и 3. Как меняется потенциальная энергия пружины маятника, модуль скорости груза и жёсткость пружины при движении груза маятника от точки 2 к точке 1?
Рис. 1
Для каждой величины определите соответствующий характер её изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.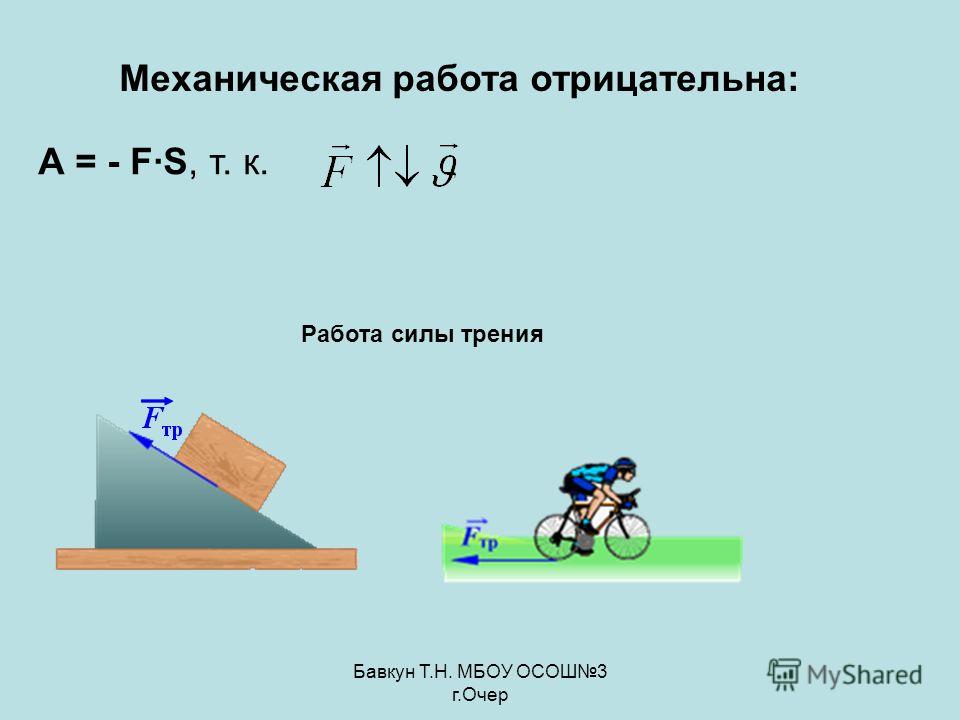
Точка 2 представляет собой положение устойчивого равновесия маятника. Когда груз находится в точке 2, пружина не деформирована. Решение
Точка 1, напротив, соответствует сжатой пружине. При движении груза от точки 2, в которой он имеет максимальную скорость, к точке 1 пружина сжимается, тормозя груз, то есть модуль скорости груза уменьшается (2).
При этом потенциальная энергия пружины увеличивается (1) по формуле:
Eпот =
Жесткость пружины является характеристикой пружины, не зависящей от фазы колебания, поэтому жесткость пружины не изменяется (3).
Потенциальная энергия пружины маятника | Модуль скорости груза | Жесткость пружины |
1 | 2 | 3 |
Ответ: 123.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Коэффициент трения — обзор
8.4 Коэффициент трения
Коэффициент трения (COF) является эмпирическим измерением — он должен быть измерен экспериментально и не может быть получен расчетами. Более грубые поверхности обычно имеют более высокие эффективные значения. Как статические, так и кинетические COF зависят от пары контактирующих поверхностей.
Большинство сухих материалов в комбинации имеют коэффициент тучности от 0,3 до 0,6. Значения вне этого диапазона редки, но, например, тефлон может иметь коэффициент ниже 0.04. Нулевое значение означает полное отсутствие трения, исключительное свойство — даже левитационные транспортные средства имеют сопротивление. Резина при контакте с другими поверхностями может давать COF от 1 до 2. Иногда утверждают, что μ всегда меньше 1, но это неверно. В то время как в большинстве соответствующих приложений μ <1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальная сила поверхности на объект. Например, поверхности, покрытые силиконовым каучуком или акриловым каучуком, имеют коэффициент трения, который может быть существенно больше 1.
В то время как в большинстве соответствующих приложений μ <1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальная сила поверхности на объект. Например, поверхности, покрытые силиконовым каучуком или акриловым каучуком, имеют коэффициент трения, который может быть существенно больше 1.
Хотя часто утверждается, что COF является «материальным свойством», его лучше классифицировать как «системное свойство». В отличие от истинных свойств материала (т. Е. Проводимости, диэлектрической проницаемости, предела текучести), коэффициент трения для любых двух материалов зависит от системных переменных, таких как температура, скорость, атмосфера, а также от того, что сейчас обычно называют временем старения и разрушения; а также от геометрических свойств интерфейса между материалами. Например, медный штифт, скользящий по толстой медной пластине, может иметь коэффициент трения от 0.6 на низких скоростях (скольжение металла по металлу) до значений ниже 0,2 на высоких скоростях, когда поверхность меди начинает плавиться из-за нагрева от трения. Последняя скорость, конечно, не определяет однозначно COF; если диаметр штифта увеличивается так, что нагрев от трения быстро устраняется, температура падает, штифт остается твердым, а коэффициент трения повышается до значения при испытании на «низкой скорости».
Последняя скорость, конечно, не определяет однозначно COF; если диаметр штифта увеличивается так, что нагрев от трения быстро устраняется, температура падает, штифт остается твердым, а коэффициент трения повышается до значения при испытании на «низкой скорости».
Обычно вертикальную силу ( F z ) связывают с общей механической мощностью ( P ) через COF μ , предполагая, что все тепло генерируется трением.Поверхностное тепло, создаваемое трением инструмента о материал, можно просто оценить по формуле. 8.1, предполагая постоянное давление равным p плечо [Па] [19]. Обратите внимание, что это выражение не учитывает вклад боковой поверхности штифта:
[8.1] Qs = 23πμpshoulderωrs2 = 23μFzωrs
, где r s — радиус уступа инструмента. Если мы предположим, что мощность генерируется только трением (отсюда P = Q s ), мы можем оценить COF с помощью
[8.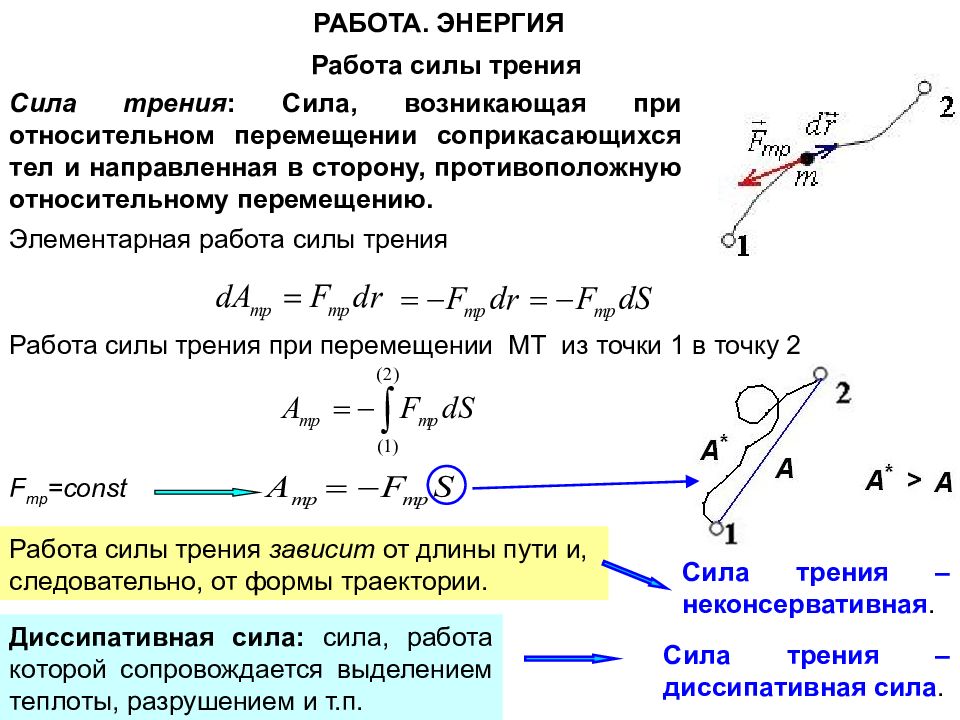 2] μ = 3p2Fzωrs
2] μ = 3p2Fzωrs
На рисунке 8.5 показано изменение COF, рассчитанного по формуле. 8.2 для разных параметров сварки.
Рисунок 8.5. Изменение коэффициента трения в зависимости от параметров сварки [19]
На COF явно больше влияет скорость вращения, чем скорость продвижения, поскольку вертикальная сила F z и мощность P больше зависят от скорость продвижения, чем скорость вращения, и они оба увеличиваются, когда скорость продвижения увеличивается.В литературе по тепловому моделированию мы находим всевозможные значения коэффициента трения. Некоторые из них реалистичны, например, предложенный в [20] ( μ = 0,4 для параметров сварки 300 мм / мин, 1500 об / мин и диаметра уступа 20 мм). Однако значение, предложенное в [21], кажется очень низким ( μ = 0,15 для параметров сварки 139,7 мм / мин, 500 об / мин и диаметра уступа 25,4 мм). Тем не менее, гипотезы, на которых основаны эти вычисления, безусловно, слишком упрощены. Очевидно, что влиянием деформации материала можно пренебречь.
Очевидно, что влиянием деформации материала можно пренебречь.
Жесткость фрикционного контакта разнородных упругих тел (Журнальная статья)
Ли, Джин Хэн, Гао, Яньфэй, Бауэр, Аллан Ф., Сюй, Хайтао и Фарр, Джордж М. Жесткость фрикционного контакта разнородных упругих тел. США: Н. П., 2017.
Интернет. DOI: 10.1016 / j.jmps.2017.12.010.
Ли, Джин Хэн, Гао, Яньфэй, Бауэр, Аллан Ф., Сюй, Хайтао и Фарр, Джордж М. Жесткость фрикционного контакта разнородных упругих тел. Соединенные Штаты. DOI: https: //doi.org/10.1016/j.jmps.2017.12.010
Ли, Цзинь Хэн, Гао, Яньфэй, Бауэр, Аллан Ф., Сюй, Хайтао и Фарр, Джордж М. Пт.
«Жесткость фрикционного контакта разнородных упругих тел». Соединенные Штаты. DOI: https: //doi.org/10.1016/j. jmps.2017.12.010. https://www.osti.gov/servlets/purl/1423063.
jmps.2017.12.010. https://www.osti.gov/servlets/purl/1423063.
@article {osti_1423063,
title = {Жесткость фрикционного контакта разнородных упругих тел},
author = {Ли, Цзинь Хэн и Гао, Яньфэй и Бауэр, Аллан Ф. и Сюй, Хайтао и Фарр, Джордж М.},
abstractNote = {Классическая зависимость Снеддона между нормальной контактной жесткостью и размером контакта действительна для осесимметричного контакта без трения, в котором два контактирующих тела аппроксимируются упругими полупространствами.Отклонение от этого результата критически влияет на точность методов наноиндентирования с измерением нагрузки и смещения. Это исследование дает подробное численное и аналитическое исследование поправок, необходимых для решения Снеддона, когда существует конечное кулоновское трение между упругим полупространством и жестким штампом с плоским концом круглой или некруглой формы. Из-за линейности кулоновского трения поправочный коэффициент оказывается функцией коэффициента трения, коэффициента Пуассона и формы контакта, но не зависит от размера контакта. При моделировании методом конечных элементов первостепенное значение имеют два вопроса: адекватность сетки вблизи контактной кромки и методология реализации трения. Хотя размеры зон прилипания или скольжения сильно отличаются от методов штрафа или лагранжевых методов, расчетные контактные жесткости почти такие же и могут быть значительно больше, чем в решении Снеддона. Для контакта с круглым пуансоном численные решения удивительно хорошо согласуются с предыдущим аналитическим решением. Для некруглого контакта пуансона результаты могут быть представлены с использованием эквивалентности между задачей контакта и механикой разрушения двух материалов.Наконец, было обнаружено, что поправочный коэффициент является произведением поправочного коэффициента для кругового контакта и мультипликативного коэффициента, который зависит только от формы пуансона, но не от коэффициента трения или коэффициента Пуассона.},
При моделировании методом конечных элементов первостепенное значение имеют два вопроса: адекватность сетки вблизи контактной кромки и методология реализации трения. Хотя размеры зон прилипания или скольжения сильно отличаются от методов штрафа или лагранжевых методов, расчетные контактные жесткости почти такие же и могут быть значительно больше, чем в решении Снеддона. Для контакта с круглым пуансоном численные решения удивительно хорошо согласуются с предыдущим аналитическим решением. Для некруглого контакта пуансона результаты могут быть представлены с использованием эквивалентности между задачей контакта и механикой разрушения двух материалов.Наконец, было обнаружено, что поправочный коэффициент является произведением поправочного коэффициента для кругового контакта и мультипликативного коэффициента, который зависит только от формы пуансона, но не от коэффициента трения или коэффициента Пуассона.},
doi = {10.1016 / j.jmps.2017.12.010},
journal = {Журнал механики и физики твердого тела},
число =,
объем = 112,
place = {United States},
год = {2017},
месяц = {12}
}
(PDF) Влияние модуля Юнга и шероховатости поверхности на трение между частицами сыпучих материалов
Материалы 2018,11, 217 9 из 10
Ссылки
1.
Cundall, P.A .; Strack, O.D.L. Дискретная численная модель для гранулированных сборок. Геотехника
1979
, 29,
47–65. [CrossRef]
2.
Ni, W .; Cheng, Y.T .; Лукич, M.J .; Weiner, A.M .; Lev, L.C .; Граммон Д.С. Влияние отношения твердости к модулю Юнга
на трение и износ двухслойных покрытий. Прил. Phys. Lett.
2004
, 85, 4028–4030.
[CrossRef]
3.Оберле, Т. Износ металлов. J. Met. 1951,3, 438–439. [CrossRef]
4.
Leyland, A .; Мэтьюз, А. О значении отношения H / E в контроле износа: нанокомпозитное покрытие
— подход к оптимизированному трибологическому поведению. Носите 2000 246, 1–11. [CrossRef]
5.
Riedo, E .; Брюн, Х. Зависимость модуля Юнга наноскопического коэффициента трения в твердых покрытиях.
Заяв. Phys. Lett. 2003,83, 1986–1988. [CrossRef]
6.
Pohlman, N.А .; Severson, B.J .; Оттино, J.M .; Люптоу, Р. Влияние шероховатости поверхности в гранулах:
Влияние на угол естественного откоса и отсутствие сегрегации. Phys. Rev. E
Phys. Rev. E
2006
, 73, 031304. [CrossRef]
[PubMed]
7. Horn, H.M .; Дир, Д.У. Фрикционные характеристики минералов. Геотехника 1962,12, 319–335. [CrossRef]
8.
Скиннер, A.E. Заметка о влиянии межчастичного трения на сопротивление сдвигу случайной сборки
сферических частиц.Геотехника 1969,19, 150–157. [CrossRef]
9.
Procter, D.C .; Бартон Р.Р. Измерения угла межчастичного трения. Геотехника
1974
, 24, 581–604.
[CrossRef]
10.
Cole, D.M .; Mathisen, L.U .; Hopkins, M.A .; Кнапп, Б. Нормальный и скользящий контактные опыты на гнейсе.
Гранул. Matter 2010,12, 69–86. [CrossRef]
11.
Cavarretta, I .; Coop, M.R .; О’Салливан, К. Влияние характеристик частиц на поведение крупнозернистых почв
.Геотехника 2010,60, 413–423. [CrossRef]
12.
Cavarretta, I .; Rocchi, I .; Куп, М. Новый аппарат межчастичного трения для сыпучих материалов.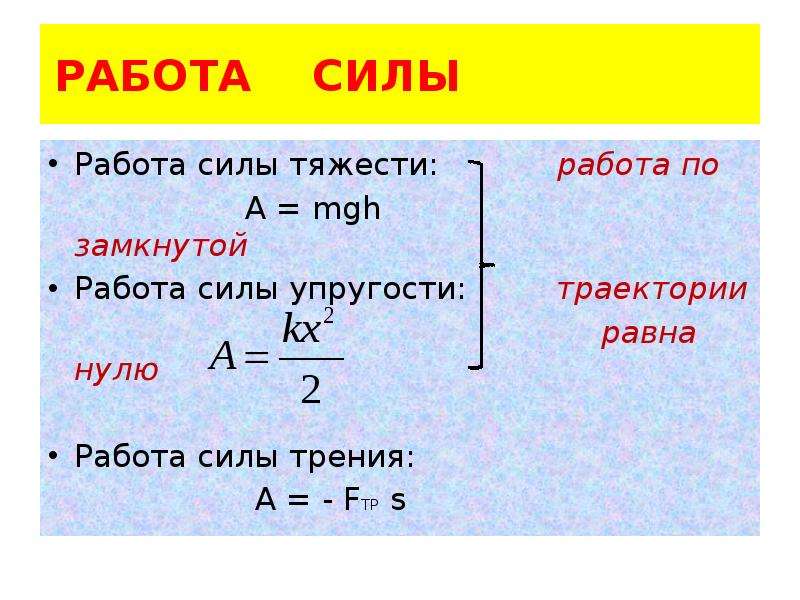 Может.
Может.
Геотек. J. 2011,48, 1829–1840. [CrossRef]
13.
Senetakis, K .; Coop, M.R .; Тодиско, М. Коэффициент трения между частицами на контактах кварцевых минералов песка Leighton
Buzzard. Почвы найдены. 2013, 53, 746–755. [CrossRef]
14.
Сенетакис, К.; Sandeep, C.S .; Тодиско, М. Динамическое трение между частицами известнякового щебня.
Трибол. Int. 2017,111, 1–8. [CrossRef]
15.
Senetakis, K .; Coop, M .; Тодиско, М. Поведение тангенциальной нагрузки-отклонения на контактах частиц почвы.
Geotechnol. Lett. 2013,3, 59–66. [CrossRef]
16.
Senetakis, K .; Куп, М.Р.Микромеханическое экспериментальное исследование жесткости скольжения между зернами
кварцевых минералов.Exp. Мех. 2015,55, 1187–1190. [CrossRef]
17.
Нарделли В. Экспериментальное исследование микромеханического контактного поведения почв. Кандидат наук. Диссертация,
Городской университет Гонконга, Гонконг, Китай, март 2017 г.
18.
Nardelli, V .; Coop, M.R .; Andrade, J.E .; Пакканелла, Ф. Экспериментальное исследование микромеханики
песка Эглин. Пудра Технол. 2017, 312, 166–174. [CrossRef]
19. Байерли Дж. Трение горных пород.Pure Appl. Geophys. 1978, 116, 615–626. [CrossRef]
20.
Yang, L .; Wang, D .; Guo, Y .; Лю, С. Трибологические свойства частиц кварцевого песка при гидроразрыве пласта.
Трибол. Int. 2016, 102, 485–496. [CrossRef]
21.
Sandeep, C.S .; Todisco, M.C .; Сенетакис, К. Поведение при касательном контакте выветрившегося вулканического оползня
материала из Гонконга. Почвы найдены. 2017,57, 1097–1103. [CrossRef]
22.
Сандип, К.S .; Сенетакис, К. Исследование микромеханических характеристик скольжения типичных зерен кварца и
полностью разложившихся вулканических гранул, подвергнутых многократному сдвигу. Энергия
2017
, 10, 370. [CrossRef]
23.
Sandeep, C.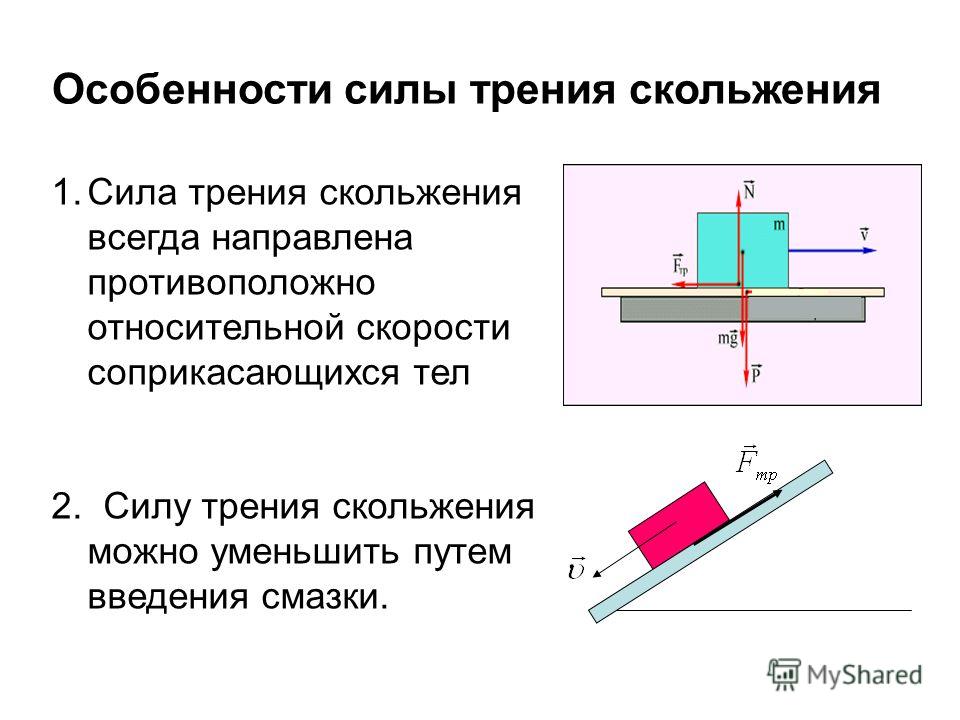 S .; Сенетакис, К. Зерновая механика кварцевого песка при нормальном и тангенциальном нагружении.
S .; Сенетакис, К. Зерновая механика кварцевого песка при нормальном и тангенциальном нагружении.
Трибол. Int. 2018, 117, 261–271. [CrossRef]
24.
Sazzad, M.M .; Судзуки, К. Влияние межчастичного трения на циклическое поведение сыпучих материалов с использованием
2D DEM.J. Geotech. Geoenviron. Англ. 2011, 137, 545–549. [CrossRef]
25.
Huang, X .; Hanley, K.J .; О’Салливан, К .; Квок, С.Ю. Изучение влияния межчастичного трения на поведение критического состояния
с помощью DEM. Int. J. Numer. Анальный. Методы Геомех. 2014,38, 1276–1297. [CrossRef]
26.
Otsubo, M .; О’Салливан, К .; Hanley, K.J .; Сим, W.W. Влияние шероховатости поверхности частиц на упругую жесткость
и динамический отклик. Геотехника 2017, 67, 452–459.[CrossRef]
% PDF-1.4
%
1127 0 объект>
эндобдж
xref
1127 119
0000000016 00000 н.
0000004040 00000 н.
0000004182 00000 п.
0000004228 00000 п.
0000004264 00000 н.
0000004415 00000 н.
0000004503 00000 н.
0000005066 00000 н.
0000005219 00000 п.
0000005367 00000 н.
0000005514 00000 н.
0000015993 00000 п.
0000016334 00000 п.
0000016634 00000 п.
0000016968 00000 н.
0000016999 00000 н.
0000034987 00000 п.
0000035542 00000 п.
0000035998 00000 п.
0000036587 00000 п.
0000036618 00000 п.
0000042997 00000 п.
0000043219 00000 п.
0000043416 00000 п.
0000043699 00000 н.
0000043773 00000 п.
0000043851 00000 п.
0000043929 00000 п.
0000043973 00000 п.
0000044103 00000 п.
0000044135 00000 п.
0000044213 00000 п.
0000044256 00000 п.
0000044334 00000 п.
0000044464 00000 п.
0000044516 00000 п.
0000044594 00000 п.
0000044636 00000 п.
0000044714 00000 п.
0000044844 00000 п.
0000044875 00000 п.
0000044953 00000 п.
0000044995 00000 п.
0000045073 00000 п.
0000045203 00000 п.
0000045254 00000 п.
0000045332 00000 п.
0000045374 00000 п.
0000045452 00000 п.
0000045582 00000 п.
0000045623 00000 п.
0000045701 00000 п.
0000045743 00000 п.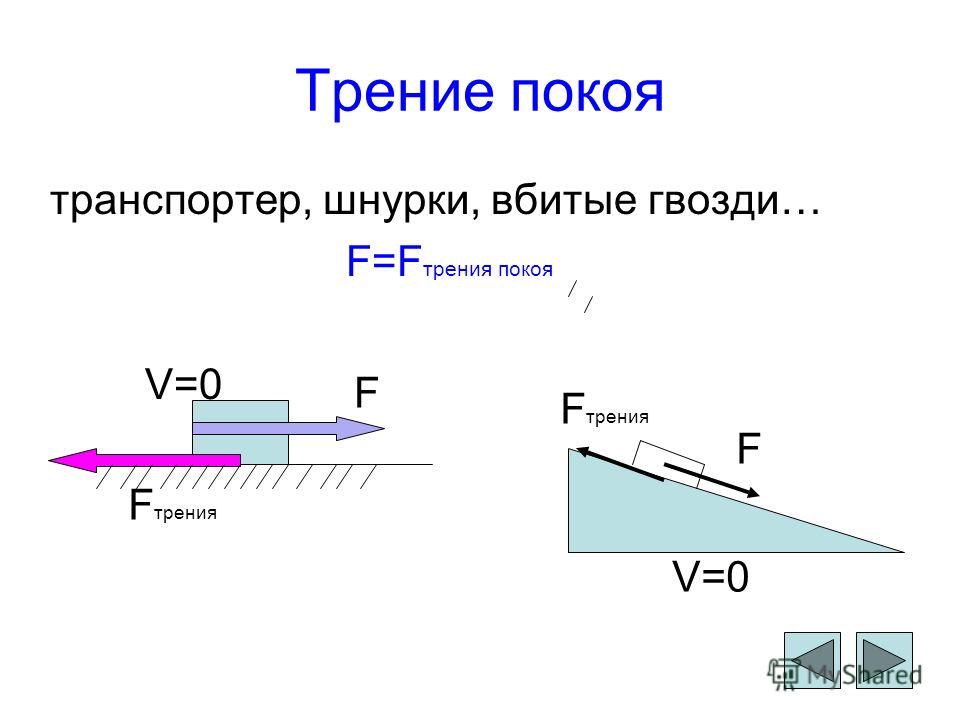
0000045821 00000 п.
0000045951 00000 п.
0000046008 00000 п.
0000046086 00000 п.
0000046128 00000 п.
0000046206 00000 п.
0000046298 00000 п.
0000046327 00000 п.
0000046369 00000 п.
0000046461 00000 п.
0000046493 00000 п.
0000046536 00000 п.
0000046628 00000 п.
0000046663 00000 п.
0000046715 00000 п.
0000046743 00000 п.
0000046787 00000 п.
0000046820 00000 н.
0000046864 00000 н.
0000046891 00000 п.
0000046935 00000 п.
0000047027 00000 п.
0000047064 00000 п.
0000047108 00000 п.
0000047162 00000 п.
0000047206 00000 п.
0000047251 00000 п.
0000047295 00000 п.
0000047350 00000 п.
0000047394 00000 п.
0000047434 00000 п.
0000047478 00000 п.
0000047570 00000 п.
0000047613 00000 п.
0000047657 00000 п.
0000047749 00000 п.
0000047801 00000 п.
0000047845 00000 п.
0000047880 00000 п.
0000047924 00000 п.
0000047962 00000 п.
0000048006 00000 п.
0000048029 00000 п.
0000048073 00000 п.
0000048101 00000 п.
0000048145 00000 п.
0000048237 00000 п.
0000048296 00000 н.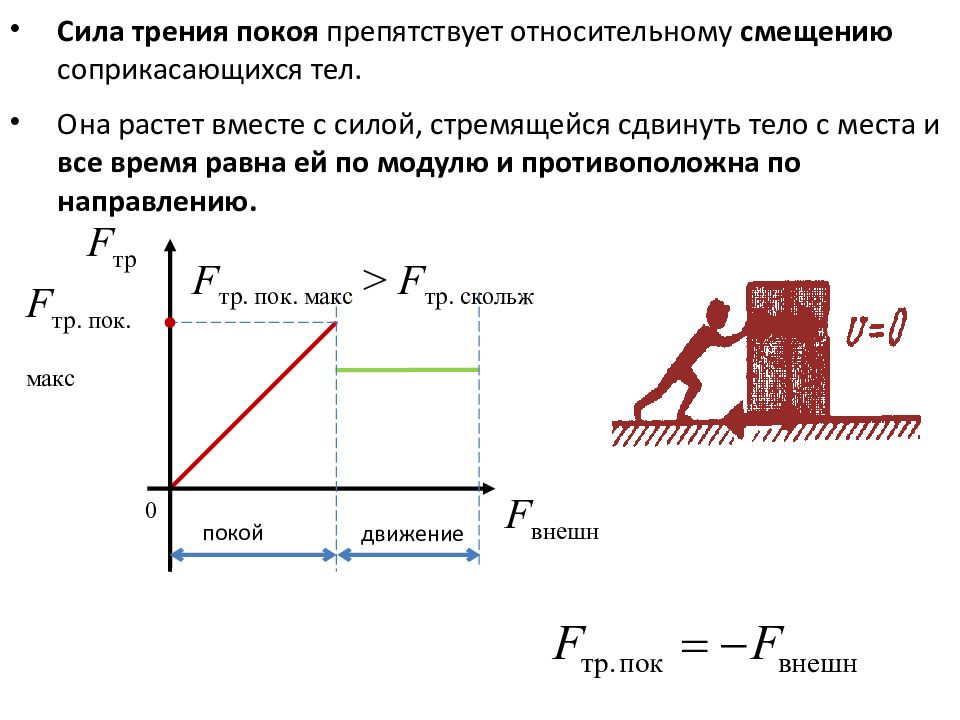
0000048340 00000 п.
0000048432 00000 н.
0000048493 00000 п.
0000048537 00000 п.
0000048629 00000 н.
0000048672 00000 н.
0000048716 00000 п.
0000048808 00000 п.
0000048866 00000 н.
0000048910 00000 п.
0000049002 00000 п.
0000049055 00000 п.
0000049099 00000 н.
0000049151 00000 п.
0000049195 00000 п.
0000049253 00000 п.
0000049306 00000 п.
0000002676 00000 н.
трейлер
] >>
startxref
0
%% EOF
1245 0 obj> поток
xV Pu «xpzLjt! @» ~ yQ9xr & MF et ( LS6NO ٛٙ}> yo
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Связь между трением и вязкоупругими свойствами резины по JSTOR
Abstract
В данной статье описывается трение нескольких типов резины о твердые поверхности в широком диапазоне температур и скоростей скольжения.Максимальная скорость не превышала нескольких сантиметров в секунду, так что нагрев трением был незначительным. Результаты показывают, что трение увеличивается со скоростью скольжения до максимального значения, а затем падает. Применение преобразования Вильямса, Ландела и Ферри (1955) показывает, что фрикционное поведение резины, скользящей при различных скоростях и температурах по заданной поверхности, можно полностью описать одной « эталонной кривой » и температурой стеклования материала. .Основная кривая на шероховатой абразивной дорожке, как правило, показывает два пика — один из них происходит со скоростью, зависящей от частоты, с которой неровности дорожки деформируют резиновую поверхность. Этот максимум отсутствует на гладкой дорожке и, таким образом, отражает потери деформации, вызванные прохождением неровностей по поверхности резины. Другой пик обычно наблюдается при гораздо более низких скоростях; он совпадает по положению с единственным максимумом, полученным на гладкой поверхности. Введение тонкого порошка (MgO) на поверхность раздела между резиной и гусеницей устраняет этот пик как на гладких, так и на шероховатых поверхностях; поэтому это связано с молекулярной адгезией.Сравнение с релаксационным спектром каучука дает фундаментальное расстояние скачка порядка 60 Å. Таким образом, кажется, что трение возникает из-за потерь на адгезию и деформацию, и что оба они напрямую связаны с вязкоупругими свойствами резины.
Информация для издателя
Королевское общество — это самоуправляемое товарищество многих самых выдающихся ученых мира, представляющих все области науки, техники и медицины, и старейшая научная академия, которая постоянно существует.Основная цель Общества, отраженная в его учредительных документах 1660-х годов, заключается в признании, продвижении и поддержке передового опыта в науке, а также в поощрении развития и использования науки на благо человечества. Общество сыграло роль в некоторых из самых фундаментальных, значительных и изменяющих жизнь открытий в истории науки, и ученые Королевского общества продолжают вносить выдающийся вклад в науку во многих областях исследований.
% PDF-1.2
%
1817 0 объект
>
эндобдж
xref
1817 76
0000000016 00000 н.
0000001875 00000 н.
0000001978 00000 н.
0000002849 00000 н.
0000003207 00000 н.
0000003576 00000 н.
0000004697 00000 н.
0000004821 00000 н.
0000005114 00000 п.
0000006228 00000 п.
0000007349 00000 н.
0000007644 00000 п.
0000007928 00000 п.
0000007952 00000 н.
0000009458 00000 п.
0000009482 00000 н.
0000010778 00000 п.
0000010802 00000 п.
0000012047 00000 п.
0000012071 00000 п.
0000013349 00000 п.
0000013373 00000 п.
0000013489 00000 п.
0000014803 00000 п.
0000014827 00000 п.
0000016089 00000 п.
0000016113 00000 п.
0000016381 00000 п.
0000016674 00000 п.
0000017948 00000 н.
0000017972 00000 п.
0000017994 00000 п.
0000018016 00000 п.
0000019280 00000 п.
0000019304 00000 п.
0000020871 00000 п.
0000020894 00000 п.
0000021804 00000 п.
0000021828 00000 п.
0000024214 00000 п.
0000024237 00000 п.

