Содержание
Модули — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Базовые сведения о модуле
К оглавлению…
Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:
Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Основные свойства модуля:
Некоторые методы решения уравнений с модулями
К оглавлению…
Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:
При этом данный способ не является единственным. Например, для уравнения вида:
Предпочтительным способом решения будет переход к совокупности:
А для уравнений вида:
Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:
Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:
- Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.

- Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять.
- Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.
Как раскрыть модуль в модуле в уравнении. Уравнения с модулем. Решение неравенств с модулем
Инструкция
Если модуль представлен в виде непрерывной функции, то значение ее аргумента может быть как положительным, так и отрицательным: |х| = х, х ≥ 0; |х| = — х, х
Модуль нулю, а модуль любого положительного числа – ему . Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Возведенный в степень аргумент одновременно находится под знаком корня того же порядка – он решается при помощи : √a² = |a| = ±a.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Модуль нуля равен нулю, а модуль любого положительного числа – ему самому. Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя целое положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Отрицательным модуль быть не может, поэтому любое отрицательное число преобразуется в положительное: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается изменение порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т.к. оно будет влиять на знак выражения.
Модуль – это абсолютная величина выражения. Чтобы хоть как-то обозначить модуль, принято использовать прямые скобки. То значение, которое заключено в ровных скобках, и является тем значением, которое взято по модулю. Процесс решения любого модуля заключается в раскрытии тех самых прямых скобок, которые математическим языком именуются модульными скобками. Их раскрытие происходит по определенному ряду правил. Также, в порядке решения модулей, находятся и множества значений тех выражений, которые находились в модульных скобках. В большей части всех случаев, модуль раскрывается таким способом, что выражение, которое было подмодульным, получает и положительные, и отрицательные значения, в числе которых также и значение ноль. Если отталкиваться от установленных свойств модуля, то в процессе составляются различные уравнения или же неравенства от исходного выражения, которые затем необходимо решить. Разберемся же с тем, как решать модули.
Их раскрытие происходит по определенному ряду правил. Также, в порядке решения модулей, находятся и множества значений тех выражений, которые находились в модульных скобках. В большей части всех случаев, модуль раскрывается таким способом, что выражение, которое было подмодульным, получает и положительные, и отрицательные значения, в числе которых также и значение ноль. Если отталкиваться от установленных свойств модуля, то в процессе составляются различные уравнения или же неравенства от исходного выражения, которые затем необходимо решить. Разберемся же с тем, как решать модули.
Процесс решения
Решение модуля начинается с записи исходного уравнения с модулем. Чтобы ответить на вопрос о том, как решать уравнения с модулем, нужно раскрыть его полностью. Для решения такого уравнения, модуль раскрывается. Все модульные выражения должны быть рассмотрены. Следует определить при каких значениях неизвестных величин, входящих в его состав, модульное выражение в скобках обращается в ноль. Для того чтобы это сделать, достаточно приравнять выражение в модульных скобках к нулю, а затем высчитать решение образовавшегося уравнения. Найденные значения нужно зафиксировать. Таким же способом нужно определить еще и значение всех неизвестных переменных для всех модулей в данном уравнении. Далее необходимо заняться определением и рассмотрением всех случаев существования переменных в выражениях, когда они отличны от значения ноль. Для этого нужно записать некоторую систему из неравенств соответственно всем модулям в исходном неравенстве. Неравенства должны быть составлены так, чтоб они охватывали все имеющиеся и возможные значения для переменной, которые находят на числовой прямой. Затем нужно начертить для визуализации эту самую числовую прямую, на которой в дальнейшем отложить все полученные значения.
Практически все сейчас можно сделать в интернете. Не является исключением из правил и модуль. Решить онлайн его можно на одном из многочисленных современных ресурсов. Все те значения переменной, которые находятся в нулевом модуле, будут особым ограничением, которое будет использовано в процессе решения модульного уравнения. В исходном уравнении требуется раскрыть все имеющиеся модульные скобки, при этом, изменяя знак выражения, таким образом, чтобы значения искомой переменной совпадали с теми значениями, которые видно на числовой прямой. Полученное уравнение необходимо решить. То значение переменной, которое будет получено в ходе решения уравнения, нужно проверять на ограничение, которое задано самим модулем. Если значение переменной полностью удовлетворяет условие, то оно является правильным. Все корни, которые будут получены в ходе решения уравнения, но не будут подходить по ограничениям, должны быть отброшены.
В исходном уравнении требуется раскрыть все имеющиеся модульные скобки, при этом, изменяя знак выражения, таким образом, чтобы значения искомой переменной совпадали с теми значениями, которые видно на числовой прямой. Полученное уравнение необходимо решить. То значение переменной, которое будет получено в ходе решения уравнения, нужно проверять на ограничение, которое задано самим модулем. Если значение переменной полностью удовлетворяет условие, то оно является правильным. Все корни, которые будут получены в ходе решения уравнения, но не будут подходить по ограничениям, должны быть отброшены.
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля
. Итак, модулем числа a
называется само это число, если a
неотрицательно и -a
, если число a
меньше нуля. Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1.
Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b
1) |x + 2| = 4, т. к. 4 > 0, то
к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
2) |x 2 – 5| = 11, т.к. 11 > 0, то
x 2 – 5 = 11 или x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 нет корней
3) |x 2 – 5x| = -8 , т.к. -8
3.
Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x)
или f(x) = -g(x)
.
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x 2 .
1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
2. Решение:
x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:
|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому
|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6.
Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
Нет корней.
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля
. Итак, модулем числа a
называется само это число, если a
неотрицательно и -a
, если число a
меньше нуля. Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1.
Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
2) |x 2 – 5| = 11, т.к. 11 > 0, то
x 2 – 5 = 11 или x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 нет корней
3) |x 2 – 5x| = -8 , т.к. -8
3.
Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т. е. g(x) ≥ 0. Тогда будем иметь:
е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x)
или f(x) = -g(x)
.
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x 2 .
1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
2. Решение:
x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
Данное уравнение равносильно двум следующим:
x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:
|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому
|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6.
Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Вконтакте
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а
обозначается как |a|
.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
Графически это можно выразить следующим образом: |a| = OA.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
Особенности решения уравнений с модулем
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5
, если, А больше или равняется нулю.
5-А
, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Решение уравнений и неравенств c модулем
Версия для печати
1. Определение модуля
Модулем числа называется расстояние от точки, изображающей это число до нуля.
По определению `abs(f(x))>=0`, причём x — любое действительное число (`x in R`) из области допустимых значений (ОДЗ). 4`;
4`;
1.3 Модуль неизвестного числа
`abs(x)=[({(x >= 0),(abs(x) = x):}), ({(x
1.4 Упражнения к определению модуля
1.4.1 Решить уравнение `abs(2x-1)=2x-1`
`2x-1>=0`;
`x >= 1/2`
Ответ: `[1/2; +infty)`
1.4.2 Решить уравнение `abs(7x-14)=14-7x`
`7x-14
Ответ: `(-infty; 2]`
1.4.3 Решить уравнение `abs(3x-19)=1`
`[(3x-19=1), (3x-19=-1) :}`;
`[(x=20/3), (x=6) :}`
Ответ: `{6; 20/3}`
1.4.4 Решить уравнение `abs(5x-11)=3x+4`
`{( 3x+4 >= 0 ), ( [(5x-11=3x+4), (5x-11=-3x-4):}) :}`;
`{(x >= -4/3), ( [(x=15/2), (x=7/8):} ) :}`;
Ответ: `{7/8; 15/2}`
1.4.5 Решить неравенство `abs(x+4) <=1`
`-1
`-5
Ответ: `[-5; -3]`
1.4.
 2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;
2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;
Сравним `4/3 vv sqrt5-1`
`4 vv 3sqrt5-3`; `7 vv 3sqrt5`; `49 vv 45 (>)`
`4/4 > sqrt5-1`
Ответ: 2
3. Решение неравенств, содержащих неизвестную функцию под знаком модуля
3.1 Смысл неравенства меньше либо равно
`abs(f(x)) <= varphi(x)`
Если `varphi(x)
Если `varphi(x) >= 0` — то необходимо решить систему: `{(varphi(x) >= 0), (-varphi(x)
`{(varphi(x) >= 0), (f(x) = -f(x)) :}`
Примеры с модулем на неравенства со смыслом меньше либо равно
3.1.1 Решить неравенство `abs(1-3x^2) <= 4x`
`{(x >= 0), (1-3x^2 <= 4x), (1-3x^2 >= -4x) :}`; `{(x >= 0), (3x^2+4x -1 >= 0), (3x^2 — 4x -1 <= 0) :}`
Ответ: `[(sqrt7-2)/3; (sqrt7+2)/3 ]`
3.
 10`
10`
`111 > 100`
`9 < 10`
`-37/20 < -5/3`
`-3/2 > -5/3`
Итоговое объединение двух систем: `x < -5/3 uu [-3/2; 2] uu x>=2`
Ответ: `(-infty; -5/3) uu (-3/2; +infty)`
3.1.3 Найти область определения функции `f(x)=sqrt(1/2-abs(3/(5-x))`
`D_f(x)`:
`1/2-abs(3/(5-x)) >= 0`;
`abs(3/(5-x))
` -1/2
`{( 3/(5-x) <= 1/2), ( 3/(5-x) >= -1/2) :}`; `{( 3/(5-x) — 1/2 <= 0), ( 3/(5-x) + 1/2 >= 0):}`;
`{( (6-5+x)/(2(5-x)) <= 0 ), ( (6+5-x)/(2(5-x)) >= 0 ):}`; `2 > 0`; `{( (x +1)/(5-x) <= 0 ), ( (11-x)/(5-x) >= 0 ):}`;
Ответ: `(-infty; -1] uu [11; +infty)`
3.
 2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
В ответ: `[-1; 1/2]` (б)
В ответ `[ ( a: (1/2; 1) uu (1; +infty)), ( б: [-1; 1/2]) :}`
Ответ: `[-1; 1) uu (1; +infty)`
4. Уравнения и неравенства, содержащие неизвестные под несколькими модулями
4.1 Решить неравенство `abs(x-4)-2abs(1-x) >= 1`
На числовом луче отметим значения x, при которых подмодульные значения обращаются в «0»: `x=1; x=4`. Луч разбился на три интервала.
Необходимо на каждом интервале найти решение данного неравенства, то есть решить совокупность трёх систем неравенств:
`[
(
{
(x <= 1), (4-x-2(1-x) >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2(1-x) >= 1) :}
),
(
{(x > 4), (x-4+2(1-x) >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (4-x-2+2x >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2-2x >= 1) :}
),
(
{(x > 4), (x-4+2-2x >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (x+1 >= 0)
:}
),
(
{(1 < x <= 4), (5-3x >= 0) :}
),
(
{(x > 4), (-x-3 >= 0) :}
)
:}` ;
`[
(
{
(x <= 1), (x >= -1)
:}
),
(
{(1 < x <= 4), (x <= 5/3) :}
),
(
{(x > 4), (x <= -3) :}
)
:}` ;
Ответ: `[-1; 5/3]`
4.
 2 -3abs(x)+1)`
2 -3abs(x)+1)`
Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`
6.9 Решить неравенство `3x — abs(x+8) — abs(1-x) <= -6`
Ответ: `(-infty; 1]`
Много задач с решениями на неравенства с модулем можно посмотреть здесь:
Решения неравенств с модулем
Время | Деятельность учителя | Деятельность ученика | ||
Слайд-1-2 | 1.Организационный момент 2.Актуализация знаний | 1мин 3мин | «Просто «думать» не умеет никто. Думать можно только над конкретным вопросом. Умение решать задачи в большой мере сводится к обучению тому, над чем надо думать в ходе решения». Доктор педагогических наук, профессор М.Волович Ребята, приглашаю вас к сотрудничеству и предлагаю работать вместе на сегодняшнем уроке. Продолжаем учиться решать. Формируем математическую интуицию, которая поможет ориентироваться в способах решения уравнений. На уроке можно ошибаться, сомневаться, консультироваться. Дать самому себе установку: «Понять и быть тем первым, который увидит ход решения». На слайде записаны уравнения. Что записано? Как называются эти уравнения? | Приветствие учителя. Дежурный докладывает об отсутствующих. Уравнения. Уравнения, содержащие модуль . |
слайд 3-5 мини-проекты Постановка проблемы | 2мин 3мин | Итак тема нашего урока. Чем мы будем заниматься на уроке и какие поставим цели? Сегодня на уроке мы повторим теоретический материал о модуле и его свойствах, геометрический смысл модуля. Научимся решать уравнения, содержащие модуль. Поработаем над основными понятиями, встречающимися в данной теме. — Дайте определение модуля. — Объясните геометрический смысл модуля. — Назовите свойства модуля. — Чему равен ? — Чему равен ? 1) Можно ли свести решение данных уравнений к решению линейных уравнений? 2).Как бы вы сгруппировали данные уравнения по способам решения?( слайд 2-выше записаны уравнения с модулем). Работают в парах, заполняют таблицу. В ходе рассуждений сделали выводы: 1).Если f(x)=g(x) то есть указали способ решения уравнений 3 и 8. 2).Если то должно выполняться условие: , так как модуль величина неотрицательная, тогда по определению модуля То есть указали способ решения уравнений 4 и 9. Как же можно решить уравнение 5,12? Разве уравнение 11 имеет отношение к теме «Модуль»? А как же решить уравнение 6? Каковы ваши предложения по применению метода интервалов? . | Формулируют тему урока. Повторить, отработать, обобщить способы решения уравнений с модулем. Учащиеся показывают и рассказывают информационные мини- проекты | |
Работают в парах .заполняют таблицу № | уравнения | Способ решения | ||
1 | 1,7,10 | На основании определения модуля | ||
2 | 2 | Не имеет решения | ||
3 | 3,8 | │f(x)│=│g(x)│f (x) =g(x) | ||
4 | 4,9 | g(x) ≥0, f(x)│=g(x), f(x)│=—g(x), | ||
5 | 5,12 | Определение модуля(два случая) | ||
6 | 11 | Свойство модуля=│х│ | ||
7 | 6 | Метод интервалов | ||
3.Физкультминутка 4.Актуализация деятельности учащихся | 1 мин | Немного отдохнем Ваша задача: решить предлагаемые уравнения, проанализировать способы их решения, провести классификацию уравнений, содержащих модуль по способам решения, составить таблицу « Решение уравнений, содержащих модуль». (Вначале более простые примеры выбирают те учащиеся, которым труднее даётся предмет; более сложные примеры выбирают те учащиеся, у которых есть математические способности. После обмена примерами, более сильные учащиеся могут выступать в роли консультантов.) Каждой группе даются карточки с уравнениями (см приложение №1). Каждая группа получает инструкцию. Прежде, чем приступить к работе над проектом, внимательно ознакомьтесь с инструкцией. | Выполняют упражнение(звучит музыка) Работа в группах( 7 групп ) Решают уравнения | |
5.Работа над проектом | 20мин | Инструкция по работе над проектом. 1. Решить уравнения. 2. Проанализировать способы решения. 3. Провести классификацию данных уравнений: а) сгруппировать примеры по способам решения; б) определить, в чём заключается общий вид уравнений в каждой группе; в) дать название каждой группе уравнений. 4. Создать проект таблицы: « Решение уравнений, содержащих модуль». 5. Подготовить защиту проекта. | 1группа-1,2,4 уравнения. 2 группа-3 ,13 ; 3 группа-12 ;9 4группа-10, 7; 5 группа-8 ,11 6 группа-5, 14 7группа- 6 | |
6.Защита проектов | 10мин | Оценочный лист. (5-бальная система) Владеет докладчик терминологией, которую использует своём проекте | ||
Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи | ||||
Выполнила ли группа все поставленные перед ней задачи | ||||
Творческие способности докладчика | ||||
Оформление проекта | В процессе обсуждения участники других групп записывают само уравнение и название метода решения, дома их решают. | |||
7.Домашнее задание | 1мин | Сформировать 2 группы (по3 человека), которые представят результаты исследования в виде презентации к следующему уроку. Задание на карточках. | ||
8 Рефлексия | 1мин | Какая задача стояла перед нами в начале урока? Можно ли считать,что мы ее решили? Сможем ли мы теперь решать уравнения аналогичные данным? Заполните опросный лист(см приложение 2) | Учащиеся отвечают на вопросы, заполняют опорный лист |
Внеклассный урок — Уравнения и неравенства с модулем
Уравнения и неравенства с модулем
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа –6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х|, |а| и т.д.
(Подробнее – в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1. Решить уравнение
|10х – 5| = 15.
Решение.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15
│10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20
│10х = –15 + 5 = –10
↕
│х = 20 : 10
│х = –10 : 10
↕
│х = 2
│х = –1
Ответ: х1 = 2, х2 = –1.
Пример 2. Решить уравнение
|2х + 1| = х + 2.
Решение.
Поскольку модуль – число неотрицательное, то х + 2 ≥ 0. Соответственно:
х ≥ –2.
Составляем два уравнения:
│2х + 1 = х + 2
│2х + 1 = –(х + 2)
Решаем:
│2х + 1 = х + 2
│2х + 1 = –х – 2
↕
│2х – х = 2 – 1
│2х + х = –2 – 1
↕
│х = 1
│х = –1
Оба числа больше –2. Значит, оба являются корнями уравнения.
Ответ: х1 = –1, х2 = 1.
Пример 3. Решить уравнение
|х + 3| – 1
————— = 4
х – 1
Решение.
Уравнение имеет смысл, если знаменатель не равен нулю – значит, если х ≠ 1. Учтем это условие. Наше первое действие простое – не просто освобождаемся от дроби, а преобразуем ее так, чтобы получить подмодульное выражение в чистом виде:
|х + 3| – 1 = 4 · (х – 1),
|х + 3| – 1 = 4х – 4,
|х + 3| = 4х – 4 + 1,
|х + 3| = 4х – 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число – то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х – 3 ≥ 0
4х ≥ 3
х ≥ 3/4
Таким образом, у нас появилось второе условие: корень или корни уравнения должны быть не меньше 3/4.
В соответствии с правилом модуля составляем совокупность двух уравнений и решаем их:
│х + 3 = 4х – 3
│х + 3 = –(4х – 3)
↕
│ х + 3 = 4х – 3
│ х + 3 = –4х + 3
↕
│х – 4х = –3 – 3
│х + 4х = 3 – 3
↕
│х = 2
│х = 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения должен быть не меньше 3/4, но не может быть равен 1. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.
Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.
Ответ: х = 2.
Неравенства с модулем.
Пример 1. Решить неравенство:
|х — 3| < 4
Решение.
Правило модуля гласит:
|а| = а, если а ≥ 0.
|а| = –а, если а < 0.
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая:
х – 3 ≥ 0 и х – 3 < 0.
1) При х – 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х – 3 < 4.
2) При х – 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:
–(х – 3) < 4. Раскрыв скобки, получаем:
–х + 3 < 4.
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
│ х – 3 ≥ 0
│ х – 3 < 4
и
│ х – 3 < 0
│–х + 3 < 4
Решим их:
│х ≥ 3
│ х < 7
и
│х < 3
│х > –1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х < 7 U –1 < х < 3.
Определяем наименьшее и наибольшее значения. Это –1 и 7. При этом х больше –1, но меньше 7. Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от –1 до 7, исключая эти крайние числа.
Ответ: –1 < х < 7.
Или: х ∈ (–1; 7).
Дополнения.
1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х — 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа – к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
–1 < х < 7.
2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:
Для этого наше неравенство надо представить в следующем виде:
–4 < х – 3 < 4.
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число –4 являются границами решения неравенства.
Далее мы просто переносим влево и вправо число –3 с обратным знаком, оставляя х в одиночестве:
–4 + 3 < х < 4 + 3
–1 < х < 7.
Пример 2. Решить неравенство
|х – 2| ≥ 5
Решение.
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны –3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ: –3 ≥ х ≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
–5 ≥ х – 2 ≥ 5
–5 + 2 ≥ х ≥ 5 + 2
Ответ тот же: –3 ≥ х ≥ 7.
Или: х ∈ [–3; 7]
Пример решен.
Пример 3. Решить неравенство:
6х2 – |х| – 2 ≤ 0
Решение.
Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х2 – х – 2 ≤ 0.
Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:
6х2 – (–х) – 2 ≤ 0.
Раскрываем скобки:
6х2 + х – 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
│6х2 – х – 2 ≤ 0
│ х ≥ 0
и
│6х2 + х – 2 ≤ 0
│ х < 0
Надо решить неравенства в системах – а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.
Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х2 – х – 2 = 0.
Как решается квадратное уравнение – см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х1 = –1/2, х2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от –1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[–1/2; 2/3].
Теперь решим второе квадратное уравнение:
6х2 + х – 2 = 0.
Его корни:
х1 = –2/3, х2 = 1/2.
Вывод: при х < 0 корнями исходного неравенства являются также все числа от –2/3 до 1/2.
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от –2/3 до 2/3, включая и эти крайние числа.
Ответ: –2/3 ≤ х ≤ 2/3.
Или: х ∈ [–2/3; 2/3].
Презентация — Решение уравнения с модулем
Слайды и текст этой онлайн презентации
Слайд 1
Решение уравнения с модулем
Родионова Г. М., учитель математики МБУ «Школа №82» г.о.Тольятти
М., учитель математики МБУ «Школа №82» г.о.Тольятти
Слайд 2
Определение модуля
Слайд 3
Определение модуля
Слайд 4
Определение модуля
Слайд 5
График функции
Слайд 6
Решение уравнений с модулем
Слайд 7
Решение уравнений с модулем
Слайд 8
Уравнение с модулем
Решить уравнение
Решение:
Для раскрытия двух модулей рассмотрим
следующие 4 случая:
Найдем нули
подмодульных
выражений
I способ.
Слайд 9
или
или
или
Слайд 10
Решений нет
Решений нет
Ответ: [-1;3]
Слайд 11
Решите уравнение
II способ.
Так как обе части уравнения неотрицательные,
то при возведении их в квадрат получим
уравнение равносильное данному.
Из определения модуля следует. Что последнее
равенство выполнимо, если
т.е. когда
Ответ: [-1;3]
Слайд 12
III способ — графический
Перепишем данное уравнение в
следующем виде:
Далее изобразим графики функций
И укажем абсциссы их общих точек. Графики совпадают при
Графики совпадают при
Ответ:
Слайд 13
III способ — графический
Ответ: [-1;3]
Слайд 14
IVспособ — графический
Найдем абсциссы общих точек графика
функции
и прямой
Для построения первого графика
достаточно взять несколько точки
с абсциссами х 3, после
чего последовательно соединить их до
получения ломаной.
Слайд 15
Ответ: [-1;3]
IVспособ — графический
Слайд 16
V способ
Числа -1 и 3 разбивают числовую прямую на
Три интервала, на каждом из которых
подмодульные выражения имеют определенный знак.
Найдем решение уравнения в каждом из
полученных промежутков:
Слайд 17
или
или
Слайд 18
Нет решения
Ответ: [-1;3]
Слайд 19
VIспособ
На числовой прямой найдем все точки с
координатой (х) , сумма расстояний от
которой до точек с координатами (-1) и (3)
равна 4.
Слайд 20
Литература:
Алгебра 9кл: учеб. для общеобразоват. учреждений/
Мордкович А.Г .– М.: Мнемозина, 2017.
Журнал «Математика в школе» №3,2010 , стр.31.
Алгебра: Нестандартные задачи: экспресс-
репетитор для подготовки к ГИА: 9-й кл./Г.В.
Сычева, Н.В. Гусева,В.А. Гусев,-М.:АСТ:Астрель
; Владимир: ВКТ, 2010
для общеобразоват. учреждений/
Мордкович А.Г .– М.: Мнемозина, 2017.
Журнал «Математика в школе» №3,2010 , стр.31.
Алгебра: Нестандартные задачи: экспресс-
репетитор для подготовки к ГИА: 9-й кл./Г.В.
Сычева, Н.В. Гусева,В.А. Гусев,-М.:АСТ:Астрель
; Владимир: ВКТ, 2010
Решение уравнений содержащих неизвестную под знаком модуля
МБОУ покровская средняя общеобразовательная школа № 1 с УИОП Иванова Саргылана Семеновна учитель математики МБОУ «ПСОШ № 1 с УИОП» Стаж работы: 15 лет Категория: высокая
решение уравнений, содержащих неизвестную под знаком модуля
способы решения уравнений
ознакомление учащихся с теоретическими основами решения уравнений с модулем, рекомендациями к решению, алгоритмирование процесса решения уравнений содержащих неизвестную под знаком модуля
ВВЕДЕНИЕ
Решение уравнений.
1.1.Определение модуля. Решение по определению
1.2. Решение уравнений по правилам
1.3. Задачи с несколькими модулями. Последовательное и параллельное раскрытие модулей
1.4. Метод интервалов в задачах с модулями
1.5. Вложенные модули
1.6. Модули и квадраты
1.7. Модули неотрицательных выражений
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
Решение уравнений по правилам
1-е правило: | f ( x )| = g ( x )
2-е правило: | f ( x )| = g ( x )
2 способ:
1 способ:
Пример. Решить уравнение | x 2 – 7 x + 11| = x + 1. Решение. Избавимся от модуля двумя описанными выше способами:
Как видим, в обоих случаях приходится решать те же самые два квадратных уравнения , но в первом случае их сопровождают квадратные неравенства , а во втором – линейное. Поэтому второй способ для данного уравнения проще. Решая квадратные уравнения, находим корни первого , оба корня удовлетворяют неравенству . Дискриминант второго уравнения отрицателен, следовательно, уравнение корней не имеет.
Поэтому второй способ для данного уравнения проще. Решая квадратные уравнения, находим корни первого , оба корня удовлетворяют неравенству . Дискриминант второго уравнения отрицателен, следовательно, уравнение корней не имеет.
Ответ : .
Способ освобождения от модуля –
замена переменной
Пример . Решить уравнение:
Решение. Заметим, что , тогда уравнение примет вид:
Пусть , тогда решим квадратное уравнение:
Его корни , условию удовлетворяет первый корень.
Возвращаясь к переменной х , получаем уравнение
решая которое находим:
Ответ : .
Задачи с несколькими модулями.
Два основных подхода к решению.
«последовательное»
раскрытие модулей
«параллельное» раскрытие модулей
Сначала один из модулей изолируется в одной части уравнения (или неравенства) и раскрывается одним из описанных ранее методов. Затем то же самое повторяется с каждым из получившихся в результате уравнений с модулями и так продолжается, пока мы не избавимся ото всех модулей.
Затем то же самое повторяется с каждым из получившихся в результате уравнений с модулями и так продолжается, пока мы не избавимся ото всех модулей.
Можно снять сразу все модули в уравнении или неравенстве и выписать все возможные сочетания знаков подмодульных выражений. При снятии модуля может получить один из двух знаков – плюс или минус. Эти области определяются знаками выражений под модулями.
Пример . Решить уравнение:
Решение.
Уединим второй модуль и раскроем его, пользуясь первым способом , то есть просто определением абсолютной величины :
К полученным двум уравнениям применяем второй способ освобождения от модуля:
Наконец, решаем получившиеся четыре линейных уравнения и отбираем те их корни, которые удовлетворяют соответствующим неравенствам :
Ответ: -1;
Пример . Решить уравнение:
Решение.
Рассмотрим 4 возможных набора знаков выражений под модулями.
Лишь первый и третий из этих корней удовлетворяют соответствующим неравенствам, а значит, и исходному уравнению.
Ответ: -1;
Метод интервалов в задачах с модулями.
Пусть имеется уравнение, в которое входят три модуля от линейных выражений; например: | x – a | + | x – b | + | x – c | = m .
Первый модуль равен x – a при x ³ a и a – x при x a . Второй равен x – b или b – x при x ³ b и x b соответственно. Аналогично раскрывается и третий модуль. Нарисуем эти области и возьмем их пересечения.
В частности , если все выражения под модулями рациональны, то достаточно отметить на оси их корни, а также точки, где они не определены, то есть корни их знаменателей. Отмеченные точки и задают искомые промежутки знакопостоянства.
Отмеченные точки и задают искомые промежутки знакопостоянства.
Пример . Решить уравнение:
Решение.
Найдем нули функции x+2=0 или x+3=0 , откуда x=-2 , x=-3 . Рассмотрим 3 возможных набора знаков выражений под модулями.
.
Решаем задачу на каждом интервале:
Ответ:
Итак, данное уравнение не имеет решений.
Вложенные модули
Последовательное раскрытие модулей наиболее эффективно в «задачах-матрешках», где внутри одного модуля находится другой, а то и несколько.
Пример . Решить уравнение:
Решение.
Освободимся от внешнего модуля, получим:
Второе уравнение совокупности решений не имеет, так как модуль всегда положителен, а первое уравнение
равносильно совокупности:
Ответ: 0; 2.
Модули неотрицательных выражений.
Пример 1 . Решить уравнение:
Решить уравнение:
Решение.
Нетрудно догадаться, что все выражения, стоящие под знаком второго, третьего и т.д. модулей положительны. И поскольку модуль положительного выражения равен самому этому выражению, получим
Ответ: 0
Пример 2 . Решить уравнение:
Решение.
Воспользуемся тождеством , и получим уравнение , решая которое методом интервалов получим ответ
Ответ:
В процессе работы над темой «Решение уравнений содержащих неизвестную под знаком модуля» :
- Изучили литературу по данному вопросу. Познакомились с алгебраическим подходом к решению уравнений, содержащих неизвестную под знаком модуля. Исследовали количество решений уравнения, в зависимости от параметров входящих в её условие.
- Изучили литературу по данному вопросу.
- Познакомились с алгебраическим подходом к решению уравнений, содержащих неизвестную под знаком модуля.

- Исследовали количество решений уравнения, в зависимости от параметров входящих в её условие.
и пришли к выводу:
В ряде случаев при решении уравнений с модулем, возможно, решать уравнения по правилам.
модулей для дифференциальных уравнений
модулей для дифференциальных уравнений
Содержание
Учебное пособие по вспомогательному приложению
Численное решение дифференциальных уравнений
Спринты мирового класса
Модель логистического роста
Модели хищника-жертвы
Линейные однородные дифференциальные уравнения второго порядка
с постоянными коэффициентами
Движение пружины
Системы с принудительной пружиной I
Матричные операции
Собственные значения и собственные векторы
Траектории линейных систем
Маятник
Свинец в теле
Усиление и фазовый сдвиг
Система Ван дер Поля
Учебное пособие по вспомогательному приложению
- Назначение:
Чтобы изучить основы Maple V, Release 4 или Release 5
для использования в модулях дифференциальных уравнений.
- Предварительные требования:
Никто Доступно для:
Клен
Численные решения дифференциальных уравнений.
- Назначение:
Получить опыт работы с численными методами аппроксимации
решение для
задачи начального значения первого порядка. - Предварительные требования:
Изучите базовое руководство для своей системы компьютерной алгебры. Доступно для:
Клен
Спринты мирового класса
- Назначение:
Чтобы исследовать применимость линейного дифференциала
уравнение как модель для
процесс спринта, и чтобы проиллюстрировать важность
параметров в моделировании. - Предварительные требования:
Учебник для вашего вспомогательного приложения и способность решать
линейный
дифференциальное уравнение с постоянными коэффициентами. Доступно для:
Клен
Модель логистического роста
- Назначение:
Изучить стандартную модель роста населения в
стесненная среда.
- Предварительные требования:
Разделение переменных. Доступно для:
Клен
Модели Хищник-Жертва
- Назначение:
Разработать и изучить модель Лотки-Вольтерры.
для взаимодействий хищник-жертва в качестве прототипа первого порядка
система дифференциальных уравнений. - Предварительные требования:
Модуль по численным решениям
дифференциальные уравнения. Доступно для:
Клен
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Назначение:
Чтобы исследовать качественное поведение
решения начальных задач видаy "+ ay '+ by = 0, у (0) = у0, у '(0) = у1.В частности, чтобы определить, как решения зависят от
знаков и величин коэффициентов a и b и на
первоначальные условия. - Предварительные требования:
Учебник по вспомогательному приложению и
знание символической формы решений дифференциала
уравнения вида y «+ ay ‘+ by = 0 .
Доступно для:
Клен
Пружинное движение
- Назначение:
Чтобы исследовать
математическая модель
y » + (c / m) y ‘+ (K / m) y = 0
для пружинного движения и изучения эффекта
повышенного демпфирования. - Предварительные требования:
Знание линейных однородных
дифференциальные уравнения с постоянной
коэффициенты. Доступно для:
Клен
Системы с принудительной пружиной I
- Назначение:
Чтобы изучить эффекты внешней движущей силы
на простом линейном осцилляторе, с демпфированием или без него. - Предварительные требования:
Модуль Spring Motion и знания
символической формы решений дифференциальной
уравнения вида y «+ ay ‘+ by = f (t) ,
где f — функция синуса или косинуса. Доступно для:
Клен
Матричные операции
- Назначение:
Поэкспериментировать с
матричные операции, особенно
умножение, инверсия и
детерминанты, и исследовать
приложения к решениям систем
линейные уравнения. В процессе
В процессе
изучая эти матричные операции, мы
научится пользоваться помощником
приложение для проведения матрицы
вычисления. - Предварительные требования:
Базовое понимание линейных комбинаций векторов,
знакомство с матричным умножением. Доступно для:
Клен
Собственные значения и собственные векторы
- Назначение:
Чтобы поэкспериментировать и изучить свойства
собственные значения и собственные векторы и их применение к
дифференциальные уравнения. - Предварительные требования:
Модуль матричных операций и
концепция приведенной формы эшелона строк. Доступно для:
Клен
Траектории линейных систем.
- Назначение:
Для исследования траекторий на фазовой плоскости
однородных линейных систем 2×2 первого порядка
дифференциальные уравнения вида X ‘= AX. - Предварительные требования:
Модуль матричных операций и
понимание смысла собственных значений и
собственные векторы матрицы A.
Доступно для:
Клен
Маятник
- Назначение:
Чтобы исследовать фазовую плоскость для второго порядка
нелинейное дифференциальное уравнение, в частности стандартное
модель для демпфированных и незатухающих маятников. - Предварительные требования:
Модуль Spring Motion. Доступно для:
Клен
Свинец в теле
- Назначение:
Разработать и изучить модель отсека
на количество свинца в организме человека и изучить
трехмерная управляемая линейная система. - Предварительные требования:
Модуль по траекториям линейных
Уравнения. Доступно для:
Клен
Усиление и фазовый сдвиг
- Назначение:
Чтобы изучить взаимосвязь между частотой
внешняя движущая сила и параметры затухающей
линейный осциллятор. - Предварительные требования:
Модуль по принудительному пружинному движению.
Доступно для:
Клен
Система ван дер Поля
- Назначение:
Чтобы исследовать модель Ван дер Поля для нелинейного
электрическая схема — в частности, для изучения предельного цикла
явление. - Предварительные требования:
Модуль по принудительному пружинному движению. Доступно для:
Клен
| CCP Home |
Ресурсы |
Ресурсы для учителей |
Модуль 4 — Линейные уравнения
Уроки:
Цели обучения:
LTLT: Я могу интерпретировать линейные данные и решать реальные проблемы, связанные с линейными отношениями.
LT1: Я могу идентифицировать графики и уравнения, которые представляют линейные данные.
LT2: Я могу вычислить наклон прямой.
LT3: Я могу найти решения линейных уравнений.
LT4: Я могу решать линейные уравнения, используя свойства равенства, распределительного свойства и комбинируя одинаковые термины.
LT5: Я могу определить точку пересечения оси Y с помощью графика или уравнения.
LT6: Я могу писать линейные уравнения в форме пересечения наклона.
LT7: Я могу написать линейное уравнение для представления реальных данных.
LT8: Я могу решить систему линейных уравнений.
Игры:
Описание модуля:
В Модуле 4 учащиеся расширяют то, что они уже знают о единицах измерения и пропорциональных отношениях, до линейных уравнений и их графиков. Учащиеся понимают связь между пропорциональными отношениями, линиями и линейными уравнениями в этом модуле. Учащиеся учатся применять навыки, приобретенные в 6 и 7 классах, в отношении символической записи и свойств равенства, чтобы расшифровывать и решать уравнения с одной переменной, а затем с двумя переменными.
Проекты:
Стандарты:
8.EE.5 График пропорциональных соотношений, интерпретируя единичную ставку как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график расстояние-время с уравнением расстояние-время, чтобы определить, какой из двух движущихся объектов имеет большую скорость.
8.EE.6 Используйте аналогичные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b.
8.EE.7 Решите линейные уравнения с одной переменной.
Архив уроков:
Суб-финн на выезде — 26.01.2017
Начальный модуль алгебры 4: Системы линейных уравнений и неравенства в двух переменных
Цель обучения: Учащиеся будут решать системы линейных уравнений и неравенств с двумя переменными, используя различные методы.
Модуль включает:
Предварительная оценка,
Введение: системы линейных уравнений и неравенств с двумя переменными,
Раздел 1: Решение систем линейных уравнений,
Раздел 2: Решение систем линейных уравнений методом подстановки.
Раздел 3: Решение систем линейных уравнений методом исключения.
Раздел 4: Графические системы линейных неравенств.
Пост-оценка.
- Дата:
- 2013
- Тип первичного материала:
- Модуль онлайн-курса
- Другие типы материалов:
- Тренировка и практика, Презентация, Викторина / Тест, Моделирование, Учебное пособие
- Учреждение:
- Колледж полуострова Кенай / Университет Аляски
- Название проекта:
- За пределами Анкориджа: расширение возможностей развития и повышения квалификации персонала
- TAACCCT Раунд:
- 1
- Субъектов:
- Начальная алгебра, система координат, графики, линии, системы, линейные уравнения, переменные, метод подстановки, метод исключения, неравенства
Промышленность / Род занятий
- Отраслевой партнер:
- Необходимые партнеры-работодатели: Архитектурно-дизайнерские бюро УСХ; Харви Х.
 Хайтауэр, архитектор; DOWL HKM; и UMIAQ
Хайтауэр, архитектор; DOWL HKM; и UMIAQ - Сектор промышленности:
- Развитие образования
- Род занятий:
- Все профессии (00-0000)
Информация об образовании / обучении
- Использование в образовательных целях:
- Модуль позволяет учащимся улучшить свои знания базовой математики перед колледжем без затрат на обучение, обычно связанных с курсами коррекционной математики.
- Требуемое время:
- Примерно 6 часов (самостоятельно)
- Тип интерактивности:
- Активно — требует, чтобы пользователь отвечал на подсказки, вопросы и т. Д.
- Примечание о качестве:
- Экспертная и внешняя проверка.
- Примечание курса:
- Основы дошкольной математики: начальная алгебра
Доступность
- Специальные возможности:
- Текстовый доступ — преобразование текста в речь
- Text Adjust — совместимый
- Настройка текста — настройка шрифта и цветов
- Макет чтения — перекомпоновка текста
- Макет чтения — номера страниц соответствуют печатному материалу
- Макет чтения — перекомпоновка текста
- Порядок чтения — Макет цифрового ресурса
- Структурная разметка — текст навигации
- Структурная разметка — Списки
- Структурная разметка — приложение для чтения электронных книг
- Разметка таблицы
- цвета, совместимые со вспомогательными технологиями
- Контрастность не менее 4.
 5: 1.
5: 1. - Язык — разметка
- Язык — разметка отрывка
- Недекоративные изображения имеют замещающий текст
- Декоративные изображения с нулевым замещающим текстом
- Синхронизированная текстовая дорожка
- Расшифровка стенограммы с аудиоконтентом
- Немерцающее содержимое
- Содержание STEM (например, математика, химия) Разметка
- Интерактивное — разметка
- Интерактивный — текстовые подсказки
Авторские права / Лицензии
Математическое моделирование модулей — термоэлектрические
11.0 Математическое моделирование термоэлектрических модулей охлаждения
11.1 ВВЕДЕНИЕ: Работа термоэлектрических охлаждающих устройств может быть описана математически, а характеристики устройства могут быть легко смоделированы на персональном компьютере. Поскольку полупроводниковый материал, используемый при изготовлении модуля, имеет несколько свойств, зависящих от температуры, необходимо учитывать влияние температуры на работу модуля, если необходимо разработать реалистичную модель. Мы не пытались дать очень подробное описание методов компьютерного моделирования, а скорее представить основные алгебраические выражения, необходимые для моделирования работы термоэлектрического модуля.
Мы не пытались дать очень подробное описание методов компьютерного моделирования, а скорее представить основные алгебраические выражения, необходимые для моделирования работы термоэлектрического модуля.
Ferrotec America провела всесторонний анализ многих термоэлектрических охлаждающих модулей в широком диапазоне температур. Это исследование привело к разработке математических моделей, которые можно использовать для надежного прогнозирования характеристик модуля в типичных условиях эксплуатации. Представленные здесь данные основаны на работе модуля в нормальной воздушной атмосфере с теплопроводящей смазкой (компаунд для теплоотвода), используемой на стыках горячего и холодного модуля. Эти условия применимы к большинству применений термоэлектрического охлаждения.Следует отметить, что для модулей с метаболизированными внешними поверхностями может наблюдаться небольшое улучшение характеристик, если модули монтируются с припоем, а не с термопастой. Кроме того, когда модули работают в вакууме, можно увидеть небольшое или умеренное увеличение производительности, особенно в случае многоступенчатых устройств.
11.2 ТЕМПЕРАТУРНО-ЗАВИСИМЫЕ СВОЙСТВА МАТЕРИАЛА: Существует ряд параметров, связанных с термоэлектрическими материалами и модулями, которые обычно необходимо учитывать в математической модели.Однако, поскольку фактические данные тестирования модуля использовались для получения нескольких важных коэффициентов, некоторыми факторами можно пренебречь, что упрощает процесс моделирования. Элементы, которые должны быть включены в модель, включают коэффициент Зеебека , эффективный модуля (SM), электрическое сопротивление (RM) и теплопроводность (KM).
Значения SM, RM и KM могут быть математически выражены полиномиальными уравнениями. Указанные коэффициенты уравнения, применимые в диапазоне от -100 ° C до + 150 ° C, были получены из стандартного модуля на 71 пару и 6 ампер.Другие конфигурации модулей можно легко смоделировать, применив простой поправочный коэффициент, как описано в параграфе 11.2.4. Обратите внимание, что при использовании различных уравнений значения температуры должны быть указаны в градусах Кельвина.
Альтернативный метод оценки температурно-зависимых свойств модуля, который может быть полезен при определенных обстоятельствах, включает использование табличных данных модуля. Значения, представляющие средние характеристики SM, RM и KM для выбранных модулей в широком диапазоне температур, можно найти в Приложении A в конце этого руководства.Хотя этот метод несколько менее точен, чем расчетные значения, он обеспечивает относительно простой подход к прогнозированию производительности модуля.
11.2.1 КОЭФФИЦИЕНТ SEEBECK: Когда на термоэлектрическом устройстве поддерживается разность температур, на входных клеммах можно определить напряжение. Величина результирующего напряжения, называемая ЭДС Зеебека, пропорциональна разнице температур. Коэффициент Зеебека как функция температуры может быть выражен полиномом третьего порядка:
S M = s 1 + s 2 T + s 3 T 2 + s 4 T 3
Где:
S M — коэффициент Зеебека модуля в вольтах / ° K
T — средняя температура модуля, ° K
Коэффициенты для модуля на 71 цикл, 6 ампер
с 1 = 1. 33450 × 10 -2
33450 × 10 -2
с 2 = -5,37574 × 10 -5
с 3 = 7,42731 × 10 -7
с 4 = -1,27141 × 10 -9
Приведенное выше полиномиальное выражение представляет коэффициент Зеебека, когда разность температур в модуле равна нулю (DT = Th — Tc = 0). Когда DT> 0, коэффициент Зеебека должен быть вычислен как для температуры Th, так и для Tc, используя выражения:
| S MTh или S MTc = с 1 T + | с 2 T 2 | + | с 3 T 3 | + | с 4 T 4 |
| 2 | 3 | 4 |
S M = (S MTh — S MTc ) / DT
Где:
S MTh — коэффициент Зеебека модуля при температуре горячей стороны Th
S MTc — коэффициент Зеебека модуля при температуре холодной стороны Tc
11. 2.2 СОПРОТИВЛЕНИЕ МОДУЛЯ: Электрическое сопротивление термоэлектрического модуля как функция температуры может быть выражено полиномами третьего порядка для двух условий (a) и (b):
2.2 СОПРОТИВЛЕНИЕ МОДУЛЯ: Электрическое сопротивление термоэлектрического модуля как функция температуры может быть выражено полиномами третьего порядка для двух условий (a) и (b):
| (а) при DT = 0: | R M = r 1 + r 2 T + r 3 T 2 + r 4 T 3 | |||||||||
| б) при DT> 0: |
| |||||||||
Где:
R M — сопротивление модуля в Ом
R MTh — сопротивление модуля при температуре горячей стороны Th
R MTc — сопротивление модуля при температуре холодной стороны Tc
T — средняя температура модуля, ° K
Коэффициенты для модуля на 71 цикл, 6 ампер
r 1 = 2. 08317
08317
r 2 = -1,98763 × 10 -2
r 3 = 8,53832 × 10 -5
r 4 = -9,03143 × 10 -8
11.2.3 ТЕПЛОПРОВОДНОСТЬ МОДУЛЯ: Теплопроводность термоэлектрического модуля как функция температуры может быть выражена полиномами третьего порядка для двух условий (a) и (b):
| а) при DT = 0: | K M = k 1 + k 2 T + k 3 T 2 + k 4 T 3 | |||||||||
| б) при DT> 0: |
| |||||||||
Где:
K — теплопроводность модуля, Вт / ° K
K MTh — теплопроводность при температуре горячей стороны Th
K MTc — теплопроводность при температуре холодной стороны Tc
T — средняя температура модуля в ° K
Коэффициенты для модуля на 71 цикл, 6 А
к 1 = 4. 76218 × 10 -1
76218 × 10 -1
к 2 = -3,89821 × 10 -6
к 3 = -8,64864 × 10 -6
к 4 = 2,20869 × 10 -8
11.2.4 ПРЕОБРАЗОВАНИЕ ПАРАМЕТРОВ ДЛЯ ДРУГИХ КОНФИГУРАЦИЙ МОДУЛЯ: Показанные параметры SM, RM и KM рассчитаны для термоэлектрического модуля на 71 пару, 6 ампер. Если необходимо моделировать новую или другую конфигурацию модуля, необходимо применить коэффициент преобразования к каждому из этих параметров, как показано ниже:
| ||||||
|
Где:
S новый — коэффициент Зеебека для нового модуля
R новый — электрическое сопротивление нового модуля
K новый — теплопроводность нового модуля
N новый — количество пар в новом модуле
I новый — оптимальный или максимальный ток нового модуля
11. 3 РАСЧЕТ ХАРАКТЕРИСТИК ТЕРМОЭЛЕКТРИЧЕСКОГО МОДУЛЯ: Существует пять переменных параметров, применимых к термоэлектрическому модулю, которые влияют на его работу. К этим параметрам относятся:
3 РАСЧЕТ ХАРАКТЕРИСТИК ТЕРМОЭЛЕКТРИЧЕСКОГО МОДУЛЯ: Существует пять переменных параметров, применимых к термоэлектрическому модулю, которые влияют на его работу. К этим параметрам относятся:
| I — | входной ток модуля выраженный в амперах |
| Вин — | входное напряжение модуля, выраженное в вольтах |
| Чт — | температура горячей стороны модуля, выраженная в ° K |
| TC — | температура холодной стороны модуля, выраженная в ° K |
| Qc — | Подвод тепла к модулю (или отвод тепла от него), выраженный в ваттах. |
Для расчета производительности модуля необходимо установить по крайней мере три из этих переменных на определенные значения. Две общие схемы расчета включают либо (а) фиксацию значений Th, I и Qc, либо (б) фиксацию значений Th, I и Tc. Для человека, ориентированного на компьютер, может быть разработана относительно простая процедура вычислений для постепенного перехода через серию фиксированных значений для получения выходных данных о производительности модуля в диапазоне рабочих условий.
Две общие схемы расчета включают либо (а) фиксацию значений Th, I и Qc, либо (б) фиксацию значений Th, I и Tc. Для человека, ориентированного на компьютер, может быть разработана относительно простая процедура вычислений для постепенного перехода через серию фиксированных значений для получения выходных данных о производительности модуля в диапазоне рабочих условий.
11.4 РАСЧЕТЫ ДЛЯ ОДНОСТУПЕНЧАТЫХ МОДУЛЕЙ: Эти уравнения математически описывают характеристики одноступенчатого термоэлектрического модуля, как показано на рисунке (11-l).При вводе числовых данных не забывайте, что значения температуры должны быть выражены в градусах Кельвина (° K). Расчеты различных параметров следует выполнять в указанном порядке.
Рисунок (11-1)
a) Разница температур (DT) по модулю в ° K или ° C составляет:
DT = T h — T c
b) Тепловая накачка (Qc) модулем в ваттах составляет:
Q c = (S M × T c × I) — (0. 5 × I 2 × R M ) — (K M × DT)
5 × I 2 × R M ) — (K M × DT)
c) Входное напряжение (Vin) модуля в вольтах:
В дюйм = (S M × DT) + (I × R M )
d) Входная электрическая мощность (вывод) модуля в ваттах составляет:
P дюйм = V дюйм × I
e) Тепло, отбрасываемое модулем (Qh) в ваттах, составляет:
Q ч = P дюйм + Q c
f) Коэффициент полезного действия (COP) холодильника:
COP = Q c / P дюйм
11.5 РАБОТА В РЕЖИМЕ НАГРЕВА: Термоэлектрические модули могут работать в режиме нагрева путем изменения полярности подаваемого постоянного тока. При таком использовании ТЕ-модуль действует как «тепловой насос», и при определенных условиях может быть достигнута эффективность нагрева, превышающая 100 процентов. При нагревании объекта небольшой массы происходит быстрое повышение температуры, поэтому необходимо соблюдать осторожность, чтобы избежать перегрева модуля или объекта. В режиме нагрева, показанном на рисунке (11-2), теплоотвод и объект фактически находятся в противоположных положениях, при этом объект теперь имеет температуру (Th), а теплоотвод — температуру (Tc).
В режиме нагрева, показанном на рисунке (11-2), теплоотвод и объект фактически находятся в противоположных положениях, при этом объект теперь имеет температуру (Th), а теплоотвод — температуру (Tc).
Рисунок (11-2) a) Тепловой поток к объекту (Qh) определяется выражением:
Q h = (S M × T h × I) + (0,5 × I 2 × R M ) — (K M × (T h — T ) в ))
b) Коэффициент полезного действия нагревателя (COPH):
COPH = Q ч / P дюйм
11.5.1 Характеристики режима нагрева стандартного модуля на 71 пару, 6 ампер графически представлены на рисунках (11-3) и (11-4).Эти графики иллюстрируют производительность модуля при температуре радиатора 25 ° C.
Рисунок (11-3)
Тепловыделение при различных температурах объектов горячей стороны
Рисунок (11-4)
Коэффициент полезного действия в режиме нагрева
11. 6 ДРУГИЕ ХАРАКТЕРИСТИКИ ТЕРМОЭЛЕКТРИЧЕСКИХ УСТРОЙСТВ: Есть много других свойств термоэлектрических устройств, которые можно описать математически.Далее следуют несколько характеристик, которые могут быть интересны в конкретных ситуациях. Помните, что значения температуры должны быть выражены в ° K.
6 ДРУГИЕ ХАРАКТЕРИСТИКИ ТЕРМОЭЛЕКТРИЧЕСКИХ УСТРОЙСТВ: Есть много других свойств термоэлектрических устройств, которые можно описать математически.Далее следуют несколько характеристик, которые могут быть интересны в конкретных ситуациях. Помните, что значения температуры должны быть выражены в ° K.
a) Максимальная тепловая насосная мощность (Qmax) термоэлектрического модуля в ваттах определяется следующим выражением. Обратите внимание, что DT = 0 при условии максимального Qc и, следовательно, Tc = Th.
| Q макс = | S M 2 × T C 2 |
| 2 × R M |
b) Максимальный перепад температур (DTmax) в ° K может быть выражен, как показано ниже.Однако для получения точного значения DTmax потребуется выполнить серию итерационных вычислений, сравнивающих Tc с DTmax при фиксированном значении Th.
| DT макс = | S M 2 × T C 2 |
| 2 × R M × K M |
c) Достоинства (Z) — это мера общих характеристик термоэлектрического устройства или материала.Z всегда выше для необработанного термоэлектрического полупроводникового материала, чем для реального модуля, работающего в тепловой системе. Поскольку на рабочий модуль влияют межфазные, кондуктивные, конвективные и другие потери, эффективный показатель качества ниже, чем у сырья. Знак отличия может быть выражен:
Где :
a — коэффициент Зеебека материала, об / ° K
p — удельное электрическое сопротивление материала в Ом-см
k — теплопроводность материала в Вт / см-° К
d) Оптимальный ток (Iopt) в амперах, необходимый для обеспечения максимальной скорости отвода тепла (Qmax), составляет:
для сырья | Для модуля TE | ||||||
|
Где :
a — площадь поперечного сечения отдельного термоэлектрического элемента в сантиметрах.
l — длина (высота) отдельного термоэлектрического элемента в сантиметрах
R — сопротивление отдельного термоэлектрического элемента в омах.
11.7 МОДЕЛИРОВАНИЕ КОМПЛЕКСНЫХ ТЕРМОЭЛЕКТРИЧЕСКИХ СИСТЕМ ОХЛАЖДЕНИЯ: Информация, представленная в предыдущих параграфах, описывает математическое моделирование термоэлектрических модулей в отличие от полных тепловых систем. Путем включения расчетов модуля в более сложную модель системы можно точно смоделировать общие тепловые характеристики.Два источника утечки тепла, которые нельзя упускать из виду в полной тепловой модели, включают (а) теплопроводность между охлаждаемым объектом и радиатором и (б) теплопроводность через зажимные винты, если таковые имеются, которые физически соединяют радиатор и охлаждение. объект.
Теплопроводность между радиатором и объектом обычно включает передачу тепла через воздушный зазор, окружающий область установки модуля. Фактическое значение утечки тепла можно рассчитать, используя уравнение в параграфе 8.4.1, где площадь (A) — это «открытая» площадь поверхности, не покрытая термоэлектрическими модулями, расстояние ( x ) — это ширина воздушного зазора, а теплопроводность (K) — это значение для воздуха.
Фактическое значение утечки тепла можно рассчитать, используя уравнение в параграфе 8.4.1, где площадь (A) — это «открытая» площадь поверхности, не покрытая термоэлектрическими модулями, расстояние ( x ) — это ширина воздушного зазора, а теплопроводность (K) — это значение для воздуха.
Теплопроводность через зажимные винты также можно рассчитать с помощью того же уравнения. В этом случае площадь (A) — это площадь поперечного сечения всех крепежных винтов, рассчитанная на основе шагового диаметра винта , а (K) — это теплопроводность материала винта.
Добавление и редактирование уравнений — справочная служба Digication
Для наших пользователей в области математики, науки и техники мы сделали возможным включение математических уравнений в красивом формате в электронные портфолио. Уравнения можно добавить с помощью кнопки на панели инструментов текстового формата или с помощью специальной кнопки модуля уравнений в библиотеке.
Добавление уравнения в модуль отформатированного текста
Чтобы добавить уравнение в модуль Rich Text, сначала нажмите кнопку Edit (1) сбоку от модуля.
Поместите курсор в то место, где вы хотите разместить уравнение, а затем нажмите кнопку «Уравнение» на панели инструментов «Формат текста» (2).
При нажатии кнопки Equation откроется редактор Equation Editor (3). В отведенном месте вы можете ввести свое уравнение или вставить его на языке LaTeX, ASCIIMath или MathML.
Уравнение появится в окне предварительного просмотра (4) и в модуле Rich Text (5), обработанном в соответствии с синтаксисом, введенным в редакторе формул.
Использование модуля Equation
Чтобы добавить уравнение с помощью инструмента «Уравнения», перейдите на страницу, на которой вы хотите разместить уравнение, и нажмите кнопку Добавить содержимое (1).
В своей библиотеке прокрутите вниз и нажмите кнопку Equation (2).
Модуль Rich Text будет размещен на вашей странице с уже открытым редактором формул.Отсюда процесс ввода и оформления вашего уравнения будет таким же, как если бы вы вводили его в существующий модуль Rich Text.
Стилизация уравнения
Чтобы стилизовать уравнение, нажмите кнопку Настройки в модуле Rich Text. На панели настроек щелкните Расширенная настройка .
В раскрытых параметрах расширенной настройки щелкните Уравнение (3), чтобы развернуть параметры стиля.Доступные свойства стиля:
- Размер шрифта
- Цвет шрифта
- Прокладка
- Цвет границы
- Цвет фона
|
CAMCLE: Модули | Хофстра | Нью-Йорк
Сегменты каждого модуля следующие.
Модуль A: Основы алгебры и решение уравнений
Решение полиномиальных уравнений; Решение уравнений с рациональными выражениями; Решение уравнений с радикальными выражениями; Разрешение неравенств; Решение системы уравнений
Модуль 1: Основы готовности к исчислению
Алгебраическая готовность к исчислению; Понимание функций; Состав функций; Графики типичных функций; Преобразования функций
Модуль 2: Основы тригонометрии
Круговое определение триггерных функций; Тригонометрические идентичности и отношения *; Графики функций синуса, косинуса и касания; Преобразования графиков тригонометрических функций; Графики взаимных тригонометрических функций; Использование обратных тригонометрических функций *; Приложения прямоугольной тригонометрии; Области треугольников и законы синусов и косинусов; Решение тригонометрических уравнений *
Модуль 3: Моделирование с помощью математики
Преобразование обычных ситуаций в математические уравнения или решения неравенств; Создание функций, моделирующих ситуацию и интерпретацию их графиков; Определение экстремальных значений ситуации на основе графика функции моделирования; Перевод задач, связанных с оценками, в математические модели
Модуль 4: Начало исчисления
Предел функции при приближении x к константе; Предел функции при приближении x к бесконечности; Признание непрерывности функции в точке или в течение интервала: определение вертикальных и горизонтальных асимптот; Средняя и мгновенная скорость изменения функции; Определение производной функции, включая синус и косинус *; Касательные линии *
Модуль 5 *: Готовность к расчетам не только
Правило мощности, правило продукта и правила отношения для производных финансовых инструментов; Цепное правило дифференцирования композиции функций; Нахождение экстремальных значений функции; Теорема о среднем значении; Неявная дифференциация; Решение связанных проблем скорости
Модуль 6 *: Опережая вычисления
Поиск первообразных; U-замещение; Основная теорема исчисления; Приложения, использующие определенные интегралы; Аппроксимация площади под кривой; Нахождение точного значения площади, ограниченной двумя кривыми;
Модуль 7: Предгорья исчисления II
Работа с выражениями и уравнениями, содержащими экспоненциальные функции; Обратные функции; Понимание логарифма как обратной функции при решении экспоненциального уравнения; Понимание экспоненциальных функций; Функция логарифма как обратная функция
Модуль 8: Прогресс в исчислении II
Производные и интегралы, включая экспоненциальные функции; Производные и интегралы, включая логарифмические функции; Производные и интегралы, включая обратные тригонометрические функции; Сигма-нотация; Геометрические последовательности и серия
.



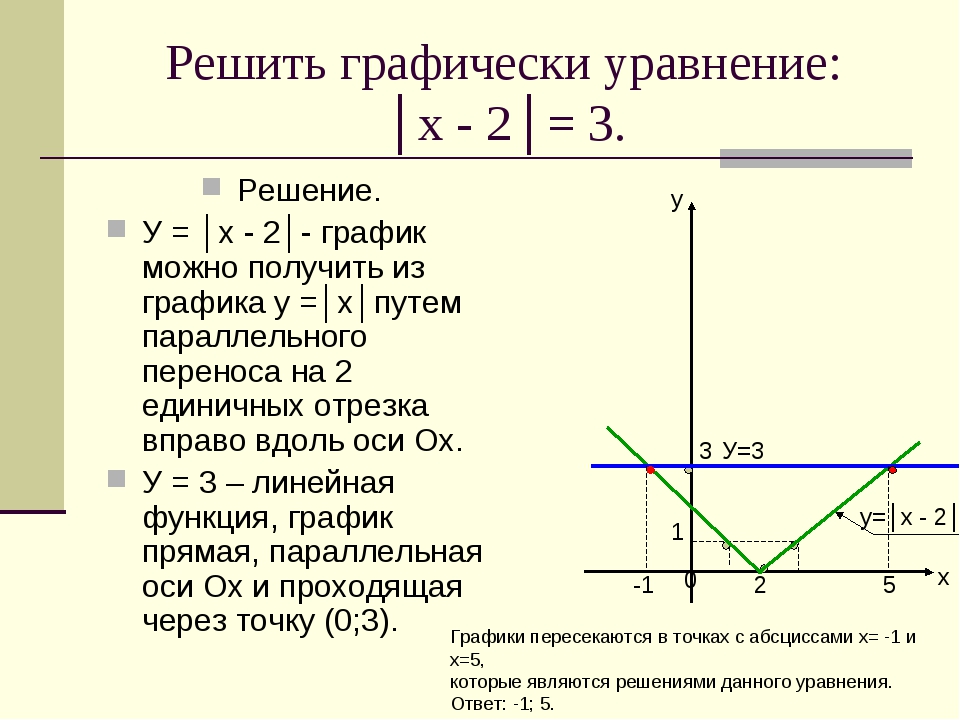 Сформулируйте.
Сформулируйте.

 Провести защиту вашего проекта.
Провести защиту вашего проекта.
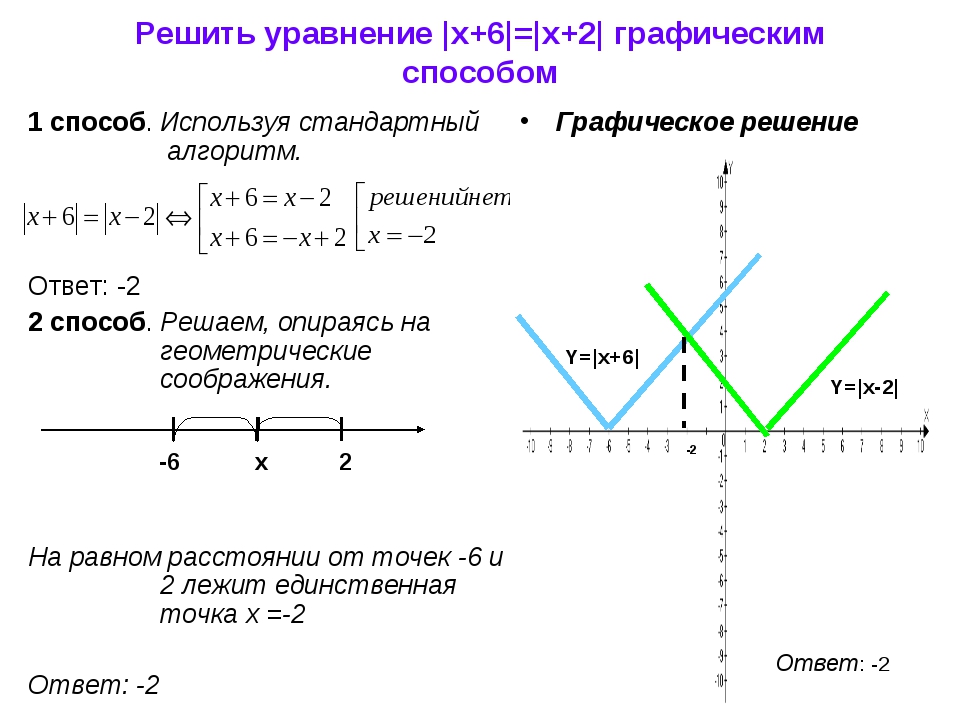

 comLouisiana PASSLPSS платье CodeLPSS Foster Care ProgramMedia RequestLafayette Magnet AcademiesLouisiana Школа FinderMySchoolAppsMySchoolBucksNew ResidentsOrganizational ChartPayrollPublic Информация OfficerPupil Прогрессирование PlanPupil Прогрессирование план поддержка DocumentsPublic отчеты RequestPublic Школа ChoiceRegistrationRisk ManagementSafety Дрель ReportingScholarshipsSchool HoursSpecial диетических потребности FormStudent допустимого использования PolicyStudent AccidentStudent HandbookStudent счет Meal возврат FormSupply ListsTalented Преподаватель Биллу процедур RightsTechnology ClassesTitle IX и политикиЗапросы на расшифровку текстаWisdomwhereWorld Book Online
comLouisiana PASSLPSS платье CodeLPSS Foster Care ProgramMedia RequestLafayette Magnet AcademiesLouisiana Школа FinderMySchoolAppsMySchoolBucksNew ResidentsOrganizational ChartPayrollPublic Информация OfficerPupil Прогрессирование PlanPupil Прогрессирование план поддержка DocumentsPublic отчеты RequestPublic Школа ChoiceRegistrationRisk ManagementSafety Дрель ReportingScholarshipsSchool HoursSpecial диетических потребности FormStudent допустимого использования PolicyStudent AccidentStudent HandbookStudent счет Meal возврат FormSupply ListsTalented Преподаватель Биллу процедур RightsTechnology ClassesTitle IX и политикиЗапросы на расшифровку текстаWisdomwhereWorld Book Online