Всего вопросов: 20
Вопрос 1. На графике изображена зависимость скорости движения слона от времени. Чему равна скорость движения слона?
Вопрос 2. На рисунке изображен график зависимости координаты тела от времени движения.
Используя график, определите начальную координату тела.
Вопрос 3. Используя рисунок, определите характер и скорость движения тела.
Вопрос 4. Какой из приведенных ниже графиков соответствует равномерному движению?
Вопрос 5. Используя график зависимости пути от времени для равномерного прямолинейного движения тела, определите скорость тела.
Вопрос 6. Используя график зависимости пути от времени для равномерного прямолинейного движения тела, определите скорость тела.
Вопрос 7. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 8. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 9. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 10. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси Ох, от времени. Чему равен модуль перемещения тела к моменту времени t=10 с?
Вопрос 11. На рисунке представлены три графика зависимости пройденного пути от времени. Какое из тел двигалось с меньшей скоростью?
Вопрос 12. На рисунке представлен график зависимости координат от времени для трех тел. В каком из нижеприведенных соотношений между собой находятся скорости этих тел?
Вопрос 13.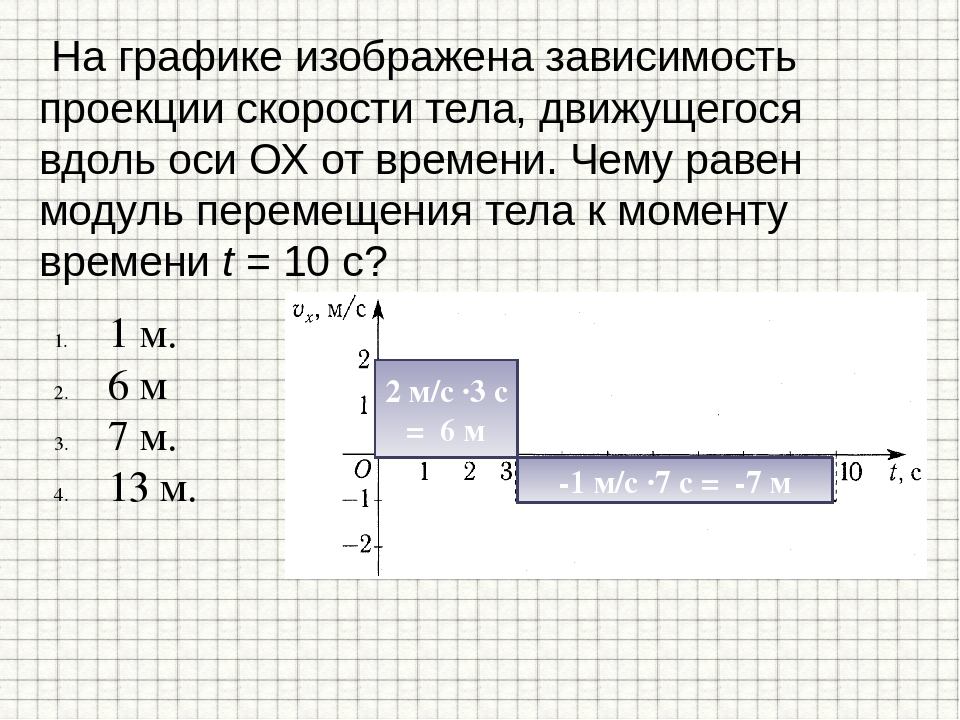 На рисунке представлен график зависимости координат от времени для трех тел. В каком из нижеприведенных соотношений находятся между собой абсолютные значения скоростей тел?
На рисунке представлен график зависимости координат от времени для трех тел. В каком из нижеприведенных соотношений находятся между собой абсолютные значения скоростей тел?
Вопрос 14. На рисунке приведены графики движения двух тел
Отношение скоростей равно:
Вопрос 15. Какой из нижеприведенных интервалов времени соответствует движению с наибольшей по модулю скоростью?
Вопрос 16. На рисунке представлен график зависимости скорости прямолинейного движения от времени. Перемещение и путь, пройденные точкой за 8 с движения, равны:
Вопрос 17. На рисунке приведена зависимость координаты тела от времени. Путь и перемещение тела за первые 3 с движения составляют:
Вопрос 18. На рисунке приведены графики движения велосипедиста I и мотоциклиста II в системе отсчета, связанной с землей. Определить скорость мотоциклиста относительно велосипедиста (в м/с).
Вопрос 19. Координата движущегося тела изменяется с течением времени так, как показано на рисунке. Какой из нижеприведенных графиков наиболее точно отражает зависимость проекции скорости этого тела от времени?
Вопрос 20. Какой из нижеприведенных графиков соответствует зависимости пройденного пути от времени, для тела проекция скорости которого изменяется так, как показано на рисунке?
Содержание
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х х(t) изображён на рисунке. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ, от времени.
А1-1. Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х = х(t) изображён на рисунке. В момент времени t=0 проекция её скорости vх и ускорения ах на ось ОХ удовлетворяют соотношениям
1) vx > 0; ax > 0 2) vx > 0; ax 3) vx 0 4) vx
А1-2. Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х = х(t) изображён на рисунке. В момент времени t=0 проекция её скорости vх и ускорения ах на ось ОХ удовлетворяют соотношениям
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х = х(t) изображён на рисунке. В момент времени t=0 проекция её скорости vх и ускорения ах на ось ОХ удовлетворяют соотношениям
1) vx = 0; ax > 0 2) vx > 0; ax 3) vx 0 4) vx
А1-3. Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х = х(t) изображён на рисунке. В момент времени t=0 проекция её скорости vх и ускорения ах на ось ОХ удовлетворяют соотношениям
1) vx > 0; ax > 0 2) vx > 0; ax 3) vx 0 4) vx
А1-4. Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени х = х(t) изображён на рисунке. В момент времени t=0 проекция её скорости vх и ускорения ах на ось ОХ удовлетворяют соотношениям
1) vx > 0; ax > 0 2) vx 0
3) vx > 0; ax
А2-1. На рисунке приведён график зависимости скорости движения тела от времени.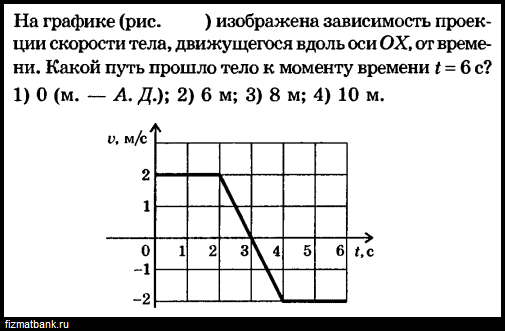 Определите перемещение тела за первые 8 с движения.
Определите перемещение тела за первые 8 с движения.
1) 4 м 2) 8 м
3) 16 м 4) 0 м
А2-2. На рисунке приведён график зависимости скорости тела от времени при прямолинейном движении. Найдите перемещение тела за первые 6 с.
1) 6 м 2) 0 м
3) 3 м 4) 2 м
А2-3. На рисунке приведён график зависимости скорости тела от времени при прямолинейном движении. Найдите путь, пройденный телом за первые 6 с.
1) 6 м 2) 0 м
3) 3 м 4) 2 м
А3-1. Тело движется вдоль оси Ох, причем проекция скорости (x меняется с течением времени по закону, приведенному на графике. Какой путь прошло тело за время от 4 до 16 с?
1) 16 м 2) 28 м
3) 36 м 4) 40 м
А3-2. На рисунке приведён график изменения мгновенной скорости тела в зависимости от времени. Найдите путь, пройденный телом за 5 с.
1) 1,5 м 2) 7,5 м
3) 5 м 4) 2,5 м
А3-3. Материальная точка, график движения которой представлен на рисунке, за 7 секунд прошла путь.
1) 35 м 2) 30 м
3) 25 м 4) 15 м
А3-4. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ, от времени. Какой путь прошло тело к моменту времени t = 6 с?
1) 0 м 2) 6 м
3) 8 м 4) 10 м
А4-1. Автомобиль, трогаясь с места, движется с ускорением 3 м/с2. Через 4 с скорость автомобиля будет равна:
1) 12 м/с 2) 0,75 м/с
3) 48 м/с 4) 6 м/с
А4-2. Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Определите примерно ускорение пули внутри ствола, если считать ее движение равноускоренным.
1) 312 км/с2 2) 114 км/с2
3) 1248 м/с2 4) 100 м/с2
А4-3. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2. На этом спуске его скорость увеличивается на 18 м/с. Велосипедист заканчивает свой спуск после его начала через
1) 0,07 с 2) 7,5 с
3) 15 с 4) 21,6 с
А4-4. Одной из характеристик автомобиля является время t его разгона с места до скорости 100 км/ч. Два автомобиля имеют такие времена разгона, что t1=2t2. Ускорение первого автомобиля по отношению к ускорению второго автомобиля
Одной из характеристик автомобиля является время t его разгона с места до скорости 100 км/ч. Два автомобиля имеют такие времена разгона, что t1=2t2. Ускорение первого автомобиля по отношению к ускорению второго автомобиля
1) меньше в 2 раза 2) больше в
·2 раз
· 3) больше в 2 раза 4) больше в 4 раза
А4-5. Мотоциклист и велосипедист одновременно начинают равноускоренное движение из состояния покоя. Ускорение мотоциклиста в 3 раза больше, чем ускорение велосипедиста. Во сколько раз больше времени понадобится велосипедисту, чтобы достичь скорости 50 км/ч?
Ускорение мотоциклиста в 3 раза больше, чем ускорение велосипедиста. Во сколько раз больше времени понадобится велосипедисту, чтобы достичь скорости 50 км/ч?
1) в 1/3 раза 2) в
·3 раза
3) в 3 раза 4) в 9 раз
А4-6. Ускорение мотоциклиста в три раза больше, чем велосипедиста. Во сколько раз бoльшую скорость разовьет мотоциклист за то же время?
1) в 1,5 раза 2) в
·3 раз
3) в 3 раза 4) в 9 раз
А5-1. Каково ускорение точки, если её координата зависит от времени по следующему закону:
1) a = c 2) a = 2c
3) a = c / 2 4) a = 2c + b
А5-2. Зависимость пути от времени для прямолинейно движущегося тела имеет вид: s(t)=2t+3t2, где все величины выражены в СИ. Ускорение тела равно.
1) 1 м/с2 2) 2 м/с2
3) 3 м/с2 4) 6 м/с2
А5-3. Зависимость координаты материальной точки от времени задаётся уравнением x(t) = At2 + Bt + C, где А, В, С числовые коэффициенты. Скорость и ускорение тела равны соответственно
1) А и С 2) В и А
3) В и С 4) В и 2А
А5-4. Движение легкового автомобиля задано уравнением: х = 150 + 30 t + 0,7t2, м. Чему равна начальная скорость автомобиля?
Движение легкового автомобиля задано уравнением: х = 150 + 30 t + 0,7t2, м. Чему равна начальная скорость автомобиля?
1) 0,7 м/с 2) 1,4 м/с
3) 30 м/с 4) 150 м/с
А6-1. Определите путь, пройденный телом от начала движения, если оно в конце пути имело скорость 10 м/с, а ускорение постоянно и равно 1 м/с2.
1) 15 м 2) 50 м
3) 10 м 4) 20 м
А6-2. Определите ускорение тела при равноускоренном движении, если скорость тела в конце пути равна 10 м/с, а путь, пройденный телом от начала движения, равен 10 м.
1) 5 м/с2 2) 2 м/с2
3) 4 м/с2 4) 3 м/с2
А6-3. При равноускоренном движении без начальной скорости с ускорением 1 м/с2 тело прошло путь 4,5 м. Его скорость в конце пути стала равна
1) 2,25 м/с 2) 3 м/с
3) 5 м/с 4) 9 м/с
А7-1. Движение материальной точки задано уравнением х = 5 – t + t2. Уравнением, выражающим зависимость скорости этой точки от времени, будет
1) v = 5 – 2t 2) v = 2t -1
3) v = 2t – 2 4) v = 5 + 2t
А7-2. Уравнение движения имеет вид х = 6t – 2t2 (м). Скорость тела станет равна нулю через.
Уравнение движения имеет вид х = 6t – 2t2 (м). Скорость тела станет равна нулю через.
1) 0,5 с 2) 1,5 с
3) 2 с 4) 3 с
A7-3. Материальная точка движется вдоль оси X по закону х = 5 + 4t — 2t2 (м). Определите координату точки, в которой скорость обращается в нуль.
1) 3м 2) 5 м
3) 7м 4) 9,5 м
А7-4. Движение тела описывается уравнением x = 2 + 4t – 2t2. В какой момент времени проекция его скорости будет равна нулю? Каковы его координата x и проекция перемещения Sx в этот момент?
1) t = 2 c, x = –2 м, Sx = 4 м 2) t = 1 c, x = 2 м, Sx = 4 м
3) t = 1 c, x = 2 м, Sx = 2 м 4) t = 1 c, x = 4 м, Sx = 2 м
А7-5. По шероховатой поверхности прямолинейно движется тело массой 1 кг. Используя график зависимости скорости движения тела от времени, запишите уравнение перемещения тела для промежутка времени, соответствующего условию а = 0.
1) S = 2t – 0,5t2 2) S = 2t – t2
3) S = 2t 4) S = 0,5t2
А8-1. На рисунке представлены графики скорости трёх тел, движущихся прямолинейно. Какое из трёх тел прошло наименьший путь за 3 с?
Какое из трёх тел прошло наименьший путь за 3 с?
1) I 2) II
3) III 4) пути трёх тел одинаковы
А8-2. На рисунке представлены графики зависимости проекций скоростей четырех тел на ось ОХ от времени. Наибольшее перемещение за 3 секунды совершит.
1) тело I 2) тело II
3) тело III 4) тело IV
А8-3. На рисунке изображены графики зависимости скорости движения четырёх автомобилей от времени. Какой из автомобилей (1, 2, 3 или 4) прошёл наибольший путь за первые 15 с движения?
1) 1 2) 2
3) 3 4) 4
Подготовка РайДр Тема «Кинематика. Динамика» 13 PAGE 14515
1.1.6 Прямолинейное равноускоренное движение
13 EMBED Equation.3 1415
|
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
|
⇐ ПредыдущаяСтр 5 из 7Следующая ⇒ График ускорения
График скорости
График перемещения
График координаты
|
На каком графике представлена проекция ускорения тела в интервале времени от 30 до 40 с?
Банк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
Подробнее
2,5 2,5. a x, м/с 2 2,5
Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
Подробнее
Образовательный портал «РЕШУ ЕГЭ» (
Вариант 2593766 1. Тело, брошенное вертикально вверх со скоростью через некоторое время упало на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени? Ось ОХ
Подробнее
ОЛИМПИАДА ПО ФИЗИКЕ Вариант А
ОЛИМПИАДА ПО ФИЗИКЕ 7 Вариант А. С какой горизонтальной скоростью нужно бросить камень с вершины горы, склон которой образует угол с горизонтом, чтобы он упал на склон горы на расстоянии L от вершины?
Подробнее
Задания 25 по физике (часть 1)
Задания 25 по физике (часть 1) 1. Если подвесить к легкой упругой пружине некоторый груз, то пружина, находясь в равновесии, окажется растянутой на 10 см. Чему будет равен период свободных колебаний этого
Если подвесить к легкой упругой пружине некоторый груз, то пружина, находясь в равновесии, окажется растянутой на 10 см. Чему будет равен период свободных колебаний этого
Подробнее
Образовательный портал «РЕШУ ЕГЭ» (
Объяснение явлений 1. На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным
Подробнее
КИНЕМАТИКА задания типа В Стр. 1 из 5
КИНЕМТИК задания типа В Стр. 1 из 5 1. Тело начало движение вдоль оси OX из точки x = 0 с начальной скоростью v0х = 10 м/с и с постоянным ускорением a х = 1 м/c 2. Как будут меняться физические величины,
Подробнее
Класс Фамилия, имя (полностью) Дата 2015 г.
Класс Фамилия, имя (полностью) Дата 05 г Инструкция по выполнению работы На выполнение работы по физике отводится 90 минут Работа состоит из частей, включающих в себя 0 заданий Часть содержит 5 заданий
Подробнее
Физика ЕГЭ 2015 Тренировочный вариант 2
Часть 1 1. После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси 0x показано на рисунке. Направления векторов скорости бруска, его ускорения
После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси 0x показано на рисунке. Направления векторов скорости бруска, его ускорения
Подробнее
Диагностическая работа
Физика. Демоверсия. 10 класс 2 Диагностическая работа для мониторинга образовательных достижений учащихся по ФИЗИКЕ Район Город (населенный пункт) Школа Класс Фамилия Имя Отчество Демоверсия. 10 класс
Подробнее
Физика ЕГЭ 2015 Тренировочный вариант 1
Часть 1 1. Тело начинает двигаться из начала координат вдоль оси Ох, причем проекция скорости v x меняется с течением времени по закону, приведенному на графике. Через 2 с ускорение тела равно 1) 0 м/с
Подробнее
Диагностическая работа по ФИЗИКЕ
Диагностическая работа по ФИЗИКЕ 0 класс.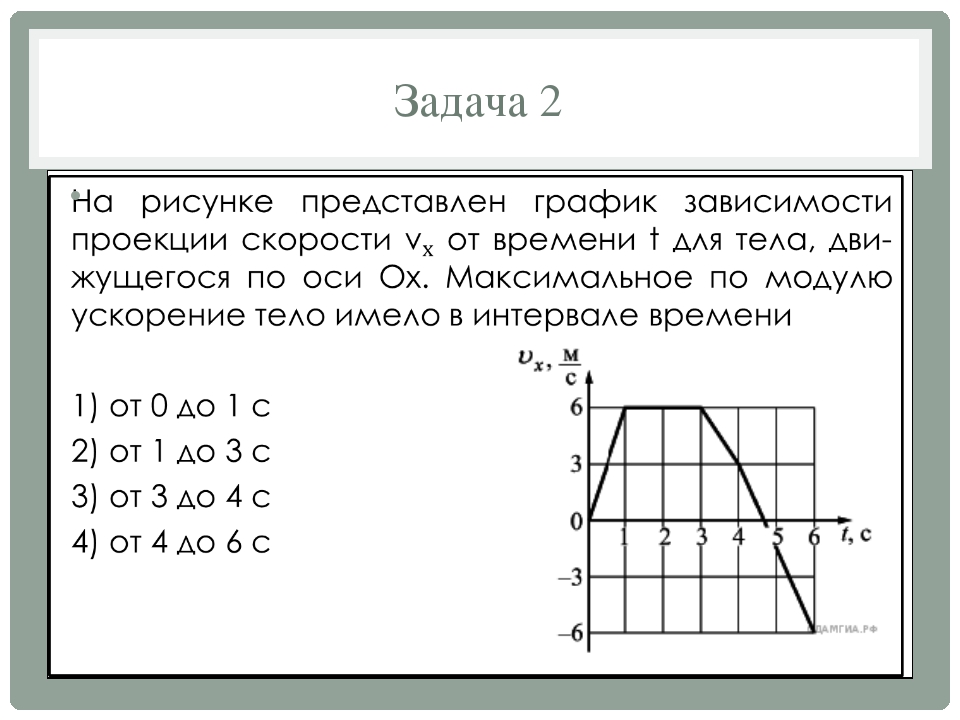 Разделы: «Механика», «МКТ и термодинамика», «Электродинамика» Инструкция по выполнению работы Для выполнения экзаменационной работы по физике отводится 40 минут.
Разделы: «Механика», «МКТ и термодинамика», «Электродинамика» Инструкция по выполнению работы Для выполнения экзаменационной работы по физике отводится 40 минут.
Подробнее
Решение задач ЕГЭ части С: Электростатика
С1.1. Около небольшой металлической пластины, укрепленной на изолирующей подставке, подвесили на шелковой нити легкую металлическую незаряженную гильзу. Когда пластину подсоединили к клемме высоковольтного
Подробнее
Решение задач ЕГЭ части С: Динамика
С1.1. Два одинаковых бруска, связанные легкой пружиной, покоятся на гладкой горизонтальной поверхности стола. В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость
Подробнее
Вариант Задание 1
Параграфы 88-93 повторить выполнить упражнение 12.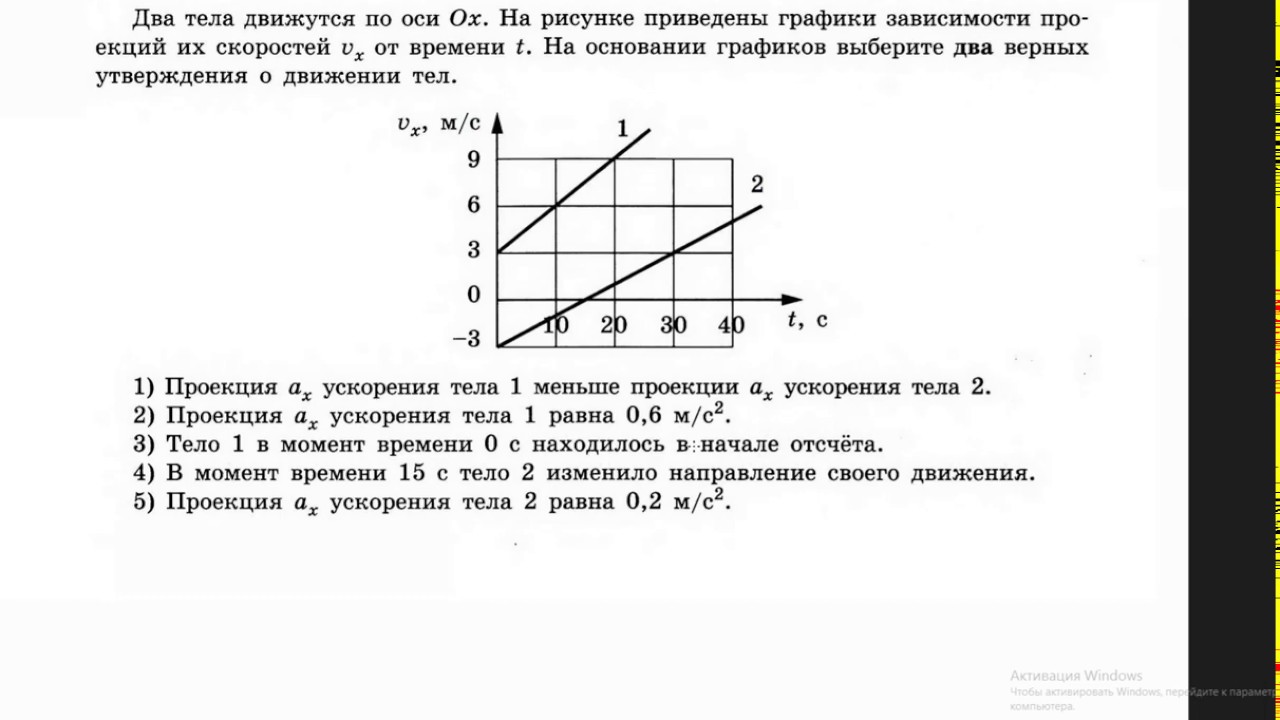 Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
Подробнее
Отложенные задания (25)
Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из
Подробнее
F в этой системе отсчёта равно
Отложенные задания (88) Мяч, брошенный вертикально вверх со скоростью υ, через некоторое время упал на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени движения?
Подробнее
Название кадра. frame117. Задание
frame117 Автомобиль стартует с места с постоянным ускорением а = 1 м/с2.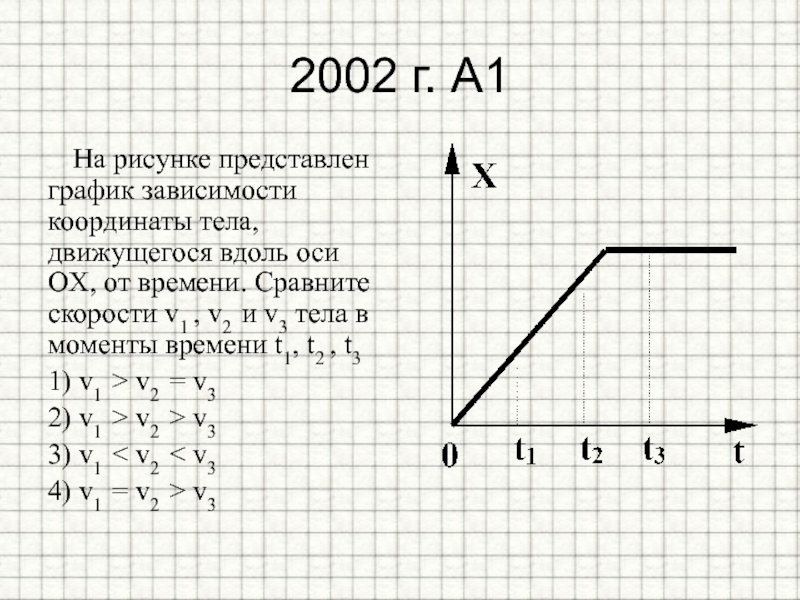 Какой путь проходит автомобиль за первые десять секунд движения? 50 м frame118 Коробка массой m = 2 кг подвешена на невесомой нити
Какой путь проходит автомобиль за первые десять секунд движения? 50 м frame118 Коробка массой m = 2 кг подвешена на невесомой нити
Подробнее
t,, с v x, м/с 0 0,2 0,4 0,6 0,8
Вариант 3811175 1. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с. 2. К
Подробнее
ДИНАМИКА задания типа В Страница 1 из 6
ДИНМИК задания типа В Страница 1 из 6 1. Спутник движется вокруг Земли по круговой орбите радиусом R. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. (M
Подробнее
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 4
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 4 1.1. Ускорение свободного падения на Луне равно 1,7 м/с 2. Каким будет период колебаний математического маятника на Луне, если на Земле он равен 1 с? Зависит ли ответ от массы
Каким будет период колебаний математического маятника на Луне, если на Земле он равен 1 с? Зависит ли ответ от массы
Подробнее
ЗАДАЧИ С4 Тема: «Электродинамика»
ЗАДАЧИ С4 Тема: «Электродинамика» Полное решение задачи должно включать законы и формулы, применение которых необходимо и достаточно для решения, а также математические преобразования, расчеты с численным
Подробнее
Курсы подготовки к ЕГЭ по физике
Курсы подготовки к ЕГЭ по физике Механика. Задание 9 Учитель физики: Бабчик И.И. Учебное заведение: МБОУ лицей 1 г. Сургут, 019 г. Задание 9. Основные вопросы 1 1. Кинематика Задача 1 Задача 7. Движение
Подробнее
«Физика», осень 2017 г. Вариант 1
З А Д А Ч А 1. ствола Первый (отборочный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по общеобразовательному предмету Снаряд вылетел со скоростью «Физика», осень 217 г. 32 Вариант
32 Вариант
Подробнее
Равномерное прямолинейное движение.
Двигаясь
прямолинейно, одно тело за каждую
секунду проходит путь 5 м.
Другое тело, двигаясь по прямой в одном
направлении, за каждую секунду проходит
путь 10 м. Движения этих тел
1) равномерные
2) неравномерные
3)
первого — неравномерное, второго —
равномерное
4) нельзя сказать
о характере движения тел
П
о
графику зависимости пройденного пути
от времени определите скорость
велосипедиста в момент времени t = 2 с.
1) 2
м/с 2) 3 м/с 3) 6 м/с 4) 18 м/с
Н
а
рисунке представлены графики зависимости
пройденного в одном направлении пути
от времени для трех тел.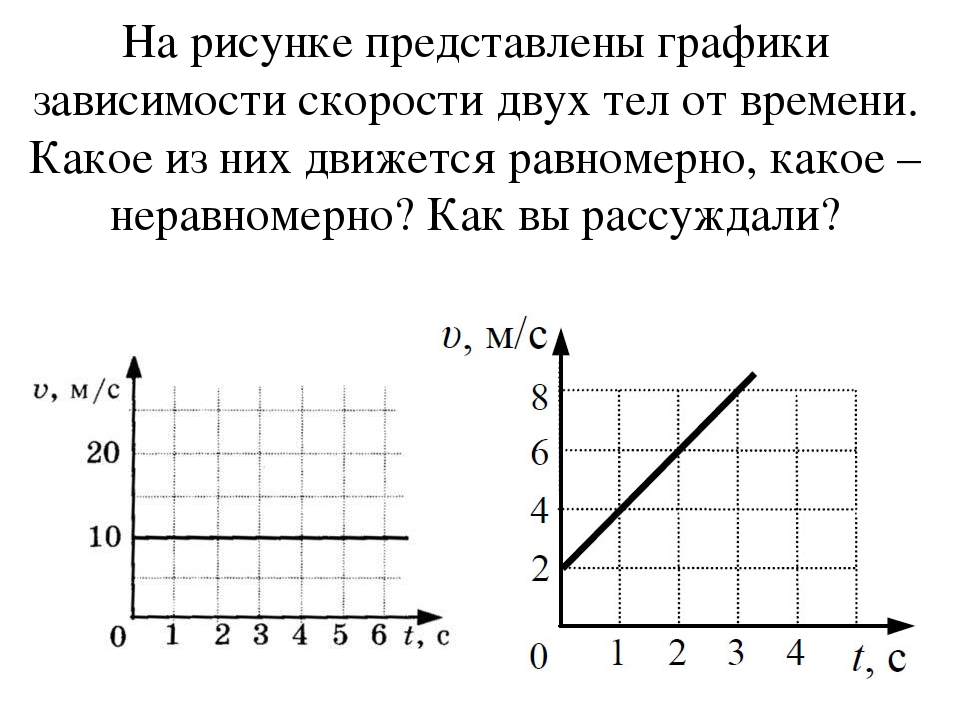 Какое из тел
Какое из тел
двигалось с большей скоростью?
1) 1
2) 2 3) 3 4) скорости всех тел одинаковы
Н
а
рисунке представлены графики зависимости
координаты х
от времени для трех тел. Какое из тел
двигалось с большей скоростью?
1) 1 2) 2 3) 3 4) Скорости всех тел одинаковы
На
рисунке представлен график зависимости
координаты х
от времени для трех тел. В каком из
нижеприведенных соотношений между
собой находятся скорости этих тел?
1)
2)
3)
4)
Координата
тела меняется с течением времени
согласно формулев единицах СИ. Чему равна координата
тела через 5 с после начала движения?
1) -20 м 2) -10 м
3) 10 м 4) 30 м
Тело движется
равномерно в сторону, противоположную
оси ОX, величина скорости тела равна
28,8 км/ч,
начальная
координата 40 м.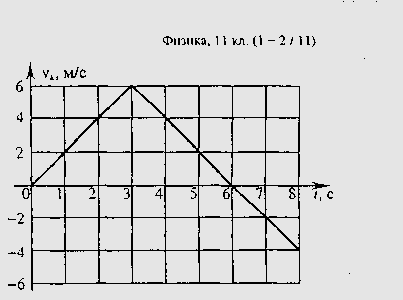 Координата тела и
Координата тела и
пройденный им путь через 5 с после
начала движения равны
1)184 м, 144 м
2) -104 м, 144 м 3) 80 м, 40 м
4) 0 м, 40 м
Т
ело
движется в соответствии с уравнением.
Определите скорость этого тела через
3 с.
1) 5 м/с 2) 29 м/с
3) 8 м/с 4) 19 м/с
На
графике изображена зависимость
координаты х
тела,
движущегося вдоль оси ОХ, от времени.
Каковы начальная координата и скорость
тела?
1) 1 м, 2 м/с 2) 0
м, 1 м/с
3) -1 м, 1 м/с 4) —
2 м, 3/4 м/с
Н
а
рисунке показан график зависимости
координаты х
тела,
движущегося прямолинейно, от времени.
Определите координату и скорость тела
в момент времени 5 с.
1) 4 м,
2,4 м/с 2) 12 м, 2,4 м/с
3) 12 м,
1,6 м/с 4) 4 м, 1,6 м/с
Н
а
графике изображена зависимость
координаты х
тела,
движущегося вдоль оси ОХ, от времени.
Каковы скорость тела и уравнение
движения?
1)
0,1 м/с, х = 30 + 0,1
t
2)
0,1 м/с,
х = 30 — 0,1
t
3)
10 м/c,
х = 30 + 10
t
4)
10 м/c,
х = 30 — 10
t
Н
а
рисунке приведен график зависимости
проекции скорости некоторого тела от
времени. Определите проекцию перемещения
этого тела за 5 с после начала движения.
1)
5 м 2) 13 м 3) -1 м 4) 9 м
а)
Тело, двигаясь прямолинейно и равномерно
в плоскости, перемещается из точки А с
координатами (1; 2) в точку В с координатами
(4; -2) за время 10 с. Модуль скорости
тела равен
1)
0,3 м/с 2) 0,5 м/с 3) 0,7 м/с 4)
2,5 м/с
б) Тело, двигаясь
прямолинейно и равномерно в плоскости,
перемещается из точки А с координатами
(1; 2) в точку В с координатами (4; -1) за
время 10 с.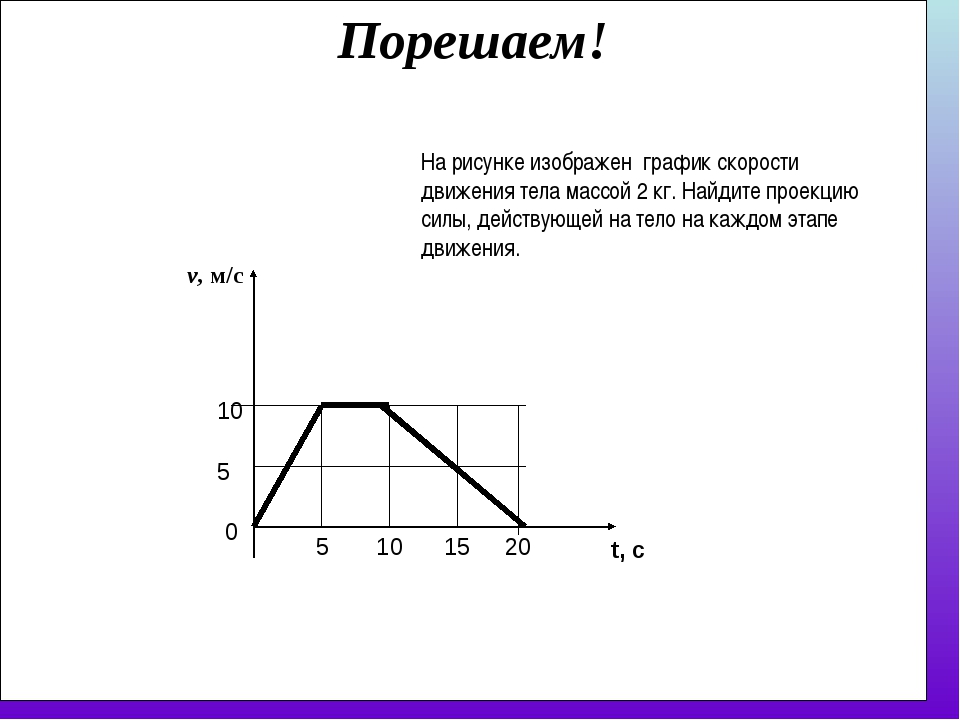 Скорость тела направлена
Скорость тела направлена
к оси ОХ под углом
1) 30º 2) 45º
3) 60º 4) 135º
Поезд длиной 200 м
въезжает в тоннель длиной 300 м, двигаясь
равномерно со скоростью 10 м/с. Через
какое время поезд выйдет полностью из
тоннеля?
1) 10 с
2) 20 с 3) 30 с 4) 50 с
а)
Материальная точка движется в плоскости
равномерно прямолинейно по закону:,
где х,
y—координаты
тела, в м,
t
— время, в с.
Каково значение скорости тела?
1) 1 м/с
2) З м/с 3) 5 м/с 4) 7 м/с
б)
Материальная точка движется в плоскости
ОХY
так, что ее координаты х
и y
меняются по закону
(м), время t
выражено в секундах. Чему равна скорость
тела?
1) 10 м/с 2)
6 м/с 3) 8 м/с 4) 14 м/с
а)
Координаты материальной точки, движущейся
в плоскости, изменяются в зависимости
от времени по закону,
где a,
b,
c
– числа, не равные нулю. Траектория
Траектория
точки выражается уравнением
1)
2)
3)
4)
б) Тело
движется в плоскости так, что все время
находится на прямой, идущей через начало
системы координат. Какое из уравнений
правильно описывает его траекторию (а
и b
не равны нулю)?
1)
2)
3)
4)
Какая
функция υ(t)
описывает зависимость скорости от
времени t
при равномерном прямолинейном движении?
1) υ
= 5t
2) υ
=
5/t
3) υ
= 5
4) υ
= -5
Две
материальные точки движутся по оси ОХ
по законам:
х1= 5 + 5t,
х2 = 5 -5t
(х—
в метрах, t
— в секундах). Чему равно расстояние
между ними через 2 с?
1) 5 м
2) 10 м 3) 15 м 4) 20 м
а) По оси ОХ движутся
две точки: первая по закону х1(t) = 5+2t,
вторая – по закону х2(t) = 2 — t.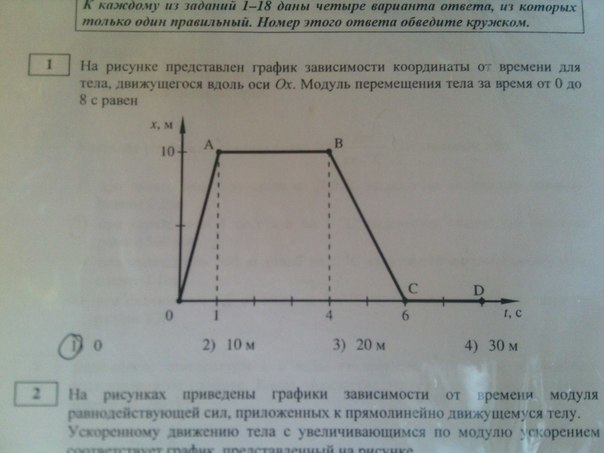
В какой момент времени они встретятся?
1) 1 с 2) 2 с
3) 3 с 4) точки не встретятся
б) По оси ОХ движутся
две точки: первая по закону х1(t) = 10+2t,
вторая – по закону х2(t) = 4+5t.
В какой момент времени они встретятся?
1) 2 с 2) 4 с
3) 6 с 4) точки не встретятся
Н
а
рисунке изображен график зависимости
координаты тела, движущегося по прямой,
от времени. На основании графика можно
утверждать, чтона участке 1 тело
покоится, на участке 2 – движется
равномернона участке 1
движение является равномерным, на
участке 2 – скорость тела меняетсяна участке 1 тело
движется равномерно, на участке 2 –
покоитсяна участке 1 тело
движется равномерно, на участке 2 –
также равномерно
Из двух пунктов,
расстояние между которыми 100 м
одновременно навстречу друг другу
начали двигаться два тела. Скорость
Скорость
одного из них 20 м/с.
Какова скорость второго тела, если тела
встретились через 4 с?
1) 5 м/с 2) 10 м/с
3) 15 м/с 4) 20 м/с
Товарный поезд,
двигаясь со скоростью 36 км/ч, проехал
станцию. Через 0,5 ч в том же направлении
начал движение скорый поезд со скоростью
72 км/ч. Через какое время после выхода
товарного поезда его нагонит скорый?
1)
1,33 ч 2) 0,5 ч 3) 1,17 ч 4) 1 ч
Цель
летит горизонтально на высоте 10 км
с постоянной скоростью 600 м/с. Ее
засекли, когда она была в зените и
пустили ракету в упреждающую точку.
Через какое время цель будет сбита,
если скорость ракеты постоянна и равна
1 км/с?
1)
11,5 с 2) 12,5 с 3) 13,5 с
4) 14,5 с
Вражеский корабль
движется по прямому курсу со скоростью
5 м/с. Кратчайшее расстояние между
Кратчайшее расстояние между
торпедным катером и курсом корабля
6000 м. Какое расстояние должно быть
между кораблем и катером при выстреле,
чтобы поразить корабль торпедой,
движущейся со скоростью 12 м/с по
кратчайшему расстоянию?
1) 8000 м 2)
7500 м 3) 7000 м 4) 6500 м
Т-2. Перемещение. Определение координаты движущегося тела.
Т-2. Перемещение и путь. Определение координаты движущегося тела.
Вариант 1.
Автомобиль дважды проехал вокруг Москвы по кольцевой дороге, длина которой 109 км. Чему равны пройденный автомобилем путь l и модуль его перемещения S?
А. l = 109 км, S = 0 км. Б. l = 218 км, S = 0 км.
В. l = S = 218 км. Г. l = S =0 км.
Камень брошен из окна второго этажа с высоты 4 м и падает на Землю на расстоянии 3 м от стены дома.
 Чему равен модуль перемещения камня?
Чему равен модуль перемещения камня?
А. 3 м. Б. 4 м. В. 5 м. Г. 7 м.
3. Плот равномерно плывет по реке со скоростью 6 км/ч. Человек движется поперек плота со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?
А. 2 км/ч. Б. 7 км/ч. В. 10 км/ч. Г. 14 км/ч.
4. К перекрестку приближаются грузовая машина со скоростью v1 = 10 м/c и легковая машина со скоростью v2 = 20 м/с (рис.А). Какое направление имеет вектор v21скорости легковой машины в системе отсчета грузовика (рис.Б)?
А.1. Б.2. В.3. Г.4.
5. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ от времени. Чему равен модуль перемещения тела к моменту времени t = 10 с?
А. 1 м. Б. 6 м. В.7 м. Г. 13 м.
6. Лодка переплывает реку шириной 600 м, причем рулевой держит курс таким образом, что лодка все время плывет перпендикулярно берегам. Скорость лодки относительно воды 5 м/с, скорость течения реки 3 м/с. Через сколько времени лодка достигнет противоположного берега?
Скорость лодки относительно воды 5 м/с, скорость течения реки 3 м/с. Через сколько времени лодка достигнет противоположного берега?
А. 120 с. Б. 150 с.
В. 1,5 м/с. Г. 2,5 м/с.
Т-2. Перемещение. Определение координаты движущегося тела.
Вариант 2.
Спортсмен пробежал дистанцию 400 м и возвратился к месту старта. Чему равен путь , пройденный спортсменом, и модуль его перемещения S?
А. = S = 0 м. Б. = S = 400 м.
В. = 400 м, S = 0 м. Г. = 0 м, S = 400 м.
Камень брошен из окна второго этажа с высоты 3 м и падает на Землю на расстоянии 4 м от стены дома. Чему равен модуль перемещения камня?
А. 7 м. Б. 5 м. В. 4 м. Г. 3 м.
Кран равномерно поднимает груз вертикально вверх со скоростью 0,3 м/с и одновременно равномерно и прямолинейно движется по горизонтальным рельсам со скоростью 0,4 м/с. Чему равна скорость груза в системе отсчета, связанной с Землей?
А. 0,1 м/с Б. 0,35м/с. В. 0,5 м/с. Г. 0,7 м/с
0,1 м/с Б. 0,35м/с. В. 0,5 м/с. Г. 0,7 м/с
4. Капля дождя, летящая с постоянной скоростью вертикально вниз, попадает на вертикальную поверхность стекла вагона, движущегося с постоянной скоростью u (рис.А). Какая из траекторий на рисунке Б соответствует следу капли на стекле?
А.1. Б.2. В.3. Г.4.
5. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ от времени. Какой путь прошло тело к моменту времени t=10 с?
А. 1 м. Б. 6 м. В.7 м. Г. 13 м.
6. Скорость движения моторной лодки, плывущей относительно берега по течению, равна 3 м/с, а скорость этой же лодки, плывущей против течения, равна 2 м/с. Чему равна скорость течения?
А. 0,5 м/с. Б. 1м/с.
В. 1,5 м/с. Г. 2,5 м/с.
Образование — МБОУ СОШ №71
Реализуемые уровни образования
Начальное общее образование
Основное общее образование
Среднее общее образование
Формы обучения
Очная
Нормативные сроки обучения
Начальное общее образование — 4 года
Основное общее образование — 5 лет
Среднее общее образование — 2 года
Сроки действия государственной аккредитации образовательных программ
8370 (21. 05.2015 — 06.03.2025)
05.2015 — 06.03.2025)
Образовательные программы
I. В МБОУ СОШ № 71 реализуется основная образовательная программа начального общего образования, разработанная в соответствии с Федеральным государственным образовательным стандартом начального общего образования.
Название образовательной программы: Основная общеобразовательная программа — образовательная программа начального общего образования (ОП НОО)
Описание образовательной программы: Основная образовательная программа начального общего образования МБОУ СОШ №71 (ООП НОО) разработана в соответствии с требованиями федерального государственного образовательного стандарта начального общего образования к структуре основной образовательной программы, определяет содержание и организацию образовательного процесса на уровне начального общего образования. В целевом разделе программы представлены цели и задачи реализации ООП НОО, планируемые результаты освоения учащимися ООП НОО, система оценки достижения планируемых результатов освоения ООП НОО. В содержательном разделе представлены программа формирования универсальных учебных действий; основное содержание учебных предметов; программа духовно-нравственного развития, воспитания учащихся; программа формирования экологической культуры, здорового и безопасного образа жизни; программа коррекционной работы. Организационный раздел содержит учебный план начального общего образования, план внеурочной деятельности, описание системы условий реализации ООП НОО.
В содержательном разделе представлены программа формирования универсальных учебных действий; основное содержание учебных предметов; программа духовно-нравственного развития, воспитания учащихся; программа формирования экологической культуры, здорового и безопасного образа жизни; программа коррекционной работы. Организационный раздел содержит учебный план начального общего образования, план внеурочной деятельности, описание системы условий реализации ООП НОО.
II. В МБОУ СОШ № 71 реализуется основная образовательная программа основного общего образования, разработанная в соответствии с Федеральным государственным образовательным стандартом основного общего образования.
Название образовательной программы: Основная общеобразовательная программа — образовательная программа основного общего образования (ОП ООО)
Описание образовательной программы: Основная образовательная программа основного общего образования МБОУ СОШ № 71 (ООП ООО) разработана в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования к структуре основной образовательной программы, определяет содержание и организацию образовательного процесса на уровне основного общего образования. В целевом разделе программы представлены цели и задачи реализации ООП ООО, планируемые результаты освоения учащимися ООП ООО, система оценки достижения планируемых результатов освоения ООП ООО. В содержательном разделе представлены программа развития универсальных учебных действий, основное содержание учебных предметов, программа воспитания и социализации учащихся, программа коррекционной работы. Организационный раздел содержит учебный план основного общего образования, план внеурочной деятельности, описание системы условий реализации ООП ООО.
В целевом разделе программы представлены цели и задачи реализации ООП ООО, планируемые результаты освоения учащимися ООП ООО, система оценки достижения планируемых результатов освоения ООП ООО. В содержательном разделе представлены программа развития универсальных учебных действий, основное содержание учебных предметов, программа воспитания и социализации учащихся, программа коррекционной работы. Организационный раздел содержит учебный план основного общего образования, план внеурочной деятельности, описание системы условий реализации ООП ООО.
III. В МБОУ СОШ № 71 реализуется образовательная программа среднего общего образования, разработанная в соответствии с федеральным компонентом государственного стандарта среднего общего образования, Федеральным базисным учебным планом и примерными учебными программами для образовательных учреждений РФ.
Название образовательной программы: Образовательная программа среднего общего образования «Гражданственность через школьное образование».
Описание образовательной программы: Образовательная программа среднего общего образования МБОУ СОШ №71 разработана в соответствии с требованиями действующего федераль¬ного законодательства, регулирующего обучение в соответствии с требованиями Федерального компонента государственного стандарта общего образования. В целевом разделе программы представлены цели и задачи реализации образовательной программы среднего общего образования, цели изучения учебных предметов федерального компонента государственного стандарта среднего общего образования, требования к уровню подготовки выпускников. В содержательном разделе представлены общие учебные умения, навыки и способы деятельности; обязательный минимум содержания основных образовательных программ по учебным предметам; система воспитательной работы; система дополнительного образования. Организационный раздел содержит учебный план, описание условий реализации образовательной программы основного общего образования.
IV. В МБОУ СОШ № 71 реализуется основная образовательная программа среднего общего образования, разработанная в соответствии с Федеральным государственным образовательным стандартом среднего общего образования.
Название образовательной программы: Основная общеобразовательная программа — образовательная программа среднего общего образования (ОП СОО)
Описание образовательной программы: Основная образовательная программа среднего общего образования МБОУ СОШ № 71 (ООП СОО) разработана в соответствии с требованиями федерального государственного образовательного стандарта среднего общего образования к структуре основной образовательной программы, определяет содержание и организацию образовательного процесса на уровне основного общего образования. В целевом разделе программы представлены цели и задачи реализации ООП СОО, планируемые результаты освоения учащимися ООП СОО, система оценки достижения планируемых результатов освоения ООП СОО. В содержательном разделе представлены программа развития универсальных учебных действий, основное содержание учебных предметов, программа воспитания и социализации учащихся, программа коррекционной работы. Организационный раздел содержит учебный план основного общего образования, план внеурочной деятельности, описание системы условий реализации ООП СОО.
V. Дополнительные образовательные программы:
1. Дополнительная общеобразовательная программа «Смысловое чтение». Имеет духовно-нравственную обще-интеллектуальную направленность, реализуется в 1-х – 4-х классах общеобразовательной школы. Программа рассчитана на 4 года. Количество часов в неделю – 1. За год: в 1классе – 33 часа, во 2 классе — 34 часа, в 3 классе — 34 часа, в 4 классе — 34 часа. Всего реализуется в объеме 135 часов. Программа направлена на обучение учеников критическому аудированию, пониманию, анализу, сравнению, генерации текстов как в устной, так и в письменной форме, разработана в соответствии с требованиями к результатам учебной деятельности в рамках реализации ФГОС НОО.
2. Дополнительная общеобразовательная программа «Юный исследователь». Предназначена для работы с детьми 1-4 классов. Программа интегрирует, обеспечивает полноту и цельность содержания программ по предметам, она рассчитана на 4 года. Количество часов в неделю – 1. За год: в 1классе – 33 часа, во 2 классе — 34 часа, в 3 классе — 34 часа, в 4 классе — 34часа. Всего реализуется в объеме 135 часов. Программа направлена на формирование у младших школьников проектной компетентности, личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
Всего реализуется в объеме 135 часов. Программа направлена на формирование у младших школьников проектной компетентности, личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
3. Дополнительная образовательная программа «Гуманитарный курс «Эссе по обществознанию: теория и практика». Ориентирована на систематизацию и расширение знаний, обучающихся 11 классов по теории, признакам эссе, как жанра сочинения по обществознанию. Она направлена на формирование у выпускников 11 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
4. Дополнительная образовательная программа «Решение графических задач в курсе общей физики». Для обучающихся 11 класса направлена на углубление и систематизацию знаний учащихся 11 классов по физике, их профессиональное самоопределение. Материал излагается на теоретической и практической основах, включающей вопросы классической механики, молекулярной физики, электродинамики, оптики и квантовой физики. Курс » Решение графических задач по физике» рассчитан на 24 часа (2 часа в неделю для 11 классов). Программа курса составлена в пределах федерального государственного образовательного стандарта.
Материал излагается на теоретической и практической основах, включающей вопросы классической механики, молекулярной физики, электродинамики, оптики и квантовой физики. Курс » Решение графических задач по физике» рассчитан на 24 часа (2 часа в неделю для 11 классов). Программа курса составлена в пределах федерального государственного образовательного стандарта.
5. Дополнительная образовательная программа «Игровой английский». Программа «Игровой английский» предназначена для детей младшего школьного возраста. Главный акцент в обучении делается на развитие творческих способности учащихся. По окончании программы учащиеся научатся основам иностранного языка, получат знания об истории и традициях страны изучаемого языка, разовьют коммуникативные умения и навыки. Программа курса рассчитана на 10 часов, разработана в соответствии с требованиями к результатам учебной деятельности в рамках реализации ФГОС НОО.
6. Дополнительная образовательная программа «Особенности выполнения творческих заданий по развитию речи». Предназначена для совершенствования речевой деятельности на основе овладения знаниями об устройстве языка и особенностях его употребления в разных условиях общения, на базе усвоения основных норм русского литературного языка, речевого этикета обучающихся 11 классов. Программа рассчитана на 20 часов. Она направлена на формирование у выпускников 11 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов в пределах федерального государственного образовательного стандарта.
Предназначена для совершенствования речевой деятельности на основе овладения знаниями об устройстве языка и особенностях его употребления в разных условиях общения, на базе усвоения основных норм русского литературного языка, речевого этикета обучающихся 11 классов. Программа рассчитана на 20 часов. Она направлена на формирование у выпускников 11 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов в пределах федерального государственного образовательного стандарта.
7. Дополнительная образовательная программа «Лесная школа». Направлена на формирование положительного отношения к школе, стимулирование познавательной активности школьников; знакомство обучающихся с нормами школьной жизни, содействие принятию требований учителя и ритма учебной деятельности, овладению правилами поведения на уроке и перемене, формирование личностных УУД. Программа рассчитана на 34 часа. Она направлена на формирование у первоклассников личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов в пределах ФГОС НОО.
8. Дополнительная образовательная программа «Информационные технологии». Направлена на овладение основами программирования, развитие у обучающихся качеств, которые помогут им в учебе и профессиональном самоопределении. Программа рассчитана на 68 часов. Она направлена на формирование у обучающихся 10-11 классов личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, необходимых для профессий, связанных с информационными технологиями, в пределах федерального государственного образовательного стандарта.
9. Дополнительная образовательная программа «Вернисаж творчества». Направлена на формирование творческой личности младших школьников, способствует развитию пространственного воображения благодаря работе с различными материалами в разных техниках. В процессе изобразительной деятельности формируются познавательные, личностные, регулятивные и коммуникативные универсальные учебные действия в пределах федерального государственного образовательного стандарта.
10. Дополнительная образовательная программа «Применение информационных технологий для решения задач по информатике». Предназначена для систематизации и расширения знаний, обучающихся 9 классов по наиболее значимым направлениям развития информационных технологий: компьютерной графике, 3D – моделированию, алгоритмизации и программированию. Она направлена на формирование у выпускников 9 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, необходимых для профессий, связанных с информационными технологиями, в пределах федерального государственного образовательного стандарта. Программа рассчитана на 24 часа.
11. Дополнительная образовательная программа «Мир информатики». Направлена на овладение трудовыми умениями и навыками при работе на компьютере обещающихся 4х классов, приобретение опыта практической деятельности по созданию информационных объектов, полезных для человека и общества, умением работать с различными видами информации и освоение основ проектно-творческой деятельности. Программа рассчитана на 34 часа, разработана в соответствии с требованиями к результатам учебной деятельности в рамках реализации ФГОС НОО.
Программа рассчитана на 34 часа, разработана в соответствии с требованиями к результатам учебной деятельности в рамках реализации ФГОС НОО.
12. Дополнительная образовательная программа «Расширяем границы познания по обществознанию». Предназначена для расширения знаний по теории и систематизации опыта познавательной и практической деятельности, решения развивающих и творческих задач, проектной деятельности в учебном процессе и социальной практике обучающихся 9 классов. Она направлена на формирование у учащихся 9 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
13. Дополнительная образовательная программа «Курс «Решение поливариантных задач по геометрии, задач с параметрами, олимпиадных задач, задач повышенной сложности». Направлена на мотивирование старшеклассников к освоению математики на повышенном уровне. Курс предусматривает знакомство обучающихся с нестандартными способами решения математических задач. Программа рассчитана на 34 часа. Она направлена на формирование у выпускников 11 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
Программа рассчитана на 34 часа. Она направлена на формирование у выпускников 11 класса личностных, метапредметных (регулятивных, познавательных, коммуникативных) и предметных результатов, в пределах федерального государственного образовательного стандарта.
14. Дополнительная образовательная программа «Школа будущего первоклассника». Представляет программу предшкольной подготовки будущих первоклассников, разработана в соответствии с программой подготовки дошкольника к школьному обучению «Предшкольная пора» под ред. Н.Ф. Виноградовой и направлена на подготовку старшего дошкольника к достижению личностных, метапредметных (регулятивных, познавательных, коммуникативных) результатов и предметных результатов в пределах федерального государственного образовательного стандарта.
Учебный план
Учебный план на 2020-2021 у.г.
Сведения об обеспеченности образовательного процесса учебной литературой МБОУ СОШ №71 на 2020-2021 учебный год в соответствии с «Федеральным перечнем учебников «
Аннотации к рабочим программам дисциплин
Начальное общее образование: аннотации, рабочие программы дисциплин.
Основное общее образование: аннотации, рабочие программы дисциплин.
Среднее общее образование (ФК ГОС): аннотации, рабочие программы дисциплин.
Среднее общее образование (ФГОС): аннотации, рабочие программы дисциплин.
Календарный учебный график
Календарный учебный график на 2020-2021
Приказ о внесении изменений в КУГ на 2020-2021 у.г.
Документы, разработанные образовательной организацией для обеспечения образовательного процесса, в том числе с применением электронного обучения и дистанционных образовательных технологий
Положение об электронном классном журнале/дневнике учащегося МБОУ СОШ №71
Положение о рабочей программе внеурочной деятельности учителя (педагогического работника)
Положение о рабочей программе учителя (педагогического работника)
Положение о формах, периодичности и порядке текущего котроля успеваемости и промежуточной аттестации учащихся МБОУ СОШ № 71
Порядок регламентации и оформления отношений МБОУ СОШ №71 и родителей (законных представителей) обучающихся, нуждающихся в длительном лечении, а также детей-инвалидов в части организации обучения по основным общеобразовательным программам на дому
Положение о порядке обучения по индивидуальному учебному плану в МБОУ СОШ №71
Положение о применении электронного обучения, дистанционных образовательных технологий при реализации образовательных программ в МБОУ СОШ №71
Программа внеурочной деятельности начального общего и основного общего образования на 2020-2021 учебный год (ФГОС)
Положение о Совете профилактики
План профилактической работы с учащимися и их семьями на 2020-2021 учебный год
План работы по профилактике правонарушений и безнадзорности несовершеннолетних совместно с отделением по делам несовершеннолетних на 2020-2021 учебный год
Приказ «Об утверждении Положения о постановке обучающихся и семей на внутришкольный учет»
Положение об индивидуальном проекте обучающихся ООО (9 класс) в соответствии с требованиями ФГОС ООО МБОУ «Средняя общеобразовательная школа №71»
Положение об индивидуальном проекте обучающихся в соответствии с требованиями ФГОС СОО МБОУ «Средняя общеобразовательная школа № 71»
Положение об осуществлении функций классного руководителя педагогическими работниками «Средняя общеобразовательная школа № 71»
Реализуемые образовательные программы
I. Основная общеобразовательная программа — образовательная программа начального общего образования (ФГОС НОО для 1-4 классов)
II. Основная общеобразовательная программа — образовательная программа основного общего образования (ФГОС ООО для 5-9 классов)
III. Образовательная программа среднего общего образования «Гражданственность через школьное образование» (ФК ГОС СОО для 11 класса)
IV. Основная общеобразовательная программа- образовательная программа среднего общего образования (ФГОС СОО для 10 класса)
Численность обучающихся в МБОУ СОШ № 71 по реализуемым образовательным программам
Общая численность обучающихся: 539
1. Основная общеобразовательная программа — образовательная программа начального общего образования
за счет бюджетных ассигнований федерального бюджета — 0
за счет бюджетов субъектов Российской Федерации — 249
за счет местных бюджетов — 0
по договорам об образовании за счет средств физических и (или) юридических лиц — 0
2. Основная общеобразовательная программа — образовательная программа основного общего образования
за счет бюджетных ассигнований федерального бюджета — 0
за счет бюджетов субъектов Российской Федерации — 250
за счет местных бюджетов — 0
по договорам об образовании за счет средств физических и (или) юридических лиц — 0
3. Образовательная программа среднего общего образования «Гражданственность через школьное образование»
за счет бюджетных ассигнований федерального бюджета — 0
за счет бюджетов субъектов Российской Федерации — 40
за счет местных бюджетов — 0
по договорам об образовании за счет средств физических и (или) юридических лиц — 0
4. Дополнительные образовательные программы:
за счет бюджетных ассигнований федерального бюджета: 0
за счет бюджетов субъектов Российской Федерации:
дополнительная общеобразовательная программа «Смысловое чтение» — 139
дополнительная общеобразовательная программа «Юный исследователь» – 20
дополнительная образовательная программа «Решение графических задач в курсе общей физики» — 0
дополнительная образовательная программа «Лесная школа» — 0
дополнительная образовательная программа «Информационные технологии» — 8
дополнительная образовательная программа «Вернисаж творчества» — 9
дополнительная образовательная программа «Мир информатики» — 0
дополнительная образовательная программа «Курс «Решение поливариантных задач по геометрии, задач с параметрами, олимпиадных задач, задач повышенной сложности» — 28
за счет местных бюджетов: 0
по договорам об образовании за счет средств физических и (или) юридических лиц:
дополнительная образовательная программа «Гуманитарный курс «Эссе по обществознанию: теория и практика» — 6
дополнительная образовательная программа «Особенности выполнения творческих заданий по развитию речи» — 11
дополнительная образовательная программа «Применение информационных технологий для решения задач по информатике» — 14
дополнительная образовательная программа «Расширяем границы познания по обществознанию» — 7
дополнительная образовательная программа «Школа будущего первоклассника» — 17
дополнительная образовательная программа «Игровой английский» — 0
Численность обучающихся, являющихся иностранными гражданами — 0
Языки, на которых осуществляется образование
Русский язык (Устав МБОУ СОШ № 71, п. 3.2).
Лицензия на осуществление образовательной деятельности
Дополнительные документы
Совместная деятельность:
Договор о сетевой форме реализации образовательных программ между МБОУ СОШ № 71 и МБОУ СОШ № 74
Договор о совместной деятельности МБУ «МВК» и МБОУ СОШ № 71
Соглашение о совместной деятельности (сотрудничестве) между МБУ «Центр психолого-педагогической, медицинской и социальной помощи» и МБОУ СОШ № 71
Соглашение о совместной деятельности МБУ «Централизованная городская библиотека им. П.П. Бажова» и МБОУ СОШ №71
Договор об организации совместной деятельности МБУ «Центральная городская детская библиотека им. А.П. Гайдара» и МБОУ СОШ №71
Дополнительные программы:
Программа развития образовательного учреждения «Профессионализм. Инновации. Качество»
Независимая оценка качества образования — все материалы находятся в соответствующем разделе сайта:
«Независимая оценка качества образования«
Административные регламенты предоставления муниципальных услуг:
Административный регламент предоставления муниципальной услуги «Предоставление информации о текущей успеваемости учащегося, ведение электронного дневника и электронного журнала успеваемости Муниципальным бюджетным общеобразовательным учреждением «Средняя общеобразовательная школа № 71» городского округа «Город Лесной» Свердловской области»
Административный регламент предоставления муниципальной услуги «Предоставление информации об образовательных программах и учебных планах, рабочих программах учебных курсов, предметов, дисциплин (модулей), годовом календарном учебном графике Муниципальным бюджетным общеобразовательным учреждением «Средняя общеобразовательная школа № 71» городского округа «Город Лесной»Свердловской области»
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
Phy 235 Глава 11
Глава 11
Динамика жесткого
Кузов
Получаем
элементы тензора инерции из уравнения.11.13a:
Аналогично
а также
Аналогично
и
Таким образом,
тензор инерции
г.
основные моменты инерции
полученный путем решения
Расширение
определитель дает кубическое уравнение в l :
Решение
численно дает
Чтобы найти
главные оси, подставляем в (см. пример 11.3):
Для i = 1 имеем
Решение
сначала для
и замена во вторую дает
Подстановка
в третий теперь дает
или
Итак,
главная ось, связанная с
является
Выполняется
таким же образом дает две другие главные оси:
г.
матрица вращения
(1)
Момент
тензора инерции преобразуется по
(2)
То есть
или
(3)
Если
,
.Потом,
(4)
Первоначально:
Таким образом,
(1)
Из уравнения.(11.102)
С
, имеем
(2)
Из уравнения.(11,131)
(2) становится
(3)
Из (1) мы можем построить следующий треугольник
из которых
Подстановка в (3) дает
Если установить
в уравнении для эффективной энергии получаем
(1)
Переставив, это уравнение можно записать как
(2)
, который является кубическим по cos q .
В ( q )
имеет вид, показанный на схеме. Два корня происходят в регионе
, и один корень лежит вне этого диапазона и, следовательно,
воображаемый.
Устойчивость
вращений твердого тела
г.
вращение твердого тела устойчиво, если система при возмущении от ее
состояние равновесия, совершает небольшие колебания вокруг него.Считайте, что мы используем главные оси
вращение для описания движения, и мы выбираем эти оси так, чтобы I 3 > I 2 > I 1 . Если система вращается вокруг оси x 1 , мы можем записать вектор угловой скорости как
Рассмотрим, что происходит, когда мы применяем небольшое возмущение.
вокруг двух других главных осей, так что угловая скорость становится равной
Соответствующие уравнения Эйлера:
Поскольку мы говорим о малых
отклонения от состояния равновесия лм будут небольшими и могут быть установлены на 0.Таким образом, второе уравнение можно использовать для вывода, что
Остальные уравнения можно переписать как
Последнее уравнение можно дифференцировать, чтобы получить
Член в скобках положительный, так как мы приняли
что I 3 > I 2 > I 1 .Это дифференциальное уравнение имеет следующее решение:
где
Когда мы смотрим на возмущение вокруг оси x 3 , мы находим следующий дифференциал
уравнение
Решение дифференциального уравнения второго порядка имеет вид
Мы видим, что возмущения вокруг оси x 2 и оси x 3 колеблются вокруг положения равновесия.
значения л = м = 0.Таким образом, мы заключаем, что вращение вокруг оси x 1 является стабильным.
Похожее
вычисления могут выполняться для вращения вокруг оси x 2 и оси x 3 . Полученные в этих случаях частоты возмущений равны
равно
Мы видим, что первая частота — мнимое число, а
вторая частота — действительное число.Таким образом, вращение вокруг оси x 3 стабильно, но вращение вокруг оси x 2 нестабильно.
Пример:
Проблема 11.34
Рассмотреть
симметричное твердое тело, свободно вращающееся вокруг своего центра масс. Момент трения ( Н f = -b w ) замедляет
вращение. Найдите компонент
угловая скорость вдоль оси симметрии как функция времени.
Эйлер
уравнение, описывающее вращение объекта вокруг оси симметрии,
скажем, ось x , это
где
компонент
крутящего момента по Ox .Поскольку объект симметричен относительно
ось x , мы имеем
, и выше
уравнение становится
В течение 1 секунды движение равновесия.Равнопросмотренное движение
Данный видеоурок посвящен теме «Скорость прямолинейного эквивалентного движения. График скорости». Во время занятия ученикам придется вспомнить такую физическую величину, как ускорение. Затем они учатся определять скорость прямого конного движения. После учитель расскажет, как построить график скорости.
Напомним, что такое ускорение.
Определение
Ускорение — это физическая величина, которая характеризует изменение скорости за определенный период времени:
То есть ускорение — это величина, которая определяется изменением скорости, во время которого это изменение произошло.
Еще раз о том, что такое уравновешенный механизм
Рассмотрим задачу.
Автомобиль увеличивает скорость каждую секунду. Автомобиль движется одинаково?
На первый взгляд кажется, что да, потому что через равные промежутки времени скорость увеличивается на равные величины. Давайте посмотрим на движение «Читать дальше» на 1 с. Возможен такой случай, что первые 0,5 с автомобилем двигались равномерно, а на вторых 0,5 с увеличивали свою скорость. Возможна и другая ситуация: автомобиль разгоняется первым, а остальные движутся равномерно.Такое движение не будет равноценным.
По аналогии с равномерным движением вводим правильную формулировку эквивалентного движения.
Равно Это движение называется, при котором тело меняет свою скорость за любые равные периоды на одно и то же значение.
Часто равномерно называют такое движение, при котором тело движется с постоянным ускорением. Простейший пример эквивалентного движения — свободное падение тела (тело падает под действием силы тяжести).
Воспользовавшись уравнением ускорения, удобно записать формулу для расчета мгновенной скорости любого интервала и для любого момента времени:
Уравнение скорости в проекциях:
Это уравнение позволяет определить скорость в любой момент движения тела. При работе с законом изменения скорости во времени необходимо учитывать направление скорости относительно выбранной СО.
К вопросу о направлении скорости и ускорении
При равномерном движении направление скорости и движения всегда совпадают. В случае равновесного движения направление скорости не всегда совпадает с направлением ускорения, а направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону по одной прямой (рис.1).
Рис. 1. Скорость и ускорение направлены в одну сторону по одной прямой.
В этом случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, запуск и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны по одной прямой (рис. 2).
Рис. 2. Скорость и ускорение направлены в разные стороны по одной прямой.
Такое движение иногда называют приспособляемым. В этом случае говорят, что тело тормозит. В конце концов, он либо останавливается, либо начинает двигаться в обратном направлении. Пример такого движения — камень, стоящий вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).
Рис. 3. Скорость и ускорение взаимно перпендикулярно
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли.В этом случае траектория движения будет круговой.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
Скорость (проекции скорости) — закон изменения скорости (проекции скорости) во времени для равновесной прямой, представленный графически.
Рис. 4. Графики зависимости проекции скорости от времени для равновесной прямой
Разберем различные графики.
Первый. Уравнение проекции скорости:. С увеличением времени увеличивается и скорость. Обратите внимание, что на графике, где одна из осей — время, а другая — скорость, будет прямая линия. Эта линия начинается с точки, характеризующей начальную скорость.
Вторая — это зависимость в отрицательном значении проекции ускорения, когда движение медленное, то есть сначала снижается скорость модуля. В этом случае уравнение выглядит так:
График начинается с точки и продолжается до точки пересечения оси времени.В этот момент скорость тела становится нулевой. Это означает, что тело остановилось.
Если вы внимательно посмотрите на уравнение скорости, то вспомните, что аналогичная функция была в математике:
Где и — какие-то постоянные, например:
Рис. 5. График работы
Это уравнение прямое, что подтверждают рассмотренные нами графики.
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи.На первом графике зависимость скорости от времени связана с тем, что при начальной скорости, равной нулю, проекция ускорения больше нуля.
Запишите это уравнение. Да и сам тип графика довольно простой (график 1).
Рис. 6. Различные случаи эквивалентного движения
Еще два случая равны запрашиваемому движению , представленному на следующих двух диаграммах. Второй случай — это ситуация, когда тело сначала двигалось с отрицательной проекцией ускорения, а затем начало ускоряться в положительном направлении оси.
Третий случай — это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси. При этом модуль скорости постоянно увеличивается, кузов разгоняется.
График ускорения
Равноправное движение — это движение, при котором ускорение тела не изменяется.
Рассмотрим графику:
Фиг.7. График зависимости проекции ускорения от времени
Если какая-либо зависимость постоянна, то на графике она изображена прямой, параллельной оси абсцисс. Прямые I и II — это прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсциссы (проекция ускорения положительна), а прямая II ниже (проекция ускорения отрицательная). Если бы движение было равномерным, проекция ускорения совпадала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченная осями графика и перпендикулярно оси абсцисс, равна:
Произведение ускорения и времени — это изменение скорости за это время.
Рис. 8. Изменение скорости
Площадь фигуры, ограниченная осями, зависимостью и перпендикулярной оси абсцисс, численно равна изменяющейся скорости тела.
Мы использовали слово «численно», так как единицы измерения площади и изменения скорости не совпадают.
На этом уроке мы познакомились с уравнением скорости и научились графически изобразить это уравнение.
Библиография
- Кикооин И.К., Кикооин А.К. Физика: Учебник для 9 класса средней школы. — М .: «Просвещение».
- Пририкин А.В., Годник Е.М., Физика. 9 кл .: Учебник для общего образования. учреждений / А.В. Pryrickin, E.M. Genther. — 14-е изд., Стереотип. — М .: Капля, 2009. — 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. — 2-е издание красное. — Х .: Веста: Издательство «Рокки», 2005. — 464 с.
- Интернет-портал «class-fizika.narod.ru» ()
- Интернет-портал «YouTube.com» ()
- Интернет-портал «Fizmat.by» ()
- Интернет-портал «Sverh-zadacha.ucoz.ru» ()
Домашнее задание
1. Что такое эквивалентное движение?
2. Опишите движение тела и определите путь, пройденный телом за 2 с от начала движения:
3.На каком из графиков показана зависимость проекции скорости тела от времени на уравновешенное движение?
В этом разделе мы рассмотрим совершенно особый вид неравномерного движения. Исходя из противостояния равномерному движению, неравномерное движение — это движение с разной скоростью по любой траектории. В чем особенность равновесного движения? Это неравномерное движение, но «ЧРЕЗВЫЧАЙНО ускоряет» . Ускорение связано с увеличением скорости. Вспомните слово «равный», мы получим равный прирост скорости.А как понять «равный прирост скорости», как оценить скорость равной или нет? Для этого нам нужно будет получить время, оценить скорость через тот же интервал времени. Например, машина начинает движение, в первые две секунды развивает скорость до 10 м / с, в следующие две секунды 20 м / с, еще через две секунды она уже движется со скоростью 30 м / с. . Каждые две секунды скорость увеличивается и каждый раз на 10 м / с. Это движение равновесия.
Физическая величина, характеризующая, во сколько раз увеличивается скорость, называется ускорением.
Можно ли считать велосипедиста эквивалентным, если после остановки в первую минуту его скорость 7 км / ч, во вторую — 9 км / ч, в третью — 12 км / ч? Это невозможно! Велосипедист разгоняется, но не одинаково, сначала разгоняется до 7 км / ч (7-0), затем 2 км / ч (9-7), затем 3 км / ч (12-9).
Обычно движение с нарастающей скоростью называется ускоренным. Движение с убывающей скоростью — замедленное движение. Но в физике любое движение с изменяющейся скоростью называется ускоренным движением.Машина начинает со сцены (скорость растет!), Или тормозит (скорость уменьшается!), В любом случае движется с ускорением.
Равно запрошенное движение — это движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) то же
Ускорение кузова
Ускорение характеризует изменение скорости. Это число, которое изменяет скорость в секунду. Если ускорение тела в модуле велико, значит, тело быстро набирает скорость (при разгоне) или быстро теряет ее (при торможении). Ускорение — Это физическая величина вектора, численно равная отношению изменения скорости к периоду времени, в течение которого это изменение произошло.
В следующей задаче определяем ускорение. В начальный момент времени скорость составляла 3 м / с, в конце первой секунды скорость корабля была 5 м / с, в конце второй — 7 м / с, в конце первой секунды. третья 9 м / с и т.д. Очевидно. Но как мы определились? Считаем разницу в скорости в одну секунду.В первой секунде 5-3 = 2, во второй второй 7-5 = 2, в третьей 9-7 = 2. А что делать, если на каждую секунду нет скоростей? Такая задача: начальная высота по скорости 3 м / с, в конце второй секунды — 7 м / с, в конце четвертой 11 м / с. В этом случае необходимо 11-7 = 4, затем 4/2 = 2. Разность скоростей делим на промежуток времени.
Эта формула чаще всего используется при решении задач в модифицированном виде:
Формула не записывается в векторном виде, поэтому знак «+» пишут, когда тело ускоряется, знак «-» — когда замедляется.
Направление вектора ускорения
Направление вектора ускорения показано на чертежах.
На этом рисунке машина движется в положительном направлении по оси OX, вектор скорости всегда совпадает с направлением движения (направленным вправо). Когда векторное ускорение совпадает с направлением скорости, это означает, что автомобиль разгоняется. Разгон положительный.
При ускорении направление ускорения совпадает с направлением скорости.Разгон положительный.
На этом рисунке машина движется в положительном направлении по оси OX, вектор скорости совпадает с направлением движения (направленным вправо), ускорение не совпадает с направлением скорости, а значит, машина медленная. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное.Например, теплоход за первую секунду снизил скорость с 9 м / с до 7 м / с, за вторую секунду до 5 м / с, за третью до 3 м / с. Скорость меняется на «-2м / с». 3-5 = -2; 5-7 = -2; 7-9 = -2м / с. Здесь появляется отрицательное значение ускорения.
При решении задач, Если тело тормозит, то ускорение в формулу подставляется знаком «минус» !!!
Перемещение с эквивалентным механизмом
Дополнительная формула под названием strong
Формула в координатах
Соединение со средней скоростью
При равновесном движении средняя скорость может быть рассчитана как начальная и конечная скорость среднего луча.
Это правило следует формуле, которую очень удобно использовать при решении многих задач
Передаточный путь
Если тело движется одинаково, начальная скорость равна нулю, пути, проходящие через последовательные равные интервалы, связаны как последовательное количество нечетных чисел.
Главное помнить
1) что такое уравновешенное движение;
2) что характеризует ускорение;
3) Ускорение — вектор. Если тело ускоряется, ускорение положительное, если замедляется — ускорение отрицательное;
3) направление вектора ускорения;
4) формулы, единицы измерения в си
Упражнения
Два поезда идут навстречу друг другу: один ускоряется на север, другой замедляется на юг.Как поезда ускоряются?
Одинаково на север. Потому что на первом поезде ускорение совпадает с движением, а на втором — с противоположным движением (он замедляется).
За первую секунду равновесного движения тело проходит 1 м, а за вторую — 2 м. Определите путь, пройденный телом за первые три секунды движения.
Задание №1.3.31 из «Сборника заданий для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\ (S_1 = 1 \) м, \ (s_2 = 2 \) м, \ (s -? \)
Решение проблемы:
Обратите внимание, что условие не говорит, имеет ли тело начальную скорость или нет. 2)) (2)) \ Right) \ hfill \\\\
\ \ Конец (Собрано) \\ Вправо.2) \ Справа))) (2) \ hfill \
\ Конец (Собран) \ Справа. \\]
В этой системе два уравнения и два неизвестных, что означает, что она (система) может быть решена. Мы не будем пытаться решить ее в целом, поэтому подставим известные нам числовые данные.
\ [\ left \ (\ begin (собрано)
1 = (\ Upsilon _0) + 0,5A \ hfill \
2 = (\ Upsilon _0) + 1, 5A \ hfill \
\ End (Собранный) \ Right. \\]
Связанная со вторым уравнением сначала, получаем:
Если подставить значение ускорения в первое уравнение, получим:
\ [(\ Upsilon _0) = 0.5 \\; м / с \\]
Теперь, чтобы узнать путь, пройденный телом за три секунды, необходимо записать уравнение движения тела.
В результате ответ будет равен:
Ответ: 6 мес.
Если вам непонятен вариант решения и у вас возник какой-то вопрос или вы обнаружили ошибку, то смело оставляйте комментарий ниже.
1) Аналитический метод.
Считаем трассу простой. Подключите уравнение движения велосипедиста.Поскольку велосипедист двигался равномерно, его уравнение движения:
(Начало координат помещается в начальную точку, поэтому начальная координата велосипедиста равна нулю).
Мотоциклист двигался одинаково. Он тоже начал движение с места старта, поэтому его начальная координата равна нулю, начальная скорость мотоциклиста тоже равна нулю (мотоциклист начал движение от остальных).
Учитывая, что мотоциклист начал движение позже, уравнение движения мотоциклиста:
При этом скорость мотоциклиста была изменена законом:
В момент, когда мотоциклист догнал велосипедиста, их координаты равны, т.е.е. или:
Решая это уравнение относительно, находим время встречи:
Это квадратное уравнение. Определить дискриминант:
Определить корни:
Подставить числовые значения и вычислить по формуле:
Второй корень отбрасывается как несоответствующий физическим условиям задачи: мотоциклист не смог догнать велосипедиста при температуре 0,37 ° C после старта велосипедиста, так как он покинул точку старта только через 2 секунды после того, как велосипедист тронулся с места. .
Итак, время, когда мотоциклист догнал велосипедиста:
Подставим это значение времени в формулу закона изменения скорости мотоциклиста и найдем значение его скорости в этой точке:
2) графический метод.
На одной координатной плоскости строим графики изменения координат времени велосипедиста и мотоциклиста (график для координаты велосипедиста — красный, для мотоциклиста — зеленый). Видно, что зависимость координаты от велосипедиста является линейной функцией, а график этой функции прямой (случай равномерного прямого движения).Мотоциклист двигался одинаково, поэтому зависимость координат мотоциклиста от времени является квадратичной функцией, которая представляет собой парабол с графиком.
Движение по прямой с ускорением — материалы исследования для IIT JEE
Скорость тела определяется как скорость смещения во времени, а ускорение определяется как скорость изменения скорости во времени. Ускорение — это векторная величина.Движение может быть равноускоренным или неравномерно ускоренным, в зависимости от того, как скорость изменяется со временем.
Равномерное ускорение
Ускорение тела называется равномерным, если его скорость изменяется на равную величину с равными интервалами.
Неравномерное ускорение
Ускорение тела называется неравномерным, если его скорость изменяется на неравную величину через равные промежутки времени.
Средняя скорость
Среднее ускорение
Иллюстрация:
Частица движется со скоростью v (t) = (1/2) kt 2 по прямой. Найти среднюю скорость частицы за время T.
Решение:
Иллюстрация:
Частица, имеющая начальную скорость, движется с постоянным ускорением «а» в течение времени t.
(a) Найдите смещение частицы за последнюю 1 секунду.
(b) Оцените его для u = 2 м / с, a = 1 м / с 2 и t = 5 сек.
Решение:
(a) Дано смещение частицы в момент времени t s = ut + 1 / 2at 2
В момент времени (t — 1) смещение частицы определяется выражением
S ‘= u (t-1) + 1 / 2a (t-1) 2
Итак, смещение за последнюю 1 секунду составляет,
S т = S — S ‘
= ut + 1/2 при 2 — [u (t-1) +1/2 a (t-1) 2 ]
= ut + 1/2 при 2 — ut + u — 1 / 2a (t — 1) 2
= 1/2 при 2 + u — 1/2 a (t + 1-2t) = 1/2 при 2 + u — 1/2 при 2 — a / 2 + при
S = и + а / 2 (2т — 1)
(б) Полагая значения u = 2 м / с, a = 1 м / с 2 и t = 5 с, получаем
S = 2 + 1/2 (2 x 5-1) = 2 + 1/2 x 9
= 2 + 4.5 = 6,5 м
Иллюстрация:
Положение частицы, движущейся вдоль оси x, определяется выражением x = 3t — 4t 2 + t 3 , где x выражается в метрах, а t — в секундах.
(a) Найдите положение частицы при t = 2 с.
(b) Найдите смещение частицы за интервал времени от t = 0 до t = 4 с.
(c) Найдите среднюю скорость частицы в интервале времени от t = 2 с до t = 4 с.
(d) Найдите скорость частицы при t = 2 с.
Решение:
(a) x (t) = 3t — 4t 2 + t 3
=> x (2) = 3 x 2 — 4 x (2) 2 + (2) 3 = 6 — 4 x 4 + 8 = -2 м.
(б) х (в) = 0
X (4) = 3 x 4 — 4 x (4) 2 + (4) 3 = 12 м.
Смещение = x (4) — x (0) = 12 м.
(c)
(d) dx / dt = 3 — 8t + 3t 2
v (2) (dx / dt) 2 = 3-8 x 2 + 3 x (2) 2 = -1 м / с
Иллюстрация:
Двум поездам требуется 3 секунды, чтобы обогнать друг друга при движении в противоположном направлении, и только 2,5 секунды, если скорость одного увеличивается на 50%. Время, которое потребуется, чтобы обогнать другого, двигаясь в том же направлении с исходной скоростью, составляет
.
(а) 10 с (б) 12 с
(в) 15 сек (г) 18 сек
Решение:
Используя уравнение,
т = д / в р
Есть,
3 = d / v 1 + v 2
2.5 = d / 1,5v 1 + v 2
Решая получаем,
v 1 = 2d / 15 и v 2 = d / 5
Когда они идут в одном направлении,
v r = v 2 — v 1 = d / 15
Таким образом, t = d / v r = d / (d / 15) = 15 с
На основании вышеизложенного мы заключаем, что вариант (c) верен.
Анализ равномерно ускоренного движения
Ящик-I:
Для равноускоренного движения с начальной скоростью u и начальным положением x 0 .
График скорости и времени
В любом случае tanθ = a 0
График положения и времени
Начальное положение x тела в каждом случае x 0 (> 0)
Корпус II:
Для равномерно замедленного движения с начальной скоростью u и начальным положением x 0 .
График скорости-времени
В любом случае tanθ = -a 0
График положения и времени
Начальное положение x тела в каждом случае x 0 (> 0)
Иллюстрация:
Частица движется прямолинейно с изменяющимся во времени ускорением a = 4 — 2t, где a в м / с 2 и t в секундах.Если частица начинает движение со скоростью -3 м / с от x = 0. Нарисуйте кривые a-t, v-t и x-t для частицы.
Решение:
а = 4-2 т
v = 4т-т 2 -3
x = 2 т 2 — т 3 /3 — 3 т
Разгон
Ускорение — это скорость изменения скорости во времени. Понятие ускорения понимается под неравномерным движением.Это векторная величина.
Среднее ускорение — это изменение скорости в единицу времени за интервал времени.
Мгновенное ускорение определяется как
Вектор ускорения при неравномерном движении
Предположим, что в момент t 1 частица, как на рисунке выше, имеет скорость, а в момент t 2 скорость равна. Среднее ускорение при движении определяется как
Переменное ускорение
Ускорение в любой момент получается из среднего ускорения путем сокращения временного интервала ближе к нулю.Поскольку Δt стремится к нулю, среднее ускорение приближается к предельному значению, которое представляет собой ускорение в тот момент, называемое мгновенным ускорением, которое является векторной величиной.
т.е. мгновенное ускорение является производной от скорости.
Следовательно, мгновенное ускорение частицы в любой момент — это скорость, с которой ее скорость изменяется в этот момент. Мгновенное ускорение в любой точке — это наклон кривой v (t) в этой точке, как показано на рисунке выше.
Уравнения движения
Взаимосвязь между различными параметрами, такими как скорость смещения, ускорение, может быть получена с использованием концепции среднего ускорения и концепции среднего ускорения и мгновенного ускорения.
Когда ускорение постоянное, различие между средним ускорением и мгновенным ускорением теряет смысл, поэтому мы можем написать
где — скорость в момент t = 0, а — скорость в некоторый момент времени t
Сейчас,
Следовательно,
…… (2)
Это первое полезное уравнение движения.
Аналогично смещению
… … (3)
, в котором положение частицы в момент t 0 и средняя скорость между t 0 и более поздним моментом времени t. Если при t 0 и t скорость частицы равна
… … (4)
Из уравнений (3) и (4) получаем,
… … (5)
Это второе важное уравнение движения.
Теперь из уравнения (2) возведем обе части этого уравнения в квадрат, получим
[Используя уравнение (4)]
Используя уравнение (3), получаем,
… … (6)
Это еще одно важное уравнение движения.
Осторожно: Выведенное выше уравнение движения возможно только при равномерно ускоренном движении, то есть движении с постоянным ускорением.
См. Это моделирование движения по прямой
Иллюстрация:
Ядро атома гелия (альфа-частица) движется внутри прямой полой трубки длиной 2.0 метров в длину, который является частью ускорителя частиц. (а) Если предположить равномерное ускорение, какова длина частицы в трубе, если она входит со скоростью 1000 м / сек и улетает со скоростью 9000 м / сек? б) Каково его ускорение в течение этого интервала?
Решение:
(a) Выберем ось x, параллельную трубке, положительным направлением которого является то, в котором движется частица, и ее начало на входе в трубку. Нам даны x и v x , и мы ищем t.Топор ускорения не задействован. Следовательно, мы используем уравнение 3, x = x 0 +
Получаем
x = v 0 + ½ (v x 0 ) + v x ) t, с x 0 = 0 или
t = 2x / (v x0 + v x) ,
t = ((2) (2,0 метра)) / ((1000 + 9000) метров / сек) = 4,0 / 10 -4 сек Ответ.
(b) Ускорение следует из уравнения 2, v x = v x 0 + a x t
=> ax = (v 0 -v x0 ) / t = ((9000-1000) метров / сек) / (4.0 × 10 (-4) сек)
= 2,0 × 10 7 м / с 2 Отв.
Пауза: Однако приведенные выше уравнения движения являются универсальными и могут быть выведены с использованием дифференциального исчисления, как указано ниже:
Или,
Пусть при t = 0,
тогда,
Или,
Далее мы знаем, что
или
Интегрирующий,
Или,
At, t = 0, x = x 0 , тогда c ‘= x 0
Следовательно,
Таким образом, мы получили то же уравнение движения, используя математический анализ.
Чтобы понять использование исчисления при решении кинематических задач, мы можем взглянуть на следующие иллюстрации.
Иллюстрация:
Смещение x частицы, движущейся в одном измерении под действием постоянной силы, связано со временем t уравнением t = √x + 3, где x выражается в метрах, а t — в секундах. Найдите смещение частицы, когда ее скорость равна нулю.
Решение:
Здесь t = √x + 3 => √x = t — 3
Возводя обе стороны в квадрат, получаем x = t 2 — 6t + 9,
Как известно скорость, v = dx / dt
Отсюда получаем v = dx / dt = 2t — 6
Положим v = 0, получим, 2t — 6 = 0
Итак, t = 3с
При t = 3 с, x = t 2 — 6t + 9 = 9 — 6 (3) + 9 = 0
Следовательно, смещение частицы равно нулю, когда ее скорость равна нулю.
Иллюстрация:
Частица стартует из точки с начальной скоростью v 1 и достигает с конечной скоростью v 2 в точке B, которая находится на расстоянии «d» от точки A. Путь прямой. Если ускорение пропорционально скорости, найдите время, которое проходит частица от точки A до точки B.
Решение:
Здесь ускорение a пропорционально скорости v.
Следовательно, α v
=> a = kv, где k постоянно
=> дв / дт = кв…………… (1)
=> (dv / ds) (ds / dt) = kv => (dv / ds) v = kv
Из уравнения (1),
дв / в = кдт
или,
Или, ln (v 2 / v 1 ) = kt
Или, t = ln (v 2 / v 1 ) / k
= [d ln (v 2 / v 1 ) / (v 2 -v 1 )]
|
Вопрос 1 : —
Если автомобиль в состоянии покоя равномерно разгоняется до скорости 144 км / ч за 20 с, он преодолевает расстояние:
(а) 20 м (б) 800 м
(в) 400 м (г) 1200 м
Вопрос 2 : —
Если тело массой 3 кг падает вниз, через 1 секунду другой мяч падает вниз с той же точки.Какое расстояние между ними через 3 сек.
(а) 25 м (б) 20 м
(в) 50 м (г) 9,8 м
Вопрос 3 : —
Два тела разной массы m a и m b падают с двух разных высот a и b. Отношение времени, которое потребовалось этим двоим, чтобы преодолеть эти расстояния, составляет:
(а) а: б (б) б: а
(c) a 2 : b 2 (d) √a: √b
Вопрос 4 : —
Мячу требуется t секунд, чтобы упасть с высоты h 1 и 2t секунд, чтобы упасть с высоты h 2 .Тогда h 1 / h 2 будет:
(а) 0,5 (б) 0,25
(в) 2 (г) 4
Связанные ресурсы
Чтобы узнать больше, купите учебные материалы по кинематике, включая учебные заметки, исправления, видеолекции, решенные вопросы за предыдущий год и т. Д. Также просмотрите дополнительные учебные материалы по физике здесь.
Движение в двух измерениях | Безграничная физика
Постоянная скорость
Объект, движущийся с постоянной скоростью, должен иметь постоянную скорость в постоянном направлении.
Цели обучения
Изучите термины для постоянной скорости и их применимость к ускорению
Основные выводы
Ключевые моменты
- Постоянная скорость означает, что движущийся объект движется по прямой с постоянной скоростью.
- Эта строка может быть представлена алгебраически как: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] представляет положение объекта в [latex] \ text {t} = 0 [/ latex], а наклон линии указывает скорость объекта.
- Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Ключевые термины
- постоянная скорость : Движение, которое не меняется ни по скорости, ни по направлению.
Движение с постоянной скоростью — одна из простейших форм движения. Этот тип движения возникает, когда объект движется (или скользит) в присутствии небольшого или незначительного трения, подобно тому, как хоккейная шайба скользит по льду.Чтобы иметь постоянную скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории.
Второй закон Ньютона ([latex] \ text {F} = \ text {ma} [/ latex]) предполагает, что когда к объекту прикладывается сила, объект будет испытывать ускорение. Если ускорение равно 0, объект не должен подвергаться воздействию внешних сил. Математически это можно представить следующим образом:
[латекс] \ text {a} = \ frac {\ text {dv}} {\ text {dt}} = 0 ~ \ Rightarrow ~ \ text {v} = \ text {const} [/ latex].
Если объект движется с постоянной скоростью, график зависимости расстояния от времени ([latex] \ text {x} [/ latex] vs. [latex] \ text {t} [/ latex]) показывает такое же изменение в положение по каждому интервалу времени. Поэтому движение объекта с постоянной скоростью представлено прямой линией: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] — это смещение, когда [latex] \ text {t} = 0 [/ latex] (или в точке пересечения оси Y).
Движение с постоянной скоростью : Когда объект движется с постоянной скоростью, он не меняет ни направления, ни скорости, и поэтому отображается как прямая линия на графике как расстояние во времени.
Вы также можете получить скорость объекта, если знаете его траекторию во времени. Имея график, как в, мы можем вычислить скорость по изменению расстояния с течением времени. Графически скорость можно интерпретировать как наклон линии. Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Постоянное ускорение
Анализ двумерного движения снаряда выполняется путем разбиения его на два движения: по горизонтальной и вертикальной осям.
Цели обучения
Анализировать двумерное движение снаряда по горизонтальной и вертикальной осям
Основные выводы
Ключевые моменты
- Постоянное ускорение при движении в двух измерениях обычно происходит по образцу снаряда.
- Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, с учетом только (вертикального) ускорения силы тяжести.
- Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.
Ключевые термины
- кинематика : или относящиеся к движению или кинематике
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, подверженное только силе тяжести. Объект называется снарядом, а его путь называется его траекторией. Движение падающих предметов — это простой одномерный тип движения снаряда, при котором нет горизонтального движения. В двумерном движении снаряда, например футбольного мяча или другого брошенного объекта, есть как вертикальная, так и горизонтальная составляющие движения.
Движение снаряда : Бросок камня или удар ногой по мячу, как правило, создает образец движения снаряда, который имеет как вертикальную, так и горизонтальную составляющую.
Самый важный факт, который следует помнить, это то, что движения по перпендикулярным осям независимы и поэтому могут быть проанализированы отдельно. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения, одно по горизонтальной оси, а другое — по вертикали. Чтобы описать движение, мы должны иметь дело со скоростью и ускорением, а также со смещением.2} [/ latex] (мы предполагаем, что движение происходит на достаточно малых высотах у поверхности земли, чтобы ускорение свободного падения было постоянным). Поскольку ускорение свободного падения происходит в вертикальном направлении только , [latex] \ text {a} _ \ text {x} = 0 [/ latex]. 2 + 2 \ text {a} _ \ text {y} (\ text {y} — \ text {y} _0) [/ latex]
Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.Горизонтальное движение простое, потому что [latex] \ text {a} _ \ text {x} = 0 [/ latex] и [latex] \ text {v} _ \ text {x} [/ latex], таким образом, является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. Движения [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] можно рекомбинировать, чтобы получить общую скорость в любой заданной точке траектории.
Графический анализ одномерного движения
Цели обучения
К концу этого раздела вы сможете:
- Опишите прямолинейный график с точки зрения его наклона и интервала y .
- Определите среднюю или мгновенную скорость по графику положения в зависимости от времени.
- Определите среднее или мгновенное ускорение по графику зависимости скорости от времени.
- Постройте график зависимости скорости отвремя из графика положения относительно времени.
- Постройте график зависимости ускорения от времени из графика зависимости скорости от времени.
График, как и картинка, стоит тысячи слов. Графики содержат не только числовую информацию; они также раскрывают отношения между физическими величинами. В этом разделе используются графики перемещения, скорости и ускорения в зависимости от времени, чтобы проиллюстрировать одномерную кинематику.
Склоны и общие отношения
Прежде всего, обратите внимание, что графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная.Когда две физические величины нанесены друг против друга на таком графике, горизонтальная ось обычно считается независимой переменной , а вертикальная ось — зависимой переменной . Если мы назовем горизонтальную ось осью x , а вертикальную ось — осью y , как на рисунке 1, прямолинейный график будет иметь общий вид
.
[латекс] y = \ text {mx} + b \\ [/ latex]
Здесь м — это наклон , определяемый как подъем, разделенный на пробег (как показано на рисунке) прямой линии.Буква b используется для точки пересечения y , которая является точкой, в которой линия пересекает вертикальную ось.
График смещения от времени (
a = 0, поэтому v постоянно)
Время обычно является независимой переменной, от которой зависят другие величины, такие как смещение. График смещения в зависимости от времени, таким образом, будет иметь x по вертикальной оси и t по горизонтальной оси.Рисунок 2 — это именно такой прямолинейный график. На нем показан график перемещения в зависимости от времени для реактивного автомобиля на очень плоском высохшем дне озера в Неваде.
Используя соотношение между зависимыми и независимыми переменными, мы видим, что наклон на приведенном выше графике — это средняя скорость [латекс] \ bar {v} \\ [/ latex], а точка пересечения — смещение в нулевой момент времени, то есть x 0 . Подставляя эти символы в [latex] y = \ text {mx} + b \\ [/ latex], получаем
[латекс] x = \ bar {v} t + {x} _ {0} \\ [/ latex]
или
[латекс] x = {x} _ {0} + \ bar {v} t \\ [/ latex].
Таким образом, график смещения в зависимости от времени дает общую взаимосвязь между смещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации.
Наклон x по сравнению с т
Наклон графика смещения x от времени t — это скорость v .
[латекс] \ text {slope} = \ frac {\ Delta x} {\ Delta t} = v \\ [/ latex]
Обратите внимание, что это уравнение аналогично уравнению, полученному алгебраически из других уравнений движения в уравнениях движения для постоянного ускорения в одном измерении.
Из рисунка видно, что автомобиль имеет водоизмещение 400 м в момент времени 0,650 м при т, = 1,0 с и так далее. Его смещение в моменты времени, отличные от указанных в таблице, можно увидеть на графике; кроме того, информация о его скорости и ускорении также может быть получена из графика.
Пример 1. Определение средней скорости по графику смещения в зависимости от времени: Jet Car
Найдите среднюю скорость автомобиля, положение которого показано на рисунке 2.
Стратегия
Наклон графика x против т. — это средняя скорость, поскольку наклон равен подъему за пробег. В данном случае подъем = изменение рабочего объема, а бег = изменение во времени, так что
[латекс] \ text {slope} = \ frac {\ Delta x} {\ Delta t} = \ bar {v} \\ [/ latex].
Поскольку наклон здесь постоянный, любые две точки на графике могут использоваться для определения наклона. (Вообще говоря, точнее всего использовать две широко разнесенные точки на прямой.Это связано с тем, что любая ошибка при чтении данных с графика пропорционально меньше, если интервал больше.)
Решение
1. Выберите две точки на линии. В этом случае мы выбираем точки, помеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Учтите, однако, что вы можете выбрать любые две точки.)
2. Подставьте значения x и t выбранных точек в уравнение. Помните, что при вычислении изменения (Δ) мы всегда используем конечное значение минус начальное значение.
[латекс] \ bar {v} = \ frac {\ Delta x} {\ Delta t} = \ frac {\ text {2000 m} — \ text {525 m}} {6 \ text {.} \ Text { 4 s} -0 \ text {.} \ Text {50 s}} \\ [/ latex],
дает
[латекс] \ bar {v} = \ text {250 м / с} [/ латекс].
Обсуждение
Это впечатляюще большая сухопутная скорость (900 км / ч или около 560 миль / ч): намного больше, чем типичное ограничение скорости на шоссе в 60 миль / ч (27 м / с или 96 км / ч), но значительно скромнее. рекорда 343 м / с (1234 км / ч или 766 миль / ч), установленного в 1997 году.
Графики движения, когда
a постоянна, но a ≠ 0
Графики на Рисунке 3 ниже представляют движение автомобиля с реактивным двигателем, когда он набирает максимальную скорость, но только в то время, когда его ускорение является постоянным. Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально составляют 200 м и 15 м / с соответственно.
График смещения в зависимости от времени на рис. 3 (а) представляет собой кривую, а не прямую линию.Наклон кривой становится более крутым с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости смещения от времени — это мгновенная скорость в этой точке. Его можно найти, проведя прямую касательную к кривой в интересующей точке и взяв наклон этой прямой. Касательные линии показаны для двух точек на рисунке 3 (а). Если это делается в каждой точке кривой и значения наносятся в зависимости от времени, то получается график зависимости скорости от времени, показанный на рисунке 3 (b).Кроме того, наклон графика зависимости скорости от времени — это ускорение, которое показано на Рисунке 3 (c).
Пример 2. Определение мгновенной скорости по уклону в точке: Реактивный автомобиль
Рассчитайте скорость реактивного автомобиля за время 25 с, найдя наклон графика x против тонн на графике ниже.
Наклон графика x против t — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке — это наклон касательной в этой точке.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке. Этот принцип проиллюстрирован на рисунке 5, где Q — точка при t = 25 с.
Решение
1. Найдите касательную к кривой при t = 25 с.
2. Определите конечные точки касательной. Они соответствуют позиции 1300 м за 19 с и позиции 3120 м за 32 с.
3. Подставьте эти конечные точки в уравнение, чтобы найти наклон: v .
[латекс] \ text {slope} = {v} _ {Q} = \ frac {{\ Delta x} _ {Q}} {{\ Delta t} _ {Q}} = \ frac {\ left (\ text {3120 m} — \ text {1300 m} \ right)} {\ left (\ text {32 s} — \ text {19 s} \ right)} \\ [/ latex]
Таким образом,
[латекс] {v} _ {Q} = \ frac {\ text {1820 m}} {\ text {13 s}} = \ text {140 м / с.} \\ [/ latex]
Обсуждение
Это значение, приведенное в таблице этого рисунка для v при t = 25 с.Значение 140 м / с для v Q показано на рисунке 5. Таким образом можно получить весь график v и t .
Продолжая этот шаг дальше, отметим, что наклон графика зависимости скорости от времени — это ускорение. Склон делится на подъем, разделенный бегом; на графике v против t , подъем = изменение скорости Δ v и бег = изменение во времени Δ t .
Наклон против vs. т
Наклон графика зависимости скорости v от времени t — это ускорение a .
[латекс] \ text {slope} = \ frac {\ Delta v} {\ Delta t} = a \\ [/ latex]
Поскольку график зависимости скорости от времени на Рисунке 3 (b) представляет собой прямую линию, ее наклон везде одинаковый, что означает, что ускорение является постоянным. Ускорение в зависимости от времени показано на рисунке 3 (c).
Дополнительную общую информацию можно получить из рисунка 5 и выражения для прямой линии, [latex] y = \ text {mx} + b \\ [/ latex].
В данном случае вертикальная ось y равна V , точка пересечения b равна v 0 , наклон м равен a , а горизонтальная ось x равна t . Подстановка этих символов дает
[латекс] v = {v} _ {0} + \ text {at} \\ [/ latex].
Общая зависимость скорости, ускорения и времени снова была получена из графика. Обратите внимание, что это уравнение также было выведено алгебраически из других уравнений движения в уравнениях движения для постоянного ускорения в одном измерении.
Неслучайно те же уравнения получаются графическим анализом и алгебраическими методами. Фактически, важный способ обнаружить физические взаимосвязи — это измерить различные физические величины, а затем построить графики одной величины относительно другой, чтобы увидеть, коррелированы ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны в виде гладких графиков, подобных приведенным выше. Из таких графиков иногда можно постулировать математические отношения.Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых соотношений.
Графики движения с непостоянным ускорением
Теперь рассмотрим движение реактивного автомобиля от 165 м / с до максимальной скорости 250 м / с, как показано на рисунке 6. Время снова начинается с нуля, а начальное смещение и скорость составляют 2900 м и 165 м. / с соответственно. (Это были окончательное смещение и скорость автомобиля в движении, показанные на Рисунке 3.) Ускорение постепенно снижается с 5,0 м / с 2 до нуля при наезде на 250 м / с. Наклон графика x против t увеличивается до t = 55 с, после чего наклон остается постоянным. Точно так же скорость увеличивается до 55 с, а затем становится постоянной, поскольку ускорение уменьшается до нуля на 55 с и остается нулевым после этого.
Пример 3. Расчет ускорения по графику зависимости скорости от времени
Рассчитайте ускорение реактивного автомобиля за время 25 с, найдя крутизну зависимости v vs. t график на рисунке 6 (б).
Стратегия
Наклон кривой при t = 25 с равен наклону касательной прямой в этой точке, как показано на рисунке 6 (b).
Решение
Определите конечные точки касательной по рисунку, а затем подставьте их в уравнение, чтобы найти наклон, a .
[латекс] \ text {slope} = \ frac {\ Delta v} {\ Delta t} = \ frac {\ left (\ text {260 м / с} — \ text {210 м / с} \ right)} {\ left (\ text {51 s} -1.{2} \\ [/ латекс].
Обсуждение
Обратите внимание, что это значение для a согласуется со значением, приведенным на рисунке 6 (c) при t = 25 с.
График перемещения в зависимости от времени можно использовать для построения графика зависимости скорости от времени, а график зависимости скорости от времени можно использовать для построения графика зависимости ускорения от времени. Мы делаем это, находя наклон графиков в каждой точке. Если график линейный (то есть линия с постоянным наклоном), легко найти наклон в любой точке, и у вас есть наклон для каждой точки.Графический анализ движения может использоваться для описания как частных, так и общих характеристик кинематики. Графики также можно использовать для других тем по физике. Важным аспектом изучения физических отношений является их графическое отображение и поиск лежащих в основе отношений.
Проверьте свое понимание
График зависимости скорости от времени захода корабля в гавань показан ниже. (а) Опишите движение корабля на основе графика. б) Как будет выглядеть график ускорения корабля?
Решение
(a) Корабль движется с постоянной скоростью, а затем начинает замедляться с постоянной скоростью.В какой-то момент скорость его замедления снижается. Он поддерживает эту более низкую скорость замедления до тех пор, пока не перестанет двигаться.
(b) График ускорения в зависимости от времени покажет нулевое ускорение на первом отрезке, большое и постоянное отрицательное ускорение на втором отрезке и постоянное отрицательное ускорение.
Сводка раздела
- Графики движения можно использовать для анализа движения.
- Графические решения дают идентичные решения математическим методам вывода уравнений движения.
- Наклон графика смещения x от времени t — это скорость v .
- Наклон графика скорости v против t графика — это ускорение a .
- Средняя скорость, мгновенная скорость и ускорение могут быть получены путем анализа графиков.
Концептуальные вопросы
1. (a) Объясните, как можно использовать график положения в зависимости от времени на Рисунке 9, чтобы описать изменение скорости во времени.Определите: (b) время ( t a , t b , t c , t d или t e ), при котором мгновенная скорость равна наибольшее, (c) время, в которое оно равно нулю, и (d) время, когда оно отрицательно.
Рисунок 9.
2. (a) Изобразите график зависимости скорости от времени, соответствующий графику перемещения от времени, представленному на рисунке 10. (b) Определите время или время ( t a , t b , т в и т. д.), при которой мгновенная скорость максимальна. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
3. (a) Объясните, как можно определить ускорение с течением времени на основе графика зависимости скорости от времени, такого как на рисунке 11. (b) На основании графика, как ускорение изменяется с течением времени?
4. (a) Изобразите график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на рисунке 12. (b) Определите время или времена ( t a , t b , т в и т. д.), при котором ускорение наибольшее. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
Рисунок 12.
5. Рассмотрим график зависимости скорости от времени человека в лифте, показанный на рисунке 13. Предположим, что лифт изначально находится в состоянии покоя. Затем он ускоряется в течение 3 секунд, поддерживает эту скорость в течение 15 секунд, затем замедляется в течение 5 секунд, пока не остановится. Ускорение для всей поездки не является постоянным, поэтому мы не можем использовать уравнения движения из уравнений движения для постоянного ускорения в одном измерении для всей поездки.(Однако мы могли бы использовать их в трех отдельных разделах, где ускорение является константой.) Нарисуйте графики: (а) положения в зависимости от времени и (б) ускорения в зависимости от времени для этой поездки.
6. Цилиндр толкается и катится по наклонной плоскости. Если начало координат является начальной точкой, нарисуйте положение, скорость и ускорение цилиндра в зависимости от времени, когда он поднимается, а затем опускается по плоскости.
Задачи и упражнения
Примечание: всегда есть неопределенность в цифрах, взятых из графиков.Если ваши ответы отличаются от ожидаемых значений, проверьте их, чтобы увидеть, находятся ли они в пределах оцененных вами неопределенностей извлечения данных.
1. a) Взяв наклон кривой на рисунке 14, убедитесь, что скорость реактивного вагона составляет 115 м / с при т = 20 с. (b) Взяв наклон кривой в любой точке на Рисунке 15, убедитесь, что ускорение реактивного автомобиля составляет 5,0 м / с 2 .
2. Используя приблизительные значения, рассчитайте наклон кривой на рисунке 16, чтобы убедиться, что скорость при t = 10.0 с составляет 0,208 м / с. Предположим, что все значения известны с 3 значащими цифрами.
3. Используя приблизительные значения, рассчитайте наклон кривой на Рисунке 16, чтобы убедиться, что скорость при t = 30,0 с составляет 0,238 м / с. Предположим, что все значения известны с 3 значащими цифрами.
4. Взяв наклон кривой на рисунке 17, убедитесь, что ускорение составляет 3,2 м / с 2 при t = 10 с.
Рисунок 17.
5. Постройте график смещения для маршрутного поезда метро, как показано на рисунке 2 из ускорения (снова показано ниже).Ваш график должен показывать положение поезда в километрах от t = 0 до 20 с. Вам нужно будет использовать информацию об ускорении и скорости, приведенную в примерах к этому рисунку.
Поезд метро в Сан-Паулу, Бразилия, замедляет ход при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки, Flickr)
6. (a) Взяв наклон кривой на рисунке 11, найдите скорость бегуна при t = 2.5 с. (b) Повторить через 7,5 с. Эти значения должны соответствовать графику на Рисунке 18.
7. График v ( t ) показан для бегового спринтера мирового класса в беге на 100 м. (См. Рисунок 21). а) Какова его средняя скорость в первые 4 с? (b) Какова его мгновенная скорость при t = 5 с? (c) Каково его среднее ускорение между 0 и 4 с? (г) Сколько у него времени для забега?
8. На рисунке 22 показан график смещения частицы за 5 с.Нарисуйте соответствующие графики скорости и ускорения.
- независимая переменная:
- переменная, относительно которой измеряется зависимая переменная; обычно наносится по оси x —
- зависимая переменная:
- переменная, которая измеряется; обычно наносится по оси y —
- наклон:
- разница в y -значение (подъем), деленное на разницу в x -значение (разбег) двух точек на прямой
- y-перехват:
- — значение y , когда x = 0, или когда график пересекает ось y
Избранные решения проблем и упражнения
1.{3} \ text {m}} {\ left (40 \ text {.} \ Text {0–20} .0 \ right) \ text {s}} = \ text {238 м / с} \\ [/ латекс]
Рисунок 23.
5.
7. (а) 6 м / с (б) 12 м / с (в) 3 м / с 2 (г) 10 с
Tc 1 скорость движения равномерное прямолинейное движение. Прямолинейное равномерное движение. Зависимость скорости, координат и пути от времени
ТС -1 Прямолинейное равномерное движение.
I опция .
1. Велосипедист, двигаясь равномерно, преодолевает 20 м за 2 с.Определите, по какому пути он пойдет при движении с той же скоростью за 10 секунд.
А. 60 м. Б. 100 м. С. 150 м.
2
… На рисунке показан график зависимости пути при движении велосипедиста от времени. Определите по этому графику путь, который проехал велосипедист за промежуток времени от 1 до 4 с.
3. Используя график, определите скорость велосипедиста в момент времени t = 2 с.
4
… На рисунке изображены графики движения трех тел.Какое из этих тел движется с наибольшей модульной скоростью в момент времени t = 5 с?
5. По графику определить скорость движения первого тела в момент времени t = 5 с.
А. 2 с, 5 м.
Б. 4 с, 10 м.
H. 5 с, 15 м.
7. Запишите уравнение движения
второго тела по графику.
И.
.
Б.
.
В.
.
9. Лодка плывет против течения реки. Какова скорость лодки относительно берега, если скорость лодки относительно воды 4 м / с, а скорость реки 3 м / с?
А. 7 м / с. Б. 5 м / с. В. 1 м / с.
10. Первые 40 км поезд прошел со скоростью 80 км / ч, а следующие 50 км со скоростью 100 км / ч. Определите среднюю скорость поезда в пути.
А. 95 км / ч. Б. 85 км / ч. ЧАС.90 км / ч.
ТС-1. Прямолинейное равномерное движение.
I
I опция.
Автомобиль, двигаясь равномерно, преодолел 50 м за 2 секунды. Какой путь он пройдет за 20 секунд, двигаясь с той же скоростью?
И
… 500 м. 1000 м.х. 250 м.
2. Определить из графика зависимости пути от времени путь, пройденный телом за промежуток времени от 3 до 5 с.
Определите скорость движения тела в данный момент по графику
т = 4 с.
4
… На рисунке изображены графики движения трех тел. Какое из этих тел движется с наименьшей скоростью в момент времени t = 2 с.
5. По расписанию движения определить скорость движения второго тела в момент времени 6 с.
6. В расписании определить время и место заседания первого и второго органов.
А. 2 с, 10 м.
Б. 1 с, 5 м.
7.Запишите уравнение движения первого тела по графику.
И.
.
Б.
.
В.
.
8. Движение тела описывается уравнением
… На каком из графиков показана зависимость координат этого тела от времени?
9. Эскалатор метро движется вниз со скоростью 0,7 м / с. Какова скорость пассажира относительно земли, если он поднимается со скоростью 0,7 м / с относительно эскалатора?
А.0 м / с. Б. 1,4 м / с. В. 1 м / с.
10. Автомобиль проехал первые 20 км со скоростью 50 км / ч, а следующие 60 км со скоростью 100 км / ч. Определите среднюю скорость автомобиля в пути.
А. 90 км / ч. Б. 80 км / ч. Высота 70 км / ч.
Равномерное движение — это движение с постоянной скоростью, то есть когда скорость не меняется (v = const) и не происходит ускорения или замедления (a = 0).
Прямое движение Это движение по прямой, то есть траектория прямолинейного движения является прямой линией.
Равномерное прямолинейное движение — это движение, при котором тело совершает одни и те же движения за любые равные промежутки времени. Например, если мы разделим некоторый временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одно и то же расстояние для каждого из этих интервалов.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как движение тела. То есть вектор смещения совпадает по направлению с вектором скорости.В этом случае средняя скорость за любой период времени равна мгновенной скорости:
V cp = v
Пройденное расстояние при прямолинейном движении равно модулю движения. Если положительное направление оси OX совпадает с направлением движения, то проекция скорости на ось OX равна значению скорости и положительна:
V x = v, то есть v \ u003e 0
Проекция смещения на ось OX составляет:
S = vt = x — x 0
где x 0 — начальная координата тела, x — конечная координата тела (или координата тела в любой момент)
Уравнение движения , то есть зависимость координат тела от времени x = x (t) принимает вид:
X = x 0 + vt
При положительном направлении оси OX противоположна направлению движения тела, то проекция скорости тела на ось OX отрицательна, скорость меньше нуля (v
X = x 0 — vt
Временная зависимость скорости, координаты и путь
Зависимость проекции скорости тела от времени показана на рис.1.11. Поскольку скорость постоянна (v = const), график скорости представляет собой прямую, параллельную оси времени Ot.
Рисунок: 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция смещения на координатную ось численно равна площади прямоугольника OABS (рис. 1.12), так как величина вектора смещения равна произведению вектора скорости на время, в течение которого перемещение было произведено.
Рисунок: 1.12. Зависимость проекции движения тела от времени при равномерном прямолинейном движении.
График движения во времени показан на рис. 1.13. На графике видно, что проекция скорости составляет
В = с 1 / t 1 = tg α
где α — угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (чем дольше тело движется за меньшее время).Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
Tg α = v
Рисунок: 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. На рисунке видно, что
Tg α 1> tg α 2
, следовательно, скорость тела 1 выше скорости тела 2 (v 1> v 2).
Tg α 3 = v 3
Если тело покоится, то график координаты представляет собой прямую линию, параллельную оси времени, то есть
X = x 0
Рисунок: 1.14. Зависимость координат тела от времени при равномерном прямолинейном движении.
М .: 2014. — 128с. М .: 2005. — 128с.
В данное руководство включены обучающие задания, тесты для самоконтроля, самостоятельной работы, тесты и примеры решения типовых задач.Предлагаемые дидактические материалы составлены в полном соответствии со структурой и методикой учебника А.В. Перышкин, М.Е. Гутник «Физика. 9 класс».
Формат: pdf ( 2014 г.
, 128с.)
Размер: 2,8 МБ
Часы, скачать:
02
Формат: pdf ( 2005 г.
, 128с.)
Размер: 6,8 МБ
Загрузить: 02
.09.2016, ссылки удалены по просьбе издательства «Дрофа» (см. Примечание)
Содержание
Предисловие 3
УЧЕБНЫЕ ЗАДАНИЯ
ТК-1.Путь и проезд 5
ТК-2. Прямолинейное равномерное движение 6
ТК-3. Относительность движения 8
ТК-4. Прямолинейное равноускоренное движение 10
ТК-5. Законы Ньютона 13
ТК-6. Кузова свободного падения 16
ТК-7. Закон всемирного тяготения. Движение тела по кругу. Искусственные спутники Земли 17
ТК-8. Импульс тела. Закон сохранения импульса 19
TK-9. Механические колебания и волны. Звук 20
ТК-10. Электромагнитное поле 22
ТК-11. Строение атома и атомного ядра 24
ТЕСТЫ ДЛЯ САМОКОНТРОЛЯ
TS-1.Прямолинейный равномерный механизм 25
ТС-2. Прямолинейный равноускоренный механизм 28
ТС-3. Законы Ньютона 31
TS-4. Органы свободного падения 34
TS-5. Закон всемирного тяготения. Движение тела по кругу. Искусственные спутники Земли. … 35
ТС 6. Тело импульс. Закон сохранения импульса 38
ТС-7. Механические колебания 39
ТС-8. Механические волны. Звук 42
ТС-9. Электромагнитное поле 45
ТС-10. Строение атома и атомного ядра 48
НЕЗАВИСИМЫЕ РАБОТЫ
CP-1.Путь и путешествие 52
CP-2. Прямолинейный равномерный механизм 55
СР-3. Прямолинейное равномерное движение. Графические задания 58
СР-4. Относительность движения 61
CP-5. Прямолинейное равноускоренное движение 64
СР-6. Прямолинейное равноускоренное движение. Графические задания 66
СР-7. Законы Ньютона 71
CP-8. Свободно падающие тела 73
CP-9. Закон всемирного тяготения. Искусственные спутники Земли 74
CP-10. Движение тела по кругу 75
СР-11. Импульс тела.Закон сохранения импульса 77
CP-12. Механические колебания 79
СР-13. Механические волны. Звук G 80
CP-14. Электромагнитное поле 82
СР-15. Строение атома и атомного ядра 86
ТЕСТОВЫЕ ДОКУМЕНТЫ
КР-1. Прямолинейное равноускоренное движение 89
КР-2. Законы Ньютона 93
КР-3. Закон всемирного тяготения. Движение тела по кругу. Искусственные спутники Земли 97
КР-4. Закон сохранения импульса 101
КР-5.Механические колебания и волны 105
КР-6. Электромагнитное поле 109
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Законы взаимодействия и движения тел 113
Механические колебания и волны 117
Электромагнитное поле 118
ОТВЕТЫ
Практические задания 119
Тесты самоконтроля 120
Самостоятельная работа 121
Тесты 124
Ссылки 126
Пособие включает обучающие задания (ТЗ), тесты на самоконтроль (ТС), самостоятельную работу (СР), контрольную работу (КР), примеры решения типовых задач.
Учебный комплект предусматривает организацию всех основных этапов учебно-познавательной деятельности школьников в соответствии с требованиями ФГОС: применение и актуализация теоретических знаний, самоконтроль качества усвоения знаний. материал, использование алгоритмов решения задач, выполнение самостоятельных и контрольно-оценочных работ.
Учебные задания (ТК 1-11) для всех разделов 9-го класса курса физики содержат комплекс качественных, экспериментальных и графических задач, ориентированных на формирование ведущих понятий и основных закономерностей курса.Задания подобраны таким образом, чтобы дать студенту возможность осмыслить существенные особенности концепции, рассмотреть физическое явление на уровне фактов, физических величин и физических законов. Авторы постарались составить учебные задания в виде небольшой проблемной книги, которая дополняет систему типовых упражнений учебника и позволяет организовать дифференцированное выполнение уроков и домашних заданий.
Тесты на самоконтроль (ТС 1-10) с выбором ответа предназначены для оперативного, тематического контроля на основе урока и самоконтроля знаний.В зависимости от конкретных условий (подготовка к уроку, организация многоуровневого обучения и др.) Преподаватель может варьировать набор тестовых заданий и определять время их выполнения.

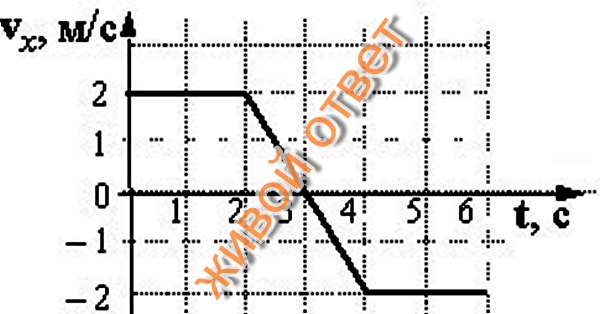 На графике представлена зависимость проекции скорости автомобиля от времени.
На графике представлена зависимость проекции скорости автомобиля от времени.
 На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален в интервале времени
На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален в интервале времени
 Проекция её скорости на вертикальное направление меняется со временем согласно графику на рисунке. Через сколько секунд стрела упадёт на землю?
Проекция её скорости на вертикальное направление меняется со временем согласно графику на рисунке. Через сколько секунд стрела упадёт на землю?
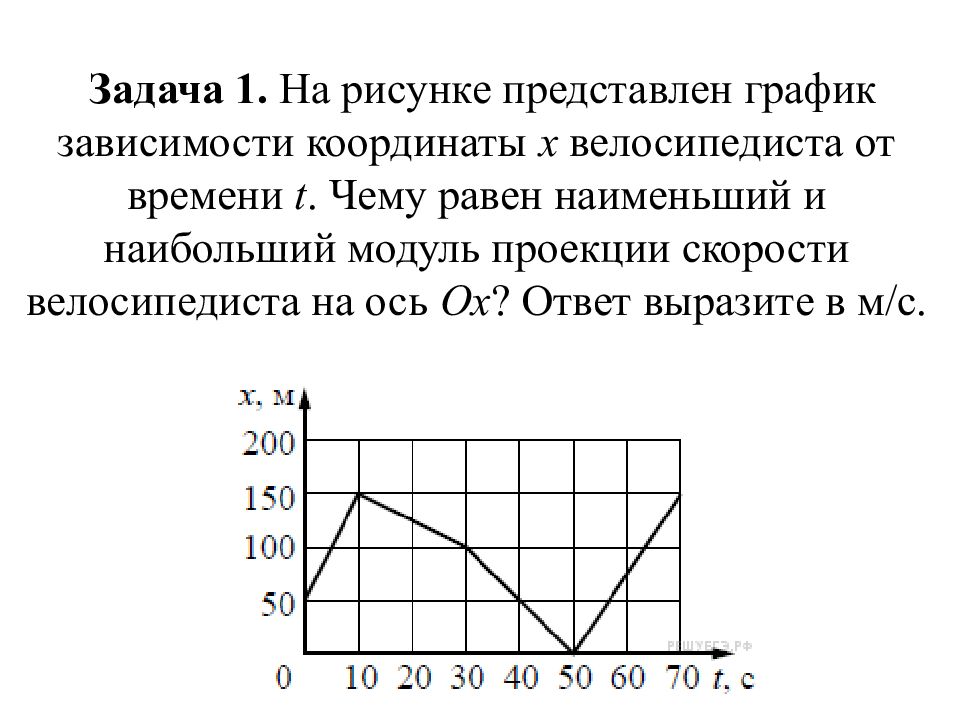
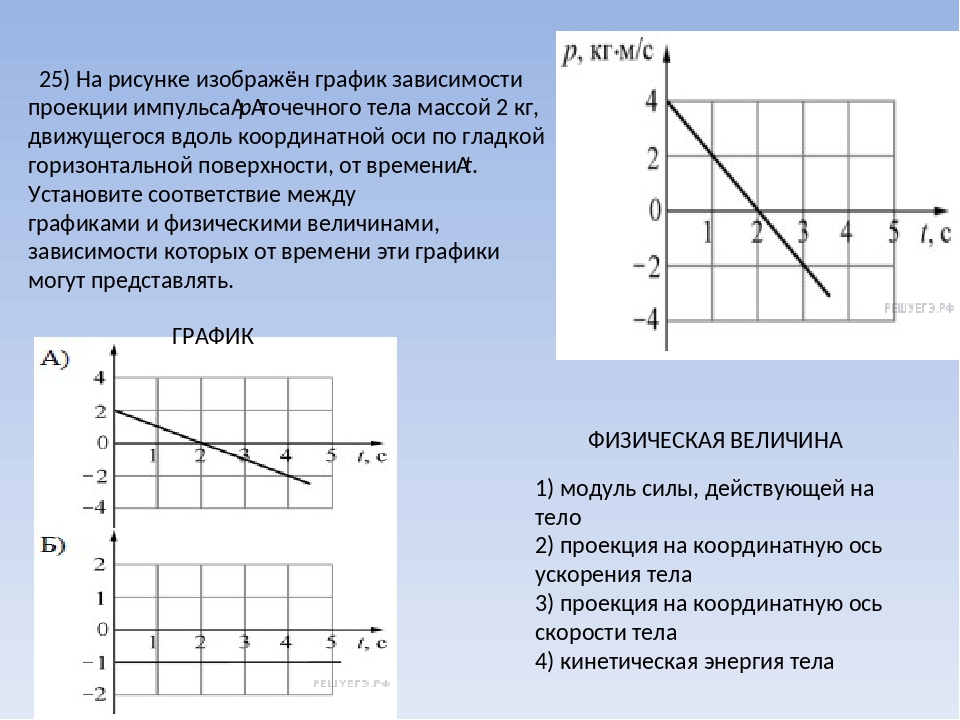 Проекция его скорости меняется по закону, приведённому на графике. Путь, пройденный телом за 1 с, равен
Проекция его скорости меняется по закону, приведённому на графике. Путь, пройденный телом за 1 с, равен
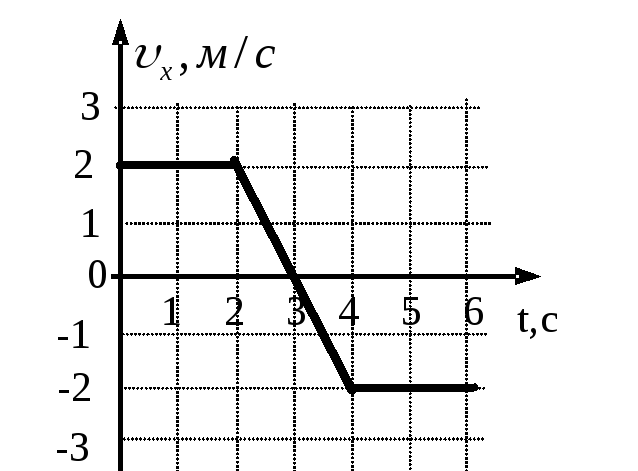 По графику зависимости проек-ции скорости тела от времени установите, какой путь прошло тело за время от 0 до 4 с.
По графику зависимости проек-ции скорости тела от времени установите, какой путь прошло тело за время от 0 до 4 с.
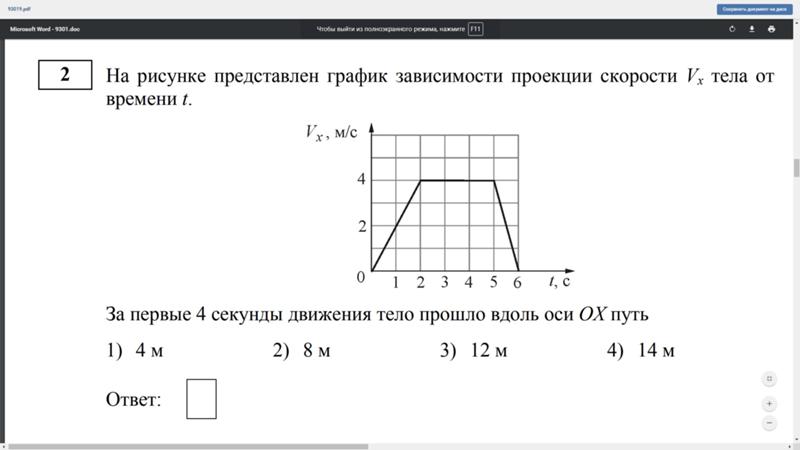 Какое тело прошло наименьший путь за 3 с?
Какое тело прошло наименьший путь за 3 с?
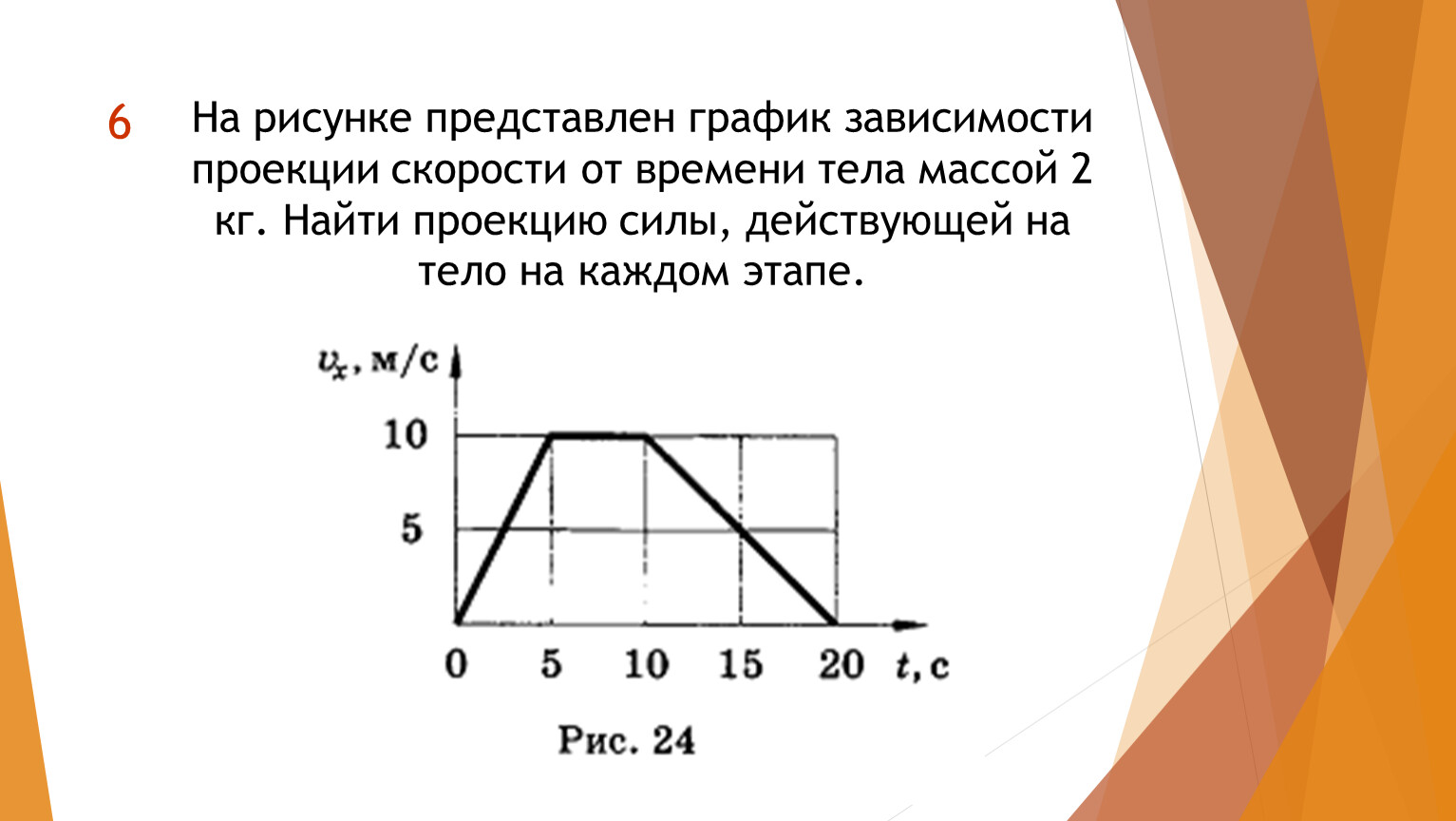 Какой путь прошло тело к моменту времени t = 6 с?
Какой путь прошло тело к моменту времени t = 6 с?