Содержание
EF18831 | СПАДИЛО.РУ
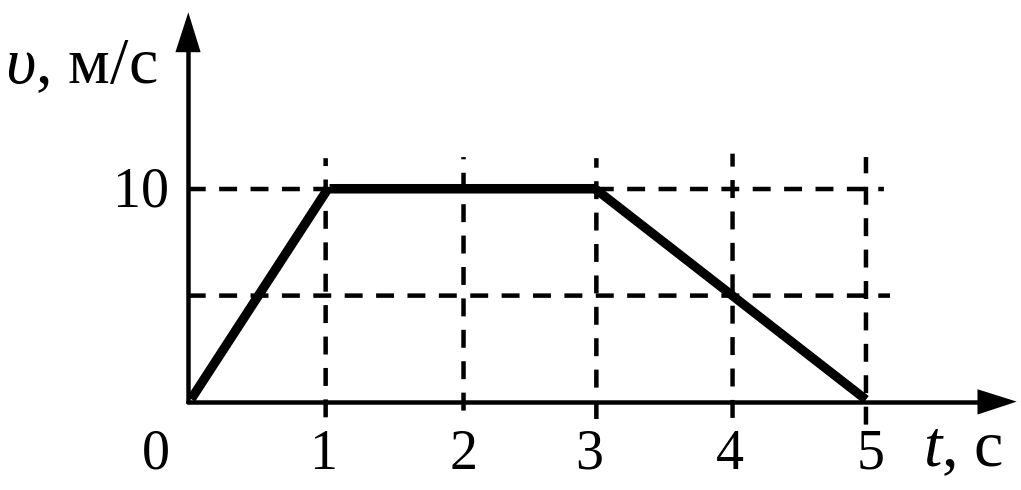
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
📜Теория для решения: Равномерное прямолинейное движение Перемещение и путь при равноускоренном прямолинейном движении
Решение
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с.
 В это время тело двигалось равномерно (с нулевым ускорением).
В это время тело двигалось равномерно (с нулевым ускорением). - От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику.
 Начальная скорость — 10 м/с, конечная — 0 м/с.
Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
s1+ s2= 100 + 100 = 200 (м)
Ответ: 200
Входная 11кл — A на рисунке представлен график зависимости модуля скорости тела от времени. Какой путь пройден телом за вторую секунду мм мм На левом рисунке представлены вектор скорости тела и вектор равнодействующей всех сил, действующих на тело.
Вариант 1
A 1. На рисунке представлен график зависимости модуля скорости тела от времени. Какой путь пройден телом за вторую секунду мм мм На левом рисунке представлены вектор скорости тела и вектор равнодействующей всех сил, действующих на тело.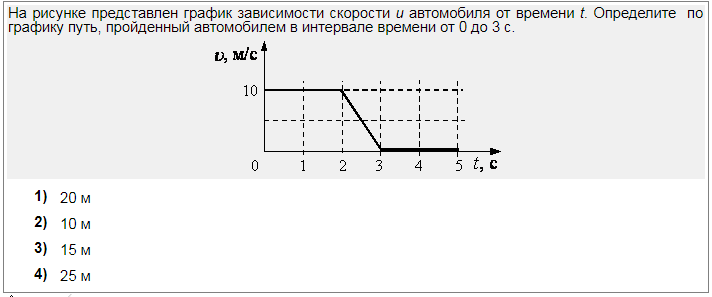 Какой из четырех векторов на правом рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчета
Какой из четырех векторов на правом рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчета
1) 3 2) 2 3) 1 4) 4
A 3. Камень массой 1 кг брошен вертикально вверх. В начальный момент его энергия равна 200 Дж. На какую максимальную высоту поднимется камень Сопротивлением воздуха пренебречь.
1) 10 мм мм Какое из утверждений правильно
A. Диффузия наблюдается только в газах и жидкостях.
B. Диффузия наблюдается только в твердых телах.
C. Диффузия наблюдается в газах, жидкостях и твердых телах.
1) A 2) B 3) C 4) ни A, ни B, ни C
A 5. Идеальный газ получил количество теплоты 300 Дж и совершил работу
100 Дж. При этом внутренняя энергия газа
1) увеличилась на 400 Дж
2) увеличилась на 200 Дж
3) уменьшилась на 200 Дж
4) уменьшилась на 400 Дж
A 6. Расстояние между двумя точечными электрическими зарядами уменьшили в 2 раза, и один из зарядов уменьшили в 2 раза. Сила взаимодействия между зарядами) увеличилась в 2 раза
2) увеличилась в 4 раза
3) увеличилась враз) не изменилась
A 7. Сила тока в проводнике постоянна и равна 0,5 А. Заряд 60 Кл пройдет по проводнику за время
Сила тока в проводнике постоянна и равна 0,5 А. Заряд 60 Кл пройдет по проводнику за время
1) 2 с 2) 30 с 3) 1 мин 4) 2 мин
B 1. В закрытом сосуде находится идеальный газ. Как при охлаждении сосуда с газом изменятся величины давление газа, его плотность и внутренняя энергия Для каждой величины определите соответствующий характер изменения
1) увеличилась
2) уменьшилась
3) не изменилась. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Давление газа
Плотность газа
Внутренняя энергия газа
?
?
?
C 1. Два свинцовых шара массами m
1
=
100 г и m
2
= 200 г движутся навстречу друг другу со скоростями v
1
= 4 мс и
v
2
= 5 мс. Какую кинетическую энергию будет иметь второй шар после их неупругого соударения
Вариант 2
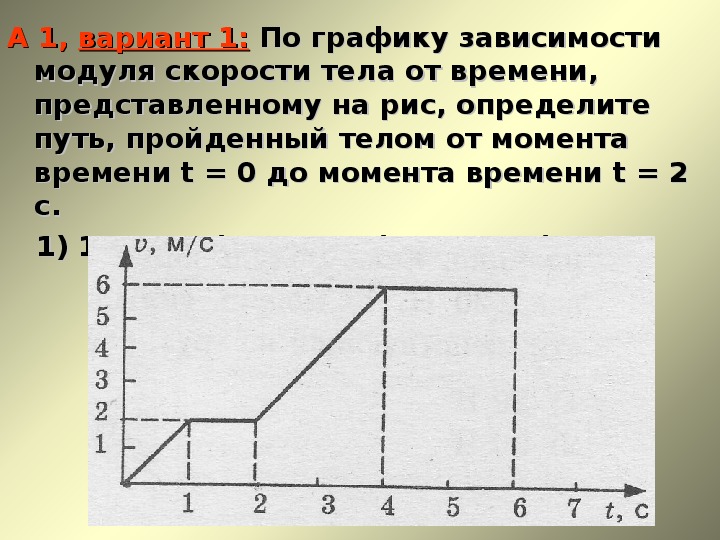
A 1. По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 см мм м
A 2.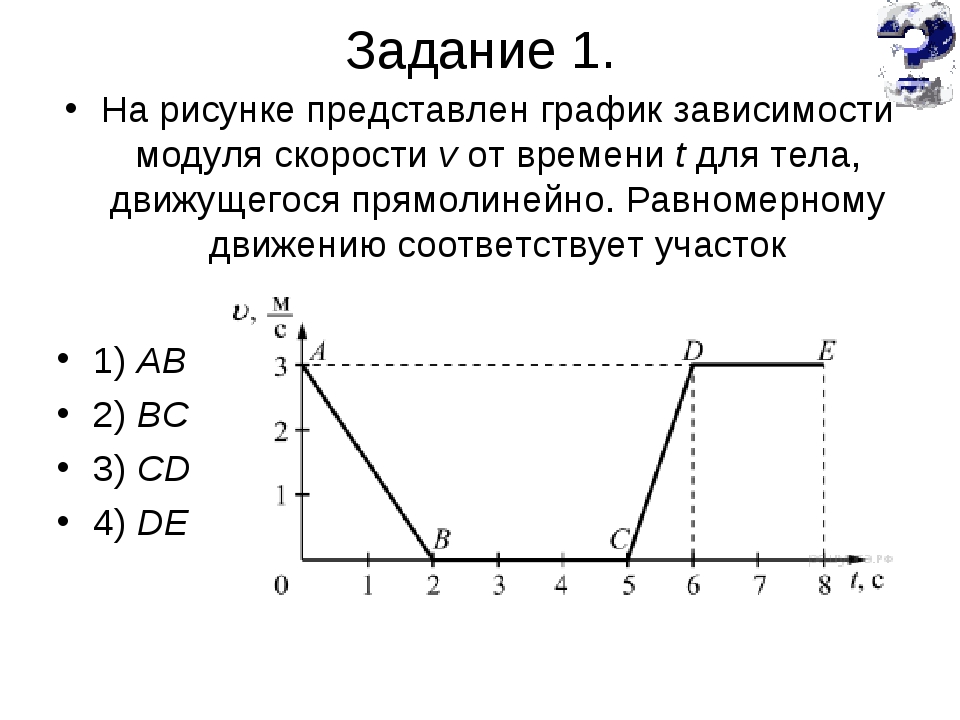 Материальная точка движется по окружности с постоянной по модулю скоростью почасовой стрелке. В какой точке траектории ускорение тела направлено по стрелке
Материальная точка движется по окружности с постоянной по модулю скоростью почасовой стрелке. В какой точке траектории ускорение тела направлено по стрелке
1) 1 2) 2 3) 3 4) 4
A 3. Тележка движется со скоростью 3 мс. Еѐ кинетическая энергия равна
27 Дж. Какова масса тележки
1) 6 кг 2) 9 кг 3) 18 кг 4) 81 кг
A 4. Броуновским движением называется
1) упорядоченное движение слоев жидкости (или газа)
2) упорядоченное движение твердых частиц вещества, взвешенных в жидкости или газе)
3) конвекционное движение слоев жидкости при ее нагревании
4) хаотическое движение твердых частиц вещества, взвешенных в жидкости (или газе)
A 5. В процессе эксперимента газ отдал окружающей среде количество теплоты, равное 3 кДж. При этом внутренняя энергия газа уменьшилась на 13 кДж. Следовательно, газ расширился, совершив работу кДж 2) 10 кДж 3) 13 кДж 4) 16 кДж
A 6. Как изменится сила кулоновского взаимодействия двухточечных заряженных тел при увеличении расстояния между ними в 3 раза и увеличении заряда одного из тел в 3 раза
1) увеличится враз) увеличится враз) не изменится
4) уменьшится в 3 раза
A 7. Сила тока в проводнике постоянна и равна 0,5 АЗа минут по проводнику пройдет заряд
Сила тока в проводнике постоянна и равна 0,5 АЗа минут по проводнику пройдет заряд
1) 600 Кл 2) 40 Кл 3) 100 Кл 4) 10 Кл
B 1. В сосуде под поршнем находится идеальный газ. Если при нагревании газа его давление остается постоянным, то как изменятся величины объем газа, его плотность и внутренняя энергия Для каждой величины определите соответствующий характер изменения
1) увеличилась
2) уменьшилась
3) не изменилась. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Объем газа
Плотность газа
Внутренняя энергия газа
?
?
?
C 1. Шары массами 6 и 4 кг, движущиеся навстречу друг другу со скоростью 2 мс каждый относительно Земли, соударяются, после чего движутся вместе. Определите, какое количество теплоты выделится в результате соударения
Инструкция по проверке и оценке работ учащихся по физике Вариант 1 Часть А Номер задания Правильный ответ Баллы
1 3
1 2
1 1
3 2
1 4
3 1
5 2
1 6
1 1
7 4
1 Часть В За полный правильный ответ ставится
2 балла, 1 балл – допущена одна ошибка за неверный ответ (более одной ошибки) или его отсутствие – 0 баллов. Номер задания Правильный ответ Баллы В 232 2 Выставление оценок
Номер задания Правильный ответ Баллы В 232 2 Выставление оценок
11-12 баллов – «5»
8-10 баллов – «4»
5-7 баллов – «3»
Часть С Критерии оценивания выполнения задания Баллы Приведено полное правильное решение, включающее следующие элементы 1) верно записано краткое условие задачи
2) записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом 3) выполнены необходимые математические преобразования и расчѐты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение по частям (с промежуточными вычислениями)
3 Правильно записаны необходимые формулы, проведены вычисления, и получен ответ верный или неверный, но допущена ошибка в записи краткого условия или переводе единиц в СИ, или представлено правильное решение только в общем виде, без каких-либо числовых расчѐтов, или записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, нов математических преобразованиях или вычислениях допущена ошибка
2 Записаны и использованы не все исходные формулы, необходимые для решения задачи, или записаны все исходные формулы, нов одной из них допущена ошибка
1 Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в
1, 2, 3 балла
0 Максимальный балл
3 Два свинцовых шара массами m
1
= 100 г и m
2
= 200 г движутся навстречу друг другу со скоростями v
1
= 4 мс и
v
2
= 5 мс. Какую кинетическую энергию будет иметь второй шар после их неупругого соударения Решение Запишем формулу для нахождения кинетической энергии шара после соударения По закону сохранения импульса откуда Имеем Ответ 0,4 Дж.
Какую кинетическую энергию будет иметь второй шар после их неупругого соударения Решение Запишем формулу для нахождения кинетической энергии шара после соударения По закону сохранения импульса откуда Имеем Ответ 0,4 Дж.
Вариант 2 Часть А Часть В За полный правильный ответ ставится 2 балла, 1 балл – допущена одна ошибка за неверный ответ (более одной ошибки) или его отсутствие – 0 баллов. Номер задания Правильный ответ Баллы В 121 2 Выставление оценок
11-12 баллов – «5»
8-10 баллов – «4»
5-7 баллов – «3» Номер задания Правильный ответ Баллы
1 2
1 2
3 1
3 1
1 4
4 1
5 2
1 6
4 1
7 1
1
Часть С Критерии оценивания выполнения задания Баллы Приведено полное правильное решение, включающее следующие элементы 1) верно записано краткое условие задачи
2) записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом 3) выполнены необходимые математические преобразования и расчѐты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение по частям (с промежуточными вычислениями)
При этом допускается решение по частям (с промежуточными вычислениями)
3 Правильно записаны необходимые формулы, проведены вычисления, и получен ответ верный или неверный, но допущена ошибка в записи краткого условия или переводе единиц в СИ, или представлено правильное решение только в общем виде, без каких-либо числовых расчѐтов, или записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, нов математических преобразованиях или вычислениях допущена ошибка
2 Записаны и использованы не все исходные формулы, необходимые для решения задачи, или записаны все исходные формулы, нов одной из них допущена ошибка
1 Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в
1, 2, 3 балла
0 Максимальный балл
3 Шары массами 6 и 4 кг, движущиеся навстречу друг другу со скоростью 2 мс каждый относительно Земли, соударяются, после чего движутся вместе. Определите, какое количество теплоты выделится в результате соударения. Решение Согласно закону сохранения импульса Отсюда скорость шаров после удара Согласно закону сохранения энергии можно найти выделявшееся количество теплоты как изменение кинетической энергии системы тел дои после взаимодействия Отсюда Ответ 19,2 Дж.
Решение Согласно закону сохранения импульса Отсюда скорость шаров после удара Согласно закону сохранения энергии можно найти выделявшееся количество теплоты как изменение кинетической энергии системы тел дои после взаимодействия Отсюда Ответ 19,2 Дж.
Тесты | Образовательная социальная сеть
Слайд 1
ГИА 2013
Слайд 2
Задания части 1 с выбором ответов
Слайд 3
Снежинка падает с высоты 1 километр. Основная часть потенциальной энергии снежинки за время падения переходит в: 1 кинетическую энергию снежинки 2 тепловую энергию 3 химическую энергию кристалликов льда, из которых состоит снежинка 4 другие (не указанные в пунктах выше) виды энергии
Слайд 4
В простейшем опыте с эбонитовой палочкой, заряженной трением о шерсть, мы видим, как маленькие бумажки притягиваются к такой палочке. Палочка имеет отрицательный заряд. Следовательно, бумажки: 1 Заряжены положительно 2 Заряжены отрицательно 3 Никак не заряжены, ведь друг с другом они не взаимодействуют 4 Суммарный заряд бумажки равен нулю, но одни части её заряжены положительно, а другие отрицательно
Слайд 5
Несколько одинаковых резисторов по 20 Ом соединили, как показано на рисунке. Найдите сопротивление между точками А и В: 1 8 Ом 2 12 Ом 3 20 Ом 4 10 Ом
Найдите сопротивление между точками А и В: 1 8 Ом 2 12 Ом 3 20 Ом 4 10 Ом
Слайд 6
Юноша бросает камень с балкона Пизанской башни с одинаковой начальной скоростью в первом случае вертикально вверх, а во втором — отвесно вниз. Сопротивление воздуха пренебрежимо мало. В каком случае скорость камня в момент его падения на землю рядом с башней будет больше: 1 скорости камня в обоих случаях будут одинаковы 2 в первом случае 3 во втором случае 4 ответ зависит от массы камня
Слайд 7
Расстояние от Солнца до Земли в 390 раз больше расстояния от Луны до Земли. Масса Солнца в 300 000 раз больше массы Земли. Сравните силы, с которыми Луна притягивается к Солнцу и к Земле. 1 силы , с которыми Луну притягивают Солнце и Земля, примерно равны 2 сила , с которой Луну притягивает Солнце, примерно вдвое больше, чем сила, с которой Луну притягивает Земля 3 сила , с которой Земля притягивает Луну, примерно в 770 раз больше силы, с которой Луну притягивает Солнце 4 Земля притягивает Луну примерно в 1,3 раза сильнее, чем Солнце
Слайд 8
Найдите общее сопротивление цепи, изображённой на рисунке (сопротивление между точками А и В).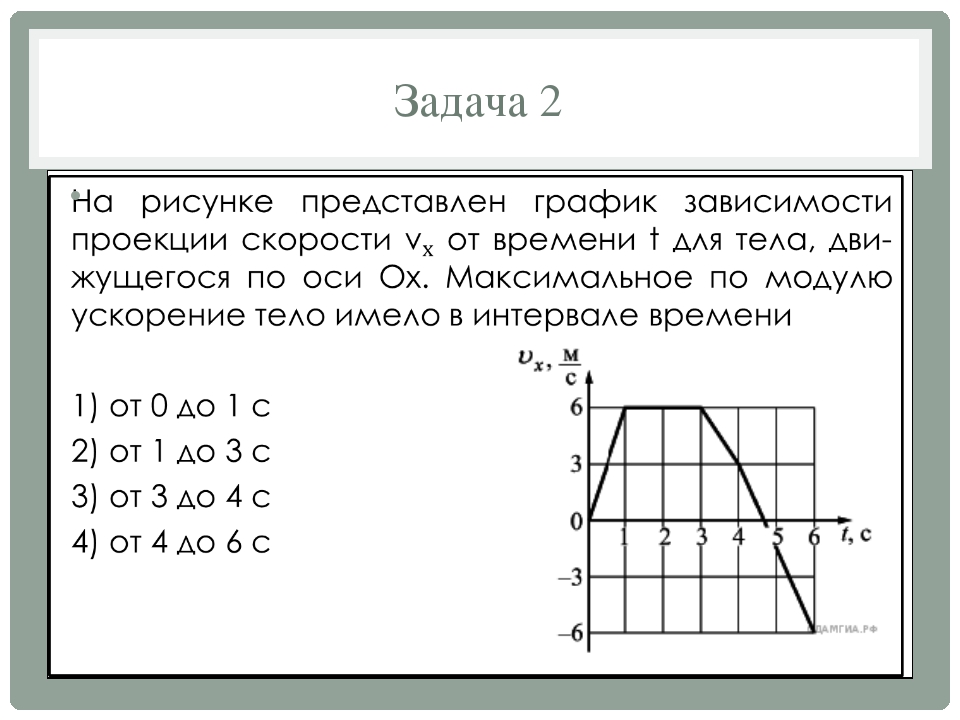 1 123 Ом 2 2,54 Ом 3 3,21 Ом 4 105,3 Ом
1 123 Ом 2 2,54 Ом 3 3,21 Ом 4 105,3 Ом
Слайд 9
Тело движется прямолинейно. На рисунке представлен график зависимости ускорения тела от времени. Какой участок (какие участки) соответствует равномерному движению тела? 1 AB 2 EF 3 BC и DE 4 DE
Слайд 10
По ручью плывёт увлекаемый течением бумажный кораблик. Работа какой силы (по перемещению кораблика) при этом отрицательна: 1 сила сопротивления воздуха 2 сила Архимеда 3 сила притяжения Земли 4 сила сопротивления воды
Слайд 11
Тело движется прямолинейно. На левом рисунке представлен график зависимости скорости тела от времени. Зависимость какой величины от времени представлена на правом рисунке: 1 ускорения 2 модуля средней скорости 3 перемещения 4 пройденного пути
Слайд 12
Вторая часть ( задание на выбор соответствия)
Слайд 13
найди соответствие Физическая величина Единица измерения А. Электрическое напряжение Б. Электрическое сопротивление С. Электрический заряд 1. кулон 2.ватт 3. ампер 4 вольт 5 ом
ампер 4 вольт 5 ом
Слайд 14
найди соответствие Учёный Физическое явление Ньютон Торричелли Кулон Существование давления Взаимодействие заряженных тел Движение и его причины
Слайд 15
Найди соответствие ФИЗИЧЕСКОЕ ЯВЛЕНИЕ УЧЕНЫЙ А) электромагнитная индукция Б) взаимосвязь между силой и деформацией 1) Лоренц 2) Фарадей 3) Ньютон 4) Гук
Слайд 16
найди соответствие ОПИСАНИЕ ПРИБОРОВ НАЗВАНИЕ ПРИБОРОВ А. Прибор, измеряющий мгновенную скорость тела Б. Прибор, измеряющий силу, действующую на тела В. Прибор, измеряющий ускорение Г. Прибор, измеряющий атмосферное давление 1) гигрометр 2) спидометр 3) динамометр 4) измерительная линейка 5) акселерометр 6) барометр-анероид
Слайд 17
Груз массой m , подвешенный к пружине, совершает колебания с периодом T и амплитудой . Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза? Для каждой величины определите соответствующий характер изменения: 1) увеличилась; 2) уменьшилась; 3) не изменилась.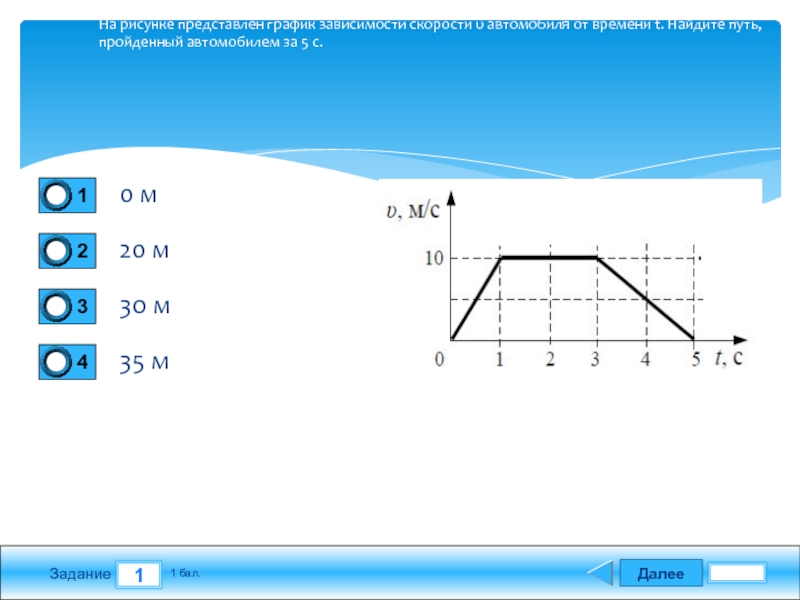 Период колебаний Максимальная потенциальная энергия пружины Частота колебаний
Период колебаний Максимальная потенциальная энергия пружины Частота колебаний
Слайд 18
. В сосуде под поршнем находится газ . Если при нагревании газа его давление остается постоянным, то как изменятся величины: объем газа, его плотность и внутренняя энергия? Для каждой величины определите соответствующий характер изменения: 1) увеличилась; 2) уменьшилась; 3) не изменилась. Объем Плотность Внутренняя энергия
Слайд 19
Как изменяется заряд и массовое число радиоактивного ядра в результате его -распаде? Установите соответствие между физическими величинами и характером их изменения. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ЧАСТОТА ИХ ИЗМЕНЕНИЯ А ) заряд ядра Б) массовое число 1 ) увеличится 2) не изменится
Слайд 20
Воздушный шарик вносят с мороза в тёплую комнату. При этом изменяются температура шарика, его объём, давление внутри шарика и некоторые другие физические характеристики. (Возможно, вам даже приходилось видеть, как такие шарики лопаются). Установите соответствие между физической величиной и характером её изменения. К каждой позиции левого столбца подберите нужную позицию правого и запишите в таблицу выбранные цифры под соответствующими буквами (цифры могут повторяться). Физическая величина Изменения А) Объём шарика 1. Увеличивается Б) Масса шарика 2. Практически не изменяется В) Внутренняя энергия газа в шарике 3. Уменьшается
К каждой позиции левого столбца подберите нужную позицию правого и запишите в таблицу выбранные цифры под соответствующими буквами (цифры могут повторяться). Физическая величина Изменения А) Объём шарика 1. Увеличивается Б) Масса шарика 2. Практически не изменяется В) Внутренняя энергия газа в шарике 3. Уменьшается
Слайд 21
По мере повышения температуры воды от -50 до +50 вода находилась сначала в твердом состоянии, затем происходил процесс плавления, и нагревание жидкой воды. Изменялась ли внутренняя энергия воды во время этих трех процессов и если изменялась, то как? ФИЗИЧЕСКИЕ ПРОЦЕССЫ ИХ ИЗМЕНЕНИЯ А ) нагревание льда Б) плавление льда В) нагревание жидкой воды 1 ) остаётся неизменной 2) увеличивается 3) уменьшается
Слайд 22
Что представляют собой следующие виды излучения? Излучение Частица А) альфа-излучение Б) бета-излучение В) гамма-излучение 1) поток электронов 2) электромагнитные волны 3) ядра атома гелия
Слайд 23
Длинную витую стальную пружину закрепили в растянутом состоянии (относительное удлинение невелико по сравнению с длиной пружины) между клеммами электрической цепи и охладили на 30∘C. Напряжение между клеммами оставалось неизменным на протяжении всего эксперимента. Физическая величина Характер изменения А) Ток в пружине Б) Сила, с которой пружина действует на клеммы А и В В) Масса 1.Увеличивается 2.Практически не изменяется 3. Уменьшается
Напряжение между клеммами оставалось неизменным на протяжении всего эксперимента. Физическая величина Характер изменения А) Ток в пружине Б) Сила, с которой пружина действует на клеммы А и В В) Масса 1.Увеличивается 2.Практически не изменяется 3. Уменьшается
Слайд 24
1) Кольцо из серебра можно расплавить в алюминиевой посуде. 2) Для нагревания на 10ОС оловянной ложки потребуется большее количество теплоты, чем для нагревания серебряной ложки, имеющей такую же массу. 3) Для плавления 3 кг цинка, взятого при температуре плавления, потребуется такое же количество теплоты, что и для плавления 2 кг меди при температуре ее плавления. 4) Стальной шарик будет плавать в расплавленном свинце при частичном погружении. 5) Алюминиевая проволока утонет в расплавленной меди.
Слайд 25
На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох. 1) Участок DE соответствует неравномерному движению тела. 2) Участок FG соответствует состоянию покоя тела. 3) В момент времени t 1 тело двигалось по направлению оси Ох. 4) Момент времени t 3 соответствует остановке тела. 5) В интервале времени от t 1 до t 2 тело изменило направление своего движения.
3) В момент времени t 1 тело двигалось по направлению оси Ох. 4) Момент времени t 3 соответствует остановке тела. 5) В интервале времени от t 1 до t 2 тело изменило направление своего движения.
Слайд 26
1) Модуль перемещения тела в момент времени t 3 равен нулю. 2) В момент времени t 1 тело имело максимальное ускорение. 3) В момент времени t 2 тело имело максимальную по модулю скорость. 4) Момент времени t 3 соответствует остановке тела. 5) На участке ВС тело двигалось равномерно.
Слайд 27
1) Удельная теплоёмкость вещества в твердом состоянии меньше удельной теплоемкости вещества в жидком состоянии. 2) Температура плавления вещества равна t 1 . 3) В точке Б вещество находится в жидком состоянии. 4) В процессе перехода из состояния Б в состояние В внутренняя энергия вещества не изменяется. 5) Участок графика ГД соответствует процессу кипения вещества.
На рисунке представлен график зависимости модуля скорости v автомобиля от времени t определите путь, пройденный автомобилем за первую секунду движения
Решение задания смотри на фотографии
Вот задача которую целый день решал кучу бумаги извел и вроде решил но как то мудрено у меня получилось
хотелось бы узнать как простым способом решить эту задачу
ото боюсь в следующий раз не повторю свой подвиг ))
задача Автомобиль проехал половину пути со скоростью 90 км/ч. 5*15*V2=913 K
5*15*V2=913 K
При соединении одинаковых по номиналу резисторов параллельно формула для определения эквивалентного сопротивления упрощается и принимает вид
Rэ = R/n
где Rэ – эквивалентное сопротивление;
R – номинал резисторов;
n – количество параллельно соединенных резисторов.
Найдем эквивалентное сопротивление для всего участка:
R = 60/3+60/2+60 = 110 Ом
Тогда, общий ток:
I = U/R = 220/110 = 2 А
Так как номиналы резисторов одинаковые, то при параллельном соединении через каждый из них потечет одинаковый ток.
Остается только найти его.
Ток через резисторы 1, 2 и 3 [здесь и далее подразумевается через каждый из резисторов]:
I123 = I/3 = 2/3 A
Ток через резисторы 4 и 5:
I45 = I/2 = 2/2 = 1 A
Ток через резистор 6 является общим и равен:
I = 2 A
F = m * ( g + a ) => 100 кг * ( 10 Н/кг + 0,1 м/с^2 ) = 1010 Н
Ответ:1010 Н = 1,01 кН
4.
 На рисунке представлен график зависимости модуля равнодействующей силы F, действующей на тело, от времени. 6. Две силы F1 30 Н и F2 40 Н приложены к одной точке тела. Угол между векторами F1 и F2 равен 900.DOC724 байта
На рисунке представлен график зависимости модуля равнодействующей силы F, действующей на тело, от времени. 6. Две силы F1 30 Н и F2 40 Н приложены к одной точке тела. Угол между векторами F1 и F2 равен 900.DOC724 байта
Первый закон Ньютона. Масса. Сила
Вариант 1
Какая из названных ниже величин векторная? 1. Масса. 2. Сила.
А. Только первая. Б. Только вторая. В. Первая и вторая. Г. Ни первая, ни вторая.
Равнодействующая всех сил, действующих на тело, равна нулю. Движется это тело или находится в состоянии покоя?
А. Тело находится в состоянии покоя. Б. Тело движется равномерно прямолинейно или находится в состоянии покоя. В. Тело движется равномерно прямолинейно. Г. Тело движется равноускоренно.
3. На рис. А представлены направления векторов скорости v и ускорения а мяча. Какое из представленных на рис. Б направлений имеет вектор равнодействующей F всех сил, приложенных к мячу?
А. 1. Б. 2. В. 3. Г. F-0.
4. На рисунке представлен график зависимости модуля равнодействующей силы F, действующей на тело, от времени.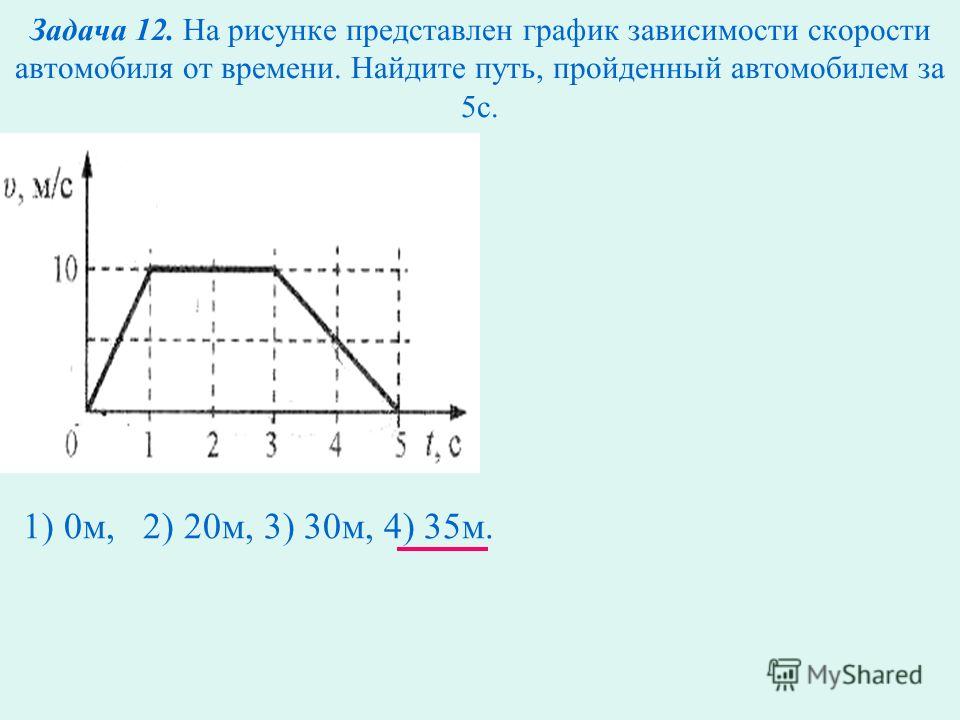 Чему равно изменение скорости тела массой 2 кг за 3 с?
Чему равно изменение скорости тела массой 2 кг за 3 с?
А. 9 м/с. Б. 12 м/с. В. 18 м/с. Г. 36 м/с.
5. На экспериментальной установке, изображенной на рисунке, установлены два шара массами mx и mэ (mэ = 0,1 кг), скрепленные сжатой легкой пружиной. Чему равна масса mx если после пережигания нити l1 = 0,5 м, 12 == 1м?
А. 0,025 кг. Б. 0,05 кг. В. 0,2 кг. Г. 0,4 кг.
6. Две силы F1 = 30 Н и F2 = 40 Н приложены к одной точке тела. Угол между векторами F1 и F2 равен 900. Чему равен модуль равнодействующей этих сил?
А. 10Н. Б.50Н. В.70Н. Г.35Н.
Вариант 2
1. Какая из названных ниже величин скалярная? 1. Масса. 2. Сила.
А. Только первая. Б. Только вторая. В. Первая и вторая. Г. Ни первая, ни вторая.
2. Векторная сумма всех сил, действующая на движущийся мяч относительно инерциальной системы отсчета, равна нулю. Какова траектория движения мяча?
А. Точка. Б. Прямая. В. Парабола. Г. Траектория может быть любой.
3. На рис. А представлены направления векторов скорости и Т равнодействующей всех сил, приложенных к мячу. Какое из представленных на рис. Б направлений имеет вектор ускорения а?
Какое из представленных на рис. Б направлений имеет вектор ускорения а?
А. 1. Б. 2. В. 3. Г. а = 0.
4. На рисунке представлен график зависимости модуля равнодействующей силы F, действующей на прямолинейно движущееся тело, от времени. Чему равно изменение скорости тела массой 2 кг за 4 с?
А. 4 м/с. Б. 8 м/с. В. 16 м/с. Г. 32 м/с.
5. На экспериментальной установке, изображенной на рисунке, установлены два шара массами mx и mэ (mэ = 0,1 кг), скрепленные сжатой легкой пружиной. Чему равна масса mx, если после пережигания нити l1 = 1 м, 12 = 0,5м?
А. 0,025 кг. Б. 0,05 кг. В. 0,2 кг. Г. 0,4 кг.
6. Две силы F1 = 2 Ни F2 = 3 Н приложены к одной точке тела. Угол между векторами F1 и F2 равен 90°. Чему равен модуль равнодействующей этих сил?
А. 1 Н. Б. 13 EMBED Equation.3 1415 Н. В. 5Н. Г. 13 Н.
13 EMBED Word.Picture.8 1415
13 EMBED Word.Picture.8 1415
Root Entry
Приложенные файлы
- 20720369
Размер файла: 87 kB Загрузок: 0
По графику зависимости модуля скорости от времени, представленному на рисунке, определите модуль ускорения прямолинейно движущегося тела в момент времени t = 2
Физика, 9 класс Фамилия, имя___________________________________
Вариант 1
1
По графику зависимости модуля скорости от времени, представленному на рисунке, определите модуль ускорения прямолинейно движущегося тела в момент времени t = 2 с.
| 1) | 2 м/с2 | 2) | 5 м/с2 | 3) | 7,5 м/с2 | 4) | 30 м/с2 |
2
Велосипедист едет со скоростью 36 км/ч относительно Земли. Скорость ветра относительно Земли 2 м/с. Какова скорость ветра относительно велосипедиста, если он движется навстречу ветру?
| 1) | 8 м/с | 2) | 12 м/с | 3) | 34 км/ч | 4) | 38 км/ч |
3
Как будет двигаться тело массой 2 кг под действием силы 4 Н в инерциальной системе отсчёта?
| 1) | равномерно со скоростью 2 м/с |
| 2) | равномерно со скоростью 0,5 м/с |
| 3) | равноускоренно с ускорением 0,5 м/с2 |
| 4) | равноускоренно с ускорением 2 м/с2 |
4
Конькобежец массой 80 кг скользит по льду. Определите силу трения скольжения, действующую на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,02.
Определите силу трения скольжения, действующую на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,02.
| 1) | 1,6 H | 2) | 16 H | 3) | 40 H | 4) | 400 H |
5
Сила тяготения между двумя телами увеличится в 2 раза, если, не меняя расстояния между телами, массу одного из них
| 1) | увеличить в раз |
| 2) | уменьшить в раз |
| 3) | увеличить в 2 раза |
| 4) | уменьшить в 2 раза |
6
Три тела разного объема полностью погрузили в одну и ту же жидкость (см. рисунок). При этом
рисунок). При этом
| 1) | наибольшая архимедова сила действует на тело 1 |
| 2) | наибольшая архимедова сила действует на тело 2 |
| 3) | наибольшая архимедова сила действует на тело 3 |
| 4) | на все тела действуют одинаковые архимедовы силы |
7
На рисунке представлен график смещения x частиц от положения равновесия в зависимости от расстояния S, на которое распространилась гармоничная волна. Какой стрелкой на графике правильно отмечена длина волны?
8
Для обращения в пар 2 кг спирта при температуре кипения затрачивается 1800 кДж теплоты. При конденсации 1 кг спирта (при той же температуре)
| 1) | выделяется 900 кДж теплоты |
| 2) | поглощается 900 кДж теплоты |
| 3) | выделяется 1800 кДж теплоты |
| 4) | поглощается 1800 кДж теплоты |
9
В опыте по исследованию зависимости температуры T нафталина от времени t были использованы кристаллы нафталина.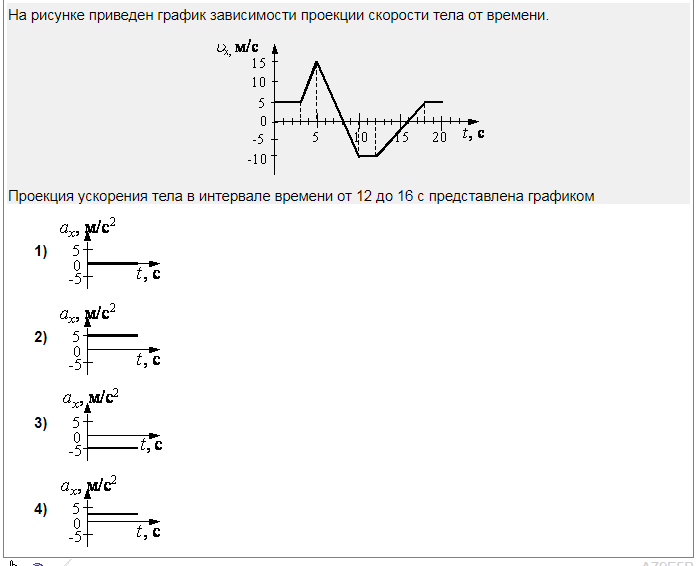 Полученный график представлен на рисунке. Какому участку графика соответствует нагревание твердого нафталина? Считать скорость подвода тепла постоянной.
Полученный график представлен на рисунке. Какому участку графика соответствует нагревание твердого нафталина? Считать скорость подвода тепла постоянной.
| 1) | аb |
| 2) | bс |
| 3) | cd |
| 4) | таких участков нет |
10
Поля какой природы обнаруживаются около неподвижного положительно заряженного шара?
| 1) | только магнитное |
| 2) | электрическое и гравитационное |
| 3) | электрическое и магнитное |
| 4) | только гравитационное |
11
В электрическую цепь включены три проводника одинакового поперечного сечения из одного и того же материала, но разной длины: первый – 1 м, второй – 2 м, третий – 3 м.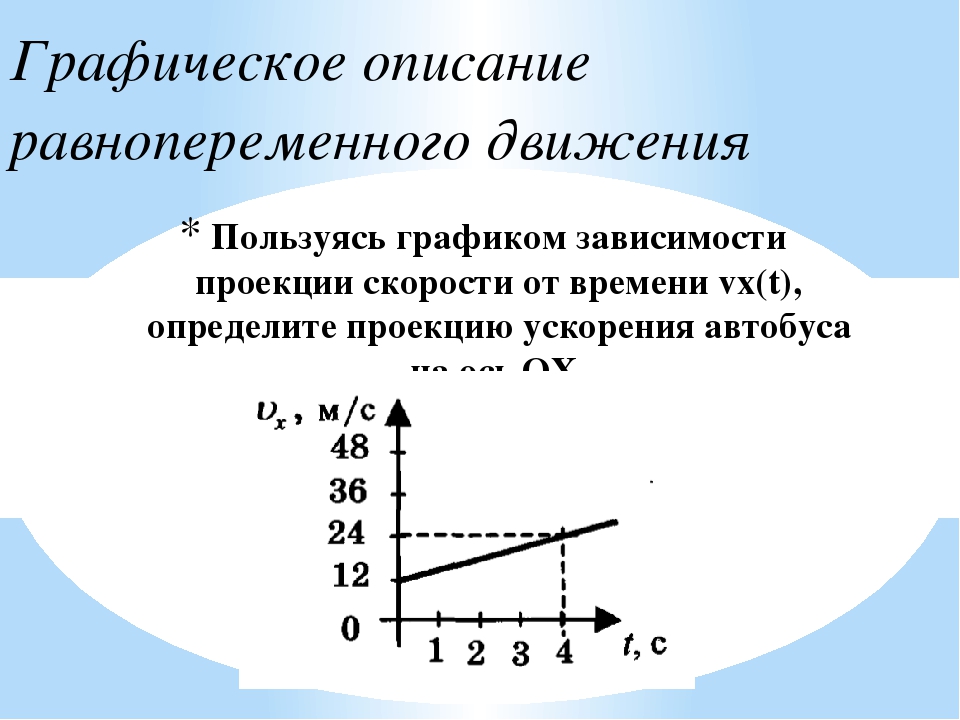 Между собой проводники соединены последовательно. В каком проводнике выделяется большее количество тепла?
Между собой проводники соединены последовательно. В каком проводнике выделяется большее количество тепла?
| 1) | первом |
| 2) | втором |
| 3) | третьем |
| 4) | во всех одинаковое |
12
В электрической цепи (см. рисунок) амперметр А1 показывает силу тока 2А, амперметр А2 показывает силу тока 0,5А. Ток, протекающий через лампу, равен
| 1) | 2,5 А |
| 2) | 2 А |
| 3) | 1,5 А |
| 4) | 0,5 А |
13
Угол падения луча на зеркальную отражающую поверхность равен 10. Угол между падающим и отраженным лучом равен
Угол между падающим и отраженным лучом равен
| 1) | 0 | 2) | 5 | 3) | 10 | 4) | 20 |
| Ответы на задания В1, В2 и В3 запишите в указанном месте, а затем впишите в бланк тестирования справа от номера задания, начиная с первой клеточки. Каждую цифру или запятую пишите в отдельной клеточке в соответствии с образцом. |
В1
Установите соответствие между физическими величинами и единицами измерения этих величин в системе СИ: к каждой позиции из первого столбца подберите соответствующую позицию из второго столбца, обозначенную цифрой.
| ^ | еДИНИЦы ИЗМЕРЕНИЯ | ||
| А) | количество теплоты | 1) | Джоуль (1 Дж) |
| Б) | удельная теплота плавления | 2) | Джоуль на килограмм (1 Дж/кг) |
| В) | удельная теплоёмкость вещества | 3) 4) | Ватт (1 Вт) Вольт (1 В) |
| 5) | Джоуль на килограмм-градус (1 Дж/(кгС)) | ||
Запишите в таблицу выбранные цифры.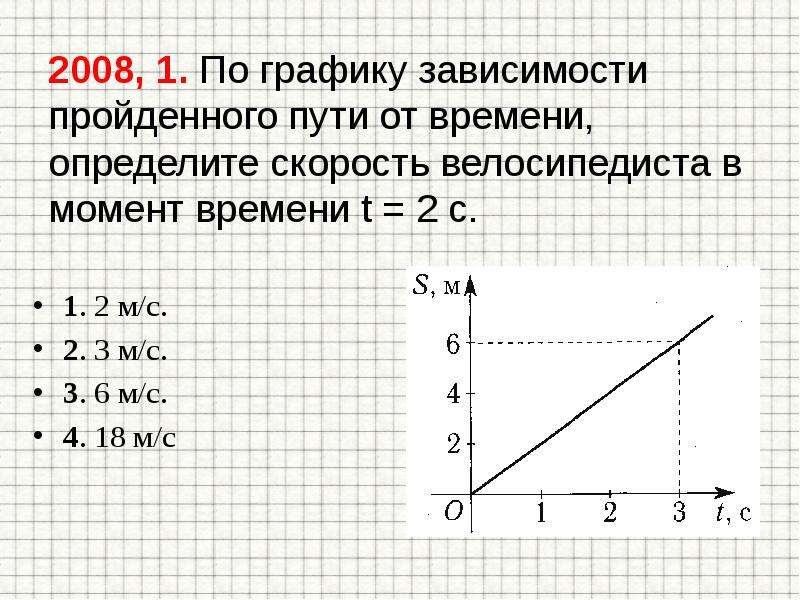
В2
Камень свободно падал вниз в течение 4 с. С какой высоты упал камень, если начальная скорость равна нулю? Принять g = 10 м/с2.
Ответ: _____ м.
В бланк запишите только число.
В3
Платформа с закрепленным на ней орудием покоится на гладких рельсах. Общая масса платформы с орудием равна 20 т. Из орудия, горизонтально вдоль рельсов, выпущен снаряд массой 20 кг со скоростью 500 м/c. Определите скорость платформы сразу после выстрела.
Ответ: __________ м/с .
В бланк запишите только число.
~EndLATTest
16.6 Стоячие волны и резонанс
На протяжении этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое. При определенных условиях волны могут подпрыгивать взад и вперед через определенную область, фактически становясь стационарными. Они называются стоячими волнами .
Другой связанный эффект известен как резонанс. В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызывать движение большой амплитуды.Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс хорош — например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызывать движение большой амплитуды.Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс хорош — например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
Стоячие волны
Иногда кажется, что волны не двигаются; скорее, они просто вибрируют на месте. Вы можете увидеть неподвижные волны, например, на поверхности стакана с молоком в холодильнике. Вибрация двигателя холодильника создает волны на молоке, которые колеблются вверх и вниз, но не движутся по поверхности. (Рисунок) показывает эксперимент, который вы можете попробовать дома.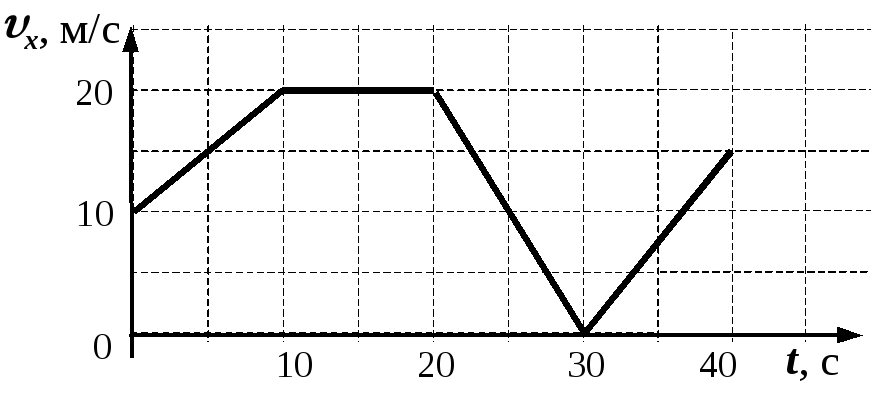 Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны.Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на (Рисунок) для двух идентичных волн, движущихся в противоположных направлениях. Волны движутся друг сквозь друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны.Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на (Рисунок) для двух идентичных волн, движущихся в противоположных направлениях. Волны движутся друг сквозь друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Рисунок 16.25 Стоячие волны образуются на поверхности миски с молоком, установленной на ящичном веере. Вибрация вентилятора заставляет поверхность молока колебаться. Волны видны из-за отражения света от лампы.
рисунок 16.26 Временные снимки двух синусоидальных волн. Красная волна движется в направлении -x, а синяя волна движется в направлении + x.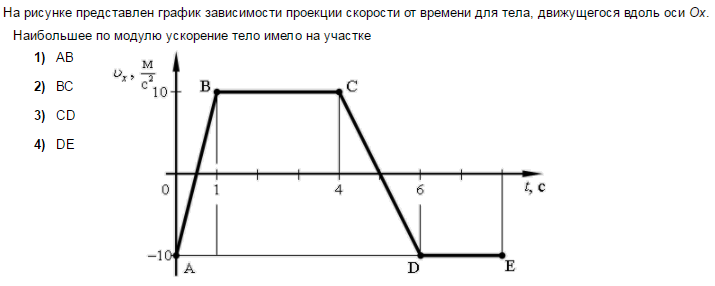 Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точках [latex] x = 0 \, \ text {m}, 3 \, \ text {m}, 6 \, \ text {m}, 9 \, \ text {m}, 12 \ , \ text {m}, 15 \, \ text {m} [/ latex] и обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени.Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точках [latex] x = 0 \, \ text {m}, 3 \, \ text {m}, 6 \, \ text {m}, 9 \, \ text {m}, 12 \ , \ text {m}, 15 \, \ text {m} [/ latex] и обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени.Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию [латекс] {y} _ {1} (x, t) = A \, \ text {sin} (kx- \ omega t) [/ latex], а вторая волна имеет волну функция [латекс] {y} _ {2} (x, t) = A \, \ text {sin} (kx + \ omega t) [/ latex]. Волны интерферируют и образуют результирующую волну
[латекс] \ begin {array} {c} y (x, t) = {y} _ {1} (x, t) + {y} _ {2} (x, t), \ hfill \\ y (x, t) = A \, \ text {sin} (kx- \ omega t) + A \, \ text {sin} (kx + \ omega t). \ hfill \ end {array} [/ latex]
\ hfill \ end {array} [/ latex]
Это можно упростить с помощью тригонометрического идентификатора
[латекс] \ text {sin} (\ alpha ± \ beta) = \ text {sin} \, \ alpha \, \ text {cos} \, \ beta ± \ text {cos} \, \ alpha \, \ текст {sin} \, \ beta, [/ latex]
, где [latex] \ alpha = kx [/ latex] и [latex] \ beta = \ omega t [/ latex], что дает нам
[латекс] y (x, t) = A [\ text {sin} (kx) \ text {cos} (\ omega t) — \ text {cos} (kx) \ text {sin} (\ omega t) + \ text {sin} (kx) \ text {cos} (\ omega t) — \ text {cos} (kx) \ text {sin} (\ omega t)], [/ latex]
, что упрощается до
[латекс] y (x, t) = [2A \, \ text {sin} (kx)] \ text {cos} (\ omega t).[/ латекс]
Обратите внимание, что результирующая волна является синусоидальной волной, которая является функцией только положения, умноженной на функцию косинуса, которая является функцией только времени. Графики x ( x , t ) как функции x для различных времен показаны на (Рисунок). Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна является суммой двух волн. По мере того, как красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и деструктивной интерференции.
Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна является суммой двух волн. По мере того, как красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и деструктивной интерференции.
Первоначально в момент времени [latex] t = 0, [/ latex] две волны находятся в фазе, и в результате получается волна, которая в два раза превышает амплитуду отдельных волн. Волны также находятся в фазе в момент времени [latex] t = \ frac {T} {2}. [/ latex] На самом деле волны находятся в фазе в любом целом числе кратном половине периода:
[латекс] t = n \ frac {T} {2} \, \ text {where} \, n = 0,1,2,3 \ text {…}. \, \ Text {(в фазе)}. [/ латекс]
В других случаях две волны [latex] 180 \ text {°} (\ pi \, \ text {radians}) [/ latex] не совпадают по фазе, и результирующая волна равна нулю.Это происходит на
[латекс] t = \ frac {1} {4} T, \ frac {3} {4} T, \ frac {5} {4} T \ text {,…}, \ frac {n} {4} T \, \ text {где} \, n = 1,3,5 \ text {…}. \, \ Text {(не в фазе)}. [/ латекс]
\, \ Text {(не в фазе)}. [/ латекс]
Обратите внимание, что некоторые положения результирующей волны x всегда равны нулю, независимо от фазового соотношения. Эти позиции называются узлами . Где встречаются узлы? Рассмотрим решение суммы двух волн
[латекс] y (x, t) = [2A \, \ text {sin} (kx)] \ text {cos} (\ omega t). [/ латекс]
Нахождение позиций, в которых функция синуса равна нулю, обеспечивает положение узлов.
[латекс] \ begin {array} {ccc} \ hfill \ text {sin} (kx) & = \ hfill & 0 \ hfill \\ \ hfill kx & = \ hfill & 0, \ pi, 2 \ pi, 3 \ pi \ text {,…} \ hfill \\ \ hfill \ frac {2 \ pi} {\ lambda} x & = \ hfill & 0, \ pi, 2 \ pi, 3 \ pi \ text {,…} \ hfill \ \ \ hfill x & = \ hfill & 0, \ frac {\ lambda} {2}, \ lambda, \ frac {3 \ lambda} {2} \ text {,…} = n \ frac {\ lambda} {2} \ quad n = 0,1,2,3 \ text {,…}. \ hfill \ end {array} [/ latex]
Есть также позиции, где y колеблется между [латексом] y = \ text {±} A [/ latex]. Это пучностей . Мы можем найти их, посчитав, какие значения x приводят к [latex] \ text {sin} (kx) = \ text {±} 1 [/ latex].
Это пучностей . Мы можем найти их, посчитав, какие значения x приводят к [latex] \ text {sin} (kx) = \ text {±} 1 [/ latex].
[латекс] \ begin {array} {ccc} \ hfill \ text {sin} (kx) & = \ hfill & ± 1 \ hfill \\ \ hfill kx & = \ hfill & \ frac {\ pi} {2}, \ frac {3 \ pi} {2}, \ frac {5 \ pi} {2} \ text {,…} \ hfill \\ \ hfill \ frac {2 \ pi} {\ lambda} x & = \ hfill & \ frac {\ pi} {2}, \ frac {3 \ pi} {2}, \ frac {5 \ pi} {2} \ text {,…} \ hfill \\ \ hfill x & = \ hfill & \ frac { \ lambda} {4}, \ frac {3 \ lambda} {4}, \ frac {5 \ lambda} {4} \ text {,…} = n \ frac {\ lambda} {4} \ quad n = 1 , 3,5 \ текст {,…}.\ hfill \ end {array} [/ latex]
В результате получается стоячая волна, как показано на (Рисунок), где показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях. Результирующая волна выглядит как синусоидальная волна с узлами в целых кратных полуволнах. Пучины колеблются между [латексом] y = \ text {±} 2A [/ latex] из-за члена косинуса, [latex] \ text {cos} (\ omega t) [/ latex], который колеблется между [латексом] ± 1 [/ латекс].
Результирующая волна кажется неподвижной, без видимого движения в направлении x , хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x .(Рисунок) показывает различные снимки результирующей волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
Рисунок 16.27 Когда две одинаковые волны движутся в противоположных направлениях, результирующая волна является стоячей волной. Узлы появляются в целых числах, кратных половине длины волны. Пучины появляются с нечетными числами, кратными четверти длины волны, где они колеблются между [латексом] y = \ text {±} A. [/ latex] Узлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами. Когда струна защипывается, импульсы проходят по струне в противоположных направлениях. Концы струн фиксируются на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на (Рисунок).
Концы струн фиксируются на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на (Рисунок).
Рисунок 16.28 Лабораторная установка для создания стоячих волн на струне. У струны есть узел на каждом конце и постоянная линейная плотность. Длина между фиксированными граничными условиями равна L. Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.
Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f .Другой конец струны проходит над шкивом без трения и привязан к подвешенной массе. Величина натяжения тетивы равна весу подвешенной массы. Струна имеет постоянную линейную плотность (масса на длину) [латекс] \ mu [/ latex], а скорость, с которой волна распространяется по струне, равна [латексу] v = \ sqrt {\ frac {{F} _ {T }} {\ mu}} = \ sqrt {\ frac {mg} {\ mu}} [/ latex] (рисунок). Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны.Начиная с нулевой частоты и медленно увеличивая частоту, появляется первая мода [латекс] n = 1 [/ латекс], как показано на (Рисунок). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами [латекс] {\ lambda} _ {1} = 2L [/ latex ]. Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны.Начиная с нулевой частоты и медленно увеличивая частоту, появляется первая мода [латекс] n = 1 [/ латекс], как показано на (Рисунок). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами [латекс] {\ lambda} _ {1} = 2L [/ latex ]. Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
.
[латекс] {f} _ {1} = \ frac {v} {{\ lambda} _ {1}} = \ frac {v} {2L}, [/ latex]
, где скорость волны [латекс] v = \ sqrt {\ frac {{F} _ {T}} {\ mu}}.[/ latex] Сохранение постоянного напряжения и увеличение частоты приводит ко второй гармонике или режиму [latex] n = 2 [/ latex]. Этот режим представляет собой полноразмерный [латекс] {\ lambda} _ {2} = L [/ latex], а частота в два раза превышает основную частоту:
[латекс] {f} _ {2} = \ frac {v} {{\ lambda} _ {2}} = \ frac {v} {L} = 2 {f} _ {1}.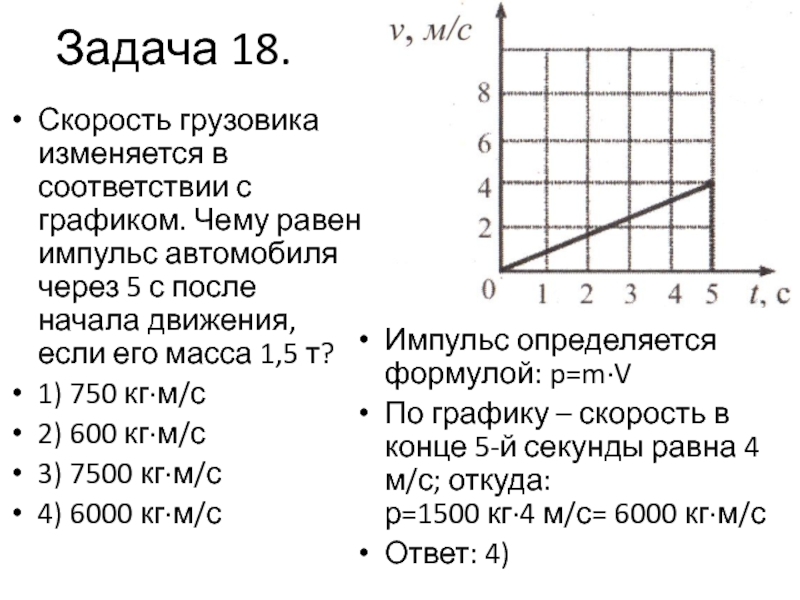 [/ латекс]
[/ латекс]
Рисунок 16.29 Стоячие волны, созданные на цепочке длиной L. Узлы возникают на каждом конце цепочки. Узлы — это граничные условия, которые ограничивают возможные частоты, возбуждающие стоячие волны.(Обратите внимание, что амплитуды колебаний поддерживаются постоянными для визуализации. Возможные модели стоячих волн на струне известны как нормальные режимы. Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды по мере увеличения частоты.)
Следующие две моды, или третья и четвертая гармоники, имеют длины волн [латекс] {\ lambda} _ {3} = \ frac {2} {3} L [/ latex] и [латекс] {\ lambda} _ {4} = \ frac {2} {4} L, [/ latex], управляемый частотами [латекс] {f} _ {3} = \ frac {3v} {2L} = 3 {f} _ {1} [/ latex] и [latex] {f} _ {4} = \ frac {4v} {2L} = 4 {f} _ {1}.[/ latex] Все частоты выше частоты [latex] {f} _ {1} [/ latex] известны как обертоны . Уравнения для длины волны и частоты можно резюмировать как:
[латекс] {\ lambda} _ {n} = \ frac {2} {n} L \ quad n = 1,2,3,4,5 \ text {…} [/ latex]
[латекс] {f} _ {n} = n \ frac {v} {2L} = n {f} _ {1} \ quad n = 1,2,3,4,5 \ text {…} [/ латекс]
Модели стоячей волны, которые возможны для струны, первые четыре из которых показаны на (Рисунок), известны как нормальные моды с частотами, известными как нормальные частоты. Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота нормального режима струны [latex] n = 2 [/ latex] — это первый обертон (или вторая гармоника). Частота нормальной моды [latex] n = 3 [/ latex] — это второй обертон (или третья гармоника) и так далее.
Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота нормального режима струны [latex] n = 2 [/ latex] — это первый обертон (или вторая гармоника). Частота нормальной моды [latex] n = 3 [/ latex] — это второй обертон (или третья гармоника) и так далее.
Решения, показанные как (Уравнение) и (Уравнение), предназначены для строки с граничным условием узла на каждом конце.Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. (Уравнение) и (Уравнение) подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример
Стоячие волны на струне
Рассмотрим строку [латекс] L = 2.00 \, \ text {m}. [/ latex] прикреплен к струнному вибратору с регулируемой частотой, как показано на (Рисунок). Волны, создаваемые вибратором, проходят по струне и отражаются фиксированным граничным условием на шкиве. Струна, имеющая линейную массовую плотность [латекс] \ mu = 0,006 \, \ text {кг / м,} [/ latex], проходит через шкив без трения с незначительной массой, а натяжение обеспечивается за счет 2,00 -кг подвесная масса. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые струнный вибратор должен быть настроен, чтобы произвести первые три нормальные моды стоячих волн.
Струна, имеющая линейную массовую плотность [латекс] \ mu = 0,006 \, \ text {кг / м,} [/ latex], проходит через шкив без трения с незначительной массой, а натяжение обеспечивается за счет 2,00 -кг подвесная масса. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые струнный вибратор должен быть настроен, чтобы произвести первые три нормальные моды стоячих волн.
Рисунок 16.30 Струна, прикрепленная к струнному вибратору с регулируемой частотой.
Стратегия
- Скорость волны можно найти с помощью [latex] v = \ sqrt {\ frac {{F} _ {T}} {\ mu}}. [/ latex] Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет составлять половину волны. Вторую можно найти, добавив половину длины волны.
 Это самая короткая длина, которая приведет к образованию узла на границах. Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на (Рисунок).
Это самая короткая длина, которая приведет к образованию узла на границах. Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на (Рисунок). - Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны.
Рисунок 16.31 (a) На рисунке представлен второй режим строки, который удовлетворяет граничным условиям узла на каждом конце строки.(b) Этот рисунок не может быть нормальным режимом для струны, потому что он не удовлетворяет граничным условиям. На одном конце есть узел, а на другом — пучность.
Решение
- Начните со скорости волны на струне. Натяжение равно весу подвешенной массы. Даны линейная массовая плотность и масса подвешенной массы:
[латекс] v = \ sqrt {\ frac {{F} _ {T}} {\ mu}} = \ sqrt {\ frac {mg} {\ mu}} = \ sqrt {\ frac {2 \, \ текст {кг} (9,8 \ frac {\ text {m}} {\ text {s}})} {0.
 006 \ frac {\ text {kg}} {\ text {m}}}} = 57,15 \, \ text {m / s}. [/ латекс]
006 \ frac {\ text {kg}} {\ text {m}}}} = 57,15 \, \ text {m / s}. [/ латекс] - Первая нормальная мода с узлами на каждом конце — это половина длины волны. Следующие две моды находятся путем добавления половины длины волны.
- Частоты первых трех режимов находятся с помощью [latex] f = \ frac {{v} _ {w}} {\ lambda}. [/латекс]
[латекс] \ begin {array} {} \\ {f} _ {1} = \ frac {{v} _ {w}} {{\ lambda} _ {1}} = \ frac {57.15 \, \ text {m / s}} {4.00 \, \ text {m}} = 14.29 \, \ text {Hz} \ hfill \\ {f} _ {2} = \ frac {{v} _ {w}} { {\ lambda} _ {2}} = \ frac {57.15 \, \ text {m / s}} {2,00 \, \ text {m}} = 28,58 \, \ text {Hz} \ hfill \\ {f} _ {3} = \ frac {{v} _ { w}} {{\ lambda} _ {3}} = \ frac {57.15 \, \ text {m / s}} {1.333 \, \ text {m}} = 42.87 \, \ text {Hz} \ hfill \ конец {array} [/ latex]
Значение
Три режима стоя в этом примере были созданы путем поддержания натяжения струны и регулировки частоты возбуждения. Сохранение постоянного натяжения струны приводит к постоянной скорости. Те же самые режимы можно было бы получить, сохраняя постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу.)
Те же самые режимы можно было бы получить, сохраняя постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу.)
Проверьте свое понимание
Уравнения для длин волн и частот мод волны, создаваемой на струне:
[латекс] \ begin {array} {} \\ {\ lambda} _ {n} = \ frac {2} {n} L \ quad n = 1,2,3,4,5 \ text {…} \ , \ text {and} \ hfill \\ {f} _ {n} = n \ frac {v} {2L} = n {f} _ {1} \ quad n = 1,2,3,4,5 \ текст {…} \ hfill \ end {array} [/ latex]
были получены путем рассмотрения волны на струне, где были симметричные граничные условия узла на каждом конце. Эти режимы являются результатом двух синусоидальных волн с идентичными характеристиками, за исключением того, что они движутся в противоположных направлениях, ограниченных областью L с узлами, необходимыми на обоих концах.Будут ли работать те же уравнения при наличии симметричных граничных условий с пучностями на каждом конце? Как бы выглядели нормальные режимы для среды, которая могла бы свободно колебаться на каждом конце? Не беспокойтесь, если вы не можете представить себе такую среду, просто рассмотрите две синусоидальные волновые функции в области длиной L с пучностями на каждом конце.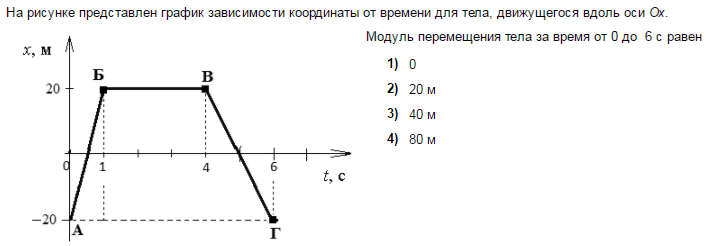
Да, уравнения будут одинаково хорошо работать для симметричных граничных условий среды, свободно колеблющейся на каждом конце, где на каждом конце есть пучности.Ниже показаны нормальные режимы первых трех режимов. Пунктирная линия показывает положение равновесия среды.
Обратите внимание, что первая мода составляет две четверти или половину длины волны. Вторая мода — это четверть длины волны, за которой следует половина длины волны, за которой следует четверть длины волны, или одна полная длина волны. Третья мода — полторы длины волны. Это тот же результат, что и у строки с узлами на каждом конце. Уравнения для симметричных граничных условий одинаково хорошо работают как для фиксированных граничных условий, так и для свободных граничных условий.К этим результатам мы вернемся в следующей главе, когда будем обсуждать звуковую волну в открытой трубе.
Свободные граничные условия, показанные в последней проверке понимания, могут показаться трудными для визуализации. Как может быть система, которая может свободно колебаться на каждом конце? На (Рисунок) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим). В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия.При соответствующей частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, составляющих одну четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При правильной частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности. Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и примите во внимание (рисунок).
Как может быть система, которая может свободно колебаться на каждом конце? На (Рисунок) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим). В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия.При соответствующей частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, составляющих одну четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При правильной частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности. Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и примите во внимание (рисунок).
Рисунок 16.32 (a) Металлический стержень длиной L (красный), поддерживаемый двумя опорами (синими) на каждом конце. При движении с соответствующей частотой стержень может резонировать с длиной волны, равной длине стержня с узлом на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца. При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с пучностями на каждом конце.
При движении с соответствующей частотой стержень может резонировать с длиной волны, равной длине стержня с узлом на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца. При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с пучностями на каждом конце.
Рисунок 16.33 Длину волны можно измерить между двумя ближайшими повторяющимися точками. На волне на веревке это означает одинаковую высоту и наклон. (a) Длина волны измеряется между двумя ближайшими точками, где высота равна нулю, а наклон является максимальным и положительным. (b) Длина волны измеряется между двумя идентичными точками, где высота максимальна, а наклон равен нулю.
Обратите внимание, что изучение стоячих волн может стать довольно сложным. На (Рисунок) (а) показана мода стоячей волны [латекс] n = 2 [/ латекс], и это приводит к длине волны, равной L . В этой конфигурации режим [латекс] n = 1 [/ латекс] также был бы возможен с стоячей волной, равной 2 L . Можно ли получить режим [latex] n = 1 [/ latex] для конфигурации, показанной в части (b)? Ответ — нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия. Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы.Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн. Следует отметить, что когда система приводится в действие на частоте, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
В этой конфигурации режим [латекс] n = 1 [/ латекс] также был бы возможен с стоячей волной, равной 2 L . Можно ли получить режим [latex] n = 1 [/ latex] для конфигурации, показанной в части (b)? Ответ — нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия. Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы.Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн. Следует отметить, что когда система приводится в действие на частоте, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, производимый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле.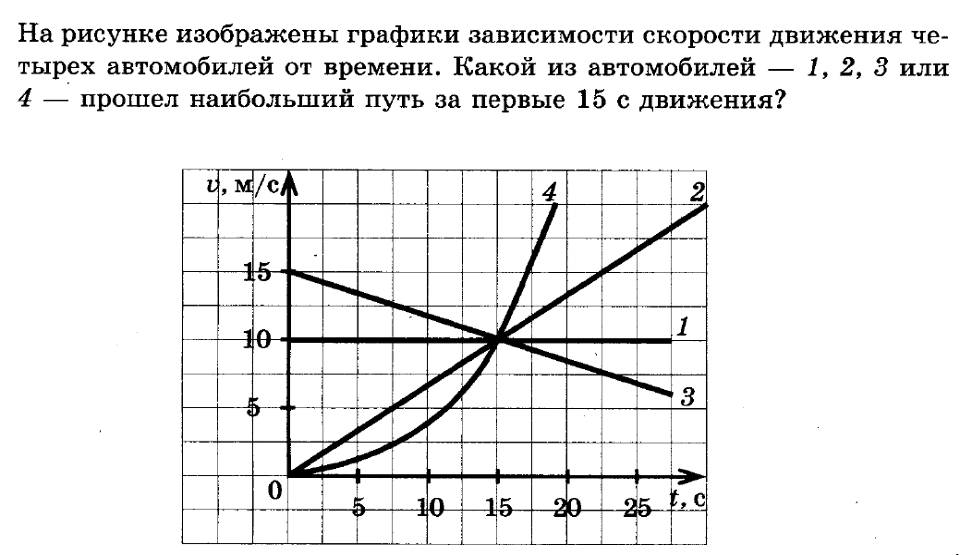 Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, для поиска частот звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, для поиска частот звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире.Воздух в трубке, например, в музыкальном инструменте, таком как флейта, может быть вызван резонансом и производить приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения дает доказательства наличия условий, подходящих для резонанса, стоячих волн, а также конструктивных и деструктивных помех. Здание может колебаться в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, создавая резонанс, в результате которого одно здание рушится, а соседние — нет.Часто здания определенной высоты разрушаются, в то время как другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто можно увидеть, что спортзалы, супермаркеты и церкви страдают от повреждений, в то время как отдельные дома страдают гораздо меньше. Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Когда волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникает конструктивная интерференция.Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше — повреждены.
2.8: Графический анализ одномерного движения
График, как и изображение, стоит тысячи слов. Графики содержат не только числовую информацию; они также раскрывают отношения между физическими величинами. В этом разделе используются графики перемещения, скорости и ускорения в зависимости от времени, чтобы проиллюстрировать одномерную кинематику.
Склоны и общие отношения
Прежде всего обратите внимание на то, что графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная.Когда две физические величины наносятся друг на друга на таком графике, горизонтальная ось обычно считается независимой переменной, а вертикальная ось — зависимой переменной. Если мы назовем горизонтальную ось осью x, а вертикальную ось — осью y, как на рисунке \ (\ PageIndex {1} \), прямолинейный график будет иметь общий вид
\ [y = mx + b. \]
Здесь \ (m \) — наклон, определяемый как подъем, деленный на длину прямой линии (рисунок \ (\ PageIndex {1} \)).Буква \ (b \) используется для обозначения точки пересечения, то есть точки, в которой линия пересекает вертикальную ось.
Рисунок \ (\ PageIndex {1} \): прямолинейный график. Уравнение прямой: \ (y = mx + b \).
График смещения от времени (
a = 0, поэтому v постоянно)
Время обычно является независимой переменной, от которой зависят другие величины, такие как смещение. График смещения в зависимости от времени, таким образом, будет иметь x на вертикальной оси и t на горизонтальной оси.Рисунок \ (\ PageIndex {2} \) — это именно такой прямолинейный график. На нем показан график перемещения в зависимости от времени для реактивного автомобиля на очень плоском высохшем дне озера в Неваде.
Рисунок \ (\ PageIndex {2} \): График перемещения в зависимости от времени для автомобиля с реактивным двигателем на соляных равнинах Бонневилля.
Используя соотношение между зависимыми и независимыми переменными, мы видим, что наклон на графике выше — это средняя скорость \ (\ bar {v} \), а точка пересечения — это смещение в нулевой момент времени, то есть \ (x_0 \). Подставляя эти символы в \ (y = mx + b \), получаем
\ [x = \ bar {v} t + x_0 \]
или
\ [x = x_0 + \ bar {v} t.\]
Таким образом, график смещения в зависимости от времени дает общую взаимосвязь между смещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации.
НАКЛОН \ (X \) VS. \ (Т \)
Наклон графика смещения \ (x \) от времени \ (t \) — это скорость \ (v \).
\ (\ displaystyle slope = \ frac {Δx} {Δt} = v \)
Обратите внимание, что это уравнение аналогично уравнению, полученному алгебраически из других уравнений движения в уравнениях движения для постоянного ускорения в одном измерении.
Из рисунка видно, что автомобиль имеет водоизмещение 25 м за 0,50 с и 2000 м за 6,40 с. Его смещение в остальное время можно увидеть на графике; кроме того, информация о его скорости и ускорении также может быть получена из графика.
Пример \ (\ PageIndex {1} \): определение средней скорости по графику смещения в зависимости от времени: реактивный автомобиль
Найдите среднюю скорость автомобиля, положение которого показано на рисунке \ (\ PageIndex {2} \).
Стратегия
Наклон графика зависимости \ (x \) от \ (t \) — это средняя скорость, поскольку наклон равен подъему за пробег. В этом случае подъем = изменение положения, бег = изменение во времени, так что
\ [\ displaystyle slope = \ frac {Δx} {Δt} = \ bar {v}. \ nonumber \]
Поскольку наклон здесь постоянный, любые две точки на графике могут использоваться для определения наклона. (Вообще говоря, точнее всего использовать две широко разнесенные точки на прямой.Это связано с тем, что любая ошибка при чтении данных с графика пропорционально меньше, если интервал больше.)
Решение
- Выберите две точки на линии. В этом случае мы выбираем точки, обозначенные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Учтите, однако, что вы можете выбрать любые две точки.)
- Подставьте значения x и t выбранных точек в уравнение. Помните, что при вычислении изменения (Δ) мы всегда используем конечное значение минус начальное значение.\ [\ displaystyle \ bar {v} = \ frac {Δx} {Δt} = \ frac {2000 m − 525 m} {6.4 s − 0.50 s}, \ nonumber \], что дает \ [\ displaystyle v− = 250 m / с. \ nonumber \]
Обсуждение
Это впечатляюще большая сухопутная скорость (900 км / ч или около 560 миль / ч): намного больше, чем типичное ограничение скорости на шоссе в 60 миль / ч (27 м / с или 96 км / ч), но значительно скромнее. рекорда 343 м / с (1234 км / ч или 766 миль / ч), установленного в 1997 году.
Графики движения, когда a постоянно, но a 0
Графики на рисунке \ (\ PageIndex {3} \) ниже представляют движение автомобиля с реактивным двигателем, когда он набирает максимальную скорость, но только в то время, когда его ускорение является постоянным.Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально составляют 200 м и 15 м / с соответственно.
Рисунок \ (\ displaystyle \ PageIndex {3} \): Графики движения автомобиля с реактивным двигателем за период времени, когда его ускорение является постоянным. (a) Наклон графика \ (\ displaystyle x \) vs. \ (\ displaystyle t \) — это скорость. Это показано в двух точках, а полученные мгновенные скорости нанесены на следующий график.2 \) на заданном временном интервале.
Рис. \ (\ Displaystyle \ PageIndex {4} \): реактивный автомобиль ВВС США едет по рельсовому пути. (кредит: Мэтт Тростл, Flickr)
График смещения в зависимости от времени на рисунке \ (\ PageIndex {3a} \) представляет собой кривую, а не прямую линию. Наклон кривой становится более крутым с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости смещения от времени — это мгновенная скорость в этой точке. Его можно найти, проведя прямую касательную к кривой в интересующей точке и взяв наклон этой прямой.Касательные линии показаны для двух точек на рисунке \ (\ PageIndex {3a} \). Если это делается в каждой точке кривой и значения наносятся в зависимости от времени, то получается график зависимости скорости от времени, показанный на рисунке \ (\ PageIndex {3b} \). Кроме того, наклон графика зависимости скорости от времени — это ускорение, которое показано на рисунке \ (\ PageIndex {3c} \).
Пример \ (\ PageIndex {2} \):
Рассчитайте скорость реактивного автомобиля за 25 с, найдя наклон зависимости \ (\ displaystyle x \) vs.\ (\ displaystyle t \) график на графике ниже
Рисунок \ (\ displaystyle \ PageIndex {5} \): наклон графика \ (x \) vs. \ (t \) — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке — это наклон касательной в этой точке.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке. Этот принцип проиллюстрирован на рисунке, где Q — точка в \ (\ displaystyle t = 25 s \).
Решение
- Найдите касательную к кривой в точке \ (\ displaystyle t = 25 s \).
- Определите конечные точки касательной. Они соответствуют позиции 1300 м за 19 с и позиции 3120 м за 32 с.
- Подставьте эти конечные точки в уравнение, чтобы найти наклон, v .
\ (\ displaystyle slope = v_Q = \ frac {Δx_Q} {Δt_Q} = \ frac {(3120 м − 1300 м)} {(32 s − 19 s)} \)
Таким образом,
\ (\ displaystyle v_Q = \ frac {1820 m} {13 s} = 140 м / с.\)
Обсуждение
Это значение v at \ (\ displaystyle t = 25 s \), приведенное в таблице на этом рисунке. Значение 140 м / с для \ (\ displaystyle v_Q \) показано на рисунке. Таким образом можно получить весь график \ (\ displaystyle v \) vs. \ (\ displaystyle t \).
Продолжая этот шаг, отметим, что наклон графика зависимости скорости от времени — это ускорение. Склон делится на подъем, разделенный бегом; на графике \ (\ displaystyle v \) vs. \ (\ displaystyle t \), рост = изменение скорости \ (\ displaystyle Δv \) и бег = изменение во времени \ (\ displaystyle Δt \).
СКЛОН V VS. Т
Наклон графика зависимости скорости \ (\ displaystyle v \) от времени \ (\ displaystyle t \) равен ускорению \ (\ displaystyle a \).
\ (\ displaystyle slope = \ frac {Δv} {Δt} = a \)
Поскольку график зависимости скорости от времени на рисунке \ (\ PageIndex {3b} \) представляет собой прямую линию, ее наклон везде одинаковый, что означает, что ускорение постоянно. Ускорение в зависимости от времени показано на рисунке (c).
Дополнительную общую информацию можно получить из рисунка и выражения для прямой линии \ (\ displaystyle y = mx + b.\)
В этом случае вертикальная ось \ (\ displaystyle y \) равна \ (\ displaystyle V \), точка пересечения \ (\ displaystyle b \) равна \ (\ displaystyle v_0 \), наклон \ (\ displaystyle m \ ) — это \ (\ displaystyle a \), а горизонтальная ось \ (\ displaystyle x \) — это \ (\ displaystyle t \). Подставляя эти символы, получаем
\ [v = v_0 + at. \ nonumber \]
Общая зависимость скорости, ускорения и времени снова была получена из графика. Обратите внимание, что это уравнение также было получено алгебраически из других уравнений движения в уравнениях движения для постоянного ускорения в одном измерении.
Неслучайно те же уравнения получаются графическим анализом и алгебраическими методами. Фактически, важный способ обнаружить физические взаимосвязи — это измерить различные физические величины, а затем построить графики одной величины относительно другой, чтобы увидеть, коррелированы ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны в виде гладких графиков, подобных приведенным выше. Из таких графиков иногда можно постулировать математические отношения.Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых соотношений.
Графики движения с непостоянным ускорением
Теперь рассмотрим движение реактивного автомобиля от 165 м / с до максимальной скорости 250 м / с, как показано на рисунке \ (\ PageIndex {6} \). Время снова начинается с нуля, а начальное положение и скорость составляют 2900 м и 165 м / с соответственно. (Это были конечное положение и скорость автомобиля в движении, показанные на рисунке \ (\ PageIndex {4} \)). Ускорение постепенно уменьшается от \ (\ displaystyle 5.2 \) до нуля при скорости 250 м / с. Наклон графика \ (\ displaystyle x \) vs. \ (\ displaystyle t \) увеличивается до тех пор, пока не \ (\ displaystyle t = 55 s \), после чего наклон становится постоянным. Точно так же скорость увеличивается до 55 с, а затем становится постоянной, поскольку ускорение уменьшается до нуля на 55 с и остается нулевым после этого.
Рисунок \ (\ displaystyle \ PageIndex {3} \) заканчивается. (а) Наклон этого графика — скорость; он показан на следующем графике. (б) Скорость постепенно приближается к своему максимальному значению.Наклон этого графика — ускорение; он нанесен на окончательный график. (c) Ускорение постепенно снижается до нуля, когда скорость становится постоянной.
Пример \ (\ PageIndex {3} \): Расчет ускорения по графику зависимости скорости от времени
Рассчитайте ускорение реактивного автомобиля за время 25 с, найдя наклон графика \ (\ displaystyle v \) vs. \ (\ displaystyle t \) на рисунке \ (\ PageIndex {6b} \).
Стратегия
Наклон кривой в \ (\ displaystyle t = 25 s \) равен наклону касательной прямой в этой точке, как показано на рисунке \ (\ PageIndex {6b} \).2. \)
Обсуждение
Обратите внимание, что это значение для a согласуется со значением, приведенным на рисунке (c) в точке \ (\ displaystyle t = 25 s \).
График перемещения в зависимости от времени можно использовать для построения графика зависимости скорости от времени, а график зависимости скорости от времени можно использовать для построения графика зависимости ускорения от времени. Мы делаем это, находя наклон графиков в каждой точке. Если график линейный (то есть линия с постоянным наклоном), легко найти наклон в любой точке, и у вас есть наклон для каждой точки.Графический анализ движения может использоваться для описания как частных, так и общих характеристик кинематики. Графики также можно использовать для других тем по физике. Важным аспектом изучения физических отношений является их графическое отображение и поиск лежащих в основе отношений.
Упражнение \ (\ displaystyle \ PageIndex {1} \): проверьте свое понимание
График зависимости скорости от времени захода корабля в гавань показан ниже.
- Опишите движение корабля на основе графика.
- Как будет выглядеть график ускорения корабля?
Рисунок \ (\ displaystyle \ PageIndex {7} \)
- Ответьте на
(a) Корабль движется с постоянной скоростью, а затем начинает замедляться с постоянной скоростью. В какой-то момент скорость его замедления снижается. Он поддерживает эту более низкую скорость замедления до тех пор, пока не перестанет двигаться.
Решение b
График ускорения в зависимости от времени покажет нулевое ускорение на первом отрезке, большое и постоянное отрицательное ускорение на втором отрезке и постоянное отрицательное ускорение.
Рисунок \ (\ Displaystyle \ PageIndex {8} \)
Резюме
- Графики движения можно использовать для анализа движения.
- Графические решения дают идентичные решения математическим методам вывода уравнений движения.
- Наклон графика смещения \ (\ displaystyle x \) от времени \ (\ displaystyle t \) равен скорости \ (\ displaystyle v \).
- Наклон графика зависимости скорости \ (\ displaystyle v \) от времени \ (\ displaystyle t \) — это ускорение \ (\ displaystyle a \).
- Средняя скорость, мгновенная скорость и ускорение могут быть получены путем анализа графиков.
Глоссарий
- независимая переменная
- переменная, относительно которой измеряется зависимая переменная; обычно наносится по оси \ (x \)
- зависимая переменная
- переменная, которая измеряется; обычно наносится по оси \ (y \) —
- уклон
- разница в \ (y \) — значении (росте), деленном на разницу в \ (x \) — значении (пробеге) двух точек на прямой
- Y-перехват
- значение \ (y \), когда \ (x \) = 0 или когда график пересекает ось \ (y \)
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
1.3 Язык физики: физические величины и единицы
Точность, прецизионность и значащие числа
Наука основана на экспериментах, требующих точных измерений. Достоверность измерения можно описать с точки зрения его точности и прецизионности (см. Рисунок 1.19 и рисунок 1.20). Точность — это насколько измерение близко к правильному значению для этого измерения.Например, предположим, что вы измеряете длину стандартного листа бумаги для принтера. На упаковке, в которой вы приобрели бумагу, указано, что она имеет длину 11 дюймов, и предположим, что указанное значение верное. Вы трижды измеряете длину бумаги и получаете следующие размеры: 11,1 дюйма, 11,2 дюйма и 10,9 дюйма. Эти измерения довольно точны, потому что они очень близки к правильному значению 11,0 дюймов. Напротив, если бы вы получили размер в 12 дюймов, ваше измерение не было бы очень точным.Вот почему измерительные приборы калибруются на основе известного измерения. Если прибор постоянно возвращает правильное значение известного измерения, его можно безопасно использовать для поиска неизвестных значений.
Рис. 1.19. Механические весы с двумя чашами используются для сравнения различных масс. Обычно объект неизвестной массы помещается в одну чашу, а объекты известной массы — в другую. Когда стержень, соединяющий две посуды, расположен горизонтально, массы в обеих посуде равны.Известные массы обычно представляют собой металлические цилиндры стандартной массы, например 1 грамм, 10 грамм и 100 грамм. (Серж Мелки)
Рисунок 1.20. В то время как механические весы могут считывать массу объекта только с точностью до десятых долей грамма, некоторые цифровые весы могут измерять массу объекта с точностью до ближайшей тысячной доли грамма. Как и в других измерительных приборах, точность шкалы ограничивается последними измеренными цифрами. Это сотые доли в изображенной здесь шкале. (Splarka, Wikimedia Commons)
«Точность» указывает, насколько хорошо повторные измерения чего-либо дают одинаковые или похожие результаты.Следовательно, точность измерений означает, насколько близки друг к другу измерения, когда вы измеряете одно и то же несколько раз. Один из способов анализа точности измерений — определение диапазона или разницы между самым низким и самым высоким измеренными значениями. В случае размеров бумаги для принтера наименьшее значение составляло 10,9 дюйма, а максимальное значение — 11,2 дюйма. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,3 дюйма. Эти измерения были достаточно точными, потому что они варьировались всего на долю дюйма.Однако, если бы измеренные значения были 10,9 дюймов, 11,1 дюймов и 11,9 дюймов, тогда измерения не были бы очень точными, потому что есть много отклонений от одного измерения к другому.
Измерения в бумажном примере точны и точны, но в некоторых случаях измерения точны, но не точны, или они точны, но неточны. Давайте рассмотрим систему GPS, которая пытается определить местоположение ресторана в городе. Думайте о расположении ресторана как о самом центре мишени в яблочко.Затем представьте каждую попытку GPS определить местонахождение ресторана как черную точку в яблочко.
На рис. 1.21 вы можете видеть, что измерения GPS разнесены далеко друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность измерительной системы с высокой точностью. Однако на Рисунке 1.22 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от целевого местоположения.Это указывает на высокую точность измерительной системы с низкой точностью. Наконец, на рис. 1.23 GPS является точным и точным, что позволяет определить местонахождение ресторана.
Рис. 1.21. Система GPS пытается определить местонахождение ресторана в центре мишени. Черные точки представляют каждую попытку определить местоположение ресторана. Точки расположены довольно далеко друг от друга, что указывает на низкую точность, но каждая из них находится довольно близко к фактическому местоположению ресторана, что указывает на высокую точность.(Темное зло)
Рис. 1.22 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, но они находятся довольно далеко от фактического местоположения ресторана, что указывает на низкую точность. (Темное зло)
Рис. 1.23 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, и они находятся недалеко от фактического местоположения ресторана, что указывает на высокую точность. (Темное зло)
Неопределенность
Точность и прецизионность измерительной системы определяют неопределенность ее измерений.Неопределенность — это способ описать, насколько ваше измеренное значение отклоняется от фактического значения, которое имеет объект. Если ваши измерения не очень точны или точны, то неопределенность ваших значений будет очень высокой. В более общем плане неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать пробег вашего автомобиля, вы можете сказать, что это 45 000 миль, плюс-минус 500 миль. Сумма плюс или минус — это неопределенность в вашей стоимости.То есть вы указываете, что фактический пробег вашего автомобиля может составлять от 44 500 миль до 45 500 миль или где-то между ними. Все измерения содержат некоторую неопределенность. В нашем примере измерения длины бумаги мы можем сказать, что длина бумаги составляет 11 дюймов плюс-минус 0,2 дюйма или 11,0 ± 0,2 дюйма. Неопределенность измерения, A , часто обозначается как δA («дельта A »),
.
Факторы, способствующие неопределенности измерения, включают следующее:
- Ограничения измерительного прибора
- Навыки человека, производящего измерение
- Неровности в измеряемом объекте
- Любые другие факторы, влияющие на результат (в значительной степени зависящие от ситуации)
В примере с бумагой для принтера неточность может быть вызвана: тем фактом, что наименьшее деление на линейке равно 0.1 дюйм, человек, использующий линейку, имеет плохое зрение или неуверенность, вызванную бумагорезательной машиной (например, одна сторона бумаги немного длиннее другой). Хорошей практикой является тщательное рассмотрение всех возможных источников неопределенности в измерение и уменьшение или устранение их,
Процент неопределенности
Один из методов выражения неопределенности — это процент от измеренного значения. Если результат измерения A выражается с погрешностью δ A , погрешность в процентах составляет
.
1.2% неопределенность = δAA × 100%.% Неопределенность = δAA × 100%.
Рабочий Пример
Расчет процента неопределенности: мешок яблок
В продуктовом магазине продаются 5-фунтовые пакеты с яблоками. Вы покупаете четыре пакета в течение месяца и каждый раз взвешиваете яблоки. Вы получите следующие размеры:
- Неделя 1 Вес: 4,8 фунта 4,8 фунта
- Вес 2 недели: 5,3 фунта 5,3 фунта
- Вес на 3 неделе: 4,9 фунта 4,9 фунта
- 4 неделя вес: 5.4 фунта 5,4 фунта
Вы определили, что вес 5-фунтового мешка имеет погрешность ± 0,4 фунта. Какова погрешность в процентах от веса мешка?
Стратегия
Во-первых, обратите внимание, что ожидаемое значение веса мешка, AA, составляет 5 фунтов. Неопределенность этого значения, δAδA, составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной неопределенности веса
% Неопределенности = δAA × 100%.% Неопределенности = δAA × 100%.
Решение
Подставьте известные значения в уравнение
% Неопределенности = 0.4 фунта5 фунтов × 100% = 8%.% Погрешности = 0,4 фунта5 фунтов × 100% = 8%.
Обсуждение
Можно сделать вывод, что вес мешка с яблоками составляет 5 фунтов ± 8 процентов. Подумайте, как изменился бы этот процент неопределенности, если бы мешок с яблоками был вдвое меньше, но неопределенность в весе осталась бы прежней. Совет для будущих расчетов: при вычислении процентной погрешности всегда помните, что вы должны умножить дробь на 100 процентов. Если вы этого не сделаете, у вас будет десятичное количество, а не процентное значение.
Неопределенность в расчетах
Есть неопределенность во всех вычислениях на основе измеренных величин. Например, площадь пола, рассчитанная на основе измерений его длины и ширины, имеет неопределенность, потому что и длина, и ширина имеют неопределенности. Насколько велика неопределенность в том, что вы вычисляете умножением или делением? Если измерения в расчетах имеют небольшую погрешность (несколько процентов или меньше), то можно использовать метод сложения процентов.Этот метод гласит, что процент неопределенности в величине, вычисленной путем умножения или деления, представляет собой сумму процентных погрешностей в элементах, использованных для выполнения расчета. Например, если пол имеет длину 4,00 м и ширину 3,00 м с погрешностями 2 процента и 1 процент соответственно, то площадь пола составляет 12,0 м 2 и имеет погрешность 3 процента ( выраженная как площадь, это 0,36 м 2 , которое мы округляем до 0,4 м ( 2 , поскольку площадь пола дается с точностью до одной десятой квадратного метра).
Для быстрой демонстрации точности и неопределенности измерений в зависимости от единиц измерения попробуйте это моделирование. У вас будет возможность измерить длину и вес стола, используя единицы измерения в миллиметрах и сантиметрах. Как вы думаете, что обеспечит большую точность, точность и неопределенность при измерении стола и блокнота в моделировании? Подумайте, как природа гипотезы или вопроса исследования может повлиять на точность измерительного инструмента, необходимого для сбора данных.
Прецизионность измерительных инструментов и значащих цифр
Важным фактором точности измерений является точность измерительного инструмента. В общем, точный измерительный инструмент — это инструмент, который может измерять значения с очень маленькими приращениями. Например, рассмотрите возможность измерения толщины монеты. Стандартная линейка может измерять толщину с точностью до миллиметра, а микрометр может измерять толщину с точностью до 0,005 миллиметра. Микрометр — более точный измерительный инструмент, поскольку он может измерять очень небольшие различия в толщине.Чем точнее измерительный инструмент, тем точнее и точнее могут быть измерения.
Когда мы выражаем измеренные значения, мы можем перечислить только столько цифр, сколько мы первоначально измерили с помощью нашего измерительного инструмента (например, линейки, показанные на рисунке 1.24). Например, если вы используете стандартную линейку для измерения длины палки, вы можете измерить ее дециметровой линейкой как 3,6 см. Вы не можете выразить это значение как 3,65 см, потому что ваш измерительный инструмент не был достаточно точным, чтобы измерить сотую долю сантиметра.Следует отметить, что последняя цифра в измеренном значении была определена каким-то образом лицом, выполняющим измерение. Например, человек, измеряющий длину палки линейкой, замечает, что длина палки находится где-то между 36 и 37 мм. Он или она должны оценить значение последней цифры. Правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой погрешностью. Например, последнее измеренное значение 36,5 мм состоит из трех цифр или трех значащих цифр.Количество значащих цифр в измерении указывает на точность измерительного инструмента. Чем точнее инструмент измерения, тем большее количество значащих цифр он может сообщить.
Рисунок 1.24 Показаны три метрические линейки. Первая линейка измеряется в дециметрах и может измерять до трех дециметров. Вторая линейка имеет длину в сантиметрах и может измерять три целых шесть десятых сантиметра. Последняя линейка в миллиметрах и может измерять тридцать шесть целых пять десятых миллиметра.
Нули
Особое внимание уделяется нулям при подсчете значащих цифр.Например, нули в 0,053 не имеют значения, потому что они всего лишь заполнители, которые определяют местонахождение десятичной точки. В 0,053 есть две значащие цифры — 5 и 3. Однако, если ноль встречается между другими значащими цифрами, нули имеют значение. Например, оба нуля в 10.053 значимы, поскольку эти нули были фактически измерены. Таким образом, заполнитель 10.053 содержит пять значащих цифр. Нули в 1300 могут иметь значение, а могут и не иметь значения, в зависимости от стиля написания чисел.Они могут означать, что число известно до последнего нуля, или нули могут быть заполнителями. Итак, 1300 может иметь две, три или четыре значащих цифры. Чтобы избежать этой двусмысленности, запишите 1300 в экспоненциальном представлении как 1,3 × 10 3 . Только значащие цифры приведены в множителе x для числа в экспоненциальном представлении (в форме x × 10yx × 10y). Таким образом, мы знаем, что 1 и 3 — единственные значащие цифры в этом числе. Таким образом, нули имеют значение, кроме случаев, когда они служат только в качестве заполнителей.В таблице 1.4 приведены примеры количества значащих цифр в различных числах.
| Номер | Значимые цифры | Обоснование |
|---|---|---|
| 1,657 | 4 | Нет нулей, и все ненулевые числа всегда значимы. |
| 0,4578 | 4 | Первый ноль — это только местозаполнитель для десятичной точки. |
| 0,000458 | 3 | Первые четыре нуля — это заполнители, необходимые для представления данных с точностью до десятитысячных. |
| 2000,56 | 6 | Три нуля здесь значимы, потому что они встречаются между другими значащими цифрами. |
| 45 600 | 3 | Без подчеркивания или научного обозначения мы предполагаем, что последние два нуля являются заполнителями и не имеют значения. |
| 15895 00 0 | 7 | Два подчеркнутых нуля значимы, а последний ноль — нет, так как он не подчеркнут. |
| 5,457 × 10 13 | 4 | В экспоненциальном представлении все числа перед знаком умножения являются значащими |
| 6.520 × × 10 –23 | 4 | В экспоненциальном представлении все числа, указанные перед знаком умножения, значимы, включая нули. |
Значимые цифры в расчетах
При объединении измерений с разной степенью точности и точности количество значащих цифр в окончательном ответе не может быть больше количества значащих цифр в наименее точном измеренном значении. Существует два разных правила: одно для умножения и деления, а другое — для сложения и вычитания, как описано ниже.
Для умножения и деления: Ответ должен иметь такое же количество значащих цифр, что и начальное значение с наименьшим количеством значащих цифр.Например, площадь круга можно вычислить по его радиусу, используя A = πr2A = πr2. Посмотрим, сколько значащих цифр будет у площади, если в радиусе всего две значащие цифры, например, r = 2,0 м. Тогда, используя калькулятор, который хранит восемь значащих цифр, вы получите
A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2. A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2.
Но поскольку радиус состоит только из двух значащих цифр, вычисленная площадь имеет значение только до двух значащих цифр или
, даже если значение ππ имеет значение не менее восьми цифр.
Для сложения и вычитания : ответ должен иметь такие же числовые разряды (например, разряды десятков, разряды единиц, разряды десятков и т. Д.), Что и наименее точное начальное значение. Предположим, вы купили в продуктовом магазине 7,56 кг картофеля, измеренного по шкале с точностью 0,01 кг. Затем вы бросаете в свою лабораторию 6,052 кг картофеля, измеренного по шкале с точностью до 0,001 кг. Наконец, вы идете домой и добавляете 13,7 кг картофеля, измеренное на весах с точностью до 0.1 кг. Сколько у вас сейчас килограммов картошки и сколько значащих цифр уместно в ответе? Масса находится простым сложением и вычитанием:
7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кг 7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кг
Наименьшее измерение — 13,7 кг. Это измерение выражается с точностью до 0,1 десятичного знака, поэтому наш окончательный ответ также должен быть выражен с точностью до 0,1. Таким образом, ответ следует округлить до десятых, получая 15,2 кг. То же самое и с недесятичными числами.Например,
6527,23 + 2 = 6528,23 = 6528,6527,23 + 2 = 6528,23 = 6528.
Мы не можем указать десятичные разряды в ответе, потому что 2 не имеет значимых десятичных знаков. Следовательно, мы можем отчитаться только до одного места.
Рекомендуется оставлять лишние значащие цифры при вычислении и округлять до правильного числа значащих цифр только в окончательных ответах. Причина в том, что небольшие ошибки из-за округления при вычислении иногда могут привести к значительным ошибкам в окончательном ответе.В качестве примера попробуйте вычислить 5,098– (5.000) × (1010) 5,098– (5.000) × (1010), чтобы получить окончательный ответ только на две значащие цифры. Учет всего значимого во время расчета дает 48. Округление до двух значащих цифр в середине расчета изменяет его до 5 100 — (5.000) × (1000) = 100, 5 100 — (5.000) × (1000) = 100, что является способом выключенный. Точно так же вы бы избегали округления в середине вычислений при подсчете и ведении бухгалтерского учета, когда нужно аккуратно сложить и вычесть много маленьких чисел, чтобы получить, возможно, гораздо большие окончательные числа.
Значимые цифры в этом тексте
В этом учебнике предполагается, что большинство чисел состоит из трех значащих цифр. Кроме того, во всех проработанных примерах используется постоянное количество значащих цифр. Вы заметите, что ответ, данный для трех цифр, основан на вводе как минимум трех цифр. Если на входе меньше значащих цифр, в ответе также будет меньше значащих цифр. Также уделяется внимание тому, чтобы количество значащих цифр соответствовало создаваемой ситуации.В некоторых темах, таких как оптика, будет использоваться более трех значащих цифр. Наконец, если число является точным, например, 2 в формуле, c = 2πrc = 2πr, это не влияет на количество значащих цифр в вычислении.
Рабочий Пример
Приближение огромных чисел: триллион долларов
Дефицит федерального бюджета США в 2008 финансовом году был немногим больше 10 триллионов долларов. Большинство из нас не имеют представления о том, сколько на самом деле стоит даже один триллион.Предположим, вам дали триллион долларов банкнотами по 100 долларов. Если вы составили стопки по 100 купюр, как показано на рис. 1.25, и использовали их для равномерного покрытия футбольного поля (между концевыми зонами), сделайте приблизительное представление о том, насколько высокой станет стопка денег. (Здесь мы будем использовать футы / дюймы, а не метры, потому что футбольные поля измеряются в ярдах.) Один из ваших друзей говорит, что 3 дюйма, а другой говорит, что 10 футов. Как вы думаете?
Рис. 1.25. Банковская пачка содержит сто банкнот по 100 долларов и стоит 10 000 долларов.Сколько банковских стеков составляет триллион долларов? (Эндрю Мэджилл)
Стратегия
Когда вы представляете себе ситуацию, вы, вероятно, представляете себе тысячи маленьких стопок по 100 завернутых банкнот по 100 долларов, которые вы могли бы увидеть в фильмах или в банке. Поскольку это величина, которую легко оценить, давайте начнем с нее. Мы можем найти объем стопки из 100 купюр, узнать, сколько стопок составляют один триллион долларов, а затем установить этот объем равным площади футбольного поля, умноженной на неизвестную высоту.
Решение
- Рассчитайте объем стопки из 100 купюр. Размеры одной банкноты составляют примерно 3 на 6 дюймов. Пачка из 100 таких банкнот имеет толщину примерно 0,5 дюйма. Таким образом, общий объем стопки из 100 купюр равен
объем стопки = длина × ширина × высота, объем стопки = 6 дюймов × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов. 3. объем стопки = длина × ширина × высота, объем стопки = 6 дюйма × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов 3. Подсчитайте количество стопок.Обратите внимание, что триллион долларов равен 1 × 1012 $ 1 × 1012, а стопка из ста 100-долларовых банкнот равна 10000, 10000 долларов или 1 × 104 доллара 1 × 104. Количество стопок у вас будет
.
1,3 $ 1 × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков. 1 доллар × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков.
Вычислите площадь футбольного поля в квадратных дюймах. Площадь футбольного поля составляет 100 ярдов × 50 ярдов 100 ярдов × 50 ярдов, что дает 5 000 ярдов 25 000 ярдов2.Поскольку мы работаем в дюймах, нам нужно преобразовать квадратные ярды в квадратные дюймы
.
Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 1 фут × 12 дюймов 1 фут = 6 480 000 дюймов 2, Площадь ≈6 × 106 дюймов 2 Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 0,1 фут × 12 дюймов 1 фут = 6 480000 дюймов 2, Площадь ≈6 × 106 дюймов 2.
Это преобразование дает нам 6 × 106 дюймов 26 × 106 дюймов 2 для площади поля. (Обратите внимание, что в этих расчетах мы используем только одну значащую цифру.)
- Рассчитайте общий объем купюр.Объем всех стопок по 100 долларов составляет 9 дюймов 3 / стопка × 108 стопок = 9 × 108 дюймов 39 дюймов / стопка × 108 стопок = 9 × 108 дюймов 3
- Рассчитайте высоту. Чтобы определить высоту купюр, используйте следующее уравнение
объем купюр = площадь поля × высота денег Высота денег = объем купюр Площадь поля Высота денег = 9 × 108 дюймов 36 × 106 дюймов 2 = 1,33 × 102 дюймов Высота денег = 1 × 102 дюйма = 100 дюймы объем купюр = площадь поля × высота денег Высота денег = объем купюр площадь поля Высота денег = 9 × 108 дюймов36 × 106 дюймов 2 = 1,33 × 102 дюйма Высота монеты = 1 × 102 дюйма = 100 дюймовВысота денег будет около 100 дюймов. Преобразование этого значения в футы дает
.
100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов
Обсуждение
Окончательное приблизительное значение намного выше, чем первоначальная оценка в 3 дюйма, но другая ранняя оценка в 10 футов (120 дюймов) была примерно правильной. Как это приближение соответствует вашему первому предположению? Что это упражнение может сказать вам с точки зрения приблизительных оценок, и тщательно рассчитанных приближений?
В приведенном выше примере окончательное приблизительное значение намного выше, чем ранняя оценка первого друга в 3 дюйма.Однако ранняя оценка другого друга в 10 футов (120 дюймов) была примерно верной. Как это приближение соответствует вашему первому предположению? Что это упражнение может предложить о значении приблизительных оценок , и тщательно рассчитанных приближений?
% PDF-1.6
%
1065 0 объект
>
эндобдж
804 0 объект
>
эндобдж
1062 0 объект
> поток
2007-12-19T11: 32: 44-05: 002007-11-20T10: 09: 06-05: 00Acrobat PDFMaker 8.1 для Word2007-12-19T11: 32: 44-05: 00Acrobat Distiller 8.Приложение 1.0 (Windows) / pdf
конечный поток
эндобдж
1147 0 объект
> / Кодировка >>>>>
эндобдж
1051 0 объект
>
эндобдж
1103 0 объект
>
эндобдж
1138 0 объект
>
эндобдж
1139 0 объект
>
эндобдж
1140 0 объект
> / Pa0 + 1> / A0 1145 0 R / A3 1146 0 R / A3 + 1> / A0 + 1> / Pa4 + 1> / Pa1 + 1 >>>
эндобдж
1141 0 объект
>
эндобдж
1142 0 объект
>
эндобдж
1143 0 объект
>
эндобдж
1144 0 объект
>
эндобдж
1145 0 объект
>
эндобдж
1146 0 объект
>
эндобдж
1104 0 объект
>
эндобдж
1177 0 объект
>
эндобдж
1178 0 объект
>
эндобдж
1179 0 объект
>
эндобдж
1180 0 объект
>
эндобдж
1184 0 объект
>
эндобдж
1185 0 объект
>
эндобдж
1105 0 объект
>
эндобдж
1106 0 объект
>
эндобдж
1107 0 объект
>
эндобдж
1111 0 объект
>
эндобдж
1112 0 объект
>
эндобдж
1088 0 объект
>
эндобдж
1087 0 объект
>
эндобдж
1057 0 объект
>
эндобдж
1058 0 объект
>
эндобдж
1059 0 объект
>
эндобдж
1060 0 объект
>
эндобдж
1061 0 объект
>
эндобдж
760 0 объект
> / ProcSet [/ PDF / Text] / ExtGState >>> / Тип / Страница >>
эндобдж
762 0 объект
> / ProcSet [/ PDF / Text] / ExtGState >>> / Тип / Страница >>
эндобдж
1239 0 объект
> / ColorSpace> / Font> / ProcSet [/ PDF / Text / ImageB] / ExtGState >>> / Type / Page >>
эндобдж
1251 0 объект
> поток
H \ = k @ w
`Y / ݭ M1A @ I]) H z $ c7 R ~ Ġ & = _ VyV ‘; C’ @ dJpNxMh = Y
Роль водорода и топливных элементов в глобальной энергетической системе
Водородные технологии пережили циклы завышенных ожиданий, за которыми следовало разочарование.Тем не менее, все больше данных свидетельствует о том, что эти технологии представляют собой привлекательный вариант для глубокой декарбонизации глобальных энергетических систем, и что недавние улучшения в их стоимости и производительности также указывают на экономическую жизнеспособность. Этот документ представляет собой всесторонний обзор потенциальной роли, которую водород может играть в обеспечении электроэнергией, теплом, промышленности, транспорта и хранения энергии в низкоуглеродной энергетической системе, а также оценку статуса водорода в том, что касается его способности выполнять эту задачу. потенциал.Возникающая картина является весьма многообещающей: водород хорошо зарекомендовал себя в определенных нишах, таких как вилочные погрузчики, а сейчас появляются и основные области применения. Транспортные средства, работающие на водороде, коммерчески доступны в нескольких странах, и было продано 225 000 систем домашнего отопления на топливных элементах. Это шаг вперед по сравнению с ситуацией пятилетней давности. Этот обзор показывает, что проблемы, связанные со стоимостью и производительностью, остаются, и для того, чтобы водород стал действительно конкурентоспособным, по-прежнему требуются значительные улучшения.Но такая конкурентоспособность в среднесрочной перспективе больше не кажется нереалистичной перспективой, что полностью оправдывает растущий интерес и политическую поддержку этих технологий во всем мире.
Эта статья в открытом доступе
Подождите, пока мы загрузим ваш контент…
Что-то пошло не так. Попробуй еще раз?
Общая модель батареи — Simulink
Извлечение параметров батареи из таблиц данных
На этом рисунке показаны подробные параметры, извлеченные из данных Panasonic.
Паспорт батареи NiMH-HHR650D.
Номинальную емкость и внутреннее сопротивление можно узнать из
таблицы спецификаций. Остальные подробные параметры взяты из Типичного
График характеристик разряда.
Параметр | Значение | ||||
|---|---|---|---|---|---|
Номинальная внутренняя емкость | 905 905 | ||||
Номинальное напряжение (a) | | ||||
Номинальная мощность | | ||||
Максимальная мощность (б) | | ||||
Напряжение полного заряда (в) | | ||||
Номинальный ток разряда (г) | 3 A | ||||
Емкость при номинальном напряжении (а) | | ||||
Экспоненциальное напряжение (е) | Вольт | 9en0009 Емкость (e) | |
Эти параметры являются приблизительными и зависят от точности точек
полученный из разряда
изгиб.
Кривые расхода, полученные на основе этих параметров, отмеченных значком
пунктирные линии на следующих рисунках аналогичны паспорту
кривые.
Для представления температурных эффектов литий-ионных (Li-ion) аккумуляторов,
дополнительная кривая нагнетания при температуре окружающей среды, отличная от
номинальная температура и параметры теплового отклика.Дополнительные кривые расхода обычно не приводятся в технических данных и могут
требуют проведения простых экспериментов. Следующие примеры показывают
параметры, извлеченные из литий-железо-фосфата A123 ANR26650M1 и
Паспорта литий-кобальто-оксидных батарей Panasonic CGR 18 650 AF.
Технические характеристики A123 ANR26650M1 включают в себя требуемую разрядку
точки кривой и другие необходимые параметры.
Эти параметры взяты из таблицы данных литий-ионного аккумулятора A123.
температурно-зависимая модель батареи.
| Параметр | Значение | |
|---|---|---|
Номинальное напряжение (c) | | 3 |
Максимальная вместимость (d) | | |
Напряжение полного заряда (а) | | |
Номинальный ток разряда | | |
Емкость при номинальном напряжении (c) | | |
Экспоненциальная зона (b) | ||
Номинальная температура окружающей среды | | |
Вторая температура окружающей среды | | |
| ||
Начальное напряжение разряда при 0 ° C (e) | | |
Напряжение при максимальной мощности 90% при 0 ° C | | |
Экспоненциальная зона при 0 ° C (f) | [ | |
Тепловое сопротивление, ячейка-окружающая среда | | |
Тепловая постоянная времени, от ячейки к окружающей среде | |
На рисунке пунктирными линиями показаны кривые разряда, полученные из
моделирование при различных температурах окружающей среды. Исполнение модели очень
близко к результатам таблицы данных.
Тот же подход для извлечения параметров применяется к Panasonic
Литий-ионный CGR18650AF с этими характеристиками.
Эти параметры извлекаются для модели батареи.
| Параметр | Значение | ||
|---|---|---|---|
Номинальное напряжение (с) | | ||
Максимальная емкость (d) | | ||
Напряжение полного заряда (a) | | ||
Номинальный ток разряда | | ||
Внутреннее сопротивление (расчетное) | | | |
Экспоненциальная зона (b) | [ | ||
Номинальная температура ° C | |||
Вторая температура окружающей среды | | ||
Максимальная производительность при 0 ° C (ч) | | ||
Начальное напряжение разряда при 0 ° C (e) | | ||
Напряжение при максимальной емкости 90% при 0 ° C | | ||
Экспоненциальная зона при 0 ° C (ж) | [ | ||
Тепловое сопротивление, ячейка-окружающая среда | | ||
Тепловая постоянная времени, от ячейки к окружающей среде | |
На рисунке показано хорошее совпадение смоделированных кривых расхода
(представлены пунктирными линиями) и кривые таблицы данных. Точность
модель зависит от того, насколько точны выбранные точки из техпаспорта разряда
кривые есть.
Моделирование ячеек в серии и / или параллельно
Для моделирования последовательной и / или параллельной комбинации ячеек на основе параметров
одной ячейки используйте преобразование параметра, показанное в следующей таблице
может быть использован. Переменная Nb_ser соответствует количеству
ячеек последовательно, а Nb_par соответствует количеству
ячеек параллельно.
| Параметр | Значение | ||
|---|---|---|---|
Номинальное напряжение | 1.18 * Nb_ser | ||
Номинальная мощность | 6,5 * Nb_par | ||
Максимальная емкость | 7 * Nb_par | 7 * Nb_par | |
Номинальный ток разряда | 1,3 * Nb_par | ||
Внутреннее сопротивление | 0.002 * Nb_ser / Nb_par | ||
Пропускная способность при номинальном напряжении | 6,25 * Nb_par | ||
Экспоненциальная зона | p4, 1,3 * Nb 9059 | 9_Ser2 * Nb 9059 Fall9 ! Время изучать физику … Падения Возьмите карандаш, вытяните руку и отпустите. Все мы знаем, что карандаш упадет. Хорошо, а как насчет того, чтобы уронить шар для боулинга? Это то же самое? Нет, подождите! Как насчет арбуза, упавшего с высокого здания? Почему ты бы так поступил? Я бы сделал это, чтобы увидеть это.Или, может быть, даже более экстремально, человек выпрыгивает из самолета. Все эти примеры можно рассматривать как «падение», но не все падения одинаковы. Итак, приступим к делу. Вот все, что вам нужно знать о падающих вещах. Держитесь за свои места. Вероятно, это будет больше, чем вы просили. Не волнуйтесь, математика (в основном) будет на простом уровне. Падение без сопротивления воздуха Я собираюсь поговорить о сопротивлении воздуха внизу. Однако я хочу начать с простейшего случая, когда объект, падающий у поверхности Земли, имеет незначительную силу сопротивления воздуха.На самом деле, это упрощение во многих случаях не только приблизительно верно, но и является одним из ключевых компонентов природы науки. Если мы хотим построить научную модель (наука — это все о создании моделей), лучше всего начать с чего-то без дополнительных сложностей. Если вы хотите смоделировать массу на пружине, предположите, что пружина безмассовая. Если вы хотите смоделировать корову, вы должны считать, что это сфера (обязательная шутка о сферической корове). Эти упрощения — первый шаг к построению более сложных моделей. Постоянна ли сила тяжести? Это одна вещь, которая всплывает довольно часто. Люди говорят, что если вы уроните два объекта разной массы, у них будет одинаковая сила тяжести. Хорошо, первая проблема — это слово «гравитация» — что это означает? Это может означать много разных вещей. Два наиболее распространенных значения: гравитационная сила или гравитационное поле. Начнем с гравитационного поля. Это мера гравитационного эффекта от объекта с массой. Поскольку гравитационное взаимодействие — это сила между двумя массами, вы можете думать об этом как о «половине» этого взаимодействия (с одной массой).Если у вас есть объект около поверхности Земли, то этот объект будет иметь гравитационное взаимодействие в зависимости от гравитационного поля Земли. Вблизи поверхности Земли гравитационное поле представлено символом g и имеет значение около 9,8 ньютонов на килограмм. Нет. Значение g не является ускорением свободного падения. Да, это правда, что 9,8 н / кг соответствует единицам измерения в метрах на секунду в квадрате. Также верно и то, что свободно падающий (без сопротивления воздуха) объект падает с ускорением 9.8 м / с 2 — но это все равно гравитационное поле. Неважно, какой объект вы поместите возле поверхности Земли, гравитационное поле, создаваемое Землей, постоянно и направлено в сторону центра Земли. |
