наибольший общий делитель 18 и 24

Вы искали наибольший общий делитель 18 и 24? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и наибольший общий делитель 24 и 18, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «наибольший общий делитель 18 и 24».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как наибольший общий делитель 18 и 24,наибольший общий делитель 24 и 18,наибольший общий делитель чисел 24 и 18,найди наибольший общий делитель чисел 24 и 18,найдите наибольший делитель чисел 24 и 18,найдите наибольший общий делитель чисел 18 и 24,найдите наибольший общий делитель чисел 24 и 18,найдите нод чисел 24 и 18,найти наибольший общий делитель чисел 18 и 24,найти наибольший общий делитель чисел 24 и 18,найти нод 24 и 18,нод 18,нод 18 24,нод 18 и 24,нод 24 18,нод 24 и 18,нод чисел 18 и 24,нод чисел 24 и 18,нок чисел 18 и 24,нок чисел 24 и 18. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и наибольший общий делитель 18 и 24. Просто введите задачу в окошко и нажмите
«решить» здесь (например, наибольший общий делитель чисел 24 и 18).

Где можно решить любую задачу по математике, а так же наибольший общий делитель 18 и 24 Онлайн?

Решить задачу наибольший общий делитель 18 и 24 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Наибольший общий делитель — презентация онлайн

1.

Наибольший общий делитель.

Назовите и запишите делители числа 18
1
2
18
18
3
9
6
из чисел
простые?числа?
А как Какие
называются
оставшиеся
составные
4
5
9
13
14
17
21
27
Незнайка записал разложение
числа
на простые множители:
120=2*3*4*5
Это верно?
120=2*2*2*3*5
Назовите все делители
120
120 : 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20,
24, 30, 40, 60, 120

6. Запишите делители чисел 18 и 24

18: 1, 2, 3, 6, 9, 18
24: 1, 2, 3, 4, 6, 8, 12, 24
Подчеркните
общие делители
этих чисел.
Укажите
наибольший
общий делитель
этих
чисел.
НОД(18;24) = 6

7. Внимание!

Определение.
Наибольшим общим делителем двух
натуральных чисел называется самое
большое натуральное число, на
которое делится каждое из данных
чисел.
НОД (а, в)

8. Верно ли Незнайка сделал записи?

1) НОД(15,20)=3;
2) НОД(30,45)=5;
3) НОД(4,10)=2;
4) НОД(23,7)=0,7;
5) НОД(12,6)=6.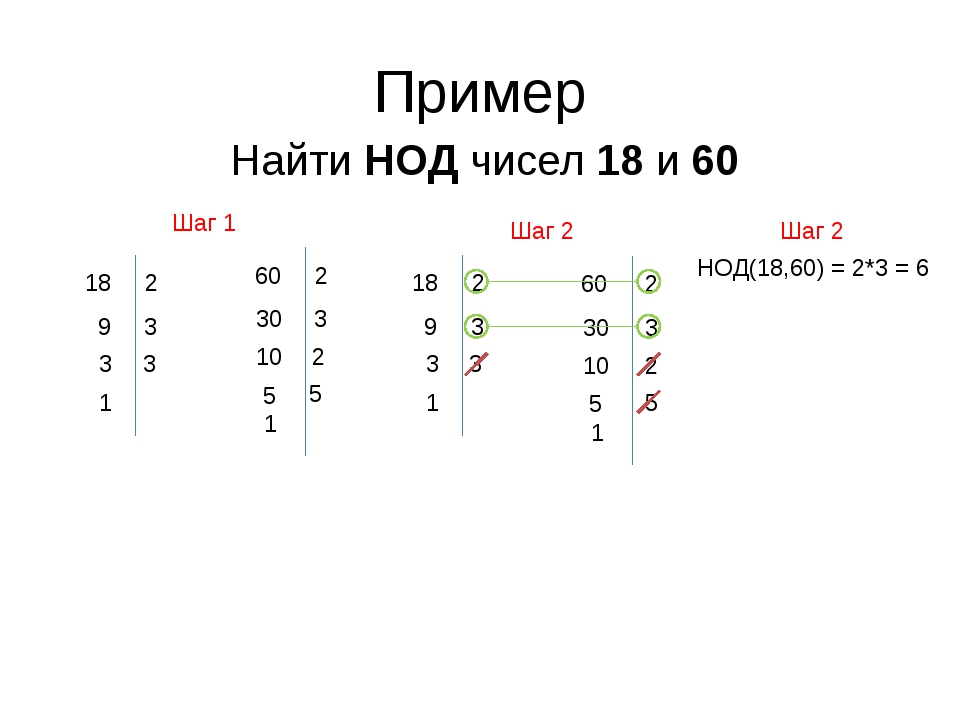
Проверка:
1) является ли это число натуральным;
2) является ли это число общим делителем
рассматриваемых чисел;
3) наибольшее ли оно из общих делителей.

9. Попросим Незнайку найти НОД двух чисел 84 и 112.

84 2
42 2
21 3
77
1
112
56
28
14
7
1
2
2
2
2
7
Долго?..
• Разложите на простые
множители.
• Подчеркните общие множители
в полученных разложениях.
• Найдите их произведение.
НОД(84;112)=2*2*7=28

10. Алгоритм нахождения НОД:

1. Разложите данные числа на простые
множители.
2. Найдите (подчеркните) общие
множители в полученных
разложениях.
3. Найдите произведение общих
простых множителей.
На зарядку солнышко поднимает нас,
поднимаем руки мы по команде «раз».
А над нами весело шелестит листва,
Опускаем руки мы по команде «два».
Задание 1.
Назовите общие простые множители чисел по их
разложениям:
а) 15 = 3*5;
60 = 2*2*3*5.
б) 36 = 2*2*3*3;
78 = 2*3*13.
в) 54 = 2*3*3*3;
90 = 2*3*3*5.
Задание 2. Найдите:
а) НОД (15;60) = 15
б) НОД (36;78) = 6
в) НОД (54;90) = 6
Ребята, помогите мне
выполнить ЗАДАНИЕ 3.
Найдите:
НОД (16, 24) =
НОД (100, 40) =
НОД (54, 90) =

14. Проверка задания 3:

а) 16
8
4
2
1
2
2
2
2
24
12
6
3
1
2
2
2
3
НОД (16, 24) = 8
б) 100
50
25
5
1
2
2
5
5
40
20
10
5
1
2
2
2
5
НОД (100, 40) = 20
в) 54
27
9
3
1
2
3
3
3
90
45
15
5
1
2
3
3
5
НОД (54, 90) = 18

15. Подведём итоги:

1.
2.
3.
4.
5.
6.
С каким новым понятием вы сегодня
познакомились?
Дайте определение НОД.
Какими способами можно найти НОД?
Как найти НОД по определению?
Как найти НОД через разложение на множители?
Известно, что НОД (а, в) = 14. Найдите несколько
возможных ситуаций для а и в.

Наибольший общий делитель. Взаимно простые числа 6 класс онлайн-подготовка на Ростелеком Лицей

Наибольший общий делитель. Взаимно простые числа.

Рассмотрим задачу. Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Гусиные лапки», если надо использовать все конфеты?

Решение: Каждое из чисел 48 и 36 делится на число подарков. Поэтому сначала выпишем все делители числа 48.

Получим: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.

Затем выпишем все делители числа 36.

Получим: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Общими делителями чисел 48 и 36 являются числа: 1, 2, 3, 4, 6, 12. Наибольшим из этих чисел является число 12. Его называют наибольшим общим делителем чисел 48 и 36.

Значит, можно составить 12 подарков. В каждом подарке будет 4 конфеты «Ласточка» (48:12 = 4) и 3 конфеты «Гусиные лапки» (36:12 = 3).

Наибольшим общим делителем чисел a и b, называется наибольшее число, на которое делятся без остатка числа а и b.

Например, у чисел 12 и 8 наибольший общий делитель (НОД) равен 4, а у чисел 20 и 35 НОД равен 5.

Найдем наибольший общий делитель чисел 24 и 35.

Делителями 24 будут 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут 1, 5, 7, 35.

Видим, что числа 24 и 35 имеют только один общий делитель – число 1. Такие числа называют взаимно простыми.

Взаимно простыми числами называют натуральные числа, если их общий делитель равени1 1.

Например, у чисел 5 и 8, 11 и 18, 16 и 27 НОД равен 1.

Наибольший общий делитель можно найти, не выписывая всех делителей данных чисел.

1. Для нахождения наибольшего общего делителя двух или более чисел, например 36 и 24, надо:

   
   

   Разложить их на простые множители

   
   

   36 = 2 * 2 * 3 * 3; 24 = 2 * 2 * 2 * 3.

2. В группах множителей, входящих в разложение этих чисел, оставить только совпадающие множители

   
   

   (2 * 2 * 3) и (2 * 2 * 3)

3. Найти произведение оставшихся множителей.

   
   

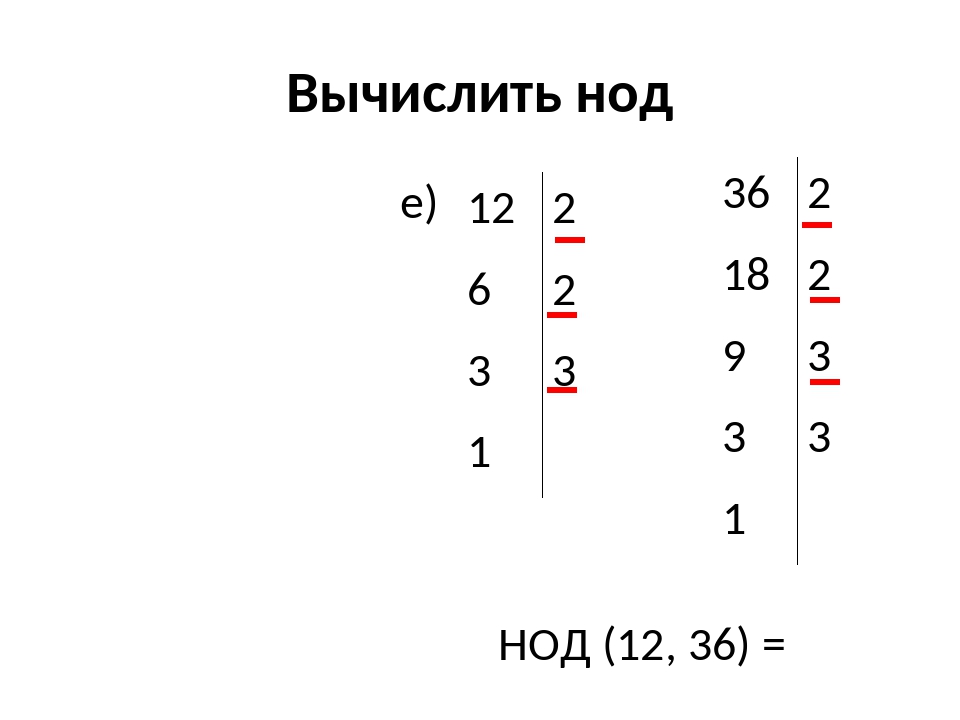
   2 * 2 * 3 = 12

   
   

   Наибольший общий делитель чисел 36 и 24 равен 12.

Рассмотрим задачу. Мальчики на 8 марта купили 54 розы и 36 гвоздик. Какое наибольшее количество букетов могут составить мальчики?

Решение:

Разложим на простые множители каждое из чисел:

54 = 2 * 3 * 3 * 3; 36 = 2 * 2 * 3 * 3.

В каждом разложении присутствует произведение 2 * 3 * 3 = 18, которое и будет наибольшим общим делителем. Значит, мальчики могут составить 18 букетов, в каждом из которых будет 54:18 = 3 розы и 36:18 = 2 гвоздики.

Калькулятор и примеры нахождения наибольшего общего делителя

Примеры нахождения НОД с помощью разложения на простые множители

В примерах показано как можно находить наибольщий общий делитель чисел (НОД) с помощью разложения на простые множители.

Пример Найти наибольший общий делитель чисел 585 и 360

НОД(585, 360) = 2^{min(0, 3)} * 3^{min(2, 2)}*5^{min(1, 1)}*13^{min(1, 0)}= 45

a = 585 = 3² * 5 * 13;

b = 360 = 2³ * 3² * 5

Пример Наибольший общий делитель чисел 680 и 612

НОД(680, 612) = 2^{min(3, 2)} * 3^{min(0, 2)}*5^{min(1, 0)}*17^{min(1, 1)}= 68

a = 680 = 2³ * 5 * 17;

b = 612 = 2² * 3² * 17

Пример Наибольший общий делитель чисел 675 и 825

НОД(675, 825) = 3^{min(3, 1)} * 5^{min(2, 2)}*11= 75

a = 675 = 3³ * 5²;

b = 825 = 3*5²*11

Пример Наибольший общий делитель чисел 7920 и 594

НОД(7920, 594) = 2^{min(4, 1)} * 3^{min(2, 3)}*5^{min(1, 0)}*11= 198

a = 7920 = 2⁴*3²*5*11;

b = 594 = 2*3³*11

Пример Найти наибольший общий делитель трех чисел 60, 80 и 48

НОД(60, 80, 48) = 2^{min(3, 4, 4)} * 3^{min(1, 0, 1)}*5^{min(1, 1, 0)}= 8

a = 60 = 2³ * 3 * 5;

b = 80 = 2⁴ * 5;

c = 48 = 2⁴ * 3

Пример Наибольший общий делитель чисел 195, 156 и 260

НОД(195, 156, 260) = 2^{min(0, 2, 2)} * 3^{min(1, 1, 0)}*5^{min(1, 0, 1)}*13^{min(1, 1, 1)}= 13

a = 195 = 3 * 5 * 13;

b = 156 = 2² * 3 * 13;

c = 260 = 2² * 5 * 13

Пример Найти наибольший общий делитель трех чисел 324, 111 и 432

НОД(324, 111, 432) = 2^{min(2, 0, 4)} * 3^{min(4, 1, 3)}*37^{min(0, 1, 0)}= 3

a = 324 = 2² * 3⁴;

b = 111 = 3 * 37;

c = 432 = 2⁴ * 3³

Пример Наибольший общий делитель чисел 320, 640 и 960

НОД(320, 640, 960) = 2^{min(6, 7, 6)} * 3^{min(0, 0, 1)}*5^{min(1, 1, 1)}= 320

a = 320 = 2⁶ * 5;

b = 640 = 2⁷ * 5;

c = 960 = 2⁶ * 3 *5

keepslide.

com — НОД И НОК ЧИСЕЛ
учитель математики МОУ… | Facebook

НОД И НОК ЧИСЕЛ
учитель математики МОУ лицея №1 Бугаева Вера Михайловна г.Комсомольска–на–Амуре

Наибольший обЩий делитель
Наибольшее натуральное число на которое де-лятся без остатка числа a и b, называют наи-большим общим делителем чисел a и b. Например: НОД чисел 48 и 36 равен 12, т.е. наи- большему из натуральных чисел, ко- торое делит нацело и 48, и 36. НОД(48;36)=12.

ПОМНИ!
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо: разложить их на простые множители; из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел; найти произведение оставшихся множителей. Например: НОД (96, 72)=24 96=2 • 2 • 2 • 2 • 2 • 3, 72=2 • 2 • 2 • 3 • 3 Остались множители: 2 • 2 • 2 • 3=24.

ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№1. Найдите НОД чисел: а)108 и 72; б) 150 и 225 . Решение. Разложим числа на простые множители: 108 2 72 2 150 2 225 5 54 2 36 2 75 5 45 5 27 3 18 2 15 5 9 3 9 3 9 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 Найдем одинаковые множители ( выделены одним цветом) НОД(108; 72) = 36, т.к. НОД(150; 225) = 75, т.к. 2 • 2 • 3 • 3 = 36. 5 • 5 • 3 = 75.

Числа правят миром. Пифагор
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Взаимно простые числа
Найти наибольший общий делитель чисел: а) 22 и 39; б) 56 и 31; в) 73 и 45; г) 44 и 63. Если вы решали все примеры верно, то в ответе всегда получалась 1.

Наименьшее общее кратное
Наименьшим общим кратным натуральных чи-сел a и b называют наименьшее натуральное число, которое кратно и a, и b. Например: НОК чисел 75 и 60 равен300, т.е. наименьшему из натуральных чисел, которые делятся без остатка на числа 75 и 60. НОК(75 и 60) =300

ПОМНИ!
Чтобы найти наименьшее общее кратное несколь- ких натуральных чисел , надо: разложить их на простые множители; выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложений остальных чисел; найти произведение получившихся множите- лей.

•
Давайте попрактикуемся
№2. Найдите НОК чисел: а) 108 и 72; б) 150 и 225. Решение. Разложим числа на простые множители: 108 2 72 2 150 2 225 5 54 2 36 2 75 5 45 5 27 3 18 2 15 5 9 3 9 3 9 3 3 3 3 3 3 3 3 3 1 1 1 1 НОК(150; 225) = 5 • 5 • 3 • 3 • 2 = 450 НОК(108; 72) = 2 • 2 • 3 • 3 • 3 • 2 = 216

Реши самостоятельно
№1. Найдите: а) НОД (81 и 243) б) НОК(15 и 18) в) НОД(72 и 108) г) НОК(36 и 48) д) НОД(168 и 180) е) НОК(252 и 360) ж) НОД(360 и 1050) з) НОК(396 и 180) и)НОД(270;450 и 555) к) НОК(72;120 и 264)

Позволяет решать различные задачи
Сокращение дробей
Отыскание общего знаменателя дробей
Применение НОД и нок чисел
№2. Сократите дроби: а) ; б) ; в) ; г) . №3. Приведите дроби к общему знаменателю: а) и ; б) и .

ПРОВЕРЬ СЕБЯ
№1. а) 81; б) 90; в) 36 ; г) 144; д) 12; е)2520 ; ж) 30; з) 1980; и) 15; к) 3960. №2. а) ; б) ; в) ; г) . №3. и ; и . Попытайся сократить такую дробь: . Трудно? А как выполнить это задание быстро и легко, не раскладывая числа на простые множители? Оказывается это возможно осуществить с помощью алгоритма Евклида.

Алгоритм евклида
Во многих случаях, когда числитель и знаменатель делятся на число (например на 19, на 37 и т.д.), а признака делимости мы не знаем, НОК числителя и знаменателя находят с помо-щью, так называемого, алгоритма Евклида. Суть его проста: делится большее число на меньшее. Затем меньшее делится на первый остаток. При этом получается второй остаток. Дальше первый остаток делится на второй и процесс продолжается. Он конечен и последний неравный нулю остаток и будет наибольший общим делителем. Прием этот занимателен, он называется –алгоритм Евклида – реко-мендуем его испробовать. Продемонстрируем его на примере.

Сократить дробь: .
Для того, чтобы сократить данную дробь найдем с помощью алгоритма Евкли- да НОД чисел 5959 и 13433. Делим 13433 на 5959. 13433 5959 11918 2 5959 1515 4545 3 1515 1414 1414 1 1414 101 101 14 404 = 404 0 Последний неравный нулю остаток, т. е. 101 и будет наибольшим общим дели- телем. Разделим на 101 числитель и знаменатель. Получим дробь: .

РЕШИ самостоятельно
№1. С помощью алгоритма Евклида сократить дроби: а) б) в) г) д) ; ; ; ; . №2. Найдите НОД чисел: а) 2304 и 5220; б) 8136 и 12250; в) 1348 и 1126; г) 42628 и 33124; д) 71004 и 154452. №3. Какой наименьшей длины должна быть доска, чтобы ее можно было раз- резать поперек на части, равные 20см и 27см, не получив обрезков? №4. Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если имеется 12 зайцев, 24 лисицы, 16 морковок и 48 яблок? №5. Найдите НОК и НОД чисел, затем сравните произведение этих чисел с произведением НОК и НОД: а) 14 и21; б) 24 и 36; в) 32 и 48; г) 18 и24; д) 25 и 35.

РЕШАЕМ И ПРОВЕРЯЕМ
№1.
№2.
№3.
№4.
№5.
а) НОД (14; 21) = 7; б) НОД (24; 36) = 12; НОК (14; 21) = 42. НОК (24; 36) = 72. в) НОД (32; 48) = 16; г) НОД (18; 24) = 6; НОК (32; 48) = 96. НОК (18; 24) = 72. д) НОД (25; 35) = 5; НОК (25; 35) =175.

Замечательное свойство НОК и НОД
Заметили ли вы, что для любых натуральных чисел a и b выпол- няется равенство: НОД(a;b) НОК(a;b) = a b Это свойство позволяет по заданным числам и известному НОД находить НОК этих чисел. a b НОК(a;b) =
НОД(a;b)

Предлагаю решить задачи
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в коробке. Какое наименьшее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну? Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Белочка», если надо использовать все конфеты? Сколько конфет «Ласточка» и «Белочка» будет в каждом подар-ке? Для поездки за город работникам завода было выделено несколько ав-тобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе? Конфеты «Сладкая математика» продаются по 12 штук в коробке, а кон-феты «Геометрия с орехами» – по 15 штук в коробке. Какое наимень-шее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну? Коля, Серёжа и Ваня регулярно ходили в кинотеатр. Коля бывал в нём каждый 3-й день, Серёжа — каждый 7-й, Ваня — каждый 5-й. Сегодня все ребята были в кино. Когда все трое встретятся в кинотеатре в сле-дующий раз?

ответы
№1. НОД (36; 48) = 12; 36 : 12 = 3 (шт) конфет «Белочка» 48 : 12 = 4 (шт) конфет « Ласточка»
№2. НОД (424; 477) = 53; (424 + 477) : 53 = 17 (чел)
№3. 5 коробок «Сладкая математика», 4 коробки «Геометрия с ореха- ми» . НОК(15; 12) = 60, 60 : 12 = 5, 60 : 15 = 4.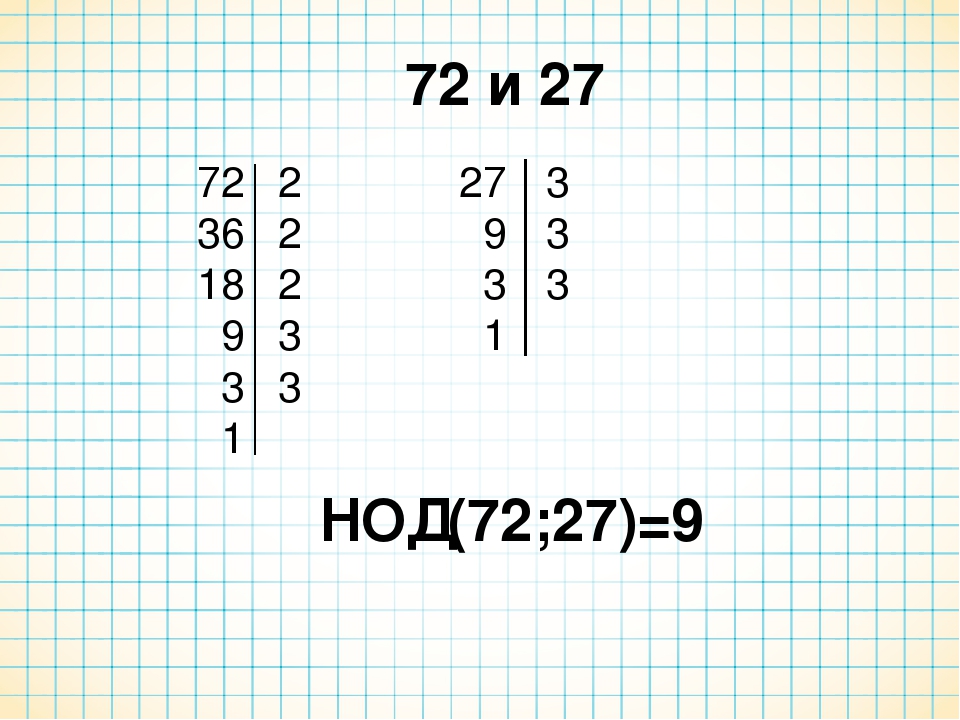
№4. На 105 день. НОК (3; 5; 7) = 105.
Спасибо за работу ! Успехов в учебе!

Наибольший Общий Делитель

Давайте вспомним, что означают эти буквы: аббревиатура «НОД» расшифровывается как «Наибольший Общий Делитель».

Делитель – это число, на которое другое число делится без остатка.

Обычно необходимо найти НОД для двух чисел. Иногда эту задачу усложняют и ищут НОД для трех, четырех и более чисел.

Например:

Два числа: 9 и 12

Три числа: 9, 12 и 24

Дадим определение:

Наибольший Общий Делитель (НОД) – это такое наибольшее число, на которое исследуемые числа делятся без остатка.

Найдем НОД для чисел 9 и 12

Запишем все делители этих чисел:

12 – ( 1, 2, 3, 4, 6, 12)

9 – ( 1, 3, 9)

Сравним оба ряда. В обоих рядах наибольшим одинаковым числом является 3. Это число и будет НОД для этой пары чисел. Оба этих числа делятся на 3 без остатка:

12 : 3 = 4

9 : 3 = 3

Таким образом, НОД (12 и 9) = 3

Зачем нужен НОД?

Например, чтобы упростить большую дробь.

Вот числа 9 и 12. Наибольший Общий Делитель для них будет число 3.

Если у нас будет дробь 9/12, то её можно упростить, разделив числитель и знаменатель на НОД, т.е. на 3, получим:

9/12 = (9 ∶ 3)/(12 ∶ 3) = 3/4

Согласитесь, что с дробью 3/4 гораздо удобнее проводить дальнейшие вычисления, чем с 9/12 .

Чтобы найти НОД двух чисел, существует несколько способов.

Один мы рассмотрели выше, когда нашли НОД для пары чисел 12 и 9.

Рассмотрим теперь другой, самый наглядный способ. Он подходит для нахождения НОД любых чисел (и маленьких, и больших).

Например, найти НОД для чисел 24 и 18.

Решение:

Разложим эти два числа на простые множители:

24 I 2             18 I 2

12 I 2               9 I 3

  6 I 2               3 I 3

  3 I 3               1 I

  1 I

Итак, получаем разложения:

24 = 2 · 2 · 2 · 3

18 = 2 · 3 · 3

Теперь ищем в этих разложениях одинаковые пары чисел, подчеркнем эти пары:

24 = 2 · 2 · 2 · 3

18 = 2 · 3 · 3

Получили две пары: (2 и 2) и (3 и 3). Остальные числа в рядах не имеют совпадений.

Получаем, что общими множителями чисел 24 и 18 являются числа 2 и 3.

Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:

2 · 3 = 6

Получаем: НОД (24 и 18) = 6

Именно на это число мы можем разделить 24 и 18 без остатка:

24 : 6 = 4

18 : 6 = 3

Это число является их делителем. И именно это число будет их наибольшим делителем, т.е. НОДом.

Теперь возьмем числа побольше.

Например,

Найти НОД для чисел 72 и 128.

Решение:

Разложим эти два числа на простые множители:

128 I 2                 72 I 2

  64 I 2                 36 I 2

  32 I 2                 18 I 2

  16 I 2                   9 I 3

    8 I 2                   3 I 3

    4 I 2                   1 I

    2 I 2

    1 I

Итак, получаем разложения:

128 = 2 · 2 · 2 · 2 · 2 · 2 · 2

  72 = 2 · 2 · 2 · 3 · 3

Теперь ищем в этих разложениях одинаковые пары чисел, выделим эти пары подчеркиванием:

128 = 2 · 2 · 2 · 2 · 2 · 2 · 2

  72 = 2 · 2 · 2 · 3 · 3

Получили три пары: (2 и 2), (2 и 2) и (2 и 2). Остальные числа в рядах не имеют совпадений.

Получаем, что общими множителями чисел 128 и 72 являются числа 2, 2 и 2.

Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:

2 · 2 · 2 = 8

Получаем: НОД (128 и 72) = 8

Именно на это число делятся исследуемые числа без остатка:

128 : 8 = 16

72 : 8 = 9

И именно это число будет их наибольшим делителем, т.е. НОДом.

Немного усложним задачу и найдем НОД для трех чисел.

Например,

Найти НОД для чисел 36, 24 и 18.

Решение:

Разложим эти три числа на простые множители:

24 I 2             18 I 2            36 I 2

12 I 2               9 I 3            18 I 2

  6 I 2               3 I 3              9 I 3

  3 I 3               1 I                 3 I 3

  1 I                                       1 I

Итак, получаем разложения:

24 = 2 · 2 · 2 · 3

18 = 2 · 3 · 3

36 = 2 · 2 · 3 · 3

Теперь ищем в этих разложениях одинаковые тройки чисел, выделим эти тройки подчеркиванием:

24 = 2 · 2 · 2 · 3

18 = 2 · 3 · 3

36 = 2 · 2 · 3 · 3

Получили две тройки: (2, 2 и 2) и (3, 3 и 3). Остальные числа в рядах не имеют совпадений.

Получаем, что общими множителями чисел 36, 24 и 18 являются числа 2 и 3.

Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:

2 · 3 = 6

Получаем: НОД (36, 24 и 18) = 6

Именно на это число мы можем разделить 36, 24 и 18 без остатка:

24 : 6 = 4

18 : 6 = 3

36 : 6 = 6

Это число является их делителем. И именно это число будет их наибольшим делителем, т.е. НОДом.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Наибольший общий делитель | Методическая разработка по алгебре (6 класс) по теме:

Слайд 1

Наибольший общий делитель Математика – 6 МОУ «СОШ № 48» г.Астрахани Учитель математики Бакреу Н.Н. 2010 г.

Слайд 2

Назовите составные числа 2534, 157, 783, 111, 27453, 25890, 37455 2534 783 111 27453 25890 37455 04/11/17

Слайд 3

Разложите на простые множители 84 84 2 42 2 21 3 7 7 1 84 = 2 ³ · 3 · 7

Слайд 4

Найдите НОД НОД (42; 35) 42 2 35 5 21 3 7 7 7 7 1 1 НОД (42; 35) = 7

Слайд 5

Найдите НОД НОД (20; 50) = НОД(24; 12) = НОД (60; 45) = НОД (9; 11) = НОД (15; 130) НОД (56; 7) = 10 12 15 1 5 7

Слайд 6

Найдите взаимно простые числа 45 и 11 100 и 25 37 и 111 67 и 7 12 и 15

Слайд 7

Самостоятельная работа Вариант 1 Вариант 2 1. Разложите на простые множители 1782 2268 2. Найдите НОД: НОД (96; 72) НОД (98; 35) НОД (17; 40) НОД(24; 19) НОД(840;1008;256) НОД(625;1050;750)

Слайд 8

Докажите, что данные числа не взаимно простые НОД(15; 2780) НОД(15; 2780) = 5 НОД(98; 14) НОД(98; 14) = 7 НОД(216; 6) НОД(216; 6) = 6 04/11/17

Слайд 9

Найдите НОД НОД (25; 200) НОД (32; 16) НОД (27; 9) НОД (28; 70) НОД (18; 36 ) 28 9 18 25 16 7 04/11/17

Слайд 10

Найдите числа, кратные данным 15 21 35 26 72 101 70 144 505 63 60 52 04/11/17

Слайд 11

Найдите кратные чисел Кратные 3 и 5: 15, 30, 45, 60, 75,… Кратные 2 и 13: 26, 52, 78,… Кратные 5 и 9: 45, 90, 135,… Кратные 12 и 24: 24, 48, 72,… Кратные 12 и 18: 36, 72,… НОК (3; 5) = 15 НОК (2; 13) = 26 04/11/17

Слайд 12

Найдите НОК НОК (3; 8) НОК (5; 7) НОК (11; 6) НОК (31; 3) НОК (9; 10) НОК (12; 6) 24 35 66 93 90 12 04/11/17

Слайд 13

Найдите НОД НОД (2 1 ; 14 ) НОД ( 4 2; 6) НОД ( 7 7; 11 ) НОД (2 0 ; 3 0) НОД (18; 45) 1 0 11 9 25 7 6 04/11/17

Слайд 14

Найдите НОК НОК ( 2 ; 6 ) НОК ( 3 ; 7) НОК ( 5 ; 8 ) НОК ( 2 ; 9 ) НОК ( 12 ; 36 ) НОК ( 44 ; 4 ) 12 21 40 18 36 44 04/11/17

Слайд 15

Найдите НОК НОК ( 2 ; 7 ) НОК ( 13 ; 3 ) НОК ( 5 ; 11 ) НОК ( 8 ; 17 ) НОК ( 24 ; 7 ) НОК ( 28 ; 3 ) 14 39 55 136 168 84 04/11/17

Слайд 16

Литература Математика — 6. Тесты. И.В. Гришина, Изд. «Лицей», 2006 г. Математика – 6.Н.Я.Виленкин и др., изд. Мнемозина, Москва, 2007. http://aida.ucoz.ru Библиотека www.prometheaplanet.com

GCF из 18 и 24

---

На этой странице мы определим GCF для 18 и 24, научим вас различным способам вычисления GCF для 18 и 24, и
покажу, для чего можно использовать GCF 18 и 24.

Что такое GCF для 18 и 24?
GCF — это сокращение от Greatest Common Factor. Следовательно, GCF 18 и 24 совпадает с наибольшим общим фактором.
18 и 24. GCF 18 и 24 — это наибольшее положительное целое число, на которое можно разделить 18 и 24.Кроме того, как 18, так и 24 имеют набор факторов, и GCF является наибольшим фактором, который является общим для 18 и 24.

---

Сравните коэффициенты, чтобы получить GCF 18 и 24
Согласно приведенному выше определению, чтобы найти GCF 18 и 24, вы можете сравнить множители 18 с
множитель 24, чтобы увидеть, какой фактор является наибольшим. Когда мы это сделали, мы обнаружили
что наибольший общий коэффициент (GCF) 18 и 24 равен 6.

---

Используйте LCM, чтобы получить GCF 18 и 24
Наименьшее общее кратное (НОК) 18 и 24 равно 72.Вы можете найти НОК 18 и 24, разделив произведение 18 и 24 на НОК 18 и 24.
Вот формула и математика:

Произведение из 18 и 24 LCM 18 и 24

= GCF

18 × 24 72

= 6

---

Используйте компьютерную таблицу, чтобы получить GCF 18 и 24
Если у вас есть компьютер, вы также можете использовать электронную таблицу в Excel или Numbers, чтобы вычислить GCF 18 и 24. Вы хотите напечатать
= gcf (18, 24) в ячейку, чтобы получить ответ.

gcf (18, 24) = 6

---

Используйте GCF 18 и 24 для упрощения дроби
GCF 18 и 24 можно использовать для многих вещей. Вы можете, например, упростить дробь, разделив числитель и знаменатель на
GCF как это:

18 ÷ 6 24 ÷ 6

=

---

Используйте GCF 18 и 24, чтобы упростить соотношение
Точно так же вы можете использовать GCF 18 и 24, чтобы упростить соотношение, разделив каждую часть отношения на
GCF выглядит следующим образом:

= 18: 24
= (18 ÷ 6): (24 ÷ 6)
= 3: 4

---

Используйте GCF 18 и 24, чтобы найти LCM 18 и 24
Поскольку использование наименьшего общего кратного (НОК) является одним из способов найти НОК 18 и 24, вы можете использовать НОК 18 и 24, чтобы найти НОК 18 и 24. НОК 18 и 24 можно, например, использовать для сложения и вычитания дробей со знаменателями 18 и 24.
НОК 18 и 24 является произведением 18 и 24, разделенного на НОК 18 и 24. Вот математика:

Произведение из 18 и 24 GCF из 18 и 24

= LCM

18 × 24 6

= 72

Вот и все! Мы надеемся, что эта страница выполнила свою задачу по определению GCF 18 и 24, показав вам, как рассчитать GCF,
примеры его использования и его отношение к LCM.

Калькулятор GCF
Используйте Калькулятор GCF для решения проблемы, аналогичной описанной на этой странице.

GCF из 18 и 25
Вот следующий GCF в нашем списке, который мы вычислили и объяснили для вас.

---

Авторские права |
Политика конфиденциальности |
Заявление об ограничении ответственности |
Контакт

Калькулятор GCF (наибольший общий коэффициент)

Калькулятор GCF вычисляет наибольший общий коэффициент от двух до шести различных чисел. Читайте дальше, чтобы найти ответ на вопрос: «Каков наибольший общий коэффициент данных чисел?», Узнайте о нескольких методах поиска GCF, включая разложение на простые множители или алгоритм Евклида, решите, какой из них вам больше всего нравится, и убедитесь сами, что наш калькулятор GCF поможет вам сэкономить время при работе с большими числами!

Что такое GCF?

Определение наибольшего общего множителя — наибольший целочисленный множитель, который присутствует между набором чисел .Он также известен как наибольший общий делитель , наибольший общий знаменатель ( GCD ), наибольший общий делитель ( HCF ) или наибольший общий делитель ( HCD ). Это важно в некоторых приложениях математики, таких как упрощение многочленов, где часто бывает необходимо выделить общие множители. Далее нам нужно знать, как найти GCF.

Как найти наибольший общий множитель

Существуют различные методы, которые помогут вам найти GCF.Некоторые из них — детская игра, другие — более сложные. Стоит знать их все, чтобы вы могли решить, что вам больше нравится:

• Используя список факторов,
• Разложение чисел на простые множители,
• алгоритм Евклида,
• Бинарный алгоритм (алгоритм Штейна),
• Использование нескольких свойств GCF (включая наименьшее общее кратное, LCM).

Хорошая новость в том, что вы можете оценить НОД с помощью простых математических операций, без корней и логарифмов! В большинстве случаев это просто вычитание, умножение или деление.

GCF finder — список факторов

Основной метод, используемый для оценки наибольшего общего делителя, — это найти все множители данных чисел. Факторы — это просто числа, умножение которых дает исходное значение. В общем, они могут быть как положительными, так и отрицательными, например 2 * 3 совпадает с (-2) * (-3) , оба равны 6. С практической точки зрения мы рассматриваем только положительные . Более того, речь идет только о целых числах.В противном случае вы можете найти бесконечную комбинацию различных дробей, являющихся факторами, что в нашем случае бессмысленно. Зная это, давайте оценим наибольший общий знаменатель чисел 72 и 40 .

1. Факторы 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 ,
2. Факторы 40 : 1, 2, 4, 5, 8, 10, 20, 40 ,
3. Перечислите все общие множители: 1, 2, 4, 8 ,
4. Наибольший общий делитель: 8 , максимальное значение сверху.

Давайте попробуем что-нибудь посложнее. Мы хотим найти ответ на вопрос: «Какой наибольший общий множитель для 33264 и 35640 ?» Все, что нам нужно сделать, это повторить предыдущие шаги:

1. Факторы 33264 : 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, 21, 22, 24, 27, 28, 33, 36, 42, 44, 48, 54, 56, 63, 66, 72, 77, 84, 88, 99, 108, 112, 126, 132, 144, 154, 168, 176, 189, 198, 216, 231, 252, 264, 297, 308, 336, 378, 396, 432, 462, 504, 528, 594, 616, 693, 756, 792, 924, 1008, 1188, 1232, 1386, 1512, 1584, 1848, 2079, 2376, 2772, 3024, 3696, 4158, 4752, 5544, 8316, 11088, 16632, 33264 ,
2. Факторы 35640 : 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 15, 18, 20, 22, 24, 27, 30, 33, 36, 40 , 44, 45, 54, 55, 60, 66, 72, 81, 88, 90, 99, 108, 110, 120, 132, 135, 162, 165, 180, 198, 216, 220, 264, 270, 297 , 324, 330, 360, 396, 405, 440, 495, 540, 594, 648, 660, 792, 810, 891, 990, 1080, 1188, 1320, 1485, 1620, 1782, 1980, 2376, 2970, 3240 , 3564, 3960, 4455, 5940, 7128, 8910, 11880, 17820, 35640 ,
3. Список всех общих делителей: 1, 2, 3, 4, 6, 8, 9, 11, 12, 18, 22, 24, 27, 33, 36, 44, 54, 66, 72, 88, 99, 108, 132, 198, 216, 264, 297, 396, 594, 792, 1188, 2376 ,
4. Окончательный результат: 2376 .

Как видите, чем больше факторов, тем больше времени занимает процедура и легко ошибиться. Стоит знать, как работает этот метод, но вместо этого мы рекомендуем использовать наш калькулятор GCF, просто чтобы убедиться, что результат правильный.

Факторизация на простые множители

Другая часто используемая процедура, которую можно рассматривать как калькулятор наибольшего общего делителя, использует разложение на простые множители. Этот метод в некоторой степени родственен ранее упомянутому.Вместо того, чтобы перечислять все возможные факторы, мы находим только те, которые являются простыми числами. В результате произведение всех общих простых чисел является ответом на нашу проблему, и, что более важно, всегда есть один уникальный способ разложить любое число на простые. Итак, теперь давайте найдем наибольший общий знаменатель 72 и 40 , используя разложение на простые множители:

1. Основные множители числа 72 равны: 2, 2, 2, 3, 3 ,
2. Основные множители числа 40 : 2, 2, 2, 5 ,
3. Другими словами, мы можем написать: 72 = 2 * 2 * 2 * 3 * 3 и 40 = 2 * 2 * 2 * 5 ,
4. Общая часть в обоих случаях равна 2 * 2 * 2 = 8 , и это наибольший общий коэффициент.

Мы видим, что для этого простого примера результат согласуется с предыдущим методом. Посмотрим, работает ли он одинаково хорошо для более сложного случая. Что такое GCF для 33264 и 35640 ?

1. Основные множители 33264 : 2, 2, 2, 2, 3, 3, 3, 7, 11 ,
2. Основные множители числа 35640 : 2, 2, 2, 3, 3, 3, 3, 5, 11 ,
3. Мы можем использовать обозначение экспоненты для записи продуктов как: 33264 = 2⁴ * 3³ * 7 * 11 , 35640 = 2³ * 3⁴ * 5 * 11 ,
4. Общее произведение двух чисел: 2³ * 3³ * 11 .Мы также можем записать его более компактным и сложным способом с учетом факториалов: (3!) ³ * 11 . Проверьте, дает ли наш калькулятор GCD такой же результат: 2376 .

Алгоритм Евклида

Идея, лежащая в основе алгоритма Евклида, гласит, что если число k является наибольшим общим множителем чисел A и B , то k также является GCF для разности этих чисел A - В .Следуя этой процедуре, мы наконец достигнем 0. В результате наибольший общий делитель будет последним ненулевым числом. Еще раз взглянем на наши примеры — числа 40 и 72 . Каждый раз, когда мы производим вычитание, мы сравниваем два числа, упорядочивая их от наибольшего до наименьшего значения:

• GCF из 72 и 40 : разница 72-40 равна 32 ,
• GCF из 40 и 32 : 40-32 = 8 ,
• GCF из 32 и 8 : 32-8 = 24 ,
• GCF из 24 и 8 : 24-8 = 16 ,
• GCF из 16 и 8 : 16-8 = 8 ,
• GCF из 8 и 8 : 8-8 = 0 СТОП!

На нашем последнем шаге вычитанием мы получаем 0.Это означает, что мы находим наш Наибольший общий делитель и его значение в предпоследней строке вычитаний: 8 .

А как насчет более сложного случая с 33264 и 35640 ? Попробуем решить ее с помощью алгоритма Евклида:

• GCF из 35640 и 33264 : 35640 - 33264 = 2376 ,
• GCF из 33264 и 2376 : 33264 - 2376 = 30888 ,
• GCF из 30888 и 2376 : 30888 - 2376 = 28512 ,
• GCF из 28512 и 2376 : 28512 - 2376 = 26136 ,
• GCF из 26136 и 2376 : 26136 - 2376 = 23760 ,
• GCF из 23760 и 2376 : 23760 - 2376 = 21384 ,
• GCF из 21384 и 2376 : 21384 - 2376 = 19008 ,
• GCF из 19008 и 2376 : 19008 - 2376 = 16632 ,
• GCF из 16632 и 2376 : 16632 - 2376 = 14256 ,
• GCF из 14256 и 2376 : 14256 - 2376 = 11880 ,
• GCF из 11880 и 2376 : 11880 - 2376 = 9504 ,
• GCF из 9504 и 2376 : 9504 - 2376 = 7128 ,
• GCF из 7128 и 2376 : 7128 - 2376 = 4752 ,
• GCF из 4752 и 2376 : 4752 - 2376 = 2376 ,
• GCF из 2376 и 2376 : 2376 - 2376 = 0 СТОП!

Как и в предыдущем примере, НОД для 33264 и 35640 является последней отличной от нуля разницей в процедуре, которая равна 2376 .

Как видите, базовая версия этого искателя GCF очень эффективна и проста, но имеет один существенный недостаток. Чем больше разница между приведенными числами, тем больше шагов необходимо для достижения последнего шага. По модулю — это эффективная математическая операция, которая решает проблему, потому что нас интересует только остаток, меньший обоих чисел. Давайте повторим алгоритм Евклида для наших примеров, используя по модулю вместо обычного вычитания:

• GCF из 72 и 40 : 72 mod 40 = 32 ,
• GCF из 40 и 32 : 40 mod 32 = 8 ,
• GCF из 32 и 8 : 32 mod 8 = 0 СТОП!

Наибольший общий знаменатель 8 .А что насчет другого?

• GCF из 35640 и 33264 : 35640 мод. 33264 = 2376 ,
• GCF из 33264 и 2376 : 33264 mod 2376 = 0 СТОП!

GCD из 35640 и 33264 — это 2376 , и он находится всего за два шага вместо 15. Неплохо, не так ли?

Алгоритм двоичного наибольшего общего делителя

Если вам нравятся более простые арифметические операции, чем те, которые используются в алгоритме Евклида (например,грамм. по модулю), двоичный алгоритм (или алгоритм Штейна) определенно для вас! Все, что вам нужно использовать, это сравнение, вычитание и деление на 2. При оценке наибольшего общего множителя двух чисел имейте в виду следующие тождества:

1. gcd (A, 0) = A , мы используем тот факт, что каждое число делит ноль, и наблюдение с последнего шага в алгоритме Евклида — одно из чисел упало до нуля, и наш результат был предыдущим,
2. Если и A , и B равны, это означает, что gcd (A, B) = 2 * gcd (A / 2, B / 2) , поскольку 2 является общим множителем,
3. Если только одно из чисел четное, скажем, A , тогда gcd (A, B) = gcd (A / 2, B) .На этот раз 2 не является общим делителем, поэтому мы можем продолжить сокращение, пока оба числа не станут нечетными,
4. Если и A , и B нечетные и A> B , то gcd (A, B) = gcd ((A-B) / 2, B) . На этот раз мы объединяем две функции в один шаг. Первый выводится из алгоритма Евклида, определяющего наибольший общий делитель разности обоих чисел и меньшего. Во-вторых, возможно деление на 2, так как разность двух нечетных чисел четная, и согласно шагу 3 мы можем уменьшить четное.
5. Шаги 2–4 повторяются до достижения шага 1 или A = B . Результатом будет 2ⁿ * A , где n — количество множителей 2, найденных на втором этапе.

Как обычно, давайте попрактикуемся в алгоритме с нашими наборами чисел. Начнем с 40 и 72 :

• Они оба равны gcf (72, 40) = 2 * gcf (36, 20) = 2² * gcf (18, 10) = 2³ * gcf (9, 5) =… ,
• Остальные числа нечетные, поэтому … = 2³ * gcf ((9-5) / 2, 5) = 2³ * gcf (2, 5) ,
• 2 ровно, поэтому мы можем уменьшить его: … = 2³ * gcf (1, 5) ,
• 1 и 5 нечетны, поэтому: … = 2³ * gcf ((5-1) / 2, 1) = 2³ * gcf (2, 1) ,
• Удалите 2 из четного числа: … = 2³ * gcf (1, 1) = 2³ = 8 .

На самом деле, мы могли бы остановиться на третьем шаге, так как НОД 1 и любое число равно 1.
Хорошо, а как найти наибольший общий множитель для 33264 и 35640 с помощью двоичного метода?

• Два четных числа: gcf (35640, 33264) = 2 * gcf (17820, 16632) = 2² * gcf (8910, 8316) = 2³ * gcf (4455, 4158) =… ,
• Один четный, один нечетный: … = 2³ * gcf (4455, 2079) ,
• Два нечетных: … = 2³ * gcf ((4455-2079) / 2, 2079) = 2³ * gcf (1188, 2079) ,
• Один четный нечетный: … = 2³ * gcf (594, 2079) = 2³ * gcf (297, 2079) ,
• Два нечетных: … = 2³ * gcf ((2079-297) / 2, 297) = 2³ * gcf (891, 297) ,
• Два нечетных: … = 2³ * gcf ((891-297) / 2, 297) = 2³ * gcf (297, 297) = 2³ * 297 = 2376 .

Номера Coprime

Мы знаем, что простые числа — это числа, у которых есть только два положительных целых делителя: 1 и само себя. Итак, вопрос в том, что такое взаимно простые числа? Мы можем определить их как чисел, не имеющих общих делителей . Точнее, 1 — их единственный общий делитель, но поскольку мы опускаем 1 в разложении на простые множители, можно сказать, что у них нет общих делителей. Другими словами, мы можем написать, что числа A и B взаимно просты, если gcf (A, B) = 1 .На самом деле это не означает, что любое из них является простым числом, просто список общих факторов пуст. Примеры взаимно простых чисел: 5 и 7 , 35 и 48 , 23156 и 44613 .

Интересный факт: можно вычислить вероятность того, что два случайно выбранных числа взаимно просты. Хотя это довольно сложно, общий результат составляет около 61% . Вы удивлены? Просто проверьте это на себе — представьте два случайных числа (скажем, из пяти цифр), воспользуйтесь нашим калькулятором наибольшего общего коэффициента и выясните, будет ли результат 1 или нет.Повторите игру несколько раз и оцените, какой процент взаимно простых чисел вы нашли.

Наибольший общий знаменатель более двух чисел

Теперь, когда мы знаем о многочисленных методах нахождения наибольшего общего делителя двух чисел, вы можете спросить: «как найти наибольший общий делитель трех или более чисел?» . Оказывается, это не так сложно, как может показаться на первый взгляд. Что ж, перечисление всех факторов для каждого числа — определенно простой метод, потому что мы можем просто найти самый большой из них.Однако вы быстро поймете, что по мере увеличения числа фигур на это уходит все больше и больше времени.

Метод факторизации простых чисел имеет аналогичный недостаток, но поскольку мы можем сгруппировать все простые числа, например, в порядке возрастания, мы можем представить способ получения результата немного быстрее, чем раньше.

С другой стороны, если вы предпочитаете использовать двоичные или евклидовы алгоритмы для оценки ОКФ нескольких чисел, вы также можете использовать теорему, которая гласит, что:

gcf (a, b, c) = gcf (gcf (a, b), c) = gcf (gcf (a, c), b) = gcf (gcf (b, c), a) .

Это означает, что мы можем вычислить НОД любых двух чисел, а затем снова запустить алгоритм, используя результат и третье число, и продолжать, пока остаются какие-либо цифры. Неважно, какие два мы выберем в первую очередь.

Наименьшее общее кратное

Еще одно понятие, тесно связанное с НОД, — наименьшее общее кратное. Чтобы найти наименьшее общее кратное, мы используем тот же процесс, который мы использовали для поиска GCF. Как только мы сведем числа к разложению на простые множители, мы ищем наименьшую степень каждого множителя, а не наибольшую степень.Затем мы умножаем наибольшие степени, и в результате получаем наименьшее общее кратное или НОК. Это можно сделать вручную или с помощью калькулятора LCM.

Наибольший общий коэффициент можно оценить с помощью LCM. Допустимо следующее выражение:

gcf (a, b) = | a * b | / см (а, б) .

Может быть удобно сначала найти наименьшее общее кратное из-за сложности и продолжительности. Естественно, его можно вычислить любым способом, поэтому стоит знать, как найти GCD и LCM.

Свойства GCD

Мы уже представили несколько свойств наибольшего общего знаменателя. В этом разделе мы перечислим самые важные:

• Если отношение двух чисел a и b ( a> b ) является целым числом, тогда gcf (a, b) = b ,

• gcf (a, 0) = a , используется в алгоритме Евклида,

• gcf (a, 1) = 1 ,

• Если a и b не имеют общих множителей (они взаимно просты), то gcf (a, b) = 1 ,

• Все общие множители a и b также являются делителями gcf (a, b) ,

• Если b * c / a является целым числом и gcf (a, b) = d , то a * c / d также является целым числом,

• Для любого целого числа k : gcf (k * a, k * b) = k * gcf (a, b) , используется в двоичном алгоритме,

• Для любого положительного целого числа k : gcf (a / k, b / k) = gcf (a, b) / k ,

• gcf (a, b) * lcm (a, b) = | a * b | ,

• gcf (a, lcm (b, c)) = lcm (gcf (a, b), gcf (a, c)) ,

• пкм (a, gcf (b, c)) = gcf (lcm (a, b), lcm (a, c)) .

Система приходской школы Лафайет}

Быстрые ссылки Выберите страницу: Видение на 2020 год 2007-2018 Отчеты округа ХиндсШкольные библиотеки и медиацентрРуководство по исключению и ограничению участия2020-2021 Административный календарь округа2020-2021 годШкольный календарь округа на 2019-2020 годы Принятый бюджет2019-2020 Взвешенные курсы2020-2021 Предлагаемый бюджет504 Поиск детей и соответствие требованиям 504 координатор Ускоренный читатель ) Руководящие принципы округаАвтоматическая аварияСправочные документыМеню для завтрака и обедаBullyingBidМаршруты автобусовСтаж в автобусеМеста остановок автобусовЦентральный офис / школьный справочникПроцессы чартерной школыГорячая линия по борьбе с жестоким обращением с детьмиПоследствия поведенияУчебная программа для колледжа и диплом о профессиональной работеДепартамент A-ZРабота по работе с сотрудниками UPGrading ScaleHCIS Часто задаваемые вопросыЗдоровье и безопасностьДомашняя зонаПолитика выбора учебных материаловJBCE School ChoiceLafayetteCheckbook.comLouisiana PASSLPSS платье CodeLPSS Foster Care ProgramMedia RequestLafayette Magnet AcademiesLouisiana Школа FinderMySchoolAppsMySchoolBucksNew ResidentsOrganizational ChartPayrollPublic Информация OfficerPupil Прогрессирование PlanPupil Прогрессирование план поддержка DocumentsPublic отчеты RequestPublic Школа ChoiceRegistrationRisk ManagementSafety Дрель ReportingScholarshipsSchool HoursSpecial диетических потребности FormStudent допустимого использования PolicyStudent AccidentStudent HandbookStudent счет Meal возврат FormSupply ListsTalented Преподаватель Биллу процедур RightsTechnology ClassesTitle IX и политикиЗапросы на расшифровку текстаWisdomwhereWorld Book Online

Калькулятор GCF

Как найти GCF из двух или более чисел?

Есть несколько способов найти GCF двух целых чисел.Те же процедуры можно применить к более чем двум целым числам. Например, давайте найдем GCF, равный 16 и 24 долларам.

• Перечисление факторов.
  фактор 16 $: 1,2,4,8,16 $; Фактор
  24 $: 1,2,3,4,6,8,12,24 $.

Общие множители для 16 $ и 24 $: 1,2,4,8 $. Итак, наибольший общий делитель 16 и 24 долларов равен 8 долларам.

• Использование разложения на простые множители.
  $ 16 = 2 \ times2 \ times 2 \ times 2 $
  $ 24 = 2 \ times 2 \ times 2 \ times 3.$ 90 263

Общие простые множители $ 16 $ и $ 24 $: 2, 2, 2 $. Итак, GCF — это произведение общих простых множителей, $ 2 \ times2 \ times \ times2 = 8 $.

• Евклидов алгоритм.
  $ 24-16 = 8 $
  $ 16-8-8 = 0 $
  Итак, GCF в размере 16 $ и 24 $ равен 16 $.

Вкратце, алгоритм Евклида можно описать следующим образом: сначала мы вычитаем меньшее число, в данном случае $ 16 $, из большего числа, в данном случае $ 24 $, и повторяем процедуру вычитания, пока результат не станет меньше. чем исходное небольшое количество.Далее мы используем исходное маленькое число, в данном случае 16 $, как новое большее число и повторяем процедуру вычитания, пока не достигнем нуля.
Когда мы достигаем нуля, GCF данных чисел становится меньшим числом, в данном случае $ 8 $, которое мы нашли непосредственно перед нулевым результатом.
Как мы знаем, диаграмма Венна представляет отношения между наборами чисел или объектов с помощью перекрывающихся кругов. В некоторых случаях диаграмма Венна может помочь нам найти наибольший общий фактор. Например, на диаграмме ниже показаны простые множители 16 и 24 долларов.Мы видим, что общие простые множители находятся в обоих кругах. Итак, GCF $ 16 $ и $ 24 $ — это произведение в множестве пересечений, $ 2 \ times2 \ times2 = 8 $.

Факторное дерево также можно использовать для нахождения GCF. Во-первых, определите общие факторы. У чисел 16 $ и 24 $ есть общие множители 2,2 $ и 2 $.
GCF — это произведение общих простых множителей. Если числа не имеют общих факторов с использованием факторного дерева, то GCF этих чисел составляет 1 доллар США.

Работа GCF с шагами показывает полный пошаговый расчет для
нахождение наибольшего общего делителя данного набора целых чисел: 5, 20, 40, 80, 100 $ с использованием разложения на простые множители.Для любого другого набора чисел просто укажите список чисел и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор GCF для создания работы, проверки результатов, полученных вручную, или для эффективного выполнения домашних заданий.

Шлюз

Veuillez réessayer dans quelques instants. Si le problème persiste,
veuillez communiquer avec le service de soutien Technique de Alberta Education (доступный
en anglais seulement).

Телефон :		780-427-5318
		(Composer d’abord le 310-0000 pour obtenir une ligne sans frais)
Телекопье:		780-427-1179
Adresse de Courriel:		cshelpdesk @ gov.ab.ca

Что такое GCF 18 и 24?

Что такое GCF 24 и 24?

Каков GCF для 24 и 24.

GCF для 24 и 24 составляет 24 ..

Каков GCF для 18, 24 и 32?

Заключительный шаг: наибольшее число общего множителя Мы нашли множители и разложение на простые множители 18 и 32. Наибольшее число общих множителей — это число GCF.Итак, наибольший общий делитель 18 и 32 равен 2.

Что такое делители 18?

Факторы 18: 1, 2, 3, 6, 9, 18. Факторы 19: 1, 19.

Что такое GCF 16 24?

Метод 2: GCF 16 и 24 путем перечисления общих факторов Общие факторы 24 и 16: 1, 2, 8 и наибольшее из них 8.

Что такое GCF 15 и 30?

Пример: Каков наибольший общий делитель 15 и 30? Общие делители 15 и 30 — это 1, 3, 5 и 15.Наибольший общий делитель равен 15.

Сколько 6 раз делится на 18?

Факторы 18: 1, 2, 3, 6, 9, 18.

Какие множители 18 и 24?

Рассмотрим множители 18 и 24. Общие множители — это 1, 2, 3, 6. которые делятся точно на оба (или все) числа.

Каков GCF для 24 18 и 12?

6 Как вы можете видеть, когда перечисляете множители каждого числа, 6 — это наибольшее число, на которое делятся 12, 18 и 24.

Что такое GCF для 18 и 27?

Множители 27 — это 1, 3, 9, 27. Общие делители 18 и 27 — это 1, 3 и 9. Наибольший общий делитель 18 и 27 равен 9.

Что такое GCF 24 и 25?

Наибольший общий коэффициент (GCF) для 24 и 25, обозначение CGF (24,25), равен 1.

Что такое GCF для 18 и 30?

Наибольший общий делитель (НОД) 18 и 30 равен 6. Теперь мы вычислим простые множители 18 и 30, а затем найдем наибольший общий делитель (наибольший общий делитель (НОД)) чисел, сопоставив наибольший общий делитель. из 18 и 30.

Что такое HCF 16 18 и 24?

2Как вы можете видеть, когда перечисляете множители каждого числа, 2 — это наибольшее число, на которое делятся 16, 18 и 24.

Что такое HCF для 18 24 и 42?

6 Метод общих множителей Сначала найдите все множители заданных чисел по отдельности. Следовательно, общие множители для 18, 24 и 42 равны 1, 2, 3 и 6. HCF для 18, 24 и 42 равняется 6.

Каков GCF для 18, 24 и 36?

Наибольший общий делитель 18, 24 и 36 равен 6.

Каков ВПК 24 20?

Мы нашли множители и разложение на простые множители 24 и 20. Наибольшее общее число множителей — это число GCF. Таким образом, наибольший общий множитель 24 и 20 равен 4.

Что такое GCF для 15 и 18?

3 GCF для 15 и 18 равно 3.

Что такое GCF для 36 24?

12GCF 24 и 36 составляет 12, самый высокий среди общих факторов.

Является ли 18 идеальным квадратом?

В математике квадрат — это произведение целого числа на себя.Например, произведение числа 2 само по себе равно 4. В этом случае число 4 называется полным квадратом. Квадрат числа обозначается как n × n…. Пример 1. IntegerPerfect square17 x 1728918 x 1832419 x 1936120 x 2040021 другие строки

Каковы множители 18 и 3?

Наибольший общий множитель (GCF) 3 и 18 равен 3.

Что такое GCF 24 и 72?

GCF 72 и 24 путем перечисления общих факторов GCF 72 и 24 равно 24.

Что такое GCF для 18 и 45?

9 Между 18 и 45 GCF равен 9, и вот откуда вы это знаете.

Калькулятор наибольшего общего коэффициента

Укажите числа, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы найти GCF.

Связанный калькулятор LCM | Калькулятор коэффициентов

Какой наибольший общий коэффициент (GCF)?

В математике наибольший общий делитель (GCF), также известный как наибольший общий делитель, двух (или более) ненулевых целых чисел a и b , является наибольшим положительным целым числом, на которое можно разделить оба целых числа. .Обычно обозначается как GCF (a, b). Например, GCF (32, 256) = 32.

.

Метод простой факторизации

Есть несколько способов найти наибольший общий делитель заданных целых чисел. Один из них включает в себя вычисление простых множителей каждого целого числа, определение общих факторов и умножение этих факторов для нахождения НОД. См. Пример ниже.

EX:	GCF (16, 88, 104) 16 = 2 × 2 × 2 × 2 88 = 2 × 2 × 2 × 11 104 = 2 × 2 × 2 × 13 ОКФ (16, 88, 104) = 2 × 2 × 2 = 8

Факторизация на простые множители эффективна только для меньших целочисленных значений.Большие значения сделают простое разложение каждого из них и определение общих факторов гораздо более утомительным.

Евклидов алгоритм

Другой метод, используемый для определения GCF, включает использование алгоритма Евклида. Этот метод является гораздо более эффективным, чем использование разложения на простые множители. Алгоритм Евклида использует алгоритм деления в сочетании с наблюдением, что НОД двух целых чисел также может делить их разность. Алгоритм следующий:

GCF (а, а) = а GCF (a, b) = GCF (a-b, b), когда a> b GCF (a, b) = GCF (a, b-a), когда b> a

На практике:

1. Для двух положительных целых чисел a и b, где a больше, чем b , вычтите меньшее число b из большего числа a , чтобы получить результат c .
2. Продолжайте вычитать b из a , пока результат c не станет меньше b .
3. Используйте b в качестве нового большого числа и вычтите окончательный результат c , повторяя тот же процесс, что и в шаге 2, пока остаток не станет 0.
4. Если остаток равен 0, GCF — это остаток от шага, предшествующего нулевому результату.

EX:	GCF (268442, 178296) 268442–178296 = 178296– = 88150 — 88150 = 1996 88150 — 1996 × 44 = 326 1996 г. — 326 × 6 = 40 326 — 40 × 8 = 6 6–4 = 2 4 — 2 × 2 = 0

Из приведенного выше примера видно, что GCF (268442, 178296) = 2.Если бы присутствовало больше целых чисел, тот же процесс был бы выполнен, чтобы найти GCF следующего целого числа и GCF двух предыдущих целых чисел. Ссылаясь на предыдущий пример, если вместо этого желаемое значение было GCF (268442, 178296, 66888), после того, как было обнаружено, что GCF (268442, 178296) равно 2, следующим шагом будет вычисление GCF (66888, 2). В этом конкретном случае ясно, что GCF также будет 2, давая результат GCF (268442, 178296, 66888) = 2.

.