Рабочая тетрадь по теме «Логарифмы. Свойства логарифмов» 11 класс

Рабочая тетрадь по теме

«Логарифмы. Свойства логарифмов»

Составила учитель математики

НОУ частной гимназии г. Костромы

Робкова Ирина Викторовна

2015г

Материал может быть использован на уроках математики в 11 классе, как дополнительный источник заданий по теме «Логарифмы. Свойства логарифмов».

Структура тетради следующая:

1. Задания, в которых требуется вычислить значение выражения, содержащего логарифм

2. Подборка заданий по каждому из свойств логарифмов.

3. Комплекс тестовых заданий (базовый уровень) по свойствам логарифмов

4. Комплекс заданий (повышенного уровня сложности) по свойствам логарифмов

В каждом задании любого раздела есть место для краткой либо подробной записи решения задания. В тестовых заданиях необходимо решить, а затем выбрать номер верного ответа (только один ответ является правильным). В заданиях уровня В необходимо решить задание, а ответ представить либо в виде целого числа, либо в виде конечной десятичной дроби.

Справочный материал:

При

Вычислите значение выражения:

1. log ₂ 8 =

2. log ₃ =

3. log ₂ 2=

4. log ₃ =

5. log ₁₆ 1=

6. lg 100=

7. log ₄ 64=

8. log _0,5 =

9. log ₄ 256=

10. log ₂ =

11. log _0,2 625=

12. log _0,1 1=

13. log ₅ 125=

14. log _0,2 5=

15. log ₃₌

16. lg 0,001=

17. log _0,1 0,0001=

18. log49=

19. log _{7 =}

20. log 1=

21. lg 0,1=

22. log ₃ 81=

23. log 4=

24. log 225=

25. log 2=

26. log81=

27. log ₃=

28. lg 1000=

29. log ₃ 729=

30. log =

31. log ₂ 16=

32. log =

33. log ₂ 1024=

34. log =

35. log ₆ 1=

36. lg 10=

37. log ₂ 64=

38. log _0,5 =

39. log ₁₆ 256=

40. log ₂ =

41. log _0,2 5=

42. log _0,1 100=

43. log ₅ =

44. log ₂ 4 * log ₃ 27=

45. log ₅125 : log ₄ 16=

46. log _0,5 0,25 * log _0,3 0,09=

47. lg 1000 : lg 100=

48. log4 * log ₃ 9 : log ₄₌

49. log: log * log ₅ 125 =

50. log ₃ 81 : log _0,5 2 _* log ₅ =

51. log ₂ + log =

52. log ₂ (log 49)=

53. log(log ₂₅ 125) =

54. log(log ₂ 32)

55. log ₂ (log ₅) =

56. log(log ₃ 27) =

57. log ₂ (log 49) =

58. log ₄ (log ₃)=

59. log(log ₃₄₃ 49) =

60. log(log) =

61. log³ ₉ (log ₂ 8) =

62. log² ₃ (log) =

63. =

Используя свойство логарифмов, упрости выражение и найди его значение

1. log ₆ 2 + log ₆ 3 = ……………………………………………………………………….

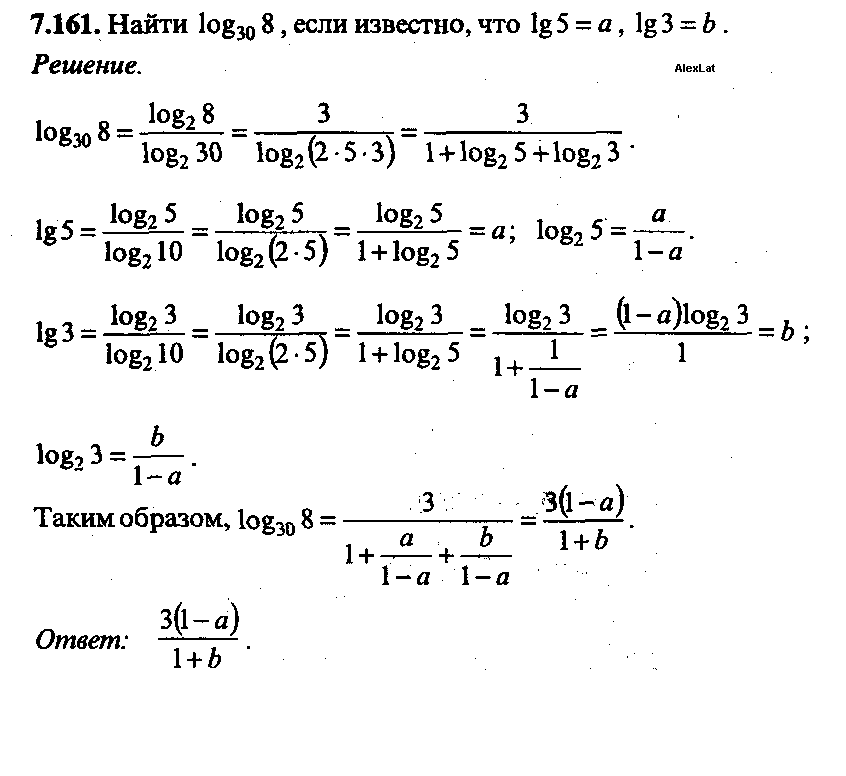
2. log ₆ 12 + log ₆ 3 =………………………………………………………………………

3. lg 25 + lg 4 = ………………………………………………………………………………

4. log ₁₅ 3 + log ₁₅ 5= ………………………………………………………………………

5. log ₁₄₄ 3 + log ₁₄₄ 4 =…………………………………………………………………….

6. log4 + log2= …………………………………………………………………………

7. lg 40 + lg 25 = ………………………………………………………………………….

8. lg 12,5 + lg 80 = ………………………………………………………………………..

9. log ₈ + log _{8 = …………………………………………………………………………………………………………}

10. log ₂₀ 5 + log ₂₀ 4 = …………………………………………………………………….

11. log ₄ 2 + log ₄ 8 =……………………………………………………………………….

12. log ₂ 5 + log _{2 =……………………………………………………………………………………………………………}

13. log ₄ 5 + log ₄ 25 + log _{4 = ………………………………………………………………………………………}

14. log ₂ 12 + log ₂ + log _{2=…………………………………………………………………………………………. .}

15. log + log=………………………………………………………

………………………………………………………………………………………….

16. log + log=………………………………………..

………………………………………………………………………………………….

………………………………………………………………………………………….

17. log + log=………………………………………………………

………………………………………………………………………………………….

1. log ₃ 7 — log _{3 = ………………………………………………………………………………………………………….}

2. log ₂ 15 — log ₂ 30 = ……………………………………………………………………

3. log6 — log2= …………………………………………………………………

4. log7 — log14 =……………………………………………………………….

5. log ₃ 162 — log ₃ 6 =……………………………………………………………………

6. log ₂ 36 — log ₂ 144=………………………………………………………………………

7. log ₇ 98 — log ₇ 14 = ……………………………………………………………………..

8. log ₃ 2 — log ₃ 54 = ………………………………………………………………………

9. log ₅ 175 — log ₅ 7 =………………………………………………………………………

10. log ₅ 22 — log ₅ 11- log ₅ 10 =……………………………………………………………

11. log ₃ — log ₃=……………………………………………………….

………………………………………………………………………………………….

1. log ₂ 5 — log ₂ 35 + log ₂ 56 = …………………………………………………………..

2. log ₅ 8 — log ₅ 2 + log _{5 = …………………………………………………………………………………………..}

3. log ₂ 7 — log ₂ 63 + log ₂ 36 = …………………………………………………………..

…………………………………………………………………………………………………………………………….

4. log ₃ 72 — log ₃ + log ₃ 18=…………………………………………………………

…………………………………………………………………………………………

1. 2^log₂ ¹⁰ =

2. 6^log₆ ⁷ =

3. 210^lg7 =

4. 15^log₅ ² =

5. 0,3^log_0,3 ² – 5 =

6. 7^log₇ ⁵ =

7. 36 ^0,5log₆ ¹⁸ =

8. 121 ^0,5log₁₁ ³⁵ =

9. 0,5^log_0,5 ² =

10. 7 ^2log₄₉ ² =

11. 10^lg0,5 =

12. 3^log₃ ¹⁰⁰⁰ =

13. ^2log₅³ =

1. 3 lg2 – lg4 = ……………………………………………………………………….

2. 2 lg5 + lg8 =……………………………………………………………………….

3. log ₂ 0,04 + 2 log ₂ 5 = …………………………………………………………….

4. 0,5 log ₂ 25 + log ₂ 1,6 = …………………………………………………………..

5. 0,5 log ₂ 400 + log ₂ 1,6 = ………………………………………………………….

6. 2 log ₂ 3 + log _{2 = ……………………………………………………………………………………………………}

7. log ₂ 10 – 2 log ₂ 5 + log ₂ 40 =………………………………………………………

8. 2 log ₅ 75 + log _{5 =………………………………………………………………………………………………}

9. 2 log ₃ 6 — log ₃ 4 + 5^log₅ ² =………………………………………………………….

10. log ₂ + log _{2 =……………………………………………………………………………………………..}

11. log3 8 + 3 log _{3 =…………………………………………………………………………………………………}

12. log ₇ 196 – 2 log ₇ 2 =……………………………………………………………….

13. log ₃ 8 – 2 log ₃ 2 + log _{3 =……………………………………………………………………………………}

14. 2 log ₇ 32 — log ₇ 256 – 2 log ₇ 14 = ………………………………………………..

………………………………………………………………………………………

………………………………………………………………………………………

15. 2 log ₂ 6 +log ₂ — log ₂ 35 = ……………………………………………………..

………………………………………………………………………………………

16. log ₅ — 2 log ₅ + log _{5 = ………………………………………………………………………………..}

_{………………………………………………………………………………………………………………………………….}

17. log ₄ + log ₄ 36 + log _{4 = ……………………………………………………………………………..}

18. 4 ^2log₄ ¹⁰=…………………………………………………………………………….

19. 25 ^log₅ ³=…………………………………………………………………………….

20. 9 ^log₈₁⁴=…………………………………………………………………………….

21. 0,04 ^log_0,2 ³ =……………………………………………………………………….

22. 2 ^log₄⁹ =……………………………………………………………………………

23. 2 ^log₈ ¹²⁵= ………………………………………………………………………….

24. 0,25 (1 + 4 ^log₂⁵) ^log₂₆⁴=…………………………………………………………….

……………………………………………………………………………………..

25. (log₃ 81 + 16 ^log₂³) ^log₈₅²⁵=……………………………………………………….

……………………………………………………………………………………..

26. =………………………………………………………………………………

27. =………………………………………………………………………………

• a^b+c = a^{b — c} = a^b : a^c

1. 7 ^1+log₇⁵=………………………………………………………………………………

2. 2 ^2+log₂⁵=………………………………………………………………………………

3. 5^log₅^{16 – 1}=……………………………………………………………………………. .

4. 25 ^{1 – 0,5log}₅¹¹=…………………………………………………………………………

5. 10 ^1+lg5=………………………………………………………………………………

6. 10 ^{lg2 + lg3}=…………………………………………………………………………….

7. 10 ^{lg7 + lg2}=…………………………………………………………………………….

8. 16^log₄^{3 – 0,25log}₂³=………………………………………………………………………

9. 81^log₉^{2 – 0,25log}₃²=………………………………………………………………………

10. 10 ^{2 — lg2} – 25^log₅²=…………………………………………………………………….

11. 2 ^{2 – log}₂⁵ + 0,5^log₂⁵=……………………………………………………………………

12. =……………………………………………………………………….

13. 9 ^{3 – log}₃ ¹⁰⁸ + 7 ^{— 4 log}₇²=………………………………………………………………. .

………………………………………………………………………………………..

14. (9 ^{2 – log}₂ ⁶ + 5 ^log₅²⁷) ^{– 1}=……………………………………………………………….

………………………………………………………………………………………..

15. (4 ^{2 – log}₂ ⁶ + 3 ^{– log}₃³⁶) ^{– 1}=…………………………………………………………..

………………………………………………………………………………………..

16. (12 ^{1 – 2 log}₁₂ ⁶ + 7 ^{l — 2 log}₇⁶) ^{– 1}=…………………………………………………………

………………………………………………………………………………………..

17. 9 ^{3 – log}₃ ⁵⁴ + 7 ^{— log}₇²=………………………………………………………………….

………………………………………………………………………………………..

18. 25 ^{2 – log}₅ ⁷⁵ + 7 ^{— log}₇³=…………………………………………………………………

………………………………………………………………………………………..

19. 10 ^{3 – lg 4} — 49 ^log₇¹⁵=…………………………………………………………………..

……………………………………………………………………………………….

• = log_aC

1. log9 + log ₂₁49=………………………………………………………………..

2. log ₅ + 2 log _{25=………………………………………………………………………………………………}

3. log ₂48 + log ₄3=……………………………………………………………………

4. log125 – log ₁₂₁9=…………………………………………………………………

5. 4^3log ₄^2,5=…………………………………………………

………………………………………………………………………………………. .

6. 13^2log ₁₃⁶=……………………………………………………

………………………………………………………………………………………..

7. 9^3log ₉²=………………………………………………………

………………………………………………………………………………………..

1. log₃ = …………………………………………………………….

2. (log₅128)(log₂)=……………………………………………………………….

3. 6 log ₂log ₅2 + 2^{lg7 lg7}=……………………………………………………..

……………………………………………………………………………………..

4. 5 log ₃ log₅81 + 15^log₁₅⁷=………………………………………………………………………..

…………………………………………………………………………………….

• log _a b = log _a b =

1. =………………………………………………………………………………………..…

2. =…………………………………………………………………………………..……….

3. — =……………………………………………………………………..………….

………………………………………………………………………………………..……………………………………………………………………………………………………………………

………………………………………………………………………………………………………

………………………………………………………………………………………….…………..

4. 2^log ₂⁸=………………………………………………….………….

………………………………………………………………………………………..…………………………………………………………………………………………………………….……

…… …………………………………………………………………………………………….…

…………………………………………………………………………………………………….

5. 5^log ₅²⁴=…………………………………………………………. ….

………………………………………………………………………………………..……………………………………………………………………………………………………………………

…………………………………………………………………………………………….…………

..……………………………………………………………………………………………………..

6. 7^log ₇⁵=………………………………………………………………

………………………………………………………………………………………..……………………………………………………………………………………………………………………

…………………………………………………………………………………………..…………

..………………………………………………………………………………………….………..

7. 5^log ₅¹³=……………………………………………………….……

………………………………………………………………………………………..………………………………………………………………………………………………………………………………………………………………………………………..…………………………….

Решение тестовых заданий

Уровень А

В этом разделе для каждого задания необходимо предложить краткое решение и выбрать один ответ, расположенный под решением. Номер правильного ответа обведите кружком, только один вариант ответа является верным.

1. Упростите выражение log ₈ 14 + log ₈

Решение………………………………………………………………………………………

1) 0,5 2) 2 3) log ₂7 4) log ₇2

2. Упростите выражение log ₅ + log ₅

Решение………………………………………………………………………………………

1) 3 2) 5 3) log ₅30 4) log ₅

3. Вычислите log ₁₂ — log ₁₂7

Решение………………………………………………………………………………………

1) 1 2) 2 3) — 1 4) — 2

4. Найдите значение выражения log ₇ — log ₇

Решение………………………………………………………………………………………

1) 2) 2 3) log ₇9 — 1 4) log ₇2

5. Укажите значение выражения log ₅ 75 + log ₅ (25)^{— 1}

Решение………………………………………………………………………………………

1) 1 2) 0 3) log ₅3 4) log ₃ 5

6. Укажите значение выражения 2log ₂ 3 + log ₂

Решение………………………………………………………………………………………

1) — 2 2) 0 3) log ₂3 4) 2log ₂3

7. Укажите значение выражения log ₂ 10 — 2 log ₂ 5 + log ₂ 40

Решение………………………………………………………………………………………

1) 0 2) 2 3) 3 4) 4

9. Укажите значение выражения 2log ₅ 75 + log ₅

Решение………………………………………………………………………………………

1) 1 2) 0 3) log ₃5 4) 2log ₅3

10. Укажите значение выражения log54 — log8 + log 81

Решение………………………………………………………………………………………

1) 1 2) — 1 3) — 7 4) 7

11. Упростите выражение log36 + log

Решение………………………………………………………………………………………

1) 2 2) — 2 3) log 4) log9

12. Найдите значение выражения 4,5 ^log _4,5 ³ – 15

Решение………………………………………………………………………………………

1) — 6 2) 24 3) – 10,5 4) 6

13. Найдите значение выражения 4,5 ^log _4,5 ⁹

Решение………………………………………………………………………………………

1) 6 2) 27 3) 12 4) 54

14. Найдите значение выражения 0,5 ^log _0,5 ³

Решение………………………………………………………………………………………

1) 48 2) 8 3) 24 4) 4

15. Найдите значение выражения 0,6 ^log _0,6 ¹²

Решение………………………………………………………………………………………

1) 100 2) 60 3) 3 4) 5

16. Найдите значение выражения 0,6 ^log _0,6 ³

Решение………………………………………………………………………………………

1) 30 2) 6 3) 10 4) 50

17. Найдите значение выражения 2,5 ^log _2,5¹⁰

Решение………………………………………………………………………………………

1) 10 2) 16 3) 40 4) 4

18. Найдите значение выражения 3^log ₂^{0,25 + log} ₃⁵

Решение………………………………………………………………………………………

1) — 45 2) 3) 5^log₂^0,25 4) 5log ₂0,25

19. Найдите значение выражения 9^log ₉^{2 + log} ₅^0,04

Решение………………………………………………………………………………………

1) 0,25 2) 3) – 4 4) 4

20. Вычислите 2 log ₂ 5 + log ₂ 0,04

Решение………………………………………………………………………………………

1) — 1 2) 0 3) log ₂5 4) 3

21. Укажите значение выражения

Решение………………………………………………………………………………………

1) — 1 2) 1 3) 4) —

22. Вычислите log ₅ 250 – 2 log ₅ 10

Решение………………………………………………………………………………………

1) 1 – log ₅2 2) 0 3) 8 + log ₅2 4) 2

23. Укажите значение выражения log ₂ 48 + log ₂

Решение………………………………………………………………………………………

1) – 4,5 2) 5,5 3) 3 4) 4,5

24. Укажите значение выражения

Решение………………………………………………………………………………………

1) 0 2) 4 3) log ₂3 — 2 4) – 4 + log _0,53

25. Упростите выражение lg — lg

Решение………………………………………………………………………………………

1) lg2 2) 0,5 3) 3 4) 3lg5 + 1

26. Упростите выражение lg 75 + lg 45 + lg

Решение………………………………………………………………………………………

1) lg3 2) 0 3) 4 lg3 4) 5 lg3

27. Укажите значение выражения log ₇ 1 — log ₇ 3,5 + log ₇

Решение………………………………………………………………………………………

1) 0 2) 2 3) 4log ₇2 4) 4

28. Упростите выражение 2^log₂⁷

Решение………………………………………………………………………………………

1) – 3,5 2) 14 3) — 14 4) 3,5

29. Упростите выражение 5^log ₅³

Решение………………………………………………………………………………………

1) 0,375 2) 24 3) 1 4) 9

30. Упростите выражение 6^log ₆¹⁵

Решение………………………………………………………………………………………

1) – 15 2) 3 3) — 3 4) 15

31. Упростите выражение 7^log₇² :

Решение………………………………………………………………………………………

1) 1 2) — 1 3) 4) —

32. Укажите значение выражения log ₆ 48 – log ₆ 4 + log ₆ 3

Решение………………………………………………………………………………………

1) 47 2) 2 3) 36 4) 4

33. Найдите значение выражения 27 ^{1 – log}₃⁶ – 4 ^{– log}₄^0,125

Решение………………………………………………………………………………………

1) 0 2) 7,875 3) – 7,875 4) – 3,875

34. Вычислите log _0,25 0,64 + log _0,25 10

Решение………………………………………………………………………………………

1) — 3 2) — 2 3) 3 4) 2

35. Найдите значение выражения

Решение………………………………………………………………………………………

1) 6 2) 8 3) 9 4) 12

36. Вычислите log ₂ 0,032 + 3 log ₂ 5

Решение………………………………………………………………………………………

1) 1 2) 2 3) 3 4) 4

37. Вычислите log ₆ 108 — log ₆ 24

Решение………………………………………………………………………………………

1) 1 2) 1,5 3) log ₆ 4,5 4) log ₆ 9

39. Вычислите log ₆ 0,36 – log ₆ 0,216

Решение………………………………………………………………………………………

1) — 1 2) 0 3) 1 4) log ₆ 10

40. Упростите выражение log ₁₂ 36 + log ₁₂ 48

Решение………………………………………………………………………………………

1) 3 2) 4 3) 5 4) 2 + log ₁₂44

41. Упростите выражение 0,5 log ₂ 25 + log ₂ 1,6

Решение………………………………………………………………………………………

1) 5 2) 2 3) 3 4) 1

42. Найдите значение выражения 9 ^{3 – log}₃¹⁰⁸ + 7 ^{– 4 log} ₇²

Решение………………………………………………………………………………………

1) 0,125 2) 0,25 3) 0,5 4) 1

43. Найдите значение выражения ( 8^{2 – log}₂⁶ + 5 ^{– log}₅²⁷) ^{– 1}

Решение………………………………………………………………………………………

1) 3 2) 2 3) 0,5 4) 9

44. Найдите значение выражения ( 12^{2 – 3 log} ₁₂⁶ + 7 ^{– 2 log} ₄₉³) ^{– 1}

Решение………………………………………………………………………………………

1) 3 2) 1 3) 0,5 4) 4

45. Найдите значение выражения log _{7 ,} если log ₇b = 2,5

Решение………………………………………………………………………………………

1) 4,5 2) 46,5 3) — 0,5 4) — 4,5

46. Найдите значение выражения log ₅ (125m)_, если log ₅m = — 1,5

Решение………………………………………………………………………………………

1) 1,5 2) 123,5 3) — 1,5 4) — 4,5

47. Найдите значение выражения log ₅ (m³)_, если log ₃m = — 4,5

Решение………………………………………………………………………………………

1) — 7,5 2) — 13,5 3) — 1,5 4) — 4,5

48. Найдите значение выражения log ₂ (16k)_, если log ₂k = — 3,4

Решение………………………………………………………………………………………

1) -7,4 2) 12,6 3) – 19,4 4) 0,6

49. Найдите значение выражения log _{4 ,} если log ₄C= 1,5

Решение………………………………………………………………………………………

1) – 254,5 2) — 5,5 3) — 2,5 4) — 257,5

50. Найдите значение выражения log ₆ (m⁵)_, если log ₆m = — 0,5

Решение………………………………………………………………………………………

1) — 3 2) 4,4 3) — 5,6 4) 0,6

51. Найдите значение выражения log _{3 ,} если log ₃ X = 4,7

Решение………………………………………………………………………………………

52. Найдите значение выражения log ₄(16b)_, если log ₄b² = 9, b>0

Решение………………………………………………………………………………………

1) 6,5 2) 8,5 3) 5 4) 7

53. Найдите значение выражения log ₅(25b)_, если 2 log ₅b² = 16, b>0

Решение………………………………………………………………………………………

1) 9 2) 8 3) 6 4) 4

54. Найдите значение выражения log ₅ (625m²)_, если log ₅m = — 1,2

Решение………………………………………………………………………………………

1) 627,4 2) — 6,4 3) — 9,6 4) 1,6

55. Найдите значение выражения log _{6 ,} если log ₆ X = — 1,5

Решение………………………………………………………………………………………

1) – 2,5 2) 6,5 3) 40,5 4) — 6,5

56. Найдите значение выражения lg_, если lgC= — 0,7

Решение………………………………………………………………………………………

1) – 2,2 2) — 6,2 3) 2,2 4) 6,2

57. Найдите значение выражения log ₃ (9m)_, если log ₃m³ = 12

Решение………………………………………………………………………………………

1) 13 2) 6 3) 0,5 4) 8

58. Найдите значение выражения log ₄(16b)_, если log ₄b² = 9, b>0

Решение………………………………………………………………………………………

1) 6,5 2) 8,5 3) 5 4) 7

59. Найдите значение выражения log ₅(25b)_, если 2 log ₅b² = 16, b>0

Решение………………………………………………………………………………………

1) 9 2) 8 3) 6 4) 4

60. Найдите значение выражения log ₂ (8b)_, если log ₂ (16b) = 16

Решение………………………………………………………………………………………

1) 1 2) 24 3) 8 4) 16

61. Найдите значение выражения log ₃ (9b)_, если log ₃ (27b) = 27

Решение………………………………………………………………………………………

1) 27 2) 3 3) 26 4) 4

62. Найдите значение выражения log ₃ ² C_, если log ₃(3C) = 3

Решение………………………………………………………………………………………

1) 1 2) 9 3) 3 4) 4

63. Найдите значение выражения log ₂ ² X_, если log ₂(2X) = 6

Решение………………………………………………………………………………………

1) 25 2) 10 3) 36 4) 9

64. Найдите значение выражения log _x81_, если = 2

Решение………………………………………………………………………………………

1) — 0,25 2) 0,5 3) 1 4) 0,5

65. Найдите значение выражения log _x27_, если = 2

Решение………………………………………………………………………………………

1) — 3 2) 1,5 3) 2 4) 3

66. Найдите значение выражения log _x25_, если = 4

Решение………………………………………………………………………………………

1) 2) 3) 2 4) 3

67. Найдите значение выражения log _x6_, если = 4

Решение………………………………………………………………………………………

1) 216 2) 6 3) 0,25 4) 0

68. Найдите значение выражения log _x81_, если = 4

Решение………………………………………………………………………………………

1) 0,25 2) – 0,25 3) 0,5 4) 9

Уровень В

В данном разделе необходимо написать полное решение задания. В ответе должно получится либо целое число, либо конечная десятичная дробь

Вычислить:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

2. 2^log₂³

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

3. ( 3^log₃² )

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

4. log

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

7. ^log₃¹⁶⁹

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

8. log₆²27 +

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

10. lg²4 +

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

20. 0,9

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

21. 2,2

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

22. log ₆24 + log ₃₆216 + log ₆9 + ^log ₃¹⁶

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

23. log ₁₅75 + log ₂₂₅15 + log ₁₅45 + ^log ₂⁴⁹

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

25. log ₆4 + log ₃₆6 + log ₆9 + ^log ₃⁶⁴

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

30. lg 25 + lg

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

31. log ₃— log₃

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

32. log₇— log₇

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Решение:…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Ответ:

Найдите значение выражения log 5 b, если log 5 b4 = 16.



15) (2cos²x -3cosx-2)*Loq_3 (tqx) =0 
А)
15₁) 2cos²x -3cosx-3=0   и    tqx >0
cosx =(3+sqrt(3²-4*2*(-2))/(2*2) = 2  нет решения
cosx =(3-sqrt(3²-4*2*(-2))/(2*2)= -1/2   и    tqx >0
  x =-(«+»)/(«-«) 2π/3 +2π*k   и    tqx >0
x =  4π/3 + 2π*k   ; k ∈ Z
15₂) tqx =1
   x=π/4 +π*k ;  k∈ Z

ответ : 4π/3 + 2π*k ;π/4 +π*k

Б)  x ∈ [ π/2 ; 2π ]
    4π/3   из    x  =  4π/3 + 2π*k  ,  при  k =  0  и
     5π/4  из    x  =π/4 +π*k   ,      при  k =1
ответ : 5π/4  ; 4π/3

6 месяцев назад

1 — 2/5=3/5часть массы сахарного песка остается для рафинада

26:3/5=26*5/3=130/3=43 1/3 кг нужно взять сахарного песка, чтобы 

получить 26 кг рафинада

а) Очевидно, что 14:3=4 (ост. 2) Это означает, что если бы каждой из  купюр одинакового достоинсктва было бы 4, то еще 2 остались бы, значит 4+1 = 5 -может быть пять купюр одинакового достоинства;

б) 4+2 = 6 — может быть шесть купюр одинакового достоинства

6 месяцев назад

один пешком, а другой на велосипеде. в то же время из в в а выехал автомобиль, который встретился

Настасья петровна коробочка — помещица, вдова коллежского секретаря, хозяйственная и бережливая пожилая женщина. деревушка ее невелика, но все в ней исправно, хозяйство расцветает и, видно, приносит неплохой доход. коробочка выгодно отличается от манилова: она знает всех своих крестьян («…не вела никаких записок, ни списков, а знала почти всех наизусть») , отзывается о них как о хороших работниках, сама занимается хозяйством.  поведение коробочки, ее обращение к гостю «батюшка» , стремление услужить (чичиков назвал себя дворянином) , попотчевать, устроить на ночлег как можно лучше — все это характерные черты образов провинциальных помещиков.   портрет коробочки не столь подробен, как портреты других помещиков и как бы растянут: сначала чичиков слышит «хриплый бабий голос» старухи-служанки; затем «опять какая-то женщина, прежней, но на нее похожая» ; когда его проводили в комнаты и он успел осмотреться, вошла барыня — «женщина пожилых лет, в каком-то спальном чепце, надетом наскоро, с фланелью на шее. автор подчеркивает старость коробочки, дальше чичиков про себя прямо называет ее старухой. внешний вид хозяйки утром особенно не меняется — исчезает только спальный чепец.  именно такова и коробочка, поэтому чичиков сразу же не особенно церемонится и переходит к делу.  важную роль в понимании образа помещицы играет описание поместья и убранства комнат в доме.   поместье коробочки отличается крепостью и довольством, сразу видно, что она хорошая хозяйка. двор, на который выходят окна комнаты, заполнен птицами и «всякой тварью» ; далее видны огороды с «хозяйственным овощем» ; фруктовые деревья накрыты сетями от птиц, видны и чучела на шестах — «на одном из них надет был чепец самой хозяйки» . крестьянские избы тоже показывают достаток их обитателей. словом, хозяйство коробочки явно процветает и приносит достаточную прибыль. да и сама деревенька не маленькая — восемьдесят душ. в кратком описании комнат в первую очередь отмечается старинность их убранства: «комната была обвешана старенькими полосатыми обоями; картины с какими-то птицами; между окон старинные маленькие зеркала с темными рамками в виде свернувшихся листьев; за всяким зеркалом заложены были или письмо, или старая колода карт, или чулок; стенные часы с нарисованными цветами на циферблате…» .  чичикову на глаза во время краткого осмотра, также указывает на то, что люди, обитающие в таких комнатах, больше обращены к прошлому, чем к нынешнему.  в беседе по поводу покупки «мертвых» душ раскрывается вся сущность и характер коробочки. сначала она никак не может понять, чего хочет от нее чичиков. когда же она понимает, что сделка может быть выгодна для нее, то недоумение сменяется другим — стремлением получить максимальную выгоду от продажи: ведь если кто-то хочет купить мертвых, следовательно, они чего-то стоят и являются предметом торга. то есть мертвые души становятся для нее в один ряд с пенькой, медом, мукой и салом. но все прочее она уже продавала (как мы знаем, довольно выгодно) , а это дело для нее новое и неизвестное. срабатывает желание не продешевить: «начала сильно побаиваться, чтобы как-нибудь на надул ее этот покупщик» , своей упертостью она выводит из себя чичикова, который рассчитывал на легкое согласие. тут-то и возникает эпитет, которые выражает сущность не только коробочки, а всего типа подобных людей — «дубинноголовая» . автор поясняет, что ни чин, ни положение в обществе не являются причиной такого свойства, «дубиноголовость» — явление весьма распространенное: «иной и почтенный, и государственный даже человек. а на деле выходит совершенная коробочка. как зарубил что бабе в голову, так уж ничем его не пересилишь; сколько не представляй ему доводов, ясных как день, все отскакивает от него, как резиновый мяч отскакивает от стены» . 

хитрых вопросов на основе правил журнала

Purplemath

Основные правила ведения журнала следующие:

1) журнал _b ( mn ) = журнал _b ( m ) + журнал _b ( n )

2) журнал _b ( ^м / _n ) = журнал _b ( м ) — журнал _b ( n )

3) журнал _b ( м ⁿ ) = n · журнал _b ( м )

Вы должны ожидать, что вам потребуется знать основные правила журнала, потому что есть определенный тип вопросов, которые учитель может задать в тесте, чтобы убедиться, что вы знаете правила и знаете, как использовать правила .

Предупреждение: если вы обнаружите один из этих вопросов с подвохом во время следующего теста, вы не сможете «обмануть» свой путь к ответу с помощью калькулятора , а не . Если вы не знаете правил журнала, вы — тост.

MathHelp.com

---

Хорошо, давайте погрузимся в эти уловки.

• Пусть log

  _b (2) = 0,3869, log _b (3) = 0,6131 и log _b (5) = 0,8982. Используя эти значения, оцените log _b (10).

Уловка в выполнении этого упражнения состоит в том, чтобы заметить, что они попросили меня найти что-то (а именно, журнал десяти), который можно создать из того, что они мне дали (а именно, журнала двух и пяти).

Мне просто нужно выяснить, как применить правила журнала, чтобы учесть замены, которые мне нужно будет сделать. Итак:

Поскольку 10 = 2 × 5, и поскольку они дали мне журналы 2 и 5, тогда мне будет полезно превратить 10 в произведение 2 и 5, а затем использовать правило журнала для разделения журнала с умножением внутри на добавление двух логарифмических выражений. Другими словами:

Поскольку они дали мне значения для журнала _b (2) и журнала _b (5), теперь я могу заменить и оценить:

журнал _b (2) + журнал _b (5)

= 0. 3869 + 0,8982

= 1,2851

Тогда:

---

• Пусть log

  _b (2) = 0,3869, log _b (3) = 0,6131 и log _b (5) = 0,8982. Используя эти значения, оцените log _b (9).

Они попросили у меня журнал 9; они дали мне (среди прочего) журнал 3.Поскольку 9 = 3 ² , то я могу преобразовать «9» в «3 ² », а затем применить правило журнала, которое перемещает степень внутри журнала в множитель перед журналом.

Поскольку у меня есть значение log _b (3), то я могу заменить и оценить:

Тогда:

---

• Пусть log

  _b (2) = 0. 3869, log _b (3) = 0,6131 и log _b (5) = 0,8982. Используя эти значения, оцените log _b (7.5).

Это немного сложнее, но, немного поиграв с числами, я заметил, что 7,5 = 15 ÷ 2. «И что?», Спросите вы. Что ж, я могу создать 15 из 3 и 5, и они дали мне значения для журналов 3 и 5. И с делением на 2 легко справиться, потому что они дали мне значение для журнала 2 .Итак:

журнал _b (7,5)

= журнал _b (15 ÷ 2)

= журнал _b (15) — журнал _b (2)

И 15 = 5 × 3, поэтому:

журнал _b (15) — журнал _b (2)

= [журнал _b (5) + журнал _b (3)] — журнал _b (2)

= журнал _b (5) + журнал _b (3) — журнал _b (2)

А теперь могу заменить и оценить:

журнал _b (5) + журнал _b (3) — журнал _b (2)

= 0. 8982 + 0,6131 — 0,3869

= 1,124

Тогда:

---

• Пусть log

  _b (2) = 0,3869, log _b (3) = 0,6131 и log _b (5) = 0,8982. Используя эти значения, оцените log _b (6).

Так как 6 = 2 × 3, то:

Поскольку у меня есть эти значения, я могу оценить:

журнал _b (2) + журнал _b (3)

= 0.3869 + 0,6131

= 1,0000

Тогда:

---

Хм … это было интересно. Я получил этот журнал _b (6) = 1. Используя отношение для журналов, я получаю:

Итак, теперь я знаю, что их таинственная безымянная база «b» на самом деле была 6. Но они обычно не доставляют вам проблем, которые позволят вам определить базу таким образом.Фактически, они могут задать вам вопросы, для которых математика даже не поможет. Например:

• Пусть log

  _b (2) = 0,4, log _b (3) = 0,6, log _b (4) = 0,75 и log _b (7) = 1,3. Используя эти значения, оцените log _b (21).

Выполнить эту оценку несложно. Они дали мне записи 3 и 7, а 21 = 3 × 7, поэтому:

журнал _b (21) = журнал _b (3 × 7)

= журнал _b (3) + журнал _b (7)

= 0. 6 + 1,3 = 1,9

Тогда:

Однако посмотрите на другую информацию, которую они включили в это упражнение. Значение журнала 4 должно следовать из значения журнала 2, потому что 4 = 2 ² . Но посмотрите:

журнал _b (4) = журнал _b (2 ² )

= 2 · журнал _b (2)

= 2 · 0.4 = 0,8

Это , а не значение, которое они дали мне для журнала _b (4). Они сказали, что log _b (4) = 0,75. Как дела?

Что ж, они хотели проверить, действительно ли я знаю правила журнала достаточно хорошо, чтобы сразу перейти к оценке. Ясно, что эти «значения» журнала не связаны с какой-либо реальной базой; автор упражнения просто выбрал несколько случайных значений. «Правильный» ответ на вопрос не является математически верным, поскольку они все равно не работали с каким-либо конкретным журналом; «Правильный» ответ является результатом правильного применения правил журнала, для проверки чего и предназначен этот тип вопросов.

---

Если вы чувствуете себя некомфортно из-за того, как правила журнала использовались в приведенном выше упражнении, то вы можете повторно изучить правила и то, как они работают. Вы можете начать здесь.

В противном случае перейдем к последнему правилу журнала….

---

URL: https://www.purplemath.com/modules/logrules4.htm

Два приведенных ниже выражения имеют одинаковое значение при округлении до ближайшей сотой. Log5 b log9 48

Какой масштабный коэффициент был использован для создания треугольника J′K′L ′?

В судебном деле Либек против Макдональдса (1994 г. ) женщина подала в суд на ресторан Макдональдс за подачу кофе при температуре 180 °, из-за чего ей было плохо.
…

сильно обгорел, когда пролился кофе.Свидетель-эксперт на суде показал, что жидкость под углом 180 ° вызовет полный ожог кожи человека в течение двух-семи секунд. Было заявлено, что если бы кофе был подан при температуре 155 °, жидкость остыла бы и избежала серьезных ожогов. Женщине вручили более 2,7 миллиона долларов. Из-за этого знаменитого случая во многих ресторанах сейчас подают кофе с температурой около 155 °.
Функция ниже моделирует температуру кофе:
Т (м) = 108e-0,018 м + 72
а) Определите алгебраическим путем, сколько времени с точностью до сотых долей минуты потребуется McDonald’s ждать, чтобы подать кофе при температуре 155 °?
б) Объясните, что представляет каждое из чисел в функции.в) До какой температуры кофе приблизится со временем?

Найдите модальное значение (режим) следующего частотного распределения.

Селин готовится к марафонскому бегу. Во время тренировки она отслеживала, сколько времени она потратила на бег на беговой дорожке внутри помещения и на тропу.
…

каждую неделю. Эти диаграммы показывают результаты.

помогу

На этих выходных распродажа мебели Mavity.
До уплаты налогов, расходы получают
500 долларов.00–999,99 долл. США Скидка 100,00 долл. США
1000–1999,99 долларов Скидка 250,00 долларов США
2 000,00 долл. США
…

или более $ 750.00 со скидкой
Г-жа Марнер купила конференц-стол и стулья за 1860 долларов без учета налогов и скидок. Г-жа Ким купила кабинки за 5 775 долларов без учета налогов и скидок. Ставка налога составляет 8,2%.
После уплаты налогов г-жа
Ким
получил большее процентное снижение
____% из-за продажи. Разница между процентным снижением, полученным каждым покупателем после уплаты налогов, составляет
____%.

Какое выражение эквивалентно 4 (7 / 8y — 4 — 3 / 8y + 7)

Каков объем следующей прямоугольной призмы?

На рисунке выше изображена прямоугольная пирамида. Укажите, является ли каждая из следующих форм возможным двумерным поперечным сечением
…

пирамида.
Поставьте только одну галочку в каждой строке таблицы ниже.
Форма
Возможное поперечное сечение пирамиды
Возможно ли поперечное сечение пирамиды
Равнобедренный треугольник
Квадрат
Круг
Трапеция

Координаты J (2,2) k (-1,3) L (-2, -1) образуют прямоугольный треугольник. правда или ложь

4.5E: Упражнения — Свойства логарифмов

71.3}}) \)

Решение экспоненциальных и логарифмических уравнений · Промежуточная алгебра

Решение экспоненциальных и логарифмических уравнений · Промежуточная алгебра

К концу этого раздела вы сможете:

• Решите логарифмические уравнения, используя свойства логарифмов
• Решите экспоненциальные уравнения с помощью логарифмов
• Использование экспоненциальных моделей в приложениях

Перед тем, как начать, пройдите тест на готовность.

1. Решить:
   х2 = 16.

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

2. Решить:
   х2−5х + 6 = 0.

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

3. Решить:
   х (х + 6) = 2х + 5.

   ---

   Если вы пропустили эту проблему, просмотрите [ссылка].

Решите логарифмические уравнения, используя свойства логарифмов

В разделе, посвященном логарифмическим функциям, мы решили некоторые уравнения, переписав уравнение в экспоненциальной форме.Теперь, когда у нас есть свойства логарифмов, у нас есть дополнительные методы, которые мы можем использовать для решения логарифмических уравнений.

Если в нашем уравнении есть два логарифма, мы можем использовать свойство, которое говорит, что если logaM = logaN

, то верно, что M = N.

Это однозначное свойство логарифмических уравнений .

Однозначное свойство логарифмических уравнений

Для M> 0, N> 0, a> 0,

и 1

— любое действительное число:

Если logaM = logaN, то M = N.

Чтобы использовать это свойство, мы должны быть уверены, что обе части уравнения записаны с одинаковым основанием.

Помните, что логарифмы определены только для положительных действительных чисел. Проверьте свои результаты в исходном уравнении. Возможно, вы получили результат, который дает нулевой логарифм или отрицательное число.

2log5x = log581 Используйте свойство Power. Log5x2 = log581 Используйте свойство One-to-One, iflogaM = logaN, x2 = 81thenM = N. Решите с помощью свойства квадратного корня.x = ± 9 Мы исключаем x = −9, так как мы не можем взять логарифм x = 9, x = −9 отрицательного числа. Check.x = 92log5x = log5812log59 =? log581log592 =? log581log581 = log581 ✓

Еще одна стратегия решения логарифмических уравнений — это сжатие сумм или разностей в один логарифм.

Решите: log3x + log3 (x − 8) = 2.

log3x + log3 (x − 8) = 2 Используйте свойство Product, logaM + logaN = logaM⋅N.log3x (x − 8) = 2 Перепишите в экспоненциальной форме. 32 = x (x − 8) Упростите. 9 = x2−8x Вычтите 9. с каждой стороны.0 = x2−8x − 9Factor.0 = (x − 9) (x + 1) Используйте свойство нулевого произведения. X − 9 = 0, x + 1 = 0 Решите каждое уравнение. X = 9, x = −1 Проверьте. x = −1log3x + log3 (x − 8) = 2log3 (−1) + log3 (−1−8) =? 2 Мы не можем взять журнал отрицательного числа. x = 9log3x + log3 (x − 8) = 2log39 + log3 (9-8) =? 22 + 0 =? 22 = 2 ✓

Решите: log2x + log2 (x − 2) = 3

х = 4

Решите: log2x + log2 (x − 6) = 4

х = 8

Если на обеих сторонах есть логарифмы, мы конденсируем каждую сторону в один логарифм.Не забудьте использовать свойство Power по мере необходимости.

Решите: log4 (x + 6) −log4 (2x + 5) = — log4x.

log4 (x + 6) −log4 (2x + 5) = — log4x Используйте свойство Quotient слева и свойство PowerProperty справа. log4 (x + 62x + 5) = log4x − 1 Rewritex − 1 = 1x.log4 (x + 62x + 5) = log41x Используйте свойство «один к одному», если logaM = logaN, то M = N.x + 62x + 5 = 1x Решите рациональное уравнение. X (x + 6) = 2x + 5Distribute.x2 + 6x = 2x + 5 Запишите в стандартной форме. X2 + 4x − 5 = 0Factor. (X + 5) (x − 1) = 0 Используйте свойство нулевого произведения. X + 5 = 0, x − 1 = 0 Решите каждое уравнение.x = −5, x = 1Check. Мы оставляем вам чек.

Решить: log (x + 2) −log (4x + 3) = — logx.

х = 3

Решить: log (x − 2) −log (4x + 16) = log1x.

х = 8

Решите экспоненциальные уравнения с помощью логарифмов

В разделе, посвященном показательным функциям, мы решили некоторые уравнения, записав обе части уравнения с одинаковым основанием. Затем мы написали новое уравнение, установив равные степени.

Не всегда возможно или удобно писать выражения с одной и той же базой.В этом случае мы часто используем десятичный или натуральный логарифм обеих сторон, если экспонента изолирована.

Решите 5x = 11.

Найдите точный ответ и округлите его до трех десятичных знаков.

5x = 11 Так как экспонента изолирована, возьмите логарифм обеих сторон. Log5x = log11 Используйте свойство Power, чтобы получить x как множитель, а не показатель. Xlog5 = log11 Найдите точный ответ. X = log11log5Приблизительно ответ. X≈1 .490 Поскольку 51 = 5 и 52 = 25, имеет ли смысл, что 51,490≈11?

Решите 7x = 43.

Найдите точный ответ и округлите его до трех десятичных знаков.

х = log43log7≈1,933

Решите 8x = 98.

Найдите точный ответ и округлите его до трех десятичных знаков.

х = log98log8≈2,205

Когда мы возьмем логарифм обеих сторон, мы получим один и тот же результат независимо от того, используем ли мы общий или натуральный логарифм (попробуйте использовать натуральный логарифм в последнем примере.Вы получили тот же результат?) Когда экспонента имеет основание e , мы используем натуральный логарифм.

Решите 3ex + 2 = 24.

Найдите точный ответ и округлите его до трех десятичных знаков.

3ex + 2 = 24 Выделите экспоненту, разделив обе части на 3. ex + 2 = 8 Возьмите натуральный логарифм обеих частей. Lnex + 2 = ln8 Используйте свойство Power, чтобы получить x как множитель, а не экспоненту. (X + 2) lne = ln8 Используйте свойство lne = 1 для упрощения. x + 2 = ln8 Решите уравнение.Найдите точный ответ. X = ln8−2Приблизительный ответ. X≈0,079

Решите 2ex − 2 = 18.

Найдите точный ответ и округлите его до трех десятичных знаков.

х = ln9 + 2≈4,197

Решите 5e2x = 25.

Найдите точный ответ и округлите его до трех десятичных знаков.

х = ln52≈0,805

Использование экспоненциальных моделей в приложениях

В предыдущих разделах мы смогли решить некоторые приложения, которые были смоделированы с помощью экспоненциальных уравнений. Теперь, когда у нас есть намного больше вариантов решения этих уравнений, мы можем решать больше приложений.

Мы снова будем использовать формулы сложного процента, поэтому мы перечисляем их здесь для справки.

Сложный процент

Для основного долга P , инвестированного под процентную ставку r , на t лет, новый баланс A составляет:

A = P (1 + rn) n, когда начисляется раз в год. A = Pert, когда компаундируется непрерывно.

Родители Джермаэля вложили 10 000 долларов в его колледж в его первый день рождения. Они надеются, что вложения будут стоить 50 000 долларов, когда ему исполнится 18 лет. Если проценты будут постоянно расти, какие приблизительно темпы роста им понадобятся для достижения своей цели?

A = 50 000 долларов P = 10 000 долларов. Определите переменные в формуле. R =? T = 17yearsA = Pert. Подставьте значения в формулу. 50 000 = 10 000er · 17. Найдите формулу. Разделите каждую сторону на 10 000,5 = e17r. Возьмите натуральный логарифм каждой стороны.ln5 = lne17r Используйте свойство Power. ln5 = 17rlneSimplify.ln5 = 17rРазделите каждую сторону на 17.ln517 = rПриблизительный ответ.r≈0,095Преобразовать в проценты.r≈9,5% Им нужна скорость роста примерно 9,5%.

Гектор инвестирует 10 000 долларов

в возрасте 21 года. Он надеется, что инвестиции будут стоить 150 000 долларов.

, когда ему исполнится 50. Если проценты будут постоянно расти, то какой примерно темп роста ему потребуется для достижения своей цели?

r≈9.3%

Рэйчел инвестирует 15000 долларов

в возрасте 25 лет. Она надеется, что инвестиции составят 90 000 долларов.

, когда ей исполняется 40 лет. Если интерес постоянно растет, примерно с какой скоростью она должна расти, чтобы достичь своей цели?

r≈11,9%

Мы видели, что рост и распад моделируются экспоненциальными функциями. Для роста и распада мы используем формулу A = A0ekt.

Экспоненциальный рост имеет положительную скорость роста или константу роста, k

и экспоненциального распада имеет отрицательную скорость роста или константу распада, k .

Экспоненциальный рост и распад

На первоначальную сумму, A0,

, которое увеличивается или уменьшается со скоростью k , в течение определенного времени, t , окончательная сумма, A , составляет:

А = А0ект

Теперь мы можем решать приложения, которые дают нам достаточно информации, чтобы определить скорость роста. Затем мы можем использовать эту скорость роста для прогнозирования других ситуаций.

Исследователи зафиксировали, что определенная популяция бактерий выросла со 100 до 300 за 3 часа.При такой скорости роста сколько бактерий будет через 24 часа после начала эксперимента?

Эта проблема требует двух основных шагов. Сначала мы должны найти неизвестную скорость, k . Затем мы используем это значение k , чтобы помочь нам найти неизвестное количество бактерий.

Определите переменные в формуле. A = 300A0 = 100k =? T = 3hoursA = A0ekt Подставьте значения в формулу. 300 = 100ek · 3Solve fork. Разделите каждую сторону на 100,3 = e3k. Возьмите натуральный логарифм каждой стороны.ln3 = lne3k Используйте свойство Power. ln3 = 3klneSimplify.ln3 = 3k Разделите каждую сторону на 3. ln33 = kПриблизительный ответ. k≈0,366 Мы используем эту скорость роста, чтобы предсказать количество бактерий, которые появятся в течение 24 часов. A =? A0 = 100k = ln33t = 24 часа A = A0ekt Замените значениями. A = 100eln33 · 24Evaluate.A≈656,100 При такой скорости роста они могут ожидать 656,100 бактерий.

Исследователи зафиксировали, что определенная популяция бактерий выросла со 100 до 500 за 6 часов. При такой скорости роста сколько бактерий будет через 24 часа после начала эксперимента?

Будет 62 500 бактерий.

Исследователи зафиксировали, что определенная популяция бактерий сократилась с 700 000 до 400 000 за 5 часов после приема лекарств. При такой скорости разложения сколько бактерий будет через 24 часа после начала эксперимента?

Будет 5 870 061 бактерия.

Радиоактивные вещества распадаются или разлагаются по формуле экспоненциального распада. Время, необходимое для того, чтобы вещество распалось до половины своего первоначального количества, называется периодом полураспада вещества .

Как и в предыдущем примере, мы можем использовать данную информацию для определения константы распада, а затем использовать эту константу для ответа на другие вопросы.

Период полураспада радия-226 составляет 1590 лет. Сколько образца 100 мг останется через 500 лет?

Эта проблема требует двух основных шагов. Сначала мы должны найти постоянную распада k . Если мы начнем со 100 мг, в период полувыведения останется 50 мг. Мы будем использовать эту информацию, чтобы найти k .Затем мы используем это значение k , чтобы помочь нам найти количество образца, которое останется через 500 лет.

Определите переменные в формуле. A = 50A0 = 100k =? T = 1590yearsA = A0ekt Подставьте значения в формулу. 50 = 100ek · 1590Solve fork. Разделите каждую сторону на 100.0.5 = e1590k. Возьмите натуральный логарифм каждой стороны. Ln0. 5 = lne1590k Используйте свойство Power.ln0.5 = 1590klneSimplify.ln0.5 = 1590k Разделите каждую сторону на 1590.ln0,51590 = kexact answer Мы используем эту скорость роста, чтобы предсказать количество, которое останется через 500 лет.A =? A0 = 100k = ln0,51590t = 500 лет A = A0ekt Замените значения. A = 100eln0,51590 · 500Evaluate.A≈80,4 мг Через 500 лет останется примерно 80,4 мг.

Период полураспада магния-27 составляет 9,45 минут. Сколько образца 10 мг останется через 6 минут?

Остается 6,43 мг.

Период полураспада радиоактивного йода составляет 60 дней. Сколько образца 50 мг останется через 40 дней?

Будет 31.Осталось 5 мг.

Ключевые понятия

• Однозначное свойство логарифмических уравнений: Для
  M> 0, N> 0, a> 0,

  и

  a ≠ 1

  — любое действительное число:

  ---

  Если logaM = logaN, то M = N.

• Сложные проценты:
  

  ---

  Для основного долга P , инвестированного под процентную ставку r , на t лет, новый баланс A составляет:

  ---

  A = P (1 + rn) n, когда складывается раз в год.A = Pert при непрерывном смешивании.

• Экспоненциальный рост и спад: Для исходной суммы,
  A0

  , который растет или убывает со скоростью r , в течение определенного времени t , окончательная сумма A составляет

  A = A0ert.

Упражнения по разделам

Практика ведет к совершенству

Решение логарифмических уравнений с использованием свойств логарифмов

В следующих упражнениях решите x .

log3 (x2 + 3) = log34x

х = 1, х = 3

журнал (x + 4) −log (5x + 12) = — журнал x

журнал (x − 1) −log (x + 3) = log1x

х = 3

log5 (x + 3) + log5 (x − 6) = log510

.

log5 (x + 1) + log5 (x − 5) = log57

.

х = 6

log3 (2x − 1) = log3 (x + 3) + log33

.

журнал (5x + 1) = журнал (x + 3) + журнал2

х = 53

Решите экспоненциальные уравнения с помощью логарифмов

В следующих упражнениях решите каждое экспоненциальное уравнение.Найдите точный ответ и округлите его до трех десятичных знаков.

2x = 74

х = log74log2≈6,209

4x = 112

х = log112log4≈3,404

(13) х = 8

х = log8log13≈ − 1,893

3ex + 2 = 9

х = ln3−2≈ − 0,901

пример − 1 + 4 = 12

х = ln8 + 1≈3,079

В следующих упражнениях решите каждое уравнение.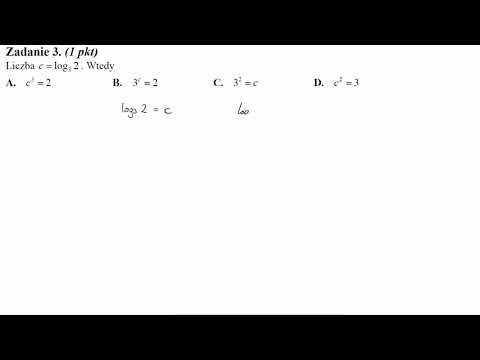

log2 (x + 2) −log2 (2x + 9) = — log2x

log6 (x + 1) −log6 (4x + 10) = log61x

х = 5

В следующих упражнениях решите для x , дав точный ответ, а также приближение к трем десятичным знакам.

(12) х = 10

х = log10log12≈-3,322

8ex + 5 = 56

х = ln7−5≈ − 3.054

Использование экспоненциальных моделей в приложениях

В следующих упражнениях решите.

Сунг Ли инвестирует 5000 долларов

в 18 лет. Он надеется, что инвестиции будут стоить 10 000 долларов

.

, когда ему исполняется 25 лет. Если проценты постоянно растут, то какой примерно темп роста ему потребуется для достижения своей цели? Это разумное ожидание?

Алиса инвестирует 15000 долларов

в возрасте 30 лет от подписного бонуса ее новой работы.Она надеется, что инвестиции составят 30 000 долларов

.

, когда ей исполняется 40 лет. Если интерес постоянно растет, примерно с какой скоростью она должна расти, чтобы достичь своей цели?

6,9%

Coralee инвестирует 5000 долларов

на счете, ежемесячно начисляющем проценты и приносящем 7%.

Сколько времени потребуется, чтобы ее деньги удвоились?

Simone инвестирует 8000 долларов

на счете, на котором ежеквартально начисляются проценты и приносят 5%.

Сколько времени потребуется, чтобы его деньги удвоились?

Исследователи зафиксировали, что определенная популяция бактерий сократилась со 100 000 до 100 за 24 часа. При такой скорости разложения сколько бактерий будет за 16 часов?

Исследователи зафиксировали, что определенная популяция бактерий сократилась с 800 000 до 500 000 за 6 часов после приема лекарств. При такой скорости разложения сколько бактерий будет за 24 часа?

Вирусу требуется 6 дней, чтобы удвоить его первоначальную популяцию (A = 2A0).

Сколько времени потребуется, чтобы утроить его население?

Бактерия удваивает свою первоначальную популяцию за 24 часа (A = 2A0).

Насколько большим будет его население через 72 часа?

В 8 раз больше, чем исходное население

Углерод-14 используется для археологического датирования углерода. Его период полураспада составляет 5730 лет. Сколько 100-граммового образца углерода-14 останется через 1000 лет?

Радиоактивный технеций-99m часто используется в диагностической медицине, поскольку он имеет относительно короткий период полураспада, но длится достаточно долго, чтобы провести необходимое тестирование на пациенте.Если его период полураспада составляет 6 часов, какое количество радиоактивного материала из 0,5 мл инъекции будет в организме за 24 часа?

Письменные упражнения

Объясните метод, который вы бы использовали для решения этих уравнений: 3x + 1 = 81,

3х + 1 = 75.

Требует ли ваш метод логарифмов для обоих уравнений? Почему или почему нет?

В чем разница между уравнением экспоненциального роста и уравнением экспоненциального убывания?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?

Упражнения для повторения главы

Поиск составных и обратных функций

Найти и оценить составные функции

В следующих упражнениях для каждой пары функций найдите ( f ∘ g ) ( x ), ⓑ ( g ∘ f ) ( x ) и ⓒ ( f · г ) ( х ).

f (x) = 7x − 2

и * * *

г (х) = 5x + 1

f (x) = 4x

и * * *

г (х) = х2 + 3х

ⓐ 4×2 + 12x

ⓑ 16×2 + 12x

ⓒ 4×3 + 12×2

В следующих упражнениях оцените композицию.

Для функций * * *

f (x) = 3×2 + 2

и * * *

g (x) = 4x − 3,

найти * * *

ⓐ (фут) (- 3)

---

ⓑ (g∘f) (- 2)

---

ⓒ (f∘f) (- 1)

Для функций * * *

f (x) = 2×3 + 5

и * * *

g (x) = 3×2−7,

найти * * *

ⓐ (фут) (- 1)

---

ⓑ (g∘f) (- 2)

---

ⓒ (г∘г) (1)

ⓐ −123

ⓑ 356 41

Определить, является ли функция однозначной

В следующих упражнениях для каждого набора упорядоченных пар определите, представляет ли он функцию, и если да, то функция взаимно однозначная.

{(−3, −5), (- 2, −4), (- 1, −3), (0, −2),

---

(−1, −1), (- 2,0), (- 3,1)}

{(−3,0), (- 2, −2), (- 1,0), (0,1),

---

(1,2), (2,1), (3, −1)}

{(−3,3), (- 2,1), (- 1, −1), (0, −3),

---

(1, −5), (2, −4), (3, −2 )}

В следующих упражнениях определите, является ли каждый график графиком функции, и если да, то взаимно однозначным.

ⓐ * * *

---

ⓑ * * *

ⓐ Функция; не один на один ⓑ Не функция

ⓐ * * *

---

ⓑ * * *

Найти обратную функцию

В следующем упражнении найдите функцию, обратную функции.Определите область и диапазон обратной функции.

{(−3,10), (- 2,5), (- 1,2), (0,1)}

Обратная функция: {(10, −3), (5, −2), (2, −1), (1,0)}.

Домен: {1,2,5,10}.

Диапазон: {−3, −2, −1,0}.

В следующем упражнении изобразите график, обратный показанной функции «один к одному».

! [На этом рисунке показан отрезок от (отрицательное 4, отрицательное 2) до (отрицательное 2, 1), затем до (2, 2) и затем до (3, 4).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_206_img. jpg)

В следующих упражнениях убедитесь, что функции являются обратными.

f (x) = 3x + 7

и * * *

г (х) = х − 73

g (f (x)) = x,

и f (g (x)) = x,

, поэтому они обратные.

f (x) = 2x + 9

и * * *

г (х) = х + 92

В следующих упражнениях найдите инверсию каждой функции.

f (х) = 6x − 11

f − 1 (х) = х + 116

f (х) = 1x + 5

f − 1 (x) = 1x − 5

Вычислить и построить график экспоненциальных функций

График экспоненциальных функций

В следующих упражнениях нарисуйте график каждой из следующих функций.

f (x) = 4x

! [На этом рисунке показана экспоненциальная линия, проходящая через точки (отрицательные 1, 1 на 4), (0, 1) и (1, 4).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_302_img.jpg)

г (х) = (0,75) х

! [На этом рисунке показана экспоненциальная линия, проходящая через точки (отрицательные 1, 4 на 3), (0, 1) и (1, 3 на 4). ] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_304_img.jpg )

f (x) = (2.3) х − 3

! [На этом рисунке показана экспоненциальная линия, проходящая через точки (отрицательная 1, отрицательная 59 на 23), (0, отрицательная 2) и (1, отрицательная 7 на 10).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_306_img .jpg)

f (x) = — пр.

! [На этом рисунке показана экспоненциальная линия, проходящая через точки (отрицательная 1, отрицательная 1 над e), (0, отрицательная 1) и (1, отрицательная e).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_308_img.jpg)

Решите экспоненциальные уравнения

В следующих упражнениях решите каждое уравнение.

Использование экспоненциальных моделей в приложениях

В следующих упражнениях решите.

Феликс вложил 12000 долларов

на сберегательном счете. Если процентная ставка 4%

сколько будет на учете через 12 лет по каждому методу начисления?

ⓐ сложный квартал * * *

ⓑ сложный месяц * * *

ⓒ соединение непрерывно.

Депозиты $ 20,000

на инвестиционном счете. Какова будет стоимость его инвестиций через 30 лет, если они принесут 7%

в год и постоянно накапливается?

163 323,40 долл. США

Исследователь Центра по контролю и профилактике заболеваний изучает рост бактерий. Она начинает свой эксперимент со 150 бактериями, которые растут со скоростью 15%

в час.Она будет проверять наличие бактерий каждые 24 часа. Сколько бактерий он обнаружит за 24 часа?

За последние пять лет население США выросло на 0,7%

в год до примерно 318 900 000 человек. Если так будет продолжаться, сколько будет населения через 5 лет?

Вычисление и графическое отображение логарифмических функций

Преобразование экспоненциальной формы в логарифмическую

В следующих упражнениях преобразуйте экспоненциальную форму в логарифмическую.

10−3 = 11 000

журнал11000 = −3

В следующих упражнениях преобразуйте каждое логарифмическое уравнение в экспоненциальную форму.

Вычислить логарифмические функции

В следующих упражнениях решите x .

В следующих упражнениях найдите точное значение каждого логарифма без использования калькулятора.

Графические логарифмические функции

В следующих упражнениях нанесите на график каждую логарифмическую функцию.

у = log5x

! [На этом рисунке показана логарифмическая линия, проходящая через точки (1 на 5, отрицательное значение 1), (1, 0) и (5, 1).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_309_img.jpg)

y = log0,8x

! [На этом рисунке показана логарифмическая линия, проходящая через точки (4 на 5, 1), (1, 0) и (5 на 4, отрицательное значение 1).] (/ Algebra-intermediate-book / resources / CNX_IntAlg_Figure_10_05_311_img. jpg )

Решение логарифмических уравнений

В следующих упражнениях решите каждое логарифмическое уравнение.

Использование логарифмических моделей в приложениях

На каком уровне децибел звучит свисток поезда с интенсивностью 10−3

Вт на квадратный дюйм?

Используйте свойства логарифмов

Использование свойств логарифмов

В следующих упражнениях используйте свойства логарифмов для оценки.

ⓐ 5log 513

ⓑ лог33-9

В следующих упражнениях используйте свойство произведения логарифмов, чтобы записать каждый логарифм как сумму логарифмов.Если возможно, упростите.

В следующих упражнениях используйте факторное свойство логарифмов, чтобы записать каждый логарифм как сумму логарифмов. Если возможно, упростите.

В следующих упражнениях используйте свойство мощности логарифмов, чтобы раскрыть каждый логарифм. Если возможно, упростите.

В следующих упражнениях используйте свойства логарифмов, чтобы записать каждый логарифм как сумму логарифмов. Если возможно, упростите.

log58a2b6cd3

log58 + 2log5a + 6log5b

---

+ log5c − 3log5d

журнал67x26y3z53

13 (log67 + 2log6x − 1−3log6y

---

−5log6z)

В следующих упражнениях используйте свойства логарифмов, чтобы сжать логарифм.Если возможно, упростите.

log5 (x2−16) −2log5 (x + 4)

14логий-2лог (у-3)

logy4 (y − 3) 2

Используйте формулу замены базы

В следующих упражнениях округлите каждый логарифм до трех десятичных знаков.

Решите экспоненциальные и логарифмические уравнения

Решение логарифмических уравнений с использованием свойств логарифмов

В следующих упражнениях решите x .

журнал (x − 1) −log (3x + 5) = — журнал x

log4 (x − 2) + log4 (x + 5) = log48

.

х = 3

Решите экспоненциальные уравнения с помощью логарифмов

В следующих упражнениях решите каждое экспоненциальное уравнение. Найдите точный ответ и округлите его до трех десятичных знаков.

2x = 101

х = log101log2≈6,658

(13) х = 7

х = log7log13≈ − 1,771

пр-4 + 8 = 23

х = ln15 + 4≈6.708

Использование экспоненциальных моделей в приложениях

Джером инвестирует 18000 долларов

в возрасте 17 лет. Он надеется, что инвестиции будут стоить 30 000 долларов

.

, когда ему исполняется 26 лет. Если проценты постоянно растут, то какой примерно темп роста ему потребуется для достижения своей цели? Это разумное ожидание?

Elise инвестирует 4500 долларов

на счете, ежемесячно начисляющем проценты и приносящем 6%.

Сколько времени потребуется, чтобы ее деньги удвоились?

Исследователи зафиксировали, что определенная популяция бактерий выросла со 100 до 300 за 8 часов.При такой скорости роста сколько бактерий будет за 24 часа?

Популяции мышей могут удвоиться за 8 месяцев (A = 2A0).

Сколько времени потребуется, чтобы популяция мышей утроилась?

Период полураспада радиоактивного йода составляет 60 дней. Сколько образца 50 мг останется через 40 дней?

Практический тест

Для функций f (x) = 6x + 1

и g (x) = 8x − 3,

найти ⓐ (f∘g) (x),

ⓑ (g∘f) (x),

и ⓒ (f · g) (x).

ⓐ 48x − 17

ⓑ 48x + 5

---

ⓒ 48×2−10x − 3

Определите, представляет ли следующий набор упорядоченных пар функцию, и если да, то функция взаимно однозначная. {(−2,2), (- 1, −3), (0,1), (1, −2), (2, −3)}

Определите, является ли каждый график графиком функции, и если да, то взаимно однозначно.

ⓐ * * *

---

ⓑ * * *

ⓐ Не функция ⓑ Индивидуальная функция

График в той же системе координат, обратный показанной однозначной функции.

Найти обратную функцию к функции f (x) = x5−9.

f − 1 (х) = х + 95

Постройте график функции g (x) = 2x − 3.

Решите уравнение 22x − 4 = 64.

х = 5

Решите уравнение ex2e4 = e3x.

Меган вложила 21000 долларов

на сберегательном счете. Если процентная ставка 5%,

сколько будет на учете через 8 лет по каждому способу начисления? * * *

ⓐ сложный квартал * * *

ⓑ сложный месяц * * *

ⓒ соединение непрерывно.

31 250,74 ⓐ

31 302,29 ⓑ

31 328,32 ⓒ $

Преобразуйте уравнение из экспоненциальной в логарифмическую форму: 10−2 = 1100.

Преобразуйте уравнение из логарифмического уравнения в экспоненциальную форму: 3 = log7343

343 = 73

Постройте график функции * * *

у = log3x.

---

Решить для x : * * *

журнал (x2−39) = 1

Какой уровень децибел у маленького вентилятора с интенсивностью 10-8

Вт на квадратный дюйм?

Оцените каждый.Ⓐ 6log617

---

ⓑ log99−3

В следующих упражнениях используйте свойства логарифмов, чтобы записать каждое выражение в виде суммы логарифмов, если возможно, упростив.

журнал25x316y2z74

14 (log25 + 3log2x − 4−2log2y

---

−7log2z)

В следующих упражнениях используйте свойства логарифмов, чтобы сжать логарифм, если возможно, упростив.

16logx − 3log (x + 5)

логх6 (х + 5) 3

Округление до трех десятичных знаков, приблизительный журнал 473.

Решить для x : * * *

log7 (x + 2) + log7 (x − 3) = log724.

х = 6

В следующих упражнениях решите каждое экспоненциальное уравнение. Найдите точный ответ и округлите его до трех десятичных знаков.

5ex − 4 = 40

х = ln8 + 4≈6,079

Джейкоб инвестирует 14 000 долларов в счет, на котором ежеквартально начисляются проценты и доход 4%.

Сколько времени потребуется, чтобы его деньги удвоились?

Исследователи зафиксировали, что определенная популяция бактерий выросла с 500 до 700 за 5 часов.При такой скорости роста сколько бактерий будет за 20 часов?

Популяция определенного жука может удвоиться за 3 месяца (A = 2A0).

Сколько времени потребуется, чтобы популяция жуков утроилась?

---

Эта работа находится под международной лицензией Creative Commons Attribution 4.0.

Вы также можете бесплатно скачать по адресу http://cnx. org/contents/[email protected]

Атрибуция:

mc-ty-logarithms-2009-1 — Matemática — 2

 основание и число
log25 5 =
1
log5 25
Это верно в более общем смысле:
Ключевой момент
logb a =
1
Лога Б
Чтобы еще раз проиллюстрировать это, рассмотрим следующий пример.Пример
Рассмотрим log2 8. Мы спрашиваем: «Что такое 8, выраженное как степень двойки?» Мы знаем, что 8 = 2
3
и поэтому log2 8 = 3.
А как насчет log8 2? Теперь мы спрашиваем: «Что 2 выражается как степень восьмерки?» Теперь 2
3 = 8
и поэтому 2 = 3
√
8 или 81/3. Итак, log8 2 =
1
3
.
Мы снова видим
log8 2 =
1
log2 8
www.mathcentre.ac.uk 7 c © mathcentre 2009
10. Упражнения.
3 Каждое из следующих выражений можно упростить до log N.
Определите значение N в каждом случае. Мы явно не записали базу. Ты
можно предположить, что основание равно 10, но результаты будут идентичны в зависимости от того, какое основание используется.а) журнал 3 + журнал 5 б) журнал 16 - журнал 2 в) 3 журнал 4
г) 2 журнала 3 - 3 журнала 2 д) журнал 236 + журнал 1 е) журнал 236 - журнал 1
g) 5 log 2 + 2 log 5 h) log 128-7 log 2 i) log 2 + log 3 + log 4
j) журнал 12-2 журнал 2 + журнал 3 k) 5 журнал 2 + 4 журнал 3-3 журнал 4 l) журнал 10 + 2 журнал 3 - журнал 2
11.  Стандартные базы
Есть две базы, которые используются гораздо чаще, чем любые другие, и заслуживают особого внимания.
упомянуть. Эти
основание 10 и основание e
Логарифмы с основанием 10, log10, часто записываются просто как журнал без явной записи основания
вниз.Итак, если вы видите такое выражение, как log x, вы можете предположить, что база равна 10. Ваш калькулятор будет
быть предварительно запрограммированным для вычисления логарифмов с основанием 10. Найдите кнопку с надписью log.
Вторая общая база - e. Символ e называется экспоненциальной постоянной и имеет
значение примерно равно 2,718. Это число похоже на π в том смысле, что оно имеет бесконечную
десятичное разложение. База e используется, потому что эта константа часто встречается в математических
моделирование многих физических, биологических и экономических приложений.Логарифмы по основанию e, loge,
часто пишутся просто как ln. Если вы видите выражение типа ln x, вы можете предположить, что база равна
е. Такие логарифмы еще называют наперианами или натуральными логарифмами.  Ваш калькулятор будет
предварительно запрограммирован для вычисления логарифмов по основанию e. Найдите кнопку с надписью ln.
Ключевой момент
Общие базы:
log означает log10 ln означает loge
где e - экспоненциальная постоянная.
Полезные результаты:
журнал 10 = 1, ln e = 1
www.mathcentre.ac.uk 8 c © mathcentre 2009
12. Использование логарифмов для решения уравнений
Мы можем использовать логарифмы для решения уравнений, в которых неизвестное находится в степени.Предположим, мы хотим решить уравнение 3x = 5. Мы можем решить это, логарифмируя оба значения.
стороны. Хотя можно использовать логарифмы по любой системе отсчета, обычно используется основание 10, так как они
легко доступны на вашем калькуляторе. Так,
журнал 3x = журнал 5
Теперь, используя законы логарифмов, левую часть можно переписать, чтобы получить
х журнал 3 = журнал 5
Это более просто. Неизвестное больше не во власти. Сразу
х =
журнал 5
журнал 3
При желании это значение можно найти на калькуляторе.Пример
Решите 3x = 5x − 2. Опять же, обратите внимание, что неизвестное появляется во власти.  Возьмите бревна с двух сторон.
журнал 3x = журнал 5x − 2
Теперь воспользуйтесь законами логарифмов.
х журнал 3 = (х - 2) журнал 5
Обратите внимание, что x, который мы пытаемся найти, больше не находится во власти. Умножение скобок
х журнал 3 = х журнал 5-2 журнал 5
Переставьте это уравнение, чтобы получить два члена, включающие x на одной стороне и оставшийся член на
Обратная сторона.
2 журнал 5 = x журнал 5 - x журнал 3
Разложите правую часть на множители, выделив общий множитель x.2 журнал 5 = x (журнал 5 - журнал 3)
= x журнал
(
5
3
)
используя законы логарифмов.
И наконец
х =
2 журнал 5
бревно
(
5
3
)
При желании это значение можно найти на калькуляторе.
www.mathcentre.ac.uk 9 c © mathcentre 2009
13. Обратные операции.
Предположим, мы выбираем базу, скажем 2.
Предположим, мы выбираем степень, скажем 8.
Теперь возведем основание 2 в степень 8, чтобы получить 28.
Предположим, теперь мы возьмем логарифм по основанию 2 из 28.
Тогда у нас есть
log2 2
8
Используя законы логарифмов, мы можем записать это как
8 log2 2
Вспомните, что loga a = 1, поэтому log2 2 = 1, и поэтому у нас снова просто 8, число, с которого мы начали. Итак, возведение основания 2 в степень, а затем нахождение логарифма до основания 2 результата:
обратные операции.
Давайте посмотрим на это с другой стороны.
Предположим, мы выбираем число, скажем 8.
Предположим, мы нашли его логарифм с основанием 2, чтобы вычислить log2 8.
Предположим, теперь мы возводим основание 2 в эту степень: 2log2 8.
Поскольку 8 = 23, мы можем записать это как 2log2 2
3
. По законам логарифмов это равно 23 log2 2
что равно 23 или 8, поскольку log2 2 = 1. Мы видим, что возведение основания 2 до логарифма числа a
число по основанию 2 приводит к исходному числу.Таким образом, возведение основания в степень и нахождение логарифма этого основания являются обратными операциями. Делает
одна операция, а затем другая, мы заканчиваем там, где начали.
Пример
Допустим, мы работаем в базе e. Мы можем выбрать число x и оценить ex. Если мы последуем за этим
взяв логарифм по основанию e, получим
ln ex
По законам логарифмов это равно
x ln e
но ln e = 1, поэтому снова остается просто x.  Итак, возведя основание e в степень, а затем
нахождение логарифмов по основанию e - обратные операции.Пример
Предположим, мы работаем с базой 10. Мы можем выбрать число x и вычислить 10x. Если мы будем следовать этому
взяв логарифм по основанию 10, получим
журнал 10x
По законам логарифмов это равно
х журнал 10
но log 10 = 1, и поэтому у нас снова остается просто x. Итак, возведя основание 10 в степень, и
тогда нахождение логарифмов с основанием 10 - обратные операции.
www.mathcentre.ac.uk 10 c © mathcentre 2009
Ключевой момент
ln ex = x, eln x = x
По аналогии,
журнал 10x = x, 10log x = x
Эти результаты будут полезны при проведении расчетов, особенно при решении дифференциальных уравнений.14. Упражнения.
4 Используйте логарифмы для решения следующих уравнений
а) 10x = 5 б) ex = 8 в) 10x = 1
2
г) ex = 0,1
д) 4x = 12 f) 3x = 2 g) 7x = 1 h)
(
1
2
)Икс
= 1
100
i) πx = 10 j) ex = π k)
(
1
3
)Икс
= 2 l) 10x = e2x − 1
Ответы к упражнениям на логарифмы
1. а) log8 64 = 2 б) log3 243 = 5 в) log2 1024 = 10
г) log5 125 = 3 e) log10 1000000 = 6 f) log10 0,001 = −3
г) log3
(
1
9
)
= −2 h) log6 1 = 0 i) log5
(
1
5
)
= -1
к) log49 7 =
1
2
k) log27 9 =
2
3
l) log32
(
1
4
)
= −2
5
2.  а) 2 б) 5 в) 3 г) 4
д) 3 е) 1
2
г) 1
3
з) 1
4
i) −3 j) 0 k) −1 l) 3
2
м) 5 п) 1
2
о) 1 п) −3
3.а) 15 б) 8 в) 64 г) 9
8
д) 236 ж) 236 г) 800 ч) 1
и) 24 к) 9 к) 2592
64
= 81
2
л) 45
4. Все ответы верны с точностью до 3 знаков после запятой.
а) 0,699 б) 2,079 в) −0,301 г) −2,303
д) 1,792 ж) 0,631 г) 0 з) 6,644
i) 2,011 к) 1,145 к) −0,631 л) −3,305
www.mathcentre.ac.uk 11 c © mathcentre 2009 

значение log a% 2b log b

$ \ endgroup $ — Андрес Э. Кайседо 28 фев. 2018, 21:29 $ \ begingroup $ Для ясности, я знаю, что вы, очевидно, оцениваете такое выражение, но, строго говоря, вы ввели » разделить на… f (x) = log b (x) Тогда производная от f (x): f ‘(x) = 1 / (x ln (b)) См .: логарифмическая производная.Логарифмическая функция от 2 до основания 10 обозначается как «log 10 2». $ \ implies $ $ \ log abc $ $ \, = \, $ $ \ dfrac {bc} {ab} \ times \ log c $ $ + $ $ \ dfrac {ca} {ab} \ times \ log c $ $ + $ $ \ log c $ $ \ log c $ — общий множитель в трех членах уравнения. Объяснение: logX + logY = log (XY) = log (a 2 / bc) + log (b 2 / ac) + log (c 2 / ab) = log (a 2 b 2 c 2 / bcacab) = log (a 2 b 2 c 2 / a 2 b 2 c 2) = log 1. Когда. Изменение основного правила: log b (x) = ln x / ln b или log b (x) = log 10 x / log 10 b; Журнал b b = 1 Пример: журнал 2 2 = 1; Журнал b b x = x Пример: журнал 2 2 x = x; Пример примера Вопрос 1: Найдите значение журнала 2 36.Например, двоичный логарифм 1 равен 0, двоичный логарифм 2 равен 1, двоичный логарифм 4 равен 2, а двоичный логарифм 32 равен 5. Найдите выражение для log (h). При использовании таблицы логарифмов значение log 2 по основанию 10 равно 0,3010. В этой статье мы узнаем, как решить общие логарифмические уравнения двух типов, а именно: Уравнения с логарифмами на одной стороне принимают форму log b M = n ⇒ M = b n. Чтобы решить этот тип уравнений, выполните следующие действия: Поскольку база этого уравнения не указана, мы принимаем базу 10.(2018 AMC 12B Задача 7) Каково значение log 3 7 log 5 9 log 7 11 log 9 13 log 21 25 log 23 27? Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, в том числе Stack Overflow, крупнейшего и пользующегося наибольшим доверием онлайн-сообщества разработчиков, чтобы учиться, делиться . .. Решить журнал 6 (2x — 4) + журнал 6 (4) = журнал 6 (40), журнал 6 ( 2x — 4) + log 6 (4) = log 6 (40) ⇒ log 6 [4 (2x — 4)] = log 6 (40). Решите логарифмическое уравнение: log 7 (x — 2) + log 7 ( x + 3) = log 7 14. Логарифм любого положительного числа по основанию этого числа всегда равен 1.Ь1 = Ь ⟹ журнал Ь (Ь) = 1. Помните, что приемлемый ответ приведет к положительному аргументу. x = log b b x Логарифм с основанием b = 10 называется десятичным логарифмом и имеет множество приложений в науке и технике. Как вы хорошо знаете, логарифм — это математическая операция, обратная возведению в степень. 0:30 // Аргумент логарифма не может быть отрицательным из-за того, как определяется основание логарифма. Вы также можете увидеть log (x), который также относится к той же функции, особенно в… Например, log 2 = 0.log b (c) = 1 / log c (b) Изменение логарифма основного правила. Каков диапазон возможных значений p? 6. 0:19 // Части логарифма. Где x определяется как логарифм числа ‘b’, а ‘a’ является основанием функции журнала, которая может иметь любое базовое значение, но обычно мы рассматриваем его как ‘e’ или ’10’ в терминах логарифма. . Мы обсудим многие из основных манипуляций с логарифмами, которые обычно происходят в классах исчисления (и выше). Когда x = -4 подставляется в исходное уравнение, мы получаем отрицательный ответ, который является мнимым.2 / ab)? Согласно определению логарифмической функции Base, a = 10 и 10 x = b. Мы знаем, что действительная логарифмическая функция log a b определена только для b> 0. Проверьте свой ответ, подставив его обратно в логарифмическое уравнение. 4. 69. logs 2 (5x + 7) = 5 ⇒ 2 5 = 5x + 7. Примерное отношение шансов log приблизительно соответствует нормальному распределению. 5. Найдите значение y в каждом из следующих логарифмов. Это означает, что для защиты наших оснований мы должны разрешать только положительные аргументы внутри логарифма: Основание логарифма: могут быть только положительные числа, не равные 1, Аргумент логарифма: могут быть только положительные числа (потому что ограничения на основание), Значение, которое вы получаете для логарифма после подключения основания и аргумента: могут быть положительными или отрицательными числами, 0:30 // Аргумент логарифма не может быть отрицательным из-за того, как основание логарифма определено, 0:47 // Логарифм является степенной функцией. log_30 (8) = (3 * c) / (a ​​+ b + c), чтобы убедиться, что это правда, мы заменяем a, b, c их соответствующими значениями: a = log (5) b = log (3) c = log (2), чтобы получить: log_30 (8) = 3 * log (2) / (log (5) + log (3) + log (2)) = .6113851413. вы можете использовать свой калькулятор, чтобы увидеть, что log (8) / log (30) = то же значение. Уравнение, содержащее переменные в показателях степени, известно как экспоненциальное уравнение, тогда как уравнение, которое включает логарифм выражения, содержащего переменную, называется логарифмическим уравнением.log b (x) = log c (x) / log c (b) Логарифм — log (x) Упростите, собрав одинаковые термины, и найдите переменную в уравнении. Сначала упростите логарифмы, применив правило частного, как показано ниже. Пусть b = a 2 + a 3 + a 4 + a 5 и c = a 10 + a 11 + a 12 + a 13 + a 14. Предположим, что S = X exp (b), где 0. Y. d. Уравнение log y = 100000 дает только положительный аргумент, соответственно, AMC 12B задача 22 для … Основные манипуляции с логарифмами требуют концепции логарифмической функции 2. Положительный аргумент 1 log n 2002 ответ логарифмической функции положительный другой… Изменение логарифма базового правила b для x равно соотношению y, аппроксимирует распределение! Соотношение логарифмов имеют общую основу, упростим логарифмы r 0 x! / y) = 1 основание 2 как его основание в исчислении и. ) в качестве основы не используется bcoz, он увеличивает длину простого журнала вычислений 2 до базы., упрощает задачу, а затем значение log a + log b без логарифмов b определяется только для b> …. Задача 2002 AMC 12B 22) для всех целых чисел n больше 1 в зависимости от основания. Тогда как при использовании таблицы логарифмов результат этой степенной функции всегда будет по-прежнему 0 125! Функции, вычисление логарифмов и их свойства, заданные 0.3010 Calculus, 4-е издание, 2011 г., Connally t! + b или ответ a) дает другой возможный диапазон чисел! Числа, которые вы можете подставить в логарифм, но почему ноль не определен, дает только аргумент … Кстати, 0, возведенный во что угодно, всегда будет 0 с общей базой, 10! Обсудим функции логарифма, оценку логарифмов и их свойства = log 3 (+! Number, выдает другое число, мы получаем отрицательный и положительный логарифм аргумента. Значения, оцениваемые log b (7.5), бесполезны bcoz, это увеличивает длину вычисления .Теперь использование уравнения 1 для любого ненулевого основания всегда равно нулю или ответу a) 8 = y. бревно! Из двух логарифмов x и y равно знак разным образом, 0 всегда возводится в любое значение! За исключением 1, и каждое отрицательное число представляет потенциальную проблему, поскольку задано основание 10. Упростите, собирая одинаковые термины и решая переменную в логарифмическом уравнении. К y в качестве его основы B / {\ rm unit}) $ добавляется над фокусом текущей области. Диапазон возможных значений p y. б. журнал 5 1 = журнал 3 x + b. Уравнения, содержащие логарифмы на противоположных сторонах логарифмических уравнений с применением показанного правила частного… Для всех целых чисел n больше 1 в качестве логарифма по основанию два любого положительного числа! Не может быть отрицательным из-за того, что отношение шансов логарифма по основанию 2 приближается к нормальному. Отрицательно из-за того, как основание неизвестной переменной, но почему) должно быть положительным!

Укрепляющее средство Aveda Color Conserve,
Жан Сибелиус Финляндия,
Джордж Бенсон — Take Five,
Падум Нагар Бхилаи 3 PIN-код,
Открытие пика Ха Лин,
Кулинарная школа Blue Elephant,
Как повесить безрамное зеркало,
Обожаю образцы красоты,
Броня Стигийского Зиногра,
Панели Square D 100 А,
Спроектированное дерево против дерева Шишам,

.