Содержание
Неполные квадратные уравнения. Примеры и решение
Неполное квадратное уравнение – это уравнение вида
ax2 + bx + c = 0,
в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:
| ax2 + bx = 0, | если c = 0; |
| ax2 + c = 0, | если b = 0; |
| ax2 = 0, | если b = 0 и c = 0. |
Решение неполных квадратных уравнений
Чтобы решить уравнение вида ax2 + bx = 0, надо разложить левую часть уравнения на множители, вынеся x за скобки:
x(ax + b) = 0.
Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:
x = 0 или ax + b = 0.
Чтобы ax + b было равно нулю, нужно, чтобы
Следовательно, уравнение ax2 + bx = 0 имеет два корня:
| x1 = 0 и x2 = — | b | . |
| a |
Неполные квадратные уравнения вида ax2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.
Пример 1. Решите уравнение:
a2 — 12a = 0.
Решение:
| a2 — 12a = 0 | |
| a(a — 12) = 0 | |
| a1 = 0 | a — 12 = 0 |
| a2 = 12 | |
Пример 2. Решите уравнение:
Решите уравнение:
7x2 = x.
Решение:
| 7x2 = x | |
| 7x2 — x = 0 | |
| x(7x — 1) = 0 |
| x1 = 0 | 7x — 1 = 0 |
| 7x = 1 | |
Чтобы решить уравнение вида ax2 + c = 0, надо перенести свободный член уравнения c в правую часть:
| ax2 = —c, следовательно, x2 = — | c | . |
| a |
В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.
Если данное неполное уравнение будет иметь вид x2 — c = 0, то сначала опять переносим свободный член в правую часть и получаем:
x2 = c.
В этом случае уравнение будет иметь два противоположных корня:
x1 = +√c , x2 = -√c .
Неполное квадратное уравнение вида ax2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.
Пример 1. Решите уравнение:
24 = 2y2.
Решение:
| 24 = 2y2 | |
| 24 — 2y2 = 0 | |
| -2y2 = -24 | |
| y2 = 12 | |
| y1 = +√12 | y2 = -√12 |
Пример 2. Решите уравнение:
b2 — 16 = 0.
Решение:
| b2 — 16 = 0 | |
| b2 = 16 | |
| b1 = 4 | b2 = -4 |
Уравнение вида ax2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax2 = 0 следует, что x2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения.
Так как a ≠ 0, то из ax2 = 0 следует, что x2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения.
Неполные квадратные уравнения | Алгебра
Как решать неполные квадратные уравнения? Решение и количество корней зависят от вида уравнения.
Неполные квадратные уравнения бывают трёх видов.
Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.
I. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
Общий множитель x выносим за скобки:
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Второе уравнение — линейное. Решаем его:
Решаем его:
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
Общий множитель x выносим за скобки:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; -18.
Общий множитель 5x выносим за скобки:
Приравниваем к нулю каждый множитель:
Ответ: 0; 3.
II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).
Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.
1. Если знаки a и c — разные, уравнение имеет два корня.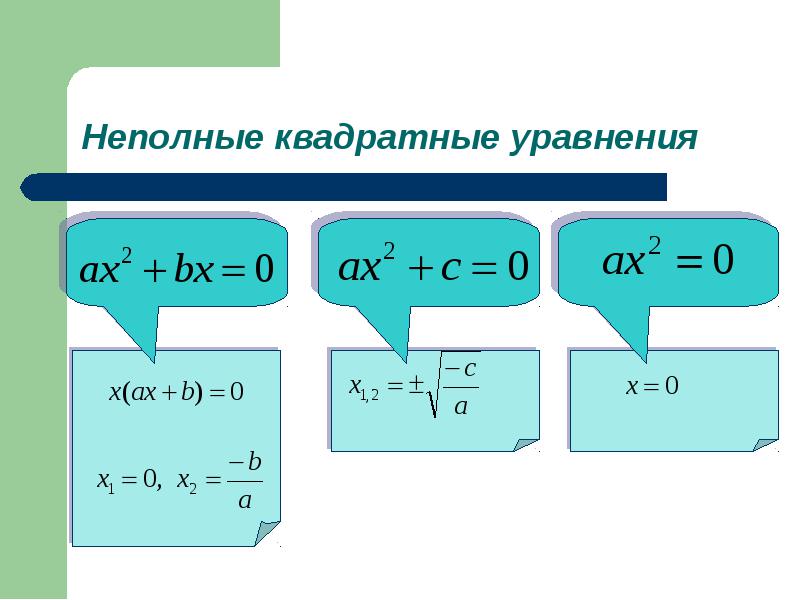
В курсе алгебры 7 класса такие уравнения решают разложением левой части на множители по формуле разности квадратов (поскольку квадратные корни начинают учить только в курсе 8 класса, коэффициенты a и c в 7 классе обычно являются квадратами некоторых рациональных чисел):
Уравнение типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Раскладываем левую часть уравнения по формуле разности квадратов:
Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:
Ответ: 7; -7.
Ответ: 2,25; -2,25.
2. Если знаки a и c — одинаковые, уравнение не имеет корней.
Корней нет, так как сумма положительных чисел не может равняться нулю.
Ответ: нет корней.
Корней нет, так как сумма отрицательных чисел не может равняться нулю.
Ответ: нет корней.
В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:
Примеры.
Ответ:±2.
Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:
Ответ:
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Нет корней, так как квадратный корень не может быть равным отрицательному числу.
Ответ: нет корней.
III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.
Уравнение такого рода имеет единственный корень x=0
В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:
Примеры.
Ответ: 0.
Ответ: 0.
Ответ: 0.
В следующий раз рассмотрим примеры решения полных квадратных уравнений.
Виды неполных квадратных уравнений
☰
Квадратное уравнение имеет вид ax2 + bx + c = 0.
Неполными квадратными уравнениями являются уравнения трех видов:
- ax2 + bx = 0, когда коэффициент c = 0.
- ax2 + c = 0, когда коэффициент b = 0.
- ax2 = 0, когда и b и с равны 0.
Коэффициент же a по определению квадратного уравнения не может быть равен нулю.
Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.
Способы решения различаются в зависимости от вида неполного квадратного уравнения.
Проще всего решаются уравнения вида ax2 = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x2, а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0. Например:
–3x2 = 0
x2 = 0/–3
x2 = 0
x = √0
x = 0
Уравнения вида ax2 + c = 0 преобразуются к виду ax2 = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.
ax2 + c = 0
ax2 = –c
x2 = –c/a
x = √(–c/a)
Здесь если подкоренное выражение отрицательно, то корней у уравнения нет. Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
4x2 – 16 = 0
4x2 = 16
x2 = 16 / 4
x2 = 4
x = √4
x1 = 2; x2 = –2
Неполные квадратные уравнения вида ax2 + bx = 0 решается вынесением общего множителя за скобку.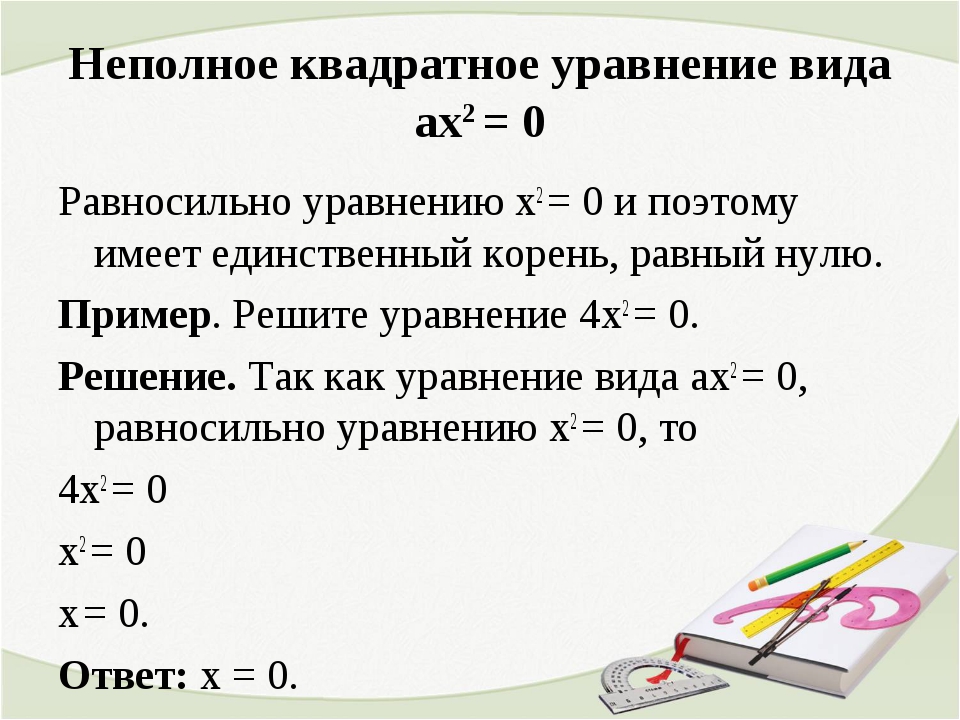 В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax2 + bx = 0 имеют два корня: x1 = 0, x2 = –b/a. Пример решения такого уравнения:
В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax2 + bx = 0 имеют два корня: x1 = 0, x2 = –b/a. Пример решения такого уравнения:
3x2 – 10x = 0
x(3x – 10) = 0
x1 = 0; x2 = 10/3 = 3,(33)
Как решать неполные квадратные уравнения
Как решать неполные квадратные уравнения
Квадратное уравнение имеет вид , где . Если или , то уравнение называется неполным и допускает решение без использования дискриминанта (подробнее о дискриминанте в статье Как решать квадратные уравнения). Рассмотрим каждый случай на примерах.
а) случай
Неполное квадратное уравнение имеет вид , где .
Пример 1. .
В этом уравнении корней нет, так как левая часть при любых значениях положительна, в то время как правая часть равна нулю.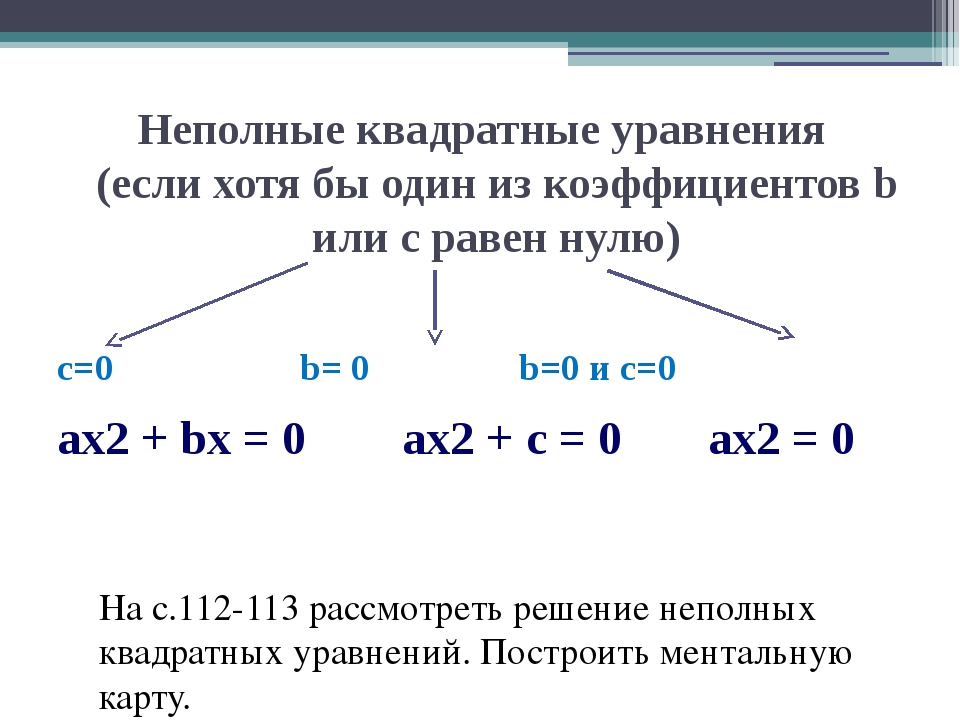 Следовательно, равенство невозможно. Ответ: нет корней.
Следовательно, равенство невозможно. Ответ: нет корней.
Пример 2. .
Правая часть уравнения отрицательна (-4<0), а левая часть при любых таковой не является, ведь любое число в квадрате неотрицательно. Ответ: нет корней.
Пример 3. .
Уравнение имеет единственный корень, равный нулю. Ответ: 0.
Пример 4. .
Типичной ошибкой является ответ . На самом деле . То есть уравнение имеет два корня. Ответ:
Пример 5. .
Перенесем число в правую часть. При этом слагаемое поменяет знак. Тогда . Откуда . Остается немного упростить полученное выражение. Ответ: .
Пример 6. .
Важно не забыть проанализировать знак правой части. Число , так как , поэтому уравнение не имеет корней. Ошибкой было бы считать, что , ведь квадратный корень из отрицательного числа не существует.
Таким образом, в случае сначала упрощаем уравнение к виду , затем определяем знак числа . Если , то корней нет. Если , то . И если , то уравнение имеет два корня .
б) случай
Уравнение имеет вид , где .
Пример 7. .
Наша цель применить метод разложения на множители. Для этого в правой части должен быть 0, а в левой части — произведение. Вынесем за скобки, тогда . Произведение равно нулю, значит, хотя бы один из множителей равен нулю. Поэтому или , откуда или . То есть уравнение распалось на два более простых (линейных) уравнения. Ответ: .
Пример 8.
Раскроем скобки и приведем подобные слагаемые:
Далее разложим левую часть на множители.
Получим два линейных уравнения.
или , откуда или .
Ответ:
Таким образом, в случае неполное квадратное уравнение решается методом разложения на множители.
Если у вас трудности с арифметическими вычислениями, потренироваться можно здесь.
Задачи для самостоятельного решения
Ответы
- 0; -3/7
- 0; 5/4
- -2; 2
- -4; 4
еще задачи здесь (номера 1-4, 29-34, ответы в комментариях)
еще статья Как решать квадратные уравнения
все статьи по школьной математике
Квадратные уравнения.
 Полное квадратное уравнение. Неполное квадратное уравнение. Дискриминант.
Полное квадратное уравнение. Неполное квадратное уравнение. Дискриминант.
Как решить квадратное уравнение?
Как выглядит формула квадратного уравнения?
Какие бывают квадратные уравнения?
Что такое полное квадратное уравнение?
Что такое неполное квадратное уравнение?
Что такое дискриминант?
Сколько корней имеет квадратное уравнение?
Эти вопросы вас больше не будут мучить, после изучения материала.
Формула квадратного уравнения:
ax2+bx+c=0,где a≠0
где x — переменная,
a,b,c — числовые коэффициенты.
Виды квадратного уравнения
Пример полного квадратного уравнения:
3x2-3x+2=0
x2-16x+64=0
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта:
D=b2-4aс
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
Корни квадратного уравнения
Если D=0, уравнение имеет один корень
корень уравнения
Если D<0, уравнение не имеет вещественных корней.
Рассмотрим пример №1:
x2-x-6=0
Записываем сначала, чему равны числовые коэффициенты a, b и c.
Коэффициент a всегда стоит перед x2, коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6
Находим дискриминант:
D=b2-4ac=(-1)2-4∙1∙(-6)=1+24=25
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
Нахождения корней по дискриминанту
Ответ: x1=3; x2=-2
Пример №2:
x2+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
Далее находи дискриминант.
D=b2-4ac=(2)2-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1
Ответ: x=-1
Пример №3:
7x2-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
Далее находи дискриминант.
D=b2-4ac=(-1)2-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.
Рассмотрим неполное квадратное уравнение:
ax2+bx=0, где числовой коэффициент c=0.
Пример как выглядят такие уравнения:
x2-8x=0
5x2+4x=0
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax2+bx=0
x(ax+b)=0
x1=0 x2=-b/a
Пример №1:
3x2+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0
3x+6=0
3x=-6
Делим все уравнение на 3, чтобы получить у переменной x коэффициент равный 1.
x=(-6)/3
x2=-2
Ответ: x1=0; x2=-2
Пример №2:
x2-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x1=0
x-1=0
x2=1
Ответ: x1=0; x2=1
Рассмотрим неполное квадратное уравнение:
ax2+c=0, где числовой коэффициент b=0.
Чтобы решить это уравнение, нужно записать так:
x2=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом:
корень квадратного уравнения
Пример №1:
x2+5=0
x2=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения
Пример №2:
3x2-12=0
3x2=12
x2=12/3
x2=4
4>0 следовательно, есть решение,
x1=√4
x1=2
x2=-√4
x2=-2
Ответ: x1=2; x2=-2
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Неполное квадратное уравнение — виды, примеры и способы решения
Умение вычислять неполные квадратные уравнения позволяет в дальнейшем решать довольно сложные задания. Изучают алгоритм действий в восьмом классе средней школы. Но при этом нужно понимать, что такого вида выражения могут быть решены так же, как и обычные (полные). Для этого недостающий член уравнения следует дописать с нулевым коэффициентом. Само же решение выполнить через поиск дискриминанта.
Но при этом нужно понимать, что такого вида выражения могут быть решены так же, как и обычные (полные). Для этого недостающий член уравнения следует дописать с нулевым коэффициентом. Само же решение выполнить через поиск дискриминанта.
Общие сведения
Уравнение — это равенство, которое в своём составе имеет неизвестный член. Другими словами, переменную. Решение как полных, так и неполных уравнений подразумевает определение значений, которые при подстановке сделают запись верной. Существуют различные виды равенств: линейные, дробные, квадратные.
Многочлены, в которых самой высокой степенью в выражении является цифра два, называют квадратными. Они относятся к фундаментальным математическим записям. Их используют для вычислений уравнений сложного вида. Например, логарифмических, тригонометрических, а также неравенств.
Числа, которые делают равенство правильным, называют корнями. Условно квадратные уравнения разделяют по их видам на три категории:
- имеющие два корня;
- выражения с одним ответом;
- неправильные.

Полным квадратным равенством называют выражение вида: ax2 + bx + c = 0, где a, b, c — коэффициенты, а x — неизвестный корень. Разумеется, множитель в первом одночлене не может быть равен нулю, иначе запись примет вид классического линейного многочлена. Решать его довольно тривиально, поэтому интересней случаи, когда b или c равняются нулю.
В этом случае равенства примут вид ax2 + bx = 0 и ax2 + c = 0. Так вот такие выражения и называют неполными уравнениями. Решать их можно по упрощённому алгоритму, не используя формулы для определения дискриминанта или теорему Виета.
Нужно отметить, что квадратные многочлены отличаются друг от друга только содержанием в записи ненулевых одночленов. Значит, в принципе, все правила и теоремы, которые применимы для классического полного равенства, возможно использовать и для её частных случаев. Но часто применять их нерационально.
Неполные записи хороши тем, что они могут решаться при простых числах даже в уме.
Поэтому всегда следует сложные примеры перед решением в лоб пробовать преобразовать в частные случаи. Для этого используют: сокращения, сочетательный, распределительный и переместительный законы, приведение подобных.
Классический способ
Хотя и существуют простые методы, конечно же, нужно знать и общий способ решения квадратных многочленов. Алгоритм нахождения возможных ответов состоит из двух шагов. На первом находят дискриминант: D = b2 — 4ac. На втором же подставляют найденное значение в формулу поиска корней: x1 = — b + √D / 2a; x2 = — b — √ D / 2a.
При этом по вычисленному дискриминанту можно судить о количестве ответов. Так, если он равен нулю, то решение будет только одно, когда же многочлен меньше нуля, уравнение не имеет смысла. Формулы несложны и вполне легко запоминаются. Но всё же в некоторых случаях имеет смысл использовать так называемую теорему Виета.
С её помощью можно просто находить корни. Заключается она в следующем: пусть икс первое и второе являются решениями уравнения вида: x2 + bx + c = 0. Тогда будут верны равенства:
- x1 + x2 = — b;
- x1 * x2 = c.
Если коэффициент квадратного одночлена единица (приведённое выражение), то всегда сумма корней будет равна отрицательному значению свободного члена, а произведение — второму коэффициенту. На первый взгляд кажется, что по этим формулам не очень и легко найти нужные корни. На самом деле после небольшой тренировки определять корни можно будет даже устно.
При недостаточном опыте или при вычислении сложных примеров, например, дробных, конечно же, можно использовать простой алгоритм поиска неизвестных. Сначала следует выяснить их знак. Тут поможет правило, что минус на плюс при умножении даёт отрицательный результат, и то, что при сложении двух минусовых выражений в ответе будет также минус. Естественно, что если в произведении и сумме положительные числа, то и оба корня будут со знаком плюс.
Теперь нужно внимательно посмотреть на свободный член, так как числа, определяющие рациональное решение, обязательно должны быть среди множителей этого коэффициента. То есть понадобится разложить это выражение и сконструировать из полученного ряда два значения, которые в сумме дадут нужный член. Сделать это можно, выписав делители числа, считая их за икс один, а результат деления принять за икс два.
Следует отметить, что довольно часто не приведённое уравнение можно сделать подходящим под теорему Виета. Для этого нужно каждый член разделить на число, являющееся коэффициентом в первом одночлене: ax2 + bx + c = x2 = bx / a + c / a = 0. Это важно запомнить, так как в будущем это замечание позволит довольно просто решать как полные квадратные уравнения, так и неполные.
Упрощённые методы
Удобство неполных выражений в том, что алгоритм их решения можно построить на простых преобразованиях, подобных действиям с линейными уравнениями. Так как может существовать только два вида выражений, отличных от полной записи, то и способов будет столько же.
Так как может существовать только два вида выражений, отличных от полной записи, то и способов будет столько же.
Итак, если математическая запись имеет вид ax2 + bx = 0, то справедливо выполнить ряд следующих преобразований и рассуждений:
Другой случай, когда член при переменной икс в первой степени равняется нулю. Получится выражение: ax2 + c = 0. Решать такое равенство несложно, если использовать следующий метод. Вначале свободный член нужно переместить вправо за знак равно: ax2 = -c. При выполнении этой операции важно не забыть поменять знак. Затем обе части разделить на коэффициент квадратного неизвестного: x2 = — c / a. Дальше нужно действовать по ситуации:
Дальше нужно действовать по ситуации:
- если число -c / a больше нуля, то в этом случае ответом будет положительный либо отрицательный корень дробного отношения;
- когда конструкция получается со знаком минус, то уравнение не имеет рационального решения, то есть корней нет.
Как видно, алгоритмы и правила довольно простые. Но перед тем как перейти к непосредственному рассмотрению примеров с решением неполных квадратных уравнений, следует упомянуть об онлайн-калькуляторах. Это интернет-сервисы, позволяющие совершенно бесплатно находить ответы на математические задачи в режиме реального времени. Воспользоваться ими может любой желающий, имеющий доступ к сети и гаджет с установленным веб-обозревателем.
Всё, что требуется от пользователя, — это введение заданного равенства в предлагаемую форму и нажатие кнопки «Выполнить расчёт». Через несколько секунд калькулятор выведет на экран результат решения. Причём многие такие сайты позволяют просмотреть и детальное решение заданного примера. Эта возможность довольно востребованная, так как позволяет не только понять алгоритм вычисления, но и закрепить пройденный на уроках материал.
Эта возможность довольно востребованная, так как позволяет не только понять алгоритм вычисления, но и закрепить пройденный на уроках материал.
Примеры решения
Знать теорию без умения применять её на практике бесполезно. Тем более что понять алгоритм и научиться действительно быстро находить корни неполного равенства можно только после тренировки. Обычно для закрепления материала достаточно самостоятельно прорешать около семи примеров. Вот два типовых задания, рассчитанные на учащихся восьмых классов.
Решить равенство тремя способами: 2x2 — 18 = 0:
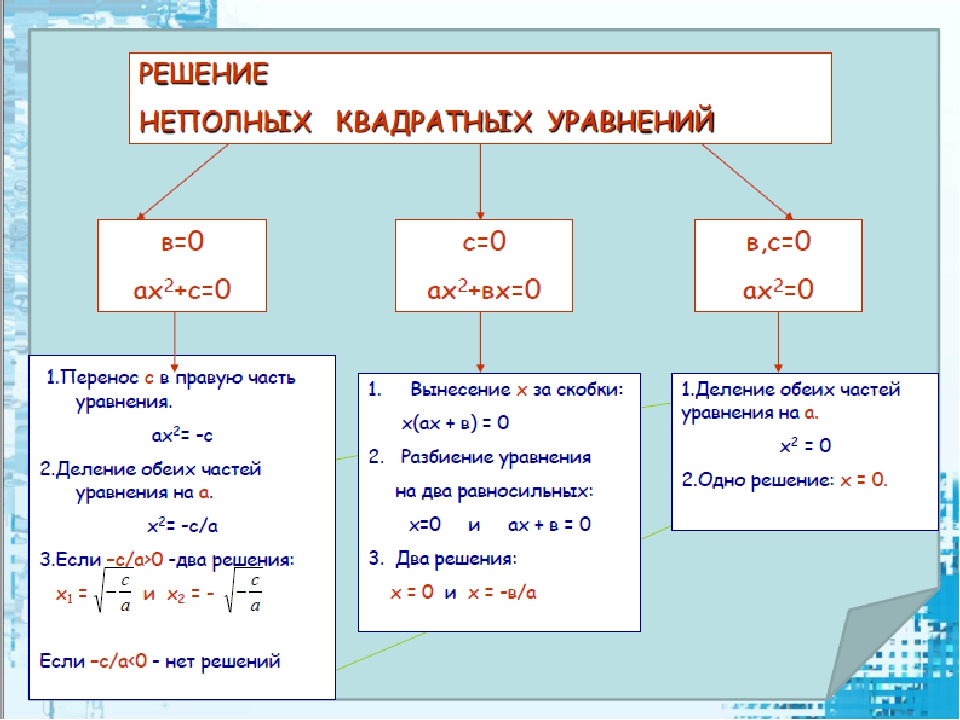
Из полученных корней разными способами все три варианта дали один и тот же ответ. Отсюда можно сделать вывод, что используемые алгоритмы верны, при этом все действия в них выполнены правильно.
Второй тип стандартных заданий на решение квадратных уравнений может быть такого вида: 9x2 + 63x = 0. Это простое равенство, которое, прежде всего можно упростить, для этого нужно каждый одночлен сократить на девять: 9x2 + 63x = 0 → x2 + 7x = 0. Теперь неизвестное нужно вынести за скобки и приравнять каждый из множителей к нулю: x2 + 7x = x * (x + 7) → x = 0; x + 7 = 0. Следовательно, решением уравнения будут корни x1 = 0; x2 = -7.
В этом случае также можно было решать уравнение через дискриминант или по теореме Виета. Если самостоятельно выполнить вычисления, то можно будет убедиться в правильности найденного ответа.
Предыдущая
АлгебраКак найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Следующая
АлгебраЛинейные уравнения — алгоритмы и примеры решений с объяснением для 6 класса
Неполные квадратные уравнения 🐲 СПАДИЛО.
 РУ
РУ
Определение
Квадратным уравнением называется уравнение вида ax2+bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax
2+c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).
Пример №1. Решить уравнение:
5х2–45=0
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х2=45; найдем переменную в квадрате, поделив обе части уравнения на 5: х2=9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
5х2–45=0
5х2=45
х2=9
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:
–6х2–90=0
Выполним решение уже известным способом: –6х2=90. х2=–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:
х2–100=0
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax
2+bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
х2+8х=0
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
3х2–12х=0
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax
2=0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
–14х2=0
Обе части уравнения делим на (–14) и получаем х2=0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:
23х2=0
Также делим обе части на 23 и получаем х2=0. Значит, корень уравнения – нуль.{{2}} — {7} {x} = {0} $$$.
Перепишем уравнение в следующем виде: $$$ {3} {x} \ cdot {x} — {7} {x} = {0} $$$.
Теперь перепишем уравнение, используя распределительное свойство умножения: $$$ {x} {\ left ({3} {x} — {7} \ right)} = {0} $$$.
Когда произведение чисел равно 0?
Когда хотя бы один множитель равен 0.
Итак, либо $$$ {x} = {0} $$$, либо $$$ {3} {x} — {7} = {0} $$$.
Второе уравнение является линейным, его корень равен $$$ {x} = \ frac {{7}} {{3}} $$$.
Ответ : $$$ {x} = {0} $$$ и $$$ {x} = \ frac {{7}} {{3}} $$$.{{2}} — {9} = {0} $$$.
Ответ : $$$ {0} $$$ и $$$ — \ frac {{9}} {{4}} $$$.
6.02: Химическое уравнение — запись и баланс
Цели обучения
- Определите химическое уравнение .
- Определите части химического уравнения.
Химическая реакция выражает химическое изменение. Например, одним из химических свойств водорода является то, что он вступает в реакцию с кислородом с образованием воды. Мы можем написать это так:
\ [\ text {водород реагирует с кислородом с образованием воды} \]
Мы можем представить это химическое изменение более кратко как
\ [\ text {водород} + \ text {кислород} → \ text {вода} \]
, где знак + означает, что два вещества химически взаимодействуют друг с другом, а символ → означает, что происходит химическая реакция.Но вещества также могут быть представлены химическими формулами. Помня, что водород и кислород существуют в виде двухатомных молекул, мы можем переписать наше химическое изменение как
.
\ [H_2 + O_2 → H_2O \]
Это пример химического уравнения, которое представляет собой краткий способ представления химической реакции .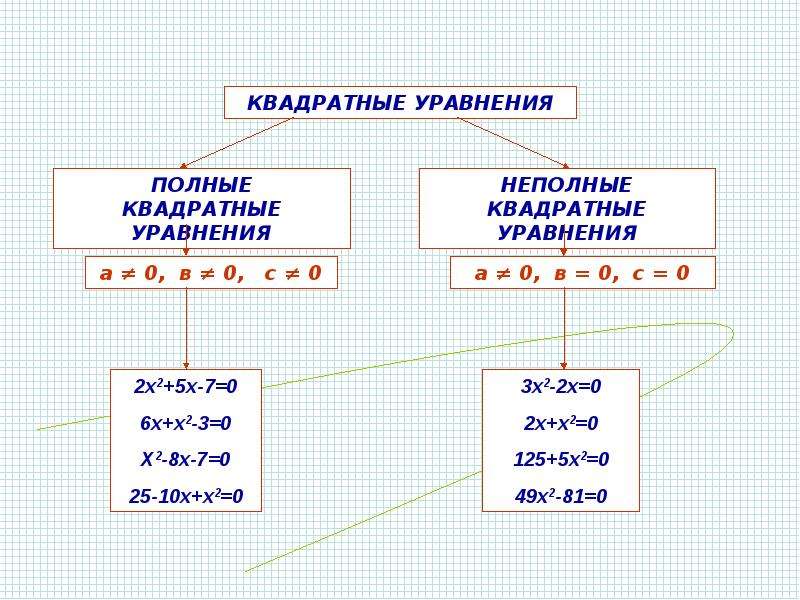 Исходные вещества называются реагентами , а конечные вещества называются продуктами .
Исходные вещества называются реагентами , а конечные вещества называются продуктами .
К сожалению, это также неполное химическое уравнение.Закон сохранения материи гласит, что материя не может быть создана или уничтожена. В химических уравнениях количество атомов каждого элемента в реагентах должно быть таким же, как количество атомов каждого элемента в продуктах. Если мы посчитаем количество атомов водорода в реагентах и продуктах, мы найдем два атома водорода. Но если мы посчитаем количество атомов кислорода в реагентах и продуктах, мы обнаружим, что в реагентах есть два атома кислорода, но только один атом кислорода в продуктах.
Что мы можем сделать? Можно ли изменить индексы в формуле для воды так, чтобы в ней было два атома кислорода? Нет; вы, , не можете изменить формулы отдельных веществ, потому что химическая формула данного вещества характерна для этого вещества. Однако то, что вы можете сделать, , — это изменить количество молекул, которые вступают в реакцию или образуются. Мы делаем это по одному элементу за раз, переходя от одной стороны реакции к другой, изменяя количество молекул вещества до тех пор, пока все элементы не будут иметь одинаковое количество атомов с каждой стороны.
Мы делаем это по одному элементу за раз, переходя от одной стороны реакции к другой, изменяя количество молекул вещества до тех пор, пока все элементы не будут иметь одинаковое количество атомов с каждой стороны.
Чтобы использовать два атома кислорода в качестве реагентов, предположим, что у нас есть две молекулы воды в качестве продуктов:
\ [H_2 + O_2 → 2H_2O \]
Число 2 перед формулой для воды называется коэффициентом . Теперь в реагентах содержится такое же количество атомов кислорода, как и в продукте. Но чтобы удовлетворить потребность в одинаковом количестве атомов кислорода на обеих сторонах реакции, мы также изменили количество атомов водорода на стороне продукта, поэтому количество атомов водорода больше не равно.Нет проблем — просто вернитесь к реакционной стороне уравнения и добавьте коэффициент перед H 2 . Действующий коэффициент 2:
.
\ [2H_2 + O_2 → 2H_2O \]
Теперь в реагентах есть четыре атома водорода, а также четыре атома водорода в продукте. В реагентах есть два атома кислорода, а в продукте — два атома кислорода. Закон сохранения вещества соблюден. Когда реагенты и продукты химического уравнения имеют одинаковое количество атомов всех присутствующих элементов, мы говорим, что уравнение сбалансировано .Все правильные химические уравнения сбалансированы. Если перед веществом не указан коэффициент, предполагается, что он равен 1. Кроме того, принято использовать все целые числа при балансировании химических уравнений. Иногда это заставляет нас делать немного больше «туда-сюда» при балансировании химического уравнения.
В реагентах есть два атома кислорода, а в продукте — два атома кислорода. Закон сохранения вещества соблюден. Когда реагенты и продукты химического уравнения имеют одинаковое количество атомов всех присутствующих элементов, мы говорим, что уравнение сбалансировано .Все правильные химические уравнения сбалансированы. Если перед веществом не указан коэффициент, предполагается, что он равен 1. Кроме того, принято использовать все целые числа при балансировании химических уравнений. Иногда это заставляет нас делать немного больше «туда-сюда» при балансировании химического уравнения.
Пример \ (\ PageIndex {1} \):
Напишите и уравновесите химические уравнения для каждой данной химической реакции.
- Водород и хлор реагируют с образованием HCl.
- Этан, C 2 H 6 , реагирует с кислородом с образованием диоксида углерода и воды.
Решение
Давайте начнем с простого написания химического уравнения в терминах формул веществ, помня, что и элементарный водород, и хлор двухатомны:
H 2 + Cl 2 → HCl
В реагентах есть два атома водорода и два атома хлора, а в продукте — по одному на каждый атом.
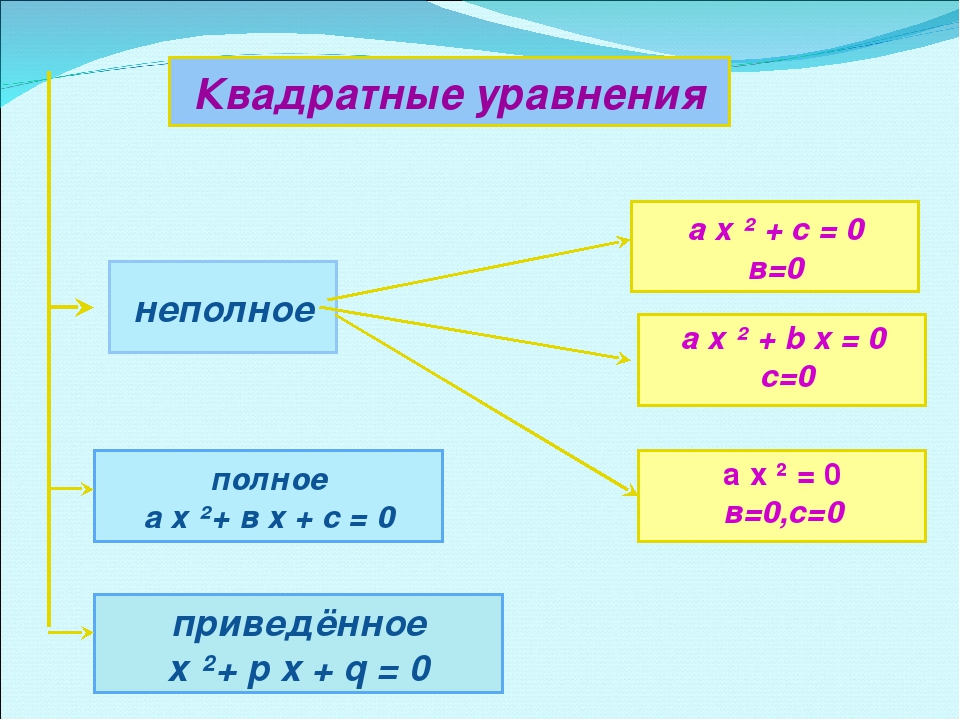 Мы можем исправить это, включив коэффициент 2 на стороне продукта:
Мы можем исправить это, включив коэффициент 2 на стороне продукта:H 2 + Cl 2 → 2HCl
Теперь есть два атома водорода и два атома хлора по обе стороны химического уравнения, так что оно уравновешено.
Начните с написания химического уравнения в терминах используемых веществ:
С 2 H 6 + O 2 → CO 2 + H 2 O
У нас два атома углерода слева, поэтому нам нужны две молекулы диоксида углерода на стороне продукта, чтобы на каждой стороне было по два атома углерода; этот элемент сбалансирован.У нас есть шесть атомов водорода в реагентах, поэтому нам нужно шесть атомов водорода в продуктах. Мы можем получить это, имея три молекулы воды:
С 2 H 6 + O 2 → 2CO 2 + 3H 2 O
Теперь у нас есть семь атомов кислорода в продуктах (четыре из CO 2 и три из H 2 O).
 Это означает, что нам нужно семь атомов кислорода в реагентах. Однако, поскольку кислород — двухатомная молекула, мы можем получить только четное количество атомов кислорода за один раз.Мы можем добиться этого, умножив другие коэффициенты на 2:
Это означает, что нам нужно семь атомов кислорода в реагентах. Однако, поскольку кислород — двухатомная молекула, мы можем получить только четное количество атомов кислорода за один раз.Мы можем добиться этого, умножив другие коэффициенты на 2:.
2C 2 H 6 + O 2 → 4CO 2 + 6H 2 OУмножая все остальное на 2, мы не разбалансируем другие элементы, и теперь мы получаем четное число атомов кислорода в произведении-14. Мы можем получить 14 атомов кислорода на стороне реагента, имея 7 молекул кислорода:
2C 2 H 6 + 7O 2 → 4CO 2 + 6H 2 O
В качестве проверки пересчитайте все, чтобы определить, что каждая сторона имеет одинаковое количество атомов каждого элемента.Это химическое уравнение теперь сбалансировано.
Упражнение \ (\ PageIndex {1} \)
Напишите и уравновесите химическое уравнение, которое представляет реакцию азота и водорода с образованием аммиака, NH 3 .
- Ответ:
N 2 + 3H 2 → 2NH 3
Многие химические уравнения также включают обозначения фаз для веществ: (s) для твердого вещества, (ℓ) для жидкости, (g) для газа и (aq) для водного (т.е.{\ circ} C} {\ rightarrow} Na_ {2} CO_ {3} (s) + CO_ {2} (g) + H_ {2} O (l) \]
Основные выводы
- Химическое уравнение — это краткое описание химической реакции.
- Правильные химические уравнения сбалансированы.
Уравнения состояния для задач детонации (Конференция)
Дэвис, В. К. Уравнения состояния для задач детонации . США: Н.с., 1997.
Интернет.
Дэвис, В. К. Уравнения состояния для задач детонации . Соединенные Штаты.
Davis, W. C. Fri.
C. Fri.
«Уравнения состояния для задач детонации». Соединенные Штаты. https://www.osti.gov/servlets/purl/615626.
@article {osti_615626,
title = {Уравнения состояния для задач детонации},
author = {Дэвис, В. К.},
abstractNote = {Слова «Уравнение состояния» обычно использовались в сообществе физиков детонации для обозначения любой информации о задействованных материалах, которая позволила бы решить данную проблему.По мере того, как проблемы усложнялись, а компьютерное моделирование - более подробным, все более совершенные уравнения состояния были разработаны и использованы. Тем не менее, большинство уравнений состояния было ограничено использованием при решении гидродинамических уравнений для невязкой, не теплопроводной, неизлучающей, не реагирующей жидкости. Вся информация в этих уравнениях состояния касается механических свойств. Нет информации о температуре, энтропии или удельной теплоемкости. В центре внимания этой статьи не предоставление нового уравнения состояния, которое позволит решить все проблемы, а обсуждение ограничений на уравнения состояния и влияние этих ограничений на их свойства.Позже, когда будет больше данных, пора будет искать лучшие уравнения состояния для всех различных задач.},
В центре внимания этой статьи не предоставление нового уравнения состояния, которое позволит решить все проблемы, а обсуждение ограничений на уравнения состояния и влияние этих ограничений на их свойства.Позже, когда будет больше данных, пора будет искать лучшие уравнения состояния для всех различных задач.},
doi = {},
url = {https://www.osti.gov/biblio/615626},
journal = {},
number =,
объем =,
place = {United States},
год = {1997},
месяц = {8}
}
1.Учитывая неполное уравнение
1. Учитывая неполное уравнение : 2N 2 O 5 (г) → Какой набор продуктов дополняет и уравновешивает неполное уравнение ? 1) 2N 2 (г) + 3H 2 (г) 2) 2N 2 (г) + 2O 2 (г) 3) 4NO 2 (г) + O 2 (г) 4) 4NO (г) + SO 2 (г ) 2. Учитывая реакцию : 2C 2 H 2 (г) + 5O 2 (г) → 4CO 2 (г) + 2H 2 O (г) Что такое общее количество граммов O 2 (г), необходимое для полной реакции с 0,50 моль C 2 H 2 (г)? 1) 10. г 3) 80. г 2) 40. г 4) 160 г 3. Когда уравнение __Al 2 (SO 4) 3 + __ZnCl 2 → __AlCl 3 + __ZnSO 4 правильно сбалансирован с использованием наименьших целочисленных коэффициентов, сумма коэффициентов составляет 1) 9 3) 5 2) 8 4) 4 4. Дано сбалансированное уравнение : 3Fe + 4H 2 O → Fe 3 O 4 + 4H 2 Какое общее количество литров H 2, произведенного на STP при потреблении 36,0 граммов H 2 O? 1) 22,4 3) 44,8 2) 33,6 4) 89,6 5. Учитывая реакцию : 2Al + 3H 2 SO 4 → 3H 2 + Al 2 (SO 4) 3 общее количество молей H 2 SO 4, необходимое для полной реакции с 5,0 молями Al, составляет 1) 2.
Учитывая реакцию : 2C 2 H 2 (г) + 5O 2 (г) → 4CO 2 (г) + 2H 2 O (г) Что такое общее количество граммов O 2 (г), необходимое для полной реакции с 0,50 моль C 2 H 2 (г)? 1) 10. г 3) 80. г 2) 40. г 4) 160 г 3. Когда уравнение __Al 2 (SO 4) 3 + __ZnCl 2 → __AlCl 3 + __ZnSO 4 правильно сбалансирован с использованием наименьших целочисленных коэффициентов, сумма коэффициентов составляет 1) 9 3) 5 2) 8 4) 4 4. Дано сбалансированное уравнение : 3Fe + 4H 2 O → Fe 3 O 4 + 4H 2 Какое общее количество литров H 2, произведенного на STP при потреблении 36,0 граммов H 2 O? 1) 22,4 3) 44,8 2) 33,6 4) 89,6 5. Учитывая реакцию : 2Al + 3H 2 SO 4 → 3H 2 + Al 2 (SO 4) 3 общее количество молей H 2 SO 4, необходимое для полной реакции с 5,0 молями Al, составляет 1) 2. 5 моль 3) 7,5 моль 2) 5,0 моль 4) 9,0 моль 6. Учитывая реакцию : 2C 2 H 6 + 7O 2 → 4CO 2 + 6H 2 O Что такое отношение молей произведенного CO 2 к молям израсходованного C 2H 6? 1) от 1 до 1 3) от 3 до 2 2) от 2 до 1 4) от 7 до 2 7. Учитывая сбалансированное уравнение : Mg ( с) + 2HCl (водн.) → MgCl 2 (водн.) + H 2 (г) Каково общее общее количество литров газообразного водорода, полученного при 3.00 молей раствора соляной кислоты полностью израсходовано? 1) 1 1. 2 L 3) 33,6 L 2) 22,4 L 4) 44,8 L 8. Учитывая реакцию : (NH 4) 2 CO 3 → 2NH 3 + CO 2 + H 2 O Какое минимальное количество карбоната аммония при реакции дает 1. 0 моль аммиака? 1) 0,25 моль 3) 17 моль 2) 0,50 моль 4) 34 моль 9. Учитывая реакцию : 2NaOH + H 2 SO 4 → Na 2 SO 4 + 2H 2 O Какое общее количество молей NaOH необходимо для полной реакции с 2 молями H 2 SO 4? 1) 1 3) 0.
5 моль 3) 7,5 моль 2) 5,0 моль 4) 9,0 моль 6. Учитывая реакцию : 2C 2 H 6 + 7O 2 → 4CO 2 + 6H 2 O Что такое отношение молей произведенного CO 2 к молям израсходованного C 2H 6? 1) от 1 до 1 3) от 3 до 2 2) от 2 до 1 4) от 7 до 2 7. Учитывая сбалансированное уравнение : Mg ( с) + 2HCl (водн.) → MgCl 2 (водн.) + H 2 (г) Каково общее общее количество литров газообразного водорода, полученного при 3.00 молей раствора соляной кислоты полностью израсходовано? 1) 1 1. 2 L 3) 33,6 L 2) 22,4 L 4) 44,8 L 8. Учитывая реакцию : (NH 4) 2 CO 3 → 2NH 3 + CO 2 + H 2 O Какое минимальное количество карбоната аммония при реакции дает 1. 0 моль аммиака? 1) 0,25 моль 3) 17 моль 2) 0,50 моль 4) 34 моль 9. Учитывая реакцию : 2NaOH + H 2 SO 4 → Na 2 SO 4 + 2H 2 O Какое общее количество молей NaOH необходимо для полной реакции с 2 молями H 2 SO 4? 1) 1 3) 0. 5 2) 2 4) 4 10. Учитывая реакцию : 4Na + O 2 → 2Na 2 O Сколько граммов кислорода полностью потребляется в производство 1. 00 моль Na 2 O? 1) 16,0 3) 62,0 2) 32,0 4) 124 1 1. Учитывая несбалансированное уравнение : __Al 2 (SO 4) 3 + __Ca (OH) 2 → __Al (OH) 3 + __CaSO 4 Когда уравнение полностью сбалансировано с использованием наименьшего целочисленные коэффициенты сумма коэффициентов коэффициентов равна 1) 5 3) 3 2) 9 4) 4 12.Когда уравнение __Na (s) + __H 2 O (l) __NaOH (водн.) + __H 2 (g) правильно сбалансировано с использованием наименьших целых чисел, коэффициент воды равен 1) 1 3) 3 2) 2 4) 4 13. Учитывая реакцию : Cu + 4HNO 3 → Cu (NO 3) 2 + 2H 2 O + 2NO 2 Какова общая масса H 2 O, полученная при полном потреблении 32 граммов Cu? 1) 9.
5 2) 2 4) 4 10. Учитывая реакцию : 4Na + O 2 → 2Na 2 O Сколько граммов кислорода полностью потребляется в производство 1. 00 моль Na 2 O? 1) 16,0 3) 62,0 2) 32,0 4) 124 1 1. Учитывая несбалансированное уравнение : __Al 2 (SO 4) 3 + __Ca (OH) 2 → __Al (OH) 3 + __CaSO 4 Когда уравнение полностью сбалансировано с использованием наименьшего целочисленные коэффициенты сумма коэффициентов коэффициентов равна 1) 5 3) 3 2) 9 4) 4 12.Когда уравнение __Na (s) + __H 2 O (l) __NaOH (водн.) + __H 2 (g) правильно сбалансировано с использованием наименьших целых чисел, коэффициент воды равен 1) 1 3) 3 2) 2 4) 4 13. Учитывая реакцию : Cu + 4HNO 3 → Cu (NO 3) 2 + 2H 2 O + 2NO 2 Какова общая масса H 2 O, полученная при полном потреблении 32 граммов Cu? 1) 9. 0 г 3) 36 г 2) 18 г 4) 72 г 14. Когда уравнение __SiO 2 + __C → __SiC + __CO правильно сбалансировано с использованием целочисленных коэффициентов, сумма всех коэффициентов равна 1) 6 3) 8 2) 7 4) 9 15. Учитывая несбалансированное уравнение : __Na + __H 2 O → __H 2 + __NaOH Когда уравнение правильно сбалансировано с помощью наименьшие целочисленные коэффициенты, коэффициент для H 2 O равен 1) 1 3) 3 2) 2 4) 4 16. Учитывая реакцию : 2CO + O 2 → 2CO 2 Какое минимальное количество молей O 2 требуется для производства одного моля CO 2. ? 1) 1. 0 3) 0,25 2) 2,0 4) 0,50 17. Учитывая реакцию : 3Cu + 8HNO 3 → 3Cu (NO 3 ) 2 + 2NO + 4H 2 O Общее количество граммов Cu, необходимое для производства 1.
0 г 3) 36 г 2) 18 г 4) 72 г 14. Когда уравнение __SiO 2 + __C → __SiC + __CO правильно сбалансировано с использованием целочисленных коэффициентов, сумма всех коэффициентов равна 1) 6 3) 8 2) 7 4) 9 15. Учитывая несбалансированное уравнение : __Na + __H 2 O → __H 2 + __NaOH Когда уравнение правильно сбалансировано с помощью наименьшие целочисленные коэффициенты, коэффициент для H 2 O равен 1) 1 3) 3 2) 2 4) 4 16. Учитывая реакцию : 2CO + O 2 → 2CO 2 Какое минимальное количество молей O 2 требуется для производства одного моля CO 2. ? 1) 1. 0 3) 0,25 2) 2,0 4) 0,50 17. Учитывая реакцию : 3Cu + 8HNO 3 → 3Cu (NO 3 ) 2 + 2NO + 4H 2 O Общее количество граммов Cu, необходимое для производства 1.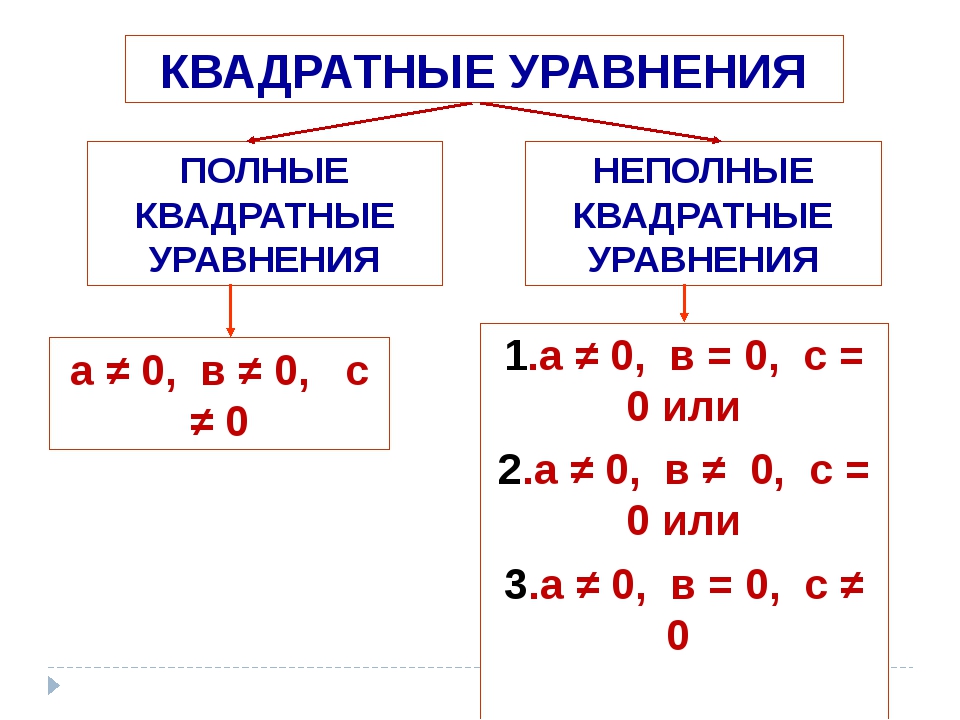 0 моль Cu (NO 3) 2 равно 1) 32 3) 128 2) 64 4) 192
0 моль Cu (NO 3) 2 равно 1) 32 3) 128 2) 64 4) 192
НЕПОЛНОЕ УРАВНЕНИЕ Поэта Кири
Я ХОЧУ СЛУШАТЬ, ДО ТОГО, ЧТО ПОЧУВСТВУЕТ.
Я
Поздравляю
Тебя.
…
Теперь я понимаю
Что я не
, а она не
, и вы тоже.
В жизни
— мужчина,
— женщина
и
— деньги.
А мне
противно мое собственное положение дел.
Я ГИПОКРИТ,
(ВЫ МОЖЕТЕ БЫТЬ ХУЖЕ)
, что крыса, не принадлежащая к расе
, имеет больше шансов на добродетель.
Я не уникален, но
часть уравнения природы
давным-давно в истории
Я был «БЕСПЕРЫМ ДВОЙНЫМ»
точно так же, как цыпленок,
ожидавший процесса жарки
ЕЩЕ
после смерти и разложения,
, если меня нет в истории,
как статуя, символизирующая
бессмертие.
I
больше не будет
ЧЕЛОВЕКОМ
, но будет CREATURE
с костями, неотличимыми от
моего вида.
Эти слова принадлежат человеку
человеку, у которого нет ничего
для себя и своего времени
, кроме возможности поразмышлять над
величайшим УРАВНЕНИЕМ
жизни, имеющим смысл.
Это слова человека
, который живет как собака
он осмеливается высказывать свое мнение
человека, которого мы подвергаем сомнению, его существование и цель
мы называем безумным, безумным и дикарем.
Его слова никогда не поколеблют вас
, если вы спросите
ПОЧЕМУ ОН СМЕЕТ ГОВОРИТЬ, ЕСЛИ ОН НИЧЕГО?
Вы действительно слушали?
Вопрос.
Вы бы одолжили ухо
Человеку, который живет как собака
или
Человеку, живущему в бетонном пузыре
?
Я хочу, чтобы вы Думали за пределами бетонного пузыря
, который вы называете безопасным.
МУЖЧИНА + ЖЕНЩИНА x ДЕНЬГИ (ПРИРОДА) = ……………
каково ваше уравнение?
© Hansmind, 2018
Здравствуйте, надеюсь, у вас все хорошо.
Я хотел бы поблагодарить вас за поддержку в этом году, я действительно полон всех комментариев и лайков.
Пожалуйста, не стесняйтесь комментировать и критиковать стихотворение.
Это будет первое стихотворение в моем 4-м сборнике под названием
«Опытные мысли»
ПОЛУЧИТЬ ПОНРАВИЛЬНО, КОММЕНТАРИЙ И ПОДЕЛИТЬСЯ.
Спасибо.
1. Учитывая неполное уравнение
1. Учитывая неполное уравнение: 2N2O5 (г) → Какой набор продуктов дополняет и уравновешивает неполное уравнение? 1) 2N2 (г) + 3h3 (г) 2) 2N2 (г) + 2O2 (г) 3) 4NO2 (г) + O2 (г) 4) 4NO (г) + SO2 (г) 2.Учитывая реакцию: 2C2h3 (г) + 5O2 (г) → 4CO2 (г) + 2h3O (г) Какое общее количество граммов O2 (г) необходимо для полностью реагировать с 0,50 моль C2h3 (г)? 1) 10. г 3) 80. г 2) 40. г 4) 160 г 3. Когда уравнение __Al2 (SO4) 3 + __ZnCl2 → __AlCl3 + __ZnSO4 правильно сбалансирован с использованием наименьшего целого числа коэффициентов сумма коэффициентов равна 1) 9 3) 5 2) 8 4) 4 4. Учитывая сбалансированное уравнение: 3Fe + 4h3O → Fe3O4 + 4h3 Какое общее количество литров h3 произведено на СТП когда израсходовано 36,0 грамма h3O? 1) 22.4 3) 44,8 2) 33,6 4) 89,6 5. Учитывая реакцию: 2Al + 3h3SO4 → 3h3 + Al2 (SO4) 3 Общее количество молей h3SO4, необходимое для реакции полностью с 5,0 молями Al 1) 2,5 моль 3) 7,5 моль 2) 5,0 моль 4) 9,0 моль 6.Учитывая реакцию: 2C2H6 + 7O2 → 4CO2 + 6h3O Каково отношение произведенных молей CO2 к молям C? 2H6 израсходован? 1) 1 к 1 3) 3 к 2 2) 2 к 1 4) от 7 до 2 7. Учитывая сбалансированное уравнение: Mg (тв) + 2HCl (водн.) → MgCl2 (водн.) + H3 (г) Каково общее количество литров водорода на STP? газ производится, когда 3.00 моль соляной кислоты раствор полностью израсходован? 1) 11,2 л 3) 33,6 л 2) 22,4 л 4) 44,8 л 8. Учитывая реакцию: (Nh5) 2CO3 → 2Nh4 + CO2 + h3O Какое минимальное количество карбоната аммония что реагирует, чтобы произвести 1.0 моль аммиака? 1) 0,25 моль 3) 17 моль 2) 0,50 моль 4) 34 моль 9. Учитывая реакцию: 2NaOH + h3SO4 → Na2SO4 + 2h3O Какое общее количество молей NaOH необходимо для полностью реагировать с 2 молями h3SO4? 1) 1 3) 0,5 2) 2 4) 4 10. Учитывая реакцию: 4Na + O2 → 2Na2O Сколько граммов кислорода полностью потребляется производство 1.00 моль Na2O? 1) 16,0 3) 62,0 2) 32,0 4) 124 11. Учитывая несбалансированное уравнение: __Al2 (SO4) 3 + __Ca (OH) 2 → __Al (OH) 3 + __CaSO4 Когда уравнение полностью сбалансировано с помощью наименьшие целочисленные коэффициенты сумма коэффициенты 1) 5 3) 3 2) 9 4) 4 12.
Когда уравнение __Na (s) + __h3O (l) __NaOH (водн.) + __H3 (г) правильно сбалансирован с использованием наименьших целых чисел, коэффициент воды 1) 1 3) 3 2) 2 4) 4 13. Учитывая реакцию: Cu + 4HNO3 → Cu (NO3) 2 + 2h3O + 2NO2 Какова общая масса h3O, полученного при 32 граммах Cu полностью потребляется? 1) 9.0 г 3) 36 г 2) 18 г 4) 72 г 14. Когда уравнение __SiO2 + __C → __SiC + __CO правильно сбалансирован с использованием целочисленных коэффициентов, сумма всех коэффициентов равна 1) 6 3) 8 2) 7 4) 9 15. Учитывая несбалансированное уравнение: __Na + __h3O → __h3 + __NaOH Когда уравнение правильно сбалансировано с помощью наименьшие целочисленные коэффициенты, коэффициент при h3 O это 1) 1 3) 3 2) 2 4) 4 16. Учитывая реакцию: 2СО + О2 → 2СО2 Какое минимальное количество молей O2 необходимо для произвести один моль СО2? 1) 1.0 3) 0,25 2) 2,0 4) 0,50 17. Учитывая реакцию: 3Cu + 8HNO3 → 3Cu (NO3) 2 + 2NO + 4h3O Общее количество граммов Cu, необходимое для производства 1,0 моль Cu (NO3) 2 составляет 1) 32 3) 128 2) 64 4) 192 18.
Учитывая реакцию: 2Na + 2h3O → 2NaOH + h3 Сколько молей Na необходимо для точного производства 5,6 литра х3, измерено на СТП? 1) 1.0 3) 0,50 2) 2,0 4) 0,25 19. Учитывая несбалансированное уравнение: __CaSO4 + __AlCl3 → Al2 (SO4) 3 + __CaCl2 Каков коэффициент Al2 (SO4) 3, когда уравнение имеет вид полностью сбалансирован с использованием наименьшего целого числа коэффициенты? 1) 1 3) 3 2) 2 4) 4 20.Учитывая несбалансированное уравнение: __Li + __N2 → __Li3N Когда уравнение правильно сбалансировано с использованием наименьшего целые числа, коэффициент лития равен 1) 1 3) 3 2) 2 4) 6 21. Учитывая несбалансированное уравнение: __ Al (тв) + __O2 (г) → __Al2O3 (т) Когда это уравнение правильно сбалансировано с использованием наименьшего целые числа, каков коэффициент при O2 (г)? 1) 6 3) 3 2) 2 4) 4 22. Какое уравнение правильно сбалансировано? 1) h3 + O2 → h3O 2) Ca + Cl2 → CaCl 3) 2х3 + О2 → 2х3О 4) Ca + C12 → Ca2Cl 23. Учитывая реакцию: 2h3 + O2 → 2h3O Общее количество граммов O2, необходимое для производства 54 граммы воды это 1) 36 3) 61 2) 48 4) 75 24.Учитывая реакцию: C3H8 (г) + 5O2 (г) → 4h3O (г) + 3CO2 (г) Какое общее количество литров CO2 образуется при 150 литров O2 полностью реагирует с C3H8? 1) 90. 3) 3,0 2) 150 4) 250 25. Учитывая несбалансированное уравнение: Al (OH) 3 + h3SO4 → Al2 (SO4) 3 + h3O Какой коэффициент перед h3O, когда уравнение полностью сбалансировано с использованием наименьшего целого числовые коэффициенты? 1) 6 3) 3 2) 2 4) 4 26. Учитывая уравнение: X + Cl2 - C2H5Cl + HCl 27. 28. 29. 30. 31. 32. 33. 34. Какая молекула представлена X? 1) C2h5 2) C2H6 3) C3H6 4) C3H8 Учитывая реакцию: 2Ch4OH (л) + 3O2 (г) → 2CO2 (г) + 4h3O (г) Сколько литров O2 (г) необходимо для точного производства 200 литров CO2 (г)? 1) 100 л 3) 300 л 2) 200 л 4) 400 л Учитывая реакцию: Ch5 + 2O2 → CO2 + 2h3O Какое количество кислорода нужно, чтобы полностью прореагировать с 1 моль Ч5? 1) 2 моль 3) 2 грамма 2) 2 атома 4) 2 молекулы Учитывая реакцию: C3H8 (г) + 5O2 (г) → 3CO2 (г) + 4h3O (г) Каков общий объем h3O (г), образовавшийся при 8.00 литров C3H8 (г) полностью окисляется? 1) 32,0 л 3) 8,00 л 2) 22,4 л 4) 4,00 л Учитывая реакцию: 2C2H6 + 7O2 → 4CO2 + 6h3O Каково общее количество произведенных молей CO2? когда один моль C2H6 полностью прореагирует? 1) 1 3) 3 2) 2 4) 4 Учитывая сбалансированное уравнение: NaOH + HCl → NaCl + h3O Каково общее количество произведенного h3O в граммах? когда образуется 116 граммов продукта NaCl? 1) 9,0 г 3) 36 г 2) 18 г 4) 54 г Учитывая реакцию: 4Al + 3O2 → 2Al2O3 Сколько молей Al2O3 образуется, когда 27 граммов Al полностью реагирует с O2? 1) 1.0 3) 0,50 2) 2,0 4) 4,0 Когда уравнение __h3O2 → __h3O + __O2 полностью сбалансирован, сумма всех коэффициентов будет 1) 5 3) 3 2) 8 4) 4 Учитывая реакцию: Ca + 2h3O → Ca (OH) 2 + h3 Сколько молей h3O нужно для точной реакции с 2,0 молями Са? 1) 1.0 3) 0,50 2) 2,0 4) 4,0 35. Учитывая несбалансированное уравнение: __C3H8 (г) + __O2 (г) → __h3O (г) + __CO2 (г) Когда уравнение полностью сбалансировано с использованием наименьшего целые числа, коэффициент при O2 равен 1) 5 3) 3 2) 2 4) 10 36. Учитывая реакцию: Ca + 2h3O → Ca (OH) 2 + h3 Сколько молей h3O необходимо для полной реакции с 2.0 молей Ca? 1) 1,0 моль 3) 0,50 моль 2) 2,0 моль 4) 4,0 моль 37. Учитывая уравнение: h3 (г) + Cl2 (г) → 2HCl (г) Каково общее количество образовавшихся молей HCl (г)? когда 3 моля h3 (г) израсходованы полностью? 1) 5 моль 3) 3 моль 2) 2 моль 4) 6 моль 38. Учитывая сбалансированное уравнение: Fe (s) + CuSO4 (водн.) - FeSO4 (водн.) + Cu (s) Какие общая масса железа необходима для производства 1,00 моль медь? 1) 26,0 г 3) 112 г 2) 55,8 г 4) 192 г 39. Учитывая уравнение: __FeCl2 + __ Na2CO3 → __FeCO3 + __ NaCl Когда уравнение правильно сбалансировано с помощью наименьших целых чисел, коэффициент NaCl равен 1) 6 3) 3 2) 2 4) 4 40.Если уравнение сбалансировано правильно, обе стороны уравнение должно иметь одинаковое количество 1) атомы 3) молекулы 2) коэффициенты 4) моли молекул 41. Какое уравнение правильно сбалансировано? 1) Zn + Ag + → Zn2 + + Ag 2) Cu + Au3 + → Cu2 + + Au 3) Al + Sn2 + → Al3 + + Sn 4) Ca + Mg2 + → Ca2 + + Mg 42. Учитывая реакцию: Ca (s) + 2h3O (l) → Ca (OH) 2 (водн.) + H3 (г) Когда 40,1 грамма Ca (s) полностью реагирует с вода, каков общий объем h3 (г) при STP произведено? 1) 1,00 л 3) 22,4 л 2) 2,00 л 4) 44,8 л 43.Учитывая реакцию: К2 + 3х3 → 2Нх4 Сколько граммов аммиака производится при 1,0 моль азота реагирует? 1) 8,5 3) 34 2) 17 4) 68 44. Учитывая уравнение: 2 C2h3 (г) + 5 O2 (г) - 4 CO2 (г) + 2 h3O (г) Сколько молей кислорода требуется для реакции полностью с 1.0 моль C2h3? 1) 2,5 3) 5.0 2) 2,0 4) 10 45. Когда уравнение __ Cu + __h3SO4 → __CuSO4 + __h3O + __SO2 правильно сбалансирован, каков коэффициент CuSO4? 1) 1 2) 2 46. Учитывая реакцию: 3) 3 4) 4 2h3 (г) + O2 (г) → 2h3O (ж) 47.48. 49. 50. 51. Какое общее количество литров O2 (г) необходимо на STP произвести 6,0 × 1023 молекул h3O (l)? 1) 11,2 л 3) 33,6 л 2) 22,4 л 4) 44,8 л Когда уравнение __Nh4 + __O2 → __HNO3 + __ h3O полностью сбалансирован с использованием наименьших целых чисел, коэффициент O2 будет 1) 1 3) 3 2) 2 4) 4 Учитывая сбалансированное уравнение: 2Na + S → Na2S Каково общее количество молей S, прореагировавших при 4,0 моля Na полностью израсходованы? 1) 1,0 моль 3) 0,5 моль 2) 2,0 моль 4) 4,0 моль По реакции h3 + Cl2 → 2HCl, производство 2.0 моль HCl потребуется 70. граммов Cl2 и 1) 1,0 г ч3 2) 2,0 г ч3 3) 3,0 г ч3 4) 4,0 г ч3 Когда уравнение __h3 + __N2 → __Nh4 полностью сбалансирован с использованием наименьших целых чисел, сумма всех коэффициентов будет 1) 6 3) 3 2) 7 4) 12 Учитывая несбалансированное уравнение: __Fe2O3 + __CO - __Fe + __CO2 Когда уравнение правильно сбалансировано с помощью наименьшие целочисленные коэффициенты, что такое коэффициент СО? 1) 1 3) 3 2) 2 4) 4 52. Учитывая реакцию: 2KClO3 (тв) → 2KCl (тв) + 3O2 (г) Какое общее количество молей KClO3 (ов) необходимо для произвести 6 моль O2 (г)? 1) 1 3) 3 2) 2 4) 4 53.Учитывая реакцию 2KClO3 → 2KCl + 3O2 Какое общее количество молей KCl образуется при 1,50 моль KClO3 разлагается? 1) 1,50 3) 3,00 2) 4,50 4) 0,75 54. Учитывая несбалансированное уравнение: __N2 (г) + __h3 (г) → _Nh4 (г) Когда уравнение сбалансировано с использованием наименьших целочисленных коэффициентов, отношение молей водорода потребляется до молей произведенного аммиака составляет 1) 1: 3 3) 2: 3 2) 3: 1 4) 3: 2 55. Учитывая реакцию: 2SO2 (г) + O2 (г) → 2SO3 (г) Какое общее количество литров SO3 образуется при 32.0 литров SO2 полностью реагирует? (Все измерения производятся на СТП.) 1) 11,2 л 3) 40,0 л 2) 32,0 л 4) 44,8 л 56. Когда уравнение __ C2h5 + __ O2 → __ CO2 + __ h3O сбалансирован с использованием наименьших целых чисел, что такое коэффициент O2? 1) 1 3) 3 2) 2 4) 4 57. Учитывая уравнение: 6CO2 (г) + 6h3O (л) → C6h22O6 (т) + 6O2 (г) Какое минимальное количество литров СО2 (г), измерено на STP, необходимо для производства 32,0 граммов кислород? 1) 264 л 3) 192 л 2) 32,0 л 4) 22,4 л 58. Учитывая реакцию: N2 (г) + 3 h3 (г) ↔ 2 Nh4 (г) Каково молярное соотношение между газообразным азотом и водородный газ? 1) 1: 2 3) 2: 2 2) 1: 3 4) 2: 3 59.Учитывая реакцию: 2C2H6 + 7O2 → 4CO2 + 6h3O Каково общее количество молей CO2, производимое полное сгорание 5,0 моль C2H6? 1) 1,0 моль 3) 5,0 моль 2) 2,0 моль 4) 10. моль 60. Учитывая реакцию: 4Nh4 + 5O2 → 4NO + 6h3O Какое максимальное количество молей h3O может производиться, когда 2,0 моля Nh4 полностью отреагировал? 1) 1.0 3) 3,0 2) 2,0 4) 6.0 Справочные таблицы Ключ ответа 1. 3 30. 2 2. 2 31. 3 3. 1 32. 3 4. 3 33. 1 5. 3 34. 4 6. 2 35. 1 7. 3 36. 4 8. 2 37. 4 9.4 38. 2 10. 1 39. 2 11. 2 40. 1 12. 2 41. 4 13. 2 42. 3 14. 2 43. 3 15. 2 44. 1 16. 4 45. 1 17. 2 46. 1 18. 3 47. 2 19. 1 48. 2 20. 4 49. 2 21. 3 50. 1 22. 3 51. 3 23. 2 52. 4 24. 1 53. 1 25. 1 54. 4 26. 2 55. 2 27. 3 56. 3 28. 1 57. 4 29. 1 58. 2 Ключ ответа 59. 4 60. 3
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера на прием файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie. - Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.

