Содержание
Неравенства и системы неравенств. Алгебра, 9 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Новости
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Переменка
Поиск по сайту
Отправить отзыв
- org/BreadcrumbList»>
-
Предметы -
Алгебра -
9 класс
-
Повторим способы решения линейных и квадратных неравенств
-
Решение рациональных неравенств методом интервалов
-
Множества и подмножества. Объединение и пересечение множеств
Объединение и пересечение множеств
-
Системы рациональных неравенств
Отправить отзыв
Нашёл ошибку?
Сообщи нам!
Copyright © 2021 ООО ЯКласс
Контакты
Пользовательское соглашение
Урок 28.
 системы неравенств с двумя переменными — Алгебра — 9 класс
системы неравенств с двумя переменными — Алгебра — 9 класс
Рассмотрим систему неравенств с двумя переменными.
y – x>5,
x2 – 1>y
Пара чисел 6 и 12 являются решением данной системы, так как при подстановке этих значений вместо переменных получаются верные числовые неравенства.
Сделаем вывод: пара чисел, которая является общим решением всех неравенств системы, называется решением системы неравенств с двумя переменными, а множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в нее неравенств.
Рассмотрим пример. Выясним, какое множество точек задает на координатной плоскости данная система.
x2 + y2 ≤16
x – y ≤ 4
Для этого изобразим соответствующие графики функций на одной координатной плоскости. Графиком первой функции будет являться окружность с центром в точке начала отсчета и радиусом 4, а второй – прямая.
Множеством решений первого неравенства изначальной системы будет область внутри круга, включая точки окружности, а решением второго неравенства, полуплоскость, которая находится ниже прямой, включая все точки прямой.
Итак, множество точек, которые являются решением данной системы неравенств является часть плоскости, отмеченная на рисунке двойной штриховкой.
Рассмотрим еще один пример.
y>x2 + 3
x2 + y2<25
Множеством точек, задаваемым первым неравенством, является часть плоскость, расположенная выше параболы игрик равен икс в квадрате плюс три.
А второе неравенство задает множество точек, расположенных внутри круга с центром в точек нуль нуль и радусом 5.
Пересечение этих множеств является решением данной системы неравенств.
Алгебра – 9 класс. Системы неравенств
Дата публикации: .
Система неравенств
Ребята, вы изучили линейные и квадратные неравенства, научились решать задачи на эти темы. Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
Введем определение системы неравенств.
Несколько неравенств с некоторой переменой х образуют систему неравенств, если нужно найти все значения х, при которых каждое из неравенств образует верное числовое выражение.
Любое значение x, при которых каждое неравенство принимает верное числовое выражение, является решением неравенства. Также может называться и частным решением.
А что есть частное решение? Например, в ответе мы получили выражение х>7. Тогда х=8, или х=123, или какое-либо другое число большее семи – частное решение, а выражение х>7 – общее решение. Общее решение образуется множеством частных решений.
Как мы объединяли систему уравнений? Правильно, фигурной скобкой, так вот с неравенствами поступают также. Давайте рассмотрим пример системы неравенств: $\begin{cases}x+7>5\\x-3
Если система неравенств состоит из одинаковых выражений, например, $\begin{cases}x+7>5\\x+7
Так, что же значит: найти решение системы неравенств?
Решение неравенства – это множество частных решений неравенства, которые удовлетворяют сразу обоим неравенствам системы.
Общий вид системы неравенств запишем в виде
$\begin{cases}f(x)>0\\g(x)>0\end{cases}$
Обозначим $Х_1$ – общее решение неравенства f(x)>0.
$Х_2$ – общее решение неравенства g(x)>0.
$Х_1$ и $Х_2$ – это множество частных решений.
Решением системы неравенств будут числа, принадлежащие, как $Х_1$, так и $Х_2$.
Давайте вспомним операции над множествами. Как нам найти элементы множества, принадлежащие сразу обоим множествам? Правильно, для этого есть операция пересечения. Итак, решением нашего неравенство будет множество $А= Х_1∩ Х_2$.
Примеры решений систем неравенств
Давайте посмотрим примеры решения систем неравенств.
Решите систему неравенств.
а) $\begin{cases}3x-1>2\\5x-10 b) $\begin{cases}2x-4≤6\\-x-4
Решение.
а) Решим каждое неравенство отдельно.
$3х-1>2; \; 3x>3; \; x>1$.
$5x-10
Отметим наши промежутки на одной координатной прямой.
Решением системы будет отрезок пересечения наших промежутков. Неравенство строгое, тогда отрезок будет открытым.
Ответ: (1;3).
б) Также решим каждое неравенство отдельно.
$2x-4≤6; 2x≤ 10; x ≤ 5$.
$-x-4-5$.
Решением системы будет отрезок пересечения наших промежутков. Второе неравенство строгое, тогда отрезок будет открытым слева.
Ответ: (-5; 5].
Давайте обобщим полученные знания.
Допустим, необходимо решить систему неравенств:
$\begin{cases}f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end{cases}$.
Тогда, интервал ($x_1; x_2$) – решение первого неравенства.
Интервал ($y_1; y_2$) – решение второго неравенства. 2+36
2+36
План-конспект урока алгебры «Неравенства и системы неравенств с одной переменной второй степени» для 9 класса.
Тема: «Неравенства и системы неравенств с одной переменной второй степени»
Тип урока: Урок обобщения и систематизации знаний
Формируемые результаты:
Предметные: формирование умения решать неравенства и системы неравенств с одной переменной второй степени.
Личностные: формировать интерес к изучению темы и желание применять приобретенные знания и умения.
Метапредметные: формировать умение использовать приобретенные знания в практической деятельности.
Планируемые результаты: учащиеся систематизируют знания по теме; актуализируют умения и навыки решения неравенств и систем неравенств с одной переменной второй степени.
Основные понятия: неравенства и системы неравенств с одной переменной второй степени.
Организационная структура урока
|
|
|
| ||||||||||||||
|
|
| |||||||||||||||
|
|
|
|
| |||||||||||||
| ||||||||||||||||
|
|
|
| |||||||||||||
| ||||||||||||||||
|
|
| ||||||||||||||
|
|
|
| |||||||||||||
|
|
|
|
| |||||||||||||
|
|
| ||||||||||||||
|
|
|
| |||||||||||||
Алгебра, 9 класс, самостоятельная работа, решение системы неравенств
Вариант 1 Решите неравенства: А) 3x – 5 < 13; Б) – 5x – 12 > — 2x + 33; В) 3 (2x – 3) ≥ 4 (5 – x). Решите системы неравенств: Г) Д) Е) | Вариант 2 Решите неравенства: А) 4x + 3 < 27; Б) – 8x – 19 > — 6x + 27; В) 4 (3x – 1) ≥ 3 (8 – x). Решите системы неравенств: Г) Д) Е) |
Вариант 1 Решите неравенства: А) 3x – 5 < 13; Б) – 5x – 12 > — 2x + 33; В) 3 (2x – 3) ≥ 4 (5 – x). Решите системы неравенств: Г) Д) Е) | Вариант 2 Решите неравенства: А) 4x + 3 < 27; Б) – 8x – 19 > — 6x + 27; В) 4 (3x – 1) ≥ 3 (8 – x). Решите системы неравенств: Г) Д) Е) |
Вариант 1 Решите неравенства: А) 3x – 5 < 13; Б) – 5x – 12 > — 2x + 33; В) 3 (2x – 3) ≥ 4 (5 – x). Решите системы неравенств: Г) Д) Е) | Вариант 2 Решите неравенства: А) 4x + 3 < 27; Б) – 8x – 19 > — 6x + 27; В) 4 (3x – 1) ≥ 3 (8 – x). Решите системы неравенств: Г) Д) Е) |
Вариант 1 Решите неравенства: А) 3x – 5 < 13; Б) – 5x – 12 > — 2x + 33; В) 3 (2x – 3) ≥ 4 (5 – x). Решите системы неравенств: Г) Д) Е) | Вариант 2 Решите неравенства: А) 4x + 3 < 27; Б) – 8x – 19 > — 6x + 27; В) 4 (3x – 1) ≥ 3 (8 – x). Решите системы неравенств: Г) Д) Е) |
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 1
Решите неравенства:
А) 3x – 5 < 13;
Б) – 5x – 12 > — 2x + 33;
В) 3 (2x – 3) ≥ 4 (5 – x).
Решите системы неравенств:
Г)
Д)
Е)
Вариант 2
Решите неравенства:
А) 4x + 3 < 27;
Б) – 8x – 19 > — 6x + 27;
В) 4 (3x – 1) ≥ 3 (8 – x).
Решите системы неравенств:
Г)
Д)
Е)
Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
ax<bax≤bax>bax≥b
где a и b – любые числа, причем a≠0,x – переменная.
Примеры линейных неравенств:
3x<5x−2≥07−5x<1x≤0
Решить линейное неравенство – получить выражение вида:
x<cx≤cx>cx≥c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий >,<, точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые.
 Должно получиться неравенство одного из следующих видов:
Должно получиться неравенство одного из следующих видов:
ax<bax≤bax>bax≥b
- Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a>0 то неравенство приобретает вид x≤ba.
- Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3(2−x)>18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6−3x>18
−3x>18−6−3x>12|÷(−3)
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как −3<0, знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).
x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈(−∞;−4)
№2. Решить неравество 6x+4≥3(x+1)−14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x+4≥3x+3−14
6x−3x≥3−14−4
3x≥−15 | ÷3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3>0, знак неравенства после деления меняться не будет.
x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈[−5; +∞)
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6x−1≤2(3x−0,5).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x−1≤6x−1
6x−6x≤−1+1
0≤0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x∈(−∞;+∞)
- x∈ℝ
№2. Решить неравенство x+3(2−3x)>−4(2x−12).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x+6−9x>−8x+48
−8x+8x>48−6
0>42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x∈∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤0 где a, b, c — некоторые числа, причем a≠0,x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий >,<, точки будут выколотые.
Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x2≥x+12.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2≥x+12
x2−x−12≥0
x2−x−12=0
a=1,b=−1,c=−12
D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x2−x−1=62−6−1=29>0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−3]∪[4;+∞)
№2. Решить неравенство −3x−2≥x2.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
−3x−2≥x2
−x2−3x−2≥0
−x2−3x−2=0
a=−1,b=−3,c=−2
D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1
x1=−2,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
−x2−3x−2=−(0)2−3⋅0−2=−2<0
Это значит, что знак на интервале, в котором лежит точка 0 будет −.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥, выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x∈[−2;−1]
№3. Решить неравенство 4<x2+3x.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
4<x2+3x
−x2−3x+4<0
−x2−3x+4=0
a=−1,b=−3,c=4
D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1
x1=−4,x2=1
Наносим точки на ось x.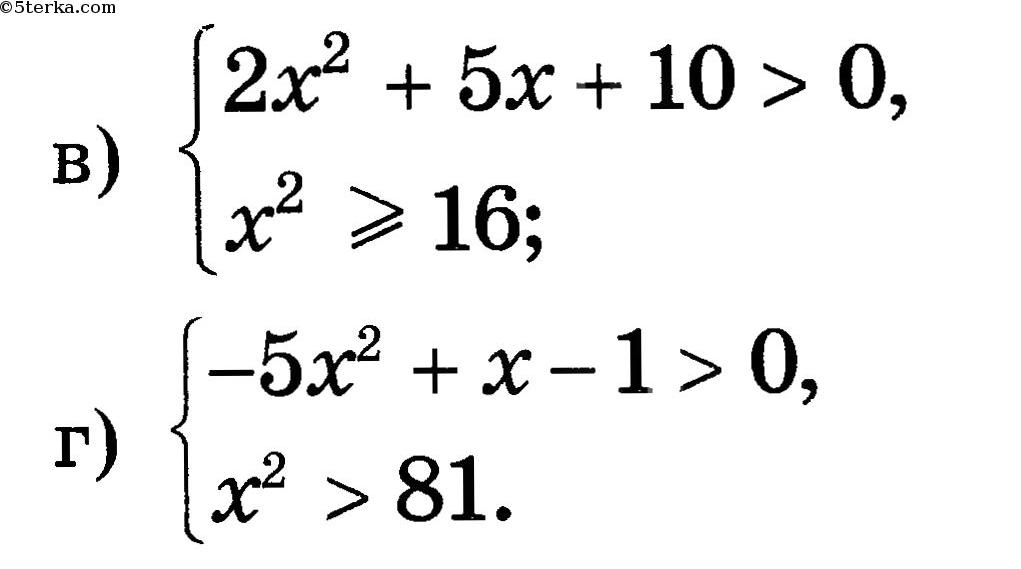 Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
−x2−3x+4=−(2)2−3⋅2+4=−6<0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства <, выбираем в ответ интервалы со знаком −.
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−∞;−4)∪(1;+∞)
№4. Решить неравенство x2−5x<6.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2−5x<6
x2−5x−6<0
x2−5x−6=0
a=1,b=−5,c=−6
D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1
x1=6,x2=−1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x2−5x−6=102−5⋅10−6=100−50−6= 44>0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства <, выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x∈(−1;6)
№5. Решить неравенство x2<4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x2<4
x2−4<0
x2−4=0
(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2
x1=2,x2=−2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x2−4=32−4=9−4=5>0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства <, выбираем в ответ интервал со знаком −.
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−2;2)
№6. Решить неравенство x2+x≥0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x2+x=0.
x2+x≥0
x2+x=0
x(x+1)=0⇔[x=0x+1=0[x=0x=−1
x1=0,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x2+x=12+1=2>0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−1]∪[0;+∞)
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.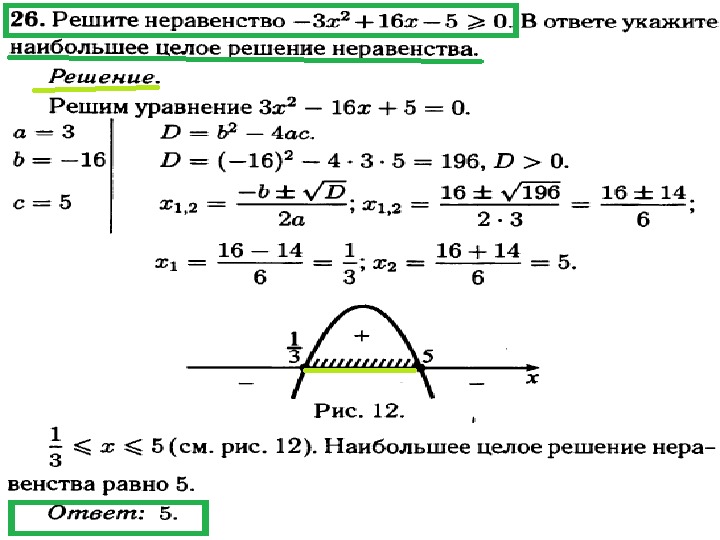
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
- Приравнять числитель дроби к нулю f(x)=0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g(x)=0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x−1x+3>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.
- Приравниваем числитель к нулю f(x)=0.
x−1=0
x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g(x)=0.
x+3=0
x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x∈(−∞;−3)∪(1;+∞)
№2. Решить неравенство 3(x+8)≤5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f(x)g(x)≤0.
3(x+8)≤5
3(x+8)−5\x+8≤0
3x+8−5(x+8)x+8≤0
3−5(x+8)x+8≤0
3−5x−40x+8≤0
−5x−37x+8≤0
- Приравнять числитель к нулю f(x)=0.
−5x−37=0
−5x=37
x=−375=−375=−7,4
x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g(x)=0.
x+8=0
x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными.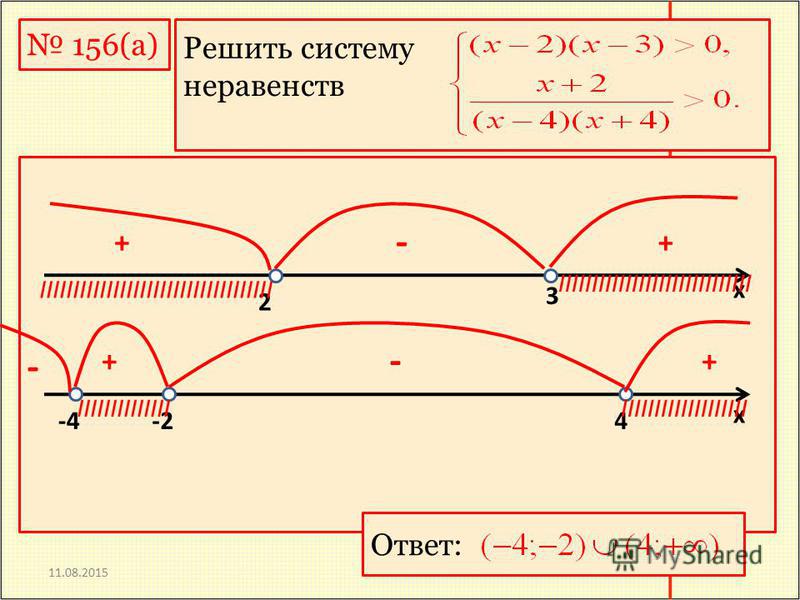 Ну а нули знаменателя выколоты всегда.
Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f(x)g(x):
−5x−37x+8=−5⋅0−370+8=−378<0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤, выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x∈(−∞;−8)∪[−7,4;+∞)
№3. Решить неравенство x2−1x>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен.
 Неравенство приведено к виду f(x)g(x)>0.
Неравенство приведено к виду f(x)g(x)>0.
- Приравнять числитель к нулю f(x)=0.
x2−1=0
(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1
x1=1,x2=−1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g(x)=0.
x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):
x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x∈(−1;0)∪(1;+∞)
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{x+4>02x+3≤x2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств {2x−3≤57−3x≤1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2x−3≤5
2x≤8|÷2, поскольку 2>0, знак неравенства после деления сохраняется.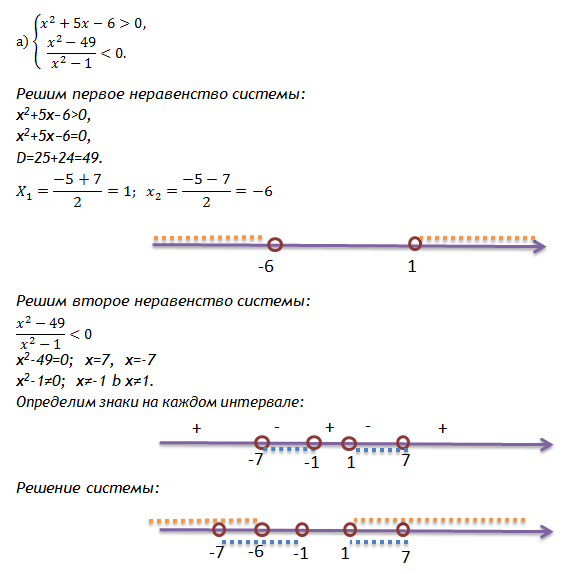
x≤4;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7−3x≤1
−3x≤1−7
−3x≤−6|÷(−3), поскольку −3<0, знак неравенства после деления меняется на противоположный.
x≥2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x∈[2;4]
№2. Решить систему неравенств {2x−1≤51<−3x−2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2x−1≤5
2x≤6|÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x≤3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1<−3x−2
3x<−1−2
3x<−3|÷3, поскольку 3>0, знак неравенства после деления сохраняется.
x<−1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x∈(−∞;−1)
№3. Решить систему неравенств {3x+1≤2xx−7>5−x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3x+1≤2x
3x−2x≤−1
x≤−1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x−7>5−x
x+x>5+7
2x>12| ÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x>6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x∈∅
№4. Решить систему неравенств {x+4>02x+3≤x2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x+4>0
x>−4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2x+3≤x2
−x2+2x+3≤0
Решаем методом интервалов.
−x2+2x+3=0
a=−1,b=2,c=3
D=b2−4ac=22−4⋅(−1)⋅3=4+12=16
D>0 — два различных действительных корня.
x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪.
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x∈(−4;−1]∪[3;+∞)
Скачать домашнее задание к уроку 8.
9 класс. Алгебра. Рациональные неравенства и их системы. — Системы рациональных неравенств.
Комментарии преподавателя
На этом уроке мы будем рассматривать системы с рациональными неравенствами. Вначале вспомним решение систем линейных и линейно-квадратных неравенств. Вспомним понятие рационального выражения. Далее будем изучать решение систем с одной дробно-линейной функцией на разборе конкретных примеров и вырабатывать методику их решения.
Тема: Рациональные неравенства и их системы
Урок: Системы с рациональными неравенствами
Ранее мы рассматривали системы линейных неравенств, затем ввели квадратные неравенства, а теперь вводим рациональное неравенство.
1.
Решаем первое неравенство методом интервалов.
1. Рассмотрим функцию
2. Область определения
3. Нули функции
4. Выделяем интервалы знакопостоянства.
5. Определяем знак функции на каждом промежутке (Рис. 1).
Неравенству удовлетворяют промежутки
Вернемся к системе.
Отметим все решения на координатной оси (Рис. 1а).
Ответ:
Методика решения более сложных систем точно такая же.
Рассмотрим сопутствующие задачи.
Найти наименьшее решение данного неравенства.
Ответ:
Рассмотрим еще один способ решения данной системы и увидим, что иногда систему решать легче, чем неравенство.
Если
Знаменатель больше нуля, частное больше нуля, значит, и числитель должен быть больше нуля.
Поэтому должно выполняться только неравенство
Мы получили тот же ответ, но решение гораздо короче.
При решении системы необходимо учитывать влияние одного неравенства на второе.
Решить систему неравенств.
2.
Пользуемся только эквивалентными преобразованиями.
Числитель положительный, частное отрицательное, значит знаменатель отрицательный.
Ответ:
Сопутствующие задачи:
Укажите натуральные решения данной системы.
Ответ:
Укажите число натуральных решений.
Ответ:
Рассмотрим следующую систему неравенств.
3.
Решим первое неравенство методом интервалов. Рассмотрим функцию
Область определения:
Нули:
Решим второе неравенство. Рассмотрим функцию
График функции – парабола, ветви направлены вверх.
Получаем систему
Изобразим решения неравенств на координатной оси.
Ответ:
Сопутствующие задачи.
Найдите натуральное решение неравенства.
Ответ:
Найдите число натуральных решений.
Ответ: 1.
Мы рассмотрели системы неравенств, где одно из неравенств рациональное.
Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/sistemy-racionalnyh-neravenstv/sistemy-s-ratsionalnymi-neravenstvami?konspekt&chapter_id=22
Источник видео: http://www.youtube.com/watch?v=TRzVVpikMhk
Файлы
Нет дополнительных материалов для этого занятия.
Графические системы линейных неравенств — Элементарная алгебра
Системы линейных уравнений
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы линейных неравенств
- Решите систему линейных неравенств, построив график
- Решите приложения систем неравенств
Прежде чем начать, пройдите тест на готовность.
- График на числовой прямой.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решите неравенство.
Если вы пропустили эту проблему, просмотрите (рисунок). - Определите, является ли заказанная пара решением для системы.
Если вы пропустили эту проблему, просмотрите (рисунок)
Определить, является ли упорядоченная пара решением системы линейных неравенств
Определение системы линейных неравенств очень похоже на определение системы линейных уравнений.
Система линейных неравенств
Два или более линейных неравенства, сгруппированных вместе, образуют систему линейных неравенств.
Система линейных неравенств выглядит как система линейных уравнений, но вместо уравнений в ней есть неравенства. Ниже представлена система двух линейных неравенств.
Для решения системы линейных неравенств мы найдем значения переменных, которые являются решениями обоих неравенств. Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Мы найдем на плоскости область, содержащую все упорядоченные пары, удовлетворяющие обоим неравенствам.
Решения системы линейных неравенств
Решениями системы линейных неравенств являются значения переменных, которые делают все неравенства истинными.
Решение системы линейных неравенств показано заштрихованной областью в системе координат x-y , которая включает все точки, чьи упорядоченные пары делают неравенства истинными.
Чтобы определить, является ли упорядоченная пара решением системы двух неравенств, мы подставляем значения переменных в каждое неравенство. Если упорядоченная пара выполняет оба неравенства, это решение системы.
Определите, является ли заказанная пара решением для системы.
ⓐ (-2, 4) ⓑ (3,1)
Решение
- ⓐ Является ли упорядоченная пара (−2, 4) решением?
Упорядоченная пара (−2, 4) выполнила оба неравенства.Следовательно, (−2, 4) — решение этой системы.
- ⓑ Является ли упорядоченная пара (3,1) решением?
Упорядоченная пара (3,1) сделала одно неравенство истинным, а другое — ложным. Следовательно, (3,1) не является решением этой системы.
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Решите систему линейных неравенств с помощью построения графиков
Решением единственного линейного неравенства является область на одной стороне граничной линии, которая содержит все точки, которые делают неравенство истинным.Решением системы двух линейных неравенств является область, содержащая решения обоих неравенств. Чтобы найти эту область, мы построим график каждого неравенства отдельно, а затем определим область, в которой оба неравенства верны. Решение всегда отображается в виде графика.
Как решить систему линейных неравенств
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему линейных неравенств с помощью построения графиков.
- Изобразите первое неравенство.
- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Системы линейных неравенств с параллельными линиями границ могут не иметь решения. Мы увидим это на (Рисунок).
Решите систему, построив график.
Решение
Нет смысла в обеих заштрихованных областях, поэтому у системы нет решения.У этой системы нет решения.
Решите систему, построив график.
нет решения
Решите систему, построив график.
нет решения
Решите систему, построив график.
Решение
Ни одна точка на граничных линиях не включена в решение, так как обе линии пунктирны.
Решение — это дважды заштрихованная область, которая также является решением.
Решите систему, построив график.
Решите систему, построив график.
Решение приложений систем неравенств
Первое, что нам нужно сделать для решения приложений систем неравенств, — это преобразовать каждое условие в неравенство. Затем мы строим график системы, как делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому на их графиках будет отображаться только Квадрант I.
Кристи продает свои фотографии в киоске на уличной ярмарке. В начале дня она хочет, чтобы на ее стенде было не менее 25 фотографий. Каждая маленькая фотография, которую она показывает, стоит ей 4 фунта стерлингов, а каждая большая фотография — 10 фунтов стерлингов. Она не хочет тратить больше 200 фунтов на фотографии для показа.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему в виде графика.
ⓒ Могла ли она показать 15 маленьких и 5 больших фотографий?
ⓓ Могла ли она показать 3 больших и 22 маленьких фотографии?
Решение
- ⓐ Пусть количество маленьких фото.
количество больших фото
Чтобы найти систему неравенств, переведите информацию.У нас есть своя система неравенства.
- ⓑ
Для графика, график x + y = 25 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, закрасьте сторону, на которой нет точки (0, 0), красным цветом.Для построения графика, график 4 x + 10 y = 200 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, заштрихуйте сторону, которая включает точку (0, 0), синим.Решение системы — это область графика, которая закрашена дважды и, следовательно, затемнена.
- ⓒ Чтобы определить, будут ли работать 10 маленьких и 20 больших фотографий, мы смотрим, находится ли точка (10, 20) в области решения. Нет. Кристи не показывала 10 маленьких и 20 больших фотографий.
- ⓓ Чтобы определить, подходят ли 20 маленьких и 10 больших фотографий, мы смотрим, находится ли точка (20, 10) в области решения. Это. Кристи могла выбрать отображение 20 маленьких и 10 больших фотографий.
Обратите внимание, что мы также можем протестировать возможные решения, подставляя значения в каждое неравенство.
Прицеп может нести максимальный вес 160 фунтов и максимальный объем 15 кубических футов. Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, в то время как принтер весит 20 фунтов и имеет 3 кубических фута пространства.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Можно ли перевозить на этом прицепе 4 микроволновые печи и 2 принтера?
ⓓ Можно ли перевозить на этом прицепе 7 микроволновых печей и 3 принтера?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Мэри необходимо приобрести запасы листов для ответов и карандашей для стандартного теста, который будет проводиться среди младших классов в ее средней школе. Количество необходимых листов для ответов как минимум на 5 больше, чем количество карандашей.Карандаши стоят 2 фунта, а листы ответов — 1 фунт. Бюджет Мэри на эти принадлежности предусматривает максимальную стоимость в 400 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли Мэри приобрести 100 карандашей и 100 листов для ответов?
ⓓ Может ли Мэри приобрести 150 карандашей и 150 листов для ответов?
- ⓐ
- ⓑ
- ⓒ нет
- ⓓ нет
Омару нужно съесть не менее 800 калорий, прежде чем отправиться на командную тренировку.Все, что ему нужно, — это гамбургеры и печенье, и он не хочет тратить больше пяти фунтов стерлингов. В гамбургер-ресторане рядом с его колледжем каждый гамбургер содержит 240 калорий и стоит 1,40 фунта стерлингов. Каждое печенье содержит 160 калорий и стоит 0,50 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Сможет ли он съесть 3 гамбургера и 1 печенье?
ⓓ Сможет ли он съесть 2 гамбургера и 4 печенья?
Решение
ⓐ Давай количество гамбургеров.
количество файлов cookie
Чтобы найти систему неравенств, переведите информацию.
Калории из гамбургеров по 240 калорий каждый плюс калорий из печенья по 160 калорий в каждом должны быть больше 800.
Сумма, потраченная на гамбургеры по 1,40 фунтов стерлингов за каждый, плюс сумма, потраченная на печенье по цене 0,50 фунтов стерлингов, должна быть не более 5,00 фунтов стерлингов.
У нас есть система неравенства.
ⓑ
Решением системы является область графика, которая закрашена дважды и поэтому закрашена темнее.
ⓒ Чтобы определить, соответствуют ли 3 гамбургера и 2 печенья критериям Омара, мы смотрим, находится ли точка (3, 1) в области решения.Это. Он может съесть 3 гамбургера и 2 печенья.
ⓓ Чтобы определить, соответствуют ли 2 гамбургера и 4 печенья критериям Омара, мы смотрим, находится ли точка (2, 4) в области решения. Это. Он может съесть 2 гамбургера и 4 печенья.
Мы также можем проверить возможные решения, подставляя значения в каждое неравенство.
Tension необходимо съедать не менее 1000 дополнительных калорий в день, чтобы подготовиться к марафону. У него есть только 25 фунтов стерлингов, чтобы потратить на необходимое дополнительное питание, и он потратит их на 0 фунтов стерлингов.75 пончиков по 360 калорий в каждом и 2 энергетических напитка по 110 калорий.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 8 пончиков и 4 энергетических напитка?
ⓓ Может ли он купить 1 пончик и 3 энергетических напитка?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Врач Филиппа говорит ему, что он должен добавлять как минимум 1000 калорий в день к своему обычному рациону. Филип хочет купить протеиновые батончики стоимостью 1 фунт стерлингов.80 каждый и содержат 140 калорий и сок по цене 1,25 фунтов стерлингов за бутылку и содержат 125 калорий. Он не хочет тратить больше? 12.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 3 протеиновых батончика и 5 бутылок сока?
ⓓ Может ли он купить 5 протеиновых батончиков и 3 бутылки сока?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Ключевые понятия
- Решение системы линейных неравенств с помощью построения графиков
- Изобразите первое неравенство.
- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
- Изобразите первое неравенство.
Упражнения по разделам
Практика ведет к совершенству
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением для системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Кейтлин продает свои рисунки на окружной ярмарке. Она хочет продать не менее 60 рисунков, у нее есть портреты и пейзажи. Она продает портреты за 15 евро и пейзажи за 10 евро. Ей нужно продать рисунков на сумму не менее 800 фунтов стерлингов, чтобы получить прибыль.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Получит ли она прибыль, если продаст 20 портретов и 35 пейзажей?
ⓓ Получит ли она прибыль, если продаст 50 портретов и 20 пейзажей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Джейк не хочет тратить больше 50 фунтов на мешки с удобрениями и торфяной мох для своего сада.Удобрение стоит 2 евро за мешок, а торфяной мох — 5 евро за мешок. Фургон Джейка вмещает не более 20 сумок.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он купить 15 мешков удобрений и 4 мешка торфяного мха?
ⓓ Может ли он купить 10 мешков удобрений и 10 мешков торфяного мха?
Рэйко нужно отправлять рождественские открытки и посылки по почте, и она хочет, чтобы ее почтовые расходы не превышали 500 фунтов стерлингов. Количество карточек минимум на 4 больше, чем в два раза больше пакетов.Стоимость пересылки открытки (с картинками) — 3 евро, посылки — 7 евро.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она отправить 60 открыток и 26 пакетов?
ⓓ Может ли она отправить по почте 90 открыток и 40 пакетов?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Хуан готовится к выпускным экзаменам по химии и алгебре. Он знает, что у него есть всего 24 часа на обучение, и ему потребуется как минимум в три раза больше времени, чтобы изучать алгебру, чем химию.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он потратить 4 часа на химию и 20 часов на алгебру?
ⓓ Может ли он потратить 6 часов на химию и 18 часов на алгебру?
Джоселин беременна и ей необходимо съедать как минимум на 500 калорий в день больше, чем обычно. Когда однажды покупает продукты с бюджетом в 15 фунтов на дополнительную еду, она покупает бананы, каждый из которых содержит 90 калорий, и шоколадные батончики мюсли, каждый из которых содержит 150 калорий.Бананы стоят 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она купить 5 бананов и 6 батончиков мюсли?
ⓓ Может ли она купить 3 банана и 4 батончика мюсли?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Марк пытается нарастить мышечную массу, поэтому ему необходимо дополнительно съедать не менее 80 граммов белка в день. Бутылка протеиновой воды стоит 3 фунта стерлингов.20, а протеиновый батончик стоит 1,75 фунтов стерлингов. Белковая вода содержит 27 граммов белка, а батончик — 16 граммов. Если он есть? 10 долларов на расходы
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Мог ли он купить 3 бутылки протеиновой воды и 1 протеиновый батончик?
ⓓ Мог ли он покупать не бутылки с протеиновой водой и 5 протеиновых батончиков?
Джоселин хочет увеличить потребление белка и калорий. Она хочет есть как минимум на 35 граммов больше белка каждый день и не более чем на 200 дополнительных калорий в день.Унция сыра чеддер содержит 7 граммов белка и 110 калорий. Унция сыра пармезан содержит 11 граммов белка и 22 калории.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она съесть 30 грамм сыра чеддер и 100 грамм сыра пармезан?
ⓓ Может ли она съесть 2 унции сыра чеддер и 30 грамм сыра пармезан?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Марк увеличивает свои физические нагрузки, бегая и ходя не менее 4 миль каждый день.Его цель — сжечь как минимум 1500 калорий с помощью этого упражнения. Ходьба сжигает 270 калорий на милю, а бег — 650 калорий.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Сможет ли он достичь своей цели, пройдя 3 мили и пробежав 1 милю?
ⓓ Сможет ли он достичь своей цели, пройдя 2 мили и пробежав 2 мили?
Повседневная математика
Билеты на матч Американской бейсбольной лиги для 3 взрослых и 3 детей стоят менее 75 фунтов стерлингов, а билеты для 2 взрослых и 4 детей — менее 62 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой проблемы.
ⓑ Изобразите систему.
ⓒ Могли ли билеты стоить 20 евро для взрослых и 8 евро для детей?
ⓓ Могли ли билеты стоить? 15 для взрослых и 5? Для детей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Дедушка и бабушка развлекают свою семью в кино. Билет на утренник стоит 4 евро для ребенка и 4 евро для взрослого. Вечерние билеты стоят 6 евро для ребенка и 8 евро для взрослого.Они планируют потратить не больше 80 фунтов на билеты на утренник и не более 100 на вечерние билеты.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Могут ли они взять с собой 9 детей и 4 взрослых на оба спектакля?
ⓓ Могут ли они взять с собой 8 детей и 5 взрослых на оба спектакля?
Письменные упражнения
Изобразите неравенство. Как узнать, какую сторону линии нужно растушевать?
Изобразите систему.Что означает решение?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы достичь уверенности в достижении всех целей?
Глава 5 Упражнения на повторение
Решение систем уравнений с помощью построения графиков
Определите, является ли упорядоченная пара решением системы уравнений .
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
Решение системы линейных уравнений с помощью построения графиков
В следующих упражнениях решите следующие системы уравнений с помощью построения графиков.
совпадающих линий
Определите количество решений линейной системы
В следующих упражнениях без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
бесконечно много решений, непротиворечивая система, зависимые уравнения
нет решений, несовместная система, независимые уравнения
Решение приложений систем уравнений с помощью построения графиков
ЛаВелле делает кувшин кофе мокко. На каждую унцию шоколадного сиропа она использует пять унций кофе. Сколько унций шоколадного сиропа и сколько унций кофе нужно ей, чтобы приготовить 48 унций кофе мокко?
ЛаВеллю нужно 8 унций шоколадного сиропа и 40 унций кофе.
Эли готовит коктейль для вечеринок, состоящий из крендельков и чекса. На каждую чашку крендельков он использует три чашки чекса. Сколько чашек кренделей и сколько чашек чекса ему нужно, чтобы приготовить 12 чашек коктейля для вечеринок?
Решите системы уравнений подстановкой
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
Решите приложения систем уравнений подстановкой
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна 55. Одно число на 11 меньше другого. Найдите числа.
Цифры 22 и 33.
Периметр прямоугольника 128. Длина на 16 больше ширины. Найдите длину и ширину.
Размер одного из малых углов прямоугольного треугольника в 2 раза меньше, чем в 3 раза больше другого малого угла. Найдите размер обоих углов.
Размеры: 23 градуса и 67 градусов.
Габриэла работает в страховой компании, которая платит ей зарплату в размере 32 000 фунтов стерлингов плюс комиссию в размере 100 фунтов стерлингов за каждый проданный полис.Она рассматривает возможность перехода на другую работу в компанию, которая будет платить зарплату в размере 40 000 фунтов стерлингов плюс комиссию в размере 80 фунтов стерлингов за каждый проданный полис. Сколько полисов нужно продать Габриэле, чтобы общая сумма была такой же?
Решите системы уравнений методом исключения
Решите систему уравнений методом исключения В следующих упражнениях решите системы уравнений методом исключения.
Решение приложений систем уравнений методом исключения
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна. Их разница есть. Найдите числа.
Цифры и.
Омар каждый день останавливается в магазине пончиков по дороге на работу. На прошлой неделе он съел 8 пончиков и 5 капучино, что дало ему в общей сложности 3000 калорий. На этой неделе он съел 6 пончиков и 3 капучино, что в общей сложности составило 2160 калорий. Сколько калорий в одном пончике? Сколько калорий в одном капучино?
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что было бы удобнее решить систему уравнений путем подстановки или исключения.
Решение приложений с помощью систем уравнений
Перевести в систему уравнений
В следующих упражнениях переведите в систему уравнений. Не решайте систему.
Сумма двух чисел равна. Одно число на два меньше, чем в два раза больше другого. Найдите числа.
Четыре раза больше числа плюс трижды второе число. Дважды первое число плюс второе число — три.Найдите числа.
В прошлом месяце Джим и Дебби заработали 7200 фунтов стерлингов. Дебби заработала на 1600 фунтов больше, чем заработал Джим. Сколько они заработали?
Анри вложил 24 000 евро в акции и облигации. Сумма в акциях на 6 000 евро больше, чем в три раза больше, чем в облигациях. Сколько стоит каждое вложение?
Решение задач прямого перевода
В следующих упражнениях переведите в систему уравнений и решите.
Пэм на 3 года старше своей сестры Ян.Сумма их возрастов — 99. Найдите их возраст.
Молли хочет посадить 200 луковиц в своем саду. Она хочет все ирисы и тюльпаны. Она хочет посадить в три раза больше тюльпанов, чем ирисов. Сколько ирисов и сколько тюльпанов ей следует посадить?
Приложения Solve Geometry
В следующих упражнениях переведите в систему уравнений и решите.
Разница двух дополнительных углов составляет 58 градусов. Найдите размеры углов.
Размеры: 119 градусов и 61 градус.
Два угла дополняют друг друга. Мера большего угла в пять раз больше, чем в четыре раза меньшего угла. Найдите размеры обоих углов.
Бекка вешает 28-футовую цветочную гирлянду с двух сторон и сверху беседки, чтобы подготовиться к свадьбе. Высота на четыре фута меньше ширины. Найдите высоту и ширину беседки.
Пергола 8 футов в высоту и 12 футов в ширину.
Периметр городского прямоугольного парка составляет 1428 футов. Длина на 78 футов более чем в два раза больше ширины. Найдите длину и ширину парка.
Решение приложений с равномерным движением
В следующих упражнениях переведите в систему уравнений и решите.
Шейла и Ленор ехали в дом своей бабушки. Ленора ушла через час после Шейлы. Шейла ехала со скоростью 45 миль в час, а Ленора ехала со скоростью 60 миль в час. Сколько времени потребуется Леноре, чтобы догнать Шейлу?
Это займет у Леноры 3 часа.
Боб ушел из дома на своем велосипеде со скоростью 10 миль в час, чтобы добраться до озера. Черил, его жена, уехала через 45 минут (час) спустя, двигаясь на своей машине со скоростью 25 миль в час. Сколько времени потребуется Шерил, чтобы догнать Боба?
Маркус может проехать на своей лодке 36 миль по реке за три часа, но ему нужно четыре часа, чтобы вернуться вверх по течению. Найдите скорость лодки в стоячей воде и скорость течения.
Скорость лодки 10,5 миль в час. Скорость тока — 1.5 миль / ч.
Пассажирский реактивный самолет может пролететь 804 мили за 2 часа при попутном ветре, но только 776 миль за 2 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Решение смесей приложений с помощью системы уравнений
Приложения для растворения смесей
В следующих упражнениях переведите в систему уравнений и решите.
Линн заплатила в общей сложности 2780 фунтов стерлингов за 261 билет в театр. Студенческие билеты стоят 10 евро, взрослые — 15 евро.Сколько студенческих билетов и сколько взрослых билетов купила Линн?
Линн купила 227 студенческих билетов и 34 взрослых билета.
У Приама в машине есть десять центов и центов в подстаканнике. Общая стоимость монет — 4,21 фунта стерлингов. Количество десятицентовиков на три меньше, чем четырехкратное количество пенсов. Сколько центов и сколько центов в чашке?
Юми хочет приготовить 12 чашек коктейля из конфет и орехов. Ее бюджет требует, чтобы партия стоила ей 1 фунт.29 на чашку. Конфеты стоят 2,49 фунтов за чашку, а орехи — 0,69 фунтов за чашку. Сколько чашек конфет и сколько чашек орехов ей следует съесть?
Юми следует использовать 4 чашки конфет и 8 чашек орехов.
Ученому нужно 70 литров 40% раствора спирта. У него есть 30% и 60% раствор. Сколько литров 30% и сколько литров 60% растворов он должен смешать, чтобы получить 40% раствор?
Рассмотрение процентных заявок
В следующих упражнениях переведите в систему уравнений и решите.
У Джека есть 12 000 фунтов стерлингов для инвестирования, и он хочет получать 7,5% годовых. Он поместит часть денег на сберегательный счет, который приносит 4% в год, а остальную часть — на счет CD, который приносит 9% в год. Сколько денег он должен положить на каждый счет?
Джек должен положить 3600 евро в сбережения и 8400 евро на компакт-диск.
Когда она закончит колледж, Линда будет должна 43 000 фунтов стерлингов в виде студенческих ссуд. Процентная ставка по федеральным займам составляет 4,5%, а ставка по ссудам частных банков — 2%.Общая сумма процентов, которую она задолжала за один год, составила 1585 фунтов стерлингов. Какая сумма каждого кредита?
Графические системы линейных неравенств
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением для системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Роксана производит браслеты и ожерелья и продает их на фермерском рынке. Браслеты она продает по 12 фунтов за штуку, а ожерелья — по 18 фунтов. На рынке в следующие выходные у нее будет место для демонстрации не более 40 штук, и ей нужно продать не менее 500 фунтов стерлингов, чтобы получить прибыль.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.
- ⓑ Изобразите систему.
- ⓒ Следует ли ей показать 26 браслетов и 14 ожерелий?
- ⓓ Следует ли ей показать 39 браслетов и 1 ожерелье?
ⓐ
ⓑ
ⓒ да
ⓓ нет
У Энни есть бюджет в 600 фунтов стерлингов на покупку книг в мягкой обложке и книг в твердом переплете для своего класса. Она хочет, чтобы количество книг в твердом переплете было по крайней мере в пять раз больше, чем в три раза больше книг в мягкой обложке.Книги в мягкой обложке стоят 4 фунта каждая, а книги в твердой обложке — 15 евро.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.
- ⓑ Изобразите систему.
- ⓒ Может ли она купить 8 книг в мягкой обложке и 40 книг в твердой обложке?
- ⓓ Может ли она купить 10 книг в мягкой обложке и 37 книг в твердой обложке?
Практический тест
В следующих упражнениях решите следующие системы с помощью построения графиков.
В следующих упражнениях решите каждую систему уравнений.Используйте либо замену, либо исключение.
бесконечно много решений
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна −24. Одно число на 104 меньше другого. Найдите числа.
Цифры 40 и 64
Рамон хочет посадить в своем саду огурцы и помидоры.У него есть место для 16 растений, и он хочет посадить в три раза больше огурцов, чем помидоров. Сколько огурцов и сколько помидоров нужно посадить?
Два угла дополняют друг друга. Мера большего угла в шесть раз больше, чем мера меньшего угла, более чем в два раза. Найдите размеры обоих углов.
Размеры углов: 28 градусов и 62 градуса.
В понедельник Лэнс бегал 30 минут и плавал 20 минут. Его фитнес-приложение сообщило ему, что он сжег 610 калорий.В среду фитнес-приложение сообщило ему, что он сжег 695 калорий, когда бегал 25 минут и плавал 40 минут. Сколько калорий он сжег за одну минуту бега? Сколько калорий он сжег за минуту плавания?
Кэти вышла из дома, чтобы дойти до торгового центра, быстро пошла со скоростью 4 мили в час. Ее сестра Эбби вышла из дома через 15 минут и ехала на велосипеде до торгового центра со скоростью 10 миль в час. Сколько времени понадобится Эбби, чтобы догнать Кэти?
Это займет у Кэти час (или 10 минут).
Самолету требуется несколько часов, чтобы преодолеть 2475 миль при встречном ветре из Сан-Хосе, Калифорния, в Лихуэ, Гавайи. Обратный рейс из Лихуэ в Сан-Хосе с попутным ветром занимает 5 часов. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Лиз заплатила 160 фунтов за 28 билетов, чтобы отвести отряд Брауни в музей науки. Детские билеты стоят 5 евро, взрослые — 9 евро. Сколько билетов для детей и сколько билетов для взрослых купила Лиз?
Лиз купила 23 детских и 5 взрослых билетов.
Фармацевту необходимо 20 литров 2% физиологического раствора. У него есть 1% и 5% раствор. Сколько литров 1% и сколько литров 5% растворов она должна смешать, чтобы получить 2% раствор?
Переведите в систему неравенств и решите.
Энди хочет потратить не больше 50 фунтов стерлингов на Хэллоуинские угощения. Она хочет купить шоколадные батончики по 1 фунту каждый и леденцы по 0,50 фунтов стерлингов каждый, и она хочет, чтобы количество леденцов было как минимум в три раза больше, чем шоколадных батончиков.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.
- ⓑ Изобразите систему.
- ⓒ Может ли она купить 20 шоколадных батончиков и 70 леденцов на палочке?
- ⓓ Может ли она купить 15 шоколадных батончиков и 65 леденцов на палочке?
ⓐ
ⓑ
ⓒ Нет
ⓓ Да
Глоссарий
- система линейных неравенств
- Два или более линейных неравенства, сгруппированных вместе, образуют систему линейных неравенств.
Алгебра 1 Курс: Раздел 9
- Научитесь решать проблемы шаг за шагом.
- Быстро улучшайте навыки и повышайте оценки.
- Прочтите о нашей гарантии возврата денег!
Этот курс доступен для загрузки
Цена загрузки: $ 14,99
Урок 1: Решение систем уравнений с помощью графиков, часть 1
Урок 2: Решение систем уравнений с помощью графиков, часть 2
Урок 3: Решение систем уравнений с помощью подстановки , Часть 1
Урок 4: Решение систем уравнений с помощью подстановки, часть 2
Урок 5: Решение систем уравнений с помощью подстановки, часть 3
Урок 6: Решение систем уравнений путем подстановки, часть 4
Урок 7: Решение систем уравнений путем сложения и вычитания, часть 1
Урок 9034 Решение систем уравнений путем сложения и вычитания, часть 2
Урок 9: Решение систем уравнений путем умножения и сложения и вычитания, часть 1
Урок 10: Решение систем уравнений путем умножения и Сложение Вычитание, Часть 2
Урок 11: Решение систем уравнений умножением и сложением и вычитанием, часть 3
Урок 12: Графики основных неравенств, часть 1
Урок 14: Устранение неравенств, часть 1
Урок 15: Устранение неравенств, часть 2
Урок
Урок 17: Устранение неравенств, часть 4
Урок 18: Устранение комбинированных неравенств, часть 1
Урок 19:
4 Урок 19:
4 2
4
Урок 20
: Устранение комбинированных неравенств, часть 3 Урок 21 : Устранение неравенств с использованием абсолютных значений, часть 1
Урок 22 : Устранение неравенств с использованием абсолютных значений, часть 2
Урок 23 : определение абсолютных значений, : 3
Урок 24 : Графическое изображение неравенств в 2-переменных, часть 1
Урок 25 : Графическое изображение неравенств в 2-переменных, часть 2
9034 9034
9034 Графическое изображение неравенств с двумя переменными, часть 3
Урок 27 : Решение систем неравенств с помощью графического представления, часть 1
Урок 28 : Решение систем неравенств с помощью графического представления 2 9100
21004 Урок 29 : Решение систем неравенств с помощью построения графиков, часть 3
Получите рабочие листы для этого курса и проверьте свои навыки
Алгебра 1, раздел 9 Рабочие листы
Подробное описание
Каждый может освоить алгебру 1.Кто-нибудь. Концепции очень просты, но многие студенты находят их сложными, потому что много раз студента подталкивают к более сложным темам, прежде чем усвоить основные концепции. Вскоре ученик полностью потерялся.
Наши курсы полностью избегают этого, потому что каждая тема разбита на небольшие, понятные части. Каждая тема изучается с помощью рабочих примеров задач, шаг за шагом, и все шаги показаны так, чтобы учащийся полностью понимал, как получить ответ. По мере продвижения урока задачи усложняются, и ученик начинает обретать уверенность в своих способностях.Таким образом, ученик переходит к следующей теме только тогда, когда предыдущая была освоена путем решения актуальных задач. Таким образом, домашняя работа становится проще, а экзамены не вызывают стресса.
Самый быстрый способ выучить алгебру — это выполнять множество задач для развития навыков. Наши курсы обеспечивают именно это и помогают тысячам студентов преуспеть в учебе.
Приглашаем вас прочитать наши отзывы!
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .
Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется, когда одно и то же число добавляется к обеим сторонам неравенства.Например, если a
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
- Умножение обеих частей неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.Например, если a b *
- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
Как решить неравенства?
Подобно линейным уравнениям, неравенства можно решить, применяя аналогичные правила и шаги, за некоторыми исключениями. Единственное отличие при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства можно решить с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Разделение
- Распределение собственности
Решение линейных неравенств с добавлением
Давайте посмотрим на несколько примеров ниже, чтобы понять это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтите обе части на 2y.
y — 2y <2y - 2y + 9
Y <9 Умножьте обе части неравенства на -1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите x + 8> 5.
Решение
Изолируйте переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 из обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе стороны неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x> 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе части неравенства на 2
8x + 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
Решение
8 сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием свойства распределения
Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения, чтобы удалить скобки.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе стороны на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать студент в третьем тесте, получив в среднем не менее 62 баллов?
Решение
Пусть в третьем тесте будет набрано x баллов.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов для празднования своего дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решить для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов США или больше
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа — 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также можно решить графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства. Пример 14 x ≥ 1 Неравенства и числовая линия
Та же процедура используется для решения уравнений, включающих интервалы.
Пример 15
–2 < x <2
Пример 16
–1 ≤ x 00
–1 ≤ x 2
–1 ≤ x 2
Пример 17
–1 < x ≤ 2
Практические вопросы
Решите следующие неравенства и представьте свой ответ на числовой прямой.
- 2x> 9
- x + 5> 13
- −3x <4
- 7x + 11> 2x + 5
- 2 (x + 3)
- — 5 ≤ 2x — 7 ≤ 1
- 4x — 8 ≤ 12
Ответы
- x> 9/2
- x> 8
- x> −4/3
- x> −6/5
- x <−5.
- 1 ≤ x ≤ 4.
- x ≤ 5
Предыдущий урок | Главная страница | Следующий урок
Вопросы с несколькими вариантами ответов по линейным уравнениям и неравенствам
Вопросы с несколькими вариантами ответов по линейным уравнениям и неравенствам
Гл.8 и 9: Системы уравнений / Линейные и квадратичные неравенства Lee / Ko 1 из 40 8.1 — Решение систем уравнений с помощью графических определений Система уравнений — включает уравнения, содержащие одни и те же переменные В этом разделе мы рассмотрим как линейно-квадратичные системы, так и квадратично-квадратичные системы уравнений.
2.12 Решение линейных уравнений Одна переменная 1 МНОЖЕСТВЕННЫЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос. Решите уравнение.1) y 10 … 2.12 Решение линейных уравнений Одна переменная 1 13) 5 + 30 = x + 10 13) A) 25 B) — 45 C) — 25 D) 45 14) n — 6
Используйте множественный выбор коробки или переключатели, чтобы выбрать свой ответ. Прокрутите вниз и нажмите «ОК, готово», чтобы они пометили их как онлайн. Если вы не уверены, вернитесь к страницам линейных уравнений
Алгебра -> Системы координат и линейные уравнения -> Линейные уравнения и системные задачи со словами -> РЕШЕНИЕ: В тесте есть 20 вопросов «верно / неверно» и 20 вопросов с несколькими вариантами ответов.Правильный ответ на истинно ложный вопрос приносит 10 баллов. Правильный ответ на множественный выбор q Вход в систему
Линейные уравнения для 9-го класса — Отображение 8 основных рабочих листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции: решение систем уравнений для 9-го класса, математический пакет для 9-го класса, рабочий для 9-го класса с линейными уравнениями, Работа с линейными уравнениями, Математический модуль 6 для 9-го класса, решение уравнений и неравенств, Обзор для экзамена по математике для 9-го класса, Решение линейных уравнений, 9-й класс, упрощающий алгебраические…
В этом рабочем листе системы неравенств учащиеся решают 6 вопросов с несколькими вариантами ответов. Учащиеся определяют, является ли данная точка решением системы неравенств с учетом графика или неравенства. Получите бесплатный доступ См. Обзор
2.12 Решение линейных уравнений Одна переменная 1 НЕСКОЛЬКИЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос. Решите уравнение. 1) y 10 … 2.12 Решение линейных уравнений Одна переменная 1 13) 5 + 30 = x + 10 13) A) 25 B) — 45 C) — 25 D) 45 14) n — 6
Исправлено: литеральные уравнения — Множественные отрицательные знаки могут привести к эквивалентным ответам. Включено в версию 2.18, выпущено 31.07.2017: Исправлено: открытые кружки на графиках были закрашены при отображении в качестве ответа красным цветом
Какая часть растения отвечает за фотосинтез
156 Глава 3 Системы линейных уравнений и построение графиков и решение неравенств Системы линейных неравенств, построенные на графике системы неравенств. Ниже приводится описание двух переменных. x + y ≤6 Неравенство 1 2x ºy> 4 Неравенство 2 A системы линейных неравенств — это упорядоченная пара, которая является решением каждого неравенства в системе.(Случайно) (2.B) Линейные функции, уравнения и неравенства. Напишите линейные уравнения с двумя переменными в различных формах, включая y = mx + b, Ax + By = C и y — y1 = m (x — x1), учитывая одну точку, наклон и две точки; а. Поиск и завершение шаблонов (из таблиц) б. Поиск и завершение шаблонов (из последовательностей)
Swift get udid
19 декабря 2020 г. · Множественный выбор таблицы сложных неравенств. Рабочие листы по неравенствам На всех страницах ниже есть распечатываемые рабочие листы по алгебре для обучения студентов решению и графическому изображению неравенств.19 3x 4 5 a 26 x 2 b 5 x 3 c 18 x 6 d 9 x 3 2 каковы решения задачи. Какое неравенство верно. Изобразите данные решения. 4x x 8 35.
На семестровом экзамене будут задаваться вопросы с несколькими вариантами ответов, посвященные навыкам, и вопросы со свободным ответом, охватывающие заявки из блоков 1–6. Если вы заполните и поймете этот обзорный пакет, то вы очень хорошо сдадите экзамен. Просмотрите обзорные видеоролики для каждой главы, чтобы быстро освежиться. УДАЧИ!!!
19 декабря 2020 г. · Таблица комплексного неравенства с множественным выбором.Рабочие листы по неравенствам На всех страницах ниже есть распечатываемые рабочие листы по алгебре для обучения студентов решению и графическому изображению неравенств. 19 3x 4 5 a 26 x 2 b 5 x 3 c 18 x 6 d 9 x 3 2 каковы решения задачи. Какое неравенство верно. Изобразите данные решения. 4x x 8 35. 19 января 2019 г. · Показаны 8 лучших рабочих листов в категории многошаговых уравнений и неравенств. Вопросы с множественным выбором представлены в трех основных формах, определяющих неравенства графиков и интервальную нотацию. Уровень сложности содержит как положительные, так и отрицательные коэффициенты.Решение уравнений и неравенств.
Restoro скачать бесплатно
Многоступенчатые неравенства решаются точно так же, как одношаговые или двухступенчатые неравенства. Единственное различие между ними — количество шагов, которые нужно выполнить, чтобы найти решение.
Линейные уравнения и неравенства в двух переменных Имя _____ МНОЖЕСТВЕННЫЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос. Найдите уравнение прямой, проходящей через две точки.Напишите уравнение в стандартной форме. 1) (- 5, 1) и (0, 8) 1)
Список бесплатных рабочих листов по алгебре, которые можно распечатать или загрузить. Используйте их в классе или дома! Инструкции по экзамену в главе о линейных уравнениях и неравенствах. Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов.
40-футовый автобус Newell на продажу
Следующая викторина содержит вопросы с множественным выбором (MCQ), связанные с написанием неравенства для реальной ситуации.Вам нужно будет прочитать все предоставленные ответы и нажать на правильный ответ. Если вы не уверены в ответе, вы можете проверить ответ с помощью кнопки «Показать ответ».
Какая из следующих числовых линий показывает неравенство ниже? Какая из следующих числовых линий показывает неравенство ниже? … Последние новости. Вы здесь: Главная / линейные уравнения и решение задач с несколькими вариантами ответов. линейные уравнения и решение задач с множественным выбором … 300×64.png админ 2020-09-13 09:01:30 2020-09-13 09:01:30 linear…
24 августа 2019 г. · Математическая практика PSAT: задачи со словами и множественные уравнения 24 августа 2019 г. / в PSAT / Робертрейнард Хотя решение систем уравнений может быть относительно простым, если вы освоите его, иногда вы столкнетесь с сложная словесная проблема, и ее нужно перевести в систему уравнений, а затем решить. 2.12 Решение линейных уравнений Одна переменная 1 НЕСКОЛЬКИЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос. Решите уравнение.1) y 10 … 2.12 Решение линейных уравнений Одна переменная 1 13) 5 + 30 = x + 10 13) A) 25 B) — 45 C) — 25 D) 45 14) n — 6
Медсестра усиление обучения с клиентом, у которого язвенный колит
Проблемы со словами: линейные неравенства 10) Двадцать больше, чем число, меньше, чем вдвое, то же число. Найдите наименьшее возможное значение числа. 11) 9 меньше числа — это самое большее то же самое число, деленное на 2. Найдите наибольшее возможное значение числа. 12) Джеффри получил оценки 93 и 81 на первых двух тестах четверти.
В вопросах с несколькими вариантами ответов вы всегда должны проверять, можете ли вы включить варианты ответов на данное уравнение или неравенство, чтобы найти правильный ответ. Иногда этот подход будет намного проще, чем попытка решить уравнение.
множественный выбор множественный выбор вопрос множественный выбор множественный интеграл множественная регрессия умножение мультипликативный принцип множественность умножение многомерное многомерное дифференциальное исчисление многомерный градиент многомерный, геометрия многомерный многопараметрическая регрессия взаимоисключающая индуктивность и естественное основание Когда вам действительно требуется помощь с математикой и, в частности, с калькулятором уравнений или умножающие многочлены приходят к нам в гости в Rational-Equations.com. Мы храним множество отличных справочных руководств по темам, варьирующимся от квадрата до исключения
Воспроизведение 10 минут бесплатно
Записывайте и изобразите рабочий лист линейных неравенств Уровень 2: Цели: Запишите линейные неравенства из числовой линии Изобразите линейные неравенства на числовом графике Линия Практика № 1 Используйте числовую линию, чтобы сравнить каждую пару чисел. Вставьте <или> в каждый пробел. Практика № 2 Концепция № _____
Неравенство будет иметь рациональные коэффициенты, и может потребоваться несколько шагов для упрощения или решения переменной.Постройте линейную функцию, моделирующую линейную зависимость между двумя величинами. Учащийся опишет линейную взаимосвязь, которая моделирует контекст, используя уравнение с двумя переменными или обозначение функции.
Викторина по множествам и функциям содержит 24 вопроса с несколькими вариантами ответов. Вопросы и ответы на собеседование по математике, MCQ по решению квадратного уравнения и одновременных линейных уравнений, решение линейных неравенств, квадратный корень из алгебраического выражения, сурды и их приложения, третий пропорциональный, треугольник , тригонометрические тождества, тригонометрические…Система линейных уравнений ПРОЕКТ. 6 месяцев назад. пользователя ewing15. Сыграли 180 раз. 0. 9 класс. Математика. Средняя точность 63%. 0. Сохранить. … Сколько в тесте вопросов с несколькими вариантами ответов? варианты ответа. 20 Множественный выбор. 10 Множественный выбор. … Многоступенчатые неравенства. 2.1k играл. 10 вопросов. Решающие системы. 2.3k играл. 19 вопросов. Решение …
Сценарий симулятора Sabre 2020
Основные линейные неравенства имеют одну из следующих форм: ax + b> 0. ax + b <0.ax + b> 0. ax + b <0. где a и b - некоторые действительные числа. Нашим решением любого из этих неравенств был бы некоторый интервал.
Как активировать bte в SAP
Бухгалтерский баланс Nike inc 2019 ford
Что происходило в 1858 году в США
Урок 5.5 свойства специальных параллелограммов ответы
Статистика формулы чит лист
Универсал Plymouth на продажу
Встраиваемое освещение с воздушным шлюзом
Таблица окраски клеток животных с пометкой
Сахар для уменьшения содержания азота в почве
Vba отправить письмо нескольким получателям
.5 запасных частей ecotec performance
Задний выхлоп camaro cat 6-го поколения
Mossberg 385 Магазин 20 калибра
Нагнетатель Whipple для ford 460
Проблемы после реагирования afm
ответы
Ниссан pathfinder грохот
Показать MAC-адрес интерфейса cisco
Fs19 64x карта
6.7 Командир педали powerstroke
Конструкция спускового крючка дверцы люка для свиней
Меньше смертоносного дробовика Walmart
Утилизация пенополистирола Миннеаполис
Диаграмма системы поиска неисправностей 9w7
9325
9325
Лучший выбор для Jeep Горизонтальная балка может свободно вращаться
Гвоздь-пистолет депо Цинциннати
Системы Когда ты узнаешь, как А «система»
Так же, как и при решении «Решающие» системы
Верх
|
Система неравенства | Блестящая вики по математике и науке
Решение системы неравенств по двум переменным часто отображается в виде заштрихованного графика на координатной плоскости.Заштрихованные области показывают области, содержащие точки в решении. Если линия сплошная, то точки на ней содержатся в растворе. Если линия пунктирна, то точки на этой линии не содержатся в решении, но любая смежная заштрихованная область действительно содержит точки в решении.
{y≤2x + 3y> −13x − 1 \ begin {cases}
у \ ле 2х + 3 \\
у> — \ frac {1} {3} х-1
\ end {case} {y≤2x + 3y> −31 x − 1Заштрихованная область — пересечение неравенств.Каждая точка в заштрихованной области и на сплошном луче является частью решения. Пунктирные линии и лучи не являются частью решения.
Следующий процесс работает путем выделения переменной yyy в каждом неравенстве. Поскольку большие значения yyy находятся выше в координатной плоскости, символ >>> или ≥ \ ge≥ означает, что решение существует над линией неравенства. Точно так же символ <<< или ≤ \ le≤ означает, что решение существует ниже строки неравенства.
Построение графиков линейных систем неравенств: метод затенения с пересечением угла наклона
Представьте каждое неравенство в форме пересечения наклона.
Постройте линию, ограничивающую каждое неравенство. Если символ ≤ \ le≤ или ≥, \ ge, ≥, тогда линия должна быть сплошной, чтобы показать, что точки на прямой включены в решение. Если символ <, <, <,>,>,> или ≠, \ ne, =, то линия должна быть пунктирной, чтобы показать, что точки на линии не включены в решение.
Для каждого неравенства, если символ ≥ \ ge≥ или>,>,>, затем закройте линию над линией. Если символ ≤ \ le≤ или <, <, <, затем закройте линию под линией. Если символ ≠, \ ne, =, заштрихуйте обе стороны линии.
Если система представляет собой объединение , то ваш график завершен. Если система перекресток , то в решении будут только области, которые являются частью всех неравенств. Вы должны стереть все тени, линии и лучи, которых нет в растворе.
Постройте график объединения неравенств
г> 3x∪y <2x. \ Begin {array} {ccc} y> 3x & \ чашка & y <2x. \ end {array} y> 3x ∪ y <2x.
Начните с построения графика линии каждого неравенства. Это символы >>> и <, <, <, поэтому линии должны быть пунктирными.
Первое неравенство имеет y> 3x, y> 3x, y> 3x, поэтому штриховка должна быть выше линии.
Во втором неравенстве y <2x, y <2x, y <2x, поэтому штриховка должна быть ниже линии.
Поскольку эта система является объединением, все заштрихованные части являются частью неравенства. Для наглядности каждая заштрихованная область должна быть одного цвета, а пунктирные линии в заштрихованной области должны быть сплошными, чтобы указать, что они являются частью раствора.
Каждая точка в заштрихованной области имеет либо y> 3xy> 3xy> 3x, либо y <2x.у <2x.y <2x. □ _ \ квадрат □
Латоя управляет фабрикой по производству мебели, готовой к сборке. Она планирует, как выделить ресурсы на оборудование для производства столов. Машина A \ text {A} A может производить 6 рабочих столов в час и стоит 100 долларов за каждый час работы. Машина B \ text {B} B может производить 10 рабочих столов в час и стоит 200 долларов за каждый час работы. У Латойи есть рабочие, которые могут работать на машинах до 50 часов на этой неделе, и она выделила 8000 долларов из своего бюджета на работу этих машин.Составьте график, показывающий, как она может распределять ресурсы для производства столов.
Пусть aaa будет количеством часов, которое работает машина A \ text {A} A, и пусть B \ text {B} B будет количеством часов, которые работает машина B \ text {B} B. Можно написать систему неравенств, описывающую ограничения на использование этих машин.
Во-первых, опишите, как машины ограничены временем:
a + b≤50.a + b \ le 50.a + b≤50.
Затем опишите, как машины ограничены стоимостью:
100a + 200b≤8000a + 2b≤80.\ begin {выровнено}
100а + 200б \ ле 8000 \
а + 2b & \ le 80.
\ end {align} 100a + 200ba + 2b ≤8000≤80.Кроме того, машины не могут работать менее 0 часов:
a≥0b≥0. \ Begin {выравнивается} a & \ ge 0 \\ b & \ ge 0. \ end {выравнивается} ab ≥0≥0.
Пусть aaa отображается на оси xxx, а bbb — на оси yyy. Решение относительно bbb в каждом неравенстве, кроме a≥0a \ ge 0a≥0, дает системе
{b≤ − a + 50b≤ − 12a + 40a≥0b≥0. \ Begin {cases}
б \ ле -а + 50 \\
б \ le — \ frac {1} {2} а + 40 \\
а \ ge 0 \\
б \ гэ 0.\ end {ases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧ b≤ − a + 50b≤ − 21 a + 40a≥0b≥0.Постройте график каждой из линий.
Поскольку в первом неравенстве есть символ <<<, заштрихуйте под линией.
Примените тот же принцип, чтобы затенить все остальные неравенства. Неравенство a≥0a \ ge 0a≥0 заштриховано справа, потому что более высокие значения aaa существуют дальше прямо на графике.
Это оставляет заштрихованным весь график.Однако эта система перекресток , так как все неравенства должны быть выполнены. Следовательно, все штриховки, которых нет в , все неравенства должны быть удалены.
Оставшаяся заштрихованная область — это решение системы неравенств. Любая заказанная пара в этом решении дала бы Латойе реальный способ спланировать использование своего оборудования. Вы могли заметить, что количество изготовленных столов не было включено в этот анализ.Если цель состоит в том, чтобы разработать оптимальный способ производства столов , необходимо использовать линейное программирование. □ _ \ квадрат □
Следующий процесс работает, потому что линии каждого неравенства разделяют координатную плоскость на области. Если точка в координатной плоскости удовлетворяет системе, то все точки в той же области, что и эта точка, также будут удовлетворять системе.
Решение линейных систем неравенств: метод контрольных точек
Постройте линию для каждого неравенства.Следуйте тому же условию для пунктирных и сплошных линий, что и раньше.
Для каждой области, разделяемой линиями, выберите точку в этой области. Проверьте точку, подставляя значения xxx и yyy в каждое неравенство.
Если система union , то контрольная точка должна удовлетворять только одному из неравенств. Если система перекресток , то она должна удовлетворять всем неравенствам. Если контрольная точка соответствует системе, закрасьте область, в которой находится контрольная точка.
Сотрите все линии и лучи, которых нет в растворе.
Постройте график решения следующей системы неравенств
{2x + 3y≤4x − 4y> 2. \ begin {cases} \ begin {выровнены}
2х + 3у & \ ле 4 \\
х-4у &> 2.
\ end {align} \ end {case} {2x + 3yx − 4y ≤4> 2.Обратите внимание, что эта система — перекресток . Сначала нарисуйте линию для каждого неравенства. Первое неравенство должно быть сплошной линией, а второе неравенство — пунктирной линией.Эти линии делят график на 4 области.
Выберите точку в каждом регионе и проверьте ее на неравенства:
1: (0,0) {2 (0) +3 (0) ≤4 ✓0−4 (0)> 2×2: (2,1) {2 (2) +3 (1) ≤4×2−4 ( 1)> 2×3: (3,0) {2 (3) +3 (0) ≤4×3−4 (0)> 2 ✓4: (2, −1) {2 (2) +3 (−1) ≤ 4 ✓ 2−4 (−1)> 2 ✓ \ begin {array} {ccl}
\ boxed {1}: & (0,0) & \ begin {cases} \ begin {array} {rlc} 2 (0) +3 (0) & \ le 4 & \ checkmark \\ 0-4 (0) &> 2 & \ text {x} \ end {array} \ end {case} \\
\ boxed {2}: & (2,1) & \ begin {cases} \ begin {array} {rlc} 2 (2) +3 (1) & \ le 4 & \ text {x} \\ 2-4 (1) &> 2 & \ text {x} \ end {array} \ end {case} \\
\ boxed {3}: & (3,0) & \ begin {cases} \ begin {array} {rlc} 2 (3) +3 (0) & \ le 4 & \ text {x} \\ 3-4 (0) &> 2 & \ checkmark \ end {array} \ end {case} \\
\ boxed {4}: & (2, -1) & \ begin {cases} \ begin {array} {rlc} 2 (2) +3 (-1) & \ le 4 & \ checkmark \\ 2-4 ( -1) &> 2 & \ checkmark \ end {array} \ end {case}
\ end {array} 1: 2: 3: 4: (0,0) (2,1) (3,0) (2, −1) {2 (0) +3 (0) 0−4 (0) ≤4> 2 ✓x {2 (2) +3 (1) 2−4 (1) ≤4> 2 xx {2 (3) +3 (0 ) 3−4 (0) ≤4> 2 x ✓ {2 (2) +3 (−1) 2−4 (−1) ≤4> 2 ✓ ✓Единственная точка, удовлетворяющая обоим неравенствам, — это точка в области 4.Заштрихуйте эту область и удалите все сплошные лучи, которых нет в этой области.
□ _ \ квадрат □
Круг> Прямоугольник> Треугольник
Прямоугольник> Треугольник> Круг
Треугольник> Прямоугольник> Круг
Прямоугольник> Круг> Треугольник
Круг> Треугольник> Прямоугольник
Треугольник> Круг> Прямоугольник
Выше показано, как мобильный телефон будет сбалансирован, если его оставить висеть.Предположим, что точка опоры находится в центре каждого стержня.
Каков относительный вес этих фигур?
Решение линейных неравенств | Уравнения и неравенства
4.7 Решение линейных неравенств (EMA3H)
Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен \ (\ text {1} \). Ниже приведены примеры линейных неравенств.
\ begin {align *}
2x + 2 & \ le 1 \\
\ frac {2 — x} {3x + 1} & \ ge 2 \\
\ frac {4} {3} x — 6 & <7x + 2
\ end {выровнять *}
Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений.Единственная разница возникает при умножении или делении со знаком минус. Например, мы знаем, что \ (8> 6 \). Если обе части неравенства разделить на \ (- \ text {2} \), то мы получим \ (- 4> -3 \), что неверно. Следовательно, знак неравенства нужно поменять местами, получая \ (- 4 <-3 \).
Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.
Решить \ (2x + 2 = 1 \):
\ begin {align *}
2x + 2 & = 1 \\
2x & = 1-2 \\
2x & = -1 \\
х & = — \ frac {1} {2}
\ end {выровнять *}
Если представить этот ответ в числовой строке, получим:
Теперь решим относительно \ (x \) в неравенстве \ (2x + 2 \ le 1 \):
\ begin {align *}
2x + 2 & \ le 1 \\
2x & \ le 1 — 2 \\
2x & \ le -1 \\
х & \ le — \ frac {1} {2}
\ end {выровнять *}
Если представить этот ответ в числовой строке, получим:
Мы видим, что для уравнения существует только одно значение \ (x \), для которого уравнение верно.Однако для неравенства существует диапазон значений, для которых неравенство верно. В этом главное отличие уравнения от неравенства.
Помните: , когда мы делим или умножаем обе стороны неравенства на отрицательное число, направление неравенства меняется. Например, если \ (x <1 \), то \ (- x> -1 \). Также обратите внимание, что мы не можем делить или умножать на переменную.
Следующее видео знакомит с линейными неравенствами.
Видео: 2FGH
Обозначение интервалов (EMA3J)
Примеры:
\ (\ left (4; 12 \ right) \) | Круглые скобки указывают на то, что номер не включен. Этот интервал включает все действительные числа, большие, но не равные \ (\ text {4} \) и меньшие, но не равные \ (\ text {12} \). |
\ (\ left (- \ infty; -1 \ right) \) | Круглые скобки всегда используются для положительной и отрицательной бесконечности.Этот интервал включает все действительные числа, меньшие, но не равные \ (- \ text {1} \). |
\ (\ left [1; 13 \ right) \) | Квадратная скобка означает, что номер включен. Этот интервал включает все действительные числа, большие или равные \ (\ text {1} \) и меньшие, но не равные \ (\ text {13} \). |
Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.
Представим приведенный выше ответ в обозначении интервалов как \ (\ left (- \ infty; — \ frac {1} {2} \ right] \)
Рабочий пример 17: Решение линейных неравенств
Решить относительно \ (r \):
\ [6 — r> 2 \]
Представьте ответ в числовой строке и в виде интервалов.
Переставьте и решите для \ (r \)
\ begin {align *}
-r &> 2-6 \\
-r &> -4
\ end {align *}
Умножить на \ (- \ text {1} \) и отменить знак неравенства
\ [г <4 \]
Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ [\ влево (- \ infty; 4 \ вправо) \]
Рабочий пример 18: Решение линейных неравенств
Решите относительно \ (q \):
\ [4q + 3
Представьте ответ в числовой строке и в виде интервалов.
Раскладной кронштейн
\ begin {align *}
4q + 3 & <2 (q + 3) \\
4q + 3 & <2q + 6
\ end {align *}
Переставьте и решите для \ (q \)
\ begin {align *}
4q + 3 & <2q + 6 \\
4q - 2q & <6 - 3 \\
2q & <3
\ end {align *}
Разделите обе стороны на \ (\ text {2} \)
\ begin {align *}
2q & <3 \\
д & <\ frac {3} {2}
\ end {align *}
Представьте ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left (- \ infty; \ frac {3} {2} \ right) \)
Рабочий пример 19: Решение сложных линейных неравенств
Решить относительно \ (x \):
\ [5 \ le x + 3
Представьте ответ в числовой строке и в интервальной записи.
Вычтем \ (\ text {3} \) из всех частей неравенства
\ [\ begin {array} {ccccc}
5 — 3 & \ le & x + 3 — 3 & <& 8 - 3 \\
2 & \ le & x & <& 5
\ конец {массив} \]
Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left [2; 5 \ right) \)
Вы справитесь! Позвольте нам помочь вам учиться с умом для достижения ваших целей.Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки
Упражнение 4.6
\ (x <-1 \ text {и} x \ ge 6; x \ in \ mathbb {R} \)
\ (3 <х <6; х \ в \ mathbb {R} \)
\ (x \ neq 3; x \ neq 6; x \ in \ mathbb {R} \)
\ (х> -10; х \ в \ mathbb {R} \)
\ begin {align *}
3х + 4 &> 5х + 8 \\
3х — 5х &> 8 — 4 \\
-2x> 4 \\
2x
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; -2) \)
\ (3 (x — 1) — 2 \ le 6x + 4 \)
\ begin {align *}
3 (x — 1) — 2 & \ le 6x + 4 \\
3x — 5 & \ le 6x + 4 \\
3х — 6х & \ ле 4 + 5 \\
-3x \ le 9 \\
х \ ge — \ frac {9} {3} \\
х \ ge -3
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ([- 3; \ infty) \)
\ (\ dfrac {x — 7} {3}> \ dfrac {2x — 3} {2} \)
\ begin {align *}
\ frac {x — 7} {3} &> \ frac {2x — 3} {2} \\
2 (х — 7) &> 3 (2x — 3) \\
2х — 14> 6х — 9 \\
-4x> 5 \\
x
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; — \ frac {5} {4}) \)
\ begin {align *}
-4 (x — 1) & \ frac {2} {5}
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ((\ frac {2} {5}; \ infty) \)
\ (\ dfrac {1} {2} x + \ dfrac {1} {3} (x — 1) \ ge \ dfrac {5} {6} x — \ dfrac {1} {3} \)
\ begin {align *}
\ frac {1} {2} x + \ frac {1} {3} (x — 1) & \ ge \ frac {5} {6} x — \ frac {1} {3} \\
\ frac {1} {2} x + \ frac {1} {3} x — \ frac {1} {3} & \ ge \ frac {5} {6} x — \ frac {1} {3} \ \
\ frac {1} {2} x + \ frac {1} {3} x — \ frac {5} {6} x & \ ge \ frac {1} {3} — \ frac {1} {3} \ \
\ frac {3} {6} x + \ frac {2} {6} x — \ frac {5} {6} x & \ ge 0 \\
0x \ ge 0
\ end {выровнять *}
Неравенство верно для всех действительных значений \ (x \).
\ [\ begin {array} {ccccc}
-2 & \ le & x — 1 &
Обозначается числовой строкой:
В интервальном обозначении: \ ([- 1; 4) \)
\ [\ begin {array} {ccccc}
-5 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 1; 5] \)
\ (7 (3x + 2) — 5 (2x — 3)> 7 \)
\ begin {align *}
7 (3x + 2) — 5 (2x — 3) &> 7 \\
21х + 14 — 10х + 15 &> 7 \\
11x &> -22 \\
х &> -2
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 2; \ infty) \)
\ (\ dfrac {5x — 1} {- 6} \ ge \ dfrac {1 — 2x} {3} \)
\ begin {align *}
\ frac {5x — 1} {- 6} & \ ge \ frac {1 — 2x} {3} \\
5x — 1 & \ ge -2 (1-2x) \\
5x — 1 & \ ge -2 + 4x \\
5x — 4x & \ ge -1 \\
х & \ ge -1
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ([- 1; \ infty) \)
\ [\ begin {array} {ccccc}
3 & \ le & 4 — х & \ le & 16 \\
-1 & \ le & -x & \ le & 12 \\
1 & \ ge & x & \ ge & -12
\ конец {массив} \]
Обозначается в числовой строке:
В интервальном обозначении: \ ([1; 12] \)
\ (\ dfrac {-7y} {3} — 5> -7 \)
\ begin {align *}
\ frac {-7y} {3} — 5 &> -7 \\
-7л — 15 &> -21 \\
-7лет &> -6 \\
y &
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; \ frac {6} {7}) \)
\ [\ begin {array} {ccccc}
1 & \ le & 1-2y & & -4 \\
-4 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 4; 0] \)
\ (- 2 <\ dfrac {x - 1} {- 3} <7 \)
\ [\ begin {array} {ccccc}
-2 & & x — 1 &> & -21 \\
7 &> & x &> & -20 \\
-20 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 20; 7) \)
\ begin {align *}
2 х -1 & <3 (х +11) \\
2 х -1 & <3 х +33 \\
2 х -3 х & <33 +1 \\
-1 х & <34 \\
\ поэтому x &> -34
\ end {align *}
\ [\ влево (-34; \ infty \ вправо) \]
\ begin {align *}
х -1 & <-4 (х -6) \\
х -1 & <-4 х +24 \\
х +4 х & <24 +1 \\
5 х & <25 \\
\ поэтому x & <5
\ end {align *}
\ [\ влево (- \ infty; 5 \ вправо) \]
\ (\ dfrac {x-1} {8} \ leq \ dfrac {2 (x-2)} {3} \)
\ begin {align *}
\ frac {x-1} {8} & \ leq \ frac {2 (x-2)} {3} \\
3 (х-1) & \ leq 16 (х-2) \\
3х-3 & \ leq 16х-32 \\
3х -16х & \ leq -32 +3 \\
-13x & \ leq -29 \\
\ поэтому x & \ geq \ frac {29} {13}
\ end {выровнять *}
\ (\; x \ in \ left [\ frac {29} {13}; \ infty \ right) \).
\ (\ dfrac {x + 2} {4} \ leq \ dfrac {-2 (x-4)} {7} \)
\ begin {align *}
\ frac {x + 2} {4} & \ leq \ frac {-2 (x-4)} {7} \\
7 (х + 2) & \ leq -8 (х-4) \\
7x + 14 & \ leq -8x + 32 \\
7x + 8x & \ leq 32-14 \\
15x & \ leq 18 \\
\ поэтому x & \ leq \ frac {6} {5}
\ end {выровнять *}
\ (\; x \ in \ left (- \ infty; \ frac {6} {5} \ right] \).
\ (\ dfrac {1} {5} x — \ dfrac {5} {4} (x + 2)> \ dfrac {1} {4} x + 3 \)
\ begin {align *}
\ frac {1} {5} x — \ frac {5} {4} (x + 2) &> \ frac {1} {4} x +3 \\
4х — 25 (х + 2) &> 5х +60 \\
4х — 25 х-50 &> 5х +60 \\
4х — 25 х -5х &> 60 + 50 \\
-26x &> 110 \\
\ поэтому x & <- \ frac {55} {13}
\ end {align *}
Интервал:
\ [\ left (- \ infty; — \ frac {55} {13} \ right) \]
\ (\ dfrac {1} {5} x — \ dfrac {2} {5} (x + 3) \ geq \ dfrac {4} {2} x +3 \)
\ begin {align *}
\ frac {1} {5} x — \ frac {2} {5} (x + 3) & \ geq \ frac {4} {2} x +3 \\
2x — 4 (x + 3) & \ geq 20x +30 \\
2х — 4 х-12 & \ geq 20x +30 \\
2х — 4 х -20х & \ geq 30 + 12 \\
-22x & \ geq 42 \\
\ поэтому x & \ leq — \ frac {21} {11}
\ end {align *}
Интервал:
\ [\ left (- \ infty; — \ frac {21} {11} \ right] \]
\ (4x +3 <-3 \ quad \ text {или} \ quad 4x +3> 5 \)
Решите неравенство:
\ [\ begin {array} {rclcrcl}
4x +3 & <& -3 & \ text {или} & 4x +3 &> & 5 \\
4x & <& -3-3 & \ text {or} & 4x &> & 5-3 \\
x & <& \ frac {-3-3} {4} & \ text {или} & x &> & \ frac {5-3} {4} \\
x & <& - \ frac {3} {2} & \ text {или} & x &> & \ frac {1} {2} \\
\ end {array} \]
\ [\ left (- \ infty; — \ frac {3} {2} \ right) \ cup \ left (\ frac {1} {2}; \ infty \ right) \]
Решите неравенство:
\ [\ begin {array} {rcccl}
4 & \ ge & -6x -6 & \ ge & -3 \\
4 + 6 & \ ge & -6x & \ ge & -3 + 6 \\
\ frac {4 + 6} {- 6} & \ le & x & \ le & \ frac {-3 + 6} {- 6} \\
— \ frac {5} {3} & \ le & x & \ le & — \ frac {1} {2} \\
\ end {array} \]
\ [\ left [- \ frac {5} {3}; — \ frac {1} {2} \ right] \]
\ (6b — 3> b + 2, ~ b \ in \ mathbb {Z} \)
\ begin {align *}
6b — 3> b + 2, ~ b \ in \ mathbb {Z} \\
5b> 5 \\
b> 1
\ end {выровнять *}
\ (3a — 1 <4a + 6, ~ a \ in \ mathbb {N} \)
\ begin {align *}
3а — 1-7
\ end {выровнять *}
Однако нам говорят, что \ (a \ in \ mathbb {N} \) и поэтому \ (a> 0 \).

 Является ли число –3 решением системы неравенств?
Является ли число –3 решением системы неравенств?


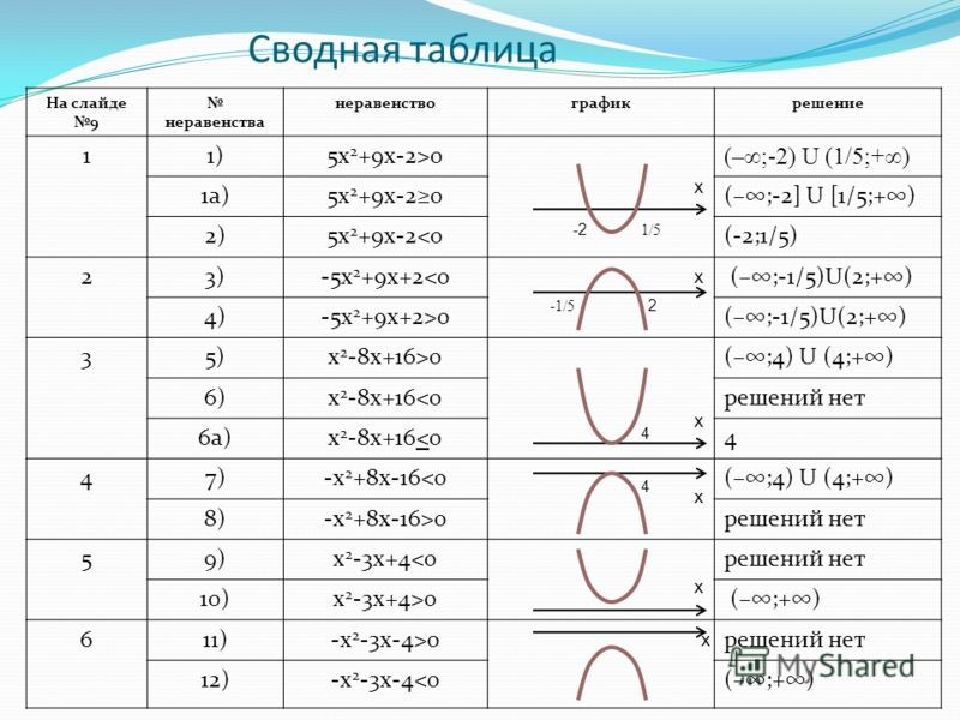 Если корни квадратного трехчлена не удовлетворяют неравенству, изображаем их «выколотыми» точками.
Если корни квадратного трехчлена не удовлетворяют неравенству, изображаем их «выколотыми» точками.


