Содержание
Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике
Часть 1.
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков , .
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие – левее точки на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .
Обратите внимание, многие, назвав первую точку вместо второй точки указывают точку , что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные – правее точки , включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что .
Пример 3.

Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные – выше точки , включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:
Пример 4.
Решить неравенство:
Решение:
Кратко:
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению , так как область значений функции –
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
Если не очень понятно, загляните сюда –>+ показать
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.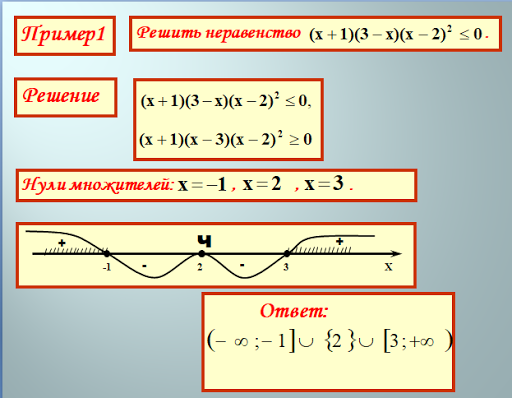
Поэтому
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Примеры решения простейших тригонометрических неравенств
Часть 2.
Начало здесь.
Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические уравнения (часть III).
Кстати, для сдающих ЕГЭ по математике, – умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Примеры решения простейших тригонометрических неравенств
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.
Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1. Для этого мы мысленно соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.
Заметим, кстати, что дуга повторяет дугу равно через пол круга, то есть через (период функции – это ).
Все подходящие значения можно записать в виде следующего двойного неравенства:
или так
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов . Указываем все значения тангенса, большие или равные – выше (включая саму точку).
«Транслируем» отмеченные точки оси тангенсов на тригонометрический круг.
Все подходящие значения можно записать в виде следующего двойного неравенства:
или такого (разницы – никакой):
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси котангенсов . Указываем все значения котангенса, большие или равные – правее (включая саму точку).
«Транслируем» отмеченные точки оси котангенсов на тригонометрический круг:
Все подходящие значения можно записать в виде следующего двойного неравенства:
Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки (значение тангенса в этих точках не определено)?
А, решая тригонометрическое неравенство с котангенсом, – мы не включаем в ответ точки (значение котангенса в этих точках не определено).
Пример 4.
Решить неравенство:
Решение:
Проверьте себя
Помните, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например, задание 2).
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
Если у вас есть вопросы, – пожалуйста, – пишите в комментариях!
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2
Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.

Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Определение 4
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1
Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2
Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3
Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5
Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4
Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5
Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6
Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 6
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.
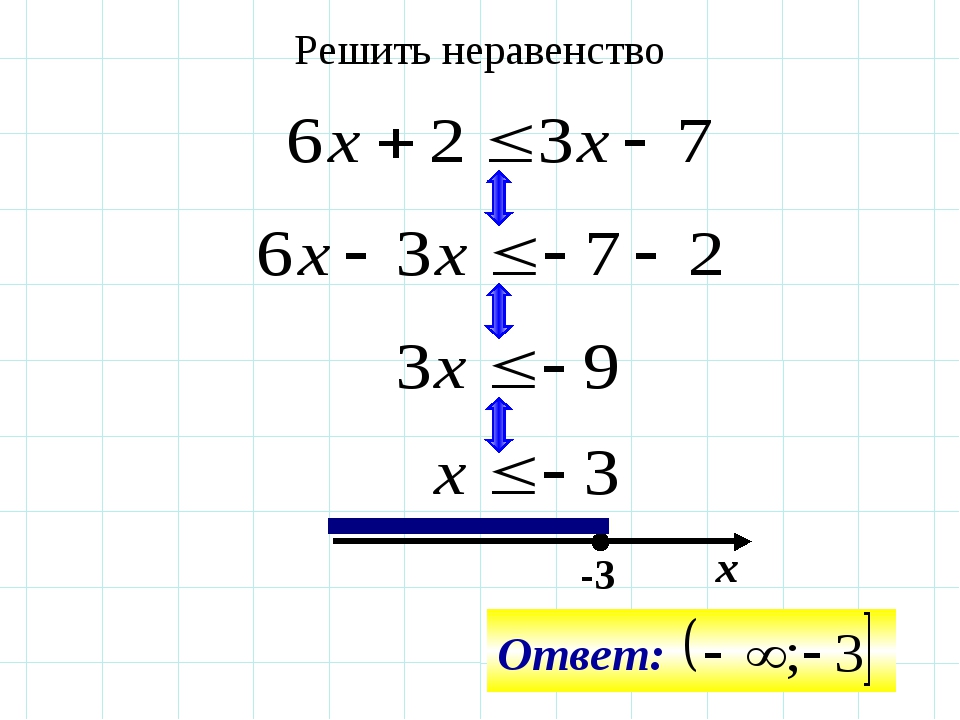
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7
- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8
Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Пример 7
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8
Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Пример 9
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Линейные неравенства, решение и примеры
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Линейные неравенства — это неравенства вида:
- ax + b < 0,
- ax + b > 0,
- ax + b ≥ 0,
- ax + b ≤ 0,
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.
Типы неравенств
- Строгие — используют только больше (>) или меньше (<):
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
- Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно):
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы:
- a ≠ b — означает, что a не равно b.

- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
- Если а > b , то b < а. Также наоборот: а < b, то b > а.
- Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
- Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
- Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять из-за возможных исключений. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
- Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
- Если а > b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа < nb и
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
- Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие данного правила или квадратный пример: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то
Если а < b , то
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Важно знать
Два неравенства можно назвать равносильными, если у них одинаковые решения.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
|
Решение линейных неравенств
Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.
Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак < , ≤ , ≥ , а и b — действительные числа, a ≠ 0.
Определение 2. Неравенства называют линейными с одной переменной, когда ax < c или ax > c , где x — переменная, a, c — некоторые числа.
Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x < c можно записать в форме нестрогого неравенства: ax ≤ c, ax ≥ c . Такое уравнение принято называть линейным. Его главные различия:
Такое уравнение принято называть линейным. Его главные различия:
- форма записи ax + b > 0 — в первом и ax > c — во втором;
- допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.
Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.
Определение 3. Линейные неравенства с одной переменной x выглядят так:
- ax + b < 0,
- ax + b > 0,
- ax + b ≤ 0,
- ax + b ≥ 0,
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Для решения ax + b < 0 (≤, >, ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.
Алгоритм решения ax + b < 0 при a ≠ 0
- перенесем число b в правую часть с противоположным знаком,
- получим равносильное: ax < −b;
- произведем деление обеих частей на число не равное нулю.

Когда a положительное, то знак остается, если a — отрицательное, знак меняется на противоположный.
Рассмотрим пример: 4x + 16 ≤ 0.
Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.
- Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
- Произведем деление обеих частей на 4. Меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4.
- Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.
Ответ: x ≤ −4 или числовой промежуток (−∞, −4].
При решении ax + b < 0, когда а = 0, получается 0 * x + b < 0. На рассмотрение берется b < 0, после выясняется верное оно или нет.
Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b < 0. При подстановке любого t вместо x, получаем 0 * t + b < 0 , где b < 0. Если оно верно, то для решения подойдет любое значение. Когда b < 0 неверно, тогда данное уравнение не имеет решений, так как нет ни одного значения переменной, которое может привести к верному числовому равенству.
Числовое неравенство вида b < 0 (≤, > , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
- Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
- Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.
Ответ: промежуток (− ∞ , + ∞).
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов это:
- введение функции y = ax + b;
- поиск нулей для разбиения области определения на промежутки;
- отметить полученные корни на координатной прямой;
- определение знаков и отмечание их на интервалах.
Алгоритм решения ax + b < 0 (≤, >, ≥) при a ≠ 0 с использованием метода интервалов:
- найдем нули функции y = ax + b для решения уравнения ax + b = 0.
Если a ≠ 0, тогда решением будет единственный корень — х₀;
- начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
- определим знаки функции y = ax + b на промежутках.
Для этого найдем значения функции в точках на промежутке;
- если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если < или ≤ н — над отрицательным промежутком.
Рассмотрим пример: −3x + 12 > 0.
Как решаем:
- В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
−6x = −12,
x = 2.
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
- Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6 < 0 . Знак на промежутке является отрицательным.
- Выполним решение со знаком >. Штриховку сделаем над положительным промежутком.
По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x < 4.
Ответ: (−∞, 4) или x < 4.
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
- во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
- во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
- во время решения ax + b > 0 произвести определение промежутка, где график изображается выше Ох;
- во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
- Так как коэффициент при x отрицательный, данная прямая является убывающей.
- Координаты точки пересечения с Ох равны −√3 : 5.
- Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
- Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.
Ответ: (−∞, −√3 : 5) или x < −√3 : 5.
Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!
Чтобы ребенок чувствовал себя увереннее на сложных контрольных и улучшил оценки в школе, запишите его на уроки математики в Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Урок 50. тригонометрические неравенства — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №50. Тригонометрические неравенства.
Перечень вопросов, рассматриваемых в теме
- решение простейших тригонометрических неравенств с помощью тригонометрической окружности;
- решение тригонометрических неравенств, сводимых к квадратным;
- решение тригонометрических неравенств методом интервалов.
Глоссарий по теме
- Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Тангенсом угла называется отношение к
Угол может выражаться и в градусах и в радианах.
- Арккосинусом числа называется такое число α, что: . Арккосинус числа m обозначают: .
- Арксинусом числаназывается такое число α, что: и . Арксинус числа m обозначают:.
- Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни под ред. А.Б. Жижченко. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 334-337.
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. 353-367.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
1. Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства .
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на (получим неравенство , то решением его будет множество точек, в которых . Это числа .
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
Рассмотрим теперь значение (рис.3).
Рисунок 3 – Решение неравенства
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1) , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением :
(для строгого неравенства) – множество интервалов;
(для нестрогого неравенства) – множество отрезков.
Если значение a= – 1,то получим следующую картинку (рис. 4):
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства является любое действительное число. Если неравенство строгое, то решением неравенства является любое действительное число, кроме чисел вида .
Наконец, если , то решением неравенства является любое действительное число.
Решение неравенства рассмотрим более коротко.
Очевидно, что если , то решением неравенства является любое действительное число.
Если , то решением неравенства является любое действительное число, а решением неравенства является любое действительное число, за исключением чисел вида .
Если , то решением неравенства являются числа вида , а неравенство решений не имеет. То же самое можно сказать о решении неравенств и в случае .
Случай рассмотрим более подробно (рис. 5).
Рисунок 5 – Решение неравенства
Решение неравенства для :
(для строгого неравенства) — множество интервалов;
(для нестрогого неравенства) — множество отрезков.
2. Теперь рассмотрим решение неравенств и .
Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для неравенство решений не имеет, а решением неравенства является любое действительное число.
Для неравенство решений не имеет, а решением неравенства является любое действительное число.
Рассмотрим случай более подробно.
Рассмотрим решение неравенства (рис. 6).
Рисунок 6 – Решение неравенства
Множество решений этого неравенства:
.
Теперь рассмотрим неравенство (рис. 7).
Рисунок 7 – Решение неравенства
Множество решений этого неравенства:
.
3. Теперь рассмотрим решение простейших неравенств и .
Сначала рассмотрим неравенство (рис. 8).
Рисунок 8 – Решение неравенства
Множество решений этого неравенства:
.
Соответственно, множество решений неравенства :
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Решите неравенство. Заполните пропуски
Решение:
Ведем новую переменную: .
Вспомогательное неравенство имеет вид:
, .
Вернемся к исходной переменной: .
Второе неравенство решений не имеет. Решением первого неравенства является:
.
Ответ: .
Пример 2.
Решите неравенство. Найдите коэффициенты
Решение:
Выразим
Рисунок 9 – решение неравенства
Ответ:
Простейшие тригонометрические уравнения и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.
Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi
n\).
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi
n\).
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi
x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi
n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm
\dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \
n\in\mathbb{Z}\). Отметим эти точки на окружности:
Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств
вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x
>\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x
<\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x
\geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x =
\dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x
\leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x =
\sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности:
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n —
\text{ четном}\\ -\sin \alpha, \text{при } n — \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n —
\text{ четном}\\ -\cos \alpha, \text{при } n — \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\
x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq
n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c — \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases}
\sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt]
\cos \dfrac x2=1
\end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned}
&\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt]
&\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered}
\right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[
\begin{gathered} \begin{aligned}
&x=\pi+6\pi n\\
&x=2\pi +6\pi m
\end{aligned} \end{gathered}
\right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi
+6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p,
p\in\mathbb{Z}\).
Простейшие неравенства | Алгебра
Простейшие линейные неравенства — это неравенства вида x>a; x≥a; x<a; x≤a.
Решение простейшего линейного неравенства можно изобразить на числовой прямой в виде числового промежутка и записать в виде интервала.
Неравенства бывают строгие и нестрогие.
Строгие неравенства — это неравенства со знаками больше (>) или меньше (<).
Нестрогие неравенства — это неравенства со знаками больше либо равно(≥) или меньше либо равно(≤).
При изображении на числовой прямой решения строгого неравенства точку выкалываем (она рисуется пустой внутри), точку из нестрогого неравенства закрашиваем (для запоминания можно использовать ассоциацию).
Числовой промежуток, соответствующий решению неравенства x<a или x≤a находится слева от точки a (штриховка идет от точки a влево, к минус бесконечности).
Числовой промежуток — решение неравенства x>a или x≥a — лежит справа от точки a (штриховка идет от точки a вправо, на плюс бесконечность) (для запоминания можно использовать ассоциацию).
Скобка, соответствующая точке a строгого неравенства x>a или x<a — круглая.
В нестрогом неравенстве x≥a или x≤a точка a — с квадратной скобкой.
Бесконечность и минус бесконечность в любом неравенстве всегда записываются с круглой скобкой.
Если обе скобки в записи круглые, числовой промежуток называется открытым. Концы открытого промежутка не являются решением неравенства и не включаются в ответ.
Конец промежутка с квадратной скобкой включается в ответ.
Запись промежутка всегда ведётся слева направо, от меньшего — к большему.
Решение простейших линейных неравенств схематически можно представить в виде схемы:
Рассмотрим примеры решения простейших линейных неравенств.
Читают: «икс больше двенадцати».
Решение:
Неравенство нестрогое, на числовой прямой 12 изображаем выколотой точкой.
К знаку неравенства мысленно пририсовываем стрелочку: —>. Стрелочка указывает, что от 12 штриховка уходит вправо, к плюс бесконечности:
Так как неравенство строгое и точка x=12 выколотая, в ответ 12 записываем с круглой скобкой.
Ответ:
Читают: «икс принадлежит открытому промежутку от двенадцати до бесконечности».
Читают: «икс больше минус трёх целых семи десятых»
Решение:
Неравенство нестрогое, поэтому -3,7 на числовой прямой изображаем закрашенной точкой. Мысленно пририсовываем к знаку неравенства стрелочку: —≥. Стрелочка направлена вправо, поэтому штриховка от -3,7 идёт вправо, на бесконечность:
Так как неравенство нестрогое и точка x= -3,7 закрашенная, -3,7 в ответ записываем с квадратной скобкой.
Ответ:
Читают: «икс принадлежит промежутку от минус трёх целых семи десятых до бесконечности, включая минус три целых семь десятых».
Читают: «икс меньше нуля целых двух десятых» (или «икс меньше чем нуль целых две десятых»).
Решение:
Неравенство строгое, 0,2 на числовой прямой изображаем выколотой точкой. К знаку неравенства мысленно пририсовываем стрелочку: <—. Стрелочка подсказывает, что от 0,2 штриховка уходит влево, к минус бесконечности:
Неравенство строгое, точка выколотая, 0,2 — с круглой скобкой.
Ответ:
Читают: «икс принадлежит открытому промежутку от минус бесконечности до нуля целых двух десятых».
Читают: «икс меньше либо равен пяти».
Решение:
Неравенство нестрогое, на числовой прямой 5 изображаем закрашенной точкой. К знаку неравенства мысленно пририсовываем стрелочку: ≤—. Направление штриховки — влево, к минус бесконечности:
Неравенство нестрогое, точка закрашенная, 5 — с квадратной скобкой.
Ответ:
Читают: «икс принадлежит промежутку от минус бесконечности до пяти, включая пять».
Решение вопросов со словами о неравенстве
(Вы можете сначала прочитать Введение в неравенство и решение неравенств.)
В алгебре у нас есть вопросы о неравенстве, например:
Сэм и Алекс играют в одной футбольной команде.
В минувшую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Как английский язык превращается в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте набросок, если нужно
- Присвойте буквы значениям
- Найдите или обработайте формулы
Мы также должны записать , что на самом деле требуется для , чтобы мы знали, куда мы идем и когда мы приедем!
Лучший способ узнать это — на примере, поэтому давайте попробуем наш первый пример:
Сэм и Алекс играют в одной футбольной команде.
В минувшую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?
Письма о назначении:
- количество голов, забитых Алексом: A
- количество голов, забитых Сэмом: S
Мы знаем, что Алекс забил на 3 гола больше, чем Сэм, поэтому: A = S + 3
А мы знаем, что вместе они забили меньше 9 голов: S + A <9
Нас спрашивают, сколько голов мог бы забить Алекс: A
Решить:
Начать с: S + A <9
A = S + 3, поэтому: S + (S + 3) <9
Упростить: 2S + 3 <9
Вычтем 3 с обеих сторон: 2S <9 - 3
Упростить: 2S <6
Разделите обе стороны на 2: S <3
Сэм забил менее 3 голов, что означает, что Сэм мог забить 0, 1 или 2 гола.
Алекс забил на 3 гола больше, чем Сэм, поэтому Алекс мог забить 3, 4 или 5 голов .
Чек:
- Когда S = 0, тогда A = 3 и S + A = 3, и 3 <9 правильно
- Когда S = 1, тогда A = 4 и S + A = 5, и 5 <9 правильно
- Когда S = 2, тогда A = 5 и S + A = 7, и 7 <9 правильно
- (Но когда S = 3, тогда A = 6 и S + A = 9, а 9 <9 неверно)
Еще много примеров!
Пример: Из 8 щенков девочек больше, чем мальчиков.
Сколько может быть девочек-щенков?
Письма о назначении:
- Количество девочек: г
- количество мальчиков: б
Мы знаем, что есть 8 щенков, поэтому: g + b = 8, что может быть преобразовано в
б = 8 — г
Мы также знаем, что девочек больше, чем мальчиков, поэтому:
г> б
У нас спрашивают количество щенков девочек: г
Решить:
Начать с: g> b
b = 8 — g , поэтому: g> 8 — g
Добавьте g к обеим сторонам: g + g> 8
Упростить: 2g> 8
Разделите обе стороны на 2: г> 4
Итак, девочек может быть 5, 6, 7 или 8.
А может быть 8 девочек? Тогда бы вообще не было мальчиков, и вопрос по этому поводу не ясен (иногда вопросы такие).
Чек
- Когда g = 8, тогда b = 0 и g> b правильно (но разрешено ли b = 0?)
- Когда g = 7, тогда b = 1 и правильное g> b
- Когда g = 6, тогда b = 2 и g> b правильно
- Когда g = 5, тогда b = 3 и g> b правильно
- (Но если g = 4, то b = 4 и g> b неверно)
Быстрый пример:
Пример: Джо участвует в гонке, в которой ему нужно ехать на велосипеде и бегать.
Он проезжает на велосипеде дистанцию 25 км, а затем пробегает 20 км. Его средняя скорость бега составляет половину его средней скорости езды на велосипеде.
Джо завершает гонку менее чем за 2,5 часа, что мы можем сказать о его средней скорости?
Письма о назначении:
- Средняя скорость движения: с
- Итак, средняя скорость езды на велосипеде: 2 с
Формулы:
- Скорость = Расстояние Время
- Что можно изменить на: Время = Расстояние Скорость
Нас спрашивают о его средних скоростях: с и 2 с
Гонка делится на две части:
1.Велоспорт
- Расстояние = 25 км
- Средняя скорость = 2с км / ч
- Итак Время = Расстояние Средняя скорость = 25 2 с часов
2. Работает
- Расстояние = 20 км
- Средняя скорость = с км / ч
- Итак Время = Расстояние Средняя скорость = 20 с часов
Джо завершает гонку менее чем за 2,5 часа
- Общее время <2½
- 25 2s + 20 s <2½
Решить:
Начать с: 25 2s + 20 s <2½
Умножить все члены на 2 с: 25 + 40 <5 с
Упростить: 65 <5 с
Разделите обе стороны на 5: 13
Поменять местами стороны: с> 13
Значит, его средняя скорость бега больше 13 км / ч, а его средняя скорость езды на велосипеде больше 26 км / ч
В этом примере мы можем использовать сразу два неравенства:
Пример: скорость
v м / с шара, брошенного прямо в воздух, определяется как v = 20 — 10t , где t — время в секундах.
В какое время скорость будет от 10 до 15 м / с?
Письма:
- скорость в м / с: v
- время в секундах: t
Формула:
У нас спрашивают время t , когда v находится между 5 и 15 м / с:
10 10 <20 - 10 т <15 Решить: Начать с: 10 <20 - 10т <15 Вычтите 20 из каждого: 10-20 <20-10t - 20 <15-20 Упростить: −10 <−10t <−5 Разделим каждое на 10: −1 <−t <−0.5 Изменить знаки и отменить неравенства: 1> t> 0,5 Лучше сначала показать меньшее число Таким образом, скорость составляет от 10 до 15 м / с между 0,5 и 1 секундой позже. И достаточно жесткий пример для завершения: Какой может быть ширина и длина комнаты? Сделайте набросок: мы не знаем размеров столов, только их площадь, могут они идеально поместиться или нет! Письма о назначении: Формула для периметра: 2 (Ш + Д) , и мы знаем, что это 16 м Мы также знаем, что площадь прямоугольника равна ширине, умноженной на длину: Площадь = Ш × Д И площадь должна быть больше или равна 7: Нас спрашивают о возможных значениях W и L
,
поэтому поменяйте местами: 0,5 Пример: прямоугольная комната вмещает не менее 7 столов, каждый из которых имеет площадь 1 квадратный метр.Периметр комнаты 16 м.
Решим:
Начать с: Ш × Д ≥ 7
Заменитель L = 8 — W: W × (8 — W) ≥ 7
Expand: 8W — W 2 ≥ 7
Переместите все термины в левую часть: W 2 — 8W + 7 ≤ 0
Это квадратное неравенство.Ее можно решить разными способами, здесь мы решим ее, заполнив квадрат:
Переместите числовой член — 7 в правую часть неравенства: W 2 — 8W ≤ −7
Заполните квадрат в левой части неравенства и уравновесите его, прибавив такое же значение к
правая часть неравенства: W 2 — 8W + 16 ≤ −7 + 16
Упростить: (W — 4) 2 ≤ 9
Извлеките квадратный корень из обеих частей неравенства: −3 ≤ W — 4 ≤ 3
Да, у нас есть два неравенства, потому что 3 2 = 9 И (−3) 2 = 9
Добавьте 4 к обеим сторонам каждого неравенства: 1 ≤ W ≤ 7
Таким образом, ширина должна быть между 1 м и 7 м (включительно), а длина — 8 — ширина .
Чек:
- Скажем, W = 1, тогда L = 8−1 = 7 и A = 1 x 7 = 7 м 2 (подходит ровно для 7 таблиц)
- Скажем, W = 0,9 (меньше 1), тогда L = 7,1 и A = 0,9 x 7,1 = 6,39 м 2 (7 не подходят)
- Скажем, W = 1,1 (чуть больше 1), тогда L = 6,9 и A = 1,1 x 6,9 = 7,59 м 2 (7 легко помещаются)
- Аналогично для W около 7 м
Simple English Wikipedia, бесплатная энциклопедия
Неравенство — это когда один объект равен: [1] [2]
- Меньше, чем другие (a a меньше b )
- Больше, чем другой (a> b {\ displaystyle a> b} означает, что a больше, чем b )
- Не меньше другого (a≥b {\ displaystyle a \ geq b} означает, что a не меньше b , то есть больше или равно b )
- Не больше другого (a≤b {\ displaystyle a \ leq b} означает, что a не больше b , или меньше или равно b )
Иногда используется неравенство назовите утверждение, что одно выражение меньше, больше, не меньше или не больше другого.
Неравенство 1 Это решение уравнения x + 4> 12
Неравенство в математике — это когда два решения или ответа сравниваются на большее или меньшее чем. Это когда сравниваются два или все же множество решений, не равных по количеству. Решить неравенство — значит найти его решения. Когда вы подставляете число в переменную, и утверждение истинно, тогда это решение. Когда вы подставляете число в переменную, и тогда утверждение неверно, число не является решением этого утверждения.
Решение неравенства — это поиск решения данной переменной. Это поиск относительного порядка набора. Неравенство может иметь множество решений, но обычно мы ищем только решения в виде вещественных чисел. Правильный способ читать неравенство — слева направо, как и другие уравнения, но с той лишь разницей, что они имеют разные правила для каждого уравнения.
Например, рассмотрим неравенство x + 4> 12, где x — действительное число. Во-первых, нужно найти x и убедиться, что это действительно решение.Ответ будет x> 8, и это верное утверждение. Это выражение касается положения x в наборе действительных чисел. Числовая линия — это один из способов показать местоположение относительно всех других действительных чисел. [3] (См. Рисунок Неравенство 1)
Линейное неравенство Пример линейного неравенства
Существует пять различных видов неравенства:
- Первый вид — это линейные неравенства, которые представляют собой неравенства, различающие выражения на меньшее или равное, меньшее или большее или равное, большее чем.Он заключается в том, что если мы заменим неравенство отношением равенства, то результатом будет линейное уравнение.
- Второй вид — это комбинации неравенств, которые должны удовлетворять неравенствам. Здесь нужно сначала иметь число в наборах решений, так что числа, удовлетворяющие неравенствам, будут значениями в пересечении двух наборов решений. [4]
- Третий вид — это неравенства, включающие абсолютные значения, что означает, что значения можно перефразировать как комбинации неравенств, включающих абсолютные значения.
- Четвертый вид неравенств называется полиномиальными неравенствами, что означает, что они непрерывны и их графики не имеют скачков или разрывов.
- И последнее, но не менее важное, это рациональные неравенства, которые означают, что это форма одного многочлена, деленного на другой многочлен. Другими словами, графики рациональных функций не имеют разрывов и не представлены в нулях знаменателя.
абсолютное значение Пример, показывающий абсолютное значение
Пример добавления неравенств.
Есть четыре способа решить квадратные уравнения:
- Сложите или вычтите одинаковое число с обеих сторон.
- Сдвиньте стороны и измените расположение знака неравенства.
- Умножьте одинаковое число с обеих сторон.
- Разделите одинаковое положительное или отрицательное число на обе стороны. пример умножения неравенства
Кроме того, для решения неравенства потребуется два шага. Первый — упростить, используя обратное сложение или вычитание.Второй — еще больше упростить, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число символ неравенства необходимо перевернуть. [5] [6]
Примеры решения неравенств [изменить | изменить источник]
Неравенство 2 Решение уравнения -6y
Неравенство — это математическое утверждение, объясняющее, что эти два значения не равны и различны. Уравнение a ≠ b означает, что a не равно b .Неравенство одинаково с любым уравнением, с той (единственной) разницей, что неравенство не использует знак равенства, а символы неравенства. Неравенство b> a означает, что b больше a. Ограничения скорости, знаки и другие используют неравенство, чтобы выразить их.
Решая неравенство, человек должен иметь верное утверждение. Когда вы делите или умножаете неравенство с отрицательным числом с обеих сторон, утверждение неверно. Чтобы утверждение было правильным с отрицательным числом, нужно изменить направление символа неравенства.Когда число является положительным числом, переворачивать символ не нужно. Неравенство — это правдивое заявление.
Например, начните с истинного утверждения -6 y <-12. Когда обе стороны разделены на -6, результат станет y <2. В этом утверждении символ необходимо перевернуть, чтобы получить истинное утверждение, которое дает y> 2 как правильный ответ. В числовой строке (см. Рисунок Неравенство 2) замкнутый заштрихованный кружок указывает на то, что он включен в набор решений.Открытый кружок указывает на то, что он не входит в набор решений. [7]
Прочтите: Опишите решения проблемы неравенства
Цели обучения
- Изобразите неравенства на числовой прямой
- Изобразите неравенства в обозначении интервалов
Обозначьте неравенства на числовой прямой
Во-первых, давайте определимся с важной терминологией. Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем.В этих утверждениях используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Первый способ, с которым вы, вероятно, знакомы — основное неравенство.Например:
- [latex] {x} \ lt {9} [/ latex] указывает список чисел, которые меньше [latex] 9 [/ latex]. Вы бы предпочли написать [latex] {x} \ lt {9} [/ latex] или попытаться перечислить все возможные числа, которые меньше [latex] 9 [/ latex]? (Большинство людей ответят первым)
- [латекс] -5 \ le {t} [/ latex] указывает все числа, которые больше или равны [latex] -5 [/ latex].
Обратите внимание, как размещение переменной слева или справа от знака неравенства может изменить, ищете ли вы больше или меньше.
Например:
- [латекс] x \ lt5 [/ latex] означает все действительные числа, которые меньше 5, тогда как;
- [latex] 5 \ lt {x} [/ latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex] x \ gt {5} [/ latex] обратите внимание, как неравенство по-прежнему указывает то же направление относительно x. Этот оператор представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.
Второй способ — график с использованием числовой прямой:
И третий способ — с интервалом.
В этом разделе мы подробно рассмотрим второй и третий способы. Опять же, эти три способа написать решения неравенства:
- неравенство
- интервал
- график
Знаки неравенства
В поле ниже показан символ, значение и пример для каждого знака неравенства. Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
| Символ | слов | Пример |
|---|---|---|
| [латекс] \ neq [/ латекс] | не равно | [латекс] {2} \ neq {8} [/ latex], 2 равно не равно и 8 . |
| [латекс] \ gt [/ латекс] | больше | [латекс] {5} \ gt {1} [/ latex], 5 больше 1 |
| [латекс] \ lt [/ латекс] | менее | [латекс] {2} \ lt {11} [/ latex], 2 меньше 11 |
| [латекс] \ geq [/ латекс] | больше или равно | [латекс] {4} \ geq {4} [/ latex], 4 больше или равно 4 |
| [латекс] \ leq [/ латекс] | меньше или равно | [латекс] {7} \ leq {9} [/ latex], 7 меньше или равно 9 |
Неравенство [латекс] x> y [/ latex] можно также записать как [latex] {y} <{x} [/ latex].Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут.
Графическое изображение неравенства
Неравенства также можно изобразить на числовой прямой. Ниже приведены три примера неравенств и их графики. Графики — очень полезный способ визуализировать информацию, особенно когда эта информация представляет собой бесконечный список чисел!
[латекс] х \ leq -4 [/ латекс]. Это переводится во все действительные числа в числовой строке, которые меньше или равны [латекс] 4 [/ латекс].
[латекс] {x} \ geq {-3} [/ латекс]. Это переводится во все действительные числа в числовой строке, которые больше или равны -3.
Каждый из этих графиков начинается с круга — открытого или закрытого (заштрихованного) круга. Эта точка часто называется конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств , которые больше или равны [latex] \ displaystyle \ left (\ geq \ right) [/ latex] или меньше или равны [latex] \ displaystyle. \ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для больше (>) или меньше (<). Дело в , а не в части решения.
Затем график бесконечно продолжается в одном направлении. Это показано линией со стрелкой в конце. Например, обратите внимание, что для графа [latex] \ displaystyle x \ geq -3 [/ latex], показанного выше, конечной точкой является [latex] −3 [/ latex], представленная замкнутым кружком, поскольку неравенство равно . больше или равно [латекс] -3 [/ латекс].Синяя линия нарисована справа от числовой, потому что значения в этой области больше, чем [latex] −3 [/ latex]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Пример
График неравенства [латекс] x \ ge 4 [/ латекс]
Показать решение
Мы можем использовать числовую линию, как показано. Поскольку значения для [latex] x [/ latex] включают [latex] 4 [/ latex], мы помещаем сплошную точку на числовой строке в [latex] 4 [/ latex].
Затем мы рисуем линию, которая начинается с [latex] x = 4 [/ latex] и, как указано стрелкой, продолжается до положительной бесконечности, что показывает, что набор решений включает в себя все действительные числа, большие или равные [latex] 4 [/ латекс].
В этом видео показан пример построения графика неравенства.
Пример
Напишите неравенство, описывающее все действительные числа в числовой строке, которые меньше [latex] 2 [/ latex], затем нарисуйте соответствующий график.
Показать решение
Нам нужно начинать слева и работать вправо, поэтому мы начинаем с отрицательной бесконечности и заканчиваем на [latex] 2 [/ latex]. Мы не будем включать ни то, ни другое, потому что бесконечность не является числом, и неравенство не включает [латекс] 2 [/ латекс].
Неравенство: [латекс] x \ lt2 [/ латекс]
Чтобы нарисовать график, сначала поместите открытую точку на числовой прямой, а затем нарисуйте линию, идущую влево. Нарисуйте стрелку в самой левой точке линии, чтобы указать, что она продолжается до бесконечности.
Изобразите неравенства, используя обозначение интервала
Другой широко используемый и, возможно, самый краткий метод описания неравенств и решений неравенств называется интервальной нотацией . Согласно этому соглашению, наборы строятся с использованием круглых или квадратных скобок, каждая из которых имеет свое значение.Решения для [latex] x \ geq 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex]. Этот метод широко используется и будет присутствовать в других курсах математики, которые вы, возможно, пройдете.
Основная концепция, которую следует запомнить, заключается в том, что круглые скобки представляют решения, которые больше или меньше числа, а скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «равны».”Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [ / латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, чем [latex] 1 [/ latex] включительно. В таблице ниже представлены возможные варианты.Не забывайте читать неравенства слева направо, как текст.
В таблице ниже описаны все возможные неравенства, которые могут возникнуть, и способы их записи с использованием интервальной записи, где a и b — действительные числа.
| Неравенство | слов | Интервальное обозначение |
|---|---|---|
| [латекс] {a} \ lt {x} \ lt {b} [/ латекс] | все действительные числа от a до b , кроме a и b | [латекс] \ влево (а, б \ вправо) [/ латекс] |
| [латекс] {x} \ gt {a} [/ латекс] | Все действительные числа больше a , но не включая a | [латекс] \ left (a, \ infty \ right) [/ latex] |
| [латекс] {x} \ lt {b} [/ латекс] | Все действительные числа меньше b , но не включая b | [латекс] \ влево (- \ infty, b \ right) [/ латекс] |
| [латекс] {x} \ ge {a} [/ латекс] | Все действительные числа больше a , включая a | [латекс] \ left [a, \ infty \ right) [/ latex] |
| [латекс] {x} \ le {b} [/ латекс] | Все действительные числа меньше b , включая b | [латекс] \ влево (- \ infty, b \ right] [/ латекс] |
| [латекс] {a} \ le {x} \ lt {b} [/ латекс] | Все вещественные числа от a до b , включая a | [латекс] \ влево [а, б \ вправо) [/ латекс] |
| [латекс] {a} \ lt {x} \ le {b} [/ латекс] | Все вещественные числа от a до b , включая b | [латекс] \ слева (a, b \ справа] [/ латекс] |
| [латекс] {a} \ le {x} \ le {b} [/ latex] | Все вещественные числа от a до b , включая a и b | [латекс] \ слева [a, b \ справа] [/ латекс] |
| [латекс] {x} \ lt {a} \ text {или} {x} \ gt {b} [/ latex] | Все действительные числа меньше a или больше b | [латекс] \ left (- \ infty, a \ right) \ чашка \ left (b, \ infty \ right) [/ latex] |
| Все вещественные числа | Все вещественные числа | [латекс] \ left (- \ infty, \ infty \ right) [/ latex] |
Пример
Опишите неравенство [латекс] x \ ge 4 [/ latex], используя обозначение интервала
Показать решение
Решения для [latex] x \ ge 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex].
Обратите внимание на использование кронштейна слева, потому что 4 включены в набор решений.
Пример
Используйте обозначение интервала, чтобы указать все действительные числа, большие или равные [латекс] -2 [/ латекс].
Показать решение
Используйте скобку слева от [latex] -2 [/ latex] и скобки после бесконечности: [latex] \ left [-2, \ infty \ right) [/ latex]. Скобка указывает, что [latex] -2 [/ latex] включен в набор со всеми действительными числами от [latex] -2 [/ latex] до бесконечности.
Подумай об этом
В предыдущих примерах вам давали неравенство или описание одного со словами и просили нарисовать соответствующий график и записать интервал. В этом примере вам дается интервал и предлагается написать неравенство и нарисовать график.
Дано [латекс] \ left (- \ infty, 10 \ right) [/ latex], запишите соответствующее неравенство и нарисуйте график.
В поле ниже запишите, считаете ли вы, что сначала будет проще нарисовать график или сначала записать неравенство.
Показать решение
Сначала нарисуем график.
Интервал читается как «все действительные числа меньше 10», поэтому мы начнем с того, что поставим точку на 10 и проведем линию влево со стрелкой, указывающей, что решение продолжает отрицательную бесконечность.
Чтобы записать неравенство, мы будем использовать <, поскольку круглые скобки указывают, что 10 не включено. [латекс] x <10 [/ латекс]
В следующем видео вы увидите примеры того, как записывать неравенства тремя представленными здесь способами: в виде неравенства, в интервальной нотации и с помощью графика.
публикаций: устранение неравенств в один шаг | Конечная математика
Неравенства похожи на уравнения в том, что они показывают взаимосвязь между двумя выражениями. Мы решаем и графически изображаем неравенства аналогично уравнениям. Однако есть некоторые отличия, о которых мы поговорим в этой главе. Основное отличие состоит в том, что для линейных неравенств ответом является интервал значений, тогда как для линейного уравнения ответом чаще всего является одно значение.
При написании неравенств используются следующие символы
> больше
[латекс] \ ge [/ latex] больше или равно
<меньше
[латекс] \ le [/ latex] меньше или равно
Запишите и изобразите неравенства в одной переменной на числовой прямой
Начнем с простого неравенства x> 3
Мы читаем это неравенство как «x больше 3». Решение — это набор всех действительных чисел больше трех.Мы часто представляем множество решений неравенства числовой линией.
Рассмотрим еще одно простое неравенство [латекс] x \ le4 [/ latex]
Мы читаем это неравенство как «x меньше или равно 4». Решение — это набор всех действительных чисел, которые равны четырем или меньше четырех. Построим это множество решений на числовой прямой.
В графе мы используем пустой кружок для конечной точки строгого неравенства (x> 3) и закрашенный кружок, если включен знак равенства (x [latex] \ le [/ latex] 4).
Пример 1
На числовой прямой нанесите следующие неравенства.
- х <−3
- [латекс] x \ ge6 [/ латекс]
- x> 0
- [латекс] x \ le8 [/ латекс]
Решения
- Неравенство x <−3 представляет все действительные числа, которые меньше −3. Число −3 не входит в решение и обозначено белым кружком на графике.
- Неравенство [латекс] x \ ge6 [/ latex] представляет все действительные числа, которые больше или равны шести.Число шесть включено в решение и обозначено на графике замкнутым кружком.
- Неравенство x > 0 представляет все действительные числа, которые больше нуля. Число ноль не входит в решение и отображается на графике белым кружком.
- Неравенство [латекс] x \ le8 [/ latex] представляет все действительные числа, которые меньше или равны восьми. Число восемь включено в решение и обозначено на графике замкнутым кружком.
Пример 2
Напишите неравенство, которое представлено на каждом графике.
Решения
- x <−12
- x > 540
- x <65
- [латекс] x \ ge83 [/ латекс]
В реальной жизни неравенство проявляется повсюду. Вот несколько простых примеров реальных приложений.
Пример 3
Запишите каждое утверждение в виде неравенства и обозначьте его числовой прямой.
- Чтобы получить бесплатную проверку, на вашем текущем счете необходимо поддерживать баланс не менее $ 2500.
- Чтобы кататься на американских горках «Thunderbolt», вы должны быть ростом не менее 48 дюймов.
- Чтобы получить бесплатный вход в зоопарк Сан-Диего, вам должно быть меньше 3 лет.
- Ограничение скорости на межштатной автомагистрали составляет 65 миль в час.
Решения
- Неравенство записывается как [латекс] х \ ge2500 [/ латекс]. Слова «как минимум» означают, что в набор решений включена стоимость 2500 долларов.
- Неравенство записывается как [latex] x \ ge48 [/ latex]. Слова «по крайней мере» означают, что значение 48 дюймов включено в набор решений.
- Неравенство записывается как x <3.
- Ограничение скорости означает наивысшую допустимую скорость, поэтому неравенство записывается как [latex] x \ le65 [/ latex].
Чтобы решить неравенство, мы должны изолировать переменную с одной стороны от знака неравенства. Чтобы изолировать переменную, мы используем те же базовые методы, которые используются при решении уравнений.Для неравенств этого типа:
x — a < b или x — a > b
Мы изолируем x, добавив константу a к обеим сторонам неравенства.
Пример 4
Решите каждое неравенство и изобразите набор решений.
- х − 3 <10
- х − 1> −10
- [латекс] x − 1 \ le − 5 [/ латекс]
- [латекс] x − 20 \ ge14 [/ латекс]
Решения
- Чтобы решить неравенство x- 3 <10 Упростите:
x <13 - Решить неравенство x — 1> -10
- Решить неравенство [латекс] x-1 \ le-5 [/ latex].Упростить:
[латекс] x \ le-4 [/ латекс] - Решить неравенство [латекс] x-20 \ le14 [/ latex]
Для неравенств этого типа:
x + 1 b
Мы выделяем x, вычитая константу a с обеих сторон неравенства.
Пример 5
Решите каждое неравенство и изобразите набор решений.
- [латекс] x + 2 <7 [/ латекс]
- [латекс] x + 8 \ le-7 [/ латекс]
- [латекс] x + 4> 13 [/ латекс]
Решения
- Чтобы решить неравенство x + 2 <7, вычтите 2 с обеих сторон неравенства. x + 2 — 2 <7 - 2
Упростить: x <5 - Чтобы решить неравенство [латекс] x + 8 \ le – 7 [/ latex], вычтите 8 с обеих сторон неравенства. [латекс] x + 8 — 8 \ le-7 — 8 [/ latex] Упростить:
[латекс] x \ ge – 15 [/ латекс] - Чтобы решить неравенство x + 4> 13, вычтите 4 с обеих сторон неравенства. x + 4-4> 13-4 Упростить:
x > 9
Рассмотрим проблему:
[латекс] \ frac {x} {5} \ le 3 [/ latex]
Чтобы найти решение, умножаем обе части на 5:
[latex] (5) \ frac {x} {5} \ le 3 (5) [/ latex]
Получаем
[латекс] х \ ле 15 [/ латекс].
Ответ неравенства может быть выражен четырьмя различными способами:
- Обозначение неравенства Ответ просто выражается как x <15.
- Обозначение набора Ответ: x | x <15. Вы читаете это как «набор всех значений x, таких, что x является действительным числом меньше 15».
- Интервальное обозначение использует скобки для обозначения диапазона значений в решении. Решение интервального обозначения для нашей задачи — (-∞, 15). Обозначение интервалов также использует понятие бесконечности ∞ и отрицательной бесконечности −∞.Круглые или открытые скобки «(» и «)» означают, что число рядом со скобкой не входит в набор решений. Квадратные или закрытые скобки «[» и «]» означают, что число рядом со скобкой включено в набор решений.
- График решения показывает решение в виде вещественной числовой прямой. Закрашенный кружок на номере указывает, что номер включен в набор решений. Белый кружок указывает на то, что номер не входит в набор. Для нашего примера здесь нарисован график решения.
Пример 6
- [−4,6] говорит, что решения — это все числа от −4 до 6 , включая −4 и 6.
- (8,24) говорит, что решением являются все числа от 8 до 24, но не включает числа 8 и 24.
- [3,12) говорит, что решением являются все числа от 3 до 12, включая 3, но не включая 12.
- (−5, ∞) говорит, что решением являются все числа больше −5, , исключая −5.
- (−∞, ∞) говорит, что решение — все действительные числа.
Решаем неравенство
[латекс] 2x \ ge 12 [/ latex] делением обеих сторон на 2:
[латекс] \ frac {2x} {2} \ ge \ frac {12} {2} [/ латекс]
Упростить:
[латекс] x \ ge 6 [/ латекс]
Давайте запишем решение в четырех различных обозначениях, которые вы только что выучили:
| Обозначение неравенства | [латекс] x \ ge 6 [/ латекс] |
| Обозначение набора | [латекс] {x | x \ ge 6} [/ латекс] |
| Интервальное обозначение | [латекс] [6, [/ латекс] ∞] |
| График решения |
Мы решаем неравенство аналогично решению обычного уравнения.Мы можем складывать или вычитать числа по обе стороны неравенства. Мы также можем умножать или делить положительные числа по обе стороны неравенства, не меняя решения.
Что-то другое происходит, если мы умножаем или делим на отрицательные числа. В этом случае знак неравенства меняет направление.
Например, чтобы решить −3x <9
Делим обе части на –3. Знак неравенства меняется с <на>, потому что мы делим на отрицательное число.
[латекс] \ frac {-3x} {- 3} \ gt \ 6 \ frac {9} {- 3} [/ латекс]
[латекс] x \ gt \ -3 [/ латекс]
Мы можем объяснить, почему это происходит, на простом примере.Мы знаем, что два меньше трех, поэтому можем записать неравенство.
2 <3
Если мы умножим оба числа на −1, мы получим −2 и −3, но мы знаем, что −2 больше −3.
−2> −3
Вы видите, что умножение обеих сторон неравенства на отрицательное число привело к изменению направления знака неравенства. Это также происходит, если мы делим на отрицательное число.
Пример 7
Решите каждое неравенство. Приведите решение в обозначениях неравенств и интервалов.
- [латекс] 4x \ lt 24 [/ латекс] [латекс] \ displaystyle {4} {x} lt {24} [/ latex]
- [латекс] -9x \ le \ frac {3} {5} [/ латекс]
- [латекс] \ displaystyle- {5} {x} \ le {21} [/ latex]
- [латекс] \ displaystyle {12} {x} \ gt- {30} [/ latex]
Решения
- [latex] \ displaystyle {4} {x} \ lt {24} [/ latex] Разделите обе стороны на 4: [latex] \ displaystyle \ frac {{{4} {x}}} {{4}} \ lt \ frac {{24}} {{4}} [/ latex] Упростите, чтобы получить ответ:
[latex] \ displaystyle {x} \ lt {6} [/ latex] - [латекс] \ displaystyle- {9} {x} \ le- \ frac {{3}} {{5}} [/ latex] Разделите обе стороны на –9:
[латекс] \ displaystyle \ frac {{- {9} {x}}} {{- {9}}} \ ge- \ frac {{3}} {{5}} (- \ frac {{1}} {{9}}) [/ latex] .Направление неравенства изменилось. Чтобы получить ответ, упростите:
[latex] \ displaystyle {x} \ ge \ frac {{1}} {{15}} [/ latex] - [латекс] \ displaystyle- {5} {x} \ le {21} [/ latex] Разделите обе стороны на –5:
[латекс] \ displaystyle \ frac {{- {5} {x}}} {{ — {{5}}}} \ ge \ frac {{21}} {{- {{5}}}} [/ latex] Направление неравенства изменено. Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ ge- \ frac {{21}} {{5}} [/ latex] - [latex] \ displaystyle {12} {x} \ gt- {30} [/ latex] Разделите обе стороны на 12: [latex] \ displaystyle \ frac {{{12} {x}}} {{12}} \ gt- \ frac {{30}} {{12}} [/ latex] Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ gt- \ frac {{5}} {{2}} [/ латекс]
Пример 8
Решите каждое неравенство.Приведите решение в обозначениях неравенств.
- [латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le- {12} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex]
Решения
- [латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex] Умножьте обе стороны на 2: [латекс] \ displaystyle {2} (\ frac {{x}} {{2}}) \ gt {40} ({2}) [/ latex] Упростить: [latex] \ displaystyle {x} \ gt {80} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le {12} [/ latex] Умножьте обе стороны на –3:
[латекс] \ displaystyle- {3} (\ frac {{x}} {{- {3}}}) \ ge- {12} (- {3}) [/ latex] Направление неравенства изменено.Для упрощения: [latex] \ displaystyle {x} \ ge {36} [/ latex] - [латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex] Умножьте обе стороны на 25 [латекс] \ displaystyle {25} ( \ frac {{x}} {{25}}) \ lt \ frac {{3}} {{2}} ({25}) [/ latex] Упростить:
[латекс] \ displaystyle {x} \ lt \ гидроразрыв {{75}} {{2}} [/ latex] или 37,5 - [латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex] Умножьте обе стороны на –7: [латекс] \ displaystyle (- {7}) \ frac {{x}} {{- {7}}} \ le {9} (- {7}) [/ latex] Направление неравенства изменено. Упростите: [latex] \ displaystyle {x} \ le- {63} [/ латекс]
.
- Ответом на неравенство часто бывает интервал значений.Распространенные неравенства:
- ge больше или равно
- le меньше или равно
- Решение неравенств с помощью сложения и вычитания работает так же, как решение уравнения. Чтобы решить, мы изолируем переменную на одной стороне уравнения.
- Есть четыре способа изобразить неравенство:
- Обозначение уравнения x ge 2
- Установить обозначение x ge 2
- Интервальное обозначение [2, ∞) Закрытые скобки «[» и «]» означают включение, круглые скобки «(« и »)» означают исключение.
- График решения
- При умножении или делении обеих сторон неравенства на отрицательное число необходимо обратить неравенство.
ck12, Algebra, Linear Inequalities, «
Solving One-Step Inequalities», под лицензией CC BY-NC 3.0.
Построение графиков линейных неравенств: примеры — ChiliMath
Теперь мы готовы применить предложенные шаги для построения графика линейного неравенства из предыдущего урока.Давайте рассмотрим четыре (4) примера, охватывающих различные типы символов неравенства.
Пример 1: Изобразите линейное неравенство y> 2x-1.
Во-первых, убедитесь, что переменная y сама по себе находится слева от символа неравенства, что и имеет место в этой задаче. Затем нужно построить граничную линию, на мгновение изменив символ неравенства на символ равенства.
Постройте график линии y> 2x-1 по оси xy, используя предпочитаемый вами метод.Поскольку символ неравенства просто больше, чем «>», а не больше, чем , или равен «≥», граничная линия будет пунктирной или пунктирной. Итак, вот как это должно выглядеть на данный момент.
Последний шаг — заштриховать либо выше, либо ниже границы. На основе предложенных шагов нам сказали заштриховать верхнюю сторону граничной линии, если у нас есть символы неравенства> (больше) или ≥ (больше или равно). Всегда помните, что «больше» означает «верх».
Чтобы проверить, верен ли ваш окончательный график неравенства, мы можем выбрать любых точек в заштрихованной области. Для этого возьмем точку (−1, 1).
Оцените значения x и y точки, входящей в неравенство, и посмотрите, верно ли утверждение. В точке (−1,1) значения x = -1 и y = 1.
Поскольку контрольная точка из заштрихованной области дает истинное утверждение после проверки с исходным неравенством, это показывает, что наш окончательный график верен!
Пример 2: Постройте линейное неравенство y \ ge -x + 2.
Переменная y находится слева. Это хорошо! Обратите внимание, у нас есть символ «больше или равно». «Равный» аспект символа говорит нам о том, что граница будет сплошной. Итак, давайте изобразим прямую y = -x + 2 в декартовой плоскости.
Как и в примере 1, мы закрасим верхнюю часть ограничительной линии, потому что у нас есть случай «больше чем».
Убедитесь, что наш график правильный, выбрав точку (4,2) в заштрихованной части, и оцените значения x и y точки в данном линейном неравенстве.
Из выбранной контрольной точки, x = 4 и y = 2
У нас есть верное утверждение, которое дает нам уверенность в правильности нашего окончательного графика неравенства.
Пример 3: Постройте график решения линейного неравенства \ large {y <{1 \ over 2} x - 1}.
Если посмотреть на проблему, то символ неравенства — «меньше чем», а не «меньше или равно». Из-за этого график граничной линии будет прерывистым или штриховым. Кроме того, «меньше» означает, что мы закрасим область ниже линии .Вот и все!
Вот график граничной линии \ large {y = {1 \ over 2} x — 1}.
Поскольку символ неравенства на меньше (<), мы закрашиваем область под пунктирной линией.
Я предоставлю вам убедиться, что это правильный график, выбрав любые контрольные точки из заштрихованной области и сверив их с исходным линейным равенством.
Пример 4: Постройте график решения линейного неравенства y \ le — {2 \ over 3} x + 2.
Поскольку мы уже рассмотрели несколько примеров, я считаю, что вы почти можете решить это в своей голове. Вы можете произвести впечатление на своего учителя, предложив такое короткое решение.
Я вижу, что символ неравенства «меньше или равен» (≤), что делает границу сплошной. Более того, решение находится ниже границы из-за его аспекта «меньше чем». Вот правильный график неравенства.
В приведенных выше примерах вы видели линейные неравенства, в которых переменные y всегда находятся слева.Вы даже можете думать о них как о линейных неравенствах в форме пересечения наклона линии.
X и Y находятся на одной стороне символа неравенства
На этот раз нас интересуют примеры, в которых переменные x и y расположены по одну сторону от символа неравенства.
Мы можем назвать их линейными неравенствами в Стандартной форме . Ниже приведены четыре общих случая, когда A, B и C — это просто числа или константы.
Что нам нужно сделать, так это переписать данное неравенство или изменить его так, чтобы переменная y оставалась в левой части.Другими словами, мы собираемся найти y через x. После этого мы можем применить предложенные шаги для построения графика линейного неравенства, как обычно.
Давайте рассмотрим несколько примеров.
Пример 5: Изобразите линейное неравенство в стандартной форме 4x + 2y <8.
Начните решение относительно y в неравенстве, сохраняя y-переменную слева, в то время как остальная часть материала перемещается в правую сторону. Сделайте это, вычтя обе части на 4x и разделив все неравенство на коэффициент при y, равный 4.Поскольку делим на положительное число, направление символа неравенства остается прежним.
Поскольку у нас есть символ «меньше чем» (<) и , а не символ «меньше или равно» (≤), граничная линия будет пунктирной или пунктирной.
На всякий случай, если вы забыли, где взять граничную линию, измените на время неравенство на символ равенства, то есть с y <-2x + 4 на y = -2x + 4. Затем изобразите уравнение линии, используя любой из этих методов.
Итак, следующий очевидный шаг — решить, какую область затенять. Будет ли это выше или ниже границы? Мы закрасим нижнюю часть граничной линии, потому что у нас есть случай « меньше » после того, как мы преобразовали исходную проблему неравенства в форму, в которой y находится слева.
Мы можем проверить, правильно ли мы построили график, выбрав любые контрольные точки, найденные в заштрихованной области. Лучшая контрольная точка — это исходная точка, которая является точкой (0,0), потому что ее легко вычислить.
Контрольная точка (0,0) означает x = 0 и y = 0. Оцените эти значения в преобразованном неравенстве или исходном неравенстве, чтобы убедиться, что вы получили истинное утверждение.
Это действительно работает! Итак, мы заштриховали правильную область, которая находится под пунктирной линией.
Пример 6: Изобразите линейное неравенство в стандартной форме 3x — 6y \ le 12.
Чтобы переменная y оставалась слева, я бы вычел обе части на 3 x , а затем разделил все неравенство на коэффициент при y, который равен — 6 .
ПОМНИТЕ: При делении неравенства на отрицательное число мы должны изменить или переключить направление символа неравенства.
«Новое» неравенство будет иметь сплошную границу из-за символа «≥», где оно имеет компонент «равно». Кроме того, поскольку y «больше», это означает, что я закрашу область над линией.
Возможно, вас заинтересует:
Решение линейных неравенств
Шаги по построению графика линейных неравенств
Графические системы линейных неравенств
Решение сложных неравенств
Решение линейных неравенств (алгебра 1, линейные неравенства) — Mathplanet
График линейного неравенства по одной переменной представляет собой числовую прямую.Используйте открытый кружок для <и> и замкнутый кружок для ≤ и ≥.
График для x> -3
График для x ≥ 2
Неравенства, имеющие одно и то же решение, называются эквивалентными. Есть свойства неравенств, а также свойства равенства. Все перечисленные ниже свойства верны и для неравенств, содержащих ≥ и ≤.
Свойство сложения неравенства гласит, что добавление одного и того же числа к каждой стороне неравенства дает эквивалентное неравенство
$$ Если \: x> y, \: то \: x + z> y + z $$
$$ Если \: x Свойство неравенства вычитания говорит нам, что вычитание одного и того же числа из обеих частей неравенства дает эквивалентное неравенство. $$ Если \: x> y, \: то \: x-z> y-z $$ $$ Если \: x Свойство неравенства умножения говорит нам, что умножение обеих сторон неравенства на положительное число дает эквивалентное неравенство. $$ Если \: x> y \: и \: z> 0, \: то \: xz> yz $$ $$ Если \: x Умножение каждой стороны неравенства на отрицательное число, с другой стороны, не приводит к эквивалентному неравенству, если мы также не изменим направление символа неравенства $$ Если \: x> y \: и \: z <0, \: то \: xz $$ Если \: x То же самое и со свойством деления неравенства. Деление обеих частей неравенства на положительное число дает эквивалентное неравенство. $$ Если \: x> y \: и \: z> 0, \: то \: \ frac {x} {z}> \ frac {y} {z} $$ $$ Если \: x И деление на обе стороны неравенства с отрицательным числом дает эквивалентное неравенство, если знак неравенства перевернут. $$ Если \: x> y \: и \: z <0, \: then \: \ frac {x} {z} <\ frac {y} {z} $$ $$ Если \: x Чтобы решить многоступенчатое неравенство, вы делаете то же самое, что и при решении многоступенчатого уравнения.Возьмите что-то одно, желательно начать с изоляции переменной от констант. При решении многоступенчатых неравенств важно не забывать обращать знак неравенства при умножении или делении на отрицательные числа. Пример Решите неравенство $$ — 2 \ влево (x + 3 \ вправо) <10 $$ $$ — 2x-6 <10 $$ $$ — 2x-6 \, {\ color {green} {+ \, 6} <10 \,} {\ color {green} {+ \, 6}} $$ $$ — 2x <16 $$ $$ \ frac {-2x} {{\ color {green} {-2}}} \: {\ color {blue} {>}} \: \ frac {16} {{\ color {green} {- 2}}} $$ $$ x> -8 $$ Видеоурок Решите линейное неравенство $$ -2 \ влево (x + 2 \ вправо)> 4 — x $$ Процедура решения линейных неравенств с одной переменной Нам нужно быть осторожными с смыслом равенства при умножении или делении на отрицательные числа. Ниже приведены несколько примеров решения уравнений, включающих неравенства. Решить x + 2 Ответ Нам нужно вычесть «2» из обеих частей неравенства. `x + 2 <4` ` x <4-2` `x <2` График этого решения выглядит следующим образом: Решить `x / 2> 4` Ответ Нам нужно умножить обе части неравенства на `2`. `x / 2> 4` `x> 4xx2` `x> 8` Вот график этого решения: Решить 2 x ≤ 4 Ответ Нам нужно разделить обе части неравенства на `2`. `2x <= 4` `x <= 4 / 2` `x <= 2` Вот график этого решения: Решите неравенство 3-2 x ≥ 15 Ответ В этом примере нам нужно вычесть 3 с обеих сторон; затем разделите обе части на «-2» (не забудьте изменить направление неравенства). `3-2x> = 15` `-2x> = 15-3` `-2x> = 12` `х <= 12 / (- 2)` `x <= - 6` Вот график этого решения: (Обратите внимание на изменение смысла из-за деления на отрицательное Проверить: Всегда проверяйте свое решение, и вы можете быть уверены, что ваш ответ правильный. В этом случае любое число меньше «-6» должно «работать» в исходном уравнении, а любое число больше «-6» не должно работать. Возьмем `x = -10` (удобное число меньше` -6`) LHS `= 3 — 2 (-10) = 3 + 20 = 23`. Это больше, чем «15», так что это правда. Теперь возьмем `x = 0` (удобное число больше, чем` -6`) LHS `= 3 — 2 (0) = 3`. Это НЕ больше 15, как мы и надеялись. Итак, мы можем быть уверены, что наш ответ правильный. Решите неравенство `3/2 (1-x)> 1/4-x` Ответ `3/2 (1-x)> 1/4-x` Умножение обеих сторон на 4 дает: `6 (1-x)> 1-4x` `6-6x> 1-4x` `-6x + 4x> 1-6` `-2x> -5` ` x <5/2` (Обратите внимание на изменение смысла последней строки из-за деления на отрицательное Вот график этого решения: Проверка: Принимая x = 0 (что должно работать): «» LHS «= 3/2 (1 — 0) = 3/2` «» RHS «= 1 / 4` Верно, что `3/2> 1 / 4`, так что это хорошо. Теперь возьмем x = 3 (удобное число больше 5/2, которое не должно работать): «» LHS «= 3/2 (1-3) = -3` «RHS» = 1/4 — 3 = -2 3 / 4` Неверно, что `-3> -2 3 / 4` и поэтому` x = 3` не работает, как мы надеялись. Мы можем быть уверены, что наш ответ (`x <5 / 2`) правильный. Решить −1 <2 x + 3 <6 Ответ `- 1 <2x + 3 <6` Вычтем `3` со всех трех сторон `- 1 — 3 <2x + 3 - 3 <6 - 3` `- 4 <2x <3` Разделить все стороны на `2` `-2 График решения: Решить 2 x < x — 4 ≤ 3 x + 8 Ответ Другой способ решения более сложных неравенств с 3 `2x Тогда, решая каждое из этих неравенств, получаем: LHS неравенство: `x <- 4` RHS неравенство: `x — 4 ≤ 3x + 8` `- 4 ≤ 2x + 8` `- 12 ≤ 2x` `x ≥ -6` Принимая во внимание, что окончательное решение должно удовлетворять обоим `x <-4` и` x ≥ -6` Эти две части выглядят так: Рассматривая область пересечения двух частей, получаем `-6 ≤ x <-4` Это график окончательного решения: Решите следующие неравенства для x : 1.Решить 3 — 3 x <- 1 Ответ `3 — 3x <-1` `- 3x ` x> 4/3 ~~ 1,333 … ` Вот график решения: 2. Решите −2 ( x + 4)> 1 — 5 x Ответ `-2 (x + 4)> 1 — 5x` `-2x — 8> 1 — 5x `3x — 8> 1` `3x> 9` `x> 3` График решения: 3. Решить `x / 5-2> 2/3 (x + 3)` Ответ `x / 5-2> 2/3 (x + 3)` Умножить на 5: `х-10> 10/3 (х + 3)` Умножить на 3: `3x-30> 10 (x + 3)` `3x-30> 10x + 30` `3x> 10x + 60` `-7x> 60` `x <(- 60) / 7 ~~ -8.57` График решения: 4. Решить x — 1 <2 x + 2 <3 x + Ответ Нам нужно найти пересечение «истинных» значений. 2.Решение линейных неравенств
аналогично решению основных уравнений. (См. Решение уравнений.) Пример 1
Пример 2
Пример 3
Пример 4
номер) Пример 5
номер). Неравенства с тремя членами
Пример 6
Пример 7
членов (сторон) — переписать неравенство как
3x + 8`
неравенств, получаем: Упражнения
`
1

 Знак неравенства при этом не меняется.
Знак неравенства при этом не меняется.