25. Неравенства с модулем | Контрольные работы по математике и другим п

I тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:

где (3.27)

Решение зависит от знака числа А.

1. Если то неравенство (3.27) не имеет решений.

2. Если то неравенство (3.27) равносильно системе неравенств

где (3.28)

1. Если то неравенство (3.28) не имеет решений.

2. Если то неравенство (3.28) равносильно уравнению

3. Если , то неравенство (3.28) равносильно системе неравенств

где (3.29)

1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения

2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что

3. Если то неравенство (3.29) равносильно совокупности

где (3.30)

1. Если то решением неравенства (3.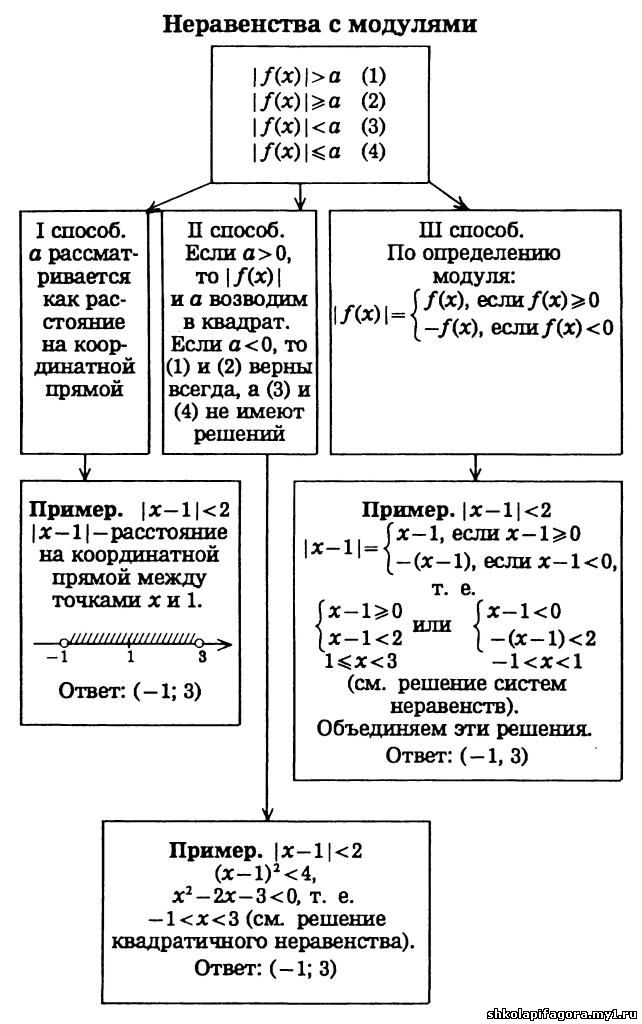 30) является множество всех значений Х из ОДЗ выражения

2. Если то неравенство (3.30) равносильно совокупности

II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:

(3.31)

Где – некоторые выражения с переменной Х.

Для решения неравенств типа (3.31) можно использовать следующие способы.

1-й способ: используя определение модуля, получаем равносильную совокупность систем:

2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения

1. Если

(3.32)

То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).

2. Если

То решением является множество всех значений Х, которые удовлетворяют системе

3. Если решение определяется системой

Ответом в решении неравенства (3. 31) является объединение всех решений, полученных на этапах 1–3.

3-й способ: метод интервалов.

Для решения необходимо:

1) найти значения Х, для которых

2) найденные значения Х нанести на числовую ось;

3) определить знак выражения на всех полученных промежутках;

4) нарисовать кривую знаков;

5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;

6) в ответе неравенства указать совокупность полученных решений.

III тип: Неравенство содержит несколько модулей и решается двумя способами:

1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.

2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.

IV тип: Неравенство вида

где (3.33)

Решается двумя способами:

1-й способ: метод интервалов.

2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:

Решение неравенства (3.33) сводится к решению неравенства

Аналогично решают неравенства IV типа (3.33), если они заданы со знаками

V тип: Неравенства, решаемые заменой переменной.

В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.

Пример 1. Решить неравенства:

1) 2)

3) 4)

5) 6)

Решение. 1) Решаем как неравенство I типа:

Получаем ответ:

2) Решаем как неравенство I типа:

Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду

Его решение: это и есть ответ.

3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:

Получаем ответ:

4) Заданное неравенство может быть записано в виде

Заменим переменную Решаем неравенство

Его решение

Возвращаемся к переменной Х и решаем совокупность

Получаем

Т. е. приходим к ответу

5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде

Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).

ОДЗ:

Рис. 3.10

А) рассмотрим неравенство на 1-м промежутке. Получаем систему

(3.34)

Решаем неравенство

Получаем

Система (3.34) сводится к системе

На данном промежутке решений нет.

Б)

Если , то С учетом рассматриваемого промежутка имеем:

Получаем

В)

Решением является промежуток:

Объединим полученные решения и приходим к ответу:

6)

ОДЗ:

Введем новую переменную:

тогда и приходим к неравенству вида

Решаем его

Используем метод интервалов (рис. 3.11).

Рис. 3.11

Запишем полученное решение в виде совокупности:

Вернемся к переменной Х:

(3. 35)

– выполняется при любых

С учетом ОДЗ второе неравенство системы (3.35) равносильно системе

Получаем ответ:

< Предыдущая		Следующая >

Уравнения и неравенства, содержащие знак модуля

Е.П. Нелин, В.А. Лазарев

 АЛГЕБРА

и начала математического

анализа

10 класс

Учебник для

общеобразовательных

учреждений. Базовый и

профильный уровень

§ 5. Уравнения и неравенства, содержащие знак модуля

(Оформление и автор интерактивных технологий Морозова Е.)

Объяснение и обоснование

     Решать любое уравнение или неравенство, содержащее знак модуля, можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений.

        В зависимости от выбранного способа решения получаем разные записи решения.

Пример            Решите уравнение | 2x – 4 | = 6.

I способ (по определению модуля)

II способ (использование геометрического смысла модуля)

     Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.

     Общая схема решения уравнений и неравенств, содержащих знак модуля — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида

|f (x)| + |g (x)| = a  (a > 0).

     Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции f (x) и g (x) будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства

f (x) ≥ или ≤0,                              (1)

g (x) ≥ или ≤0.                             (2)

     Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции f (x)), а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции g (x)). Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций f (x) и g (x), то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).

     Чтобы продолжить решение неравенств f (x) ≥или≤0 и g (x) ≥или≤ 0 методом интервалов, необходимо найти нули функций f (x) и g (x), то есть найти нули всех подмодульных функций (это и есть второй ориентир).

     Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир).

     В каждом из полученных промежутков знаки функций f (x) и g (x) не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы). 

     Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Вопросы для контроля

1. Объясните, какими способами можно решать уравнения и неравенства, содержащие знак модуля. Проиллюстрируйте эти способы на примерах.
2. Обоснуйте специальные соотношения. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.
3. Обоснуйте обобщения использования геометрического смысла модуля. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.

Упражнения

Решите уравнения и неравенства, содержащие знак модуля (1–15).

Постройте график функции

ТЕСТ

Уравнения и неравенства

 

 

 

Решение неравенств и уравнений с модулем

Рассмотрены способы решения сложных неравенств с параметрами, приведен алгоритм

Просмотр содержимого документа

«Решение неравенств и уравнений с модулем»

 

Решение

неравенств с параметрами

Метод замены множителей.

(МЗМ)

 

МЕТОД ЗАМЕНЫ МНОЖИТЕЛЯ (МЗМ)

Решение неравенств с модулями повышенной сложности стандартными школьными методами оказывается весьма сложным и громоздким, что вызывает у школьников определенные трудности.

Одним из эффективных и доступных методов решения таких неравенств и их систем является метод замены множителя .

Суть метода замены множителей (МЗМ) состоит в том, чтобы с помощью равносильных преобразований заменить каждый множитель в области его существования на более простой множитель, в конечном счете, рациональный и имеющий те же интервалы знакопостоянства

Решение последних легко осуществляется методом интервалов для рациональных функций.

, ≥, Решение неравенства (1) зависит только от знаков, входящих в него сомножителей. .»

Важно отметить , что метод замены множителя реализуется только при приведении исходного неравенства к каноническому виду:

(1)

где множители представляют собой рациональные функции; знак сравнения обозначает один из знаков: , ≥,

Решение неравенства (1) зависит только от знаков, входящих в него сомножителей.

.

Условия равносильности для МЗМ

Примеры решения неравенств модулем с применением

метода замены множителей (МЗМ)

• Решить неравенство

|х 2 -7х+2| ≤|х 2 +5х-2|

|х 2 -7х+2| ≤|х 2 +5х-2|

 

Применим МЗМ.

(х 2 -7х+2- х 2 -5х+2) (х 2 -7х+2+ х 2 +5х-2) ≤0;

(-12х+4) (2 х 2 -2х) ≤0;

-4(3х-1)(х-1) ≤0;

х (3х-1) (х-1) ≥0

2.

3.

4.

5.

6. Решить неравенство

Примеры для самостоятельного решения

ответы

СПАСИБО ЗА ВНИМАНИЕ!

ТВОРЧЕСКИХ

ВАМ

УСПЕХОВ!

Неравенства с модулем.

Новый взгляд на решение

Математика является символом мудрости науки,

эталоном совершенства и красоты в науке.

Российский философ, профессор   А.В. Волошинов

    Наиболее сложно решаемыми задачами школьной математики являются неравенства, содержащие переменные под знаком модуля. Для успешного решения таких неравенств необходимо хорошо знать свойства модуля и иметь навыки их использования.

Основные понятия и свойства

    Модуль (абсолютная величина) действительного числа обозначается и определяется следующим образом:

    К простым свойствам модуля относятся следующие соотношения:

,  ,    и  .

    Отметим, что последние два свойства справедливы для любой четной степени.

    Кроме того, если  , где  , то    и  

    Более сложные свойства модуля, которые можно эффективно использовать при  решении уравнений и неравенств с модулями, формулируются посредством следующих теорем:  

    Теорема 1. Для любых аналитических функций  и    справедливо неравенство  .   

    Теорема 2. Равенство равносильно неравенству  .

   

    Теорема 3. Равенство равносильно неравенству .

    Наиболее распространенными в школьной математике неравенствами, содержащие неизвестные переменные под знаком модуля, являются неравенства вида и  , где  некоторая положительная константа.

    Теорема 4. Неравенство равносильно двойному неравенству , а решение неравенства    сводится к решению совокупности неравенств    и  .                                         

    Данная теорема является частным случаем теорем 6 и 7.   

    Более сложными неравенствами, содержащие модуль, являются неравенства вида  ,  и  .

    Методы решения таких неравенств можно сформулировать посредством следующих трех теорем.   

    Теорема 5. Неравенство равносильно совокупности двух систем неравенств  

  и                  (1)

    Доказательство.  Так как  , то

,      или   .

    Отсюда вытекает справедливость (1).   

    Теорема 6. Неравенство равносильно системе неравенств  

               (2)

    Доказательство.  Так как  , то из неравенства   следует, что  . При таком условии неравенство   будет равносильно неравенству   и при этом вторая система неравенств (1) окажется несовместной.

    Теорема доказана.   

    Теорема 7. Неравенство равносильно совокупности одного неравенства и двух систем неравенств   

,        и                    (3)  

    Доказательство.  Поскольку , то неравенство всегда выполняется, если  .

    Пусть  , тогда неравенство будет равносильно неравенству  , из которого вытекает совокупность двух неравенств    и .

    Теорема доказана.

    Рассмотрим типовые примеры решения задач на тему «Неравенства, содержащие переменные под знаком модуля».

Решение неравенств с модулем

    Наиболее простым  методом решения неравенств с модулем является метод, основанный на раскрытии модулей. Этот метод является универсальным, однако в общем случае его применение может привести к весьма громоздким вычислениям. Поэтому учащиеся должны знать и другие (более эффективные) методы и приемы решения таких неравенств. В частности, необходимо иметь навыки применения теорем, приведенных в настоящей статье. 

Пример 1. Решить неравенство

.               (4) 

Решение. Неравенство (4) будем решать «классическим» методом – методом раскрытия модулей. С этой целью разобьем числовую ось точками    и    на интервалы и рассмотрим три случая.

1.  Если , то , , , и неравенство (4) принимает вид    или  .

Так как здесь  рассматривается случай , то является решением неравенства (4).

2. Если  , то из неравенства (4) получаем   или  . Так как  пересечение интервалов    и   является пустым, то на рассматриваемом интервале решений неравенства (4) нет.

3. Если  , то неравенство (4) принимает вид   или . Очевидно, что   также является решением неравенства (4).

Ответ:  ,  .   

Пример 2. Решить неравенство  .  

Решение. Положим, что  . Так как  , то заданное неравенство принимает вид    или   . Поскольку  , то    и отсюда следует    или  .                                         

Однако  , поэтому    или .

Ответ:  .

Пример 3. Решить неравенство

.               (5) 

Решение.      Так как  , то неравенство (5) равносильно неравенствам    или  . Отсюда, согласно теореме 4, имеем совокупность неравенств     и  .

Ответ:  ,  .

Пример 4. Решить неравенство

.               (6)

Решение. Обозначим  . Тогда из неравенства (6) получаем неравенства    ,  ,    или  .

Отсюда, используя метод интервалов, получаем  . Так как , то здесь имеем систему неравенств

               (7)

Решением первого неравенства системы (7) является объединение двух интервалов    и  , а решением второго неравенства – двойное неравенство  . Отсюда следует, что решение системы неравенств (7) представляет собой объединение двух интервалов  и  .

Ответ:  ,

Пример 5. Решить неравенство

.               (8)

 

Решение. Преобразуем неравенство (8) следующим образом:

,   ,

  или   .

Применяя метод интервалов, получаем решение неравенства (8).

Ответ: .

Примечание. Если в условии теоремы 5 положить  и , то получим .

Пример 6. Решить неравенство

.               (9)

Решение. Из неравенства (9) следует  . Преобразуем неравенство (9) следующим образом:

,  ,

,    или   

.

Так как  , то    или  .

Ответ:  .

 

Пример 7. Решить неравенство 

.               (10)

Решение. Так как    и  , то      или  .

В этой связи   и неравенство (10) принимает вид

  или

.               (11)

Отсюда  следует, что  или  . Так как  , то   и из неравенства (11) вытекает    или  .

Ответ: .

Примечание.  Если к левой части неравенства (10) применить теорему 1, то получим . Отсюда и из неравенства (10) следует, что    или 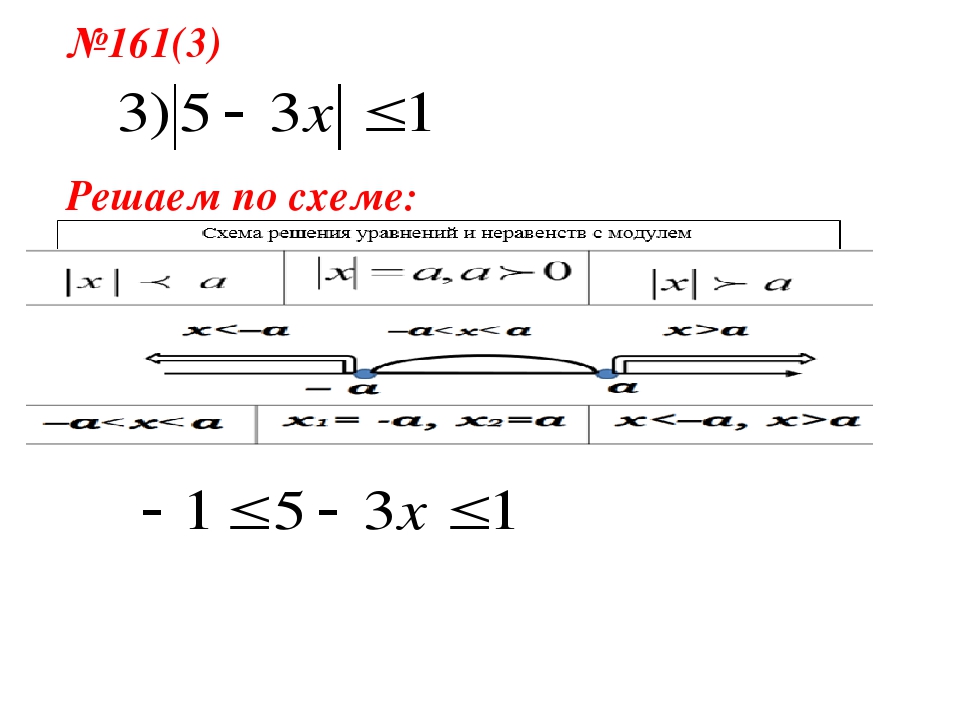 . Так как  , то неравенство (10) принимает вид    или  . 

   

Пример 8. Решить неравенство

.               (12)   

Решение.  Так как , то и из неравенства (12) следует  или . Однако , поэтому    или  . Отсюда получаем    или  .

Ответ:  .

    

Пример 9. Решить неравенство

 

                                                     .                                        (13)

Решение.  Согласно теореме 7 решением неравенства (13) являются    или  .

Пусть теперь  .  В таком случае   и неравенство (13) принимает вид    или  .

Если объединить интервалы и  , то получим решение неравенства (13) вида  .

Ответ:  .

 

Пример 10. Решить неравенство

.                (14)

Решение.    Перепишем неравенство (14) в равносильном виде: . Если к левой части данного неравенства применить теорему 1, то получим неравенство  .

Отсюда и из теоремы 1 следует, что неравенство (14) выполняется для любых значений  .

Ответ:  любое число.

   

Пример 11. Решить неравенство

.               (15)

Решение. Применяя теорему 1 к левой части неравенства (15), получаем . Отсюда и из неравенства (15) вытекает уравнение , которое имеет вид  .

Согласно теореме 3, уравнение равносильно неравенству . Отсюда получаем .

Ответ:  .

Пример 12. Решить неравенство

.               (16)

Решение. Из неравенства (16), согласно теореме 4, получаем систему неравенств  

    или      

При решении неравенства воспользуемся теоремой 6 и получим систему неравенств    из которой следует .  

Рассмотрим неравенство . Согласно теореме 7, получаем совокупность неравенств   и .  Второе неравенство совокупности справедливо для любого действительного  .

Следовательно, решением неравенства (16) являются  .

Ответ:  .

Пример 13. Решить неравенство

.               (17)

Решение.  Согласно теореме 1 можно записать

               (18)

Принимая во внимание неравенство (17), делаем вывод о том, что оба неравенства (18) обращаются в равенства, т.е. имеет место система уравнений

По теореме 3 данная система уравнений равносильна системе неравенств

   или    

Ответ:  .

   

Пример 14. Решить неравенство

.               (19)

Решение. Так как , то .  Умножим обе части неравенства (19) на выражение , которое для любых значений  принимает только положительные значения. Тогда получим неравенство, которое равносильно неравенству (19), вида    

.

Отсюда получаем    или , где .  Так как  и ,  то решением неравенства (19) являются   и .

Ответ: , .

    Для более глубокого изучения методов решения неравенств с модулем можно посоветовать обратиться к учебным пособиям, приведенных в списке рекомендованной литературы.

Рекомендуемая литература

1. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.

2. Супрун В.П. Математика для старшеклассников: методы решения и доказательства неравенств. – М.: Ленанд / URSS, 2018. – 264 с.

3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS, 2017. – 296 с. 

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение системы неравенств с модулем

Решим систему неравенств с модулем из варианта №50 А. Ларина.

Решим каждое неравенство системы по отдельности, а потом совместим решения обоих неравенств на одной координатной прямой.

1. Решим первое неравенство системы.

Чтобы решить неравенство, содержащее модули, нужно раскрыть модули.

Приравняем каждое подмодульное выражение к нулю и найдем точки, в которых подмодульные выражения меняют знак.

Нанесем эти значения на числовую прямую:

Мы получили три промежутка. Найдем знаки каждого подмодульного выражения на каждом промежутке:

Раскроем модули на каждом промежутке (мы можем граничные точки  и  включать в оба промежутка):

а)

На этом промежутке оба подмодульных выражения отрицательны, поэтому мы раскрываем модули с противоположным знаком:

(1)

Так как исходное неравенство «превращается» в неравенство (1) только при , получим систему неравенств:

.

Решим первое неравенство, и получим систему:

.

Решением системы неравенств является промежуток:

б)

На этом промежутке первое подмодульное выражение положительно, а второе отрицательно, поэтому первый модуль мы раскрываем с тем же знаком, а второй с противоположным.

Получаем неравенство:

(2)

Так как исходное неравенство «превращается» в неравенство (2) только при , получим систему неравенств:

или

Решением системы неравенств является промежуток:

в)

На этом промежутке оба подмодульных выражения положительны, поэтому оба модуля мы раскрываем с тем же знаком.

Получаем неравенство:

(3)

Так как исходное неравенство «превращается» в неравенство (3) только при , получим систему неравенств:

или

Решением системы является промежуток:

Объединим три промежутка и получим решение первого неравенства исходной системы:

2. Решим второе неравенство системы.

Приведем левую часть неравенства к общему основанию. Сначала разложим на множители знаменатель первой дроби:

Решим это неравенство методом интервалов.

Найдем корни числителя и знаменателя и нанесем их на числовую ось.

На самом правом промежутке , поэтому знаки расставим так:

Нас интересуют промежутки со знаком «-«:

следовательно, решение этого неравенства:

Совместим решения первого и второго неравенств исходной системы на одной координатной прямой и найдем их пересечение:

 

Ответ: [-2;1)(2;2,4]

И.В. Фельдман, репетитор по математике.

18. Решение линейных неравенств с модулем Краткосрочный план

Актуализация опорных знаний. Устный опрос.

1. Что является решением неравенства

2. Что является решением неравенства

3. В каком случае неравенство с модулем
имеет бесконечное множество решений?

4. Приведите примеры неравенства, не
имеющие решений.

Предложите учащимся письменно решить несколько
неравенств с модулем, постепенно усложняя задание.

Приложение 1

Задание
1.
Имеет ли решение неравенство:

а)                   б)                  

в)

г)                д)            

е) ?

Задание 2. Запишите в виде двойного неравенства неравенство
с модулем:

а) ;               б)                          в)

Задание 3. Запишите в виде неравенства с модулем двойное
неравенство:

а)           б)                    в)

Решить неравенство, изобразить геометрически
решение, записать в виде числового промежутка:

Задание 4.а)                   б)

-45 < 15x < 45	15x < -45 или 15x>45
-3 < x < 3	x < -3 или x>3

            

Ответ:
                   

 Ответ:

Задание
5. а)                  б)  

— 84 < — 28x < 84	28x < -84 или 28x>84
— 3< x < 3	x < -3 или  x>3

           

Ответ:
                  

Ответ:

Задание 6. а)                         б) 

-11 < 11x < 11	11x < -11  или  11x>11
-1 < x < 1	x < -1  или  x>1

             

Ответ:
                    

Ответ:

После
окончания выполнения, попросить обменяться тетрадями с соседом.4`;

1.3 Модуль неизвестного числа

`abs(x)=[({(x >= 0),(abs(x) = x):}), ({(x

1.4 Упражнения к определению модуля

1.4.1 Решить уравнение `abs(2x-1)=2x-1`

`2x-1>=0`;

`x >= 1/2`

Ответ: `[1/2; +infty)`

1.4.2 Решить уравнение `abs(7x-14)=14-7x`

`7x-14
Ответ: `(-infty; 2]`

1.4.3 Решить уравнение `abs(3x-19)=1`

`[(3x-19=1), (3x-19=-1) :}`;

`[(x=20/3), (x=6) :}`

Ответ: `{6; 20/3}`

1.4.4 Решить уравнение `abs(5x-11)=3x+4`

`{( 3x+4 >= 0 ), ( [(5x-11=3x+4), (5x-11=-3x-4):}) :}`;

`{(x >= -4/3), ( [(x=15/2), (x=7/8):} ) :}`;

Ответ: `{7/8; 15/2}`

1.4.5 Решить неравенство `abs(x+4) <=1`

`-1


`-5
Ответ: `[-5; -3]`

1.4.2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;

Сравним `4/3 vv sqrt5-1`

`4 vv 3sqrt5-3`; `7 vv 3sqrt5`; `49 vv 45 (>)`




`4/4 > sqrt5-1`




Ответ: 2

3. Решение неравенств, содержащих неизвестную функцию под знаком модуля

3.1 Смысл неравенства меньше либо равно

`abs(f(x)) <= varphi(x)`

Если `varphi(x)


Если `varphi(x) >= 0` — то необходимо решить систему: `{(varphi(x) >= 0), (-varphi(x)


`{(varphi(x) >= 0), (f(x) = -f(x)) :}`

Примеры с модулем на неравенства со смыслом меньше либо равно

3.1.1 Решить неравенство `abs(1-3x^2) <= 4x`

`{(x >= 0), (1-3x^2 <= 4x), (1-3x^2 >= -4x) :}`; `{(x >= 0), (3x^2+4x -1 >= 0), (3x^2 — 4x -1 <= 0) :}`

Ответ: `[(sqrt7-2)/3; (sqrt7+2)/3 ]`

3. 10`

`111 > 100`

`9 < 10`

`-37/20 < -5/3`

`-3/2 > -5/3`

Итоговое объединение двух систем: `x < -5/3 uu [-3/2; 2] uu x>=2`

Ответ: `(-infty; -5/3) uu (-3/2; +infty)`

3.1.3 Найти область определения функции `f(x)=sqrt(1/2-abs(3/(5-x))`

`D_f(x)`:

`1/2-abs(3/(5-x)) >= 0`;



`abs(3/(5-x))


` -1/2

`{( 3/(5-x) <= 1/2), ( 3/(5-x) >= -1/2) :}`; `{( 3/(5-x) — 1/2 <= 0), ( 3/(5-x) + 1/2 >= 0):}`;

`{( (6-5+x)/(2(5-x)) <= 0 ), ( (6+5-x)/(2(5-x)) >= 0 ):}`; `2 > 0`; `{( (x +1)/(5-x) <= 0 ), ( (11-x)/(5-x) >= 0 ):}`;

Ответ: `(-infty; -1] uu [11; +infty)`

3.2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`

В ответ: `[-1; 1/2]` (б)




В ответ `[ ( a: (1/2; 1) uu (1; +infty)), ( б: [-1; 1/2]) :}`

Ответ: `[-1; 1) uu (1; +infty)`

4. Уравнения и неравенства, содержащие неизвестные под несколькими модулями

4.1 Решить неравенство `abs(x-4)-2abs(1-x) >= 1`

На числовом луче отметим значения x, при которых подмодульные значения обращаются в «0»: `x=1; x=4`. Луч разбился на три интервала.

Необходимо на каждом интервале найти решение данного неравенства, то есть решить совокупность трёх систем неравенств:




`[
(
{
(x <= 1), (4-x-2(1-x) >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2(1-x) >= 1) :}
),
(
{(x > 4), (x-4+2(1-x) >= 1) :}
)
:}` ;

`[
(
{
(x <= 1), (4-x-2+2x >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2-2x >= 1) :}
),
(
{(x > 4), (x-4+2-2x >= 1) :}
)
:}` ;

`[
(
{
(x <= 1), (x+1 >= 0)
:}
),
(
{(1 < x <= 4), (5-3x >= 0) :}
),
(
{(x > 4), (-x-3 >= 0) :}
)
:}` ;

`[
(
{
(x <= 1), (x >= -1)
:}
),
(
{(1 < x <= 4), (x <= 5/3) :}
),
(
{(x > 4), (x <= -3) :}
)
:}` ;

Ответ: `[-1; 5/3]`

4.2 -3abs(x)+1)`

Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`

6.9 Решить неравенство `3x — abs(x+8) — abs(1-x) <= -6`

Ответ: `(-infty; 1]`

Много задач с решениями на неравенства с модулем можно посмотреть здесь:

Решения неравенств с модулем

Абсолютные неравенства — объяснение и примеры

Абсолютное значение неравенства подчиняется тем же правилам, что и абсолютное значение чисел . Разница в том, что у нас есть переменная в априорном и константа во втором.

В этой статье будет представлен краткий обзор неравенств по абсолютным значениям, за которым будет следовать пошаговый метод для решения неравенств по абсолютным значениям .

Наконец, есть примеры различных сценариев для лучшего понимания.

Что такое абсолютное неравенство?

Прежде чем мы научимся решать неравенства по абсолютным значениям, давайте вспомним абсолютное значение числа.

По определению, абсолютное значение числа — это расстояние значения от начала координат, независимо от направления. Абсолютное значение обозначается двумя вертикальными линиями, охватывающими число или выражение.

Например, , абсолютное значение x выражается как | х | = a, откуда следует, что x = + a и -a.Теперь давайте посмотрим, что влечет за собой неравенство абсолютных ценностей.

Абсолютное неравенство — это выражение с абсолютными функциями, а также со знаками неравенства. Например, выражение | x + 3 | > 1 — неравенство по абсолютной величине, содержащее символ «больше».

На выбор доступны четыре различных символа неравенства. Они меньше ( <), больше (> ), меньше или равны ( ≤ ) и больше или равны ( ≥ ).Таким образом, неравенства по абсолютной величине могут иметь любой из этих четырех символов.

Как разрешить абсолютные неравенства?

Шаги решения неравенств абсолютных значений во многом аналогичны решению уравнений абсолютных значений. Однако есть некоторая дополнительная информация, которую вам необходимо иметь в виду при решении вопросов неравенства абсолютных значений.

Ниже приведены общие правила, которые следует учитывать при решении неравенств абсолютных значений:

• Выделите слева выражение абсолютного значения.
• Решите положительную и отрицательную версии неравенства абсолютных значений.
• Когда число по другую сторону знака неравенства отрицательное, мы либо заключаем, что все действительные числа являются решениями, либо неравенство не имеет решения.
• Когда число на другой стороне положительное, мы устанавливаем составное неравенство, удаляя столбцы абсолютных значений.
• Тип знака неравенства определяет формат формируемого сложного неравенства.Например, если проблема содержит знак больше или больше / равно, настройте составное неравенство, которое имеет следующую форму:

(значения в столбцах абсолютных значений) <- (число на другой стороне) ИЛИ (Значения в полосах абсолютных значений)> (Число на другой стороне).

• Точно так же, если проблема содержит знак меньше или меньше / равно, задайте составное трехчастное неравенство следующего вида:

— (Число с другой стороны знака неравенства) <( количество в столбцах абсолютных значений) <(Число с другой стороны знака неравенства)

Пример 1

Решите неравенство для x: | 5 + 5x | — 3> 2.

Решение

Выделите выражение абсолютного значения, добавив 3 к обеим сторонам неравенства;

=> | 5 + 5x | — 3 (+ 3)> 2 (+ 3)

=> | 5 + 5x | > 5.

Теперь решите как положительную, так и отрицательную «версии» неравенства следующим образом;

Мы примем символы абсолютного значения, решив уравнение обычным способом.

=> | 5 + 5x | > 5 → 5 + 5x> 5.

=> 5 + 5_x_> 5

Вычтем 5 с обеих сторон

5 + 5x (- 5)> 5 (- 5) 5x> 0

Теперь разделим обе стороны на 5

5x / 5> 0/5

x > 0.

Таким образом, x > 0 — одно из возможных решений.

Чтобы найти отрицательную версию неравенства абсолютного значения, умножьте число с другой стороны знака неравенства на -1 и переверните знак неравенства:

| 5 + 5x | > 5 → 5 + 5x <- 5 => 5 + 5x <-5 Вычтем 5 с обеих сторон => 5 + 5x (−5) <−5 (- 5) => 5x <−10 => 5x / 5 < −10/5 => х <−2.

x > 0 или x <−2 - два возможных решения неравенства.В качестве альтернативы мы можем решить | 5 + 5x | > 5 по формуле:

(значения в столбцах абсолютных значений) <- (число на другой стороне) ИЛИ (значения в столбцах абсолютных значений)> (число на другой стороне).

Иллюстрация:

(5 + 5x) <- 5 OR (5 + 5x)> 5

Решите приведенное выше выражение, чтобы получить;

x <−2 или x > 0

Пример 2

Решить | x + 4 | — 6 <9

Решение

Выделите абсолютное значение.

| x + 4 | — 6 <9 → | x + 4 | <15

Так как в нашем выражении абсолютного значения знак неравенства меньше, мы задаем трехкомпонентное решение для составного неравенства как:

-15

-19

Пример 3

Решить | 2x — 1 | — 7 ≥ -3

Решение

Сначала выделите переменную

| 2x — 1 | — 7≥-3 → | 2x — 1 | ≥4

Мы установим составное неравенство «или» из-за знака «больше или равно» в нашем уравнении.

2 — 1≤ — 4 или 2x — 1 ≥ 4

Теперь решим неравенства;

2x — 1 ≤ -4 или 2x — 1 ≥ 4

2x ≤ -3 или 2x ≥ 5

x ≤ -3/2 или x ≥ 5/2

Пример 4

Решить | 5x + 6 | + 4 <1

Решение

Выделите абсолютное значение.

| 5x + 6 | + 4 <1 → | 5x + 6 | <-3

Поскольку число на другой стороне отрицательное, проверьте также обратное, чтобы определить решение.

| 5x + 6 | <-3

Положительный <отрицательный (ложный). Следовательно, это абсолютное неравенство не имеет решения.

Пример 5

Решить | 3x — 4 | + 9> 5

Решение

Выделите абсолютное значение.

| 3x — 4 | + 9> 5 → | 3x — 4 | > -4

| 5x + 6 | <-3

Поскольку, положительное <отрицательное (истина). Следовательно, все решения этого неравенства по абсолютной величине - действительные числа.

Предыдущий урок | Главная страница | Следующий урок

Решение абсолютных уравнений и неравенств (Алгебра 1, Линейные неравенства) — Mathplanet

Абсолютное число числа a записывается как

$$ \ осталось | a \ right | $$

And представляет собой расстояние между a и 0 на числовой прямой.

Уравнение абсолютного значения — это уравнение, которое содержит выражение абсолютного значения. Уравнение

$$ \ осталось | x \ right | = a $$

Имеет два решения x = a и x = -a, потому что оба числа находятся на расстоянии a от 0.

Чтобы решить уравнение абсолютного значения как

$$ \ осталось | x + 7 \ вправо | = 14 $$

Вы начинаете с того, что превращаете его в два отдельных уравнения, а затем решаете их по отдельности.

$$ x + 7 = 14 $$

$$ x + 7 \, {\ color {green} {- \, 7}} \, = 14 \, {\ color {green} {- \, 7}} $$

$$ x = 7 $$

или

$$ x + 7 = -14 $$

$$ x + 7 \, {\ color {green} {- \, 7}} \, = -14 \, {\ color {green} {- \, 7}} $$

$$ x = -21 $$

Уравнение абсолютного значения не имеет решения, если выражение абсолютного значения равно отрицательному числу, поскольку абсолютное значение никогда не может быть отрицательным.

Неравенство

$$ \ осталось | х \ право | <2 $$

Представляет расстояние между x и 0, которое меньше 2

Тогда как неравенство

$$ \ осталось | x \ right |> 2 $$

Представляет расстояние между x и 0, которое больше 2

Вы можете записать неравенство по абсолютным значениям как составное неравенство.

$$ \ осталось | x \ right | <2 \: или

$$ — 2

Это верно для всех неравенств по абсолютным значениям.

$$ \ осталось | ax + b \ right | 0 $$

$$ = — c

$$ \ осталось | ax + b \ right |> c, \: где \: c> 0 $$

$$ = ax + b <-c \: или \: ax + b> c $$

Вы можете заменить> выше на ≥ и <на ≤.

При решении неравенства абсолютного значения необходимо сначала выделить выражение абсолютного значения на одной стороне неравенства, прежде чем решать неравенство.

---

Пример

Решите неравенство абсолютных значений

$$ 2 \ влево | 3x + 9 \ вправо | <36 $$

$$ \ frac {2 \ left | 3x + 9 \ right |} {2} <\ frac {36} {2} $$

$$ \ осталось | 3x + 9 \ вправо | <18 $$

$$ — 18 <3x + 9 <18 $$

$$ — 18 \, {\ color {green} {- \, 9}} <3x + 9 \, {\ color {green} {- \, 9}} <18 \, {\ color {green} { - \, 9}} $$

$$ — 27 <3x <9 $$

$$ \ frac {-27} {{\ color {green} 3}} <\ frac {3x} {{\ color {green} 3}} <\ frac {9} {{\ color {green} 3} } $$

$$ — 9

---

Видеоурок

Решите уравнение абсолютного значения

$$ 4 \ влево | 2x -1 \ вправо | -2 = 10 $$

Неравенство абсолютных значений

Неравенство абсолютных значений

Абсолютное неравенство

Вот шаги, которые необходимо выполнить при решении абсолютного значения
неравенства:

1. Выделите выражение абсолютного значения в левой части
   неравенство.
2. Если число с другой стороны знака неравенства равно
   отрицательный, ваше уравнение либо не имеет решения, либо все действительные числа являются решениями.
   Используйте знак каждой стороны неравенства, чтобы решить, какой из этих случаев
   держит. Если число по другую сторону знака неравенства положительное,
   перейти к шагу 3.
3. Удалите полосы абсолютных значений, установив составное неравенство.
   Тип знака неравенства в задаче подскажет нам, как настроить
   сложное неравенство.

Если ваша проблема имеет знак больше, чем (ваша проблема
теперь говорит, что абсолютное значение больше числа), затем установите
сложное неравенство «или», которое выглядит следующим образом:

(количество внутри абсолютного значения) <- (число на другом боковая сторона)
ИЛИ

(количество внутри абсолютного значения)> (число на другой стороне)

Такая же установка используется для ³
знак.


Если ваше абсолютное значение на меньше числа , тогда
установить составное неравенство из трех частей, которое выглядит так:

— (число на другой стороне) <(количество внутри абсолютного значение) <(число на другой стороне)

Такая же установка используется для £
знак

4. Решите неравенства.

Сначала этот процесс может немного сбивать с толку, так что будьте
пациент, пока учится решать эти задачи. Давайте посмотрим на несколько примеров.

Пример 1: | x + 4 | — 6 <9

Шаг 1: Изолировать абсолют значение	| х + 4 | — 6 <9 | x + 4 | <15
Шаг 2: Номер включен другая сторона отрицательная?	Нет, это положительное число, 15.Переходим к шагу 3.
Шаг 3: Установить сложное неравенство	Знак неравенства в нашей задаче меньше знак, поэтому мы установим неравенство из 3 частей: -15
Шаг 4: Решить составное неравенство	-19 <х <11

Пример 2: | 2x 1 | — 7 ³
-3

Шаг 1: Изолировать абсолют значение	| 2x 1 | — 7 ³ -3 | 2x 1 | ³ 4
Шаг 2: Is число на другой стороне отрицательное число?	Нет, это положительное число, 4.Переходим к шагу 3.
Шаг 3: Установить сложное неравенство	Знак неравенства в нашей задаче больше или знак равенства, поэтому составим составное неравенство со словом «или же»: 2x 1 £ -4 или 2x 1 ³ 4
Шаг 4: Решить неравенства	2x 1 £ -4 или 2x 1 ³ 4 2x £ -3 или 2x ³ 5 x £ -3/2 или x ³ 5/2

Пример 3: | 5x + 6 | + 4 <1

Шаг 1: Изолировать абсолютное значение	| 5x + 6 | + 4 <1 | 5x + 6 | <-3
Шаг 2: Is число на другой стороне отрицательное число?	Да, это отрицательное число, -3. Посмотрите на признаки каждой стороны неравенства для определения решения проблемы: | 5x + 6 | <-3 положительный <отрицательный Это утверждение неверно, поэтому решения нет. к этой проблеме.

Пример 4: | 3x 4 | + 9> 5

Шаг 1: Изолировать абсолютное значение	| 3х 4 | + 9> 5 | 3x 4 | > -4
Шаг 2: Is число на другой стороне отрицательное число?	Да, это отрицательное число, -4. Посмотрите на признаки каждой стороны неравенства для определения решения проблемы: | 3x 4 | > -4 положительный> отрицательный Это утверждение всегда верно, поэтому решение проблема — все действительные числа

Абсолютное неравенство значений — ChiliMath

В этом уроке мы узнаем, как решать неравенства абсолютных значений, используя стандартный подход, который обычно преподают на уроках алгебры.То есть выучите правила и правильно их применяйте. Есть четыре случая , задействованных при решении неравенств абсолютных значений.

ВНИМАНИЕ: Во всех случаях предполагается, что значение «a» положительное, то есть a> 0.

---

Четыре (4) случая, которые следует учитывать при решении абсолютных неравенств

ДЕЛО 1 :

ДЕЛО 2 :

ДЕЛО 3 :

Абсолютное значение любого числа равно нулю (0) или положительному, которое никогда не может быть меньше или равно отрицательному числу.

Ответ в этом случае всегда нет решения .

ДЕЛО 4 :

Абсолютное значение любого числа либо ноль (0), либо положительное. Имеет смысл, что оно всегда должно быть больше любого отрицательного числа.

Ответ в этом случае всегда , все действительные числа .

---

Примеры решения абсолютных неравенств

Пример 1 : Решите неравенство абсолютных значений.

Если вы еще не знакомы с различными случаями, я предлагаю вам сохранить копию приведенного выше списка случаев для справки.Это определенно поможет вам легко решить проблемы.

Проблема предполагает, что существует значение «x», которое может сделать утверждение истинным. Что ж, абсолютное значение чего-либо всегда равно нулю или положительному значению, которое никогда не бывает меньше отрицательного числа. Это утверждение должно быть ложным, следовательно, нет решения . Это пример case 3 .

Выберите несколько тестовых значений для проверки:

• Если x положительный, скажем, x = 5;

• Если x отрицательно, скажем, x = -5;

---

Пример 2 : Решите неравенство абсолютных значений.

Если задуматься, любое значение «x» может сделать утверждение истинным. Проверьте несколько чисел, включая ноль, а также любые отрицательные или положительные числа. Что вы получаете?

Помните, что выражение абсолютного значения даст нулевой или положительный ответ, который всегда больше отрицательного числа. Следовательно, ответ , все действительные числа . Это case 4 .

---

Пример 3 : Решите неравенство абсолютных значений.

Это неравенство «меньше чем» по абсолютной величине, которое является примером случай 1 .Избавьтесь от символа абсолютного значения, применив правило. Затем решите возникшее линейное неравенство.

Цель состоит в том, чтобы изолировать переменную «x» посередине. Для этого вычтем левую, среднюю и правую части неравенства на 6.

Ответ в виде символа неравенства утверждает, что решения — это все значения x от -8 до -4, но не включая сами значения -8 и -4.

Мы также можем записать ответ в интервальной нотации, используя круглые скобки, чтобы обозначить, что -8 и -4 не являются частью решений.

Или напишите ответ в числовой строке, где мы используем белые кружки, чтобы исключить -8 и -4 из решения.

---

Пример 4 : Решите неравенство абсолютных значений.

Это неравенство «меньше или равно» по абсолютной величине, которое все еще подпадает под случай 1 . Очистите символ абсолютного значения с помощью правила и решите линейное неравенство.

Выделите переменную «x» посередине, сложив все стороны на 6, а затем разделив на 3 (коэффициент при x).

Символ неравенства предполагает, что решением являются все значения x от -3 до 7, а также включая конечные точки -3 и 7. Мы включаем конечные точки, потому что мы используем символ «≤».

Чтобы записать ответ в виде интервалов, мы будем использовать квадратные скобки вместо обычных скобок, чтобы обозначить, что -3 и 7 являются частью решения.

И, наконец, мы будем использовать закрашенные или закрашенные кружки, чтобы показать, что включены -3 и 7.

---

Пример 5 : Решите неравенство абсолютных значений.

Это пример неравенства «больше чем» по абсолютной величине, который является примером case 2 . Давайте удалим выражение абсолютного значения, используя приведенное ниже правило.

Как видите, мы решаем два отдельных линейных неравенства.

В интервальной записи слово « или » заменяется символом «\ чашка», означающим « объединение ». Объединение наборов означает, что мы собираем неперекрывающиеся элементы двух или более наборов решений.

Ответ в интервальной нотации станет более понятным, если вы посмотрите, как он выглядит на числовой строке. В случае 2 стрелки всегда будут в противоположных направлениях. Белые кружки означают, что -3 и 7 не включены в решения, которые являются следствием символа «>«.

---

Пример 6 : Решите неравенство абсолютных значений.

Разбейте это на два линейных неравенства и решите каждое отдельно. Вот правило для case 2 .

Вот решение.

Для обозначения интервалов мы используем квадратные скобки, чтобы включить в решение -2 и 3.

Закрашенные или закрашенные кружки означают, что -2 и 3 являются частью решения. В случае 2 стрелки всегда будут указывать в противоположных направлениях.

---

Возможно, вас заинтересует:

Решение уравнений абсолютных значений

Функции построения графиков абсолютных значений

2.6: Решение абсолютных уравнений и неравенств

Из графика видно, что обе функции совпадают, где \ (x = −5 \) и \ (x = 1 \).Решения соответствуют точкам пересечения.

Для применения теоремы необходимо изолировать абсолютное значение. Общие шаги для решения уравнений абсолютных значений приведены в следующем примере.

Не все уравнения абсолютных значений имеют два решения.

Пример \ (\ PageIndex {4} \):

Решите: \ (| 7 x — 6 | + 3 = 3 \).

Решение

Начните с выделения абсолютного значения.

Только ноль имеет нулевое абсолютное значение, \ (| 0 | = 0 \).Другими словами, \ (| X | = 0 \) имеет одно решение, а именно \ (X = 0 \). Поэтому установите аргумент \ (7x — 6 \) равным нулю, а затем решите относительно \ (x \).

Геометрически одно решение соответствует одной точке пересечения.

Рисунок \ (\ PageIndex {4} \)

Ответ :

Решение: \ (\ frac {6} {7} \).

Если дано уравнение с двумя абсолютными значениями вида \ (| a | = | b | \), то \ (b \) должно быть таким же, как \ (a \), или наоборот. Например, если \ (a = 5 \), то \ (b = \ pm 5 \) и мы имеем:

Другими словами, если два выражения абсолютного значения равны, то аргументы могут быть одинаковыми или противоположными.

Абсолютные неравенства

Начнем с рассмотрения решений следующего неравенства:

\ (| х | \ leq 3 \)

Абсолютное значение числа представляет собой расстояние от начала координат. Следовательно, это уравнение описывает все числа, расстояние от которых до нуля меньше или равно \ (3 \). Мы можем построить график этого набора решений, заштриховав все такие числа.

Рисунок \ (\ PageIndex {6} \)

Конечно, мы можем видеть, что существует бесконечно много решений для \ (| x | ≤3 \), ограниченных \ (- 3 \) и \ (3 \).Выразите этот набор решений, используя обозначение набора или обозначение интервала следующим образом:

В этом тексте мы будем выражать решения в интервальной нотации. В общем, для любого алгебраического выражения \ (X \) и любого положительного числа \ (p \):

Эта теорема верна и для строгих неравенств. Другими словами, мы можем преобразовать любое неравенство абсолютных значений, включающее « меньше », в составное неравенство, которое можно решить обычным образом.

Пример \ (\ PageIndex {7} \):

Решите и изобразите набор решений: \ (| x + 2 | <3 \).

Решение

Ограничьте аргумент \ (x + 2 \) символами \ (- 3 \) и \ (3 \) и решите.

Здесь мы используем открытые точки для обозначения строгих неравенств на графике следующим образом.

Рисунок \ (\ PageIndex {7} \)

Ответ :

Используя обозначение интервалов, \ ((- 5,1) \).

Решение \ (| x + 2 | <3 \) можно интерпретировать графически, если мы положим \ (f (x) = | x + 2 | \) и \ (g (x) = 3 \), а затем определим где \ (f (x)

Рисунок \ (\ PageIndex {7} \)

Решение состоит из всех \ (x \) — значений, где график \ (f \) находится ниже графика \ (g \). В этом случае мы видим, что \ (| x + 2 | <3 \), где \ (x \) - значения находятся между \ (- 5 \) и \ (1 \). Чтобы применить теорему, мы должны сначала выделить абсолютное значение.

Пример \ (\ PageIndex {8} \):

Решить: \ (4 | x + 3 | — 7 ≤ 5 \).

Решение

Начните с выделения абсолютного значения.

Затем примените теорему и перепишите неравенство абсолютных значений как составное неравенство.

Решить.

Заштрихуйте решения на числовой прямой и представьте ответ в виде интервалов. Здесь мы используем закрытые точки для обозначения инклюзивных неравенств на графике следующим образом:

Рисунок \ (\ PageIndex {8} \)

Ответ :

Используя обозначение интервалов, \ ([- 6,0] \)

Упражнение \ (\ PageIndex {3} \)

Решите и изобразите набор решений: \ (3 + | 4 x — 5 | <8 \).

Ответ

Обозначение интервалов: \ ((0, \ frac {5} {2}) \)

Рисунок \ (\ PageIndex {9} \)

www.youtube.com/v/sX6ppL2Fbq0

Затем мы исследуем решения неравенства, которое включает « больше », как в следующем примере:

\ (| х | \ geq 3 \)

Это неравенство описывает все числа, расстояние от которых до начала координат больше или равно \ (3 \). На графике мы можем заштриховать все такие числа.

Рисунок \ (\ PageIndex {10} \)

Существует бесконечно много решений, которые можно выразить с помощью обозначений множеств и интервалов следующим образом:

В общем случае для любого алгебраического выражения \ (X \) и любого положительного числа \ (p \):

Теорема верна и для строгих неравенств.Другими словами, мы можем преобразовать любое неравенство абсолютных значений, включающее « больше », в составное неравенство, описывающее два интервала.

Пример \ (\ PageIndex {9} \):

Решите и изобразите набор решений: \ (| x + 2 |> 3 \).

Решение

Аргумент \ (x + 2 \) должен быть меньше \ (- 3 \) или больше \ (3 \).

3} \\ {x <- 5} \ quad \ quad \ quad \ quad \ quad \: x> 1 \ end {array} \)

Рисунок \ (\ PageIndex {11} \)

Ответ :

Используя обозначение интервалов, \ ((- ∞, −5) ∪ (1, ∞) \).

Решение \ (| x + 2 |> 3 \) можно интерпретировать графически, если мы положим \ (f (x) = | x + 2 | \) и \ (g (x) = 3 \), а затем определим где \ (f (x)> g (x) \) путем построения графиков как \ (f \), так и \ (g \) на одном и том же наборе осей.

Рисунок \ (\ PageIndex {12} \)

Решение состоит из всех \ (x \) — значений, где график \ (f \) находится над графиком \ (g \). В этом случае мы видим, что \ (| x + 2 |> 3 \), где \ (x \) — значения меньше \ (- 5 \) или больше \ (1 \). Чтобы применить теорему, мы должны сначала выделить абсолютное значение.

Пример \ (\ PageIndex {10} \):

Решить: \ (3 + 2 | 4x — 7 | ≥ 13 \).

Решение

Начните с выделения абсолютного значения.

Затем примените теорему и перепишите неравенство абсолютных значений как составное неравенство.

Решить.

Заштрихуйте решения на числовой прямой и представьте ответ, используя интервальную нотацию.

Рисунок \ (\ PageIndex {13} \)

Ответ :

Используя обозначение интервалов, \ ((- ∞, 12] ∪ [3, ∞) \)

Упражнение \ (\ PageIndex {4} \)

Решить и построить график: \ (3 | 6 x + 5 | — 2> 13 \).

Ответ

Используя обозначение интервалов, \ (\ left (- \ infty, — \ frac {5} {3} \ right) \ cup (0, \ infty) \)

Рисунок \ (\ PageIndex {14} \)

www.youtube.com/v/P6HjRz6W4F4

До этого момента наборы решений линейных неравенств по модулю состояли из одного ограниченного интервала или двух неограниченных интервалов. Это не всегда так.

Пример \ (\ PageIndex {11} \):

Решить и построить график: \ (| 2x − 1 | +5> 2 \).

Решение

Начните с выделения абсолютного значения.

2} \\ {| 2 х — 1 | > — 3} \ end {array} \)

Обратите внимание, что у нас абсолютное значение больше отрицательного числа. Для любого действительного числа x абсолютное значение аргумента всегда будет положительным. Следовательно, любое действительное число решит это неравенство.

Рисунок \ (\ PageIndex {15} \)

Геометрически мы можем видеть, что \ (f (x) = | 2x − 1 | +5 \) всегда больше, чем \ (g (x) = 2 \).

Рисунок \ (\ PageIndex {16} \)

Ответ :

Все действительные числа, \ (ℝ \).

Пример \ (\ PageIndex {12} \):

Решить и построить график: \ (| x + 1 | + 4≤3 \).

Решение

Начните с выделения абсолютного значения.

В этом случае мы видим, что изолированное абсолютное значение должно быть меньше или равно отрицательному числу. Опять же, абсолютное значение всегда будет положительным; отсюда можно сделать вывод, что решения нет.

Геометрически мы можем видеть, что \ (f (x) = | x + 1 | +4 \) никогда не меньше, чем \ (g (x) = 3 \).

Рисунок \ (\ PageIndex {17} \)

Ответ : \ (Ø \)

Таким образом, существует три случая для уравнений и неравенств абсолютных значений. Отношения \ (=, <, \ leq,> \) и \ (≥ \) определяют, какую теорему применять.

Случай 1: Уравнение абсолютного значения:

Рисунок \ (\ PageIndex {18} \)

Случай 2. Неравенство абсолютных значений, предполагающее, что «

меньше .«

Рисунок \ (\ PageIndex {19} \)

Случай 3. Неравенство абсолютных значений, включающее «

больше ».

Рисунок \ (\ PageIndex {20} \)

Примеры абсолютных неравенств — MathLearnIt.com

---

Неравенство абсолютного значения немного отличается от уравнения абсолютного значения, примеры которого
можно увидеть на абсолютное значение
уравнения стр.

Когда у нас было равенство, что-то вроде | x | =
4 , г.

решить это означало найти, какие значения x являются расстоянием
4 от нуля.

Решения были точными цифрами.

В данном случае решения: x = 4 , & nbspand
x = -4 .

Решения абсолютного неравенства значений

Решения примеров неравенства абсолютных значений вместо этого будут выглядеть примерно так: | x | <4 .

Решить это значит найти, какие значения x меньше расстояния
чем 4 от нуля.

Решениями являются любые значения x между -4 и
4 .
Итак, мы ищем интервал значений с неравенствами по абсолютной величине.

Решение такого абсолютного неравенства требует записи неравенства абсолютных значений в виде двойного неравенства .

Вот это:

-4 < x <4

Что на числовом графике будет представлено так.

Белый кружок на каждом конце означает, что сами 4 и -4 НЕ будут входить в число
значения решений.

---

Примеры абсолютных неравенств,
Решение

(1,1)

Решить | x — 2 | <6 .

Решение

В этом примере предлагается найти значение или значения x , что
приведет к тому, что расстояние от x до 2 будет
строго меньше 6 .

Итак, думайте о расстоянии, принимая за отправную точку ноль.

Если размер расстояния от x до 2 не
достигнет 6 в положительном направлении, тогда он не достигнет -6 в отрицательном направлении, идя
либо в другую сторону.

Итак, исходная форма в этом примере может быть записана как двойное неравенство, а затем решена как таковая.

-6 < x — 2 <6

-6 + 2 < x — 2 + 2
<6 + 2

-4 < x <8

Это решение, интервал различных значений x
между -4 и 8 .

Но не сами -4 и 8 .

Это также можно записать как x ∈ (-4 , 8 ).

(1,2)

Решить | 2 x + 3 | < 5 .

Решение

Примеры абсолютного неравенства значений, такие как этот, следуют тому же подходу, что и пример (1.1), с
исходная установка представляет собой двойное неравенство.

Хотя на этот раз неравенство меньше ИЛИ равно

-5 < 2 x + 3 < 5

-5-3 < 2 x + 3-3 < 5-3

-8 < 2 x < 2

\\ bf {\\ frac {-8} {2}}
< \\ bf {\\ frac {2 \\ boldsymbol {x}} {2}}
< \\ bf {\\ frac {2} {2}}

-4 < x < 1

Это тоже интервал, который также можно записать как x ∈
[-4, 1] .

Квадратные скобки означают, что в отличие от примера (1.1),

x Решения также могут быть значениями на каждом конце
интервал, -4 & nbspand 1 .

На числовом графике это показано как:

Темные кружки в конечных точках показывают, что -4 и 1 включены как
решений, поскольку исходное неравенство было меньше или равно.

(1,3)

Решить | x | > 4 .

Решение

Набор для решения примеров неравенств абсолютных значений, которые включают символ «больше», представляет собой
немного отличается от символа «меньше».

Если подумать о | x | > 4 .

Он спрашивает, какие значения x являются расстоянием больше, чем
& nbsp4 от нуля.

Мы можем наблюдать эти значения на числовом графике.

Значения x , которые находятся на расстоянии более 4
от нуля:

x <-4 или x >
4 .

Итак, что нужно сделать, чтобы решить пример «больше, чем», — это установить составное неравенство с помощью «или», затем
продолжить.

(1,4)

Решить | x — 2 | > 6 .

Решение

x -2 <-6 или x -2> 6

x — 2 + 2 <-6 + 2 или x — 2 + 2> 6 + 2

x <-4 или x >
8

Это сложное неравенство является решением.

x значения меньше -4 или больше 8
сделать истинным исходное неравенство по абсолютной величине.

1. Дом

›

2. Функции

›
Примеры абсолютных неравенств

---

Вернуться к началу страницы

абсолютных величин неравенств | Блестящая вики по математике и науке

Здесь мы рассмотрим определение абсолютного значения числа.Чтобы «отменить» знаки абсолютного значения, мы могли бы получить положительное или отрицательное значение, поскольку абсолютное значение −5-5 −5 совпадает с абсолютным значением 5 5 5, которое равно 5 5 5. Это становится методом, в котором у нас есть несколько случаев.

Основные шаги (для работы с линейными / множественными линейными неравенствами абсолютных значений):

1. «Отменить» знаки абсолютного значения, сделав выражения внутри знака абсолютного значения отрицательными или положительными.
2. Возьмите все полученные неравенства (это все наборы решений) и найдите набор решений.Чтобы выяснить набор решений с учетом набора наборов решений из случаев, которые вы разработали, рассмотрите исходную проблему как кусочную функцию, поэтому у вас есть варианты. Какие значения xx x делают левую часть отрицательной? Положительный? Нуль? Все это дополнительные ограничения на xx x, и вы будете пересекаться между этими дополнительными ограничениями на xx x и «окончательным» неравенством, полученным в результате работы, которую вы проделали. Это дает то, что я называю «ограниченным окончательным» неравенством.
3. Наконец, вы берете объединение всех «ограниченных финальных» неравенств для вашего окончательного набора решений.

Мы рассмотрим, как это сделать, в следующих трех примерах.

Решить ∣x + 3∣ <7 | х + 3 | <7 ∣x + 3∣ <7.

---

Случай 1: x + 3x + 3x + 3 неотрицательно, или x ≥ − 3x \ geqslant -3x⩾ − 3
Свойство абсолютного значения говорит нам, что ∣a∣ = a | a | = a∣a∣ = a для неотрицательного aaa, поэтому в этом случае
∣x + 3∣ <7 ⟹ x + 3 <7 ⟹ x <4.| x + 3 | <7 \ следует x + 3 <7 \ следует x <4.∣x + 3∣ <7⟹x + 3 <7⟹x <4. Теперь у нас есть два неравенства, и решение для этого случая - пересечение обоих неравенств. Это потому, что xxx должен удовлетворять обоим, поскольку они зависят друг от друга ((((только потому, что x≥ − 3x \ geq -3x≥ − 3, мы имеем x <4) x <4) x <4). Следовательно, решение для этого случая: −3≤x <4-3 \ leq x <4−3≤x <4.

Случай 2: x + 3x + 3x + 3 отрицательно, или x <−3x <-3x <−3
Опять же, ∣a∣ = −a | a | = -a∣a∣ = −a для отрицательного значения aaa, поэтому
∣x + 3∣ <7 ⟹ - (x + 3) <7 ⟹ x> −10.| x + 3 | <7 \ подразумевает - (x + 3) <7 \ подразумевает x> -10.∣x + 3∣ <7⟹− (x + 3) <7⟹x> −10.
По той же причине, что и выше, мы должны взять пересечение обоих неравенств, которое составляет −10

Наконец, возьмем объединение этих неравенств, поскольку они не зависят друг от друга:
-10 <х <4. □ -10 <х <4. \ _ \ квадрат-10 <х <4. □

Решить 2∣x + 2∣ − ∣x + 5∣⩽4 2 | x + 2 | — | x + 5 | \ leqslant 4 2∣x + 2∣ − ∣x + 5∣⩽4.

---

Случай 1: x + 2> 0 и x + 5> 0 ⟹ x> −2 x + 2> 0 \ text {and} x + 5> 0 \ подразумевает x> -2x + 2> 0 и x +5> 0⟹x> −2
В этом случае имеем
2 (x + 2) — (x + 5) ⩽42x + 4 − x − 5⩽4x − 1⩽4x⩽5⇒ − 2

Случай 2: x + 2> 0 и x + 5⩽0 x + 2> 0 \ text {and} x + 5 \ leqslant 0 x + 2> 0 и x + 5⩽0
Так как это всегда верно что x + 5> x + 2, x + 5> x + 2, x + 5> x + 2, этот случай невозможен.

Случай 3: x + 2⩽0 и x + 5> 0 ⟹ −5 0 \ подразумевает -5 0⟹ − 5 В этом случае имеем
−2 (x + 2) — (x + 5) ⩽4−2x − 4 − x − 5⩽4−3x − 9⩽4−3x⩽13x⩾ − 133⇒ − 133⩽x⩽ − 2.\ begin {выровнено}
-2 (x + 2) — (x + 5) & \ leqslant 4 \\
-2x — 4 — x — 5 & \ leqslant 4 \\
-3x — 9 & \ leqslant 4 \\
-3x & \ leqslant 13 \\
х & \ geqslant \ dfrac {-13} {3} \\
\ Rightarrow \ dfrac {-13} {3} \ leqslant x & \ leqslant -2.
\ end {align} −2 (x + 2) — (x + 5) −2x − 4 − x − 5−3x − 9−3xx⇒3−13 ⩽x ⩽4⩽4⩽4⩽13⩾3 −13 ⩽ −2.

Случай 4: x + 2⩽ и x + 5⩽ ⟹ x⩽ − 5 x + 2 \ leqslant \ text {and} x + 5 \ leqslant \ влечет x \ leqslant -5x + 2⩽ и x + 5⩽ ⟹x⩽ − 5
В этом случае имеем
−2 (x + 2) + (x + 5) ⩽4−2x − 4 + x + 5⩽4 − x + 1⩽4 − x⩽3x⩾3, \ begin {align}
-2 (x + 2) + (x + 5) & \ leqslant 4 \\
-2x — 4 + x + 5 & \ leqslant 4 \\
-x +1 & \ leqslant 4 \\
-x & \ leqslant 3 \\
х & \ geqslant 3,
\ end {align} −2 (x + 2) + (x + 5) −2x − 4 + x + 5 − x + 1 − xx ⩽4⩽4⩽4⩽3⩾3,
что невозможно, поскольку x⩽ − 5.2 — \ dfrac {1} {2} & <0 \\ \ left (x + 1 + \ dfrac {1} {\ sqrt {2}} \ right) \ left (x + 1 - \ dfrac {1} {\ sqrt {2}} \ right) & <0. \ end {align} (x + 2) 2−2 (x + 2) +1 (x + 2−1) 2 (x + 1) 2 (x + 1) 2−21 (x + 1 + 2). 1) (x + 1−2 1) <21 <21 <21 <0 <0. Чтобы решить это квадратное неравенство, мы можем использовать диаграмму знакового анализа.

Мы знаем, что неравенство будет равно нулю, когда один множитель всего выражения равен нулю, а именно при −1−12-1 — \ frac {1} {\ sqrt {2}} −1−2 1 и −1 +12 -1 + \ frac {1} {\ sqrt {2}} −1 + 2 1, поэтому мы хотим знать, является ли каждый фактор положительным или отрицательным при определенных значениях xxx, которые меньше −1−12. -1 — \ frac {1} {\ sqrt {2}} −1−2 1, больше −1−12-1 — \ frac {1} {\ sqrt {2}} −1−2 1 и меньше -1 + 12 -1 + \ frac {1} {\ sqrt {2}} -1 + 2 1 и больше -1 + 12 \ frac {1} {\ sqrt {2 }} 2 1.Мы также используем свойства, умноженные на отрицательное, дают положительное, умноженное на положительное — положительное, а умноженное на отрицательное — отрицательное. Чтобы убедиться, что левая часть меньше нуля, мы ищем xx x, которые дают нам отрицательные значения левой части.

Мы видим, что левая часть квадратного неравенства меньше нуля, когда −1−12

Мы видим, что левая часть квадратичного неравенства меньше нуля, когда −3−12 (((Обратите внимание, что эти неравенства удовлетворяют x <−2.) x <-2.) x <- 2.)

Теперь у нас есть два сложных неравенства (1) и (2), оба из которых являются решениями; xxx может лежать в любом интервале, в результате чего окончательное решение установлено

.

−3−12

8

-16

Ни один из других вариантов

16

Максимальное значение

для всех действительных чисел xxx

∣3x + 8∣ − ∣4x∣? | 3x + 8 | — | 4x | ? ∣3x + 8∣ − ∣4x∣?

Отправьте свой ответ

Y = ∣x∣ − ∣x + 1∣ + ∣x + 2∣ − ∣x + 3∣ + ⋯ + ∣x + 2016∣ Y = | x | — | x + 1 | + | х + 2 | — | x + 3 | + \ cdots + | x + 2016 | Y = ∣x∣ − ∣x + 1∣ + ∣x + 2∣ − ∣x + 3∣ + ⋯ + ∣x + 2016∣

Найдите минимальное значение Y Y Y.