Содержание
Учебный проект «Нестандартные приемы решения квадратных уравнений»
Введение
Тема «Квадратные уравнения» является одной из самых актуальных. Квадратные
уравнения – это фундамент, на котором покоится величественное здание алгебры.
Они находят широкое применение в разных разделах математики.
В школьном курсе изучаются формулы корней квадратного уравнения, с помощью
которых можно решать любые квадратные уравнения. Однако, имеются и другие приемы
решения квадратных уравнений, которые позволяют очень быстро и рационально
решать квадратные уравнения.
Проблемный вопрос: существуют ли кроме общепринятых приемов решения
квадратных уравнений другие, которые позволяют быстро и рационально решать
квадратные уравнения?
Гипотеза: установление связи между коэффициентами и корнями
квадратного уравнения позволит найти эффективные приемы быстрого решения
квадратного уравнения.
Цель: установив связь между коэффициентами и корнями квадратного
уравнения, найти новые рациональные приемы решения уравнений
Задачи:
- Изучить литературу по истории приемов решения квадратных уравнений
- Обобщить накопленные знания о квадратных уравнениях и способах их
решения.
- Установить зависимость корней квадратного уравнения от его коэффициентов
и найти эффективные приемы быстрого решения квадратного уравнения, в том
числе с большими коэффициентами. - Сделать выводы.
- Разработать дидактический материал для проведения практикума по решению
квадратных уравнений с использованием новых приемов в помощь ученикам,
увлеченным математикой и учителям, ведущим факультативные занятия.
Объект исследования: квадратные уравнения
Предмет изучения: методы и приемы решения квадратных уравнений, в том
числе с большими коэффициентами
Глава 1.
Изучение литературы
Основной материал, связанный с изучением темы «Квадратные уравнения»
находится в УМК под ред.С.А.Теляковского. В учебнике разобраны все основные
вопросы по теме:
1. Определение и виды квадратных уравнений
2. Основные методы решения квадратных уравнений
Однако, дополнительный материал, связанный с историей вопроса о возникновении
квадратных уравнений можно найти в «Энциклопедия по математике»
«Занимательная математика», М. , 2007. Способы решения задач на квадратные
, 2007. Способы решения задач на квадратные
уравнения в полном объёме раскрыты в изданиях «Сборник элективных курсов»
Волгоград, 2006 г.
Изученная литература позволила приобрести новые интересные знания по истории
возникновения квадратного уравнения, приобрести опыт по решению различных
квадратных уравнений и перейти к следующему этапу в исследовании – перенести
полученные знания в нестандартную ситуацию.
Глава 2.
Изучение истории вопроса о квадратных уравнениях
Глава 3.
Обобщение имеющихся знаний о квадратных уравнениях и способах их решения
Глава 4.
Нестандартные приемы решения квадратных уравнений
Дидактический материал по применению нестандартных приемов
решения квадратных уравнений.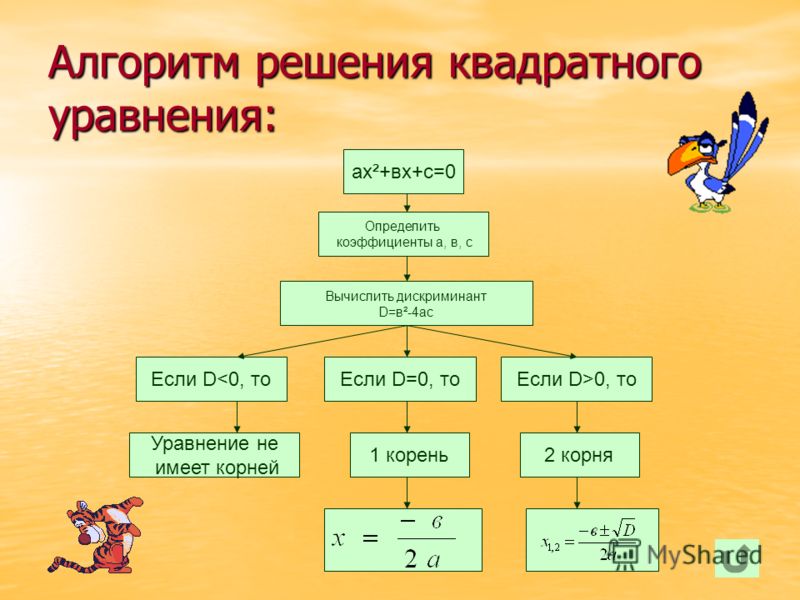
1. Найди наиболее рациональным способом корни уравнения:
4х2 – 13х + 9 =0
(1; 2,25)1978х2 – 1984х + 6=0
(1; 6/1978)4х2 + 11х + 7 = 0
(-1; -7/4)319х2 + 1988х +1669=0
(-1; -1669/319)1999х2 + 2000х+1=0
(-1; -1/1999)
2. Решить квадратные уравнения с большими коэффициентами
313х2 +326х+13=0
(-1; -13/313)839х2– 448х -391=0
(1; -391/839)345х2 – 137х – 208=0
(1;.-208/345)939х2+978х+39=0
(-1; -39/939)
3. Используя полученные знания, установи соответствие:
1) х2+5х+6=0
2) 6х2-5х+1=0
3) 2х2-5х+3=0
4) 3х2-5х+2=0
5) х2-5х+6=0
6) 6х2+5х+1=0
7) 2х2+5х+2=0
8) 3х2+5х+2=01) 1/6;1/2
2) 1; 3/2
3) 1; 2/3
4) -2; -3
5) -1/3 ; -1/2
6) -1; -3/2
7) -1; -2/3
8) 2;3
Глава 5.
Анализ работы учащихся по решению квадратных уравнений нестандартными способами
Разработаны критерии оценки проведенного практикума:
- За каждое верно выполненное задание ставится 1 балл;
- Наиболее возможное количество набранных баллов-17
- Если ученик набирает менее
7 баллов, то выставляется оценка «2»
от 7 до 11 баллов «3»
от 12 до 15 баллов «4»
от 16-17 баллов «5»
Результаты практикума.
Выполняли работу – 11человек
Набрали баллов
от 16-17 – 5человек (45%)
от 12-15– 6человек (55%)
Менее 12 – 0 человек
Средний балл – 4,45
Процент качества – 100%
Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.
Выводы по результатам проведения практикума
Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие
выводы:
- нестандартные приемы решения квадратных уравнений заслуживают внимания;
- позволяют экономить время решения, что обусловлено применением тестовой
системы экзаменов.
Глава 6.
Выводы
В процессе работы над проектом, была создана система нестандартных приемов
решения квадратных уравнений и разработан банк заданий, на основе которого
проведена успешная апробация этих приемов.
Данный материал можно рекомендовать для внеклассных и факультативных занятий
по математике. Учителя могут использовать его как методическое пособие при
изучении темы «Решение квадратных уравнений», а также, для контроля за знаниями
учащихся.
Материалом этого проекта могут воспользоваться и те, кто любит математику и
хочет знать о математике больше.
Литература
- Выгодский М.Я
. Справочник по элементарной математике. – М.
государственное издательство физико-математической литературы, 1970.
. Сборник задач по алгебре для
8-9 классов: учебное пособие для учащихся школ и классов с углубленным
изучением математики:4-е изд.-М. : Просвещение, 1997.
: Просвещение, 1997.
. Алгебра. Учебник для 8 класса. М.,
Просвещение, 2001.
. Дополнительные главы к школьному
учебнику. 8 класс М., Просвещение, 1996.
. Математический калейдоскоп. – М.: Бюро «Квантум»,
2005.
НЕОБЫЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
НЕОБЫЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
Василенко А.М. 1Яковлева Е.А. 1
1
Поздина Н.Б. 1
1
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
«Уравнение – это золотой ключ, открывающий все математические сезамы»
С. Коваль
Коваль
Математическое образование, получаемое в школе, очень важная часть жизни современного человека. Практически всё, что окружает нас так или иначе связано с математикой. Решение многих практических задач сводится к решению уравнений различных видов.
Уравнения – это наиболее объёмная тема всего курса алгебры. В прошлом учебном году на уроках алгебры мы познакомилась с квадратными уравнениями. Квадратные уравнения находят широкое применение при решении различных задач, как в области математики, так и в области физики и химии.
В школьном курсе математики изучается основные способы решения квадратных уравнений. Однако, имеются и другие приёмы решения квадратных уравнений, некоторые из которых позволяют быстро, рационально решать их.
Нами было проведено анкетирование среди 84 учащихся 8-9 классов по двум вопросам:
По результатам анкетирование были получены следующие результаты:
Проанализировав полученные результаты, мы пришли к выводу, что большинство учащихся используют при решении квадратных уравнений формулы корней с использование дискриминанта и недостаточно осведомлены о способах решения квадратных уравнений.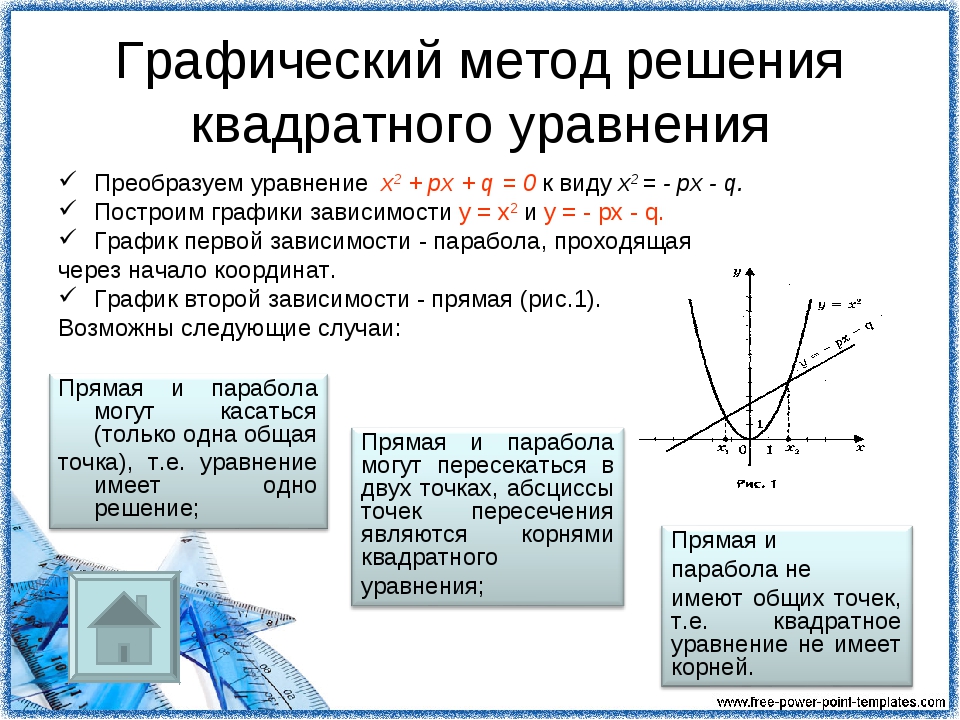
Таким образом, выбранная нами тема является актуальной.
Мы поставили перед собой цель: изучить нетрадиционные способы решения квадратных уравнений, познакомить учащихся 8 и 9 классов с различными способами решения, выработать умение выбирать рациональный способ решения квадратного уравнения.
Для достижения указанной цели нужно решить следующие задачи:
-
собрать информацию о различных способах решения квадратных уравнений, -
освоить найденные способы решения, -
составить программу для решения квадратных уравнений по формулам корней квадратного уравнения в Excel, -
разработать дидактический материал для проведения урока или внеурочного мероприятия по нестандартным методам решения квадратных уравнений, -
провести занятие «Необычные способы решения квадратных уравнений» с учащимися 8 – 9 классов.
Объект исследования: квадратные уравнения.
Предмет исследования: различных способы решения квадратных уравнений.
Считаем, что практическая значимость работы состоит в возможности использования банка приёмов и способов решения квадратных уравнений на уроках математики и внеурочной деятельности, а также в ознакомлении учащихся 8 — 9 классов с данных материалом.
ГЛАВА 1. НЕОБЫЧНЫЕ МЕТОДЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
-
- СВОЙСТВА КОЭФФИЦИЕНТОВ (a,b,c)
Метод основан на свойствах коэффициентов a,b,c:
-
Если a+b+c=0, то = 1, =
Пример:
-6х2 + 2х +4=0, то = 1, = = .
-
Если a – b+c=0, то = -1, = —
Пример:
2017х2 + 2001х +16 =0, то = -1, -.
-
- ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ (a,b,c)
Справедливы следующие зависимости коэффициентов a,b,c:
Если b=a2+1, c=a, то х1=-а; x2 = — .
Если b=-(a2+1), a=c, то x1=a; x2 =.
Если b=a2-1, c=-a, то x1=-a; x2 = .
Если b=-(a2-1), -a=c, то x1=a; x2 = — .
Решим следующие уравнения:
-
5x2 + 26x + 5 = 0
x1= -5
x2= — 0,2.
-
13x2 — 167x + 13 = 0
x1=13 x2=
-
14x2 + 195x — 14 = 0
x1= — 14 x2=
-
10x2 — 99x — 10 = 0
x1=10 x2=-0,1.
-
- «ПЕРЕБРОС» ГЛАВНОГО КОЭФФИЦИЕНТА
Коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Далее корни находятся по теореме Виета. Найденные корни делятся на ранее переброшенный коэффициент, благодаря этому мы находим корни уравнения.
Найденные корни делятся на ранее переброшенный коэффициент, благодаря этому мы находим корни уравнения.
Пример:
2х2 – 3х + 1 = 0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 3у + 2 = 0.
Согласно теореме Виета
у1 = 2 , х1 = 2/2 , x1 = 1,
у2 = 1; x2 = 1/2; x2 = 0,5.
Ответ: 0,5; 1.
-
- ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ
Если в уравнении аx2 + bx + c = 0 перенести второй и третий члены в правую часть, то получим ax2 = –bx–c .
Построим графики зависимостей у = aх2 и у = –bx–c в одной системе координат.
График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая.
Возможны следующие случаи:
-
прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; -
прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение;
е. уравнение имеет одно решение;
-
прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Решим следующие уравнения:
1) х2 + 2х – 3 = 0
х2 = — 2х + 3
В одной системе координат построим график функции у =х2 и график функции у = — 2х+3. Обозначив абсциссы точек пересечения, получим ответ.
Ответ: х1= — 3, х2 =1.
2) х2 + 6х +9 = 0
х2 = — 6х — 9
В одной системе координат построим график функции у = х2 и график функции у = -6х — 9. Обозначив абсциссу точки касания, получим ответ.
Обозначив абсциссу точки касания, получим ответ.
Ответ: х= — 3.
3) 2х2 + 4х +7=0
2х2 = — 4х — 7
В одной системе координат построим график функции у =2х2 и график функции
у = — 4х — 7.
Парабола у =2х2 и прямая у = — 4х — 7 не имеют общих точек, следовательно уравнение не имеет корней.
Ответ: нет корней.
-
- РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ
Решим уравнение aх2 +bх+c=0:
-
Построим точки S(-b:2a,(a+c):2a)- центр окружности и точку А(0,1). -
Провести окружность радиуса SA.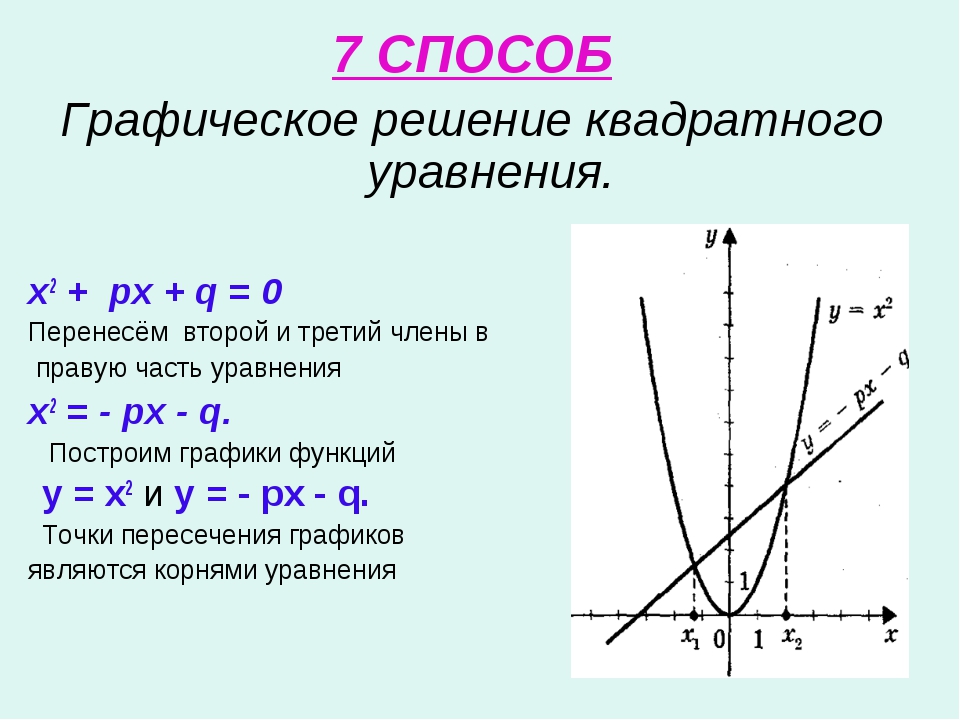
-
Абсциссы точек пересечения с осью Ох есть корни исходного уравнения.
При этом возможны три случая:
1) Радиус окружности больше ординаты центра (AS>SK, или R>), окружность пересекает ось Ох в двух точках..B(х1; 0) и D(х2;0), где х1 и х2 – корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SВ, или R = ), окружность касается оси Ох в точке B(х1; 0 ), где х1 – корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра (AS < SВ, или R < ), окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.
а) AS > SВ или R > , б) AS = SВ или R = в) AS < SВ, или R < .
Два решения х1 и х2. Одно решение х1.. Не имеет решения.
Пример 1: 2х2 –8х + 6 = 0.
Решение: Определим координаты точки центра окружности по формулам:
у = = .
Проведём окружность радиуса SA, где А (0;1).
Ответ: х1 = 1 , х2 = 3.
Пример 2: х2 –6х + 9 = 0.
Решение: Найдём координаты S: x=3, y=5.
Ответ: x=3.
Пример 3: х2 + 4х + 5 = 0.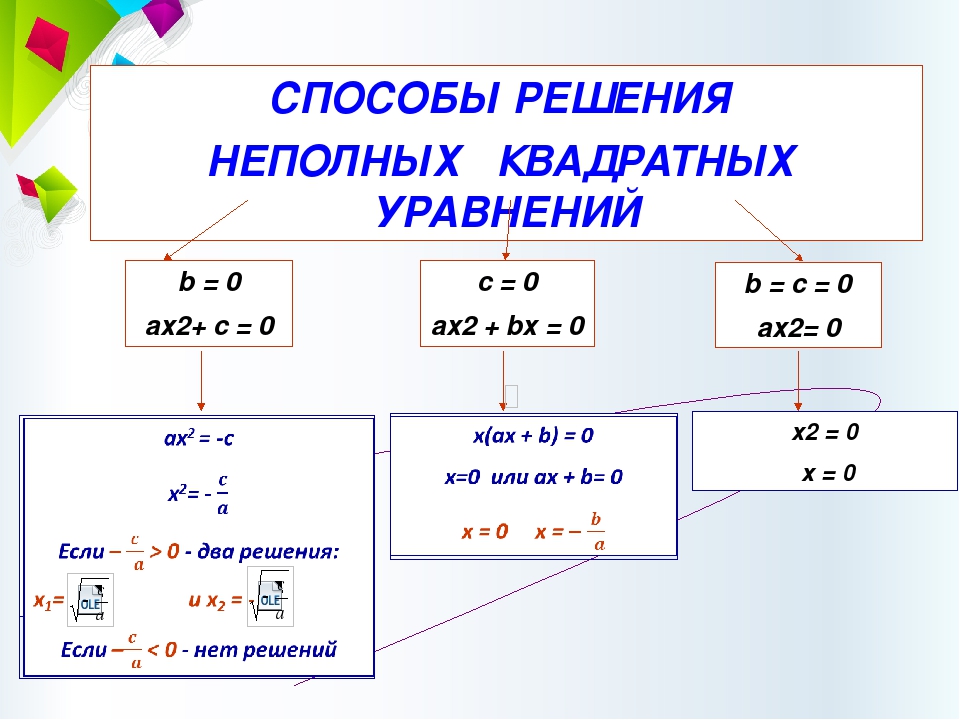
Решение: Координаты центра окружности: х= — 2 и y = 3.
Ответ: нет корней
-
- РЕШЕНИЕ С ПОМОЩЬЮ НОМОГРАММЫ
Номограмма (от греческого «nomos» – закон и грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещённый на стр. 83 сборника: Брадис В.М. «Четырехзначные математические таблицы». — М., “ДРОФА”, 2000. Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0 (см. Приложение 1).
Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам: ОВ = , АВ =
Полагая ОС = р, ЕD = q, ОЕ = а (все в см), из подобия треугольников САН и СDFполучим пропорцию откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
Пример 1:z2 — 9z + 8 = 0.
На шкале p находим отметку -9, а на шкале q отметку 8. Проводим через эти метки прямую, которая пересекает кривую шкалу номограммы в отметках 1 и 8. Следовательно, корни уравнения 1 и 8.
Ответ: 1; 8.
Именно данное уравнение решено в таблице Брадиса стр. 83 (см. Приложение 1).
Пример 2: 2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение:
z2 — 4,5z + 1 = 0. Номограмма даёт корни z1 = 4 иz2 = 0,5.
Ответ: 4; 0,5.
Пример 3:x2 – 25x + 66 = 0
Коэффициенты p и q выходят за пределы шкалы. Выполним подстановку x = 5z, получим уравнение:
z2 – 5z + 2,64 = 0,
которое решаем посредством номограммы.
Получим z1 = 0,6 и z2 = 4,4,
откудаx1 = 5 z1 = 3,0 иx2 = 5 z2 = 22,0.
Ответ: 3; 22.
Пример 4: z2 + 5z – 6 = 0, номограмма даёт положительный корень z1=1, а отрицательный корень находим, вычитая положительный корень из — p, т.е. z2= — p –1= — 5 – 1= -6.
Z=1
Ответ: 1; -6.
Пример 5: z2 – 2z – 8 = 0, номограмма даёт положительный корень z1=4, а отрицательный равен z2= — p –4 =
Z=4
= 2 – 4= -2.
Ответ: 4; -2.
ГЛАВА 2. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛАМ КОРНЕЙ С ПОМОЩЬЮ EXCEL
РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛАМ КОРНЕЙ С ПОМОЩЬЮ EXCEL
Мы решили составить программу для решения квадратного уравнения с помощью Excel – это широко распространенная компьютерная программа. Нужна она для проведения расчётов, составления таблиц и диаграмм, вычисления простых и сложных функций. Она входит в состав пакета Microsoft Office.
Лист программы Excel, где отображены формулы:
Лист программы Excel, где показан конкретный пример решения квадратного уравнения x2 – 14x – 15 = 0:
ГЛАВА 3. СРАВНЕНИЕ РАЗНЫХ СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАКЛЮЧЕНИЕ
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Уолтер Варвик Сойер
В ходе работы мы собрали материал и изучили способы решения (нахождения корней) квадратных уравнений. Решение уравнений разными способами представлено в Приложении 2.
Решение уравнений разными способами представлено в Приложении 2.
Изучая разные способы решения квадратных уравнений, мы сделали вывод, что для каждого уравнения можно подобрать свой наиболее эффективный и рациональный вариант нахождения корней. Каждый из способов решения уникален и удобен в определённых случаях. Некоторые способы решения позволяют сэкономить время, что немаловажно при решении заданий на ОГЭ, другие – помогают решить уравнение с очень большими коэффициентами. Мы постарались сравнить разные способы решения, составив таблицу, в которой отразили плюсы и минусы каждого из способов.
Нами разработан раздаточный материал. Познакомиться с банком заданий по теме можно в Приложении 3.
Используя Microsoft Excel, мы составили электронную таблицу, которая позволяет автоматически рассчитывать корни квадратного уравнения по формулам корней.
Мы провели урок, посвященный необычным способам решения квадратных уравнений, для учащихся 9 классов. Ученикам очень понравились способы, они отметили, что полученные знания пригодятся им в дальнейшем обучении. Результатом проведённого урока стали работы учащихся, в которых они представили различные варианты решения квадратных уравнений (см. Приложение 4).
Материал нашей работы можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его для небольшого элективного курса «Необычные способы решение квадратных уравнений».
Материалом работы могут воспользоваться и те, кто любит математику и те, кто хочет знать о математике больше.
ЛИТЕРАТУРА
-
Брадис В. М. «Четырехзначные математические таблицы для средней школы», М.: Дрофа, 2000. -
Виленкин Н.Я. «Алгебра для 8 класса», М.: Просвещение, 2000. -
Галицкий М.Л. «Сборник задач по алгебре», М.: Просвещение 2002. -
Глейзер Г. И. «История математики в школе», М.: Просвещение, 1982. -
Звавич Л.И. «Алгебра 8 класс», М.: Мнемозина, 2002. -
Макарычев Ю.Н. “Алгебра 8 класс”, М.: Просвещение, 2015. -
Плужников И. «10 способов решения квадратных уравнений» // Математика в школе. — 2000.- № 40. -
Пресман А.А. «Решение квадратного уравнения с помощью циркуля и линейки»//М., Квант, №4/72, c.34. -
Савин А.П. «Энциклопедический словарь юного математика»,
М.: Педагогика, 1989.
Интернет ресурсы:
http://revolution.allbest.ru/
http://mat.1september.ru/2001/42/no42_01.htm
ПРИЛОЖЕНИЕ 1
«СБОРНИК БРАДИСА В.М.»
ПРИЛОЖЕНИЕ 2
«РЕШЕНИЕ УРАВНЕНИЯ ВСЕМИ СПОСОБАМИ»
Исходноеуравнение: 4х2+3х -1 = 0.
1.Формула корней квадратного уравнения с использованием дискриминанта D
4х2+3х -1 = 0
D = b2 – 4ac = 9+16 = 25 > 0, => уравнение имеет два корня
x1,2 =
x1 ==
x2 ==-1
2.Теорема Виета
4х2+3х -1 = 0, поделим уравнение на 4, чтобы оно стало приведённым
х2+х -=0
+ =-
* =-
х1 = -1
х2 =
3. Метод выделения полного квадрата
4х2+3х -1 = 0
(4х2+2*2х *+)-1=0
(2х + )2 -=0
(2х + — )( 2х + + )=0, произведение =0, когда один из множителей=0
(2х — )=0 (2х +2)=0
х1 = х2 = -1
4. Способ группировки
4х2+3х -1 = 0
4х2+4х-1х-1=0
4х(х+1)-1(х+1)=0
(4х-1)( х+1)=0, произведение =0, когда один из множителей=0
(4х-1)=0 ( х+1)=0
х1 = х2 = -1
5. Свойства коэффициентов
4х2+3х -1 = 0
Если a — b+c=0, то = -1, = —
4-3-1=0, => = -1, =
6. Метод «переброски» главного коэффициента
4х2+3х -1 = 0
y2+3y — 4 = 0
Теорема Виета:
+ =- 3
* =- 4
y1 = -4
y2 = 1
Разделим найденные корни на главный коэффициент и получим корни нашего уравнения:
х1 = -1
х2 =
7. Способ решения квадратных уравнений с помощью циркуля и линейки
4х2+3х -1 = 0
Определим координаты точки центра окружности по формулам:
у = =
х1 = -1
х2 =
8. Графический способ решения
4х2+3х -1 = 0
4х2= — 3x + 1
В одной системе координат построим график функции у = 4х2и график функции
-3
у = — 3х+1. Обозначив абсциссы точек пересечения, получим ответ:
x
х1 = -1
=
9. С помощью номограммы
4х2+3х -1 = 0, разделим коэффициенты уравнения 1/на 4, получим уравнение
1/4
х2 +х -= 0.
Номограмма даёт положительный корень = ,
а отрицательный корень находим, вычитая положительный корень из — p, т.е.
x2= — p –=- -= -1.
10. Решение данного уравнения в EXCEL
ПРИЛОЖЕНИЕ 3
«ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ ТЕМЫ
“РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ”»
10х2+ 2017х + 2007 = 0 -1 -200,7
-10х2+ 7х + 3 = 0 -1 0,3
354х2-52х -302 = 0 1 —
100х2-99х-1 = 0 1 -0,01
5х2+ 9х + 4 = 0 -1 -0,8
2017х2+ х -2016 = 0 -1
22х2+10х-12 = 0 -1
5432х2-3087х-2345 = 0 1 —
4х2+ 2х -6с = 0 1 -1,5
55х2-44х -11= 0 1 -0,2
6х2— 7х — 3 = 0 — , 1,5
4х2-17х-15 = 0 -0,75, 5
4271х2-4272х + 1 = 0 1,
3х2+10х + 7 = 0 -1, — 2
5х2— 11х + 2 = 0 2, 0,2
2х2— 11х + 15 = 0 2,5, 3
4х2+ 4х -3= 0 -1,5, 0,5
5х2 -12х + 7 = 0 1,4, 1
2х2+ 13х + 15 = 0 -1,5 -5
3х2-7х + 2 = 0 1/3 2
ПРИЛОЖЕНИЕ 4
«РАБОТЫ УЧАЩИХСЯ»
Просмотров работы: 3248
Презентация «10 способов решения квадратных уравнений» по математике – проект, доклад
Слайд 1
10 способов решения квадратных уравнений
2 3 4 5 6 7 8 9
Слайд 2
История развития квадратных уравнений.
Квадратные уравнения в Древнем Вавилоне: Х2+Х=3/4 Х2-Х=14,5
Слайд 3
Как составлял и решал Диофант квадратные уравнения. Отсюда уравнение: (10+х)(10-х) =96 или же: 100 — х2 =96 х2 — 4=0 (1)
Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Слайд 4
Квадратные уравнения в Индии. ах2 + bх = с, а>0. (1)
Слайд 5
Квадратные уравнения у ал – Хорезми. 1) «Квадраты равны корнями», т.е. ах2 + с = bх. 2) «Квадраты равны числу», т.е. ах2 = с. 3) «Корни равны числу», т.е. ах = с. 4) «Квадраты и числа равны корням», т.е. ах2 + с = bх. 5) «Квадраты и корни равны числу», т.е. ах2 + bx = с. 6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Слайд 6
Квадратные уравнения в Европе ХIII — ХVII вв. х2 +bх = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Слайд 7
О теореме Виета. «Если В + D, умноженное на А — А2, равно ВD, то А равно В и равно D». На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место (а + b)х — х2 = ab, т.е. х2 — (а + b)х + аb = 0, то х1 = а, х2 = b.
Слайд 8
Способы решения квадратных уравнений.
1. СПОСОБ: Разложение левой части уравнения на множители. Решим уравнение х2 + 10х — 24 = 0. Разложим левую часть на множители: х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2). Следовательно, уравнение можно переписать так: (х + 12)(х — 2) = 0 Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
Слайд 9
2. СПОСОБ: Метод выделения полного квадрата. Решим уравнение х2 + 6х — 7 = 0. Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 6х в следующем виде: х2 + 6х = х2 + 2• х • 3. полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2• х • 3 + 32 = (х + 3)2. Преобразуем теперь левую часть уравнения х2 + 6х — 7 = 0, прибавляя к ней и вычитая 32. Имеем: х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16. Таким образом, данное уравнение можно записать так: (х + 3)2 — 16 =0, (х + 3)2 = 16. Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
Слайд 10
3. СПОСОБ: Решение квадратных уравнений по формуле. Умножим обе части уравнения ах2 + bх + с = 0, а ≠ 0 на 4а и последовательно имеем: 4а2х2 + 4аbх + 4ас = 0, ((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0, (2ax + b)2 = b2 — 4ac, 2ax + b = ± √ b2 — 4ac, 2ax = — b ± √ b2 — 4ac,
Слайд 11
4. СПОСОБ: Решение уравнений с использованием теоремы Виета. Как известно, приведенное квадратное уравнение имеет вид х2 + px + c = 0. (1) Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид x1 x2 = q, x1 + x2 = — p а) x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = — 3 0 и p= 8 > 0. б) x2 + 4x – 5 = 0; x1 = — 5 и x2 = 1, так как q= — 5 0; x2 – 8x – 9 = 0; x1 = 9 и x2 = — 1, так как q = — 9
Слайд 12
5. СПОСОБ: Решение уравнений способом «переброски». Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Умножая обе его части на а, получаем уравнение а2х2 + аbх + ас = 0. Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.
Слайд 13
• Пример. Решим уравнение 2х2 – 11х + 15 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 11у + 30 = 0. Согласно теореме Виета у1 = 5 х1 = 5/2 x1 = 2,5 у2 = 6 x2 = 6/2 x2 = 3. Ответ: 2,5; 3.
Слайд 14
6. СПОСОБ: Свойства коэффициентов квадратного уравнения. А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. 1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а. Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение x2 + b/a • x + c/a = 0. Согласно теореме Виета x1 + x2 = — b/a, x1x2 = 1• c/a. По условию а – b + с = 0, откуда b = а + с. Таким образом, x1 + x2 = — а + b/a= -1 – c/a, x1x2 = — 1• ( — c/a), т.е. х1 = -1 и х2 = c/a, что и требовалось доказать.
Слайд 15
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
В. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Слайд 16
7. СПОСОБ: Графическое решение квадратного уравнения. Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px — q. Построим графики зависимости у = х2 и у = — px — q.
Слайд 17
• Пример Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2). Решение. Запишем уравнение в виде х2 = 3х + 4. Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Ответ: х1 = — 1; х2 = 4
Слайд 18
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки. нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Слайд 19
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (6,а рис. ) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0. 2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения. 3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Слайд 20
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы. z2 + pz + q = 0. Криволинейная шкала номограммы построена по формулам (рис.11): Полагая ОС = р, ED = q, ОЕ = а (все в см.), Из подобия треугольников САН и CDF получим пропорцию
Слайд 21
• Примеры. 1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис.12). 2) Решим с помощью номограммы уравнение 2z2 — 9z + 2 = 0. Разделим коэффициенты этого уравнения на 2, получим уравнение z2 — 4,5z + 1 = 0. Номограмма дает корни z1 = 4 и z2 = 0,5. 3) Для уравнения z2 — 25z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
Слайд 22
10. СПОСОБ: Геометрический способ решения квадратных уравнений. • Примеры. 1) Решим уравнение х2 + 10х = 39. В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15). Для искомой стороны х первоначального квадрата получим
Слайд 23
у2 + 6у — 16 = 0. Решение представлено на рис. 16, где у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9. Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис.16).
Нестандартные методы решения задач по математике Текст научной статьи по специальности «Математика»
НЕСТАНДАРТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ПО МАТЕМАТИКЕ
А.С. Меджидов
НОУ ВПО «Социально-педагогический институт», г. Дербент
Сфера математики была и остается наименее изученной. Можно сказать, что на современном этапе развития науки и образования необходимой составляющей выпускника является умение решать уравнения по математике нестандартными методами. Это, в свою очередь, развивает у обучаемых нестандартность мышления, что является неотъемлемой частью инновационной школы.
Ключевые слова: метод, уравнение, метод функциональной подстановки, метод тригонометрической подстановки, комбинированные методы.
На современном этапе развития образования на занятиях по математике в математических классах лицеев, гимназий и общеобразовательных школ, всё большее внимание уделяется изучению инновационных, нестандартных методов решения уравнений и неравенств из различных разделов математики (алгебра, тригонометрия и геометрия). В известной степени это вызвано тем, что в последние годы имеет место устойчивая тенденция к усложнению заданий, предлагаемых на вступительных экзаменах по математике в ведущих высших учебных заведениях Российской Федерации.
Целью нашего исследования является рассмотрение нестандартных методов решения задач по математике, которые имеют довольно-таки широкое распространение. Многие из приведенных здесь задач предлагались совсем недавно на вступительных экзаменах в ВУЗы Российской Федерации.
По мнению Пирютко О.Н.,метод функциональной подстановки является, пожалуй, самым распространенным методом решения сложных задач школьной математики. Суть метода состоит в введении новой переменной у = /(х), применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является
тригонометрическая подстановка.[3]
Барвенов С.А., считает, что основная трудность решения задач методом функциональной подстановки заключается в том, что зачастую трудно угадать вид самой подстановки и вид уравнений (или неравенств), где эту подстановку можно использовать. В настоящем разделе предлагаются наиболее распространенные уравнения и неравенства, которые эффективно решаются методом функциональной подстановки. [2]
Задачи и решения.
Пример 1 .Решить уравнение
л/х — х + 2 + л/х — х + 7 = л/ 2х — 2х + 21.
Решение.у2 +5у = 6, у2 + 5у — 36 = 0 и ух = -9, у2= 4 .
Рассмотрим два уравнения х2 -х+ 2 = -9ш2 — х + 2 = 4.
Первое уравнение корней не имеет, а из второго получаем х1 = -1 и х2=2.
Подстановкой убеждаемся в том, что найденные значения переменной х являются корнями
исходного уравнения.
Метод тригонометрической подстановки. Пирютко О.Н. к числу нестандартных методов решения алгебраических уравнений относит метод, основанный на применении тригонометрической подстановки. Использование такого метода целесообразно в том случае когда искомые уравнения напоминают известные тригонометрические формулы. Это относится преимущественно к уравнениям (системам уравнений), решение которых обычными приемами весьма затруднительно и которые после введения тригонометрических подстановок сводятся к несложным тригонометрическим уравнениям. Суть тригонометрической подстановки состоит в замене неизвестной переменной х тригонометрической функцией, например х = cosco или х = со, а также в замене х некоторой функцией от sin со , cos со или со.
Полученные корни тригонометрических уравнений позволяют находить корни исходных уравнений как в тригонометрической, так и в алгебраической форме. Следует особо отметить, что тригонометрические уравнения имеют, как правило, бесконечное число корней, а исходные уравнения — конечное их число. [3]
Задачи и решения.
Пример 2.Решить уравнение
8х3 — 6х -1 = 0.
Решение. Поскольку х = 0 не является корнем уравнения, то разделим обе его части на 2 х. Тогда
9 1
4х = — + 3 = 0.
2х
Если х < —1 или х>1, то левая часть уравнения будет больше 4, а правая его часть -меньше 4 . Следовательно, корни уравнения находятся на отрезке -1 < х < 1.
Пусть x = cosí¿>, где 0 < со < л . Тогда уравнение принимает вид тригонометрического уравнения
8cos3<»-6cos<z>-l = 0,
4cos3®-3cos¿y = —,
2
cos3<» = —.
2
1 ж
Решением уравнения cos3íy = — являются со = —(6п±\), где п — целое число. Однако л 5л 1л
0<со <л, поэтому сох = —, со2 = — и соъ = . , х2 = cosco2 и
х3 = cosco3.
_ п 5л In
Ответ: х = cos—, х, = cos— и х, = cos—.
1 9 9 3 9
Барвенов С.А. рассматривает методы, основанные на монотонности функций. При решении уравнений типа f (х) = g(х) в ряде случаев весьма эффективным является метод, который использует монотонность функций y = f (х) и y = g(х) . Если функция y = f (х) непрерывна и возрастает (убывает) на отрезке а < х < Ъ , а функция у = g(.x) непрерывна и убывает (возрастает) на этом же отрезке, то уравнение f(х) = g(x) на отрезке а<х<Ь может иметь не более одного корня.
Напомним, что функция y = f (х) называется возрастающей (или убывающей) на отрезке а < х < Ъ , если для любых хх, х2, удовлетворяющих неравенствам а < хг < х2 < Ъ,
выполняется неравенство /(х1)< /(х2) (соответственно, /(X)> /(Х2)). Если функция у = /(х) является на отрезке а<х<Ь возрастающей или убывающей, то она называется монотонной на этом отрезке.
В этой связи при решении уравнения /(х) = g(х) необходимо исследовать функции у = / (х) и у = g(x) на монотонность, и если одна из этих функций на отрезке а <х <Ь убывает, а другая функция возрастает, то необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Если, например, функция у = /(х) возстает, а у = %(х) убывает для а<х<Ь и при этом / (а) > g(a), то корней уравнения /(х) = g(x) среди а <х<Ь нет. Особенно такой метод эффективен в том случае, когда обе части уравнения /(х) = g(х) представляют собой весьма «неудобные» для совместного исследования функции. Кроме того, если функция у = / (х) является монотонной на отрезке а <х <Ь и уравнение /(х) = с (где с — некоторая константа) имеет на этом отрезке корень, то этот корень единственный. [4]
Задачи и решения.
Пример 3. Решить уравнение \о%2{1-х) = х-\.
Решение. Областью допустимых значений уравнения являются х < 7. Рассмотрим функции /(х) = \о%)2(1 — х) и g(x) = x-1. Известно, что функция у = /(х) для х<7 является
убывающей, а функция у = g (х) — возрастающей. В этой связи уравнение может иметь только один корень, т.е. х = 3 , который легко находится подбором.
Ответ: х = 3 .
Барвенов С.А. приводит также комбинированные методы. При решении сложных задач по математике используются самые разнообразные нестандартные методы, большинство из которых трудно поддаются классификации. Как правило, такие методы ориентированы на решение относительно узкого круга задач, однако их знание и умение ими пользоваться необходимы для успешного решения математических задач повышенной сложности. В настоящем разделе приведены задачи, решение которых базируется на применении оригинальных (эффективных, но сравнительно редко встречающихся) комбинированных методов. [1, 2]
Задачи и решения.
Пример 4.Решить уравнение
х3 — (л/2 + 1)х2 +2 = 0.
Решение. Рассмотрим уравнение с параметром а вида х3 — (а + 1)х2 +а2 = 0,
которое совпадает с уравнением при а = 42 . Перепишем уравнение в виде квадратного уравнения относительно неизвестной переменной а, т.е.
а2 -ах2 +х3 -х2 =0.
Решением уравнения относительно а являются
а1,2
х2 ± л/х4 -4х3 +4х2 _ х2 + х(х — 2)
2 2
т.е. а1=х2—х и а2=х. Поскольку а = V2, то получаем два уравнения относительно переменной х вида х2-х их = 42. Отсюда получаем три корня исходного уравнения,
1±л/і + 4л/2
т.е. х, 7 =——————:—————- и х = 42 .
1,2 2 3
Подводя итоги о нестандартных методах решения задач по математике, можно отметить лишь то, что рассмотренные нами методы — это всего лишь небольшая часть существующих на данном этапе развития математики методов, таких как: методы, основанные на применении численных неравенств,методы решения функциональных уравнений,методы решения симметрических систем уравнений и др. [4]
Применение нестандартных методов решения задач по математике требует от старшеклассников и абитуриентов нетрадиционного мышления, необычных рассуждений. Незнание и непонимание таких методов существенно уменьшает область успешно решаемых задач по математике,тем более, что имеющая место тенденция к усложнению конкурсных заданий по математике стимулирует появление новых оригинальных (нестандартных) подходов к решению математических задач. Следует отметить, что знание нестандартных методов и приемов решения задач по математике способствует развитию у обучаемых нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и др.).
Литература
1. Назаров А.И. Задачи-ловушки. Мн.: Аверсэв, 2006.
2. Барвенов С.А. Математика для старшеклассников. Мн.: Аверсэв, 2004.
3. Пирютко О.Н. Типичные ошибки на централизованном тестировании. Мн.: Аверсэв, 2006.
4. Барвенов С.А. Методы решения алгебраических уравнений. Мн.: Аверсэв, 2006.
Исследовательская работа «Способы решения квадратных уравнений»
LnRiLWZpZWxke21hcmdpbi1ib3R0b206MC43NmVtfS50Yi1maWVsZC0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWZpZWxkLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWZpZWxkLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1maWVsZF9fc2t5cGVfcHJldmlld3twYWRkaW5nOjEwcHggMjBweDtib3JkZXItcmFkaXVzOjNweDtjb2xvcjojZmZmO2JhY2tncm91bmQ6IzAwYWZlZTtkaXNwbGF5OmlubGluZS1ibG9ja311bC5nbGlkZV9fc2xpZGVze21hcmdpbjowfQ==
LnRiLWhlYWRpbmcuaGFzLWJhY2tncm91bmR7cGFkZGluZzowfQ==
LnRiLWJ1dHRvbntjb2xvcjojZjFmMWYxfS50Yi1idXR0b24tLWxlZnR7dGV4dC1hbGlnbjpsZWZ0fS50Yi1idXR0b24tLWNlbnRlcnt0ZXh0LWFsaWduOmNlbnRlcn0udGItYnV0dG9uLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1idXR0b25fX2xpbmt7Y29sb3I6aW5oZXJpdDtjdXJzb3I6cG9pbnRlcjtkaXNwbGF5OmlubGluZS1ibG9jaztsaW5lLWhlaWdodDoxMDAlO3RleHQtZGVjb3JhdGlvbjpub25lICFpbXBvcnRhbnQ7dGV4dC1hbGlnbjpjZW50ZXI7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2xpbms6aG92ZXIsLnRiLWJ1dHRvbl9fbGluazpmb2N1cywudGItYnV0dG9uX19saW5rOnZpc2l0ZWR7Y29sb3I6aW5oZXJpdH0udGItYnV0dG9uX19saW5rOmhvdmVyIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazpmb2N1cyAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6dmlzaXRlZCAudGItYnV0dG9uX19jb250ZW50e2ZvbnQtZmFtaWx5OmluaGVyaXQ7Zm9udC1zdHlsZTppbmhlcml0O2ZvbnQtd2VpZ2h0OmluaGVyaXQ7bGV0dGVyLXNwYWNpbmc6aW5oZXJpdDt0ZXh0LWRlY29yYXRpb246aW5oZXJpdDt0ZXh0LXNoYWRvdzppbmhlcml0O3RleHQtdHJhbnNmb3JtOmluaGVyaXR9LnRiLWJ1dHRvbl9fY29udGVudHt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2ljb257ZGlzcGxheTppbmxpbmUtYmxvY2s7dmVydGljYWwtYWxpZ246bWlkZGxlO2ZvbnQtc3R5bGU6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9faWNvbjo6YmVmb3Jle2NvbnRlbnQ6YXR0cihkYXRhLWZvbnQtY29kZSk7Zm9udC13ZWlnaHQ6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9fbGlua3tiYWNrZ3JvdW5kLWNvbG9yOiM0NDQ7Ym9yZGVyLXJhZGl1czowLjNlbTtmb250LXNpemU6MS4zZW07bWFyZ2luLWJvdHRvbTowLjc2ZW07cGFkZGluZzowLjU1ZW0gMS41ZW0gMC41NWVtfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSJiMjUwMWU1OTFkMDVlMzQyYWMzMTg2MTgxZjkzMmZkYiJdIHsgdGV4dC1hbGlnbjogY2VudGVyOyB9IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249ImIyNTAxZTU5MWQwNWUzNDJhYzMxODYxODFmOTMyZmRiIl0gLnRiLWJ1dHRvbl9fbGluayB7IGJhY2tncm91bmQtY29sb3I6IHJnYmEoIDI1NSwgMjU1LCAyNTUsIDEgKTtib3JkZXItcmFkaXVzOiAyMXB4O2NvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7Ym9yZGVyOiAycHggc29saWQgcmdiYSggOTksIDEyOSwgMjQwLCAxICk7Zm9udC1zaXplOiAxNnB4O2NvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iYjI1MDFlNTkxZDA1ZTM0MmFjMzE4NjE4MWY5MzJmZGIiXSAudGItYnV0dG9uX19pY29uIHsgZm9udC1mYW1pbHk6IGRhc2hpY29uczsgfSAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iZTM0M2ZjNmUzZTgzOWQ5MWIxNmFjMzA0NTFjZGI2ZTUiXSB7IGZvbnQtc2l6ZTogMTNweDtmb250LXN0eWxlOiBpdGFsaWM7IH0gIC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSJlMzQzZmM2ZTNlODM5ZDkxYjE2YWMzMDQ1MWNkYjZlNSJdIGEgeyB0ZXh0LWRlY29yYXRpb246IG5vbmU7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gLndwLWJsb2NrLXRvb2xzZXQtYmxvY2tzLWNvbnRhaW5lci50Yi1jb250YWluZXJbZGF0YS10b29sc2V0LWJsb2Nrcy1jb250YWluZXI9IjZmN2QzNjU3NDcwNzUyMzI0MmI2MWFiNDc3NzM3NDY2Il0geyBwYWRkaW5nOiAyNXB4OyB9IC50Yi1ncmlkLC50Yi1ncmlkPi5ibG9jay1lZGl0b3ItaW5uZXItYmxvY2tzPi5ibG9jay1lZGl0b3ItYmxvY2stbGlzdF9fbGF5b3V0e2Rpc3BsYXk6Z3JpZDtncmlkLXJvdy1nYXA6MjVweDtncmlkLWNvbHVtbi1nYXA6MjVweH0udGItZ3JpZC1pdGVte2JhY2tncm91bmQ6I2QzOGEwMztwYWRkaW5nOjMwcHh9LnRiLWdyaWQtY29sdW1ue2ZsZXgtd3JhcDp3cmFwfS50Yi1ncmlkLWNvbHVtbj4qe3dpZHRoOjEwMCV9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tdG9we3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1zdGFydH0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1jZW50ZXJ7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpjZW50ZXJ9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tYm90dG9te3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1lbmR9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSI1NTRjZjYzNTlmYzhiMGNlMTE0OGMwYWRiMzEwYmQ0YiJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMSkgeyBncmlkLWNvbHVtbjogMSB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSI1NTRjZjYzNTlmYzhiMGNlMTE0OGMwYWRiMzEwYmQ0YiJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMikgeyBncmlkLWNvbHVtbjogMiB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSI1NTRjZjYzNTlmYzhiMGNlMTE0OGMwYWRiMzEwYmQ0YiJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMykgeyBncmlkLWNvbHVtbjogMyB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSI1NTRjZjYzNTlmYzhiMGNlMTE0OGMwYWRiMzEwYmQ0YiJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgNCkgeyBncmlkLWNvbHVtbjogNCB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSI1NTRjZjYzNTlmYzhiMGNlMTE0OGMwYWRiMzEwYmQ0YiJdIC5qcy13cHYtbG9vcC13cmFwcGVyID4gLnRiLWdyaWQgeyBncmlkLXRlbXBsYXRlLWNvbHVtbnM6IG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpO2dyaWQtYXV0by1mbG93OiByb3cgfSAud3B2LXBhZ2luYXRpb24tbmF2LWxpbmtzW2RhdGEtdG9vbHNldC12aWV3cy12aWV3LXBhZ2luYXRpb24tYmxvY2s9ImNkZmQ0YzQ3MzdiMjg5OGViYTQ0NDNkZDU5YTFiZjUwIl0geyB0ZXh0LWFsaWduOiBsZWZ0O2p1c3RpZnktY29udGVudDogZmxleC1zdGFydDsgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249IjdmMmRhZjQ0NjQ4YjI1NDhhNWQzZjkyM2M1MTNhZTI1Il0geyB0ZXh0LWFsaWduOiBjZW50ZXI7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iN2YyZGFmNDQ2NDhiMjU0OGE1ZDNmOTIzYzUxM2FlMjUiXSAudGItYnV0dG9uX19saW5rIHsgYmFja2dyb3VuZC1jb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO2JvcmRlci1yYWRpdXM6IDIxcHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTtib3JkZXI6IDJweCBzb2xpZCByZ2JhKCA5OSwgMTI5LCAyNDAsIDEgKTtmb250LXNpemU6IDE2cHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTsgfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSI3ZjJkYWY0NDY0OGIyNTQ4YTVkM2Y5MjNjNTEzYWUyNSJdIC50Yi1idXR0b25fX2ljb24geyBmb250LWZhbWlseTogZGFzaGljb25zOyB9IC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSJjYThjNDY0NWQ0OTBhMmM2ZjE0N2JjYTY4MmQ1YjRlYiJdIHsgZm9udC1zaXplOiAxM3B4O2ZvbnQtc3R5bGU6IGl0YWxpYzsgfSAgLnRiLWZpZWxkW2RhdGEtdG9vbHNldC1ibG9ja3MtZmllbGQ9ImNhOGM0NjQ1ZDQ5MGEyYzZmMTQ3YmNhNjgyZDViNGViIl0gYSB7IHRleHQtZGVjb3JhdGlvbjogbm9uZTsgfSBoMy50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iNWZkYjdlM2Y5ODY1NDRjNGZlMTMwNDhkZmYzZDM2ZTYiXSAgeyBmb250LXNpemU6IDE2cHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTsgfSAgaDMudGItaGVhZGluZ1tkYXRhLXRvb2xzZXQtYmxvY2tzLWhlYWRpbmc9IjVmZGI3ZTNmOTg2NTQ0YzRmZTEzMDQ4ZGZmM2QzNmU2Il0gYSAgeyBjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApO3RleHQtZGVjb3JhdGlvbjogbm9uZTsgfSBoMi50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iMDg1ZGJiYmMwZGVmZWFkYzI3YjIzYjU3MzdhY2U2NDUiXSAgeyBjb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO2JhY2tncm91bmQtY29sb3I6IHJnYmEoIDYsIDE0NywgMjI3LCAxICk7cGFkZGluZy10b3A6IDIwcHg7cGFkZGluZy1ib3R0b206IDIwcHg7cGFkZGluZy1sZWZ0OiAyNXB4O21hcmdpbi10b3A6IDIwcHg7bWFyZ2luLWJvdHRvbTogMjBweDsgfSAgaDIudGItaGVhZGluZ1tkYXRhLXRvb2xzZXQtYmxvY2tzLWhlYWRpbmc9IjA4NWRiYmJjMGRlZmVhZGMyN2IyM2I1NzM3YWNlNjQ1Il0gYSAgeyBjb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO3RleHQtZGVjb3JhdGlvbjogbm9uZTsgfSAudGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSB7IGdyaWQtdGVtcGxhdGUtY29sdW1uczogbWlubWF4KDAsIDAuNzJmcikgbWlubWF4KDAsIDAuMjhmcik7Z3JpZC1hdXRvLWZsb3c6IHJvdyB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDJuICsgMSkgeyBncmlkLWNvbHVtbjogMSB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDJuICsgMikgeyBncmlkLWNvbHVtbjogMiB9IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iMzRmMGE0ZDQ1MjcyYTczOTQ1NmM5MmYwZDlmZjdkYTAiXSB7IHRleHQtYWxpZ246IGNlbnRlcjsgfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSIzNGYwYTRkNDUyNzJhNzM5NDU2YzkyZjBkOWZmN2RhMCJdIC50Yi1idXR0b25fX2xpbmsgeyBiYWNrZ3JvdW5kLWNvbG9yOiByZ2JhKCAyNTUsIDI1NSwgMjU1LCAxICk7Ym9yZGVyLXJhZGl1czogMjFweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApO2JvcmRlcjogMnB4IHNvbGlkIHJnYmEoIDgwLCAxMTMsIDIxOCwgMSApO2ZvbnQtc2l6ZTogMTZweDtsaW5lLWhlaWdodDogMjNweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApOyB9IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249IjM0ZjBhNGQ0NTI3MmE3Mzk0NTZjOTJmMGQ5ZmY3ZGEwIl0gLnRiLWJ1dHRvbl9faWNvbiB7IGZvbnQtZmFtaWx5OiBkYXNoaWNvbnM7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iMzRmMGE0ZDQ1MjcyYTczOTQ1NmM5MmYwZDlmZjdkYTAiXSAudGItYnV0dG9uX19pY29uOjpiZWZvcmUgeyBjb250ZW50OiAnXGY0NjcnOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iNjY4YWUxODU1YjI1YjE2MmViOGU0NjAyN2U4NGVlZDYiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iYTA5M2Y4MGI5ODk4OGY0NDg2N2JjOTJiYzhiMmJjY2UiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iYjIwN2JlMWYwOWI1Y2ZlYWVkZTZhNzE5ODhhNzQyNzUiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iNjYwNzcwMDhmOGIzODIyNjg4ZTQyN2Q5ZTAzOWYyMWYiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IGgzLnRiLWhlYWRpbmdbZGF0YS10b29sc2V0LWJsb2Nrcy1oZWFkaW5nPSI0MDIzN2JiYTNhYjRmMjdjYmJiYWY4ZmRlZDk1ZGQ0ZSJdICB7IGZvbnQtc2l6ZTogMTZweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApOyB9ICBoMy50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iNDAyMzdiYmEzYWI0ZjI3Y2JiYmFmOGZkZWQ5NWRkNGUiXSBhICB7IGNvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7dGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbi50Yi1ncmlkLWNvbHVtbltkYXRhLXRvb2xzZXQtYmxvY2tzLWdyaWQtY29sdW1uPSIzMDM0ZmJlODg2YzExMDU0ZTk1YjQ2YjA5ZDNlNDExMiJdIHsgZGlzcGxheTogZmxleDsgfSAudGItY29udGFpbmVyIC50Yi1jb250YWluZXItaW5uZXJ7d2lkdGg6MTAwJTttYXJnaW46MCBhdXRvfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtY29udGFpbmVyLnRiLWNvbnRhaW5lcltkYXRhLXRvb2xzZXQtYmxvY2tzLWNvbnRhaW5lcj0iNzk5MDAxN2I5ZDJhNjk3MTQ5OTcxOTJkMTJjZGY5MzAiXSB7IHBhZGRpbmc6IDI1cHg7Ym94LXNoYWRvdzogNXB4IDVweCAxMHB4IDAgcmdiYSggMCwgMCwgMCwgMC41ICk7IH0gLnRiLWZpZWxkW2RhdGEtdG9vbHNldC1ibG9ja3MtZmllbGQ9Ijc5MzY1OWQ4MmY4Zjk2YjU1NmE1NzY3YmQzMDM2Njc4Il0geyBtYXJnaW4tdG9wOiAzMHB4O21hcmdpbi1ib3R0b206IDMwcHg7IH0gIC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSI3OTM2NTlkODJmOGY5NmI1NTZhNTc2N2JkMzAzNjY3OCJdIGEgeyB0ZXh0LWRlY29yYXRpb246IG5vbmU7IH0gIGgxLnRiLWhlYWRpbmdbZGF0YS10b29sc2V0LWJsb2Nrcy1oZWFkaW5nPSI0ZjVhNjYwNTg5ZjhhMmViOGU3YTg1MDIwOTBkODFkYyJdIGEgIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1jb250YWluZXIudGItY29udGFpbmVyW2RhdGEtdG9vbHNldC1ibG9ja3MtY29udGFpbmVyPSJlZDM4MzJhYTYyMDFjYmVjNWIxZTViOTAyZGMwNjdlMiJdIHsgcGFkZGluZzogMjVweDsgfSBAbWVkaWEgb25seSBzY3JlZW4gYW5kIChtYXgtd2lkdGg6IDc4MXB4KSB7IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30udGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iNTU0Y2Y2MzU5ZmM4YjBjZTExNDhjMGFkYjMxMGJkNGIiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iNTU0Y2Y2MzU5ZmM4YjBjZTExNDhjMGFkYjMxMGJkNGIiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDIpIHsgZ3JpZC1jb2x1bW46IDIgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iNTU0Y2Y2MzU5ZmM4YjBjZTExNDhjMGFkYjMxMGJkNGIiXSAuanMtd3B2LWxvb3Atd3JhcHBlciA+IC50Yi1ncmlkIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMC41ZnIpIG1pbm1heCgwLCAwLjVmcik7Z3JpZC1hdXRvLWZsb3c6IHJvdyB9IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gICAudGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSB7IGdyaWQtdGVtcGxhdGUtY29sdW1uczogbWlubWF4KDAsIDAuNWZyKSBtaW5tYXgoMCwgMC41ZnIpO2dyaWQtYXV0by1mbG93OiByb3cgfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDIpIHsgZ3JpZC1jb2x1bW46IDIgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19ICAgICAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC1jb2x1bW4udGItZ3JpZC1jb2x1bW5bZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbj0iMzAzNGZiZTg4NmMxMTA1NGU5NWI0NmIwOWQzZTQxMTIiXSB7IGRpc3BsYXk6IGZsZXg7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gIC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IH0gQG1lZGlhIG9ubHkgc2NyZWVuIGFuZCAobWF4LXdpZHRoOiA1OTlweCkgeyAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19IC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99LnRiLWdyaWQsLnRiLWdyaWQ+LmJsb2NrLWVkaXRvci1pbm5lci1ibG9ja3M+LmJsb2NrLWVkaXRvci1ibG9jay1saXN0X19sYXlvdXR7ZGlzcGxheTpncmlkO2dyaWQtcm93LWdhcDoyNXB4O2dyaWQtY29sdW1uLWdhcDoyNXB4fS50Yi1ncmlkLWl0ZW17YmFja2dyb3VuZDojZDM4YTAzO3BhZGRpbmc6MzBweH0udGItZ3JpZC1jb2x1bW57ZmxleC13cmFwOndyYXB9LnRiLWdyaWQtY29sdW1uPip7d2lkdGg6MTAwJX0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi10b3B7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpmbGV4LXN0YXJ0fS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWNlbnRlcnt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmNlbnRlcn0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1ib3R0b217d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpmbGV4LWVuZH0gLndwdi12aWV3LW91dHB1dFtkYXRhLXRvb2xzZXQtdmlld3Mtdmlldy1lZGl0b3I9IjU1NGNmNjM1OWZjOGIwY2UxMTQ4YzBhZGIzMTBiZDRiIl0gID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDFuKzEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iNTU0Y2Y2MzU5ZmM4YjBjZTExNDhjMGFkYjMxMGJkNGIiXSAuanMtd3B2LWxvb3Atd3JhcHBlciA+IC50Yi1ncmlkIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMWZyKTtncmlkLWF1dG8tZmxvdzogcm93IH0gLnRiLWJ1dHRvbntjb2xvcjojZjFmMWYxfS50Yi1idXR0b24tLWxlZnR7dGV4dC1hbGlnbjpsZWZ0fS50Yi1idXR0b24tLWNlbnRlcnt0ZXh0LWFsaWduOmNlbnRlcn0udGItYnV0dG9uLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1idXR0b25fX2xpbmt7Y29sb3I6aW5oZXJpdDtjdXJzb3I6cG9pbnRlcjtkaXNwbGF5OmlubGluZS1ibG9jaztsaW5lLWhlaWdodDoxMDAlO3RleHQtZGVjb3JhdGlvbjpub25lICFpbXBvcnRhbnQ7dGV4dC1hbGlnbjpjZW50ZXI7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2xpbms6aG92ZXIsLnRiLWJ1dHRvbl9fbGluazpmb2N1cywudGItYnV0dG9uX19saW5rOnZpc2l0ZWR7Y29sb3I6aW5oZXJpdH0udGItYnV0dG9uX19saW5rOmhvdmVyIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazpmb2N1cyAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6dmlzaXRlZCAudGItYnV0dG9uX19jb250ZW50e2ZvbnQtZmFtaWx5OmluaGVyaXQ7Zm9udC1zdHlsZTppbmhlcml0O2ZvbnQtd2VpZ2h0OmluaGVyaXQ7bGV0dGVyLXNwYWNpbmc6aW5oZXJpdDt0ZXh0LWRlY29yYXRpb246aW5oZXJpdDt0ZXh0LXNoYWRvdzppbmhlcml0O3RleHQtdHJhbnNmb3JtOmluaGVyaXR9LnRiLWJ1dHRvbl9fY29udGVudHt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2ljb257ZGlzcGxheTppbmxpbmUtYmxvY2s7dmVydGljYWwtYWxpZ246bWlkZGxlO2ZvbnQtc3R5bGU6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9faWNvbjo6YmVmb3Jle2NvbnRlbnQ6YXR0cihkYXRhLWZvbnQtY29kZSk7Zm9udC13ZWlnaHQ6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9fbGlua3tiYWNrZ3JvdW5kLWNvbG9yOiM0NDQ7Ym9yZGVyLXJhZGl1czowLjNlbTtmb250LXNpemU6MS4zZW07bWFyZ2luLWJvdHRvbTowLjc2ZW07cGFkZGluZzowLjU1ZW0gMS41ZW0gMC41NWVtfSAgIC50Yi1ncmlkLC50Yi1ncmlkPi5ibG9jay1lZGl0b3ItaW5uZXItYmxvY2tzPi5ibG9jay1lZGl0b3ItYmxvY2stbGlzdF9fbGF5b3V0e2Rpc3BsYXk6Z3JpZDtncmlkLXJvdy1nYXA6MjVweDtncmlkLWNvbHVtbi1nYXA6MjVweH0udGItZ3JpZC1pdGVte2JhY2tncm91bmQ6I2QzOGEwMztwYWRkaW5nOjMwcHh9LnRiLWdyaWQtY29sdW1ue2ZsZXgtd3JhcDp3cmFwfS50Yi1ncmlkLWNvbHVtbj4qe3dpZHRoOjEwMCV9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tdG9we3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1zdGFydH0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1jZW50ZXJ7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpjZW50ZXJ9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tYm90dG9te3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1lbmR9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMWZyKTtncmlkLWF1dG8tZmxvdzogcm93IH0gLndwLWJsb2NrLXRvb2xzZXQtYmxvY2tzLWdyaWQudGItZ3JpZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWdyaWQ9IjhjNjc5MTU2YzE0ZTgxYWQ0OTYwYWFjNTM0ODVlMjYxIl0gID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDFuKzEpIHsgZ3JpZC1jb2x1bW46IDEgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19ICAgICAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC1jb2x1bW4udGItZ3JpZC1jb2x1bW5bZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbj0iMzAzNGZiZTg4NmMxMTA1NGU5NWI0NmIwOWQzZTQxMTIiXSB7IGRpc3BsYXk6IGZsZXg7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gIC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IH0g
Мастер-класс по математике «Нестандартные способы решения квадратных уравнений» (с презентацией)
Пояснительная записка.
Методическая разработка предназначена для проведения факультативного занятия по алгебре в 8-ом классе. Ее материалы полезны для расширения математических знаний обучающихся, дают им возможность более совершенно решать задания, способствуют подготовке к ОГЭ и ЕГЭ.
Цель:
Способствовать овладению обучающимися нестандартными способами решения квадратных уравнений.
Задачи:
Образовательные: (формирование познавательных УУД ): научить использовать нестандартные способы решения полных квадратных уравнений и определять условия, когда их применение наиболее рационально.
Воспитательные: (формирование коммуникативных и личностных УУД): умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблемы, строить продуктивное взаимодействие между сверстниками, воспитывать ответственность и уважение.
Развивающие: (формирование регулятивных УУД ): умение обрабатывать и использовать информацию, выбирать способы решения, контроль и оценка процесса и результатов деятельности.
Организация деятельности учеников на занятии: отчасти самостоятельно определяют тему, цель занятия, проблему, над которой нужно работать, самостоятельно, работая в парах, пытаются применить алгоритм решения полных квадратных уравнений нестандартными способами, знакомятся с условиями применения этих способов, решают задания, отвечают на вопросы, делают заключение о необходимости применения различных способов решения квадратных уравнений, оценивают себя и свою деятельность.
Ход урока.
1. Организационный момент.
Приветствие: (учитель) Здравствуйте, ребята!
А теперь тихонько сели,
На меня все посмотрели.
И вокруг все оглянулись
Всем красиво улыбнулись!
А я всем желаю удачного занятия! (Слайд 1)
2. Определение темы занятия.
(учитель): Чем сегодня мы с Вами будем заниматься, давайте попробуем угадать.
Историческая справка: Их решали в Древнем Вавилоне, Древней Греции, Индии. С 13-17 век к их решению свои усилия прилагали и европейцы. Итальянцы: Фибоначчи, Тарталья, Кардано. Франсуа Виет здесь очень постарался и сей объект решению поддался. (Слайд 2)
О какой математической модели идет здесь речь? Ваша версия? (об уравнениях)
О каких именно уравнениях сегодня пойдет речь, мы узнаем из следующего слайда. На экране уравнения расположены в двух столбиках. (Слайд 3)
x² + y²= 9 x² + 4х = 0
2х + 5 = 0 2x² — 5х – 3 = 0
Х + у = 4 4x² — 81 = 0
x³ = 27 x² = 25
a² = 0
(x — 3)² = 49
Дайте, характеристику уравнениям второго столбика (квадратные уравнения с одной переменной). Итак, тема занятия частично определена. «Квадратные уравнения». Записать тему в тетради. (Слайд 4)
3. Актуализация знаний.
Дайте определение квадратного уравнения
Назовите виды квадратных уравнений.
Определения полного и неполного квадратных уравнений.
Задание (на интерактивной доске предложены квадратные уравнения, распределить по столбикам полные и неполные квадратные уравнения)
Перечислить способы решения неполных квадратных уравнений на примерах уравнений, записанных в столбик «Неполные квадратные уравнения»
x² — 6х + 8 = 0 (Слайд 5)
x² — 8х = 0
8 x² — 7х + 3 = 0
x² — 25 = 0
2 x² = 0
2 + 9х = — 7x²
18 — x² = 14
х ( х – 5 ) = — 4
Учащиеся делают вывод, что решение неполных квадратных уравнений им уже известно. Значит, речь на занятии пойдет о полных квадратных уравнениях.
(Слайд 6)
Обучающимся предлагают оценить умения по решению полных квадратных уравнений. Перечисляются способы решения полных квадратных уравнений и напротив каждого способа учащиеся ставят знак «+» или «-».
В ходе обсуждения способов решения учащиеся приходят к выводу, что не умеют решать квадратные уравнения 3 способами. 4 способа известны им потому, что их изучают в школьном курсе алгебры. А такие способы как «Способ, основанный на свойстве коэффициентов, закономерности коэффициентов, переброски» неизвестны потому, что являются нестандартными. Учащиеся делают окончательное заключение о теме занятия и записывают ее.
«Нестандартные способы решения полных квадратных уравнений» (Слайд 7)
Далее учащиеся под руководством учителя ставят цель перед собой: овладение нестандартными способами решения полных квадратных уравнений.
Намечают организацию своей деятельности, определив задачи
Узнать:
При каких условиях применяют данный способ решения полных квадратных уравнений
Как решать данным способом (освоить алгоритм решения)
Зачем необходимы различные способы решения. (Слайд 8)
1. Овладение новым знанием:
Эпиграфом к данному разделу стали слова английского философа (Слайд 9)
Весь материал — в архиве.
Перечень тем проектов для учащихся 8-9 классов:
Учитель: Баязитова Б.Е. (русский язык, литература)
1.Роль русского языка в многонациональной России.
2.Одиночество Чацкого в пьесе А.С.Грибоедова «Горе от ума».
3.Белые ночи» Ф.М.Достоевского в иллюстрациях русских художниках.
4.Роль художественной детали в создании образов помещиков из поэмы Н.В.Гоголя «Мертвые души».
5.Бал как элемент дворянского быта на страницах романа А.С.Пушкина «Евгений Онегин».
6.Анна Родионовна Яковлева в жизни и творчестве А.С.Пушкина.
7.Цена жизни по роману Д.Сэлинджера «Над пропастью во ржи».
8.Библейская легенда о блудном сыне и ее трансформация в повести А.С.Пушкина «Станционный смотритель».
9.Дружба в жизни человека (на основе материала лирики А.С.Пушкина).
10.Дневник Татьяны Лариной.
Учитель: Богданова М.П. (биология)
1. Моделирование условий для разведения экзотических растений в домашних условиях.
2. Влияние корма на окрас раковины улитки Ахотин.
3. Вторая жизнь просроченным семенам.
4. Исследование освещенности классных кабинетов в школе.
5. Видовое разнообразие грибов на территории города Стрежевой.
6. Царство пыли. Что в ней скрыто.
7. Вторая жизнь ТБО.
8. Влияние электролита батареек на всхожесть семян кресс салата.
9. Проект озеленения пришкольной территории МОУ СОШ №3 г. Стрежевой.
10. Выявление информированности населения города Стрежевой о раздельном сборе мусора.
Учителя: Бобровская Н.М., Пастиева К.В. (история)
|
Направление
|
Темы
|
|
1.Краеведение
2.Семейная летопись
3.Общие темы по Первой мировой войне и Второй мировой войне
4. Роль личности в истории России
|
«История малой Родины»
Исследование происхождения семейной фамилии, переселений, генеалогическое древо
«Неизвестные страницы Первой мировой войны» и «Второй мировой войны»
«Неизвестный подвиг» — труженики тыла- наши земляки.
Судьба реформаторов в России: Сперанский М. М., Столыпин П.А., Витте С.Ю. и др.
|
Учитель: Валова Н.А. (информатика)
- Семейный бюджет
- Влияние социальных сетей на подростка
- Демонстрационная программа по математике «Движение во времени»
- QR-код – двухмерный штрих-код
- Мультфильм своими руками
Учитель: Воробьева Е.В. (литература)
- ДЕТИ ВЕЛИКОЙ ОТЕЧЕСТВЕННОЙ ВОЙНЫ В ПРОИЗВЕДЕНИЯХ ХУДОЖЕСТВЕННОЙ ЛИТЕРАТУРЫ 20 ВЕКА
- КРЫЛАТЫЕ ВЫРАЖЕНИЯ И АФОРИЗМЫ НА СТРАНИЦАХ «КАПИТАНСКОЙ ДОЧКИ» А.С. ПУШКИНА
- СУДЬБЫ ЛЮДЕЙ, ПОХОЖИХ НА АНДРЕЯ СОКОЛОВА ( ПО М.ШОЛОХОВУ «СУДЬБА ЧЕЛОВЕКА»)
- «СВЕТ МОЙ, ЗЕРКАЛЬЦЕ! СКАЖИ…» (ПО ПРОИЗВЕДЕНИЯМ В.ЖУКОВСКОГО, А.ПУШКИНА, Н. ГОГОЛЯ И ДР.)
Учитель: Еремеева В.А. (английский язык)
1.День, когда я родился.
2.Английский календарь. Что могут рассказать названия месяцев и дней недели.
3. Что могут рассказать банкноты о своем народе ( на примере американского доллара).
4. Поэтический перевод стихотворений с английского языка на русский.
5. Шотландский танец-обряд, соревнование или разговор?
6.Аббревиатура как лингвистическая особенность оn-line общения.
7. История самых известных песен России и Британии ( например, «В лесу родилась елочка», и “Happy Birthday”).
8.Почему англичане дарят подарки на Рождество, а мы на Новый год?
9. Пути изучения английского языка с помощью Интернета.
10. «Слова-ловушки» переводчика
Учителя: Кошкарева В.А., Овсянникова С.В., Шоцкая Е.В. (физкультура)
- Где и как растут чемпионы.
- Спортивные традиции в семье как фактор физического воспитания личности.
- Сила есть — ума не надо? Или спорт учебе не помеха.
- Закаливание в спортивной практике.
- Питание спортсменов во время соревнований и в восстановительном периоде.
- Составление суточного пищевого рациона спортсменов.
- Основные гигиенические правила подготовки юных спортсменов.
- Рациональный распорядок дня для спортсменов.
- Гигиенические требования к местам занятий физической культурой.
- Определение суточного расхода энергии спортсмена
Учитель: Малышенко А.Л. (математика)
Равносильные преобразования неравенств: теория и практика.
Равносильные преобразования уравнений: теория и практика.
Равносоставленные многоугольники.
Развитие понятия числа. Понятие о действительных числах и действиях над ними.
Различные способы доказательства теоремы Пифагора
Решение задач на смеси и сплавы
Сложные проценты
Способы решения систем уравнений с двумя переменными.
Стандартные и нестандартные методы решения неравенств.
Стандартные и нестандартные методы решения уравнений.
Статистические исследования.
Сценарий математического праздника, викторины, нетрадиционного урока с использованием мультимедийных технологий.
Теория игр. Кубик Рубика.
Теория чисел
Треугольник Паскаля
Треугольник Эйлера-Бернулли
Функции в окружающем мире
Характеристические свойства окружности.
Частота и вероятность событий.
Чем геометрия Лобачевского отличается от геометрии Евклида.
Учитель: Петрова Л.А. (география)
- Антропогенные катастрофы в природе.
- География международного туризма.
- География миграций в России.
- География на купюрах.
- Есть ли в России реальная возможность использования альтернативных источников энергии?
- Зачем предприятиям нашего города нужны очистные сооружения?
- Перепись населения в школе
- Мировые города – главные центры активности мирового сообщества.
- Похож ли мой город на город моей бабушки?
- Растения в государственной символике стран.
- Растения и животные в мире геральдики.
- Российская Арктика (географическое положение, физико-географические особенности, научные исследования, проблемы).
Учитель Сагитова В.В. (физика)
Кристаллы.
Устройство и принцип работы амперметра.
Устройство и принцип работы вольтметра.
Влажность воздуха и влияние ее на жизнедеятельность человека.
Влияние наушников на слух человека.
Вода внутри нас.
Нахождение своего роста с помощью математического маятника.
Необычные свойства обычной воды.
Физика в игрушках.
Энерго — и ресурсосбережение в школе и дома.
Энергосберегающие лампы: за и против.
Сравнение ламп накаливания и энергосберегающих ламп.
Учитель: Трофимова О.М. (математика)
Примерные темы исследовательских работ по математике для учащихся 9 класса:
Алгоритмический подход к решению геометрических задач.
Вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа.
Виды уравнений и способы их решения.
Вписанные и описанные окружности. Вневписанные окружности.
График дробно-линейной функции.
Загадки арифметической прогрессии.
Замечательные точки треугольника.
Золотое сечение
Информация, кибернетика и математика.
Иррациональные неравенства.
Иррациональные уравнения.
Использование тригонометрических формул при измерительных работах
История развития учения об уравнениях.
Летопись открытий в мире чисел и фигур.
Математика – царица или слуга для других наук.
Метод подобия в задачах на построение.
Методы решения текстовых задач.
Методы решения уравнений 4 степени.
Можно ли считать мир геометрически правильным.
На правильном пути по ступенькам прогрессии.
Неравенства и системы неравенств с двумя переменными.
Неравенства с параметром.
Нестандартные задачи по алгебре.
Нестандартные задачи по геометрии.
Нестандартные решения уравнений
Нестандартные способы нахождения площадей некоторых многоугольников.
Нестандартные способы решения квадратных уравнений.
О среднем арифметическом, о среднем гармоничном, о среднем геометрическом, о среднем квадратичном.
Парабола и я
Последовательности и прогрессии в жизни.
Построение графиков сложных функций
Презентации избранных вопросов алгебры или геометрии.
Приложения математики в экономике.
Применение векторов к доказательству свойств и признаков параллелограмма.
Применение векторов к доказательству теорем о треугольниках.
Применение подобия к доказательству и решению задач.
Применение свойств квадратичной функции при решении задач.
Прогрессии в нашей жизни
Простые и сложные проценты
Путешествие в историю математики.
Примерные темы проектов по математике для учащихся 9 класса:
Равносильные преобразования неравенств: теория и практика.
Равносильные преобразования уравнений: теория и практика.
Равносоставленные многоугольники.
Развитие понятия числа. Понятие о действительных числах и действиях над ними.
Различные способы доказательства теоремы Пифагора
Решение задач на смеси и сплавы
Сложные проценты
Способы решения систем уравнений с двумя переменными.
Стандартные и нестандартные методы решения неравенств.
Стандартные и нестандартные методы решения уравнений.
Статистические исследования.
Сценарий математического праздника, викторины, нетрадиционного урока с использованием мультимедийных технологий.
Теория игр. Кубик Рубика.
Теория чисел
Треугольник Паскаля
Треугольник Эйлера-Бернулли
Уравнения высших степеней.
Уравнения с параметром.
Уравнения с переменной под знаком модуля.
Функции в окружающем мире
Характеристические свойства окружности.
Частота и вероятность событий.
Чем геометрия Лобачевского отличается от геометрии Евклида.
Учитель: Усольцева Л.А. (информатика)
- Сравнение мобильных операционных систем iOS и Android.
- Социальные сети в жизни учащихся нашей школы.
- Искусственный интеллект фантастика или реальность.
- Технологии в облаках.
- Эволюция компьютерного вируса.
- Влияние компьютера на здоровье человека.
- Спам и защита от него.
- Интернет-зависимость — проблема современного общества.
- История развития операционной системы WINDOWS.
- История программирования в лицах.
- Моделирование геометрических операций в графических редакторах.
- Применение в цифровой электронике двоичной, восьмеричной и шестнадцатеричной систем счисления.
- Как возникли различные системы счисления.
- Графика в среде программирования PascalABC
- Влияние интернета, СМИ на формирование нравственности.
Как решать квадраты, не представленные в стандартной форме — Видео и стенограмма урока
Стандартная квадратичная форма
Оба способа, которыми мы знаем, как решать квадратичные уравнения, требуют, чтобы уравнение было в стандартной форме ( y = ax 2 + bx + c ) , а этот определенно не так. Но не позволяйте этому смущать вас! Не паникуйте и не думайте, что вам нужно сделать что-то безумное. Все, что нам нужно сделать, это использовать свои навыки алгебры, чтобы перемещать вещи и возвращать это уравнение в стандартную форму.
Давайте начнем с распределения -2 x на ( x — 1) внутри круглых скобок, чтобы изменить это выражение только на сложение. Это дает нам следующее: -2 x 2 + 2 x + 5 + x = 0, и теперь остается только объединить одинаковые термины, чтобы получить нашу стандартную квадратичную форму, -2 x . 2 + 3 х + 5 = 0.
Теперь мы можем начать думать о решении этой проблемы, и эти числа не так уж и плохи, поэтому давайте попробуем разложить на множители. Это означает, что сначала нужно вычленить отрицательное из всего в трехчлене, чтобы получить следующее: — (2 x 2 — 3 x — 5) = 0, а затем найти пару чисел, у которых есть произведение -10 и сумма -3. Если выписать множители -10 и найти пару, соответствующую нашим критериям, получится, что -5 и +2 — наши победители. Это означает, что мы можем использовать метод площади, чтобы исключить это.Подстановка этих значений в четыре квадранта и последующее извлечение наибольшего общего множителя из каждого столбца и строки дает нам факторизованную форму уравнения как — (2 x — 5) ( x + 1) = 0.
Свойство нулевого произведения
Это изменяет уравнение в нашей задаче на следующее: 0 = 2 x — 5 или 0 = x + 1, что теперь позволяет нам использовать свойство нулевого произведения. Свойство нулевого произведения говорит о том, что всякий раз, когда мы умножаем две вещи и получаем ноль, одна из вещей, с которой мы начали, должна была быть нулевой.Это означает, что в данном случае либо 2 x — 5 = 0, либо x + 1 = 0. Теперь достаточно нескольких быстрых обратных операций, чтобы определить, что наши два ответа — 5/2 или -1.
x = -1 — допустимое решение, но не имеет особого смысла для нашей игры. Мы хотим посмотреть на наш ответ 5/2, и похоже, что мы немного отстали. Нам нужно отойти немного дальше. Давайте попробуем выровнять наш выстрел и посмотрим, даст ли это желаемый результат. Чуть ниже… хорошо. Но помните, что это последний уровень, поэтому наше новое уравнение, вероятно, не будет выглядеть лучше, чем предыдущее, и, конечно же, это немного безумно:
2 x (3 x — 5) = x + 30
Это даже не равно нулю, но ничего страшного! Нам все еще нужно сделать то же самое, что и раньше — использовать алгебру, чтобы вернуть эту квадратичную форму обратно в стандартную форму.Сначала умножение на свойство распределения, затем использование обратных операций для перемещения всего в левую часть уравнения и, наконец, объединение подобных членов дает нам квадратное уравнение стандартной формы 6 x 2-11 x -30 = 0.
Квадратичная формула
Давайте продолжим и воспользуемся квадратной формулой для этой формулы, потому что числа намного больше, чем предыдущая. Это означает, что мы должны сначала правильно определить a , b и c как коэффициенты на нашем трехчлене. A , первый коэффициент, равен 6, следующий, b , равен -11, а константа на конце, c , равна -30. Теперь нам нужно подставить эти значения в формулу, и теперь нам нужно очень внимательно следить за порядком операций, чтобы получить два наших ответа.
Выполняя этот шаг за раз, — -11 превратится в +11, внутренняя часть квадратного корня (так называемый дискриминант) имеет показатель степени, который мы можем сделать в первую очередь. -11 * -11 это 121.Тогда 4 * 6 * -30 будет -720. Продолжая порядок операций, умножение в нижней части (2 * 6) дало бы мне 12. Выполнение минус-отрицания превращается в плюс-положительный, что означает, что мы получаем 11 +/- квадратный корень из 841/12, и оказывается, что квадратный корень из 841 равен 29, что означает, что я могу разделить два ответа на 11 + (29/12) или 11 — (29/12). Выполнение этого и последующее упрощение дробей дает нам два ответа: 10/3 или -3/2.
Мы снова можем более или менее игнорировать наш отрицательный корень здесь просто, как то, что произойдет, если рогатка сломается, и сосредоточиться на положительном корне в 10/3, что, похоже, будет работать.Я чувствую себя довольно уверенно, идя на этот снимок. Давайте сделаем это … и да, мы получили это! Вы победили Furious Fowls . Вы эксперт по квадратичным решениям и готовы решать любые квадратные уравнения!
Резюме урока
Давайте рассмотрим, чему нас научил Furious Fowls . Мы можем решить квадратные уравнения двумя способами: факторизуя и используя свойство нулевого продукта или используя формулу корней квадратного уравнения. Оба эти способа требуют, чтобы квадратное выражение было в стандартной форме, поэтому, если выражение изначально не в стандартной форме, используйте алгебру, чтобы преобразовать его в стандартную форму, прежде чем вы начнете решать уравнение.
Цели урока
По завершении этого урока вы сможете решать квадратные уравнения с помощью факторизации или использования квадратной формулы.
Бобсон Вонг | Учитель математики
Последнее обновление: пятница, 10 января 2020 г.
Опубликовано: воскресенье, 5 января 2020 г.
Решение квадратных уравнений (уравнения, которые могут быть записаны в форме ax 2 + bx + c = 0, где a ≠ 0) является основной темой в алгебре старших классов.Как правило, студенты в США изучают несколько методов их решения (разложение на множители, построение графиков, завершение квадрата или использование формулы квадратного уравнения). По моему опыту, многие студенты не только изо всех сил пытаются выучить четыре совершенно разных метода, но и вынуждены бороться с определением того, какой метод лучше всего работает для данного квадратного уравнения.
Несколько месяцев назад математик По-Шен Ло опубликовал в Интернете статью и видео (оба можно посмотреть на http://www.poshenloh.com/quadratic/), в которых описывался другой способ решения квадратных уравнений.Хотя он разработал ее независимо, другие математики, в том числе древние вавилоняне и греки, а также Джон Сэвидж в статье 1989 года Mathematics Teacher , разработали аналогичные методы (Лох описывает их более подробно на http://www.poshenloh.com/ квадратично связаны /).
В этом году я преподаю алгебру I классу старшеклассников и второкурсников, многие из которых повторяют этот курс. Я решил обучить своих учеников методу, описанному Ло. Попутно я внес несколько изменений в соответствии с потребностями моих учеников, наиболее заметной из которых было добавление визуального элемента в метод, чтобы помочь ученикам запоминать и понимать шаги.В этой статье описаны уроки, которые я бы использовал для обучения этому методу, и то, как студенты отреагировали на него. (Эти описания отражают изменения, которые я внес после первоначального обучения этим концепциям.)
Урок 1: Понимание графика квадратичной функции
Чтобы понять, как решать квадратные уравнения, учащиеся должны быть знакомы с характеристиками графиков квадратичных функций. Поскольку многие из моих студентов уже видели эти графики раньше, я смог быстро просмотреть многие из их характеристик.Если бы я обучал студентов, которые раньше не видели квадратичные функции, я бы представил это упражнением, в котором студенты работают в группах по два или три человека, чтобы построить график нескольких квадратичных функций с использованием технологий и записать свои уравнения в стандартной и факторизованной форме, а также их x перехватов, сумма перехватов x и произведение x-перехватов. Это можно сделать с помощью таблицы, подобной таблице 1 ниже:
Уравнение (разложенная форма) | Уравнение (стандартная форма) | Набросок графика | Уравнение оси симметрии | x -перехват | Сумма x -перехватов | Произведение x -перехватов |
( x — 2) ( x — 8) = 0 | x 2 -10 x + 16 = 0 | х = | ||||
( x — 4) ( x — 3) = 0 | x 2 -7 x + 12 = 0 | х = | ||||
( x + 1) ( x -5) = 0 | x 2 -4 x -5 = 0 | х = | ||||
… | … | … | … | … | … | … |
Таблица 1.Характеристики квадратных уравнений
Поскольку студенты еще не научились факторингу, я бы дал им уравнения как в стандартной, так и в факторизованной форме. Чтобы упростить эту задачу, здесь a = 1 во всех случаях. Здесь цель состоит в том, чтобы учащиеся могли определить сумму и произведение пересечений по оси x, а также уравнение оси симметрии с учетом уравнения в стандартной форме.
Урок 2: Обобщение характеристик квадратичной функции
После предыдущего урока учащиеся должны прийти к следующим выводам (все из которых имеют решающее значение для решения квадратных уравнений) для уравнения y = ax 2 + bx + c :
- Перехваты x графа являются противоположностями чисел в факторизованной форме многочленов.
- Ось симметрии расположена на полпути между пересечениями x и является средним значением.
- Сумма x -перехватов составляет половину противоположности b .
- Произведение x -перехватов равно c .
Учащимся может быть сложно использовать правильную терминологию (они могут сказать что-то вроде «число в скобках меняется со знаком в ответах»). Чтобы побудить студентов к мозговому штурму, я сначала разрешаю им использовать неформальный язык.После того, как студенты сделают свои наблюдения, я ввожу некоторую терминологию, чтобы помочь студентам точно описать свое мнение обо мне:
- нулей функции f — это значения x , которые делают уравнение f ( x ) = 0 истинным (другими словами, что приводит к выходу из 0).
- пересечений по оси x графика функции — это точки, в которых график пересекает ось y.
- корней уравнения — это значения переменной, которые делают его истинным.
Учащиеся не должны ссылаться на «нули графика» или «корни функции». Функции имеют нули, графики имеют точки пересечения по оси x, а уравнения имеют корни. Однако все эти термины связаны. Чтобы подчеркнуть этот словарный запас, я бы даже провел урок или часть урока, делая примеры, в которых ученики заполняют пробелы в предложениях, используя правильные термины.Например:
1. Заполните пропуски правильными словами: __________ __________ y = ( x — 3) ( x + 4) равны 3 и –4.
РЕШЕНИЕ: Нули функции y = ( x — 3) ( x + 4) равны 3 и –4.
2. Заполните пропуски правильными словами: __________ __________ y = ( x + 5) ( x — 6) равны (–5, 0) и (6, 0).
РЕШЕНИЕ: Интерпретации x графика y = ( x + 5) ( x — 6) равны (–5, 0) и (6, 0).
3. Заполните пропуски правильными словами: __________ __________ ( x + 12) ( x + 13) = 0 равны –12 и –13.
РЕШЕНИЕ: Корни уравнения ( x + 12) ( x + 13) = 0 равны –12 и –13.
На этом уроке учащиеся также должны заполнить таблицу, аналогичную таблице 2, чтобы они лучше познакомились с характеристиками квадратичных функций с учетом их графиков или уравнений.Эта таблица может содержать уравнения в факторизованной форме, чтобы учащиеся могли умножать многочлены (желательно с использованием прямоугольной или пространственной модели, о которой я писал на http://bobsonwong.com/blog/21-think-inside-the-box-2) .
Уравнение (разложенная форма) | Уравнение (стандартная форма) | Набросок графика | Уравнение оси симметрии | x -перехват | Сумма x -перехватов | Произведение x -перехватов |
y = ( x — 1) ( x — 5) | х = | |||||
х = | 2, 6 | |||||
y = x 2 -12 x + 20 | х = 6 | 12 | 20 | |||
… | … | … | … | … | … | … |
Таблица 2.Заполнение характеристик квадратичных функций
Урок 3: Определение характеристик квадратичной функции по ее графику
На следующем уроке учащимся необходимо определить характеристики квадратичной функции с учетом других характеристик. Студенты должны работать с графиками квадратичных функций, помеченных различными характеристиками, и просить их найти недостающие характеристики, помеченные как переменные. Ниже приведены некоторые примеры.
4. Найдите значения u и m :
РЕШЕНИЕ: учащимся дают интерцепты x и просят найти их среднее значение ( м, ) и расстояние между средним значением и каждым корнем ( и ). Здесь x 1 = 6-2 = 4 и x 2 = 6 + 2 = 8. После выполнения нескольких примеров с положительными корнями учащиеся должны проработать примеры с положительным и отрицательным корнем, а также примеры с двумя отрицательными корнями.
5. Найдите значения x 1 и x 2 :
РЕШЕНИЕ: Студентам дается уравнение оси симметрии ( x = 6), которое соответствует среднему значению интерцептов x , и их просят найти интерцепты x , которые помечены x 1 и x 2 . График показывает, что x 1 = 6-2 = 4 и x 2 = 6 + 2 = 8.Опять же, учащимся следует также проработать другие примеры с положительными и отрицательными корнями.
Урок 4: Определение нулей квадратичной функции по их произведению и среднему
6. Найдите значения u , x 1 и x 2 :
РЕШЕНИЕ: Студентам дается среднее значение и произведение x-точек пересечения, и их просят найти точки пересечения x . Они должны увидеть из графика, что x -перехватывания равны x 1 = 5 — u и x 2 = 5 + u .Они могут написать уравнение, которое выражает произведение интерцептов x двумя способами:
x 1 · x 2 = 16
(5 — u ) (5 + u ) = 16
25 — u 2 = 16, поэтому u 2 = 9, или u = 3.
(ПРИМЕЧАНИЕ: хотя u = ± 3, мы можем игнорировать отрицательный корень, поскольку график симметричен, а корни равны x = 5 ± u .)
Таким образом, x 1 = 5 — u = 5 — 3 = 2 и x 2 = 5 + u = 5 + 3 = 8.
Эта немного упрощенная версия метода, описанного Ло, приводит к следующему уроку, на котором студенты начинают решать квадратные уравнения.
Как и в Уроке 3, здесь учащиеся также должны выполнить несколько примеров со всеми положительными, положительными и отрицательными корнями и всеми отрицательными корнями.
Урок 5: Решение квадратных уравнений с
a = 1 и целыми корнями
На этом уроке студенты решают квадратные уравнения, в которых a = 1, а корни — целые числа.Этот урок будет работать лучше всего, если произведение корней достаточно велико, чтобы учащиеся не могли легко угадать факторы, например:
7. Решите относительно x : x 2 — 20 x + 96 = 0.
РЕШЕНИЕ: Я настоятельно рекомендую студентам нарисовать график, подобный приведенному ниже, для решения этих задач.
Из предыдущего урока учащиеся должны прийти к следующим выводам из уравнения:
- сумма корней равна — b = — (- 20) = 20.
- Среднее значение корней (т. Е. Сумма корней, деленная на 2) составляет 20/2 = 10.
- Произведение корней равно c = 96.
Вот где этот метод действительно экономит время. Используя обычно преподаваемый метод «угадывай и проверь», ученики должны найти два числа, которые умножаются на 96 и складываются в 20. Это может быть утомительно и неприятно! Этот метод обеспечивает более систематическую процедуру. Из графика мы видим, что корни равны x 1 = 10 — u и x 2 = 10 + u .Учащиеся могут написать уравнение, которое выражает произведение корней двумя способами :
x 1 · x 2 = c
(10 — u ) (10 + u ) = 96
100- u 2 = 96, поэтому u 2 = 4, или u = 2.
Таким образом, x 1 = 10 — u = 10-2 = 8 и x 2 = 10 + u = 10 + 2 = 12.
Урок 6: Решение квадратных уравнений с
a = 1 и дробными средними
Иногда корни имеют дробные средние значения, например :
8. Решите относительно x : x 2 — 21 x + 98 = 0.
РЕШЕНИЕ:
Из уравнения мы видим, что сумма корней — b = — (- 21) = 21, поэтому среднее значение корней составляет 21/2. Кроме того, произведение корней c = 98.Из графика мы видим, что корни равны x 1 = 21/2 — u и x 2 = 21/2 + u .
Хотя это может показаться концепцией, которую можно включить в предыдущий урок, я обнаружил, что дополнительный день помог студентам освоиться с идеями, лежащими в основе этого метода. Кроме того, многим ученикам неудобно использовать дроби, поэтому этот урок дает ученикам больше времени и практики.
Урок 7: Решение квадратных уравнений с
a = 1 и иррациональными корнями
На следующем уроке учащиеся решают квадратные уравнения с иррациональными корнями, например следующие:
9.Решить относительно x : x 2 + 9 x + 5 = 0.
РЕШЕНИЕ:
Урок 8: Решение квадратных уравнений с помощью
и ≠ 1
На этом уроке учащиеся решают квадратные уравнения, в которых a For 1. Для этих задач учащиеся сначала должны разделить все уравнение на a . Это сделает задачу более сложной, чем предыдущие, но я обнаружил, что студенты, которые борются с дробями, могут использовать калькулятор для выполнения операций с дробями (большинство графических калькуляторов можно настроить так, чтобы преобразовать результат в дробь в наименьших значениях) или преобразовать их. дроби в десятичные.
10. Решите относительно x : 2 x 2 + 8 x + 3 = 0.
РЕШЕНИЕ: Разделив уравнение на a = 2, мы получим x 2 + 4 x + 3/2 = 0. Здесь среднее значение корней равно –4/2 = –2, а произведение составляет 3/2.
Урок 9: Решение квадратных уравнений с мнимыми корнями
Для студентов, которым необходимо решать уравнения с мнимыми корнями (в штате Нью-Йорк, где я преподаю, эти уравнения преподаются в Алгебре II, а не в Алгебре I), следующий урок будет включать вопросы, подобные следующему: :
11.Решить относительно x : x 2 — 8 x + 17 = 0.
РЕШЕНИЕ:
x 1 · x 2 = c
(4 — u ) (4 + u ) = 17
16 — u 2 = 17
u 2 = –1
u = i
x 1 = 4 + i, x 2 = 4- i
Поскольку корни мнимые, на графике нет пересечений x , поэтому горизонтальная линия здесь не является осью x .Мне было интересно, что точки x 1 и x 2 представляют графически, поэтому я провел небольшое исследование по построению графиков сложных корней на квадратных уравнениях. Эта визуализация комплексных корней требует графического отображения квадратных уравнений в трех измерениях с осью z , представляющей мнимые числа. К счастью, я нашел несколько ссылок:
Учителя, у которых есть время, могут быть заинтересованы в дальнейшем изучении этих ресурсов.
Заключение: преимущества и ограничения метода
В целом, я считаю, что метод решения квадратных уравнений, описанный Ло, имеет несколько преимуществ по сравнению с другими процедурами, которым я учил в математике в старших классах:
- Как указывает Ло, учащиеся могут использовать один метод для решения всех квадратных уравнений.Конечно, студенты также могут использовать квадратную формулу для решения любого квадратного уравнения, но, по моему опыту, ученикам легче управлять этим методом. Многим ученикам сложно правильно подставить формулу. Алгебраические манипуляции, используемые в этом методе, обычно проще и легче запомнить, чем те, которые требуются для подстановки в формулу корней квадратного уравнения. Я обнаружил, что многие студенты, которым было очень трудно правильно подставить квадратную формулу, добились большего успеха с этим методом.
- Как и в случае с квадратной формулой, учащимся не нужно угадывать и проверять или использовать метод « ac », чтобы разложить на множители. Они могут найти корни x 1 и x 2 , а затем разложить полином на множители как ( x — x 1 ) ( x — x 2 ).
- Графическая интерпретация, которую я описываю здесь, усиливает связь между осью симметрии и корнями уравнения.Построение уравнения имеет решающее значение для помощи студентам в запоминании процедуры, поскольку она требует нескольких шагов, но я думаю, что это проще, чем пытаться запомнить кажущуюся произвольной формулой. (Раньше я учил песню, чтобы помочь ученикам запомнить квадратную формулу, но этот метод не требует от учеников пения!) Кроме того, построение графиков помогает ученикам объяснять свою работу людям, которые не знакомы с этим методом. Это особенно важно для меня, поскольку в конце года мои ученики сдают государственный тест, который будет оцениваться другими учителями.
- Студенты сразу получают ответ в виде m ± u (если корни действительные) или m ± ui (если корни мнимые). Они избегают упрощения выражений вроде. Используя этот метод, студенты определят, что м = 2 и u =.
Этот метод также имеет некоторые ограничения:
- Студенты должны работать с дробями. Я обнаружил, что многие студенты борются с дробями.Чтобы обойти это, я посоветовал им использовать калькулятор. Графические калькуляторы, такие как TI-NSpire и TI-83/84, позволяют студентам преобразовывать десятичные дроби в дроби или выполнять операции с дробями и сохранять результат как дробь. Однако, если корни иррациональны, то работа с десятичным представлением становится проблематичной, если учащимся нужно выражать ответы в простейшей радикальной форме.
- Студентам, возможно, придется рационализировать знаменатели. При использовании квадратичной формулы знаменатель будет рациональным (кроме случаев, когда a иррационально).Используя этот метод, учащиеся могут найти квадратный корень из дроби, если — ≠ 1 (см. Пункт 10 выше). Если учителя предпочитают, чтобы ответы выражались рациональными знаменателями, им придется показать учащимся, как рационализировать знаменатели
- Учащимся может быть трудно запомнить шаги. Как я сказал ранее, построение графика решения может помочь учащимся понять и запомнить этот метод.
Короче, планирую использовать этот метод для решения квадратных уравнений в будущем.Жду ваших комментариев и предложений!
Новый способ упростить квадратные уравнения
Итак, легко представить, что математики, должно быть, исчерпали проблему. Просто не может быть лучшего способа вывести квадратную формулу.
Введите По-Шен Ло, математика из Университета Карнеги-Меллона в Питтсбурге, который нашел более простой способ — тот, который, кажется, остался незамеченным за эти 4000 лет.
Подход Ло не полагается на завершение квадрата или другие сложные математические трюки.В самом деле, это достаточно просто, чтобы работать как общий метод, а это означает, что учащимся вообще не нужно запоминать формулу. «Этот вывод может демистифицировать квадратичную формулу для студентов во всем мире», — говорит он.
Новый подход прост. Он начинается с наблюдения, что если квадратное уравнение можно разложить на множители следующим образом:
Тогда правая часть равна 0, когда x = R или когда x = S. Тогда это были бы корни квадратичной.
Умножение правой части дает
Это верно, когда -B = R + S и когда C = RS.
А теперь самое интересное. Ло указывает, что числа R и S в сумме дают -B, когда их среднее значение равно -B / 2.
«Итак, мы ищем два числа вида -B / 2 ± z, где z — одна неизвестная величина», — говорит он. Затем мы можем умножить эти числа вместе, чтобы получить выражение для C. Итак,
Тогда простая перестановка дает
Это означает, что решение квадратного уравнения будет:
Voilà! Это квадратная формула.
[Более общую версию можно получить, разделив уравнение Ax2 + Bx + C = 0 на A, чтобы получить x2 + B / Ax + C / A = 0, а затем повторить описанный выше процесс.]
Это очень важно улучшение предыдущего метода, и Лох показывает почему на простом примере.
Найдите корни следующего квадратичного уравнения: x2 — 2x + 4 = 0
Традиционным методом было бы вычислить значения для A, B и C и подставить их в формулу корней квадратного уравнения. Но подход Ло решает проблему интуитивно.Первый шаг — подумать, что два корня уравнения должны быть равны -B / 2 ± z = 1 ± z
И поскольку их произведение должно быть C = 4, мы можем написать:
Итак, корни are
Попытка решить ту же проблему с использованием традиционного метода намного сложнее. Давай, попробуй! Новый подход намного проще и интуитивно понятнее, не в последнюю очередь потому, что он вообще не требует запоминания формулы.
Интересный вопрос: почему никто раньше не наткнулся на этот метод и широко не распространял его.
Ло говорит, что он «был бы очень удивлен, если бы этот подход полностью ускользнул от человеческих открытий до настоящего времени, учитывая 4000-летнюю историю этой темы и миллиарды людей, которые столкнулись с формулой и ее доказательством. техника, конечно, широко не преподается и не известна «.
Ло безуспешно искал в истории математики подход, похожий на его. Он изучил методы, разработанные древними вавилонянами, китайцами, греками, индийцами и арабами, а также современными математиками с эпохи Возрождения до наших дней.Похоже, что никто из них не сделал этого шага, хотя алгебра проста и известна веками.
Так почему именно сейчас? Ло считает, что это связано с тем, как традиционный подход доказывает, что квадратные уравнения имеют два корня. «Возможно, причина в том, что на самом деле математически нетривиально сделать обратное утверждение: у него всегда два корня, и эти корни имеют сумму -B и произведение C», — говорит он.
Ло, преподаватель математики и известный популяризатор, обнаружил свой подход при анализе учебных программ по математике для школьников с целью разработки новых объяснений.Вывод возник из этого процесса.
Теперь вопрос в том, насколько широко и быстро это распространится. Чтобы ускорить внедрение, Ло сняла видео об этом методе. В любом случае, вавилонские налоговые вычислители наверняка были бы впечатлены.
Ссылка: arxiv.org/abs/1910.06709: Простое доказательство квадратичной формулы
Поправка: мы внесли поправку в предложение, чтобы сказать, что метод никогда не был широко распространен, и включили цитату Ло.
Учебный план по квадратикам, согласованный с Общими основными государственными стандартами
% PDF-1.7
%
1 0 obj
>
эндобдж
2 0 obj
> поток
2017-10-12T18: 05: 54-07: 002017-10-12T18: 05: 54-07: 002017-10-12T18: 05: 54-07: 00Appligent AppendPDF Pro 5.5uuid: 9a20473d-a6f5-11b2-0a00- 782dad000000uuid: 9a2077e4-a6f5-11b2-0a00-20d2a7a2ff7fapplication / pdf
Prince 9.0 rev 5 (www.princexml.com) AppendPDF Pro 5.5 Ядро Linux 2.6 64-битная 2 октября 2014 Библиотека 10.1.0
конечный поток
эндобдж
5 0 obj
>
эндобдж
3 0 obj
>
эндобдж
8 0 объект
>
эндобдж
9 0 объект
>
эндобдж
10 0 obj
>
эндобдж
11 0 объект
>
эндобдж
12 0 объект
>
эндобдж
36 0 объект
>
эндобдж
37 0 объект
>
эндобдж
38 0 объект
>
эндобдж
39 0 объект
>
эндобдж
40 0 объект
>
эндобдж
61 0 объект
> / Повернуть 0 / Тип / Страница >>
эндобдж
62 0 объект
> / Повернуть 0 / Тип / Страница >>
эндобдж
63 0 объект
> / Повернуть 0 / Тип / Страница >>
эндобдж
64 0 объект
> / Повернуть 0 / Тип / Страница >>
эндобдж
65 0 объект
> / Повернуть 0 / Тип / Страница >>
эндобдж
78 0 объект
> поток
xX ے64_ + 5 ؖ Мп
eRveaHI> 8 ݭ Fjӧ [z} fW,; z7 {o \ JIvc = SJȆ-gJ6h ہ- V + u ^ tRők ^ 7Boox’zɶz> b3
Примеры квадратных уравнений в реальном мире
Квадратичное уравнение выглядит так:
Квадратные уравнения появляются во многих реальных ситуациях!
Здесь мы собрали для вас несколько примеров и решаем каждый из них разными методами:
Каждый пример следует за тремя основными этапами:
- Возьмите описание реального мира и составьте несколько уравнений
- Решить!
- Используйте здравый смысл для интерпретации результатов
Шары, стрелы, ракеты и камни
Когда вы бросаете мяч (или стреляете стрелой, запускаете ракету или бросаете камень), он поднимается в воздух, замедляясь при движении, а затем снова падает все быстрее и быстрее…
… и квадратное уравнение всегда подскажет вам его положение!
Пример: бросание мяча
Мяч бросается вверх с высоты 3 м над землей со скоростью 14 м / с. Когда он падает на землю?
Игнорируя сопротивление воздуха, мы можем вычислить его высоту, сложив эти три вещи:
(Примечание: t — время в секундах)
| Высота от 3 м: | 3 | |
| Он движется вверх со скоростью 14 метров в секунду (14 м / с): | 14т | |
| Гравитация тянет его вниз, меняя его положение на около 5 м в секунду в квадрате: | −5 т 2 | |
| (Примечание для энтузиастов: -5t 2 упрощено от — (½) при 2 с a = 9.8 м / с 2 ) |
Сложите их и получите высоту h в любой момент t :
ч = 3 + 14т — 5т 2
И мяч ударится о землю при нулевой высоте:
3 + 14т — 5т 2 = 0
Квадратичное уравнение!
В «Стандартной форме» это выглядит так:
−5 т 2 + 14 т + 3 = 0
Еще лучше, если мы умножим все члены на −1:
5т 2 — 14т — 3 = 0
Давайте решим…
Есть много способов решить эту проблему, здесь мы будем множить ее, используя «Найти два числа, которые
умножьте, чтобы получить a × c , и сложите, чтобы получить b «метод в Factoring Quadratics:
a × c = −15 и b = −14 .
Множители −15: −15, −5, −3, −1, 1, 3, 5, 15
Попробовав несколько комбинаций, мы обнаружим, что −15 и 1 работают.
(−15 × 1 = −15,
и −15 + 1 = −14)
Перепишите середину с −15 и 1: 5t 2 — 15t + t — 3 = 0
Фактор первых двух и последних двух: 5t (t — 3) + 1 (t — 3) = 0
Общий коэффициент равен (t — 3) 🙁 5t + 1) (t — 3) = 0
И два решения: 5t + 1 = 0 или t — 3 = 0
t = −0.2 или t = 3
«t = −0,2» — отрицательное время, что в нашем случае невозможно.
«t = 3» — это тот ответ, который нам нужен:
Мяч падает на землю через 3 секунды!
Вот график Параболы h = −5t 2 + 14t + 3
Показывает высоту мяча против раз
Несколько интересных моментов:
(0,3) При t = 0 (на старте) мяч находится на высоте 3 м
(-0.2,0) говорит, что -0,2 секунды ДО того, как мы бросили мяч, он находился на уровне земли. Этого никогда не было! Так что наш здравый смысл говорит игнорировать это.
(3,0) говорит, что через 3 секунды мяч оказывается на уровне земли.
Также обратите внимание, что мяч летит почти на 13 метров в высоту .
Примечание: вы можете точно определить, где находится верхняя точка!
Метод объяснен в разделе «Графические квадратные уравнения» и состоит из двух этапов:
Найдите где (по горизонтальной оси) вершину, используя −b / 2a :
- t = −b / 2a = — (- 14) / (2 × 5) = 14/10 = 1.4 секунды
Затем найдите высоту, используя это значение (1.4)
- h = −5t 2 + 14t + 3 = −5 (1,4) 2 + 14 × 1,4 + 3 = 12,8 метров
Таким образом, мяч достигает наивысшей точки 12,8 метра за 1,4 секунды.
Пример: новый спортивный велосипедВы создали новый спортивный велосипед! Теперь вы хотите сделать их много и продать с прибылью. |
Ваши затраты будут:
- 700 000 долл. США на установку производства, рекламу и т. Д.
- 110 $ на изготовление каждого велосипеда
На основе аналогичных велосипедов можно ожидать, что продаж будут следовать этой «кривой спроса»:
- Штучные продажи = 70,000 — 200P
Где «P» — цена.
Например, если выставить цену:
- по 0 долларов, вы просто раздаете 70000 велосипедов
- за 350 долларов, велосипеды вообще не продашь
- за 300 долларов вы можете продать 70000 — 200 × 300 = 10000 велосипедов
Итак… какая лучшая цена? А сколько нужно сделать?
Составим уравнения!
Сколько вы продаете, зависит от цены, поэтому используйте «P» в качестве переменной «Цена».
- Штучные продажи = 70,000 — 200P
- Продажи в долларах = Единицы × Цена = (70,000 — 200P) × P = 70,000P — 200P 2
- Затраты = 700,000 + 110 x (70,000 — 200P) = 700,000 + 7,700,000 — 22,000P = 8,400,000 — 22,000P
- Прибыль = Затраты на продажу = 70,000P — 200P 2 — (8,400,000 — 22,000P) = -200P 2 + 92,000P — 8,400,000
Прибыль = −200P 2 + 92,000P — 8,400,000
Да, квадратное уравнение.Давайте решим эту проблему, завершив квадрат.
Решить: −200P
2 + 92,000P — 8,400,000 = 0
Шаг 1 Разделите все члены на -200
P 2 — 460P + 42000 = 0
Шаг 2 Переместите числовой член в правую часть уравнения:
P 2 — 460P = -42000
Шаг 3 Заполните квадрат в левой части уравнения и уравновесите его, добавив такое же число в правую часть уравнения:
(b / 2) 2 = (−460/2) 2 = (−230) 2 = 52900
P 2 — 460P + 52900 = −42000 + 52900
(П — 230) 2 = 10900
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
P — 230 = ± √10900 = ± 104 (с точностью до целого числа)
Шаг 5 Вычтем (-230) с обеих сторон (другими словами, прибавим 230):
P = 230 ± 104 = 126 или 334
Что это нам говорит? В нем говорится, что прибыль НУЛЯ при цене 126 долларов США или 334 900 долларов США.
Но мы же хотим знать максимальную прибыль, не так ли?
Это ровно посередине! по цене 230 долл. США
А вот график:
Прибыль = −200P 2 + 92,000P — 8,400,000
Лучшая цена продажи $ 230 , и можно ожидать:
- Штучные продажи = 70 000 — 200 x 230 = 24 000
- Продажи в долларах = 230 долларов x 24 000 = 5 520 000 долларов
- Затраты = 700 000 + 110 x 24 000 = 3 340 000 долларов
- Прибыль = 5 520 000 долларов США — 3 340 000 долларов США = 2 180 000 долларов США
Очень прибыльное предприятие.
Пример: малая стальная рама
Ваша компания собирается изготавливать рамы как часть нового продукта, который они запускают.
Рама будет вырезана из куска стали, и для снижения веса конечная площадь должна быть 28 см 2
Внутренняя часть рамы должна быть 11 см на 6 см
Какой должна быть ширина металла x ?
Площадь стали перед резкой:
Площадь = (11 + 2x) × (6 + 2x) см 2
Площадь = 66 + 22x + 12x + 4x 2
Площадь = 4x 2 + 34x + 66
Площадь стали после вырезания середины 11 × 6:
Площадь = 4x 2 + 34x + 66 — 66
Площадь = 4x 2 + 34x
Давайте решим это графически!
Вот график 4x 2 + 34x:
Требуемая область 28 показана горизонтальной линией.
Площадь равна 28 см 2 когда:
x равно около -9,3 или 0,8
Отрицательное значение x не имеет смысла, поэтому ответ:
x = 0,8 см (прибл.)
Пример: речной круиз
Трехчасовой речной круиз идет на 15 км вверх по течению и обратно. Течение реки 2 км / час. Какова скорость лодки и сколько длилось путешествие вверх по течению?
Следует подумать о двух скоростях: скорость, которую лодка развивает в воде, и скорость относительно земли:
- Пусть x = скорость лодки в воде (км / ч)
- Пусть v = скорость относительно земли (км / ч)
Поскольку река течет вниз по течению со скоростью 2 км / ч:
- при движении вверх по течению v = x − 2 (скорость снижена на 2 км / ч)
- при движении вниз по течению v = x + 2 (скорость увеличена на 2 км / ч)
Мы можем превратить эти скорости во времена, используя:
время = расстояние / скорость
(чтобы проехать 8 км со скоростью 4 км / ч, нужно 8/4 = 2 часа, верно?)
И мы знаем, что общее время составляет 3 часа:
общее время = время на входе + время на выходе = 3 часа
Сложите все вместе:
общее время = 15 / (x − 2) + 15 / (x + 2) = 3 часа
Теперь мы используем наши навыки алгебры, чтобы найти «x».
Во-первых, избавьтесь от дробей, умножив на (x-2) (x + 2) :
3 (х-2) (х + 2) = 15 (х + 2) + 15 (х-2)
Развернуть все:
3 (x 2 −4) = 15x + 30 + 15x − 30
Переместите все влево и упростите:
3x 2 — 30x — 12 = 0
Это квадратное уравнение! Решим его с помощью дискриминантной формулы:
Где a , b и c
из квадратного уравнения
в «стандартной форме»: ax 2 + bx + c = 0
Решить 3x
2 — 30x — 12 = 0
Коэффициенты: a = 3 , b = −30 и c = −12
Квадратичная формула: x = [−b ± √ (b 2 −4ac)] / 2a
Вставьте a, b и c: x = [- (- 30) ± √ ((- 30) 2 −4 × 3 × (−12))] / (2 × 3)
Решить : x = [30 ± √ (900 + 144)] / 6
x = [30 ± √ (1044)] / 6
х = (30 ± 32.31) / 6
x = −0,39 или 10,39
Ответ: x = −0,39 или 10,39 (до 2 знаков после запятой)
x = −0,39 не имеет смысла для этого реального вопроса, но x = 10,39 просто идеально!
Ответ: Скорость лодки = 10,39 км / ч (с точностью до 2 знаков после запятой)
Итак, путь вверх по течению = 15 / (10,39−2) = 1,79 часа = 1 час 47 минут
И путь вниз по течению = 15 / (10.39 + 2) = 1,21 часа = 1 час 13мин
Пример: параллельные резисторы
Два резистора включены параллельно, как на этой схеме:
Общее сопротивление было измерено на уровне 2 Ом, и известно, что один из резисторов на 3 Ом больше, чем другой.
Каковы номиналы двух резисторов?
Формула для вычисления общего сопротивления «R T »:
1 R T
знак равно
1 R 1 + 1 R 2
В данном случае имеем R T = 2 и R 2 = R 1 + 3
1
2
знак равно
1
р 1
+
1
Р 1 +3
Чтобы избавиться от дробей, мы
можно умножить все члены на 2R 1 (R 1 + 3), а затем упростить:
Умножьте все члены на 2R 1 (R 1 + 3): 2R 1 (R 1 +3) 2 = 2R 1 (R 1 +3) R 1 + 2R 1 (R 1 +3) R 1 +3
Затем упростите: R 1 (R 1 + 3) = 2 (R 1 + 3) + 2R 1
Развернуть: R 1 2 + 3R 1 = 2R 1 + 6 + 2R 1
Переместите все термины влево: R 1 2 + 3R 1 — 2R 1 — 6 — 2R 1 = 0
Упростить: R 1 2 — R 1 — 6 = 0
Да! Квадратное уравнение!
Давайте решим это, используя наш Решатель квадратного уравнения.
- Введите 1, −1 и −6
- И вы должны получить ответы −2 и 3
R 1 не может быть отрицательным, поэтому ответ будет R 1 = 3 Ом .
Два резистора на 3 Ом и 6 Ом.
Прочие
Квадратные уравнения полезны во многих других областях:
Форма параболического зеркала, телескопа-рефлектора или спутниковой антенны определяется квадратным уравнением.
Квадратные уравнения также необходимы при изучении линз и изогнутых зеркал.
И многие вопросы, связанные со временем, расстоянием и скоростью, требуют квадратных уравнений.
Math Genius изобрел дико простой новый способ решения квадратных уравнений
Если вы изучали алгебру в старшей школе (или изучаете ее прямо сейчас), велика вероятность, что вы знакомы с квадратной формулой. Если нет, возможно, вы подавили это.
К этому моменту миллиарды из нас должны были выучить, запомнить и реализовать этот громоздкий алгоритм для решения квадратных уравнений, но, по словам математика По-Шен Ло из Университета Карнеги-Меллона, на самом деле существует более простой и лучший способ. все это время, хотя он оставался почти полностью скрытым в течение тысяч лет.
В новой исследовательской статье Ло отмечает квадратную формулу как «замечательный триумф ранних математиков», восходящий к истокам древневавилонского периода около 2000 г. до н.э., но также открыто признает некоторые из ее древних недостатков.
«К сожалению, для миллиардов людей во всем мире квадратичная формула также является их первым (и, возможно, единственным) опытом довольно сложной формулы, которую они должны запомнить», — пишет Ло.
Эта трудная задача, которую выполняли студенты-математики, насчитывающие примерно четыре тысячелетия, не меньше, возможно, не была полностью необходимой, как это бывает. Конечно, всегда были альтернативы квадратичной формуле, такие как разложение на множители, завершение квадрата или даже разрыв миллиметровой бумаги.
Но квадратичная формула обычно считается наиболее полным и надежным методом решения квадратичных задач, даже если она немного непостижима. Вот как это выглядит:
Эту формулу можно использовать для решения квадратных уравнений стандартной формы, где ax 2 + bx + c = 0.
В сентябре Ло проводил мозговой штурм математики за квадратными уравнениями, когда он натолкнулся на новый, упрощенный способ вывода той же формулы — альтернативный метод, который он описывает в своей статье как «вычислительно эффективный, естественный и легко запоминающийся алгоритм для решения общих квадратных уравнений» .
«Я был ошеломлен», — говорит Ло об открытии. «Как такое может быть, что я никогда не видел этого раньше и никогда не видел этого ни в одном учебнике?»
В новом методе Ло он начинает со стандартного метода попытки разложить квадратичное x² + bx + c на множители как (x -) (x -), что сводится к поиску двух чисел, которые нужно подставить в пробелы с суммой −b. и продукт c. Он использует технику усреднения, которая концентрируется на сумме, в отличие от более распространенного способа сосредоточения внимания на произведении двух чисел, составляющих c, что требует догадок для решения проблем.
«Сумма двух чисел равна 2, когда их среднее значение равно 1.» Ло объясняет на своем сайте.
«Итак, мы можем попытаться найти числа, которые равны 1 плюс некоторая сумма и 1 минус такая же сумма. Все, что нам нужно сделать, это определить, существует ли такая сумма au, что 1 + u и 1 — u работают как два числа, а u может быть равно 0. »
Согласно Ло, действительное значение для u всегда может быть определено с помощью альтернативного квадратичного метода Ло интуитивно понятным способом, что позволяет решить любое квадратное уравнение.
В статье Ло он признает, что «был бы очень удивлен, если бы этот подход полностью ускользнул от человеческих открытий до настоящего времени, учитывая 4000-летнюю историю этой темы», но говорит об альтернативной технике, которая сочетает в себе впервые предложенные шаги. Вавилонскими, греческими и французскими математиками — «определенно не широко преподается и не известно (автор не смог найти доказательств этого в английских источниках)».
Однако, с тех пор как в октябре Ло впервые поделился своей предпечатной статьей с описанием простого доказательства в Интернете, его внимание привлекла исследовательская статья 1989 года, которая является наиболее похожей предыдущей работой, которую он нашел, — в некоторой степени оправдывающей его недоверие. что этот альтернативный метод до сих пор не был найден.
«Другая работа совпадала почти во всех вычислениях с очевидной логической разницей в предположении, что каждый квадратичный фактор может быть разложен на множители, и педагогической разницей в выборе знака», — пояснил Лох в электронном письме ScienceAlert.
Все, что остается решить, — это загадка, почему этот метод не стал более широко известен до этого, поскольку он дает нам, по словам Ло, «восхитительный альтернативный подход к решению квадратных уравнений, который является практичным. для интеграции во все основные учебные программы «.
(Не говоря уже, конечно, о том, что это может просто означать, что никому больше не нужно запоминать квадратичную формулу.)
Мы до сих пор не знаем, как это ускользало от более широкого внимания на протяжении тысячелетий, но если инстинкты Ло верны, математика учебники могут оказаться на грани исторического переписывания — и мы не относимся легкомысленно к открытиям, которые меняют учебники.
«Я хотел как можно шире поделиться им со всем миром, — говорит Ло, — потому что он может демистифицировать сложную часть математики, которая заставляет многих людей думать, что, возможно, математика не для них».«
Этот исследовательский документ доступен на веб-сайте предварительной печати arXiv.org, и вы можете прочитать здесь обобщенное объяснение простого доказательства По-Шен Ло.
Примечание редактора (27 декабря 2019 г.): более ранняя версия этого В статье цитируется устаревшая версия веб-сайта Ло, что приводит к несоответствиям с его объяснением. Сейчас мы исправили ее и приносим извинения за любые непреднамеренные ошибки.
Советы по решению квадратных уравнений
Обновлено 8 декабря 2020 г.
Ли Джонсон
Каждый студент, изучающий алгебру на более высоком уровне, должен научиться решать квадратные уравнения.Это тип полиномиального уравнения, которое включает степень 2, но не выше, и имеет общую форму: ax 2 + bx + c = 0. Вы можете решить это с помощью формулы квадратного уравнения, факторизации или завершения квадрата.
TL; DR (слишком долго; не читал)
Сначала найдите факторизацию для решения уравнения. Если его нет, но коэффициент b делится на 2, заполните квадрат.2 + bx + c = 0
В этом примере a = 1, b = 6 и c = 9. Задача факторизации состоит в том, чтобы найти два числа, которые складываются вместе, чтобы дать число в точке b и умножьте вместе, чтобы получить число на месте c .
Итак, представляя числа как d и e , вы ищете числа, которые удовлетворяют:
d + e = b
Или, в данном случае, b = 6:
d + e = 6
d × e = c
Или, в данном случае, с c = 9:
d × e = 9
Сосредоточьтесь на поиске чисел, которые являются множителями c , а затем сложите их вместе, чтобы узнать, равны ли они b .2 + 6x + 9 \\ \ end {align}
Факторизация эффективно проходит через этот процесс в обратном порядке, но может быть сложно выработать правильный способ разложить квадратное уравнение на множители, и этот метод не идеален для каждого квадратичного уравнения. уравнение по этой причине. Часто приходится угадывать факторизацию, а затем проверять ее.
Проблема в том, что теперь любое из выражений в скобках будет равно нулю, если вы выберете значение x . Если любая скобка равна нулю, все уравнение равно нулю, и вы нашли решение.Посмотрите на последний этап [( x + 3) ( x + 3) = 0], и вы увидите, что скобки обнуляются только тогда, когда x = −3. Однако в большинстве случаев квадратные уравнения имеют два решения.
Факторизация становится еще более сложной задачей, если не равно единице, но сначала лучше сосредоточиться на простых случаях.
Заполнение квадрата для решения уравнения
Заполнение квадрата помогает вам решать квадратные уравнения, которые нелегко разложить на множители.2 = 16
Теперь решите уравнение относительно x . Извлеките квадратный корень из обеих частей, чтобы получить:
x + 4 = \ sqrt {16}
Вычтите 4 с обеих сторон, чтобы получить:
x = \ sqrt {16} — 4
Корень может быть положительным или отрицательное, и взятие отрицательного корня дает:
x = -4 — 4 = -8
Найдите другое решение с положительным корнем:
x = 4 — 4 = 0
Следовательно, единственным ненулевым решением является −8. Для подтверждения сверьте это с исходным выражением.2–4 × 1 × 5}} {2 × 1} \\ & = \ frac {-6 ± \ sqrt {36 — 20}} {2} \\ & = \ frac {-6 ± \ sqrt {16} } {2} \\ & = \ frac {-6 ± 4} {2} \ end {выровнено}
Принятие положительного знака дает:
\ begin {align} x & = \ frac {-6 + 4} {2} \\ & = \ frac {-2} {2} \\ & = -1 \ end {выровнено}
И если принять отрицательный знак, получим:
\ begin {align} x & = \ frac {- 6 — 4} {2} \\ & = \ frac {-10} {2} \\ & = -5 \ end {align}
Какие два решения уравнения.

 к. можно использовать для решения абсолютно всех квадратных уравнений
к. можно использовать для решения абсолютно всех квадратных уравнений

