Содержание
График обратной функции
Свойство симметрии графиков обратных функций
Пусть функция f(x) определена на некотором множестве X, и имеет множество значений Y: . И пусть она имеет на множестве X обратную функцию f -1: . Тогда графики прямой и обратной функций, построенные при значениях их аргументов и , соответственно, симметричны относительно прямой .
Доказательство
Пусть – произвольная точка графика прямой функции , с аргументом, принадлежащим множеству X:
(1) .
Построим точку , симметричную точке относительно прямой , и выразим ее координаты через координаты точки A.
График обратной функции y = f –1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x.
Для этого через точку A проводим прямую, перпендикулярную прямой . Пусть C – точка пересечения этих прямых. Далее, на проведенной прямой, откладываем точку S, симметричную точке A относительно прямой . При этом
;
.
Из точек A и S опустим перпендикуляры на оси координат. Поскольку прямая составляет угол с осями координат, то и перпендикулярная ей прямая AS также составляет угол с осями координат. Тогда и пересекутся в точке D, принадлежащей прямой . При этом углы у оснований треугольников DAC и SDC равны . По этой причине они являются равнобедренными. А поскольку , то они конгруэнтны. Тогда , и, следовательно,
(2) .
В треугольниках и углы при вершинах O и D равны , а при вершинах равны . Поэтому они равнобедренные и подобные. А поскольку они имеют общее основание OD, то они конгруэнтны. Тогда
(3) .
Используя (2) и (3) имеем:
;
.
Итак, мы выразили координаты симметричной точки S через координаты точки A:
(4) ;
(5) .
Поскольку точка принадлежит графику функции f, то ее координаты связаны уравнением:
(1) .
Поскольку, по условию, f имеет обратную функцию, то
.
Подставляя (4) и (5) находим:
.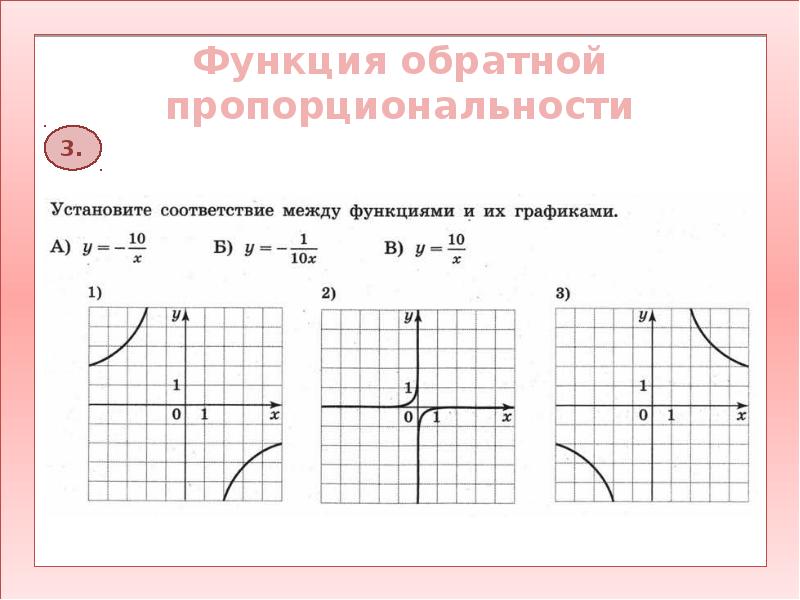
То есть мы получили, что симметричная точка S принадлежит графику обратной функции.
Так как мы выбрали точку A произвольно, то это относится ко всем точкам графика .
Все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику обратной функции .
Далее мы можем поменять и местами. В результате получим, что
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику функции .
Отсюда следует, что графики функций и симметричны относительно прямой .
Свойство доказано.
Примеры графиков обратных функций
Некоторые функции являются непрерывными и строго монотонными на всей области определения. Поэтому они имеют обратные функции, и их графики симметричны относительно прямой . Например, кубическая парабола строго возрастает для всех x. Поэтому она имеет обратную функцию , график которой симметричен графику параболы относительно прямой .
Существуют функции, которые не являются монотонными на всей области определения. Однако можно указать интервал X, на котором такая функция определена, непрерывна и строго монотонна. В этом случае можно выполнить операцию сужения функции на множество X: . То есть рассматривать только значения аргумента, принадлежащие интервалу X. Тогда на этом интервале она будет иметь обратную функцию. В результате графики суженной функции и обратной функции будут симметричны относительно прямой .
Однако можно указать интервал X, на котором такая функция определена, непрерывна и строго монотонна. В этом случае можно выполнить операцию сужения функции на множество X: . То есть рассматривать только значения аргумента, принадлежащие интервалу X. Тогда на этом интервале она будет иметь обратную функцию. В результате графики суженной функции и обратной функции будут симметричны относительно прямой .
Например, квадратичная парабола, , определена и непрерывна для всех x, но не является монотонной. Но она строго возрастает при , то есть на множестве . Тогда сужение параболы имеет обратную функцию . Их графики симметричны относительно прямой .
Тригонометрическая функция также не является монотонной, но она непрерывна и строго возрастает при . Тогда ее сужение имеет обратную функцию . Их графики также симметричны относительно прямой .
Ниже приводятся графики некоторых элементарных функций. Для некоторых из них выполнена операция сужения, и построен график обратной функции.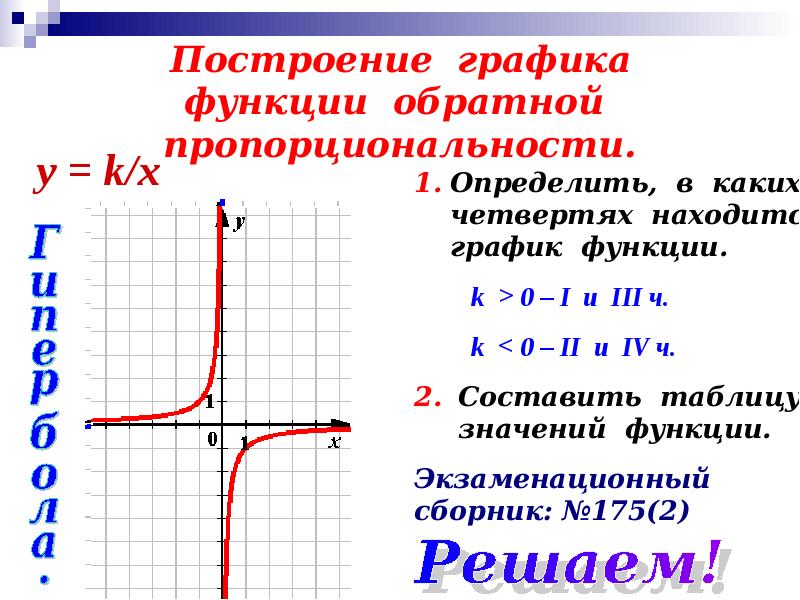
График параболы y = x2 и обратной функции – квадратного корня .
График кубической параболы y = x2 и обратной функции – кубического корня .
График показательной функции с основанием 2, y = 2x и обратной функции – логарифма с основанием 2, y = log2 x.
График экспоненты y = ex и обратной функции – натурального логарифма y = ln x.
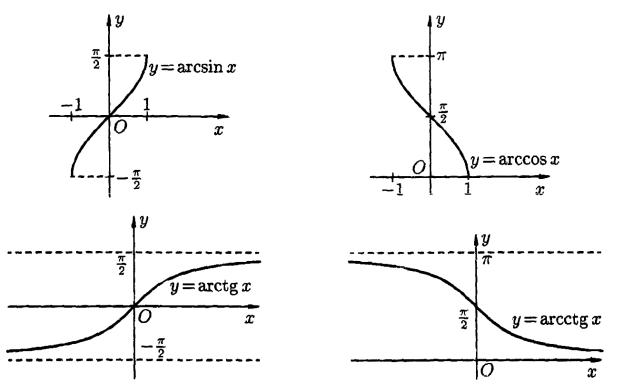
График синуса y = sin x и обратной функции – арксинуса y = arcsin x.
График косинуса y = cos x и обратной функции – арккосинуса y = arccos x.
График тангенса y = tg x и обратной функции – арктангенса y = arctg x.
График котангенса y = ctg x и обратной функции – арккотангенса y = arcctg x.
Автор: Олег Одинцов. Опубликовано:
3.1.4 Обратная функция. График обратной функции
Видеоурок 1: Обратные функции. Введение
Введение
Видеоурок 2: Обратные функции (Пример 1)
Видеоурок 3: Обратные функции (Пример 2)
Лекция: Обратная функция. График обратной функции
Рассмотрим некоторую функцию у = f(x), которая возрастает или же убывает, то есть является монотонной. Для нее будет иметься некоторая функция х = g(y), которая будет называться обратной функцией.
Что такое обратная функция?
Давайте рассмотрим некое уравнение: соs(х) = 1/2.
Решением данного уравнения будет: x = ±arccos(1/2) + 2πk, k ϵ Z.
Косинус и арккосинус — это наглядный пример обратных функций.
Давайте рассмотрим обратные функции на примере.
Например, мы имеем функцию у = 3х + 2.
Для данной функции и область определения, и область значения может принимать все множество действительных чисел. Более того, данная функция является монотонно возрастающей на всем участке.
А теперь давайте из данной зависимости выразим «х». В результате этого получим:
х = у/3 — 2/3.
Полученная зависимость будет называться обратной функцией для той, что давалась изначально, только теперь мы получили зависимость «х» от «у».
Если записать второе уравнение в привычном нам виде, то есть заменить «х» на «у» и наоборот, получим:
у = х/3 — 2/3.
На графике изобразим первоначальную функцию, обратную ей, и функцию у = х.
Можно заметить, что обратные функции симметричны относительно прямой у = х.
Свойства взаимообратных функций
1.
2. Первое свойство дает понять, что область определения второй функции такая же, как и область значения первой.
3. Графики любых взаимообратных функций всегда будут симметричны относительно биссектрисы первой и третьей четверти.
4. Обратные функции имеют одинаковую монотонность.
Графики основных обратных функций
1. Степенная функция
Ниже представлены графики, полученные для положительного показателя степени и для отрицательного показателя степени:
2. Обратные логарифмические функции и их графики:
Обратные логарифмические функции и их графики:
Взаимно обратные функции: алгоритм вывода формулы, примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X \xrightarrow{f} Y$.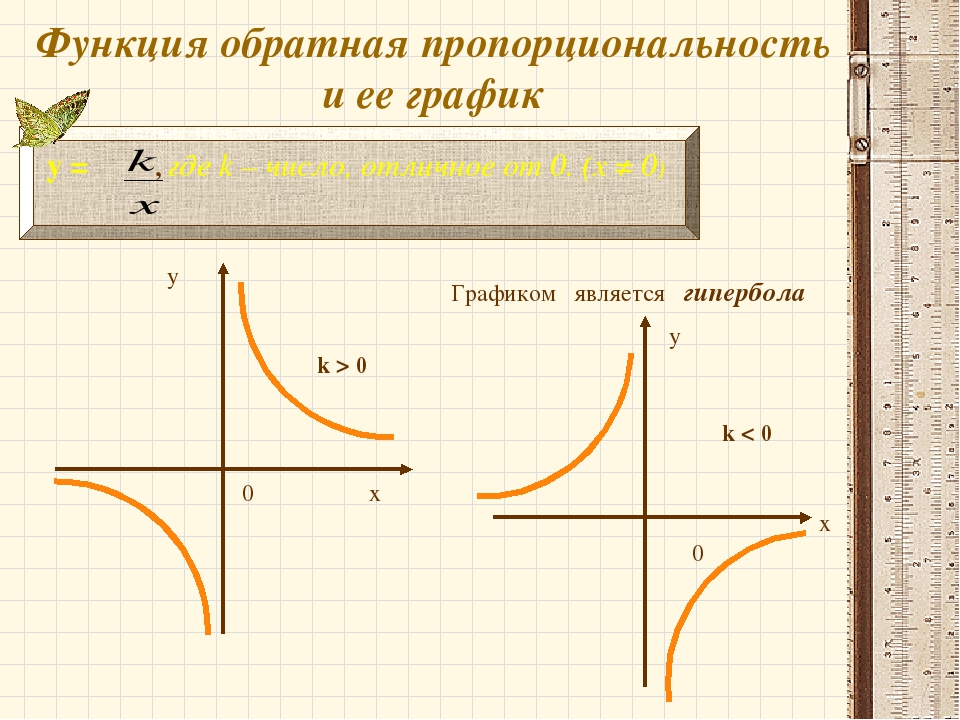 {-1}$ называют обратной функцией к f.
{-1}$ называют обратной функцией к f.
Например: аналитическое выражение для функции $X \xrightarrow{f} Y$, заданной таблицей $y = f(x) = \frac{x}{2}$. Обратное соответствие $Y \xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X \xrightarrow{f} Y$ и $Y \xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = \frac{x}{2}$
Шаг 1. 2+1$
2+1$
Шаг 2. Находим y из полученной формулы: $y = \sqrt{\frac{x-1}{2}}$ — искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
Задайте формулой функцию, обратную данной.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = \frac{x+4}{5}$ — искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = \frac{-x+2}{3}$ — искомая обратная функция
в) y = 4x+1, где $-1 \le x \le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = \frac{x-1}{4}$
Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac{x-1}{4} \le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$
Итак, искомая обратная функция: $y = \frac{x-1}{4}$, где -3 $\le x \le 21$
г) $y=- \frac{1}{2} x+7$, где $2 \le x \le 9$
Меняем аргумент и значение: $x=-\frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция
Пример 2. 2+3$
2+3$
Область определения: $x \ge 1$
Область значений: $y \ge 3$
Презентация на тему: «Обратные функции и их графики»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Обратные функции и их графики
Номер слайда 2
Номер слайда 3
Вопросы: Какая функция называется обратимой?Любая ли функция обратима?Какая функция называется обратной данной?Как связаны область определения и множество значений функции и обратной ей функции?Если функция задана аналитически, как задать формулой обратную функцию?Если функция задана графически, как построить график обратной ей функции?
Номер слайда 4
Обратимая и обратная функции.
Номер слайда 5
Какая из функций обратима?3) y = 2x + 5 4) y = -x2 + 7
Номер слайда 6
Алгоритм нахождения обратной функции Убедиться, что функция монотонна.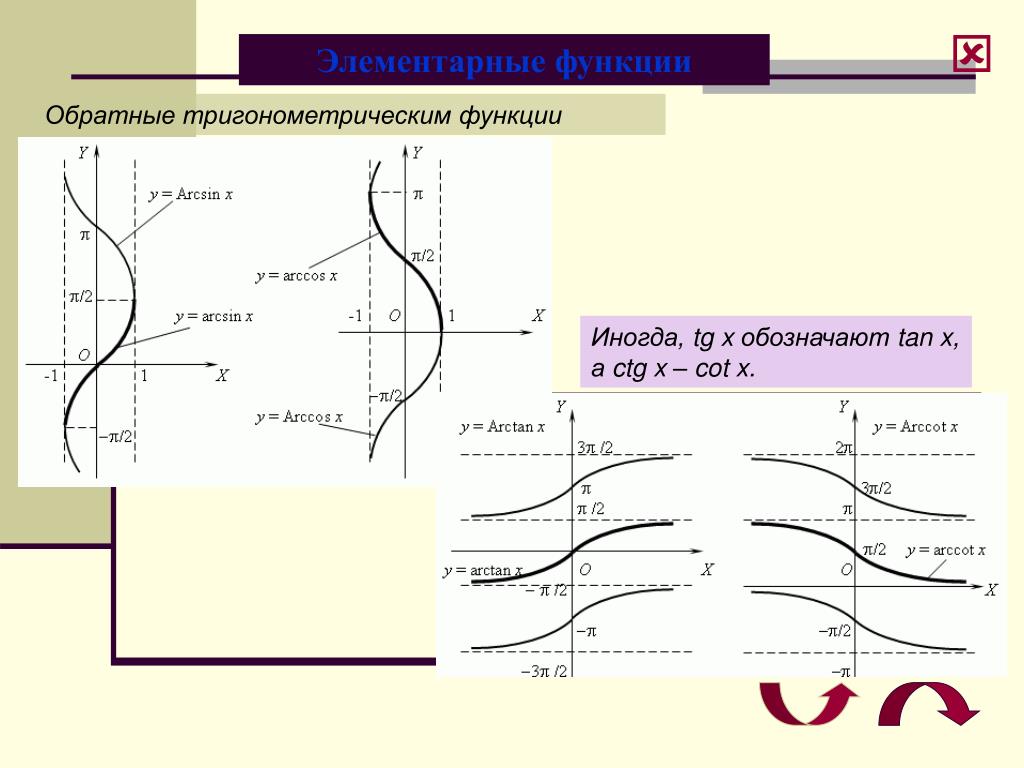 Выразить переменную х через у. Переобозначить переменные. Вместо х=f -1(y) пишут y=f -1(x)
Выразить переменную х через у. Переобозначить переменные. Вместо х=f -1(y) пишут y=f -1(x)
Номер слайда 7
Обратные функции их свойства и графики. Обратные функции – определение и свойства. Доказательство леммы о взаимной монотонности прямой и обратной функций
3
Графики взаимно обратных функций Теорема. Пусть f и g взаимно обратные функции. Графики функций y=f(x) и x=g(y) симметричны друг другу относительно биссектрисы угла хоу. Доказательство. По определению взаимно обратных функций формулы y=f(x) и x=g(y) выражают одну и ту же зависимость между переменными х и у, а значит, эта зависимость изображается одним и тем же графиком некоторой кривой С. Кривая С является графиком функции y=f(x). Возьмем произвольную точку Р(a; b) С. Это означает, что b=f(a) и одновременно a=g(b). Построим точку Q, симметричную точке Р относительно биссектрисы угла хоу. Точка Q будет иметь координаты (b; a). Так как a=g(b), то точка Q принадлежит графику функции y=g(x): действительно, при х=b значение у=а равно g(x). Таким образом, все точки, симметричные точкам кривой С относительно указанной прямой, лежат на графике функции у=g(x). Примеры функций графики которых взаимно обратны: у=е х и у=lnx; y=x 2 (x 0) и y= ; у=2x 4 и у= +2.
Доказательство. По определению взаимно обратных функций формулы y=f(x) и x=g(y) выражают одну и ту же зависимость между переменными х и у, а значит, эта зависимость изображается одним и тем же графиком некоторой кривой С. Кривая С является графиком функции y=f(x). Возьмем произвольную точку Р(a; b) С. Это означает, что b=f(a) и одновременно a=g(b). Построим точку Q, симметричную точке Р относительно биссектрисы угла хоу. Точка Q будет иметь координаты (b; a). Так как a=g(b), то точка Q принадлежит графику функции y=g(x): действительно, при х=b значение у=а равно g(x). Таким образом, все точки, симметричные точкам кривой С относительно указанной прямой, лежат на графике функции у=g(x). Примеры функций графики которых взаимно обратны: у=е х и у=lnx; y=x 2 (x 0) и y= ; у=2x 4 и у= +2.
4
Производная обратной функции Пусть f и g взаимно обратные функции. Графики функций y=f(x) и x=g(y) симметричны друг другу относительно биссектрисы угла хоу. Возьмем точку х=а и вычислим значение одной из функций в этой точке: f(a)=b.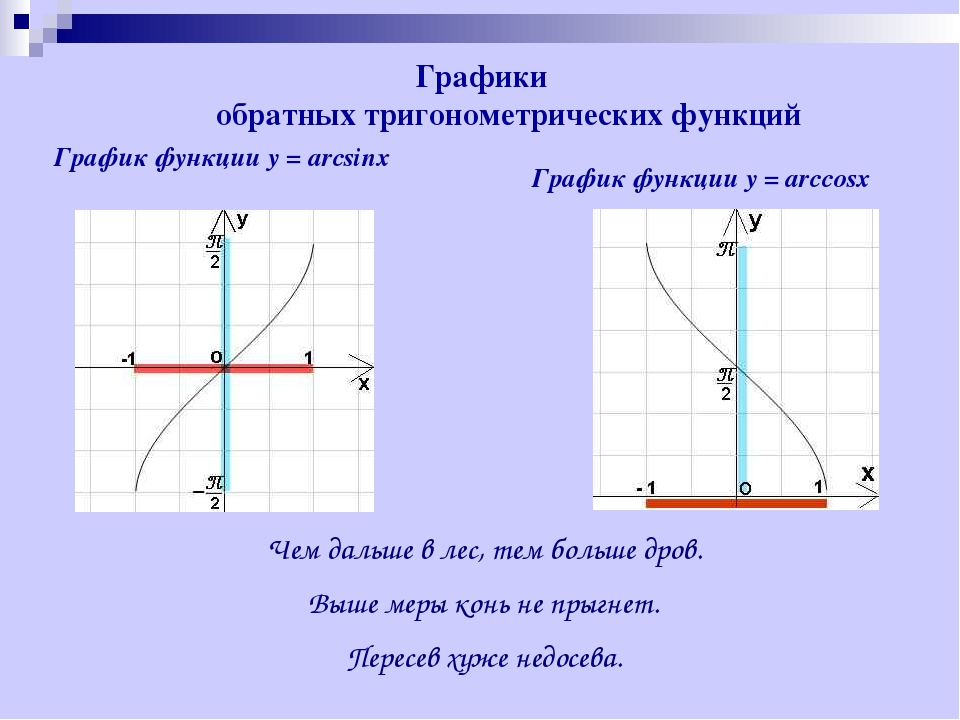 Тогда по определению обратной функции g(b)=a. Точки (a; f(a))=(a; b) и (b; g(b))=(b; a) симметричны относительно прямой l. Так как кривые симметричны, то и касательные к ним симметричны относительно прямой l. Из симметрии угол одной из прямых с осью х равен углу другой прямой с осью у. Если прямая образует с осью х угол α, то ее угловой коэффициент равен k 1 =tgα; тогда вторая прямая имеет угловой коэффициент k 2 =tg(α)=ctgα=. Таким образом, угловые коэффициенты прямых, симметричных относительно прямой l, взаимно обратны, т.е. k 2 =, или k 1 k 2 =1. Переходя к производным и учитывая, что угловой коэффициент касательной является значением производной в точке касания делаем вывод: Значения производных взаимно обратных функций в соответствующих точках взаимно обратны, т.е.. Пример 1. Докажите, что функция f(x)=x 3, обратима. Решение. y=f(x)=x 3. Обратной функцией будет функция y=g(x)=. Найдем производную функции g:. Т.е. =. Задание 1. Докажите, что функция, заданная формулой, обратима 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Тогда по определению обратной функции g(b)=a. Точки (a; f(a))=(a; b) и (b; g(b))=(b; a) симметричны относительно прямой l. Так как кривые симметричны, то и касательные к ним симметричны относительно прямой l. Из симметрии угол одной из прямых с осью х равен углу другой прямой с осью у. Если прямая образует с осью х угол α, то ее угловой коэффициент равен k 1 =tgα; тогда вторая прямая имеет угловой коэффициент k 2 =tg(α)=ctgα=. Таким образом, угловые коэффициенты прямых, симметричных относительно прямой l, взаимно обратны, т.е. k 2 =, или k 1 k 2 =1. Переходя к производным и учитывая, что угловой коэффициент касательной является значением производной в точке касания делаем вывод: Значения производных взаимно обратных функций в соответствующих точках взаимно обратны, т.е.. Пример 1. Докажите, что функция f(x)=x 3, обратима. Решение. y=f(x)=x 3. Обратной функцией будет функция y=g(x)=. Найдем производную функции g:. Т.е. =. Задание 1. Докажите, что функция, заданная формулой, обратима 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
5
Пример 2. Найдите функцию, обратную функции у=2х+1. Решение. Функция у=2х+1 возрастающая, следовательно, она имеет обратную. Выразим х через у: получим.. Перейдя к общепринятым обозначениям, Ответ: Задание 2. Найдите обратные функции для данных функций 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Найдите функцию, обратную функции у=2х+1. Решение. Функция у=2х+1 возрастающая, следовательно, она имеет обратную. Выразим х через у: получим.. Перейдя к общепринятым обозначениям, Ответ: Задание 2. Найдите обратные функции для данных функций 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Лекция 20 ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ. Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то () (). Например, () = > = = (), так
Что будем изучать: Урок на тему: Исследование функции на монотонность. Убывающие и возрастающие функции. Связь производной и монотонности функции. Две важные теоремы о монотонности. Примеры. Ребята, мы
Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
6 Задачи, приводящие к понятию производной Пусть материальная точка движется по прямой в одном направлении по закону s f (t), где t — время, а s — путь, проходимый точкой за время t Отметим некоторый момент
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Геометрический смысл производной Рассмотрим график функции y=f(x) и касательную в точке P 0 (x 0 ; f(x 0)). Найдем угловой коэффициент касательной к графику в этой точке. Угол наклона касательной Р 0
Квадратичная функция в различных задачах Дихтярь МБ Основные сведения Квадратичной функцией (квадратным трёхчленом) называется функция вида у ax bx c, где abc, заданные числа и Квадратичные функции у
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Пусть имеем функцию определенную на множестве X и пусть точка X — внутренняя точка те точка для которой существует окрестность X Возьмем любую точку и обозначим через называется
Лекция 5 Производные основных элементарных функций Аннотация: Даются физическая и геометрическая интерпретации производной функции одной переменной Рассматриваются примеры дифференцирования функции и правила
1 СА Лавренченко Лекция 12 Обратные функции 1 Понятие обратной функции Определение 11 Функция называется взаимно-однозначной, если она не принимает никакое значение более одного раза, те из следует при
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Глава 5 Исследование функций с помощью формулы Тейлора Локальный экстремум функции Определение Функция = f (достигает в точке с локального максимума (минимума), если можно указать такое δ >, что ее приращение
МОДУЛЬ «Применение непрерывности и производной. Применение производной к исследованию функций». Применение непрерывности.. Метод интервалов.. Касательная к графику. Формула Лагранжа. 4. Применение производной
Применение производной к исследованию функций». Применение непрерывности.. Метод интервалов.. Касательная к графику. Формула Лагранжа. 4. Применение производной
Лекция 9. Производные и дифференциалы высших порядков, их свойства. Точки экстремума функции. Теоремы Ферма и Ролля. Пусть функция y дифференцируема на некотором отрезке [b]. В таком случае ее производная
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
Глава 1. Пределы и непрерывность 1. Числовые множества 1 0. Действительные числа Из школьной математики Вы знаете натуральные N целые Z рациональные Q и действительные R числа Натуральные и целые числа
Лекция 19 ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x)
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
Тема 8.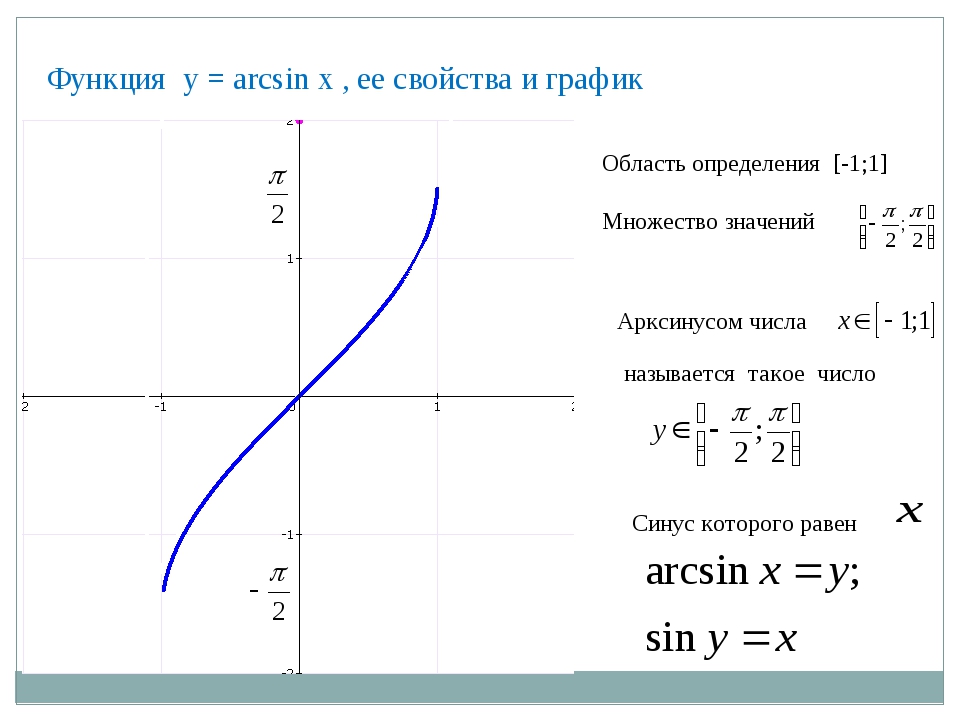 Показательная и логарифмическая функции. 1. Показательная функция, ее график и свойства В практике часто используются функции y=2 x,y=10 x,y=(1 2x),y=(0,1) x и т. д., т. е. функция вида y=a x,
Показательная и логарифмическая функции. 1. Показательная функция, ее график и свойства В практике часто используются функции y=2 x,y=10 x,y=(1 2x),y=(0,1) x и т. д., т. е. функция вида y=a x,
44 Пример Найти полную производную сложной функции = sin v cos w где v = ln + 1 w= 1 По формуле (9) d v w v w = v w d sin cos + cos cos + 1 sin sin 1 Найдем теперь полный дифференциал сложной функции f
Задания для самостоятельного решения. Найдите область определения функции 6x. Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через точку М (;) графика функции. Найдите тангенс угла
Тема Числовая функция, ее свойства и график Понятие числовой функции Область определения и множество значений функции Пусть задано числовое множество X Правило, сопоставляющее каждому числу X единственное
Лекция 23 ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКА ФУНКЦИИ ТОЧКИ ПЕРЕГИБА График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале График
Тема Теория пределов Практическое занятие Числовые последовательности Определение числовой последовательности Ограниченные и неограниченные последовательности Монотонные последовательности Бесконечно малые
Числовые функции и числовые последовательности Д. В. Лыткина АЭС, I семестр Д. В. Лыткина (СибГУТИ) математический анализ АЭС, I семестр 1 / 35 Содержание 1 Числовая функция Понятие функции Числовые функции.
В. Лыткина АЭС, I семестр Д. В. Лыткина (СибГУТИ) математический анализ АЭС, I семестр 1 / 35 Содержание 1 Числовая функция Понятие функции Числовые функции.
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА класс (профиль) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Â. À. Äàëèíãåð ÌÀÒÅÌÀÒÈÊÀ: ÎÁÐÀÒÍÛÅ ÒÐÈÃÎÍÎÌÅÒÐÈ ÅÑÊÈÅ ÔÓÍÊÖÈÈ. ÐÅØÅÍÈÅ ÇÀÄÀ УЧЕБНОЕ ПОСОБИЕ ДЛЯ СПО -е издание, исправленное и дополненное Ðåêîìåíäîâàíî Ó åáíî-ìåòîäè åñêèì îòäåëîì ñðåäíåãî ïðîôåññèîíàëüíîãî
А.В. Землянко Математика. Алгебра и начала анализа Воронеж СОДЕРЖАНИЕ ТЕМА 1. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ… 6 1.1. Числовая функция… 6 1.2. График функции… 9 1.3. Преобразование графиков функции…
Тема. Функция. Способы задания. Неявная функция. Обратная функция. Классификация функций Элементы теории множеств. Основные понятия Одним из основных понятий современной математики является понятие множества.
Пусть задано числовое множество D R. Если каждому числу x D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x D. Множество D, называется
Функции нескольких переменных 11. Определение функции нескольких переменных. Предел и непрерывность ФНП 1. Определение функции нескольких переменных ОПРЕДЕЛЕНИЕ. Пусть X = { 1 n i X i R } U R. Функция
МАТЕМАТИКА ДЛЯ ВСЕХ Ю.Л.Калиновский Contents 1 Графики функций. Часть I……………………………… 5 1.1 Введение 5 1.1.1 Понятие множества………………………………………. 5 1.1.
Практическая работа 6 Тема: «Полное исследование функций. Построение графиков» Цель работы: научиться исследовать функции по общей схеме и строить графики. В результате выполнения работы студент должен:
Глава 8 Функции и графики Переменные и зависимости между ними. Две величины и называются прямо пропорциональными, если их отношение постоянно, т.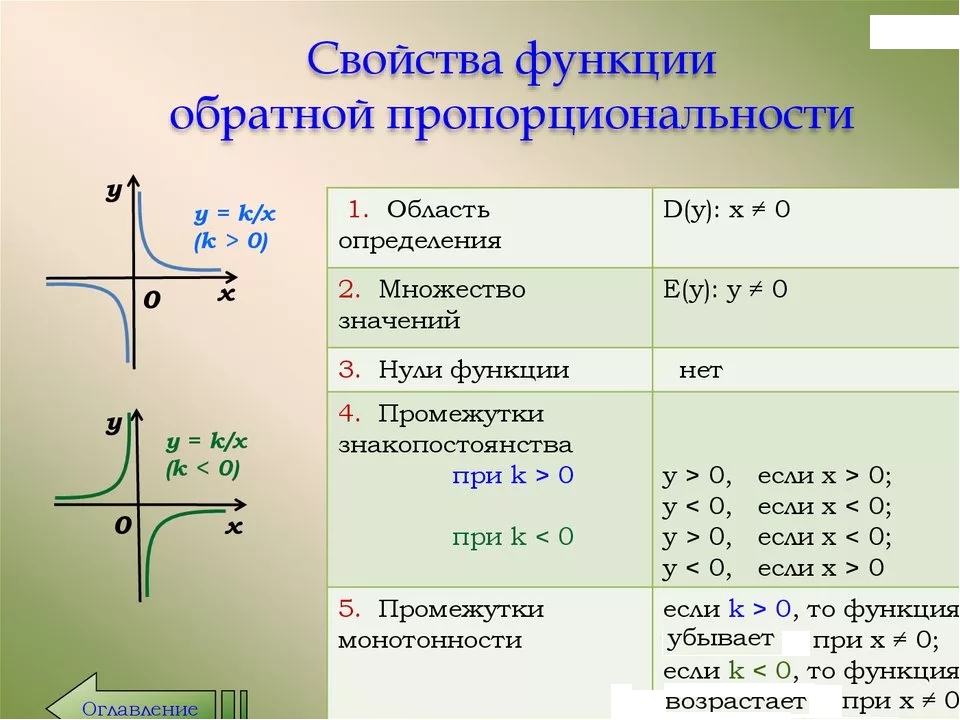 е. если =, где постоянное число, не меняющееся с изменением
е. если =, где постоянное число, не меняющееся с изменением
ЛЕКЦИЯ 2. Операции с подпространствами, число базисов число базисов и число подпространств размерности k. Основные результаты Лекции 2. 1) U V, U + V, dim(u + V). 2) Подсчет числа плоскостей в F 4 2.
Вопрос 5. Функция, способы задания. Примеры элементарных функций и их графики. Пусть даны два произвольных множества Х и Y. Функция это правило, по которому каждому элемента из множества X можно найти
Лекция 4 ЧИСЛОВЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ Понятие функции Способы задания функции Основные свойства функций Сложная функция 4 Обратная функция Понятие функции Способы задания функции Пусть D
Лекции Глава Функции нескольких переменных Основные понятия Некоторые функции многих переменных хорошо знакомы Приведем несколько примеров Для вычисления площади треугольника известна формула Герона S
Непрерывность функций Непрерывность функции в точке Односторонние пределы Определение Число A называется пределом функции f(x) слева при стремлении x к a, если для любого числа существует такое число
Научно-исследовательская работа Математика «Применение экстремальных свойств функции для решения уравнений» Выполнила: Гудкова Елена обучающаяся 11 класса «Г» МБОУ СОШ «Аннинский Лицей» п. г.т. Анна Руководитель:
г.т. Анна Руководитель:
Федеральное агентство по образованию —— САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АИ Сурыгин ЕФ Изотова ОА Новикова ТА Чайкина МАТЕМАТИКА Элементарные функции и их графики Учебное
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести
Функция Понятие функции Способы задания функции Характеристики функции Обратная функция Предел функции Предел функции в точке Односторонние пределы Предел функции при x Бесконечно большая функция 4 Лекция
Раздел Дифференциальное исчисление функции одной и нескольких переменных Функция действительного аргумента Действительные числа Целые положительные числа называются натуральными Добавим к натуральным
Сергей А Беляев стр 1 Математический минимум Часть 1 Теоретическая 1 Верно ли определение Наименьшим общим кратным двух целых чисел называется наименьшее число, которое делится на каждое из заданных чисел
Раздел 2 Теория пределов Тема Числовые последовательности Определение числовой последовательности 2 Ограниченные и неограниченные последовательности 3 Монотонные последовательности 4 Бесконечно малые и
Дифференцирование неявно заданной функции Рассмотрим функцию (,) = C (C = const) Это уравнение задает неявную функцию () Предположим, мы решили это уравнение и нашли явное выражение = () Теперь можно
Тестовые задания для подготовки к ЭКЗАМЕНУ по дисциплине «Математика» для студентов заочного отделения Производной функции y=f() называется: f A) B) f C) f f Если в некоторой окрестности точки функция
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ В результате измерения физических величин (время, площадь, объем, масса, скорость и т. д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь
д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь
Математический анализ Раздел: Введение в анализ Тема: Понятие функции (основные определения, классификация, основные характеристики поведения) Лектор Рожкова С.В. 2012 г. Литература Пискунов Н.С. Дифференциальное
Занятие 7 Теоремы о среднем. Правило Лопиталя 7. Теоремы о среднем Теоремы о среднем это три теоремы: Ролля, Лагранжа и Коши, каждая следующая из которых обобщает предыдущую. Эти теоремы называют также
Лекция подготовлена доц Мусиной МВ Непрерывность функции Пусть функция y = f(x) определена в точке x и в некоторой окрестности этой точки Функция y = f(x) называется непрерывной в точке x, если существует
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Понятие производной, ее геометрический и физический смысл Задачи, приводящие к понятию производной Определение Касательной S к линии y f (x) в точке A x ; f (
13. Частные производные высших порядков Пусть = имеет и определенные на D O. Функции и называют также частными производными первого порядка функции или первыми частными производными функции. и в общем
Функции и называют также частными производными первого порядка функции или первыми частными производными функции. и в общем
Министерство образования Республики Беларусь УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯНКИ КУПАЛЫ» Ю.Ю. Гнездовский, В. Н. Горбузов, П.Ф. Проневич ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
Лекция Глава Множества и операции над ними Понятие множества Понятие множество относится к наиболее первичным понятиям математики не определяемым через более простые Под множеством понимают совокупность
Лекция 8 Дифференцирование сложной функции Рассмотрим сложную функцию t t t f где ϕ t t t t t t t f t t t t t t t t t Теорема Пусть функции дифференцируемы в некоторой точке N t t t а функция f дифференцируема
Лекция 3 Экстремум функции нескольких переменных Пусть функция нескольких переменных u = f (x, x) определена в области D, и точка x (x, x) = принадлежит данной области Функция u = f (x, x) имеет
Вопрос. Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных
2.2.7. Применение дифференциала к приближенным вычислениям. Дифференциал функции y = зависит от х и является главной частью приращения х. Также можно воспользоваться формулой: dy d Тогда абсолютная погрешность:
Глава 6 Дифференциальное исчисление функции одной переменной Задачи приводящие к понятию производной Задача о скорости неравномерного прямолинейного движения S — закон неравномерного прямолинейного движения
Прямая на плоскости Общее уравнение прямой. Прежде чем вводить общее уравнение прямой на плоскости введем общее определение линии. Определение. Уравнение вида F(x,y)=0 (1) называется уравнением линии L
Определение. Уравнение вида F(x,y)=0 (1) называется уравнением линии L
КОМИТЕТ ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЛЕНИНГРАДСКОЙ ОБЛАСТИ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ЛЕНИНГРАДСКОЙ ОБЛАСТИ «ВОЛХОВСКИЙ АЛЮМИНИЕВЫЙ КОЛЛЕДЖ» Методическое
Производная и правила дифференцирования Пусть функция y = f получила приращение y f 0 f 0 соответствующее приращению аргумента 0 Определение Если существует предел отношения приращения функции y к вызвавшему
ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Математическое моделирование» À.Í. Êàíàòíèêîâ, À.Ï. Êðèùåíêî
ОБРАТНЫЕ ФУНКЦИИ Задачи, в которых участвуют обратные функции, встречаются в самых различных разделах математики и в ее приложениях Важную область математики составляют обратные задачи в теории интегральных
Система задач по теме «Уравнение касательной» Определите знак углового коэффициента касательной, проведенной к графику функции y f (), в точках с абсциссами a, b, c а) б) Укажите точки, в которых производная
Взаимно обратные функции.
Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения, область значений этой функции, тогда на интервале определена непрерывная строго монотонная функция с областью значений, которая
является обратной для
.
Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.
Функции
f
и
g
называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений. Решения как раз и записываются через обратные функции.
Рассмотрим
несколько примеров нахождения обратных функций
.
Начнём с линейных взаимно обратных функций.
Найти функцию, обратную для.
Эта функция линейная, её графиком является прямая. Значит, функция монотонна на всей области определения. Поэтому, искать обратную ей функцию будем на всей области определения.
Значит, функция монотонна на всей области определения. Поэтому, искать обратную ей функцию будем на всей области определения.
.
Выразим
x
через
y
(другими словами, решим уравнение относительно
x
).
— это и есть обратная функция, правда здесь
y
– аргумент, а
x
– функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы
x
и
y
, будем писать
.
Таким образом, и — взаимно обратные функции.
Приведём графическую иллюстрацию взаимно обратных линейных функций.
Очевидно, что графики симметричны относительно прямой
(биссектрисы первой и третьей четверти). Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
Найти функцию, обратную.
Эта функция квадратная, графиком является парабола с вершиной в точке.
.
Функция возрастает при и убывает при. Значит, искать обратную функцию для заданной можно на одном из двух промежутков.
Пусть, тогда, и, меняя местами х и у, получаем обратную функцию на заданном промежутке: .
Найти функцию, обратную.
Эта функция кубическая, графиком является кубическая парабола с вершиной в точке.
.
Функция возрастает при. Значит, искать обратную функцию для заданной можно на всей области определения.
, и, меняя местами х и у, получаем обратную функцию.
Проиллюстрируем это на графике.
Перечислим
свойства взаимно обратных функций
и.
и.
Из первого свойства видно, что область определения функции совпадает с областью значений функции и наоборот.
Графики взаимно обратных функций симметричны относительно прямой.
Если возрастает, то и возрастает, если убывает, то и убывает.
Найдите область значений каждой из взаимно обратных функций и, если указаны их области определения:
Найдите функцию, обратную данной. Постройте на одной системе координат графики этих взаимно обратных функций:
Является ли данная функция обратной по отношению к самой себе:
Задайте функцию, обратную данной и постройте её график:
Для заданной функции найдите обратную функцию:
Для заданной функции найдите обратную и постройте графики заданной и обратной функции:
Выясните, существует ли обратная функция для заданной функции. Если да, то задайте обратную функцию аналитически, постройте график заданной и обратной функции:
Найдите область определения и область значений функции, обратной для функции, если:
Являются ли функции взаимно обратными, если:
Соответственные выражения, которые обращаются друг в друга. Чтобы разобраться в том, что это означает, стоит рассмотреть конкретный пример. Допустим, имеем y = cos(x). Если взять от аргумента косинус, то можно найти значение y. Очевидно, для этого необходимо иметь икс. Но что если изначально дан игрек? Именно тут дело доходит до сути вопроса. Для решения задачи требуется использование обратной функции. В нашем случае это арккосинус.
Чтобы разобраться в том, что это означает, стоит рассмотреть конкретный пример. Допустим, имеем y = cos(x). Если взять от аргумента косинус, то можно найти значение y. Очевидно, для этого необходимо иметь икс. Но что если изначально дан игрек? Именно тут дело доходит до сути вопроса. Для решения задачи требуется использование обратной функции. В нашем случае это арккосинус.
После всех преобразований получим: x = arccos(y).
То есть, чтобы найти функцию, обратную данной, достаточно просто выразить из нее аргумент. Но это работает только при условии, если полученный результат будет иметь единственное значение (об этом дальше).
В общем виде можно записать этот факт так: f(x) = y, g(y) = x.
Определение
Пусть f — функция, областью определения которой является множество X, а областью значений — множество Y. Тогда, если существует g, чьи области выполняют противоположные задачи, то f является обратимой.
Кроме того, в таком случае g — единственна, что означает, что существует ровно одна функция, удовлетворяющая этому свойству (не более, не менее). Тогда ее называют обратной функцией, и на письме обозначают так: g(x) = f -1 (x).
Тогда ее называют обратной функцией, и на письме обозначают так: g(x) = f -1 (x).
Другими словами, их можно рассматривать как двоичное отношение. Обратимость имеет место быть только тогда, когда одному элементу множества соответствует одно значение из другого.
Не всегда существует обратная функция. Для этого каждый элемент y є Y должен соответствовать не более чем одному x є X. Тогда f называется взаимно-однозначной или инъекцией. Если f -1 принадлежит Y, то каждый элемент этого множества должен соответствовать некоторому x ∈ X. Функции с таким свойством называются сюръекциями. Оно выполняется по определению, если Y — изображение f, но это не всегда так. Чтобы быть обратной, функция должна быть как инъекцией, так и сюръекцией. Такие выражения называются биекциями.
Пример: квадратные и корневые функции
Функция определена на }
Взаимно обратные функции, их графики.
Взаимно обратные функции.
Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения , область значений этой функции , тогда на интервале определена непрерывная строго монотонная функция с областью значений , которая является обратной для .
Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений . Решения как раз и записываются через обратные функции.
Рассмотрим несколько примеров нахождения обратных функций.
Начнём с линейных взаимно обратных функций.
Найти функцию, обратную для .

Эта функция линейная, её графиком является прямая. Значит, функция монотонна на всей области определения. Поэтому, искать обратную ей функцию будем на всей области определения.
.
Выразим x через y (другими словами, решим уравнение относительно x).
— это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать .
Таким образом, и — взаимно обратные функции.
Приведём графическую иллюстрацию взаимно обратных линейных функций.
Очевидно, что графики симметричны относительно прямой (биссектрисы первой и третьей четверти). Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
Найти функцию, обратную .
Эта функция квадратная, графиком является парабола с вершиной в точке .
.
Функция возрастает при и убывает при . Значит, искать обратную функцию для заданной можно на одном из двух промежутков.
Пусть , тогда , и, меняя местами х и у, получаем обратную функцию на заданном промежутке: .
Проиллюстрируем это на графике.
Найти функцию, обратную .
Эта функция кубическая, графиком является кубическая парабола с вершиной в точке .
.
Функция возрастает при . Значит, искать обратную функцию для заданной можно на всей области определения.
, и, меняя местами х и у, получаем обратную функцию .
Проиллюстрируем это на графике.
Перечислим свойства взаимно обратных функций и .
и .
Из первого свойства видно, что область определения функции совпадает с областью значений функции и наоборот.
Графики взаимно обратных функций симметричны относительно прямой .
Если возрастает, то и возрастает, если убывает, то и убывает.
Для заданной функции найдите обратную функцию:
Для заданной функции найдите обратную и постройте графики заданной и обратной функции: Выясните, существует ли обратная функция для заданной функции. Если да, то задайте обратную функцию аналитически, постройте график заданной и обратной функции: Найдите область определения и область значений функции , обратной для функции , если:
Найдите область значений каждой из взаимно обратных функций и , если указаны их области определения:
Являются ли функции взаимно обратными, если:
Найдите функцию, обратную данной.
 Постройте на одной системе координат графики этих взаимно обратных функций:
Постройте на одной системе координат графики этих взаимно обратных функций:Является ли данная функция обратной по отношению к самой себе: Задайте функцию, обратную данной и постройте её график:
Задайте функцию, обратную данной и постройте её график:
Рассмотрите данную функцию на каждом из указанных промежутков. Если она на этом промежутке имеет обратную функцию, то задайте её аналитически, укажите её область определения и область значений, постройте её график.
на
на
на
на
на
на
на
на
на
на
на
на
на
на
на
на
На каждом из указанных промежутков найдите, если это возможно, функцию, обратную данной:
на ; на на ;
на ; на на ;
на ; на на ;
на ; на на ;
Даны взаимно обратные функции и .

. Решите уравнения:
. Решите уравнения:
. Решите уравнения:
. Решите уравнения:
Постройте график функции и определите, существует ли для неё обратная функция. Если да, то на том же чертеже постройте график обратной функции и задайте её аналитически.
Дана функция , график которой изображён на рисунке. Постройте график обратной функции и найдите области определения и области значений обоих функций.
Понятие об обратной функции: график функции и теорема
Мы уже сталкивались с задачей, когда по заданной функции f и заданному значению её аргумента необходимо было вычислить значение функции в этой точке. Но иногда приходится сталкиваться с обратной задачей: найти по известной функции f и её некоторому значению y значение аргумента, в котором функция принимает данное значение y.
Функция, которая, принимает каждое свое значение в единственной точке своей области определения, называется обратимой функцией. Например, линейная функция будет являться обратимой функцией. А квадратичная функция или функция синус не будет являться обратимыми функциями. Так как одно и то же значение функция может принимать при различных аргументах.
Обратная функция
Положим, что f есть некоторая произвольная обратимая функция. Каждому числу из области её значений y0, соответствует лишь одно число из области определения x0, такое что f(x0) = y0.
Если теперь мы каждому значению х0 поставим в соответствие значение y0, то получим уже новую функцию. Например, для линейной функции f(x) = k * x + b функция g(x) = (x — b)/k будет являться обратной.
Если некоторая функция g в каждой точке х области значений обратимой функции f принимает значение у такое, что f(y) = x, то говорят, что функция g – есть обратная функция к f.
Если у нас будет задан график некоторой обратимой функции f, то для того чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции f и обратной к ней функции g будут симметричны относительно прямой, заданной уравнением y = x.
Если функция g является обратной к функции f, то функция g будет являться обратимой функцией. А функция f будет обратной к функции g. Обычно говорят, что две функции f и g взаимно обратные друг к другу.
На следующем рисунке представлены графики функций f и g взаимно обратных друг к другу.
Выведем следующую теорему: если функция f возрастает (или убывает) на некотором промежутке A, то она обратима. Обратная к а функция g, определенная в области значений функции f, также является возрастающей (или соответственно убывающей) функцией. Данная теорема называется теоремой об обратной функции.
Нужна помощь в учебе?
Предыдущая тема: Логарифмическая функция: основные свойства и графики
Следующая тема:   Производная и первообразная показательной функции: число е и примеры
{2} [/ latex] ограничен доменом [latex] \ left [0, \ infty \ right) [/ latex], в котором эта функция взаимно однозначно, и построим график, как на рисунке 7. {- 1} \ left (x \ right) = \ sqrt {x} [/ latex].{-1} \ left (x \ right) [/ latex] — это график [латекса] f \ left (x \ right) [/ latex], отраженного относительно диагональной линии [латекс] y = x [/ latex], которую мы назовем идентификационной линией, показанной на рисунке 8.
{- 1} \ left (x \ right) = \ sqrt {x} [/ latex].{-1} \ left (x \ right) [/ latex] — это график [латекса] f \ left (x \ right) [/ latex], отраженного относительно диагональной линии [латекс] y = x [/ latex], которую мы назовем идентификационной линией, показанной на рисунке 8.
Рис. 8. Функции квадратного и квадратного корня в неотрицательной области
Эта взаимосвязь будет соблюдаться для всех однозначных функций, поскольку она является результатом функции и ее обратного обмена входами и выходами. Это эквивалентно смене ролей вертикальной и горизонтальной осей.{-1} \ left (x \ right) [/ латекс].
Рисунок 9
Решение
Это взаимно однозначная функция, поэтому мы сможем набросать обратную. Обратите внимание, что показанный график имеет видимую область [латекс] \ left (0, \ infty \ right) [/ latex] и диапазон [latex] \ left (- \ infty, \ infty \ right) [/ latex], так что обратный будет иметь домен [latex] \ left (- \ infty, \ infty \ right) [/ latex] и диапазон [latex] \ left (0, \ infty \ right) [/ latex].
Если отразить этот график по линии [latex] y = x [/ latex], точка [latex] \ left (1,0 \ right) [/ latex] отражается в [latex] \ left (0,1 \ right) [/ latex] и точка [latex] \ left (4,2 \ right) [/ latex] отражает в [latex] \ left (2,4 \ right) [/ latex].{-1} [/ latex], тогда [latex] f \ left (f \ left (x \ right) \ right) = x [/ latex], и мы можем вспомнить несколько функций, обладающих этим свойством. Идентификационная функция выполняет, как и обратная функция, потому что
[латекс] \ frac {1} {\ frac {1} {x}} = x [/ латекс]
Любая функция [латекс] f \ left (x \ right) = c-x [/ latex], где [latex] c [/ latex] является константой, также равна своей собственной обратной.
Обратные функции: Графики
Особенностью пары обратной функции является то, что их упорядоченные пары перевернуты.Например, f (x) = 2x + 1 и его обратная функция, f − 1 (x) = x − 12, имеют следующие упорядоченные пары:
f (x) = 2x + 1: (0, 1), (1, 3), (2, 5), (3, 7)
f − 1 (x) = x − 12: (1, 0) , (3, 1), (2, 5), (7, 3)
При построении графика функции будут отражением друг друга на линии y = x, как показано ниже.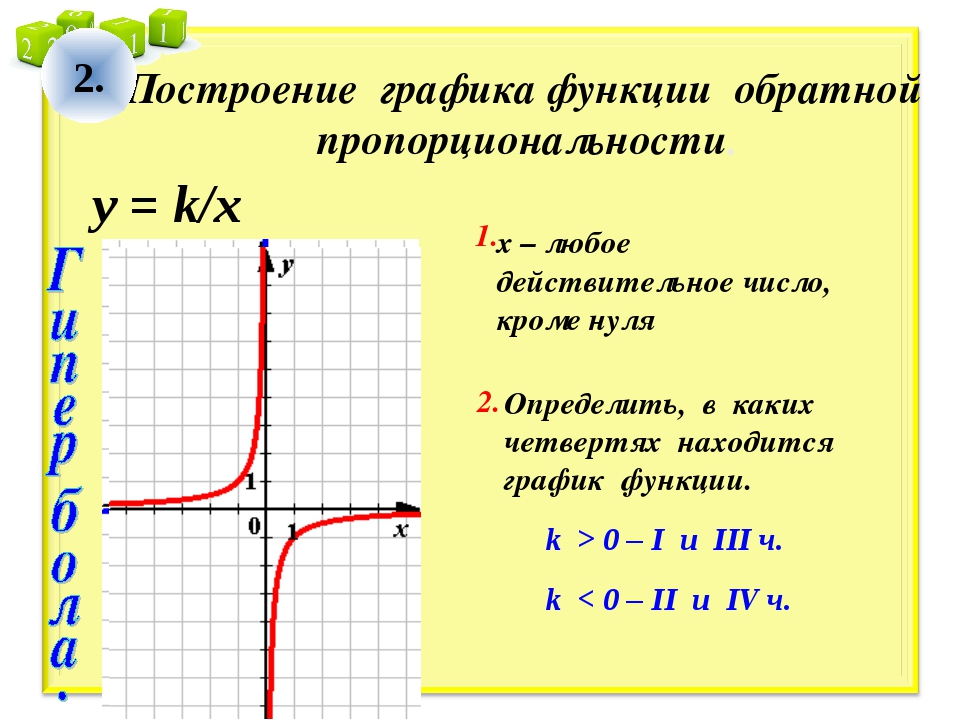
ГРАФИКИ ОБРАТНЫХ ФУНКЦИЙ:
У обратных функций есть графики, которые являются отражениями от линии y = x и, таким образом, имеют перевернутые упорядоченные пары.
Давайте воспользуемся этой характеристикой, чтобы идентифицировать обратные функции по их графикам.
РУКОВОДСТВО ПО ВЫЯВЛЕНИЮ ОБРАТНЫХ ФУНКЦИЙ ПО ИХ ГРАФАМ:
1. Нарисуйте оба графика на одной координатной сетке.
2. Проведите линию y = x и обратите внимание на симметрию.
а. Если симметрия не очевидна, функции не являются обратными функциями.
г. Если симметрия очевидна, перейдите к шагу 3 для проверки.
3.Сравните координаты как минимум четырех точек, чтобы определить, поменялись ли они местами. В таком случае функции обратные.
Пример 1. Нарисуйте графики f (x) = 2x 2 и g (x) = x2 для x≥0 и определите, являются ли они обратными функциями.
Шаг 1. | |
Шаг 2: Проведите линию y = x и найдите симметрию. Если симметрия не заметна, функции не обратные. Если симметрия заметна, дважды проверьте с шага 3. В этом случае симметрия очевидна, поэтому переходите к шагу 3. | |
Шаг 3: Сравните координаты по крайней мере четырех точек, чтобы увидеть, поменялись ли координаты местами. Поскольку выбранные четыре точки показывают, что координаты f (x) обратны координатам g (x), функции являются обратными функциями. |
Пример 2: Нарисуйте графики f (x) = 3x 2 -1 и g (x) = x + 13 для x≥0 и определите, являются ли они обратными функциями.
Шаг 1. Постройте оба графика на одной координатной сетке. | |
Шаг 2: Проведите линию y = x и найдите симметрию. Если симметрия не заметна, функции не обратные.Если симметрия заметна, дважды проверьте с шага 3. В этом случае симметрия очевидна, поэтому переходите к шагу 3. | |
Шаг 3: Сравните координаты по крайней мере четырех точек, чтобы увидеть, поменялись ли координаты местами. Поскольку выбранные четыре точки показывают, что координаты f (x) НЕ обратны координатам g (x), функции НЕ являются обратными функциями. Более пристальный взгляд на линию y = x покажет, что она немного отцентрована. |
Обратный Разделы: Определение Охват вашего учебника Обратная функция Как только вы нашли обратное Вы знаете, что это Поскольку синие точки ( Находка Наверное, ваш учебник
Вы можете увидеть на последней
Даже не зная, что Верх
|
Функции и их инверсии — рабочие примеры
Обратные функции
Часть 1. Что такое обратная функция?
Пусть $ f $ будет функцией $ 1-1 $ с областью определения $ A $ и диапазоном $ B.{-1} (x).
долл. США
Обратите внимание, что определить обратную функцию этой формы не так просто. Итак, рассмотрим следующий пошаговый подход к поиску обратного:
| Шаг 1: | Замените $ f (x) $ на $ y. $ (Это просто для , запишите меньше по мере продолжения) $$ y = \ frac {x + 4} {3x-2} $$ |
| Шаг 2: | Поменяйте ролями $ x $ и $ y. $ $$ x = \ frac {y + 4} {3x-2} $$ |
| Шаг 3: | Найдите $ y, $, которое будет искомой обратной функцией.{-1} (x)) & = f \ left (\ frac {4 + 2x} {3x-1} \ right) \\ & = \ frac {\ left (\ frac {4 + 2x} {3x-1} \ right) + 4} {3 \ left (\ frac {4 + 2x} {3x-1} \ right) -2} \ \ & = \ frac {\ left (\ frac {4 + 2x + 4 (3x-1)} {3x-1} \ right)} {\ left (\ frac {3 (4 + 2x) — 2 (3x-1) )} {3x-1} \ right)} \\ & = \ frac {\ left (\ frac {4 + 2x + 12x-4)} {3x-1} \ right)} {\ left (\ frac {12 + 6x — 6x + 2)} {3x-1} \верно)} \\ & = \ frac {\ cancel {14} x} {\ cancel {3x-1}} \ cdot \ frac {\ cancel {3x-1}} {\ cancel {14}} \\ & = х \ end {align *}   В качестве упражнения: попробуйте самостоятельно убедиться, что $ (f ^ {- 1} \ circ f) (x) = x $.{-1} (х) = \ sqrt {x} \ end {выровнять *} |

обратных функций
обратных функций
Содержание: Эта страница соответствует § 1.7 (стр. 150)
текста.
Предлагаемые задачи из текста
с.158 # 1-4, 5, 8, 9, 12, 13, 15, 18, 21, 22, 27, 31, 34, 37, 46, 48, 51, 71, 74, 83
Определение обратной функции
Графики обратных функций
Существование инверсии
Поиск инверсий
Определение обратной функции
Прежде чем определять инверсию функции, нам нужно иметь правильный мысленный образ функции.
Рассмотрим функцию f (x) = 2x + 1. Мы знаем, как вычислить f при 3, f (3) = 2 * 3 + 1 = 7. В этом разделе это
помогает думать о f как о преобразовании 3 в 7, а f превращает 5 в 11 и т. д.
Теперь, когда мы думаем о f как о «действующем» на числа и преобразовывающем их, мы можем определить обратное к
f как функция, которая «отменяет» то, что сделала f. Другими словами, функция, обратная f, должна вернуть 7 к
3, и вернем -3 к -2 и т. Д.
Пусть g (x) = (x — 1) / 2.Тогда g (7) = 3, g (-3) = -2 и g (11) = 5, поэтому кажется, что g отменяет то, что сделал f, по крайней мере
для этих трех значений. Чтобы доказать, что g является обратным к f, мы должны показать, что это верно для любого значения x в
область f. Другими словами, g должен вернуть f (x) к x для всех значений x в области определения f. Итак, g (f (x))
= x должно выполняться для всех x в области определения f. Чтобы проверить это условие, убедитесь, что формула для g (f (x))
упрощается до x.
г (f (x)) = g (2x + 1) = (2x + 1 -1) / 2 = 2x / 2 = x.
Это упрощение показывает, что если мы выберем любое число и позволим f действовать им, то применение g к результату восстанавливает
наш оригинальный номер. Нам также нужно увидеть, что этот процесс работает в обратном порядке, или что f также отменяет то, что делает g.
f (g (x)) = f ((x — 1) / 2) = 2 (x — 1) / 2 + 1 = x — 1 + 1 = x. (1/3)
Используйте калькулятор для вычисления значений f (g (4)) и g (f (-3)). g — величина, обратная f, но из-за округления
ошибка, калькулятор может не вернуть точное значение, с которого вы начали. Попробуйте f (g (-2)). Ответы будут отличаться для
разные компьютеры. Однако на нашей тестовой машине f (g (4)) вернул 4; g (f (-3)) вернул 3; но, f (g (-2)) вернул
-1.9999999999999991, что довольно близко к -2.
Калькулятор может дать нам хорошее представление о том, что g является обратной величиной f, но мы не можем проверить все возможные значения.
из х.
(b) Докажите, что g является обратным к f, упростив формулы для f (g (x) и g (f (x)).
Вернуться к содержанию
Графики обратных функций
Мы видели примеры отражений в плоскости. Отражение точки (a, b) относительно оси x равно (a, -b),
а отражение (a, b) вокруг оси y равно (-a, b). Теперь мы хотим поразмышлять о прямой y = x.
Отражение точки (a, b) относительно прямой y = x — это точка (b, a) .
Пусть f (x) = x 3 + 2. Тогда f (2) = 10 и точка (2,10) находится на графике f. Обратное к f должно
возьмите 10 обратно к 2, то есть f -1 (10) = 2, поэтому точка (10,2) находится на графике f -1 . Точка
(10,2) — отражение на прямой y = x точки (2,10). Тот же аргумент можно сделать для всех пунктов
графики f и f -1 .
График f -1 — это отражение относительно линии y = x графика f.
Вернуться к содержанию
Существование инверсии
Некоторые функции не имеют обратных функций. Например, рассмотрим f (x) = x 2 . Есть два числа
что f принимает значение 4, f (2) = 4 и f (-2) = 4. Если бы f имел обратный, то тот факт, что f (2) = 4, означал бы, что
Функция, обратная f, возвращает 4 к 2. С другой стороны, поскольку f (-2) = 4, функция, обратная f, должна привести 4 к -2.Следовательно, не существует функции, обратной f.
Посмотрите на ту же задачу с точки зрения графиков. Если бы у f был обратный, то его график был бы отражением
график функции f относительно прямой y = x. График f и его отражение относительно y = x показаны ниже.
Обратите внимание, что отраженный график не проходит тест вертикальной линии,
так что это не график функции.
Это обобщает следующим образом: функция f имеет обратную тогда и только тогда, когда ее график отражается относительно
line y = x, результат — график функции (проходит тест вертикальной линии).Но это можно упростить.
Прежде чем отображать график, мы можем сказать, пересечется ли какая-либо вертикальная линия более одного раза, посмотрев
как горизонтальные линии пересекают исходный график!
Тест горизонтальной линии
Пусть f — функция.
Если какая-либо горизонтальная линия пересекает график f более одного раза, то f не имеет обратной.
Если ни одна горизонтальная линия не пересекает график f более одного раза, то f действительно имеет обратный.
Свойство иметь обратное очень важно в математике, и у него есть название.
Определение : Функция f равна взаимно однозначно тогда и только тогда, когда f имеет инверсию.
Следующее определение эквивалентно, и оно чаще всего дается для однозначного определения.
Альтернативное определение : Функция f равна взаимно однозначно , если для каждых a и b в ее домене
f (a) = f (b) влечет a = b.(1/3) (кубический корень из x). Ответ
Вернуться к содержанию
Поиск инверсий
Пример 1. Сначала рассмотрим простой пример f (x) = 3x + 2 .
График f представляет собой линию с наклоном 3, поэтому он проходит тест горизонтальной линии и имеет инверсию.
Чтобы вычислить f для числа x, необходимо выполнить два шага. Сначала мы умножаем x на 3, затем прибавляем 2.
Считая обратную функцию отменой того, что сделала f, мы должны отменить эти шаги в обратном порядке.
Шаги, необходимые для вычисления f -1 , состоят в том, чтобы сначала отменить добавление 2 путем вычитания 2. Затем мы отменим
умножение на 3 путем деления на 3.Следовательно, f -1 (x) = (x — 2) / 3.
Шаги по поиску обратной функции f.
- Заменить f (x) на y в уравнении, описывающем функцию.
- Поменять местами x и y. Другими словами, замените каждый x на y и наоборот.
- Решить относительно y.
- Заменить y на f -1 (x).
Пример 2. f (x) = 6 — x / 2
| Шаг 1 | у = 6 — х / 2. |
| Шаг 2 | х = 6 — у / 2. |
| Шаг 3 | х = 6 — у / 2. у / 2 = 6 — х. y = 12 — 2x. |
| Шаг 4 | f -1 (x) = 12 — 2x. |
Шаг 2 часто сбивает студентов с толку. Мы могли бы пропустить шаг 2 и найти x вместо y, но тогда мы бы получили
с формулой в y вместо x. Формула будет такой же, но переменная будет другой. Избежать
это мы просто меняем ролями x и y перед тем, как решить.
Пример 3. f (x) = x 3 + 2
Это функция, с которой мы работали в упражнении 1. Из ее графика (показанного выше) мы видим, что у нее есть
обратный. (Фактически, обратное ему было дано в упражнении 1.)
Шаг 1 y = x 3 + 2. Шаг 2 х = у 3 + 2. Шаг 3 х — 2 = у 3 .(1/3).
Упражнение 3:
График f (x) = 1-2x 3 , чтобы увидеть, что у него есть обратное. Найдите f -1 (x). Ответ
Вернуться к содержанию
OpenAlgebra.com: обратные функции
Начнем с определения: Обратные функции — Функции f (x) и g (x) являются обратными, если обе
для всех x в домене g и f соответственно.Другими словами, если вы составите обратные функции, результат будет x .
Убедитесь, что данные функции инвертированы .
При проверке того, что две функции инвертированы, вы должны получить исходное значение x , сложив оба способа.
Определить, являются ли данные функции инверсными .
Если f и g являются обратными функциями, то g можно записать с использованием обозначений
который гласит: « g равно f, обратное .» Внимание: В этом контексте -1 указывает обратную функцию, а не отрицательную экспоненту.
Найдите время, чтобы просмотреть функции один-к-одному (1-1), потому что оказывается, что если функция 1-1, то у нее есть обратная функция. Следовательно, мы можем рассматривать тест горизонтальной линии как тест, который определяет, имеет ли функция инверсию или нет.
Далее мы в общих чертах описываем процедуру нахождения обратных функций .
Шаг 1 : Замените f (x) на y .
Шаг 2 : поменять местами x и y .
Шаг 3 : Решите полученное уравнение относительно y .
Шаг 4 : Замените y обозначением, обратным f .
Шаг 5 : (Необязательно) Убедитесь, что функции инвертированы.
Найти функцию, обратную заданной .
Теперь, когда вы знаете определение обратной функции и как ее найти, мы теперь обратим наше внимание на их графики.Для любой однозначной функции f , где
и мы имеем следующее свойство.
Симметрия обратных функций — Если ( a , b ) — это точка на графике функции f , то ( b , a ) — это точка на графике ее обратной функции. Кроме того, два графика будут симметричными относительно линии y = x .
На следующем графике видно, что функции
имеют симметрию при построении графика на одном и том же наборе осей.
Обратите внимание, что (2, 3) — точка на f , а (3, 2) — точка на обратном. Другими словами, чтобы построить график обратного, все, что вам нужно сделать, это переключить координаты каждой упорядоченной пары. Мы использовали этот факт, чтобы найти обратные, и это будет очень важно в следующей главе, когда мы разработаем определение логарифма.
Дан график функции 1-1, нарисуйте ее обратную и линию симметрии .
Видео на YouTube:
Обратные функции
Вы использовали обратных функций с первых дней изучения алгебры, чтобы уравновесить вещи.Теперь, когда вы обладаете более высокими математическими знаниями, вы можете лучше понять, почему и как они работают.
Что такое обратная функция?
Обратная функция для f ( x ), обозначенная f -1 ( x ) (которая читается как « f , обратная x »), содержит тот же домен и элементы диапазона как исходная функция, f ( x ). Однако наборы меняются.Другими словами, домен f ( x ) — это диапазон f -1 ( x ), и наоборот. Фактически, для каждой упорядоченной пары ( a , b ), принадлежащей f ( x ), существует соответствующая упорядоченная пара ( b , a ), которая принадлежит f — 1 ( x ). Например, рассмотрим эту функцию, г :
Обратная функция — это набор всех упорядоченных пар в обратном порядке:
Только взаимно однозначные функции обладают обратными функциями.Поскольку эти функции имеют элементы диапазона, каждый из которых соответствует только одному элементу домена, нет опасности, что их обратные значения не будут функциями. Тест горизонтальной линии — это быстрый способ определить, является ли график графиком взаимно однозначной функции. Он работает так же, как тест вертикальной линии: если произвольная горизонтальная линия может быть проведена поперек графика f ( x ) и пересекает f более чем в одном месте, то f не может быть единым- to-one функция.
Обратные функции обладают уникальным свойством, заключающееся в том, что при составлении их исходных функций обе функции отменяются. Математически это означает, что
Графики обратных функций
Поскольку функции и обратные функции содержат одни и те же числа в упорядоченной паре, только в обратном порядке, их графики будут отражением друг друга по линии y = x , как показано на рисунке 1.
Рисунок 1 Обратные функции симметричны относительно прямой y = x .
Нахождение обратных функций
Чтобы найти обратную функцию для взаимно-однозначной функции, выполните следующие действия:
1. Перепишите функцию, используя y вместо f ( x ).
2. Переключите переменные x и y ; оставьте все остальное в покое.
3. Решите новое уравнение относительно y .
4. Замените y на f −1 ( x ).
5. Убедитесь, что полученная обратная функция взаимно однозначна. Если это не так, ограничьте домен прохождением теста горизонтальной линии.
Пример 1: Если, найти f −1 ( x ).
Выполните пять перечисленных выше шагов, начиная с перезаписи f ( x ) как y :
Обратите внимание на ограничение x ≥ 0 для f −1 ( x ).

 Постройте оба графика на одной координатной сетке.
Постройте оба графика на одной координатной сетке. 
 Например, предположим, что ваша функция состоит из этих
Например, предположим, что ваша функция состоит из этих