Содержание
Правильная пирамида — урок. Геометрия, 10 класс.
Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой.
Боковые грани правильной пирамиды — равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды называется апофемой.
Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром.
Все грани тетраэдра — равные равносторонние треугольники.
В средней школе нужно уметь решать задачи, где дана:
— правильная треугольная пирамида;
— правильная четырёхугольная пирамида;
— правильная шестиугольная пирамида.
Правильная треугольная пирамида
Основание правильной треугольной пирамиды — равносторонний треугольник.
Вершина пирамиды проецируется в точку пересечения медиан.
Запомни:
\(BN:NK = 2:1\),
\(KD\) — апофема,
∢ \(NKD\) и ∢ \(NLD\) — двугранные углы при основании пирамиды,
∢ \(DCN\) и ∢ \(DBN\) — углы между боковым ребром и плоскостью основания пирамиды.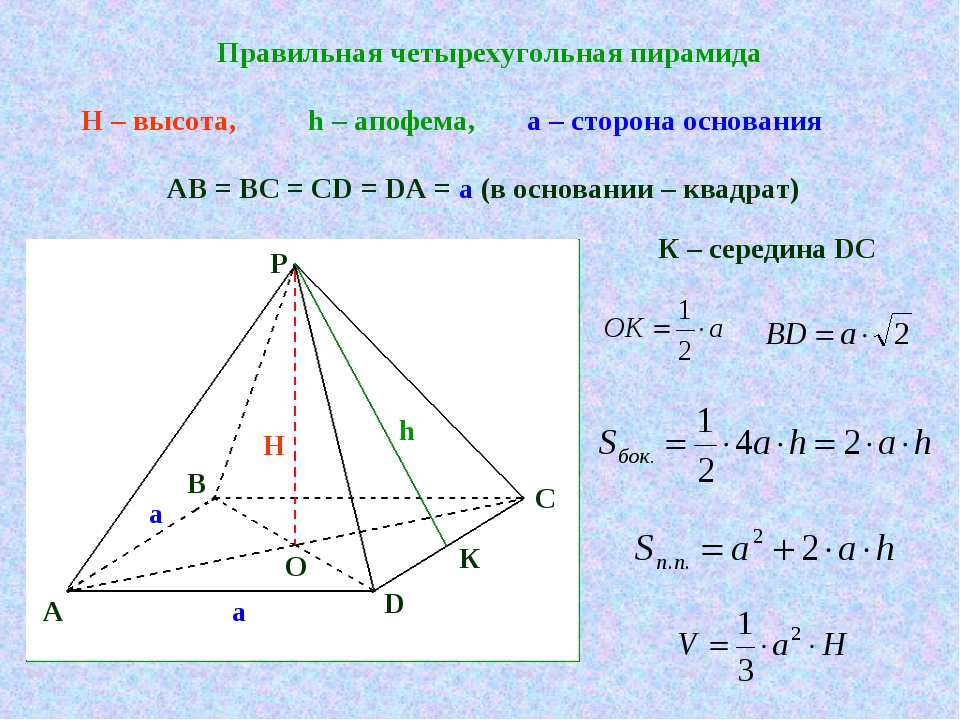
Правильная четырёхугольная пирамида
Основание правильной четырёхугольной пирамиды — квадрат.
Вершина пирамиды проецируется в точку пересечения диагоналей основания (квадрата).
\(ML\) — апофема,
∢ \(MLO\) — двугранный угол при основании пирамиды,
∢ \(MCO\) — угол между боковым ребром и плоскостью основания пирамиды.
Правильная шестиугольная пирамида
Основание правильной шестиугольной пирамиды — правильный шестиугольник.
Вершина пирамиды проецируется в точку пересечения диагоналей основания (шестиугольника).
\(SE = h\) — апофема,
∢ \(OES\) — двугранный угол при основании пирамиды.
Для вычисления площади боковой поверхности правильной пирамиды существуют две формулы:
Sб=12Pоснования⋅hиSб=Sоснованияcosϕ, где \(P\) — периметр основания, \(h\) — апофема, ϕ — двугранный угол при основании.
Объём пирамиды \(V =\) 13Sосн⋅H, где \(H\) — высота пирамиды.
Обрати внимание!
Не путай \(h\) — апофему с \(H\) — высотой пирамиды!
Урок 64. пирамида — Математика — 4 класс
Математика, 4 класс
Урок № 64. Пирамида
Перечень вопросов, рассматриваемых в теме:
— пирамида – объёмная фигура, многогранник
— элементы пирамиды
— виды пирамид
Глоссарий по теме:
Пирамида – геометрическая фигура, основание которой – многоугольник, а грани – треугольники, имеющие общую вершину.
Вершина – общая точка всех боковых граней.
Основание – многоугольник.
Боковые грани – треугольники.
Боковые ребра – отрезки, соединяющие вершину с вершинами основания.
Основная и дополнительная литература по теме урока:
- Математика: 4 класс: учебник в 2 ч. Ч.1/ В.Н. Рудницкая, Т.В. Юдачева. – М. Вентана-Граф, 2015.
 с.85-87
с.85-87 - Математика: 4 класс: учебник в 2 ч. Ч.2/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова.–М. Просвещение, 2016.с.112-113
- Готовимся к Всероссийской проверочной работе. Математика. Рабочая тетрадь 4 класс/ под.ред. Рыдзе О.А. – М.; Просвещение, 2016. – с.27-35
Теоретический материал для самостоятельного изучения
Посмотри внимательно на геометрические фигуры. Их можно разделить на группы.
Первая группа – плоские фигуры (это фигуры, которые можно целиком расположить на плоской поверхности). Все эти фигуры-многоугольники.
Вторая группа – объёмные фигуры (это фигуры, которые занимают определенное пространство, возвышаются над плоской поверхностью.) Объемные фигуры в математике еще называют пространственными фигурами или геометрическими телами.
Сегодня на уроке мы будем изучать объемную фигуру. А какую? Вы узнаете, расшифровав слово. Каждое число обозначает место буквы в алфавите.
Мы рассмотрим понятие «пирамида» с математической точки зрения. Давайте выделим элементы пирамиды. У пирамиды есть основание. Основание пирамиды – многоугольник.
Давайте выделим элементы пирамиды. У пирамиды есть основание. Основание пирамиды – многоугольник.
У этой пирамиды в основании лежит треугольник.
Эта часть пирамиды называется боковой гранью.
Боковые грани пирамиды-треугольники.
Фигура, поверхность которой состоит из многоугольников, называется многогранником. Значит пирамида-многогранник
Это – боковое ребро Боковые рёбра – это отрезки, соединяющие вершину пирамиды с вершинами основания.
Общая точка боковых граней пирамиды называется вершиной пирамиды.
Итак, пирамида – это геометрическая фигура, основание которой многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Пирамиды бывают разных видов. Называют пирамиду по ее основанию. Если в основании лежит треугольник, то пирамиду называют треугольной, четырёхугольник – четырёхугольной, пятиугольник – пятиугольной.
.
Это развёртки треугольной и четырёхугольной пирамиды. Вы сами сможете изготовить модель пирамиды, если перечертите на клетчатую бумагу эти развертки, вырежете и перегнете по красным линиям и проклеите там, где потребуется.
Задания тренировочного модуля:
1.Заполните таблицу
Вид пирамиды | всего вершин | боковые рёбра | боковые грани |
Треугольная пирамида | |||
Четырёхугольная пирамида |
Правильный ответ.
всего вершин | боковые ребра | боковые грани | |
Треугольная пирамида | 4 | 3 | 3 |
Четырёхугольная пирамида | 5 | 4 | 4 |
2. Выберите предметы, которые имеют форму пирамиды.
Правильный ответ.
Пирамида. Формулы и свойства
Определение.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
| Рис.1 |
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.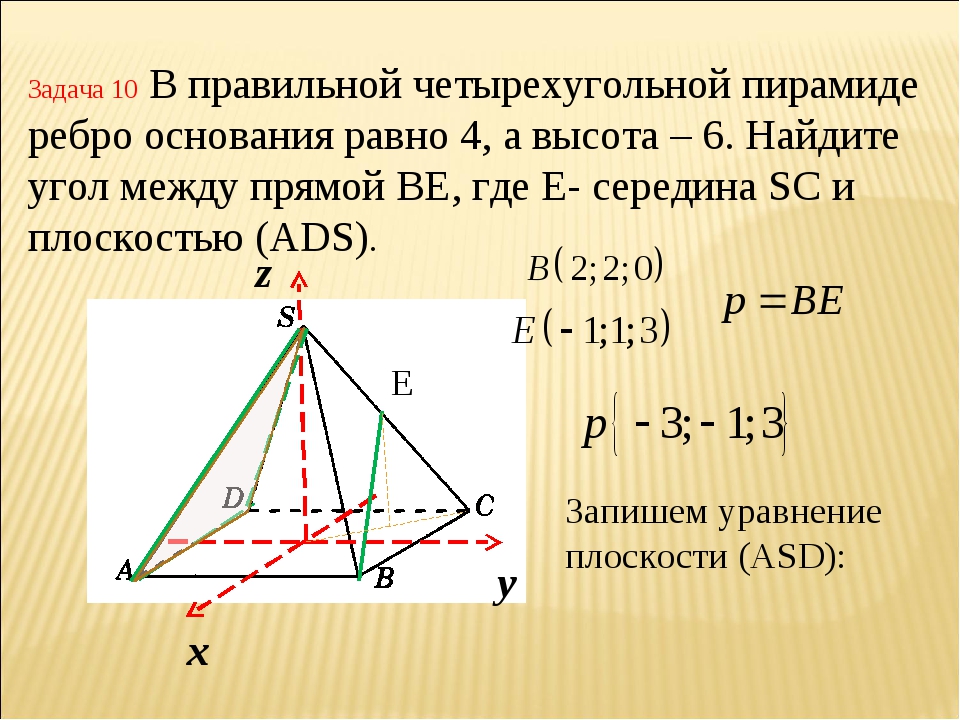
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.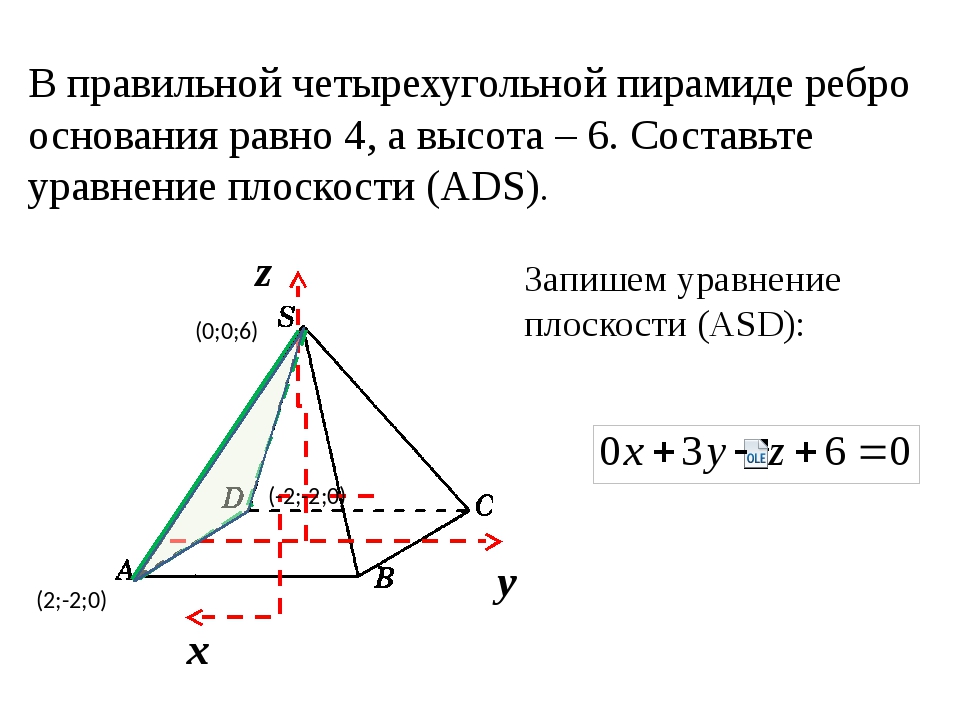
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
Правильная пирамида с четырехугольником в основании
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача.
Диагональ основания правильной четырехугольной пирамиды равна 4 см, а боковая грань образует с основанием угол 60 градусов. найдите объем пирамиды.
Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
Ответ: 8√6 / 3 см3.
Задача.
Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны α. Найти площадь полной поверхности пирамиды.
Решение.
Поскольку пирамида правильная, то ее высота проецируется в центр основания.
Значит KN = a/2
Соответственно, треугольник OKN — прямоугольный. Значит
ON = KN / cos α = a / 2cos α
Поскольку пирамида правильная, то треугольник DOC — равнобедренный. Значит его площадь равна
Sт = DC * ON / 2
Sт = ( a * a / 2cos α) / 2 = a2 / 4cos α
Откуда площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней
Sб = 4a2 / 4cos α
Sб = a2 / cos α
Откуда площадь полной поверхности равна
Sп = a2 / cos α + a2 = a2 ( 1 + 1 / cos α )
Ответ: площадь полной поверхности правильной четырехугольной пирамиды равна a2 ( 1 + 1 / cos α )
Правильная пирамида с четырехугольником в основании |
Описание курса
| Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
формула для правильной треугольной и четырехугольной
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3. Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
Пирамида, вписанная в конус. Свойства пирамиды, вписанной в конус
Определение 1. Пирамидой, вписанной в конус, называют такую пирамиду, у которой основание вписано в основание конуса, а вершина совпадает с вершиной конуса (рис. 1).
Определение 2. Если пирамида вписана в конус, то конус называют описанным около пирамиды.
Рис. 1
1
Замечание. Если пирамида вписана в конус, ее боковые ребра равны и являются образующими конуса, вершина пирамиды лежит на оси конуса, а высота пирамиды равна высоте конуса.
Теорема 1. Около пирамиды можно описать конус тогда и только тогда, когда выполнены следующие два условия:
- Около основания пирамиды можно описать окружность;
- Основанием перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды, является центр описанной около основания пирамиды окружности.
Доказательство. Поскольку перпендикуляр, опущенный из вершины конуса на плоскость его основания, проходит через центр основания конуса, то для пирамиды, вписанной в конус, справедливость обоих условий теоремы вытекает из определения конуса, описанного около пирамиды.
Теперь рассмотрим пирамиду SA1A2 … An , для которой выполнены условия 1 и 2 теоремы, и докажем, что около нее можно описать конус.
Пусть O – центр круга, окружность которого описана около основания A1A2 … An пирамиды. Поскольку отрезок SO перпендикулярен плоскости основания пирамиды, то, соединив все точки этого круга с вершиной пирамиды S , мы получим конус с осью OS, описанный около пирамиды SA1A2 … An (рис. 2).
Рис.2
Теорема доказана.
Поскольку около любого правильного многоугольника можно описать окружность, то из доказанной теоремы 1 непосредственно вытекает
Следствие 1. Около любой правильной пирамиды можно описать конус.
Теорема 2. Около пирамиды можно описать конус тогда и только тогда, когда все боковые ребра пирамиды равны.
Доказательство. Действительно, если пирамида вписана в конус, то ее боковые ребра являюся образующими конуса, и, значит, равны между собой.
Рассмотрим теперь пирамиду SA1A2 … An высоты h , у которой все боковые ребра
SA1 = SA2 = … = SAn = l ,
и докажем, что около ее основания можно описать окружность. Пусть точка O – основание перпендикуляра, опущенного из вершины S на плоскость основания пирамиды (рис. 3).
Рис.3
Все прямоугольные треугольники SOA1 , SOA2 , … , SOAn равны, поскольку у них равны гипотенузы SA1 , SA2 , … , SAn , а катет SO является общим. Следовательно,
OA1 = OA2 = … = OAn .
Отсюда вытекает, что многоугольник A1A2 . .. An вписан в окружность с центром в точке O . Радиус этой окружности можно найти по теореме Пифагора
.. An вписан в окружность с центром в точке O . Радиус этой окружности можно найти по теореме Пифагора
.
По теореме 1 около такой пирамиды можно описать конус.
Доказательство теоремы 2 завершено.
Отношение объемов конуса и вписанной в него правильной
n — угольной пирамиды
Задача. Найти отношение объемов конуса и вписанной в него правильной n — угольной пирамиды.
Решение. Поскольку и объем конуса, и объем пирамиды вычисляются по формуле
,
а высота конуса равна высоте описанной около него пирамиды , то для объемов конуса и описанной около него правильной n — угольной пирамиды справедливо равенство
Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле
то справедливо равенство
Ответ.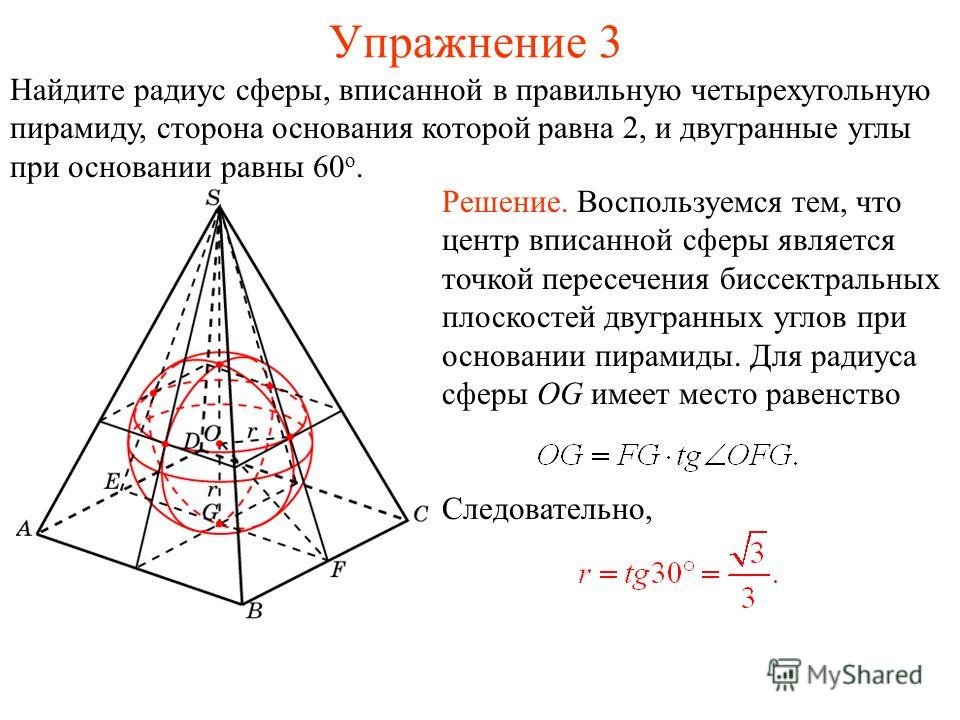
Следствие 2. Отношение объема правильной треугольной пирамиды к объему конуса, описанного около данной пирамиды, равно
Следствие 3. Отношение объема правильного тетраэдра к объему конуса, описанного около данного тетраэдра, равно
Следствие 4. Отношение объема правильной четырехугольной пирамиды к объему конуса, описанного около данной пирамиды, равно
Следствие 5. Отношение объема правильной шестиугольной пирамиды к объему конуса, описанного около данной пирамиды, равно
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
4.7. Пирамида
Определение 4.9.
Многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой.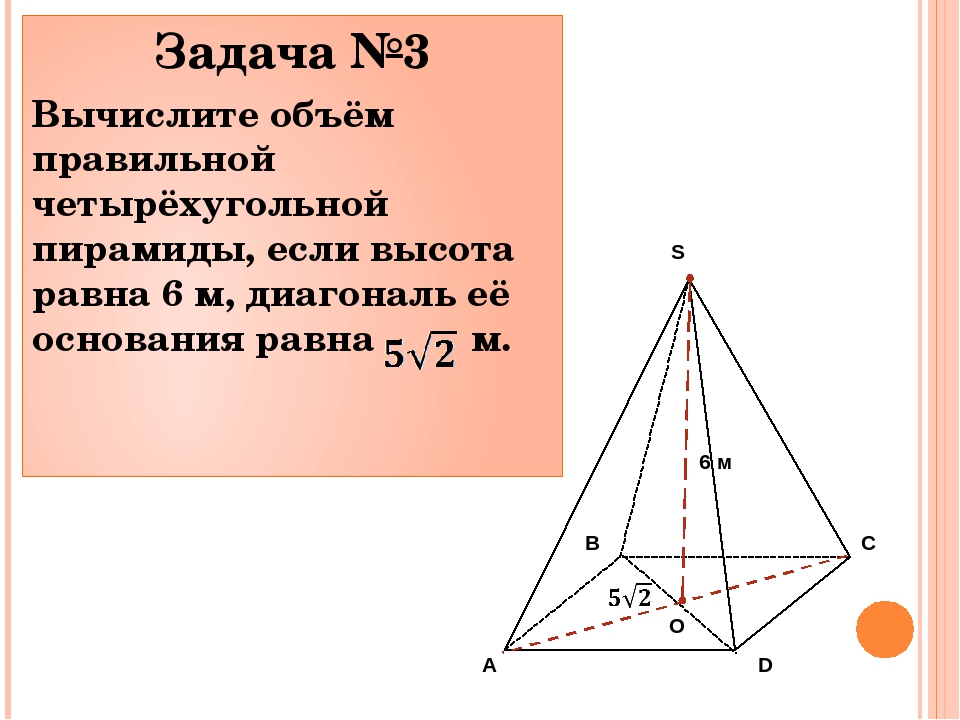
Грани, отличные от основания, называются боковыми. Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. В зависимости от числа сторон основания пирамида называется треугольной, четырехугольной, пятиугольной и т. д.
Определение 4.10.
Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением.
Теорема 4.10.
Если все боковые ребра пирамиды равны, то ее высота проходит через центр круга, описанного вокруг основания.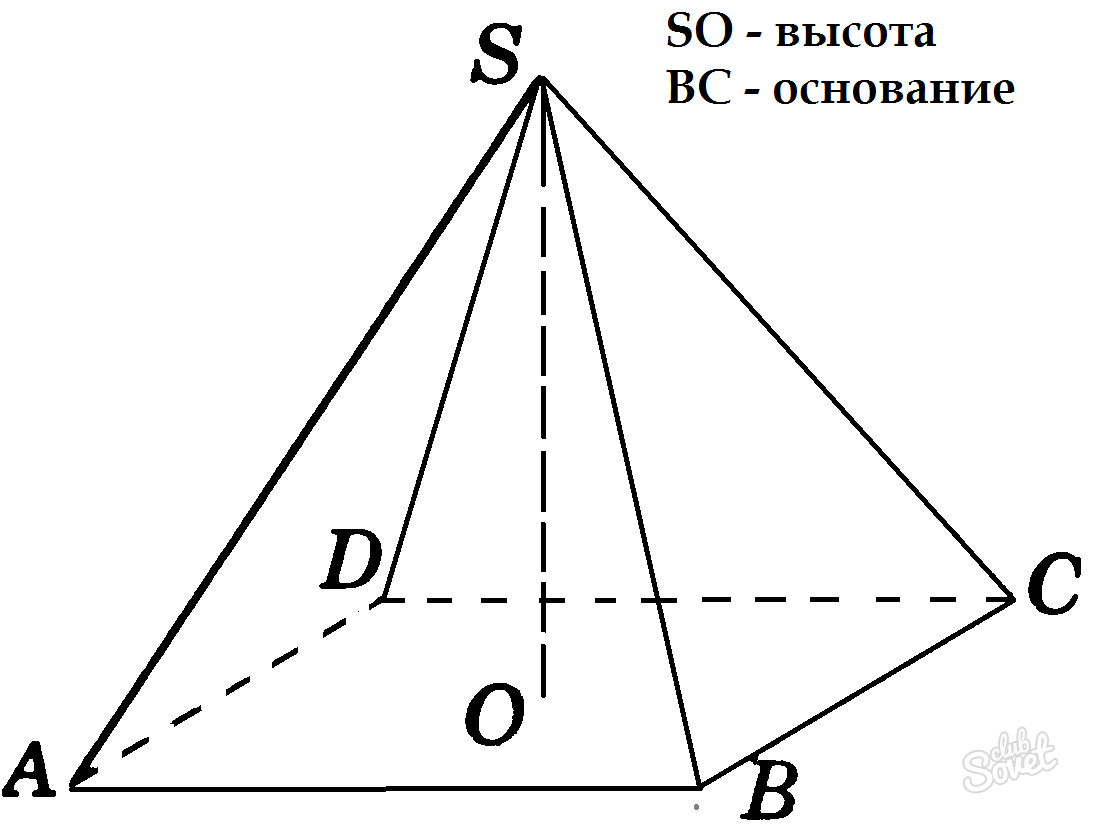
Теорема 4.11.
Если все боковые грани пирамиды одинаково наклонены к плоскости основания, а высота проходит внутри пирамиды, то высота проходит через центр вписанного в основание пирамиды круга.
Теорема 4.12.
Если все боковые грани наклонены к плоскости основания под одинаковым углом φ, то
Эта формула справедлива, в частности, для правильной пирамиды.
Теорема 4.14.
Если пирамиду пересечь плоскостью, параллельной плоскости основания, (чертеж 4.7.3), то:
-
боковые ребра и высота делятся этой плоскостью на пропорциональные отрезки в отношении -
площади сечения и основания пирамиды относятся как квадраты их расстояний до вершины пирамиды:
Математическая задача: правильная четырехугольная пирамида
Сколько квадратных метров нужно, чтобы покрыть форму правильной четырехугольной пирамиды краем основания 10 метров, если отклонение боковых краев от плоскости основания составляет 68 °? Рассчитайте отходы 10%.
Правильный ответ:
Чтобы решить эту математическую задачу со словами, вам понадобятся следующие знания:
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2
Сопутствующие математические задачи и вопросы:
- Пирамида — угол
Рассчитайте поверхность правильной четырехугольной пирамиды, край основания которой составляет 6 см, и отклонение от плоскости плоскости боковины основания составляет 50 градусов. - Тетраэдрическая пирамида
Рассчитайте объем и поверхность правильной тетраэдрической пирамиды, если площадь содержимого основания составляет 20 см. 2 , а угол отклонения боковых граней от плоскости основания составляет 60 градусов. - Крыша
Крыша башни имеет форму правильной четырехугольной пирамиды, длина основания которой составляет 11 м, а боковая стенка животного с основанием расположена под углом 57 °. Посчитайте, сколько кровли нам нужно, чтобы покрыть всю крышу, если мы рассчитываем на 15% отходов - 4-сторонняя пирамида
Рассчитайте объем и поверхность 4-сторонней правильной пирамиды, у которой длина основания составляет 4 см. Угол от плоскости боковины и плоскости основания составляет 60 градусов.
Угол от плоскости боковины и плоскости основания составляет 60 градусов. - Крыша дома
Крыша дома имеет форму правильной четырехугольной пирамиды с краем основания 17 м. Сколько м 2 нужно для покрытия кровли, если уклон крыши 57 ° и мы рассчитываем 11% отходов, стыков и перекрытий площади кровли? - Четырехугольная пирамида
Правильная четырехугольная пирамида имеет край основания a = 1,56 дм и высоту h = 2,05 дм. Рассчитайте: а) угол отклонения плоскости боковины от плоскости основания б) угол отклонения боковой кромки от плоскости основания - Четырехугольная призма
Высота правильной четырехугольной призмы v = 10 см, отклонение диагональ корпуса от основания 60 °.Определите длину краев основания, поверхности и объем призмы. - Пирамида 8
Вычислите объем и площадь поверхности правильной четырехугольной пирамиды со стороной основания 9 см и боковой стенкой с основанием под углом 75 °. - Четырехугольная пирамида
Вычислите площадь поверхности и объем правильной четырехугольной пирамиды: стороны оснований (внизу, вверху): a1 = 18 см, a2 = 6 см, угол α = 60 ° (угол α — это угол между боковой стенкой и базовая плоскость. ) S =? , V =?
) S =? , V =? - Диагональ основания
В обычной 4-сторонней пирамиде боковой край образует угол 55 ° с диагональю основания. Длина боковой кромки восемь метров. Вычислите площадь поверхности и объем пирамиды. - Восьмиугольная пирамида
Найдите объем правильной восьмиугольной пирамиды с высотой v = 100 и углом бокового ребра к плоскости основания α = 60 °. - Боковые грани
Обычная четырехгранная пирамида имеет высоту тела 2 дм, а противоположные боковые грани образуют угол 70 °.Вычислите площадь поверхности и объем пирамиды. - Четырехугольная пирамида
В правильной четырехугольной пирамиде высота составляет 6,5 см, а угол между основанием и боковой стенкой составляет 42 °. Рассчитайте площадь поверхности и объем тела. Округлите вычисления до 1 знака после запятой. - Башня
Вершина башни представляет собой правильную шестиугольную пирамиду с базовым краем длиной 8 метров и высотой 5 метров. Сколько м 2 листов потребуется для покрытия верхней части башни, если учесть 8% листовых отходов? - Тетраэдрическая пирамида
Определите поверхность правильной тетраэдрической пирамиды, если ее объем V = 120, а угол боковой стенки с плоскостью основания составляет α = 42 ° 30 ‘.
- Клумба
Клумба имеет форму усеченной пирамиды, нижний край цоколя а = 10 м, верхний цоколь б = 9 м. Угол отклонения кромки от основания альфа = 45 °. Какой объем нужен для изготовления этой клумбы? Сколько растений можно посадить, если 1 м 2 = - Четырехугольная призма
Рассчитайте объем (V) и поверхность (S) правильной четырехугольной призмы, высота которой составляет 28,6 см, и отклонение диагонали тела от основания плоскость 50 °.
Треугольная пирамида — определение, формула и примеры
В этом уроке мы узнаем о типах пирамид, уделяя особое внимание треугольным пирамидам. площадь поверхности треугольной пирамиды, сеть треугольной пирамиды с помощью некоторых решенных примеров, а также несколько сложных и интерактивных вопросов для проверки вашего понимания.
Трехмерная фигура, у которой все грани — треугольники, известна как треугольная пирамида.
Знаете ли вы, что одна из самых старых пирамид, известных человеку, — это «Великая пирамида Гизы»? Он был построен примерно в 2550 году до нашей эры в Египте.Они входят в число семи чудес света.
Это пирамиды, хорошо, но это тоже треугольные пирамиды?
Давайте узнаем!
План урока
Что такое треугольная пирамида?
Краткое описание
Треугольная пирамида — это пирамида с треугольным основанием, ограниченная четырьмя треугольными гранями, где 3 грани пересекаются в одной вершине.
В правильной треугольной пирамиде все грани представляют собой равносторонние треугольники, известные как тетраэдры.
В правой треугольной пирамиде основание представляет собой равносторонний треугольник, а другие грани — равнобедренные треугольники.
В неправильной треугольной пирамиде основанием является разносторонний или равнобедренный треугольник.
Сетки треугольной пирамиды
Давайте займемся небольшим занятием.
Возьмите лист бумаги.
Вы можете увидеть две отдельные сети треугольной пирамиды, показанной ниже.
Скопируйте это на лист бумаги.
Обрежьте его по краю и сложите, как показано на рисунке ниже.
Сложенная бумага образует треугольную пирамиду.
Моделирование ниже иллюстрирует треугольную пирамиду в 3D.
Щелкните край треугольной пирамиды и перетащите ее.
Вы сможете увидеть все четыре грани по мере его вращения.
Кроме того, вы сможете просматривать сети треугольных пирамид, перемещая ползунок.\ circ \), поскольку они треугольные.
Если треугольная пирамида специально не указана как неправильная, все треугольные пирамиды считаются правильными треугольными пирамидами.
Какие части треугольной пирамиды?
- У него 4 грани, 6 кромок и 4 угла.
- В каждой вершине пересекаются по 3 ребра.
- Треугольная пирамида не имеет параллельных граней.
- Правильная треугольная пирамида имеет равносторонние треугольники на всех гранях. Имеет 6 плоскостей симметрии.
- Треугольные пирамиды бывают правильными, неправильными и прямоугольными.
Каковы формулы треугольной пирамиды?
Треугольная пирамида Объем:
| \ (\ begin {align} \ frac {1} {3} \ text {Base Area} \ times \ text {Height} \ end {align} \) |
Площадь поверхности треугольной пирамиды (общая):
| \ (\ begin {align} \ text {Base Area} + \! \ Frac {1} {2} \ text {(Perimeter} \! \ Times \! \ Text {Slant Height}) \ end {align} \) |
Теперь рассмотрим правильную треугольную пирамиду , составленную из равносторонних треугольников со стороной \ (a \) .2 \) Калькулятор треугольной пирамиды Изучите калькулятор треугольной пирамиды ниже, чтобы найти площадь поверхности и объем правильной треугольной пирамиды:
- Треугольная пирамида имеет 4 грани, 6 ребер и 4 угла. Все четыре грани имеют треугольную форму.
- Тетраэдр представляет собой треугольную пирамиду с равносторонними равносторонними треугольниками на каждой грани.
Сид узнал, что две треугольные пирамиды совпадают.Он начал наблюдать за их соответствием.
В то время как он поместил основания обоих треугольников в положение, чтобы увидеть, перекрываются ли они, две конгруэнтные треугольные пирамиды слиплись вдоль его основания и образовали треугольную бипирамиду.
Сколько граней, ребер и вершин у этой бипирамиды?
Решение
Если мы откроем изображение выше, чтобы увидеть сеть треугольной бипирамиды, мы увидим это:
Имеется 6 треугольных граней, 9 ребер и 5 вершин. 2 \\
& = \ Sqrt {3} \ times 6 \ times 6 \\
& = 62.35
\ end {align} \]
| \ (\ следовательно \) Общая площадь = 62,35 единиц 2 |
Решая вопросы о треугольной пирамиде, Шрея застрял. Давайте поможем ей прийти к окончательному ответу.
Вот вопрос: «Сумма длины ребер правильной треугольной пирамиды составляет 60 единиц. Найдите площадь поверхности одной из ее граней».
Решение
Мы знаем, что треугольная пирамида имеет 6 граней.2 \
& = \ frac {\ sqrt {3}} {4} \ times 10 \ times 10 \\
& = 25 \ sqrt {3} \\
& = 43,30
\ end {align} \]
| \ (\ следовательно \) Площадь одной из его граней = 43,30 единиц 2 |
Вы уже знакомы с формулами треугольной пирамиды для определения объема, а также общей площади поверхности.
Вы также могли заметить, что для определения общей площади поверхности и объема необходимо знать край.2} & = 6 \ times \ sqrt {3} \ times \ sqrt {2} \\
a & = 6 \ sqrt {6}
\ end {align} \]
| \ (\ следовательно \) Длина ребра треугольной пирамиды равна \ (6 \ sqrt6 \) |
- Новая форма образуется путем совмещения грани треугольной пирамиды точно над одной треугольной гранью квадратной пирамиды. Сколько вершин, ребер и граней будет у новой формы?
- В Рохане есть палатка в форме неправильной треугольной пирамиды.Объем палатки v куб. См, высота h см. Какова будет площадь основания его палатки?
Интерактивные вопросы о треугольной пирамиде
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции Треугольной пирамиды.Математическое путешествие вокруг Треугольной пирамиды начинается с того, что ученик уже знает, и продолжается творческой выработкой новой концепции в молодых умах. Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Сколько треугольников образуют треугольную пирамиду?
Четыре треугольника образуют треугольную пирамиду.
2. Является ли пирамида треугольной призмой?
Призма — это многогранник с параллельными верхним и нижним основаниями и прямоугольными боковыми гранями.Пирамида имеет одно основание и треугольные боковые грани, которые пересекаются в центральной вершине. Треугольная пирамида — это геометрическое тело с треугольным основанием, и все остальные грани также являются треугольниками с общей вершиной.
3. Почему пирамида представляет собой треугольник?
Каждая сторона пирамиды (каждое основание и вершина) образует треугольник . Треугольник , основанный на , пирамида имеет четыре треугольные стороны. Это означает, что три стороны пирамиды имеют одинаковый размер, и пирамида выглядит так же, если вы ее повернете.Форма пирамиды позволяет равномерно распределять вес по всей конструкции.
4. Составлена ли пирамида из равносторонних треугольников?
Когда основание представляет собой треугольник, пирамида представляет собой треугольную пирамиду. У него четыре грани, включая основание. Когда грани представляют собой равносторонние треугольники, это правильная треугольная пирамида.
Правые пирамиды, правые конусы и сферы | Измерения
На рисунке ниже изображена сфера.{3} \\
& = \ frac {4} {3} \ pi (\ text {512}) \\
& = \ frac {2048} {3} \ pi \\
& = \ text {2 144,6605 …}
\ end {align *}
Следовательно, объем сферы равен \ (\ text {2 144,66} \) единиц 3 . {2} (\ text {7}) \\
& = \ frac {1} {3} \ pi (\ text {4}) (\ text {7}) \\
& = \ frac {28} {3} \ pi \\
& = \ текст {29,3215…}
\ end {выровнять *}
Следовательно, объем конуса равен \ (\ text {29,32} \) единиц 3 .
На рисунке изображена пирамида с квадратным основанием. Вертикальная высота пирамиды составляет \ (H = \ text {8} \) единиц, а наклонная высота составляет \ (h = \ text {8,94} \) единиц; каждая сторона основания пирамиды составляет \ (b = \ text {8} \) единиц.{2} (\ text {8}) \\
& = \ frac {1} {3} (\ text {64}) (\ text {8}) \\
& = \ frac {512} {3} \\
& \ приблизительный \ текст {170,6666 …}
\ end {выровнять *}
Следовательно, объем квадратной пирамиды равен: \ (\ text {170,67} \) единиц 3 .
Найдите площадь поверхности и объем показанного здесь конуса. Округлите ответы до ближайшего целого числа.
Площадь конуса:
\ begin {align *}
A _ {\ text {cone}} & = \ pi r (r + h) \\
& = \ пи (5) (5 + 20) \\
& = \ текст {392,69908. {2} (\ sqrt {375}) \\
& = \ текст {506,97233.{3} $} \).
Твердое тело внизу состоит из куба и квадратной пирамиды. Найдите его объем и площадь поверхности (с точностью до десятичного знака \ (\ text {1} \)):
Высота куба равна \ (\ text {5} \) \ (\ text {cm} \).Поскольку общая высота объекта равна \ (\ text {11} \) \ (\ text {cm} \), высота пирамиды должна быть \ (\ text {6} \) \ (\ text {cm} \).
Сначала проработаем том:
\ begin {align *}
\ text {Объем} & = \ text {объем куба} + \ text {объем квадратной пирамиды} \\
& = s ^ {3} + \ frac {1} {3} bH \\
& = (5) ^ {3} + \ frac {1} {3} (5) ^ {2} (6) \\
& = \ текст {175} \ text {см $ ^ {3} $}
\ end {выровнять *}
Для площади поверхности отметим, что одна грань куба покрыта пирамидой. {3} $} \).
Объем квадратной пирамиды с учетом стороны основания и высоты Калькулятор
- Цель использования
- Каков объем квадратной пирамиды с учетом края основания и высоты наклона. Округлите ответ до ближайшей десятой, не используя в ответах никаких единиц измерения.
[1] 2020/05/20 05:26 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / — /
- Комментарий / запрос
- облегчить чтение и понимание / нет устарело
[2] 2019/05/11 01:24 Женский / До 20 лет / Начальная школа / Младший ученик средней школы / Немного /
- Цель использования
- Домашнее задание
[3] 2019/03/22 08:11 Женский / Моложе 20 лет / Начальная школа / Младший школьник / Немного /
- Цель использования
- домашнее задание
[4 ] 2018/10/20 17:14 Женский / До 20 лет / Начальная школа / Младший школьник / Не совсем /
- Цель использования
- основной класс
[5] 2018/03/01 22 : 46 Женский / До 20 лет / Старшая школа / Университет / Аспирант / Полезный /
- Цель использования
- Как решить sque пирамида
[6] 2017/03/07 13:39 Женский / До 20 лет / Начальная школа / Неполные старшие классы / — /
- Цель использования
- Моя проблема заключалась в проблеме … V = 1/3 Ач; V = 45 и h = 5. Найдите A. [Объем пирамиды]
- Комментарий / запрос
- Я понятия не имею, как найти этот ответ, и пока сдамся.
[7] 2014/10/01 15:00 Мужчина / Моложе 20 лет / Старшая школа / Университет / Аспирант / Не совсем /
- Цель использования
- математический проект
[8] 06.06.2014 10:45 Женский / До 20 лет / Начальная школа / Младший школьник / Не совсем /
- Цель использования
- Предварительная алгебра
[9 ] 2014/05/20 01:10 Мужской / До 20 лет / Начальная школа / Младший школьник / Маленький /
- Комментарий / Запрос
- Фонд должен быть более ясным
[10] 2014/04/07 00:33 Мужчина / Уровень 20 лет / Средняя школа / Университет / аспирант / Немного /
Треугольная пирамида: определение, формула и примеры — Видео и стенограмма урока
Формула объема
для треугольной пирамиды
Объем объекта — это количество места внутри объекта, поэтому объем треугольной пирамиды — это количество места внутри пирамиды.Объем треугольной пирамиды можно определить по формуле V = 1/3 A H , где A = площадь основания треугольника, а H = высота пирамиды или расстояние от основание пирамиды до вершины.
Например, если бы у нас была треугольная пирамида высотой 12 единиц, а площадь основания составляла 24 квадратных единицы, тогда объем пирамиды был бы V = (1/3) (24) (12) = 96 куб.
Формула площади поверхности для треугольной пирамиды
Площадь поверхности объекта — это общая площадь поверхности объекта.Таким образом, площадь поверхности треугольной пирамиды — это площадь всех ее граней и основания вместе взятых. Когда у нас есть правильная треугольная пирамида, все грани пирамиды имеют одинаковую площадь. Следовательно, площадь поверхности правильной треугольной пирамиды можно найти, добавив площадь основания в 3 раза больше площади одной из граней. То есть SA = A + 3 a , где A — это площадь основания пирамиды, а a — площадь одной из граней пирамиды.
Чтобы найти площадь треугольника, мы используем формулу A = 1/2 bh , где b — основание треугольника, а h — высота треугольника.
Следовательно, наша формула площади поверхности принимает вид SA = A + 3 (1/2 bh ) = A + 3/2 bh , где b — основание одной из пирамид. Faces, которая также является длиной одной из сторон основания пирамиды, а h — высота одной из граней пирамиды.
Например, если у нас есть правильная треугольная пирамида с гранями, имеющими высоту = 10 единиц и основание = 6 единиц, а площадь основания пирамиды составляет 16 квадратных единиц, то площадь поверхности пирамиды равна SA = 16 + (3/2) (6) (10) = 106 квадратных единиц. Это говорит нам о том, что если вы сложите все площади граней пирамиды и основания пирамиды, вы получите 106 квадратных единиц.
Когда у нас есть неправильная пирамида, мы просто вычисляем площади каждой из граней пирамиды и основания пирамиды по отдельности, а затем складываем их все.То есть SA = Площадь основания + Площадь грани 1 + Площадь грани 2 + Площадь грани 3.
Примеры
Рассмотрим треугольник Рубика. Треугольник Рубика — это правильная треугольная пирамида. От основания пирамиды до вершины 3 дюйма. Площадь основания треугольника Рубика составляет 6,5 квадратных дюймов. Высота одной из граней составляет 3,5 дюйма, а основание одной из граней — 4 дюйма. Зная эту информацию, мы можем найти объем и площадь треугольника Рубика.
Объем = 1/3 AH = (1/3) (6.5) (3) = 6.5 кубических единиц
Площадь поверхности = A + (3/2) bh = 6.5 + (3/2 ) (4) (3.5) = 27,5 квадратных единиц
Рассмотрим еще один пример. Найдите объем и площадь следующей правильной треугольной пирамиды.
Сначала мы найдем объем, поэтому нам нужна площадь основания пирамиды и высота пирамиды. Мы видим, что A = 8.7 квадратных сантиметров и H = 9 см. Поэтому мы подставляем эти значения в нашу формулу объема, чтобы получить V = (1/3) (8,7) (9) = 26,1, поэтому наш объем составляет 26,1 кубических сантиметра.
Теперь мы находим нашу площадь поверхности. Это правильная треугольная пирамида, поэтому нам нужны основание и высота одной из наших граней и площадь основания пирамиды. Из рисунка мы видим, что A = 8,7 квадратных сантиметра, b = 10 см, а h = 7 см. Мы подставляем эти значения в нашу формулу, чтобы получить SA = 8.7 + (3/2) (10) (7) = 113,7. Следовательно, площадь нашей пирамиды составляет 113,7 квадратных сантиметра.
Краткое содержание урока
Треугольные пирамиды — это пирамиды с треугольным основанием. Стороны треугольной пирамиды называются гранями , а точка, где все грани встречаются, называется вершиной . У нас есть формулы для расчета объема и площади поверхности треугольной пирамиды.
Чтобы найти объем, мы используем формулу V = (1/3) A H , где A = площадь основания пирамиды и H = высота пирамиды.Чтобы найти площадь правильной треугольной пирамиды, воспользуемся формулой SA = A + (3/2) b h , где A = площадь основания пирамиды, b = основание одной из граней, а х = высота одной из граней.
Ключевые термины
Пирамида — трехмерная форма, имеющая многоугольник в качестве основания и треугольники в качестве сторон, все они встречаются в общей точке
Грани — треугольные стороны пирамиды
Основание — нижний многоугольник пирамиды
Вершина — точка пересечения всех треугольных граней на пирамиде
Треугольная пирамида — пирамида с треугольником в основании
Правильная треугольная пирамида — пирамида, имеющая основание с равными по длине сторонами
Неправильная треугольная пирамида — пирамида с основанием с разной длиной сторон
Объем — сколько места внутри объекта
Площадь поверхности — общая площадь поверхности объекта
Результаты обучения
После этого урока вы должны уметь:
- 9 0014 Сопоставьте следующие термины с соответствующими частями пирамиды: грань, основание, вершина
- Как отличить правильную треугольную пирамиду от неправильной
- Объясните, как найти объем и площадь любой треугольной пирамиды
Площадь поверхности и объем пирамид, призм, цилиндров и конусов (Геометрия, Площадь) — Mathplanet
Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела.Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.
Объем — это мера того, сколько фигура может вместить, и измеряется в кубических единицах. Объем говорит нам кое-что о вместимости фигуры.
Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть как прямоугольные, так и треугольные призмы.
Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем твердое тело, как картонную коробку, и расплющиваем его, чтобы найти все включенные геометрические формы.
Чтобы найти объем призмы (не имеет значения, прямоугольная она или треугольная), мы умножаем площадь основания, называемую площадью основания B, на высоту h.
$$ V = B \ cdot h $$
Цилиндр — это труба, состоящая из двух параллельных конгруэнтных окружностей и прямоугольника, основанием которого является окружность окружности.{2} \ cdot h $$
Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех- или четырехсторонней поверхности соответственно в основании. Когда мы вычисляем площадь поверхности пирамиды ниже, мы берем сумму площадей четырех треугольников и базового квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.
Объем пирамиды составляет одну треть объема призмы.
$$ V = \ frac {1} {3} \ cdot B \ cdot h $$
Основание конуса — круг, и это легко увидеть.{3} $$
Видеоурок
Найти площадь поверхности цилиндра радиуса 4 и высоты 8
Найти объем конуса высотой 5 и радиусом 3
Пирамида | Encyclopedia.com
Ресурсы
Пирамида — это искусственно созданное геометрическое тело, форма которого прославилась царскими гробницами Древнего Египта. Это твердое тело с основанием в виде трех- или четырехстороннего многоугольника (трех- или четырехугольника соответственно), боковые грани которого представляют собой треугольники (стороны трехугольника) с общей вершиной (вершиной пирамиды).Размеры этих треугольников классифицируют форму как обычно равнобедренную, но иногда и как равностороннюю. В случае египетской пирамиды Хеопса основание представляет собой почти идеальный квадрат 755 футов (230 м) на ребре, а грани треугольников приблизительно равносторонние.
Некоторые древние египетские пирамиды: пирамида Хуфу (Великая пирамида) в Гизе, пирамида Нефериркаре Какай в Абу-Сире и ступенчатая пирамида Джозера в Саккаре. Другие древние пирамиды находятся в Китае, Франции, Южной Америке, Мексике, Украине, Судане и Боснии и Герцеговине.
Основанием пирамиды может быть любой многоугольник с тремя или более гранями, а имена пирамид соответствуют количеству ребер в основании. Когда основание представляет собой треугольник, пирамида представляет собой треугольную пирамиду. Он также известен как тетраэдр, поскольку он имеет четыре грани, включая основание. Когда эти грани представляют собой равносторонние треугольники, это квадратная пирамида, в основе которой лежит квадрат.
Чаще всего встречаются пирамиды правильной формы. Эти пирамиды имеют правильный многоугольник для основания и равнобедренные треугольники для боковых граней.Однако не все пирамиды правильные.
Высоту пирамиды можно измерить двумя способами: от вершины по линии, перпендикулярной основанию, и от вершины по линии, перпендикулярной одному из краев основания. Последняя мера называется наклонной высотой. Однако, если боковые грани не являются конгруэнтными треугольниками, наклонная высота может варьироваться от грани к грани и не будет иметь большого значения для пирамиды в целом. Если слово наклон не включено, термин высота (или высота) относится к высоте.
Если помимо конгруэнтности боковые грани равнобедренные, пирамида будет правильной. В правильной пирамиде прямоугольных треугольников можно встретить в изобилии. Предположим, у вас есть правильная пирамида с высотой VC и наклонной высотой VD. Здесь треугольники VCD, VDE, VCE и CDE являются прямоугольными треугольниками. Если в любом из этих треугольников известны две стороны, можно использовать теорему Пифагора (форму уравнения которой имеет следующий вид: a 2 + a 2 = c 2 , где c — длина гипотенузы, а и b — длины двух других сторон), чтобы вычислить третью.Это, в свою очередь, может быть использовано в других треугольниках для определения еще других неизвестных сторон. Например, если правильная квадратная пирамида имеет наклонную высоту в две единицы и основание из двух единиц на краю, боковые края должны быть 5 единиц, а высота — 3 единицы.
Существуют формулы для вычисления боковой и общей площади некоторых специальных пирамид, но в большинстве случаев проще вычислить площади различных граней и сложить их.
Объем — другое дело.Вычислить объем без формулы может быть очень сложно. К счастью, существует довольно примечательная формула, возраст которой насчитывает не менее 2300 лет.
В предложении 7 книги XII его Elements греческий математик Евклид Александровский (ок. 325 – ок. 265 г. до н.э. показал, что «Любая призма с треугольным основанием делится на три равные друг другу пирамиды с треугольным оснований ». Это означает, что каждая из трех пирамид, на которые была разделена призма, имеет одну треть объема призмы.Поскольку объем призмы равен площади, B, ее основания, умноженной на высоту, h: объем пирамиды составляет одну треть от этого, или Bh / 3.
Пирамиды, основания которых представляют собой многоугольники с более чем тремя сторонами, можно разделить на треугольные пирамиды, и к каждой из них применяется формула Евклида. Тогда, если B — это сумма площадей треугольников, в которые входит многоугольник.
КЛЮЧЕВЫЕ ТЕРМИНЫ
Высота — Расстояние от вершины, перпендикулярно основанию.
Пирамида — Тело с многоугольным основанием и треугольными боковыми гранями.
Высота наклона — Расстояние от вершины, перпендикулярное краю основания.
