Отрезок и прямая: Точка, прямая, отрезок, луч, угол. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Прямая, отрезок, луч, плоскость

Главная
Геометрия
Начальные геометрические сведения
Прямая, отрезок, луч, плоскость

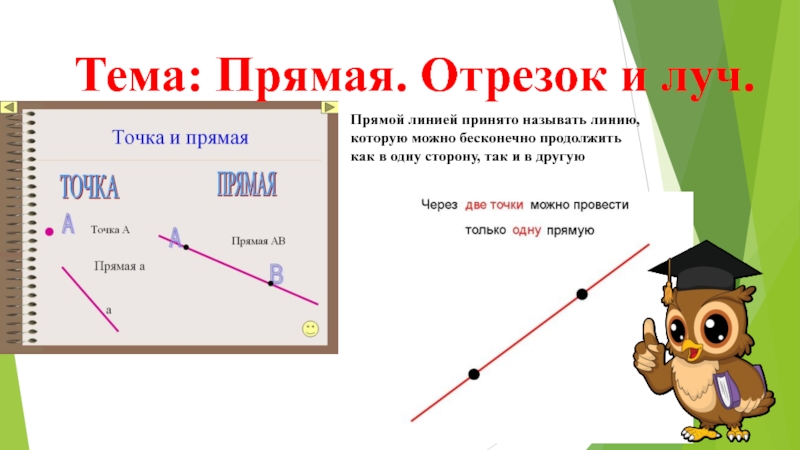
Прямая и точка

Прямая бесконечна. Через две точки можно провести только одну прямую. Две прямые могут пересекаться, а могут и не пересекаться. Пересекаются прямые только в одной точке. В двух точках пересечься они не могут, так как через две точки можно провести только одну прямую.

Через точки A и B проходит прямая AB. Двигай точки A и B.

Плоскость

Плоскость — это поверхность, состоящая из прямых, соединяющих две любые точки поверхности.

Через точки A,B,C и D проходит плоскость. Двигай точки A, B и C.

Отрезок

Отрезок — это все точки прямой, расположенные между двумя заданными точками, которые называются концами отрезка.

Перед тобой отрезок AB. Двигай точки A и B.

Длина отрезка

Длина отрезка — это число, показывающее, во сколько раз отрезок длиннее, чем выбранный единичный отрезок.

Здесь AB — отрезок, CD — единичный отрезок. Длина отрезка AB показывают ризки на отрезке AB. Двигай точки A, B, C и D.

Расстояние между двумя точками

Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.

Здесь A и B — точки, CD — единичный отрезок. Расстояние между точками A и B показывают ризки на отрезке AB. Двигай точки A, B, C и D.

Луч и дополнительные полупрямые

Луч (полупрямая) — это часть прямой. Любая точка прямой делит прямую на две таких части — два луча (две полупрямых). Такие два луча называются дополнительные полупрямые.

Здесь AB — это луч (двигай луч). Здесь точка D — это упомянутая точка, которая делит прямую. CD — это луч (двигай луч). CE — дополнительная полупрямая к лучу CD.

Равные фигуры

Равные фигуры — это фигуры, которые при наложении совмещаются всеми своими точками. Если фигуры совмещаются после зеркального отражения, то это тоже равные фигуры.

Фигуры FGHIJ и KLMNO равны фигуре ABCDE. Двигай точки A, B, C, D, E.

Середина отрезка

Середина отрезка — это точка, которая делит отрезок на два равных отрезка.

Точка C — середина отрезка AB. Двигай точки A и B.

Презентация — Математика 1 класс «Линии: кривая, прямая. Луч — Отрезок

Слайды и текст этой онлайн презентации

Слайд 1

2014 год,
13 октября,
понедельник.

Слайд 2

К задуманному числу прибавили 1 и получили 5. Какое число задумали?
Какое число при счёте следует за числом 6?
Число на 1 меньше, чем 8.
Какое число имеет соседей 3 и 4?
Какое число предшествует числу 7?

Слайд 3

1
2
3
4
5
6
7
8
9
10

Слайд 4

Ежик по лесу шел, На обед грибы нашел: Два — под березой, Один — у осины, Сколько их будет В плетеной корзине?
2+1=3

Слайд 5

Три ромашки-желтоглазки, Два веселых василька Подарили маме дети. Сколько же цветов в букете?
3+2=5

Слайд 6

1
1
2

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Отдыхай-ка

Слайд 11

Слайд 12

Линии: кривая, прямая. Луч. Отрезок. Точка.

Слайд 13

На какие две группы можно разделить эти линии? Сколько прямых линий? Сколько кривых линий? Каких линий больше?

Слайд 14

Сказка
В стране Геометрии жила-была точка.
Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям.

Слайд 15

Прямая линия начала хвастаться: «Я самая длинная У меня ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на неё. Сама-то она малюсенькая. Вышла она да так увлеклась, что не заметила и наступила на прямую линию. И вдруг исчезла прямая линия. На её месте появился луч.

Слайд 16

Он тоже был длинный, но всё же не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч. И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало и конец.

Слайд 17

Вот так маленькая точка смогла изменить жизнь больших линий.

Слайд 18

Слайд 19

Слайд 20

! Прямую линию мы проводим по линейке.

Слайд 21

Сколько линий можно провести через одну точку?

Слайд 22

Сколько линий можно провести через две точки?

Слайд 23

Отдыхай-ка

Слайд 24

Слайд 25

С.15

Слайд 26

Слайд 27

Что мы узнали? Что повторили?

Слайд 28

Оцени свою работу на уроке.

Слайд 29

Наше настроение

Точка, линия, прямая, луч, отрезок, ломанная.

Точка, линия, прямая, луч, отрезок, ломанная На рисунке 3 объекта отрезок прямой ремешок

Прямой называется линия (множество точек имеющих лишь длину) которая не искривляется и не имеет ни начала ни конца.

Отрезок это прямая ограниченная с двух концов.

Луч это прямая ограниченная с одного конца.

Точка не имеет никаких измерительных характеристик, в задачах важно только ее местоположение.

Отметим три точки на прямой

Прямая не является трехмерной фигурой, более того она не искривляется, а бесконечно продолжается не имея ни ширины ни высоты в 1 плоскости. Поэтому и точки можно ставить на протяжении всей бесконечной длины где угодно, это повлияет только на длину отрезков, отсекаемых этими точками.

Количество отрезков

Так как точек три, расположим их произвольно на прямой и назовем а, b, c. Таким образом три точки ограничивают прямую, превращая в отрезки три раза, то есть мы имеем три отрезка

Количество лучей

Теперь разберемся с лучами. Прямая не ограниченна ни с начала ни с конца, а луч должен быть ограничен с одной стороны.

если мы поставим на прямой 1 точку соответственно ограничив ее в этой точке то получим 2 луча,
если поставим 2 точки мы ограничим прямую в двух местах, логично было бы предположить что и лучей у нас будет больше 2х, но ограничив в двух местах мы получили отрезок, т. к. он ограничен с двух сторон, и 2 луча, т. к. имеем еще начало и конец прямой, которые не ограничены,
если поставим три точки? правильно, ситуация повторится, только увеличится количество отрезков

Ответ

Прямая на которой отмечены три точки делится этими точками на три отрезка и два луча.

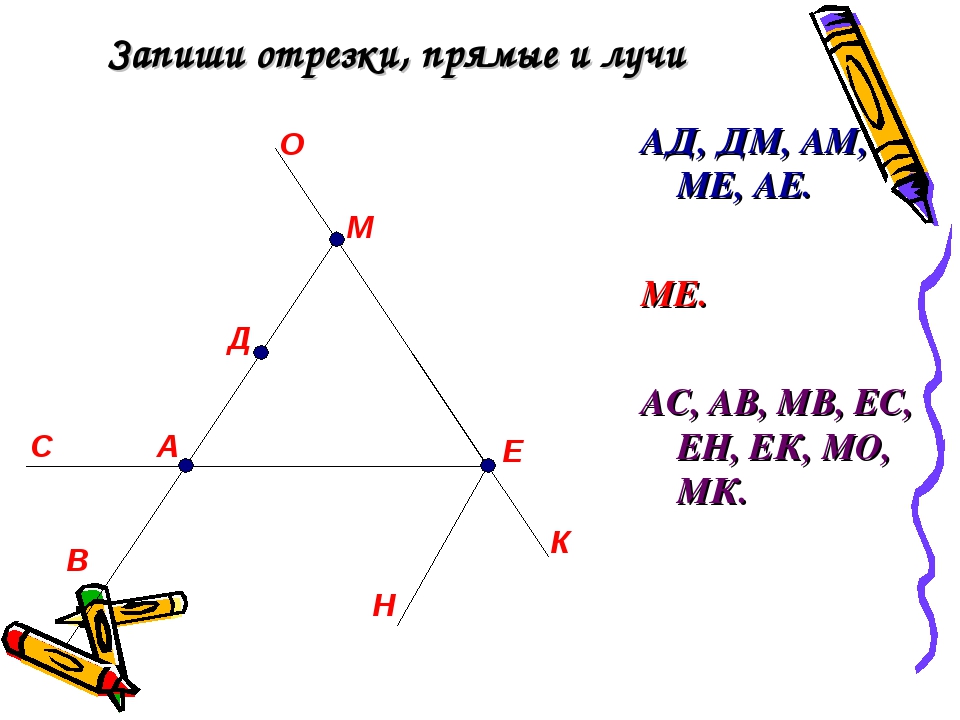
Нарисуем прямую и отметим на ней три точки А, В, С. (см. рисунок)

Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками.

Или проще говоря, отрезок это часть прямой, ограниченная двумя точками.

На рисунке получилось три отрезка:

АВ (рис. 1)

АС (рис. 3)

Луч – часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки. Любая точка на прямой разделяет прямую на два луча.

Точка А делит прямую на лучи: а и АС. (рис. 4)

Точка В делит прямую на лучи: ВА и ВС. (рис. 5)

Точка С делит прямую на лучи: СА и с. (рис. 6)

Получилось три отрезка и шесть лучей.

ПОВТОРЯЕМ ТЕОРИЮ

16. Заполните пропуски.

1) Точка и отрезок являются примерами геометрических
фигур.
2) Измерить отрезок означает подсчитать, сколько единых отрезков
в нем помещается.
3) Если на отрезке АВ ометить точку С, то длинна отрезка АВ равна сумме длин
отрезков АС +СВ

4) Два отрезка называют равными, если они совпадают при наложении
.
5) Равные отрезки имеют равные
длины.
6) Расстоянием между точками А и В называют длину отрезка
АВ.

РЕШАЕМ ЗАДАЧИ

17. Обозначьте отрезки, изображенные на рисунке, и измерьте их длины.

18. Проведите все возможные отрезки с концами в точках A, B, C и D. Запишите обозначения всех проведенных отрезков.

AB, ВC, СD, АD, АС, ВD

19. Запишите все отрезки, изображенные на рисунке.

20. Начертите отрезки СК и АD так, чтобы СК=4 см 6 мм, АD=2 см 5 мм.

21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм. Какова длина отрезка АЕ?

АЕ=ВЕ-ВА= 5 см 3 мм — 3см 8мм = 1 см 5мм

22. Выразите данную величину в указанных единицах измерения.

23. Запишите звенья ломаной и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

24. Отметьте точку В, расположенную на 6 клеток левее и на 1 клетку ниже точки А; точку С, расположенную на 3 клетки правее и на 3 клетки ниже точки В; точку D, расположенную на 7 клеток правее и на 2 клетки выше точки С. Соедините последовательно отрезками точки А, В, С и D.

Образовалась ломаная АВСD, состоящая из 3 звеньев.

25. Вычислите длину ломаной, изображенной на рисунке.

а) 5*36 = 180 мм
б) 3*28 = 84 мм
в) 10*10+15*4 = 160 мм

26. Постройте ломаную DСЕК так, чтобы DС=18 мм, СЕ=37 мм, ЕК=26 мм. Вычислите длину ломаной.

27. Известно, что АС=17 см, ВD=9см, ВС=3 см. Вычислите длину отрезка АD.

28. Известно, что МК=KN=NP=PR=RT=3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длины.

29. На прямой отметили точки так, что расстояние между двумя любыми соседними точками равно 4 см, а между крайними точками — 36 см. Сколько точек отмечено?

30. Начертите, не отрывая карандаша от бумаги, фигуры, изображенные на рисунке. По каждой линии можно проводить карандашом только один раз.

Отрезок. Длина отрезка. Треугольник.

1. В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия
— наука об «измерении земли». Это слово происходит от латинских слов: geo — земля и metr — мера, мерить. В геометрии изучаются различные геометрические объекты
, их свойства, их связи с окружающим миром. Простейшие геометрические объекты — это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.

Если приложить к двум точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок,
который называют АВ или ВА (читаем: «а — бэ», «бэ- а»). Точки А и В называются концами отрезка
(рисунок 1). Расстояние между концами отрезка, измеренное в единицах длины, называется длиной
отрез
ка
.

Единицы длины: м — метр, см — сантиметр, дм — дециметр, мм — миллиметр, км — километр и др. (1 км = 1000 м; 1м =10 дм; 1 дм = 10 см; 1 см = 10 мм).
Для измерения длины отрезков используют линейку, рулетку. Измерить длину отрезка, значит, выяснить, сколько раз в нем укладывается та или иная мера длины.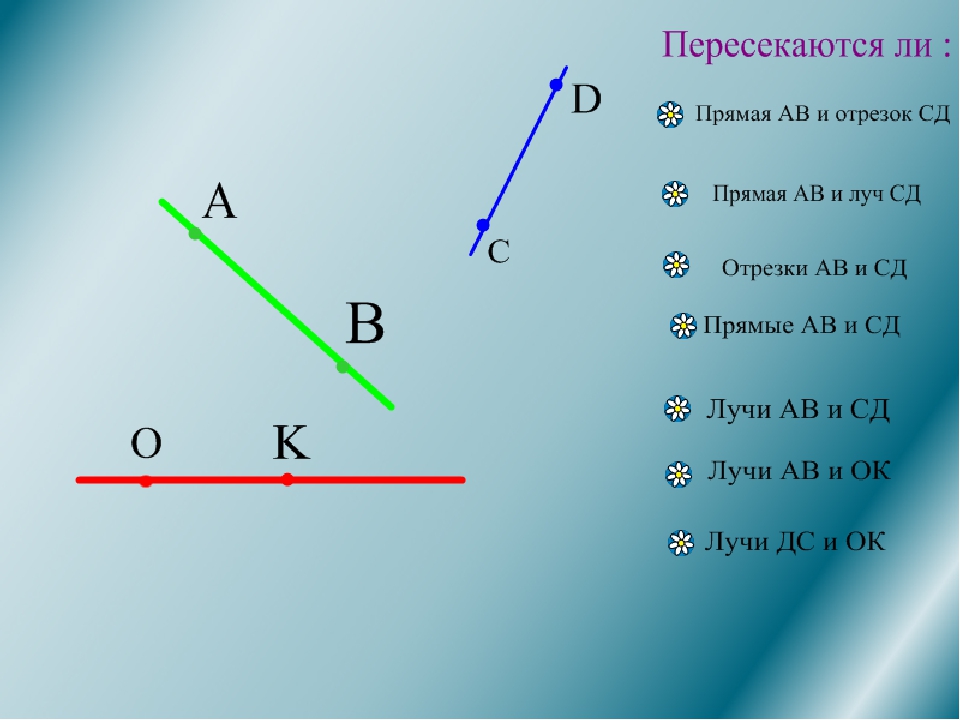

Равными
называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2). Например, можно вырезать реально или мысленно один из отрезков и приложить к другому так, чтобы совпали их концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равные длины. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют различные длины, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка. Сравнивать отрезки наложением можно, используя циркуль.

Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то мы получим представление о прямой
АВ (рисунок 3). Любая точка, лежащая на прямой, разбивает ее на два луча
(рисунок 4). Точка С разбивает прямую АВ на два луча
СА и СВ. Тоска С называется началом луча
.

2. Если три точки, не лежащие на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником.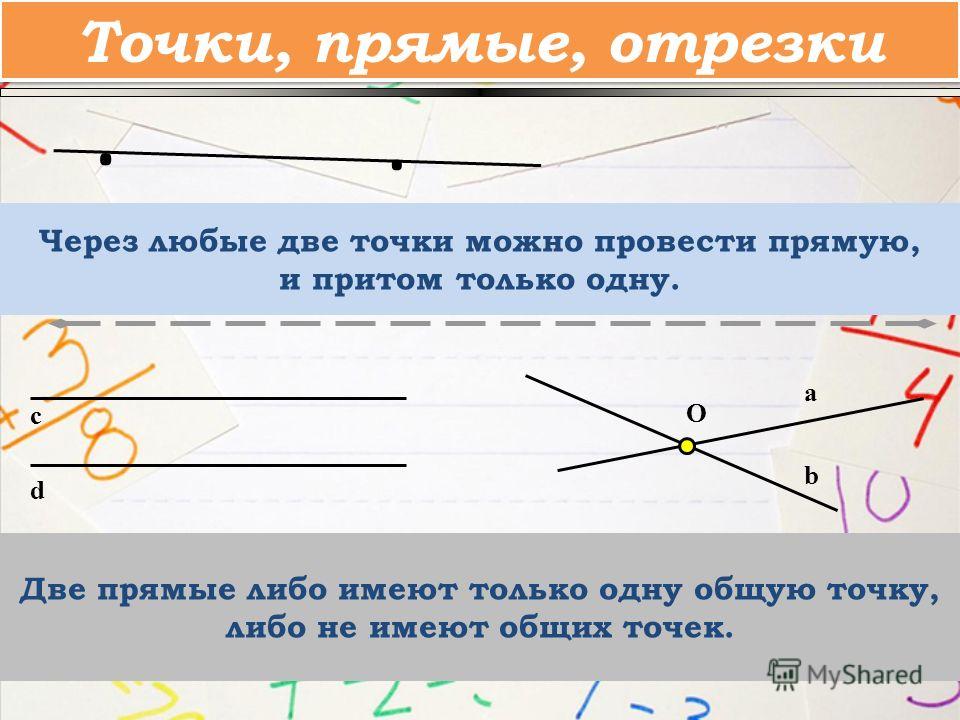
Данные точки называются вершинами
треугольника, а отрезки, их соединяющие, сторонами
треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM — стороны треугольника, точки F, N, M — вершины треугольника. Стороны всех треугольников обладают следующим свойством: длина любой из сторон треугольника всегда меньше суммы длин двух других его сторон.

Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости
. Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).

Блок 1. Дополнительный

Мир, в котором мы живем, все, что нас окружает, древние называли природой или космосом. Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).

Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т. д. Однако все перечисленные объекты имеют размеры, в отличие от них размеры геометрической точки считаются равными нулю (её измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить. Можно также сказать, в каком месте она находится. Поставив авторучкой в тетради точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A
,
B
,
C
,
D
,
(читают «точка а, точка бэ, точка цэ, точка дэ»
) (рисунок 7).

Провода, висящие на столбах, видимая линия горизонта (граница между небом и землей или водой), русло реки, изображенное на карте, гимнастический обруч, струя воды, бьющая из фонтана дают нам представление о линиях.

Различают замкнутые и незамкнутые линии, гладкие и негладкие линии, линии с самопересечением и без самопересечения (рисунки 8 и 9).

Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т. д. дают нам представление о поверхностях
(рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.

Тело человека, камень, кирпич, головка сыра, мяч, ледяная сосулька и т.д. дают нам представление о геометрических
телах (рисунок 11).

Наиболее простая из всех линий — это прямая
. Приложим к листу бумаги линейку и проведем карандашом вдоль неё прямую линию. Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение — длину, а два других ее измерения равны нулю (рисунок 12).

При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом. Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать прямую также двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую n
на рисунке 13 можно обозначить: АВ или ВА, А
D
или
D
А,
D
В или В
D
.

Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать прямой). На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут. Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой m, ее называют общей
точкой. В точке D прямые AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:

Через любые две точки всегда

можно провести прямую и причем только одну

.

Из всех видов линий, соединяющих любые две точки, наименьшую длину имеет отрезок, концами которого служат данные точки (рисунок 14).

Фигура, которая состоит из точек и соединяющих их отрезков называется ломаной

(рисунок 15). Отрезки, образующие ломаную, называются звеньями
ломаной, а их концы — вершинами
ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG.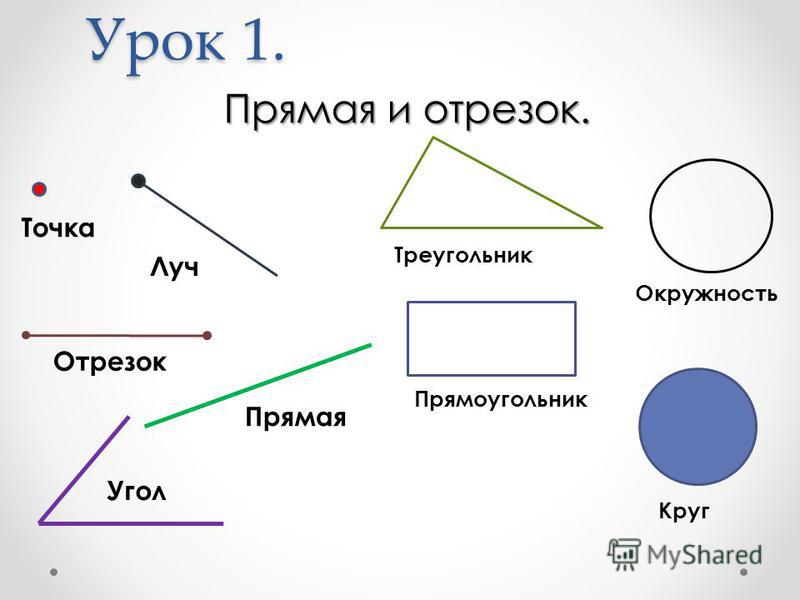 Длиной ломаной называется сумма длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.

Замкнутая ломаная называется многоугольником
, ее вершины называются вершинами многоугольника
, а ее звенья сторонами
многоугольника (рисунок 16). Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любой, например, многоугольник (семиугольник) ABCDEFG , многоугольник (пятиугольник) RTPKL:

Сумма длин всех сторон многоугольника называется периметром

многоугольника и обозначается латинской буквой
p
(читаем: пэ
). Периметры многоугольников на рисунке 13:

P ABCDEFG = AB + BC + CD + DE + EF + FG + GA.

P RTPKL = RT + TP + PK + KL + LR.

Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью

(рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ,
… (читаем: плоскость альфа, бетта, гамма, дельта, и т. д.
).

Блок 2. Словарь.

Составьте словарь новых терминов и определений из §2. Для этого в пустые строки таблицы впишите слова из списка терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.

Блок 3. Установите соответствие (УС).

Геометрические фигуры.

Блок 4. Самопроверка.

Измерение отрезка с помощью линейки.

Напомним, что измерить отрезок АВ в сантиметрах, значит, сравнить его с отрезком длиной 1см и узнать, сколько таких отрезков по 1см помещается в отрезке АВ. Чтобы измерить отрезок в других единицах длины, поступают подобным же образом.

Для выполнения заданий работайте по плану, приведенному в левой колонке таблицы. При этом правую колонку рекомендуем закрыть листом бумаги. Затем вы сможете сопоставить свои выводы с решениями, приведенными в таблице справа.

Блок 5. Установление последовательности действий (УП).

Построение отрезка заданной длины.

Вариант 1
. В таблице записан перепутанный алгоритм (перепутанный порядок действий) построения отрезка заданной длины (например, построим отрезок ВС = 7см). В левом столбце указание к действию в правом результат выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.

Вариант 2.
В следующей таблице приведен алгоритм построения отрезка КМ = n см, где вместо n
можно подставить любое число. В этом варианте нет соответствия между действием и результатом. Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат. Ответ запишите в виде: 2а, 1в, 4б и т.д.

Вариант 3.
Используя алгоритм варианта 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.

Блок 6. Фасетный тест.

Отрезок, луч, прямая, плоскость.

В задачах фасетного теста используются рисунки и записи под номерами 1 — 12, приведённые в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО». Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Например, задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6, з
атем к нему добавляется условие под номером 15, требование задачи стоит под номером 19.»

13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;

14) провести через каждые две точки прямую;

15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;

16) количество различных отрезков на рисунке;

17) количество различных лучей на рисунке;

18) количество различных прямых на рисунке;

19) количество получившихся различных плоскостей;

20) длина отрезка АС в сантиметрах;

21) длина отрезка АВ в километрах;

22) длина отрезка DC в метрах;

23) периметр треугольника PRQ;

24) длина ломаной QPRMN;

25) частное периметров треугольников RMN и PRQ;

26) длина отрезка ED;

27) длина отрезка BE;

28) количество получившихся точек пересечения прямых;

29) количество получившихся треугольников;

30) количество частей, на которые оказалась разделена плоскость;

31) периметр многоугольника, выраженный в метрах;

32) периметр многоугольника, выраженный в дециметрах;

33) периметр многоугольника, выраженный в сантиметрах;

34) периметр многоугольника, выраженный в миллиметрах;

35) периметр многоугольника, выраженный в километрах;

РАВНО (равна, имеет вид):

а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8∙b; з) 800∙b; и) 8000∙b; к) 80∙b; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28

Блок 7. Давай поиграем.

7.1. Математический лабиринт.

Лабиринт состоит из десяти комнат с тремя дверьми каждая. В каждой из комнат находится по одному геометрическому объекту (он нарисован на стене комнаты). Сведения об этом объекте находятся в «путеводителе» по лабиринту. Читая его, надо переходить в ту комнату, о которой написано в путеводителе. Проходя по комнатам лабиринта, рисуйте свой маршрут. В двух последних комнатах имеются выходы.

Путеводитель по лабиринту

Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.
Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.
Геометрический объект этой комнаты составлен из четырёх отрезков, имеющих три общие точки.
Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.
В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.
Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.

Представление об этом геометрическом объекте даёт полет артиллерийских снарядов

(траектория движения).

В этой комнате находится геометрический объект с тремя вершинами, но это не горные

Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье

оружие коренных жителей Австралии). В физике эту линию называют траекторией

движения тела.

Представление об этом геометрическом объекте даёт поверхность озера в

безветренную погоду.

Теперь можете выходить из лабиринта.

В лабиринте находятся геометрические объекты: плоскость, незамкнутая линия, прямая, треугольник, точка, замкнутая линия, ломаная, отрезок, луч, четырёхугольник.

7.2. Периметр геометрических фигур.

В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти — и шестиугольники. С помощью линейки (в миллиметрах) определите периметры некоторых из них.

7.3. Эстафета геометрических объектов.

В заданиях эстафеты есть пустые рамки. В них запишите пропущенное слово. Затем перенесите это слово в другую рамку, куда показывает стрелка. При этом можно изменять падеж этого слова. Проходя по этапам эстафеты, выполняйте требуемые построения. Если эстафету пройдёте правильно, то в конце получите слово: периметр
.

7.4. Крепость геометрических объектов.

Прочитайте § 2, выпишите из его текста названия геометрических объектов. Затем впишите эти слова в пустые клетки «крепости».

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

A
B
C

точка 1, точка 2, точка 3

1
2
3

Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие?
A
A
A

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

a
b
c

Линия может быть

замкнутой, если её начало и конец находятся в одной точке,
разомкнутой, если её начало и конец не соединены

замкнутые линии

разомкнутые линии

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

самопересекающейся
без самопересечений

самопересекающиеся линии

линии без самопересечений

прямой
ломанной
кривой

прямые линии

ломанные линии

кривые линии

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

прямая линия AB

B
A

Прямые могут быть

пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
параллельными, если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча
A
A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

луч AB

B
A

Лучи совпадают, если

расположены на одной и той же прямой,
начинаются в одной точке,
направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

C
B
A

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки

B
A

прямая линия AB

B
A

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
B
A
✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB

B
A

Задача: где прямая
, луч
, отрезок
, кривая
?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE

вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E

звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE

звено AB и звено BC являются смежными

звено BC и звено CD являются смежными

звено CD и звено DE являются смежными

A
B
C
D
E
64
62
127
52

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

замкнутая ломанная линия, не имеющая самопересечения, ABCDEF

многоугольник ABCDEF

вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F

вершина A и вершина B являются соседними

вершина B и вершина C являются соседними

вершина C и вершина D являются соседними

вершина D и вершина E являются соседними

вершина E и вершина F являются соседними

вершина F и вершина A являются соседними

сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF

сторона AB и сторона BC являются смежными

сторона BC и сторона CD являются смежными

сторона CD и сторона DE являются смежными

сторона DE и сторона EF являются смежными

сторона EF и сторона FA являются смежными

A
B
C
D
E
F
120
60
58
122
98
141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.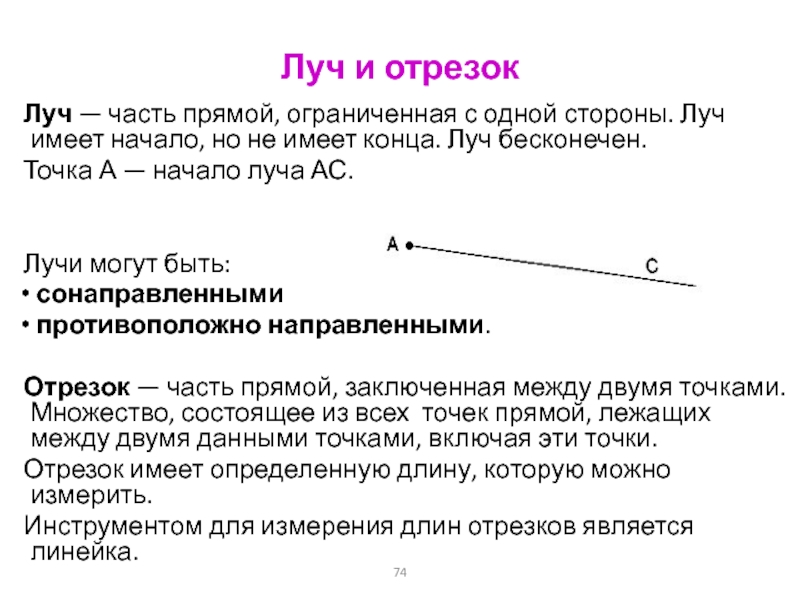 д.

Введение в геометрию. Точка, прямая и отрезок

2. Глава 1 Начальные геометрические сведения.

Введение в геометрию.
Точка, прямая и отрезок.

3. Евклид (Eνκλειδηζ) (365-300 до н.э.) древнегреческий математик , автор первого из дошедших до нас теоретических трактатов по

математике «Начала» (13 книг).
Евклид. Рельеф работа Андреа
Пизано. Около 1334-1340 г.г.

4. Страницы «Начал» Евклида. Издание 1482 г.

Платон (477-347 до н.э.) —
древнегреческий философ, ученик Сократа и
учитель Евклида.
Многих мыслителей и
философов привлекала
знаменитая Академия
Платона. Уважение к
геометрии было
настолько велико, что
по преданию, у входа в
Академию Платона
имелась надпись:
Однажды Царь Птолемей I
сам захотел одолеть премудрости
геометрии, но довольно скоро
обнаружил, что изучение математики
– слишком тяжелое бремя.
Птолемей спросил Евклида:
«Нельзя ли постигнуть все тайны
науки как-нибудь проще?»
Евклид ответил:
Евдем Родосский
(IV век до н.э.)
объясняет происхождение термина
«геометрия» так: «Геометрия была
открыта египтянами и возникла при
измерении Земли. Это измерение
было им необходимо вследствие
разлития реки Нила, постоянно
смывавшего границы».

9. от древнегреческих слов «ge»- «земля» и «metreo»- «измеряю»

Геометрия – это наука, занимающаяся изучением
геометрических фигур и их свойств.
Какие геометрические фигуры вам известны?
прямая
куб
ломаная
цилиндр
отрезок
шар
луч
конус
прямоугольник
пирамида
квадрат
параллелепипед
По какому принципу данные геометрические
фигуры записаны в двух различных группах?
прямая
куб
ломаная
цилиндр
отрезок
шар
луч
конус
прямоугольник
пирамида
квадрат
параллелепипед
Часть геометрии, в которой рассматриваются
фигуры
НА ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
Называется
Planum (лат) –
равнина, местность
(в 7-9 классах)
Sterio (лат) телесный, пространственный
(в 10-11 классах)

11. Быстренько, не задумываясь, выберите из предложенных пяти фигур ту, которая вам больше понравилась.

Геометрия изучает фигуры и их свойства.
А могут ли фигуры рассказать о нас?
Быстренько, не задумываясь,
выберите из предложенных пяти фигур ту,
которая вам больше понравилась.
Ломаная (Зигзаг)
Прямоугольник
Квадрат
Круг
Треугольник

12. Вот что говорят фигуры о нас

Соответствует трудолюбие, усердие, потребность
доводить начатое дело до конца, упорство. Любит
раз и навсегда заведенный порядок.
Это временная форма личности, ищет лучшее
положение.
Поэтому
любознателен,
пытлив,
интересно все происходящее, и смел.
Символ лидерства. Способен концентрироваться на
главной цели. Энергичен, неудержим, сильная
личность.
Самая
доброжелательная
фигура.
Способен
сопереживать, сочувствовать. Счастлив тогда, когда
все ладят друг с другом.
Символ творчества. Нравится комбинировать,
создавать что-то новое, оригинальное. Самый
восторженный и возбудимый.

13. Фигуры много знают о нас. Поэтому и мы должны узнать о них как можно больше.

Что же мы будем изучать в 7 классе?
Поможет нам в этом –
учебник. Авторы нашего
учебника: Л. С. Атанасян,
В. Ф. Бутузов, С, Б.
Кадомцев, Э. Г. Позняк,
И. И. Юдина.
Глава 1. Начальные геометрические
сведения.
Глава 2. Треугольники.
Глава 3. Параллельные прямые.
Глава 4. Соотношения между сторонам
и углами треугольника
Логическая цепочка:
начальные понятия –определения –
аксиомы — теоремы

14. – гимнастика для ума — витамин для мозга — язык геометрии

Без чертежа не изготовить ни
одной машины, не построить
здания. На нем можно
изъясняться, не прибегая к
словам. Древние математики
часто рисовали чертеж и вместо
доказательства писали только
одно слово: «СМОТРИ!»
Архимед (287-212 до н.э.) –
древнегреческий философ и
ученый. Уроженец и гражданин
Сиракуз (остров Сицилия).
Образование получил в
Александрии. Архимеду
принадлежит ряд важнейших
математических и физических
открытий (закон Архимеда).

15. Смерть Архимеда. Копия XVIII в. с римской мозаики II в.

По преданию, последними словами
Архимеда были:
«НЕ ТРОНЬ МОИХ ЧЕРТЕЖЕЙ!».
Предание гласит: во II
Пуническую войну во время
обороны своего родного города
Сиракузы Архимед придумал
множество механических устройств,
которые наводили ужас на
нападавших римлян, таки не
сумевших взять город приступом и
победивших лишь с помощью
предательства. В глубокой
задумчивости Архимед рисовал на
песке геометрические фигуры когда
на него напали римские воины.
Обозначение
.
А, В, С, Е, D, N, M …
.
a, b, c, d, AB, CD, NM …

17. Начальные геометрические сведения

Через одну точку
можно
провести
сколько
угодно
различных прямых
Через любые две
точки можно
провести прямую, и
притом только одну

18. Начальные геометрические сведения

А
a
А a
В a
С a
К
В
С
Е
D
К a
Е a

19. Начальные геометрические сведения

1
2
Две прямые либо
Параллельны
имеют одну общую
точку, либо не имеют
общих точек
Пересекаются

20. Отрезок – часть прямой ограниченная двумя точками. Эти точки называются концами отрезка ( отрезок содержит все точки прямой,

Начальные геометрические сведения
От резок – част ь прямой ограниченная двумя
точками. Эт и т очки называют ся концами от резка (
от резок содержит все т очки прямой, лежащие
между его концами и концы от резка)

21. Начальные геометрические сведения

A
C M
AC AM AO
CM CO
MO
O

22. Закрепление

23. Закрепление

1.
2.
3.
4.
1. Начертите прямую.
Как ее можно
обозначить?
2. Отметьте точку Т, не лежащую на
данной прямой, и точки D, E, K,
лежащие на этой прямой.

25. Специальные символы, позволяющие кратко записывать какое-либо утверждение.

є — принадлежит, «лежит»
є — не принадлежит, «не лежит»
3. Используя символы, запишите
предложение:
«Точка D принадлежит прямой AB,
точка C не принадлежит прямой a »
D є AB,
Cє
a
4. Используя рисунок и символы
є и є , запишите , какие точки
принадлежат прямой а, а какие –
нет.
-Сколько прямых можно провести через заданную точку А?
-Сколько прямых можно провести через две точки?
— Через любые две точки можно провести прямую?
СВОЙСТВО ПРЯМОЙ: Через любые две точки можно
провести прямую и притом только одну.
5. Начертите прямые a и b (XYи MK),
пересекающиеся в точке О.
пересечение
(XY ∩ MK = О)
Специальный символ: ∩-
a∩b=О
«Прямые a и b (XYи MK)
пересекаются в точке О».
Сколько общих точек может быть у двух прямых?
Задание:
сделать рисунки и обдумать ответ
6. На прямой a отметьте
последовательно точки О, A, B, C.
Запишите все получившиеся отрезки.
7. Начертите прямые a и b,
пересекающиеся в точке М. На прямой a
отметьте точку N, отличную от точки М.
—
Являются ли прямые М N и a различными прямыми?
Может ли прямая b проходить через точку N?
8. Дана прямая EF, A є EF, B є EF.
Может ли прямая АВ не пересекать
отрезок EF?
Проверь себя
6. ОА, ОВ, ОС, АВ, АС, ВС, ОА.
7.
a
b
М
N
a∩b=М
Nєa
a) прямая МN и прямая a совпадают, то есть это одна и та же
прямая.
b) прямая b не может проходить через точку N, т.к. она уже
проходит через точку M, а через точки М и N можно провести
прямую и притом только одну (это прямая а).
F
В
Е
8. Не может
На рисунке выделена
часть прямой,
ограниченная двумя
точками. Как называется эта фигура?
Определение: часть прямой, ограниченная двумя точками,
называется отрезком. Точи, ограничивающие отрезок,
называются его концами.
Обозначение: отрезок АС или СА
точки А и С – концы отрезка
Рассмотрите рисунок.
Что вы видите?
Запишите с помощью
символов.
О точке А, принадлежащей отрезку СB, говорят также, что точка
А лежит между точками С и B (если А – внутренняя
точка отрезка), а также, что отрезок AС содержит
точку А.
Обозначение: С – А – В – «точка А лежит между
точками С и B »
Решаем по учебнику:
страница 7 № 2, 5, 6.
Дополнительные задачи:
1. Сколько точек пересечения могут
иметь три прямые? Рассмотрите все
возможные случаи и сделайте
соответствующие рисунки.
2. На плоскости даны три точки. Сколько
прямых можно провести через эти
точки так, чтобы на каждой прямой
лежали хотя бы две из данных точек?
Рассмотрите все возможные случаи и
сделайте рисунки.

32. Обозначения

Запись
Чтение
A, B, C, …
Точка A, точка B, точка C, …
a, b, c, …
AB, CD, …
Прямая a, прямая b, …
Прямая AB, прямая CD, …
A a
B a
Точка A принадлежит прямой a.
Или прямая а проходит через
точку А.
Точка B не принадлежит прямой
a. Или прямая а не проходит
через точку В

33. Обозначения

Запись
a∩b=М
Чтение
Прямая а и прямая b
пересекаются в точке М.
Или прямая а и прямая b имеют
общую точку М.
АВ ∩ СD = О Прямая АВ и прямая СD
пересекаются в точке О.
Или прямая АВ и прямая СD
имеют общую точку О.
(часть
Отрезок МТ
прямой) МТ

34. Обозначения

Запись
с || d
Чтение
Прямая с и прямая d
параллельные.
a│b
Прямая а и прямая b
перпендикулярные.
С – А – В Точка А лежит между
точками С и B

35. Провешивание прямой на местности (от слова «веха») – практический способ проведения прямых на местности.

Провешивание прямой на мест ност и
(от слова «веха»)
– практический способ
проведения прямых на местности.
Проверь себя
б) одна
1.а) три
в) две
г) ни одной
2. а) одна прямая
б) три прямые

КРОССВОРД
Вставь пропущенное слово: «Через любые две
точки можно провести … ; и при том только
одну».
Математический знак
Название книги, в которой впервые был
систематизирован геометрический материал.
Геометрическая фигура на плоскости.
Геометрическая фигура в пространстве.
Раздел геометрии.
Математический знак ∩
Первоначальное понятие в геометрии.
Часть прямой, ограниченная двумя точками.
Древнегреческий математик.
Геометрическая фигура на плоскости.

38. Математический диктант (с последующей проверкой).

1. Начертите прямую и обозначьте ее буквой b.
а) Отметьте точку М, лежащую на прямой b.
б) Отметьте точку N, не лежащую на прямой b.
в) Используя символы и , запишите предложение: «Точка М лежит на
прямой b, а точка N не лежит на ней».
2. Начертите прямые а и b, пересекающиеся в точке М. На прямой а
отметьте точку N, отличную от точки М.
а) Являются ли прямые MN и а различными прямыми?
б) Может ли прямая b проходить через точку N?
(Ответы обоснуйте)

39. Проверка математического диктанта

М b; N b.

40. Проверка математического диктанта

1. Параграф 1 учебника пункты 1 и 2 прочитать, подготовить
ответы на вопросы 1, 2, 3 на странице 25. Пункт 2 на уроке
мы не рассматривали, дома самостоятельно с ним
познакомитесь.
2. В тетради решить задачи № 1, 3, 4, 7.
3. Дополнительная задача (за нее можно получить хорошую
отметку!)
Задача: Сколько различных прямых можно провести через
четыре точки? Рассмотрите все возможные случаи и
сделайте рисунки.
Что узнали нового, чему научились, что понравилось.
Оцените свою работу на уроке, нарисовав в тетради
следующие знаки:
• Старался, и всё получалось.
• Старался, но не всё получалось.
• Не старался.

Отрезок

Отрезок. Длина отрезка. Треугольник.

1. В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия — наука об «измерении земли». Это слово происходит от латинских слов: geo – земля и metr — мера, мерить. В геометрии изучаются различные геометрические объекты, их свойства, их связи с окружающим миром. Простейшие геометрические объекты – это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.

Если приложить к двум точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок, который называют АВ или ВА (читаем: «а – бэ», «бэ– а»). Точки А и В называются концами отрезка (рисунок 1). Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрезка.

Единицы длины: м – метр, см — сантиметр, дм – дециметр, мм – миллиметр, км – километр и др. (1 км = 1000 м; 1м =10 дм; 1 дм = 10 см; 1 см = 10 мм). Для измерения длины отрезков используют линейку, рулетку. Измерить длину отрезка, значит, выяснить, сколько раз в нем укладывается та или иная мера длины.

Равными называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2). Например, можно вырезать реально или мысленно один из отрезков и приложить к другому так, чтобы совпали их концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равные длины. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют различные длины, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка. Сравнивать отрезки наложением можно, используя циркуль.

Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то мы получим представление о прямой АВ (рисунок 3). Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется началом луча.

2. Если три точки, не лежащие на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником. Данные точки называются вершинами треугольника, а отрезки, их соединяющие, сторонами треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM – стороны треугольника, точки F, N, M – вершины треугольника. Стороны всех треугольников обладают следующим свойством: длина любой из сторон треугольника всегда меньше суммы длин двух других его сторон.

Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости. Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).

Блок 1. Дополнительный

Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т.д. Однако все перечисленные объекты имеют размеры, в отличие от них размеры геометрической точки считаются равными нулю (её измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить. Можно также сказать, в каком месте она находится. Поставив авторучкой в тетради точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A, B, C, D, (читают «точка а, точка бэ, точка цэ, точка дэ») (рисунок 7).

Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т.д. дают нам представление о поверхностях (рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.

Наиболее простая из всех линий – это прямая. Приложим к листу бумаги линейку и проведем карандашом вдоль неё прямую линию. Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение – длину, а два других ее измерения равны нулю (рисунок 12).

При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом. Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать прямую также двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую n на рисунке 13 можно обозначить: АВ или ВА, АD или DА, DВ или ВD.

Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать прямой). На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут . Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой m, ее называют общей точкой. В точке D прямые AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:

Через любые две точки всегда можно провести прямую и причем только одну.

Фигура, которая состоит из точек и соединяющих их отрезков называется ломаной (рисунок 15). Отрезки, образующие ломаную, называются звеньями ломаной, а их концы — вершинами ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG. Длиной ломаной называется сумма длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.

Замкнутая ломаная называется многоугольником, ее вершины называются вершинами многоугольника, а ее звенья сторонами многоугольника (рисунок 16). Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любой, например, многоугольник (семиугольник) ABCDEFG , многоугольник (пятиугольник) RTPKL:

Сумма длин всех сторон многоугольника называется периметром многоугольника и обозначается латинской буквой p (читаем: пэ). Периметры многоугольников на рисунке 13:

P_ABCDEFG = AB + BC + CD + DE + EF + FG + GA.

P_RTPKL= RT + TP + PK + KL + LR.

Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью (рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ,… (читаем: плоскость альфа, бетта, гамма, дельта, и т.д.).

Блок 2. Словарь.

Блок 3. Установите соответствие (УС).

Геометрические фигуры.

Блок 4. Самопроверка.

Измерение отрезка с помощью линейки.

Блок 5. Установление последовательности действий (УП).

Построение отрезка заданной длины.

Вариант 1. В таблице записан перепутанный алгоритм (перепутанный порядок действий) построения отрезка заданной длины (например, построим отрезок ВС = 7см). В левом столбце указание к действию в правом результат выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.

Вариант 2. В следующей таблице приведен алгоритм построения отрезка КМ = n см, где вместо n можно подставить любое число. В этом варианте нет соответствия между действием и результатом. Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат. Ответ запишите в виде: 2а, 1в, 4б и т.д.

Вариант 3. Используя алгоритм варианта 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.

Блок 6. Фасетный тест.

Отрезок, луч, прямая, плоскость.

В задачах фасетного теста используются рисунки и записи под номерами 1 – 12, приведённые в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО». Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Например, задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6, затем к нему добавляется условие под номером 15, требование задачи стоит под номером 19.»

Содержание теста.

13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;

14) провести через каждые две точки прямую;

15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;

ТО:

16) количество различных отрезков на рисунке;

17) количество различных лучей на рисунке;

18) количество различных прямых на рисунке;

19) количество получившихся различных плоскостей;

20) длина отрезка АС в сантиметрах;

21) длина отрезка АВ в километрах;

22) длина отрезка DC в метрах;

23) периметр треугольника PRQ;

24) длина ломаной QPRMN;

25) частное периметров треугольников RMN и PRQ;

26) длина отрезка ED;

27) длина отрезка BE;

28) количество получившихся точек пересечения прямых;

29) количество получившихся треугольников;

30) количество частей, на которые оказалась разделена плоскость;

31) периметр многоугольника, выраженный в метрах;

32) периметр многоугольника, выраженный в дециметрах;

33) периметр многоугольника, выраженный в сантиметрах;

34) периметр многоугольника, выраженный в миллиметрах;

35) периметр многоугольника, выраженный в километрах;

РАВНО (равна, имеет вид):

а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8∙b; з) 800∙b; и) 8000∙b; к) 80∙b; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28

Блок 7. Давай поиграем.

7.1. Математический лабиринт.

Путеводитель по лабиринту

Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.

Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.

Геометрический объект этой комнаты составлен из четырёх отрезков, имеющих три общие точки.

Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.

В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.

Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.

Представление об этом геометрическом объекте даёт полет артиллерийских снарядов

(траектория движения).

В этой комнате находится геометрический объект с тремя вершинами, но это не горные

вершины.

Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье

оружие коренных жителей Австралии). В физике эту линию называют траекторией

движения тела.

Представление об этом геометрическом объекте даёт поверхность озера в

безветренную погоду.

Теперь можете выходить из лабиринта.

7.2. Периметр геометрических фигур.

В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти – и шестиугольники. С помощью линейки (в миллиметрах) определите периметры некоторых из них.

7.3. Эстафета геометрических объектов.

7.4. Крепость геометрических объектов.

точка и прямая линия, отрезок, луч, ломаная линия

К основным геометрическим фигурам на плоскости относятся точка и прямая линия. Отрезок, луч, ломаная линия — простейшие геометрические фигуры на плоскости.

Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:

Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезок изображается так:

Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:

Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.

Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.

Выше изображена трехзвенная ломаная линия.

Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:

Четырехзвенная замкнутая ломаная линия — четырехугольник

Трехзвенная замкнутая ломаная линия — треугольник

Плоскость, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.

Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:

Плоскость,прямая,луч,отрезок. — Математика — Презентации

Плоскость , прямая , луч , отрезок .

5 класс.

Цели урока:

Цель урока:

1. Сформировать у учащихся понятие отрезок, прямая, луч.

2 . Научить строить отрезок, прямую по двум точкам.

3. Научить определять принадлежность точки отрезку, прямой, лучу.

4. Продолжить работу над развитием навыков устного счёта.

5. Повторить решение задач на части.

Какое число нужно

вписать в

последнюю клетку?

+23

+15

+24

:10

Плоскость ,прямая ,луч ,отрезок .

Прямые обозначают так :

прямая m

прямая р

прямая АВ

прямая CD

Взаимное расположение прямых.

Через любые две точки можно провести прямую, и притом только одну.

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Луч

Если провести прямую и поставить на ней точу, то мы разделим её на две части, каждая из которых называется лучом. Точка является началом обоих этих лучей.

Луч

Обычно луч обозначается маленькой латинской буквой или двумя заглавными латинскими буквами . При этом на пером месте ставится буква, обозначающая начало луча.

Отрезок.

Отрезок – часть прямой, ограниченная двумя точками. Точки A и B – концы отрезка

Отрезок с концами А и В обозначают АВ или ВА.

Он содержит точки А и В и все точки прямой, лежащие между точками А и В.

Сколько есть

отрезков

соединяющих

точки С и К ?

Любые две точки можно

соединить только

одним отрезком.

Какие точки лежат

на отрезке EF?

Точки N,M, E, F лежат

на отрезке EF.

Какие точки

не лежат

на отрезке EF?

Точки Y, D, P

не лежат

на отрезке EF.

Какие из точек

лежат на отрезке KL

и на прямой KL?

Точки K, L, G лежат

на отрезке KL и на прямой КL.

Какие точки

лежат на прямой KL и

не лежат на отрезке KL?

Какие точки

лежат на прямой KL и

не лежат на отрезке KL?

Точка V лежит на прямой KL и

не лежит на отрезке KL.

Какие из точек

лежат на луче MN?

Точки M, N, S,Q

лежат на луче MN.

Отметьте в тетради точки С и D

и проведите прямую СD.

Отметьте на отрезке СD

точку М.

Решение:

Ответь на вопрос:

Лежит ли точка М на прямой СD?

Домашнее задание:

п.2.1 стр. 77-79 читать

№ 339-341(устно), № 360.

Определение линейного сегмента — Математическая открытая ссылка

Определение: прямая линия, соединяющая два
точек, не выходя за их пределы.

Попробуй это
Отрегулируйте сегмент линии ниже, перетащив оранжевую точку на конечную точку, и посмотрите, как ведет себя сегмент PQ.

См. Рисунок выше. Отрезок PQ соединяет точки P и Q.
Точки P и Q называются «конечными точками» отрезка.Слово «сегмент» обычно означает «кусок» чего-либо, а здесь оно означает «кусок».
полный
линия, которая обычно простирается до бесконечности в обоих направлениях.

Отрезок линии одномерный. Он имеет измеримую длину, но нулевую ширину. Если вы начертите линейный сегмент карандашом, осмотр под микроскопом покажет, что карандашный след имеет измеримую ширину. Карандашная линия — это просто способ проиллюстрировать идею на бумаге. Однако в геометрии отрезок линии не имеет ширины.

Наименование отрезков

Сегменты линии обычно называют двумя способами:

По конечным точкам.
На рисунке выше сегмент линии будет называться PQ, потому что он соединяет две точки P и Q.
Напомним, что точки обычно обозначаются одними заглавными (заглавными) буквами.
Сокращенный способ записать это:
Это читается как «отрезок линии PQ». Полоса над двумя буквами указывает на то, что это отрезок линии, а не линия, которая продолжается вечно в обоих направлениях.
Одной буквой.
Вышеупомянутый сегмент будет называться просто «y». По соглашению, это обычно одна строчная (строчная) буква.
Этот метод часто используется для обозначения сторон
треугольники и прочее
полигоны.

Строений

В главе о конструкциях
есть анимированные демонстрации того, как выполнять различные конструкции
относящиеся к линейным сегментам с использованием только циркуля и линейки. См .:

Координатная геометрия

В другом разделе математики, называемом координатной геометрией, точки, определяющие линию, расположены на плоскости, используя их
координаты — два числа, которые показывают, где находится точка.
Подробнее см. Определение отрезка линии (координатная геометрия).

Если мы знаем координаты двух конечных точек отрезка линии,
мы можем вычислить расстояние между ними и таким образом найти длину отрезка.
См. Расстояние между двумя точками (координатная геометрия)

Другие темы строки

линий и линейных сегментов

Изучение линий и сегментов

Вы научитесь определять пересекающиеся, параллельные и перпендикулярные линии.

Вобаул:

Узнать | Деятельность

Учиться

Художники используют сетки. Пересекающиеся отрезки линий помогают им увеличивать или уменьшать рисунки.

Линия

Линейный сегмент

Ray

В сетке две пересекающиеся линии пересекаются в точке P.

Параллельные прямые никогда не пересекаются. Синие линии параллельны.

Перпендикуляр линий пересекаются под прямым углом. Красная линия перпендикулярна каждой синей линии.

Деятельность

Эти прямые параллельны, пересекаются или перпендикулярны?

Воспользуйтесь картой района Фенуэй Бостона, чтобы ответить на следующие вопросы.

Укажите, параллельна ли каждая пара улиц или перпедикулярна

Куинсберри-стрит и Питерборо-стрит
ул. Ван-Несс и ул. Килмарнок,

Могли бы вы добраться от угла Джерси и Питерборо до Оверленд-стрит, не пересекая Ван-Несс? Объяснять.

Проверьте свои ответы.

Геометрия: сегменты

Сегменты и лучи находятся под подмножеством линий.Сегмент — это часть линии, имеющая две конечные точки и имеющую определенную длину. С другой стороны, луч также является частью линии, имеющей одну конечную точку, а другое направление продолжается бесконечно. На рисунке 1 изображены сегмент и луч.

Запоминание терминов

Конгруэнтный
— того же размера и формы.
Расстояние
— числовое значение, описывающее расстояние между двумя объектами.
Конечная точка
— точка, расположенная в конце отрезка, определяющая его предел.
Противоположный
— реверс по положению или направлению.
Подмножество
— часть набора.
Вертикальный
— положение вверх-вниз.

Определение сегмента

Сегмент — это набор точек, состоящий из двух точек линии, называемых конечными точками, и всех точек линии между конечными точками .Обычно он используется для обозначения длины, высоты или ширины определенного объекта и расстояния между двумя объектами. Он называется с помощью метки его конечных точек и вставки линии (() ̅) над буквами. На рисунке 2 показан отрезок AB, который также можно записать как (AB) ̅.

Пример 1

Розыгрыш (CD).

Пояснение:

Нарисуйте две точки и обозначьте их буквами C и D.

Соедините две точки прямо друг с другом.

Пример 2

Сколько сегментов в строке ниже?

Пояснение:

Используйте точки на линии как конечные точки сегментов.

Сегменты: (QR), (RS), (ST), (QS), (RT) и (QT).

Середина сегмента

Средняя точка сегмента — это точка, которая делит линейный сегмент на две совпадающие части.Он расположен в центре сегмента. На рисунке 3 показана середина сегмента.

Примечание. Две вертикальные линии показывают, что расстояния от средней точки до обеих конечных точек равны.

Пример 3

Длина (XY) равна 12, а Z — средняя точка (XY). Найдите длину (XZ).

Пояснение:

Средняя точка Z делит (XY) на две равные части: (XZ) и (YZ).

Длина (XZ) равна ½ длины (XY), что составляет ½ 12 = 6.

Пример 4

O — середина (NP). Если (NO) = 9, какова длина (NP)?

Ответ: 18

Пояснение:

Средняя точка O делит (NP) ̅ на две равные части: (NO) ̅ и (PO) ̅.

с Длина (NP) ̅ в два раза больше длины (NO) ̅, что составляет 2 9 = 18.

Сложение и вычитание сегментов

На рисунке 4 показаны три коллинеарные точки E, F и G, образующие сегмент.

Точки E и G составляют конечные точки сегмента, который является (EG), а точка F между ними делит (EG) на два сегмента: (EF) и (FG). Сумма длин (EF) и (FG) равна длине (EG).Следовательно, (EF) + (FG) = (EG) . Выражение представляет сегмент, если точка F находится между точками E и G.

Следующие выражения справедливы также для длин сегментов:

(EF) = (EG) — (FG)

(FG) = (EG) — (EF)

Пример 5

Найдите длину (JL) на рисунке.

Пояснение:

Точки J и L являются конечными точками (JL), а точка K находится между точками J и L.

Следовательно, (JK) + (KL) = (JL).

(JL) = 6 + 4 = 10.

Пример 6

Длина (UV) равна 13, а W находится между точками U и V. Если (WU) = 5, какова длина (VW)?

Точки U и V являются конечными точками (UV), а точка W находится между точками U и V.

Следовательно, (UW) + (VW) = (UV).

(UW) = (WU) = 5

Итак, (VW) = (UV) — (UW) = 13-5 = 8.

Определение луча

Луч состоит из точки на прямой и всех точек с одной стороны от точки. У него только одна конечная точка. Лучи обычно используются в физике для обозначения направления, а также силы. Называя луч, рассмотрите две точки на луче: одна — это конечная точка, а другая — любая точка на луче.Метка конечной точки должна быть первой буквой имени луча и помещать знак стрелки вправо (()) над буквами. На рисунке 5 показан луч, помеченный как (RY).

Противоположные лучи — это два луча, которые лежат на одной линии и имеют общий конец и не имеют других общих точек. На Рисунке 6 (RS) ̅ и (ST) ̅ — противоположные лучи.

Пример 7

Ничья (AE).

Пояснение:

Нарисуйте две точки и обозначьте их буквами A и E.

Соедините две точки прямо друг с другом и продолжите линию от точки E.

Пример 8

Найдите количество лучей, которые могут быть найдены в линии.

Пояснение: 12

Считайте две точки на линии точками луча.

Лучи, указывающие вправо, могут называться (MB), (BP), (PC), (MP), (BC) и (MC).

Лучи, указывающие налево, могут называться (CP), (PB), (BM), (CB), (PM) и (CM).

В этой линии 12 лучей.

линий, сегментов линий и лучей — математика для 3-го класса

Узнайте о линиях, сегментах линий и лучах

Вы знаете, что такое геометрия?

Геометрия — это математика форм и пространств.

😃 В геометрии мы работаем с различными формами.

(Вы можете назвать каждую из этих фигур? Попробуйте! 🤗)

В геометрии мы также работаем с более простыми вещами, такими как точек, линий, отрезков линий, и лучей .

Это строительных блоков геометрии. 😺

В этом уроке давайте узнаем о каждом из них. 😎

Что такое очки?

🤓 Посмотрите на эти точки.

Каждая из этих точек называется точкой .

Точка — это любое место в космосе. Он не имеет длины, высоты или ширины .

👉 Очки обозначаются одиночными заглавными буквами как .

Например, это точка А.

👉 Кончик карандаша можно рассматривать как острие.

👉 Каждое место на фигуре представляет собой точку.

Что такое линии?

😃 Посмотрите на это изображение. Он показывает горизонт.

Можете ли вы сказать, где заканчивается горизонт с обеих сторон? 🤔

Нет, не можем. 🤓

Это потому, что горизонт продолжается с обеих сторон. Это никогда не кончится. Это линия .

Линия — это прямой путь точек, который вечно продолжается в обоих направлениях.

В геометрии рисуется линия со стрелками на обоих концах.

Как вы думаете, мы можем измерить длину линии? 🤔

Нет! 😁 Мы не можем.

✅ Поскольку линия никогда не заканчивается, мы не можем измерить ее длину .

👉 Чтобы назвать линию, используйте любые две точки на ней.

Например, чтобы назвать эту линию, мы используем две точки на ней, A и B, и называем ее Line AB или Line BA.

При написании имени поместите двустороннюю стрелку поверх этикетки.

Что такое линейные сегменты?

🤓 Посмотрите на края этой шахматной доски.

Каждое ребро представляет собой отрезок линии .

Отрезок — это прямой путь с двумя конечными точками.

Отрисовывается линейный сегмент с точками на обоих концах.

Можно ли измерить длину отрезка линии? 🤔

Да! Ты можешь! 🤗

✅ Это потому, что в определенной точке отрезок линии заканчивается .

👉 Чтобы назвать сегмент линии , используйте его конечные точки.

Например, этот линейный сегмент может называться Линейный сегмент AB или Линейный сегмент BA .

При написании имени поместите строку поверх этикетки.

Что такое лучи?

Посмотрите на эти лучи света. 🌞

Мы знаем, где начинаются лучи.

Но вы можете сказать, где кончаются эти лучи? 🤔

Нет! Мы не можем.

Это потому, что луч начинается в одной точке и продолжает идти в обратном направлении вечно.

Луч — это прямой путь из точек, который начинается в одной точке и продолжается в одном направлении вечно.

✅ У луча одна конечная точка.

Рисуется луч с точкой на одном конце и стрелкой на другом.

Можете ли вы измерить длину луча? 🤔

Нет! 😎 Вы не можете.

✅ Это потому, что луч, как линия, никогда не заканчивается.

👉 Чтобы назвать луч , начните с его конечной точки и закончите в любой точке на другой стороне.

✅ Помните! Существует только один способ назвать луч , который начинается с его конечной точки.

Например, этот луч можно назвать Ray XY (но не Ray YX).

При написании имени поместите одностороннюю стрелку поверх этикетки.

Смотри и учись

Поздравляем! 👏 Теперь вы знаете, что такое прямые, отрезки и лучи. Начните свою практику ниже.

Линейный сегмент

Часть прямой называется отрезком.

На самом деле, значение сегмента линии происходит от двух слов «Линия» и «Сегмент».

Значение «Линия» — прямой путь.
Значение сегмента — это часть.

Сегмент линии графически представлен линией с двумя конечными точками.Она также известна как линия между двумя точками.

Представительство

Графически сегмент линии представлен линией с двумя конечными точками.
Отрезок линии записывается математически на основе графического представления. Итак, напишите названия точек по очереди и выведите на обе точки линию.

Формация

Отрезок линии геометрически формируется двумя различными способами.

Часть прямой

Сегмент линии — это, по сути, выделенная часть прямой линии.

$ \ overleftrightarrow {EF} $ — прямая на плоскости, обозначающая любые две точки ($ P $ и $ Q $) на этой прямой. Затем извлеките маленькую линию в точках $ P $ и $ Q $ из прямой.

Маленькая линия, которая содержит конечные точки $ P $ и $ Q $, является частью прямой $ \ overleftrightarrow {EF} $. Поэтому геометрически он называется отрезком прямой.

На основе графического представления отрезка, отрезок в этом примере записывается как $ \ overline {PQ} $, а его длина в математике записывается как $ PQ $.

Линия между точками

Линия, соединяющая любые две точки на плоскости, считается отрезком. Это соображение вызвано двумя основными причинами.

Маленькая линия содержит две конечные точки.
Расстояние между двумя конечными точками можно измерить, и оно равно длине небольшой линии.

$ M $ и $ N $ — две точки на плоскости, соединяющие их линией. Расстояние между двумя точками равно длине линии.Более того, это похоже на отрезок прямой. Следовательно, линию, соединяющую любые две точки на плоскости, можно рассматривать как отрезок.

Отрезок линии в математике записывается как $ \ overline {MN} $, а его длина обозначается как $ MN $.

2. Определения

Аналитический
Основы геометрии

2. Параметрические уравнения

Роберт С. Уилсон

Определения

(векторное сложение точек)
Пусть A = ( x ₁, y ₁) и пусть B = ( x ₂,
y ₂) по двум точкам.Определить

A + B = ( x ₁ + x ₂, y ₁ +
y ₂)

(Скалярное умножение точек)
Пусть A = ( x , y ) и пусть r будет действительным числом. Определить

rA = ( rx , ry )

Пусть A и B будут двумя точками.Отрезок линии
между A и B — набор точек вида

C = (1- т ) A + tB

верх

где

0 т 1

A и B называются конечными точками
отрезок между A и B .

Набор
очки формы

C = (1- т ) A + tB

, где t > 1 — это точки на другом
сторона из B из A , и множество таких точек, где t <0 — это точки на
другая сторона из A из B .

верх

Набор
очки формы

(1- т ) A + tB

, где t > 0 — это набор точек на линии, определяемый параметрами A и B , которые находятся на той же стороне из A как B .

Набор
очки формы

(1- т ) A + tB

верх

, где t <0 — набор точек на
линия определяется A и B , которые находятся на противоположной стороне A , чем B .

верх

Набор баллов
формы

(1- т ) A + tB

, где t > 0 называется лучом от A до B .

верх

Учитывая
линия, уравнение которой равно

топор + на = c

набор точек,
координаты удовлетворяют

верх

топор + по < c

— это набор точек
одна сторона линии , а набор
точки, координаты которых
удовлетворить

топор + по > c

— это набор точек на
другая сторона линии .

Пусть A , B , и C будут тремя неколлинеарными точками. Угол
между AB и AC — это набор точек, которые находятся на
та же сторона AB , что и C , и та же сторона AC , что и B . Если точка находится в углу между
AB и AC , считается, что это внутри угла .
Точки, которых нет внутри
угла, а не на лучах, начинающихся с A и проходящих через B и C , называются вне угла.

Треугольник — это фигура, определяемая
три точки, состоящие из
три линии
отрезки, соединяющие три точки.Эти три точки называются тремя вершинами , а отрезки линий между
вершины называются сторонами треугольника.

Пусть A , B , и C будут тремя неколлинеарными точками. Интерьер
треугольник ABC — это набор точек, которые находятся на
та же сторона AB , что и C , та же сторона AC , что и B , и та же сторона BC , что A .Очки в интерьере
треугольник считается внутри треугольника .
Точки, которых нет внутри
говорят, что треугольник находится на за пределами треугольника .

верх

Сегмент ЛЭП

ElectricLineSegment — это абстрактный класс, который собирает информацию о конфигурации и возможности подключения проводников. ElectricLineSegment Объекты классифицируются по напряжению и относятся к воздушным или подземным проводам.

ElectricLineSegment представляет цепи, часто называемые фидерами. Первичные проводники берут начало в главном распределительном центре и питают одну или несколько подстанций. Вторичные сети питаются от пяти или более первичных фидеров, чтобы поддерживать нагрузку трансформатора на уровне 125 процентов в случае сбоя. Конденсаторы уменьшают падение напряжения на фидере.

Системы управления фидерами

созданы для определения того, к какой цепи принадлежит данное электрическое устройство (т.е.какому источнику или, в замкнутой системе, источники питают его энергией), и какие из его электрических фаз находятся под напряжением на первичной стороне. Эта информация может использоваться для создания схем цепей и визуального различения различных систем подачи. Подтипы этих объектов ElectricLineSegment являются первичными, вторичными, однофазными и трехфазными.

ElectricLineSegment наследует атрибуты от абстрактного класса ElectricComplexEdge .

Ассоциации: ElectricLine

Подтипы: нет

Названия моделей: нет

Атрибуты:

ElectricLineObjectID: длинное целое число — ID объекта связанной ElectricLine.

ElectricTraceWeight: длинное целое число — используется Feeder Manager для определения состояния устройства и другой информации, влияющей на подключение цепи. Feeder Manager требует, чтобы этому полю было присвоено имя модели MMELECTRICTRACEWEIGHT.

FeederID: текст — идентификатор Feeder Manager, присвоенный фидерам и устройствам, которые участвуют в определенной цепи распределения. Feeder Manager использует в этом поле название модели FEEDERID.

FeederID2: текст — Идентификатор Feeder Manager назначается, если устройство поставляется со вторым питателем. Feeder Manager использует в этом поле название модели FEEDERID2.

FeederInfo: длинное целое число — назначенная Feeder Manager информация о фазе, описывающая фазу цепи.Feeder Manager использует в этом поле название модели FEEDERINFO.

LabelText: text — Предоставляет текст для аннотации строки. Специальные средства автоматического обновления ArcFM Update Primary Conductor Text и взаимосвязи используют имя модели LABELTEXT в этом поле.

NeutralMaterial: текст — Материал нейтрального провода; значения домена включают все, алюминиевый проводник, медь и т. д.

NeutralSize: текст — Размер нейтрального провода; значения домена включают 1/0 AWG, 1000 Concentric Neutral и т. д.

NominalVoltage: длинное целое число — Код, указывающий напряжение системы; Значения домена включают 7,2 кВ с заземлением по оси Y, 24,9 кВ с заземлением по оси Y, 2400 дельта и т. д. В автоматическом обновлении ArcFM Inherit Nominal Voltage используется название модели NOMINALVOLTAGE в этом поле.

Рабочее напряжение: длинное целое число — Код, обозначающий стандартный уровень, на котором в настоящее время работает система, который может изменяться выше или ниже номинального напряжения; значения домена включают 120 вольт, 480 вольт и т. д.Feeder Manager и Electric Tracing используют в этом поле название модели OPERATINGVOLTAGE. В Structural Analysis для воздушных проводов в этом поле используется название модели OPERATINGVOLTAGE.

PhaseDesignation: длинное целое число — Код, указывающий наличие фаз; значения домена включают A, AB, AC и т. д. Значительное количество инструментов ArcFM требует, чтобы этому полю было присвоено имя модели PHASEDESIGNATION. Поскольку от этого имени модели зависит большая часть функциональности, его всегда следует назначать.Ниже приведены несколько примеров инструментов, для которых требуется имя модели поля PHASEDESIGNATION.

Conduit Manager — Требуется это название модели, если вы хотите разместить разные фазы одного проводника в разных воздуховодах.
Расчет конструкций — требуется это название модели для воздушных проводов.
Feeder Manager / Electric Tracing — Требуется это название модели, если вы хотите отслеживать фазировку проводов.
QA Validation Rules — Фаза банковского модуля и Фаза на преобразователе. Правила проверки банка требуют это название модели.
Phase Swap — Требуется это название модели для идентификации поля, содержащего информацию о фазах.

Международная модель данных

В дополнение к перечисленным выше атрибутам в международной модели электрических данных используются следующие атрибуты.

CapacityToGround — Емкостное реактивное сопротивление относительно нейтрали или земли любого сегмента линии (Ом на единицу длины карты)

ConductorMaterial — Материал, из которого изготовлен проводник

Размер проводника — Размер проводника

ConnectionOKIndicator — указывает, способен ли сегмент линии и готов к подключению к нагрузке или другому сегменту линии

InsulationType — Тип изоляции жилы

InsulationVoltage — Выдерживаемое напряжение изоляции проводника (В)

MaxContinousCurrent — Постоянный ток проводника (Амперы)

NumberConductorPerPhase — Количество проводников на фазу

OuterDiameter — Наружный диаметр проводника

OutOfOrderIndicator — Указывает, обесточен ли сегмент линии (например, выведен из эксплуатации для обслуживания)

RatedCurrent — Номинальный постоянный ток проводника, включая любое снижение номинального тока, требуемое для особых условий (Амперы)

Реактивное сопротивление — Реактивное сопротивление проводника прямой последовательности (Ом на единицу длины карты)

Сопротивление — Сопротивление проводника прямой последовательности (Ом на единицу длины карты)