Содержание
понятие, сущность, примеры и задача
Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча.
Если взять произвольную прямую a, и отметим на ней некоторую точку О, то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.
Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k.
Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.
При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.
На рисунке представлен луч ОС.
Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.
Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми.
Задача:
Проведите прямую, и отметьте на ней точки A B и на отрезке AB отметьте точку C. Среди лучей АB, BC, CA, AC и BA найдите пары совпадающих лучей.
Решение:
Лучи совпадают, если они лежат на одной прямой и имеют общее начало и ни один из них не является продолжением другого луча.
По рисунку видно, что этим условиям удовлетворяют лучи AB и AC, а также лучи BC и BA. Следовательно, они являются совпадающими.
Ответ: AB и AC, BC и BA.
Нужна помощь в учебе?
Предыдущая тема: Провешивание прямой на местности: примеры и картинки
Следующая тема:   Угол: понятие, определение и виды углов на рисунках
Координатная прямая (числовая прямая), координатный луч
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
Определение 1
Луч — это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.
Прямую обычно изображают горизонтально, указывая направление направо.
На примере мы видим, что O является началом луча.
Пример 1
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Пример 2
Определение 2
Единичный отрезок — это расстояние от 0 до точки, выбранной для измерения.
Пример 3
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 — например, 2, 3, 4, 5…
Пример 4
Определение 3
Координатный луч – это шкала, которая может длиться до бесконечности.
Зачастую его изображают лучом с началом в точке O, и откладывают единственный единичный отрезок. Пример указан на рисунке.
Пример 5
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Вы можете записывать числа как удобно – под лучом или над ним.
Пример 6
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто — прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 7
Проведите луч в противоположную сторону, дополнив его до прямой
Пример 8
Отложите единичные отрезки по примеру, указанному выше
С левой стороны запишите натуральные числа 1, 2, 3, 4, 5… с противоположным знаком. Обратите внимание на пример.
Пример 9
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Пример 10
Определение 4
Координатная прямая – это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Определение 5
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Пример 11
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа. Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π(=3,141592…).
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Определение 6
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Согласно правилу,
Определение 7
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Следует отметить, что знак, стоящий перед числом, зависит от размещения точки на прямой. Точкам, лежащим правее начала отсчета, соответствуют положительные числа, а точкам, лежащим левее, — отрицательные.
Координаты точек на координатной прямой
Определение 8
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.
Перед тем, как завершить статью, следует упомянуть о принятых обозначениях координаты точки. Координату принято записывать в круглых скобках справа от буквы, которой обозначена точка. Например, если точка M имеет координату – 6, то можно записать как M(-6) , а запись вида M(53+7) значит, что координатой является 53+7
5.4.4. Изображение чисел на координатном луче.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 1.4k. Опубликовано
- Луч Ох с началом отсчета в точке О, на котором указаны единичный отрезок и направление, называют координатным лучом.

- Число, соответствующее точке координатного луча, называется координатой этой точки. Например, А(3). Читают: точка А с координатой 3.
Примеры.
1) Отметить на координатном луче точки А(4), В(8), С(12).
Выбираем единичный отрезок — одну клетку.
- Тогда 1 клетка будет соответствовать числу 1;
- 4 клетки от начала отсчета будут соответствовать числу 4;
- 8 клеток — числу 8, а 12 клеток — числу 12.
Читают: точка А с координатой 4. Точка В с координатой 8. Точка С с координатой 12.
2) Изобразить на координатном луче все правильные дроби со знаменателем, равным 12.
Выбираем единичный отрезок — 12 клеток. Тогда одна клетка будет равна одной двенадцатой доли единичного отрезка, равного 12 клеткам.
Тогда одна клетка будет равна одной двенадцатой доли единичного отрезка, равного 12 клеткам.
Любому числу координатного луча соответствует единственная точка. И если под и над точкой стоят два числа, то это означает, что эти два числа равны между собой (смотрите тему: «Сокращение обыкновенных дробей»).
3) Начертить координатный луч, выбрать единичный отрезок, равный 6 клеткам и отметить точки: А( 1/6), В(2/3), С(1½), D (21/3).
За единичный отрезок мы взяли 6 клеток.
- 1 клетка — это одна шестая часть единичного отрезка, т. е дробь 1/6.
- 2 клетки — две шестые части единичного отрезка или дробь 1/3 (2/6=1/3).
- 3 клетки — три шестые части единичного отрезка или дробь ½ (3/6=½).
- 4 клетки — четыре шестые части единичного отрезка или дробь 2/3 (4/6=2/3).

- 5 клеток — пять шестых частей единичного отрезка или несократимая дробь 5/6.
- 6 клеток — шесть шестых или один единичный отрезок (6/6=1).
Число 1½ означает, что ½ единичного отрезка (3 клетки) следует откладывать не от нуля, а от 1 целой.
Число 21/3 изображаем так: отсчитываем 2 целые единицы (2·6=12 клеток) и еще 2 клетки.
4) На координатном луче отметить точки: А(5/8), В(1¾), С(2½).
Смотреть видео в хорошем разрешении на моём канале.
Онлайн урок: Координатный луч по предмету Математика 5 класс
Мы уже поговорили про координатный луч, но важно понять, почему он “координатный” и как определены координаты в данном случае.
Обычно можно услышать слово “координаты” в географическом контексте.
Когда мы узнаем координаты, а это два числа, то можем однозначно сказать, про какую точку на карте идет речь.
Другими словами, в географическом смысле, координаты являются числами, определяющими положение точки на карте.
В случае с координатным лучом все даже проще.
Ведь если карта — двумерный объект, то есть, если перед нами лежит карта, нам нужно одно число, чтобы определить, как высоко расположена точка, а второе число, чтобы определить насколько она смещена вправо или влево, то на луче точка может быть лишь дальше или ближе от его начала.
Координата точки на координатном луче соответствует количеству единичных отрезков между этой точкой и точкой начала отсчета.
Посмотрим еще раз на рисунок из прошлой главы:
Точка А находится на расстоянии одного единичного отрезка от точки начала отсчета.
Точке А соответствует число 1
Точка В находится на расстоянии двух единичных отрезков от точки начала отсчета.
И точке В соответствует число 2
Аналогично каждой следующей точке соответствует число на единицу больше.
Число, соответствующее точке на координатном луче, называют координатой этой точки.
Заметим теперь, как соответствуют друг другу натуральный ряд и координатный луч.
За исключением точки начала отсчета, каждой точке соответствует натуральное число.
Если смотреть от начала отсчета, то координата следующей точки после данной равна следующему натуральному числу после координаты данной точки.
На том же самом рисунке мы видим, что следующее число за координатой точка В (2) , за точкой В идет точка С и координата точки С (3)
Допустим мы знаем, что точки P и Q — соседние, причем Q находится дальше от точки начала отсчета, чем P.
И также мы знаем, что координата точки P равняется 276
Тогда мы сможем сказать координату точки Q, это будет следующее натуральное число после числа 276, то есть ответ: 277
Аналогичная логика работает и в другую сторону.
Координата точки, идущей перед данной, является предыдущим натуральным числом по отношению к координате данной точки.
Так, если координата точки В — это 2, то координата точки А будет числом, на единицу меньшим, чем 2, то есть единицей.
Допустим, точки E и R соседние.
Также известно, что R находится дальше от точки начала отсчета, чем Е; а также известна координата точки R, она равна 315
Чтобы найти координату точки Е достаточно взять предыдущее натуральное число от числа 315, это будет число 314
Эти примеры показывают, как натуральный ряд ложится на координатный луч.
Отметим, что именно луч идеально соответствует натуральным числам, ведь и луч, и натуральный ряд ограничены с одной стороны (с начала), но продолжаются бесконечно.
Если же нам надо найти координату точки безотносительно соседних точек, то достаточно отсчитать количество единичных отрезков между данной точкой и точкой начала отсчета.
Найдем координату точки Н.
Между ей и точкой О (началом отсчета) 4 единичных отрезка, значит, координата точки Н равна 4
Координатный луч. Шкала — НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ВЕЛИЧИНЫ — Математика 5 класс — А.С. Истер
Раздел 1 НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ВЕЛИЧИНЫ
§ 18. Координатный луч. Шкала
Начертим луч ОХ горизонтально вправо от точки О и запишем у его начала число 0 (рис. 51).
равна единичному отрезку. Против точки K запишем число 1. Говорят, что точка K соответствует числу 1, или число 1 изображен точкой K. Коротко это записывают так: K(1). Число 1 называют координатой точки K.
Число 1 называют координатой точки K.
Чтобы изобразить на луче число 2, надо отложить от начала луча один за одним два единичных отрезка, число 3 — три единичных отрезка и т. д. Таким образом, каждому натуральному числу и числу 0 соответствует одна определенная точка луча ОХ. Достали координатный луч. Точка О, что соответствует началу координатного луча, называется точкой отсчета.
Если точка L на луче соответствует числу 6 (рис. 51), то длина отрезка OL равна 6 единицам.
Координатный луч позволяет сравнивать натуральные числа. Если координатный луч направлен слева направо, то из двух натуральных чисел большем соответствует точка, которая лежит справа, а меньшем — влево.
Пример 1. 2 < 5, так как точка А(2) лежит слева от точки B(5) (рис. 52).
Рис. 51
Выберем какой-либо отрезок АВ, длину которого примем за единицу. Такой отрезок называется единичным отрезком. Отложим от начала луча отрезок ВK, что
Рис. 52
52
Рис. 53
Пример 2. На рисунке 53 точками обозначены натуральные числа х, при которых неравенство х < 5 будет правильной.
Длины отрезков измеряют линейкой с большими и малыми делениями (рис. 54). Они разбивают линейку на равные части. Длине каждого деления соответствует определенная единица измерения. Например, на линейке, изображенной на рисунке 54, большой делении соответствует 1 см, а малой — 1 мм.
Рис. 54
Рис. 55
Рис. 56
Рис. 57
Систему таких делений вместе с соответствующими числами называют шкале. Шкалы бывают не только на линейках, они могут быть различной формы. На рисунке 55 представлена шкала комнатного термометра. Каждая его деление соответствует одному градусу Цельсия (пишут 1 °С). Термометр показывает 18 °С. Координатный луч, линейка, комнатный термометр — примеры прямолинейных шкал. Шкалы часов (рис. 56), спидометра (рис. 57) — криволинейные.
Шкалы часов (рис. 56), спидометра (рис. 57) — криволинейные.
Чтобы прочитать показания на шкале, надо знать цену деления. Так, на рисунке 57 между числами 20 и 40 — четыре деления. Поэтому цена одного деления (40 — 20) : 4 = 5.
Начальный уровень
606. Каким числам соответствуют точки А, В, С и D на координатном луче (рис. 58 и рис. 59)?
Рис. 58
Рис. 59
607. Начерти координатный луч, единичный отрезок которого равен 1 см, и отметить на нем числа 0, 1, 3, 5, 6.
608. Начерти координатный луч, единичный отрезок которого равен 2 см, и отметить на нем числа 0, 1, 3, 4, 6.
Средний уровень
609. Каким числам соответствуют точки М, N, K, Q на рисунке 60 и рисунке 61?
Рис. 60
Рис. 61
610. Каким числам соответствуют точки на рисунке 62 и рисунке 63?
Рис. 62
62
Рис. 63
611. Отметить на координатном луче точки А(3), B(7), C(2), T(10).
612. Отметить на координатном луче точки М(1), L(6), K(5), Г(9).
613. Запиши показатели термометров на рисунках 64— 67.
Рис. 64
Рис. 65
Рис. 66
Рис. 67
614. Начерти координатный луч с началом в точке O. За возьми единичный отрезок длиной 1 см. Отметить на луче точки А, В, С, D, если OA = 5 см, ОВ = 8 см, ОС = 2 см, OD = 4 см. Каким числам соответствуют точки А, В, С и D?
615. На каком расстоянии от начала отсчета содержатся точки A, B, C и D (рис. 68)?
Рис. 68
616. Названия приборы, имеющие шкалы.
617. Интервал времени соответствует наименьшей делении на циферблате часов (рис. 56)?
618. Запиши все натуральные числа, которые лежат на координатном луче между числами:
1) 99 и 108;
2) 998 и 1003.
619. Какая из двух точек на координатном луче размещена слева от другой: та, что соответствует числу 108, и, что числу 119?
620. Какая из двух точек на координатном луче размещена справа от другой: та, что соответствует числу 987, и, что числу 992?
621. Точка М координатного луча соответствует числу 10. Названия четыре числа, которым соответствуют точки, расположенные на координатном луче:
1) справа от точки М; 2) слева от точки М.
622. На рисунке 69 показано шкалу спидометра. Какова скорость автомобиля в каждый из моментов, когда стрелка указывает на точки М, N, K, L, Г?
Рис. 69
Достаточный уровень
623. Между числами 40 и 60 на шкале 4 деления. Найди цену деления этой шкалы.
624. Между числами 500 и 1000 на шкале 5 делений. Найди цену деления этой шкалы.
625. Начерти координатный луч и отметить на нем все натуральные числа, которые:
1) меньше 8; 2) меньше 10 и больше 5.
626. Начерти координатный луч и отметить на нем все натуральные числа, которые:
Начерти координатный луч и отметить на нем все натуральные числа, которые:
1) меньше 6; 2) больше 3 и меньше 7.
627. Запиши, какую температуру будет показывать термометр, изображенный на рисунке 70, если столбик:
1) опустится на 3 деления;
2) опустится на 2 деления;
3) поднимется на 4 деления;
4) поднимется на 5 делений.
628. Длина единичного отрезка координатного луча равна 4 см. На нем обозначены точки М(37) и N(40). Какова длина отрезка MN?
629. На координатном луче отмечены точки A(42) и B(56). Длина отрезка AB равна 7 см. Найди длину единичного отрезка этого луча.
630. Начерти координатный луч и отметить на нем точку А(5). Отметить на координатном луче точки, удаленные от точки А на 3 единичных отрезка.
631. Сравни числа а и b с числами 6 и 10 (рис. 71). Результат запиши с помощью знака неравенства.
Рис. 70
Рис. 71
Рис. 72
72
632. Сравни числа а и b с числом 8 (рис. 72) и между собой.
633. Какое число стоит в конце стрелки на рисунке 73?
Рис. 73
634. Начерти в тетради отрезок, длина которого 12 см. Над одним концом отрезка напишите число 0, а над другим 24. Раздели отрезок на 4 равные части. Назови числа, которые соответствуют каждой делении. Отметить на полученной шкале числа 3, 7, 10, 15, 19, 23.
Упражнения для повторения
635. Заполни пустые кружочки:
Рис. 74
636. Два мотоциклиста выехали одновременно из одного города в противоположных направлениях. Один ехал со скоростью 65 км/час. Скорость второго — на 5 км/ч больше. Каким было расстояние между мотоциклистами через 4 ч?
637. Малыш нарисовал прямоугольник со сторонами 9 см и 12 см, а Карлсон закрасил треть этого прямоугольника. Какая площадь осталась незакрашенной?
Какая площадь осталась незакрашенной?
Домашняя самостоятельная работа № 4
1. Обчисли значение выражения 24 + 32 : 8.
А) 24; Б) 28; В) 7; Г) 20.
2. Среди лучей, изображенных на рисунке 75, названия пару доповняльних лучей.
A) АМ и AK; Б) AN и AM;
B) AK и AB; Г) AN и AB.
Рис. 75
3. Какому числу соответствует точка K на рисунке 76?
A) 3; Б) 5;
B) 6; Г) 4.
Рис. 76
4. В кафе есть 4 вида пирожных и напитки: чай, кофе, сок. Сколькими способами можно выбрать одно пирожное и один напиток?
А) 7; Б) 12; В) 24; Г) 18.
5. 5 ящиков слив и 2 ящика яблок вместе весят 92 кг. Один ящик яблок весит 16 кг. Сколько весит один ящик слив?
А) 12 кг; Б) 14 кг; В) 10 кг; Г) 16 кг.
Рис. 77
6. На рисунке 77 точка K принадлежит отрезку АВ, АВ = 52 см, АK = 17 см. Вычислите длину отрезка KВ.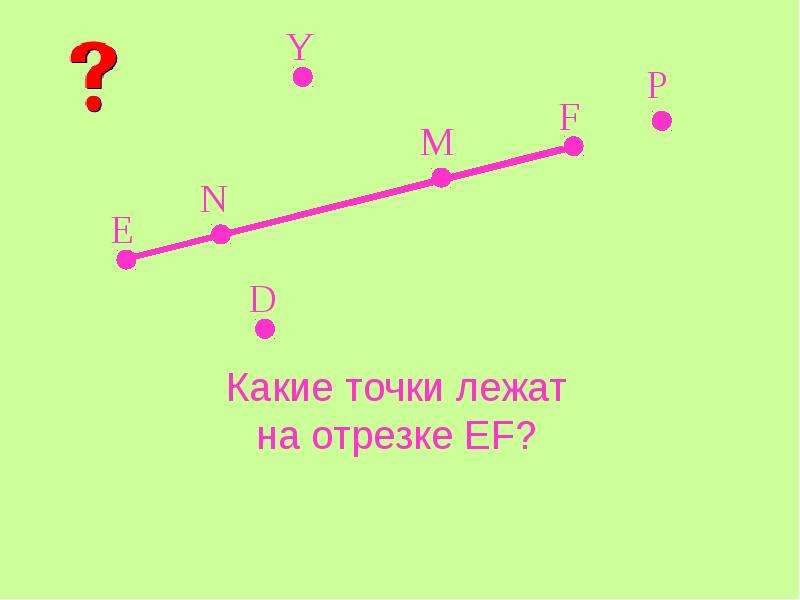
A) 45 см; Б) 25 см;
B) 35 см; Г) 69 см.
7. Сколько разных чотирицифрових чисел можно составить, используя цифры 8 и 9, если цифры могут повторяться?
А) 12; Б) 8; В) 10; Г) 16.
8. Ученик планировал решить 60 задач за 6 дней, но решал каждый день на 2 задачи больше, чем планировал. За сколько дней ученик решил все задачи?
А) 5 дней; Б) 4 дня; В) 3 дня; Г) 8 дней.
9. На рисунке 78 АВ = 40 см, ВМ = 32 см, АN = 19 см. Найдите длину резкая MN.
A) 12 см; Б) 11 см;
B) 10 см; Г) 9 см.
10. В турнире играют 8 шахматистов. Каждый сыграл с каждым из соперников по одной партии. Сколько всего партий было сыграно на турнире?
А) 56; Б) 14; В) 28; Г) 24.
Рис. 78
11. Точка K принадлежит отрезку АВ (см. рис. 77), длина которого 28 см. Длина отрезка АК в три раза меньше длины отрезка КВ. Найдите длину отрезка КВ.
А) 7 см; Б) 12 см; В) 14 см; Г) 21 см.
12. Сколькими способами можно выбрать 2 белые и 1 розовую розу из 10 белых и 8 розовых роз?
А) 80; Б) 720; В) 160; Г) 360.
Задания для проверки знаний № 4 (§14 — §18)
1. Начерти прямую а. Обозначь точку L, принадлежащую прямой а, и точку М, которая этой прямой не принадлежит.
2. Начерти отрезок АВ длиной 7 см 2 мм, обозначь на нем точку К. Запиши все отрезки, которые образовались на рисунке, и измерь длину каждого.
3. Начерти координатный луч. За единичный отрезок возьми 2 клетки. Отметить на этом луче числа 0, 1, 3, 6, 10.
4. Из букв разрезной азбуки составлено слово «учитель». Сколькими способами можно составить пару из одной гласной и одной согласной букв этого слова?
5. Запиши все натуральные числа, которые лежат на координатном луче между числами 996 и 1002.
6. На отрезке АВ длиной 40 см отмечены точки С и D так, что АС = 12 см, ВБ = 18 см. Найди длину отрезка CD.
7. Найди значение выражения
(1 102 200 — 870 796) : 68 + 512 ∙ 309.
8. Сколько различных трехзначных чисел можно составить, используя цифры 1, 2, 3, 4, если цифры не повторяются.
11. Точка K принадлежит отрезку АВ (см. рис. 77), длина которого 28 см. Длина отрезка АК в три раза меньше длины отрезка КВ. Найдите длину отрезка КВ.
А) 7 см; Б) 12 см; В) 14 см; Г) 21 см.
12. Сколькими способами можно выбрать 2 белые и 1 розовую розу из 10 белых и 8 розовых роз?
А) 80; Б) 720; В) 160; Г) 360.
Задания для проверки знаний № 4 (§14 — §18)
1. Начерти прямую а. Обозначь точку L, принадлежащую прямой а, и точку М, которая этой прямой не принадлежит.
2. Начерти отрезок АВ длиной 7 см 2 мм, обозначь на нем точку К. Запиши все отрезки, которые образовались на рисунке, и измерь длину каждого.
3. Начерти координатный луч. За единичный отрезок возьми 2 клетки. Отметить на этом луче числа 0, 1, 3, 6, 10.
4. Из букв разрезной азбуки составлено слово «учитель». Сколькими способами можно составить пару из одной гласной и одной согласной букв этого слова?
5. Запиши все натуральные числа, которые лежат на координатном луче между числами 996 и 1002.
Запиши все натуральные числа, которые лежат на координатном луче между числами 996 и 1002.
6. На отрезке АВ длиной 40 см отмечены точки С и D так, что АС = 12 см, ВБ = 18 см. Найди длину отрезка CD.
7. Найди значение выражения
(1 102 200 — 870 796) : 68 + 512 ∙ 309.
8. Сколько различных трехзначных чисел можно составить, используя цифры 1, 2, 3, 4, если цифры не повторяются.
9. Дополнительное задание. Сколькими способами можно выбрать альбом и 3 марки из 4 разных альбомов и 9 разных марок?
10. Дополнительное задание. На отрезке АВ длиной 24 см обозначено точку М так, что длина отрезка АМ на 2 см больше длины отрезка МВ. Найди длины отрезков АМ и МВ.
Урок 25. обобщение и систематизация знаний по теме «наглядные представления о геометрических фигурах» — Математика — 5 класс
Математика
5 класс
Урок № 25
Обобщение и систематизация знаний по теме «Наглядные представления о геометрических фигурах»
Перечень рассматриваемых вопросов:
-понятие отрезка, прямой, луча;
-изображение чисел точками на координатной прямой;
-измерение длины отрезка;
-единицы длины.
Тезаурус
Луч – прямая линия, которая имеет начало, но не имеет конца.
Координатный луч – это луч, на котором задано направление, а также отмечены начало отсчёта и единичный отрезок.
Начало отсчёта –особая точка, обычно обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек
Единичный отрезок–величина, принимаемая за единицу при геометрических построениях.
Прямая – линия, которую можно бесконечно продолжить как в одну, так и в другую сторону.
Отрезок – часть прямой, ограниченная двумя точками.
Обязательная литература
Никольский С. М. Математика. 5класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272с.
Дополнительная литература
1.Чулков П. В. Математика: тематические тесты. 5класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. //И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.
Теоретический материал для самостоятельного изучения
«Человек – мера всех вещей», – сказал древнегреческий ученый Протагор. Эту фразу можно отнести и к математике, ведь в качестве измерительных инструментов использовались чаще всего шаг, человеческая рука или нога. Такие «приборы» были удобны тем, что они у человека всегда были при себе. Но у разных людей локти, руки и ступни имеют разную длину, поэтому и были начаты поиски единой системы мер.
Сегодня мы повторим метрические единицы длины.
Между различными единицами длины метрической системы существуют следующие соотношения:
1 км = 1000 м
1 м = 1000 мм
1 м = 100 см
1 м = 10 дм
1 дм = 10 см
1 см = 10 мм
Используя полученные знания, осуществим перевод 4792 мм в другие метрические единицы длины. Эта длина соответствует 4м 7дм 9см 2мм, или 4м 79см 2мм.
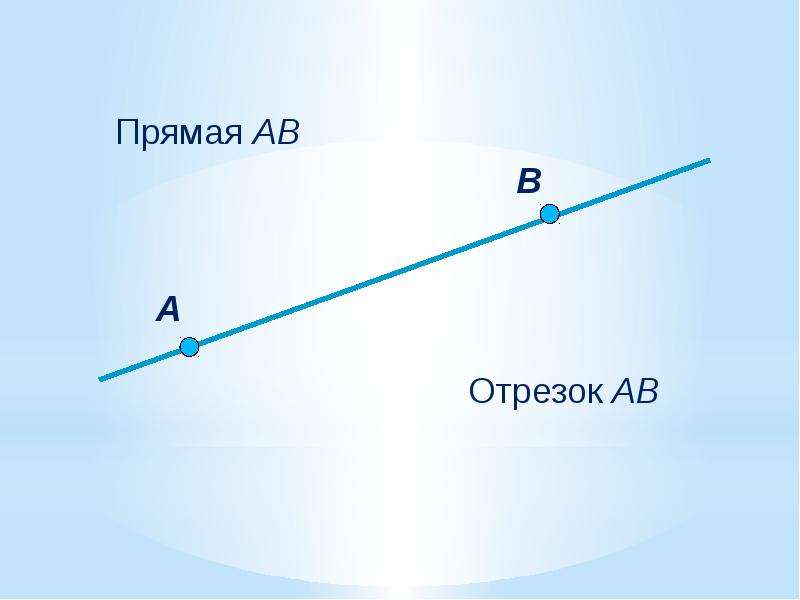
А теперь вспомним, что такое луч. Луч –это прямая линия, которая имеет начало, но не имеет конца. А теперь вспомним, что такое луч. Луч – это прямая линия, которая имеет начало, но не имеет конца. Луч стоит отличать от понятий «прямая» и «отрезок». Прямая – это линия, которую можно бесконечно продолжить как в одну, так и в другую сторону. Отрезок –это часть прямой, ограниченная двумя точками.
Если же начало луча обозначить точкой О сверху, а снизу под началом луча подписать число 0 и отложить единичный отрезок ОА, где под точкой А записать число 1, и далее в право отложить какое-то количество единичных отрезков, то мы получим координатный луч. Координатный луч – это луч, на котором задано направление, а также отмечены начало отсчёта и единичный отрезок.
С помощью координатного луча можно изобразить натуральные числа. Для этого отмечаем на координатном луче точку и задаём её координаты в соответствии с количеством единичных отрезков, отсчитываемых от нуля. Например, точка С имеет координату 3, так как у неё третий единичный отрезок от нуля.
Натуральные числа можно сравнить с помощью координатного луча. Так, например, число C больше числа А, так как лежит правее. Ведь если на координатном луче точка лежит правее, она будет соответствовать большему числу.
Решим задачу.
На отрезке AB отмечена точка C.
Найдите длину отрезка АС, если АВ = 27 см и ВС = 7 см.
Отрезок – это геометрическая фигура, которая являет собой часть прямой, заключенной между двумя точками.
Точка С лежит на отрезке. Значит, мы точно знаем порядок расположения точек: точка C лежит между точками A и B.
Получаем, что длина отрезка АС равна:
АС = АВ – BC = 27 – 7 = 20 см
Ответ: АС = 20 см.
Итак, сегодня мы вспомнили понятие координатный луч; повторили, как изображать числа точками на координатном луче; за крепили зависимость между единицами метрической системы.
Вычисление расстояния, измерение длины по рисунку
На плане участка клетками изображены клумбы, каждая из которых имеет форму квадрата со стороной 10 м. Ширина всех тропинок между клумбами – 1 м.
Найдите длину пути от точки А до точки В, изображенных на плане.
Решение: двигаясь по проложенному маршруту, можно понять, что путь пролегает через четыре клумбы по 10 м, при этом одну клумбу проходят с двух сторон и четыре раза пересекают тропинки шириной 1 м. Поэтому длина пути равна: 10 + 1 + 10 + 1 + 10 + 1 + 10 + 1 + 10 = 54 м.
Ответ: 54 м.
Тренировочные задания
№1. Какая координата будет соответствовать точке, на которую указывает стрелка?
Чтобы ответить на вопрос, нужно сложить координаты первой точки, то есть 37 с тем числом единиц, на которые перемещают исходную точку, то есть 22.
Таким образом, правильный ответ: 37 + 22 = 59.
№2. Дан отрезок АС = 8 см. На прямой АС отмечены точки, находящиеся на расстоянии 3 см от какого-либо из концов отрезка АС. Сколько таких точек?
Решение: начертим прямую. Отметим точки А и С.
Посмотрим на точку А. Отметим точки, которые лежат на расстоянии 3 см от точки А (В1иВ2).
Таких точек может быть две. Так как от точки А мы можем пойти на 3 см налево или на 3 см направо.
Посмотрим теперь на точку С и отметим точки, находящиеся на расстояние 3см (В3 и В4).
Таких точек также может быть две, так как от точки С мы можем пойти на 3 см налево или на 3 см направо.
Таким образом, правильный ответ: 4 точки.
Как найти Координаты Точки? Примеры
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
А вот и координаты увлекательных уроков математики: на интерактивной платформе и в комфортном темпе!
Запишите ребенка на бесплатный вводный урок в онлайн-школу Skysmart, чтобы закрыть пробелы по школьной программе и не бояться контрольных.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Правила координат:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
В детской школе Skysmart ученики чертят графики на специальной онлайн-доске вместе с учителем. А еще решают задачки в интерактивном формате и смело задают вопросы, которые бывает неловко спросить перед всем классом.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься весело и в удовольствие уже завтра!
геометрических терминов — бесплатная справка по математике
Балл:
Точка указывает местоположение и не имеет размера или размера. Точка обозначается точкой и обычно обозначается выбранной буквой. На рисунке ниже точки помечены ближайшей буквой.
Линия:
Линия — это набор точек, проходящих в двух противоположных направлениях без конца. Линия одномерная и не имеет ширины. Он идентифицируется путем обозначения двух точек на линии или написания выбранной строчной буквы после строки.
Обозначение, например, AB (написанное с помощью символа линии <---> над буквами), читается как «линия AB» и относится к линии, которая имеет точки A и B.
Самолет:
Плоскость — это плоская поверхность, не имеющая толщины и простирающаяся без конца во ВСЕХ направлениях. Это двухмерный объект. Самолет представлен параллелограммом и может быть назван путем написания заглавной буквы выбора в одном из его углов. Я подробно расскажу о том, что такое параллелограмм, в будущих уроках.А пока подумайте о параллелограмме как о «оконном стекле». Для простоты вы можете представить себе плоскость как бесконечно большой лист бумаги.
На схеме ниже показаны три точки, линия и плоскость.
Линейный сегмент:
Линейный сегмент — это часть линии, имеющей две точки, называемые конечными точками. У него также есть точки между конечными точками. У линейного сегмента нет набора НЕПРЕРЫВНЫХ точек, как у линии. Конечная точка означает, что линия имеет начало и конец.Обозначение отрезка линии на полосе над любой буквой по выбору. Скажем, AB имеет полосу над ним, вы бы прочитали это как «отрезок AB».
Луч:
Луч — это часть линии, имеющая одну конечную точку и набор всех точек с одной стороны от конечной точки. Луч всегда обозначается двумя буквами по выбору. Первая буква должна быть конечной точкой. Над буквами рисуем стрелку с концом.
Угол:
Угол — это объединение двух лучей, имеющих одинаковую конечную точку.Конечная точка угла называется вершиной; лучи называются сторонами угла.
В геометрии есть несколько дополнительных терминов, которые также необходимо понимать. Они определяют отношения между геометрическими объектами:
Коллинеарные точки: точки, лежащие на одной линии.
Копланарные точки: точки, лежащие в одной плоскости.
Противоположные лучи: 2 луча, лежащих на одной линии, с общей конечной точкой и не имеющей других общих точек.Противоположные лучи образуют прямую линию и / или прямой угол, равный 180 °.
Параллельные линии: две копланарные линии, которые не пересекаются.
Теорема о перпендикулярном биссектрисе (доказательство, обратное, примеры и видео)
Теорема о перпендикулярном биссектрисе (доказательство, обратное и примеры)
- Определения
Перпендикуляр
Все хорошее изучение начинается со словарного запаса, поэтому мы сосредоточимся на двух важных словах теоремы. Перпендикуляр означает два отрезка, лучи, линии или любую их комбинацию, которые пересекаются под прямым углом. Линия считается перпендикулярной, если она пересекает другую линию и образует прямые углы.
Биссектриса
Биссектриса — это объект (линия, луч или отрезок), который разрезает другой объект (угол, отрезок линии) на две равные части. Биссектриса не может делить линию пополам, потому что по определению линия бесконечна.
Биссектриса перпендикулярная
Соединяя эти два значения вместе, мы получаем понятие серединного перпендикуляра , линии, луча или отрезка, который делит пополам угол или отрезок прямой под прямым углом.
Прежде чем беспокоиться о том, что это серединный перпендикуляр к углу , подумайте: какова мера прямого угла? 180 °; это означает, что линия, разделяющая этот угол на две равные части и образующая два прямых угла, является серединным перпендикуляром угла.
Теорема о биссектрисе о перпендикуляре
Хорошо, мы заложили основу. Итак, сложив все вместе, что говорит теорема о срединном перпендикуляре ?
Если точка находится на серединном перпендикуляре отрезка прямой, то она равноудалена от конечных точек отрезка.
Как это работает?
Предположим, у вас есть большой квадратный участок земли со стороной 1000 метров. Вы построили гигантскую радиобашню высотой 300 метров прямо посреди вашей земли. Вы планируете транслировать рок-музыку днем и ночью.
В любом случае, это место для вашей радиомачты означает, что у вас будет 500 метров земли слева и 500 метров земли справа. Ваша радиомачта представляет собой серединный перпендикуляр к длине вашей земли.
Вы должны укрепить вышку проволокой, чтобы она не опрокинулась при сильном ветре.Их называют растяжками. Какой длины должна быть растяжка сверху вниз с каждой стороны?
Поскольку вы построили серединный перпендикуляр, вам не нужно проводить измерения с каждой стороны. Достаточно одного измерения, которое можно рассчитать с помощью геометрии. Используйте теорему Пифагора для прямоугольных треугольников:
Ваша башня 300 метров. Можно выйти на 500 метров, чтобы закрепить конец провода. Башня встречает вашу землю под углом 90 °. Итак:
300 м2 + 500 м2 = c2
90 000 + 250 000 = c2
340 000 = c2
340 000 = с
583.095 м = с
Вам нужны оттяжные тросы длиной 583,095 метра, чтобы проложить путь от вершины башни до края вашей земли. Вы повторяете операцию на высоте 200 метров и высоте 100 метров.
Для каждой выбранной высоты вы обрежете растяжку одинаковой длины для левой и правой стороны вашей радиомачты, потому что башня является серединным перпендикуляром вашей земли.
Доказательство теоремы о серединном перпендикуляре
Обратите внимание на удивительную силу двух слов, «серединный перпендикуляр», потому что эту теорему можно доказать только с помощью отрезка HM и его серединного перпендикуляра WA.
Нам дан отрезок HM, и мы разделили его пополам (разделили ровно пополам) линией WA. Эта линия делит HM пополам под углом 90 °, потому что это данность. Это означает, что если мы проведем линейный сегмент от точки W до точки H, мы сможем создать прямоугольный треугольник WHA, а другой линейный сегмент WM создаст прямоугольный треугольник WAM.
Что у нас теперь? У нас есть два прямоугольных треугольника, WHA и WAM, общая сторона WA, со всеми этими конгруэнциями:
- WA ≅ WA (по рефлексивному свойству)
- ∠WAH ≅ ∠WAM (углы 90 °; дано)
- HA ≅ AM (биссектриса; дано)
Как это выглядит? Мы надеемся, что вы сказали Side Angle Side , потому что это именно то, что есть.
Постулат «Боковой угол» гласит: «Если две стороны и прилегающий угол одного треугольника совпадают с двумя сторонами и прилегающим углом другого треугольника, то эти два треугольника конгруэнтны».
Это означает, что стороны WH и WM равны, потому что CPCTC (соответствующие части конгруэнтных треугольников равны). БАМ! Проверено!
Практическое испытание
Теперь вы можете разобраться с теоремой сами. Вы либо утонете, либо поплывете на этом.Вот отрезок линии WM. Построим серединный перпендикуляр SI.
Как вы можете доказать, что SW ≅ SM? Вы знаете, что делать?
- Постройте линейные сегменты SW и SM.
- Что теперь есть? Два прямоугольных треугольника, SWI и SIM. У них прямые углы, ∠SIW и ∠SIM.
- Определите WI и IM как конгруэнтные, потому что они являются двумя частями линейного сегмента WM, которые были разделены пополам SI.
- Определить SI как конгруэнтный самому себе (по рефлексивному свойству).
Что это дает? Две конгруэнтные стороны и включенный угол — что это за постулат? Постулат SAS , конечно же! Следовательно, отрезок SW ≅ SM.
Итак, ты утонул или ПЛАВАТЬ?
Обращение к теореме о серединном перпендикуляре
Обратите внимание, что теорема построена как утверждение «если, то». Это сразу наводит на мысль, что вы можете написать обратное, переключив части:
Если точка равноудалена от конечных точек отрезка прямой, то она находится на серединном перпендикуляре отрезка.
Мы тоже можем это показать. Постройте отрезок HD. Поместите случайную точку над ней (но все же где-нибудь между точками H и D) и назовите ее точкой T. Если точка T находится на одинаковом расстоянии от точек H и D, это обратное утверждение говорит, что она должна лежать на серединном перпендикуляре к HD.
Вы можете доказать или опровергнуть это, проведя перпендикулярную линию из точки T через сегмент HD. Там, где ваша перпендикулярная линия пересекает HD, назовите это Точкой U.
.
Если точка T находится на на том же расстоянии от точек H и D, то HU ≅ UD.Если точка T находится на расстоянии , а не на том же расстоянии от точек H и D, то HU ≇ UD.
Символ ≇ означает «не соответствует».
Вы можете пройти этапы создания двух прямоугольных треугольников △ THU и △ TUD и доказать, что углы и стороны совпадают (или не совпадают), так же, как и в исходной теореме.
Вы должны идентифицировать прямые углы, конгруэнтные стороны вдоль исходного отрезка HD и рефлексивную конгруэнтную сторону TU. Когда вы дойдете до пары соответствующих сторон, которые не совпадают, тогда вы узнаете, что точка T не находится на серединном перпендикуляре.
Только точки, лежащие на серединном перпендикуляре, будут равноудалены от конечных точек отрезка. Все остальное приземляется с БУХОМ.
Краткое содержание урока
После того, как вы проработали все ракурсы, доказательства и мультимедиа, теперь вы можете вспомнить теорему о срединном перпендикуляре и проверить обратное утверждение теоремы. Вы также узнали, что означают слова «перпендикуляр», «биссектриса» и «обратное».
Следующий урок:
Соответствие прямоугольных треугольников
точек, линий и плоскостей | Систры
Терминология и символы
Понятия точек, линий, плоскостей, сегментов линий и лучей имеют решающее значение для создания отличной основы для понимания геометрии.Символика особенно важна.
Геометрия начинается с трех неопределенных терминов — слов без формального определения, но с общим соглашением о том, что они собой представляют.
A Точка — это место в пространстве, которое не имеет измерения. Он представлен точкой и помечен заглавной буквой. На изображении ниже обозначено множество точек.
A Строка имеет одно измерение (оно продолжается вечно). Он представлен линией с двумя наконечниками стрелок.Через любые две точки проходит ровно одна линия. Вы можете использовать любые две точки на этой линии, чтобы назвать его. Вы рисуете мини-линию с двумя стрелками над двумя точками, когда называете линию. Строка также может быть названа одной строчной буквой скрипта.
Сколько линий на изображении выше пересекаются в точке K?
A Самолет имеет два измерения. Он нарисован как фигура, которая выглядит как стена или пол, но продолжается в обоих направлениях до бесконечности.Чтобы назвать плоскость, вы пишете слово «плоскость», а затем перечисляете три неколлинеарные точки. Крыша на фото выше плоская, как и бетонная стена, которая включает точку L.
Крышу можно было назвать самолетом BFG, но не самолетом NBG. Почему нет?
Сегменты и лучи являются определенными терминами. Их можно описать известными словами точка, линия и плоскость.
Сегмент AB состоит из конечных точек A и B и любых точек между A и B на линии AB.Буквы можно поменять местами, не затрагивая сегмент, на который вы ссылаетесь.
Луч AB состоит из конечной точки A и всех точек на прямой AB, которые лежат на той же стороне A, что и B. Буквы не могут быть перевернуты, или вы имеете в виду другой луч. На изображении выше луч GB содержит точку N, а луч BG — нет.
Если точка C лежит на прямой AB между A и B, то луч Ca и луч CB являются противоположными лучами. Например, на фото выше луч CD и луч CH — это противоположные лучи, образующие линию DH.
Важно, чтобы вы попрактиковались в рисовании фигур в своем учебнике по геометрии, чтобы понимать, что они изображают. Нарисуйте пересекающиеся линии и обозначьте их, как в книге. Нарисуйте плоскости, пересекающиеся плоскости, противоположные лучи и т. Д.
Используйте складную плоскость Point Line Plane, чтобы делать подробные заметки для интерактивной записной книжки.
% PDF-1.4
%
224 0 объект
>
эндобдж
xref
224 92
0000000016 00000 н.
0000003112 00000 н.
0000003197 00000 н.
0000003435 00000 п.
0000003957 00000 н.
0000004035 00000 н.
0000004111 00000 п.
0000004186 00000 п.
0000004263 00000 н.
0000004482 00000 н.
0000007240 00000 н.
0000007586 00000 н.
0000007994 00000 н.
0000008241 00000 н.
0000011840 00000 п.
0000012219 00000 п.
0000012622 00000 п.
0000012894 00000 п.
0000013117 00000 п.
0000016134 00000 п.
0000016481 00000 п.
0000016894 00000 п.
0000017546 00000 п.
0000017785 00000 п.
0000017838 00000 п.
0000017875 00000 п.
0000018622 00000 п.
0000018670 00000 п.
0000019323 00000 п.
0000019370 00000 п.
0000019418 00000 п.
0000020401 00000 п.
0000020557 00000 п.
0000023195 00000 п.
0000023490 00000 н.
0000023842 00000 п.
0000024155 00000 п.
0000030399 00000 п.
0000030840 00000 п.
0000031262 00000 п.
0000031507 00000 п.
0000036639 00000 п.
0000037015 00000 п.
0000037531 00000 п.
0000037926 00000 п.
0000038580 00000 п.
0000039278 00000 п.
0000039696 00000 п.
0000039774 00000 п.
0000040045 00000 п.
0000041135 00000 п.
0000041335 00000 п.
0000042489 00000 п.
0000042970 00000 п.
0000043387 00000 п.
0000043679 00000 п.
0000044691 00000 п.
0000044742 00000 п.
0000045964 00000 п.
0000046226 00000 п.
0000046605 00000 п.
0000047030 00000 п.
0000047534 00000 п.
0000048883 00000 н.
0000051777 00000 п.
0000062076 00000 п.
0000063031 00000 п.
0000074587 00000 п.
0000077279 00000 п.
0000077858 00000 п.
0000078053 00000 п.
0000078647 00000 п.
0000078713 00000 п.
0000079742 00000 п.
0000079964 00000 н.
0000080253 00000 п.
0000080483 00000 п.
0000080637 00000 п.
0000084824 00000 н.
0000102422 00000 н.
0000104181 00000 п.
0000122651 00000 н.
0000124411 00000 н.
0000126539 00000 н.
0000127614 00000 н.
0000128658 00000 н.
0000129785 00000 н.
0000130043 00000 н.
0000147641 00000 н.
0000149365 00000 н.
0000151314 00000 н.
0000002136 00000 п.
трейлер
] / Назад 634491 >>
startxref
0
%% EOF
315 0 объект
> поток
hb«b`XAb, lpy tF ޑ bAuXu: hy2 UT5MtcӒS2SuY9X8% yxDD2
ŊK4d — «rsblm: Mebfa խ acLJLIK (./ CV`2 & ‘7ѾQKEY) — [QCluI @ V5U ݧ jl \ mfiU`rE # B21ohljnkl1tXX5T
Ul-8 \ r; GQ`-4HmEVP $ d%
ȵwpDsX & N
Объекты базовой геометрии: точка, линия, отрезок линии, луч, угол и плоскость
Геометрия — это раздел математики, который включает изучение форм, размеров и взаимного расположения фигур. Геометрия состоит из двух частей: плоская геометрия и твердотельная геометрия.
Плоская геометрия: Работает с двумерными или двухмерными объектами, такими как линия, круг, треугольник и т. Д.Эти фигуры легко нарисовать на бумаге. 2D-формы имеют только два измерения, а именно длину и ширину.
Сплошная геометрия: Он работает с трехмерными или трехмерными объектами с некоторой глубиной, такими как куб, сфера, кубоид, призма и т. Д. Эти формы немного сложно нарисовать на бумаге. Трехмерные формы имеют три измерения, а именно длину, ширину и глубину.
Прежде чем приступить к реальной геометрии, мы должны понять следующие основные термины. Эти термины относятся к основным объектам, составляющим геометрические формы.
Точка: Ниже приведены свойства точки,
- Это место в космосе.
- У острия нет длины, ширины или толщины.
- Обычно обозначается точкой.
- Очки обычно называются с большой буквы.
Например, на показанном рисунке мы представляем точки как «точку A, точку B и точку C».
Строка: Ниже приведены свойства строки,
- Линия — это группа точек.
- Линия имеет длину, но не ширину.
- Точки на линии могут продолжаться бесконечно.
- Обычно он представлен линией с двумя стрелками над буквами, обозначающими точки.
- Две стрелки используются, чтобы показать, что линия продолжается бесконечно.
Например, на показанном рисунке мы представляем линию как «XY». Мы также можем назвать ее линией «YX».
Полезная информация о строках
- Для данной точки существует бесконечное количество линий, проходящих через нее.Эти линии называются параллельными линиями.
- Есть одна и только одна линия, проходящая через две разные точки.
- Точка пересечения двух различных линий.
- Три или более точки считаются коллинеарными, если они лежат на одной линии.
- Три или более точки считаются неколлинеарными, если они не лежат на одной линии.
- Через любую линию проходит бесконечное количество плоскостей.
- Ровно одна плоскость проходит через три неколлинеарных точки.
- Две различные пересекающиеся линии лежат на одной плоскости.
- Две или более прямых называются компланарными, если они лежат в одной плоскости.
- Две или более прямых считаются некомпланарными, если они не лежат в одной плоскости.
- Если две или более точки лежат на плоскости, вся прямая лежит в плоскости
- A-X-B означает, что точки «A, X, B» лежат на одной прямой и что точка X находится между A и B.
- Пересечение двух плоскостей представляет собой линию
- Прямая, которая пересекает две или более данных копланарных прямых в разных точках, называется трансверсалью данных прямых.
- Линия, которая перпендикулярна отрезку и проходит через середину отрезка, называется серединным перпендикуляром отрезка.
- Каждая точка на серединном перпендикуляре сегмента равноудалена от двух конечных точек сегмента.
Линейный сегмент: Ниже приведены свойства линейного сегмента,
- Сегмент линии — это часть линии.
- Он имеет две конечные точки с заглавными буквами, обозначающими точки.
- Линейный сегмент имеет длину, но не ширину.
- Линия не имеет конечных точек, тогда как сегмент линии имеет конечные точки.
- Обычно обозначается линией над буквами, обозначающими точки
Например, на показанном рисунке мы представляем отрезок линии как «XY».
Разница между линией и отрезком линии
| Линия | Линейный сегмент |
|---|---|
| Линия — это группа точек. | Сегмент линии — это часть линии. |
| Линия не имеет конечных точек. | У отрезка линии есть конечные точки. |
| Точки на линии могут продолжаться бесконечно. | Определены точки на линии. |
| Он представлен линией с двумя стрелками над буквами, обозначающими точки. | Представлен простой линией над буквами, обозначающими точки. |
Луч: Следующие свойства луча,
- Луч — это набор точек, которые начинаются в одной точке и бесконечно продолжаются в одном направлении.
- Луч имеет длину, но не ширину.
- Он имеет конечную точку и стрелку, изображенную заглавными буквами.
Например, на показанном рисунке мы представляем луч как «MN».
Угол: Два луча, имеющие общую или одинаковую конечную точку, образуют угол.
- Угловая точка угла называется вершиной.
- Две прямые стороны называются дугами. Угол — это степень поворота между каждой рукой.
Например, на показанном рисунке мы представляем угол A. Два луча AB и AC имеют общую конечную точку A.
Плоскость: Это ровная ровная поверхность, похожая на лист бумаги.
- Он простирается во веки веков во всех направлениях.
- Он имеет бесконечную ширину и длину.
- Мы можем использовать стрелки, чтобы показать, что он простирается во всех направлениях навсегда.
— Поделись с друзьями! —
Коллинеарно
Точки коллинеарны, если они лежат на одной линии.
Что делает точки коллинеарными?
Две точки всегда лежат на одной прямой, так как мы можем провести через них четкую (одну) линию.
Три точки коллинеарны, если они лежат на одной линии.
Точки A, B и C не лежат на одной прямой. Мы можем провести линию через A и B, A и C, B и C, но не через все 3 точки.
Компланарные точки лежат в одной плоскости. На диаграмме ниже точки A, B, U, W, X и Z лежат в плоскости M, а точки T, U, V, Y и Z лежат в плоскости N.
- Точки A, Z и B лежат на одной прямой. Точно так же точки T, U и V коллинеарны, поскольку они лежат на отдельной прямой.
- Точки X и Y коллинеарны, хотя лежат в разных плоскостях. (Следует отметить, однако, что можно построить плоскость, содержащую X и Y.)
- Поскольку вы можете провести линию через любые две точки, существует множество пар точек, которые коллинеарны на диаграмме.
- Набор точек, которые не являются коллинеарными (не коллинеарными) в одной плоскости, — это точки A, B и X.
- Набор точек, которые не лежат на одной прямой и находятся в разных плоскостях: T, Y, W и B.
Особенности коллинеарных точек
1. Точка на прямой, которая находится между двумя другими точками на той же прямой, может интерпретироваться как начало двух противоположных лучей.
Точка C находится между точками A и B на AB (вверху). Используя эти точки, мы можем сформировать два противоположных луча, CA и CB.
2. Длина сегмента. Постулат сложения сегментов гласит, что если A, B и C являются точками на одной прямой, где B находится между A и C, то AB + BC = AC.
Пример:
Если AC = 27 и BC = 11 на диаграмме выше, то мы можем найти AB.
3. Коллинеарные точки лежат на одной прямой, поэтому наклон между любыми двумя точками должен быть одинаковым.
Пример:
Если (1, 2), (3, 6) и (5, k) коллинеарные точки, каково значение k?
Мы можем найти значение k, сначала найдя наклон между двумя известными точками. Затем мы можем решить для k, приравняв наклон, который мы только что нашли, к выражению для наклона, включающему k как неизвестное:
Используя точки (1, 2) и (3, 6), чтобы найти наклон прямой, мы получаем
Наклон между (3, 6) и (5, k) составляет
Так как точки лежат на одной прямой, наклоны для этих двух точек равны, поэтому
к = 10
Таким образом, значение k равно 10, а координата коллинеарной точки 3 rd равна (5, 10).
4. Есть только 2 вершины, коллинеарные для любого выпуклого многоугольника на плоскости.
Для представленного ниже 6-стороннего выпуклого многоугольника, называемого шестиугольником, вы можете провести 5 линий от каждой вершины к другим 5 вершинам. Однако никакая комбинация любых трех вершин не может оставаться на одной линии.
Пересечение луча и отрезка линии в 3D — CodeFull
Эта страница содержит методы для выполнения различных тестов на перекрестках. Хотя в нем нет записи для ray vs.Я попробовал предложенный тест пересечения луча и пересечения луча (стр. 782 Рендеринга в реальном времени, 3-е издание), и в моем случае он не сработал.
Я немного осмотрелся и, основываясь на адаптации этого ответа, наконец нашел метод, который отлично работает. Для данного луча (с начальной, конечной точкой и направлением) и отрезка линии с заданными начальной и конечной точками мы выполняем тест на пересечение 3D-линий. Однако обратите внимание, что в различных графических API-интерфейсах всегда есть некоторая ошибка при преобразовании точек экрана в линии (потому что нет отображения 1-1 из пикселей экрана в точные трехмерные точки в пространстве).Следовательно, при проведении испытаний на пересечение необходимо учитывать некоторую степень допуска. Это особенно важно на этапе раннего отклонения алгоритма проверки пересечений. Тест на раннее отклонение проверяет, являются ли две 3D-линии совмещенными. В противном случае сообщение о пересечении не будет.
После нахождения точки пересечения мы должны проверить, находится ли эта точка между начальной и конечной точками отрезка прямой. Это можно сделать, сравнив длину линейного сегмента с суммой расстояний точки пересечения от начальной и конечной точки линейного сегмента соответственно.Если длина «почти» равна, это означает, что исходный луч пересечется с отрезком прямой.
Вот псевдокод описываемого процесса (адаптированный из исходного ответа):
const double coPlanerThreshold = 0,7; // Некоторое пороговое значение, зависящее от приложения
const double lengthErrorThreshold = 1e-3;
bool пересечение (Луч луч, сегмент LineSegment)
{
Vector3 da = ray.End — ray.Origin; // Ненормализованное направление луча
Vector3 db = сегмент.Конец — отрезок.Начало;
Vector3 dc = segment.Start — ray.Origin;
if (Math.Abs (dc.Dot (da.Cross (db)))> = coPlanerThreshold) // Линии не копланарны
вернуть ложь;
двойной s = dc.Cross (db) .Dot (da.Cross (db)) / da.Cross (db) .LengthSquared;
if (s> = 0.0 && s <= 1.0) // Значит, у нас есть пересечение { Пересечение Vector3 = ray.Origin + s * da; // Смотрим, лежит ли это на сегменте если ((пересечение - отрезок.Start) .LengthSquared + (пересечение - segment.End) .LengthSquared <= segment.LengthSquared + lengthErrorThreshold) вернуть истину; } вернуть ложь; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 20 21 22 23 24 25 | const двойной coPlanerThreshold = 0.7; // Некоторое пороговое значение, зависящее от приложения const double lengthErrorThreshold = 1e-3; bool пересечение (Луч луч, сегмент LineSegment) { Vector3 da = ray. |
