Пересечение круги эйлера: Пересечение и объединение множеств — урок. Алгебра, 9 класс. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Задачи на пересечение и объединение множеств (Круги Эйлера)

Круги Эйлера – задачи на пересечение или объединение множеств

Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

«Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.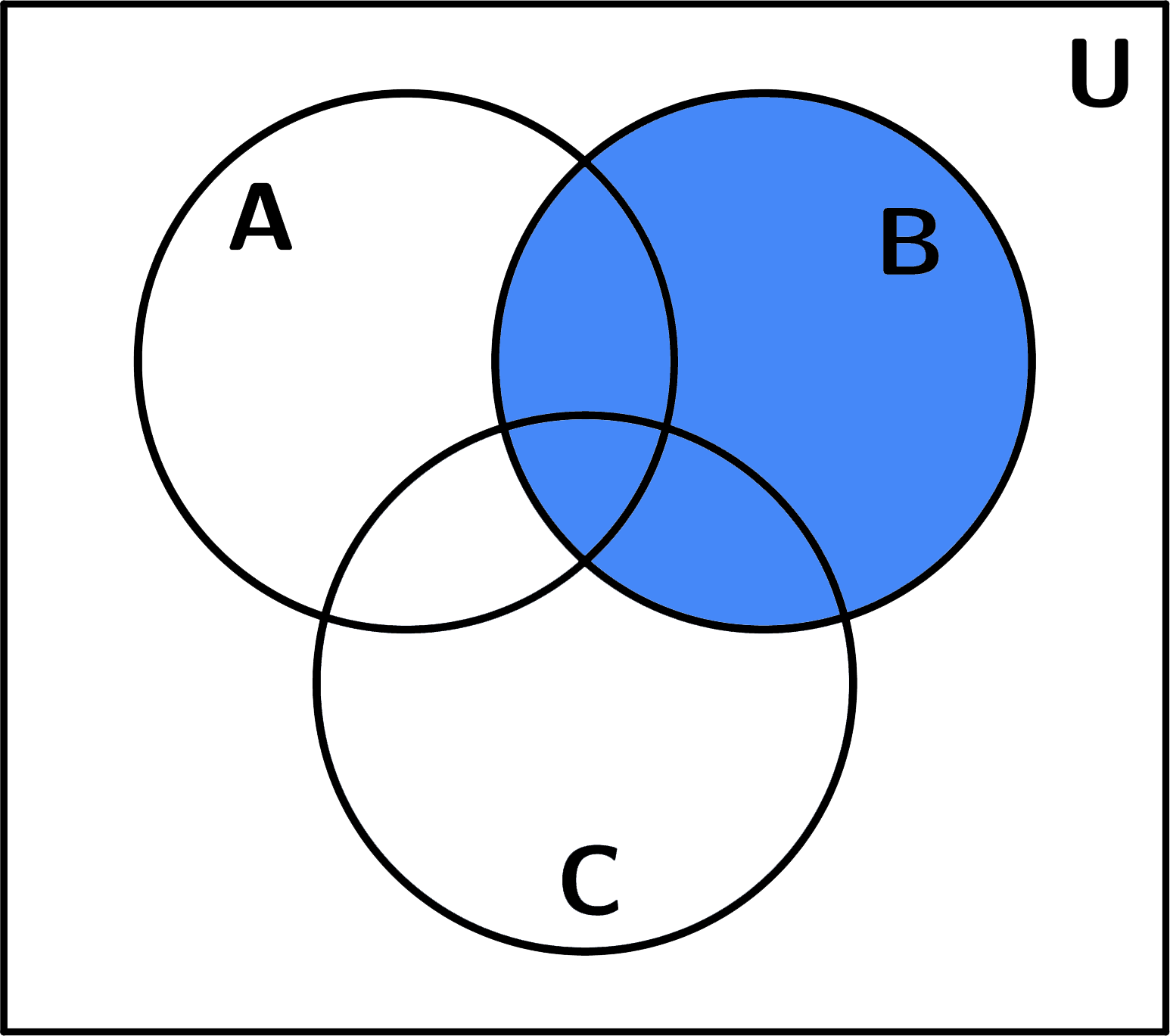
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:

Ответ. 5 человек смотрели только «Стиляги».

Любимые мультфильмы

Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

Решение

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».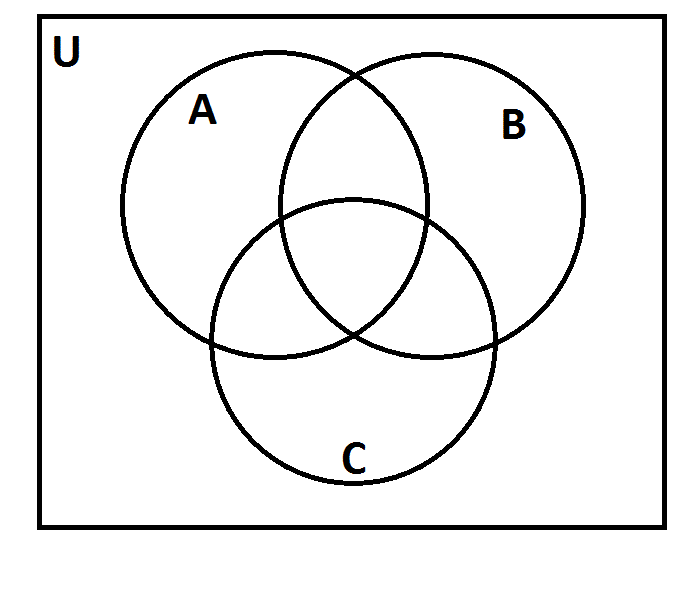
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

«Мир музыки»

В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?

Решение

Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:

Ответ: 6 покупателей купили диски и Максим, и Земфиры.

Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение

Учитывая условия задачи, чертеж будет таков:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ. 8 книг прочитал только Рон.

Пионерский лагерь

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение

Изобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке.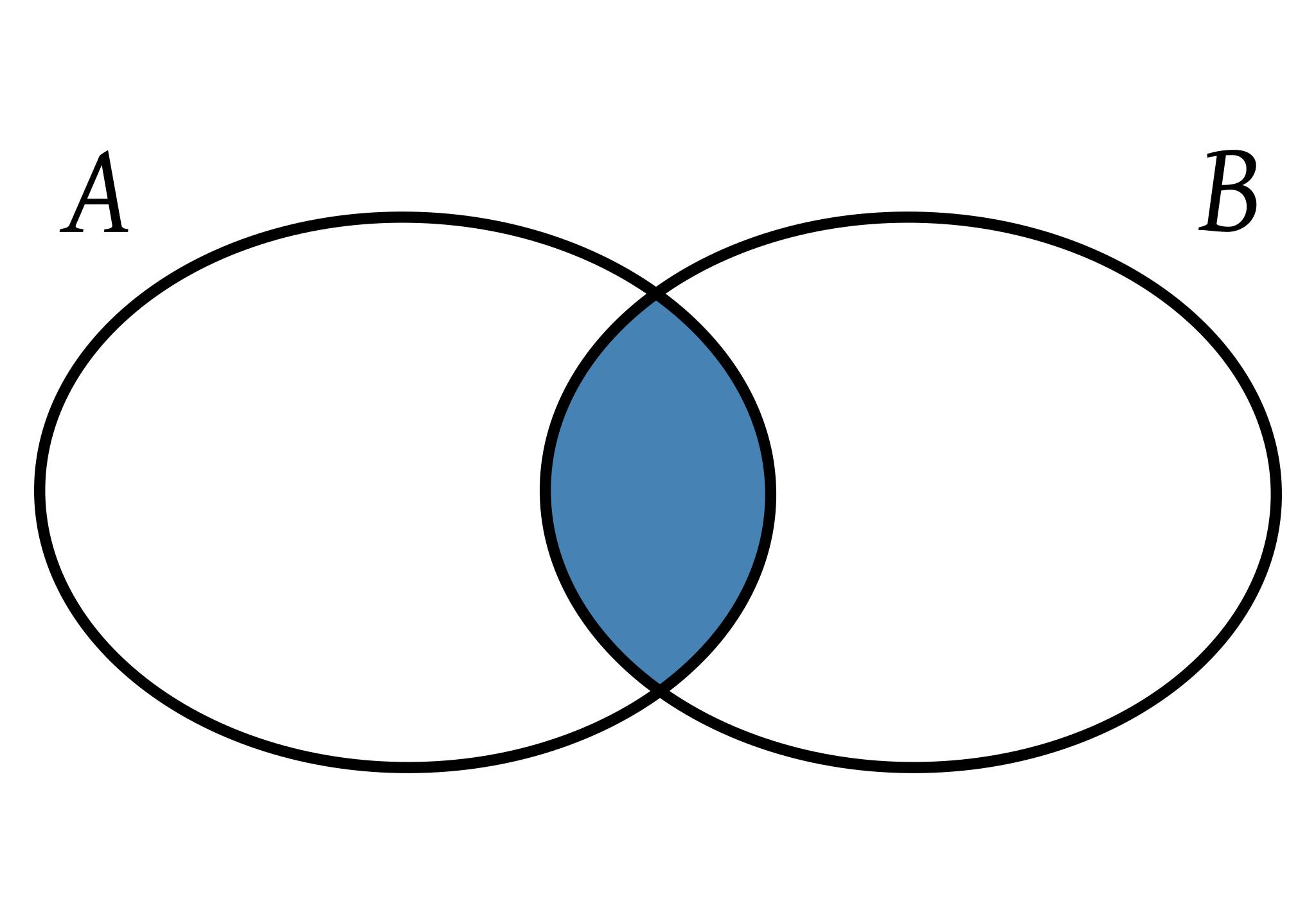 Только спортом заняты 5 человек.
Ответ. 5 человек заняты только спортом.

Экстрим

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Решение

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде.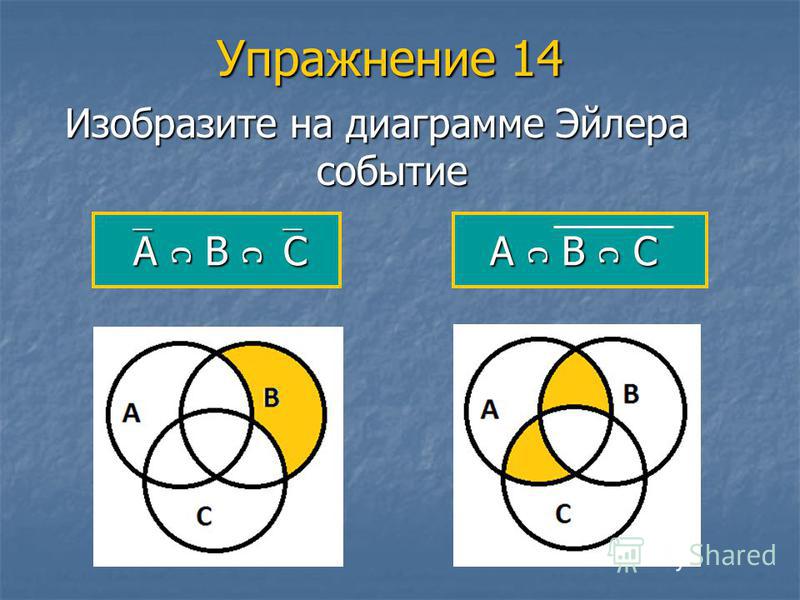 Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

«Обитаемый остров» и «Стиляги»

Любимые мультфильмы

«Мир музыки»

Пионерский лагерь

Экстрим

Круги Эйлера, диаграммы Венна | Онлайн калькулятор

Для наглядного геометрического моделирования множеств и отношений между ними используется диаграммы Венна также иногда их называют кругами Эйлера или диаграммами Эйлера – Венна.

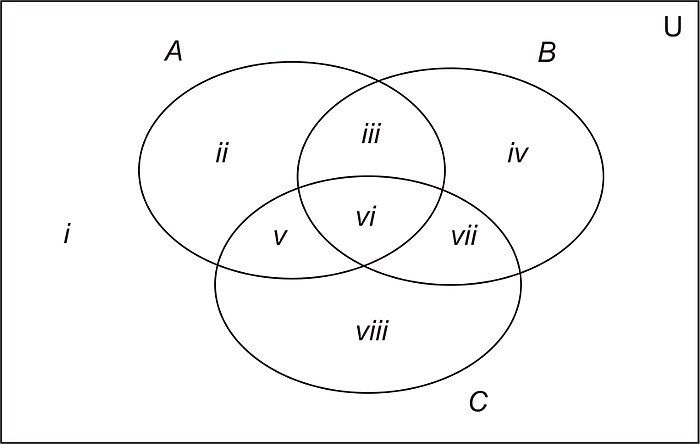
Универсальное множество изображают в виде прямоугольника (универсум), а множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 и более множеств). Диаграмма Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

С помощью диаграмм Венна удобно иллюстрировать операции над множествами. Примеры команд:
(A union B) intersect C
symmetric difference of S and T
(complement S) intersect (A union B)
(A intersection B) union C
(A intersection B) union C’
(A union B’) intersection C
(A intersection B) union (A intersection C)

Используйте следующие правила ввода основных обозначений операций над множествами:
Дополнение: ¯A = A’
Пересечение: (A∩B) = (A intersection B)
Объединение: (А⋃B) = (A union B)
Симметрическая разность: (A∆B) = (symmetric difference of A and B)
Относительное дополнение: (A\B) = (A\B)

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Смотрите также

Решение.

Воспользуемся кругами Эйлера — Решение

Занятие по
подготовке к ГИА по математике по решению
задач с помощью кругов Эйлера. Теория
графов. ( учитель Артемова Л.И.)

С
портивный
класс

В
классе 38 человек. Из них 16 играют в
баскетбол, 17 — в хоккей, 18 — в футбол.
Увлекаются двумя видами спорта —
баскетболом и хоккеем — четверо,
баскетболом и футболом — трое, футболом
и хоккеем — пятеро. Трое не увлекаются
ни баскетболом, ни хоккеем, ни футболом.

Сколько
ребят увлекаются одновременно тремя
видами спорта?

Сколько
ребят увлекается лишь одним из этих
видов спорта?

Решение.

В
оспользуемся
кругами Эйлера.

Пусть
большой круг изображает всех учащихся
класса,

а
три меньших круга Б, Х и Ф изображают
соответственно баскетболистов, хоккеистов
и футболистов.

Тогда
фигура Z, общая часть кругов Б, Х и Ф,
изображает ребят, увлекающихся тремя
видами спорта.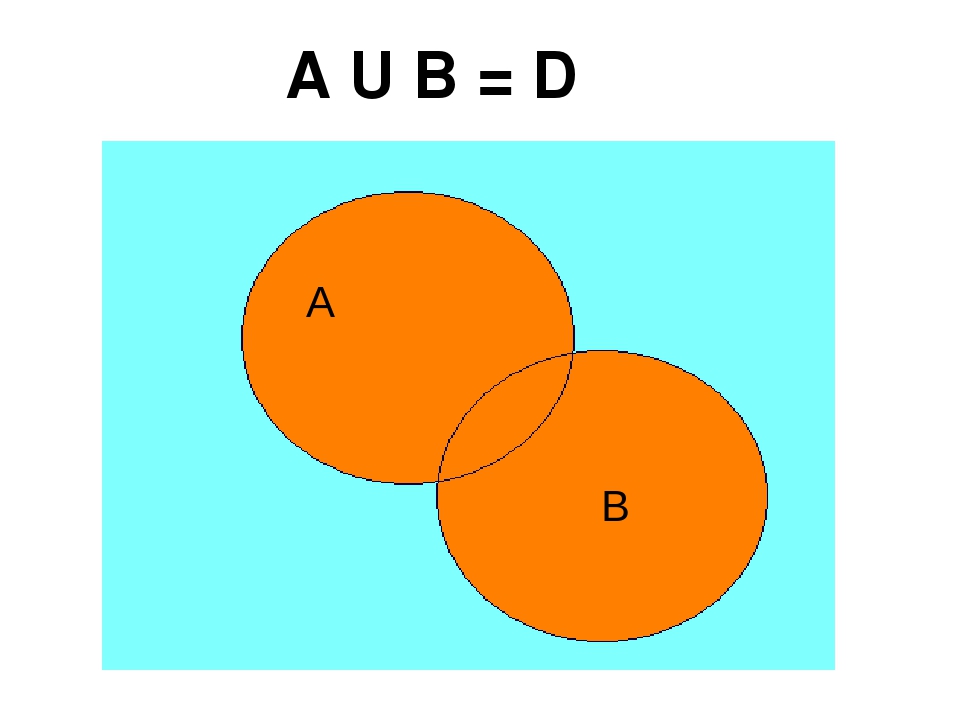

Из
рассмотрения кругов Эйлера видно, что
одним лишь видом спорта —

баскетболом
занимаются

16
— (4 + z + 3) = 9 — z;

одним
лишь хоккеем

17
— (4 + z + 5) = 8 — z;

одним
лишь футболом

18
— (3 + z + 5) = 10 — z.

Составляем
уравнение, пользуясь тем, что класс
разбился на отдельные группы ребят;
количества ребят в каждой группе обведены
на рисунке рамочкам:

3
+ (9 — z) + (8 — z) + (10 — z) + 4 + 3 + 5 + z = 38,

z
= 2.

Таким
образом, двое ребят увлекаются всеми
тремя видами спорта.

Складывая
числа 9 — z, 8 — z и 10 — z, где z = 2, найдем
количество ребят, увлекающихся лишь
одним видом спорта: 21 человек.

Ответ.

Двое
ребят увлекаются всеми тремя видами
спорта человека.

Увлекающихся
лишь одним видом спорта: 21 человек.

Круги
Эйлера – задачи на пересечение или
объединение множеств

Это
новый тип задач, в которых требуется
найти некоторое пересечение множеств
или их объединение, соблюдая условия
задачи.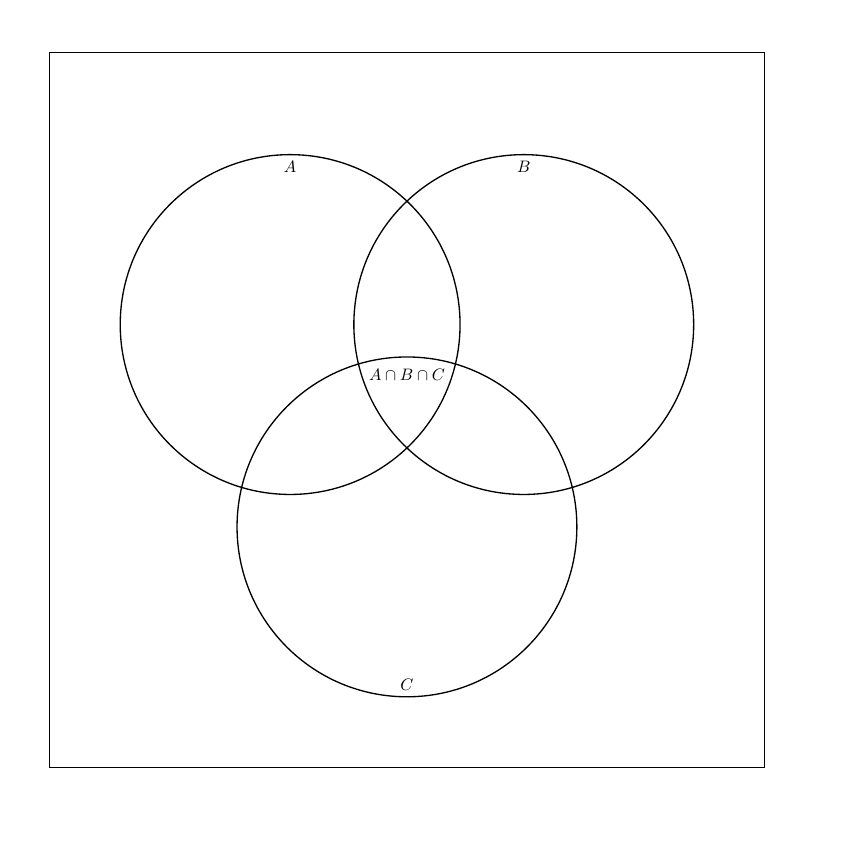

Круги
Эйлера — геометрическая схема, с помощью
которой можно изобразить отношения
между подмножествами, для наглядного
представления.

Метод
Эйлера является незаменимым при решении
некоторых задач, а также упрощает
рассуждения. Однако, прежде чем приступить
к решению задачи, нужно проанализировать
условие. Иногда с помощью арифметических
действий решить задачу легче.

«Обитаемый
остров» и «Стиляги»

Некоторые
ребята из нашего класса любят ходить в
кино. Известно, что 15 ребят смотрели
фильм «Обитаемый остров», 11 человек –
фильм «Стиляги», из них 6 смотрели и
«Обитаемый остров», и «Стиляги». Сколько
человек смотрели только фильм «Стиляги»?

Решение

Чертим
два множества таким образом:

6
человек, которые смотрели фильмы
«Обитаемый остров» и «Стиляги», помещаем
в пересечение множеств.

15
– 6 = 9 – человек, которые смотрели только
«Обитаемый остров».

11
– 6 = 5 – человек, которые смотрели только
«Стиляги».

Получаем:

Ответ.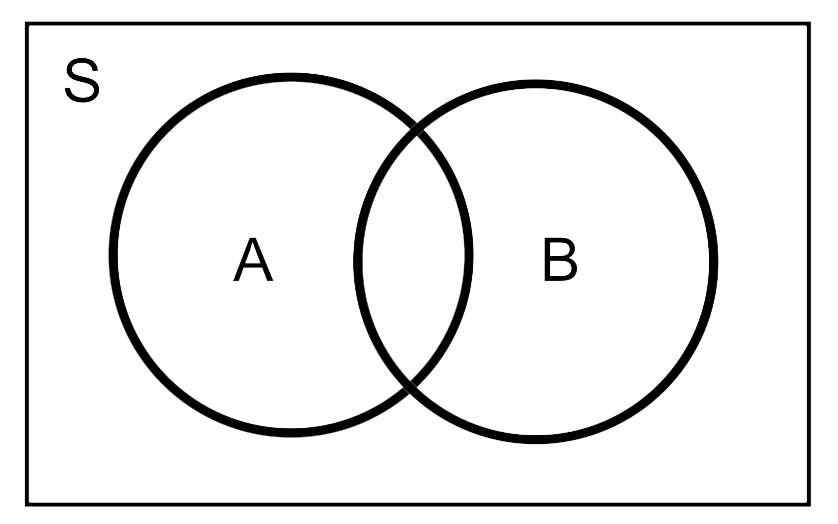
5 человек смотрели только «Стиляги».

Любимые
мультфильмы

Среди
школьников шестого класса проводилось
анкетирование по любимым мультфильмам.
Самыми популярными оказались три
мультфильма: «Белоснежка и семь гномов»,
«Губка Боб Квадратные Штаны», «Волк и
теленок». Всего в классе 38 человек.
«Белоснежку и семь гномов» выбрали 21
ученик, среди которых трое назвали еще
«Волк и теленок», шестеро – «Губка Боб
Квадратные Штаны», а один написал все
три мультфильма. Мультфильм «Волк и
теленок» назвали 13 ребят, среди которых
пятеро выбрали сразу два мультфильма.
Сколько человек выбрали мультфильм
«Губка Боб Квадратные Штаны»?

Решение

В
этой задаче 3 множества, из условий
задачи видно, что все они пересекаются
между собой. Получаем такой чертеж:

Учитывая
условие, что среди ребят, которые назвали
мультфильм «Волк и теленок» пятеро
выбрали сразу два мультфильма, получаем:

21
– 3 – 6 – 1 = 11 – ребят выбрали только
«Белоснежку и семь гномов».

13
– 3 – 1 – 2 = 7 – ребят смотрят только
«Волк и теленок».

Получаем:

38
– (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят
только «Губка Боб Квадратные Штаны».

Делаем
вывод, что «Губка Боб Квадратные Штаны»
выбрали 8 + 2 + 1 + 6 = 17 человек.

Ответ.
17 человек выбрали мультфильм «Губка
Боб Квадратные Штаны».

«Мир
музыки»

В
магазин «Мир музыки» пришло 35 покупателей.
Из них 20 человек купили новый диск певицы
Максим, 11 – диск Земфиры, 10 человек не
купили ни одного диска. Сколько человек
купили диски и Максим, и Земфиры?

Решение

Изобразим
эти множества на кругах Эйлера.

Теперь
посчитаем: Всего внутри большого круга
35 покупателей, внутри двух меньших
35–10=25 покупателей. По условию задачи
20 покупателей купили новый диск певицы
Максим, следовательно, 25 – 20 = 5 покупателей
купили только диск Земфиры. А в задаче
сказано, что 11 покупателей купили диск
Земфиры, значит 11 – 5 = 6 покупателей
купили диски и Максим, и Земфиры:

Ответ:
6 покупателей купили диски и Максим, и
Земфиры.

Гарри
Поттер, Рон и Гермиона

На
полке стояло 26 волшебных книг по
заклинаниям. Из них 4 прочитал и Гарри
Поттер, и Рон. Гермиона прочитала 7 книг,
которых не читали ни Гарри Поттер, ни
Рон, и две книги, которые читал Гарри
Поттер. Всего Гарри Поттер прочитал 11
книг. Сколько книг прочитал Рон?

Решение

Учитывая
условия задачи, чертеж будет таков:

Так
как Гарри Поттер всего прочитал 11 книг,
из них 4 книги читал Рон и 2 книги –
Гермиона, то 11 – 4 – 2 = 5 – книг прочитал
только Гарри. Следовательно,

26
– 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.

Ответ.
8 книг прочитал Рон.

Пионерский
лагерь

В
пионерском лагере 70 ребят. Из них 27
занимаются в драмкружке, 32 поют в хоре,
22 увлекаются спортом. В драмкружке 10
ребят из хора, в хоре 6 спортсменов, в
драмкружке 8 спортсменов; 3 спортсмена
посещают и драмкружок и хор. Сколько
ребят не поют, не увлекаются спортом,
не занимаются в драмкружке? Сколько
ребят заняты только спортом?

Решение

Изобразим
множества следующим образом:

70
– (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют,
не увлекаются спортом, не занимаются в
драмкружке. Только спортом заняты 5
человек.

Ответ.
5 человек заняты только спортом.

Экстрим

Из
100 ребят, отправляющихся в детский
оздоровительный лагерь, кататься на
сноуборде умеют 30 ребят, на скейтборде
– 28, на роликах – 42. На скейтборде и на
сноуборде умеют кататься 8 ребят, на
скейтборде и на роликах – 10, на сноуборде
и на роликах – 5, а на всех трех – 3.
Сколько ребят не умеют кататься ни на
сноуборде, ни на скейтборде, ни на
роликах?

Решение

Всеми
тремя спортивными снарядами владеют
три человека, значит, в общей части
кругов вписываем число 3. На скейтборде
и на роликах умеют кататься 10 человек,
а 3 из них катаются еще и на сноуборде.
Следовательно, кататься только на
скейтборде и на роликах умеют 10-3=7 ребят.
Аналогично получаем, что только на
скейтборде и на сноуборде умеют кататься
8-3=5 ребят, а только на сноуборде и на
роликах 5-3=2 человека. Внесем эти данные
в соответствующие части. Определим
теперь, сколько человек умеют кататься
только на одном спортивном снаряде.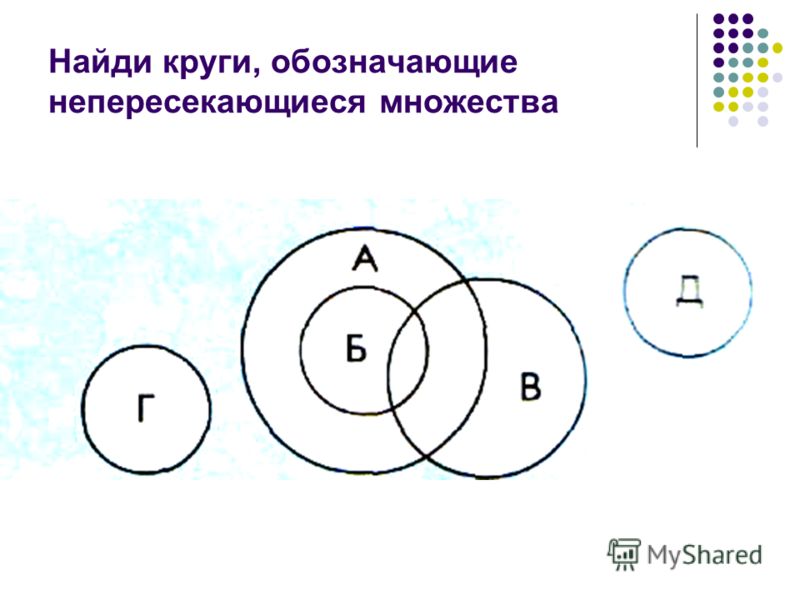
Кататься на сноуборде умеют 30 человек,
но 5+3+2=10 из них владеют и другими снарядами,
следовательно, только на сноуборде
умеют кататься 20 ребят. Аналогично
получаем, что только на скейтборде умеют
кататься 13 ребят, а только на роликах –
30 ребят. По условию задачи всего 100 ребят.
20+13+30+5+7+2+3=80 – ребят умеют кататься хотя
бы на одном спортивном снаряде.
Следовательно, 20 человек не умеют
кататься ни на одном спортивном снаряде.

Ответ.
20 человек не умеют кататься ни на одном
спортивном снаряде.

Задача:
В классе учатся 40 человек. Из них по
русскому языку имеют «тройки» 19 человек,
по математике – 17 человек и по физике
– 22 человека. Только по одному предмету
имеют «тройки»: по русскому языку – 4
человека, по математике – 4 человека и
по физике – 11 человек. Семь человек
имеют «тройки» и по математике и по
физике, из них пятеро имеют тройки и по
русскому языку. Сколько человек учатся
без «троек». Сколько человек имеют
«тройки» по двум из трёх предметов.
Рассмотрим решение с помощью следующего
слайда

Теория
графов

Теория
графов – наука сравнительно молодая.
Первая работа по теории графов принадлежит
Леонарду Эйлеру. Она появилась в 1736 году
в публикациях Петербургской Академии
Наук и начиналась с рассмотрения задачи
о кенигсбергских мостах. Графы придали
условиям наглядность, упростили решение
и выявили сходство задач. Сейчас почти
в любой отрасли науки и техники
встречаешься с графами: в электротехнике
при построении электрических схем, в
химии – при изучении молекул и их
цепочек, в экономике – при решении задач
выбора оптимального пути для потоков
грузового транспорта. Граф – это фигура,
состоящая из точек и линий.

Решим
следующую задачу:

В
школьном драматическом кружке решили
ставить гоголевского «Ревизора». И тут
разгорелся жаркий спор. Всё началось с
Ляпкина-Тяпкина.

–
Ляпкиным-Тяпкиным
буду я! Решительно заявил Дима. С раннего
детства я мечтал воплотить этот образ
на сцене.

– Ну
хорошо, согласен уступить эту роль, если
мне дадут сыграть Хлестакова, проявил
великодушие Гена.

– …
А мне – Осипа,
– не уступил ему в великодушии Дима.

–
Хочу быть
Земляникой или Городничим, – сказал
Вова.

–
Нет, Городничим
буду я, – хором закричали Алик и Боря.
– или Хлестаковым, добавили они
одновременно.

Удастся
ли распределить роли так. Чтобы исполнители
были довольны?

Изобразим
каждого участника драматического кружка
точкой, а все их пожелания будем изображать
линиями. Видно, что Осипа будет играть
Дима, Вова – Землянику, Гена – Ляпкина
– Тяпкина, Алик и Боря – Хлестакова и
Городничего.

Решите
с помощью графов следующую задачу: В
первенстве класса по настольному теннису
6 участников: Андрей, Борис, Виктор,
Галина, Дмитрий и Елена. Первенство
проводят по круговой системе – каждый
из участников играет с каждым из остальных
один раз.

13
Из 100 туристов, отправляющихся в
заграничное путешествие, немецким
языком владеют 30 человек, английским —
28, французским — 42. Английским и немецким
одновременно владеют 8 человек, английским
и французским — 10, немецким и французским
— 5, всеми тремя языками — 3.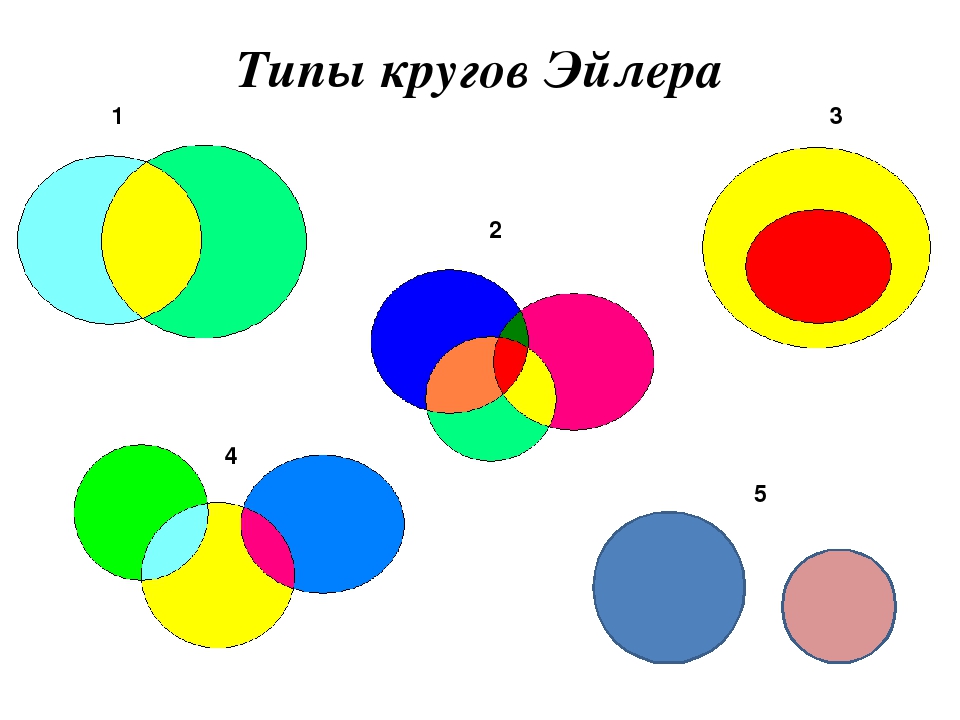 Сколько
туристов не владеют ни одним языком?

Выразим
условие этой задачи графически. Обозначим
кругом тех кто знает английский, другим
кругом — тех, кто знает французский, и
третим кругом — тех, кто знают немецкий.
Тогда, например, те, кто владеет и
английским и немецким, «попадут»
в общую часть первого и третьего круга.

Всеми
тремя языками владеют три туриста,
значит, в общей части кругов вписываем
число 3. Английским и французским языками
владеют 10 человек, а 3 из них владеют еще
и немецким. Следовательно, только
английским и французским владеют 10-3=7
человек.

Аналогично
получаем, что только английским и
немецким владеют 8-3=5 человек, а немецким
и французским 5-3=2 туриста. Вносим эти
данные в соответствующие части.

Определим
теперь, сколько человек владеют только
одним из перечисленных языков. Немецкий
знают 30 человек, но 5+3+2=10 из них владеют
и другими языками, следовательно, только
немецкий знают 20 человек. Аналогично
получаем, что одним английским владеют
13 человек, а одним французским — 30 человек.

По
условию задачи всего 100 туристов.
20+13+30+5+7+2+3=80 туристов знают хотя бы один
язык, следовательно, 20 человек не владеют
ни одним из данных языков.

Ответ:
только английским владеет 13 человек,
только французским — 30, только немецким
— 20 человек. 20 человек не знают ни одного
из этих языков.

Задачи
на круги Эйлера

Задача
1. Про учеников школы, которые участвовали
в физико-математическом конкурсе,
известно, что 7 из них справились с
задачами и по математике и по физике,
11 из них справились с задачами по
математике, 9 из них справились с задачами
по физике. Сколько учеников принимали
участие в конкурсе?

Задача
2. В одной семье было много детей. 7 из
них любили капусту, 6 — морковь, 5 — горох,
4 — капусту и морковь, 3 — капусту и горох,
2 — морковь и горох, один — и капусту, и
морковь, и горох. Сколько детей было в
семье?

Задача
3. На полу комнаты площадью 24 м2 лежат
три ковра. Площадь одного из них — 10 м2,
другого — 8 м2, третьего — 6 м2. Каждые два
ковра перекрываются по площади 3 м2, а
площадь участка пола, покрытого всеми
тремя коврами, составляет 1 м2. Найдите
площадь участка пола: а) покрытого первым
и вторым коврами, но не покрытого третьим
ковром; б) покрытого только одним первым
ковром; в) не покрытого коврами.

Задача
4. На спортивные соревнования в Летней
математической школе ходили 220 школьников.
При этом некоторые из них участвовали
в чемпионатах, а остальные были зрителями.
В легкоатлетической эстафете приняли
участие 30 человек, в соревнованиях по
волейболу — 26, пионерболу — 32, футболу —
31, шахматам — 28 и теннису — 36 человек. 53
школьника приняли участие более чем в
одном соревновании; из них 24 школьника
участвовали 3 или более раз, 9 школьников
— не менее 4 раз и 3 школьника — даже 5 раз
(в последнюю тройку входит и один чудак,
который выступал во всех шести
соревнованиях). Сколько школьников были
зрителями?

Разнобой

Задача
5. Дано 6 гирь: две зеленых, две красных,
две синих.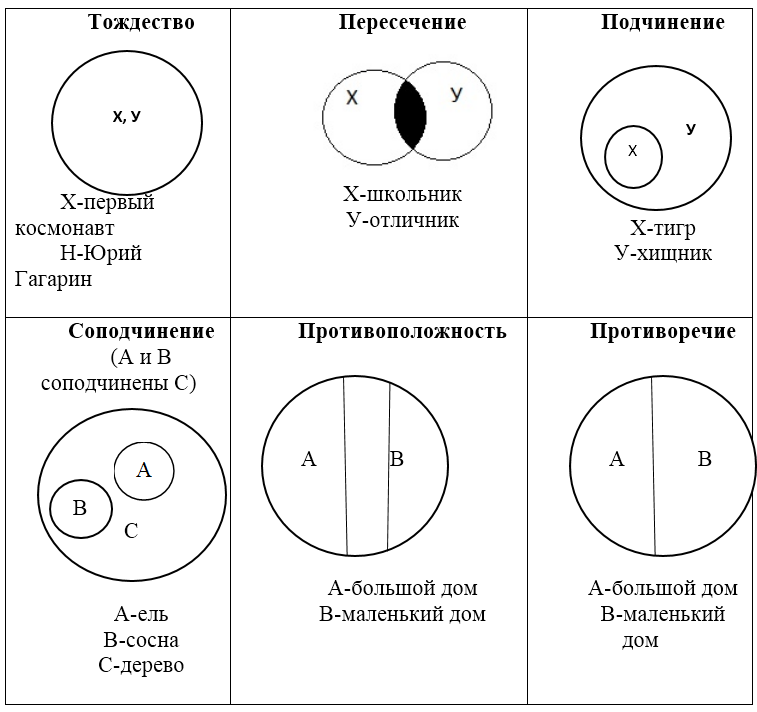 В каждой паре одна гиря
тяжелая, а другая легкая, причём все
тяжелые гири весят одинаково и все
легкие тоже. Можно ли за 2 взвешивания
на чашечных весах найти все тяжелые
гири?

Задача
6. На плоскости расположено 11 шестерёнок,
соединенных в кольцо. Могут ли все
шестерёнки вращаться одновременно?

Решение логических задач с помощью кругов эйлера

Муниципальное общеобразовательное учреждение

лицей № 8 «Олимпия»

Дзержинского района г. Волгограда

Телефоны (8442) 58-80-83, 51-81-31 адрес электронной почты lyceum8@mail.ru

Решение логических задач с помощью кругов Эйлера

Выполнил:

Назаретян Сюзана Горовна,

ученица 5 Б класса

Учитель:

Кокиева Лилия Диляверовна, учитель

математики высшей категории

Волгоград, 2011

Оглавление	С.
Введение……………………………………………………………………………………	3 — 4
Глава I. Логические задачи и круги Эйлера ……………..…….……	5 — 9
1.1. Трудно решать логические задачи? …..…………………….	5 — 6
1.2. Немного о множествах ………..……………………………	6 — 8
1.3. Из истории кругов Эйлера …….……..…………………….	8 — 9
Глава II. Решение логических задач с помощью кругов Эйлера…..	7 — 14
2.1. Задачи на пересечение и объединение двух множеств…….	9 —12
2.2. Задачи на пересечение и объединение трёх множеств . …..	12 — 14
Заключение………………………………………………………………………………..	15
Список источников и литературы……………………………………………….	16
Приложения ………………………………………………………………………………	17—20

Введение.

Сколько гостей Вам встречать, если собираются друзья с 15 угощениями и 20 украшениями? Может ли хватить всем места за столом, вмещающем 22 человека? Первое, что приходит на ум, это 35 человек. А причём здесь 22 человека? Есть подвох? Конечно! Ведь надо рассмотреть несколько вариантов.

Как узнать количество учащихся класса, посещающих одновременно две или три секции, если известны количества участников каждой секции отдельно? Можно ли научиться решать такие задачи, планируя результат? Хочется ответить положительно.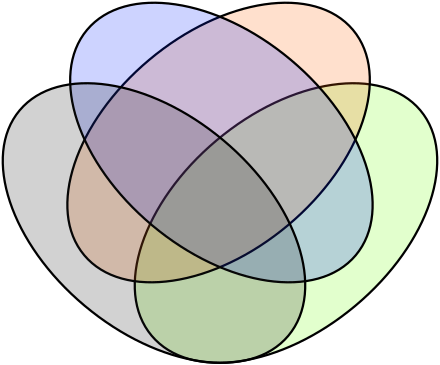

А как решить такую задачу: «Министерство послало в один из лицеев инспектора для проверки, как в нём ведётся преподавание иностранных языков. Сотрудник министерства в отчёте записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трёх языков: французский, немецкий и испанский. Причём все три языка изучают 5 человек; немецкий и испанский 10;французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчёт, был уволен. Почему?»? Такое длинное условие: пока дочитали до конца – забыли начало. Что делать?

Оказывается, такие задачи решаются с помощью кругов Эйлера. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.

Актуальность нашей работы заключается в том, чтобы такие задачи не ставили нас «в тупик» и мы могли их решать.

С учетом этого и была выбрана темаисследования: «Решение логических задач с помощью кругов Эйлера».

Объект исследования — логические задачи.

Предмет исследования —использование кругов Эйлера для решения логических задач .

Гипотеза исследования. Можно решать логические задачи определённого вида специальными способами и в 5 – 6 классах.

Целью нашего исследования является исследование механизма решения определённых логических задач при помощи кругов Эйлера.

Для достижения цели исследования и обоснования гипотезы нам необходимо решить ряд задач:

Найти необходимые сведения о пересечении и объединении множеств, о кругах Эйлера.
Рассмотреть способы решения логических задач на пересечение и объединение двух и трёх множеств.
Вывести в общем виде способ решения логических задач определённого вида с помощью кругов Эйлера.
Научиться решать конкретные логические задачи с помощью кругов Эйлера.
Создать модели «Круги Эйлера» для решения задач с двумя и тремя множествами в помощь учащимся.

Методы исследования:

1. Поиск, анализ и синтез различных источников информации.

2. Интервьюирование, беседы.

Практическая значимость заключается в расширении аппарата для решения логических задач. Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике. Применение кругов Эйлера придает задачам наглядность и простоту.

Теоретическая значимость заключается в разработке способа действий при решении логических задач с помощью кругов Эйлера в общем виде.

Здесь будет выводиться история переписки.

Глава I. Логические задачи и круги Эйлера

1.1. Трудно решать логические задачи?

Логика – это искусство рассуждать, умение делать правильные выводы.

Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь.

Решение логических задач – одно из важнейших средств развития мыслительных способностей.

Логические задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей, начиная с детского сада и заканчивая старшими классами средней школы. Логические задачи допускают изложение в занимательной, игровой форме. С другой стороны, такие задачи труднее, для их решения часто не требуется глубоких знаний, а следует применить смекалку.

Вдоль овражка
Шла фуражка,
Две косынки,
Три корзинки
И от них не отставала
Белоснежная панама.
Посчитай поскорей
Сколько было детей?

Задача предполагает несколько решений. Потому что мы точно не знаем, носил ли кто — нибудь и головной убор, и корзинку.
1 Решение. Предполагается, что каждый ребёнок носил 1 предмет.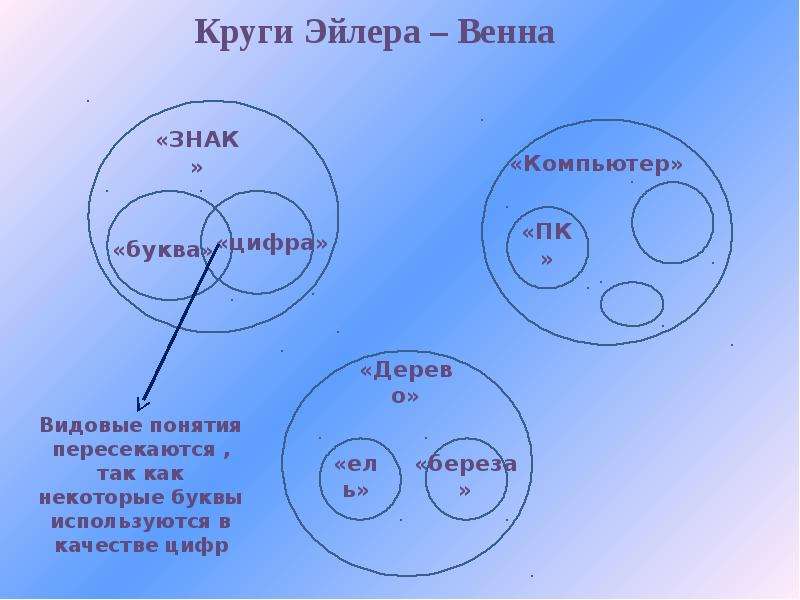 Значит, детей было 7.
2 Решение. Предполагается, что 1 из детей нёс корзинку и головной убор. Следовательно, детей было 6.
3 Решение. Предполагается, что 2 из детей носили и корзинку, и головной убор. Следовательно, детей было 5 .
4 Решение. Предполагается, что 3 из детей носили и корзинку, и головной убор. Следовательно, детей было 4.

1.2. Немного о множествах

Множество – одно из основных понятий математики. Его смысл выражается словами: совокупность, собрание, класс, набор, команда и т.д. Этот смысл поясняется многочисленными примерами. Так, можно говорить о множестве всех учащихся 5-го класса, о множестве всех жителей Волгограда, о множестве всех натуральных чисел, о множестве корней данного уравнения. Основатель теории множеств немецкий математик Георг Кантор (1845–1918) так определил множество – «многое, мыслимое как единое, целое».

Множества обозначаются прописными буквами латинского алфавита А, В, С, …

О предметах, составляющих множество, говорят, что они принадлежат этому множеству или являются его элементами.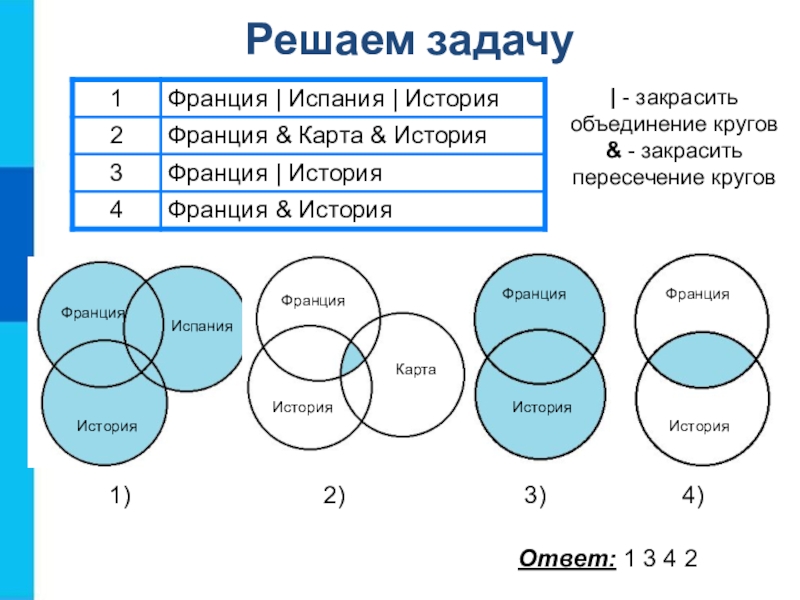 Множества, элементами которых являются числа, называются числовыми множествами.

Множество может быть задано перечислением всех его элементов в произвольном порядке. Такое множество называют конечным. Мы будем рассматривать только конечные множества.

Множество, в котором нуль элементов, называют пустым.

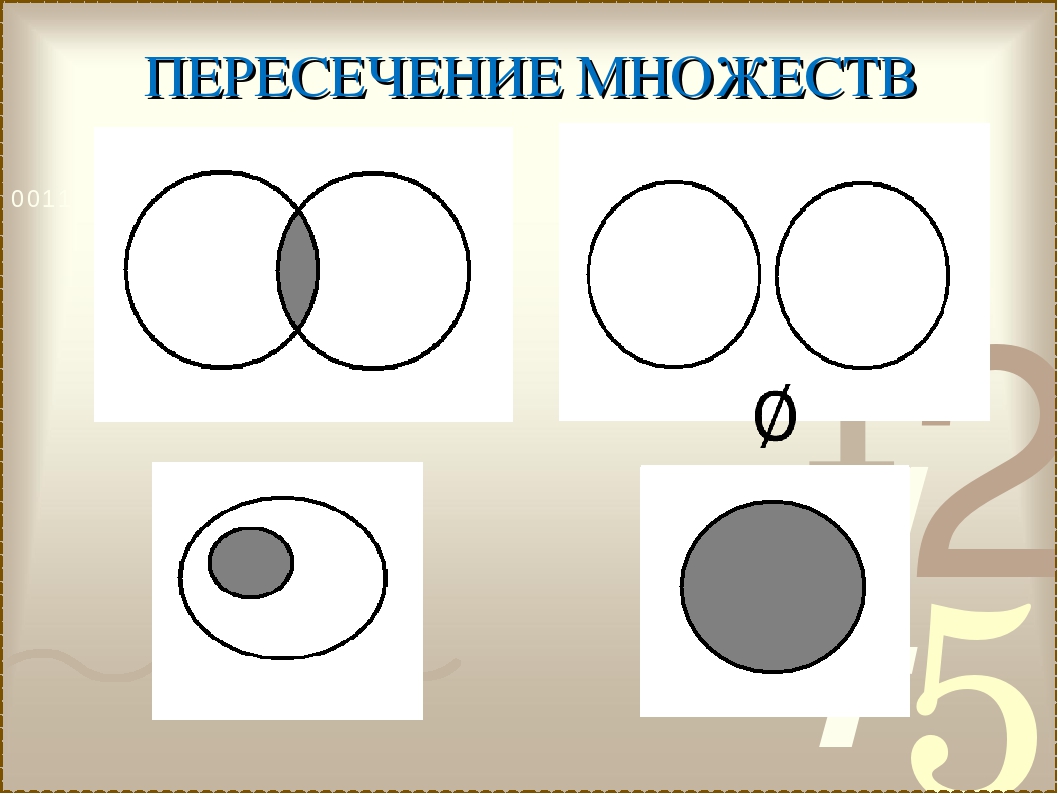
Над множествами, как и над числами, производят операции. Рассмотрим некоторые из них: пересечение, объединение и разность.

Пересечение множеств

Возьмем множество X, состоящее из букв а, б, в, г, д, и множество Y, состоящее из букв г, д, е, ж:

X = {а, б, в, г, д}, Y= {г, д, е, ж}.

Эти множества имеют общие элементы гид. Множества X и Y называются пересекающимися множествами. Множество общих элементов X и Y называют пересечением множеств X и Y и обозначают с помощью знака :Х Y={г, д} (рис.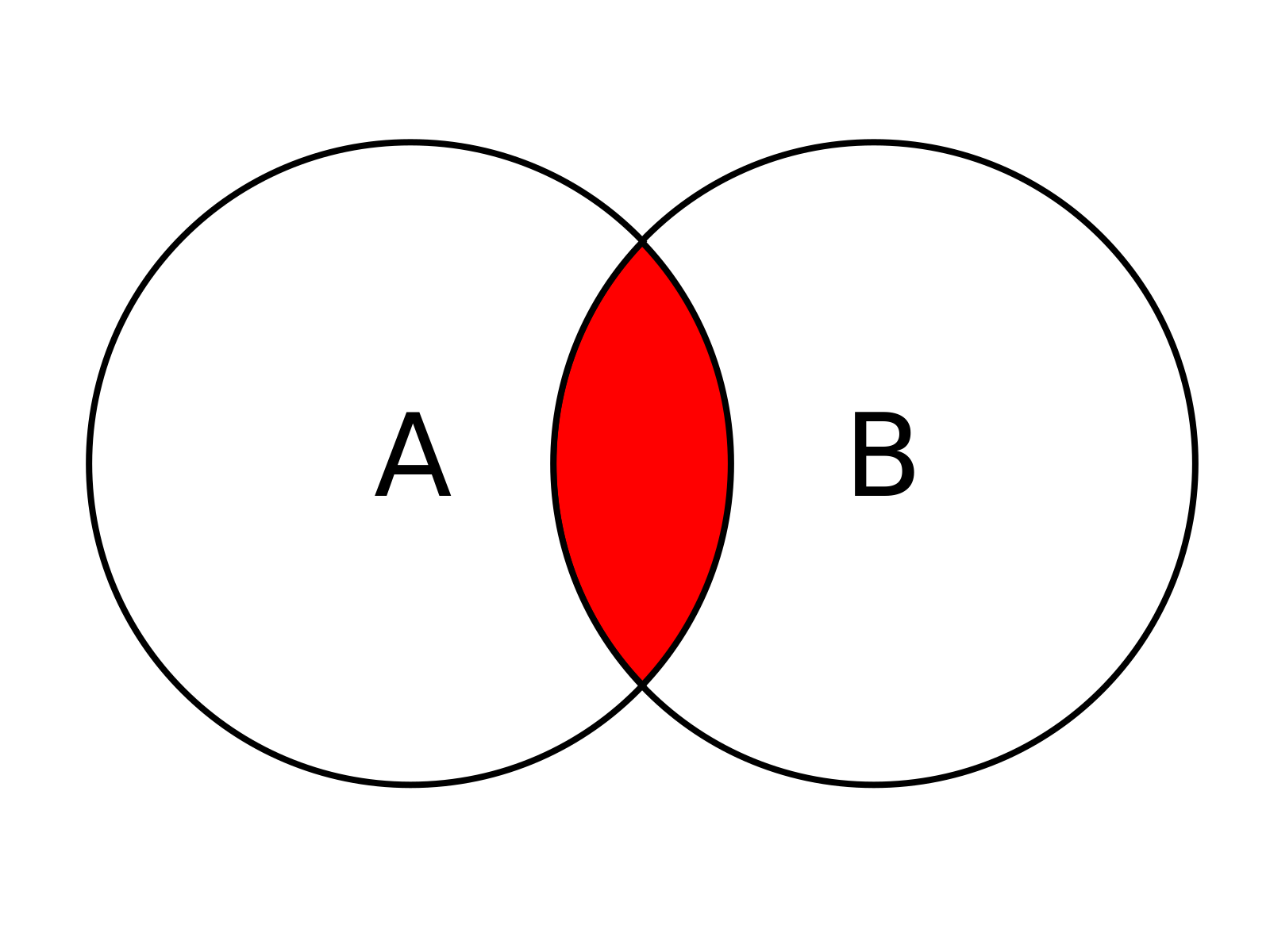 1).

Пусть множество А = {1, 3, 5}. Множества А и X не имеют ни одного общего элемента. В таком случае множества А и X называются непересекающимися множествами. Пересечением множеств А и X является пустое множество: А  Х=  (рис. 2).

Пересечением множеств называется новое множество, состоящее
из элементов, принадлежащих одновременно нескольким множествам

Рис. 1

Рис. 2

Объединение множеств

Если из элементов множеств X и Y составить новое множество, состоящее из всех элементов этих множеств и не содержащее других элементов, то получится объединение множеств Х и Y, которое обозначают с помощью знака :

X и Y= {а, б, в, г, д, е, ж) (рис. 4).

Объединение множеств А и X не является пустым:

А X = {1, 3, 5, а, б, в, г, д) (рис.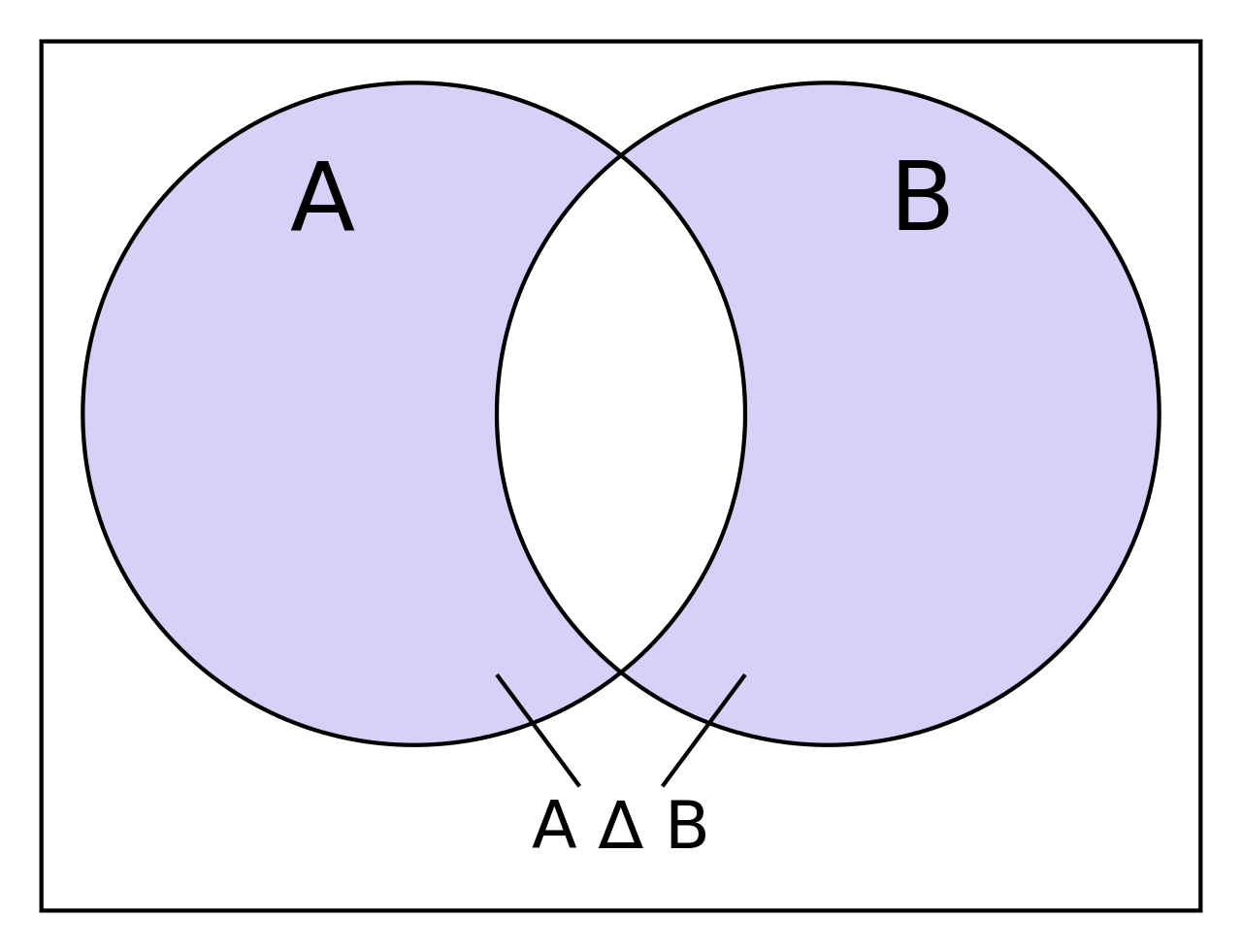 5).

Объединением множеств называется новое множество, состоящее
из элементов, принадлежащих хотя бы одному из множеств.

Рис. 3

Рис. 4

Разность

Разность множеств X и Y — это множество всех элементов из X, не являющихся элементами из Y.Разность обозначают Х\Y = {а, б, в} (рис. 5).

Рис. 5

1.3. Из истории кругов Эйлера

Часто множество изображают кругами, эти круги обычно называют «кругами Эйлера» по имени величайшего математика Леонарда Эйлера.

Леонард Эйлер (Euler) (1707 – 1783 г.г.) – математик, механик, физик и астроном. По происхождению швейцарец, а работал в основном в Росси и в Германии. В 1726 году был приглашен в Петербургскую АН и в 1727 году переехал в Россию. В 1741 – 1766 годах работал в Берлине, член Берлинской АН. Эйлер – ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.

Одним из первых, кто разрабатывал метод решения задач с помощью кругов Эйлера, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил швейцарский математик Леонард Эйлер (1707 – 1783). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказывает о кругах, которые «очень подходят для того, чтобы облегчить наши размышления». После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848).

Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов пользовался и немецкий математик Эрнест Шредер (1841 – 1902). Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Глава II. Решение логических задач с помощью кругов Эйлера

2.1. Задачи на пересечение и объединение двух множеств

К Лене на День Рождения пришли гости с подарками. Получилось так, что подарили только букеты цветов и воздушные шарики. Шесть гостей подарили букеты цветов, четыре — воздушные шарики.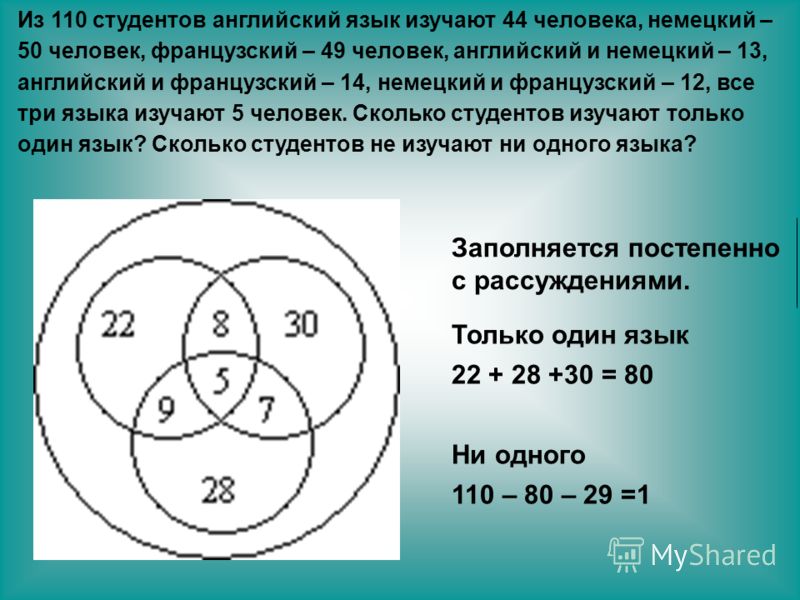 Сколько было гостей?
Задача предполагает несколько решений. Потому что мы точно не знаем, брал ли кто — нибудь из гостей два подарка.

1 Решение. Предполагается, что каждый гость с одним подарком. Следовательно, гостей 10.

2 Решение. Предполагается, что 1 из гостей пришел и с шариком, и с букетом цветов. Следовательно, 6 + 3 = 9 гостей.

3 Решение. Предполагается, что 2 из гостей пришли с двумя подарками. Следовательно, гостей 8.

4 Решение. Предполагается, что 3 из гостей пришли и с шариком, и с букетом цветов. Следовательно, 6 + 1 = 7.

5 Решение. Предполагается, 4 из гостей пришли с 2 подарками. Следовательно, 4 + 2 = 6 гостей.

)2)

) 4)

В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:

а) пересечении; б) объединении?

Ответ: а) от 0 до 30; б) от 40 до 70.

«;Ёлки»; и «;Неудержимый»;: Некоторые ребята из нашего класса любят ходить в кино. Известно, что 12 ребят смотрели фильм «Ёлки», 9 человек – фильм «Неудержимый», из них 6 смотрели и «Ёлки», и «Неудержимый». Сколько человек смотрели только фильм «Неудержимый»?
Сначала заполняем пересечение. Это будет число 6. Потом заполняем множество ребят, смотревших фильм «Ёлки». Это будет число 6. Так как 6 из двенадцати к тому же ещё смотрели фильм «Неудержимый». После заполняем множество ребят, смотревших фильм «Неудержимый». Это будет число 3. Так как 6 из 9 к тому же ещё смотрели фильм «Ёлки».
Ответ: 3 человека смотрели только фильм «Неудержимый».

20 человек знают английский и 10 — немецкий, из них 5 знают и английский, и немецкий. Сколько человек всего?

Способ 1. С помощью модели «Круги Эйлера» (Приложение 1).

10+20 – 5=25 человек.

Способ 2.

1) 20 – 5 = 15(чел.) – знают только английский язык;

2) 10 – 5 = 5 (чел.) – знают только немецкий язык;

3) 15+5+5 = 25 (чел.) – всего.

Можно решать и короче:

20 – 5 = 15(чел.) – знают только английский язык;
10+15 = 25 (чел.) — знают немецкий и только английский

2.2. Задачи на пересечение и объединение трёх множеств

В классе всего 36 человек. Учащиеся посещают математический, физический и химический кружки, причем, математический кружок посещают 18 человек, физический — 14 человек, химический — 10 человек. Кроме того, известно, что все три кружка посещают 2 человека, математический и физический -8,математический и химический — 5, физический и химический — 3.

Сколько учеников класса не посещают никаких кружков?

Способ 1. На рисунке большой круг изображает множество всех учеников класса. Внутри этого круга расположены три пересекающихся круга меньшего диаметра: эти круги изображают соответственно множества членов математического, физического и химического кружков. Эти круги обозначены буквами М, Ф, Х.

Общей части всех трех кругов соответствует множество ребят, посещающих все три кружка, поэтому она обозначена МФХ.

Через обозначено множество ребят, посещающих математический и физический кружки, но не посещающих химический кружок. Аналогичным образом обозначены и все остальные области. Здесь для удобства обозначений мы будем отсутствие отмечать чертой над символом.

Теперь обратимся к числовым данным (см. Приложение 2).

В область МФХ впишем число 2, т.к. все три кружка посещают 2 ученика. Далее известно, что ребят, посещающих математический и физический кружки, было 8. Значит, в область МФ надо вписать число 8. Но область МФ состоит из двух частей: и МФХ, причем в МФХ входят 2 человека. Значит, на долю остается 6 человек.

Теперь рассмотрим множество МХ, на которое приходится 5 человек. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 3.

Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество входит 18 – (2+3+6) = 7 человек.

Рассмотрим множество ФХ, на которое приходится 3 человека. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 1.

Рассмотрим множество Ф, в которое входят 14 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 1. Значит, в четвертое подмножество входит 14 – (2+1+6) = 5 человек.

36 – (10+7+6+5) = 8 человек. Таким образом, в классе 8 ребят, не посещающих никаких кружков.

? 8

Способ 2. С помощью модели «Круги Эйлера» (Приложение 1).

Представим множества учащихся, посещающих математический, физический и химический кружки, в виде кругов, вырезанных из плотной бумаги. Будем считать, что площадь каждого из этих кругов равна числу учащихся, посещающих соответствующий кружок. Наложим круги друг на друга так, чтобы было понятно, что есть учащиеся, посещающие один, два или три кружка. Вычислим площадь получившейся фигуры:

14 + 18 + 10 – ((8 + 5 + 3)  2) – 2 = 8 (чел. )— не посещают кружки.

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста.

Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек,а одним французским — 30.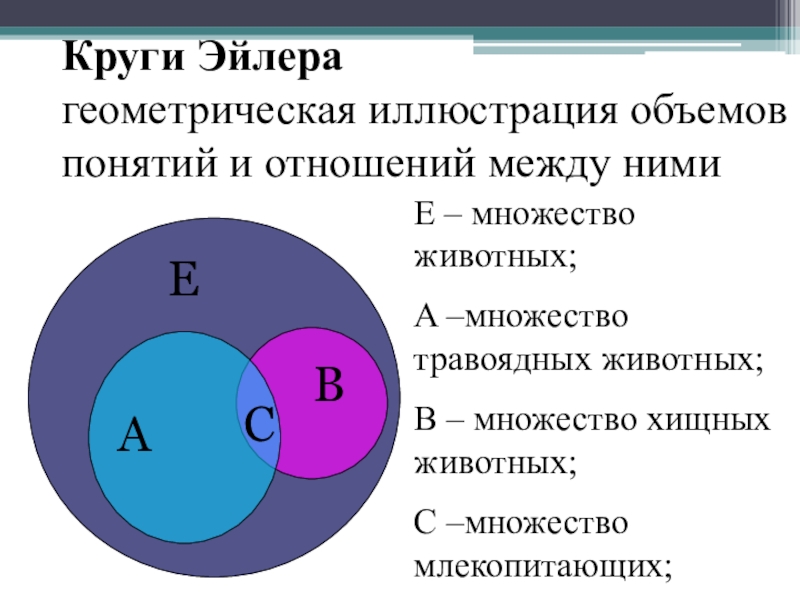

Всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Заключение

Существует множество приемов, которые используются при решении текстовых логических задач (Приложение 3). Очень часто решение задачи помогает найти рисунок, он делает решение простым и наглядным. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще.

Подобные задачи часто имеют практический характер, что немаловажно в современной жизни. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь.

Нами созданы модели «Круги Эйлера» для решения логических задач на пересечение двух и трёх множеств, которыми можно пользоваться как на месте (за партой), так и у доски (Приложение 4).

Поиск готовых способов решения выделенных логических задач, самостоятельное описание способа действий при использовании кругов Эйлера для их решения, а также попытки рассмотрения другой формы представления данных условия позволили нам решить поставленные задачи.

Цель была достигнута. С результатами работы были ознакомлены наши одноклассники, что позволило решать логические задачи этого вида не только нам.

Теперь наши одноклассники решают такие задачи, используя не только модели, но и памятку со способом действий, написанных нами.

Теперь мы точно будем знать, сколько друзей нам надо встречать в гости. От 20 до 35! А значит, и за стол всех всё же можно будет посадить.

Данная тема, безусловно, расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных задач.

Литература

Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей Текст/ Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993. с. 42. – ISBN 5-7084-0023-4
Занимательная математика. 5 – 11 классы. Текст: (Как сделать уроки нескучными) / Авт. – сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. с.32-38. – 10000 экз. –5-7057-0482-8
Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. Текст/ И.Я Депман. М.: Просвещение, 1999. с. 189 – 191, 231. – 10000 экз. – ISBN 5-09-007107-1
Смыкалова, Е.В. Дополнительные главы по математике для учащихся 5 класса. Текст: СПб: СМИО Пресс, 2009. с.14-20. – 2000 экз. – ISBN 5-7704-0055-2
Фарков, А.В. Математические олимпиады в школе.5–11 классы.Текст / А.В. Фарков. М.: Айрис–пресс, 2007. с. 27, 34, 61. – 7000 экз. – ISBN 978-5-8112-2394-7
Энциклопедия для детей. Т. 11. Математика Текст/ Глав.ред. М.Д. Аксёнова. М.: Аванта +,2001. с. 537 — 542. – 20000экз. – ISBN 5-8483-0015-1
Иванищев, Д. М. Поляна загадок – математика царица.

Дистанционная обучающая олимпиада по математике (ДООМ)

Сопова, С. С. Диаграмма Эйлера-Вена и «;дерево»;. Взаимодополнение.

Приложение 1

Модель «Круги Эйлера» на пересечение двух множеств

На листе бумаги нарисовать два круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 1 () (), № 2 ().

На бумаге цвета 2 обвести и вырезать детали № 2, № 3 () ().

 — окошко для названия множества,  — окошко для числа

Модель «Круги Эйлера» на пересечение трёх множеств

На листе бумаги нарисовать три круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 5 () (), № 2, № 1, № 4.

На бумаге цвета 2 обвести и вырезать детали № 6 (), (), № 2, № 1, № 3.

На бумаге цвета 3 обвести и вырезать детали № 7 (), (), № 4 (), № 1 (),

№ 3 ().

Приложение 2.

Способ действий при решении задач

на пересечение и объединение трёх множеств с помощью кругов Эйлера

Начертить три пересекающихся круга. Обозначить множества: A, B, C.
Начертить большой круг, в котором окажутся три маленьких. Это общее количество объектов – множество Е.
Начертить отдельное множество D – подмножество множества E Это те, кто не является элементом множеств А, В и С.
Найти часть круга, являющуюся общей для всех трёх множеств (№1) и записать данные.
Найти часть круга, являющуюся общей для двух множеств (№1 и №2) и записать данные в №2.

Найти часть круга, являющуюся общей для двух множеств (№1 и №3) и записать данные в №3.

Найти часть круга, являющуюся общей для двух множеств (№1 и №4) и записать данные в №4.

Найти часть круга, отвечающую за каждое множество в отдельности:

5 = А – (1 + 2 + 4), 6 = В – (1 + 2 + 3), 7 = С – (1 + 3 + 4).

Должно выполняться: 1 + 2 + 3 + 4 + 5 + 6 + 7 + D = E/
Записываем ответ на вопрос задачи.

Приложение 3.

Задача (/). а)На 3 курсе факультета обучается 81 студент. Многие из них выбрали одинаковые дисциплины, посещают одни и те же лекции и хорошо знают друг друга. б) 43 студента посещают лекции по философии, в)32 — по логике и г)41 — по естествознанию. д) Философию и логику выбрали 11 человек. е) Философию и естествознание посещает 21 студент, ж)а логику и естествознание — 16. з) 4 человека выбрали только философию и логику.

Сколько студентов посещают лекции:

1) по всем трём предметам,

2)только по философии и естествознанию,

3)только по логике и естествознанию,

4)только по философии,

5)только по естествознанию,

6)только по логике,

7)не выбрали ни одну из этих дисциплин.

Каждое высказывание из условия записать в виде логического выражения, строго подписывая друг под другом элементы. Решать систему будем с тех уравнений, где меньше всего неизвестных, попарно вычитая уравнения. При решении стремимся убрать как можно больше неизвестных.

1) Возможные варианты перебираем с учетом

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

з) 0 + 0 + 0 + + 0 + 0 + 0 + 0 = 4

2) Четко видно, что = 4. Подписываем под чертой вычисленные значения и убираем использованные уравнения. Ниже приведен подробный ход решения.

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

и) 4

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

и) 4 7

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

и) 4 14 9 7

а) + + + + + + + = 81

и) 18 12 11 4 14 9 7

0) + + ++ + + + = 81

и) 18 12 11 4 14 9 7 6

Ответ:1) по всем трём предметам, , 7

2)только по философии и естествознанию, , 14

3)только по логике и естествознанию, , 9

4)только по философии, , 18

5)только по естествознанию, , 11

6)только по логике, , 12

7)не выбрали ни одну из этих дисциплин, , 6

Приложение 4

Отчёт о проделанной работе перед коллегами

В кругах Эйлера | SKVOT

Работа креатора — это не только генерить идеи. Но и вовремя включить критическое мышление — чтобы найти в концепциях противоречия и отбросить то, что не выживет.

Инструменты есть не только для креативного, но и для логического мышления. И круги Эйлера — как раз из этого списка. Рассказываем, что это, и на примере креативных проектах показываем принцип работы кругов.

Рисовать, чтобы думать

Круги Эйлера — это шесть простых геометрических схем, которые помогают разобраться в соотношении понятий. Математик Леонард Эйлер придумал их еще в XVIII веке и предположил, что этот инструмент упростит размышления любому, кто мыслит.

Эйлер предложил шесть типов отношений: равнозначность, подчинение, соподчинение, пересечение, противоречие, противоположность. Вот как они объясняются с помощью окружностей:

По сути, круги Эйлера — способ визуализировать отношения между любыми объектами, группами объектов и даже абстрактными понятиями. Например, чтобы искать точки пересечения между любителями «Звездных войн», жителями швейцарских горных сел и посетителями музыкального фестиваля Sziget.

Чем больше понятий, тем сложнее представить их связи мысленно, цифрами, списками — и тем эффективнее делать схему. Например, в сериале «Теория большого взрыва» Говард при помощи кругов Эйлера объясняет Леонарду, почему ему стоит забить на поиски идеальной женщины:

Круги Эйлера используют для решения логических задач уже в средней школе. Но схемы универсальны — и действительно пригодятся любому, кто размышляет.

Нарисуй, распечатай, запомни круги Эйлера — и используй, если нужно:

— Разработать стратегию и проверять, как идея/проект с ней соотносятся.
— Анализировать контент конкурентов, кампании каннских победителей, рекламу Superbowl — и понять ключевые схемы.
— Выбрать tone of voice, героя истории, стиль вижуала, маскот для бренда, месседж для слогана.
— Найти противоречия и логические ямы в брифе, сценарии, посте для соцсетей.
— Освоить новый скил, но с направлением определиться трудно.

Эйлер на кейсах

Самый надежный способ разобраться в механизме системы, которую придумал Эйлер, — найти примеры в готовых кейсах. Увидишь, как работает равнозначность в стратегии бренда или пересечение в поисках героя для рекламного ролика, — поймешь, как использовать этот подход в своих целях.

#1. Равнозначность

У Эйлера этот тип взаимодействия понятий выглядит как два круга, которые полностью совпадают. Одно равно другому, как ни назови. Стивен Хокинг = автор книги «Краткая история времени». Или «Пираты Карибского моря: на странных берегах» = самый дорогой фильм в истории (пока).

Один рекламный ролик не сможет за минуту убедить пользователей, что пиво = Guinness, мыло = Dove, а детское масло = Johnson’s Baby. Нужна эффективная (часто многолетняя) маркетинговая стратегия, которая приведет к этому убеждению.

В идеале название бренда будет однозначно ассоциироваться с целой индустрией или продуктом. Слышишь «мебель для самостоятельной сборки» — сразу понимаешь, что это IKEA. Видишь пошаговый гайд по сборке — точно IKEA. А с помощью этих прочных связей бренд может говорить на самые разные темы: экологичность, ресайклинг, домашний уют и социальная ответственность.

#2. Подчинение

Допустим, общее понятие — это большой круг. Внутри него находится другой, маленький, и это — частность большого. Зимних олимпийских видов спорта много, и бобслей, например, один из них.

Такой тип отношений — мощный инструмент для рекламного месседжа. Особенно если его целью оказывается инклюзия: включение незаметной, неожиданной, уязвимой группы в сообщество. Nike на протяжении нескольких лет топит за спорт как удовольствие, независимо от телосложения, опыта, целей и происхождения. И на уровне продукта, и на уровне рекламных кампаний.

Коллекцию Victory Swim разработали для спортсменок-мусульманок — и Nike промит ее идеальным роликом, где женщины в хиджабах участвуют в соревнованиях, серфят, занимаются дайвингом и учат дочек плавать. И становятся частью сообщества Nike:

#3. Соподчинение

Графический ключ к этому соотношению — большой круг, внутри которого помещаются несколько маленьких. Маленькие понятия на равных и полностью включены в какое-то общее. Например, актеры, получившие Оскар, — Хоакин Феникс, Гэри Олдман, Леонардо Ди Каприо.

Если поместишь ключевое понятие в не самую очевидную область и будешь искать соподчинение в ней, выйдет крутой экспириенс. Например, очевидно было с началом пандемии находить параллели в прошлом — в частности, с эпидемией «испанки».

Креаторы латвийского агентства Nord DDB во время весеннего локдауна разработали серию принтов о бедах, которые мы уже пережили (а значит, есть все шансы пережить и жесткий карантин). Среди самых страшных событий прошлого: шлепанцы на носки и кроксы с платформой. Реально страшно:

#4. Пересечение

Эта диаграмма Эйлера — самая культовая и попсовая: ее растащили в коуч-пособия и мемы. Суть в том, что объем одного понятия частично совпадает с объемом другого — у них есть что-то общее.

Это крутой визуальный инструмент для поиска инсайта. Если представить бренд как исходный круг и строить вокруг него пересечения с ценностями и потребностями ЦА, попадешь в область, где совпадение будет максимальным.

Например, у Starbucks есть фишка: писать имя посетителя на кофейном стаканчике. Этот факт даже не про кофе, он — маленькая деталь в общем объеме информации о бренде. Но среди посетителей кофеен точно есть те, кто хочет сказать свое имя — и услышать его от бариста. Значит, нужно найти героя, который только в Starbucks может назвать себя как угодно, а не так, как написано в паспорте.

#5. Противоречие

В отличие от противоположности, противоречие держится на конфликте. Круг разделен пополам. Одна его часть утверждает, что не является второй частью. И наоборот.

На этом принципе строятся самые остроумные рекламные войны между брендами: Audi vs BMW, Pepsi vs Coca Cola, Old Spice vs Axe. Чаще это противостояние скрытое — борьба стратегий, разделение целевых аудиторий, — но иногда начинается прямой троллинг конкурента.

Рекламная борьба между McDonald’s и Burger King — самая долгая и зрелищная. Клоун, маскот Мака, шифруется и приходит в Burger King за воппером. Потом Burger King показывает, что весь год снимал рекламу вопперов, заслоняя ими бигмаки. Конкуренты меряются вкусом и размером бургеров, близостью ресторанов уже больше 20 лет.

А зарывают топор войны только ради социально важных поступков, но и тогда это соревнование в благородстве. В начале осеннего локдауна французский Burger King опубликовал в медиа призыв покупать в McDonald’s и других сетях фастфуда — чтобы индустрия выжила. Конечно, воппер будет лучшим решением, но и бигмак сойдет.

#6. Противоположность

Понятия с противоположными характеристиками Эйлер представляет как две части круга, между которыми остается свободное пространство — это все остальное. Проза и поэзия — две противоположности, а между ними: верлибр и ритмическая проза, например.

Противоположности — это мирные антонимы, которые не вступают в конфликт и не строят свою идентичность на отрицании друг друга. Это холодное, а это горячее. Это промышленное, а это DIY.

Wunderman Thompson построили на противоположности крутую кампанию для West Australian Ballet. В качестве промо новой постановки «Дракула» на стенах общественных туалетов разместили необычные принты. Изображение вампира в зеркале не отражается — постер пустой. Тут Дракула есть — там нет:

Логический вывод

В системе Эйлера — шесть простых геометрических схем, которые нарисует от руки даже ребенок. По отдельности каждая из них определяет только одно взаимодействие. Но если берешься за большую тему, в твоей схеме могут сочетаться сразу несколько типов соотношений.

Например, целевая аудитория бренда — подростки от 13 до 18. Среди них есть те, кто использует инстаграм, и те, кто использует тикток. Тиктокеры и инста-teens входят в целевую по принципу соподчинения. Но есть небольшая группа, которая зависает в обеих соцсетях — и между собой они взаимодействуют по принципу пересечения.

Тестить мир на противоречия и связи — суперполезно и суперувлекательно. Хорошие новости: ты не сможешь остановиться. Плохие новости: ты не сможешь остановиться.

Доказать законы алгебры высказываний можно:

построив таблицу истинности для правой и левой частей закона;

выполнив эквивалентные преобразования над правой и левой частями формулы для приведения их к одному виду;

с помощью диаграмм Эйлера-Венна.

Леонард Эйлер при решении задач изображал множества с помощью кругов, и в его честь этот метод был назван «методом кругов Эйлера». Однако такой прием очень полезен и при решении логических задач, когда с помощью кругов изображаются высказывания. Стоит отметить, что этим методом математики пользовались и до Эйлера. Так, в трудах Лейбница были обнаружены изображения таких кругов. Но, как уже говорилось, достаточно основательно этот метод был развит Эйлером. После Эйлера метод получил развитие в работах других ученых, однако наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика». Поэтому такие схемы называют «диаграммами Эйлера-Венна».

После Эйлера этот метод развивал чешский математик Бернард Больцано (1781-1858), только, в отличие от Эйлера, он рисовал не круглые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841-1902).

Любое высказывание на диаграмме изображается кругом, а его отрицание — частью плоскости, находящейся вне круга.

Рисунок 5. Диаграмма Эйлера -Венна

Если у нас есть два высказывания X и Y, то их на диаграмме изображают двумя кругами, как правило, разного цвета.

Рисунок 6. Логическое умножение двух высказываний X и Y

Ярким желтым цветом на диаграмме закрашено логическое умножение (конъюнкция) двух высказываний, а их логическое сложение (дизъюнкция) изображено на следующем рисунке. Другими словами логическое умножение — это пересечение кругов, а логическое сложение изображается как объединение кругов.

Рисунок 7. Логическое сложение двух высказываний X и Y

Давайте посмотрим, как с помощью диаграмм Эйлера-Венна можно доказать, что

В соответствии с приоритетом логических операций, сначала требуется выполнить A Λ B (1 шаг), затем (2 шаг), (3 шаг) и, наконец, выполнить сложение высказываний, полученных на шагах 1 и 3 (4 шаг).

Шаг 1	Шаг 2	Шаг 3	Шаг 4

Рисунок 8. Доказательство на диаграммах Эйлера-Венна

На рисунке 8 (2 шаг) заштриховано высказывание , результат изображен голубым цветом с белой штриховкой (3 шаг). Из последнего рисунка (4 шаг) непосредственно видно, что .

С доказательством некоторых логических законов на диаграммах Эйлера-Венна и с помощью таблиц истинности можно ознакомиться по ссылке .

Доказательство законов коммутативности

Доказательство закона ассоциативности

Доказательство закона дистрибутивности

Доказательство закона де Моргана

Создание диаграммы Венна — Служба поддержки Office

Чтобы быстро добавить к графическому элементу SmartArt внешний вид и оформление дизайнера, вы можете изменить цвета диаграммы Венна. Вы также можете добавить эффекты, такие как свечение, сглаживание или объемные эффекты.

К кругам графического элемента SmartArt можно применять сочетания цветов, основанные на Цвета темы.

Щелкните графический элемент SmartArt, цвет которого нужно изменить.

В разделе Работа с рисунками SmartArt на вкладке Конструктор в группе Стили SmartArt нажмите кнопку Изменить цвета.

Если вкладка Работа с рисунками SmartArt или Конструктор не отображается, выделите графический элемент SmartArt.

Совет: (СОВЕТ.) Если навести указатель мыши на эскиз, можно увидеть, как изменяются цвета рисунка SmartArt.

Изменение цвета линии или стиля границы круга

В графическом элементе SmartArt щелкните правой кнопкой мыши границу круга, которую требуется изменить, и выберите пункт Формат фигуры.

В диалоговом окне Формат фигуры выполните одно из указанных ниже действий.

Чтобы изменить цвет границы круга, нажмите кнопку Цвет линии на левой панели, в области Цвет линии нажмите кнопку Цвет

и выберите нужный цвет.

Чтобы изменить тип линии границы круга, нажмите кнопку тип линии в левой области, в области стиль линии , а затем выберите нужные стили линий.

Изменение цвета фона круга на диаграмме Венна

Щелкните графический элемент SmartArt, который нужно изменить.

Щелкните правой кнопкой мыши границу круга и выберите команду Формат фигуры.

В левой области диалогового окна Формат фигуры нажмите кнопку Заливка, а затем в области Заливка выберите пункт сплошная заливка.

Нажмите кнопку Цвет

и выберите нужный цвет.

Для выбора цвета фона, который не входит в Цвета темы, нажмите кнопку Другие цвета, а затем щелкните необходимый цвет на вкладке Обычные либо создайте собственный цвет на вкладке Спектр. Пользовательские цвета и цвета на вкладке Обычные не обновляются при последующем изменении тема документа.

Чтобы увеличить прозрачность фигур на диаграмме, переместите ползунок Прозрачность или введите число в поле рядом с ним. Значение прозрачности можно изменять от 0 (полная непрозрачность, значение по умолчанию) до 100 % (полная прозрачность).

Диаграммы Венна

и диаграммы Эйлера, объясненные на примерах

Диаграммы

Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многих людей смущает понимание разницы. Хотя оба типа диаграмм основаны на теории множеств, есть некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья развеет ваши сомнения относительно диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы сделать ее более ясной.

Венн против Эйлера: определение

Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между набором наборов. Но диаграмма Эйлера показывает только отношения, существующие в реальном мире.

Диаграммы Венна и

Диаграммы Эйлера Примеры

Начнем с очень простого примера. Давайте рассмотрим надмножество животных с млекопитающими и птицами как подмножества. Диаграмма Венна показывает пересечение двух множеств, хотя такой возможности не существует в реальном мире.Диаграмма Эйлера, с другой стороны, не показывает пересечения.

Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии.

Теперь давайте рассмотрим более сложный пример с колодой карт. Опять же, важно помнить о различии между двумя типами диаграмм: всех возможных комбинаций и реальных комбинаций. Давайте возьмем карты в качестве расширенного набора, а черные карты, красные карты и ромбы — в качестве подмножества.

Как одни и те же данные представлены по-разному с помощью диаграмм Венна и диаграмм Эйлера

Как показано в приведенном выше примере, диаграммы Венна показывают четыре пересечения, для которых нет данных, потому что они должны отображать все возможные комбинации.

Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера , и наоборот. Ознакомьтесь с этой замечательной вики-статьей о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера.Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.

Рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставит вам все необходимые инструменты. Вы можете быстро начать работу, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели.Благодаря такому количеству супер крутых функций вы не ошибетесь с Creately.

Диаграммы Венна и Эйлера | Давайте поговорим о науке

Диаграммы Венна

Иногда мы используем картинки для рисования наборов. Один тип изображения называется Диаграмма Венна . Диаграммы Венна помогают визуально показать отношения между наборами. Обычно диаграммы Венна имеют два перекрывающихся круга. Но вы можете нарисовать диаграммы Венна с тремя или более перекрывающимися замкнутыми кривыми.Диаграммы Венна не всегда показывают, что конкретно входит в набор. Например, на картинке ниже показаны наборы K и L:

Каждый кружок представляет все элементы набора. Имея только картинку, вы можете задать вопросы о подмножествах , пересечении и соединении .

K ⊆ L (находится ли K внутри L)? НЕТ.

L ⊆ K (находится ли L внутри K)? НЕТ.

Вопросы 1: Что такое K ∩ L? (Какая область внутри обоих наборов?) Нарисуйте изображение, а затем закрасьте его. Ответы даны внизу страницы.

Вопросы 2: Что такое K ∪ L? (Какова общая площадь набора K, набора L или обоих?) Закрасьте картинку, чтобы показать свой ответ.

Попробуйте это с наборами:

E = {1, 3, 8, 9, 14, 17}

F = {0, 14, 3, 5, 10, 20}

Вопросы 3: Используйте диаграмму Венна, чтобы показать наборы E и F .

Что такое E ∩ F ?

Что такое E ∪ F ?

Кем был Венн?

Джон Венн (1834-1923) был английским логиком . Логик — это тот, кто изучает способы логического мышления.Его помнят за изобретение диаграммы, названной в его честь — диаграммы Венна.

Венн был воспитан его отцом, который был преподобным англиканской церкви. Его мать умерла, когда он был очень молод. Он поступил в Кембриджский университет, где на втором курсе получил стипендию по математике. Несмотря на то, что в школе он действительно хорошо разбирался в математике, после ее окончания он стал преподобным, как его отец и дед.

Венн никогда не переставал думать о математике.После нескольких лет религиозной работы он вернулся в Кембридж, где преподавал логику и вероятность. В 1867 году он женился, и у него родился сын — Джон. Его сын Джон в конце концов стал президентом Королевского колледжа Кембриджского университета, где вместе со своим отцом выполнял важные исследовательские проекты.

Диаграммы Венна были впервые опубликованы в 1880 году в статье под названием «О схематическом и механическом представлении предложений и рассуждений». в «Философском журнале и журнале науки».«

Диаграммы Эйлера

Другой способ показать множества и их отношения — использовать диаграмму Эйлера . Эти диаграммы похожи на диаграммы Венна, но имеют тенденцию быть более сложными. Они часто показывают подмножества, а также пересечение и объединение. В диаграмме Эйлера размер и форма кругов / овалов не важны. Важно то, как они перекрываются или не перекрываются.

Вопрос 4:

Является ли какой-либо набор подмножеством (⊆) другого?

Если да, то какой?

Вопрос 5:

A) Цвет в N ∪ Q

B) Тень в M ∩ R

C) Цвет в P ∩ N ∩ Q

D) Тень в M ∪ P ∪ R

Возможно ли N ∩ R ? Нет! N и R не перекрываются.В теории множеств мы называем это пустым набором или пустым набором , потому что он ничего не содержит. Символ для нулевого набора — ∅ . Вот еще один пример нулевого набора:

G — количество жирафов в классе миссис Браун. B = {} = ∅

Приложения диаграмм Венна и Эйлера

Диаграммы Венна и Эйлера полезны в самых разных контекстах. Оба типа диаграмм помогают нам визуализировать концепции и отношения. Это может помочь нам легче понять сложную информацию.Эти диаграммы используют одну и ту же структуру для представления различных типов контента.

Например, диаграммы Венна часто используются для решения математических задач. Представление вопроса в виде диаграммы Венна часто упрощает понимание и решение. Компании часто используют диаграммы Венна для сравнения продуктов, анализа конкурентов и принятия решений. Диаграммы Венна представляют собой множество других видов практической информации, от химии до географии. Их можно использовать даже для юмора или для представления сложных философских вопросов.Диаграммы Венна и Эйлера — простой способ представить все виды информации.

ОТВЕТОВ

Вопрос 1:

Что такое K ∩ L? (Какая область внутри обоих наборов?) Закрасьте картинку, чтобы показать свой ответ.

Вопрос 2:

Что такое K ∪ L? (Какова общая площадь набора K, набора L или обоих?) Закрасьте картинку, чтобы показать свой ответ.

Вопрос 3:

Используйте диаграмму Венна, чтобы показать наборы E и F .

E ∩ F = {3, 14}

E ∪ F = {0, 1, 3, 5, 8, 9, 10, 14, 17, 20}

Вопрос 4:

Является ли какой-либо набор подмножеством (⊆) другого?

Если да, то какой?

Да, R является подмножеством P ( R ⊆ P )

Вопрос 5:

A) Цвет в N ∪ Q

B) Тень в M ∩ R

C) Цвет в P ∩ N ∩ Q

D) Тень в M ∪ P ∪ R

Диаграммы и круги Венна

Диаграммы и круги Венна

Сатьядев Нандакумар
Вт 17 июл 11:42:14 2018

Диаграммы Венна дают наглядное представление о взаимосвязях между
наборы.Мы часто видим диаграммы Венна с кружками, которые изображают
отношения, которые могут возникать между 2 наборами или 3 наборами. Например,
следующая диаграмма Венна иллюстрирует отношения между 3
наборы.

Можем ли мы нарисовать диаграмму Венна, изображающую все отношения, которые могут
существует между 4 наборами с использованием кругов?

Характеристика Эйлера

Эйлерова характеристика геометрической фигуры определяется как V-E + F,
где V — количество вершин, E — количество ребер, а F —
количество лиц (регионов).

Для любой плоской фигуры характеристика Эйлера равна 2. (Попробуйте
квадрат: V = 4, E = 4, F = 2, что дает V-E + F = 2, и треугольник: V = 3, E = 3, F = 2,
что дает V-E + F = 2 или следующий рисунок с V = 4, E = 5, F = 3.)

Характеристика Эйлера и диаграммы Венна

Любая диаграмма Венна является плоской фигурой, поэтому V-E + F будет 2. Мы можем проверить
что на Рисунке 1, где V = 6, E = 12, F = 8, что дает V-E + F = 2.

Ключевой момент заключается в следующем: два различных круга могут пересекаться только в
ровно 0, 1 или 2 балла.Для диаграмм Венна нам необходимо
рассматривать только пары окружностей, которые пересекают друг друга ровно в 2
точки.

Чтобы упростить количество случаев, предположим, что каждая отдельная пара
кругов соответствует отдельной паре пересечений
точки. [сноска]

Попробуем ввести на рисунок четвертый кружок. Четвертый
вводимый круг приносит еще 6 вершин. Таким образом
V = 12. Каждая вершина имеет степень 4. (рисунок).

Легко устанавливаемый факт, что для любого графа сумма
степени вершин в два раза больше числа ребер.Следовательно, E = 24. Но
поскольку нам нужна плоская фигура, мы должны иметь F = 2-V + E = 2-12 + 24 = 14.

Таким образом, невозможно представить 16 регионов с помощью диаграмм Венна.
состоящий из 4-х кружков.

(Эллипсы, овалы, треугольники и т. Д. Могут использоваться для представления
отношения между 4 наборами.)

Более 4 комплектов

Количество пар, образованных n кругами, равно n (n-1) / 2. Количество
вершин на фигуре пересечения, следовательно, n (n-1), если Venn
диаграмма существует как плоская фигура. Количество ребер — 2n (n-1).п = 2.

Поскольку 2 ⁿ асимптотически больше n (n-1), единственный
два значения n, для которых может выполняться уравнение: n = 2 и
п = 3.

Вклад Венна

Однажды в разговоре я
и мой друг задавался вопросом
заслужил ли Джон Венн бессмертную славу за столь тривиальную концепцию. В
в свете приведенного выше обсуждения легче оценить
вклад — он дал

геометрический
схема для изображения отношений между n наборами для произвольного n (!!)
Конечно, ему пришлось использовать рекурсивную схему с использованием странных форм.

Сноска: через точку могут проходить 3 круга. Но если
отметим, что любая подколлекция из 3 кругов из 4 должна быть действительной
Диаграмма Венна для 3-х наборов, можно сделать вывод, что конфигурации, в которых
3 или более кружков, проходящих через точку, не имеют значения.

ОБРАТНАЯ СВЯЗЬ: Вас не убедил аргумент? Напишите мне
доработки / исправления по адресу [email protected].

Диаграммы Эйлера и Венна: они не только для развлечения

(источник) К тому времени, когда вы дочитаете этот пост в блоге, вы должны быть в третьей группе.Диаграммы Венна и Эйлера (произносится как «масленка») невероятно популярны в Интернете как забавные диаграммы. Они предлагают простой способ изобразить концепции теории множеств. Итак, в чем разница между ними? Почему они смешные? Полезны ли они для реальных данных? Оба типа диаграмм используются для отображения концепций теории множеств:

Union — комбинация двух наборов. В диаграммах Венна и Эйлера.
Intersection — Входит в оба из двух наборов. В диаграммах Венна и Эйлера.
Разница — Все, кроме пересечения двух наборов. В диаграммах Венна и Эйлера.
Относительное дополнение — В одном наборе, а не в другом. В диаграммах Венна и Эйлера.
Абсолютное дополнение — Все, чего нет в другом наборе. Только в диаграммах Эйлера.
Подмножество — Набор, полностью содержащийся в другом наборе. Только в диаграммах Эйлера.
Disjoint — Два набора без общих элементов. Только в диаграммах Эйлера.Все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна. Диаграммы Эйлера имеют только те комбинации пересечений, которые действительно существуют в реальном мире. Диаграммы Венна представляют все гипотетически возможные логические отношения между категориями. Диаграммы Венна по определению должны отображать все возможные комбинации пересечений, что создает некоторые интересные проблемы с компоновкой. Когда есть три круга, отображается каждое пересечение, но как только вы попадаете в четыре категории, круги перестают работать.Эллипсы могут работать до пяти категорий, но помимо пяти необходимо использовать странные формы, чтобы вплетаться и выходить из всех комбинаций пересечений. Пять уже довольно сложно читать, но как только эти странные формы вступают в игру, чтение диаграмм становится почти невозможным, а текстовые описания отношений часто легче понять. Это подводит нас к тому, почему так много забавных диаграмм. Диаграмма Венна позвоночных и беспозвоночных, которую мы показали вам ранее, предполагает, что некоторые животные могут одновременно иметь позвоночник и не иметь позвоночника.Хотя это может быть и не смешно, любой, кто учился в шестом классе по естествознанию, может сказать вам, что это довольно глупо. С более интересным предметом указание на несуществующие отношения может быть довольно забавным. Некоторые диаграммы достигают юмора, помещая что-то в категорию, к которой это не относится, или к той, в которой вы обычно не ожидали бы этого. Креативная маркировка (как на диаграмме Эйлера ниже) тоже всегда помогает. Мы знаем, что диаграммы Эйлера могут быть забавными, но могут ли они быть полезными? Некоторые диаграммы включают количественную информацию, используя площадь каждой части диаграммы.Хорошим примером этого является Глобальная карта социальных сетей за 2011 год по данным Global Web Index. Сами по себе диаграммы Эйлера, подобные этой, дают вам довольно хорошее общее представление о задействованных значениях. Считать из них точное количество было бы немного сложно, но для получения общего обзора они хороши. На этом конкретном рисунке эти диаграммы Эйлера используются как малые кратные, что позволяет сравнивать регионы. Почему в инфографике нет более серьезных диаграмм Эйлера / Венна? Они хорошо демонстрируют совпадение категорий.Они выглядят «круто» — многие дизайнеры считают это важным. Они разумно демонстрируют количество. Они демонстрируют сложные и интересные отношения в простой для понимания манере. Если вы дизайнер и вам нужны интересные диаграммы, внимательно изучите свои данные. Возможно, вы сможете использовать диаграмму Эйлера или Венна. Дрю Скау — кандидат компьютерных наук, студент-визуализатор UNCC, со степенью бакалавра архитектуры.

Все о диаграмме Венна

Определение диаграммы Венна

Диаграмма Венна (также известная как диаграмма набора или логика ) может показывать различия, сходства и перекрывающиеся отношения между наборами, т.е.е., группы данных. Чаще всего его используют для описания общих черт между противоборствующими фракциями — например, в приведенном ниже примере диаграммы Венна мы можем увидеть общие характеристики клеток растений и животных.

Исходные клетки растений против клеток животных — https://owlcation.com/stem/Plant-Cells-vs-Animal-Cells-With-Diagrams

Набор данных визуализируется как совокупность фиксированных точек внутри замкнутой окружности (обычно кругов, но иногда эллипсов, сфер или даже треугольников): визуально описывает одну категорию, которую имеют все включенные данные.В приведенном выше примере окружность, содержащая характеристики клеток животных, имеет точки данных: неправильная / круглая, центросомы, центриоли, лизосомы, ядро, клеточная мембрана, цитоплазма, митохондрии, аппарат Гольджи и рибосомы. Только или из этих точек данных / характеристик являются общими для растительных клеток, визуализированных в синем пересечении.

Нравится, как выглядит этот пример диаграммы Венна? Начни и создай свой собственный!

Основная точка интереса диаграмм Венна — это пересечение — данные, которые попадают в более чем одну категорию (в приведенном выше примере это поясняется меткой «обе», хотя следует помнить, что пересечение — это , а не . собственный, отдельный набор данных).Диаграммы Венна могут состоять из нескольких пересечений и наборов кругов, но наиболее часто используется трехкружная или тройная диаграмма Венна.

Одним из факторов популярности тройного Венна является то, что он создает в центре изогнутый треугольник идеальной и постоянной ширины, известный как «треугольник Рело». Эта форма очаровала инженеров, математиков, архитекторов и графических дизайнеров своими математическими возможностями и визуальной красотой и использовалась эрудитами от немецкого инженера Франца Рёло (в честь которого они теперь названы) для производства кинетических машин и Леонардо Да. Винчи за проектирование карты.

Начните создавать свои собственные диаграммы и бизнес-графику.

Попробуйте Vizzlo бесплатно

Развитие и история диаграммы Венна

В той или иной форме диаграммы в стиле Венна существуют еще со средневековья. Абстрактное визуальное представление соединений и пересечений различных множеств — невероятно старая концепция, поскольку существует глубокое человеческое стремление показать, что принадлежит, а что нет. Как и большинство логических сред, он рос и органически изменялся с годами, уточнялся, перефокусировался и перенаправлялся в круговую диаграмму, с которой мы так хорошо знакомы сегодня.

Первым математиком, напрямую связавшимся с этим стилем диаграмм, был немецкий эрудит и философ Готфрид Вильгельм Лейбниц примерно в конце 1600-х годов. Лейбниц был, по сути, одним из первых приверженцев многих концепций визуализации данных: он верил в символическое представление сложных мыслей, чтобы не только лучше передавать эти идеи, но и оставлять меньше места для человеческих ошибок, неверной интерпретации и возникающих споров. Для Лейбница этого удалось добиться путем вычисления и визуализации разногласий в формализованных логических диаграммах.

Диаграмма Эйлера

Примерно сто лет спустя знаменитый швейцарский математик Леонард Эйлер стал широко известен тем, что использовал перекрывающиеся круги для представления логических выводов (или силлогистических рассуждений). Эти круги используются для изображения четырех категоричных положений силлогизма:

Универсальное подтверждение «Все графики Vizzlo выглядят красиво»
Универсальный отрицательный «Ни один из графиков Vizzlo не является трудным для создания»
Особо утвердительное «Некоторые из Vizzard Vizzlo включают диаграммы Венна»
Особо отрицательный «Некоторые из Vizzard Vizzlo не являются диаграммами Венна»

Замечание на полях: Знаете ли вы, что в соответствии с логической семантикой в английском языке до конца XVI века было четыре слова, обозначающие «да» и «нет» ?! Универсальное Утверждение было бы сказано как «Да», Универсальное Отрицательное как «Нет», Частное Утверждение как «Да» и Частное Отрицательное как «Нет».»

Чтобы было ясно, стало обычной практикой данных, а именно: группировать диаграммы Эйлера и Венна под более известным названием «диаграмма Венна», чтобы избежать путаницы — только в очень технических математических ситуациях может потребоваться разграничение между ними.

Современная диаграмма Венна

Диаграмма Венна, которую мы знаем сегодня, была разработана английским математиком Джоном Венном.В 1880 году он опубликовал статью под названием «О схематическом и механическом представлении суждений и рассуждений». В нем Венн предложил изменить диаграмму Эйлера, чтобы она стала более полной визуализацией вероятности, потребовав отображения всех возможностей. Однако название «диаграмма Венна» было придумано американским философом Кларенсом Ирвингом лишь несколько лет спустя, в 1918 году.

С тех пор диаграмма Венна стала центром обширных исследований многих других известных ученых, в том числе А.W.F. Эдвардс, Бранко Грунбаум и Генри Джон Стивен Смит. Они стали важной визуализацией для математических исследований, будь то традиционная трехкружная диаграмма или более сложные версии, включая сферы и эллипсы, для таких областей, как теория множеств, теория логики, вращательная симметрия и изучение сложных форм и чисел, таких как тессеракт.

Что НЕ является диаграммой Венна?

Для такой простой диаграммы Венна с годами неправильно обозначали. Фактически, сейчас мы чаще всего обращаемся почти исключительно к диаграммам Эйлера, когда обсуждаем «Венн.”

Диаграммы Венна по сути являются более специфическим типом диаграмм Эйлера. Вот удобная диаграмма Эйлера, наглядно описывающая, что все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна:

Золотое правило Венна состоит в том, что он всегда визуализирует всех возможностей, даже если ни один из данных не укладывается в эти пересечения, тогда как диаграмма Эйлера визуализирует только категории, для которых есть данные. Если бы мы заставили приведенную выше диаграмму соответствовать параметрам диаграммы Венна, мы должны были бы представить себе, что существуют некоторые диаграммы Венна, которые не являются диаграммами Эйлера.Чтобы поместить это в контекст, это похоже на утверждение, что некоторые животные не пингвины, и поэтому некоторые пингвины не являются животными.

Чтобы продемонстрировать это различие на практике, представим, что трое друзей сравнивают свои домашние задания. Люси подготовила два домашних задания: одно по теме «Прокариоты и эукариоты» по естествознанию и одно по теме «Вероятность и статистика» по математике. Анвар также подготовил домашнее задание по математике на тему «Вероятность и статистика», но выбрал для науки тему «Клетки животных и клетки растений».Янс написал отличное эссе на тему «Митоз и мейоз» для Science, но совершенно забыл, что его домашнее задание по математике вообще нужно.

Если оранжевый набор данных представляет Янса, розовый набор данных представляет Анвара, а синий набор данных представляет Люси, мы можем организовать эту информацию двумя разными способами.

Диаграмма Эйлера показывает всего возможностей, по которым у нас уже есть фактические данные. Мы знаем, что Анвар и Люси выполнили домашнее задание по математике на тему «Вероятность и статистика», и пересечение показывает это.Мы знаем, что Янс не создавал никаких домашних заданий по математике, как Анвар и Люси, и что они не выбрали ту же тему, что и он, для науки, поэтому набор данных Янса не пересекается с другими.

Диаграмма Венна показывает ту же информацию — темы, которые трое друзей изучали индивидуально, и математическую тему, которую выбрали Анвар и Люси. Однако у нас также есть пересечения, которые не содержат данных, но представляют всех других возможностей.

Оранжевое пересечение слева представляет собой случай, когда Янс вместе с Анваром помнит свою домашнюю работу по математике, а также науку, но в этом гипотетическом результате Люси забывает завершить работу по математике.Зеленый перекресток справа олицетворяет ту же судьбу Анвара. Центральное пересечение показывает вероятность того, что все трое друзей не забудут работать над «Вероятностью и статистикой» для математики, а также над различными темами для естествознания, и никто не получит наказание…

Готовы создать свою собственную диаграмму Венна? Вот небольшой ярлык для страницы Vizzard специально для вас.

Для построения диаграммы Венна между двумя наборами данных должны быть как общие черты, так и различия.Если вся информация по категориям идентична, ваша диаграмма будет выглядеть так:

Даже с двумя наборами данных, если содержащаяся информация не имеет различий, две кривые будут полностью перекрываться, образуя только один круг.

Противоположная проблема, два набора данных без общих черт, также не будут создавать диаграмму Венна (но вполне приемлемую диаграмму Эйлера, показывающую непересекающихся множеств ).

Удивительно, но то, что выглядит столь же знакомым, как приведенный ниже пример, также математически не считается диаграммой Венна.

Как объяснялось ранее, одним из ключевых требований диаграммы Венна является то, что она должна отображать все возможные логические результаты. Поскольку в приведенном выше примере нет пересечения, в котором встречаются только желтый и красный или только синий и оранжевый, это не может считаться полным отображением универсальной логики.

Сводка

Подводя итог, диаграмма Венна:

Тип диаграммы Эйлера
Схема с двумя или более наборами данных, изображенными в пределах окружности
Используется для визуализации различий и общих черт между этими наборами данных
Используется для выработки всех логических выводов
Невероятно быстрое изготовление с использованием диаграммы Венна Vizzlo Vizzard

Vizzlo очень проста, и вы можете попробовать ее бесплатно.

Начните создавать свои собственные диаграммы и бизнес-графику.

Попробуйте Vizzlo бесплатно

Развлечения с диаграммами Венна и Эйлера

Диаграмма Венна — это математическая иллюстрация, которая показывает все возможные математические или логические отношения между множествами. Диаграмма Эйлера похожа на диаграмму Венна, но не обязательно показывает все возможных пересечений множеств. Диаграмма Эйлера часто более полезна для отображения данных реального мира, потому что не все наборы частично перекрываются со всеми другими наборами.

Я использовал апплет «Трехкруговая диаграмма Венна», чтобы составить диаграмму пищевых предпочтений в моей семье. У меня есть один ребенок, который не ест много мяса или овощей, а другой не любит углеводы. Это классическая диаграмма Венна, которая объясняет, почему я не готовлю так часто, как раньше.

Этот рисунок обозначен как диаграмма Венна, но на самом деле это диаграмма Эйлера, потому что истинное счастье нигде не пересекается с ношением брюк. По крайней мере, для человека, который составил диаграмму.

Больше диаграмм после прыжка.

Если круги не пересекаются, это не диаграмма Венна. Что может быть очень печально, если вы — круг. Этот дизайн был найден на футболках без резьбы. Однако диаграммы Эйлера могут перекрываться или нет. Но Эйлер не то, что имел в виду синий круг.

На прошлой неделе я наткнулся на это очень полезное изображение, с которого я начал поиски различий между диаграммой Венна и диаграммой Эйлера. Это объясняет географическую терминологию, используемую в той области восточной Атлантики, которая сбивает американцев с толку.Автор обозначил этот предмет как «Великая британская диаграмма Венна», а затем пояснил, что на самом деле это диаграмма Эйлера. Несомненно, люди более знакомы с Венном. Но независимо от того, насколько географически точны географические названия, ирландские комментаторы предсказуемо возражали против включения во все, что помечено словом «британский». Еще одну такую диаграмму, которая включает больше островов, можно найти здесь.

Эти кисло-сладкие каракули — настоящие диаграммы Венна. Их подготовила Джессика Хэги из Indexed, блога, полного замечательных диаграмм и графиков, сделанных на учетных карточках.

Роб Харвилла использовал диаграммы Венна и другие диаграммы, чтобы деконструировать песню «This Is Why I’m Hot» Мимса из The Villlage Voice. Диаграммы ясно показывают, что тексты вообще не имеют смысла. Тем не менее, на момент написания песня была номером один.

Кстати о музыке, вот футболка для музыкальных снобов с двухкомпонентной диаграммой Венна. Со страницы товара:

Нет ничего хорошего, если это нравится другим. Мы только что доказали это математически.У меня есть теория, что карикатуристы удосужились изучать на уроках математики только диаграммы Венна.

У Рэндалла Манро из xkcd самые странные любовные записки. Эта классическая диаграмма Венна настолько мила и проста, что с до он начал заполнять зоны.

Диаграммы Венна и диаграммы Эйлера — это еще два из множества удобных обучающих устройств, которые используются в странных или комедийных целях. См. Также столовые приборы периодического действия, дополнительные столовые приборы периодического действия и развлечения с блок-схемами.

VennMaster: Пропорциональные диаграммы Эйлера для функционального анализа микрочипов методом GO | BMC Bioinformatics

Было продемонстрировано Чоу и Раски [14, 15], что задача визуализации пересекающихся наборов выборок с помощью пропорциональных площадям диаграмм Эйлера, как правило, не может быть идеально решена для более чем двух наборов с кругами на плоскости. Поэтому мы определили функцию стоимости, отражающую конфликтующие ограничения перекрытия кругов и мощности множества пересечений, и искали наилучшие компромиссные решения, используя эволюционный и ройный подходы для оптимизации [подробности см. В дополнительном файле 1].

Функция стоимости

Мы предлагаем функционал стоимости E , отображающий центры правильных многоугольников (или окружностей) на значение ошибки, описывающее качество решения. Функция E включает компромисс между правильными графическими областями пересечения и истинными размерами набора. Сначала проблема разбивается на непересекающиеся, независимо решаемые подзадачи. Этого можно достичь, найдя компоненты связности графа пересечений, у которого есть по одной вершине для каждого набора и ребра, соединяющие пересекающиеся множества.Связанные компоненты можно найти с помощью поиска в глубину (сравните [16, 17]), который занимает O ( n + m ) шагов, где n — количество вершин (наборов), а m — это количество ребер (которое может быть не более n ( n — 1) / 2). Результирующая сложность составляет O ( n ²) для разделения проблемы. В дальнейшем предполагается, что у всех наборов есть хотя бы один пересекающийся партнер.Пусть A ₁ … A _м ⊆ UMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae8hfXxfaaa @ 376F @ последовательность пересекающихся подмножеств общего набора генов UMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae8hfXxfaaa @ 376F @ и пусть G ₁… G _м ⊆ ℝ ² — графическое двумерное представление наборов.

Для идеально решаемого случая мощность каждого пересекающегося подмножества A ( I ) = ∩ _i∈I A _i для I ⊆ {1 … м } пропорционально соответствующей графической площади пересечения G ( I ) = η площадь (∩ _i∈I G _i) так что | A ( I ) | = G ( I ) для коэффициента пропорциональности η > 0.Определить A (∅) = UMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae8hfXxfaaa @ 376F @. Функция возможных ошибок, реализованная в Kestler et al. [3], это E = ∑ _{I ⊆ {1 … m }} w _{| I |} f ( I ) с частичными ошибками

f1 (I) = d (G (I), | A (I) |) {αif A (I) = ∅βif A (I) ≠ ∅, G (I) = 0γotherwiseMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOzay2aaSbaaSqaaiabigdaXaqabaGccqGGOaakcqWGjbqscqGGPaqkcqGH9aqpcqWGKbazcqGGOaakcqWGhbWrcqGGOaakcqWGjbqscqGGPaqkcqGGSaaldaabdaqaaiabdgeabjabcIcaOiabdMeajjabcMcaPaGaay5bSlaawIa7aiabcMcaPmaaceaabaqbaeaabmWaaaqaaGGaciab = f7aHbqaaiabbMgaPjabbAgaMjabbccaGiabdgeabjabcIcaOiabdMeajjabcMcaPiabg2da9iabgwGigdqaaaqaaiab = j7aIbqaaiabbMgaPjabbAgaMjabbccaGiabdgeabjabcIcaOiabdMeajjabcMcaPiabgcMi5kabgwGiglabcYcaSaqaaiabdEeahjabcIcaOiabdMeajjabcMcaPiabg2da9iabicdaWaqaaiab = n7aNbqaaiabb + gaVjabbsha0jabbIgaOjabbwgaLjabbkhaYjabbEha3jabbMgaPjabbohaZjabbwgaLbqaaaaaaiaawUhaaaaa @ 6EC4 @

с функцией расстояния d ( г , c ) и константы α , β , γ ≥ 0, допускающие разные веса для трех случаев: нежелательные графические перекрытия, отсутствующие графические пересечения и отклонения площади.

Эффект от использования различных настроек параметров для выделения различных аспектов данных показан на рисунке 5. Веса w _k, k = 1 … m были ранее выбраны как w _k = 1 / ( k — 1) (для k > 1) и d ( g , c ) = ( g — c ) ².

Рисунок 5

Влияние различных настроек параметров на функционал стоимости . Пример с тремя наборами A = {1, 2, 3}, B = {2, 4, 5} и C = {3, 4, 6} таким образом, что имеется попарное перекрытие одного элемент, но не среди всех трех наборов, т. е. | A ∩ B | = | A ∩ C | = | B ∩ C | = 1 и | A ∩ B ∩ C | = 0.Это означает, что невозможно найти идеальное решение, удовлетворяющее всем ограничениям, а только приблизительные, на которые влияет относительный вес частичных затрат. На левой диаграмме показаны настройки α = 0 и β = γ = 1, так что нежелательные пересечения (серая область в центре) игнорируются. Для диаграммы справа a было установлено на 50, таким образом показывая меньшую серую область за счет большего отклонения области.

Функция ошибок f ₁ взвешивает (потенциально большое) пересечение двух больших множеств намного сильнее, чем (потенциально маленькое) пересечение двух маленьких множеств или маленькое с большим множеством.Поскольку размер пересечения последовательности наборов ограничен ее наименьшим набором, мы предлагаем нормализовать частичные ошибки этой верхней границей. Более того, f ₁ не принимает во внимание, что едва заметное пересечение (где пересечение должно быть) хуже, чем слишком большое графическое перекрытие (сравните Рисунок 5). Функция ошибок, компенсирующая эти два эффекта, может быть определена как

f2 (I) = d (G (I), | A (I) |) mini∈I | Ai | {αif A (I) = ∅βif A (I ) ≠ ∅, G (I) <| A (I) | γ в противном случае.MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOzay2aaSbaaSqaaiabikdaYaqabaGccqGGOaakcqWGjbqscqGGPaqkcqGH9aqpjuaGdaWcaaqaaiabdsgaKjabcIcaOiabdEeahjabcIcaOiabdMeajjabcMcaPiabcYcaSmaaemaabaGaemyqaeKaeiikaGIaemysaKKaeiykaKcacaGLhWUaayjcSdGaeiykaKcabaGagiyBa0MaeiyAaKMaeiOBa42aaSbaaeaacqWGPbqAcqGHiiIZcqWGjbqsaeqaamaaemaabaGaemyqae0aaSbaaeaacqWGPbqAaeqaaaGaay5bSlaawIa7aaaakmaaceaabaqbaeaabmWaaaqaaGGaciab = f7aHbqaaiabbMgaPjabbAgaMjabbccaGiabdgeabjabcIcaOiabdMeajjabcMcaPiabg2da9iabgwGigdqaaaqaaiab = j7aIbqaaiabbMgaPjabbAgaMjabbccaGiabdgeabjabcIcaOiabdMeajjabcMcaPiabgcMi5kabgwGiglabcYcaSaqaaiabdEeahjabcIcaOiabdMeajjabcMcaPiabgYda8maaemaabaGaemyqaeKaeiikaGIaemysaKKaeiykaKcacaGLhWUaayjcSdaabaGae83SdCgabaGaee4Ba8MaeeiDaqNaeeiAaGMaeeyzauMaeeOCaiNaee4DaCNaeeyAaKMaee4CamNaeeyzaugabaaaaaGaay5EaaGaeiOla4caaa @ 8 442 @

Обычно следует выбирать β > γ . MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = xfr = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGafmyrauKbaKaaaaa @ 2CF6 @ ( I ) определяется как верхняя граница перекресток I ⊆ {1… м }. Это условие диктует, что максимально возможная ошибка пересечения> k наборов должна быть меньше, чем максимально возможная ошибка пересечения k наборов. Пусть M будет верхней границей частичной ошибки f ₁ в приведенном выше случае. M может быть макс. _i d (0, | A _i |) / | A _i | макс { α , β , γ }.Таким образом, приведенное выше уравнение может быть сформулирована как

(Mk) wkM≥Σj = к + 1 м (MJ) wjM, i≤k Условия могут быть выполнены (так что равенство выполняется) путем определения веса с обратной стороны, начиная с w _m = 1 до w ₁:

wk = 2m − k − 1 (mk), 1≤k Оценка функция ошибки требует вывода ( Lm 2 ^{м -1}) шагов вычислений при использовании полигоны с L ребрами (пересечение двух полигонов с M и N ребрами можно вычислить за O ( M + N ) с помощью алгоритма О’Рурка [18]).Для задач с ≥ 8 категориями сложность может быть уменьшена из-за ограничений по времени и пространству, наблюдая только множества пересечений I с | I | = K для верхней границы K . Вероятность того, что для сильно пересекающейся группы множеств существует идеальная диаграмма (вплоть до высокого уровня пересечений), тем не менее очень мала. Размер диаграммы Эйлера определяется как количество граней, которые эта диаграмма должна отражать все пересечения, встречающиеся в данных e ( I ) = | { I ⊆ {1… м } | A ( I ) ≠ ∅} |

Текущая реализация позволяет наблюдать частичную ошибку f для каждого набора пересечений A ( I ), I ⊆ {1 … m }. Далее мы предлагаем некоторые расширения предыдущей схемы визуализации:

i) Чтобы обеспечить лучшую адаптацию и сокращение нежелательных областей (отмеченных серым), пространство решений было расширено за счет возможности оптимизации для изменения площадей многоугольников. в определенном диапазоне, так что условия порядка область ( G _{π (1)}) ≤… ≤ площадь ( G _{π ( м )}) были сохранены с перестановкой π такой, что | A _{π (1)} | ≤ … ≤ | A _{π ( м )} |. Множества одинаковой мощности были представлены равными графическими областями. Допускалось только радиальное масштабирование полигонов. К сожалению, эта стратегия не улучшила визуальное представление, даже несмотря на то, что текущая реализация пренебрегала критериями порядка и, следовательно, имела больше свободы для адаптации (найденные решения, конечно, не были более информативными).= Сг с центрами полигонов a ₁.MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGafmyrauKbauaacqGH9aqpcqWGfbqrcqGHRaWkiiGacqWF0oazcuWGfbqrgaqcaaaa @ 330A @

с параметром весовой δ ≥ 0.

Чтобы избежать локальных минимумов, функции затрат Е сведено к минимуму по центрам многоугольников (форма и ориентация многоугольников остаются неизменными) с использованием алгоритма оптимизации роя [19] и эволюционной стратегии с самоадаптирующейся скоростью мутаций [20].

Оптимизация роя частиц

Оптимизация роя частиц (PSO) [19] — это биологически мотивированный метод оптимизации, подобный эволюционным стратегиям [20] и генетическим алгоритмам. Рой состоит из N взаимодействующих частиц, так что каждая частица j = 1 … N представляет решение x ^{( j )} ∈ ℝ ⁿ в n — размерное пространство, имеющее приспособленность f ( x ^{( j )}).Кроме того, каждая частица имеет вектор скорости v ^{( j )} ∈ ℝ ⁿ, который определяет ее текущее движение в пространстве для каждой оси. Вначале, при t = 0, местоположения выбираются равномерно из единичного гиперкуба n [0, 1] ⁿ, до которого масштабируется эта задача ограниченной оптимизации. Скорости выбираются независимо из диапазона [ -v _max , v _макс] для постоянного v _max> 0.Роя эволюционирует с течением времени в дискретных шагов по времени с правилами обновления для местоположений

х + 1 (к) = х (к) + В.Т. (к) MathType @ СПР @ 5 @ 5 @ + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbeGae8hEaG3aa0baaSqaaiabdsha0jabgUcaRiabigdaXaqaaiabcIcaOiabdQgaQjabcMcaPaaakiabg2da9iab = Hha4naaDaaaleaacqWG0baDaeaacqGGOaakcqWGQbGAcqGGPaqkaaGccqGHRaWkcqWF2bGDdaqhaaWcbaGaemiDaqhabaGaeiikaGIaemOAaOMaeiykaKcaaaaa @ 425B @

и скорости

VT + 1 (к) = VT (J) + cglobU [0,1] (х (Glob) -xt (к)) + clocU [0,1] (х (J, LOC) -xt (к)) MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbeGae8NDay3aa0baaSqaaiabdsha0jabgUcaRiabigdaXaqaaiabcIcaOiabdQgaQjabcMcaPaaakiabg2da9 IAB = zha2naaDaaaleaacqWG0baDaeaacqGGOaakcqWGQbGAcqGGPaqkaaGccqGHRaWkcqWGJbWydaWgaaWcbaGaem4zaCMaemiBaWMaem4Ba8MaemOyaigabeaat0uy0HwzTfgDPnwy1egaryqtHrhAL1wy0L2yHvdaiqaakiab + rr8vjabcUfaBjabicdaWiabcYcaSiabigdaXiabc2faDjabcIcaOiab = Hha4naaDaaaleaacqWG0baDaeaacqGGOaakcqWGNbWzcqWGSbaBcqWGVbWBcqWGIbGycqGGPaqkaaGccqGHsislcqWF4baEdaqhaaWcbaGaemiDaqhabaGaeiikaGIaemOAaOMaeiykaKcaaOGaeiykaKIaey4kaSIaem4yam2aaSbaaSqaaiabdYgaSjabd + gaVjabdogaJbqabaGccqGFueFvcqGGBbWwcqaIWaamcqGGSaalcqaIXaqmcqGGDbqxcqGGOaakcqWF4baEdaqhaaWcbaGaemiDaqhabaGaeiikaGIaemOAaOMaeiilaWIaemiBaWMaem4Ba8Maem4yamMaeiykaKcaaOGaeyOeI0Iae8hEaG3aa0baaSqaaiabdsha0bqaaiabcIcaOiabdQgaQjabcMcaPaaakiabcMcaPaaa @ 888D @

с положительными константами ускорения _{с Глоб} и c _loc. (Glob) MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = xfr = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbeGae8hEaG3aa0baaSqaaiabdsha0bqaaiabcIcaOiabdEgaNjabdYgaSjabd + gaVjabdkgaIaaaca @ 360 местное лучшее решение для одной частицы J является х (у, LOC) MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbeGae8hEaG3aa0baaSqaaiabdsha0bqaaiabcIcaOiabdQgaQjabcYcaSiabdYgaSjabd + gaVjabdogaJjabcMcaPaaaaaa @ 36F6 @.Скорости ограничены интервалом [ -v _max , v _макс] для каждой оси. Взаимодействие между частицами регулируется влиянием глобального и локального оптимума на член скорости. UMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae8hfXxfaaa @ 376F @ [0, 1) является равномерной случайной генерацией случайной величиной числа из интервала [0, 1).Одним из вариантов метода является ограничение местоположения ограничивающей рамкой [0,1] ⁿ и изменение знака компонентов скорости соответствующих размеров, так что частицы отскакивают от стены.

Эволюционная оптимизация

Поколение содержит N человека, каждый из которых представляет допустимое решение проблемы. На следующем этапе каждый человек мутируется, и его пригодность оценивается с помощью ранее определенной функции затрат E .Индивидуум воспроизводится с частотами, пропорциональными его рангу приспособленности, таким образом производя потомство до тех пор, пока не будет достигнут исходный размер поколения. Лучший человек всегда без изменений передается новому поколению. Процесс мутации и репликации повторяется до тех пор, пока лучший человек не изменится на протяжении определенного количества шагов.

Лицо состоит из параметра вектора v1t ⋯ vmt∈ℝ2MathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbeGae8NDay3aa0baaSqaaiabigdaXaqaaiabdsha0baakiabl + Uimjab = zha2naaDaaaleaacqWGTbqBaeaacqWG0baDaaGccqGHiiIZtuuDJXwAK1uy0HMmaeHbfv3ySLgzG0uy0HgiuD3BaGabaiab + 1risnaaCaaaleqabaGaeGOmaidaaaaa @ 43A9 @ представляющей полигональные центры и вектор σ т ∈ ℝ + mMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWefv3ySLgznfgDOjdaryqr1ngBPrginfgDObcv39gaiqaacqWFDeIudaqhaaWcbaGaey4kaScabaGaemyBa0gaaaaa @ 38FC @ описывая частоту мутаций для каждого параметра.Первая популяция инициализируется равномерно распределенными случайными значениями, так что каждый параметр остается в определенном диапазоне, т.е. многоугольники должны быть заключены в ограничивающую рамку [0, 1] ², а параметры мутации должны содержаться в интервале [ τ _нижний, τ _верх] с 0 < τ _нижний < τ _верх.

На стадии мутации параметры мутации сами мутировали

сг (т + 1) = σiteN (0, τ) = 1 … mMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaqbaeqabeGaaaqaaGGaciab = n8aZnaaDaaaleaacqWGPbqAaeaacqGGOaakcqWG0baDcqGHRaWkcqaIXaqmcqGGPaqkaaGccqGH9aqpcqWFdpWCdaqhaaWcbaGaemyAaKgabaGaemiDaqhaaOGaemyzau2aaWbaaSqabeaat0uy0HwzTfgDPnwy1egaryqtHrhAL1wy0L2yHvdaiqaacqGFneVtcqGGOaakcqaIWaamcqGGSaalcqWFepaDcqGGPaqkaaaakeaacqWGPbqAcqGH9aqpcqaIXaqmcqGGUaGlcqGGUaGlcqGGUaGlcqWGTbqBaaaaaa @ 53FD @

и ограничена интервалом [ τ _ниже, τ _верх].Постоянный параметр мета-мутации τ > 0 является заранее заданной константой. Затем обновляются положения полигонов

vi (t + 1) = vit + [N (0, σi (t + 1)) N (0, σi (t + 1))] i = 1 … mMathType @ MTEF @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaqbaeqabeGaaaqaaGqabiab = zha2naaDaaaleaacqWGPbqAaeaacqGGOaakcqWG0baDcqGHRaWkcqaIXaqmcqGGPaqkaaGccqGH9aqpcqWF2bGDdaqhaaWcbaGaemyAaKgabaGaemiDaqhaaOGaey4kaSYaamWaaeaafaqabeGabaaabaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae4xdX7KaeiikaGIaeGimaaJaeiilaWccciGae03Wdm3aa0baaSqaaiabdMgaPbqaaiabcIcaOiabdsha0jabgUcaRiabigdaXiabcMcaPaaakiabcMcaPaqaaiab + 1q8ojabcIcaOiabicdaWiabcYcaSiab9n8aZnaaDaaaleaacqWGPbqAaeaacqGGOaakcqWG0baDcqGHRaWkcqaIXaqmcqGGPaqkaaGccqGGPaqkaaaacaGLBbGaayzxaaaabaGaemyAaKMaeyypa0JaeGymaeJaeiOla4IaeiOla4IaeiOla4IaemyBa0gaaaaa @ 68DA @

, где NMathType @ СПР @ 5 @ 5 + = feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasa acPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaWenfgDOvwBHrxAJfwnHbqeg0uy0HwzTfgDPnwy1aaceaGae8xdX7eaaa @ 3761 @ (0, с ) представляет собой обычно распространяется случайная величина со средним значением 0 и дисперсией σ .После каждой мутации все параметры ограничиваются указанными выше условиями.

Эволюционный отбор и создание потомства выполняются путем присвоения каждой особи ранга r = 1 … N в соответствии с ее пригодностью, определенной в соответствии со значением функционала стоимости E или E ‘, так что лучший индивид (тот, у кого самые низкие затраты или самая высокая приспособленность) имеет r = 1. Затем каждый индивид повторяется количество раз, обратно пропорциональное его ранговому значению.Следовательно, особь с рангом r будет иметь не более [ qN / r ] (для фиксированного 0 < q <1) потомков. Начиная с наивысшего ранга r = 1, новая популяция заполняется до тех пор, пока не будет достигнут размер N и не будет завершено новое поколение. Все, кроме первой особи (наиболее приспособленные из последнего поколения), мутируют.

Процесс оптимизации останавливается, когда функционал стоимости лучшего человека не улучшается за определенное количество шагов или количество поколений превышает верхнюю границу.

Реализация VennMaster

Подход к визуализации был реализован как платформенно-независимое приложение Java с открытым исходным кодом, которое доступно в Интернете [9]. Приложение позволяет интерактивное исследование диаграмм Эйлера было протестировано в Windows XP, Linux и Mac OS X с использованием Java Runtime Environment 1.5 [21].

Когда кто-то касается многоугольника курсором, его область выделяется, и отображаются имена задействованных групп и мощность множества пересечений.Среди множества других параметров, включающих стратегию эволюции и функцию ошибок, можно настроить количество ребер многоугольников. Эти настройки можно экспортировать и импортировать в формате XML [22]. Кроме того, в информационном поле отображается список генов выбранного набора (ов) пересечений. Неразрешенные пересечения (для которых не существует соответствующего пересечения многоугольников) перечислены в поле «Несоответствия». К каждому набору или набору пересечений можно прикрепить текстовую метку (см. Рисунок 3).Метки и многоугольники можно перемещать перетаскиванием (функция стоимости будет обновлена немедленно). Таким образом, пользователь может интерактивно изменять конфигурацию и может перезапустить процесс оптимизации в измененной компоновке. Установленные позиции можно заблокировать, чтобы оптимизатор не сдвинул их. Процессом оптимизации можно управлять через диалоговое окно параметров (см. Дополнительную информацию [9]). Пропорциональные диаграммы Эйлера могут быть сохранены в формате JPEG или SVG (масштабируемая векторная графика (SVG) — это графический формат на основе XML [23]).

Интеграция с GoMiner

GoMiner [4] — это инструмент для биологической интерпретации «омических» данных, включая данные микрочипов экспрессии генов. Омические эксперименты часто генерируют списки из десятков или сотен генов, экспрессия которых различается в разных образцах. GoMiner использует онтологию генов для идентификации биологических процессов, функций и клеточных компонентов, представленных в этих списках, и группирует гены в биологически согласованные категории. Возможность импорта файлов из GoMiner была включена в программное обеспечение для анализа функциональных категорий дифференциально экспрессируемых генов.Для файлов GoMiner категории были предварительно отфильтрованы, чтобы количество генов во включенных категориях находилось в определенном определяемом диапазоне и не превышало заданное значение FDR или p -значение. В качестве альтернативы можно использовать простой формат файла с разделителями табуляцией с парой элемент / группа в каждой строке. Текущая версия позволяет экспортировать профиль ошибок, в котором перечислены все частичные ошибки для каждой непустой комбинации наборов I ⊆ {1 … n }, так что G ( I )> 0 или A ( I ) ≠ ∅.Каждая строка содержит значения I , | I | , G ( I ), | A ( I ) | и f ( I ).

VennMaster был недавно интегрирован в программное обеспечение GoMiner (см. Рисунок 6). Эта интеграция обеспечивает удобный интерфейс для пользователя и устраняет накладные расходы на выполнение операций ввода-вывода файлов и управление внешними файлами.

Задачи на пересечение и объединение множеств (Круги Эйлера)

Круги Эйлера – задачи на пересечение или объединение множеств

Решение

Любимые мультфильмы

Решение

«Мир музыки»

Решение

Решение

Пионерский лагерь

Решение

Экстрим

Решение

Любимые мультфильмы

«Мир музыки»

Пионерский лагерь

Экстрим

Круги Эйлера, диаграммы Венна | Онлайн калькулятор

Смотрите также

Решение.

Решение логических задач с помощью кругов эйлера

Логика – это искусство рассуждать, умение делать правильные выводы.

В кругах Эйлера | SKVOT

Рисовать, чтобы думать

Эйлер на кейсах

Логический вывод

Создание диаграммы Венна — Служба поддержки Office

и диаграммы Эйлера, объясненные на примерах

Венн против Эйлера: определение

Диаграммы Венна и

Диаграммы Венна и Эйлера | Давайте поговорим о науке

Диаграммы Венна

Диаграммы Эйлера

Приложения диаграмм Венна и Эйлера

Диаграммы и круги Венна

Характеристика Эйлера

Характеристика Эйлера и диаграммы Венна

Более 4 комплектов

Вклад Венна

Диаграммы Эйлера и Венна: они не только для развлечения

Все о диаграмме Венна

Определение диаграммы Венна

Развитие и история диаграммы Венна

Диаграмма Эйлера

Современная диаграмма Венна

Что НЕ является диаграммой Венна?

Сводка

Развлечения с диаграммами Венна и Эйлера

VennMaster: Пропорциональные диаграммы Эйлера для функционального анализа микрочипов методом GO | BMC Bioinformatics

Функция стоимости

Оптимизация роя частиц

Эволюционная оптимизация

Реализация VennMaster

Интеграция с GoMiner

Добавить комментарий Отменить ответ