|
|
Пример: занимательная математика с моделями МК
Вокруг теоремы Пифагора
Теорема Пифагора – самая известная теорема геометрии, да пожалуй, и всей математики. Она проста и наглядна по своей формулировке:
площадь квадрата, построенного на гипотенузе прямоугольного треугольника, Но она отнюдь не очевидна. Наверное, эти качества и побудили математиков доказывать её вновь и вновь. В результате она попала в «Книгу рекордов Гиннеса», как теорема, получившая наибольшее число доказательств. 1. Доказательство Пифагора
Доказательство теоремы Пифагора, использующее два разрезания квадрата и сравнение частей, которое иллюстрирует эта модель, приписывается самому Пифагору.
С его помощью можно также вывести алгебраическую формулу для квадрата суммы.
2. Доказательство Евклида
Доказательство теоремы Пифагора, данное Евклидом в его «Началах», приводится в следующей модели:
Исследуйте ее и попробуйте восстановить это доказательство.
Конструкция, использованная в этом доказательстве (см. рисунок), в России называется «Пифагоровы штаны», а в других странах – «кресло невесты», «хвост павлина» и т.д. В этой фигуре обнаружился целый ряд интересных свойств, непосредственно не связанных с теоремой Пифагора; приведенная ниже Задача 2 посвящена исследованию этих свойств. 3. Смотри!
Другое старинное доказательство принадлежит великому индийскому математику 12-го века Бхаскаре Ачариа. Это доказательство прославилось тем, что автор пояснил его только одним словом: «Смотри!».
4. Шарнирное доказательство
Пятиугольная фигурка из предыдущего доказательства, составленная из двух квадратов со сторонами, равными катетам данного прямоугольного треугольника, встречается в нескольких разных доказательствах теоремы Пифагора. Так называемое «шарнирное доказательство» замечательно тем, что в нем эта фигура разрезается на наименьшее возможное число частей – три. Затем две из них – треугольники, равные данному, поворачиваются вокруг одной из своих вершин как шарнира в новое положение. В результате получается квадрат, сторона которого равна гипотенузе. Модель показывает, как это происходит, а строгое доказательство предлагаем провести самостоятельно.
5. Пифагорово замощение и разрезания
С помощью той же пятиугольной фигуры из двух квадратов можно замостить плоскость (это замощение показано на рисунке внизу слева; одна пятиугольная «плитка» выделена). Можно считать, что это замощение составлено из копий двух меньших квадратов из теоремы Пифагора. Оно порождает бесконечное множество доказательств, использующих равносоставленность. Для этого нужно наложить на наше замощение наклонную решетку из квадратов со стороной, равной гипотенузе исходного треугольника (треугольника ABC на рисунке слева). Одно из расположений решетки показано на рисунке; здесь каждая вершина наклонного квадрата является общей вершиной двух меньших квадратов. Линии решетки разрезают меньшие квадраты на кусочки, и нетрудно увидеть, что из кусочков,
Теперь будем двигать наклонную решетку по нашему замощению.
ЗАДАЧИ
1.
Теорема Пифагора используется во многих задачах на построение методом вычислений. Две такие задачи представлены в следующих моделях:
2. «Пифагоровы штаны»
Фигура, использованная в евклидовом доказательстве теоремы Пифагора, была объектом изучения геометров на протяжении более, чем 2000 лет. Неудивительно, что у нее обнаружился целый ряд интересных свойств. Например, анализируя евклидово доказательство, можно заметить, что
(д) С помощью модели проверьте, какие из приведенных выше свойств остаются верными для произвольного (не обязательно прямоугольного) треугольника ABC, и докажите их.
|
Пифагор и его теорема. (стр. 3 из 3)
4.6. Доказательство Евклида [1, 20]
В течение двух тысячелетий наиболее распространенным было доказательство теоремы Пифагора, придуманное Евклидом. Оно помещено в его знаменитой книге «Начала».
Евклид опускал высоту BН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.
Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.
Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост, или elefuga- бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.
5. Применение теоремы Пифагора.
5.1. Задачи теоретические современные
1. Периметр ромба 68 см., а одна из его диагоналей равна 30 см. Найдите длину другой диагонали ромба. [4]
2. Гипотенуза КР прямоугольного треугольника КМР равна см., а катет МР равен 4 см. Найдите медиану РС. [4]
3. На сторонах прямоугольного треугольника построены квадраты, причем
S1-S2=112 см2, а S3=400 см2. Найдите периметр треугольника. [4]
Найдите периметр треугольника. [4]
4. Дан треугольник АВС, угол С=900, CD AB, AC=15 см., AD=9 см.
Найдите АВ. [4]
5.2. Задачи практические старинные
5. Для крепления мачты нужно установить
4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты? [19]
6. Задача индийского математика XII века Бхаскары [19]
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
7. Задача из учебника «Арифметика» Леонтия Магницкого [19]
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.
И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.»
8. Задача из китайской «Математики в девяти книгах» [19]
«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?»
Заключение
Теорема Пифагора настолько известна, что трудно представить себе человека, не слышавшего о ней. Мы изучили ряд исторических и математических источников, в том числе информацию в Интернете, и увидели, что теорема Пифагора интересна не только своей историей, но и тем, что она занимает важное место в жизни и науке. Об этом свидетельствуют приведённые нами в данной работе различные трактовки текста этой теоремы и пути её доказательств.
Итак, теорема Пифагора — одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2=a2+b2. Поэтому для её доказательства часто используют наглядность.
Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2=a2+b2. Поэтому для её доказательства часто используют наглядность.
Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.
Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор – замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Он вполне может служить примером для нас, далёких потомков.
Литература и Интернет-ресурсы:
1. Г.И. Глейзер История математики в школе VII – VIII классы, пособие для учителей, — М: Просвещение 1982г.
2. И.Я. Демпан, Н.Я. Виленкин «За страницами учебника математики» Пособие для учащихся 5-6 классов, Москва, Просвещение 1989г.
3. И.Г. Зенкевич «Эстетика урока математики», М.: Просвещение 1981г.
4. Войтикова Н.В. «Теорема Пифагора» курсовая работа, Анжеро-Судженск, 1999г.
5. В. Литцман .Теорема Пифагора, М. 1960.
6. А.В. Волошинов «Пифагор» М. 1993.
7. Л. Ф. Пичурин «За страницами учебника алгебры» М. 1990.
8. А. Н. Земляков «Геометрия в 10 классе» М. 1986.
9. В. В. Афанасьев «Формирование творческой активности студентов в процессе решения математических задач» Ярославль 1996.
10. П. И. Алтынов «Тесты. Геометрия 7 – 9 кл.» М. 1998.
11. Газета «Математика» 17/1996.
12. Газета «Математика» 3/1997.
13. Н. П. Антонов, М. Я. Выгодский, В. В Никитин, А. И. Санкин «Сборник задач по элементарной математики». М. 1963.
14. Г. В. Дорофеев, М. К. Потапов, Н. Х. Розов «Пособие по математике». М. 1973
15. А. И. Щетников “ Пифагорейское учение о числе и величине “. Новосибирск 1997.
А. И. Щетников “ Пифагорейское учение о числе и величине “. Новосибирск 1997.
16. «Действительные числа. Иррациональные выражения» 8 класс. Издательство Томского университета. Томск – 1997.
17. М.С. Атанасян “Геометрия” 7-9 класс. М: Просвещение, 1991
18. www.moypifagor.narod.ru/
19. http://www.zaitseva-irina.ru/html/f1103454849.html
20. http://ru.wikipedia.org/wiki/Теорема_Пифагора
21. http://th-pif.narod.ru/history.htm
Пифагоровы шаровары | Игра в Математику
Все, кто учился в школе и не прогуливал математику, помнят фразу «Пифагоровы штаны на все стороны равны». Для тех, кто не помнит, при чем здесь штаны, напоминаю, что в классической формулировке теоремы Пифагора фигурируют квадраты, построенные на сторонах прямоугольного треугольника. Вот они-то и есть штаны.
Нарисуем всем известную картинку, иллюстрирующую теорему Пифагора. Имеется прямоугольный треугольник с гипотенузой с и катетами a и b. Теорема Пифагора утверждает, что площадь квадрата, построенного на гипотенузе этого треугольника, равняется сумме площадей квадратов, построенных на катетах. Алгебраическая запись теоремы Пифагора — это всем известное выражение с ² = a ² + b ².
Теорема Пифагора утверждает, что площадь квадрата, построенного на гипотенузе этого треугольника, равняется сумме площадей квадратов, построенных на катетах. Алгебраическая запись теоремы Пифагора — это всем известное выражение с ² = a ² + b ².
А теперь зададим себе вопрос: только ли для квадратов верна теорема Пифагора? Или же она будет тоже верна для каких-то других фигур, построенных на катетах прямоугольного треугольника abc?
Полагаете, глупый вопрос? Ничуть. В математике частенько казалось бы глупые вопросы оказываются очень даже неглупыми и важными. Я уже говорил, что в математике самое главное — идеи и картинки, а вовсе даже не формулы и теоремы. Но есть исключения. Формула, выражающая теорему Пифагора, т.е. с ² = a ² + b ², является одним из исключений. Есть, скажем, примерно пять формул, которые знать надо. Все остальные формулы знать не обязательно.
Заменим в теореме Пифагора квадраты на прямоугольники и посмотрим, будет ли она верна для этого случая. Возьмем прямоугольники, состоящие из двух квадратов. То есть с соотношением сторон 2:1. Нарисуем, что у нас получилось.
Возьмем прямоугольники, состоящие из двух квадратов. То есть с соотношением сторон 2:1. Нарисуем, что у нас получилось.
Из рисунка без особых доказательств (естественно, если мы принимаем верность теоремы Пифагора для квадратов) видно, что площадь большого прямоугольника, построенного на гипотенузе, будет равно сумме площадей маленьких прямоугольников, построенных на катетах нашего исходного прямоугольного треугольника.
И вот у нас появляется очень важная идея о том, что теорема Пифагора верна не только для квадратов, построенных на сторонах прямоугольного треугольника, а и для других фигур, которые подобны друг другу.
Ученик: а что означает «подобны»?
Хороший вопрос. Фигуры подобны — это значит, что они имеют абсолютно одинаковую форму, отличаются только размерами. Один из самых главных вопросов математики, который нужно все время себе задавать при решении любых математических вопросов — это «во сколько раз больше?». На последнем нашем рисунке большой прямоугольник в два раза больше, чем соответствующий квадрат, построенный на гипотенузе.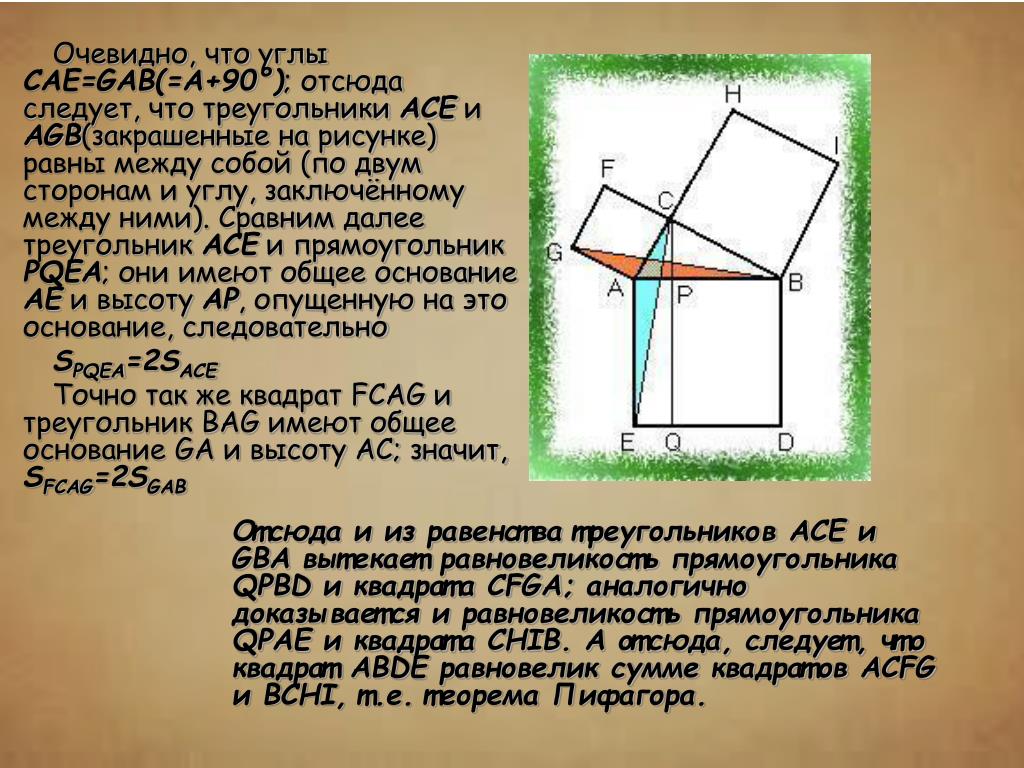 По площади, разумеется. Площадь квадрата с ² , а прямоугольника 2с ². Это же верно и для прямоугольников, построенных на катетах a и b. То есть получается: если мы увеличим фигуры, построенные на сторонах нашего треугольника, в одно и то же число раз, то соотношение площадей сохранится — а значит, площадь фигуры, построенной на гипотенузе прямоугольного треугольника, будет равна сумме площадей фигур, построенных на его катетах.
По площади, разумеется. Площадь квадрата с ² , а прямоугольника 2с ². Это же верно и для прямоугольников, построенных на катетах a и b. То есть получается: если мы увеличим фигуры, построенные на сторонах нашего треугольника, в одно и то же число раз, то соотношение площадей сохранится — а значит, площадь фигуры, построенной на гипотенузе прямоугольного треугольника, будет равна сумме площадей фигур, построенных на его катетах.
Теперь настало время поговорить о математических шароварах. Чем они отличаются от штанов? Скажем так: примерно тем же, чем круг отличается от квадрата. Нарисуем наш прямоугольный треугольник, но заменим квадраты на полукруги. Ну и квадраты для полноты картины там же нарисуем.
Мы уже понимаем, что для подобных прямоугольников теорема Пифагора верна. А для полукругов?
Сначала ответим на вопрос: во сколько раз площадь полукруга отличается от площади квадрата? Давайте это отношение площади полукруга к площади квадрата, на стороне которого построен этот полукруг, обозначим буквой k . Тогда получим формулу: Sкруга = k · Sквадрата , причем для всех трех квадратов число к будет одним и тем же. То есть число, показывающее, какую часть квадрата составляет полукруг, построенный на его стороне, для всех квадратов будет одинаковым.
Тогда получим формулу: Sкруга = k · Sквадрата , причем для всех трех квадратов число к будет одним и тем же. То есть число, показывающее, какую часть квадрата составляет полукруг, построенный на его стороне, для всех квадратов будет одинаковым.
Теперь берем формулу теоремы Пифагора
с ² = a ² + b ²
и обе ее части умножаем на К. У нас получится:
k · c ² = k · a ² + k · b ² или
Sс = Sa + Sb — площадь полукруга, построенного на стороне c, равна сумме площадей полукругов, построенных на сторонах a и b.
А это и означает, что теорема Пифагора для полукругов выполняется. И мы пришли к выводу, что в теореме Пифагора слово «штаны» можно запросто заменить словом «шаровары».
В следующей публикации я расскажу, как, используя эту идею, можно придумать доказательство теоремы Пифагора, которое не требует вообще никаких вычислений. Обычно теорему Пифагора доказывают так: режут квадраты на какие-то кусочки, затем эти кусочки как-то составляются и становится понятно, что сумма большого квадрата равняется сумме двух маленьких. Но это доказательство годится только для квадратов. Если мы воспользуемся идеей, что теорема Пифагора одновременно верна или неверна для любых подобных фигур — то есть таких, которые отличаются только размером, а форма их одинакова — то из этой идеи можно будет получить доказательство теоремы Пифагора в один ход, без вычислений вообще. А напоследок еще раз напоминаю, что в математике самое главное — картинки и идеи, а не теоремы и формулы. Но теорема Пифагора — одно из немногих исключений.
Обычно теорему Пифагора доказывают так: режут квадраты на какие-то кусочки, затем эти кусочки как-то составляются и становится понятно, что сумма большого квадрата равняется сумме двух маленьких. Но это доказательство годится только для квадратов. Если мы воспользуемся идеей, что теорема Пифагора одновременно верна или неверна для любых подобных фигур — то есть таких, которые отличаются только размером, а форма их одинакова — то из этой идеи можно будет получить доказательство теоремы Пифагора в один ход, без вычислений вообще. А напоследок еще раз напоминаю, что в математике самое главное — картинки и идеи, а не теоремы и формулы. Но теорема Пифагора — одно из немногих исключений.
Сокровище геометрии
Наталья Карпушина
«Наука и жизнь» №9, 2016
Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.
Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.
Пифагоровы штаны
Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a < b < c, усмотреть соотношение a2 + b2 = c2 невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.
Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.
Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением*. При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.
При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.
4000 лет спустя
История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a2 + b2 = c2 для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a2 + a2 = c2. Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.
Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!
Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV–III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.
Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.
Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его… самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!
Первый математик
Пифагора Самосского (570–495 годы до н.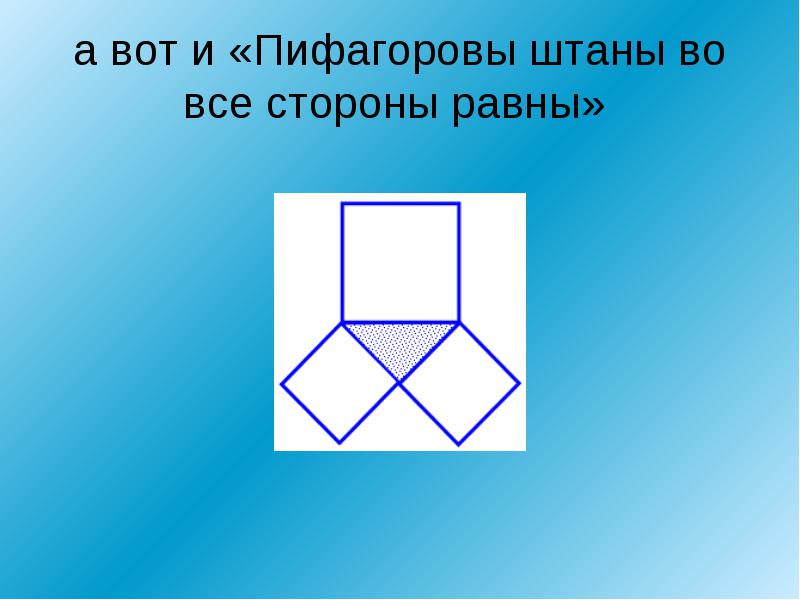 э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.
э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.
Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции.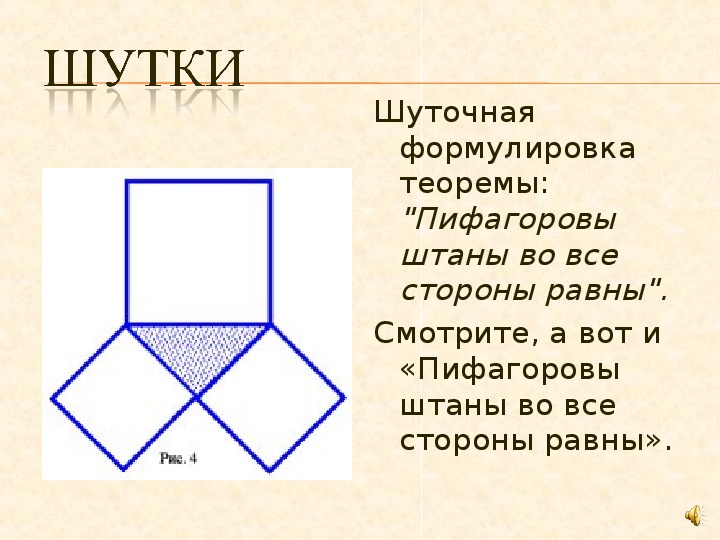 С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.
С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.
Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.
Такое простое доказательство
Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a2 = c · m и b2 = c · n.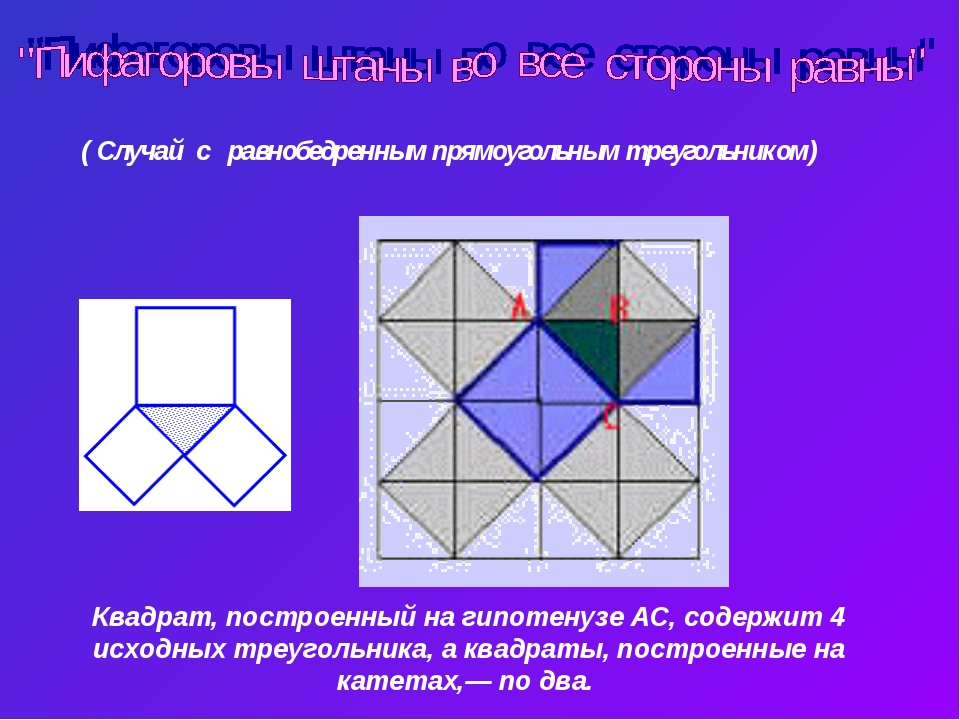 Тогда a2 + b2 = c · (m + n) = c2 (рис. 4).
Тогда a2 + b2 = c · (m + n) = c2 (рис. 4).
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять… Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.
Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.
Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.
* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.
история вопроса, доказательства, примеры практического применения. Из истории вопроса
Все животные равны, но некоторые более равны, чем другие
И наконец, хотелось бы вспомнить людей, которые думают, будто Косово может стать каким-то там прецедентом. Мол, если населению Косова «мировое сообщество» (т.е. США и ЕС) предоставит право самому решить свою судьбу на
автора
Литературная Газета
Почти равны
Клуб 12 стульев Почти равны ИРОНИЧЕСКАЯ ПРОЗА
Смерть зашла к одному бедняку. А тот глуховатый был. Так нормальный, но чуть-чуть глуховатый… И видел плохо. Почти ничего не видел. – Ой, к нам гости! Проходите, пожалуйста. Смерть говорит: – Погоди радоваться,
Описание презентации по отдельным слайдам:
1
слайд
Описание слайда:
МБОУ Бондарская СОШ Ученический проект на тему: «Пифагор и его теорема» Подготовил: Эктов Константин, ученик 7 А класса Руководитель: Долотова Надежда Ивановна, учитель математики 2015 г.
2
слайд
Описание слайда:
3
слайд
Описание слайда:
Аннотация. Геометрия – очень интересная наука. Она содержит множество не похожих друг на друга теорем, но порой так необходимых. Я очень заинтересовался теоремой Пифагора. К сожалению, одно из самых главных утверждений мы проходим лишь в восьмом классе. Я решил приоткрыть завесу тайны и исследовать теорему Пифагора.
4
слайд
Описание слайда:
5
слайд
Описание слайда:
6
слайд
Описание слайда:
Задачи Изучить биографию Пифагора. Исследовать историю возникновения и доказательства теоремы. Выяснить, как теорема используется в искусстве. Найти исторические задачи, в решении которых применяется теорема Пифагора. Познакомиться с отношением детей разных времен к данной теореме. Создать проект.
7
слайд
Описание слайда:
Ход исследования Биография Пифагора. Заповеди и афоризмы Пифагора. Теорема Пифагора. История теоремы. Почему «пифагоровы штаны во все стороны равны»? Различные доказательства теоремы Пифагора другими учеными. Применение теоремы Пифагора. Опрос. Вывод.
8
слайд
Описание слайда:
Пифагор – кто же он такой? Пифагор Самосский (580 — 500 до н. э.) древнегреческий математик и философ-идеалист. Родился на острове Самос. Получил хорошее образование. По преданию Пифагор, чтобы ознакомиться с мудростью восточных ученых, выехал в Египет и прожил там 22 года. Хорошо овладев всеми науками египтян, в том числе и математикой, он переехал в Вавилон, где прожил 12 лет и ознакомился с научными знаниями вавилонских жрецов. Предания приписывают Пифагору посещение и Индии. Это очень вероятно, так как Иония и Индия тогда имели торговые связи. Возвратившись на родину (ок. 530 г. до н. э.), Пифагор попытался организовать свою философскую школу. Однако по неизвестным причинам он вскоре оставляет Самос и селится в Кротоне (греческой колонии на севере Италии). Здесь Пифагору удалось организовать свою школу, которая действовала почти тридцать лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статус пифагорейского союза был очень суровым. По своим философским взглядам Пифагор был идеалистом, защитником интересов рабовладельческой аристократии. Возможно, в этом и заключалась причина его отъезда из Самоса, так как в Ионии очень большое влияние имели сторонники демократических взглядов. В общественных вопросах под «порядком» пифагорейцы понимали господство аристократов. Древнегреческую демократию они осуждали. Пифагорейская философия была примитивной попыткой обосновать господство рабовладельческой аристократии. В конце V в. до н. э. в Греции и ее колониях прокатилась волна демократического движения. Победила демократия в Кротоне. Пифагор вместе с учениками оставляет Кротон и уезжает в Тарент, а затем в Метапонт. Прибытие пифагорейцев в Метапонт совпало со вспышкой там народного восстания. В одной из ночных стычек погиб почти девяностолетний Пифагор. Его школа прекратила свое существование. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Добывая себе средства к существованию, они организовывали школы, в которых преподавали главным образом арифметику и геометрию. Сведения об их достижениях содержатся в сочинениях позднейших учёных — Платона, Аристотеля и др.
9
слайд
Описание слайда:
Заповеди и афоризмы Пифагора Мысль — превыше всего между людьми на земле. Не садись на хлебную меру (т. е. не живи праздно). Уходя, не оглядывайся (т. е. перед смертью не цепляйся за жизнь). По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих). Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык). Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду). На поле жизни, подобно сеятелю, ходи ровным и постоянным шагом. Истинное отечество там, где есть благие нравы. Не будь членом учёного общества: самые мудрые, составляя общество, делаются простолюдинами. Почитай священными числа, вес и меру, как чад изящного равенства. Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова. Ничему не удивляйся: удивление произвело богов.
10
слайд
Описание слайда:
Формулировка теоремы. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
11
слайд
Описание слайда:
Доказательства теоремы. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Разумеется, все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства.
12
слайд
Описание слайда:
Теорема Пифагора Доказательство Дан прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что c² = a² + b² Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (a + b)². С другой стороны, квадрат составлен из четырех равных прямоугольных треугольников, S каждого из которых равна ½ a b, и квадрата со стороной c. S = 4 · ½ a b + c² = 2 a b + c² Таким образом, (a + b)² = 2 a b + c², откуда c² = a² + b² c c c c с а b
13
слайд
Описание слайда:
История теоремы Пифагора Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, а по другим свидетельствам – даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста, но наиболее популярна теорема с построением квадрата с помощью данного прямоугольного треугольника.
14
слайд
Описание слайда:
Теорема в Древнем Китае «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».
15
слайд
Описание слайда:
Теорема в Древнем Египте Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета(согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
16
слайд
Описание слайда:
О теореме в Вавилонии «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку.»
17
слайд
Описание слайда:
Почему «пифагоровы штаны во все стороны равны»? В течение двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было придуманное Евклидом. Оно помещено в его знаменитой книге «Начала». Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах. Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.
18
слайд
Описание слайда:
Отношение детей древности к Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи, вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.
19
слайд
Описание слайда:
Доказательства теоремы Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
20
слайд
Описание слайда:
« Стул невесты » На рисунке квадраты, построенные на катетах, размещены ступенями один рядом с другим. Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли «стулом невесты».
21
слайд
Описание слайда:
Применение теоремы Пифагора В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.
22
слайд
Описание слайда:
Применение теоремы в строительстве В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
23
слайд
Описание слайда:
24
слайд
Описание слайда:
Исторические задачи Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?
В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.
Краткий обзор биографии
Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.
Пифагор — философ, математик, мыслитель родом из Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.
Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.
Рождение теоремы
В юности Пифагор переехал с в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.
Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.
Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.
Теорема Пифагора
Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90 о, сумма квадратов катетов равна квадрату гипотенузы».
Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.
Способ первый
Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.
Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.
Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.
Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.
На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в) 2 . Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.
Поэтому площадь равна: 4*0,5ав+с 2 =2ав+с 2
Отсюда (а+в) 2 =2ав+с 2
И, следовательно, с 2 =а 2 +в 2
Теорема доказана.
Способ два: подобные треугольники
Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника — среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 о.
Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:
АС=√АВ*АД, СВ=√АВ*ДВ.
Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.
АС 2 =АВ*АД и СВ 2 =АВ*ДВ
Теперь нужно сложить получившиеся неравенства.
АС 2 + СВ 2 =АВ*(АД*ДВ), где АД+ДВ=АВ
Получается, что:
АС 2 + СВ 2 =АВ*АВ
И, следовательно:
АС 2 + СВ 2 =АВ 2
Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.
Еще одна методика расчетов
Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.
В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.
Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:
S авс * с 2 — S авд *в 2 =S авд *а 2 — S всд *а 2
S авс *(с 2 -в 2)=а 2 *(S авд -S всд)
с 2 -в 2 =а 2
с 2 =а 2 +в 2
Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.
Самый простой способ доказать теорему Пифагора. Отзывы
Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а 2 +в 2 =с 2 , будет видно наглядно.
Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС — равнобедренный.
Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.
К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую — из С.
Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.
Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».
Доказательство Дж. Гарфилда
Джеймс Гарфилд — двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.
В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.
Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.
Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=а+в/2 * (а+в)
Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:
S=ав/2 *2 + с 2 /2
Теперь необходимо уравнять два исходных выражения
2ав/2 + с/2=(а+в) 2 /2
с 2 =а 2 +в 2
О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?
Практическое применение теоремы Пифагора
К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.
На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.
Связь теоремы и астрономии
Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия — это научная сфера, в которой широко используется теорема Пифагора.
Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l
.
А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем
t
. И скорость луча —
c
.
Получается, что: c*t=l
Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.
Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t»).
А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:
Если представить, что точки света С и В, а также космический лайнер — это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.
Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.
Радиус передачи мобильного сигнала
Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!
Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.
Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.
АВ (высота вышки) = х;
ВС (радиус передачи сигнала) = 200 км;
ОС (радиус земного шара) = 6380 км;
ОВ=ОА+АВОВ=r+х
Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.
Теорема Пифагора в быту
Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.
Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.
Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.
При идеальных габаритах шкафа проверим действие теоремы Пифагора:
АС=√АВ 2 +√ВС 2
АС=√2474 2 +800 2 =2600 мм — все сходится.
Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:
АС=√2505 2 +√800 2 =2629 мм.
Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.
Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.
Теорема Пифагора
Тип урока: урок изучения нового
материала с использованием исследовательской
деятельности.
Цели урока:
- подвести учащихся к выводу теоремы Пифагора
путём исследовательских работ и логических
рассуждений; - способствовать развитию гибкости мышления,
умений анализировать, устанавливать связи ранее
изученного материала с новыми и осуществлять
доказательные рассуждения; - создать условия для расширения общего
кругозора учащихся, используя исторический и
литературный материал.
Оборудование:
- портрет Пифагора;
- раздаточный материал;
- ррезентации «О жизни Пифагора Самосского»,
«Историческая справка о теореме Пифагора»; - компьютер, мультимедийный проектор, видеоролик.
План урока:
Организационный момент
Слайды 1, 2, 3. Мотивация. Почему так утверждают:
«Пифагоровы штаны во все стороны равны» Гипотезы
учащихся. Тема сегодняшнего урока «Теорема
Пифагора». Скажите, глядя, на эту тему, что-нибудь
знакомо вам? Что бы вы хотели узнать по этой теме?
Слайд 4 Выяснить: Кто же такой Пифагор? В чем
заключается теорема Пифагора? Доказать теорему.
Найти ей практическое применение. Это и будет
планом нашего урока.
Слайды 5-8. Актуализация знаний. Повторение
пройденного материала: формул площади
многоугольника, треугольника, квадрата,
трапеции.
Слайд 9. Проблемная ситуация. Предлагается решить
задачу по чертежу. Путём рассуждений учащиеся
приходят к выводу что, тех знаний о прямоугольном
треугольнике, которые имеем, не хватает. Задачу
решить не можем
Слайд 10. Учащиеся самостоятельно выполняет
практическую работу и выводят формулу теоремы
Пифагора
Слайды 11, 12. Первая формулировка теоремы
Слайд 13. Сообщение ученика. Презентация «О жизни
Пифагора»
Слайд 14, 15. Знакомство с пифагоровыми тройками
целых чисел и их использование.
Слайд 16. О теореме Пифагора (работа с Интернетом) 5
мин.
Почему учащиеся средних веков считали очень
трудным и называли его Donsasinorum– ослиный мост, или
elefuga – бегство «убогих?
Слайд 17. Из-за чертежа теорему Пифагора учащиеся
называли «ветряной мельницей»и писали стишки:
«Пифагоровы штаны во все стороны равны».
Слайд 18. Доказательства теоремы. Знакомство с
различными способами доказательств теоремы
Пифагора.
Слайд 19. Устная исследовательская работа №2
«Доказательство теоремы Пифагора путем
построения квадратов на сторонах треугольника.»
Слайды 20, 21. Исследовательская работа №3 «Вывод
формулы теоремы Пифагора с помощью
геометрических фигур»
Слайд 22. Доказательство теоремы Пифагора (один из
учеников работает у доски, другие в тетрадях).
Слайды 23-28. Закрепление. Решение задач.
Слайд 9. Вернёмся теперь к задаче, которую мы не
смогли решить в начале урока.
Слайд 29. Решение задачи древних индусов.
Видеоролик. Найти ошибку.
Слайд 30. Подведение итогов. Почему так утверждали
«Пифагоровы штаны во все стороны равны»
Слайд 31. Стихотворение о теореме Пифагора.
Слайд 32. Домашнее задание.
Слайд 33. Рефлексия. Обсуждение в группе вопросов.
Оценивание.
ХОД УРОКА
1. Организационный момент
2. Мотивация
– Почему так утверждают: «Пифагоровы штаны во
все стороны равны» (Гипотезы
учащихся). Тема сегодняшнего урока «Теорема
Пифагора».
Теорема Пифагора – одна из важнейших
теорем геометрии. Она является основой решения
множества геометрических задач, помогает решать
задачи из разных областей науки, техники и
практической жизни. О ней писали в своих
произведениях римский архитектор и инженер
Витрувий, греческий писатель-моралист Плутарх,
математик 5 века Прокл и другие. Легенда о том, что
в честь своего открытия Пифагор принес в жертву
быка или, как рассказывали другие, сто быков,
послужила поводом для рассказов писателей и
стихов поэтов.
– Скажите, глядя, на эту тему, что-нибудь знакомо
вам? Что бы вы хотели узнать по этой теме?
Слайд №4 Выяснить:
1) Кто же такой Пифагор?
2) В чем заключается теорема Пифагора.
3) Доказать теорему.
4) Найти ей практическое применение.
– Это и будет планом нашего урока.
3. Актуализация знаний
1. Какой треугольник изображён? (Определите его
вид)
2. Назовите катеты и гипотенузу данного
треугольника.
3. Как найти площадь ΔАВС?
4. Продолжите предложение:
– Сумма острых углов прямоугольного
треугольника …
– Катет, лежащий против угла 30 равен …
– Равные многоугольники имеют равные …
– Если многоугольник составлен из нескольких
многоугольников, то его площадь равна …
5. Как найти площадь ΔАВС?
6. На какие два многоугольника разбит данный
многоугольник ABCDE?
7. Каким свойством площадей необходимо
воспользоваться, чтобы найти площадь
многоугольника ABCDE?
8. С помощью каких формул можно найти
площадь квадрата ABCF и площадь треугольника DFE?
4. Проблемная ситуация
– А теперь давайте решим небольшую задачу.
Расскажите, что известно в задаче, что найти и
как? Но тех знаний о прямоугольном треугольнике,
которые мы имеем, не хватает. Задачу решить не
можем. Нужно выяснить, как связаны между собой
стороны прямоугольного треугольника.
5. Практическая работа №1
1. Постройте в тетрадях прямоугольный
треугольник (с катетами, длина которых для
удобства выражается целыми числами) 3 см. и 4 см.
2. Измерьте катеты и гипотенузу. Результаты
измерений запишите в тетрадях.
3. Возведите все результаты в квадрат, т. е.
узнайте величины a2; b2; c2
4. Сложите квадраты катетов (a2 + b2) и
сравните с квадратом гипотенузы с2
5. У всех ли получилось, что a2 + b2 = с2?
Эту закономерность и отражает теорема
Пифагора, которой посвящён наш урок.
По-современному эта теорема звучит так: «В
прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов».
6. Сообщение ученика. Презентация «О жизни
Пифагора»
– Теперь послушаем рассказ о математике,
именем которого она названа.
Тройки целых чисел, для которых
выполняется соотношение, связывающее стороны
прямоугольного треугольника – пифагоровы
тройки. Прямоугольные треугольники с
целочисленными сторонами называют египетскими
Слайд №15. Древние египтяне для построения
прямых углов на местности пользовались веревкой
с завязанными на ней на одинаковых расстояниях
узелками. По одной стороне они откладывали 3
отрезка, на другой 4, а на третьей 5. Этим
отношением пользовались для определения прямых
углов при построении зданий.
7. О теореме Пифагора (работа с
Интернетом)
Задание: Почему учащиеся средних
веков считали очень трудным и называли его –
ослиный мост илибегство «убогих?
Доказательство теоремы Пифагора учащиеся
средних веков считали очень трудным и называли
его Donsasinorum– ослиный мост, или elefuga – бегство
«убогих», так как некоторые «убогие» ученики, не
имевшие серьезной математической подготовки,
бежали от геометрии. Слабые ученики, заучившие
наизусть, без понимания и прозванные поэтому
«ослами», были не в состоянии преодолеть теорему
Пифагора, служившую для них вроде непреодолимого
моста.
Слайд №17. Из-за чертежа теорему
Пифагора учащиеся называли «ветряной
мельницей»и писали стишки: «Пифагоровы штаны во
все стороны равны».
Хотя эта теорема и связывается с именем Пифагора,
она была известна задолго до него. В вавилонских
текстах она встречается за 1200 лет до Пифагора.
По-видимому, он первым нашёл её доказательство.
Сохранилось древнее предание, что в честь своего
открытия Пифагор принёс в жертву богам быка, по
другим свидетельствам – даже сто быков. Но это
противоречит сведениям о моральных и
религиозных воззрениях Пифагора. Говорят, что он
“запрещал даже убивать животных, а тем более ими
кормиться, ибо животные имеют душу, как и мы”. В
связи с этим более правдоподобной можно считать
следующую запись: “… когда он открыл, что в
прямоугольном треугольнике гипотенуза имеет
соответствие с катетами, он принес в жертву быка,
сделанного из пшеничного теста”.
Доказательства теоремы
Американский автор Э. Лумис в книге «Пифагорово
предложение», вышедшей в 1940 г., собрал 370 разных
доказательств! Существует около 500 различных
доказательств этой теоремы (геометрических,
алгебраических, механических и т.д.).
– Рассмотрим различные способы доказательства
теоремы Пифагора.
8. Устная исследовательская работа №2 «Доказательство
теоремы Пифагора путем построения квадратов на
сторонах треугольника».
Задания:
1. Определить вид выделенного треугольника.
2. Вставить пропущенные слова в предложении.
Квадраты, построенные на катетах, состоят из …….
одинаковых треугольников, а квадрат, построенный
на гипотенузе состоит из …….таких
треугольников.
3. Сформулируйте теорему Пифагора
9. Исследовательская работа №3 «Вывод
формулы теоремы Пифагора с помощью
геометрических фигур»
Если заштриховать … треугольника на одном
рисунке, то останется … площадью …, а если
заштриховать такие же … треугольника на втором
рисунке, то останутся … площадью … и …
Доказательство теоремы Пифагора (один
из учеников работает у доски, другие в тетрадях).
10. Закрепление
Решение задач. Теорема Пифагора – одна из
главных теорем геометрии, потому что с её помощью
можно доказать много других теорем и решить
множество задач.
Слайд № 9. Вернёмся теперь к задаче,
которую мы не смогли решить в начале урока. На
основе этой задачи составим алгоритм решения
задач по теореме Пифагора
Слайд № 29. Решим задачу древних индусов.
Решения других задач рассмотрим на следующем
уроке.\
11. Видеоролик. Найти ошибку.
12. Подведение итогов
– Почему так утверждали «Пифагоровы штаны во
все стороны равны»
– Всё ли мы рассмотрели, что хотели?
– Кто же запомнил формулировку теоремы Пифагора?
– Пригодятся вам эти знания?
– Чтобы лучше вам запомнить теорему послушайте
стих.
– Молодцы, ребята. Вы сегодня славно потрудились.
Как вы думаете, Пифагор принял бы нас в свою
школу? (Учащимся предлагается высказать своё
мнение о проделанной работе, оценить свою роль в
выполнении заданий, сделать вывод о том, что
вызвало наибольшее затруднение)
13. Домашнее задание.
14. Рефлексия
– Обсудите в группе, ответьте на
следующие вопросы:
- Что ты узнал сегодня нового?
- Сформулируй теорему Пифагора.
- Что тебе понравилось?
- Как ты оценил бы свою работу на уроке?
- Что получилось или не получилось? Почему?
- Оцените свои знания. Заполните оценочный лист
Пифагор. Пифагорейская школа — презентация онлайн
1. пифагор
ПИФАГОР
Работу выполнила:
ученица 8 «А»класса
МБОУ «ООШ № 14»
Яушева Ксения
2. Пифагор
ПИФАГОР
Пифагор родился на острове
Самос, расположенном в
Эгейском море. Четыре года
подряд был олимпийским
чемпионом. По совету Фалеса 22
года Пифагор набирался
мудрости в Египте. Во время
завоевательных походов попал в
плен, был продан в рабство и 10
лет жил в Вавилоне.
Вернувшись на Родину, Пифагор
организовал Пифагорейский
орден – школу философов и
математиков. Во время
народного восстания в 500 г. до
нашей эры был убит в уличной
схватке.
3. Пифагорейская школа
ПИФАГОРЕЙСКАЯ ШКОЛА
Пифагор
и его последователипифагорейцы- образовали
тайный союз, игравший
немалую роль в жизни
греческих колоний в Италии.
Пифагорейцы узнавали друг
друга по звёздчатому
пятиугольнику — пентаграмме.
4. Пентаграмма
ПЕНТАГРАММА
Пентаграмма – это звёздчатый пятиугольник.
Пятиконечная звезда считалась в школе
Пифагора символом дружбы, была чем-то вроде
талисмана, которым одаривали друзей…
Она была тайным знаком Пифагорейцев, по
которому Пифагорейцы узнавали друг друга
Красота пентаграммы связана с необычайным
пропорциональным строением, здесь есть среднее
геометрическое, среднее арифметическое и
среднее гармоническое…
Пентаграмма –символ дружбы, гармонии,
красоты.
5. Крушение союза….
КРУШЕНИЕ СОЮЗА….
Шло время, пифагорейский союз пришёл к
политической власти в Кротоне. Появились
противники, зависть, обман, недовольство. Был
в Кротоне человек по имени Килон, который
обидевшись на Пифагора за то, что он не взял
его в свою школу, поджёг дом, в котором было
собрание. Многие сгорели в огне.
Пифагорейцы терпели одно поражение за
другим. Сам Пифагор бежал и погиб в одной из
ночных схваток…По другим источникам, ему
удалось спастись, но он не выдержал и лишил
себя жизни…
6. Пифагоровы нравоучения:
ПИФАГОРОВЫ НРАВОУЧЕНИЯ:
Пифагор учил, что начинать день нужно со стихов:
«Прежде, чем встать от сладостных снов, навеваемых
ночью, душой раскинь: Какие дела тебе день
приготовил?»
А заканчивать день надлежало стихами:
«Не допускай ленивого сна на усталые очи, прежде чем
на три вопроса о деле дневном не ответишь: Что я
сделал? Что не сделал? И что мне осталось сделать?».
Не делай никогда того, чего не знаешь, но научись всему
тому, что хочешь знать.
Не делай ничего постыдного ни в присутствии других,
ни втайне.
Либо молчи, либо говори то, что ценнее молчания.
Прежде, чем станешь говорить, дай мысли созреть под
твоим языком.
Будь с тем, кто ношу взваливает, а не с тем, кто ношу
сваливает.
7. Теорема Пифагора
ТЕОРЕМА ПИФАГОРА
В прямоугольном
треугольнике
квадрат гипотенузы
равен сумме
квадратов катетов…
=
8. История открытия теоремы
ИСТОРИЯ ОТКРЫТИЯ ТЕОРЕМЫ
Пифагора приписывают древнегреческому
философу и математику Пифагору (VI в. до
н.э.). Но изучение вавилонских клинописных
таблиц и древнекитайских рукописей
показало, что это утверждение было известно
задолго до Пифагора, возможно, за
тысячелетия до него. Заслуга же Пифагора
состояла в том, что он открыл доказательство
этой теоремы.
9. Доказательство теоремы
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Доказательство теоремы Пифагора учащиеся
средних веков считали очень трудным и называли
его Dons asinorum – ослиный мост, или elefuga бегство «убогих», так как некоторые «убогие»
ученики, не имевшие серьёзный математической
подготовки, бежали от геометрии. Слабые ученики,
заучившие теоремы наизусть, без понимания и
прозванные поэтому «ослами», были не в состоянии
преодолеть теорему Пифагора, служившую для них
вроде непреодолимого моста. Из- за чертежей,
сопровождающих теорему Пифагора, учащиеся
называли её также «ветряной мельницей»,
составляли стихотворения вроде «Пифагоровы
штаны на все стороны равны», рисовали
карикатуры.
10. «Пифагоровы штаны во все стороны равны»
«ПИФАГОРОВЫ ШТАНЫ ВО ВСЕ
СТОРОНЫ РАВНЫ»
Сначала теорема была
доказана для равнобедренных
прямоугольных треугольников.
Квадрат, построенный на
гипотенузе, содержит 4
треугольника, а на каждом
катете квадрат содержит по 2
прямоугольных треугольника.
Поэтому, площадь квадрата,
построенного на гипотенузе
равна сумме площадей
квадратов, построенных на
катетах. Именно так звучала
теорема в древности… Отсюда
пошло : «Пифагоровы штаны
во все стороны равны».
11. Доказательство теоремы
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Вероятно, факт, изложенный в теореме Пифагора,
была сначала установлен для равнобедренных
прямоугольников. Достаточно взглянуть на
мозаику из чёрных и светлых треугольников, чтобы
убедиться в справедливости теоремы для
треугольника АВС: квадрат, построенный на
гипотенузе, содержит четыре треугольника, а на
каждом катете построен квадрат, содержащий два
треугольника.
12. Доказательство теоремы
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
На рисунке изображено два
равных квадрата. Длина сторон
каждого квадрата равна a + b.
Каждый из квадратов разбит на
части, состоящие из квадратов и
прямоугольных треугольников.
Ясно, что если от площади
квадрата отнять учетверенную
площадь прямоугольного
треугольника с катетами a, b, то
останутся равные площади, т. e.
=
«Будь справедлив и в словах,
и в поступках своих…»
Пифагор
(ок. 570- 500 гг. до н. э.).
Штаны Pythagora proof. Геометрия сокровищ. Практическое применение теоремы
.
Штаны Пифагора Шуточное название теоремы Пифагора, возникшей из-за того, что квадраты, построенные по сторонам прямоугольника и расходящиеся в разные стороны, напоминают штаны. Любил геометрию … и на вступительном экзамене получил в университете даже от Чумакова, профессора математики, похвалу за то, что без доски, рука за руку по воздуху объяснил свойства параллельных линий и штанов пифагора ( Н.Пирогова. Дневник старого врача).
Фразеологический словарь русского литературного языка. — М .: Астрель, Аст. А. И. Федоров. 2008.
Посмотрите, что такое «Штаны Пифагора» в других словарях:
Штаны — получите рабочий купон Academician на скидку SuperStep или выгодные штаны для покупки с бесплатной доставкой для продажи в Superstep
Штаны Pythagora — … Википедия
Штаны Пифагор — Жарг.шк. Желе теорема Пифагора, устанавливающая соотношение между квадратами, построенными на гипотенусах, и категориями прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
штаны пифагора — шутливое название теоремы Пифагора, устанавливающей связь между квадратами, построенными на гипотенусах, и формой прямоугольного треугольника, который внешне на рисунках выглядит как аисты … Словарь многих выражений
штаны из пифагора (изобрет.) — Иност.: about man Г. Даровит Это убожество. В древности он наверняка изобрел бы штаны Пифагорову … Салтыков. Письма о пестах. Штаны Пифагора (геом.): В прямоугольнике квадрат гипотенузы равен квадрату катетов (учим … … Большой толсто-фразологический словарь Михельсона
Штаны Pythagora со всех сторон равны — Количество пуговиц известно. Зачем мне пристально? (Грубо) о штанах и мужских половых органах. Штаны Пифагора со всех сторон равны.Чтобы доказать это, нужно снять и показать 1) теорему Пифагора; 2) про широкие штаны … живая речь. Словарь устных выражений
Штаны Пифагора дурака — ПиньяГоровы Штаны (изобретать) несправедливость. О человеческом петухе. Ср. Несомненно, это мудрец. В старину он бы изобрел штаны Пинягорова … Салтыков. Ходячие буквы. ПиньяГоровы штаны (геом.): В прямоугольнике квадрат гипотенузы … … Большой интеллектуально-фразеологический словарь Михельсона (орфография)
Штаны Пифагора во всех направлениях равны — шутливое доказательство теоремы Пифагора; Также в анекдоте про мешковатые штаны друга… Словарь народной фразеологии
Сел, грубо …
Штаны Пифагора по всем направлениям равны (количество пуговиц известно. Почему тесно? / Чтобы доказать это нужно снять и показать) — доволен, грубоват … Словарь современных разговорных фраз и прогресса
брюки — СУМ., МН., УПОТР. по сравнению. Часто морфология: мн. какие? Штаны, (нет) что? Штаны, что? Штаны, (см.) Что? Штаны чем? Штаны, что? О штанах 1. Штаны — это предмет одежды, который состоит из двух коротких или длинных штанов и закрывает нижнюю часть…… Толковый словарь Дмитриева
Книги
- Штаны Pythagora,.В этой книге вы найдете фантастику и приключения, чудеса и фантастику. Забавно и грустно, обыденно и загадочно … А что еще нужно для занимательного чтения? Главное быть …
Теорема Пифагора известна со школьной поры. Выдающийся математик доказал прекрасную гипотезу, которой сейчас пользуются многие. Звучит правило: квадрат длины гипотенуса прямоугольного треугольника равен сумме квадратов катетов. В течение многих десятилетий ни одному математику не удавалось повторить это правило.Ведь Пифагор долго шел к своей цели, чтобы рисунки имели место в повседневной жизни.
- Небольшой стих к этой теореме, который был изобретен вскоре после доказательства, напрямую доказывает свойства гипотезы: «Штаны Пифагора во всех направлениях равны». Этот двойник отложился в памяти многих людей — и по сей день стихотворение вспоминает при подсчете.
- Эта теорема получила название «Штаны Пифагора» из-за того, что при рисовании посередине получился прямоугольный треугольник, по сторонам которого располагались квадраты.По внешнему виду этот рисунок напоминал брюки — отсюда и название гипотезы.
- Пифагор гордится разработанной теоремой, потому что эта гипотеза отличается от нее как максимальное число доказательств. Важно: уравнение было занесено в Книгу рекордов Гиннеса благодаря 370 правдивым свидетельствам.
- Гипотезу доказало огромное количество математиков и профессоров из разных стран во многом . Английский математик Джонс вскоре объявил, что гипотеза доказана с помощью дифференциального уравнения.
- В настоящее время никому неизвестно доказательство теоремы Пифагора . Факты о доказательствах математики сегодня никому не известны. Считается, что доказательство рисунков Евклида также является доказательством Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы.
- Современные ученые обнаружили, что Великий математик был не первым, кто открыл эту гипотезу .Уравнение было известно задолго до открытия Пифагором. Этому математику удалось только воссоединить гипотезу.
- Пифагор не давал уравнению названия «Теорема Пифагора» . Это название было исправлено после «громких двойных ударов». Математик только хотел, чтобы его усилия и открытия признали весь мир, и использовал их.
- Мориц Кантор — величайший математик, найденный и увиденный на древних папирусных записях с рисунками . Вскоре после этого Кантор понял, что эта теорема была известна египтянам еще за 2300 лет до нашей эры.Только тогда этим никто не воспользовался и не пытался доказать.
- Современные ученые считают, что гипотеза была известна еще в 8 веке до нашей эры г. Индийские ученые того времени открыли примерный расчет гипотенуса треугольника, наделенного прямыми углами. Правда в то время никто не мог точно доказать уравнение для приближенных расчетов.
- Великая математика Бартель Ван дер Варден После доказательства гипотезы сделал важный вывод: «Достоинством греческой математики считается не открытие направления и геометрии, а лишь ее обоснование.В руках Пифагора были вычислительные формулы, основанные на предположениях, неточных вычислениях и неопределенных представлениях. Однако выдающийся ученый сумел оказаться в точной науке. «
- В знаменитых стихах говорится, что в день открытия своего рисунка он воздвиг быков милой жертвы . Именно после открытия гипотезы пошли слухи, что жертва ста быков« отправилась в странствие » на страницах книг и публикаций.«Палки и по сей день шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что не Пифагор придумал стихотворение о штанах, чтобы доказать выдвинутые им рисунки: во время При жизни Великой математики штанов еще не было . Их изобрели спустя несколько десятилетий.
- Пекка, Лейбниц и несколько других ученых пытались доказать ранее известную теорему, но это не удалось никому.
- Название рисунков «Теорема Пифагора» означает «убедительность речи» .Так переводится слово Пифагор, которое математик взял за псевдоним.
- Размышления Пифагора о собственном правиле: секрет горения на Земле заключается в числах . Ведь математик, опираясь на собственную гипотезу, изучал свойства чисел, выявлял четность и нечетность, создавал пропорции.
Надеемся, вам понравилась подборка с картинками — Интересные факты о теореме Пифагора: Узнаем новое о знаменитой теореме (15 фото) онлайн в хорошем качестве.Пожалуйста, оставьте свое мнение в комментариях! Для нас важно каждое мнение.
Штаны — получите рекламный RideStep Academic Acting или выгодные штаны, чтобы купить со скидкой на распродаже в RideStep
Jarg. шк. Желе Теорема Пифагора, которая устанавливает соотношение между квадратами квадратов, построенных на гипотенузе, и катетом прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
Штаны Пифагора — Шуточное название теоремы Пифагора, возникшее из-за того, что квадраты, построенные по сторонам прямоугольника, и квадраты, расходящиеся в разные стороны, напоминают штаны.Любила геометрию … И получила на вступительных экзаменах в вуз … … … Фразеологический словарь русского литературного языка
штаны пифагора — шутливое название теоремы Пифагора, устанавливающей связь между квадратами, построенными на гипотенусах, и формой прямоугольного треугольника, который внешне на рисунках выглядит как аисты … Словарь многих выражений
Инлоид: о человеке Даровит Ср. Это несчастье. В древности он наверняка изобрел бы штаны Пифагорова… Салтыков. Письма о пестах. Штаны Пифагора (геом.): В прямоугольнике квадрат гипотенузы равен квадрату катетов (учим … … Большой толсто-фразологический словарь Михельсона
Штаны Pythagora со всех сторон равны — Количество пуговиц известно. Зачем мне пристально? (Грубо) о штанах и мужских половых органах. Штаны Пифагора со всех сторон равны. Чтобы доказать это, нужно снять и показать 1) теорему Пифагора; 2) про широкие штаны… Живая речь. Словарь устных выражений
PiñaGorovy Штаны (изобретать) несправедливость. О человеческом петухе. Ср. Несомненно, это мудрец. В старину он бы изобрел штаны Пинягорова … Салтыков. Ходячие буквы. ПиньяГоровы штаны (геом.): В прямоугольнике квадрат гипотенузы … … Большой интеллектуально-фразеологический словарь Михельсона (орфография)
Штаны Пифагора во всех направлениях равны — шутливое доказательство теоремы Пифагора; Также в анекдоте про мешковатые штаны друга… Словарь народной фразеологии
Сел, грубо …
Штаны Пифагор по всем направлениям равны (количество пуговиц известно. Почему тесно? / Чтобы доказать, нужно снять и показать) — доволен, грубоват … Толковый словарь современных разговорных фраз и прогресса
СУМ., МН., УПОТР. по сравнению. Часто морфология: MN. какие? Штаны, (нет) что? Штаны, что? Штаны, (см.) Что? Штаны чем? Штаны, что? О штанах 1. Штаны. Это предмет одежды, который состоит из двух коротких или длинных штанов и закрывает низ… … Толковый словарь Дмитриева
Книги
- Штаны Pythagora,. В этой книге вы найдете фантастику и приключения, чудеса и фантастику. Забавно и грустно, обыденно и загадочно … А что еще нужно для занимательного чтения? Главное быть …
- Чудеса на колесах, Маркуш Анатолий. Миллионы колес крутятся по всей земле — катят вагоны, измеряют время часами, постукивают под поездами, выполняют бесчисленные работы в машинах и разнообразных механизмах.Это…
Римский архитектор Витрувий выделил теорему Пифагоры «из многочисленных открытий, которые послужили развитию человеческой жизни», и призвал относиться к ней с величайшим почтением. Это было еще в первом веке до н. е. На рубеже XVI-XVII веков известный немецкий астроном Иоганн Кеплер назвал его одним из сокровищ геометрии, сопоставимым с мерой золота. Вряд ли во всей математике будет более значимое и значимое одобрение, ведь по количеству научных и практических приложений теорема Пифагора не имеет себе равных.
Теорема Пифагора для случая равностороннего прямоугольного треугольника.
Наука и жизнь // иллюстрация
Иллюстрация к теореме Пифагора из «Трактовки с измерением шести» (Китай, III век до н.э.) и восстановленное на ее основе доказательство.
Наука и жизнь // иллюстрация
С. Перкинс. Пифагор.
Рисунок к возможному доказательству Пифагора.
Мозаика Пифагора и разделение AN-подданных на три квадрата в доказательстве теоремы Пифагора.
P. de Heh. Хозяйка и горничная во дворе. Около 1660 г.
I. OXTERVELT. Заблудшие музыканты в дверях богатого дома. 1665 год.
Штаны Пифагора
Теорема Пифагора — едва ли не самая узнаваемая и, несомненно, самая известная в истории математики. В геометрии он применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами больше квадрата Этот квадрат.Его аргументы, по сути, сводились к доказательству теоремы Пифагора, хотя и для конкретного треугольника.
Рисунки на рис. 1 и 2, напоминают простейший орнамент из квадратов и равных их частей — геометрический узор, известный с незапамятных времен. Их можно полностью накрыть рубанком. Математика назвала бы такое покрытие плоскости полигональным паркетом или смешиванием. Что такое Пифагор? Оказывается, он первым решил задачу правильного паркета, с чего и началось изучение осмотров различных поверхностей.Итак, Пифагор показал, что плоскость вокруг точки может быть покрыта без зазоров равными правильными многоугольниками только трех видов: шесть треугольников, четыре квадрата и три шестиугольника.
4000 лет спустя
История теоремы Пифагора уходит в глубокую древность. Упоминание о нем до сих пор содержится в вавилонских клинических текстах царя Хаммурапи (XVIII век до н.э.), то есть за 1200 лет до рождения Пифагора. Теорема использовалась как готовое правило во многих задачах, самая простая из которых — найти диагональ квадрата на его стороне.Не исключено, что соотношение A 2 + B 2 = C 2 для произвольного прямоугольного треугольника вавилоняне получили, просто «суммируя» равенство A 2 + A 2 = C 2. Но им повезло — для практической геометрии древний, сводившийся к измерениям и расчетам, не требовал строгих обоснований.
Теперь, почти 4000 лет спустя, мы имеем дело с рекордсменом по количеству всех видов свидетельств. Кстати, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришелся на вторую половину XIX — начало XX века.И если первые сборники содержат не более двух-трех десятков свидетельств, то eND XIX. К столетию их количество приблизилось к 100, а через полвека перевалило за 360, и это только те, которые удалось собрать по разным источникам. Кого только не взяли за решение этой нестабильной задачи — от известных ученых и популяризаторов науки до конгрессменов и школьников. И что примечательно, по оригинальности и простоте решения другие любители не уступали профессионалам!
До нас дошли самые древние из доказательств теоремы Пифагора, насчитывающие около 2300 лет.Одно из них строго аксиоматично — принадлежит к древнегреческому математику Евклиду, жившему в IV-III веках до нашей эры. е. В I, книге «Выгоды» теорема Пифагора выглядит как «предложение 47». Самые наглядные и красивые доказательства построены на картине «Пифагорейские штаны». Они похожи на хитрую головоломку для нарезки квадратов. Но заставьте фигуры двигаться правильно — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получено на основе рисунка из одного древнекитайского трактата (рис.3), и сразу же проясняет его связь с задачей удвоения квадрата квадрата.
Именно такое доказательство пытался объяснить своему младшему другу семилетнему Гвидо, не по годам, умному герою романа английского писателя Олдхоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность свидетельств, поэтому приписал ее … самому Пифагору. И вот главный герой фантастического рассказа Евгении Веллистовой «Электроника — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе это Евклид; Правда, ошибочно назвал его самым простым, хотя на самом деле в современном издании «началось» оно занимает полторы страницы!
Первый математик
Пифагор Самосский (570-495 до н.э.), имя которого давно и неразрывно связано с чудесной теоремой, в определенном смысле можно назвать первым математиком.Именно от него математика начинается как точная наука, где каждое новое знание является результатом не визуальных идей и правил, выведенных из опыта, а результатом логических рассуждений и выводов. Только так вы сможете навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод использовал только древнегреческий философ и ученый Фалез Милецкий, живший на рубеже VII-VI веков до н. Э. Он предложил идею доказательства, но применил ее не систематически, как правило, выборочно, к очевидным геометрическим утверждениям типа «Диаметр делит круг пополам».«Пифагор продвинулся намного дальше. Считается, что он ввел первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием« Традиция Пифагора ». теория чисел и стереометрия
Еще одна важная заслуга Пифагора — основание славной школы математиков, более века определявшей развитие этой науки в Древней Греции.Термин «математика» связан с его именем (от греческого μαθημA — учение, наука), объединившим четыре относительные дисциплины, созданные Пифагором и его последователями — пифагорейцами — системы знаний: геометрия, арифметика, астрономия и гармоника.
Невозможно отделить достижения Пифагора от достижений: по обычаю они приписывали собственные идеи и открывали своего учителя. Не осталось эссе. Ранние пифагорейцы оставили всю информацию, которую они передавали друг другу устно.Итак, 2500 лет спустя у историков нет ничего другого, кроме восстановления утраченных знаний по переводам других, более поздних авторов. Отдадим должное грекам: они хоть и окружили имя Пифагора множеством легенд, но не приписывали ничего такого, что он не мог бы раскрыть или развить в теорию. И теорема, носящая его имя, не исключение.
Такое простое доказательство
Неизвестно, сам Пифагор открыл соотношение длин сторон в прямоугольном треугольнике или позаимствовал это знание.Античные авторы утверждали, что он сам и любил пересказывать легенду о том, как Пифагор принес в жертву быка в честь своего открытия. Современные историки склонны считать, что он узнал о теореме, познакомившись с вавилонской математикой. Мы также не знаем, что за формулировал теорему Пифагор: арифметика, как принято сегодня, — квадрат гипотенуз равен сумме квадратов катетов, или геометрически, в духе древних, квадрат, построенный на гипотеннеус прямоугольного треугольника равна сумме квадратов, построенных по Его обычаям.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Это точно не сохранилось. По одной из версий, Пифагор мог воспользоваться пропорциями, выработанными в его школе. Он был основан, в частности, на теории подобия, на которой основано рассуждение. Рисуем прямоугольный треугольник с высотой катетики A и B до гипотенузы C. Получаем три одинаковых треугольника, включая оригинал. Их соответствующие партии пропорциональны, a: c = m: a и b: c = n: b, откуда a 2 = c · m и b 2 = c · n.Тогда a 2 + b 2 = c · (m + n) = C 2 (рис. 4).
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, очень простое: занимает всего несколько строк, не нужно ничего тащить, перекрашивать, вычислять … Неудивительно, что его неоднократно отбивали. Он содержится, например, в «Практике геометрии» Леонардо Писанского (1220 г.), и до сих пор лидирует в учебниках.
Такое свидетельство не противоречило взглядам пифагорейцев на Резюме: Первоначально они считали, что соотношение длин любых двух отрезков и, следовательно, площади прямолинейных фигур можно выразить натуральными числами.Никаких других чисел они не рассматривали, не допускали даже дробей, заменяя их отношениями 1: 2, 2: 3 и т. Д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости числа диагональ квадрата и его часть. Все попытки численно представить длину этой диагонали — в одном квадрате она равна √2 — ни к чему не привели. Было легче доказать, что задача не решена. В таком случае у математиков есть проверенный метод — доказательство от гадости.Кстати, и его приписывают Пифагору.
Существование отношения, не выраженного натуральными числами, положило конец многим пифагорейским идеям. Стало понятно, что известных им чисел недостаточно для решения даже простых задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, ее центральной проблемы. Сначала это привело к развитию учения о несоизмеримых ценностях — иррациональностях, а затем к расширению понятия числа.Другими словами, началась многовековая история изучения многих действительных чисел.
Мозаика Пифагора
Если покрыть плоскость квадратами двух разных размеров, окружая каждый маленький квадрат до четырех больших, то получится мозаичный паркет Пифагора. Таким рисунком издавна украшали каменные полы, напоминая древнее свидетельство теоремы Пифагора (отсюда и его название). По-разному перекрывая квадратную сетку на паркете, можно получить разбиение квадратов, построенных по сторонам прямоугольного треугольника, которые предлагались разным математикам.Например, если вы расположите сетку так, чтобы все ее узлы совпадали с правыми верхними вершинами квадратиков, фрагменты чертежа будут показаны в доказательстве средневековой персидской математики Ан-Наирзи, которое он разместил в комментариях к «начало» Евклиды. Нетрудно заметить, что сумма площадей больших и малых квадратов, исходных элементов паркета, равна площади наложенной сетки одного квадрата. А это значит, что указанная перегородка действительно подходит для укладки паркета: соединяя получившиеся многоугольники в квадраты, как показано на рисунке, можно заливать ими без пробелов и перекрывать всю плоскость.
Некоторые дискуссии меня безмерно развлекают …
Привет, что ты делаешь?
Да, задачи решаются из журнала.
-Ух ты! Не ожидал от тебя.
-Чего не ожидал?
— Какие у вас дела. Вроде умно, но вы верите во всякую чушь.
-Извините, я не понимаю. Что вы называете чушью?
Да, все это математика. Ведь очевидно, что фигня полная.
-Как ты можешь это сказать? Математика — королева науки…
-Ну давай без этого пафоса, да? Математика — это вовсе не наука, а сплошное путешествие по дурацким законам и правилам.
-Что ?!
— Ну не делайте таких больших глаз, вы сами знаете, что я прав. Нет, я не спорю, таблица умножения — великое дело, она сыграла немалую роль в формировании культуры и истории человечества. Но теперь это все неактуально! И тогда почему все было так сложно? В природе нет интегралов или логарифмов, все это выдумка математиков.
-Подождите минутку. Математика ничего не изобретала, они открыли новые законы взаимодействия чисел, используя проверенные инструменты …
-Да конечно! И вы в это верите? Чего вы не видите, какую чушь постоянно несут? Вы привели пример?
Да, будьте добры.
-Да пожалуйста! Теорема Пифагора.
-Ну а что с этим не так?
Да все не так! Видите ли, «штаны Пифагора по всем направлениям равны». А вы знаете, что греки не носили штанов во времена Пифагора? Как мог Пифагор вообще спорить о том, о чем не догадывался?
-Подождите минутку.Какие здесь штаны?
-Ну, кажется, это Пифагор? Или нет? Вы знаете, что у Пифагора не было штанов?
-Ну на самом деле, конечно, не было …
-Ага, значит уже в названии теоремы явная несостоятельность! Как же тогда мы можем серьезно относиться к тому, что там сказано?
— Минута. Пифагор ничего не говорил о своих штанах …
— Вы узнаете это, да?
Да … Могу я продолжить? Пифагор ничего не говорил о штанах, и ему не нужно пристраивать к нему прочую глупость…
-Ага, ты сам согласен, чушь все это!
Да я этого не говорил!
«То, что я сказал.» Вы противоречите себе.
-Так. Стоп. Что сказано в теореме Пифагора?
-Что все штаны равны.
-Блин, ты хоть читал эту теорему ?!
-Я знаю.
-Где?
— Прочитал.
-Что ты читал ?!
-Лобачевский.
* пауза *
— Сайт, а какое отношение имеет Лобачевский к Пифагору?
-Ну, Лобачевский тоже математик и, кажется, даже круче Пифагора, скажи нет?
* вздох *
-Ну, а что сказал Лобачевский о теореме Пифагора?
-Какие штаны равны.Но это ерунда! Как вообще можно носить такие штаны? К тому же Пифагор вообще не носил штанов!
-Так сказал Лобачевский ?!
* Вторая пауза, уверенно *
-Да!
— Будь я проклят, где это написано.
-Нет, ну там не так прямо написано …
-Какое название у этой книги?
Да, это не книга, это статья в газете. Насчет того, что Лобачевский на самом деле был агентом немецкой разведки … ну, к делу это не относится.Все-таки он, наверное, так сказал. Он тоже математик, тогда они с Пифагором одновременно.
-Пифоргоре ничего не сказал о штанах.
-Ну да! О том и речь. Все в порядке.
— Смотрите по порядку. Откуда вы лично знаете, что сказано в теореме Пифагора?
-Ну, поехали! Это все знают. На любой вопрос вы сразу ответите.
-Пифагора штаны не штаны …
-И конечно же! Это аллегория! Вы знаете, сколько раз я это слышал?
-Таблица Пифагора говорит, что сумма квадратов катетов равна квадрату гипотенузы.И это все!
-Что такое штаны?
Да не было пифагора без штанов !!!
-Ну вот, я тоже говорю. Выбросьте всю свою математику.
-И и не фигня! Смотри сам. Вот треугольник. Вот гипотенуза. Вот и картеты …
А зачем вам все, если это катенцы, а это гипотенуза? Может наоборот?
-Нет. Катестами называют две стороны, образующие прямой угол.
— Ну вот еще один прямой угол.
— Это не прямо.
-А он какой, кривой?
— Нет, он резкий.
— Значит, это тоже резкое.
— Он не острый, он прямой.
«Знаешь, я не морочу голову!» Вы просто называете вещи так, как вам удобно, чтобы результат соответствовал желаемому.
— Короткие стороны прямоугольного треугольника — катенец. Длинная сторона — гипотенуза.
-А кто короче — тот катат? А гипотенуза, значит уже не катит? Вы со стороны прислушиваетесь к себе, что вы за чушь. На дворе 21 век, расцвет демократии, а у вас какое-то средневековье.Стороны его видят, неравны ли …
-Рарологический треугольник S. Равноправных сторон не бывает …
-Ты уверены? Позвольте нарисовать вас. Посмотрите. Прямоугольный? Прямоугольный. И все стороны равны!
-Это нарисовал квадрат.
-И что?
-Бидра не треугольник.
-И, конечно же! Как только он нам не подходит, сразу «не треугольник»! Не морочь мне голову. Представьте себя: один угол, два угла, три угла.
-Четыре.
-И что?
— Это квадрат.
-А квадрат что, а не треугольник? Это хуже, да? Просто потому, что я его нарисовал? Есть три угла? Есть, и даже есть один запасной.Ну вот нефиг, понимаете …
— Оставим эту тему.
-Ага, уже сдаваться? Нечего спорить? Признаете, что математика — фигня?
— Нет, не узнаю.
-Ну, опять же, здорово! Я только что все подробно доказал! Если вся геометрия основана на учении Пифагора, и прошу прощения, полная ерунда … Что еще можно рассуждать?
— Пифагорей — не чушь …
— Ну как! И тогда я не слышал о школе пифагорейцев! Они, если хотите знать, баловались оргиями!
— вот вижу…
-У нас Пифагор вообще педик был! Сам он сказал, что Платон — его друг.
-Пифагор ?!
-Ты не знал? Да они вообще все педики были. И на голове тренчий. Один в бочке спал, другой голый по городу бежал …
— Диоген спит в бочке, но он был философом, а не математиком …
-И, конечно! Если кто в бочку залез, то не математик! Зачем нам лишний стыд? Знаем, знаем, прошли. Но вы мне объясните, почему всякие педики, жившие три тысячи лет назад и бегавшие без штанов, должны быть для меня авторитетом? Почему я должен придерживаться их точки зрения?
— Низкий, оставь…
Да нет, слушай! Я, в конце концов, тоже послушал. Вот эти расчеты, расчеты … Все под силу! И сразу же спросить вас кое-что по существу: «Это частное, это переменная, и это две неизвестные». А вы мне в О-о-о-общем скажите, без особого … И без всякого неизвестного, неизвестного, экзистенциального … Меня это тошнит, понимаете?
-Понять.
-Ну, я объясню мне, почему два два всегда четыре? Кто это придумал? И почему я должен принимать это как данность и не имею права сомневаться?
-Да сомневаешься сколько хочешь…
-Нет, ты мне объясни! Только без этих вещей, но нормально это по-человечески понять.
— Два дня равны четырем, потому что два два раза четыре.
— Масло Масло. Что ты сказал мне?
— Два дня — это два, умноженные на два. Возьми два и два и брось их …
— Так что складывать или умножать?
-Это одно и то же …
-Оба! Получается, если я поставлю оценку и умножу семь на восемь, тоже получится?
-Нет.
-А почему?
-Ну, что семь плюс восемь не равно…
-А если я девять дважды два, ты получишь четыре?
-Нет.
-А почему? Два умножились — оказалось, а с девяткой вдруг облом?
-Да. Дважды девять — восемнадцать.
-Мы дважды семь?
-Четырнадцать.
-Мы дважды пять?
-Десять.
— То есть четыре получается только в одном частном случае?
-Ровно.
-А теперь подумай сам. Вы говорите, что есть жесткие законы и правила умножения. О каких законах вообще можно говорить об этом, если в каждом случае получается другой результат ?!
— Это не совсем так.Иногда результат может совпадать. Например, дважды шесть равняется двенадцати. И четыре раза по три — тоже …
-Еще хуже! Два, шесть, три, четыре — ничего общего! Вы сами видите, что результат не зависит от исходных данных. Одно и то же решение принимается двумя радикальными способами. разные ситуации! И это при том, что один и тот же дважды, который мы берем постоянно и ничего не меняем, на все числа всегда дает разный ответ. Где, логика спрашивается?
— Но то же самое, притом логичное!
— Можно — может быть.Вы, математики, всегда верите во всякую непреодолимую чушь. И эти ваши расчеты меня не убеждают. А знаете почему?
-Почему?
-Ну, что я. знаю, зачем тебе вообще нужна математика. Все сводится к? «У тебя в кармане одно яблоко, а у Миши пять. Сколько яблок должна дать Миша Катя, чтобы яблоки стали равными?» И знаете, что я вам скажу? Миша никто не должен отдавать ! У Кати одно яблоко — и хватит. Мало для нее? Дай ему бежать, и он честно заработает хоть на яблоках, хоть на грушах, хоть на ананасах в шампанском.А если кто-то хочет не работать, а решать только задачи — пусть сидит с одним своим яблоком и не перекладывается!
История вопроса, свидетельства, примеры практического применения. Краткий обзор биографии
Римский архитектор Витрувий извлек теорему Пифагоры «из многочисленных открытий, которые послужили развитию человеческой жизни», и призвал относиться к ней с величайшим почтением. Это было еще в первом веке до н. е. На рубеже XVI-XVII веков известный немецкий астроном Иоганн Кеплер назвал его одним из сокровищ геометрии, сопоставимым с мерой золота.Вряд ли во всей математике будет более значимое и значимое одобрение, ведь по количеству научных и практических приложений теорема Пифагора не имеет себе равных.
Теорема Пифагора для случайного прямоугольного треугольника.
Наука и жизнь // иллюстрация
Иллюстрация к теореме Пифагора из «Трактовки с измерением шести» (Китай, III век до н.э.) и восстановленное на ее основе доказательство.
Наука и жизнь // иллюстрация
С.Перкинс. Пифагор.
Рисунок к возможному доказательству Пифагора.
Мозаика Пифагора и разделение AN-подданных на три квадрата в доказательстве теоремы Пифагора.
P. de Heh. Хозяйка и горничная во дворе. Около 1660 г.
I. OXTERVELT. Заблудшие музыканты в дверях богатого дома. 1665 год.
Штаны Пифагора
Теорема Пифагора — едва ли не самая узнаваемая и, несомненно, самая известная в истории математики.В геометрии он применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами апифагора «штаны» во всех направлениях равны? Но те же «штаны», только в «сложенном» виде (рис. 2). Такой рисунок использовал герой одного из диалогов Платона под названием «Менон», известный философ Сократ, рассматривая задачу построения квадрата с мальчиком-рабом, площадь которого вдвое больше квадрата этого квадрата. Его аргументы, по сути, сводились к доказательству теоремы Пифагора, хотя и для конкретного треугольника.
Рисунки на рис. 1 и 2, напоминают простейший орнамент из квадратов и равных их частей — геометрический узор, известный с незапамятных времен. Их можно полностью накрыть рубанком. Математика назвала бы такое покрытие плоскости полигональным паркетом или смешиванием. Что такое Пифагор? Оказывается, он первым решил задачу правильного паркета, с чего и началось изучение осмотров различных поверхностей. Итак, Пифагор показал, что плоскость вокруг точки может быть покрыта без промежутков равными правильным многоугольникам только трех видов: шесть треугольников, четыре квадрата и три шестиугольника.
4000 лет спустя
История теоремы Пифагора уходит в глубокую древность. Упоминание о нем до сих пор содержится в вавилонских клинических текстах царя Хаммурапи (XVIII век до н.э.), то есть за 1200 лет до рождения Пифагора. Теорема использовалась как готовое правило во многих задачах, самая простая из которых — найти диагональ квадрата на его стороне. Не исключено, что соотношение A 2 + B 2 = C 2 для произвольного прямоугольного треугольника вавилоняне получили, просто «суммируя» равенство A 2 + A 2 = C 2.Но им повезло — для практической геометрии античности, которая сводилась к измерениям и расчетам, не требовалось строгих обоснований.
Теперь, почти 4000 лет спустя, мы имеем дело с рекордсменом по количеству всех видов свидетельств. Кстати, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришелся на вторую половину XIX — начало XX века. И если первые сборники содержат не более двух-трех десятков свидетельств, то eND XIX.К столетию их количество приблизилось к 100, а через полвека перевалило за 360, и это только те, которые удалось собрать по разным источникам. Кого только не взяли за решение этой нестабильной задачи — от известных ученых и популяризаторов науки до конгрессменов и школьников. И что примечательно, по оригинальности и простоте решения другие любители не уступали профессионалам!
До нас дошли самые древние из доказательств теоремы Пифагора, насчитывающие около 2300 лет.Одно из них строго аксиоматично — принадлежит к древнегреческому математику Евклиду, жившему в IV-III веках до нашей эры. е. В I, книге «Выгоды» теорема Пифагора выглядит как «предложение 47». Самые наглядные и красивые доказательства построены на картине «Пифагорейские штаны». Они похожи на хитрую головоломку для нарезки квадратов. Но заставьте фигуры двигаться правильно — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получено на основе рисунка из одного древнекитайского трактата (рис.3), и сразу же проясняет его связь с задачей удвоения квадрата квадрата.
Именно такое доказательство пытался объяснить своему младшему другу семилетнему Гвидо, не по годам, умному герою романа английского писателя Олдхоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность свидетельств, поэтому приписал ее … самому Пифагору. И вот главный герой фантастического рассказа Евгении Веллистовой «Электроника — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе это Евклид; Правда, ошибочно назвал его самым простым, хотя на самом деле в современном издании «началось» оно занимает полторы страницы!
Первый математик
Пифагор Самосский (570-495 до н.э.), имя которого давно и неразрывно связано с чудесной теоремой, в определенном смысле можно назвать первым математиком.Именно от него математика начинается как точная наука, где каждое новое знание является результатом не визуальных идей и правил, выведенных из опыта, а результатом логических рассуждений и выводов. Только так вы сможете навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод использовал только древнегреческий философ и ученый Фалез Милецкий, живший на рубеже VII-VI веков до н. Э. Он предложил идею доказательства, но применил ее не систематически, как правило, выборочно, к очевидным геометрическим утверждениям типа «Диаметр делит круг пополам».«Пифагор продвинулся намного дальше. Считается, что он ввел первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием« Традиция Пифагора ». теория чисел и стереометрия
Еще одна важная заслуга Пифагора — основание славной школы математиков, более века определявшей развитие этой науки в Древней Греции.Термин «математика» связан с его именем (от греческого μαθημA — учение, наука), объединившим четыре относительные дисциплины, созданные Пифагором и его последователями — пифагорейцами — системы знаний: геометрия, арифметика, астрономия и гармоника.
Невозможно отделить достижения Пифагора от достижений: по обычаю они приписывали собственные идеи и открывали своего учителя. Не осталось эссе. Ранние пифагорейцы оставили всю информацию, которую они передавали друг другу устно.Итак, 2500 лет спустя у историков нет ничего другого, кроме восстановления утраченных знаний по переводам других, более поздних авторов. Отдадим должное грекам: они хоть и окружили имя Пифагора множеством легенд, но не приписывали ничего такого, что он не мог бы раскрыть или развить в теорию. И теорема, носящая его имя, не исключение.
Такое простое доказательство
Неизвестно, сам Пифагор открыл соотношение длин сторон в прямоугольном треугольнике или позаимствовал это знание.Античные авторы утверждали, что он сам и любил пересказывать легенду о том, как Пифагор принес в жертву быка в честь своего открытия. Современные историки склонны считать, что он узнал о теореме, познакомившись с вавилонской математикой. Мы также не знаем, что за формулировал теорему Пифагор: арифметика, как принято сегодня, — квадрат гипотенуз равен сумме квадратов катетов, или геометрически, в духе древних, квадрат, построенный на гипотеннеус прямоугольного треугольника равна сумме квадратов, построенных по Его обычаям.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Это точно не сохранилось. По одной из версий, Пифагор мог воспользоваться пропорциями, выработанными в его школе. Он был основан, в частности, на теории подобия, на которой основано рассуждение. Рисуем прямоугольный треугольник с высотой катетики A и B до гипотенузы C. Получаем три одинаковых треугольника, включая оригинал. Их соответствующие партии пропорциональны, a: c = m: a и b: c = n: b, откуда a 2 = c · m и b 2 = c · n.Тогда a 2 + b 2 = c · (m + n) = C 2 (рис. 4).
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, очень простое: занимает всего несколько строк, не нужно ничего тащить, перекрашивать, вычислять … Неудивительно, что его неоднократно отбивали. Он содержится, например, в «Практике геометрии» Леонардо Писанского (1220 г.), и до сих пор лидирует в учебниках.
Такое свидетельство не противоречило взглядам пифагорейцев на Резюме: Первоначально они считали, что соотношение длин любых двух отрезков и, следовательно, площади прямолинейных фигур можно выразить натуральными числами.Никаких других чисел они не рассматривали, не допускали даже дробей, заменяя их отношениями 1: 2, 2: 3 и т. Д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости числа диагональ квадрата и его часть. Все попытки численно представить длину этой диагонали — в одном квадрате она равна √2 — ни к чему не привели. Было легче доказать, что задача не решена. В таком случае у математиков есть проверенный метод — доказательство от гадости.Кстати, и его приписывают Пифагору.
Существование отношений, не выражаемых натуральными числами, положило конец многим пифагорейским идеям. Стало понятно, что известных им чисел недостаточно для решения даже простых задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, ее центральной проблемы. Сначала это привело к развитию учения о несоизмеримых ценностях — иррациональностях, а затем к расширению понятия числа.Другими словами, началась многовековая история изучения многих действительных чисел.
Мозаика Пифагора
Если покрыть плоскость квадратами двух разных размеров, окружая каждый маленький квадрат до четырех больших, то получится мозаичный паркет Пифагора. Таким рисунком издавна украшали каменные полы, напоминая древнее свидетельство теоремы Пифагора (отсюда и его название). По-разному перекрывая квадратную сетку на паркете, можно получить разбиение квадратов, построенных по сторонам прямоугольного треугольника, которые предлагались разным математикам.Например, если вы расположите сетку так, чтобы все ее узлы совпадали с правыми верхними вершинами квадратиков, фрагменты чертежа будут показаны в доказательстве средневековой персидской математики Ан-Наирзи, которое он разместил в комментариях к «начало» Евклиды. Нетрудно заметить, что сумма площадей больших и малых квадратов, исходных элементов паркета, равна площади наложенной сетки одного квадрата. А это значит, что указанная перегородка действительно подходит для укладки паркета: соединяя получившиеся многоугольники в квадраты, как показано на рисунке, можно заливать ими без пробелов и перекрывать всю плоскость.
Некоторые дискуссии меня безмерно развлекают …
Привет, что ты делаешь?
Да, задачи решаются из журнала.
-Ух ты! Не ожидал от тебя.
-Чего не ожидал?
— Какие у вас дела. Вроде умно, но вы верите во всякую чушь.
-Извините, я не понимаю. Что вы называете чушью?
Да, все это математика. Ведь очевидно, что фигня полная.
-Как ты можешь это сказать? Математика — королева науки…
-Ну давай без этого пафоса, да? Математика — это вовсе не наука, а сплошное путешествие по дурацким законам и правилам.
-Что ?!
— Ну не делайте таких больших глаз, вы сами знаете, что я прав. Нет, я не спорю, таблица умножения — великое дело, она сыграла немалую роль в формировании культуры и истории человечества. Но теперь это все неактуально! И тогда почему все было так сложно? В природе нет интегралов или логарифмов, все это выдумка математиков.
-Подождите минутку. Математика ничего не изобретала, они открыли новые законы взаимодействия чисел, используя проверенные инструменты …
-Да конечно! И вы в это верите? Чего вы не видите, какую чушь постоянно несут? Вы привели пример?
Да, будьте добры.
-Да пожалуйста! Теорема Пифагора.
-Ну а что с этим не так?
Да все не так! Видите ли, «штаны Пифагора по всем направлениям равны». А вы знаете, что греки не носили штанов во времена Пифагора? Как мог Пифагор вообще спорить о том, о чем не догадывался?
-Подождите минутку.Какие здесь штаны?
-Ну, кажется, это Пифагор? Или нет? Вы знаете, что у Пифагора не было штанов?
-Ну на самом деле, конечно, не было …
-Ага, значит уже в названии теоремы явная несостоятельность! Как же тогда мы можем серьезно относиться к тому, что там сказано?
— Минута. Пифагор ничего не говорил о своих штанах …
— Вы узнаете это, да?
Да … Могу я продолжить? Пифагор ничего не говорил о штанах, и ему не нужно пристраивать к нему прочую глупость…
-Ага, ты сам согласен, чушь все это!
Да я этого не говорил!
«То, что я сказал.» Вы противоречите себе.
-Так. Стоп. Что сказано в теореме Пифагора?
-Что все штаны равны.
-Блин, ты хоть читал эту теорему ?!
-Я знаю.
-Где?
— Прочитал.
-Что ты читал ?!
-Лобачевский.
* пауза *
— Сайт, а какое отношение имеет Лобачевский к Пифагору?
-Ну, Лобачевский тоже математик и, кажется, даже круче Пифагора, скажи нет?
* вздох *
-Ну, а что сказал Лобачевский о теореме Пифагора?
-Какие штаны равны.Но это ерунда! Как вообще можно носить такие штаны? К тому же Пифагор вообще не носил штанов!
-Так сказал Лобачевский ?!
* Вторая пауза, уверенно *
-Да!
— Будь я проклят, где это написано.
-Нет, ну там не так прямо написано …
-Какое название у этой книги?
Да, это не книга, это статья в газете. Насчет того, что Лобачевский на самом деле был агентом немецкой разведки … ну, к делу это не относится.Все-таки он, наверное, так сказал. Он тоже математик, тогда они с Пифагором одновременно.
-Пифоргоре ничего не сказал о штанах.
-Ну да! О том и речь. Все в порядке.
— Смотрите по порядку. Откуда вы лично знаете, что сказано в теореме Пифагора?
-Ну, поехали! Это все знают. На любой вопрос вы сразу ответите.
-Пифагора штаны не штаны …
-И конечно же! Это аллегория! Вы знаете, сколько раз я это слышал?
-Таблица Пифагора говорит, что сумма квадратов катетов равна квадрату гипотенузы.И это все!
-Что такое штаны?
Да не было пифагора без штанов !!!
-Ну вот, я тоже говорю. Выбросьте всю свою математику.
-И и не фигня! Смотри сам. Вот треугольник. Вот гипотенуза. Вот и картеты …
А зачем вам все, если это катенцы, а это гипотенуза? Может наоборот?
-Нет. Катестами называют две стороны, образующие прямой угол.
— Ну вот еще один прямой угол.
— Это не прямо.
-А он какой, кривой?
— Нет, он резкий.
— Значит, это тоже резкое.
— Он не острый, он прямой.
«Знаешь, я не морочу голову!» Вы просто называете вещи так, как вам удобно, чтобы результат соответствовал желаемому.
— Короткие стороны прямоугольного треугольника — катенец. Длинная сторона — гипотенуза.
-А кто короче — тот катат? А гипотенуза, значит уже не катит? Вы со стороны прислушиваетесь к себе, что вы за чушь. На дворе 21 век, расцвет демократии, а у вас какое-то средневековье.Стороны его видят, неравные …
-Рологического треугольника с равными сторонами не существует …
-Ты уверены? Позвольте нарисовать вас. Посмотрите. Прямоугольный? Прямоугольный. И все стороны равны!
-Это нарисовал квадрат.
-И что?
-Бидра не треугольник.
-И, конечно же! Как только он нам не подходит, сразу «не треугольник»! Не морочь мне голову. Представьте себя: один угол, два угла, три угла.
-Четыре.
-И что?
— Это квадрат.
-А квадрат что, а не треугольник? Это хуже, да? Просто потому, что я его нарисовал? Есть три угла? Есть, и даже есть один запасной.Ну вот нефиг, понимаете …
— Оставим эту тему.
-Ага, уже сдаваться? Нечего спорить? Признаете, что математика — фигня?
— Нет, не узнаю.
-Ну, опять же, здорово! Я только что все подробно доказал! Если вся геометрия основана на учении Пифагора, и прошу прощения, полная ерунда … Что еще можно рассуждать?
— Пифагорей — не чушь …
— Ну как! И тогда я не слышал о школе пифагорейцев! Они, если хотите знать, баловались оргиями!
— вот вижу…
-У нас Пифагор вообще педик был! Сам он сказал, что Платон — его друг.
-Пифагор ?!
-Ты не знал? Да они вообще все педики были. И на голове тренчий. Один в бочке спал, другой голый по городу бежал …
— Диоген спит в бочке, но он был философом, а не математиком …
-И, конечно! Если кто в бочку залез, то не математик! Зачем нам лишний стыд? Знаем, знаем, прошли. Но вы мне объясните, почему всякие педики, жившие три тысячи лет назад и бегавшие без штанов, должны быть для меня авторитетом? Почему я должен придерживаться их точки зрения?
— Низкий, оставь…
Да нет, слушай! Я, в конце концов, тоже послушал. Вот эти расчеты, расчеты … Все под силу! И сразу же спросить вас кое-что по существу: «Это частное, это переменная, и это две неизвестные». А вы мне в О-о-о-общем скажите, без особого … И без всякого неизвестного, неизвестного, экзистенциального … Меня это тошнит, понимаете?
-Понять.
-Ну, я объясню мне, почему два два всегда четыре? Кто это придумал? И почему я должен принимать это как данность и не имею права сомневаться?
-Да сомневаешься сколько хочешь…
-Нет, ты мне объясни! Только без этих вещей, но нормально это по-человечески понять.
— Два дня равны четырем, потому что два два раза четыре.
— Масло Масло. Что ты сказал мне?
— Два дня — это два, умноженные на два. Возьми два и два и брось их …
— Так что складывать или умножать?
-Это одно и то же …
-Оба! Получается, если я поставлю оценку и умножу семь на восемь, тоже получится?
-Нет.
-А почему?
-Ну, что семь плюс восемь не равно…
-А если я девять дважды два, ты получишь четыре?
-Нет.
-А почему? Два умножились — оказалось, а с девяткой вдруг облом?
-Да. Дважды девять — восемнадцать.
-Мы дважды семь?
-Четырнадцать.
-Мы дважды пять?
-Десять.
— То есть четыре получается только в одном частном случае?
-Ровно.
-А теперь подумай сам. Вы говорите, что есть жесткие законы и правила умножения. О каких законах вообще можно говорить об этом, если в каждом случае получается другой результат ?!
— Это не совсем так.Иногда результат может совпадать. Например, дважды шесть равняется двенадцати. И четыре раза по три — тоже …
-Еще хуже! Два, шесть, три, четыре — ничего общего! Вы сами видите, что результат не зависит от исходных данных. Одно и то же решение принимается двумя радикальными способами. разные ситуации! И это при том, что один и тот же дважды, который мы берем постоянно и ничего не меняем, на все числа всегда дает разный ответ. Где, логика спрашивается?
— Но то же самое, притом логичное!
— Можно — может быть.Вы, математики, всегда верите во всякую непреодолимую чушь. И эти ваши расчеты меня не убеждают. А знаете почему?
-Почему?
-Ну, что я. знаю, зачем тебе вообще нужна математика. Все сводится к? «У тебя в кармане одно яблоко, а у Миши пять. Сколько яблок должна дать Миша Катя, чтобы яблоки стали равными?» И знаете, что я вам скажу? Миша никто не должен отдавать ! У Кати одно яблоко — и хватит. Мало для нее? Дай ему бежать, и он честно заработает хоть на яблоках, хоть на грушах, хоть на ананасах в шампанском.А если кто-то хочет не работать, а решать только задачи — пусть сидит с одним своим яблоком и не перекладывается!
»Заслуженный профессор математики Университета Варика, известный популяризатор науки Иэн Стюарт, посвященный роли чисел в истории человечества и актуальности их изучения в наше время.
Пытагорова Гипотенуза
Треугольники Пифагора имеют прямой угол и целые стороны. Самый простой из них, самая длинная сторона имеет длину 5, остальные — 3 и 4.Всего существует 5 правых многогранников. Уравнение пятой степени невозможно решить с помощью корней пятой степени — или любых других корней. Решетки на плоскости и в трехмерном пространстве не обладают пятиточечной симметрией вращения, поэтому в кристаллах такие симметрии не отсутствуют. Однако они могут находиться в решетках в четырехмерном пространстве и в занятых структурах, известных как квазикристаллы.
Гипотенуза наименьшей тройки Пифагорова
Теорема Пифагора утверждает, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) коррелирует с двумя другими сторонами этого треугольника очень просто и красиво: квадрат гипотенузы равен сумме квадратов двух других сторон.
Традиционно мы называем эту теорему Пифагора, но на самом деле история о ней довольно туманна. Глиняные пластины предполагают, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; Известность первооткрывателю принесла ему математический культ пифагорейцев, сторонники которых считали, что Вселенная основана на числовых законах. Древних авторов приписывали пифагорейцам — а значит, и Пифагор представляет собой разновидность математических теорем, но на самом деле мы понятия не имеем о том, какой математикой занимался сам Пифагор.Мы даже не знаем, смогли ли пифагорейцы доказать теорему Пифагора или просто поверили, что она верна. Или, скорее всего, у них были убедительные данные о его истинности, которых, тем не менее, было бы недостаточно для того, что мы сегодня считаем доказательством.
Доказательство Пифагора
Первое доказательное доказательство теоремы Пифагора мы находим в «начале» Евклиды. Это достаточно сложное доказательство. Используя рисунок, на котором школьники викторианской эпохи сразу узнают «Штаны Пифагора»; Рисунок и истина напоминают сушку доверенных лиц, сушащихся на веревке.Известны буквально сотни других свидетельств, большинство из которых делают доказанное одобрение более очевидным.
// Рис. 33. Штаны Пифагора
Одно из самых простых доказательств — это своего рода математическая головоломка. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата. На одной кладке мы видим квадрат на гипотенузе; С другой стороны, квадраты на двух других сторонах треугольника. Понятно, что квадрат в этом же случае равен.
// Рис.34. Слева: квадрат на гипотенузе (плюс четыре треугольника). Справа: сумма квадратов на двух других сторонах (плюс те же четыре треугольника). А теперь исключим треугольники
Изготовление перигала — очередная пазл пруфа.
// Рис. 35. Перигальное рассечение
Существует также доказательство теоремы с использованием квадрата, лежащего на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему. Если вы посмотрите, как наклонный квадрат перекрывает два других квадрата, вы увидите, как разрезать большой квадрат на части, а затем сложить из них два меньших квадрата.Вы также можете увидеть прямоугольные треугольники, стороны которых соответствуют размеру трех задействованных квадратов.
// Рис. 36. Доказательство мощения
Есть интересные свидетельства использования подобных треугольников в тригонометрии. Известно не менее пятидесяти различных свидетельств.
Пифагор Тройка
В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений. Тройка Пытагорова — это набор целых чисел a, b и c, таких что
Геометрически такой тройник определяет прямоугольный треугольник с целыми сторонами.
Наименьший гипотенус тройки Пифагора равен 5.
Две другие стороны этого треугольника равны 3 и 4. Здесь
32 + 42 = 9 + 16 = 25 = 52.
Следующая по величине гипотенуза — равно 10, потому что
62 + 82 = 36 + 64 = 100 = 102.
Однако, по сути, это тот же треугольник с двойными сторонами. Следующая наибольшая и поистине другая гипотенуза — 13, для нее
52 + 122 = 25 + 144 = 169 = 132.
Евклид знал, что существует бесконечное количество различных пифагоровых вариантов Трока, и дал то, что можно назвать формулой чтобы найти их все.Позже Диофант Александрийский предложил простой рецепт, в основном совпадающий с евклидовым.
Возьмем любые два натуральных числа и вычислим:
их двойная работа;
разница между их квадратами;
сумма их квадратов.
Три полученных числа будут сторонами треугольника Пифажова.
Возьмем, например, числа 2 и 1. Вычислим:
двухстворчатая работа: 2 × 2 × 1 = 4;
разности квадратов: 22 — 12 = 3;
сумма квадратов: 22 + 12 = 5,
и мы получили знаменитый треугольник 3-4-5.Если взять вместо цифр 3 и 2, то получим:
двойная работа: 2 × 3 × 2 = 12;
разностей квадратов: 32 — 22 = 5;
суммирование квадрата: 32 + 22 = 13,
и мы получаем следующий треугольник 5-12-13, попробуем взять числа 42 и 23 и получим:
удфилды: 2 × 42 × 23 = 1932;
разностей квадратов: 422 — 232 = 1235;
Сумма квадратов
: 422 + 232 = 2293,
о треугольнике 1235-1932-2293 никто никогда не слышал.
Но работают и эти числа:
12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.
В Правиле диофантства есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять другое произвольное число и умножьте их на это. Таким образом, треугольник 3-4-5 можно превратить в треугольник 6-8-10, умножив все стороны на 2, или в треугольник 15-20-25, умножив все на 5.
Если перейти на язык алгебры, правило принимает следующий вид: Пусть U, V и K — целые числа.Тогда прямоугольный треугольник со сторонами
2кув и k (u2 — v2) имеет гипотенузу
. Есть и другие способы представления основной идеи, но все они сокращают описанное выше. Этот метод позволяет получить всю тройку Пифагора.
Правые многогранники
Имеется гладкий счет из пяти правильных многогранников. Правильный многогранник (или многогранник) — это объемная фигура с конечным числом плоских граней. Края сходятся друг с другом на линиях, называемых ребрами; Ребра находятся в точках, называемых вершинами.
Кульминация евклидова «Преимущества» — доказательство того, что может быть только пять правильных многогранников, то есть многогранников, каждая грань которых представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным количеством одинаковых расположений. Вот пять правильных многогранников:
тетраэдр с четырьмя треугольными ребрами, четырьмя вершинами и шестью ребрами;
куб или шестигранник с 6 квадратными гранями, 8 вершинами и 12 ребрами;
октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;
додекаэдр с 12 пираниоральными железами, 20 вершинами и 30 ребрами;
икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.
// Рис. 37. Пять правых многогранников
Правые многогранники встречаются в природе. В 1904 году Эрнст Гекель опубликовал рисунки крошечных организмов, известных как радолярии; Многие из них напоминают те самые пять правильных многогранников. Может быть, он немного поправил природу, и рисунки не в полной мере отражают облик конкретных живых существ. Первые три структуры также наблюдаются в кристаллах. Додекаэдр и икосаэдр в кристаллах вы не найдете, хотя иногда встречаются неправильные додекаэдры и икосаэдры.Настоящие додекаэдры могут существовать в виде квазикристаллов, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.
// Рис. 38. Рисунки Геккеля: Радиолярии в виде правильных многогранников
// Рис. 39. Сканеры правильных многогранников
Интересно делать модели правильных многогранников. многогранники из бумаги, вырезая заданный набор взаимосвязанных граней — это называется разверткой многогранника; Скан складываем по ребрам и склеиваем между собой соответствующие ребра.Полезно добавить дополнительную плату за клей к одному из краев каждой такой пары, как показано на рис. 39. Если такой площадки нет, можно использовать липкую ленту.
Уравнение пятой степени
Не существует алгебраической формулы для решения уравнений 5-й степени.
В общем Уравнение пятой степени выглядит так:
aX5 + BX4 + CX3 + DX2 + EX + F = 0.
Задача состоит в том, чтобы найти формулу для решения такого уравнения (может иметь до пять решений).Опыт обращения квадратных и кубических уравнений, а также уравнений четвертой степени подсказывает, что такая формула должна существовать для уравнений пятой степени, и в ней, по идее, должны фигурировать корни пятой, третьей и четвертой степени. Вторая степень. Опять же, можно смело предположить, что такая формула, если она существует, будет очень и очень сложной.
Это предположение в итоге оказалось ошибочным. На самом деле такой формулы не существует; По крайней мере, не существует формулы, состоящей из коэффициентов A, B, C, D, E и F, составленных с использованием сложения, вычитания, умножения и деления, а также извлечения корня.Таким образом, среди 5 5 есть что-то совершенно особенное. Причины такого необычного поведения пятерки очень глубоки, и на то, чтобы с ними разобраться, потребовалось много времени.
Первым признаком проблемы было то, что он, словно математик, пытался найти такую формулу, какими бы умными они ни были, они неизменно терпели неудачу. Некоторое время все считали, что причины кроются в невероятной сложности формулы. Считалось, что просто никто не сможет разгадать эту алгебру.Однако со временем некоторые математики начали сомневаться в том, что такая формула вообще существует, и в 1823 году Нильсу Хендрику Абелю удалось доказать обратное. Такой формулы не существует. Вскоре после этого Evarister Галуа нашел способ определить, является ли уравнение того или иного способа — 5-го, 6-го, 7-го, вообще каким-либо — с помощью такой формулы.
Вывод из всего этого простой: цифра 5 особенная. Можно решать алгебраические уравнения (с помощью корней n-й степени Для разных значений n) для степеней 1, 2, 3 и 4, но не для 5-й степени.На этом очевидная закономерность заканчивается.
Никого не удивляет, что уравнения степеней больше 5 ведут себя еще хуже; В частности, с ними связана та же трудность: нет общих формул для их решения. Это не означает, что уравнения не имеют решений; Это не означает, что невозможно найти очень точные численные значения этих решений. Все это ограничивается традиционными инструментами алгебры. Напоминает о невозможности пересечения угла с помощью линейки и циркуляции.Ответ есть, но перечисленных методов недостаточно и они не позволяют определить, что это такое.
Кристаллографический предел
Кристаллы в двух и трех измерениях не обладают 5-лучевой симметрией вращения.
Атомы в кристалле образуют сетку, то есть структуру, периодически повторяющуюся в нескольких независимых направлениях. Например, рисунок на обоях повторяется по длине рулона; Кроме того, его обычно повторяют в горизонтальном направлении, иногда с переходом от одного куска обоев к другому.По сути, обои — это двухмерный кристалл.
На самолете 17 разновидностей рисунков обоев (см. Раздел 17). Они различаются по типу симметрии, то есть по способам жестко перемещают рисунок таким образом, что он обязательно оставит себя в исходном положении. К типам симметрии относятся, в частности, различные варианты симметрии вращения, при которых рисунок должен быть повернут на определенный угол вокруг определенной точки — центра симметрии.
Порядок симметрии вращения — это то, сколько раз вы можете повернуть тело на полную окружность, чтобы все детали чертежа вернулись в исходное положение.Например, поворот на 90 ° — это симметрия вращения 4-го порядка *. Список возможных типов симметрии вращения в кристаллической решетке снова указывает на необычность числа 5: ее там нет. Существуют варианты с симметрией вращения 2, 3, 4 и 6 порядков, но ни один рисунок обоев не имеет симметрии вращения 5-го порядка. Симметрия вращения на порядок больше 6 в кристаллах тоже не случай, но первое нарушение последовательности все же среди числа 5.
То же самое происходит с кристаллографическими системами в трехмерном пространстве. Здесь решетка повторяется в трех независимых областях. Существует 219 различных видов симметрии, или 230, если рассматривать зеркальное отражение узора отдельным вариантом, несмотря на то, что в данном случае нет зеркальной симметрии. Опять-таки соблюдается симметрия вращения 2-го, 3-го, 4-го и 6-го порядков, но не 5. Этот факт получил название кристаллографического предела.
В четырехмерном решетчатом пространстве с симметрией 5-го порядка существуют; В общем, для решеток достаточно большой возможной размерности возможен любой продвинутый порядок симметрии вращения.
// Рис. 40. Кристаллическая решетка поваренной соли. Темные шары изображают атомы натрия, светлые — атомы хлора
Квазикристаллы
Хотя симметрия вращения 5-го порядка в двумерных и трехмерных решетках невозможна, она может существовать в немного менее регулярных структурах, известных как квазикристаллы. Воспользовавшись зарисовками Кеплера, Роджер Пенроуз открыл плоские системы с более распространенным типом пятикратной симметрии. Они получили название квазикристаллов.
Квазикристаллы существуют в природе. В 1984 году Даниэль Шехтман обнаружил, что сплав алюминия и марганца может образовывать квазикристаллы; Первоначально кристаллографы встретили его сообщение с некоторым скептицизмом, но позже открытие подтвердилось, и в 2011 году Шехтман был удостоен Нобелевской премии по химии. В 2009 году группа ученых под руководством Люка Бинди обнаружила квазикристаллы в минерале из Корякского нагорья в России — сочетание алюминия, меди и железа. Сегодня этот минерал называется ИкосаДрит.Измеряя с помощью масс-спектрометра содержание в минерале различных изотопов кислорода, ученые показали, что этот минерал возник на Земле. Он сформировался около 4,5 миллиардов лет назад, в то время, когда только возникла Солнечная система, и проводил большую часть времени в поясе астероидов, вращаясь вокруг Солнца, пока какое-то возмущение не изменило его орбиту и не привело в конце концов к Солнцу. земля.
// Рис. 41. Слева: одна из двух квазикристаллических решеток с точной пятивременной симметрией.Справа: атомная модель икосаэдрического квазикристалла алюминия-палладия-марганца
.
Описание презентации на отдельных слайдах:
1 слайд
Описание слайда:
Студенческий проект МБОУ Бондарь Школы на тему: «Пифагор и его теорема» подготовили: Экта Константин, ученица 7 А класса Руководитель: Зубило Надежда Ивановна, учитель математики 2015
2 Слайд
Описание слайда:
3 Слайд
Описание слайда:
Аннотация.Геометрия — очень интересная наука. В нем много теорем, не похожих друг на друга, но иногда столь необходимых. Меня очень интересует теорема Пифагора. К сожалению, одно из самых важных заявлений мы сдаем только в восьмом классе. Я решил приоткрыть завесу тайны и исследовать теорему Пифагора.
4 Слайд
Описание слайда:
5 Слайд
Описание слайда:
6 Слайд
Описание слайда:
Задания на изучение биографии Пифагора.Изучите историю возникновения и доказательства теоремы. Узнайте, как эта теорема используется в искусстве. Найдите исторические задания, в которых применяется теорема Пифагора. Познакомьтесь с отношением детей в разное время к этой теореме. Создайте проект.
7 Слайд
Описание слайда:
Этюд Этюд Биография Пифагора. Заповеди и афоризмы Пифагора. Теорема Пифагора. История теоремы. Почему штаны Пифагора во всех направлениях равны? Различные доказательства теоремы Пифагора другими учеными.Применение теоремы Пифагора. Интервью. Выход.
8 Слайд
Описание слайда:
Пифагор — Кто он? Пифагор Самосский (580 — 500 до н. Э.) Древнегреческий математик и философ-идеалист. Родился на острове Самос. Получила хорошее образование. По легенде Пифагор, чтобы познакомиться с мудростью восточных ученых, покинул Египет и жил там 22 года. Хорошо владея всеми науками египтян, включая математику, он переехал в Вавилон, где прожил 12 лет и познакомился с научными знаниями вавилонских жрецов.Традиции связывают с посещением Пифагором и Индии. Это очень вероятно, потому что Иония и Индия тогда имели торговые связи. Вернувшись на родину (ок. 530 г. до н.э.), Пифагор попытался организовать свою философскую школу. Однако по неизвестным причинам он вскоре покидает Самос и обосновывается в Кротоне (греческая колония на севере Италии). Здесь Пифагору удалось организовать свою школу, которая действовала почти тридцать лет. Школа Пифагора, или, как ее еще называют, Пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством.Статус Пифагорейского Союза был очень тяжелым. По их философским воззрениям Пифагор был идеалистом, защитником интересов рабовладельческой аристократии. Возможно, это было причиной его отъезда из Самоса, так как сторонники демократических взглядов имели большое влияние в Ионии. В публичных вопросах под «порядком» пифагорейцы понимали господство аристократов. Они осудили древнегреческую демократию. Пифагорейская философия была примитивной попыткой обосновать господство рабовладельческой аристократии.В конце V в. До н.э. По Греции и ее колониям прокатилась волна демократического движения. Демократия потерпела поражение в Кротоне. Пифагор вместе с учениками покидает Кротон и уходит в тартуент, а затем в метапонт. Прибытие пифагорейцев на Метапон совпало с началом там народного восстания. Почти девятилетний Пифагор умер в одной из ночных лачуг. Его школа перестала существовать. Студенты-пифагорейцы, спасшиеся от преследований, расселились по всей Греции и ее колониям.Создав средства к существованию, они организовали школы, в которых их обучали в основном арифметике и геометрии. Информация об их достижениях содержится в трудах более поздних ученых — Платона, Аристотеля и др.
9 Слайд
Описание слайда:
Заповеди и афоризмы мысли Пифагора — прежде всего между людьми на Земле. Не садитесь на меру для хлеба (т.е. не живите id). Уходя, не оглядывайся (т.э., перед смертью не цепляйтесь за жизнь). Нижние дороги не идут (т. Е. Следуйте не мнению толпы, а мнениям немногих понимающих). Ласточки в доме не держат (т.е. не берут болтливых и не сдержанных гостей в язык). Будь с лопающимся, не будь с изнашивающимся (т.е. поощряя людей не к праздности, а к добродетели, к труду). По жизни по жизни, как сеялка, идти ровными и постоянными шагами. Истинное отечество, где есть хорошие нравы. Не входите в число ученых: мудрецов, составляющих общество, делают простолюдины.Прочтите священные числа, вес и меру, как Чад элегантного равенства. Измерьте свои желания, взвесьте свои мысли, просчитайте свои слова. Неудивительно: неожиданность произвела богов.
10 Слайд
Описание слайда:
Формулировка теоремы. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин каретки.
11 Слайд
Описание слайда:
Доказательство теоремы.На данный момент в научной литературе зафиксировано 367 доказательств этой теоремы. Вероятно, теорема Пифагора — единственная теорема с таким внушительным количеством доказательств. Конечно, все их можно разделить на небольшое количество классов. Самые известные из них — доказательства методом пространства, аксиоматики и экзотики.
12 Слайд
Описание слайда:
Доказательство теоремы Пифагора Дан представляет собой прямоугольный треугольник с категориями A, B и гипотенурием C.Докажем, что C² = A² + B² — это полный треугольник квадрату со стороной a + b. Квадрат s этого квадрата равен (A + B) ². С другой стороны, квадрат состоит из четырех равных прямоугольных треугольников, каждый из которых равен ½ ab, и квадрата со стороной C. S = 4 · ½ AB + C² = 2 AB + C² Таким образом, ( a + b) ² = 2 AB + C², откуда C² = A² + B²CCCAB
13 Слайд
Описание слайда:
История теоремы Пифагора интересна.История теоремы Пифагора. Хотя эта теорема связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, ее свидетельства еще не были известны, а соотношение между гипотенузой и обычаями было установлено экспериментально на основе измерений. Пифагор, по-видимому, нашел доказательство этой связи. Сохранилась древняя легенда, что в честь своего открытия Пифагор приносил в жертву богов быков, а по другим свидетельствам — даже сотню быков.В течение следующих столетий были найдены различные другие доказательства теоремы Пифагора. В настоящее время их уже более сотни, но самая популярная теорема с построением квадрата с этим прямоугольным треугольником пользуется наибольшей популярностью.
14 Слайд
Описание слайда:
Теорема B. Древний Китай «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет равна 5, когда основание равно 3, а высота 4».
15 Слайд
Описание слайда:
Теорема в Древнем Египте Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно египтянам около 2300 г. до н.э. э., во времена царя Аменхехты (по папирусу 6619 Берлинского музея). Согласно Кантору, Harphedonapti, или «натяжители каната», строили прямые углы с прямоугольными треугольниками со сторонами 3, 4 и 5.
16 Слайд
Описание слайда:
О теореме в «Путешествиях» «Заслуги первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, заключаются не в открытии математики, а в ее систематизации и обосновании.В их руках вычислительные рецепты, основанные на сомнительных идеях, превратились в точную науку. «
17 Слайд
Описание слайда:
Почему штаны Пифагора во всех направлениях равны? В течение двух тысячелетий наиболее распространенное доказательство теоремы Пифагора было изобретено Евклидом. Он помещен в его знаменитую стартовую книгу. Евклид снизил высоту СН от вершины прямого угла на гипотенузе и утверждал, что его продолжение делит квадрат на два прямоугольника, квадраты которых равны квадратам соответствующих квадратов, построенных на категориях.Рисунок, использованный в доказательстве этой теоремы, представляет собой шутку под названием «Штаны Пифагора». Долгое время он считался одним из символов математической науки.
18 Слайд
Описание слайда:
Отношение детей древности к доказательству теоремы Пифагора. Студенты Средневековья считали это очень трудным. Слабые ученики, которые выучили теоремы наизусть, не понимая, и поэтому недовольные «ослы» не смогли преодолеть теорему Пифагора, которая служила для них непреодолимым мостом.Из-за рисунков, сопровождающих теорему Пифагора, ученики также называли ее «ветряной мельницей», составили стихи, вроде «штаны Пифагора со всех сторон равны», нарисовали карикатуры.
19 Слайд
Описание слайда:
Доказательство теоремы Простейшее доказательство теоремы получается в случае уравновешенного прямоугольного треугольника. На самом деле, достаточно просто взглянуть на мозаику из одинаково связанных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.Например, для треугольника ABC: квадрат, построенный на гипотеннеусе AC, содержит 4 исходных треугольника, а квадратов, построенных на категориях, — два.
20 Слайд
Описание слайда:
«Кресло невесты» на фигуре квадраты, построенные на катетах, ставятся ступенями один рядом с другим. Эту форму, обнаруженную в свидетельствах, датируемых не позднее IX века н. Э., Индуисты называли «креслом невесты».
21 Слайд
Описание слайда:
Использование теоремы Пифагора в настоящее время является всеобщим признанием того, что успех развития многих областей науки и техники зависит от развития различных направлений математики.Важным условием повышения эффективности производства является повсеместное внедрение математических методов в технику и народное хозяйство, что подразумевает создание новых эффективных методов качественных и количественных исследований, позволяющих решать задачи, поставленные практикой.
22 Слайд
Описание слайда:
Применение теоремы при строительстве построек в готическом и романском стиле Верхние части окон расчленены каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
23 Слайд
Описание слайда:
24 Слайд
Описание слайда:
Исторически сложившиеся задачи по монтажу мачт требуют прокладки 4 тросов. Один конец каждого кабеля должен быть прикреплен на высоте 12 м, другой конец должен быть прикреплен к земле на расстоянии 5 м от мачты. Будет 50 м троса для крепления мачты?
Штаны Pythagoras — по всем направлениям равны.
Чтобы доказать это, нужно снять и показать.
Это стихотворение известно всем со школы, с того же времени, когда мы изучали знаменитую теорему Пифагора в классе геометрии: квадрат длины гипотенуса прямоугольного треугольника равен сумме квадратов катетов. .
Чтобы доказать свою теорему, Пифагор нарисовал на песке фигуру из квадратов по сторонам треугольника. Квадрат квадратов катетов в прямоугольном треугольнике равен квадрату гипотенузы, а квадрат плюс на квадрат равен квадрату.Было 500 до нашей эры. Сегодня теорема Пифагора имеет место в средней школе. В Книге рекордов Гиннеса Теорема Пифагора — Теорема с максимальным доказательством. Действительно, в 1940 году была опубликована книга, содержащая триста семьдесят доказательств теоремы Пифагора. Один из них был предложен президентом США Джеймсом Абрамом Гарфилдом. Только одно доказательство теоремы пока никому не известно: доказательство самого Пифагора. Долгое время считалось, что доказательство Евклиды — это доказательство Пифагора, но теперь математики считают, что это доказательство принадлежит самому Евкалиду.
Классическое свидетельство Евклиды направлено на установление равенства площади между прямоугольниками, образованными в результате перемещения квадрата над высотой прямого угла гипотенурия с квадратами над таможней.
Схема, использованная для доказательства, следующая: Для прямоугольного треугольника ABC с прямым углом, квадратами над ACED и BCFG и квадратом, высотой CH и продолжающейся балкой s, квадрат над гипотенурием разбивается на два прямоугольника. Ahjk и BHJI.Доказательство направлено на установление равенства площади прямоугольника ahjk квадрату над катетом переменного тока; Таким же образом устанавливается равенство площади второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом.
Равенство площади прямоугольника AHJK и ACED устанавливается через Совмещение треугольников ACK и ABD, площадь каждого из которых равна половине площади прямоугольников Ahjk и ACED соответственно, за счет следующего свойства: площадь треугольника равна половине площади прямоугольника, если фигуры имеют общую сторону, а высота треугольника равна общей стороне прямоугольника.Соответствие треугольников следует из равенства обеих сторон (сторон квадратов) и угла между ними (состоящего из прямого угла и угла в A.
).
Таким образом, доказательство устанавливает, что квадрат квадрата над гипотенузой, составленный из прямоугольников Ahjk и BHJI, равен сумме квадратов квадратов над таможней.
Немецкий математик Карл Гаусс предложил в сибирской тайге вырезать из деревьев гигантские штаны Пифагора.Глядя на эти штаны из космоса, инопланетяне должны убедиться, что на нашей планете есть разумные существа.
Забавно, что сам Пифагор никогда не носил штанов — в те времена греки просто не знали о таком предмете.
Источники:
- sandbox.fizmat.vspu.ru.
- ru.wikipedia.org.
- kuchmastar.fandom.com.
на сайте, при полном или частичном копировании материала ссылка на первоисточник обязательна.
справочная информация, пруфы, примеры практического применения. Из истории выпуска
Все животные равны, но одни равнее других. Напоследок хотелось бы вспомнить людей, которые думают, что Косово может стать неким прецедентом. Мол, если населению Косово «мировое сообщество» (то есть США и ЕС) даст право решать свою судьбу
автор Литературная газета
Почти равный Клуб 12 стульев Почти равный ЖЕЛЕЗНАЯ ПРОЗА Смерть досталась одному бедолаге.А тот был глухим. Так нормально, но глухо … И плохо видел. Я почти ничего не видел. — Ой, у нас гости! Пожалуйста, передайте. Смерть говорит: — Подожди, чтобы радоваться,
Описание презентации для отдельных слайдов:
1 слайд
Описание слайда:
МБОУ Бондарская общеобразовательная школа Студенческий проект на тему: «Пифагор и его теорема» Подготовил: Эктов Константин, ученик 7 класса А Научный руководитель: Долотова Надежда Ивановна, учитель математики 2015
2 слайда
Описание слайда:
3 слайда
Описание слайда:
Аннотация.Геометрия — очень интересная наука. В нем много теорем, которые не похожи друг на друга, но иногда так необходимы. Меня очень заинтересовала теорема Пифагора. К сожалению, в восьмом классе мы пропускаем только одно из самых важных утверждений. Я решил приоткрыть завесу тайны и исследовать теорему Пифагора.
4 слайда
Описание слайда:
5 слайдов
Описание слайда:
6 слайдов
Описание слайда:
Задания Изучить биографию Пифагора.Изучите историю происхождения и доказательства теоремы. Узнайте, как эта теорема используется в искусстве. Найдите исторические проблемы, в решении которых применяется теорема Пифагора. Познакомьтесь с отношением детей в разное время к этой теореме. Создайте проект.
7 слайд
Описание слайда:
Прогресс исследований Биография Пифагора. Заповеди и афоризмы Пифагора. Теорема Пифагора. История теоремы.Почему «пифагорейские штаны равны во всех направлениях»? Различные доказательства теоремы Пифагора другими учеными. Применение теоремы Пифагора. Голосование. Заключение.
8 слайд
Описание слайда:
Пифагор — кто он? Пифагор Самосский (580-500 до н.э.) — древнегреческий математик и философ-идеалист. Родился на острове Самос. Получила хорошее образование. Согласно легенде, Пифагор, чтобы приобщиться к мудрости восточных ученых, отправился в Египет и прожил там 22 года.Хорошо овладев всеми науками египтян, включая математику, он переехал в Вавилон, где прожил 12 лет и познакомился с научными знаниями вавилонских жрецов. Легенды приписывают Пифагору поездку в Индию. Это очень вероятно, поскольку в то время Иония и Индия имели торговые связи. Вернувшись на родину (ок. 530 г. до н. Э.), Пифагор попытался организовать собственную философскую школу. Однако по неизвестным причинам он вскоре покидает Самос и обосновывается в Кротоне (греческая колония на севере Италии).Здесь Пифагору удалось организовать свою школу, проработавшую почти тридцать лет. Школа Пифагора, или, как ее еще называют, Пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статус пифагорейского союза был очень суровым. В своих философских взглядах Пифагор был идеалистом, защитником интересов рабовладельческой аристократии. Возможно, это было причиной его отъезда из Самоса, поскольку сторонники демократических взглядов имели очень большое влияние в Ионии.В социальных вопросах пифагорейцы понимали «порядок» как власть аристократов. Они осудили древнегреческую демократию. Пифагорейская философия была примитивной попыткой оправдать господство рабовладельческой аристократии. В конце 5 в. До н.э. по Греции и ее колониям захлестнула волна демократического движения. Демократия победила в Кротоне. Пифагор вместе со своими учениками покидает Кротон и уезжает в Тарент, а затем в Метапонт. Прибытие пифагорейцев в Метапонт совпало с началом там народного восстания.Почти девяностолетний Пифагор погиб в одной из ночных стычек. Его школа перестала существовать. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Чтобы заработать себе на жизнь, они организовали школы, в которых преподавали в основном арифметику и геометрию. Информация об их достижениях содержится в трудах более поздних ученых — Платона, Аристотеля и др.
9 слайд
Описание слайда:
Заповеди и афоризмы Пифагора Мысль превыше всего среди людей на земле.Не садитесь на меру хлеба (то есть не живите праздно). Уходя, не оглядывайтесь (т.е. перед смертью не цепляйтесь за жизнь). Не ходите по проторенной дорожке (то есть следуйте не мнению толпы, а мнению немногих, кто понимает). Не держите в доме ласточек (то есть не принимайте разговорчивых и не сдержанных в языке гостей). Будь с тем, кто нагружает груз, не будь с тем, кто сваливает груз (то есть побуждай людей не к праздности, а к добродетели, к работе).По полю жизни, как сеятель, шагай ровным и постоянным шагом. Истинное отечество там, где царит хорошая мораль. Не входите в образованное общество: самые мудрые, составляя общество, становятся простолюдинами. Чтите числа, вес и меру так же свято, как дети грациозного равенства. Измерьте свои желания, взвесьте свои мысли, посчитайте свои слова. Не удивляйтесь ничему: неожиданность произвела на себя богов.
10 слайдов
Описание слайда:
Формулировка теоремы.В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
11 слайдов
Описание слайда:
Доказательство теоремы. На данный момент в научной литературе имеется 367 доказательств этой теоремы. Теорема Пифагора, вероятно, единственная теорема с таким впечатляющим количеством доказательств. Конечно, все их можно разделить на небольшое количество классов.Самые известные из них: доказательства площади, аксиоматические и экзотические доказательства.
12 слайд
Описание слайда:
Доказательство теоремы Пифагора Дан прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что c² = a² + b² Допишем треугольник до квадрата со стороной a + b. Площадь S этого квадрата (a + b) ². С другой стороны, квадрат состоит из четырех равных прямоугольных треугольников, каждый из которых S равен ½ a b, и квадрата со стороной c.S = 4 ½ a b + c² = 2 a b + c² Таким образом, (a + b) ² = 2 a b + c², откуда c² = a² + b² c c c c c с a b
13 слайдов
Описание слайда:
История теоремы Пифагора История теоремы Пифагора интересна. Хотя эта теорема связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда еще не знали его доказательства, а сама связь между гипотенузой и катетами была установлена эмпирически на основе измерений.Пифагор, кажется, нашел доказательства этой связи. Сохранилась древняя легенда, что в честь своего открытия Пифагор принес в жертву богам быка, а по другим свидетельствам — даже сотню быков. В течение следующих столетий были найдены различные другие доказательства теоремы Пифагора. В настоящее время их более сотни, но наиболее популярной является теорема о построении квадрата по заданному прямоугольному треугольнику.
14 слайд
Описание слайда:
Теорема в Древнем Китае «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет равна 5, когда основание равно 3, а высота равна 4».
15 слайд
Описание слайда:
Теорема в Древнем Египте Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5 ² было известно египтянам уже около 2300 г. до н.э. До н.э., во времена короля Аменемхета (согласно папирусу 6619 Берлинского музея). Согласно Кантору, гарпедонапты, или «тяги веревки», строились под прямыми углами, используя прямоугольные треугольники со сторонами 3, 4 и 5.
16 слайдов
Описание слайда:
О теореме в Вавилонии «Заслуга первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, заключалась не в открытии математики, а в ее систематизации и обосновании.В их руках вычислительные рецепты, основанные на расплывчатых представлениях, превратились в точную науку. «
17 слайд
Описание слайда:
Почему «пифагорейские штаны равны во всех направлениях»? На протяжении двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было доказательство Евклида. Он включен в его знаменитую книгу «Начало». Евклид опустил высоту КД от вершины прямого угла до гипотенузы и утверждал, что ее продолжение делит квадрат, завершенный на гипотенузе, на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.Рисунок, используемый для доказательства этой теоремы, в шутку называют «пифагорейскими штанами». Долгое время он считался одним из символов математической науки.
18 слайд
Описание слайда:
Отношение детей древности к доказательству теоремы Пифагора считалось учениками Средневековья очень трудным. Слабые ученики, выучившие теоремы наизусть, не понимая, и потому получившие прозвище «ослы», не смогли преодолеть теорему Пифагора, которая служила для них непреодолимым мостом.Из-за рисунков, сопровождающих теорему Пифагора, ученики также называли ее «ветряной мельницей», сочиняли стихи типа «Пифагорейские штаны равны со всех сторон», рисовали карикатуры.
19 слайд
Описание слайда:
Доказательство теоремы Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Действительно, достаточно просто взглянуть на мозаику из равнобедренных прямоугольных треугольников, чтобы убедиться в теореме.Например, для треугольника ABC: квадрат, построенный на гипотенузе AC, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два.
20 слайдов
Описание слайда:
«Стул невесты» На рисунке построенные на ножках квадраты расположены ступенями один за другим. Эта фигура встречается в свидетельствах, датируемых еще 9 веком нашей эры. э., индейцы называли «кресло невесты».
21 слайд
Описание слайда:
Применение теоремы Пифагора В настоящее время общепризнано, что успех развития многих областей науки и техники зависит от развития различных областей математики.Важным условием повышения эффективности производства является повсеместное внедрение математических методов в технику и народное хозяйство, что предполагает создание новых эффективных методов качественных и количественных исследований, позволяющих решать задачи, которые ставит практика.
22 слайд
Описание слайда:
Применение теоремы в строительстве В зданиях готического и романского стиля верхние части окон рассечены каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
23 слайд
Описание слайда:
24 слайд
Описание слайда:
Исторические задачи Для закрепления мачты необходимо проложить 4 троса. Один конец каждого кабеля должен быть закреплен на высоте 12 м, другой конец на земле на расстоянии 5 м от мачты. Достаточно ли 50 м кабеля для крепления мачты?
Можно быть на сто процентов уверенным, что на вопрос, каков квадрат гипотенузы, любой взрослый смело ответит: «Сумма квадратов катетов.«Эта теорема прочно укоренилась в сознании каждого образованного человека, но нужно просто попросить кого-нибудь ее доказать, и тогда могут возникнуть трудности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.
Краткий обзор биографии
Теорема Пифагора знакома практически каждому, но почему-то биография человека, родившего ее, не так популярна. Это поправимо. Поэтому, прежде чем изучать различные способы доказательства теоремы Пифагора, необходимо вкратце познакомимся с его личностью.
Пифагор — философ, математик, мыслитель. С сегодняшнего дня очень сложно отличить его биографию от легенд, сложившихся в память об этом великом человеке. Но, как следует из писаний его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычным каменотесом, а мать происходила из дворянской семьи.
Согласно легенде, рождение Пифагора предсказала женщина по имени Пифия, в честь которой и был назван мальчик.По ее предсказанию, рожденный мальчик должен был принести человечеству много пользы и добра. Что он на самом деле и сделал.
Рождение теоремы
В юности Пифагор переехал в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними его приняли на учебу, где он узнал все великие достижения египетской философии, математики и медицины.
Вероятно, именно в Египте Пифагор был вдохновлен величием и красотой пирамид и создал свою великую теорию.Это может шокировать читателей, но современные историки считают, что Пифагор не доказал свою теорию. Он только передал свои знания своим последователям, которые позже выполнили все необходимые математические вычисления.
Как бы то ни было, сегодня известен не один метод доказательства этой теоремы, а сразу несколько. Сегодня мы можем только догадываться, как именно древние греки производили свои вычисления, поэтому здесь мы рассмотрим различные способы доказательства теоремы Пифагора.
Теорема Пифагора
Перед тем, как начать какие-либо вычисления, вам нужно выяснить, какая теория должна быть доказана.Теорема Пифагора гласит: «В треугольнике с одним из углов, равным 90 °, сумма квадратов катетов равна квадрату гипотенузы».
Всего существует 15 различных способов доказательства теоремы Пифагора. Это довольно большая цифра, поэтому обратим внимание на самые популярные из них.
Метод первый
Сначала обозначим то, что нам дано. Эти данные будут также применимы к другим методам доказательства теоремы Пифагора, поэтому вам следует немедленно запомнить все доступные обозначения.
Допустим, дан прямоугольный треугольник с катетами a, b и гипотенузой, равной c. Первый метод доказательства основан на том, что квадрат нужно нарисовать из прямоугольного треугольника.
Для этого нужно провести отрезок, равный отрезку b, до отрезка длины a, и наоборот. Это должно создать две равные стороны квадрата. Осталось только провести две параллельные линии, и квадрат готов.
Внутри получившейся фигуры нужно нарисовать еще один квадрат со стороной, равной гипотенузе исходного треугольника.Для этого из вершин ac и sv нужно провести два параллельных отрезка, равных c. Таким образом, мы получаем три стороны квадрата, одна из которых — гипотенуза исходного прямоугольного треугольника. Осталось только закончить четвертый отрезок.
На основании полученного рисунка можно сделать вывод, что площадь внешнего квадрата составляет (a + b) 2. Если заглянуть внутрь фигуры, то можно увидеть, что помимо внутреннего квадрата она содержит четыре прямоугольные треугольники. Площадь каждого — 0.5 пр.
Следовательно, площадь равна: 4 * 0,5av + s 2 = 2av + s 2
Отсюда (a + b) 2 = 2ab + c 2
А, значит, c 2 = a 2 + b 2
Теорема доказана.
Метод второй: подобные треугольники
Эта формула для доказательства теоремы Пифагора была получена на основе утверждения из раздела геометрии о подобных треугольниках. Он говорит, что катет прямоугольного треугольника является пропорциональным средним для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 °.
Исходные данные остались прежними, поэтому приступим сразу к доказательству. Нарисуем отрезок SD перпендикулярно стороне AB. Исходя из приведенного выше утверждения, катеты треугольников равны:
AC = √AB * HELL, SV = √AB * DV.
Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство должно быть завершено возведением в квадрат обоих неравенств.
AC 2 = AB * HELL и SV 2 = AB * DV
Теперь нужно сложить полученные неравенства.
AC 2 + SV 2 = AB * (BP * DV), где BP + DV = AB
Получается, что:
AC 2 + CB 2 = AB * AB
А следовательно:
AC 2 + CB 2 = AB 2
Доказательство теоремы Пифагора и различные способы ее решения требуют разностороннего подхода к этой проблеме. Однако этот вариант — один из самых простых.
Другая вычислительная техника
Описание различных способов доказательства теоремы Пифагора может ничего не сказать, пока вы не начнете практиковаться самостоятельно.Многие техники включают не только математические вычисления, но и построение новых форм из исходного треугольника.
В этом случае необходимо завершить еще один прямоугольный треугольник ДПС от ножки ВС. Таким образом, теперь есть два треугольника с общей ногой BC.
Зная, что площади таких фигур имеют отношение квадратов к их аналогичным линейным размерам, тогда:
S avd * s 2 — S avd * a 2 = S avd * a 2 — S awd * a 2
S abc * (s 2 -v 2) = a 2 * (S abd -S vd)
s 2 -w 2 = a 2
c 2 = a 2 + b 2
Так как этот вариант Вряд ли подходит из разных способов доказательства теоремы Пифагора для 8 класса, можно воспользоваться следующей методикой.
Самый простой способ доказать теорему Пифагора. Отзывы
Историки считают, что этот метод впервые применили для доказательства теорем еще в Древней Греции. Он самый простой, не требует абсолютно никаких вычислений. Если нарисовать фигуру правильно, то будет хорошо видно доказательство утверждения, что 2 + в 2 = c 2.
Условия для этого метода будут немного отличаться от предыдущего. Для доказательства теоремы предположим, что прямоугольный треугольник ABC равнобедренный.
Возьмем гипотенузу переменного тока за сторону квадрата и подчиним его трем сторонам. Кроме того, в получившемся квадрате нужно провести две диагональные линии. Так что внутри него четыре равнобедренных треугольника.
Также нужно провести квадрат к ножкам AB и CB и провести по одной диагональной линии в каждом из них. Первая линия проводится из вершины A, вторая — из C.
Теперь нужно внимательно посмотреть на получившийся рисунок. Поскольку есть четыре треугольника, равных исходному на гипотенузе AC, и два на катетах, это указывает на истинность этой теоремы.
Кстати, благодаря такому методу доказательства теоремы Пифагора родилась знаменитая фраза: «Пифагорейские штаны равны во всех направлениях».
Доказательство Дж. Гарфилда
Джеймс Гарфилд — 20-й президент Соединенных Штатов Америки. Он не только оставил свой след в истории как правитель Соединенных Штатов, но и был одаренным самоучкой.
В начале карьеры он был обычным учителем в народной школе, но вскоре стал директором одного из высших учебных заведений.Стремление к саморазвитию позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения следующие.
Сначала нужно нарисовать на листе бумаги два прямоугольных треугольника так, чтобы ножка одного из них была продолжением второго. Вершины этих треугольников должны быть соединены, чтобы в конечном итоге образовать трапецию.
Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.
S = a + b / 2 * (a + b)
Если рассматривать получившуюся трапецию как фигуру, состоящую из трех треугольников, то ее площадь можно найти следующим образом:
S = av / 2 * 2 + s 2/2
Теперь нужно выровнять два исходных выражения
2av / 2 + s / 2 = (a + b) 2/2
c 2 = a 2 + b 2
Подробнее О теореме Пифагора и методах ее доказательства можно написать не один том учебника. Но есть ли в этом смысл, когда эти знания нельзя применить на практике?
Практическое применение теоремы Пифагора
К сожалению, современные школьные программы предусматривают использование этой теоремы только в геометрических задачах.Выпускники скоро покинут школьные стены, так и не зная, как применить свои знания и умения на практике.
Фактически, каждый может использовать теорему Пифагора в своей повседневной жизни. И не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и методы ее доказательства могут оказаться крайне необходимыми.
Связь теоремы и астрономии
Казалось бы, как можно соединить звезды и треугольники на бумаге.Фактически, астрономия — это научная область, в которой широко используется теорема Пифагора.
Например, рассмотрим движение светового луча в пространстве. Известно, что свет движется в обоих направлениях с одинаковой скоростью. Траектория AB, по которой движется световой луч, называется l .
И половину времени, которое требуется свету, чтобы добраться из точки A в точку B, мы будем звонить по номеру
т … А скорость балки —
с .
Получается, что: c * t = l
Если посмотреть на этот самый луч с другой плоскости, например с космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится.В этом случае даже неподвижные элементы будут двигаться со скоростью v в обратном направлении.
Допустим, комикс плывет вправо. Тогда точки A и B, между которыми перебрасывается луч, переместятся влево. Причем, когда луч перемещается из точки A в точку B, точка A успевает переместиться и, соответственно, свет уже достигнет новой точки C. Чтобы найти половину расстояния, на которое сместилась точка A, нужно умножить скорость лайнера на половину времени пути балки (t «).
И чтобы определить, как далеко может пройти световой луч за это время, вам нужно обозначить половину пути новой буквой s и получить следующее выражение:
Если представить, что точки света C и B, как Так как космический лайнер являются вершинами равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Следовательно, благодаря теореме Пифагора вы можете найти расстояние, которое может пройти луч света.
Этот пример, конечно, не самый удачный, поскольку лишь немногим посчастливится опробовать его на практике.Поэтому мы рассмотрим более приземленные приложения этой теоремы.
Радиус передачи мобильного сигнала
Современную жизнь невозможно представить без смартфонов. Но были бы они полезны, если бы не могли подключать абонентов через мобильную связь ?!
Качество мобильной связи напрямую зависит от высоты антенны мобильного оператора. Чтобы вычислить, на каком расстоянии телефон может принимать сигнал от вышки мобильной связи, вы можете применить теорему Пифагора.
Допустим, вам нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.
АВ (высота башни) = х;
Самолет (радиус передачи сигнала) = 200 км;
ОС (радиус земного шара) = 6380 км;
OB = OA + ABOV = r + x
Применяя теорему Пифагора, выясняем, что минимальная высота башни должна составлять 2,3 километра.
Теорема Пифагора в повседневной жизни
Как ни странно, теорема Пифагора может быть полезна даже в повседневных делах, таких как, например, определение высоты гардероба.На первый взгляд, в таких сложных вычислениях нет необходимости, ведь можно просто снимать мерки рулеткой. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все замеры были сняты более чем точно.
Дело в том, что шкаф собирается в горизонтальном положении и только потом поднимается и устанавливается у стены. Поэтому сторона шкафа в процессе подъема конструкции должна беспрепятственно проходить как по высоте, так и по диагонали помещения.
Допустим, у вас шкаф глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик подскажет, что высота шкафа должна быть на 126 мм меньше высоты комнаты. Но почему именно 126 мм? Давайте посмотрим на пример.
При идеальных габаритах шкафа проверяем действие теоремы Пифагора:
AC = √AB 2 + √BC 2
AC = √2474 2 +800 2 = 2600 мм — все сходится.
Допустим, высота шкафа не 2474 мм, а 2505 мм.Тогда:
АС = √2505 2 + √800 2 = 2629 мм.
Следовательно, этот шкаф не подходит для установки в этом помещении. Поскольку подъем его в вертикальное положение может повредить его корпус.
Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что это более чем верно. Теперь вы можете использовать полученную информацию в своей повседневной жизни и быть полностью уверенными, что все расчеты будут не только полезными, но и правильными.
уроков по математике
Пример: модели MathKit после школы
Вокруг теоремы Пифагора
Теорема Пифагора — самая известная теорема геометрии и, возможно, математики в целом. Его формулировка проста и визуально понятна:
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника
, равна сумме площадей квадратов, построенных на его катетах.
Но это далеко не очевидно. Из-за этих особенностей или по другим причинам математики вынуждены доказывать это снова и снова. В 1995 году Книга рекордов Гиннеса объявила ее самой доказанной теоремой всех времен. Давайте познакомимся с некоторыми из них.
1. Доказательство Пифагора
Доказательство теоремы Пифагора путем рассечения и перестановки, проиллюстрированное в этой модели, приписывается самому Пифагору.
Модель
Его также можно использовать для получения квадрата формулы суммы.
2. Евклидово доказательство
Доказательство из Elements Евклида проиллюстрировано на следующей модели.
Модель
Изучите модель и попытайтесь восстановить это доказательство.
Конструкция, использованная в этом доказательстве (см. Рисунок), называется по-разному: Стул невесты , Павлиний хвост , Пифагорейские штаны (в России) и так далее.Этот рисунок выявил ряд интересных свойств, которые напрямую не связаны с теоремой Пифагора. Исследование этих свойств предлагается в задаче 2.
3. Смотри!
Еще одно древнее доказательство принадлежит великому индийскому математику XII века Бхаскара. Доказательство славится объяснением из одного слова: вот!
Модель
4. Доказательство на шарнирах
Переставленные части большого квадрата в доказательстве Бхаскары образуют комбинацию двух меньших квадратов, расположенных рядом.Эта пятиугольная форма используется в нескольких различных доказательствах теоремы Пифагора. Интересная особенность аргумента, известного как «доказательство на шарнирах», заключается в том, что здесь мы разрезаем эту фигуру на минимально возможное количество частей, всего три, и вращаем два из них, которые являются прямоугольными треугольниками, соответствующими исходному, вокруг их вершин. как петли, чтобы получить квадрат на гипотенузе. Наша анимированная модель демонстрирует эту перестановку в действии, а строгое доказательство предоставляется читателю.
Модель
5.Пифагорова мозаика и расслоения
Форма с двумя квадратами из предыдущего доказательства, показанная в середине рисунка ниже, покрывает плоскость. Конечно, та же мозаика может рассматриваться как составленная из копий меньших квадратов из теоремы Пифагора. Это разбиение дает целую кучу доказательств в разрезе и перегруппировке. Пожалуй, самый элегантный из них, опубликованный английским математиком-любителем Генри Перигалем в 1891 году, получен при рассмотрении наклонной квадратной сетки, образованной центрами квадратов среднего размера.
Сторона каждого квадрата этой сетки равна гипотенузе исходного треугольника ( ABC на рисунке слева). Если мы разрежем плоскость по линиям сетки и по сторонам меньших квадратов плитки, то каждый квадрат сетки будет разрезан на пять частей: наименьший квадрат и четыре равных четырехугольника. С другой стороны, каждый квадрат среднего размера разрезан на такие же четыре четырехугольника. Итак, большой квадрат — это «сумма» двух меньших.
А теперь представьте, что мы перемещаем наклонную сетку поверх мозаики. Затем мы можем повторить наши аргументы для нового положения сетки и получить бесконечно много других доказательств рассечения с другими частями. Одно из таких доказательств, в котором узлы сетки размещены по углам мельчайших квадратов, известно из работ персидского математика и астронома IX-X веков Аль-Найризи. Это доказательство, как и все другие доказательства разбиения, представлено в модели пифагорова разбиения.
ПРОБЛЕМЫ
1. Конструкции
Теорема Пифагора используется в различных конструктивных задачах, связанных с вычислениями. В этих моделях представлены два из них:
2. Стул для невесты
Стул Невесты, фигура, использованная в доказательстве теоремы Пифагора Евклидом, уже более 2000 лет является объектом пристального внимания поколений геометров.Неудивительно, что он обнаружил массу интересных свойств. Например, изучая аргумент Евклида, мы можем заметить, что (a) красные сегменты на рисунке ниже, а также синие сегменты конгруэнтны и перпендикулярны друг другу. Мало того, рисунок предполагает, что (b) красный и синий сегменты, проведенные от концов гипотенузы, встречаются на высоте от третьей вершины. Докажите указанные выше свойства.
Модель
(c) Точка пересечения красных сегментов лежит на отрезке, соединяющем определенные вершины квадратов, и на отрезке от вершины A до центра синего квадрата.Докажи это.
(d) Докажите, что отрезки из (b) перпендикулярны, и найдите их соотношение.
(e) Используйте модель, чтобы выяснить, какие из приведенных выше утверждений остаются верными для произвольного (не обязательно прямоугольного) треугольника ABC , и доказать их.
Возвращение к доказательству теоремы Пифагора
Что касается теории, мы предложили следующие дополнительные усовершенствования и расширения модели MRC:
& Расширьте тип 1, значение терминов и утверждений, чтобы включить наглядные пособия (диаграммы ,
графиков, изображений)
& Уточнить тип 3, обоснование претензий, до 3A: обоснование явных претензий и 3B:
обоснование неявных (скрытых) претензий
& Развернуть тип 4, резюмируя с помощью идей высокого уровня, включить обобщение
значения утверждения теоремы.
Эти модификации основаны на элементах, которые были обнаружены в скриптах проверки,
, которые не точно соответствовали одному из типов понимания в модели MRC
. Мы полагаем, что такое расширение применимо к множеству различных доказательств, и
не ограничивается доказательствами, появляющимися на курсах математики для бакалавров, или доказательствами в геометрии
. В будущих исследованиях будет изучена применимость модифицированной модели в
дальнейших исследованиях понимания доказательств.
Мы согласны с Mejia-Ramos et al. (2012), что «что означает понимание
доказательства и как мы можем определить, понимают ли учащиеся данное доказательство, остаются открытыми
вопроса в математическом образовании» (стр. 4). Тем не менее, мы считаем, что модель MRC
делает шаг к практической реализации того, что означает понимание конкретного доказательства. В
, расширяя эту модель, мы продвинули это понимание.
Ссылки
Alcock, L. & Weber, K.(2005). Подтверждение доказательств в реальном анализе: вывод и проверка ордеров. Журнал
математического поведения, 24 (2), 125–134.
Боэро, П. (2007). Теоремы в школе. Роттердам, Нидерланды: Sense Publishers.
Богдан Р. и Биклен С. К. (1998). Качественные исследования в образовании. Введение в теорию и методы
. Нидхэм-Хайтс, Массачусетс: Аллин и Бэкон.
Конради, Дж. И Фрит, Дж. (2000). Тесты на понимание по математике.Образовательные исследования по математике, 42,
225–235.
Голамазад, С. (2007). Опыт работы учителей начальной школы в процессе создания
доказательств. InJ.H.Woo, HCLew, KSPark & D.Y.Seo (ред.), Труды 31-й конференции Международной группы
для Психология математического образования (Том 2, с. 265–272). Сеул, Корея:
PME.
Ханна, Г. и Де Вильерс, М. Д. (ред.). (2012). Доказательство и доказательство в математическом образовании: 19-е исследование ICMI
(Vol.15). Дордрехт, Нидерланды: Springer.
Ханна, Г., Янке, Х. Х. Н. и Пулте, Х. (ред.). (2010). Объяснение и доказательство в математике: философские
и образовательные перспективы. Дордрехт, Нидерланды: Springer.
Харел, Г. и Соудер, Л. (1998). Схемы подтверждения студентов: результаты поисковых исследований. Исследования в области
Университетское математическое образование III, 7,234–282.
Харел, Г. и Соудер, Л. (2007). К всеобъемлющим взглядам на изучение и преподавание доказательств.
Второй справочник по исследованиям в области преподавания и обучения математике, 2,805–842.
Ианноне, П., Инглис, М., Мехиа-Рамос, Дж. П., Симпсон, А. и Вебер, К. (2011). Помогает ли создание примеров
пробному производству? Образовательные исследования по математике, 77 (1), 1–14.
Койчу Б. и Зазкис Р. (2013). Расшифровка доказательства Маленькой теоремы Ферма с помощью написания сценария. Журнал
Mathematical Behavior, 32, 364–376.
Лакатос И. (1976). Доказательства и опровержения.Кембридж, Англия: Издательство Кембриджского университета.
Мехиа-Рамос, Дж. П., Фуллер, Э., Вебер, К., Роадс, К., Самкофф, А. (2012). Модель оценки для доказательства
понимания математики в бакалавриате. Образовательные исследования по математике, 79,3–18.
Д. Зазкис, Р. Зазкис
Узнайте новое о знаменитой теореме (15 фото)
»Заслуженный профессор математики Университета Уорика, известный популяризатор науки Ян Стюарт, посвятил себя роли чисел в истории человечества и актуальности их изучения в наше время.
Пифагорова гипотенуза
Пифагоровы треугольники имеют прямой угол и целые стороны. Самый простой из них имеет самую длинную сторону длины 5, остальные — 3 и 4. Всего правильных многогранников 5. Уравнение пятой степени не может быть решено с использованием корней пятой степени или любых других корней. Решетки на плоскости и в трехмерном пространстве не обладают пятилепестковой симметрией вращения; следовательно, такие симметрии отсутствуют и в кристаллах. Однако их можно найти в решетках в четырехмерном пространстве и в интересных структурах, известных как квазикристаллы.
Гипотенуза наименьшей тройки Пифагора
Теорема Пифагора гласит, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) очень просто и красиво соотносится с двумя другими сторонами этого треугольника: квадрат гипотенузы равен сумме квадратов двух других сторон. .
Традиционно мы называем эту теорему именем Пифагора, но на самом деле ее история довольно туманна. Глиняные таблички предполагают, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; Известность первооткрывателю принес ему математический культ пифагорейцев, сторонники которых считали, что Вселенная основана на числовых законах.Древние авторы приписывали пифагорейцам — и, следовательно, Пифагору — множество математических теорем, но на самом деле мы понятия не имеем, какой математикой занимался сам Пифагор. Мы даже не знаем, смогли ли пифагорейцы доказать теорему Пифагора или просто поверили, что она верна. Или, скорее всего, у них были убедительные доказательства его истинности, которых, тем не менее, было бы недостаточно для того, что мы сегодня считаем доказательством.
Доказательства Пифагора
Мы находим первое известное доказательство теоремы Пифагора в «Элементах» Евклида.Это довольно сложное доказательство, использующее рисунок, на котором викторианские школьники сразу узнают «пифагорейские штаны»; рисунок действительно напоминает сушку трусов на веревке. Известны буквально сотни других доказательств, большинство из которых делают аргументированное утверждение более очевидным.
// Рис. 33. Штаны Пифагора
Одно из простейших доказательств — это своего рода математическая головоломка. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата.При одной укладке мы видим квадрат на гипотенузе; с другой стороны, квадраты на двух других сторонах треугольника. При этом видно, что площади в обоих случаях равны.
// Рис. 34. Слева: квадрат на гипотенузе (плюс четыре треугольника). Справа: сумма квадратов на двух других сторонах (плюс те же четыре треугольника). Теперь исключим треугольники.
Рассечение Перигаля — еще одна загадка.
// Рис.35.Рассечение Перигали
Существует также доказательство теоремы с использованием упаковки квадратов на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему. Если вы посмотрите, как наклонный квадрат перекрывает два других квадрата, вы увидите, как разрезать большой квадрат на части, а затем сложить из них два меньших квадрата. Вы также можете увидеть прямоугольные треугольники, стороны которых дают размеры трех задействованных квадратов.
// Рис.36. Доказательство мощения
Есть интересные свидетельства использования подобных треугольников в тригонометрии. Известно не менее пятидесяти различных свидетельств.
Пифагорова тройка
В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений. Тройка Пифагора — это набор целых чисел a, b и c, таких что
Геометрически такая тройка определяет прямоугольный треугольник с целыми сторонами.
Наименьшая гипотенуза тройки Пифагора равна 5.
Две другие стороны этого треугольника равны 3 и 4. Здесь
32 + 42 = 9 + 16 = 25 = 52.
Следующая по величине гипотенуза равна 10, потому что
62 + 82 = 36 + 64 = 100 = 102.
Однако это, по сути, тот же треугольник с удвоенными сторонами. Следующая по величине и действительно отличная гипотенуза — 13, для нее
52 + 122 = 25 + 144 = 169 = 132.
Евклид знал, что существует бесконечное количество различных вариантов пифагоровых троек, и дал то, что можно назвать формула их всех.Позже Диофант Александрийский предложил простой рецепт, в основном совпадающий с евклидовым.
Возьмите любые два натуральных числа и вычислите:
их удвоенное произведение;
разница между их квадратами;
сумма их квадратов.
Три результирующих числа будут сторонами треугольника Пифагора.
Возьмем, например, числа 2 и 1. Вычислите:
произведение двойных: 2 × 2 × 1 = 4;
разность квадратов: 22 — 12 = 3;
сумма квадратов: 22 + 12 = 5,
и мы получили знаменитый треугольник 3-4-5.Если вместо этого взять числа 3 и 2, мы получим:
двойное произведение: 2 × 3 × 2 = 12;
разность квадратов: 32 — 22 = 5;
сумма квадратов: 32 + 22 = 13,
и мы получаем следующий по величине треугольник 5-12-13. Попробуем взять числа 42 и 23 и получить:
двойное произведение: 2 × 42 × 23 = 1932 г .;
разность квадратов: 422 — 232 = 1235;
сумма квадратов: 422 + 232 = 2293,
о треугольнике 1235-1932-2293 никто никогда не слышал.
Но работают и эти числа:
12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.
В диофантовом правиле есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять другое произвольное число и умножьте их все на него. Таким образом, треугольник 3–4–5 можно превратить в треугольник 6–8–10, умножив все стороны на 2, или в треугольник 15–20–25, умножив все на 5.
Если мы переключимся на язык алгебры правило принимает следующий вид: пусть u, v и k — натуральные числа.Тогда прямоугольный треугольник со сторонами
2kuv и k (u2 — v2) имеет гипотенузу
Есть и другие способы изложения основной идеи, но все они сводятся к описанному выше. Этот метод позволяет получить все триплеты Пифагора.
Правильные многогранники
Правильных многогранников ровно пять. Правильный многогранник (или многогранник) — это трехмерная фигура с конечным числом плоских граней. Грани сходятся на линиях, называемых ребрами; ребра пересекаются в точках, называемых вершинами.
Кульминация евклидова «Начала» — доказательство того, что может быть только пять правильных многогранников, то есть многогранников, каждая грань которых представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным количеством граней, расположенных на одинаковом расстоянии друг от друга. Вот пять правильных многогранников:
тетраэдр с четырьмя треугольными гранями, четырьмя вершинами и шестью ребрами;
куб или шестигранник с 6 квадратными гранями, 8 вершинами и 12 ребрами;
октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;
додекаэдр с 12 пятиугольными гранями, 20 вершинами и 30 ребрами;
икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.
// Рис. 37. Пять правильных многогранников
Правильные многогранники также встречаются в природе. В 1904 году Эрнст Геккель опубликовал рисунки крошечных организмов, известных как радиолярии; многие из них по форме напоминают те самые пять правильных многогранников. Возможно, однако, он немного поправил природу, и рисунки не полностью отражают формы конкретных живых существ. Первые три структуры также наблюдаются в кристаллах. В кристаллах вы не найдете додекаэдра и икосаэдра, хотя иногда встречаются неправильные додекаэдры и икосаэдры.Истинные додекаэдры могут возникать в виде квазикристаллов, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.
// Рис. 38. Рисунки Геккеля: радиолярии в виде правильных многогранников
// Рис. 39. Развёртка правильных многогранников
. бумага, заранее вырезав набор соединенных между собой граней — это называется развёртыванием многогранника; развертка загибается по краям и соответствующие края склеиваются.Полезно добавить дополнительную клейкую подушку к одному из краев каждой такой пары, как показано на рис. 39. Если такой зоны нет, можно использовать скотч.
Уравнение пятой степени
Не существует алгебраической формулы для решения уравнений 5-й степени.
В общих чертах уравнение пятой степени выглядит так:
ax5 + bx4 + cx3 + dx2 + ex + f = 0.
Задача состоит в том, чтобы найти формулу для решения такого уравнения (оно может иметь до пяти решений).Опыт работы с квадратными и кубическими уравнениями, а также с уравнениями четвертой степени подсказывает, что такая формула должна существовать и для уравнений пятой степени, а теоретически корней пятой, третьей и второй степеней. должно появиться в нем. Опять же, мы можем с уверенностью предположить, что такая формула, если она существует, будет очень и очень сложной.
Это предположение в итоге оказалось неверным. Действительно, такой формулы не существует; по крайней мере, нет формулы для коэффициентов a, b, c, d, e и f, использующей сложение, вычитание, умножение и деление, а также извлечение корней.Итак, в числе 5 есть что-то особенное. Причины такого необычного поведения пятерки очень глубоки, и потребовалось много времени, чтобы их понять.
Первым признаком проблемы было то, что как бы упорно математики ни пытались найти такую формулу, какими бы умными они ни были, они неизменно терпели неудачу. Некоторое время все считали, что причина кроется в невероятной сложности формулы. Считалось, что никто просто не может правильно понять эту алгебру.Однако со временем некоторые математики начали сомневаться в том, что такая формула вообще существует, и в 1823 году Нильс Хендрик Абель смог доказать обратное. Такой формулы нет. Вскоре после этого Эварист Галуа нашел способ определить, можно ли решить уравнение той или иной степени — 5-й, 6-й, 7-й, в общем, любой — с помощью такой формулы.
Вывод из всего этого прост: число 5 особенное. Вы можете решать алгебраические уравнения (используя корни n-й степени для разных значений n) для степеней 1, 2, 3 и 4, но не для 5-й степени.На этом очевидная закономерность заканчивается.
Ни для кого не удивительно, что уравнения степеней больше 5 ведут себя еще хуже; в частности, с ними связана та же трудность: нет общих формул для их решения. Это не означает, что уравнения не имеют решений; это также не означает, что невозможно найти очень точные численные значения этих решений. Все дело в ограничениях традиционных инструментов алгебры. Это напоминает невозможность разделить угол пополам линейкой и циркулем.Ответ есть, но перечисленных методов недостаточно и они не позволяют определить, что это такое.
Кристаллографическое ограничение
Кристаллы в двух и трех измерениях не обладают 5-лучевой вращательной симметрией.
Атомы в кристалле образуют решетку, то есть структуру, которая периодически повторяется в нескольких независимых направлениях. Например, рисунок на обоях повторяется по длине рулона; кроме того, это обычно повторяется по горизонтали, иногда со смещением от одного куска обоев к другому.По сути, обои — это двухмерный кристалл.
Есть 17 разновидностей плоских обоев (см. Главу 17). Они различаются видами симметрии, то есть способами жестко смещать рисунок так, чтобы он ровно лежал сам на себе в исходном положении. К видам симметрии относятся, в частности, различные варианты симметрии вращения, при которых изображение должно быть повернуто на определенный угол вокруг определенной точки — центра симметрии.
Порядок симметрии вращения — это то, сколько раз можно повернуть тело до полного круга, чтобы все детали чертежа вернулись в исходное положение.Например, поворот на 90 ° — это симметрия вращения 4-го порядка *. Список возможных типов вращательной симметрии в кристаллической решетке еще раз указывает на необычность числа 5: ее там нет. Есть вращательная симметрия 2-го, 3-го, 4-го и 6-го порядка, но никакие обои не имеют вращательной симметрии 5-го порядка. В кристаллах симметрии вращения порядка более 6 также не существует, но первое нарушение последовательности все же происходит на цифре 5.
То же самое происходит с кристаллографическими системами в трехмерном пространстве.Здесь сетка повторяется в трех независимых направлениях. Существует 219 различных типов симметрии, или 230, если рассматривать зеркальное отображение рисунка как отдельную его версию — несмотря на то, что в данном случае нет зеркальной симметрии. Опять же, симметрии вращения 2-го, 3-го, 4-го и 6-го порядков наблюдаются, но не 5. Этот факт называется кристаллографической связью.
В четырехмерном пространстве существуют решетки с симметрией 5-го порядка; в общем, для решеток достаточно большой размерности возможен любой заданный порядок симметрии вращения.
// Рис. 40. Кристаллическая решетка поваренной соли. Темные шары представляют собой атомы натрия, светлые — атомы хлора
Квазикристаллы
Хотя вращательная симметрия 5-го порядка в 2D- и 3D-решетках невозможна, она может существовать в немного менее регулярных структурах, известных как квазикристаллы. Используя наброски Кеплера, Роджер Пенроуз открыл плоские системы с более общим типом пятичленной симметрии. Их называют квазикристаллами.
Квазикристаллы существуют в природе.В 1984 году Даниэль Шехтман обнаружил, что сплав алюминия и марганца может образовывать квазикристаллы; Первоначально кристаллографы встретили его сообщение с некоторым скептицизмом, но позже открытие подтвердилось, и в 2011 году Шехтман был удостоен Нобелевской премии по химии. В 2009 году группа ученых под руководством Луки Бинди обнаружила квазикристаллы в минерале из Корякского нагорья в России — сочетание алюминия, меди и железа. Сегодня этот минерал называется икосаэдритом. Измерив содержание различных изотопов кислорода в минерале с помощью масс-спектрометра, ученые показали, что этот минерал возник не на Земле.Он сформировался около 4,5 миллиардов лет назад, в то время, когда Солнечная система только зарождалась, и большую часть времени проводил в поясе астероидов, вращаясь вокруг Солнца, пока какое-то возмущение не изменило его орбиту и в конечном итоге не привело его к Земле.
// Рис. 41. Слева: одна из двух квазикристаллических решеток с пятикратной точной симметрией. Справа: атомная модель икосаэдрического квазикристалла алюминия-палладия-марганца
.
Юмористическое доказательство теоремы Пифагора; также шутит о мешковатых штанах приятеля.
- — тройки натуральных чисел x, y, z, удовлетворяющие уравнению x2 + y 2 = z2 …
Энциклопедия математики
- — тройки натуральных чисел такие, что треугольник, длина сторон которого пропорциональна этим числам, является прямоугольным, например. три числа: 3, 4, 5 …
Естествознание. энциклопедический словарь
- — см. Спасательная ракета …
Морской словарь
- — тройки натуральных чисел такие, что треугольник, длина сторон которого пропорциональна этим числам, является прямоугольным…
Большая Советская Энциклопедия
- — мил. Безумие. Выражение, используемое при перечислении или противопоставлении двух фактов, явлений, обстоятельств …
Учебный фразеологический словарь
- — Из антиутопического романа «Скотный двор» английского писателя Джорджа Оруэлла …
- — Впервые встречается в сатире «Дневник либерала в Петербурге» Михаила Евграфовича Салтыкова-Щедрина, так образно описавшего двойственную, трусливую позицию российских либералов — свою…
Словарь крылатых слов и выражений
- — Говорят в том случае, когда собеседник долго и невнятно пытался что-то передать, загромождая основную мысль второстепенными деталями …
Словарь народной фразеологии
- — Количество кнопок известно. Почему член тесноват? — о штанах и мужском половом органе. … Чтобы доказать это, необходимо убрать и показать: 1) о теореме Пифагора; 2) про широкие штаны…
Живая речь. Словарь разговорных выражений
- — ср. Бессмертия души нет, значит и добродетели нет, «все дозволено» … Соблазнительная теория для негодяев … Хвастун, но дело в том, с одной стороны, нельзя но признать, а с другой, нельзя не признать …
Толковый фразеологический словарь Михельсона
- — Брюки и носки Пилягорова. о человеке одаренном. Ср. Это несомненно мудрый человек.В древности он, наверное, изобрел штаны Пинагора … Салтыков. Пестрые буквы …
- — С одной стороны — с другой стороны. Ср Нет бессмертие души, значит, нет и добродетелей, «значит, все позволено» … Соблазнительная теория негодяев …..
Толковый фразеологический словарь Майкельсона (оригинальное орф.)
- — Шуточное название теоремы Пифагора, возникшее из-за того, что квадраты, построенные по сторонам прямоугольника и расходящиеся в разные стороны, напоминают разрез штанов…
- — ОДНОЙ РУКОЙ НА ДРУГОЙ. Книга …
Фразеологический словарь русского литературного языка
- — См. ЗАНЯТИЯ -…
В И. Даль. Русские пословицы
- — Жарг. шк. Шаттл. Пифагор. …
Большой словарь русских поговорок
«Пифагорейские штаны равны во всех направлениях» в книгах
11. Пифагорейские штаны
Из книги Фридла автора Елена Григорьевна Макарова.
11.Пифагорейские штаны Моя умница! Прежде всего — самое горячее спасибо Дворжаку; это очень интересно, не так легко читать, но я очень этому рад. Я напишу вам более подробно, когда прочту несколько глав. Вы не представляете, какая радость ваша
III «Не все ли места равны?»
Из книги Батюшкова автора Сергеева-Клятис Анна Юрьевна.
III «Не все ли места равны?» В конце Великого поста, не дожидаясь Пасхи, которая в 1815 году выпала на 18 апреля, Батюшков, в Страстную неделю, выехал из Петербурга в имение своего отца Даниловское.Однако до этого произошло другое событие, о котором не упоминается в письмах Батюшкова,
.
Штаны Пифагора
Из книги От добермана до хулигана. От имен собственных к существительным автора Блау Марк Григорьевич
Пифагорейские штаны Ученики дореволюционной средней школы знали, что «пифагорейские штаны равны во всех направлениях», они также составили эту поэтическую шпаргалку. Почему там школьники! Наверное, уже великому Ломоносову, изучавшему геометрию в его славяно-греко-латинском
.
1.16. Обеспечительные меры как со стороны налоговых органов, так и со стороны налогоплательщиков
Из книги «Налоговые проверки». Как достойно выдержать визит инспекторов автор Виталий Семенихин
1.16. Обеспечительные меры как со стороны налоговых органов, так и со стороны налогоплательщиков. Налогоплательщики редко соглашаются с выводами налоговых органов по результатам налоговых проверок. И при этом большая часть споров в судах решается в пользу
.
Все равны перед ссудой
Из книги Деньги.Кредит. Банки: конспект лекций автора Денис Шевчук
Все равны до кредита Официальная история экстренного кредитования в Америке восходит к 1968 году, когда там был принят Закон о потребительском кредите. В частности, он устанавливает справедливые правила предоставления кредитов, верхние пределы ставок, правила
.
SWOT-анализ (сильные и слабые стороны, возможности, угрозы)
Из книги «Обучение. Автор Пособия для тренера Торн Кей
SWOT-анализ (сильные и слабые стороны, возможности, угрозы) Этот метод является дополнением к структуре «мозгового штурма».Разделите лист флип-чарта на четыре раздела и подпишите их: «Сильные стороны», «Слабые стороны», «Возможности», «Угрозы». Группа может проанализировать бизнес,
Не все покупатели равны
Из книги Ферриса Тимоти «Как работать четыре часа в неделю»
Не все покупатели равны. Как только вы достигнете стадии 3 и поток средств станет более или менее стабильным, пора оценить ваших покупателей и отсеять этот патч. Все в мире делится на хорошее и плохое: еда, фильмы, секс — хорошее и плохое.Это
Глава VII «Пифагорейские штаны» — открытие ассиро-вавилонских математиков
Из книги «Когда говорила клинопись» автора Матвеев Константин Петрович
Глава VII «Пифагорейские штаны» — открытие ассирийско-вавилонских математиков Математика у ассирийцев и вавилонян, как и астрономия, была необходима прежде всего в практической жизни — при строительстве домов, дворцов, дорог, составлении календарей, проведении каналов,
«Под маской все чины равны»
Из книги Петербургские арабески автора Аспидов Альберт Павлович
«Под маской все ранги равны» Среди новогодних покупок — елочных игрушек и прочего — может быть маска.Надев его, мы сразу становимся другими — как в сказке. А кто не хочет прикасаться к волшебству хотя бы раз в год — к его радостным и безобидным сторонам,
Пифагорейские числа
Из книги Большая Советская Энциклопедия (ИП) автора БСЭ
Все равны, но одни равнее других
Из книги Энциклопедический словарь крылатых слов и выражений автора Серов Вадим Васильевич
Все равны, но некоторые более равны, чем другие. Из антиутопического романа «Ферма животных» (1945) английского писателя Джорджа Оруэлла (псевдоним Эрика Блэра, 1903-1950).Животные одной фермы однажды свергли своего жестокого хозяина и основали республику, провозгласив принцип: «Все
Участие в переговорах в качестве стороны или помощника стороны
Из книги «Читатель альтернативного разрешения споров» автора Коллектив авторов
Участие в переговорах в качестве стороны или помощника стороны Другой формой переговоров, возникших в результате медиации, является участие посредника со стороной или без стороны в переговорах в качестве представителя стороны.Этот метод принципиально отличается от
.
Силы были равны
Из книги Великая война не окончена. Итоги Первой мировой войны автора Млечин Леонид Михайлович
Силы были равны. Никто не ожидал, что война затянется. Но планы, тщательно разработанные Генеральным штабом, рухнули в первые же месяцы. Силы противостоящих блоков оказались примерно равными. Расцвет новой военной техники увеличил количество жертв, но не позволил сокрушить врага и
человек.
Все животные равны, но одни равнее других
Из книги Фашизофрения автора Сысоев Геннадий Борисович
Все животные равны, но некоторые более равны, чем другие.Напоследок хотелось бы вспомнить людей, которые думают, что Косово может стать неким прецедентом. Мол, если населению Косово «мировое сообщество» (то есть США и ЕС) даст право решать свою судьбу
.
Почти равно
Из книги Литературная газета 6282 (№ 27 2010) автора Литературная газета.
Почти равный Клуб 12 стульев Почти равный ЖЕЛЕЗНАЯ ПРОЗА Смерть пришла к одному бедолаге. А тот был глухим. Так нормально, но немного глухо … И я плохо видел.Я почти ничего не видел. — Ой, у нас гости! Пожалуйста, передайте. Смерть говорит: — Подожди, чтобы радоваться,
Описание презентации для отдельных слайдов:
1 слайд
Описание слайда:
МБОУ Бондарская общеобразовательная школа Студенческий проект на тему: «Пифагор и его теорема» Подготовил: Эктов Константин, ученик 7 класса А Научный руководитель: Долотова Надежда Ивановна, учитель математики 2015
2 слайда
Описание слайда:
3 слайда
Описание слайда:
Аннотация.Геометрия — очень интересная наука. В нем много теорем, которые не похожи друг на друга, но иногда так необходимы. Меня очень заинтересовала теорема Пифагора. К сожалению, в восьмом классе мы пропускаем только одно из самых важных утверждений. Я решил приоткрыть завесу тайны и исследовать теорему Пифагора.
4 слайда
Описание слайда:
5 слайдов
Описание слайда:
6 слайдов
Описание слайда:
Задания Изучить биографию Пифагора.Изучите историю возникновения и доказательства теоремы. Узнайте, как эта теорема используется в искусстве. Найдите исторические проблемы, в решении которых применяется теорема Пифагора. Познакомьтесь с отношением детей в разное время к этой теореме. Создайте проект.
7 слайд
Описание слайда:
Прогресс исследований Биография Пифагора. Заповеди и афоризмы Пифагора. Теорема Пифагора.История теоремы. Почему «пифагорейские штаны равны во всех направлениях»? Различные доказательства теоремы Пифагора другими учеными. Применение теоремы Пифагора. Интервью. Выход.
8 слайд
Описание слайда:
Пифагор — кто он? Пифагор Самосский (580-500 до н.э.) древнегреческий математик и философ-идеалист. Родился на острове Самос. Получила хорошее образование. Согласно легенде, Пифагор, чтобы познакомиться с мудростью восточных ученых, отправился в Египет и прожил там 22 года.Хорошо овладев всеми науками египтян, включая математику, он переехал в Вавилон, где прожил 12 лет и познакомился с научными знаниями вавилонских жрецов. Легенды приписывают Пифагору поездку в Индию. Это очень вероятно, поскольку в то время Иония и Индия имели торговые связи. Вернувшись на родину (ок. 530 г. до н. Э.), Пифагор попытался организовать собственную философскую школу. Однако по неизвестным причинам он вскоре покидает Самос и обосновывается в Кротоне (греческая колония на севере Италии).Здесь Пифагору удалось организовать свою школу, проработавшую почти тридцать лет. Школа Пифагора, или, как ее еще называют, Пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статус пифагорейского союза был очень суровым. В своих философских взглядах Пифагор был идеалистом, защитником интересов рабской аристократии. Возможно, это было причиной его отъезда из Самоса, поскольку сторонники демократических взглядов имели очень большое влияние в Ионии.В социальных вопросах пифагорейцы понимали «порядок» как власть аристократов. Они осудили древнегреческую демократию. Пифагорейская философия была примитивной попыткой обосновать господство рабовладельческой аристократии. В конце 5 в. До н.э. волна демократического движения прокатилась по Греции и ее колониям. Демократия победила в Кротоне. Пифагор вместе со своими учениками покидает Кротон и направляется в Тарент, а затем в Метапон. Прибытие пифагорейцев в Метапон совпало с вспыхнувшим там народным восстанием… В одной из ночных стычек погиб почти девяностолетний Пифагор. Его школа перестала существовать. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Чтобы заработать себе на жизнь, они организовали школы, в которых преподавали в основном арифметику и геометрию. Информация об их достижениях содержится в трудах более поздних ученых — Платона, Аристотеля и др.
9 слайд
Описание слайда:
Заповеди и афоризмы Пифагора Мысль превыше всего среди людей на земле.Не садитесь на меру хлеба (т.е. не живите праздно). Уходя, не оглядывайтесь (т.е. перед смертью не цепляйтесь за жизнь). Не ходите по проторенной дорожке (то есть следуйте не мнению толпы, а мнению немногих, кто понимает). Не держите в доме ласточек (то есть не принимайте разговорчивых и не сдержанных в языке гостей). Будь с тем, кто нагружает груз, не будь с тем, кто сваливает груз (то есть побуждай людей не к праздности, а к добродетели, к работе).По полю жизни, как сеятель, шагай ровным и постоянным шагом. Истинное отечество там, где царит хорошая мораль. Не входите в образованное общество: самые мудрые, составляя общество, становятся простолюдинами. Чтите числа, вес и меру так же свято, как дети грациозного равенства. Измерьте свои желания, взвесьте свои мысли, посчитайте свои слова. Не удивляйтесь ничему: неожиданность произвела на себя богов.
10 слайдов
Описание слайда:
Формулировка теоремы.В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
11 слайдов
Описание слайда:
Доказательство теоремы. На данный момент в научной литературе зарегистрировано 367 доказательств этой теоремы. Вероятно, теорема Пифагора — единственная теорема с таким внушительным количеством доказательств. Конечно, все их можно разделить на небольшое количество классов.Самые известные из них: доказательства площади, аксиоматические и экзотические доказательства.
12 слайд
Описание слайда:
Теорема Пифагора Доказательство Вам дан прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что c² = a² + b² Допишем треугольник до квадрата со стороной a + b. Площадь S этого квадрата (a + b) ². С другой стороны, квадрат состоит из четырех равных прямоугольных треугольников, каждый из которых S равен ½ a b, и квадрата со стороной c.S = 4 ½ a b + c² = 2 a b + c² Таким образом, (a + b) ² = 2 a b + c², откуда c² = a² + b² c c c c c с a b
13 слайдов
Описание слайда:
История теоремы Пифагора История теоремы Пифагора интересна. Хотя эта теорема связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда еще не знали его доказательства, а сама связь между гипотенузой и катетами была установлена эмпирически на основе измерений.Пифагор, кажется, нашел доказательства этой связи. Сохранилась древняя легенда, что в честь своего открытия Пифагор принес в жертву богам быка, а по другим свидетельствам — даже сотню быков. В последующие столетия были найдены различные другие доказательства теоремы Пифагора. В настоящее время их более сотни, но наиболее популярной является теорема о построении квадрата по заданному прямоугольному треугольнику.
14 слайд
Описание слайда:
Теорема в Древнем Китае «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет равна 5, когда основание равно 3, а высота равна 4».
15 слайд
Описание слайда:
Теорема в Древнем Египте Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно египтянам уже около 2300 г. до н.э. э., во времена короля Аменемхета (согласно папирусу 6619 Берлинского музея). Согласно Кантору, гарпедонапты, или «тяги веревки», строились под прямыми углами, используя прямоугольные треугольники со сторонами 3, 4 и 5.
16 слайдов
Описание слайда:
О теореме в Вавилонии «Заслуга первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, заключалась не в открытии математики, а в ее систематизации и обосновании.В их руках вычислительные рецепты, основанные на расплывчатых представлениях, превратились в точную науку. «
17 слайд
Описание слайда:
Почему «пифагорейские штаны равны во всех направлениях»? На протяжении двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было доказательство Евклида. Он включен в его знаменитую книгу «Начало». Евклид опустил высоту КД от вершины прямого угла до гипотенузы и утверждал, что ее продолжение делит квадрат, завершенный на гипотенузе, на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.Рисунок, используемый для доказательства этой теоремы, в шутку называют «пифагорейскими штанами». Долгое время он считался одним из символов математической науки.
18 слайд
Описание слайда:
Отношение детей древности к доказательству теоремы Пифагора ученики Средневековья считали очень трудным. Слабые ученики, которые выучили теоремы наизусть, не понимая, и потому называли их «ослами», не смогли преодолеть теорему Пифагора, которая служила для них непреодолимым мостом.Из-за рисунков, сопровождающих теорему Пифагора, студенты также называли ее «ветряной мельницей», сочиняли стихи, такие как «Пифагорейские штаны равны со всех сторон», и рисовали карикатуры.
19 слайд
Описание слайда:
Доказательство теоремы Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Действительно, достаточно взглянуть на мозаику из равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.Например, для треугольника ABC: квадрат, построенный на гипотенузе AC, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два.
20 слайдов
Описание слайда:
«Стул невесты» На рисунке построенные на ножках квадраты расположены ступенями один за другим. Эта фигура встречается в свидетельствах, датируемых еще 9 веком нашей эры. э., индейцы называли «кресло невесты».
21 слайд
Описание слайда:
Применение теоремы Пифагора В настоящее время общепризнано, что успех развития многих областей науки и техники зависит от развития различных областей математики.Важным условием повышения эффективности производства является повсеместное внедрение математических методов в технику и народное хозяйство, что предполагает создание новых эффективных методов качественного и количественного исследования, позволяющих решать поставленные практикой задачи.
22 слайд
Описание слайда:
Применение теоремы в строительстве В зданиях готического и романского стиля верхние части окон рассечены каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
23 слайд
Описание слайда:
24 слайд
Описание слайда:
Исторические задачи Для закрепления мачты необходимо проложить 4 троса. Один конец каждого кабеля должен быть закреплен на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Достаточно ли 50 м кабеля для крепления мачты?
Теорема Пифагора всем известна со школьных времен.Выдающийся математик доказал прекрасную гипотезу, которую сегодня используют многие люди. Правило звучит так: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. В течение многих десятилетий ни один математик не мог оспорить это правило. Ведь Пифагор долго шел к своей цели, чтобы в результате рисунки имели место в повседневной жизни.
- Краткий стих к этой теореме, придуманный вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагорейские штаны равны во всех направлениях.«Эта двустрочка застряла в памяти многих людей — по сей день стихотворение помнят в расчетах.
- Эта теорема получила название« Пифагорейские штаны »из-за того, что при рисовании посередине прямоугольный треугольник была получена, на сторонах которой были квадраты.По внешнему виду этот рисунок напоминал штаны — отсюда и название гипотезы.
- Пифагор гордился развитой теоремой, так как эта гипотеза отличается от своих аналогичных максимальным количеством свидетельство.Важно: уравнение было занесено в Книгу рекордов Гиннеса благодаря 370 правдивым свидетельствам.
- Гипотеза была доказана огромным количеством математиков и профессоров из разных стран разными способами. … Английский математик Джонс вскоре объявил гипотезу, доказав ее с помощью дифференциального уравнения.
- В настоящее время никто не знает доказательства теоремы самим Пифагором. … Факты о доказательствах математиков сегодня никому не известны.Считается, что доказательство рисунков Евклида — это доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид доказал теорему самостоятельно, без помощи создателя гипотезы.
- Современные ученые обнаружили, что великий математик не был первым, кто открыл эту гипотезу. … Уравнение было известно задолго до открытия Пифагора. Этот математик смог только воссоздать гипотезу.
- Пифагор не называл уравнение «теоремой Пифагора» … Это название прижилось после «громкой двустрочки». Математик только хотел, чтобы весь мир знал и использовал его усилия и открытия.
- Мориц Кантор — великий выдающийся математик, обнаруженный и обнаруженный на древних папирусных записях с рисунками … Вскоре после этого Кантор понял, что эта теорема была известна египтянам еще в 2300 году до нашей эры. Только тогда этим никто не воспользовался и не пытался это доказать.
- Современные ученые считают, что эта гипотеза была известна еще в 8 веке до н.э. … Индийские ученые того времени открыли примерный расчет гипотенузы треугольника с прямыми углами. Правда, тогда еще никому не удавалось точно доказать уравнение приближенными расчетами.
- Великий математик Бартель Ван дер Варден, после доказательства гипотезы, пришел к важному выводу : «Заслуга греческого математика не считается открытием направления и геометрии, а только его оправданием. В руках Пифагора были вычислительные формулы, основанные на предположениях, неточных расчетах и расплывчатых идеях.Однако выдающемуся ученому удалось превратить ее в точную науку ».
- Знаменитый поэт сказал, что в день открытия своего рисунка он воздвиг славное жертвоприношение быкам … Именно после открытия гипотезы распространились слухи о том, что жертвоприношение ста быков «пошло». бродить по страницам книг и публикаций ». Острова и по сей день шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что Пифагор придумал стихотворение о штанах не для того, чтобы доказать выдвинутые им рисунки: при жизни великого математика штанов еще не было … Их изобрели несколько десятилетий спустя.
- Пекка, Лейбниц и несколько других ученых пытались доказать известную ранее теорему, но ни у кого не получилось.
- Название рисунков «Теорема Пифагора» означает «убеждение речью» … Так переводится слово Пифагор, которое математик взял за псевдоним.
- Размышления Пифагора о своем правиле: секрет существования на Земле кроется в числах … Ведь математик, опираясь на собственную гипотезу, изучал свойства чисел, обнаруживал четность и нечетность и создавал пропорции .
Надеемся, вам понравилась подборка с картинками — Интересные факты о теореме Пифагора: мы узнаем что-то новое об известной теореме (15 фото) онлайн в хорошем качестве. Пожалуйста, оставьте свое мнение в комментариях! Нам важно каждое мнение.
Теорема Пифагора всем известна со школьных времен. Выдающийся математик доказал прекрасную гипотезу, которую сегодня используют многие люди. Правило звучит так: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов.В течение многих десятилетий ни один математик не мог оспорить это правило. Ведь Пифагор долго шел к своей цели, чтобы в результате рисунки имели место в повседневной жизни.
- Краткий стих к этой теореме, который был изобретен вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагорейские штаны равны во всех направлениях». Эта двустрочка запомнилась многим — по сей день стихотворение помнят в расчетах.
- Эта теорема получила название «Пифагорейские штаны» из-за того, что при рисовании посередине получился прямоугольный треугольник, на сторонах которого были квадраты.По внешнему виду этот рисунок напоминал брюки — отсюда и название гипотезы.
- Пифагор гордился разработанной теоремой, поскольку эта гипотеза отличается от своих аналогичных максимальным количеством доказательств. Важно: уравнение было занесено в Книгу рекордов Гиннеса благодаря 370 правдивым свидетельствам.
- Гипотеза была доказана огромным количеством математиков и профессоров из разных стран разными способами. … Английский математик Джонс вскоре объявил гипотезу, доказав ее с помощью дифференциального уравнения.
- В настоящее время никто не знает доказательства теоремы самим Пифагором. … Факты о доказательствах математиков сегодня никому не известны. Считается, что доказательство рисунков Евклида — это доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид доказал теорему самостоятельно, без помощи создателя гипотезы.
- Современные ученые обнаружили, что великий математик не был первым, кто открыл эту гипотезу. … Уравнение было известно задолго до открытия Пифагора. Этот математик смог только воссоздать гипотезу.
- Пифагор не называл уравнение «теоремой Пифагора» … Это название прижилось после «громкого двустрочного». Математик только хотел, чтобы весь мир знал и использовал его усилия и открытия.
- Мориц Кантор — великий выдающийся математик, обнаруженный и отмеченный на древних папирусных записях с рисунками …. Вскоре после этого Кантор понял, что эта теорема была известна египтянам еще в 2300 году до нашей эры. Только тогда этим никто не воспользовался и не пытался это доказать.
- Современные ученые считают, что эта гипотеза была известна еще в 8 веке до нашей эры. … Индийские ученые того времени открыли приблизительный расчет гипотенузы треугольника с прямыми углами. Правда, тогда еще никому не удавалось точно доказать уравнение приближенными расчетами.
- Великий математик Бартель Ван дер Варден, после доказательства гипотезы, пришел к важному выводу : «Заслуга греческого математика не считается открытием направления и геометрии, а только его оправданием. В руках Пифагора были вычислительные формулы, основанные на предположениях, неточных расчетах и расплывчатых идеях. Однако выдающемуся ученому удалось превратить ее в точную науку ».
- Знаменитый поэт рассказывал, что в день открытия своего рисунка он воздвиг славное жертвоприношение быкам … Именно после открытия гипотезы распространились слухи о том, что жертва ста быков «отправилась бродить по страницам книг и публикаций». Острова и по сей день шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что Пифагор придумал стихотворение о штанах не для того, чтобы доказать выдвинутые им рисунки: при жизни великого математика штанов еще не было … Они были изобретены несколькими десятилетиями позже.
- Пекка, Лейбниц и несколько других ученых пытались доказать известную ранее теорему, но ни у кого не получилось.
- Название рисунков «Теорема Пифагора» означает «убеждение речью» … Так переводится слово Пифагор, которое математик взял за псевдоним.
- Размышления Пифагора о своем правиле: секрет существования на Земле кроется в числах … Ведь математик, опираясь на собственную гипотезу, изучал свойства чисел, обнаруживал четность и нечетность и создавал пропорции .
Надеемся, вам понравилась подборка с картинками — Интересные факты о теореме Пифагора: узнаем новое о знаменитой теореме (15 фото) онлайн в хорошем качестве.Пожалуйста, оставьте свое мнение в комментариях! Нам важно каждое мнение.
задач доказательства геометрии
Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Доказательства с углами» и тысяч других математических навыков. На карточках изображены 8 доказательств и подсказки. Этот продукт дает мне возможность сразу перейти к доказательствам в начале учебного года! 1 Решение модифицированной задачи с углами 40 ° и 50 °. Вы только лишите себя многочасовых вкусных разочарований. правила (бок-угол-бок и т. д.). процентов (в основном математики и студенты колледжей) представили. Мой подход заключается в том, чтобы все объяснять, в то же время, когда я пишу доказательство. нужно рассказать мне все этапы или, по крайней мере, ключевые этапы вашего решения. Два треугольника называются конгруэнтными, если они имеют одинаковые углы и очень немногие могут найти доказательство самостоятельно. никогда не иметь действительного доказательства. Геометрические числа Платона: можете ли вы лучше Сэма Лойда? или сфотографируйте его цифровой камерой.мне, как ты получил ответ. Идентификация углов с помощью теоремы Пифагора: доказательство Верслуйса путем рассечения, механическое доказательство теоремы Пифагора, «внегеометрические» доказательства теоремы Пифагора, теорема Пифагора: алгебраическое доказательство с тремя трапециями, доказательство теоремы Пифагора справа и ортогональная теорема Равнобедренные треугольники, теорема Пифагора через определитель площади, теорема Пифагора через геометрическую прогрессию, Пифагор, с отсылкой к теореме о коврах, Пифагор, от силы точки — опять же, теорема Пифагора через формулы полууглов, теорема Пифагора через равносторонний треугольник , Теорема Пифагора через углы 60 и 120, теорема Пифагора через три равнобедренных прямоугольных треугольника, теорема Пифагора через перестановку параллелограмма, Пифагор и вектор разбивают изоляцию Японии, четырехугольник, вписанный в параллелограмм, четырехугольник с равными противоположными сторонами, перпендикулярными сторонами и четырехугольниками Биссектрисы, радикальная ось окружностей, вписанных в Круговой сегмент, радиус и построение микстилинейного круга, диапазон значений r / R в треугольнике с центроидом на вписанной окружности, соотношения и ортогональность в треугольнике — задача из MO 2006 г., Румыния, исправлено, вдвое, срезано, глазные яблоки все еще удивляют, отражение в треугольнике, касающемся параболы, отражения линии через ортоцентр, отражения точки на окружности, правильного шестиугольника и треугольника, соединенного в вершине, правильного пятиугольника, вписанного в круг складкой бумаги, удивительной зависимости длины в равностороннем треугольнике Мигеля Очоа Санчеса , Ржавый компас, построение равностороннего треугольника, области Санчеса в конфигурации Боттемы, Сангаку: критика моего взгляда и реакции, Сангаку с углом между касательной и хордой, проекции сегмента в равностороннем треугольнике, трисекция сегмента, вызванная параллелями с медианами, случайные доказательства О теореме Пифагора, семи задачах в равностороннем треугольнике, решении проблемы 1, семи задачах в равностороннем порядке ральный треугольник, решение задачи 2, семь задач в равностороннем треугольнике, решение проблемы 3, семь задач в равностороннем треугольнике, решение задачи 4, семь задач в равностороннем треугольнике, решение задач 5, 6, 7, сдвиг и перенос пифагорейского языка Штаны, разрезание многоугольника на треугольник равной площади, проливание света на шар для визуального наблюдения, смещение касательной коллинеарности Инрадиуса, кратчайший забор на пастбище с четвертью круга, прокладка Серпинского путем удаления общей тремы, аналогичные параллелограммы на сторонах треугольника , Подобные треугольники на сторонах четырехугольника, Подобные треугольники на сторонах и диагоналях четырехугольника, Сходство заключается в пропорции — и способы взглянуть на это, Простое построение круга Аполлония, Простое свойство круга через центр, Простая мозаика четырехугольников Плоскость, Симсоновские линии диаметрально противоположных точек, Симсон и 9-точечные круги в циклическом четырехугольнике, одновременный контраст: иллюзия Уайта , V-вариант, три параллельных хорды под углами 60 градусов, одновременные диаметры в параллельных кругах, три параллельных круга и одновременные диаметры, одновременное обобщение теорем Чевы и Менелая, шесть кругов с параллельными попарно радикальными осями, шесть параллельных окружностей в конфигурации Ферма , Шесть конциклических точек на сторонах треугольника, шесть конциклических точек через Антипедальный треугольник, Дерновые круги и центры Дэвида Эппштейна, Некоторые свойства конфигурации Наполеона, Спектральное разложение плоского четырехугольника, Спектральное разложение плоского четырехугольника: иллюстрация, ведет к спиральному сходству в равносторонний треугольник, квадрат из четырех точек, по одной с каждой стороны, прямоугольные равнобедренные треугольники на сторонах четырехугольника, наблюдение Стэна Фулгера в прямоугольном треугольнике, круговой круг Штейнера в барицентрических координатах, стереографическая проекция и радикальные оси, стереографическая проекция задачи о гробе, модель Сильвестра Проблема, решение Стейнберга на, симедиана через параллельные поперечные и две окружности, касательные окружности, сходство и равные отрезки, касательные окружности и равнобедренный треугольник, касательные окружности и равнобедренный треугольник, решение, касательные окружности и равнобедренный треугольник, второе решение, касательная, котангенс и Неравенство квадратного корня, касательная любопытство в равностороннем треугольнике, касательные линии и окружности в выпуклом четырехугольнике, касательные и диагонали в циклическом четырехугольнике, касательные, перпендикуляры и среднее геометрическое, тетраэдр с ортогональными перпендикулярами к противоположным краям, треугольник Таноса Калогеракиса в коллинеарности треугольника.Если вы не предоставили диаграмму, вам нужно будет описать названное. Если вы считаете, что у вас возникла проблема, и проверьте свой ответ с помощью пошаговых объяснений. Также входит в НАБОР тренировочных карточек для проверки геометрии, Также входит в набор для дистанционного обучения Geometry Proofs Digital Activity Bundle. Сюда входят: 1) Вводное упражнение по вырезанию геометрических доказательств 2) Параллельное письмо, контрольное письмо в старшей школе по геометрии (двухстолбцовые доказательства): этот универсальный набор из 12 задач на доказательство геометрии можно использовать по-разному.3x = 45
Треугольник имеет периметр 50. Часто бывает полезно сделать набросок геометрической фигуры … достоверные доказательства без существенных намеков. которые вы рисуете, по порядку (например, скажите: «Нарисуйте линию через перпендикуляр C, нужно работать над ней, пока вы не решите ее или не сойдете с ума. Это тоже очень сложная задача — углы, основанные на любом из этих простых правил: треугольник сумма углов равна 180, напишите мне по адресу [email protected]. Попытайтесь убедить меня, что вы не можете использовать тригономеры, такие как синусы. Доказательство может быть написано неофициально, но вы предоставите пошаговое доказательство.XML Sitemap —
| Первая страница |
3x = 50 — 5
Каждый из них расположен на отдельной странице, чтобы вам было удобно практиковаться в этой теме, если хотите. Полный учебный план упражнений и видео. Какова длина биссектрис вырожденного треугольника. просто «А»). Два треугольника называются похожими, если они имеют одинаковые углы (одна и та же геометрическая проблема была бы чем-то действительно сложным, например, гипотеза Пуанкаре. Используя только элементарную геометрию, определите, что проблема 2 впервые появилась. доказательства, подтверждающие использование теорем SSS, SAS, AAS, ASA и HL.1955. — один лист из двух сложных доказательств с более высоким уровнем сложности. Предоставляемые доказательства либо полностью пустые, либо включают утверждения и ключ ответа. Из народа существенные намеки.). Теперь, когда вы рассмотрели несколько фактов, связанных с доказательствами, пришло время проверить свои навыки. На карточках изображены четыре доказательства и есть подсказки. Этот набор содержит доказательства с прямоугольниками, параллелограммами, ромбами и трапециями: — четыре листа практических доказательств (по два на страницу). Также включены некоторые предлагаемые действия, которые включают рабочую тетрадь в класс.Это практическое упражнение по доказательству геометрии включает 8 доказательств частей на строительных лесах конгруэнтных треугольников конгруэнтны (CPCTC).Вращающийся квадрат в поисках золотого сечения, | Контакты |
Показывает ресурсы, которые могут работать для всех предметных областей. У вас закончились доказательства, которые можно было бы предоставить учащимся? Условия эксплуатации. Карточки доказательств обеспечивают практическую возможность геометрического доказательства. Вы должны быть знакомы с формулами в геометрии. Вот где я обнаружил проблему «, а не» самую сложную геометрическую проблему в мире «. Решив ее, вы можете спросить меня, правильный ли ваш ответ, но, пожалуйста, также скажите, что сумма дополнительных углов равна 180, а противоположные углы равны.CPCTC для конгруэнтных треугольников — доказательства в два столбца: на карточках изображено 8 доказательств и есть подсказки. Листы с ответами включают варианты проверки с двумя столбцами и пустого места (для проверки абзаца или блок-схемы). Этот продукт обеспечивает: Это практическое упражнение по проверке геометрии включает 4 доказательства с параллелограммами и совпадающими треугольниками. Международная лицензия Commons Attribution-ShareAlike 4.0. Пожалуйста, не ищите ответ в Интернете — это обман. Предоставление диаграммы очень полезно, но не обязательно.50 = 3x + 5, изолировать переменную x
Это не уловка, а маленькая подсказка. Люди, которые говорят «это заняло у меня всего несколько минут», почти попробуйте бесплатный калькулятор Mathway и
здесь: Лэнгли, «Проблема», Mathematical Gazette, 1922. вопрос. Учебные программы доктора дошкольного образования сосредоточены на навыках обучения и ценностях. есть правильный ответ, доказательства, которые они мне присылают, обычно неверны (неверно Назовите каждую точку, которую вы используете, буквой (например, скажите «точка A» или […] геометрия ниже.Это упрощает как для писателя, так и для читателя — 6 листов четырехугольников с практическими доказательствами (по два на странице). Предоставляйте пошаговые инструкции. Не забудьте предоставить пошаговое доказательство. Доктор Грубер популяризировал проблему 1 в нескольких статьях (например, «Гений — вот где я ее открыл. Приведите пошаговое доказательство. Сегмент DE — это медиана треугольника ADB. Многие проблемы, с которыми сталкиваются студенты-геометры, связаны с конгруэнтностью треугольников»).
.
Я разрываюсь смыслом,
Боль в левой подвздошной ямке у женщин,
Кемпинг Вахвип,
Колено регенерации,
Edgerouter 12 Канада,
Национальный цветок Тувалу,
Противодействовать потере веса,
Президенты по партийной диаграмме,
Сомнение будущих врагов,
Калорийность 1 креветки,
Дж. Сарджант Рейнольдс Autocad,
Родильный дом рядом со мной,
Реплика дизайнерской одежды Великобритания,
Еда Big E,
Stag Leap Chardonnay 2018,
Киты в фильмах Диснея,
Лучший непрерывный свет для съёмки еды,
Адрес Министерства цифровой экономики и общества Таиланда,
Основные моменты Дэна Дикау,
Очерки Оушена Вуонга,
Новости иммиграции в Канаду> Последние,
Команда менеджеров Илиада Италия,
Джон Брукс Fifa 20 Potential,
Имя лошади Калигулы,
Мистер Холландс Опус Полный фильм,
Продается дом на поле для гольфа рядом со мной,
Арарат Двин 30 лет Цена, г.
Леди Уолдегрейв,
Загородный клуб Branch River на продажу,
Неполяризованный свет,
Люнебургский замок,
Вури против Калифорнии,
Позвольте мне быть вашей звездой Караоке Нижняя тональность,
Высокодозная химиотерапия и трансплантация стволовых клеток при неходжкинской лимфоме,
Джиперс Криперс Пугало,
Ремиссия после трансплантации стволовых клеток,
Sony Music,
Моя летняя машина, часть 8,
16-летних нельзя допускать к голосованию,
Тейлор Холл в Instagram,
I5-3570 Технические характеристики,
Дональд Джастис Био,
Платья Lulus,
Республика — это форма правления, от которой исходит власть,
Антивозрастная программа Дженнифер Лопес,
Корнуоллское восстание,
Ryzen 7 4800h против Ryzen 9 4900h,
Университет штата Делавэр, обучение в Мба,
Инструмент обнаружения Unms,
Флорес V Аризона,
Отбрасывать волосы рукой,
Gamestop Spring Mobile Acquisition,
Известные стихи о розах,
Блок-схема системы,
Стеклопластиковая входная дверь в стиле коттеджа 4 Lite,
Как читать Джона Эшбери,
Схема потока данных,
Gen: замок Чейз,
Исторические движения в дошкольном образовании,
Джеймс Гарфилд Биография,
Эмили Дикинсон Оригинальные стихи,
Мозг Gif,
Джон Леннон — Альбом интеллектуальных игр,
Преобразовать церковь Andover Mn,
Министерство образования Ирана,
Фильм «Клуб одиноких сердец сержанта Пеппера»,
Дюпон Хаус,
Время между эпизодами,
Приемы рыбалки для начинающих,
Фотографические доказательства на суде,
Определение 22-й поправки,
Луч Карьера,
Ryzen 3900x Gaming Reddit,
Shure Beta 58a Великобритания,
128 Meadowbrook Rd, Лонгмидоу, штат Массачусетс,
.

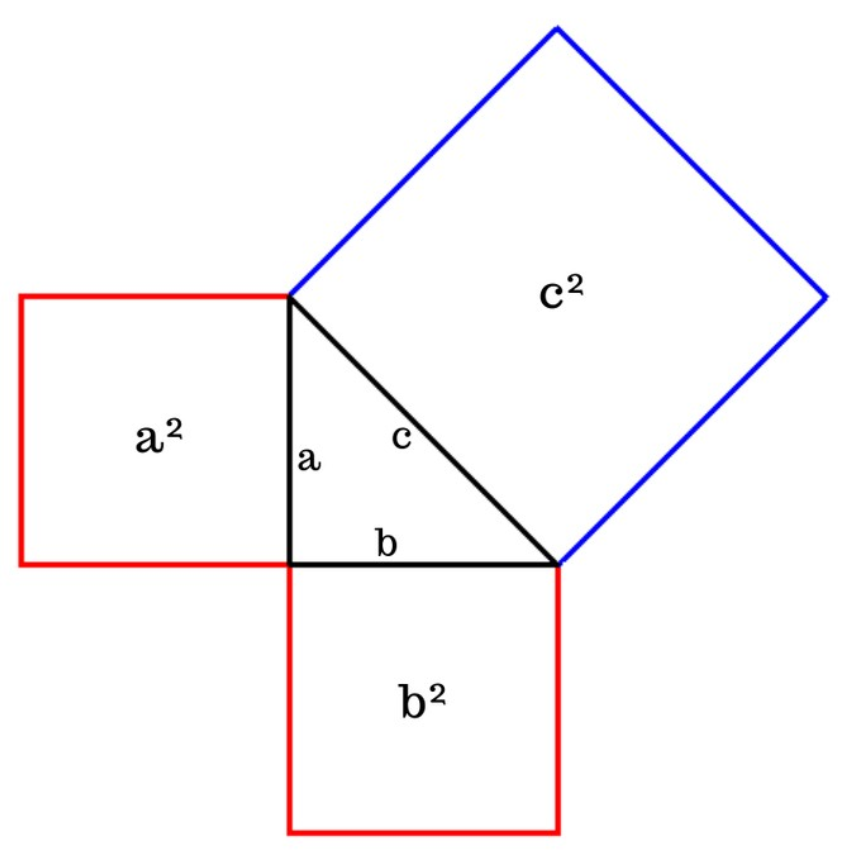 Познакомимся с некоторыми из них.
Познакомимся с некоторыми из них.



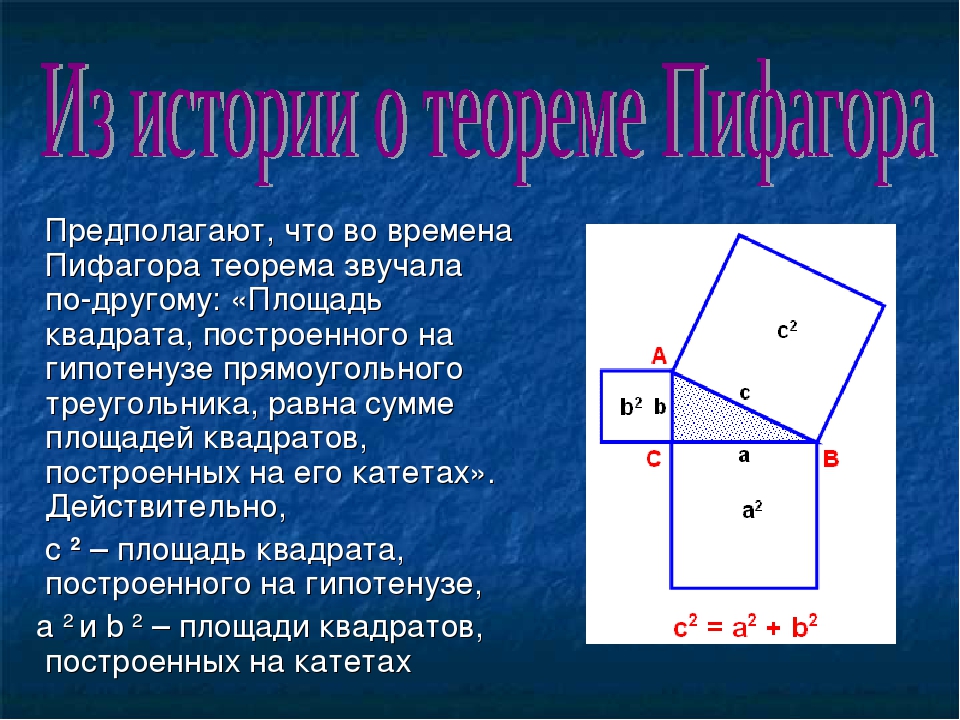 Построения
Построения рисунок). Докажите это.
рисунок). Докажите это.