Площадь через интеграл круга: Площадь кругового сектора — mathfordev — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Площадь кругового сектора — mathfordev

Площадь всего круга, как известно, выражается формулой «пи-эр-квадрат».
С чего вдруг. Разбираемся. Найдем сначала площадь верхней половины круга.
Рассмотрим рисунок:
На рисунке изображен круг с центром в начале координат, ограниченный окружностью радиуса R. Уравнение окружности, чей центр лежит в начале координат (точке (0; 0)), выглядит так:
x² + y² = R².
Верхняя половина круга ограничена линией y = (R² — x²)^1/2. Я вынес x² в правую часть уравнения окружности и взял квадратный корень. Для нижней части уравнение будет y = -(R² — x²)^1/2. Таким образом, площадь верхней половины круга можно найти как определенный интеграл от функции y = (R² — x²)^1/2 в интервале (-R; R). Но сначала найдем неопределенный интеграл:
Для того, чтобы найти второй интеграл, применим интегрирование по частям, которое выражается формулой:
Получаем:
Подставляем его в исходное выражение:
Перекидываем интеграл из правой части равенства в левую и делим на два:
Теперь можно найти определенный интеграл и, следовательно, площадь полукруга:
Площадь круга, очевидно, в два раза больше площади полукруга.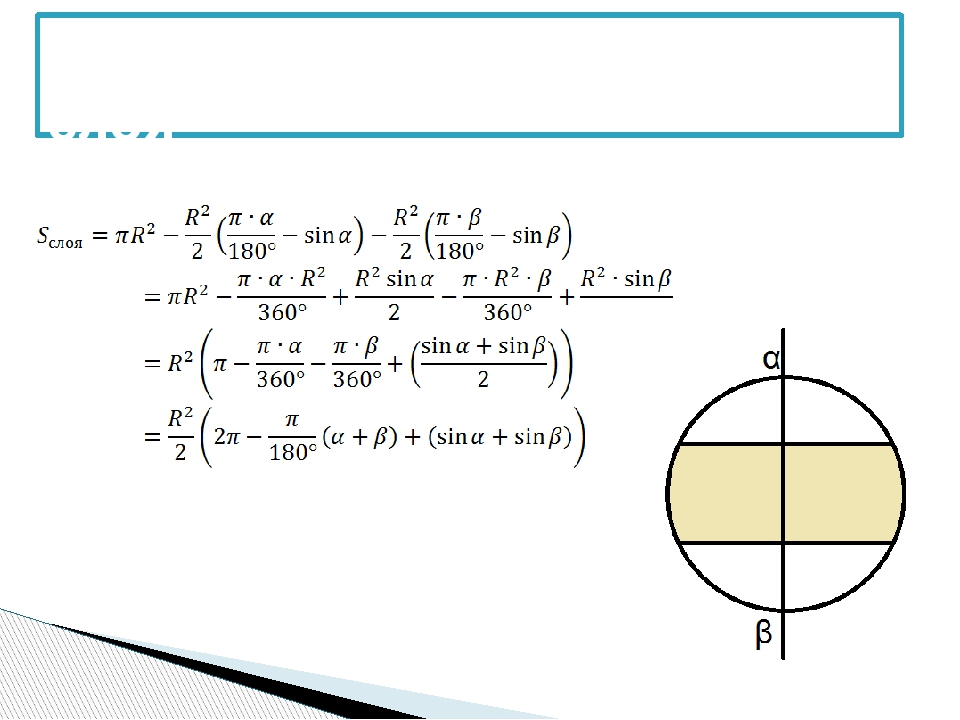
Можно подойти несколько по-другому и найти сразу площадь произвольного криволинейного сектора.
Рассмотрим круговой сектор, дуга которого α радиан. Одна сторона сектора лежит на оси Oy, а другая на луче OM. Точка M (Rcosθ; Rsinθ) проецируется в точку M_x (Rcosθ; 0) на оси Ox. Чтобы найти площадь кругового сектора, изображенного на рисунке, нужно вычислить интеграл, чья формула была получена ранее, на интервале от 0 до Rcosθ и вычесть площадь треугольника OMM_x.
Площадь треугольника OMM_x:
Вычтем ее и получим:

Радиан — мера угла, альтернативная градусу. Если градус — 1/360 доля круга, то полкруга как угол в 18 веке стали принимать как π радиан. Следовательно радиан — это такой угол, если полкруга (180 градусов) поделить на π. Что-то около 57 градусов. Составим пропорцию, зная что весь круг как угол равен 2π, через α обозначив угол произвольного сектора, а через S — его площадь:
Найдем S:
Пропорциональность углового размера кругового сектора и его площади исходит из того, что круг симметричная фигура.

Современные математики не знают, что такое интеграл (дополнено)

Читаем Википедию:
Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другие.
После прочтения этого текста вы точно поняли, что такое интеграл?
Я акцентирую внимание на вот этом смысловом контуре: «…интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых«.

В этом контуре отсутствует самый важный признак интеграла. То есть, оболочка есть, а «внутренности» нету!

Слово «бесконечно» не означает вообще ничего. Есть такой эпитет, который обычно используют дети, чтобы придать значимость слову большой. Они говорят: «Ого-го какой большой!» Так вот «бесконечность» это «ого-го» в смысле и огромности, и малости.

Приведу пример. Возьмем площадь круга. Любого круга, хоть маленького, хоть большого. Этот круг ограничен линией, характеризуемой длиной и называемой окружностью.

Так вот. Если к площади нашего круга прибавить длину окружности чуть большего радиуса, чем описанная вокруг круга окружность, то на сколько увеличится площадь круга? Правильно, ни на сколько не увеличится. Площадь круга никак не изменится. То есть, не получит никакого приращения своей площади. То есть, приращение площади круга в виде длины окружности равно нулю.

Но ведь у этой окружности есть длина. Она никак не равна нулю. Ее можно измерить и получить некое значение отличное от нуля. И отношение площади круга к длине окружности тоже далеко не ноль и не бесконечность…

Теперь внимательно следим за руками. Я покажу вам фокус. Приращение площади круга, в виде длины окружности, равно нулю. Я могу заменить это предложение другим предложением: «У площади круга нет никакого приращения». Смысл один и тот же. Но куда-то исчез ноль! Единица, деленная на ноль — есть бесконечность. Это знают все. А единица, деленная на «нет никакого приращения» чему равна? Где тут наша бесконечность? Куда подевалась-то?

Еще разок. Пишем две дроби. В числителе обеих дробей — единица, например. В знаменателе одной дроби написан значок «ноль», в знаменателе другой дроби ничего нет. Просто числитель и дробная черта. Первую дробь определяют как бесконечность. Вторая дробь к бесконечности не имеет никакого отношения…

Берем два значения одной и той же переменной. Приближаем их другк другу. Приближаем их к одному и тому же значению. Хлоп! Они приняли одно и то же значение. Чему равна разность между этими двумя одинаковыми значениями? Нулю. А чему равно частное между этими же значениями? Единице. Вот это новость! Отсутствие разницы между двумя одинаковыми значениями можно, оказывается, описать двумя различными числами. Нулем и единицей. Но ноль не равен единице, а смысл их, в данном случае, одинаков! Тут есть один нюанс. Ноль участвует в разности, а единица в частном. При нуле в частном появляется какая-то бесконечность, а при единице в частном никакой бесконечности нету, но при написании обеих единиц в виде разности опять появляется ноль…

Теперь идем дальше. Нет, это будет оченьмногабукав… Ладно я сокращу. В другой статье опишу подробнее, если эта статья получит отклики. Смысл вот в чем. Площадь круга можно раздробить на мелкие кусочки различными способами. Я покажу только два наиболее характерные. Этот круг можно порезать на колечки одной (как вариант) толщины, а можно покромсать ножиком «взад и поперек». То есть можно создать разные слагаемые (смотрим определение интеграла) дифференцируя эту площадь по радиусу (нарезая колечки), а можно эти слагаемые создавать, дифференцируя площадь круга по множеству независимых аргументов (кромсая бессистемно).

Итак. Берем два пакета. В один пакет накладываем колечки, полученные путем дифференцирования площади круга по радиусу. Во второй пакет складываем кусочки, которые мы покромсали бессистемно.

Мы хотим получить тот же круг, который мы дифференцировали (разбивали на части) двумя способами: по радиусу (колечки разного диаметра) и по многим аргументам (бессистемно).

Производим интегрирование по дифференциалу радиуса. Вытаскиваем колечки от самого малого диаметра до самого большого. В результате получаем исходный круг исходной площади.

Из второго пакета достаем один из кусочков… ВСЕ! Дальше мы не знаем какой доставать кусок и куда прикладывать к первому. Поэтому мы объявляем, что этот кусок и есть исходный круг, к которому надо приложить НЕКУЮ КОНСТАНТУ ИНТЕГРИРОВАНИЯ, которая есть все то, что осталось во втором пакете. И в результате мы получим круг исходной площади.

Но второй случай не есть интегрирование. Это есть сумма. Она никак не связана с интергрированием потому, что куски разнородные! Хотя я немного утрирую. .. На самом деле и суммирование (сложение) и умножение — есть два частных случая интегрирования. Именно поэтому в алгоритм и дифференцирования, и интегрирования входят одновременно оба арифметических действия: и сложение (вычитание) и умножение (деление).

То есть два арифметических действия — есть два частных случая одного и того же действия, которое современной математикой пока не рассмотрено. Потому, что в математике пока нет «Структурного анализа». Но те люди, которые на данном этапе окопались в «верхах» математической науки считают, что им все это не требуется. Хотя, возможно, у них есть другая, подпольная математика, не доступная гоям, в которой есть и этот «структурный анализ» но под другим названием…

P.S.

mishin05
9 апр, 2018 17:05 (местное)Я просто фигею от этой логики: «АСАД — ЖИВОТНОЕ, КОТОРОЕ УБИЛО 70 СИРИЙЦЕВ ХИМОРУЖИЕМ, А МЫ, КАК НАСТОЯЩИЕ ЧЕЛОВЕКИ ЗА ЭТО У@УЯРИМ ЕЩЕ НЕСКОЛЬКО СОТ СИРИЙЦЕВ СВОИМИ РАКЕТАМИ. ПОТОМУ, ЧТО МЫ НЕ ИЗВЕРГИ И НЕ ЖИВОТНЫЕ!»

Шизофреники рулят. ..

Отсюда

P.P.S. Покажу скриншот из работы Леонарда Эйлера. Очень интересный скриншот, если понять, что означают фразы, написанные великим математиком:

Последним предложением Эйлер троллит своих оппонентов из подражания которым и выпестовались современные «математики».)

Как правильно найти площадь фигуры. Определенный интеграл. Как вычислить площадь фигуры. Треугольник. Через основание и высоту

Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур — любая из них обладает площадью. Площади фигур — это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Величина эта всегда бывает выражена положительным числом. Единицей измерения служит площадь квадрата, чья сторона равняется единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она разбита, на площадь одного квадрата.

Другие определения данного понятия выглядят следующим образом:

1. Площади простых фигур — скалярные положительные величины, удовлетворяющие условиям:

У равных фигур — равные величины площадей;

Если фигура делится на части (простые фигуры), то ее площадь — сумма площадей данных фигур;

Квадрат, имеющий стороной единицу измерения, служит единицей площади.

2. Площади фигур сложной формы (многоугольников) — положительные величины, имеющие свойства:

У равных многоугольников — одинаковые величины площадей;

В случае, если многоугольник составляют несколько других многоугольников, его площадь равняется сумме площадей последних. Это правило справедливо для неперекрывающихся многоугольников.

В качестве аксиомы принято утверждение, что площади фигур (многоугольников) — положительные величины.

Определение площади круга дается отдельно как величины, к которой стремится площадь вписанного в окружность данного круга — при том, что число его сторон стремится к бесконечности.

Площади фигур неправильной формы (произвольных фигур) не имеют определения, определяются лишь способы их вычисления.

Вычисление площадей уже в древности было важной практической задачей при определении размеров земельных участков. Правила вычисления площадей за несколько сотен лет были сформулированы греческими учеными и изложены в «Началах» Евклида как теоремы. Интересно, что правила определения площадей простых фигур в них — те же, что и в настоящее время. Площади имеющих криволинейный контур, рассчитывались с применением предельного перехода.

Вычисление площадей простых прямоугольника, квадрата), знакомых всем со школьной скамьи, достаточно просто. Необязательно даже запоминать содержащие буквенные обозначения формулы площадей фигур. Достаточно помнить несколько простых правил:

2. Площадь прямоугольника вычисляется умножением его длины на ширину. При этом необходимо, чтобы длина и ширина были выражены в одних и тех же единицах измерения.

3. Площадь сложной фигуры вычисляем, разделив ее на несколько простых и сложив полученные площади.

4. Диагональ прямоугольника делит его на два треугольника, чьи площади равны и равняются половине его площади.

5. Площадь треугольника вычисляется как половина произведения его высоты и основания.

6. Площадь круга равняется произведению квадрата радиуса на всем известное число «π».

7. Площадь параллелограмма вычисляем как произведение смежных сторон и синуса лежащего между ними угла.

8. Площадь ромба — ½ результата умножения диагоналей на синус внутреннего угла.

9. Площадь трапеции находим умножением ее высоты на длину средней линии, которая равняется среднему арифметическому оснований. Другой вариант определения площади трапеции — перемножить ее диагонали и синус лежащего между ними угла.

Детям в начальной школе для наглядности часто даются задания: найти площадь нарисованной на бумаге фигуры с помощью палетки или листа прозрачной бумаги, разграфленной на клеточки. Такой лист бумаги накладывается на измеряемую фигуру, считается число полных клеточек (единиц площади), поместившихся в ее контуре, затем число неполных, которое делится пополам.

Как найти площадь фигуры?

Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.

Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.

Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.

Площадь треугольника

Обозначения:

Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).
Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r

Площадь квадрата

Обозначения:

Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2

Площадь прямоугольника

Обозначения:

S — определяемая площадь,
a, b — длины сторон прямоугольника.

Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники. В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.

Площадь параллелограмма

Обозначения:

S — искомая площадь,
a, b — длины сторон,
h — длина высоты данного параллелограмма,
d1, d2 — длины двух диагоналей,
α — угол, находящийся между сторонами,
γ — угол, находящийся между диагоналями.

Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2

Площадь ромба

Обозначения:

S — искомая площадь,
a — длина стороны,
h — длина высоты,
α — меньший угол между двумя сторонами,
d1, d2 — длины двух диагоналей.

Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2

Площадь трапеции

Обозначения:

Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h

Площадь выпуклого четырехугольника

Обозначения:

Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)

Площадь круга

Обозначения:

Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2

Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4

Площадь сложной фигуры

Сложную можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.

Обозначение:

S — площадь кольца,
R, r — радиусы внешней окружности и внутренней соответственно,
D, d — диаметры внешней окружности и внутренней соответственно.

Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).

Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).

Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.

Площадь закрашенной фигуры

Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б». Скажем так, «рамку» маленького квадрата. Для этого:

Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
Аналогичным образом находим площадь фигуры «Б».
Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.

Теперь вы знаете, как находить площади разных фигур.

Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.

Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.

Формулы для нахождения площади любого треугольника представлены несколькими вариантами:

1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.

На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:

По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.

3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:

Прямоугольник

Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:

Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:

Квадрат

Площадь квадрата определяют как вторую степень длины стороны:

Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.

Площадь квадрата можно найти другим способом, например, если использовать диагональ:

Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:

Параллелограмм

Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.

Формулы площади параллелограмма таковы:

Ромб

Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:

Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:

Трапеция

Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:

Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.

Цилиндр и параллелепипед

Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:

Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:

Кольцо

Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:

Площадь кольца, с использованием длин диаметров, определяют следующим образом:

Многоугольник

Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:

где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.

Если вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.

Геометрическая форма комнаты

Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:

Прямоугольные.
Квадратные.
Сложной конфигурации (например, круглые).
С нишами и выступами.

Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.

Помещение прямоугольной или квадратной формы

Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:

S комнаты=A*B, где

А — длина помещения.

В — ширина помещения.

Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.

Помещение со сложной конфигурацией

Если ваша комната не попадает под определение «типичной», т.е. имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем. Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:

Формула нахождения площади круга:

S комн.=π*R 2 , где

R — радиус помещения.

Формула нахождения площади треугольника:

S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где

Р — полупериметр треугольника.

А, В, С — длины его сторон.

Отсюда Р=А+В+С/2

Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.

Площадь помещения с выступами и нишами

Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.

Площадь стены находится по формуле:

S стен = Р х С, где

Р — периметр

С — высота

Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.

Комната с многоуровневым потолком

Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.

Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:

Найти размеры всех прямых участков стен.
Найти площадь пола.
Перемножить длину и высоту вертикальных участков.
Суммировать получившееся значение с площадью пола.

Пошаговая инструкция по определению общей

площади помещения

Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
Визуально разделите комнату на участки правильной и неправильной формы. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете убедитесь, что луч лежит ровно на поверхности стены.
Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.= S стен+S пола+S потолка

В геометрии площадь фигуры является одной из основных численных характеристик плоского тела. Что такое площадь, как ее определять у различных фигур, а также какие свойства она имеет — все эти вопросы мы рассмотрим в данной статье.

Что такое площадь: определение

Площадь фигуры — это число единичных квадратов в этой фигуре; неформально выражаясь, это размер фигуры. Чаще всего, площадь фигуры обозначается как «S». Её можно измерить с помощью палетки или прибора планиметр. Также площадь фигуры можно вычислить, зная основные ее размеры. Например, площадь треугольника можно вычислить по трем различным формулам:

Площадь прямоугольника равна произведению его ширины на длину, а площадь круга равна произведению квадрата радиуса на число π=3,14.

Свойства площади фигуры

площадь равна у равных фигур;
площадь всегда неотрицательна;
единицей измерения площади является площадь квадрата со стороной, равной 1 единице длины;
если фигура разделена на две части, то общая площадь фигуры равна сумме площадей составляющих ее частей;
фигуры, равные по площади, называются равновеликими;
если одна фигура принадлежит другой фигуре, то площадь первой не может превосходить площади второй.

Как найти площадь поверхности вращения с помощью интеграла

Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой
поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная
фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).

Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой.
Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь
поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов,
образованных вращением вокруг оси прямых x = a и
x = b.

Заметим, что тело вращения и соответственно его поверхность могут быть образованы также
вращением фигуры не вокруг оси Ox, а вокруг оси Oy.

Пусть в прямоугольных координатах на плоскости уравнением y = f(x)
задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1. Найти площадь поверхности параболоида, образованную
вращением вокруг оси Ox дуги параболы
, соответствующей
изменению x от x = 0 до
x = a.

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Прежде чем воспользоваться формулу для нахождения площади поверхности вращения,
напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда
найденную только что производную:

Далее по формуле (1) находим:

Ответ: длина дуги кривой равна

Пример 2. Найти площадь поверхности, образуемой вращением
вокруг оси Ox астроиды
.

Решение. Достаточно вычислить площадь поверхности, получающейся от вращения
одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды
выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности
вращения:

Производим интегрирование от 0 до a:

Ответ: площадь поверхности вращения равна
.

Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими
уравнениями

Тогда площадь поверхности вращения вычисляется по формуле

(2).

Пример 3. Найти площадь поверхности вращения, образованной вращением
вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a.
Циклоида задана параметрическими уравнениями

Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды
и уравнение прямой
y = a, найдём

Из этого следует, что границы интегрирования соответствуют

Теперь можем применить формулу (2). Найдём производные:

Запишем подкоренное выражение в формуле, подставляя найденные производные:

Найдём корень из этого выражения:

Подставим найденное в формулу (2):

Произведём подстановку:

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы

Ответ: площадь поверхности вращения равна
.

Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:

Площадь поверхности вращения вычисляется по формуле:

(3).

Пример 4. Найти площадь поверхности, образованной вращением
лемнискаты
вокруг полярной оси.

Решение. Действительные значения для ρ получаются при
, то есть при
(правая ветвь
лемнискаты) или при
(левая ветвь лемнискаты).

Решение. Дифференциал корня из формулы площади поверхности вращения равен:

В свою очередь произведение функции, которой задана лемниската, на синус угла равно

Поэтому площадь поверхности вращения найдём следующим образом:

Начало темы «Интеграл»

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.

Определение 1

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.

Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):

S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt

Определение 2

Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.

Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Пример 1

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:

Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z

При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2

Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.

Ответ: S(G)=6π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:

φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z

Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.

Разберем еще одну задачу.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 2

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.

Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).

Составим таблицу итоговых значений:

t0	0	π8	π4	3π8	π2	5π8	3π4	7π8	π
x0=φ(t0)	3	2.36	1.06	0.16	0	-0.16	-1.06	-2.36	-3
y0=ψ(t0)	0	0.11	0.70	1.57	2	1.57	0.70	0.11	0

t0	9π8	5π4	11π8	3π2	13π8	7π4	15π8	2π
x0=φ(t0)	-2.36	-1.06	-0.16	0	0.16	1.06	2.36	3
y0=ψ(t0)	-0.11	-0.70	-1.57	-2	-1.57	-0.70	-0.11	0

После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:

φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z

Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.

∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96

Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.

Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.

Применение метода Монте-Карло для вычисления площади круга

1. Срединная формула прямоугольников

Срединная формула прямоугольников Введем обозначение I d Пусть -непрерывны на [ ] Разделим отрезок [ ] равных частичных отрезков [ ] где на Введем обозначения ( ) ( ) ( ) интеграл I в виде Представим где

Подробнее

МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ

Кременчугский национальный университет имени Михаила Остроградского МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ Математические методы вычислений на ЭВМ А.П. Черный, д.т.н., профессор http:\\sue.kdu.edu.u 2 ЛЕКЦИЯ

Подробнее

Тема7. «Численное интегрирование.»

Министерство образования Республики Беларусь УО «Витебский государственный технологический университет» Тема7. «Численное интегрирование.» Кафедра теоретичской и прикладной математики. разработана доц.

Подробнее

ТЕМА 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ТЕМА 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Понятие непрерывной случайной величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Математическое ожидание непрерывной случайной величины

Подробнее

Численное интегрирование

Численное интегрирование — — Численное интегрирование. Постановка задачи Задача вычисления интегралов возникает во многих областях прикладной математики. Требуется вычислить определенный интеграл I d.

Подробнее

12. Определенный интеграл

58 Определенный интеграл Пусть на промежутке [] задана функция () Будем считать функцию непрерывной, хотя это не обязательно Выберем на промежутке [] произвольные числа,, 3,, n-, удовлетворяющие условию:

Подробнее

Численное интегрирование

Математическое моделирование объектов теплоэнергетики Лекция 2 Численное интегрирование Введение 2 На практике достаточно большое число задач сводится к вычислению значения определенного интеграла некоторой

Подробнее

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. Интегральные суммы и определённый интеграл Пусть дана функция y = f (), определённая на отрезке [, b ], где < b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

Подробнее

Лабораторная работа 3.2

Лабораторная работа 3.2 ФОРМУЛЫ, ИМЕНА, МАССИВЫ. ФОРМУЛЫ НАД МАССИВАМИ. ОСНОВНЫЕ ФУНК- ЦИИ Задание 1. Выполните вычисления по следующим формулам: A= 4 x 2 3 3x 2x, B= x y z, C= x y z 1 x, x y считая заданными

Подробнее

Тема6. «Определенный интеграл»

Министерство образования Республики Беларусь УО «Витебский государственный технологический университет» Тема6. «Определенный интеграл» Кафедра теоретической и прикладной математики. разработана доц. Е.Б.Дуниной

Подробнее

МЕТОДЫ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИ

МЕТОДЫ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИ Интерполяция Интерполяция способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений Пусть в ходе эксперимента при изменении

Подробнее

2. «Простая» статистика

2. «Простая» статистика 1 2. «Простая» статистика В большинстве статистических расчетов приходится работать с выборками случайной величины: либо с данными эксперимента, либо с результатами моделирования

Подробнее

Дифференцирование функций, заданных таблично. x 1 1,2 1,3 1,55 y(x) ,5 16,5

Дополнение к Вычислительному практикуму. Глава 1 1 Дифференцирование функций, заданных таблично Для функции, заданной таблицей, найти разностные производные всех типов. Найти эластичность этой функции,

Подробнее

4 Сеточные методы. 4.1 Основные понятия.

4 Сеточные методы. 4.1 Основные понятия. Для решения многих численных задач требуется введение дискретных функций, определенных в точках. Пространством, в котором определены данные функции, будет являться

Подробнее

Моделирование процесса перколяции

Моделирование процесса перколяции Мейер Никита Владимирович Санкт-Петербургский государственный университет Прикладная математика и информатика Вычислительная стохастика и статистические модели Научный

Подробнее

1. Численные методы решения уравнений

1. Численные методы решения уравнений 1. Системы линейных уравнений. 1.1. Прямые методы. 1.2. Итерационные методы. 2. Нелинейные уравнения. 2.1. Уравнения с одним неизвестным. 2.2. Системы уравнений. 1.

Подробнее

Интерполирование функций

Постановка задачи, основные понятия Конечные разности и их свойства Интерполяционные многочлены Оценка остаточного члена интерполяционных многочленов Постановка задачи, основные понятия Пусть, то есть

Подробнее

АППРОКСИМАЦИЯ. y i y 0 y 1 y 2 y n. i x 0 x 1 x 2 x n

АППРОКСИМАЦИЯ На практике часто приходится сталкиваться с задачей сглаживания экспериментальных данных задача аппроксимации. Основная задача аппроксимации построение приближенной (аппроксимирующей) функции

Подробнее

6.7. Статистические испытания

Лекция.33. Статистические испытания. Доверительный интервал. Доверительная вероятность. Выборки. Гистограмма и эмпирическая 6.7. Статистические испытания Рассмотрим следующую общую задачу. Имеется случайная

Подробнее

, (3.4.3) ( x) lim lim

3.4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВЫБОРОЧНЫХ ЗНАЧЕНИЙ ПРОГНОЗНЫХ МОДЕЛЕЙ До сих пор мы рассматривали способы построения прогнозных моделей стационарных процессов, не учитывая одной весьма важной особенности.

Подробнее

3724 РЯДЫ. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

3724 РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 1 РАБОЧАЯ ПРОГРАММА РАЗДЕЛОВ «РЯДЫ КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ» 11 Числовые ряды Понятие числового ряда Свойства числовых рядов Необходимый признак сходимости

Подробнее

МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ

Подробнее

Квадратурные и кубатурные формулы

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Пензенский государственный университет» Квадратурные и кубатурные формулы Методические

Подробнее

Лекция 9. Тема Введение в теорию оценок.

Лекция 9 Тема Введение в теорию оценок. Содержание темы Предмет, цель и метод задачи оценивания Точечные выборочные оценки, свойства оценок Теоремы об оценках Интервальные оценки и интеграл Лапласа Основные

Подробнее

Непрерывные случайные величины.

Тема Непрерывные случайные величины. Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной. В частных случаях это может быть не один промежуток, а объединение нескольких

Подробнее

)? (Вероятность попадания непрерывной СВ

Случайные величины. Определение СВ ( Случайной называется величина, которая в результате испытания может принимать то или иное значение, заранее не известное).. Какие бывают СВ? ( Дискретные и непрерывные.

Подробнее

ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ

Глава 0 ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ Т-00 Вычисление членов последовательности по рекуррентной формуле Т-00 Составление рекуррентной формулы Т-00 Формула общего члена Т-004 Составление арифметической прогрессии

Подробнее

ξ i; i высота. Тогда площадь каждой полоски

Тема КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ Лекция КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА Задачи приводящие к понятию криволинейного интеграла первого рода Определение и свойства криволинейного интеграла первого рода Вычисление

Подробнее

Аппроксимация таблично заданных функций

Аппроксимация таблично заданных функций Таблично заданные функции. Зависимость разрядного напряжения газового промежутка с однородным полем от расстояния между электродами Расстояние между шарами, см Диаметр

Подробнее

Линия тренда. Прогноз в EXCEL Линия тренда

Линия тренда. Прогноз в EXCEL На практике при моделировании различных процессов в частности, экономических, физических, технических, социальных широко используются те или иные способы вычисления приближенных

Подробнее

Вычисление площади поверхности вращения с помощью определенного интеграла. Площадь поверхности вращения при параметрически заданной линии. Вычисление площади поверхности вращения, заданной в полярных координатах

Поэтому сразу перейду к основным понятиям и практическим примерам.

Посмотрим на лаконичную картинку

И вспомним: что можно вычислить с помощью определённого интеграла
?

В первую очередь, конечно, площадь криволинейной трапеции
. Знакомо со школьных времён.

Если же данная фигура вращается вокруг координатной оси, то речь уже идёт о нахождении объёма тела вращения
. Тоже просто.

Что ещё? Не так давно была рассмотрена задача о длине дуги кривой
.

И сегодня мы научимся рассчитывать ещё одну характеристику – ещё одну площадь. Представьте, что линия вращается
вокруг оси . В результате этого действия получается геометрическая фигура, называемая поверхностью вращения
. В данном случае она напоминает такой горшок без дна. И без крышки. Как бы сказал ослик Иа-Иа, душераздирающее зрелище =)

Чтобы исключить двусмысленную трактовку, сделаю занудное, но важное уточнение:

с геометрической точки зрения наш «горшок» имеет бесконечно тонкую
стенку и две
поверхности с одинаковыми площадями – внешнюю и внутреннюю. Так вот, все дальнейшие выкладки подразумевают площадь только внешней поверхности
.

В прямоугольной системе координат площадь поверхности вращения рассчитывается по формуле:

или, если компактнее: .

К функции и её производной предъявляются те же требования, что и при нахождении длины дуги кривой
, но, кроме того, кривая должна располагаться выше
оси . Это существенно! Нетрудно понять, что если линия располагается под
осью , то подынтегральная функция будет отрицательной : , и поэтому к формуле придётся добавить знак «минус» дабы сохранить геометрический смысл задачи.

Рассмотрим незаслуженно обойденную вниманием фигуру:

Площадь поверхности тора

В двух словах, тор – это бублик
. Хрестоматийный пример, рассматриваемый практически во всех учебниках по матану, посвящён нахождению объёма
тора, и поэтому в целях разнообразия я разберу более редкую задачу о площади его поверхности
. Сначала с конкретными числовыми значениями:

Пример 1

Вычислить площадь поверхности тора, полученного вращением окружности вокруг оси .

Решение
: как вы знаете, уравнение задаёт окружность
единичного радиуса с центром в точке . При этом легко получить две функции:

– задаёт верхнюю полуокружность;
– задаёт нижнюю полуокружность:

Суть кристально прозрачна: окружность
вращается вокруг оси абсцисс и образует поверхность
бублика. Единственное, здесь во избежание грубых оговорок следует проявить аккуратность в терминологии: если вращать круг
, ограниченный окружностью , то получится геометрическое тело
, то есть сам бублик. И сейчас разговор о площади его поверхности
, которую, очевидно, нужно рассчитать как сумму площадей:

1) Найдём площадь поверхности, которая получается вращением «синей» дуги вокруг оси абсцисс. Используем формулу . Как я уже неоднократно советовал, действия удобнее проводить поэтапно:

Берём функцию и находим её производную
:

И, наконец, заряжаем результат в формулу:

Заметьте, что в данном случае оказалось рациональнее удвоить интеграл от чётной функции
по ходу решения, нежели предварительно рассуждать о симметрии фигуры относительно оси ординат.

2) Найдём площадь поверхности, которая получается вращением «красной» дуги вокруг оси абсцисс. Все действия будут отличаться фактически только одним знаком. Оформлю решение в другом стиле, который, само собой, тоже имеет право на жизнь:

3) Таким образом, площадь поверхности тора:

Ответ
:

Задачу можно было решить в общем виде – вычислить площадь поверхности тора, полученного вращением окружности вокруг оси абсцисс, и получить ответ . Однако для наглядности и бОльшей простоты я провёл решение на конкретных числах.

Если вам необходимо рассчитать объём самого бублика, пожалуйста, обратитесь к учебнику, в качестве экспресс-справки:

Согласно теоретической ремарке, рассматриваем верхнюю полуокружность. Она «прорисовывается» при изменении значения параметра в пределах (легко видеть, что на данном промежутке), таким образом:

Ответ
:

Если решить задачу в общем виде, то получится в точности школьная формула площади сферы , где – её радиус.

Что-то больно простая задачка, даже стыдно стало…. предлагаю вам исправить такую недоработку =)

Пример 4

Вычислить площадь поверхности, полученной вращением первой арки циклоиды вокруг оси .

Задание креативное. Постарайтесь вывести или интуитивно догадаться о формуле вычисления площади поверхности, полученной вращением кривой вокруг оси ординат. И, конечно, снова следует отметить преимущество параметрических уравнений – их не нужно как-то видоизменять; не нужно заморачиваться с нахождением других пределов интегрирования.

График циклоиды можно посмотреть на странице Площадь и объем, если линия задана параметрически
. Поверхность вращения будет напоминать… даже не знаю с чем сравнить… что-то неземное – округлой формы с остроконечным углублением посередине. Вот для случая вращения циклоиды вокруг оси ассоциация в голову мгновенно пришла – продолговатый мяч для игры в регби.

Решение и ответ в конце урока.

Завершаем наш увлекательный обзор случаем полярных координат
. Да, именно обзор, если вы заглянете в учебники по математическому анализу (Фихтенгольца, Бохана, Пискунова, др. авторов), то сможете раздобыть добрый десяток (а то и заметно больше) стандартных примеров, среди которых вполне возможно найдётся нужная вам задача.

Как вычислить площадь поверхности вращения,
если линия задана в полярной системе координат?

Если кривая задана в полярных координатах
уравнением , и функция имеет непрерывную производную на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле , где – угловые значения, соответствующие концам кривой.

В соответствии с геометрическим смыслом задачи подынтегральная функция , а это достигается только при условии ( и заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона , иными словами кривая должна располагаться выше
полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.

Пример 5

Вычислить площадь поверхности, образованной вращением кардиоиды вокруг полярной оси.

Решение
: график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат
. Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке (что, собственно, обусловлено и вышесказанным замечанием).

Поверхность вращения будет напоминать яблочко.

Техника решения стандартна. Найдём производную по «фи»:

Составим и упростим корень:

Надеюсь, с заштатными

Если кривая задана параметрическими уравнениями , то площадь поверхности, полученной вращением данной кривой вокруг оси , рассчитывается по формуле . При этом «направление прорисовки» линии, о которое было сломано столько копий в статье , безразлично. Но, как и в предыдущем пункте, важно чтобы кривая располагалась выше
оси абсцисс – в противном случае функция , «отвечающая за игреки», будет принимать отрицательные значения и перед интегралом придётся поставить знак «минус».

Пример 3

Вычислить площадь сферы, полученной вращением окружности вокруг оси .

Решение
: из материалов статьи о площади и объемё при параметрически заданной линии
вы знаете, что уравнения задают окружность с центром в начале координат радиуса 3.

Ну а сфера

, для тех, кто забыл, – это поверхность шара
(или шаровая поверхность
).

Придерживаемся наработанной схемы решения. Найдём производные:

Составим и упростим «формульный» корень:

Что и говорить, получилась конфетка. Ознакомьтесь для сравнения, как Фихтенгольц бодался с площадью эллипсоида вращения
.

Ответ
:

Если решить задачу в общем виде, то получится в точности школьная формула площади сферы , где – её радиус.

Что-то больно простая задачка, даже стыдно стало…. предлагаю вам исправить такую недоработку =)

Пример 4

Вычислить площадь поверхности, полученной вращением первой арки циклоиды вокруг оси .

Решение и ответ в конце урока.

Как вычислить площадь поверхности вращения,

если линия задана в полярной системе координат?

Если кривая задана вполярных координатах
уравнением , и функция имеет непрерывную производную на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле , где – угловые значения, соответствующие концам кривой.

Пример 5

Вычислить площадь поверхности, образованной вращением кардиоиды вокруг полярной оси.

Поверхность вращения будет напоминать яблочко.

Техника решения стандартна. Найдём производную по «фи»:

Составим и упростим корень:

Надеюсь, с заштатными тригонометрическими формулами
ни у кого не возникло затруднений.

Используем формулу:

На промежутке , следовательно: (о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой
).

Ответ
:

Интересное и короткое задание для самостоятельного решения:

Пример 6

Вычислить площадь шарового пояса ,

Что такое шаровой пояс? Положите на стол круглый неочищенный апельсин и возьмите в руки нож. Сделайте два параллельных
разреза, разделив тем самым фрукт на 3 части произвольных размеров. Теперь возьмите серединку, у которой сочная мякоть обнажилась с обеих сторон. Данное тело называется шаровым слоем
, а ограничивающая её поверхность (оранжевая кожура) – шаровым поясом
.

Читатели, хорошо знакомые с полярными координатами
, легко представили чертёж задачи: уравнение задаёт окружность с центром в полюсе радиуса , от которой лучи
отсекают меньшую
дугу. Данная дуга вращается вокруг полярной оси и таким образом получается шаровой пояс.

Теперь можно с чистой совестью и лёгким сердцем съесть апельсинку, на этой вкусной ноте и завершим занятие, не портить же вам аппетит другими примерами =)

Решения и ответы:

Пример 2:
Решение

: вычислим площадь поверхности, образованной вращением верхней ветви
вокруг оси абсцисс. Используем формулу
.

В данном случае:
;

Таким образом:

Ответ
:

Пример 4:
Решение

: используем формулу
. Первая арка циклоиды определена на отрезке
.

Найдём производные:

Составим и упростим корень:

Таким образом, площадь поверхности вращения:

На промежутке
, поэтому

Первый интеграл
интегрируем по частям

:

Во втором интеграле используем
тригонометрическую формулу

.

Ответ
:

Пример 6:
Решение

: используем формулу:

Ответ
:

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как вычислить определенный интеграл

по формуле трапеций и методом Симпсона?

Численные методы – достаточно большой раздел высшей математики и серьезные учебники по данной теме насчитывают сотни страниц. На практике, в контрольных работах традиционно предлагаются для решения некоторые задачи по численным методам, и одной из распространенных задач является – приближенное вычисление определенных интегралов
. В этой статье я рассмотрю два метода приближенного вычисления определенного интеграла – метод трапеций
и метод Симпсона
.

Что нужно знать, чтобы освоить данные методы? Прозвучит забавно, но можно вообще не уметь брать интегралы. И даже вообще не понимать, что такое интегралы. Из технических средств потребуется микрокалькулятор. Да-да, нас ждут рутинные школьные расчёты. А еще лучше – закачайте мой калькулятор-полуавтомат для метода трапеций и метода Симпсона
. Калькулятор написан в Экселе и позволит в десятки раз уменьшить время решения и оформления задач. Для экселевских чайников прилагается видеомануал! К слову, первая видеозапись с моим голосом.

Сначала зададимся вопросом, а зачем вообще нужны приближенные вычисления? Вроде бы можно найти первообразную функции и использовать формулу Ньютона-Лейбница, вычислив точное значение определенного интеграла. В качестве ответа на вопрос сразу рассмотрим демонстрационный пример с рисунком.

Вычислить определенный интеграл

Всё было бы хорошо, но в данном примере интеграл не берётся – перед вами неберущийся, так называемый интегральный логарифм
. А существует ли вообще этот интеграл? Изобразим на чертеже график подынтегральной функции :

Всё нормально. Подынтегральная функция непрерывна
на отрезке и определенный интеграл численно равен заштрихованной площади. Да вот только одна загвоздка – интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы. При этом задача встречается в двух формулировках:

1) Вычислить определенный интеграл приближенно, округляя результат до определённого знака после запятой
. Например, до двух знаков после запятой, до трёх знаков после запятой и т.д. Предположим, получился приближенный ответ 5,347. На самом деле он может быть не совсем верным (в действительности, скажем, более точный ответ 5,343). Нашазадача состоитлишь в том
, чтобы округлить результат до трёх знаков после запятой.

2) Вычислить определенный интеграл приближенно, с определённой точностью
. Например, вычислить определённый интеграл приближенно с точностью до 0,001. Что это значит? Это значит, что если получен приближенный ответ 5,347, то все
цифры должны быть железобетонно правильными
. А точнее говоря, ответ 5,347 должен отличаться от истины по модулю (в ту или другую сторону) не более чем на 0,001.

Существуют несколько основных методов приближенного вычисления определенного интеграла, который встречается в задачах:

Метод прямоугольников
. Отрезок интегрирования разбивается на несколько частей и строится ступенчатая фигура (гистограмма
), которая по площади близка к искомой площади:

Не судите строго за чертежи, точность не идеальна – они лишь помогают понять суть методов.

В данном примере проведено разбиение отрезка интегрирования на три отрезка:
. Очевидно, что чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. Метод прямоугольников даёт грубое приближение площади, видимо, поэтому очень редко встречается на практике (припомнил только один практический пример). В этой связи я не буду рассматривать метод прямоугольников, и даже не приведу простую формулу. Не потому, что лень, а по причине принципа моего решебника: что крайне редко встречается в практических задачах, то – не рассматривается.

Метод трапеций
. Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломаной
линией:

Таким образом, наша площадь (синяя штриховка) приближается суммой площадей трапеций (красный цвет). Отсюда и название метода. Легко заметить, что метод трапеций даёт значительно лучшее приближение, чем метод прямоугольников (при одинаковом количестве отрезков разбиения). И, естественно, чем больше более мелких промежуточных отрезков мы рассмотрим, тем будет выше точность. Метод трапеций время от времени встречается в практических заданиях, и в данной статье будет разобрано несколько примеров.

Метод Симпсона (метод парабол)
. Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.

Чертеж строить не вижу смысла, поскольку визуально приближение будет накладываться на график функции (ломаная линия предыдущего пункта – и то практически совпала).

Задача на вычисление определенного интеграла по формуле Симпсона – самая популярное задание на практике. И методу парабол будет уделено значительное внимание.

Пример:
Найти объем шара радиуса
R
.

В поперечных сечениях шара
получаются окружности переменного радиуса у. В зависимости от текущей
координаты х этот радиус выражается по формуле .

Тогда функция площадей сечений имеет вид:
Q
(x
) =
.

Получаем объем шара:

Пример:
Найти объем произвольной пирамиды с высотой Н и площадью основания
S
.

При пересечении пирамиды
плоскостями, перпендикулярными высоте, в сечении получаем фигуры,
подобные основанию. Коэффициент подобия этих фигур равен отношению
x
/
H
, где х — расстояние от плоскости сечения до вершины пирамиды.

Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.

Отсюда получаем функцию площадей сечений:

Находим объем пирамиды:

Объем тел вращения.

Рассмотрим кривую, заданную уравнением
y
=
f
(x
). Предположим, что функция
f
(x
) непрерывна на отрезке [
a
,
b
]. Если соответствующую ей криволинейную трапецию с основаниями а и
b
вращать вокруг оси Ох, то получим так называемоетело вращения
.

y
=
f
(x
)

Площадь поверхности тела вращения.

М
i
B

Определение:

Площадью поверхности вращения
кривой
АВ вокруг данной оси называют предел, к которому стремятся площади
поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к
нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу АВ на
n
частей точками
M
0
,
M
1
,
M
2
, … ,
M n
. Координаты вершин полученной ломаной имеют координаты
x i
и
y i
.
При вращении ломаной вокруг оси получим поверхность, состоящую из
боковых поверхностей усеченных конусов, площадь которых равна
D
P i
. Эта площадь может быть найдена по формуле
:

Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой
поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная
фигура, образованная вращением отрезка AB
кривой вокруг оси Ox
(рисунок ниже).

Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой.
Тело, образованное вращением этой трапеции вокруг то же оси Ox
, и есть тело вращения. А площадь
поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов,
образованных вращением вокруг оси прямых x
= a

и
x
= b

.

Вычисление площади поверхности вращения, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y
= f
(x
)

задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1.
Найти площадь поверхности параболоида, образованную
вращением вокруг оси Ox
дуги параболы
, соответствующей
изменению x
от x
= 0
до
x
= a

.

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Ответ: длина дуги кривой равна

Пример 2.
Найти площадь поверхности, образуемой вращением
вокруг оси Ox
астроиды
.

Производим интегрирование от 0 до a
:

Вычисление площади поверхности вращения, заданной параметрически

Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими
уравнениями

Тогда площадь поверхности вращения вычисляется по формуле

(2).

Пример 3.
Найти площадь поверхности вращения, образованной вращением
вокруг оси Oy
фигуры, ограниченной циклоидой и прямой y
= a

.
Циклоида задана параметрическими уравнениями

Из этого следует, что границы интегрирования соответствуют

Теперь можем применить формулу (2). Найдём производные:

Запишем подкоренное выражение в формуле, подставляя найденные производные:

Найдём корень из этого выражения:

Подставим найденное в формулу (2):

Произведём подстановку:

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы

Ответ: площадь поверхности вращения равна
.

Вычисление площади поверхности вращения, заданной в полярных координатах

Пусть кривая, вращением которой образована поверхность, задана в полярных координатах.

Приветствую вас, уважаемые студенты вуза Аргемоны!

Сегодня мы продолжим учиться материализации предметов. В прошлый раз мы вращали плоские фигуры и получали объёмные тела. Некоторые из них — очень даже заманчивые и полезные. Думаю, что многому, что изобретает маг, можно в дальнейшем найти применение.

Сегодня мы будет вращать кривые. Понятно, что таким образом мы можем получить какой-то предмет с очень тонкими гранями (колбочка или флакон для зелий, ваза для цветов, стакан для напитков и т.п.), потому как вращающаяся кривая именно такого рода предметы и может сотворить. Другими словами, вращением кривой мы можем получить какую-то поверхность — замкнутую со всех сторон или нет. Почему прямо сейчас вспомнилась дырявая чаша, из которой всё время пил сэр Шурф Лонли-Локли.

Вот мы и сотворим дырявую чашу и недырявую, и подсчитаем площадь сотворённой поверхности. Думаю, для чего-то она (вообще площадь поверхности) ведь будет нужна — ну хотя бы для нанесения специальной магической краски. А с другой стороны, площади магических артефактов могут потребоваться для расчёта приложенных к ним магических сил или ещё чего-то. Мы научимся это находить, а уж где применить — найдём.

Итак, форму чаши вполне нам может дать кусок параболы. Возьмём самую простейшую y=x 2 на промежутке .
Видно, что при вращении её вокруг оси OY получается как раз чаша. Без дна.

Заклинание для расчёта площади поверхности вращения выглядит следующим образом:

Здесь |y| — это расстояние от оси вращения до любой точки кривой, которая вращается. Как известно, расстояние — это перпендикуляр.
Немного труднее со вторым элементом заклинания: ds — это дифференциал дуги. Эти слова нам ничего не дают, поэтому не будем заморачиваться, а перейдём на язык формул, где этот дифференциал явно представлен для всех известных нам случаев:
— декартовой системы координат;
— записи кривой в параметрическом виде;
— полярной системы координат.

Для нашего случая расстояние от оси вращения до любой точки на кривой равно х.2. Для нашего случая площадь круга будет равна пи), но вычислим его по новой формуле — для проверки.
Расстояние от оси вращения до любой точки этого кусочка кривой также равно х.

Ну вот, расчёты наши верны, что радует.

А теперь домашнее задание
.

1. Найти площадь поверхности, полученной вращением ломаной ABC, где A=(1; 5), B=(1; 2), C=(6; 2), вокруг оси ОХ.
Совет. Записать все отрезки в параметрическом виде.
AB: x=1, y=t, 2≤t≤5
BC: x=t, y=2, 1≤t≤6
Кстати, на что похож получившийся предмет?

2. Ну а теперь придумайте что-то сами. Трёх предметов, думаю, хватит.

исчислений — Площадь под четвертью круга по интегрированию

исчисление — Площадь под четвертью круга по интегрированию — Mathematics Stack Exchange

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

0
+0
Авторизоваться
Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил
5 лет, 7 месяцев назад

Просмотрено
21к раз

$ \ begingroup $

Как можно определить площадь под четвертью круга путем интегрирования. 2} \: dx.2.
\ end {align}

Создан 08 окт.

Оливье Олоа

11k1818 золотых знаков188188 серебряных знаков307307 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

Вот более быстрое решение.2 $$

Создан 10 дек.

W. ZhuW. Чжу

1,14711 золотых знаков77 серебряных знаков1919 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

пусть круг: $ x ^ 2 + y ^ 2 = r ^ 2 $, затем рассмотрим плиту площадью $ dA = ydx $, затем площадь четверти круга
$$ A_ {1/4} = \ int_0 ^ r ydx = \ int_0 ^ r \ sqrt {r ^ 2-x ^ 2} dx $$
$$ = \ frac12 \ left [x \ sqrt {r ^ 2-x ^ 2} + r ^ 2 \ sin ^ {- 1} \ left (x / r \ right) \ right] _0 ^ r $$

$$ = \ frac12 \ left [0 + r ^ 2 (\ pi / 2) \ right] = \ frac {\ pi} {4} r ^ 2 $$
или используйте двойную интеграцию:
$$ = \ iint rdr d \ theta = \ int_0 ^ {\ pi / 2} \ d \ theta \ int_0 ^ R rdr = \ int_0 ^ {\ pi / 2} \ d \ theta (R ^ 2/2) = (R ^ 2/2) (\ pi / 2) = \ frac {\ pi} {4} R ^ 2 $$

Создан 10 дек.

$ \ endgroup $

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie

Настроить параметры

Определение площади круга

Как, вероятно, известно большинству людей, читающих этот блог, площадь круга определяется как

, где — отношение диаметра круга к его длине, а — радиус круга.Но как мы можем найти , доказав эту хорошо известную формулу? Для этого мы можем использовать так называемую интеграцию , которая является ветвью исчисления.

Площадь под кривой

Площадь под любой кривой между осью x, кривой и линиями (см. Рисунок ниже) задается как

где — функция (кривая), а ширина — бесконечно малая. Фактически, мы суммируем серию прямоугольников площади от нижнего до верхнего предела.

Уравнение окружности

Чтобы сделать это для круга, нам нужно написать уравнение для круга. Чтобы упростить задачу, мы центрируем круг в начале координат. В этом случае, если круг имеет радиус, уравнение, описывающее этот круг, будет просто

Следовательно, чтобы найти площадь круга, все, что нам нужно сделать, это проинтегрировать между ними, а затем умножить ответ на 4 (так как у нас есть нашел только площадь четверти круга).

Чтобы найти площадь круга, в принципе все, что нам нужно сделать, это просуммировать прямоугольники от до между осью x и кругом, а затем умножить ответ на 4.

Интеграция для этого —

Это не интеграл, который мы можем сделать, поэтому мы, кажется, застряли!

Изменение переменных для использования «полярных координат»

К счастью, есть способ обойти эту проблему. Вместо того, чтобы использовать координаты xy (более корректно известные как декартовы координаты ), мы можем изменить систему координат на нечто, называемое полярными координатами , и когда мы это сделаем, мы получим интеграл, который мы можем делать.

Чтобы увидеть, как перейти от декартовых координат к полярным, рассмотрите рисунок ниже.

Мы запишем координаты в терминах двух новых переменных, где — радиус круга, а — угол между линией от центра круга к точке и осью x. Когда мы это сделаем, мы можем написать это и.

Затем, чтобы определить положительную площадь квадранта, мы можем вместо этого интегрировать, используя. Чтобы увидеть, как мы это делаем, рассмотрим рисунок ниже.

Одна из причин, по которой метод использования полярных координат проще, заключается в том, что теперь у нас есть только одна переменная, так как радиус является постоянной величиной.Когда мы использовали в качестве переменных, перемещение по окружности включало изменение обеих переменных , но с полярными координатами изменяется только одна переменная,.

Вместо того, чтобы находить площадь прямоугольника и суммировать их, мы рассматриваем срез круга, где угол в срезе равен бесконечно малому углу, а радиус каждого среза равен. Это показано заштрихованной областью на рисунке выше. Затем мы суммируем эти срезы между углом и. Но при использовании исчисления мы не используем градусы, а скорее должны использовать радиан и , которые, как я объяснил в этом блоге, являются более естественной единицей измерения угла.

По мере того, как становится бесконечно малым, срез становится треугольником, а площадь треугольника определяется выражением. Высота, конечно, всего лишь радиус, а как быть с основанием? База — это длина дуги, которую вы помните из определения радиана.

Интеграл, который мы хотим сделать, поэтому равен

Но помните, что это площадь только положительного квадранта, поэтому площадь всего круга будет , 4 умноженная на это, или

, как в известной формуле. b_af (x) dx.2} dx. \ nonumber \]

В этом разделе мы изучаем аналогичные формулы для площади и длины дуги в полярной системе координат.

Области областей, ограниченных полярными кривыми

Мы изучили формулы для площади под кривой, заданной в прямоугольных координатах, и параметрически заданных кривых. Теперь обратимся к выводу формулы для площади области, ограниченной полярной кривой. Напомним, что доказательство основной теоремы исчисления использовало понятие суммы Римана для аппроксимации площади под кривой с помощью прямоугольников.Для полярных кривых мы снова используем сумму Римана, но прямоугольники заменены секторами круга.

Рассмотрим кривую, заданную функцией \ (r = f (θ), \), где \ (α≤θ≤β. \) Наш первый шаг — разделить интервал \ ([α, β] \) на n подынтервалов равной ширины. Ширина каждого подынтервала определяется формулой \ (Δθ = (β − α) / n \), а точка разделения i -я \ (θ_i \) задается формулой \ (θ_i = α + iΔθ \ ). Каждая точка разделения \ (θ = θ_i \) определяет линию с наклоном \ (\ tan θ_i \), проходящую через полюс, как показано на следующем графике.

Рисунок \ (\ PageIndex {1} \): Разбиение типичной кривой в полярных координатах.

Отрезки соединены дугами постоянного радиуса. Это определяет сектора, площади которых можно рассчитать с помощью геометрической формулы. Затем площадь каждого сектора используется для аппроксимации площади между последовательными линейными сегментами. Затем мы суммируем площади секторов, чтобы приблизительно определить общую площадь. Этот подход дает приближение суммы Римана для общей площади. Формула для площади сектора круга показана на следующем рисунке.2 dθ. \ label {areapolar} \ end {align} \]

Пример \ (\ PageIndex {1} \): поиск области полярной области

Найдите площадь одного лепестка розы, определяемую уравнением \ (r = 3 \ sin (2θ). \)

Решение

График \ (r = 3 \ sin (2θ) \) следует.

Рисунок \ (\ PageIndex {3} \): График \ (r = 3 \ sin (2θ). \)

Когда \ (θ = 0 \), мы имеем \ (r = 3 \ sin (2 ( 0)) = 0 \). Следующее значение, для которого \ (r = 0 \) равно \ (θ = π / 2 \). Это можно увидеть, решив уравнение \ (3 \ sin (2θ) = 0 \) для \ (θ \).{π / 2} _0 \\ [4pt] & = \ dfrac {9} {4} (\ dfrac {π} {2} — \ dfrac {\ sin 2π} {4}) — \ dfrac {9} {4 } (0− \ dfrac {\ sin 4 (0)} {4}) \\ [4pt] & = \ dfrac {9π} {8} \ end {align *} \]

Упражнение \ (\ PageIndex {1} \)

Найдите площадь внутри кардиоиды, определяемую уравнением \ (r = 1− \ cos θ \).

Подсказка: Используйте уравнение \ ref {areapolar}. Обязательно определите правильные пределы интеграции перед оценкой.

Ответ: \ (А = 3π / 2 \)

Пример \ (\ PageIndex {1} \) включал поиск площади внутри одной кривой.Мы также можем использовать уравнение \ ref {areapolar}, чтобы найти площадь между двумя полярными кривыми. Однако нам часто нужно найти точки пересечения кривых и определить, какая функция определяет внешнюю кривую или внутреннюю кривую между этими двумя точками.

Пример \ (\ PageIndex {2} \): поиск области между двумя полярными кривыми

Найдите площадь вне кардиоиды \ (r = 2 + 2 \ sin θ \) и внутри круга \ (r = 6 \ sin θ \).

Решение

Сначала нарисуйте график, содержащий обе кривые, как показано.

Рисунок \ (\ PageIndex {4} \): Область между кривыми \ (r = 2 + 2 \ sin θ \) и \ (r = 6 \ sin θ. \)

Чтобы определить пределы интегрирования, сначала найдите точки пересечения, установив две функции равными друг другу и решив для \ (θ \):

\ [\ begin {align *} 6 \ sin θ & = 2 + 2 \ sin θ \\ [4pt] 4 \ sin θ & = 2 \\ [4pt] \ sin θ & = \ dfrac {1} {2 } \ end {align *}. \]

Это дает решения \ (θ = \ dfrac {π} {6} \) и \ (θ = \ dfrac {5π} {6} \), которые являются пределами интегрирования.{5π / 6} _ {π / 6} \)

\ (= 9 (\ dfrac {5π} {6} — \ dfrac {\ sin (10π / 6)} {2}) — 9 (\ dfrac {π} {6} — \ dfrac {\ sin (2π / 6)} {2}) — (3 (\ dfrac {5π} {6}) — 4 \ cos \ dfrac {5π} {6} — \ dfrac {\ sin (10π / 6)} {2}) + ( 3 (\ dfrac {π} {6}) — 4 \ cos \ dfrac {π} {6} — \ dfrac {\ sin (2π / 6)} {2}) \)

\ (= 4π \).

Упражнение \ (\ PageIndex {2} \)

Найдите площадь внутри круга \ (r = 4 \ cos θ \) и вне круга \ (r = 2 \).

Подсказка: Используйте уравнение \ ref {areapolar} и воспользуйтесь преимуществом симметрии.

Ответ: \ (A = \ dfrac {4π} {3} +2 \ sqrt {3} \)

В примере \ (\ PageIndex {2} \) мы нашли область внутри круга и вне кардиоиды, сначала найдя точки их пересечения. Обратите внимание, что решение уравнения непосредственно для \ (θ \) дало два решения: \ (θ = \ dfrac {π} {6} \) и \ (θ = \ dfrac {5π} {6} \). Однако на графике есть три точки пересечения. Третья точка пересечения — начало координат.Причина, по которой эта точка не появилась в качестве решения, заключается в том, что начало координат находится на обоих графиках, но для разных значений \ (θ \). Например, для кардиоиды получаем

\ [\ begin {align *} 2 + 2 \ sin θ = 0 \\ [4pt] \ sin θ = −1, \ end {align *}. \]

, поэтому значения для \ (θ \), которые решают это уравнение, равны \ (θ = \ dfrac {3π} {2} + 2nπ \), где \ (n \) — любое целое число. Для круга получаем

\ [6 \ sin θ = 0. \]

Решения этого уравнения имеют вид \ (θ = nπ \) для любого целого значения \ (n \).2} дт. \]

В полярных координатах мы определяем кривую уравнением \ (r = f (θ) \), где \ (α≤θ≤β. \) Чтобы адаптировать формулу длины дуги для полярной кривой, мы используем уравнения

\ [x = r \ cos θ = f (θ) \ cos θ \]

\ [y = r \ sin θ = f (θ) \ sin θ, \]

и заменим параметр \ (t \) на \ (θ \). { 2π} _0 \ sqrt {2 + 2 \ cos θ} \, dθ.π_0 \\ [4pt] & = 16 \ end {align *} \]

Упражнение \ (\ PageIndex {3} \)

Найдите общую длину дуги \ (r = 3 \ sin θ \).

Подсказка: Используйте уравнение \ ref {arcpolar1}. Чтобы определить правильные пределы, составьте таблицу значений.

Ответ: \ (s = 3π \)

5. Центроид площади интегрированием

М. Борна

Типичная (прямая) Проблема

В конструкции откидной плиты у нас есть бетонная стена (с вырезанными дверями и окнами), которую нам нужно поднять.Мы не хотим, чтобы стена треснула, когда мы ее поднимаем, поэтому нам нужно знать центр масс стены. Как найти центр масс такой неровной формы?

Конструкция с наклонно-перегородкой (также называемая откидной или откидной)

В этом разделе мы увидим, как найти центр тяжести области с прямыми сторонами, а затем расширим концепцию на области с изогнутыми сторонами, где мы будем использовать интеграцию .

Момент

Момент массы является мерой ее тенденции вращаться вокруг точки.Ясно, что чем больше масса (и чем больше расстояние от точки), тем больше будет тенденция к вращению.

Момент определяется как:

Момент = масса × расстояние от точки

Пример 1

В этом случае будет общий момент около O:

(По часовой стрелке в данной работе считается положительным.)

` М = 2 × 1 — 10 × 3 = -28 \ «кгм» `

Центр масс

Теперь мы стремимся найти центр масс системы, и это приведет к более общему результату.

Пример 2

У нас есть 3 гири по 10 кг, 5 кг и 7 кг на расстоянии 2 м, 2 м и 1 м от точки O, как показано.

Мы хотим заменить эти массы одной единственной массой, чтобы получить эквивалентный момент. Где мы должны разместить эту единую массу?

Ответ

Общий момент `= 10 × 2 + 5 × 4 + 7 × 5 = 75 \» кг.м «`

Если сложить массы, получится: `10 + 5 + 7 = 22 \» кг «`

Для равноценного момента нам понадобится:

`22 бар (d) = 75`

где
bar (d) — это расстояние от центра масс до точки вращения.

т. Е. `Bar (d) = 75/22 приблизительно 3,4 \ text [м]`

Таким образом, наша эквивалентная система (с одной массой `22 \» кг «`) будет иметь:

Центр масс (центроид) тонкой пластины

1) Прямоугольник:

Центроид (очевидно) будет точно в центре пластины в точке (2, 1).

2) Больше Сложные формы :

Мы делим сложную форму на прямоугольники и находим bar (x) (координата центра тяжести x ) и bar (y) (координата центра тяжести y ), принимая моменты относительно Координаты y- и x- соответственно.

Поскольку это тонкие пластины с однородной плотностью, мы можем просто вычислить моменты, используя площадь .

Пример 3

Найдите центр тяжести фигуры:

Ответ

Мы разделим область на 2 прямоугольника и предположим, что масса каждого прямоугольника сосредоточена в центре.

Левый прямоугольник: «» Площадь «= 3 × 2 = 6 \» кв. Ед. «`. Центр `(-1/2, 1)`

Правый прямоугольник: «» Площадь «= 2 × 4 = 8 \» кв. Ед. «`.Центр `(2, 2)`

Если взять моменты относительно оси y , получим:

`6 (- 1/2) +8 (2) = (6 + 8) barx`
-3 + 16 = 14 бар x
бар x = 13/14 шт

Теперь, относительно оси x :

`6 (1) +8 (2) = (6 + 8) бары`
`6 + 16 = 14бары`

`бары = 22/14`
`= 1 4 / 7`

Итак, центроид находится по адресу: `(13/14, 1 4/7)`

Мы будем использовать этот процесс для решения проблемы конструкции наклонной плиты , упомянутой в начале этого раздела.

В целом можно сказать:

`bar (x) = (» суммарные моменты в «\ x» -направлении «) /» общая площадь «`

`bar (y) = (» суммарные моменты в «\ y» -направлении «) /» общая площадь «`

Эта идея более широко используется в следующем разделе.

Центроид для криволинейных участков

Рассматривая сначала простой случай, мы стремимся найти центроид для области, определяемой функцией f ( x ), и вертикальные линии x = a и x = b , как указано на следующем рисунке.

Чтобы найти центроид, мы используем ту же основную идею, что и для случая с прямыми сторонами выше. Указанный «типичный» прямоугольник находится в единицах «x» от оси «y», и он имеет ширину «Δx» (которая становится «dx» при интегрировании) и высоту y = f ( x ). .

Обобщая вышеупомянутый случай прямоугольных областей, мы умножаем эти 3 значения (`x`,` f (x) `и` Deltax`, что дает нам площадь каждого тонкого прямоугольника, умноженную на его расстояние от оси `x`. ), затем добавьте их.d y \ f (y) \ dy`

Обратите внимание, что на этот раз интегрирование ведется по «y», а расстояние «типичного» прямоугольника от оси «x» составляет единицы «y». Также обратите внимание, что нижний и верхний пределы интеграла — это «c» и «d», которые находятся на оси «y».

Конечно, могут быть прямоугольные участки, которые нужно рассматривать отдельно. (Для упрощения я использовал другую кривую для случая «bary».)

Альтернативный метод: В зависимости от функции может быть проще использовать следующую альтернативную формулу для координаты y- , которая получена из учета моментов в направлении x (обратите внимание на « dx » в интеграле, а верхний и нижний пределы соответствуют оси x для этого альтернативного метода).2) / 2 дх`

Это верно, поскольку для нашей тонкой полосы (шириной `dx`) центроид будет составлять половину расстояния от верха до низа полосы. b x \ (y_2-y_1) \ dx`

Для координаты y у нас есть 2 разных способа сделать это.2`

`= 2,29`

В этом примере метод 2 проще, чем метод 1, но это не всегда так.

На поиске областей путем интеграции

Разделив на $ l $ и извлекая квадратный корень, имеем
\ [
\ text {среднее квадратичное} = \ frac {1} {\ sqrt 3} \, др.
\]

Здесь среднее арифметическое $ \ frac {1} {2} al $; и соотношение
квадратичного среднего арифметического (это отношение называется
форм-фактор ) равен $ \ dfrac {2} {\ sqrt 3} = 1.2} $, поскольку он вращается вокруг оси $ x $, между
$ x = 0 $ и $ x = 4 $.

(9) Найдите объем, генерируемый синусоидальной кривой.
вращается вокруг оси $ x $. Найдите также площадь
его поверхность.

(10) Найдите площадь участка кривой
$ xy = a $ находится между $ x = 1 $ и $ x = a $. Найти
средняя ордината между этими пределами.

(11) Покажите, что среднее квадратичное значение функции
$ y = \ sin x $, между пределами $ 0 $ и $ \ pi $ радиан, равно $ \ dfrac {\ sqrt2} {2} $.
Найдите также среднее арифметическое того же
функционировать в одних и тех же пределах; и показать, что
форм-фактор $ = 1.{0,21x} $.
Найдите площадь между кривой и
ось $ x $, от ординаты в точке $ x = 2 $ до ординаты
при $ x = 8 $. Найдите также высоту средней ординаты
кривой между этими точками.

(15) Покажите, что радиус круга, площадь
что в два раза больше площади полярной диаграммы, равно
к среднему квадратичному значению всех значений $ r $ для этого
полярная диаграмма.

(16) Найдите объем, образованный кривой
$ y = ± \ dfrac {x} {6} \ sqrt {x (10-x)} $ вращается вокруг оси $ x $.2 \ pi $. Отсюда и
ответ следует.

(14) Площадь 62,6 $ кв. Средняя ордината — 10,42 доллара.

(16) 436,3 $. (Это твердое тело имеет форму груши.)

5.3 Двойные интегралы в полярных координатах — том 3 исчисления

Цели обучения

5.3.1 Распознавать формат двойного интеграла в полярной прямоугольной области.
5.3.2 Вычислить двойной интеграл в полярных координатах с помощью повторного интеграла.
5.3.3. Распознавать формат двойного интеграла по общей полярной области.
5.3.4 Используйте двойные интегралы в полярных координатах для вычисления площадей и объемов.

Двойные интегралы иногда намного легче вычислить, если мы изменим прямоугольные координаты на полярные. Однако, прежде чем мы опишем, как сделать это изменение, нам нужно установить понятие двойного интеграла в полярной прямоугольной области.

Полярные прямоугольные области интеграции

Когда мы определили двойной интеграл для непрерывной функции в прямоугольных координатах — скажем, gg по области RR в плоскости xyxy — мы разделили RR на подпрямоугольники со сторонами, параллельными осям координат.Эти стороны имеют либо постоянные значения xx, либо постоянные значения yy. В полярных координатах форма, с которой мы работаем, представляет собой полярный прямоугольник, стороны которого имеют постоянные значения rr и / или постоянные значения θθ. Это означает, что мы можем описать полярный прямоугольник, как на рис. 5.28 (a), с R = {(r, θ) | a≤r≤b, α≤θ≤β} .R = {(r, θ) | a≤ r≤b, α≤θ≤β}.

В этом разделе мы ищем возможность интегрирования по полярным прямоугольникам. Рассмотрим функцию f (r, θ) f (r, θ) над полярным прямоугольником RR. Разделим интервал [a, b] [a, b] на миллиметровые подинтервалы [ri − 1, ri] [ri − 1, ri ] длины Δr = (b − a) / mΔr = (b − a) / m и разделим интервал [α, β] [α, β] на nn подинтервалов [θj − 1, θj] [θj − 1, θj ] ширины Δθ = (β − α) / n.Δθ = (β − α) / n. Это означает, что круги r = rir = ri и лучи θ = θjθ = θj для 1≤i≤m1≤i≤m и 1≤j≤n1≤j≤n делят полярный прямоугольник RR на меньшие полярные подпрямоугольники RijRij (рисунок 5.28 (б)).

Рис. 5.28 (a) Полярный прямоугольник RR (b), разделенный на подпрямоугольники Rij.Rij. (c) Крупный план подпрямоугольника.

Как и раньше, нам нужно найти площадь ΔAΔA полярного подпрямоугольника RijRij и «полярный» объем тонкого прямоугольника над Rij.Rij. Напомним, что в окружности радиуса r, r длина ss дуги, ограниченная центральным углом θθ радиан, равна s = rθ.s = rθ. Обратите внимание, что полярный прямоугольник RijRij очень похож на трапецию с параллельными сторонами ri − 1Δθri − 1Δθ и riΔθriΔθ и шириной Δr.Δr. Следовательно, площадь полярного подпрямоугольника RijRij равна

.
ΔA = 12Δr (ri − 1Δθ + r1Δθ) .ΔA = 12Δr (ri − 1Δθ + r1Δθ).

Упрощая и полагая rij * = 12 (ri − 1 + ri), rij * = 12 (ri − 1 + ri), имеем ΔA = rij * ΔrΔθ.ΔA = rij * ΔrΔθ. Следовательно, полярный объем тонкой рамки над RijRij (рис. 5.29) равен

.
f (rij *, θij *) ΔA = f (rij *, θij *) rij * ΔrΔθ.f (rij *, θij *) ΔA = f (rij *, θij *) rij * ΔrΔθ.

Рисунок 5.29 Определение объема тонкой рамки над полярным прямоугольником Rij.Rij.

Используя ту же идею для всех подпрямоугольников и суммируя объемы прямоугольных ящиков, мы получаем двойную сумму Римана как

∑i = 1m∑j = 1nf (rij *, θij *) rij * ΔrΔθ.∑i = 1m∑j = 1nf (rij *, θij *) rij * ΔrΔθ.

Как мы видели ранее, мы получаем лучшее приближение к полярному объему твердого тела над областью RR, когда позволяем mm и nn становиться больше. Следовательно, мы определяем полярный объем как предел двойной суммы Римана,

V = limm, n → ∞∑i = 1m∑j = 1nf (rij *, θij *) rij * ΔrΔθ.V = limm, n → ∞∑i = 1m∑j = 1nf (rij *, θij *) rij * ΔrΔθ.

Это становится выражением для двойного интеграла.

Определение

Двойной интеграл функции f (r, θ) f (r, θ) по полярной прямоугольной области RR в плоскости rθrθ определяется как

∬Rf (r, θ) dA = limm, n → ∞∑i = 1m∑j = 1nf (rij *, θij *) ΔA = limm, n → ∞∑i = 1m∑j = 1nf (rij *, θij * ) rij * ΔrΔθ.∬Rf (r, θ) dA = limm, n → ∞∑i = 1m∑j = 1nf (rij *, θij *) ΔA = limm, n → ∞∑i = 1m∑j = 1nf ( rij *, θij *) rij * ΔrΔθ.

5,8

Опять же, как и в случае двойных интегралов по прямоугольным областям, двойной интеграл по полярной прямоугольной области может быть выражен как повторный интеграл в полярных координатах.Следовательно,

∬Rf (r, θ) dA = ∬Rf (r, θ) rdrdθ = ∫θ = αθ = β∫r = ar = bf (r, θ) rdrdθ.∬Rf (r, θ) dA = ∬Rf (r , θ) rdrdθ = ∫θ = αθ = β∫r = ar = bf (r, θ) rdrdθ.

Обратите внимание, что выражение для dAdA заменяется на rdrdθrdrdθ при работе в полярных координатах. Другой способ взглянуть на полярный двойной интеграл — это заменить двойной интеграл в прямоугольных координатах. Когда функция ff задана в терминах xx и y, y, используя x = rcosθ, y = rsinθ, anddA = rdrdθx = rcosθ, y = rsinθ, и dA = rdrdθ изменяет ее на

.
∬Rf (x, y) dA = ∬Rf (rcosθ, rsinθ) rdrdθ.∬Rf (x, y) dA = ∬Rf (rcosθ, rsinθ) rdrdθ.

Обратите внимание, что все свойства, перечисленные в разделе Двойные интегралы по прямоугольным областям для двойного интеграла в прямоугольных координатах, сохраняются и для двойного интеграла в полярных координатах, поэтому мы можем использовать их без колебаний.

Пример 5.24

Рисование полярной прямоугольной области

Нарисуйте полярную прямоугольную область R = {(r, θ) | 1≤r≤3,0≤θ≤π} .R = {(r, θ) | 1≤r≤3,0≤θ≤π}.

Решение

Как видно из рисунка 5.30, r = 1r = 1 и r = 3r = 3 — это окружности радиуса 1 и 31 и 3, а 0≤θ≤π0≤θ≤π покрывает всю верхнюю половину плоскости. Следовательно, область RR выглядит как полукруглая полоса.

Рисунок 5.30 Полярная область RR находится между двумя полукругами.

Теперь, когда мы нарисовали полярную прямоугольную область, давайте продемонстрируем, как вычислить двойной интеграл по этой области, используя полярные координаты.

Пример 5.25

Вычисление двойного интеграла по полярной прямоугольной области

Вычислить интеграл ∬R3xdA∬R3xdA по области R = {(r, θ) | 1≤r≤2,0≤θ≤π}.R = {(r, θ) | 1≤r≤2,0≤θ≤π}.

Решение

Сначала мы нарисуем фигуру, аналогичную рис. 5.30, но с внешним радиусом 2.2. Из рисунка видно, что у нас

∬R3xdA = ∫θ = 0θ = π∫r = 1r = 23rcosθrdrdθ Используйте повторный интеграл с правильными пределами интегрирования. = ∫θ = 0θ = πcosθ [r3 | r = 1r = 2] dθ Интегрируйте сначала относительно. = ∫θ = 0θ = π7cosθdθ = 7sinθ | θ = 0θ = π = 0. R3xdA = ∫θ = 0θ = π∫r = 1r = 23rcosθrdθ Используйте повторный интеграл с правильными пределами интегрирования. = ∫θ = 0θ = πcosθ [r3 | r = 1r = 2] dθ Интегрируйте сначала по отношению к тору.= ∫θ = 0θ = π7cosθdθ = 7sinθ | θ = 0θ = π = 0.

КПП 5.17

Нарисуйте область R = {(r, θ) | 1≤r≤2, −π2≤θ≤π2}, R = {(r, θ) | 1≤r≤2, −π2≤θ≤π2}, и оцените ∬RxdA.∬RxdA.

Пример 5.26

Вычисление двойного интеграла путем преобразования из прямоугольных координат

Вычислите интеграл ∬R (1 − x2 − y2) dA∬R (1 − x2 − y2) dA, где RR — единичная окружность на плоскости xyxy.

Решение

Область RR представляет собой единичный круг, поэтому мы можем описать ее как R = {(r, θ) | 0≤r≤1,0≤θ≤2π}.R = {(r, θ) | 0≤r≤1,0≤θ≤2π}.

Используя преобразование x = rcosθ, y = rsinθ, x = rcosθ, y = rsinθ и dA = rdrdθ, dA = rdrdθ, получаем

∬R (1 − x2 − y2) dA = ∫02π∫01 (1 − r2) rdrdθ = ∫02π∫01 (r − r3) drdθ = ∫02π [r22 − r44] 01dθ = ∫02π14dθ = π2.∬R ( 1 − x2 − y2) dA = ∫02π∫01 (1 − r2) rdrdθ = ∫02π∫01 (r − r3) drdθ = ∫02π [r22 − r44] 01dθ = ∫02π14dθ = π2.

Пример 5.27

Вычисление двойного интеграла путем преобразования из прямоугольных координат

Вычислить интеграл ∬R (x + y) dA∬R (x + y) dA, где R = {(x, y) | 1≤x2 + y2≤4, x≤0} .R = {(x, y ) | 1≤x2 + y2≤4, x≤0}.

Решение

Мы видим, что RR — это кольцевая область, которая может быть преобразована в полярные координаты и описана как R = {(r, θ) | 1≤r≤2, π2≤θ≤3π2} R = {(r, θ) | 1≤r≤2, π2≤θ≤3π2} (см. Следующий график).

Рисунок 5.31 Кольцевая область интеграции R.R.

Следовательно, используя преобразование x = rcosθ, y = rsinθ, x = rcosθ, y = rsinθ и dA = rdrdθ, dA = rdrdθ, получаем

∬R (x + y) dA = ∫θ = π / 2θ = 3π / 2∫r = 1r = 2 (rcosθ + rsinθ) rdrdθ = (∫r = 1r = 2r2dr) (∫π / 23π / 2 (cosθ + sinθ) dθ) = [r33] 12 [sinθ − cosθ] | π / 23π / 2 = -143.∬R (x + y) dA = ∫θ = π / 2θ = 3π / 2∫r = 1r = 2 (rcosθ + rsinθ) rdrdθ = (∫r = 1r = 2r2dr) (∫π / 23π / 2 (cosθ + sinθ) dθ) = [r33] 12 [sinθ − cosθ] | π / 23π / 2 = -143.

КПП 5.18

Вычислите интеграл ∬R (4 − x2 − y2) dA∬R (4 − x2 − y2) dA, где RR — окружность радиуса 22 на плоскости xyxy.

Общие полярные области интеграции

Чтобы оценить двойной интеграл непрерывной функции с помощью повторных интегралов по общим полярным областям, мы рассматриваем два типа областей, аналогичные типу I и типу II, как обсуждалось для прямоугольных координат в двойных интегралах по общим областям.Полярные уравнения чаще записываются как r = f (θ) r = f (θ), чем θ = f (r), θ = f (r), поэтому мы описываем общую полярную область как R = {(r, θ) | α≤θ≤β, h2 (θ) ≤r≤h3 (θ)} R = {(r, θ) | α≤θ≤β, h2 (θ) ≤r≤h3 (θ)} (см. следующий рисунок).

Рисунок 5.32. Общая полярная область между α <θ <βα <θ <β и h2 (θ)

Теорема 5.8

Двойные интегралы по общим полярным областям

Если f (r, θ) f (r, θ) непрерывно в общей полярной области DD, как описано выше, то

∬Df (r, θ) rdrdθ = ∫θ = αθ = β∫r = h2 (θ) r = h3 (θ) f (r, θ) rdrdθ∬Df (r, θ) rdrdθ = ∫θ = αθ = β ∫r = h2 (θ) r = h3 (θ) f (r, θ) rdrdθ

5.9

Пример 5.28

Вычисление двойного интеграла по общей полярной области

Вычислите интеграл ∬Dr2sinθrdrdθ∬Dr2sinθrdrdθ, где DD — область, ограниченная полярной осью и верхней половиной кардиоиды r = 1 + cosθ.r = 1 + cosθ.

Решение

Мы можем описать область DD как {(r, θ) | 0≤θ≤π, 0≤r≤1 + cosθ} {(r, θ) | 0≤θ≤π, 0≤r≤1 + cosθ} как показано на следующем рисунке.

Рис. 5.33. Область DD — это верхняя половина кардиоиды.

Следовательно, имеем

∬Dr2sinθrdθ = ∫θ = 0θ = π∫r = 0r = 1 + cosθ (r2sinθ) rdrdθ = 14∫θ = 0θ = π [r4] r = 0r = 1 + cosθsinθdθ = 14∫θ = 0θ = π (1+ cosθ) 4sinθdθ = −14 [(1 + cosθ) 55] 0π = 85.∬Dr2sinθrdrdθ = ∫θ = 0θ = π∫r = 0r = 1 + cosθ (r2sinθ) rdrdθ = 14∫θ = 0θ = π [r4] r = 0r = 1 + cosθsinθdθ = 14∫θ = 0θ = π (1 + cosθ) 4sinθdθ = −14 [(1 + cosθ) 55] 0π = 85.

КПП 5.19

Вычислить интеграл

∬Dr2sin22θrdrdθ, где D = {(r, θ) | -π4≤θ≤π4≤r≤2cos2θ} .∬Dr2sin22θrdrdθ, где D = {(r, θ) | -π4≤θ≤π4≤r≤2cos2θ}.

Полярные области и объемы

Как и в прямоугольных координатах, если твердое тело SS ограничено поверхностью z = f (r, θ), z = f (r, θ), а также поверхностями r = a, r = b, θ = α , r = a, r = b, θ = α и θ = β, θ = β, мы можем найти объем VV SS путем двойного интегрирования, как

V = ∬Rf (r, θ) rdrdθ = ∫θ = αθ = β∫r = ar = bf (r, θ) rdrdθ.V = ∬Rf (r, θ) rdrdθ = ∫θ = αθ = β∫r = ar = bf (r, θ) rdrdθ.

Если основание твердого тела можно описать как D = {(r, θ) | α≤θ≤β, h2 (θ) ≤r≤h3 (θ)}, D = {(r, θ) | α≤ θ≤β, h2 (θ) ≤r≤h3 (θ)}, то двойной интеграл для объема становится

V = ∬Df (r, θ) rdrdθ = ∫θ = αθ = β∫r = h2 (θ) r = h3 (θ) f (r, θ) rdrdθ.V = ∬Df (r, θ) rdrdθ = ∫ θ = αθ = β∫r = h2 (θ) r = h3 (θ) f (r, θ) rdrdθ.

Проиллюстрируем эту идею несколькими примерами.

Пример 5.29

Определение объема с помощью двойного интеграла

Найдите объем твердого тела, лежащего под параболоидом z = 1 − x2 − y2z = 1 − x2 − y2 и над единичной окружностью на плоскости xyxy (см. Следующий рисунок).

Рисунок 5.34. Параболоид z = 1 − x2 − y2z = 1 − x2 − y2.

Решение

Методом двойного интегрирования мы видим, что объем является повторным интегралом вида ∬R (1 − x2 − y2) dA∬R (1 − x2 − y2) dA, где R = {(r, θ) | 0≤r≤1,0≤θ≤2π} .R = {(r, θ) | 0≤r≤1,0≤θ≤2π}.

Это интегрирование было показано ранее в примере 5.26, поэтому объем равен π2π2 кубических единиц.

Пример 5.30

Поиск объема с помощью двойного интегрирования

Найдите объем твердого тела, лежащего под параболоидом z = 4 − x2 − y2z = 4 − x2 − y2 и над диском (x − 1) 2 + y2 = 1 (x − 1) 2 + y2 = 1 на xyxy-плоскость.См. Параболоид на рис. 5.35, пересекающий цилиндр (x − 1) 2 + y2 = 1 (x − 1) 2 + y2 = 1 над плоскостью xyxy.

Рис. 5.35. Определение объема твердого тела с параболоидной крышкой и круглым основанием.

Решение

Сначала измените диск (x − 1) 2 + y2 = 1 (x − 1) 2 + y2 = 1 на полярные координаты. Раскладывая квадратный член, получаем x2−2x + 1 + y2 = 1.x2−2x + 1 + y2 = 1. Затем упростим, чтобы получить x2 + y2 = 2x, x2 + y2 = 2x, что в полярных координатах становится r2 = 2rcosθr2 = 2rcosθ, а затем либо r = 0r = 0, либо r = 2cosθ.г = 2cosθ. Аналогичным образом уравнение параболоида меняется на z = 4 − r2.z = 4 − r2. Следовательно, мы можем описать диск (x − 1) 2 + y2 = 1 (x − 1) 2 + y2 = 1 на xyxy-плоскости как область

D = {(r, θ) | 0≤θ≤π, 0≤r≤2cosθ}. D = {(r, θ) | 0≤θ≤π, 0≤r≤2cosθ}.

Следовательно, объем твердого тела, ограниченного сверху параболоидом z = 4 − x2 − y2z = 4 − x2 − y2 и ниже r = 2cosθr = 2cosθ, равен

V = ∬Df (r, θ) rdrdθ = ∫θ = 0θ = π∫r = 0r = 2cosθ (4 − r2) rdrdθ = ∫θ = 0θ = π [4r22 − r44 | 02cosθ] dθ = ∫0π [8cos2θ− 4cos2θ] dθ = [52θ + 52sinθcosθ − sinθcos3θ] 0π = 52π.V = ∬Df (r, θ) rdrdθ = ∫θ = 0θ = π∫r = 0r = 2cosθ (4 − r2) rdrdθ = ∫θ = 0θ = π [4r22 − r44 | 02cosθ] dθ = ∫0π [8cos2θ − 4cos2θ] dθ = [52θ + 52sinθcosθ − sinθcos3θ] 0π = 52π.

Обратите внимание, что в следующем примере интегрировать полярные координаты не всегда просто. Сложность интеграции зависит от функции, а также от региона, в котором нам нужно выполнить интеграцию. Если область имеет более естественное выражение в полярных координатах или если ff имеет более простую первообразную в полярных координатах, то изменение полярных координат уместно; в противном случае используйте прямоугольные координаты.

Пример 5.31

Определение объема с помощью двойного интеграла

Найдите объем области, которая лежит под параболоидом z = x2 + y2z = x2 + y2 и над треугольником, ограниченным прямыми y = x, x = 0, y = x, x = 0 и x + y = 2x + y = 2 в плоскости xyxy (рисунок 5.36).

Решение

Сначала исследуйте область, в которой нам нужно установить двойной интеграл и сопутствующий параболоид.

Рис. 5.36. Определение объема твердого тела под параболоидом и над заданным треугольником.

Область DD — это {(x, y) | 0≤x≤1, x≤y≤2 − x}. {(X, y) | 0≤x≤1, x≤y≤2 − x}. Преобразуя прямые y = x, x = 0, y = x, x = 0 и x + y = 2x + y = 2 в xyxy-плоскости в функции от rr и θ, θ, получаем θ = π / 4 , θ = π / 4, θ = π / 2, θ = π / 2 и r = 2 / (cosθ + sinθ), r = 2 / (cosθ + sinθ) соответственно.Изобразив область на плоскости xyxy, мы видим, что она выглядит как D = {(r, θ) | π / 4≤θ≤π / 2,0≤r≤2 / (cosθ + sinθ)}. D = { (r, θ) | π / 4≤θ≤π / 2,0≤r≤2 / (cosθ + sinθ)}. Теперь преобразование уравнения поверхности дает z = x2 + y2 = r2.z = x2 + y2 = r2. Следовательно, объем твердого тела определяется двойным интегралом

.
V = ∬Df (r, θ) rdrdθ = ∫θ = π / 4θ = π / 2∫r = 0r = 2 / (cosθ + sinθ) r2rdrdθ = ∫π / 4π / 2 [r44] 02 / (cosθ + sinθ ) dθ = 14∫π / 4π / 2 (2cosθ + sinθ) 4dθ = 164∫π / 4π / 2 (1cosθ + sinθ) 4dθ = 4∫π / 4π / 2 (1cosθ + sinθ) 4dθ.V = ∬Df ( r, θ) rdrdθ = ∫θ = π / 4θ = π / 2∫r = 0r = 2 / (cosθ + sinθ) r2rdrdθ = ∫π / 4π / 2 [r44] 02 / (cosθ + sinθ) dθ = 14∫ π / 4π / 2 (2cosθ + sinθ) 4dθ = 164∫π / 4π / 2 (1cosθ + sinθ) 4dθ = 4∫π / 4π / 2 (1cosθ + sinθ) 4dθ.

Как видите, этот интеграл очень сложный. Таким образом, вместо этого мы можем вычислить этот двойной интеграл в прямоугольных координатах как

V = ∫01∫x2 − x (x2 + y2) dydx. V = ∫01∫x2 − x (x2 + y2) dydx.

Оценка дает

V = ∫01∫x2 − x (x2 + y2) dydx = ∫01 [x2y + y33] | x2 − xdx = ∫0183−4x + 4×2−8x33dx = [8×3−2×2 + 4×33−2×43] | 01 = 43. V = ∫01∫x2 − x (x2 + y2) dydx = ∫01 [x2y + y33] | x2 − xdx = ∫0183−4x + 4×2−8x33dx = [8×3−2×2 + 4×33−2×43] | 01 = 43.

Чтобы ответить на вопрос, как находятся формулы для объемов различных стандартных твердых тел, таких как сфера, конус или цилиндр, мы хотим продемонстрировать пример и найти объем произвольного конуса.

Пример 5.32

Определение объема с помощью двойного интеграла

Используйте полярные координаты, чтобы найти объем внутри конуса z = 2 − x2 + y2z = 2 − x2 + y2 и выше xy-plane.xy-plane.

Решение

Область DD для интегрирования является основанием конуса, который выглядит как окружность на плоскости xy (см. Следующий рисунок).

Рис. 5.37. Определение объема твердого тела внутри конуса и над плоскостью xyxy.

Мы находим уравнение круга, полагая z = 0: z = 0:

0 = 2-х2 + у22 = х2 + у2х2 + у2 = 4.0 = 2-х2 + у22 = х2 + у2х2 + у2 = 4.

Это означает, что радиус круга равен 2,2, поэтому для интегрирования мы имеем 0≤θ≤2π0≤θ≤2π и 0≤r≤2.0≤r≤2. Подставляя x = rcosθx = rcosθ и y = rsinθy = rsinθ в уравнение z = 2 − x2 + y2z = 2 − x2 + y2, получаем z = 2 − r.z = 2 − r. Следовательно, объем конуса

∫θ = 0θ = 2π∫r = 0r = 2 (2 − r) rdrdθ = 2π43 = 8π3∫θ = 0θ = 2π∫r = 0r = 2 (2 − r) rdrdθ = 2π43 = 8π3 кубических единиц.

Анализ

Обратите внимание, что если бы мы нашли объем произвольного конуса с радиусом aa единиц и высотой hh единиц, то уравнение конуса было бы z = h − hax2 + y2.z = h — hax2 + y2.

Мы все еще можем использовать рисунок 5.37 и установить интеграл как ∫θ = 0θ = 2π∫r = 0r = a (h − har) rdrdθ.θ = 0θ = 2π∫r = 0r = a (h − har) rdrdθ .

Вычисляя интеграл, получаем 13πa2h.13πa2h.

КПП 5.20

Используйте полярные координаты, чтобы найти повторный интеграл для определения объема твердого тела, окруженного параболоидами z = x2 + y2z = x2 + y2 и z = 16 − x2 − y2.z = 16 − x2 − y2.

Как и в случае с прямоугольными координатами, мы также можем использовать полярные координаты для поиска областей определенных регионов с помощью двойного интеграла.Как и раньше, нам нужно понять область, площадь которой мы хотим вычислить. Построение графика и определение региона могут быть полезны для понимания ограничений интеграции. Как правило, формула площади при двойном интегрировании будет иметь вид

.
AreaA = ∫αβ∫h2 (θ) h3 (θ) 1rdrdθ. AreaA = ∫αβ∫h2 (θ) h3 (θ) 1rdrdθ.

Пример 5.33

Нахождение площади с помощью двойного интеграла в полярных координатах

Оцените площадь, ограниченную кривой r = cos4θ.r = cos4θ.

Решение

Набросок графика функции r = cos4θr = cos4θ показывает, что это полярная роза с восемью лепестками (см. Следующий рисунок).

Рис. 5.38. Нахождение области полярной розы с восемью лепестками.

Используя симметрию, мы видим, что нам нужно найти площадь одного лепестка, а затем умножить ее на 8,8. Обратите внимание, что значения θθ, для которых график проходит через начало координат, являются нулями функции cos4θ, cos4θ, и они являются нечетными кратными π / 8.π / 8. Таким образом, один из лепестков соответствует значениям θθ в интервале [−π / 8, π / 8]. [- π / 8, π / 8]. Следовательно, площадь, ограниченная кривой r = cos4θr = cos4θ, равна

A = 8∫θ = −π / 8θ = π / 8∫r = 0r = cos4θ1rdrdθ = 8∫ − π / 8π / 8 [12r2 | 0cos4θ] dθ = 8∫ − π / 8π / 812cos24θdθ = 8 [14θ + 116sin4θcos4θ | −π / 8π / 8] = 8 [π16] = π2.A = 8∫θ = −π / 8θ = π / 8∫r = 0r = cos4θ1rdrdθ = 8∫ − π / 8π / 8 [12r2 | 0cos4θ] dθ = 8∫ − π / 8π / 812cos24θdθ = 8 [14θ + 116sin4θcos4θ | −π / 8π / 8] = 8 [π16] = π2.

Пример 5.34

Нахождение области между двумя полярными кривыми

Найдите площадь, ограниченную кругом r = 3cosθr = 3cosθ и кардиоидой r = 1 + cosθ.r = 1 + cosθ.

Решение

Прежде всего, нарисуйте графики региона (рис. 5.39).

Рис. 5.39. Нахождение области, заключенной как в круг, так и в кардиоиду.

Мы можем видеть симметрию графа, что нам нужно найти точки пересечения. Приравнивая два уравнения друг к другу, получаем

3cosθ = 1 + cosθ. 3cosθ = 1 + cosθ.

Одна из точек пересечения θ = π / 3.θ = π / 3. Область над полярной осью состоит из двух частей: одна часть определяется кардиоидой от θ = 0θ = 0 до θ = π / 3θ = π / 3, а другая часть определяется кругом от θ = π / 3θ = π. / 3 до θ = π / 2.θ = π / 2. По симметрии общая площадь в два раза больше площади над полярной осью.Таким образом, имеем

A = 2 [∫θ = 0θ = π / 3∫r = 0r = 1 + cosθ1rdrdθ + ∫θ = π / 3θ = π / 2∫r = 0r = 3cosθ1rdrdθ]. A = 2 [∫θ = 0θ = π / 3∫r = 0r = 1 + cosθ1rdrdθ + ∫θ = π / 3θ = π / 2∫r = 0r = 3cosθ1rdrdθ].

Оценивая каждую деталь отдельно, находим, что площадь составляет

A = 2 (14π + 9163 + 38π − 9163) = 2 (58π) = 54πквадратных единиц. A = 2 (14π + 9163 + 38π − 9163) = 2 (58π) = 54πквадратных единиц.

КПП 5.21

Найдите площадь, заключенную внутри кардиоиды r = 3−3sinθr = 3−3sinθ и вне кардиоиды r = 1 + sinθ.r = 1 + sinθ.

Пример 5.35

Вычисление неправильного двойного интеграла в полярных координатах

Вычислите интеграл ∬R2e − 10 (x2 + y2) dxdy.∬R2e − 10 (x2 + y2) dxdy.

Решение

Это неправильный интеграл, потому что мы интегрируем по неограниченной области R2.R2. В полярных координатах всю плоскость R2R2 можно рассматривать как 0≤θ≤2π, 0≤θ≤2π, 0≤r≤∞.0≤r≤∞.

Используя замену переменных из прямоугольных координат в полярные, получаем

∬R2e − 10 (x2 + y2) dxdy = ∫θ = 0θ = 2π∫r = 0r = ∞e − 10r2rdrdθ = ∫θ = 0θ = 2π (lima → ∞∫r = 0r = ae − 10r2rdr) dθ = (∫ θ = 0θ = 2πdθ) (lima → ∞∫r = 0r = ae − 10r2rdr) = 2π (lima → ∞∫r = 0r = ae − 10r2rdr) = 2πlima → ∞ (−120) (e − 10r2 | 0a) = 2π (−120) lima → ∞ (e − 10a2−1) = π10.∬R2e − 10 (x2 + y2) dxdy = ∫θ = 0θ = 2π∫r = 0r = ∞e − 10r2rdrdθ = ∫θ = 0θ = 2π (lima → ∞∫r = 0r = ae − 10r2rdr) dθ = (∫ θ = 0θ = 2πdθ) (lima → ∞∫r = 0r = ae − 10r2rdr) = 2π (lima → ∞∫r = 0r = ae − 10r2rdr) = 2πlima → ∞ (−120) (e − 10r2 | 0a) = 2π (−120) lima → ∞ (e − 10a2−1) = π10.

КПП 5.22

Вычислите интеграл ∬R2e − 4 (x2 + y2) dxdy.∬R2e − 4 (x2 + y2) dxdy.

Раздел 5.3. Упражнения

В следующих упражнениях выразите регион DD в полярных координатах.

122.

DD — это область диска радиуса 22 с центром в начале координат, лежащая в первом квадранте.

123.

DD — это область между окружностями радиуса 44 и 55 с центром в начале координат, лежащая во втором квадранте.

124.

DD — это область, ограниченная осью yy и x = 1 − y2.x = 1 − y2.

125.

DD — это область, ограниченная осью xx и y = 2 − x2.y = 2 − x2.

126.

D = {(x, y) | x2 + y2≤4x} D = {(x, y) | x2 + y2≤4x}

127.

D = {(x, y) | x2 + y2≤4y} D = {(x, y) | x2 + y2≤4y}

В следующих упражнениях дается график полярной прямоугольной области DD.Выразите DD в полярных координатах.

128.

130.

132.

На следующем графике область DD расположена ниже y = xy = x и ограничена x = 1, x = 5, x = 1, x = 5 и y = 0.y = 0.

133.

На следующем графике область DD ограничена y = xy = x и y = x2.y = x2.

В следующих упражнениях вычислите двойной интеграл ∬Rf (x, y) dA∬Rf (x, y) dA по полярной прямоугольной области D.D.

134.

f (x, y) = x2 + y2, D = {(r, θ) | 3≤r≤5,0≤θ≤2π} f (x, y) = x2 + y2, D = {(r, θ) | 3≤r≤5,0≤θ≤2π}

135.

f (x, y) = x + y, D = {(r, θ) | 3≤r≤5,0≤θ≤2π} f (x, y) = x + y, D = {(r, θ) | 3≤r≤5,0≤θ≤2π}

136.

f (x, y) = x2 + xy, D = {(r, θ) | 1≤r≤2, π≤θ≤2π} f (x, y) = x2 + xy, D = {(r, θ) | 1≤r≤2, π≤θ≤2π}

137.

f (x, y) = x4 + y4, D = {(r, θ) | 1≤r≤2,3π2≤θ≤2π} f (x, y) = x4 + y4, D = {(r, θ) | 1≤r≤2,3π2≤θ≤2π}

138.

f (x, y) = x2 + y23, f (x, y) = x2 + y23, где D = {(r, θ) | 0≤r≤1, π2≤θ≤π} .D = {( r, θ) | 0≤r≤1, π2≤θ≤π}.

139.

f (x, y) = x4 + 2x2y2 + y4, f (x, y) = x4 + 2x2y2 + y4, где D = {(r, θ) | 3≤r≤4, π3≤θ≤2π3}. D = {(r, θ) | 3≤r≤4, π3≤θ≤2π3}.

140.

f (x, y) = sin (arctanyx), f (x, y) = sin (arctanyx), где D = {(r, θ) | 1≤r≤2, π6≤θ≤π3} D = { (г, θ) | 1≤r≤2, π6≤θ≤π3}

141.

f (x, y) = arctan (yx), f (x, y) = arctan (yx), где D = {(r, θ) | 2≤r≤3, π4≤θ≤π3} D = { (г, θ) | 2≤r≤3, π4≤θ≤π3}

142.

∬Dex2 + y2 [1 + 2arctan (yx)] dA, D = {(r, θ) | 1≤r≤2, π6≤θ≤π3} ∬Dex2 + y2 [1 + 2arctan (yx)] dA, D = {(r, θ) | 1≤r≤2, π6≤θ≤π3}

143.

∬D (ex2 + y2 + x4 + 2x2y2 + y4) arctan (yx) dA, D = {(r, θ) | 1≤r≤2, π4≤θ≤π3} ∬D (ex2 + y2 + x4 + 2x2y2 + y4) arctan (yx) dA, D = {(r, θ) | 1≤r≤2, π4≤θ≤π3}

В следующих упражнениях интегралы были преобразованы в полярные координаты.Убедитесь, что тождества верны, и выберите самый простой способ вычисления интегралов в прямоугольных или полярных координатах.

144.

∫12∫0x (x2 + y2) dydx = ∫0π4∫secθ2secθr3drdθ∫12∫0x (x2 + y2) dydx = ∫0π4∫secθ2secθr3drdθ

145.

∫23∫0xxx2 + y2dydx = ∫0π / 4∫2secθ3secθrcosθdrdθ∫23∫0xxx2 + y2dydx = ∫0π / 4∫2secθ3secθrcosθdrdθ

146.

∫01∫x2x1x2 + y2dydx = ∫0π / 4∫0tanθsecθdrdθ∫01∫x2x1x2 + y2dydx = ∫0π / 4∫0tanθsecθdrdθ

147.

∫01∫x2xyx2 + y2dydx = ∫0π / 4∫0tanθsecθrsinθdrdθ∫01∫x2xyx2 + y2dydx = ∫0π / 4∫0tanθsecθrsinθdrdθ

В следующих упражнениях преобразуйте интегралы в полярные координаты и вычислите их.

148.

∫03∫09 − y2 (x2 + y2) dxdy∫03∫09 − y2 (x2 + y2) dxdy

149.

∫02∫ − 4 − y24 − y2 (x2 + y2) 2dxdy∫02∫ − 4 − y24 − y2 (x2 + y2) 2dxdy

150.

∫01∫01 − x2 (x + y) dydx∫01∫01 − x2 (x + y) dydx

151.

∫04∫ − 16 − x216 − x2sin (x2 + y2) dydx∫04∫ − 16 − x216 − x2sin (x2 + y2) dydx

152.

Вычислите интеграл ∬DrdA∬DrdA, где DD — это область, ограниченная полярной осью и верхней половиной кардиоиды r = 1 + cosθ.r = 1 + cosθ.

153.

Найдите площадь области DD, ограниченную полярной осью и верхней половиной кардиоиды r = 1 + cosθ.г = 1 + cosθ.

154.

Вычислите интеграл ∬DrdA, ∬DrdA, где DD — это область, ограниченная частью четырехлистной розы r = sin2θr = sin2θ, расположенной в первом квадранте (см. Следующий рисунок).

155.

Найдите общую площадь области, ограниченной четырехлистной розой r = sin2θr = sin2θ (см. Рисунок в предыдущем упражнении).

156.

Найдите площадь области D, D, которая является областью, ограниченной y = 4 − x2, y = 4 − x2, x = 3, x = 3, x = 2, x = 2 и y = 0. у = 0.

157.

Найдите площадь области D, D, которая является областью внутри диска x2 + y2≤4×2 + y2≤4 и правее линии x = 1.x = 1.

158.

Определить среднее значение функции f (x, y) = x2 + y2f (x, y) = x2 + y2 в области DD, ограниченной полярной кривой r = cos2θ, r = cos2θ, где −π4≤θ≤ π4 − π4≤θ≤π4 (см. следующий график).

159.

Определить среднее значение функции f (x, y) = x2 + y2f (x, y) = x2 + y2 в области DD, ограниченной полярной кривой r = 3sin2θ, r = 3sin2θ, где 0≤θ≤π20 ≤θ≤π2 (см. Следующий график).

160.

Найти объем твердого тела, расположенного в первом октанте и ограниченного параболоидом z = 1−4×2−4y2z = 1−4×2−4y2 и плоскостями x = 0, y = 0, x = 0, y = 0 и z = 0. z = 0.

161.

Найдите объем твердого тела, ограниченного параболоидом z = 2−9×2−9y2z = 2−9×2−9y2 и плоскостью z = 1.z = 1.

162.

Найдите объем твердого тела S1S1, ограниченного цилиндром x2 + y2 = 1×2 + y2 = 1 и плоскостями z = 0z = 0 и z = 1.z = 1.
Найдите объем твердого тела S2S2 вне двойного конуса z2 = x2 + y2, z2 = x2 + y2, внутри цилиндра x2 + y2 = 1, x2 + y2 = 1 и над плоскостью z = 0.г = 0.
Найдите объем твердого тела внутри конуса z2 = x2 + y2z2 = x2 + y2 и ниже плоскости z = 1z = 1, вычитая объемы твердых тел S1S1 и S2.S2.

163.

Найдите объем твердого тела S1S1 внутри единичной сферы x2 + y2 + z2 = 1×2 + y2 + z2 = 1 и над плоскостью z = 0.z = 0.
Найдите объем твердого тела S2S2 внутри двойного конуса (z − 1) 2 = x2 + y2 (z − 1) 2 = x2 + y2 и над плоскостью z = 0.z = 0.
Найдите объем твердого тела вне двойного конуса (z − 1) 2 = x2 + y2 (z − 1) 2 = x2 + y2 и внутри сферы x2 + y2 + z2 = 1.х2 + у2 + z2 = 1.

Для следующих двух упражнений рассмотрим сферическое кольцо, представляющее собой сферу с цилиндрическим отверстием, вырезанным таким образом, чтобы ось цилиндра проходила через центр сферы (см. Следующий рисунок).

164.

Если сфера имеет радиус 44, а цилиндр — 2,2, найдите объем сферического кольца.

165.

Цилиндрическое отверстие диаметром 66 см просверливается в сфере радиуса 55 см таким образом, чтобы ось цилиндра проходила через центр сферы.Найдите объем получившегося сферического кольца.

166.

Найдите объем твердого тела, лежащего под двойным конусом z2 = 4×2 + 4y2, z2 = 4×2 + 4y2, внутри цилиндра x2 + y2 = x, x2 + y2 = x и над плоскостью z = 0. z = 0.

167.

Найдите объем твердого тела, лежащего под параболоидом z = x2 + y2, z = x2 + y2, внутри цилиндра x2 + y2 = x, x2 + y2 = x и над плоскостью z = 0. z = 0 .

168.

Найдите объем твердого тела, лежащего под плоскостью x + y + z = 10x + y + z = 10 и над диском x2 + y2 = 4x.х2 + у2 = 4х.

169.

Найдите объем твердого тела, лежащего под плоскостью 2x + y + 2z = 82x + y + 2z = 8 и над единичным кругом x2 + y2 = 1.x2 + y2 = 1.

170.

Радиальная функция ff — это функция, значение которой в каждой точке зависит только от расстояния между этой точкой и началом системы координат; то есть f (x, y) = g (r), f (x, y) = g (r), где r = x2 + y2.r = x2 + y2. Докажите, что если ff — непрерывная радиальная функция, то ∬Df (x, y) dA = (θ2 − θ1) [G (R2) −G (R1)], ∬Df (x, y) dA = (θ2 − θ1) ) [G (R2) −G (R1)], где G ′ (r) = rg (r) G ′ (r) = rg (r) и (x, y) ∈D = {(r, θ) | R1≤r≤R2,0≤θ≤2π}, (x, y) ∈D = {(r, θ) | R1≤r≤R2,0≤θ≤2π}, где 0≤R1

171.

Используйте информацию из предыдущего упражнения, чтобы вычислить интеграл ∬D (x2 + y2) 3dA, ∬D (x2 + y2) 3dA, где DD — это единичный диск.

172.

Пусть f (x, y) = F ′ (r) rf (x, y) = F ′ (r) r — непрерывная радиальная функция, определенная на кольцевой области D = {(r, θ) | R1≤r≤ R2,0≤θ≤2π}, D = {(r, θ) | R1≤r≤R2,0≤θ≤2π}, где r = x2 + y2, r = x2 + y2, 0

173.

Примените предыдущее упражнение для вычисления интеграла ∬Dex2 + y2x2 + y2dxdy, ∬Dex2 + y2x2 + y2dxdy, где DD — это кольцевая область между окружностями радиусов 11 и 22, расположенными в третьем квадранте.

174.

Пусть ff будет непрерывной функцией, которая может быть выражена в полярных координатах только как функция θθ; то есть f (x, y) = h (θ), f (x, y) = h (θ), где (x, y) ∈D = {(r, θ) | R1≤r≤R2, θ1 ≤θ≤θ2}, (x, y) ∈D = {(r, θ) | R1≤r≤R2, θ1≤θ≤θ2}, где 0≤R1

175.

Примените предыдущее упражнение, чтобы вычислить интеграл ∬Dy2x2dA, ∬Dy2x2dA, где D = {(r, θ) | 1≤r≤2, π6≤θ≤π3}.D = {(r, θ) | 1≤r≤2, π6≤θ≤π3}.

176.

Пусть ff будет непрерывной функцией, которая может быть выражена в полярных координатах только как функция θθ; то есть f (x, y) = g (r) h (θ), f (x, y) = g (r) h (θ), где (x, y) ∈D = {(r, θ) | R1≤r≤R2, θ1≤θ≤θ2} (x, y) ∈D = {(r, θ) | R1≤r≤R2, θ1≤θ≤θ2} с 0≤R1

177.

Вычислить ∬Darctan (yx) x2 + y2dA, ∬Darctan (yx) x2 + y2dA, где D = {(r, θ) | 2≤r≤3, π4≤θ≤π3}.D = {(r, θ) | 2≤r≤3, π4≤θ≤π3}.

178.

Сферический колпачок — это область сферы, которая находится выше или ниже данной плоскости.

Покажите, что объем сферической крышки на рисунке ниже равен 16πh (3a2 + h3) .16πh (3a2 + h3).
Сферический сегмент — это твердое тело, образованное пересечением сферы с двумя параллельными плоскостями. Если расстояние между плоскостями h, h, покажите, что объем сферического сегмента на рисунке ниже равен 16πh (3a2 + 3b2 + h3) .16πh (3a2 + 3b2 + h3).

179.

В статистике совместная плотность для двух независимых, нормально распределенных событий со средним μ = 0μ = 0 и стандартным распределением σσ определяется как p (x, y) = 12πσ2e − x2 + y22σ2.p (x, y) = 12πσ2e − x2 + y22σ2. Рассмотрим (X, Y), (X, Y), декартовы координаты шара в положении покоя после того, как он был выпущен из положения на оси z в направлении xyxy-плоскости. Предположим, что координаты мяча независимо распределены нормально со средним значением μ = 0μ = 0 и стандартным отклонением σσ (в футах).Вероятность того, что мяч остановится не далее чем в футе от начала координат, определяется выражением P [X2 + Y2≤a2] = ∬Dp (x, y) dydx, P [X2 + Y2≤a2] = ∬Dp (x, y) dydx, где DD — диск радиуса a с центром в начале координат. Докажите, что P [X2 + Y2≤a2] = 1 − e − a2 / 2σ2.P [X2 + Y2≤a2] = 1 − e − a2 / 2σ2.

180.

Двойной несобственный интеграл ∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx может быть определен как предельное значение двойные интегралы ∬Dae (−x2 + y2 / 2) dA∬Dae (−x2 + y2 / 2) dA по дискам DaDa радиусов a с центром в начале координат, поскольку a неограниченно возрастает; то есть ∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = lima → ∞∬Dae (−x2 + y2 / 2) dA.∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = lima → ∞∬Dae (−x2 + y2 / 2) dA.

Используйте полярные координаты, чтобы показать, что ∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = 2π.∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = 2π .
Докажите, что ∫ − ∞∞e − x2 / 2dx = 2π, ∫ − ∞∞e − x2 / 2dx = 2π, используя соотношение ∫ − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = (∫ − ∞∞e − x2 / 2dx) (∫ − ∞∞e − y2 / 2dy). − ∞∞∫ − ∞∞e (−x2 + y2 / 2) dydx = (∫ − ∞∞e − x2 / 2dx) (∫ − ∞∞e − y2 / 2dy).

Исчисление II — Область с полярными координатами

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-8: Область с полярными координатами

В этом разделе мы рассмотрим области, ограниченные полярными кривыми.2} \, d \ theta}} \]

Обратите внимание, что мы используем \ (r \) в интеграле вместо \ (f \ left (\ theta \ right) \), поэтому убедитесь и сделайте соответствующую замену при выполнении интеграла.

Рассмотрим пример.

Пример 1 Определите площадь внутреннего цикла \ (r = 2 + 4 \ cos \ theta \).

Показать решение

Мы построили график этой функции, когда впервые начали рассматривать полярные координаты. Для этой задачи нам также необходимо знать значения \ (\ theta \), где кривая проходит через начало координат.Мы можем получить их, установив уравнение равным нулю и решив.

\ [\ begin {align *} 0 & = 2 + 4 \ cos \ theta \\ \ cos \ theta & = — \ frac {1} {2} \ hspace {0.5in} \ Rightarrow \ hspace {0.5in} \ theta = \ frac {{2 \ pi}} {3}, \ frac {{4 \ pi}} {3} \ end {align *} \]

Вот эскиз этой кривой с заштрихованной внутренней петлей.

Вы понимаете, почему нам нужно было знать значения \ (\ theta \), где кривая проходит через начало координат? Эти точки определяют, где начинается и заканчивается внутренний цикл, и, следовательно, также являются пределами интегрирования в формуле.{\ frac {{4 \ pi}} {3}} \\ & = 4 \ pi — 6 \ sqrt 3 = 2,174 \ end {align *} \]

Вы ведь следили за работой, проделанной в этом интеграле, не так ли? В этом разделе вы встретите довольно много интегралов триггерных функций, поэтому при необходимости вернитесь к разделам «Интегралы, включающие триггерные функции» и сделайте быстрый обзор.

Итак, вот как мы определяем области, которые заключены одной кривой, но как насчет ситуаций, подобных следующему эскизу, где мы хотим найти область между двумя кривыми.2} \ right) \, d \ theta}} \]

Давайте посмотрим на пример.

Пример 2 Определите площадь, которая находится внутри \ (r = 3 + 2 \ sin \ theta \) и снаружи \ (r = 2 \).

Показать решение

Вот набросок области, которую мы ищем.

Чтобы определить эту область, нам нужно знать значения \ (\ theta \), для которых две кривые пересекаются. Мы можем определить эти точки, задав два уравнения и решив их.

\ [\ begin {align *} 3 + 2 \ sin \ theta & = 2 \\ \ sin \ theta & = — \ frac {1} {2} \ hspace {0.5in} \ Rightarrow \ hspace {0.5in} \ theta = \ frac {{7 \ pi}} {6}, \ frac {{11 \ pi}} {6} \ end {align *} \]

Вот эскиз фигуры с добавленными углами. {{\, \ frac {{7 \ pi}} {6}}} {{\ frac {1} {2} \ left ({7 + 12 \ sin \ theta — 2 \ cos \ left ({2 \ theta} \ right)} \ right) \, d \ theta}} \\ & = \ left.{\ frac {{7 \ pi}} {6}} \\ & = \ frac {{11 \ sqrt 3}} {2} + \ frac {{14 \ pi}} {3} = 24,187 \ end {align *} \]

Давайте поработаем небольшую модификацию предыдущего примера.

Пример 3 Определите площадь области вне \ (r = 3 + 2 \ sin \ theta \) и внутри \ (r = 2 \).

Показать решение

На этот раз мы ищем следующий регион.

Итак, это область, которую мы получаем, используя пределы от \ (\ frac {{7 \ pi}} {6} \) до \ (\ frac {{11 \ pi}} {6} \).{\ frac {{11 \ pi}} {6}} \\ &
= \ frac {{11 \ sqrt 3}} {2} — \ frac {{7 \ pi}} {3} = 2,196 \ end {align *} \]

Обратите внимание, что для этой области «внешняя» и «внутренняя» функции противоположны!

Сделаем еще одну последнюю модификацию этого примера.

Пример 4 Определите площадь, которая находится внутри как \ (r = 3 + 2 \ sin \ theta \), так и \ (r = 2 \).

Показать решение

Вот эскиз для этого примера.

Мы не сможем решить эту задачу таким же образом, как в предыдущих двух. Нет никаких ограничений, которые позволили бы нам ограничивать эту область по мере того, как мы увеличиваемся от одного к другому. Помните, что по мере увеличения \ (\ theta \) область, за которой мы следуем, должна быть закрыта. Однако единственные два диапазона для \ (\ theta \), с которыми мы можем работать, охватывают область из двух предыдущих примеров, а не эту область.

Однако в данном случае это не является серьезной проблемой.Есть два способа решить эту проблему. Мы посмотрим на них обоих.

Решение 1
В этом случае заметим, что круг разделен на две части, и мы следуем за верхней частью.