Формула Герона для нахождения площади треугольника: определение, примеры

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

Формула площади

Площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c).

S = √p(p-a)(p-b)(p-c)

Полупериметр (p) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.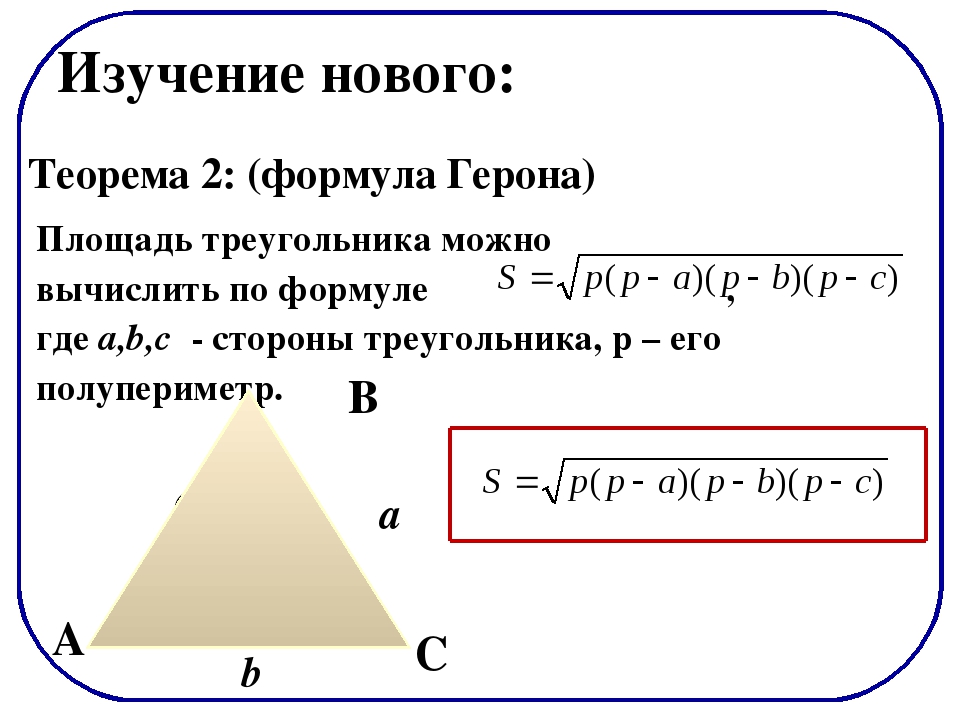

Примеры задач

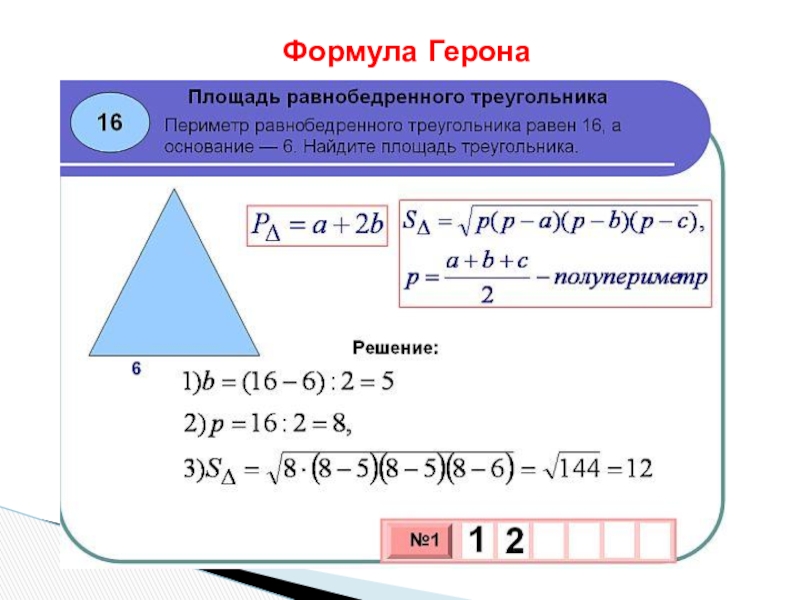
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр: p = (6 + 8 + 10) / 2 = 12 см.
Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
S = √12 ⋅ (12 – 6)(12 – 8)(12 – 10) = √12 ⋅ 6 ⋅ 4 ⋅ 2 = 24 см².

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c, известный катет – a, а неизвестный – b. Применим Теорему Пифагора, чтобы найти длину катета b:
b² = c² – a² = 15² – 9² = 144 см², следовательно, b = 12 cм.

Полупериметр треугольника равен: p = (9 + 12 + 15) / 2 = 18 см.
Остается только использовать формулу для нахождения площади:
S = √18 ⋅ (18 – 9)(18 – 12)(18 – 15) = √18 ⋅ 9 ⋅ 6 ⋅ 3 = 54 см².

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Вывод формулы Герона

      Утверждение 1. Площадь произвольного треугольника можно найти по формуле Герона:

где   a , b , c   – длины сторон треугольника, а   p   – полупериметр треугольника, т.е.

.

      Доказательство.

Рис.1

      Поскольку (рис.1)

то

      Воспользовавшись теоремой косинусов, получаем:

      Следовательно,

      Таким образом,

что и требовалось доказать.

Вывод формулы Брахмагупты

      Утверждение 2. Площадь четырёхугольника, вписанного в окружность, можно найти по формуле Брахмагупты:

где   a , b , c , d   – длины сторон четырёхугольника, а   p   – полупериметр, т.е.

      Доказательство.

Рис.2

      Если угол   D   четырёхугольника   ABCD   обозначить буквой   φ   (рис.2), то, поскольку сумма противоположных углов вписанного четырёхугольника равна   π ,   угол   B   будет равен   π – φ .   По этой причине

      Следовательно,

      Применяя теорему косинусов к треугольнику   ACD ,   получаем:

AC ² = a² + b² – 2bc cos φ .

      Применяя теорему косинусов к треугольнику   ABC ,   получаем:

AC ² =
= c² + d ² – 2cd cos (π – φ) =
= c² + d ² + 2cd cos φ .

      Следовательно,

где буквами   A   и   B   обозначены выражения

      Поэтому

Преобразуем каждую скобку

B + A = 2 (ab +cd) +
+ a² + b² – c² – d² =
= a² + 2ab + b² –
– (c² – 2cd + d²) =
= (a + b)² – (c – d)² =
= (a + b + c – d)
(a + b – c + d) =
= (2p – 2d)(2p – 2c) =
= 4(p – d)(p – c) ;

B – A = 2 (ab +cd) –
– (a² + b² – c² – d²) =
= – (a² – 2ab + b²) +
+ (c² + 2cd + d²) =
= (c + d)² – (a – b)² =
= (c + d + a – b)
(c + d – a + b) =
= (2p – 2b)(2p – 2a) =
= 4(p – b)(p – a) .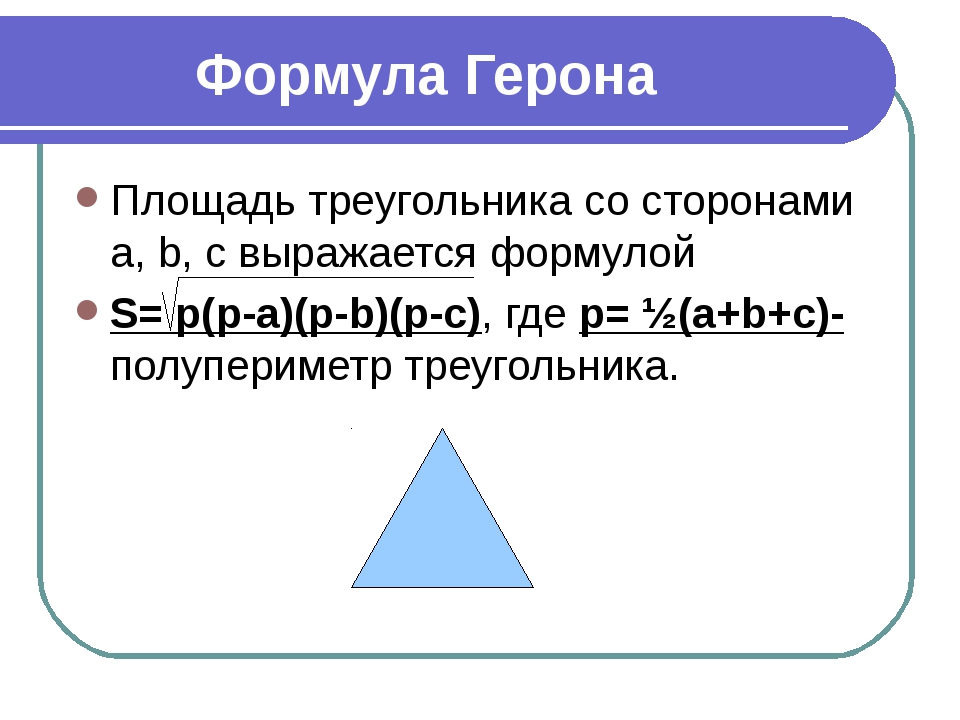

Буквой   p   здесь обозначен полупериметр четырехугольника   ABCD

Подставляя преобразованные выражения в формулу для   S² , получаем

      Таким образом,

что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Площадь треугольника. Формула Герона

План-конспект урока математики по теме

«Формулы площадей треугольников. Формула Герона», 9-й класс

Цель:изучить формулу Герона, организовать самостоятельно – познавательную деятельность учащихся при изучении темы.

Задачи:

Образовательная:

— Расширить знания о формулах площади треугольников; учить применять формулы Герона  при решении задач

— Совершенствовать навыки решения задач;

— Обеспечить усвоение задач, входящих в содержание темы урока.

Развивающая:

-развивать логическое мышление, развивать навыки и умения работать в парах и группах; развивать навыков самоорганизации и участия в работе группы и творческие способности учащихся.

Воспитательная:

-повышать интерес к изучению математики, сознательное отношение к учебе, уважительное отношение друг к другу, умение слушать ответы товарищей, воспитывать стремление к непрерывному совершенствованию своих знаний.

Формируемые УУД

Личностные:  учатся замечать и признавать свои ошибки, прислушиваться к мнениям одноклассников, анализировать, овладевать  историческими и математическими знаниями и умениями, навыками их применения в реальной жизни, осознавать ценности исторических и математических знаний как важнейшего компонента научной картины мира,  рефлексия.

Коммуникативные: планирование учебного сотрудничества с учителями и сверстниками, приобретают умения организовать сотрудничество с партнёром, осуществлять оценку действий партнера, умение с достаточной полнотой и точностью выражать свои мысли.

Регулятивные: осознание качества и уровня усвоения пройденного материала.  Оценивают умение  сотрудничать с учителем и одноклассниками.

Познавательные: устанавливают причинно-следственные связи между объектами, осуществляют подведение под понятие , проводят сравнение, классификацию объектов, выбирают наиболее эффективный способов решения задач.

Планируемые образовательные результаты

Метапредметные. Понимать связь математики с искусством, поэзией, философией, научиться чувствовать красоту формул и теорем, развивать интерес к истории математических открытий.

Личностные. Грамотно излагать свои мысли, анализировать, сравнивать, развивать познавательный интерес через творческие задания. Уметь самостоятельно приобретать новые знания и практические умения, управлять своей познавательной деятельностью. Развивать активность и находчивость при решении  поставленных задач, умение работать в коллективе. 

Предметные. Понимать формулу Герона. Знать, как находить площадь треугольника по трем сторонам.

Тип урока: формирование новых знаний и умений.

Формы работы учащихся: фронтальная, индивидуальная, парная, групповая.

Необходимое техническое оборудование: компьютер, интерактивное оборудование.

Дидактические средства: учебник, презентация, модели треугольников.

Методы и приемы: фронтальная работа, сочетающаяся с обще классной; частично-поисковый метод; индивидуальная работа, работа парами и группами. 

1. Мотивационно-организационный этап

— Добрый день! Располагайтесь поудобнее, начинаем наш урок.

2. Актуализация опорных знаний

А) Проверка домашнего задания

Б) Математический диктант (проверка формул площадей фигур)

В) Работа в парах:

1) Найдите площадь прямоугольника со сторонами 2 см и 3 см

2) Найдите площадь прямоугольного треугольника с катетами 3 см и 2 см

3) Найдите площадь правильного треугольника со стороной 2 см

4) Найдите площадь ромба, диагонали которого равны 3 см и 4 см

Найдите площадь треугольника со сторонами 2 см и  см, если угол между сторонами составляет 60°

Найдите площадь треугольника, стороны которого 13 см, 14 см, 15 см.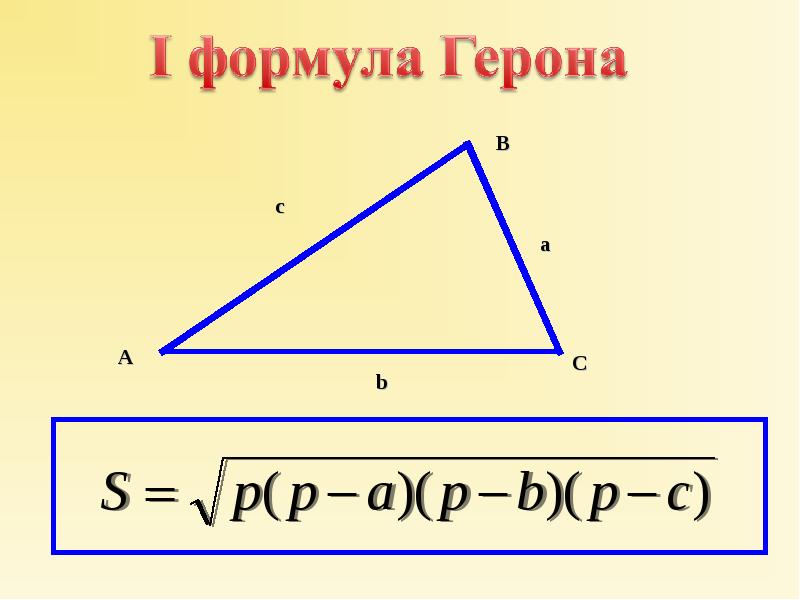

3. Создание проблемной ситуации

Ученики, решив первые пять задач, затрудняются решить последнюю задачу. Предлагают разные варианты, но ничего не получается.

При решении возникла проблема: не хватает знаний.

Учитель: Сегодня на уроке мы рассмотрим ещё один способ вычисления площади треугольника: с помощью формулы Герона, которая позволяет вычислить площадь треугольника, зная лишь его стороны, что может очень пригодиться, особенно в практических вычислениях.

4. Сообщение темы и целей урока

— Давайте сформулируем тему урока?

— А какова цель нашего урока? (Ответы детей.)

— Верно, цель урока: изучить теорему Герона и рассмотреть способы решения типовых задач.

Теорема:

Площадь произвольного треугольника можно вычислить по формуле: , где  – полупериметр,  – длины сторон треугольника.

Доказательство

Рассмотрим произвольный треугольник  (пусть  – острые, напомним, что в треугольнике всегда есть хотя бы два острых угла). Обозначим в нём: . Проведём высоту , а также обозначим:  (см. Рис. 2.).

Рис. Иллюстрация к теореме

Воспользуемся следствием из теоремы Пифагора для прямоугольных треугольников :  (1), :  (2).

Приравняв правые части в формулах (1) и (2), получаем:

, откуда: . Так как  (3), то получаем:  (4).

 Сложим формулы (3) и (4):

.

Теперь вернёмся к формуле (1) и подставим в неё полученное выражение для :

Теперь вспомним, что полупериметр выражается формулой: . Отсюда: . Тогда преобразуем полученную формулу:

.

Отсюда высота равна: .

Запишем известную нам формулу для площади треугольника: .

чтд

Учитель: А теперь давайте решим задачу, с которой возникли трудности.

В треугольнике  известны стороны: ; ; .

Найти: .

Решение:

Ответ: 84.

Комплекс упражнений для глаз. Минутка отдыха

Закрепление материала

1. Найти площадь  , если  ,   и  .

Решение.  Так как здесь  , то согласно теореме 1 получаем

.

Ответ:  .

2. Боковые стороны треугольника равны 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равна: а) 25 см; б) 11 см.

Решение

а) ,

 (см²).

S =  ∙ 25 ∙ h, 300 =  ∙ 25 h, h =  = 24 (см).

Ответ. 24 см.

б) ,

 (см²).

S =  ∙ 11 ∙ h, 132 =  ∙ 11 ∙ h, h =  = 24 (см).

Ответ. 24 см.

 Учитель: А теперь предлагаю самостоятельно решить задачу по вариантам.

Вариант 1

1. Найдите наименьшую высоту треугольника со сторонами 5, 5, 6.

Вариант 2

1. Найдите наименьшую высоту треугольника со сторонами 17, 65, 80.

8. Подведение итогов урока

— Я благодарю вас за работу.

Поработали вы плодотворно, я могу оценить вашу работу так: …

9. Рефлексия урока

Карточка для рефлексии

Ответьте на вопросы:

Данная тема мне понятна.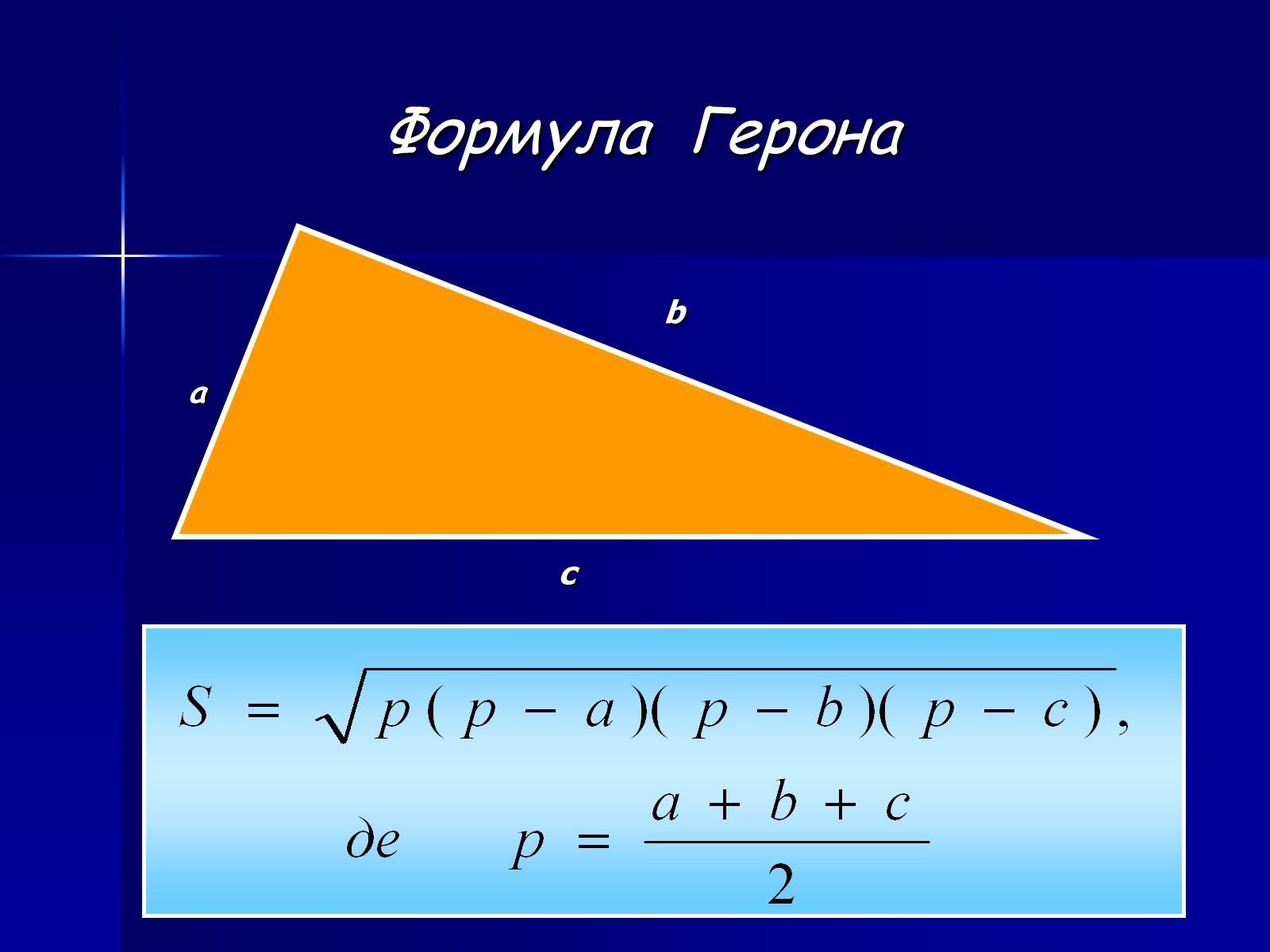

Я хорошо понял теорему Герона о вычислении площади треугольника по трем его сторонам.

Я знаю, как пользоваться формулой для вычисления площади треугольника по трем сторонам.

Я сумею найти______________________________

Поработали вы плодотворно, я могу оценить вашу работу …

10. Домашнее задание (разноуровневое домашнее задание)

Уровень 1

Найдите площадь треугольника по трем сторонам: 17, 65, 80; 

Уровень 2. В треугольнике АВС даны три стороны: , . Найдите часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины В.

Учитель: На этом наш урок закончен. Желаю всем успеха.

Формула Герона | Математика, которая мне нравится

Герон Александрийский

Герон Александрийский жил во второй половине первого века нашей эры. О Героне известно довольно мало. Однако до нас дошли некоторые его труды и копии его трудов, на основании которых Герона вполне заслуженно считают величайшим инженером. Он изобрел автоматические двери, которые производили огромное впечатление на людей, приходивших в храмы, первый торговый автомат, наливавший за монетку определенное количество святой воды, механических певчих птиц, автоматический театр, самострельный арбалет, паровую турбину и многое другое.

К сожалению, в средние века многие его изобретения оказались никому не нужными.

Формула Герона, которая позволяет вычислить площадь треугольника по длинам его сторон, в действительности была открыта Архимедом. Однако это не умаляет того, что сделал этот человек.

О Героне сняты мультфильмы. Один из них советский, 1979 года, “Герон’’, другой — 13-я серия из французского мультсериала, посвященная Герону, “Жили-были первооткрыватели. Герон Александрийский’’. Если честно, мультфильмы я вообще не очень люблю, а вот документальный фильм о Героне, “Древние открытия: удивительные машины. Герон’’, посмотрела с большим удовольствием. Вы можете его тоже посмотреть вот здесь: http://www.cinemaplayer. ru/29479-_drevnie_otkryitiya_udivitelnyie_mashinyi___Ancient_Discoveries_Surprising_Machines.html

А теперь рассмотрим формулу Герона. Приведу самое простое ее доказательство, основанное на теореме Пифагора, доступное восьмикласснику.

Теорема. Площадь треугольника, длины сторон которого равны и , находится по формуле

где — полупериметр треугольника.

Доказательство. Рассмотрим треугольник , . Пусть — высота треугольника , проведенная из вершины , . Тогда , и по теореме Пифагора из треугольников и соответственно имеем:

откуда

Вспоминая, что , получаем и .
Сложим последнее равенство с равенством , получим

или

Теперь найдем высоту треугольника:

Поскольку

то

Подставляем эти выражения в найденное выражение для :

Учитывая то, что , получаем требуемое.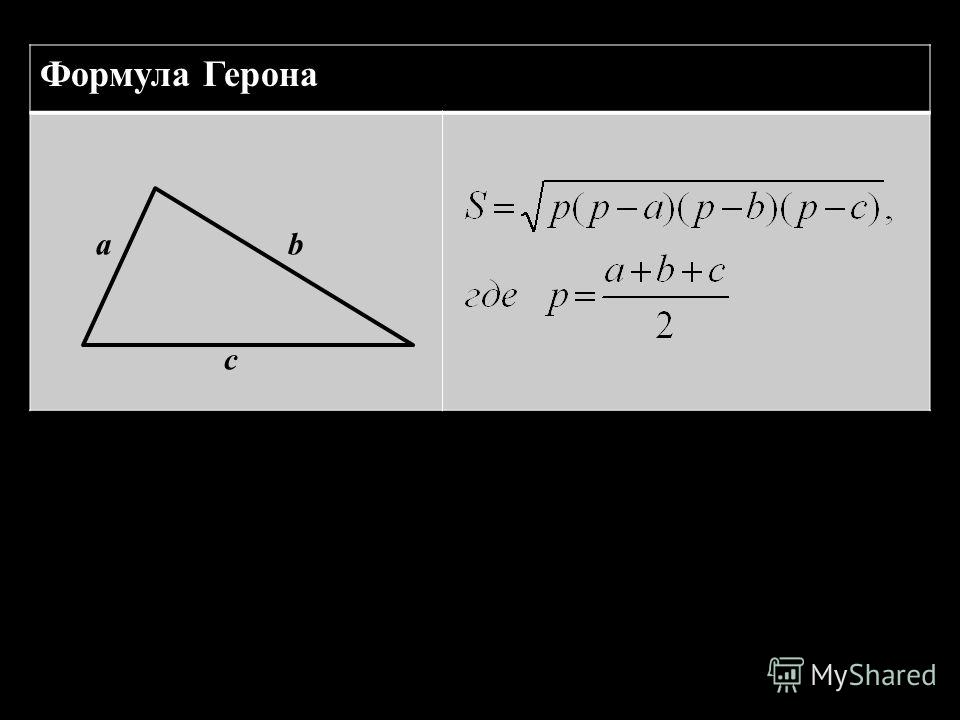

Источник: http://ru.wikipedia.org/wiki/Герон

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции. — Формула Герона для нахождения площади треугольника.

Комментарии преподавателя

История формулы Герона

На данном уроке мы изучим формулу Герона, позволяющую вычислять площадь треугольника по его сторонам.

До этого мы умели вычислять площадь треугольника, зная его основание и высоту:  и катеты (для прямоугольного треугольника): . Формула Герона – это новая формула, которая связывает площадь треугольника и длины всех трёх его сторон.

Открыта эта формула была, по всей видимости, ещё Архимедом в  веке до н.э., но его доказательство не дошло до наших дней. А вот в «Метрике» Герона Александрийского ( век до н.э.) она есть.

Герона (см. Рис. 1) интересовали треугольники с целочисленными сторонами, площадь которых также является целым числом. Такие треугольники в его честь называют героновыми.

Простейший геронов треугольник – так называемый египетский треугольник (со сторонами 3, 4 и 5).

Рис. 1. Герон Александрийский (Источник)

Теорема

Площадь произвольного треугольника можно вычислить по формуле: , где  – полупериметр,  – длины сторон треугольника.

Доказательство

Рассмотрим призвольный треугольник  (пусть  – острые, напомним, что в треугольнике всегда есть хотя бы два острых угла). Обозначим в нём: . Проведём высоту , а также обозначим:  (см. Рис. 2.).

Рис. 2. Иллюстрация к теореме

Воспользуемся следствием из теоремы Пифагора для прямоугольных треугольников :  (1), :  (2).

Приравняв правые части в формулах (1) и (2), получаем:

, откуда: . Так как  (3), то получаем:  (4).

 Сложим формулы (3) и (4):

.

Теперь вернёмся к формуле (1) и подставим в неё полученное выражение для :

.

Теперь вспомним, что полупериметр выражается формулой: . Отсюда: . Тогда преобразуем полученную формулу:

.

Отсюда высота равна: .

Запишем известную нам формулу для площади треугольника: .

Доказано.

Задача 1

Стороны треугольника равны . Найти высоты этого треугольника.

Доказательство

Рассмотрим треугольник . Проведём в нём высоты . Напомним, что все высоты треугольника пересекаются в одной точке.

Рис. 3. Иллюстрация к задаче

Формула Герона и её доказательство

Вычислим площадь треугольника с помощью формулы Герона.

.

Тогда площадь треугольника:

.

Теперь запишем формулу для площади треугольника через высоту:

.

Аналогично находим остальные высоты: , .

Ответ:.

Задачи на применение формулы Герона

Задача 2

Дан , его основание , боковые стороны  и  соответственно .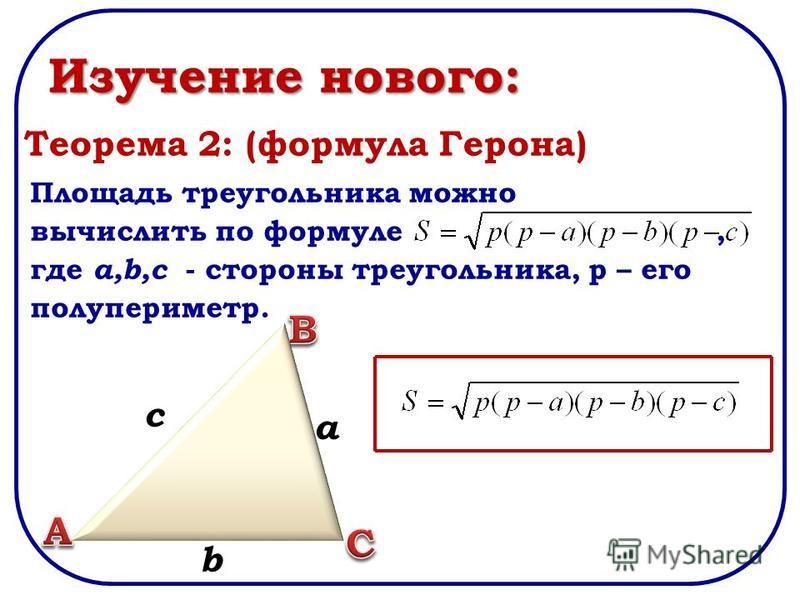 Точка , лежащая внутри треугольника, находится на расстоянии  от стороны  и  от стороны . Найти расстояние от точки  до стороны  (см. Рис. 4).

Решение

Рис. 4. Иллюстрация к задаче

Рассмотрим треугольник : в нём – высота. Обозначим: . Тогда: .

Найдём площадь треугольника .

Для начала найдём площадь треугольника  через формулу Герона:

.

Теперь вычислим площадь треугольника : .

Площадь треугольника: : .

Теперь, учитывая следующее соотношение: , получаем: .

Теперь найдём расстояние от точки  до стороны : .

Ответ: .

ИСТОЧНИК

http://x-uni.com/geometriya/8-klass/video/formula-gerona-dlya-nahozhdeniya-ploschadi-treugolnika

http://www.youtube.com/watch?v=zp82OIuz93g

http://v.5klass.net/zip/823d1fb40b3ed49403a117ef8517c666.zip

http://kak-kak2.ru/img/605c9fb504028311913e985a5ea8d1e1.jpg

http://hijos.ru/2012/10/03/formula-gerona/

http://www. calc.ru/Formula-Gerona.html

Формулы площади треугольника

Формулы площади треугольника

Подождите пару секунд пока подгрузятся формулы

Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!

Через основание и высоту

$$S= \frac{1}{2} ah $$
\(S\) — площадь треугольника

\(a\) — основание

\(h\) — высота

\(a =\)   
\(h =\)

Через две стороны и угол

$$S= \frac{1}{2} ab sin \alpha $$
\(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\( \alpha \) — угол между сторонами \(a\) и \(b\)

\(a =\)   
\(b =\)   
\( \alpha =\)

Формула Герона

$$S= \sqrt{p(p-a)(p-b)(p-c)} $$
\(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(a =\)   
\(b =\)   
\(c =\)

Через радиус вписанной окружности

$$S= rp $$
\(S\) — площадь треугольника

\(r\) — радиус вписанной окружности

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(r =\)   
\(p =\)

Через радиус описанной окружности

\(S= \frac{abc}{4R} \)

\(S\) — площадь треугольника

\(R\) — радиус описанной окружности

\(a\) — сторона

\(b\) — сторона

\(c\) — сторона

\(a =\)  
\(b =\)

\(c =\)  
\(R =\)

Площадь прямоугольного треугольника

$$S= \frac{1}{2} ab $$
\(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(a =\)   
\(b =\)

Площадь прямоугольного треугольника

$$S= de $$
\(S\) — площадь треугольника

\(d =\)   
\(e =\)

Формула Герона для прямоугольного треугольника

$$ S= (p-a)(p-b) $$
\(S\) — площадь треугольника

\(a\) — сторона

\(b\) — сторона

\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)

\(a =\)   
\(b =\)   
\(p =\)

Площадь равнобедренного треугольника

$$S= \frac{1}{2} a^2 sin \alpha$$
\(S\) — площадь треугольника

\(a\) — сторона

\(\alpha\) — угол между боковыми сторонами

\(a =\)   
\( \alpha =\)

Площадь равнобедренного треугольника

\(a\) — сторона

\(b\) — сторона

\(\alpha\) — угол между боковыми сторонами и основанием

\(a =\)   
\(b =\)   
\( \alpha =\)

Площадь равнобедренного треугольника

$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$
\(S\) — площадь треугольника

\(b\) — сторона

\(\alpha\) — угол между боковыми сторонами и основанием

\(b =\)   
\(\alpha =\)

Формула Герона для равнобедренного треугольника

a =   
b =

Площадь равностороннего треугольника

$$S= \frac{ \sqrt{3}a^2}{4} $$
\(S\) — площадь треугольника

\(a\) — сторона

\(a =\)

Площадь равностороннего треугольника

$$S= \frac{3 \sqrt{3}R^2}{4}$$
\(S\) — площадь треугольника

\(R\) — радиус описанной окружности

\(R =\)

Площадь равностороннего треугольника

$$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника

\(r\) — радиус вписанной окружности

\(r =\)

Площадь равностороннего треугольника

$$S= \frac{h^2}{\sqrt{3}}$$
\(S\) — площадь треугольника

\(h\) — высота

\(h =\)

Площадь треугольника онлайн расчет

Данная страница посвящена достаточно распространенному информационному ресурсу  — описанию и расчету площади произвольного треугольника. Отличие от других ресурсов, это расчет площади онлайн, непосредственно в процессе прочтения статьи

Площадь через высоту и основание

Это самая простая для запоминания формула. Словами эта формула звучит так — площадь треугольника равна половине произведения основания треугольника на его высоту.

В случае прямоугольного треугольника это выражение приобретает еще более простой смысл: Площадь прямоугольного треугольника равна половине произведения двух катетов 

площадь через стороны треугольника

Площадь треугольника выраженная через стороны известна очень давно —  она фигурирует в книгах, датированных 1 веком до нашей эры. 

Эту формулу можно выразить по разному, благо формул расчета параметров треугольника достаточно.

Но если попытаться мыслить категориями времен до нашей эры, когда не было формул в современном преставлении, не было переменных и знаков корня, то единственной аксимомой, на базе которого, Герон, создал свою формулу, была теорема Пифагора. А так как в те времена, еще не знали иррациональных чисел, да к отрицательным  у ученых было достаточно скептическое видение, то для размышлений использовались целые числа. 

Самого доказательства здесь не будет, предположив только что Герон, дополнял произвольный пифагоровый треугольник до прямоугольника высчитывал его площадь, и делил на два. 

Площадь через координаты вершин

Когда известны координаты вершин треугольника, формула площади может быть выражена вот такой формулой

Определитель третьего порядка  легко раскладывается, и поэтому  расчет площади даже в ручном режиме не вызовет никаких затруднений.

Площадь через две стороны и угол между ними

Площадь через сторону и два угла

Редко встречающаяся задача,  но и для таких исходных данных  высчитали формулу. Внимательный читатаель сразу видит «ошибку». Заголовок гласит, что площадь узнается через сторону и два угла, то есть через три переменных, а в формуле присутствут все четыре. Как же так?

На самом деле ошибки никакой нет, зная одну из основных аксиом треугольника, гласящая, что сумма внутренних углов  треугольника всегда(!!) равна 180 градусов

Поэтому нет ничего сложного, зная два угла треугольника, узнать третий.

Площадь через медианы треугольника

Заменив квадраты сторон на дополнительные переменные,  система превращается в систему линейных уравнений, которые легко решить.

А узнав все стороны, легко определить площадь по сторонам треугольника

Как её выводили  неизвестно, то что что она по своему элеганта, это не подвергается сомнению.

Площадь треугольника — Формула Герона

Основная формула для определения площади треугольника полезна только в том случае, если вы знаете основание и высоту.

Итак, что вы будете делать, если вам известны только три длины сторон?

Всего два шага.

Шаг 1: Вычислите половину периметра треугольника и назовите его s.

Шаг 2: Используйте s в следующей формуле:

Давайте воспользуемся формулой, чтобы определить площадь треугольника выше.

Шаг 1: Периметр треугольника равен 12 + 22 + 16 = 50

Следовательно, значение s равно половине 50 или 25.

Шаг 2: Замените s в формуле площади на 25 и решите.

A =

A =

A =

A = 93,7 м ²

Вот еще пара примеров, которые стоит попробовать.

Пример 1:

Шаг 1: Определите половину периметра.

s =

Шаг 2: Используйте s в формуле Герона.

A =

A =

A =

A = 24 шт. ²

Теперь у этого треугольника есть основание и высота. Итак, давайте сравним нашу работу с формулой, с которой вы, возможно, более знакомы для решения.
A =

A =

A = 24 единицы ²

Здесь мы имеем тот же ответ, что и при использовании метода Герона.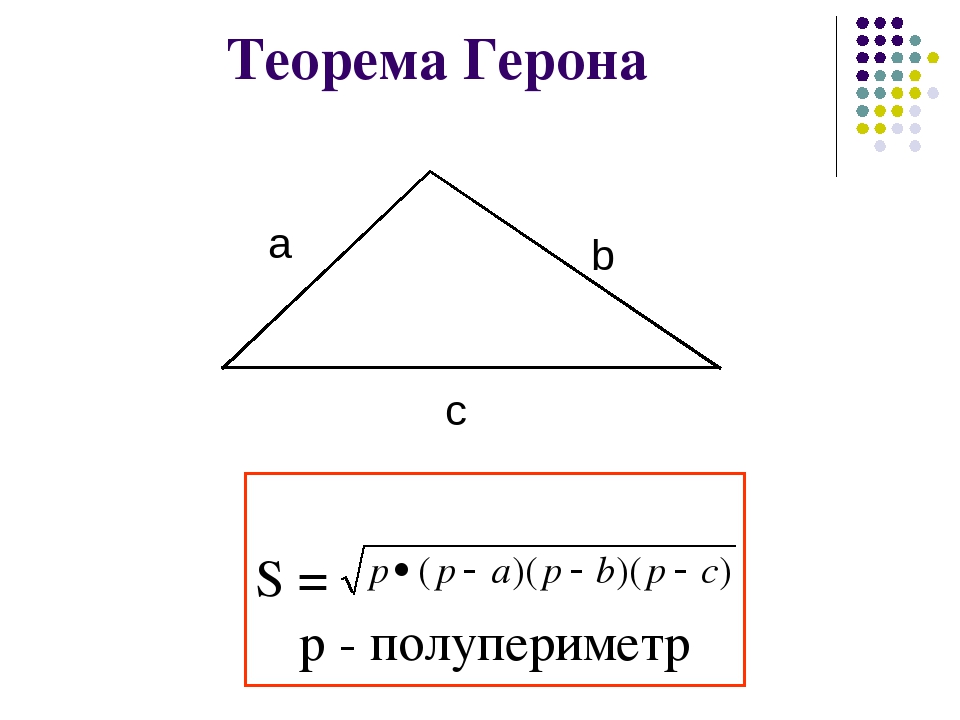

Пример 2:

Шаг 1. Определите половину периметра. s =

s =

s = 15,5

Шаг 2: Используйте s в формуле Герона.

Если решение нерационально, ответ можно округлить. В этом примере мы округлили до ближайшей десятой.

Давайте рассмотрим

Если вам даны три стороны треугольника, вы можете использовать периметр и формулу Герона для определения площади. Всего два шага.

Шаг 1: Определите половину периметра.

Шаг 2: Используйте три длины стороны и половину периметра в формуле Герона.

На некоторых площадях будут иррациональные номера. Это означает, что они не могут быть представлены в виде дроби. Вместо этого это десятичные дроби, которые никогда не заканчиваются и никогда не повторяются. Когда это происходит, площадь можно округлить до любого числового значения, о котором вас могут попросить.

Формула Герона. Калькулятор | Формула

Если вам интересно, как рассчитать площадь треугольника, зная его три стороны, вы попали в нужное место — калькулятор формул Герона может сделать это в кратчайшие сроки. Просто введите заданные вами значения — например, стороны треугольника — и наш инструмент подскажет вам ответ. Если вам интересно узнать о формуле площади Герона, вы прочтете об этом ниже. Кроме того, там можно найти доказательства формул Герона, поэтому продолжайте прокручивать, чтобы узнать больше об этой полезной, но не очень известной формуле.

Формула площади Герона: уравнение площади треугольника с заданными 3 сторонами

Формула Герона, также известная как формула Героя, — это формула для вычисления площади треугольника с учетом трех сторон треугольника.Впервые он был упомянут в книге Герона Metrica , написанной ок. 60 г. н.э., представлявший собой сборник формул для расчета поверхностей и объемов различных объектов. Базовая формулировка:

площадь = √ (s * (s - a) * (s - b) * (s - c))

где
s — полупериметр — половина периметра треугольника:

s = (a + b + c) / 2

Однако существуют и другие формы этой формулы — если вы не хотите рассчитывать полупериметр вручную, вы можете использовать формулу только с длинами сторон:

площадь = 0. 25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))

Доказательство формулы Герона

Есть много способов доказать формулу площади Герона, но вам нужно знать некоторые основы геометрии. Вы можете использовать:

Существуют и другие доказательства, но они более сложные или используют законы, которые не так популярны (например, тригонометрическое доказательство с использованием закона котангенсов).

В этом доказательстве нам нужно использовать формулу площади треугольника:

площадь = (c * h) / 2

Все значения в формуле должны быть выражены в терминах сторон треугольника: c — это сторона, поэтому она соответствует условию, но мы мало знаем о нашем росте.Итак, чтобы получить доказательство формулы Герона, нам нужно найти h в терминах сторон.

1. Из теоремы Пифагора мы знаем, что:

   h² + (c - d) ² = a² и h² + d² = b² , согласно рисунку выше

2. Вычитание этих двух уравнений дает:

   c² - 2 * c * d = a² - b² , из которого можно вывести формулу для d в терминах сторон треугольника:

   d = (-a² + b² + c²) / (2 * c)

3. Следующий шаг — найти высоту по сторонам треугольника. Снова воспользуйтесь теоремой Пифагора:

   h² = b² - d²

   h² = b² - ((-a² + b² + c²) / (2 * c)) ² — это уже в терминах сторон, но давайте попробуем уменьшить его до более красивой формы, применив различие тождественности квадратов:

   h² = ((2 * b * c) - a² + b² + c²) * ((2 * b * c) - a² + b² + c²) / (4 * c⁴)

   h² = ((b + c) ² - a²) * (a² - (b - c) ²) / (4 * c²)

   h² = (b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²)

4. Примените эту формулу к первому уравнению, уравнению для площади треугольника:

   площадь = (c * h) / 2 = 0.5 * в * в

   площадь = 0,5 * c * √ ((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²))

   площадь = 0,25 * √ ((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c)

Вот, пожалуйста! Это доказательство площади Heron. Преобразование окончательного уравнения в форму с помощью полупериметра — тривиальная задача.

Посмотрите на рисунок — a, b, c — стороны треугольника, а α, β, γ — углы, противоположные этим сторонам.Чтобы найти доказательство формулы Герона с помощью тригонометрии, нам нужно использовать другую формулу площади треугольника с учетом двух сторон и угла между ними:

площадь = 0,5 * a * b * sin (γ)

1. Чтобы вывести доказательство формулы Герона в этом случае, нам нужно выразить синус угла через стороны треугольника. Мы можем использовать закон косинусов:

   c² = a² + b² - 2 * a * b * cos (γ)

2. Благодаря этому закону мы получаем косинус, зависящий от стороны.Но как найти формулу для синуса? Это легко, просто используйте базовое соотношение между функциями синуса и косинуса — тригонометрическое тождество Пифагора:
   sin² (γ) + cos² (γ) = 1 , поэтому формула для косинуса равна

   .

   sin (γ) = √ (1 - cos² (γ)) = (√ (4 * a² * b² - (a² + b² -c²) ²)) / (2 * a * b)

3. Теперь вы можете подставить синус в формулу площади треугольника:

   площадь = 0,5 * a * b * sin (γ)

   площадь = 0. 25 * √ (4 * a² * b² - (a² + b² - c²) ²))

   площадь = 0,25 * √ (2 * a * b - (a² + b² - c²) * (2 * a * b + (a² + b² - c²)))

   площадь = 0,25 * √ (c² - (a - b) ²) * (- c² + (a + b) ²)

   площадь = 0,25 * √ (c - a + b) * (c + a - b) * (- c + a + b) * (c + a + b)

который должен был доказать.

Отлично! Теперь вы понимаете, почему эта формула верна, поэтому не ждите больше и попробуйте калькулятор формул Герона!

Как пользоваться калькулятором формул Герона?

Это действительно просто! Просто выполните эти два простых шага:

1. Введите указанные значения в соответствующие поля .Предположим, что a = 12 дюймов, b = 5 дюймов и c = 13 дюймов.
2. Неизвестное значение появляется в мгновение ока! В нашем примере область треугольника — это пропущенное значение, которое мы хотим найти. Калькулятор формул Герона выяснил, что площадь такого треугольника равна 30 кв.

Помните, что почти в каждом калькуляторе вы можете изменить единицы измерения простым щелчком мыши по названию единицы. Также вы можете использовать наш инструмент, чтобы узнать недостающую сторону треугольника, зная две стороны и площадь.Однако существуют два таких треугольника, которые удовлетворяют условию, поэтому мы показываем только одно решение — например, треугольники со сторонами 12, 13, 5 и 12, 13, 24,515 будут иметь одинаковую площадь, равную 30.

Формула I Херона. — Доктора математики

Существует красивая формула площади треугольника, которую многие студенты, к сожалению, никогда не видят. В этом посте мы рассмотрим эту формулу и три способа ее доказать. В следующий раз я покажу несколько примеров того, насколько это может быть полезно.(Кстати, вы также увидите ее под названием «Формула героя», основанная на другом переводе имени ее создателя на греческом.) В конце концов, в этой серии статей мы столкнемся с некоторыми очень практическими проблемами, связанными с поиском местности.

Формула

Вот хороший вводный вопрос из 1995 года (когда Ask Dr. Math было меньше года):

 Площадь треугольников по формуле героя

Я занимаюсь серфингом около недели, и это первый сайт, который я посетил, где действительно была такая область.В настоящее время я создаю (пробую) программный пакет для управления объектами.

Вопрос.
Если бы человек дал  три измерения треугольника  (в футах) и, по крайней мере, отметил базовое измерение, не зная углов, потому что две другие линии должны были бы где-то пересекаться, есть ли формула, которая могла бы вычислить площадь? Размер площади крыши, например, до пяти измерений, квадраты, прямоугольники и прямоугольники нечетного размера - нормально, но у меня проблема с двумя другими. Когда вы спрашиваете высоту треугольника, вы получаете ответ «что?».Пентагоны, знающие только пять измерений?

Спасибо за возможность хотя бы отправить это. Иногда помогает просто попытка изложить проблему в письменной форме.  

Доктор Кен ответил:

 Здравствуйте!

Вот одна из моих любимых формул в математике: это формула  Герона  (иногда называемая формулой Герона  ) для площади треугольника. Если 3 стороны равны a, b и c, тогда пусть s = (a + b + c) / 2. Буква s обозначает полупериметр  . Тогда площадь треугольника равна

                     Sqrt {s (s-a) (s-b) (s-c)}.Что касается вашего вопроса о пятиугольнике, я не уверен, что понимаю, что вы имеете в виду. Вам даны только пять длин сторон? Если это так, то вы не можете определить, что это за площадь, только по этой информации (пятиугольник - это не такая же жесткая фигура, как треугольник). 

Как вы, возможно, знаете из теоремы сравнения SSS, треугольник полностью определяется длинами его сторон, так что это все, что вам нужно, чтобы найти площадь. Это не верно для многоугольников с большим количеством сторон. Позже мы будем искать способы найти такие области, некоторые из которых включают разбиение их на треугольники и использование Heron.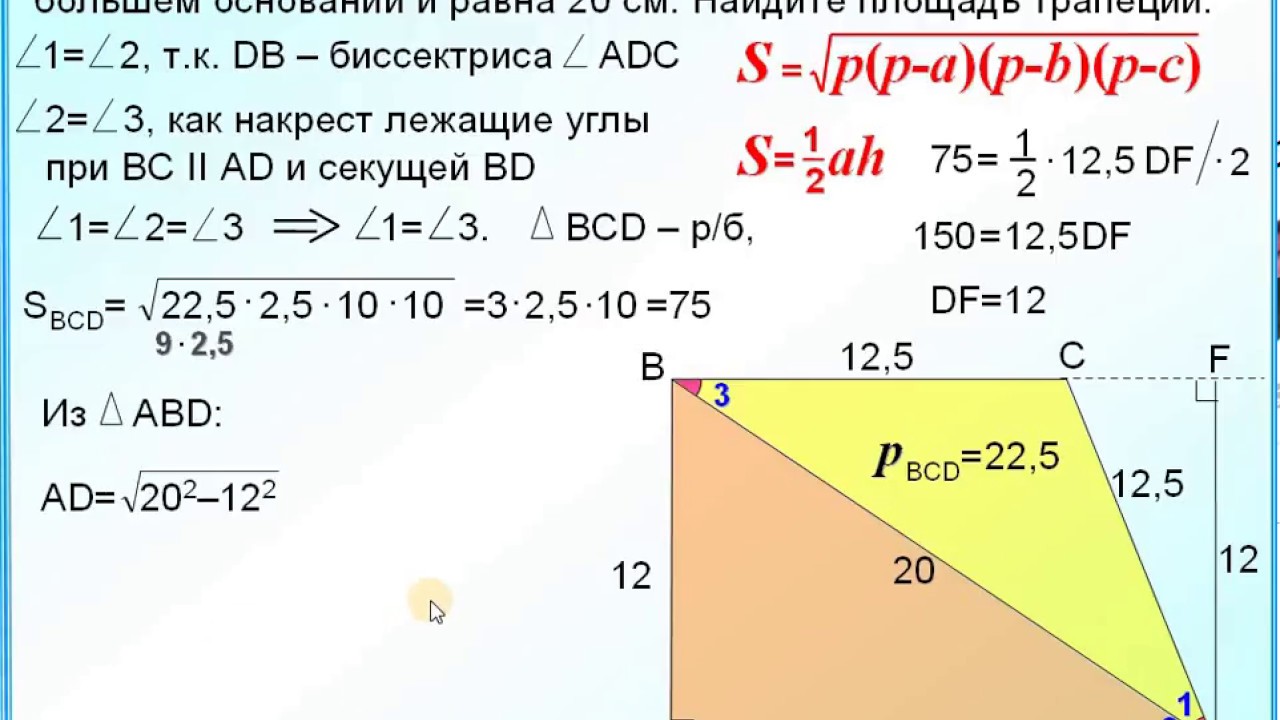

Формула легко запоминается, но нелегко доказать (и поэтому одна из немногих, которые мне приходится запоминать, а не воссоздавать при необходимости).

Вот наш треугольник со сторонами a , b и c :

Сначала вычисляем полупериметр (половину суммы сторон): \ (s = \ frac {a + b + c} {2} \). Тогда площадь треугольника будет $$ K = \ sqrt {s (s-a) (s-b) (s-c)}. $$

Если мы заменим s в формуле на его определение, мы получим эту форму, которая немного менее запоминается, но не менее интересна: $$ K = \ sqrt {\ frac {a + b + c} {2} \ cdot \ frac {-a + b + c} {2} \ cdot \ frac {a-b + c} {2} \ cdot \ frac {a + bc} {2}}.

$

Итак, почему это должно работать? Нас об этом спрашивали несколько раз, поэтому вот три доказательства: одно с использованием тригонометрии, одно с использованием теоремы Пифагора и одно с использованием кругов и треугольников. Если вы не следуете одному доказательству, попробуйте следующее. Второй покажет, как я часто работаю с формулой для тех, кто ее не знает, так что это полезно не только для доказательства.

Доказательство # 1: Закон косинусов

Во-первых, вопрос от 1997 года:

 Доказательство формулы героя

Не могли бы вы сказать мне, где найти доказательство формулы Героя или помочь о том, как ее получить? Я учитель, и мой класс над этим работает.2 (A / 2) = ----------
                    до н.э

Теперь мы можем вернуться к формуле для площади треугольника:

  (1/2) bc.sin (A) = bc.sin (A / 2) .cos (A / 2)

                   bc.sqrt [s (s-a) (s-b (s-c)]
                 знак равно
                              до н.э
                 = sqrt [s (s-a) (s-b) (s-c)] 

Непонятно, откуда вы это знаете (это верно для многих доказательств в их окончательной форме), но это прекрасно, как части формулы попадают на свои места пополам!

Доказательство # 2: теорема Пифагора

Год спустя мы получили такой вопрос:

 Выводы формулы Герона

Я понимаю, как использовать теорию Герона, но как именно она получена? 

Доктор Роб сослался на доказательство выше, а затем дал одно, которое я обычно использую:

 Другое доказательство использует теорему Пифагора вместо тригонометрических функций синуса и косинуса. 2) / 16
      = - (c + [a + b]) * (c- [a + b]) * (c + [a-b]) * (c- [a-b]) / 16
      = (a + b + c) * (a + b-c) * (a-b + c) * (- a + b + c) / 16
      = (2 * s) * (2 * s-2 * c) * (2 * s-2 * b) * (2 * s-2 * a) / 16
      = s * (s-a) * (s-b) * (s-c)
    K = sqrt [s * (s-a) * (s-b) * (s-c)] 

Алгебра там получилась довольно сложной, хотя основная идея проста. Позвольте мне продемонстрировать, как этот метод работает в качестве вычисления в конкретном случае, для тех, кто не выучил (или не забыл) формулу:

Предположим, мы знаем, что стороны треугольника равны 5, 7 и 8, и хотим найти площадь.2. $$ Решая это для x , находим \ (x = \ frac {5} {2} \). (Оно превратилось в линейное уравнение, которое очень легко решить.)

Применяя теорему Пифагора к любому треугольнику, мы находим \ (h = \ frac {5} {2} \ sqrt {3} \).

Наконец, площадь равна $$ \ frac {1} {2} bh = \ frac {1} {2} \ cdot 8 \ cdot \ frac {5} {2} \ sqrt {3} = 10 \ sqrt {3 }. $$

Это намного проще, чем , доказывающий формулу , но немного сложнее, чем , используя ее.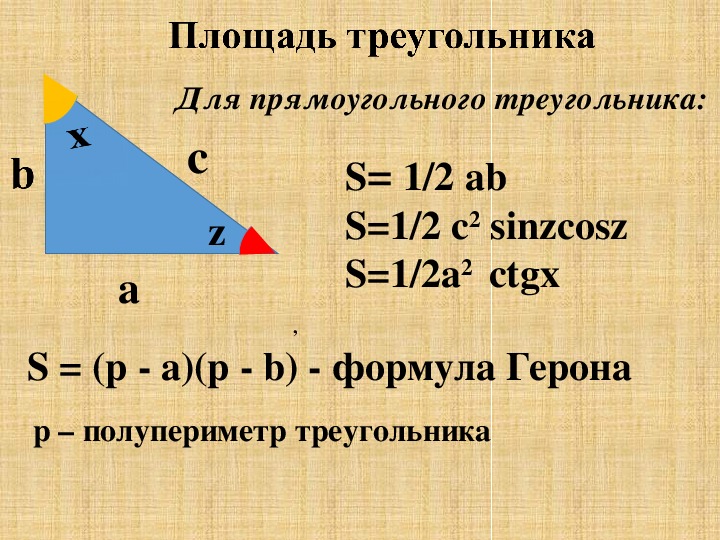

В качестве альтернативного подхода вы можете написать уравнение, в котором AD + DC = 8, и решить напрямую для h ; но это радикальное уравнение, которого большинство из нас предпочло бы избежать! (Впрочем, в следующий раз я продемонстрирую это.)

Доказательство № 3: Выписанные круги

Наконец, в 2000 году мы получили запрос на чисто геометрическое доказательство:

 Геометрическое доказательство формулы Герона

Как мне доказать формулу Героя (n), используя окружность с центром P и радиусом R, вписанную в треугольник ABC? 

Доктор Флор взял это (хотя его ответ может быть не тем, к чему должен был привести намек). Обратите внимание, что вписанная окружность или вписанная окружность (внутренне) касается сторон треугольника, в то время как вневписанная окружность касается одной стороны и продолжений двух других сторон.

 Я знаю метод геометрического доказательства формулы Герона с помощью вписанной окружности треугольника, но в этом методе я также использую одну из вневписанных окружностей.  Я научился этому методу у Пола Ю из Атлантического университета Флориды.

Сначала я нарисовал для вас треугольники и два круга. Обратите внимание, что я изменил имена: у вписанной окружности   центр I и радиус r (в то время как вневписанная окружность   (напротив A) имеет центр I 'и радиус r') вместо вашего центра P и радиуса R.

Найдите минутку, чтобы сориентироваться; Найдите треугольник ABC и центры двух окружностей.

 Далее стороны треугольника записываются как a = BC, b = AC и c = AB. Я использую s = (a + b + c) / 2 для полупериметра.

1. Из того факта, что две касательные к окружности совпадают, мы видим, что AE = AG, CG = CF и BE = BF. Так, например:

   AE + EB + CG = c + CG = s

и, следовательно, CG = s-c.

Таким же образом:

   CF = s-c
   AG = AE = s-a
   BE = BF = s-b 

Мы уже начинаем видеть, как формула обретает форму в виде трех различий.

 2. Снова из того факта, что две касательные к окружности совпадают, мы видим, что AE '= AG, BE' = BJ и CG '= CJ.  Это дает нам:

   AG '+ AE' = AB + BJ + CJ + AC = 2 с

И мы можем сделать вывод, что AG '= AE' = s. И, например,
   BE '= s-c. 

Они появляются повсюду. Но пока мы не знаем никаких территорий.

 3. И I, и I 'лежат на биссектрисе внутреннего угла 
 Кусочки собираются вместе!
 На этом рисунке желтые треугольники - это пара, использованная выше, а зеленые - следующие:
 5. Мы также можем видеть, что треугольники AIG и AI'G 'похожи.2 = ---------------
                s

а также

            (s-a) (s-b) (s-c)
   r = sqrt (---------------) . ........... [3]
                   s 
 Теперь у нас есть формула для inradius  r  ABC. Посмотрите на этот крупный план ABC:
.
 Площади треугольников AIB, BIC и CIA равны соответственно \ (\ displaystyle \ frac {cr} {2} \), \ (\ displaystyle \ frac {ar} {2} \) и \ (\ displaystyle \ frac {br} {2} \), поэтому их сумма, площадь ABC, равна \ (\ displaystyle K = \ frac {ar} {2} + \ frac {br} {2} + \ frac {cr} {2 } = \ frac {a + b + c} {2} r = sr \).Итак…
 7. Нетрудно увидеть, что площадь ABC, назовем ее K, равна s * r. Комбинируя это с [3], мы находим формулу Герона:

   К = sqrt (s (s-a) (s-b) (s-c)) 
 И вот формула!
 В следующий раз мы воспользуемся этим полезным и удивительным образом.
 Формула Герона | Блестящая вики по математике и науке 
 Найдите площадь треугольника ниже.
 Imgur
 Поскольку длина трех сторон равна 6, полупериметр равен s = 6 + 6 + 62 = 9s = \ frac {6 + 6 + 6} {2} = 9s = 26 + 6 + 6 = 9. Следовательно, площадь треугольника
.
 A = 9 × (9-6) × (9-6) × (9-6) = 93. □ A = \ sqrt {9 \ times (9-6) \ times (9-6) \ times (9-6)} = 9 \ sqrt {3}. \ _ \ SquareA = 9 × (9-6) × (9−6) × (9−6) = 93. □
 Найдите площадь треугольника ниже.
 Imgur
 Поскольку три стороны равны 4, 5 и 7, полупериметр равен s = 4 + 5 + 72 = 8s = \ frac {4 + 5 + 7} {2} = 8s = 24 + 5 + 7 = 8. Следовательно, площадь треугольника
.
 A = 8 × (8−4) × (8−5) × (8−7) = 46.□ A = \ sqrt {8 \ times (8-4) \ times (8-5) \ times (8-7)} = 4 \ sqrt {6}. \ _ \ SquareA = 8 × (8−4) × (8−5) × (8−7) = 46. □
 Какова площадь треугольника со сторонами 13, 14 и 15?
 Поскольку три стороны имеют длину 13, 14 и 15, полупериметр равен s = 13 + 14 + 152 = 21s = \ frac {13 + 14 + 15} {2} = 21s = 213 + 14 + 15 = 21. Следовательно, площадь треугольника
.
 A = 21 × (21−13) × (21−14) × (21−15) = 84. □ A = \ sqrt {21 \ times (21-13) \ times (21-14) \ times (21-15)} = 84. \ _ \ squareA = 21 × (21-13) × (21-14) × (21−15) = 84.□
 Найдите площадь треугольника ниже.
 Imgur
 Поскольку три стороны имеют длину 6, 8 и 10, полупериметр равен s = 6 + 8 + 102 = 12s = \ frac {6 + 8 + 10} {2} = 12s = 26 + 8 + 10 = 12. Следовательно, площадь треугольника
.
 A = 12 × (12−6) × (12−8) × (12−10) = 24. □ A = \ sqrt {12 \ times (12-6) \ times (12-8) \ times (12-10)} = 24. \ _ \ squareA = 12 × (12-6) × (12-8) × (12−10) = 24. □
 Найдите площадь треугольника с длинами сторон 4,134,134,13 и 151515.
 У нас есть a = 4, b = 13, c = 15a = 4, b = 13, c = 15a = 4, b = 13, c = 15 и s = 4 + 13 + 152 = 16s = \ frac {4 + 13 + 15} {2} = 16 = 24 + 13 + 15 = 16. Следовательно,
 А = 16 (16-4) (16-13) (16-15) = 24. □ A = \ sqrt {16 (16-4) (16-13) (16-15)} = 24. \ _ \ squareA = 16 (16-4) (16-13) (16-15) = 24 . □
 Найдите площадь треугольника, обведенного черным. 
 Изображение
 Мы можем использовать теорему Пифагора, чтобы найти, что длины сторон равны 5,29,210 5, \ sqrt {29}, 2 \ sqrt {10} 5,29, 210.2} \\
 & = \ frac {1} {4} \ sqrt {2704} \\
 & = 13. \ _ \ квадрат
 \ end {align} A = 41 2 (a2b2 + a2c2 + b2c2) - (a4 + b4 + c4) = 41 2 (25 × 29 + 25 × 40 + 29 × 40) −252−292−402 = 41 2704 = 13. □
 Примечание. Этот треугольник появляется в составных фигурах, что является более простым подходом.
 Найдите площадь треугольника ниже. 
 Imgur
 Поскольку длина трех сторон равна 6, полупериметр равен s = 6 + 6 + 62 = 9s = \ frac {6 + 6 + 6} {2} = 9s = 26 + 6 + 6 = 9.Следовательно, площадь треугольника
.
 A = 9 × (9-6) × (9-6) × (9-6) = 93. □ A = \ sqrt {9 \ times (9-6) \ times (9-6) \ times (9-6)} = 9 \ sqrt {3}. \ _ \ SquareA = 9 × (9-6) × (9−6) × (9−6) = 93. □
 Найдите площадь треугольника ниже. 
 Imgur
 Поскольку три стороны равны 4, 5 и 7, полупериметр равен s = 4 + 5 + 72 = 8s = \ frac {4 + 5 + 7} {2} = 8s = 24 + 5 + 7 = 8. Следовательно, площадь треугольника
.
 A = 8 × (8−4) × (8−5) × (8−7) = 46.□ A = \ sqrt {8 \ times (8-4) \ times (8-5) \ times (8-7)} = 4 \ sqrt {6}. \ _ \ SquareA = 8 × (8−4) × (8−5) × (8−7) = 46. □
 Какова площадь треугольника со сторонами 13, 14 и 15? 
 Поскольку три стороны имеют длину 13, 14 и 15, полупериметр равен s = 13 + 14 + 152 = 21s = \ frac {13 + 14 + 15} {2} = 21s = 213 + 14 + 15 = 21. Следовательно, площадь треугольника
.
 A = 21 × (21−13) × (21−14) × (21−15) = 84. □ A = \ sqrt {21 \ times (21-13) \ times (21-14) \ times (21-15)} = 84. \ _ \ squareA = 21 × (21-13) × (21-14) × (21−15) = 84.□
 Найдите площадь треугольника ниже. 
 Imgur
 Поскольку три стороны имеют длину 6, 8 и 10, полупериметр равен s = 6 + 8 + 102 = 12s = \ frac {6 + 8 + 10} {2} = 12s = 26 + 8 + 10 = 12. Следовательно, площадь треугольника
.
 A = 12 × (12−6) × (12−8) × (12−10) = 24. □ A = \ sqrt {12 \ times (12-6) \ times (12-8) \ times (12-10)} = 24. \ _ \ squareA = 12 × (12-6) × (12-8) × (12−10) = 24. □
 Колонна Формула Герона | Японская математика в период Эдо 
 Площадь треугольника можно вычислить, когда найдены длины его трех сторон.Предполагая, что площадь треугольника равна S, и пусть
 где  a ,  b  и  c  - длины трех сторон треугольника, тогда следует, что
 . Формулу можно доказать следующим образом:
 Площадь треугольника 
 Чтобы найти площадь треугольника с тремя сторонами, длина которого равна  a ,  b  и  c , опустите перпендикуляр из A на сторону BC, пусть основание перпендикуляра будет H, и положим AH =  h. .Площадь △ ABC равна, и если мы представим  ah , используя только  a ,  b  и  c , мы получим формулу Герона.
 Глядя на рисунок, мы знаем, что 、 h  2  = c  2  -x  2  = b  2  - (a-x)  2  верно, и поэтому мы получаем
 из c  2  -x  2  = b  2  -a  2  + 2ax-x  2 .
 Затем, используя
 следует, что
 4a  2  h  2  = 4a  2  c  2  - (c  2  + a  2  -b  2 )  2  
 = (2ac + c  2  + a  2  -b  2 ) (2ac-c  2  -a  2  + b  2 ) = {(c + a)  2  -b  2 } {b  2  - (приблизительно)  2 } 
 = (c + a + b) (c + a-b) (b + c-a) (b-c + a)
 Здесь, полагая a + b + c = 2s, получаем 4a  2  h  2  = 2s (2s-2b) (2s-2a) (2s-2c) = 16s (sa) (sb) (sc) . 
 Следовательно, получено из
 a  2  h  2  = 4s (s-a) (s-b) (s-c).
 С другой стороны, как, получаем 
.
 Используя эту формулу, мы можем легко вычислить площадь любого треугольника, все стороны которого представлены натуральными числами. Как описано в столбце «Теорема Пифагора», когда площадь этого треугольника также является натуральным числом, он называется треугольником Герона.
 Треугольники с тремя сторонами (4,13,15), (3,25,26), (9,10,17), (7,15,20), (6,25,29), (11,13, 20), (5,29,30), (13,14,15) и т. Д. Являются треугольниками Герона; пожалуйста, подтвердите это, используя формулу Герона.
 Радиус вписанной окружности треугольника 
 Как показано на рисунке, круг с радиусом  r  с точкой O в качестве центра вписан в треугольник ABC с тремя сторонами длиной  a ,  b  и  c  соответственно. В этом случае O называется внутренним центром, и отсюда следует, что AMO≡ △ ANO, △ BNO≡ △ BLO и △ CLO≡ △ CMO.
 Радиус вписанной окружности треугольника можно вычислить, когда найдены длины его трех сторон.Из рисунка следует, что △ ANO≡ △ AMO, △ CMO≡ △ CLO и △ BLO≡ △ BNO. Таким образом, получаем
;
  как   a  +  b  +  c  = 2 ( l  +  m  +  n )
 , получаем
.
 Следовательно, получаем
 по формуле Герона. 
 Наконец, приведем формулу для вычисления вписанного четырехугольника окружности.
 Площадь вписанного четырехугольника круга 
 Используя тот факт, что  x  +  y  = 180 ° или свойство вписанного четырехугольника, а площадь △ ABD равна  ad  sin  x , а площадь △ BCD равна  bc  sin  y , и представляя BD  2  двумя способами, используя закон косинусов, мы можем исключить sin  x , sin  y  и т. Д., от выражения общей площади.
 Как показано на рисунке, предполагая, что длины четырех сторон равны  a, b, c, d, , и допуская, площадь четырехугольника ABCD равна.
 Мы хотели бы, чтобы вы попробовали доказать эту формулу. Для справки: 
 Если C и D перекрываются, четырехугольник становится треугольником с d = 0, а формула меняется на формулу Герона.
 Решение проблем с помощью формулы Херона 
 Введение 
 Формула Герона для определения площади треугольника со сторонами длины
 a, b, c равно
 где
 Очень жаль, что эта тема практически исчезла
 из школьной программы сегодня.Расчет с учетом имеющихся расчетов
 и компьютеры, больше не может быть причиной для отказа от формулы.
 В дальнейшем я надеюсь показать несколько интересных и сложных
 задачи с использованием формулы Герона.
 Будет ли кто-нибудь доказывать или доказывать
 формула для конкретного класса будет зависеть от класса. Первоначально,
 исследование с помощью формулы Херона может включать вычислительные области
 используя формулу и сравнивая результаты - много
 поскольку мы осмысленно ставим аналогичные упражнения с пифагорейскими
 Теорема задолго до того, как ее доказательство или демонстрация будут полностью поняты.
 Например, одно упражнение может заключаться в том, чтобы ученики измерили
 стороны и высота на нескольких треугольниках и, с помощью калькулятора,
 вычислить площади с помощью обеих формул
 Сравнение результатов может привести к интуиции о
 области треугольников и понимание того, когда одна формула может
 быть более применимым, чем другие.
 Формула Герона 
 Демонстрация и доказательство формулы Герона могут быть выполнены.
 из элементарного рассмотрения геометрии и алгебры.Я представлю здесь алгебраическое доказательство. Альтернативные доказательства и выводы предлагаются на веб-сайте Джвильсона, Формула Герона, а особенно краткое геометрическое доказательство приводится в Формуле Герона, Геометрическое доказательство.
 Я буду
 предположим теорему Пифагора и формулу площади для треугольника
, где  b  - длина основания, а  h  - высота этого основания.
 база.
 У нас
 итак, для справки в будущем,
 2s = a + b + c 
 2 (s - a) = - a + b + c 
 2 (s - b) = a - b + c 
 2 (s - c) = a + b - c
 У нашего треугольника есть хотя бы одна сторона, для которой высота
 лежит «внутри» треугольника.Для удобства сделайте это
 сторона длиной  c . Это не будет иметь никакого значения, просто проще.
 Пусть p + q = c, как указано. Тогда
 Эта демонстрация формулы Герона проста и элементарна.
 Работа над ним со студентами может дать плодотворные идеи
 стратегия, симметрия, планирование и наблюдение.Теперь перейдем к
 рассмотрим некоторые задачи и исследования, для которых формула Герона
 является полезным.
 Проблема: 
 Покажите, что максимальная площадь треугольной области с фиксированной
 периметр получается равносторонним треугольником.
 Комментарий. Я бы адаптировал формулировку и контекст этой проблемы
 в зависимости от фона студентов. Выше я упоминал
 исследовательское исследование, в ходе которого студенты изучали разные
 треугольные области, которые могут быть сформированы с периметром 100
 ноги.Теперь расширите это. Попросите учащихся организовать стол, за которым
 длины сторон систематически меняются.
 Чтобы что-то «систематически» варьировать, нужно
 для определения переменной, которую можно упорядочить в таблице. Например,
 исследовать более решаемую проблему равнобедренных треугольников.
 Пусть сторона длиной  a  будет основанием и будет изменяться от 2 до
 48 с шагом 2, как показано ниже
 
 Эту таблицу можно создать с помощью калькулятора всего за несколько
 минут, и данные открывают много возможностей для обсуждения,
 правдоподобные рассуждения и постановка проблемы.
 Например, в четырех строках таблицы будут отображаться треугольники.
 с целыми областями. Есть ли другие треугольники (не равнобедренные)
 с периметром 100, имеющим целые стороны и целую площадь?
 Между прочим, глядя на эту таблицу и интерпретируя ее,
 студенты могут понять, что для любой выбранной длины
 для основания равнобедренный треугольник будет иметь наибольшую площадь для
 все треугольники с периметром в 100 единиц, которые можно было построить
 на этой базе.
 Когда таблица будет заполнена, подумайте о том, чтобы ученики
 построить график длиной  и  по оси абсцисс и
 площадь по оси ординат. Полученная кривая дает больше возможностей
 для правдоподобных рассуждений.
 Вернемся теперь к тому, чтобы показать, что равносторонний
 треугольник имеет наибольшую площадь для любого фиксированного периметра.
 и равенство наступает, когда s - a = s - b = s - c, то есть a = b
 = с.Поскольку произведение всегда меньше этой константы, это
 константа - это максимум для продукта и максимальная площадь
 треугольник с фиксированным периметром 2s -
 Равносторонний треугольник имеет максимальную площадь. Например,
 максимальная площадь для всех треугольников, имеющих периметр 100, составляет
 Формула Герона для треугольной площади 
Формула Герона для треугольной площади
 СОДЕРЖАНИЕ
 
 Главная страница
Ссылки и ссылки
 ТЕОРЕМА
 
 
 Рисунок 6
 
 Для треугольника со сторонами длиной  a ,  b  и  c  и площадью  K  имеем
  K  = sqrt [ s  ( s - a ) ( s - b ) ( s - c )],
где  s  = ( a  +  b  +  c ) - полупериметр треугольника.
 ДОКАЗАТЕЛЬСТВО
 
Пусть  ABC  - произвольный треугольник. Кроме того, пусть сторона  AB  будет не меньше длины двух других сторон (Рисунок 6).
 Поскольку доказательство формулы Герона является «окольным» и длинным, мы разделим доказательство на три основные части.
 Часть А
 
Пусть  O  будет центром вписанной окружности. Пусть  r  будет радиусом этой окружности (рисунок 7).Как видим,  OD  =  OE  =  OF  =  r .
 Теперь, применив обычную формулу для площади треугольников, получим:
Площадь ( AOB ) = (основание) (высота) = ( AB ) ( OD ) =  кр 
 Площадь ( BOC ) = (основание) (высота) = ( BC ) ( OE ) =  ar 
 Площадь ( COA ) = (основание) (высота) = ( AC ) ( OF ) =  br 
Так,
  K  = Площадь ( ABC ) = Площадь ( AOB ) + Площадь ( BOC ) + Площадь ( COA )
Путем подстановки
  K  =  cr  +  ar  +  br  =  r  ( a  +  b  +  c ) =  rs 
 
 Рисунок 7
 
 Часть B
 
Теперь, используя предложение 1, мы видим, что  ABC  теперь состоит из трех пар конгруэнтных треугольников, а именно
  AOD  соответствует  AOF 
  BOD  соответствует  BOE 
и  COE  соответствует  COF 
 Эти сравнения следуют AAS. Поскольку соответствующие части конгруэнтных треугольников конгруэнтны, имеем
  AD  =  AF ,  BD  =  BE  и  CE  =  CF 
в то время как & lt  AOD  = & lt  AOF , & lt  BOD  = & lt  BOE  и & lt  COE  = & lt  COF .
 Теперь вытяните основание треугольника  AB  до точки  G , так что  AG  =  CE .Сейчас,
  BG  =  BD  +  AD  +  AG  =  BD  +  AD  +  CE  по конструкции
= (2  BD  + 2  AD  + 2  CE )
= [( BD  +  BE ) + ( AD  +  AF ) + ( CE  +  CF )] по совпадению
= [( BD  +  AD ) + ( BE  +  CE ) + ( AF  +  CF )]
= [ AB  +  BC  +  AC ]
= ( c  +  a  +  b ) =  с 
 Теперь, поскольку  BG  =  s ,
  с  -  с  =  BG  -  AB  =  AG 
  с  -  b  =  BG  -  AC 
= ( BD  +  AD  +  AG ) - ( CF  +  AF )
= ( BD  +  AD  +  CE ) - ( CE  +  AD ) =  BD , поскольку  AF = AD ,  CF  =  CE  и  AG  =  CE  .Так же,
  s  -  a  =  BG  -  BC 
= ( BD  +  AD  +  AG ) - ( BE  +  CE )
= ( BD  +  AD  +  CE ) - ( BD  +  CE ) =  AD , поскольку  BD  =  BE  и  AG  =  CE .
 Эти равенства просто помогают нам визуализировать сегменты  s  -  a ,  s  -  b  и  s  -  c .
 Часть C
 
Теперь постройте  OL  так, чтобы он был перпендикулярен  OB , пересекая  AB  в точке  K  (рисунок 8).
 
 Рисунок 8
 
 Затем постройте  AM  так, чтобы он был перпендикулярен  AB , пересекая  OL  в точке  H  (рисунок 9).
 
 Рисунок 9
 
 Затем подключите  BH  (Рисунок 10).
 
 Рисунок 10.
 
 По предложению 4 четырехугольник AHBO является вписанным четырехугольником.
По предложению 5 мы знаем, что & lt  AHB  + & lt  AOB  = 180 градусов.  (*) 
 Пожалуйста, не расстраивайтесь со следующей алгеброй. Это можно визуализировать с помощью рисунка 10.
 Теперь давайте сосредоточимся на углах около  O .
Из сравнений в части B мы видим, что
& lt  FOA  = & lt  DOA , & lt  DOB  = & lt  EOB  и & lt  EOC  = & lt  FOC .  (**) 
Очевидно,
& lt  FOA  + & lt  DOA  + & lt  DOB  + & lt  EOB  + & lt  EOC  + & lt  FOC  = 360 градусов.
По  (**) ,
2 & lt  DOA  + 2 & lt  DOB  + 2 & lt  FOC  = 360 градусов,
или же
& lt  DOA  + & lt  DOB  + & lt  FOC  = 180 градусов. (***) 
 Очевидно, & lt  DOA  + & lt  DOB  = & lt  AOB .  (****) 
Подставляя  (****)  в  (***) , мы видим, что & lt  AOB  + & lt  FOC  = 180 градусов.  (*****) 
Из номеров  (*)  и  (*****) , & lt  AHB  = & lt  FOC .
 Теперь мы видим, что треугольник  COF  похож на треугольник  BHA .
Подобными треугольниками
  AB / AH  =  CF / OF  =  AG / r 
так как  CF  =  AG  и  OF  =  r .
 Эквивалентно,
  AB / AG  =  AH / r   (V *) 
 Точно так же треугольник  KAH  аналогичен  KDO .Это потому, что & lt  KAH  и & lt  KDO  оба имеют угол 90 градусов, а & lt  AKH  = & lt  DKO .
Снова подобными треугольниками,
  AH / AK  =  OD / KD  =  r / KD 
Переставляем урожайность:
  AH / r  =  AK / KD 
 Комбинируя это с  (V *) , получаем:
  AB / AG  =  AK / KD   (V **) 
так как обе стороны равны  AH / r .
 Теперь посмотрим на треугольник  BOK . По предложению 2 мы видим, что треугольник  ODB  и треугольник  KDO  подобны.
Аналогичными треугольниками  KD / r  =  r / BD 
Это,
( KD ) ( BD ) =  r   2   (V ***) 
 Теперь прибавьте 1 к обеим сторонам  (V **) :
[ AB / AG ] + 1 = [ AK / KD ] + 1
Эквивалентно,
[ AB  +  AG ] /  AG  = [ AK  +  KD ] /  KD 
или же
  BG / AG = AD / KD 
 Умножение этого уравнения слева на  BG / BG  и справа на  BD / BD  дает:
[( BG ) ( BG )] / [( AG ) ( BG )] = [( AD ) ( BD )] / [( KD ) ( BD ) ]
Подставляя сюда  (V ***)  и упрощая, получаем
[( BG )  2 ] / [( AG ) ( BG )] = [( AD ) ( BD )] / [ r   2 ]
Перекрестное умножение:
  r   2  ( BG )  2  = ( AG ) ( BG ) ( AD ) ( BD )
Подставляя сегменты, полученные в части B, в приведенное выше уравнение, мы получаем:
  r   2   s   2  = ( s - c ) ( s ) ( s - a ) ( s - b ) =  s  ( s - a ) ( s - b ) ( s - c )
Следовательно,
  rs  = sqrt [ s  ( s - a ) ( s - b ) ( s - c )]
 Из Части A площадь треугольника  ABC = K = rs .