Все формулы площади равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

Формула площади равнобедренной трапеции через стороны и угол, (S ):

2. Формулы площади равнобедренной трапеции если в нее вписана  окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S ):

Площадь трапеции

Площадь трапеции, формулы и калькулятор для вычисления площади в режиме онлайн и сводная таблица с формулами площади трапеции. Приведены формулы для всех типов трапеций и частные случаи для равнобедренных трапеций.

Таблица с формулами площади трапеции (в конце страницы)

— Вычисления   (показано)
  (скрыто)

— примечания   (показано)
  (скрыто)

Площадь для всех видов трапеции

1

Площадь трапеции по высоте и двум основаниям

… подготовка …

a — основание

b — основание

h — высота

2

Площадь трапеции по высоте и средней линии

… подготовка …

m — средняя линия

h — высота

3

Площадь трапеции по четырем сторонам

. .. подготовка …

a — основание

b — основание

c — сторона

d — сторона

4

Площадь трапеции по диагонали и углу между диагоналями

… подготовка …

d₁ — диагональ

d₂ — диагональ

α° — угол между диагоналями

5

Площадь трапеции через ее основания и углы при основании

… подготовка …

a — основание

b — основание

α° — угол при основании

β° — угол при основании

Площадь равнобедренной трапеции

6

Площадь равнобедренной трапеции через ее стороны

. .. подготовка …

a — сторона

b — сторона

c — сторона

7

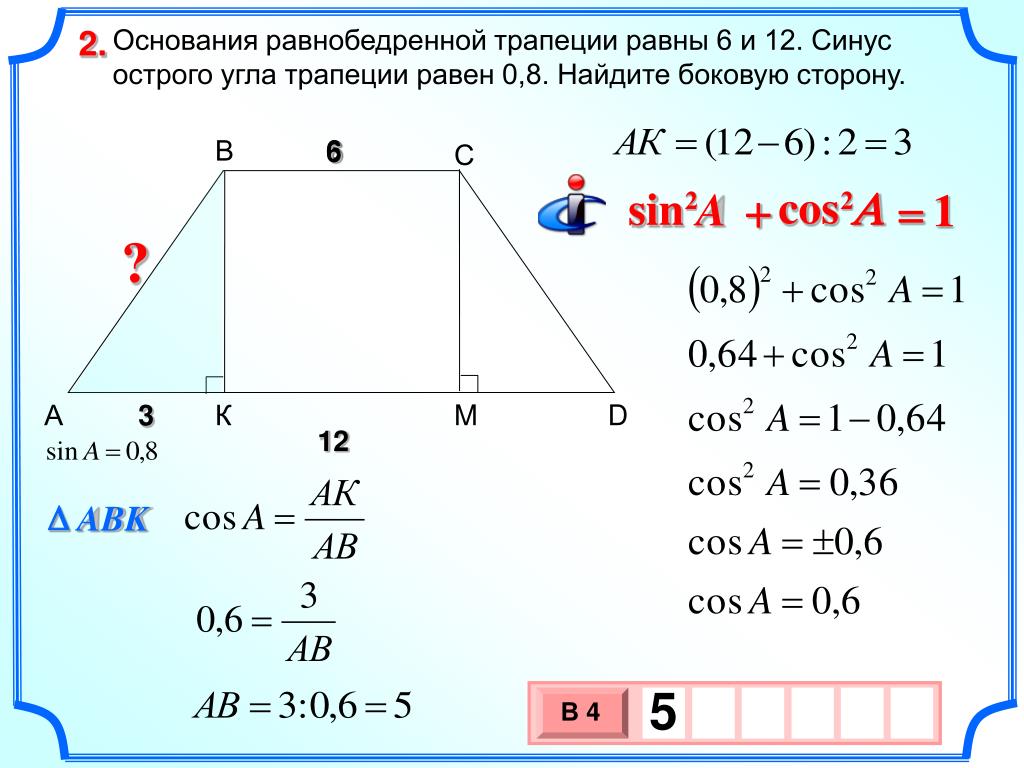
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании

… подготовка …

a — основание

c — сторона

α° — угол при основании

8

Площадь равнобедренной трапеции через большее основание, боковую сторону и угол при большем основании

… подготовка …

b — основание

c — сторона

α° — угол при основании

9

Площадь равнобедренной трапеции через основания и угол при основании

. .. подготовка …

a — основание

b — основание

α° — угол при основании

10

Площадь равнобедренной трапеции через диагонали и угол между диагоналями

… подготовка …

d — диагональ

α° — угол между диагоналями

11

Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

… подготовка …

m — средняя линия

c — сторона

α° — угол между сторонами

12

Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.

… подготовка …

r — радиус вписанной окружности

α° — угол между сторонами

13

Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.

… подготовка …

a — основание

b — основание

r — радиус вписанной окружности

14

Площадь равнобедренной трапеции через ее основания и угол при большем основании

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.

… подготовка …

a — основание

b — основание

α° — угол при основании

15

Площадь равнобедренной трапеции через стороны

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.

… подготовка …

a — основание

b — основание

c — сторона

16

Площадь равнобедренной трапеции через основания и среднюю линию

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.

… подготовка …

a — основание

b — основание

m — средняя линия

Примечание:

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади трапеции

В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.

Определения

Площадь трапеции – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу

Трапеция – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу.

Основания трапеции – это параллельные стороны трапеции. Трапеция имеет большое и малое основание.

Средняя линия трапеции – это отрезок соединяющий середины боковых сторон трапеции и при этом всегда параллельный основаниям трапеции.

Высота трапеции – это отрезок проведенный между основаниями трапеции под углом 90 градусов к каждому из снований.

Сумма углов трапеции равна 360 градусов.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.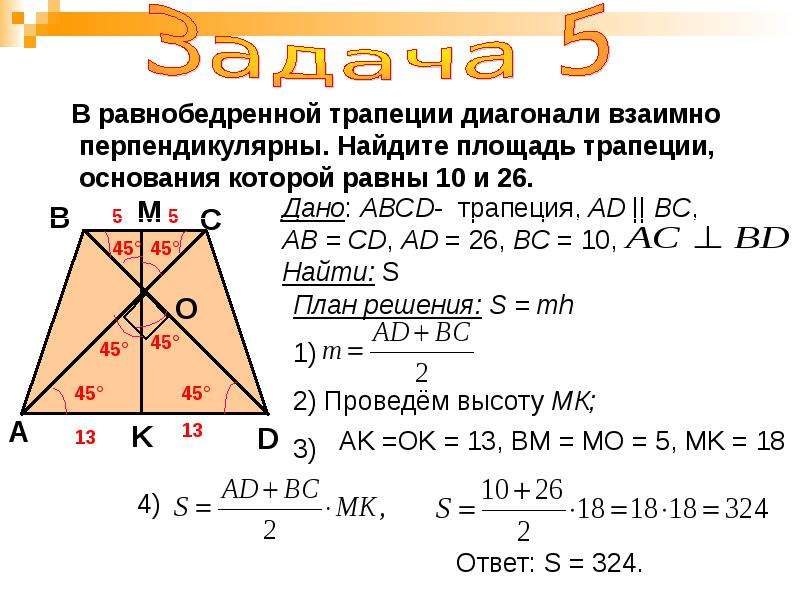

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Площадь равнобедренной трапеции | Треугольники

Площадь равнобедренной трапеции можно найти с помощью любой из формул для нахождения площади трапеции в общем случае. Благодаря свойствам равнобедренной трапеции некоторые из этих формул могут быть упрощены.

I Площадь трапеции равна произведению полусуммы оснований на высоту.

Как и для случая произвольной трапеции, площадь равнобедренной трапеции ABCD, AD∥BC, AB=CD,

Если AD=a, BC=b, BF=h, то формула площади трапеции принимает вид

II. Площадь трапеции равна произведению её средней линии на высоту.

Это верно, в частности, для равнобедренной трапеции.

Если MN — средняя линия трапеции ABCD, BF — её высота, то площадь трапеции равна

Если MN=m, BF=h, то

III.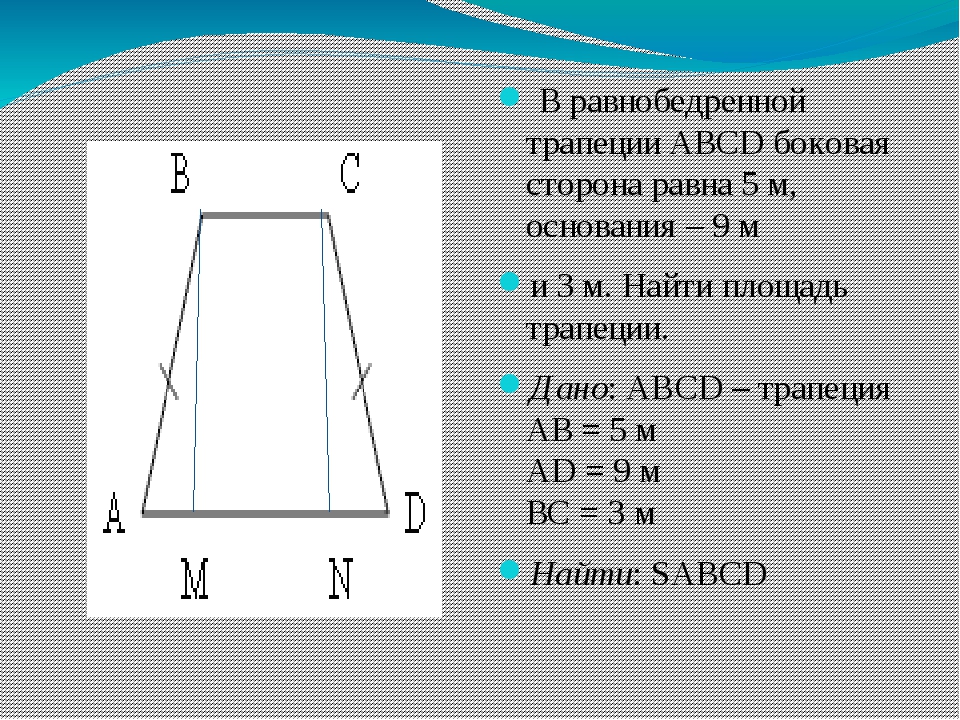 Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

Поскольку диагонали равнобедренной трапеции равны, площадь равнобедренной трапеции равна половине произведения квадрата её диагонали на синус угла между диагоналями.

Для равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O,

Если AC=d, ∠COD=φ

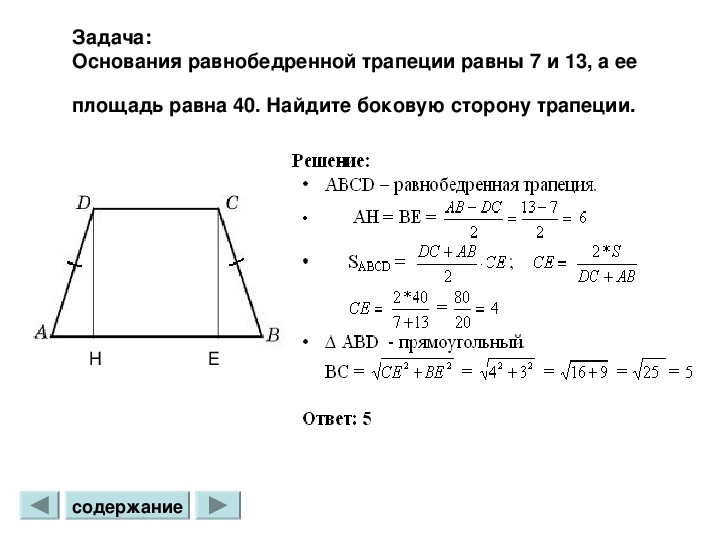
VI. Площадь равнобедренной трапеции с перпендикулярными диагоналями.

1) Если диагонали равнобедренной трапеции перпендикулярны, так как sin 90º=1, предыдущая формула принимает вид:

2) Площадь равнобедренной трапеции, диагонали которой перпендикулярна, равна квадрату её высоты.

В равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O, проведем высоту FK через точку пересечения диагоналей.

Прямоугольные треугольники AOD и BOC — равнобедренные (с основаниями AD и BC). Поэтому их высоты OK и OF являются также медианами.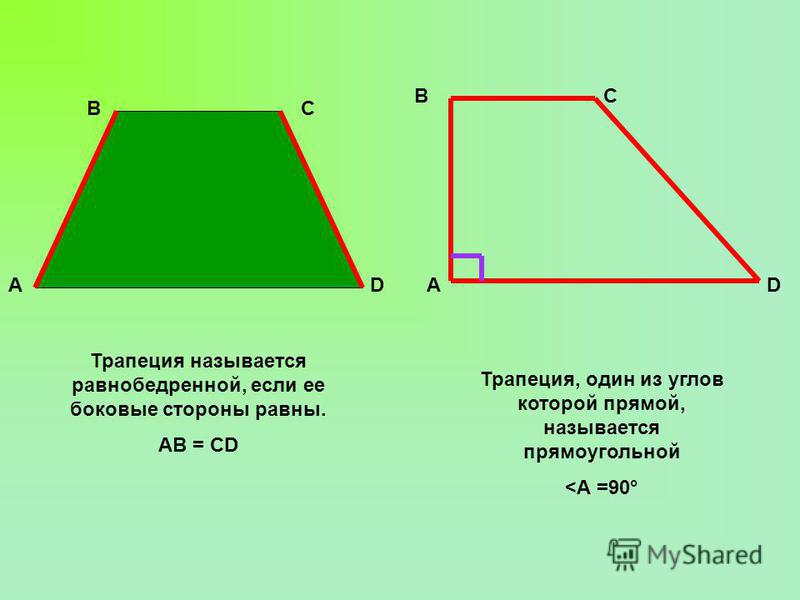 Следовательно, по свойству медианы, проведенной к гипотенузе

Таким образом, формула для нахождения площади равнобедренной трапеции с перпендикулярными диагоналями:

V. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

Так как в трапецию ABCD можно вписать окружность, то

AD+BC=AB+CD, то есть p=AD+BC или p=AB+CD=2AB.

Таким образом, площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению суммы оснований на радиус окружности.

Если обозначить основания трапеции AD=a, BC=b, то

Также площадь равнобедренной трапеции, в которую можно вписать окружность, равна удвоенному произведению боковой стороны на радиус окружности.

Если обозначить боковые стороны AB=CD=c, то формула площади трапеции в этом случае

Так как высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями, то площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению среднего арифметического и среднего геометрического её оснований:

Площадь равнобедренной трапеции

1.  Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

Формула площади равнобедренной трапеции через стороны и угол, (S ):

Формула площади равнобедренной трапеции через стороны и угол

2. Формулы площади равнобедренной трапеции если в нее вписана  окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3.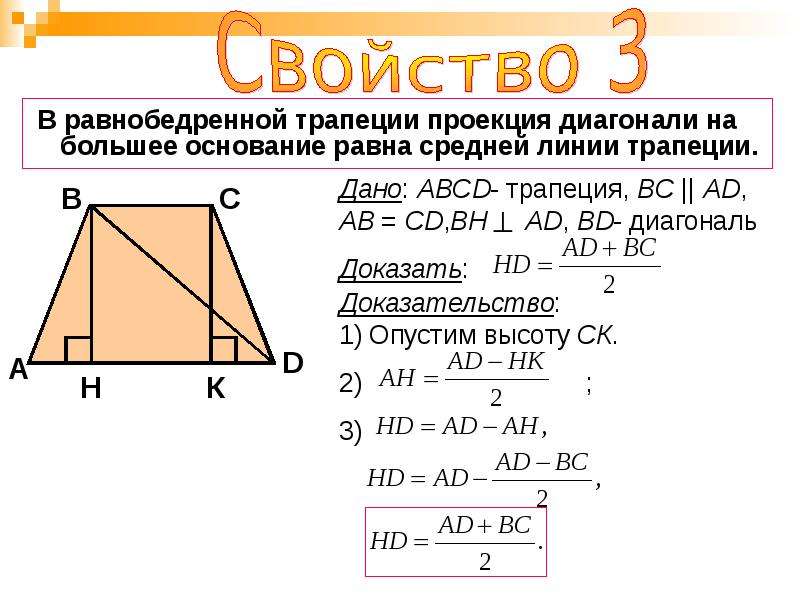  Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5.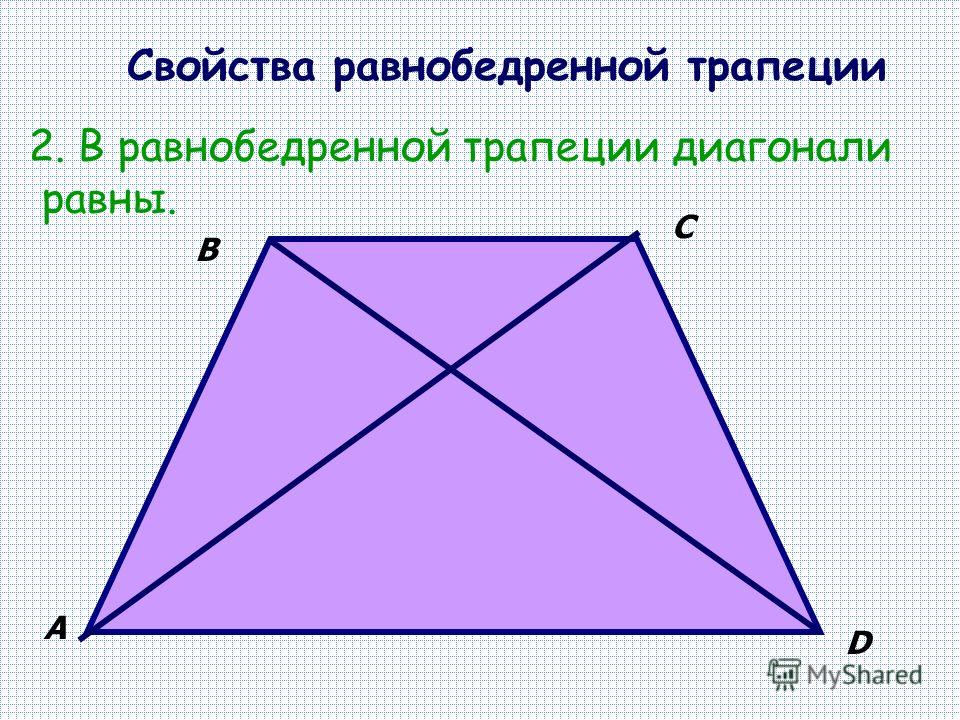  Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S ):

Площадь трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.

Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.

Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.

Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.

Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем.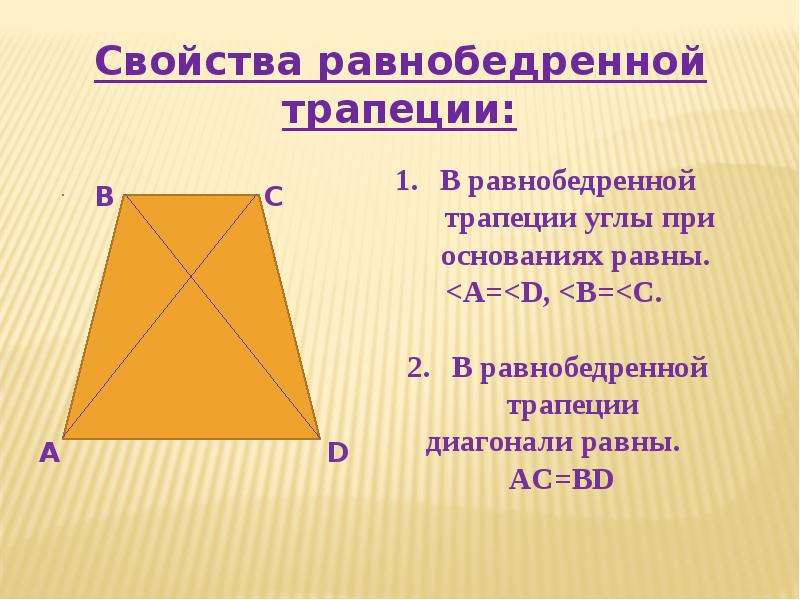 Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a²-x²=c²-y² или x²-y²=a²-c².
x²-(d-b-x)²=a²-c² — Подставляем вместо х полученное выше выражение d-b-y.
x²-d²+bd+dx-b²+bd-bx-x²+dx-bx=a²-c² — Раскрываем скобки.
x²-d²+2bd+2dx-b²-2bx-x²=a²-c² — Приводим подобные слагаемые.
2dx-2bx=a²-c²+d²+b²-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a²-c²+(d-b)² — Выносим общие множители.

Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:

Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.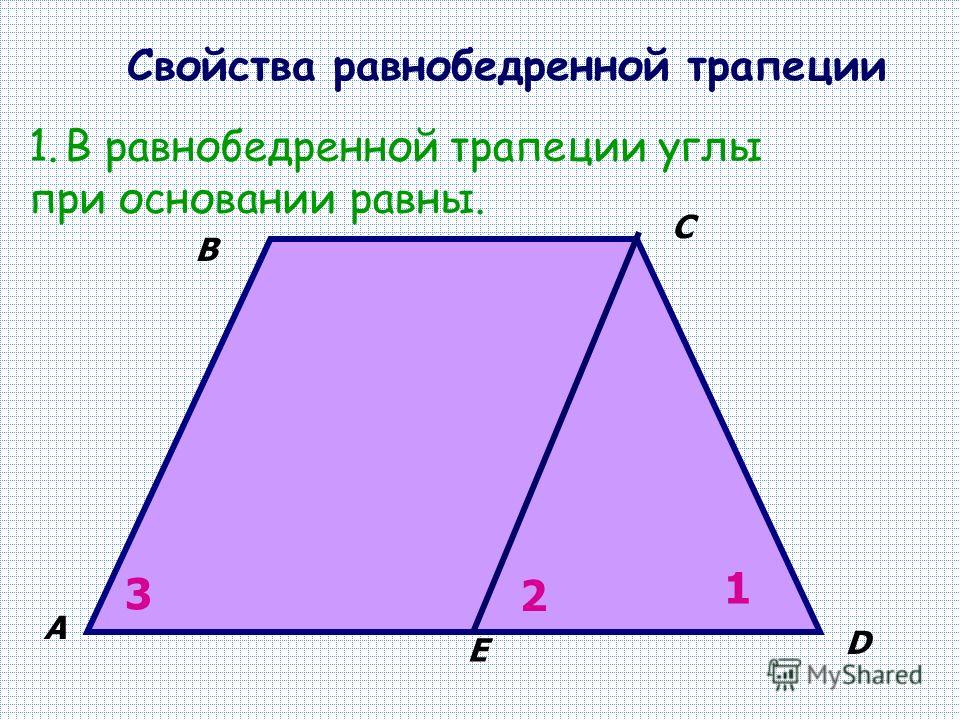

Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону и среднюю линию
Тогда площадь трапеции равна

Площадь трапеции

На данной странице вы можете ознакомиться со всеми формулами для нахождения площади трапеции, как обычной, так и равнобедренной или неправильной. Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.

Площадь трапеции по высоте и двум основаниям

Формула нахождения площади трапеции по высоте и двум основаниям:

$S = \frac{a + b}{2} \cdot h$,

$S$ — площадь трапеции, где

$a$ — малое основание трапеции,

$b$ — большее основание трапеции,

$h$ — высота трапеции.

Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:

$S = m \cdot h$, где

$S$ — площадь трапеции,

$m$ — средняя линия,

$h$ — высота трапеции.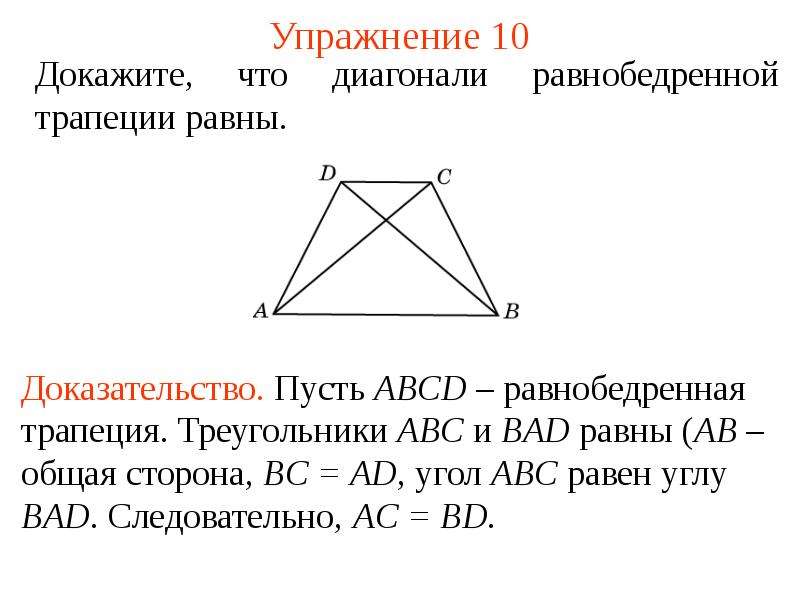 2}$, где

$S$ — площадь трапеции,

$a$ — малое основание,

$b$ — большее основание,

$c, d$ — боковые стороны.

Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:

$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где

$S$ — площадь трапеции,

$d1$ — первая диагональ,

$d2$ — вторая диагональ,

$α$ — угол между диагоналями.

Площадь трапеции через ее основание и углы

Формула нахождения площади трапеции через ее основание и углы при основании:

$S = \frac12 \cdot (b^2 — g^2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где

$S$ — площадь трапеции,

$b$ — большее основание,

$g$ — малое основание,

$α$ — первый угол при основании,

$γ$ — второй угол при основании. 2}{4}}$, где

$S$ — площадь трапеции,

$AB$ — малое основание,

$CD$ — большее основание,

$AC = DB$ — боковая сторона.

Площадь равнобедренной трапеции через малое основание

Формула нахождения площади равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании

$S = c \cdot \sin (α) \cdot (a + c \cdot \cos (α))$, где

$S$ — площадь трапеции,

$a$ — малое основание,

$c$ — боковая сторона

$α$ — угол.

Площадь равнобедренной трапеции через большее основание, боковую сторону и угол

$S = c \cdot \sin (α) \cdot (b — c \cdot \cos (α))$, где

$S$ — площадь трапеции,

$α$ — угол при большем основании,

$c$ — боковая сторона,

$b$ — большее основание.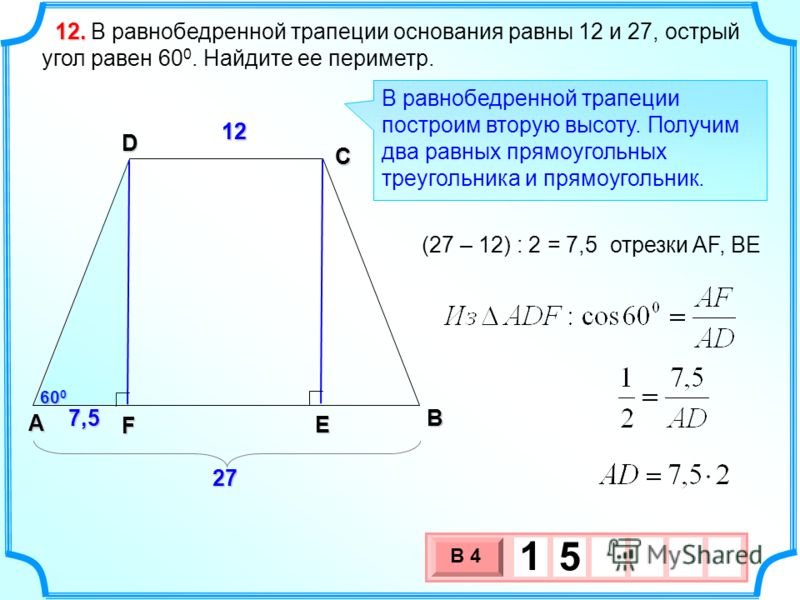 2 \cdot \sin (α)$, где

$S$ — площадь трапеции,

$D$ — диагональ трапеции,

$α$ — угол между диагоналями.

Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:

$S = m \cdot c \cdot \sin (α)$, где

$S$ — площадь трапеции,

$m$ — средняя линия трапеции,

$c$ — боковая сторона,

$α$ — угол при основании.

Чтобы проверить правильность своего решения и ответа или найти какие-либо ошибки в действиях необходимо решить пример данной задачи. Для наглядности выполним пример задачи на нахождение равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании. 2}{\sin (α)}$, где

$S$ — площадь трапеции,

$R$ — радиус вписанной окружности,

$α$ — угол между сторонами.

Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности

Формула нахождения площади равнобедренной трапеции через два ее основания и радиус вписанной окружности:

$S = r \cdot (a + b)$, где

$S$ — площадь трапеции,

$r$ — радиус вписанной окружности,

$a$ — малое основание,

$b$ — большее основание

Площадь равнобедренной трапеции через ее основания и угол при большем основании

Формула нахождения площади равнобедренной трапеции через ее основания и угол при большем основании:

$S = \frac {d \cdot b} {\sin (α)}$, где

$S$ — площадь трапеции,

$d$ — малое основание,

$b$ — большее основание,

$α$ — угол при большем основании.

Площадь равнобедренной трапеции через основания и среднюю линию

Формула нахождения площади равнобедренной трапеции через основания и среднюю линию:

$S = m \cdot \sqrt {a \cdot b}$, где

$S$ — площадь трапеции,

$m$ — средняя линия,

$a$ — малое основание,

$b$ — большее основание.

Для того, чтобы сверить свой ответ и решение с онлайн-калькулятором и найти какие-либо свои ошибки, будет полезно рассмотреть пример решения данной задачи на нахождение площади равнобедренной трапеции через заданные основания и среднюю линию.

Пример 3

Дано: малое основание $a = 5$ cм, большее основание $b = 8$ см, $m = 6$ см.2$

Как найти площадь трапеции: формулы и примеры

Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.

Что нужно знать про трапецию?

Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.

В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.

Формулы площади трапеции

Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.

Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.

Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.

Рассмотрим еще один вариант: в трапеции проведены диагонали d₁и d₂, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d₁d₂ *sinα.

Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c² – ( ( 1/2(b – a)) * ((b – a)² + c² – d²) )².

Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.

Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.

Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r²/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30⁰: S = 8r².

Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d₁ и d₂, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h².

Формула площади криволинейной трапеции

Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.

Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫^b_af(x)dx = F(x)│^b_a = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.

Примеры задач

Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.

Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.

Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.

Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.

Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ² = АР² + РХ²). И высчитать его площадь: S_APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см².

Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.

Все это позволит вам утверждать, что S_AMPC = S_APX = 54 см².

Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.

Решение:  Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.

Введем еще одно обозначение – ОЕ = х. А также высоту h₁ для треугольника ТМЕ и высоту h₂ для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).

Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h₁ = 1/5(b + х) * h₂. Преобразуем и получим: h₁/ h₂ = 1/5 * ((b + х)/(х + а)).

Раз треугольники ТМЕ и АЕС подобные, имеем h₁/ h₂ = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х² – а²) = (b² – х²) ↔ 6х² = b² + 5а² ↔ х = √(5а² + b²)/6.

Таким образом, ОЕ = х = √(5а² + b²)/6.

Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Как найти площадь трапеции

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Площадь трапеции — пояснения и примеры

Напомним, трапеция , также называемая трапецией , , представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон.Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.

В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — ногами. Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.

Проще говоря, основание и высота трапеции перпендикулярны друг другу.

Трапеции могут быть как правыми трапециями, (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины).Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.

Из этой статьи вы узнаете:

• Как найти площадь трапеции,
• Как вывести формулу площади трапеции и
• Как найти площадь трапеции с помощью трапеции формула площади.

Как найти площадь трапеции?

Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости.Это пространство, заключенное в 2D-геометрии.

На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника. Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.

Вывести формулу площади трапеции

Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )

= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )

= ¹ / ₂ × h × ( AB + 2 BC + CD )

= ¹ / ₂ × h × ( FE + AD )

Но, FE = b ₁ и AB = b ₂

Следовательно, Площадь a трапеция ADEF ,

= ¹ / ₂ × h × (b ₁ + b ₂ ) ……………….(Это формула площади трапеции)

Формула площади трапеции

Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.

Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).

Площадь = ½ h (b ₁ + b ₂ )

Где h — высота, а b _1, и b ₂ — параллельные стороны трапеции.

Как определить площадь неправильной трапеции?

Неправильная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, вам нужно найти сумму оснований и умножить ее на половину высоты.

В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.

Как найти периметр трапеции?

Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.

Пример 1

Рассчитайте площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.

Решение

Пусть b ₁ = 14 см и b ₂ = 10 см

Площадь трапеции = ½ h (b ₁ + b ₂ ) см ²

= ½ x 5 (14 + 10) см ²

= ½ x 5 x 24 см ²

= 60 см ²

Пример 2

Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.

Раствор

Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. Единиц

= ½ x 30 x (60 + 40) мм ²

= ½ x 30 x 100 мм ²

= 1500 мм ²

Пример 3

Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.

Раствор

Площадь трапеции = ½ часа (b ₁ + b ₂ ) кв.единицы измерения.

⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов

⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы

⇒ 322 = 23h

Разделите обе стороны на 23.

h = 14

Итак, высота трапеции составляет 14 дюймов.

Пример 4

Учитывая, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м ² .

Решение

Пусть b ₁ = 25 м

Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. Единиц

⇒ 352 м ² = ½ x 16 м x (25 m + b ₂ ) кв. Единиц

⇒ 352 = 8 x (25 + b ₂ )

⇒ 352 = 200 + 8b ₂

Вычтите 200 с обеих сторон.

⇒ 152 = 8b ₂

Разделите обе стороны на 8, чтобы получить;

b ₂ = 19

Следовательно, длина другого основания трапеции составляет 19 м.

Пример 5

Рассчитайте площадь трапеции, показанной ниже.

Решение

Поскольку стороны (непараллельные стороны) трапеции равны, высоту трапеции можно рассчитать следующим образом;

Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.

⇒ (27-15) / 2 см

⇒ 12/2 см = 6 см

12 ² = h ² + 6 ² По теореме Пифагора высота (h) рассчитывается как;

144 = h ² + 36.

Вычтем 36 с обеих сторон.

h ² = 108.

h = 10,39 см.

Следовательно, высота трапеции 10,39 см.

Теперь вычислите площадь трапеции.

Площадь трапеции = ½ ч (b ₁ + b ₂ ) кв. единицы измерения.

= ½ x 10,39 x (27 + 15) см ² .

= ½ x 10,39 x 42 см ² .

= 218,19 см ² .

Пример 6

Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м ² , найдите высоту и основание трапеции.

Решение

Пусть высота = x

Другая база равна 10 м, чем высота = x + 10.

Площадь трапеции = ½ h (b ₁ + b ₂ ) Кв. единицы измерения.

Путем подстановки

480 = ½ * x * (x + 10 + 18)

480 = ½ * x * (x + 28)

Удалите скобки с помощью свойства распределения.

480 = ½x ² + 14x

Умножьте каждый член на 2.

960 = x ² + 28x

x ² + 28x — 960 = 0

Решите квадратное уравнение, чтобы получить;

x = — 48 или x = 20

Подставьте положительное значение x в уравнение высоты и основания.

Высота: x = 20 м.

Другая база = x + 10 = 10 + 20 = 30 м.

Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.

Практические задачи

1. Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота — 15 единиц.
2. Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
3. Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше, чем другое основание?

Предыдущий урок | Главная страница | Следующий урок

Равнобедренная трапеция — Калькулятор геометрии

Видео с вопросом: Определение области равнобедренной трапеции

Стенограмма видео

𝐴𝐵𝐶𝐷 — это равнобедренная трапеция, где 𝐴𝐵 равно 𝐴𝐷 равно 𝐷𝐶 равно восьми сантиметрам, а 𝐵𝐶 равно 16 сантиметрам.Найдите область, дающую ответ с двумя десятичными знаками.

Итак, на схеме у нас есть трапеция 𝐴𝐵𝐶𝐷 и несколько слов о названии этой формы. В США и Канаде вы знаете это как трапецию. А в остальном мире это будет трапеция. Нам говорят, что есть три равные стороны. 𝐴𝐵 𝐴𝐷 и 𝐷𝐶 все восемь сантиметров. В трапеции у нас будет пара параллельных сторон. Здесь это будут и 𝐵𝐶. Мы можем заметить, что наши длины 𝐷𝐶 и 𝐴𝐵 одинаковы, поэтому нам говорят, что это равнобедренная трапеция.Равнобедренная трапеция имеет одну пару конгруэнтных непараллельных сторон. Чтобы найти площадь трапеции, мы используем формулу, согласно которой площадь трапеции равна 𝐴 плюс 𝐵 в два раза больше, где 𝐴 и 𝐵 — основание, а ℎ — высота перпендикуляра.

Однако, глядя на нашу диаграмму, мы видим, что нам не сообщается перпендикулярная высота. Но это можно будет решить, если мы знаем основание треугольника и воспользуемся теоремой Пифагора. Чтобы найти длину основания этого треугольника, мы можем заметить, что на прямой у нас есть восьмисантиметровый отрезок.Мы знаем, что основание двух треугольников будет одинаковой длины, поскольку у нас есть равнобедренная трапеция. И то и другое мы можем назвать 𝑥. И мы знаем, что эти три длины в сумме дают 16 сантиметров. Следовательно, у нас должно быть четыре сантиметра, восемь сантиметров и четыре сантиметра. Если мы внимательно посмотрим на один из треугольников в нашей трапеции, у нас будет гипотенуза восьми сантиметров и двух других длин.

Здесь мы можем использовать теорему Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов на двух других сторонах.Подстановка наших значений даст нам восемь квадратов, равных восьми в квадрате плюс четыре в квадрате, где ℎ, конечно, высота треугольника, а не гипотенуза. Таким образом, 64 равно в квадрате плюс 16. Чтобы найти ℎ в квадрате само по себе, мы вычитаем 16 из обеих частей. Следовательно, 48 равно в квадрате. И, наконец, чтобы найти, мы извлекаем квадратный корень из обеих частей, что дает нам, что ℎ равно корню 48. Мы оставляем наш ответ в этой форме корня, поскольку мы еще не закончили использовать это значение каждого в наших вычислениях. .

Теперь мы можем работать с областью нашей трапеции, используя формулу. Подставляя наши значения, мы получаем восемь плюс 16 больше, чем двукратный корень 48. Восемь плюс 16 равняются 24. Итак, у нас 24 больше, чем двукратный корень 48. И мы могли бы упростить наши 24 над двумя как 12. Итак, у нас 12-кратный корень 48. Обратите внимание, в вопросе нам было предложено указать значение с точностью до двух десятичных знаков. Итак, мы можем пойти дальше и использовать наш калькулятор, чтобы упростить наш ответ. Получаем ответ 83,138438 и т. Д. Квадратных сантиметров. А теперь, чтобы найти ответ с двумя десятичными знаками, мы проверяем третью десятичную цифру, чтобы узнать, пять или больше.А поскольку это так, то наш ответ составляет 83,14 квадратных сантиметра для площади.

Вычислить площадь нарисованной равнобедренной трапеции класс 9 по математике CBSE

Подсказка : Мы можем решить эту проблему двумя простыми способами. Первый способ — использовать прямоугольники. Второй метод основан на использовании стандартной формулы площади трапеции. Мы знаем, что площадь трапеции равна \ [= \ dfrac {1} {2} (a + b) d \], где \ [a \] и \ [b \] — длина двух параллельных сторон, \ [d \] — перпендикулярное расстояние между двумя параллельными сторонами.

Полный пошаговый ответ :
Давайте посмотрим на второй способ.
У нас есть формула для определения площади трапеции \ [= \ dfrac {1} {2} (a + b) d \].
Из данной диаграммы имеем \ [a = 3 \], \ [b = 7 \] и \ [d = 4 \]. Подставляя, мы получаем
\ [= \ dfrac {1} {2} (a + b) d \]
\ [= \ dfrac {1} {2} \ times (3 + 7) \ times 4 \]
By БОДМА решаем расчетную часть в скобках, получаем:
\ [= \ dfrac {1} {2} \ times 10 \ times 4 \]
Умножение,
\ [= \ dfrac {1} {2} \ times 40 \]
Делим, получаем
\ [= 20 \; c {m ^ 2} \]
Следовательно, площадь данной равнобедренной трапеции равна \ [20 \; c {m ^ 2} \]. 2} \]».

Примечание : Мы используем второй метод, который легко решить и выполнить прямую замену. Так как площадь указана в квадратных единицах. Учитывая, что длина сторон дана в сантиметрах, мы имеем площадь в квадратном сантиметре. Равнобедренная трапеция — это трапеция, в которой базовые углы равны, и поэтому длина левой и правой сторон также равна. Эта концепция используется при решении первого метода. Мы также можем решить эту проблему, разделив на два треугольника, что немного сложно, поэтому используйте вышеуказанный метод для решения этого типа проблемы.

Вы в одном шаге от ответа!

Подпишитесь бесплатно!

Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!

Площадь трапеции.Определение, формула и калькулятор

Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике

Количество квадратных единиц, необходимое для полного заполнения
трапеция.
Формула: Средняя ширина × высота

Попробуйте это Перетащите оранжевые точки, чтобы переместить трапецию и изменить ее размер. Как размер трапеции
изменяется, пересчитывается площадь.

Формула площади

Площадь трапеции равна средней ширине, умноженной на высоту, или по формуле:

где
b1, b2 — длины каждого основания,
h — высота (высота)

Напомним, что основания — это две параллельные стороны трапеции.Высота (или высота) трапеции — это
перпендикулярное расстояние
между двумя базами.

В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и длины основания, поэтому, как вы можете видеть, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.

Вывод формулы

См. Раздел «Как получить формулу площади трапеции».

Калькулятор

Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.

Введите любые три значения, и будет вычислено недостающее.
Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.

Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.

Определение высоты по площади

Как найти высоту (высоту) трапеции, задайте две базы и площадь.Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту). Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу:

Где a — это площадь, а b1, b2 — две базы.

Нахождение базы в районе

Как найти основание трапеции, укажите одно из оснований, высоту и площадь.
Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту).Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу:

Где a — площадь, b — известная база, а h — высота (высота).

Если известно медианное значение

Напомним, что
медиана (м) трапеции
— отрезок, соединяющий середины непараллельных сторон. Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции

Где м, — это медиана, а х — высота (высота).

Площадь в виде сложной формы

Другой способ найти площадь трапеции — рассматривать ее как более простые формы, а затем добавлять или вычитать их площади, чтобы найти результат. Для
Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника:

Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».

Координатная геометрия

В координатной геометрии, если вы знаете координаты четырех вершин,
вы можете рассчитать различные его свойства, в том числе площадь и периметр.Для получения дополнительной информации см. Площадь и периметр трапеции (Координатная геометрия).

Что попробовать

1. На рисунке выше нажмите «скрыть детали»
2. Перетащите оранжевые точки на вершинах, чтобы получилась трапеция произвольного размера.
3. Рассчитайте площадь по формуле
4. Теперь попробуйте оценить площадь трапеции, просто глядя на
   квадратов внутри нее
5. Когда вы закончите, нажмите «Показать подробности», чтобы увидеть, насколько близко вы подошли.

Другие полигоны

Общий

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с полигонами

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Калькулятор площади трапеции

Если у вас когда-либо были проблемы с запоминанием формул в классе геометрии, эта область калькулятора трапеции обязательно вам поможет. Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все другие ее свойства, такие как длины сторон или внутренние углы. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!

Вы также можете воспользоваться нашим калькулятором окружности, чтобы проанализировать геометрию круга более подробно.

Что такое трапеция?

Трапеция — это четырехсторонняя геометрическая форма, две стороны которой параллельны друг другу. Эти две стороны ( a и b на изображении выше) называются основаниями трапеции. Две другие стороны ( c и d ) называются ножками. х — высота трапеции.

Сумма всех внутренних углов трапеции дает 360 °. Кроме того, углы на одной стороне опоры называются смежными и всегда составляют в сумме 180 °:

α + β = 180 °

γ + δ = 180 °

Как найти площадь трапеции?

Площадь трапеции находится по следующей формуле:

A = (a + b) * h / 2

Вы можете заметить, что для трапеции с a = b (и, следовательно, c = d = h) формула упрощается до A = a * h , что в точности соответствует формуле для площади прямоугольника.

Как найти периметр трапеции?

Вы также можете использовать вычислитель площади трапеции, чтобы найти периметр этой геометрической формы. Просто сложите все стороны вместе:

P = a + b + c + d

Использование калькулятора площади трапеции: пример

Предположим, вы хотите вычислить площадь определенной трапеции. Все данные:

α = 30 °

γ = 125 °

h = 6 см

a = 4 см

P = 25 см

1. Рассчитайте оставшиеся внутренние углы.