ВОПРОСЫ К ЗАЧЕТУ. 2.Решите уравнения. 22. Уравнение ах 2 + вх + с = 0 не имеет корней, если

ID_6041 1/26 neznaika.pro

1 Графики функций Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. На рисунках изображены

Подробнее

Формулы сокращенного умножения

Класс 7.3, 7.5 Учебник: Алгебра (Макарычев Н.В.) Тема модуля «Формулы сокращенного умножения. Функции» В тесте проверяются теоретическая и практическая части. Формулы сокращенного умножения ТЕМА Знать

Подробнее

ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ

М- 8 класс Рабочая тетрадь 8 глава стр. 1 Глава 8 ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ Т-801 Установление вида зависимостей в физических формулах и законах Т-80 Выражение одной переменной через другие Т-803 Вычисление

Подробнее

Квадратные уравнения

И. В. Яковлев Материалы по математике MathUs.ru Содержание Квадратные уравнения 1 Неполные квадратные уравнения………………………. 1 2 Выделение полного квадрата………………………….

Подробнее

ID_6684 1/8 neznaika.pro

Уравнения, неравенства, системы с параметром Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.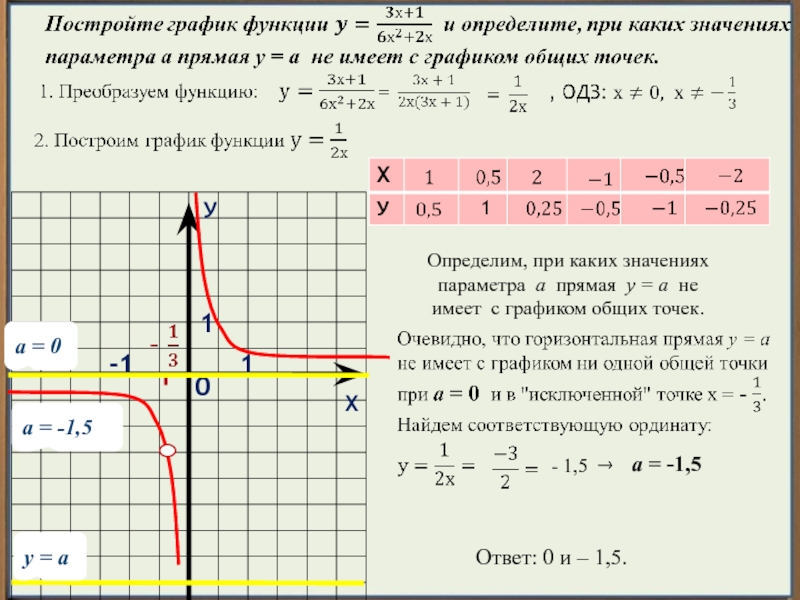

Подробнее

Тема 1.4 Функции, их свойства и графики

Тема.4 Функции, их свойства и графики Автор: Переверзьева Н.С. Преподаватель математики Лицей 6 Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины Узнать методы

Подробнее

Квадратные уравнения

И. В. Яковлев Материалы по математике MathUs.ru Содержание Квадратные уравнения 1 Неполные квадратные уравнения………………………. 1 2 Выделение полного квадрата………………………….

Подробнее

Тема 41 «Задания с параметром»

Тема 41 «Задания с параметром» Основные формулировки заданий с параметром: 1) Найти все значения параметра, при каждом из которых выполняется определенное условие. ) Решить уравнение или неравенство с

Подробнее

М А Т Е М А Т И К А В Ш К О Л Е

Контрольная работа 1. «Основные понятия и свойство алгебраической дроби», «Сложение и вычитание алгебраических дробей с одинаковыми и разными знаменателями» 1. Найдите значение перемененной х, при котором

Подробнее

Задание 18. Задачи с параметром

Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных

Подробнее

Квадратичная функция

Квадратичная функция Функция вида y=ax +bx+c, где а 0, называется квадратичной. Значения х, при которых функция принимает значение, равное 0, называют нулями функции. Если b=c=0, то функция принимает вид

Подробнее

= 1 е) f(9) = 27; f(1) = 3

Глава 8 ФУНКЦИИ И ГРАФИКИ Алгоритмы А- Задание стандартных функций А- Понятие функции. График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем

Подробнее

ID_4970 1/7 neznaika.pro

Уравнения, неравенства, системы с параметром Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.

Подробнее

3. Прямая на плоскости

3 Прямая на плоскости В 3 представлены типов задач на прямую на плоскости, использующие все основные уравнения прямой, а также формулы расстояния между двумя точками, расстояния от точки до прямой, угла

Подробнее

Тематическое планирование 8 класса

Тип урока : Урок изучения нового материала ИН Комбинированный урок- К Урок применения знаний и умений ПЗУ Урок закрепления изученного ЗИ Урок обобщения и систематизации знаний ОСЗ Урок проверки и коррекции

Подробнее

УРАВНЕНИЯ.

ФУНКЦИИ. НЕРАВЕНСТВА

МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ) Т.А. ПОЛЕВАЯ, И.Н. РОМАШОВА, С.А. ПОЛЕВАЯ УРАВНЕНИЯ. ФУНКЦИИ. НЕРАВЕНСТВА МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ-ИНОСТРАНЦЕВ

Подробнее

КАЛЕНДАРНО — ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

КАЛЕНДАРНО — ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ урока тема урока 1 Повторение за курс 6 класса. Решение 2 Повторение за курс 6 класса. Положительные и отрицательные числа. 3 Повторение за курс 6 класса. Пропорции.

Подробнее

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ В результате изучения курса алгебры в 8АВ, 8 ГД (группа А) классе учащийся научится знать/понимать: значение математической науки для решения задач, возникающих в теории и практике;

Подробнее

Пояснительная записка

Пояснительная записка Основой для рабочей программы по алгебре на 05-06 учебный год в 8а классе МКОУ ГСОШ является авторская программа А. Г. Мордковича для общеобразовательных учреждений (Программы. Математика.

Подробнее

РАЗДЕЛ 14. ЗАДАЧИ С ПАРАМЕТРАМИ

РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных

Подробнее

Алгоритм решения квадратных неравенств

Алгоритм решения квадратных неравенств 1) Привести неравенство к стандартному виду : 2) Решить квадратное уравнение (т.е. найти точки пересечения параболы с осью Ох):,, если D > 0, то (две точки пересечения

Подробнее

и x 1x 2, в частности сумму одинаковых

Тема Квадратное уравнение Формулы Виета Два алгебраических выражения, соединенных знаком «=», образуют равенство Равенство, справедливое при всех допустимых значениях входящих в него переменных, называется

Подробнее

1) y=-x 2 +7x-14 2) y=x 2-7x+14 3) y=x 2 +7x+14 4) y=-x 2-7x-14

5. 1: Установите соответствие между графиками функций и формулами, которые их задают. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру. ФОРМУЛЫ Графики 1) y=-x 2 +7x-14 2)

Подробнее

Степенная функция. Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия.

Степенная функция Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия. Если k=2, то y=x 2 квадратичная функция, ее график парабола.

Подробнее

Инструкция по выполнению работы

Проект Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 009 года (в новой форме) по АЛГЕБРЕ Демонстрационный вариант 009 года

Подробнее

11.

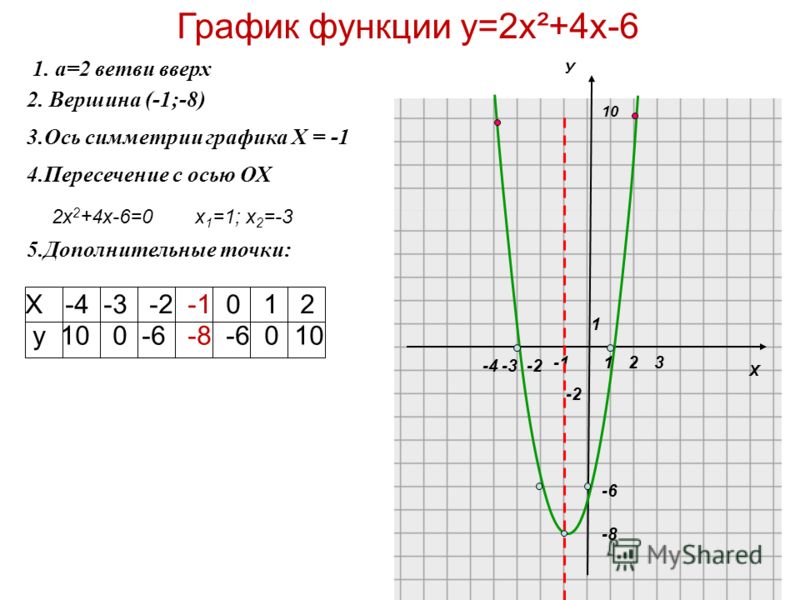1. Функции Базовый уровень.

111 Функции Базовый уровень Оглавление 11101 Системы координат 1110 Понятие функции 7 1110 Область определения функции 10 11104 Область (множество) значений функции 1 11105 Возрастание и убывание функции

Подробнее

Глава 11 ТЕСТОВЫЕ ЗАДАНИЯ

Глава ТЕСТОВЫЕ ЗАДАНИЯ Т-0 Исследование функции по графику Т-0 Соответствие между графиком рациональной функции и формулой Т-0 Построение графика по свойствам Т-04 Параллельный перенос графика Т-05 Симметричное

Подробнее

Примеры решений контрольных работ

Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 3. Аналитическая геометрия на плоскости 1. Составить уравнения прямых, проходящих через точку A(4; 1) a) параллельно прямой

Подробнее

Образцы базовых задач по ЛА

Образцы базовых задач по ЛА Метод Гаусса Определенные системы линейных уравнений Решите систему линейных уравнений методом Гаусса x 6 y 6 8, 6 x 6 y 6 Решите систему линейных уравнений методом Гаусса 6

Подробнее

Геометрический смысл производной

Геометрический смысл производной Рассмотрим график функции y=f(x) и касательную в точке P 0 (x 0 ; f(x 0 )).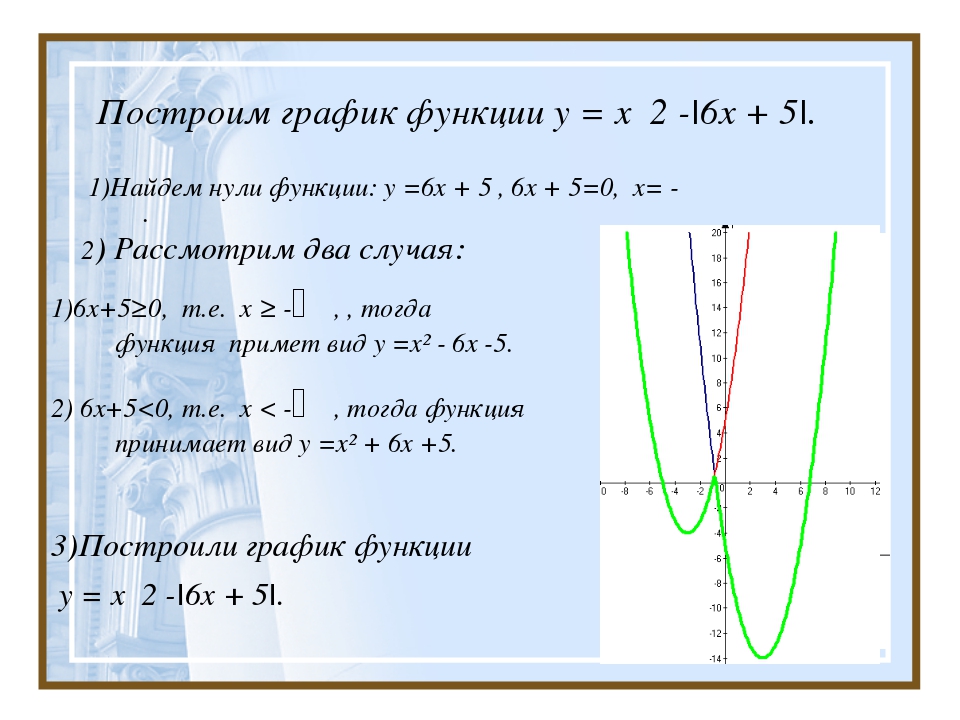 Найдем угловой коэффициент касательной к графику в этой точке. Угол наклона касательной Р 0

Подробнее

ВАРИАНТ 16 M Доказать, что прямые

ВАРИАНТ 16 1 Через точки M 1 (3 4) и M (6 ) проведена прямая Найти точки пересечения этой прямой с осями координат Составить уравнения сторон треугольника для которого точки A ( 1 ) B ( 3 1) C (0 4) являются

Подробнее

Содержание. Неравенства… 20

Содержание Уравнение…………………………………….. Целые выражения………………………………. Выражения со степенями……………………….. 3 Одночлен………………………………………

Подробнее

Математика (БкПл-100, БкК-100)

Математика (БкПл-100, БкК-100) М.П. Харламов 2009/2010 учебный год, 2-й семестр Лекция 9.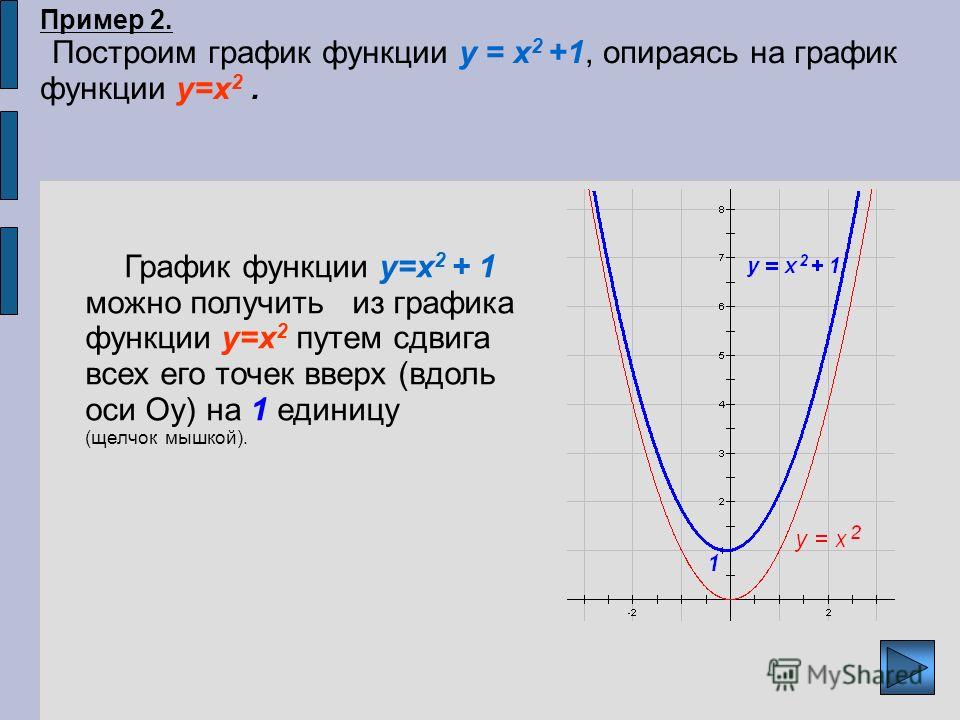 Элементы аналитической геометрии 1 Что изучает аналитическая геометрия? Аналитическая геометрия изучает свойства

Подробнее

Уравнения прямой и плоскости

Уравнения прямой и плоскости Уравнение прямой на плоскости.. Общее уравнение прямой. Признак параллельности и перпендикулярности прямых. В декартовых координатах каждая прямая на плоскости Oxy определяется

Подробнее

Лабораторная работа №7

Тема:
«Вычисление
функций одной переменной в Excel»

Цель занятия:
получить практические навыки вычисления
функций одной переменной у=f(x)
и построения их графиков в Excel

Отрабатываемые
вопросы:

1.Создание
формул для вычисления функций одной
переменной.

2.Построение
графиков функций.

Организационно
– методические указания

В Excel
удобно осуществлять построение различных
функций на плоскости и поверхностей в
пространстве.

1.Построение
прямой.
Рассмотрим построение данной функции
в Excel
на примере уравнения у=2х+1
в диапазоне
: х[0; 3]
с шагом х=0,25. Решение
задачи
включает следующие этапы.

1.1. Ввод данных.
Для этого
значения аргумента Х
и функции У
следует
представить в таблице, первый
столбец
которой будет заполнен значениями Х ,
а второй
– функцией У.
Для этого в
ячейку А1 вводим заголовок Аргумент,
а в ячейку В1
– заголовок Прямая.

В ячейку А2 вводится
первое значение аргумента 0,
а в ячейку A3
вводится второе значение аргумента с
учетом шага построения (0,25).
Затем, выделив
блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).

Далее вводим
уравнение прямой: в ячейку В2 вводим
формулу: =2*A2+1,
затем копируем
эту формулу в ячейки В2:В14. В результате
должна быть получена следующая таблица
исходных данных и результатов (рис.3.17.)
.

Рис.3.17.Построение
прямой

1.2. Построение
графика функции. Выделите диаграмму и,
используя вкладку Вставка

График, постройте
график
функции у=2х+1
(рис.3.18.).

Рис.3.18. График
прямой

1.3.
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).

2.Решение
уравнения второго порядка.
Примерами уравнений второго порядка
являются: парабола,
гипербола, окружность,
эллипс и другие.
В качестве
примера рассмотрим построение параболы
вида: у =х²
в диапазоне
х[–3;
+3] с шагом х=0,5. 2
(рис.3.20).

Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).

Рис.3. 19.Построение
параболы

Рис.3.20. График
параболы

Рис.3.21. График
гиперболы

3.Построение
гиперболы.
В простейшем
случае уравнение гиперболы имеет вид
y=k/x.
Задача построения гиперболы аналогична
построению параболы.

Рассмотрим
построение гиперболы y=1/x
в диапазоне х[0,1:
10,1] с шагом х=0,5. Выполните
все вышеуказанные действия самостоятельно
(рис.3.21).

Задания для
самостоятельного выполнения

1. Построить график
   функции Зх+2у–4=0 в диапазоне х[–1;
   3] с шагом =0,25.

2. Построить график
   функции Зх–5у+15=0 в диапазоне х[–1;
   3] с шагом =0,25.

3. Построить график
   функции У=е2х в диапазоне х[0.1;
   2] с шагом =0,2.

4. Построить график
   функции У=2х в диапазоне х[–2;
   2] с шагом =0,5.

5. Построить график
   функции У=lnx в диапазоне х[0.5;
   10] с шагом =0,5.

6. Построить график
   функции Зх+2у–4=0 в диапазоне х[–1;
   3] с шагом =0,25.

7. Построить график
   функции y=2cos3x в диапазоне х[0.1;
   1.8] с шагом =0,1.

8. Построить график
   функции y=x2 в диапазоне х[–3;
   3] с шагом =0,25.

9. Построить график
   функции y=1/2x в диапазоне х[0.1;
   10] с шагом =0,25.

10. Построить верхнюю
    часть параболы у2=х в диапазоне x[0;
    4] с шагом =0,25.

11. Построить гиперболу
    y =1/2х в диапазоне х
    [0,1; 5,1] с шагом =0,25

12. Построить верхнюю
    полуокружность эллипса x4/4+у2=1 в диапазоне
    х
    [–2,25; 2,25] с шагом =0,25.

13. Постройте параболу:
    у2=6х в диапазоне х
    [0; 4] с шагом =0,25.
    Найдите координаты фокуса и уравнение
    директрисы.

14. Постройте параболу:
    х2=8у в диапазоне x
    [–2,25; 2,25] с шагом =0,25.
    Найдите координаты фокуса и уравнение
    директрисы.

График линейной функции — презентация онлайн

1. Линейная функция и её график

2. Повтори:

• Линейной функцией называется
функция вида у=kх+b, где k,b-числа,
х-независимая переменная( аргумент),
у-зависимая переменная (функция).

3. Какие из функций

1.
2.
3.
4.
5.
6.
7.
2у=3:х-2
у=3-5х
у+х=0
у=1,4х-3
у=х
у=5
у=1/2х являются линейными?
Проверь себя: 2,3,4,5,6

5. Алгоритм построения графика линейной функции

Чтобы построить график линейной функции нужно:
Задать два значения
аргумента х (любых, выбираем сами!!!;
Найти два соответствующих значения
функции у;
Построить точки в системе координат;
Провести через них прямую линию.

6. Построить график функции у=-2х+2

• Решение:
• Построение
у
У=-2х+2
х
0
-2
у
2
6
х
у= -2х+2

7. Задание

• Найдите значение линейной функции у=2х-1 при
заданном значении аргумента х=0;2;4;-1.
Алгоритм выполнения:
т.к. значение аргумента (х) задано, то
1. Вместо х подставляем конкретное значение
2. Вычисляем значение у.
Х=0 У=2*0-1=-1.
Х=2 у= 2*2-1=3
Х=4 у=2*4-1=7
х=-1 у= 2*(-1)-1=-2-1=-3
Задание
• Функция задана у=2х-1 Найдите значение аргумента
при заданном значении функции у=11,-3, 0
Алгоритм выполнения:
т.к. дано значение функции (у), значит
1. Вместо у подставляем конкретное значение
2. Решаем уравнение, что найти значение х.
У=11
2х-1=11
2х=11+1
2х=12
х=12/2
х=6
У=-3
2х-1=-3
2х=-3+1
2х=-2
х=-2/2
х=-1
У=0
2х-1=0
2х=0+1
2х=1
х=1/2
х=0,5

9.

Постройте график линейной функции у=-3-х и у = — х

уу
• У = -3 – х
х
0
3
у
-3
-6
У= — х — 3
у= -3-х
у=-х
х
х
у= — х
х
0
6
у
0
-6

10. Постройте график линейной функции у = х – 3 и у = х

• у=х–3
у
х
0
3
у
-3
0
У=х-3
У=х
х
У=х-3
у= х
х
0
6
у=у х
0
6

11. Построить график линейной функции у= kх+b при k=0 , b=5 т.е. у=5

у
У=5
х

12. Ответить устно на вопросы:

• Что называется линейной функцией?
• Что является графиком линейной функции?
• Сколько точек нужно взять, чтобы построить
прямую?
• Как называется переменная х и
переменная у?

13. Домашнее задание

• №854(1,2), 858 (1;2), 856

Графики функций квадратного корня

Родительская функция функций формы

ж

Икс

знак равно

Икс

—

а

+

б

является

ж

Икс

знак равно

Икс

.

Обратите внимание, что

домен

из

ж

Икс

знак равно

Икс

является

Икс

≥

0

и

диапазон

является

у

≥

0

.

График

ж

Икс

знак равно

Икс

—

а

+

б

можно получить, переведя график

ж

Икс

знак равно

Икс

к

а

единиц вправо, а затем

б

единиц вверх.

Пример:

Нарисуйте график

у

знак равно

Икс

—

1

+

2

из родительского графа

у

знак равно

Икс

.

Решение:

Шаг 1. Нарисуйте график

у

знак равно

Икс

.

Шаг 2.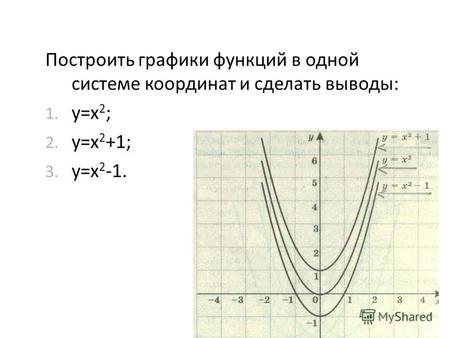 Переместите график

у

знак равно

Икс

от

1

единицы справа, чтобы получить график

у

знак равно

Икс

—

1

.

Шаг 3. Переместите график

у

знак равно

Икс

—

1

от

2

единиц до получения графика

у

знак равно

Икс

—

1

+

2

.

Область определения функции

у

знак равно

Икс

—

1

+

2

является

Икс

≥

1

.

Диапазон функции

у

знак равно

Икс

—

1

+

2

является

у

≥

2

.

Интеграция

: площадь и кривые

Интеграция

и функция площади

Площадь между графиком функции y = f (x)
а ось x, начиная с x = 0, называется функцией площади A (x)

Пример

Найдите площадь под графиком y = 2x
между x = 2 и x = 4

Область между 2 и 4 можно описать как
область между x = 0 и x = 4 минус
область между x = 0 и x = 2

у = 2x

Определенные интегралы

Площадь графика y = f (x)
между x = a и x = b равно

Пример

Найдите заштрихованную область как определенный интеграл.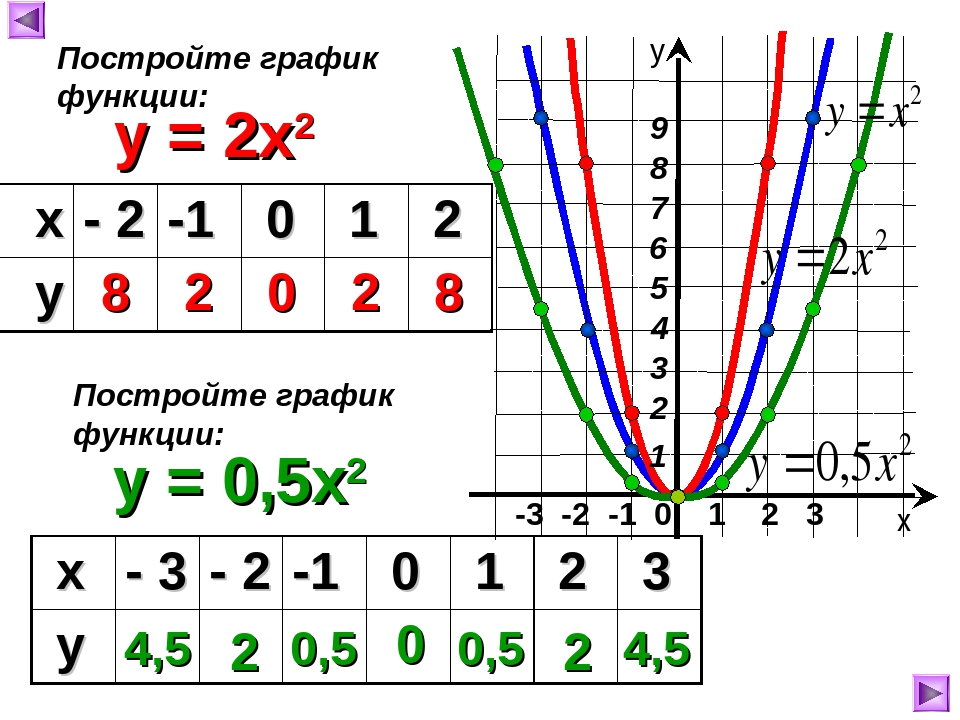

Площадь между кривой и осью Y

Иногда необходимо найти
область между функцией и
ось ординат.

Это дается как

Не всегда можно выразить функцию
y = f (x) через x = f (y).

Также может быть проще вычислить

и вычтите это как составную площадь.

Основная теорема исчисления

Примеры

Оценить

Оценить

Найдите положительное значение z: —

Области, ограниченные графиком и осью абсцисс.

При вычислении площади, заключенной между графиком и осью абсцисс: —

• Всегда рисовать эскиз
• Рассчитать площади выше и ниже оси x по отдельности
• Игнорировать отрицательные знаки и добавить.

Пример
Вычислите площадь, заключенную на графике y = x + 2.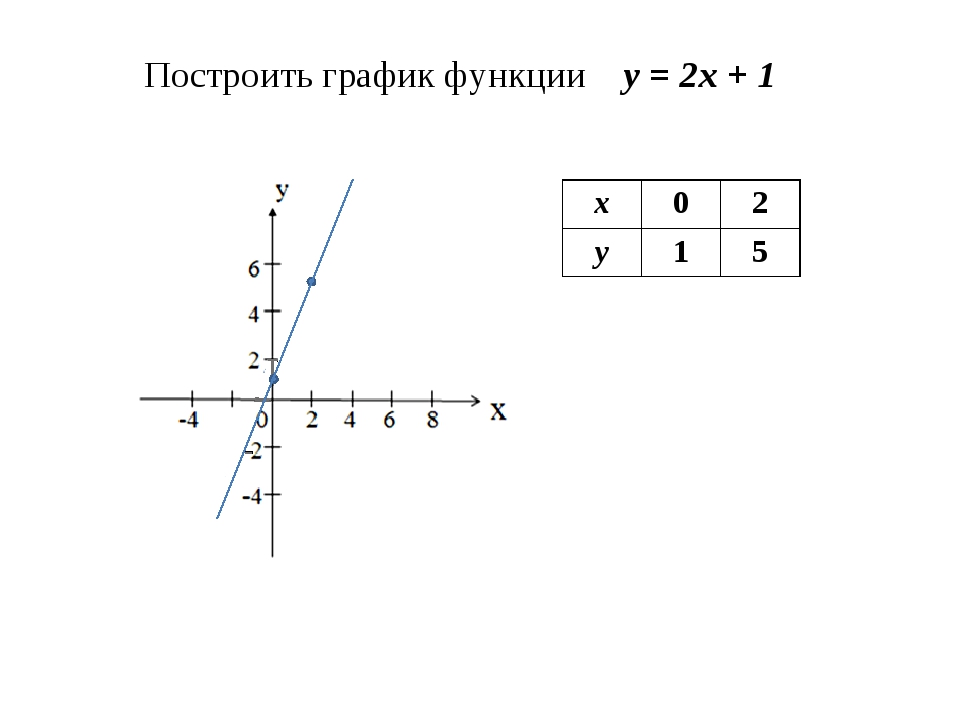
и ось x для -6 ​​≤ x ≤1

График отсекает ось абсцисс в точке (-2, 0)

Площадь ниже оси x =

Площадь над осью абсцисс =

Область между двумя графиками

Область между двумя графиками можно найти путем вычитания
область между нижним графиком и осью x от
область между верхним графиком и осью абсцисс.

Пример

Рассчитать область, заштрихованную между графиками
у = х + 2 и у = х ²
.

Графики пересекаются в точках (-1, 1) и (2,4).

Площадь между верхней кривой и осью абсцисс

Площадь между нижней кривой и осью абсцисс

Всего:

Формула для площади между двумя графиками

Пример

Рассчитайте затененную область между
параболы с уравнениями

y = 1 + 10x — 2x ² и
у = 1 + 5х — х ² . (Высшее 2002, стр. 2)

Эскиз кривой

В процессе построения кривой выполняются следующие шаги:

\ (1. \) Домен

Найдите область определения функции и определите точки разрыва (если есть).

\ (2. \) Перехватывает

Определите точки пересечения \ (x- \) и \ (y — \) функции, если это возможно. Чтобы найти точку пересечения \ (x — \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x.\) Аналогично, мы устанавливаем \ (x = 0 \), чтобы найти точку пересечения \ (y — \). Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо). \)

\ (3. \) Симметрия

Определите, является ли функция четной, нечетной или ни одной, и проверьте периодичность функции. Если \ (f \ left ({- x} \ right) = f \ left (x \ right) \) для всех \ (x \) в области, то \ (f \ left (x \ right) \) является четный и симметричный относительно оси \ (y — \).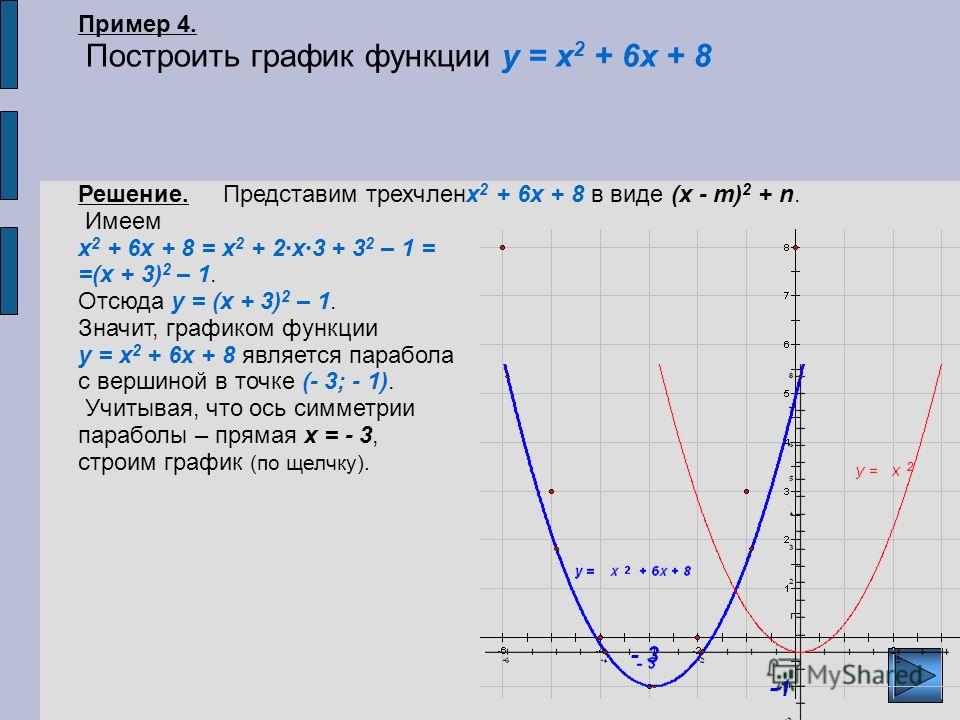 \ prime \ left (x \ right) \) и найдите критические точки функции. (Помните, что критические точки — это точки, в которых первая производная равна нулю или не существует.) Определите интервалы, в которых функция увеличивается и уменьшается с помощью теста первой производной.

\ (6. \) Локальный максимум и минимум

Используйте первый или второй производный тест, чтобы классифицировать критические точки как локальный максимум или локальный минимум. Вычислите значения \ (y — \) локальных экстремальных точек.

\ (7.2} — 6x + 2 = 0, \; \;} \ Rightarrow

{D = 36 — 4 \ cdot 3 \ cdot 2 = 12, \; \;} \ Rightarrow
{{x_ {1,2}} = \ frac {{6 \ pm \ sqrt {12}}} {6}} = {1 \ pm \ sqrt 3 \ приблизительно 0,42; \; 1,58.}
\]

При прохождении через точку \ (x = 1 — {\ large \ frac {{\ sqrt 3}} {3} \ normalsize}, \) производная меняет знак с плюса на минус (рисунок \ (1a \)). Следовательно, эта точка является максимальной. Аналогично устанавливается, что \ (x = 1 + {\ large \ frac {{\ sqrt 3}} {3} \ normalsize} \) является точкой минимума.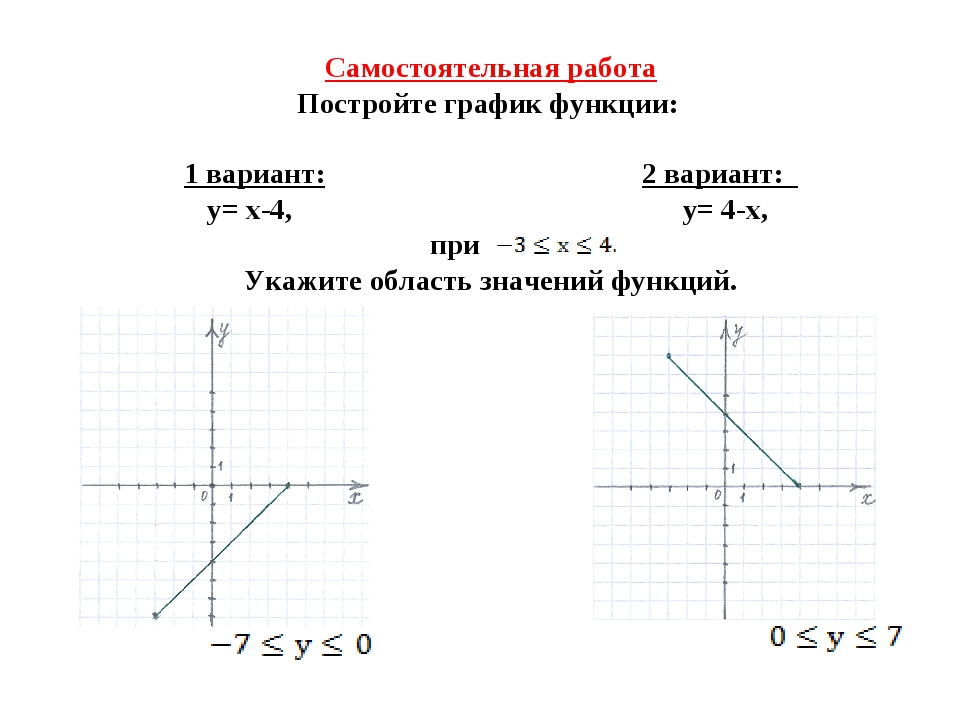 2}} \ right]}
+ {2 — \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} ​​- \ sqrt 3 + \ cancel {1}}
— {\ frac {{\ sqrt 3}} {9} — \ cancel {3}}
+ {2 \ sqrt 3 — \ cancel {1} ​​+ \ cancel {2}}
— {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 — \ sqrt 3 — 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]

Аналогично находим, что

\ [
{y \ left ({1 + \ frac {{\ sqrt 3}} {3}} \ right)}
= — {\ frac {{2 \ sqrt 3}} {9} \ приблизительно -0 , 38.}
\]

Таким образом, функция имеет локальный максимум в точке

\ [\ left ({1 — \ frac {{\ sqrt 3}} {3}, \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({0,42; \ ; 0,38} \ вправо). \]

Соответственно, локальный минимум достигается в точке

.

\ [\ left ({1 + \ frac {{\ sqrt 3}} {3}, — \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({1,58; \; — 0,38} \ вправо) \]

Интервалы увеличения / уменьшения следуют из рисунка \ (1a. \)

Рассмотрим вторую производную:

\ [
{y ^ {\ prime \ prime} \ left (x \ right) = {\ left ({3 {x ^ 2} — 6x + 2} \ right) ^ \ prime}}
= {6x — 6;}
\]

\ [
{y ^ {\ prime \ prime} \ left (x \ right) = 0, \; \;} \ Rightarrow
{6x — 6 = 0, \; \;} \ Rightarrow
{x = 1 .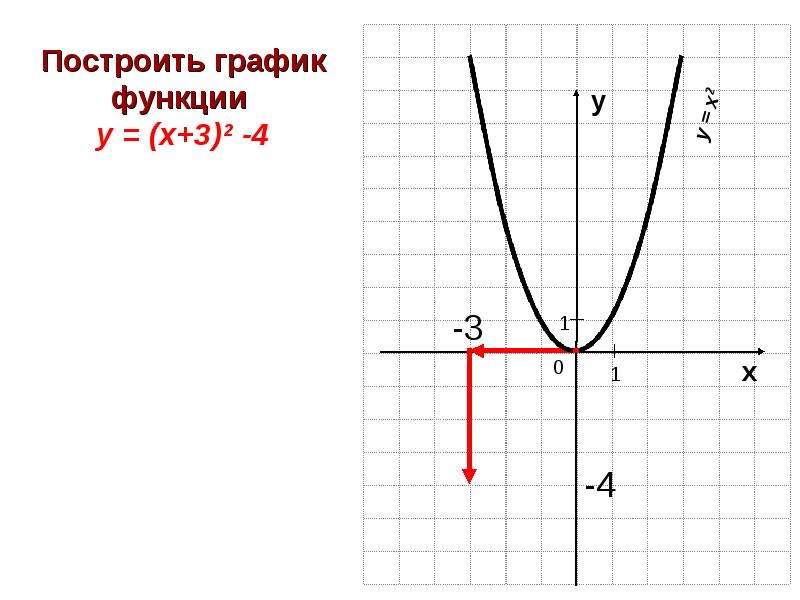 2}}
= {\ left ({x + 2} \ right) \ left ({2x — \ cancel {2} + x + \ cancel {2}} \ right)}
= {3x \ left ({x + 2} \ вправо).}
\]

Стационарных точек

\ [
{y ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{3x \ left ({x + 2} \ right) = 0, \; \;} \ Rightarrow
{ {x_1} = 0, \; {x_2} = — 2.}
\]

Производная меняет знак, как показано на рисунке \ (3a. \). Следовательно, \ (x = -2 \) — точка максимума, а \ (x = 0 \) — точка минимума. В этих экстремальных точках функция имеет следующие значения:

\ [
{y \ left ({- 2} \ right) = — 4,} \; \; \; \ kern-0.3}}} = 0, \; \;} \ Rightarrow
{{x_1} = — \ sqrt 3, \; {x_2} = \ sqrt 3.}
\]

При прохождении через эти точки вторая производная меняет знак. Следовательно, обе точки являются точками перегиба. Функция строго выпуклая вниз в интервалах \ (\ left ({- \ infty, — \ sqrt 3} \ right) \) и \ (\ left ({\ sqrt 3, + \ infty} \ right) \) и соответственно, строго выпукло вверх в интервале \ (\ left ({- \ sqrt 3, \ sqrt 3} \ right).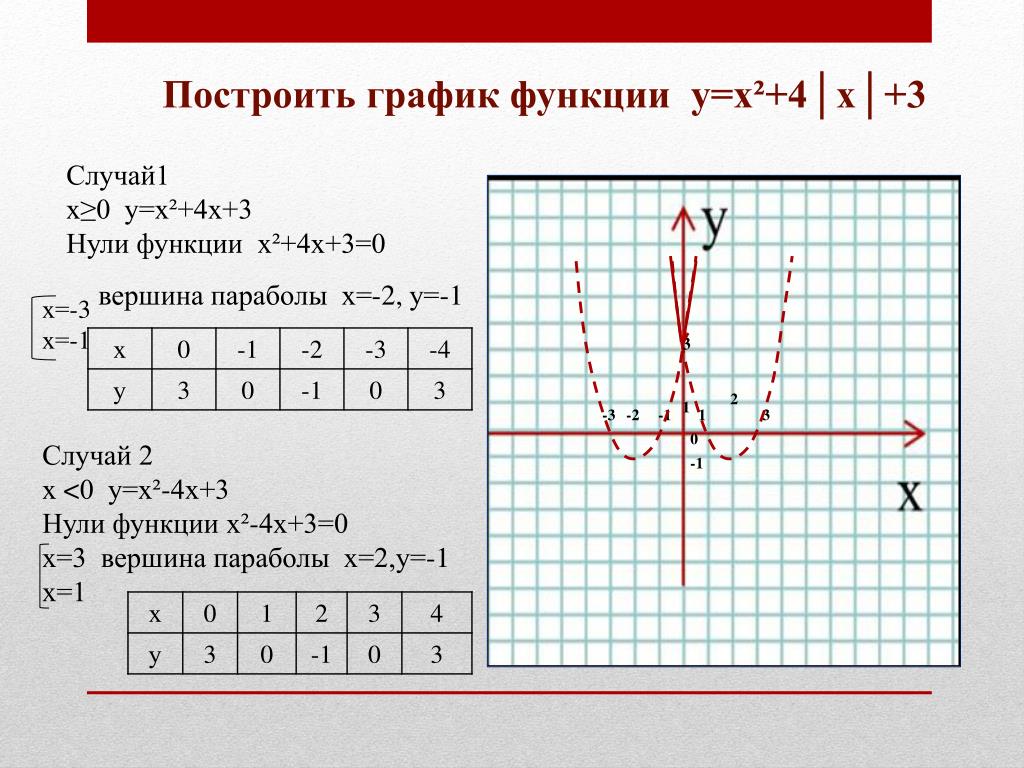 2} + 1}} {{\ cancel {1} ​​- \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 — 2 \ sqrt 2 + 2 + 1}} {{- \ sqrt 2}}} = {\ frac {{4 — 2 \ sqrt 2}} {{- \ sqrt 2}}} = {\ frac {{4 — 4 \ sqrt 2}} {2}} = {2 \ left ({1 — \ sqrt 2} \ right) \ приблизительно {- 0.2} + 1}} {{\ cancel {1} ​​+ \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 + 2 \ sqrt 2 + 2 + 1}} {{\ sqrt 2} }} = {\ frac {{4 + 2 \ sqrt 2}} {{\ sqrt 2}}} = {\ frac {{4 + 4 \ sqrt 2}} {2}} = {2 \ left ({1 + \ sqrt 2} \ right) \ приблизительно {4.83}} \]

Теперь мы можем нарисовать график функции (рисунок \ (5b \)).

python — Как построить y = 1 / x как единый график

На этот вопрос уже есть ответы :

Закрыт 4 года назад.

Есть ли простой способ построить график функции, стремящейся к бесконечности как положительного, так и отрицательного, в виде единого графика, не соединяющего оба конца положительного и отрицательного?

Например, построение y = 1 / x с использованием этого кода дает результирующий график:

  импортировать numpy как np
импортировать matplotlib. pyplot как plt

def f (x):
    возврат 1 / x
fx_name = r '$ f (x) = \ frac {1} {x} $'

x = np.setdiff1d (np.linspace (-10,10,100), [0]) # чтобы удалить ноль
у = f (х)
plt.plot (x, y, label = fx_name)
plt.легенда (loc = 'верхний левый')
plt.show ()
  

Но мне хотелось бы получить такой результат, которого я добился, построив два отдельных домена:

  импортировать numpy как np
импортировать matplotlib.pyplot как plt

def f (x):
    возврат 1 / x
fx_name = r '$ f (x) = \ frac {1} {x} $'

xfn = np.setdiff1d (np.linspace (-10,0,100), [0])
xfp = np.setdiff1d (np.linspace (0,10,100), [0])
yfn = f (xfn)
yfp = f (xfp)

yf = plt.plot (xfn, yfn, label = fx_name)
plt.plot (xfp, yfp, color = yf [0] .get_color ())
plt.legend (loc = 'верхний левый')
plt.показывать()
  

Есть кратчайшие пути?
Большое спасибо.

Решение

Включить ноль в массив домена и подавить деление на ноль. Это приводит к тому, что один элемент возвращаемого массива совмещенных доменов обозначается как «inf», а «inf» не отображается.

  импортировать numpy как np
импортировать matplotlib.pyplot как plt

def f (x):
    с np.errstate (div = 'ignore', invalid = 'ignore'):
        возврат 1 / x
fx_name = r '$ f (x) = \ frac {1} {x} $'

x = np.linspace (-10,10,101)
у = f (х)
plt.сюжет (x, y, label = fx_name)
plt.legend (loc = 'верхний левый')
plt.show ()
  

Я предпочитаю этот метод, поскольку он позволяет избежать ручных манипуляций с массивом и может быть легко повторно использован для других функций, которые используют тот же домен (например, y = 1 / (x + 2)). Спасибо всем за вклад.

.