Содержание
Самостоятельная работа Вариант 1 — Самостоятельная работа
Самостоятельная
работа.
Вариант 1.
Выполните сложение:
а) 78
639 + 85 089; б) 68
677 388 + 5 068 075 009.
Выполните сложение,
выбирая удобный порядок действий:
а) 49 617
+ 999 + 383; б)
52 681+4861 + 139.Точка А
лежит между
точками М
и N. Выполните
чертеж и вычислите длину отрезка MN,
если АМ
= 28мм и AN
= 35мм.Найдите периметр
многоугольника ABCD,
если AB
= 46 см, ВС=
13см, CD
= 24 см и AD
= 50 см.Разложите по
разрядам число; а) 576; б) 3 875 025 110.
Самостоятельная
работа.
Вариант 2.
Выполните сложение:
а) 69
928 + 48 096; б) 80
679 084 + 5 075 460 350.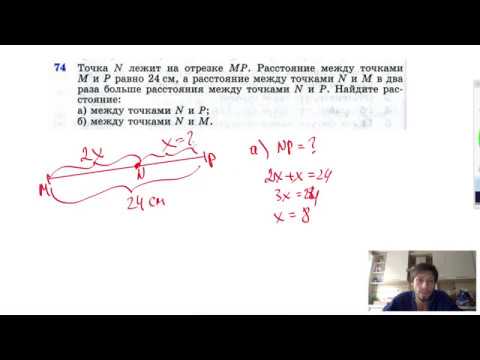
Выполните сложение,
выбирая удобный порядок действий: а)
695 + 2305 + 57 908; б)
89 716 + 9688 + 312.Точка X
лежит между
точками А и
В. Выполните
чертеж и вычислите длину отрезка АВ,
если АХ
= 39 мм и ХВ=17
мм.Найдите периметр
многоугольника ABCDE,
если АВ
= 38 м, ВС = 34
м, CD
= 36 м, DЕ
= 35 м и АЕ
= 37 м.Разложите по
разрядам число: а) 2 507; б) 18 703 205 003.
Самостоятельная
работа.
Вариант 3.
Выполните сложение:
a)
78 935 + 54 367; б)
3 087 657 707 + 30 876
577.Выполните сложение,
выбирая удобный порядок действий: а)
302 + 58 758+1698; б)
197 + 2414 + 47 586.Точка Y
лежит между
точками A
и B.
Выполните чертеж и вычислите длину
отрезка АВ,
если AY
= 43 см и YB
= 38 см.
Найдите периметр
многоугольника ABDKE,
если АВ
= 43 см, BD=42
см, DK
= 44 см, КЕ = 41
см и EA
= 40 см.Разложите по
разрядам число: а)
45 308; 6)253
605 814 022.
Самостоятельная
работа.
Вариант 4.
Выполните сложение:
а)
238 756 + 489
445;
б) 7
688 323 051+94 516 826 989.Выполните сложение,
выбирая удобный порядок действий: а)
1888 + 87 239+1112; б)
437 + 637 849 + 62 151.На отрезке CD
отмечены
точки А и В
так, что точка
А лежит
между точками В
и D.
Найдите длину
отрезка CD,
если СВ = 15
см, ВА=14 см
и AD
= 12
см.Вычислите периметр
пятиугольника ABCDE,
если АВ
=32 см, BC=CD
= 35 см и AE
= DE
= 47 см.
Разложите по
разрядам число: а) 56 409; б) 18 609 037 020.
5 класс. Математика. Никольский. Учебник. Ответы к стр. 83
Измерение величин
Измерение отрезков
Ответы к стр. 83
367. Точка С расположена на прямой между точками A и B. Длина отрезка AC равна 8 см, длина отрезка CB на 3 см больше длины отрезка AC. Найдите длину отрезка AB.
1) 8 + 3 = 11 (см) – длина отрезка СВ
2) 8 + 11 = 19 (см) – длина отрезка АВ
О т в е т: отрезок АВ 19 см.
368. Точка A расположена на прямой между точками B и C. Длина отрезка CB на 3 см больше длины отрезка AC. Найдите длину отрезка AB.
Точка А делит отрезок ВС на отрезок ВА и отрезок АС. Тогда длина отрезка АВ = ВС – АС. Но длина отрезка СВ = АС + 3 (см). Подставляем в первое выражение длину отрезка СВ из второго выражение: АВ = ВС – АС = (АС + 3) – АС = АС + 3 – АС = 3 (см).
Но длина отрезка СВ = АС + 3 (см). Подставляем в первое выражение длину отрезка СВ из второго выражение: АВ = ВС – АС = (АС + 3) – АС = АС + 3 – АС = 3 (см).
О т в е т: отрезок АВ 3 см.
369. На прямой даны точки A, B и C, причем AB = 6 см, AC = 13 см. Найдите длину отрезка BC, если:
а) точки B и C лежат по одну сторону от точки A;
б) точки B и C лежат по разные стороны от точки A.
а) Получается отрезок АС, разделённый точкой В на отрезки АВ и ВС. Тогда длина отрезка ВС = АС – АВ = 13 – 6 = 7 (см).
О т в е т: отрезок ВС 7 см.
б) Получается отрезок ВС, разделённый точкой А на отрезки ВА и АС. Тогда длина отрезка ВС = ВА + АС = 6 + 13 = 19 (см).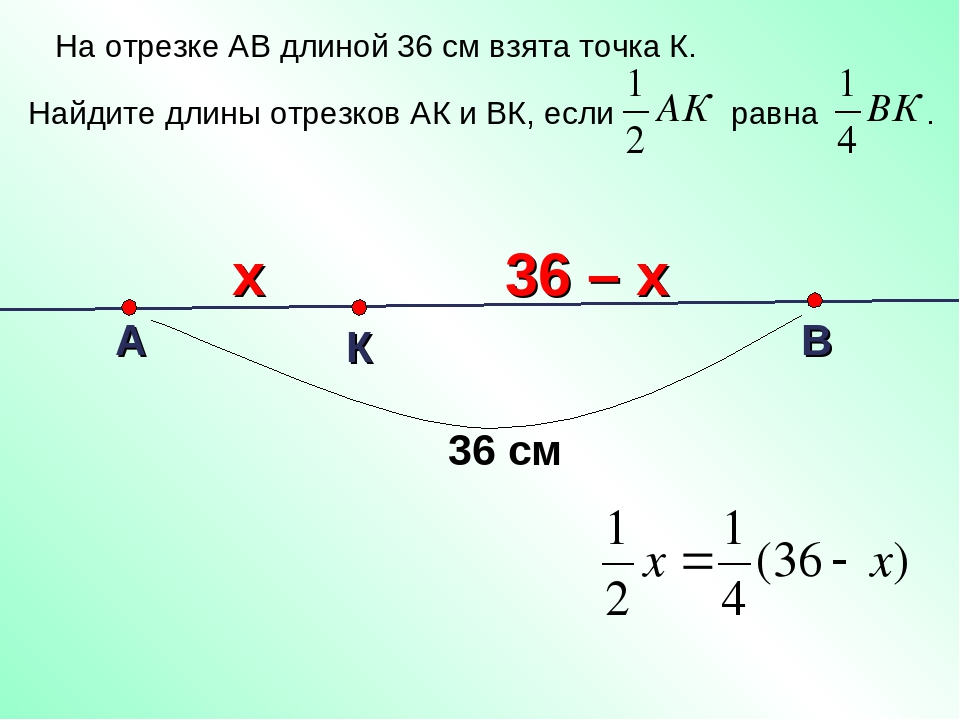
О т в е т: отрезок ВС 19 см.
370. На прямой даны три точки A, B и C, причем AB = 13 см, AC = 4 см. Найдите длину отрезка BC. (Задача имеет два решения.)
Так как АВ > АС, то возможно 2 решения: точка В не может делить отрезок АС на отрезки АВ и ВС, поскольку отрезок АВ будет больше исходного отрезка АС.
1) Точка С делит отрезок АВ на отрезки АС и СВ. Тогда длина отрезка ВС = АВ – АС = 13 – 4 = 9 (см).
О т в е т: отрезок ВС 9 см.
2) Точка А делит отрезок СВ на отрезки СА и АВ. Тогда длина отрезка ВС = СА + АВ = 4 + 13 = 17 (см).
О т в е т: отрезок ВС 17 см.
371. На прямой даны три точки A, B и C, причем AB = 83 см, AC = 97 см. Найдите длину отрезка BC. Сколько решений имеет задача?
Найдите длину отрезка BC. Сколько решений имеет задача?
Так как АС > АВ, то возможно 2 решения: точка С не может делить отрезок АВ на отрезки АС и СВ, поскольку отрезок АС будет больше исходного отрезка АВ.
1) Точка В делит отрезок АС на отрезки АВ и ВС. Тогда длина отрезка ВС = АС – АВ = 97 – 83 = 14 (см).
О т в е т: отрезок ВС 14 см.
2) Точка А делит отрезок ВС на отрезки ВА и АС. Тогда длина отрезка ВС = ВА + АС = 83 + 97 = 180 (см).
О т в е т: отрезок ВС 180 см.
372. На луче AM отложили отрезки AB и AC, AC = 89 см. Найдите длину отрезка BC, если:
а) AB на 15 см длиннее AC;
б) AB на 15 см короче AC.
а) В этом случае точка С лежит между точками А и В и делит отрезок АВ на отрезки АС и СВ, поскольку исходный отрезок АВ не может быть меньше отрезка АС. Тогда:
Тогда:
1) АВ = АС + 15 = 89 + 15 = 104 (см)
2) ВС = АВ – АС = 104 – 89 = 15 (см)
О т в е т: отрезок ВС 15 см.
б) В этом случае точка В лежит между точками А и С и делит отрезок АС на отрезки АВ и ВС, поскольку исходный отрезок АС не может быть меньше отрезка АВ. Тогда:
1) АВ = АС – 15 = 89 – 15 = 74 (см)
2) ВС = АС – АВ = 89 – 74 = 15 (см)
О т в е т: отрезок ВС 15 см.
373. Объясните на примере, как измерить длину отрезка с точностью до 1 см.
а) с недостатком; б) с избытком; в) с округлением.
Если приложить шкалу сантиметровой линейки к отрезку АВ так, что отметка «0» совпадёт с точкой А, то окажется, что точка В не совпадает с делением шкалы на отметке «6» или «7». При этом величины 6 см и 7 см отличаются от АВ не более чем на 1 см и называются приближёнными значениями длины АВ с точностью до 1 см.
а) длина отрезка АВ равна 6 см с недостатком с точностью до 1 см;
б) длина отрезка АВ равна 7 см с избытком с точностью до 1 см;
в) длина отрезка АВ равна 7 см с округлением с точностью до 1 см, поскольку точка В находится ближе к отметке «7», а не «6».
374. Измерьте длину и ширину тетради с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением.
а) длина 20 см, ширина 16 см;
б) длина 21 см, ширина 17 см;
в) длина 21 см, ширина 17 см.
375. Отметьте в тетради две точки. Определите на глаз расстояние между ними. Начертите отрезок с концами в этих точках и измерьте приближенно его длину.
AB ≈ 7 см.
376. С помощью линейки измерьте отрезки, изображенные на рисунке 53, с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением.
АВ = 2 см 5 мм, СD = 3 см 3 мм, EF = 2 см 8 мм
а) АВ ≈ 2 см, СD ≈ 3 см, EF ≈ 2 см;
б) АВ ≈ 3 см, СD ≈ 4 см, EF ≈ 3 см;
в) АВ ≈ 3 см, СD ≈ 3 см, EF ≈ 3 см.
377. Рейка длиной 147 см разрезана на 4 равные части. Какую длину имеет каждая часть с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением?
147 : 4 = 36 (ост. 3)
а) 36 см;
а) 37 см;
б) 37 см.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Урок 1. прямая и отрезок — Геометрия — 7 класс
Геометрия
7 класс
Урок № 1
Прямая и отрезок
Перечень рассматриваемых вопросов:
- Исторические сведения о возникновении и предмете изучения геометрии, значение геометрии.
- Знакомство с особенностями геометрических задач, аксиомами и теоремами.
- Различие между плоскими и пространственными фигурами;
- Формулировка основных определений и описание понятий: «отрезок», «расстояние между двумя точками», «принадлежит прямой» и «лежит между».

- Взаимное расположение трёх точек, прямых.
- Изображение с помощью чертежных инструментов прямых, отрезков, лучей.
- Измерение расстояния на местности провешиванием прямой.
Тезаурус:
Геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
Отрезок – это часть прямой, ограниченная точками, вместе с этими точками.
Концы отрезка – это точки, ограничивающие отрезок.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М.
 Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с. - Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
«Геометрия – неотъемлемая часть мировой сокровищницы человеческой мысли», – однажды сказал российский математик Игорь Фёдорович Шарыгин.
С этих слов мы и начнём изучать новый раздел математики, который называется геометрия.
Геометрия – одна из древнейших наук, которая возникла из потребностей человека. Её название состоит из двух древнегреческих слов: гео – земля и метрео – измеряю, получается: «землю измеряю». Действительно, слово «геометрия» связано с измерениями, как на земельных участках, так и при строительстве зданий. Многие факты добывались опытным путем, поэтому геометрия не являлась точной наукой во времена своего зарождения.
Многие факты добывались опытным путем, поэтому геометрия не являлась точной наукой во времена своего зарождения.
Геометрические сведения стали доказываться только благодаря древнегреческому учёному Фалесу, который жил в VI веке до нашей эры.
Спустя некоторое время, уже в III веке до нашей эры, другой греческий учёный Евклид написал «Начала». Эта книга стала основой изучения геометрии на долгое время, а наука в честь учёного была названа евклидовой геометрией.
Сегодня геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
В школе изучается два курса геометрии – планиметрия, в ней рассматриваются свойства фигур на плоскости, и стереометрия, в ней рассматриваются свойства фигур в пространстве.
Аксиомы планиметрии.
В каждой науке есть свои термины, понятия, геометрия не исключение. В геометрии есть основные положения, которые принимаются в качестве исходных и носят название аксиом и основные понятия, определение которым не даётся, например, точка и прямая, но их свойства выражены в аксиомах. Это всё является фундаментом геометрии, на котором строятся другие понятия и доказываются теоремы.
Это всё является фундаментом геометрии, на котором строятся другие понятия и доказываются теоремы.
Рассмотрим некоторые из аксиом.
1. Аксиомы принадлежности.
Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
2. Аксиомы расположения.
Из трех точек на прямой одна и только одна лежит между двумя другими.
3. Аксиомы измерения.
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
В целом аксиомы разделены на 5 групп, 3 из которых, частично, представлены вашему вниманию.
В 7 классе вы будете изучать планиметрию. Давайте перечислим некоторые понятия из этого раздела геометрии. Поговорим о точках, прямых, отрезках, вспомним, как они обозначаются.
Обычно прямую обозначают малой латинской буквой (например, a), а точки большими латинскими буквами, например, A.
Если на прямой отметить точки, например, A и B, то прямую в можно обозначить двумя заглавными буквами AB или BA.
Часть прямой, ограниченной точками, включая эти точки, называют отрезком. В нашем случае получаем отрезок AB или BA.
Точки, ограничивающие отрезок, называются концами отрезка. В нашем случае концами отрезка являются точки A и B.
Варианты взаимного расположения точек и прямой: точки могут лежать на прямой или не лежать на ней.
Например, точки A и B лежат на прямой a, точки C и D не лежат на прямой a. При этом в записи используют следующее обозначение:
Это можно прочитать таким образом: «точка A и B принадлежат прямой a (ϵ – знак принадлежности), также точки C и D не принадлежат прямой a (перечёркнутый знак принадлежности)».
При этом через точки А и В нельзя провести прямую, не совпадающую с прямой а, из этого делаем вывод, что через любые две точки можно провести только одну прямую.
Рассмотрим, как располагаются прямые на плоскости.
Прямые могут иметь только одну общую точку, тогда говорят, что прямые пересекаются или не иметь общих точек, тогда говорят, что прямые не пересекаются.
прямые пересекаются – прямые не пересекаются
Провешивание прямой.
Решим задачу. Построим с помощью линейки отрезок длиннее, чем она сама. Приём, который мы будем использовать, называется провешиванием прямой.
Рассмотрим, в чём он заключается. Для этого приложим к листу бумаги линейку и отметим три точки А, В, С, при этом, точка С пусть лежит между точками А и В. Далее передвинем линейку так, чтобы её конец оказался около точки С, отметим точку D. Все построенные точки А, В, С, D лежат на одной прямой. Теперь проведём отрезок АВ, потом отрезок ВD, в результате получим отрезок АD длиннее, чем линейка.
Для построения на местности отмечают две точки, например, А и В, ставят в них шесты (вехи), третий шест ставят в точку С так, чтобы её закрывали уже ранее поставленные шесты.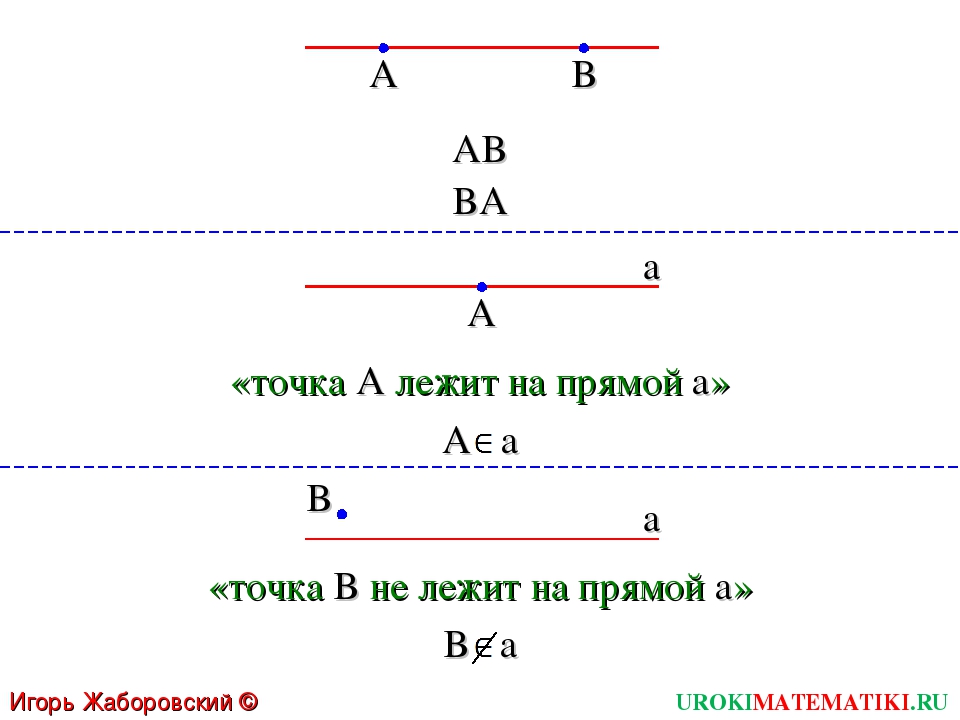
Так можно прокладывать линии высоковольтных передач, трассы и т. д.
Разбор заданий тренировочного модуля.
1. Сколько отрезков образуется при пересечении прямых на рисунке?
Объяснение:
Посмотрите на рисунок. На нём изображены 4 пересекающиеся прямые, точки пересечения разбивают прямые на отрезки: прямая с разбивается на 3 отрезка АЕ, АВ, ЕВ. Аналогично все прямые разбиваются на 3 отрезка. В результате получаем, что каждая из четырёх прямых, разбивается точками пересечения на 3 отрезка, значит: 4 · 3 = 12
Ответ: 12.
2. Выберите правильные варианты ответа. С чем пересекается прямая m?
Варианты ответа:
с прямой n
с отрезком АВ
с отрезком СL
с отрезком АС
Решение: при выполнении задания, нужно помнить, что прямая бесконечно продолжается в обе стороны, а отрезок ограничен точками, поэтому, если продолжить прямую m и n, то становится понятно, что они пересекутся между собой. Кроме того, прямая m пересечётся и с отрезком АВ. Следовательно, получается 2 ответа: прямая m пересекается с прямой n и отрезком АВ.
Кроме того, прямая m пересечётся и с отрезком АВ. Следовательно, получается 2 ответа: прямая m пересекается с прямой n и отрезком АВ.
Ответ: прямая m пересекается с прямой n; прямая m пересекается с отрезком АВ.
Урок 24. соотношения между сторонами и углами треугольника. неравенство треугольника — Геометрия — 7 класс
Геометрия
7 класс
Урок № 24
Соотношения между сторонами и углами треугольника. Неравенство треугольника
Перечень рассматриваемых вопросов:
- Установление соотношений между сторонами и углами треугольника.
- Формулирование неравенства треугольника.
- Теоремы о сравнении сторон и углов треугольника, их применение при решении задач.
- Проведение исследования о существовании треугольника с заданными элементами.
Тезаурус
Каждая сторона треугольника меньше суммы двух других сторон.
В треугольнике против большей стороны лежит больший угол. Против большего угла лежит большая сторона.
Против большего угла лежит большая сторона.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее, на уроках геометрии, вы познакомились с различными фигурами, в том числе и с треугольником.
Сегодня мы продолжим изучать треугольники и рассмотрим соотношение между его элементами.
Теорема: В треугольнике против большей стороны лежит больший угол.
Дано: ∆АВС.
AB > AC.
Доказать:
∠С > ∠В
Доказательство:
Отложим на стороне AB отрезок, равный стороне AC.
Так как AD < AB, то точка D лежит между точками A и B.
Следовательно, угол 1 является частью угла C и, значит,
∠C > ∠1.
Угол 2 – внешний угол треугольника BDC, поэтому ∠2 > ∠B (по свойству внешнего угла треугольника).
∠1 = ∠2 как углы при основании равнобедренного ∆ADC (по свойству равнобедренного треугольника).
→∠C > ∠1, ∠1 = ∠2, ∠2 > ∠B →∠C > ∠B.
Теорема доказана.
Справедлива и теорема, обратная данной. Против большего угла лежит большая сторона.
Дано: ∆АВС.
∠С > ∠В
Доказать:
AB > AC.
Доказательство:
Предположим, что АВ = АС или АВ < АС. Если АВ = АС → ∆АВС – равнобедренный (по определению равнобедренного треугольника) →∠С = ∠В (по свойству равнобедренного треугольника). Что противоречит условию, т. к. ∠С > ∠ В.
Если АВ < АС → ∠С < ∠В (по теореме доказанной выше: против большей стороны лежит больший угол) Что противоречит условию, т. к. ∠С > ∠В.
Поэтому наше предположение неверное → AB > AC.
Теорема доказана.
Докажем два следствия из этих теорем.
1 следствие. В прямоугольном треугольнике гипотенуза больше катета.
Дано: ∆АВС – прямоугольный.
∠В = 90°
Доказать: АС > СВ.
Доказательство: ∠В > ∠А, т. к. ∠В = 90° ( по условию), ∠А –острый → АС > СВ (по обратной теореме о соотношениях между сторонами и углами треугольника: против большего угла лежит большая сторона).
к. ∠В = 90° ( по условию), ∠А –острый → АС > СВ (по обратной теореме о соотношениях между сторонами и углами треугольника: против большего угла лежит большая сторона).
Что и требовалось доказать.
Докажем второе следствие из этих теорем.
2 следствие:
Если два угла треугольника равны, то треугольник равнобедренный. Это следствие называется признак равнобедренного треугольника.
Дано: ∆АВС
∠А = ∠С
Доказать: ∆АВС – равнобедренный
Доказательство:
Докажем, что АВ = ВС.
Пусть АВ > ВС →∠С > ∠А (по теореме доказанной выше: против большей стороны лежит больший угол), противоречит условию, т. к. ∠А = ∠С . → АВ = ВС →∆АВС – равнобедренный (по определению равнобедренного треугольника).
Что и требовалось доказать.
Докажем теорему по соотношению между сторонами треугольника.
Теорема:
Каждая сторона треугольника меньше суммы двух других сторон.
Дано:
∆АВС
Доказать: АВ < АС + СВ.
Доказательство:
Продолжим сторону AC и отложим отрезок CD = BC.
∆BCD – равнобедренный (по определению равнобедренного треугольника) →∠1 = ∠2 (по свойству равнобедренного треугольника).
В ∆ABD: ∠ABD > ∠1 (так как угол 1 часть угла АВD), →∠ABD > ∠2 (так как ∠1 = ∠2).
Так как против большего угла лежит большая сторона (по теореме о соотношениях между сторонами и углами треугольника) → AB < AD, AD = AC + CD, т.к. CD = BC, поэтому AD = AC + CВ → AB < AC + СВ.
Что и требовалось доказать.
Сформулируем следствие из этой теоремы.
Для любых трёх точек A, B и C, не лежащих на одной прямой, справедливы неравенства: AB < AC + CB, AC < AB + BC, BC < BA + AC.
Решим задачу на доказательство, используя теоремы о соотношениях между углами и сторонами треугольника.
Докажем, что в произвольном треугольнике, если медиана и высота проведены из одной вершины, то эта медиана не меньше высоты, проведённой из то же вершины.
Дано: ∆АВС.
ВМ – медиана,
ВН – высота.
Доказать: ВМ ≥ ВН.
Доказательство:
Рассмотрим случай, когда АВ ≠ ВС. То ВМ и ВН не совпадают (т. к. по свойству равнобедренного треугольника, высота и медиана совпадают, если проведены к его основанию).
Рассмотрим ∆ВНМ – прямоугольный (по определению прямоугольного треугольника), т. к. ∠Н = 90°, при этом угол в 90° единственный в данном треугольнике (по теореме о сумме углов треугольника) → ∠Н – самый большой → ВМ > ВН (по обратной теореме о соотношениях между сторонами и углами треугольника).
Рассмотрим ещё случай АВ = ВС → ∆АВС – равнобедренный (по определению равнобедренного треугольника). То ВМ = ВН (по свойству равнобедренного треуголника, высота и медиана совпадают, если проведены к его основанию)→ ВМ ≥ ВН.
То ВМ = ВН (по свойству равнобедренного треуголника, высота и медиана совпадают, если проведены к его основанию)→ ВМ ≥ ВН.
Что и требовалось доказать.
Разбор заданий тренировочного модуля.
1 Дано: ABC, равнобедренный, вычислите чему равна третья сторона треугольника, если две других равны 8 см и 4 см?
Объяснение: По определению равнобедренного треугольника, две его боковые стороны равны, следовательно это будет сторона равная 4 см или 8см.
Сторона 4см не может быть, т. к. 8см = 4 см + 4 см., что противоречит теореме о соотношениях между сторонами треугольника: каждая сторона треугольника меньше суммы двух других сторон.
Предположим, что боковые стороны равны 8 см. Тогда, по теореме о соотношениях между сторонами треугольника, каждая сторона треугольника меньше суммы двух других сторон, получим следующее соотношение между сторонами треугольника:
4 см < 8 см + 8 см
8 см < 8 см + 4 см.
Соотношение верно, следовательно, третья сторона равна 8 см.
Ответ: третья сторона равна 8 см.
2. Дано: ∆АВК – равнобедренный, ВК – основание треугольника, его периметр равен 29 см, разность двух сторон равна 5 см, при этом один из его внешних углов – острый. Найдите длину боковой стороны АВ и основания ВК.
Объяснение: т. к. по условию, один из внешних углов острый, то один из внутренних углов будет тупым, а это может быть, в равнобедренном треугольнике, только вершина над основанием треугольника (следствие из теоремы о сумме углов треугольника). → Основание ВК – самая длинная сторона треугольника АВК (по теореме о соотношении между углами и сторонами треугольника). → ВК – АВ = 5 см →ВК = 5см + АВ.
По определению равнобедренного треугольника, две его боковые стороны равны → АВ = АК. Периметр треугольника – сумма длин трёх его сторон.
Р∆АВК = АВ + АК + ВК = 29 см (по условию).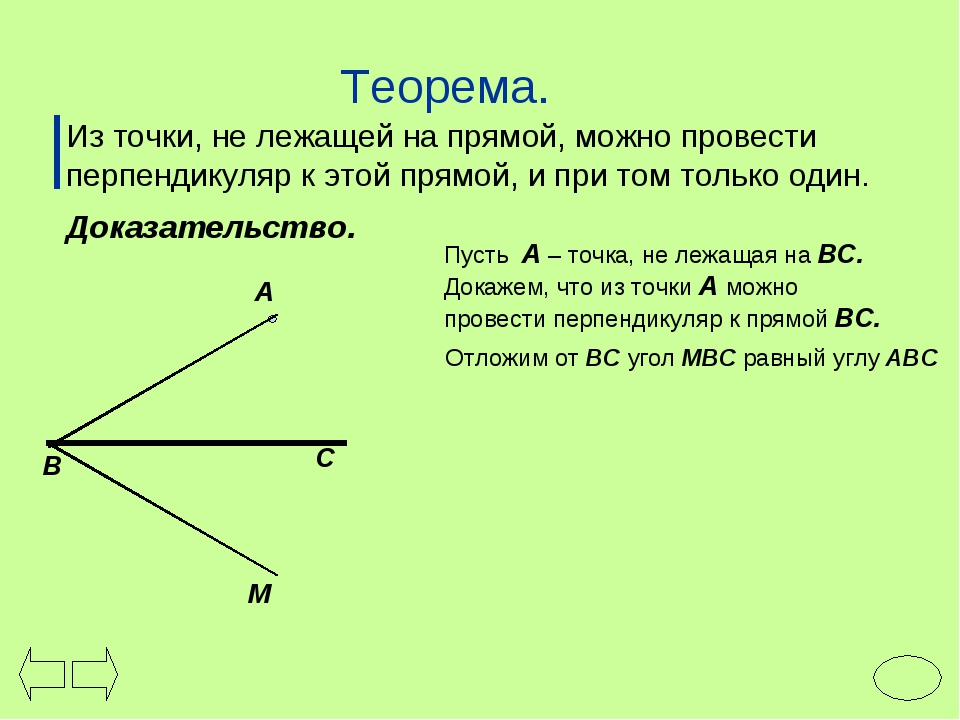
2АВ + ВК = 29 см
2АВ +5см + АВ = 29 см
3АВ = 24 см
АВ = 8 см, ВК = 8 + 5 =13 см.
Ответ: ВК = 13 см; АВ = 8 см.
Движение переводит плоскость в плоскость.
Геометрия
Реферат
на тему:
“Преобразования фигур”
Выполнил: ученик 10 Б класса
Халиуллин А.Н.
Проверила: Исрафилова Р.Х.
Малояз 2003 год
План:
I. Преобразование.
II. Виды преобразований
Гомотетия
Подобие
Движение
III. Виды движения
Симметрия относительно точки
Симметрия относительно прямой
Симметрия относительно плоскости
Поворот
Параллельный перенос в пространстве
I. Преобразование — смещение каждой точки данной фигуры каким-нибудь образом, и получение новой фигуры.
II. Виды преобразования в пространстве: подобие, гомотетия, движение.
Подобие
Преобразование фигуры F называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз, т.е. для любых точек X и Y фигуры F и точек X’, Y’ фигуры F’, в которые он переходят, X’Y’ = k * XY.
Свойства подобия: 1. Подобие переводит прямые в прямые, полупрямые – в полупрямые, отрезки – в отрезки.
Подобие сохраняет углы между полупрямыми
Подобие переводит плоскости в плоскости.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Гомотетия
Гомотетия – простейшее преобразование относительно центра O с коэффициентом гомотетии k. Это преобразование, которое переводит произвольную точку X’ луча OX, такую, что OX’ = k*OX.
Свойство гомотетии: 1. Преобразованием гомотетии переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k=1).
Доказательство. Действительно, пусть O – центр гомотетии и a — любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости a. Преобразование гомотетии переводит точку A в точку A’ на луче OA, а точку B в точку B’ на луче OB, причем OA’/OA = k, OB’/OB = k, где k – коэффициент гомотетии. Отсюда следует подобие треугольников AOB и A’OB’. Из подобия треугольников следует равенство соответственных углов OAB и OA’B’, а значит, параллельность прямых AB и A’B’. Возьмем теперь другую прямую AC в плоскости a. Она при гомотетии перейдет а параллельную прямую A’C’. При рассматриваемой гомотетии плоскость aперейдет в плоскость a’, проходящую через прямые A’B’, A’C’. Так как A’B’||AB и A’C’||AC, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, плоскости a и a’ параллельны, что и требовалось доказать.
Движение
Движением — преобразование одной фигуры в другую если оно сохраняет расстояние между точками, т.е. переводит любые две точки X и Y одной фигуры в точки X , Y другой фигуры так, что XY = X Y
Свойства движения: 1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.Это значит, что если A, B, C, лежащие на прямой, переходят в точки A1,B1,C1. То эти точки также лежат на прямой; если точка B лежит между точками A и C, то точка B1 лежит между точками A1 и C1.
Доказательство. Пусть точка B прямой AC лежит между точками A и C. Докажем, что точки A1,B1,C1 лежат на одной прямой.
Если точка A1,B1,C1 не лежат на прямой, то они являются вершинами треугольника. Поэтому A1C1 < A1B1 + B1C1. По определению движения отсюда следует, что AC<AB+BC. Однако по свойству измерения отрезков AC=AB+BC.
Мы пришли к противоречию. Значит, точка B1 лежит на прямой A1C1. Первое утверждение теоремы доказано.
Покажем теперь, что точка B1 лежит между A1 и C1. Допустим, что точка A1 лежит между точками B1 и C1. Тогда A1B1 + A1C1 = B1C1, и, следовательно, AB+AC=BC. Но это противоречит неравенству AB+BC=AC. Таким образом, точка A1 не может лежать между точками B1 и C1.
Аналогично доказываем, что точка C1 не может лежать между точками A1 и B1.
Так как из трех точек A1,B1,C1 одна лежит между двумя другими, то этой точкой может быть только B1. Теорема доказана полностью.
При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки
При движении сохраняются углы между полупрямыми.
Доказательство. Пусть AB и AC – две полупрямые, исходящие из точки A, не лежащие на оной прямой. При движении эти полупрямые переходят в некоторые полупрямые A1B1 и A1C1. Так как движение сохраняет расстояние, то треугольники ABC и A1B1C1 равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов BAC и B1A1C1, что и требовалось доказать.
Движение переводит плоскость в плоскость.
Докажем это свойство. Пусть a — произвольная плоскость. Отметим на ней любые три точки A, B, C, не лежащие на одной прямой. Проведем через них плоскость a’.
Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a’.
Пусть X — произвольная точка плоскости a. проведем через нее какую-нибудь прямую a в плоскости a, пересекающую треугольник ABXC в двух точках Y и Z. Прямая а перейдет при движении в некоторую прямую a’. Точки Y и Z прямой a перейдут в точки Y’ и Z’, принадлежащие треугольнику A’B’C’, а значит, плоскости a’.
Итак прямая a’ лежит в плоскости a’. Точка X при движении переходит в точку X’ прямой a’, а значит, и плоскости a’, что и требовалось доказать.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
III. Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.
Теория познания, основанная на поведенческих моделях / Хабр
Я не знаю, как она точно называется. Феноменология, эмпирио-критицизм, махизм — вот близкие течения. Ближе будет рациональность по Юдковскому. Формализация данной теории называется AIXI.
Идейно похоже на научный метод, но немножко шире. Придумал не я, лишь немного систематизирую и прохожусь по известным мне возражениям.
В какой-то мере данный подход альтернативен философским течениям материализма и идеализма, а кроме того, он лежит в основе одной из теорий ИИ.
Немного бэкграунда
Я занимаюсь системами обучения с подкреплением — то есть системами управления, которым мы ставим некоторую цель, и которые, не зная, как работает мир, этой цели достигают. Соответственно, возникает вопрос: а как должна быть устроена система познания, чтобы она работала в таких условиях? А как должно быть устроено познание у человека, чтобы он мог изучать мир и достигать целей? Я читал статьи по рациональному мышлению, но они выглядят недостаточно строгими и точными. Читал о научном методе, читал его критику. Работаю в data science и потому наслышался вещей вроде «машинное обучение хорошо работает, если ты хорошо знаешь предметную область», что весьма разумно, но совершенно не объясняет, откуда люди узнают предметную область, при нулевых знаниях на старте. Читал статьи людей, которые предлагали свой метод познания, называемый диалектикой и противопоставляющий себя блэкбокс-анализу. Читал идеалистов, которые полагают, что разум и материя принципиально несводимы друг к другу. И потому хочу описать целостную теорию познания — настолько конкретно, чтобы её можно было свести к программному коду.
Итак, как она устроена и работает.
Эмпиризм
Мы познаём мир через некие «сенсоры». То есть какую-то информацию мы объявляем «наблюдением», логики в нём не ищем, обоснований не требуем — относимся так, как будто нам этот массив данных сформировал некий датчик. Если датчик сбоит — значит, информация будет искажена, зашумлена, смещена. Мы всё равно её считаем своим сенсорным входом. «Датчик сбоит» — это уже возможный вывод, а мы пока никаких выводов не делаем.
Далее, мы про некоторые утверждения говорим «они относятся к реальности» — в случае, если из этого утверждения можно вывести какие-то прогнозы. Пусть даже прогнозы вероятностные — это неважно. Если высказывание хоть как-то меняет наши ожидания по поводу того, что мы увидим на сенсорах — оно касается реальности. Если же нет — значит, высказывание не о реальности. В сомнительных случаях имеет смысл уточнять, что имел в виду автор теории, в терминах прогноза опыта. Например, утверждение «я положил яблоко в холодильник» относится к реальности в том смысле, что я ожидаю или увидеть завтра это яблоко в холодильнике, или увидеть его следы, если кто-то его забрал. Может, реально я и не клал яблоко, и я его не найду. Всё равно, это утверждение про наш мир, просто оно ложное.
А какое утверждение не относится к реальности? Например, теорема Пифагора. Если мы вспомним определения точек и прямых, то окажется, что это абстракции. То есть в реальном мире нет никаких точек и прямых, это выдумка математиков. Но если сопоставить вымышленным точкам и прямым реальные объекты, и находиться пространстве, достаточно близком к Евклидовому, то выводы теоремы Пифагора будут применимы к наблюдаемым объектам.
Вероятности
Вероятность мы интерпретируем в контексте теории принятия решений, то есть высказывание P(A)=1/3 — значит, что если мы будем ставить на подобные события (то есть любые с P=1/3) деньги с коэффициентом 2/3 к 1/3, то в среднем выйдем в ноль, если 3/4 к 1/4, то будем выигрывать, а 1/2 к 1/2 — то проигрывать.
Это называется «субъективная интерпретация теории вероятностей», то есть, условно, это не монетка имеет свойство падать орлом с вероятностью 1/2. Это мы плохо умеет предсказывать падающие монетки. А вот робот с высокочастотной камерой и знанием физики ещё в воздухе смог бы сказать, выпадет ли орёл или решка.
Сравнение гипотез
Мы называем утверждения, относящиеся к реальности, гипотезами или моделями. Иногда — теориями, если это модель, у которой очень большая вероятность. Хорошая модель — это такая, которая хорошо угадывает будущие наблюдения, и это главный критерий. Все остальные критерии важны лишь в той мере, в которой позволяют оценить главный без прямого эксперимента.
«Хорошо угадывать» — значит, назначать высокую вероятность тем исходам, которые фактически произойдут. Если первая модель присвоила более высокие, чем вторая, исходы тому, что затем фактически случилось — значит, первая модель лучше.
Как заранее узнать, что одна модель лучше другой? Посмотреть, какая модель лучше предсказывает.x» будет в первом случае очень простым, во втором довольно сложным и потому маловероятным.
Идеальный способ выбрать априорные вероятности — это перебрать разные способы измерения сложности, и выбрать тот, результаты которого лучше всего соотносятся с идеей «проставить равные априорные вероятности, а затем скорректировать априорные вероятности огромным числом наблюдений». То есть наша задача — подобрать такие приоры, чтобы за минимальное число фактов оказываться сильно уверенными именно в той теории, в которой мы в противном случае тоже оказались бы сильно уверены, просто за намного большее число наблюдений.
Генерация моделей (upd)
Новые модели получаются путём выбора из пространства алгоритмов. В идеале мы перебираем все алгоритмы (их бесконечно много) и каждому проставляем свою вероятность быть «той самой истинной моделью» и работаем со всей композицией сразу. На практике нужна какая-нибудь эвристика, которая позволит перебрать конечное множество алгоритмов, и среди них найти достаточно хорошие. Тут никаких абсолютных правил нет — каждый извращается как умеет, и эвристика применима лишь ограниченно. Примеры эвристик: перебор алгоритмов, начиная с самого короткого. Или генерация рандомных алгоритмов и применение к ним генетического алгоритма (отбор наилучших, удаление наихудших, смешивание наилучших в надежде получить что-то ещё лучше, элемент случайности в виде мутаций). То есть мы не всегда можем найти более точную модель, но если мы её каким-то образом получили, то всегда можем проверить, правда ли она более точная.
Алгоритмы не существуют сами по себе — их надо записывать на языках программирования. Соответственно, нужно выбрать язык. Есть два основных критерия поиска.
Во-первых, важно, чтобы на данном языке было удобно искать оптимальный алгоритм. Например, если мы возьмём язык вроде C++, то мы не сможем напрямую скрещивать или мутировать две программы — если мы смешаем их коды, то получится что-то, что даже не скомпилируется. А есть язык Brainfuck — код на нём выглядит как-то так: «2517214», причём «2», «5», «7» — это отдельные действия, то есть любая строка из цифр от 1 до 8 является работоспособным Brainfuck кодом. Для эволюционного поиска BF явно удобнее, чем C++. Если мы сумеем создать язык программирования, который был бы целиком дифференцируемым, как нейросеть, и при этом Тьюринг-полным, мы могли бы искать наиболее точные модели через градиентный спуск.
Во-вторых, разные языки задают разные априорные вероятности моделей. Например, если в языке экспонента вынесена в базовые функции, но она будет казаться чем-то простым и вероятным. А если нет, то придётся её подбирать как-нибудь, например, бесконечным рядом, и в результате все модели с экспонентой будут сильно заштрафованы. То есть в идеале нужно подобрать язык, который бы мог лаконично и точно описать предметную область, и при этом был бы Тьюринг-полным (то есть быть таким, чтобы через него можно было выразить любой другой язык). Для большинства задач, для которых мы применяем компьютеры, лучше всего подходят языки высокого уровня — в них есть специальные функции для наиболее распространённых операций. Поэтому с точки зрения априорных вероятностей лучше всего использовать язык высокого уровня.
В любом случае, как бы мы ни задали язык, если у системы AIXI будет достаточно времени и наблюдений, то она найдёт такую модель, которая будет включать в себя некий оптимальный язык под задачу и лаконичную модель, записанную на этом языке. Системы deep learning действуют аналогично: выделение признаков первыми слоями нейросети — это как раз создание чего-то вроде языка, который лаконично описывает предметную область.
Ну и основной метод тестирования этой модели и смежных: запрограммировать и запустить на решение тестовых задач. Если модель нельзя запрограммировать, то нужно закодить хотя бы малый её кусочек.
Здесь приведён программный код модели и пример её применения — к сожалению, это не строго теоретический AIXI, а его адаптация к реальности, чтобы он работал быстрее и точнее. Выбран язык наподобие Brainfuck, но число операций больше, и для ускорения поиска использованы эвристики эволюции, бустинга (создаём несколько моделей, каждая следующая исправляет ошибки предыдущей) и пост-обработки (выходные данные подаются на вход какой-нибудь обычной системе машинного обучения, вроде линейной регрессии).
Распространённые контраргументы и вопросы
* Этот метод поверхностный, он не даёт глубины. Он не вскрывает глубинные закономерности.
— Полагаю, если метод «вскрывает глубинные закономерности», то он сразу ложный, так как претендует на невозможное. Простая проверка. У нас есть чёрный ящик. Допустим, это программа. Всё, что мы можем с ней сделать — это подать на вход одно число и получить в ответ другое. Это вся доступная информация.
Мы видим закономерность: когда мы подаём X, на выходе получается Y=2X. Во всех наших тестах. Значит ли это, что внутри программы так и написано, return 2X? Ничего подобного. Там может быть return X+X, return 3X-X, return 2X+1-1 и куча других вариантов.
Пока метод, «вскрывающий глубинные закономерности» не научится отличать программу с X+X от программы с 3X-X и всех остальных вариантов, он не «вскрывает глубинные закономерности».
* Он позволяет увидеть лишь простые/линейные/не-динамические закономерности
— Модель — это всегда некий алгоритм, то есть штука, принимающая на вход одну последовательность и выдающая другую. Любую закономерность, которую мы можем записать, можно записать в виде алгоритма (в противном случае понятие алгоритма не полно, и туда надо записать ещё и такую закономерность, которая «неалгоритмична»). GPT-3 — нейросеть, предсказывающая конец текста по началу — построена именно как поведенческая модель, а уж предсказание текста точно не может быть чем-то простым/линейным/не-динамическим
* Подход не позволяет увидеть причинно-следственные связи
— Данный подход действительно не включает причинность как базовый элемент. Тем не менее, подход отвечает на вопросы «что будет, если я нажму кнопку А», «что будет, если я нажму кнопку Б». Это вполне тянет на эмпирическое определение причинности.
* Данный подход к познанию — не единственный возможный, есть другие.
— Я утверждаю, что они или не лучше, или хуже описанного. В любом случае, можно провести прямой эксперимент: два игрока формализуют свои подходы до уровня программного кода, а затем запускают их на куче «чёрных ящиков». Затем смотрим, какой подход лучше предсказывает поведение чёрного ящика, либо лучше угадывает их программный код, либо лучше ими манипулирует. Две основные тестовые площадки — это kaggle и openAI Gym, но можно придумать ещё что-то своё.
* Этот подход к познанию не даёт 100% гарантий чего-либо.
— Да, именно так, и я не видел подхода, который давал бы, и при этом не был ещё более косячным.
* Данный подход не пригоден к изучению людей, потому что их нельзя изучать только по поведению.
— Данный подход рассматривает речь людей как разновидность поведения. Мы «додумываем», что думают и чувствуют другие люди, но это лишь «скрытая переменная», полезная для предсказания, но непроверяемая. А ещё у людей есть априорная информация об устройстве мозгов других людей — не в смысле «упавшая с неба», а в смысле «вколоченная в мозги эволюцией, которая размножала лишь самых социально приспособленных».
* Как этот подход относится к этике?
— Параллельно. Поведенческие модели — это что-то типа карты реальности. А этика — это «куда мы хотим ехать». Так что это разные вещи.
* Ты не можешь всё проверять сам, тебе придётся опираться на слова других людей.
— Я могу к этому относиться как к сенсорным данным. Ну есть у меня термодатчик, я знаю, что иногда он довольно точен, но иногда, при каких-то условиях барахлит, а иногда показывает вовсе не температуру, а что-то другое. Так и со словами людей.
* Люди так не мыслят.
— Чтобы знать, как мыслят люди, надо построить модель мышления, запустить её и сравнить результаты. Рефлексия не очень надёжна. Это с одной стороны. С другой — описанный метод затратен, там что реальные живые существа и ИИ будут использовать какие-то упрощения, в ущерб качеству. Реальные машины не содержат в себе цикл Карно, и не потому, что он чем-то плох.
* Как вы решаете проблему индукции?
— Применяем абдукцию. Не выводим из частного общее, а из кучи «частных» делаем модель для прогноза другой кучи «частных». Затем проверяем точность модели.
* Не станет ли пользователь этой модели солипсистом?
— Вообще, подход неявно включает в себя познающего субъекта и окружающую реальность. Это не соответствует шаблону солипсизма. Но некоторые проблемы солипсизма возможны — например, такой подход даст совершенно бессмысленный ответ на вопрос «что я буду видеть, если я умру». Но может, проблема не в ответе, а в вопросе
* Такой подход не даёт полноты — он пригоден для изучения лишь узкой области.
— Такой подход, будучи запрограммирован, автоматом даёт нам «теорию всего» — с полным покрытием, но очень большой погрешностью. А потом позволяет её уточнять. Поясню. Допустим, мы сделали робота, у него все датчики — это одна видеокамера. И все актуаторы — это одна рука. Все вопросы о будущем, которые может задать робот, выглядят так: что я увижу через свою видеокамеру, если до этого я видел то-то, и рукой двигал так-то. Этот вопрос — вполне корректный вопрос для машинного обучения, чем дольше будет жить робот, тем точнее он будет в своих прогнозах. То есть моделью мира будет нейросеть, которая обучена на прошлом опыте, и она при любых вводных будет выдавать какие-то плюс-минус осмысленные картинки будущего.
* но наука так не работает! У нас нет Теории Всего, это эмпирический факт.
— Ага=( У нас к каждой научной теории вдогонку идёт не очень формализованная теория по её интерпретации. Есть механика Ньютона? Отлично, а теперь давайте опишем, что такое «масса» в терминах того, какие предметы надо взять в руки, на какие весы положить, и что делать, если весов рядом нет. И окажется, что понятия «массы» в квантмехе и астрофизике инструментально различаются. Нет у нас единого набора инструментов, который бы и для микромира хорошо работал, и для астрономических величин. Приходится эти концепции состыковывать в воображении учёного. Я не считаю, что проблема именно в массе. Я считаю, что проблема в том, что мы не можем просто провести кучу измерений, загнать данные в нейросеть и на выходе получить Теорию Всего — потому что мы не можем провести кучу измерений одним и тем же оборудованием, то есть у нас нет единого массива сенсоров
* Очень прагматичный подход. Ориентирован на эксплуатацию мира, а не изучение.
— В этом подходе познание примерно равно эксперимент примерно равно эксплуатация. Я не вижу смысла в других критериях истинности, кроме как «это полезная модель, чтобы достигать цели» и «это точная модель, чтобы делать прогнозы».
* Этот подход не работает для гуманитарных наук.
— Ну, во-первых, это повод спросить, а правда ли они науки. Во-вторых, некоторые гуманитарные науки реально что-то предсказывают. Например, есть теория прайминга в психологии. Если на товаре будет написано «не менее 10 в одни руки», у человека будет склонность купить именно 10 единиц товара. Теория немного шире, но сосредоточимся на одной конкретной закономерности. Она проверяема экспериментально? Да, можно поделить магазины на две группы, и в одной из них делать соответствующую вывеску про 10 единиц, а в другой — нет.
* Этот подход не работает для исторических наук
— Прошлого в каком-то смысле не существует. Оно есть лишь в виде следов. Мы додумываем прошлое. Иногда исторические теории можно проверить, например, некоторые теории предсказывают, что в некоем месте удастся найти древний город. Если мы колеблемся между несколькими историческими теориями, то гипотетически могут быть факты, которые склонят нас к какой-то из них.
* Основной вопрос философии?
— Если его свести в вопросу «что я увижу в случае таком-то», то на него будет конкретный ответ (или конкретное «не знаю»), иначе выглядит как что-то, не имеющее отношения к реальности. Если свести его к вопросу «мыслят ли люди мозгом» и далее к вопросу «если повредить мозг, то сохранятся ли наблюдаемые признаки мышления, то есть поведение», то ответ тоже очевиден, и его даёт чистая эмпирика
* Есть ли яркий пример того, как эта теория познания полезна?
— Всё машинное обучение на ней работает. Да, в машинном обучении редко применяется концепция сложности модели, и не происходит перебора во всём множестве алгоритмов. Поэтому теория AIXI несколько шире, чем практически применимый машинлёрнинг. Кроме того, существуют разные интерпретации квантмеха. Одни и те же формулы, но разные интерпретации. Так вот, крупная группа учёных вообще отказываются от интерпретации (говорят «заткнись и считай»), то есть действуют в духе описанной поведенческой теории познания.
* Как «поведенческая» теория относится к логическим категориям?
— На входе и выходе модели мы используем либо сырые данные (циферки с датчиков), либо данные, категоризованные какой-либо иной системой. Внутри модели может быть что угодно. Обычно там математика, но может быть любая другая система вывода, если такая найдётся. Нейросети вполне способны создавать свои «категории» из элементарных блоков, так что это вполне посильная задача
* Это теория не строит «объективную» модель мира. В ней всегда есть точка зрения.
— Да. Если повезёт, то данные будут собраны со многих «точек зрения», и теория будет применима независимо от того, откуда мы смотрим на мир. Но модели мира вообще без «точки зрения» у нас нет. Впрочем, в практической деятельности всегда есть конкретные действующие лица и выгодоприобретатели, так что не вижу проблемы.
* В чём отличие от научного метода и научной практики?
— Наука стремится создать единую непротиворечивую картину мира. То есть в научных журналах не публикуют статьи вида «вот это лекарство лечит от болезни, с вероятностью 80%, а с вероятностью 20% — нет. Через полгода и десять мегабаксов мы обновим цифры». P-value хуже, чем 0.05 в науке большая редкость.
Кроме того, наука ориентируется в основном на эксперимент. А «поведенческий анализ» больше опирается на наблюдения. Не потому, что они лучше, а потому, что они дешевле и доступнее. Если есть возможность, лучше ставить эксперименты.
Меньше внимания к объяснению, больше к прогнозу. Неважно, что человек не понял теорию — главное, он может вести по ней расчёты. Появится интерпретируемость? Хорошо, но это не главное.
У наук есть конкретный предмет познания, а у «поведенческого анализа» предмет — это всё, что приходит через сенсоры, то есть «поведенческий анализ» всегда пытается строить «Теорию Всего».
Интерпретация теории вероятности — субъективная (монетка упадёт орлом к вероятностью 50% — это факт не о монетке, а о моём незнании), а в «настоящей» науке — обычно частотная.
При достаточном времени и статистике данный метод примерно сводится к науке в современном понимании.
* Ваш метод буржуазный/либеральный/идеалистический/материалистический/ещё какой-то.
— Этот метод не относится напрямую к обществу. Он может работать и в коллективе, и у одного человека, и у нечеловеческого ИИ. Данному методу неважно, какие способы обобщения использовать — хорошо бы иметь большую «библиотеку» абстракций, но при нужде можно всё разработать с нуля.
* Ваш метод догматичен, вы узко смотрите, вы не видите того-то и того-то.
— Возможно, то, чего мы не видим — не более, чем чей-то глюк. Если мы не видим какую-то реально важную штуку, то будет некая группа задач, где наш метод работает систематически плохо, а какой-то другой — хорошо. Для пользователей данного метода это будет выглядеть так: часть людей использует стратегию, которая необъяснимым образом постоянно приводит их к успеху. На этом весь догматизм кончится и начнутся попытки скопировать удачную стратегию
* Этот подход предполагает, что всё можно оцифровать и измерить, а это не так.
— Оцифровка — довольно искусственная операция. Например, мне нужно сделать систему, которая предсказывает, будет ли у человека болеть какая-либо часть тела. Нам нужно оцифровать боль. Самый простой способ — если есть боль, то записываем 1, иначе 0. Способ посложнее — если есть какие-то градации сильнее/слабее, то можно присвоить им числа. 0 — нет боли, 1 — чуть-чуть болит, 2 — средне болит, 3 — сильно, 4 — ужас-кошмар. Оцифровка — это наш способ разложить сходные наблюдения по кучкам, не более того.
* Ваш подход не учитывает, что мы можем взломать код чёрного ящика или спросить о нём разработчика.
— При взломе мы всё равно будет использовать какие-то средства воздействия и средства наблюдения. Их мы и назовём сенсорами и актуаторами. При общении с разработчиком мы всё равно используем какой-то канал связи — он и будет нашим сенсорным входом. То есть если мы сделаем что-то из вышеперечисленного, то мы изменим границы чёрного ящика: теперь туда входит и наше средство взлома, и предполагаемый разработчик.
* Ваш подход основан на аксиомах, точно так же, как подход такой-то. Вы просто верите в какие-то другие штуки.
— Вышеописанный подход опирается на априорные вероятности, а не аксиомы. Разница в том, что априорные вероятности — это первичные допущения, и по ходу работы они точно изменятся. Мы используем матаппарат, а значит, и аксиомы теории вероятностей, чтобы измерять точность. Это не значит, что мы находимся во власти исходных допущений — это значит, что мы используем язык матстата, чтобы выражать свои мысли. Его можно использовать для описания практически любого правила, по которому оценивается качество модели.
новые штрихи к портрету • Айк Акопян • Новости науки на «Элементах» • Астрофизика, Черные дыры
В апреле 2019 года коллаборация Телескопа горизонта событий (Event Horizon Telescope, EHT) опубликовала первое «фото» ближайших окрестностей сверхмассивной черной дыры, находящейся в центре гигантской эллиптической галактики M87. Галактика удалена от нас примерно на 53 млн световых лет, а размер запечатленной области составляет несколько световых дней. Такой феноменальной разрешающей способности удалось добиться благодаря тому, что EHT — это не один телескоп, а система из нескольких крупных радиотелескопов, расположенных на разных континентах, но работающих как единое целое. Коллаборация продолжала работать, и сейчас, спустя два года ученые представили новую порцию данных. Им удалось запечатлеть поляризованное излучение от аккреционного диска вокруг этой черной дыры, тщательный анализ которого позволил многое понять про структуру магнитного поля в ее окрестностях. В некотором смысле этот результат даже важнее, чем «портрет» черной дыры, полученный два года назад, так как он позволил достаточно надежно определить режим, в котором аккрецирует эта дыра. По удачному совпадению недавно же была опубликована и статья нескольких научных групп, работающих на самых разных телескопах (как наземных, так и космических), которые провели наблюдения бьющего из этой черной дыры джета в широкой области электромагнитного диапазона. Из нее следует, что до полного понимания всех процессов, которые порождают джеты и и происходят внутри них, довольно далеко, но зато сейчас теоретики получили новые ограничения на параметры своих теорий.
Предыстория
Черные дыры — объекты с самой высокой плотностью энергии в нашей Вселенной: в достаточно малом по астрофизическим меркам объеме сконцентрирована гравитационная и вращательная энергия огромного количества вещества, которое когда-то сформировало эту дыру. Сейчас известно, что существуют черные дыры как минимум двух классов: дыры звездных масс (их массы обычно обычно попадают в промежуток от нескольких до нескольких десятков масс Солнца) и сверхмассивные черные дыры (СМЧД), обитающие в центрах галактик (их массы измеряются миллионами или даже миллиардами масс Солнца). Вопрос о существовании черных дыр промежуточной массы (порядка 104–105 масс Солнца) пока открыт.
Радиус горизонта событий черной дыры пропорционален ее массе (\(r_g=2GM/c^2\), подробнее об этом см., например, в задаче Испарение черных дыр). Размер «звездных» черных дыр лежит в диапазоне от нескольких до пары десятков километров. А вот радиус горизонта СМЧД — это уже поистине астрономическая величина: от нескольких радиусов Юпитера (сотни тысяч км, это порядка одной световой секунды) до нескольких десятков астрономических единиц (1 а. е. ≈ 1,5·1011 м, то есть речь идет о миллиардах километров — или световых часах).
Распространено представление о черных дырах как о чрезвычайно «прожорливых» объектах, которые поглощают оказавшееся поблизости вещество и благодаря этому только увеличивают свою массу. Если не вдаваться в детали, то дело примерно так и обстоит. Тем удивительнее, что природа умеет «извлекать» энергию из этих объектов в процессе аккреции. Вокруг СМЧД в центрах галактик вещество из межзвездного пространства постепенно теряет момент импульса и формирует аккреционный поток, который медленно, но верно падает на черную дыру.
По мере приближения к горизонту событий вещество теряет гравитационную энергию и из-за этого нагревается. Изначально холодный неионизированный газ нагревается до миллиардов кельвинов. При этом средняя энергия электронов и протонов становится во много раз больше энергии связи в атомах — вещество полностью ионизируется. В результате медленное и размеренное течение межзвездного водорода в нескольких световых годах от горизонта событий на расстоянии нескольких световых дней от него становится очень горячим электрон-протонным супом, движущимся со скоростью, близкой к скорости света. Что важно, нагретая плазма имеет свойство излучать, и это излучение можно попытаться увидеть! А что еще важнее, если в аккреционном диске присутствуют магнитные поля, то это излучение еще и поляризовано и, измерив поляризацию, можно узнать структуру магнитного поля. Но об этом ниже.
Почему вообще в аккреционном диске должны существовать магнитные поля? Причин может быть несколько (к примеру, генерация магнитных полей в результате так называемого «динамо» в аккреционных дисках, см. работы M. Liska et al., 2020. Large-scale poloidal magnetic field dynamo leads to powerful jets in GRMHD simulations of black hole accretion with toroidal field и A. Brandenburg et al., 1995. Dynamo-generated Turbulence and Large-Scale Magnetic Fields in a Keplerian Shear Flow), но самой важной является эффект сохранения магнитного потока. Идею можно проиллюстрировать на следующем примере. Рассмотрим большой объем обычного водорода и начнем его сжимать (рис. 2). Если в этом объеме присутствует магнитное поле, то поначалу оно никак не будет чувствовать электрически нейтральный водород, так как магнитное поле взаимодействует только с зарядами. В результате силовые линии никак не будут чувствовать сжатия, оставаясь неизменными. Однако в какой-то момент из-за сжатия вещество нагреется и начнет ионизироваться.
В среднем, ионизированный газ (плазма), также электронейтрален, но электроны и протоны в нем не связаны и могут перемещаться независимо друг от друга. Точнее, почти независимо: у движения частиц в плазме есть два важных свойства. Во-первых, если в какой-то области окажется больше электронов, чем протонов, то возникнет электрическое поле, которое притянет протоны, и баланс восстановится. Во-вторых, если в системе есть магнитное поле, то частицы не могут свободно перемещаться поперек его силовых линий (подробно этот эффект обсуждался в задаче Северное сияние). А магнитные силовые линии, в свою очередь, не могут свободно «скользить» в плазме. В результате магнитное поле и частицы в плазме оказываются связанными друг с другом. Этот эффект называется «вмороженностью» магнитного поля в плазму. В итоге частицы плазмы в магнитном поле ведут себя подобно бисеру на нитке: они свободно перемещаются вдоль силовых линий, но не могут перемещаться поперек них.
«Вмороженность» магнитных линий в плазму означает, что, если плазма, приближаясь к горизонту событий, уплотняется, то силовые линии будут завлекаться за веществом, а сила поля будет увеличиваться (как показано на рис. 2). Первые идеи о том, что магнитные поля могут быть принципиально важны в таких аккрецирующих системах появились еще в 1970 годах (см., например, статью G. Bisnovatyi-Kogan, A. Ruzmaikin, 1974. The accretion of matter by a collapsing star in the presence of a magnetic field).
Однако вопрос о роли магнитного поля в процессе аккреции оставался открытым.
К 90-м годам стало понятно: магнитные поля необходимы, чтобы объяснить, почему аккреция происходит в принципе (S. Balbus, J. Hawley, 1991. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis; см. также задачу Аккреция вопреки). Дело в том, что для того, чтобы вещество аккрецировало на черную дыру (а не просто вращалось по кеплеровским орбитам, как планеты вокруг звезд), необходимо трение между слоями. Однако было совершенно непонятно, что может вызывать это трение — обычной силы вязкости недостаточно, чтобы объяснить тот темп аккреции, который наблюдался напрямую. Решением стала так называемая магниторотационная неустойчивость. В этом механизме магнитное поле играет роль инициатора турбулентности, которая и вызывает аномально сильное трение, достаточное, чтобы объяснить высокий темп аккреции.
От теории к симуляциям
Чтобы аккреция шла, достаточно даже очень слабого магнитного поля, поскольку оно усиливается из-за магниторотационной неустойчивости (J. Stone et al., 1996. Three-dimensional Magnetohydrodynamical Simulations of Vertically Stratified Accretion Disks). Поэтому важный вопрос о том, насколько сильно на самом деле поле в аккреционных дисках и насколько оно влияет на крупномасштабную динамику процесса аккреции, оставался без ответа.
К концу XX века астрофизики поняли, что модель тонкого диска (диск Шакуры — Сюняева, см. N. Shakura, R. Sunyaev, 1973. Black holes in binary systems. Observational appearance, а также задачу Дисковая аккреция), предложенная еще в 1970 годах, в которой все происходит в тонкой дискообразной области, применима далеко не ко всем аккрецирующим системам. Ключевым предположением в модели тонкого диска являлась радиационная эффективность: вся энергия нагрева плазмы эффективно излучается из диска в виде фотонов, что позволяет веществу сплюснуться в тонкий диск. Но в аккреционных системах типа черной дыры M87* в центре галактики M87 или черной дыры в центре нашей Галактики это предположение неверно: вещества слишком мало, и нагрев происходит слишком быстро, из-за чего вещество не успевает «остыть» и сплюснуться в диск. В результате возникла модель толстого диска. Несмотря на аналитическую сложность, она неплохо годится для численных симуляций, поскольку для моделирования толстого диска не требуется огромное разрешение, которое нужно в случае с тонкими дисками.
В XXI веке из численных симуляций стало ясно, что есть два режима аккреции толстого диска (рис. 4, также см. статьи R. Narayan et al., 2012. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: role of outflows, F. Foucart et al., 2017. How important is non-ideal physics in simulations of sub-Eddington accretion on to spinning black holes? и B. Ripperda et al., 2020. Magnetic Reconnection and Hot Spot Formation in Black Hole Accretion Disks): режим стандартной и нормальной эволюции (англ. — Standard And Normal Evolution, SANE; в переводе с английского sane буквально означает «здравый») и режим магнитодоминирующего диска (англ. — Magnetically Arrested Disk, MAD; в переводе mad означает «сумасшедший»). В режиме SANE магнитное поле очень слабое и играет лишь промежуточную роль: оно запускает процесс турбулентности, но в остальном динамика диска полностью определяется движением вещества. Из-за этого в SANE-моделях магнитные поля турбулентны и менее структурированы, а джеты в таких симуляциях достаточно слабые. В режиме MAD, который характеризуется тем, что сила магнитного поля достаточно большая и давление магнитного поля сопоставимо с давлением вещества, силовые линии структурированы и играют не просто важную роль в формировании джета и аккреции, но способны на время затормозить аккрецию и даже запустить ее в обратном направлении, делая ее прерывистой и непостоянной.
Однако эти модели до поры до времени не подтверждались наблюдениями и «существовали» лишь в виде симуляций, результат которых зависит от начальных условий (пример симуляции можно посмотреть на этом видео).2\)). Легко посчитать, что угловой размер горизонта событий — 10−5 угловых секунд (то есть примерно 10 микросекунд дуги). Чтобы понять, насколько эта величина мала, достаточно представить, что вы пытаетесь увидеть десятирублевую монету на поверхности Луны, находясь на Земле.
В оптике есть достаточно простой способ оценить, какого размера телескоп понадобится, чтобы оптически разрешить объект данного углового размера: на длине волны \(\lambda\) минимальный угловой размер (в радианах) детали, который вы можете разглядеть с помощью телескопа с диаметром зеркала (апертурой) \(D\), равен \(\lambda /D\). Ярче всего вещество вокруг черной дыры светит в радиодиапазоне, на частоте примерно несколько сотен ГГц, поэтому легче всего наблюдать именно на соответствующей длине волны (примерно 1 мм). Чтобы разрешить горизонт событий на этой длине волны, необходим телескоп, диаметр которого сравним с размерами Земли!
Ясно, что телескоп такого размера построить невозможно (по крайней мере, в обозримом будущем). Однако люди нашли изящный способ «обойти» эту проблему. Этот способ — радиоинтерферометрия (см. задачу Как ловить тень черной дыры). Если синхронизировать работу радиотелескопов в разных точках Земли с высокой точностью (ошибка синхронизации должна быть меньше, чем период радиоволны), то эти телескопы могут работать вместе — так, как если бы это был один телескоп, размеры которого сопоставимы с расстоянием между телескопами.
Подходящих кандидатов для наблюдений оказалось всего два: уже упоминавшиеся Sgr A* в центре нашей Галактики и M87* в центре галактики M87. Вторая дыра в ~2000 раз дальше от нас, но она и примерно во столько же раз массивнее, что делает наблюдаемый угловой размер ее горизонта событий сравнимым с Sgr A*. Казалось бы, нет разницы, какую из черных дыр наблюдать. Но нет: легкие — а значит и маленькие — черные дыры обладают существенным недостатком: происходящее в их непосредственной окрестности слишком быстро меняется. Период обращения вещества вблизи горизонта событий СМЧД Sgr A* составляет около часа, а для M87* это время ближе к одному месяцу. Это означает, что изображение M87* более стационарно и при помощи радиоинтерферометрии его гораздо легче запечатлеть.
Вся эта «теория», граничащая местами с научной фантастикой, воплотилась в реальность благодаря усилиям коллаборации Телескопа горизонта событий (Event Horizon Telescope, EHT). Это глобальная сеть радиотелескопов, расположенных на разных континентах и работающих по принципу радиоинтерферометрии как один большой телескоп размером с земной шар. Ученым потребовалось более десяти лет работы, чтобы получить «фото» горизонта событий сверхмассивной черной дыры в центре галактики M87 в радиодиапазоне (рис. 5, подробности — в новости Черная дыра галактики M87: портрет в интерьере, «Элементы», 14.04.2019). Саму дыру мы, конечно, не видим: это изображение формируется светом, излученным горячей плазмой в аккреционном диске и/или джете вокруг черной дыры, значительно искаженным из-за сильно искривленного пространства-времени вокруг горизонта событий.
То, что раньше можно было изучать лишь теоретически, стало возможным наблюдать непосредственно и сравнивать с теоретическими предсказаниями! И здесь довольно быстро после громкого триумфа наблюдателей пришел отрезвляющий ответ от теоретиков. Теперь, когда имелись наблюдения, они получили возможность сделать большое количество симуляций с разными параметрами (разным вращением черной дыры, режимом аккреции, направлением оси вращения и т. д.) и сравнить их с наблюдениями!
На самом деле, сами по себе такие симуляции — это уже непростая задача. Проблем здесь несколько. Во-первых, магнитогидродинамические симуляции, которые еще и учитывают искривленное пространство-время вокруг черных дыр (так называемые GRMHD-алгоритмы), очень сложны в реализации и необыкновенно дороги с вычислительной точки зрения. Была проделана отдельная большая работа по сравнению основных результатов GRMHD-программ разных научных групп между собой, чтобы понять, насколько эти алгоритмы близки друг к другу (O. Porth et al., 2019. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project). Во-вторых, магнитная гидродинамика, методы которой используются для симуляций и построения изображений, лишь аппроксимирует плазму — как некую замагниченную жидкость определенной температуры. В реальности это не совсем так: плазма вокруг сверхмассивных черных дыр бесстолкновительная (то есть она не является жидкостью в строгом смысле этого слова), а электроны и протоны могут вообще иметь разные температуры! Поэтому для построения изображения делается огромное количество допущений и приближений, которые в свою очередь добавляют свободные параметры.
Оказалось, что численные модели предсказывают примерно одинаковую картину (The Event Horizon Telescope Collaboration, 2019. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring): «бублик» с асимметричными краями, возникающими из-за релятивистского усиления излучения в одном из направлений и ослабления в другом. Железно удалось подтвердить только то, что черная дыра вращается (но это мы и так знали благодаря наличию у нее джета; об этом еще будет сказано ниже). Из сравнений с симуляциями с множествами открытых параметров и настроек понять, какое у черной дыры магнитное поле, в каком режиме протекает аккреция (MAD или SANE), как направлен аккреционный диск относительно джета и многое другое, так и не удалось.
Поляризованный свет в конце тоннеля
Чтобы еще больше ограничить множество возможных параметров, нужны были какие-нибудь более детальные наблюдения этой черной дыры. И тут самое время вспомнить о том, что помимо интенсивности и частоты (наблюдения на другой длине волны также проводились и будут вскоре опубликованы) у света есть поляризация. Именно ее и удалось измерить для M87*. Две статьи с этими результатами были опубликованы некоторое время назад в журнале The Astrophysical Journal Letters.
Заряженные частицы в плазме находятся в постоянном движении. Электроны рассеиваются на протонах и друг на друге из-за кулоновского взаимодействия, а любое ускорение или торможение заряженной частицы влечет за собой излучение электромагнитных волн — света. Такое излучение называют тормозным (нем. bremsstrahlung, см. задачу Тормозное излучение). В среднем тормозное излучение не поляризовано, так как рассеяние в плазме происходит во всех направлениях и поляризации отдельно взятых волн налагаются друг на друга, производя в сумме неполяризованный свет.
Но если в плазме есть магнитные поля, то все гораздо интереснее. В магнитном поле релятивистские электроны могут излучать так называемое синхротронное излучение (см. задачу Синхротронное излучение в Крабовидной туманности). Его поляризация — если она есть — определяется направлением внешнего магнитного поля. А поляризовано это излучение может быть, потому что масштабы магнитного поля значительно превосходят масштабы плазмы (то есть для огромного количества частиц направление магнитного поля, а следовательно, и плоскость поляризации, будет одинаковым). В реальности, конечно, наблюдаемый свет лишь частично поляризован. Процент поляризованного света называют долей поляризации (англ. fractional polarization).
Наблюдаемый от черной дыры M87* свет был поляризован местами на 30%, что означает достаточно сильное и структурированное магнитное поле (рис. 6).
Из этих данных о магнитном поле можно сделать несколько выводов. Во-первых, большая доля поляризации говорит о том, что магнитное поле в аккреционном диске не хаотично и турбулентно, как предсказывали многие SANE-модели, а структурировано. Во-вторых, спиральная структура поляризации означает, что магнитное поле преимущественно сонаправлено с осью вращения (рис. 7), что полностью вписывается в предсказания многих MAD-моделей.
Все это означает, что новые данные позволяют уверенно «закрыть» длящуюся десятилетия дихотомию: они однозначно указывают, что аккреционный диск M87* находится в MAD-режиме с сильным структурированным магнитным полем, направленным вдоль оси вращения (рис. 8).
Помимо всего этого плоскость поляризации может вращаться по мере распространения волны сквозь замагниченную плазму из-за фарадеевского вращения. Это позволяет определить не только направление магнитного поля, но и его величину, а также плотность и температуру плазмы. Эти результаты как раз-таки оказались очень ожидаемыми: величина магнитного поля варьируется от нескольких до нескольких десятков Гаусс, плотность — от 104 до 107 частиц на кубический сантиметр, а температура в наблюдаемой области лежит в диапазоне 1010–1011 К.
Джет галактики M87 крупным планом
Джеты — это уникальные индикаторы сверхмассивных черных дыр во Вселенной. Их можно наблюдать (а значит — и изучать) во всех возможных диапазонах электромагнитного излучения — от радио- в ГГц (длина волны ~см) до высокоэнергичного гамма-излучения, кванты которого имеют энергию порядка ТэВ (длина волны ~10−18 см). Процессы, порождающие джеты и происходящие внутри них, чрезвычайно энергичные: ученые детектируют высокоэнергичные нейтрино и космические лучи, предположительно произведенные в недрах этих джетов. Самое удивительное, что несмотря на свою протяженность (многие джеты превосходят в размере галактику, в которой они родились), источник энергии джета немногим превосходит саму черную дыру. Так, в галактике M87 джет тянется на десятки тысяч световых лет, тогда как область, в которой он «ускоряется», имеет размер немногим больше светового дня! Как именно работает центральный источник, который запускает джет, размеры которого на несколько порядков превосходят размер самого источника? Что именно излучает в джете в таком необыкновенно широком диапазоне? Как при этом производятся нейтрино и космические лучи экстремальных энергий? Все эти вопросы во многом пока остаются загадкой.
Вблизи горизонта событий быстро вращающейся черной дыры пространство-время «завлекается» за ее вращением. Поэтому в этой области ничто не может находиться в состоянии покоя (без вращения). Эта область называется эргосферой черной дыры, и уже давно известны теоретические механизмы (например, процесс Пенроуза, см. Penrose process), при которых вещество с помощью особенностей этой области может забирать энергию вращения у черной дыры, постепенно ее останавливая. Похожий процесс может отвечать и за «запуск» джета с помощью закручивания магнитных силовых линий в эргосфере черной дыры (см. видео; R. Blandford, R. Znajek, 1977. Electromagnetic extraction of energy from Kerr black holes).
До сих пор при этом не до конца ясно, как именно такая структура остается стабильной на всем своем протяжении, как полость джета заполняется плазмой (сильное магнитное поле имеет свойство выталкивать плазму) и как именно эта плазма излучает. В недавней наблюдательной кампании десяток телескопов, работающих в диапазонах от радио- до высокоэнергичного гамма-излучения, было детально изучено излучение джета в галактике М87 (рис. 9). Статья с описанием этих результатов также была опубликована в одном из недавних номеров журнала The Astrophysical Journal Letters. Гамма-телескопы имеют очень плохую разрешающую способность, и поэтому понять, из какой области джета конкретно приходят высокоэнергичные фотоны, можно только по неявным признакам.
Простейшей моделью до сих пор являлась теория самосогласованного синхротронно-комптоновского излучения. Согласно ей, в некоторой компактной области вокруг черной дыры (размер этой области — несколько радиусов Шварцшильда) лептоны излучают низкоэнергичное синхротронное излучение (см. задачу Синхротронное излучение в Крабовидной туманности) на фоне магнитных полей джета и диска. Затем те же энергичные лептоны в джете сталкиваются с низкоэнергичными фотонами, «выкидывая» их на высокие энергии (этот процесс называется обратным комптоновским рассеянием). У этой модели есть серьезное ограничение: всё это может происходить лишь в довольно небольшой области вокруг основания джета, где плотность лептонов и их энергии достаточно велики.
Как показали результаты последних наблюдений, эта модель не согласуется с интенсивным гамма-излучением джета M87. Чтобы объяснить его высокую интенсивность в гамма-диапазоне (1042 эрг/с), требуется огромное количество энергичных гамма фотонов, сконцентрированных в очень маленькой области размером в несколько радиусов черной дыры. Однако при этом возникают теоретические проблемы: при такой большой плотности гамма-фотоны могут взаимодействовать с низкоэнергичными (например, оптическими) фотонами и рождать огромное количество электрон-позитронных пар, увеличивая при этом количество материи в джете, но уменьшая интенсивность излучения. Эта проблема в астрофизике высоких энергий известна как проблема компактности, и раннее в основном обсуждалась в контексте источников гамма-всплесков. Однако теперь, после детальных наблюдений и оценок светимости на различных диапазонах, эта проблема остро встала и применительно к джету галактики М87 — область, в которой обязано происходить ускорение лептонов и интенсивное излучение в гамма-диапазоне, должна быть в десятки раз больше, чем предполагалось раннее. Но это очень сложно обосновать теоретически, так как далеко от черной дыры и магнитные поля, и плотность материи сильно меньше, чем в ее непосредственной окрестности.
В общем, вопрос о природе излучения в джетах тоже пока остается открытым, но в этом вечном «пинг-понге» между наблюдателями и теоретиками мячик теперь на стороне теоретиков.
Третьей уже не будет
Данные, полученные коллаборацией EHT по итогам наблюдения за M87*, позволили ученым значительно сузить и во многом прояснить понимание деталей процесса аккреции на сверхмассивные черные дыры. Но многие вопросы пока еще остаются открытыми. С точки зрения крупномасштабной динамики до сих пор непонятно, какие черные дыры производят джеты, а какие — нет. От чего и как это зависит? Могут ли джеты периодически «включаться» и «выключаться» — даже при постоянной аккреции (см., например, S. Ressler et al., 2021. Magnetically modified spherical accretion in GRMHD: reconnection-driven convection and jet propagation)?
Нам, как наблюдателям, одновременно очень повезло и не повезло. Не повезло нам потому, что сверхмассивных черных дыр достаточно большого углового размера, подходящих для наблюдения с Земли, всего две — Sgr A* и M87* (данные по Sgr A* обрабатываются и будут опубликованы позже). Третьей такой черной дыры скорее всего не существует, а сделать радиоинтерферометрию на порядки точнее не удастся, скорее всего, еще очень долго.
Но в то же время нам крупно повезло, что в относительно близких окрестностях Млечного Пути вообще нашлась активная сверхмассивная черная дыра, и у M87* мы видим отчетливый энергичный джет, а у нашей собственной дыры Sgr A* джета нет. Означает ли это, что черная дыра в центре Галактики аккрецирует в другом режиме? Отличаются ли свойства аккрецирующего вещества и магнитного поля? Или это результат какого-то геометрического эффекта, из-за которого джет очень слабый и мы не можем его наблюдать? Дальнейшие наблюдения Телескопа горизонта событий наверняка помогут нам приблизиться к ответам на эти вопросы.
Источники:
1) The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring // The Astrophysical Journal Letters. 2021. DOI: 10.3847/2041-8213/abe71d.
2) The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon // The Astrophysical Journal Letters. 2021. DOI: 10.3847/2041-8213/abe4de.
3) The EHT MWL Science Working Group. Broadband Multi-wavelength Properties of M87 during the 2017 Event Horizon Telescope Campaign // The Astrophysical Journal Letters. 2021. DOI: 10.3847/2041-8213/abef71.
Айк Акопян
| Axiom | Манипулятивная | Обсуждение | ||
|---|---|---|---|---|
| II, 1 |
|
Это говорит нам, что если точка B находится между A и C , | ||
| II, 2 |
|
Эта аксиома устанавливает, что между любыми двумя точками на прямой существует | ||
| II, 3 |
|
Это говорит о том, что если точка B находится между точками A и | ||
| II, 4 |
|
Эта аксиома устанавливает, что точки на прямой всегда можно расставить по порядку. | ||
| II, 5 |
|
Эта аксиома устанавливает, что прямая линия, пересекающая одну сторону треугольника, должна |
Гильбертс
Гильбертс
ТОС и гл. 0 и гл. 1 Аксиома | Гл. 2 Нейтральная геометрияЧ. 2 Содержание | Гл. 3 TransformationalCh. 3 Содержание 3.1.1 Введение | Гл. 4 Проективная геометрияЧ. 4 Содержание 4.1.1 Введение 4.1.2 Историческое 4.2.1 Аксиомы 4.2.2 Основные теоремы 4.3 Двойственность 4.4 Теорема Дезарга 4.5.1 Гармонические наборы 4.5.2 Музыкальные и гармонические наборы 4.6.1 Определения проективности 4.6.2 Основная теорема 4.6.3 Проективность / Гармонические множества 4.6.4 Альтернативная конструкция 4.7.1 Коники 4.7.2 Теорема Паскаля 4.7.3 Касательные к коникам | Другие темы 5 Сферическая геометрияЧ. 6 Фрактальная геометрияЧ. 7 Топология | ПриложенияИнтернет-ресурсыIndexGeometer’s Sketchpad / GeoGebraJavaSketchpad / GeoGebraHTML Видео-лекции Логический обзор Рекомендации Благодарности |
Приложение А. Аксиомы Гильберта для евклидовой геометрии
Распечатка
Математика — это игра, в которую играют согласно
определенные правила с бессмысленными пометками на бумаге.
Дэвид Гильберт (18621943)
Вступительное примечание. Набор аксиом Гильберта является примером того, что
называется синтетическая геометрия . Синтетический
геометрия имеет промежуточность и конгруэнтность как неопределенные термины, свойства
конгруэнтность дана в аксиомах, не имеет
аксиомы для измерения расстояния и угла. Однако Axiom V.1 связана с
измерение длины путем сравнения двух произвольных отрезков.
Неопределенные термины балла,
линия, самолет
лежать между 90 285 и
соответствие.
(Некоторые веб-браузеры неправильно отображают некоторые символы, угол отображается как
∠, конгруэнтный
отображается как ≅ ,
а греческие символы альфа и бета отображаются как
α ,
β .)
Группа I.Аксиомы Заболеваемость
I.1. Для каждых двух точек A, B, существует линия м
который содержит каждую из точек A, B .
I.2. На каждые две точки A, B, не больше
чем одна линия м , содержащая каждую из точек A, B .
I.3. На прямой есть как минимум две точки. Там
существуют как минимум три точки, не лежащие на одной линии.
I.4. Для любых трех точек A, B, C , которые не лежат на одном и том же
линии существует плоскость a , содержащая
каждая из точек A, B, C. Для каждой плоскости существует точка, которая
это содержит.
I.5. Для любых трех точек A, B, C , которые не лежат на одном и том же
линии, существует не более одной плоскости, содержащей каждую из трех
точки A, B, C .
I.6.Если две точки A, B отрезка м лежат в плоскостиα , то каждая точка м лежит в плоскости
Альфа .
I.7. Если два самолетаα ,
β есть точка
A общего, то у них есть еще хотя бы одна общая точка B .
I.8. Существует не менее четырех точек, не лежащих на плоскости.
Группа II.Аксиомы порядка
II.1. Если точка B находится между точками A и C , то
A, B, C — три отдельные точки на линии, а B также находится между
C и A.
II.2. Для любых двух различных точек A, и C, там
существует в
по крайней мере одна точка B на линии AC такая, что C находится между
A и B .
II.3. Из любых трех точек на прямой существует не более одной,
лежит между двумя другими.
II.4. Пусть A, B, C — три точки, которые не лежат на прямой и
пусть м будет линией в плоскости ABC , которая не соответствует ни одному из
точки A, B, C . Если линия м проходит через точку
сегмент AB , он также проходит через точку сегмента AC или
отрезок г. до н.э.
Группа III. Аксиомы конгруэнтности
III.1. Если A, B — две точки на линии м и A ‘
точка на той же или на другой линии м ‘ тогда всегда возможно
найти точку B ‘ на заданной стороне линии от м’ до A ‘
таким образом, что сегмент AB конгруэнтен сегменту A’B ‘.В
символы AB
≅ A’B ‘.
III.2. Если два сегмента конгруэнтны третьему, они конгруэнтны.
друг другу.
III.3. На линии м пусть AB и BC будут двумя отрезками.
которые кроме B не имеют ничего общего. Кроме того, на том же или
на другой линии m ‘ пусть A’B’ и B’C ‘ будут двумя сегментами
которые кроме B ‘ также не имеют ничего общего.В том случае, если
AB
≅
A’B ‘ и BC
≅ B’C ‘, , затем AC≅
A’C ‘.
III.4. Позволять
∠ ( h, k) — угол в
самолетα и м ‘ прямая на плоскости
α ‘ и
пусть определенная сторона м ‘ дюймα ‘
быть данным.Пусть h ‘ будет лучом на линии m’ , который исходит из
точка О ‘. Тогда существует в плоскостиα ‘
один-единственный луч k ‘ такой, что угол
∠ ( ч, к)
конгруэнтно углу
∠ ( h ‘, k’) и при
одновременно все внутренние точки угла
∠ ( ч ‘, к’)
лежат на заданной стороне м ‘.
Символически
∠ ( ч,
л)
≅
∠ ( ч ‘, к’).
Каждый угол конгруэнтен сам себе.
III.5. Если для двух треугольников ABC и A’B’C ‘ сравнения
AB
≅
A’B ‘, AC
≅
A’C ‘,∠ BAC
≅
∠ B’A’C ‘ удерживайте, затем сравнение∠ ABC
≅
∠ A’B’C ‘
тоже доволен.
Группа IV.Аксиома параллелей
IV. Пусть м будет любой линией, а A будет точкой не на ней. потом
в плоскости есть не более одной линии, определяемой м и A ,
который проходит через A и не пересекает м .
Группа V. Аксиомы непрерывности
V.1. ( Аксиома меры или Аксиома Архимеда ) Если AB
и CD — любые сегменты, тогда существует номер n такой, что
n сегментов CD , построенных непрерывно от A , вдоль
Луч из A через B пройдет за точку B .
V.2. ( Аксиома полноты строки ) Расширение набора
указывает на линию с ее отношениями порядка и конгруэнтности, которые сохраняли бы
отношения, существующие между исходными элементами, а также фундаментальные
свойства порядка линий и конгруэнтности, вытекающие из аксиом I-III, и
форма V.1 невозможна.
Определенные термины
- Рассмотрим две точки A и B на линии м .Набор
две точки A и B называются
сегмент . Точки между A и B называются
точки отрезка AB , или также говорят, что ложь
внутри сегмента AB . - Пусть A, A ‘, O, B будут четырьмя точками прямой м , так что O
находится между A и B , но не между A и A ‘.Тогда говорят, что точки A, A ‘ лежат на линии m на одной
и с той же стороны точки O и точек A, B говорят, что
лежат на прямой m по разные стороны от точки O . Совокупность
точки линии м , лежащие на той же стороне O , являются
называется луч , исходящий из О. - Пусть α будет плоскостью и h, k
любые два различных луча, исходящие из O вα
и лежащих на разных линиях.Пара лучей h, k называется
угол и обозначается
∠ ( ч, к)
или же
∠ ( к, з) . - Пусть луч h лежит на прямой h ‘, а луч k — на прямой.
строка к ‘. Лучи h и k вместе с точкой O
разделите точки плоскости на две области. Все точки, лежащие на
та же сторона у k ‘, что и у h , а также лежащие на
та же сторона h ‘, что и у k , как считается, лежит в
интерьер угол
∠ ( ч, к) . - Если A, B, C — три точки, которые не лежат на одной прямой, то
система из трех сегментов AB, BC, CA, и их конечных точек называется
треугольник ABC.
_____________
Гильберт, Дэвид, Основы геометрии (Grundlagen der Geometrie) ,
Второе английское издание пер. пользователя Unger, L. LaSalle: Open Court Publishing
Компания, 1971 (1899).
% PDF-1.6
6 0 obj
>
эндобдж
9 0 объект
>
/ Длина 11 0 R
>>
поток
«Fh>»:> 8.:>: # H: # DtGEѼdt] fDtGDs # «= A4GDtGDu> .: 6.GF»: 0e Wdt # hC # JIY` $ ADAB 8Ga $$ Q 쎂 I $ GRMQuGtEGGh: 9g # : 6ydta: # h3: aa4CDBL H «H #, $ JP
«+ * DDDDDDDDDDDDDhxIHGyyF #: 6mD | GDt] @ e8YDx $ G @) ՛ 4 Dt #: H 莈 쎂 A:»: # EBЌ $ «8ЈAIt (r8hDDDDDDDDDDDDDDDDDD | Ga>,
GAGA2> G2: XAE @ 0 # B.! Ѓ.dtGHIb; IvIg_-C ## EB
DtGFtc #. $ GVGDt] G @ dt * R: 2: + #:
GD} -%: L! @Q! D
$ HKC_ (pR $ I M $ «DAEMrP8B} 莋: ##: ѹ»> Adt # R> HY0RT
$$ BG3A0A $ &%, tE: EU_eTLQVawGDqh # 6.: 8 # :. 莍. «:,: # H #:»: 1НАЛОГ I:
G @ $ GhX — $! B # G
$ «, / _ * ԡI (𱕢
, CDtGRty: #> yGF # A t] I $ G (a AYHJI8 (dqDDDDBqR, / p (p + E | E9CAEldF &! H ##: 0 莍 tmѴG #: + 0, G) Lpa2:. @ A
# «Dw» 8) I \ 4I * (p @ H w2F 剔 9Mp18cqhGkDGGT} DtaL (rGEtGE8A2) H #: / 0 I) (dt ## dqPADatG0 (#XA
H) G $ + @
«Dh MDL8S9XGIDtY 莈 $] L&G @ Q I 쏂 GAqBY @@ hD» 😯
8APIL @ ESPBEyC9N PAT * xI W; aF: aQ1 + # Dty $ GGDx # «: 7фG: # hDtGF2: #: #. Sgʲ +) ʲ +
rÌ 莈 莍 AdtAdt Dr HVG @ # JGAhA TAl! `EH $ TbPYSQSHdh-Z
XAGA0 #C (b «» (B «» «! DpH $% S% + A% eU! C) 8X & H $ S &) ye * $» BB «qŤD!; F; * SCM) +! K (# ~ 3XAAi & b *) 6S @.5Ng} GПGGH «PD ~ +! S @ Hq
> GH & SAAM # H # V «: 3GG + h) ZZQh +]
GA! «: Av &: — H (菣 R>» :: MeQ #> AY, Kki @ $
XzV
N * | «: A $»: ѩ} UW [## Ap $ f _ =} 2-I «: TE (bv #; Af (X! Te4ZDtq
hԈ! MZE «: MH $ + v: # Ȅ» «» «# m2PL $ DuYMJc # Db% Dyaw34 = -h3V (d» «» — JM6,) j;! FK #lSaGYeL
WϣcP (b
4HeFFD # P1` $ A @: DuG} h «: —
Аксиомы Гильберта для геометрии евклидовой плоскости
Неопределенный
Условия
точка, линия, частота, промежуточность, совпадение
Аксиомы
- Аксиомы
Заболеваемость
Постулат I.1.
За каждую точку
P
и для
каждая точка Q не равна P , существует единственная линия \ (\ ell \), в которую входят точки
P и
Вопрос .
Постулат I.2.
Для каждой прямой \ (\ ell \) существует не менее двух различных точек
P
а также
Q инцидент с \ (\ ell \).
Постулат I.3.
Существует не менее трех различных точек.
с тем свойством, что ни одна линия не связана со всеми тремя из них.
II.
Аксиомы промежуточности
Постулат B.1.
Если точка
B находится между точкой
А и точка
С
затем точки A ,
Б , г.
C — три отдельные точки на линии, и
B тогда также находится между
C и
А .
Постулат B.2.
Для двух разных точек
B и
D , есть точки
A, C и E на линии
BD такой, что
B находится между
А и
D,
C находится между
Группа
D и
D
лежит между
B
а также
E .
Постулат B.3.
Если
А,
Группа
C — три различные точки, лежащие на одной прямой, затем одна и
только одна из точек находится между двумя другими.
Постулат B.4. (Разделение самолетов
Аксиома)
Для каждой линии \ (\ ell \) и для любых трех точек
А ,
B , и
С
которые не лежат на \ (\ ell \):
а)
Если A и B находятся на одной стороне \ (\ ell \) и B
и C находятся на одной стороне \ (\ ell \), тогда A и C находятся на одной стороне от \ (\ ell \).
б)
Если A и B находятся на противоположных сторонах \ (\ ell \) и B
и C находятся на противоположных сторонах \ (\ ell \), тогда A и C находятся на одной стороне \ (\ ell \).
- Аксиомы
Сравнение
Постулат C.1.
Если
A и B — разные точки и
A ‘ — это точка, тогда для каждого луча r , исходящего из A’ , существует
уникальная точка B ‘ на r такая, что \ (B’ \ ne A ‘\) и такая, что AB и
A’B ‘ конгруэнтны.
Постулат C.2.
Если сегмент
A’B ‘и сегмент
A «B» конгруэнтны
тот же отрезок AB, затем отрезки
Группа
A «B» конгруэнтны друг другу.
Постулат C.3.
На линии
м, пусть
Группа
BC — два отрезка, которые, кроме
для B не имеют общих точек. Кроме того, на той же или другой линии
м ‘,
пусть A’B ‘и
B’C ‘- два сегмента, которые, кроме
для B ‘, не имеют общих точек.В
в этом случае, если \ (AB \ cong A’B ‘\) и
\ (BC \ cong B’C ‘\), то
\ (AC \ cong A’C ‘\).
Постулат C.4.
Если \ (\ angle BAC \) — угол, и если \ (\ overrightarrow {B’C ‘} \) — луч, то существует
ровно один луч \ (\ overrightarrow {B’A ‘} \) на каждой стороне прямой \ (\ overleftrightarrow {B’C’} \) такой, что
\ (\ угол B’A’C ‘\ cong \ angle BAC \).
Постулат C.5.
Если \ (\ angle A \ cong \ angle B \) и
\ (\ angle A \ cong \ angle C \), затем \ (\ angle B \ cong \ angle C \).Более того, каждый
угол конгруэнтен сам себе.
Постулат C.6. ( SAS )
Если две стороны и включенный угол
один треугольник конгруэнтен соответственно двум сторонам и включенному углу
другой треугольник, затем два треугольника совпадают.
- Аксиомы
Непрерывность
Аксиома Архимеда
Если
AB
и CD — любые сегменты, то там
существует число n такое, если
сегмент CD отключается n раз на луче \ (\ overrightarrow {AB} \), исходящем из A , тогда точка E
достигнуто где \ (n \ cdot CD \ cong AE \) и B
находится между A и E .
Аксиома Дедекинда
Предположим, что множество всех точек на
строка \ (\ ell \) — это объединение \ (\ Sigma_1 \ cup \ Sigma_2 \) двух непустых подмножеств
такая, что никакая точка \ (\ Sigma_1 \) не находится между двумя точками \ (\ Sigma_2 \) и
наоборот . Тогда есть единственная точка,
O , лежит на \ (\ ell \)
такое, что O находится между \ (P_1 \) и \ (P_2 \) тогда и только тогда, когда \ (P_1 \ in
\ Sigma_1 \) и \ (P_2 \ in \ Sigma_2 \) и \ (O \ ne P_1, \, P_2 \).
Следующие два принципа вытекают из
Аксиома Дедекинда, но в разы более полезна.
Элементарный
Принцип непрерывности:
Если одна конечная точка сегмента находится внутри
круг, а другой — снаружи, тогда отрезок пересекает круг.
Циркуляр
Принцип непрерывности:
Если один круг имеет одну точку внутри и
одна точка вне другого круга, затем два круга пересекаются в двух точках.
- Аксиома параллелей
Пусть \ (\ ell \) — произвольная линия и
P точка не на нем. Тогда есть не более одной строки
который проходит через P и не
пересекаются с \ (\ ell \).
Коллинеарность
Точки коллинеарны, если они лежат на одной линии.
Что делает точки коллинеарными?
Две точки всегда лежат на одной прямой, поскольку мы можем провести через них четкую (одну) линию.
Три точки коллинеарны, если они лежат на одной линии.
Точки A, B и C не лежат на одной прямой. Мы можем провести линию через A и B, A и C, B и C, но не через все 3 точки.
Компланарные точки лежат в одной плоскости. На схеме ниже точки A, B, U, W, X и Z лежат в плоскости M, а точки T, U, V, Y и Z лежат в плоскости N.
- Точки A, Z и B лежат на одной прямой. Точно так же точки T, U и V коллинеарны, поскольку они лежат на отдельной прямой.
- Точки X и Y коллинеарны, хотя лежат в разных плоскостях. (Однако следует отметить, что можно построить плоскость, содержащую X и Y.)
- Поскольку вы можете провести линию через любые две точки, существует множество пар точек, которые коллинеарны на диаграмме.
- Набор точек, которые не коллинеарны (не коллинеарны) в одной плоскости: A, B и X.
- Набор точек, которые не коллинеарны и находятся в разных плоскостях: T, Y, W и B.
Особенности коллинеарных точек
1. Точка на прямой, которая находится между двумя другими точками на той же прямой, может интерпретироваться как начало двух противоположных лучей.
Точка C находится между точками A и B на AB (вверху). Используя эти точки, мы можем сформировать два противоположных луча, CA и CB.
2. Длина сегмента. Постулат сложения сегментов гласит, что если A, B и C — точки на одной прямой, где B находится между A и C, то AB + BC = AC.
Пример:
Если AC = 27 и BC = 11 на диаграмме выше, то мы можем найти AB.
3. Коллинеарные точки лежат на одной прямой, поэтому наклон между любыми двумя точками должен быть одинаковым.
Пример:
Если (1, 2), (3, 6) и (5, k) коллинеарные точки, каково значение k?
Мы можем найти значение k, сначала найдя наклон между двумя известными точками. Затем мы можем решить для k, приравняв наклон, который мы только что нашли, к выражению для наклона, включающему k как неизвестное:
Используя точки (1, 2) и (3, 6), чтобы найти наклон прямой, мы получаем
Наклон между (3, 6) и (5, k) составляет
Поскольку точки лежат на одной прямой, наклоны для этих двух точек равны, поэтому
к = 10
Таким образом, значение k равно 10, а координата коллинеарной точки 3 rd равна (5, 10).
4. Есть только 2 вершины, коллинеарные для любого выпуклого многоугольника на плоскости.
Для представленного ниже 6-стороннего выпуклого многоугольника, называемого шестиугольником, вы можете провести 5 линий от каждой вершины к другим 5 вершинам. Однако никакая комбинация любых трех вершин не может оставаться на одной линии.
Если A B C — это три точки на прямой, такие как AB 5 см, BC 3 см и AC 8 см, одна из которых находится между двумя другими
Нокаут NEET Май 2024 г.
Персонализированный наставник AI и адаптивное расписание,
Материал для самообучения,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
₹ 40000 / —
купить сейчас
Нокаут NEET Май 2025 г.
Персонализированный наставник AI и адаптивное расписание,
Материал для самообучения,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
₹ 45000 / —
купить сейчас
Основа NEET + Нокаут NEET 2024
Персонализированный наставник AI и адаптивное расписание,
Материал для самообучения,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
54999 ₹ / —
42499 ₹ / —
купить сейчас
NEET Foundation + Knockout NEET 2024 (простая установка)
Персонализированный наставник AI и адаптивное расписание,
Материал для самообучения,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
3999 / —
купить сейчас
NEET Foundation + Knockout NEET 2025 (простая установка)
Персонализированный наставник AI и адаптивное расписание,
Материал для самообучения,
Неограниченные пробные тесты и персонализированные аналитические отчеты,
Круглосуточная поддержка в чате сомнений.
3999 / —
купить сейчас
| Срок | Определение
| |
| Срок | Определение
| |
| Срок | Определение
| |
| Срок | Определение
| |
| Posted in Разное | ||
