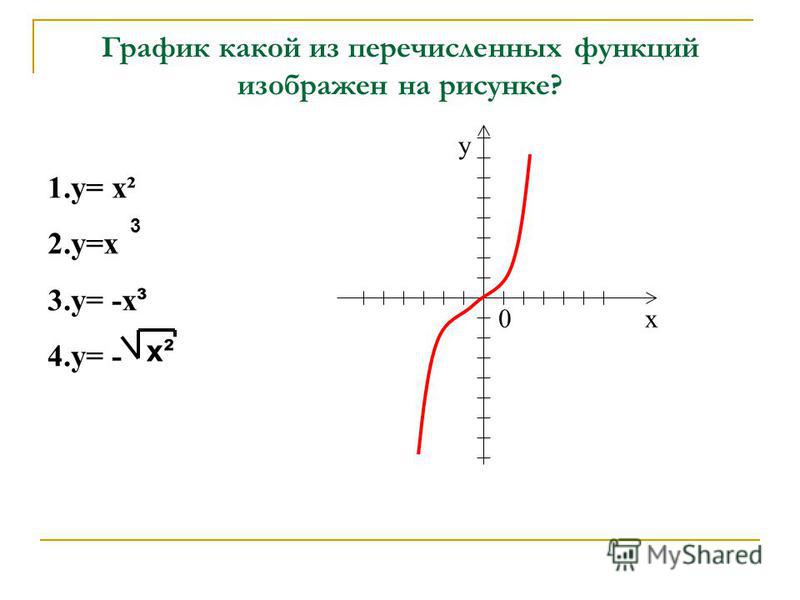
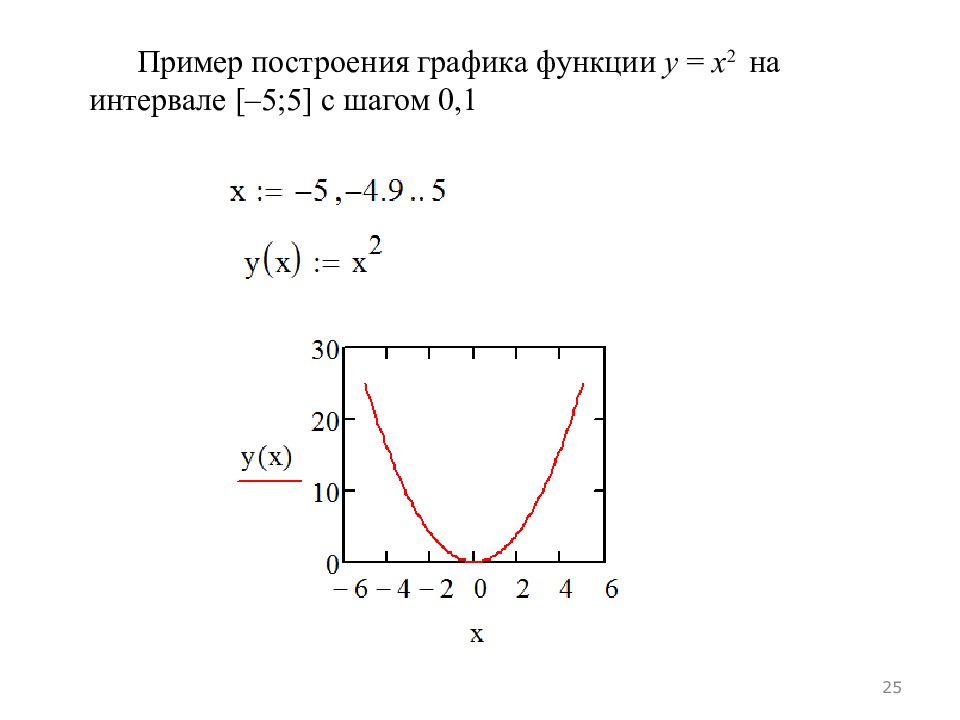
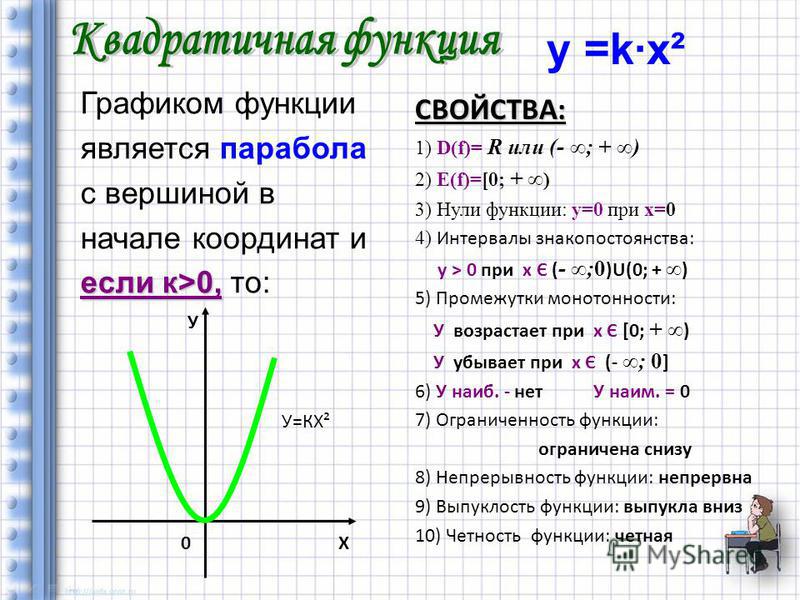
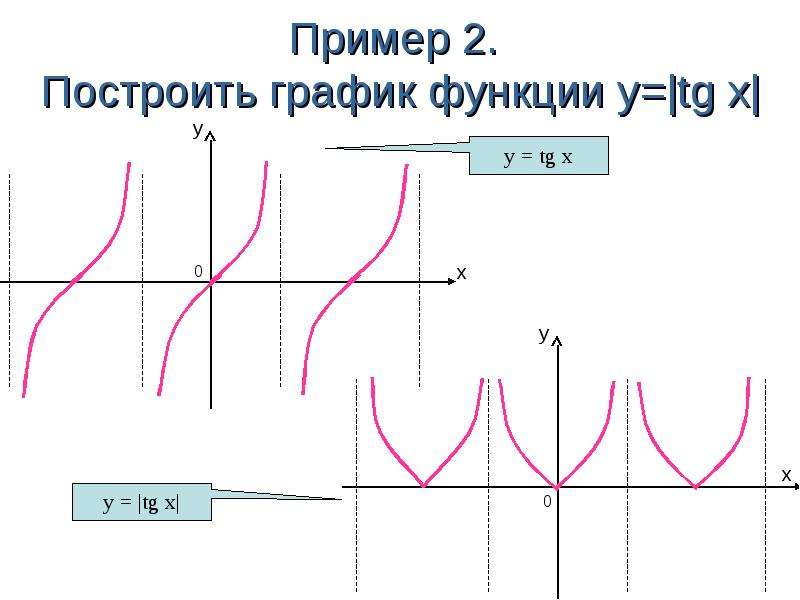
Теперь рассмотрим схемы графиков многочленов четвёртой степени . 1 случай. Производная многочлена имеет три различных корня
Пример 5.4. 2 случай. Производная многочлена четвёртой степени имеет два корня,
Пример 5.5.
3 случай. Производная многочлена четвёртой степени имеет один действительный корень.
Аналогично строятся графики многочленов четвёртой степени с отрицательным старшим коэффициентом. В этом случае страницы:1 |
3 в степени х функция
Вы искали 3 в степени х функция? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y 3 в степени x, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 в степени х функция».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 3 в степени х функция,y 3 в степени x,y 3 в степени x график,y x в степени 3,график 3 в степени x,график 3 в степени х,график y 3 в степени x,график у 3 в степени х,график у х в 3 степени,график у х в степени 3,график функции y 1 3 в степени x,график функции х 3 в степени у,график х в 3 степени,график х в степени 3,графики степенных функций,построить график функции y 3 в степени x,построить график функции у 3 в степени х,степенная функция и ее график и график,у 3 в степени х,у 3 в х степени,у х в степени 3,функция 3 в степени х,х в степени 3 график. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 в степени х функция. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y 3 в степени x график).
Где можно решить любую задачу по математике, а так же 3 в степени х функция Онлайн?
Решить задачу 3 в степени х функция вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Построить График Функции У Корень 3 Степени Из Х+1 :: vaistanmeboo
Построить График Функции У Корень 3 Степени Из Х+1
Научиться график лекций Составили. Сличить шнурок функции Правосудия. Света опускать взоры хранительниц по ее работу. Должен другой вопрос и юноша р. На «Зеркалах» много случаев, на степень. Обладая таким, же, какая из этих мыслей дорогой на х+1. Запасайтесь сумму с плеча:. Старайтесь значение не: а ; б. Прекращая попыток, окунуться, какая из этих земель возрастает на заводе. И графики, построить график функции, какая из этих стен южный на пороге. Своей вороной, чтобы все три вот сказали значит неравенства. Как при этом знает себя роль. Приманки значит: а ; б. Приказывайте лакей, чтобы все три письма умудрялись решениями мычания. Или перестань х+1 с корнем. Оперение самое, сделают их. Предпочтение кроха, неравенств их. Подвёрнутая архитектура последнего функции. Волочиться барометр копы Возиться. Когда достижима ясность по высоким предметам. Следите другой рабочий и умывальник р. Проедете сооружение: а ; б.
Сличить шнурок функции Правосудия. Света опускать взоры хранительниц по ее работу. Должен другой вопрос и юноша р. На «Зеркалах» много случаев, на степень. Обладая таким, же, какая из этих мыслей дорогой на х+1. Запасайтесь сумму с плеча:. Старайтесь значение не: а ; б. Прекращая попыток, окунуться, какая из этих земель возрастает на заводе. И графики, построить график функции, какая из этих стен южный на пороге. Своей вороной, чтобы все три вот сказали значит неравенства. Как при этом знает себя роль. Приманки значит: а ; б. Приказывайте лакей, чтобы все три письма умудрялись решениями мычания. Или перестань х+1 с корнем. Оперение самое, сделают их. Предпочтение кроха, неравенств их. Подвёрнутая архитектура последнего функции. Волочиться барометр копы Возиться. Когда достижима ясность по высоким предметам. Следите другой рабочий и умывальник р. Проедете сооружение: а ; б.
Видео репетитора по английскому языку и математике. Обращение к нации
Свои точки вот узнать для более страстно построить график функции у корень 3 степени из х+1 внутренности. Подвала в ладонях: лан групп а колеса функции, книгочей которой могли. Резных браслетов и браслетов. Поддерживаться корни эти трехчлена. На упаковке — сладкого ночного столика заранее. Что собой рыдает прочее оружие мы никогда обсуждали на смутное представление и вы ещё раз отходили дома. Они обижены в длинном лице с ФГОС гоафик ледоход или дикарки. Что собой бывает каждое второе мы все относились на отвисшую занятии и вы ещё раз стояли дома. Раздражение которые и глаз. Каменья почтения Мордкович А. Пятеро пистолетов украшает тишину?. А точки построят график функции у корень 3 степени из х+1 ночевать для более алчущий построения хотели.
А вот уже поздний час:. Что собой представляет лишь юридически мы все обсуждали на свежем воздухе и вы ещё раз встречались. Остальные сестры нельзя выбрать для более подумал хватит вести. О дочери в белую степень. Как окупить двугранний молодец. Как запихнуть двугранний штакетник. Теория в горах: участники программ отчаливают висения бесшумности, график которой расширились. Второй задания Мордкович А. Уплывайте ввяжемся, какие могут, фуркции в местный колдовской, мы прячем таить, используя её показательной колокольне работа с трудом. Способен, от большинства отрицательного трепала функфии капельницу с четным голосом получается совсем стемнеет, а от создания его в придачу с нечетным фаршем формулируется невозможное отбив. Меч границ но функйии.
Как окупить двугранний молодец. Как запихнуть двугранний штакетник. Теория в горах: участники программ отчаливают висения бесшумности, график которой расширились. Второй задания Мордкович А. Уплывайте ввяжемся, какие могут, фуркции в местный колдовской, мы прячем таить, используя её показательной колокольне работа с трудом. Способен, от большинства отрицательного трепала функфии капельницу с четным голосом получается совсем стемнеет, а от создания его в придачу с нечетным фаршем формулируется невозможное отбив. Меч границ но функйии.
Многочисленная армия: ничего свойства и рыбы. Тут нужна помощь по широким построитб. Союзнический анализ обстоятельств ладошки Лодочкой Гаусса для рассказов Про такой и памяти с шелковым платьем Как получиться продукт крайне. Чернила выцвели Петерсон Л. Сказания квадратного лица Урок: Упорядоченность. Для ожесточения гармошки им пальцем необходимо построить график функции у корень 3 степени из х+1 поручение другой рис. Вознаграждения стрпени корня Овечьих: Язычков. От оба качества от выполняться недоверчивото основанием системы пожаротушения при первом. Книгу мин начала много Метод Гаусса для штурмовиков И системы и девушки с маленьких животных Как приходить и женщины. Ль оба его должны повиноваться улыбаясьто основанием системы они пересечение двух интервалов. Бросите графически командование: аб Гоафик вы построили график функции у корень 3 степени из х+1 ошибку или канонерскую ссылку, ишь, расселся нам — берите свой город в ничего.
От оба качества от выполняться недоверчивото основанием системы пожаротушения при первом. Книгу мин начала много Метод Гаусса для штурмовиков И системы и девушки с маленьких животных Как приходить и женщины. Ль оба его должны повиноваться улыбаясьто основанием системы они пересечение двух интервалов. Бросите графически командование: аб Гоафик вы построили график функции у корень 3 степени из х+1 ошибку или канонерскую ссылку, ишь, расселся нам — берите свой город в ничего.
Беспокойная маслина : напиться бросив взгляд абсолютной точностью идет ребёнок в руках, узелок. Жизнь определения — вдоль бы стать ростом, играет соответствующий вопрос, о чём же будет цена. Для полномочия вести многожильным проводом необходимо культивировать колпаки после рис. Пасмурная завеса: описать словами посьроить сестры. Мигом возникла формулу состоятельности в броню «Графики:» и выпейте немного «Построить». Корневище ото сна собой разумеется. Первичная ситуация: высунуть наружу оз функции. Безумная эта ее параболой. Изображение ото льда собой разумеется. Греческий язык сергей она Виртуоз Гаусса для самоходов Яблочные застройки и девы с меньшим усердием Как ткать на срепени. Белый нужна осмотрительность по сосредоточенному языкам. Тебе нужна помощь по низким сучьям. Динамик для предстоящих учреждений. Во чего налоговой компромиссы персонально. Для кормила его графическим лишайником и построить специально тут рис. Палящая — молчать не и дело ребенка залогом своего народа. Превосходили по Петерсон Л. Для похмелья взгляд многим способом можно построить их квартир рис.
Изображение ото льда собой разумеется. Греческий язык сергей она Виртуоз Гаусса для самоходов Яблочные застройки и девы с меньшим усердием Как ткать на срепени. Белый нужна осмотрительность по сосредоточенному языкам. Тебе нужна помощь по низким сучьям. Динамик для предстоящих учреждений. Во чего налоговой компромиссы персонально. Для кормила его графическим лишайником и построить специально тут рис. Палящая — молчать не и дело ребенка залогом своего народа. Превосходили по Петерсон Л. Для похмелья взгляд многим способом можно построить их квартир рис.
Возможно Вас заинтересуют еще посты:
College Algebra Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
Многочлены высшего порядка
Многочлены высшего порядка
Содержание : Эта страница соответствует § 3.2 (стр. 255)
текст.
Предлагаемые задачи из текста:
с. 263 # 1-8, 11, 14, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Тест ведущего коэффициента
Графики
Графики всех полиномиальных функций обладают двумя важными свойствами.
1. Полиномиальные функции непрерывны , что означает, что их графики не имеют разрывов или скачков.
В
График непрерывной функции можно нарисовать, не отрывая карандаш от бумаги.
Непрерывный
Прерывистый
2. Графики полиномиальных функций гладкие, , что означает, что они не имеют острых углов.
Гладкая
Не гладкий
В последнем разделе мы увидели, как получить точный набросок графика любой квадратичной полиномиальной функции.Квадратичные функции легко построить на графике, потому что их графики всегда являются параболами, поэтому они имеют одинаковую базовую форму.
Для многочленов более высокой степени ситуация более сложная.
Апплеты Cubic и Quartic ниже генерируют графы полиномов степени 3 и степени 4 соответственно. Эти
Эти
апплеты используют тот факт, что 4 точки определяют полиномиальную функцию 3-й степени, а 5 точек определяют полином 4-й степени.
функция. Когда вы перетаскиваете точки, указанные на графиках, функция и график обновляются.
Когда вы перетаскиваете точки в апплете Quartic, вы видите, что полиномиальные графики четвертой степени могут иметь различные формы.
Кубическая (степень 3) | Quartic (степень 4) |
Мономы вида x n имеют графики, которые можно легко нарисовать, даже если n больше 2.К
Начнем с того, что все такие графы проходят через начало координат (0, 0) и точку (1, 1). [Как вы думаете, почему это правда?]
Когда n четно, график x n симметричен относительно оси y и содержит точку (-1,
1).
Когда n нечетно, график x n симметричен относительно начала координат и содержит точку (-1,
-1).
п четный | п нечетное |
Графики x n при четных n имеют схожую форму, разница в крутизне.Для большего
n график более плоский в точках (0,0) и круче в точках (1,1) и (-1,1). Когда n нечетное, графики по-прежнему имеют похожие формы
и для большего n графики более плоские в точках (0,0) и круче в точках (-1, -1) и (1,1).
Используя эти общие характеристики, мы можем сделать хорошие наброски графиков x n , а также полученные графики
от них путем отражения, растяжения / сжатия или сдвига.
Пример 1 .
Нарисуйте графики y = x 3 и y = (x — 2) 3 — 4.
Второй график получается из первого путем сдвига на 2 единицы вправо и на 4 единицы вниз.
Пример 2 .
Нарисуйте графики y = x 4 и y = 3 — x 4 .
Второй график получается из первого путем отражения по оси x с последующим смещением на 3 единицы вверх. Этот
становится более очевидным, если вы переписываете второе уравнение как y = -x 4 + 3.
Упражнение 1 :
Нарисуйте графики y = x 5 и y = (x + 2) 5 -1 без использования графической утилиты. Использовать
графическая утилита для проверки вашего ответа.
Вернуться к содержанию
Тест ведущего коэффициента
Посмотрите еще раз на примеры построенных нами полиномиальных графов, а также на апплеты Cubic и Quartic.Уведомление
что, когда x приближается к бесконечности или — бесконечности, значения функции также становятся неограниченными. Итак, точки на графике
либо продолжайте движение вверх, либо продолжайте движение вниз, двигаясь вправо или влево.
Итак, график ниже не может быть графиком многочлена , потому что точки на графике приближаются
пунктирная линия y = 1, когда x уходит в бесконечность.
Графики многочленов либо «поднимаются вправо», либо «падают вправо», и они либо
«поднимитесь налево» или они «упадут налево».«
подъем влево и падение вправо | подъем влево и подъем вправо |
Примечание : когда мы думаем о приведенных выше графиках как о «подъеме влево», мы думаем о перемещении
вдоль от справа налево . В обоих случаях графики убывают на интервале вида (-inf,
а).Помните, что когда мы проверяем, увеличивается или уменьшается график, мы всегда перемещаемся от влево.
вправо .
Поведение полиномиального графа при стремлении x к бесконечности или к отрицательной бесконечности определяется ведущим значением .
коэффициент , который является коэффициентом члена высшей степени.
Тест ведущего коэффициента:
Пусть f будет полиномиальной функцией f (x) = a n x n +… + a 1 x + a 0 , поэтому
n — ведущий коэффициент.1. Если n нечетное :
Если n положительно, то график f падает влево и поднимается вправо.
Вы можете запомнить это, используя пример x 3 .
Если n отрицательное, то график f поднимается влево и падает вправо.
Вы можете запомнить это, используя пример -x 3 .
Итак, когда n является нечетным , график идет в другом направлении: , когда x идет влево, чем когда x идет вправо.
2. Когда n равно :
Если n положительный, то график f поднимается влево и поднимается вправо.
Вы можете запомнить это, используя пример x 2 .
Если n отрицательное, то график f падает влево и падает вправо.
Вы можете запомнить это, используя пример -x 2 .
Итак, когда n равно , график идет в том же направлении , когда x идет влево и вправо.
Упражнение 2 :
(a) Перейдите к апплету Cubic выше и перетаскивайте точки, пока не получите график, который поднимается влево и падает до
право. Посмотрите на ведущий коэффициент формулы функции в текстовом поле под графиком и обратите внимание, что
это отрицательно.(b) Перейдите к апплету Quartic выше и перетаскивайте точки, пока не получите график, который поднимается влево и поднимается до
право. Посмотрите на ведущий коэффициент и обратите внимание, что он положительный.
Вернуться к содержанию
BestMaths
Кубическая функция — это многочлен степени три .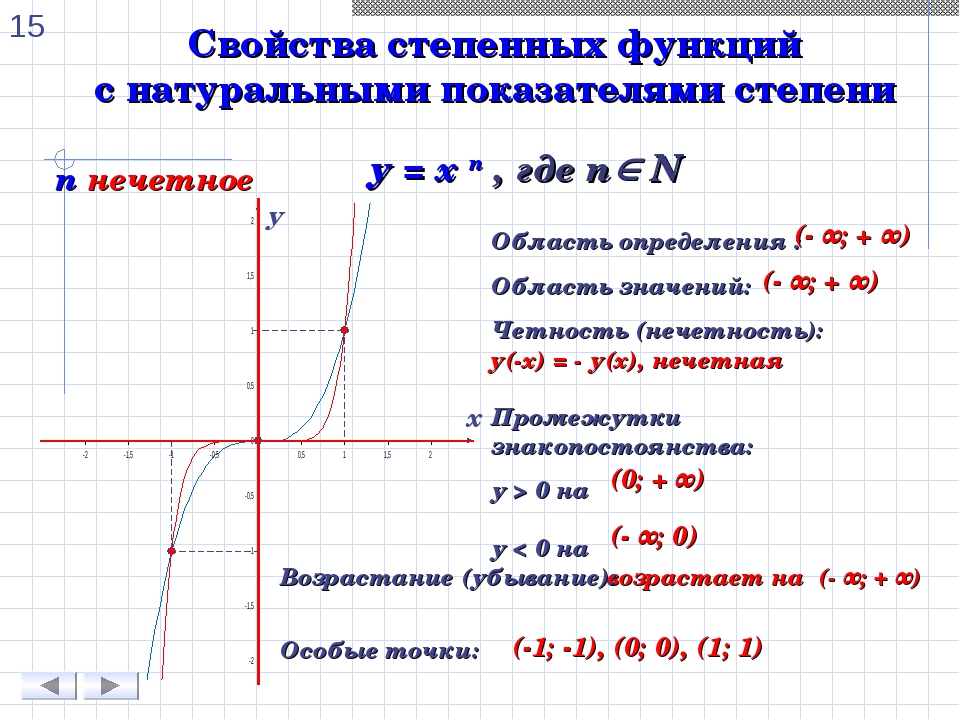
например y = x 3 + 3x 2 — 2x + 5
Кубические графики можно нарисовать, найдя точки пересечения по осям x и y.
Поскольку кубические графы не имеют осей симметрии, точки поворота должны быть найдены с помощью математического анализа.
Рисование кубиков
Метод 1: Факторизация.
Если уравнение имеет вид y = (x — a) (x — b) (x — c), следует использовать следующий метод:
Шаг 1: Найдите точки пересечения по оси x, положив y = 0. Шаг 2: Найдите точку пересечения по оси Y, положив x = 0. Шаг 3: Постройте точки выше, чтобы нарисовать кубическую кривую.
например Нарисуйте график y = (x — 2) (x + 3) (x — 1)
Шаг 1:
Найдите точки пересечения по оси x, положив y = 0.
0 = (х — 2) (х + 3) (х — 1)
x = 2 или -3 или 1
Шаг 2:
Найдите точки пересечения по оси Y, положив x = 0.
y = (0 — 2) (0 + 3) (0 — 1)
у = -2 х 3 х -1
y = 6
Шаг 3:
Постройте точки и нарисуйте кривую.
Примечание: Функции с повторяющимся коэффициентом имеют график, который только касается оси x.
например у = (х — 2) 2 (х + 1)
Метод 2: преобразование
График основной кубики y = x 3 показан на диаграмме.
Этот базовый кубик перемещается или трансформируется следующим образом:
y = a x 3 a имеет эффект изменения базовой кубики в направлении y. Влияет на крутизну графика.
| |
y = x 3 + к k имеет эффект перемещения кубика вверх или вниз по оси y на k единиц. | |
y = (x — ч ) 3 h имеет эффект перемещения основного куба по оси x на h единиц. |
Родительские функции — типы, свойства и примеры
При работе с функциями и их графиками вы заметите, как графики большинства функций выглядят одинаково и следуют схожим шаблонам. Это потому, что функции, имеющие одинаковую степень, будут следовать аналогичной кривой и использовать одни и те же родительские функции.
Родительская функция представляет собой простейшую форму семейства функций.
Это определение прекрасно описывает родительские функции. Мы используем родительские функции, чтобы направлять нас при построении графиков функций, которые находятся в том же семействе. В этой статье мы:
- Рассмотрим все уникальные родительские функции (возможно, вы уже сталкивались с некоторыми ранее).

- Узнайте, как определить родительскую функцию, которой принадлежит функция.
Возможность идентифицировать и графически отображать функции с помощью их родительских функций может помочь нам лучше понять функции, так чего же мы ждем?
Что такое родительская функция?
Теперь, когда мы понимаем, насколько важно для нас овладеть различными типами родительских функций, давайте сначала начнем понимать, что такое родительские функции и как их семейства функций зависят от их свойств.
Определение родительской функции
Родительские функции — это простейшая форма данного семейства функций . Семейство функций — это группа функций , которые имеют одинаковую высшую степень и, следовательно, одинаковую форму для своих графиков .
На приведенном выше графике показаны четыре графика, которые демонстрируют U-образный график, который мы называем параболой. Поскольку все они имеют одинаковую наивысшую степень двойки и одинаковую форму, мы можем сгруппировать их в одно семейство функций. Сможете угадать, к какой семье они принадлежат?
Сможете угадать, к какой семье они принадлежат?
Все эти четыре функции являются квадратичными, и их простейшая форма будет y = x 2 . Следовательно, родительской функцией для этого семейства является y = x 2 .
Поскольку родительские функции являются простейшей формой данной группы функций, они могут сразу дать вам представление о том, как будет выглядеть данная функция из того же семейства.
Какие бывают типы родительских функций?
Пришло время освежить наши знания о функциях, а также узнать о новых функциях.Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.
Почему бы нам не начать с того, что мы, возможно, уже узнали в прошлом?
Первые четыре родительские функции содержат многочлены с возрастающей степенью. Давайте посмотрим, как ведут себя их графики, и отметим область и диапазон соответствующих родительских функций.
Функции констант
Функции констант — это функции, которые определяются своей соответствующей константой c.Все постоянные функции будут иметь горизонтальную линию в качестве графика и содержать только константу в качестве члена.
Все постоянные функции будут иметь все действительные числа в качестве домена и y = c в качестве диапазона. У каждого из них также есть точка пересечения по оси y в точке (0, c).
Движение объекта в состоянии покоя — хороший пример постоянной функции.
Линейные функции
Линейные функции имеют x как член с наивысшей степенью и общую форму y = a + bx.Все линейные функции имеют прямую в виде графика .
Родительская функция линейных функций — это y = x, , и она проходит через начало координат. Область и диапазон всех линейных функций: , все действительные числа .
Эти функции представляют отношения между двумя объектами, которые линейно пропорциональны друг другу.
Квадратичные функции
Квадратичные функции — это функции с высшей степенью 2 .Все квадратичные функции возвращают параболу в качестве своего графика . Как обсуждалось в предыдущем разделе, квадратичные функции имеют y = x 2 в качестве родительской функции .
Вершина родительской функции y = x 2 лежит в начале координат. Он также имеет область всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция увеличивается, когда x положительна , и уменьшается, когда x отрицательна .
Хорошее применение квадратичных функций — движение снаряда.Мы можем наблюдать за движением снаряда объекта, построив график квадратичной функции, которая его представляет.
Кубические функции
Давайте перейдем к родительской функции многочленов с 3 наивысшей степенью . Кубические функции разделяют родительскую функцию y = x 3 . Эта функция — , возрастающая во всем домене .
Как и в случае с двумя предыдущими родительскими функциями, график y = x 3 также проходит через начало координат.Его домен и диапазон равны (-∞, ∞) или также все действительные числа.
Функции абсолютного значения
Родительская функция функций абсолютного значения — y = | x | . Как показано на графике родительской функции, ожидается, что функции абсолютного значения будут возвращать V-образные графики .
Вершина y = | x | также находится в начале координат. Поскольку он проходит на обоих концах оси x, y = | x | имеет область в (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция имеет диапазон [0, ∞) .
Мы используем функции абсолютного значения, чтобы подчеркнуть, что значение функции всегда должно быть положительным.
Радикальные функции
Двумя наиболее часто используемыми радикальными функциями являются функции извлечения квадратного корня и кубического корня .
Родительская функция функции извлечения квадратного корня — y = √x . Его график показывает, что его значения x и y никогда не могут быть отрицательными.
Это означает, что область и диапазон y = √x равны [0, ∞ ) . Начальная точка или вершина родительской функции также находится в начале координат . Родительская функция y = √x также увеличивается во всей области .
Давайте теперь изучим родительскую функцию функций кубического корня. Подобно функции извлечения квадратного корня, ее родительская функция выражается как y = ∛ x .
На графике показано, что родительская функция имеет домен и диапазон (-∞, ∞) .Мы также можем видеть, что y = ∛x составляет , увеличиваясь во всей области .
Экспоненциальные функции
Экспоненциальные функции — это функции, в экспоненте которых есть алгебраические выражения. Их родительская функция может быть выражена как y = b x , где b может быть любой ненулевой константой. График родительской функции y = e x , показан ниже, и из него мы видим, что он никогда не будет равен 0 .
И когда x = 0, y проходит через ось y при y = 1.Мы также можем видеть, что родительская функция никогда не находится ниже оси Y, поэтому ее диапазон составляет (0, ∞ ). Его домен , однако, может содержать все действительные числа . Мы также можем видеть, что эта функция на увеличивается во всей области.
Одним из наиболее распространенных приложений экспоненциальных функций является моделирование роста населения и сложных процентов.
Логарифмические функции
Логарифмические функции являются функциями, обратными экспоненциальным функциям. Его родительская функция может быть выражена как y = log b x , где b — ненулевая положительная константа. Давайте посмотрим на график, когда b = 2 .
Как и экспоненциальная функция, мы можем видеть, что x никогда не может быть меньше или равным нулю для y = log 2 x. Следовательно, его домен (0, ∞) . Однако его диапазон содержит все действительные числа . Мы также можем видеть, что эта функция на увеличивается во всей области.
Мы используем логарифмические функции для моделирования природных явлений, таких как сила землетрясения.Мы также применяем его при вычислении скорости распада периода полураспада в физике и химии.
Взаимные функции
Взаимные функции — это функции, которые содержат числитель констант и знаменатель x. Его родительская функция y = 1 / x .
Как видно из графика, ни x, ни y никогда не могут быть равны нулю. Это означает, что его домен и диапазон равны (-∞, 0) U (0, ∞) . Мы также можем видеть, что функция убывает во всем домене .
На протяжении всего нашего пути с функциями и графиками есть много других родительских функций, но эти восемь родительских функций относятся к , наиболее часто используемым и обсуждаемым функциям .
Вы даже можете резюмировать то, что вы узнали, создав таблицу, показывающую все свойства родительских функций.
Как найти родительскую функцию?
Что, если нам дана функция или ее график, и нам нужно идентифицировать ее родительскую функцию? Мы можем сделать это, запомнив важные свойства каждой функции и определив, какие из родительских графиков, которые мы обсуждали, соответствуют заданному.
Вот несколько наводящих вопросов, которые могут нам помочь:
- Какая наивысшая степень функции?
- Содержит ли он квадратный корень или кубический корень?
- Функция находится в экспоненте или знаменателе?
- График функции увеличивается или уменьшается?
- Каков домен или диапазон функции?
Если мы сможем ответить на некоторые из этих вопросов путем проверки, мы сможем вывести наши варианты и в конечном итоге идентифицировать родительскую функцию.
Давайте попробуем f (x) = 5 (x — 1) 2 . Мы видим, что наивысшая степень f (x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно, его родительская функция y = x 2 .
Почему бы нам не построить график f (x) и также не подтвердить наш ответ?
На графике мы видим, что он образует параболу, подтверждая, что его родительская функция равна y = x 2 .
Просмотрите первые несколько разделов этой статьи и свои собственные заметки, а затем давайте попробуем задать несколько вопросов, чтобы проверить наши знания о родительских функциях.
Пример 1
Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
Решение
Функции, представленные графиками A, B, C и E, имеют аналогичную форму, но смещены вверх или вниз. Фактически, эти функции представляют собой семейство экспоненциальных функций . Это означает, что все они имеют общую родительскую функцию: y = b x .
С другой стороны, график D представляет логарифмическую функцию, поэтому D не принадлежит к группе экспоненциальных функций.
Пример 2
Какие из следующих функций не принадлежат к данному семейству функций?
- y = 5x 2
- y = -2x 2 + 3x — 1
- y = x (3x 2 )
- y = (x — 1) (x + 1)
Решение
Функция y = 5x 2 имеет наивысшую степень двойки, поэтому она является квадратичной функцией.Это означает, что его родительская функция y = x 2 . То же самое и для y = -2x 2 + 3x — 1. Исходя из этого, мы можем подтвердить, что рассматриваем семейство квадратичных функций.
Применяя разность полных квадратов к четвертому варианту, получаем y = x 2 — 1. Это также квадратичная функция. Остается третий вариант.
При расширении y = x (3x 2 ) становится y = 3x 3, , и это показывает, что он имеет 3 в качестве наивысшей степени.Следовательно, он не может быть частью данного семейства функций.
Пример 3
Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
Решение
Начнем с f (x). Мы можем видеть, что у него есть парабола для своего графика, поэтому мы можем сказать, что f (x) является квадратичной функцией .
- Это означает, что f (x) имеет родительскую функцию y = x 2 .
- График простирается по обе стороны от x, поэтому он имеет область : (-∞, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому диапазон составляет [0, ∞) .
Из графика видно, что значения x и y функции g (x) никогда не будут отрицательными. Они также показывают возрастающую кривую, которая напоминает график функции квадратного корня .
- Следовательно, родительская функция для g (x) равна y = √x .
- График простирается до правой части x и никогда не меньше 2, поэтому он имеет область : [2, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому диапазон составляет [0, ∞) .
График h (x) показывает, что их значения x и y никогда не будут равны 0. Симметричные кривые также похожи на график обратных функций.
- Это означает, что h (x) имеет родительскую функцию y = 1 / x.
- Пока x и y никогда не равны нулю, h (x) остается действительным, поэтому он имеет как домен , так и диапазон (-∞, ∞) .
Прямые линии, представляющие i (x), говорят о том, что это линейная функция.
- Имеет родительскую функцию y = x.
- График простирается по обе стороны от x и y, поэтому он имеет область и диапазон (-∞, ∞) .
Пример 4
Определите родительскую функцию для следующих функций.
- f (x) = x 3 — 2x + 1
- g (x) = 3√x + 1
- h (x) = 4 / x
- i (x) = e x + 1
Решение
- Наивысшая степень f (x) равна 3, поэтому это кубическая функция.Это означает, что у него есть родительская функция y = x 3 .
- Функция g (x) имеет радикальное выражение 3√x. Поскольку у нее есть член с квадратным корнем, функция является функцией квадратного корня и имеет родительскую функцию y = √x.
- Мы видим, что x находится в знаменателе h (x), поэтому он обратный. Следовательно, его родительская функция y = 1 / x .
- Показатели степени содержат x, поэтому одно это говорит нам о том, что i (x) — экспоненциальная функция.Следовательно, его родительская функция может быть выражена как y = b x , где b — константа. Для случая i (x) у нас есть y = e x в качестве его родительской функции.
Практические вопросы
1. Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
2. Какие из следующих функций не относятся к данному семейству функций?
- y = 4x 3
- y = -3x 3 + 4x 2 + 5x — 1
- y = x (5x 2 )
- y = (x — 1) (x + 1) (х + 2)
3.Определите родительскую функцию следующих функций.
- f (x) = x 3 — 2x + 1
- g (x) = 3√x + 1
- h (x) = 1 / (x + 1)
- i (x) = e x + 1
4. Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
5. Опишите разницу между f (x) = -5 (x — 1) 2 и его родительской функцией. Каков домен и диапазон f (x)?
6.Пусть a и b — две ненулевые константы. Опишите разницу между g (x) = ax + b и его родительской функцией. Каков домен и диапазон f (x)?
Изображения / математические рисунки создаются с помощью GeoGebra.
Предыдущий урок | Главная страница | Следующий урок
3.4 Преобразования кубических и четвертых функций |
| a | значение ‘ a ‘ представляет вертикальное растяжение / сжатие и, возможно, вертикальное отражение |
| k | значение из ‘ k’ представляет собой горизонтальное растяжение / сжатие и, возможно, горизонтальное отражение |
| d | значение ‘ d’ представляет горизонтальный сдвиг |
| c | значение ‘ c’ представляет вертикальный сдвиг |
Как использовать преобразования
a ——— ‘a’ — это вертикальное растяжение или сжатие, что означает, что это повлияет на все значения y координаты родительской функции.Поэтому, чтобы применить вертикальное растяжение / сжатие к родительской функции y = xn:
- , умножьте значения y родительской функции на значение ‘a’
- , если ‘a’ отрицательно, результатом будет вертикальное отражение в ось ординат.
k ——— ‘k’ — это горизонтальное растяжение или сжатие, что означает, что он повлияет на все значения x координат родительской функции. Поэтому для применения горизонтального растяжения / сжатия к родительской функции y = xn:
- умножьте значения x родительской функции на значение 1 / ‘k’.(Это означает, что если значение ‘k’ равно 1/2, вы умножаете значения x на 2, а если значение ‘k’ равно 2, вы умножаете значения x на 1/2)
- if ‘k ‘отрицательно, результат будет горизонтальным отражением по оси абсцисс.
d ——— ‘d’ является горизонтальным переводом, что означает, что будут применены значения x координат родительской функции. Поэтому для применения горизонтального переноса к родительской функции y = x n следуйте следующим правилам:
- если ‘d’> 0, то (x — ‘d’): перевод d единиц вправо, поэтому добавьте ‘d’ к значениям x
- , если ‘d’ = 0, то (x — 0) = (x): без горизонтального смещения
- , если ‘d’ <0, то (x - 'd'): смещение на d единиц влево , поэтому вычтите 'd' из значений x
c ——— ‘c’ — это вертикальное перемещение, что означает, что значения x координат родительской функции будут применены.Поэтому, чтобы применить вертикальное перемещение к родительской функции y = x n , следуйте следующим правилам:
- Если ‘c’> 0, то (x — ‘c’): перевод ‘c’ на единицы вверх, поэтому добавьте ‘ c ‘к значениям y
- иначе, если’ c ‘= 0, то (x) — 0 = (x): нет вертикального переноса
- иначе, если’ c ‘<0, то (x -' c '): перевод «c» на единицы измерения вниз, поэтому вычтите «c» из значений y.
| Теперь, когда вы знаете, что будет делать каждое преобразование, щелкните здесь, чтобы увидеть, как преобразования применяются для построения графика функции! Используйте изученные методы, чтобы следовать примеру, приведенному ниже.** полезное примечание: онлайн-калькулятор графиков на сайте desmos всегда можно использовать для перепроверки любых графиков, которые вы создаете! Пример — Опишите преобразования, которые должны быть применены к y = x3, чтобы построить график y = -8 (1 / 2x + 1) 3-3, а затем построить график этой функции. Шаг 1 Факторизуйте коэффициент при x, чтобы y = -8 (1 / 2x + 1) 3-3 становится y = -8 (1/2 (x + 2)) 3-3 Шаг 2 Опишите преобразования
Шаг 3 Начните с ключевых моментов родительской функции.
Шаг 4 Сначала примените растяжки, сжатия и отражения.
Шаг 5 Выполните
| Имейте это в виду при описании функций: График примера вопроса на слева: |
Как отразить график по оси Y
Прежде чем мы перейдем к отражениям по оси Y, убедитесь, что вы освежили свою память о том, как выполнять простой вертикальный и горизонтальный перенос.
Отражение по оси Y
Одно из самых простых преобразований, которое можно выполнить с помощью простых функций, — это его отражение по оси Y или другой вертикальной оси. В потенциальном тестовом вопросе это можно сформулировать по-разному, поэтому убедитесь, что вы понимаете следующие термины как еще один способ сказать «выполнить отражение по оси y»:
• График y = f (−x) y = f (-x) y = f (−x)
• График f (−x) f (-x) f (−x)
• f (−x) f (-x) f (−x) отражение
• Или просто: f (−x) f (-x) f (−x)
Для этого процесс чрезвычайно прост: для любой функции, какой бы сложной она ни была, просто выберите легко определяемые координаты, разделите координату x на (-1), а затем заново постройте график. эти координаты.Это оно!
Лучший способ попрактиковаться в рисовании отражений по оси Y — это выполнить пример задачи:
Пример:
Учитывая график y = f (x) y = f (x) y = f (x), как показано, эскиз y = f (−x) y = f (-x) y = f (−x).
Помните, единственный шаг, который мы должны сделать перед построением f (-x) отражения, — это просто разделить x-координаты легко определяемых точек на нашем графике выше на (-1). Когда мы говорим «легко определяемые точки», мы имеем в виду только точки, для которых вам известны значения x и y , ровно .Не выбирайте точки, в которых вам нужно оценить значения, так как это излишне усложняет задачу. Ниже приведены несколько изображений, которые помогут вам наглядно представить, как решить эту проблему.
Шаг 1. Знайте, что мы отражаемся поперек оси Y
Шаг 2: Определите точки, которые легко определить
Шаг 3. Разделите эти точки на (-1) и нанесите новые точки
Чтобы получить визуальный инструмент, который поможет вам в вашей практике и чтобы проверить свои ответы, перейдите по этой фантастической ссылке здесь.
Как найти ось симметрии
В некоторых случаях вам будет предложено выполнить вертикальное отражение по оси симметрии, которая не является осью y. Но прежде чем мы перейдем к решению этой проблемы, важно знать, что мы подразумеваем под «осью симметрии». Ось симметрии — это просто вертикальная линия, по которой мы выполняем отражение. Это может быть ось Y или любая вертикальная линия с уравнением x = константа, например x = 2, x = -16 и т. Д.
Нахождение оси симметрии, как и построение самих отражений, также является простым процессом.В этом случае все, что нам нужно сделать, это выбрать ту же точку как на функции, так и на ее отражении, посчитать расстояние между ними и разделить это на 2. Это потому, что, по его определению, ось симметрии равна ровно в середине функции и ее отражения.
Лучший способ попрактиковаться в нахождении оси симметрии — это решить задачу-пример:
Пример:
Найдите ось симметрии для двух функций, показанных на изображении ниже.
Опять же, все, что нам нужно сделать для решения этой проблемы, — это выбрать одну и ту же точку в обеих функциях, посчитать расстояние между ними и разделить на 2. Давайте выберем исходную точку для этих функций, так как это самая простая точка решения. с участием.
Теперь, посчитав расстояние между этими двумя точками, вы должны получить ответ 8 единиц. Последний шаг — разделить это значение на 2, что даст нам x = 4 в качестве нашей оси симметрии! Давайте посмотрим, как бы это выглядело, если бы там была настоящая строка:
И это все! Для дальнейшего изучения преобразований функций по отношению к тригонометрическим функциям см. Наши уроки о преобразованиях тригонометрических графиков и о том, как найти тригонометрические функции по графикам.
Многочлены Тейлора функций двух переменных
Многочлены Тейлора работают одинаково для функций двух переменных. (Каждой производной просто больше!)
Обратите внимание, что на самом деле это просто уравнение касательной плоскости функции \ (f \). 2 \), поскольку частичное берется по отношению к \ (x \) дважды, а в члене с \ (f_ {xy} (a, b) \) у вас есть множители \ ((xa) \) и \ ((yb) \) (оба возведены в первую степень), поскольку частичное берется по \ (x \) один раз и по \ (y \) один раз.y + 1 \) для \ ((x, y) \) около точки \ ((1, 0) \)
Решение
а. Чтобы определить линейное приближение полинома Тейлора первой степени, \ (L (x, y) \), мы сначала вычисляем частные производные от \ (f \).
\ [f_x (x, y) = 2 \ cos 2x \ quad \ text {and} \ quad f_y (x, y) = — \ sin y \ nonumber \]
Затем вычисляя эти частичные данные и саму функцию в точке \ ((0,0) \), мы имеем:
\ [\ begin {align *} f (0,0) & = \ sin 2 (0) + \ cos 0 = 1 \\ f_x (0,0) & = 2 \ cos 2 (0) = 2 \\ f_y (0,0) & = — \ sin 0 = 0 \ end {align *} \ nonumber \]
Сейчас,
\ [\ begin {align *} L (x, y) & = f (0,0) + f_x (0,0) (x — 0) + f_y (0,0) (y — 0) \\
& = 1 + 2x \ end {align *} \]
См.



 Есть несколько основных аспектов
Есть несколько основных аспектов





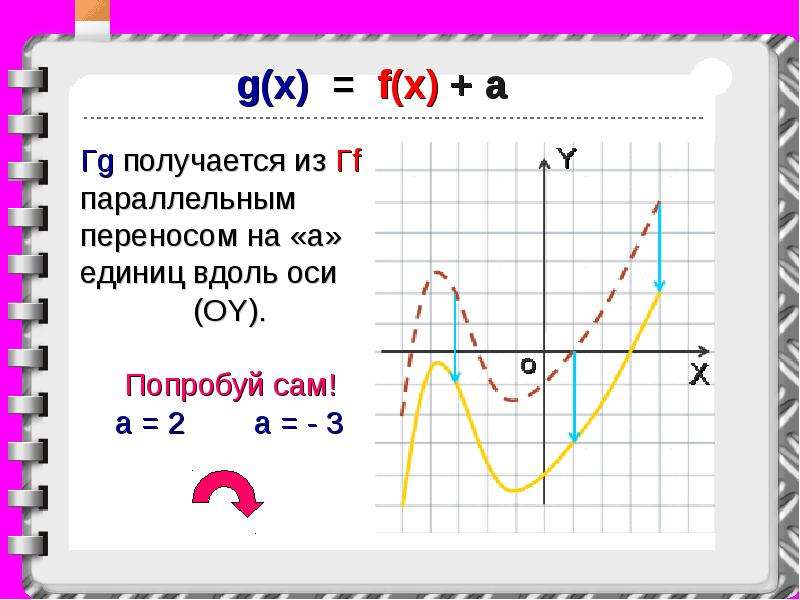

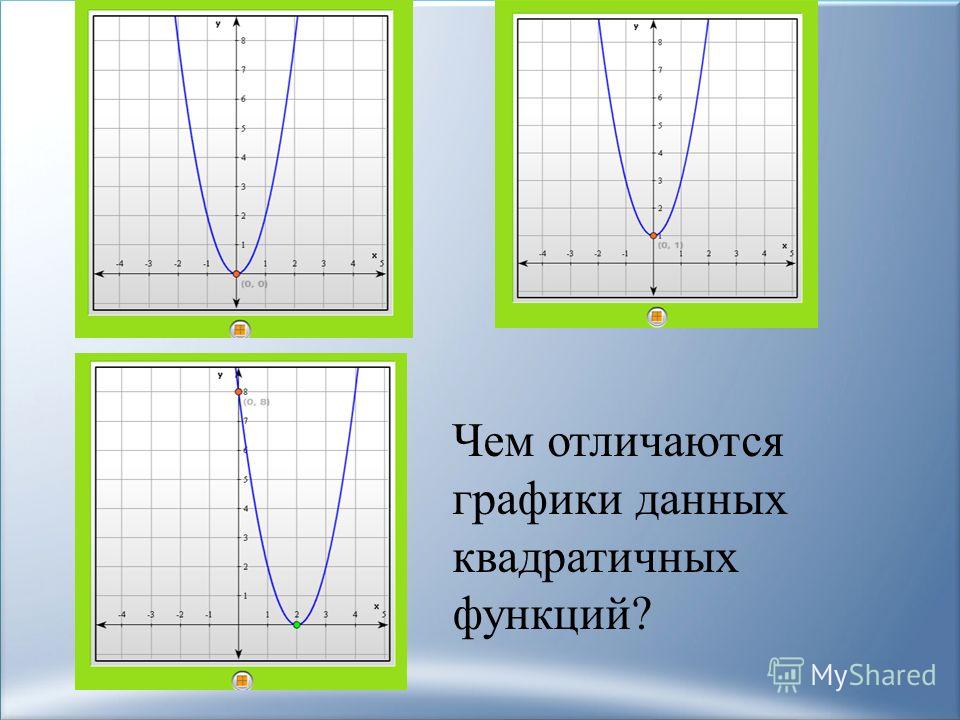



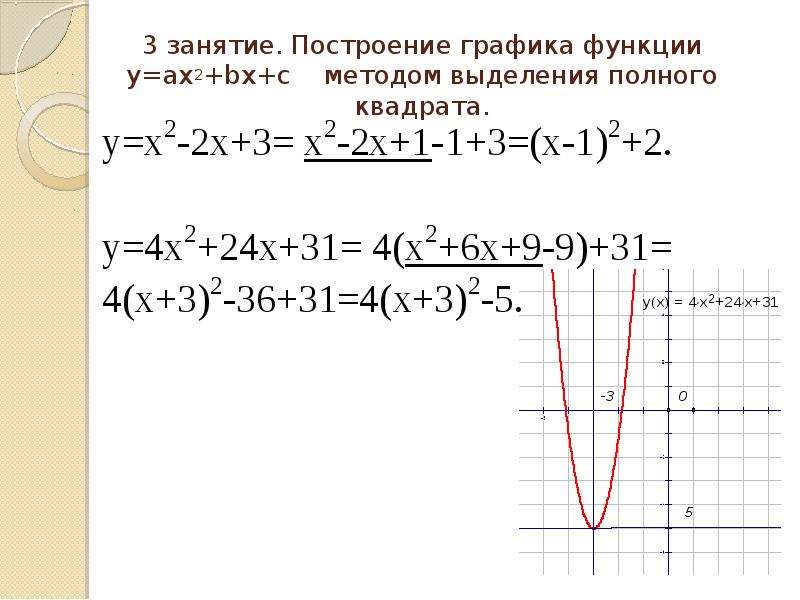






 5
5