Содержание
y x 2 2x 3 график функции
Вы искали y x 2 2x 3 график функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и график функции y x 2 2x 3, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y x 2 2x 3 график функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 2 2x 3 график функции,график функции y x 2 2x 3,график функции y x2 2x 3,построить график функции y x2 2x 3,постройте график функции y x 2 2x 3,постройте график функции y x 2 3x 2,постройте график функции y x 2x 3,постройте график функции y x2 2x 3. 2 — 2x — 3′)
2 — 2x — 3′)
plt.ylabel(‘Ось y’)
plt.xlabel(‘Ось x’)
plt.grid()
plt.axis([-10, 16, -10, 10])
plt.scatter(x1, y1, s = 1, c = ‘b’)
plt.scatter(x1, -y1, s = 1, c= ‘b’)
plt.plot(x2, y2, ‘r—‘)
plt.plot(x2, -y2, ‘r—‘)
plt.show()
Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0.
Далее, мы отбираем по этой маске значения из наших массивов x и y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)). 2$
2$
9
6,25
4
2,25
1
0,25
0
0,25
1
2,25
4
6,25
9
Отметим полученные точки на координатной плоскости и соединим их кривой:
Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.
Свойства параболы y=x²
1. Область определения $x \in (- \infty;+ \infty)$ — все действительные числа.
2. Область значений $y \in [0;+ \infty)$ — все неотрицательные действительные числа.
3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$.
4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.
5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$. 2$, кроме двух точек с $ x \neq \pm 1 $.
2$, кроме двух точек с $ x \neq \pm 1 $.
Построить график функции у=-x²+2x+8 (парабола) – решение и ответ
Формулировка задания: Построить график функции у = -x² + 2x + 8.
Решение:
Для построения графика параболы нужно построить таблицу значений x и y.
Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:
x = 0 ⇒
y = -0² + 2 ⋅ 0 + 8 = 8
Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:
y = 0 ⇒
-x² + 2x + 8 = 0
a = -1, b = 2, c = 8
D = 2² – 4 ⋅ (-1) ⋅ 8 = 36
x1 = (-2 + 6) / (-2) = -2
x2 = (-2 – 6) / (-2) = 4
Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:
Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:
x = 1 ⇒
y = -1² + 2 ⋅ 1 + 8 = 9
x = -1
y = -(-1)² + 2 ⋅ (-1) + 8 = 5
Таблица значений теперь выглядит следующим образом:
Отметим полученные точки на координатной плоскости:
Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними.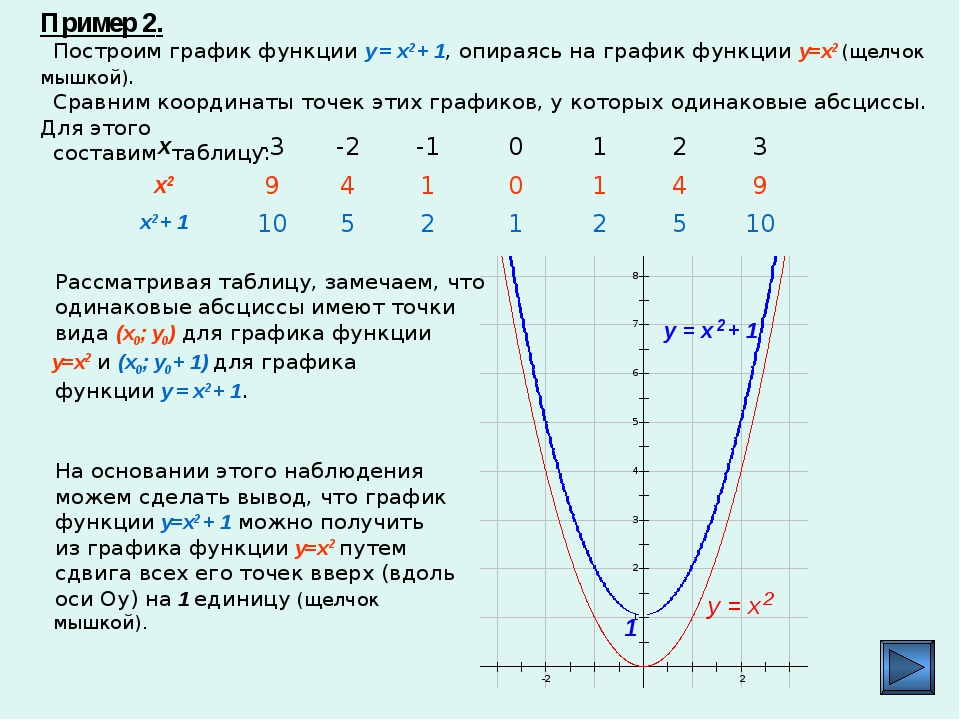 Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
(4 – (-2)) / 2 = 6 / 2 = 3
xв = -2 + 3 = 1
Точка с таким значением x уже есть в таблице значений. Осталось построить график:
Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Функции | Презентация к уроку (алгебра, 9 класс) по теме:
Слайд 1
Построение графиков квадратичной функции, содержащей модуль
Слайд 2
Актуализация опорных знаний
Определение квадратичной функцииАлгоритм построения квадратичной функцииКак, зная график функции y=f(x) построить графики следующих функций:y=f(-x)y=-f(x)y=f(x+m)y=f(x)+ny=f(x+m)+ny=kf(x)y=|f(x)|y=f(|x|)
Слайд 3
Устно Дан график функции y = x2 – 4x + 3.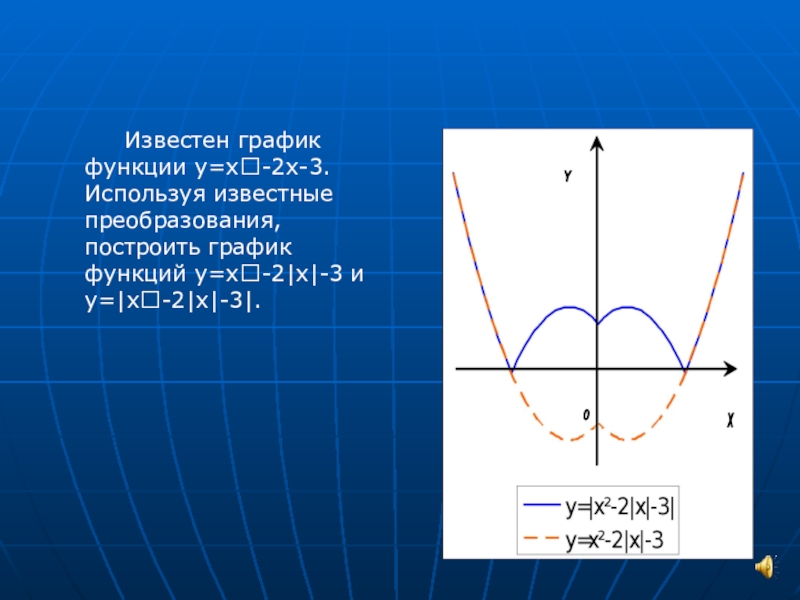 Составьте формулу функции, график которой:
Составьте формулу функции, график которой:
1) симметричен данному относительно оси: а) x; б) y; 2) получается из данного параллельным переносом на 3) получается из данного растяжением в 2 раза от оси а) x; б) y 4) получается из данного сжатием в 2 раза к оси а) x; б) y
1а) y = –x2 + 4x – 3; 1б) y = x2 + 4x + 3 2 y = x2 – 6x + 6;3а) y = 0,25×2 – 2x + 3; 3б) y = 2×2 – 8x + 6; 4а) y = 4×2 – 8x + 34б) y = 0,5×2 – 2x + 1,5;
Слайд 4
Найдите соответствия:
Слайд 5
Построить график функции y=|-2×2 +8x -6|
1. Построим график функции y= -2×2 +8x -6Ветви параболы направлены внизВершина в точке:Ось симметрии: х=2Нули функцииХ1 =1, Х2 =3
х
0
1
2
3
4
у
-6
-0
2
0
-6
2. отразим части параболы, расположенные в нижней части полуплоскости, симметрично относительно оси абсцисс.
Слайд 6
0 1 x
Y
6
2
1
-1
-2
-3
-4
-5
-6
Построим график функции y =| — 2 x 2+6 x -2 | 1. Сначала построим график функции y = — 2 x 2+8 x -6 Преобразуем трехчлен:
Сначала построим график функции y = — 2 x 2+8 x -6 Преобразуем трехчлен:
2. отразим части параболы, расположенные в нижней части полуплоскости, симметрично относительно оси абсцисс.
Применение преобразований при построении графика функции
Слайд 7
Аналитическое построение
Построить график функции y=|x|xПо определению модуля: y = x2 ,x>0 — x2 ,x0 x
y
x>0
x
Слайд 8
Построим график функции y=|x2-5x|+x-3 с помощью узловых точек
x2-5x=0, x(x-5)=0, x=0 илиx=5x=0или x=5 разбивают числовую прямую на три промежуткаI. x=-1; (-1)2 -5(-1)>0 y=x2-5x+x-3 =x2-4x-3 Строим параболу и выделяем ту часть, которая находится на промежуткеII. x=1; 12 -5*10 y=x2-4x-3 Эту параболу уже строили, поэтому выделим ту часть, которая находится на промежуткеВыделенные части являются графиком функции
| || |||
0 5 x
Слайд 9
Постройте графики функций:
Вариант 1
Вариант 2
Вариант 3
Вариант 4
а) y=|x2 -4|б) y=|2x-x2 |
а)y=|x2 -1|б) y=|x2 +2x-1|
а) y=|(x-3)2 -1| б) y=x2 -|x-1|
а) y=|-(x+2)2 +3|б) y=|2+4|x|-x2|
Слайд 10
Вариант 1а) y=|x2 -4| б) y=|2x-x2 |
Вариант 2а) y=|x2 -1| б) y=|x2 +2x-1|
Вариант3а) y=|(x-3)2 -1| б) y=x2 -|x-1|
Вариант 4а) y=|-(x+2)2 +3| б) y=|2+4|x|-x2|
Проверь себя !
Слайд 11
Основные преобразования графиков:
параллельные переносы; симметрии относительно осей координат;растяжения (сжатия) от (к) осей (осям) координат; преобразования, связанные с модулями.
Слайд 12
Алгоритм построения графика функции у = ах2 + bх +с.
1.
Определить направление ветвей параболы.
2.
Найти координаты вершины параболы (т; п).
3.
Провести ось симметрии.
4.
Определить точки пересечения графика функции с осью Ох, т.е. найти нули функции.
5.
Составить таблицу значений функции с учетом оси симметрии параболы.
Слайд 13
Перенос вдоль оси ординат
График функции y= f (x) + b при b >0 можно получить параллельным переносом вдоль оси ординат графика функции y= f (x) на b единиц вверх. График функции y=f(x)-b при b>0 можно получить параллельным переносом вдоль оси ординат графика функции y=f(x) на b единиц вниз
0 1 x
y= x2 +2
y=x2
0 1 x
y= x2 -2
y=x2
Y
2
1
Y
1
-2
Слайд 14
Перенос вдоль оси ординат
График функции y= f(x)+b при b >0 можно получить так :1. построить график функции y= f (x)2.перенести ось абсцисс на b единиц вверхГрафик функции y=f(x)-b при b>0 можно получить так:1. построить график функции y=f(x)2 перенести ось абсцисс на единиц вниз
построить график функции y= f (x)2.перенести ось абсцисс на b единиц вверхГрафик функции y=f(x)-b при b>0 можно получить так:1. построить график функции y=f(x)2 перенести ось абсцисс на единиц вниз
Y
2
0 1 x
0 1 x
На b вверх
0 1 x
Вниз На b
Y
1
-2
0 x
Слайд 15
Перенос вдоль оси абсцисс
График функции y= f (x + c) можно получить параллельным переносом вдоль оси абсцисс графика функции y= f (x) на |c| единиц влево при c >0 .График функции y=f(x+c) можно получить параллельным переносом вдоль оси абсцисс графика функции y=f(x) на |c| единиц вправо при c-2 0 1 x
y=x2
y=(x+2)2
0 1 2 x
y=x2
y=(x-2)2
Y
1
Y
1
Слайд 16
Перенос вдоль оси абсцисс
График функции y= f (x + c) при c >0 можно получить так :1.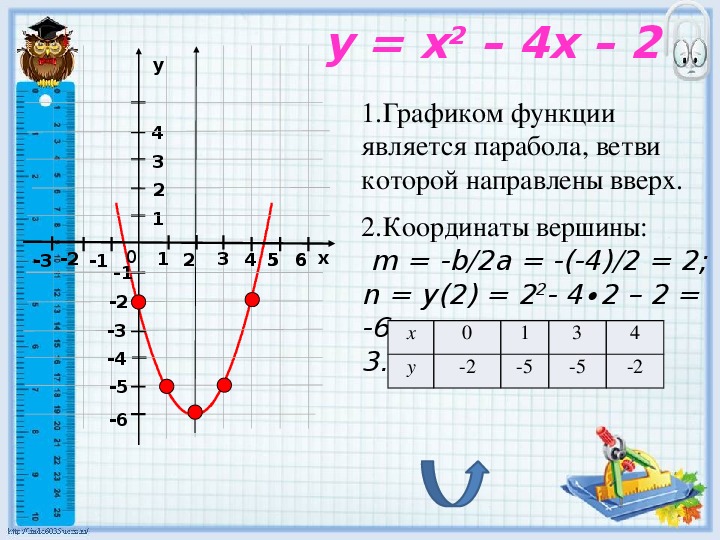 построить график функции y= f (x)2.перенести ось ординат на |b| единиц вправоГрафик функции y=f(x+c) при c0 1 x
построить график функции y= f (x)2.перенести ось ординат на |b| единиц вправоГрафик функции y=f(x+c) при c0 1 x
y
1
0
0 1 x
y
1
y
1
0
y
1
Слайд 17
Сжатие ( растяжение ) графика вдоль оси ординат
График функции y= b f (x) при b>1 можно получить растяжением графика функции y= f (x) вдоль оси ординатГрафик функции y=bf(x) при 00 1 x
y=x2
y=2×2
0 1 x
y=x2
y=0,5×2
Y
1
Y
1
Слайд 18
Симметрия относительно оси абсцисс
0 1 x
y=x2
y=-x2
Чтобы построить график фунуции y= -f(x): 1. Строим график функции y=f(x)2. Отражаем его симметрично относительно оси абсцисс.
Слайд 19
график функции y = f(|x|), y = |f(x)|
график функции y = f(|x|) получается из графика функции y = f(x) следующим преобразованием: 1) точки графика, имеющие неотрицательные абсциссы – неподвижны; 2) точки графика, имеющие отрицательные абсциссы заменяются на точки, полученные из неподвижных отражением относительно оси y.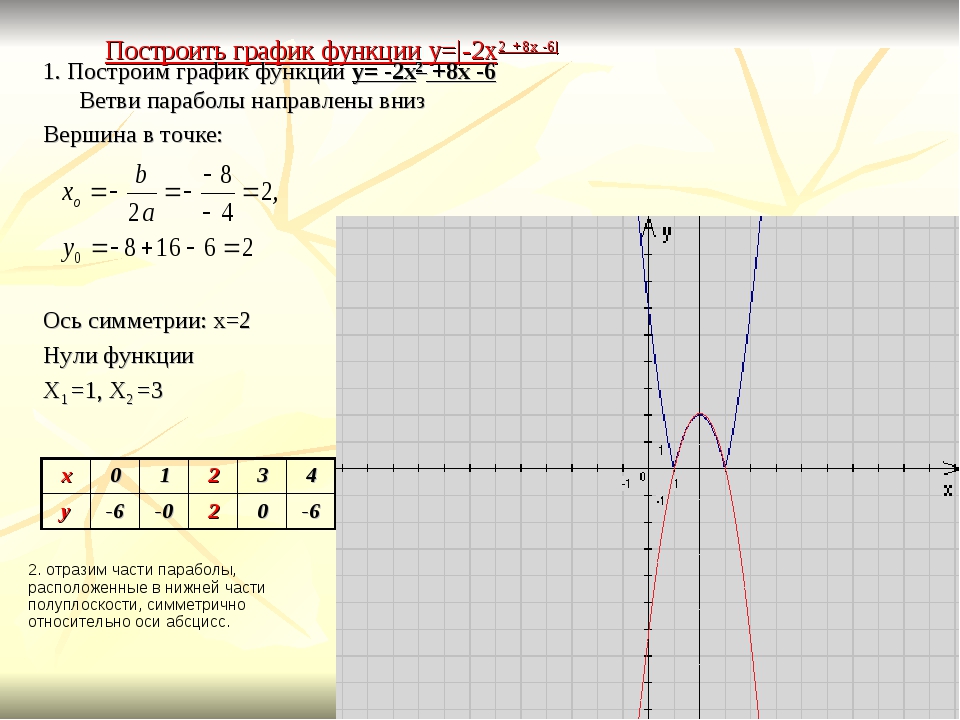 график функции y = |f(x)| получается из графика функции y = f(x) следующим преобразованием: 1) точки графика, имеющие неотрицательные ординаты – неподвижны; 2) точки графика, имеющие отрицательные ординаты, отражаются относительно оси x.
график функции y = |f(x)| получается из графика функции y = f(x) следующим преобразованием: 1) точки графика, имеющие неотрицательные ординаты – неподвижны; 2) точки графика, имеющие отрицательные ординаты, отражаются относительно оси x.
Слайд 20
Функция, содержащая операцию « взятие модуля»
Чтобы построить график функции y= |f( x) |:1. Строим график функции y= f(x),2.Часть графика, расположенную в верхней полуплоскости сохраняем.3. Часть графика, расположенную в нижней полуплоскости. отображаем симметрично относительно оси абсцисс в верхнюю полуплоскость.
0 x
y
Графики функции. 9-й класс
Цель урока – повторить и систематизировать
знания об изученных функциях и их графиках.
Для достижения цели поставлены три задачи:
– обучающая: повторить свойства изученных
функций, а также их графики.
– развивающая: развивать математическую
речь, логическое мышление, познавательный
интерес к предмету, воображение, память;
– воспитательная: воспитывать
аккуратность, внимание к слову учителя.
Структура урока
| № | Этапы урока | Деятельность уч-ся | Время |
| 1 | Организационный момент | 1 | |
| 2 | Математический диктант | Письменная | 5-7 |
| 3 | Проверка математического диктанта | Письменная, устная работа | 10 |
| 4 | Решение задач на построение графиков
функций | Решение задач Письмена, устная работа | 15 |
| 5 | Самостоятельная работа. | Сам. работа. | 7-8 |
| 6 | Подведение итогов. Рефлексия. | Обсуждение результатов деятельности на
уроке | 3 |
| 7 | Домашнее задание. | Обсуждение | 1 |
Тип урока: обобщения и систематизации знаний.
Оборудование и оформление: проектор, таблица,
сигнальные карточки, шаблоны функций у = х?, у = х?
Ход урока
1. Оргмомент.
Объявление темы и цели урока. Запись в тетради
даты, темы.
2. Математический диктант.
Диктант проводится с целью выявления пробелов
в знаниях учащихся, для того, чтобы в дальнейшем
их можно было ликвидировать. Учащиеся получают
Учащиеся получают
два чистых листа бумаги и копирку и выполняют
работу под копирку в двух экземплярах.
Задания математического диктанта.
- Постойте график функции
1 вар: y=(x-1)?; 2 вар: y= -x?+3.
Как называются графики этих функций?
- Запишите формулу для вычисления координаты х
вершины параболы. - Постройте график функции
1 вар: y= | x |; 2 вар: y= | x -1|.
- Как называется график функции, в каких
четвертях расположен график функции - 1 вар: у = 2 вар:
у = – ? Запишите
уравнение прямой в общем виде. - На рисунке изображён график функции у = х2–
х -6. Используя график функции, решите неравенство
(слайд 2)
1 вар: х2 – х-6 >0 2 вар: х2 – х – 6 <0 .
3. Проверка.
По окончании математического диктанта
учащиеся сдают 1 лист с ответами учителю, а другой
оставляют у себя для проверки. Проверка
Проверка
проводится с помощью средств обратной связи –
сигнальных карточек.
На слайде 3 несколько видов графиков,
один ученик называет свой вариант ответа, другие
сигнализируют своё согласие или не согласие
сигнальными карточками (зелёный цвет – согласны,
красный – не согласны с ответом товарища). С
помощью этого слайда идёт проверка вопросов №
1,3,4.
Последний вопрос проверяется по слайду 2.
При проверке не просто называются верные
ответы, но также идёт обсуждение ошибок. В конце
ученики выставляют себе оценки по следующим
критериям:
“5” – 6 верных ответов,
“4” – 4,5 верных ответов,
“3” – 3 верных ответа,
“2” – 1,2 верных ответа.
Учитель может перепроверить оценки учеников,
т.к. у него есть листы с ответами.
4. Решение задач на построение графиков
функций.
А) Построение графиков линейной функции: у=2х+3,
у=2х-2, у = – х, у = – х+3.
При построении ученики отвечают на вопросы.
Когда графики функций вида у = кх +в параллельны?
На что указывает число в в уравнении прямой?
По графику определите координаты точек
пересечения графиков функций с осью ординат.
(Слайд 3)
Б) Построение графиков функций у = х2, у
= х2, у = (х+3)2-2,
у = х2-2. Построение графиков
производится с использованием шаблонов графиков
функций.
При построении графиков функций ученики
рассказывают свойства этих функций.
Выполните задания: график какой функции
изображён на рисунке? (Слайд 5)
В) Построение графика функции y = ах2 +
вх + с
Постройте график функции y =x2-5x+6. Ученики
выполняют построение по алгоритму. Один ученик
работает у доски.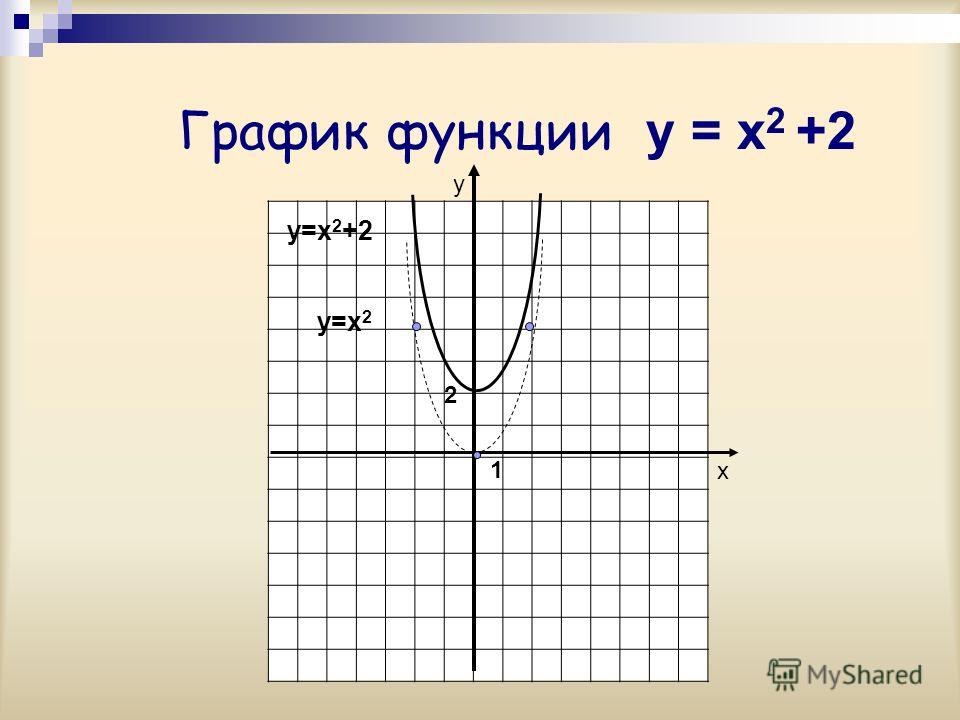
Выполните задание: квадратичная функция y = ax2
+ bx + c задана графиком, изображённым на
рисунке. Определите знаки коэффициентов a, b
и c. (Слайд 6)
1) a > 0, b < 0, c > 0;
2) a > 0, b > 0, c > 0;
3) a > 0, b < 0, c = 0;
4) a > 0, b = 0, c < 0.
По графику квадратичной функции найдите все
значения x, при которых (Слайд 7)
Г) Построение графиков функций, содержащих знак
модуля:
у = | x -1|+2; y=|x2-x-6|
Чтобы построить график функции y=|f(x)|,
достаточно построить график функции y=f(x) и ту
часть графика, которая расположена в нижней
полуплоскости, симметрично отразить
относительно оси 0x. (Слайд 8)
5.
 Самостоятельная работа.
Самостоятельная работа.
Задания самостоятельной работы
дифференцированы по сложности. (Слайд 9)
1 уровень: 1 вар: y=(x+2)2-4, y= х3-2;
2 вар: y=(x-4)2-1, y= (х+5)3.
2 уровень: 1 вар: y = 4x – х2, у = ;
2 вар: y = x2– 6х, у = -.
3 уровень: 1 вар: y =x2-2x-3, y =|2х-1|;
2 вар: y =-x2-2x-3, y =|0,5х+1|.
6. Подведение итогов.
Оценки за урок.
Рефлексия.
Включаем светофор: если на уроке ученику было
всё понятно и не возникли вопросы, то он
поднимает сигнальную линейку зелёного цвета, в
противном случае – красную.
7. Домашнее задание. (Слайды 10, 11)
1. Повторить свойства функции у = и построить график у =
2.
3. Построить график функции вида y=f(x).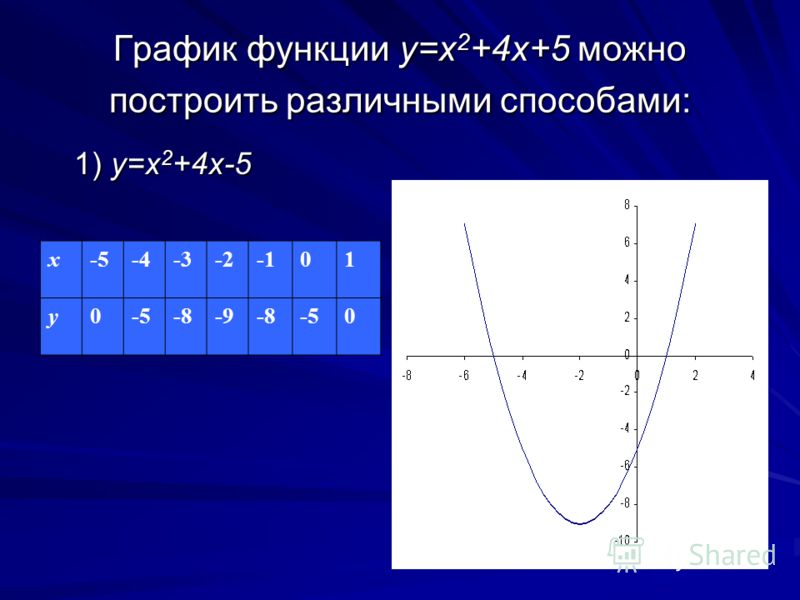
y = x2
— |x| -3
4. Объясните построение графика функции (На оценку “5”)
Презентация
Квадратичная функция и её график
График функции
2
y = ax .
График функции
2
y = ax + bx + c.
Лабораторнографическая работа
у
y = ax2,
a>0
x≤0
( ;0]
0
x≥0
[0; )
y = ax2,
a
х
Задача: Построить график функции y = x2 – 2x + 3 и
сравнить с графиком функции y = x2
Построение.
1.Графиком функции y = x2 – 2x + 3 является парабола, ветви которой
направлены вверх.
2.Составим таблицу значений функции y = x2 – 2x + 3
x
-3
-2
-1
0
y = x2 – 2x + 3
18
11
6
3
1
2
2
3
3
6
3. Построим график функции y = x2 – 2x + 3
4.Сравним графики y = x2 – 2x + 3 и y = x2
y = x2 – 2x + 3 = x2 – 2x + 1+ 2 = (x – 1)2 + 2
Вывод: Графиком функции y = x2 – 2x + 3 является парабола,
получаемая сдвигом параболы y = x2 на единицу вправо и на две
единицы вверх.
Графиком функции
y = ax2+bx+c
является парабола,
получаемая сдвигом
параболы y = ax2
вдоль координатных
осей.
Ось симметрии
у
y = ax2+bx+c,
a>0
0
х
Вершины параболы
y = ax2+bx+c
x0
b
2a
y y x 0 a x b x c
2
0
0
0
y = ax2+bx+c,
a
Задания
Дана функция y = ax2 +bx + c.
1. Найдите координаты точек пересечения графика
функции с осями координат.
2. Постройте график данной функции.
3. С помощью графика найдите:
a) множество значений х, на котором функция:
1) возрастает, 2) убывает, 3) принимает
положительные
значения,
4)
принимает
отрицательные значения;
a) значения переменной х, при которых функция
принимает наибольшее и наименьшее значение.
4. Проходит ли график данной функции через точки
A(m; n), B(-m; n), C(-m; -n), D(m; -n).
Вариант 1.
2
-x
y=
+ 6x – 5;
m = 2; n = 3
Вариант 2.
y=
2
0,5x
+ 3x – 0,5;
m = 1; n = 4
ПРИМЕР 1 Изобразите функцию вида y = ax 2 График y = 2x 2. Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для.
Презентация на тему: «ПРИМЕР 1 График функции вида y = ax 2 График y = 2x 2. Сравните график с графиком y = x 2. ШАГ РЕШЕНИЯ 1 Составьте таблицу значений для.» — стенограмма презентации :
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
ПРИМЕР 1 График функции вида y = ax 2 График y = 2x 2.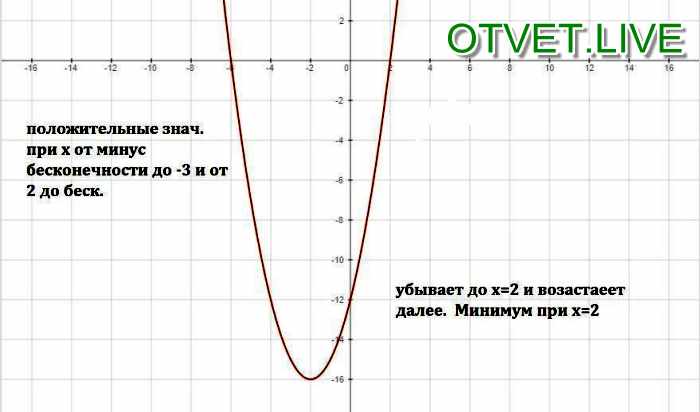 Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для y = 2x 2. ШАГ 2 Постройте точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для y = 2x 2. ШАГ 2 Постройте точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
2
ПРИМЕР 1 Изобразите функцию вида y = ax 2 ШАГ 4 Сравните графики y = 2x 2 и y = x 2. Оба они открываются и имеют одинаковую вершину и ось симметрии. График y = 2x 2 уже, чем график y = x 2.
3
ПРИМЕР 2 Изобразите функцию вида y = ax 2 + c График y = — сравните график с графиком x 2 + 3 1212 y = x 2 ШАГ РЕШЕНИЯ 1 Составьте таблицу значений для y = — x 2 + 3 1212 ШАГ 2 Нанесите точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
4
ПРИМЕР 2 Постройте график функции вида y = ax 2 ШАГ 4 Сравните графики y = — и y = x 2.Оба графика имеют одну и ту же ось симметрии. Однако график y = — открывается вниз и шире, чем график y = x 2.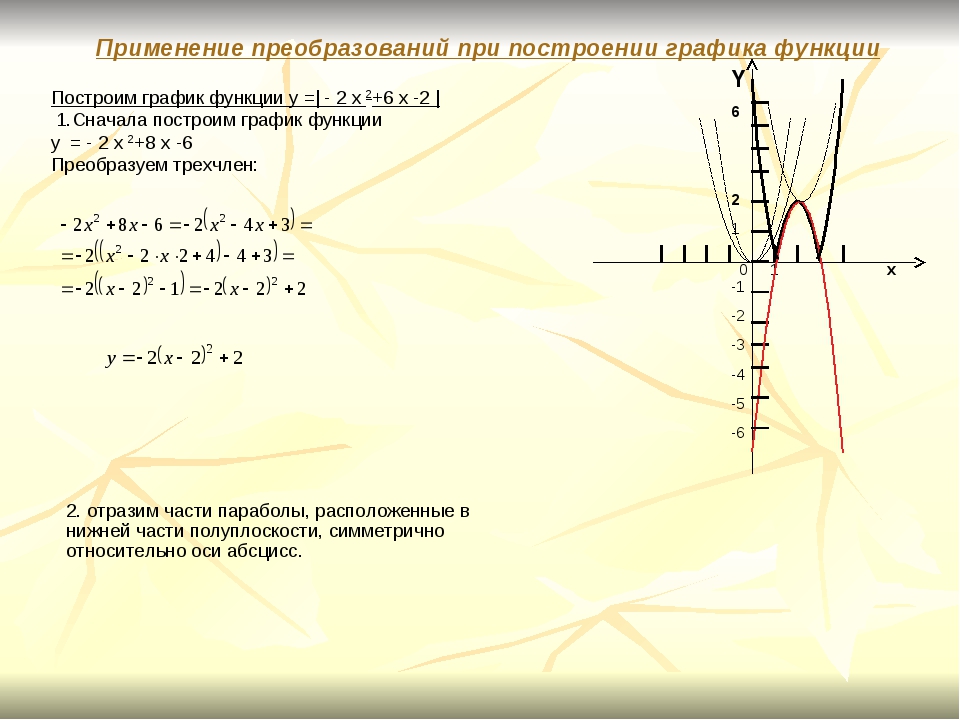 Кроме того, его вершина на 3 единицы выше. х 2 + 3 1212 1212
Кроме того, его вершина на 3 единицы выше. х 2 + 3 1212 1212
5
РЕКОМЕНДАЦИИ для примеров 1 и 2 Изобразите функцию. Сравните график с графиком y = x 2. 1. y = — 4x 2 РЕШЕНИЕ ШАГ 1 Составьте таблицу значений y = — 4x 2. X — 2 — 102 Y — 16-40 — 16 — 4
6
ПРАКТИЧЕСКИЕ ПРАКТИКИ для примеров 1 и 2 ШАГ 2 Обозначьте точки из таблицы.ШАГ 3 Проведите плавную кривую через точки. ШАГ 4 Сравните графики y = — 4x 2 и y = x 2. Та же ось симметрии и вершина, раскрывается вниз и уже. ОТВЕТ
7
РЕКОМЕНДАЦИИ для примеров 1 и 2 2. y = — x 2 — 5 РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для y = — x 2 — 5. X — 2 — 102 Y — 9 — 6 — 5 — 9 — 6 ШАГ 2 Нанесите точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.ШАГ 4 Сравните графики y = — x 2-5 и y = x 2.
8
ПРАКТИЧЕСКИЕ ПРАКТИКИ для примеров 1 и 2 ОТВЕТ Ось симметрии та же, вершина смещена на 5 единиц вниз и открывается вниз.
9
РЕКОМЕНДАЦИИ для примеров 1 и 2 3. f (x) = РЕШЕНИЕ ШАГ 1 X — 4 — 20 — 4 2 Y — 2 4264 ШАГ 2 Нанесите точки из таблицы.ШАГ 3 Проведите плавную кривую через точки. ШАГ 4 x 2 + 2 1414 Составьте таблицу значений для f (x) = x 2 + 2 1414 Сравните графики f (x) = и y = x 2. x 2 + 2 1414
10
РЕКОМЕНДУЕМЫЕ ПРАКТИКИ для примеров 1 и 2 ОТВЕТ Одна и та же ось симметрии, вершина смещена на 2 единицы вверх, раскрывается и становится шире.
Преобразования квадратичных функций | Колледж алгебры
Результаты обучения
- График вертикальных и горизонтальных сдвигов квадратичных функций
- График вертикального сжатия и растяжения квадратичных функций
- Напишите уравнение преобразованной квадратичной функции, используя форму вершин
- Определить вершину и ось симметрии для данной квадратичной функции в форме вершины
Стандартная форма квадратичной функции представляет функцию в форме
[латекс] f \ left (x \ right) = a {\ left (x-h \ right)} ^ {2} + k [/ latex]
где [латекс] \ left (h, \ text {} k \ right) [/ latex] — вершина. 2 [/ латекс]
2 [/ латекс]
Величина [латекс] а [/ латекс] указывает на растяжение графика. Если [latex] | a |> 1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается дальше от оси [latex] x [/ latex] –, поэтому график сужается, появляется вертикальная растяжка. Но если [latex] | a | <1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается ближе к оси [latex] x [/ latex] –, поэтому график кажется шире, но на самом деле есть вертикальное сжатие.{2}} {4a} \ end {align} [/ latex]
На практике, однако, обычно легче запомнить, что [latex] h [/ latex] является выходным значением функции, когда входным значением является [latex] h [/ latex], поэтому [latex] f \ left (h \ right) = f \ left (- \ dfrac {b} {2a} \ right) = k [/ latex].
Попробуйте
Сетка координат наложена на квадратную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение пути мяча. Стрелок забивает корзину?
(кредит: модификация работы Дэна Мейера)
Показать решение
Путь проходит через начало координат и имеет вершину в [latex] \ left (-4, \ text {} 7 \ right) [/ latex], поэтому [latex] \ left (h \ right) x = — \ frac { 7} {16} {\ left (x + 4 \ right)} ^ {2} +7 [/ латекс].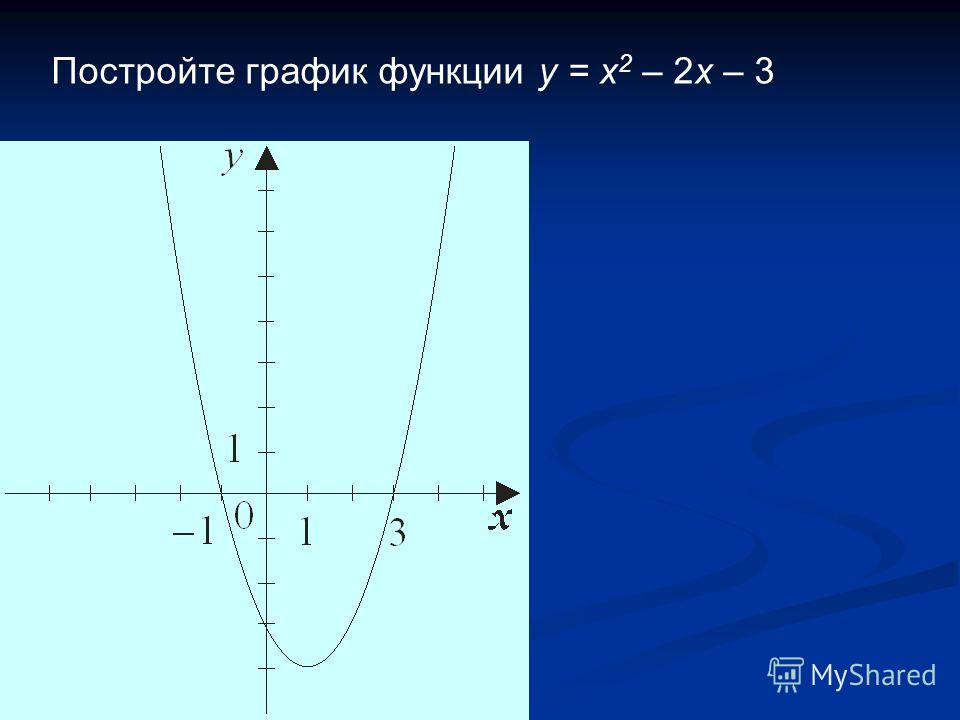 Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.
Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Графические уравнения, система уравнений с программой «Пошаговое решение математических задач»
Описание
Команда plot генерирует график практически любой функции или отношения, обнаруживаемого в математике средней школы и колледжа.Он будет отображать функции, заданные в форме y = f (x), например y = x 2 или y = 3x + 1, а также отношения вида f (x, y) = g (x, y) , например x 2 + y 2 = 4.
Чтобы использовать команду построения графика, просто перейдите к основному
страницу графика, введите свое уравнение (в терминах x и y), введите набор
значения x и y, для которых должен быть построен график, и нажмите «График»
кнопка. Ваше уравнение будет автоматически построено, и будет показан ответ.
Ваше уравнение будет автоматически построено, и будет показан ответ.
в вашем браузере в течение нескольких секунд.2 = 1 от x = -2 до x = 2, y = -1,8 до y = 1,8
Опции (только расширенная страница)
Деления
Значения: отмечен или не отмечен
По умолчанию: установлен
Если галочки отмечены, на осях графика будут отображаться отметки и числовые шкалы.
Линии сетки
Значения: установлен или не установлен
По умолчанию: не установлен
Если установлен флажок Линии сетки, на график будет наложена синяя сетка.
Оси
Значения: Нет или Автоматическая исходная точка или Исходная точка в (#, #)
По умолчанию: Автоматическая исходная точка
Параметр «Оси» управляет внешним видом и расположением осей на графике. Если отмечено «Нет», оси не будут отображаться вообще. Когда установлен флажок «Автоматическое начало координат», будут отображаться оси. Две оси обычно пересекаются в точке (0,0), но иногда эта точка пересечения может быть расположена в другом месте. Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке.
Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке.
Соотношение сторон
Значения: Один к одному или Золотое сечение или #: #
По умолчанию: Один к одному
Параметр Соотношение сторон управляет соотношением высоты графика к его ширине. Когда установлен флажок «Один к одному», соотношение составляет 1: 1, и масштабы на двух осях будут идентичными. Это гарантирует, что круги, например, действительно будут отображаться на экране круглыми. Когда выбрано золотое сечение, соотношение сторон составляет 1: 1 / г, где g — золотое сечение (приблизительно 1.6180). Это якобы дает соотношение высоты к ширине, которое особенно «приятно» для глаз. Когда выбрано #: # и введены два значения, будет применяться указанное соотношение сторон. Это полезно, если сюжет сильно сжат в одном или другом направлении и его необходимо «растянуть», чтобы сделать его более четким.
Родительские функции — Типы, свойства и примеры
При работе с функциями и их графиками вы заметите, как графики большинства функций выглядят одинаково и следуют схожим шаблонам.Это потому, что функции, имеющие одинаковую степень, будут следовать аналогичной кривой и использовать одни и те же родительские функции.
Родительская функция представляет собой простейшую форму семейства функций.
Это определение прекрасно описывает родительские функции. Мы используем родительские функции, чтобы направлять нас при построении графиков функций, которые находятся в том же семействе. В этой статье мы:
- Рассмотрим все уникальные родительские функции (возможно, вы уже сталкивались с некоторыми ранее).
- Узнайте, как определить родительскую функцию, которой принадлежит функция.
Возможность идентифицировать и графически отображать функции с помощью их родительских функций может помочь нам лучше понять функции, так чего же мы ждем?
Что такое родительская функция?
Теперь, когда мы понимаем, насколько важно для нас овладеть различными типами родительских функций, давайте сначала начнем понимать, что такое родительские функции и как их семейства функций зависят от их свойств.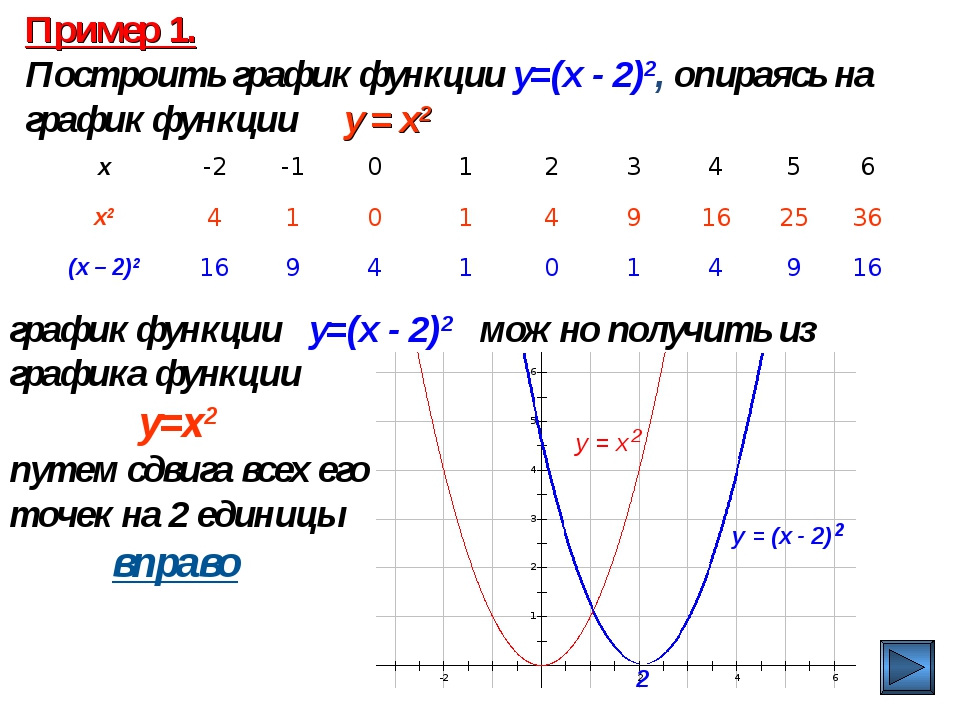
Определение родительской функции
Родительские функции — это простейшая форма данного семейства функций . Семейство функций — это группа функций, которые имеют одинаковую наивысшую степень и, следовательно, одинаковую форму для своих графиков .
На приведенном выше графике показаны четыре графика, которые демонстрируют U-образный график, который мы называем параболой. Поскольку все они имеют одинаковую высшую степень двойки и одинаковую форму, мы можем сгруппировать их в одно семейство функций.Сможете угадать, к какой семье они принадлежат?
Все эти четыре функции являются квадратичными, и их простейшая форма будет y = x 2 . Следовательно, родительской функцией для этого семейства является y = x 2 .
Поскольку родительские функции являются простейшей формой данной группы функций, они могут сразу дать вам представление о том, как будет выглядеть данная функция из того же семейства.
Какие бывают типы родительских функций?
Пришло время освежить наши знания о функциях, а также узнать о новых функциях.Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.
Почему бы нам не начать с тех, которые мы, возможно, уже узнали в прошлом?
Первые четыре родительские функции содержат многочлены с возрастающей степенью. Давайте посмотрим, как ведут себя их графики, и отметим область и диапазон соответствующих родительских функций.
Функции констант
Функции констант — это функции, которые определяются своей соответствующей константой c.Все функции-константы будут иметь горизонтальную линию в качестве графика и содержать только константу в качестве члена.
Все постоянные функции будут иметь все действительные числа в качестве домена и y = c в качестве диапазона. У каждого из них также есть точка пересечения по оси y в точке (0, c).
Движение объекта в состоянии покоя — хороший пример постоянной функции.
Линейные функции
Линейные функции имеют x как член с наивысшей степенью и общую форму y = a + bx.Все линейные функции имеют прямую линию в виде графика .
Родительская функция линейных функций — это y = x, , и она проходит через начало координат. Область и диапазон всех линейных функций: , все действительные числа .
Эти функции представляют отношения между двумя объектами, которые линейно пропорциональны друг другу.
Квадратичные функции
Квадратичные функции — это функции с 2 в качестве высшей степени .Все квадратичные функции возвращают параболу в виде графика . Как обсуждалось в предыдущем разделе, у квадратичных функций y = x 2 в качестве родительской функции .
Вершина родительской функции y = x 2 лежит в начале координат. Он также имеет область всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция увеличивается, когда x положительна , и уменьшается, когда x отрицательна .
Он также имеет область всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция увеличивается, когда x положительна , и уменьшается, когда x отрицательна .
Хорошее применение квадратичных функций — движение снаряда.Мы можем наблюдать за движением снаряда объекта, построив график квадратичной функции, которая его представляет.
Кубические функции
Давайте перейдем к родительской функции многочленов с 3 в качестве высшей степени . Кубические функции имеют общую родительскую функцию y = x 3 . Эта функция на увеличивается по всему домену .
Как и в случае с двумя предыдущими родительскими функциями, график y = x 3 также проходит через начало координат.Его домен и диапазон — это (-∞, ∞) или все действительные числа.
Функции абсолютного значения
Родительская функция функций абсолютного значения — y = | x | .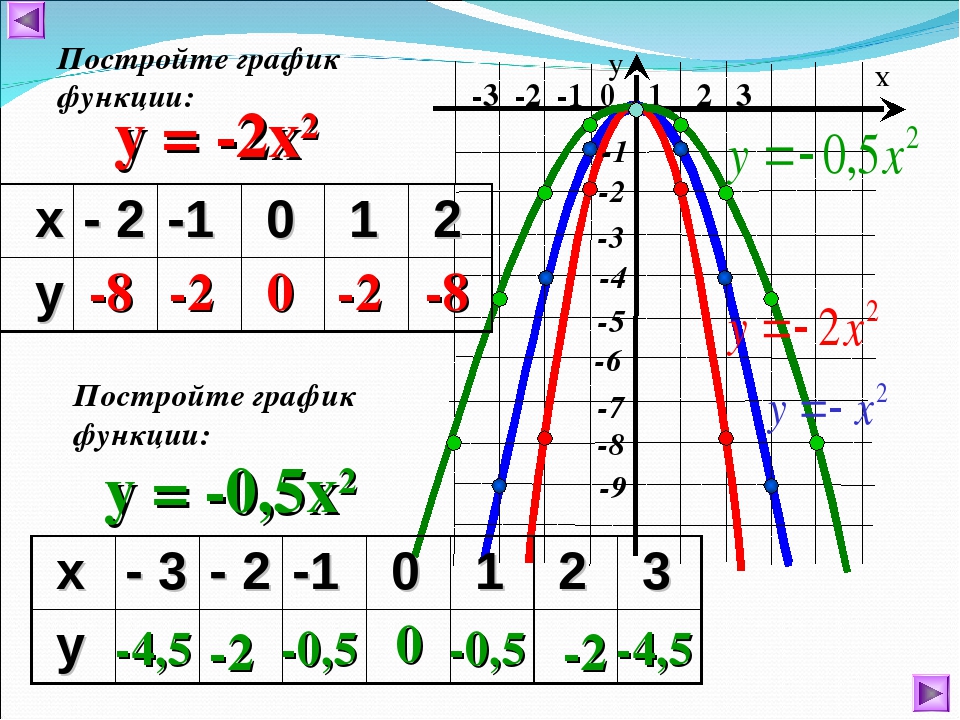 Как показано на графике родительской функции, функции абсолютного значения должны возвращать V-образные графики .
Как показано на графике родительской функции, функции абсолютного значения должны возвращать V-образные графики .
Вершина y = | x | также находится в начале координат. Поскольку он проходит на обоих концах оси x, y = | x | имеет область в (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция имеет диапазон [0, ∞) .
Мы используем функции абсолютного значения, чтобы подчеркнуть, что значение функции всегда должно быть положительным.
Радикальные функции
Двумя наиболее часто используемыми радикальными функциями являются функции извлечения квадратного корня и кубического корня .
Родительская функция функции извлечения квадратного корня — y = √x . Его график показывает, что его значения x и y никогда не могут быть отрицательными.
Это означает, что область и диапазон y = √x равны [0, ∞ ) . Начальная точка или вершина родительской функции также находится в в начале координат . Родительская функция y = √x также увеличивается на во всей области .
Начальная точка или вершина родительской функции также находится в в начале координат . Родительская функция y = √x также увеличивается на во всей области .
Давайте теперь изучим родительскую функцию функций кубического корня. Подобно функции извлечения квадратного корня, ее родительская функция выражается как y = ∛ x .
На графике показано, что родительская функция имеет домен и диапазон (-∞, ∞) .Мы также можем видеть, что y = ∛x составляет , увеличиваясь во всей области .
Экспоненциальные функции
Экспоненциальные функции — это функции, в экспоненте которых есть алгебраические выражения. Их родительская функция может быть выражена как y = b x , где b может быть любой ненулевой константой. График родительской функции, y = e x , показан ниже, и из него мы видим, что он никогда не будет равен 0 .
И когда x = 0, y проходит через ось y при y = 1.Мы также можем видеть, что родительская функция никогда не находится ниже оси Y, поэтому ее диапазон составляет (0, ∞ ). Его домен , однако, может быть полностью действительным числом . Мы также можем видеть, что эта функция на увеличивается во всем домене.
Одним из наиболее распространенных приложений экспоненциальных функций является моделирование роста населения и сложных процентов.
Логарифмические функции
Логарифмические функции являются функциями, обратными экспоненциальным функциям. Его родительская функция может быть выражена как y = log b x , где b — ненулевая положительная константа. Давайте посмотрим на график, когда b = 2 .
Как и экспоненциальная функция, мы можем видеть, что x никогда не может быть меньше или равным нулю для y = log 2 x. Следовательно, его домен (0, ∞) . Однако его диапазон содержит все действительные числа . Мы также можем видеть, что эта функция на увеличивается во всем домене.
Следовательно, его домен (0, ∞) . Однако его диапазон содержит все действительные числа . Мы также можем видеть, что эта функция на увеличивается во всем домене.
Мы используем логарифмические функции для моделирования природных явлений, таких как сила землетрясения.Мы также применяем его при вычислении скорости распада периода полураспада в физике и химии.
Взаимные функции
Взаимные функции — это функции, которые содержат числитель констант и знаменатель x. Его родительская функция — y = 1 / x .
Как видно из графика, ни x, ни y никогда не могут быть равны нулю. Это означает, что его домен и диапазон равны (-∞, 0) U (0, ∞) . Мы также можем видеть, что функция на убывает во всей области .
На протяжении всего нашего пути с функциями и графиками есть много других родительских функций, но эти восемь родительских функций относятся к , наиболее часто используемым и обсуждаемым функциям .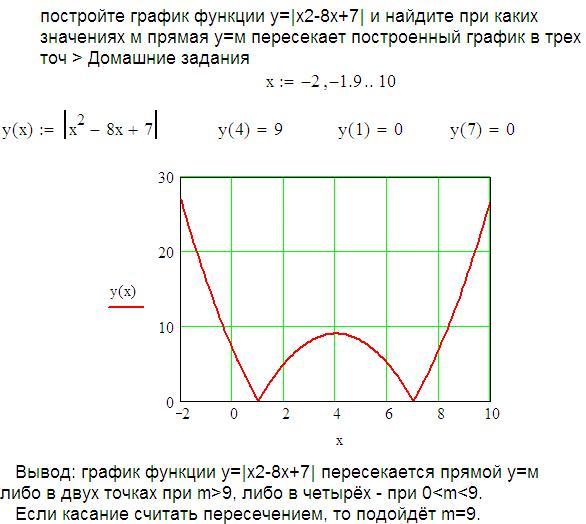
Вы даже можете резюмировать то, что вы узнали, создав таблицу, показывающую все свойства родительских функций.
Как найти родительскую функцию?
Что делать, если нам дана функция или ее график, и нам нужно идентифицировать ее родительскую функцию? Мы можем сделать это, запомнив важные свойства каждой функции и определив, какие из родительских графиков, которые мы обсуждали, соответствуют заданному.
Вот несколько наводящих вопросов, которые могут нам помочь:
- Какая наивысшая степень функции?
- Содержит ли он квадратный корень или кубический корень?
- Функция находится в экспоненте или знаменателе?
- График функции увеличивается или уменьшается?
- Каков домен или диапазон функции?
Если мы сможем ответить на некоторые из этих вопросов путем проверки, мы сможем вывести наши варианты и в конечном итоге идентифицировать родительскую функцию.
Давайте попробуем f (x) = 5 (x — 1) 2 .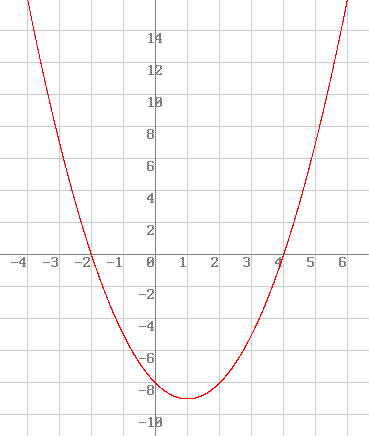 Мы видим, что наивысшая степень f (x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно, его родительская функция y = x 2 .
Мы видим, что наивысшая степень f (x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно, его родительская функция y = x 2 .
Почему бы нам не построить график f (x) и также не подтвердить наш ответ?
На графике мы видим, что он образует параболу, подтверждая, что его родительская функция равна y = x 2 .
Просмотрите первые несколько разделов этой статьи и свои собственные заметки, а затем давайте попробуем задать несколько вопросов, чтобы проверить наши знания о родительских функциях.
Пример 1
Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
Решение
Функции, представленные графиками A, B, C и E, имеют аналогичную форму, но смещены вверх или вниз. Фактически, эти функции представляют собой семейство из экспоненциальных функций .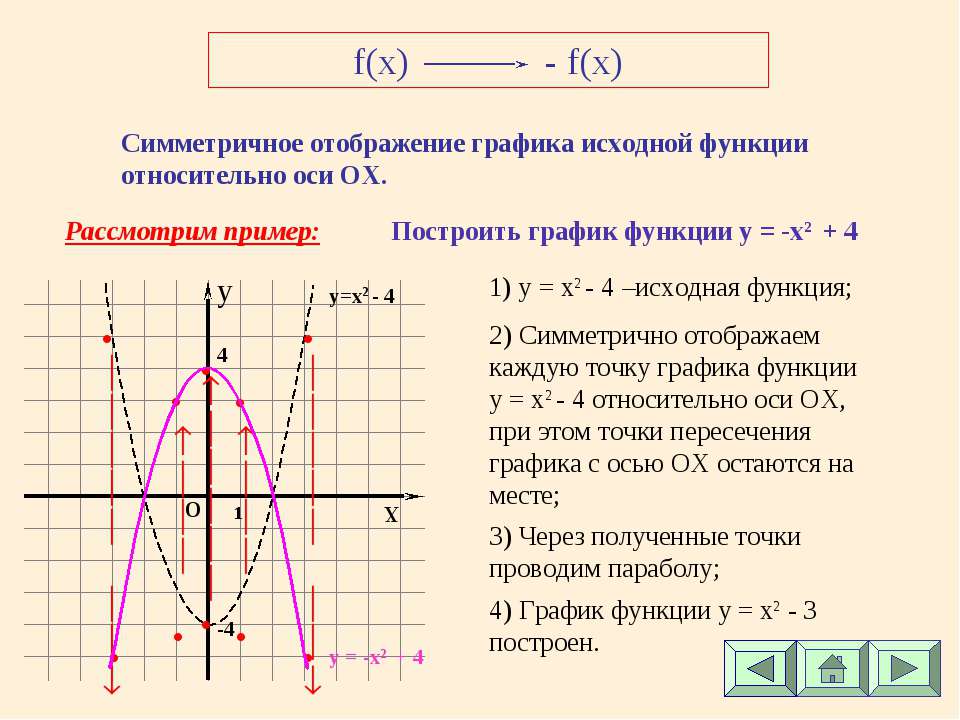 Это означает, что все они имеют общую родительскую функцию: y = b x .
Это означает, что все они имеют общую родительскую функцию: y = b x .
С другой стороны, график D представляет логарифмическую функцию, поэтому D не принадлежит к группе экспоненциальных функций.
Пример 2
Какие из следующих функций не принадлежат к данному семейству функций?
- y = 5x 2
- y = -2x 2 + 3x — 1
- y = x (3x 2 )
- y = (x — 1) (x + 1)
Решение
Функция y = 5x 2 имеет наивысшую степень двойки, поэтому она является квадратичной функцией.Это означает, что его родительская функция y = x 2 . То же самое и для y = -2x 2 + 3x — 1. Исходя из этого, мы можем подтвердить, что рассматриваем семейство квадратичных функций.
Применяя разность полных квадратов к четвертому варианту, получаем y = x 2 — 1. Это также квадратичная функция.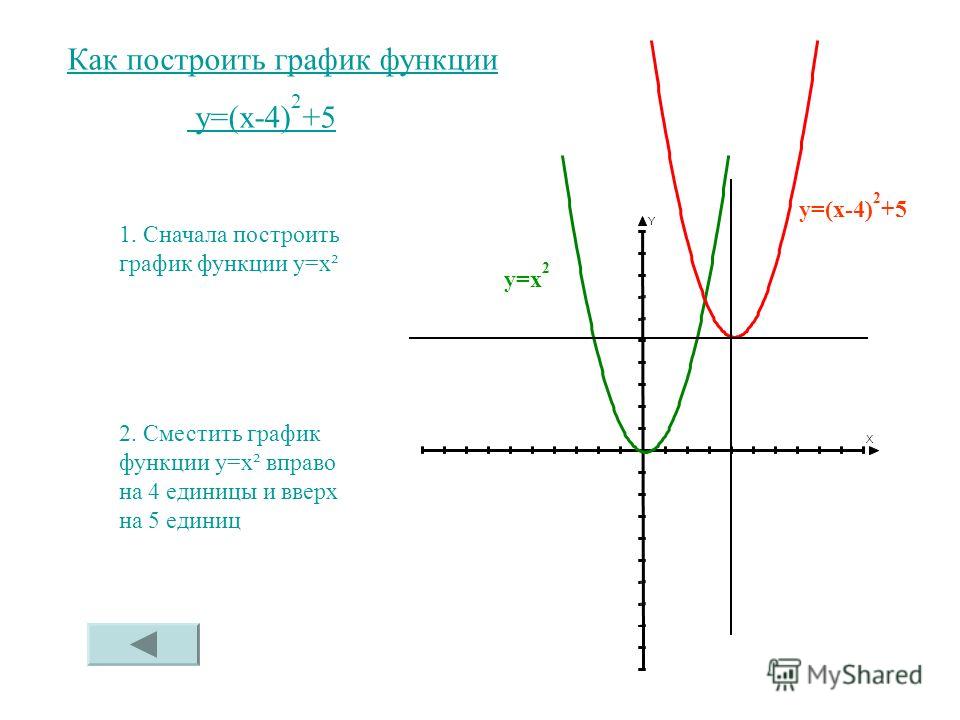 Остается третий вариант.
Остается третий вариант.
При расширении y = x (3x 2 ) становится y = 3x 3, , и это показывает, что он имеет 3 в качестве наивысшей степени.Следовательно, он не может быть частью данного семейства функций.
Пример 3
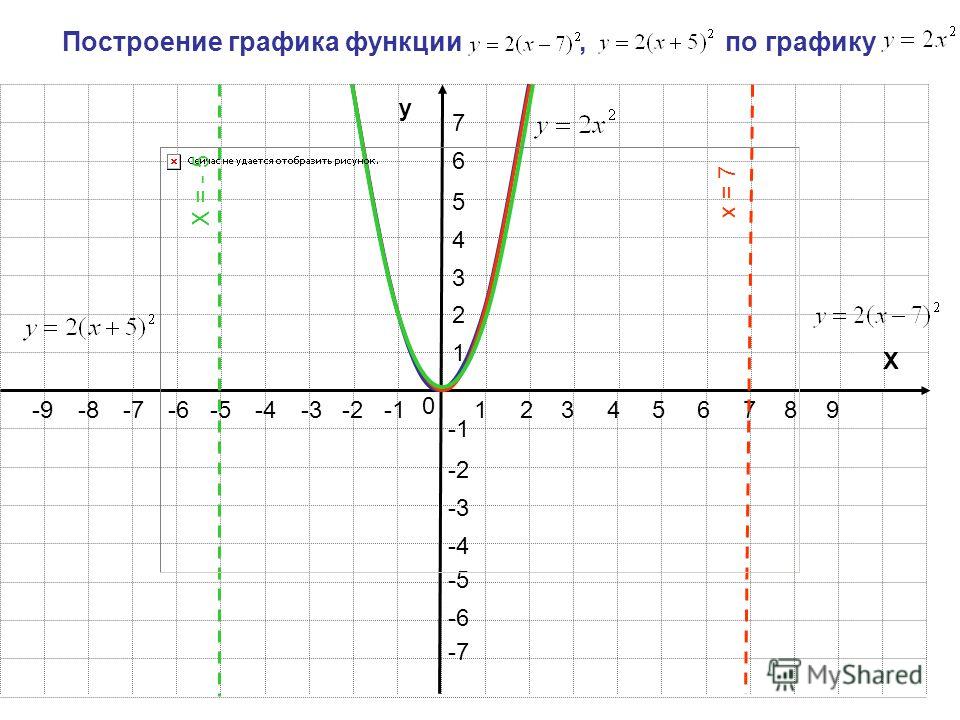
Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
Решение
Начнем с f (x). Мы можем видеть, что у него есть парабола для своего графика, поэтому мы можем сказать, что f (x) является квадратичной функцией .
- Это означает, что f (x) имеет родительскую функцию y = x 2 .
- График простирается по обе стороны от x, поэтому он имеет область (-∞, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0, ∞) .
Основываясь на графике, мы видим, что значения x и y функции g (x) никогда не будут отрицательными. Они также показывают возрастающую кривую, которая напоминает график функции квадратного корня .
- Следовательно, родительская функция для g (x) равна y = √x .
- График простирается до правой части x и никогда не меньше 2, поэтому он имеет область [2, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0, ∞) .
График h (x) показывает, что их значения x и y никогда не будут равны 0. Симметричные кривые также похожи на график обратных функций.
- Это означает, что h (x) имеет родительскую функцию y = 1 / x.
- До тех пор, пока x и y никогда не равны нулю, h (x) по-прежнему действителен, поэтому он имеет как домен , так и диапазон (-∞, ∞) .
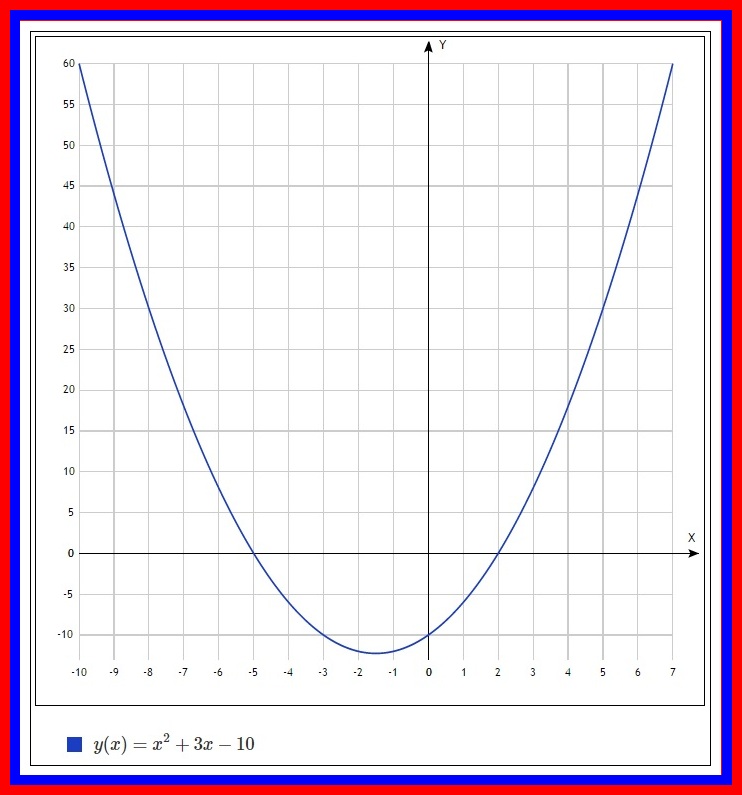
Прямые линии, представляющие i (x), говорят о том, что это линейная функция.
- Он имеет родительскую функцию y = x.
- График простирается по обе стороны от x и y, поэтому он имеет область и диапазон (-∞, ∞) .
Пример 4
Определите родительскую функцию для следующих функций.
- f (x) = x 3 — 2x + 1
- g (x) = 3√x + 1
- h (x) = 4 / x
- i (x) = e x + 1
Решение
- Наивысшая степень f (x) равна 3, поэтому это кубическая функция.Это означает, что у него есть родительская функция y = x 3 .
- Функция g (x) имеет радикальное выражение 3√x. Поскольку у нее есть член с квадратным корнем, функция является функцией с квадратным корнем и имеет родительскую функцию y = √x.
- Мы видим, что x находится в знаменателе h (x), поэтому он обратный.
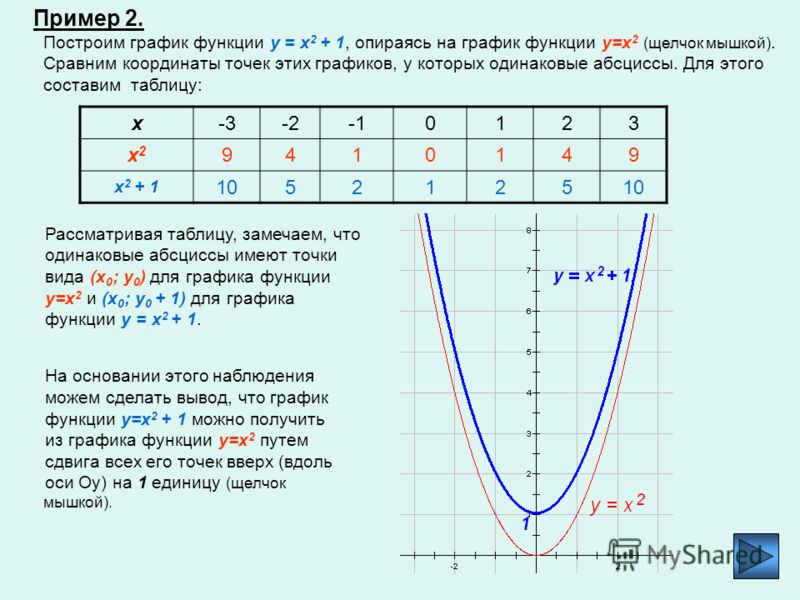 Следовательно, его родительская функция — y = 1 / x .
Следовательно, его родительская функция — y = 1 / x . - Показатели функции содержат x, поэтому одно это говорит нам о том, что i (x) — экспоненциальная функция.Следовательно, его родительская функция может быть выражена как y = b x , где b — константа. Для случая i (x) у нас есть y = e x в качестве его родительской функции.
Практические вопросы
1. Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
2. Какие из следующих функций не относятся к данному семейству функций?
- y = 4x 3
- y = -3x 3 + 4x 2 + 5x — 1
- y = x (5x 2 )
- y = (x — 1) (x + 1) (x + 2)
3.Определите родительскую функцию следующих функций.
- f (x) = x 3 — 2x + 1
- g (x) = 3√x + 1
- h (x) = 1 / (x + 1)
- i (x) = e x + 1
4.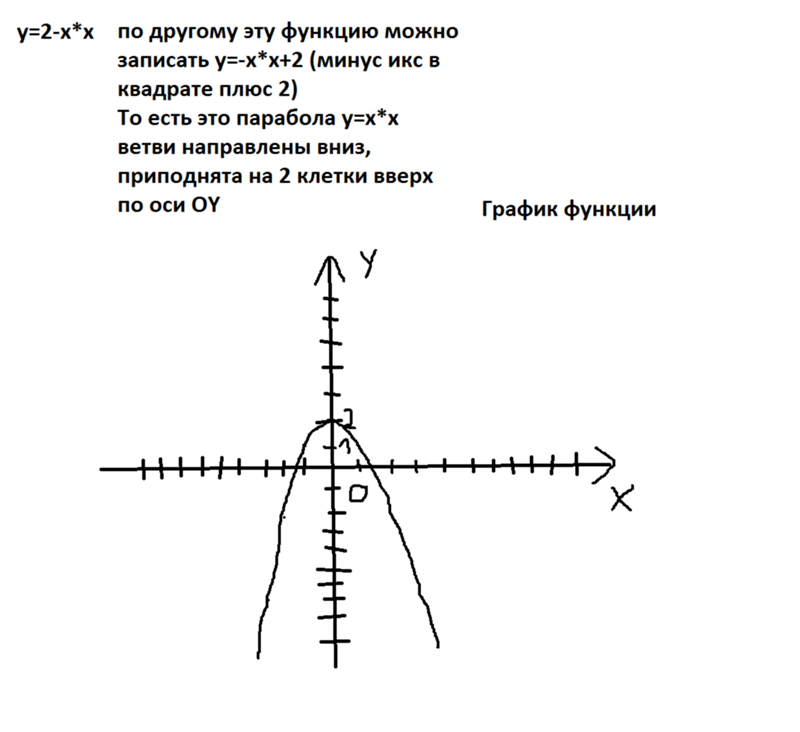 Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
5. Опишите разницу между f (x) = -5 (x — 1) 2 и его родительской функцией. Каков домен и диапазон f (x)?
6.Пусть a и b — две ненулевые константы. Опишите разницу между g (x) = ax + b и его родительской функцией. Каков домен и диапазон f (x)?
Изображения / математические рисунки создаются с помощью GeoGebra.
Предыдущий урок | Главная страница | Следующий урок
Mathscene — Функции 1 — Урок 3
Mathscene — Функции 1 — Урок 3
| 2007 Rasmus ehf и Jhann sak | Функции | Печать |
Урок 3
.
Функции второй степени
Давайте снова посмотрим на многочлены второй степени.Самая простая форма функции — f (x)
= х 2 . График представляет собой
параболу часто называют основной параболой.
Обратите внимание, что график симметричен относительно оси y-
ось. Ось ординат называется осью симметрии этой функции.
Теперь посмотрим, как коэффициенты влияют на внешний вид графика.
Коэффициент x 2 равен
обычно называется a. Если мы посмотрим на
параболы с разными значениями a мы видим, что некоторые шире, а некоторые
уже основной параболы, где a = 1.
Вот графики парабол, где a = 4, 2,
ог.
а = 4
а = 2
а =
а =
Вот параболы с
отрицательные значения
а = −4
а = −2
а = —
а = —
Если значение a равно
положительный график изгибается вверх (как улыбка!) Чем больше значение
уже график.
По мере того, как становится мало
график становится более плоским и плоским до тех пор, пока, когда a не станет отрицательным, он не станет меньше (
как хмурый взгляд! ).
Пример 1
Теперь нарисуем график
из f (x) = x 2 + 1 и
сравните его с g (x) = x 2 .
| x | f (x) = х 2 + 1 | |
| -2 | (-2) 2 + 1 = 5 | |
| -1 | (-1) 2 + 1 = 2 | |
| 0 | 0 + 1 = 1 | |
| 1 | 1 2 + 1 = 2 | |
| 2 | 2 2 + 1 = 5 |
Значения функции (
y) в таблице значений для f (x) = x 2 +1 все
на единицу выше соответствующих значений в таблице значений для g (x) = x 2
и график был переведен по вертикали на 1 единицу.
Обратите внимание, что график f (x) =
x 2 + 1 не пересекает
ось абсцисс. Это говорит нам о том, что уравнение x 2
+ 1 = 0 не имеет решения. Мы уже знаем это, поскольку число в квадрате никогда не бывает
отрицательное, поэтому x 2 никогда не может быть равно -1.
Пример
2
Нарисуйте график f (x) = x 2
— 1 и сравните с g (x)
= х 2 .
| x | f (x) = х 2 — 1 | |
| -2 | (-2) 2 — 1 = 3 | |
| -1 | (-1) 2 — 1 = 0 | |
| 0 | 0 — 1 = -1 | |
| 1 | 1 2 — 1 = 0 | |
| 2 | 2 2 — 1 = 3 |
Теперь значения функции в
все таблицы f (x) на единицу ниже соответствующих значений в таблице для
g (x) = x 2 и график
опустился на одну единицу.
Обратите внимание, что в этом примере
график f (x) = x 2
— 1 пересекает ось x в двух местах.
Это означает, что уравнение
x 2 — 1 = 0 имеет два
решения,
х 2 — 1 = 0
х 2 = 1
х = 1
, которые равны x = −1 и x
= 1.
Пример
3
Нарисуйте график f (x)
= (x + 1) 2 (или f (x)
= x 2 + 2x + 1) и сравните
это к основной параболе g (x) = x 2 .
| x | f (x) = (х + 1) 2 | |
| -3 | (-3 + 1) 2 = 4 | |
| -2 | (-2 + 1) 2 = 1 | |
| -1 | (-1 + 1) 2 = 0 | |
| 0 | (0 + 1) 2 = 1 | |
| 1 | (1 + 1) 2 = 4 |
Здесь мы прибавили 1 к x
и мы видим, что функция
значения в таблице значений сдвинуты на одну строку вверх по сравнению с базовыми
функция.
График f (x) — это
так же, как если бы мы переместили график g (x) = x 2 на одну единицу
Слева.
Мы говорим, что основной граф
переведено на -1 единиц по горизонтали. Ось симметрии теперь x
= -1.
Пример
4
Нарисуйте
график f (x) = (x — 2) 2
— 1 (или f (x) = x 2
— 4x + 3) и сравните его с базовым графиком g (x) = x 2 .
Если использовать тот же метод, что и в предыдущем
Например, мы можем предположить, что график переместился на две единицы вправо и одну
блок вниз. Теперь проверим это, составив таблицу
значения, начиная с x = 0 и
рисование графика.
| x | f (x) = (х — 2) 2 — 1 | |
| 0 | (0–2) 2 — 1 = 3 | |
| 1 | (1-2) 2 — 1 = 0 | |
| 2 | (2–2) 2 — 1 = -1 | |
| 3 | (3–2) 2 — 1 = 0 | |
| 4 | (4–2) 2 — 1 = 3 |
Обратите внимание, что ось симметрии теперь x = 2.
Мы можем найти, где график пересекает ось Y
без рисования графика. Мы делаем это, вычисляя f (0)
= 3 или путем умножения скобок и
видя, что постоянный член (член без x) равен 3.
f (x) = (x — 2) 2 — 1 = x 2
— 4х + 4 — 1 = х 2
— 4x + 3
или
f (0) = (x — 2) 2 — 1 = 4 — 1 = 3
Пример
5
Найдите график зависимости f (x) = (x — 2) 2
— 1 пересекает ось абсцисс.Положим y = f (x) = 0, а затем решим уравнение
для x.
| (x — 2) 2 — 1 = 0 | Первый переместите -1 над знаком равенства. |
| (x — 2) 2 = 1 | Далее, извлеките квадратный корень из обеих частей уравнения. Помните + и -. |
| х — 2 = 1 = 1 | Наконец переместите 2 на другую сторону и упростите результат.  |
| х = 2 1 |
Точки пересечения:
х = 2 -1
= 1 и x = 2 + 1 = 3.
Легко видеть, что запись функции в виде f (x)
= (x — 2) 2 — 1 дает нам много информации.
Он сообщает нам, как переводится основной график
вертикально и горизонтально.
Он также сообщает нам, где находится ось симметрии.
Наконец, мы можем легко найти точки
пересечение с осями x и y.
Общий вид уравнения, записанного в этом
путь:
е (х) = а (х + г) 2 + s
a — коэффициент при x 2
как мы уже видели.
ось симметрии имеет уравнение x = −r (или, можно сказать, то же
значение как r, но с обратным знаком).
Поэтому важно знать, как
перепишите функцию
f (x) =
ax 2 + bx + c в виде
f (x) = a (x + r) 2 + s
Пример
6
Теперь давайте посмотрим, как мы можем изменить секунду
функция степени от одной формы к другой.
Записываем f (x) = x 2 — 4x + 3 в виде f (x) = (x — 2) 2 .
— 1.
По сравнению с общей формой:
f (x) = ах 2
+ bx + c
f (х) = х 2
— 4x + 3
Здесь a
= 1
og b = −4
и c = 3 (поэтому график пересекает ось y в 3).
Посмотрите на правило возведения скобки в квадрат:
(x q) 2 = p 2
2xq
+ q 2 .
Мы видим, что коэффициент при x
составляет 2кв.
В нашем примере коэффициент при x равен
−4, что означает 2q = — 4 и, следовательно,
q = −2.
Если посчитать
(х — 2) 2
получаем x 2
— 4x + 4.
(х
— 2) 2 = х 2
— 4x + 4.
Если мы вычтем 1 с обеих сторон
мы получили :
(х — 2) 2
−1 = x 2 — 4x +
4−1 = x 2 — 4x
+ 3
Обобщая метод:
| f (x) = x 2 — 4x + 3 | Половина коэффициент при x равен −4 / 2 = −2, который мы возводим в квадрат (4) и добавить к уравнению. |
| = (x 2 — 4x + 2 2 ) — 2 2 + 3 | |
| = (х — 2) 2 — 4 + 3 | Если мы прибавив 4 к уравнению, мы также должны вычесть 4, чтобы уравнение без изменений Теперь упростим −4 + 3 = −1 |
| = (х — 2) 2 — 1 |
Из приведенного выше примера можно сделать вывод, что
график полинома второй степени, где a = 1 (f (x) = x 2 + bx + c) имеет ось симметрии в:
x = −b / 2 и обрезает y
ось, где y = c.
Пример
7
Найдите ось симметрии графика f (x) =
2x 2 — 12x + 10.
В этом случае a = 2, поэтому правило из предыдущего примера не применяется. Ни один
так же легко переписать функцию, как раньше.
Вместо этого мы переводим функцию вниз на 10
единиц путем вычитания 10 из уравнения. Перемещение графика по вертикали не
изменить положение оси симметрии.
Назовем эту новую функцию g (x) и найдем, где
g (x) отсекает ось x.
2x 2
— 12x = 0
2х (х — 6) = 0
Это уравнение имеет решения x = 0 и 6, поэтому
график g (x) пересекает ось x
в 0 и 6. Ось симметрии должна быть посередине этих двух точек, что
находится в x = 3 .
Пример
8
Записываем функцию f (x) = 2x 2
— 12x + 10 в виде
е (х) = а (х + г) 2 + s.
| f (x) = 2x 2 — 12x + 10 | Дубль 2 вне скобки. Половина коэффициента при x равно −6 / 2 = −3, поэтому добавьте 3 2 внутри скобок. Мы действительно добавили 18, поэтому теперь нам нужно вычесть 23 2 = 18 за пределами скобки. |
| = 2 (x 2 — 6x + 3 2 ) — 2 3 2 + 10 | |
| = 2 (x 2 — 6x + 9) — 18 + 10 | |
| = 2 (х — 3) 2 — 8 |
Теперь мы, как и раньше, видим, что ось симметрии
находится в x = 3.
Коэффициенты x В приведенном выше примере (f (x)
= 2x 2 — 12x + 10)
равны a = 2, b = −12 и c = 10. Чтобы найти ось симметрии, мы
множитель 2 вынес за скобки. Это соответствует делению на 2. Тогда мы
завершил квадрат делением коэффициента при x
(−6) на 2.
Общая формула оси симметрии
функция
f (x) = ax 2
+ bx + c — это
следовательно:
Пример
9
Найдите вершину параболы f (x) = 2x 2
— 12x + 10.
Вершина (в которой вращается парабола) лежит
на оси симметрии, поэтому мы знаем значение x вершины (3).
Мы нашли
значение y путем вычисления f (3).
ф (3) = 23 2
— 123 + 10 = 18 — 36 + 10 = −8.
Вершина параболы равна (3,
−8).
Примечание: Если a> 0, вершина является точкой минимума. Если
a <0 вершина является точкой максимума.
Попробуйте пройти тест 3 по функциям I.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
Quadratics
Квадратики — многочлены степени 2.
Они бывают разных форм, но всегда имеют квадрат.
Примеры
Квадратичное выражение:
Квадратное уравнение:
Квадратичная функция:
Квадратичный график:
Квадратичное неравенство:
Квадратичное отображение:
Квадратичные графики
Квадратичные графики имеют отличительную U-образную форму
называется параболой.
Улыбка положительной параболы:
у = ах 2
Отрицательные параболы нахмурились!
у = — ах 2
Рисование парабол вида y = ax
2
Выберите значения для x и поместите их в таблицу.
Разработать соответствующий для y.
Постройте эти точки и соедините их плавной кривой.
Пример
Заполните таблицу значений для
уравнение y = x 2
Построение этих точек и объединение их плавной кривой дает
Обратите внимание, насколько симметричен график!
Пример
Заполните таблицу значений для
уравнение y = -5x 2
Построение этих точек и объединение их плавной кривой дает
Снова обратите внимание на симметричность графика!
Работа в обратном направлении
Пример
Найдите уравнение следующей параболы
вида y = ax 2
График имеет вид y = ax 2
Данная координата (2, 1)
Итак, x = 2 и y = 1 находятся на кривой
.
Заменить и решить
Параболы вида y = a (x-b)
2
Пример
Заполните таблицу значений для
уравнение y = (x-2) 2
Нанесение этих точек и объединение их плавной кривой дает
На этот раз график симметричен, когда x = 2
Точка поворота (2,0)
Ось симметрии b
в уравнении y = a (x-b) 2
Пример
Найдите уравнение следующей параболы
вида y = a (x-b) 2
График имеет вид y = a (x-b) 2
Данная координата (2, 3)
Итак, x = 2 и y = 3 находятся на кривой
.
Подставляем и решаем
Параболы вида y = a (x-b)
2 + c
Пример
Заполните таблицу значений уравнения
у = -2 (х + 3) 2 + 2
Обратите внимание, что ось симметрии x = — 3
Работа в обратном направлении
Пример
Найдите уравнение следующей параболы
вида y = a (x-b) 2 + c
График имеет вид y = a (x-b) 2 + c
Данная координата (-3, -2)
Итак, x = -3 и y = -2 находятся на кривой
.
На графике b = -2, поскольку это ось симметрии.
Заменить x = -3, y = -2 и b = -2
Точка (-2, -5) также находится на кривой.
Итак, c = -5
Заменить на -2 = a + c
Подставляя a, b и c в исходное уравнение
у = а (х-б) 2 + с
Ось симметрии
Это квадрат в законченной квадратной форме.
Завершение квадрата
Параболы формы y = ax
2 + bx + c
Пример
Заполнить таблицу значений
для уравнения y = 2x 2 + 3x — 2
Поворотные точки
Положительные параболы имеют минимальную точку поворота.
Пример
Найдите точку поворота квадратичной
у = х 2 + 3х + 2
Точка поворота находится на оси симметрии.
Отрицательные параболы имеют максимальную точку поворота.
Корни
Корень уравнения — это значение, которое удовлетворяет требованиям
уравнение, когда его выражение установлено равным нулю.
Например, 0 = x 2 + 2x -3
Максимально возможное количество корней
совпадает со степенью многочлена
поэтому у квадратичной может быть не более двух корней.
Не все квадраты имеют корни.
Чтобы найти корни квадратичной,
Нарисуйте график и посмотрите, где он пересекает ось x.
или
Установить y = 0 и разложить на множители (если возможно)
Пример
На графике видно, что уравнение y = x 2 + 2x –3 имеет корни
х = -3 и х = 1
Это то же самое, что установить y на ноль и разложить на множители: —
Любая скобка может равняться 0, поэтому необходимо учитывать обе:
Таблица Excel
Построение парабол
Чтобы нарисовать график
y = ax 2 + bx + c
- Определите форму как U (a> 0) или ∩ (a <0)
- Найдите корни уравнения.
(ах 2 + bx + c = 0)
- Отметьте корни на вашей оси.
- Отметьте точку (0, c) на вашей оси.
- Найдите ось симметрии.
(½ пути между корнями)
- Используйте это значение x, чтобы найти точку поворота.
- Соедините значения плавной кривой.
Пример
Эскиз y = x 2 — 2x — 3
Это будет U-образная форма, так как a = 1
Он обрежет ось Y на (0, -3)
Пример
Эскиз y = 3-2x-x 2
Это будет форма ∩, так как a = -1
Он обрежет ось Y в точке (0,3)
Квадратные уравнения
Стандартная форма Квадратные уравнения имеют вид
Чтобы найти решение квадратного уравнения:
Перепишем выражение в стандартной квадратичной форме
Факторизуйтесь, если можете:
{Не забудьте найти общие множители и разницу двух квадратов}
Используйте квадратные формулы
Примеры
Решить 3x — 6x 2 = 0
Решить 49 — 9x 2 = 0
Решить 15x 2 — x — 6 = 0
Решить 15x 2 — x + 1 = 7
Факторизация квадратичных расчетов
Квадратичная формула
Если квадратичная величина не факторизуется,
попробуйте квадратичную формулу:
Пример
Решить 2 + 4x -5x 2 = 0
Дайте свой ответ в виде сурда.
Пример
Найдите корни 2 + 4x -5x 2
Ответьте правильно с точностью до двух знаков после запятой.
Не все квадраты разложить на множители
Дискриминант
Примеры
Дискриминант
б 2 — 4ac
= 3 2 — 4x1x4
= 9–16
= — 7
b 2 — 4ac <0
Нет настоящих корней
b 2 — 4ac
= 3 2 — 4x1x (-2)
= 9 +8
= 17
b 2 — 4ac> 0
Два отличных настоящих корня
б 2 — 4ac
= 6 2 — 4x1x9
= 36–36
= 0
b 2 — 4ac = 0
Корни равные и настоящие
Работа в обратном направлении
Пример
Корни (x — 1) (x + k) = -4 равны.
Найдите значения k.
Сначала разложим скобки
Касание
Касательная к кривой касается кривой только в одной точке.
Чтобы проверить касание, установите две функции равными друг другу
и найдем получившийся дискриминант.
Если b 2 — 4ac> 0, линия обрывается в двух разных точках.
Это не касательная.
Если b 2 — 4ac <0, линия не касается кривой.
Это не касательная.
Если b 2 — 4ac = 0, линия касается кривой только в одной точке.
Это касательная.
Примеры
© Александр Форрест
Графические квадратные уравнения
Квадратное уравнение в стандартной форме
( a , b и c может иметь любое значение, за исключением того, что a не может быть 0.)
Вот пример:
Графики
Вы можете построить квадратное уравнение с помощью функции Grapher, но для того, чтобы действительно понять, что происходит, вы можете построить график самостоятельно. Читать дальше!
Простейший квадратичный
Простейшее квадратное уравнение:
f (х) = х 2
И график у него тоже простой:
Это кривая f (x) = x 2
Это парабола.
Теперь давайте посмотрим, что произойдет, когда мы введем значение «а»:
f (x) = ах 2
- Большие значения сгибают кривую внутрь
- Меньшие значения a расширяют его наружу
- И отрицательные значения a переворачивают вверх дном
«Генерал» квадратичный
Перед построением графика мы переставляем уравнение, из этого:
f (x) = ах 2 + bx + c
К этому:
f (x) = a (x-h) 2 + k
Где:
Другими словами, вычислите h (= −b / 2a), затем найдите k , вычислив все уравнение для x = h
Но почему?
В этой новой форме замечательно то, что h и k показывают нам самую низкую (или очень высокую) точку, называемую вершиной :
А также кривая симметрична (зеркальное отображение) относительно оси , которая проходит через x = h , что упрощает построение графика
Итак…
- h показывает, насколько далеко влево (или вправо) кривая сместилась от x = 0
- k показывает, насколько далеко вверх (или вниз) кривая сместилась от y = 0
Давайте посмотрим, как это сделать:
Пример: График f (x) = 2x
2 — 12x + 16
Во-первых, отметим:
- а = 2,
- b = −12, и
- с = 16
Итак, что мы знаем?
- a положительный, значит, это «восходящий» график (U-образный)
- a равно 2, поэтому он немного «раздавлен» по сравнению с графиком x 2
Далее посчитаем h:
h = −b / 2a = — (- 12) / (2×2) = 3
И теперь мы можем вычислить k (используя h = 3):
k = f ( 3 ) = 2 (3) 2 — 12 · 3 + 16 = 18−36 + 16 = −2
Итак, теперь мы можем построить график (с настоящим пониманием!):
Мы также знаем: вершина равна (3, −2), а ось равна x = 3
От графика к уравнению
Что делать, если у нас есть график и мы хотим найти уравнение?
Пример: вы только что построили некоторые интересные данные, и они выглядят квадратично:
Просто зная эти два момента, мы можем придумать уравнение.
Во-первых, мы знаем h и k (в вершине):
(ч, к) = (1, 1)
Итак, давайте представим это в следующей форме уравнения:
f (x) = a (x-h) 2 + k
f (x) = a (x − 1) 2 + 1
Затем вычисляем «а»:
Мы знаем точку (0, 1.5) , поэтому: f (0) = 1.5
И a (x − 1) 2 + 1 при x = 0 это: f (0) = a (0−1) 2 + 1
Они оба равны f (0) , поэтому сделайте их равными: a (0−1) 2 + 1 = 1.5
Упростить: a + 1 = 1,5
а = 0,5
Итак, вот результирующее квадратное уравнение:
f (x) = 0,5 (x − 1) 2 + 1
Примечание. Это может быть не правильное уравнение для данных, но это хорошая модель и лучшее, что мы можем придумать.
.
