Открытая Математика. Функции и Графики. Алгебраические операции над функциями

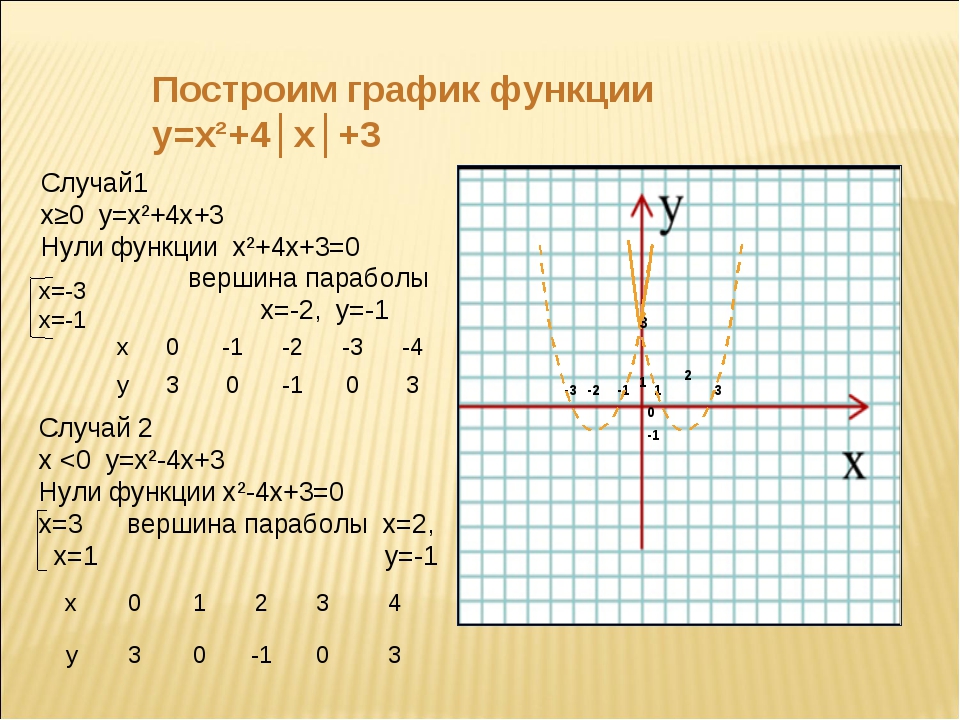
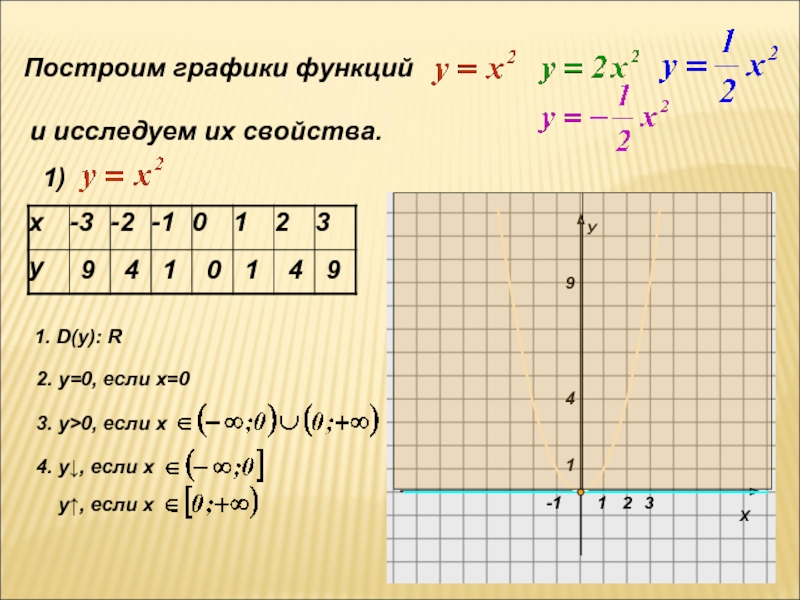
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.

Графики функций y = x + sin x и y = x sin x.

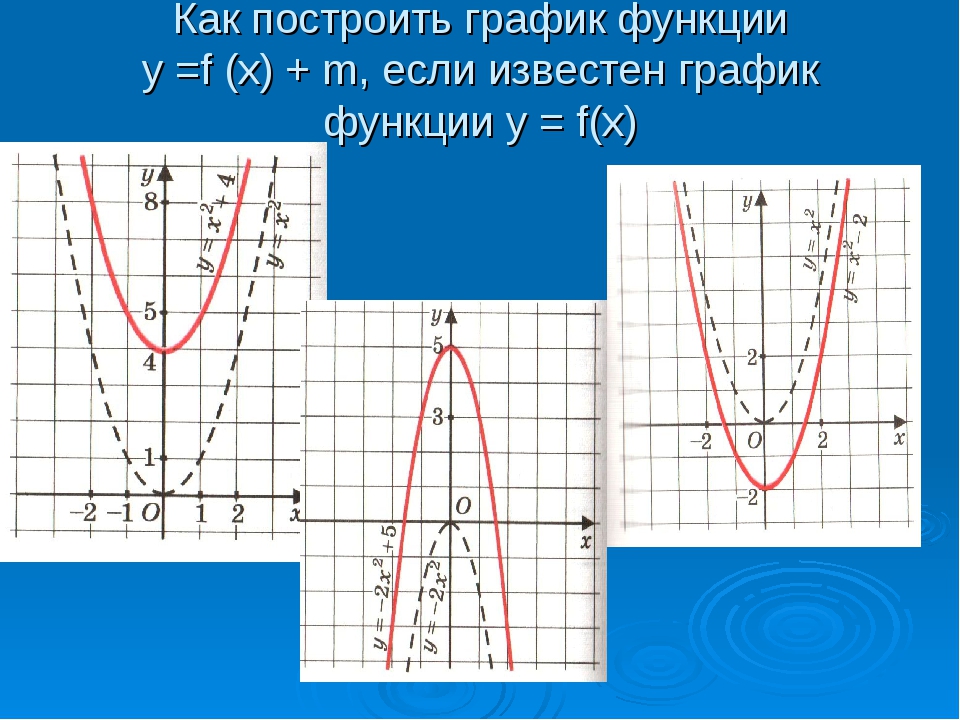
Правило построения графика функции 1f(x),
если график функции f(x)
уже построен.

• Если x = a – вертикальная асимптота графика функции f(x),
  то есть limx→a+0f(x)=∞ или limx→a-0f(x)=∞,
  то limx→a+01f(x)=0 или соответственно limx→a-01f(x)=0.
  
  Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции f(x),
   x = a будет нулем функции 1f(x).




• Если у графика функции f(x)
  есть горизонтальная асимптота y = 0 при x→∞,
  то limx→∞1f(x)=∞.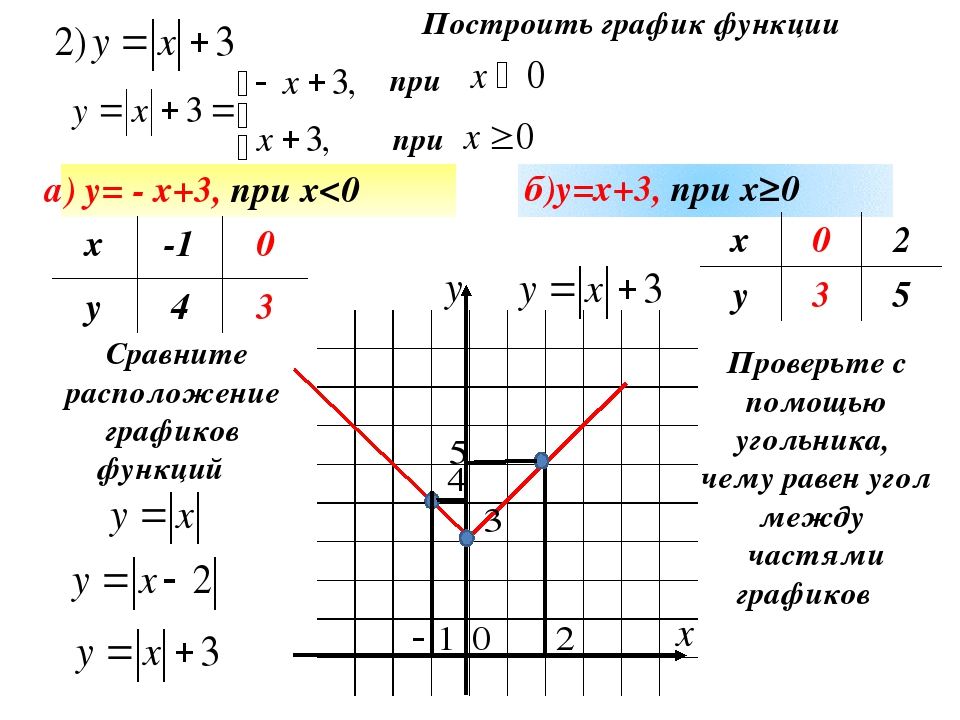




• Если у графика функции f(x)
  есть горизонтальная асимптота y = b при x→∞,
  то график функции 1f(x)
  будет иметь горизонтальную асимптоту y=1b.




• Если график функции f(x) пересекает ось абсцисс в точке (x0; 0),
  то есть x0
  – нуль функции f(x):
   f(x0)=0,
  то x=x0
  – вертикальная асимптота графика функции y=1f(x).




• Если точка (x0; y0)
  – точка максимума (минимума) функции f(x)
  и y0≠0,
  то (x0; 1y0)
  – точка минимума (максимума) функции 1f(x).




• Промежуткам возрастания (убывания) графика функции f(x)
  соответствуют промежутки убывания (возрастания) графика функции 1f(x).

Графики функций y=log2|x2-1|
и y=log|x2-1|2.

Калькулятор функций

Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|. По определению,

|fx|={fxпри  fx≥0,-fxпри  fx<0.

Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.

Преобразование графиков функций

Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0  f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси OY.

Множество точек, удовлетворяющее уравнению |y| = sin x + 0,5.

Равенство |y| = f (x) не задает функции, так как при f (x) > 0 существуют два значения y = ± f (x), удовлетворяющие ему. Множество точек, задаваемое уравнением |y| = f (x), рисуется следующим образом: строится график функции f (x), отбрасывается его часть, находящаяся ниже оси абсцисс, оставшаяся часть дополняется своим симметричным отражением относительно оси абсцисс.

Как построить график функции в Wolfram|Alpha

Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20

Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если не задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot.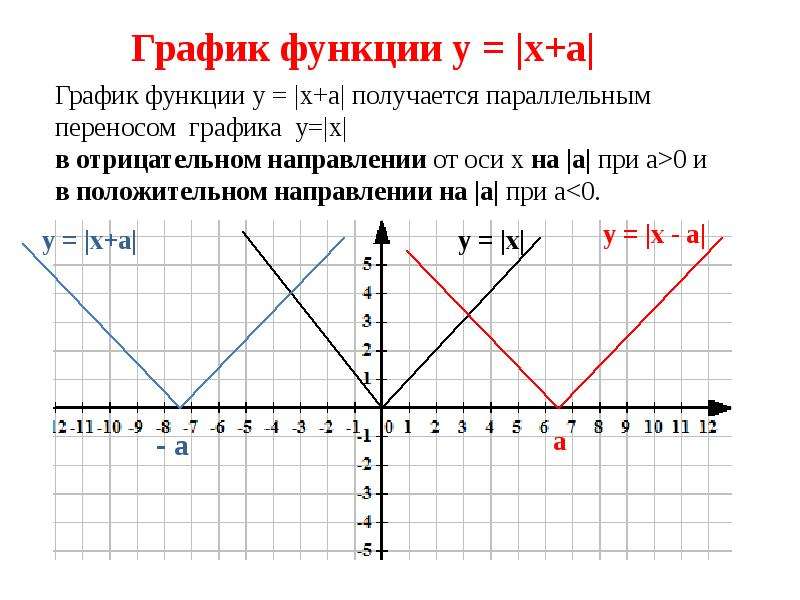 Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

Сравните:

Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.

Одновременно в Wolfram | Alpha можно строить графики нескольких функций.

Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:

Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:

Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. 2 cos(x) для x от -6 до 6 и y от -2 до 2

Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:

А что, если вы захотите построить одновременно несколько графиков функций двух переменных?

Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:

Новой функцией Wolfram | Alpha является возможность строить графики действительной и мнимой частей комплексно-значных функций двух переменных:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.

Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.

Источник by Sam Blake

Опубликовано в блоге Web in Math

Как построить график: 4 бесплатных приложения

4 бесплатных математических инструмента для создания графиков, которые позволяют создавать их, просто вводя функции, выражения и уравнения. Эти инструменты включает в себя простой и удобный интерфейс, и, как предоставляется, красочный интерфейс, а также возможность вводить нужные функции или выражения. Кроме того, эти инструменты позволяют сохранять созданные графики в различных форматах: PNG, JPG, PDF — и многих другое.  Эти инструменты подходят для преподавателей и студентов. Graph Graph представляет собой бесплатное программное обеспечение для создания графиков для Windows, позволяя рисовать графики в системе координат. Можно создать график с использованием часто используемых математических функций, линейных, тригонометрических и т.д. ПО включает регулируемый масштаб, с помощью которого можно легко настроить значение системы координат, как большие, так и малые. Есть возможность применять различные цвета для выделения разных участков графика. Можно рассчитать площадь и длину пути. Инструмент позволяет настроить функции, а также константы. Мало того, он позволяет добавлять текстовые метки, включающие различные шрифты, изображения и объекты. График можно сохранить в различных форматах, таких как JPG, PNG, PDF, SVG, BMP, EMF, GIF. График можно распечатать. Лучшей частью этой бесплатной программы является то, что она позволяет создавать анимацию, с помощью которой можно показать изменения на графике при изменении значения. Скачать Graph Functy Functy — другое бесплатное обеспечение для создания математических графиков для Windows, которое позволяет создавать и визуализировать 3D декартовы и сферические математические функции в реальном масштабе времени. Оно позволяет вводить математические функции, мгновенно показывая вид на график и предоставляя вам возможность редактировать нанесенные диапазоны значений, используемых в функциях, X, Y или Z. Есть функция просмотра, где можно вращать, перемещать, масштабировать, а также оценить график. Это бесплатное программное обеспечение поддерживает анимированные функции с временной переменной. Можно сохранить и экспортировать созданный график в PLY-формат, так что он может использоваться в дальнейшем с другими приложениями по 3D моделированию. Скачать Functy Calc5 Calc5 является бесплатным онлайн-инструментом для создания математических графиков, который позволяет построить 2D и 3D графики, просто введя нужные математические функции.  Он предоставляет современный математический калькулятор графиков и поддерживает вычислительные операции. Можно делать символьные вычисления: дифференцирование, интегрирование и многое другое. Есть опции масштабирования и панорамирования при создании 2D графика. Введите требуемую функцию, нажмите на OK, и график будет готов. Для сохранения созданного графика можно сделать скриншот экрана, поскольку инструмент не имеет функции сохранения графиков. Попробовать Calc5 Desmos Graphing Calculator Desmos Graphing Calculator — другой бесплатный онлайн-инструмент, позволяющий создавать простые и сложные графики, просто введя выражения и уравнения вручную или с помощью клавиатуры приложения. Интерфейс яркий и удобный, где можно нарисовать несколько графиков. Бесплатный инструмент позволяет настроить формат бумаги графика, в зависимости от ваших требований. Требуется зарегистрироваться на  бесплатном веб-сервисе, чтобы сохранять и делиться созданными графиками с друзьями и коллегами.  Есть три способа сохранения графика: можно отправить по электронной почте, встроить или сохранить график в виде изображения в формате PNG. График можно и напечатать. Инструмент доступен как приложение для браузера Chrome. Попробовать Desmos Graphing Calculator  Поделиться:     Оставьте свой комментарий! Добавить комментарий < Предыдущая   Следующая >

Построение графика с помощью элементарных преобразований.

Построение графика функции

y=f(kx) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; b=0)

Рассмотрим сначала два частных случая при b=0,т.е. функция имеет вид y=f(kx) .

1. При |k|>1 график функции y=f(x) сжимается в |k| раз вдоль оси OX относительно оси OY.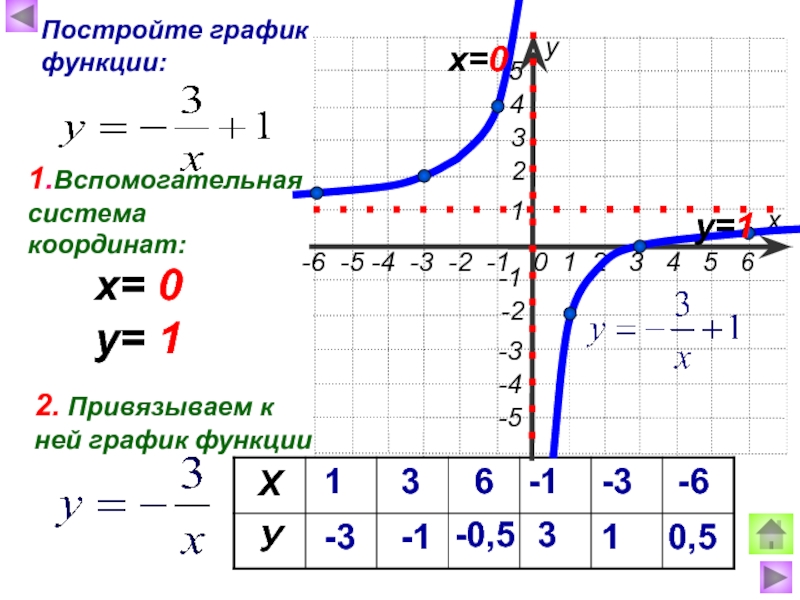

2. При |k|<1 график функции y=f(x) растягивается в раз вдоль оси OX относительно оси OY .

При k<0 полученный график дополнительно отображаем симметрично относительно оси OY.

Рассмотрим примеры:

Построить график функции	Построить график функции

Построение графика функции

y=f(x+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; k=1)

При b>0 график функции y=f(x) сдвигается влево вдоль оси OX на b единиц.

При b<0 график функции y=f(x) сдвигается вправо вдоль оси OX на |b| единиц

Рассмотрим примеры:

Построить график функции ( b>0 )	Построить график функции ( b<0 )

Построение графика функции

y=f(kx+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0)

Рассмотрим общий случай : y=f(kx+b) .

Сначала вынесем коэффициент k за скобку: .
Именно число определяет сдвиг вдоль оси OX , а не b ,
как полагают некоторые абитуриенты.

Теперь строим график функции y=f(x) .
Затем строим график функции y=f(kx) , после чего сдвигаем полученный график вдоль оси OX на
единиц влево или вправо в зависимости от знака этого числа.

Рассмотрим пример: построить график функции

Построение графика функции

y=A·f(kx+b)+B
с помощью элементарных преобразоаний
графика функции y=f(x)

Комбинируя методы построения графиков, рассмотренные в предыдущих случаях, можно по известному графику функции
y=f(x)
построить график функции y=A·f(kx+b)+B с помощью растяжений, сжатий по горизонтали и вертикали,
параллельных переносов вдоль осей координат,
а также симметрий относительно координатных осей тех графиков,
которые получаются из первоначального графика последовательно применением подходящего преобразования.

Рассмотрим примеры.

Построить график функции	Построить график функции

Построить график функции c помощью GeoGebra

В поисках решения,  как же предложить всем желающим, создавать графики уравнения или строить произвольные графики функций, я перелопатил многое:   искал скрипты, писал сам и пытался изучить язык metapost и научить гостей сайта, но в к конечном  итоге я нашел ту «жемчужину» которая помогла мне.

Речь идет о бесплаьной программе Geogebra, сайт которого размещен по адресу http://www.geogebra.org/

Программа написана на Java, поэтому является кроссплатформенным решением, то работает как на Linux-совместимых ( Ubuntu, Red Hat  и прочее), так и на Windows операционных системах.

Рабочее окно GeoGebra выглядит вот так

 

 

Функционал  программы очень обширен,  но в основном на 100% процентов  эту программу будут использовать  преподаватели для создания учебных материалов, студенты для создания дипломных работ, и школьники  при защите курсовых или для понимания той или иной задачи.

Программа может строить:

— Многоугольники и рассчитывать  площади

— Вектора и вычисления с ними

— поворот точки или фигуры вокруг начала координат  или другой произвольной точки

— зеркальное отображени фигуры.

— биссектриссу угла

— много другое, вплоть до анимационных картинок для  показания физических процессов.

 

Но самое главная возможность, на мой взгляд это  построение графика любого уравнения  от одного или двух переменных.

Рассмотрим примеры

Открываем GeoGebra  и внизу в поле Ввод пишем уравнение третьей степени

и получаем следующее

Поставив точку на пересечении графика уравнения и оси абсцисс  мы можем получить  координаты

Точка А имеет координаты (-2.46:0)

То есть один из корней уравнения третьей степени  будет иметь значение -2.46 и это легко проверяется подстановкой в исходное уравнение.

 

С помощью программы можно  создавать  более сложные графики как здесь

 

так и анимационные ролики, которые можно увидеть в форуме создателей GeoGebra.

Программа GeoGebra почему то незаслуженно забыта на российских просторах,  и ни один из более менее популярных ресурсах, посвященных учебе, об этой программе не говорит.Хотя для возникновения интереса у школьников, для понимания геометрических а иногда и алгебраических задач это незаменимая программа.

 

Успехов в изучении программы!

 

• Построить ненаправленный граф по матрице >>

Wolfram | Примеры альфа: домен и диапазон

---

Домен и диапазон

Найдите область и диапазон математического выражения.

Вычислить область определения функции:

Вычислить диапазон функции:

Укажите ограничение на независимую переменную:

Вычислить как домен, так и диапазон:

Вычислить область и диапазон функции нескольких переменных:

Другие примеры

Wolfram | Примеры альфа: приложения исчисления

---

Другие примеры

Асимптоты

Вычислить горизонтальные, вертикальные или наклонные асимптоты.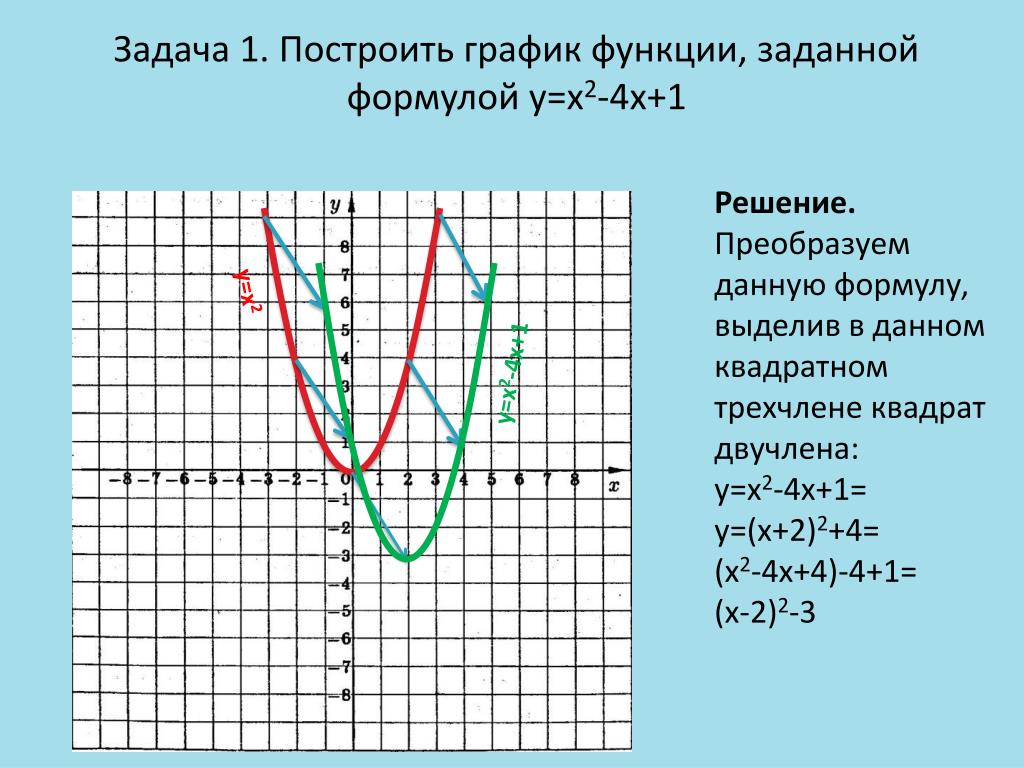

Вычислить асимптоты функции:

Другие примеры

---

Другие примеры

Касательные и нормали

Вычислить касательную линию к кривой или вычислить касательную плоскость или нормальную линию к поверхности.

Найдите касательную к графику функции в точке:

Найдите нормаль к кривой, заданной уравнением:

Другие примеры

---

Другие примеры

Бугорки и углы

Вычислить и визуализировать куспиды и углы функции.

Найдите точки возврата на графике функции:

Найдите углы на графике функции:

Другие примеры

---

Другие примеры

Стационарные точки

Вычисляйте и визуализируйте стационарные точки функции.

Найдите стационарные точки функции:

Найдите стационарные точки функции нескольких переменных:

Другие примеры

---

Другие примеры

Точки перегиба

Вычислить и визуализировать точки перегиба функции.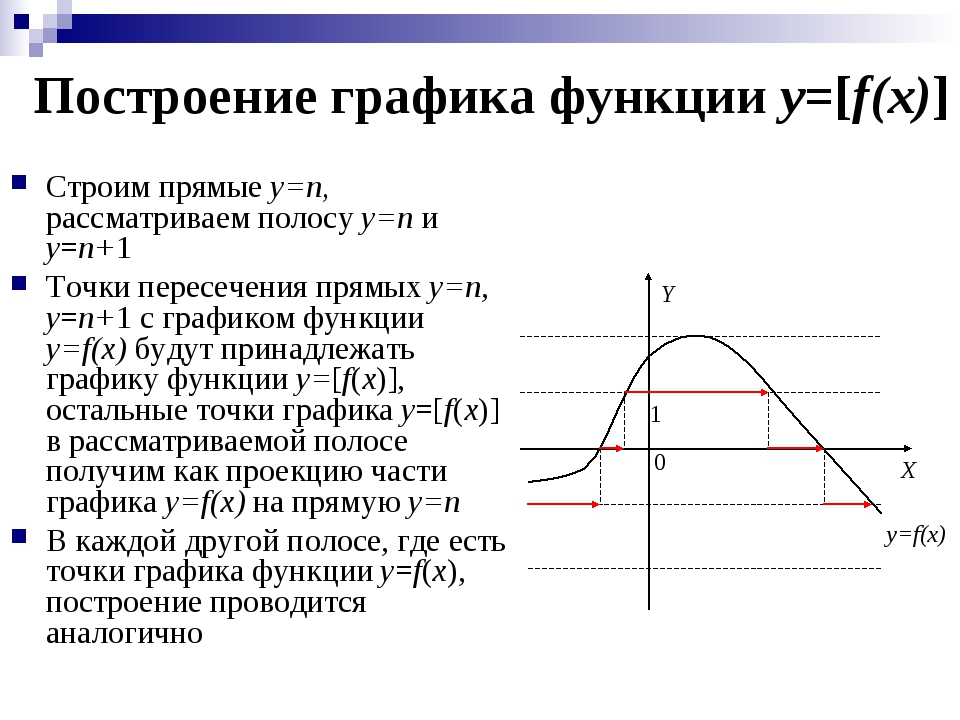

Найдите точки перегиба функции:

Найдите точки перегиба в указанном домене:

Другие примеры

---

Другие примеры

Оптимизация

Найдите глобальные и локальные экстремумы и стационарные точки функций или наложите ограничение на функцию и вычислите ограниченные экстремумы.

Свернуть или развернуть функцию:

Минимизируйте или максимизируйте функцию нескольких переменных:

Свернуть или развернуть функцию с ограничением:

Другие примеры

---

Другие примеры

Площадь между кривыми

Вычисляет площади замкнутых областей, ограниченных областей между пересекающимися точками или областей между указанными границами.

Вычислите площадь, ограниченную двумя кривыми:

Укажите ограничения для переменной:

Другие примеры

---

Другие примеры

Длина дуги

Вычислить длину дуги в различных системах координат и размерах.

Вычислите длину дуги кривой:

Другие примеры

---

Другие примеры

Поверхности и твердые тела революции

Вычислите площадь поверхности вращения или объем тела вращения.

Вычислить свойства поверхности вращения:

Вычислить свойства твердого тела вращения:

Другие примеры

---

Другие примеры

Кривизна

Вычисляет кривизну функций и параметризованных кривых в различных системах координат и измерениях.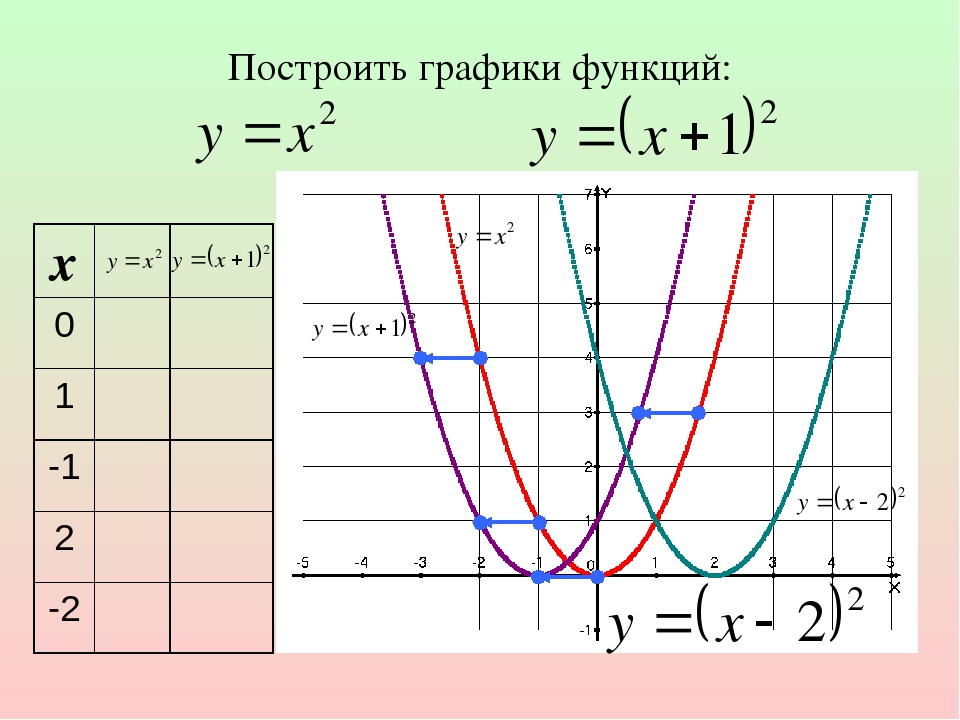

Вычислите кривизну плоской кривой:

Вычислить кривизну пространственной кривой в точке:

Другие примеры

---

Другие примеры

Седловые точки

Вычислить и визуализировать седловые точки функции.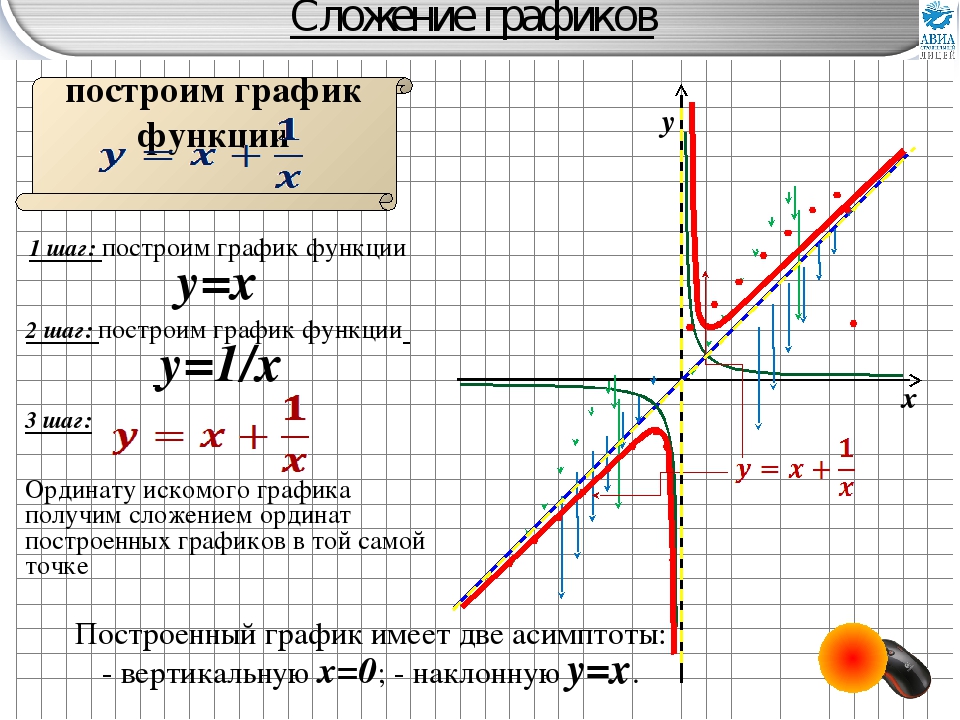

Найдите седловые точки функции:

Найдите точку перевала, ближайшую к указанной точке:

Другие примеры

Изучение студентами функций и их графиков с помощью Desmos — Technology Tools for Teaching in Higher Education, The Practical Handbook Series

Ана Дафф

Графический калькулятор

Desmos — это открытый онлайн-инструмент с обширной числовой и визуальной универсальностью. Это позволяет пользователю строить и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, функции графиков и создавать модели регрессии из наборов данных, среди других возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент слайдера, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к конкретным компонентам.

Преимущества обучения с использованием Desmos

• Открытый и бесплатный ресурс без регистрации или подписки
• Позволяет статические и динамические графические демонстрации и количественный анализ двумерных моделей
• Можно предварительно организовать демонстрации и мероприятия
• Требует от пользователей легко приобретаемых технических навыков
• Позволяет легко делиться демонстрациями с другими пользователями

Ресурсы

• Ноутбук или мобильное устройство (Android или iOS)
• Интернет-браузер или приложение Desmos Graphing Calculator

Шаг 1.Создайте учетную запись на Desmos.com (необязательно)

Перейдите на сайт Desmos.com и перейдите по ссылке «Начать построение графиков». У вас есть возможность создать учетную запись и войти в систему, что позволит вам сохранять, называть и искать свою работу. Последующие шаги по реализации будут основаны на предположении, что вы вошли в свою учетную запись, чтобы воспользоваться этими функциями. Однако графические возможности Desmos не ограничиваются держателями учетных записей, и в этом случае можно сохранить доступ к своей работе, создав ссылку для общего доступа и сохранив ее для дальнейшего использования.

Шаг 2. Откройте Графический калькулятор Desmos и создайте график

Щелкните График без названия и введите название графика (доступно только зарегистрированным пользователям). Введите краткое описание действия: поместите курсор в строку 1, щелкните +
(Добавить элемент), затем примечание «» и добавьте описание в строку 1.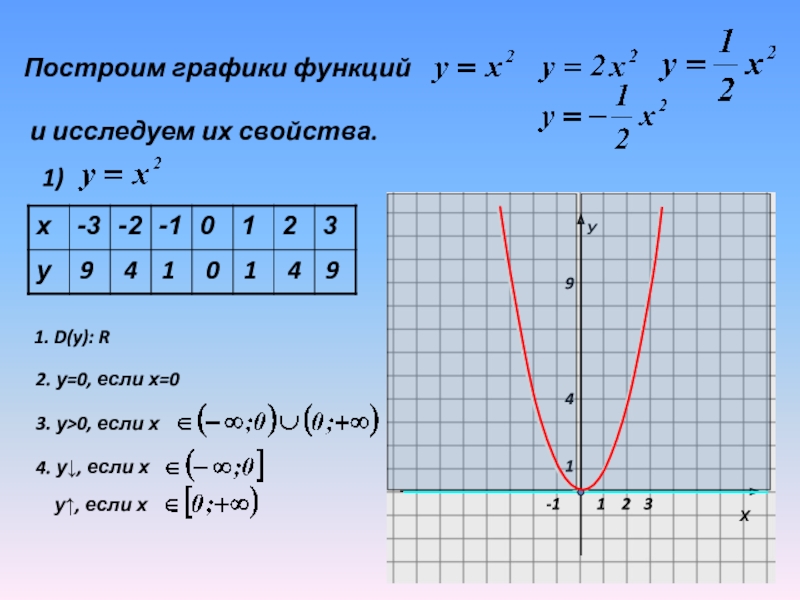

Шаг 3. Укажите функцию, функциональные компоненты или данные, моделируемые функцией

Desmos позволяет пользователю явно указывать функцию (функции) и моделировать данные с помощью функции с использованием регрессии.Если вы используете упражнение как часть оценивания, попросите учащихся импортировать случайно сгенерированные данные (например, из документа Excel), чтобы в результирующих функциях была изменчивость.

Шаг 4. Создайте набор инструкций

Позвольте результатам обучения направлять ваш набор инструкций. Обратите внимание, что задачи могут включать статическое и динамическое исследование модели, включая визуализацию изменений с помощью ползунка. Для лучшего прогресса задачи можно организовать по папкам и руководствоваться примечаниями инструктора, встроенными в график Desmos.Оба могут быть добавлены, нажав
+ (Добавить элемент), затем папку или заметку.

Шаг 4.

Предложите учащимся изучить руководства по графическим инструментам Desmos

Раздел справки предоставляет большой банк подробных и интерактивных учебных ресурсов для новых и опытных пользователей Desmos. Студенты могут научиться создавать ползунки и таблицы, определять ограничения домена и диапазона и выполнять регрессию, следуя простым интерактивным турам, предоставляемым Desmos. Библиотека видеоуроков обширна и легко доступна для поиска, а Руководство пользователя Desmos предоставляет базовое руководство по инструментам Desmos.

Шаг 5. Поделитесь графиком (ами) со своими учениками

Нажмите на инструмент «Поделиться своим графиком», расположенный в верхнем левом углу. Созданная ссылка отправит студентов на график и позволит каждому студенту просматривать и изменять его отдельно от других пользователей, не влияя на созданный вами график. Обратите внимание, что вы также можете использовать этот инструмент, чтобы сохранить изображение графика (за некоторыми исключениями) и встроить его в другие платформы.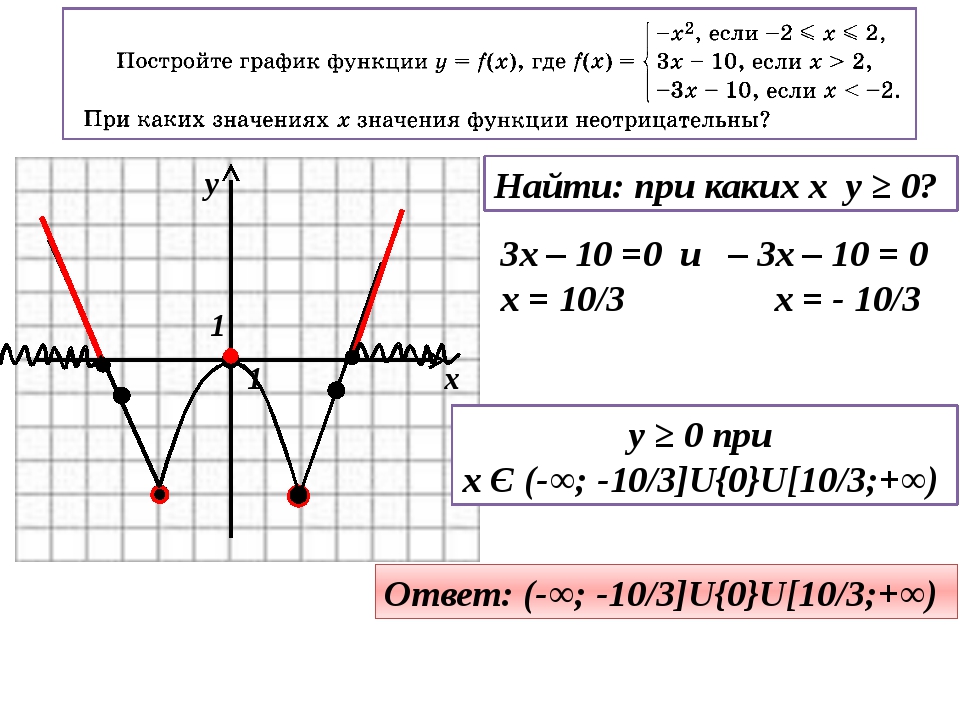

Шаг 6. Включение Калькулятора Графа Десмоса в оценки

Включите результаты исследований учащихся и извлеченные уроки в оценки с помощью инструмента «Поделитесь своим графиком», с помощью которого учащиеся обмениваются ссылками или изображениями своих работ внутри, непосредственно или как часть отдельного документа для отправки.Обратите внимание, что ссылка будет включать график в том виде, в котором он был на момент создания ссылки.

• Избегайте путаницы, сводя к минимуму двусмысленность- Разработайте инструкции, соответствующие результатам обучения. Разбейте занятие на компоненты и распределите их по папкам. По мере необходимости направляйте учащихся к конкретным ресурсам в ходе упражнения по темам, которые могут нуждаться в разъяснении. Воспользуйтесь преимуществами обширной библиотеки обучающих видео от Desmos и его пользователей (доступных через любую поисковую систему с «выбранной темой Desmos +») в качестве ресурса для студентов по конкретным задачам.
• Помните о времени и требуемых навыках — Проверьте, сколько времени вам потребуется, чтобы выполнить задание, затем умножьте это время на три. На протяжении всего теста размышляйте о своих знаниях учеников, диапазоне их навыков, связанных с технологиями и контентом, и соответствующим образом корректируйте деятельность.
• Поощряйте решение проблем и устранение неполадок с помощью одноранговой поддержки — Покажите учащимся, как делиться работой с помощью инструмента «Поделиться своим графиком», чтобы искать помощи у других во время упражнения.Наблюдая за работой учащегося, будет легче определить, где учащийся допустил ошибку или где он наткнулся на камень преткновения.

Цифровые ресурсы

Руководство пользователя Desmos

Примеры изучения функций с помощью Desmos в действии:

Экичи, Селил и Плайли, Крис. «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Интернет.

Годин, Шон. «В чем проблема? Ищу лжецов.Бюллетень — Ассоциация математиков Онтарио 56.4 (2018): 11–13. Интернет.

Хойлс, Селия. «Преобразование математической практики учащихся и учителей с помощью цифровых технологий». Исследования в области математического образования. 20.3 1–20. Интернет.

Набб, Кейт и Муравска, Жаклин. «Мотивация расчетов с помощью одного вопроса». ПРИМУС 29.10 (2019): 1140–1153. Интернет.

Shahriari, Razieh et al. «Влияние использования технологий на понимание студентами математики и алгебры в колледже.”ProQuest Dissertations Publishing, 2019. Web.

Ана Дафф — научный сотрудник факультета бизнеса и информационных технологий Технического университета Онтарио, где она преподает математические курсы первого года обучения. Ее исследовательский опыт связан с математикой, в которой она имеет докторскую степень. из Университета Оттавы. До Технологического университета Онтарио она преподавала математику в Оттавском университете, Королевском военном колледже Канады и Международной школе Белграда в Сербии. Она также имеет обширный опыт в разработке и управлении крупномасштабными программами мобилизации и обучения сообществ в Канаде и за рубежом в неправительственном и государственном секторах.

Quick-R: создание графика

В R графики обычно создаются в интерактивном режиме.

# Создание графика
attach (mtcars)
plot (wt, mpg)
abline (lm (mpg ~ wt))
title («Регрессия MPG по весу»)

Функция plot () открывает окно графика и отображает зависимость веса от миль на галлон.
Следующая строка кода добавляет к этому графику линию регрессии.Последняя строка добавляет заголовок.

нажмите для просмотра

Сохранение графиков

Вы можете сохранить график в различных форматах из меню
Файл -> Сохранить как .

Вы также можете сохранить график с помощью кода, используя одну из следующих функций.

Функция	Вывод на
pdf («mygraph.pdf»)	pdf файл
выигрыш.метафайл («mygraph.wmf»)	метафайл Windows
png («mygraph.png»)	файл png
jpeg («mygraph.jpg»)	файл jpeg
BMP («mygraph.bmp»)	файл BMP
постскриптум («mygraph.ps»)	постскриптум

Подробнее см. «Ввод / вывод».

Просмотр нескольких графиков

Создание нового графика с помощью команды высокоуровневого построения (plot, hist, boxplot и т. Д.) Обычно перезаписывает предыдущий график. Чтобы этого избежать, перед созданием нового графика откройте новое окно графика. Чтобы открыть новое окно графика, используйте одну из функций ниже.

Функция	Платформа
окна ()	Окна
X11 ()	Unix
кварцевый ()	Mac

Вы можете открыть несколько окон графиков одновременно.Подробнее см. Справку (dev.cur) .

Либо, открыв первое окно графика, выберите History -> Recording из меню окна графика.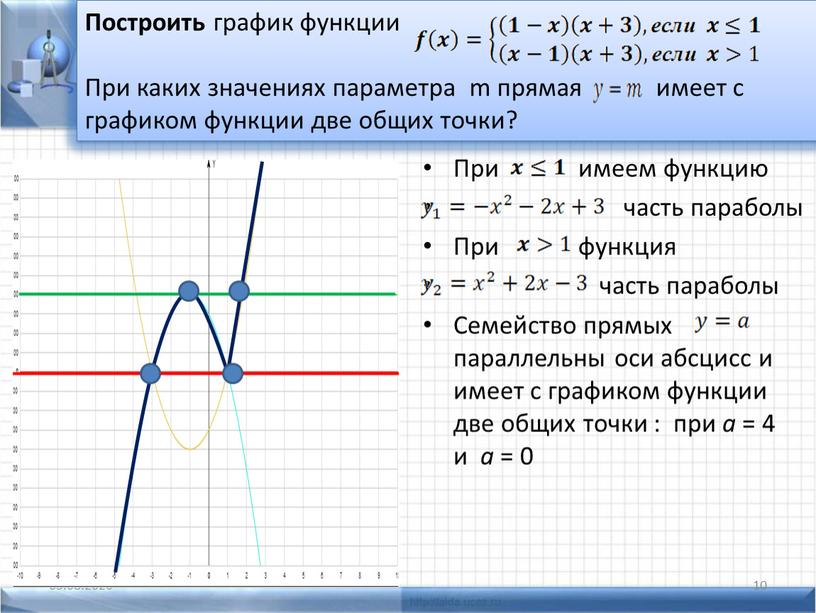 Затем вы можете использовать Предыдущий и Следующий , чтобы перемещаться по графикам, которые вы создали.

Графические параметры

Вы можете указать шрифты, цвета, стили линий, оси, справочные линии и т. Д., Указав графические параметры. Это обеспечивает широкую степень настройки.Графические параметры описаны в разделе Advanced Graphs. Раздел Advanced Graphs также включает более подробное описание настройки осей и текста.

к практике

Попробуйте выполнить упражнения по созданию графиков в этом курсе по визуализации данных в R.

Лучшее бесплатное программное обеспечение для построения графиков: для загрузки и онлайн

Когда дело доходит до лучших бесплатных программ для построения графиков программ, у вас есть множество инструментов для рисования и создания любых типов математических и статистических графиков, диаграмм и диаграмм (таких как линейный график, столбчатая и круговая диаграмма, гистограмма, диаграмма рассеяния, диаграмма в виде прямоугольников и усов) бесплатно.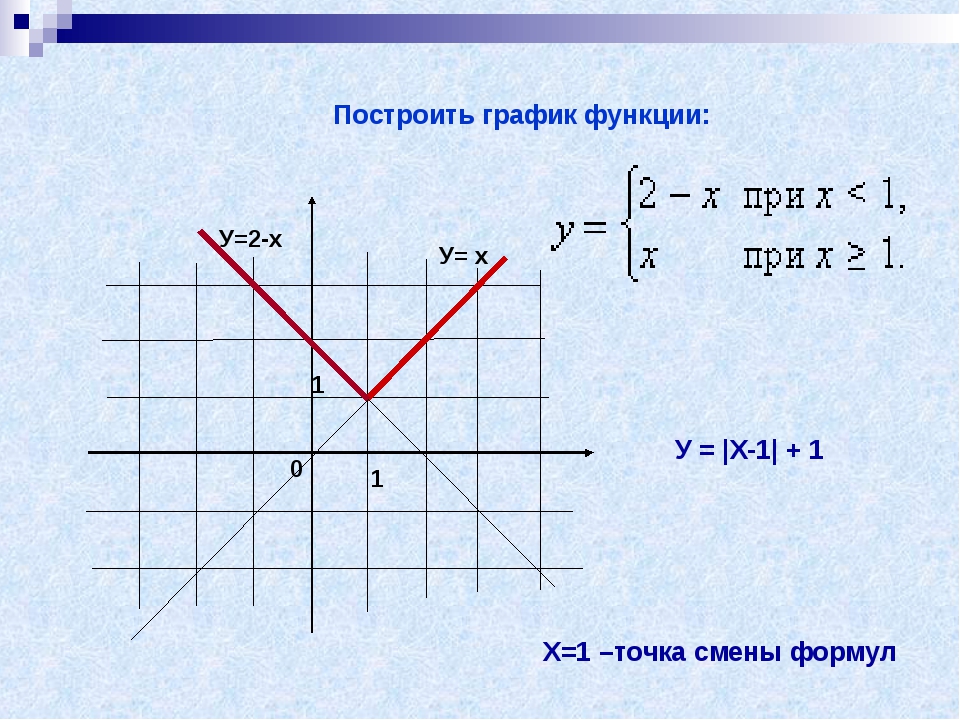

Бесплатное программное обеспечение для построения графиков данных бывает трех типов:

• локальные конструкторы диаграмм для бесплатной загрузки (для Mac, Windows и Linux)
• онлайн-конструкторы диаграмм и диаграмм
• с открытым исходным кодом программы.

Кроме того, вы можете найти бесплатное и простое программное обеспечение для создания трехмерных графиков, которое позволяет создавать профессиональные диаграммы для различных целей в статистике, математике, науке о данных, маркетинге и т. Д.

Вот список лучших бесплатных программ для построения графиков. легкий и профессиональный способ.

1. Meta-chart.com

Если вы ищете простую и абсолютно легкую в использовании онлайн-программу для бесплатного построения графиков , Meta-chart.com может быть вашим ответом. Все, что вам нужно, это данные, и вы можете начать строить диаграммы и графики с нуля.

Самое приятное то, что вы можете создавать и публиковать свои диаграммы в Интернете без каких-либо затрат. Диаграммы и графики создаются за считанные минуты. Для использования программы не нужно регистрироваться. Однако, если вы решите зарегистрироваться, вы можете сохранить свои графики и поделиться ими со всем миром.

Основные преимущества и особенности:

• Большое количество возможных типов графиков и диаграмм — вы можете создавать линейные диаграммы, простые и многополосные диаграммы, круговые диаграммы, гистограммы, диаграммы разброса, диаграммы с прямоугольниками и усами, диаграммы с областями, сплайн графики, прямоугольные и усовые диаграммы, счетные диаграммы и т. д.
• Вы можете ввести данные вручную или импортировать файлы электронных таблиц (CSV) .
• Очень красивые и визуально привлекательные дизайны и графики.
• Абсолютно просто в использовании онлайн-программного обеспечения для построения графиков.
• Поделитесь бесплатно своими собственными графиками и диаграммами.
• Вы можете использовать обычную или трехмерную диаграмму типа .

Веб-сайт: www.meta-chart.com

2. График

График предназначен для тех, кому требуется с открытым исходным кодом и бесплатно загружаемое программное обеспечение для построения графиков для Windows или Mac. Это одна из самых популярных бесплатных программ для рисования математических и статистических графиков.

Вы можете нарисовать графики функций и выполнить некоторые математические вычисления над функциями.Система имеет множество встроенных функций, например sin, cos, log и т. д. Вы можете выбрать цвет, ширину и стиль линий графиков.

Graph — это приложение для Windows, но его также можно запустить на Mac через Wine.

Основные преимущества и особенности:

• Функции рисования — вы можете отображать стандартные функции, параметрические и полярные функции.
• Нарисуйте соотношение — программа может показать любое уравнение и неравенство.
• Оттенки , которые можно создавать с помощью разных стилей и цветов.
• Точечный ряд и линии тренда.
• Взаимодействуйте с другими программами, такими как Windows Bitmap, Portable Network Graphics, JPEG, Windows Enhanced Metafile, Portable Document Format (PDF) и другими.
• Вы можете создавать свои собственные пользовательские функции.
• Анимация, показывающая, что происходит с функцией.

Веб-сайт: http://www.padowan.dk/

3. Infogr.am

Infogr.am — это захватывающая бесплатная программа для построения графиков, доступная в Интернете, .По сути, это платная онлайн-программа с бесплатной версией. Они могут предложить вам простоту использования и очень креативные шаблоны графиков.

Вы можете строить не только красивые диаграммы, но и инфографику, карты и отчеты. Это отличный инструмент для визуализации маркетинговых данных, онлайн-публикаций, образовательных целей, бизнес-отчетности и т. Д.

Варианты дизайна сразу видны.

Ключевые преимущества и особенности бесплатного плана:

• Более 35 типов диаграмм , включая круговые диаграммы, гистограммы и линейные диаграммы, столбчатые таблицы, диаграммы с областями, точечные диаграммы, пузырьковые диаграммы, древовидные карты, финансовые графики и облака слов.
• Публикуйте свой контент — позволяет добавлять визуализации данных на ваш веб-сайт с помощью встраиваемых материалов.
• Импорт данных — вы можете импортировать файлы электронных таблиц (CSV, XLSX) со своего компьютера или из облачного хранилища.
• 2 типа карт — доступ к карте мира и карте США.
• Размер библиотеки 10.
• Простой и удобный интерфейс.

Веб-сайт: https://infogram.com

4.Gnuplot

Gnuplot — популярное портативное бесплатное программное обеспечение для построения графиков , которое можно загрузить. Он широко используется на многих платформах, включая MS Windows, Linux, Unix и OSX . Он также сохраняет поддержку старых систем, таких как VMS, Ultrix, OS / 2 и MS-DOS. Исходный код защищен авторским правом, но распространяется бесплатно.

Он был создан, чтобы помочь ученым и студентам визуализировать отношения данных и математические функции. Однако теперь он поддерживает множество неинтерактивных приложений, таких как веб-скрипты.

Gnuplot поддерживает как 2D, так и 3D типы графиков. Среди основных стилей 2D-графиков — закрашенные кривые, полосы ошибок, гистограммы, гистограммы, пошаговые функции, многоосные шкалы, круги, прямоугольные диаграммы и многие другие.

Основные преимущества и возможности:

• Отображение 2D-функций и точек данных в различных стилях (точки, линии, планки погрешностей).
• Построение трехмерных точек данных и поверхностей во многих стилях (контурный график, сетка).
• Алгебраические вычисления.
• Подбор модели на основе данных.
• Поддержка многих операционных систем, форматов графических файлов и устройств вывода.

Веб-сайт: http://www.gnuplot.info/

5. Desmos

Desmos — это бесплатный онлайн-калькулятор нового поколения для всех учащихся и учителей.Он имеет впечатляющее количество функций и возможностей.

Программа позволяет вам строить графики функций, исследовать преобразования, строить данные, оценивать уравнения и многое другое — и все это бесплатно. Вы можете изучать уравнения, создавать и публиковать полноцветные графики.

Desmos — невероятно мощный инструмент для построения графиков. Он также поддерживает виртуальную клавиатуру с часто используемыми математическими символами. Вы также можете использовать физическую клавиатуру.

Основные преимущества и особенности:

• Мощные настройки графика для настройки графика в соответствии с вашими требованиями.
• Производные и дифференциальное исчисление всего несколькими нажатиями клавиш: d / dx.
• Функциональная нотация для установления связей между выражениями, таблицами и другими математическими объектами.
• Неравенства для автоматического затенения над или под линиями и кривыми.
• Многие статистические возможности , такие как исследование формы, центра и разброса наборов данных, запуск моделей линейной регрессии, создание и построение статистических диаграмм, таких как линейный график, гистограмма, точечная диаграмма и многие другие и т. Д.
• Интегралы, точки построения, полярные графики и многие другие функции.

Веб-сайт: https://www.desmos.com/

6. Orange

Orange — это инструмент машинного обучения, статистики и визуализации данных с открытым исходным кодом для новичков и профессионалов. Он включает в себя визуальное программирование, анализ данных и интерактивную визуализацию данных. Кроме того, его также можно использовать как библиотеку Python.

Вы можете влюбиться в этот инструмент, который позволяет принимать бизнес-решения, не тратя много времени на анализ и сравнение чисел.

Orange — это , идеально подходящий для визуализации данных , и в нем есть все: ряд типов графиков, статистических распределений, тепловых карт, деревьев решений, иерархическая кластеризация, линейные проекции, прямоугольная диаграмма, диаграммы рассеяния и многое другое.

Это бесплатно загружаемое программное обеспечение для Windows, Mac OS и Linux .

Основные преимущества и возможности:

• Вы можете выполнять простой анализ данных с интеллектуальной визуализацией данных.
• Широкий спектр виджетов визуализации, таких как точечная диаграмма, прямоугольная диаграмма, гистограмма, визуализации для конкретных моделей, такие как дендрограмма, силуэтный график и т. Д.
• Визуальное программирование и графический пользовательский интерфейс, позволяющий сосредоточиться на исследовательском анализе данных вместо кодирования.
• Используется в школах, университетах и ​​на курсах профессионального обучения по всему миру.
• В Orange доступны различные надстройки для добычи данных.

Веб-сайт: https://orange.biolab.si/

7. GeoGebra

GeoGebra входит в число лучших программ с открытым исходным кодом и бесплатного построения графиков для всех уровней образования, объединяющих электронные таблицы и графики. , геометрия, алгебра, статистика, математика и исчисления в одном удобном инструменте.

GeoGebra — ведущий поставщик программного обеспечения для математики, поддерживающего образование в области науки, статистики, технологий, инженерии и математики во всем мире.

Вы можете легко решать уравнения, создавать конструкции, функции графиков, анализировать данные и изучать трехмерную математику! Вы можете использовать программу онлайн или скачать ее на свой компьютер.

Основные преимущества и особенности:

• Очень простой в использовании интерфейс с множеством мощных функций.
• Предоставляет широкий спектр различных представлений для математических объектов: представление алгебры, представление графики, представление электронной таблицы, представление 3D-графики, представление , представление CAS, представление калькулятора вероятности и т. Д.
• Доступно на многих языках для миллионов наших пользователей по всему миру.
• Прямой ввод различных уравнений и координат.
• Вы можете использовать его бесплатно онлайн или загрузить для Windows, Mac и Linux .

Веб-сайт: https://www.geogebra.org

8. AmCharts

AmCharts также является одним из впечатляющих бесплатных инструментов для построения графиков, которые могут удивить своей простотой.Этот расширенный инструмент построения диаграмм может удовлетворить любые потребности в визуализации данных.

Их решения для построения графиков включают линейную диаграмму, диаграмму площадей, прямоугольников и усов, столбцы, столбцы, водопад, Mekko, цилиндры, трапеции, свечи, составные (обычные, 100% или 3D) и многие другие типы графиков.

Кроме того, AmCharts поддерживает как онлайн, так и офлайн.

Основные преимущества и особенности:

• Расширенные серийные диаграммы для отображения сложных визуализаций данных. Программа объединяет различные типы графиков на одной диаграмме.
• Улучшенные временные шкалы.
• Микрокарты и спарклайны.
• Функциональный инструмент с интерактивными возможностями, параметрами экспорта и загрузкой внешних данных.
• Адаптивная и удобная для мобильных устройств программа.
• Настраиваемая и гибкая, богатая опциями аннотации. Поддерживает темы и стили CSS.
• Многоязычный — почти 30 языков включены в продукт.

Веб-сайт: https://www.amcharts.com

Хотите больше бесплатных программ для построения графиков?

Вот список других хороших бесплатных решений:

9. Mondrian — универсальная программа для визуализации статистических данных. Он предлагает выдающиеся интерактивные методы визуализации данных практически любого типа.

10. LabPlot — KDE-приложение для интерактивного построения графиков и анализа научных данных. Он предоставляет простой способ создавать, управлять и редактировать графики, а также выполнять анализ данных. Доступно для Linux, Windows и Mac OS X.

11. MathGV — бесплатная программа для построения графиков математических функций с открытым исходным кодом для Windows XP, Vista и Windows 7.

12. Euler Math Toolbox — простая математическая программа, объединяющая числовые и символьные инструменты в одном бесплатном пакете. Программа работает на Windows 7, 8 или 10, 32 или 64 бит.

13. MagicPlot Student — современная программа для построения графиков для школьников. Легкое приложение для анализа данных, построения графиков и нелинейной подгонки. Доступно для Windows, Mac OS X и Unix-подобных платформ.

14. Meta-calculator.com — бесплатное онлайн-программное обеспечение для построения графиков, которое позволяет построить график любого уравнения, найти его пересечения, создать таблицу значений и т. Д.

15. Mathway — предоставляет студентам инструменты, необходимые для понимания и решения их математических задач.

Если вы поклонник бесплатного программного обеспечения, наш пост о 10 лучших бесплатных инструментах для создания карт разума может быть вам полезен.

Какая ваша любимая бесплатная программа для построения графиков? Поделитесь своими мыслями о поле ниже.

Онлайн-справка — Быстрая справка

Графические функции Последнее обновление: 04.09.2019 Создание новой функциональной диаграммы Origin поддерживает построение четырех видов функций: 2D-функции, 2D-параметрические функции, 3D-функции и 3D-параметрические функции. Нажмите Файл: Новое: График функции или Нажмите кнопку функционального графика на стандартной панели инструментов. Когда вы выбрали график функции из меню, откроется диалоговое окно, позволяющее вам определить функцию. Чтобы построить 3D параметрическую функцию, выберите меню Файл: Новое: График функции: Параметрический график функции 3D , чтобы открыть диалоговое окно Создать трехмерный график параметрической функции .В этом диалоговом окне введите сетку сетки , установите масштаб для двух параметров, введите параметрические уравнения для переменных X, Y и Z, а затем определите константы, которые можно использовать в определении функции в нижней таблице, если нужный. Нажмите ОК, чтобы получить график. См. Больше [образцы функций 3D] Примечание: После построения графика функции вы можете переопределить или настроить график функции на вкладке Функция диалогового окна Подробная информация о графике , который можно открыть, дважды щелкнув график функции в окне графика. Добавить график функции к существующему графику При активном окне графика щелкните Файл: Новый: График функции или щелкните кнопку графика функции на стандартной панели инструментов, как описано выше. Выберите Добавить в активный график в раскрывающемся списке внизу диалогового окна. Примечание: Если вы выберете 3D-график функции, когда активным окном графика является 2D, этот раскрывающийся список не будет отображаться. Альтернативный метод добавления графика функции к существующему графику При активном графике щелкните Insert: Function Plot or Insert: Parametric Plot . Примечание: В более старых версиях это находится в разделе График: добавить график функции . Ключевые слова: график математических функций, трехмерный график параметрической функции, двухмерный график параметрической функции, график функции, сетка Требуется минимальная исходная версия: 9. 0SR0

R plot () Функция (добавление заголовков, меток, изменение цветов и наложение горшков)

В этой статье вы научитесь использовать функцию построения графика в R. Она используется для построения графиков в соответствии с типом переданного объекта.

Наиболее часто используемой функцией построения графиков в программировании на R является функция plot () . Это универсальная функция, то есть у нее есть много методов, которые вызываются в соответствии с типом объекта, переданного в функцию plot () .

В простейшем случае мы можем передать вектор, и мы получим диаграмму рассеяния величины и индекса. Но обычно мы передаем два вектора и строим диаграмму рассеяния этих точек.

Например, команда plot (c (1,2), c (3,5)) построит точки (1,3) и (2,5) .

Вот более конкретный пример, где мы строим график диапазона синусоидальной функции от -pi до pi .

  x <- seq (-pi, pi, 0.1)
сюжет (x, sin (x))
  

---

Добавление заголовков и осей надписей

Мы можем добавить заголовок к нашему графику с параметром main . Точно так же xlab и ylab можно использовать для маркировки оси x и оси y соответственно.

  сюжет (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)")
  

---

Изменение цвета и типа графика

Выше мы видим, что график состоит из круглых точек и имеет черный цвет.Это цвет по умолчанию.

Мы можем изменить тип графика с помощью аргумента типа . Он принимает следующие строки и имеет заданный эффект.

 "п" - баллов
"l" - линии
«б» - и точки, и линии
«c» - пустые точки, соединенные линиями
«о» - точки и линии, нанесенные поверх черточки
«s» и «S» - ступеньки лестницы
"h" - вертикальные линии в виде гистограммы
«n» - не создает точек или линий
 

Точно так же мы можем определить цвет, используя col .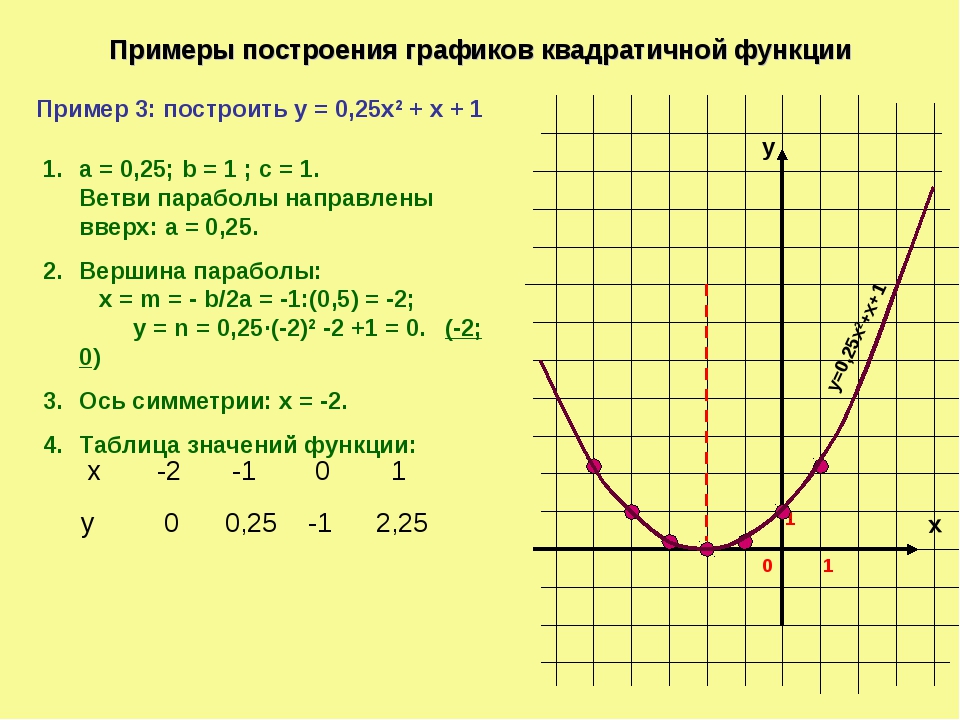

  сюжет (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)",
type = "l",
col = "синий")
  

---

Наложение графиков с помощью функции legend ()

Вызов plot () несколько раз приведет к построению текущего графика в том же окне вместо предыдущего.

Однако иногда мы хотим наложить графики, чтобы сравнить результаты.

Это стало возможным с помощью функций lines () и points () для добавления линий и точек соответственно к существующему графику.

  сюжет (x, sin (x),
main = "Наложение графиков",
ylab = "",
type = "l",
col = "синий")
строки (x, cos (x), col = "red")
легенда ("верхний край",
с («грех (х)», «соз (х)»),
fill = c ("синий", "красный")
)
  

Мы использовали функцию legend () , чтобы правильно отобразить легенду.Посетите функцию legend (), чтобы узнать больше.

Также посетите функцию plot (), чтобы узнать больше о различных аргументах, которые может принимать функция plot () и другие примеры.