Содержание
Пошаговое построение сечения четырехугольной пирамиды
Сегодня научимся строить сечения четырехугольной правильной пирамиды. Использовать для построения будем метод следов. Пользоваться этим методом неудобно и даже иногда невозможно, когда сечение имеет малый наклон или не имеет наклона к плоскости основания. Если такой случай вам попадется, лучше использовать метод внутреннего проецирования.
Задача 1. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .
Задача 1. Дано
Шаг 1. Через точки и , принадлежащие плоскости грани , проведем прямую . Определим точку плоскости основания пирамиды, которая бы принадлежала и секущей плоскости. Для этого проведем продолжение ребра и найдем точку его пересечения с прямой – точка .
Задача 1. Шаг 1.
Шаг 2. Аналогично найдем вторую точку секущей плоскости в плоскости основания: проводим прямую , находим ее пересечение с продолжением ребра – точка .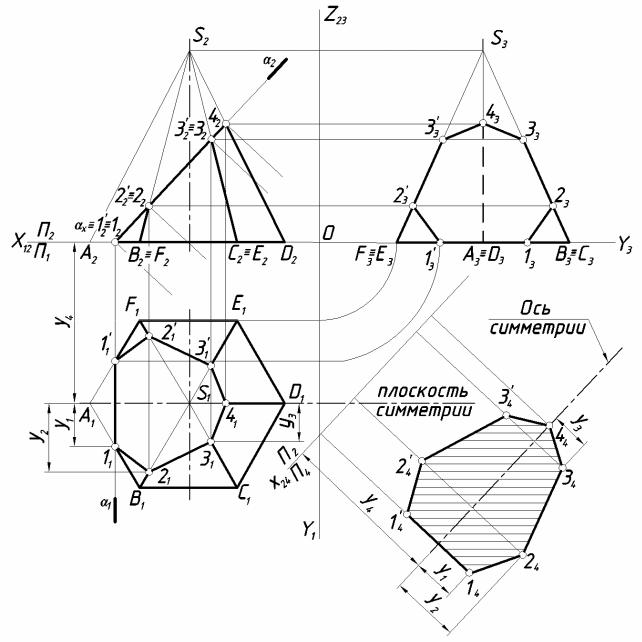
Задача 1. Шаг 2.
Шаг 3. Через две точки можно провести прямую, и, так как точки и принадлежат и секущей плоскости, и плоскости основания, то и прямая, проведенная через них, будет принадлежать обеим плоскостям. А раз эта прямая лежит в плоскости основания, то определим точки пересечения этой прямой с другими прямыми плоскости основания, например, с продолжением ребра – точка , и продолжением ребра – точка . Значит, точки и – тоже точки плоскости сечения, а за счет того, что прямая лежит в плоскости грани , точка также принадлежит плоскости этой грани. Аналогично, так как прямая принадлежит плоскости грани , то и точка – точка этой же плоскости. Теперь можно соединить точки и – как точки одной плоскости, и соединить точки и .
Задача 1. Шаг 3.
Шаг 4. Пересечение прямых и даст нам последнюю точку искомого сечения – точку .
Задача 1. Шаг 4.
Проводим отрезки , , завершая построение:
Многоугольник сечения
Окончательный вид сечения:
Окончательный вид
Задача 2. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .
Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .
Задача 2. Дано
Шаг 1. Проводим прямую , она принадлежит грани , так как точки и принадлежат ей.
Задача 2. Шаг 1.
Шаг 2. Прямая пересечет прямую , и точка их пересечения благодаря принадлежности прямой будет лежать в плоскости основания.
Задача 2. Шаг 2.
Шаг 3. Точки и принадлежат плоскости основания, проведем через них прямую , найдем точку пересечения этой прямой ребра – точку . Продлим прямую до пересечения с прямой , получим точку . Точка принадлежит плоскости , тк как этой плоскости принадлежит прямая .
Задача 2. Шаг 3.
Шаг 4. Соединим точки и . Найдем место пересечения данной прямой ребра – точку .
Задача 2. Шаг 4.
Шаг 5. Соединяем полученные точки отрезками.
Задача 2. Шаг 5.
Окончательный вид с другого ракурса:
Окончательный вид сечения
Задача 3. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .
Задача 3. Дано
Шаг 1. Соединим и , как точки одной плоскости.
Задача 3. Шаг 1.
Шаг 2. Прямая принадлежит плоскости грани , следовательно, пересечет прямую этой же грани . Найдем точку их пересечения , продлив ребро .
Задача 3. Шаг 2.
Шаг 3. Точки и – “одного поля ягоды” – обе принадлежат плоскости грани . Поэтому соединим их, отметив точку пересечения с ребром – .
Задача 3. Шаг 3.
Шаг 4. Точки и принадлежат плоскости основания, соединяем их. Прямая лежит в плоскости основания и пересечет прямую в точке .
Задача 3. Шаги 4-5.
Шаг 5. Точки и соединяем, так как обе они принадлежат плоскости , и получаем последнюю точку сечения – на ребре .
Шаг 6. Соединяем точки отрезками.
Задача 3. Шаг 6.
Окончательный вид сечения:
Окончательный вид сечения
Задача 4. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .
Задача 4. Дано.
Шаг 1-2. Точки и принадлежат грани , соединим их отрезком (прямой). Точки и принадлежат грани основания, также соединим их.
Задача 4. Шаги 1-2
Шаг 3. Прямая пересечет продолжение ребра в точке . Точка , таким образом, принадлежит плоскости грани .
Задача 4. Шаг 3.
Шаг 4. Соединяем точки и , проводя прямую . Она пересечет ребро в точке .
Задача 4. Шаг 4.
Шаг 5. Соединяем полученные точки на ребрах отрезками:
Задача 4. Шаг 5.
Окончательный вид с удобного ракурса:
Окончательный вид
Построение сечений
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур.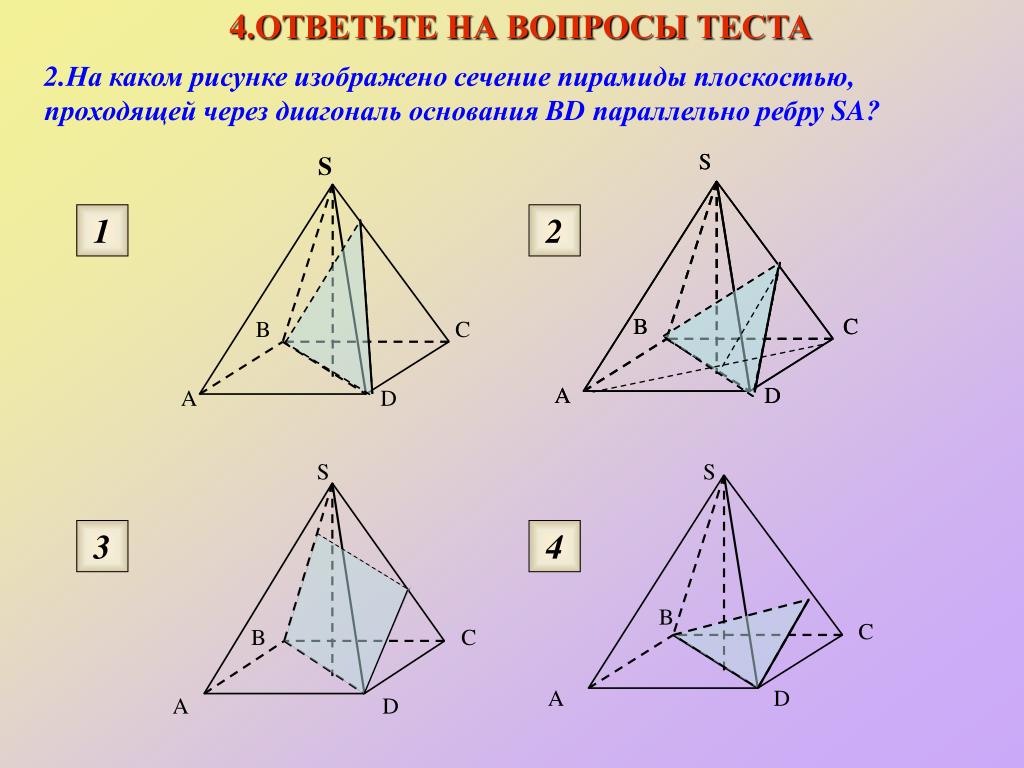 \circ\).
\circ\).
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая \(a\), не лежащая в плоскости \(\pi\), параллельна некоторой прямой \(p\), лежащей в плоскости \(\pi\), то она параллельна данной плоскости.
2. Пусть прямая \(p\) параллельна плоскости \(\mu\). Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\), то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\).
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]
5. Пусть прямая \(l\) лежит в плоскости \(\lambda\). Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\), не лежащей на прямой \(l\), то прямые \(l\) и \(s\) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
7. Теорема о трех перпендикулярах.
Пусть \(AH\) – перпендикуляр к плоскости \(\beta\). Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\). Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA’\) и \(BB’\) (точки \(A’, B’\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A’B’\) – проекция прямой \(a\) на плоскость \(\mu\). Точка \(M=a\cap
A’B’\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\).
Причем заметим, что все точки \(A, B, A’, B’, M\) лежат в одной плоскости.
Пример 1.
Дан куб \(ABCDA’B’C’D’\). \(A’P=\dfrac 14AA’, \ KC=\dfrac15 CC’\). Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\).
Решение
1) Т.к. ребра куба \(AA’, CC’\) перпендикулярны \((ABC)\), то точки \(A\) и \(C\) — проекции точек \(P\) и \(K\).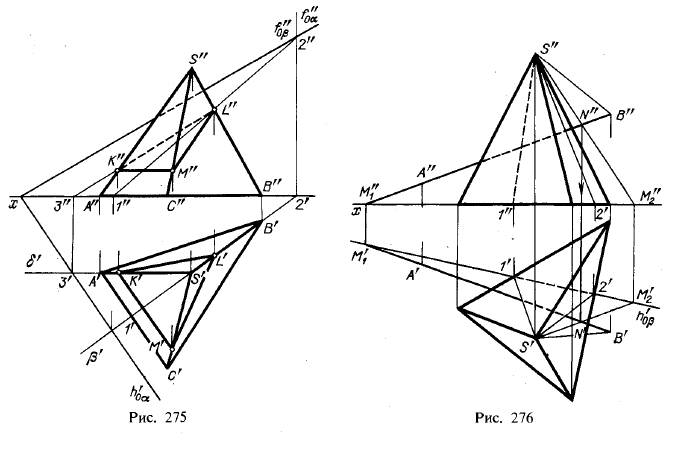 \circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
\circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
Если обозначить ребро куба за \(a\), то \(PA=\dfrac34a, \ KC=\dfrac15a,
\ AC=a\sqrt2\). Тогда:
\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow
EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]
Пример 2.
Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\), высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\), считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\), считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\).
Решение
1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\) пересечения медиан основания. Найдем проекцию прямой \(MN\) на плоскость \(ABC\). Т.к. \(DO\perp (ABC)\), то и \(NO\perp (ABC)\). Значит, \(O\) – точка, принадлежащая этой проекции.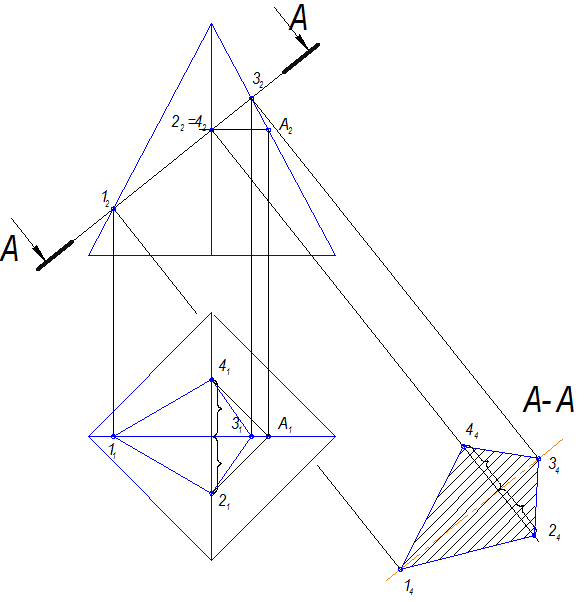 Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\). Точка \(Q\) будет лежать на медиане \(AK\).
Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\). Точка \(Q\) будет лежать на медиане \(AK\).
Действительно, т.к. \(MQ\) и \(NO\) перпендикулярны \((ABC)\), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\) лежат в одной плоскости \(ADK\), то и точка \(Q\) будет лежать в этой плоскости. Но еще (по построению) точка \(Q\) должна лежать в плоскости \(ABC\), следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\).
Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\). \(L\) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\).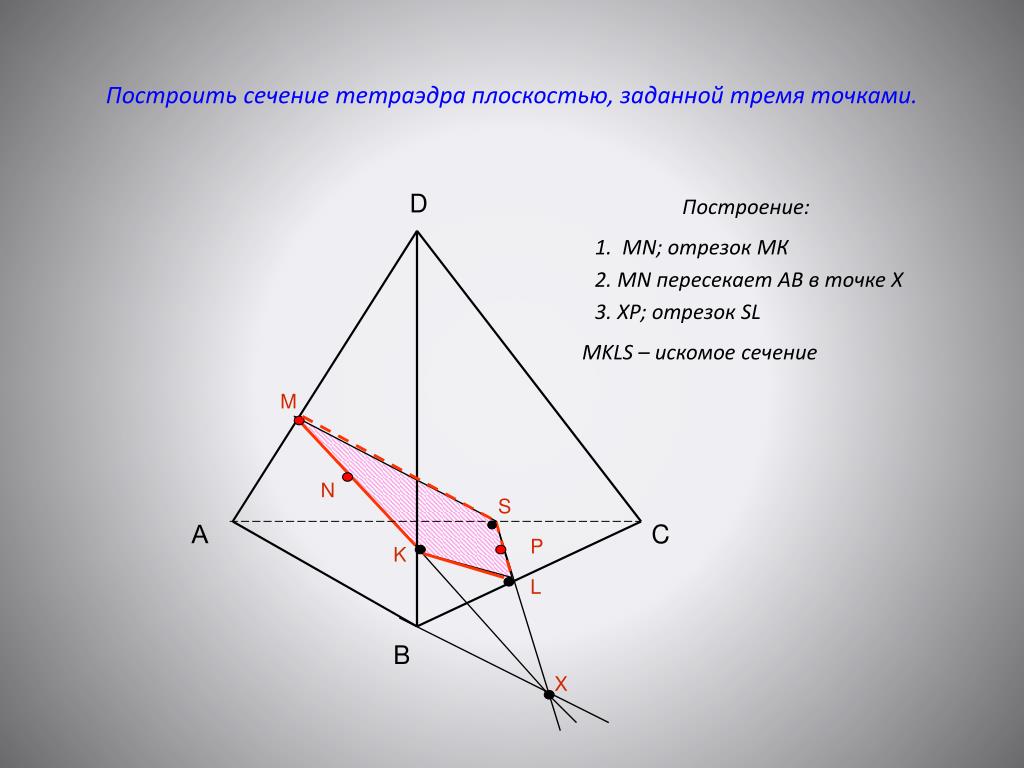 \circ, \ \angle L\) – общий). Значит,
\circ, \ \angle L\) – общий). Значит,
\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a}
=\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow
x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]
Следовательно, \(OL>OK\), значит, точка \(L\) действительно лежит вне отрезка \(AK\).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\)).
Пример 3
Дана правильная четырехугольная пирамида \(SABCD\). Найдите сечение пирамиды плоскостью \(\alpha\), проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\).
Решение
1) Обозначим середину ребра \(SA\) за \(M\). Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\). Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\).
Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\). Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\).
Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\), она должна содержать некоторую прямую, параллельную \(BD\). Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\). Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel
BD\) (\(K\in SB, P\in SD\)). Тогда, соединив точки \(C, P, M, K\), получим сечение пирамиды плоскостью \(\alpha\).
2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\). Таким образом мы полностью определим построенное сечение.
Заметим, что так как \(KP\parallel BD\), то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\). Но \(SB=SD\), значит и \(SK=SP\). Таким образом, можно найти только \(SP:PD\).
Рассмотрим \(\triangle ASC\). \circ\), то \(\triangle
ABD=\triangle CBD\), следовательно, \(AD=CD\), следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\).
Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\); наклонная \(BK\perp AC\), значит и проекция \(HK\perp AC\). Но мы уже определили, что \(DK\perp AC\). Таким образом, точка \(H\) лежит на отрезке \(DK\).
Соединив точки \(A\) и \(H\), получим отрезок \(AN\), по которому плоскость \(\alpha\) пересекается с гранью \(DAC\). Тогда \(\triangle
ABN\) – искомое сечение пирамиды плоскостью \(\alpha\).
2) Определим точное положение точки \(N\) на ребре \(DC\).
Обозначим \(AB=CB=DB=x\). Тогда \(BK\), как медиана, опущенная из вершины прямого угла в \(\triangle ABC\), равна \(\frac12 AC\), следовательно, \(BK=\frac12 \cdot \sqrt2 x\).
Рассмотрим \(\triangle BKD\). Найдем отношение \(DH:HK\).
Заметим, что т.к. \(BH\perp (DAC)\), то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\).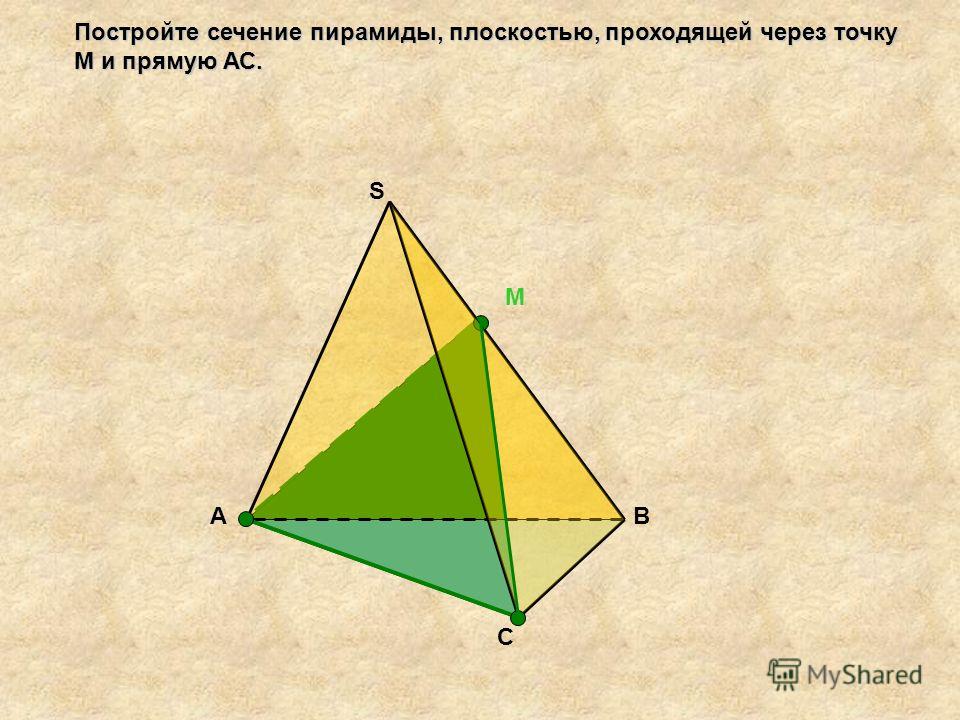 Тогда \(\triangle DBH\sim \triangle DBK\), следовательно
Тогда \(\triangle DBH\sim \triangle DBK\), следовательно
\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x
\Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]
Рассмотрим теперь \(\triangle ADC\). Медианы треугольника точной пересечения делятся в отношении \(2:1\), считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\).
Сечение пирамиды плоскостью — Энциклопедия по машиностроению XXL
СЕЧЕНИЕ ПИРАМИДЫ ПЛОСКОСТЬЮ [c.98]
На рис. 100, а показана линия (1-2-3) сечения пирамиды плоскостью Р(Рг) -1- П2, которая строится по точкам Ь — 22 — З2 пересечения фронтальных проекций рёбер с проекцией секущей плоскости. [c.92]
Рис. 1.3.1. Пример на двойное проецирование двух точек А и В Рис. 1.3.2. Сечение пирамиды плоскостью, заданной точками А, В, С Рис. 1.3.3. Сечение композиции из двух элементов плоскостью, заданной тремя точками А, В, С 1.3.3. Сечение композиции из двух элементов плоскостью, заданной тремя точками А, В, С
|
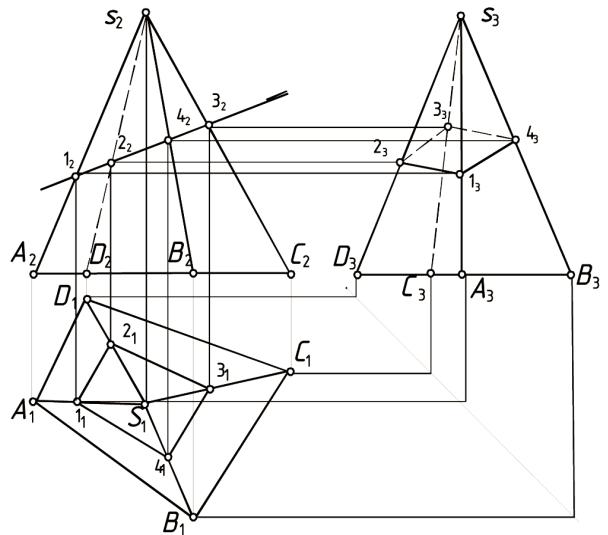
Пример 1.3.2. Изображение произвольной пирамиды полное. Основание и любая боковая грань могут быть выбраны за основные плоскости, тогда все остальные грани будут определенными элементами первого порядка, так как они заданы двумя элементами нулевого порядка. Значит, на пирамиде определены все инциденции. Построим сечение пирамиды плоскостью, заданной тремя точками А, В, С (рис. 1.3.2). Решение осуществляется способом построения горизонтальных следов прямых, лежащих в сечении.
[c.34]
Пример 1.3.3. На рис. 1.3.3. приведено условие позиционной задачи композиционного типа. Дана фигура, составленная из двух прямоугольных параллелепипедов. Обе исходные фигуры составляют полное изображение. Проверим, будет ли полной композиция из этих фигур. Тем же способом, что и в предыдущем примере, попытаемся построить сечение пирамиды плоскостью, заданной тремя точками А, В, С. Разрешимость задачи может свидетельствовать о полноте изображения. Для этого определим следы каждой грани заданной формы с плоскостью AB . Как видим, решение такой задачи оказывается достаточно простым.
[c.34]
Разрешимость задачи может свидетельствовать о полноте изображения. Для этого определим следы каждой грани заданной формы с плоскостью AB . Как видим, решение такой задачи оказывается достаточно простым.
[c.34]
Для нанесения на развертку точек О, Е м Р, соответствующих вершинам О, Е и Е сечения пирамиды плоскостью 2, нужно предварительно определить их натуральные расстояния от вершины 5, для чего следует перенести точки О, Е я Е на соответствующие натуральные величины боковых ребер. [c.202]
Построение натуральной величины сечения пирамиды плоскостью. [c.78]
Как строят сечение пирамиды плоскостью, проходящей через ее вершину [c.86]
На рис.111, (Я показана линия (1 — 2 — 3) сечения пирамиды плоскостью (3(Р2) -L П2, которая строится по точкам Ь — 22 — Зо пересечения фронтальных [c.121]
Пересечение следа с основанием определяет фигуру (4] — 5] — Vi) сечения пирамиды плоскостью 3 и точки N] N2, М] -> Мт пересечения прямой / с пирамидой. [c.122]
[c.122]
В качестве вспомогательных выбирают плоскости, пересекающие поверхности по прямым линиям или окружностям, и по возможности применяют проецирующие плоскости. Например, для определения точек пересечения (АВ) с поверхностью пирамиды на рис. 148 использована фронтально-проецирующая плоскость Р. Построив горизонтальную проекцию 1-2-3 фигуры сечения пирамиды плоскостью Р, находим горизонтальные проекции тип точек пересечения прямой с поверхностью пирамиды, а по ним — фронтальные т и п. [c.146]
Сечение пирамиды плоскостью. Если секущая плоскость параллельна основанию пирамиды (рис. 249), то в сечении получается многоугольник, подобный основанию. В остальных случаях форма фигуры сечения зависит от положения секущей плоскости относительно граней пирамиды. [c.139]
Строят сечение пирамиды плоскостью Р. Оно представляет собой треугольник, подобный треугольнику основания пирамиды. [c.106]
Строят сечение пирамиды плоскостью Р. Горизонтальная проекция его представляет собой треугольник, подобный треугольнику основания пирамиды.
[c.125]
Горизонтальная проекция его представляет собой треугольник, подобный треугольнику основания пирамиды.
[c.125]
Сечение пирамиды плоскостью, параллельной основанию, есть многоугольник, подобный основанию пирамиды, и [c.115]
Сечение пирамиды плоскостью [c.151]
Секущая плоскость 9 пересекает стороны основания АВ и АС в точках L я М, а боковое ребро в точке К- Таким образом, сечение пирамиды плоскостью [c.235]
Построить сечение пирамиды плоскостью, проходящей через вершину (рис. 261) и [c.243]
Построить сечение пирамиды плоскостью, проходящей через точку А, перпендикулярно тому ребру пирамиды, на котором задана точка А (рис. 259 [9—16]). [c.244]
Построить сечение пирамиды плоскостью (рис. 288 [3, 4]) 1) DEF, 2) A F, 3) EFG, [c.244]
На НИС.102, а показано построение на пирамиде ОК1 линии сечения АВС плоскостью Р(ОЕР) способом рёбер. [c.94]
[c.94]
Пример 1.3.5. Определить сечение пирамиды вертикаль- ной плоскостью а. [c.39]
Построение аксонометрической проекции сечения пирамиды проще всего проделать с помощью следа (линии пересечения) данной плоскости на плоскости основания пирамиды (в данном случае на координатной плоскости хОу). Этот след определен точками 1 и 2. Тогда при помощи точки 3 лег- [c.233]
При пересечении призмы или пирамиды плоскостью в сечении получается плоская фигура, ограниченная линиями пересечения секущей плоскости с гранями призмы или пирамиды. [c.77]
На рисунке 12.51 показаны два чертежа одного предмета— треугольной пирамиды с призматическим отверстием. Изображения на рисунке 12.51, а — только виды. Изображения на рисунке 12.51, б — главный вид, часть вида сверху и часть горизонтального разреза А—А, профильный разрез. Чертеж на рисунке 12.51, б значительно более нагляден, информативен, чем чертеж на рисунке 12.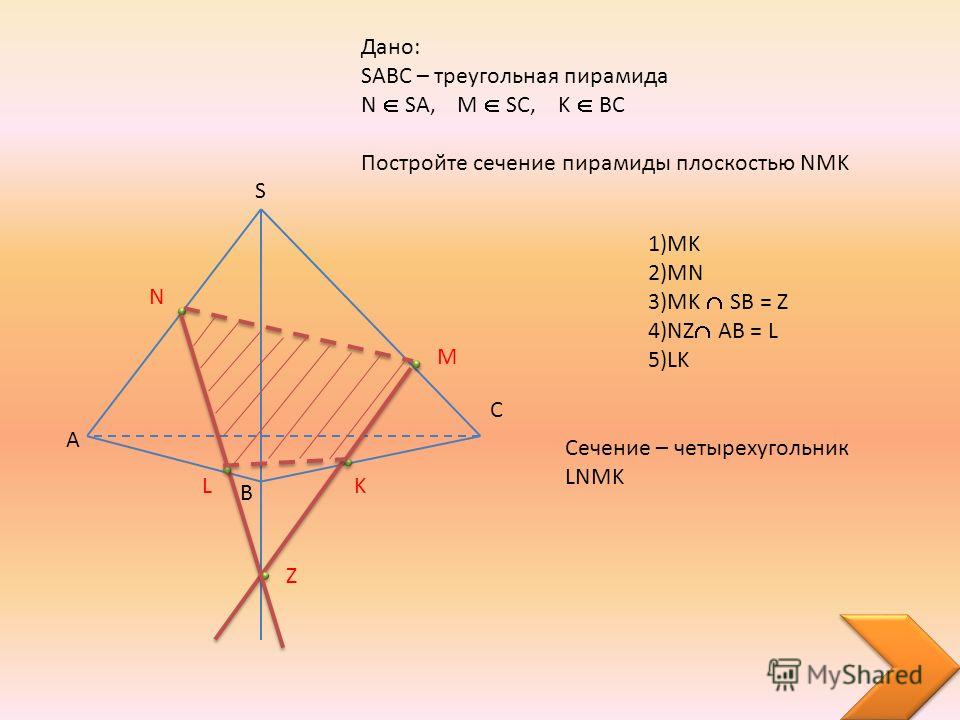 51, а. Для более четкого представления условностей разрезов рассмотрим построение проекций некоторых точек. Пусть задана проекция п. Точка N находится на сечении пирамиды секущей горизонтальной плоскостью разреза А—А. Ее фронтальную проекцию я строим в проекционной связи на фронтальной проекции — фронтальном следе секущей плоскости разреза А—А. По положению проекции I видно, насколько ниже секущей плоскости разреза А—А расположена точка I боковой грани призматического отверстия.
[c.181]
51, а. Для более четкого представления условностей разрезов рассмотрим построение проекций некоторых точек. Пусть задана проекция п. Точка N находится на сечении пирамиды секущей горизонтальной плоскостью разреза А—А. Ее фронтальную проекцию я строим в проекционной связи на фронтальной проекции — фронтальном следе секущей плоскости разреза А—А. По положению проекции I видно, насколько ниже секущей плоскости разреза А—А расположена точка I боковой грани призматического отверстия.
[c.181]
Построить проекции сечения треугольной пирамиды плоскостью, [c.279]
Рассматривая конус, как предел вписанной в него пирамиды с той же вершиной, убеждаемся, что центр тяжести конуса лежит на отрезке, соединяющем вершину конуса с центром тяжести основания, на расстоянии трех четвертей длины этого отрезка от вершины. Можно также сказать, что центр тяжести конуса совпадает с центром тяжести сечения конуса плоскостью, параллельной основанию и проведенной на расстоянии одной четверти высоты конуса от основания.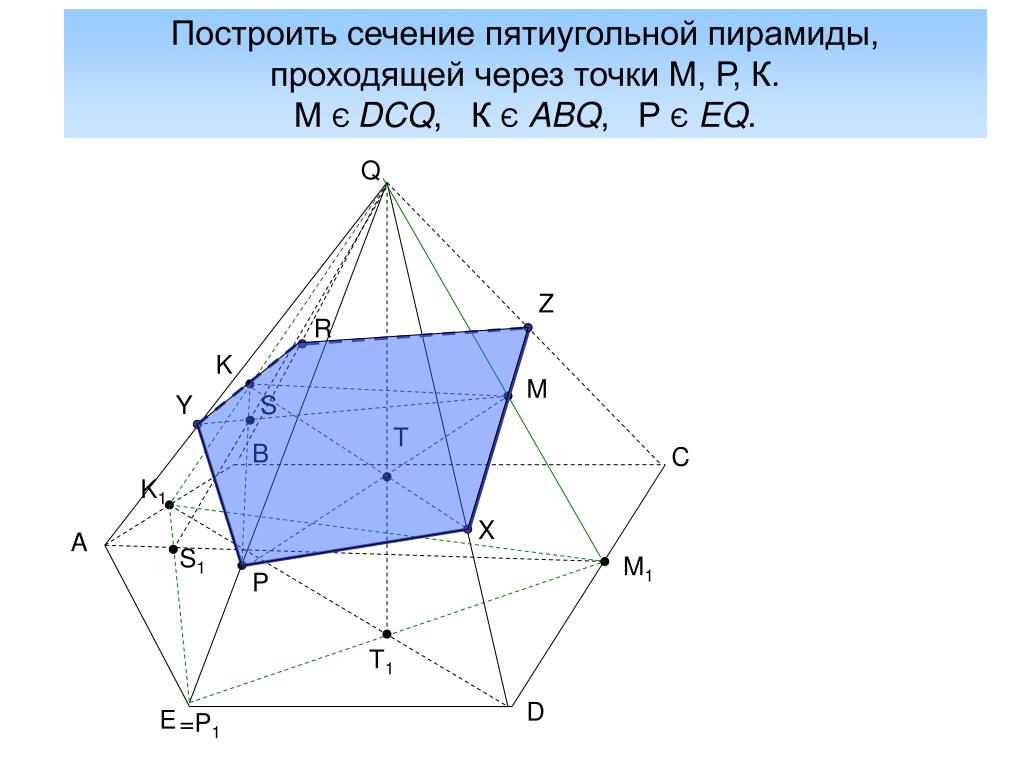 [c.278]
[c.278]
Построения фигуры сечения пирамиды и конуса в принципе аналогичны. В этом случае на плоских основаниях пирамиды и конуса наносят изображения сечений, выполненные на горизонтальной плоскости проекций, в качестве вторичных проекций. [c.326]
Грани призмы являются плоскостями уровня. Поэтому построение линии пересечения поверхностей многогранников выполним способом граней. Сначала строим сечение пирамиды плоскостью Г верхней грани призмы. Из полученного треугольного сечения выделяем ломаную 1234, раеполо-женную в пределах верхней грани призмы. Затем строим треу10льное [c.117]
Возьмем прямую (V — 1 ) и найдем её пересечение 2(2г -> 21) с плоскостью основания (СКВ). Построим также З2 = /2 П (02К2Ь2) -> З1 и след (2 — З1). Пересечение следа с основанием определяет фигуру (41-5) — У]) сечения пирамиды плоскостью Р и точки N1 -> N2, М) М2 пересечения прямой / с пирамидой. [c.93]
ООП Построить горизонтальную проек-Оии цию сечения пирамиды плоскостью ос. Построить полную развертку поверхности верхней части пирамиды (черт. 348).
[c.96]
Построить полную развертку поверхности верхней части пирамиды (черт. 348).
[c.96]
Определим координаты центра тяжести пирамиды. Для этого рассмотрим 1лементарный объем, полученный сечением пирамиды плоскостями, параллельными плоскости xSy, на расстояниях г и z- -dz от вершины. Имеем [c.123]
Фронтальная проекция KyLyMv сечения пирамиды — также отрезок прямой, так как использована фронтально-проецирующая плоскость сечения.
[c.96]Сечение пирамиды или призмы (черт. Ill) может быть построено и с помощью теоремы Дезарга ( 2), если предварительно определена точка пересечения одного из ребер с заданной плоскостью 0L, например точка 1=ЗАг а и прямая т = аГ р (Р — плоскость основания многогранника). В перспективно-коллинеарном соответствии двух плоскостей а и линия т их пересечения является осью коллинеации, а вершина S пирамиды — центром.
[c.51]
АГ П помощью косоугольного проеци-1 рования определить вид (треугольник или четырехугольник) сечения пирамиды VAB плоскостью а KLM) (черт. 156).
[c.44]
156).
[c.44]
Пример I. Построить проекции сечения пирамиды SAB DE фронтально проецирующей плоскостью S (рис. в0). [c.62]
Пример 4. Построить проекции и натуральный вид сечения пирамиды 5ЛВС плоскостью 0 М, N, Р) общего положения (рис. 98). [c.97]
Пусть требуется построить сечение пирамиды SAB DE фронталь-но проецирующей плоскостью Й(Й2) (рис. 49). [c.41]
Рассмотрим пример построения сечения пирамиды SAB DE плоскостью общего положения Г(т 11 п), заданной двумя параллельными прямыми т, п (рис. 50). Анализ расположения ребер и граней данного многогранника относительно плоскостей проекций показывает, что ребро SE — горизонтально проецирующая прямая, грани AB DE, ABS — фронтально проецирующие плоскости, грани DSE — [c.42]
Пирамида с вырезом. Как пример построения сечений несколькими плоскостями рассмотрим (рис. 6.10) построение пирамиды с вырезом, который образован тремя плоскостями — горизонтальной 7 (С ), фронтально-проецирующей R R )vi профильной Q (QJ. Горизонтальная плоскость Т (Г ,) пересекает боковую поверхность пирамиды по пятиугольнику с горизонтальной проегшией к—l—g—f—4—k, стороны которого параллельны проекциям сторон основания пирамиды. Фронтально-проецирующая гьдоскость R (R ) в пределах выреза пересекает боковую поверхность пирамиды по ломаной линии с горизонтальной проекцией 3—8—9 —10—2vi с профильной проекцией 3″8″9″10″2″. Профильная плоскость Q (Q ) пересекает в пределах выреза боковую поверхность пирамиды по ломаной с го-
[c.78]
Горизонтальная плоскость Т (Г ,) пересекает боковую поверхность пирамиды по пятиугольнику с горизонтальной проегшией к—l—g—f—4—k, стороны которого параллельны проекциям сторон основания пирамиды. Фронтально-проецирующая гьдоскость R (R ) в пределах выреза пересекает боковую поверхность пирамиды по ломаной линии с горизонтальной проекцией 3—8—9 —10—2vi с профильной проекцией 3″8″9″10″2″. Профильная плоскость Q (Q ) пересекает в пределах выреза боковую поверхность пирамиды по ломаной с го-
[c.78]
На рис. 113, а показано построение на пирамиде VGKL линии сечения AB плоскостью P(DEF) способом рёбер. [c.122]
Предположим, что сечение построено. Если принять плоскость 0 основания пирамиды за плоскость проекций, а ее вершину S за центр проектирования, то шестиугольйик АВС. .. можно рассматривать как центральную проекцию сечения I II III… Наоборот, приняв плоскость сечения за плоскость проекций и сохранив центр проектирования в той же точке S, можно шестиугольник I II III. .. рассматривать как центральную проекцию основания ЛВС. .. Следовательно, основание пирамиды и любое ее плоское сечение гомологичны. Гомологичными будут и их горизонтальные проекции — шести-
[c.91]
.. рассматривать как центральную проекцию основания ЛВС. .. Следовательно, основание пирамиды и любое ее плоское сечение гомологичны. Гомологичными будут и их горизонтальные проекции — шести-
[c.91]
Урок 18. сечения многогранников — Геометрия — 11 класс
Геометрия, 11 класс
Урок №18. Сечения многогранников
Перечень вопросов, рассматриваемых в теме:
Решение задач, сводящихся к доказательству, связанному с построением сечения многогранника
Построение сечения многогранников
Решение задач на нахождение площадей сечений многогранников
Площадь
треугольника S=½hа
трапеции S=½h(а+b)
параллелограмма S=hа
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.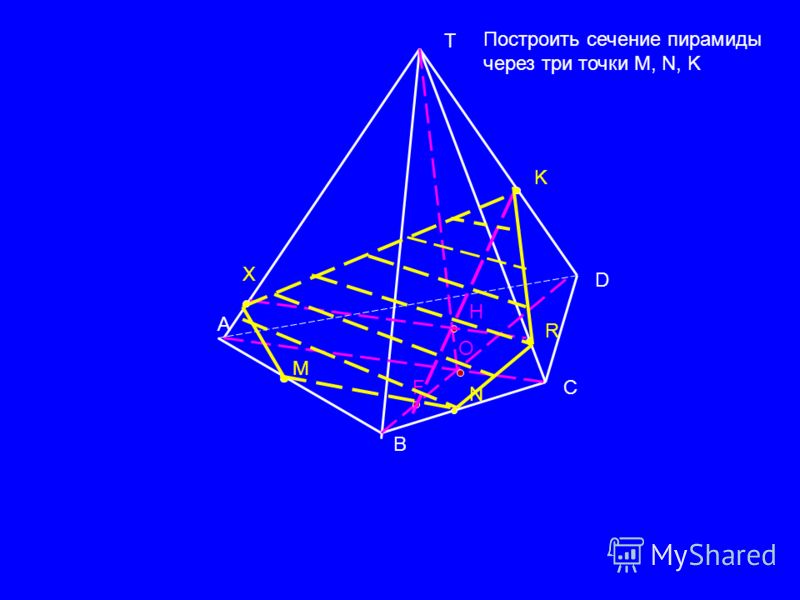 Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурс:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек.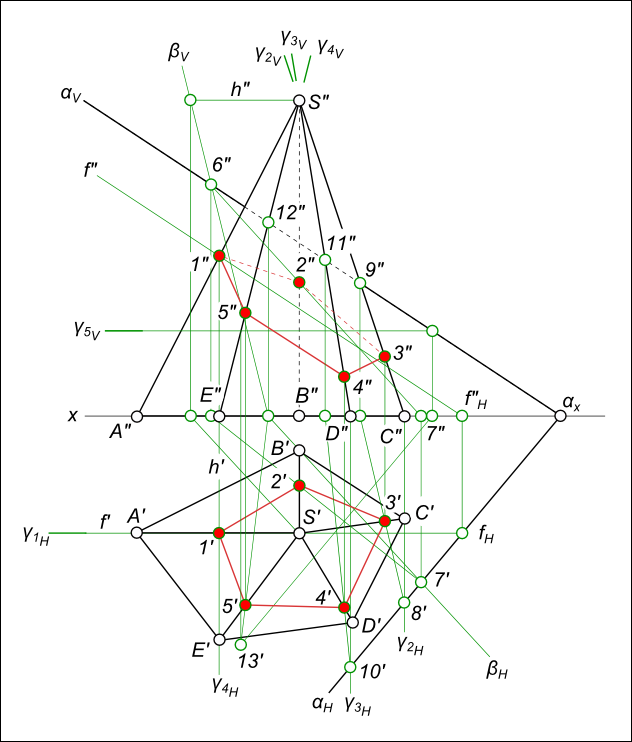 Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
Примеры и разбор решения заданий тренировочного модуля
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Решение:
сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN.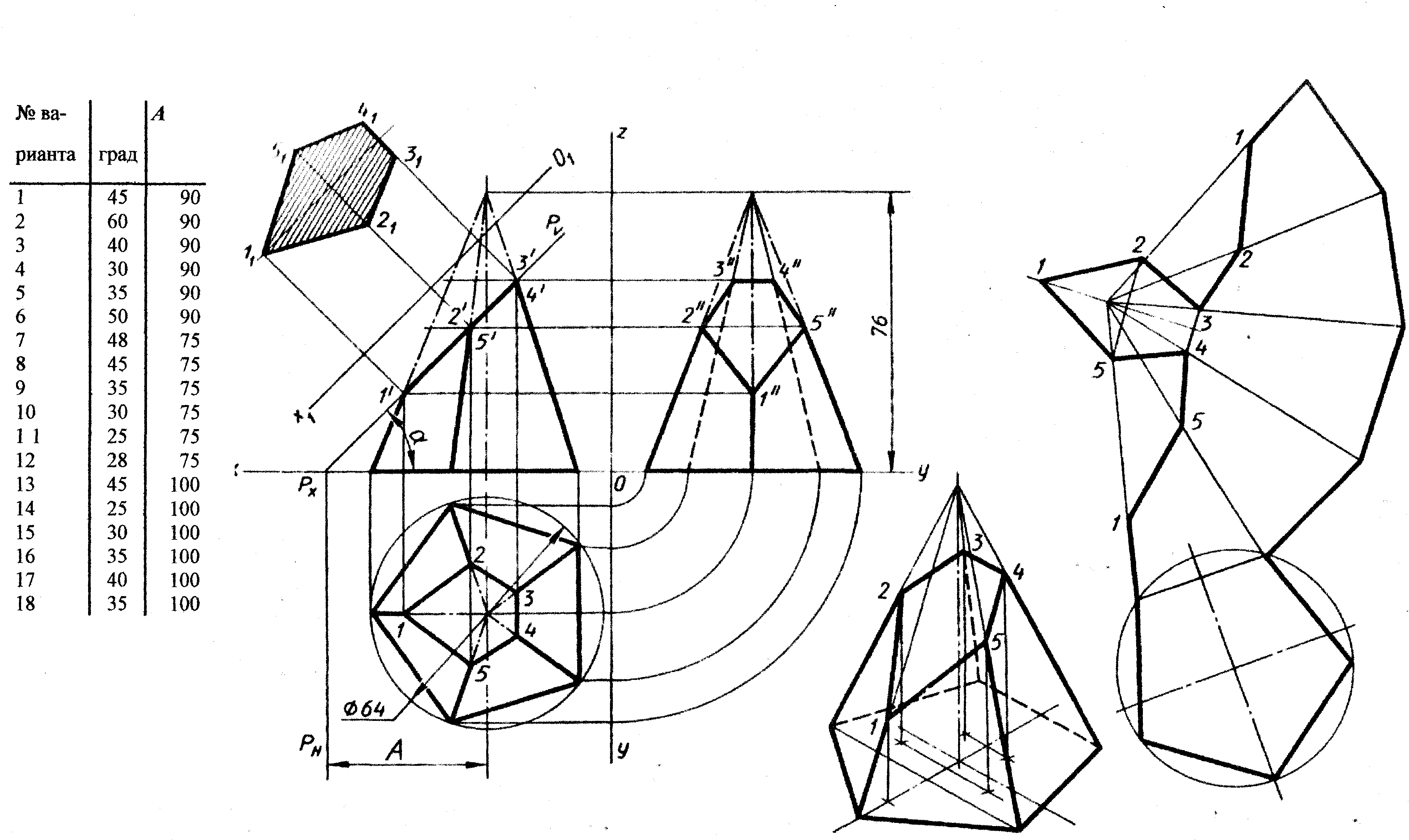 Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a2/8
Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a2/8
Ответ:3 a2/8
№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .
Решение:
боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.
То есть большая боковая грань содержит большую сторону основания.
По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна .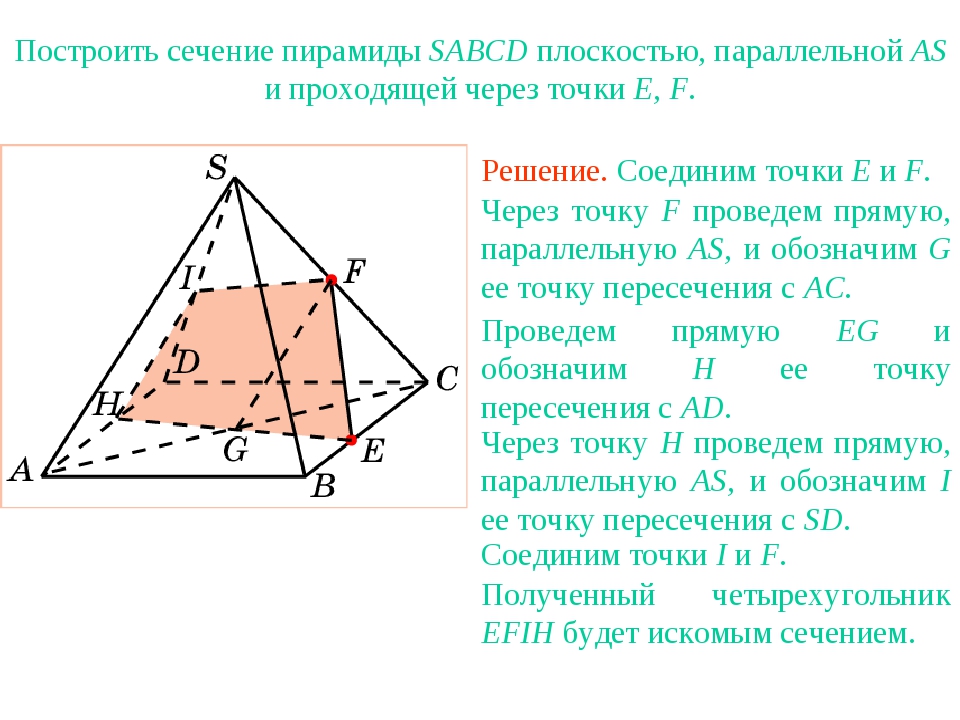
Найдем площадь основания, а оно равно площади сечения, по формуле .
Мы воспользуемся второй формулой. Получим, что площадь основания равна .
Ответ: 15 /4 см2
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Решение:
пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна
S=BD*SO/2= 3 =6
откуда ah=2 .
Площадь сечения DPQ равна
Ответ:
№4
Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .
Решение:
пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция). Следовательно, и LK⊥AC.
Следовательно, и LK⊥AC.
Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .
Тогда по теореме косинусов для △KLB: KL2=729/4⇒KL=27/2
Значит, SALC=567/4=141,75
Ответ : 141,75
№5
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.
Решение:
По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы, тогда
по теореме Пифагора.
Тогда
Ответ: 8
Сечение пирамиды плоскостью
ИНЖЕНЕРНАЯ ГРАФИКА
Методические рекомендации и контрольные задания
для студентов инженерно-технологического факультета
заочной формы обучения
Составила: Тарасенко В.С.
Рассмотрено и утверждено
на заседании кафедры
«___ »___________2012 г.
Протокол №___
Гродно, 2012
Форматы чертежей и оформление чертежных листов
Размеры чертежных листов выбирают в зависимости от габаритных размеров чертежа, но не произвольно. Форматы листов определяются размерами внешней рамки чертежа, выполненной тонкой линией.
Рисунок 1.
ГОСТ 2.301-68 устанавливает 5 основных листов чертежей и других конструкторских документов: А0, А1, А2, А3, А4. Размеры сторон основных форматов приведены в таблице:
| Обозначение формата | Размеры сторон формата, мм |
| АО | 841×1189 |
| А1 | 594×841 |
| А2 | 420×594 |
| A3 | 297×420 |
| А4 | 210×297 |
Формат А4 располагают только вертикально (основная надпись внизу листа).
Основную надпись помещают в правом нижнем углу чертежа. Форма, размеры и содержание граф основной надписи установлены ГОСТ 2.104–68. Основная надпись на чертежах и схемах должна соответствовать рисунку:
Рисунок 2.
Шрифты чертежные
Чертежи, схемы и другие конструкторские документы содержат необходимые надписи: названия изделий, размеры, данные о материале, обработке поверхностей детали, технические требования, характеристики и другие надписи. Типы и размеры шрифта установлены ГОСТ 2.304-81.
Размер шрифта h определяется высотой прописных (заглавных) букв в миллиметрах, измеряемой перпендикулярно к основанию строки. Установлены следующие размеры шрифта: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Шрифты могут быть выполнены без наклона или с наклоном около 75˚ к основанию строки. Ширина g буквы определяется по отношению к размеру шрифта h, например
Студентам необходимо выполнить шрифты на вспомогательной сетке, образованной вспомогательными линиями, в которую вписываются буквы. Построение шрифта на вспомогательной сетке показано на рисунке:
Построение шрифта на вспомогательной сетке показано на рисунке:
Рисунок 3.
Линии чертежа
Согласно ГОСТ 2.303-68 на чертежах применяются следующие типы линий:
Рисунок 4.
Выбранные толщины линий должны быть одинаковыми для всех изображений на данном чертеже, выполненных в одном и том же масштабе.
Образец выполнения задания «Линии чертежа. Шрифты» приведен на рисунке
Перед решением задания № 2 самостоятельно проработать темы: Проектирование точки. Точка в системе двух плоскостей проекций. Проекция отрезка прямой линии. Проекции точки и прямой, расположенных на плоскости.
Проекции пирамид и призм
Построение проекции правильной четырехугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой четырехугольник без искажения. Фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки S’ (вершины, пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию S» вершины.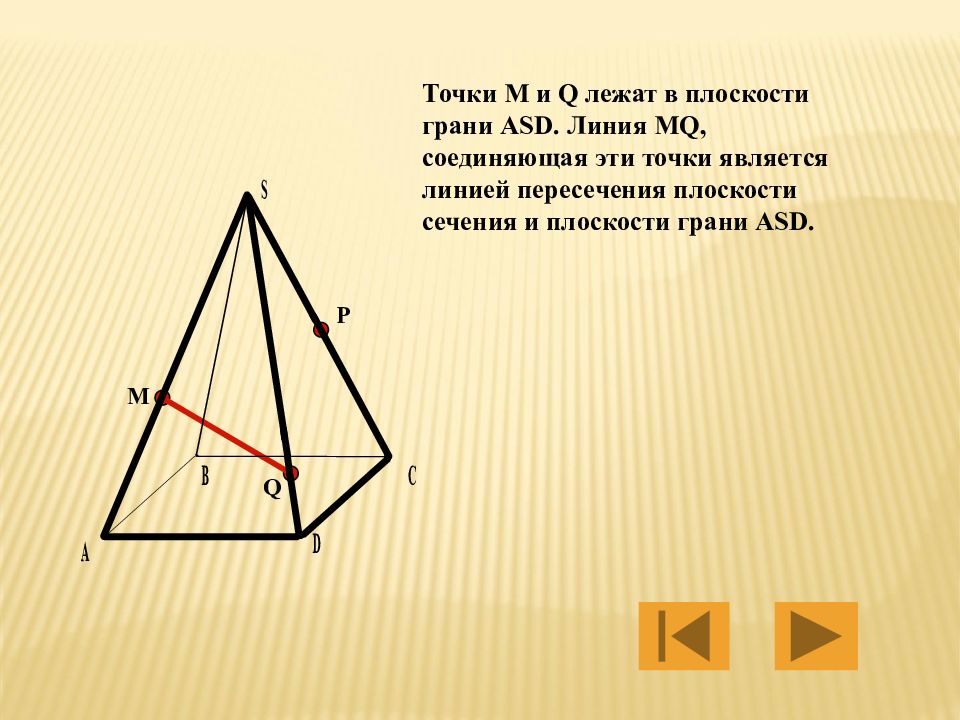 Соединяя точку S» с точками 1″, 2″, 3″ и 4″, получают фронтальные проекции ребер пирамиды.
Соединяя точку S» с точками 1″, 2″, 3″ и 4″, получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки S’ с горизонтальными проекциями точек 1′, 2′, 3′ и 4′.
Рисунок 5.
Пусть, например, дана фронтальная проекция А» точки А, расположенной на грани пирамиды 1″, S», 2″ и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через А» вспомогательную прямую, проходящую через вершину пирамиды и точку N», расположенную на ее грани. Горизонтальную проекцию N’ S ‘ вспомогательной прямой находят, применяя линию связи, искомая горизонтальная проекция А’ точки А находится на пересечении линии связи, проведенной из точки А» с горизонтальной проекцией N’S’ вспомогательной прямой.
Изометрическая проекция пирамиды выполняется следующим образом.
Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — длину диагонали 24. Из точки О пересечения диагоналей проводят ось z и на ней откладывают высоту пирамиды.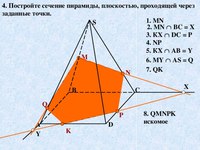 Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Изометрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От начала координат О по оси х откладывают координату хА, из ее конца параллельно оси у — координату уА и из конца этой координаты параллельно оси z — третью координату zA. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х; откладывают координату хВ и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.
Содержание работы. На листе чертежной бумаги формата A3 вычертить три проекции пирамиды и призмы. Построить проекции точек, расположенных на поверхности этих тел. Нанести размеры. Условия работы даны в заданиях.
№ 1 № 2
№ 3 № 4
№ 5 № 6
№ 7 № 8
№ 9 № 10
№ 11 № 12
№ 13 № 14
№ 15 № 16
| Вариант | h | d | a |
3. Перед решением задания №3 самостоятельно проработать темы: сечение тел плоскостями, построение натуральной величины, построение аксонометрических проекций.
Перед решением задания №3 самостоятельно проработать темы: сечение тел плоскостями, построение натуральной величины, построение аксонометрических проекций.
Сечение пирамиды плоскостью.
Правильная шестиугольная пирамида, пересеченная фронтально-проецирующей плоскостью α», показана на рисунке.
Фронтальная проекция сечения совпадает с фронтальным следом f0α»плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости α» с ребрами пирамиды. Действительный вид фигуры сечения в этом примере найдем способом перемен плоскостей проекций.
Развертка боковой поверхности усеченной пирамиды с фигурой сечения и фигурой основания приведена на рисунке.
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку S0 (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки S'»E'» или S'»B'», так как эти ребра параллельны профильной плоскости и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например А0 откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок А’В’). Точки A0-E0 соединяют прямыми с вершиной S0. Затем от вершины S0 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки S'»E'» или S'»B'», так как эти ребра параллельны профильной плоскости и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например А0 откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок А’В’). Точки A0-E0 соединяют прямыми с вершиной S0. Затем от вершины S0 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
Рисунок 6.
На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — S'»5′» и S»2′». Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к горизонтальной плоскости и проходящей через вершину S.
Полученные точки 10, 20, 30 и т.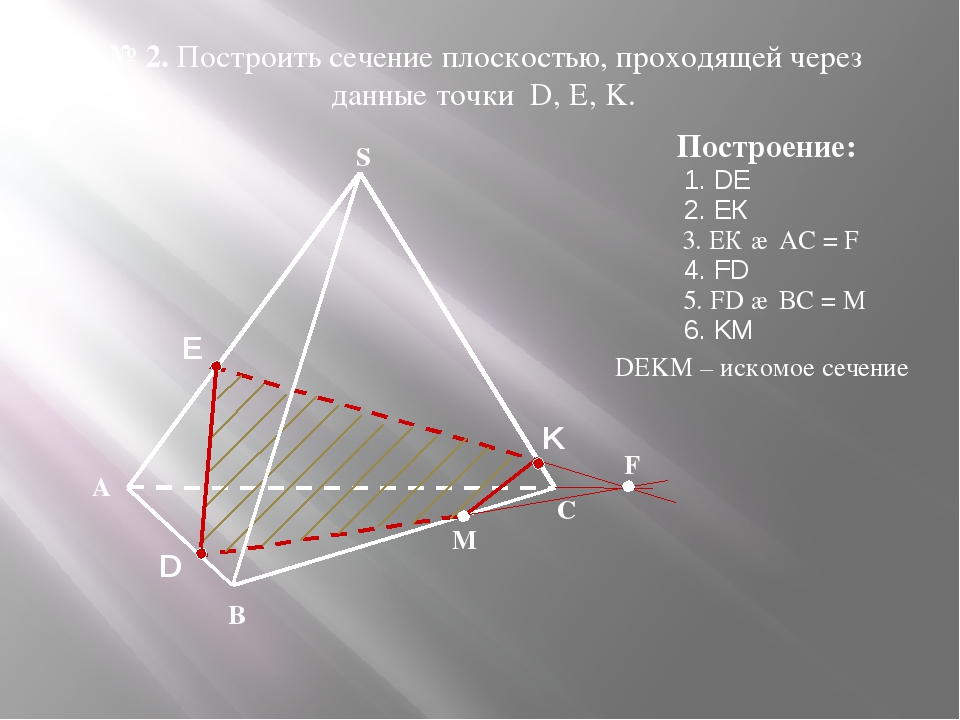 д. соединяют прямыми и пристраивают фигуры основания и сечения. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
д. соединяют прямыми и пристраивают фигуры основания и сечения. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
Построение изометрической проекции усеченной пирамиды начинают с построения изометрической проекции основания пирамиды по размерам, взятым с горизонтальной проекции комплексного чертежа.
Рисунок 7.
Затем на плоскости основания по координатам точек 1′-6′ строят горизонтальную проекцию сечения (тонкие линии на основании пирамиды, рисунок 2).
Рисунок 8.
Из вершины полученного шестиугольника проводят вертикальные прямые, на которых откладывают координаты, взятые фронтальной или профильной проекции призмы, например, отрезки К1, К2, К3 и т. д. Полученные точки 1-6 соединяем, получаем фигу сечения. Соединив точки 1-6 с вершинами шестиугольника, основания пирамиды, получим изометрическую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.
Содержание работы. На листе чертежной бумаги формата A3 вычертить три проекции пирамиды. Провести фронтальный след секущей плоскости. Построить горизонтальную и профильную проекции фигуры сечения. Способом вращения вокруг выбранной оси построить действительный вид фигуры сечения. Построить развертку усеченной пирамиды. Построение изометрии усеченной пирамиды будет проводиться на занятиях совместно с преподавателем.
На листе чертежной бумаги формата A3 вычертить три проекции пирамиды. Провести фронтальный след секущей плоскости. Построить горизонтальную и профильную проекции фигуры сечения. Способом вращения вокруг выбранной оси построить действительный вид фигуры сечения. Построить развертку усеченной пирамиды. Построение изометрии усеченной пирамиды будет проводиться на занятиях совместно с преподавателем.
Условия работы даны в задании.
№1 №2 №3 №4
№5 №6 №7 №8
№ 9 № 10 № 11 № 12
№ 13 № 14 № 15 № 16
4. Перед решением задания №4 самостоятельно проработать темы: взаимное пересечение тел.
Построить сечение пирамиды плоскостью p. Пирамида
Для построения натуральной величины фигуры сечения (рис. 4) применен способ перемены плоскостей проекций. В качестве дополнительной плоскости принята плоскость H
1
, параллельная плоскостиР
и перпендикулярная плоскостиV
. Полученная проекция треугольника1
1
2
1
3
1
является натуральной величиной фигуры сечения.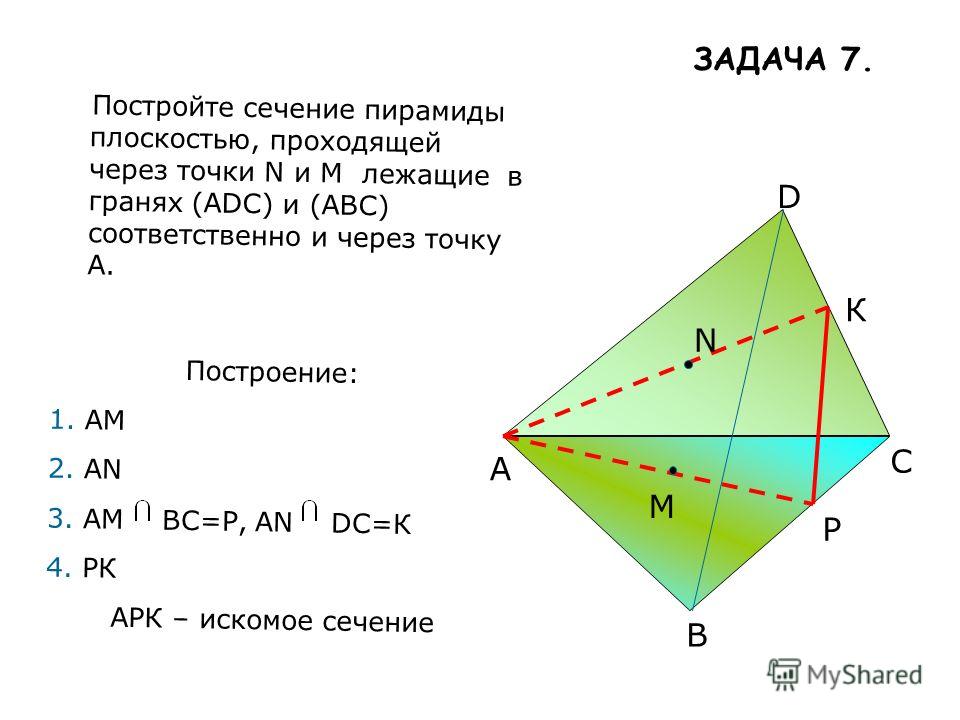
Пирамида с вырезом
В качестве примера построения сечений многогранника несколькими плоскостями рассмотрим построение пирамиды с вырезом, который образован тремя плоскостями −
P
,
R
, иT
(рис. 5).
Плоскость P
, параллельная горизонтальной плоскости проекций, пересекает поверхность пирамиды по пятиугольнику 1-2-3-K-6
.
На горизонтальной плоскости проекций стороны пятиугольника параллельны проекциям сторон основания пирамиды. Построив горизонтальную проекцию пятиугольника, отмечаем точки4
и5
.
Фронтально-проецирующая плоскостьR
пересекает пирамиду по пятиугольнику 1-2-7-8-9
. Чтобы найти горизонтальные проекции точек8
и9
,
проведем через них дополнительные образующиеSM
иSN
.
Вначале на фронтальной проекции−
s
′
m
′
иs
′
n
′,
а затем на горизонтальной−
sm
иsn
.
Фронтально-проецирующая плоскостьΤ
пересекает пирамиду по пяти-
угольнику 5-4-8-9-10
.
Построив горизонтальную проекцию выреза, строим его профильную проекцию.
Построение проекций линии пересечения цилиндра плоскостью
При пересечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих, рис. 6). Если секущая плоскость перпендикулярна к оси вращения, в результате сечения получится окружность (рис. 7). В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс (рис. 8).
6). Если секущая плоскость перпендикулярна к оси вращения, в результате сечения получится окружность (рис. 7). В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс (рис. 8).
Рассмотрим пример | построения проекций линии сечения | цилиндра | ||||
фронтально- | ||||||
проецирующей | ||||||
стью Q | ||||||
ется эллипс (рис. 9). | ||||||
Фронтальная | ||||||
ция линии сечения в этом | ||||||
случае совпадает с фрон- | ||||||
тальным следом плоскости | ||||||
Qv | ||||||
горизонтальной проекцией | ||||||
поверхности | цилиндра | |||||
окружностью. | Профильная | |||||
проекция линии | строится | |||||
по двум имеющимся про- | ||||||
екциям −
горизонтальной и фронтальной.
В общем случае построение линии пересечения поверхности плоскостью сводится к нахождению общих точек, принадлежащих одновременно секущей плоскости и поверхности.
Для нахождения этих точек применяют метод дополнительных секущих плоскостей:
1.
Проводят дополнительную плоскость;
2.
Строят линии пересечения дополнительной плоскости с поверхностью и дополнительной плоскости с заданной плоскостью;
3.
Определяют точки пересечения полученных линий.
Дополнительные плоскости проводят таким образом, чтобы они пересекали поверхность по наиболее простым линиям.
Нахождение точек линии пересечения начинают с определения характерных (опорных) точек. К ним относятся:
1.
Верхние и нижние точки;
2.
Левая и правая точки;
3.
Точки границы видимости;
4.
Точки, характеризующие данную линию пересечения (для эллипса
−
точки большой и малой осей).
Для более точного построения линии пересечения необходимо построить еще и дополнительные (промежуточные) точки.
В рассматриваемом примере точки 1
и8
являются нижней и верхней точками. Для горизонтальной и фронтальной проекций точка1
будет левой точкой, точка8
−
правой. Для профильной проекции точки4
и5
−
точки границы видимости: точки, расположенные ниже точек4
и5
на профильной проекции будут видимыми, все остальные−
нет.
Точки 2, 3
и6, 7
−
дополнительные, которые определяются для большей точности построения. Профильная проекция фигуры сечения – эллипс, у которого малая ось−
отрезок 1-8,
большая−
4-5
.
Построение проекций линий пересечения конуса плоскостью
В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.
Если секущая плоскость проходит через вершину конуса, в его сечении получается пара прямых −
образующих (треугольник) (рис. 10, а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 10, б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 10, в, г, д) в зависимости от величины угла наклона секущей плоскости.
Эллипс получается в том случае, когда угол β
наклона секущей плоскости меньше угла наклонаα
образующих конуса к его основанию(β
Если углы α
иβ
равны,
то есть секущая плоскость параллельна одной из образующих конуса, в сечении получается парабола (рис. 10, г).
Если секущая плоскость направлена под углом, который изменяется в пределах 90° β>α
, то в сечении получается гипербола. В этом случае секу-
щая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная (рис.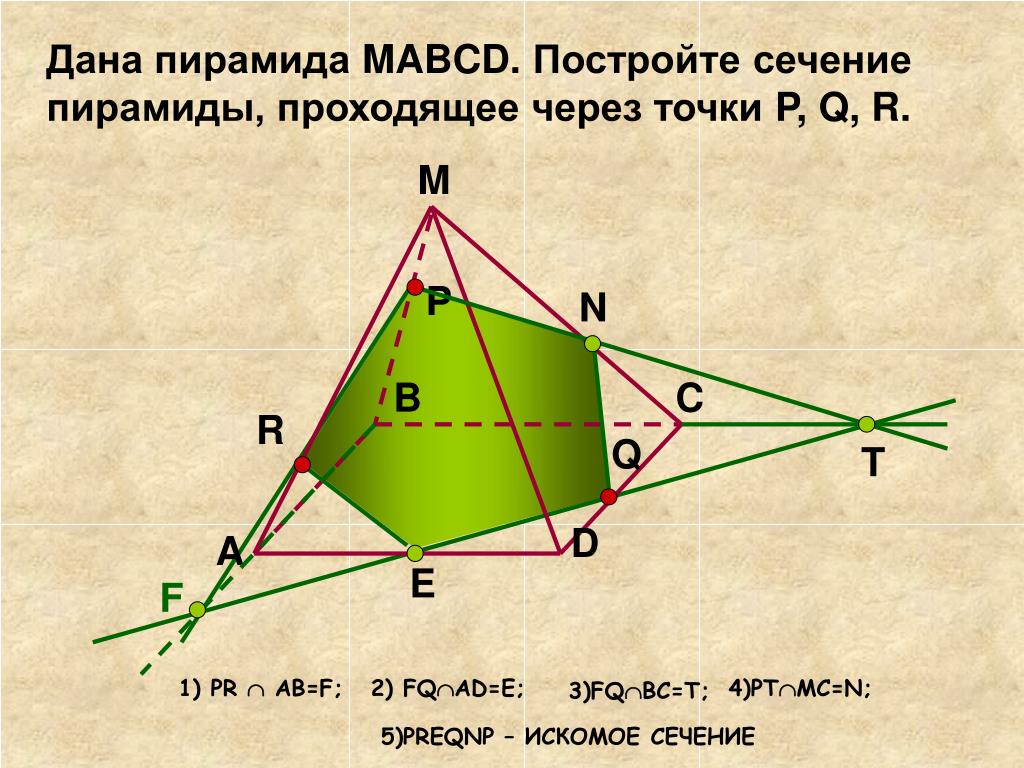 10, д).
10, д).
Известно, что точка принадлежит поверхно- | ||||
сти, если она принадлежит какой-нибудь линии | ||||
поверхности. Для конуса наиболее графически | ||||
простыми линиями являются прямые (образую- | ||||
щие) и окружности. Следовательно, если по усло- | ||||
вию задачи требуется найти горизонтальные про- | ||||
екции точек A | ||||
конуса, то нужно через точки провести одну из | ||||
этих линий. | ||||
Горизонтальную проекцию точки A | ||||
с помощью образующих. Для этого через точку A | ||||
и вершину конуса S | ||||
фронтально-проецирующую плоскостьP(Pv). ки b Рассмотрим пример построения проекций линии пересечения конуса фронтально-проецирующей плоскостьюP(Pv), Фронтальная проекция линии сечения совпадает с фронтальным следом плоскости Pv Для удобства решения задачи обозначим крайние образующие конуса и определим характерные (опорные) точки. Нижняя точка 1 | ||||
Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.
Пример.
Построить сечение плоскостью (MNP)
Треугольник MNP — сечение пирамиды
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.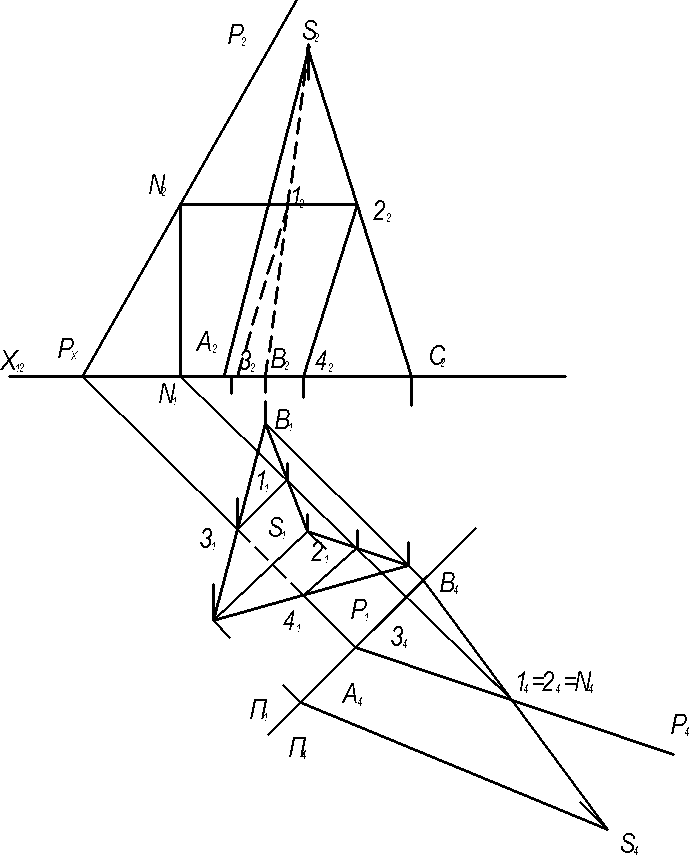
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
Треугольник BKL — искомое сечение.
Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.
Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.
Продолжим прямую NP.
Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P.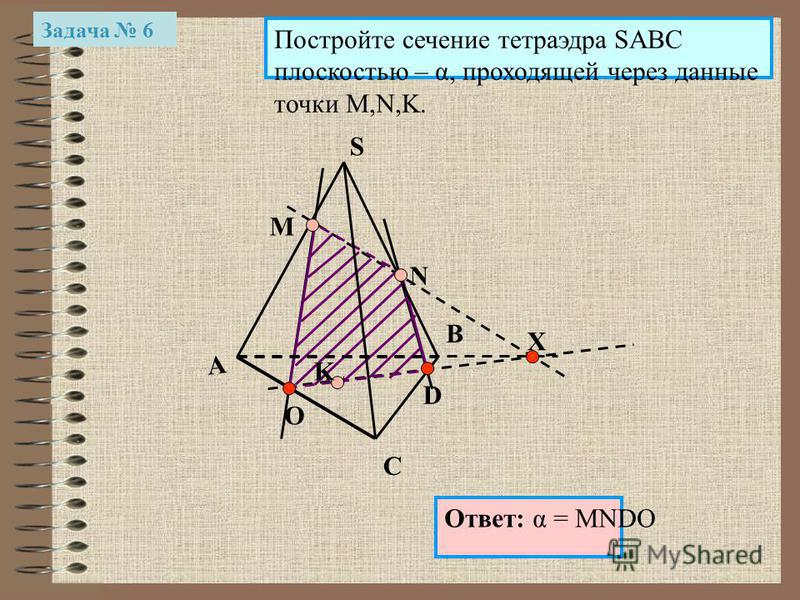 Значит, ищем пересечение NP с прямой BC.
Значит, ищем пересечение NP с прямой BC.
Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.
Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).
Через H и точку M, лежащую в этой же плоскости, можем провести прямую.
Получим след MT.
T — точка пересечения прямых MH и AC.
Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).
4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.
Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.
Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости.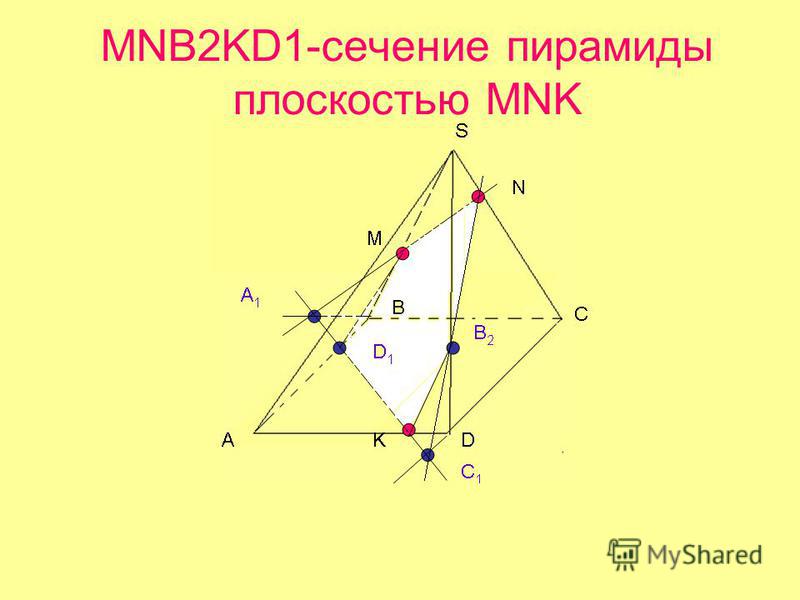 У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.
У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.
Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.
Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.
Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.
Таким образом, получили все то же сечение MNPT.
Рассмотрим еще один пример такого рода.
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).
Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).
Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Правильная шестиугольная пирамида, пересеченная фронтально-проецирующей плоскостью Р,
показана на рис. 180.
Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным сле-
дом P v
плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости Р
с ребрами пирамиды.
Действительный вид фигуры сечения в этом примере определяется способом совмещения.
Развертка боковой поверхности усеченной пирамиды с фигурой сечения и фигурой основания приведена на рис. 180, б.
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку s l
(вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R,
равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s»e»
или s»b»,
так как эти ребра параллельны плоскости W
и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например а 1 , откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника – основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab).
Далее по дуге окружности от любой точки, например а 1 , откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника – основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab).
Точки a
1 …f 1
соединяют прямыми с вершиной s 1 . Затем от вершины a 1
на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
На профильной проекции усеченной пирамиды имеются действительные длины только двух от-
резкое – s»5
и s»2.
Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н
и проходящей через вершину s. Например, повернув отрезок s»6″
около оси до положения, параллельного плоскости W,
получим на этой плоскости его действительную длину. Для этого достаточно через точку 6″
провести горизонтальную прямую до пересечения с действительной длиной ребра SE
или SB.
Отрезок s»6 0 ″
(см. рис. 180).
Полученные точки 1 1 2 1
, 3 1
, и т.д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
Построение изометрической проекции усеченной пирамиды начинают с построения изометрической проекции основания пирамиды по размерам, взятым с горизонтальной проекции комплексного чертежа. Затем на плоскости основания по координатам точек 1…6
строят горизонтальную проекцию сечения (см. тонкие синие линии на рис. 180, а, в).
Из вершин полученного шестиугольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фронтальной или профильной проекций призмы, например, отрезки К { , К 2 , К 3
и т.д. Полученные точки 1…6
соединяем, получаем фигуру сечения. Соединив точки 1…6
с вершинами шестиугольника, основания пирамиды, получим изометрическую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.
Невидимые ребра изображают штриховыми линиями.
Пример сечения треугольной неправильной пирамиды фронтально-проецирующей плоскостью показан на рис. 181.
Все ребра на трех плоскостях проекций изображены с искажением. Горизонтальная проекция
основания представляет собой его действительный вид, так как основание пирамиды расположено на плоскости Н
.
Действительный вид 1
0 , 2 0 , 3
0 фигуры сечения получен способом перемены плоскостей проекций. В данном примере горизонтальная плоскость проекций Н
заменена новой плоскостью, которая параллельна плоскости Р;
новая ось х 1
совмещена со следом Р V
(рис. 181, а).
Развертку поверхности пирамиды строят следующим образом. Способом вращения находят действительную длину ребер пирамиды и их отрезков от основания до секущей плоскости Р.
Например, действительные длины ребра SC
иего отрезка СЗ
равны соответственно длине фронтальной проекции s»c»
ребра и отрезка c 1 ′3 1
после поворота.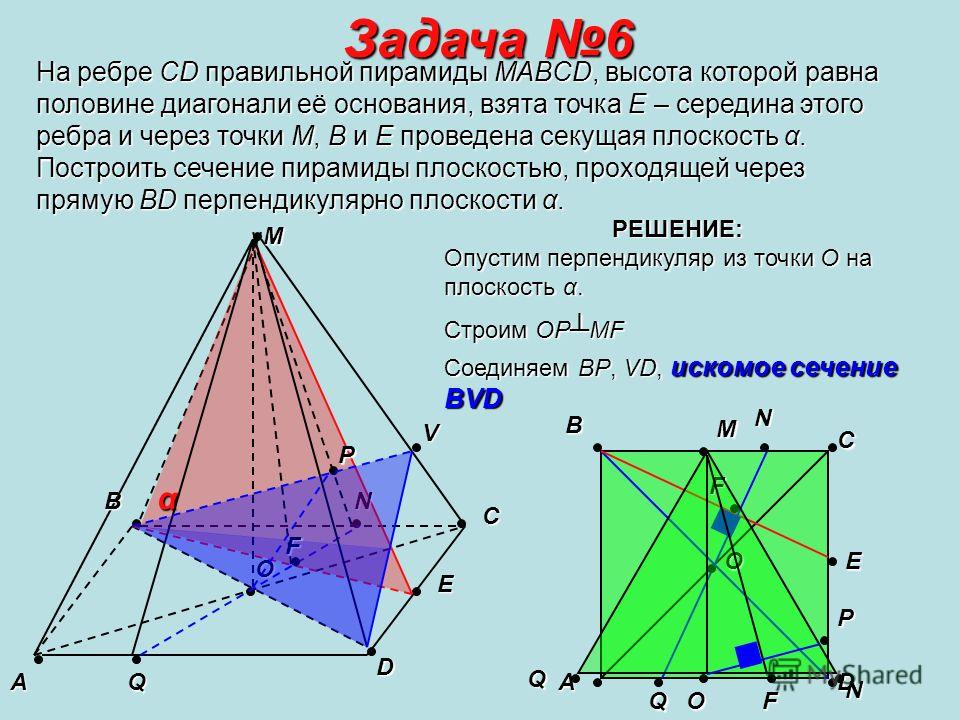
Затем строят развертку треугольной неправильной пирамиды (рис. 181, в). Для этого из произвольной точки S
проводят прямую, на кот, откладывают действительную длину ребра SA.
Из точки s
делают засечку радиусом R 1 ,
равным действительной длине ребра SB,
а из точки засечку радиусом R 2 ,
равным стороне основания пирамиды АВ,
в результате чего получают точку b 1
и грань s 1 b 1 a 1 .
Затем из точек s
и b 1
как из центров, делают засечки радиусами, равными действительной длине ребра SC
и стороне ВС
получают грань s 1 b 1 с 1
пирамиды. Также строится грань s 1 с 1 a 1
.
От точек а 1 b 1
и с 1
откладывают действительные длины отрезков ребер, которые берут на фронтальной проекции (отрезки а 1 ′1 1 ′, b 1 ′2 1 ′,с 1 ′3 1 ′
). Используя метод триангуляции, пристраивают основание и фигуру сечения.
Для построения изометрической проекции усеченной пирамиды (рис. 181, б) проводят изометрическую ось х.
181, б) проводят изометрическую ось х.
По координатам т
и п
строят основание пирамиды ABC.
Сторона основания АС
параллельна оси х
или совпадает с осью х.
Как и в предыдущем примере, строят изометрическую проекцию горизонтальной проекции фигуры сечения 1 2 2 2 3 2
(используя точки I, III и IV). Из этих точек проводят вертикальные прямые, на которых откладывают отрезки, взятые с фронтальной или профильной проекции призмы К 1 , К 2
и К 3 .
Полученные точки 1
, 2, 3
соединяют прямыми между собой и с вершинами основания.
Определение.
Боковая грань
— это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение.
Боковые ребра
— это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение.
Высота пирамиды
— это перпендикуляр, опущенный из вершины на основание пирамиды.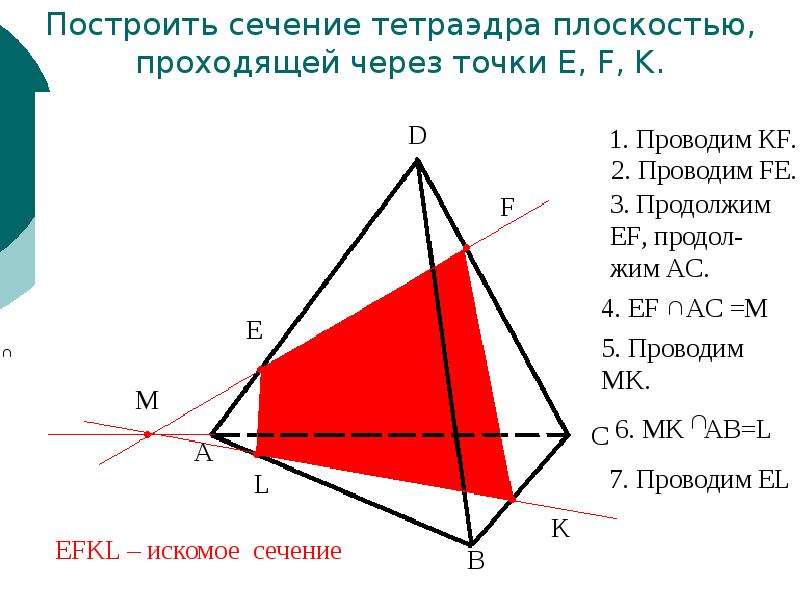
Определение.
Апофема
— это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение.
Диагональное сечение
— это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение.
Правильная пирамида
— это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула.
Объём пирамиды
через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.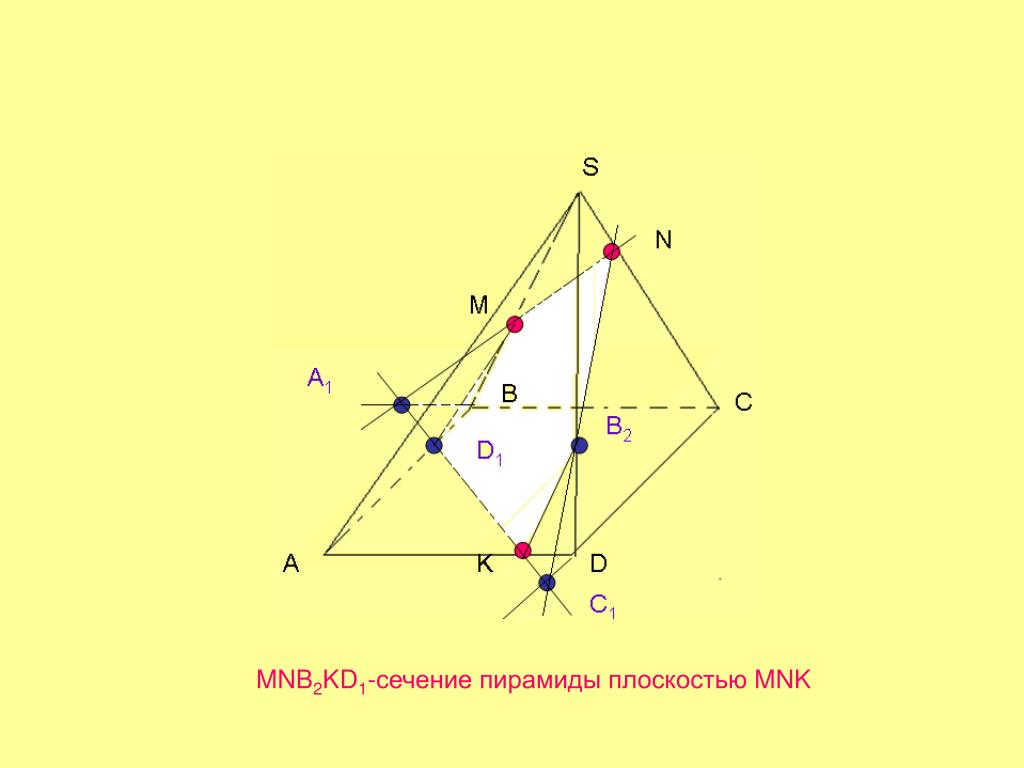
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n
, где n
— это количество углов в основании пирамиды.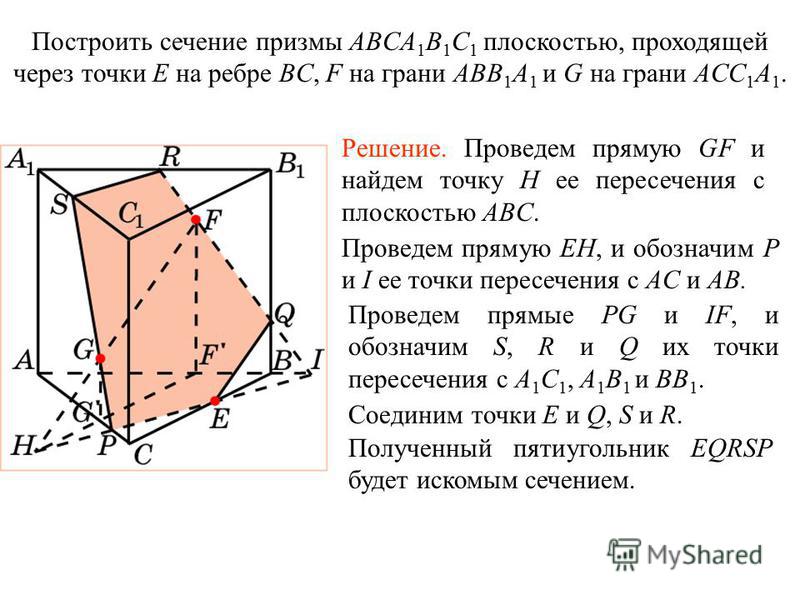
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение.
Усеченная пирамида (пирамидальная призма)
— это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение.
Треугольная пирамида (четырехгранник)
— это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол
.
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника
(GM).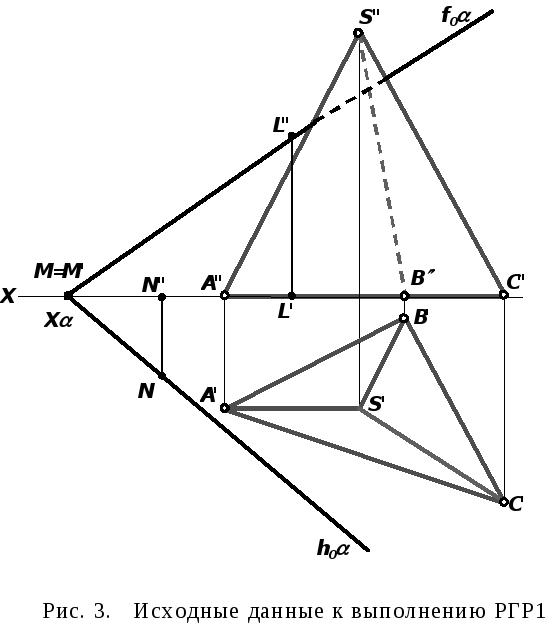
Бимедианой
называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение.
Наклонная пирамида
— это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение.
Прямоугольная пирамида
— это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение.
Остроугольная пирамида
— это пирамида в которой апофема больше половины длины стороны основания.
Определение.
Тупоугольная пирамида
— это пирамида в которой апофема меньше половины длины стороны основания.
Определение.
Правильный тетраэдр
— четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение.
Прямоугольный тетраэдр
называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол
и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение.
Равногранный тетраэдр
называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение.
Ортоцентричный тетраэдр
называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение.
Звездная пирамида
называется многогранник у которого основой является звезда.
Определение.
Бипирамида
— многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.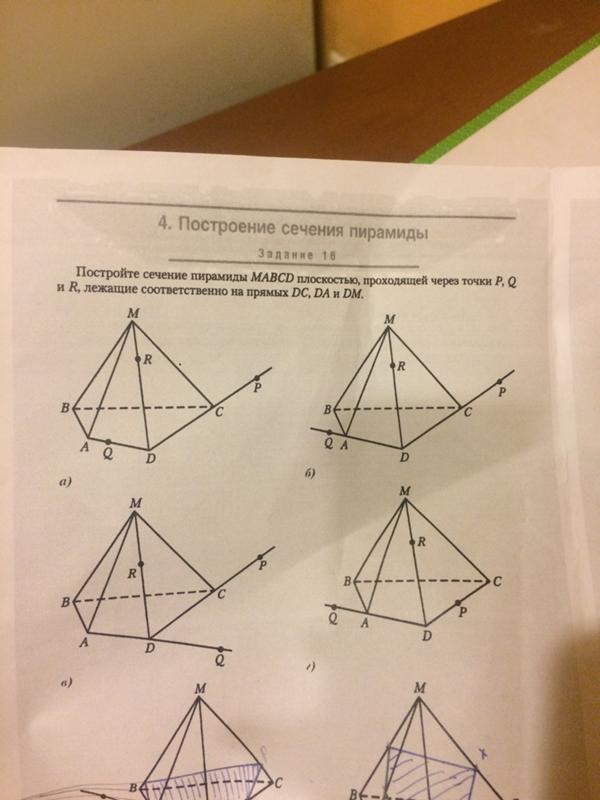
PPT — Постройте сечение пирамиды, плоскостью, проходящей через точку М и прямую АС. PowerPoint Presentation
Постройте сечение пирамиды, плоскостью, проходящей через точку М и прямую АС. S М А В С
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. S Р К А В F С
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. S М N K А В С
D 1)МN (CBD) 2)ABC∩CBD=CB N 3) MN∩CB=Q 4) KQ(АВС) 5) KQ∩AB=L 6) KQ∩AC=R 7) NR (ACD) 8) ML (ABD) 9) NRLM – искомое сечение M Q C B K L R A
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. S N М B C K Z A D L
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. S M N X B C Q P А D K Y
Постройте сечение куба плоскостью МРК.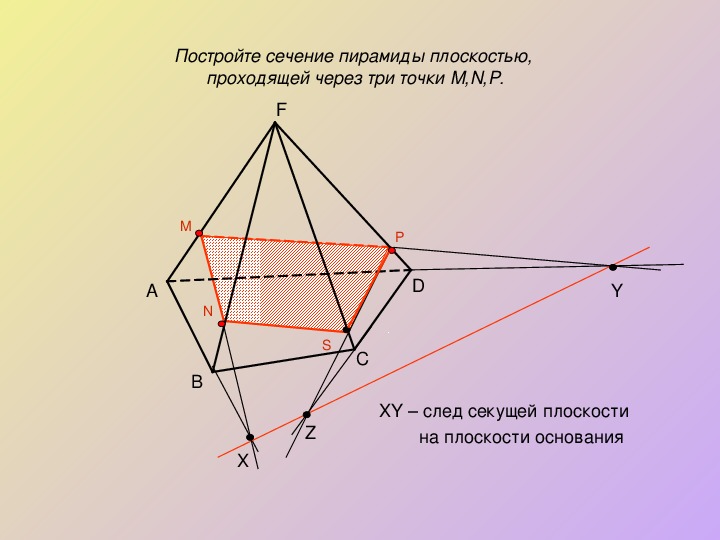 B2 Z B1 C1 L Р A1 D1 D2 К В С М А D
B2 Z B1 C1 L Р A1 D1 D2 К В С М А D
Дан куб ABCDA1B1C1D1.Через точки С, D1и середину ребра АА1 проведена секущая плоскость.Найдите площадь сечения, если ребро куба равно 4. B1 C1 D1 А1 В С D А
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МРК. M K C2 P L N A2
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МB1К. Z S K M L T
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МPК. K E S P M X L
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МPК. Y K R P S M Z H E
Построить сечение куба, плоскостью, проходящей через заданные точки.
Построить сечение куба, плоскостью, проходящей через заданные точки. C1 B1 N A1 D1 K M B C A D
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МPК.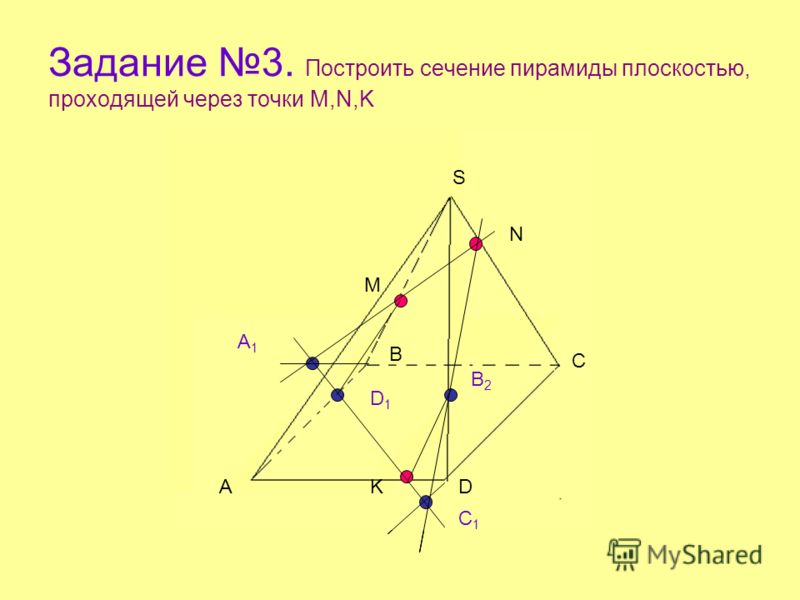 L M L1 Y1 Y P T K E
L M L1 Y1 Y P T K E
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МPК. H M W Y F Q P K L F1
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью МPК. М К Р
B1 C1 A1 D1 B C D A Постройте сечение куба плоскостью А1PС. Р1 Р
B1 C1 A1 D1 B C D A Постройте сечение призмы плоскостью МPК. Р М К
B1 C1 A1 D1 B C D A Постройте сечение призмы плоскостью МPК. Точка Р принадлежит плоскости АА1D1D М К Р
Постройте сечение призмы плоскостью МPК. B1 C1 Р М A1 D1 B C D A К
C1 A1 D1 B C D A Постройте сечение призмы плоскостью МPК. B1 Р М К
№63 -2005 ЕГЭ (сборник задач) : Дан куб .Через точки М, К и середину Е проведена секущая плоскость. ………. (Постройте сечение ) J Z B1 C1 М A1 D1 К P L B C X м1 D A Е Т
(Постройте сечение ) J Z B1 C1 М A1 D1 К P L B C X м1 D A Е Т
Для учителя • С 10 слайда упрощается объяснение, так как подразумевается, что ученики видят плоскость в которой находятся точки. • Для дидактического материала быстро можно распечатать заготовки слайда.
Домашняя работа • на «3» — построить сечение на бумажном носителе без описания; • на «4» — построить сечение с пошаговым описанием построения( см.слайд 4) • на «5» – построить сечение с полным обоснованием (пошаговым описанием построения и ссылками на аксиомы и теоремы).
Вариант 1 Ф.И. ________________ класс______ 1) 2) 3) 4)
Вариант 2 Ф.И._________________ класс_____ 1) 2) 3) 4)
Вариант 1 ответы 1) 2) 3) 4)
Вариант 2 ответы 1) 2) 3) 4)
Зачетная работа( вариант) • В-1 В-2 1.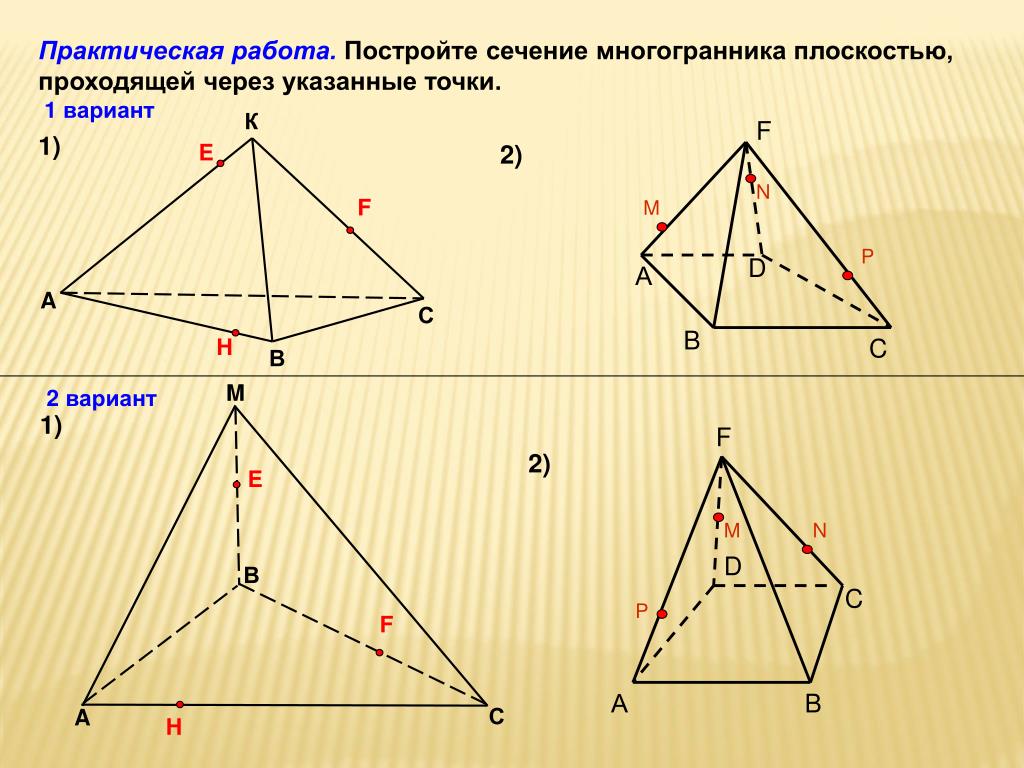 сл.№5 1. сл.№6 2. сл.№ 10 2.сл.№11 3. сл.№16 3. сл.№17 2. Теоретический вопрос.
сл.№5 1. сл.№6 2. сл.№ 10 2.сл.№11 3. сл.№16 3. сл.№17 2. Теоретический вопрос.
Существование плоскости С1. Какова бы ни была плоскость , существуют точки, принадлежащие этой плоскости, и точки , не принадлежащие ей. Т.15.1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. С2.Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Т.15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну. С3.Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Математических изображений | Плоские развертки геометрических тел (5): Пирамида и пирамидальная усеченная форма
Пирамида — это многогранник с многоугольной гранью (известной как основание), а другие грани — это треугольники, встречающиеся в общей точке (вершине пирамиды).
пирамида). Эти грани (боковые грани) представляют собой треугольники.
Частный случай — когда основание вписано в круг. В первой математике мы можем поиграть с пирамидами, в основе которых лежит правильный многоугольник.
Если вершина находится выше центра этого круга, то можно сказать, что пирамида является правой пирамидой.Правильная пирамида — это правая пирамида, основание которой — правильный многоугольник.
Главный интерес этой страницы — увидеть, как пирамиду можно превратить в плоскость.
Плоская развертка или сетка пятиугольной пирамиды:
Другой пример, сетка шестиугольной пирамиды:
Чтобы рассчитать площадь боковой поверхности пирамиды, нам нужна высота наклона. Наклонная высота пирамиды, если расстояние между вершиной и вершиной
центр стороны основания.Это высота боковой грани. Существует связь между наклонной высотой и высотой пирамиды.
(Теорема Пифагора).
Мы собираемся вычислить площадь боковой поверхности пирамиды. Если P — периметр основания, формула для бокового
Площадь поверхности пирамиды (боковые грани — треугольники) аналогична формуле для площади треугольника:
Когда мы изучаем площадь боковой поверхности конуса, формула будет аналогичной (как Кеплера и площадь круга.)
Самая правильная пирамида — тетраэдр — платоновое тело, состоящее из четырех равносторонних треугольников.
Тогда тетраэдр — это частный случай треугольной пирамиды.
А это плоская сетка тетраэдра:
Когда мы разрезаем пирамиду плоскостью, параллельной основанию, мы получаем пирамидальную усеченную пирамиду (или усеченную пирамиду).
Например, это шестиугольная усеченная фигура:
А вот его сетка самолета:
Другой пример:
Как и раньше, для вычисления площади боковой поверхности усеченного конуса нам нужна высота склона:
Если P — периметр нижнего основания, а p — периметр верхнего основания, формула для площади боковой поверхности аналогична формуле для площади
трапеция (боковые грани равны трапеции):
В приведенных выше примерах основания были правильными многоугольниками.Но мы можем рассматривать пирамиды, основания которых не являются правильными многоугольниками. В следующей математике
основания — неправильные многоугольники (хотя они вписаны в круг и являются выпуклыми многоугольниками). Каждый раз мы меняем количество
стороны основания генерируется новая призма
со случайно нарисованными сторонами:
БОЛЬШЕ ССЫЛКИ
Плоские развертки конусов и усеченного конуса. Как рассчитать площадь боковой поверхности.
Плоские развертки конусов, срезанных косой плоскостью.Сечение представляет собой эллипс.
Мы изучаем разные цилиндры и видим, как они превращаются в плоскость. Затем мы объясним, как рассчитать площадь боковой поверхности.
Плоские сетки призм с правильным основанием с разным бортовым номером, разрезанные наклонной плоскостью.
Мы изучаем разные призмы и видим, как они превращаются в плоскую сеть. Затем мы объясним, как рассчитать площадь боковой поверхности.
Первый рисунок плоской сети правильного додекаэдра был опубликован Дрером в его книге «Underweysung der Messung» («Четыре книги измерений»), опубликованной в 1525 году.
Первый рисунок плоской сетки правильного октаэдра был опубликован Дрером в его книге «Underweysung der Messung» («Четыре книги измерений»), опубликованной в 1525 году.
Первый рисунок плоской сетки правильного тетраэдра был опубликован Дрером в его книге «Underweysung der Messung» («Четыре книги измерений»), опубликованной в 1525 году.
Объем тетраэдра равен одной трети призмы, в которой он находится.
Первый рисунок плоской сетки правильного тетраэдра был опубликован Дрером в его книге «Underweysung der Messung» («Четыре книги измерений»), опубликованной в 1525 году.
Объем октаэдра в четыре раза больше объема тетраэдра. Его легко вычислить, и тогда мы можем получить объем тетраэдра.
Двенадцать вершин икосаэдра лежат в трех золотых прямоугольниках. Тогда мы можем вычислить объем икосаэдра
Некоторые свойства этого платонического тела и его отношение к золотому сечению. Построение додекаэдров разными методами.
Вы можете снять фаску с куба, и тогда вы получите многогранник, похожий (но не равный) усеченному октаэдру.Также можно получить ромбический додекаэдр.
Очень простая техника построения сложных и красочных многогранников.
Трехмерные фигуры
Трехмерные фигуры
Вернуться к содержанию
Обзор базовой геометрии — Урок 9
Обзор урока
Плоскости: параллельные, перпендикулярные и прочие
Точка, линия и плоскость — неопределенные термины. Несколько предположений
были созданы вокруг них с помощью постулата «точка-линия-плоскость»
в уроке 1.Для самолетов мы должны добавить еще три предположения ниже.
|
Самолеты не имеют неровностей и, как линии, продолжаются вечно.Три (неколлинеарные) точки определяют плоскость.
Также определяют три точки: треугольник; линия и точка не на линии;
и две пересекающиеся линии. Ровно один самолет содержит их.
Таким образом, стул на трех ножках стабилен, но большее количество ножек может вызвать
стул качаться.
Поскольку линии не имеют толщины, плоскости также не имеют толщины.
Линия, не лежащая на плоскости, может пересекать плоскость не более чем в одной точке.
| Мера наименьшего из всех возможных углов определяет угловая мера между линией и плоскостью. |
| Если линия l пересекает плоскость X в точке P , то линия l перпендикулярна плоскости X ( л X ) тогда и только тогда, когда l перпендикулярно каждой линии в X , которая содержит П . |
| Теорема о перпендикуляре прямой и плоскости: Если линия перпендикулярна двум разным линиям в их точке пересечения, то он перпендикулярен плоскости, которая содержит эти прямые. |
Две плоскости являются параллельными плоскостями тогда и только тогда, когда у них нет точек.
общие или они идентичны.
Опять же, это всеобъемлющее определение не используется повсеместно.
Расстояние между параллельными плоскостями — это длина сегмента
перпендикулярно плоскостям с концами в каждой плоскости.
Расстояние между плоскостью и точкой не на ней измеряется.
по перпендикулярному отрезку от точки к плоскости.
Когда две плоскости пересекаются, образуются четыре двугранных угла .
Меру этих углов можно указать, построив
лучей, перпендикулярных линии пересечения, и измеряя те
углы образовались.
Косые линии — это не компланарные линии, которые не пересекаются.
Так же, как есть разница между многоугольником и многоугольной областью,
мы различаем поверхность трехмерной фигуры и пространство
он включает.С этого мы начинаем твердую геометрию .
Коробка , поверхность прямоугольного твердого тела , или
параллелепипед — одна из важнейших трехмерных фигур.
Коробка имеет шесть граней , каждая из которых представляет собой прямоугольную область.
Противоположные грани лежат в параллельных плоскостях.
Куб — это прямоугольник с квадратными областями всех граней.
Края , — это линейные сегменты, где грани встречаются друг с другом.
Концами ребер являются вершин .Коробка имеет 12 ребер и 8 вершин.
На рисунке справа показано типичное двухмерное изображение.
а также
Тессерак или гиперкуб — четырехмерный аналог куба.
На рисунке слева показано двухмерное представление этого четырехмерного объекта.
Более подробную информацию о них можно найти
видел и
нашел.
Многие люди с трудом верят, что такое может существовать, поэтому такие книги, как
Плоская земля
(Эбботт, 1884 г.),
Sphereland
(Бюргерс, 1983), и
Флаттерленд
(Стюарт, 2001) были
написано.
Цилиндрические твердые тела / поверхности: призмы и цилиндры
| Цилиндрическое тело — это набор точек между областью и его переводное изображение в пространстве, включая регион и его изображение. Цилиндрическая поверхность является границей цилиндрического твердого тела. Цилиндр представляет собой поверхность цилиндрического твердого тела с круглым основанием. Призма — это поверхность цилиндрического твердого тела с многоугольным основанием. |
Цилиндрические твердые тела имеют два основания , которые конгруэнтны и параллельны плоскостям.
Поверхность без оснований известна как боковая поверхность .
Высота или высота — это расстояние между плоскостями.
баз. Если вектор трансляции перпендикулярен плоскостям
основания, цилиндрическое тело — это правый цилиндр или правая призма ,
в противном случае это косой .Призмы названы по форме их
база. Неосновные грани призмы известны как боковые грани , которые
сходятся на боковых краях . Правая призма, основание которой — правильный многоугольник
это обычная призма .
Конические тела / поверхности: пирамиды и конусы
| Коническое тело — это набор точек на любом сегменте между областью (основание ) и точка (вершина ) не в плоскости база. Коническая поверхность является границей конического твердого тела. Пирамида — это поверхность конического твердого тела с многоугольным основанием. Конус — это поверхность конического твердого тела с круглым основанием. |
Конические тела имеют только одно основание .
Пирамиды имеют боковых граней, соединяют вершины основания.
многоугольник с вершиной . В конусе боковой кромкой является любой отрезок.
конечными точками которого являются вершина и точка на основной окружности.Треугольные, неосновные грани пирамиды — это боковых граней .
Пирамиды и конусы также могут быть правыми или наклонными .
Правая пирамида с правильным многоугольным основанием тоже правильная .
Конус также имеет ось , которая является
линия (не сегмент) через вершину и центр основания.
высота коники — это расстояние между вершиной и вершиной.
самолет, содержащий базу.
В правильной пирамиде высота наклона
высота любой боковой грани (треугольника).Только в правом конусе она равна длине бокового края.
Конус или пирамида могут быть усеченными — многие стаканы
усеченные конусы. Усеченный конус тоже
известен
в виде усеченного конуса .
Сферы и прочие предметы круглые
| Сфера — это набор точек в пространстве на определенное расстояние ( радиус ) от точки ( центр ). |
Сферы имеют нулевых оснований .Сферу можно рассматривать как трехмерный аналог круга.
Дважды радиус составляет диаметр .
Hypersphere или 4-ball — это четырехмерный аналог сферы.
(Аналог намеренно пишется по-другому, но здесь тоже правильно.)
Шар (круг, сфера, гиперсфера) размером n называется шаром n .
| Плоское сечение трехмерной фигуры — это пересечение этой фигуры с плоскостью. |
Сфера и плоскость могут пересекаться очень немногими способами. Во-первых, самолет мог
касайтесь сферы только в точке. Эта плоскость должна быть касательной в этой точке.
таким образом линия, содержащая центр сферы и точку
пересечение будет нормальным (перпендикулярным) к плоскости. Во-вторых,
плоскость пересекается более чем в одной точке, и в этом случае пересечение
это круг. Это пересечение называется малым кругом .
если плоскость не содержит центр круга, в этом случае
он известен как большой круг .Большие круги делят сферы на полушарий и , буквально полусферы.
Маршруты большого круга очень
важны в навигации, потому что они содержат кратчайшее расстояние
между двумя точками на поверхности.
Геодезическая — это общий термин для кратчайшего расстояния между двумя точками.
Метрика — это термин из общей теории относительности. Так мы измеряем пространство-время.
В терминах дифференциального исчисления это:
dx 2 + dy 2 + dz 2 — c 2 dt 2 . Antipode с точностью до наоборот или наоборот; также точки сферы, такие
как земля, которые диаметрально противоположны (противоположные концы диаметра).
Земля представляет собой сплюснутый сфероид (в форме M & M, то есть сплющенный на полюсах).
и из трех взаимно перпендикулярных радиусов повторяется тем длиннее).
Вытянутый сфероид больше похож на футбольный мяч или сигару
(из трех взаимно перпендикулярных радиусов повторяется тем короче).В эллипсоиде три взаимно перпендикулярных радиуса имеют разную длину.
Посмотреть этот сайт
для некоторых диаграмм и определений, включая тор , или пончик.
Гипотеза Кеплера
К 1606 году Кеплер начал работу над тем, что стало известно как
Гипотеза Кеплера
после получения письма от Харриота
которые работали над проблемой не менее 15 лет.
Сэр Уолтер Рэли
фактически предложил это своему помощнику Харриоту.Проблема заключается в наиболее эффективном расположении упаковки.
для пушечных ядер или, в конечном счете, атомов в кристалле,
хотя тогда о строении атома было мало что известно.
В конце концов Кеплер предположил, что
гранецентрированная кубическая (FCC) [и эквивалентно
гексагональная плотная упаковка (HCP)]
оба дали оптимальную плотность упаковки сфер.
В конце концов, эта проблема стала частью C проблемы 18 Гильберта.
знаменитый список из 23 человек, созданный в 1900 году.
До 1990-х годов это оставалось одним из последних
нерешенные проблемы дискретной геометрии.В 1990 г. У-И Сян разослал препринты, а в 1992 г.
представил для публикации 100-страничное доказательство, которое осталось
неприемлемым в математическом сообществе из-за его
нечеткость и отсутствие логической прогрессии.
Хотя он был опубликован в
International Journal of Mathematics , у некоторых есть
«сомнения в серьезности судейства»
поскольку « Journal редактируется коллегами Сяна из Беркли».
Это «нельзя считать доказательством».»
( Гипотеза Кеплера , Джордж Спиро, 2003, стр. 150.)
Примерно в 1996 году Хейлз начал противоречивое доказательство, которое следует
вычислительный подход.
9 августа 1998 г. Сэм Хейлз объявил
доступность
статей и препринтов, доказывающих гипотезу Кеплера.
В январе 1999 г. недельный семинар, посвященный исключительно гипотезе Кеплера.
был проведен в Институте перспективных исследований в Принстоне, где эксперты
чистил его со всех сторон. Они требовали публикации в
Анналы математики .В конечном итоге он был (будет?) Опубликован, но
с беспрецедентной оговоркой о том, что судьи не могут
проверить доказательство.
Конические секции
Nappes является множественным числом от Nappe .
Конус называется двойным, если мы говорим о полном конусе.
который больше похож на песочные часы или две «круговые пирамиды»
соединились в их вершинах.
Одиночная «круговая пирамида» — это то, что большинство студентов подумают как конус.
Выше показано пересечение плоскости с конусом — двойным
ворсанный конус. Эти loci (наборы точек) представляют собой конические секции.
Loci имеет множественное число для , locus (набор точек).
Эти конические сечения ( круг , эллипс , парабола ,
и гипербола ) будут изучены более подробно в алгебре II.
См. Эту веб-страницу для получения более подробной информации.
Платоновы тела
| Платоново тело — это выпуклые многогранники с все грани одинаковые многоугольники. Как показано ниже, их ровно пять. |
Платоновы тела также известны как правильные многогранники.
Тетраэдр также известен как треугольная пирамида .
Шестигранник также известен как куб .
Дуалы особенно важны в кристаллографии, где
рассеянное излучение
(электроны,
нейтроны,
рентгеновские лучи)
лучше всего изучать в обратном пространстве.
Глядя на таблицу выше, подумайте о формуле Эйлера
который связывает количество граней, вершин и ребер любых многогранников:
F + V = E + 2.
Нетрудно показать, что правильных многогранников всего пять.
(выпуклый и грани все тот же правильный многоугольник).
Подумайте, сколько одинаковых правильных многоугольников может сойтись в одной вершине.
Нам всегда нужно больше двух, если мы собираемся сложить его и
оградить любое пространство.
Для треугольников (с углом 60 °) шесть составят мозаику плоскости.
Следовательно, необходимо учитывать три, четыре и пять, и результаты могут быть
рассматриваемый выше как тетраэдр, октаэдр и икосаэдр.Для квадратов (с углом 90 °) четыре будут разбивать плоскость мозаикой.
Следовательно, нужно рассматривать только три, и куб является результатом.
Для пятиугольника (с углом 108 °) четыре превышают 360 °.
Следовательно, нужно рассматривать только три, и в результате получается додекаэдр.
Три шестиугольника (с углом 120 °) образуют мозаику на плоскости.
Таким образом, мы исчерпали все возможности, в результате
правильные многогранники или платоновы тела.
Эта ссылка
ведет на страницу, описывающую пять платоновых тел, вместе с
цветные фигурки.Этот сайт
есть твердые тела, которые можно вращать.
Этот сайт
ссылки на многие другие хорошие сайты.
Древние связывали пять платоновых тел с огнем (4), землей (6),
воздух (8), вода (20) и космос (12).
Твердые тела Архимеда
| В Archimedian Solid твердое тело выпуклое, все вершины идентичны, все грани — правильные многоугольники, но не все одинаковые. |
Твердые тела Архимеда можно классифицировать по набору чисел, который указывает
количество сторон многоугольников в каждой вершине.Таким образом, {3,6,6} будет обозначать один треугольник и два шестиугольника в каждой вершине.
Остальные двенадцать: {3,8,8}; {4,6,6}; {3,10,10}; {5,6,6};
{3,3,4,4}; {3,3,5,5}; {3,4,4,4}; {4,6,8}; {3,4,4,5}; {4,6,10}; {3,3,3,3,4};
и {3,3,3,3,5}.
Эта (неработающая) ссылка
ведет на страницу с описанием тринадцати архимедовых или полурегулярных тел,
в комплекте с цветными фигурами.
C 60 — высокосимметричная молекула чистого углерода.
Форма такая же, как у футбольного мяча или
Archimedian Solid усеченный икосаэдр: {5,6,6}.C 60 часто упоминается как Buckyballs.
Технически это твердое тело Архимеда представляет собой усеченный изокаэдр года.
Это имя происходит от имени Ричарда Бакминстера Фуллера,
известен своими геодезическими куполами.
Степан центр
в Нотр-Дам является местным примером.
C 60 является одним из класса известных соединений
как фуллерены также называют в честь американского архитектора выше.
Молекула C 60 была открыта в 1985 году, когда группа
пытался понять спектры поглощения межзвездной пыли.Их работа принесла им Нобелевскую премию по химии 1996 года.
Изначально производился в очень малых количествах или извлекался из сажи.
теперь доступен и является центром множества разнообразных исследований.
Длинные углеродные трубки называются
нанотрубки также были произведены.
C 60 представляет собой новую, неожиданную кристаллическую форму твердого
углерод. Другие формы: тетраэдрическая углеродная связь в алмазе.
и соединение листового типа в графите имеет гораздо более долгую историю.Видеть
На этой странице представлена краткая, хорошо задокументированная история C 60 .
Пентамино
Пентамино.
Мои исследовательские интересы связаны с утроением пентамино из
подмножество 9 из 12.
Можете ли вы утроить все 9 в наборе или даже все 12?
Можете ли вы втрое повторить данное пентамино со всеми 220 подмножествами?
Симметрия, виды и сети
Отражения меняют ориентацию, таким образом, как двумерные фигуры, трехмерные фигуры могут
также быть прямо конгруэнтным или противоположно конгруэнтным .Это особенно важно в органической химии, где ориентация
из четырех связей вокруг углерода (тетраэдр) имеет решающее значение для жизни.
Посмотри это
ссылка для получения дополнительной информации (загрузить
плагин звонка).
Я думал, что в последние годы была распространена диетическая добавка с обоими изомерами,
и много людей погибло,
но триптофан
похоже, в конечном итоге возникла другая (димерная) проблема.
Архитекторы часто рисуют масштабные виды или планы зданий.Некоторые могут назвать эти отметками .
Этот сайт
есть сети для многих твердых тел и другие лакомые кусочки.
| Сетка представляет собой двумерную фигуру, которую можно складывать на сегменты или изогнутый на своих границах в трехмерную поверхность. |
Раскраска карты
http://www.ams.org/notices/199807/thomas.pdf
Сколько цветов необходимо и сколько цветов достаточно, чтобы раскрасить любую карту на плоскости?
На сфере (4)?
На ленте Мебиуса (6)?
На торе (7)?
Карты с границами, состоящими только из прямых или окружностей
может понадобиться еще меньше цветов! (Смотрите рисунок справа.)
За исключением плоскости / сферы, эти вопросы были
легко ответить.
Как и сеть, карта представляет собой двумерное приближение для трехмерной фигуры.
Когда это карта земли, часто встречаются различные искажения.
Если вы взяли глобус и разрезали его примерно через каждые 15 ° долготы,
в результате пробок (см. рисунок слева) можно было уложить ровно. Это было бы
довольно точно, но довольно неудобно — разные части
одна и та же страна будет на разных глубинах и фактической форме
этих стран трудно увидеть.Исторически сложилось так, что проекция Меркатора , созданная
обычно используется фламандский картограф 1569 года.
Особенно искажены участки земли у полюсов, что приводит к
Африка (11 миллионов миль 2 ) размером с Гренландию
(менее 1 миллиона миль 2 ).
Это происходит потому, что проекция Меркатора на самом деле является чистой
для цилиндра, а не для сферы. Преобразование может быть сгенерировано расширением
лучи из центра Земли на боковую грань цилиндра.Как указано выше, это преобразование не является изометрией.
Однако он сохраняет промежуточность и коллинеарность,
по линиям долготы и широты.
Таким образом, четыре направления (север, юг, восток и запад)
находятся на перпендикулярных линиях.
Изучив карты, Фрэнсис Гатри в 1852 году предположил, что любой
карту на сфере или плоскости можно выделить / раскрасить
всего четыре цвета. Легко видеть, что необходимы четыре цвета (см. Справа).Однако доказательство достаточности части было завершено только в 1976 году.
Даже тогда доказательство, предоставленное Haken и Appel , было спорным.
уже много лет. Споры возникли из-за того, что они использовали компьютер
чтобы доказать, что нужны были только четыре цвета
для каждого из 1952 типов возможных карт. Проблема была встроена в
теория графов
перед этим анализом.
| Теорема о четырех цветах . Предположим, что области, имеющие общую границу некоторой длины, должны иметь разные цвета.Тогда любая карта регионов на плоскости или сфере может быть раскрашенным таким образом, чтобы потребовалось всего четыре цвета. Предположено Гутри в 1852 году; доказано Хакеном и Аппелем в 1976 году. |
Ниже представлен раздаточный материал для домашнего задания 9.8 №26.
(Где-то добавить угол наклона / склонения и
график для двугранных углов.)
Моделирование определенных форм, объектов и элементов зданий в 3D
Чтобы создать 3D-модель в SketchUp, вы постоянно переключаетесь между инструментами рисования, видами, компонентами и организационными инструментами.В этой статье вы найдете несколько примеров, иллюстрирующих способы совместного использования этих инструментов для моделирования определенной формы или объекта.
Примеры иллюстрируют несколько различных приложений для создания 3D-моделей в SketchUp: деревообработка, моделирование деталей или абстрактных объектов и создание зданий. Примеры упорядочены от простого к сложному.
Рисунок стула
В следующем видео вы видите три способа нарисовать 3D-модель стула.В первых двух примерах вы видите два метода создания одного и того же стула:
- Вычитание: Выдавите прямоугольник до высоты стула. Затем используйте инструмент «Толкать / тянуть» (), чтобы вырезать форму стула.
- Добавка: Начните с моделирования сиденья стула. Затем выдавите спинку и ноги с помощью инструмента Push / Pull.
В третьем примере вы видите, как создать более подробную и сложную модель, используя компоненты для упрощения моделирования ножек стула и ступенек на спинке стула.
Совет: Вы можете использовать советы и приемы, продемонстрированные в этих примерах стульев, для создания всевозможных других сложных трехмерных моделей.
Чертеж чаши, купола или сферы
В этом примере вы смотрите на один из способов нарисовать чашу и как применить технику создания чаши к куполу или сфере.
Вкратце, чтобы создать чашу, вы рисуете круг на плоскости земли и профиль формы чаши прямо над кругом.Затем вы используете инструмент Follow Me, чтобы превратить контур в чашу, следуя за исходным кругом на плоскости земли.
Вот как работает процесс, шаг за шагом:
- С помощью инструмента Окружность () нарисуйте окружность на плоскости земли. Эти шаги будут проще, если вы начнете с исходной точки осей рисования. Размер этого круга не имеет значения.
- Наведите указатель мыши на начало координат, чтобы он привязался к исходной точке, а затем переместите курсор вверх по синей оси.
- Начиная с синей оси, нарисуйте круг, перпендикулярный кругу на плоскости земли (т. Е. Привязанный к красной или зеленой оси). Чтобы облегчить вывод, двигайтесь по орбите так, чтобы зеленая или красная ось проходила примерно слева направо вдоль экрана. Если инструмент «Окружность» не остается в зеленом или красном направлении вывода, нажмите и удерживайте клавишу Shift , чтобы заблокировать вывод. Радиус этого второго круга представляет собой внешний радиус вашей чаши.
- С помощью инструмента Смещение () создайте смещение этой второй окружности.Расстояние смещения представляет собой толщину чаши. Посмотрите на следующий рисунок, чтобы увидеть, как ваша модель выглядит в этот момент.
- С помощью инструмента Line () нарисуйте две линии: одну, которая делит внешний круг пополам, и другую, разделяющую внутренний круг, созданный с помощью инструмента «Смещение».
- С помощью инструмента Eraser () сотрите верхнюю половину второго круга и лицо, представляющее внутреннюю часть чаши. Когда вы закончите, у вас будет профиль чаши.
- С помощью инструмента Select () выберите край круга на базовой плоскости. Это путь, по которому инструмент Follow Me завершит чашу.
- С помощью инструмента Follow Me () щелкните профиль чаши. Ваша чаша готова, и вы можете удалить круг на плоскости земли. На следующем рисунке показан профиль чаши слева и чаши справа.
Примечание: Почему нужно рисовать две линии, чтобы разделить смещенные окружности? Когда вы рисуете круг с помощью инструмента Круг (или кривую с помощью инструмента Дуга, или кривую линию с помощью инструмента От руки), вы фактически рисуете круг (или дугу, или кривую), состоящий из нескольких сегментов, которые действовать как единое целое.Чтобы удалить часть сегмента окружности, дуги или кривой, необходимо нарушить непрерывность. Первая линия, которую вы рисуете, создает конечные точки, которые разрывают сегменты внешнего круга, но не внутреннего круга. Проведение второй линии через внутренний круг разбивает внутренний круг на две непрерывные линии.
Вы можете использовать те же шаги, чтобы создать купол, просто нарисовав свой профиль вверх ногами. Чтобы создать сферу, вам совсем не нужно изменять второй круг для создания профиля.Посмотрите следующее видео, чтобы узнать, как создать сферу.
Создание конуса
В SketchUp можно создать конус, изменив размер грани цилиндра или выдавив треугольник по круговой траектории с помощью инструмента «Следуй за мной».
Чтобы создать конус из цилиндра, выполните следующие действия:
- С помощью инструмента Окружность нарисуйте окружность.
- Используйте инструмент Push / Pull , чтобы выдавить круг в цилиндр.
- Выберите инструмент Перемещение ().
- Щелкните по сторонам света на верхнем крае цилиндра, как показано слева на рисунке. Кардинальная точка выравнивается с красной или зеленой осью и действует как маркер изменения размера. Чтобы найти кардинальную точку, наведите курсор инструмента «Перемещение» на край верхнего цилиндра; когда подсветка края круга исчезает, это указывает на кардинальную точку.
- Переместите край к центру, пока он не сузится до конуса.
- Щелкните в центре, чтобы завершить конус, как показано слева на рисунке.
Вот шаги для моделирования конуса путем выдавливания треугольника по круговой траектории:
- Нарисуйте круг на плоскости земли. Вам будет проще совместить треугольник с центром круга, если вы начнете рисовать круг от начала координат осей.
- С помощью инструмента Line () нарисуйте треугольник, перпендикулярный окружности. (См. Изображение слева на следующем рисунке.
- С помощью инструмента Select () выберите грань круга.
- Выберите инструмент Follow Me () и щелкните треугольную грань, которая создает конус почти мгновенно (если на вашем компьютере достаточно памяти). Вы можете увидеть конус справа на следующем рисунке.
Создание пирамидальной скатной крыши
В SketchUp вы можете легко нарисовать шатровую крышу, которая представляет собой простую пирамиду. На этом примере вы видите, как добавить крышу и к простому однокомнатному дому.
Чтобы нарисовать пирамиду (поднять пирамидальную шатровую крышу):
- С помощью инструмента Прямоугольник () нарисуйте прямоугольник, достаточно большой, чтобы покрыть ваше здание.Чтобы создать настоящую пирамиду, создайте квадрат вместо прямоугольника. Механизм вывода SketchUp подскажет, когда вы прямоугольник, квадрат или золотое сечение.
- С помощью инструмента Line () проведите диагональную линию от одного угла до противоположного.
- Проведите еще одну диагональную линию от одного угла до другого. На рисунке вы видите, как линии образуют X. В этом примере лица показаны в рентгеновском представлении, поэтому вы можете увидеть, как прямоугольник покрывает план этажа.
- Выберите инструмент Перемещение () и наведите указатель мыши на центральную точку, пока не отобразится зеленая точка вывода.
- Щелкните по центральной точке.
- Переместите курсор в синем направлении (вверх), чтобы поднять крышу или пирамиду, как показано на рисунке. Если вам нужно зафиксировать перемещение в синем направлении, нажмите клавишу со стрелкой вверх при перемещении курсора.
- Когда ваша крыша или пирамида достигнет желаемой высоты, щелкните, чтобы завершить перемещение.
Совет: При создании модели дома или многоэтажного здания разделите стены и крышу или каждый этаж здания в отдельные группы.Таким образом, вы можете редактировать их по отдельности или скрыть крышу, чтобы посмотреть на план внутреннего этажа. См. «Организация модели» для получения подробной информации о группах.
В SketchUp самый простой способ создать 3D-модель здания — это использовать его контуры. После того, как у вас есть посадочное место, вы можете разделить посадочное место и выдавить каждую секцию до нужной высоты.
Вот несколько советов по поиску следов здания:
- Если вы моделируете существующее здание, обведите контур здания с помощью инструментов рисования.Если здание не закрыто деревьями, вы можете найти аэрофотоснимок на Google Maps и отследить снимок. В SketchUp вы можете захватывать изображения из Google и загружать их непосредственно в модель, как показано на следующем рисунке.
- Если у вас нет аэрофотоснимка существующего здания, которое вы хотите смоделировать, возможно, вам придется попробовать старомодный маршрут: измерить внешний вид, чтобы создать отпечаток, и нарисовать его с нуля. Если буквально измерить все здание нецелесообразно, вы можете использовать такие приемы, как измерение одного кирпича для оценки его габаритных размеров или фотографирование объекта или человека, длина которого вам известна.См. Раздел «Измерение углов и расстояний до точной модели» для получения более подробной информации.
Если вы можете начать со снимка своего следа, следующие шаги проведут вас через процесс отслеживания этого следа. Сначала настройте вид снимка:
- Выберите Камера> Стандартные виды> Сверху в строке меню.
- Выберите « Камера»> «Масштабирование с», чтобы убедиться, что вы можете видеть все в своем файле.
- Используйте инструменты «Панорама» и «Масштаб», чтобы создать хороший вид на верхнюю часть здания, которое вы хотите смоделировать.Вы должны четко видеть здание, чтобы отследить его след. См. Просмотр модели для получения подробной информации об использовании этих инструментов.
- Выберите «Просмотр»> «Стиль лица»> «X-Ray » в строке меню. В режиме рентгеновского снимка вы можете увидеть вид сверху здания через грани, которые вы рисуете для создания контура.
После настройки снимка попробуйте следующие шаги, чтобы отследить след здания:
- Установите оси рисования в угол здания.Подробнее см. Регулировка осей рисования.
- С помощью инструмента Прямоугольник () нарисуйте прямоугольник, определяющий часть вашего здания. Щелкните угол, а затем щелкните противоположный угол, чтобы нарисовать прямоугольник. Если контур вашего здания включает углы, отличные от 90 градусов, кривые или другие формы, которые вы не можете обвести с помощью инструмента «Прямоугольник», используйте любые другие инструменты рисования, которые вам понадобятся, чтобы обвести след вашего здания.
- Продолжайте рисовать прямоугольники (или линии и дуги) до тех пор, пока весь контур здания не будет определен перекрывающимися или смежными прямоугольниками, как показано слева на следующем рисунке.Убедитесь, что нет зазоров и дырок; если есть, заполните их большим количеством прямоугольников.
- С помощью инструмента Eraser () удалите все края внутри контура здания. Когда вы закончите, у вас должна получиться одна грань, определяемая периметром прямых краев. Вы можете отключить просмотр рентгеновских лучей, как показано справа на следующем рисунке, чтобы четко видеть ваши лица и окончательный отпечаток.
- У некоторых простых зданий высота внешней стены одна, но у большинства их больше одной.После завершения создания контура используйте инструмент Line , чтобы разделить контур здания на несколько граней, каждая из которых соответствует разной высоте внешней стены, как показано на следующем рисунке. Затем вы можете использовать инструмент Push / Pull () для выдавливания каждой области до нужной высоты здания.
Создание многогранника
В этом примере вы видите, как создать многогранник, который повторяет грани, выровненные вокруг оси.
Чтобы проиллюстрировать, как вы можете создать сложную форму с базовыми повторяющимися элементами, в этом примере показано, как создать многогранник, называемый ромбикосододекаэдром , , который состоит из пятиугольников, квадратов и треугольников, как показано на рисунке.
Следующие шаги объясняют, как создать эту форму, повторяя грани вокруг оси:
- Установите правильный угол между первым квадратом и пятиугольником, а также между первым треугольником и квадратом. См. «Точное измерение углов и расстояний до модели» для получения подробной информации об измерении углов с помощью инструмента Транспортир.
- Отметьте точную центральную точку пятиугольника, которая показана здесь на зеленой поверхности, которая была временно добавлена к компоненту пятиугольника.Это ось, вокруг которой будут выровнены копии.
- Создайте квадрат и треугольник, а затем сгруппируйте два компонента. Дополнительные сведения о компонентах см. В разделе «Разработка компонентов и динамических компонентов». Чтобы узнать о группах, см. Организация модели.
- Предварительно выберите объекты, которые вы хотите скопировать и повернуть (в данном случае группу, которую вы только что создали).
- Выберите инструмент Повернуть ().
- Совместите курсор поворота с гранью пятиугольника и щелкните его центральную точку, как показано на следующем рисунке.
- Щелкните указателем поворота в точке, где сходятся концы квадрата, треугольника и пятиугольника.
- Нажмите клавишу Ctrl , чтобы включить функцию копирования инструмента «Повернуть». Курсор поворота изменится и появится знак плюса (+).
- Переместите курсор, чтобы повернуть выделение вокруг оси. Если вы изначально щелкнули по точке, где сошлись концы квадрата, треугольника и пятиугольника, новая группа защелкнется в своем новом положении, как показано на следующем рисунке.
- Щелкните, чтобы завершить операцию поворота.
- Продолжайте вращать копии вокруг оси, пока форма не будет завершена. При построении ромбикосододекаэдра вам необходимо сгруппировать различные компоненты вместе и повернуть копии этих групп вокруг различных граней компонентов.
Совет: Если компонент, вокруг которого вы вращаете, не находится в красной, зеленой или синей плоскости, убедитесь, что курсор инструмента «Повернуть» выровнен с гранью компонента, прежде чем щелкнуть центральную точку.Когда курсор выровнен, нажмите и удерживайте клавишу Shift , чтобы заблокировать это выравнивание при перемещении курсора в центральную точку.
ПИРАМИДНАЯ СХЕМА ВЫБИРАЕТ ТЫСЯЧИ ИНВЕСТИЦИЙ В «САМОЛЕТНУЮ ИГРУ»
В Plane Game, новейшей и самой популярной финансовой пирамиде Южной Флориды, нет «супер-спасателей». Билеты стоят 1500 долларов, и хотя пилот должен заработать 12000 долларов, большинство пассажиров отправляются в поездку.
Соблазненные обещанием мгновенного обогащения, тысячи людей вложили деньги в игру в пирамиду в надежде получить быструю прибыль в размере 12 000 долларов, заявили власти.Большинство ушли на 1500 долларов беднее.
«Это жадность, большая жадность», — сказал агент под прикрытием из офиса шерифа округа Палм-Бич. «Мне их ни капли не жалко. Никто им руки не выкручивает».
Во вторник агенты шерифа арестовали шестерых организаторов игры на вербовочном собрании в Лейк-Уорт. Еще семеро были арестованы полицией Бойнтон-Бич 13 марта. Государственная прокуратура также следит за митингами в Бока-Ратон.
Игра в самолет незаконна.По законам Флориды это определено как разновидность лотереи. Любому, кого поймают за игрой, грозит штраф в размере 1000 долларов и тюремное заключение сроком до года.
«Люди уже должны знать, что это незаконно, — сказал Джек Фриз, представитель прокуратуры округа Палм-Бич. «Но некоторым из них все равно. Что за штраф в тысячу долларов, если вы можете выиграть 12 000 долларов?»
Большинство тех, кто играет в игру, в остальном являются законопослушными гражданами, сказал агент шерифа.
«В основном это люди со средним достатком из всех слоев общества», — сказал он.«Они учителя, медсестры, домохозяйки, продавцы автомобилей. Но все они думают, что могут получить что-то бесплатно».
The Plane Game — это тонко замаскированный взлет на цепях пирамид, которые существуют уже много лет. Стоимость авиабилета 1500 долларов. Игроки входят в игру как «пассажиры». По мере прохождения игры они становятся членами экипажа, вторыми пилотами и, в конечном итоге, пилотами.
Предполагается, что каждый пилот получит 12 000 долларов. Когда это происходит, пилот выбывает из игры, а второй пилот становится пилотом.
Но пассажиры не получают ни цента, пока не станут пилотами. Даже в этом случае они не получат свои 12000 долларов, если восемь новых пассажиров не заплатят 1500 долларов. Чтобы новые пассажиры получали деньги, необходимо нанять еще 64 пассажира. Эти 64 пассажира не заработают денег, если в игру не войдут еще 512 пассажиров.
«Чем больше людей привлекается, тем труднее и труднее заполнять самолет», — сказал представитель шерифа Джо Брэдшоу. «Вы делаете ставку на то, что заполните самолет до того, как он упадет.И рано или поздно он должен рухнуть ».
Организаторы не сообщают потенциальным игрокам об опасностях игры. Они также не упоминают тот факт, что на каждого человека, собравшего 12000 долларов, восемь человек теряют свои вложения в 1500 долларов.
«Лишь немногие зарабатывают деньги», — сказал один агент под прикрытием. «Многие люди встревожены. Большинство из них в конце концов просто сдаются».
Те, кто сдаются, не всегда уходят тихо.Некоторые звонят властям.
«Нам позвонили 15 человек и сказали, что их ограбили», — сказал агент шерифа. «Именно тогда мы решили провести расследование».
Недовольные игроки помогли детективам сорвать вербовку во вторник в доме на Марк Драйв в Лейк-Уорт. Среди 30 человек, явившихся на встречу, были два агента под прикрытием, выдававшие себя за потенциальных «пассажиров».
Агенты выслушали выступление руководителей групп. На этой встрече лидеры изменили название игры на Семинар «Живая мастерская».
«Они изменили терминологию, но это была та же игра», — сказал агент. «Это был всего лишь вопрос семантики».
После того, как группа была разбита на секции, в нее вошли депутаты. Шесть организаторов были увезены в СИЗО, где им были предъявлены уведомления о явке в суд. Всем остальным разрешили вернуться домой.
Никакие деньги не переходили из рук в руки во время встречи, сказали агенты. Вместо этого люди, которые согласились присоединиться к игре, устраивали секретные встречи с лидерами групп.
«На секретных встречах вы должны отдать администратору 15 100-долларовых купюр в конверте.Только наличные. Они не принимают чеки ».
В« Самолетной игре »нет ни в чем не повинных жертв, — сказал агент. Все знают правила заранее.
« Они знают, что делают неправильно, — сказал агент ». Лидеры неоднократно заявляли, что то, что они делают, незаконно. Они используют кодовые имена вместо настоящих ».
Большинство игроков также знают, что проигравших намного больше, чем победителей, сказал агент.
« Они думают, что они не станут теми, кто обжечься «, — сказал он.
По словам следователей, игра в самолет возникла в Нью-Йорке и переехала в Калифорнию. Его корни в Южной Флориде восходят к округу Мартин. Сообщается, что в округе Дейд прошли приемы на работу, в которых приняло участие до 1000 человек.
В то время как наиболее распространенная игра требует, чтобы пассажиры вложили 1500 долларов, в одной из разновидностей игры взимается плата в 5000 долларов и выплата в размере 40 000 долларов.
«Один парень прошел через это девять раз», — сказал агент. «Он завершил строительство двух самолетов за 5000 долларов и семи самолетов за 1500 долларов.Он заработал около 130 000 долларов «.
Власти не имеют возможности узнать, насколько широко распространена игра в самолет, но по оценкам одного агента, в нее вовлечено не менее 1000 жителей округа Палм-Беч.
Двигайтесь вперед, используя наклонный самолет — Урок
(0 оценок)
Спасибо за оценку!
Быстрый просмотр
Уровень оценки: 4
(3-5)
Требуемое время: 45 минут
Зависимость урока: Нет
Тематические области:
Геометрия, Физические науки, Решение проблем, Рассуждения и доказательства, Наука и технологии
Ожидаемые характеристики NGSS:
Резюме
Учащиеся изучают построение пирамиды, узнавая о простой машине, называемой наклонной плоскостью.Они также узнают о другой простой машине, шурупе, и о том, как ее использовать в качестве подъемного или крепежного устройства. Во время соответствующей практической деятельности учащиеся видят, как угол наклона и сила тяги могут облегчить (или усложнить) подтягивание объекта вверх по наклонной плоскости.
Эта инженерная программа соответствует научным стандартам нового поколения (NGSS).
Инженерное соединение
Инженеры используют простые машины, чтобы строить более высокие, прочные и долговечные здания.В конструкции многих устройств используются наклонные плоскости. Например, пандусы представляют собой наклонные плоскости, которые облегчают людям в инвалидных колясках перемещение на более высокое место вместо использования лестницы. Парковочные гаражи спроектированы с использованием наклонных плоскостей для перевода автомобилей на следующий уровень парковки. Винты используются, чтобы поднять что-либо или скрепить две или более вещей вместе. Инженеры проектируют машины на основе больших винтов, такие как буровые установки для подъема масла или грязи, и используют винты меньшего размера для скрепления вместе широкого диапазона предметов, от космического корабля до электрической зубной щетки.
Цели обучения
После этого урока учащиеся должны уметь:
- Опишите наклонные плоскости и то, как инженеры используют их в повседневной работе.
- Определите винт как наклонную плоскость, обернутую вокруг стержня.
- Объясните, как можно использовать винт для перемещения вверх материалов, например камня.
- Опишите, как инженеры принимают во внимание простые машины при разработке современных проектов.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными предметами K-12,
образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) ,
проект Д2Л (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика;
внутри типа по подтипу, затем по классу, и т. д. .
NGSS: научные стандарты нового поколения — наука
| Ожидаемые характеристики NGSS | ||
|---|---|---|
3-ПС2-1.Спланируйте и проведите расследование, чтобы получить доказательства воздействия сбалансированных и неуравновешенных сил на движение объекта. (Класс 3) Вы согласны с таким раскладом? Спасибо за ваш отзыв! | ||
| Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов. | ||
| Этот урок посвящен следующим аспектам трехмерного обучения NGSS: | ||
| Наука и инженерная практика | Основные дисциплинарные идеи | Пересекающиеся концепции |
| Совместно спланируйте и проведите расследование для получения данных, которые послужат основой для доказательств, используя справедливые тесты, в которых контролируются переменные и количество рассмотренных испытаний. Соглашение о выравнивании: В научных исследованиях используются различные методы, инструменты и техники. Соглашение о выравнивании: | Каждая сила действует на один конкретный объект и имеет как силу, так и направление. На покоящийся объект обычно действует несколько сил, но они складываются, чтобы получить нулевую чистую силу на объект.Силы, которые не равны нулю, могут вызвать изменение скорости или направления движения объекта. (Граница: на этом уровне используется качественное и концептуальное, но не количественное сложение сил.) Соглашение о согласовании: Соприкасающиеся предметы оказывают друг на друга силу. Соглашение о выравнивании: | Причинно-следственные связи обычно выявляются. Соглашение о выравнивании: |
Государственные стандарты Common Core — математика
- Представляйте и решайте задачи, связанные с умножением и делением.
(Оценка
3)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Умножайте или делите для решения словесных задач, связанных с мультипликативным сравнением, например.g., используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного.
(Оценка
4)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Применяйте и расширяйте предыдущие представления о делении, чтобы делить единичные дроби на целые числа и целые числа на единичные дроби.(Оценка
5)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ
Колорадо — математика
- Представляйте и решайте задачи, связанные с умножением и делением.(Оценка
3)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Умножайте или делите для решения словесных задач, связанных с мультипликативным сравнением.(Оценка
4)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Решайте реальные проблемы, связанные с делением единичных дробей на ненулевые целые числа и делением целых чисел на единичные дроби.(Оценка
5)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Больше подобной программы
Just Plane Simple
Этот урок знакомит студентов с тремя из шести простых машин, используемых многими инженерами.Эти машины включают наклонную плоскость, клин и винт.
Смотрите, как он скользит!
Учащиеся используют наклонные плоскости при воссоздании сложной задачи поднять каменный монолит, чтобы построить пирамиду. Они сравнивают толкание и тягу блоков разного размера вверх по наклонной плоскости, определяют угол наклона и изучают изменения, которые происходят при увеличении или уменьшении угла…
Инженерное дело: простые машины
Студенты знакомятся с шестью типами простых машин — клином, колесом и осью, рычагом, наклонной плоскостью, винтом и шкивом — в контексте построения пирамиды, получая общее представление об инструментах, которые использовались с тех пор. древние времена и используются до сих пор.
Преимущество машин
На этом уроке учащиеся узнают о работе с точки зрения физики и видят, что работа облегчается благодаря использованию простых машин. Уже сталкиваясь с простыми машинами каждый день, учащиеся узнают об их широко распространенном использовании для улучшения повседневной жизни.
Предварительные знания
Общие сведения о пирамидах. Знакомство с шестью простыми машинами, представленными в Уроке 1 этого раздела.
Введение / Мотивация
Простые машины помогают нам легче выполнять задачу.Какие из простых машин мы изучали? (Возможные ответы: клин, колесо и ось, рычаг, наклонная плоскость, винт и шкив.) Сегодня мы рассмотрим две из шести простых машин — наклонную плоскость и винт.
Наклонная плоскость часто является самой простой из всех простых машин , потому что она не перемещается, когда вы ее используете; он просто сидит на месте. Наклонная плоскость предназначена для перемещения чего-либо с более низкой высоты на более высокую. Наклонная плоскость может быть такой же простой, как подъездная дорожка или лестница.Вы когда-нибудь пользовались одним из них?
Наклонная плоскость помогает поднимать предметы на более высокий уровень. Вы когда-нибудь пытались поднять по лестнице что-нибудь тяжелое? Это довольно сложно! Как насчет того, чтобы поднять этот предмет по лестнице? Так проще? Это точно! Перенести тяжелый предмет по лестнице легче, чем по лестнице, а поднимать его по гладкому пандусу еще проще. Почему это так? (Ответ: Необязательно так много поднимать ногами.)
авторское право
Авторское право © Wikimedia Commons https: // commons.wikimedia.org/wiki/File:Approaching_the_Top_of_the_Ladder_to_Balcony_House,_Mesa_Verde_National_Park_(4851976994).jpg
Однако всегда есть компромисс, чтобы переместить что-то таким образом, чтобы потребовалось меньше усилий. В наклонной плоскости компромисс — расстояние. Если вы сравните длину лестницы с длиной пандуса, ведущего на второй этаж здания, вы обнаружите, что длина лестницы намного короче. Расстояние до пандуса больше, но для подъема требуется меньше усилий.Вы испытали это механическое преимущество ? Люди из древних культур поняли это давным-давно, когда построили пирамиды , используя длинные пандусы, чтобы помочь им перемещать тяжелые камни на вершину! Сегодня инженеры-механики используют наклонные плоскости во многих инженерных конструкциях для перемещения вверх, таких как гаражи, эвакуаторы, конвейерные ленты и эскалаторы.
Винт — другая форма наклонной плоскости; это просто наклонная плоскость, обернутая вокруг стержня, как спираль .(Если возможно, раздайте ученикам несколько винтов.) Винт также является второй простой машиной, которую мы собираемся изучить сегодня. Можете ли вы вспомнить повседневные примеры наклонных плоскостей или винтов? (Ответы: лестница, пандус, горка, лестница, болт, винт, дрель.)
Хотя винт считается простой машиной, работа зависит от другой простой машины, рычага. Вы когда-нибудь видели или использовали винт, чтобы скрепить дерево? Как вкрутить шуруп в дерево? Ну, вы воспользуетесь отверткой или дрелью.Отвертка — это рычаг, который помогает вкрутить шуруп в дерево. Винт — это просто цилиндр, вокруг которого намотана наклонная плоскость. Заостренный конец винта работает как клин (еще одна простая машина!), Но винт отличается от клина, потому что он получает свою силу от поворота рычагом, а не от приложения прямой силы, чтобы толкнуть его в объект.
Винт может действовать двумя способами: он может поднимать груз и может скреплять два или более объекта вместе.Пример использования винта для подъема груза — это когда он используется для заправки масла. Нефть, поступающая из глубокой скважины, легко откачивается с помощью винтового насоса. Архимед был известным математиком и изобретателем, который более двух тысяч лет назад сконструировал винт Архимеда — машину, которую поворачивали лошади или люди для подъема воды.
Когда мы используем шуруп для закрепления предметов, он преобразует вращательное движение, при котором шуруп поворачивается, в прямолинейное движение шурупа по дереву или другому материалу.Это то, что дает винту механическое преимущество . Чтобы превратить винт в твердый материал, требуется меньше усилий, чем для того, чтобы вбить клин в тот же материал. Сегодня инженеры используют винты во многих инженерных приложениях и конструкциях, таких как буровые установки, которые поднимают масло, грязь или воду. Вы когда-нибудь видели, чтобы домкрат поднимал машину, чтобы поменять спущенное колесо? Ну, это тоже пример винта. Инженеры также используют винты в качестве крепежа для больших объектов, таких как спортивные стадионы или самолеты, и для небольших объектов, таких как столы или MP3-плееры.Сегодня мы познакомимся поближе с двумя простыми машинами — наклонной плоскостью и винтовой. Как вы думаете, как они могли помочь в строительстве древних пирамид? После урока перейдите к упражнению «Смотри, как слайд»! для учащихся воссоздают сложную задачу поднять каменный монолит для построения пирамиды с использованием наклонных плоскостей.
Предпосылки и концепции урока для учителей
Механическое преимущество
Механическое преимущество машины — это отношение нагрузки к приложенной силе.Другими словами, механическое преимущество определяет, сколько силы нам нужно для выполнения задачи. Например, чем больше механическое преимущество машины, тем меньше силы требуется для выполнения такой задачи, как перемещение объекта. Верно и обратное. Математически механическое преимущество (MA) = нагрузка ÷ приложенная сила. Хорошим механическим преимуществом является то, что больше 1.
Плоскость наклонная
Назначение наклонной плоскости как простой машины — переместить что-либо с меньшей высоты на большую с меньшими усилиями.Объект, просто помещенный на наклонную поверхность, часто скользит по поверхности (см. Рис. 1) из-за силы, действующей в направлении вниз. Другими словами, силы в этом сценарии неуравновешены (т.е. отсутствует сила, направленная вверх, чтобы противодействовать силе, направленной вниз, и, следовательно, объект будет скользить вниз). Скорость, с которой объект скользит вниз, зависит от того, насколько наклонена поверхность; чем больше наклон поверхности, тем быстрее предмет будет скользить по ней. Это измеряется углом наклона .Студенты могут найти это с помощью транспортира. Трение также влияет на движение объекта по склону. Трение — это сила, которая оказывает сопротивление движению, когда один объект соприкасается с другим. Теперь представьте, что вы находитесь с обратной стороны объекта и применяете силу, чтобы удерживать объект в одном и том же месте (не двигаясь). Чтобы удерживать объект в неподвижном состоянии, сила, которую вы должны приложить, должна была бы равняться направленной вниз силе силы тяжести. Это был бы пример сбалансированных сил.Если вы хотите подтолкнуть силу вверх, вам нужно будет превысить силу тяжести.
Рис. 1: На этой диаграмме показано, как древние культуры использовали наклонные плоскости для перемещения тяжелых камней на вершину своих пирамид. Сила тяжести, трения и тяговое усилие — все это влияет на то, насколько легко (или сложно) вытащить тележку по наклонной плоскости. Авторское право
Авторские права © 2005 Трэвис Рейли, Программа ITL, Инженерный колледж, Университет Колорадо в Боулдере
Чтобы понять движение объекта по наклонной плоскости, важно проанализировать силы, действующие на него.Сила тяжести (также известная как вес) действует в направлении вниз. Когда угол наклона больше и круче наклон, приходится преодолевать больший весовой компонент. При меньшем уклоне весовая составляющая легче преодолевается и требует меньших усилий.
Механическое преимущество наклонной плоскости зависит от ее наклона и высоты. Чтобы найти идеальное механическое преимущество наклонной плоскости, разделите длину склона на его высоту.
Наклонная плоскость дает механическое преимущество, заключающееся в уменьшении силы, необходимой для перемещения объекта на определенную высоту; это также увеличивает расстояние, на которое должен перемещаться объект.Объект, движущийся вверх по наклонной плоскости, должен перемещаться по всей длине наклона плоскости, чтобы переместиться на расстояние высоты. Например, если у вас есть пандус с длиной склона 20 метров, который поднимается на 5 метров в высоту, то ваш компромисс — это перемещение на расстояние 20 метров вместо подъема прямо на 5 метров, и ваше идеальное механическое преимущество составляет 4.
Винт
Винт — это простая машина, имеющая две цели. Его можно использовать для скрепления двух или более предметов вместе или для подъема тяжелого предмета.В большинстве случаев для поворота винта используется рычаг. Хороший пример — отвертка. Это окружность рычага или отвертки и шаг винта, которые определяют механическое преимущество винта.
Шаг винта — это расстояние между соседними резьбами на этом винте. Шаг можно рассчитать, разделив определенное расстояние на количество витков резьбы на винте. Например, если у вас есть винтовая застежка с 5 резьбой на дюйм винта, то шаг винта будет 1/5.Один полный оборот винта в предмет равен расстоянию шага винта. Или, в этом примере, один поворот винта переместит винт на расстояние 1/5 дюйма.
Идеальное механическое преимущество винта находится приблизительно при делении окружности рычага на шаг винта. Например, если ключ на 8 дюймов используется для затяжки болта с шагом 1/5 дюйма, то идеальное механическое преимущество составляет π * 8 дюймов / (1/5 дюйма) = 126.
Если тот же самый винт с шагом 1/5 повернуть отверткой с диаметром окружности 1 дюйм, то идеальное механическое преимущество станет 1 ÷ 1/5 или 5.
Сопутствующие мероприятия
- Смотрите слайд! — Учащиеся воссоздают сложную задачу поднять каменный монолит, чтобы построить пирамиду, используя наклонные плоскости. Они сравнивают толкание и тягу блоков или предметов разного размера вверх по наклонной плоскости. Они определяют угол наклона и изучают изменения, которые происходят при увеличении или уменьшении угла.
Закрытие урока
Сегодня мы узнали о двух простых машинах; наклонная плоскость и винт.Кто может мне привести пример наклонной плоскости? (Возможные ответы: пандус, лестница, эскалатор.) Как наклонная плоскость помогает нам в работе? (Возможный ответ: мы толкаем предметы вверх по наклонной плоскости.) Каков компромисс? (Ответ: Расстояние) Какими двумя способами используются винты? (Ответ: скреплять предметы или что-то поднимать.) Какая еще простая машина часто помогает нам использовать винт? (Ответ: рычаг.) Что сконструировал инженер, использующий наклонную плоскость или винт? (Возможные ответы: гараж, пандус, эскалатор, буровая установка, удерживание частей чего-либо вместе, например самолета или MP3-плеера.)
Проведите итоговую оценку, как описано в разделе «Оценка».
На других уроках этого раздела студенты изучают каждую простую машину более подробно и видят, как каждую из них можно использовать в качестве инструмента для построения пирамиды или современного здания.
Словарь / Определения
угол наклона: угол на дне пандуса, образованный пандусом и горизонтальной линией (см. рисунок 1).
трение: сила, препятствующая движению между двумя контактирующими телами.
наклонный: наклонный, наклонный или наклонный. Отклоняться от горизонтали.
наклонная плоскость: простая машина, поднимающая объект на большую высоту. Обычно это прямая наклонная поверхность и отсутствие движущихся частей, таких как пандус, наклонная дорога или лестница.
механическое преимущество: преимущество, полученное за счет использования простых машин, позволяющих выполнять работу с меньшими усилиями.Облегчение задачи (что означает меньшее усилие), но может потребоваться больше времени или места для работы (большее расстояние, веревка и т. Д.). Например, приложение меньшей силы на большем расстоянии для достижения того же эффекта, что и приложение большой силы на небольшом расстоянии. Отношение выходной силы, оказываемой машиной, к приложенной к ней входной силе.
Мезоамерика: регион, простирающийся на юг и восток от центральной Мексики и включающий части Гватемалы, Белиза, Гондураса и Никарагуа.В доколумбовые времена он был населен различными цивилизациями, такими как майя и ольмеки.
монолит: большой каменный блок, особенно используемый в архитектуре или скульптуре.
Шаг (винта): расстояние по вертикали между двумя витками резьбы винта.
сила тяги: причина движения или изменения.
пирамида: массивная структура древнего Египта и Мезоамерики, использовавшаяся для склепа или гробницы.Типичная форма — это квадратное или прямоугольное основание на земле со сторонами (гранями) в форме четырех треугольников, которые встречаются в точке наверху. Мезоамериканские храмы имеют ступенчатые стороны и плоскую вершину, увенчанную камерами.
пандус: наклонная поверхность или проезжая часть, соединяющая разные уровни.
Винт: простая машина, которая поднимает или скрепляет материалы. Часто цилиндрический стержень, нарезанный спиральной резьбой.
простая машина: машина с небольшим количеством движущихся частей или без них, которая используется для облегчения работы (дает механическое преимущество).Например, клин, колесо и ось, рычаг, наклонная плоскость, винт или шкив.
уклон: наклонная линия, поверхность, плоскость, положение или направление. Величина или степень отклонения от горизонтали.
спираль: кривая, которая огибает фиксированную центральную точку (или ось) на постоянно увеличивающемся или уменьшающемся расстоянии от этой точки.
Оценка
Оценка перед уроком
Таблица «Знай / Хочу знать / Учиться» (KWL): Создайте классную диаграмму KWL, чтобы помочь организовать изучение новой темы.На большом листе бумаги или классной доске нарисуйте таблицу с заголовком «Простые машины: наклонные плоскости и винты». Нарисуйте три столбца с названиями K, W и L, представляющие, что учащиеся знают о наклонных плоскостях и винтах, что хотят, чтобы знал о наклонных плоскостях и винтах, и что изучил о наклонных плоскостях и винтах и их механических преимуществах . Заполняйте разделы K и W во время введения к уроку по мере появления фактов и вопросов.Заполните L-часть в конце урока.
Оценка после введения
Неформальное обсуждение: Запрашивайте, объединяйте и обобщайте ответы студентов на доске.
- Какие бывают примеры наклонных самолетов в повседневной жизни? (Возможные ответы: пандус для инвалидных колясок, тротуарный бордюр, который превращается в пандус для колясок и велосипедов, горка на детской площадке, горка, которая выбрасывает жевательные шарики из машины, лестница, эскалатор.)
- Какие бывают примеры винтов? (Возможные ответы: буровая установка, автомобильный домкрат, болт, винты, скрепляющие части чего-либо, например самолета или MP3-плеера.)
- Как инженеры используют наклонные плоскости и винты в современных конструкциях? (Возможные ответы: наклонные плоскости включены в конструкцию конвейерных лент или пандусов, используемых для перемещения предметов вверх. Парковочные гаражи спроектированы с использованием больших наклонных плоскостей. Винты используются для скрепления объектов вместе, таких как самолеты и компьютеры, а также для подъема материала. , как при бурении на масло, воду или грязь.)
Итоги урока Оценка
Таблица KWL (Заключение): Как класс, завершите столбец L таблицы KWL, как описано в разделе «Оценка перед уроком».Составьте список всего, что студенты узнали о наклонных плоскостях и винтах, а также об их механических преимуществах. Были ли даны ответы на все вопросы W? Что нового они узнали?
Заключительное обсуждение: Попросите учащихся объяснить, почему легче вытащить тележку или заблокировать длинный неглубокий пандус, чем подниматься по ступеням, лестнице или крутому пандусу. Попросите их привести примеры механических преимуществ использования наклонной плоскости или винта.
Bingo: Раздайте каждому студенту лист бумаги со списком терминов лексики урока.Попросите каждого ученика обойти комнату и найти ученика, который сможет определить один словарный термин. Студенты должны найти разных студентов для каждого слова. Когда студент завершает все условия, он кричит «Бинго!». Продолжайте, пока двое или трое (или большинство) учеников не сыграют в лото. Спросите студентов, которые кричали «Бинго!» дать определения словарных терминов.
Использование уравнений: Предоставьте учащимся дополнительные примеры задач (аналогичные примерам, приведенным в предыстории урока), чтобы они сами вычислили механическое преимущество наклонной плоскости и винта.Попросите их использовать уравнения, приведенные в разделе «Предпосылки урока», для определения механического преимущества наклонной плоскости и винта.
- Примеры: Пандус для инвалидов имеет длину 24 фута и поднимается на 2 фута в высоту. В чем механическое преимущество рампы? (Ответ: 24/2 = 12)
- Стандартный винт ¼-20 имеет резьбу 20 / дюйм. В чем механическое преимущество использования отвертки с окружностью 2 дюйма? (Ответ: 2 / (1/20) = 40)
Исследование : Попросите учащихся самостоятельно исследовать сбалансированные и несбалансированные силы дома.Попросите их выполнить следующие действия и ответить на заданные вопросы:
- Постройте две наклонные плоскости из повседневных материалов в вашем доме (например, ящиков для хлопьев, книг и т. Д.). Убедитесь, что у одного крутой склон, а у другого более пологий.
- Выберите катящийся предмет (например, мрамор, игрушечную машинку и т. Д.).
- Неуравновешенные силы: Поместите объект на вершину наклонной плоскости и наблюдайте, что он делает. Скатывается? Если да, то почему? (Ответ: объект должен скатиться в обеих плоскостях, потому что неуравновешенные силы вызывают движение объекта в направлении действующей силы.)
- Уравновешенные силы: Теперь приложите палец к нижней части объекта, чтобы удерживать его на месте. Проделайте это с обоими самолетами. В каком самолете вам нужно было приложить больше силы, чтобы уравновесить силы? (Ответ: более крутая плоскость.) Когда силы уравновешены, движется ли объект? (Ответ: Нет. Уравновешенные силы заставляют объект оставаться на одном месте.)
Мероприятия по продлению урока
Предложите учащимся развить свое понимание наклонных плоскостей, обсуждая различные варианты использования пандусов.В какой ситуации вы могли бы сделать пандус короче / длиннее, мельче / круче? Когда можно добавить трение, чтобы пандус работал лучше? Нарисуйте разные пандусы для разных целей. Чем они отличаются?
Попросите учащихся взглянуть на ассортимент различных винтов и вычислить механическое преимущество каждого. Какой из них имеет наибольшее механическое преимущество и наименьшее? Попросите их вкрутить в дерево разные крепежи. Можете ли вы почувствовать и увидеть разницу в механическом преимуществе винта с близкой резьбой по сравнению с винтом.тот, у которого нити дальше друг от друга?
Предложите учащимся исследовать винт Архимеда и написать краткий отчет, описывающий, как работает это устройство, рисовать эскизы и приводить собственные примеры повседневных способов его использования для помощи людям.
Рекомендации
Хендерсон, Том. Урок 3: Силы в двух измерениях: наклонные плоскости. The Physics Classroom (учебник физики в средней школе). По состоянию на 25 января 2006 г.http://www.compadre.org/precollege/items/detail.cfm?ID=2014
Райт, Ричард. Дамы и господа … наклонный самолет! PCS Education Systems, Inc. По состоянию на 25 января 2006 г. http://www.weirdrichard.com/inclined.htm
Авторские права
© 2005 Регенты Университета Колорадо.
Авторы
Трэвис Рейли; Малинда Шефер Зарске; Лоуренс Э.Карлсон; Жаклин Ф. Салливан; Дениз У. Карлсон, при участии студентов, участвовавших в курсе подготовки инженерного корпуса К-12 весной 2005 года.
Программа поддержки
Комплексная программа преподавания и обучения, Инженерный колледж, Университет Колорадо в Боулдере
Благодарности
Содержание этих программ электронных библиотек было разработано в рамках Комплексной программы преподавания и обучения в рамках гранта GK-12 Национального научного фонда.0338326. Однако это содержание не обязательно отражает политику Национального научного фонда, и вам не следует предполагать, что оно одобрено федеральным правительством.
Последнее изменение: 30 апреля 2021 г.
Новейшая схема незаконных пирамид растет и растет, но не исчезает
Undated (AP) _ ″ Самолет ″, новейший поворот в вековой незаконной схеме пирамиды, появляется в сообществах по всей стране, и власти призывают ничего не подозревающих игроков нельзя морочить с ума.
″ В этих схемах пирамидального типа жертвы по большей части столь же жадны, как и промоутеры ″, — сказал Спенсер Бараш, помощник главного юрисконсульта Государственной комиссии по ценным бумагам в Оклахоме, где есть десятки игр ″ Airplane ″. возникла.
«Самолет» похож на перекати-поле Оклахомы, плывущее по улице ».
Существуют вариации, но типичная игра« Самолет »начинается с« пилота », который убеждает двух человек заплатить ему вступительный взнос, чтобы он был ″ соавтором. — пилоты.″ По сообщениям, гонорар достигает 1500 долларов, но обычно составляет 100 долларов.
Вторые пилоты, в свою очередь, набирают по два игрока каждый. Эти четверо, которые также платят взнос, становятся «бортпроводниками», и каждый набирает по два «пассажира» снова за 100 долларов.
Когда самолет заполнен — скажем, 14 входов — у пилота есть 1400 долларов, и пирамида делится пополам: вторые пилоты становятся пилотами, бортпроводники становятся вторыми пилотами, а пассажиры становятся бортпроводниками. Вновь набранные пассажиры платят пилоту по 100 долларов каждый, и пирамида продолжает дробиться и расти.
Конечно, чем дольше работает пирамида, тем труднее найти желающих. Те, кто еще не пилоты, потеряют свои деньги, когда пирамида рухнет.
Такие игры называются пирамидами, потому что несколько прибыльных наверху поддерживаются множеством плательщиков внизу.
Где началась игра — загадка, но об этом сообщили в Майами; Тампа, штат Флорида; Оксфорд, штат Миссисипи; Рочестер, штат Нью-Йорк; Торонто; Лос-Анджелес; Монреаль; Индиана; Колорадо; Теннесси; Грузия; Южная Каролина и Техас.
«Самолет отличается от других сделок многоуровневой пирамиды тем, что у него нет общего промоутера», — сказал Бараш. ″ Это просто много маленьких самолетиков. Она распространяется из уст в уста ».
Игра стала настолько популярной в Университете Оклахомы, что комиссия Бараша послала приказ о прекращении противоправных действий межбратскому совету и попросила его разослать приказ всем братствам.
«Люди, с которыми я разговаривала, сказали, что это происходит в общежитиях уже пару месяцев», — сказала Линда Линн, репортер студенческой газеты Oklahoma Daily.
Один студент, первокурсник, который отказался назвать свое имя, назвал игру грабежом после того, как его самолет сложился, и он потерял свой вступительный взнос в размере 50 долларов.
«Это совсем не гарантировано, это совершенно случайно», — сказал студент. ″ Это было действительно популярно, и все этим занимались. Я даже не думал о том, что делаю. Когда я подумал об этом, я понял, что напортачил. В начале этого месяца «
″ Самолет ″ был настоящей модой в Университете Флориды в Гейнсвилле, где студенты увидели в нем способ заработать деньги на весенние каникулы.
По данным полиции, в этом могло быть задействовано до 1000 студентов. Не было никаких арестов, хотя такие схемы караются до года тюремного заключения и штрафом в 1000 долларов во Флориде.
«Он начинает выдыхаться», — сказал лейтенант полиции Гейнсвилла Алан Морроу. ″ Это получает плохую огласку, и люди не хотят терять деньги. Причуды приходят и уходят в кампусе. ″
Но это не только университетские городки.
Полиция Стэнтона, штат Калифорния, 12 марта разогнала игру «Самолет» в магазине нестандартных автомобилей и обвинила 132 человека в соответствии с городским кодексом, выступившими против открытия игорных заведений.Полиция вернула 9000 долларов наличными, бухгалтерскими книгами и квитанциями, сообщил капитан полиции Леонард Хаворт.
Власти считают, что в играх сложно бороться. Игроки отказываются сотрудничать, потому что боятся потерять свои инвестиции, и многие люди не видят в этом ничего плохого.
Инвестиции могут быть небольшими, и те, кто приходит рано, могут зарабатывать деньги.
″ Но если посмотреть на совокупный эффект и то, как обманывают этих людей, определенно есть причина, по которой они закрываются, из общественных интересов, — сказал Бараш.
«Это игра, но она так не продается», — сказал он. ″ Единственный способ добиться успеха в этих вещах — это продать их людям, вводящим в заблуждение. ″
Почтовая служба США, которая контролирует финансовые пирамиды, такие как цепные письма, знает об игре, но не имеет юрисдикции, потому что письма не используется, сказал Пит Уиллер, региональный руководитель инспекторов в Ньюарке, штат Нью-Джерси,
Таким образом, прекращение игр оставлено на усмотрение местных властей и властей штата, которые надеются, что увлечение исчезнет.И у таких, как Бараш, есть совет для тех, кто думает присоединиться к такой игре: «Наш девиз в Оклахоме — это звучит слишком хорошо, чтобы быть правдой, но это так».
Кто построил пирамиды?Вопрос Марк Ленер и Захи Хавасс пытались решить загадку, где Следующие ниже интервью с Марком Ленером и Захи Хавасс обращаются к МАРК ЛЕНЕР, археолог, Восточный институт Чикагского университета, NOVA: В своей обширной работе и исследованиях в Гизе вы хоть раз задавали вопросы ЛЕНЕР: No.Но сомневался ли я когда-нибудь, были ли они божественными или супер Все, что я нашел, все больше убеждает меня в том, что это действительно НОВА: Геродот, греческий историк, писал, что 100000 рабочих построили ЛЕНЕР: Да, ну, во-первых, Геродот утверждает, что ему это сказали. Он Один из Итак, из-за нашего сопоставления и из-за нашего подхода, на который мы смотрели, Что ж, работая таким образом, я призываю любого присоединиться к этой задаче, Одна из вещей, которые эксперимент NOVA показал мне, что ни одна книга не может, — это просто Но проблема уже не существует: 5000 человек действительно возьмут на себя строительство и Совсем недавно со мной связалась строительная фирма DMJM — NOVA: Вы упомянули надписи в Гизе, которые указывают, кто построил LEHNER: Одно из самых убедительных доказательств, которые у нас есть, — это граффити на Были ли это призывники милитаристского толка? Конечно, они не были рабами. А на самом деле становится все интереснее. Потому что в некоторых памятниках вы найдете НОВА: Откуда пришли банды? Были ли они местными жителями или они LEHNER: Есть некоторые свидетельства того, что людей меняли туда и обратно. В любом случае, мы думаем, что это был опыт новобранцев. Но есть НОВА: Некоторые теории о том, кто построил пирамиды, предполагают, что строители LEHNER: Одна вещь, которая поражает меня, когда я читаю об этих идеях, — что это ЗАХИ ХАВАСС, генеральный директор Гизы НОВА: Давайте рассмотрим вопрос о том, кто построил пирамиды. HAWASS: Нам повезло, потому что мы нашли все свидетельства НОВА: Греческий историк Геродот утверждал в 500 г. до н. Э. что 100000 человек ГАВАСС: Геродот, когда приехал сюда, встретил гидов, которые рассказывают истории и прочее. НОВА: А как вы пришли к этому номеру? HAWASS: Я пришел к этому числу, основываясь на размере проекта пирамиды, НОВА: На ваших раскопках на рабочем кладбище вы сказали, что нашли HAWASS: Мы нашли 600 скелетов. И мы обнаружили, что эти люди, номер один, НОВА: Откуда вы это знаете? HAWASS: Потому что у нас есть команда из Национального исследовательского центра, которая НОВА: Над погребальной камерой Хуфу есть надпись, которая идентифицирует HAWASS: Говорят, что надписи внутри пяти разгрузочных камер НОВА: А что там говорят? HAWASS: Рабочие, участвовавшие в строительстве Великой пирамиды, были NOVA: Но как насчет надписей в помещениях для разгрузки в Хуфу и HAWASS: Говорят, что эти надписи написаны людьми, которые |



