Содержание
4 класс, уравнение, решение уравнений, примеры и задачи
Дата публикации: .
Решение уравнений
1. Реши уравнения на сложение и вычитание целых чисел.
| 5456 — х = 2343 | х + 3217 = 7898 | у — 4325 = 346 |
| 9949 — y = 6957 | 1202 — y = 722 | y + 4890 = 8979 |
2. Реши уравнения на умножение и деление целых чисел.
| 45 * х = 225 | х * 18 = 108 | у : 25 = 12 |
| 44 * y = 176 | 224 : y = 32 | y * 40 = 360 |
3. Реши уравнения на сложение и вычитание дробей.
| 3 1⁄8 — х = 2 1⁄8 | х + 4 1⁄3 = 7 3⁄9 | у — 5 8⁄7 = 1⁄14 |
| 12 1⁄15 — y = 1 1⁄5 | 4 1⁄2 — y = 2 1⁄8 | y + 13 1⁄4 = 2 4⁄8 |
4. Реши уравнения на умножение и деление дробей.
Реши уравнения на умножение и деление дробей.
| 45 * х = 225 | х * 17 = 108 | у : 25 = 12 |
| 49 * y = 176 | 224 : y = 32 | y * 40 = 360 |
Текстовые задачи и уравнения
Составь уравнения к задачам и реши их.
1. Автобус проехал 2 часа со скоростью 60 км/час и ещё 3 часа – со скоростью 70 км/час. Какое расстояние проехал автобус за все время?
2. Одновременно в противоположных направлениях из города выехали велосипедист и мотоциклист и продолжили движение в течении 3 часов. Мотоциклист двигался со скоростью 40 км/час, а велосипедист – со скоростью 15 км/час. Сколько километров проехал мотоциклист? Сколько километров проехал велосипедист? На сколько километров мотоциклист проехал больше, чем велосипедист?
3. Из деревни А в село Б вышел пешеход. Через 2 часа он остановился на отдых и отдыхал в течении одного часа. Затем он продолжил свой путь и пришел в село Б через 6 часов после часового отдыха. Какова скорость пешехода, если расстояние между деревней А и селом Б равно Х км?
Какова скорость пешехода, если расстояние между деревней А и селом Б равно Х км?
4. В городе есть 4 улицы: Южная, Северная, Восточная и Западная. На Южной улице живет 10 % от всех жителей города. На Восточной живет на 1 3⁄5 больше, чем на Южной улице. На Северной улице живет в 2 раза больше, чем на Южной улице. Сколько жителей живет на каждой улице, если всего городе зарегистрировано 1 миллион человек?
1. Запиши числа, которые содержат:
| 9 | сот. | 1 | дес. | 2 | ед. | = _____ | 3 | сот. | 0 | дес. | 7 | ед. | = _____ | |
| 6 | сот. | 0 | дес. | 6 | ед. | = _____ | 3 | сот. | 5 | дес. | 0 | ед. | = _____ | |
| 0 | сот. | 5 | дес. | 0 | ед. | = _____ | 9 | сот. | 8 | дес. | 5 | ед. | = _____ | |
4. Заполни таблицу.
| e | 300 | 356 | 353 | 389 | 342 | 384 | 382 |
| e-90 | … | … | … | … | … | … | … |
| f | 451 | 451 | 461 | 441 | 431 | 471 | 481 |
| f+80 | … | … | … | … | … | … | … |
Заполните таблицу
| Слагаемое | 410 | 109 | 358 | ||||
| Слагаемое | 301 | 259 | 758 | 420 | 294 | 273 | 193 |
| Сумма | 772 | 816 | 881 | 689 |
Заполните таблицу
| Уменьшаемое | 161 | 972 | 291 | 494 | 741 | ||
| Вычитаемое | 284 | 216 | 714 | 269 | 161 | ||
| Разница | 32 | 6 | 178 | 33 |
4. Вычисли и выполни проверку.
Вычисли и выполни проверку.
| 458 | 146 | 185 | 164 | 703 | |||||
| — | 132 | + | 15 | — | 50 | + | 10 | — | 58 |
| … | … | … | … | … | |||||
| 773 | 374 | 308 | 659 | 351 | |||||
| + | 241 | — | 214 | + | 247 | — | 487 | + | 220 |
| … | … | … | … | … | |||||
4. Вычисли и выполни проверку.
| 375 | 319 | 782 | 684 | 862 | |||||
| — | 198 | — | 226 | — | 737 | — | 522 | — | 622 |
| … | … | … | … | … | |||||
| 627 | 325 | 777 | 597 | 908 | |||||
| — | 139 | — | 307 | — | 121 | — | 496 | — | 720 |
| … | … | … | … | … | |||||
Реши уравнения
| 9 | + | x | = | 26 | y | + | 26 | = | 68 | x | + | 7 | = | 93 | ||
| x | = | … | y | = | … | x | = | … |
Реши уравнения
| 15 | — | x | = | 8 | y | — | 13 | = | 24 | x | — | 9 | = | 56 | ||
| x | = | … | y | = | … | x | = | … |
Реши уравнения
| 37 | — | x | = | 13 | y | + | 21 | = | 45 | x | — | 32 | = | 58 | ||
| x | = | … | y | = | … | x | = | … |
84. Сколько единиц каждого разряда в числах:
Сколько единиц каждого разряда в числах:
7808, 426, 931 тыс., 21011, 975, 350 тыс., 252, 4919, 628 тыс.?
Урок 21. решение уравнений — Математика — 4 класс
Математика, 4 класс
Урок 21. Решение уравнений
Перечень вопросов, рассматриваемых в теме:
- Что такое уравнение?
- Как решить уравнение, где в ответе не число, а числовое выражение.
- Что такое корень уравнения?
- Как найти неизвестное вычитаемое?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Обязательная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63
Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63
2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27
3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78
Теоретический материал для самостоятельного изучения:
Рассмотрите записи:
376 + 282; (х — у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 — 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
Алгоритм:
- Вспомнить компоненты действия данного уравнения.
- Определить неизвестный компонент.
- Вспомнить правило нахождения неизвестного компонента.
- Применить правило и найти неизвестный компонент.
- Записать ответ.
- Сделать проверку
Используя алгоритм, решите первое уравнение
24 + х = 49
х = 49 — 24
х = 25
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Нет.
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 — 30, после чего получаем уравнение известного вам вида
24 + х = 49
х = 49 — 24
х = 25
Проверка:
24 + 25 = 79 — 30
49 = 49
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
75 — х = 9 ∙ 7
Применяем алгоритм решения составных уравнений:
- Найти значение числового выражения: 75 — х = 9 ∙ 7
75 — х = 63
- Вспомнить компоненты действия данного уравнения: 75 — х = 63
3. Определить неизвестный компонент.
Определить неизвестный компонент.
Неизвестно – вычитаемое.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
х = 75 — 63
6. Записать ответ.
х = 12
7. Сделать проверку.
75 — 12 = 9 ∙ 7
63 = 63
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
х + 390 = 70 ∙ 6
х + 390 = 420
х = 420 — 390
х = 30
Проверка:
30 + 390 = 70 ∙ 6
420 = 420
Ответ: неизвестное число — 30
Урок математики в 4 классе «Решение уравнений нового вида» — Разработки уроков — Методические разработки — Методические разработки
Корякова Людмила Николаевна, учитель начальных классов
Урок математики
в 4 классе
Тема: Решение уравнений нового вида.
Цель: Способствовать развитию умения решать сложные
уравнения, где неизвестное выражено суммой или разностью чисел.
Задачи:
·
формировать
умения решать сложные уравнения, где неизвестное выражено суммой или разностью
чисел;
·
развивать
логическое мышление и умение анализировать;
·
применять
элементы здоровьесберегающих технологий на уроке;
·
воспитывать
коллективизм, взаимопомощь.
Тип урока: Усвоение новых знаний.
Оборудование: Карточки уравнений; карточка с геометрическим
материалом; доска; учебник.
Ход урока:
I.
Организационный момент:
1.
Приветствие
гостей.
2.
Упражнение на
развитие внимания, памяти: Я покажу вам карточку и буду держать её 5 секунд.
Назовите по порядку, какие вы запомнили предметы. Сколько их? (на карточке треугольник, квадрат, круг,
прямоугольник, овал)
3.
Я желаю
получить такую оценку каждому из вас на уроке.
— А для этого надо отгадать эти анаграммы и вы
узнаете, чем мы будем заниматься сегодня на уроке.
Анаграммы:
ЕШАРЬТ
ТОАГЫДАВЬТ МСЕТЬАК
(решать) (отгадывать) (смекать)
II.
Актуализация
знаний. Устный счет.
1.
— Назови
компоненты при сложении. Как найти неизвестное слагаемое?
— Как называются компоненты при вычитании?
— Как найти уменьшаемое? Вычитаемое?
2.
Даны
выражения, подумайте с чего начинается решение выражений, где больше чем одно
действие (с порядка действий):
Задание: расставь действия в выражениях
a + b – (d + k) : m – n
3 4 1
2 5
500 – (280 + 120) = 100
2 1
(600 – 327) + 27 = 300
1 2
3.
Реши задачи:
А) К неизвестному числу прибавить 700 и получится
сумма 1800
1. Составь уравнение.
2. Чему равно неизвестное число?
Х + 700 = 1800
Х = 1100
Б) Из неизвестного числа вычли 60 и получили разность
150
1. Составь уравнение.
2. Чему равно неизвестное число?
Х – 60 = 150
Х = 210
III.
Решение
уравнений.
Мы с вами повторили решение простых уравнений, теперь
переходим к решению более сложных.
У
доски:
120
+ Х = 200 – 75
120
+ Х = 125
Х
= 125 – 120
Х
= 5
120
+ 5 = 200 – 75
125 = 125
IV.
Физминутка
«Близнецы»
Дети встают между партами, кладут друг другу руки на
плечи и закрывают глаза. По моему сигналу они выполняют следующие команды:
·
присесть
·
встать
·
встать на
пальчики, опуститься
·
наклониться влево
·
наклониться
вправо
·
прогнуться назад
·
постоять на
правой ноге, согнув левую ногу в колене
·
постоять на левой
ноге, согнув правую ногу в колене
·
открыть глаза и
тихо сесть
Задание на ошибку:
(х + 29) – 48 = 90
Диалог:
·
Что случилось?
·
Что вы увидели
нового для себя?
·
Какая возникла
проблема?
·
Давайте попробуем
её решить?
Составление плана решения уравнения:
1. Расставим порядок действий. Если бы это был пример, с
Расставим порядок действий. Если бы это был пример, с
чего бы вы начали его решение?
(х + 29) – 48 = 90
1 2
2. Установим название компонентов по последнему действию.
Где находится неизвестное число?
(х + 29) – 48 = 90
3. Вырази чему равен неизвестный компонент?
Х + 29 = 90 + 48 – такое уравнение мы умеем решать?
Х + 29 = 138 – получили простое уравнение.
Х = 138 – 29
Х = 109
(109 + 29) – 48 = 90
1 2
90 = 90
4. Так чем мы будем заниматься сегодня на уроке? (Решать
уравнения нового вида, где неизвестное выражено суммой или разностью)
V.
Еще раз
назовите тему нашего урока? (Решение уравнений нового вида)
Повторим алгоритм решения уравнений:
1. Расстановка порядка действий.
2. Установление названия компонентов по последнему
действию.
3. Найди уменьшаемое, вычитаемое, слагаемое.
4. Проверка (порядок действий).
VI.
Цель: Да,
сегодня мы научимся решать эти уравнения, где неизвестное будет выражено суммой
или разностью.
VII.
Закрепление
нового материала (у доски)
140 – (а + 25) = 40 а + 25 = 140 – 40 а + 25 = 100 а = 100 – 25 а = 75 _________________ 140 – (75 + 25) = 40 40 = 40
| 340 + (190 – х) = 400 190 – х = 400 – 340 190 – х = 60 х = 190 – 60 х = 130 _______________ 340 + (190 – 130) = 400
|
Физминутка
«Клоуны»
Дети свободно стоят между партами; по моей команде:
·
брови свести и
развести;
·
глаза прищурить,
затем широко открыть;
·
губы максимально
открыть в импровизированной улыбке, а затем поджать;
·
шею вытянуть,
затем опустить;
·
руками обнять
себя, погладить и пожелать успехов в учебе.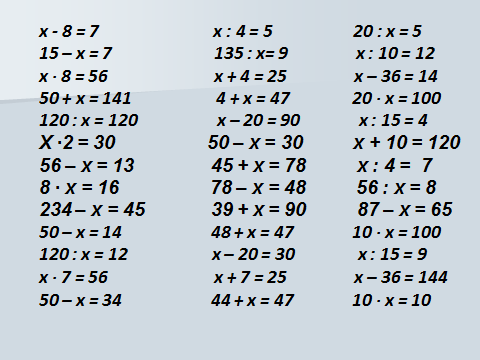
VIII.
Работа в
парах сменного состава.
(Каждому ребенку раздать карточки с уравнением вида:
100 – (х + 25) = 52)
— Что главное при работе в паре? (Помочь своему
товарищу)
IX.
Объясни как
решал уравнение? (Устно)
Физминутка
для глаз:
·
обведи глазами
синий кружок по часовой стрелке;
·
красный – против
часовой стрелке; (Повторить 2-3 раза)
X.
Самостоятельная
работа (Разноуровневые задания)
1 уровень
на «3»:
189 – (х – 80) = 39
х – 80 = 189 – 39
2 уровень
на «4»:
350 – (45 + а) = 60
3 уровень
на «5»:
Составь по задаче уравнение и реши его: Из числа 280
вычесть сумму чисел х и 40 равно 80
280 – (х + 40) = 80
х + 40 = 280 – 80
х + 40 = 200
х = 200 – 40
х = 160
________________
280 – (160 + 40) = 80
80 = 80
XI.
Проверка
разноуровневых заданий (по образцу):
1 уровень:
189 – (х – 80) = 39
х – 80 = 189 – 39
х – 80 = 150
х = 150 +80
х = 230
_________________
189 – (230 – 80) = 39
39 = 39
2 уровень:
350 – (45 + а) = 60
45 + а = 350 – 60
45 +а = 290
а = 290 – 45
а = 245
__________________
350 – (45 + 245) = 60
60 = 60
3 уровень:
280 – (х + 40) = 80
х + 40 = 280 – 80
х + 40 = 200
х = 200 – 40
х = 160
________________
280 – (160 + 40) = 80
80 = 80
XII.
Оцениваю
детей.
XIII.
Рефлексия
урока.
Как вы себя чувствовали сегодня на уроке?
— комфортно
— тревожно
Покажите мне карточками, чтобы я увидела всех. Почему?
Почему?
С чем связана твоя тревога?
XIV.
Домашнее
задание.
1 уровень
на «3»: стр. 92 № 9
2 уровень
на 4»: стр. 93 № 14
3 уровень
на «5»: стр. 96 на смекалку:
Подумай и попробуй исследовать и решить это уравнение самостоятельно 60 х + 180 = 420, составь план решения.
4 класс. Математика. Решение уравнений. — Решение уравнений.
Комментарии преподавателя
В уравнении значение разности представлено числовым выражением. Цель урока – научиться решать уравнения данного вида.
Разность неизвестного числа и числа 11 равна частному чисел 48 и 3. Решим это уравнение, то есть найдем значение неизвестного, при котором равенство будет верным. Сначала найдем значение частного . Запишем уравнение в упрощенном виде: левую часть уравнения перепишем без изменений, а справа запишем значение частного – 16.
Вспомним, как связаны компоненты при вычитании. Чтобы найти неизвестное уменьшаемое, надо к значению разности прибавить вычитаемое.
27 – это корень уравнения. Проверим, верно ли мы нашли корень уравнения, для этого подставим вместо неизвестного числа корень 27. Должно получиться верное равенство.
Проверка:
Выполним вычисления.
Значение разности и значение частного равны. Уравнение решено верно. Корень уравнения – 27.
Слева в равенстве разность с неизвестным числом, а справа произведение чисел 20 и 7. Мы можем вычислить значение произведения. .
Мы можем вычислить значение произведения. .
Чтобы найти уменьшаемое, прибавим к разности вычитаемое:
Корень уравнения 205. Выполним проверку.
Проверка:
Результаты совпали, значит, уравнение решено верно и корень уравнения – 205.
Это уравнение с неизвестным вычитаемым. Значение разности представлено суммой чисел. Можем найти значение суммы. .
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть значение разности:
Это корень уравнения.
Проверка:
Значение разности и значение суммы совпали, значит, уравнение решено верно, корень уравнения – 45.
На уроке мы учились решать уравнения нового вида: с неизвестным уменьшаемым и неизвестным вычитаемым.
Источник конспекта: http://interneturok. ru/ru/school/matematika/4-klass/tema-2/reshenie-uravneniy-nahozhdenie-neizvestnogo-umenshaemogo?konspekt
ru/ru/school/matematika/4-klass/tema-2/reshenie-uravneniy-nahozhdenie-neizvestnogo-umenshaemogo?konspekt
Источник видео: http://www.youtube.com/watch?v=91wXWaIqd48
Файлы
Нет дополнительных материалов для этого занятия.
Конспект урока для 4 класса на тему «Решение уравнений разными способами»
Урок математики по системе Л. В. Занкова
Учитель МОУ гимназии №9 Сизонова Ирина Александровна
ТЕМА: Решение уравнений разными способами.
Цели: научиться решать уравнения разными способами, сравнить решение задачи алгебраическим и арифметическим способами; повторить соотношение единиц измерений длины, времени; отработать вычислительные навыки с многозначными числами; воспитывать ответственность, внимание, чувство товарищества.
Личностные УУД — принимать ситуацию неуспеха и понимать ситуацию успеха, находить причины ситуации неуспеха, формирование учебной мотивации.
Регулятивные УУД — уметь определять и формулировать цель на уроке; проговаривать последовательность действий на уроке; работать по коллективно составленному плану.
Коммуникативные УУД- уметь оформлять свои мысли в устной форме; слушать и принимать речь других; совместно договариваться о правилах поведения и общения в группе; высказывать свою точку зрения по инициативе учителя; эффективно сотрудничать, осуществляя взаимопомощь и взаимоконтроль.
Познавательные УУД — осуществлять расширенный поиск информации и представлять информацию в предложенной форме; делать выводы по аналогии и проверять эти выводы.
Предметные УУД — продолжить работу по формированию решения задач; отрабатывать приемы вычислительных навыков с многозначными числами, внетабличное умножение и деление; повторить порядок действий в выражениях. Развивать интеллектуальные способности: внимание, память, мышление, познавательный интерес через индивидуальные способности, самостоятельность, используя проблемные ситуации и творческий характер заданий. Уметь решать текстовые задачи арифметическим и алгебраическим способом.
Уметь решать текстовые задачи арифметическим и алгебраическим способом.
Оборудование: Учебник И.И. Аргинская Математика 4 класс
Карточки с примерами
Тесты «Решение простых текстовых задач»
Карточки для работы в парах сменного состава
Таблица классов и разрядов
Корабль (рисунок)
Таблицы законов.
Ход урока.
Оргмомент.
Давайте проверим готовность к уроку и прочитаем стихотворение:
Математику, друзья,
Не любить никак нельзя,
Очень строгая наука,
Очень точная наука,
Интересная наука –
Математика.
— Ребята, вы хотели бы полететь в космос?
— Давайте полетим на Солнце! (а если вечером, когда Солнце сядет, ведь не так жарко, заодно погреемся).
— А кто знает, какова температура на Солнце?
Запишем в тетрадях: 6000º
— Да, действительно очень жарко. У нас летом + 30º, и то мы страдаем от жары. А посчитайте, на сколько делений поднимется столбик градусника, чтобы от нашей Т 30º достичь солнечной Т в 6000º.
— а теперь посчитайте, какой высоты будет градусник, который сможет показать самую низкую Т в — 20º, а самую высокую в + 6000º, если одно деление равно 1 мм. (6020 мм)
Запишем:
— А сколько это см? дм? м? (6 м – высота 2-х этажного дома)
602 см 60 дм 2 см 6 м 2 см
— А кто знает, какое расстояние от Земли до Солнца?
150.000.000 км
— Вот какое огромное число, а расстояние это даже трудно представить. Единицами, какого класса представлено число? (таблица разрядов и классов).
— Если бы мы решили поехать на карете, нам понадобилось бы 500 лет.
Запишите, сколько это веков. (5 веков)
— А потом люди придумали автомобиль. Теперь на эту дорогу понадобилось бы времени в 5 раз меньше. Сколько лет? Запишите. (100 лет)
— На самолете пришлось бы лететь 10 лет. Запишем, сколько это месяцев. (120 мес.)
— А вот на космическом корабле можно преодолеть это расстояние за 1 год. Сколько дней? (365 дней).
— А солнечный луч пробегает это расстояние всего за 8 минут. Посчитайте, в котором часу взошло солнышко, если его первый луч разбудил нашу Олю в 7 часов утра? (6 ч 52 мин)
Поменяйтесь тетрадями и проверьте ответы. (на переносной доске записаны правильные ответы).
И так, мы выяснили, что на Солнце лететь нельзя: и далековато, и жарковато. А Солнце – это планета? (да, это звезда, раскаленный газовый шар, нет атмосферы)
Сегодня я предлагаю поиграть в игру, которая называется «Космическая академия». Представим, что наш класс – это космическая академия и мы готовимся для полетов в космос.
Представим, что наш класс – это космическая академия и мы готовимся для полетов в космос.
— Какими чертами должен обладать космонавт? (умный, точный в расчетах, хороший товарищ, умеющий решать трудные задачи).
— И сегодня мы будем решать примеры и уравнения, задачи, а еще думать, смекать, соображать.
— Нас уже ждет корабль, на котором полетят те, кто наберет определенное количество баллов. Вы готовы к испытаниям?
ЗАРЯДКА ДЛЯ УМА.
1) 5 ∙ 37 ∙ 20 = 3700 15 ∙ 18 = 270
4 ∙ 9 ∙ 25 = 900 25 ∙ 4 ∙ 29 ∙ 3 = 8700
12 ∙ 25 = 300 997 ∙452 + 3 ∙ 452 = 452000
23 ∙ 11 = 253
2) стр 121 №№ 509, 512.
— Ни кому неизвестное число увеличилось вдвое. Решило оно полюбоваться на себя в зеркало. Подошло это число к зеркалу и увидело там 811. Скажите, каким было это число до увеличения вдвое?
Устно посчитали, реакцию проверили. Вы сказали, что будущие космонавты должны быть точны в расчетах, поэтому ко всему надо относиться с предельным вниманием. (Знаете ли вы, что в 1962 году американцы подорвали свою ракету, стартовавшую к Венере, так как с некоторым опозданием ученые обнаружили в программе действовавшей ракету ошибку: был пропущен один знак. Казалось бы мелочь, но она могла обернуться катастрофой). Почему я вам об этом рассказала?
Вы сказали, что будущие космонавты должны быть точны в расчетах, поэтому ко всему надо относиться с предельным вниманием. (Знаете ли вы, что в 1962 году американцы подорвали свою ракету, стартовавшую к Венере, так как с некоторым опозданием ученые обнаружили в программе действовавшей ракету ошибку: был пропущен один знак. Казалось бы мелочь, но она могла обернуться катастрофой). Почему я вам об этом рассказала?
РАБОТА НА КАРТОЧКАХ.
Возьмите карточку, найдите значение выражений.
№1 №2 №3
3076 ∙ 54 = 166104 6750 ∙ 24 = 162000 5075 ∙ 38 = 19285
48024 : 24 = 2001 84042 : 21 = 4002 62100 : 30 = 2070
728 ∙ 60 = 43680 1477 ∙ 50 = 73850 767 ∙ 40 = 30680
(3 б + 1 б за скорость)
— Самопроверка (ответы на доске)
— Выпишите внизу значение третьего выражения, округлите его до сотен.
— Что значит округлить до сотен?
— Назовите приближенное число?
— Найдите разность между точным и приближенным числом.
— На сколько изменился результат, округляя числа? №1 №2 №3
— Это больше или меньше разрядного числа? (меньше 100, значит, наши действия по округлению чисел правомерны).
РАБОТАЕМ ПО ТЕМЕ УРОКА
— К нам в гости пожаловали инопланетяне У и Х. Где мы их встречали? Они просят нас среди выражений найти уравнение.
— что такое уравнение? Докажите, что вы выбрали уравнение.
48 – 7 ∙ 6 = 6 (12 + m) + 75
44 + (а – 85) > 105 4 (х + 2) = 32
РЕШЕНИ УРАВНЕНИЙ РАЗНЫМИ СПОСОБАМИ ЭТО И ЕСТЬ ТЕМА НАШЕГО УРОКА.
4 (х + 2) = 32 прочитайте по-разному.
Как можно решить это уравнение?
4х + 4 ∙ 2 = 32 (о чем говорит нам распределительный закон умножения – а(в + с) = ав + ас))
4(х + 2) : 4 = 32 : 4 (назвать свойство равенства а = в и с ≠ 0, ас = вс, ас = вс, а:с = в:с) как по другому?
Х + 2 = 32 : 4 (значение компонентов. Что неизвестно? Как найти?)
Что неизвестно? Как найти?)
— Что значит решить уравнение? Найдите корень уравнения? Х = 6
— Какой способ решения вам больше нравиться?
РЕШЕНИЕ УРАВНЕНИЙ.
(у + 1) ∙ 6 = 36 5х + 220 = 3х + 360 3(х – 1) + 12 = 18
У кого — решает уравнение на основе распределительного закона
— на основе свойства равенств
— на основе знания компонентов
(3 человека на переносных досках)
Решите уравнения разными способами. Кто решал по другому?
ПРОВЕРКА ФРОНТАЛЬНАЯ:
— Прочитайте уравнение, корень которого составляет 7 дес.
— Корень которого составляет 5 ед 1 разряд.
— Корень которого равен значению частного 75 и 25.
ФИЗКУЛЬМИНУТКА.
Пришло время отдохнуть, размяться, проявить внимание, взаимовыручку, чувство товарищества. (пары сменного состава)
(пары сменного состава)
РЕШЕНИЕ ЗАДАЧИ.
Пока вы работали в парах, к нам из центра управления полетами пришло сообщение, в котором просят решить такую задачу. (Чтение текста учителем)
Для полетов в космос построили 540 машин, причем луноходов в 8 раз больше, чем планетоходов. Сколько луноходов и сколько планетоходов построили?
Луноходы ? в 8 раз больше
540 машин
Планетоходы ?
Что обозначает число 540?
Что знаем о луноходах?
Что надо узнать в задаче?
Как можно решить задачу?
Решите задачу удобным для вас способом (2 человека на доске).
1 способ
Пусть х – количество планетоходов, тогда х ∙ 8 – количество луноходов. Всего машин было х + х ∙ 8, по условию задачи машин 540, составим уравнение х + х ∙ 8 = 540
х = 60 (пл)
60 ∙ 8 = 480 (лун)
2 способ
1 + 8 = 9 ч – 540 (м)
540 : 9 = 60 (пл)
60 ∙ 8 = 480 (лун)
Сравнить.
С геометрической планеты пришли тесты – проверка готовности к полетам. Вы готовы ответить на вопросы?
Проверка
№ 25 № 26
212434 321313
— Подсчитайте количество баллов.
— У кого от 10 до 25 баллов, значит, вы готовы к полету на орбитальную станцию, кто это?
— Как проходила подготовка к полетам? Чему учились?
1 ряд – займите места на космическом корабле
2 ряд 3 ряд
В расчетное время,
Стартуя с земли,
К загадочным звездам
Летят корабли.
Представим:
Чуть-чуть помечтали –
И все космонавтами стали!
Группе 4 «Б» класса объявляется благодарность за добросовестную подготовку к полету в космос. Счастливого пути!
Счастливого пути!
Тесты Уравнения и неравенства (4 класс) по теме математики
Сложность: знаток.Последний раз тест пройден 17 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Найдите уравнение:
- Правильный ответ
- Неправильный ответ
- Вы и еще 84% ответили правильно
- 84% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Чему равно уменьшаемое, если вычитаемое равно 458, а разность равна 349 ?
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Чему равен множитель, если один из множителей равен 25, а произведение равно 5000?
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Верно ли, что 2340 : 4 < 630?
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Решите уравнение 7 * (12 — 2) + x = 75
- Правильный ответ
- Неправильный ответ
- Вы и еще 86% ответили правильно
- 86% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Чему равно слагаемое, если известное слагаемое равно 358, а сумма равна 800 ?
- Правильный ответ
- Неправильный ответ
- Вы и еще 77% ответили правильно
- 77% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Найдите неравенство, решением которого является число 10.

- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Решите уравнение х + 12 * 3 = 40.
- Правильный ответ
- Неправильный ответ
- Вы и еще 85% ответили правильно
- 85% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Замените двойное неравенство двумя неравенствами: 4 < y ≤ 14.
- Правильный ответ
- Неправильный ответ
- Вы и еще 53% ответили правильно
- 53% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Верно ли, что 28 ×32 ≤ 730?
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Маруся Зазон
9/10
Валентина Полухина
10/10
Максим Андреев
7/10
Наталья Бирюк
9/10
Андрей Кот
9/10
Ярик Дюжев
10/10
Ксюша Тараканова
10/10
Алмас Нургалиев
10/10
Кристина Хуртира
9/10
Гелена Черняховская
10/10
ТОП-3 тестакоторые проходят вместе с этим
Тесты по теме «Уравнения и неравенства» (4 класс) рассчитаны на учеников младшей школы, которые хотят проверить или закрепить свои знания по теме. Данная подборка тестов поможет выявить пробелы в выученном материале и качественно подготовиться к уроку. Вопросы теста проверяют умение решать неравенства и устанавливать, будет ли то или иное число решением. Более сложные вопросы посвящены решению показательных неравенств и уравнений.
Тест «Уравнения» по математике поможет ребенку справиться со сложной темой, лучше понять ее. Его целесообразно использовать для систематизации знаний и самооценивания.
Его целесообразно использовать для систематизации знаний и самооценивания.
Рейтинг теста
Средняя оценка: 4.2. Всего получено оценок: 623.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Контрольная работа 1. Контрольная работа по математике 4 класс 2 четверть
Математика 4 класс
Контрольные работы
Контрольные работы 4 класс. 2 четверть
Вариант 1
1) Выполни вычисления.
| 24 618 + 4 536 = | 32 879 — 19 586 = |
| 7518 * 3 = | 16002 : 7 = |
Решение: 24 618 + 4 536 = 29 154
32 879 — 19 586 = 13 293
7 518 * 3 = 22 554
16 002 : 7 = 2 286
2) Выполни вычисления и сделай проверку:
28км 640м — 9км 890м =
Решение:
- 1) 28км 640м — 9км 890м = 18км 750м
- Ответ: 18км 750м
3) Реши уравнение
х — 180 = 20 * 6
Решение:
- 1) х = (20 * 6) + 180
- 2) x = 120 + 180
- 3) x = 300
4) Восстанови пропущенные цифры:
Решение:
Вариант 2
1) Выполни вычисления.

| 42 731 + 23 895 = | 97 586 — 33 569 = |
| 8 416 * 4 = | 32 568 : 6 = |
Решение: 42 731 + 23 895 = 66 626
97 586 — 33 569 = 64 017
8 416 * 4 = 33 664
32 568 : 6 = 5 428
2) Выполни вычисления и сделай проверку:
29т 350кг + 18т 980кг =
Решение:
- 1) 29т 350кг + 18т 980кг = 48т 330кг
- Ответ: 48т 330кг
3) Реши уравнение
x + 60 = 16 * 6
Решение:
- 1) x = (16 * 6) — 60
- 1) x = 96 — 60
- 1) x = 36
4) Восстанови пропущенные цифры:
Решение:
Вариант 3
1) Выполни вычисления.

| 32 746 + 5 825 = | 43 568 — 28 173 = |
| 3416 * 4 = | 18512 : 8 = |
Решение: 32 746 + 5 825 = 38571
43 568 — 28 173 = 15 395
3 416 * 4 = 13 664
18 512 : 8 = 2 314
2) Выполни вычисления и сделай проверку:
17км 830м — 8км 540м =
Решение:
- 1)17км 830м — 8км 540м = 9км 290м
- Ответ: 9км 290м
3) Реши уравнение
470 — х = 30 * 4
Решение:
- 1) х = 470 — (30 * 4)
- 2) x = 470 — 120
- 3) x = 350
4) Восстанови пропущенные цифры:
Решение:
Вариант 4
1) Выполни вычисления.

| 53 846 + 14 653 = | 87 476 — 65 339 = |
| 4216 * 3 = | 43047 : 9 = |
Решение: 53 846 + 14 653 = 68 499
87 476 — 65 339 = 22 137
4 216 * 3 = 12 648
43 047 : 9 = 4 783
2) Выполни вычисления и сделай проверку:
13т 640кг + 27т 580кг =
Решение:
- 1) 13т 640кг + 27т 580кг = 41т 220кг
- Ответ: 41т 220кг
3) Реши уравнение
90 + х = 1 800 : 10
Решение:
- 1) 90 + х = (1 800 : 10) — 90
- 2) x = 180 — 90
- 3) x = 90
- Ответ:
4) Восстанови пропущенные цифры:
Решение:
На странице использованы материалы из книги С. И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
Простые задачи
Составные задачи
Вы здесь: Главная → Задания → 4 класс Это исчерпывающая коллекция бесплатных распечатываемых заданий по математике для 4 класса, организованных по таким темам, как сложение, вычитание, математика в уме, разряд, умножение, деление, деление в столбик, множители, измерения, дроби и десятичные дроби. Они генерируются случайным образом, их можно распечатать из вашего браузера и включать в себя ключ ответа.Рабочие листы подходят для любой математической программы четвертого класса, но особенно хорошо подходят для математической программы IXL для четвертого класса и их новых уроков внизу страницы. Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати. Все рабочие листы содержат ключ ответа на 2-й странице файла. Ментальное прибавлениеМентальное вычитаниеДобавление в столбцы
Вычитание в столбцахРазрядное значение / округление
Римские цифры Это совершенно необязательно, так как римские цифры не включены в Умножение умножения
Умножить по столбцамПсихологическое отделение
Длинное деление
ФакторыЕдиницы измеренияОбычные единицы Метрические единицы Следующие рабочие листы немного выходят за рамки Общих основных стандартов для 4-го класса и являются необязательными.
ФракцииДобавление фракции Вычитание дроби Дроби к смешанным числам или ст. Сравнение дробей Эквивалентные дроби Десятичные числаСложение десятичных чисел Десятичное вычитание Если вы хотите иметь больший контроль над такими параметрами, как количество проблем, размер шрифта, интервал проблем или диапазон чисел, просто |
Номер 4 класса
Расширьте понимание эквивалентности дробей и заказа
4.NF.A.1 Объяснение
почему дробь a / b эквивалентна дроби (nxa) / (nxb) при использовании
модели визуальной фракции, обращая внимание на то, как количество и размер
части различаются, хотя сами две фракции одинаковы
размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.
Постройте дробную стену
Эквивалентные дроби: домино
Также включен в математических центров четвертого класса
Эквивалентные дроби на сетке умножения Эквивалентные дроби: Установить эквивалентную дробь модели RollIs it Equivalent?
4.NF.A.2 Сравните две дроби с разными числителями и разными знаменателями, например путем создания общих знаменателей или числителей, или путем сравнения с эталонной дробью, такой как ½. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений при помощи символов>, = или <. и обосновать выводы, например, используя модель визуальной фракции.
Доли дня рождения
Кто больше ел?
Также включен в математических центров четвертого класса
Сложение фракций с помощью шаблонных блоков Проблемы со смыслом или бессмыслицей Плитка шоколада Питера
b.Разлагайте дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение с помощью уравнения. Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8
D e составить фракцию
Pizza Share
г. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью и / или используя свойства операций и взаимосвязь между сложением и вычитанием.
Сложить и сравнить: смешанные числа
Также включен в математических центров четвертого класса
Проблемы со словами: сложение и вычитание смешанных чисел Переименование дробей больше единицы Вычитание и сравнение: смешанные числа
d. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели, например, используя модели визуальных дробей и уравнения для представления проблемы.
Вычесть и сравнить
Также включен в математических центров четвертого класса
Задачи со словами: сложение и вычитание дробей Запись и решение: сложение и сравнение дробей
4.NF.B.4 Применяйте и расширяйте предыдущие представления о умножении, чтобы умножить дробь на целое число:
a. Дробь a / b следует понимать как кратное 1 / b. Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 x (1/4), записав вывод с помощью уравнения 5/4 = 5 x (1/4).
Фракции треугольника
Также включен в математических центров четвертого класса
Умножение единичной дроби на целое число Четырехугольные дроби
b.Поймите, что кратное a / b является кратным 1 / b, и используйте это понимание для умножения дроби на целое число. Например, используйте модель визуальной дроби, чтобы выразить 3 x (2/5) как 6 x (1/5), распознавая этот продукт как 6/5. (Обычно n x (a / b) = (nxa) / b).
Умножение дроби на целое число
г. Решайте задачи со словами, связанные с умножением дроби на целое число, например с помощью моделей и уравнений визуальной фракции для представления проблемы.Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?
Математическая литература Ссылка: Full House
Также включен в математических центров четвертого класса
Задачи со словами: умножение дроби на целое число Задачи со словами: умножение смешанного числа на целое число
Иллюстративная математика
Иллюстративная математика
4 класс
4.О.А. 4 класс — Операции и алгебраическое мышление
4. О.А.А. Для решения задач используйте четыре операции с целыми числами.
4.OA.A.1. Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте $ 35 = 5 \ times 7 $ как утверждение, что 35 в 5 раз больше 7 и 7 раз больше 5. Представьте словесные утверждения мультипликативных сравнений как уравнения умножения.
4.OA.A.2. Умножайте или делите для решения словесных задач, включающих мультипликативное сравнение, например.g., используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного.
4.OA.A.3. Решите многоступенчатые задачи со словами, поставленные с целыми числами и получив ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
4. О.А.Б. Ознакомьтесь с факторами и мультипликаторами.
4.OA.B.4. Найдите все пары факторов для целого числа в диапазоне 1–100. Помните, что целое число является кратным каждому из его факторов. Определите, является ли данное целое число в диапазоне 1–100 кратным заданному однозначному числу. Определите, является ли данное целое число в диапазоне 1–100 простым или составным.
4.OA.C. Создавайте и анализируйте шаблоны.
4.OA.C.5. Создайте рисунок числа или фигуры, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например, учитывая правило «сложить 3» и начальное число 1, сгенерируйте термины в результирующей последовательности и обратите внимание, что термины чередуются между нечетными и четными числами. Неформально объясните, почему числа будут и дальше меняться таким образом.
-
Пока нет задач, иллюстрирующих этот стандарт.
4.NBT. 4 класс — Число и операции в десятичной системе счисления
4.NBT.A. Обобщите понимание разрядов для многозначных целых чисел.
4.NBT.A.1. Помните, что в многозначном целом числе цифра в одном месте в десять раз больше, чем в месте справа. Например, узнайте, что $ 700 \ div 70 = 10 $, применив концепции числового значения и деления.
4.NBT.A.2. Чтение и запись многозначных целых чисел с использованием десятичных цифр, числовых имен и расширенной формы. Сравните два многозначных числа на основе значений цифр в каждом месте, используя символы $> $, = и $
<$ для записи результатов сравнения.
4.NBT.A.3. Используйте понимание разрядов, чтобы округлить многозначные целые числа до любого места.
4.NBT.B. Используйте понимание разрядов и свойства операций для выполнения многозначной арифметики.
4.NBT.B.4. Плавно складывайте и вычитайте многозначные целые числа, используя стандартный алгоритм.
4.NBT.B.5.Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядах и свойствах операций. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей.
4.NBT.B.6. Находите частные и остатки целых чисел с четырехзначными дивидендами и однозначными делителями, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между умножением и делением.Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
4. Н.Ф. 4 класс — Число и операции — Дроби
4. Н.Ф.А. Расширьте понимание эквивалентности и упорядочения дробей.
4.NF.A.1. Объясните, почему дробь $ a / b $ эквивалентна дроби $ (n \ times a) / (n \ times b) $, используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две фракции имеют одинаковый размер.Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.
4.NF.A.2. Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравните с эталонной дробью, такой как 1/2. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов $> $, = или $
<$ и обоснуйте выводы, например, используя модель визуальной дроби.
4.NF.B. Постройте дроби из единичных дробей, применяя и расширяя предыдущее понимание операций над целыми числами.
4.NF.B.3. Дробь $ a / b $ с $ a> 1 $ понимается как сумма дробей $ 1 / b $.
4.NF.B.3.a. Под сложением и вычитанием дробей следует понимать соединение и разделение частей, относящихся к одному целому.
4.NF.B.3.b. Разложите дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение с помощью уравнения.Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: $ \ frac38 = \ frac18 + \ frac18 + \ frac18 $; $ \ frac38 = \ frac18 + \ frac28 $; $ 2 \ frac18 = 1 + 1 + \ frac18 = \ frac88 + \ frac88 + \ frac18. $
4.NF.B.3.c. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью и / или используя свойства операций и взаимосвязь между сложением и вычитанием.
4. Н.Ф.B.3.d. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели, например, используя модели визуальных дробей и уравнения для представления проблемы.
4.NF.B.4. Применяйте и расширяйте предыдущие представления об умножении, чтобы умножить дробь на целое число.
4.NF.B.4.a. Дробь $ a / b $ понимается как кратное 1 / b $.Например, используйте модель визуальной дроби, чтобы представить $ 5/4 $ как произведение $ 5 \ times (1/4) $, записав вывод уравнением $ 5/4 = 5 \ times (1/4). $
4.NF.B.4.b. Поймите кратное $ a / b $ как кратное $ 1 / b $, и используйте это понимание, чтобы умножить дробь на целое число. Например, используйте модель визуальной дроби, чтобы выразить $ 3 \ times (2/5) $ как $ 6 \ times (1/5) $, распознавая этот продукт как $ 6/5 $.(В общем, $ n \ times (a / b) = (n \ times a) /b.$)
4.NF.B.4.c. Решайте задачи со словами, включающие умножение дроби на целое число, например, используя визуальные модели дробей и уравнения для представления проблемы. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?
4.NF.C. Изучите десятичную систему обозначений дробей и сравните десятичные дроби.
4.NF.C.5. Выразите дробь со знаменателем 10 как эквивалентную дробь со знаминателем 100 и используйте этот метод, чтобы сложить две дроби с соответствующими знаменателями 10 и 100. Например, выразите 3/10 $ как 30/100 $ и сложите 3/10 + 4 / 100 = 34/100 $.
4.NF.C.6. Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите $ 0,62 $ как $ 62/100 $; описать длину как $ 0.62 $ метра; найдите 0,62 доллара на числовой диаграмме.
4.NF.C.7. Сравните два десятичных знака с сотыми, исходя из их размера. Помните, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов $> $, = или $
<$ и обоснуйте выводы, например, используя визуальную модель.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
4. MD. 4 класс — Измерения и данные
4.MD.A. Решайте проблемы, связанные с измерением и преобразованием измерений из более крупной единицы в меньшую.
4.MD.A.1. Знать относительные размеры единиц измерения в рамках одной системы единиц, включая км, м, см; кг, г; фунт, унция; л, мл; час, мин, сек. В рамках единой системы измерения выразите измерения в большей единице через меньшую единицу. Запишите эквиваленты измерений в таблицу из двух столбцов. Например, знайте, что 1 фут в 12 раз больше 1 дюйма. Выразите длину 4-футовой змеи как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, в которой перечислены пары чисел $ (1, 12) $, $ ( 2, 24) $, $ (3, 36) $,…
4.MD.A.2. Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкости, массами объектов и деньгами, включая задачи, связанные с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, данных в большей единице, в единицах меньшего размера. . Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерений.
4.MD.A.3. Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах.Например, найдите ширину прямоугольной комнаты с учетом площади пола и длины, просмотрев формулу площади как уравнение умножения с неизвестным коэффициентом.
4.MD.B. Представляйте и интерпретируйте данные.
4.MD.B.4. Постройте линейный график для отображения набора данных измерений в долях единицы $ (1/2, 1/4, 1/8) $. Решайте задачи, связанные с сложением и вычитанием дробей, используя информацию, представленную на линейных графиках. Например, с помощью линейного графика найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземплярами в коллекции насекомых.
4.MD.C. Геометрические измерения: понимание понятий угла и измерения углов.
4.MD.C.5. Распознавайте углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимайте концепции измерения углов:
4.MD.C.5.a. Угол измеряется относительно окружности с центром в общем конце лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают окружность.Угол, который составляет 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов.
4.MD.C.5.b. Угол, который поворачивается на $ n $ углов в один градус, называется угловой мерой $ n $ градусов.
4.MD.C.6. Измерьте углы в целых градусах с помощью транспортира.Нарисуйте углы указанной меры.
4.MD.C.7. Считайте угловую меру аддитивной. Когда угол разбивается на неперекрывающиеся части, угловая мера целого является суммой угловых величин частей. Решайте задачи сложения и вычитания, чтобы найти неизвестные углы на диаграмме в реальных и математических задачах, например, используя уравнение с символом для неизвестной угловой меры.
4.Г. 4 класс — Геометрия
4.Г.А. Нарисуйте и обозначьте линии и углы, а также классифицируйте формы по свойствам их линий и углов.
4.G.A.1. Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах.
4.G.A.2. Классифицируйте двумерные фигуры по наличию или отсутствию параллельных или перпендикулярных линий либо по наличию или отсутствию углов заданного размера. Считайте прямоугольные треугольники категорией и определяйте прямоугольные треугольники.
4.G.A.3. Признайте линию симметрии двумерной фигуры как линию, проходящую через фигуру, так что фигуру можно сложить вдоль линии на совпадающие части. Определите линейно-симметричные фигуры и проведите линии симметрии.
Рабочие листы по математике для 4-х классов
Рабочие листы для сложения
Это главная страница для дополнительных рабочих листов. Перейдите по ссылкам на рабочие листы «Космический корабль» Математическое добавление, рабочие листы для сложения с несколькими цифрами, рабочие листы без дополнительных операций и другие темы для сложения.Эти дополнительные рабочие листы бесплатны для личного использования или использования в классе.
Дополнительные рабочие листы
Рабочие листы вычитания
Это главная страница рабочих листов вычитания. Следуйте ссылкам на рабочие листы космического корабля по математическому вычитанию, тесты на вычитание по времени, рабочие листы для многозначного вычитания, простые рабочие листы заимствования и перегруппировки, а также математические рабочие листы со смешанными задачами сложения и вычитания
Рабочие листы вычитания
Рабочие листы умножения
Это главная страница рабочих листов умножения.Уберите пальцы, потому что это первая математическая операция, требующая запоминания фактов. Вы найдете рабочие листы умножения для восьми простых правил папы для освоения таблицы умножения, умножения RocketMath, многозначного умножения, квадратов и других тем рабочего листа умножения. Все эти рабочие листы умножения включают ключи ответов, их можно сразу распечатать и использовать в классе или дома.
Рабочие листы умножения
Рабочие листы деления
Это главная страница рабочих листов деления.Это включает в себя рабочие листы космического корабля Math Division, рабочие листы с многозначным делением, рабочие листы квадратного корня, кубические корни, рабочие листы смешанного умножения и деления. Эти рабочие листы деления бесплатны для личного использования или использования в классе.
Рабочие листы деления
Таблица умножения
Пытаетесь запомнить факты умножения? Эта страница содержит таблицы умножения для печати, которые идеально подходят для справки. Существуют различные варианты каждой таблицы умножения с фактами от 1-9 (продукты 1-81), 1-10 (продукты 1-100), 1-12 (продукты 1-144) и 1-15 (продукты 1-255). .Каждая из этих таблиц умножения представляет собой SVG с высоким разрешением, поэтому факты умножения печатаются красиво!
Таблица умножения
Таблица умножения
Вы ищете печатную таблицу умножения, в которой есть больше, чем просто факты? Один с некоторыми дополнительными математическими фактами о множителях? Или уникальный дизайн? В цвете? Все таблицы умножения на этой странице представляют собой файлы SVG с высоким разрешением, которые прекрасно печатаются на вашем принтере и являются отличным ресурсом для изучения таблиц умножения в классе начальной школы или дома!
Таблица умножения
Рабочие листы семейства фактов
Рабочие листы семейства фактов сосредоточены на наборах связанных математических фактов, а не на конкретных операциях.Обучайте своих детей сложению и вычитанию одновременно и укрепляйте отношения в семье фактов! На каждом уровне представлены две группы фактов, позволяющие постепенно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов.
Рабочие листы о семье
Рабочие листы продольного деления
Вводные рабочие листы продольного деления, рабочие листы продольного деления с остатками и без остатков, продольные деления с десятичными знаками. Все эти листы с длинным делением содержат подробные, развернутые ответы.
Рабочие листы с длинным делением
Графические дроби
Отличное введение в дроби с использованием круговой графики. Студентов просят определить числовые формы дробей из графики или создать свои собственные представления.
Графические дроби
Уменьшение фракций
Практические рабочие листы для уменьшения фракций. Таблицы с различными дробями в этом разделе предназначены для сокращения простых дробей, неправильных дробей и смешанных дробей.
Уменьшение дробей
Сравнение дробей
Практические рабочие листы для сравнения дробей.Задачи о дробях на этих листах требуют, чтобы дети сравнивали одинаковые и непохожие знаменатели, неправильные дроби и смешанные дроби.
Сравнение дробей
Сложение дробей
Рабочие листы для сложения дробей с общими знаменателями, с разными знаменателями, как простые дроби и как смешанные дроби. Полная работа с шагами показана для каждой проблемы в клавишах ответов.
Сложение дроби
Вычитание дробей
Рабочие листы для вычитания дробей с общими знаменателями, с разными знаменателями, как простые дроби и как смешанные дроби.Ключи полного ответа, которые показывают работу!
Вычитание дроби
Умножение дробей
Эти рабочие листы по математике предоставляют практические навыки умножения дробей. Включает проблемы с целыми и без целых, а также с перекрестной отменой и без нее. Каждый рабочий лист PDF-файлов здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ!
Умножение на дробь
Разделение на фракции
Таблицы деления на фракции с разделением на две части.Включает простые дроби, смешанные дроби и неправильные дроби, а также задачи, для решения которых используется шаг перекрестного умножения.
Дробное деление
Дроби как десятичные числа
Рабочие листы для преобразования дробей в десятичные числа, в том числе с использованием деления в столбик.
Дроби как десятичные
Проблемы со словами
На этой странице есть проблемы со словами, охватывающие ряд трудностей для всех основных операций, включая проблемы с большими значениями, а также с неиспользованной информацией.Задачи со словами — отличный способ применить эти математические факты на практике и развить настоящее понимание того, что означают операции в реальном мире!
Текстовые задачи
Задачи с денежным словом
Реальные задачи на сложение, вычитание, умножение и деление, связанные с деньгами. Отличное первое введение в прикладную математику для студентов, знакомых с десятичной арифметикой!
Проблемы с денежным словом
Отрицательные числа
Эти рабочие листы с отрицательными числами объединяют отрицательные числа с другими целыми числами (как положительными, так и отрицательными) с помощью основных математических операций, умножения отрицательных чисел с многозначными числами и деления в столбик с отрицательными числами.
Отрицательные числа
Проценты
Рабочие листы для практики использования и расчета процентов от других чисел, включая преобразование между дробями и процентами.
Проценты
Округление чисел
В этом разделе представлены рабочие листы округления для округления целых чисел и округления десятичных чисел, начиная с относительно простых задач, которые вводят алгоритм округления, а затем переходят к более сложным задачам, где учащиеся должны определить правильную цифру разряда для проверки, а также правильную цифру для округления в большую или меньшую сторону..
Округление чисел
Номера для заказа
Практикуйтесь в рабочих таблицах порядковых номеров с несколькими номерами в порядке возрастания (от наибольшего к наименьшему) и убывания (от наименьшего к наибольшему). Включает целые, десятичные и отрицательные числа. Аналогичные наборы рабочих листов с порядковыми номерами представлены как в горизонтальном, так и в вертикальном форматах.
Номера для заказа
Стандартная, расширенная и словесная форма
Практические рабочие листы для преобразования чисел между стандартной формой (цифры), развернутой формой (числовое значение) и словоформой (полное или устное представление).
Стандартная, развернутая и словесная форма
Среднее, Медиана, Диапазон
Рабочие листы для определения среднего, медианы, режима и диапазона для наборов чисел. Проблемы включают в себя наборы всех положительных целых чисел, всех отрицательных целых чисел и наборы смешанных знаков, а также практику использования калькулятора.
Среднее, Медиана, Диапазон
Отсутствующие операции
Рабочие листы, где есть ответы, но операция отсутствует. Это отличный способ выучить семейства фактов «наоборот» или обеспечить подкрепление, если запоминание с помощью других упражнений, кажется, застопорилось.
Отсутствующие операции
Римские цифры
Рабочие листы с римскими цифрами, включая преобразование римских цифр, упорядочивание римских цифр и завершение шаблонов римских цифр. Римские цифры — идеальная тема для учащихся 3-го, 4-го и 5-го классов, и эти рабочие листы дают возможность попрактиковаться как в чтении, так и в написании римских цифр, а также в базовых навыках восприятия чисел.
Римские цифры
Таблица римских цифр
Если вы пытаетесь научиться читать и писать римские цифры, пытаетесь найти причудливый способ записать год своего рождения, или если вам просто нужна «шпаргалка» для быстрой справки, каждая римских цифры Таблица с числами на этой странице поможет вам быстро освоить эту древнюю систему счисления.Все диаграммы печатаются на одной странице с версиями для 1-10, 1-100 и 1-1000 с правилами для римских цифр и без них. Пытаетесь понять, что должна означать эта странная римская цифра после Суперкубка? Ознакомьтесь с новой таблицей римских цифр Суперкубка!
Таблица римских цифр
Судоку
Судоку для детей и взрослых, включая легкие и сложные трудности, злые судоку, самурайские судоку и многое другое!
Судоку
Magic Square
Головоломки Magic Square — отличное введение в логику и решение задач… Попробуйте эти 3×3, 4×4 и 5×5, чтобы повысить свои математические навыки!
Магический квадрат
Головоломки с числовой сеткой
Этот раздел включает в себя рабочие листы математической логики в виде сетки, включающие сложение, вычитание, умножение и деление для разных классов и уровней навыков. Существуют версии этих логических головоломок с пропущенными числами, а также с пропущенными операциями.
Пазлы с числовой сеткой
Рабочие листы экспонентов
Вводит квадраты, кубы и экспоненты, смешанные с другими основными операциями.Включает практику, которая построит сайт-память общих экспоненциальных членов
Рабочие листы экспонентов
Рабочие листы для порядка операций
Базовая геометрия
Простая маркировка линий, углов и треугольников. Опознавательные формы
Базовая геометрия
Определение аналогового времени
Практические рабочие листы для определения времени аналоговых часов, включая чтение времени и рисование циферблатов.
Определение аналогового времени
Истекшее время аналогового сигнала
Рабочие таблицы, в которых сравниваются два аналоговых тактовых сигнала и определяется, сколько времени прошло между ними.
Аналоговое истекшее время
Больше и меньше
Практические рабочие листы для сравнения чисел. Эти рабочие листы содержат больше и меньше операций, сравнения и проверки на равенство для многозначных чисел, времени и многого другого!
Больше и меньше
Бумага для рукописного ввода
Шаблоны на бумаге для рукописного ввода с разной высотой линий, включая 3-строчную практическую бумагу с обычным и широким макетами, чистый лист для рассказов и обычную линованную бумагу для старшеклассников.Ознакомьтесь с пронумерованными пустыми шаблонами проверки правописания!
Бумага для рукописного ввода
Миллиметровая бумага
Миллиметровая бумага, сетка и точечная бумага для печати бесплатно для математических задач, поделок, зентанглинга, ландшафтного дизайна, архитектуры или просто рисования. Все стили миллиметровой бумаги включают дюймовые и сантиметровые вариации. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов.
Миллиметровая бумага
Координатная плоскость
Пустые координатные плоскости на этой странице включают варианты с метками на оси или на краю сетки, а также версии с метками квадрантов.Вы можете найти полные 4-х квадрантные координатные плоскости, а также только пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Координатная плоскость
Измерение в дюймах
Эти рабочие листы для измерения дюймов (обычных единиц) помогут развить навыки выполнения линейных измерений либо отдельной точки, либо измерения длины объекта. Существуют различные измерительные рабочие листы с задачами, подходящие для учеников детского сада, первого, второго или третьего класса математики.
Дюймы измерения
Метрические измерения
Таблицы метрических измерений для определения измеренных положений и измерения объектов в сантиметрах и миллиметрах на линейке. Эти рабочие листы являются отличной практикой для учеников первого, второго, третьего и четвертого классов, а также могут предоставить практическую практику вычитания при измерении длины предметов на линейке.
Метрические измерения
Преобразование единиц измерения в метрической системе СИ
В этих таблицах используются дроби единиц для преобразования значений единиц измерения из одного измерения в другое.Этот подход более распространен на уроках химии, физики или других естественных наук и требует от студентов сосредоточиться на отмене единиц, чтобы достичь решения с правильным значением и правильными единицами.
Преобразование единиц метрической системы СИ
Преобразование в обычные единицы
Практика преобразования обычных единиц измерения расстояния (дюймы в футы), объема (унции в галлоны) и массы (унции в фунты). В этих таблицах также используются дроби единиц для преобразования единиц измерения из одного измерения в другое.Этот подход более распространен на уроках химии, физики или других естественных наук и требует от студентов сосредоточиться на отмене единиц, чтобы достичь решения с правильным значением и правильными единицами.
Преобразование обычных единиц
Обычная и метрическая
В этих таблицах используются дробные единицы для преобразования значений между единицами СИ (метрическая) и обычными единицами. В этом разделе рассматривается практика преобразования дюймов в метры, литров в галлоны и граммов в фунты.
Обычные и метрические
Picture Math Division
В этих распечатываемых рабочих листах используются изображения и группировка для построения концептуального понимания деления, и они являются прекрасным первым введением в эту часто сбивающую с толку операцию. Эти рабочие листы начинаются с простых задач с изображением деления, когда для составления числовых предложений вычитания требуются только базовые навыки счета, но более поздние рабочие листы требуют, чтобы учащиеся создали аналогичную сеточную иллюстрацию, чтобы продемонстрировать свое понимание концепций деления, включая остатки.Это прекрасное первое знакомство с разделением для учащихся третьего или четвертого класса.
Математический отдел изображений
Деньги
Эти печатные денежные таблицы содержат реалистичные монеты и купюры в задачах для идентификации монет, внесения сдачи, подсчета монет, сравнения денежных сумм. Они развивают базовые навыки признания и счета в детском саду и в первом классе, чтобы подготовиться к полноценной денежной практике, необходимой для перехода во второй класс.
Деньги
Проверка математики космического корабля
Страницы проверки космического корабля (в комплекте с космическим кораблем!) Для отслеживания прогресса на листах математики космического корабля или ракетной математики для каждой из четырех основных операций.
Проверка математики космического корабля
Добавление цвета по номеру
Эти рабочие листы с дополнительными раскрасками требуют, чтобы учащиеся решали простые математические факты, чтобы найти правильный цвет, который нужно закрасить, чтобы показать картинку собственного творчества. Вы найдете постоянно растущий набор тематических страниц, посвященных праздникам и сезонам, которые я буду добавлять со временем … Почаще проверяйте обновления, или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Цвет сложения по номеру
Вычитание цвета по номеру
Эти рабочие листы для вычитания раскраски требуют от учащихся решить простые математические факты, чтобы найти правильный цвет, который нужно закрасить, чтобы показать картину своего собственного творчества.Вы найдете постоянно растущий набор тематических страниц, посвященных праздникам и сезонам, которые я буду добавлять со временем … Почаще проверяйте обновления, или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Вычитание цвета по номеру
Умножение цвета на число
Ищете рабочие листы, которые сделают изучение математики в День святого Валентина немного более увлекательным? На этой странице собраны рабочие листы для умножения цвета на числа, подходящие для учащихся третьего, четвертого или пятого классов.
Умножение цвета на число
Деление цвета по номеру
Ищете рабочие листы, которые сделают изучение математики в День святого Валентина немного более увлекательным? На этой странице собраны листы с цветным разделением чисел, подходящие для учащихся третьего, четвертого или пятого классов.
Цвет деления по номеру
День святого Валентина
Ищете рабочие листы, которые сделают изучение математики в День святого Валентина немного более увлекательным? На этой странице представлена коллекция цветных по номерам рабочих листов, подходящих для детей от детского сада до четвертого класса, включая операции сложения, вычитания, умножения и деления.Также есть сборник простых математических упражнений с забавными темами ко Дню святого Валентина.
День Святого Валентина
День Земли
Ищете рабочие листы, которые сделают изучение математики в День Земли немного более увлекательным? На этой странице представлена коллекция цветных по номерам рабочих листов, подходящих для детей от детского сада до четвертого класса, включая операции сложения, вычитания, умножения и деления. Также есть сборник простых математических упражнений с забавными темами, посвященными Дню Земли.
день Земли
ул.Patrick’s Day
Когда дело доходит до математики, вы не можете полагаться исключительно на удачу ирландцев, но этот День святого Патрика делает его немного веселее! На этой странице представлена коллекция цветных по номерам рабочих листов, подходящих для детей от детского сада до четвертого класса, включая операции сложения, вычитания, умножения и деления. Есть также сборник простых математических упражнений с забавными темами трилистника Дня Святого Патрика.
День Святого Патрика
Весна
Какое лучшее время года, чтобы начать развивать новые математические навыки, чем Весна! На этой странице представлена коллекция цветных по номерам рабочих листов, подходящих для детей от детского сада до четвертого класса, включая операции сложения, вычитания, умножения и деления.Существует также коллекция простых весенних математических листов с забавными весенними цветочными темами, а также таблица умножения, диаграмма сотен, миллиметровая бумага и координатная плоскость!
Весна
Диаграмма квадратного корня
Если вы ищете список точных квадратных корней или полную таблицу квадратных корней от 1 до 100, таблица квадратного корня с этой страницы поможет вам найти радикалы! Существуют как цветные, так и черно-белые версии диаграмм в формате PDF для печати.
Диаграмма квадратного корня
Диаграмма дробей
В этом уникальном отображении эквивалентных дробей значения дробей объединяются в числовой прямой для создания элегантной симметрии. Он не только выделяет дроби в их наименьшей, наиболее сокращенной форме, но и обеспечивает удобный десятичный эквивалент для наиболее часто используемых дробей. Это действительно одна из лучших справочных таблиц, которые я создал за 10 лет создания математических ресурсов!
График фракций
Пазлы для поиска слов
Используйте эти математические головоломки для поиска слов, чтобы познакомить школьников со словарем и терминами с новыми математическими концепциями! Эти головоломки для поиска слов включают наборы для различных уровней обучения Common Core, а также конкретные темы по геометрии, алгебре и многому другому!
Пазлы с поиском слов
Диаграмма вероятности
Диаграмма привязки вероятности для справки о проблеме Word! На этой иллюстрированной таблице описаны сценарии с монетами, игральными костями и игральными картами.Он включает в себя шансы на наиболее вероятный и наименее вероятный исход.
Диаграмма вероятности
Таблица измерений
Эта таблица измерений является хорошим справочным пособием при решении проблем со словами, связанных с преобразованием единиц объема, длины или температуры из одной системы в другую. Значения отображаются на одной шкале как в обычной, так и в метрической системе. Отлично подходит для измерения на кухне и приготовления пищи!
Таблица измерений
Числовая строка
Числовая строка может быть мощным инструментом для изучения отрицательных чисел, соотношений или просто вводных операций сложения и вычитания.PDF-файлы числовых линий на этой странице включают различные диапазоны (10, 12, 15, 20, 15 и 100) как начиная с нуля, так и с отрицательными диапазонами. Полный набор линий с дробными числами, отмеченных общими знаменателями, входит в диапазоны от -5 до 5. Существуют также числовые строки для конкретных приложений для истекшего времени, температуры и денег, а также пустые числовые строки для обычных диапазонов и дробей.
Числовая строка
Рабочие листы по математике для четвертого класса
Четвертый класс — это переходный этап, на котором акцент смещается с многих основных математических фактов на приложения.По-прежнему уделяется большое внимание более сложной арифметике, такой как задачи деления в столбик и длинное умножение, и в этом разделе вы найдете множество математических листов по этим темам. В этом наборе рабочих листов 4-го класса есть больше рабочих листов с дробями, включая сокращение и сравнение дробей, а также обязательно ознакомьтесь с Калькулятором дробей, который предоставит много помощи при решении задач с дробями. Проценты — еще одна тема, которую изучают в 4-м классе, и рабочие листы с процентным соотношением в этом разделе могут быть решены с помощью калькулятора процентов, если у учащихся возникают проблемы с решением этих задач.Учащиеся также будут использовать многие из своих базовых математических навыков для преобразования единиц измерения в 4-м классе, и в этом разделе вы также найдете рабочие листы для преобразования единиц измерения и обычных единиц.
Рабочие листы по уравнениям
Рабочие листы с одношаговым уравнением
Этот набор рабочих листов требует от студентов решения одношаговых уравнений, включающих целые числа, дроби и десятичные дроби, путем выполнения операций сложения, вычитания, умножения или деления. Он также содержит математические загадки, определение стоимости предметов, перевод фраз в одношаговое уравнение и многое другое.
Рабочие листы с двухэтапными уравнениями
Щелкните ссылку, чтобы получить доступ к эксклюзивным рабочим таблицам по решению двухэтапных уравнений, которые включают целые числа, дроби и десятичные дроби. Ряд MCQ, уравнения в геометрии, перевод двухэтапных уравнений и многие другие упражнения доступны для практики.
Рабочие листы с многоступенчатыми уравнениями
Эти рабочие листы требуют от учащихся выполнить несколько шагов для решения уравнений. Используйте знания, полученные при решении одношаговых и двухэтапных уравнений, чтобы решить эти многоступенчатые уравнения.Сюда также включен ряд прикладных задач, основанных на геометрических формах.
Рабочие листы задач по формулам
Загрузите и распечатайте эту огромную коллекцию одношаговых, двухэтапных и многошаговых задач по уравнениям со словами, которые включают целые числа, дроби и десятичные дроби. Рабочие листы MCQ представляют собой идеальный инструмент для изучения восприятия учащимся темы.
Рабочие листы перестановки уравнений
Рабочие листы с буквенными уравнениями помогают отточить навыки, такие как перестановка буквальных уравнений, перегруппировка и оценка, включены текстовые задачи, содержащие реальные приложения, и многое другое.
Уравнение рабочего листа
Щелкните здесь, чтобы просмотреть таблицы по уравнению линии. Напишите уравнение прямой в стандартной форме, двухточечной форме, форме с пересечением и углом наклона. Загрузите полный набор рабочих листов по уравнению линии, которые также включают рабочие листы по параллельным и перпендикулярным линиям.
Таблицы построения графиков линейных уравнений
Вы всего в одном клике от огромной коллекции рабочих листов по построению графиков линейных уравнений.Постройте точки и нанесите линию на график. Используйте значения x, чтобы заполнить таблицы функций и построить график линии. Рабочие листы MCQ представляют собой идеальный инструмент для проверки знаний учащихся по этой теме.
Рабочие листы по квадратному уравнению
Щелкните ссылку, чтобы просмотреть обширный набор рабочих листов по квадратным уравнениям. Решите квадратные уравнения, разложив на множители, заполнив квадратные, квадратные формулы или методы извлечения квадратного корня. Найдите сумму и произведение корней. Проанализируйте природу корней.
Рабочие листы уравнения абсолютного значения
Используйте эти рабочие листы, чтобы научить своих студентов абсолютному значению целых чисел. Этот модуль включает в себя такие упражнения, как вычисление выражения абсолютного значения для определенного значения, таблицы ввода и вывода, построение графика функции абсолютного значения и решение различных типов уравнений абсолютного значения.
Рабочие листы систем уравнений
Решите эти системы уравнений методом исключения или замены. Уравнения содержат две или три переменные.Уравнение с двумя переменными представляет собой прямые линии, тогда как уравнения с тремя переменными представляют собой плоскость.
Задачи по математике для KidZone
[Оценка 1]
[Оценка
2]
[Класс 3]
[Оценка
4]
[5 класс]
Введение:
Задачи Word отсортированы по классам, а внутри каждой оценки — по
тема. Я всегда нахожу, что предоставление сезонного рабочего листа помогает сохранить мои
дочь взволнована своей работой.
Уровни обучения являются ориентировочными — пожалуйста, используйте свой
суждение, основанное на способностях и стремлении вашего ребенка (моя старшая дочь
всегда использовала оценку ниже, тогда как моя младшая дочь кажется оценкой
или два выше — иди разбери).Имейте в виду, что задачи по математике со словами
требуются навыки чтения, понимания и математики, чтобы ребенок, хорошо разбирающийся в
основные математические уравнения могут оказаться труднее, чем вы ожидаете, столкнувшись с
с математическими задачами со словом.
Все задачи со словами
динамические (другими словами, они создают новую проблему каждый раз, когда вы их открываете
или нажмите «Обновить» в своем браузере). Слова в частном
проблема не изменится, но цифры изменятся. Дети, которые борются
преобразование словесной задачи в математическое уравнение будет обнадеживающим
(создание уверенности), чтобы снова обратиться к одним и тем же словесным подсказкам с разными
числа, поэтому рассмотрите возможность печати пары повторений каждой проблемы.
В классе вы можете создать проблему для партнеров или группы
ученики решают вместе, а затем воссоздают то же самое
проблема для детей делать соло.
Со старшей дочкой однажды я понял, насколько она
боролся с математикой, когда ее нельзя было записать в красивом аккуратном уравнении, я
часто решали с ней математическую задачу (выполняя большую часть работы
я), а затем предоставил ей несколько повторений той же проблемы с
разные числа для нее, чтобы сделать соло.Через несколько недель она
смог сделать их без прохождения от мамы. Она одна из
те ребята, которые говорят: «Это слишком сложно!» довольно быстро так
укрепление уверенности важно — если она думает, что не может что-то сделать
она не может — если она думает, что может сделать что-то, что может. Теперь как сделать
Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? * смеяться *
Общие задачи со словами для класса 1
— Мешки с фасолью
— Ведра
— Собачьи кости
— Время в школу (рисунок
предложения)Тематические задания на слова для 1 класса
Примечание:
проблема возникает с новыми числами каждый раз, когда вы нажимаете
Задачи 2 степени со словами
Тематические задачи со словами для 2 класса
Примечание:
проблема возникает с новыми числами каждый раз, когда вы нажимаете
Задачи со словами 3-й степени
Тематические задания на слова для 3 класса
Примечание:
проблема возникает с новыми числами каждый раз, когда вы нажимаете
Задачи со словами для 4-й степени
Тематические задачи со словами для 4 класса
Примечание:
проблема возникает с новыми числами каждый раз, когда вы нажимаете
Задачи 5-го класса со словами
Тематические задачи со словами для 5 класса
Примечание:
проблема возникает с новыми числами каждый раз, когда вы нажимаете
Уравнения и выражения для 4-го класса по математике
Изучение уравнений и выражений для 4-го класса является важной прелюдией к изучению алгебры в более поздних классах.Уравнения и выражения обычно пишутся вместе с задачами со словами и не имеют переменных, которые вы обычно увидите в более поздних классах. Используйте приведенные ниже образцы в качестве моделей, чтобы задавать вопросы дома.
Какие советы по решению выражений и уравнений четвертого класса?
Часто для решения задач 4-го класса требуется несколько шагов. Поскольку четвероклассники знакомы со сложением, вычитанием, умножением и делением, ваш ребенок должен ожидать, что все четыре операции будут включены в вопросы.Используя подсказки из словесной проблемы, учащиеся могут составить уравнение, которое отражает проблему. Рассмотрим следующий пример.
Лаура зарабатывает 3 доллара в день за мытье посуды. Майк зарабатывает 4 доллара в день за уборку дома пылесосом. Какова общая сумма, которую зарабатывают Майк и Лора, если каждый из них выполняет свою работу по пять дней подряд?
Чтобы решить эту задачу, ваш ребенок должен придумать уравнение, которое выглядит следующим образом: 3 x 5 + 4 x 5. Учащиеся начнут решать эту задачу с вычисления заработка Лауры (3 x 5 = 15) и заработка Майка (4 x 5 = 20).Затем, поскольку в вопросе учащиеся должны найти общий заработок Лоры и Майка, эти две суммы складываются. Используя это уравнение, ваш ребенок обнаружит, что Лора и Майк заработали всего 35 долларов.
Задачи со словом, требующие от учащихся составить уравнения, являются сложными, поскольку содержат комбинацию математических операций. В приведенном выше примере требовалось два набора задач умножения, а также сложение. Когда ваша дочь решает задачу со словами дома, убедитесь, что она показывает свою работу для каждого шага, чтобы вы могли определить, какой шаг вызвал наибольшие трудности.
Проблемы Word с несколькими шагами
Умножение
Джорджия купила три розы по 2 доллара каждая, четыре лилии по 1 доллару каждая и одну ромашку по 3 доллара. Затем по дороге домой она теряет 5 долларов, и у нее не остается денег. С каких денег начиналась Грузия?
Ваш сын может столкнуться с этой проблемой, потому что она требует длинного уравнения с несколькими шагами и критического мышления. В виде уравнения решение будет выглядеть следующим образом: (3 x 2) + (4 x 1) + 3 + 5. Однако, поскольку это может быть непосильно для четвероклассника, разбейте его на шаги.
Ему следует начать с умножения, чтобы вычислить, сколько будет стоить каждый тип цветка. Розы стоят 6 долларов, лилии — 4 доллара, ромашка — 3 доллара. В результате уравнение упростится и будет выглядеть так: 6 + 4 + 3. Однако ему нужно помнить, что Джорджия потеряла 5 долларов по дороге домой, поэтому добавьте еще пять в уравнение: 6 + 4 + 3 + 5 = 18. Разбив задачу на этапы, ваш сын обнаружит, что Грузия начиналась с 18 долларов.
Дивизион
Майк получает 3 доллара в неделю.Он хочет купить три комикса по 2 доллара каждый и роман по 9 долларов. Сколько недель потребуется Майку, чтобы накопить достаточно денег?
Для решения этой задачи требуются как умножение, так и деление. Начните с умножения, чтобы выяснить, сколько вообще будут стоить комиксы и роман. Уравнение должно выглядеть так: 2 x 3 + 9 = 15.


