звенья, вершины, длина. Замкнутая ломаная

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки  AB,  BC,  CD  и  DE  — это звенья ломаной. Точки  A,  B,  C,  D  и  E  — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная  ABCDE  или ломаная  EDCBA.

Замкнутая и незамкнутая ломаная

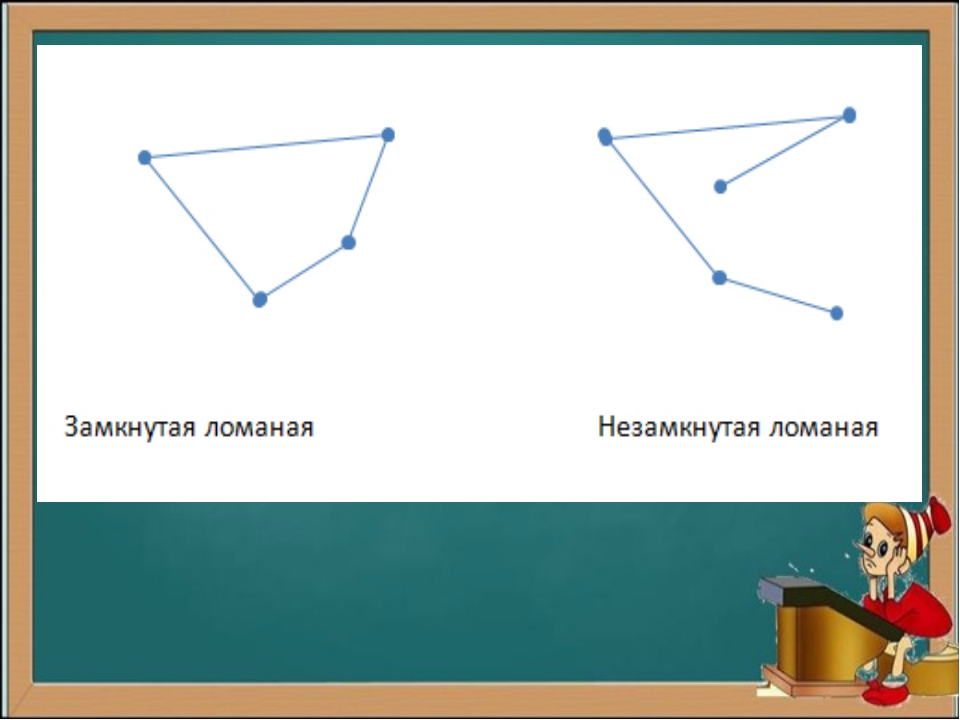
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная  ABCD.

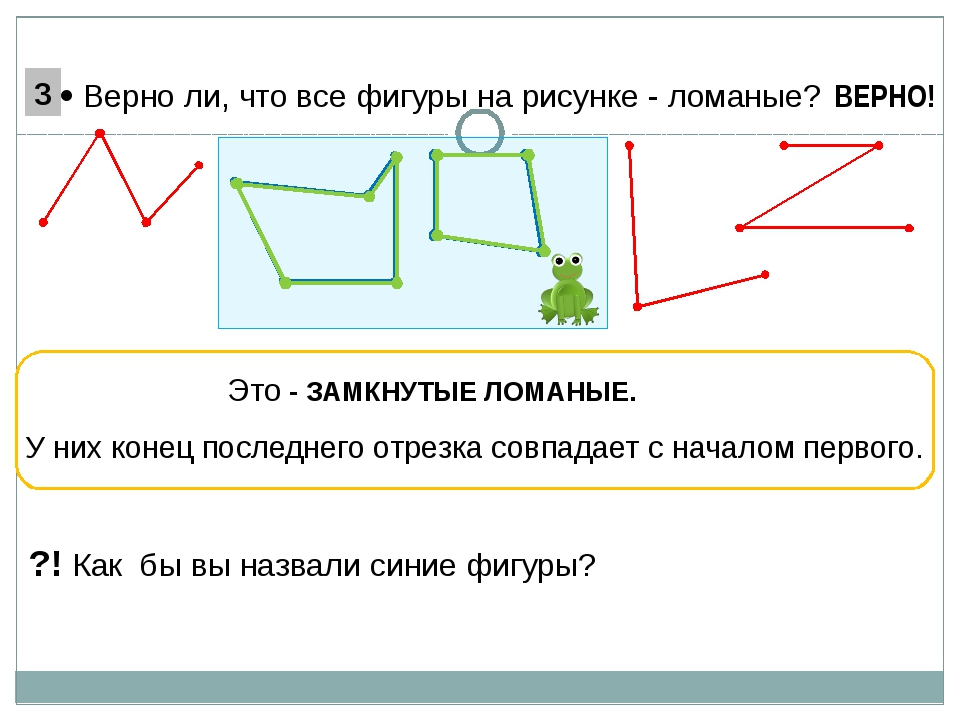
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная  ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки  F,  T,  K  — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник  ABCDE.

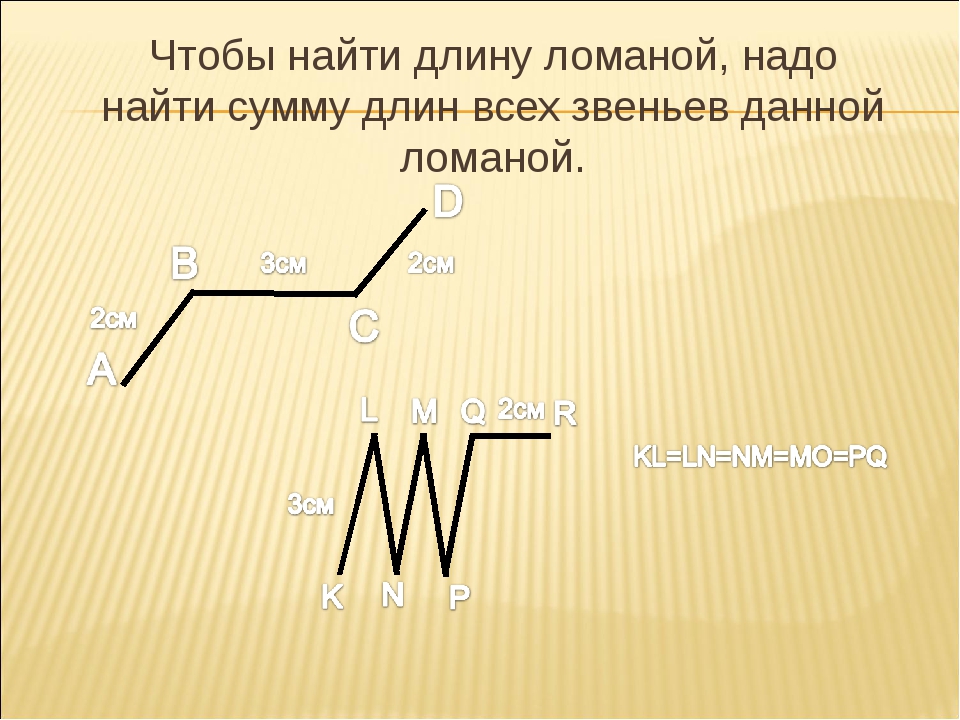
Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.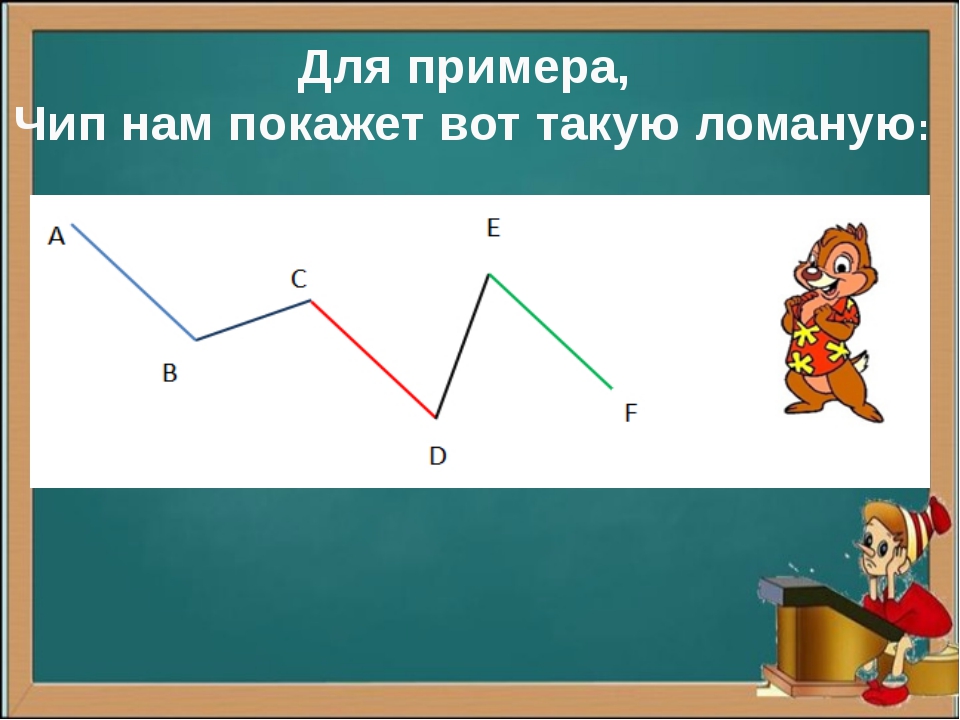

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной   ABCD  будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной  ABCD  равна  9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =

3 см + 5 см + 4 см + 5 см = 17 см.

Ответ:  17 см.

Урок 13. длина ломаной. закрепление — Математика — 2 класс

Математика, 2 класс. Урок №13.

Длина ломаной. Закрепление

Перечень вопросов, рассматриваемых в теме:

— Как найти длину ломаной?

Глоссарий по теме:

Ломаная — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.

Звенья — отрезки, из которых состоит ломаная.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина ломаной – это сумма длин всех её звеньев.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35

2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 — с.20, 21

3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 — с.20, 21, 25

Теоретический материал для самостоятельного изучения

На рисунке мы видим ломаную линию, состоящую из трёх звеньев.

Как найти длину ломаной линии? Это можно сделать двумя способами.

Первый способ. Сначала узнаем длину каждого звена с помощью линейки

Длина первого звена 4 см.

Длина второго звена 6 см.

Длина третьего звена 5 см.

Найдем сумму этих длин.

4+6+5=15 (см)

Найдем длину ломаной вторым способом.

Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.

Накладываем циркуль на второй отрезок, переносим его на прямую.

Накладываем циркуль на третий отрезок, переносим его на прямую.

Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.

Выводы: длину ломаной можно находить двумя способами.

Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.

Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка.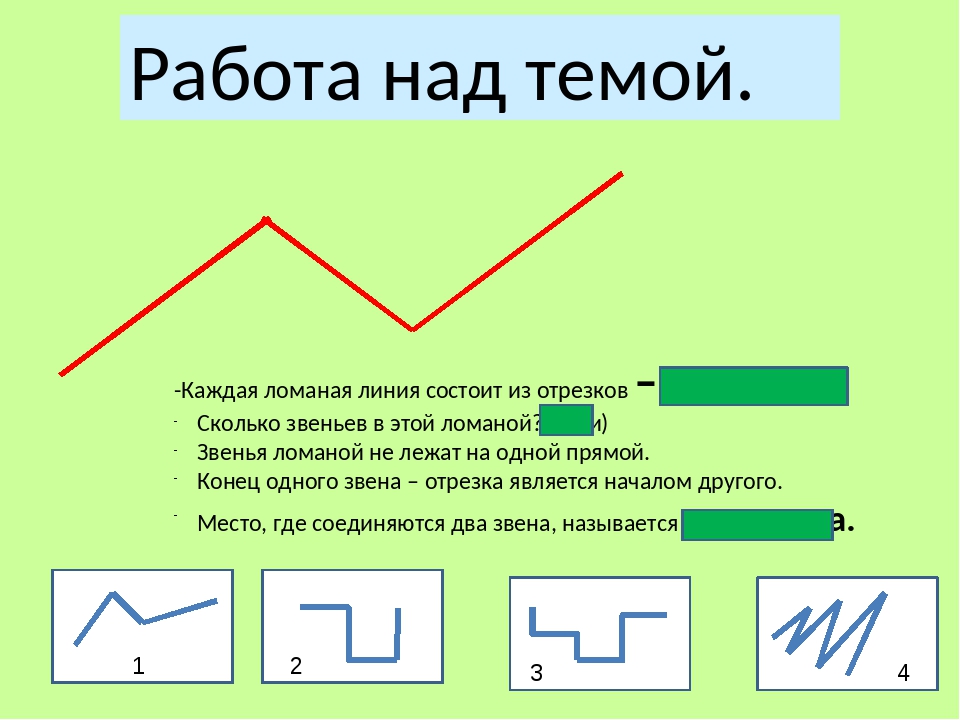 Это и будет длина всей ломаной.

Тренировочные задания.

1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см

Варианты ответов:

10 см 8 см 7 см

Правильный вариант:

10 см 8 см 7 см

2. Расположите ломаные линии по порядку: от самой короткой до самой длинной

Правильный вариант: Найдем длину каждой ломаной

6 + 2 + 2 = 10 см

7 + 5 = 12 см

2 + 1 + 3 +2 = 8 см

3 + 1 + 5 = 9 см

Расставим в порядке возрастания:

2 + 1 + 3 + 2 = 8 см

3 + 1 + 5 = 9 см

6 + 2 + 2 = 10 см

7 + 5 = 12 см

Урок математики 1 класс «Ломаная линия»

Класс: 1г класс

Тема урока: «Ломаная линия»

Тип урока: урок-исследование объекта и понятия.

Цель урока: развитие основных видов универсальных учебных действий через знакомство с

понятиями: ломаная линия, звенья ломаной линии, вершины ломаной линии.
Формируемые в рамках урока универсальные учебные действия
личностные:
•развитие логического мышления, пространственного воображения, внимания, памяти, фантазии
регулятивные:
•целеполагание в постановке учебной темы и задачи на основе соотнесения того, что уже

известно и усвоено, и того, что ещё неизвестно
•планирование — определение последовательности промежуточных целей с учётом конечного

результата

составление плана и последовательности действий
познавательные:
• выделение и формулирование познавательной цели с помощью учителя
•совершенствование математической речи
•решение рабочих задач с использованием ИКТ (ломаная линия и её виды)
•повторение понятий: отрезок, прямая линия, луч.
коммуникативные:
•развивать умение слушать и вступать в диалог
•участвовать в коллективном обсуждении проблем
Материалы и оборудование: компьютер, интерактивная доска, учебник, карандаши, линейки, счетные палочки, звездочка для рефлексии, таблички со словами (незамкнутая, замкнутая, звено, ломаная), таблички с примерами, таблички с отрезками, лучами, прямыми , ломаной
Методы работы: объяснительно – иллюстративные, частично – поисковые, словесные, наглядные, практические.
Ожидаемый результат:
•знать что такое ломаная линия, из чего она состоит, чем отличается от прямой, луча, отрезка
•знать чем отличается замкнутая ломаная от незамкнутой ломаной линии
•повышение активности учащихся на уроках для улучшения результатов обучения;
•использование учащимися приобретённых знаний и умений в практической деятельности и повседневной жизни
•обогащение математического словарного запаса

Ход урока

I. Мотивация к учебной деятельности.
  Будем вместе развивать

  Качество – внимательность.

 А поможет всё узнать

 Наша любознательность.

II. Актуализация знаний
1.- Сегодня к нам пришла в гости Точка (Рисунок Точки). Она приглашает нас в путешествие. А в какую страну вы узнаете, переставив карточки в порядке убывания чисел.
(Дети на ИКТ-доске расставляют числа, а вместе с ними перемещаются и буквы. Получилось слово Геометрия.)

т о Г я р м е и е
4 7 9 1 3 6 8 2 5

Геометрия – наука очень интересная,
Много нового она в себе таит,
Языком углов и линий говорит.
Что нам встретится в пути — вовсе неизвестно
И поэтому идти очень интересно.

— А чтобы веселее было идти, давайте решим задачи :

1. В лесную школу на урок

 Бежал, запыхавшись, щенок.

За ним две белки и трое котят –

Они учиться все хотят.

Я прошу вас, не ленитесь,

Сосчитать их потрудитесь. (6)

2. Шла овчарка по дорожке,

У неё четыре ножки.

Ей навстречу – чёрный дог.

Сколько всех собачьих ног? (8)

3. Сёстры – белочки сидели

Вшестером в дупле на ели.

К ним ещё одна примчалась –

От дождя она спасалась.

Все теперь сидят в тепле.

Сколько белочек в дупле? (7)
 

III. Создание проблемной ситуации
1. На пути нам встретился город.
— Мы узнаем, в какой город мы попали, решив примеры и расколдовав буквы.
— Прочитайте выражения и найдите их значение
4-1 (Л)              1+1 (и)
3+2 (и)              5-4 (я)
2+2 (н)
— Как же называется город? (- Город Линий)

2.Работа в группах.
— Нам надо узнать, как называются улицы в этом городе.
-Точка предлагает нам поработать в парах.
-Давайте вспомним правила работы в парах.
— Работать дружно, не ссориться, помогать друг другу.
Не смеяться над неправильным ответом.
Говорить негромко, вежливо.

У  на каждой парте столе лежит карточка с заданием, на каждом листочке линии.

— Повернитесь друг к другу, рассмотрите карточки.
-Какое задание нужно выполнить?
( — Разделить линии на группы.)
— Разделите. (Дети выполняют группировку с обсуждением в группе)
Проверка.
— Какие группы у вас получились?
( Отрезки, лучи и прямые.)
— Как называются улицы в городе Линий? (Назовите известные вам линии.)
( -Отрезок, луч, прямая)

1 ряд назовите прямые линии-2, 8

— Что вы знаете о прямой линии? (-Линия, у которой нет начала и конца. Она бесконечна, не имеет границ, т.е. её можно продолжить в любую сторону)
 

2ряд назовите лучи- 1,3

— Что такое луч? ( — Луч — это часть прямой линии, ограниченная с одной стороны)

3ряд назовите отрезки- 6,4

— Что такое отрезок? (-Отрезок — это часть прямой линии, ограниченная с двух сторон)
 

3. Формулирование темы урока
-Закройте глазки и представьте себе город Линий. Как вы думаете все ли улицы в этом городе мы назвали? (- Нет, не все. Есть и другие  линии.)
 

-Какую еще группу мы не назвали?  (Кривая линия)
— Что вы знаете про эту линию? (Для изображения этой линии не нужна линейка)
 

-Сегодня на уроке мы будем наблюдать за новым видом линий , займёмся исследованием, совершим маленькие «открытия» и, надеюсь, ответим на многие ваши вопросы.
Про эту линию точка хочет рассказать нам интересную историю.

 «Однажды я гуляла на волшебной поляне. Солнышко светило ярко-ярко. Мне захотелось побегать и попрыгать. Но вдруг я обо что-то споткнулась и  упала. Я наклонилась и увидела у себя под ногами вот эту веточку. Я взяла её в руки и увидела, что она сломалась.

-Какая интересная линия! — подумала я.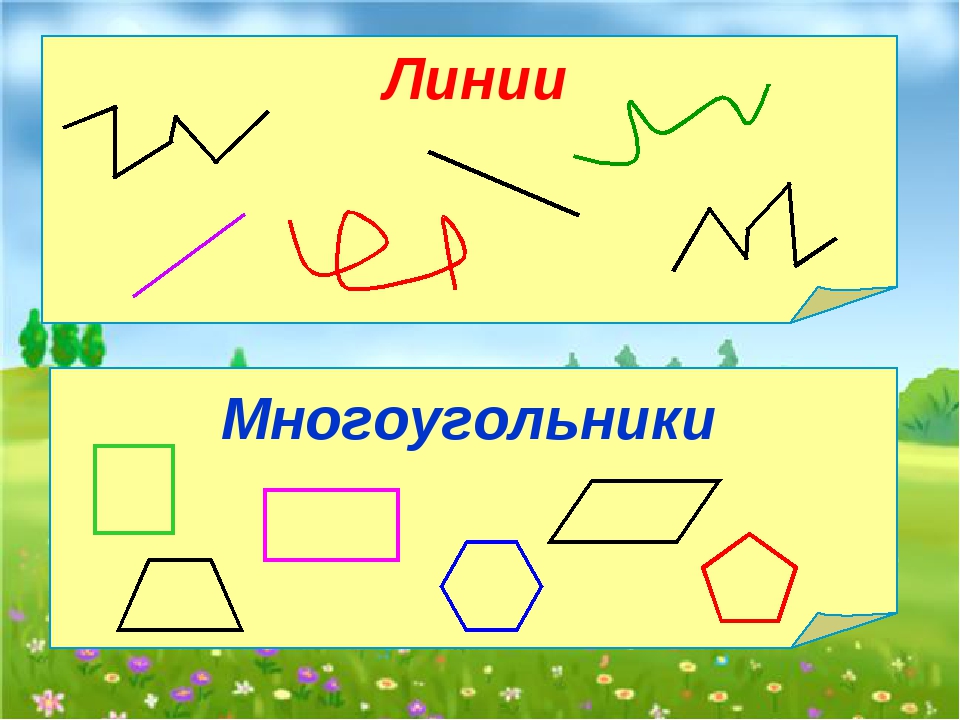 Она была прямая, а стала…»

— Как можно назвать эту линию?(Ломаная, незамкнутая)
— Определите тему нашего урока .(Ломаная линия)
— Проверьте свои предположения.

 Прочитайте тему урока на с.38 учебника.
— На какой вопрос ответили? (-Как называется эта линия.)

IV. Открытие новых знаний

1. Исследование ломаной линии путём практической работы.
— Попробуем сконструировать ломаную линию
– Возьмите в руки столько палочек, сколько раз я хлопну в ладоши (5 раз).
— Девочки убавьте одну палочку.
— Сколько палочек у мальчиков?(5) У девочек?(4)
— Постройте свою ломаную линию.
— Проверьте работу в парах друг у друга и помогите, если у кого-то не получилось.

–Кому понравились работы? Действительно, много интересных и разных ломаных!
– Сколько палочек использовали мальчики?
— Сколько палочек использовали девочки?

— Что интересного заметили, моделируя линию:
— Из чего состоит ломаная линия? (-Из отрезков. )
— Как соединяются отрезки? (-Концами)
— Как следуют? (-Последовательно друг за другом.)

Вывод: точное название линии «ломаная линия». Она состоит из отрезков, которые последовательно идут друг за другом.

В городе Линий нам встретилась бабочка, она рада нас видеть в гостях.

Ну а сейчас отдохнем вместе с ней.

Физкультминутка

2. — Когда отрезки становятся частью ломаной, у них появляется другое название. Хотите его узнать?

— Как же узнать название частей ломаной? (Спросить у учителя)
— (Части ломаной называются звеньям ломаной)
–Скажем слово вслух: «звено», много «звеньев».
– Показываю табличку «Звено».
— Сколько звеньев у нашей ломаной? (4 звена)
— На что похожа наша ломаная? (-На гору)
— Как бы вы назвали эту точку? (Учитель показывает на вершину ломаной и уточняет, что это вершина, как у горы. )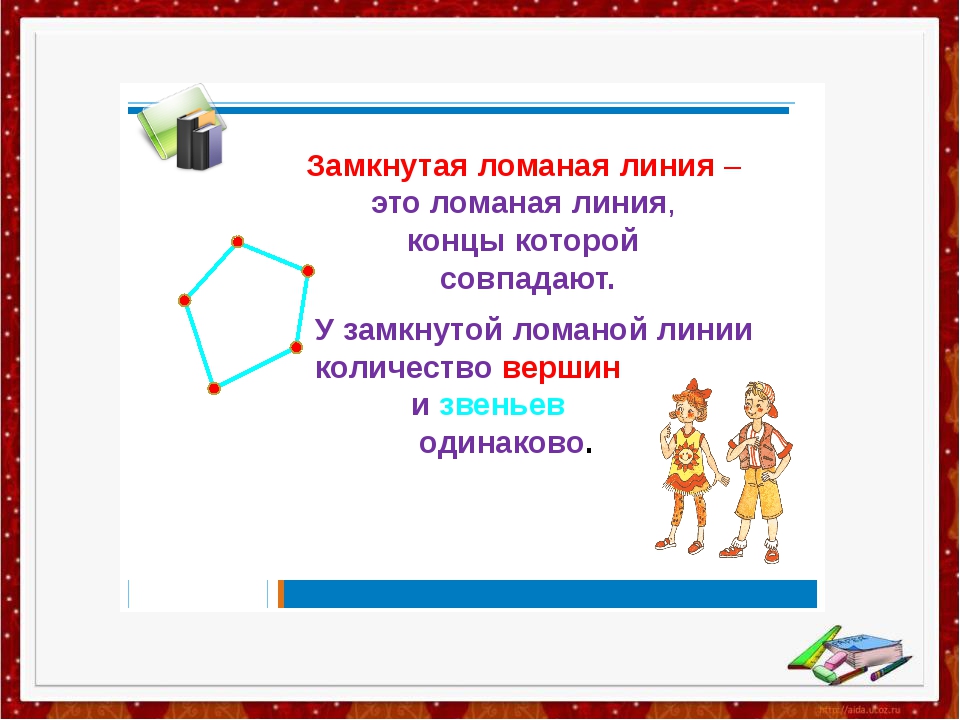

— Вершины – это точки, где соединяются звенья.
— Сколько вершин у ломаной? (3)

4. — Название линии знаем, конструировать умеем, из каких частей состоит тоже знаем. А какое важное умение нам предстоит освоить?
(-Научиться чертить ломаную линию).
-С чего можно начать построение ломаной линии?(- Поставить точки.)
-Точки у вас в тетради уже есть. Стр.

-Что надо делать дальше? (-Соединить их.)
-Как соединить? (-Конец соединить с началом.)
-Какой инструмент нам понадобится? Чем будем чертить?(-Линейка, карандаш.)
-Начертите. (Дети чертят ломаную в учебнике.)
 

— Расскажите план построения ломаной.
•Поставить точки – вершины
•Последовательно их соединить
•Дать вершинам название

-Где можно увидеть ломаную линию? (Дети рассматривают рисунки и изображения, макеты домов.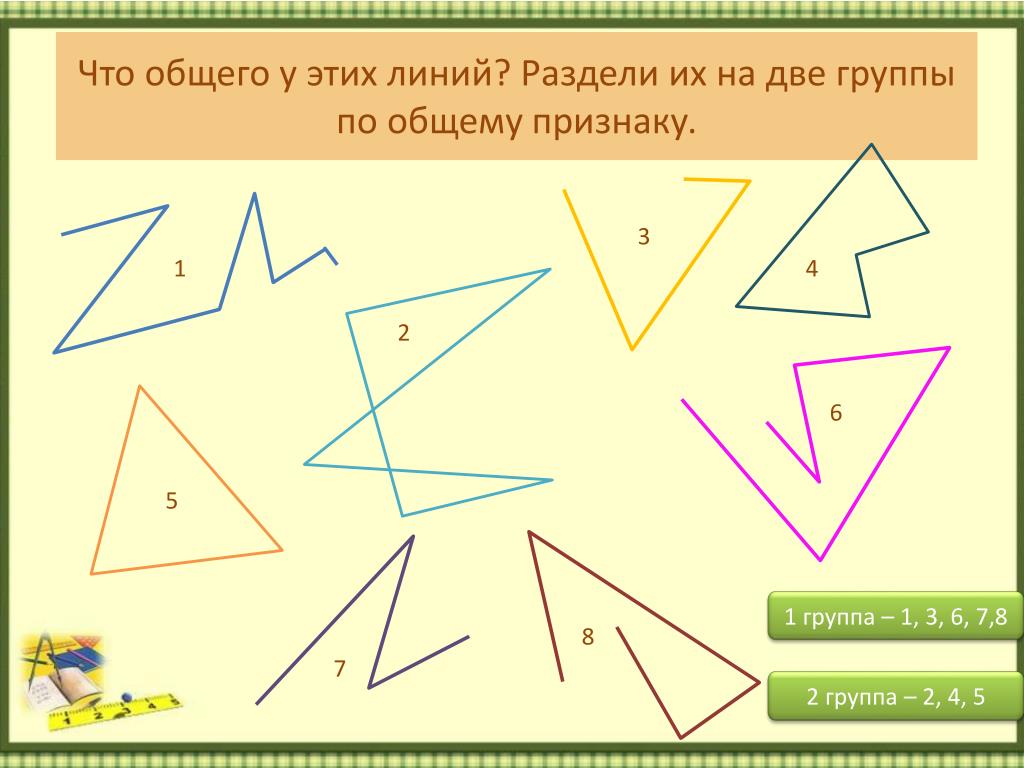 крыш:
-Вершины гор, крыши домов и др.)

Найдите на рисунке в учебнике ломаные линии

5. Виды ломаных
-Рассмотрите ломаные в учебнике . Какие бывают ломаные? (-Замкнутые и незамкнутые ломаные линии)
-Чем отличается замкнутая ломаная от незамкнутой?
-Приведите пример замкнутой ломаной линии. Где мы с ними встречаемся? (-Геометрические фигуры)

V. Обобщение знаний
-О каких линиях говорили? (-О ломаных. О кривых.)
-Из чего ломаные линии состоят?
-Как называется часть ломаной линии?
-Какие ломаные существуют?
-Все ли загадки ломаной линии мы разгадали? (-Нет)

-Ломаная линия таит в себе еще много загадок, а разгадывать мы их будем на наших следующих уроках.

Нам пора возвращаться обратно из путешествия. Вам понравилось?

VI. Рефлексия
-Кому на уроке было трудно? (учитель тоже поднимает руку)
-Кому было легко?
-Мы очень хорошо работали, и Точка прислала вам сюрприз.
-Это ваша награда за хорошую работу- «Орден Звездочки». Его получит каждый.

 Но вот загадка: -почему орден звездочки? (- Контур звездочки — это замкнутая ломаная линия)

Кто понял новый материал, и кому было интересно на уроке, тот раскрасит звездочку красным цветом, а кому было не очень интересно -синим цветом.

Покажите ваши ордена.

Оценка работы

Начало формы 

Урок по теме «Ломаная линия». 1-й класс

Цель: развитие основных видов универсальных учебных действий через
знакомство с понятиями: ломаная линия, звенья ломаной линии, вершины ломаной
линии.

Материалы и оборудование: компьютер, интерактивная доска, учебник,
карандаши, линейки, счетные палочки, звездочка для рефлексии, таблички со
словами (незамкнутая, замкнутая, звено, ломаная), таблички с примерами, таблички
с отрезками, лучами, прямыми, ломаной

Методы работы: объяснительно-иллюстративные, частично-поисковые,
словесные, наглядные, практические.

Тип урока: ОНЗ (открытие нового знания)

Система учебников «Перспектива», 1 класс. Автор учебника Л.Г.Петерсон.

Ожидаемый результат:

• знать, что такое ломаная линия, из чего она состоит, чем отличается от
  прямой, луча, отрезка;
• знать, чем отличается замкнутая ломаная от незамкнутой ломаной линии;
• повышение активности учащихся на уроках для улучшения результатов
  обучения;
• использование учащимися приобретённых знаний и умений в практической
  деятельности и повседневной жизни;
• обогащение математического словарного запаса.

Ход урока

I. Организационный момент

Проверка готовности к уроку.

– Кто готов показать, как умеем работать?

– Давайте улыбнемся друг другу. Пусть сегодняшний урок принесет нам всем
радость общения.

– На уроке, ребята, вас ожидает много интересных заданий, новых открытий, а
кто и что же помогут вам сделать эти открытия?

У: Внимание, находчивость, смекалка, учитель, дружное сотрудничество…

II. Актуализация знаний

1.– Сегодня к нам пришла в гости Точка (Рисунок Точки). Она приглашает нас в
путешествие. А в какую страну, вы узнаете, переставив карточки в порядке
убывания чисел

(Дети на ИКТ-доске расставляют числа, а вместе с ними перемещаются и буквы.
Получилось слово Геометрия.)

т о Г я р м е и е

Приложение 1>

4 7 9 1 3 6 8 2 5

Геометрия – наука очень интересная,

Треугольник, круг, квадрат уже известны вам.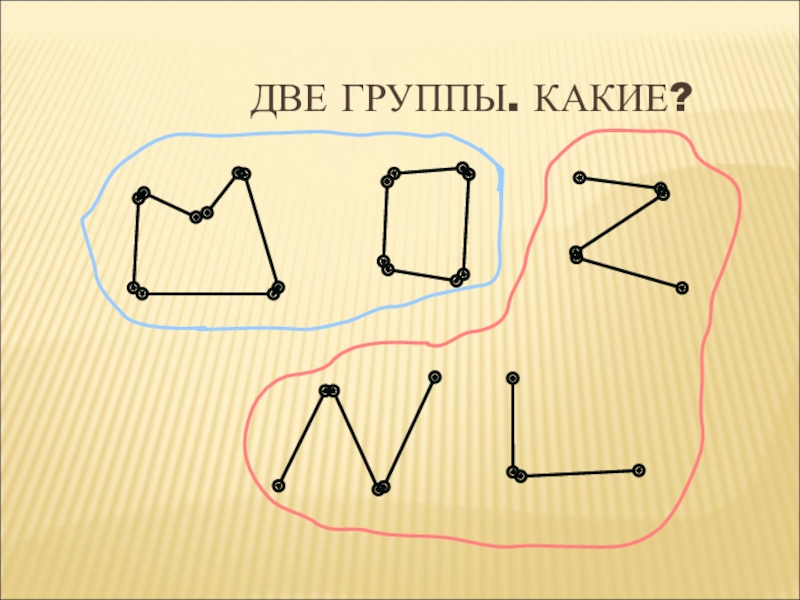

Много нового она в себе таит,

Языком углов и линий говорит.

Что нам встретится в пути – вовсе неизвестно,

И поэтому идти очень интересно.

– А чтобы веселее было идти, давайте посчитаем двойками.

– Где нам может пригодиться знание счета «2»? (Когда считаемся парами)

Счет двойками

2. – Но, чтобы запомнить все, что мы там увидим, надо быть очень внимательным
и наблюдательным. Поэтому сначала потренируем внимание и зрительную память.
Запомните, что увидите (рисунок на доске закрывается)

– Что объединяет все рисунки ? (Это геометрические фигуры) <Приложение
5>

– Какая фигура отличается от других? (Круг, шестиугольник)

– Каким по счету был 6-угольник? (пятый)

– Назовите 1 фигуру, 3-ю (Треугольник, круг)

– Назовите весь ряд.

Открывается изображение на доске.

– Какая фигура лишняя? Почему?

– Точка очень любопытна, она интересуется, правда ли, что:

– Некоторые фигуры – треугольники (покажи)

– Все фигуры-треугольники (докажи)

– Каждая фигура является квадратом (докажи)

– Некоторые фигуры-прямоугольники (покажи)

– Есть фигуры, у которых углов больше 3 (докажи)

III.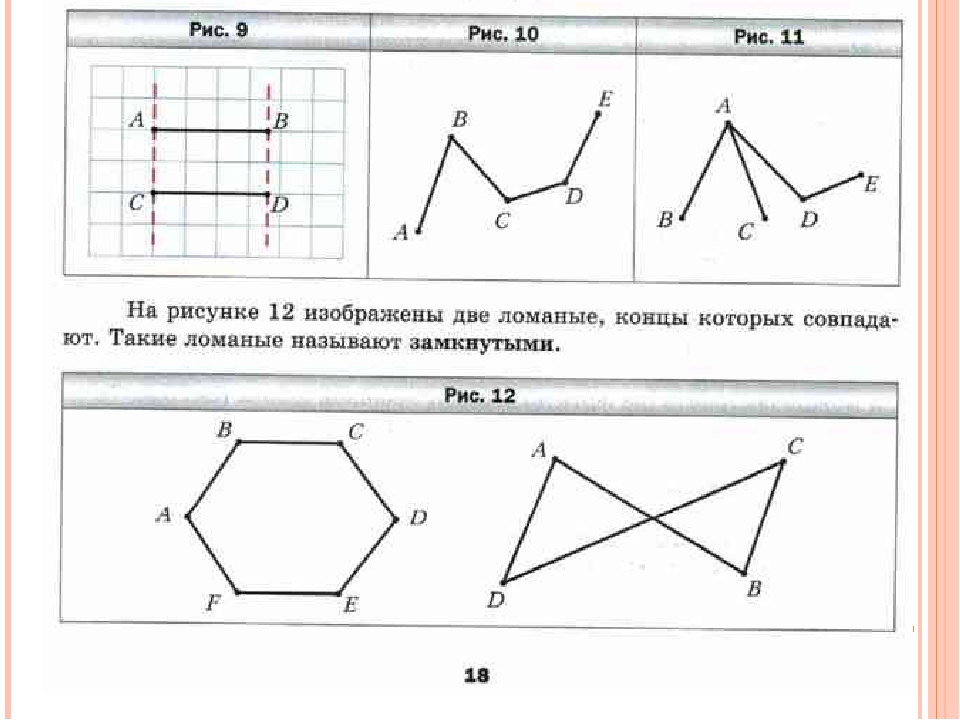 Подготовка проблемной ситуации

1. На ИКТ-доске появляется рисунок города:

– Мы узнаем, в какой город мы попали, решив примеры и расколдовав буквы.

– Прочитайте выражения и найдите их значение

4+4 (Л) 5+2 (и)

3+2 (и) 8-3 (я)

7-4 (н)

(По мере решения, выражения переворачиваются, и на доске появляется слово
ЛИНИЯ)

– Как же называется город? (Город Линий)

2.Работа в группах.

– Нам надо узнать, как называются улицы в этом городе.

– Точка предлагает нам поработать в группах.

– Давайте вспомним правила работы в группе.

– Работать дружно, не ссориться, помогать друг другу.

Не смеяться над неправильным ответом.

Говорить негромко, вежливо.

У командиров групп на столе лежат конверты с заданием, на каждом листочке
изображены разные линии.

– Повернитесь к командирам, рассмотрите карточки.

– Подумайте и скажите – какое задание можно предложить всем для работы?

(Разделить линии на группы.)

– Разделите. (Дети выполняют группировку с обсуждением в группе)

Проверка.

– Какие варианты у вас получились? (По одному ученику от каждой группы
приглашаю к ИКТ-доске для демонстрации группировок.)

– У какой группы так же? По-другому?

– На какой группировке остановимся? Почему?

(Отрезки, лучи и прямые. Нам важен не цвет и толщина линий, а их название.)

– Как называются улицы в городе Линий? (Назовите известные вам линии.)

(Отрезок, луч, прямая)

– Что вы знаете о прямой линии? (Линия, у которой нет начала и конца. Она
бесконечна, не имеет границ, т.е. её можно продолжить в любую сторону)

– Что такое отрезок? (Отрезок – это часть прямой линии, ограниченная с
двух сторон)

3.Формулирование темы урока

– Закройте глазки и представьте себе город Линий. Как вы думаете все ли улицы
в этом городе мы назвали? (Нет, не все. Есть и другие линии.)

(Меняется изображение прямой линии на ломаную)

– Откройте глаза.

– Что изменилось?

(Прямая линия превратилась в непрямую)

– Что вы знаете про эту линию? (Выявление затруднений).

– А что бы вы хотели узнать про эту линию?

• Как называется?

(План действий)

– Сегодня на уроке мы будем наблюдать за такими линиями, займёмся
исследованием, совершим маленькие «открытия» и, надеюсь, ответим на многие ваши
вопросы.

Про эту линию точка хочет рассказать нам интересную историю (Учитель
сопровождает рассказ показом, используя веточку)

– Однажды я гуляла на волшебной поляне. Солнышко светило ярко – ярко. Мне
захотелось побегать и попрыгать. Но вдруг я обо что – то споткнулась и упала. Я
наклонилась и увидела у себя под ногами вот эту веточку. Я взяла ее в руки и
увидела, что она сломалась в трех местах.

– Какая интересная линия! – подумала я. Она была прямая, а стала …
(ломаная).

– Как же называется эта линия? (Ломаная линия)

– Какая тема урока? (Ломаная линия)

Открывается тема урока на доске

– На какой вопрос ответили? (Как называется эта линия.)

IV. Открытие новых знаний

Исследование ломаной линии путём практической работы.

– Попробуем сконструировать ломаную линию

– Возьмите в руки столько палочек, сколько раз я хлопну в ладоши (6 раз).

– Девочки убавляют одну палочку.– Сколько палочек у мальчиков?(6) У
девочек?(5)

– Постройте свою ломаную линию.

– Проверьте работу в парах друг у друга и помогите, если у кого-то не
получилось.

– Хотите посмотреть, какие линии получились? Встаньте, походите по классу и
посмотрите, какие составлены линии.

–Кому понравились работы? Действительно, много интересных и разных ломаных!

– Сколько палочек использовали мальчики?

– Сколько палочек использовали девочки?

– Что интересного заметили, моделируя линию:

– Из чего состоит ломаная линия? (Из отрезков.)

– Как соединяются отрезки? (Концами.)

– Как следуют? (Последовательно друг за другом.)

– Подведу итог тому, что вы сказали:

Вывод: точное название линии «ломаная линия» Ломаная линия состоит из
отрезков, которые последовательно идут друг за другом.

Физкультминутка

– Точка предлагает нам немного отдохнуть.

(Учитель показывает карточки с выражениями. Дети находят значение выражений и
выполняют действия.) <Приложение 2>

Сколько раз ногами топнем? (2+2)

Сколько раз в ладоши хлопнем? (5-3)

Мы присядем сколько раз? (4+2)

А наклонимся сейчас? (7-4)

И подпрыгнем ровно столько.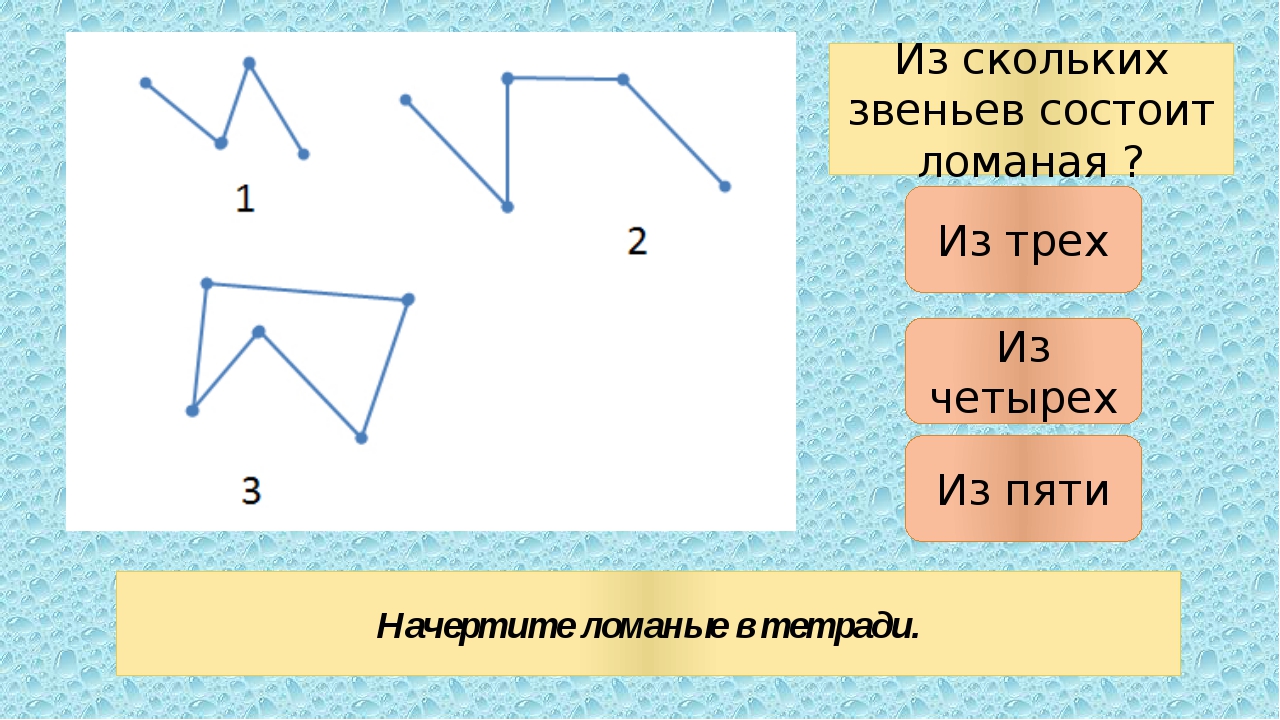 (1+3)

Ай да счет! Игра и только!

2. – Когда отрезки становятся частью ломаной, у них появляется другое
название. Хотите его узнать?

– Где можно узнать название?

– Можно спросить у учителя.

– Спросить у мамы.

– Посмотреть в энциклопедии.

– Посмотреть в Интернете.

– В учебнике.

– Кто сможет посмотреть в Интернете? (Двое ребят работает за компьютером.)

– А мы посмотрим в учебнике. Откройте учебник. Как называются части ломаной?

(В учебнике нет названия.)

– Удалось ли найти информацию в Интернете? Почему не каждому удалось найти
ответ на вопрос?

(Еще плохо умеем пользоваться компьютером, не умеем работать в Интернете, не
хватает знаний).

– На каком занятии будем получать эти знания?

(На занятии по информатике)

– Кому всё же удалось узнал название частей ломаной? (Отвечает другой ученик,
умеющий читать.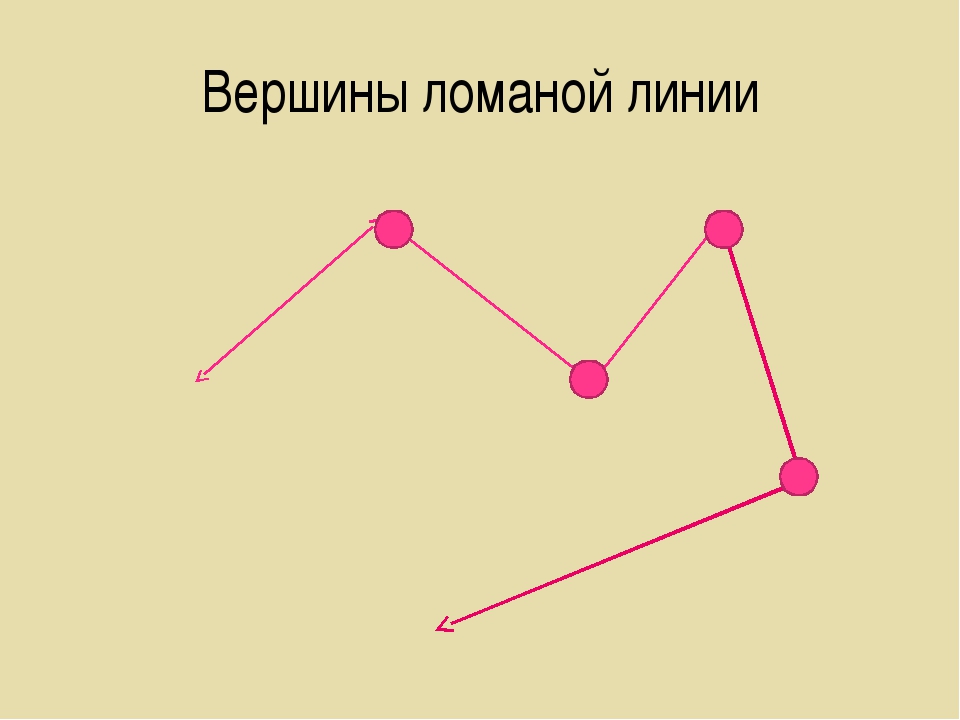

(Части ломаной называются звеньям ломаной) <Приложение
3 и Приложение 6>

– Скажем слово вслух: «звено», много «звеньев».

– Показываю табличку «Звено».

– Прикрепите слово к ломаной. (Ребенок прикрепляет табличку к звену ломаной,
начерченной на доске)

– Сколько звеньев у нашей ломаной? (4 звена)

– На что похожа наша ломаная? (На гору)

– Как бы вы назвали эту точку? (Учитель показывает на вершину ломаной и
уточняет, что это вершина, как у горы. Ученик прикрепляет табличку «Вершина»)

– Вершины – это точки, где соединяются звенья.

– Сколько вершин у ломаной? (3)

3. Работа по учебнику стр.4

– Каждая вершина имеет свое название.

– Рассмотрите ломаную в №1.

– Какой буквой обозначено начало ломаной? (А)

– Вершины ломаной? (БВГД)

– Конец ломаной? (Е)

– Получилось название нашей линии. Прочитайте его. (Ломаная АБВГДЕ)

– Как надо называть вершины ломаной? (По порядку)

Вывод:

– На какие вопросы дали ответ?

• Как называется линия?
• Как сконструировать?
• Из чего состоит?

4. – Название линии знаем, конструировать умеем, из каких частей состоит
тоже знаем. А какое важное умение нам предстоит освоить? (Научиться чертить
ломаную линию).

– С чего можно начать построение ломаной линии?(Поставить точки.)

-Точки у вас в учебнике уже есть. Назовите их.

– Что надо делать дальше? (Соединить их.)

– Как соединить? (Конец соединить с началом.)

– Какой инструмент нам понадобится? Чем будем чертить? (Линейка,
карандаш.)

– Начертите. (Дети чертят ломаную в учебнике.)

– Прочитайте название ломаной линии. (ИКЛМН)

– Расскажите план построения ломаной. (Ученики друг другу проговаривают
последовательность построения.)

• Поставить точки – вершины
• Последовательно их соединить
• Дать вершинам название

– На какие вопросы предстоит ответить?

– Где можно увидеть ломаную линию? (Дети рассматривают рисунки и изображения,
макеты домов. крыш:

– Вершины гор, крыши домов и др.)

5. Виды ломаных

– Рассмотрите ломаные в учебнике № 1. Какие бывают ломаные? (Замкнутые и
незамкнутые ломаные линии)

– Чем отличается замкнутая ломаная от незамкнутой?

– Приведите пример замкнутой ломаной линии. Где мы с ними встречаемся?
(Геометрические фигуры)

6. Применение полученных знаний.

Учебник №2.

– Что изображено? Что общего? (Ломаные линии. Есть звенья и вершины.)

– Какое задание вам придумала Точка? (Сказать сколько звеньев и вершин в
многоугольнике и записать. )

– Выполните работу самостоятельно.

Самостоятельная работа

Проверка по образцу на ИКТ-доске.

– Сколько вершин и звеньев у первой фигуры? Как называется? (так по всем
фигурам)

– От чего зависит название многоугольника? (От количества вершин и
звеньев.)

V. Обобщение знаний

– О каких линиях говорили? (О ломаных, о кривых)

– Какие задачи перед собой поставили? Ответили мы на поставленные вопросы?

– Из чего ломаные линии состоят?

– Как называется часть ломаной линии?

– Какие ломаные существуют?

– У каждого из вас есть листочек. Возьмите его. Найдите ломаные линии.

(У детей листок с рисунками различных линий. Около каждой линии стоит номер.

– Под какими они номерами?

– Все ли загадки ломаной линии мы разгадали? (Нет)

– Ломаная линия таит в себе еще много загадок, а разгадывать мы их будем на
наших следующих уроках.

– Сегодня на уроке мы исследовали ломаную линию по плану. Как вы думаете, по
нему мы можем изучать только линии?

(По этому плану мы можем изучать не только линии, но и буквы, и цифры)

VI. Рефлексия.

– Кому на уроке было трудно? (учитель тоже поднимает руку)

– Кому было легко?

– Мы очень хорошо работали, и Точка прислала вам сюрприз

– Это ваша награда за хорошую работу – «Орден Звездочки». Его получит каждый.
Но вот загадка: почему орден звездочки?

(Контур звездочки – это замкнутая ломаная линия.)

звенья, вершины и длина, разновидности

Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.

Это интересно: разность чисел — что это, как ее найти?

Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.

Звенья, вершины и длина

Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:

1. Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
2. Точки соединения концов этих отрезков называются вершинами.
3. Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
4. Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
5. Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.

Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.

Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:

1. Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
2. Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).

В целом такую совокупность принято называть ABCDE или EDCBA.

Обратите внимание: что такое луч в геометрии.

Разновидности

В геометрии принято различать несколько разновидностей по структуре:

1. Замкнутые самопересекающиеся.
2. Незамкнутые самопересекающиеся.
3. Замкнутые без самопересечений.
4. Незамкнутые без самопересечений.

Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.

Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.

Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.

Конспект урока по математике для учащихся 1 класса по теме «Точка. Линии прямая, кривая, отрезок, луч, ломаная.»

Конспект урока по математике для учащихся 1 класса по теме

«Точка. Линии: прямая, кривая, отрезок, луч, ломаная.»

Тема: Точка. Линии: прямая, кривая, отрезок, луч, ломаная.

Образовательные цели:

1. Уточнить геометрические понятия: «точка, прямая, кривая, луч, отрезок, ломаная» через предметно-практическую деятельность.

2. Упражнять в черчении линий, располагая их в пространстве в разном положении.

3. Научить измерять длину отрезков разными способами.

4. Применять сформированные понятия при выполнении различных заданий.

Развивающая цель: Развитие математической речи.

Коррекционная цель: Развитие ориентировки в пространстве, зрительно-моторной координации.

Воспитательная цель: Развитие умения анализировать свои действия и управлять ими.

Тип урока: комбинированный урок, урок-практикум.

Методы, формы, приемы: словесный, практический, наглядный.

Оборудование: тетради, линейки, карандаши, карточки, ленты, домики, табличка с правилом урока, листы бумаги, звоночек.

Ход урока

I – Организационный этап

Учитель: На какой урок нас позвал звонок?

Что мы делаем на уроках математики?

В стране «Математика» есть много разных городов.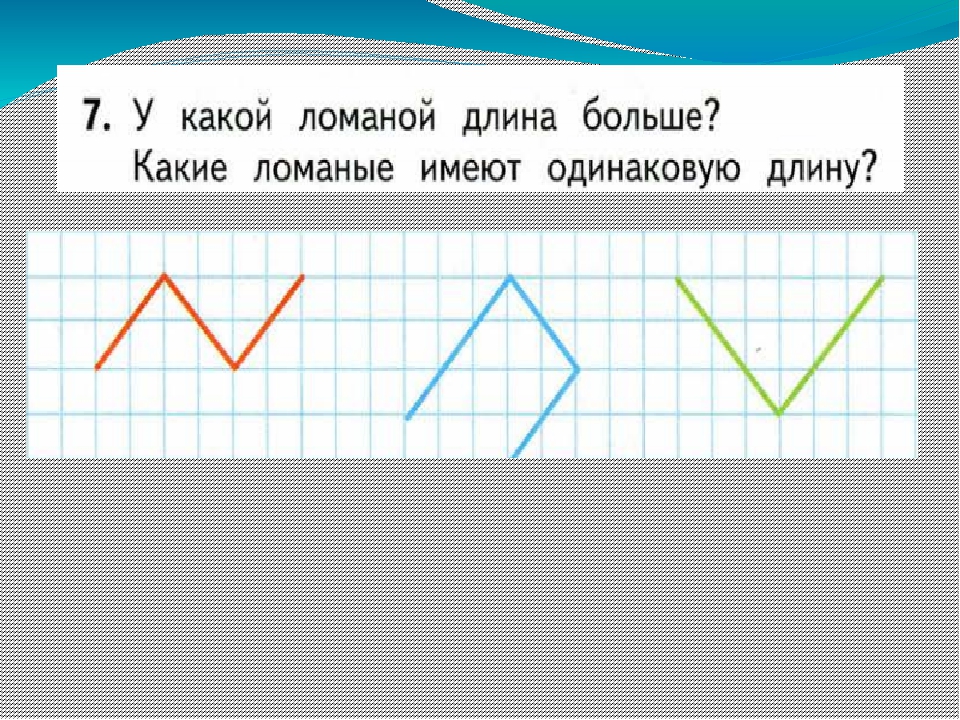

На этом уроке мы посетим город, который называется «ГЕОМЕТРИЯ».

Стихотворение читает ученица

Геометрия – наука про измерение Земли.

Без нее нельзя построить ни дома, ни корабли.

Не скроить костюм и платье, не подстричь в саду кусты.

И, поэтому, друзья, без нее никак нельзя!

Геометрия – наука, которая занимается изучением свойств разных фигур на плоскости и в пространстве.

Учитель: В городе много улиц, но мы посетим только одну. Кто там живет? Это вы сейчас узнаете и назовете тему урока.

II – Мотивация учебной деятельности учащихся. Сообщения темы, цели, задач урока и мотивация учебной деятельности школьников

1) рисование учителем на доске человечка

Точка, точка, запятая, минус рожица кривая,

Палки, палки, огуречик.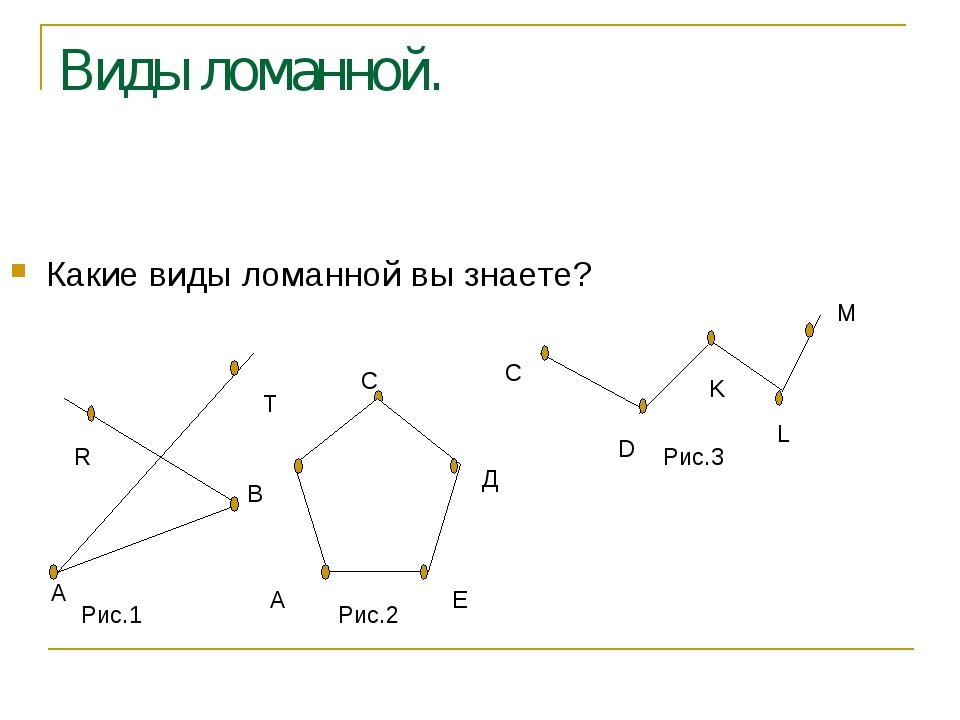 Вот и вышел человечек.

Учитель: Смотрите, к нам пришел человечек из города «Геометрия». Он хочет подсказать нам тему урока. (Что я использовала, рисуя фигуру смешного человека?)

(Ученики определяют тему урока).

Тема урока: «Точка. Линии».

А какие линии вы знаете? Как вы думаете, чем мы будем сегодня заниматься?

На уроке нам предстоит много строить и чертить. А что нам в этом поможет? (карандаш и линейка)

Стихотворения читают ученики

Я чёрный, красный, желтый, синий,

С начинкой твёрдой в середине,

Я с острым ножиком дружу

И что хочу – изображу. (Карандаш)

Всем ребятам помогаю сделать ровную черту.

Я в тетрадках уважаю чистоту и прямоту. (линейка)

Учитель: Точки и линии окружают нас повсюду. Архитектор чертит дома, используя прямые линии. Художник рисует людей, животных и растения, отражая кривые линии. Многие приборы работают, применяя луч. Посмотрите, у нас в классе многие предметы состоят из линий и точек. Нам тоже нужно хорошо знать эту тему, этим мы и займемся. Кроме того, есть много игр с точками и линиями. Это «Морской бой», «Обводки», «Точки», «Точки и отрезки», «Крестики и нолики». В конце урока научимся играть в игру «Точки».

Учитель: Проверьте все ли учебные принадлежности на месте? А очки готовы помочь вам в работе? Раз вы готовы, то начинаем. Запишем в тетрадках число. Посмотрите на дома. Как вы думаете, кто там живет? (ответы учеников).

Прочитайте правило урока: «Математику нельзя изучать, наблюдая, как это делает сосед».

Поэтому работаем все дружно, старательно, красиво и внимательно!

III – Восприятие и первичное осознание нового материала

Учитель: Кроме линейки есть и другой способ провести прямую линию – надо просто перегнуть лист. Линия сгиба — это прямая линия.

Выполним геометрическую разминку.

1. Геометрическая разминка

Учитель: Возьмите в руки лист бумаги. Какая это геометрическая фигура? Перегните ее так, чтобы получилось

1) 2 прямоугольника

2) 2 треугольника

3) треугольник и трапеция

4) 4 квадрата

5) 4 треугольника

Учитель: У вас получались линии на сгибах, которые формировали разные геометрические фигуры. А сейчас прогуляемся по улице, где живут линии.

2. Усвоение новых знаний

А) Точка

Учитель: Пора заглянуть в домик № 1. Кто там живет? (Звенит звоночек, ученица встает и рассказывает свою тему).

Рассказ ученицы про точку.

1. 1.Знаете ли вы, что точка- самая простая геометрическая фигура.

2. Ее нельзя измерить, у нее нет длины, ширины.

3. Точку можно назвать буквой, например, точка А.

4. Все линии и фигуры начинаются с точки и состоят из них.

5. Точки могут располагаться на прямой или вне прямой.

6. Через точку можно проводить разные линии.

7. А еще точка живет в русском языке. Там она заканчивает предложение.

Практическая работа № 1 «Точка»

Учитель: Поработаем с точками. Откройте тетради. Запишите число. Пропустите 3 клетки вниз и 3 клетки справа и карандашом поставьте точку. Назовем ее точка А. Через 8 клеточек поставьте вторую точку М. Мы можем сказать, что обе точки расположены на одной линии? Проверьте линейкой. Поставьте внизу посредине листа третью точку К. Можно сказать, что все 3 точки расположены на одной прямой линии? Если соединить точки А и К, К и М , что получим? А все 3 точки? А если линию замкнуть?

Упражнение «Точки в жизни»

Учитель: Давайте подумаем, а где в жизни мы встречаемся с точками. В этом вам поможет карточка с картинками. (Ученики приводят примеры. Опираясь на карточку с картинками).

Б) Прямая

Учитель: Давайте заглянем в домик № 2. Кто там живет? (Звенит звоночек, ученица встает и рассказывает свою тему).

Рассказ ученицы про прямую линию.

1. Знаете ли вы, что прямая линия может быть продолжена сколько угодно в обе стороны, то есть она не имеет концов или границ. Поэтому у нее нет имени.

2. Через одну точку можно провести сколько угодно прямых линий.

3. Через две точки можно провести только одну прямую линию.

4. Прямые могут располагаться вертикально, горизонтально и под углом, т.е. наклонно.

5. Прямые могут пересекаться, а могут идти параллельно.

Практическая работа №2 «Прямая линия»

Учитель: В тетради проведите через точки А и М линию. Какая это будет линия? Сколько таких линий можно провести через эти 2 точки? А через 1 точку? Проведите через точку К несколько прямых линий.

Практическая работа № 3

Учитель: Возьмите в руки ленты, это ваши линии. Покажите прямую линию.

Кончики свисают, т. к. у нее нет начала и конца. Расположите их горизонтально, а теперь вертикально, наклонно.

Поработайте в парах. Покажите параллельные прямые. А теперь пусть они пересекутся. Точка, где линии встретились называется точкой пересечения.

Упражнение «Прямые в жизни»

Учитель: Давайте подумаем, а где в жизни мы встречаемся с прямыми. В этом вам поможет карточка с картинками. (Ученики приводят примеры, опираясь на карточку с картинками).

В) Луч

Учитель: Отправляемся в домик № 3. (Звенит звоночек, ученик встает и рассказывает свою тему).

Рассказ ученика про луч

Знаете ли вы, что Луч – это часть прямой линии, ограниченной, с одной стороны.

1. У луча всегда есть начало, и это точка, ее можно назвать буквой.

2. Из 1 точки можно провести сколько угодно лучей.

3. А если провести 2 луча из 1 точки, то получится угол. Углы могут быть разные: прямые, острые и тупые.

Практическая работа № 4

Учитель: Возьмите ленточку только за один конец. Какая линия получилась?

Соедините 2 луча, что получили? (угол, ломаную).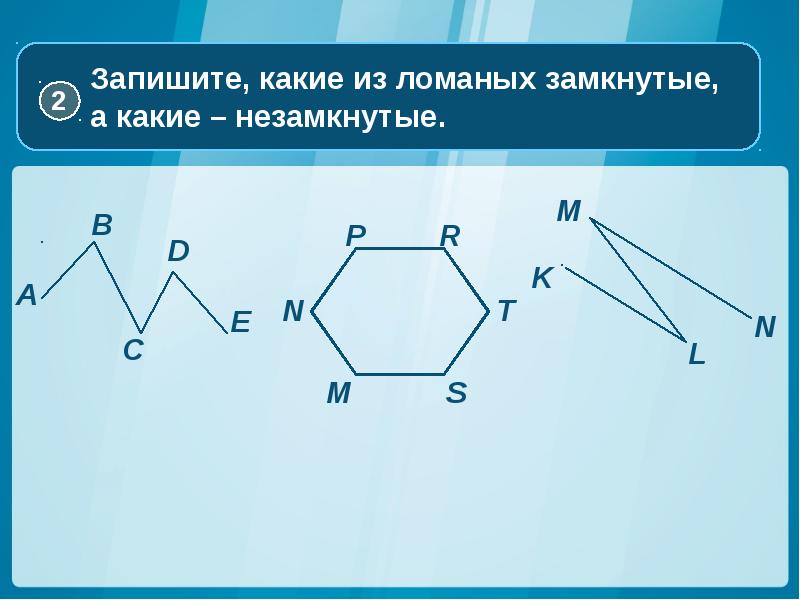 Могу я добавить свою линию? Сколько можно провести лучей из одной точки?

Практическая работа № 5

Учитель: Давайте построим лучик в тетрадях. Что надо поставить? (точку) Назовем ее точкой О. Сколько еще лучей можно провести через эту точку. Проведите. Найдите угол.

Упражнение «Лучи в жизни».

Учитель: Давайте подумаем, а где в жизни мы встречаемся с лучами. В этом вам поможет карточка с картинками. (Ученики приводят примеры, опираясь на карточку с картинками).

Г) Кривая

Учитель: Отправляемся в домик № 4. Кто там живет? (Звенит звоночек, ученик встает и рассказывает свою тему).

Рассказ ученика про кривую линию

1. Знаете ли вы, что кривые линии тоже состоят из точек?

2. Их можно проводить без инструмента, от руки.

3. Они не имеют начала и конца.

4. Они, могут быть замкнутые и незамкнутые.

5. Через 1, 2 и более точек можно провести много кривых линий.

6. Кривые линии живут в круге, овале, геометрических фигурах и других рисунках.

Практическая работа № 6

Учитель: Возьмите ленты за 2 конца, натяните. А теперь расслабьте руки. Какая получилась линия? Бросьте ленту на парту. Какую линию видите?

Практическая работа № 7

Учитель: Поставьте в тетрадях 2 точки и соедините их от руки, без линейки. Что у вас получилось? Можно еще провести кривую линию через эти 2 точки? Проведите. Сколько кривых можно провести через 1 точку? А как вы думаете, можно ли нарисовать кривую линию без точек? (Можно). Нарисуйте.

Упражнение «Кривые линии в жизни»

Учитель: Давайте подумаем, а где в жизни мы встречаемся с кривыми линиями.

(Ученики приводят примеры, опираясь на карточку с картинками).

Физкультурная пауза с лентами.

Зрительная гимнастика.

Д) Отрезок

Учитель: Чтобы познакомиться еще с одной линией, послушайте сказку.

Жила-была любопытная точка, которая хотела всё знать. Увидит любую линию и непременно спросит: «Какая это линия, длинная или короткая? Замкнутая или нет?» Подумала однажды точка: «Как же я всё смогу узнать, если всегда буду жить в одном месте?» И отправилась точка путешествовать по прямой линии. Шла она шла. Долго шла. Устала и говорит: «Скоро ли будет конец у прямой линии?»

Дайте ответ точке. Почему?

«Что же мне делать, — задумалась точка, — Не могу же я вечно гулять по прямой». «А ты позови на помощь ножницы», — подсказала прямая. Тут, откуда ни возьмись появились ножницы, щёлкнули раз, щёлкнули два, и разрезали прямую.

«Как интересно, что же получилось из моей прямой?» «Это отрезок — сказали ножницы, теперь ты на отрезке прямой.

Учитель: Отрезки прямой живут в доме № 5. (Звенит звоночек, ученик встает и рассказывает свою тему).

Рассказ ученика про отрезок.

1. Часть прямой, ограниченной с обеих сторон, называется отрезком.

2. От прямой линии можно в любом месте отрезать кусочек и получится отрезок.

3. Отрезок имеет начало и конец и его обозначают буквами.

4. Через одну точку можно провести сколько угодно отрезков прямой линий.

5. Через две точки можно провести только один отрезок.

6. Отрезок имеет определенную длину, которую можно измерить. Линейка — инструмент для измерения длин отрезков.

7. Отрезки могут быть равными и неравными по длине.

8. Отрезки могут располагаться вертикально, горизонтально и наклонно.

9. Отрезки прямой могут пересекаться.

10. Отрезки прямой могут идти параллельно.

11. Их можно складывать, делить на равные части.

Практическая работа № 8

Учитель: Возьмите ленты и покажите отрезки. Расположите их горизонтально, вертикально и наклонно. Поработайте в парах и покажите параллельные отрезки, а теперь пусть они пересекутся. Как называется их общая точка?

Практическая работа № 9

Учитель: Поставьте точку К. Постройте отрезок КМ=7 см горизонтально. Второй отрезок АС=6см, вертикально. Пусть они пересекутся. Точка О будет называться точкой пересечения. (см. карточку)

Как можно измерять отрезки? (линейкой, наложением, на глаз)

Практическая работа № 10

3) Учитель: У вас на парте полоски. Это три отрезка: красный, синий, желтый. Какой самый большой (маленький?) Как можно определить, какой самый большой, а какой самый маленький? (на глаз, наложением, измерением). Сделайте это. Какой длины самый большой отрезок? Самый маленький?

Упражнение «Отрезки в жизни».

Учитель: Давайте подумаем, а где в жизни мы встречаемся с отрезками.

(Ученики приводят примеры, опираясь на карточку с картинками).

Е) Ломаная

Учитель: У нас остался еще один домик № 6. Кто там живет?

(Звенит звоночек, ученица встает и рассказывает свою тему).

Рассказ ученицы про ломаную.

1. Линия, состоящая из нескольких отрезков и лучей, называется ломаной.

2. Знаете ли вы, что, когда отрезки соединяются, получается ломаная линия.

3. Она может состоять из 2, 3, 4 и более отрезков. Начало одного отрезка является концом другого отрезка.

4. Ломаная может быть замкнутой и незамкнутой.

5. Замкнутая ломаная на плоскости ограничивает многоугольник.

6. Отрезок ломаной называется звеном, а место соединения 2-х отрезков называется вершиной.

7. Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.

Практическая работа № 11

Учитель: Поработайте в парах. У вас вместе 6 отрезков.

Какую линию можете сложить из них? Сделайте это. Что получилось?

Практическая работа №12

Учитель: Начертите ломаную из 4 отрезков и найдите ее длину. Как называются отрезки ломаной, а места их соединения? А теперь замкните ее. Какую фигуру получили? А из 3-х, 6-ти ломаных какая получится фигура?

Упражнение «Ломаные в жизни»

Учитель: Давайте подумаем, а где в жизни мы встречаемся с ломаными.

(Ученики приводят примеры, опираясь на карточку с картинками).

IV – Первичная проверка понимания усвоенного материала

1) фронтальный опрос

Учитель: Подведем итоги работы.

1. Какая самая простая геометрическая фигура, из которой состоят все остальные?

2. Какие линии повторили?

3. Чем отличаются прямая, луч и отрезок?

4. Из чего состоит ломаная и как называются ее отрезки? А места соединения?

5. Как получить угол?

6. Чем отличается прямая от кривой линии?

2) Учитель: Подумаем, где в жизни мы встречаем все эти линии?

Поработаем с карточками.

Карточка № 1 Игра «Найди линию»

Учитель: На карточке под номерами расположены разные предметы. Запишите в тетрадях номера предметов, где есть 1. прямые линии, 2. отрезки, 3. ломаные, 4. кривые, 5. лучи.

Карточка № 2 Игра «Точки и числа»

Учитель: У каждого на столах лежит лист, на котором изображены точки и числа. Ваша задача поочередно соединять данные точки линиями, прямыми или кривыми вы должны решить сами, в порядке возрастания чисел. От меньшего к большему. Кто раньше получит рисунок. Поднимите руку.

VII – Рефлексия

Учитель: Чем мы занимались на уроке?

Повторили: «Какие бывают линии и чем они отличаются друг от друга?»

Узнали, что линии бывают замкнутые и незамкнутые.

Чертили эти линии и показывали.

Учились сравнивать отрезки.

Что нового узнали?

Точка и линии-самые простые геометрические фигуры.

Линии состоят из множества точек.

Линии располагаются на плоскости и в пространстве горизонтально, вертикально, наклонно.

Линии бывают параллельные и могут пересекаться.

VIII – Сообщение домашнего задания

Учитель: Нарисуйте примеры предметов с прямыми, кривыми, ломаными линиями и с лучами по 2-4 примера.

Приложение к уроку

Карточка

Фотографии с урока

Замкнутые самопересекающиеся ломаные

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019

В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).

Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).

И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).

Нас будут интересовать замкнутые самопересекающиеся ломаные.

Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).

Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.

Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.

Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.

Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.

Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.

Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.

Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).

Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.

Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?

Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.

Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.

Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).

Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.

Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.

Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.

Художник Мария Усеинова

Как интерпретировать и строить пунктирные графики

Линейные графики

Хорошим способом для него определить тенденцию или закономерность в его финансах может быть отображение данных на линейном графике , подобном показанному здесь для зависимости высоты растения от времени. График показывает, что с каждым днем ​​высота растения увеличивается на сантиметр. График образует идеально прямую линию. Это линейных , потому что растение растет на одно и то же количество сантиметров каждый день.

В реальной жизни точки данных обычно не увеличиваются и не уменьшаются с одинаковой постоянной скоростью, чтобы построить идеально линейный график. Скорее всего, они образуют пунктирный график , который здесь показан.

Понимание того, как построить ломаную линию, помогает нам интерпретировать информацию, которую он может предоставить, поэтому давайте посмотрим, как Майк построил свой график.

Основы

Есть несколько важных компонентов, которые необходимы каждому линейному графику.Вы можете увидеть их на графике Майка. Во-первых, ему нужен заголовок для описания информации, содержащейся в графике. Также требуется ось x , горизонтальная линия и ось y , вертикальная линия. Обе оси должны быть помечены, чтобы показать, что они представляют. В некоторые месяцы Майк приносит больше и тратит больше денег, поэтому его доллары зависят от месяца. Следовательно, его доллары — это зависимая переменная , которая идет по оси y. Чтобы увидеть взаимосвязь между его доходами и расходами, он изобразит их оба на одном и том же наборе осей, в результате чего получится график с двойной прерывистой линией .

Создание шкалы

Масштаб оси y, числа, представляющие доллары, варьируются от 500 до 1150 долларов. Эта шкала позволяет рассчитывать его ежемесячный доход, который варьируется от 525 до 1120 долларов. Это также оставляет место для его расходов, которые варьируются от 600 до 1050 долларов. Интервал этой шкалы равен 50, что можно увидеть, заметив, что число, идущее вверх по сетке, увеличивается на 50 с каждой отметкой. Он начал свою шкалу с 500 долларов, потому что было бы глупо начинать с 0 и использовать много места, чтобы подняться до 525 долларов.Он поместил символ разрыва на оси ординат ниже 500, чтобы указать, что он перескакивает от 0 до 500.

Добавление данных

Теперь, когда у него есть структура графика, он может начать добавлять точки данных. В январе у него было 1035 долларов дохода и 825 долларов расходов. Как вы можете видеть здесь, он добавил J к оси абсцисс, чтобы обозначить месяц. Пунктирная черная стрелка показывает, что он следовал вертикальной линии, проходящей через букву J вверх, и поместил красную координату посередине между линиями, обозначенными 800 и 850, чтобы показать расходы в размере 825.Затем он продолжил движение вверх по линии и поместил зеленую координату чуть выше середины между 1000 и 1050, чтобы показать свой доход 1035.

В феврале он заработал 1100 долларов и потратил 975 долларов. Здесь он добавил F вдоль оси x, чтобы представить месяц, красную координату, чтобы представить 975 долларов, и зеленую координату, чтобы представить 1100 долларов.

Интерпретация графика

Как вы можете видеть здесь, Майк завершил свой график с двойной ломаной линией, так что он может начать интерпретировать информацию, которую он предоставляет.Надеюсь, он определит, почему он не может выбраться из долгов!

Самый полезный аспект диаграммы состоит в том, что она ясно показывает его самую большую потенциальную проблему. Первые четыре месяца, с января по апрель, его доход был намного больше, чем его расходы.

Например, апрель был удачным месяцем для Майка. Это прямо перед выпускными экзаменами студентов колледжа, а у него было много дел.Поскольку зеленая координата, которая представляет его доход, довольно близка к середине между 1100 и 1150, Майк может оценить, что он заработал около 1120 долларов. Он так много работал, что у него тоже не было времени на траты денег, поэтому его расходы были низкими. Красная координата показывает, что он потратил 600 долларов. В том месяце у него был положительный баланс в размере 520 долларов.

Однако в следующем месяце его положение быстро изменилось, потому что студенты колледжа были на летних каникулах.В мае у Майка было меньше работы, к тому же у него было свободное время, чтобы тратить деньги. Его красная координата расходов, как вы можете видеть, намного выше, чем его зеленая координата дохода. Он заработал всего около 525 долларов, а потратил 1050 долларов. Это привело к остатку — 525 долларов, что полностью уничтожило деньги, которые он смог вернуть в предыдущем месяце.

В следующем месяце, как видно здесь, все еще существует очень большой отрицательный разрыв между его расходами и доходами.

В июле, а также в остальное время года зеленые координаты доходов выше, чем красные координаты расходов. Однако у них есть относительно небольшие зазоры. Самый большой разрыв, наблюдавшийся в октябре, показывает положительное сальдо около 225 долларов. Хотя это лучше, чем отсутствие положительного баланса, такая относительно небольшая сумма объясняет, почему Майк не добивается больших успехов в выплате своего долга!

Краткое содержание урока

Используя ломаную линию, Майк быстро понял, что ему нужно найти другую работу и не ходить в магазины и кофейни в начале лета! Тот факт, что такой вид отображения данных обеспечивает быстрый способ обнаружения тенденций в данных, делает их подходящими для многих реальных целей.

2.6.2: Пунктирные графики — K12 LibreTexts

Вариантом линейного графика является пунктирный график . Этот тип линейного графика используется, когда необходимо показать изменения во времени. Линия используется для соединения значений, но линия не имеет определенного наклона. Однако точки значимы, и все они представляют собой важную часть графика. Обычно вам предоставляется пунктирный график, и вы должны интерпретировать данную информацию с графика.

Интерпретация ломаной линии

1. Ответьте на приведенные ниже вопросы для следующего пунктирного графика, показывающего расстояние между автобусом и автобусной станцией с течением времени.

а. Какая была самая быстрая скорость автобуса?

Автобус разгонялся до 16 миль в час.

г. Сколько раз автобус останавливался в пути? (Не считайте начало и конец поездки.)

Автобус останавливали 4 раза.

г.Какое расстояние было от автобуса до автобуса вначале?

Автобус изначально находился в 2 милях от автобусной станции.

г. Какое общее расстояние проехал автобус?

Общее расстояние, пройденное автобусом, составило 38 миль.

2. Сэм решает провести некоторое время со своим другом Аароном. Он запрыгивает на свой велосипед и отправляется к дому Аарона, но по пути у него спустило колесо, и ему приходится пройти оставшееся расстояние. Как только он приезжает в дом Аарона, они ремонтируют спущенное колесо, играют в покер, а затем Сэм возвращается домой.По пути домой Сэм решает остановиться в торговом центре, чтобы купить книгу о том, как играть в покер. На следующем графике представлено приключение Сэма:

а) Как далеко от дома Сэма до дома Аарона?

Это 25 км от дома Сэма до дома Аарона.

б) Как далеко от дома Аарона до торгового центра?

От дома Аарона до торгового центра 15 км.

c) Когда у Сэма спустило колесо?

У Сэма спустило колесо в 10:00.

г) Как долго Сэм оставался в доме Аарона?

Сэм пробыл в доме Аарона 1 час.

д) С какой скоростью Сэм ехал от дома Аарона до торгового центра, а затем от торгового центра к дому?

Сэм двигался со скоростью 30 км / ч от дома Аарона до торгового центра, а затем со скоростью 40 км / ч от торгового центра до дома.

3. Следующий график представляет собой пример пунктирной линии, и он представляет время поездки туда и обратно, от дома до популярного кемпинга и обратно.

а) Как далеко от дома до парка для пикников?

Это 40 миль от дома до парка для пикников.

б) Как далеко от парка для пикников до кемпинга?

Это в 60 милях от парка для пикников до кемпинга.

в) В каких 2 местах машина остановилась?

Автомобиль остановился у парка для пикников и у кемпинга.

г) Как долго машина стояла у кемпинга?

Машину остановили у палаточного городка на 15 минут.

д) Когда машина прибывает на площадку для пикника?

Машина прибыла на площадку для пикников в 11:00.

е) Сколько времени понадобилось на обратный путь?

Обратный путь занял 1 час.

г) На какой скорости ехала машина от дома до парка для пикников?

Скорость автомобиля от дома до парка для пикников составляла 40 миль / ч.

ч) Какая скорость была у машины от палаточного лагеря до дома?

Скорость автомобиля от палаточного лагеря до дома составляла 100 миль / ч.

Разрыв строки — Определение и примеры разрыва строки

Определение разрыва строки

Разрыв строки — это поэтический прием, который используется в конце строки и в начале следующей строки в стихотворении. Его можно использовать без традиционной пунктуации. Также ее можно описать как точку, в которой линия делится на две половины. Иногда разрыв строки, который происходит в середине предложения, создает enjambment.

Примеры разрыва строки в литературе

Пример № 1:

Cymbeline (Уильям Шекспир)

«Своим мечом,
Который он махнул мне в горло, я взял
Его голову от него
Я абсолютен
Twas very Cloten ”

В данном отрывке есть два примера разрыва строки.Один разрыв строки разрезает линию «Я взял его голову» посередине, помещая разрыв строки в конец второй строки. Другой разрыв строки используется в четвертой строке, «я», будучи человеком, имеет абсолютное значение. Эти разрывы строк определяют визуальную форму этого текста.

Пример № 2:

Улисс (Автор Альфред Лорд Теннисон)

«Подхожу к престарелой жене, Я измеряю и получаю пособие. , и не знаю меня.
Я не могу отдохнуть от путешествия: Я выпью
Жизнь на дрожжах: Все времена, когда я наслаждался
Очень сильно, сильно пострадал , как с теми
, Кто меня любил, так и в одиночестве, на берегу, и когда
Vext тусклое море: я стал именем
Многое я видел и знал; города мужчин
И нравы, климат, советы, правительства… »

В этом отрывке много разрывов строк. Во-первых, разрыв строки разрезает фразу «Я принимаю и применяю неравные законы для дикарей» на две части в конце первой строки.Точно так же разрыв встречается в других строках, таких как «Я выпью жизнь до дна», «Все времена, когда я очень наслаждался, сильно страдал» и «Я стал именем».

Пример № 3:

Ода соловью (Автор Джон Китс)

«Мое сердце болит, и болит сонное онемение. в канализацию…
Эта ты, легкокрылая Дриада деревьев
В каком-то мелодичном сюжете…
Буковой зелени и бесчисленных теней,
Певица лета в безудержной легкости.

В этом отрывке Китс использовал разрывы строк для создания различных типов художественного эффекта. Строка также заставляет читателей сделать небольшой перерыв, что, в свою очередь, усиливает раскрытие следующих строк.

Пример № 4:

Второе пришествие (Уильям Батлер Йейтс)

«Поворот и поворот в расширяющемся круговороте
Сокол не слышит сокольничника;
Все разваливается; центр не может вместить ;
Кровавый прилив спустился, и повсюду
Церемония невиновности утоплена;
Лучшие лишены всякой убежденности, худшие
Полны страстной напряженности …
Второе пришествие! Едва ли эти слова произносятся
И какой грубый зверь, его час наконец настал… »

В этом отрывке тоже есть несколько разрывов строки.К ним относятся: «центр не может удерживаться», «и везде утопает церемония невиновности…» Поэт вводит читателей в удивительные и разнообразные идеи.

Пример № 5:

Ozymandias (Автор Перси Биши Шелли)

«Наполовину затонувший, разбитое лицо лежит, его хмурый взгляд,
И морщинистая губа, и хладнокровная насмешка,
Скажите, что его скульптор хорошо читал эти страсти
Которые еще выживают, отпечатано на этих безжизненных вещах ,
Взгляни на мои дела, Могущественные и отчаяние!
Рядом ничего не осталось. Вокруг разложения
Из этих колоссальных обломков, бескрайних и голых
Одинокие и ровные пески простираются далеко ».

Этот отрывок также является хорошим примером разрыва строки. Эти разрывы строк придают стихотворению жизненную силу, а также создают перерывы в процессе чтения.

Функция разрыва строки

Разрывы строк могут быть источником динамизма в поэзии, поскольку они обеспечивают способ, с помощью которого поэтические формы внушают содержание с силой и последовательным смыслом, что может быть невозможно в других типах текста того же уровня.Разрывы строк используются как важные поэтические приемы, потому что они часто вносят двусмысленность, а также влияют на смысл. Однако они приводят читателей к неожиданным идеям и разному пониманию, а также контролируют способ, которым они приходят к идеям.

, когда использовать пунктирную линию — повествование с данными

В этом случае и стиль линии, и слова на оси x позволяют быстро понять, какие точки данных представляют фактические данные, а какие — прогноз. Я большой сторонник толстых, жирных, сплошных линий и маркеров данных для реальных данных и тонких пунктирных линий (а иногда и незакрашенных маркеров данных, хотя я чувствовал, что здесь это выглядело слишком беспорядочно) для прогнозов и прогнозируемых данных из-за способ, которым он помогает нам интуитивно понять, на что мы смотрим, когда выполняется хорошо.

В приведенном выше предположении я предполагаю, что точки данных прогноза достаточно важны для непосредственной маркировки (другими словами, важны конкретные числовые значения; если бы это было не так, вы могли бы подойти к этому по-другому, возможно, только маркировка точки 2017 и 2022, или не помечать ни одну из них, а позволить оси Y для общей величины быть достаточно хорошей). Я могу представить, как разные люди делают здесь свой выбор в зависимости от того, на чем вы хотите, чтобы аудитория сосредоточилась, а также от личных эстетических предпочтений.Мета-точка: будьте внимательны, когда дело касается деталей дизайна в целом и использования пунктирных линий в частности.

тактика: как это сделать в моем инструменте?

Изменение форматирования одиночной линии со сплошной на точечную, как в первом примере выше, возможно и довольно просто в большинстве инструментов. Обычно это достигается с помощью меню или кода для изменения стиля линии. Если вы не знаете, как это сделать, умный поиск в Google с названием вашего инструмента и что-то вроде «поменять линию на графике на пунктирную» укажет вам на решение.

Замена сплошной части линии на пунктирную немного сложнее, но для этого есть несколько решений. Существует метод грубой силы для физического форматирования каждой отдельной точки данных (например, если вы работаете в Excel, вы должны щелкнуть один раз, чтобы выделить серию, затем щелкнуть еще раз, чтобы выделить отдельную точку данных, а затем отформатировать эту точку данных. или связанная линия индивидуально, как вы этого хотите). Как вы понимаете, это может занять много времени.Другой способ — сделать то, что будет выглядеть как одна строка, на самом деле двумя разными сериями данных, что позволит вам форматировать их по отдельности. В приведенном выше примере продаж у меня будет столбец дат с 2010 по 2022 год, чтобы установить ось абсцисс. Тогда моя первая серия для ФАКТИЧЕСКИХ данных будет иметь значения с 2010 по 2017 год. У меня будет вторая серия для моей строки ПРОГНОЗ, которая имеет значения с 2017 по 2022 год (обратите внимание на перекрытие с 2017, имеющее значения как для ФАКТИЧЕСКИХ данных, так и для ПРОГНОЗ, чтобы избежать разрыв в строке). Я полагаю, вы могли бы использовать аналогичный подход в других инструментах.

Вы можете загрузить файл Excel с приведенными выше примерами (включая как грубую силу, так и более элегантные решения, описанные выше для второго примера).

Это два случая использования, в которых я использую пунктирные линии и продвигаю их использование. Есть ли другие случаи, когда вы бы порекомендовали использовать пунктирную линию? Или дополнительные соображения, которые следует учитывать при выборе стиля линии? Оставьте комментарий со своими мыслями!

Разрыв строки — определение и примеры

Определение разрыва строки

Что такое разрыв строки? Вот быстрое и простое определение:

Разрыв строки — это конец одной строки стихов и начало новой строки.

Некоторые дополнительные ключевые сведения о переносах строк:

• Разрывы строк разделяют стихи на строки, а длина строк определяет внешний вид стихотворения на странице: длинные и тонкие, короткие и широкие или форма, полностью самостоятельная. .
• Расположение разрыва строки часто определяется количеством слогов в строке, но столь же часто оно свободно выбирается поэтом.
• Разрывы строк служат важной функцией при установке ритма стихотворения, поскольку они вставляют паузу между последним словом одной строки и первым словом следующей строки.По этой причине разрывы строк обычно происходят там, где также встречаются естественные паузы в языке, например, после знаков препинания, в конце мысли или между отдельными изображениями.

Глубокие разрывы строк

Даже больше, чем содержание стихотворения, часто именно разрывы строк делают текст узнаваемым для людей как поэзия, то есть узнаваемым в отличие от прозы, что не так. Не используйте разрывы строк таким же образом. Из-за этого строчку можно было считать фундаментальной единицей поэзии, а строчка разрывала маркер этих единиц.В следующих разделах описаны основные характеристики и условные обозначения, определяющие использование разрывов строк в поэзии.

Длина строки

Вплоть до недавнего времени, начиная с XIX века, единственным приемлемым способом разорвать линию был размер стихотворения. По этой причине полезно иметь четкое представление о том, что такое измеритель, чтобы понять, как он повлиял на использование разрывов строк. Мы предоставляем более подробную информацию о счетчике на отдельной странице, но предлагаем краткое руководство здесь.

• Метр: Рисунок из ударных и безударных слогов, создающий ритм стихотворных строк. Единицы измерения называются футами. Ноги подвержены разным нагрузкам. Например, ямб — это ступня с безударным слогом, за которым следует ударный слог (de- fine ), тогда как хорея имеет противоположное значение: ударный слог, за которым следует безударный слог ( Po -et). Поэтические метры определяются как типом , , так и числом футов, которые они содержат.Например, пентаметр ямба — это тип измерителя, обычно используемый в поэзии, который содержит пять ямбов в строке (отсюда префикс «пента», что означает пять).

В формальном стихе (поэзия со строгим размером и схемой рифм), а также в пустом стихе (не рифмованная поэзия со строгим размером) метр стихотворения определяет длину каждой строки, требуя, чтобы каждая строка содержала определенное количество символов. слоги. Итак, стихотворение, написанное ямбическим пентаметром (пять ямбов в строке), будет иметь разрыв строки через каждые десять слогов, как в следующем примере:

Могу ли я сравнить тебя с летним днем?
Ты милее и умереннее.

В произвольном стихе (стихотворении без определенного размера или схемы рифм) длина строки определяется желанием поэта создать определенный ритм или сделать больший акцент на определенных словах, вставив вокруг них больше места. В произвольном стихе, в отличие от формального или пустого стиха, длина строки может значительно варьироваться на протяжении всего стихотворения, как в следующем примере:

Многие способы танцевать Жизель, но сегодня, когда вы
смотрите, вы думаете, что она и есть искусство, существо

, которое запоминает

каждый ее жест и ощущает его отношение ко времени
всего за мгновение до этого, когда она сделала что-то

рядом с ним…

Использование заглавных букв

До XIX века первое слово каждой строки стихов, как правило, было написано с заглавной буквы, независимо от того, было ли оно началом нового предложения. Сегодня нет стандарта использования заглавных букв в начале строк; некоторые поэты делают это, а некоторые нет, хотя обычно это рассматривается как несколько формальная деталь, оставшаяся от ушедшей эпохи поэзии. Вот, например, первые строки раннего стихотворения Джона Эшбери, в котором используется заглавная буква в начале каждой новой строки, хотя позже в своей жизни Эшбери, как и многие другие современные поэты, перестал соблюдать это соглашение в своих стихах.

Сидя между морем и зданиями
Ему нравилось рисовать морской портрет.
Но точно так же, как дети представляют себе молитву.
Это просто тишина, он ожидал, что его объект
взметнется по песку и, схватив кисть,
Нанесет на холст свой собственный портрет.

Пунктуация

Хотя разрывы строк сами по себе, как правило, создают паузу в ритме стихотворения — и поэты обычно используют знаки препинания в конце строк — разрывы строк не обязательно должны иметь совпадать с использованием знаков препинания.Строки, которые с по заканчиваются знаками препинания, называются линиями с остановкой в ​​конце, а строки, которые не заканчиваются с до с знаками препинания, называются линиями с перемычкой. Например, в этих строках из Ромео и Джульетта первая, вторая и пятая строки остановлены, а третья и четвертая — замкнуты:

Когда он умрет,
Возьмите его и вырежьте звездочки,
И он сделает лицо небес таким прекрасным
Чтоб весь мир полюбил ночь
И не поклонялся яркому солнцу.

Разрывы строк и синтаксис

Синтаксис — это термин, который относится к структуре и порядку слов в предложении. Вообще говоря, поэты помещают в свои стихи разрывы строк, чтобы они не нарушали осмысленно синтаксис предложения, а вместо этого создавали паузы, имитирующие естественные паузы речи. Однако это не всегда так; некоторые поэты используют разрывы строк, чтобы намеренно создать необычную каденцию или фразу в своих стихах. Использование разрывов строк этими двумя разными способами дает совершенно разный эффект.Например, возьмем следующие два примера, в которых используются одни и те же слова, но используются разрывы строк в разных местах:

В нескольких минутах ходьбы от моей комнаты в Будапеште
под дворцовым кварталом
и заброшенной больницей в скале
была знаменитая баня называется Рудас.

vs.

В нескольких минутах ходьбы от моей комнаты
в Будапеште под дворцовым кварталом
и заброшенной больницей
в скале была
знаменитая баня Рудас.

В первом приведенном выше примере разрывы строк используются таким образом, что синтаксис предложения намного более естественен, чем во втором примере, который довольно неприятен. Но некоторые поэты хотят добиться этого резкого эффекта и используют разрывы строк, чтобы целенаправленно изменить способ, которым кто-то будет естественно читать данное предложение. Э.Е.Каммингс — поэт, который даже зашел в этом направлении настолько, что разрывал строки посреди слов. Вот отрывок из одного из стихотворений Камминга, в котором разрывы строк используются в агрессивной оппозиции естественному синтаксису:

dim
i
nu
tiv

e this park is e
mpty (everyb
body’s elsewher
e except me 6 e

Разрывы строк vs.Разрывы строф

В то время как большая часть этой статьи посвящена разрывам строк, которые отделяют одну строку стихов от другой, разрывы строк тесно связаны с разрывами строф (также называемыми «двойными разрывами строк»), которые разделяют группы строк на строфы. . Например, в первых двух строфах «Зеленых дорог» Эдварда Томаса есть два разрыва строки и один разрыв строфы:

Зеленые дороги, которые заканчиваются в лесу
В июне этого года усыпаны белыми гусиными перьями

Оставленные отметки сзади кто-то пошел в лес
Чтобы показать свой след.Но он никогда не вернулся.

Разрыв строфы, как показано выше, обычно отличается от разрыва строки через увеличенный пробел между двумя строками. Однако иногда — особенно когда стихи взяты внутри отрывка прозы — разрывы строк и строфы могут быть обозначены косой чертой (/) и двойной косой чертой (//) соответственно. В этой нотации первые две строфы «Зеленых дорог» будут выглядеть так:

Зеленые дороги, которые заканчиваются в лесу / В июне этого года усыпаны белыми гусиными перьями // Как следы, оставленные кем-то, кто пошел в лес / Чтобы показать его след.Но он никогда не вернулся.

Поэзия без разрывов строк

Некоторые поэты пишут в форме абзацев, а не используют разрыв строки. Эти типы стихов называются стихотворениями в прозе, потому что они выглядят как прозаические произведения. Вот пример стихотворения в прозе современной поэтессы Луизы Глюк:

Давным-давно, еще до того, как я был измученным художником, страдающим тоской, но неспособным сформировать прочную привязанность, задолго до этого я был славным правителем, объединяющим всех. о разделенной стране — так мне рассказала гадалка, исследовавшая мою ладонь.Она сказала, что великие дела впереди или, возможно, позади вас; в этом трудно быть уверенным. И все же, добавила она, в чем разница? Прямо сейчас вы ребенок, держась за руки с гадалкой. Все остальное — гипотеза и мечта.

Как определить, что является стихотворением, а что нет, без разрывов строк? Ответ в том, что это во многом зависит от контекста. Это стихотворение в прозе было написано известным поэтом и опубликовано в книге, окруженной другими стихотворениями. Но даже если бы это было не так, любой самодостаточный отрывок прозы, подобный этому — с началом и концом, — мог бы считаться стихотворением в прозе, если человек, написавший его, определил его таким образом.

Нетрадиционные разрывы строк

Хотя все показанные до сих пор разрывы строк были четкими переходами от одной строки к другой, некоторые разрывы строк более неоднозначны или выглядят иначе, чем те, которые обсуждались выше.

Отступ

Строки стихов обычно выравниваются по левой стороне страницы, но поэты иногда делают отступы (отодвигая их от левого поля), чтобы усложнить традиционные разрывы строк. Отступ не означает, что линия не разорвана должным образом.Скорее, отступ, как и сам разрыв строки, дополнительно сообщает формулировку или ритм стихотворения. Например, строка с большим отступом, чем другие на странице, может быть прочитана как имеющая перед ней немного более длинную паузу или отсроченное начало, как если бы поэт переводил дыхание. В следующем примере из стихотворения Джори Грэм использование отступов непоследовательно и иногда даже попадает в середину строки, создавая прерывистый ритм в стихотворении. Однако, несмотря на неравномерность отступов, каждая новая строка в этом стихотворении имеет свой собственный разрыв строки.

Тогда цикады снова как растопка, которую не возьмут.
Застрявшая спичка какой-то утопии, которую мы уже не помним,
условия —
правила. Что собирались упразднить, что
восстановили? За ними гудок в гавани,
хриплые объявления о неторопливом прибытии,
паучий девственный визг чаек, косой звук, скользкий
совершенно беззольный проступок

и затем подводные пастбища неиссякаемые фосфорные почерки
их собственных волнений теперь стирается
, борьба глубины с текущими коридорами глубины…

Пропущенные строки

«Пропущенная строка» — это термин для отдельной строки стихов, которая разделена на две отдельные строки с использованием определенного стиля отступа, так что первая строка выровнена по левой стороне страницы, но вторая строка имеет отступ так, чтобы она начиналась сразу под той точкой на странице, где закончилась первая строка. Следующий пример — отрывок из стихотворения Чарльза Райта, который часто использовал пропущенные строки:

Я стою внутри слова здесь
, поскольку это слово стоит в своем предложении,
Unshadowy, наполовину непринужденно.

Религия находится в руинах более тысячи лет.
Почему небо не должно быть в клочья,
потерянные ноты в забытых песнях?

Пропущенные линии могут использоваться по разным причинам. Они могут добавить пространство в середине строки, которое одновременно больше и меньше места, добавляемого типичным разрывом строки, а также визуально добавляют размер стихотворению.

Повторяющиеся строки

Если поэт пишет стихотворную строку, которая оказывается слишком длинной, чтобы уместиться на странице без перерыва, когда книга отправляется в печать, эта строка обычно разбивается на две строки, где вторая Строка имеет отступ, чтобы указать, что она должна быть продолжением предыдущей строки.Следующий пример представляет собой отрывок из стихотворения К. К. Уильямса, который был известен тем, что использовал повторяющиеся строки.

Девушка, которая в 1971 году, когда я жил одна, мучительно одинокая, лишенная, подавленная,
небрежно сказала мне в разговоре с друзьями, что, хотя сначала
она нашла меня —

Я могу Не помню этот термин, какой-то устаревший разговорный язык, означающий странные, неприемлемые, необычные вещи —

, она решила, что я в конце концов прав…. двенадцать лет спустя она возвращается ко мне из
ниоткуда …

Эти повторяющиеся строки — хотя они кажутся новыми, с отступом — на самом деле , а не следуют за разрывами строк. Отступ в этом случае означает, что строка с отступом является частью предыдущей строки и не должна рассматриваться сама по себе.

Примеры разрывов строк

Пример разрывов строк в Шекспировской

Макбет

Как и почти все произведения Шекспира, Макбет был написан ямбическим пентаметром.Это означает, что перенос строки происходит (более или менее) через каждые десять слогов.

Было бы время для такого слова.
Завтра, и завтра, и завтра,
Ползет этим мелким шагом изо дня в день
До последнего слога записанного времени,
И все наши вчерашние дни освещали дураков
Путь к пыльной смерти. Выходи, короткая свеча!
Жизнь — всего лишь ходячая тень, плохой игрок
Которая расхаживает и тревожит свой час на сцене
И затем больше не слышно: это сказка
Рассказанная идиотом, полная звука и ярости,
Ничего не значимая.

Пример разрывов строк в «Зеленых яйцах и ветчине» доктора Сьюза

В строках этой книги доктора Сьюза используется тетраметр ямба, так что каждая строка содержит восемь слогов.

Не люблю в доме.
Не люблю их с мышкой.
Мне они здесь и там не нравятся.
Я их нигде не люблю.
Не люблю зеленые яйца и ветчину.
Я не люблю их, Сэм-я-Ам.

Пример разрывов строк в произведении Роберта Крили «Конец»

Это короткое стихотворение состоит из трех двустиший, в которых разрывы строк используются как традиционными, так и нетрадиционными способами.Показанный здесь отрывок — это первые три строки стихотворения. Первый разрыв строки интуитивно соответствует синтаксису предложения, действуя как пауза там, где в противном случае могла бы стоять запятая. Однако второй разрыв строки происходит в точке, которая заметно расходится с тем местом, где синтаксис диктует паузу. Результатом этого объединения является то, что слова «Серый» странно висят в конце строки без какого-либо разрешения их значения.

Когда я знаю, что люди думают обо мне
, я погружаюсь в свое одиночество.Серая шляпа

, купленная ранее болгами.

Пример разрыва строки в произведении Чарльза Олсона «Я, Максим Глостерский, тебе»

Олсон был поэтом-новатором, который использовал разрывы строк нетрадиционным способом. В этом отрывке из его стихотворения «Я, Максим Глостерский, к Тебе» использование заглавных букв в начале строк и предложений непоследовательно, отступы используются идиосинкразическими способами, а разрывы строк не всегда встречаются там, где синтаксис сделайте паузу естественной.

вещь, которую вы ищете
, может лежать за изгибом
гнезда (во-вторых, убитый раз, птица! Птица!
А там! (Сильный) толчок, мачта! Полет
(птицы
) o kylix, o
Антоний Падуанский
низко низко, o благослови

крыши, старые, пологие, крутые
, на столбах коньков которых сидят чайки, с которых они уходят,

И стеллажи для отщепов
моего города!

Почему писатели используют разрывы строк?

Писатели используют разрывы строк, потому что это нормально. rt того, что делает стихотворение стихотворением.Добавляя больше пробелов в текст, поэты могут в большей степени контролировать скорость и ритм чтения их стихов, тем самым отличая их как от повседневного языка, так и от прозы. Так что во многом вопрос «почему писатели используют перенос строки» не отличается от вопроса о том, почему люди вообще пишут стихи.

Но это оставляет вопрос о том, как поэты используют разрывы строк для достижения различных эффектов, и ответ на этот вопрос иногда может иметь столько же ответов, сколько существует поэтов, пишущих сегодня.Однако чаще всего писатели используют разрывы строк, чтобы определить скорость и ритм стихотворения. Например, поэт может использовать более короткие строки и больше разрывов строк, чтобы замедлить читателя, и попросить их уделять особое внимание каждому отдельному слову, которое используется. С другой стороны, поэт может использовать длинные строки, если стиль стихотворения более разговорный или если предложения содержат сложные идеи с большим количеством предложений, поскольку более длинные строки легче и быстрее понять. В конце концов, разрывы строк можно использовать любым способом, которым поэт хочет изменить способ представления текста стихотворения читателю.

Другие полезные ресурсы для разрыва линий

Разметка дорожного покрытия | Справочник водителя

Двойные желтые линии, белые линии, сплошные и прерывистые линии

Для безопасного вождения во Флориде вы должны понимать, что означают разные линии на дороге. Их цвет и твердые они или сломанные подскажут, как водить машину в такой ситуации и что можно и что нельзя делать. Двойная желтая линия, например, говорит вам, что вы не можете пройти.

Рассматриваемые темы: Разметка тротуара

Справочник водителей Флориды — разметка тротуара

Линии, символы и слова часто наносятся на проезжую часть, чтобы помочь водителям направлять и контролировать движение.Вы должны знать, что означают разные линии и цвета, и подчиняться им, как дорожным знакам или сигналам.

Белые и желтые линии используются по краям тротуара и между полосами движения для удержания транспортных средств в очереди. Эти линии могут быть сплошными или прерывистыми (длинные тире), одинарными или двойными.

Желтые полосы движения

Желтые полосы движения разделяют полосы движения транспортных средств, движущихся в противоположных направлениях. Одиночные желтые линии могут также отмечать левый край тротуара на разделенных шоссе и улицах с односторонним движением.желтая прерывистая линия

желтая прерывистая линия

Желтая прерывистая линия разделяет полосы движения, движущегося в противоположных направлениях. Держитесь правее линии, если только вы не проезжаете впереди идущую машину. Проходя мимо, вы можете временно пересечь эту линию, когда это будет безопасно.

Двойные желтые линии: одна сплошная, одна сломанная

Сплошная желтая линия справа от пунктирной желтой центральной линии означает, что обгон или пересечение запрещены на этой полосе, за исключением поворота налево.Если ломаная линия находится ближе к вам, вы можете пересечь ломаную линию только для того, чтобы обогнать другой автомобиль, и только тогда, когда это будет безопасно.

Двойные желтые линии

Двойные сплошные желтые линии запрещают транспортным средствам, движущимся в любом направлении, пересекать линии. Вы не можете пересекать эти линии, если не поверните налево, когда это безопасно.

Белые полосы движения

Белые полосы движения разделяют полосы движения транспорта, движущегося в одном направлении.Одиночные белые линии могут также отмечать правый край тротуара.

Белая прерывистая линия

Белая прерывистая линия разделяет две полосы движения в одном направлении. После подачи сигнала (если это безопасно) вы можете пересекать эту линию при смене полосы движения.

Сплошная белая линия

Сплошная белая линия отмечает правый край проезжей части или разделяет полосы движения, движущегося в одном направлении. Вы можете двигаться в одном направлении по обе стороны от этой линии, но вам не следует пересекать линию, если только вы не должны сделать это во избежание опасности.

Двойная сплошная белая линия

Двойная белая линия разделяет две полосы движения, идущего в одном направлении. Пересечение двойной сплошной линии запрещено. Только левый поворот полоса

Сплошная полоса со стрелкой поворота

Сплошные белые линии используются для полос поворота и препятствуют смене полосы движения возле перекрестков. Стрелки часто используются с белыми линиями, чтобы показать, какой поворот может быть сделан с полосы движения.

Если вы находитесь на полосе, обозначенной изогнутой стрелкой и словом ТОЛЬКО, вы должны повернуть в направлении стрелки.Если ваша полоса отмечена как изогнутой, так и прямой стрелкой, вы можете повернуть или пойти прямо.

Реверсивные полосы

На некоторых автомагистралях есть разветвленные полосы движения для облегчения движения в час пик. Направление движения обычно меняется каждый день в определенное время. Эта разметка на тротуаре используется вместе со специальными дорожными знаками и другими знаками и символами.

Сплошная белая линия отмечает край тротуара на большинстве дорог. Стоп-линии, пешеходные переходы и парковочные места также отмечены белыми линиями.Такие символы, как стрелки, также имеют белый цвет. Одной желтой линией отмечен левый край всех разделенных дорог или дорог с односторонним движением. Бордюры часто обозначаются желтым цветом в запретных для парковки зонах возле пожарных кранов или перекрестков. Запрещается парковаться или проезжать по участкам с разметкой, указывающей на пожарные полосы или зоны безопасности.

Стрелка разметки полосы в центральной полосе на схеме ниже указывает, что движение по этой полосе может быть изменено в соответствии с местными органами управления дорожным движением из-за движения в час пик или других особых дорожных условий.

Водители с любого направления могут использовать центральную полосу для левых поворотов.

Дорога с двусторонним движением с центральной полосой

Дорога с двусторонним движением с центральной полосой для левых поворотов в любом направлении движения. Специально обозначенная центральная полоса поворота предназначена для замедления и укрытия поворачивающих транспортных средств и не может быть использована для обгона.

Водители с любого направления могут использовать центральную полосу для левых поворотов. Водители, движущиеся в любом направлении, могут использовать центральную полосу только для левых поворотов.

Назад к Руководству для водителей Флориды Содержание

Типы линий в R: lty — Easy Guides — Wiki

Различные типы линий , доступные в R , показаны на рисунке ниже. Аргумент lty может использоваться для указания типа строки . Чтобы изменить ширину строки на , можно использовать аргумент lwd .

Функция, используемая для создания этого рисунка, предоставлена ​​в конце этого документа.

Тип строки (lty) можно указать с помощью текста («пустая», «сплошная», «пунктирная», «пунктирная», «точка-тише», «длинная тире», «двойная тише») или числа (0, 1, 2, 3, 4, 5, 6) . Обратите внимание, что lty = «solid» идентично lty = 1 .

  # Сплошная линия (по умолчанию)
сюжет (1:10, 1:10, type = "l")
# Используйте пунктирную линию
сюжет (1:10, 1:10, type = "l", lty = 2)
# Изменить ширину линии
сюжет (1:10, 1:10, type = "l", lty = 2, lwd = 3)  

По умолчанию lty = 1

Используйте следующую функцию R, чтобы отобразить график типов линий , доступных в R :

  # Типы линий
# ++++++++++++++++++++++++++++++++++++++++++++
generateRLineTypes  

Этот анализ был выполнен с использованием R (вер.3.1.0).

Понравилась эта статья? Буду очень признателен, если вы поможете ему распространиться, отправив его другу по электронной почте или поделившись им в Twitter, Facebook или Linked In.

Покажи мне немного любви с кнопками «Мне нравится» ниже … Спасибо и, пожалуйста, не забудь поделиться и прокомментировать ниже !!

Avez vous aimé cet article? Je vous serais très recnaissant si vous aidiez à sa diffusion en l’envoyant par courriel à un ami or le partageant на Twitter, Facebook или Linked In.