Примеры последовательности: определения, формулы и примеры решения — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

виды числовых последовательностей и примеры

Если функция определена на множестве натуральных чисел N, то такая функция называется бесконечной числовой последовательностью. Обычно числовые последовательность обозначают как(Xn), где n принадлежит множеству натуральных чисел N.

Числовая последовательность может быть задана формулой. Например, Xn=1/(2*n). Таким образом мы ставим в соответствие каждому натуральному числу n некоторый определенный элемент последовательности (Xn).

Если теперь последовательно брать n равными 1,2,3, …., мы получим последовательность (Xn): ½, ¼, 1/6, …, 1/(2*n), …

Виды последовательности

Последовательность может быть ограниченной или неограниченной, возрастающей или убывающей.

Последовательность (Xn) называет ограниченной, если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m<=Xn

Последовательность (Xn), не являющаяся ограниченной, называется неограниченной последовательностью.

Последовательность (Xn) называется возрастающей, если для всех натуральных n выполняется следующее равенство X(n+1) > Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.

Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X(n+1) < Xn. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена.

Пример последовательности

Проверим, являются ли последовательности 1/n и (n-1)/n убывающими.

Если последовательность убывающая, то X(n+1) < Xn. Следовательно X(n+1) – Xn < 0.

1/n:

X(n+1) – Xn = 1/(n+1) – 1/n = -1/(n*(n+1)) < 0. Значит последовательность 1/n убывающая.

(n-1)/n:

X(n+1) – Xn =n/(n+1) — (n-1)/n = 1/(n*(n+1)) > 0. Значит последовательность (n-1)/n возрастающая.

Нужна помощь в учебе?

Предыдущая тема: Графический способ решения систем уравнений: алгоритм и пример решения
Следующая тема:&nbsp&nbsp&nbspЭлектронный учебник по русскому языку: все темы школьной программы

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ | Энциклопедия Кругосвет

Содержание статьи

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y₁, y₂,…, y_n,…. Значения y₁, y₂, y₃,… называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n² можно записать:

y₁ = 1²= 1;

y₂ = 2²= 4;

y₃ = 3²= 9;…y_n= n²;…

Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n-го члена:

y_n= f(n).

Пример. y_n= 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y₁ = 3; y_n= y_n_–1 + 4, если n = 2, 3, 4,….

Здесь y₁ = 3; y₂ = 3 + 4 = 7; y₃ = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: y_n= 4n – 1.

Пример 2. y₁ = 1; y₂ = 1; y_n = y_n_–2 + y_n_–1 , если n = 3, 4,….

Здесь: y₁ = 1; y₂ = 1; y₃ = 1 + 1 = 2; y₄ = 1 + 2 = 3; y₅ = 2 + 3 = 5; y₆ = 3 + 5 = 8;

Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .

На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n.

Свойства числовых последовательностей.

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {y_n} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y₁y₂y₃y_ny_n₊₁

Определение. Последовательность {y_n} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y₁ > y₂ > y₃ > … > y_n> y_n₊₁ > … .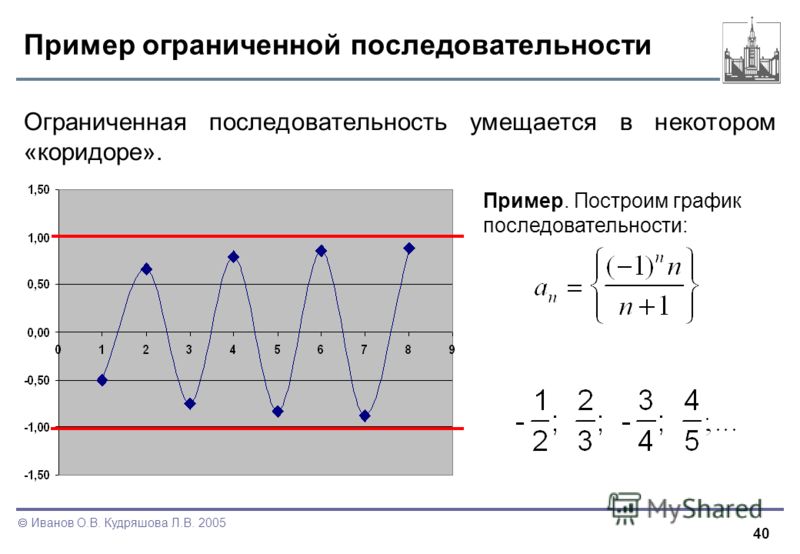

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Пример 1. y₁ = 1; y_n= n²– возрастающая последовательность.

Пример 2. y₁ = 1; – убывающая последовательность.

Пример 3. y₁ = 1; – эта последовательность не является не возрастающей не убывающей.

Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство y_n= y_n+T. Число T называется длиной периода.

Пример. Последовательность периодична с длиной периода T = 2.

Арифметическая прогрессия.

Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность {a_n}, заданная рекуррентно соотношениями

a₁ = a, a_n= a_n_–1 + d (n = 2, 3, 4, …)

(a и d – заданные числа).

Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a₁ = 1, d = 2.

Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a₁ = 20, d = –3.

Нетрудно найти явное (формульное) выражение a_nчерез n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1)d по сравнению с первым членом арифметической прогрессии, т.е.

a_n = a₁ + d(n – 1).

Это формула n-го члена арифметической прогрессии.

Используя явное выражение a_nчерез n, можно доказать следующее свойство арифметической прогрессии: если натуральные числа i, j, k, l таковы, что i + j = k + l, то a_i+ a_j= a_k+ a_l. Чтобы в этом убедиться, достаточно подставить i, j, k и l вместо n в формулу n-го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые n членов арифметической прогрессии, то суммы членов, равно отстоящих от концов, будут одинаковы:

a₁ + a_n= a₂ + a_n–₁ = a₃ + a_n_–2 = … = 2_a1 + (n – 1)d.

Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии:

S_n= a₁ + a₂ + … + a_n_–1 + a_n.

С этой целью берется еще одна такая же сумма, но слагаемые записывается в обратном порядке:

S_n = a_n + a_n–₁ + … + a₂ + a₁.

Далее она складывается почленно с исходной суммой, причем слагаемые сразу попарно группируются. В результате

2S_n = (a₁ + a_n) + (a₂ + a_n_–1) + … + (a_n + a₁) = n(2_a1 + (n – 1)d),

откуда . Это формула суммы n членов арифметической прогрессии.

Арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним – предыдущего и последующего. Действительно, так как

a_n= a_n_–1 + d;

a_n = a_n₊₁ – d.

Сложение двух последних равенств дает .

Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.

Пример. При каком значении x числа 3x + 2, 5x – 4 и 11x + 12 образуют конечную арифметическую прогрессию?

Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению

5x – 4 = ((3x + 2) + (11x + 12))/2.

Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3x + 2, 5x – 4 и 11x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.

Геометрическая прогрессия.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.

Таким образом, геометрическая прогрессия – это числовая последовательность {b_n}, заданная рекуррентно соотношениями

b₁ = b, b_n = b_n_–1q (n = 2, 3, 4…).

(b и q – заданные числа, b ≠ 0, q ≠ 0).

Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.

Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.

Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.

Геометрическая прогрессия является возрастающей последовательностью, если b1 > 0, q > 1, и убывающей, если b1 > 0, 0 q

Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.

b₁², b₂², b₃², …, b_n2,… является геометрической прогрессией, первый член которой равен b₁², а знаменатель – q².

Формула n-го члена геометрической прогрессии имеет вид

b_n= b₁q^n–¹.

Можно получить формулу суммы членов конечной геометрической прогрессии.

Пусть дана конечная геометрическая прогрессия

b₁, b₂, b₃, …, b_n

пусть S_n – сумма ее членов, т. е.

S_n= b₁ + b₂+ b₃ + … + b_n.

Принимается, что q № 1. Для определения S_nприменяется искусственный прием: выполняются некоторые геометрические преобразования выражения S_nq.

Тогда

S_nq = (b₁ + b₂ + b₃+ … + b_n_–1 + b_n)q = b₂ + b₃ + b₄ + …+ b_n+ b_nq = S_n+ b_nq – b₁.

Таким образом, S_nq = S_n + b_nq – b₁ и, следовательно,

Это формула суммы n членов геометрической прогрессии для случая, когда q ≠ 1.

При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае S_n= a₁n.

Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как

b_n= b_n-₁q;

b_n= b_n+₁/q,

следовательно, b_n2= b_n–₁ b_n+₁ и верна следующая теорема (характеристическое свойство геометрической прогрессии):

числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.

Предел последовательности.

Пусть есть последовательность {c_n} = {1/n}. Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число , или . С ростом n все члены геометрической прогрессии убывают и их значение приближается к нулю. В этом случае принято говорить, что при n, стремящемся к бесконечности, данная последовательность сходится и нуль есть ее предел. Записывается это так:

Строгое определение предела формулируется следующим образом:

Если существует такое число A, что для любого (сколь угодно малого) положительного числа ε найдется такое натуральное N (вообще говоря, зависящее от ε), что для всех n ≥ N будет выполнено неравенство |a_n– A| {a_n} сходится и A – ее предел.

Обозначается это так: .

В противном случае последовательность называется расходящейся.

Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности {c_n} = {1/n}. Пусть ε – сколь угодно малое положительное число. Рассматривается разность

Существует ли такое N, что для всех n ≥ N выполняется неравенство 1/N ? Если взять в качестве N любое натуральное число, превышающее 1/ε, то для всех n ≥ N выполняется неравенство 1/n ≤ 1/N ε , что и требовалось доказать.

Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.

Теорема 1. Если последовательность имеет предел, то она ограничена.

Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.

Теорема 3. Если последовательность {a_n} имеет предел A, то последовательности {ca_n}, {a_n+ с} и {| a_n|} имеют пределы cA, A + c, |A| соответственно (здесь c – произвольное число).

Теорема 4. Если последовательности {a_n} и {b_n} имеют пределы, равные A и B соответственно, то последовательность {pa_n + qb_n} имеет предел pA + qB.

Теорема 5. Если последовательности {a_n} и {b_n}имеют пределы, равные A и B соответственно, то последовательность {a_nb_n} имеет предел AB.

Теорема 6. Если последовательности {a_n} и {b_n} имеют пределы, равные A и B соответственно, и, кроме того, b_n ≠ 0 и B ≠ 0, то последовательность {a_n/ b_n} имеет предел A/B.

Анна Чугайнова

виды числовых последовательностей и примеры 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 9.

Последовательности.

Давай выпишем натуральные четные числа 2, 4, 6 ,8, ….

Очевидно, что следующее число равно 10, далее 12, на десятом месте будет 20, на сотом – 200 и т.д. То есть для любого натурального числа n можем указать соответствующее ему положительное четное число, равное 2n Рассмотрим еще одну последовательность, выпишем положительные дроби, числитель которых на единицу меньше знаменателя:

12;23;34;45…

То есть для каждого натурального числа n можно указать соответствующую ему дробь: nn+1. Значит, на шестом месте будет дробь 67, на двадцатом — 2021, на сотом — 100101 и т.д.

Числа, которые образуют последовательность называют членами данной последовательности.

Число, которое стоит на первом месте – первый член, на втором – второй член и т.д.

Члены последовательности обозначают a₁, a₂, a₃ …

Член, номер которого n, обозначают a_{и называют n-ым членом последовательности.}

Саму последовательность обозначают: an или cn.

Последовательности бывают конечными и бесконечными.

Все предыдущие последовательности, которые мы рассмотрели – бесконечные, а, например, последовательность нечетных двузначных чисел: 11, 13, 15, … 99 – это конечная последовательность.

Любую последовательность можно задать числами или формулой. Например, положительных четных чисел можно задать формулой a_n = 2n, а последовательность положительных нечетных чисел можно задать a_n = 2n + 1.

Рассмотрим последовательность, которая задана формулой c_n = 5n — n². Найдем первые пять членов этой последовательности:

c1=5∙1-12=4

c2=5∙2-22=6

c3=5∙3-32=6

c4=5∙4-42=4

c5=5∙5-52=0

4; 6; 6; 4; 0; …

Пусть следующая последовательность задана формулой: x_n = (-1)ⁿ ∙ 5, тогда все члены последовательности с четными номерами будут равны 5, а с нечетными номерами будут равны (-5). То есть последовательность будет выглядеть так -5; 5; -5; 5;…

Рассмотрим еще одну последовательность, первый член которой равен 3, а каждый следующий член равен квадрату предыдущего, то есть

a1=3,an+1=an2

Найдем несколько членов этой последовательности:

a2=32=9

a3=92=81

a4=812=6561

Пусть следующая последовательность задана формулой bn=n2-n. Найдем пятый и одиннадцатый члены этой последовательности. Получим:

b5=52-5=25-5=20

b11=112-11=121-11=110.

Видно, что мы можем найти любой член последовательности по заданной формуле.

Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной.

Выпишем последовательность натуральных чисел, которые при делении на 3 дают в остатке 2 и запишем рекуррентную формулу этой последовательности. Получим:

5; 8; 11; 14;…

То есть an=3n+2

Пусть задана последовательность cn=n2+2n. Число 168 является членом данной последовательности. Необходимо найти номер данного члена?

Итак, cn=168=n2+2n.

Решим уравнение:

n2+2n=168

n2+2n-168=0

n1=-14,n2=12

Так как n – это порядковый номер члена последовательности, то он может быть только натуральным числом, значит, n = 12. Следовательно, число 168 – это двенадцатый член нашей последовательности.

a12=168.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Элементы математического анализа

Числовые последовательности. Способы задания числовых последовательностей

Если каждому натуральному числу n поставлено в соответствие некоторое действительное число x_n , то говорят, что задана числовая последовательность

x₁, x₂, … x_n , …

Число x₁ называют членом последовательности с номером 1 или первым членом последовательности, число x₂ — членом последовательности с номером 2 или вторым членом последовательности, и т.д. Число x_n называют членом последовательности с номеромn .

Существуют два способа задания числовых последовательностей – с помощью формулы общего члена последовательности и с помощью рекуррентной формулы.

Задание последовательности с помощью формулы общего члена последовательности – это задание последовательности

x₁, x₂, … x_n , …

с помощью формулы, выражающей зависимость члена x_n от его номера n .

Пример 1. Числовая последовательность

1, 4, 9, … n² , …

задана с помощью формулы общего члена

x_n = n², n = 1, 2, 3, …

Задание последовательности с помощью формулы, выражающей член последовательности x_n через члены последовательности с предшествующими номерами, называют заданием последовательности с помощью рекуррентной формулы.

Пример 2 (Числа Фибоначчи). Числовая последовательность

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

может быть задана с помощью рекуррентной формулы

x_n = x_{n – 1} + x_{n – 2}, n > 2 ,

с начальными условиями

x₁ = 1, x₂ = 1 .

Возрастающие и убывающие последовательности

Определение 1. Числовую последовательность

x₁, x₂, … x_n , …

называют возрастающей последовательностью, если каждый член этой последовательности больше предшествующего члена.

Другими словами, для всех n = 1, 2, 3, … выполнено неравенство

x_{n + 1} > x_n

Пример 3. Последовательность натуральных чисел

1, 2, 3, … n, …

является возрастающей последовательностью.

Определение 2. Числовую последовательность

x₁, x₂, … x_n , …

называют убывающей последовательностью, если каждый член этой последовательности меньше предшествующего члена.

Другими словами, для всех n = 1, 2, 3, … выполнено неравенство

x_{n + 1} < x_n

Пример 4. Последовательность

заданная формулой

является убывающей последовательностью.

Пример 5. Числовая последовательность

1, – 1, 1, – 1, …

заданная формулой

x_n = (– 1)ⁿ, n = 1, 2, 3, …

не является ни возрастающей, ни убывающей последовательностью.

Определение 3. Возрастающие и убывающие числовые последовательности называют монотонными последовательностями.

Ограниченные и неограниченные последовательности

Определение 4. Числовую последовательность

x₁, x₂, … x_n , …

называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M.

Другими словами, для всех n = 1, 2, 3, … выполнено неравенство

x_n < M

Определение 5. Числовую последовательность

x₁, x₂, … x_n , …

называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m.

Другими словами, для всех n = 1, 2, 3, … выполнено неравенство

x_n > m

Определение 6. Числовую последовательность

x₁, x₂, … x_n , …

называют ограниченной, если она ограничена и сверху, и снизу.

Другими словами, существуют такие числа M и m, что для всех n = 1, 2, 3, … выполнено неравенство

m < x_n < M

Определение 7. Числовые последовательности, которые не являются ограниченными, называют неограниченными последовательностями.

Пример 6. Числовая последовательность

1, 4, 9, … n² , …

заданная формулой

x_n = n², n = 1, 2, 3, … ,

ограничена снизу, например, числом 0. Однако эта последовательность неограничена сверху.

Пример 7 . Последовательность

заданная формулой

является ограниченной последовательностью, поскольку для всех n = 1, 2, 3, … выполнено неравенство

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Предел числовой последовательности

Определение 1. Число a называют пределом числовой последовательности

a₁, a₂, … a_n , …

если для любого положительного числа ε найдется такое натуральное число N , что при всех n > N выполняется неравенство

| a_n – a | < ε .

Условие того, что число a является пределом числовой последовательности

a₁, a₂, … a_n , … ,

записывают с помощью обозначения

и произносят так: «Предел a_n при n , стремящемся к бесконечности, равен a ».

То же самое соотношение можно записать следующим образом:

a_n → a при .

Словами это произносится так: «a_n стремится к a при n , стремящемся к бесконечности».

Замечание. Если для последовательности

a₁, a₂, … a_n , …

найдется такое число a , что a_n → a при , то эта последовательность ограничена.

Определение 2. Говорят, что последовательность

a₁, a₂, … a_n , …

стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N , что при всех n > N выполняется неравенство

| a_n| > C .

Условие того, что числовая последовательность

a₁, a₂, … a_n , … ,

стремится к бесконечности, записывают с помощью обозначения

или с помощью обозначения

при .

Пример 1. Для любого числа k > 0 справедливо равенство

Пример 2 . Для любого числа k > 0 справедливо равенство

Пример 3. Для любого числа a такого, что | a | < 1, справедливо равенство

Пример 4. Для любого числа a такого, что | a | > 1, справедливо равенство

Пример 5 . Последовательность

– 1 , 1 , – 1 , 1 , … ,

заданная с помощью формулы общего члена

a_n = (– 1)ⁿ ,

предела не имеет.

Свойства пределов числовых последовательностей

Рассмотрим две последовательности

a₁, a₂, … a_n , … , и b₁, b₂, … b_n , … .

Если при существуют такие числа a и b , что

и ,

то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем

Если, кроме того, выполнено условие

то при существует предел дроби

причем

Для любой непрерывной функции f (x) справедливо равенство

Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии

Рассмотрим геометрическую прогрессию

b₁, b₂, … b_n , … ,

знаменатель которой равен q .

Для суммы первых n членов геометрической прогрессии

S_n = b₁ + b₂ + … + b_n , n = 1, 2, 3, …

справедлива формула

Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение

S = b₁ + b₂ + … + b_n + … ,

то будет справедлива формула

В случае бесконечно убывающей геометрической прогрессии знаменатель q удовлетворяет неравенству

| q | < 1 ,

поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем

Итак,

Примеры вычисления пределов последовательностей. Раскрытие неопределенностей

Определение 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .

Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.

Пример 6. Найти предел последовательности

Решение. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:

Ответ.

Пример 7 . Найти предел последовательности

Ответ.

В следующих двух примерах показано, как можно раскрыть неопределенности типа.

Пример 8 . Найти предел последовательности

Решение. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:

Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:

Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

Ответ.

Пример 9. Найти предел последовательности

Решение. В рассматриваемом примере неопределенность типа возникает за счет разности двух корней, каждый из которых стремится к. Для того, чтобы раскрыть неопределенность, домножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».

Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.

Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби,а затем сокращая дробь на n²:

Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

Ответ.

Пример 10. Найти предел последовательности

Решение. Замечая, что для всех k = 2, 3, 4, … выполнено равенство

получаем

Ответ. 1 .

Число e. Второй замечательный предел

Рассмотрим последовательность

(1)

В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой e.

Таким образом, справедливо равенство

(2)

причем расчеты показывают, что число

e = 2,718281828459045…

и является иррациональным и трансцендентным числом.

Число e играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции

y = e^x,

которую называют «экспонента».

Число e также является пределом последовательности

(3)

что позволяет вычислять число e с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.

Замечание. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

9 гифок, наглядно иллюстрирующих числовые последовательности

Говоря формальным языком, под последовательностью понимается отображение из множества натуральных чисел во множество произвольной природы. Фактически мы перенумеровываем элементы некоторого множества. В курсе математического анализа наиболее важными являются числовые последовательности, т.е. «перенумерация» некоторого подмножества из множества вещественных чисел. Если говорить сухим математическим языком, такое соотношение записывается следующим образом:

Для наглядности мы проиллюстрируем на следующем примере:

Важнейшим понятием из теории числовых последовательностей является понятие предела. Для чего же в программировании может быть использован предел числовой последовательности? Давайте рассмотрим пример поиска логарифма.

Машина изначально умела только делать логические операции с числами, записанными в двоичной системе счисления, затем ее научили делать простейшие арифметические операции, но когда дело дошло до поиска значение «более сложных» функций, таких как логарифм, в дело пошли числовые последовательности, а именно последовательности сумм рядов, которые позволяют с той или иной точностью понять, чему же равен логарифм того или иного числа. А логарифм, в свою очередь, используется, к примеру, в нейросетях.

Но об этом чуть позже.

Как же определяется предел числовой последовательности? Математическим языком это записывается следующим образом:

Число a является пределом числовой последовательности X_n , если выполняется следующие условие:

Звучит сложно для восприятия, не правда ли?

Давайте рассмотрим визуализацию сходящейся числовой последовательности, которая выглядит следующим образом

Чтобы было нагляднее понимать это определение, можно представить, что ε — это ширина трубки, которую мы можем уменьшать сколько угодно, в любом случае найдется такое N, начиная с которого все, что справа от него, будет находиться в этой трубке.

Здесь изображена конкретная ε — трубка, но видно, что каково бы ни было число ε > 0, всегда найдется N, от него зависящий, что начиная с этого номера значения последовательности x_n отличаются от 1 не более чем на ε.

Между тем расходящиеся числовые последовательности встречаются намного чаще. Давайте домножим рассмотренную выше последовательность на «переключатель» (-1)ⁿ. Получаем последовательность:

Вот ее визуализация:

У этой последовательности есть две точки «накопления» её элементов – «1» и «-1». Мы видим, что, например, для ε = 0,1 (см. чертёж) мы никогда не найдем такого N, что все точки последовательности, начиная с некоторого номера, будут попадать в интервал (a - ε; a + ε), где a — произвольно заданное число. Все четные элементы попадают в верхнюю ε — окрестность, а все нечетные в нижнюю. Предела у этой последовательности нет.

Рассмотрим более хитрые примеры расходящихся числовых последовательностей. Изобразим, например:

У этой последовательности 5 точек накопления ее элементов (также известных, как частичные пределы).

Можно рассмотреть эту же последовательность, изображенную в виде точек. По оси абсцисс отложены номера элементов:

Рассмотрим последовательность с бесконечным числом точек накопления элементов (частичных пределов).

Как видно на визуализации, множество ее частичных пределов представляет из себя весь отрезок от -1 до 1:

На анимации изображена логарифмическая шкала на 50 тысяч элементов.

Если рассмотреть эту последовательность в виде вертикальных отрезков, они плотно заполнят весь отрезок от -1 до 1.

Изобразим числовую последовательность, включающую в себя все рациональные числа от 0 до 1. Множество ее частичных пределов представляет собой отрезок [0; 1].

Ее визуализация в логарифмической шкале будет выглядеть следующим образом:

Далее рассмотрим визуализации числовых последовательностей, сходящихся к числу e :

Может быть, многие из вас знают, что последовательность s_n сходится к числу e гораздо быстрее, но насколько быстрее – представить не очень просто. В этом нам тоже помогут анимации. Давайте изобразим обе эти последовательности на одном графике:

Зачем может пригодиться число e? В математике оно всплывает крайне часто, например, для поиска факториала.

И на десерт

В заключение рассмотрим последовательность, частичными пределами которой являются все дроби вида:

На графике она будет выглядеть следующим образом:

И в вертикальных отрезках:

Видно, что точка 0 тоже является частичным пределом.

Продолжение следует…

Если вас заинтересовало наше иллюстративное объяснение темы числовых последовательностей, вы можете также посмотреть иллюстративный курс по математическому анализу.

Выражаем большую признательность за работу Алексею Никитину и Алексею Карпову.

Числовые последовательности (определение, примеры, свойства)

Вопросы
занятия:

·
познакомиться
с понятием числовой последовательности;

·
рассмотреть
способы задания числовых последовательностей.

Материал
урока.

Мы
с вами приступаем к изучению темы «Производная» и начнём с повторения понятия
числовой последовательности. С этим понятием вы знакомились в курсе алгебры
базовой школы.

Давайте
вспомним, что же такое числовая последовательность, и какими свойствами она
обладает.

Определение.

Функцию
вида y = f(x),
где x принадлежит множеству натуральных чисел называют функцией натурального
аргумента или числовой последовательностью и обозначают

y = f (n)

y₁,
y₂, y₃,…,y_n,…

(y_n).

Давайте теперь вспомним способы задания
последовательностей.

Последовательность задана аналитически,
если указана формула её n -ого члена, y_n
= f(n).

Например:

При
словесном способе задания последовательности: последовательность,
каждый её член, возможность вычисления каждого её члена можно задать словами,
не обязательно формулами.

При рекуррентном задании
последовательности задаются правила вычисления энного члена по предыдущим
членам.

Давайте вспомним свойства числовых
последовательностей.

Последовательность (y_n)
называется ограниченной сверху, если все её члены
не больше некоторого числа. Другими словами, последовательность (y_n)
ограничена сверху, если существует число M
такое, что для любого n
выполняется неравенство: y_n
≤ M.

Число M
называется верхней границей последовательности.

Например,

Последовательность (y_n)
называется ограниченной снизу, если все её члены не
больше некоторого числа. Другими словами, последовательность (y_n)
ограничена снизу, если существует число m такое, что для
любого n выполняется неравенство:
y_n ≥
m.

Число m
называется нижней границей последовательности.

Например,

Если последовательность ограничена и сверху
и снизу, то её называют ограниченной последовательностью.

Рассмотрим пример.

Таким образом, ограниченность
последовательности означает, что все члены последовательности (точнее,
соответствующие им точки прямой) принадлежат некоторому отрезку.

Последовательность (y_n)
называется возрастающей, если каждый последующий член больше
предыдущего, то есть верно неравенство

Например,

Последовательность (y_n)
называется убывающей, если каждый её член меньше предыдущего, то
есть верно неравенство

Например,

Возрастающие и убывающие
последовательности объединяют общим термином – монотонные
последовательности.

Рассмотрим несколько примеров.

Пример.

Последовательности и шаблоны — Mathigon

Многие профессии, использующие математику, заинтересованы в одном конкретном аспекте — нахождение шаблонов и способность предсказывать будущее. Вот два примера:

Геологи всего мира хотят предсказать землетрясений и извержений вулкана . Они могут попытаться найти закономерности в исторических данных сейсмографов, в атмосфере или даже в поведении животных. Например, одно землетрясение может позже вызвать афтершоки.

Банкиры также просматривают исторические данные о курсах акций, процентных ставках и курсах обмена валют, чтобы оценить, как финансовые рынки могут измениться в будущем. Возможность предсказать, пойдет ли цена акции вверх или вниз, может быть чрезвычайно прибыльной!

Профессиональные математики используют очень сложные алгоритмы для поиска и анализа всех этих закономерностей, но пока давайте начнем с чего-нибудь более простого.

Простые последовательности

В математике последовательность — это цепочка чисел (или других объектов), которые обычно следуют определенному шаблону.Отдельные элементы в последовательности называются терминами .

Вот несколько примеров последовательностей. Сможете ли вы найти их закономерности и вычислить следующие два члена?

3 , 6 +3 , 9 +3 , 12 +3 , 15 +3 , +3 +3 ,… Шаблон: «Добавьте 3 к предыдущему номеру, чтобы получить следующий «.

4 , 10 +6 , 16 +6 , 22 +6 , 28 +6 , +6 , +6 ,… Шаблон: «Добавить 6 к предыдущему числу чтобы получить следующий.»

3 , 4 +1 , 7 +3 , 8 +1 , 11 +3 , +1 , +3 ,… Шаблон:« Попеременно добавляйте 1 и добавляйте 3 к предыдущему номеру, чтобы перейти к следующему ».

1 , 2 × 2 , 4 × 2 , 8 × 2 , 16 × 2 , × 2 , × 2 ,… Шаблон: «Умножить предыдущее число на 2 , чтобы получить следующий «.

Точки (…) в конце просто означают, что последовательность может продолжаться бесконечно.Обращаясь к таким последовательностям в математике, мы часто представляем каждый член специальной переменной:

x1, x2, x3, x4, x5, x6, x7,…

Маленькое число после x называется . нижний индекс и указывает положение термина в последовательности. Это означает, что мы можем представить n -й член последовательности как xnxix2.

Треугольники и квадратные числа

Последовательности в математике не всегда должны быть числами. Вот последовательность, состоящая из геометрических фигур — треугольников увеличивающегося размера:

На каждом шаге мы добавляем еще одну строку к предыдущему треугольнику.Длина этих новых строк также увеличивается каждый раз на единицу. Вы видите узор?

1 , 3 +2 , 6 +3 , 10 +4 , 15 +5 , 21 +6 +7 , +8 ,…

Мы можем также опишите этот паттерн с помощью специальной формулы:

xn = xn − 1 + n

Чтобы получить n -ое число треугольника, мы берем предыдущий первый следующий номер треугольника и прибавляем n .Например, если n = $ {n}, формула принимает вид x $ {n} = x $ {n-1} + $ {n}.

Формула, которая выражает xn как функцию предыдущих членов последовательности, называется рекурсивной формулой . Если вы знаете первый член, последний член, второй член в последовательности, вы можете вычислить все последующие.

Другая последовательность, состоящая из геометрических фигур, — это квадратные числа . Каждый член состоит из все более крупных квадратов:

Для чисел треугольника мы нашли рекурсивную формулу, которая сообщает вам следующих членов последовательности в зависимости от предыдущих членов.Для квадратных чисел мы можем сделать еще лучше: формула, которая сообщает вам n -й член напрямую, без необходимости сначала вычислять все предыдущие:

xn =

Это называется явной формулой . Мы можем использовать его, например, для вычисления 13-го квадратного числа без предварительного нахождения предыдущих 12 квадратных чисел.

Давайте суммируем все определения, которые мы видели до сих пор:

Последовательность — это список чисел, геометрических фигур или других объектов, которые следуют определенному шаблону.Отдельные элементы в последовательности называются термами и представлены такими переменными, как xn.

Рекурсивная формула для последовательности сообщает вам значение n -го члена как функцию его предыдущего члена — первого члена. Вы также должны указать первые термины.

Явная формула для последовательности сообщает вам значение n -го члена как функцию только _n_ предыдущего члена, без ссылки на другие термины в последовательности.

Фотография последовательности действий

В следующих разделах вы узнаете о множестве различных математических последовательностей, удивительных шаблонов и неожиданных приложений.

Но сначала давайте посмотрим на кое-что совершенно другое: фотосъемка с последовательностью действий . Фотограф делает несколько снимков в быстрой последовательности, а затем объединяет их в одно изображение:

Вы видите, как лыжник формирует последовательность? Узор — это не сложение или умножение, а геометрическое преобразование.Между последовательными шагами лыжник одновременно переводится и поворачивается, отражается и расширяется.

Вот еще несколько примеров фотосъемки последовательности действий для вашего удовольствия:

Последовательности и серии — рабочие примеры

Последовательности

Последовательность $ \ {a_ {n} \} $ — это бесконечный список чисел
$$ a_ {1}, a_ {2}, a_ {3}, \ ldots, $$
где у нас есть одно число $ a_ {n} $ для каждого положительного целого числа $ n $.

Определение последовательностей.

Мы можем указать последовательность разными способами.

Выкройка.
Мы можем указать это, перечислив некоторые элементы и подразумевая, что
Показанный образец продолжается.

Пример.

Например
$$ 2, 4, 6, 8, \ ldots $$
будет последовательность, состоящая из четных положительных целых чисел.

Формула.
Мы также можем указать последовательность, указав формулу для члена, который
соответствует целому числу $ n $.

Пример.

Например, последовательность
$$ 2, 4, 6, 8, \ ldots $$
также может быть задано явной формулой
$$ a_ {n} = 2n.$$

Рекурсивно.
Наконец, мы также можем предоставить правило для получения следующего члена последовательности из предыдущих. Это называется рекурсивно определенной последовательностью .

Пример.

Например, последовательность
$$ 2, 4, 6, 8, \ ldots $$
может быть определено правилом
$$ a_ {1} = 2 \ quad \ text {and} \ quad a_ {n} = a_ {n-1} +2 \ text {for} n \ geq 2. $$

Это правило гласит, что мы получаем следующий член, беря предыдущий член и добавляя 2 доллара. Поскольку мы начинаем с числа 2, мы получаем все четные положительные целые числа.

Давайте обсудим эти способы определения последовательностей более подробно и рассмотрим несколько примеров.

Часть 1: Арифметические последовательности

Последовательность, которую мы видели в предыдущем абзаце, является примером того, что
называется арифметической последовательностью : каждый член получается
, добавив фиксированное число к предыдущему члену.

В качестве альтернативы, разница между последовательными сроками всегда является
одно и тоже.

Общая формула.

Если последовательность $ a_ {n} $ является арифметической, то существует фиксированное число $ d $, так что $ a_ {n + 1} -a_ {n} = d $ для любого $ n.$
Число $ d $ обычно называют шагом или разницей . Давайте попробуем найти формулу для члена $ a_ {n} $ арифметической последовательности в терминах $ d $ и $ a_ {1} $.

Начнем с $ a_ {n} = a_ {n-1} + d $. Применяя это снова, мы видим, что, поскольку $ a_ {n-1} = a_ {n-2} + d $, мы получаем, что $ a_ {n} = a_ {n-2} + d + d = a_ {n- 2} + 2d $. Мы можем продолжить так и получить:
\ begin {align *}
a_ {n} & = a_ {n} = a_ {n-1} + d \\
& = a_ {n-2} + d + d = a_ {n-2} + 2d \\
& = a_ {n-3} + d + d = a_ {n-3} + 3d \\
& \ vdots \\
& = a_ {2} + (n-2) d \\
& = a_ {1} + (n-1) d \\
\ end {выровнять *}
Таким образом, мы получаем, что в арифметической последовательности $ a_ {n} $ с шагами размера $ d $ формула для $ a_ {n} $ задается следующим образом:
$$ a_ {n} = a_ {1} + (n-1) d $$

Пример.Рассмотрим последовательность $ 3, 8, 13, 18, 23, 28, \ ldots $. Это арифметика? Если да, найдите формулу для $ a_ {n} $ и используйте ее, чтобы найти $ a_ {101} $, 101-й член в последовательности.

Решение.
Эта последовательность является арифметической, поскольку разница между каждым термином составляет 5 долларов США.
доллара США.
($ 8-3 = 13-8 = 18-13 = \ cdots = 5 $.) Итак, это арифметическая последовательность
с шагом $ d = 5 $ и первым членом $ a_ {1} = 3 $.

Наша формула выше дает $ a_ {n} = a_ {1} + (n-1) d = 3 + (n-1) 5 $.

Для $ a_ {101} $ мы подставляем $ n = 101 $ в эту формулу, чтобы получить $ a_ {101} = 3 + (100) 5 = 503 $.

Часть 2: Геометрические последовательности

Рассмотрим последовательность $ 2, 4, 8, 16, 32, 64, \ ldots $. Эта последовательность не арифметическая, поскольку разница между терминами не всегда одинакова.
Если мы присмотримся, то увидим, что следующий член в последовательности получается путем умножения предыдущего члена на то же число .
Соответственно, соотношение следующих друг за другом сроков всегда одинаково (а именно 2 доллара США).

Последовательность $ a_ {n} $, где есть фиксированный $ r $, так что
$ \ frac {a_ {n}} {a_ {n-1}} = r $ для всех $ n $ называется геометрическим
последовательность.{n-1} a $, или
Правило, что $ a_ {n} = r a_ {n-1} $.

Последнее правило является примером рекурсивного правила . Рекурсивно определенная последовательность — это последовательность, в которой правило для создания следующего члена в последовательности явно записано в терминах предыдущих членов.

Рассмотрим следующий (довольно известный) пример.

Пример.

Определите последовательность $ a_ {n} $ следующим образом: Пусть
$$ a_ {1} = 1 \ quad, \ quad a_ {2} = 1 \ quad \ text {и} \ quad a_ {n} =
a_ {n-1} + a_ {n-2} \ text {for} n \ geq 2.$$
Это правило гласит, что для получения следующего термина в последовательности вы должны добавить два предыдущих термина. Поскольку для этого правила требуются два предыдущих члена, нам нужно указать первые два члена последовательности $ a_ {1}, a_ {2} $, чтобы начать работу.
Используя это, мы можем начать перечислять термины в последовательности и получить $ 1, 1, 2, 3, 5, 8, 13, 21, 34, \ ldots $. (Это хорошо известная последовательность Фибоначчи .)

Пример.

Рассмотрим рекурсивно определенную последовательность
$$ a_ {1} = 1 \ quad, \ quad a_ {2} = 1 \ quad, \ quad a_ {3} = 1 \ quad
\ text {и} \ quad a_ {n} = \ frac {a_ {n-3}} {a_ {n-1} + a_ {n-2}} \ text {for} n \ geq 3.$$

Перечислите первые 7 членов этой последовательности.

Решение.
\ begin {align *}
а_ {1} & = 1 \\
а_ {2} & = 1 \\
a_ {3} & = 1 \\
a_ {4} & = \ frac {1} {1 + 1} = \ frac {1} {2} \\
a_ {5} & = \ frac {1} {1+ \ frac {1} {2}} = \ frac {1} {\ frac {3} {2}} = \ frac {2} {3} \\
a_ {6} & = \ frac {1} {\ frac {1} {2} + \ frac {2} {3}} = \ frac {1} {\ frac {7} {6}} = \ frac { 6} {7} \\
a_ {7} & = \ frac {\ frac {1} {2}} {\ frac {2} {3} + \ frac {6} {7}} = \ frac {\ frac {1} {2}} {\ frac {32} {21}} = \ frac {21} {64}
\ end {выровнять *}

Часть 4: Последовательности через списки

Метод использования списка для определения последовательности, пожалуй, самый
сложно, поскольку требует от нас взглянуть на короткий фрагмент последовательности,
и угадать шаблон или правило, которое используется для создания
термины в последовательности.
Теперь, когда мы увидели еще несколько примеров последовательностей, мы можем обсудить, как искать шаблоны и выяснять с помощью списка, как найти рассматриваемую последовательность.

Пример.

Получив список, например $ 1, 3, 9, 27, 81, \ ldots $, мы можем попытаться
ищите узор несколькими способами.
Теперь, когда мы рассмотрели арифметических, геометрических и рекурсивных
последовательности, мы можем попробовать проверить,
один из этих типов.

Арифметика?
Чтобы проверить, является ли последовательность арифметической, мы проверяем, действительно ли
разница последовательных сроков всегда одинакова.{\ text {th}} $ термин в
последовательность.

Решение.
Мы быстро видим, что эта серия не является геометрической, поскольку $ \ frac {1} {- 3} \ neq \ frac {-3} {- 7} $.

Теперь мы можем попытаться проверить, является ли последовательность арифметической. Если мы посмотрим на различия последовательных терминов, мы получим: $ -3 — 1 = -4 = -7 — (-3) = -11 — (-7) $, поэтому мы видим, что это арифметическая последовательность с разницей $ d = -4 $.
Итак, общий термин
$$ a_ {n} = a_ {1} + (n-1) d = 1 + (n-1) (-4) = — 4n + 5. $$

(Мы также могли бы попытаться определить рекурсивное определение этой последовательности.)

Последовательность

Последовательность — это список чисел в определенном порядке. Каждое число в последовательности называется

срок

. Каждый термин в последовательности имеет позицию (первый, второй, третий и т. Д.).

Например, рассмотрим последовательность

{

35 год

…

}

В этой последовательности каждое число называется термином. Номер

имеет первую позицию,

занимает вторую позицию,

занимает третье место и так далее.

иногда пишется член последовательности

Часто можно найти алгебраическое выражение для представления отношения между любым термином в последовательности и его положением в последовательности.

В приведенной выше последовательности

срок

можно рассчитать с помощью уравнения

знак равно

—

Конечные и бесконечные последовательности

Последовательность

конечный

если он имеет ограниченное количество условий и

бесконечный

если это не так.

Конечная последовательность:

{

…

}

Первый из последовательности —

и последний член

.Поскольку последовательность имеет последний член, это конечная последовательность.

Бесконечная последовательность:

{

…

}

Первый член последовательности

. «…» в конце означает, что последовательность продолжается вечно; у него нет последнего срока. Это бесконечная последовательность.

Последовательности возрастания и убывания

Возрастающая последовательность — это такая, в которой каждый член больше предыдущего. Это,

Следующие две последовательности увеличиваются.

{

…

}

{

1.5

1,75

1,825

1,9375

…

}

Убывающая последовательность — это такая, в которой каждый член больше предыдущего. Это,

< а п .

Следующие две последовательности убывают.

{

100

—

100

—

150

—

200

…

}

{

0.5

0,25

0,125

0,0625

…

}

Последовательность не может ни увеличиваться, ни уменьшаться:

{

—

…

}

Арифметические и геометрические последовательности

арифметическая последовательность

представляет собой последовательность, в которой разница между любыми двумя последовательными терминами одинакова.

Пример:

…

Здесь

общая разница

между любыми двумя последовательными сроками

геометрическая последовательность

последовательность, в которой

обычное отношение

между любыми двумя последовательными терминами то же самое.

Пример:

128

512

…

Здесь общее соотношение между любыми двумя последовательными терминами равно

Последовательность событий

Примеры

«Пока солнце не растворилось в звездах»

Подъезжая к старому заброшенному дому, Стелла почувствовала, как ее сердце тяжело бьется в груди. Родители, которых она никогда не знала, прожили здесь всю свою жизнь. Справа находился застекленный солярий, где, как она представляла, они каждый вечер сидят и играют в карты. При мысли об этом ее мысли вернулись в собственное детство.
В ее доме не было стеклянных соляриев.Нет, конечно. Она и пятеро других детей постоянно были заперты на трех двухъярусных кроватях в доме ее приемных родителей. Каждую ночь они не играли в карты. Они составили длинный список дел, которые нужно было выполнить до того, как родители вернутся домой с работы в семь часов. В противном случае все умели разбегаться и спрятаться.
Жизнь продолжалась в этом бесконечном лабиринте хлопот и страха, пока Стелле не исполнилось 18 лет. Она сразу устроилась официанткой и сняла комнату в городе.Когда она не работала официанткой, она писала. В конце концов, журнал Writers ‘Haven подобрал одну из ее историй, позволив жизни сместиться в еще одном направлении. На этот раз смена принесла замечательные перемены.
Из-за жары, последовавшей за ее подчинением в Writers ‘Haven, она почувствовала себя достаточно храброй, чтобы начать охоту за агентом. По воле судьбы одно из ее писем-запросов упало на стол Норы Робб. Несколько месяцев спустя ее дебютный роман «Жизнь без любви» произвел фурор.У Стеллы были истории за историями, скопившиеся в ее крошечной комнатке в городе. Один за другим бестселлеры давали Стелле возможность расслабиться в кресле первого класса на борту Delta Airlines и поехать в Сан-Диего, чтобы выяснить, почему ее биологические родители никогда не любили ее.
Оказывается, адрес, который ей дал следователь, вел к старому заброшенному дому, который она стояла раньше. Дом был пуст, родители ушли, а душа оставалась пустой. Почему они прогнали ее? Почему они так и не нашли ее? Стоя на разбитом тротуаре, глядя на покрытый копотью внешний вид, она подумала, что, возможно, пора принять свою жизнь такой, какая она есть.
Конечно, она не выросла, играя в джин рамми в пятницу вечером под звездами. Но сегодня она стояла у океана. И, приходя завтра, она могла пойти куда угодно и сделать что угодно. Возможно, этого было достаточно. Отвернувшись от разлагающихся руин родительской жизни, она решила не оглядываться назад, а, скорее, запрыгнуть на свою маленькую красную «Веспу» и поехать вдоль побережья, пока солнце не сольется с звездами.

Давайте рассмотрим последовательность событий в этом рассказе. В первом абзаце нас встречает женщина по имени Стелла, которая должна быть взрослой.Потому что, глядя на дом, она вспоминает тяжелое детство, наполненное «домашними делами и страхом».

Следуя последовательности, мы возвращаемся в ее детство. Затем мы видим, что ей исполняется 18 лет, и она продолжает расти и взрослеть, поскольку она официантка по вечерам и пишет в течение дня. Ее тяжелая работа окупается, потому что все эти часы за клавиатурой приводят к ее публикации в Writers ‘Haven. После этого она публикует серию бестселлеров и, наконец, взрослая женщина путешествует, чтобы раскрыть свои корни.

Обратите внимание, что последовательность событий не обязательно должна следовать по прямой. В этом рассказе мы не следовали образцу рождения, детства и взрослости. Скорее, мы перешли из взрослой жизни в детство и снова во взрослую жизнь. В некоторых случаях следование чьей-то мечте — хороший способ оживить линейную последовательность событий.

Теперь давайте посмотрим на историю, которая следует в более простом хронологическом порядке.

последовательность в предложении | Примеры предложений по Кембриджскому словарю

Эти примеры взяты из корпусов и из источников в Интернете.Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

Среди 30 последовательностей «цель / неслово» 20 последовательностей имели совместимую структуру слогов, а 10 последовательностей имели несовместимую структуру.

Взаимодействия между агентами состоят из последовательности социальных действий, выполняемых отдельными агентами.

Гиперребро называется ненаправленным, если последовательности его исходного и целевого узлов равны.

Как предполагалось ранее, поток воды будет легче проходить через незамерзшие поры, чем через ледосодержащие поры.

Эффекты тренировки, касающиеся количества достигнутых последовательностей движений пальцев, не различались между группами.

Гены примыкают друг к другу или разделены короткими межгенными последовательностями.

Были проанализированы конкатенированные последовательности atp6, nad1 (частичный) и cox1 (частичный).

Все полученные последовательности были согласованы внутри вида, хотя наблюдались также некоторые интро-специфические вариации.

Ампликоны в среднем от 4 животных (от 1 до 8) секвенировали из каждого местоположения.

Также были протестированы зонды с последовательностями петель из 22 п.н., но они показали пониженную специфичность (данные не показаны).

Различия среди нуклеотидных последовательностей были вызваны вставками / делециями 1-6 нуклеотидов и событиями замены.

Все они принимают синтаксис целевого естественного языка в качестве входного синтаксиса последовательностей символов.

Изучая детей, которые приступили к задаче развития языка, сталкиваясь с экологическими рисками, устойчивость этих последовательностей становится очевидной.

Нас могут сбить с толку последовательности, составляющие сориты.

Я сопоставил метрические последовательности, полученные из традиционного репертуара, с этой мелодией, чтобы установить еще один параметр для метрического соответствия.

Даже такая простая комбинаторная система допускает 720 пар последовательностей, большинство из которых бессмысленны.

Ограничения сделали бы некоторые последовательности грамматическими, а другие — нетраматическими.

С помощью самих инструментов археологи могут реконструировать различные действия: выбор и добычу сырья, последовательность изготовления, использование и утилизацию.

Задача состоит в том, чтобы найти наиболее дешевую стратегию последовательного выполнения действий по устранению неполадок.

148 характеристик, последовательности сборки и выбора элементов сопряжения, а также предоставляет информацию, необходимую для анализа допусков.

Полученные последовательности не показали значительной гомологии с какими-либо известными генами.

Тестирование закончилось, когда ребенок неправильно воспроизвел обе последовательности при заданной длине строки.

Последовательности слогов были представлены с частотой один каждые 750 мс для последовательного воспроизведения.

Представленный здесь подход позволяет нам детально зафиксировать набор последовательностей развития.

Если чувствительность к звуковым последовательностям применяется к словообразовательным суффиксам, мы также можем ожидать увидеть различия между отдельными суффиксами в зависимости от частоты суффиксов.

Пусть (k) — множество би-бесконечных последовательностей на k символах.

В частности, он связан с исторической перспективой, в которой внимание уделяется конкретным последовательностям и контекстам.

Перестановки, соответствующие возможному порядку колоды после одного тасования, могут иметь не более двух восходящих последовательностей.

Определим последовательности матроидов и множеств следующим образом.

Учитывая сходство проанализированных последовательностей, выравнивания нуклеотидов очевидны и здесь не показаны.

Чтобы лучше понять взаимоотношения между различными клонами, необходимо секвенировать дополнительные гены, включая некоторые ядерные локусы.

Другим объяснением может быть отсутствие у кукурузы специфических сигнальных последовательностей для транспорта в сок флоэмы.

Клоны, которые имели 2,3 т.п.н. по сравнению с контрольной плазмидой (1,8 т.п.н.), были отобраны для секвенирования.

Высота попыток изучалась многими авторами в рамках различных моделей случайности последовательностей.

Теперь мы опишем модель эволюции двоичных последовательностей на дереве.

Первые 21 — это исторически узнаваемая последовательность событий, связанных с индивидуальными действиями.

Фактически, есть исследования, свидетельствующие о том, что обнаружение ошибок, последовательность развития и согласование смысла могут быть чувствительны к социальному контексту.

Последовательности фонем для неслов, таким образом, законны как фонотактически, так и просодически.

В микросателлитах повторяющиеся последовательности разной длины в данном локусе называются аллелями, и наблюдается совместное доминирование.

Обратите внимание, что там, где это указано, ссылка относится к последовательностям неидентичных согласных символов.

Дети с аутизмом также представили больше физических — причинных обоснований в своих словесных описаниях созданных ими последовательностей изображений по сравнению с преднамеренными описаниями.

Последовательности разминки были представлены аналогично тестовым заданиям.

Первоначально в ходе анализа исследуется количество произведенных детьми отдельных действий и количество произведенных ими правильно упорядоченных последовательностей.

Фактически, существуют определенные постнатальные критические периоды и последовательности развития для появления биогенных аминов дофамина и норадреналина.

Следующие взаимодействия представляют собой определенные последовательности, содержащие предыдущее поведение.

Затем линейная или множественная регрессия была применена к последовательностям сезонов для поиска тенденций.

В качестве критерия результата использовалось количество преднамеренных наборов, упорядоченных правильно (максимальный балл составлял 3).

Некооперативные представления, по-видимому, моделируют причинные процессы или, по крайней мере, причинные процессы, которые будут происходить после определенных игровых последовательностей.

Второе соло (16–27 такты) модулируется обратно к промежуточной тонике посредством последовательностей и хроматизма, основанных на исходном мотиве.

Кроме того, метод, основанный на эволюции фронта, может быть использован для отслеживания контуров движущихся и деформируемых объектов во временных последовательностях изображений [19].

Почему и где неважно окажется полезным в цепочке жалоб и для кого?

Применение семантического критерия предполагает лексический статус исследуемых последовательностей морфем.

Сопоставление меток и / или переменных означает сопоставление обозначенных последовательностей.

Структура позволяет запускать точечные модели в пространстве с использованием временных последовательностей интерполированных, непрерывных суточных максимальных и минимальных температур.

Однако иногда полезно рассмотреть совместимые последовательности ненормированных потенциалов.

Переходим к бесконечным апериодическим сизигиям.

Характеристика замещающих последовательностей с помощью возвращаемых слов.

Мы также рассмотрели исследования с участием моделей на животных, анализ последовательностей человеческих антител и исследования с использованием компьютерного моделирования и кристаллической структуры.

Наконец, мы приводим модифицированную конструкцию вышеупомянутого каркаса, чтобы получить примеры неполных факторов с контролируемыми центральными последовательностями.

Наконец, модификация последнего семейства предоставляет примеры факторов скрещенных продуктов, которые не являются полными, но для которых центральные последовательности находятся под контролем.

Мы начнем с обсуждения последовательностей отображений в нескольких категориях, рассматривая топологические, равномерные и ограниченные дифференцируемые сопряжения как обеспечивающие морфизмы.

Две последовательности эквивалентны тогда и только тогда, когда они допускают сокращения, имеющие общее расширение.

Большая часть острова состоит из зеленосланцевых фаций с повсеместным нанесением на них отпечатков.

Последовательности отказа — это сублиторальные последовательности, которые никогда не подвергались воздействию.

Акцент в анализе делается на выявлении, корреляции и определении возраста разрезов, ограниченных несогласием.

Отдельные толщи игнимбритов имеют мощность до 200 м.

Однако в настоящее время секвенировано недостаточно интронов, чтобы это стало возможным.

Поскольку эти 18 белков значительно различались по длине, мы предоставили деревья соединения соседей как для полных белковых последовательностей, так и для доменов гомологии ольфактомедина.

Каждый начинается с конечного алфавита и правила подстановки, которое используется для определения пространства символьных последовательностей.

Мы начнем с введения некоторых целочисленных последовательностей, которые будут иметь решающее значение для нашей конструкции.

Для каждого потока было рассмотрено десять таких последовательностей.

Под этим мы подразумеваем, что не было обнаружено ранее неизвестных поверхностей, которые дали бы начало новым бифуркационным последовательностям.

Затем для этих различных начальных условий строятся (конечные) минимизирующие последовательности, простирающиеся от t0 до t.

Мы будем называть такие последовательности ограниченными последовательностями многочленов или, если контекст ясен, просто ограниченными последовательностями.

В случае гиперболических последовательностей, по существу, тот же аргумент, что и приведенный выше, позволяет нам сказать немного больше.

Выведенные последовательности белков между изоферментами показывают 50-60% гомологии внутри видов, в то время как гомология одного и того же изофермента у разных видов превышает 90%.

Прежде чем показать, как генерируются новые последовательности, мы сначала отметим, что одна действительная собственная функция уже известна для симметричного случая.

Чтобы дополнительно охарактеризовать точку вставки, были секвенированы 332 п.н. из pbs103, а 357 п.н. секвенировали из pbel3.

В четырех оставшихся полиморфизмах редкий аллель присутствует максимум в трех последовательностях из 20.

Основанный на коалесценции метод обнаружения рекомбинации по последовательностям генов.

Однако влияние рекомбинации на топологию дерева зависит главным образом от степени родства рекомбинирующих последовательностей.

Филогенетические отношения между шестью видами на основе последовательностей полос политенных хромосом.

Моделирование проводилось отдельно для каждого локуса в зависимости от количества последовательностей, длины локуса и количества сегрегационных сайтов.

Уникальные последовательности составляют лишь немногим более одной трети генома.

Наши знания о физиологических эффектах генов, для которых в настоящее время доступны последовательности, все еще ограничены.

Из 63 последовательностей, составляющих эти семейства, 12 были аннотированы как интронные последовательности.

Мы называем эти пространственно организованные последовательности законсервированными «шаблонами слов».

Таким образом, последовательности нематод в медленно эволюционирующих белках, по-видимому, не являются мутационно насыщенными.

Однако в иллюстративных целях удобнее рассматривать только идентичности для нескольких последовательностей.

Структура компактная и глобулярная и, вероятно, лишь минимально вмешивается в слитые трансактивирующие последовательности.

При оценке сходства между двумя последовательностями такого размера предпочтительным методом является матричное сравнение.

Виртуозные пассажи чередовались с более простыми, менее сложными последовательностями, чтобы создать ослепительный, но прерывистый паттерн движения.

Новая второстепенная парадигма относительно корреляции границы с земными последовательностями появляется в этом томе и поддерживается редакторами.

Запомненные последовательности формируют наш «опыт», письменной записью которого является «история», как «естественная», так и «политическая».

Кроме того, мы идентифицировали дополнительные семейства на основе кластеризации аминокислотных последовательностей, в результате чего получили 637 различных семейств.

Однако существуют пределы того, что в настоящее время может быть выведено только на основе последовательностей генов.

Почему мы восстановили такой высокий процент новых последовательностей?

Образцы анализировали электрофорезом в 12% геле для секвенирования с последующей авторадиографией.

Вместо этого мы могли бы перестроить две входные последовательности, используя парные грамматики.

За последние пять лет были полностью секвенированы геномы четырех различных эукариотических организмов.

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

Арифметических последовательностей и серии

Арифметические последовательности

Арифметическая последовательность Последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d ., Или арифметическая прогрессия, используемая при ссылке на арифметическую последовательность., Представляет собой последовательность чисел, в которой каждое последующее число является суммой предыдущее число и некоторая константа d .

an = an − 1 + d Арифметическая последовательность

И поскольку an − an − 1 = d, константа d называется общей разностью Константа d , которая получается вычитанием любых двух последовательных членов арифметической последовательности; ан-ан-1 = д.. Например, последовательность положительных нечетных целых чисел представляет собой арифметическую последовательность

1,3,5,7,9,…

Здесь a1 = 1, а разница между любыми двумя последовательными членами равна 2. Мы можем построить общий член an = an − 1 + 2, где,

a1 = 1a2 = a1 + 2 = 1 + 2 = 3a3 = a2 + 2 = 3 + 2 = 5a4 = a3 + 2 = 5 + 2 = 7a5 = a4 + 2 = 7 + 2 = 9 ⋮

В общем, учитывая первый член a1 арифметической последовательности и его общую разницу d , мы можем написать следующее:

a2 = a1 + da3 = a2 + d = (a1 + d) + d = a1 + 2da4 = a3 + d = (a1 + 2d) + d = a1 + 3da5 = a4 + d = (a1 + 3d) + d = a1 + 4d ⋮

Отсюда мы видим, что любая арифметическая последовательность может быть записана в терминах ее первого элемента, общей разности и индекса следующим образом:

an = a1 + (n − 1) d Арифметическая последовательность

Фактически, любой общий член, линейный в n , определяет арифметическую последовательность.

Пример 1

Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 ^{-го члена}: 7,10,13,16,19,…

Решение:

Начните с поиска общей разницы,

d = 10-7 = 3

Обратите внимание, что разница между любыми двумя последовательными членами равна 3. Последовательность действительно является арифметической прогрессией, где a1 = 7 и d = 3.

an = a1 + (n − 1) d = 7 + (n − 1) ⋅3 = 7 + 3n − 3 = 3n + 4

Следовательно, мы можем написать общий член an = 3n + 4. Уделите минуту, чтобы убедиться, что это уравнение описывает заданную последовательность. Используйте это уравнение, чтобы найти член 100 ^th:

а100 = 3 (100) + 4 = 304

Ответ: an = 3n + 4; а100 = 304

Общая разница арифметической последовательности может быть отрицательной.

Пример 2

Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления 75 ^{-го члена}: 6,4,2,0, −2,…

Решение:

Начните с поиска общей разницы,

d = 4−6 = −2

Затем найдите формулу для общего члена, здесь a1 = 6 и d = −2.

an = a1 + (n − 1) d = 6 + (n − 1) ⋅ (−2) = 6−2n + 2 = 8−2n

Следовательно, an = 8−2n и член 75 ^th можно рассчитать следующим образом:

a75 = 8−2 (75) = 8−150 = −142

Ответ: an = 8−2n; а100 = −142

Термины между данными членами арифметической последовательности называются средними арифметическими. Термины между данными членами арифметической последовательности.

Пример 3

Найдите все члены арифметической последовательности между a1 = −8 и a7 = 10.Другими словами, найдите все средние арифметические значения между 1 ^-м и 7 ^-м членами.

Решение:

Начните с поиска общей разницы d . В этом случае нам дается первый и седьмой член:

an = a1 + (n − 1) d Используйте n = 7. a7 = a1 + (7−1) da7 = a1 + 6d

Подставляем a1 = −8 и a7 = 10 в приведенное выше уравнение, а затем решаем общую разность d .

10 = −8 + 6d18 = 6d3 = d

Затем используйте первый член a1 = −8 и общую разность d = 3, чтобы найти уравнение для n -го члена последовательности.

an = −8 + (n − 1) ⋅3 = −8 + 3n − 3 = −11 + 3n

При an = 3n − 11, где n — положительное целое число, найдите пропущенные члены.

a1 = 3 (1) −11 = 3−11 = −8a2 = 3 (2) −11 = 6−11 = −5a3 = 3 (3) −11 = 9−11 = −2a4 = 3 (4) — 11 = 12−11 = 1a5 = 3 (5) −11 = 15−11 = 4a6 = 3 (6) −11 = 18−11 = 7} среднее арифметическое a7 = 3 (7) −11 = 21−11 = 10

Ответ: −5, −2, 1, 4, 7

В некоторых случаях первый член арифметической последовательности может не указываться.

Пример 4

Найдите общий член арифметической последовательности, где a3 = −1 и a10 = 48.

Решение:

Чтобы определить формулу для общего члена, нам нужны a1 и d. Линейная система с этими переменными может быть сформирована с использованием данной информации и an = a1 + (n − 1) d:

{a3 = a1 + (3−1) da10 = a1 + (10−1) d⇒ {−1 = a1 + 2d48 = a1 + 9d Используйте a3 = −1. Используйте a10 = 48.

Исключите a1, умножив первое уравнение на -1, и прибавьте результат ко второму уравнению.

{−1 = a1 + 2d48 = a1 + 9d ⇒ × (−1) + {1 = −a1−2d48 = a1 + 9d¯ 49 = 7d7 = d

Подставляем d = 7 в −1 = a1 + 2d, чтобы найти a1.

−1 = a1 + 2 (7) −1 = a1 + 14−15 = a1

Затем используйте первый член a1 = −15 и общую разность d = 7, чтобы найти формулу для общего члена.

an = a1 + (n − 1) d = −15 + (n − 1) ⋅7 = −15 + 7n − 7 = −22 + 7n

Ответ: an = 7n − 22

Попробуй! Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 ^{-го члена}: 32,2,52,3,72,…

Ответ: an = 12n + 1; а100 = 51

Арифметическая серия

Арифметический ряд Сумма членов арифметической последовательности.представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:

S5 = Σn = 15 (2n − 1) = [2 (1) −1] + [2 (2) −1] + [2 (3) −1] + [2 (4) −1] + [2 (5) −1] = 1 + 3 + 5 + 7 + 9 = 25

Добавлением 5 положительных нечетных целых чисел, как мы сделали выше, можно управлять. Однако рассмотрите возможность добавления первых 100 положительных нечетных целых чисел. Это было бы очень утомительно. Поэтому затем мы разработаем формулу, которую можно использовать для вычисления суммы первых n членов, обозначенных Sn, любой арифметической последовательности.В целом

Sn = a1 + (a1 + d) + (a1 + 2d) +… + an

Записывая эту серию в обратном порядке, мы имеем,

Sn = an + (an − d) + (an − 2d) +… + a1

И сложив эти два уравнения вместе, члены, содержащие d , прибавляют к нулю, и мы получаем n множителей a1 + an:

2Sn = (a1 + an) + (a1 + an) +… + (an + a1) 2Sn = n (a1 + an)

Разделив обе стороны на 2, мы получим формулу для n -й частичной суммы арифметической последовательности Сумма первых n членов арифметической последовательности, заданной формулой: Sn = n (a1 + an) 2.:

Sn = n (a1 + an) 2

Используйте эту формулу для вычисления суммы первых 100 членов последовательности, определенной как an = 2n − 1. Здесь a1 = 1 и a100 = 199.

S100 = 100 (a1 + a100) 2 = 100 (1 + 199) 2 = 10 000

Пример 5

Найдите сумму первых 50 членов заданной последовательности: 4, 9, 14, 19, 24,…

Решение:

Определите, есть ли общее различие между данными терминами.

d = 9−4 = 5

Обратите внимание, что разница между любыми двумя последовательными членами равна 5. Последовательность действительно является арифметической прогрессией, и мы можем написать

an = a1 + (n − 1) d = 4 + (n − 1) ⋅5 = 4 + 5n − 5 = 5n − 1

Следовательно, общий член an = 5n − 1. Чтобы вычислить частичную сумму 50 ^-й этой последовательности, нам понадобятся 1 ^-е и 50 ^-е слагаемые:

а1 = 4а50 = 5 (50) -1 = 249

Затем используйте формулу, чтобы определить частичную сумму 50 ^-й заданной арифметической последовательности.

Sn = n (a1 + an) 2S50 = 50. (A1 + a50) 2 = 50 (4 + 249) 2 = 25 (253) = 6,325

Ответ: S50 = 6,325

Пример 6

Вычислить: Σn = 135 (10−4n).

Решение:

В этом случае нас просят найти сумму первых 35 членов арифметической последовательности с общим членом an = 10−4n. Используйте это для определения 1 ^-го и 35 ^-го члена.

a1 = 10−4 (1) = 6a35 = 10−4 (35) = — 130

Затем используйте формулу, чтобы определить частичную сумму 35 ^-го.

Sn = n (a1 + an) 2S35 = 35⋅ (a1 + a35) 2 = 35 [6 + (- 130)] 2 = 35 (−124) 2 = −2,170

Ответ: −2,170

Пример 7

Первый ряд сидений в амфитеатре под открытым небом содержит 26 сидячих мест, второй ряд — 28 сидений, третий ряд — 30 сидячих мест и так далее. Если рядов 18, какова общая вместимость театра?

Рисунок 9.2

Римский театр (Википедия)

Решение:

Начните с поиска формулы, которая дает количество мест в любом ряду.Здесь количество мест в каждом ряду образует последовательность:

26,28,30,…

Обратите внимание, что разница между любыми двумя последовательными членами равна 2. Последовательность представляет собой арифметическую прогрессию, где a1 = 26 и d = 2.

an = a1 + (n − 1) d = 26 + (n − 1) ⋅2 = 26 + 2n − 2 = 2n + 24

Таким образом, количество мест в каждом ряду равно an = 2n + 24. Чтобы рассчитать общую вместимость 18 рядов, нам нужно вычислить частичную сумму 18 ^th.Для этого нам понадобятся 1 ^-й и 18 ^-й термины:

а1 = 26а18 = 2 (18) + 24 = 60

Используйте это, чтобы вычислить частичную сумму 18 ^-го следующим образом:

Sn = n (a1 + an) 2S18 = 18⋅ (a1 + a18) 2 = 18 (26 + 60) 2 = 9 (86) = 774

Ответ: Всего 774 места.

Попробуй! Найдите сумму первых 60 членов заданной последовательности: 5, 0, −5, −10, −15,…

Ответ: S60 = −8,550

Основные выводы

Арифметическая последовательность — это последовательность, в которой разница d между последовательными членами является постоянной.
Общий член арифметической последовательности может быть записан в терминах его первого члена a1, общей разности d и индекса n следующим образом: an = a1 + (n − 1) d.
Арифметический ряд — это сумма членов арифметической последовательности.
Частичная сумма n арифметической последовательности может быть вычислена с использованием первого и последнего членов следующим образом: Sn = n (a1 + an) 2.

Тематические упражнения

Часть A: Арифметические последовательности

Запишите первые 5 членов арифметической последовательности, учитывая их первый член и общую разницу.Найдите формулу для его общего члена.

Учитывая арифметическую последовательность, найдите формулу для общего члена и используйте ее, чтобы определить 100 ^{-й член}.

−3, −7, −11, −15, −19,…
−6, −14, −22, −30, −38,…
−5, −10, −15, −20, −25,…
−13, 23, 53, 83, 113,…
13, 0, −13, −23, −1,…
14, −12, −54, −2, −114,…
0.8, 2, 3.2, 4.4, 5.6,…
4,4, 7,5, 10,6, 13,7, 16,8,…
Найдите положительное нечетное целое число 50 ^-го.
Найдите положительное четное целое число 50 ^-е.
Найдите 40 ^{-й член} в последовательности, состоящей из всех остальных положительных нечетных целых чисел: 1, 5, 9, 13,…
Найдите 40 ^{-й член} в последовательности, состоящей из всех остальных положительных четных целых чисел: 2, 6, 10, 14,…
Какое число представляет собой член 355 в арифметической последовательности −15, −5, 5, 15, 25,…?
Какое число является членом −172 в арифметической последовательности 4, −4, −12, −20, −28,…?
Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1 + 5, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член через a1 и общую разность d .
Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1−9, где a1 = 4 и n> 1, найдите уравнение, которое дает общий член через a1 и общую разность d .

Учитывая члены арифметической последовательности, найдите формулу для общего члена.

a4 = −2310 и a21 = −252

Найдите все средние арифметические между заданными членами.

Часть B: Арифметическая серия

Рассчитайте указанную сумму по формуле для общего члена.

Оценить.

∑n = 1160 (3n)
∑n = 1121 (−2n)
∑n = 1250 (4n − 3)
∑n = 1120 (2n + 12)
∑n = 170 (19−8n)
∑n = 1220 (5 − п)
∑n = 160 (52−12n)
∑n = 151 (38n + 14)
∑n = 1120 (1.5n − 2,6)
∑n = 1175 (-0,2n-1,6)
Найдите сумму первых 200 натуральных чисел.
Найдите сумму первых 400 натуральных чисел.

Общий член для последовательности положительных нечетных целых чисел задается как an = 2n − 1, а общий член для последовательности положительных четных целых чисел задается как an = 2n. Найдите следующее.

Сумма первых 50 положительных нечетных целых чисел.
Сумма первых 200 положительных нечетных целых чисел.
Сумма первых 50 положительных четных целых чисел.
Сумма первых 200 положительных четных целых чисел.
Сумма первых k положительных нечетных целых чисел.
Сумма первых k четных положительных чисел.
Первый ряд сидений в малом театре состоит из 8 посадочных мест. После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
Первый ряд сидений в амфитеатре под открытым небом содержит 42 сиденья, второй ряд — 44 сиденья, третий ряд — 46 сидячих мест и так далее.Если рядов 22, какова общая вместимость театра?
Если в треугольной стопке кирпичей 37 кирпичей в нижнем ряду, 34 кирпича во втором ряду и так далее, с одним кирпичом наверху. Сколько кирпичей в стопке?
В каждом последующем ряду треугольной стопки кирпичей на один кирпич меньше, пока наверху не останется только один кирпич.Сколько рядов в стеке, если всего кирпичей 210?
10-летний договор о заработной плате предлагает 65 000 долларов в первый год с повышением на 3200 долларов каждый дополнительный год. Определите общую сумму обязательств по заработной плате за 10-летний период.
Башня с часами бьет в колокол количество раз, указанное в часах.В час дня он ударяет один раз, в два часа — дважды и так далее. Сколько раз за день башня с часами бьет в колокол?

Часть C: Обсуждение

Является ли последовательность Фибоначчи арифметической последовательностью? Объяснять.
Используйте формулу для n -й частичной суммы арифметической последовательности Sn = n (a1 + an) 2 и формулу для общего члена an = a1 + (n − 1) d, чтобы получить новую формулу для n -я частичная сумма Sn = n2 [2a1 + (n − 1) d].При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
Обсудите методы расчета сумм, в которых индекс не начинается с 1. Например, Σn = 1535 (3n + 4) = 1,659.
Известная история повествует о плохом поведении Карла Фридриха Гаусса в школе.В наказание учитель поручил ему сложить первые 100 целых чисел. Легенда гласит, что молодой Гаусс правильно ответил в считанные секунды. Каков ответ и как, по-вашему, он смог так быстро найти сумму?

ответов

5, 8, 11, 14, 17; ан = 3n + 2
15, 10, 5, 0, −5; ан = 20−5н
12, 32, 52, 72, 92; an = n − 12
1, 12, 0, −12, −1; ан = 32−12н
1.8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
ан = 1.2n − 0,4; а100 = 119,6

Определение последовательности по Merriam-Webster

последовательность

| \ ˈSē-kwən (t) s

, -ˌKwen (t) s \

: гимн неправильного размера между постепенным и Евангелием в мессах для особых случаев (например, Пасхи).

: непрерывная или связная серия: например,

: расширенный цикл стихотворений, объединенных единой темой.

последовательность сонетов

: три или более игральных карты обычно одной масти в последовательном порядке рангов.

: последовательность повторений мелодической фразы или гармонического паттерна в каждой новой позиции.

: набор элементов, упорядоченных так, чтобы их можно было пометить положительными целыми числами.

: точный порядок оснований в нуклеиновой кислоте или аминокислот в белке

f (1)

: последовательность связанных кадров или сцен, раскрывающих отдельный объект или этап истории фильма.

3а

: порядок наследования

: Упорядочение времен последовательных глаголов в предложении, предназначенное для выражения связных отношений, особенно между главной и подчиненной частями.

: последующее развитие

: непрерывность развития

повествовательная последовательность

переходный глагол

: для последовательного расположения

: для определения последовательности химических компонентов (таких как аминокислотные остатки или основания нуклеиновых кислот) в

виды числовых последовательностей и примеры

Виды последовательности

Пример последовательности

Нужна помощь в учебе?

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ | Энциклопедия Кругосвет

Свойства числовых последовательностей.

Арифметическая прогрессия.

Геометрическая прогрессия.

Предел последовательности.

виды числовых последовательностей и примеры 9 класс онлайн-подготовка на Ростелеком Лицей |

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Элементы математического анализа

Числовые последовательности. Способы задания числовых последовательностей

Возрастающие и убывающие последовательности

Ограниченные и неограниченные последовательности

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Предел числовой последовательности

Свойства пределов числовых последовательностей

Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии

Примеры вычисления пределов последовательностей. Раскрытие неопределенностей

Число e. Второй замечательный предел

9 гифок, наглядно иллюстрирующих числовые последовательности

И на десерт

Продолжение следует…

Числовые последовательности (определение, примеры, свойства)

Последовательности и шаблоны — Mathigon

Простые последовательности

Треугольники и квадратные числа

Фотография последовательности действий

Последовательности и серии — рабочие примеры

Последовательности

Определение последовательностей.

Пример.

Пример.

Пример.

Общая формула.

Пример.

Пример.

Пример.

Последовательность

Конечные и бесконечные последовательности

Последовательности возрастания и убывания

Арифметические и геометрические последовательности

Примеры

«Пока солнце не растворилось в звездах»

последовательность в предложении | Примеры предложений по Кембриджскому словарю

Арифметических последовательностей и серии

Арифметические последовательности

Пример 1

Пример 2

Пример 3

Пример 4

Арифметическая серия

Пример 5

Пример 6

Пример 7

Основные выводы

Тематические упражнения

Часть A: Арифметические последовательности

Часть B: Арифметическая серия

Часть C: Обсуждение

ответов

Определение последовательности по Merriam-Webster

Добавить комментарий Отменить ответ