Содержание
Линейные уравнения 7 класс | Алгебра
Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида
где a и b — числа, x — переменная.
Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).
Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.
Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:
При переносе знаки слагаемых меняем на противоположные:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -9.
Раскрываем скобки:
Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:
(Обратите внимание: хотя сумма слагаемых с переменной равна нулю, результат записываем не как 0, а как 0x).
Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.
Ответ: x — любое число.
Раскрываем скобки:
Можно сначала привести подобные слагаемые, чтобы упростить уравнение:
а уже потом перенести: неизвестные — в одну сторону, известные — в другую:
Это уравнение не имеет корней.
Ответ: нет корней.
Раскрываем скобки:
Приводим подобные слагаемые:
Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ:
В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.
Линейное уравнение с одной переменной с примерами.
п.1. Количество корней линейного уравнения с одной переменной
Линейным уравнением с одной переменной x называют уравнение вида ax = b, где a и b — действительные числа.
a называют коэффициентом при переменной , а b — свободным членом .
При решении линейных уравнений возможны три случая.
a
b
x
Количество корней
$b \in \Bbb R$ — любой
$x = \frac{b}{a}$
$x \in \Bbb R$ — любой
Бесконечное множество корней
$x \in \Bbb \varnothing $
п.2. Примеры
Пример 1. Решите уравнение 6-5x = 8(3,5-2x)
Решение:
$ 6-5x = 8(3,5-2x) \iff 6-5x = 28-16x \iff -5x+16x = 28-6 \iff $
$ \iff 11x = 22 \iff x = 2 $
Ответ: x=2
Пример 2. Решите уравнение $\frac{2}{3} x-\frac{4}{5} = 0,6x$
Решение:
$ \frac{2}{3}x-\frac{4}{5} = 0,6x | ×15 \iff 2x∙5-4∙3 = 0,6x∙15 \iff 10x-12=9x \iff $
$ \iff 10x-9x = 12 \iff x = 12 $
Ответ: x = 12
Пример 3. 2-3a)}{a} = \frac{a(a-3)}{a} = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ 0x = 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a≠0 \\ x = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$
2-3a)}{a} = \frac{a(a-3)}{a} = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ 0x = 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a≠0 \\ x = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$
Ответ: при a ≠ 0,x = a-3; при a = 0, $x \in \Bbb R$ — любой
Пример 6*. Решите уравнение (k+1)x = k
Решение:
$$ (k+1)x = k \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} k+1 ≠ 0 \\ x = \frac{k}{k+1} \end{array} \right.} \\ {\left\{ \begin{array}{c} k+1 = 0 \\ 0x = -1 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} k ≠ -1 \\ x = \frac{k}{k+1} \end{array} \right.} \\ {\left\{ \begin{array}{c} k = -1 \\ x \in \Bbb \varnothing — решений \quad нет \end{array} \right.} \end{array} \right. $$
Ответ: при k ≠ -1, $ x = \frac{k}{k+1} $, при k = -1 решений нет
Пример 7*. Решите уравнение ax+b = cx+d
Решите уравнение ax+b = cx+d
Решение:
$$ ax+b = cx+d \iff ax-cx = d-b \iff (a-c)x = d-b \iff $$
$$ \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a-c ≠ 0 \\ x = \frac{d-b}{a-c} \end{array} \right.} \\ {\left\{ \begin{array}{c} a-c = 0 \\ d-b = 0 \\ 0x = 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} a-c = 0 \\ d-b ≠ 0 \\ 0x ≠ 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a ≠ c \\ x = \frac{d-b}{a-c} \end{array} \right.} \\ {\left\{ \begin{array}{c} a = c \\ d = b \\ x \in \Bbb R — любой \end{array} \right.} \\ {\left\{ \begin{array}{c} a = c \\ d ≠ b \\ x \in \Bbb \varnothing — решений \quad нет \end{array} \right.} \end{array} \right. $$
Линейное уравнение с одной переменной, урок по алгебре в 7 классе, примеры решения
Дата публикации: .
Определение линейного уравнения с одной переменной
Ребята, в 5 классе вы проходили тему: Решение уравнений на сложение и вычитание. Мы говорили о линейных уравнениях. Уравнениях, в которых только одна переменная.
Мы говорили о линейных уравнениях. Уравнениях, в которых только одна переменная.
Например: 4x = 18; 2z — 5 = 0.
Решить уравнение – значит найти те значения переменных, при котором уравнение превращается в верное равенство. Каждое такое решение называется корнем уравнения.
Например, уравнение 3x = 12 имеет корень, равный 4. При х = 4 выражение является верным равенством. Действительно, 3 * 4 = 12.
И больше никакое значение х не удовлетворяет данному равенству.
Общий вид линейного уравнения с одной переменной х можно представить: ах + b = 0, где где а и b – любые числа, которые называются коэффициентами линейного уравнения.
Рассмотрим виды линейных уравнений.
1. a = 0 и b = 0.
Корнем уравнения может быть любое число. В этом случае говорят, что уравнение не имеет корней.
2. a ≠ 0 и b ≠ 0.
Уравнение превращается в уравнение вида ax = -b (коэффициент b перенесли на право со сменой знака).
Значит, х = (-b) : a или x = -(b : a).
Алгоритм решения линейного уравнения вида ax + b = 0, где a ≠ 0
1) Переписать уравнение так, чтобы оно приняло вид ax = -b.
2) Найти корень уравнения x = (-b) : a или x = -(b : a).
Если линейное уравнение имеет более сложном виде, например, 4х + 3 = 18 — х.
Тогда необходимо упростить уравнение через приведение подобных слагаемых.
(4x + 3) — (18 — х) = 0
4x + 3 — 18 + х = 0
5x — 15 = 0
5x = 15
x = 3.
Обобщим полученные знания в общий алгоритм.
Алгоритм решения линейного уравнения вида ax + b = сx + d, где a ≠ c
1) Перенесем все члены уравнения налево и не забудем поменять знак при переносе.
2) Раскроим скобки после переноса и приведем подобные слагаемые. В результате получим уравнение вида ax + b = 0, где a ≠ 0.
3) Найдем корень уравнения вида x = (-b) : a или x = -(b : a).
Примеры решения линейных уравнений с одной переменной
1. Решите уравнение: 7x + 21 = 0.
7х = -21
х = $\frac{(-21)}{7} = — 3$.
2. Решите уравнение: 2x -1 = 5(х + 4).
2x — 1 — 5(х + 4) = 0
2x — 1 — 5х — 20 = 0
-3х — 21 = 0
-3х = 21
x = $\frac{21}{(-3)}= -7$.
Линейные уравнения для 7 класса с помощью онлайн-решателя
Применение линейных уравнений широко распространено в нашей жизни. Они используются во многих расчетах,
строительстве сооружений и даже спорте. Линейные уравнения человек использовал еще в древности и с тех пор
их применение только возрастает.
Линейные уравнения, изучаемые в 7 классе, имеют следующий вид: \[ab=x\](ax — числа, b — переменная).\]
Множество уравнений сводятся к такому виду путем выполнения простых арифметических операций: раскрытие
скобок, перенос слагаемых, деление или умножение левой и правой части на определенное число. Чтобы хорошо
усвоить данный раздел математики необходимо решить не менее 100 уравнений. Решая уравнения (7 класс алгебра)
Решая уравнения (7 класс алгебра)
онлайн, вы будете оттачивать свои навыки и освоите все методы решения.
Так же читайте нашу статью «Решить уравнения 2 класс онлайн»
Допустим, нам дано уравнение следующего вида:
\[4(9-5x)+7x=11-2(8x+1)\]
По уравнению видно, что его можно существенно упростить, раскрыв скобки:
\[36-20x+7x=11-16x-2\]
Мы раскрыли скобки, придерживаясь основных правил: умножили множитель на каждое слагаемое в скобках; изменили
знак на противоположный, если перед скобками стоял минус.
Избавившись от скобок, выполним группировку членов уравнения:
\[-20x+7x+16x=11-2-36\]
Выполнив простые арифметические операции, получили:
\[-3x=-27\]
Еще раз произведем перенос членов:
\[x=-27\div3\]
Выполнив деление, получим результат:
\[x = — 9\]
Где можно решить уравнение онлайн решателем 7 класс?
Решить уравнение вы можете на нашем сайте pocketteacher. ru. Бесплатный онлайн решатель
ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто внести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Основные правила математики с примерами. 7 класс Алгебра. — Сайт учителя математики Косыхиной Н.В.
Основные правила математики с примерами. 7 класс Алгебра.
Содержание
Уравнения. Равносильные уравнения. Свойства
Корень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет.
 Также можно сказать, что решить уравнение — это значит найти множество его корней.
Также можно сказать, что решить уравнение — это значит найти множество его корней.
2 x + 6 =36x = 15 —корень уравнения, поскольку2 · 15 + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100 0 = 100 — неверно.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
12x = 24 : 1212x :12 = 24 : 12x = 2. x5 = 3 · 5×5 · 5 = 3 · 5x = 15
x5 = 3 · 5×5 · 5 = 3 · 5x = 15
Линейное уравнение
Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.
2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0, 5x = 8 —нелинейные уравнения
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
2x, 356x2y, 0,2a20, b, 15 — одночлены.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
2x, 356x2y, 0,2a20 — одночлены стандартного вида.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
2x, 356x2y, 0,2a20.2, 356, 0,2 —коэффициенты.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
2x2y3z , —15x2y3z, 0,5x2y3z —подобные.2x2y3z и 2x2y3 — не подобные.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
2x + 3x2y
- Одночлены, из которых состоит многочлен, называют членами многочлена.
2x + 3x2y —многочлен;2x и 3x2y — его одночлены
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Многочлен называют неполным квадратом разности.
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого и любых целых выполняются равенства:
Для любых , и любого целого выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.
Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.

- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
Поиск
Поиск
-
Школьный помощник- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая
предыдущая
вернуться на предыдущую страницу
Такой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Русский язык 6 класс
- Математика 5 класс
- Математика 6 класс
- Алгебра 7 класс
- Русский язык 7 класс
- Алгебра 8 класс
- Русский язык 5 класс
- Наименьшее общее кратное
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Деление и дроби
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Окружность и круг
- Доли. Обыкновенные дроби
- Квадратный корень из неотрицательного числа
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.
Комментарии преподавателя
Метод подстановки.
Существует несколько методов решения систем. Один из них метод подстановки. Рассмотрим пример.
Пример 1:
Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.
В данном случае удобно выразить х во втором уравнении:
Подставим полученное выражение в первое уравнение:
Преобразуем первое уравнение:
,
,
,
Подставим полученное значение во второе уравнение:
, ,
Получаем следующее решение системы:
Пример 2:
В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки. Для этого умножим оба уравнения на шесть:
Выразим у из первого уравнения:
Подставим полученное выражение во второе уравнение и выполним преобразования:
, ,
,
Подставим полученное значение в первое уравнение:
Получаем единственное решение системы, пара чисел:
Вывод:
на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.
Мы решили примеры для понимания и закрепления данной техники.
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
Метод сложения.
Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.
Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно получить одно уравнение с одной переменной. Рассмотрим метод алгебраического сложения на примере:
Пример 1:
Задана система двух линейных уравнений с двумя неизвестными, и нужно найти такую пару х и у, чтобы при подстановке ее в уравнения получились верные числовые равенства.
Несложно заметить, что в первом уравнении у стоит с минусом, а во втором – с плюсом, и если сложить эти уравнения, то у уничтожится, и мы получим одно уравнение с одной неизвестной:
+
Получаем:
Найдем значение х:
,
Подставим значение х во второе уравнение и найдем у:
Ответ: (2,4; 2,2)
Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать. Рассмотрим пример:
Пример
При сложении уравнений получим:
,
Попробуем вычесть уравнения, причем, вычтем первое из второго:
,
Ответ: (5,5; 0,5)
Вывод:
на данном уроке мы рассмотрели новый метод решения систем двух линейных уравнений – метод алгебраического сложения. Мы решили несколько примеров для закрепления данной техники.
Мы решили несколько примеров для закрепления данной техники.
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/metod-algebraicheskogo-slozheniya?konspekt&chapter_id=10
http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html
Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4
Решение линейных уравнений с одной переменной
Линейные уравнения с одной переменной — это уравнения, в которых переменная имеет показатель степени 1, который обычно не отображается (это понятно). Примером может быть что-то вроде \ (12x = x — 5 \). Для решения линейных уравнений есть одна основная цель: изолировать переменную . В этом уроке мы рассмотрим, как это делается, на нескольких примерах.
Содержание
- Примеры решения одношаговых уравнений
- Примеры решения двухэтапных уравнений
- Примеры уравнений, в которых сначала необходимо упростить
- Бесконечно много или нет решений
- Сводка
объявление
Примеры решения одношаговых линейных уравнений
После всей вашей тяжелой работы над решением уравнения вы знаете, что хотите получить окончательный ответ, например \ (x = 5 \) или \ (y = 1 \). В обоих этих случаях переменная изолирована или сама по себе.
В обоих этих случаях переменная изолирована или сама по себе.
Итак, нам нужно выяснить, как изолировать переменную. Как мы это сделаем, зависит от самого уравнения! Если его на что-то умножили, поделим. Если к нему что-то добавили, мы вычтем. Поступая так, мы постепенно будем получать переменную сама по себе.
Давайте рассмотрим пример, чтобы увидеть, как это работает.
Пример
Решите уравнение: \ (4x = 8 \)
Решение
В этом примере 4 — это умножение на \ (x \).Следовательно, чтобы изолировать \ (x \), вы должны разделить эту сторону на 4. Делая это, вы должны помнить одно важное правило: что бы вы ни делали с одной стороной уравнения, вы должны делать с другой стороной. Итак, мы разделим обе стороны на 4.
\ (\ begin {align} 4x & = 8 \\ \ dfrac {4x} {\ color {red} {4}} & = \ dfrac {8} {\ color {red} {4}} \ end {align} \)
Упрощение:
\ (х = \ в коробке {2} \)
Вот и все, один шаг, и готово. (Вот почему подобные уравнения часто называют «одношаговыми» уравнениями)
(Вот почему подобные уравнения часто называют «одношаговыми» уравнениями)
Чек
Каждый раз, когда вы решаете линейные уравнения, вы всегда можете проверить свой ответ, подставив его обратно в уравнение.Если вы получите верное утверждение, значит, ответ правильный. Это не обязательно на 100% для каждой задачи, но это хорошая привычка, поэтому мы сделаем это для наших уравнений.
В этом примере наше исходное уравнение было \ (4x = 8 \). Чтобы проверить это, убедитесь, что верно следующее:
\ (\ begin {align} 4x & = 8 \\ 4 (2) & = 8 \\ 8 & = 8 \ end {align} \)
Это верное утверждение, поэтому наш ответ правильный.
Для любого уравнения любая операция, которую вы выполняете с одной стороной, должна выполняться и с другой стороной.
Давайте попробуем еще пару примеров, прежде чем переходить к более сложным уравнениям.
Пример
Решить: \ (3x = 12 \)
Решение
Поскольку \ (x \) умножается на 3, план состоит в том, чтобы разделить на 3 с обеих сторон:
\ (\ begin {align} 3x & = 12 \\ \ dfrac {3x} {\ color {red} {3}} & = \ dfrac {12} {\ color {red} {3}} \\ x & = \ в штучной упаковке {4} \ end {align} \)
Чек
Чтобы проверить наш ответ, мы позволим \ (x = 4 \) и подставим его обратно в уравнение:
\ (\ begin {align} 3x & = 12 \\ 3 (4) & = 12 \\ 12 & = 12 \ end {align} \)
Как и раньше, поскольку это истинное утверждение, мы знаем, что наш ответ правильный.
В следующем примере вместо умножения переменной на значение из переменной вычитается значение. Чтобы «отменить» это, мы добавим это значение обеим сторонам.
Пример
Решить: \ (y-9 = 21 \)
Решение
На этот раз из y вычитается 9. Итак, мы отменим это, добавив 9 к обеим сторонам.
\ (\ begin {align} y-9 & = 21 \\ y-9 \ color {red} {+ 9} & = 21 \ color {red} {+ 9} \\ y & = 30 \ end {align} \)
Далее мы рассмотрим то, что обычно называют «двухэтапными» уравнениями.В этих уравнениях нам нужно будет отменить две операции, чтобы изолировать переменную.
Примеры двухшаговых уравнений
В каждом из приведенных выше примеров нужно было выполнить один шаг, прежде чем мы получили ответ. В следующих примерах вы увидите, как работать с уравнениями, которые вместо этого состоят из двух шагов. Если выполняется более одной операции, важно помнить порядок операций PEMDAS. Поскольку вы отменяете операции с \ (x \), вы будете работать «снаружи внутрь».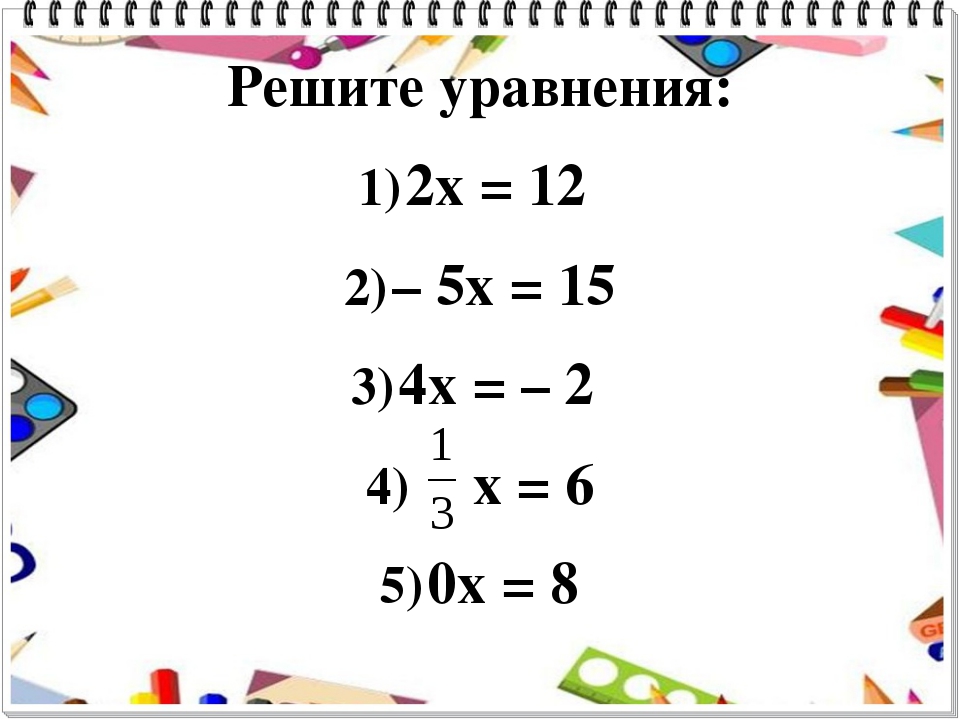 Это легче понять, когда вы увидите это на примере.
Это легче понять, когда вы увидите это на примере.
Пример
Решить: \ (2x-7 = 13 \)
Решение
Обратите внимание на две операции, выполняемые с \ (x \): он умножается на 2, а затем вычитается 7. Нам нужно будет отменить это. Но только \ (x \) умножается на 2, поэтому первым шагом будет прибавление 7 к обеим сторонам. Тогда мы можем разделить обе части на 2.
Добавление 7 к обеим сторонам:
\ (\ begin {align} 2x-7 & = 13 \\ 2x-7 \ color {red} {+ 7} & = 13 \ color {red} {+ 7} \\ 2x & = 20 \ end {align} \ )
Теперь разделите обе стороны на 2:
.
\ (\ begin {align} 2x & = 20 \\ \ dfrac {2x} {\ color {red} {2}} & = \ dfrac {20} {\ color {red} {2}} \\ x & = \ в штучной упаковке {10} \ end {align} \)
Чек
Как и в случае с более простыми задачами, вы можете проверить свой ответ, подставив свое значение \ (x \) обратно в исходное уравнение.
\ (\ begin {align} 2x-7 & = 13 \\ 2 (10) — 7 & = 13 \\ 13 & = 13 \ end {align} \)
Это правда, значит, у нас есть правильный ответ.
Давайте рассмотрим еще один пример с двумя шагами, прежде чем мы снова будем преодолевать трудности. Убедитесь, что вы понимаете каждый показанный шаг и также работаете над проблемой.
Пример
Решить: \ (5w + 2 = 9 \)
Решение
Как и выше, есть две операции: \ (w \) умножается на 5, а затем к нему прибавляется 2.Мы отменим их, сначала вычтя 2 с обеих сторон, а затем разделив на 5.
\ (\ begin {align} 5w + 2 & = 9 \\ 5w + 2 \ color {red} {- 2} & = 9 \ color {red} {- 2} \\ 5w & = 7 \\ \ dfrac { 5w} {\ color {red} {5}} & = \ dfrac {7} {\ color {red} {5}} \\ w = \ boxed {\ dfrac {7} {5}} \ end {align} \)
Дробь справа не может быть упрощена, так что это наш окончательный ответ.
Чек
Пусть \ (w = \ dfrac {7} {5} \). Тогда:
\ (\ begin {align} 5w + 2 & = 9 \\ 5 \ left (\ dfrac {7} {5} \ right) + 2 & = 9 \\ 7 + 2 & = 9 \\ 9 & = 9 \ конец {align} \)
Итак, мы снова получили правильный ответ!
Упрощение перед решением
В следующих примерах содержится больше вариативных терминов и, возможно, необходимо некоторое упрощение. В каждом случае шаги будут заключаться в том, чтобы сначала упростить обе стороны, а затем использовать то, что мы делали, чтобы изолировать переменную. Сначала мы подробно рассмотрим пример, чтобы увидеть, как все это работает.
В каждом случае шаги будут заключаться в том, чтобы сначала упростить обе стороны, а затем использовать то, что мы делали, чтобы изолировать переменную. Сначала мы подробно рассмотрим пример, чтобы увидеть, как все это работает.
Чтобы понять этот раздел, вам должно быть удобно комбинировать похожие термины.
Пример
Решить: \ (3x + 2 = 4x-1 \)
Решение
Поскольку обе части упрощены (нет скобок, которые нам нужно вычислять, и нет одинаковых членов для объединения), следующим шагом будет получение всех x на одной стороне уравнения и всех чисел на другой стороне.Применяется то же правило — что бы вы ни делали с одной стороной уравнения, вы должны делать и с другой стороной!
Можно перемещать \ (3x \) или \ (4x \). Предположим, вы переместили \ (4x \). Поскольку он положительный, вы должны вычесть его с обеих сторон:
\ (\ begin {align} 3x + 2 & = 4x-1 \\ 3x + 2 \ color {red} {- 4x} & = 4x-1 \ color {red} {- 4x} \\ -x + 2 & = -1 \ конец {выравнивание} \)
Теперь уравнение выглядит так же, как и раньше. Следующим шагом будет вычитание 2 с обеих сторон:
Следующим шагом будет вычитание 2 с обеих сторон:
\ (\ begin {align} -x + 2 \ color {red} {- 2} & = -1 \ color {red} {- 2} \\ — x = -3 \ end {align} \)
Наконец, поскольку \ (- x = -1x \) (это всегда верно), разделите обе стороны на \ (- 1 \):
\ (\ begin {align} \ dfrac {-x} {\ color {red} {- 1}} & = \ dfrac {-3} {\ color {red} {- 1}} \\ x & = 3 \ end {выровнять}\)
Чек
Вам следует воспользоваться моментом и убедиться, что следующее утверждение является верным:
\ (3 (3) + 2 = 4 (3) — 1 \)
В следующем примере нам нужно будет использовать свойство распределения перед решением.Здесь легко ошибиться, поэтому убедитесь, что вы распределили число перед круглыми скобками для всех терминов внутри.
Пример
Решить: \ (3 (x + 2) -1 = x-3 (x + 1) \)
Решение
Сначала разложите 3 и –3 и соберите одинаковые термины.
\ (\ begin {align} 3 (x + 2) -1 & = x-3 (x + 1) \\ 3x + 6-1 & = x-3x-3 \\ 3x + 5 & = — 2x-3 \ end {выровнять}\)
Теперь мы можем прибавить 2x к обеим сторонам. (Помните, что вы получите тот же ответ, если вместо этого вычтете 3x с обеих сторон)
(Помните, что вы получите тот же ответ, если вместо этого вычтете 3x с обеих сторон)
\ (\ begin {align} 3x + 5 \ color {red} {+ 2x} & = — 2x-3 \ color {red} {+ 2x} \\ 5x + 5 & = -3 \ end {align} \)
Отсюда мы можем решить, как и с другими двухэтапными уравнениями.
\ (\ begin {align} 5x + 5 \ color {red} {- 5} & = — 3 \ color {red} {- 5} \\ 5x & = — 8 \\ \ dfrac {5x} {\ color { красный} {5}} & = \ dfrac {-8} {\ color {red} {5}} \\ x & = \ dfrac {-8} {5} \\ & = \ boxed {- \ dfrac {8 } {5}} \ end {align} \)
Чек
Это был сложный вопрос, поэтому не забудьте проверить свой ответ и убедиться, что не было допущено никаких ошибок. Для этого вы убедитесь, что следующее утверждение является верным:
\ (3 \ left (- \ dfrac {8} {5} +2 \ right) -1 = \ left (- \ dfrac {8} {5} \ right) -3 \ left (- \ dfrac {8} { 5} +1 \ вправо) \)
(Примечание: это работает, но вы должны быть очень осторожны с скобками!)
Бесконечно много решений и никаких решений
Бывают случаи, когда вы выполняете все эти шаги, и возникает действительно странное решение. Например, при решении уравнения \ (x + 2 = x + 2 \) с использованием описанных выше шагов в итоге получается \ (0 = 0 \). Это, конечно, правда, но что хорошего в этом?
Например, при решении уравнения \ (x + 2 = x + 2 \) с использованием описанных выше шагов в итоге получается \ (0 = 0 \). Это, конечно, правда, но что хорошего в этом?
Если вы получите подобное утверждение, это означает, что уравнение имеет бесконечно много решений. Любой \ (x \), о котором вы можете подумать, удовлетворял бы уравнению \ (x + 2 = x + 2 \). Подходящий ответ в этом случае — «бесконечно много решений».
Другая ситуация возникает, когда вы упрощаете уравнение до утверждения, которое никогда не бывает истинным, например \ (3 = 4 \) или \ (0 = 1 \).Это происходит с уравнением \ (x + 5 = x-7 \), которое приводит к \ (5 = -7 \), что, конечно, никогда не бывает истинным. Это означает, что никакое \ (x \) не удовлетворяет этому уравнению. Другими словами «нет решения». Итого:
- Если вы получите утверждение, которое всегда истинно, например \ (5 = 5 \) или \ (0 = 0 \), то существует бесконечно много решений.
- Если вы получаете утверждение, которое всегда ложно, например \ (10 = 11 \) или \ (1 = 5 \), то решений нет.

реклама
Сводка
Решение линейных уравнений сводится к выделению переменной.В зависимости от уравнения это может занять от одного шага до многих. Всегда проверяйте, нужно ли вам сначала упростить одну или обе стороны уравнения, и всегда проверяйте свой ответ.
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
Решение линейных уравнений с одной переменной
Линейное уравнение — это уравнение прямой, записанное с одной переменной.Единственная степень переменной — 1. Линейные уравнения с одной переменной могут иметь вид [latex] ax + b = 0 [/ latex] и решаются с использованием основных алгебраических операций.
Мы начинаем с классификации линейных уравнений с одной переменной как одного из трех типов: тождественные, условные или противоречивые. Уравнение идентичности верно для всех значений переменной. Вот пример тождественного уравнения.
Уравнение идентичности верно для всех значений переменной. Вот пример тождественного уравнения.
[латекс] 3x = 2x + x [/ латекс]
Набор решений состоит из всех значений, которые делают уравнение истинным.Для этого уравнения набором решений является все действительные числа, потому что любое действительное число, замененное на [латекс] x [/ латекс], сделает уравнение истинным.
Условное уравнение верно только для некоторых значений переменной. Например, если мы должны решить уравнение [латекс] 5x + 2 = 3x — 6 [/ latex], мы имеем следующее:
[латекс] \ begin {array} {l} 5x + 2 \ hfill & = 3x — 6 \ hfill \\ 2x \ hfill & = — 8 \ hfill \\ x \ hfill & = — 4 \ hfill \ end {array} [/ латекс]
Набор решений состоит из одного числа: [латекс] \ {- 4 \} [/ латекс].Это единственное решение, поэтому мы решили условное уравнение.
Непоследовательное уравнение приводит к ложному утверждению. Например, если мы должны решить [латекс] 5x — 15 = 5 \ left (x — 4 \ right) [/ latex], мы имеем следующее:
Например, если мы должны решить [латекс] 5x — 15 = 5 \ left (x — 4 \ right) [/ latex], мы имеем следующее:
[латекс] \ begin {array} {ll} 5x — 15 = 5x — 20 \ hfill & \ hfill \\ 5x — 15 — 5x = 5x — 20 — 5x \ hfill & \ text {Subtract} 5x \ text {from обе стороны}. \ hfill \\ -15 \ ne -20 \ hfill & \ text {Ложный оператор} \ hfill \ end {array} [/ latex]
Действительно, [латекс] -15 \ ne -20 [/ латекс].Нет решения, потому что это противоречивое уравнение.
Решение линейных уравнений с одной переменной включает фундаментальные свойства равенства и основные алгебраические операции. Ниже приводится краткий обзор этих операций.
Общее примечание: линейное уравнение с одной переменной
Линейное уравнение с одной переменной можно записать в виде
[латекс] ax + b = 0 [/ латекс]
, где a и b — действительные числа, [латекс] a \ ne 0 [/ латекс].
Как сделать: дано линейное уравнение с одной переменной, используйте алгебру для его решения.

Следующие шаги используются для манипулирования уравнением и выделения неизвестной переменной, так что последняя строка читается как x = _________, если x — неизвестное. Нет установленного порядка, так как используемые шаги зависят от того, что указано:
- Мы можем складывать, вычитать, умножать или делить уравнение на число или выражение, если мы делаем то же самое с обеими сторонами знака равенства.Обратите внимание, что мы не можем делить на ноль.
- При необходимости примените свойство распределения: [latex] a \ left (b + c \ right) = ab + ac [/ latex].
- Выделите переменную на одной стороне уравнения.
- Когда переменная умножается на коэффициент на заключительном этапе, умножьте обе части уравнения на обратную величину коэффициента.
Пример 1: Решение уравнения с одной переменной
Решите следующее уравнение: [латекс] 2x + 7 = 19 [/ латекс].
Решение
Это уравнение можно записать в виде [латекс] ax + b = 0 [/ латекс], вычитая [латекс] 19 [/ латекс] с обеих сторон. Однако мы можем перейти к решению уравнения в его исходной форме, выполнив алгебраические операции.
Однако мы можем перейти к решению уравнения в его исходной форме, выполнив алгебраические операции.
[латекс] \ begin {array} {ll} 2x + 7 = 19 \ hfill & \ hfill \\ 2x = 12 \ hfill & \ text {Вычтите 7 с обеих сторон}. \ Hfill \\ x = 6 \ hfill & \ text {Умножьте обе стороны на} \ frac {1} {2} \ text {или разделите на 2}. \ hfill \ end {array} [/ latex]
Решение [латекс] x = 6 [/ латекс].
Попробуй 1
Решите линейное уравнение с одной переменной: [латекс] 2x + 1 = -9 [/ латекс].
Решение
Пример 2: Алгебраическое решение уравнения, когда переменная появляется с обеих сторон
Решите следующее уравнение: [латекс] 4 \ left (x — 3 \ right) + 12 = 15-5 \ left (x + 6 \ right) [/ latex].
Решение
Примените стандартные алгебраические свойства.
[латекс] \ begin {array} {ll} 4 \ left (x — 3 \ right) + 12 = 15-5 \ left (x + 6 \ right) \ hfill & \ hfill \\ 4x — 12 + 12 = 15 — 5x — 30 \ hfill & \ text {Применить свойство распределения}. \ Hfill \\ 4x = -15 — 5x \ hfill & \ text {Объединить похожие термины}. \ Hfill \\ 9x = -15 \ hfill & \ text {Поместите} x- \ text {термины на одну сторону и упростите}. \ hfill \\ x = — \ frac {15} {9} \ hfill & \ text {Умножьте обе стороны на} \ frac {1} {9 } \ text {, обратное 9}.\ hfill \\ x = — \ frac {5} {3} \ hfill & \ hfill \ end {array} [/ latex]
\ Hfill \\ 4x = -15 — 5x \ hfill & \ text {Объединить похожие термины}. \ Hfill \\ 9x = -15 \ hfill & \ text {Поместите} x- \ text {термины на одну сторону и упростите}. \ hfill \\ x = — \ frac {15} {9} \ hfill & \ text {Умножьте обе стороны на} \ frac {1} {9 } \ text {, обратное 9}.\ hfill \\ x = — \ frac {5} {3} \ hfill & \ hfill \ end {array} [/ latex]
Анализ решения
Эта задача требует, чтобы свойство распределения применялось дважды, а затем свойства алгебры используются для достижения последней строки, [latex] x = — \ frac {5} {3} [/ latex].
Попробуй 2
Решите уравнение с одной переменной: [латекс] -2 \ left (3x — 1 \ right) + x = 14-x [/ latex].
Решение
Системы линейных уравнений
Линейное уравнение — это уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,
Это также может быть как y = 0,5 (7 — x)
Или как y + 0,5x = 3,5
Или как y + 0,5x — 3,5 = 0 и более.
(Примечание: это одно и то же линейное уравнение!)
A Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
Вместе они представляют собой систему линейных уравнений.
Сможете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Попробуем построить и решить реальный пример:
Пример: вы против лошади
Это гонка!
Вы можете бегать 0,2 км каждую минуту.
Лошадь может бежать 0,5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.
Как далеко вы можете уйти, прежде чем лошадь вас поймает?
Мы можем составить из двух уравнений ( d = расстояние в км, t = время в минутах)
- Вы бежите на 0.2 км каждую минуту, поэтому d = 0,2t
- Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)
Итак, у нас есть система уравнений ( линейных ):
Решаем на графике:
Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут . .. Тебе всего 2 км.
.. Тебе всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Существует множество способов решения линейных уравнений!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим это с помощью алгебры!
Хммм … как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y — (−3x + y) = 6 — 2
А теперь упростим:
х + у + 3х — у = 6-2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .
И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
x = 1 и y = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. Нет x 2 , y 3 , √x и т. Д. :
Линейное против нелинейного
Размеры
| A Линейное уравнение может быть в 2 измерениях … (например, x и y ) | ||
| … или в 3-х измерениях … (делает самолет) | ||
| … или 4 размера … | ||
. .. или больше! .. или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:
Система уравнений состоит из двух или более уравнений в одной или нескольких переменных
Много переменных
Таким образом, Система уравнений может иметь многих, уравнений и многих переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | y | – | 2z | = | 3 |
| x | – | y | – | z | = | 0 |
| x | + | y | + | 3z | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений в 4 переменных,
- 9000 уравнений в 567 переменных,
- и др.

Решения
Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будут решением. Не гарантировано, но вероятно.
На самом деле есть только три возможных случая:
- Нет раствор
- Одно решение
- Бесконечно много решений
Когда нет решения , уравнения называются «несовместимыми» .
Один или бесконечно много решений называются «согласованными»
Вот диаграмма для 2 уравнения с 2 переменными :
Независимая
«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
Эти уравнения — «Зависимые» , потому что они на самом деле являются тем же уравнением , только умноженным на 2.
Итак, второе уравнение не дало новой информации .
Где верны уравнения
Уловка состоит в том, чтобы найти, где , все уравнений, истинны одновременно .
Верно? Что это значит?
Пример: вы против лошади
Линия «ты» истинна по всей ее длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t = 5 и d = 1 уравнение истинно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
- при t = 5 и d = 3, уравнение неверно (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )
Точно так же линия «лошади» также верна по всей своей длине (но больше нигде).
Но только в точке, где они пересекают (при t = 10, d = 2), они оба истинны .
Значит, они должны быть правдой одновременно …
… поэтому некоторые люди называют их «Одновременные линейные уравнения»
Решить с помощью алгебры
Для их решения принято использовать алгебру.
Вот пример «Лошади», решенный с помощью алгебры:
Пример: вы против лошади
Система уравнений:
В этом случае кажется, что проще всего установить их равными друг другу:
г = 0.2т = 0,5 (т − 6)
Начать с : 0,2t = 0,5 (t — 6)
Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3
Вычтем 0,5t с обеих сторон: −0,3t = −3
Разделим обе части на −0,3 : t = −3 / −0,3 = 10 минут
Теперь мы знаем , когда тебя поймают!
Зная t , можно вычислить d : d = 0,2t = 0,2 × 10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра и графики
Зачем использовать алгебру, если графики настолько просты? Потому что:
Более 2 переменных не могут быть решены с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение заменой
- Решение методом исключения
Мы увидим каждую с примерами по 2 переменным и 3 переменным. Вот и …
Вот и …
Решение заменой
Это шаги:
- Напишите одно из уравнений в стиле «переменная = …»
- Заменить (т.е. заменить) эту переменную в другое уравнение (а).
- Решите другое уравнение (а)
- (при необходимости повторить)
Вот пример с 2 уравнениями с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Воспользуемся вторым уравнением и переменной «y» (это выглядит как простейшее уравнение).
Напишите одно из уравнений в стиле «переменная =»… «:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 — x» в другом уравнении:
- 3x + 2 (8 — x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Развернуть 2 (8 − x) :
- 3x + 16 — 2x = 19
- у = 8 — х
Тогда 3x − 2x = x :
И на последок 19−16 = 3
Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :
И ответ:
х = 3
у = 5
Примечание: поскольку — это решение, уравнения «согласованы»
Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?
Решение подстановкой: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это несложно, сделать … просто нужно много времени !
Пример:
- х + г = 6
- г — 3у = 7
- 2x + y + 3z = 15
Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду, что делаем:
| x | + | z | = | 6 | |||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
WeI может начать с любого уравнения и любой переменной.Воспользуемся первым уравнением и переменной «x».
Напишите одно из уравнений в стиле «переменная = …»:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
Теперь замените «x» на «6 — z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
| х | = | 6 — z | ||||||||
| – | 3 года | + | z | = | 7 | |||||
| 2 (6-z) | + | y | + | 3z | = | 15 | ||||
Решите, используя обычные методы алгебры:
2 (6 − z) + y + 3z = 15 упрощается до y + z = 3 :
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
Хорошо.Мы добились некоторого прогресса, но пока не достигли этого.
Теперь повторите процесс , но только для последних 2 уравнений.
Напишите одно из уравнений в стиле «переменная = …»:
Выберем последнее уравнение и переменную z:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| z | = | 3 — х лет | |||||||
Теперь замените «z» на «3 — y» в другом уравнении:
| x | = | 6 — z | |||||||
| – | 3 года | + | 3 — х лет | = | 7 | ||||
| z | = | 3-й год | |||||||
Решите, используя обычные методы алгебры:
−3y + (3 − y) = 7 упрощается до −4y = 4 , или другими словами y = −1
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 3-й год | |||||||
Почти готово!
Зная, что y = −1 , мы можем вычислить, что z = 3 − y = 4 :
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 4 | |||||||
И зная, что z = 4 , мы можем вычислить, что x = 6 − z = 2 :
| x | = | 2 | |||||||
| y | = | -1 | |||||||
| z | = | 4 |
И ответ:
х = 2
у = -1
г = 4
Проверка: проверьте сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных … просто повторяйте одни и те же шаги снова и снова, пока не решите проблему.
Заключение: Замена работает хорошо, но требует много времени.
Решение методом исключения
Уничтожение может быть быстрее … но должно быть аккуратным.
«Исключить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
По идее, мы можем спокойно :
- умножить уравнение на константу (кроме нуля),
- прибавить (или вычесть) уравнение к другому уравнению
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг в друга?
Представьте себе два действительно простых уравнения:
х — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x — 5 = 3»:
х — 5 + 5 = 3 + 5
х = 8
Попробуйте сами, но используйте 5 = 3 + 2 в качестве второго уравнения
Он все равно будет работать нормально, потому что обе стороны равны (это то, для чего стоит знак =!)
Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. Д., Если это поможет.
Хорошо, время для полного примера. Давайте использовать 2 уравнения с 2 переменными , пример из предыдущего:
Пример:
Очень важно, чтобы все было в порядке:
| 3x | + | 2 года | = | 19 | |||
| x | + | y | = | 8 |
Сейчас… наша цель — исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножьте второе уравнение на 2:
.
| 3x | + | 2 года | = | 19 | |||
| 2 x | + | 2 y | = | 16 |
Вычтем второе уравнение из первого уравнения:
| x | = | 3 | |||||
| 2x | + | 2 года | = | 16 |
Ура! Теперь мы знаем, что такое x!
Затем мы видим, что во втором уравнении есть «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второе уравнение на ½ (т.е. разделить на 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
Вычтем первое уравнение из второго уравнения:
| x | = | 3 | |||||
| y | = | 5 |
Готово!
И ответ:
x = 3 и y = 5
А вот график:
Синяя линия — это место, где 3x + 2y = 19 истинно
Красная линия — это место, где x + y = 8 истинно
При x = 3, y = 5 (где линии пересекаются) они равны , оба истинны. Это ответ.
Вот еще один пример:
Пример:
- 2х — у = 4
- 6x — 3y = 3
Разложите аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 3 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 3 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 9 | |||
| 6x | – | 3 года | = | 3 |
0-0 = 9 ???
Что здесь происходит?
Все просто, решения нет.
| На самом деле это параллельные линии: |
И на последок:
Пример:
- 2х — у = 4
- 6x — 3y = 12
Аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 12 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 12 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 0 | |||
| 6x | – | 3 года | = | 3 |
0 — 0 = 0
Ну, это на самом деле ИСТИНА! Ноль действительно равен нулю…
… это потому, что на самом деле это одно и то же уравнение …
… значит существует бесконечное количество решений
| Это та же строка: |
Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:
- Нет раствор
- Одно решение
- Бесконечно много решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы начнем со следующего примера, давайте рассмотрим улучшенный способ решения задач.
Следуйте этому методу, и мы с меньшей вероятностью ошибемся.
Прежде всего удалите переменные в порядке :
.
- Сначала удалите x с (из уравнений 2 и 3, по порядку)
- , затем исключите y (из уравнения 3)
Вот как мы их устраняем:
У нас есть «форма треугольника»:
Теперь начните снизу и вернитесь к исходному состоянию (так называемая «обратная подстановка»)
(введите z , чтобы найти y , затем z и y , чтобы найти x ):
И решаемся:
ТАКЖЕ, мы обнаружим, что проще выполнить каких-то вычислений в уме или на бумаге для заметок, чем всегда работать в рамках системы уравнений:
Пример:
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y — z = 27
Аккуратно написано:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 2x | + | 5лет | – | z | = | 27 |
Сначала удалите x из 2-го и 3-го уравнения.
Во втором уравнении нет x … переходите к третьему уравнению:
Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге для заметок):
И получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 3 года | – | 3z | = | 15 |
Затем удалите y из 3-го уравнения.
Мы, , могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½, умноженное на 2, равно 3) …
… но мы можем избежать дробей , если мы:
- умножьте третье уравнение на 2 и
- умножьте 2-е уравнение на 3
и , затем выполняют вычитание … вот так:
И в итоге получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| z | = | -2 |
Теперь у нас есть «треугольник»!
Теперь вернемся снова вверх «с обратной заменой»:
Мы знаем z , поэтому 2y + 5z = −4 становится 2y − 10 = −4 , затем 2y = 6 , поэтому y = 3 :
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | -2 |
Тогда x + y + z = 6 становится x + 3−2 = 6 , поэтому x = 6−3 + 2 = 5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | -2 |
И ответ:
x = 5
y = 3
z = −2
Проверка: проверьте сами.
Общая консультация
Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.
Но иногда замена может дать более быстрый результат.
- Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
- Устранение проще для больших ящиков
И всегда полезно сначала просмотреть уравнения, чтобы увидеть, есть ли простой ярлык… так что опыт помогает.
Оценка: 7 — Алгебра и функции 2
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся.Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для математиков, испытывающих трудности | |
|---|---|
Стратегии | Примеры |
Вовлечение в стратегии исполнительного функционирования |
|
Примерные примеры |
|
Поощряйте и моделируйте математическую беседу |
|
Проверить понимание при использовании «математических правил»; объясните почему |
|
Обучение математике — ключевые слова |
|
Используйте сокращения, чтобы помочь учащимся запомнить шаги / процессы |
|
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? Последняя редакция 1 июля 2011 г. Ким Сьюард. |
Алгебра — линейные уравнения
Решите каждое из следующих уравнений.
Показать обсуждение
В следующих задачах мы подробно опишем первую проблему и оставим большую часть объяснений нижеприведенных проблем.
a \ (3 \ left ({x + 5} \ right) = 2 \ left ({- 6 — x} \ right) — 2x \) Показать решение
Для этой задачи нет дробей, поэтому нам не нужно беспокоиться о первом этапе процесса.На следующем шаге нужно упростить обе стороны. Итак, мы уберем все скобки, умножив числа до конца, а затем объединим похожие термины.
\ [\ begin {align *} 3 \ left ({x + 5} \ right) & = 2 \ left ({- 6 — x} \ right) — 2x \\ 3x + 15 & = — 12 — 2x — 2x \\ 3x + 15 & = — 12 — 4x \ end {align *} \]
Следующий шаг — получить все \ (x \) с одной стороны и все числа с другой стороны. С какой стороны будет идти \ (x \) — решать вам и, вероятно, будет зависеть от проблемы.Как правило, мы помещаем переменные в ту сторону, которая дает положительный коэффициент. Это делается просто потому, что часто легко потерять знак минус на коэффициенте, и поэтому, если мы убедимся, что он положительный, нам не нужно об этом беспокоиться.
Итак, для нашего случая это будет означать прибавление 4 \ (x \) к обеим сторонам и вычитание 15 с обеих сторон. Также обратите внимание, что, хотя мы фактически выполняем эти операции в это время, мы обычно выполняем эти операции в нашей голове.
\ [\ begin {align *} \ require {color} 3x + 15 & = — 12 — 4x \\ 3x + 15 {\ color {Red} — 15} {\ color {Blue} + 4x} & = — 12 — 4x {\ color {Blue} + 4x} {\ color {Red} — 15} \\ 7x & = — 27 \ end {align *} \]
На следующем этапе нужно получить коэффициент 1 перед \ (x \). В этом случае мы можем сделать это, разделив обе стороны на 7.
\ [\ begin {align *} \ frac {{7x}} {7} & = \ frac {{- 27}} {7} \\ x & = — \ frac {{27}} {7} \ end { выровнять*}\]
Теперь, если мы выполнили всю нашу работу правильно, \ (x = — \ frac {{27}} {7} \) является решением уравнения.
Последний и последний шаг — проверить решение. Как указано в схеме процесса, нам необходимо проверить решение в исходном уравнении . Это важно, потому что мы могли допустить ошибку на самом первом шаге, и если мы сделали, а затем проверили ответ в результатах этого шага, может показаться, что решение верное, хотя на самом деле мы этого не делаем. У меня нет правильного ответа из-за ошибки, которую мы сделали изначально.? 2 \ left ({- \ frac {{15}} {7}} \ right) + \ frac {{54}} {7} \\ \ frac {{24}} {7} & = \ frac {{24 }} {7} \ hspace {0.5in} {\ mbox {OK}} \ end {align *} \]
Итак, мы выполнили свою работу правильно и решение уравнения:
\ [x = — \ frac {{27}} {7} \]
Обратите внимание, что здесь мы не использовали обозначение набора решений. Для отдельных решений мы редко будем делать это в этом классе. Однако, если бы мы хотели, чтобы обозначение набора решений для этой проблемы было бы
\ [\ left \ {{- \ frac {{27}} {7}} \ right \} \]
Прежде чем переходить к следующей задаче, давайте сначала кратко прокомментируем «беспорядок» этого ответа.НЕ ожидайте, что все ответы будут красивыми простыми целыми числами. Хотя мы стараемся, чтобы большинство ответов были простыми, часто это не так, поэтому НЕ зацикливайтесь на идее, что ответ должен быть простым целым числом, что вы сразу же предполагаете, что вы сделали ошибку из-за «беспорядка» ответ.
b \ (\ displaystyle \ frac {{m — 2}} {3} + 1 = \ frac {{2m}} {7} \) Показать решение
Хорошо, с этим мы не будем так подробно объяснять проблему.
В этом случае у нас есть дроби, поэтому, чтобы облегчить нашу жизнь, мы умножим обе части на ЖК-дисплей, который в данном случае равен 21. После этого проблема будет очень похожа на предыдущую. Также обратите внимание, что знаменатели — это только числа, поэтому нам не нужно беспокоиться о делении на ноль.
Давайте сначала умножим обе стороны на ЖК-дисплей.
\ [\ begin {align *} 21 \ left ({\ frac {{m — 2}} {3} + 1} \ right) & = \ left ({\ frac {{2m}} {7}} \ right ) 21 \\ 21 \ left ({\ frac {{m — 2}} {3}} \ right) + 21 \ left (1 \ right) & = \ left ({\ frac {{2m}} {7} } \ right) 21 \\ 7 \ left ({m — 2} \ right) + 21 & = \ left ({2m} \ right) \ left (3 \ right) \ end {align *} \]
Будьте осторожны, чтобы правильно распределить 21 в скобках с левой стороны.Все, что находится внутри скобок, нужно умножить на 21, прежде чем мы упростим. На данный момент у нас есть проблема, аналогичная предыдущей, и на этот раз мы не будем утруждать себя ее объяснениями.
\ [\ begin {align *} 7 \ left ({m — 2} \ right) + 21 & = \ left ({2m} \ right) \ left (3 \ right) \\ 7m — 14 + 21 & = 6m \\ 7m + 7 & = 6m \\ m & = — 7 \ end {align *} \]
Итак, похоже, \ (m = — 7 \) — это решение.2} — 6 \ left (5 \ right) + 9}} \\ \ frac {5} {4} & = \ frac {5} {4} \ hspace {0.5in} {\ mbox {OK}} \ end {выровнять*}\]
d \ (\ displaystyle \ frac {{2z}} {{z + 3}} = \ frac {3} {{z — 10}} + 2 \) Показать решение
В этом случае ЖК-дисплей выглядит как \ (\ left ({z + 3} \ right) \ left ({z — 10} \ right) \), и также похоже, что нам нужно избегать \ (z = — 3 \) и \ (z = 10 \), чтобы не получить деление на ноль.
Приступим к работе над этой проблемой.2} — 7z — 30} \ right) \ end {align *} \]
На этом этапе давайте сделаем паузу и признаем, что здесь у нас есть z 2 . 2}}} — 14z — 60 \ \ — 20z & = — 11z — 51 \\ 51 & = 9z \\ \ frac {{51}} {9} & = z \\ & \ frac {{17}} {3} = z \ end {align * } \]
Обратите внимание, что z 2 фактически компенсировались.? 3 \ left ({- \ frac {3} {{13}}} \ right) + 2 \\ \ frac {{17}} {{13}} & = \ frac {{17}} {{13}} \ hspace {0,5 дюйма} {\ mbox {OK}} \ end {align *} \]
Иногда проверка может быть немного запутанной, но это означает, что мы ЗНАЕМ, что решение правильное.
Линейные уравнения — определение, формулы, примеры и решения
Линейные уравнения — это не что иное, как еще одно подмножество «уравнений». Любые линейные вычисления, требующие более одной переменной, могут быть выполнены с помощью линейных уравнений.Стандартная форма линейного уравнения с одной переменной имеет вид ax + b = 0. Здесь x — переменная, а a и b — константы. В то время как стандартная форма линейного уравнения с двумя переменными имеет вид ax + by = c. Здесь x и y — переменные, а a, b и c — константы.
Что такое линейное уравнение?
Математическое выражение, имеющее знак равенства со знаком «=», называется уравнением. Линейные уравнения — это уравнения степени 1.
Определение линейного уравнения
Линейное уравнение — это уравнение, записанное для двух разных переменных.Это уравнение будет линейной комбинацией этих двух переменных, и может присутствовать константа. Удивительно, но когда любое линейное уравнение отображается на графике, оно обязательно дает прямую линию — отсюда и название: линейные уравнения.
Примеры линейных уравнений
Линейное уравнение можно записать по-разному. Любое простое уравнение относительно x и y можно назвать линейным уравнением, если оно следует определенному набору правил. Например, наивысшая (и единственная) степень обеих переменных — x и y — в уравнении должна быть 1.Кроме этого, там могут быть константы (переменные нулевой степени). Чтобы лучше понять, какие уравнения можно назвать линейными или нет, взгляните на следующие уравнения.
| Уравнения | Линейные или нелинейные |
| y = 8x — 9 | линейный |
| y = x 2 -7 | Нелинейный |
| √y + x = 6 | Нелинейный |
| y + 3x — 1 = 0 | линейный |
| y 2 — x = 9 | Нелинейный |
Что такое линейное уравнение
Линейные уравнения — это широкий спектр уравнений в целом.Могут быть линейные уравнения с одной переменной, линейные уравнения с двумя переменными и так далее. В каждом уравнении одно остается постоянным: наивысшая (и единственная) степень всех переменных в уравнении должна быть 1. Кроме этого, могут присутствовать константы (переменные нулевой степени). Давайте посмотрим на следующую игру под названием «Читатель мыслей», которая поможет вам лучше понять линейные уравнения.
Appu создал игру под названием «Mind Reader». Он хочет поиграть со своими друзьями.Поэтому он просит одного из своих друзей, Кайру, придумать число, умножить его на 2 и вычесть из него 5. Затем он спрашивает ее окончательный результат. Кайра говорит: «Это 13», поэтому Аппу тут же говорит, что изначально Кайра подумал о 9. Кайра кивает, и друзья Аппу, включая Кайру, удивляются! Все хотят знать, как работает игра Mind Reader. Вы знаете, как это работает? К концу этого короткого урока вы поймете, как это работает.
Формула линейного уравнения
Формула линейного уравнения составляется от случая к случаю и основана на количестве переменных и самих переменных.Во-первых, переменные должны быть независимыми друг от друга. Предположим, у вас есть x как переменная, тогда вы не можете сохранить x 2 как другую переменную. Во-вторых, наивысшая (и единственная) степень всех переменных в уравнении должна быть 1. Кроме этого, могут присутствовать константы (переменные нулевой степени). Давайте посмотрим на стандартную форму линейного уравнения с переменными x и y:
График линейных уравнений
График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, и наоборот, тогда как график линейного уравнения с двумя переменными x и y образует прямую линию.Причина, по которой уравнение первой степени называется линейным уравнением, состоит в том, что его геометрическое представление представляет собой прямую линию. Выше приведены несколько примеров того, как мы строим линейные уравнения на графике.
Как решать линейные уравнения?
Давайте посмотрим, как решить любое уравнение. Уравнение похоже на весы с одинаковыми весами с обеих сторон. Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно все равно останется в силе. Точно так же, если мы умножим или разделим одно и то же число в обеих частях уравнения, оно все равно останется в силе.Рассмотрим уравнение 3x — 2 = 4. Мы выполним математические операции с левой и правой частями, чтобы не нарушить баланс. Теперь добавим 2 с обеих сторон, чтобы уменьшить левую до 3 раз. Это не нарушит баланс. Новое значение LHS равно 3x — 2 + 2 = 3x, а новое значение RHS равно 4 + 2 = 6. Теперь давайте разделим обе стороны на 3, чтобы уменьшить LHS до x. Таким образом, имеем x = 2 . Это всего лишь один из способов решения таких уравнений. Еще один и более эффективный способ — это графическое решение линейных уравнений.
Важные моменты
- Значения переменной, которая делает линейное уравнение истинным, называются решением или корнем линейного уравнения.
- На решение линейного уравнения не влияет добавление, вычитание, умножение или деление одного и того же числа в обе стороны уравнения.
- График линейного уравнения с одной или двумя переменными представляет собой прямую линию.
Что такое линейное уравнение? Объясните на примере.
Уравнение вида ax + by = c называется линейным уравнением. Здесь x и y — переменные, а a, b и c — константы. Примеры линейного уравнения:
- y = 4x — 3
- 7лет — 5x = 1
- г = 2
Какова формула линейного уравнения?
Стандартная форма линейного уравнения с одной переменной имеет вид ax + b = 0. Здесь x — переменная, а a и b — константы. В то время как стандартная форма линейного уравнения с двумя переменными имеет вид ax + by = c.Здесь x и y — переменные, а a, b и c — константы.
Что такое простое определение линейного уравнения?
Уравнение, которое можно записать в форме ax + by = c, называется линейным уравнением. Это стандартная форма линейного уравнения с двумя переменными x и y.
Почему это называется линейным уравнением?
Это называется линейным уравнением, потому что если вы попытаетесь построить график данного уравнения с переменными x и y на графике с осями x и y, вы получите линию в качестве результата.
