Содержание
Линейная функция, график — прямая. Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
Тестирование онлайн
Линейная функция
Определение. График
Линейной функцией называется функция вида
где k, b — некоторые числа.
Функция вида называется прямой пропорциональностью, является частным случаем линейной зависимости.
Графиком линейной функции является прямая линия.
Для построения графика достаточно знать координаты двух точек.
Свойства линейной функции
1) Область определения функции — множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке , а ось Оу — в точке (0; b).
7) — является нулем функции.
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k.
9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
При k: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k — тупой, если k=0, то прямая совпадает с осью Ох.
Для построения графика функции — прямой линии, очевидно, достаточно двух точек.
Особые случаи
1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.
2) Если k=0, получим уравнение y=b. Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейная функция
Линейной функцией называют функцию, заданную формулой
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия.
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом.
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 1, 2 и 3.
1, 2 и 3.
| k > 0 | ||||||
|
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
| k = 0 | ||||||
|
При k < 0 линейная функция (1) убывает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 7, 8 и 9.
7, 8 и 9.
| k < 0 | ||||||
|
Прямые линии
y = kx + b1 и y = kx + b2 ,
имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны.
Прямые линии
y = k1x + b1 и y = k2x + b2 ,
имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.
Прямые линии
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
|
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .
При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
Прямые, параллельные оси ординат
Прямые, параллельные оси Oy, задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
13, 14, 15.
|
Замечание 1. Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
Рассмотрим уравнение
где p, q, r – произвольные числа.
В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию.
Действительно,
что и требовалось.
В случае, когда получаем:
откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:
В случае, когда уравнение (5) решений вообще не имеет.
Замечание 2. При любом значении r1, не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4).
Замечание 3. При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4).
Пример. Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
- перпендикулярной к прямой (8).
Решение.
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
4x + 5y = 7,
задаётся уравнением
4x + 5y = – 7 .
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, прямая, перпендикулярная к прямой
4x + 5y = 7 ,
задаётся уравнением
– 5x + 4y = – 22 .
Функция прямая пропорциональность | Алгебра
Определение
Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).
Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.
Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).
Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).
Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.
Свойства функции прямой пропорциональности
1) Область определения — множество действительных чисел:
D(y): x∈(-∞;+∞) (или x∈R).
2) Область значений — множество действительных чисел:
D(y): y∈(-∞;+∞) (или y∈R).
3) Нуль функции (y=0) при x=0.
4) При k>0 функция y=kx возрастает, при k<0 — убывает.
5) При k>0 график функции проходит через I и III координатные четверти.
Функция принимает положительные значения при положительных значениях аргумента:
y>0 при x>0.
Функция принимает отрицательные значения при отрицательных значениях аргумента:
y<0 при x<0.
При k<0 график функции проходит через II и IV координатные четверти.
Функция принимает положительные значения при отрицательных значениях аргумента:
y>o при x<0.
Функция принимает отрицательные значения при положительных значениях аргумента:
y<0 при x>0.
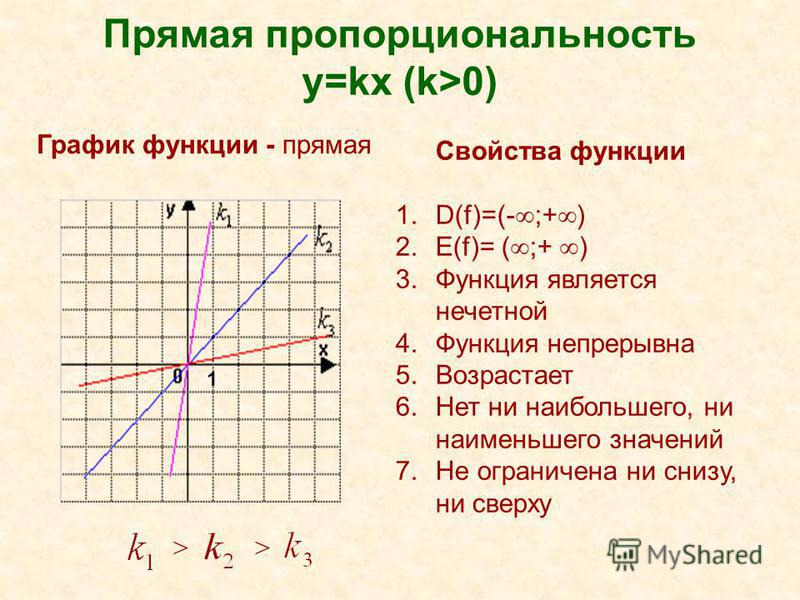
Число k называется угловым коэффициентом прямой y=kx.
k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.
Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.
При k1>0, k2>0
так как α1>α2, то k1>k2.
При k3<0, k4<0
так как α3>α4, то k4>k3.
В качестве иллюстрации рассмотрим графики четырёх функций прямой пропорциональности.
Графики функций y=x и y= -x являются биссектрисами соответственно I и III, II и IV координатных четвертей. Эти графики легко построить на листе в клеточку: каждую клеточку делим по диагонали:
Прямая пропорциональность и её график
Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.
Примером прямой пропорциональности может служить второй закон Ньютона: Ускорение тела прямо пропорционально приложенной к нему силе:
\[F=ma\]
Здесь масса — коэффициент пропорциональности. {»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
Рис. 2. График функции $y=kx$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $\left(x_0,\ y_0\right)$ и провести прямую через эту точку и начало координат.
Задачи на построение графиков функции прямой пропорциональности
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции (синусоида)
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).
Рис.1.
Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции область значений: . Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.
Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторяется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.
На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при (см. рис. 1).
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому при .
Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 3, а), то при увеличении аргумента ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрастает.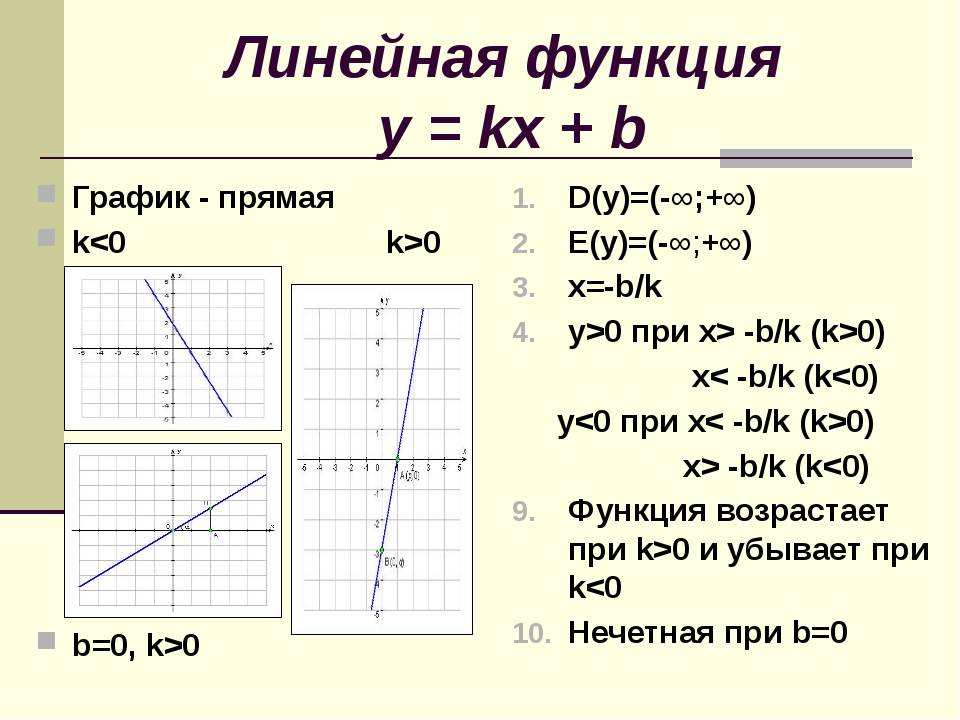 Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Рис.2 Рис.3
Если (рис.3,б), то при увеличении аргумента ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , например на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрично относительно начала координат (рис. 5).
5).
Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)
Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Такие процессы называют гармоническими колебаниями.
График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным переносом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число).
- Область значений:
-
Функция четная:
(график симметричен относительно оси ).
- Функция периодическая с периодом :
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.
Рис. 7
7
Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .
Как видим, наибольшее значение функции равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .
Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при .
Косинус — четная функция: , поэтому ее график симметричен относительно оси .
Косинус — периодическая функция с наименьшим положительным периодом : . Таким образом, через промежутки длиной вид графика функции повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .
Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 0 при , а также, учитывая период, при всех .
Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому при
Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 9, а), то при увеличении аргумента абсцисса соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Если (рис. 9, б), то при увеличении аргумента абсцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Рис.8 Рис.9
Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу
Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также
абсциссы и ординаты этих точек. Так как , то при повороте
прямоугольника около точки на угол — против часовой стрелки он перейдет в прямоугольник .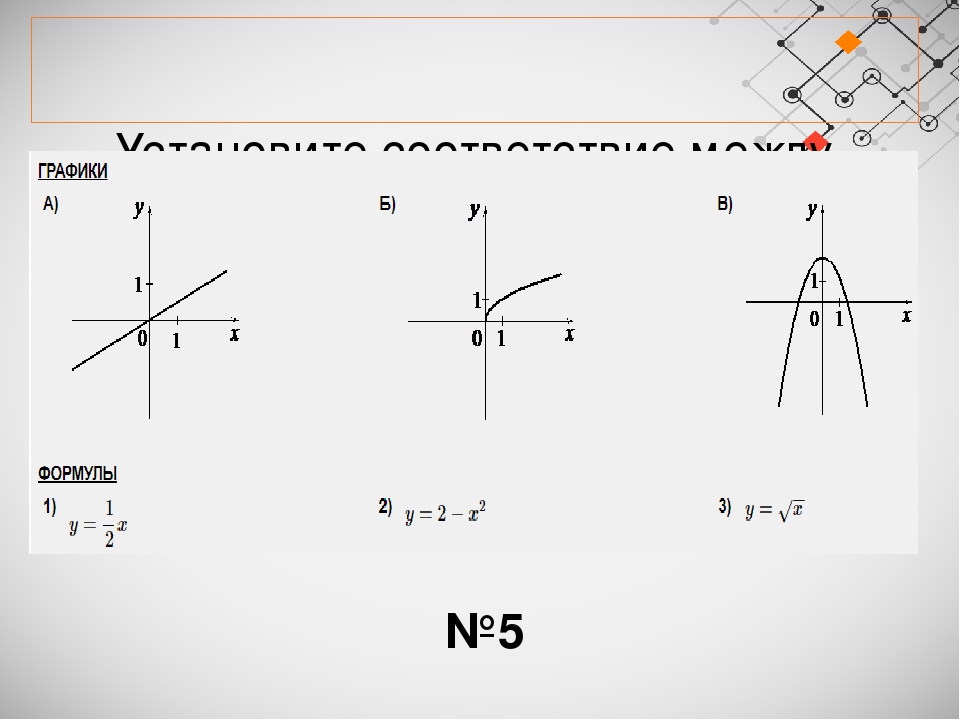 Но тогда . Следовательно, 00.
Но тогда . Следовательно, 00.
Укажем также формулы, которые нам понадобятся далее:.
Тогда,
Таким образом, .
Учитывая, что , график функции можно получить из графика функции его параллельным переносом вдоль оси на (рис. 11). Полученный график называется косинусоидой (рис. 12).
Рис.11
Рис.12
График функции (тангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Функция НАКЛОН — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции НАКЛОН в Microsoft Excel.
Описание
Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой; иными словами, наклон — это скорость изменения значений вдоль прямой.
Синтаксис
НАКЛОН(известные_значения_y;известные_значения_x)
Аргументы функции НАКЛОН описаны ниже.
-
Известные_значения_y Обязательный. Массив или диапазон ячеек, содержащих зависимые числовые точки данных. -
Известные_значения_x Обязательный. Множество независимых точек данных.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
-
Если аргументы известные_значения_y и известные_значения_x пусты или количество содержащихся в них точек не совпадает, функция НАКЛОН возвращает значение ошибки #Н/Д.

-
Уравнение наклона линии регрессии имеет следующий вид:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
-
Основной алгоритм, используемый в функциях НАКЛОН и ОТРЕЗОК, отличается от основного алгоритма функции ЛИНЕЙН. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то справедливо указанное ниже.
-
Наклон и ОТОКП возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритм НАКЛОН и ОТОКП предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.

-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
| ||
|---|---|---|
|
|
| |
|
02.
|
6
| |
|
03.01.1900
|
5
| |
|
09.01.1900
|
11
| |
|
01.01.1900
|
7
| |
|
08.01.1900
|
5
| |
|
07.01.1900
|
4
| |
|
05.
|
4
| |
|
|
|
|
|
=НАКЛОН(A3:A9;B3:B9)
|
Наклон линии линейной регрессии для точек данных в диапазонах A3:A9 и B3:B9.
|
0,305556
|
Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Если предварительно построить асимптоты кривой, то многих случаях построение графика
функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться
по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться
соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти
вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели
и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно
близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус
бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние
от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении
точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Первое, что нужно узнать о вертикальных асимптотах: они параллельны
оси Oy.
Определение. Прямая x = a
является вертикальной асимптотой графика функции, если точка x = a
является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a
является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно
из условий:
-
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности) -
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).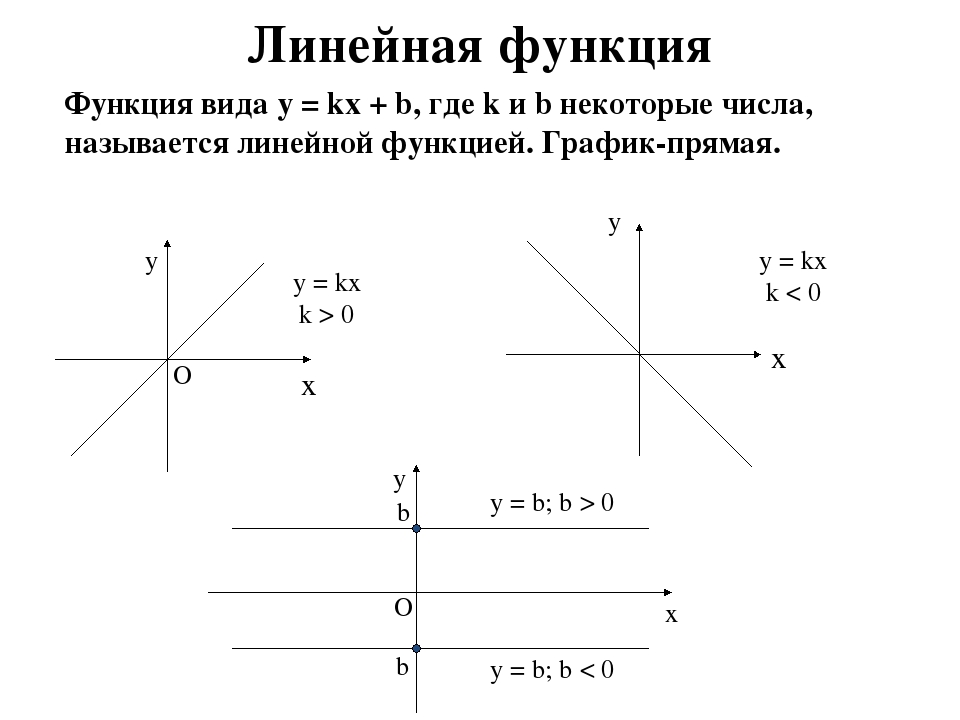
При этом функция f(x) может быть вообще не определена соответственно при
x ≥ a и
x ≤ a.
Замечание:
- символом
обозначается стремление x к a справа, причём x остаётся
больше a; - символом
обозначается стремление x к a слева, причём x остаётся меньше a.
Пример 1. График функции y=lnx
имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе
области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2.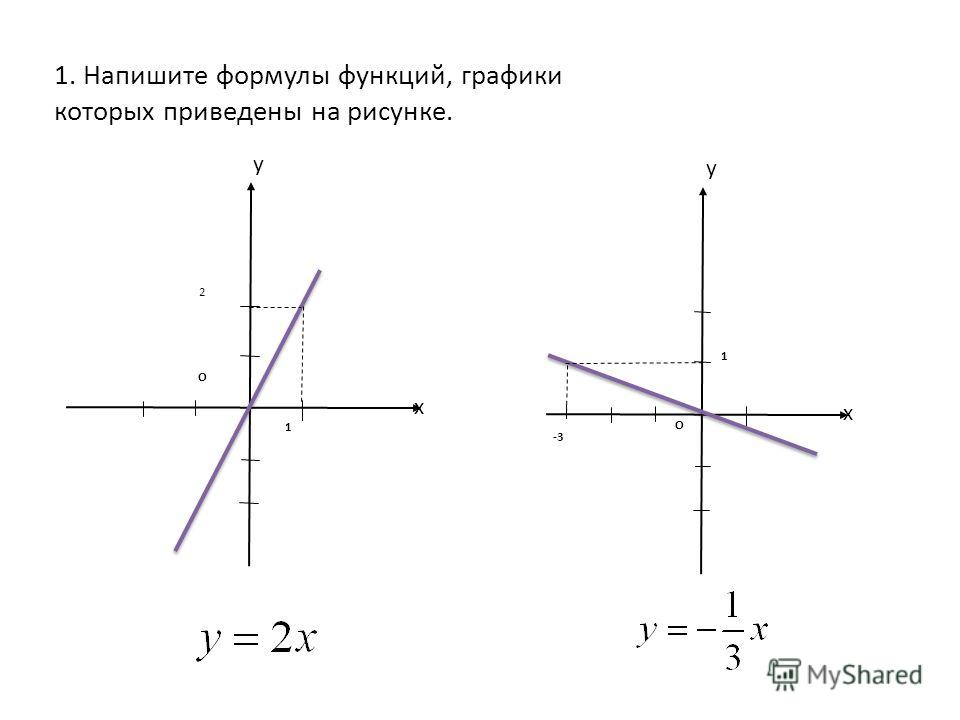 Найти асимптоты графика функции .
Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны
оси Ox.
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b),
то y = b – горизонтальная асимптота кривой y = f(x)
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную
асимпототу y = 0 (т.е.
совпадающую с осью Ox), так как предел функции при стремлении «икса»
к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении
«икса» к плюс бесконечности равен бесконечности:
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота.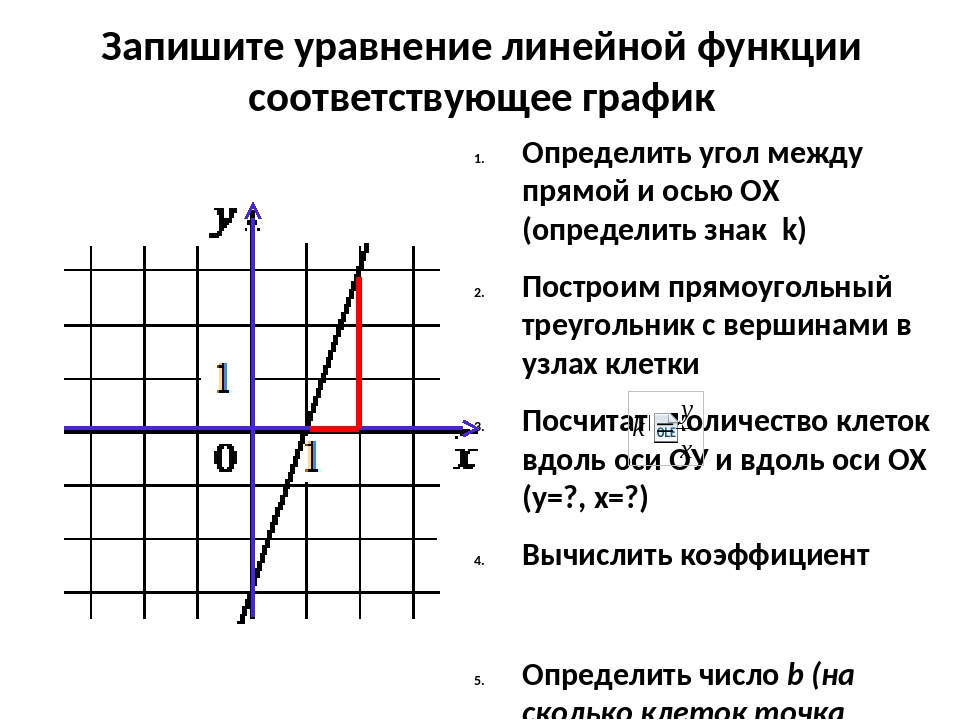 Для наклонной асимптоты необходимо больше —
Для наклонной асимптоты необходимо больше —
угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела
асимптоту y = kx + b, необходимо и
достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции
при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
и
(2)
Найденные таким образом числа k и b и являются коэффициентами
наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая
наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса
и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных,
эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только
один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус
бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то
график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b
является частным случаем наклонной y = kx + b
при k = 0.
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в
этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную
асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота
графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при
стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и
b = 0.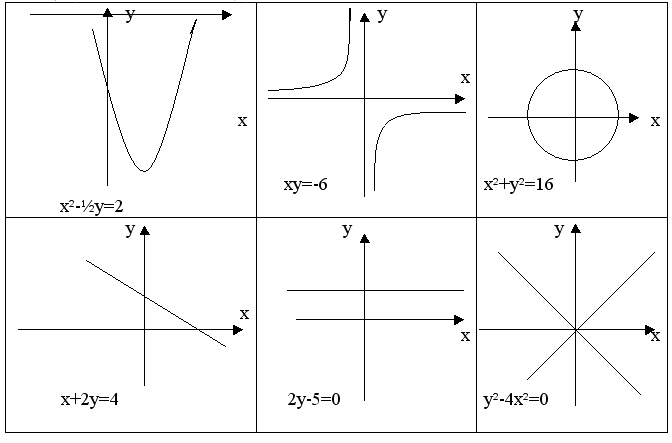
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1.
Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 — точка разрыва второго рода,
поэтому прямая x = −1 является вертикальной асимптотой
графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при
и при
будут совпадать. Таким
образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем
уравнение наклонной асимптоты:
y = −3x + 5.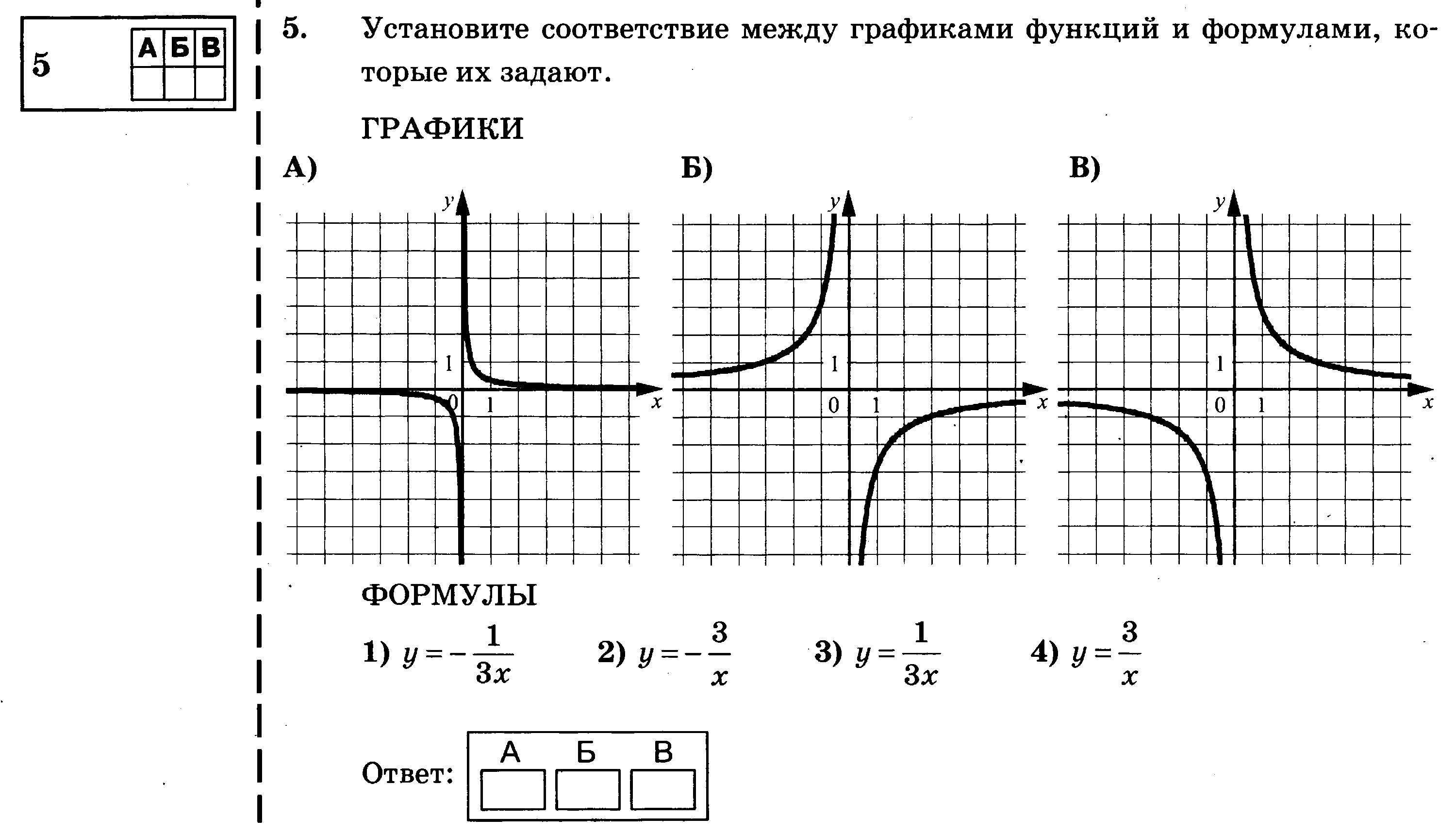
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот.
Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при
и не имеет асиптоты при
.
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения .
Так как вертикальная асимптота графика этой функции может быть только на границе области определения,
найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при
наклонной асимптотой графика данной функции является прямая y = x.
Но при найденные пределы
не изменяются. Поэтому при
наклонной асимптотой графика данной функции также является y = x.
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции
и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие
.
Функция имеет две точки разрыва: ,
. Чтобы установить вид
разрыва, найдём односторонние пределы:
Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому
график данной функции имеет две вертикальные асимптоты: x = 2 и
x = −2.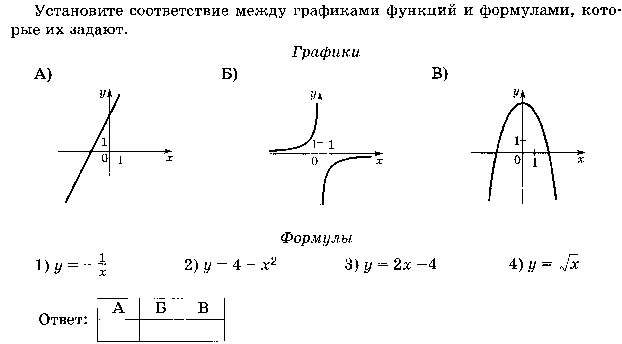
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной,
пределы при и при
совпадают. Поэтому,
определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом,
получаем уравнение наклонной асимптоты y = 2x.
Таким образом, график данной функции имеет три асимптоты: x = 2,
x = −2 и y = 2x.
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Поделиться с друзьями
Весь блок «Производная»
Уравнение прямой
Уравнение прямой обычно записывают так:
(или «y = mx + c» в Великобритании см.
ниже)
Что это означает?
y = насколько выше
x = расстояние от
м = Наклон или градиент (насколько крутая линия)
b = значение y , когда x = 0
Как найти «м» и «б»?
- b легко: просто посмотрите, где линия пересекает ось Y.

- м (Уклон) требует расчета:
| м = Изменение в Y Изменение в X |
Зная это, мы можем составить уравнение прямой:
Пример 1
м =
2
1
= 2
b = 1 (значение y при x = 0)
Итак: y = 2x + 1
Теперь вы можете воспользоваться этим уравнением…
… выберите любое значение для x и найдите соответствующее значение для y
Например, если x равен 1:
y = 2 × 1 + 1 = 3
Убедитесь сами, что x = 1 и y = 3 действительно на линии.
Или мы могли бы выбрать другое значение для x, например 7:
y = 2 × 7 + 1 = 15
Итак, когда x = 7, у вас будет y = 15
Положительный или отрицательный наклон?
Двигаясь слева направо, велосипедист должен пройти P проезд по оси P Угол наклона:
Пример 2
м =
−3
1
= −3
b = 0
Это дает нам y = −3x + 0
Нам ноль не нужен!
Итак: y = −3x
Пример 3: Вертикальная линия
Какое уравнение представляет собой вертикальная линия?
Наклон undefined . .. а где он пересекает ось Y?
.. а где он пересекает ось Y?
Фактически, это особый случай , и вы используете другое уравнение, а не « y = …», а вместо этого используете « x = …».
Как это:
x = 1,5
Каждая точка на линии имеет координату x 1,5 ,
, поэтому ее уравнение составляет x = 1,5
Взлетай и беги
Иногда используются слова «взлетать» и «бегать».
- Рост — насколько далеко вверх
- Run — это расстояние вдоль
Итак, уклон «м» равен:
м = подъем пробег
Возможно, вам будет легче запомнить.
Другие формы
Мы смотрели на форму «наклон-пересечение». Уравнение прямой можно записать многими другими способами .
Другой популярной формой является уравнение прямой линии с наклоном.
Сноска
Страна
Примечание:
В разных странах учат разным «обозначениям» (прислал мне добрые читатели):
| В США, Австралии, Канаде, Эритрее, Иране, Мексике, Португалии, Филиппинах и Саудовской Аравии используется запись: | y = mx + b |
| В Великобритания, Австралия (также), Багамы, Бангладеш, Бельгия, Бруней, Болгария, Кипр, Египет, Германия, Гана, Индия, Индонезия, Ирландия, Ямайка, Кения, Кувейт, Малайзия, Малави, Мальта, Непал , Новая Зеландия, Нигерия, Оман, Пакистан, Перу, Сингапур, Соломоновы Острова, Южная Африка, Шри-Ланка, Турция, ОАЭ, Замбия и Зимбабве | y = mx + c |
| В Афганистан, Албания, Алжир, Бразилия, Китай, Чешская Республика, Дания, Эфиопия, Франция, Ливан, Нидерланды, Косово, Кыргызстан, Норвегия, Польша, Румыния, Южная Корея, Суринам, Испания, Тунис и Вьетнам Нам: | у = ах + Ь |
| В Азербайджане, Китае, Финляндии, России и Украине : | y = kx + b |
| В Греция : | ψ = αχ + β |
| В Италия : | y = mx + q |
| В Япония : | y = mx + d |
| В Куба и Израиль : | y = mx + n |
| В Румыния : | у = gA + C |
| В Латвии и Швеции : | y = kx + m |
| В Сербии и Словении : | y = kx + n |
| В вашей стране: | сообщите нам! |
. .. но все это означает одно и то же, только разные буквы.
.. но все это означает одно и то же, только разные буквы.
Градиент (уклон) прямой
Градиент (также называемый уклоном) прямой линии показывает, насколько крута прямая линия.
Рассчитать
Для расчета градиента:
Разделите изменение высоты на изменение горизонтального расстояния
| Градиент = Изменение Y Изменение X |
Поиграйте (перетащите точки):
Примеры:
Градиент = Итак, градиент равен 1 |
Градиент = | ||
Линия круче, поэтому Градиент больше. | ||
Градиент = | ||
| Линия менее крутая, поэтому Градиент меньше. | ||
Положительно или отрицательно?
Двигаясь слева направо, велосипедист должен пройти P проезд по оси P Угол наклона:
При измерении линии:
- Если начать слева и пройти через вправо, это положительно
(но при переходе влево отрицательно). - Вверх положительный , а вниз отрицательный
Градиент = |
Эта линия идет на вниз на по мере вашего движения, поэтому градиент у нее отрицательный.
Прямо через
Градиент = |
Прямая линия (горизонтальная) имеет нулевой градиент.
Прямо вверх и вниз
Градиент = |
Последний вариант немного сложен … вы не можете разделить на ноль,
, поэтому градиент прямой вверх и вниз (вертикальной) линии будет «undefined».
Взлетай и беги
Иногда горизонтальное изменение называется «бегом», а вертикальное изменение — «подъемом» или «падением»:
Это просто разные слова, никакие вычисления не меняются.
y = mx + c — Прямолинейные графики — Edexcel — GCSE Maths Revision — Edexcel
Любое уравнение, которое можно преобразовать в форму \ (y = mx + c \), будет иметь прямолинейный график. \ (m \) — это градиент или крутизна графика, а \ (c \) — точка пересечения \ (y \) — , или точка пересечения линии с осью \ (y \). .
\ (m \) — это градиент или крутизна графика, а \ (c \) — точка пересечения \ (y \) — , или точка пересечения линии с осью \ (y \). .
Нахождение c
Графики \ (y = 2x + 1 \) и \ (y = 2x — 2 \) показаны ниже.
График \ (y = 2x + 1 \) пересекает ось \ (y \) в точке (0, 1). График \ (y = 2x — 2 \) пересекает ось \ (y \) — в точке (0, -2). Постоянный член в уравнении (+ 1 или — 2) показывает точку, где график пересекает ось \ (y \) -.
Это известно как \ (y \) — точка пересечения и обозначается буквой \ (c \) в \ (y = mx + c \).
1v4dt6jbbsq.0.0.0.1:0.1.0.$0.$1.$6″> Нахождение m
Графики \ (y = 2x \) и \ (y = 4x \) показаны ниже:
Число перед \ (x \) — это градиент графика.
Градиент — это мера крутизны.
Двигаясь по линии слева направо, вы можете подниматься вверх, спускаться вниз или вообще не меняться.
Градиент \ (= \ frac {\ text {изменение вверх}} {\ text {изменение вправо}} \) или \ (\ frac {\ text {изменение в y}} {\ text {изменение в x}} \ )
Градиенты могут быть:
- положительными — повышающимися
- 0.0.1:0.1.0.$0.$1.$15.$1″> отрицательными — понижающимися
- нулевыми — без изменений (плоская линия)
Крутые линии будут иметь высокие градиенты, такие как 5 или -8, и уравнения типа \ ( y = 5x — 4 \) или \ (y = -8x + 1 \).
Довольно плоские линии будут иметь низкие градиенты, например \ (\ frac {1} {2} \) или \ (- \ frac {3} {4} \), и уравнения типа \ (y = \ frac {1} {2 } x + 1 \) или \ (y = — \ frac {3} {4} x + 2 \).
Горизонтальные линии имеют градиент 0 и уравнения вида \ (y = 2 \).
Чтобы разработать градиент, используйте шкалы осей и найдите, на сколько единиц вы поднимаетесь или опускаетесь для каждой единицы, которую вы перемещаете вправо.
0.0.0.1:0.1.0.$0.$1.$20″> Чтобы составить уравнение линии из графика, найдите градиент и точку пересечения \ (y \).
Пример 1
Составьте уравнение этого графика.
Градиент \ (= \ frac {\ text {change up}} {\ text {change right}} \)
Градиент одинаков по всей линии, поэтому не имеет значения, где вы начинаете или заканчиваете , но обычно рекомендуется использовать две точки на линии, которые находятся далеко друг от друга.
Используя (0, 3) и (4, 7), перемещаясь по линии слева направо, мы перемещаемся на 4 единицы вверх (с 3 до 7) и на 4 единицы вправо (от 0 до 4). Итак, градиент \ (= \ frac {4} {4} = 1 \).
Пересечение \ (y \) — 3, потому что линия пересекает ось \ (y \) в точке (0, 3).
Итак, уравнение прямой в форме \ (y = mx + c \) есть \ (y = 1x + 3 \) или просто \ (y = x + 3 \).
Пример 2
Составьте уравнение этого графика.
Градиент \ (= \ frac {\ text {change up}} {\ text {change right}} \)
Использование (0, 1) и (4, −7) при перемещении по линии слева вправо, мы перемещаемся на 8 единиц вниз (от 1 до −7). Мы также перемещаемся на 4 единицы вправо (с 0 на 4).
Итак, градиент = −8 (8 единиц в отрицательном направлении) \ (\ frac {-8} {4} = -2 \).
Пересечение \ (y \) — это 1, потому что линия пересекает ось \ (y \) в точке (0, 1).
1v4dt6jbbsq.0.0.0.1:0.1.0.$0.$1.$36″> Итак, уравнение прямой \ (y = -2x + 1 \).
Пример 3
Составьте уравнение этого графика.
Градиент \ (= \ frac {\ text {change up}} {\ text {change right}} \)
Например, используя (0, −2) и (6, 0), когда мы движемся по В строке слева направо мы перемещаемся на 2 единицы вверх (от −2 до 0) и на 6 единиц вправо (от 0 до 6).
Итак, градиент \ (= \ frac {2} {6} = \ frac {1} {3} \).
Обратите внимание, что правильно упрощать дробь, но не преобразовывать ее в десятичную дробь, поскольку 0,3, 0,33 или 0,333 и т. Д. Не совсем то же самое, что \ (\ frac {1} {3} \).
Пересечение \ (y \) — равно −2, потому что прямая пересекает ось \ (y \) — в точке (0, −2).
Итак, уравнение прямой равно \ (y = \ frac {1} {3} x — 2 \).
Линейные функции и прямые
6.2 — Линейные функции и прямые линии
6.2 — Линейные функции и прямые
Линейные функции
Щелкните здесь, чтобы просмотреть функции.Линейные функции — самые простые из всех типов функций.
Линейная функция принимает на вход число x и возвращает число.
м x + b на выходе:
m и b — постоянные.
Проще говоря, x умножается на м (это называется масштабированием на коэффициент м )
а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:
f ( x ) = м x + b .
Если мы положим y = f ( x ), то это будет выглядеть так:
y = м x + b .
Это называется уравнением прямой линии , потому что если мы построим точки, которые
удовлетворить это уравнение на графике y против x , тогда,
как мы увидим ниже, все точки лежат на прямой линии.
Типичное использование линейной функции — преобразование одного набора единиц в другой.
Простой пример: если i — это расстояние в дюймах, а c — то же самое.
расстояние в сантиметрах; тогда c = 2,54 i .
Это просто масштабирование. Более сложный пример: если c — температура
измеряется в градусах Цельсия и f то же самое
температура измеряется в градусах Фаренгейта; тогда f = 1.8 c + 32.
Это масштабирование и сдвиг.
Уравнение прямой
В разделе 6.1 мы ввели декартову плоскость
с осью x , нарисованной горизонтально, и осью y , нарисованной вертикально.
Предположим, что m и b — постоянные. Мы хотим построить график линейной функции:
y = м x + b ,
на этой плоскости и покажите, что график представляет собой прямую линию. Для этого составляем следующую таблицу значений из
Для этого составляем следующую таблицу значений из
y (то есть выражения
м x + b ) по сравнению с x :
Обратите внимание на следующее:
- Каждая строка таблицы показывает точку на графике.
- В одной из строк указано, что когда x = 0, тогда y = b . Таким образом, точка (0, b )
это точка на графике. Поскольку эта точка лежит на оси y ,
число b называется точкой пересечения y . - При переходе от одной строки таблицы к следующей, значение x
увеличивается на 1, а значение y увеличивается на m . Потому что увеличение
устойчиво, точки должны лежать на прямой , а не на какой-либо другой кривой. - Более крупный
м , тем быстрее увеличивается y . Если м отрицательное, то значение
y фактически уменьшается .Номер м известен как склон .
- x не обязательно должно быть целым числом — это может быть любое действительное число. Так как
вещественные числа плотные, точки на графике
бесконечно близко друг к другу и образуют сплошную линию (т.е. без зазоров).
Вывод: Уравнение
где m и b — константы, — это уравнение прямой . м называется уклоном, а б называется |
Нахождение уравнения прямой
Учитывая график прямой, есть несколько способов найти ее уравнение.
Метод 1: Этот метод работает, только если видна точка пересечения y .
- Найдите любые две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), на линии и
подставьте их координаты в следующую формулу, чтобы получить м : - Получите b из просмотра пересечения y графика.

- Подставьте полученные числа для m и b в
уравнение y = m x + b .
Метод 2: Этот метод работает, даже если точка пересечения y не видна.
- Как и в методе 1, найдите любые две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), на линии и
подставьте их координаты в следующую формулу, чтобы получить м : - Замените полученное вами число м на
уравнение y = m x + b .Также возьмите одну из точек, скажем ( x 1 , y 1 ),
и подставляем его координаты в уравнение. Это дает:y 1 = м x 1 + b
- Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.
- Подставьте полученные числа для m и b в
уравнение y = m x + b .
Метод 3: Этот метод имеет то преимущество, что он использует только алгебру, а не геометрию,
и может применяться к любому типу функции, а не только к прямой линии:
- Найдите две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), которые находятся на линии.
Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой,
y = м x + b .Это дает:y 1 = м x 1 + b
Аналогичным образом возьмем вторую точку ( x 2 , y 2 ) и
подставляем его в уравнение прямой,
y = м x + b .
Это дает:y 2 = м x 2 + b
- Вместе эти два уравнения составляют систему двух уравнений с двумя неизвестными: m и b .
 Мы можем решить их для m и b , используя метод исключения.
Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:y 2 — y 1 = м x 2 — м x 1 ,
которое при решении для м дает то же уравнение, что и в двух других методах, а именно:
- Найти b обратной подстановкой.Чтобы быть конкретным, замените номер, который вы
полученное для м в одно уравнение системы уравнений, скажем в
y 1 = м x 1 + b .
Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.
Пример: Воспользуйтесь методом 1, чтобы найти уравнение прямой на графике справа.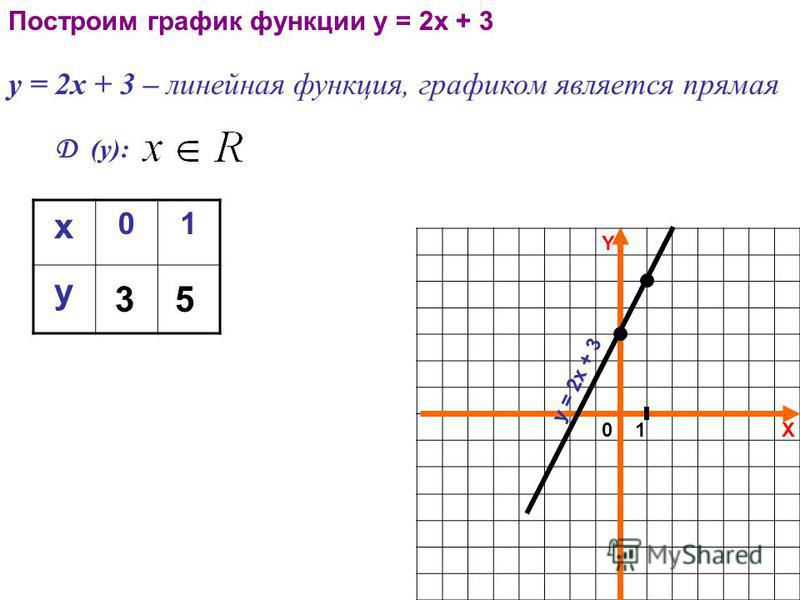
Решение: Две точки на этой линии: ( x 1 , y 1 ) = (0, 15) и
( x 2 , y 2 ) = (3, 0).
Подставляя эти координаты в формулу наклона, получаем
= -5.
При осмотре перехватчик y
б = 15.
Подставляя эти два значения для m и b в уравнение прямой линии,
y = м x + b , дает
y = −5 x + 15.
Пример: Используйте метод 3, чтобы найти уравнение прямой линии на графике справа.
Решение: Две точки на этой линии: (7, 15) и (1, 3).
Подставляем координаты точки (7, 15)
в уравнение прямой, y = m x + b ,
а затем проделайте то же самое с точкой (1, 3).
Это дает систему двух уравнений с двумя неизвестными: m и b .Неизвестный b может быть исключен путем вычитания уравнений:
Решение для м дает м = 2.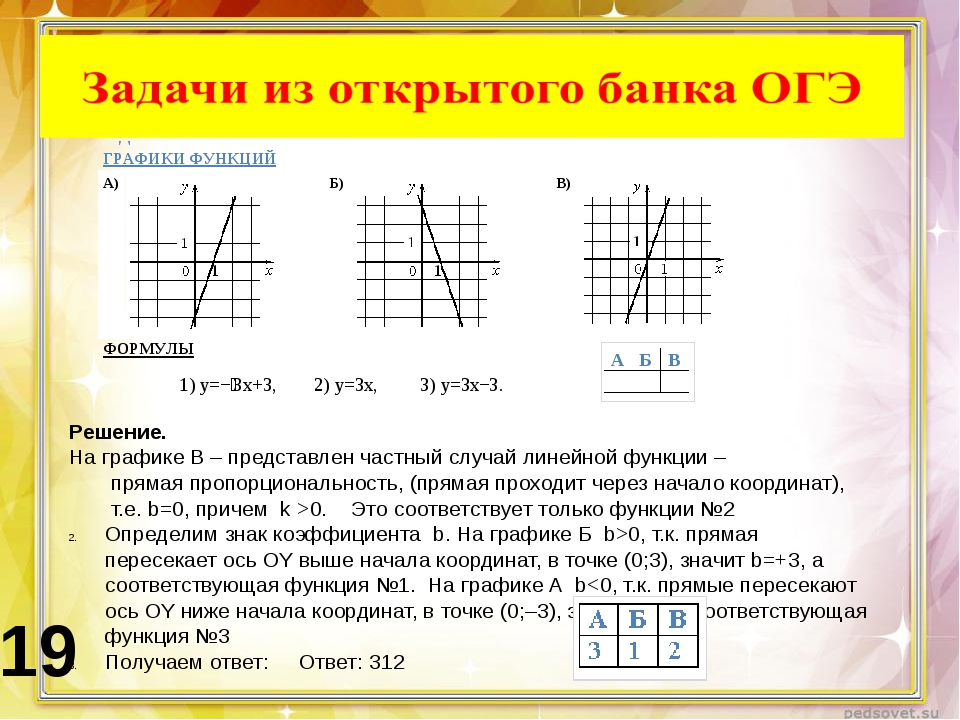 Подставляя обратно м = 2, скажем, в первое уравнение,
Подставляя обратно м = 2, скажем, в первое уравнение,
дает 15 = 7 · 2 + b , что легко решается и дает b = 1.
Подставляя эти два значения для m и b в уравнение прямой линии,
y = м x + b , дает
y = 2 x + 1.
Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Прямолинейные уравнения: форма пересечения наклона | Purplemath
Purplemath
Прямолинейные уравнения, или «линейные» уравнения, изображаются в виде прямых линий и имеют простые выражения переменных без показателей степени.Если вы видите уравнение только с x и y — в отличие от, скажем, x 2 или sqrt ( y ) — тогда вы имеете дело с уравнением прямой линии.
Существуют различные типы «стандартных» форматов прямых линий; конкретный «стандартный» формат, к которому относится ваша книга, может отличаться от формата, используемого в некоторых других книгах. (По иронии судьбы стандартного определения «стандартной формы» не существует.)
MathHelp.com
Различные «стандартные» формы часто унаследованы от нескольких веков назад, когда математики не могли обрабатывать очень сложные уравнения, поэтому они, как правило, зацикливались на простых случаях. В настоящее время вам, вероятно, не стоит слишком беспокоиться о «стандартных» формах; в этом уроке будут рассмотрены только наиболее полезные формы.
Я думаю, что наиболее полезной формой линейных уравнений является форма «наклон-пересечение»:
y = м x + b
Это называется формой пересечения уклона, потому что « м » — это наклон, а « b » дает пересечение y . (Чтобы узнать, как это уравнение используется для построения графиков, посмотрите на наклон и график.)
Мне больше всего нравится форма с пересечением склонов.Он имеет форму « y =», что упрощает его использование для построения графиков или решения текстовых задач. Просто подключите свое значение x ; уравнение уже решено для y . Кроме того, это единственный формат, который вы можете использовать в своем (в настоящее время обязательном) графическом калькуляторе; у вас должен быть формат « y =» для использования графической утилиты. Но лучшая часть формы пересечения наклона заключается в том, что вы можете считать наклон и точку пересечения прямо из уравнения. Это отлично подходит для построения графиков и может быть весьма полезно для текстовых задач.
Это отлично подходит для построения графиков и может быть весьма полезно для текстовых задач.
Партнер
Общие упражнения дадут вам некоторую информацию о линии, и вам нужно будет придумать уравнение линии. Как ты это делаешь? Вы подключаете все, что они вам дают, и решаете все, что вам нужно, например:
Найдите уравнение прямой, имеющей наклон
м = 4 и проходящей через точку (–1, –6).
Хорошо, они дали мне значение наклона; в данном случае м = 4. Кроме того, давая мне точку на линии, они дали мне значение x и значение y для этой линии: x = –1 и y = — 6.
В форме пересечения наклона прямой у меня есть y , m , x и b . Они дали мне значение m, а также значения x и y.Так что единственное, чего у меня пока нет, это значения b (что дает мне перехват y ). Затем все, что мне нужно сделать, это подключить то, что они дали мне для наклона и x и y из этой конкретной точки, а затем решить для b :
Они дали мне значение m, а также значения x и y.Так что единственное, чего у меня пока нет, это значения b (что дает мне перехват y ). Затем все, что мне нужно сделать, это подключить то, что они дали мне для наклона и x и y из этой конкретной точки, а затем решить для b :
y = м x + b
(–6) = (4) (- 1) + b
–6 = –4 + b
–2 = b
Тогда уравнение линии должно быть « y = 4 x — 2».
Что делать, если они не дадут вам уклон?
Найдите уравнение прямой, проходящей через точки (–2, 4) и (1, 2).
Ну, если у меня есть две точки на прямой, я всегда могу найти наклон; вот для чего нужна формула наклона.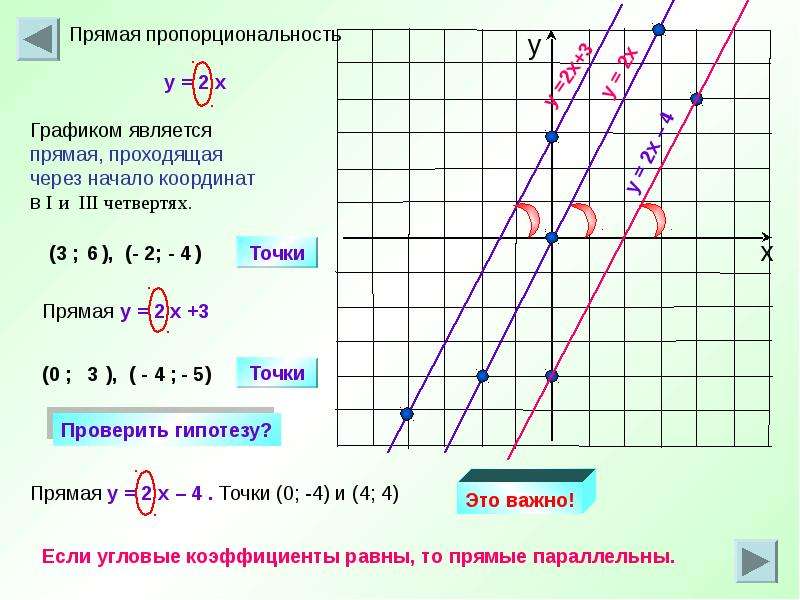
Теперь у меня есть наклон и две точки.Я знаю, что могу найти уравнение (сначала решив « b «), если у меня есть точка и наклон; это то, что я сделал в предыдущем примере. Здесь у меня и две точки , которые я использовал, чтобы найти наклон. Теперь мне нужно выбрать , одну из точек (неважно, какую из них) и использовать ее для решения b .
Используя точку (–2, 4), я получаю:
y = м x + b
4 = (- 2 / 3 ) (- 2) + b
4 = 4 / 3 + b
4 — 4 / 3 = b
12 / 3 — 4 / 3 = b
b = 8 / 3
. ..so y = (- 2 / 3 ) x + 8 / 3 .
..so y = (- 2 / 3 ) x + 8 / 3 .
С другой стороны, если я использую точку (1, 2), я получаю:
y = м x + b
2 = (- 2 / 3 ) (1) + b
2 = — 2 / 3 + b
2 + 2 / 3 = b
6 / 3 + 2 / 3 = b
b = 8 / 3
Так что неважно, какую точку я выберу.В любом случае ответ один и тот же:
Как видите, если у вас есть наклон, не имеет значения, какую точку вы используете, чтобы найти линейное уравнение.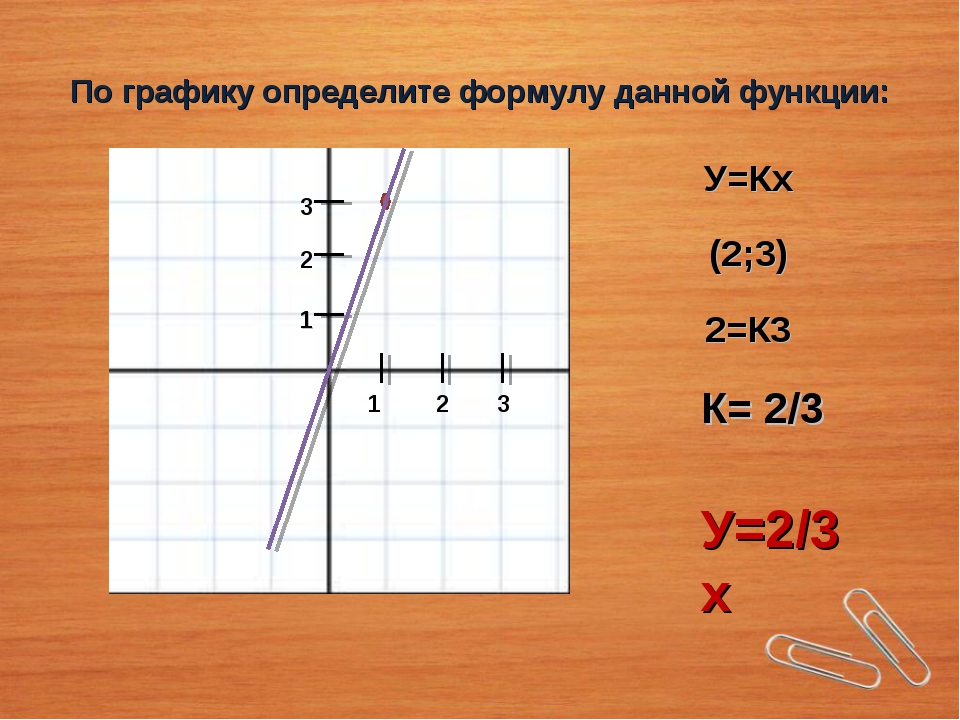 В любом случае ответ будет одинаковым.
В любом случае ответ будет одинаковым.
URL: https://www.purplemath.com/modules/strtlneq.htm
Используя уравнение прямой | Математика
Уравнение прямой обычно преподается в форме:
y = м x + c
, который кратко выражает тот факт, что если мы построим график y против x и переменные будут подчиняться соотношению этой формы, мы получим график прямой линии с градиентом или наклоном m и пересечением (где линия пересекает y- ось) c ( рис 1 )
В химии буква c часто используется для обозначения концентрации, поэтому это может сбивать с толку.Буква, используемая для обозначения точки пересечения, довольно произвольна, поэтому вполне приемлемо использовать — как и в оставшейся части этой статьи — уравнение в форме y = mx + b , поскольку b равно менее часто используемый символ. Действительно, эта форма уравнения обычно используется в некоторых других странах, и по всему миру используется несколько вариаций.
Действительно, эта форма уравнения обычно используется в некоторых других странах, и по всему миру используется несколько вариаций.
Для учащихся важно уметь использовать это уравнение и понимать концепции, лежащие в его основе, поскольку многие взаимосвязи в химии могут быть выражены в линейной форме.Эта важность даже подтолкнула математиков к разговору о « чувстве символа » — алгебраической параллели с « чувством чисел », известном как чувство числа, — которое включает в себя необходимость для каждого иметь возможность сканировать таблицу данных и предлагать символические отношения между переменные. 1
Представляем уравнение
Хотя уравнение прямой линии хорошо известно, возможно, стоит потратить некоторое время на изучение его более подробно. Проверить уравнение на конкретном примере очень просто, например:
y = 5 x + 2
Легко составить таблицу x против y для нескольких выбранных значений x , например:
Построение этих данных ( рис.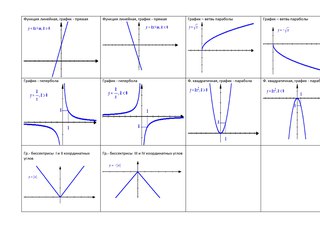 2 ) ясно показывает, что точка пересечения равна 2, а уклон м можно рассчитать как:
2 ) ясно показывает, что точка пересечения равна 2, а уклон м можно рассчитать как:
Конечно, в это упражнение можно внести больше разнообразия, включив десятичные значения.Это также имеет то преимущество, что делает результаты менее очевидными для тех, кто уже знаком с концепцией.
Может быть более удовлетворительным будет вывести уравнение, которое опять же относительно простое. Начнем с нашего определения градиента, как показано ( рис. 3) :
Мы можем переместить точку P так, чтобы она располагалась на оси y ( рис. 4 ). Немного подумав, покажем, что x 1 = 0 и y 1 = b.Затем мы заменяем x 2 и y 2 на x и y соответственно — в конце концов, это всего лишь произвольные символы, представляющие числа, которые могут меняться. Уклон м сейчас составляет:
.
Мы можем изменить это по шагам так, чтобы:
y — b = м x
и:
y = м x + b
Конечно, уравнения в химии обычно не такие простые, особенно потому, что переменные обычно не равны x и y .И не только ученые заменяют x и y более сложными символами и выражениями, математики также делают это, чтобы сделать задачи более реалистичными и, следовательно, интересными. 2
Я обычно переписываю определяющее уравнение как:
Y = м X + b
, где X является функцией x , а Y является функцией y . Это первый шаг к отходу от простых переменных x и y и приспособлен к более сложным функциям переменных, которые обычно встречаются в уравнениях, связанных с химией.Также может быть полезно разумно использовать скобки, чтобы облегчить сравнение с уравнениями, в которых градиент определяется комбинацией констант. Дальнейшая модификация дает:
Дальнейшая модификация дает:
Y = ( м ) X + b
Примеры
из химии
1. Закон Бера-Ламберта
Этот закон используется в спектрометрии и гласит, что оптическая плотность A компонента изменяется линейно как с концентрацией раствора c , так и с коэффициентом экстинкции ε, когда свет проходит через расстояние, известное как длина пути и обозначенное на л .Соотношение между этими величинами:
A = ε класс
Если мы понимаем, что ε и l будут постоянными для указанного решения в ячейке с фиксированной длиной пути, мы можем заключить эти константы в скобки и написать:
A = (ε l ) c
Если мы также поймем, что можем добавить к нему ноль, не меняя значения, мы получим:
A = (ε l ) c + 0
По сравнению с нашим определяющим уравнением Y = mX + b теперь дает:
X = c
Y = A
м = ε l
b = 0
Таким образом, построение A против c даст прямолинейный график с градиентом ε l и точкой пересечения нуля. Другими словами, график будет проходить через начало координат.
Другими словами, график будет проходить через начало координат.
2. Уравнение Нернста
Это связывает электродвижущую силу (ЭДС) E электрохимического элемента с его стандартной ЭДС E o и коэффициентом реакции Q :
, где R — газовая постоянная, а F — постоянная Фарадея. Q рассчитывается из концентраций реагирующих частиц, а n — это количество заряда, переносимого в протекающей реакции.Т — абсолютная температура.
Прежде всего, изменим уравнение так, чтобы в конце появилась уединенная постоянная E o :
Если теперь мы узнаем, что T и n будут константами для данной реакции при указанной температуре, мы можем сгруппировать константы в первом члене в скобках, чтобы получить:
Сравнение с определяющим уравнением Y = м X + b теперь дает:
, поэтому, если мы построим график E против ln Q , мы получим прямую линию и пересечем E o и градиент
3.
 Кинетика первого порядка
Кинетика первого порядка
Kinetics дает несколько примеров прямолинейных графиков. Действительно, выбор подходящей функции для построения графика — это метод определения порядка реакции. Уравнение реакций первого порядка может быть записано в нескольких эквивалентных формах, которые можно перестроить так:
ln c = ln c o — узлы
, где c o — начальная концентрация реагента, а c — концентрация после времени t .Другая присутствующая величина — это константа скорости k .
Первое, что нужно сделать при определении переменных для построения графика, — это определить константы в уравнении. Термин «константа скорости» дает здесь сильный намек, и нам также необходимо понимать, что начальная концентрация c o будет постоянной. Кроме того, если c o является константой, ln c o также будет константой.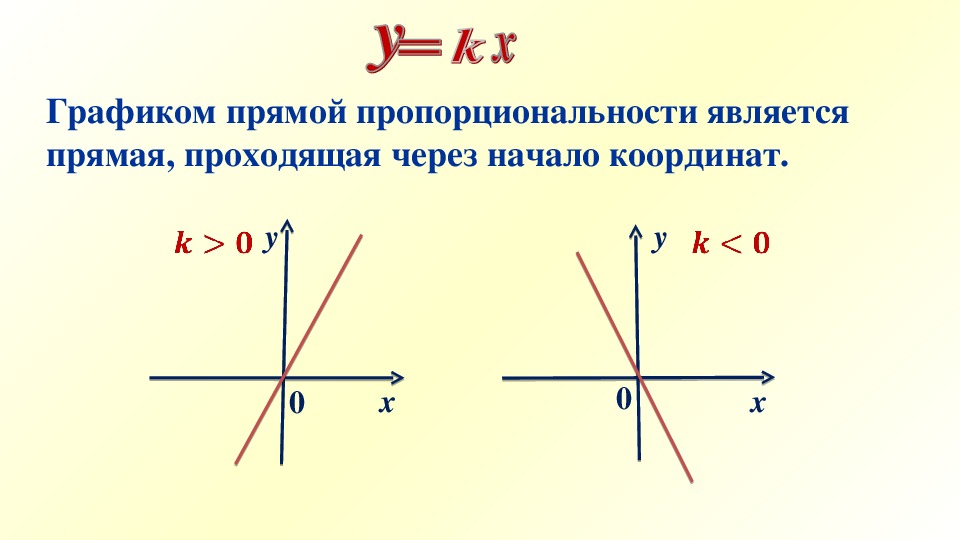 Мы перемещаем этот член в конец уравнения, так что он становится:
Мы перемещаем этот член в конец уравнения, так что он становится:
ln c = — kt + ln c o
, которое можно сравнить с определяющим уравнением Y = м X + b , чтобы получить:
Y = ln c
X = t
m = — k
b = ln c o
Следовательно, если мы построим ln c против t , мы получим прямой график с градиентом — k и пересечением ln c o .
В качестве примера рассмотрим гидролиз 1-хлор-1-метилциклоундекана в 80% этаноле при 25 o C. 3 Фактически мы можем контролировать любое количество, которое пропорционально концентрации, так что в этом случае значения c даны как относительные величины, не требующие единиц измерения. В таблице показано изменение c со временем t , а также значения ln c .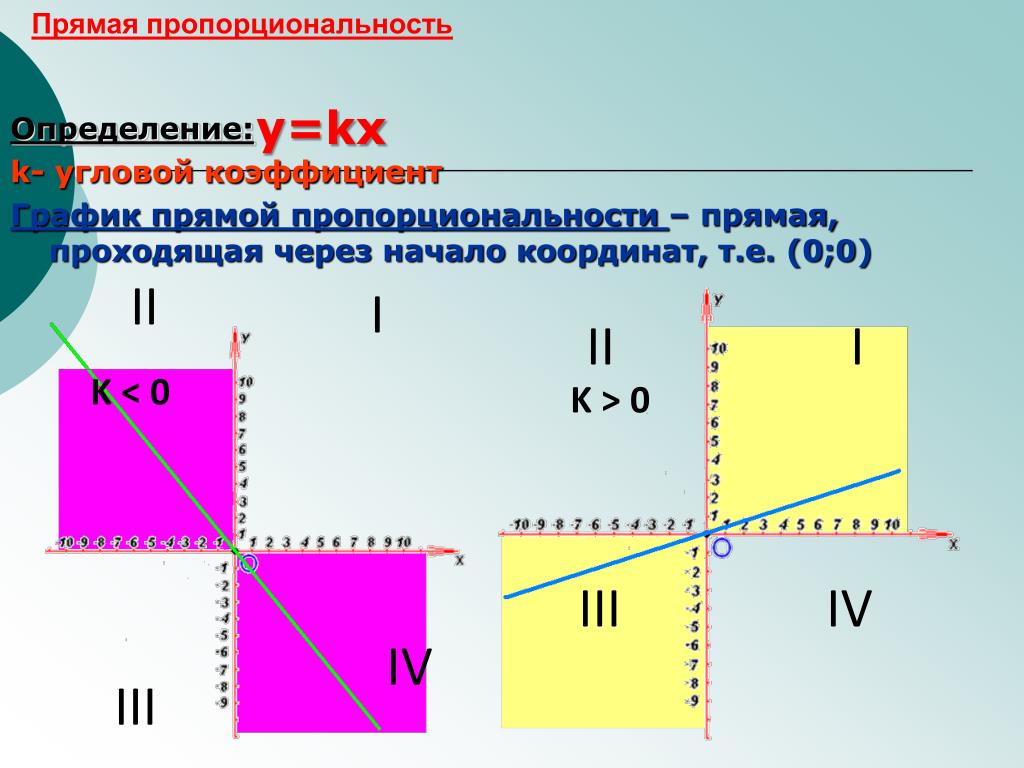
Поскольку это реакция первого порядка, график ln c (рисунок 5) против t действительно является прямой линией.График этого графика составляет -0,13 h -1 . Следовательно:
— к = -0,13 ч -1
А:
к = 0,13 час -1
Хотя этот график и результирующий градиент были сгенерированы с использованием программного обеспечения для работы с электронными таблицами, исследование показало, что вычислительные инструменты могут быть не такими эффективными, как можно было бы ожидать, для развития концептуального понимания в этой области. 4
Пол Йейтс — ведущий специалист по физическим наукам в Академии высшего образования.
Уравнение и график прямой
33
Решения уравнения первой степени
График уравнения первой степени
Константы и переменные
Раздел 2: Построение графика
Перехваты графика x и y
Форма y = ax .
Вертикальные и горизонтальные линии
y = 2 x + 6.
Это называется уравнением первой степени. Это называется так, потому что наивысший показатель степени равен 1.
Решением этого уравнения будут любые значения x и y , которые сделают уравнение — это утверждение — истинным.
Чтобы найти решение, просто позвольте x иметь любое значение, которое вам нравится.Затем уравнение определит значение y .
Например, если мы положим x = 0, то
y = 2 · 0 + 6 = 0 + 6 = 6.
Пара (0, 6) решает это уравнение.
Или, если мы выберем x = 3, то
y = 2 · 3 + 6 = 6 + 6 = 12.
Пара (3, 12) также решает это уравнение. Фактически, когда есть два неизвестных, x и y , но только одно уравнение, которое их связывает, то количество решений не ограничено.
Поскольку мы обычно сначала выбираем значение x , мы называем x независимой переменной. y будет зависимой переменной, потому что ее значение будет зависеть от значения, которое мы выбрали для x .
y будет зависимой переменной, потому что ее значение будет зависеть от значения, которое мы выбрали для x .
Задача 1. Найдите три решения уравнения первой степени y = x + 5.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
Например: (0, 5), (1, 6), (2, 7).
Задача 2. Какая из следующих упорядоченных пар решает это уравнение:
y = 3 x — 4?
(0, −4) (1, 2) (1, −1) (2, −3)
(0, −4) и (1, −1). Потому что, когда x и y имеют эти значения, уравнение верно.
График уравнения первой степени
Рассмотрим уравнение
y = 2 x + 1.
Поскольку есть две переменные, x и y , то можно ли будет на плоскости x-y нарисовать «картину» всех решений этого уравнения?
Во-первых, чтобы найти несколько решений, заполните эту таблицу. То есть вычислите значение y , которое соответствует каждому значению x :
То есть вычислите значение y , которое соответствует каждому значению x :
Теперь нанесите эти упорядоченные пары как координаты на плоскости:
Мы видим, что все эти решения лежат на одной прямой.Фактически, каждая пара ( x , y ), которая решает это уравнение, будет координатами точки на этой прямой. В этой строке каждая пара координат равна
.
( х , 2 х + 1).
y = 2 x + 1.
Таким образом, эта линия называется графиком уравнения y = 2 x + 1. А y = 2 x + 1 называется уравнением этой линии.
Другими словами, график уравнения — это график его решений. Это изображение тех значений ( x , y ), которые делают уравнение — это утверждение — истинным.
Каждое уравнение первой степени, где 1 — наивысший показатель степени, имеет в качестве графика прямую линию. (Мы доказываем это в Topics in Precalculus. )
)
По этой причине уравнение первой степени называется линейным уравнением.
Проблема 3.
а) Какой график имеет уравнение вида y = ax + b ?
Прямая линия. Это линейное уравнение.
б) Какой график имеет уравнение вида A x + B y + C = 0?
Прямая линия. Это линейное уравнение. Заглавные буквы являются условным обозначением целых коэффициентов .
Проблема 4.Что характеризует линейное уравнение ?
1 — самый высокий показатель степени.
Задача 5. Какие из следующих уравнений являются линейными?
| а) y = 4 x — 5 | б) 2 x — 3 y + 8 = 0 | c) y = x ² — 2 x + 1 | ||
| d) 3 x + 1 = 0 | e) y = 6 x + x 3 | е) y = 2 | ||
а), б), г), е).
Проблема 6.
| а) | Назовите координаты любых трех точек на прямой, уравнение которой равно |
y = 2 x — 1.
| (Выберите любое число для x ; тогда уравнение определит значение y .) |
Например, (0 −1), (1, 1), (−1, −3).
Задача 7.
а) Какая из этих упорядоченных пар решает уравнение y = 5 x — 6?
(Вы должны проверить каждую пару.)
(1, −2) (1, −1) (2, 3) (2, 4)
(1, −1) и (2, 4)
б) Какие из этих точек являются точками на графике y = 5 x — 6?
(1, −1) и (2, 4)
Проблема 8.Правда или ложь?
a) (−2, −3) находится на линии, уравнение которой составляет x + y = 5.
Ложь.
b) (2, 3) находится на линии, уравнение которой составляет x + y = 5.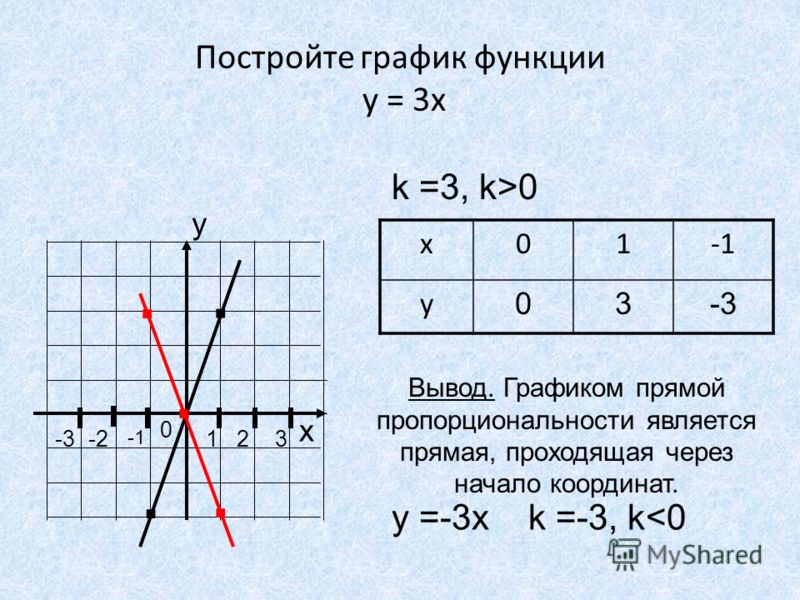
Правда.
Константы и переменные
Константа — это символ, значение которого не изменяется. Символы 2, 5,, являются константами.
Начальные буквы алфавита a, b, c обычно используются как произвольные константы , которым могут быть присвоены числовые значения; в то время как буквы x , y , z обычно используются для обозначения переменных.Например, если мы напишем
y = a x ² + b x + c ,
означает, что a , b , c — числа, а x и y — переменные.
Задача 9. Произвольные константы a и b . Каждое из следующих значений имеет вид y = ax + b .Какой номер a и какой номер b ?
| a) y = 2 x + 3. | a = 2, b = 3. | б) y = x — 4. |

 01.1900
01.1900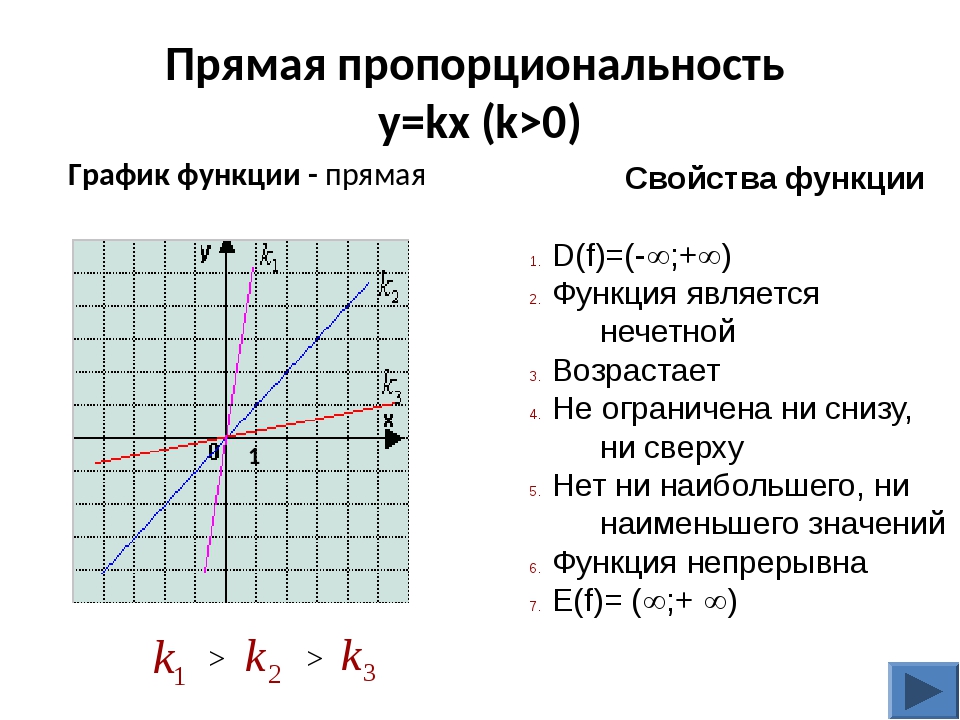 01.1900
01.1900