Содержание
Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABC
точка 1, точка 2, точка 3
123
Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAA
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abc
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
a
прямая линия AB
BA
Прямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
A
A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
a
луч AB
BA
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBA
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BA
прямая линия AB
BA
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BA
Задача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная.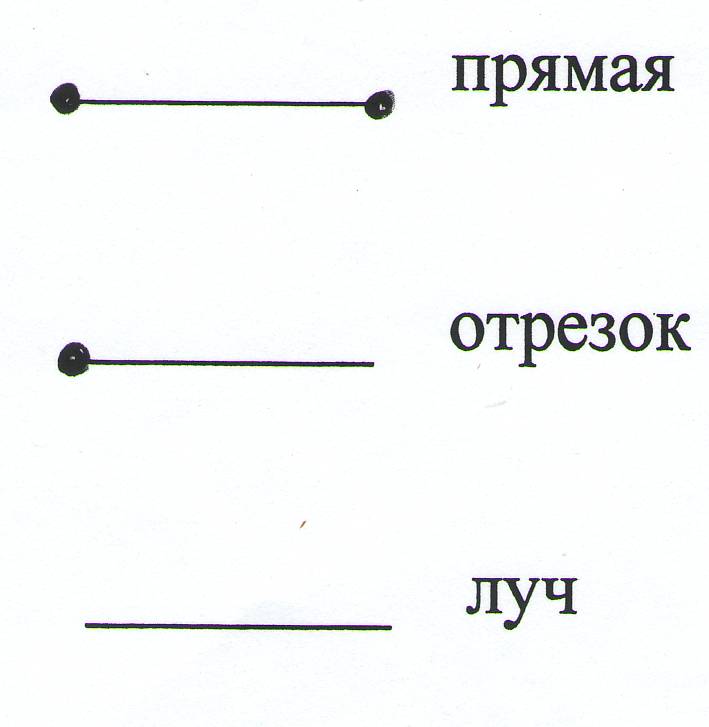 Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
Урок 21. прямая, луч, отрезок — Математика — 5 класс
Математика
5 класс
Урок №21
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Тезаурус
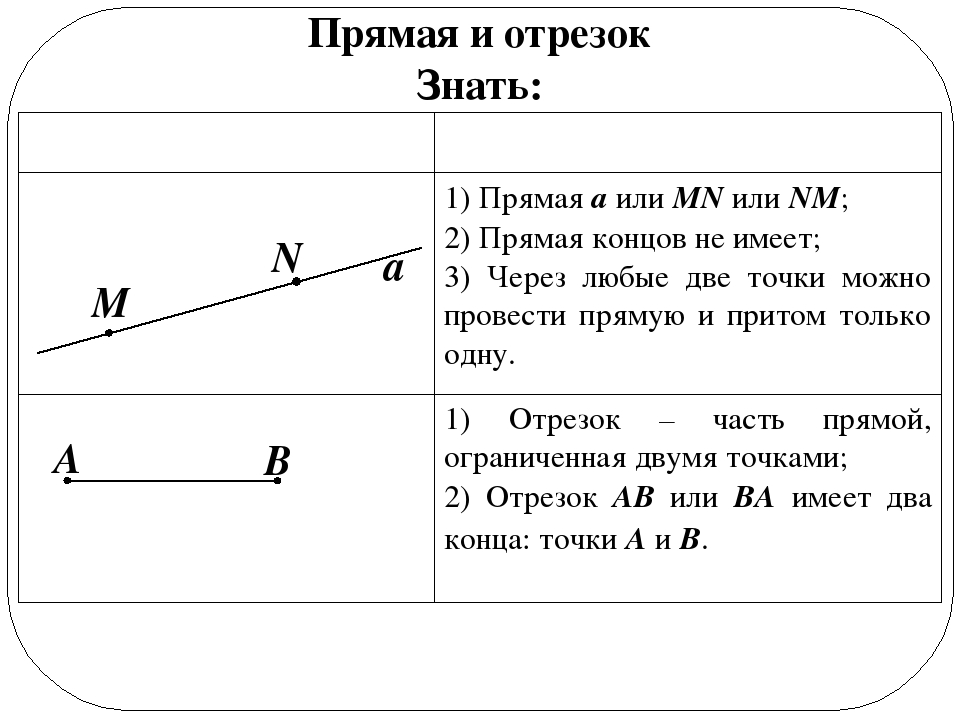
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны.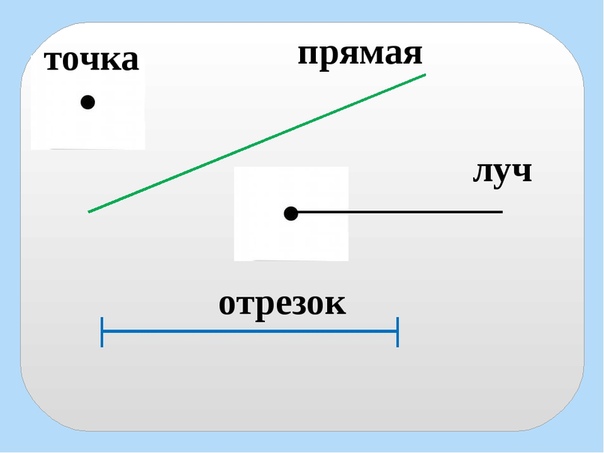 Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Это интересно
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
- Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.

- Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
- Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
- Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
Правильные ответы:
1) а – это прямая.
2) АВ – это отрезок.
3) А – это луч.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.
Линия отрезок луч отличие. Точка, линия, прямая, луч, отрезок, ломанная
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.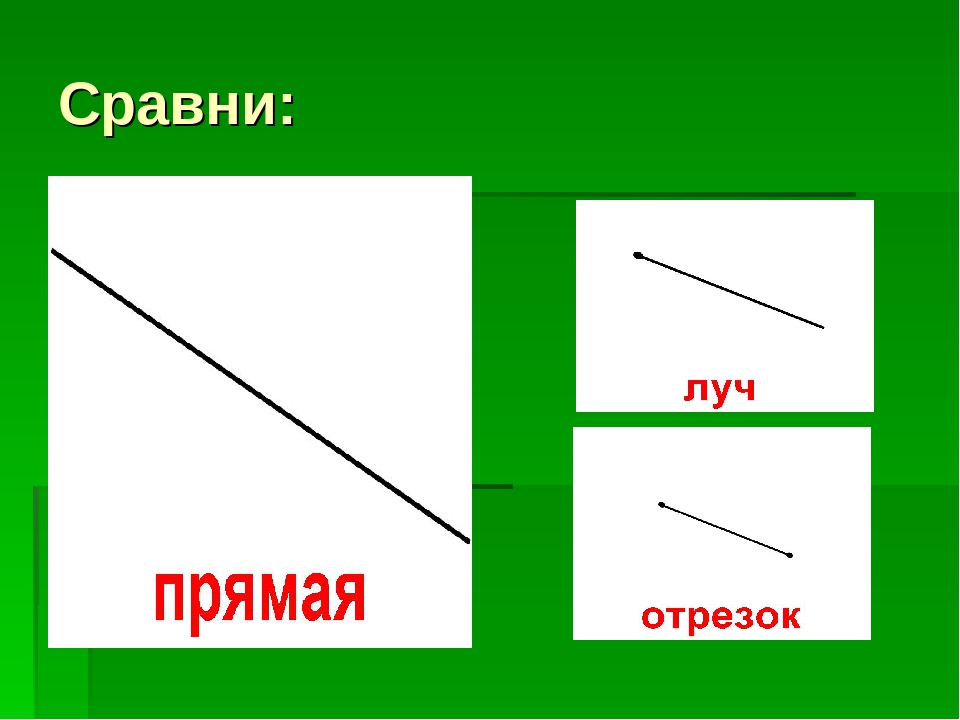
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Посещая дополнительные занятия мы поняли, что не умеем оперировать понятиями точка, линия, угол, луч, отрезок, прямая, кривая, замкнутая линии и рисовать их, точнее рисовать можем, но идентифицировать не получается.
Дети должны различать линии, кривые, окружности. Это развивает у них графику и чувство правильности при занятиях рисованием, аппликацией. Важно знать, какие основные геометрические фигуры существую, что из себя представляют. Разложите карточки перед ребенком, попросите нарисовать точно так же как на картинке. Повторите несколько раз.
На занятиях нам выдали следующие материалы:
Небольшая сказка.
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)
Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки, которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.
Так кто догадался кто вместе с котиком пришел к нам в гости?(прямая линия, луч, отрезок и точка)
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
О каких линиях вы узнали? (О прямой, луче, отрезке.)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)
(Берем две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Педагог берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец.) (Педагог отрезает другой конец нитки и показывает, что нитка не тянется.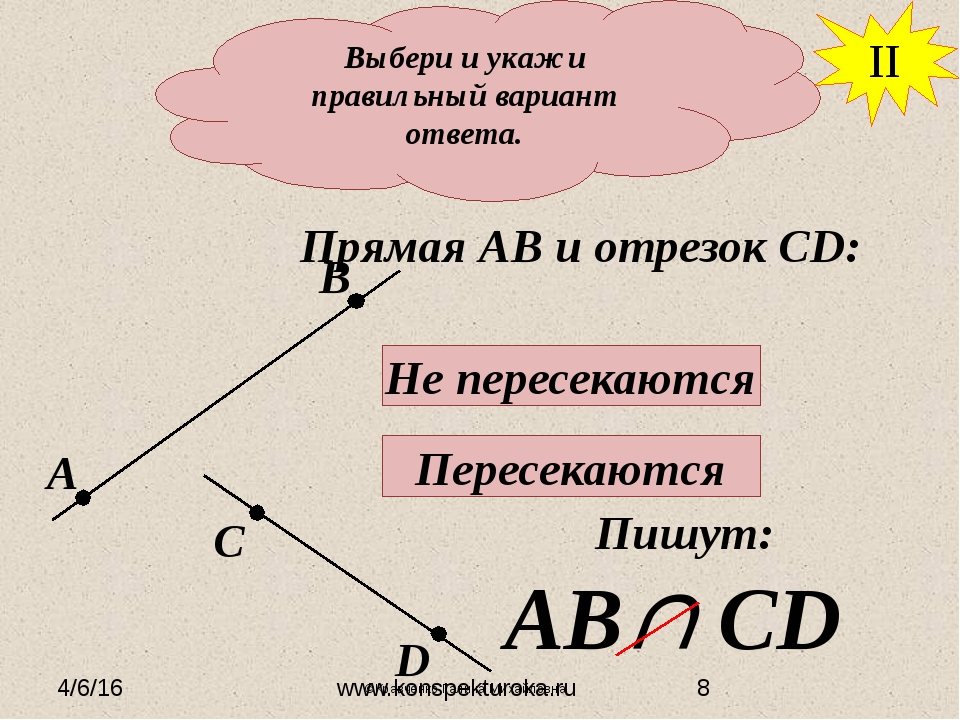 У нее есть и начало, и конец.)
У нее есть и начало, и конец.)
Как начертить прямую линию? (Провести по линейке линию.)
Как начертить отрезок? (Поставить две точки и соединить их.)
И конечно прописи:
Точка, отрезок, луч, прямая — числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Нужна помощь в учебе?
Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:   Чтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР
Отрезок — что это такое
Главная / ЧАстые ВОпросы
19 января 2021
- Отрезок — это.
 ..
.. - Разница между ним, лучом и прямой
- Вектор
- Ломаная линия
- Отрезок времени
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.
Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.
Отрезок — это геометрическая фигура
Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.
В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.
Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.
Разница между отрезком, лучом и прямой
Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:
- Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
- Луч — это часть прямой, ограниченная одной точкой. Он имеет начало и не имеет конца.
- Отрезок ограничивается двумя точками. Он имеет и начало, и конец.
Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Направленный отрезок — это вектор
Отрезки бывают двух видов:
- Ненаправленные.
- Направленные.
Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.
Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ➜ и ВА➜ — разные отрезки, так как они противоположно направленные.
Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Модулем вектора называется длина направленного отрезка. Обозначается как АВ➜. Модули векторов АВ➜ и ВА➜ равны.
Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.
Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.
Ломаная линия — это множество соединенных отрезков
Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.
Вершинами ломаной являются следующие точки:
- Точка, с которой началась ломаная.
- Точка, которой ломаная закончилась.
- Точки, в которых соединяются смежные звенья (отрезки ломаной).
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.
Любая замкнутая ломаная является геометрической фигурой — многоугольником.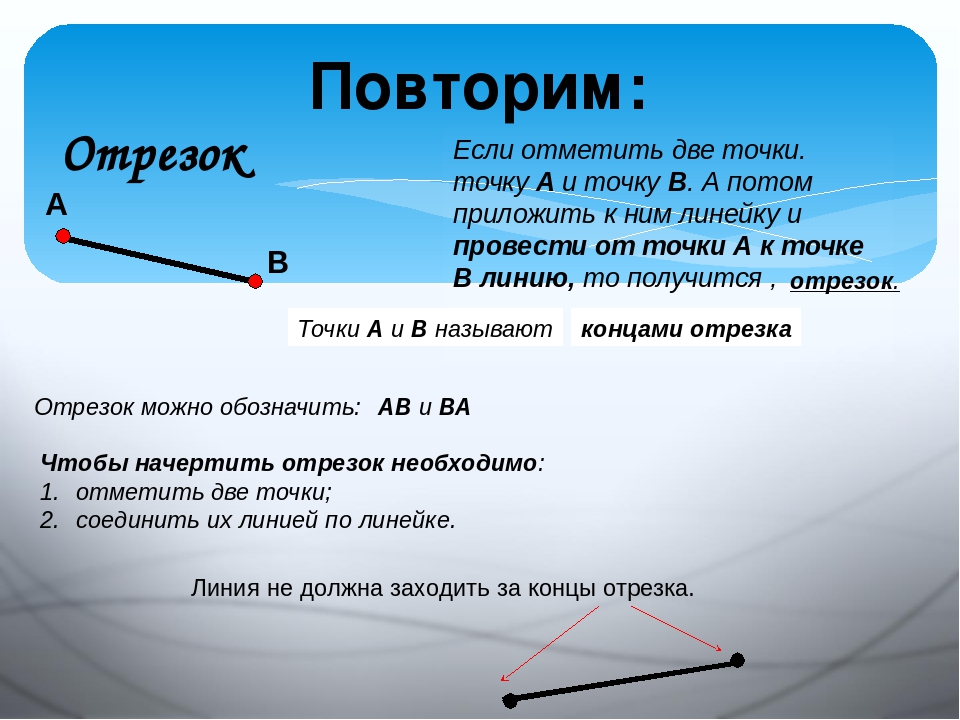
Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.
Отрезок времени
Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.
Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.
Время в целом в таком случае определяется как временная прямая.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Прямая и отрезок, измерение и сравнение отрезков
Прямая
Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины (рис. 1).
1).
Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках (рис. 2).
Понятия прямой и точки связаны тремя аксиомами геометрии:
Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются.
 В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой. - Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
В этой статье мы не будем подробно останавливаться на этих понятиях.
Отрезок
Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда
Определение 1
Отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками.
Определение 2
Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.
Отрезки будем обозначать двумя её точками концов в квадратных скобках (рис. 3).
Сравнение отрезков
Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.
Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.
Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:
Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу
(рис. 4).Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.
Длина отрезка
Помимо сравнения одних отрезков с другими также часто необходимо измерение отрезков. Измерить отрезок означает найти его длину. Для этого необходимо выбрать какой-то «эталонный» отрезок, который мы будем принимать за единицу ( к примеру отрезок, длина которого равняется 1 сантиметру). После выбора такого отрезка мы проводим с ним сравнение отрезков, длину которого нужно найти. Рассмотрим пример.
Пример 1
Найти длину следующего отрезка
если следующий отрезок равняется 1
Решение.
Для его измерения возьмем за эталон отрезок $[AB]$. Будем откладывать его на отрезок $[CM]$. Получим:
Ответ: $6$ см.
Понятие длины отрезка связаны со следующими аксиомами геометрии:
Аксиома 5: Выбрав определенную единицу измерения отрезков, длина любого отрезка будет положительна.
Аксиома 6: Выбрав определенную единицу измерения отрезков, мы можем для любого положительного числа найти отрезок, у которого длина равняется данному числу.
После определения длины отрезков у нас появляется второй способ для сравнения отрезков. Если при одном и том же выборе единицы длины отрезок $1$ и отрезок $2$ будут иметь одинаковую длину, то такие отрезки будут называться равными. Если же, без ограничения общности, отрезок 1 будет иметь длину по числовому значению меньше длины отрезка $2$, то отрезок $1$ будет меньше отрезка $2$.
Самым простым способом измерения длины отрезков является измерение, с помощью линейки.
Пример 2
Записать длины следующих отрезков:
Решение.
Измерим их с помощью линейки:
Получим.
Ответ:
- $4$ см.
- $10$ см.
- $5$ см.
- $8$ см.
Плоскость. Прямая. Луч
На этом уроке мы познакомимся с понятиями «отрезок»,
«прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых
и лучей в плоскости.
На прошлом уроке мы разобрались, как строить
отрезок. Мы уже знаем, что отрезок – это прямая линия,
ограниченная двумя точками.
Определение
Давайте начертим отрезок MN.
Если продлить этот отрезок неограниченно за точку N,
то мы получим новую фигуру, которая называется луч. У нас
получился луч MN.
Точку М называют началом
луча.
Если бы мы продлевали отрезок MN неограниченно за точку М,
то у нас бы получился луч NМ, у которого
точка N – начало луча.
Заметьте: обозначается луч большими заглавными
буквами латинского алфавита, первой буквой записывают его начало, а затем
букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не
имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде,
достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт
– это начальная точка, а след, оставленный на небе, – это прямая линия, которая
бесконечна.
Либо солнечный луч, где начальная точка – это
солнце, а конечной точки нет.
Определение
Если отрезок MN неограниченно
продлевать в обе стороны – как за точку М,
так и за точку N, то у нас получится фигура,
которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни
конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет
прямую MN на луч ОМ
и луч ОN. Лучи, на которые точка разбивает
прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить
лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго
натянуть верёвку.
В математике прямая представляется идеально ровной и
бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант:
двумя заглавными буквами латинского алфавита, например MN.
В таком случае говорят: «Прямая MN».
2-й вариант:
прямую обозначают одной малой буквой, например m, и
говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти
же две точки.
У нас это не получится. Через любые две точки можно
провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в
плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о
плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в
математике безгранична во всех направлениях. Мы рисуем фигуры на
«кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек,
отрезков, прямых и лучей в плоскости.
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на
отрезке EF, а точки L,
P, T не
лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на
луче EF, а точки А,
E, F, Т лежат на луче FЕ.
Посмотрите запись этих утверждений.
Точки А, E, F, Т лежат на прямой EF,
а точки А, P,
L – на прямой PL.
Обозначается это так:
Точка А лежит
между точками Е и F.
Точка L не лежит между точками Е и F, она
находится вне отрезка EF. Точка Е лежит между точками А
и Т, а точка А
– между точками P и L.
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят,
что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются
в точке О. Точка О
делит каждую прямую на две части. Точка О –
точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих
точек, то говорят, что они параллельны.
Запомните!
·
Прямая
бесконечна.
·
Отрезок
ограничен.
·
Луч
имеет начало, но не имеет конца.
·
Плоскость
бесконечна.
Итоги
Итак, на уроке мы с вами разобрались в отличиях
понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое
плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в
плоскости.
Разница между линией и линейным сегментом (со сравнительной таблицей)
Последнее обновление , Surbhi S
В геометрии элементарного уровня термин, с которым сталкивается каждый ученик, — «линия». Это длинная и прямая геометрическая фигура, которая простирается в обоих направлениях. Он отличается от линейного сегмента тем, что линейный сегмент имеет начальную и конечную точки, благодаря чему длина сегмента является фиксированной.
Как вы можете видеть на приведенном выше рисунке, на обоих концах линии отмечены стрелки, чтобы дать представление о ее бесконечности.Напротив, два конца отрезка отмечены кружком, который указывает на то, что он определен. Изучая геометрию, каждому ученику важно понимать разницу между линией и отрезком линии. Итак, здесь, в этой статье, мы собираемся объяснить концепцию, прочитать.
Содержимое: линия против сегмента линии
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основа для сравнения | Строка | Строка Сегмент |
|---|---|---|
| Значение | Линию можно описать как одномерную геометрическую фигуру, которая продолжается бесконечно. | Под отрезком подразумевается прямая линия, проходящая через две точки. |
| Символ | ||
| Конечные точки | Нет конечных точек. | Имеет две конечные точки. |
| Длина | Неопределено | Определено |
| На бумаге | Нет | Да |
Определение строки
Линия может пониматься как прямой, бесконечный, длинный, непрерывный путь, обозначенный стрелками, показывающими, что линия бесконечно движется в двух направлениях.Это одномерная геометрическая фигура, поскольку она имеет только длину, а не ширину и глубину. Обычно линия обозначается маленькой буквой «л».
Как вы можете видеть на рисунке выше, с обеих сторон есть стрелки. Обозначается он:
Определение линейного сегмента
Сегмент линии — это небольшой отрезок линии. Есть две точки, через которые проходит отрезок прямой, что указывает на то, что отрезок имеет определенное начало и конец. Таким образом, можно сказать, что это кратчайший путь между двумя заданными точками, который упрощает измерение отрезка с помощью линейки.Это также одномерная фигура в виде линии, имеющая только длину.
На рисунке выше показан отрезок прямой, длина которого обозначена буквой AB. Отрезок обозначается как:
.
Ключевые различия между линией и линейным сегментом
Разница между линией и линейным сегментом обсуждается в пунктах, приведенных ниже:
- Линия относится к прямой и длинной отметке на поверхности, представленной стрелками на каждом конце, показывающими, что она продолжается в двух направлениях, бесконечно.С другой стороны, сегмент подразумевает часть чего-то, так же как сегмент линии означает часть линии, которая имеет различные начало и конец.
- Хотя сегмент линии начинается в одной точке и заканчивается в другой, на линии нет конечных точек.
- Что касается длины, длина линии бесконечна, и ее невозможно измерить. И наоборот, поскольку отрезок линии имеет две конечные точки, его длину можно легко измерить.
- Отрезок линии можно нарисовать на бумаге, тогда как линию нельзя нарисовать на бумаге, ее можно только представить.
Заключение
Вкратце, сегмент линии — это сегмент с двумя конечными точками, которые при бесконечном удлинении в обоих направлениях будут называться линией. Проще говоря, ни на одной из сторон линии нет конечных точек. Оба могут быть параллельными, пересекающимися или наклонными.
В чем разница между линией и линейным сегментом?
Разница между линией и отрезком линии
В элементарной геометрии вы чаще всего будете слышать такие термины, как точка, линия, луч, углы и т. Д.Некоторые студенты обычно путаются с терминами «линия» и «линейный сегмент». Здесь я объясню вам оба термина и рассмотрю разницу между линией и сегментом линии .
Линия — это одномерная геометрическая фигура, которая представляет собой прямой и непрерывный путь и обозначается стрелками в обеих точках. Говоря простыми словами, линия бесконечна в обоих направлениях. Линия будет иметь только длину, но не ширину и глубину, и в геометрии она обозначается буквой «l».
Отрезок — это прямая линия, проходящая через обе точки. Линейный сегмент имеет определенную длину, и, как и линия, линейные сегменты также не имеют ширины и глубины.
Итак, простыми словами, сегмент линии — это небольшой сегмент линии, имеющий определенные начало и конечные точки. Отрезок — это кратчайшее расстояние между двумя точками.
Line Vs. Отрезок линии
- Линия не имеет конечной точки, а сегмент прямой имеет две конечные точки.
- Линия бесконечно удлинена с обоих концов, при этом отрезок линии имеет определенное начало и конец.
- Длину линии нельзя измерить, а длину отрезка можно измерить.
- Линия представлена буквой AB с горизонтальной линией и стрелкой вверху, а линия представлена буквой AB и горизонтальной линией вверху.
Отрезок линии — это часть линии, и оба они являются частью элементарной геометрии. Понять термины и различать их очень легко.Это основное различие между линией и отрезком линии.
Разница двух отрезков прямой с помощью циркуля и линейки или линейки
Эта конструкция показывает, как создать линейный сегмент, длина которого равна разнице между двумя заданными сегментами.
Это очень похоже на Сумму отрезков линии,
за исключением того, что второй сегмент рисуется с другой стороны от первого, фактически вычитая длины.
Два типа построения (сложение, вычитание) можно комбинировать как угодно. Например, вы можете найти результирующую длину a + b – d – f.
Что делать, если второй сегмент длиннее первого?
Если b длиннее a, то вы найдете конец конструкции слева от начала:
Расстояние PQ по-прежнему является разницей между длинами двух сегментов.
В арифметике это приведет к отрицательной длине, которой нет в евклидовой геометрии.Сегменты не могут иметь отрицательную длину.
Таким образом, точное определение того, что делает эта конструкция, — найти абсолютное значение a – b
Две вертикальные полосы означают «абсолютное значение», которое всегда положительно, независимо от того, каким образом отображается a – b.
Поэтому конструкция называется «Разница двух отрезков» — это не совсем то же самое, что арифметическое вычитание.
Проба
Доказательство этой конструкции тривиально. Это тот же рисунок, что и на последнем шаге в приведенной выше анимации.
| Аргумент | Причина | |
|---|---|---|
| 1 | Сегмент PQ соответствует данному сегменту а | Скопировано с использованием процедуры из раздела Копирование линейного сегмента. Смотрите эту страницу для доказательства. |
| 2 | Отрезок RQ соответствует данному отрезку b | Как в (1) |
| 4 | PR — разница данных отрезков a, b, c | Из (1), (2).Все сегменты коллинеарные и смежные. |
— Q.E.D
Пошаговая инструкция для печати
Вышеупомянутая анимация доступна как
распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов
или когда компьютер недоступен.
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий проблемы копирования двух сегментов линии.
Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите.Печатная продукция не защищена авторскими правами.
Другие конструкции, страницы на сайте
строки
Уголки
Треугольники
Правые треугольники
Центр треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
линий, лучей, отрезков и плоскостей
Наставник: Нарисуйте, пожалуйста,
ось координат на бумаге.Теперь пометьте оси x и y. Теперь пометьте каждую линию на оси x и y знаком
масштаб одного.
Наставник: Вы знали, что координатная ось — это плоскость?
Студент: Нет. Что такое самолет?
Наставник: Плоскость — это плоская поверхность, которая продолжается бесконечно. Лучший способ увидеть, что такое самолет
это как представить себе лист бумаги, который никогда не заканчивается.
Студент: Так же
бесконечность означает бесконечность?
Наставник: Да, это так.Бесконечность представляет собой то, что может продолжаться. Для любой
при заданном значении всегда можно найти большее значение.
Ученик: Итак, самолет простирается до конца вселенной.
Наставник: Да, но более того. Конец вселенной представляет собой конец. Что-то, что может быть
считаться бесконечным не заканчивается. На самом деле ничто из существующего не может быть бесконечным. Это просто
может продолжаться, как наша система счисления или линия.Теперь, может ли кто-нибудь вспомнить, что
линия есть?
Учащийся: линия состоит как минимум из двух точек, находящихся на прямом пути.
Наставник: Да, очень хорошо. Нарисуем один.
Наставник: А теперь у кого-нибудь есть представление о том, что такое луч?
Студент: Луч света, исходящий из лучевой пушки.
Наставник: Хорошая идея. У лучевой пушки есть отправная точка, и она продолжается вечно, если никогда не попадает в цель.Луч начинается в одной точке и продолжается до бесконечности.
Наставник: Давайте нарисуем луч.
Студент: Итак, в чем разница между линией и лучом?
Наставник: Линия уходит в бесконечность в обоих направлениях, но луч останавливается на одном конце. Если вы разрежете линию
пополам получается два луча. Теперь кто-нибудь может догадаться, что такое отрезок линии?
Студент: Это линия с двумя концами?
Наставник: Совершенно верно.Сегмент линии — это часть линии, имеющей две конечные точки. Нарисуем один на
бумага.
Разница между линией и сегментом линии (с таблицей) — спросите любую разницу
Линия без конечных точек и сегмент линии имеет две или одну конечную точку. Отрезок линии — это часть линии. Линия не имеет фиксированной точки.
Линия и линейный сегмент
Разница между линией и линейным сегментом заключается в том, что линия может быть расширена в обоих направлениях, в то время как линейный сегмент имеет фиксированную начальную и конечную точки.Он также может быть открытым с открытого конца или с обоих концов.
Продолжение линии показано стрелками на обоих концах линии. Стрелка называется лучом. Луч (стрелка) просто обозначает бесконечность линии. Линия не имеет конечной точки и может быть удлинена с обоих концов. В отличие от линии, отрезок линии имеет два определенных конца, и конец не может быть продолжен.
Пример: строка
— Показано стрелками
———- à Строка
———- à ИЛИ <————
Пример: Линия
Сегмент — показан двумя точками
.—————.
Таблица сравнения между линией и отрезком линии
| Параметры сравнения | Линия | Сегмент линии |
|---|---|---|
| Значение | Прямой бесконечный путь без ширины и ширины | Это часть линии, имеющей определенные начало и конец |
| Конечная точка | Нет | Да |
| Длина | Бесконечная | Видимые конечные точки |
| Нарисуйте на бумаге | Изображение бесконечной линии не возможно | Можно нарисовать на бумаге. |
| Измеримый | Бесконечный. Невозможно измерить на шкале | Определить геометрически |
Что такое линия?
Линия — это бесконечный, длинный, непрерывный и прямой путь, обозначенный стрелками на обоих концах. Стрелки в обоих направлениях объясняют размер длины.
Линия не имеет ширины и глубины. Линия может пересекаться, а также отображаться как параллельная.
Линия также не будет иметь кривой, как у кружков. Линии могут проходить через центральную точку, и линия играет решающую роль в диаметре круга.
Линии можно использовать по диагонали и пересекать при условии, что на обеих линиях есть две стрелки для обозначения непрерывности.
Эта линия находится в понятном геометрическом принципе. Но если мы говорим о бесконечных линиях, существующих в галактике, мы говорим о бесконечной экзистенциальной вселенной.
Что такое линейный сегмент?
Сегмент линии — это часть линии, которая должна быть изображена. У отрезка линии есть два определенных конца, которые показаны точками. Скажем, A и B — две точки.
Кратчайшее расстояние между A и B — это отрезок прямой.
Отрезок — это одномерная фигура. Например, квадрат состоит из 4 отрезков линии одинакового размера. Теперь давайте разберемся с этим на примере.
Первая точка называется AB, а другая конечная точка называется BA.
Основные различия между линией и линейным сегментом
Значение
Линия — это геометрический инструмент, а линейный сегмент — это компонент этого инструмента. Линия — это бесконечный двунаправленный непрерывный путь, обозначенный стрелками.
Сегмент линии — это отрезок линии с двумя точками, разграничивающими конец. Следовательно, отрезок прямой имеет определенное начало и конец. Также понятно, что отрезок линии — это кратчайшее измерение между двумя заданными точками, нанесенными на линию.
Конечная точка
Линия не имеет конечной точки в буквальном смысле. Но отрезок прямой, он начинается и заканчивается в разных точках. Линейный сегмент имеет 2 конечные точки.
Поскольку линия бесконечна, геометрически и научно невозможно найти начало или конец.
Длина
Длина линии бесконечна. Его длину невозможно отследить, измерить, количественно оценить по математическим, геометрическим и научным параметрам.
Поскольку линейный сегмент имеет конечную линейную часть, его можно рассчитать по их длине, ширине и ширине. К нему прилагаются дополнительные ссылки, которые прояснят то же самое.
Измерение
Невозможно измерить что-то бесконечное. Линию нельзя измерить, если это не сегмент линии.Линия может быть разбита на два или меньших отрезка.
Причина, по которой линия не может быть измерена, поскольку измерение связано с числами по отношению к объекту. Поскольку линия не выходит за пределы области видимости, применение измерения к линии невозможно. Отрезок линии можно измерить, так как он имеет номер, длину и ширину, которые необходимо определить количественно.
Рисование на бумаге
Линию можно нарисовать и показать на бумаге, но можем ли мы количественно определить и измерить ее в действительности? Можно ли измерить бесконечность? Линию можно только изобразить на бумаге, но не нарисовать.
Линия просто имеет длину, в то время как сегмент линии имеет длину, ширину и ширину. С другой стороны, часть линии, которая является отрезком линии, может быть нарисована на бумаге.
Заключение
Теории, такие как математика, геометрия, изучают вопросы, связанные с линиями и линиями. В этих двух предметах анализируются формы, размеры, положение, качества.
Сегмент линии необходим для рисования любых форм, таких как квадратный треугольник, прямоугольник и т. Д.
Подводя итог, линия является одномерной, только бесконечной длины, которая также может пересекаться параллельно.Отрезок — это составная часть линии, имеющая длину, ширину, ширину и два определенных конца. Линия определяется набором различных линейных сегментов, которые начинаются с одного конца и заканчиваются на другом.
Связанные
Что такое линейный сегмент? — [Определение, факты и пример]
Что такое линейный сегмент?
Это строчка! Он не имеет конечных точек и бесконечно распространяется в обоих направлениях.
Если вы отметите на нем две точки A и B и выделите этот сегмент отдельно, он станет отрезком прямой.
Этот линейный сегмент имеет две конечные точки A и B, длина которых фиксирована. Длина этого линейного сегмента — это расстояние между его конечными точками A и B.
Итак, сегмент линии — это отрезок или часть линии, имеющая две конечные точки. В отличие от линии, сегмент линии имеет определенную длину.
Длина отрезка линии может быть измерена в метрических единицах, таких как миллиметры, сантиметры, или в обычных единицах, таких как футы или дюймы.
Измерение отрезка линии
Чтобы измерить длину отрезка, выполните следующие действия:
Шаг 1 : Возьмите шкалу, чтобы измерить длину отрезка.Обычно меньшие отрезки линий измеряются с использованием сантиметровой шкалы.
Шаг 2 : Определите отрезок линии, который вы хотите измерить.
Шаг 3 : Поместите кончик линейки в начальную точку линейного сегмента.
Шаг 4 : Считайте число на шкале, где заканчивается отрезок линии. В данном случае это 5. Итак, длина данного отрезка линии равна 5 см.
Построение отрезка прямой с помощью линейки и циркуля
Предположим, нам нужно нарисовать отрезок длиной 5 см.Мы будем следовать данным шагам:
Шаг 1 : Проведите линию любой длины. Отметьте точку A на линии, которая является начальной точкой отрезка линии.
Шаг 2 : С помощью линейки поместите указатель циркуля на 5 см от стержня карандаша.
Шаг 3 : Поместите указатель компаса в точку A и отметьте дугу на линии острием карандаша.
Шаг 4 : Отметьте точку пересечения дуги и линии буквой B.
Шаг 5 : AB — необходимый отрезок длиной 5 см.
Пример из жизни
Стороны многоугольника, края линейки, края листа — все это примеры линейного сегмента
Интересные факты о линейном сегменте
|
Сравнение сегментов линий — A Plus Topper
Сравнение двух отрезков прямой означает поиск более короткого или более длинного отрезка. Методы сравнения длины отрезков следующие:
Сравнение наблюдением
На рисунке показаны два отрезка AB и CD.
Просто наблюдая за ними, мы легко узнаем, что отрезок CD> AB. Но это не всегда возможно, если разница между их длинами очень мала.
Сравнение с использованием разделителя
Разделитель — это геометрический инструмент, который имеет два рычага, шарнирно соединенные вместе с помощью ручки на одном конце. На других концах двух плеч есть металлические иглы. Чтобы сравнить данные отрезки AB и CD, поместим иглу одной руки разделителя в точку C и осторожно раскроем его другое плечо так, чтобы игла другого плеча попала в точку D.
Теперь осторожно поднимите перегородку, чтобы раскрытие двух рычагов осталось неизменным. Поместите одну из игл в точку A отрезка AB, и другая рука может упасть в любой точке AB. Теперь есть три возможности.
- Другая рука падает точно в B, тогда AB = CD.
- Другая рука оказывается между A и B, тогда AB> CD.
- Другой конец отходит от B, тогда AB
Сравнение путем отслеживания
Мы также можем сравнивать отрезки AB и CD методом трассировки.Проведите один из отрезков прямой так, чтобы точка C намеченного отрезка CD совпадала с точкой A отрезка AB. При этом мы наблюдаем следующее.
Измерение отрезков линии
Сегмент линии — это часть линии. Он имеет два конца и определенную длину, без ширины и без толщины. Длина отрезка линии — это расстояние, которое может измеряться в метрах, сантиметрах, миллиметрах и т. Д.
10 (миллиметры) = 1 см (сантиметр)
10 см (сантиметры) = 1 дм (дециметр)
10 дм (дециметры) = 1 м (метр)
10 м (метры) = 1 плотина (декаметр)
10 декаметров (плотина) = 1 гектометр (гм)
10 гектометров (гм) = 1 километр (км)
Для измерения отрезков линии мы используем шкалу с сантиметровыми отметками на одном крае и дюймовыми отметками на другом.
