Содержание
Прямая и обратная пропорциональность. Коэффициент и формулы
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.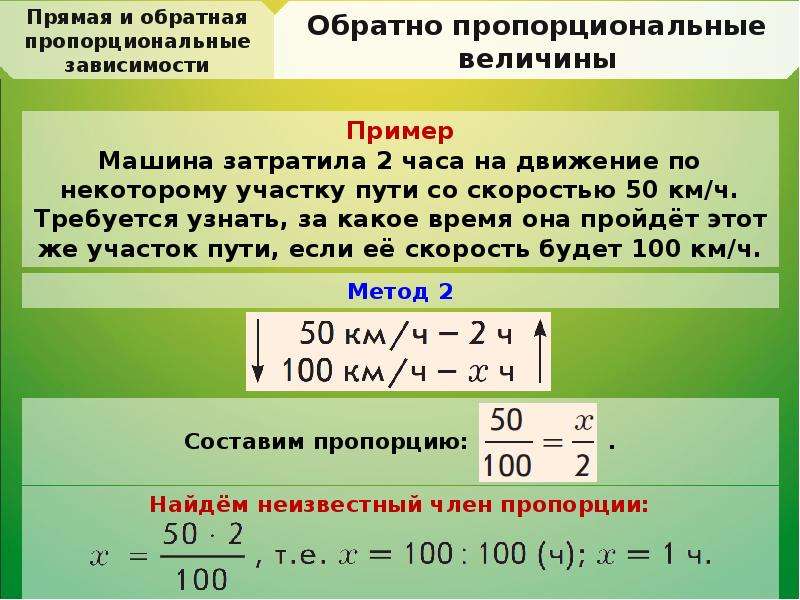
Бобкова С.Н. Прямая и обратная пропорциональные зависимости
Бобкова С.Н. Прямая и обратная пропорциональные зависимости
Автор: edu1
Методическая копилка —
Математика
МБОУ «Букреевская основная общеобразовательная школа»
Рабочие материалы выступления
на школьном этапе конкурса
«Учитель года 2013»
План — конспект открытого урока
математики в 6 классе по теме:
«Прямая и обратная
пропорциональные зависимости»
учитель математики Бобкова С. Н.
Букреевка, 2013 г.
Цель урока:
Образовательная:Закрепить понятия: пропорция, основное свойство пропорции, прямо пропорциональные величины, обратно пропорциональные величины. Закрепить умение решать задачи с помощью пропорции, познакомить с золотым сечением.
Закрепить умение решать задачи с помощью пропорции, познакомить с золотым сечением.
Продолжить формирование обще-учебных умений и навыков:
— планирование ответа;
— навыки самоконтроля;
— устный счет.
Контроль степени усвоения основных знаний, умений и навыков по данной теме.
Развивающая: Развитие умений в применении знаний в конкретной ситуации.
Развитие логического мышления, умения выделять главное, проводить обобщение, делать верные логические выводы.
Развитие умений сравнивать, правильно формулировать задачи и излагать мысли.
Развитие самостоятельной деятельности учащихся.
Воспитательная: Формирование научного мировоззрения, интереса к предмету через содержание учебного материала.
Воспитание умения работать в коллективе, культуры общения, взаимопомощи.
Воспитание таких качеств характера как настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.
Оборудование: карточки с заданиями для самостоятельной работы, презентация.
Ход урока:
1. Устная работа.
1. Что такое пропорция?
2. Как называются числа х и у в пропорции х : а = b : у?
3. Как называются числа т и п в пропорции а: т = n: b?
4. Сформулируйте основное свойство пропорции?
5. Какие ещё свойства пропорции вы знаете?
6. Какие величины называются прямо пропорциональными?
7. Какие величины называются обратно пропорциональными?
1) Верна ли пропорция:
а) 2 : 5 = 16 : 40; б) 7 : 2,1 = 2 : 0,6; в) 4 : 12 = 14 : 4,2
2) Какие числа надо вставить в «окошки», чтобы получить верную пропорцию
а) 33 : 6= : 2; б) 45 : = 15 : 3; в) : = 24 : 6; г) : = : 5.
3) Составьте верную пропорцию из чисел 10, 12, 6 и 5.
4) Повторим алгоритм решения задач на прямую
и обратную пропорциональные зависимости:
• неизвестное число обозначить буквой х
• записать условие задачи
• установить вид зависимости между величинами
• прямую пропорциональную зависимость
обозначить одинаково направленными
стрелками, а обратную пропорциональную
зависимость – противоположно направленными
стрелками.
• записать пропорцию
• найти её неизвестный член.
3. Проверка домашнего задания. Защита творческих работ (домашнее задание было составить задачу на прямую или обратно пропорциональные зависимости)
4. Решение задач
1. За 4м ткани заплатили 180р. Сколько стоят 14м этой ткани? (630 р)
2. Чтобы покрасить стены дома за 2 дня, требуется 20 маляров. За сколько дней эту работу выполнят 4 маляра? ( 10дн)
3. Пассажирский поезд, скорость которого 45км/ч, затратил на некоторый участок пути 4ч. За сколько часов пройдёт этот же участок пути товарный поезд, если его скорость 40 км/ч? ( 4,5 ч)
4. Для изготовления 18 одинаковых приборов потребовалось 27г платины. Сколько платины потребуется для изготовления28 таких приборов? ( 42г или 0,042кг)
5. В 1 кг морской воды содержится 40г соли. Сколько соли содержится в 650 г морской воды? (0,026кг)
5. Самостоятельная работа.
Составить пропорции для решения задач
I- вариант II- вариант
в) и г) а) и б)
а) На пошив 9 рубашек ушло 18,9 м ткани. Сколько метров уйдёт на пошив 12 таких рубашек?
б) 6 одинаковых труб заполняют бассейн за 24 минуты. За сколько минут заполнят бассейн 9 таких труб?
в) Бригада из 8 рабочих выполняет задание за 12 дней. Сколько рабочих сможет выполнить это задание за 8 дней, работая с той же производительностью?
г) Из 9,6 кг помидоров получают 4 л томатного соуса. Сколько литров соуса можно получить из 84 кг помидоров?
6. Знакомство с «Золотым сечением» (Демонстрация презентации).
Откройте учебник на странице 144, прочитайте исторический материал.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения.
— Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения».
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника (Прослушивание фрагмент оперы П. И. Чайковского).
И. Чайковского).
7. Рефлексия.
8. Домашнее задание: Самостоятельная работа (другой вариант)
Прямая и обратная пропорциональные зависимости
Сегодня на уроке мы продолжим работать с
пропорциями, а точнее познакомимся с прямой и обратной
пропорциональными зависимостями.
Задача
Сколько нужно сахара, чтобы сварить варенье из 5 кг черешни, если по рецепту на 2 кг ягод нужно 3 кг
сахара?
Решение:
Из решения видно, что во сколько раз больше имеется
черешни, во столько раз больше понадобится сахара.
Эту же задачу можно решить и при помощи пропорции.
Запишем кратко условие задачи в виде таблицы, обозначив за неизвестную нам
массу сахара буквой х. Смотрите, у нас есть столбик, где мы будем
записывать массу ягод, и столбик, где мы укажем соответствующую массу сахара на
массу ягод. Итак, по условию задачи известно, что по рецепту на 2 кг ягод нужно 3 кг сахара. Нам нужно узнать,
Итак, по условию задачи известно, что по рецепту на 2 кг ягод нужно 3 кг сахара. Нам нужно узнать,
сколько кг сахара потребуется на 5 кг ягод.
Такая зависимость между массой ягод и массой сахара
условно обозначается в таблице одинаково направленными стрелками. Их
направление говорит о том, что если первая величина возрастает (стрелка вверх),
то и вторая тоже возрастает (стрелка тоже вверх).
Задача
Велосипедист, двигаясь с постоянной скоростью,
проехал 10 км за 20
минут. Какой путь проедет велосипедист за 50
минут?
Решение: для наглядности
запишем кратко условие задачи в виде таблицы.
Понятно, что путь увеличится во столько раз, во
сколько раз увеличится время. Ставим стрелки в одном направлении.
Такие величины, как масса ягод для варенья и масса
сахара, время и пройденный за это время при постоянной скорости путь, и т. д.
д.
называют прямо пропорциональными величинами.
Определение
Две величины называются прямо
пропорциональными, если при увеличении (уменьшении) одной из них в несколько
раз другая увеличивается (уменьшается) во столько же раз.
Задача
Автомобиль ехал 3 часа
со скоростью 60 км/ч. За какое время он
продет это же расстояние, если будет ехать со скоростью 90 км/ч?
Решение:
Из решения видно, что во сколько раз скорость
автомобиля больше, во столько раз меньше времени тратится на этот же
путь.
Эту же задачу решим при помощи пропорции. Запишем в
таблицу кратко условие задачи. За х обозначим неизвестное нам
время.
Понятно, что чем больше скорость автомобиля, тем
меньше времени ему понадобится на преодоление этого же пути. Такая
зависимость между скоростью и временем, затраченным на пройденный путь, условно
обозначается в таблице противоположно направленными стрелками.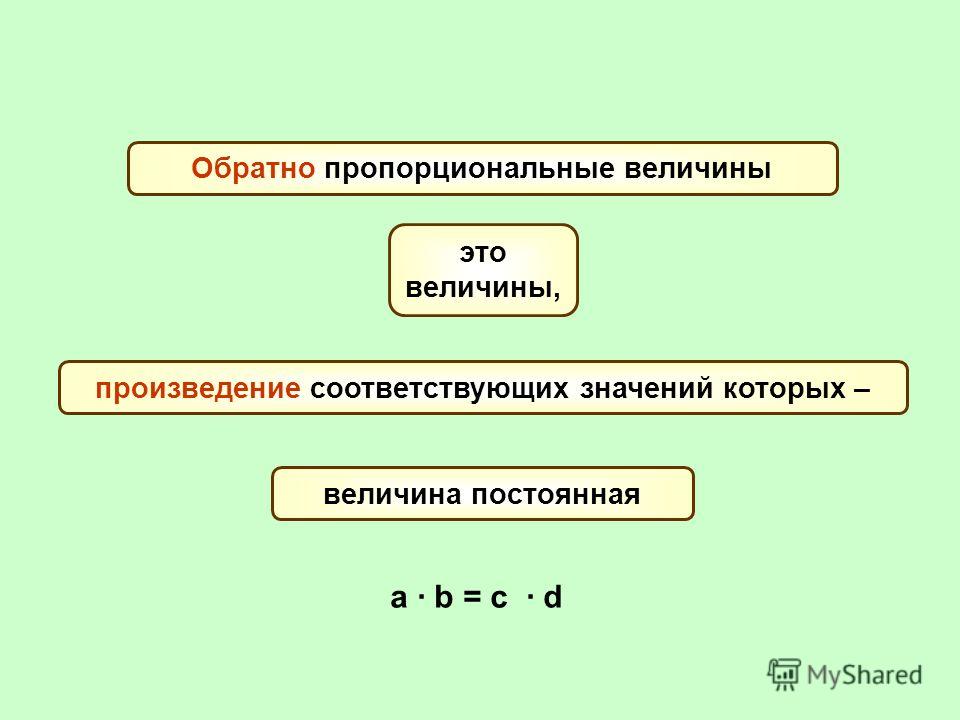 Их
Их
направление говорит о том, что если первая величина возрастает (стрелка вверх),
то вторая убывает (стрелка вниз). Составим пропорцию. Т.к. стрелки направлены в
разные стороны, то второе отношение перевернём.
Задача
5 рабочих выполнили заказ
за 132 часа. За какое время этот же заказ
смогут выполнить 12 рабочих?
Решение:
Понятно, что чем больше будет задействовано
рабочих, тем быстрее выполнится заказ. Значит, ставим стрелки в
противоположном направлении. Составим пропорцию:
Такие величины, как скорость автомобиля и время, за
которое он проедет определённый путь, число работников и время, за которое они
выполняют заказ, и т.д. называют обратно пропорциональными величинами.
Определение
Две величины называются обратно
пропорциональными, если при увеличении (уменьшении) одной из них в несколько
раз другая уменьшается (увеличивается) во столько же раз.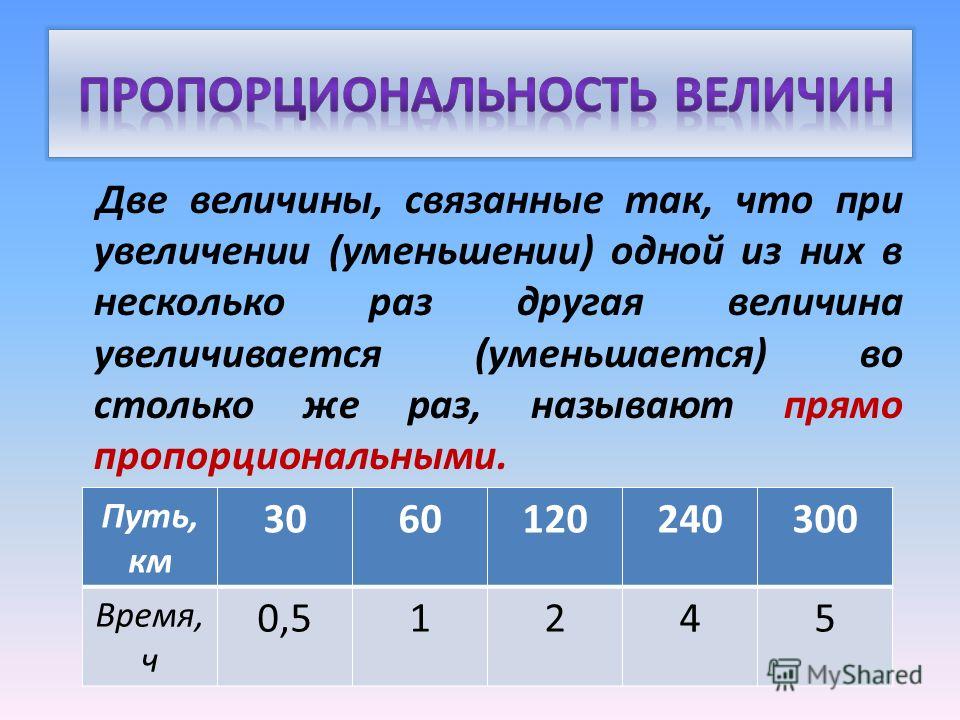
Не всякие две величины являются прямо пропорциональными
или обратно пропорциональными.
Например,
возраст человека и размер его обуви не связаны пропорциональной
зависимостью. Зависимость между величинами есть. Размер обуви с возрастом
увеличивается, но не во столько же раз.
Возраст дерева и его высота не связаны
пропорциональной зависимостью. В этом случае зависимость между величинами есть.
Действительно, высота дерева с возрастом увеличивается, но не во столько же
раз.
|
1. |
Пропорциональные и непропорциональные величины |
1 вид — рецептивный |
лёгкое |
1 Б. 
|
Следует определить, является ли пропорциональной зависимость между величинами |
|
2. |
Зависимость между величинами |
1 вид — рецептивный |
лёгкое |
1 Б. |
Необходимо определить, является ли прямо пропорциональной, обратно пропорциональной или не является пропорциональной зависимость между величинами |
|
3. 
|
Величины |
1 вид — рецептивный |
лёгкое |
2 Б. |
Необходимо выбрать величины между которыми существует прямо/обратно пропорциональная зависимость |
|
4. |
Формулы. Прямая пропорциональность |
1 вид — рецептивный |
среднее |
3 Б. 
|
Формулы. Прямая пропорциональность |
|
5. |
Формулы. Обратная пропорциональность |
1 вид — рецептивный |
среднее |
3 Б. |
Формулы. Обратная пропорциональность |
|
6. |
Лишняя формула |
1 вид — рецептивный |
среднее |
2 Б. 
|
Из данных формул следует исключить «лишнюю», обратная пропорциональность |
|
7. |
Прямо пропорциональные величины, таблица |
1 вид — рецептивный |
среднее |
4 Б. |
Прямо пропорциональные величины, таблица |
|
8. 
|
Таблица и формула (десятичные дроби) |
1 вид — рецептивный |
среднее |
4 Б. |
Следует определить зависимость между величинами, записать формулу и заполнить таблицу. Прямая пропорциональность. |
|
9. |
Таблица, формула (целые числа) |
1 вид — рецептивный |
среднее |
5 Б. 
|
Необходимо определить зависимость между величинами, записать формулу и заполнить таблицу. Обратная пропорциональность. |
Конспект урока математики на тему «Прямая и обратная пропорциональные зависимости» (6 класс)
Урок математики в 6 классе
(учитель математики Булатова О. П.)
Прямая и обратная пропорциональные зависимости
Тип урока: Урок закрепления знаний (II урок по теме)
Цель: формирование умения различать прямую и обратную пропорциональную зависимость, решать задачи на прямую и обратную пропорциональную зависимости
Формируемые результаты:
Предметные: сформировать умение решать задачи, используя прямо пропорциональные и обратно пропорциональные переменные величины.
Личностные: формировать умение объективно оценивать труд одноклассников, развивать навыки самостоятельной работы.
Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.
Планируемые результаты: Учащиеся смогут решать задачи, используя прямо пропорциональные и обратно пропорциональные переменные величины.
Основные понятия: Прямо пропорциональные переменные величины, свойство переменных величин, которые находятся в прямой пропорциональной зависимости, обратно пропорциональные переменные величины, свойство переменных величин, которые находятся в обратной пропорциональной зависимости.
Организационная структура урока
Мотивация
«Зеркало отражает верно; оно не ошибается, ибо не думает. Думать – почти всегда значит ошибаться». Пауло Коэльо
— Как вы понимаете эти слова?
Варианты детей:
Значит, для того, чтобы получить хорошие знания, надо много работать, а в процессе работы не стыдно допустить ошибку и вовремя ее исправить. Потому что каждый имеет право на ошибку!
Потому что каждый имеет право на ошибку!
Актуализация знаний
Ребята, давайте вспомним прошлый урок. Какую тему мы начали изучать?
Ответы детей. Прямая и обратная пропорциональные зависимости.
Запишем тему в тетрадь.
Какие ключевые понятия данной темы вы можете выделить?
Ответы детей: Пропорция, пропорциональная зависимость, отличие прямой и обратной пропорциональной зависимостей.
Давайте вспомним, что такое пропорция? Это равенство двух отношений.
2 учащихся к доске:
Запишите:
«8 относится к х так же как 4 относится к 3»
Выпишите крайние и средние члены пропорции
(8 и 3 — крайние; х и 4 – средние члены пропорции)
Найдите неизвестный х
(Х = 6)
За 3 часа в бассейн налилось 75 литров воды, сколько литров воды наберётся в бассейн на 5 часов?
(125 литров)
По каким критериям будем оценивать данную работу?
Запись пропорции
Умение называть крайние и средние члены пропорции
Решать уравнения, используя основное свойство пропорции
Решать задачи с помощью пропорции.

Оцениваем себя и друг друга с помощью волшебных линеечек.
С В У
Учащимся, работающим у доски выставляются оценки.
Постановка целей и плана работы.
Русский язык богат разными поговорками ,например:
Чем выше пень, тем дальше тень.
Чем больше народа (в помещении), тем меньше кислорода.
Как эти поговорки связаны с темой нашего урока?
Сформулируйте цель нашего урока.
Закрепить понятие прямой и обратной пропорциональной зависимости, уметь их различать, решать задачи на прямую и обратную пропорциональную зависимость.
На доске таблица
Соотнесите ваши знания или незнания по теме нашего урока, приклейте стикер на ту колонку, где в данный момент находитесь вы.
Приведите примеры величин являющихся прямо пропорциональными, обратно пропорциональными.
Применение знаний на практике, решение проблемы.

Решим задачу учебник стр. 136 №674
15 рабочих——— 46 дней
? рабочих ———30 дней
Определите, какая это пропорциональная зависимость.
Ответы: При увеличении одной величины, вторая уменьшается. Обратная пропорциональная зависимость.
Поэтому для того, чтобы составить пропорцию нужно расставить величины в прямой пропорциональной зависимости.
15:х = 30:46 (23 рабочих)
Сигналы рукой: всё понятно, есть вопросы, непонятно
Вопрос тем, кому не всё понятно или совсем не понятно
— Что именно вам непонятно, выявление затруднений и пробелов. Возвращение учащихся, у которых есть вопросы к темам, понятиям, которые были плохо усвоены.
№694
20 км ———-100%
14 км ———-? %
Какая это пропорциональная зависимость?
Ответы: Прямая пропорциональная зависимость. При увеличении одной величины, вторая тоже увеличивается.

20: 14= 100 : х (70%; На 30% вторая бригада отремонтировала меньше)
Сигналы рукой: всё понятно, есть вопросы, непонятно
Самостоятельная работа а парах с проверкой
Карточки
Проверка решения задач на прямую и обратную пропорциональные зависимости
Заготовили корм на 48 дней для 20 коров. Насколько дней хватит этого корма для 15 коров?
За 4 дня машинистка перепечатала 30% рукописи. Сколько дней потребуется машинистке на перепечатку 75% рукописи, если она будет работать с той же производительностью?
Двигаясь со скоростью 60 км/ч, автомобиль может пройти расстояние от пункта А до пункта В за 2 ч 20 мин. За какое время пройдет автомобиль то же расстояние, если увеличит скорость на 10 км/ч?
Домашнее задание, комментарий
№ 675, №695
Дополнительно: подобрать пословицы и поговорки на прямую и обратную пропорциональную зависимость
Подведение уроков, рефлексия
Итоги в соответствии с поставленными целями:
Какие величины называются прямо пропорциональными? Обратно пропорциональными?
Как их различить?
Как решатся задачи на прямую и обратную пропорциональную зависимость?
Возьмите стикер и соотнесите ваши знания по теме в конце урока
На доске таблица
- Не знаю
Немного знаю
Знаю и умею
Прямая и обратная пропорциональные зависимости
Прямая пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. |
Примеры:
1) — периметр квадрата, — его сторона.
= 4.
Если = 1 см, то = 41 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: «величина прямо пропорциональна величине » или «зависимость между величинами и является прямой пропорциональностью«.
2) При движении с постоянной скоростью, пройденный путь и время движения прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
| Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу. |
В рассмотренных выше примерах для величин и это число равно 4, т.к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
Обратная пропорциональная зависимость
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Примеры:
1) Если расстояние является постоянной величиной, то скорость и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и — стороны прямоугольника, а его площадь 36 см2.
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т. к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
| Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу. |
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т.к. при удвоении возраста размер обуви человека не удваивается.
6 класс. Математика. Прямая и обратная пропорциональные зависимости — Прямая и обратная пропорциональные зависимости
Комментарии преподавателя
Частное двух чисел называют отношением этих чисел.
Пропорция – это равенство двух отношений.
Велосипедист за 3 часа проезжает 75 километров. За сколько времени он проедет 150 километров с той же скоростью?
Первым действием найдем скорость велосипедиста. Затем узнаем время, за которое он проедет 150 км.
Из решения видно, что при движении с одной и той же скоростью велосипедист за большее время пройдет большее расстояние. Во сколько раз больше пройденный путь, во столько раз больше затраченное на него время. Такие величины называют прямо пропорциональными.
Определение.
Две величины называют прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Мотоциклист проехал 3 часа со скоростью 60 км/ч. За сколько часов он проедет то же расстояние со скоростью 45 км/ч?
Первым действием найдем длину пройденного пути. Вторым действием – время движения со скоростью 45 км/ч.
Вторым действием – время движения со скоростью 45 км/ч.
Мотоциклист проехал одно и то же расстояние. Во сколько раз скорость мотоциклиста больше, во столько раз меньше затраченное на движение время. Такие величины называют обратно пропорциональными.
Определение.
Две величины называют обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Длина стороны квадрата и периметр связаны прямой пропорциональной зависимостью. Периметр квадрата – это сумма длин четырех его равных сторон. Если длину стороны увеличить в несколько раз, то периметр увеличится во столько же раз.
Длина и ширина прямоугольника (при заданной площади) связаны обратной пропорциональной зависимостью. Площадь прямоугольника – это произведение длины и ширины. Поэтому, чтобы площадь оставалась неизменной при увеличении длины в несколько раз, надо ширину уменьшить во столько же раз.
Скорость автомобиля и путь, который он проедет за определенное время, связаны прямой пропорциональной зависимостью. Время в данном случае – величина постоянная, поэтому при большей скорости автомобиль пройдет больший путь.
Возраст дерева и его высота не связаны пропорциональной зависимостью. В этом случае зависимость между величинами есть. Действительно, высота дерева с возрастом увеличивается, но не во столько же раз.
Стоимость товара, купленного по одной цене, и его количество связаны прямой пропорциональной зависимостью. Чем большее количество товара купили, тем большее количество денег на него потратили.
Возраст человека и размер его обуви не связаны пропорциональной зависимостью. Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.
Дробь и ее знаменатель (при постоянном числителе) связаны обратной пропорциональной зависимостью. Чем больше знаменатель, тем меньше дробь при постоянном числителе.
Чем больше знаменатель, тем меньше дробь при постоянном числителе.
Дробь и ее числитель (если знаменатель не изменяется) связаны прямой пропорциональной зависимостью.
Весной при проведении работ по озеленению города на улице посадили липы. Принялось 95% всех посаженных лип. Сколько посадили лип, если принялось 57 лип?
Величины, о которых говорится в задаче, связаны прямой пропорциональной зависимостью. Составим краткое условие задачи, запишем пропорцию и решим ее.
Стрелки в краткой записи направлены в одну сторону. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх).
Для отопления здания школы заготовили угля на 180 дней при норме расхода 0,6 т в день. На сколько дней хватит запаса, если расход ежедневно составит 0,5 т?
Стрелки в краткой записи направлены в разные стороны. . Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в разные стороны, одно из отношений переворачиваем и приравниваем то, что получилось.
. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в разные стороны, одно из отношений переворачиваем и приравниваем то, что получилось.
Эту задачу и аналогичные ей можно решить, и не выписывая пропорцию в явном виде.
В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа?
Стрелки в краткой записи направлены в одну сторону. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх). Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в одну сторону, приравниваем полученные отношения. Составляем пропорцию. Решаем ее. Итак, ответ – 31,5 кг примесей.
Составляем пропорцию. Решаем ее. Итак, ответ – 31,5 кг примесей.
Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равны. Если две величины обратно пропорциональны, то их произведение постоянно и не равно нулю
Принтер распечатывает 27 страниц за 4,5 минуты. За какое время он распечатает 300 страниц?
Зависимость между количеством напечатанных страниц и временем прямо пропорциональная. Составим пропорцию и решим ее.
Автомобиль проехал 310 километров, истратив 25 литров бензина. Какое расстояние может проехать автомобиль с полным баком, вмещающим 40 литров бензина?
Чем большее расстояние проедет автомобиль, тем больше бензина он потратит. Соответственно, зависимость между величинами прямо пропорциональная.
Пятнадцать рабочих выполняют заказ за 4 дня. Сколько нужно рабочих, чтобы выполнить тот же заказ за 3 дня?
Сколько нужно рабочих, чтобы выполнить тот же заказ за 3 дня?
Для того чтобы выполнить заказ быстрее, количество рабочих нужно увеличить. Соответственно, зависимость обратно пропорциональная.
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/otnosheniya-i-proporcii/pryamaya-i-obratnaya-proportsionalnye-zavisimosti
источник видео — http://www.youtube.com/watch?v=ALSAtOueOSw
источник видео — http://www.youtube.com/watch?v=buKHM8w_l4M
источник видео — http://www.youtube.com/watch?v=FtTrBSJz0AY
источник видео — http://www.youtube.com/watch?v=YMuRx7h3Mus
источник видео — http://www.youtube.com/watch?v=6ADjiJrSAtQ
источник презентации — http://ppt4web.ru/matematika/prjamaja-i-obratnaja-proporcionalnye-zavisimosti.html
math_tutorial_3
3.1 Введение пропорциональности
Часто величины, входящие в уравнения, можно напрямую связать друг с другом. Мы можем написать простые отношения между этими величинами, чтобы немного упростить решение проблем.
Мы можем написать простые отношения между этими величинами, чтобы немного упростить решение проблем.
Например, возьмите уравнение для средней скорости,
Средняя скорость рассчитывается как пройденное расстояние d, деленное на затраченное время t.
Если время остается фиксированным, но я еду с большей скоростью, я буду путешествовать дальше (d больше).
Обратите внимание, что для постоянного интервала времени, если я удваиваю V (путешествую вдвое быстрее), пройденное расстояние также удваивается. Можно сказать, что скорость прямо пропорциональна пройденному расстоянию .
Общие правила:
Когда мы говорим, что переменные величины x и y прямо пропорциональны , мы имеем в виду, что при изменении x и y отношение x / y остается постоянным. Сказать, что две величины пропорциональны, значит сказать, что они прямо пропорциональны. Когда мы говорим, что переменные величины x и y равны и обратно пропорциональны , мы имеем в виду, что при изменении x и y отношение xy остается постоянным.
Когда мы говорим, что переменные величины x и y равны и обратно пропорциональны , мы имеем в виду, что при изменении x и y отношение xy остается постоянным.
Отношения прямой и обратной пропорциональности распространены в физике.
Примеры
- Объекты, движущиеся с одинаковой скоростью v, имеют импульс p, , прямо пропорциональный их массам m. (p = mv).
- Закон идеального газа (PV = nRT) гласит, что давление P составляет прямо пропорционально (абсолютной) температуре T, когда объем V остается постоянным, и обратно пропорционально объему, когда температура остается постоянной.
- Ома (V = IR) гласит, что напряжение V на резисторе прямо пропорционально электрическому току в резисторе, когда сопротивление остается постоянным.
Закон
Попробуйте сами 1
Проверьте свое понимание с помощью этих истинных / ложных вопросов
Последовательность вопросов
Вопрос
1.
 1
1
1v7QY4By0fT4r7DkTADA13wZQZ2xoe7HuQm + SLydl1b86wiKfVaWSw0KdnU9KA0CcHC2Ok8j5IJPBMtnlWSBmFvUyiRdvRGVBBXMBMFvUyiRdvRGVBBXMBoWfeQ
Вопрос
1.2
/ VmLTTVfRwqsdDP / aOCGm7X4228NafyH8cmlk4DhphCutxKFVj5 / KShUFdsqVCUyyYCBA7YVZ8tyVfLUSxIdt / omNVuTzPC7NMI6PG7pkgj + zUEVqJXTAYIz6xtRuqVGKOszbNyYBKhcMo8NvHdiwsgAEeNeENR6vF7W6iEnljlPHQa4wnDBD83Ehw32ZeAF
Правильно. Проверьте, «если я удвою x, удвоится ли и y?» В этом случае нет, если константа c не равна нулю.
Неправильно. Проверьте, «если я удвою x, удвоится ли и y?» В этом случае нет, если константа c не равна нулю.
Вопрос
1.3
ydoZie6SEZ3eL8H5M / sYVGDsA2Wvcwf + Q6Tvzyeqwh2aC + 9VGQO9T1H / Xr5Zrb6ZWl54IRePoS5a / Uxy1X5ObN2MWRExyywQSp5KiEXJQJDXr59
Правильно. В этом уравнении x обратно пропорционален y.
Неправильно. В этом уравнении x обратно пропорционален y.
Вопрос
1.4
jcO / n1Xu4byMZmKdS2DLnK1HxeRsctlbIB4ErcLnunwNCfPqoLqAAJSr1olQalKUkYz4LDCkV7JEhlSJKvH9KdA / Nz4VkJGfX1LXAj5 + Nz4VkJGfX1LXAj04 + FX1LXF30 + JGFX1LXAJ03 + JGFX1LXF30 +
Правильно.Отношение x / y 2 равно константе, поэтому они прямо пропорциональны.
Неправильно. Отношение x / y 2 равно константе, поэтому они прямо пропорциональны.
3.2 Константы пропорциональности
Когда две величины прямо пропорциональны, эти две величины связаны константой пропорциональности.
Например. Если вам платят за работу по обычной ставке R в долларах в день, деньги M, которые вы зарабатываете, прямо пропорциональны времени t, которое вы работаете.
- Ставка R — это коэффициент пропорциональности, который связывает деньги, заработанные в долларах, с отработанным временем t в днях:
- Вы можете записать эту взаимосвязь в виде уравнения, M = Rt (заработанные деньги = норма заработка x отработанное время).

- Если вы заработаете 400 долларов за 5 дней, значение R составит 400 долларов (5 дней) = 80 долларов в день.
Последовательность вопросов
Вопрос
1.5
wu0KXQ5TiVxmztloPab8mxyu3obs2NdGdtrUukmJwqSBZpyC5k7Qt4pRX7BahIfa0ENZaQ0xPn4 =
Правильно.M = (80 долларов в день) (8 дней) = 640 долларов.
Неправильно. M = (80 долларов в день) (8 дней) = 640 долларов.
Попробуйте еще раз. Подсказка: используйте значение R, вычисленное выше, чтобы найти решение.
3
Иногда константу пропорциональности можно игнорировать в задачах пропорциональности. Поскольку сумма, которую вы зарабатываете за 8 дней, в 8/5 раз больше, чем вы зарабатываете за 5 дней, эта сумма составляет
.
м8 дней = 8 дней (400 долл. США / 5 дней) = 640 долл. США
США
Мы рассмотрим эту идею подробнее в следующем разделе.
3.3 Составление соотношений пропорциональности
В простом уравнении x = zy
Если z — постоянная величина, x прямо пропорционален y.
Это отношение можно записать как
\ (х \ пропто у \)
Если две величины прямо пропорциональны, то при вычислении x / y всегда будет одно и то же значение — при условии, что в уравнении нет других непостоянных переменных.
Это означает, что мы можем написать другое отношение
x 0 / y 0 = x 1 / y 1
Следующий рабочий пример продемонстрирует, как это может быть полезно.
Рабочий пример: растяжение пружины (закон Гука)
Если вы растянете пружину на расстояние d, она окажет на вашу руку восстанавливающую силу F. Сила зависит от того, насколько вы растягиваете пружину, и это соотношение описывается уравнением
F = -kd
- Сила F равна прямо пропорциональна расстоянию d.

- Это отношение также можно записать как \ (F \ propto d \)
- -k — константа пропорциональности
Вопрос: Если пружина изначально растягивается на 2 см от ее расслабленного положения, я измеряю восстанавливающую силу 10 Н.Подсчитайте, какой была бы восстанавливающая сила, если бы я вместо этого растянул пружину на 6 см от ее положения покоя.
Решение: Чтобы решить эту проблему, вы можете сначала решить для k, используя d = 2 см и F = 10N, а затем использовать значение, чтобы найти значение F для d = 6 см, но мы сделаем это по-другому.
с
F = -kd и –k — постоянная, \ (F \ propto d \)
Это означает, что я могу использовать правило, F / d является константой
Мы можем написать новое выражение
F 0 / d 0 = F 1 / d 1
Где F 0 и d 0 представляют числовые значения для начального участка, а F 1 и d 1 представляют значения для второго участка.
Перестановка этого выражения дает,
F 1 = F 0 d 1 / d 0
Теперь вы можете решить для F 1
F 1 = 10N (6 см) / 2 см = 30N
Обратите внимание, что с помощью этого метода мы не вычисляли значение k, это не требовалось для решения проблемы.
Попробуйте сами 2
Ускорение может быть описано уравнением F = ma, где ускорение a является результатом приложенной силы F к объекту массы m.
Последовательность вопросов
Вопрос
1.6
AQuI2D1FeXwtbOBrp0eXBWfmOjFfWYyrA + 5HpdVS52BznKDjQc6FCKn7cxzG / xpKVq + NaRsFt6jV4K0gXnj6Rrw267oup7PScIxGvIfNt / EPfq1E0Yfi9T2vaWsVdjgJ1EhvGmympUATUY6Nn704XCKlKLB5YocKuZZ9eEujCNt0zF2t9fZV15G2dUOR3WsLGvN8S + 5jUFV8FibEzP7ruvIg2xIPuVIksMmvVUHmkSTVQ5 + qL19G / uzzNudOJorB8Bk3277zeiznCO6nEzyZsKmM6rXX6Lqyu01vi5s / I1YKuWLOHMY1qEmE4Bi3MfU + y03vFT2RTQE / lk34e06cl9zs416xJjyYpqKKg78Z6LbBGSuGGuNF5FJYWNug5l + yzLXXx6eWCW7fYwTo2WOQaIL0ovEW + KQE
Правильно.
Неправильно.
Попробуйте еще раз. Подсказка: масса обратно пропорциональна ускорению.
3
P’Cast: Рисование кубиками
Попробуйте сами 3
Последовательность вопросов
Вопрос
1,7
Потенциальная энергия U, запасенная в растянутой пружине, определяется уравнением:
U = ½kd 2
где k — жесткость пружины.
CJRY6 / yNMbqw7terMPmh5OHLvsILTeo9QWE3v3oDVdFumRf3BZ / y5UVykcfruJH9IO0t + X6TT0u4LYvt6ENj44X1mLzrTxtePCE + jDYGVcgeKMUdiNlWyM8QlpI5 + cJhZly1oljDvrBde / Eauba3lhM6z2Dx3qt2e9M3tWXYIrwl / PDXzAzc0DmIRMzEBfmDWNrE85so40 + hcopX33jQRyN5HGzh6ByADhQ / dyuKEBdHtWemqptx9o2GjPCdCjJsPlTajvgyXoiAzx1sU + FhLqdVcOYvvrdAZDUowiFCnERfondVURAs0LDZ8UOD6nTkDcz7iW + zLKftGEe + KCSdXzzMa672AuyWzQKDjCEKA + 6 / Ye5b5mg + AzrvndUARc + Xdy3YWEreM3O7m / 2l8sKJewn1la0ualpQ2eVLcOLyFngEwJYl
3
Правильно.
Попробуйте еще раз. Подсказка: U \ (\ propto \) d 2
Неправильно.
Прямая пропорциональность из повседневной жизни
Здесь мы перечисляем несколько важных примеров прямой пропорциональности; где у нас есть две величины, и одна всегда является фиксированным кратным другой.
Прямые пропорции играют большую роль в нашей повседневной жизни. Здесь мы рассмотрим ряд наглядных примеров. На этом этапе вы узнаете о
- ключевых определениях прямой пропорциональности
- прямых пропорциях, возникающих в ситуациях, связанных со скоростью, деньгами, топливной экономичностью вашего автомобиля и ролью \ (\ normalsize {\ pi} \).
Что такое прямая пропорциональность?
Если \ (\ normalsize {x} \) и \ (\ normalsize {y} \) — две переменные величины, которые удовлетворяют соотношению \ [\ Large {y = kx} \] для некоторого фиксированного числа \ (\ normalsize {k } \), то мы говорим, что \ (\ normalsize {y} \) прямо пропорционален \ (\ normalsize {x} \). Число \ (\ normalsize {k} \) называется константой пропорциональности . Один из важных способов размышления об этой константе \ (\ normalsize {k} \) состоит в том, что она говорит нам, насколько \ (\ normalsize {y} \) увеличивается на, если мы увеличиваем \ (\ normalsize {x} \) ровно на \ (\ normalsize {1} \).Мы будем писать \ [\ Large {y \ propto x} \], чтобы выразить, что \ (\ normalsize {y} \) прямо пропорционален \ (\ normalsize {x} \). Обратите внимание, что этот символ, однако, теряет важную информацию: точное значение константы пропорциональности.
Число \ (\ normalsize {k} \) называется константой пропорциональности . Один из важных способов размышления об этой константе \ (\ normalsize {k} \) состоит в том, что она говорит нам, насколько \ (\ normalsize {y} \) увеличивается на, если мы увеличиваем \ (\ normalsize {x} \) ровно на \ (\ normalsize {1} \).Мы будем писать \ [\ Large {y \ propto x} \], чтобы выразить, что \ (\ normalsize {y} \) прямо пропорционален \ (\ normalsize {x} \). Обратите внимание, что этот символ, однако, теряет важную информацию: точное значение константы пропорциональности.
Расстояние при ходьбе пропорционально времени.
Если мы идем с постоянной скоростью, скажем, \ (\ normalsize {6} \) км / час, то у нас есть простой пример прямой пропорциональности \ [\ Large {\ operatorname {distance} \ propto \ operatorname {time }} \], поскольку расстояние (км) = \ (6 \ times \) время (час).Константа пропорциональности, в данном случае \ (\ normalsize {6} \) км / ч, называется скоростью или скоростью . Однако олимпийский спортсмен по спортивной ходьбе будет двигаться намного быстрее, скажем, вдвое быстрее на скорости \ (\ normalsize {12} \) км / ч.
Однако олимпийский спортсмен по спортивной ходьбе будет двигаться намного быстрее, скажем, вдвое быстрее на скорости \ (\ normalsize {12} \) км / ч.
Q1 (E): Опишите связь между расстоянием и временем для спортсменов-олимпийцев, используя эту терминологию.
Q2 (M): Расстояние прямо пропорционально времени. Но время прямо пропорционально расстоянию! Какова константа пропорциональности в этом соотношении для спортсменов-олимпийцев?
Время в часах и минутах
Возможно, наиболее убедительное использование прямой пропорциональности — это соотношение между часами и минутами:
\ [\ Large {\ operatorname {time (min)} = 60 \ times \ operatorname {time (hr )}.} \]
Связь между часами и минутами настолько вездесуща, что большинство людей знают наизусть, что 15 минут — это четверть часа. Эта информация содержится в приведенном выше уравнении, которое мы можем увидеть, установив \ (\ normalsize \ mbox {time (hr)} = \ frac {1} {4}. \)
\)
\ [{\ Large \ operatorname {time ( min)} = 60 \ times \ frac {1} {4} = 15}. \]
А сколько минут в получасе? Ответ:
\ [{\ Large \ operatorname {time (min)} = 60 \ times \ frac {1} {2} = 30}. \]
Q3 (E): Сколько минут в день?
Расстояние, которое ваша машина может проехать, в зависимости от количества бензина в вашем баке.
Это другой вид пропорциональности, также включающий расстояние — теперь между тем, как далеко вы можете проехать в своей машине, и количеством бензина в вашем баке.
Если у вас нулевой газ, вы никуда не денетесь. Допустим, вы водите Holden Commodore — популярный австралийский автомобиль с объемом бака \ (\ normalsize {73} \) литров. Как далеко вы уедете, зависит от того, едете ли вы по городу или по автостраде, включен или выключен кондиционер и т. Д. Но в среднем, допустим, вы можете проехать \ (\ normalsize {12} \) км по литр (л) газа.Тогда соответствующая пропорциональность равна
\ [{\ Large \ mbox {distance (km)} \, \ propto \, \ mbox {gas (L)}} \]
с константой пропорциональности число \ (\ normalsize {12 } \) км / л, которая является мерой топливной экономичности автомобиля.
Q4 (E): Можете ли вы проехать на Holden Commodore с полным баком бензина из Брокен-Хилла в Даббо без остановки?
Диаметр и длина окружности
Прямая пропорциональность также очень важна в математике.Например, важным фактом является то, что длина окружности \ (\ normalsize {c} \) круга прямо пропорциональна его диаметру \ (\ normalsize {d} \). Фактически
\ [\ Large {\ operatorname {окружность} = \ pi \ times \ operatorname {Diameter}} \]
, где константа пропорциональности — известная константа \ (\ normalsize {\ pi} \), примерно \ ( \ normalsize {3.1415926….} \)
Итак, если вы удвоите диаметр, вы удвоите длину окружности. Другое следствие состоит в том, что если вы увеличиваете диаметр на единицу \ (\ normalsize {1} \), тогда длина окружности увеличивается на \ (\ normalsize {\ pi} \) единиц.Это не зависит от фактического размера круга, что может вызывать удивление.
Q5 (M): Если у нас есть веревка, туго обвязанная вокруг экватора Земли, и мы хотим добавить немного веревки, чтобы мы могли равномерно растянуть ее на полметра от земли, тогда какую длину веревки мы должны добавить?
Ответы
A1.
Один ответ: \ ({\ normalsize \ mbox {distance} \ propto \ mbox {time}} \). Однако это мог описать кто угодно! Более осмысленный ответ:
\ [\ Large {\ mbox {distance} = 12 \ times \ mbox {time}}.\]
Еще лучше, если вы включите единицы измерения расстояния и времени.
A2. Мы можем переставить \ (\ normalsize {\ mbox {distance} = 12 \ times \ mbox {time}} \) в
\ [{\ Large \ mbox {time} = \ frac {1} {12} \ times \ mbox {distance}}. \]
Таким образом, коэффициент пропорциональности равен \ (\ frac {1} {12} \).
A3. Связь между днями и часами — еще один пример прямой пропорциональности:
\ [{\ Large \ mbox {time (hr)} = 24 \ times \ mbox {time (days)}.} \]
Теперь мы объединяем прямая пропорциональность для минут и часов с прямой пропорциональностью для часов и дней:
\ [{\ Large \ mbox {time (min)} = 60 \ times \ mbox {time (hr)} = 60 \ times \ left (24 \ times \ mbox {time (days)} \ right)}.\]
Мы получаем новую прямую пропорциональность:
\ [{\ Large \ mbox {time (min)} = 1440 \ times \ mbox {time (days)}.
} \]
Итак, есть \ ({\ normalsize 1440 } \) минут в день.
A4. Вы можете рассчитывать проехать \ ({\ normalsize 73 \ times 12 = 876} \) км на одном баке бензина. Поскольку от Брокен-Хилла до Даббо можно добраться за \ ({\ normalsize 799 — 49 = 750} \) км, то да — вы можете совершить эту поездку без остановок.
А5. Мы увеличиваем диаметр на \ (\ normalsize {1} \), поэтому окружность должна увеличиваться на \ (\ normalsize {\ pi} \), то есть немного больше, чем \ (\ normalsize {3} \) метров.Для многих это совершенно не интуитивно!
Прямая и обратная пропорция — Прямая и обратная пропорция — Edexcel — GCSE Maths Revision — Edexcel
Прямая пропорция
Существует прямая пропорция между двумя значениями, когда одно кратно другому. Например, \ (1 \: \ text {cm} = 10 \: \ text {mm} \). При переводе сантиметров в миллиметры множитель всегда равен 10. Прямая пропорция используется для расчета стоимости бензина или обменных курсов иностранных денег.
Например, \ (1 \: \ text {cm} = 10 \: \ text {mm} \). При переводе сантиметров в миллиметры множитель всегда равен 10. Прямая пропорция используется для расчета стоимости бензина или обменных курсов иностранных денег.
Символ прямой пропорции — \ (\ propto \).
Выражение ‘t прямо пропорционально r’ можно записать с помощью символа пропорциональности:
\ [t \ propto r \]
Если \ (y = 2p \), то \ (y \) пропорционально \ (p \) и \ (y \) могут быть вычислены для \ (p = 7 \):
\ [y = 2 \ times 7 = 14 \]
Аналогично, если \ (y = 60 \), то \ (p \) можно вычислить:
\ [60 = 2p \]
bbbeg6kqb2.0.0.0.1:0.1.0.$0.$1.$9″> Чтобы найти \ (p \), разделите 60 на 2:
\ [60 \ div 2 = 30 \]
Прямая пропорция — выше
Пропорциональность может использоваться для создания уравнения.
Для этого есть четыре шага:
- запишите пропорциональную зависимость
- преобразовать в уравнение с использованием константы пропорциональности
- использовать данную информацию для нахождения константы пропорциональности
- подставить константу пропорциональности в уравнение
Пример
Значение \ (e \) прямо пропорционально \ (п\). Когда \ (e = 20 \), \ (p = 10 \). Найдите уравнение, связывающее \ (e \) и \ (p \).
- \ [e \ propto p \]
- \ [e = kp \]
- \ (20 = 10k \), поэтому \ (k = 20 \ div 10 = 2 \)
- \ [e = 2p \ ]
Это уравнение теперь можно использовать для вычисления других значений \ (e \) и \ (p \).
Если \ (p = 6 \), то \ (e = 2 \ times 6 = 12 \).
Обратная пропорция
Если одно значение обратно пропорционально другому, то оно записывается с использованием символа пропорциональности \ (\ propto \) по-другому. Обратная пропорция возникает, когда одно значение увеличивается, а другое уменьшается. Например, большее количество рабочих сократит время на выполнение задачи. Они обратно пропорциональны.
Утверждение «b обратно пропорционально m» записывается:
\ [b \ propto \ frac {1} {m} \]
Уравнения, содержащие обратные пропорции, могут использоваться для вычисления других значений.
Использование: \ (g = \ frac {36} {w} \) (поэтому \ (g \) обратно пропорционально \ (w \)).
Если \ (g = 8 \), найти \ (w \).
\ [8 = \ frac {36} {w} \]
\ [w = \ frac {36} {8} = 4.5 \]
Аналогично, если \ (w = 6 \), найти \ ( грамм\).
\ [g = \ frac {36} {6} \]
\ [g = 6 \]
Обратная пропорция — выше
Пропорциональность может использоваться для создания уравнения.
Для этого есть четыре шага:
- запишите пропорциональную зависимость
- преобразовать в уравнение с использованием константы пропорциональности
- использовать данную информацию для нахождения константы пропорциональности
- подставить константу пропорциональности в уравнение
Пример
Если \ (g \) обратно пропорционально w и когда \ (g = 4 \), \ (w = 9 \), то сформируйте уравнение, связывающее \ (g \) с \ (w \).
- \ [g \ propto \ frac {1} {w} \]
- \ [g = k \ times \ frac {1} {w} = \ frac {k} {w} \]
- \ ( 4 = \ frac {k} {9} \), поэтому \ (k = 4 \ times 9 = 36 \)
- \ [g = \ frac {36} {w} \]
Это уравнение можно использовать для вычислить новые значения \ (g \) и \ (w \).
Если \ (g = 8 \), найти \ (w \).
\ [8 = \ frac {36} {w} \]
\ [w = \ frac {36} {8} = 4.5 \]
Аналогично, если \ (w = 6 \), найти \ ( грамм\).
\ [g = \ frac {36} {6} \]
\ [g = 6 \]
Иллюстративная математика
Задача
Учебник дает следующее определение двух величин как прямо пропорциональных:
Мы говорим, что $ y $ прямо пропорционально $ x $, если $ y = kx $ для некоторой константы $ k $.
В качестве домашнего задания учащихся попросили переформулировать определение своими словами и привести пример концепции. Ниже приведены некоторые из их ответов. Обсудите каждое утверждение и пример. Переведите утверждения и примеры в уравнения, чтобы помочь вам решить, верны ли они.
- Маркус:
Это означает, что оба количества одинаковы. Когда одно увеличивается, другое увеличивается на ту же величину. Примером этого может быть количество воздуха в воздушном шаре и объем воздушного шара.
- Сэди:
Две величины пропорциональны, если одно изменение сопровождается изменением другого. Например, радиус круга пропорционален площади.
- Бен:
Когда два количества прямо пропорциональны, это означает, что если одно количество увеличивается на определенный процент, другое количество также увеличивается на тот же процент. Примером может служить рост цен на газ и рост цен на продукты питания.
- Джессика:
Когда две величины пропорциональны, это означает, что по мере увеличения одной величины другая будет также увеличиваться, и соотношение количеств одинаково для всех значений.Примером может быть длина окружности и ее диаметр, отношение значений будет равно $ \ pi. $
Комментарий IM
Задача преследует две основные цели. (1) Учащиеся понимают смысл определения прямой пропорциональности. (2) Они участвуют в SMP 3 «Приведите жизнеспособный аргумент и критикуйте рассуждения других» и SMP 6 «Заботьтесь о точности».
Когда учеников просят прочитать объяснения того или иного определения, это заставляет учащихся более глубоко изучить определение.Чтобы помочь ученикам решить, правильно ли объяснение, учителя могут посоветовать им перевести слова в уравнения и попытаться «сломать» новые формулировки. Это естественным образом приводит к необходимости уделять внимание точности языка. Многие из приведенных объяснений частично верны, но недостаточно точны. Объяснение «Две величины пропорциональны, если одно изменение сопровождается изменением другого». верно, но неполно. Объяснение: «Когда два количества прямо пропорциональны, это означает, что если одно количество увеличивается на определенный процент, другое количество также увеличивается на тот же процент.»на самом деле правильно, но не очевидно.
Студенты также должны решить, иллюстрирует ли данный пример определение. Сделайте это, студентов снова следует побуждать переводить слова в уравнения.
Чувство меры | Математика
Две переменные считаются пропорциональными, если изменение одной можно предсказать по изменению другой. Есть два различных типа пропорциональных отношений, относящихся к химикам средней школы: прямая и обратная пропорция.Прямая пропорция концептуально проще — например, если мы удвоим объем твердого тела, мы также удвоим его массу.
Эту идею, конечно, можно перевести в математическую нотацию. Предположим, что когда переменная x равна 1, соответствующая переменная y имеет значение 3; и когда x удваивается, так что его значение равно 2, y также удваивается, поэтому его значение равно 6. Мы могли бы тогда предположить, что, когда x равно 3, y будет иметь значение 9.Это действительно было бы так, если бы x прямо пропорционально y .
Следовательно, отношение y к x является постоянным:
, и это постоянное отношение известно как «константа пропорциональности». Действительно, проверка того, находятся ли две переменные в прямой зависимости, заключается в том, имеют ли они постоянное соотношение. Другими словами, если мы разделим значение одной переменной на другую, получим ли мы каждый раз одно и то же значение? Если ответ положительный, переменные изменяются прямо пропорционально друг другу, что мы можем записать как
.
y ∝ x
Если обозначить эту константу пропорциональности k , то получим
Умножение обеих сторон на x дает
y = kx
Это можно сравнить с общим уравнением прямой
y = м x + c
с уклоном м = k и пересечением c = 0.Следовательно, если две величины находятся в прямой пропорции, график зависимости одной от другой будет прямой линией, проходящей через начало координат (fig1) .
Прямая пропорция в химии
Интересным примером этого является закон Бера-Ламберта, который позволяет нам вычислить степень поглощения света, когда он проходит через раствор. Это поглощение, A, определяется уравнением
.
A = ε класс
Обратите внимание, что теперь мы используем c для представления концентрации раствора, а l представляет длину пути, то есть расстояние, которое свет проходит через раствор.Другой член в уравнении, ε , представляет собой молярный коэффициент поглощения и является константой. Для данного спектрометра, измеряющего разные растворы одного и того же вещества, длина пути и молярные коэффициенты поглощения будут постоянными, поэтому их умножение также дает константу εl . Разделив обе части уравнения на c , получим
, и поскольку это отношение является постоянным, A прямо пропорционально c .
Например: поглощение 0,01 моль дм -3 раствора брома в тетрахлорметане составляет 0,55. 1 Таким образом, оптическая плотность раствора 0,02 моль-дм –3 составляет 1,1; если мы удвоим концентрацию, абсорбция удвоится благодаря прямо пропорциональному соотношению между двумя переменными.
Обратная пропорция
Если две переменные находятся в обратной пропорции, когда мы удваиваем одну, другая уменьшается вдвое. Если x = 4, когда y = 12, и удвоение x до 8 приводит к уменьшению y вдвое до 6, мы можем ожидать, что x обратно пропорционален y .Если это так, то повторное удвоение x до 16 должно привести к тому, что y снова уменьшится вдвое до 3. В этом случае произведение двух переменных остается постоянным
xy = 4 x 12 = 8 x 6 = 16 x 3 = 48
и мы можем написать
Графическое представление двух обратно пропорциональных переменных менее полезно, чем для прямой пропорциональности, в результате получается кривая (рис. 2).
Обратная пропорция в химии
Эта идея имеет фундаментальное значение в лаборатории при разбавлении концентрированных растворов.Концентрация, c, раствора равна
.
, где n — количество растворенного вещества, а V — объем раствора. Если мы умножим обе части этого уравнения на V , мы получим
n = cV
Рассмотрим на мгновение процесс разбавления раствора. Начинаем с определенного объема раствора, а затем добавляем еще растворителя. Таким образом, количество вещества n, останется постоянным, в то время как объем, V, и концентрация, c, изменятся обратно пропорционально друг другу.
Если мы начнем с объема V 1 при концентрации c 1 и разбавим до объема V 2 при концентрации c 2, , значение n останется постоянным, поэтому у нас
c 1 V 1 = c 2 V 2
Если мы разделим обе части этого уравнения на V 2, , мы получим
, чтобы мы могли рассчитать концентрацию любого разбавленного раствора с учетом начальной концентрации, а также начального и конечного объемов.С другой стороны, если мы разделим обе части на c 2, , мы получим
, чтобы мы могли определить конечный объем, необходимый для получения раствора заданной концентрации c 2 .
Допустим, 6,7 см 3 серной кислоты 2 начальной концентрации 0,15 моль-дм -3 разбавили до 16,5 см 3 . У нас
V 1 = 6,7 см 3
В 2 = 16.5 см 3
c 1 = 0,15 моль дм -3
Таким образом, мы можем рассчитать конечную концентрацию от
Здесь следует отметить два момента. Во-первых, единицы V 1 и V 2 отменяются, оставляя нас с c 1 и c 2 , имеющими те же единицы. Во-вторых, можно ожидать, что концентрация разбавленного раствора будет меньше исходной, что и есть.Можно стать достаточно опытным в этих вычислениях, чтобы их можно было выполнять интуитивно, а не используя формальное производное уравнение.
Предположим, что мы хотим получить раствор аммиака 0,2 моль дм -3 , 2 , исходя из 500 см 3 раствора 0,5 моль дм -3 . Мы можем рассчитать требуемый окончательный объем от
с
c 1 = 0,5 моль дм -3
с 2 = 0.2 моль дм -3
V 1 = 500 см 3
, так что
На этот раз мы, конечно, ожидаем получить больший объем разбавленного раствора. Важно помнить, что это конечный объем раствора, поэтому количество воды, которое необходимо добавить, получается путем вычитания начального объема раствора из окончательного общего количества
.
1250 см 3 — 500 см 3 = 750 см 3
Линда Фишер из Университета штата Флорида, США, исследовала стратегии, используемые учителями средней математики для решения задач пропорций, 3 и обнаружила, что большинство из них склонны использовать алгебраический подход (как описано здесь), а не менее формальные методы.Сьюзан Леймон отмечает, что термин «пропорциональное рассуждение» неправильно определен, 4 и что его мастерство остается нечетким побочным продуктом обучения фракциям. Она также заявляет, что, хотя для этого требуется понимание относительно элементарных математических идей, он обеспечивает основу для понимания гораздо более сложных тем. Джейн-Джейн Ло, Джинфа Кай и Тад Ватанабе представили интересное сравнение того, как эта тема трактуется в учебниках из трех азиатских регионов и США. 5 Учебники различаются определением термина «соотношение», способом введения равных соотношений и типом включенных прикладных задач.
Пол Йейтс — советник по стратегическому академическому развитию в Честерском университете, Великобритания
МОДУЛЬ ВРЕМЕНИ M35 — пропорция
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
ПРИНУДИТЕЛЬНЫЕ ЗНАНИЯ
- Свободное владение арифметикой целых чисел и дробей.
- Знакомство с основными единицами измерения расстояния, времени, массы и объема.
- Построение прямолинейных графиков.
- Определение градиента прямолинейного графика.
- Знакомство с коэффициентами и ставками.
- Простые формулы и уравнения.
МОТИВАЦИЯ
Доктора и медсестры рассчитывают, сколько лекарства нужно ввести, используя
идеи пропорции. Например, предположим, что лекарство нужно вводить из расчета
20 микрограмм на кг в минуту.Если пациент весит 56 кг, сколько миллиграммов он должен получить за один час?
Люди, работающие в науке, финансах и во многих других областях, ищут взаимосвязи между различными интересами. Эти отношения часто оказываются либо линейными, либо гиперболическими. То есть график, связывающий эти величины, представляет собой либо прямую линию, либо гиперболу.
В этом модуле мы в основном занимаемся формулами (см. Модуль Формулы), для которых соответствующие графы являются прямыми линиями или прямоугольными гиперболами.В первом случае мы имеем прямую пропорцию, а во втором — обратную.
Рассмотрим очень простой пример: I = закон Ома, связывающий V с напряжением (разностью потенциалов), I с током и R с сопротивлением проводника.
Закон Ома лежит в основе изучения электричества. Если R — константа, I прямо пропорционален V. Если V — константа, I обратно пропорционален R. В модуле Rates and Ratios формула d = vt, соединяющая пройденное расстояние d, затраченное время t и скорость V был представлен и обсужден.Для постоянной скорости пройденное расстояние пропорционально пройденному времени, а для фиксированного расстояния затраченное время обратно пропорционально скорости.
Более сложные ситуации также рассматриваются с использованием пропорций. Известный пример из науки: для тела, движущегося с постоянным ускорением, пройденное расстояние
пропорционально квадрату путешествия во времени.
Существует огромное множество применений пропорции, и это станет очевидным из множества примеров, приведенных в разделе содержания модуля.
В этом модуле будет представлен ряд формул из физики, однако знание соответствующих физических принципов не является необходимостью для читателя.
СОДЕРЖАНИЕ
В этом модуле мы будем использовать слова «переменная» и «константа» вместо одного слова
«местоимение».
Прямая пропорция
Определение
Говорят, что переменная y прямо пропорциональна x, если
y = kx для некоторой ненулевой константы k.
Константа k называется константой пропорциональности.
Выражение «y прямо пропорционально x» символически записывается как
у х.
Иногда в литературе вместо пропорции употребляется слово вариация.
График y = kx — это прямая линия, проходящая через начало координат. Его градиент k является константой пропорциональности. (Значения, которые может принимать x, часто являются положительными действительными числами, но это не всегда так.)
Вот простой пример прямой пропорции.
Дэвид выезжает из дома с постоянной скоростью 100 км / ч.
Формула для расстояния d км, пройденного за t часов:
д = 100т.
Дэвид уйдет вдвое дальше в два раза больше, в три раза больше в три раза и так далее.
График зависимости d от t представляет собой прямую линию, проходящую через начало координат. В этом примере d прямо пропорционально t, и мы пишем d t.Константа 100 — это константа пропорциональности, и это градиент линии.
Обратите внимание, что в этом примере константа пропорциональности — это скорость, то есть коэффициент. Ставки — один из самых распространенных примеров пропорции.
Ставки, соотношения и пропорции
Ставки и коэффициенты были учтены в модуле «Ставки и коэффициенты». Идеи
этого модуля получили дальнейшее развитие и рассматриваются с другой точки зрения.
Тарифы
Все ситуации с постоянной скоростью, аналогичные приведенному выше примеру автомобиля, движущегося с постоянной скоростью, являются примерами прямой пропорциональности.
Например, если вода течет в резервуар со скоростью 5 литров / мин, количество воды V литров, которое втекает в резервуар через t минут, определяется формулой V = 5t. Таким образом, объем воды прямо пропорционален времени, в течение которого вода втекает в него.
Вот таблица значений для этой ситуации.
Как видно из таблицы, это постоянная величина.
= = = = = 5.
Таким образом, отношение V: t постоянно.
В: t = 5: 1 = 10: 2 = 15: 3 = 20: 4.
Из этого примера видно, как связаны постоянные нормы, постоянные отношения и прямая пропорция.
Передаточные числа
Предположим, что размеры прямоугольника находятся в соотношении 3: 2. Пусть x — длина прямоугольника, а y — ширина. Тогда
y: x = 3: 2 или = или y =.
Ширина y прямоугольника прямо пропорциональна длине прямоугольника.
Константа пропорциональности равна.График зависимости y от x представляет собой прямую линию, проходящую через точку
с градиентом.
ПРИМЕР
Лента шириной 3 см и длиной 1 см обрезана. Площадь отрезанной ленты Acm2 определяется формулой A = 3l. Напишите формулировку пропорции словами и символами, укажите константу пропорциональности и нарисуйте график зависимости A от l.
Решение
Так как A = 3l, A прямо пропорционально
l, и мы можем написать A l.Константа пропорциональности
равна 3.
Прямо пропорциональная собственность
Ниже приведены три важных свойства пропорции.
Применение свойств
Есть много приложений, которые иллюстрируют второе и третье свойства
прямой пропорции.
Пример объекта 2
Если автомобиль движется со скоростью 60 км / ч, расстояние Skm, пройденное за t часов, равно
S = 60т.Здесь S t и коэффициент пропорциональности 60. Перестановка дает
t = S. Следовательно, t S и коэффициент пропорциональности равен.
Пример объекта недвижимости 3
Для выращивания риса требуется 40 кг азотных удобрений на гектар, а стоимость 1 кг
составляет 50 центов. Пусть A гектаров — это площадь, n — количество требуемых килограммов удобрений, а
$ C — общая стоимость удобрений. У нас n = 40A и C = 0,5n. Это означает n A и
C n.Следовательно, C A. Мы видим, что C = 20A, поэтому C A.
Другие примеры прямой пропорции
Есть много примеров прямой пропорции. Вот несколько элементарных примеров, показывающих, насколько распространена эта идея.
Из торговли
- Когда мы читаем цену на нефть в 72 доллара за баррель, мы предполагаем, что цена определенного количества нефти прямо пропорциональна количеству баррелей. Большинство проблем с удельной стоимостью связаны прямо пропорционально.
- Сумма налога на товары и услуги, подлежащего уплате за товар, прямо пропорциональна его стоимости.Константа пропорциональности 10%.
- Для заданной процентной ставки, например 6% годовых, сумма процентов, полученных за фиксированный период, прямо пропорциональна инвестированной сумме.
- Курсы валют. Стоимость предмета в евро пропорциональна его стоимости в долларах.
Из измерения
- Преобразование единиц измерения обычно происходит прямо пропорционально. Например, преобразование сантиметров в метры или футов в метры.Есть примеры, когда преобразование единиц измерения не связано с прямой пропорцией, например, преобразование Фаренгейта в Цельсия.
- Глубина воды в контейнере, который представляет собой прямую призму с горизонтальным «основанием», прямо пропорциональна объему воды, а объем прямо пропорционален глубине воды.
- Периметр правильного многоугольника прямо пропорционален длине одной стороны.
- Длина окружности прямо пропорциональна радиусу окружности с константой пропорциональности 2π.И наоборот, радиус круга прямо пропорционален длине окружности. (C = 2πr и r =)
- На карте, нарисованной в масштабе, расстояние между любыми двумя точками на карте пропорционально расстоянию между двумя местоположениями, которые представляют точки,
с константой пропорциональности, являющейся масштабом карты.
Из науки
- Масса тела пропорциональна его объему. Константа пропорциональности равна
плотности тела.Например, плотность воды составляет 1 грамм / см3. (Формула m = ρV) - Ускорение тела пропорционально действующей на него равнодействующей силе.
Константа пропорциональности — это масса. (Формула a =) - Сила, действующая на определенный объект под действием силы тяжести, пропорциональна массе объекта. Константа пропорциональности между массой и силой известна как ускорение свободного падения.
- При постоянной силе, действующей на тело, работа, совершаемая силой, пропорциональна расстоянию, на которое движется тело.(Формула W = Fd)
- Гравитационная потенциальная энергия тела над поверхностью земли пропорциональна высоте тела над поверхностью земли. Константа пропорциональности является произведением массы и ускорения свободного падения.
- Для тела, движущегося по окружности с постоянной угловой скоростью, линейная скорость (тангенциальная скорость) пропорциональна угловой скорости. Константа пропорциональности — это радиус круга. (Формула v = ωr)
- Принцип Архимеда: Вес вытесняемой жидкости прямо пропорционален объему вытесненной жидкости.Проще говоря, принцип гласит, что выталкивающая сила, действующая на объект, равна весу жидкости, вытесняемой объектом.
- Закон Чарльза: при постоянном давлении объем V заданной массы идеального газа увеличивается или уменьшается в тот же раз, что и его температура T на шкале абсолютных температур (т. Е. Газ расширяется с увеличением температуры).
Свойства прямой пропорции могут быть успешно применены в каждом из приведенных выше примеров.Вот еще два важных примера.
Обмен валюты (пример свойства 2): конвертировать австралийские доллары в доллары США и доллары США в австралийские доллары. (Обратное значение константы пропорциональности, использованной для первого преобразования, применяется для второго.)
Преобразование единиц (пример свойства 3): измените метры на миллиметры, сначала изменив метры на сантиметры, а затем изменив сантиметры на миллиметры.
УПРАЖНЕНИЕ 1
В медицинском примере, которым начинается раздел мотивации, также используется свойство 3.
Лекарство следует вводить пациенту в дозе 20 мкг / кг / мин. Если пациент весит 56 кг, сколько миллиграммов он должен получить за один час?
УПРАЖНЕНИЕ 2
В 2008 году во время мирового финансового кризиса один австралийский доллар стоил 0,618 доллара США. Сколько стоит один доллар США в австралийских долларах?
(Подумайте о золотом сечении после выполнения этого.)
Нахождение константы пропорциональности
Если y пропорционально x, константа пропорциональности может быть найдена, если даны только одно значение x и соответствующее значение y.
ПРИМЕР
Переменная y пропорциональна переменной x. Когда x = 4, y = 11. Найдите константу пропорциональности и, следовательно, напишите формулу для y через x.
Решение
Поскольку y пропорционален x, существует постоянная k такая, что y = kx.
Когда x = 4, y = 11, поэтому 11 = 4k и k =.
Следовательно, y = x.
Процедура решения этого вопроса была следующей.
- Запишите формулировку пропорции в виде уравнения с константой k.
- Используйте информацию в вопросе, чтобы найти значение k.
- Перепишите формулу с вычисленным значением k.
Пропорциональность квадрату или кубу
Металлический шар падает с вершины высокого здания, и расстояние, с которого он падает, записывается каждую секунду.
Из физики формула для расстояния d m, на которое мяч упал за t секунд, равна
d = 4,9 т2.
В этом случае мы говорим, что d прямо пропорционально
квадрату t.Когда мы строим график зависимости d
от t, график представляет собой половину параболы.
Но что случилось с нашей прямой линией через начало координат, которую мы ожидаем от прямой пропорции? Мы можем получить прямую линию, построив график d против t2, а не против t.
| т | 0 | 1 | 2 | 3 |
| т 2 | 0 | 1 | 4 | 9 |
| д | 0 | 4.9 | 19,6 | 44,1 |
Наклон этой линии равен 4,9.
Теперь это прямая линия, проходящая через начало координат с градиентом 4.9.
Мы видим, что d пропорционально t2, и мы записываем это как d t2.
Это означает, что для любых двух значений t1 и t2 с соответствующими значениями d1 и d2,
= = 4,9.
Таким образом, еще раз соотношение является константой, а наклон линии — константой пропорциональности.
Есть много примеров, когда одна величина пропорциональна квадрату
или кубу другой. Вот еще несколько элементарных примеров:
Как мы видели выше, чтобы найти константу пропорциональности, нужна всего одна пара значений
.
ПРИМЕР
Масса, миллиграммы пластического материала, необходимого для формования твердого шара, прямо пропорциональна кубу радиуса r см шара. Если нужно 40 грамм пластика
, чтобы сделать шар радиусом 2.5 см, мяч какого размера можно сделать из 200 грамм однотипной пластмассы?
Решение
Мы знаем, что m = kr3, где k — постоянная величина, а
| м = 40 при r = 2,5 | ||
| Таким образом | 40 = к × (2,5) 3 | |
| k = 2,56. |
Итак, формула m = 2,56r3
| При m = 200, | 200 = 2,56r3 |
| r3 = 78,125 | |
| г = | |
| r ≈ 4,27 см |
УПРАЖНЕНИЕ 3
Мощность p кВт, необходимая для управления лодкой, изменяется как куб ее скорости с м / с.Если 400 кВт будут управлять лодкой со скоростью 3 м / с, какая мощность потребуется для того, чтобы та же лодка могла двигаться со скоростью 5 м / с?
Увеличение и уменьшение
Если одно количество пропорционально другому, мы можем выяснить, что происходит с одним из количеств при изменении другого.
Пусть y = kx для положительной постоянной k.
Если значение x удваивается, то значение y удваивается. Лучший способ продемонстрировать это — подставить конкретное значение x.
Например, если мы подставим x = 7, тогда y = 7k, а когда x = 14 даст y = 14k.
Аналогично, если значение x утроится, то значение y утроится. Мы можем использовать это с любым вопросом о пропорциях.
Прямая пропорциональная сводка
- y прямо пропорционально x, если существует положительная константа k такая, что y = kx.
- Символ, используемый для «пропорционально», есть. Мы пишем y x.
- Если y прямо пропорционален x, то график зависимости y от x представляет собой прямую линию, проходящую через
начало координат.Наклон линии — это коэффициент пропорциональности.
Обратная пропорция
Определение
Говорят, что переменная y обратно пропорциональна x, если
г =
для постоянного k. Число k называется константой пропорциональности.
Утверждение, что «y обратно пропорционально x», символически записывается как y.
Обратите внимание, что это также можно читать как «y прямо пропорционально».
Полезные свойства обратной пропорции отличаются от свойств прямой пропорции. Мы перечисляем здесь три важных свойства.
Скорость и время являются хорошим примером обратной пропорции.
| Мы знаем, что расстояние = скорость × время | или | d = vt | ||
| Перестановка дает время = | или | т = |
Пусть теперь расстояние между двумя городами будет 72 км.Время t часов, необходимое для преодоления этого расстояния со скоростью v км / ч, определяется формулой
.
т =
Это пример обратной пропорции. Мы пишем t и говорим, что t обратно пропорционально v с константой пропорциональности 72.
График зависимости t от v является частью прямоугольной гиперболы, но график зависимости t от
представляет собой прямую линию с градиентом 72.
ПРИМЕР
Предположим, что два города A и B находятся на расстоянии 144 км друг от друга.
a Запишите формулу для времени t часов, затрачиваемого на поездку из пункта A в пункт B со скоростью v км / ч.
b Постройте график зависимости t от v.
c Если автомобиль движется со скоростью 24 км / ч, сколько времени потребуется, чтобы завершить поездку?
d Если поездка занимает 90 минут, с какой постоянной скоростью автомобилю потребуется
, чтобы двигаться?
Решение
| c | При v = 24, t | = | ||
= 6 часов | ||||
| д | Когда t = = | , = | ||
So v | = 144 × | |||
= 96 км / ч | ||||
Есть много примеров обратной пропорции в темах, которые изучаются в школе.Например,
- Лента длиной 100 м должна быть разделена между n людьми. Длина, которую получает каждый человек, обратно пропорциональна количеству людей.
- Для цилиндров объемом 2 м3 высота цилиндра обратно пропорциональна площади основания.
- Сила между двумя заряженными объектами обратно пропорциональна квадрату расстояния между их центрами.
- Освещенность от источника света обратно пропорциональна квадрату расстояния от источника.
УПРАЖНЕНИЕ 4
Объем V см3 газа, поддерживаемого при постоянной температуре, обратно пропорционален давлению P кПа. Если объем составляет 500 см3 при давлении 80 кПа, найдите объем при давлении 25 кПа. (Это пример закона Бойля)
УПРАЖНЕНИЕ 5
Если a обратно пропорционально кубу b и a = 2, когда b = 3, найдите
а | а при b = 2 | б | b при a = |
Как и в случае с прямой пропорцией, мы можем вычислить влияние изменения другой переменной на одну переменную.
Сводка обратной пропорции
х1 у1 = х2у2 = к.
ПЕРЕАДРЕСАЦИЯ ССЫЛКИ
Пропорциональность по нескольким переменным
Часто конкретная физическая величина зависит от нескольких других переменных. Например, расстояние d, которое проезжает автомобилист, зависит как от скорости v, с которой он едет, так и от времени t, которое он едет, d = vt.
В более общем смысле, если y = kxz для положительной константы k, мы говорим, что y прямо пропорционален x и z.Аналогично, если a = для положительной константы k, мы говорим, что a прямо пропорционально b3 и обратно пропорционально c2.
ПРИМЕР
Предположим, что a прямо пропорционально b и квадрату c. Если a = 36, когда b = 3 и
c = 2, найдите a, когда b = 4 и c = 1
Решение
| a | до н.э. | ||
| т. | a | = kbc2 для некоторой константы k |
Подставляя известные значения, чтобы найти k.
| 36 | = к × 3 × 22 | ||
| к | = 3. | ||
| Отсюда | a | = 3bc2 |
Когда b = 4 и c = 1, a = 3 × 4 × 12 = 12
УПРАЖНЕНИЕ 7
Электрическое сопротивление провода R Ом прямо пропорционально его длине L м и обратно пропорционально квадрату его диаметра d мм.Некий провод длиной 100 м с
диаметром 0,4 мм имеет сопротивление 1,4 Ом.
a Найдите уравнение, связывающее R, L и D.
b Найдите сопротивление (с точностью до одного десятичного знака) провода из того же материала, если он имеет длину 150 м и диаметр 0,25 мм.
c Если длина и диаметр увеличиваются вдвое, как это повлияет на сопротивление?
d Если длина увеличена на 10%, а диаметр уменьшен на 5%, каково процентное изменение сопротивления? (Ответьте правильно с точностью до одного десятичного знака.)
Два очень важных случая прямой пропорциональности нескольким переменным — это два правила обратных квадратов.
Первый закон — основной закон гравитационной силы, второй — закон Кулона электростатической силы между двумя электрическими зарядами. Для основного закона гравитации R — это расстояние между массами m1 и m2, а для закона Кулона — это расстояние между зарядами q1 и q2.
Прочие применения пропорции
Важные примеры возникают в математике, где функция прямо пропорциональна функции.Одним из важных случаев является y 2 ax , который обеспечивает модель как экспоненциального роста, так и экспоненциального затухания.
Интересный случай пропорции — закон Снеллиуса. Когда свет преломляется через прозрачное вещество, угол падения θ связан с углом Φ преломления
уравнением
sin θ = k sin Φ для некоторой постоянной k, называемой показателем преломления.
Таким образом, чтобы получить утверждение о пропорциональности, нужно взять синус обоих углов.
Функции и исчисления
Эта тема является началом понимания учащимися приложений функций и должна начать указывать на масштабы приложений математики во многих различных областях. Это ведет ко всем аспектам изучения функций и исчисления. Графическое введение в ставки обеспечивается идеями пропорции.
ИСТОРИЯ
История пропорции начинается с древних греков. Он был разработан в Книге V Евклида и использовался для геометрии в Книге VI.Многие из вопросов, поднятых в Евклиде, не были удовлетворительно решены до работ Вейерштрасса, Кантора и Дедекинда в 19 веке. Некоторые из них обсуждаются в модуле «Ставки и коэффициенты».
Пропорция — настолько фундаментальная идея, что она проявляется в более приземленных проявлениях.
Один из таких случаев:
Правило трех
Правило трех было сокращенной версией особой формы перекрестного умножения, которую ученики часто учили наизусть.Вот пример типа проблемы.
Если три банана будут стоить 60 центов, сколько будут стоить 7 бананов? Используя правило трех, вы умножите 60 на 7 и разделите на 3.
Метод эквивалентен решению уравнения =. Без современных алгебраических обозначений язык, объясняющий, почему правило трех произведений было трудно объяснить.
Правило трех возникло у индуистских математиков Брахмагупта (около 628 г.) и Бхаскара (около 1150 г.).Он появился в Европе с 15 века и пользовался огромной популярностью у купцов. Английский арифметик XVII века писал: «Правило трех обычно называют золотым правилом; и действительно, это можно было бы так назвать; ибо как золото превосходит все другие металлы, так это правило распространяется и на все остальные в арифметике ».
Конечно, мы можем переписать решение этого вопроса, используя формулировку пропорции: «Стоимость n бананов в центах = 20n».
Греческая наука
Идеи соотношений использовались также в греческой науке.Например, Архимед
(287 — 212 гг. До н.э.) добился результатов о балансировке единого стержня. Проиллюстрируем это
на примере.
Груз весом 3 кг помещается в 120 см от точки опоры, на которой балансируется штанга. Уравновешивание может быть достигнуто, если груз массой m килограммов поместить на x см от точки опоры на другой стороне оси так, чтобы mx = 120 × 3. Следовательно, расстояние, на которое груз помещается от точки опоры, необходимое для балансировки, обратно пропорционально пропорционально весу.Современный термин для этого продукта — момент.
Трактат Архимеда «О плавающих телах» также содержит материал, в котором используются пропорции. Принцип Архимеда, упомянутый ранее в этом модуле, является примером его результатов в
в этой области.
Пропорции, естественные науки и математика
Мы кратко обсудим развитие некоторых аспектов математики и естественных наук до начала 18 века. Мы не можем попытаться дать какую-либо полную картину этого, но отметим, что наука и математика развивались очень близко друг к другу вплоть до наших дней, и пропорция была центральной концепцией в этом развитии.
Многие математические науки уходят корнями в физические науки.
Некоторый прогресс был достигнут в средневековье. Ученые Мертона в Оксфорде в середине четырнадцатого века изучали движение с постоянным ускорением, и им приписывали следующее.
Тело, движущееся с равномерно ускоренным движением в заданное время, точно на такое же расстояние, которое оно двигалось бы с постоянной скоростью, равной его мгновенной скорости в середине рассматриваемого периода времени.
Николь Оремская (1323–1382) разработала схематическое изображение движения. Он пришел к представлению пройденного расстояния в виде области, двумя измерениями которой (которые представлены перпендикулярными линиями) были время, а другим — скорость. Таким образом, он представил идею, очень похожую на прямоугольные координаты. Его выводы должны были быть подтверждены и развиты Галилеем. Эта работа была проделана задолго до того, как появилось четкое понятие координатной геометрии.
Пропорция была частью языка математики и физики со времен Галилея (1564 — 1642). Многие рукописи, происходящие от греков, пришли из Византии и арабов, и многие думали, что эти рукописи стали катализатором возрождения научной мысли в Европе. Галилей добился того, что для тела, движущегося с постоянным ускорением, пройденное расстояние пропорционально квадрату времени путешествия.
Кеплер (1571 — 1630) также был знаком с творчеством древних греков.Он последовал за Коперником и развил свои теории дальше. Его законы движения планет используют язык пропорций.
Законы Кеплера:
- Орбита каждой планеты представляет собой эллипс с Солнцем в одном из двух фокусов.
- Линия, соединяющая планету и Солнце, охватывает равные области за равные промежутки времени. В терминах пропорции это можно записать так: «Площадь, выметаемая за данный промежуток времени линией, соединяющей Солнце с планетой, пропорциональна длине временного интервала».
- Квадрат периода обращения планеты прямо пропорционален кубу большой полуоси ее орбиты.
Гюйгенс (1629 — 95) получил дополнительные результаты и обнаружил, что для тела, движущегося по круговой траектории с постоянной скоростью, v имеет ускорение, направленное к центру окружности. Сила, действующая на частицу, пропорциональна квадрату скорости и обратно пропорциональна радиусу круга.
Работа сэра Исаака Ньютона (1642–1727) является продолжением работ более ранних ученых, о которых говорилось выше.Он родился в год смерти Галилея. Он математически объяснил результаты, полученные Галилеем и Кеплером. Для достижения этих результатов он использовал разработанный им расчет. Он получил фундаментальный закон для гравитационных сил F = G, который можно читать как: «Каждая точечная масса притягивает каждую другую точечную массу силой, направленной вдоль линии, пересекающей обе точки. Сила прямо пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между точечными массами.’
Второй закон движения Ньютона также выражен в терминах пропорции.
«Изменение движения пропорционально приложенной движущей силе и происходит по прямой линии, на которой действует эта сила» (F = ma).
Пропорция оставалась ключевой идеей на протяжении XVIII и XIX веков, и ее значение, конечно же, сохраняется и по сей день.
ОТВЕТЫ НА УПРАЖНЕНИЯ
УПРАЖНЕНИЕ 1
67,2 миллиграмма
УПРАЖНЕНИЕ 2
1.618 (десятичное приближение золотого сечения)
УПРАЖНЕНИЕ 3
1852 кВт
УПРАЖНЕНИЕ 4
1600 см3
УПРАЖНЕНИЕ 5
| а | 6,75 | б | 4 |
УПРАЖНЕНИЕ 6
| а | y увеличивается примерно на 23.5% | б | x уменьшился примерно на 4,7% |
УПРАЖНЕНИЕ 7
| а | R = | б | 5,4 Ом | |||
| c | сопротивление уменьшено вдвое | д | увеличено на 21.9% |
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное).Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Прямая и обратная пропорция — Графики — WJEC — Счисление по математике GCSE (WJEC), редакция
Когда две величины находятся в прямой пропорции, при увеличении одного увеличивается другое.
Мы можем отобразить эту взаимосвязь в виде графика. Две величины, которые находятся в прямой пропорции, всегда будут давать прямолинейный график, проходящий через начало координат.
Если коэффициент пропорциональности положительный, график будет иметь положительный градиент. Если константа отрицательная, график будет иметь отрицательный градиент.
Пример 1
Заработок няни прямо пропорционален количеству отработанных часов.
Если им платят 9 фунтов стерлингов за каждый час работы, мы можем записать это в виде формулы:
\ [\ text {Earnings = 9 фунтов стерлингов} \ times \ text {часы работы} \]
Для построения графика нам понадобится три балла, мы можем использовать таблицу значений, чтобы помочь нам:
Когда часы = 0, заработок = 9 £ × 0 = 0 £
Когда часы = 1, заработок = 9 £ × 1 = 9 £
Когда часы = 2, заработок = 9 фунтов стерлингов × 2 = 18 фунтов стерлингов
фунтов стерлингов. Присвоение баллов (\ ({0} \ text {,} {~ 0} \)), (\ ({1} \ text {,} {~ 9 } \)) и (\ ({2} \ text {,} {~ 18} \)).
После того, как вы нанесете эти точки, проведите линию через все три, продлив ее как можно дальше.
Пример 2
Количество пакетов чипсов и их общая стоимость указаны в таблице.
Когда мы строим график этих точек, мы видим, что они могут быть соединены вместе в прямую линию:
Для каждой единицы на оси \ (\ text {x} \) ось \ (\ text {y} \) увеличивается на 30. Это означает, что градиент графика равен 30, и график можно записать как:
\ [\ text {y = 30 x} \]
Поиск взаимосвязей на графике
\ (\ text {y } \) прямо пропорционален \ (\ text {x} \).Из этого графика напишите уравнение, чтобы показать взаимосвязь между \ (\ text {x} \) и \ (\ text {y} \).
Когда \ (\ text {x} \) = 2, \ (\ text {y} \) = 30
\ [{30} \ text {~ ÷} {~ 2} = {15} \]
\ [\ text {y = 15 ~ \ times ~ x} \]
\ [\ text {y = 15 x} \]
Когда две величины находятся в обратной пропорции, когда одна увеличивается, другая уменьшается.
Когда мы строим график этой взаимосвязи, мы получаем изогнутый график.
Пример
\ (\ text {y} \) обратно пропорционален \ (\ text {x} \), а когда \ (\ text {x} \) = 2, \ (\ text {y} \) = 10
Нарисуйте график, заполнив таблицу значений:
1.Поскольку \ (\ text {y} \) обратно пропорционально \ (\ text {x} \), мы можем написать:
\ [\ text {y = k / x} \]
Posted in Разное
