Содержание
Урок 33. угол. виды углов: прямой, острый, тупой — Математика — 2 класс
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
— Какие бывают углы?
— Как распознавать углы?
Глоссарий по теме:
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд.
 , дораб. – М.: Просвещение, 2016. – с.3.
, дораб. – М.: Просвещение, 2016. – с.3. - Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
Теоретический материал для самостоятельного изучения
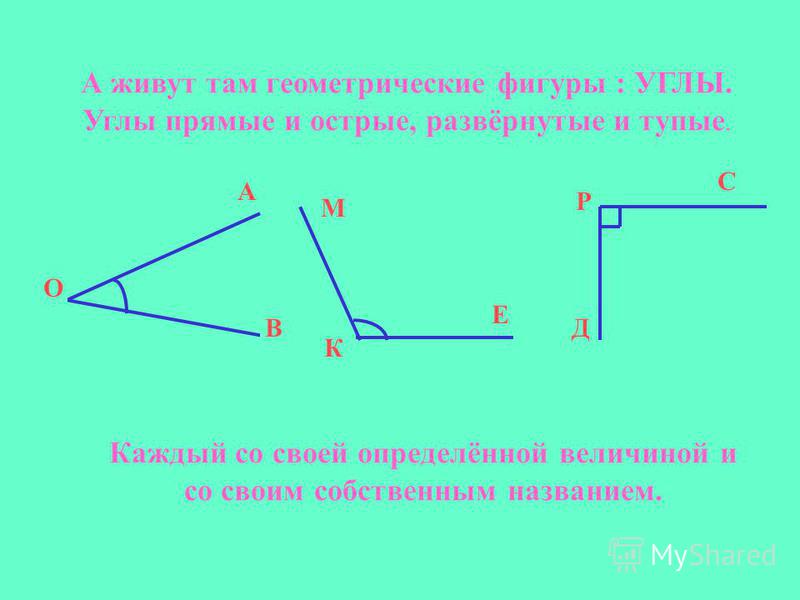
Рассмотрите фигуры и выберите лишнюю.
Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.
У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.
Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.
Угол, который больше прямого угла называется тупым углом.
Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.
Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.
Разверните лист. Линии сгиба образовали 4 прямых угла.
Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.
Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
Тренировочные задания.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.
Правильные ответы:
2. Выберите цифры, в записи которых присутствуют только прямые углы.
Правильные ответы:
Прямой угол, свойства и фигуры с прямыми углами
Прямой угол, свойства и фигуры с прямыми углами.
Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол (определение и понятие)
Геометрические фигуры с прямыми углами
Вертикальные углы, прямой угол, развернутый угол, смежные углы, тупой угол
Прямой угол (определение и понятие):
Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол – это угол, стороны которого перпендикулярны друг другу. При пересечении перпендикулярных прямых образуются прямые углы.
Прямой угол – это геометрическая фигура, которая состоит из двух перпендикулярных друг другу лучей (сторон), выходящих из одной точки (вершины).
Рис. 1. Прямой угол
Величина прямого угла может быть выражена в разных единицах измерения:
– 90°,
– π / 2 радиан,
– 100 град,
– 1/4 оборота или полного угла,
– 5400 угловых минут,
– 324000 угловых секунд.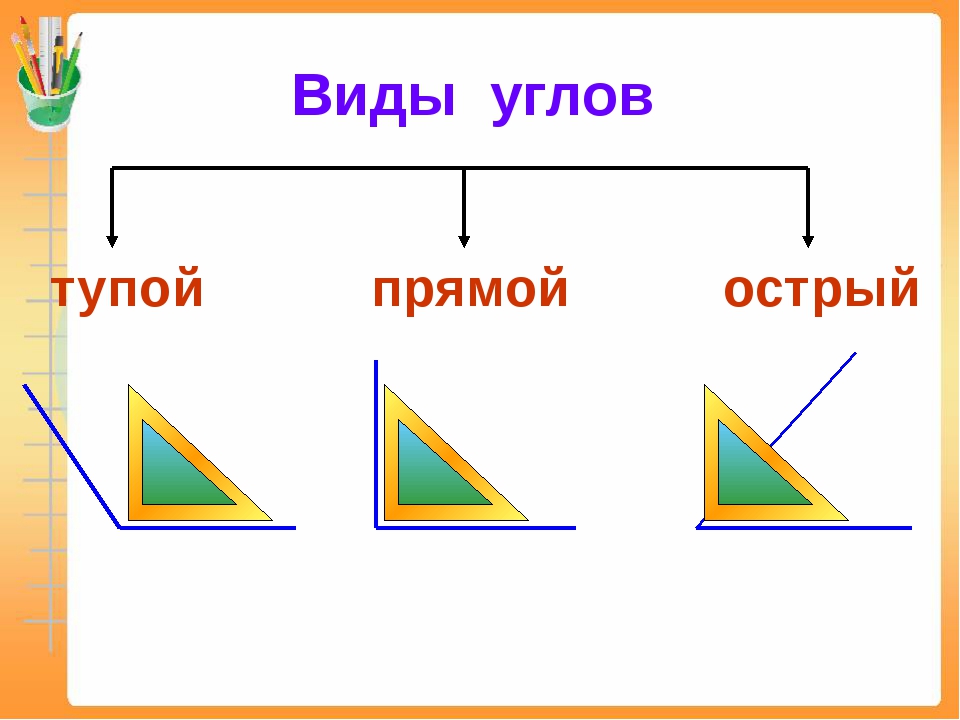
Геометрические фигуры с прямыми углами:
У некоторых геометрических фигур имеется один или несколько прямых углов.
Например, прямой угол (или прямые углы ) имеются у прямоугольного треугольника, прямоугольника, квадрата, прямоугольной трапеции.
Прямоугольный треугольник – это треугольник, у которого один угол прямой.
Рис. 2. Прямоугольный треугольник и прямой угол
Прямоугольник – параллелограмм, у которого все углы прямые.
Рис. 3. Прямоугольник и прямые углы
Квадрат – это четырёхугольник, у которого все углы прямые, все углы и стороны равны между собой.
Рис. 4. Квадрат и прямые углы
Прямоугольная трапеция – это трапеция, хотя бы один из углов которой является прямым.
Рис. 5. Прямоугольная трапеция и прямые углы
Квадрат
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www. pexels.com, https://pixabay.com
pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
1 073
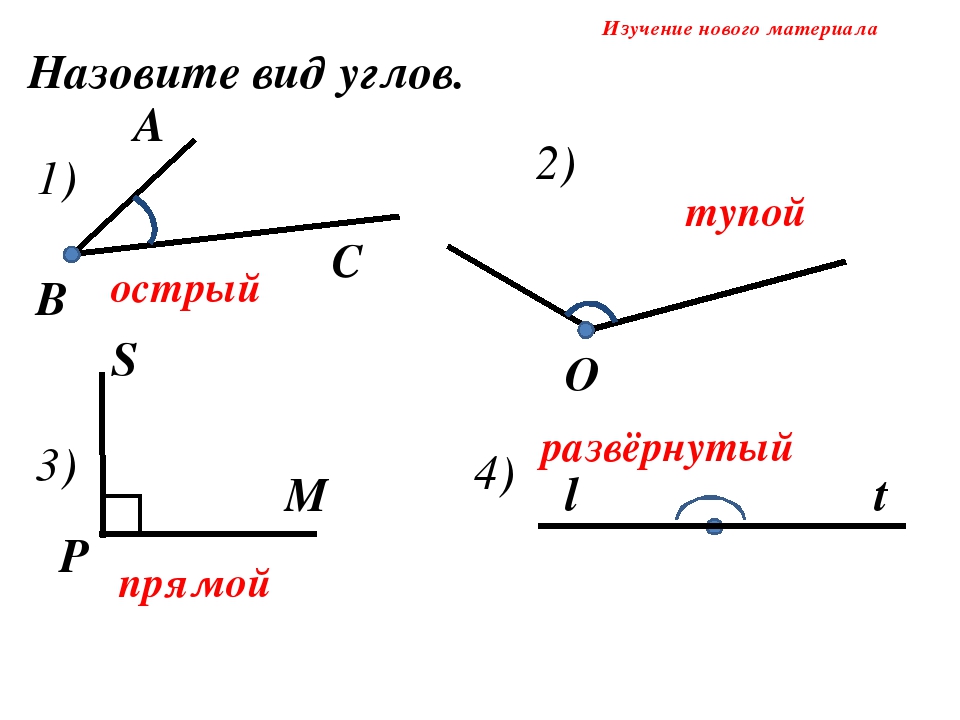
Виды углов. Прямой угол. 2-й класс
Тип урока: объяснение нового
материала.
Место урока в структуре по теме: данная тема
изучается в разделе “Табличное сложение
однозначных чисел с переходом через десяток”.
Цель урока: Познакомить учащихся с понятием
“прямой угол” и научить применять полученные
знания на практике.
Задачи урока:
1. Образовательные:
- Познакомить учащихся с понятием “прямой угол”;
- Сформировать практические навыки определения
прямого угла при помощи треугольника и без него; - Продолжить работу по совершенствованию навыка
устного счёта в пределах 100;
2. Развивающие:
- Развитие логического мышления, внимания,
памяти, пространственного воображения; - Развитие творческих умений и навыков по теме
для успешного выполнения заданий; - Развитие культуры речи и эмоций учащихся.

3. Воспитательные:
- В целях решения задач нравственного воспитания
содействовать воспитанию гуманности и
коллективизма, наблюдательности и
любознательности, развитию познавательной
активности, формированию навыков
самостоятельной работы; - В целях решения задач эстетического воспитания
содействовать развитию у учащихся чувства
прекрасного.
ХОД УРОКА
I. Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
— Ребята, сегодня мы опять отправимся в
путешествие по королевству Геометрия.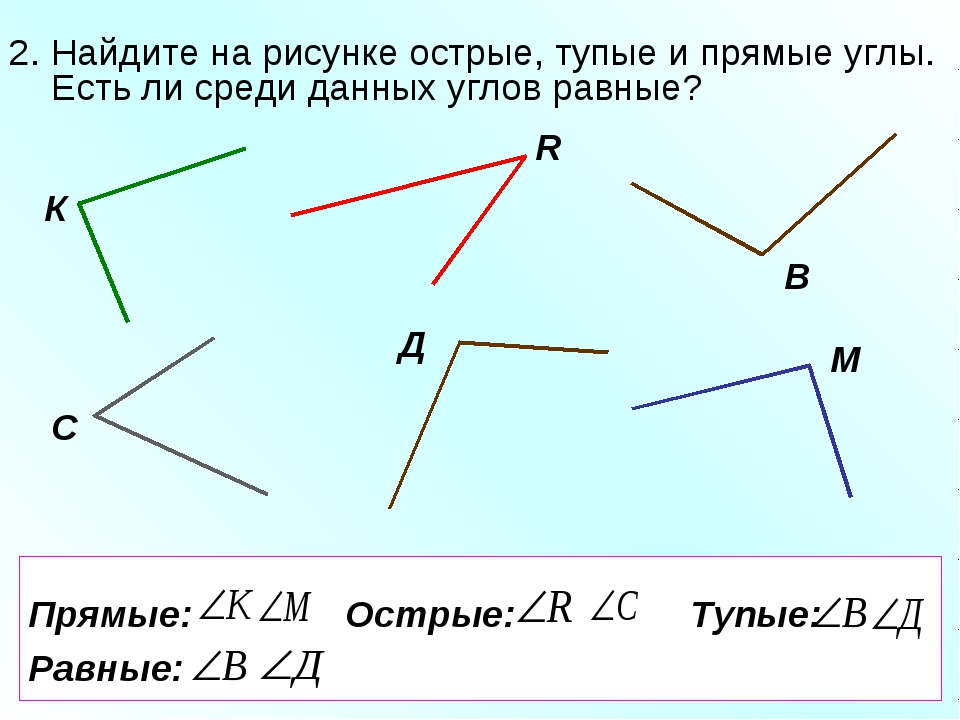
3. Устный счёт.
2 слайд
– У ворот нас встречают король Точка и его дочь
– принцесса Прямая. Прежде чем король и
принцесса познакомят нас с жителями своего
королевства, они хотят вас испытать.
II. Устный счет.
(Слайд 3)
1) Игра “Гусеница-растеряша”.
— Гусеница растеряла числа, посмотрите на
оставшиеся, разгадайте по какому правилу можно
продолжить ряд чисел. (Дети называют правило: это
чётные числа; каждое последующее число на 2
больше предыдущего).
— Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16)
(Слайд 4)
2) Игра “Математический баскетбол”.
Баскетбол — командная спортивная игра,
цель которой забросить руками мяч в подвешенную
корзину.
— Любой из вас забьёт гол, если правильно решит
пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32
– 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
Слайд 5
Задание на логику
— Сколько пятачков у 15 поросят? (15)
— Когда гусь стоит на двух ногах, то весит 4 кг.
Сколько будет весить гусь, когда встанет на одну
ногу?
6 слайд
– Вы прошли все испытания. Король и принцесса
очень довольны вами и готовы познакомить вас с
жителями королевства “Геометрия”!
(По щелчку створки ворот открываются.)
(Слайд 7)
— Ребята, перед вами жители королевства
“Геометрия”.
— Посмотрите на фигуры в каждой рамке. Какая из
них лишняя? Почему?
(Учащиеся называют лишние фигуры, обосновывают
свой выбор).
— Разделите все оставшиеся фигуры на две группы.
Как это можно сделать? (Оставшиеся фигуры можно
разделить на две группы: линии и многоугольники.)
— Назовите виды линий и многоугольников,
известные вам. (Линии: прямая, ломаная, кривая.
Многоугольники: квадрат, трапеция,
прямоугольник, четырёхугольник, пятиугольник,
шестиугольник, многоугольник).
IV. Работа над новым материалом.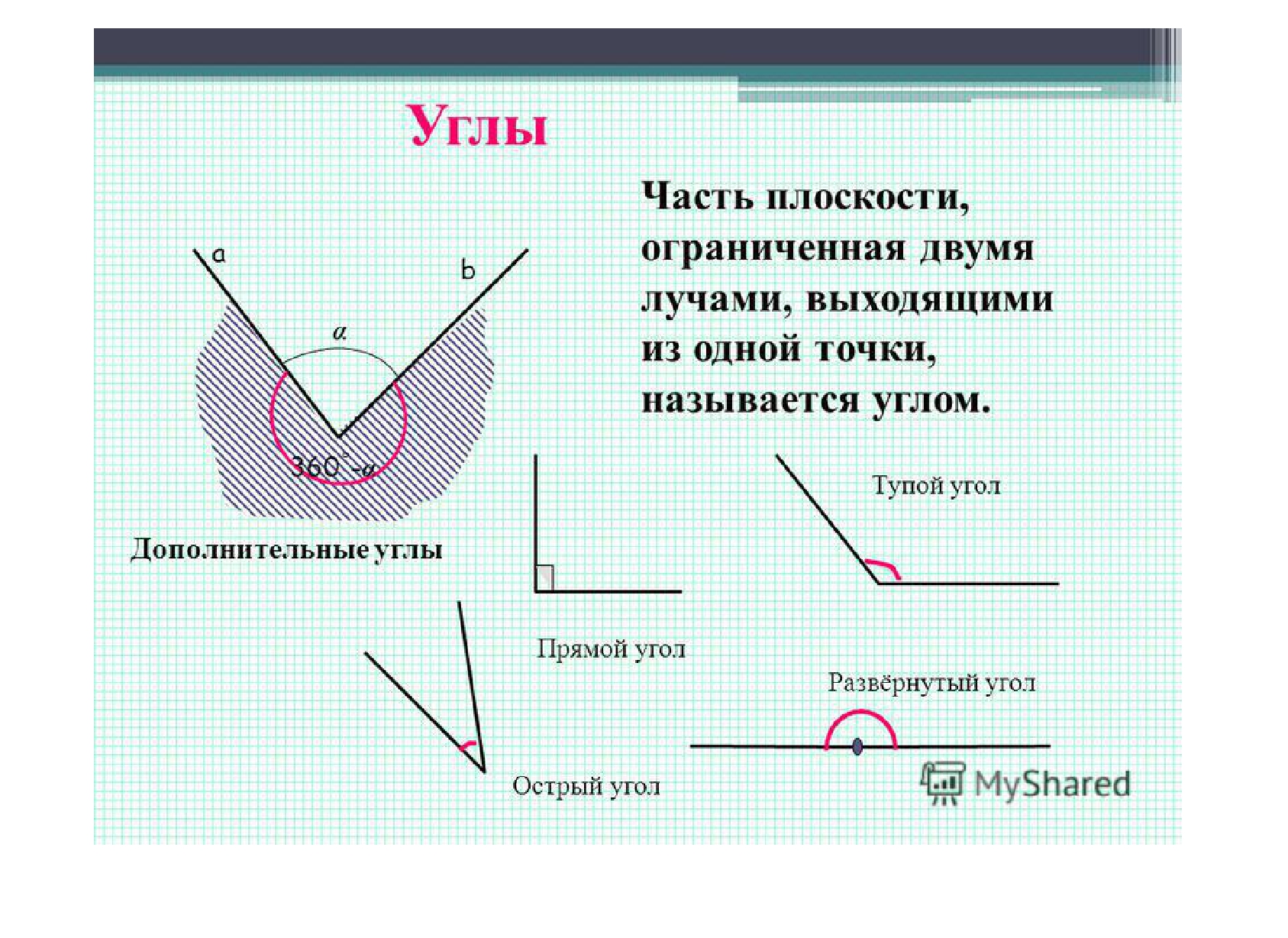
(Слайд 8)
1) — Тему урока вам подскажет кроссворд.
Кроссворд “Геометрический”.
1) Часть прямой, у которой есть начало, но нет
конца. (Луч).
2) Геометрическая фигура, не имеющая углов.
(Круг).
3) Самая маленькая геометрическая фигура.
(Точка).
4) Геометрическая фигура, имеющая форму
вытянутого круга. (Овал).
— Тема нашего урока спряталась по вертикали.
Найдите её. (Угол). (щелчок вылетают
геометрические фигуры).
— Сформулируйте пожалуйста тему нашего урока.
— Ребята, а зачем мы будем изучать углы?
— Как Вы думаете, вам эти знания пригодятся?
(Ответы детей)
— Углы окружают нас и в повседневной жизни.
Приведите свои примеры, где можно найти углы
вокруг нас.
— Ребята, а может, кто-то знает, что такое угол?
(выслушиваются мнения детей)
Правильность нашей формулировки, мы проверим
чуть позже.
— Люди, каких профессий чаще всего встречаются с
углами? (конструктор, инженер, дизайнер,
строитель, архитектор, моряк, астроном,
архитектор, портной и т.д.)
Слайд 9.
Посмотрите на рисунки: уголок соединительный
для труб и уголок канцелярский для бумаг;
угольник плотника и угольник чертёжный; угловой
стол и угловой диван.
— Ребята, а сейчас Король и Принцесса предлагают
немного поиграть.
Слайд 10.
Игра “Им угол имя подарил”.
— Угол важная фигура. Многим фигурам он помог
дать имя. Назовите фигуры.
— Что общего в названиях фигур? (что они имеют
угольник – общая часть)
— Почему первая часть слов везде разная? (потому
что углов разное количество)
Физминутка 11-16 слайды
Открываем тетради, записываем 18 января,
классная работа. (слайд 17)
Слайд 18.
— Ребята, а теперь от красных полей отступите
одну клеточку и поставьте точку О. От этой точки
От этой точки
проведите два луча.
На доске заранее нарисовать точку О (4-5). Вызвать
4-5 детей, чтобы они провели лучи на доске.
— Что за фигуры у нас получилась? (угол)
— Посмотрите, какие разные эти углы.
— Ребята, а теперь соберите правило из слов.
Работа в парах.
(Вывод: угол — это геометрическая фигура,
образованная двумя разными лучами
с общим началом).
— Ребята, а теперь посмотрите на фигуру, которую
нарисовала я.
— Это угол, или нет.
(Дети говорят – нет, еще раз возвращаемся к
правилу, после этого делаем вывод о том, что это
тоже угол – развернутый)
Слайд 19. (вывод по углу)
Плакат на доске
Точка О – вершина угла. Угол можно назвать
одной буквой, записанной около его вершины. Угол
О. Но может быть несколько углов, имеющих одну
вершину. Как быть тогда? (На листе чертеж таких
углов)
Ответы детей.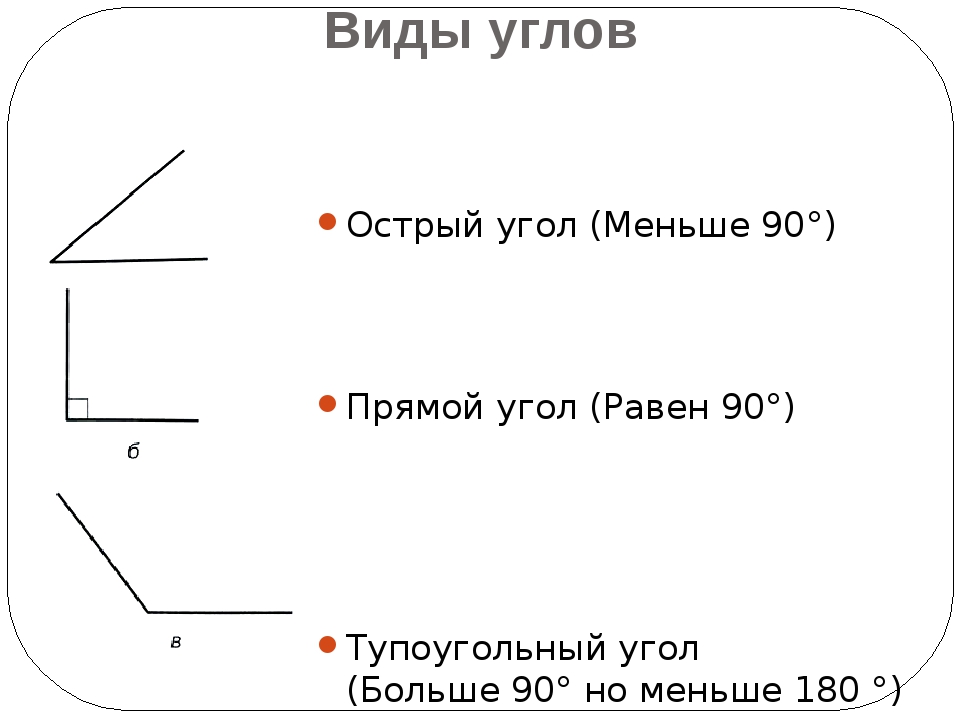
— В таких случаях если называть разные углы
одной буквой, то будет непонятно, о каком угле
идёт речь. Что этого не произошло, на каждой
стороне угла можно отметить по одной точке,
поставить около неё букву и обозначить угол
тремя буквами, при этом всегда в середине
записывают букву, обозначающую вершину угла.
Угол АОВ. Лучи АО и ОВ – стороны угла.
Плакат на доске
Слайд 20.
— Ребята, у вас на столах лежат разные виды
углов. Найдите пожалуйста одинаковые виды углов.
— Как будете искать? (Ответы детей)
Один человек на моих моделях ищет одинаковые
углы.
— Ребята, смотрите, номера 6 и 7 совпали
полностью, а 1 и 5 — нет. № 5 больше.
— Какой можно сделать вывод? После ответа детей
появляется слайд.
ВЫВОД: слайд 21
- Равные углы при наложении совпадают
- Если один угол наложить на другой и они
совпадут, то эти углы равны
Слайд 22.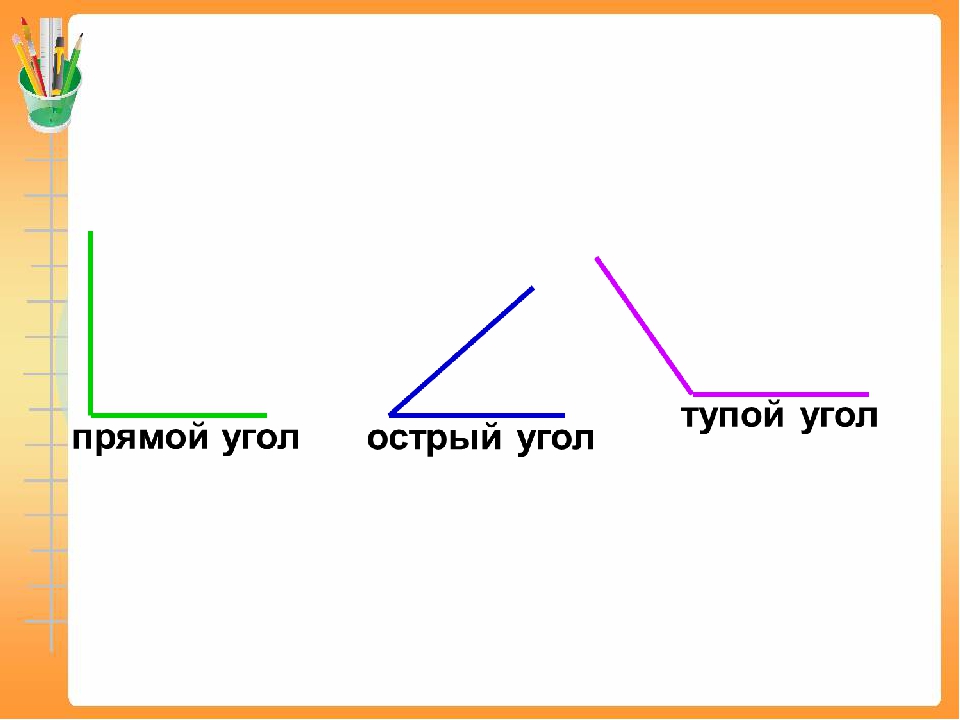
Изготовление модели прямого угла.
Слайд 23
Не всегда удобно определять прямой угол на
глаз. Для этого используют линейку-угольник.
— Каким цветом выделен угол больше прямого?
(Голубым).
— Меньше прямого? (Зелёным).
— Какой же угол из трёх предложенных прямой?
— Почему вы так решили? (Вершина и стороны угла
совпали с прямым углом на линейке-угольнике).
— Как же определить вид угла?
ВЫВОД:
- Чтобы определить вид угла, надо совместить его
вершину и сторону соответственно с вершиной и
стороной прямого угла на угольнике.
Слайд 24
— Каждый из углов имеет своё название. Острый
угол – это угол, который меньше прямого. Тупой
угол – это угол, который больше прямого.
(На доске появляются таблички с названием
углов)
— Какой угол мы будем считать главным?
Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется ПРЯМЫМ.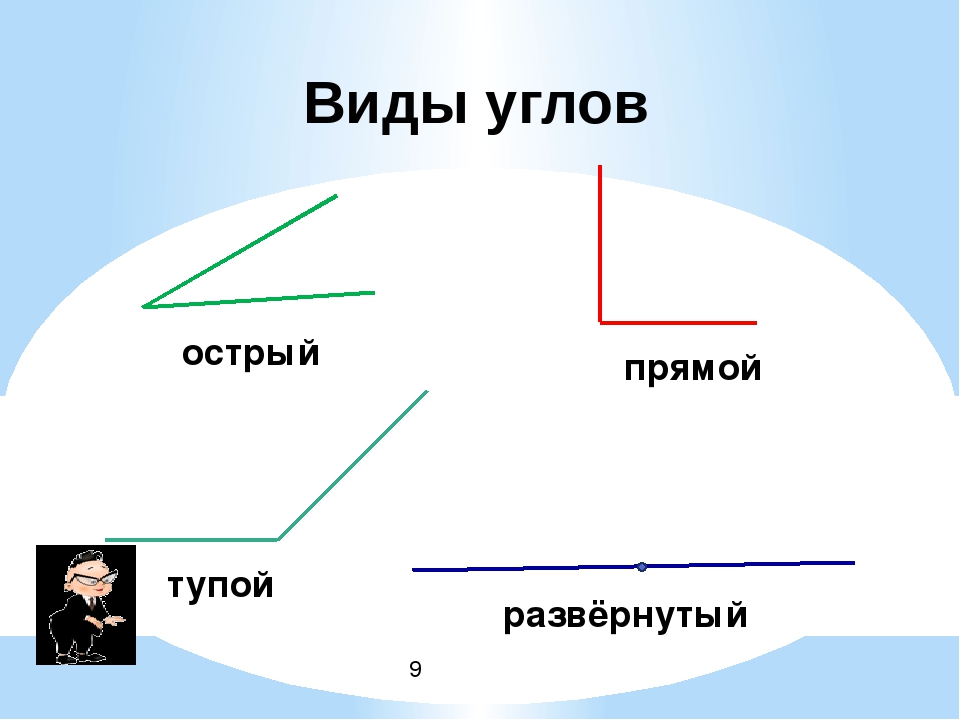
Если угол уже — ОСТРЫМ,
Если шире, то — ТУПЫМ.
Слайд 25.
— Ребята, а всегда возможно наложить углы?
— Нет. (Если начерчены в тетради…)
— Для этого существует транспортир, с помощью
которого измеряют углы. Углы измеряют в градусах.
Посмотрите на виды транспортиров.
Слайд 26.
Очень часто углы мы можем наблюдать на часах.
Углы образуют часовые стрелки.
Работа по учебнику.
Задание: Используя модель прямого
угла, найди прямые углы и выпиши их номера. (Дети
выполняют задание самостоятельно, затем один
ученик называет свой вариант ответа, все
проверяют работу).
— С помощью угольника удобно не только
определять прямые углы, но главное – строить их.
Построим прямой угол, каждый сам назовёт его
одной или тремя буквами.
Слайд 27-29 (Учитель на доске, а дети в тетрадях
строят прямой угол.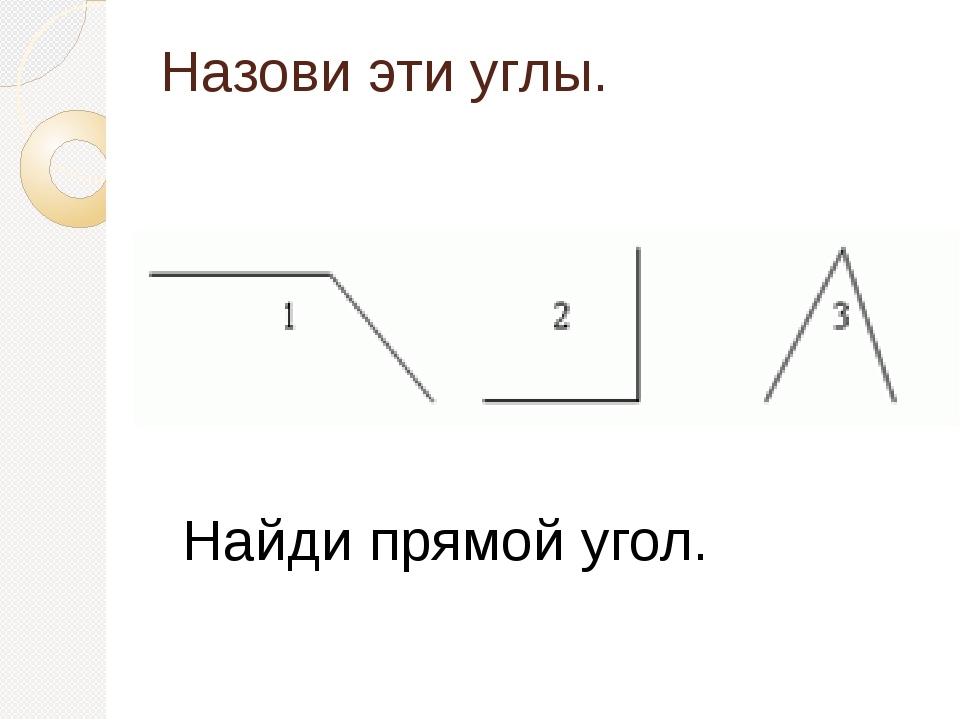 Выполняется взаимопроверка в
Выполняется взаимопроверка в
парах).
Я ОСТРЫЙ — начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим ОСТРЫЙ УГОЛ мы,
как остриё меча.
А для УГЛА ТУПОГО
Всё повторяем снова:
Из точки две прямых ведём,
Но их пошире разведём.
На чертёж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
Практическая работа по закреплению изученного.
На партах у вас проволока. Сделайте из нее
прямой угол и проверьте с помощью угольника,
затем сделайте острый и тупой.
7. Итог урока.
— Расскажите мне по схеме о том, что вам дал
сегодняшний урок математики?
8. Домашнее задание.
Урок.
 Математика 3 класс Тема: «Математика в углу (угол, виды углов)»
Математика 3 класс Тема: «Математика в углу (угол, виды углов)»
Открытый
урок.
Математика
3
класс
Тема:
«Математика в углу (угол, виды углов)»
Учитель
начальных
классов : Шеманская Лариса Ивановна
МОУ Иткульская СОШ
Задача учителя научить каждого ребенка
самостоятельно учиться, формировать у
него потребность активно относиться к
учебному процессу.
Надо, чтобы ребенок почувствовал, что
ученье — это радость, а не долг, учением
можно заниматься с увлечением, а не по
обязанности. Учитель должен сделать
так, чтобы нелегкий учебный труд приносил
школьнику радость, возбуждал желание
вновь и вновь познавать новое.
Решению этой важной задачи может помочь
игра, которая способствует развитию
умственной деятельности учащихся,
повышает их интеллектуальный уровень,
развивает их воображение и логическое
мышление, память, внимание, наблюдательность,
творческие способности.
Включение учебной задачи в игровую
ситуацию требует особой атмосферы,
определенного настроя и тона учителя.
Но самое главное — уметь найти органическую
связь игры с задачами данного урока.
Так как главная цель любой игры — помочь
сделать серьезный труд детей занимательным,
интересным и продуктивным.
Игра активизирует внимание детей к
изучаемому материалу, вызывает желание
не только участвовать в игре, но и
побеждать, а это вселяет уверенность в
свои силы. Именно игра позволяет каждому
ребенку ощутить себя личностью, проявить
и развить свою индивидуальность.
Цель: ознакомить детей с понятиями
“стороны угла”, “вершина угла”, “острый
угол”, “тупой угол”, “прямой угол”.
Учить находить прямой угол среди других
углов. Закрепить знания о геометрических
фигурах. Воспитывать интерес к предмету.
Оборудование: Линейка, угольник,
карандаш, геометрические фигуры, куски
газеты, таблички с названиями игр:
“Угадай-ка”, “Шифровая”, “Имена”,
“Строители”, “Помогай-ка”, «Кто
лишний».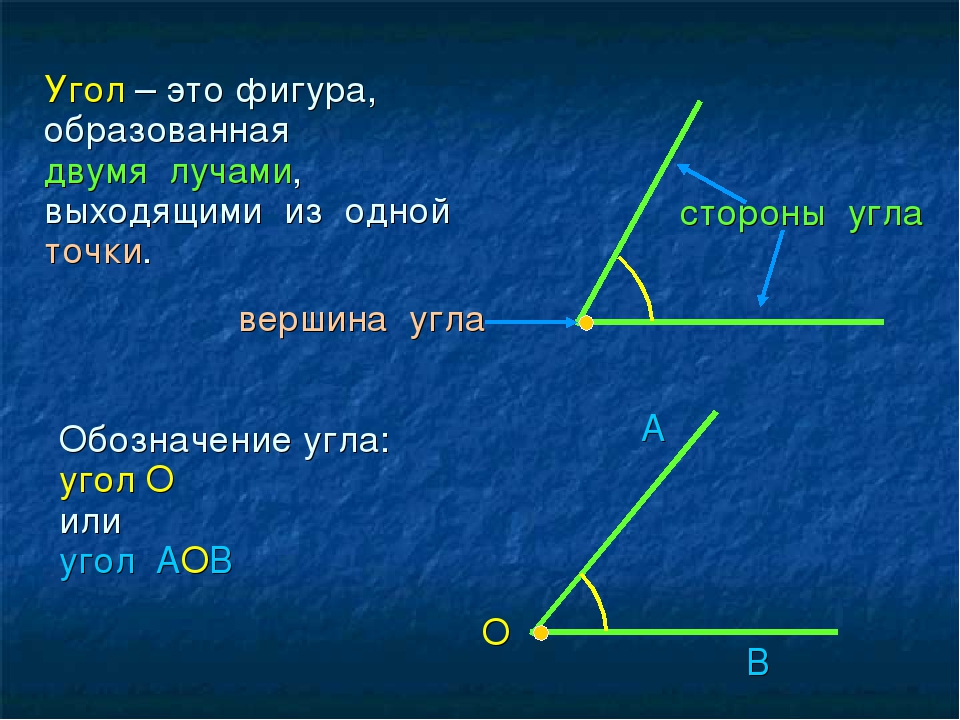 Лента, ножницы, кружок желтого
Лента, ножницы, кружок желтого
цвета, кусок алюминиевого провода, ветка
дерева.
Ход урока
I. Организация класса
II. Вступительная беседа
Ребята, сейчас у нас будет урок математики,
но урок не обычный, а урок-игра. Вы любите
играть? (Да!)
В какие игры? (Жмурки, салки, догонялки,
краски, казаки-разбойники и т.д.)
Но раз у нас урок необычный, то и игры у
нас будут необычные.
Первая игра поможет нам узнать тему
нашего урока. А называется она: “Угадай-ка”.
Я буду загадывать вам загадки о
геометрических фигурах, а вы должны их
отгадывать.
У него угла
четыре.
Все углы равны, прямые.
Ну а
по две стороны
Противоположны и
равны.
Это чудо наш угольник
Назовем
(четырехугольник).
(В нем надпись:
“Мате”.)
Он давно знакомый
мой.
Он весь ровный и прямой.
Все
четыре стороны
Одинаковой длины.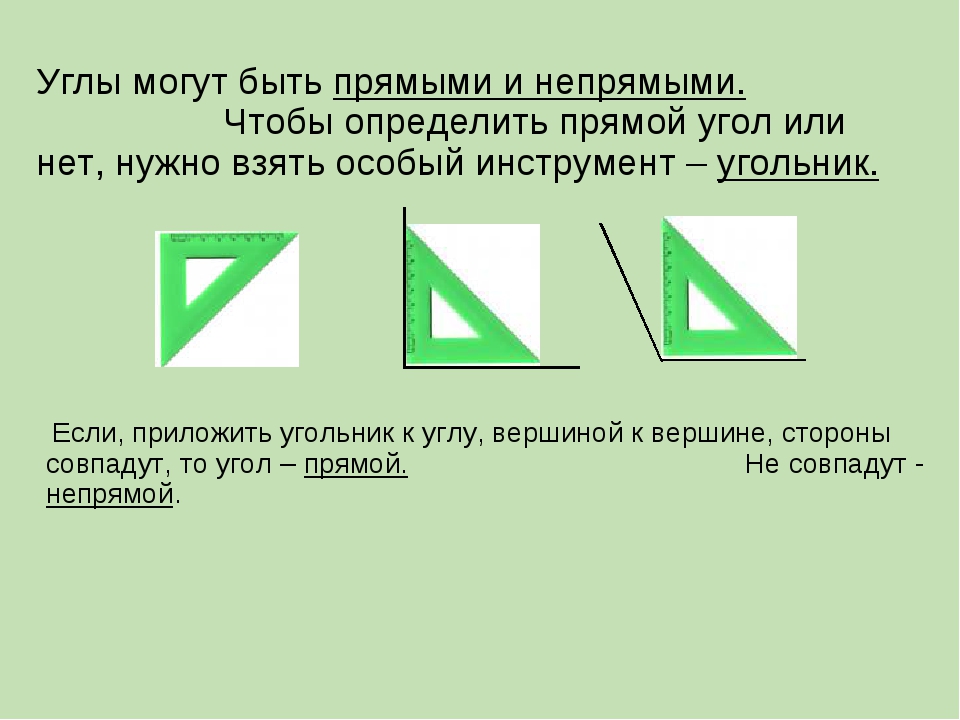
Вам
его представить рад,
А зовут его
(квадрат).
(В нем надпись: “тика”.)
Я похож, друг,
на тарелку.
Колесо кручу, как белка.
Со
стола скачусь я вдруг.
А зовусь я просто
(круг).
(В нем надпись: “в”.)
Посчитай и
посмотри:
У меня три стороны.
Три
вершины, три угла
Как зовут меня друзья?
(Треугольник)
(В нем надпись:
“углу”.)
Так как же называется наш урок-игра?
(Вывешиваю все фигуры и читаем тему
урока.)
III. Сообщение темы урока
Математика в углу. Ребята, а кто из вас
стоял в углу? За что вас туда ставили?
(Говорят дети.)
IV. Знакомство с народными традициями
Но мы математику не будем наказывать,
а наоборот, мы ее как дорогого гостя
усадим в угол. Да не в простой угол, а в
“красный угол”. Издавна дорогих гостей
усаживали на лучшее место в доме. А это
было в святом углу, т.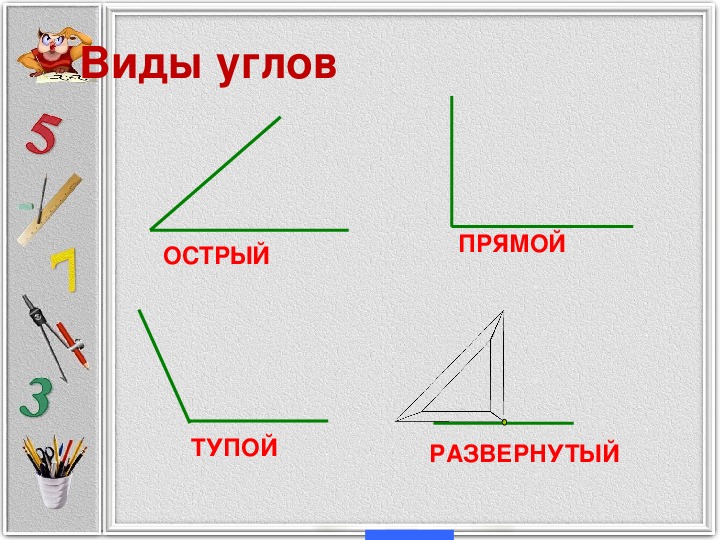 е. в углу, где висят
е. в углу, где висят
иконы: каждое утро и каждый вечер хозяева
дома обращались туда с молитвой. Поэтому
этот угол всегда украшали вышитыми
рушниками и цветами. Ученые всего мира
называют математику Царицей наук.
Поэтому мы ее и усадим в красный угол.
Ребята, вот вы стояли в углу. А кто знает,
как получается угол? (Говорят дети.)
V. Сообщение целей урока
Вот сегодня мы научимся строить углы,
узнаем их имена и научимся отличать их
друг от друга. А поможет нам в этом игра,
которая называется “Шифровка”.
V. Подготовительная работа к восприятию
нового материала
Расшифруйте слова:
НЕЙЛИКА (линейка)
ДАШРАНКА (карандаш)
ТАГАЗЕ (газета)
(Вывешиваю эти предметы.) Какой предмет
лишний? Почему? (Газета не относится к
математике.)
Все эти предметы помогут нам сегодня
сделать большое открытие. Но каждое
Но каждое
открытие надо записать в рабочий блокнот.
Это наши тетради.
VII. Работа в тетради
Запишите сегодняшнее число, классная
работа (это место нашего открытия).
VIII. Повторение пройденного
Начертите в тетради прямую линию. Теперь
“отрежем” от прямой кусок 8 см и начертим
его в тетради. Как этот кусок можно
назвать? (Отрезок). Чем отличается прямая
от отрезка или наоборот?
Отрезок имеет начало и конец, а прямая
бесконечна (учитель проделывает всю
работу с помощью ленты, ножниц и
прикрепляет все это на доске).
Теперь я разрежу прямую и к месту разреза
прикреплю желтый кружок. На что это
похоже? На луч солнца.
Правильно. Эта фигура и называется —
луч. Можно ли продолжить луч со стороны
разреза? (Нет.) А с другой стороны? (Да,
до бесконечности.) Луч имеет начало, но
не имеет конца. А вот если к солнышку
добавить еще один луч, то как вы думаете,
какая фигура получится?
Угол.
IX. Работа над новым материалом
Так что же такое угол?
Угол — это геометрическая фигура,
образованная двумя лучами, выходящими
из одной точки.
Лучи — это стороны угла.
Точка — это вершина угла.
В жизни мы каждый день встречаемся с
различными углами.
Ведь угол — это перелом (ломаю веточку),
изгиб, колено, локоть. Где еще встречаются
углы? Парта, стол, стул, книга, доска,
шкаф, портфель, дом и т.д.
Каждый угол имеет название. И сейчас мы
поиграем в игру “Имена”.
(На доске начерчены фигуры)
X. Обобщение
Углы квадрата называются прямыми.
Угол, который шире прямого, называется
тупой. Угол меньше прямого или уже
его называется острый (чертим в
тетрадях).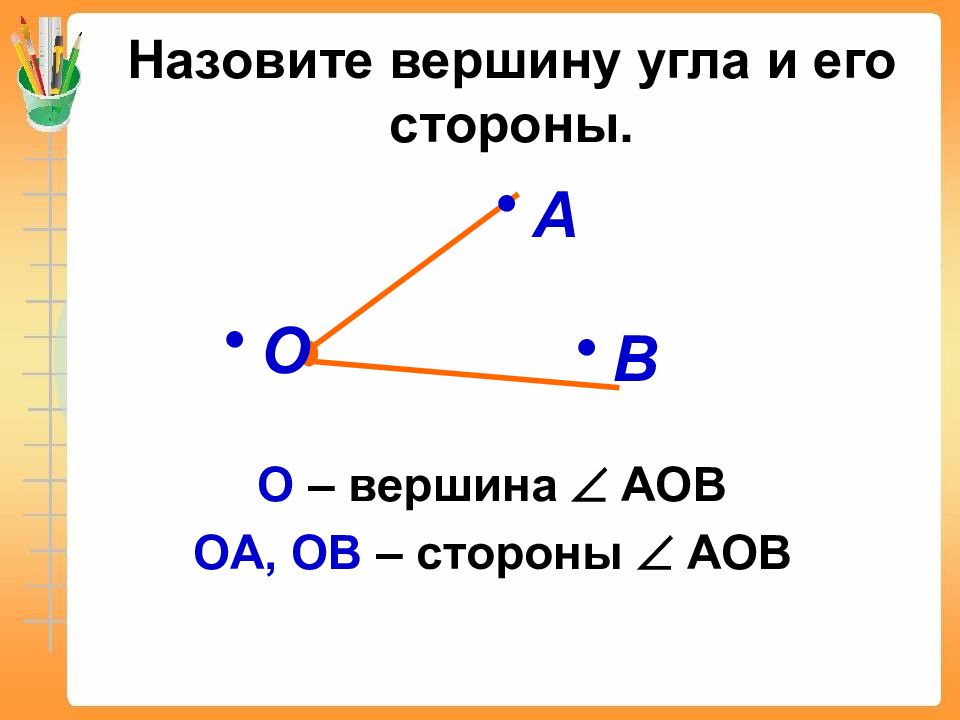
XI. Закрепление пройденного
А теперь поиграем в игру “Строители”.
(Из палочек построим прямой угол: из 2-х
палочек — один угол, из 3-х палочек —
два угла, из 4-х — четыре прямых угла.
Постройте тупой и острый угол из палочек.)
Молодцы, ребята!
Работа по учебнику
Откройте
учебник математики на стр. 119, выполним
устно задание № 401-404
(
вместе с учителем выполняют задание)
А
сейчас поиграем в игру “Помогай-ка”.
XII. Практическая работа по изготовлению
прямого угла
Наш друг карандаш построил себе домик,
но что-то в нем не так. Как вы думаете,
ребята?
(Не
ровные углы).
Правильно.
Во всех домах углы должны быть прямые.
Даже есть такая пословица: “Красна изба
углами, а обед пирогами”.
Давайте поможем Карандашу исправить
эту ошибку. Но как? Ведь у нас нет такого
инструмента, которым бы можно было
измерить прямой угол. Для этого нужен
Для этого нужен
чертежный прямоугольный треугольник
(показываю).
Пока Линеечка сходит за своим другом
Треугольником, пройдет много времени.
А Карандашу срочно нужен дом. В этом нам
поможет обыкновенная газета.
Загните любой угол газеты вот так
(показываю). А теперь сложите еще раз
так, чтобы части линии сгиба совместились.
Вот и получится прямой угол.
А вот и угольник пришел. Давайте проверим,
у всех ли получился прямой угол.
(Накладываем свои углы на прямоугольный
треугольник.)
Исправляем углы дома.
Проверяем их при помощи своих углов и
треугольника.
Дом улыбается.
Карандаш всех благодарит и приглашает
на новоселье.
На новоселье принято веселиться. И вот
Карандаш предлагает новую игру “Кто
лишний?”.
У каждого индивидуальная карточка с
разными углами под номерами.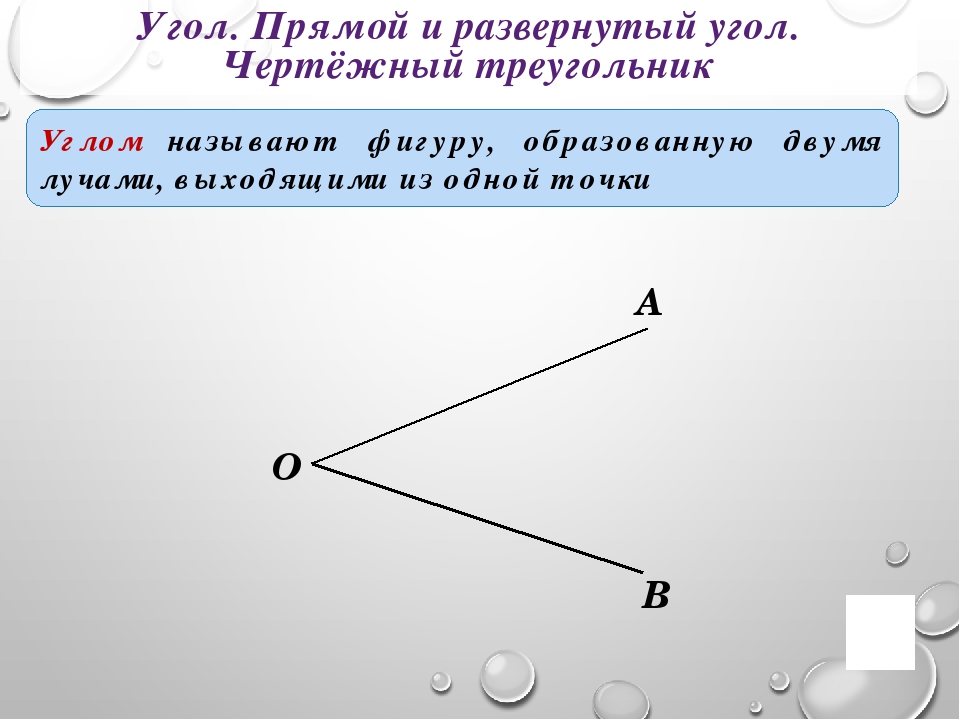 Каждый ряд
Каждый ряд
выполняет свое задание.
1 ряд — Назвать номера прямых углов. (2,
4)
2 ряд — Назвать номера тупых углов. (1)
3 ряд — Назвать номера острых углов. (3,
5)
Молодцы, ребята! Вы все хорошо справились
с работой. Ну, как говорится, всему свое
время. Пора заканчивать игру.
XIII. Итог урока
С какой же новой геометрической фигурой
мы сегодня играли? С прямым углом. А
какие еще бывают углы? Острые, тупые.
Закончить урок стихотворением:
Математику,
друзья
Не любить никак нельзя:
Очень
строгая наука,
Очень точная наука,
Интересная наука
—
Это математика.
Определение прямой угол общее значение и понятие. Что это такое прямой угол
Первое, что нужно сделать, прежде чем полностью войти в установление значения термина «прямой угол», — это обнаружить этимологическое происхождение слов, составляющих его.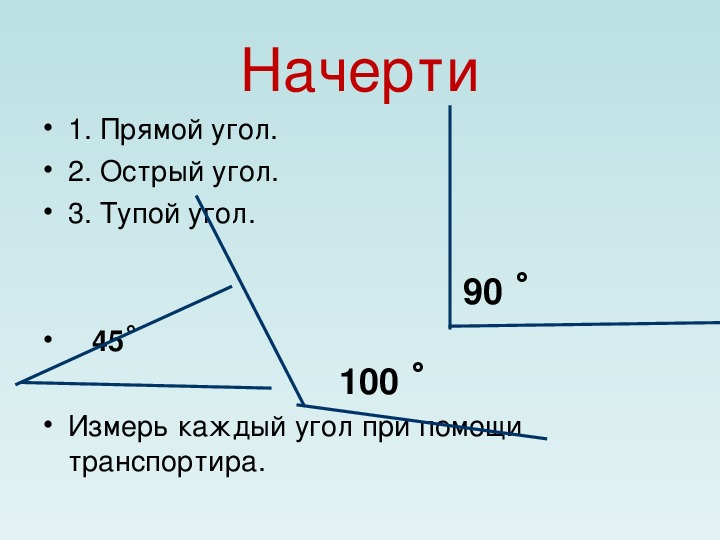 В данном случае это то, что мы можем сказать:
В данном случае это то, что мы можем сказать:
-Ангуло — это слово, которое происходит от греческого языка, в частности, от «ankulos», что можно перевести как «изогнутый» или «искривленный». Это, в свою очередь, дало форму латинскому «angulus», что является синонимом «угла».
-Recto, с другой стороны, происходит от латинского слова «rectus», что означает «право». В частности, это прилагательное происходит от глагола «regere», который можно перевести как «выпрямить».
Угол — это концепция, которая имеет несколько применений. В этом случае мы заинтересованы в том, чтобы сохранить его значение как геометрическую фигуру, образованную двумя лучами, которые разделяют вершину.
По его характеристикам можно различать разные типы углов. Прямой угол — это угол, который измеряет девяносто шестимесячных градусов (90º) . Этот угол образован двумя лучами, которые перпендикулярны друг другу и происходят в вершине, которую они разделяют.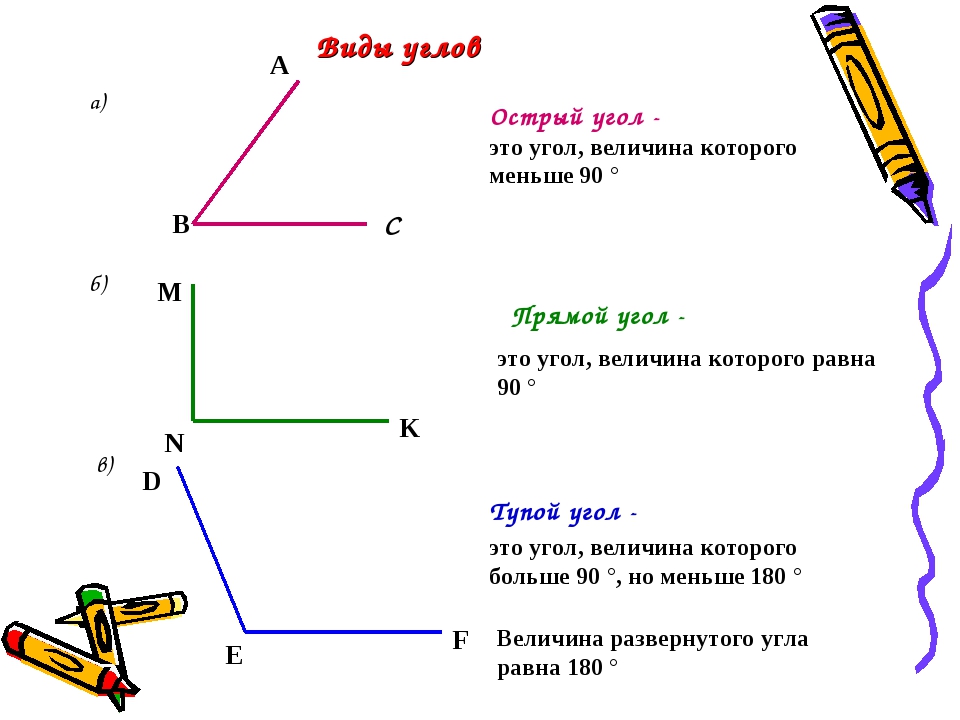
В дополнение ко всему вышесказанному, мы не можем упускать из виду другие характеристики, также очень значимые, как следующие:
— Считается, что это самый простой угол для выявления среди всех существующих.
-Это всегда одно и то же.
Мы можем найти прямые углы в разных плоских фигурах геометрии. Если мы сосредоточим наше внимание на квадрате (который имеет четыре равные и параллельные стороны), мы заметим, что его четыре внутренних угла являются прямыми углами. Это означает, что каждый угол квадрата измеряет 90º и что сумма всех его углов составляет 360º. Прямоугольные треугольники, с другой стороны, имеют прямой угол и два острых угла (которые составляют менее 90º и более 0º).
Прямые углы могут быть объединены, чтобы сформировать другой вид угла. Два прямых угла в этом кадре приводят к плоскому углу (также называемому простым углом ), который составляет 180º. Четыре прямых угла, с другой стороны, позволяют получить перигональный или полный угол: угол 360º.
Следует отметить, что прямые углы являются частью набора выпуклых углов или выступающих углов, которые охватывают все те углы, которые составляют более 0º, но менее 180º. Это означает, что острые углы и тупые углы также являются выпуклыми углами.
Также важно знать, что «Прямоугольный» — это название известного научного журнала Мадридского университета Комплутенсе. Это публикация исследований города, которая имеет раз в два года отмеченный тематический эфир и которая обычно публикуется в мае и декабре.
Он в основном состоит из статей, в которых город анализируется как таковой с разных точек зрения. То есть с архитектурной, антропологической, художественной, литературной, философской, социологической, литературной точек зрения с точки зрения человеческой географии … Таким образом, мы пытаемся показать его как пространство, полное множественности, богатства, взаимосвязи, а также мультикультурности.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.
Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.
Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.
Рис.1
Изображенный на рисунке 1 угол можно обозначить тремя способами:
Углы называют равными углами, если их можно совместить.
Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.
Рис.2
Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.3). Точку B называют основанием перпендикуляра AB.
Рис.3
Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.
Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.
Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).
Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».
Таблица 1 – Типы углов в зависимости от величины в градусах
| Прямой угол |
Свойство: Прямой угол равен 90° |
| Острый угол |
Свойство: Острый угол меньше 90° |
| Тупой угол |
Свойство: Тупой угол больше 90°, но меньше 180° |
| Развернутый угол |
Свойство: Развернутый угол равен 180° |
| Угол больший, чем развернутый |
Свойство: Такой угол больше 180°, но меньше 360° |
| Полный угол |
Свойство: Полный угол равен 360° |
| Угол, равный нулю |
Свойство: Такой угол равен 0° |
Таблица 2 – Типы углов в зависимости расположения сторон
| Вертикальные углы |
Свойство вертикальных углов: Вертикальные углы равны |
| Смежные углы |
Свойство смежных углов: Сумма смежных углов равна 180° |
| Углы с соответственно параллельными сторонами |
Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно параллельными сторонами: Сумма углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой |
| Углы с соответственно перпендикулярными сторонами |
Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой |
Определение. Биссектрисой угла называют луч, делящий угол пополам.
Биссектрисой угла называют луч, делящий угол пополам.
Задача. Доказать, что биссектрисы смежных углов перпендикулярны.
Решение. Рассмотрим рисунок 4.
Рис.4
На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку
2α + 2β = 180°.
то
α + β = 90°,
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Прямой угол
Пользователи также искали:
как начертить прямой угол,
как определить прямой угол,
прямой и непрямой угол,
прямой угол 2 класс,
прямой угол — — это 2 класс,
прямой угол определение,
прямой угол равен,
прямой угол в треугольнике,
Прямой,
прямой,
угол,
Прямой угол,
класс,
прямой и непрямой угол,
как начертить прямой угол,
прямой угол в треугольнике,
прямой угол определение,
прямой угол равен,
определить,
непрямой,
начертить,
треугольнике,
определение,
равен,
прямой угол класс,
как определить прямой угол,
прямой угол — — это класс,
прямой угол 2 класс,
прямой угол — — это 2 класс,
прямой угол,
классическая геометрия. прямой угол,
прямой угол,
…
Что такое прямой угол? — [Определение, факты и примеры]
Игры под прямым углом
Под прямым углом
Находите прямые углы в различных двухмерных формах. Помните, вы можете распознать прямые углы, глядя на перпендикулярные линии.
охватывает Common Core Curriculum 4.G.2Играть сейчасПосмотреть все игры по геометрии >>
Учитесь с помощью полной программы обучения математике K-5
Что такое прямой угол?
В геометрии, когда два луча встречаются в общей точке, они образуют угол.Точка встречи двух лучей называется вершиной.
Углы измеряются в градусах (символ: ˚)
Некоторыми распространенными типами углов являются острые, прямые и тупые углы.
Угол прямой
Когда две прямые линии пересекаются друг с другом под углом 90 ° или перпендикулярны друг другу на пересечении, они образуют прямой угол.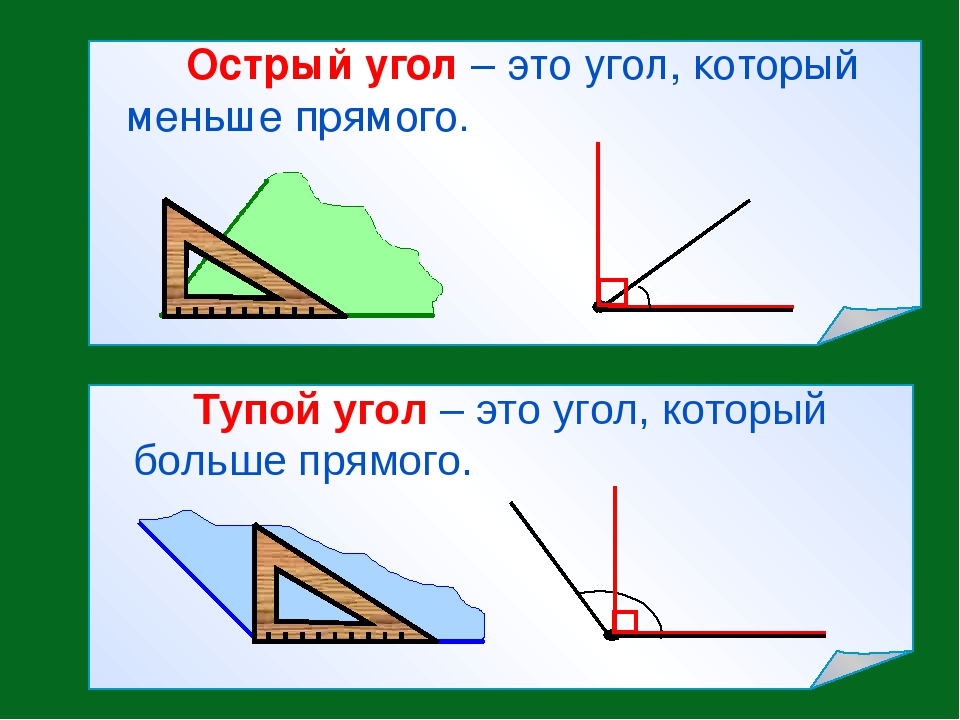 Прямой угол обозначается символом ∟.
Прямой угол обозначается символом ∟.
На данном изображении показаны различные образования прямого угла.
Мы можем найти прямые углы в формах.
Квадрат или прямоугольник имеет четыре угла с прямыми углами.
Примеры прямых углов нас окружают. Мы можем видеть прямые углы в углах комнаты, книги, куба, окон и в некоторых других местах.
Вертикальная и горизонтальная линии обычно образуют прямые углы.Однако пересекающиеся друг с другом диагональные линии тоже образуют прямые углы. Если вы нарисуете диагонали квадрата, ромба или воздушного змея, угол пересечения составит 90 градусов и, следовательно, будет прямым углом.
Пример ромба и воздушного змея с диагоналями, пересекающимися под прямым углом.
Как нарисовать прямой угол с помощью транспортира?
1 . Начните с рисования горизонтальной линии.
2 . Теперь поместите транспортир на горизонтальную линию.
Теперь поместите транспортир на горизонтальную линию.
3 . Измерьте 90˚ и отметьте его точкой.
4 . Теперь с помощью шкалы нарисуйте прямую линию от этой точки до горизонтальной линии.
Интересные факты
|
Типы углов — объяснения и примеры
Различные типы углов существуют в природе, , и каждый из них имеет большое значение в нашей повседневной жизни.
Например, , архитекторы и инженеры используют углы при проектировании машин, зданий, дорог и мостов.
В спорте спортсмены используют углы для улучшения своих результатов. Например, человек должен вращаться с диском под определенным углом, чтобы бросить его на короткое расстояние.В футболе вы должны использовать определенный угол, чтобы передать мяч следующему игроку.
Например, человек должен вращаться с диском под определенным углом, чтобы бросить его на короткое расстояние.В футболе вы должны использовать определенный угол, чтобы передать мяч следующему игроку.
Плотники и ремесленники также используют углы для изготовления таких предметов, как диваны, столы, стулья, ведра и т. Д. Художники используют углы для набросков портретов и картин. Модельеры также используют ракурсы, чтобы подобрать лучшие наряды. По этим причинам необходимо изучить различные типы углов.
(Чтобы пройти базовое объяснение углов, вы можете обратиться к предыдущей статье «Углы.”)
Различные типы углов
Углы классифицируются на основе:
Классификация углов по их величине
Существует семь типов углов, основанных на их градусном измерении. Они включают:
- нулевых углов
- острых углов
- прямых углов
- тупых углов
- прямых углов
- углов отражения
- полного угла
нулевого угла
нулевого угла (0 °) является угол образуется, когда оба плеча угла находятся в одном и том же положении.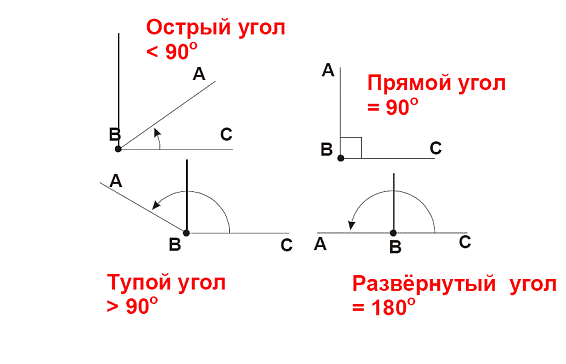
Рисунок:
∠ RPQ = 0 ° (нулевой угол)
Острый угол
Острый угол — это угол, который больше 0 °, но меньше 90 °. Типичные примеры острых углов: 15 °, 30 °, 45 °, 60 ° и т. Д.
∠ XYZ больше 0 °, но меньше 90 ° (острый угол)
Угол 90 градусов
Угол в 90 градусов, также известный как прямой угол, — это угол, размер которого равен 90 °, и называется прямым углом.Прямые углы изображаются в виде небольшой квадратной рамки между плечами угла.
Иллюстрация:
∠ ABC = 90 ° (прямой угол)
В следующем разделе (Треугольники) будет целая статья о прямоугольных треугольниках.
Тупой угол
Тупой угол — это тип угла, градусы которого больше 90 °, но меньше 180 °. Примеры тупых углов: 100 °, 120 °, 140 °, 160 °, 170 ° и т. Д.
∠ PQR — тупой угол, потому что он меньше 180 ° и больше 90 °.
Прямой угол
Как следует из названия, прямой угол — это угол, размер которого равен 180 ° (прямая линия)
Иллюстрация:
∠ XYZ = 180 ° (прямой угол)
Угол отражения
Углы отражения — это типы углов, градусы которых составляют более 180 °, но менее 360 °.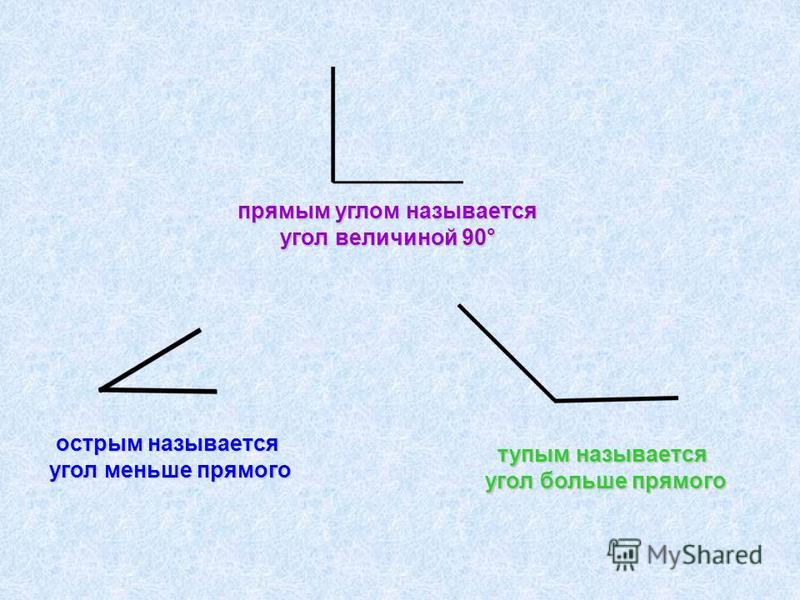 Общие примеры углов рефлекса: 200 °, 220 °, 250 °, 300 °, 350 ° и т. Д.
Общие примеры углов рефлекса: 200 °, 220 °, 250 °, 300 °, 350 ° и т. Д.
Иллюстрация:
∠ PQR больше 180 °, но меньше 360 °
Полный угол
Полный угол равен до 360 °.1 оборот равен 360 °.
Иллюстрация:
Классификация углов на основе вращения
В зависимости от направления вращения углы можно разделить на две категории, а именно;
- Положительные углы
- Отрицательные углы
Положительные углы
Положительные углы — это типы углов, измерения которых проводятся против часовой стрелки от основания.
Отрицательные углы
Отрицательные углы измеряются по часовой стрелке от основания.
Другие типы углов
Помимо рассмотренных выше углов, существуют другие типы углов, известные как парные углы. Их называют парными углами, потому что они появляются парами, чтобы показать определенное свойство.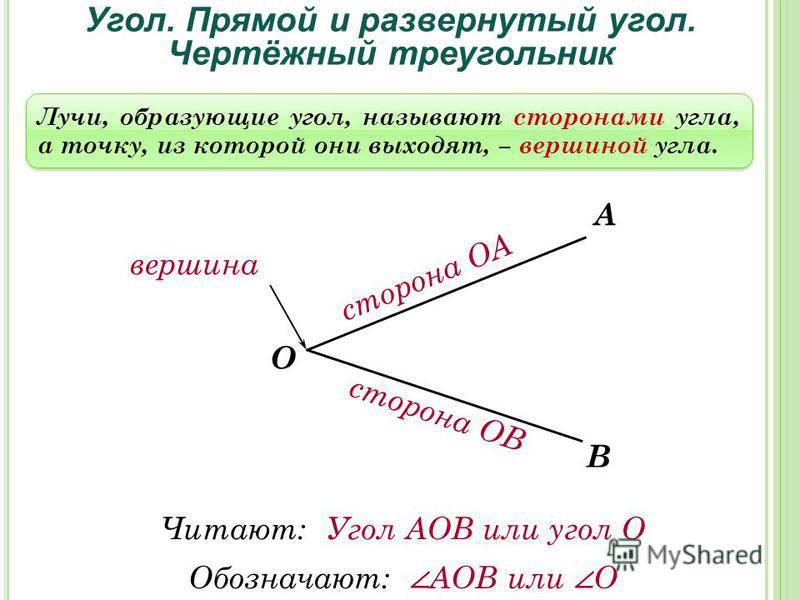 Это:
Это:
- Соседние углы имеют одинаковую вершину и плечо.
- Дополнительные углы: парные углы, которые в сумме составляют 90 °.
- Дополнительные углы: парные углы, сумма углов которых равна 180 °.
- Вертикально противоположные углы.Вертикально противоположные углы равны.
- Альтернативные внутренние углы: Альтернативные внутренние углы — это парные углы, образующиеся, когда линия пересекает две параллельные линии. Чередующиеся внутренние углы всегда равны друг другу.
- Альтернативные внешние углы : Альтернативные внешние углы — это просто вертикальные углы альтернативных внутренних углов. Альтернативные внешние углы эквивалентны.
- Соответствующие углы : Соответствующие углы — это парные углы, образующиеся, когда прямая пересекает пару параллельных прямых.Соответствующие углы также равны друг другу.
Мы видели краткий обзор различных типов углов. Далее мы увидим подробные статьи о наиболее распространенных типах углов (Дополнительные углы, Дополнительные углы и т. Д.).
Д.).
Предыдущий урок | Главная страница | Следующий урок
Прямой угол — Cuemath
В этом разделе мы исследуем мир прямых углов. Найдя ответы на вопрос, что такое сфера, как ее вычислить, и обнаружив интересные факты о прямых углах, тема станет ясной как кристалл.
Прежде чем мы начнем, давайте посмотрим, с чем недавно столкнулся Сэм.
После наблюдения угла, образованного стрелками часов в 15:00, одной четвертой части пиццы и углов комнаты, Сэм заметил, что в нескольких местах нас окружают прямые углы. Ты чувствуешь то же самое?
Наиболее распространенные прямые углы образуют вертикальная и горизонтальная линия.
Кроме того, диагональные линии, пересекающие друг друга, образуют прямой угол.
Давайте начнем наше путешествие и узнаем удивительные свойства прямых углов.
План урока
Что такое прямой угол?
Определение прямого угла: Прямой угол — это угол со значением, равным 90 градусам.
Он играет важную роль в таких областях математики, как геометрия и тригонометрия.
Когда две прямые пересекаются друг с другом под углом 90 ° или перпендикулярны друг другу на пересечении, они образуют прямой угол. Все дело в определении прямого угла.
Прямой угол обозначается символом ∟.
Форма прямого угла
Прямой угол будет похож на алфавит L.
Воспользуйтесь данным интерактивным моделированием и посмотрите, как построить прямой угол с помощью транспортира или компаса.
Примеры прямого угла в реальной жизни
Примеры прямых углов в формах, доступных вокруг нас:
- Кромки двери.
- Четыре края телевизора.
- 9:30 часов.
- Уголок стула.
Получите представление о прямых углах в формах вокруг нас из рисунка, приведенного ниже:
Эти формы чаще всего используются для получения примеров прямых углов.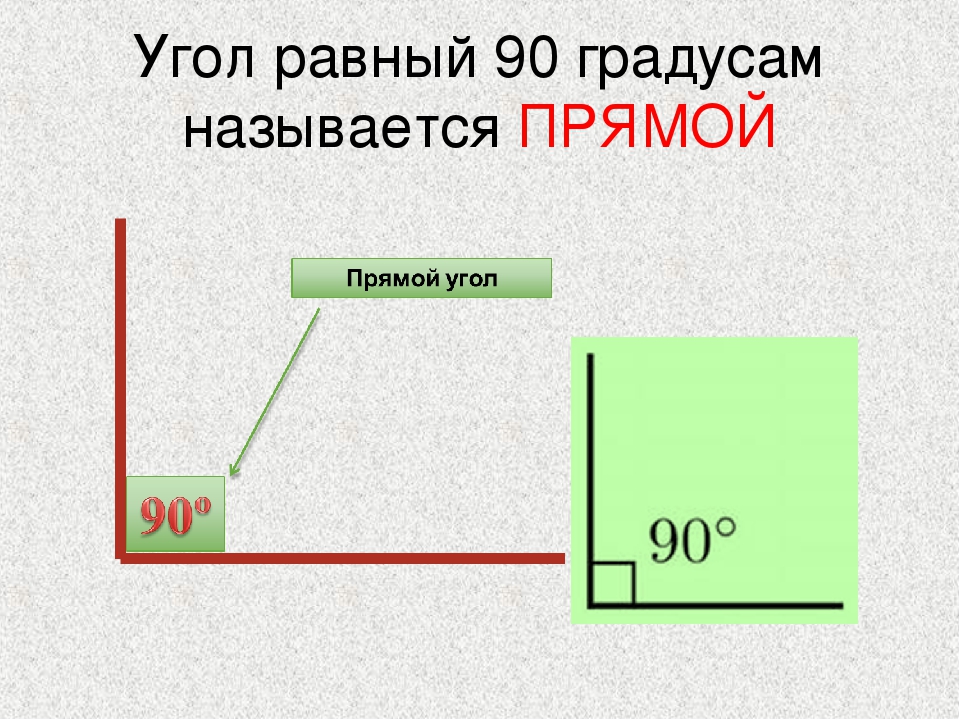
Можете ли вы найти еще несколько примеров прямых углов в формах, доступных вокруг вас?
Калькулятор прямого угла
Некоторые из устройств, используемых для измерения прямого угла: транспортир, заданные углы, угольники и т. Д.Поигравшись с симуляцией, приведенной ниже, вы увидите, как это делается.
Транспортир
Набор квадратов
Попробуйте Square
Типы углов
Существует шесть различных типов углов, а именно:
Есть еще одно место, где используется прямой угол, и это прямоугольный треугольник.
Если среди трех углов треугольника один угол равен 90 °, то этот треугольник называется прямоугольным.
Поскольку три внутренних угла прямоугольного треугольника в сумме составляют 180 градусов, и если один угол всегда равен 90 градусам, тогда два других угла всегда должны составлять в сумме 90 градусов, и они называются дополнительными углами.
Прямоугольный треугольник
Важные примечания
- Транспортир, заданные квадраты и пробный квадрат используются для измерения прямого угла в прямоугольном треугольнике.
- Существует шесть типов углов: острый угол, прямой угол, тупой угол, прямой угол, угол отражения и полный угол.
- Края двери, четыре края телевизора, 9:30 часов и угол стула — наиболее распространенные примеры прямого угла.
Решенные примеры
Тим нарисовал на бумаге несколько углов. Можете ли вы помочь ему определить правильный угол, не используя транспортир?
Решение
С точки зрения прямого угла, прямой угол выглядит как алфавит L.
Среди заданных вариантов угол в левом нижнем углу — это прямой угол
| \ (\ следовательно \) Угол в левом нижнем углу, который выглядит как L-образный угол алфавита, равен 90 |
Тревор хочет знать, какие типы углов больше прямого.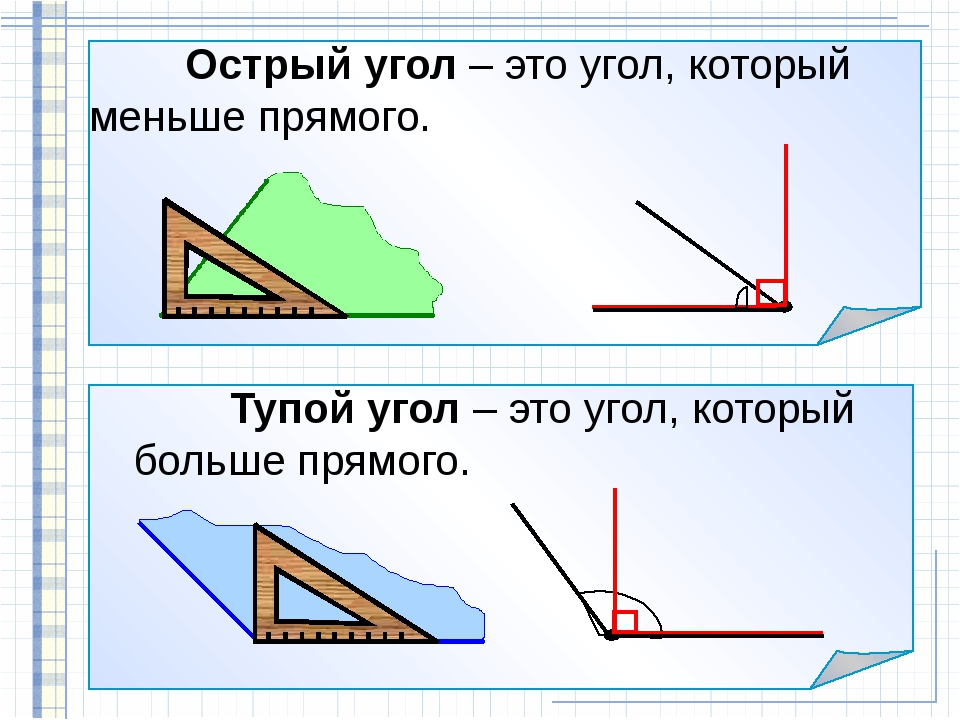 Вы можете помочь ему разобраться с этой проблемой?
Вы можете помочь ему разобраться с этой проблемой?
Решение
Согласно определению прямого угла, любой угол, размер которого превышает 90 °, больше прямого угла.
Это:
(а) Тупой угол
(б) Уголок прямой
(c) Угол отражения
(d) Угол весь
| \ (\ следовательно \) Тупой угол, Прямой угол, Угол отражения и Полный угол больше 90 ° |
Эй, вы можете написать название угла, показанного на картинке, это острый угол, тупой угол, прямой угол, угол рефлекса или весь угол?
Решение
Название угла на картинке — прямой угол.
Маленькая Фиона видела часы в своем доме, и ей было любопытно узнать угол, сделанный двумя стрелками часов в 9:00 и 15:00. Вы знаете ответ на ее вопрос?
Решение
мы можем видеть на картинке, что две стрелки часов образуют прямой угол.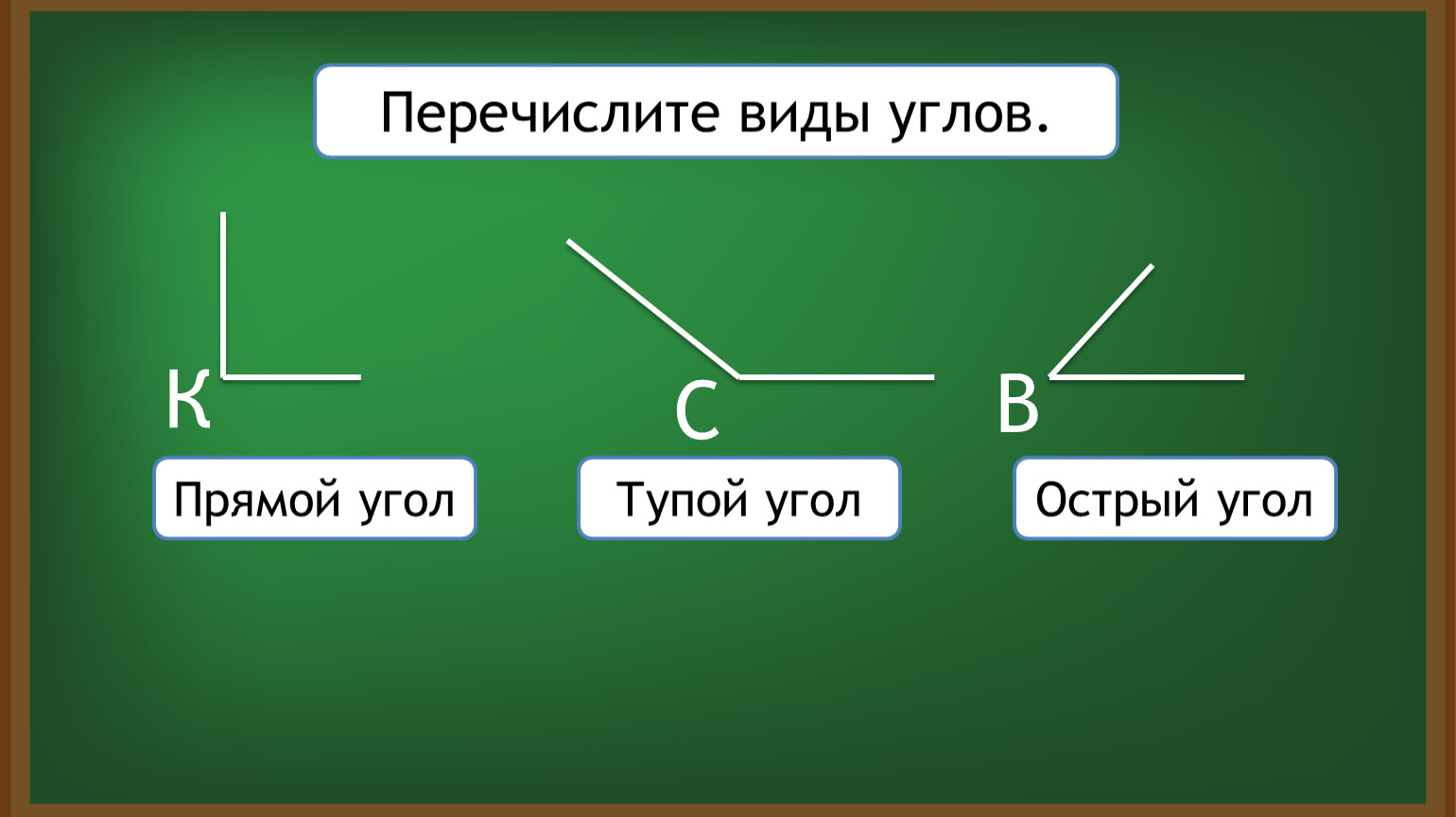
| \ (\ следовательно \) Угол, образованный двумя стрелками часов в 9:00 и 15:00, равен -Прямому углу. |
Сложные вопросы
- Назовите возможный угол, сделанный стрелками часов в 12:00 и 10:00.
- Максимальный угол угла рефлекса?
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнать о прямоугольном треугольнике с помощью моделирования и практических вопросов.Теперь вы сможете легко решать задачи с острым углом, тупым углом, типом углов, прямым углом, определением прямого угла, прямоугольным треугольником, калькулятором прямого угла, прямыми углами в формах, примерами прямых углов и меньше прямого угла.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Каковы три угла прямоугольного треугольника?
Три угла прямоугольного треугольника равны:
Два острых угла и один прямой угол.
2. Напишите виды углов?
Вот разные типы углов:
Острый угол, прямой угол, тупой угол, прямой угол, угол рефлекса и угол полного вращения или нулевой градус.
3. Что такое тупой, острый и прямой угол?
Тупой угол — это угол между 90 ° и 180 °
Острый угол — это угол от 0 ° до 90 °
А прямой угол — это угол 180 °
4.
 Что такое прямой угол, угол отражения и полный угол поворота?
Что такое прямой угол, угол отражения и полный угол поворота?
Прямой угол — это угол 90 °
Угол отражения — это угол от 180 ° до 270 °
А полный угол поворота составляет 360 ° или 0 °
Калькулятор прямоугольного треугольника
Укажите 2 значения ниже, чтобы рассчитать другие значения прямоугольного треугольника.Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д.
Калькулятор связанных треугольников | Калькулятор по теореме Пифагора
Прямой треугольник
Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Правые треугольники и отношения между их сторонами и углами являются основой тригонометрии.
В прямоугольном треугольнике сторона, противоположная углу 90 °, является самой длинной стороной треугольника и называется гипотенузой.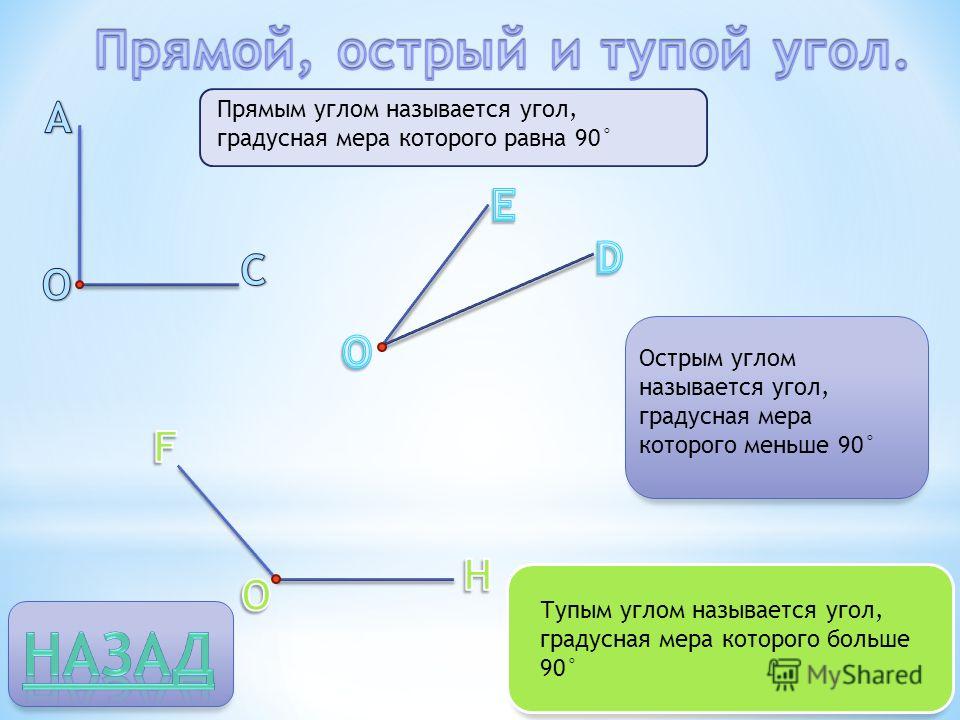 Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. . В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая является длиной от вершины прямого угла треугольника до гипотенузы треугольника.Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. . В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая является длиной от вершины прямого угла треугольника до гипотенузы треугольника.Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Если все три стороны прямоугольного треугольника имеют целые числа, он называется треугольником Пифагора. В треугольнике этого типа длины трех сторон в совокупности известны как тройка Пифагора. Примеры включают: 3, 4, 5; 5, 12, 13; 8, 15, 17 и т. Д.
Площадь и периметр прямоугольного треугольника рассчитываются так же, как и любого другого треугольника. Периметр представляет собой сумму трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Периметр представляет собой сумму трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Специальные прямоугольные треугольники
Треугольник 30 ° -60 ° -90 °:
30 ° -60 ° -90 ° относится к угловым измерениям в градусах этого типа специального прямоугольного треугольника. В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием вышеуказанного соотношения.Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сб .:
Углы: 30 °: 60 °: 90 °
Соотношение сторон: 1: √3: 2
Длина сторон: a: 5: c
Тогда, используя известные отношения сторон этого особого типа треугольника:
Как видно из вышеизложенного, знание только одной стороны треугольника 30 ° -60 ° -90 ° позволяет относительно легко определить длину любой из других сторон. Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
Треугольник 45 ° -45 ° -90 °:
Треугольник 45 ° -45 ° -90 °, также называемый равнобедренным прямоугольным треугольником, поскольку он имеет две стороны равной длины, представляет собой прямоугольный треугольник, в котором стороны, соответствующие углам, составляют 45 ° -45 ° -90 °, соблюдайте соотношение 1: 1: √2. Подобно треугольнику 30 ° -60 ° -90 °, знание длины одной стороны позволяет определить длины других сторон треугольника 45 ° -45 ° -90 °.
Углы: 45 °: 45 °: 90 °
Соотношение сторон: 1: 1: √2
Длина сторон: a: a: c
Учитывая c = 5:
треугольников 45 ° -45 ° -90 ° можно использовать для вычисления тригонометрических функций для кратных π / 4.
Острые углы и прямой угол
Расшифровка стенограммы видео по математике
00:00:03.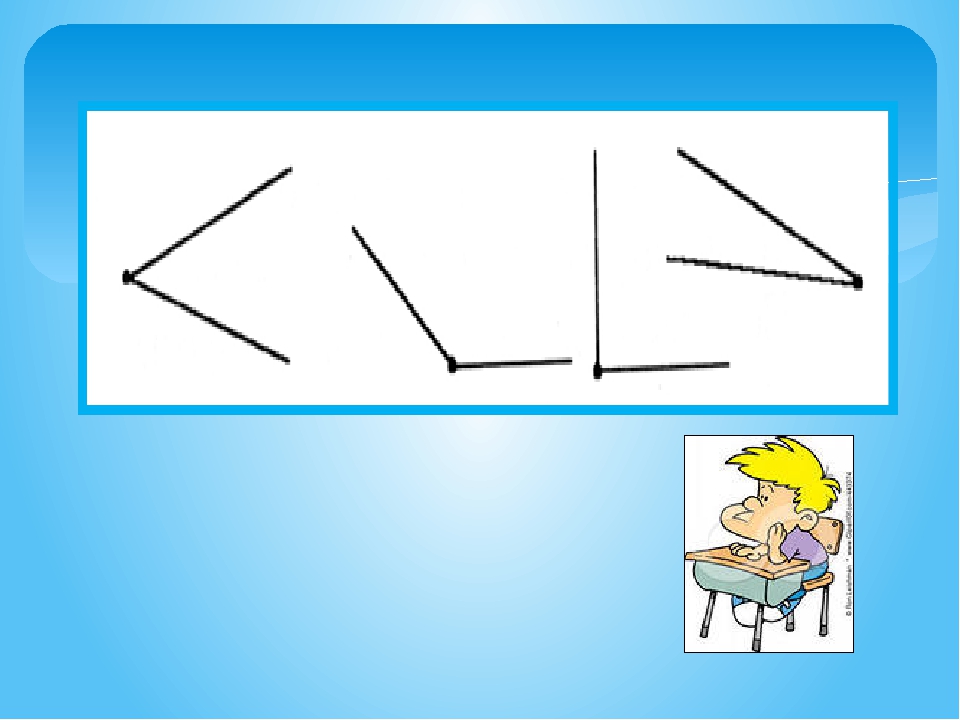 120
120
В этом уроке мы узнаем об острых углах.
00: 00: 08.100
Давайте посмотрим на этот угол.
00: 00: 11.140
Теперь, поскольку этот угол находится где-то между 0 и 90 градусами, это угол.
00: 00: 19.140
Следовательно, мы можем сказать, что acu. угол всегда больше 0 градусов и меньше 90 градусов.
00: 00: 29.010
Давайте посмотрим на несколько примеров, чтобы лучше понять это.
00:00:33.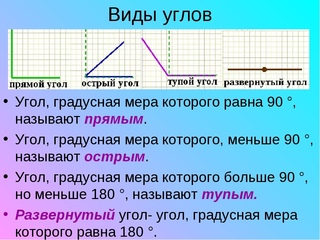 130
130
Рассмотрим этот угол в 80 градусов. Это аку. угол? Да! Это.
00: 00: 45.120
Как насчет этого угла в 35 градусов? Да! Это аку. угол.
00: 00: 54.140
Хорошо, посмотрите внимательно на этот угол.Это аку. угол?
00: 01: 02.080
Мы знаем это, аку. угол всегда больше 0 градусов. Это правда для этого угла.
00: 01: 11.020
Кроме того, оно всегда меньше 90 градусов.Опять же, это также верно для этого угла.
00: 01: 21.130
Да, это так.
00: 01: 26.230
А как насчет этого угла?
00:01:31.080
Понятно, что этот угол больше 90 градусов.
00: 01: 35.200
Следовательно, это не так.
00: 01: 39.230
На этом урок все закончился.
Что такое прямой угол? — Определение и формулы — Урок математики [видео 2021 года]
Обозначение
Прямые углы имеют особые обозначения. Это символ, из-за которого кажется, что под углом находится маленький квадрат. Выглядит это так:
Это символ, из-за которого кажется, что под углом находится маленький квадрат. Выглядит это так:
Маленькая квадратная рамка говорит вам, что это прямой угол.
Во многих местах вы увидите прямые углы. Вы увидите их в квадратах и прямоугольниках, где каждый угол представляет собой прямой угол. Одно из самых полезных мест, где вы их увидите, — это треугольники. Когда треугольник имеет прямой угол, он становится треугольником особого типа, называемым прямоугольным треугольником .У прямоугольных треугольников всегда ровно один угол, равный 90 градусам. Выглядят они так:
Правые треугольники служат основой для многих математических вещей, таких как определение расстояния вверх по склону, если вам известна только высота холма, и определение ширины холма. Без прямоугольных треугольников не было бы тригонометрии. Тригонометрические функции синуса, косинуса и тангенса основаны на прямоугольном треугольнике.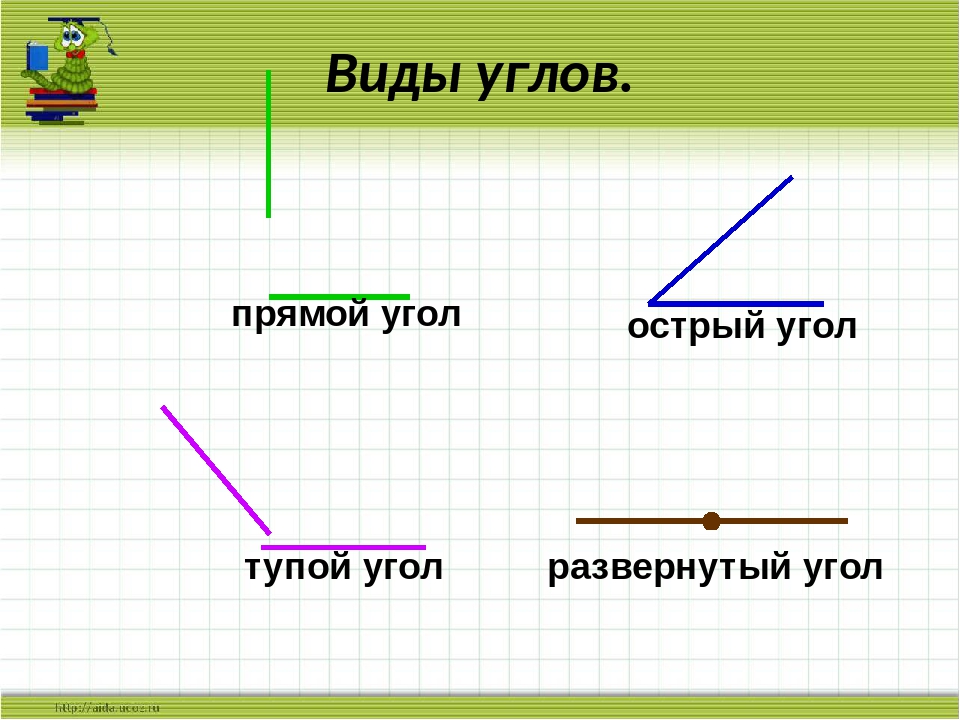
Теорема Пифагора
Одна из самых важных формул, с которыми вы когда-либо сталкивались в отношении прямоугольных треугольников, — это теорема Пифагора. Теорема Пифагора — это формула, которая связывает все три стороны прямоугольного треугольника друг с другом. Это позволяет вам найти одну сторону по двум другим.
Сторона c всегда гипотенуза или сторона, противоположная прямому углу. Гипотенуза — это всегда самая длинная сторона прямоугольного треугольника. Теорема Пифагора говорит вам, что квадрат гипотенузы такой же длины, как сумма квадратов двух других сторон.
Давайте посмотрим, как мы можем использовать теорему Пифагора, чтобы помочь нам решать проблемы. Допустим, у нас есть этот треугольник, и мы хотим найти недостающую сторону.
Недостающая сторона — это наша гипотенуза, поэтому мы можем обозначить эту сторону c .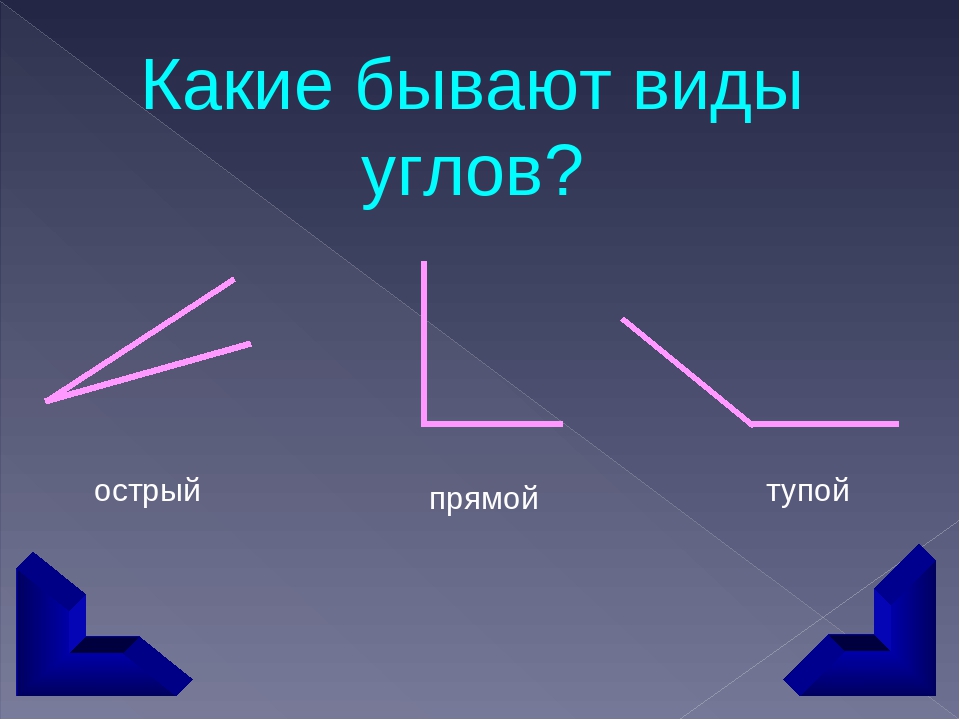 Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона тогда b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так:
Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона тогда b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так:
Мы использовали свои навыки алгебры, чтобы выделить переменную x , чтобы найти ее и найти ответ.После прохождения процесса мы видим, что наша гипотенуза равна 5.
Если бы нам дали гипотенузу и одну из сторон и попросили найти другую сторону, что мы будем делать?
Начнем так же, как и раньше. Мы обозначаем 5 как c , потому что это гипотенуза. На 4-й стороне мы обозначим b , а на стороне x мы обозначим a . Затем мы вставляем нашу информацию в теорему Пифагора и решаем относительно x .
Мы все еще используем наши навыки алгебры, чтобы найти x . На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.
На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.
Резюме урока
Прямые углы определяются как углы, которые составляют ровно 90 градусов. Самое важное место, где вы их увидите, — это треугольники. Формула, полученная из прямоугольного треугольника , является теоремой Пифагора , которая связывает все стороны прямоугольного треугольника друг с другом.Теорема Пифагора говорит вам, что квадрат гипотенузы такой же длины, как сумма квадратов двух других сторон.
Как найти угол в прямоугольном треугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.