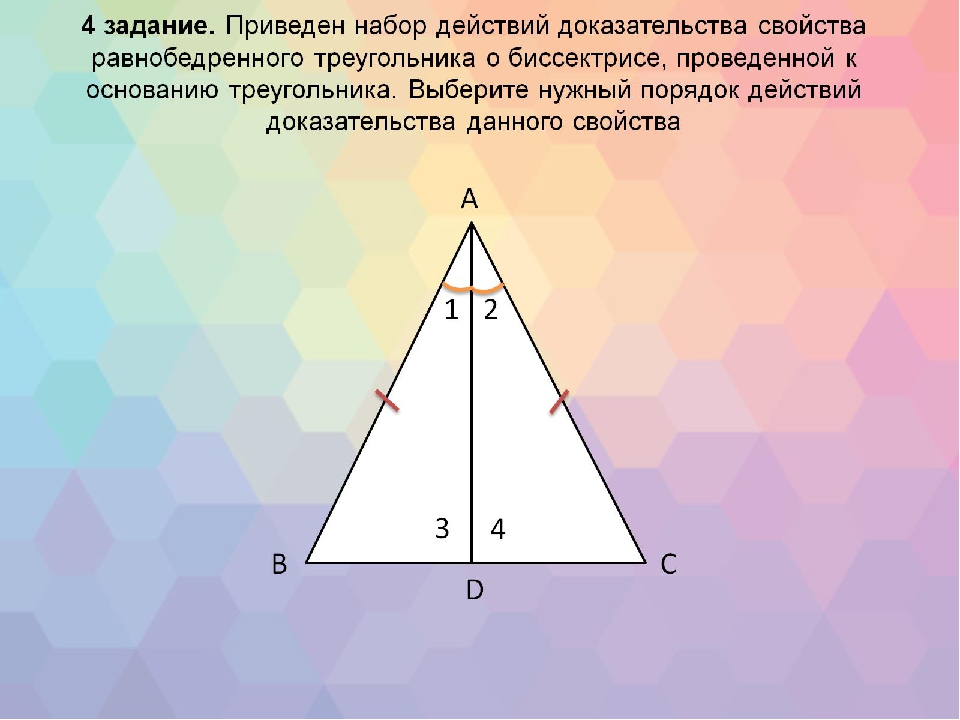
Содержание
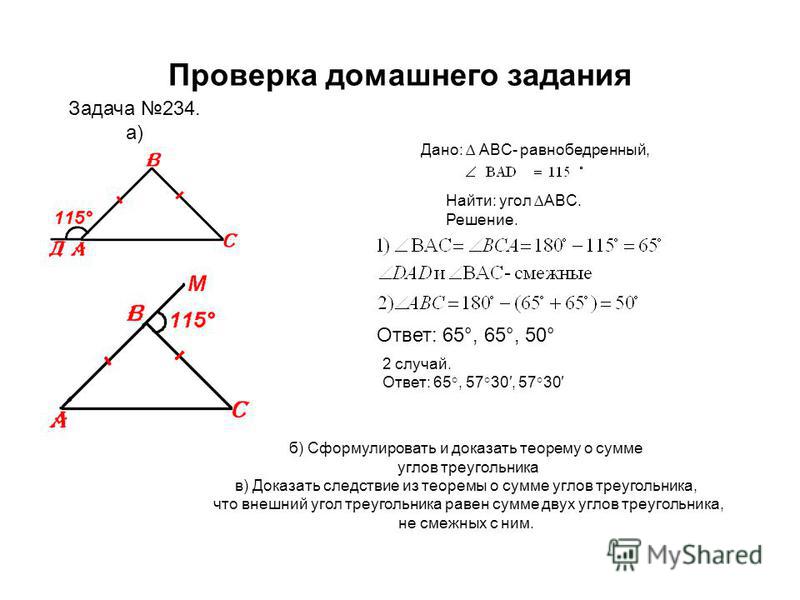
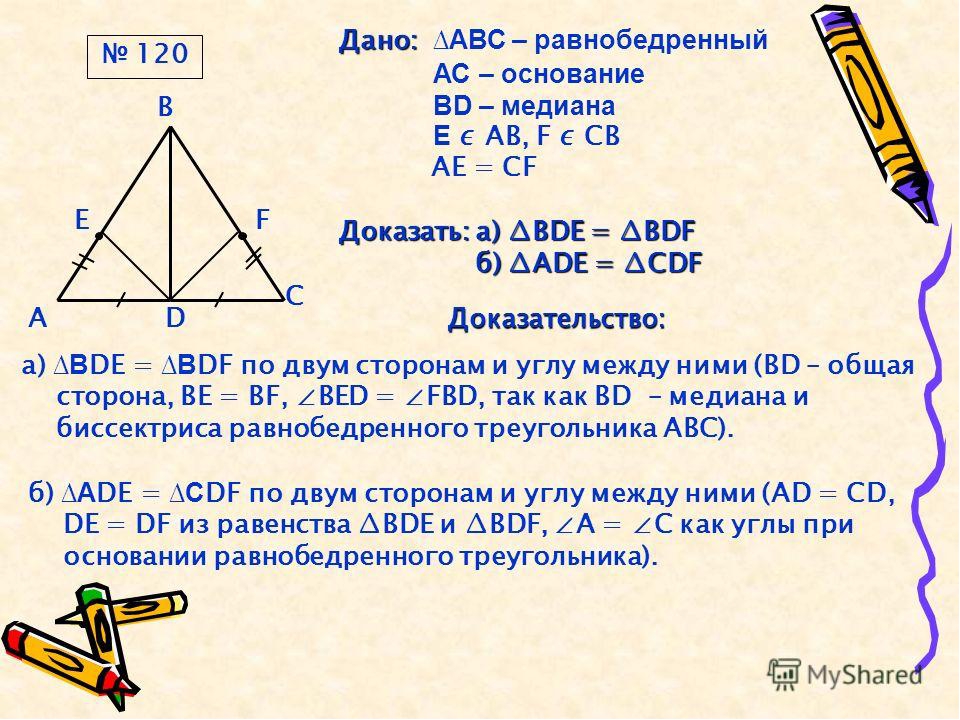
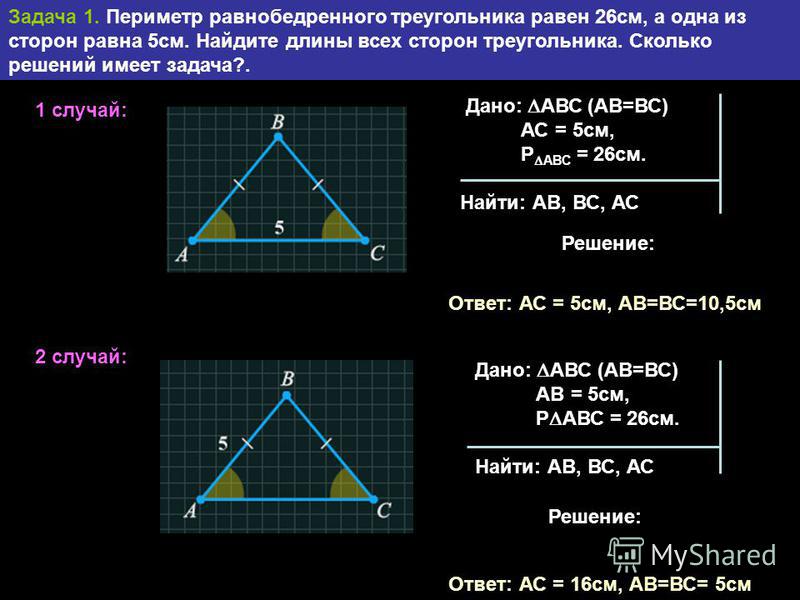
Тест репетитора по теме «равнобедренный треугольник» 7 класс
Пройдите со своим учеником небольшой тест по геометрии для 7 класса по теме: «Равнобедренный треугольник и его свойства». Если Вы репетитор по математике — задайте его своему ученику в качестве домашней работы. Обратите внимание на формат ввода ответов к задачам на вычисление. Указываются только значения величин (без наименований) в определенной единице измерения. Вопросы теста составлены лично мной. Для репетиторов математики и учеников 7 классов.
Как раскрывает тему «равнобедренный треугольник» репетитор по математике?
Подробнее об особенностях качественной репетиторской работы с данным разделом я расскажу в отдельной методической статье. Следите за новостями. На этой странице я упомяну лишь основные моменты, которые следует учесть репетитору по математике. Прежде всего это некоторое расхождение в порядке и методах доказательства признака и свойств фигуры. В учебнике Погорелова репетитор по математике найдет четкое разделение теорем об углах при основании на свойство и признак с доказательством каждого из них через инверсию обозначения треугольника.
В учебнике Атанасяна тема дается несколько иначе. Проводится биссектриса к основанию и доказывается только свойство углов. Признак же не рассматривается вообще. Если репетитор по математике захочет использовать на уроках задачи на доказательство факта равнобедренности, ему придется внимательнее их отбирать. Дидактика Атанасяна предлагает репетитору по математике номера на работу с определением (через равные стороны), а не с признаком (через углы при основании). Поэтому, например, наличие в условии задачи двух равных внешних углов треугольника — превращает ее для программы Атанасяна в категорию почти олимпиадных. Те репетиторы по математике, кто делает ставку на практику решения большого количества разных задач, обычно доказывают ученику признак (как в Погорелове) и снимают методическую проблему узкого задачного коридора. Я действую именно так. С последним учеником 7 класса мне удалось разобрать более 20 задач на равнобедренный треугольник, треть из которых — довольно содержательные и полезные номера на доказательство через равенство углов при основании. Умение показать разницу между прямой и обратной теоремой (на примере признаков и свойств фигур) говорит о репетиторе по математике как о хорошем мастере объяснений. Немногие преподаватели могут похвастаться способностью быстро и точно объяснять смысл тонких математических терминов и вопросов. Если ребенок научился отличать переход A —>B от B—>А уже в 7 классе, то, скорее всего, союз репетитора и ученика окажется продуктивным уже в ближайшей перспективе, а результаты высокими.
Умение показать разницу между прямой и обратной теоремой (на примере признаков и свойств фигур) говорит о репетиторе по математике как о хорошем мастере объяснений. Немногие преподаватели могут похвастаться способностью быстро и точно объяснять смысл тонких математических терминов и вопросов. Если ребенок научился отличать переход A —>B от B—>А уже в 7 классе, то, скорее всего, союз репетитора и ученика окажется продуктивным уже в ближайшей перспективе, а результаты высокими.
Репетитор по математике в Строгино, Колпаков А.Н.
3 свойства равнобедренного треугольника (геометрия 7 класса)
В данной публикации мы рассмотрим определение и свойства равнобедренного треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равнобедренного треугольника
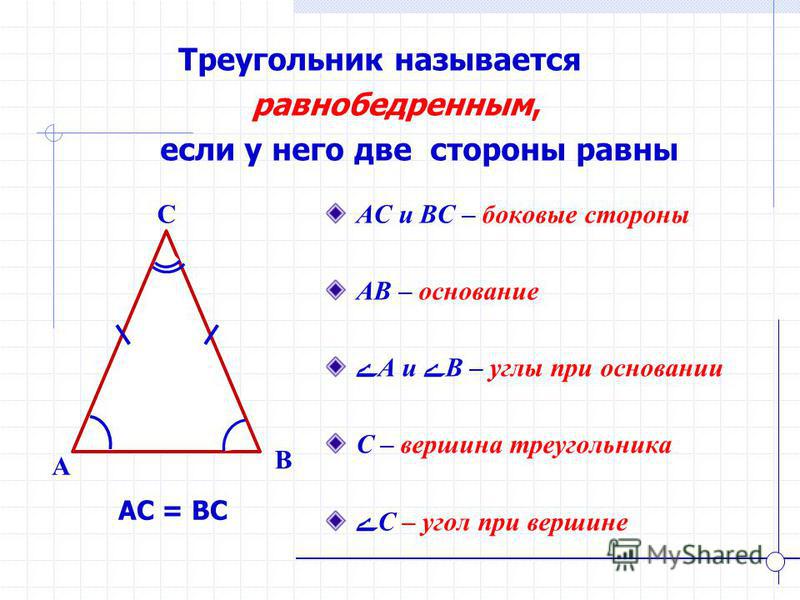
Равнобедренным называют треугольник, в котором две стороны имеют одинаковую длину (называются боковыми).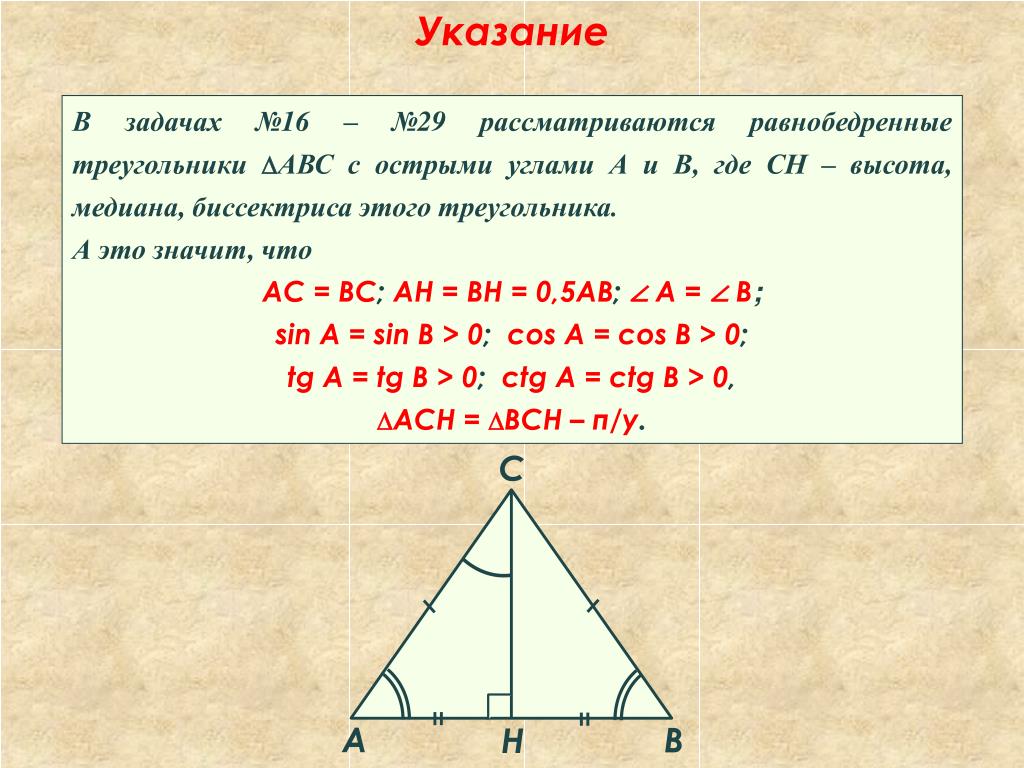 Оставшаяся третья сторона является основанием фигуры.
Оставшаяся третья сторона является основанием фигуры.
Свойства равнобедренного треугольника
Свойство 1
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны. Это значит, что α = β.
Обратная формулировка:
Если углы при основании треугольника равны, значит он является равнобедренным.
Свойство 2
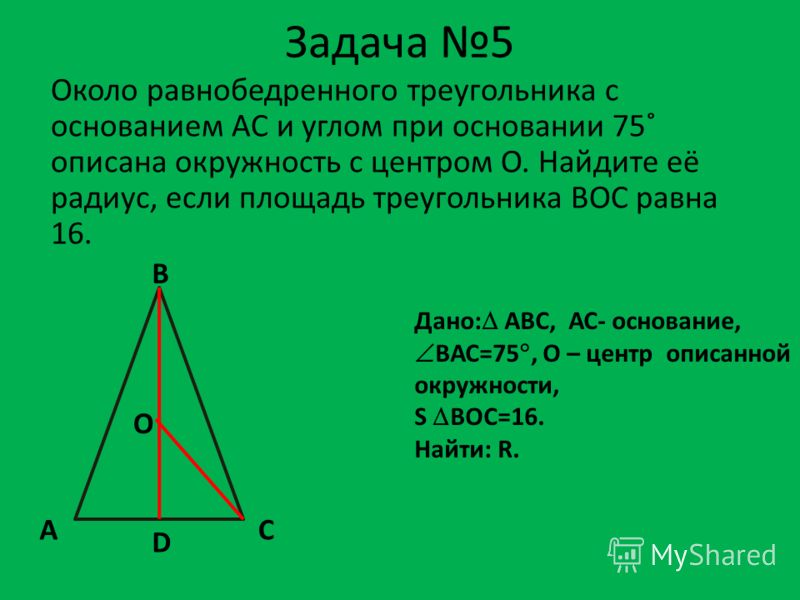
В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой угла и медианой, проведенной к основанию.
BD – медиана и высота к основанию AC, а также биссектриса угла ABC.
- BD перпендикулярна AC => ∠ADB = ∠CDB = 90°
- AD = DC
- ∠ABD = ∠DBC
Свойство 3
Центры вписанной и описанной вокруг равнобедренного треугольника окружностей лежат на одном отрезке, являющимся биссектрисой, медианой и высотой, проведенной к основанию.
- O1 и O2 – расположены на одном отрезке;
- R – радиус описанной окружности;
- r – радиус вписанной окружности.
Пример задачи
Дан равнобедренный треугольник, в котором длина основания в полтора раза больше боковой стороны. Периметр фигуры равняется 14 см. Найдите длины всех сторон.
Решение
Нарисуем чертеж согласно условиям задачи, приняв боковую сторону за a.
В таком случае, основание AC равняется 1,5a.
Периметр треугольника – это сумма всех его сторон:
AB + BC + AC = a + a + 1,5a = 3,5a = 14.
Т.е. a = 4.
Следовательно, боковая сторона равна 4 см, а основание – 6 см (4 см ⋅1,5).
Равнобедренный треугольник. Свойства, Признаки, Высота
Определение равнобедренного треугольника
Определение равнобедренного треугольника звучит проще простого:
Равнобедренным называется треугольник, у которого две стороны равны.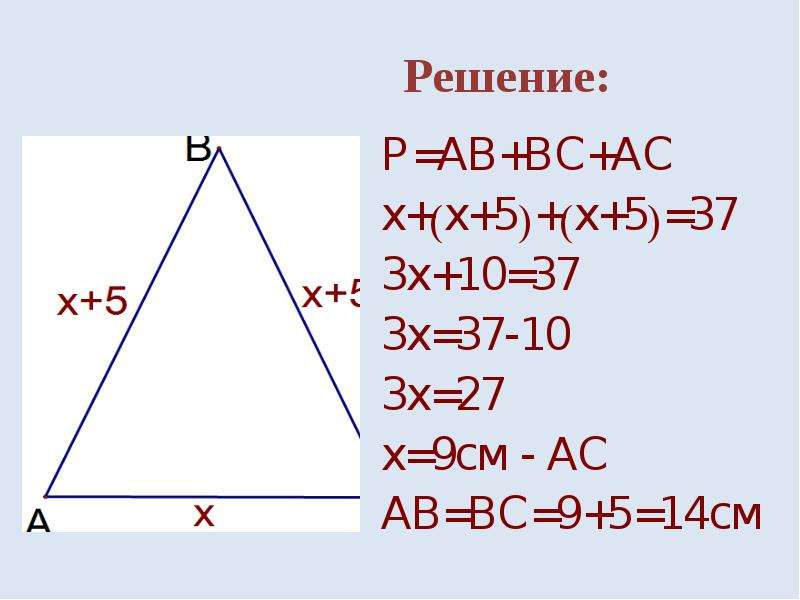 |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
∠ BАC = ∠ BСA. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.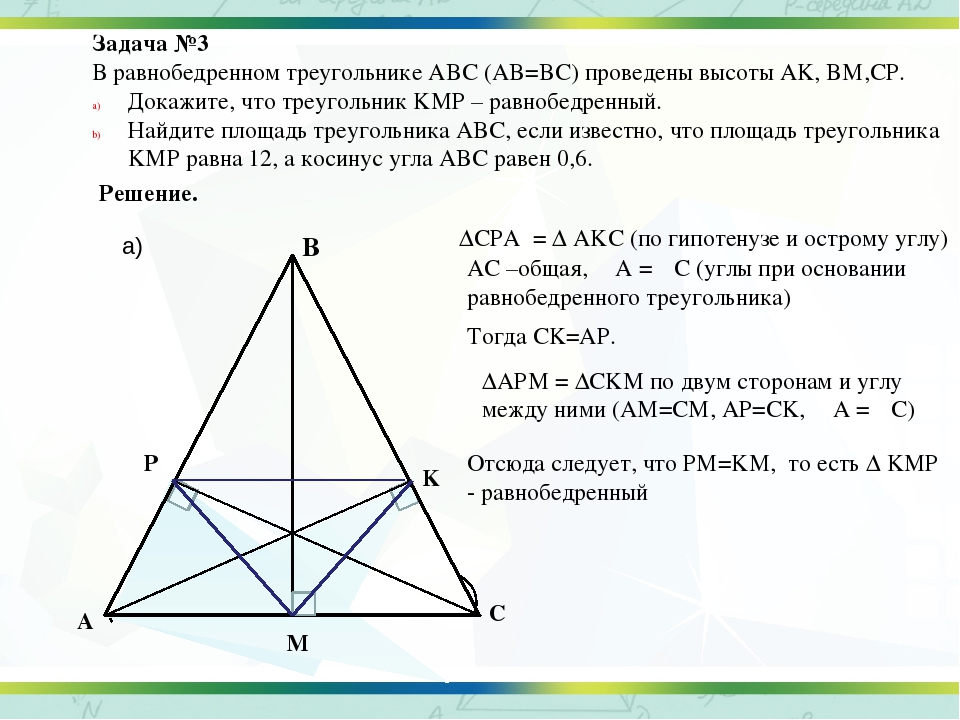
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
- Δ ABC
- Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
- Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
- Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
- Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
- AH = CH, поскольку точка H делит основание Δ ABC на две равные части
- Δ ABH = Δ BCH
- Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC
Вуаля, сразу три теоремы доказаны.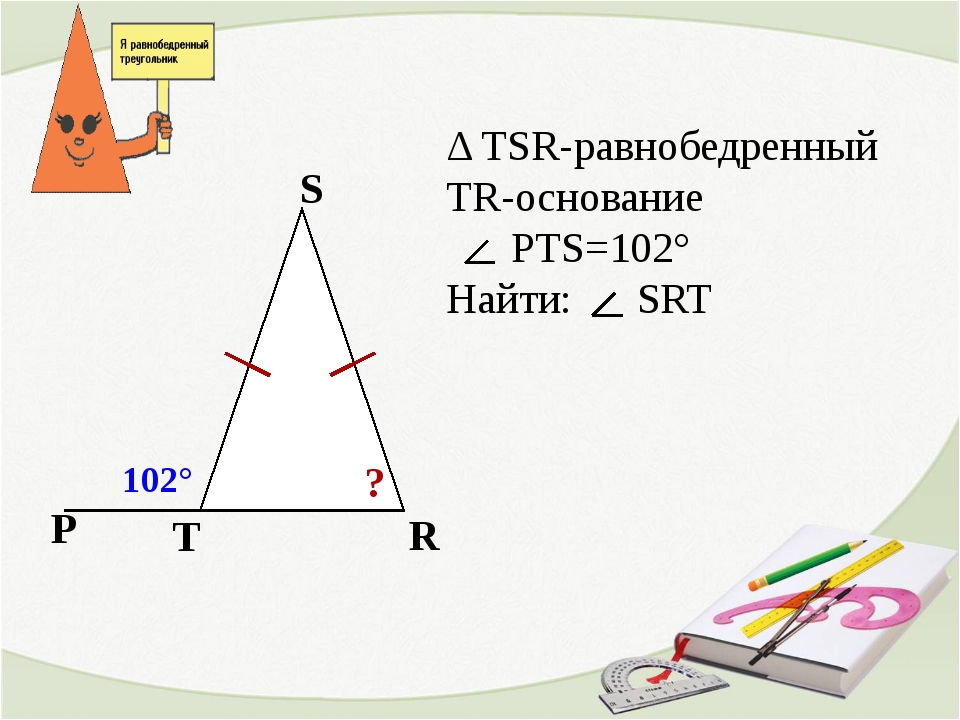
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Доказательство:
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!
- Если два угла треугольника равны, такой треугольник является равнобедренным.
Свойства углов равнобедренного треугольника
|
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике.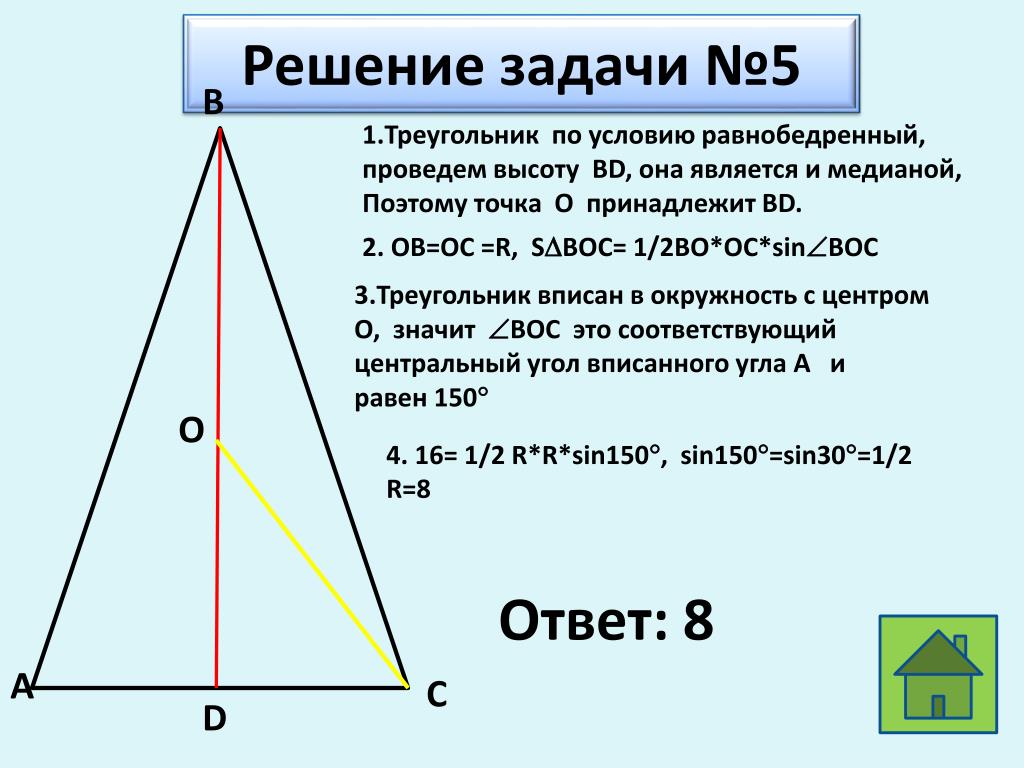 Ну… почти ничего.
Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘
Планиметрия в тезисах и решениях. 9 класс
К задачам на равнобедренный треугольник применимы все формулы п. 1.1 этой главы, разве что во всех формулах b = с, ? = ?.
1.1 этой главы, разве что во всех формулах b = с, ? = ?.
В случае равностороннего треугольника формулы значительно упрощаются, т. к. а = b = с, ? = ? = ? = 60°. Тогда
длины всех медиан, высот и биссектрис равны
Примеры решения задач
18. Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника (рис. 134). (1)
Рис. 134.
Решение. Обозначим основание треугольника через b, боковые стороны через а (см. рис.). По теореме косинусов
Тогда отношения сторон треугольника а: а: в = 1:1:?3.
Ответ: 1:1:?3.
19. Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а (рис. 135). (1)
Рис. 135.
Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:
Площадь круга:
Ответ:
20. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны (рис. 136). (2)
Найдите длину боковой стороны (рис. 136). (2)
Рис. 136.
Решение. Можно воспользоваться готовой формулой длины медианы:
Обозначим АВ через 2х, тотда ВМ = МС = х (см. рис.).
Имеем:
АВ = ВС = 6.
Задачу можно решить по-другому. Из ?ABC по теореме косинусов:
Далее, по той же теореме косинусов из ?АМВ:
Ответ: 6.
21. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см (рис. 137). (2)
Рис. 137.
Решение. Пусть данный треугольник ABC, где АВ = ВС; ВК = 3; АК = КС = 4 (см. рис.). Угол ОВС обозначим через ?. Из треугольника ВКС по теореме Пифагора находим:
Из того же треугольника следует: tg ? = 4/3. Радиус окружности R = ОС найдём из треугольника ВСО:
Ответ: 20/3 см.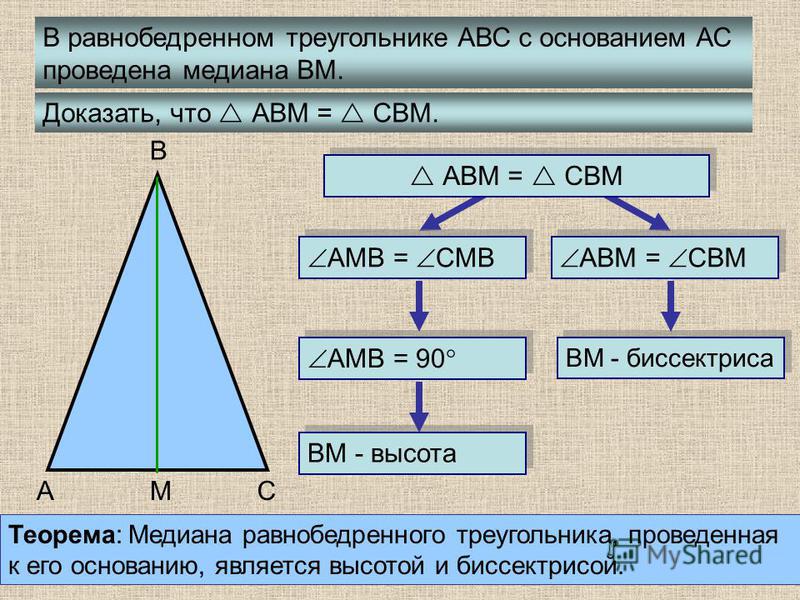
Задачи для самостоятельного решения
22. В равнобедренном треугольнике боковая сторона равна 12, а угол при вершине – 120°. Определите высоту треугольника. (1)
23. В равнобедренном треугольнике основание и опущенная на него высота равны 4. Найдите площадь описанного круга. (1)
24. В равнобедренном треугольнике высота равна 8, а основание относится к боковой стороне, как 6:5. Найдите радиус вписанной окружности. (1)
25. Длина окружности, описанной около равностороннего треугольника, равна 4. Найдите площадь заштрихованного сектора (рис. 138). (2)
Рис. 138.
26. Докажите, что сумма расстояний от любой точки равностороннего треугольника до его сторон равна длине высоты треугольника. (2)
Равнобедренный треугольник. Решение задач — презентация онлайн
А
В
равнобедренном
треугольнике
биссектриса,
проведенная к
основанию,
является
медианой и
высотой.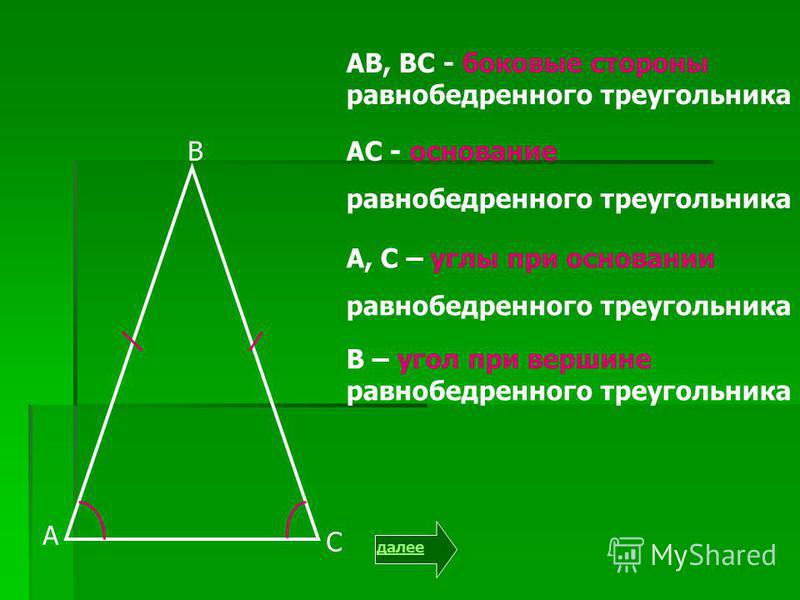
Эта
биссектриса
проведена к
В
боковой
стороне!
Эта
биссектриса
проведена к
С
В равнобедренном треугольнике построены три
боковой
биссектрисы. Которая биссектриса, проведена к основанию?
стороне!
Щелкни по ней мышкой.
В равнобедренном треугольнике биссектриса,
проведенная к основанию, является медианой и высотой.
Дано:
АВС равнобедренный, АD – биссектриса.
Доказать: АD – высота, АD – медиана.
Доказательство:
∆АВD=∆АСD (1 приз)
А
1= 2,
1 2
В
D
они смежные углы,
то они прямые.
ВD=DC,
АD- высота.
значит,
АD – медиана.
С
Найди треугольники, на которых изображена биссектриса,
которая является медианой и высотой и щелкни по ним мышкой.
С
О
А
О
А
С
В
А
В
Треугольник
равнобедренный.
ВО – биссектриса,
проведенная к
боковой стороне!
С
О
ВЕРНО. Треугольник равнобедренный.
Треугольник равнобедренный.
В
ВО – биссектриса, проведенная к основанию,
значит ВО – медиана, ВО – высота!
В
С
ВЕРНО.
Треугольник
равнобедренный.
ВО – биссектриса,
проведенная к
основанию, значит
ВО – медиана
ВО – высота!
О
С
А
А
В
Этот треугольник НЕ равнобедренный!
Биссектриса ВО не будет высотой и медианой!
О
Этот треугольник НЕ
равнобедренный! ВО высота!
Справедливы также утверждения
1. Высота равнобедренного треугольника,
проведенная к основанию, является медианой и
биссектрисой.
2. Медиана равнобедренного треугольника,
проведенная к основанию, является высотой и
биссектрисой.
В равностороннем треугольнике это свойство
верно для каждой высоты
Высоты, медианы и
С биссектрисы равностороннего
треугольника пересекаются в
одной точке.
N
D
O
А
F
В
Найти
АВD
Треугольник АВС — равнобедренный
В
? 400
А
D
ВD – медиана
Значит, ВD — биссектриса
АВD = DВС
С
DВА
Найти
А
АВD — равнобедренный
ВС – медиана
Значит, ВС — биссектриса
В
?
С
500
D
АВС = DВС
Найти
АВD
А
D
?
В
600
30
СВК — равнобедренный
ВМ – высота
Значит, ВМ — биссектриса
СВМ = КВМ
СВК = АВD
С
М
К
Найти
АВD
АВК — равнобедренный
D
ВС – медиана
Значит, ВС — биссектриса
В
?
00
12030
А
С
АВС = КВМ
АВD = 1800 — 600
К
Найти
DВА
С
АСD — равнобедренный
ВА – биссектриса
Значит, ВА — высота
А
?
В
D
АВС = DВС
Найти
АВD
СКВ — равнобедренный
АКВ — равнобедренный
ВD – медиана
Значит, ВD — биссектриса
К
550
D
С
700
1100
В
?
550
KBD = ABD
А
Найти
АВD
АКВ — равнобедренный
СКВ — равнобедренный
ВD – медиана
Значит, ВD — биссектриса
К
200
200
KBD = СBD
D
А
400
С
?
В
Дано: АВ = ВС, ВЕ – медиана треугольника АВС,
АВЕ = 40030/
Найти АВС, FEC
В
АВC — равнобедренный
ВЕ – медиана
Значит, ВЕ — биссектриса
АВЕ = СВЕ
А
900 900
Е 90
?0
F
АВС = 810
С
ВЕ – медиана
Значит, ВЕ — высота
ВЕС = 900
FЕС = 900
Дано: АВ = ВС, AE = 10см, FEC=900,
АВС = 130030/
Найти ЕВС,
АС.
АВC — равнобедренный
В
?
130030/
А
Е 900
F
ВЕ – высота
Значит, ВЕ — биссектриса
АВЕ = СВЕ
ЕВС = 65015/
С
ВЕ – высота
Значит, ВЕ — медиана
АС = 2*АЕ = 20(см)
Дано: АD = DС,
Доказать:
АDB = СDВ.
ВАС = ВCА
В
1 2
и ВD AC
АDВ = СDВ ( по 1 приз.)
АВС — равнобедренный
ВАС = ВСА
D
А
F
ВD – биссектриса
Значит, ВF — высота
С
ВD AC
Дано: АВ=ВС, АО=ОС, ОК – биссектриса ВОС
Найдите
АОК
В
АВС — равнобедренный
ВО – медиана
Значит, ВО — высота
К
ОК – биссектриса
Значит,
0
45
900
А
О
ВОК = СОК = 450
С
АОК = 1350
Дано: АВ=ВС, ОМ – биссектриса АОВ
МОС = 1350
АВО = ОВС
Докажите, что
В
АВС — равнобедренный
ВО – высота
Значит, ВО — биссектриса
АВО = ОВС
М
А
450
900
О
С
Решение задач по теме «Признаки равенства треугольников.
 Равнобедренный треугольник»
Равнобедренный треугольник»
Образовательная цель урока:
- обобщить и систематизировать изученный
материал на предыдущих уроках; - проконтролировать степень усвоения ЗУН
Воспитательные задачи.
1. Формирование мировоззрения: показать,
что источник возникновения изучаемой
дисциплины – реальный мир, что она возникла
из практических потребностей людей.
2. Формирование общеучебных навыков:
- внимания
- эстетических навыков при оформлении
записей, построении чертежа.
3. Формирование качеств личности:
- трудолюбия
- самостоятельности.
Развивающие задачи:
- развитие мыслительной деятельности,
умение анализировать, обобщать - развитие речи.
Тип урока: совершенствование знаний
умений и навыков по этой теме.
К уроку:
- Копировка и два листа для теста скрепить
скрепкой (каждому ученику). - Тесты (каждому ученику).
- Задачи в таблицах.
- Слайды для устного решения задач.
- Слайд ребус.
- Слайд для проверки графического
диктанта. - Слайды для проверки тестов.
- Индивидуальные доски.
- Слайд с домашним заданием.
Подготовительная работа:
- на доске сделать рисунки для коррекции
опорных знаний у учащихся - на боковой доске написать “ Ум без
догадки – гроша не стоит” — народная
мудрость, “Вдохновение нужно в геометрии
не меньше, чем в поэзии” — А.С.Пушкин - подготовить историческую справку о
Евклиде и Паппе.
І. Оргмомент: сегодня на уроке мы
будем решать задачи по темам “Свойства
равнобедренного треугольника” и “Признаки
равенства треугольников”. Поэтому вы
Поэтому вы
должны знать теоремы и определения, которые
изучили на предыдущих уроках и умело их
применять при решении задач. Но иногда от
ученика можно услышать признание:
Хоть ты смейся, хоть ты плачь
Не люблю решать задачи,
Потому что нет удачи
Мне на трудные задачи.
Может быть учебник скверный,
Может быть, таланта нет?
Но нашёл я способ верный:
Сразу посмотреть в ответ.
Думаю, не стоит огорчаться и падать духом,
а надо проявить упорство и настойчивость в
желании научиться решать задачи, а я вам в
этом помогу.
Тем, кто учит математику,
Тем, кто учит математике,
Тем, кто любит математику,
Тем, кто ещё не знает,
Что может любить математику,
Этот урок посвящается!
И проведём его под девизом: “Вдохновение
нужно в геометрии не меньше, чем в поэзии” —
А. С.Пушкин. Удачи вам, ребята!
С.Пушкин. Удачи вам, ребята!
ІІ. Воспроизведение и коррекция опорных
знаний у учащихся. Устный фронтальный
опрос и работа на индивидуальных досках.
- Что называется периметром треугольника?
- Как называется треугольник ABC?
Р= (написать на индивидуальной доске). - Как называется треугольник MNK?
- Напишите основание ΔMNK.
- Напишите боковые стороны ΔMNK.
- Как называется отрезок NO?
- Сформулируйте свойство высоты,
приведённой к основанию равнобедренного
треугольника. Р= (написать на
индивидуальной доске). - Что можно сказать про периметры равных
треугольников? - Напишите угол, который образуют стороны MN
и MO,ON
и OM.(Рис.1) - Напишите углы, которые прилежат к
стороне NO, MN, MO. - Напишите угол, который лежит против
стороны NO, MN, MO.
Отгадайте название геометрической фигуры,
определение и свойства которой так же
помогут решить нам на уроке несколько задач.
Показать ребус.
- Напишите радиусы окружности (Рис.2).
- Напишите диаметры окружности.
- Напишите хорды окружности.
- Что вы знаете про длины радиусов,
диаметров одной окружности?
Контроль определений окружности, радиуса,
хорды и диаметра окружности. Ответы пишут
на индивидуальных досках.
- Окружностью называется геометрическая
фигура, состоящая из всех точек плоскости,
расположенных на заданном расстоянии
отданной точки. - Хорда – это отрезок, соединяющий центр
окружности с какой – либо точкой
окружности. - Диаметр – это хорда, проходящая через
центр окружности.
- Можно провести только один диаметр.
- Диаметр окружности в два раза больше
радиуса.
Проверка графического диктанта: /\_/\_/\
(/\ – верно,_ – неверно).
ІІI.Актуализация
знаний.
При решении задач мы используем три
метода.
- Метод аналогии.
- Синтез.
- Анализ.
Метод аналогии – это не строго научный
метод, при решении любой задачи надо
вспомнить, а не встречалась ли ранее
похожая задача или теорема. Если
встречалась, то нельзя ли из неё что – то
взять для решения данной задачи или даже
целиком включить её в решение новой задачи.
Синтез – это метод рассуждения, при
котором следуют от данных к исходному (в
слепую). Из условия А, что следует?
Если верно А, то верно В,
Если верно В, то верно С,
……………………………………….
Если верно Х, то верно Z.
Анализ – это метод рассуждения, при
котором от неизвестного следуют к
известному (метод Евклида). Но мы чаще
пользуемся анализом Паппа. Это более
совершенный анализ. При анализе Паппа можно
задавать вопросы:
- Для того чтобы верно было условие В, что
достаточно сделать? - Откуда может следовать В?
- Как можно получить В?
- Что можно использовать, чтобы получить В?
И т.п.
Историческая справка.
Кто такие Евклид и Паппа?
Евклид – это величайший математик всех
времён, живший около 365 – 300 г.г. до н.э. Он
обобщил и систематизировал все известные
математические факты в уникальное собрание
“Начала”, состоящее из 15 книг дошедших до
нас. Первые 4 книги “Начал” посвящены
планиметрии. В них представлен материал,
который начинается с определений,
постулатов и аксиом. Из них выводятся
теоремы, устанавливающие все важные
свойства треугольников и других
геометрических фигур. О содержании
О содержании
остальных книг мы поговорим на других
уроках.
Паппа – это александрийский математик,
живший в ІІІ – ІV в. н.э., который изучал
жизнь и труды Евклида и писал о нём как
исключительно тихом, скромном человеке,
которому были чужды гордость и эгоизм.
И мы последуем примеру великих
математиков: будем делать для себя
маленькие открытия на уроках, решая задачи,
будем приобретать опыт в их решении. При
решении задач будем опираться на народную
мудрость “Ум без догадки – гроша не стоит”.
ІV. Воспроизведение и применение
учащимися приобретённых знаний при решении
задач. Устно по готовым рисункам.
V. Выполнение заданий стандартного типа.
- В равнобедренном треугольнике
основание относится к боковой стороне
как 3:4. Найдите стороны треугольника, если
его периметр равен 33см.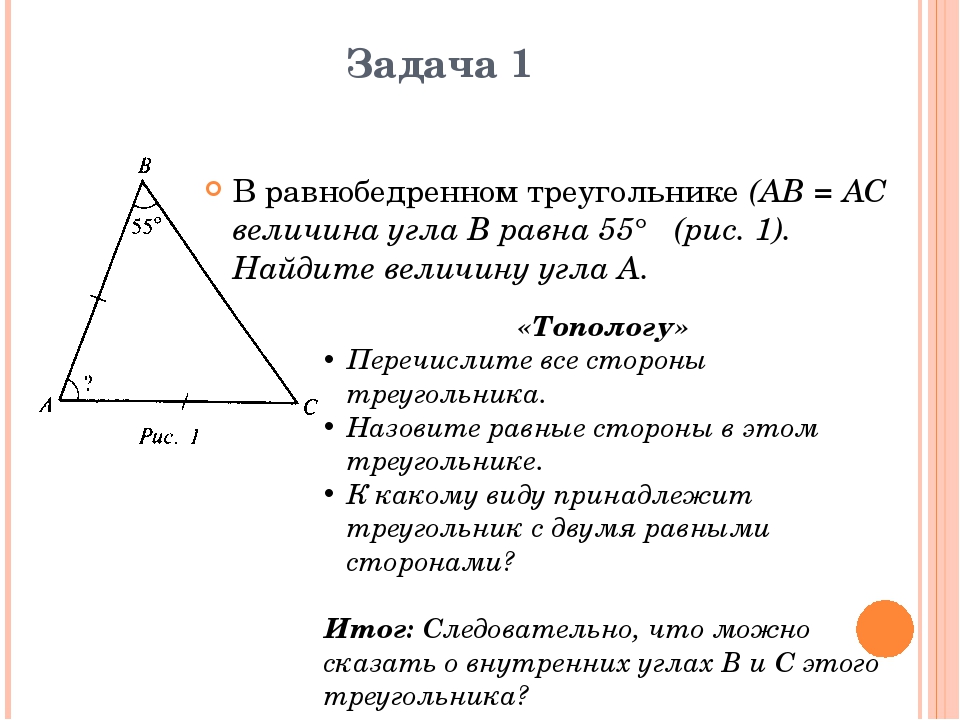 Ответ: 9см, 12см, 12см.
Ответ: 9см, 12см, 12см. - В ΔAOM
сторона AO равна
стороне OM. AM
– AO =3см. Найдите
стороны треугольника, если его периметр
равен 18см. Ответ: 5см,5см, 8см.
VІ. Контроль знаний, умений и навыков по
теме “Равнобедренный треугольник.
Признаки равенства треугольников”.
Тест.
Вариант І.
1ю Закончите чтение определения или
свойства равнобедренного треугольника (или
напишите “ не знаю”).
|
а) Треугольник называется
|
|
б) Третья сторона в равнобедренном
|
|
в) Если в треугольнике два угла равны,
|
|
г) В равностороннем треугольнике все
|
|
д) В равнобедренном треугольнике
|
2. Расстояние от A
Расстояние от A
до D равно 8см. Чему
равно расстояние от C
до B? Почему?
3. Оба треугольника равносторонние и имеют
только по одной равной стороне. Равны ли ΔOBC
и ΔDLF?
Почему?
4. Равны ли изображённые на рисунке
треугольники, если известно, что они имеют
по две равных стороны? Ответ объясните.
5. ΔDCE=ΔKFM
и оба они равносторонние. Найдите периметр ΔKFM,
если CD=10см.
Тест.
Вариант ІІ.
1. Закончите чтение определения или
свойства равнобедренного треугольника (или
напишите “ не знаю”).
|
а) Если две стороны треугольника
|
|
б) Равные стороны в равнобедренном
|
|
в) В равнобедренном треугольнике углы
|
|
г) Треугольник, у которого все стороны
|
|
д) В равнобедренном треугольнике
|
2. ΔABD и ΔCFE
ΔABD и ΔCFE
оба равнобедренные с основаниями AB
и CF и имеют по две
равных стороны. Равны ли они? Почему?
3. Чему равно расстояние от B
до M, если от A
до M равно10см?
Почему?
4. Треугольники ABD
и ACD
равносторонние. Равны ли они, если известна
только одна сторона AD=5см?
Ответ объясните.
5. Треугольники ABC
и DEF равны и оба
равнобедренные. Найдите периметр
треугольника ABC,
если DE=4см, EF=5см.
Предварительная проверка теста. Перед
проверкой собрать один лист, а второй
оставить для проверки.
Вариант І.
- а) две стороны равны
б) основанием
в) равнобедренный
г) равны
д) биссектрисой и высотой - CB=8см.
- да
- да
- PKPM=30см.
Вариант ІІ.
- а) равнобедренным
б) боковые
в) равны
г) равносторонним
д) биссектрисой и медианой - да
- BM=10см
- Да
- PABC=13см, PABC=14см.
VІІ. Подведение итогов. Доказать:
VІІІ. Домашнее задание: №165(а, б), задача
на слайде.
Вокруг задачи из учебника геометрии | Шевкин.Ru
В учебнике «Геометрия, 7 класс (В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолов; Просвещение) под номером 94 помещена задача, которая есть и в учебнике Л.С. Атанасяна и др.
Эту задачу решают в Интернете не всегда коротким способом. Давайте построим вокруг неё цепочку задач, по которой учащиеся могут продвигаться самостоятельно — от простого к сложному. Начнём не с задачи 94, а с более простых задач.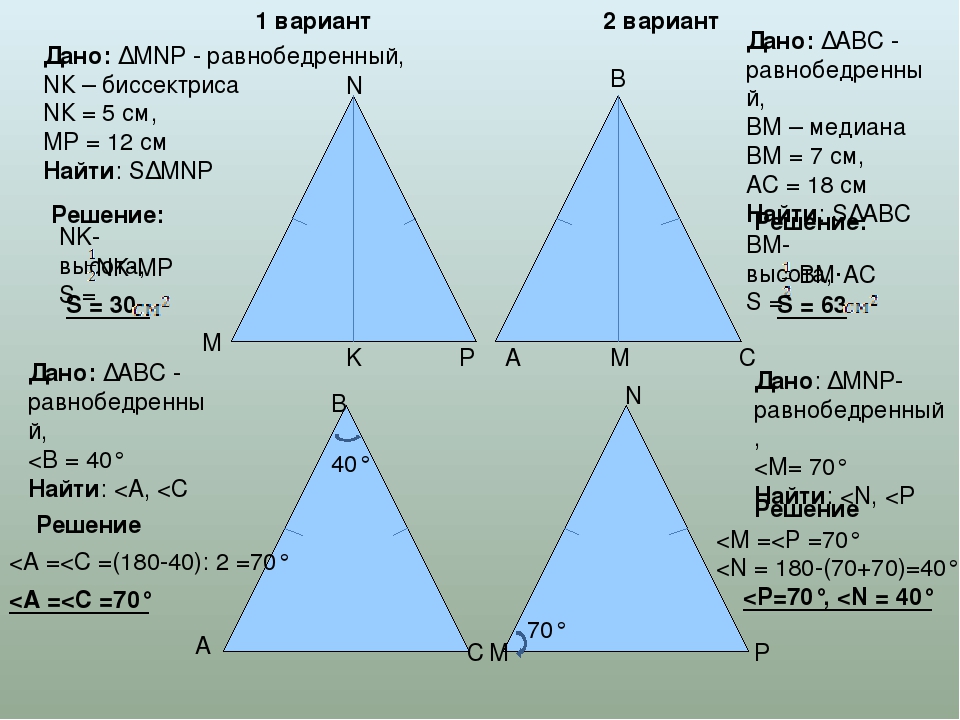
Далее приведены только условия задач.
1. На стороне AC равнобедренного треугольника ABC (AB = AC) отметили точку P. Оказалось, что
AP = PB = BC (рис. 1). Найдите угол A и докажите, что BP — биссектриса угла ABC.
2. На сторонах AC и AB равнобедренного треугольника ABC (AB = AC) отметили точки P и Q соответственно. Оказалось, что AP = PQ = QC = CB (рис. 2). Найдите угол A.
3 (94). На рисунке 3 AB = AC и AP = PQ = QR = RB = BC. Найдите угол A и докажите, что BQ = BR.
4. Равнобедренный треугольник ABC разбили на n равнобедренных треугольников, боковые стороны которых равны основанию BC треугольника ABC, а все вершины этих треугольников лежат на сторонах AB и BC треугольника ABC (как в задачах 1-3).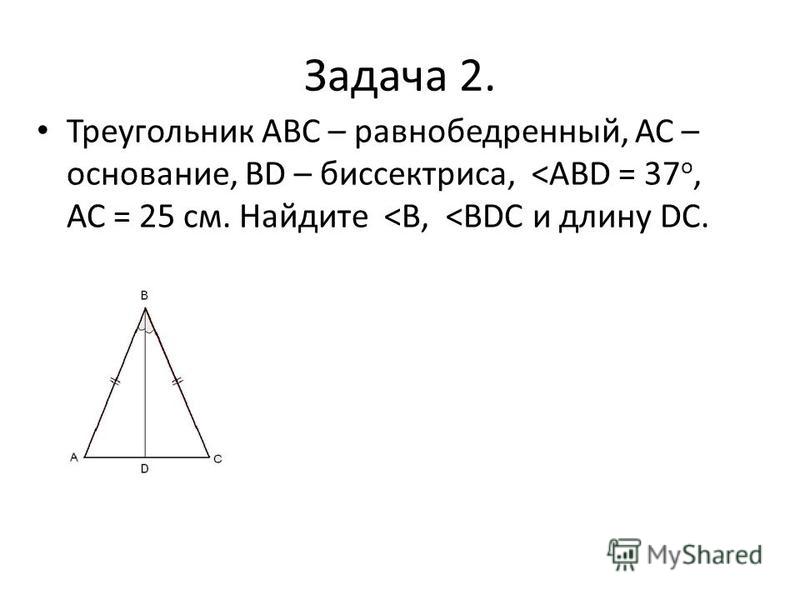 Найдите наименьшую градусную меру угла A, выражаемую натуральным числом.
Найдите наименьшую градусную меру угла A, выражаемую натуральным числом.
Для читателей старше 7 класса заметим, что равнобедренный треугольник ABC, разбитый на два равнобедренных треугольника, из задачи 1 встречается на рисунке правильного пятиугольника, в котором проведены все диагонали. На странице Задачи на правильные многоугольники есть ссылка на статью с тем же названием. Вот рисунок из этой статьи, на котором находим равнобедренный треугольник ACD, разбитый на два равнобедренных треугольника. Нижний подобен треугольнику ACD. Там же есть задача, которую можно решить при помощи этого треугольника.
И последнее наблюдение. Все равнобедренные треугольники АВС, в которых рассмотренные разбиения возможны, можно найти в правильных многоугольниках с нечётным числом сторон, если провести две наибольшие диагонали из одной вершины многоугольника. Если ещё из вершины угла при основании треугольника АВС провести наименьшую диагональ правильного многоугольника, пересекающую этот треугольник, то от него отсечётся ему подобный треугольник — последний треугольник из рассмотренного разбиения.
Ссылка на статью в разделе «Решайте с нами…» сайта www.shevkin.ru
Вокруг задачи из учебника геометрии
Теги: головоломка, задача по геометрии, математика, ОГЭ
равнобедренных треугольников — SAT Math
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.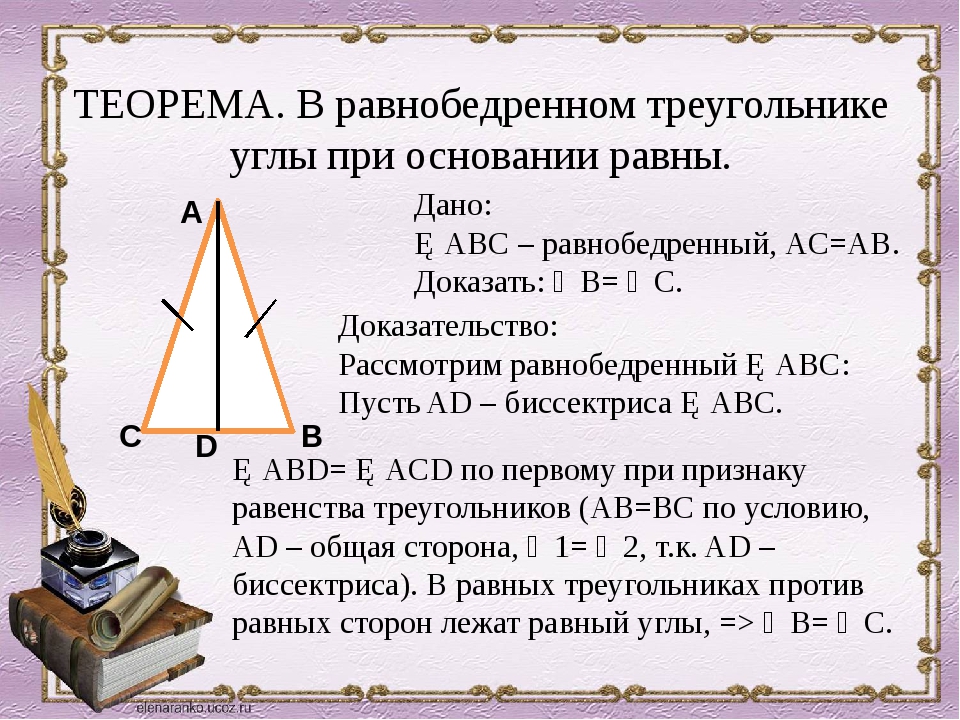 д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
равнобедренных треугольников — задача 3
Равнобедренный треугольник имеет две равные стороны и два равных угла при основании. Используя это и теорему о сумме углов треугольника, можно найти значение x, когда значения углов задаются выражениями x.
Используя это и теорему о сумме углов треугольника, можно найти значение x, когда значения углов задаются выражениями x.
По теореме о сумме углов треугольника сумма углов в треугольнике равна 180 °. Итак, сложите выражения для углов, помня, что два основных угла имеют одинаковую меру, получая уравнение: 2 * (мера базового угла) + (мера угла при вершине) = 180 °. Решите относительно x, используя методы алгебры.
Если вас попросят найти значение определенного угла, не забудьте подставить значение x в выражение желаемого угла.
Вы, вероятно, обнаружите, что во многих случаях алгебра и геометрия имеют тенденцию пересекаться.Если мы посмотрим на эту проблему, то увидим, что нас спрашивают об угле при вершине. Итак, сначала мы должны решить, какой из этих трех углов является углом при вершине.
Что ж, если эти две стороны совпадают, то у нас есть равнобедренный треугольник, что означает, что угол при вершине равен 4x. Так как же нам узнать, что такое 4x? Чтобы сделать это, мы должны выяснить, что такое X, а чтобы узнать, что такое x, мы должны использовать сумму треугольника. Похоже, мы часто этим пользуемся.
Так как же нам узнать, что такое 4x? Чтобы сделать это, мы должны выяснить, что такое X, а чтобы узнать, что такое x, мы должны использовать сумму треугольника. Похоже, мы часто этим пользуемся.
Можно сказать, что 180 градусов равны сумме этих трех углов.Опять же, поскольку это равнобедренный угол, мы знаем, что этот угол тоже должен быть 2x плюс 10 градусов. Обратите внимание, что я пишу в скобках 2x плюс 10. Это означает, что это число, и мы говорим о градусе, поэтому мы говорим об угле.
Итак, если я комбинирую одинаковые термины и поскольку вы изучаете геометрию, вы сдали алгебру, я предполагаю, что вы можете комбинировать похожие термины прямо сейчас в своей голове. 2 плюс 2 плюс 4 равно 8x, а затем 10 плюс 10 равно двадцати. Итак, все, что я здесь сделал, это сказал, что сумма этих трех углов должна составлять 180 градусов.И похоже, что нам нужно решить довольно простое уравнение.
Итак, я собираюсь вычесть 20 из обеих частей этого уравнения 180 минус 20 равно 160. 160 равно 8x, и мы видим, что можем решить это, разделив на 8, а x равно 20. И похоже, что мы ‘ все сделано правильно?
160 равно 8x, и мы видим, что можем решить это, разделив на 8, а x равно 20. И похоже, что мы ‘ все сделано правильно?
Ну, x равно 20 — это прекрасно, но это не отвечает на вопрос, найти угол при вершине. Что нам нужно сделать, так это заменить эти 20 на x. Итак, 4 умножить на 20 равно 80, что означает, что угол при вершине здесь равен 80 градусам.
Равнобедренный прямоугольный треугольник. Темы по тригонометрии
Темы | Дом
5
ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК ИЗОСЦЕЛЫ — это один из двух особых треугольников. (Другой — треугольник 30 ° -60 ° -90 °.) Студент должен знать соотношение сторон.
(Равнобедренный треугольник имеет две равные стороны. См. Определение 8 в «Некоторые теоремы плоской геометрии». Там можно найти теоремы, цитируемые ниже.)
Теорема. В равнобедренном прямоугольном треугольнике стороны находятся в соотношении 1: 1 :.
Проба . В равнобедренном прямоугольном треугольнике равные стороны составляют прямой угол. У них соотношение равенства 1: 1.
В равнобедренном прямоугольном треугольнике равные стороны составляют прямой угол. У них соотношение равенства 1: 1.
Чтобы найти отношение числа гипотенузы h , согласно теореме Пифагора имеем
ч 2 = 1 2 + 1 2 = 2.
Следовательно,
ч =.
(Урок 26 алгебры.) Следовательно, три стороны находятся в соотношении
1: 1:.
Обратите внимание: поскольку прямоугольный треугольник равнобедренный, то углы при основании равны. (Теорема 3.) Следовательно, каждый из этих острых углов равен 45 °.
(Определение углов измерения «градусами» см. В теме 12.)
Пример 1.Оцените sin 45 ° и tan 45 °.
Ответ . По любым вопросам, связанным с углом 45 °, ученику не следует обращаться к Таблице. Лучше нарисуйте треугольник и расставьте числа отношения.
Мы видим:
| sin 45 ° | = | 1 | = ½, |
по рационализации знаменателя. (Урок 26 алгебры.)
(Урок 26 алгебры.)
Проблема.Определите cos 45 ° и csc 45 °.
| cos 45 ° = | 1 | = ½. |
Таким образом, cos 45 ° равен sin 45 °; они дополняют друг друга.
| csc 45 ° = | 1 | =. |
Пример 2. Решите равнобедренный прямоугольный треугольник со стороной 6.5 см.
Ответ . Решить треугольник — значит знать все три стороны и все три угла. Поскольку это равнобедренный прямоугольный треугольник, единственная проблема — найти неизвестную гипотенузу.
Но в каждом равнобедренном прямоугольном треугольнике стороны имеют соотношение 1: 1:, как показано справа. В треугольнике слева сторона, соответствующая 1, умножена на 6,5. Следовательно, каждая сторона будет умножена на 6,5. Гипотенуза
будет 6.5. (Теорема об одном и том же кратном.)
Всякий раз, когда мы знаем числа отношения, мы используем этот метод подобных фигур для решения треугольника, а не тригонометрическую таблицу.
(В теме 6 мы будем решать прямоугольные треугольники, отношения сторон которых нам неизвестны.)
Пример 3. В равнобедренном прямоугольном треугольнике гипотенуза равна дюйму. Какова длина сторон?
Ответ . Ученик должен нарисовать треугольники и указать числа отношения.
Как умножалась сторона, соответствующая?
Согласно правилу умножения радикалов, умножается на. Следовательно, все стороны будут умножены на. И 1 =.
Следующая тема: Решение прямоугольных треугольников
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Что такое равнобедренный треугольник?
Что такое равнобедренный треугольник?
Определение: Равнобедренный треугольник определяется как треугольник, имеющий две равные стороны или две стороны одинаковой длины.
Равнобедренный треугольник также может быть равносторонним, но это не обязательно.
Определения этих треугольников обычно включают слово «только» или «точно».Эти слова имеют значение при рассмотрении вопроса о том, является ли треугольник равносторонним или равнобедренным треугольником.
Свойства равнобедренного треугольника,
Характеристики и применение
Многие треугольники, встречающиеся в реальном мире, можно считать равнобедренными, включая часть куска пиццы. Часто абстрактные или сложные формы разбиваются на более мелкие формы, такие как треугольник.
Две стороны одинаковой длины называются ножками, а третья сторона называется основанием.Часто проблема будет использовать этот словарь для передачи информации.
Знание, что у равнобедренного треугольника две стороны равны, приводит нас к первой теореме, связанной с равнобедренными треугольниками. Теперь давайте посмотрим, как найти недостающие стороны равнобедренного треугольника и вычислить их длину.
Теоремы о равнобедренном треугольнике
Теорема № 1 — Если две стороны треугольника равны, углы напротив них равны.
Это означает, что если мы знаем, что в треугольнике две стороны равны, мы знаем, что два угла также совпадают.Чтобы найти противоположный угол, вам нужно посмотреть на угол, частью которого не является сторона.
Одиночные линии на сторонах равнобедренных треугольников являются отметками, указывающими на то, что стороны имеют одинаковую длину или совпадают. Дуги в углах указывают на то, что углы имеют одинаковую меру или конгруэнтны. Обратите внимание, что основание треугольника образовано обоими конгруэнтными углами.
Обратное утверждение этой теоремы выглядит наоборот.
Теорема № 2 (обратное) — Если два угла треугольника совпадают, противоположные стороны равны.
Если мы знаем, что два угла конгруэнтны или имеют одинаковую длину, то мы знаем, что противоположные стороны равны или имеют одинаковую длину.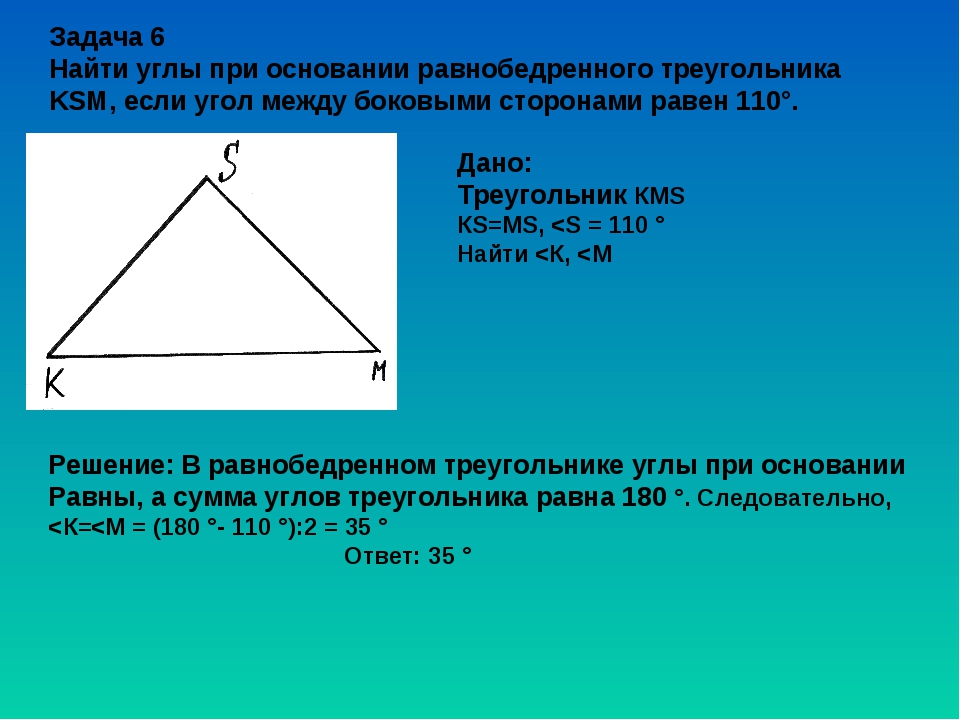
И снова совпадающие углы образуют основу, а конгруэнтные стороны — ноги.
Эти две теоремы важны для любых доказательств, которые просят вас доказать, что треугольник является равнобедренным треугольником.
Обязательно запомните данное вам определение равнобедренного треугольника. Некоторые определения позволяют доказать, что два угла совпадают, некоторым требуется дополнительный шаг, чтобы показать, что две стороны совпадают.
Решения проблем равнобедренного треугольника
Одна из распространенных проблем, связанных с равнобедренным треугольником, связана с высотой, привязанной к основанию. Высота — это линия, которая проводится от вершины одного угла к противоположной стороне, образуя прямой угол.
Когда высота проводится к основанию равнобедренного треугольника, получается два равных треугольника. Тип треугольника и место, где нарисована высота, важны. Давайте внимательно рассмотрим эту концепцию.
Когда нам дают равнобедренный треугольник, мы знаем следующие факты.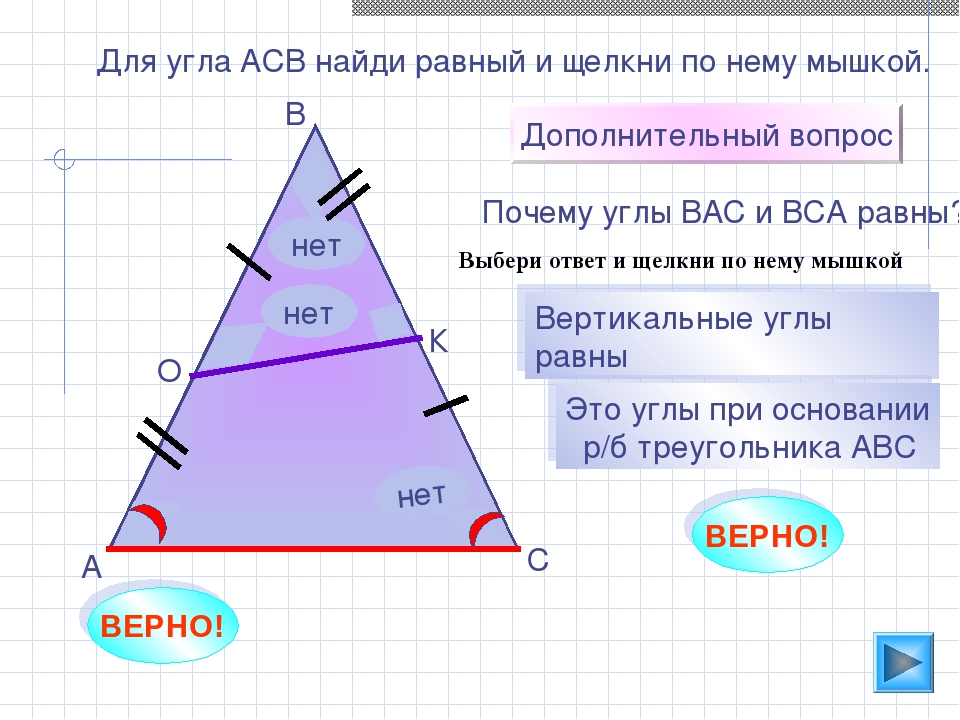
Равнобедренный треугольник имеет две конгруэнтные стороны (определение равнобедренного треугольника). Это часто будет дано вам по данной маркировке базы.Если YZ — база, то мы знаем, что XY ≅ XZ.
Поскольку мы знаем, какие стороны конгруэнтны, теперь мы знаем, какие углы конгруэнтны. ∠Y ≅ ∠Z (Если две стороны треугольника равны, углы напротив них равны).
Теперь нарисуем высоту под углом X к основанию. Это разделит исходный равнобедренный треугольник на два меньших прямоугольных треугольника.
Поскольку два прямых угла имеют одинаковую величину (90 градусов), мы можем сказать, что прямые углы совпадают.Это дает недостающую часть, чтобы доказать, что по △ XYA ≅ △ XZA by AAS.
Пример задач равнобедренного треугольника
Задача о равнобедренном треугольнике
Теорема # 1
Как найти сторону равнобедренного треугольника из уравнения x .
Обратите внимание, что два катета треугольника имеют одинаковую длину или совпадают.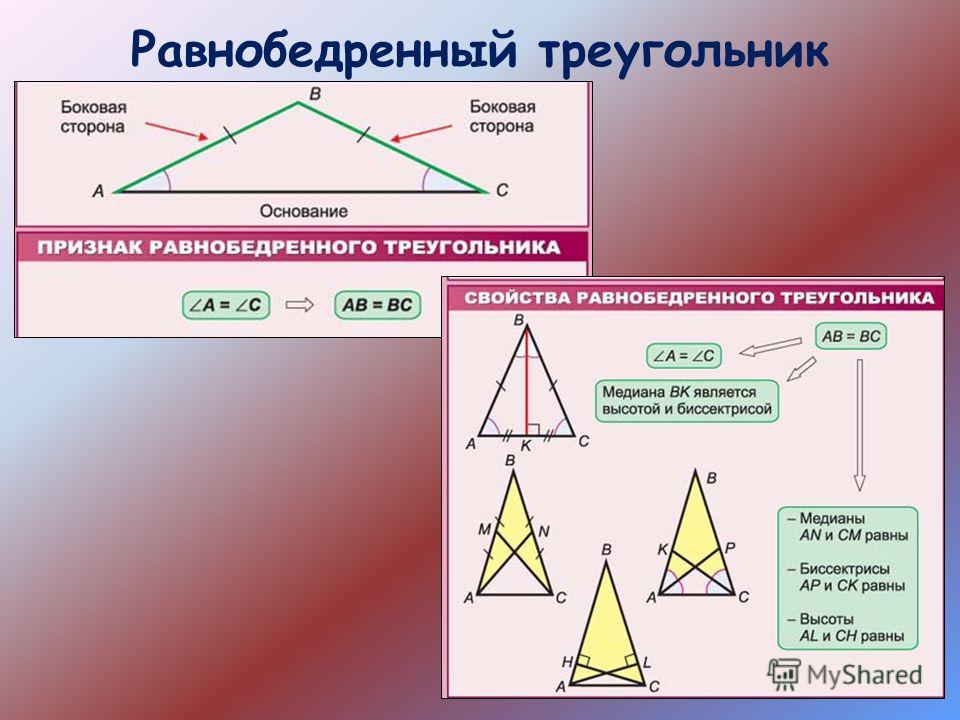 Это означает, что противоположные углы совпадают. Поскольку один из углов, противоположных опоре, равен 50 градусам, это означает, что недостающее значение также равно 50 градусам.
Это означает, что противоположные углы совпадают. Поскольку один из углов, противоположных опоре, равен 50 градусам, это означает, что недостающее значение также равно 50 градусам.
Задача о равнобедренном треугольнике
Теорема # 2
Давайте рассмотрим пример задачи, в которой это будет использоваться.
Найдите значение y .
Мы видим, что два угла равны 25 градусам. Поскольку это одна и та же мера, мы знаем, что стороны, противоположные углам, также равны по мере. Одна из сторон обозначена как 6 см . Мы знаем, что другая сторона тоже должна быть 6 см .Таким образом, значение y равно 6 см.
Пример:
Дан равнобедренный треугольник ABC с основанием BC. Найдите угол A.
Приведенная информация может помочь нам обозначить диаграмму более подробно. Мы знаем, что треугольник равнобедренный с основанием BC. Это означает, что AB и AC — ноги и конгруэнтны.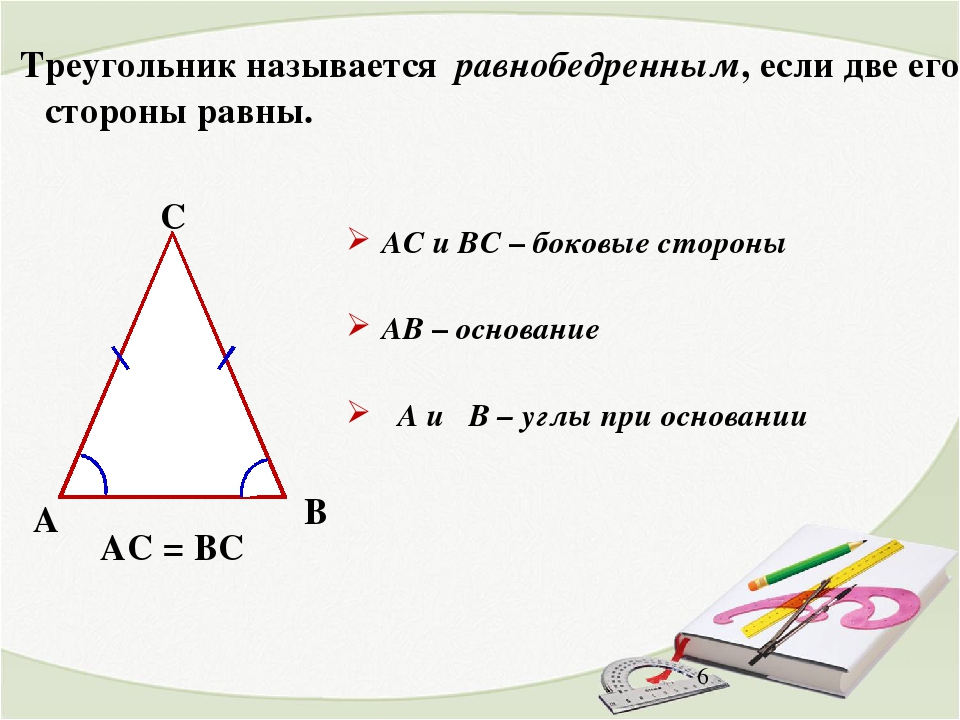 Это также означает, что противоположные углы совпадают. Поскольку один угол обозначен как 20, мы можем обозначить угол C , угол, противоположный AB, также как 20.
Это также означает, что противоположные углы совпадают. Поскольку один угол обозначен как 20, мы можем обозначить угол C , угол, противоположный AB, также как 20.
Отсутствует информация о том, что сумма углов треугольника равна 180 °. Обладая этими знаниями, мы можем закончить определение угла A .
Угол A равен 140 °
равнобедренных треугольников — Бесплатная справка по математике
В мире геометрии существует множество типов треугольников. Есть специальный треугольник, называемый равнобедренным треугольником и . В равнобедренном треугольнике базовые углы имеют одинаковую степень и, как следствие, равны (конгруэнтны).Точно так же, если два угла треугольника имеют одинаковую длину, тогда стороны , противоположные этим углам, имеют одинаковую длину. Самый простой способ определить равнобедренный треугольник — у него две равные стороны .
В равнобедренном треугольнике есть две стороны, называемые ногами, и третья сторона, называемая основанием. Угол, расположенный напротив основания, называется вершиной.
Образец A:
Угол при вершине B равнобедренного треугольника ABC составляет 120 градусов.Найдите градус каждого базового угла.
Решение:
(1) Пусть x = мера каждого базового угла.
(2) Составьте уравнение и решите относительно x.
базовый угол + базовый угол + 120 градусов = 180 градусов
x + x + 120 градусов = 180 градусов
2x + 120 = 180
2x = 180-120
2x = 60
x = 60/2
x = 30
Каждый угол основания треугольника ABC составляет 30 градусов.
Образец B:
В равнобедренном треугольнике RST угол S — это угол при вершине.Базовые углы R и T равны 64 градусам. Найдите градус угла при вершине S.
Решение:
(1) Пусть x = мера угла при вершине S.
(2) Составьте уравнение и решите относительно x.
базовый угол + базовый угол + угол при вершине S = 180 градусов
64 градуса + 64 градуса + x = 180 градусов
128 + x = 180
x = 180 — 128
x = 52
Угол при вершине S в треугольнике RST составляет 52 градуса.
Образец C:
Угол основания равнобедренного треугольника XYZ в градусах в три раза превышает градус вершины Y на 60.Найдите градус угла при вершине Y. Обратите внимание, что трудно нарисовать картинку, не зная, какие углы наибольшие.
Нам нужно составить уравнение из этой проблемы, поэтому давайте разберемся, что она пытается нам сказать. Сначала мы читаем «Степень базового угла», поэтому начнем с X =
.
Наше уравнение на данный момент: X =
Теперь мы видим «превышает в три раза … Y … на 60», что означает 3Y + 60.
Теперь наше уравнение: X = 3Y + 60
Поскольку мы знаем, что X = Z, потому что это равнобедренный треугольник, мы можем найти меры всех углов.
базовый угол + базовый угол + вершина = 180
X + Y + Z = 180
(3Y + 60) + Y + (3Y + 60) = 180
7Y + 120 = 180
7Y = 60
Y = 60/7
Y = 8,57 градуса
Угол при вершине Y треугольника XYZ равен 8,57 градуса.
Урок, проводимый г-ном Фелизом
Главная | Оставить комментарий | | |
Треугольник 80-80-20
Несколько треугольников из-за их специфических свойств служили источником для исследований, изумления и множества проблем.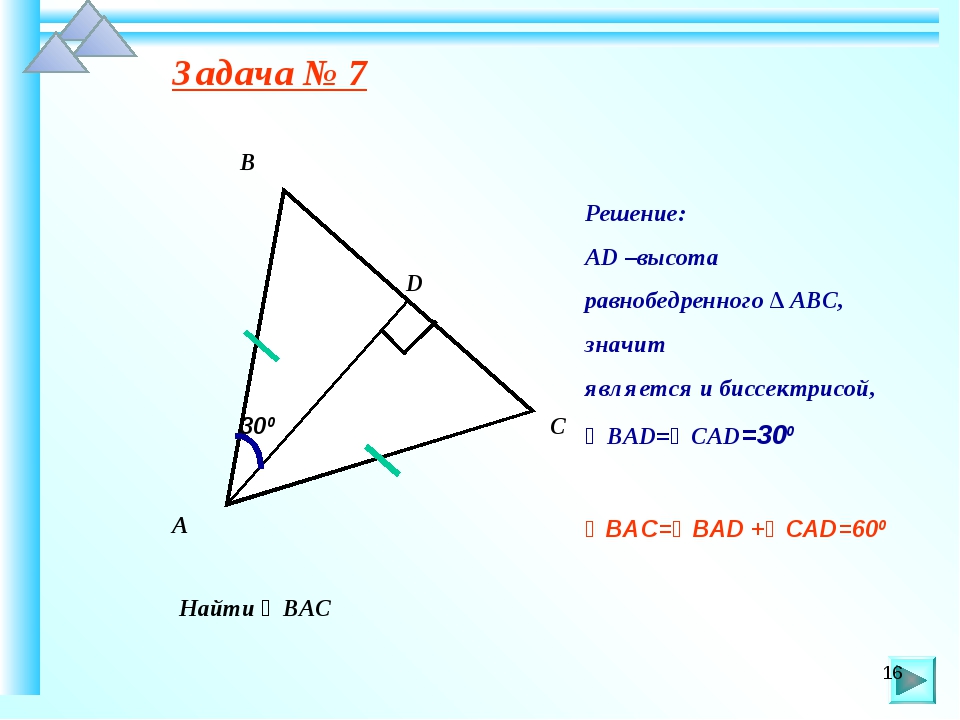 Некоторые, такие как равносторонние, правильные равнобедренные, золотые, египетские, 30-60-90, очень хорошо известны. Один треугольник, заслуживающий большего признания, вероятно, вошел в математический фольклор около 100 лет назад. Том Рике из Berkley Mathematical Circles упоминает его появление в Mathematical Gazette, том 11 (1922), стр. 173. (Его онлайн-статья также содержит дополнительные ссылки.) Это треугольник 80-80-20 (или иногда 20-80-80), то есть равнобедренный треугольник с углом при вершине 20 ° и углами основания 80 °. .
Некоторые, такие как равносторонние, правильные равнобедренные, золотые, египетские, 30-60-90, очень хорошо известны. Один треугольник, заслуживающий большего признания, вероятно, вошел в математический фольклор около 100 лет назад. Том Рике из Berkley Mathematical Circles упоминает его появление в Mathematical Gazette, том 11 (1922), стр. 173. (Его онлайн-статья также содержит дополнительные ссылки.) Это треугольник 80-80-20 (или иногда 20-80-80), то есть равнобедренный треугольник с углом при вершине 20 ° и углами основания 80 °. .
Исходная проблема повлекла за собой несколько модификаций; и каждая из них была решена многими-многими способами. Я буду добавлять решения и, возможно, проблемы, связанные с исходным. Любая помощь приветствуется.
Эта страница должна служить порталом для этого мероприятия.
Оригинальная проблема
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 50 °. Точка E находится на стороне AB такой, что ∠BCE = 60 °.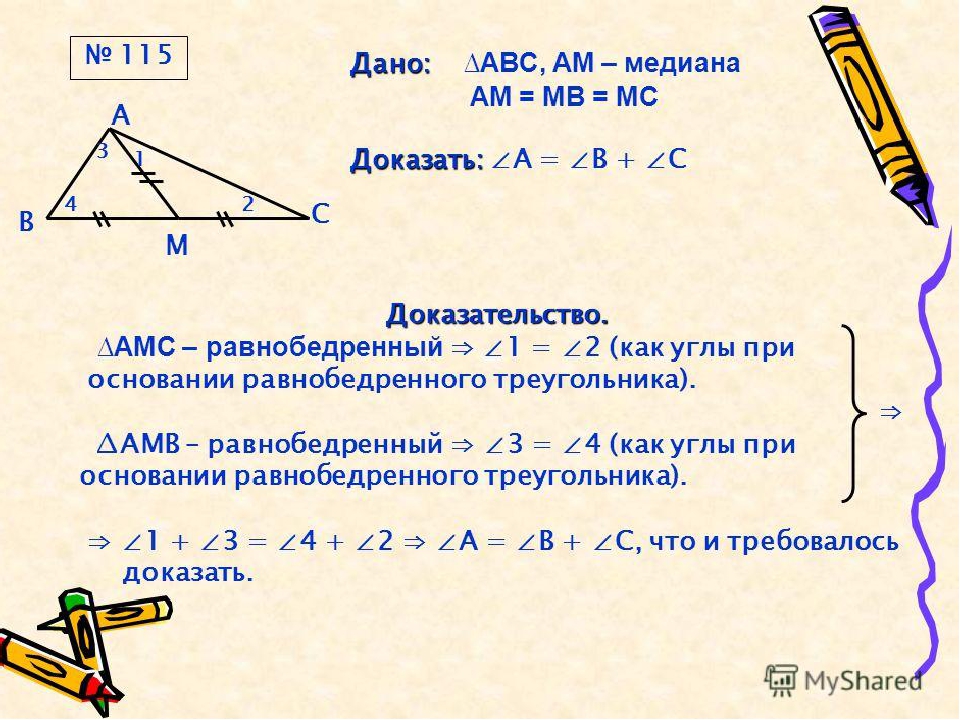 Найдите меру ∠CED.
Найдите меру ∠CED.
Решения
60-70 Вариант
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 60 °. Точка E находится на стороне AB такой, что ∠BCE = 70 °. Найдите меру ∠CED.
Решения
Равенство коротких отрезков
ABC — равнобедренный треугольник с углом при вершине ∠BAC = 20 ° и AB = AC. Нарисуйте ∠BCD = 60 °; D лежит на AB. Нарисуйте дугу с центром B и радиусом BC. Пусть эта дуга пересекает AC в точке E и AB в точке F.Докажите, что CE = DF.
Решения
Равенство длинных сегментов
ABC — равнобедренный треугольник с углом при вершине ∠BAC = 20 ° и AB = AC. Точка E находится на AB такой, что AE = BC. Найдите меру ∠AEC.
Решения
Разбиение на смежные равнобедренные треугольники
Треугольник 80-80-20 можно разделить на равнобедренный треугольник с основаниями на катетах данного треугольника. Для каких других углов при вершине A равнобедренный треугольник ABC можно аналогичным образом замощить равнобедренными треугольниками?
Решения
Раздел, начинающийся с биссектрисы основного угла
Треугольник 80-80-20 можно разделить любопытным образом: пусть BD, где D находится на AC, делит угол B пополам. Тогда AD = BC + BD.
Тогда AD = BC + BD.
Решения
Эта задача допускает обратную.
40-50 Вариант
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 40 °. Точка E находится на стороне AB такой, что ∠BCE = 50 °. Найдите меру ∠CED.
Решения
30-40 Вариант
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 30 °. Точка E находится на стороне AB такой, что ∠BCE = 40 °.Найдите меру ∠CED.
Решения
20-30 Вариант
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 20 °. Точка E находится на стороне AB такой, что ∠BCE = 30 °. Найдите меру ∠CED.
Решение
10-20 Вариант
Пусть ABC — равнобедренный треугольник (AB = AC) с ∠BAC = 20 °. Точка D находится на такой стороне AC, что ∠CBD = 10 °. Точка E находится на стороне AB такой, что ∠BCE = 20 °. Найдите меру ∠CED.
Точка E находится на стороне AB такой, что ∠BCE = 20 °. Найдите меру ∠CED.
Решения
Список литературы
- Т. Рике, Интригующая задача геометрии, Berkeley Math Circle, 5 мая 2002 г.
- Х. С. М. Коксетер и С. Л. Грейцер, Пересмотр геометрии, , MAA, 1967.
- Р. Хонсбергер, Четыре второстепенных камня из геометрии , Математические драгоценности II, MAA, 1976.
- Р. Хонсбергер, Три решения вариации старого каштана , Математические каштаны со всего света , MAA, 2001.
- К. Кноп, Девять решений одной проблемы , Квант , 1993, № 6.
- Р. Лейкин, Разделимые треугольники — что это такое? , Учитель математики , май 2001 г., стр. 392-398.
- В. В. Прасолов, Очерки чисел и цифр , МАА, 2000.
| Контакты |
| Первая страница |
| Содержание |
Copyright © 1996-2018 Александр Богомольный
.